ČESKÁ KOMORA AUTORIZOVANÝCH INŽENÝRŮ A TECHNIKŮ ČINNÝCH VE VÝSTAVBĚ
Rada pro podporu rozvoje profese ČKAIT
Autoři: doc. Ing. Jan Kaňka, Ph.D., doc. Ing. Iveta Skotnicová, Ph.D.
Stav: aktualizace 2019, vydání 2010
Anotace:
Hlavním cílem pomůcky je poskytnout základní informace z oboru stavební akustiky. Stavební akustika se zabývá vznikem zvukového vlnění, jeho šířením, vnímáním zvuku sluchem a přenosem prostorem v budovách. Vybrané fyzikální veličiny jsou hygienickými předpisy a technickými normami stanoveny jako kritéria pro posuzování budov a jejich vnitřního prostředí. Jsou stanoveny limitní hodnoty těchto kritérií pro různá prostředí, resp. různé typy konstrukcí.
Autorkou poslední aktualizace pomůcky v roce 2019 je doc. Ing. Iveta Skotnicová, Ph.D.
OBSAH
1 KRITÉRIA A LIMITY
Zvuk patří mezi fyzikální faktory životního prostředí. V budovách působí dlouhodobě a opakovaně, a proto způsobem, který významně ovlivňuje práci i odpočinek a v konečném důsledku i zdraví lidí užívajících budovu. V dnešní době lidé tráví většinu svého času v budovách. Podle údajů WHO (Světové zdravotnické organizace) se u městské populace jedná až o 90 % času. Fyzikální faktory prostředí obecně nepůsobí jen na uživatele budovy, ale i na budovu samotnou, na její konstrukce a na zařízení a věci v interiéru budovy uložené. V tomto ohledu je však působení zvuku zanedbatelné. Zvuk je vnímán jen sluchem živých organismů včetně člověka, zatímco vliv na samotné konstrukce je u tohoto faktoru téměř vyloučený. S výjimkou akustického traumatu při velmi silných podnětech (start proudového letadla, výbuchy trhavin apod.) je akustické vlnění sluchem vnímáno, aniž by došlo k poškození jemného sluchového orgánu. Tím spíše nemohou akustické vlny v běžných situacích ovlivnit pevné stavební konstrukce.
Poznání významu fyzikálních faktorů vedlo postupně k vytvoření právních předpisů pro potřebu kontroly stavu prostředí v budovách. Vybrané fyzikální veličiny jsou hygienickými předpisy a technickými normami stanoveny jako kritéria pro posuzování budov a jejich vnitřního prostředí. Jsou stanoveny limitní hodnoty těchto kritérií pro různá prostředí, resp. různé typy konstrukcí.
Kritérium lze definovat jako vybranou fyzikální veličinu, která slouží k hodnocení stavu prostředí v budově nebo jejím okolí, popřípadě může sloužit k hodnocení samotných budov a stavebních konstrukcí z hlediska jejich schopnosti stav prostředí zajišťovat či ovlivňovat.
Jako kritéria slouží takové veličiny, které mají tyto vlastnosti:
- Veličina je v úzkém vztahu s působením hodnoceného fyzikálního faktoru na konstrukce i uživatele budovy. Protože zvuk na stavební konstrukce nemá vliv, hodnotí se výhradně z hlediska působení na člověka. Příslušná kritéria proto vyjadřují míru ovlivnění akustické pohody i zdraví lidí užívajících budovu. Nemohou proto popisovat jen samotné fyzikální jevy (intenzitu, kmitočet, dynamiku působení zvuku v čase), ale nutně reagují i na fyziologické a psychologické okolnosti vnímání zvuku člověkem. Zejména přihlížejí k citlivosti příslušného smyslového orgánu – sluchu.
- Pro návrh budovy je k dispozici přiměřeně přesná a přiměřeně náročná metoda předpovědi hodnot kritéria výpočtem, který bere v úvahu všechny významné vlivy ovlivňující hodnoty kritéria.
- Pro uvedení budovy do trvalého užívání a pro běžný dozor je k dispozici přiměřeně náročný a přiměřeně přesný způsob kontroly hodnot kritéria měřením na realizovaných budovách.
- Kritéria s limitními hodnotami mají být spravedlivá ke všem účastníkům investiční výstavby tj. zejména slučitelná s příslušnými ustanoveními § 1013 zákona č. 89/2012 Sb. Občanského zákoníku [35]. Používání kritérií má účinným způsobem přispívat k ochraně zdraví a kvality života uživatelů budov i uživatelů prostoru v jejich okolí. Při tvorbě kritérií a při stanovení jejich limitních hodnot je třeba vyloučit všechny jiné zájmy, než je úsilí o zajištění optimálního prostředí v budovách. Odstavec (1) § 1013 zákona č. 89/2012 Sb. [35] je zde pro jeho důležitost citován celý.
§ 1013 Občanského zákoníku
(1) Vlastník se zdrží všeho, co působí, že odpad, voda, kouř, prach, plyn, pach, světlo, stín, hluk, otřesy a jiné podobné účinky (imise) vnikají na pozemek jiného vlastníka (souseda) v míře nepřiměřené místním poměrům a podstatně omezují obvyklé užívání pozemku; to platí i o vnikání zvířat. Zakazuje se přímo přivádět imise na pozemek jiného vlastníka bez ohledu na míru takových vlivů a na stupeň obtěžování souseda, ledaže se to opírá o zvláštní právní důvod.
Vyhovět všem požadavkům kladeným na kritéria není lehké. Některá kritéria používaná v akustice proto vznikla jako výsledek poměrně složitých manipulací s fyzikálními veličinami a jednotlivým výše uvedeným požadavkům vyhovují v různé míře. Vývoj metod hodnocení a tvorby kritérií ve stavební fyzice dosud není ukončen. Zejména v posledních letech se v tomto procesu uplatňuje u nás tendence k mezinárodnímu sjednocení v rámci Evropy.
Každému kritériu přísluší limitní hodnoty. Ty mohou být v zásadě trojího druhu:
nejnižší (minimální) požadovaná hodnota – příklad: vážená stavební neprůzvučnost Rw´ [dB]
- nejvyšší (maximální) přípustná hodnota – příklad: ekvivalentní hladina akustického tlaku LAeq [dB];
- přípustné rozmezí (interval) hodnot – příklad: standardní doba dozvuku T [s].
Limitní hodnota je hodnota kritéria, která v dané době, v dané společnosti, na daném území apod. je považována za hraniční mezi vyhovujícím a nevyhovujícím stavem. Je přirozené, že s rozvojem společnosti a techniky se limitní hodnoty mění. Volba limitní hodnoty je vždy kompromisem mezi potřebou co nejdokonalejší ochrany zdraví a kvality života uživatelů budov na jedné straně a mezi technickými a ekonomickými možnostmi stavebnictví limitní hodnoty reálně v budovách zajišťovat. Nepřiměřeně málo náročný požadavek nebude plnit svou funkci z důvodu malé ochrany uživatelů budov, avšak příliš náročný požadavek, je-li v rozporu s reálnými možnostmi jeho zajištění, vede k obcházení předpisů, resp. k neblahému stavu, kdy „úspěšně vyřešit“ akustický problém je možné jen podvodem při výpočtu nebo měření.
Posuzování prostředí v budovách se provádí porovnáním objektivně zjištěné hodnoty kritéria s limitem. Ve stadiu navrhování budov se hodnoty kritérií zjišťují výpočtem, případně měřením na modelech. Při uvádění budov do trvalého užívání (kolaudaci), nebo i v průběhu jejich užívání (například na základě stížností) se hodnoty fyzikálních kritérií zjišťují měřením. Za nejvíce spolehlivé se považují hodnoty získané měřením na skutečné stavbě, následují výsledky měření v laboratoři nebo na modelu, zatímco teoretické výpočty jsou považovány v porovnání s měřením za méně spolehlivé. Ve stádiu návrhu budovy však představuje teoretický výpočet často jedinou možnost posouzení.
Jakákoli měření i výpočty ve fyzice nemají nikdy absolutní přesnost. Výsledek je vždy zatížen nejistotou a tato nejistota by měla být vždy v protokolech z měření i u výsledku výpočtu uváděna. Vzhledem k logaritmickému charakteru hodnocení akustických veličin, kdy změna o 3 dB už představuje zdvojnásobení intenzity vlnění, nemůže být nejistota samotných výpočtů nebo měření větší než ± 1 dB. Další nejistotu však do výpočtu mohou vnášet zadané hodnoty vstupních veličin (hodnoty akustického výkonu zdrojů, jejich směrovost, hodnoty pohltivosti ploch, nad kterým se vlnění šíří apod.). Při hodnocení výsledku s nejistotami je nutno přihlédnout k účelu měření či výpočtu. Má-li měření či výpočet prokázat splnění přípustných limitů (např. při uvedení stavby do trvalého užívání – tzv. kolaudaci), je nutno tento průkaz podat nade vši pochybnost, tj. včetně započtené nejistoty ve směru k méně vyhovujícím hodnotám. Naopak má-li se prokázat, že stav nevyhovuje (např. při stížnosti uživatele stavby) a popřít tak právně existující stav úspěšně zkolaudovaného objektu, je i zde nutno prokazovat nade vši pochybnost, tedy i se započtením nejistot, ale ve směru příznivém.
Pro zajištění vyhovujícího akustického stavu vnitřního prostředí je možno použít řadu praktických postupů a opatření prováděných ve všech etapách návrhu a přípravy stavby, při vlastní výstavbě i při užívání budovy. Je pravidlem, že opatření uplatněná již ve stadiu koncepce návrhu jsou účinnější a ekonomicky výhodnější v porovnání s dodatečnými a často vynucenými změnami projektu nebo stavby v případech, kdy se na stavební akustiku při tvorbě koncepce zapomnělo. Obecně opatření proti hluku bývají výhodnější, jsou-li prováděna na samotném zdroji zvuku nebo v jeho blízkosti (taková opatření se považují za opatření aktivní), oproti opatřením v místě příjmu zvuku (kde lze hovořit o opatřeních pasivních). Zkušenosti z praxe a trhu také naznačují, že nejúčinnější nemusí být vždy ta opatření proti hluku, která jsou nejdražší.
2 FYZIOLOGICKÉ VYMEZENÍ ZVUKU
Zvuk se definuje jako mechanické vlnění prostředí, které je vnímáno sluchem. Definice tak má dvě části: fyzikální (mechanické vlnění prostředí) a fyziologickou (které vnímáme sluchem). Zvukem je jen to mechanické vlnění, které vnímáme sluchem. Spojení „slyšitelný zvuk“ je terminologicky chybný pleonasmus, protože každý zvuk je slyšitelný. Neexistuje neslyšitelný zvuk.
Mechanické vlnění částic je přítomno všude, kde je hmota. Je neoddělitelnou součástí přírodních jevů, hlasů zvířat i lidí. V souladu se zákonitostmi historického vývoje organismů, které popsal anglický přírodovědec Charles Robert Darwin (1809–1882), byly v přírodním výběru ve výhodě ty živočišné druhy, které dokázaly tuto všudypřítomnou vlastnost prostředí využít ke svému prospěchu. Tak se u vyšších organismů včetně člověka vyvinul sluch, jako nástroj registrace množství a kvality mechanického vlnění částic prostředí.
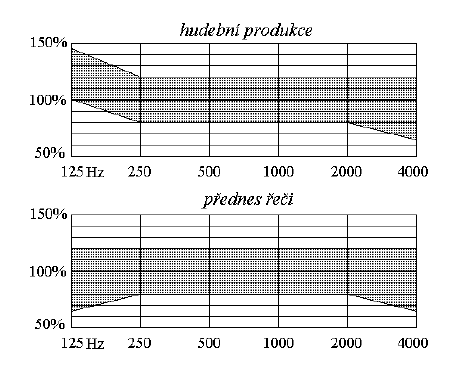
Obr. 1 Slyšitelný rozsah kmitočtů a intenzit mechanického kmitání omezený prahem slyšení a prahem bolesti a přibližné rozsahy hudby a lidské řeči. Amplituda akustické výchylky platí ve vzduchu objemové hmotnosti ρ = 1,29 kg·m-3 a pro rychlost zvuku c = 340 m·s-1
U člověka je oblast slyšení vymezena pásmem kmitočtů přibližně od 16 do 16 000 Hz a rozsahem intenzity zvuku mezi prahem slyšení, (cca 10-12 W·m-2) a prahem bolesti (cca 10 W·m-2). Jedná se o intenzity velmi malé, takže zvukové vlny se šíří prostředím bez jakékoli viditelné odezvy nebo účinku a jedinými systémy, které jsou dostatečně citlivé k tomu, aby toto vlnění zaznamenaly, jsou sluchové orgány živých organismů nebo velmi citlivá elektronická zařízení, jako je měřicí mikrofon zvukoměru. Vlnění povrchů kapalin nebo chvění pevných předmětů, které můžeme sledovat zrakem či hmatem, nejsou zvukem (i když se často spolu se zvukem tyto jevy vyskytují), protože svým kmitočtem a intenzitou neodpovídají možnosti vnímání sluchovým orgánem člověka. Amplituda výchylky částic vzduchu příslušná k rozsahu lidské řeči má hodnotu řádově nanometrů a jejich zlomků. Člověk je sluchem schopen vnímat dokonce i vlnění vzduchu s amplitudou 10-11 m. Taková amplituda je již srovnatelná s rozměry nejmenších částic hmoty – s atomy.
Zvuk se šíří v plynném, kapalném prostředí i v pevných látkách. Zvukové vlny jsou prostředím, ve kterém se šíří, v různé míře pohlcovány, odráženy, rozptylovány, soustřeďovány či tlumeny. Vhodným uspořádáním prostorů a konstrukcí v budově tak lze ovlivňovat šíření akustické energie a dosahovat jejího omezení. Člověk může slyšet i pod vodou, nebo zvukové vlny mohou dospět ke hlemýždi vnitřního ucha pevnou látkou při kostním vedení zvuku, které se zejména uplatňuje při slyšení a kontrole vlastního hlasu, většinou však, když hovoříme o slyšení, máme na mysli příjem zvuku z plynného prostředí – ze vzduchu.
Zvuk je přirozeným průvodním jevem přírodních dějů i životní aktivity člověka. Sluchem přijímá člověk významný podíl informací o světě. Zvuk je důležitým poplašným signálem, varuje před nebezpečím a je také základem řeči, která odlišila člověka od zvířat. Zvuk a sluch hrají významnou roli v adaptaci člověka na prostředí. Sluchem a hlasem navazujeme kontakt s druhými lidmi, sdělujeme své poznatky, zkušenosti i své myšlenky a plány pro budoucnost. Zvuk může být uklidňující, dráždivý, může vyvolávat smutek, vztek či radost a ve formě hudby přinášet vrcholné estetické zážitky. Zvuk a sluch hrají významnou roli v adaptaci člověka na prostředí. Sluch je smysl, který je v ustavičné pohotovosti, aby přinášel údaje o vnějším světě. Sluch varuje před nebezpečím, sluchem jsme schopni rozlišit zdroj zvuku a lokalizovat ho v prostoru. Proto je zvuk primárně pro člověka prospěšný je nesprávné ho apriorně hodnotit jako cosi nežádoucího nebo škodlivého.
Zvuk je součástí životního prostředí člověka. Moderní doba spolu s technickými revolucemi minulých staletí přinesla do tohoto prostředí velké množství nových zdrojů zvuku. Nadbytek zvuků, který je způsobován nesčetnými zdroji, jejichž činnost často jedinec nemá možnost ovlivnit, může působit způsobem, který neodpovídá lidským schopnostem a možnosti přizpůsobení. Protože organismus člověka nemá fyziologickou možnost vědomé regulace intenzity přijímaného zvukového signálu, působí tyto zvuky v plné síle, ruší člověka při práci a odpočinku, ztěžují komunikaci řečí, ruší vnímání důležitých zvukových signálů. Běžné zvuky, vyskytující se v budovách, nemohou organismus člověka přímo poškodit. Zdraví člověka ale ovlivňují zprostředkovaně prostřednictvím (někdy přestřelující) obranné reakce organismu na nežádoucí zvuk. Proto není správné příliš důrazným, okázalým a příliš častým způsobem na zvuk a na jeho případné nežádoucí účinky upozorňovat a tím u uživatelů budov zbytečně zvyšovat obavy z jeho působení. Proti nežádoucímu zvuku je třeba bojovat, ale bojovat v tichosti.
Jen při velmi vysokých intenzitách (v budovách se nevyskytujících – výbuch, třesk střelných zbraní, start letadla), nebo při dlouhodobém působení zejména v důsledku expozice na hlučném pracovišti může být zvuk příčinou trvalého poškození sluchového orgánu. Příliš časté nebo příliš silné a v nevhodnou dobu se vyskytující zvuky, které jsou nežádoucí, rušivé, obtěžující nebo lidskému zdraví škodlivé, se označují jako hluk. Hluk je nežádoucí zvuk.
3 VNÍMÁNÍ ZVUKU, VELIČINY AKUSTICKÉ IMISE
Vnímání zvuku je složitý fyziologický a psychologický proces. Sluchový orgán člověka se skládá ze zevní (boltec a zvukovod), střední (bubínek a sluchové kůstky) a vnitřní části (hlemýžď s Cortiho orgánem, který obsahuje 20 000 vláskových buněk s nervovými zakončeními) a je spojen s mozkovou kůrou sluchovým nervem.
Zvukový podnět na své cestě složitou strukturou vnějšího, středního a vnitřního ucha prochází mnoha proměnami způsobenými rozmanitými vlivy od vlnových rezonančních jevů ve zvukovodu až po složité vzájemné vazby nervových drah, které zajišťují mimo jiné prostorové slyšení a analýzu kmitočtů. Výsledkem je specifický způsob vnímání a prožívání zvuku. Při působení zvuku na člověka se uplatňuje více vlastností zvuku. Tyto vlastnosti jsou: intenzita, kmitočet, čas, informační hodnota zvuku a okolnosti jeho působení, vztah osoby příjemce ke zdroji zvuku a ke zvuku jako takovému. Základní akustické veličiny, kritéria a přípustné limity hluku jsou proto definovány takovým způsobem, aby co nejlépe popisovaly účinek zvuku na člověka a jeho sluchový orgán právě z hlediska působení všech těchto vlivů.
4 INTENZITA ZVUKU – DECIBEL
Mírou účinku mechanického vlnění vzduchu a jím přenášeného zvuku je plošná hustota akustického výkonu zvaná akustická intenzita I [W·m-2]. Prahové hodnoty akustické intenzity již byly uvedeny (viz obr. 1). Citlivost lidského sluchu při vnímání akustické intenzity není vždy stejná, ale s rostoucí intenzitou se snižuje. Při zvyšování akustické intenzity jakoby sluchový orgán stále více ztrácel schopnost vnímat v plné hodnotě její další přírůstek. Výsledkem je logaritmická závislost mezi velikostí zvukového podnětu a velikostí sluchového vjemu, kterou objevil německý fyziolog Ernst Heinrich Weber (1795–1878) a kterou později zdůvodnil jiný německý badatel, zakladatel psychofyziky Gustav Theodor Fechner (1801–1887). Weber – Fechnerův psychofyzický zákon zní: Intenzita počitku je úměrná logaritmu podnětu.
Uvedená vlastnost sluchu není samoúčelná. Umožňuje totiž člověku vnímat i velmi slabé zvukové signály s vysokou citlivostí a zároveň ho chrání před zvukem vysoké intenzity. Tato vlastnost sluchu byla důvodem k zavedení logaritmické míry (decibelové stupnice) při kvantifikaci akustických veličin. Akustická intenzita I [W·m-2] vyjádřená v decibelech se nazývá hladina akustické intenzity L [dB]
\begin{gathered}
L = 10 \log \frac{I}{I_\text{ref}} = 10 \log \frac{p^2}{p_\text{ref}^2} = 20 \log \frac{p}{p_\text{ref}}
\end{gathered}(1)
kde je
Iref = 10-12 W·m-2 … již zmíněná prahová hodnota akustické intenzity.
Podle vztahu (2) je intenzita přímo úměrná druhé mocnině akustického tlaku.
\begin{gathered}
I = \frac{P}{S} = p \cdot v = \frac{p^2}{Z}
\end{gathered}(2)
Proto je ve vztahu (1) poměr intenzit nahrazen poměrem druhých mocnin akustického tlaku.
Takto definovaná veličina se nazývá hladina akustického tlaku L [dB],
kde je
pref = 2 · 10-5 Pa … prahová hodnota akustického tlaku.
Obě veličiny – hladina akustické intenzity sledovaná ve směru šíření zvuku a hladina akustického tlaku – mají vždy stejnou hodnotu, protože jsou tak záměrně definovány. Rozdíl mezi nimi je však v kvalitě. Jako vektor je intenzita úzce spojena i se směrem šíření zvuku, zatímco akustický tlak jako skalární veličina jen popisuje stav prostředí v daném místě bez ohledu na směr šíření zvuku. Proto hladina akustického tlaku má s hladinou akustické intenzity stejnou hodnotu jen tehdy, jestliže plocha, na které zjišťujeme intenzitu, je kolmá na směr šíření zvuku. Sluchový orgán člověka je schopen přijímat zvuk z jakéhokoli směru. Vnímání zvuku tak více souvisí s tlakem než s intenzitou. To je hlavní důvod, proč se v praxi při popisu „síly“ zvuku používá veličina: hladina akustického tlaku. Spíše pro teoretické úvahy je pak vhodná představa hladiny akustické intenzity.
Je dobré si povšimnout, že v definičním vztahu (1) se logaritmuje bezrozměrné číslo (podíl akustických intenzit, resp. podíl druhých mocnin akustických tlaků). V decibelech by tak mohla být vyjádřena jakákoliv jiná fyzikální veličina (stačilo by jen stanovit její prahovou hodnotu) a v tomto smyslu má decibel obdobný charakter jako například procento.
Protože se při hladinovém vyjádření velikosti akustických veličin pracuje s logaritmy jejich hodnot, dochází při počítání s hladinami k některým skutečnostem, které se vymykají běžnému chápání kvantity. Projevuje se to například při sčítání hladin. Jsou známy hladiny L1 [dB] a L2 [dB] akustického tlaku generované dvěma různými zdroji zvuku. Úkolem je stanovit hladinu akustického tlaku při současném působení obou zdrojů. Sčítané intenzity zvuku jsou I1 [W·m-2] a I2 [W·m-2].
\begin{gathered}
L = 10 \log \Bigg( \frac{I_1}{I_0} + \frac{I_2}{I_0} \Bigg) = 10 \log \bigg(10^{\frac{L_1}{10}} + 10^{\frac{L_2}{10}} \bigg)
\end{gathered}(3)
Operace naznačená ve vztahu (3) se nazývá energetický součet.
5 KMITOČET ZVUKU – VÁHOVÁ KOREKCE ZVUKOMĚRU
Druhou důležitou vlastností zvuku je jeho kmitočtové složení. Kmitočet zvuku je počet periodických změn akustického tlaku za sekundu. Subjektivně je vnímán jako výška tónu. Tónový zvuk obsahuje jen jeden kmitočet, kde průběh hodnot akustického tlaku v čase je harmonický tj. má tvar funkce sinus nebo cosinus. Nejvyšší hodnota akustického tlaku A [Pa] při harmonickém průběhu se nazývá amplituda. Do vztahu (1) se však dosazuje efektivní hodnota, která pro harmonické vlnění činí pef = 0,707 A. Druhým parametrem harmonické závislosti akustického tlaku na čase je vlnová délka λ [m], která souvisí s kmitočtem podle vztahu
\begin{gathered}
\lambda = c \cdot T = \frac{c}{f}
\end{gathered}(4)
Vlnová délka λ [m] je dráha, kterou urazí vlna během jednoho kmitu, tedy za čas periody T [s]. Ve vztahu (4) je c [m·s-2] rychlost zvuku a f [Hz] kmitočet. Kmitočet je počet periodických změn za jednu sekundu. Při teplotě 0 °C, běžném tlaku p0 = 101,325 kPa a objemové hmotnosti vzduchu ρ0 = 1,29 kg·m-3 je rychlost zvuku ve vzduchu c0 = 331,5 m·s-1. Rychlost zvuku ve vzduchu se nepatrně mění s teplotou. Pro technické výpočty se používá hodnota c0 = 340 m·s-1 odpovídající teplotě 14,2 °C.
Skutečné zvuky v prostředí jsou čistě tónové (tj. harmonické) jen výjimečně. Průběh periodických změn akustického tlaku reálných zvuků je vždy složitější než průběh harmonický a případ od případu může nabývat nejrůznějších podob. Každý takový průběh však lze sestavit jako součet jistého počtu harmonických průběhů s různými amplitudami a vlnovými délkami pomocí Fourierova rozkladu funkce. Jean-Baptiste Joseph Fourier (1768–1830) byl francouzský matematik a fyzik. Nalezl matematický postup, kterým lze složité periodické funkce nahradit součtem konečného počtu nebo definované nekonečné řady harmonických funkcí (tedy funkcí sinus nebo cosinus). Pomocí tohoto postupu lze totiž vždy složitější periodické pohyby částic vyjádřit jako součet dílčích harmonických pohybů s různými amplitudami a úhlovými rychlostmi (a tedy i různými kmitočty, vlnovými délkami a s různými amplitudami, tj. s různou intenzitou). Jinými slovy: každý zvuk je směsí jistého počtu tónových (harmonických) zvuků o různé amplitudě a kmitočtu.
Sledováním změn hladiny akustického tlaku v závislosti na kmitočtu se zabývá kmitočtová analýza. Pro účely sledování kmitočtového složení zvuku lze oblast slyšitelných kmitočtů rozdělit na jedenáct oktávových pásem, z nichž každé je charakterizováno svým středním kmitočtem. Oktáva je interval mezi dvěma kmitočty, kde druhý je dvojnásobek prvního. Každá oktáva se nazývá podle svého středního kmitočtu. Střední kmitočty oktávových pásem jsou uvedeny v tab. 2. Hodnota hladiny akustického tlaku v oktávovém pásmu Lokt [dB] je energetickým součtem hladin akustického tlaku zvuku všech kmitočtů, které do daného pásma spadají. Této hodnotě se pak přisoudí vlastnosti zvuku o příslušném středním kmitočtu. Oktávovou analýzou tak technická akustika nahrazuje pracnou podrobnou Fourierovu analýzu kmitočtů. Jako výsledek totiž obdržíme jedenáct dílčích (pseudo)tónových složek, jejichž vlnová délka je určena středním kmitočtem oktávy a amplituda hodnotou Lokt.
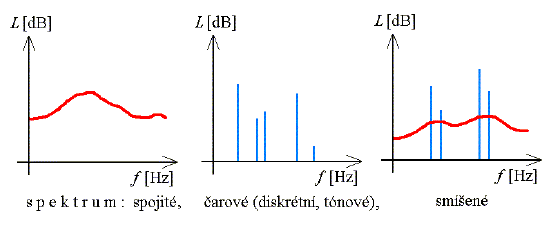
Obr. 2 Diagramy zvukových spekter
Dobrou představu o charakteru zvuku z hlediska zastoupení různých kmitočtů v daném zvuku poskytuje akustické spektrum. Akustickým spektrem se rozumí soustava hodnot sledované akustické veličiny (např. hladiny akustického tlaku) uváděná v závislosti na kmitočtu. Často se uvádí formou grafu nebo tabulky. Při výpočtech a měřeních se často pracuje jen s oktávovým spektrem v rozsahu 125 až 4 000 Hz. Z hlediska nepříznivých účinků běžných zdrojů zvuku mají ostatní pásma zpravidla menší důležitost. Zvuk s nízkým kmitočtem (16 až 63 Hz) je totiž sluchem vnímán s poměrně malou citlivostí a zvuk o vysokých kmitočtech (8 000 a 16 000 Hz) je zpravidla prostředím relativně dobře tlumen. K závadám tak nejčastěji dochází v pásmech středních kmitočtů (125 až 4 000 Hz). V případě potřeby větší přesnosti je možné se přiblížit více k realitě pomocí podrobnějšího dělení spektra na pásma třetinooktávová, devítinooktávová, případně jiným speciálním dělením. S tónovými (čárovými) spektry se můžeme setkat u hudebních nástrojů. Většina zvuků, kterými jsme obklopeni v pracovním a životním prostředí, má ale spojité spektrum. Některé stroje a technická zařízení mají spektra smíšená, tj. spojitá s výraznými tónovými složkami. Takový zvuk je našimi hygienickými předpisy hodnocen přísněji. Nejvyšší přípustné hodnoty tónového zvuku jsou o 5 dB nižší, než je tomu u zvuku bez tónových složek. Různé typy zvukového spektra jsou na obr. 2.
Při popisu zvuku a jeho účinku na člověka je třeba se vyrovnat s tou skutečností, že zvuk o různých kmitočtech je lidským sluchem vnímán s nestejnou citlivostí. Již práh slyšení je odlišný pro různé kmitočty (viz obr. 1). Při vnímání zvuku tak dochází ke zkreslení, jehož charakter navíc závisí na velikosti akustického tlaku přijímaného zvuku. Lidský sluch je nejvíce citlivý v oblasti okolo 1 000 Hz, což v podstatě odpovídá kmitočtovému obsahu lidské řeči. Relativně dobrým přiblížením k těmto vlastnostem sluchového orgánu bylo zavedení váhových filtrů, které v souladu s citlivostí lidského sluchu upravují citlivost zvukoměru. Z více původně navržených filtrů se v praxi ujal váhový filtr „A“. Zvukoměr měří hladinu akustického tlaku současně v jednotlivých kmitočtových pásmech (užších než jedna oktáva). Ke každé změřené hodnotě přičte korekci váhového filtru KA [dB] a teprve takto upravené hodnoty sečte (energeticky podle pravidel počítání s hladinami). V takovém součtu je vliv některých kmitočtů potlačen, jiných zesílen – každé pásmo má tak jinou váhu – podle přidělených korekcí. Takto vzniklá veličina je označována symbolem LA [dB] a nazývá se hladina akustického tlaku A. Velké písmeno „A“ je součástí názvu této veličiny. Jednotkou je opět decibel [dB]. Ve starší literatuře se lze setkat s praktickou poznámkou v závorce u rozměru této veličiny LA [dB(A)]. Váhové korekce jsou dány normou. Jejich hodnoty pro střední kmitočty oktávových pásem udává tab. 2. Váhové korekce se nepoužívají jen při měření zvuku, ale je nutné s nimi pracovat i v akustických výpočtech. Hladina akustického tlaku A se vypočte podle vztahu
\begin{gathered}
L_\text{A} = 10 \log \sum \limits_{\text{i}=1}^\text{n} 10^{0{,}1 (L_\text{i}+K_\text{Ai})}
\end{gathered}(5)
kde je
n … počet kmitočtových (např. oktávových) pásem.
6 PŮSOBENÍ ZVUKU V ČASE – EKVIVALENTNÍ HLADINA
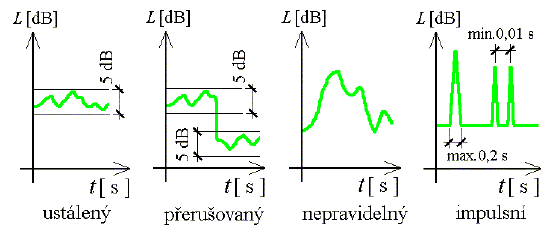
Třetí vlastností zvuku je jeho průběh a trvání v čase. Jestliže hladina akustického tlaku mění v čase svou hodnotu, je to subjektivně vnímáno jako změna hlasitosti nebo „síly“ zvuku. Sledováním takových změn se zabývá hladinová analýza. Málokterý zvuk lze charakterizovat jako ustálený (kolísající v čase v rozsahu menším než 5 dB). Většina zvuků, kterými jsme obklopeni, jsou zvuky proměnné: nepravidelné (kolísají v čase v rozsahu větším než 5 dB) nebo přerušované (hladina se mění skokem v rozsahu větším než 5 dB a v dílčích intervalech je ustálená). Zvláštním druhem proměnného zvuku je zvuk impulsní (rychlý vzestup hladiny akustického tlaku a následný pokles v trvání do 0,2 sekundy, kde interval mezi jednotlivými impulsy je větší než 0,01 sekundy) – údery kladivem, třesk pěchotních zbraní apod. Impulsní zvuk (stejně jako zvuk obsahující tónové složky) lze obtížněji vnímat jako indiferentní, a proto se takový zvuk považuje za rušivější.
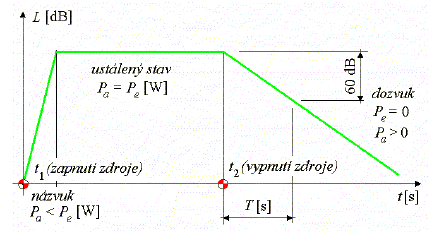
Obr. 3 Zvuk v závislosti na čase
Při působení zvuku na zdraví má rozhodující vliv celková suma akustické energie, které je jedinec dlouhodobě vystaven. Proto se proměnný zvuk hodnotí veličinou, která je označována symbolem LAeq [dB] a nazývá se ekvivalentní hladina akustického tlaku A. Její jednotkou je opět decibel. Ekvivalentní hladina akustického tlaku A se vztahuje vždy jen k určitému časovému intervalu (např. 8 hodin pracovní doby) a je definována jako hladina akustického tlaku zvuku ustáleného, který by měl v daném časovém intervalu energetický obsah stejný jako daný zvuk proměnný a tedy i předpokládané stejné škodlivé účinky. Stanoví se jako energetický průměr z hladin akustického tlaku A vyskytujících se v daném intervalu.
\begin{gathered}
L_\text{Aeq} = 10 \log \Bigg\lbrack \frac{1}{\sum \limits_{\text{i}=1}^\text{n} t_\text{i}} \sum \limits_{\text{i}=1}^\text{n} (t_\text{i}\cdot 10^{0{,}1 L_\text{Ai}}) \Bigg\rbrack
\end{gathered}(6)
kde je
n … počet dílčích intervalů.
V i-tém intervalu délky ti [sekund, minut, hodin] působila hladina LAi [dB].
Jako ekvivalentní hladina akustického tlaku A je stanovena většina hygienických limitů. Nutno poznamenat, že ekvivalentní hladina je dost zjednodušenou charakteristikou průběhu a trvání zvuku v čase. Proto tam, kde jde o posuzování rušivého účinku zvuku, často hodnotíme namísto nebo spolu s ekvivalentní hladinou i LAmax [dB] maximální hladinu akustického tlaku A dosaženou v daném časovém intervalu. Zejména při hodnocení měření zvuku se lze setkat i s dalšími veličinami. LAmin [dB] minimální hladina akustického tlaku A změřená v daném časovém intervalu charakterizuje zvukovou situaci v době, kdy měřený zdroj proměnného zvuku byl v klidu. Je tedy hodnotou zvukového pozadí. Při podrobnější hladinové analýze se používají LAX [dB] procentní hladiny akustického tlaku A. V označení této veličiny je možné za X dosadit celé číslo v intervalu od 1 do 99. Procentní hladina udává hodnotu hladiny akustického tlaku, která byla překročena v X procentech časového intervalu proběhlého měření. Některé zvukoměry jsou vybaveny procesorem, pomocí kterého automaticky počítají hodnotu ekvivalentní hladiny akustického tlaku A z velkého množství rychle za sebou následujících odečtů okamžitých hodnot hladin akustického tlaku. Takové měřicí přístroje se nazývají integrační zvukoměry.
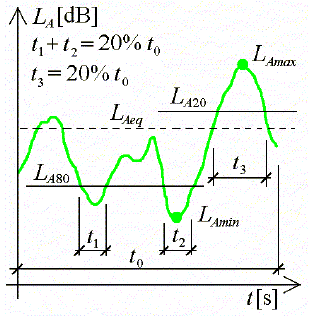
Obr. 4 K výkladu o maximálních, minimálních a procentních hladinách
Účinek zvuku závisí i na denní době, kdy zvuk působí. Naše hygienické limity pro hluk v mimopracovním prostředí jsou vesměs o 10 dB přísnější v noční době, tj. mezi 22. a 6. hodinou.
7 INFORMAČNÍ OBSAH ZVUKU A OKOLNOSTI JEHO PŮSOBENÍ – LIMITY HLUKU
Čtvrtou vlastností zvuku je jeho informační obsah. Míra rušení zvukem nezávisí jen na fyzikálních parametrech zvuku, ale je ovlivněna i postojem lidí k danému zvuku a jeho zdroji. Uživatelé budov všeobecně více tolerují hluk přicházející do budovy zvenčí ve srovnání s hlukem vznikajícím v budově. Více je tolerován hluk ze zdrojů, které jsou obecně považovány za neutišitelné, a ze zdrojů, u kterých lze obtížně určit konkrétního původce hluku (např. silniční doprava). Naopak se lze setkat se stížnostmi i na hluboce podlimitní hluk působený jinými uživateli budovy.
Menší rozmrzelost způsobí zvuk, o němž je předem známo, že bude trvat jen určitou vymezenou dobu, resp. vymezený počet opakování. Při provádění hlučných stavebních prací se vždy vyplatí předem o tom uvědomit okolí spolu s vysvětlením účelu a nezbytnosti prováděných prací a stanovení časového režimu zdroje hluku během dne i časového limitu, do kterého budou hlučné práce ukončeny. Vhodným způsobem informovaný příjemce zvuku bude vždy k jeho zdroji více tolerantní. O stupni rozmrzelosti rozhoduje i denní doba. Nejhůře je hluk snášen večer a v noci. Méně je hluk tolerován v létě než v zimě. Zkušenosti ukazují, že horší je snášenlivost hluku v menších než ve větších bytech. Významná je i vzdálenost zdroje od pozorovatele. Čím dále je zdroj zvuku od pozorovatele, tím menší je jeho emotivní obsah bez ohledu na skutečnou hodnotu hladiny akustického tlaku v místě pozorování. Zvuk vyšších kmitočtů vykazuje zpravidla větší míru rušení oproti zvuku nízkofrekvenčnímu. Přerušované zvuky více ruší v důsledku efektu očekávání, kdy pozorovatel je nadměrně vyrušován sledováním toho, zda se rušivý zvuk bude znovu opakovat.
Obtěžování hlukem je tím větší, čím více hluk upoutává naši neúmyslnou pozornost tj. čím je nejen silnější, ale i odlišnější, méně známý a méně očekávaný, čím více se u něj prosazuje nutnost identifikovat a klasifikovat ho v rámci dosavadních zkušeností. Informační hodnota zvuku může být v konkrétních případech i významnější než jeho intenzita, což lze demonstrovat na známé zkušenosti, kdy zvuková kulisa indiferentního zdroje zvuku pomáhá při učení v situacích, kdy se v okolí hovoří.
Vypracovat exaktní metodu hodnocení informačního obsahu zvuku použitelnou v praxi se zatím jeví jako neřešitelný úkol. Okolnosti působení zvuku se při hodnocení uplatňují tím způsobem, že jsou stanoveny odlišné limity hluku pro různá prostředí, různou dobu a různé zdroje. Tak existují rozdílné limity pro pracovní prostředí, pro hluk ve venkovním prostoru a uvnitř budov, kde se jiným způsobem hodnotí hluk ze zdrojů umístěných vně a uvnitř budovy. Dalšího členění limitů je dosaženo pomocí korekcí základní limitní hladiny. Tyto korekce jsou stanoveny v závislosti na druhu vykonávané práce, charakteru území, způsobu využití místností v budově, denní době apod. Přestože se hygienické předpisy čas od času mění, základní limity vycházející z poznání fyziologie a psychologie vnímání zvuku člověkem zůstávají trvale v platnosti. Bude praktické zapamatovat si alespoň tři základní limitní hodnoty: LAeq = 85, 65 a 35 dB.
Při hodnocení hluku v pracovním prostředí je důležitý limit LAeq = 85 dB. Tato hodnota se vztahuje k časovému intervalu v délce trvání pracovní směny a je-li překročena, pak se jedná o pracoviště rizikové z hlediska hluku. Po dlouhodobé (dlouholeté) expozici hlukem na takovém pracovišti může dojít ke vzniku a vývoji trvalé sluchové ztráty. Při uvádění takových pracovišť do provozu musí být věrohodně doloženo, že nelze použít jiné řešení, které by zajistilo dostatečnou ochranu pracovníků před hlukem. Pracovníci na rizikových pracovištích podléhají zvláštnímu režimu, který zahrnuje:
- používáni osobních ochranných pomůcek proti hluku;
- snížení expozice hlukem zařazením tichých přestávek nebo vystřídáním pracovníků na hlučném místě;
- pravidelné lékařské prohlídky, při kterých se audiometrickým vyšetřením včas rozpozná vznikající sluchová ztráta, což musí mít za následek přeřazení pracovníka na tiché pracoviště.
Za dodržování režimu na pracovišti rizikovém z hlediska hluku je odpovědný zaměstnavatel a jeho odpovědnost je spojena s povinností vyplácet velké náhrady pracovníkům, dojde-li v důsledku nedodržení tohoto režimu k poškození jejich sluchu. Poškození sluchu v důsledku dlouhodobé expozice v pracovním prostředí bývá nevratné, protože je spojeno s úbytkem vláskových buněk v Cortiho orgánu a tyto buňky organismus člověka nedokáže nahradit. Poškození sluchu u nás dosud nejčastější nemocí z povolání.
Asi od LAeq = 65 dB může být rušena komunikace pracovníků řečí. Rušení je však závislé na vzájemné vzdálenosti pracovníků a je nižší při možnosti vizuálního kontaktu (odezírání řeči). V mimopracovním prostředí je důležitá hodnota LAeq = 35 dB která se považuje pro většinu populace za limitní z hlediska rušení spánku.
Zásady ochrany proti hluku jsou zakotveny v zákoně č. 258/2000 Sb. o ochraně veřejného zdraví a o změně některých souvisejících zákonů [1]. Nejvyšší přípustné limity hluku stanoví nařízení vlády č. 272/2011 Sb. o ochraně zdraví před nepříznivými účinky hluku a vibrací [2]. Nejvyšší přípustné hodnoty hluku jsou stanoveny pro:
- pracoviště – místo určené nebo obvyklé pro výkon činnosti zaměstnanců;
- chráněný vnitřní prostor staveb – obytné a pobytové místnosti s výjimkou místností ve stavbách pro individuální rekreaci a ve stavbách pro výrobu a skladování;
- chráněný venkovní prostor – nezastavěné pozemky, které jsou užívány k rekreaci, sportu, léčení a výuce, s výjimkou lesních a zemědělských pozemků a venkovních pracovišť;
- chráněný venkovní prostor staveb – prostor do 2 m okolo bytových domů, rodinných domů, staveb pro školní a předškolní výchovu a pro zdravotní a sociální účely, jakož i funkčně obdobných staveb.
8 OSOBA PŘÍJEMCE ZVUKU – VÝZNAM LIMITŮ
V procesu vnímání zvuku existují značné interindividuální rozdíly. Nejde jen o rozdílnou citlivost sluchu u různých jedinců. Ta se snižuje s věkem, v důsledku chorob nebo nadměrné expozice hlukem v pracovním prostředí. Rozdíly jsou i v prožívání hlukové situace. Nejobecnější odpovědí na překročení přípustných hodnot hluku je rozmrzelost (annoyance). Jde o psychický stav, který vzniká při mimovolném vnímání nepříznivých vlivů nebo při podřizování se okolnostem, ke kterým má jedinec zamítavý postoj, protože narušují jeho soukromí, mohou představovat překážku při vykonávání práce nebo ovlivňovat jeho odpočinek. Na tyto vlivy jedinec reaguje pocity odporu, podrážděnosti, stresu a v některých případech až psychosomatickými poruchami. Zatímco rozmrzelost lze považovat za specifickou aktuální reakci na konkrétní hlukovou situaci, existuje u každého člověka určitý osobní postoj k rušivému působení hluku, určitý stupeň senzitivity, což je osobnostní charakteristika, která má dlouhodobější, resp. celoživotní trvání.
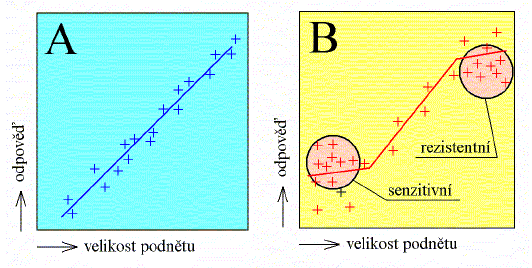
Velké interindividuální rozdíly ve vnímání a prožívání hluku jsou příčinou toho, že se často setkáme se situací, kdy hlukem postižená osoba v konkrétních podmínkách nepotvrzuje platnost bezpečných limitů, které byly stanoveny na základě statistického vyhodnocení rozsáhlého výzkumu [16]. Pro hluk je totiž charakteristické, že se z exponované populace vydělují skupiny osob velmi citlivých a velmi odolných, jejichž reakce stojí jakoby mimo kvantitativní závislosti (viz obr. 5). Působení zvuku na uživatele budov je výrazně individuálně determinováno.
Obr. 5. Vztahy mezi intenzitou podnětu a odpovědí. Typ reakce A není pro zvuk typický. Setkáváme se s typem reakce B, kde nalézáme v populaci skupinu velmi citlivých a skupinu relativně velmi odolných jedinců. Podle prof. Havránka [16]
Tato skutečnost komplikuje možnost odpovědného stanovení nejvyšších přípustných hodnot. Jestliže by se od nejvyššího přípustného limitu požadovala bezpečná ochrana celé populace včetně její senzitivní části, pak by se zcela jistě v konkrétních případech objevily nepřekonatelné potíže se zajištěním takového limitu. Například zatím není možné zcela vyloučit riziková pracoviště s hodnotou LAeq = 85 dB a vyšší. Smyslem povinných pravidelných audiometrických vyšetření pracovníků ve hlukovém v riziku je proto odhalení senzitivních jedinců dříve, než dojde k nevratnému poškození jejich sluchu, a jejich přeřazení na tiché pracoviště Naopak rezistentní jedinci mohou bez jakékoli újmy setrvat na hlučném pracovišti celá léta.
S výjimkou elektronicky zesilované hudby zvuk v mimopracovním prostředí pro svůj malý energetický obsah nemůže sám o sobě vyvolat závažnou poruchu či zdravotní potíže. Případnou „škodlivost“ přidává k takto působícímu zvuku až (někdy přestřelující) obranná reakce exponované osoby. A tato reakce je také u různých jedinců velmi rozdílná. Schopnost přivyknout určitému zvukovému režimu v obytném domě je velmi individuální a jsou známy případy, kdy rušení zvukem výtahu či výměníkové stanice bylo vyřešeno až přestěhováním senzitivního stěžovatele na jiné místo. Zkušenosti hygienické služby však také naznačují, že příčinou stížností občanů na hluk často bývají společenské problémy a mezilidské vztahy včetně sousedských sporů mezi uživateli budovy, kde odlišit senzitivního jedince od účelového stěžovatele někdy bývá obtížné. Bez nejvyšších přípustných limitů se proto nelze obejít, ale je třeba chápat je jako nezbytnou konvenci, která s přijatelnou pravděpodobností vyjadřuje statistickou závislost skutečné odpovědi lidí na konkrétní zvuk. Fyzikálně vymezený limit nemůže obsahovat všechna fyziologická a psychologická hlediska vnímání a prožívání zvuku, a proto takový limit nelze absolutizovat. Jestliže například v obytné zóně v noci lze za určitých okolností stanovit limit zvuku ve venkovním prostoru na LAeq = 50 dB neznamená to, že 49,5 dB je přijatelnou hlukovou situací pro všechny obyvatele, ani že hodnota 50,5 dB musí být nutně pro všechny obyvatele nesnesitelná.
Účelem návrhu opatření proti hluku není jen nepřekročit stanovené limity, ale v souladu s technickými a ekonomickými podmínkami daného řešení zajistit co nejlepší ochranu uživatelů budov a venkovního prostoru před nepříznivými účinky zvuku. Námitka nedostatku prostředků neobstojí, protože nejúčinnějšími prostředky ochrany nemusejí být vždy jen ta opatření, která jsou nejdražší. Na opatření proti hluku neexistuje univerzální jednoduchý recept typu „snížit hladiny pod limitní hodnoty“. Řešení je vždy výsledkem kolektivní práce projektanta, hygienika a ve složitějších případech i specialisty akustika a musí přijatelným způsobem vyvážit technické a ekonomické možnosti na jedné straně a požadavky ochrany zdraví a životní pohody na straně druhé.
9 ZDROJE ZVUKU V ŽIVOTNÍM A PRACOVNÍM PROSTŘEDÍ – VELIČINY AKUSTICKÉ EMISE
Jako zdroje zvuku se jeví předměty nebo vymezené oblasti prostředí, od kterých se do okolí šíří akustické vlnění. Charakter akustického vlnění v okolí zdroje zvuku je ovlivněn velikostí zdroje. Z tohoto hlediska rozlišujeme:
1) bodové zdroje – vlnění se šíří v kulových vlnoplochách;
2) přímkové zdroje – převažuje jeden rozměr a vlnoplochy mají tvar válce;
3) plošné zdroje – vlnoplochy jsou rovinné.
Normy definují bodový zdroj zvuku jako takový, jehož rozměry jsou velmi malé ve srovnání s vlnovou délkou vyzařovaného zvuku. Pro praktické úvahy je ale důležitá vzdálenost mezi zdrojem a místem příjmu zvuku. Je-li tato vzdálenost větší než 1,5 násobek největšího rozměru zdroje zvuku, lze přibližně tento zdroj již považovat za bodový.
Jiná možnost rozdělení zdrojů zvuku je členění na zdroje stacionární a mobilní. Stacionární zdroje (průmyslové závody, provozovny, hřiště, stadiony, staveniště) jsou zpravidla posuzovány z hlediska jejich hlučnosti přísněji ve srovnání se zdroji mobilními (doprava, zemědělské stroje). Je to dáno odlišnou reakcí obyvatelstva i možnostmi účinnějších opatření proti hluku u stacionárních zdrojů. Z časového hlediska lze rozlišovat zdroje, které působí trvale, a zdroje působící po časově omezenou dobu. U časově omezených zdrojů zvuku se známým nebo ohlášeným režimem působení (např. 1x za týden v trvání ne více než 4 hodiny ap.) lze usilovat u orgánů státní správy o výjimku z nejvyšších přípustných hodnot. Režim takového zdroje spolu s informací o jeho účelu a nezbytnosti je nutno účinným způsobem zveřejnit.
Dosud bylo pojednáno o akustických veličinách, které charakterizují zvuk v místě jeho příjmu – o veličinách akustické imise. Jsou to:
- L [dB] – hladina akustického tlaku (udávaná většinou v oktávových pásmech);
- LA [dB] – hladina akustického tlaku A;
- LAeq [dB] – ekvivalentní hladina akustického tlaku A.
Veličiny akustické imise mají při hodnocení vlivu hluku na člověka a jeho zdraví a při hodnocení ochrany lidí před hlukem naprostou prioritu a až na výjimky (např. neprůzvučnost, která je veličinou akustické izolace) by se jiná kritéria k těmto účelům neměla používat. Chceme-li však hodnotu některé z těchto veličin předpovědět výpočtem, musíme mít k dispozici údaje o zdroji zvuku. Tyto údaje poskytují veličiny akustické emise:
- LW [dB] – hladina akustického výkonu;
- Q [-] – činitel směrovosti.
Akustický výkon P [W] je množství akustické energie, kterou zdroj vyzáří do okolního prostoru za jednotku času. Akustický výkon vyjádřený v logaritmické míře se nazývá hladina akustického výkonu LW [dB] někdy také označovaná jako LP [dB].
\begin{gathered}
L_\text{W} = 10 \log \frac{P}{P_\text{ref}}
\end{gathered}(7)
kde je
Pref = 10-12 W … referenční hodnota.
Hladina akustického výkonu různých zdrojů zvuku se přednostně udává v oktávových pásmech nebo jednočíselně jako LWA [dB] (tj. s uplatněnou korekcí podle váhového filtru zvukoměru (viz kap. 5). Jednočíselný údaj však nevypovídá nic o kmitočtovém složení vyzařovaného zvuku a může proto pro většinu akustických výpočtů sloužit jen jako velmi hrubá orientace. Stejně tak nedostatečné může být, jestliže jsou údaje o zdroji zvuku vyjádřeny pomocí veličin akustické imise, např. pomocí hodnot hladin akustického tlaku změřených v jeho okolí. Takové údaje mohou být spolehlivé jedině tehdy, jestliže je přesně známo, v jakém prostředí, v jaké vzdálenosti od zdroje, za jakých podmínek atd. se měřilo.
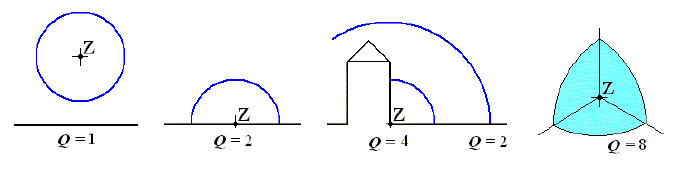
Činitel směrovosti Q [-] je bezrozměrné číslo, které charakterizuje směrové vyzařování zvuku zdrojem. Hodnota činitele směrovosti je ovlivněna odraznými plochami vyskytujícími se v blízkosti zdroje zvuku a souvisí s tím, do jak velké části prostoru je zvuk vyzařován. Nejčastěji je zdroj zvuku umístěn na odrazné ploše (terénu). Pak je zvuk vyzařován do poloprostoru a činitel směrovosti se přibližně rovná 2. Obdobně je-li zdroj umístěn u paty rozměrné staveb, pak je zvuk vyzařován do 1/4 prostoru a Q = 4 atd. Jestliže se zvuk šíří od zdroje neomezeně do všech směrů (například je-li zdrojem letadlo ve velké výšce), potom Q = 1.
Obr. 6 Hodnoty činitele směrovosti pro typické polohy zdroje zvuku
Častými zdroji zvuku v pracovním a životním prostředí jsou různé stroje a technická zařízení budov. Hodnota akustického výkonu těchto zařízení závisí nejen na jejich konstrukčním uspořádání, ale bude se měnit i v závislosti na technickém stavu, seřízení a údržbě. Díky tomu, že k vyjádření velikosti akustických veličin používáme decibelovou stupnici, nebude mít tato variabilita takový vliv na přesnost a věrohodnost akustických úvah a výpočtů, jak by se na první pohled mohlo zdát.
Příklad
Jak se musí změnit akustický výkon, aby hladina akustického výkonu vzrostla o X dB?
\begin{gathered}
L_\text{W2} - L_\text{W1} = X \\\\
10 \log \frac{P_2}{P_0} - 10 \log \frac{P_1}{P_0} = X \\\\
10 \log \frac{P_2}{P_1} = X \\\\
P_2 = P_1 \cdot 10^{0{,}1X}
\end{gathered}(8)
Dosazením X = 1 resp. X = -1 do vztahu (8) lze ukázat, že změna jednoho decibelu vyžaduje zvýšení akustického výkonu P [W] o více než 25 % resp. jeho snížení o cca 20 %. Proto také často bývá neúspěšná snaha změnit nepříznivou hlukovou situaci jen pouhým seřízením stroje (čerpadla, ventilátoru a pod.) nebo jeho výměnou za jiný stejného typu. Výrazného snížení hlučnosti lze dosáhnout jen promyšlenou změnou konstrukce stroje nebo i celé koncepce technologického procesu (např. výměna valivých ložisek za kluzná, náhrada nýtování svařováním, náhrada rázů při technologickém procesu plynulými pohyby ap.) Protože akustický výkon je úměrný ploše, která v důsledku svého chvění vyzařuje hluk, je omezení těchto ploch (např. pružným oddělením nosné konstrukce a krytu stroje od vlastního zdroje kmitání) další možností, jak snížit akustický výkon celého zařízení. Závislost vyjádřená vztahem (8) také vysvětluje velkou stabilitu hodnot akustických veličin. Například ekvivalentní hladiny akustického tlaku A hluku z pozemní dopravy jsou v nějakém místě každý den stejné i při jinak nepravidelném pohybu vozidel po městě. Aby hladina některý den vzrostla o jeden decibel, muselo by po komunikaci projet o čtvrtinu více vozidel, což je během pracovních dní vysoce nepravděpodobné. Vycházejí-li akustické výpočty ze zákonů fyziky, pak nemohou být nepřesné. Jejich nejistota není vyšší než řádově desetiny decibelů. Velké nejistoty však mohou do výpočtu zanést vstupní hodnoty, např. hodnoty hladin akustického výkonu zdrojů zvuku. Úspěšné vypracování akustického výpočtu tak závisí z větší části na úspěšnosti při získávání údajů o zdrojích zvuku, které mají být posouzeny.
10 ZÁKLADNÍ POZNATKY A ŠÍŘENÍ ZVUKU
Problematiku snižování hluku můžeme rozdělit do tří základních oblastí. První oblast představují problémy, které se vztahují ke zdroji zvuku. Některé z nich byly naznačeny v předchozí kapitole. Druhá oblast se týká cest šíření zvuku od zdroje k příjemci. Třetí oblastí je vlastní příjemce zvuku – člověk a jeho specifický způsob vnímání a prožívání hlukové situace. Obecně platí pravidlo: čím blíže ke zdroji se opatření proti hluku na jeho cestě provádí, tím obvykle bývá účinnější a často i technicky méně náročné a ekonomicky výhodnější. Dává se přednost opatřením na zdroji zvuku, kterými se sníží hodnoty akustické emise. Taková opatření se považují za aktivní. Často ale bývají v působnosti dodavatelů příslušných hlučných zařízení a týkají se převážně strojní profese. Aktivní opatření v oblasti návrhu budov spočívají v tvorbě vhodné dispozice budov a jejich souborů, kde se chráněná místa oddělí od zdrojů zvuku vzdáleností nebo stavebně. Cesty šíření zvuku mají podstatný význam pro technická řešení, protože se zde může závažným způsobem omezovat intenzita šířeného zvuku. Využije se zde útlumu zvuku vzdáleností, útlumu způsobeného ohybem zvuku přes překážku, útlumu zvukovou pohltivostí prostorů v budovách a útlumu v důsledku neprůzvučností konstrukcí. Pasivní opatření v místě příjmu zvuku se považují za méně výhodná, ale v řadě případů jsou jedině možná. Jako příklad pasivního opatření je možno uvést výměnu starých oken za okna s vyšší neprůzvučností v zástavbě těsně přiléhající k rušným městským komunikacím.
11 ŠÍŘENÍ ZVUKU VE VOLNÉM PROSTORU – VOLNÉ ZVUKOVÉ POLE
Při šíření zvuku ve volném prostoru (ve volném zvukovém poli) se akustický výkon P [W] s rostoucí vzdáleností r [m] od zdroje (s výjimkou zdroje plošného) rozprostírá na stále větší plochu S [m2]. Tím se snižuje intenzita I [W·m-2]. Od bodového zdroje se zvuk šíří v kulových vlnoplochách, kde plocha S = 4πr2. Odvození výpočtového vztahu (9) spočívá ve vynásobení obou stran příslušné rovnice číslem 1012, v jejím logaritmování a vynásobení deseti. Dále se využije skutečnosti, že referenční akustická intenzita Iref = 10-12 [W·m-2] a referenční akustický výkon Pref = 10-12 [W] mají stejnou hodnotu.
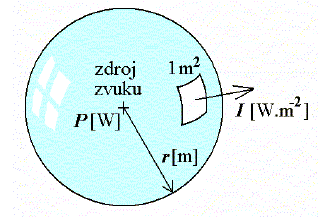
Obr. 7 K odvození vztahu (9)
\begin{gathered}
I = \frac{P}{S} = \frac{P}{4\pi r^2} \\\\
\frac{I}{10^{-12}} = \frac{P_2}{10^{-12}} \cdot \frac{I}{4\pi r^2} \\\\
10 \log = \frac{I}{I_0} = 10 \log \frac{P}{P_0} + 10 \log \frac{1}{4\pi r^2}
\end{gathered}(9)
kde Q = 1
\begin{gathered}
L = L_\text{W} + 10 \log \frac{Q}{4 \pi r^2}
\end{gathered}Jestliže se uvažuje při šíření zvuku pouze rozptyl akustického výkonu v prostoru, pak útlum se vzdáleností od zdroje je stejný pro všechny kmitočty. U většiny ostatních vlivů však útlum na kmitočtu závisí, a proto je nutné provádět kmitočtovou analýzu posuzovaného zvuku obvykle v oktávových pásmech. Tak je tomu při šíření zvuku na velké vzdálenosti (r = 100 m a více), kdy se navíc uplatní i útlum zvuku způsobený molekulární absorpcí, případně změnami teploty a prouděním vzduchu. Při akustických výpočtech se zpravidla uvažuje teplota vzduchu 14 °C, kdy je rychlost šíření zvuku c0 = 340 m·s-1. Jiným příkladem závislosti útlumu na kmitočtu může být ohyb zvuku přes překážku.
12 ÚTLUM ZVUKU VE VZDUCHU, VLIVEM VĚTRU A TEPLOTY
Útlum zvuku ve vzduchu neboli atmosférická absorpce α [dB·m-1] závisí na teplotě a relativní vlhkosti vzduchu a na kmitočtu f [Hz]. Vyjadřuje snížení hladiny akustického tlaku na jednotkovou vzdálenost od zdroje. Hodnoty α [dB·m-1] lze nalézt v ČSN ISO 9613-1 Akustika. Útlum při šíření zvuku ve venkovním prostoru. Část 1: Výpočet pohlcování zvuku v atmosféře.
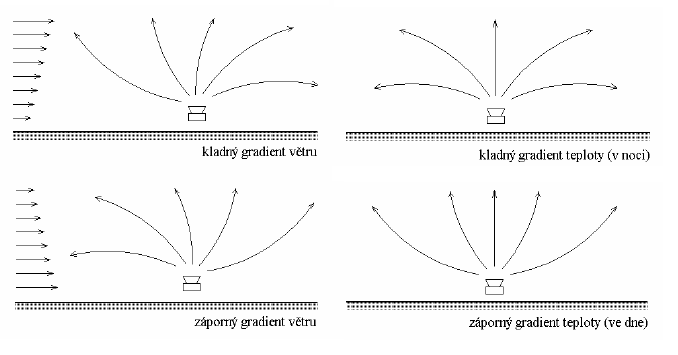
Obr. 8 Útlum nebo zesílení zvuku vlivem gradientu větru a gradientu teploty
Samotný vítr, tj. skutečnost, že vzduchová hmota se pohybuje, nemá na šíření zvuku vliv, protože rychlost větru je vždy řádově nižší oproti rychlosti zvuku. Šíření zvuku však může být ovlivněno gradientem rychlosti větru, tj. změnou rychlosti v závislosti na výšce nad terénem. Při kladném gradientu, tj. je-li rychlost ve vyšších vrstvách atmosféry vyšší, se ve směru proti větru zvukové vlny ohýbají od zemského povrchu tak, že nízko nad terénem vzniká akustický stín. Ve směru po větru se zvukové vlny ohýbají naopak k zemskému povrchu, což může být příčinou zesílení přenosu zvuku. Při záporném gradientu rychlosti zvuku je tomu naopak. Kolmo na směr větru se útlum ani zesílení přenosu zvuku neprojevují.
Rychlost zvuku se zvyšuje s teplotou. Účinek gradientu teploty je proto podobný účinku gradientu větru. Při kladném gradientu teploty obvykle v noci, tj. je-li teplota ve vyšších vrstvách atmosféry vyšší, než u zemského povrchu, se zvukové vlny ohýbají směrem k zemskému povrchu a může tak nastat zesílení přenosu. Naopak při záporném gradientu obvykle ve dne se vlny ohýbají od terénu a vytváří se zvukový stín.
Sněhová pokrývka mění pohltivost zemského povrchu. Snižuje tak účinnost zvukových vln odražených od zasněžených ploch, které měly původně nižší pohltivost zvuku. Atmosférická absorpce, útlum vlivem gradientu větru a teploty, jakož i útlum sněhem, jsou jevy závislé na proměnlivém stavu atmosféry. Při výpočtu je třeba vycházet z průměrných podmínek v dané lokalitě a často je vliv těchto jevů zanedbáván. Těmito jevy se však může někdy vysvětlit rozdílný výsledek měření zvuku oproti výsledku teoretického výpočtu.
13 ÚTLUM ZVUKU OHYBEM PŘES PŘEKÁŽKU
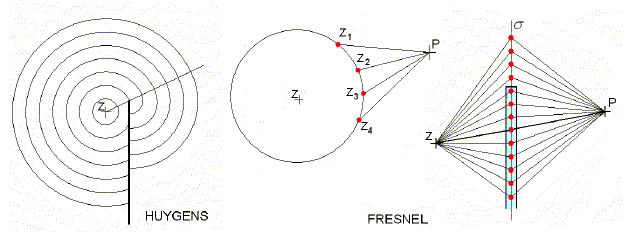
Za každou překážkou na cestě šíření zvuku, jejíž rozměry převyšují vlnovou délku, se vytváří zvukový stín, ve kterém lze pozorovat snížení intenzity zvuku oproti stavu volného šíření zvukových vln bez překážky. Útlum intenzity zvuku závisí na poloze zdroje zvuku, na poloze a geometrickém tvaru překážky, na poloze pozorovatele za překážkou a na vlnové délce zvuku. Vznik a vlastnosti zvukového stínu lze vysvětlit pomocí ohybu vlnění. Zákonitosti ohybu platí pro každé vlnění, tedy i pro vlnění elektromagnetické včetně světla, a právě pro světlo byly tyto zákonitosti nejdříve popsány. Princip šíření vlnění formuloval holandský astronom, fyzik a matematik Christian Huygens (1629–1695): Každý bod vlnoplochy je elementárním zdrojem vlnění. Výsledná vlnoplocha má tvar obálky dílčích vlnoploch. Tímto principem se vysvětluje pouze tvar vlnoploch za překážkou (viz obr. 9), nikoli však intenzita.
Augustin Jean Fresnel (1788–1827) – [čti frenel] – byl francouzský fyzik. Zdůvodnil vlnovou teorii světla a mimo jiné na základě Huygensova principu a vlnové interference vysvětlil jeho ohyb. Příslušné zákonitosti platí i pro zvuk. V oblasti praktických aplikací jeho objevů je známá Fresnelova čočka stupňovitě tvořená soustavou soustředných zobrazovacích prvků. Huygensův princip doplnil Fresnel v tomto smyslu: Při sledování intenzity je nutno přihlédnout k interferenci (skládání vlnění). K intenzitě vlnění v bodě P (viz obr. 9) přispívá každý z elementárních zdrojů vlnění – bodů vlnoplochy. Jednotlivé body vlnoplochy jsou však od bodu P různě vzdáleny. Je-li tato vzdálenost sudým násobkem půlvlny, přispěje takový elementární zdroj ke zvýšení intenzity v bodě P. Naopak při vzdálenosti rovné lichým násobkům půlvlny bude vlnění přicházející z příslušného elementárního zdroje v opačné fázi a bude intenzitu snižovat.
Obr. 9 K vysvětlení Huygensovy a Fresneloy představy ohybu vlnění
Úvahu je možno zobecnit tím, že namísto souboru elementárních zdrojů na kulové vlnoploše lze uvažovat soubor elementárních zdrojů na jakékoli ploše ležící mezi zdrojem Z a místem příjmu P. Podmínkou je jen to, aby zvolenou plochou procházely všechny možné cesty šíření vln ze zdroje Z do bodu P. S výhodou se za plochu elementárních zdrojů volí rovina σ stínící překážky. Od bodového zdroje Z se zvukové vlny šíří všemi směry a postupně zasáhnou všechny body roviny σ. Každý bod této roviny kmitá s jinou fází tak, jak k němu vlnění s různým časovým zpožděním dospělo. Každý z těchto bodů je zároveň elementárním zdrojem vlnění pro příjemce P zvuku. Celý soubor elementárních zdrojů zvuku v rovině σ musí mít v místě příjmu stejný účinek, jako původní zdroj. Přes různé body roviny σ přichází vlnění do místa příjmu po jiné dráze, a tedy s jiným fázovým zpožděním. Vlnění přicházející z místa původního zdroje přímou cestou se skládá s vlněním z jiných směrů, přičemž příspěvky od různých elementárních zdrojů v rovině σ přicházejí do místa příjmu v různé míře se shodnou fází nebo ve fázi opačné a způsobují tak buď zesílení nebo zeslabení přímého signálu. Účinek příspěvků od různých elementárních zdrojů roviny σ se tak navzájem ruší a při interferenci vlnění v místě příjmu dominuje jen přímá cesta zvuku. Tato rovnováha se poruší, postaví-li se do cesty vlnění překážka. Část elementárních zdrojů roviny σ včetně přímé cesty zvuku je vyřazena z provozu a dochází k útlumu zvuku ohybem. Výpočet útlumu zvuku ohybem využívá matematický aparát Fresnelových integrálů. Obecně útlum roste s rozdílem drah zvuku δ = a + b – c [m] (viz obr. 10) a s kmitočtem zvuku f [Hz], což je vyjádřeno hodnotou Fresnelova čísla N [-]
\begin{gathered}
N = \frac{2\delta}{\lambda} = \frac{P\delta f}{c_0}
\end{gathered}(10)
kde je
λ [m] … vlnová délka zvuku,
f [Hz] … kmitočet,
c0 [m·s-1] … rychlost zvuku ve vzduchu.
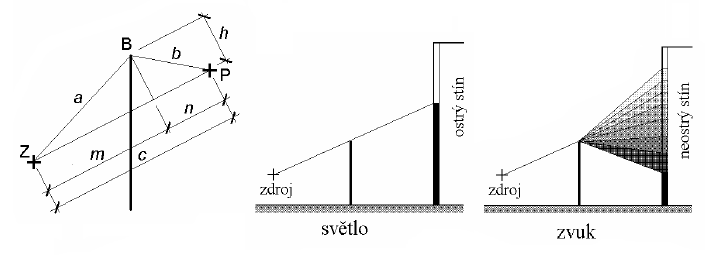
Obr. 10 Geometrické parametry ohybu vlnění a rozdíl mezi ohybem světla a zvuku
Zajímavé je srovnání mezi ohybem světla a ohybem zvuku. Vlnová délka světla je 3,8·10-7 až 7,8·10-7 m a hodnota Fresnelova čísla N vychází proto velmi vysoká již při nepatrném rozdílu drah δ [m]. U zvuku, jehož vlnová délka při šíření ve vzduchu se pohybuje v rozmezí 0,02 až 20 m, je hodnota Fresnelova čísla N v porovnání se světlem malá a menší je proto i útlum, který překážka způsobuje. Zvukové vlny zejména nízkého kmitočtu se snáze ohýbají přes překážku a zvukový stín je podstatně méně ostrý. Útlum zvuku lze zaznamenat dokonce i v místech se zápornou hodnotou dráhového rozdílu δ [m] a tedy i zápornou hodnotou Fresnelova čísla N, tj. v místech, kam světelné vlny dopadají bez omezení, takže zdroj zvuku lze z těchto míst přes překážku pozorovat.
Činitel útlumu d [-] intenzity vlnění při jeho ohybu přes překážku se definuje jako poměr intenzit
\begin{gathered}
d = \frac{I_2}{I_1}
\end{gathered}(11)
kde je
I1 resp. I2 [W·m-2] … intenzita zvuku v místě P bez uvažování resp. s uvažováním vlivu clony. Intenzita zvuku je přímo úměrná druhé mocnině efektivní hodnoty akustického tlaku pef [Pa]. Efektivní hodnota je pak přímo úměrná amplitudě akustického tlaku A [Pa] při harmonickém vlnění. Činitel útlumu lze proto vyjádřit jako poměr druhých mocnin amplitud akustického tlaku
\begin{gathered}
d = \frac{A_2^2}{A_1^2}
\end{gathered}(12)
kde je
A1 resp. A2 [Pa] … amplituda akustického tlaku v místě P bez clony, resp. se clonou.
Útlum D [dB] hladiny akustického tlaku způsobený clonou bude pak
\begin{gathered}
D = 10\log \bigg(\frac{1}{d}\bigg) = 10\log \bigg(\frac{A_1^2}{A_2^2}\bigg) = 10 \log A_1^2 - 10 \log A_2^2
\end{gathered}(13)
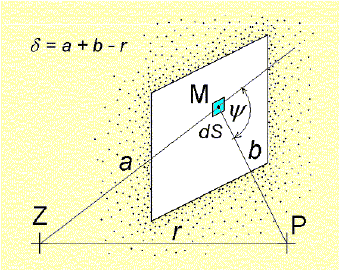
Obr. 11 K odvození Fresnelových integrálů
Pro akustický tlak při harmonickém vlnění platí vztah
\begin{gathered}
p = A \sin(\omega t - \varphi)
\end{gathered}(14)
kde je
ϕ [rad] … fáze.
Jako počátek sledování se označí okamžik, kdy vlnění dospělo do místa P po přímé cestě ze zdroje Z. Část akustického tlaku p0 [Pa], která je způsobena jen tímto přímým šířením, lze popsat vztahem
\begin{gathered}
p_0 = A_0 \sin(\omega t)
\end{gathered}(15)
kde amplituda A0 [Pa] závisí jen na výkonu zdroje a vzdálenosti r [m]. Fáze je nulová, protože na počátku sledování vlnění právě dospělo přímou cestou do místa P a je tedy na počátku vlny. Dalšími cestami volné části roviny (např. i přes bod M – viz obr. 11) dospěje vlnění do bodu P s časovým zpožděním a tedy i v odlišné fázi. Proto lze předpokládat, že akustický tlak p [Pa] v místě P vzniklý jako výsledek spolupůsobení všech cest šíření (přes všechny elementární zdroje volné části roviny σ) bude obsahovat nenulovou fázi ϕ [rad] a bude tedy odpovídat vztahu (14). Cílem následujících úvah je stanovit hodnoty amplitud akustického tlaku A1 a A2 [Pa] pro použití ve vztazích (12) a (13).
Vztah (14) lze upravit jako sinus rozdílu dvou úhlů
\begin{gathered}
p = \sin(\omega t) A \cos\varphi - \cos(\omega t) A \sin \varphi
\end{gathered}(16)
Příspěvek dp [Pa] elementární plochy dS [m2] části roviny σ v místě bodu M k hodnotě akustického tlaku v bodě P je
\begin{gathered}
dp = KdS \sin\omega \bigg(t- \frac{\delta}{c_0}\bigg)
\end{gathered}(17)
kde je
(KdS) [Pa] … amplituda zahrnující vliv A0, δ, ψ, dS
δ/c0 [s] … časové zpoždění vlny vzhledem k počátku sledování.
δ = a + b – r [m] … rozdíl drah zvuku mezi dráhou přes bod M a dráhou přímou – viz obr. 11 Vlnové číslo k [rad·m-1] je definováno jako
\begin{gathered}
k = \frac{\omega}{c_0} = \frac{2\pi}{\lambda}
\end{gathered}(18)
Vztah (9) je možno upravit roznásobením závorky a dosazením vlnového čísla
\begin{gathered}
dp = KdS \sin\bigg(\omega t - \frac{\omega \delta}{c_0}\bigg) = KdS \sin (\omega t - k\delta)
\end{gathered}(19)
Hodnota akustického tlaku p (Pa) v bodě P se získá integrací přes celou volnou část roviny σ (například přes plochu vyznačenou jako „okno“ na obr. 11).
\begin{gathered}
p = \int\limits_\delta K \sin (\omega t - k\delta)dS
\end{gathered}(20)
Integrál je možno upravit s využitím vztahu pro sinus rozdílu dvou úhlů
\begin{gathered}
p = \sin(\omega t)\int\limits_\delta K \cos (k\delta)dS - \cos(\omega t) \int\limits_\delta K \sin(k\delta)dS
\end{gathered}(21)
Integrály ve vztahu (21) jsou Fresnelovy integrály a označují se
\begin{gathered}
X = \int\limits_\delta K\cos(k\delta)dS \\\\
Y = \int\limits_\delta K\sin(k\delta)dS
\end{gathered}(22)
Vztah (21) pak bude mít tvar
\begin{gathered}
p = \sin(\omega t) X - \cos(\omega t) Y
\end{gathered}(23)
Porovnáním vztahu (23) se vztahem (16) se snadno zjistí že
\begin{gathered}
X = A\cos \varphi \\\\
Y = A \sin \varphi
\end{gathered}(24)
Hledanou druhou mocninu amplitudy A [Pa] akustického tlaku v bodě P pak lze stanovit právě pomocí Fresnelových integrálů.
\begin{gathered}
A^2 = A^2 (\sin^2\varphi + \cos^2 \varphi) = A^2 \cos^2\varphi + A^2 \sin^2\varphi = X^2 + Y^2
\end{gathered}(25)
S přihlédnutím ke vztahům (12) a (13) je pak možno pomocí Fresnelových integrálů stanovit činitel d [-] útlumu a útlum D [dB] hladiny akustického tlaku.
\begin{gathered}
d = \frac{X_2^2 + Y_2^2}{X_1^2 + Y_1^2}
\end{gathered}(26)
\begin{gathered}
D = 10\log \frac{1}{d} = 10\log(X_1^2 + Y_1^2) - 10\log(X_2^2 + Y_2^2)
\end{gathered}(27)
kde je
X1 a Y1 … hodnoty příslušných Fresnelových integrálů stanovené integrací za stavu bez clony tj. po celé rovině σ, X2 a Y2 jsou hodnoty Fresnelových integrálů stanovené integrací jen v rozsahu volné části roviny σ nezakryté clonou.
Při výpočtu Fresnelových integrálů se používá proměnná
\begin{gathered}
u = h \sqrt{\frac{2}{\lambda}\bigg(\frac{1}{m} + \frac{1}{n} \bigg)}
\end{gathered}(28)
kde je
h [m] … výška trojúhelníka ZBP,
m a n [m] … úseky základny ZP – viz obr. 10.
Fresnelovy integrály se řeší ve tvaru
\begin{gathered}
X = \int\limits_0^\text{u} \cos\bigg(\frac{\pi}{2} x^2\bigg)dx \\\\
Y = \int\limits_0^\text{u} \sin\bigg(\frac{\pi}{2} x^2\bigg)dx
\end{gathered}(29)
Hodnoty Fresnelových integrálů lze s potřebnou přesností získat jako součet jistého počtu členů alternující číselné řady. K tomu je však třeba integrály (29) upravit pomocí substituce
\begin{gathered}
t = \frac{\pi}{2}x^2
\end{gathered}(30)
na tvar
\begin{gathered}
X= \frac{1}{\sqrt{2\pi}} \int\limits_0^\text{v} \frac{\cos t}{\sqrt{t}}dt \\\\
Y= \frac{1}{\sqrt{2\pi}} \int\limits_0^\text{v} \frac{\sin t}{\sqrt{t}}dt
\end{gathered}(31)
Nová mez v proměnné t v integrálech (31) je podle vztahu (30)
\begin{gathered}
v = \frac{\pi}{2}u^2
\end{gathered}(32)
a integrály (31) lze spočítat jako součet konvergentních číselných řad
\begin{gathered}
X =\sqrt{\frac{2v}{\pi}} \bigg( 1- \frac{v^2}{5{\cdot}2!} + \frac{v^4}{9{\cdot}4!} - \frac{v^6}{13{\cdot}6!} + \frac{v^8}{17{\cdot}8!} - \text{...} \bigg) \\\\
Y =\sqrt{\frac{2v}{\pi}} \bigg( \frac{v}{3}- \frac{v^3}{7{\cdot}3!} + \frac{v^5}{11{\cdot}5!} - \frac{v^7}{15{\cdot}7!} + \frac{v^9}{19{\cdot}9!} - \text{...} \bigg)
\end{gathered}(33)
Například pro u = 1 je v = 1,5708 a integrály pak mají hodnoty
\begin{gathered}
X = 1(1 – 0{,}24674 + 0{,}02819 – 0{,}00160 + 0{,}00005 - \text{...}) \cong 0{,}7799 \\\\
Y = 1(0{,}52360 – 0{,}09228 + 0{,}00724 – 0{,}00031 + 0{,}00001 - \text{...}) \cong 0{,}4383
\end{gathered}Pro praktické použití lze hodnoty Fresnelových integrálů v závislosti na proměnné u nalézt v tab. 7.
Platí
\begin{gathered}
X(-u) = -X(u) \\\\
\lim\limits_{\text{u} \to \pm \infty} X = \pm 0{,}5 \\
\end{gathered}\begin{gathered}
Y (-u) = -Y(u) \\\\
\lim\limits_{\text{u} \to \pm \infty} Y = \pm 0{,}5 \\
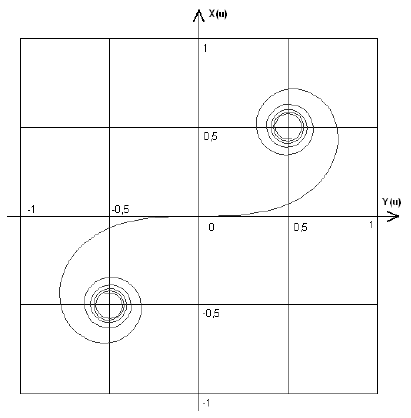
\end{gathered}Grafickým vyjádřením hodnot Fresnelových integrálů je křivka klotoida s asymptotickými body (0,5; 0,5) a (-0,5; -0,5),
kde je
u … délka oblouku křivky od počátku (0; 0) k bodu se souřadnicemi (X, Y) – viz obr. 12.
Obr. 12 Fresnelovy integrály v pravoúhlém diagramu
Mezi proměnnou u a rozdílem drah δ = a + b – c existuje souvislost popsaná níže – odvození vychází z obr. 10.
\begin{gathered}
\delta = \sqrt{m + h^2} - m + \sqrt{n^2 + h^2} - n = m \Bigg(\sqrt{1+\frac{h^2}{m^2}}-1 \Bigg) + n \Bigg(\sqrt{1+\frac{h^2}{n^2}}-1 \Bigg)
\end{gathered}(34)
Pro x <1 platí
\begin{gathered}
\sqrt{1+x} = 1 + \frac{1}{2}x - \frac{1}{2 \cdot 4}x^2 + \frac{1 \cdot 3}{2 \cdot 4 \cdot 6} x^3 - \frac{1 \cdot 3 \cdot 5}{2 \cdot 4 \cdot 6 \cdot 8} x^4 + \text{...}
\end{gathered}(35)
Při praktických aplikacích ohybu zvuku je vždy převýšení h vrcholu překážky významně nižší v porovnání se vzdálenostmi m a n. V takovém případě lze uvažovat jen první dva členy číselné řady (35) a rovnici (34) upravit
\begin{gathered}
\delta \cong \frac{h^2}{2} \bigg( \frac{1}{m} + \frac{1}{n} \bigg)
\end{gathered}(36)
Fresnelovo číslo N pak za uvedených podmínek bude rovno polovině druhé mocniny proměnné u.
\begin{gathered}
N = \frac{2 \delta}{\lambda} \cong \frac{h^2}{\lambda} \bigg( \frac{1}{m} + \frac{1}{n} \bigg) = \frac{1}{2} h^2 \frac{2}{\lambda} \bigg(\frac{1}{m} + \frac{1}{n} \bigg) = \frac{1}{2} u^2
\end{gathered}(37)
kde je
λ … délka vlny.
Z diagramu na obr. 12 vyplývá, že útlum zvuku lze stanovit i pro záporné hodnoty proměnné u, kdy výška h trojúhelníka ZBP je záporná. Taková situace nastává v případech, kdy přímá dráha zvuku od zdroje Z k místu příjmu P není clonou přerušena (viz obr. 13). V takovém případě má zápornou hodnotu i rozdíl drah δ = c – a – b a záporné je také Fresnelovo číslo N.
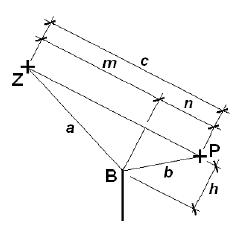
Obr. 13 Příklad situace při záporných hodnotách δ, N a u
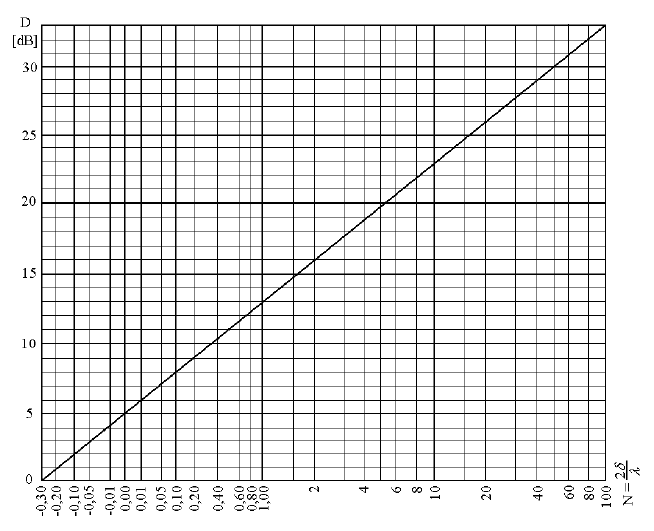
Protože přesný výpočet útlumu pomocí Fresnelových integrálů je relativně pracný, snažili se v minulosti různí autoři o zjednodušení. Jeden z možných postupů spočívá ve využití diagramu podle [25, 26]. Hodnota útlumu D [dB] se vyhledá v diagramu na obr. 14 v závislosti na Fresnelově čísle N [-].
Obr. 14 Útlum zvuku ohybem přes překážku v závislosti na Fresnelově čísle (podle prof. Maekawy)
Praktický vztah pro výpočet útlumu zvuku ohybem přes překážku nahrazující výpočet pomocí Fresnelových integrálů navrhl Čechura [12].
\begin{gathered}
D = 10\log \Bigg\lbrack (9 \lvert N \rvert + \sqrt[3]{\lvert N \rvert} + 1)^{\text{sign}\delta} + 10^{-\frac{3 \lvert N \rvert + 1}{5 \lvert N \rvert}} \Bigg\rbrack + 6
\end{gathered}(38)
kde je
N … Fresnelovo číslo
δ [m] … rozdíl drah mezi přímou cestou šíření zvuku a cestou šíření přes překážku.
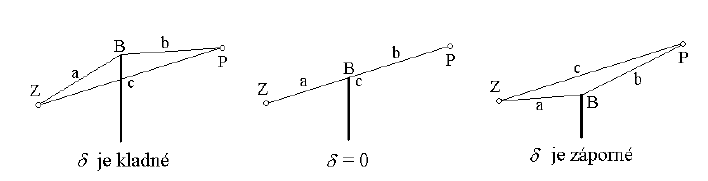
Je-li N = 0, pak se vztah (38) nahrazuje vztahem D = 6 dB. Pro kladné δ, tj. v případě, kdy stínící překážka protíná přímou cestu zvuku, je sign δ = 1. Jestliže stínící překážka neprotíná přímou cestu zvuku, pak je δ záporné a sign δ = – 1.
Obr. 15 Znaménková konvence rozdílu drah δ [m]
Platnost vztahu (38) je podmíněna těmito vlastnostmi clony:
- délka clony je nejméně dvojnásobná oproti vzdálenosti od místa P. Tloušťka clony není větší než jedna šestina vlnové délky posuzovaného zvuku;
- odraz zvuku od konstrukce akustické clony a od okolních konstrukcí je spolu s přenosem zvuku konstrukcí stěny zanedbatelný oproti zvuku šířenému ohybem vlnění nad clonou.
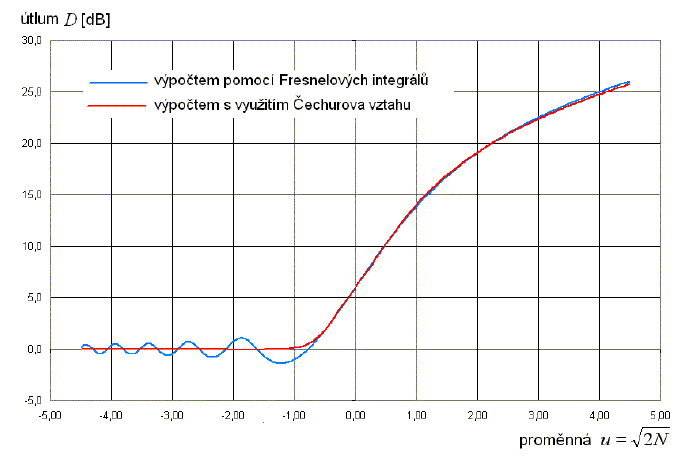
Obr. 16 Útlum D (dB) v závislosti na proměnné u
Představu o shodě výsledků mezi přesným výpočtem a výpočtem podle vztahu (38) podává obr. 16. Pro kladné hodnoty u je shoda téměř dokonalá. V oblasti záporných hodnot proměnné u vztah (38) neakceptuje periodické kolísání hodnot útlumu. V praxi se zřídka kdy řeší útlum tónového zvuku. Běžný zvuk hlučných zařízení je směsí zvuku o velkém počtu kmitočtů, kde spektrum takového zvuku bývá spojité. Zvuk se sleduje a hodnotí v kmitočtových pásmech, nejčastěji oktávových. Útlum D [dB] je závislý na kmitočtu. S kmitočtem se totiž mění hodnota proměnné u, resp. hodnota Fresnelova čísla N. V oblasti záporných hodnot proměnné u jsou tak v každém pásmu zastoupeny kmitočty, které mají útlum kladný, i kmitočty, které mají útlum záporný. Hodnoty útlumu se tak v rámci pásma vyruší, takže útlum v celém pásmu zůstává nulový. Při práci se zvukem v kmitočtových pásmech tak vztah (38) poskytuje reálnější hodnoty útlumu v porovnání s přesným výpočtem pomocí Fresnelových integrálů.
Docent Čechura už nežije, ale měl jsem příležitost nějaký čas s ním působit na stejném pracovišti. Pokud vím, tak vztah (38) vznikl jako originální odvození doc. Čechury. Domnívám se, že by bylo vhodné o vztahu (38) hovořit jako o Čechurově vztahu.
14 ŠÍŘENÍ ZVUKU V UZAVŘENÉM PROSTORU – DIFUZNÍ ZVUKOVÉ POLE
V uzavřeném prostoru (v místnosti) dochází k odrazu akustické energie od stěn, stropu a podlahy zpět směrem ke zdroji. To má za následek zvýšení hladiny akustického tlaku v porovnání se stavem, který by vznikl ve volném prostoru. Významnou roli zde hraje pohltivost zvuku povrchů, které ohraničují uzavřený prostor.
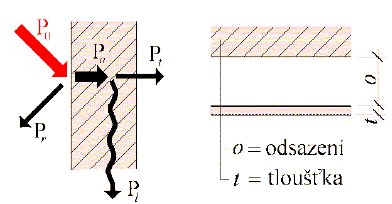
Obr. 17 Distribuce akustického výkonu po dopadu zvuku na stěnu a vysvětlení pojmů tloušťka a odsazení zvuk pohlcujícího obkladu
Při dopadu zvuku o akustickém výkonu P0 [W] na překážku se část tohoto výkonu Pr [W] odrazí a část Pa [W] pohltí. Pohlcený výkon se pak rozdělí na část výkonu Pl [W], která se ztratí (je odvedena konstrukcí mimo sledované místo nebo se promění v jiný druh energie) a na část Pt [W], která projde stěnou a je vyzářena do vedlejšího prostoru. Lze definovat
činitele odrazu
\begin{gathered}
\rho = \frac{P_\text{r}}{P_0}
\end{gathered}činitele pohltivosti
\begin{gathered}
\alpha = \frac{P_\text{a}}{P_0}
\end{gathered}a činitele prostupu (průzvučnosti)
\begin{gathered}
\tau = \frac{P_\text{t}}{P_0}
\end{gathered}Tito tři činitelé jsou bezrozměrná čísla, která mohou nabývat hodnot od nuly do jedné.
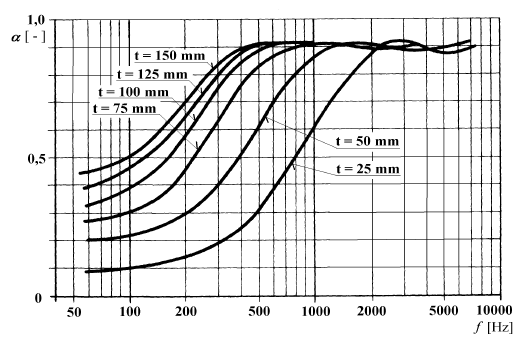
Zvuková pohltivost Ai [m2] povrchu konstrukce (i-tého povrchu) je dána součinem plochy povrchu Si [m2] a činitele pohltivosti α1 [-]. Celková zvuková pohltivost místnosti A [m2] je součtem zvukové pohltivosti všech ploch, které tuto místnost ohraničují, případně též zvukové pohltivosti předmětů a osob, které se v místnosti nacházejí. Je nutno poznamenat, že činitel pohltivosti α [-] a tudíž i pohltivost A [m2] jsou veličiny závislé na kmitočtu zvuku, a proto všechny jevy související se zvukovou pohltivostí je nutno sledovat a počítat v jednotlivých kmitočtových pásmech obvykle oktávových. Pohltivost zvuku nezávisí jen na materiálu obkladu a jeho tloušťce, ale i na odsazení (tloušťce vzduchové mezery) od tvrdého povrchu stropu nebo stěny.
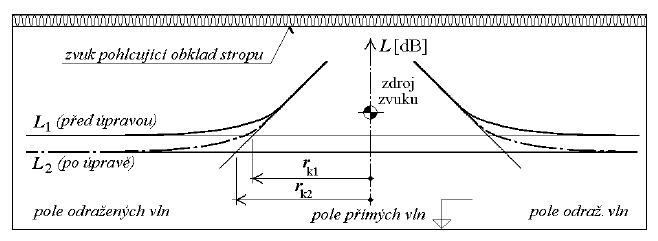
Obr. 18 K vysvětlení pojmu pole přímých vln a pole odražených vln
V bezprostředním okolí zdroje se nachází pole přímých vln. Pokles hladiny akustického tlaku se vzdáleností zde podléhá stejným zákonitostem jako ve volném prostoru a příjemce je schopen sluchem rozpoznat směr, odkud zvuk přichází. Pole přímých vln je omezeno vzdáleností rk [m], která se nazývá dozvuková vzdálenost. Ve vzdálenějších místech uzavřeného prostoru se nachází pole odražených vln, kde převládá akustické vlnění, které do uvažovaného místa dospěje po vícenásobném odrazu od ohraničujících ploch místnosti. Hodnota hladiny akustického tlaku v poli odražených vln je nezávislá na vzdálenosti od zdroje a je určena celkovou zvukovou pohltivostí místnosti A [m2]. V poli odražených vln se předpokládá difuzní charakter zvukového pole.
Představa difuzního zvukového pole je zjednodušeným modelem skutečných podmínek šíření zvuku v uzavřených prostorech, jejichž difuznost je ve skutečnosti vždy do jisté míry narušena. Toto zjednodušení zpravidla umožní dostatečně přesně výpočtem stanovit zatížení uživatelů budov hlukem, ale při sledování kvality zvuku v auditoriích (divadla, kina, koncertní sály, přednáškové síně apod.) je nutný podrobnější popis zvukového pole, kterým se zabývá prostorová akustika.
Na obr. 18 je schéma řezu uzavřeným prostorem (místností) se zdrojem zvuku uprostřed. Formou pravoúhlého diagramu je naznačeno rozložení hladin akustického tlaku v prostoru. Na svislé ose diagramu je stupnice hladin akustického tlaku L [dB], na ose vodorovné je vzdálenost r [m] od zdroje zvuku. Jestliže se zvýší celková pohltivost prostoru například obložením stropu místnosti zvuk pohlcujícím obkladem, hladina v poli odražených vln L1 [dB] se sníží na hodnotu L2 [dB]. Zároveň se zvětší dozvuková vzdálenost z hodnoty rk1 [m] na hodnotu rk2 [m]. Z vyobrazení je zřejmé, že zvýšením celkové pohltivosti prostoru nelze snížit hladinu akustického tlaku v bezprostřední blízkosti zdroje, kde se nachází pole přímých vln. Hladinu akustického tlaku L [dB] v poli odražených vln je možno stanovit pomocí vztahu (52). Jeho odvození vychází z vlastností difuzního zvukového pole a respektuje zákon zachování energie. To znamená, že akustický výkon vyzařovaný zdrojem musí být celý pohlcován ohraničujícími povrchy místnosti. Po spuštění zdroje zvuku se hladina akustického tlaku v poli odražených vln ustálí právě na takové hodnotě, která zajistí stav rovnováhy mezi vyzářeným a pohlceným akustickým výkonem.
Difuzní charakter zvuku v poli odražených vln je určen třemi vlastnostmi:
- hustota akustické energie je ve všech místech difuzního pole stejná;
- každý směr dopadu zvuku je stejně pravděpodobný;
- hustota energie zvuku je součtem hustoty energie všech zvukových vln, které současně do daného místa z různých směrů přicházejí.
Uvedené vlastnosti difuzního pole lze vyjádřit následujícími vztahy:
VLASTNOST 1: pro všechna místa v difuzním poli, která jsou určena souřadnicemi x, y, z [m] platí
\begin{gathered}
w_\Sigma (x,y,z) = \text{konst.}
\end{gathered}(39)
VLASTNOST 2: v každém místě difuzního pole platí
\begin{gathered}
\frac{dw}{d\Omega} = \text{konst.}
\end{gathered}(40)
kde je
dΩ [sterad] … elementární prostorový úhel,
dw [W·s·m-3] … elementární hustota akustické energie, která je do daného místa dodána akustickým vlněním ze směru určeného úhlem dΩ.
VLASTNOST 3: hustotu akustické energie lze vyjádřit jako součet zvukových vln přicházejících ze všech směrů
\begin{gathered}
w_\Sigma = \sum_{\text{i}=1}^\text{n} w_\text{i} = 4\pi \frac{dw}{d\Omega}
\end{gathered}(41)
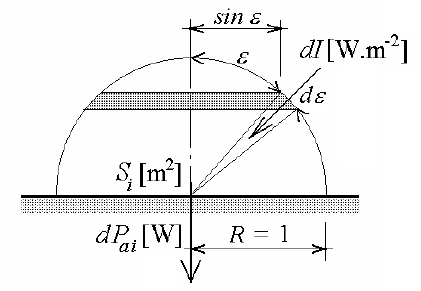
Obr. 19 K odvození vztahu (52)
Vynásobením rovnice (41) rychlostí zvuku c [m·s-1] lze obdržet
\begin{gathered}
I_\Sigma = \sum_{\text{i}=1}^\text{n} I_\text{i} = 4\pi \frac{dI}{d\Omega}
\end{gathered}(42)
kde je
dI [W·m-2] … elementární akustická intenzita, která v daném místě působí ze směru určeného prostorovým úhlem .
Veličinu IΣ [W·m-2] je možno definovat jako ekvivalentní intenzitu rovinné vlny ve volném zvukovém poli, která vzbudí stejný sluchový vjem jako difuzní zvukové pole v uzavřeném prostoru.
Na hranici difuzního pole vstupují zvukové vlny do interakce s ohraničující stěnou uzavřeného prostoru. Elementární intenzitu dI [W·m-2] příslušnou prostorovému úhlu dΩ je možno rozložit na složku dIn [W·m-2] kolmou a složku dIp [W·m-2] rovnoběžnou se stěnou.
\begin{gathered}
dI_\text{n} = dI \cos \varepsilon
\end{gathered}(43)
kde je
ε [rad] … odklon směru působení zvukové vlny od normály stěny.
Jen část dIai [W·m-2] kolmé složky intenzity je absorbována povrchem i-té plochy, která ohraničuje uzavřený prostor.
\begin{gathered}
dI_\text{ai} = \alpha_\text{i}dI_\text{n}=\alpha_\text{i}dI \cos \varepsilon
\end{gathered}(44)
kde je
αi [-] … činitel pohltivosti i-tého ohraničujícího povrchu.
Elementární akustický výkon dPai [W] pohlcený i-tou plochou Si [m2] se získá jako součin intenzity a plochy.
\begin{gathered}
dP_\text{ai} = S_\text{i} dI_\text{ai} = \alpha_\text{i}S_\text{i}dI \cos \varepsilon = A_\text{i}dI \cos \varepsilon
\end{gathered}(45)
kde je
Ai [m2] … pohltivost i-té stěny uzavřeného prostoru.
Vztah (45) lze upravit rozšířením dΩ a dosazením podle vztahu (42)
\begin{gathered}
dP_\text{ai} = A_\text{i} \frac{dI}{d\Omega} \cos \varepsilon d\Omega =A_\text{i} \frac{I_\Sigma}{4\pi} \cos \varepsilon \space d\Omega
\end{gathered}(46)
Hodnotu akustického výkonu Pai [W] pohlceného i-tou stěnou uzavřeného prostoru lze obdržet integrací vztahu (46).
\begin{gathered}
P_\text{ai} = \frac{I_\Sigma A_\text{i}}{4\pi} \int\limits_0^{\frac{\pi}{2}} \cos \varepsilon \space d\Omega
\end{gathered}(47)
Elementární prostorový úhel dΩ může být stanoven jako povrch elementárního kulového pásu podle obr. 19 dělený druhou mocninou poloměru myšlené kulové plochy. Při jednotkovém poloměru R = 1 myšlené kulové plochy lze napsat
\begin{gathered}
d\Omega = 2\pi \sin \varepsilon \space d\varepsilon
\end{gathered}(48)
a integrál (47) pak bude mít tvar (49), který lze řešit substitucí sinε = t; cosε · dε = dt
\begin{gathered}
P_\text{ai} = \frac{I_\Sigma A_\text{i}}{2} \int\limits_0^{\frac{\pi}{2}} \sin \varepsilon \cos \varepsilon \space d\varepsilon = \frac{I_\Sigma A_\text{i}}{4}
\end{gathered}(49)
Akustický výkon Pa [W] pohlcený v celém uzavřeném prostoru je roven součtu akustických výkonů pohlcených dílčími plochami. K úpravě příslušného vztahu (50) se použije výsledek integrace (49)
\begin{gathered}
P_\text{a} = \sum^\text{n}_{\text{i}=1} P_\text{ai} = \frac{I_\Sigma}{4} \sum^\text{n}_{\text{i}=1} A_\text{i} = \frac{I_\Sigma A}{4}
\end{gathered}(50)
kde je
n … počet dílčích ploch vnitřního prostoru,
\begin{gathered}
A = \sum^\text{n}_{\text{i}=1} A_\text{i} \text{ [m}^2\text{]}
\end{gathered}je celková pohltivost místnosti.
Ze zákona zachování energie plyne rovnost mezi pohlceným akustickým výkonem Pa [W] a akustickým výkonem Pe [W] vyzářeným zdrojem zvuku.
\begin{gathered}
P_\text{e} = P_\text{a} \frac{I_\Sigma A}{4}
\end{gathered}(51)
Známý vztah pro výpočet hladiny akustického tlaku L [dB] v difuzním poli lze obdržet upravením rovnice (51), jejím vynásobením hodnotou 1012, logaritmováním a vynásobením deseti.
\begin{gathered}
\frac{I_\Sigma}{10^{-12}} = \frac{P_\text{e}}{10^{-12}} \frac{4}{A}
\end{gathered}\begin{gathered}
10 \log \bigg(\frac{I_\Sigma}{I_\text{ref}} \bigg) = 10 \log \bigg( \frac{P_\text{e}}{P_\text{ref}} \bigg) = 10 \log \bigg( \frac{4}{A} \bigg)
\end{gathered}\begin{gathered}
L = L_\text{W} + 10 \log \bigg( \frac{4}{A} \bigg)
\end{gathered}(52)
kde je
Iref = 10-12 W·m-2 resp. Pref =10-12 W … referenční hodnoty akustické intenzity resp. akustického výkonu,
LW [dB] … hladina akustického výkonu zdroje.
Se vzrůstající celkovou pohltivostí A [m2] místnosti se zvyšuje i hodnota středního činitele pohltivosti αm [-] – viz vztah (54) – uzavřeného prostoru a také se postupně omezuje a ruší difuznost zvukového pole v důsledku úbytku energie odražených zvukových vln, až při extrémní hodnotě αm = 1 odražené vlny a s nimi difuzní pole zcela mizí a v celém vnitřním prostoru je pouze pole přímých vln. Tím se ruší i předpoklady, na jejichž základě byl vztah (52) odvozen. Taková situace nastává např. v bezdozvukových místnostech akustických laboratoří, které slouží k měření zvuku ve volném poli v laboratorních podmínkách. Namísto vztahu (52) se proto v prostorech s vysokou pohltivostí používá vztah (53),
kde výraz (1 – αm) kompenzuje ztrátu difuznosti při vyšších hodnotách αm.
\begin{gathered}
L = L_\text{W} + 10\log \bigg \lbrack \frac{4 (1-\alpha_\text{m})}{A} \bigg \rbrack
\end{gathered}(53)
kde je
αm [-] … střední činitel pohltivosti, který se stanoví jako průměrná hodnota ze všech povrchů v místnosti
\begin{gathered}
\alpha_\text{m}=\frac{S_1\alpha_1+S_2\alpha_2+...+S_\text{i}\alpha_\text{i}+...+S_\text{n}\alpha_\text{n}}{S_1+S_2+...+S_\text{i}+...+S_\text{n}}=\frac{\sum\limits_{\text{i}=1}^\text{n}S_\text{i}\alpha_\text{i}}{\sum\limits_{\text{i}=1}^\text{n}S_\text{i}}=\frac{A}{\sum S}
\end{gathered}(54)
kde je
Si [m2] … i-tý povrch s činitelem pohltivosti zvuku αi [-]
n … počet dílčích povrchů v místnosti. Jednotlivými povrchy mohou být např. strop, stěna, okno, dveře, koberec apod.
Hladinu akustického tlaku současně v poli přímých i odražených vln charakterizuje Berankův vztah (55) podle [8, 9], který je kombinací již uvedených vztahů (9) a (53).
\begin{gathered}
L=L_\text{W}+10\log\Bigg[\frac{Q}{4\pi r^2}+\frac{4(1-\alpha_\text{m}}{A}\Bigg]
\end{gathered}(55)
Jestliže se výraz v závorce ve vztahu (55) položí roven nule a vyjádří se r, získá se vztah pro výpočet dozvukové vzdálenosti
\begin{gathered}
r_\text{k}=\sqrt{\frac{AQ}{16\pi(1-\alpha_\text{m})}}
\end{gathered}(56)
15 KONSTRUKCE NA POHLCOVÁNÍ ZVUKU
Činitelé pohltivosti α [-] některých běžných povrchů jsou pro střední kmitočty oktávových pásem 125 až 4 000 Hz uvedeny v tab. 8. V této tabulce jsou však uvedeny jen běžné (neupravené) typy povrchů. Zvuk pohlcujícími konstrukcemi se formou obkladu zvyšuje činitel pohltivosti stropu nebo stěn místnosti, což má za následek nejen snížení hladiny akustického tlaku v poli odražených vln, ale i změnu dalších důležitých akustických vlastností místnosti v důsledku zvýšení její celkové zvukové pohltivosti, např. doby dozvuku, která je významná pro akustičnost vnitřních prostorů budov. Dnes je k dispozici poměrně široká nabídka zvuk pohlcujících úprav stropů a stěn poskytovaná tuzemskými i zahraničními firmami. Při jejich výběru je třeba zvážit i jiná než akustická hlediska, zejména hlediska provozní, estetická, požární, hlediska zdravotní nezávadnosti a hlediska ekonomická. Změřené hodnoty činitelů pohltivosti α [-] v oktávových pásmech udávají výrobci těchto konstrukcí ve svých technických podkladech formou grafu nebo tabulky obdobné tab. 8. Je dobré vědět, že zvuk pohlcující obklad není pouhým stavebním materiálem, ale je konstrukcí, o jejíchž vlastnostech rozhoduje i odsazení obkladu od povrchu, který je obkládán. Proto se lze setkat v příslušných tabulkách s několika variantami hodnot α [-] pro ten samý materiál v závislosti právě na vzdálenosti mezi ním a obkládaným povrchem.
Podle konstrukčního uspořádání a principu funkce lze zvuk pohlcující konstrukce dělit na:
- porézní konstrukce;
- kmitající membrány a desky;
- dutinové rezonátory;
- kombinované konstrukce.
16 OBKLADY Z PÓROVITÝCH MATERIÁLŮ
Obr. 20 Spektrum hodnot činitele pohltivosti zvuku α [-] pro obklad plstí z minerálních vláken různé tloušťky (podle literatury [30])
Jedná se o materiály vysoké pórovitosti, jejichž kostru tvoří vlákna nebo ztuhlá pěna. Póry musí být navzájem propojené a otevřené do volného prostoru. Používají se zejména rohože a desky z minerálních nebo organických vláken. Materiály typu pěnový polystyrén nejsou pro tyto účely vhodné pro uzavřenost jejich pórů. Póry se také nesmí uzavřít nevhodnou povrchovou úpravou (např. nátěrem). Porézní pohlcovače jsou nejvíce účinné, je-li pórovitý materiál přítomen ve vzdálenosti alespoň 1/4 vlnové délky zvuku od tvrdého povrchu stropu nebo stěny. Pohlcují proto převážně ve vysokých kmitočtech, kde vlnová délka je malá. Akustické vlastnosti obkladu je možno regulovat jeho tloušťkou h [m] případně odsazením d [m] desky pórovitého materiálu od obkládaného povrchu stropu nebo stěny. Z hygienických a estetických důvodů a také pro ochranu proti poškození se porézní pohlcovače mohou chránit zatavením do velmi tenké polyetylénové fólie, zakrytím řídkou tkaninou, pletivem, mřížovinou nebo děrovaným plechem. Procento plochy děr však musí být alespoň 25 až 35 %.
17 KMITAJÍCÍ MEMBRÁNY A DESKY
Kmitající membrána je tenká deska nebo fólie připevněná na dřevěný nebo kovový rošt, který určuje tloušťku d [m] vzduchové dutiny mezi pevným povrchem a membránou. K výrobě membrán se používá například koženka nebo novodurová, polyetylénová aj. fólie. Takováto konstrukce pohlcuje zvuk v relativně úzkém pásmu zpravidla nízkých kmitočtů v okolí rezonančního kmitočtu fr [Hz], který je ovlivněn plošnou hmotností m´ [kg·m-2] membrány a tloušťkou vzduchové mezery d [m] – viz vztah (57).
\begin{gathered}
f_\text{r}=\frac{60}{\sqrt{m'd}}
\end{gathered}(57)
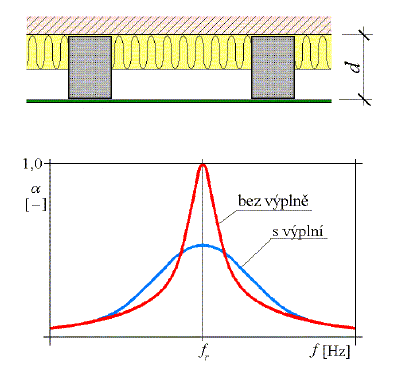
Obr. 21 Schéma konstrukce pohlcovače typu kmitající membrána a typický průběh závislosti činitele pohltivosti α [-] na kmitočtu
Užitečnou vlastností kmitajících membrán je hladký a rovný povrch. Je-li membrána málo odolná proti poškození, kryje se podobně jako porézní pohlcovače řídkým pletivem nebo mřížovinou. Krytí však nesmí bránit jejímu kmitání. Vložením porézního pohlcovače do vzduchové mezery mezi membránou a pevným povrchem je možno zvětšit šířku kmitočtového pásma pohlcování při současném snížení nejvyšší hodnoty v místě rezonančního kmitočtu (viz obr. 21). Ani tento vložený pohlcovač nesmí bránit kmitání membrány.
Zvyšováním plošné hmotnosti membrány a tloušťky vzduchové mezery se rezonanční kmitočet snižuje. Plošnou hmotnost lze zvýšit použitím tuhé kmitající desky např. dřevotřískové, azbestocementové apod. Deska však musí být k podkladu připevněna velmi měkce např. přilepením na plstěné pásy, osazením do pěnové pryže nebo přilepením na pásy koženky tak, aby byla schopna po dopadu zvukové vlny kmitat jako celek (píst). Připojení desek na rošt musí být stejně tak jako u membrán vzduchotěsné. Výhodou kmitajících membrán a desek je možnost pohlcování zvuku o nízkém kmitočtu. Tím tyto konstrukce vhodně doplňují porézní pohlcovače, které jsou naopak vysoce účinné u vyšších kmitočtů.
18 DUTINOVÉ REZONÁTORY
Pohlcování zvuku dutinovými rezonátory je založeno rovněž na principu rezonance. Při ní jsou kmitajícím prvkem částice vzduchu v otvoru spojujícím vzduchovou dutinu s vnějším prostředím. Rezonanční kmitočet je určen rozměry vzduchové dutiny a rozměry a tvarem spojovacího otvoru. Průběh závislosti činitele pohltivosti α [-] okolo rezonančního kmitočtu je obdobný jako u pohlcovačů typu kmitající membrána (viz obr. 21). Obdobně jako u předchozích typů je nutné pásmo pohlcování rozšířit vložením pórovitého materiálu do dutiny. Dutinové rezonátory používali lidé už ve starověku, jak o tom svědčí nálezy amfor zabudovaných v antických chrámech a amfiteátrech. V dnešní době se používají tvárnicové rezonátory, kde rezonanční systém je vytvořen speciální tvárnicí nebo keramickým prvkem, a děrované desky, u kterých lze rezonanční kmitočet regulovat volbou velikosti a hustoty otvorů i tloušťkou d [m] odsazení děrované desky od pevného podkladu. Na rozdíl od desek kmitajících se děrované desky připevňují k nosnému roštu pevně. K výrobě obkladů typu děrovaná deska se používají tvrdé dřevovláknité desky, ocelové či hliníkové plechy, sádrokartonové a jiné stavební desky.
Obr. 22 Schéma konstrukce tvárnicových rezonátorů a pohlcovače typu děrovaná deska
Princip pohlcování děrovanou deskou se od pohlcovače typu kmitající deska liší tím, že na místo desky či membrány kmitá vzduchový sloupec v otvorech, který má fiktivní výšku h´= h + 2Δh (viz obr. 23). Jsou-li pro uvažované kmitočtové pásmo všechny rozměry rezonátoru menší než polovina vlnové délky a hodnota činitele děrování desky
\begin{gathered}
\frac{S}{S_\text{d}}\le0{,}15
\end{gathered}pak vzduch v otvoru se chová jako nestlačitelný hmotný píst a vzduchový polštář tloušťky d jako pružina. Při kolmém dopadu zvukové vlny platí pro rezonanční kmitočet fr [Hz] rovnice
\begin{gathered}
f_\text{r}=\frac{c_\circ}{2\pi}\sqrt{\frac{S}{Vh'}}\approx54\sqrt{\frac{S}{Vh'}}
\end{gathered}(58)
Korekce 2Δh pro kruhový otvor se stanoví podle vztahu
\begin{gathered}
2\Delta h\approx\sqrt{S}\Bigg(1{,}05-\sqrt[3]{\frac{S}{S_\text{d}}}\Bigg)
\end{gathered}(59)
Korekce 2Δh pro čtvercový otvor se stanoví podle vztahu
\begin{gathered}
2\Delta h\approx\sqrt{S}\Bigg(1{,}03-\sqrt[3]{\frac{S}{S_\text{d}}}\Bigg)
\end{gathered}(60)
Pro všesměrový dopad se rezonanční kmitočet posouvá na kmitočet vyšší přibližně o polovinu oktávy. Obdobně jako u pohlcovačů typu kmitající membrána hodnota činitele pohltivosti obkladů typu děrovaná deska závisí na přítomnosti vložky porézního pohlcovače ve vzduchové dutině. Mezi děrovanou deskou a plastickou fólií, do níž je obvykle tlumící vložka zatavena, je nezbytná distanční vložka např. ze zvlněného drátěného pletiva, která zajistí zachování potřebného volného prostoru u otvorů pro činnost vzduchových sloupců v nich.
Jestliže je činitel děrování
\begin{gathered}
\frac{S}{S_\text{d}}>0{,}15
\end{gathered}pak rezonanční pohlcovač ztrácí svoji funkci ve prospěch funkce porézního pohlcovače a maximum hodnot činitele pohltivosti se přesunuje do vyšších kmitočtů.
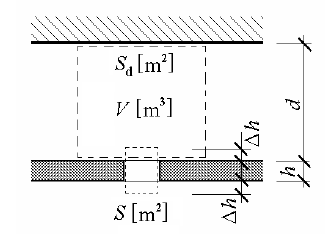
Obr. 23 Parametry detailu děrované desky – ke vztahům (58) až (60)
19 KOMBINOVANÉ KONSTRUKCE
Mezi kombinované konstrukce řadíme vícenásobné rezonanční soustavy tvořené několika rezonančními prvky řazenými za sebou a akustická tělesa, což jsou prostorové útvary vyrobené většinou z pórovitého materiálu krytého pletivem nebo tkaninou a mající tvar jednoduchých geometrických těles. Tyto předměty se zavěšují pod stropní konstrukci. Kombinované pohlcovače poskytují nejlepší efekt tj. nejvyšší hodnoty činitele pohltivosti α [-] v rozsahu co možná nejširšího pásma kmitočtů.
20 ŠÍŘENÍ ZVUKU VE ZVUKOVODU
Zvukovod je uzavřený prostor s odraznými stěnami, jehož jeden rozměr výrazně převyšuje ostatní. Nejčastějším příkladem zvukovodu v budovách je vzduchotechnické potrubí. Ocelový pozinkovaný plech, z něhož je VZT potrubí obvykle vyrobeno, velmi málo pohlcuje zvuk. Akustický výkon dopadající na stěny potrubí se z větší části odráží zpět, takže téměř nedochází k poklesu hladiny akustického tlaku se vzdáleností. Jistý útlum v přímém potrubí se projeví až při délkách nad 10 až 20 m. K významnějšímu útlumu dochází jen v místech diskontinuity potrubí, tj. při změně průřezu nebo směru potrubí a v místech jeho větvení nebo vyústění. Na principu změny průřezu jsou konstruovány tlumiče hluku výfuku spalovacích motorů.
U potrubí větších průřezů (jako je potrubí vzduchotechnické) se používají absorpční tlumiče. Jsou to části VZT potrubí, které jsou zevnitř vyloženy pórovitým zvuk pohlcujícím obkladem, případně je deskami obkladu měněn směr proudění vzduchu na způsob labyrintu. Absorpčním materiálem jsou zpravidla desky z minerální vaty, které jsou kryty děrovaným plechem, aby je dopravovaný vzduch neodvál. Absorpční tlumiče způsobují ztrátu tlaku proudícího vzduchu, takže jejich použití v systému VZT může ovlivnit potřebný výkon a volbu typu ventilátoru. Jsou však velmi účinné a lze jimi úspěšně omezit jak šíření zvuku ventilátoru, tak přenos zvuku mezi jednotlivými místnostmi v budově vzduchotechnickým potrubím. Výhodné je tlumiče umístit do VZT potrubí v blízkosti zdroje zvuku ještě ve strojovně. Vhodná délka těchto tlumičů je 1 až 2 m, takže jejich použití někdy vyžaduje zvětšení prostoru strojovny vzduchotechniky. Útlum absorpčních tlumičů závisí na kmitočtu a závisí na hodnotě činitele pohltivosti α [-] porézního materiálu, kterým je tlumič vyložen, a na příčných rozměrech tlumiče.
21 PROSTOROVÁ AKUSTIKA
Prostorová akustika se zabývá studiem akustických jevů uvnitř částečně nebo zcela uzavřených prostorů. Cílem není ochrana proti hluku, ale zajištění dobré slyšitelnosti a srozumitelnosti zvuku. Metodami prostorové akustiky se převážně řeší prostory určené k poslechu zvuku a ke sledování produkcí spojených s poslechem zvuku – kina, divadla, koncertní sály, kostely, přednáškové a soudní síně aj. Souhrnně lze tyto prostory označit jako auditoria. Při sledování kvality zvukového signálu určeného k poslechu se již nevystačí jen s modelem difuzního zvukového pole, který byl popsán v souvislosti s polem odražených zvukových vln v kap. 14. Prostorová akustika zkoumá zvukové pole podrobněji. K tomu používá metody vlnové, geometrické a statistické akustiky.
22 VLNOVÁ AKUSTIKA
V důsledku odrazu zvuku od dvou navzájem rovnoběžných stěn dochází ke stojatému vlnění při kmitočtech, pro které se vzájemná vzdálenost stěn rovná celistvému násobku půlvlny. Stojaté vlnění narušuje difuznost zvukového pole, což je příčinou změny barvy zvuku, poruch kvality a srozumitelnosti zvukového signálu.
Obr. 24 Stojaté vlnění mezi dvěma rovnoběžnými stěnami
Běžným tvarem uzavřeného prostoru (místnosti) je pravoúhlý šestistěn, který je soustavou tří dvojic navzájem rovnoběžných stěn. Navíc stojaté vlnění vzniká i vícenásobným odrazem od všech stěn místnosti a tomuto jevu se tak nevyhne ani uzavřený prostor složitějších tvarů. Z největšího rozměru místnosti lze odvodit nejnižší kmitočet, při kterém ke stojatému vlnění (vlastním kmitům prostoru) dochází. Z dalších rozměrů místnosti a jejich kombinací se odvozují další takové kmitočty. Těch je nekonečně mnoho a mají tu vlastnost, že směrem k vyšším kmitočtům se ve spektru vyskytují stále hustěji, takže od jistého kmitočtu výše již spektrum plynule vyplňují a akustické pole má opět difuzní vlastnosti. Při sledování zvuku v pásmech celé oktávy lze akustické pole v prostoru, který má objem V [m3], považovat za difuzní od kmitočtu fmin [Hz] výše
\begin{gathered}
f_\text{min}=\frac{400}{\sqrt[3]{V}}
\end{gathered}(61)
Pro pásma šířky jedné třetiny oktávy platí obdobný vztah s kmitočtem 1,5 krát vyšším:
\begin{gathered}
f_\text{min}=\frac{600}{\sqrt[3]{V}}
\end{gathered}(62)
K porušení difuznosti tedy dochází jen v oblasti nízkých kmitočtů. Pro prostor tvaru pravoúhlého šestistěnu (kvádru) o rozměrech stran lx [m], ly [m] a lz [m] lze tyto kmitočty stanovit podle vztahu
\begin{gathered}
f_\text{x,y,z}=\frac{c}{2}\sqrt{\Bigg(\frac{n_\text{x}}{l_\text{x}}\Bigg)^2+\Bigg(\frac{n_\text{y}}{l_\text{y}}\Bigg)^2+\Bigg(\frac{n_\text{z}}{l_\text{z}}\Bigg)^2}
\end{gathered}(63)
kde je
c [m·s-1] … rychlost zvuku ve vzduchu
nx, ny a nz … celá čísla od nuly do nekonečna (0, 1, 2, …) v různých kombinacích s výjimkou kombinace nx, ny , nz = 0, 0, 0.
Cílem opatření vlnové akustiky je zajistit difuznost akustického pole od co nejnižšího kmitočtu. K tomuto cíli směřují při návrhu auditorií tato opatření nebo jejich kombinace:
Volba velikosti uzavřeného prostoru. S objemem místnosti se zvyšuje difuznost akustického pole. Dobrých výsledků lze dosáhnout od vyššího objemu než 100 m3, zatímco menší místnosti mají vždy horší akustičnost.
Různoběžností stěn místnosti se omezuje stojaté vlnění. U divadel se doporučuje odchýlit jednu boční stěnu o 5 až 6 úhlových stupňů nebo obě boční stěny o 2,5 až 3 úhlové stupně.
Rozměry pravoúhlého uzavřeného prostoru (tvaru kvádru) nemají být navzájem celistvými násobky. Této podmínce vyhovuje vzájemný poměr stran kvádru např. 2:3:5, za nevyhovující lze považovat např. poměr 1:2:4.
Difuznost zvukového pole lze zvýšit obložením stěn pohlcujícím zvuk anebo členitostí jejich reliéfu pomocí říms, sloupů a polosloupů a dalších tvarů, které zajistí rozptylný (difuzní) odraz zvuku. Rozměry takových nerovností však musí být srovnatelné s vlnovou délkou zvuku, tj. větší než jeden metr.
23 GEOMETRICKÁ AKUSTIKA
Vedle zajištění difuznosti zvukového pole je třeba při návrhu auditorií odstranit nerovnoměrnost příjmu zvukového signálu různými posluchači v důsledku jejich rozdílné vzdálenosti od zdroje zvuku. U velkých sálů je potřeba zvukový signál směřující do zadních řad hlediště zesílit. To je možné dvojím způsobem:
a) elektroakusticky pomocí mikrofonu a reproduktorové soustavy,
b) stavebně vhodným uspořádáním odrazných ploch umístěných nejčastěji na stropu sálu tak, aby odrazy zvuku byly směrovány převážně do vzdálených míst hlediště.
Odražený zvuk musí ve srovnání s přímo šířeným zvukem urazit na své cestě k posluchači delší dráhu a dospěje tam tak s určitým zpožděním. Je-li zpoždění malé, lidský sluch je schopen vnímat oba signály jako jeden zvuk. Jen v takovém případě může odražený zvuk způsobit zesílení. Při větších časových rozdílech dochází k poruchám srozumitelnosti mluveného slova (směšování hlásek) a k ozvěně. Odrazy od velmi vzdálených ploch (je-li dráha odraženého zvuku více než trojnásobkem dráhy přímé) již nejsou pro srozumitelnost nebezpečné, protože odražený zvuk působí na větší vzdálenost s mnohem menší intenzitou a není vnímán rušivě v důsledku maskování. Obdobného účinku se dosáhne obložením nežádoucí odrazné plochy zvuk pohlcujícím obkladem, nebo změnou tvaru této plochy tak, aby odraz byl rozptylný nebo směřoval do jiného místa.
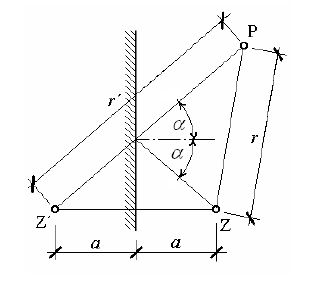
Obr. 25 Fermaův princip
Jsou-li odrazné plochy dostatečně velké (větší než vlnová délka zvuku) lze při popisu šíření zvuku aplikovat zákony geometrické optiky a představu vlnoploch nahradit představou zvukového paprsku, který vychází ze zdroje zvuku, je přímý a kolmý na kulové vlnoplochy. Úhel odrazu zvukového paprsku od odrazné plochy se rovná úhlu jeho dopadu (Fermatův princip). Dráhu odraženého paprsku můžeme konstruovat pomocí fiktivního zdroje Z´ souměrně sdruženého podle odrazné roviny. Dráha r´[m] odraženého zvuku je vzdálenost mezi body Z´ a P (viz obr. 25).
Obr. 26 Konstrukce stropu tvaru eliptického válce
K posílení signálu ve vzdálené části auditoria lze využít rovinných nebo zakřivených ploch umístěných zpravidla na stropě sálu. Na obr. 26 je naznačena konstrukce odrazné plochy tvaru eliptického válce. Jedno ohnisko elipsy je totožné se zdrojem Z zvuku a druhé F2 se umístí do prostoru pod podlahou za místem auditoria, kde chceme zvuk zesílit. Část elipsy lze přibližně nahradit kružnicí. Kromě ohnisek je nutno volit střed N odrazné eliptické plochy. Osa o půlí úhel ZNF2. Poloha středu S kružnice na této ose se získá postupným vztyčením dvou kolmic, jak vyznačeno na vyobrazení. Obdobným způsobem lze využít plochy parabolické, hyperbolické a rovinné.
Často se strop auditoria navrhuje jako kombinace několika odrazných ploch. Na obr. 27 je naznačena konstrukce ploch rovinných. Je známa poloha zdroje Z zvuku, poloha bodu N1, odkud má plocha vycházet, a požaduje se, aby odrazem od této plochy bylo zasaženo celé hlediště mezi body a a b. Konstrukce hledané části rovinné plochy N1 N2 je provedena pomocí fiktivního zdroje Z1. Bod N2 může být východiskem konstrukce další odrazné plochy N2 N3, která již bude odrážet zvuk jen do vzdálenější poloviny hlediště mezi body c a b. Konstrukce se provede pomocí fiktivního zdroje Z2. V konstrukci je možno dále pokračovat, až se pomocí částí rovinných ploch vyskládá celý strop sálu.
Obr. 27 Konstrukce stropu auditoria z rovinných ploch
Důležitou zásadou je směrování odrazů zvuku stále ve směru od zdroje do hloubky sálu. Jen tak se lze vyvarovat příliš velkých rozdílů drah a z toho plynoucího časového zpoždění odraženého zvuku způsobujícího nežádoucí směšování hlásek a ozvěnu. Stěna protilehlá jevišti bývá nejčastěji zdrojem ozvěny, a proto se opatřuje širokopásmovým zvuk pohlcujícím obkladem. Stejně tak je vhodné obložit i boční stěny zejména v zadní části hlediště nebo členit plochu těchto stěn tak, aby odraz byl difuzní. Množství zvuk pohlcujících obkladů v sále je však nutno regulovat podle zásad statistické akustiky.
24 STATISTICKÁ AKUSTIKA
Statistická akustika opět vychází z představy difuzního zvukového pole v uzavřeném prostoru tak, jak bylo popsáno v kap. 14. Kritériem akustičnosti uzavřeného prostoru z hlediska statistické akustiky je doba dozvuku T [s].
Obr. 28 K definici doby dozvuku
Po spuštění zdroje zvuku bude hladina v poli odražených vln uzavřeného prostoru postupně zvyšovat svou hodnotu. Tento jev se nazývá názvuk. Po krátké době se hladina akustického tlaku ustálí na hodnotě L [dB], při které dojde k rovnováze mezi akustickým výkonem Pe [W] emitovaným zdrojem a akustickým výkonem Pa [W] pohlcovaným ohraničujícími konstrukcemi místnosti. Hladinu L [dB] je možno stanovit pomocí vztahu (52) nebo (53). Rovnovážný stav s hladinou L [dB] v poli odražených vln zůstane v platnosti po celou dobu provozu zdroje zvuku. Po náhlém ukončení činnosti zdroje zvuku se téměř okamžitě ruší pole přímých vln. Hladina v poli odražených vln se však snižuje postupně, protože jednotlivé zvukové vlny po svých odrazech dorazí do místa sledování s větším či menším zpožděním. Tento jev se nazývá dozvuk a může trvat relativně dlouho, teoreticky nekonečně dlouhou dobu. Pozorování dozvuku však skončí, když snižující se hladina zanikne ve zvukovém pozadí daného místa. Doba, za kterou se od okamžiku ukončení činnosti zdroje zvuku sníží hladina akustického tlaku v poli odražených vln o 60 dB, se nazývá standardní doba dozvuku (zkráceně: doba dozvuku). Doba dozvuku závisí na objemu místností V [m3] a na její celkové pohltivosti A [m2] resp. na součtu ploch v místnosti (strop + stěny + podlaha) ΣS [m2] a středním činiteli pohltivosti zvuku αm [-]. Relativně jednoduchý vztah pro výpočet doby dozvuku odvodil Sabin.
\begin{gathered}
T=0{,}163\frac{V}{A}
\end{gathered}(64)
Wallace Clement Sabin (1868–1919) byl americký fyzik. Působil na Harvardské univerzitě a lze ho považovat za zakladatele moderní prostorové akustiky. Mimo jiné navrhl akustické úpravy v sále Symphony Hall v Bostonu, který je dodnes považován za jeden z nejlepších koncertních sálů světa.
Sabinův vztah je dostatečně přesný pro prostory, které nejsou opatřeny zvuk pohlcujícími obklady. Pro výpočet doby dozvuku ve více zatlumených auditoriích je vhodný vztah Eyringův.
\begin{gathered}
T=0{,}163\frac{V}{-\Sigma S\ln(1-\alpha_\text{m})}
\end{gathered}(65)
V auditoriích o větším objemu než 2 000 m3 se tento vztah doplňuje o vliv činitele útlumu zvuku ve vzduchu m [m-1].
\begin{gathered}
T=0{,}163\frac{V}{-\Sigma S\ln(1-\alpha_\text{m})+4mV}
\end{gathered}(66)
Ze vztahů (64) až (66) je patrno, že obklady pohlcujícími zvuk lze dobu dozvuku snižovat. V realizovaných prostorech je možno dobu dozvuku kontrolovat měřením. Vztah (64) pak slouží ke stanovení hodnot celkové pohltivosti místnosti A [m2] (například při měření neprůzvučnosti nebo kročejového zvuku) na základě změřených hodnot doby dozvuku. Doba dozvuku T [s] závisí na kmitočtu zvuku. Proto se sleduje v oktávových pásmech obvykle v rozsahu od 125 do 4 000 Hz.
25 RESTAURAČNÍ EFEKT
S dobou dozvuku souvisí tzv. restaurační efekt (coctail party effect). Vzniká všude tam, kde se v uzavřeném prostoru shromažďuje větší počet lidí, z nichž většina současně hovoří (jídelny, restaurace, vestibuly, hotelové haly). V důsledku hovoru více osob najednou vzniká v místnosti akustické pole s hladinou akustického tlaku, která narušuje srozumitelnost vzájemné komunikace a nutí hovořící osoby zvyšovat hlas. Tím se však dále zvyšuje hladina akustického tlaku v místnosti a jev se dále opakuje a nabývá na síle. Vzestup hladin se zastaví až po rezignaci části osob na vzájemnou komunikaci (zejména na větší vzdálenost než jen s nejbližším sousedem u stolu), případně může být limitován možnostmi akustického výkonu lidského hlasu. Tento nepříjemný a uživatele uzavřeného prostoru velice obtěžující jev lze omezit nebo i vyloučit zvýšením celkové pohltivosti.
Hodnocení srozumitelnosti při restauračním efektu je navrženo v literatuře [7]. Při takovém hodnocení je třeba předpokládat hodnoty hladin akustického výkonu LW [dB] lidského hlasu při běžné konverzaci i vzdálenost r [m], na kterou mezi sebou lidé v hodnoceném prostoru restaurace vzájemně komunikují.
Naslouchající vnímá jednak hladinu akustického tlaku přímého signálu L1 [dB] a jednak hladinu zvukového pozadí L2 [dB]. Obě hladiny se stanoví pomocí vztahů (9) a (53). Vztah (53) ale je nutno upravit vzhledem k tomu, že současně hovoří n osob.
\begin{gathered}
L=L_\text{W}+10\log n+10\log\Bigg[\frac{4(1-\alpha_\text{m})}{A}\Bigg]
\end{gathered}(67)
Za předpokladu, že polovina hostů restaurace současně mluví a druhá polovina naslouchá, se za n dosadí polovina kapacity sálu. Uplatní se korekce váhového filtru zvukoměru a stanoví se hladiny akustického tlaku A přímého signálu LA1 [dB] i zvukového pozadí LA2 [dB]. Srozumitelnost v restauraci bude záviset na rozdílu hladin ΔL [dB]
\begin{gathered}
\Delta L=L_\text{A1}-L_\text{A2}
\end{gathered}(68)
V literatuře [7] je zaveden index srozumitelnosti I [-]
\begin{gathered}
I=\frac{\Delta L+12}{30}
\end{gathered}(69)
Hodnocení pomocí indexu srozumitelnosti je uvedeno v tab. 12.
26 OPTIMÁLNÍ DOBA DOZVUKU V AUDITORIÍCH
Normy ČSN 73 0525 a ČSN 73 0527 stanoví optimální dobu dozvuku různých prostor v závislosti na jejich objemu V [m3]. Základní představu o optimálních dobách dozvuku poskytuje obr. 29. Požaduje se, aby optimální doby dozvuku bylo dosaženo ve všech šesti oktávových pásmech v rozsahu od 125 do 4 000 Hz s povolenými tolerancemi podle obr. 30.
Obr. 29 Optimální doba dozvuku různých prostor v závislosti na jejich objemu (podle ČSN 73 0525)
Obr. 30 Povolené tolerance doby dozvuku T/Topt [%] pro obsazený prostor v závislosti na středním kmitočtu oktávového pásma (podle ČSN 73 0525)
Pro některé prostory ve školách a v prostorech pro veřejné účely norma ČSN 73 0527 stanoví optimální dobu dozvuku, případně bez požadavku na dobu dozvuku požaduje akustické úpravy. Přehled je uveden v tab. 13 až 16.
27 NÁVRH AUDITORIA
Objem prostoru se stanoví podle provozních, hygienických a akustických požadavků. Z provozních a hygienických důvodů je třeba počítat s objemem nejméně 4 m3 na jedno plánované místo včetně míst pro hudebníky, členy pěveckého sboru apod. Při stanovení dolní hranice celkového objemu uzavřeného prostoru se setkáváme s těmito akustickými problémy:
- malé prostory mají zpravidla krátkou dobu dozvuku a pro hudební účely v nich nelze dosáhnout příslušné optimální doby dozvuku;
- je-li akustický výkon zdroje příliš velký (např. velký orchestr v malé zkušebně), pak snaha o snížení vysoké hladiny akustického tlaku v malém prostoru zvuk pohlcujícími obklady vede zároveň k příliš krátké době dozvuku;
- prostory s objemem menším než 100 m3 zpravidla nevyhovují z hlediska vlnové akustiky.
- Horní hranice objemu uzavřeného prostoru je limitována dosažitelným akustickým výkonem předpokládaného zdroje zvuku a možnostmi dosáhnout požadované optimální doby dozvuku. Doporučené maximální objemy jsou v tab. 17.
Základní rozměry navrhovaného prostoru by měly respektovat požadavky vlnové akustiky. Pro optimální rozložení vlastních kmitů prostoru se doporučuje prostory o objemu menším než 200 m3 navrhovat ve tvaru blížícímu se krychli, nikoli však přesně jako krychli. Vhodný poměr tří základních rozměrů prostoru je 1:1,05:1,2. Pro uzavřené prostory větších rozměrů se doporučuje poměr stran 1:1,25:1,6 nebo 1:1,5:2:5 nebo 1:1,7:2:9. Žádný z rozměrů nesmí být celistvým násobkem zbývajících dvou rozměrů.
Odrazy zvuku se prověřují grafickou studií nebo v náročnějších případech pomocí modelu na počítači. Zpoždění kteréhokoli z prvních odrazů zvuku by nemělo být větší než 0,03 s, což odpovídá maximálnímu přípustnému rozdílu drah mezi přímým a odraženým zvukem 10 m. Podlaha sálu by měla být tvarována tak, aby hlavy posluchačů byly vystaveny dopadu přímého zvuku z míst předpokládaných zdrojů. V prostorech s velkou plochou pro publikum tento požadavek může vést k většímu stoupání podlahy než je to, které by zajistilo dobrý výhled. Tvar stropu se navrhuje podle zásad geometrické akustiky. Nebezpečné jsou vyduté plochy (vnitřek kopule, válcové plochy apod.), které soustřeďují akustickou energii do jednoho místa – ohniska. V blízkosti ohniska se nesmějí nacházet posluchači. Vypouklé plochy slouží k rozptylování zvukové energie. Použijí se například v části stropu nad orchestřištěm a v místě bočních stěn hlediště. Rozptylný odraz je příznivý, protože se jím zvyšuje difuznost zvukového pole.
Navrhne se rozmístění zvuk pohlcujících konstrukcí a struktur rozptylujících zvuk včetně architektonického uspořádání upravovaných ploch. Množství pohlcovačů se kontroluje výpočtem doby dozvuku. Po realizaci akustických úprav se provede měření doby dozvuku a podle jeho výsledků se provedou korekce akustických úprav.
28 AKUSTIKA STAVEBNÍCH KONSTRUKCÍ – ZVUK V BUDOVÁCH
Akustika stavebních konstrukcí se zabývá studiem a aplikací poznatků o šíření zvuku z hlediska zvukové izolace, tj. z hlediska ochrany vnitřního prostředí budov před cizím hlukem. Z tohoto pohledu sleduje zejména akustické vlastnosti stavebních materiálů a konstrukcí.
Z hlediska hodnocení podle [2] je nutno rozlišit hluk ze zdrojů mimo budovu (venkovní hluk) a hluk ze zdrojů uvnitř budovy. Ochrana proti venkovnímu hluku metodami akustiky stavebních konstrukcí se prakticky shoduje s tím, co se v urbanistické akustice nazývá pasivní ochranou. Spočívá ve zvyšování zvukově izolačních vlastností obvodového pláště budov, zejména oken jako jeho nejslabšího prvku. Zvuk šířící se navzájem mezi prostory uvnitř budovy lze dělit dvojím způsobem:
Obr. 31 Šíření zvuku vzduchem a konstrukcí
Šíření zvuku vzduchem je charakteristické tím, že zdroj vyzařuje zvukové vlny do vzduchu v místnosti zdroje. Příkladem může být hlasitý hovor osob, reprodukovaná hudba, hra na hudební nástroje ap. Zvuk vyzařovaný zdrojem do vzduchu se šíří podle zákonitostí popsaných v kap. 14. Vytvoří se pole přímých a pole odražených vln. Při průchodu zvuku dělicí konstrukcí (příčkou, stropem) do sousední místnosti se jeho intenzita sníží. Rozhodující roli v tomto snížení intenzity hraje vlastnost dělící konstrukce – její neprůzvučnost R [dB]. Jiné místnosti, než bezprostředně sousedící s místností zdroje, zpravidla nejsou zvýšenými hodnotami zvuku zasaženy.
V porovnání se zvukem šířeným vzduchem se při šíření zvuku konstrukcí jedná o zcela jinou mechaniku vzniku a šíření zvuku v budově. Zdrojem může být např. výtahový stroj. Chvění stroje se přenáší jeho kotvením do podlahy a je nosnou konstrukcí stropu a dále i svislými konstrukcemi šířeno po budově. Zdrojem zvuku v chráněných místnostech jsou pak ve smyslu vyzařování zvukových vln do vzduchu až chvějící se stavební konstrukce. Tento zdroj je tím vydatnější, čím jsou dynamické budicí síly zdroje chvění větší, čím nižší je přenosový útlum chvění od místa buzení k místu vyzařování do chráněné místnosti a zejména čím větší je plocha konstrukcí vyzařujících zvuk. Omezování zvuku šířeného konstrukcí je proto vždy spojeno s omezením šíření chvění zejména do rozměrných stavebních konstrukcí budovy.
Zvuk výtahového stroje lze v konkrétních podmínkách jednoznačně definovat co do jeho intenzity, kmitočtového složení a relativně dobře lze i odhadnout časový režim jeho působení. Kontrola hlučnosti měřením bývá jednoznačná. Ve chráněné (např. obytné) místnosti se změří hladina akustického tlaku A při chodu stroje a porovná se s nejvyšším přípustným limitem podle [2]. Takové zvuky se považují za definovatelné. Naproti tomu však existuje v budovách řada zvuků, které vznikají náhodným způsobem při běžném užívání budovy. Vlastnosti zvuku způsobeného hlasitým hovorem osob, reprodukovanou hudbou, boucháním dveřmi, chůzí po podlaze (kročejový hluk) apod. nelze jednoznačně definovat. Nelze ani stanovit nebo uměle navodit typickou hlukovou situaci ve chráněné místnosti. To činí potíže při kontrole hlučnosti měřením. Měří-li se na základě stížnosti, stěžovatel obvykle namítne, že v době, kdy se neměřilo, bylo rušení hlukem silnější. Správnou představu o hlukové situaci uživatelů bychom snad mohli získat jen dlouhodobým monitorováním zvuku v chráněné místnosti při provozu budovy, ovšem s vyloučením zvuku způsobeného vlastními uživateli. To je prakticky nereálné.
Je zřejmé, že pro hodnocení nedefinovatelného zvuku v budovách nelze jako kritéria použít veličiny akustické imise. Proto byla do praxe zavedena kritéria, která hodnotí ochranu před rušivým hlukem v budovách pomocí kvality zvukové izolace. Jsou to veličiny vážená stavební neprůzvučnost Rw´ [dB] a vážená normalizovaná hladina akustického tlaku kročejového zvuku Lnw´ [dB] (zkráceně: vážená hladina kročejového zvuku). Obě veličiny jsou nezávislé na neustále se měnící hlukové situaci v budově a při jejich zjišťování měřením se používají umělé zdroje zvuku, které mají známé normou stanovené vlastnosti.
29 ZVUK ŠÍŘENÝ VZDUCHEM (AIRBORNE NOISE) – NEPRŮZVUČNOST STAVEBNÍ A LABORATORNÍ
Označí-li se hladina akustického tlaku v poli odražených vln v místnosti zdroje (vysílací místnosti) L1 [dB] a hladina akustického tlaku v sousední místnosti příjmu (přijímací místnosti) L2 [dB], pak na rozdíl hladin D = L1 – L2 [dB] budou mít rozhodující vliv zvukově izolační vlastnosti dělicí konstrukce charakterizované činitelem průzvučnosti τ [-], ale uplatní se též plocha S [m2] dělicí konstrukce a celková pohltivost A2 [m2] přijímací místnosti. Při hodnocení izolace proti zvuku šířenému vzduchem, kterou konstrukce oddělující navzájem obě místnosti poskytuje, se používá veličina neprůzvučnost R [dB].
\begin{gathered}
R=10\log\frac{1}{\tau}
\end{gathered}(70)
Pomocí této veličiny lze stanovit hladinu L2 [dB] akustického tlaku v místnosti příjmu. Výpočet je však nutno provádět v kmitočtových pásmech, protože neprůzvučnost je závislá na kmitočtu.
Obr. 32 Neprůzvučnost
Podle vztahu (51) je akustický výkon Pa [W] pohlcený stěnou, která obě místnosti odděluje, roven
\begin{gathered}
P_\text{a}=\frac{I_\Sigma A}{4}=\frac{I_\Sigma S\alpha}{4}
\end{gathered}(71)
kde je
IΣ [Wm-2] … intenzita v difuzním poli místnosti zdroje podle definice (42).
Tato intenzita bude v následujícím výkladu označena jako I1 [Wm-2]. Ve ztahu (71) je dále S [m2] je plocha dělící stěny a α [-] její činitel pohltivosti zvuku.
Nahradí-li se ve vztahu (71) činitel pohltivosti zvuku α [-] činitelem průzvučnosti τ [-], obdrží se rovnice pro stanovení akustického výkonu Pt [W], který prochází stěnou.
\begin{gathered}
P_\text{t}=\frac{I_1S\tau}{4}
\end{gathered}(72)
Úpravou rovnice (72) spočívající v jejím vynásobení číslem 1012, logaritmování a násobení deseti se získá vztah pro hladinu akustického výkonu LWt [W], který prochází stěnou.
\begin{gathered}
L_\text{Wt}=L_1+10\log\tau+10\log S-10\log4
\end{gathered}\begin{gathered}
L_\text{Wt}=L_1+10\log\frac{1}{\tau}+10\log S-6
\end{gathered}\begin{gathered}
L_\text{Wt}=L_1-R+10\log S-6
\end{gathered}(73)
Vztah (51) je možno dosadit do (52). Získá se tak vztah (74) pro stanovení hladiny akustického tlaku L2 [dB] v místnosti příjmu. Výpočet je však nutno provádět v kmitočtových pásmech, protože neprůzvučnost R [dB] je závislá na kmitočtu. A2 [m2] je celková pohltivost místnosti příjmu, která rovněž na kmitočtu závisí.
\begin{gathered}
L_2=L_\text{W}-10\log\Bigg(\frac{4}{A_2}\Bigg)
\end{gathered}\begin{gathered}
L_2=L_1-R+10\log S-6+10\log4-10\log A_2
\end{gathered}\begin{gathered}
L_2=L_1-R+10\log S-6+6-10\log A_2
\end{gathered}\begin{gathered}
L_2=L_1-R+10\log\Bigg(\frac{S}{A_2}\Bigg)
\end{gathered}(74)
Upravený vztah (74) se používá ke stanovení neprůzvučnosti R [dB] měřením, kde hladiny L1 a L2 vybuzené umělým zkušebním zdrojem zvuku se měří zvukoměrem a celková pohltivost A2 místnosti příjmu se vypočte ze změřené doby dozvuku T2 [s] v místnosti příjmu podle Sabinova vztahu (64).
\begin{gathered}
R=L_1-L_2+10\log\Bigg(\frac{S}{A_2}\Bigg)
\end{gathered}(75)
Pro některé dělící konstrukce existují i relativně spolehlivé metody předpovědi hodnot neprůzvučnosti výpočtem. Hodnoty neprůzvučnosti změřené na konstrukci zabudované v reálné stavbě jsou však zpravidla nižší oproti hodnotám zjištěným měřením v akustické laboratoři nebo oproti hodnotám teoreticky vypočteným. Příčinou může být odlišné provedení konstrukce na stavbě oproti laboratoři, ale zejména je příčinou uvedeného rozdílu šíření zvuku na stavbě bočními cestami, tj. cestami mimo hodnocenou konstrukci. Na obr. 33 jen cesta (1) je přímá, zatímco typy cest označené (2), (3) a (4) představují boční přenos zvuku (přes bočně navazující konstrukce), který je při měření v laboratoři vyloučen a také při výpočtu neprůzvučnosti se neuvažuje.

Obr. 33 Typy cest šíření zvuku
Rozeznává se:
- (laboratorní) neprůzvučnost R [dB] – obsahuje jen cestu (1) – s označením „bez čárky“;
- stavební neprůzvučnost R´ [dB] – obsahuje všechny typy cest (1) až (4) šíření – s označením „s čárkou“.
Vztah mezi oběma veličinami je
\begin{gathered}
R'=R-C
\end{gathered}(76)
Pro jednoduché silikátové konstrukce (z betonu, lehkých betonů, zdiva, sádry) jejichž styky jsou v celé své ploše utěsněny maltou nebo tmelem platí přibližně C = 2 až 3 dB, pro obvodové konstrukce C = 0. Kritériem pro hodnocení konstrukcí je stavební neprůzvučnost R´ [dB], protože jen tu je možno v dokončené stavbě zjišťovat měřením. Při přebírání údajů o neprůzvučnosti z technických prospektů výrobců dělících konstrukcí je třeba obě veličiny pečlivě rozlišit, protože výrobci často bez bližšího vysvětlení udávají příznivější laboratorní hodnoty, případně udávají své vlastní hodnoty korekce C (dB). Často je garance hodnot neprůzvučnosti ze strany výrobce stavebního prvku vázána na přísná pravidla provedení konstrukce na stavbě (způsob provázání zdiva, použité omítky, existence či způsob zabudování instalací do konstrukce apod.).
30 KRITÉRIUM NEPRŮZVUČNOSTI – VÁŽENÁ STAVEBNÍ NEPRŮZVUČNOST
Při poslechu hudby přes stěnu ze sousední místnosti slyšíme nejlépe kontrabas a bicí, zatímco vysoké tóny jsou potlačeny. Hodnota neprůzvučnosti R [dB] totiž zpravidla vzrůstá s kmitočtem. Proto dělicí konstrukce tlumí obvykle lépe zvuk o vyšším kmitočtu a zvuk nízkých kmitočtů snáze propouštějí. Závislost však není lineární a u různých konstrukcí a materiálů má různý průběh. V některých částech spektra může dokonce docházet k opačné závislosti (k poklesům hodnoty R se vzrůstajícím kmitočtem) v důsledku rezonance nebo vlnové koincidence. Hodnoty R se proto zjišťují v závislosti na kmitočtu v pásmech 1/3 oktávy (tj. podrobněji než v pásmech oktávových). Kmitočtový rozsah hodnocení neprůzvučnosti je dán zvukoizolačním pásmem, které zahrnuje pásma 1/3 oktávy se středními kmitočty v rozsahu 100 až 3 150 Hz. Střední kmitočty pásem 1/3 oktávy jsou uvedeny v tab. 19, kde jsou zároveň uvedeny hodnoty směrné křivky SK [dB] používané ke stanovení jednočíselné hodnoty – vážené neprůzvučnosti Rw [dB]. Jedná se o celkem 16 pásem 1/3 oktávy.
Závislost neprůzvučnosti R [dB] (změřené nebo vypočtené) na kmitočtu se zobrazuje v normalizovaném diagramu. Jedná se o pravoúhlý diagram, kde na vodorovné ose je v logaritmickém měřítku stupnice středních kmitočtů f [Hz] pásem 1/3 oktávy a na svislé ose neprůzvučnost R [dB]. Rozměry diagramu jsou normalizovány tak, že jedné oktávě na vodorovné ose odpovídá 30 mm a jednomu decibelu na svislé ose odpovídají 4 mm. Hodnoty neprůzvučnosti v jednotlivých pásmech 1/3 oktávy (je jich celkem 16) se s přesností na desetinu decibelu vynesou do diagramu. Sousední hodnoty se spojí úsečkami. Vzniklá lomená čára znázorňuje závislost neprůzvučnosti na kmitočtu.
Hodnotit zvukově izolační vlastnosti konstrukcí pomocí 16-ti číselných údajů by bylo velmi nepraktické. Proto normy (ČSN EN ISO 717-1 Akustika – Hodnocení zvukové izolace stavebních konstrukcí a v budovách – Část 1: Vzduchová neprůzvučnost) stanoví postup, kterým se z těchto 16-ti hodnot porovnáním se směrnou křivkou stanoví jednočíselné hodnocení – vážená stavební neprůzvučnost Rw´ [dB]. Postup v sobě zahrnuje preferenci těch kmitočtů, které mají na rušivost hluku větší vliv (jakási obdoba váhové funkce zvukoměru).
Obr. 34 Příklad vyhodnocení vážené neprůzvučnosti Rw [dB] ze změřených hodnot neprůzvučnosti R [dB] v pásmech 1/3 oktávy pomocí směrné křivky
Tvar směrné křivky je dán hodnotami SK [dB] v tab. 19. Jedná se vlastně o dvakrát lomenou čáru, takže je vžitý název „křivka“ vlastně z geometrického hlediska nesprávný (třebaže bude v dalším výkladu i nadále používán). Při stanovení vážené hodnoty neprůzvučnosti se směrnou křivkou pohybuje a hledá se její „správná poloha“ vyhovující dále uvedeným podmínkám. Pohyb směrnou křivkou je přípustný jen ve svislém směru s krokem jeden decibel a sledují se při něm nepříznivé odchylky hodnoceného průběhu neprůzvučnosti od této křivky. Součet těchto nepříznivých odchylek smí být nanejvýš 32 dB. K příznivým odchylkám v části spektra, kde hodnoty neprůzvučnosti jsou nad směrnou křivkou, se nepřihlíží. Hodnota posunuté směrné křivky v pásmu 500 Hz je hledaným jednočíselným údajem – váženou neprůzvučností Rw [dB]. Protože existuje zpravidla tendence dokázat, že hodnocená konstrukce má co nejlepší vlastnosti, je zájem na tom, posunout směrnou křivku co nejvýše. Pravidlo o nejvyšší přípustné hodnotě součtu nepříznivých odchylek 32 dB však pohyb směrné křivky směrem vzhůru zastaví. Na obr. 34 je provedeno hodnocení změřených hodnot neprůzvučnosti R [dB] s výsledkem Rw = 45 dB. Součet nepříznivých odchylek je
\begin{gathered}
\Sigma\Delta_\text{i}=3+3{,}5+5+6+3+3+3{,}3+2{,}5=29{,}3\text{dB}
\end{gathered}Důsledkem toho, že směrnou křivkou se pohybuje s krokem o jeden decibel, je skutečnost, že vážená hodnota Rw [dB] je vždy celé číslo bez desetinných míst. Vážená neprůzvučnost Rw [dB] tedy není fyzikální veličinou v pravém slova smyslu a také není přípustné její hodnoty dosazovat do nějakých fyzikálních rovnic. Význam této veličiny se podobá spíše bodovému hodnocení. Její dřívější název, se kterým se lze setkat ve starší literatuře „index vzduchové neprůzvučnosti“ tuto její vlastnost vyjadřoval přesněji (index = ukazatel).
ČSN EN ISO 717-1 kromě kritéria vážená neprůzvučnost uvádí doplňková kritéria – faktory přizpůsobení spektru C a Ctr [dB]. Tato kritéria pravděpodobně v budoucnosti nahradí váženou neprůzvučnost. Výhodou faktorů přizpůsobení spektru je to, že při jejich stanovení odpadá poměrně složitá manipulace se směrnou křivkou.
Faktor přizpůsobení spektru Cj [dB] se vypočte podle rovnice
\begin{gathered}
C_\text{j}=X_\text{Aj}-R_\text{W}
\end{gathered}(77)
kde je
j … číslo spektra č. 1 nebo č. 2 z tab. 20 (spektrum č. 1 se použije pro výpočet faktoru C, spektrum č. 2 se použije pro výpočet faktoru Ctr),
Rw [dB] … vážená neprůzvučnost
XAj [dB] … se vypočte podle rovnice
\begin{gathered}
X_\text{Aj}=-10\log\sum10^{0{,}1(L_\text{ij}-R_\text{i})}
\end{gathered}(78)
kde je
Lij [dB] … hladina uvedená pro i-tý kmitočet v tab. 18
Ri [dB]… hodnota neprůzvučnosti pro i-tý kmitočet.
Faktor přizpůsobení spektru se vypočte s přesností na 0,1 dB a zaokrouhlí se na celé číslo. Při uvádění výsledků výpočtu nebo měření se uvádí vážená neprůzvučnost a oba faktory přizpůsobení spektru v závorce. Příklad:
\begin{gathered}
R_\text{W}(C{;}C_\text{tr}=41(0{;}-5)\text{dB}
\end{gathered}Je-li ve stavbách požadována zvýšená ochrana proti hluku, pak ČSN 73 0532 doporučuje jako kritérium neprůzvučnosti použít součet vážené neprůzvučnosti a faktoru přizpůsobení spektru. V běžných případech se faktory přizpůsobení spektru nehodnotí.
31 ZVUK ŠÍŘENÝ KONSTRUKCÍ (STRUCTUREBORNE NOISE) – KROČEJOVÝ ZVUK
Kročejový zvuk je zvukem, který vzniká a šíří se v konstrukci stavebního objektu. Je zvukem nedefinovatelným, jehož nepravidelný charakter závisí na aktivitě lidí užívajících budovu. Chůzí po podlaze, pádem předmětů na podlahu, posunováním nábytku (židle) je stropní konstrukce dynamicky namáhána. Mechanické impulzy (rázy) v konstrukci budí ohybové vlny, které se šíří různými rychlostmi od místa impulzu a po odrazu na okrajích uvádějí konstrukce do difuzního chvění. Chvějící se konstrukce vyzařují do vzduchu ve svém okolí zvuk. K hodnocení ochrany proti kročejovému zvuku slouží veličina: normalizovaná hladina akustického tlaku kročejového zvuku – stručně: hladina kročejového zvuku Ln [dB]. Mezi laboratorní a stavební hodnotou této veličiny téměř není rozdíl.
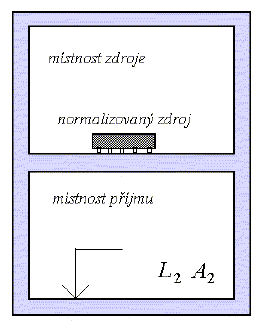
Obr. 35 K definici kročejového zvuku
Definice této veličiny se odvozuje od činnosti zařízení, které se nazývá normalizovaný zdroj kročejového zvuku. Normalizovaný zdroj kročejového zvuku se umístí do místnosti zdroje (vysílací místnosti). Zdroj obsahuje pět kovových závaží o hmotnosti 0,5 kg, která ve vzdálenostech 0,1 m od sebe dopadají v intervalech 0,1 s na povrch zkoušené konstrukce z výšky 0,04 m a udělují tak konstrukci normalizované impulzy. V místnosti příjmu (zpravidla o podlaží níže pod zkoušenou konstrukcí, ale i diagonálně a není vyloučen i přenos kročejového zvuku do vyšších podlaží) se měří hladina akustického tlaku L2 [dB]. Součástí hodnocení je také stanovení celkové pohltivosti A2 [m2] v místnosti příjmu zvuku. Hladina kročejového zvuku Ln [dB] se stanoví pomocí vztahu
\begin{gathered}
L_\text{n}=L_2+10\log\Bigg(\frac{A_2}{A_0}\Bigg)
\end{gathered}(79)
kde je
A0 = 10 m2 … referenční pohltivost.
Obdobně jako vzduchová neprůzvučnost R [dB] je i hladina kročejového zvuku Ln [dB] závislá na kmitočtu a sleduje se proto v rozsahu zvukoizolačního pásma (100 až 3 150 Hz) v pásmech 1/3 oktávy. Průběh Ln [dB] v závislosti na kmitočtu se vynese do normalizovaného diagramu a pomocí směrné křivky pro kročejový zvuk (hodnoty viz tabulka 21) se stanoví vážená hladina akustického tlaku kročejového zvuku, zkráceně: vážená hladina kročejového zvuku Lnw [dB]. Součet ΣΔi nepříznivých odchylek od směrné křivky rovněž nesmí být vyšší než 32 dB, ale pozor: nepříznivé odchylky jsou u kročejového zvuku směrem nahoru k vyšším hodnotám.
Obr. 36 Příklad vyhodnocení vážené hladiny kročejového zvuku Lnw [dB] ze změřených hodnot hladiny kročejového zvuku Ln [dB] v pásmech 1/3 oktávy pomocí směrné křivky
Samotné nosné konstrukce stropů poskytují vždy malou ochranu před kročejovým zvukem. Podstatnou roli při omezování tohoto zvuku mají konstrukce podlah. Z hlediska této funkce se podlahy dělí na plovoucí a povlakové.
Plovoucí podlahy se skládají ze dvou až tři funkčně významných vrstev. Na nosnou konstrukci stropu se klade zvukoizolační podložka. Jedná se o měkký pružný materiál většinou na bázi minerálních vláken, pružné pěny nebo rýhami či dutinami upravené pryže. U těžkých plovoucích podlah, kde následná roznášecí vrstva je vytvořena mokrým procesem je třeba zvukoizolační podložku chránit folií. Následná roznášecí vrstva je u těžkých plovoucích podlah tvořena vyztuženou betonovou či anhydritovou deskou, u lehkých plovoucích podlah deskovým materiálem (Cetris, podlahový sádrokarton, dřevotříska apod.). Od ostatních konstrukcí musí být roznášecí vrstva úplně oddělena měkkým materiálem, tedy i po stranách ve styku se stěnami, s příčkami a se stoupacím potrubím rozvodů TZB v prostupech stropní konstrukcí. Povrch roznášecí vrstvy může být chráněn vrstvou nášlapnou (parkety, keramická dlažba, laminátová či dřevěná bezespará podlaha (označení těchto nášlapných vrstev slovem „plovoucí“ je však obchodním názvem, který nemá s funkcí plovoucí podlahy jako prostředku ochrany proti kročejovému hluku nic společného).
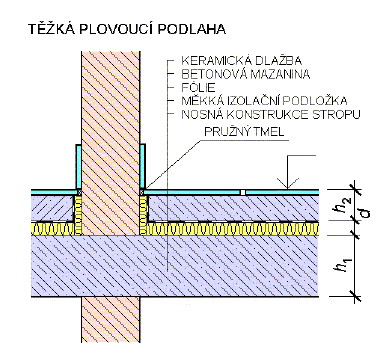
Obr. 37 Schéma řezu těžkou plovoucí podlahou
Povlakové podlahy jsou podlahy z podlahových povlaků (PVC, pryž, textil). mají různou tloušťku, mohou obsahovat měkké izolační podložky nebo jsou na samostatné izolační podložky kladeny. Zatímco plovoucí podlahy svoji zvukoizolační vrstvou brání šíření chvění do nosné konstrukce stropu a budovy, funkce povlakových podlah spočívá v omezení vzniku kročejového zvuku. Nárazy na stropní konstrukci jsou tlumeny měkkou nášlapnou vrstvou. Nejvyšší přípustné hodnoty vážené hladiny kročejového zvuku Lnw [dB] stanoví ČSN 73 0532.
ČSN EN ISO 717-2 kromě kritéria vážená hladina kročejového zvuku uvádí doplňkové kritérium – faktor přizpůsobení spektru Cl [dB]. Toto kritérium možná v budoucnosti nahradí váženou hladinu kročejového zvuku. Výhodou faktoru přizpůsobení spektru je to, že při jeho stanovení odpadá poměrně složitá manipulace se směrnou křivkou. Faktor přizpůsobení spektru Cl [dB] se vypočte podle vztahu
\begin{gathered}
C_1=L_\text{n,sum}-15-L_\text{nw}
\end{gathered}(80)
kde je
Ln,sum [dB] … energetický součet hodnot hladin kročejového zvuku,
Ln [dB] … z třetinooktávových pásem 100 až 3150,
Lnw [dB] … vážená hladina kročejového zvuku.
Plovoucí podlaha představuje dvouprvkovou konstrukci, kde jedním prvkem (deskou) je nosná konstrukce stropu a druhým prvkem (deskou) je roznášecí vrstva spolu s případnou vrstvou nášlapnou. Obě desky jsou navzájem od sebe odděleny zvukově izolační podložkou. Vlastnosti této konstrukce jsou ovlivněny rezonancí typu hmotnost – poddajnost – hmotnost a půlvlnnou rezonancí (stojatým vlněním) ve zvukově izolační podložce. Rezonanční kmitočet se stanoví podle vztahu (81), kde poměr
\begin{gathered}
\frac{E_d}{d}=s'\text{[Pa}\cdot\text{m}^{-1}]
\end{gathered}se nazývá dynamická tuhost pružné vrstvy. Dynamická tuhost pružné vrstvy je důležitou vlastností zvukově izolačních podložek. bez znalosti této veličiny, nelze správně navrhnout těžkou plovoucí podlahu. Kvalitní zvukově izolační podložky těžkých plovoucích podlah mají hodnoty dynamické tuhosti nízké. Hodnota rezonančního kmitočtu je rozhodující pro správnou funkci plovoucí podlahy. Požaduje se, aby rezonanční kmitočet byl co nejnižší, rozhodně však nižší, než 70 Hz.
\begin{gathered}
f_\text{r}=\frac{1}{2\pi}\sqrt{\frac{E_\text{d}}{d}\Bigg(\frac{1}{m'_1}+\frac{1}{m'_2}\Bigg)}
\end{gathered}(81)
Ve vztahu (81) kde je
Ed [Pa] … dynamický modul pružnosti materiálu zvukově izolační podložky
d [ m ] … tloušťka zvukově izolační podložky (ve stlačeném stavu)
m‘1 [kg·m-2] … plošná hmotnost nosné konstrukce stropu
m‘2 [kg·m-2] … plošná hmotnost konstrukce podlahy (tj. součet hmotnosti vrstev nad zvukově izolační podložkou.
Je užitečné si uvědomit rozdíl ve fungování mezery mezi vzduchovou neprůzvučností a kročejovým zvukem. U vzduchové neprůzvučnosti je mezera mezi dílčími konstrukcemi, i když je vyplněna minerálními vlákny, stále mezerou vzduchovou. Vlákna jsou ve funkci tlumení stojatého vlnění (půlvlnné rezonance) a konstrukce má stejné vlastnosti ať postupuje-li zvuk shora dolu či naopak zdola nahoru. U kročejového zvuku se výplň mezery mezi deskou nosnou a deskou roznášecí chová jako pružina, působí jen ve svislém směru ve smyslu gravitace, tedy shora dolů. O chování konstrukce zde nerozhodují pružné vlastnosti vzduchu, ale je třeba uvažovat vlastnosti konkrétního materiálu zvukově izolační podložky. Zejména uživatelé výpočetních programů někdy toto ne dostatečně rozlišují a v důsledku nesprávného zadání pak dochází k závažným chybám ve výpočtu.

Obr. 38 K rozdílu funkce mezery u neprůzvučnosti a kročejového zvuku
32 ZÁSADY NÁVRHU NEPRŮZVUČNÝCH KONSTRUKCÍ
Neprůzvučnost stavebních dělicích konstrukcí vzrůstá s jejich plošnou hmotností m´ [kg·m-2] tj. s jejich tloušťkou a je vyšší u konstrukcí z materiálů o vyšší objemové hmotnosti. Přibližně platí, že s každým zdvojnásobením plošné hmotnosti konstrukce vzrůstá neprůzvučnost o 6 dB. Podmínkou vyhovující neprůzvučnosti konstrukcí je též jejich vzduchotěsnost, tj. zejména vyloučení spár. Jejich lištování je třeba nahradit nebo doplnit tmelením.
Výhodnější jsou konstrukce ohybově měkké oproti konstrukcím ohybově tuhým. Požadavky na co největší hmotnost a zároveň co nejmenší tuhost se však většinou vzájemně vylučují. Tenké desky mají výhodu malé tuhosti, ale nejsou dost hmotné a naopak. Konstrukcí, která je zároveň hmotná i ohybově měkká, je konstrukce s násypem. Násyp dodává konstrukci dostatek hmotnosti, ale nezvyšuje její tuhost. Proto mají tradiční trámové stropy s podbíjením, záklopem a násypem tak výborné zvukově izolační vlastnosti. Navíc je-li podlaha položena na násyp prostřednictvím polštářů (trámků volně položených do násypu), je zpravidla dostatečně tlumen i kročejový zvuk. Energie chvění podlahy se přenáší do násypu, kde se mění třením mezi jednotlivými zrny násypu v teplo.
Efektivní jsou konstrukce se vzduchovou mezerou (dvojité příčky, stropy se zvukově izolačním podhledem, hmotné stěny se zvukově izolační předstěnou). Při jejich konstrukci je nutno omezit vzájemná spojení mezi dílčími konstrukcemi na nanejvýš 3 bodové spoje na 1 m2 nebo přímkové spoje (trámky roštu) s osovou vzdáleností nejméně 500 mm. Šířku vzduchové mezery je výhodné volit v rozmezí 100 až 200 mm tak, aby se vyhovělo podmínce (82). Nejlepších výsledků lze dosáhnout tehdy, jestliže jedna z dílčích stěn má vysokou plošnou hmotnost a druhá naopak je tvořena tenkou ohybově měkkou deskou upevněnou na roštu.
\begin{gathered}
d_\text{min}=0{,}73\Bigg[\frac{1}{m'_1}+\frac{1}{m'_2}\Bigg]
\end{gathered}(82)
Ve vztahu (82) pro stanovení minimální šířky vzduchové mezery kde je
m‘1 [kg·m-2] … plošná hmotnost jedné dílčí konstrukce
m‘2 [kg·m-2] … plošná hmotnost druhé dílčí konstrukce
V praxi je vždy třeba důsledně rozlišovat mezi konstrukcemi, které pohlcují zvuk a upravují tak jen akustické vlastnosti místnosti, kde jsou zabudovány, a mezi konstrukcemi, které zajišťují neprůzvučnost, tj. omezují přenos zvuku mezi dvěma místnostmi v budově. Pohlcovač zvuku nemůže být zároveň dobrou zvukově izolační konstrukcí. Porézní pohlcovače pro svoji malou hmotnost, děrované desky pro svoji průvzdušnost. Pohlcovače typu kmitající deska sice připomínají svojí konstrukcí zvukově izolační předstěnu, ale pohlcují nejvíce v oblasti rezonančního kmitočtu, což je právě oblast, kde dochází k výraznému poklesu neprůzvučnosti. Pohlcovače jsou dimenzovány tak, aby jejich rezonanční kmitočet byl v pásmu nejvyšší citlivosti sluchu (125–4 000 Hz), dvouprvkové dělící konstrukce včetně těžkých plovoucích podlah naopak musí mít rezonanční kmitočet nízký, tj. musí být v oblasti, kde zvuk vnímáme s nižší citlivostí.
Z hlediska zvukové izolace je výhodný příčný stěnový konstrukční systém, kde nosné stěny svojí hmotností, která je nutná pro zajištění stability budovy, zajistí též dostatečnou neprůzvučnost pro oddělení jednotlivých vnitřních prostorů budovy. Naopak problémy bývají u skeletů, kde snaha o maximální vylehčení výplňových příček vede někdy k podcenění zvukové izolace. Vyšší hodnoty vážené stavební neprůzvučnosti příček než Rw´= 53 dB u skeletů lze obtížně zajistit. Proto při požadavcích Rw´= 53 dB a vyšších se stává skelet nevýhodným a je lépe volit příčný stěnový konstrukční systém.
Železobetonová stropní deska tloušťky 150 mm spolu s konstrukcí těžké plovoucí podlahy nebo železobetonové prefabrikáty tloušťky 200 až 250 mm vylehčené válcovými dutinami spolu s podlahou vyhovují jako mezibytové konstrukce. Malou neprůzvučnost mají železobetonové trámové stropy, stropy vylehčené keramickými vložkami a stropy z ocelových plechů a betonu. V některých případech je proto nutné navrhovat pod těmito stropy zvukově izolační podhledy. Přílišné vylehčení nosné stropní konstrukce je v rozporu nejen s akustickými požadavky, ale zhoršuje i tepelnou stabilitu budovy, kterou hmotné stropní konstrukce svou tepelnou akumulací z velké části zajišťují.
Příčinou závažných nedostatků může být neodborná záměna materiálů. Desky z minerálních vláken typu Orsil a polystyrenbeton mají asi srovnatelné tepelně technické vlastnosti, jejich elastické vlastnosti se ale podstatně liší. Polystyrenbeton vznikne zalitím kuliček pěnového polystyrénu cementovou maltou. Jedná se o materiál, který není pružný a který na rozdíl od výborného Orsilu neposkytuje vůbec žádnou izolaci proti kročejovému zvuku. Přesto jsou známy případy, kde záměna obou materiálů byla provedena v celém objektu nebo dokonce i v celém obytném souboru s naprosto zničujícími následky pro kvalitu z hlediska šíření kročejového zvuku. I z toho důvodu je potřebné v projektech uvádět, k jakému účelu (zda jako tepelná či jako akustická izolace) je minerální vata v konstrukci navržena. Na rozdíl od tepelně technických vlastností se akustická měření na stavbách běžně provádějí a stavební úřady často vyžadují dokládat jejich výsledky při kolaudacích. Také je dnes běžně možné, že si uživatelé bytů objednají kontrolní akustická měření, na základě kterých se pak domáhají vrácení části ceny bytu. Deficit jednoho decibelu ve zvukové izolaci není z hlediska zdraví závažný, ale z právního hlediska může ve vztazích mezi developerem a nabyvatelem bytu představovat závažný problém. Dodatečná oprava závad nesprávně navržené nebo provedené zvukové izolaci představuje vždy technicky i ekonomicky velmi obtížný problém. Stejně tak neblahé jsou rekonstrukce v panelových domech hromadné bytové výstavby ze 60. až 80. let minulého století, při kterých se odstraní původní podlahový povlak (který jako relativně měkká nášlapná vrstva bránil nadměrnému vzniku kročejového zvuku) a nahradí se keramickou dlažbou přilepenou „natvrdo“ na železobetonový stropní panel. V těchto objektech lze při rekonstrukcích bytů opět navrhovat jen měkké podlahové povlaky, protože vybudování plovoucí podlahy by bylo spojeno s nežádoucím rozdílem úrovní podlahy na chodbě a v bytě.
Se zaváděním nových hlučných domácích spotřebičů včetně stále hlučnější reprodukční techniky s vysokými hladinami akustického výkonu i v nízkých kmitočtech, které vždy snáze pronikají konstrukcemi, budou v blízké budoucnosti požadavky na zvukovou izolaci spíše stoupat. Svoji roli zde také hraje používání špičkově těsněných oken, s dobrými tepelně i zvukově izolačními vlastnostmi. Jejich příliš dokonalá zvuková izolace může být paradoxně i na škodu. Brání přístupu přirozenému zvukovému pozadí města do bytu a v takovém velmi tichém prostředí pak vyniknou všechny zvuky z vnitřku budovy včetně kročejového zvuku a zvuku šířeného vzduchem z okolních prostor domu. Proto stavební místa ve velmi klidném prostředí bez dopravního hluku se jeví jako potenciálně více nebezpečná z hlediska možných stížností na zvukovou izolaci mezi byty.
PŘÍLOHA
Tab. 1 Příklady hladin akustického tlaku
| Akustický tlak p [Pa] | Akustická intenzita / [Wm-2] | Hladina akustického tlaku L [dB] | Příklad prostředí, kde se vyskytuje |
| cca 60 | cca 10 | cca 130 | práh bolesti |
| 2 | 10-2 | 100 | diskotéka |
| 0,2 | 10-4 | 80 | rušná ulice |
| 0,02 | 10-6 | 60 | kancelář |
| 0,002 | 10-8 | 40 | obývací pokoj |
| 0,0002 | 10-10 | 20 | ložnice v noci |
| 0,00002 | 10-12 | 0 | práh slyšení |
Tab. 2 Střední kmitočty oktávových pásem a hodnoty korekcí váhového filtru zvukoměru
| f [Hz] | 16 | 31.5 | 63 | 125 | 250 | 500 | 1000 | 2000 | 4000 | 8000 | 16000 |
| KA [dB] | -56,7 | -39,4 | -26,2 | -16,1 | -8,6 | -3,2 | 0,0 | +1,2 | +1,0 | -1,1 | -6,6 |
Tab. 3 Nejvyšší přípustné hodnoty hluku na pracovištích s osmihodinovou pracovní dobou (podle nařízení vlády č. 272/2011 Sb.)
| Charakteristika | Ustálený a proměnný hluk na pracovišti |
| Pracoviště | max. LAeq,8h = 85 dB *) |
| Pracoviště, na němž je vykonávána práce náročná na pozornost a soustředění, tvůrčí práce | max. LAeq,T = 50 dB |
| Pracoviště ve stavbách pro výrobu a skladování, kde hluk je způsobován větracím nebo vytápěcím zařízením těchto pracovišť | max. LAeq,8h = 70 dB |
Poznámky:
LAeq,8h = ekvivalentní hladina akustického tlaku A za 8 hodin trvání pracovní směny
LAeq,T = ekvivalentní hladina akustického tlaku A za dobu T [hodin] trvání rušivého zvuku (ta může být kratší, než doba pracovní směny)
*) jedná se jen o ochranu sluchu. Při překročení limitu LAeq,8h = 80 dB musí zaměstnavatel poskytnout zaměstnancům osobní ochranné pomůcky pracovní prostředky k ochraně sluchu účinné v oblasti kmitočtů daného hluku a zajistit jejich školení. Při překročení limitu LAeq,8h = 85 dB musí zaměstnavatel zajistit, aby zaměstnanci osobní ochranné pracovní prostředky používali.
Tab. 4 Nejvyšší přípustné hodnoty hluku ve chráněném vnitřním prostoru staveb (podle nařízení vlády č. 272/2011 Sb.)
| Charakter hluku (zdroje) | Kritérium | Limitní hodnoty | |
| v denní době 6 až 22 hodin | v noční době 22 až 6 hodin | ||
| 1) hluk pronikající vzduchem zvenčí s výjimkou ad 2) | LAeq, 8h (dB) stanovená za 8 nejhlučnějších po sobě jdoucích hodin | LAeq, 1h (dB) stanovená za nejvíce hlučnou hodinu | 40 dB + korekce podle tab. 5 |
| 2) hluk z dopravy na veřejných pozemních komunikacích, drahách, hluk z leteckého provozu | LAeq, 16h (dB) stanovená za celou denní dobu | LAeq, 8h (dB) stanovená za celou noční dobu | 40 dB + korekce podle tab. 5 |
| 3) hluk šířící se ze zdrojů uvnitř objektu a hluk ze zdrojů umístěných mimo tento objekt, který do tohoto objektu proniká jiným způsobem než vzduchem, zejména konstrukcemi nebo podložím | LAmax (dB) maximální hladina | LAmax (dB) maximální hladina | 40 dB + korekce podle tab. 5 |
| 4) hluk ze stavební činnosti uvnitř objektu | LAeq (dB) stanovená v pracovních dnech pro dobu mezi 7 a 21 hodinou | 40 dB + 15 dB + korekce podle tab. 5 | |
| 5) zvuk elektronicky zesilované hudby v prostoru pro posluchače | LAeq, 4h (dB) stanovená pro dobu T = 4 hodiny | 100 dB | |
Obsahuje-li zvuk tónové složky, nebo má-li výrazně informační charakter, přičte se další korekce – 5 dB. Za hluk s tónovými složkami se např. považuje hudba nebo zpěv, informační charakter má řeč.
V tab. 5 je výběr korekcí pro stanovení nejvyšších přípustných hodnot hluku ve chráněném vnitřním prostoru staveb, tak jak jsou stanoveny v nařízení vlády č. 272/2011 Sb.
Tab. 5 Výběr korekcí pro stanovení nejvyšších přípustných hodnot hluku ve chráněném vnitřním prostoru staveb (podle nařízení vlády č. 272/2011 Sb.)
| Druh chráněného vnitřního prostoru | Doba pobytu | korekce [dB] |
| Nemocniční pokoje | doba mezi 6.00 a 22.00 hodinou doba mezi 22.00 a 6.00 hodinou | 0 -15 |
| Lékařské vyšetřovny, ordinace | po dobu používání | -5 |
| Obytné místnosti | doba mezi 6.00 a 22.00 hodinou doba mezi 22.00 a 6.00 hodinou | 0*) -10*) |
| Přednáškové síně, učebny a pobytové místnosti škol, jeslí a staveb pro předškolní a školní výchovu a vzdělávání | po dobu používání | +5 |
*) Pro hluk z dopravy v okolí dálnic, silnic I. a II. třídy a místních komunikací I. a II. třídy, kde je hluk z dopravy na těchto komunikacích převažující, v ochranném pásmu drah a pro hluk z tramvajových a trolejbusových drah se přičítá další korekce +5 dB. Tato korekce se nepoužije ve vztahu ke chráněnému vnitřnímu prostoru staveb povolených k užívání k určenému účelu po dni 31. prosince 2005.
Tab. 6 Korekce pro stanovení nejvyšších přípustných hodnot hluku ve chráněném venkovním prostoru a chráněném venkovním prostoru staveb (podle nařízení vlády č. 272/2011 Sb.)
| Druh chráněného prostoru | Korekce [dB] | |||
| 1) | 2) | 3) | 4) | |
| Chráněný venkovní prostor staveb lůžkových zdravotnických zařízení včetně lázní | -5 | 0 | +5 | +15 |
| Chráněný venkovní prostor lůžkových zdravotnických zařízení včetně lázní | 0 | 0 | +5 | +15 |
| Chráněný venkovní prostor ostatních staveb a chráněný ostatní venkovní prostor | 0 | +5 | +10 | +20 |
Korekce uvedené v tab. 5 se navzájem nesčítají. Lze uplatnit jen jednu z uvedených korekcí.
Pro noční dobu se pro venkovní prostor staveb přičítá další korekce – 10 dB s výjimkou hluku z dopravy na železničních drahách, kde se použije korekce – 5 dB.
Pro vysoce impulsní hluk se přičte další korekce -12 dB. V případě hluku s tónovými složkami, s výjimkou hluku z dopravy na pozemních komunikacích, drahách a z leteckého provozu, se přičte další korekce -5 dB.
Vysvětlivky k tab. 6
1) Použije se pro hluk z provozu stacionárních zdrojů a hluk ze železničních stanic zajišťujících vlakotvorné práce, zejména rozřaďování a sestavu nákladních vlaků, prohlídku vlaků a opravy vozů. Pro hluk ze železničních stanic zajišťujících vlakotvorné práce, které byly uvedeny do provozu přede dnem 1. listopadu 2011, se přičítá pro noční dobu další korekce +5 dB.
2) Použije se pro hluk z dopravy na dráhách, není-li dále uvedeno jinak, na silnicích III. třídy, místních komunikacích III. třídy a účelových komunikacích ve smyslu § 7 odst. 1 zákona č. 13/1997 Sb. o pozemních komunikacích, ve znění pozdějších předpisů.
3) Použije se pro hluk z dopravy na dálnicích, silnicích I. a II. třídy a místních komunikacích I. a II. třídy v území, kde hluk z dopravy na těchto komunikacích je převažující nad hlukem z dopravy na ostatních pozemních komunikacích. Použije se pro hluk z dopravy na drahách v ochranném pásmu dráhy. Použije se pro hluk z dopravy na tramvajových a trolejbusových drahách vedených po silnicích I. a II. třídy a místních komunikacích I. a II. třídy.
4) Použije se pro stanovení hodnoty hygienického limitu staré hlukové zátěže. (Podrobněji vysvětleno v [2].)
Tab. 7 Hodnoty Fresnelových integrálů
| u | X | Y | u | X | Y | u | X | Y |
| 0,00 | 0,0000 | 0,0000 | 1,50 | 0,4453 | 0,6975 | 3,00 | 0,6057 | 0,4963 |
| 0,05 | 0,0500 | 0,0001 | 1,55 | 0,4018 | 0,6731 | 3,05 | 0,5941 | 0,5445 |
| 0,10 | 0,1000 | 0,0005 | 1,60 | 0,3655 | 0,6389 | 3,10 | 0,5616 | 0,5818 |
| 0,15 | 0,1500 | 0,0018 | 1,65 | 0,3388 | 0,5968 | 3,15 | 0,5154 | 0,5996 |
| 0,20 | 0,1999 | 0,0042 | 1,70 | 0,3238 | 0,5492 | 3,20 | 0,4663 | 0,5933 |
| 0,25 | 0,2498 | 0,0082 | 1,75 | 0,3219 | 0,4994 | 3,25 | 0,4263 | 0,5642 |
| 0,30 | 0,2994 | 0,0141 | 1,80 | 0,3336 | 0,4509 | 3,30 | 0,4057 | 0,5193 |
| 0,35 | 0,3487 | 0,0224 | 1,85 | 0,3584 | 0,4077 | 3,35 | 0,4100 | 0,4700 |
| 0,40 | 0,3975 | 0,0334 | 1,90 | 0,3945 | 0,3733 | 3,40 | 0,4385 | 0,4296 |
| 0,45 | 0,4455 | 0,0474 | 1,95 | 0,4391 | 0,3511 | 3,45 | 0,4835 | 0,4094 |
| 0,50 | 0,4923 | 0,0647 | 2,00 | 0,4883 | 0,3434 | 3,50 | 0,5326 | 0,4152 |
| 0,55 | 0,5377 | 0,0857 | 2,05 | 0,5374 | 0,3513 | 3,55 | 0,5713 | 0,4459 |
| 0,60 | 0,5811 | 0,1105 | 2,10 | 0,5816 | 0,3743 | 3,60 | 0,5880 | 0,4923 |
| 0,65 | 0,6219 | 0,1393 | 2,15 | 0,6159 | 0,4103 | 3,65 | 0,5771 | 0,5404 |
| 0,70 | 0,6597 | 0,1721 | 2,20 | 0,6363 | 0,4557 | 3,70 | 0,5419 | 0,5750 |
| 0,75 | 0,6935 | 0,2089 | 2,25 | 0,6401 | 0,5053 | 3,75 | 0,4936 | 0,5845 |
| 0,80 | 0,7228 | 0,2493 | 2,30 | 0,6266 | 0,5532 | 3,80 | 0,4481 | 0,5656 |
| 0,85 | 0,7469 | 0,2932 | 2,35 | 0,5970 | 0,5931 | 3,85 | 0,4211 | 0,5244 |
| 0,90 | 0,7648 | 0,3398 | 2,40 | 0,5550 | 0,6197 | 3,90 | 0,4223 | 0,4752 |
| 0,95 | 0,7760 | 0,3885 | 2,45 | 0,5061 | 0,6289 | 3,95 | 0,4516 | 0,4357 |
| 1,00 | 0,7799 | 0,4383 | 2,50 | 0,4574 | 0,6192 | 4,00 | 0,4984 | 0,4205 |
| 1,05 | 0,7759 | 0,4880 | 2,55 | 0,4161 | 0,5915 | 4,05 | 0,5452 | 0,4358 |
| 1,10 | 0,7638 | 0,5365 | 2,60 | 0,3889 | 0,5500 | 4,10 | 0,5737 | 0,4758 |
| 1,15 | 0,7436 | 0,5821 | 2,65 | 0,3805 | 0,5011 | 4,15 | 0,5725 | 0,5249 |
| 1,20 | 0,7154 | 0,6234 | 2,70 | 0,3925 | 0,4529 | 4,20 | 0,5417 | 0,5632 |
| 1,25 | 0,6801 | 0,6587 | 2,75 | 0,4233 | 0,4140 | 4,25 | 0,4940 | 0,5746 |
| 1,30 | 0,6386 | 0,6863 | 2,80 | 0,4675 | 0,3915 | 4,30 | 0,4494 | 0,5540 |
| 1,35 | 0,5923 | 0,7050 | 2,85 | 0,5171 | 0,3900 | 4,35 | 0,4276 | 0,5101 |
| 1,40 | 0,5431 | 0,7135 | 2,90 | 0,5624 | 0,4101 | 4,40 | 0,4383 | 0,4623 |
| 1,45 | 0,4933 | 0,7111 | 2,95 | 0,5942 | 0,4481 | 4,45 | 0,4771 | 0,4323 |
Tab. 8 Hodnoty činitele pohltivosti zvuku α [-] vybraných povrchů a konstrukcí [12]
| Konstrukce (tloušťka [mm] / odsazení [mm]) | Kmitočet f [Hz] | |||||
| 125 | 250 | 500 | 1000 | 2000 | 4000 | |
| beton hutný | 0,010 | 0,016 | 0,019 | 0,023 | 0,035 | 0,05 |
| beton vylehčený | 0,20 | 0,22 | 0,23 | 0,25 | 0,21 | 0,26 |
| beton s olejovým nátěrem | 0,01 | 0,014 | 0,016 | 0,017 | 0,018 | 0,02 |
| čalouněné křeslo zvuková pohltivost v m2 na jeden kus | 0,15 | 0,20 | 0,20 | 0,25 | 0,30 | 0,30 |
| čalouněné křeslo obsazené zvuková pohltivost v m2 na jeden kus | 0,25 | 0,30 | 0,40 | 0,45 | 0,45 | 0,40 |
| dřevěné křeslo zvuková pohltivost v m2 na jeden kus | 0,02 | 0,02 | 0,03 | 0,04 | 0,04 | 0,05 |
| dřevěné křeslo obsazené zvuková pohltivost v m2 na jeden kus | 0,20 | 0,25 | 0,30 | 0,35 | 0,35 | 0,35 |
| dřevotřísková deska (20/50 až 150) | 0,30 | 0,25 | 0,10 | 0,08 | 0,05 | 0,04 |
| dřevotřísková deska (odsazení = 0 mm) | 0,08 | 0,08 | 0,09 | 0,10 | 0,10 | 0,10 |
| dřevovláknitá měkká deska (15/0) | 0,10 | 0,15 | 0,55 | 0,52 | 0,50 | 0,45 |
| deska z pěnového polystyrénu (18 až 32/0) | 0,02 | 0,02 | 0,03 | 0,08 | 0,14 | 0,29 |
| koberec bouclé (5/0) | 0,08 | 0,10 | 0,10 | 0,21 | 0,43 | 0,78 |
| koberec kokosový (6/0) | 0,17 | 0,06 | 0,11 | 0,19 | 0,37 | 0,80 |
| koberec plyšový (10/0) | 0,13 | 0,11 | 0,15 | 0,30 | 0,63 | 0,90 |
| linoleum (-/0) | 0,02 | 0,025 | 0,03 | 0,035 | 0,04 | 0,04 |
| okenní otvor zasklený | 0,30 | 0,20 | 0,15 | 0,10 | 0,06 | 0,04 |
| omítka malovaná hlinkou (-/0) | 0,02 | 0,02 | 0,02 | 0,03 | 0,04 | 0,04 |
| omítka s olejovým nátěrem (-/0) | 0,01 | 0,01 | 0,02 | 0,02 | 0,02 | 0,02 |
| otvor jeviště s dekoracemi | 0,20 | 0,30 | 0,30 | 0,30 | 0,30 | 0,30 |
| publikum v hledišti (plocha obsazená publikem) | 0,41 | 0,48 | 0,54 | 0,57 | 0,56 | 0,53 |
| překližka laťová (18/70) | 0,27 | 0,08 | 0,11 | 0,09 | 0,09 | 0,20 |
| sádrokartonová deska (9,5/100) | 0,11 | 0,13 | 0,05 | 0,02 | 0,02 | 0,03 |
| vlysy dřevěné (-/0) | 0,03 | 0,04 | 0,06 | 0,12 | 0,10 | 0,17 |
| vodní hladina | 0,01 | 0,01 | 0,01 | 0,01 | 0,02 | 0,02 |
| zdivo cihelné režné (-/0) | 0,024 | 0,025 | 0,032 | 0,042 | 0,049 | 0,07 |
Tab. 9 Dovolený rozdíl drah mezi přímým a odraženým zvukem
| Rozdíl drah [m] | Časové zpoždění [s] | Vliv na srozumitelnost |
| méně než 10 | méně než 0,03 | zesílení zvuku – vnímáno jako jeden zvuk |
| 10 až 17 | 0,03 až 0,05 | směšování hlásek |
| 17 až 34 | 0,05 až 0,1 | ozvěna |
| více než 34 | více než 0,1 | jednoslabičná ozvěna |
Tab. 10 Činitel útlumu zvuku m [m-1] pro oktávová pásma v normálních atmosférických podmínkách (tlak 101,325 kPa, teplota 20 °C) [6]
| f [Hz] | Relativní vlhkost [%] | ||||||||||
| 10 | 15 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | |
| 1 000 | 0,0041 | 0,0025 | 0,0018 | 0,0013 | 0,0012 | 0,0011 | 0,0012 | 0,0012 | 0,0012 | 0,0013 | 0,0013 |
| 2 000 | 0,0137 | 0,0095 | 0,0067 | 0,0041 | 0,0031 | 0,0027 | 0,0024 | 0,0023 | 0,0023 | 0,0022 | 0,0023 |
| 4 000 | 0,0297 | 0,0295 | 0,0242 | 0,0161 | 0,0118 | 0,0094 | 0,0079 | 0,0069 | 0,0063 | 0,0058 | 0,0055 |
Tab. 11 Hodnoty hadiny akustického výkonu LW [dB] a činitel směrovosti Q [-] lidské řeči
| f [Hz] | 125 | 250 | 500 | 1 000 | 2 000 | 4 000 |
| LW [dB] | 62 | 67 | 69 | 68 | 63 | 62 |
| Q [-] | 1,2 | 1,5 | 1,8 | 2,0 | 2,5 | 3,5 |
Tab. 12 Hodnoty indexu srozumitelnosti a jejich hodnocení
| ΔL = LA1 – LA2 [dB] | index srozumitelnosti I [-] | srozumitelnost je |
| menší než – 12 | 0,00 | nulová |
| – 12 až – 1,5 | 0,00 až 0,35 | nevyhovující |
| – 1,5 až +1,5 | 0,35 až 0,45 | unavující |
| + 1,5 až +6,0 | 0,45 až 0,60 | dobrá |
| + 6,0 až +18,0 | 0,60 až 1,00 | velmi dobrá |
| větší než 18,0 | 1,00 | dokonalá |
Tab. 13 Požadavky na dobu dozvuku Topt [s] v prostorech škol
| Prostor | objem V [m3] orientačně | Topt [s] |
| učebna posluchárna | do 250 | 0,70 |
| jazyková učebna | 130 až 180 | 0,45 |
| audiovizuální učebna | 200 | 0,60 |
| učebna hudební výchovy | 200 | 0,90 |
| učebna hudební výchovy při reprodukované hudbě | 200 | 0,50 |
| učebna hry na individuální hudební nástroje a sólového zpěvu | 80 až 200 | 0,70 |
| učebna orchestrální hry hudebních škol | > 600 | 1,00 |
Tab. 14 Prostory ve školách, kde se požaduje širokopásmový obklad stropu
| Prostor | objem V [m3] orientačně |
| sborovna nebo konferenční místnost | |
| učebna pracovní výuky | 130 |
| školní dílna základních škol | 280 |
| učebna techniky administrativy | 130 |
| učebna gymnastiky a tance | |
| tělocvična a plavecká učebna všech typů škol | |
| herna mateřských škol a školních družin | 130 až 200 |
| denní místnost jeslí | 150 |
| školní jídelna, menza | |
| komunikační prostory před učebnami a posluchárnami |
Tab. 15 Požadavky na dobu dozvuku Topt [s] v prostorech pro veřejné účely
| Prostor | Topt [s] |
| tělocvičny | 1,3 |
| plavecké haly | 1,3 |
| sportovní haly | 1,3 |
| přepážkové haly pošt, spořitelen a bank | 1,2 |
| haly a dvorany veřejných budov | 1,4 |
| nádražní haly | 1,4 |
| letištní haly | 1,4 |
| čítárny a studovny | 1,2 |
Tab. 16 Prostory pro veřejné účely, kde se požaduje širokopásmový obklad stropu
| Prostor |
| obchodní domy |
| nákupní středisko |
| hotelová hala hotelová společenská hala |
| hotelové salónky |
| hotelová restaurace |
Tab. 17 Maximální objemy prostorů doporučené z hlediska možného akustického výkonu zdrojů živé hudby a řeči
| Účel využití | Řeč | Hudební divadlo | Komorní hudba | Symfonická hudba | Varhanní hudba |
| maximální objem [m3] | 5 000 | 15 000 | 5 000 | 25 000 | 30 000 |
Tab. 18 Přehled rušivého hluku v budově
| Hluk v budově (v závorce kritérium) | Šířený vzduchem | Šířený konstrukcí | |
| nedefinovatelný | hlasitý hovor, reprodukovaná hudba, hra na hudební nástroje (Rw´ [dB]) | kročejový hluk (Lnw´ [dB]) | |
| definovatelný opatření: | hluk technického zařízení budovy (LAmax [dB]) | ||
| zvětšit neprůzvučnost stěn strojovny | pružně uložit stroje | ||
Tab. 19 Střední hodnoty f [Hz] pásem 1/3 oktávy v rozsahu zvukoizolačního pásma a hodnoty SK [dB] směrné křivky pro neprůzvučnost
| č. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| f [Hz] | 100 | 125 | 160 | 200 | 250 | 315 | 400 | 500 | 630 | 800 | 1 000 | 1 250 | 1 600 | 2 000 | 2 500 | 3 150 |
| SK [dB] | 33 | 36 | 39 | 42 | 45 | 48 | 51 | 52 | 53 | 54 | 55 | 56 | 56 | 56 | 56 | 56 |
Tab. 20 Spektra hladin akustického tlaku k výpočtu faktorů přizpůsobení
| č. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| f [Hz] | 100 | 125 | 160 | 200 | 250 | 315 | 400 | 500 | 630 | 800 | 1 000 | 1 250 | 1 600 | 2 000 | 2 500 | 3 150 |
| č.1 dB | -29 | -26 | -23 | -21 | -19 | -17 | -15 | -13 | -12 | -11 | -10 | -9 | -9 | -9 | -9 | -9 |
| č.2 dB | -20 | -20 | -18 | -16 | -15 | -14 | -13 | -12 | -11 | -9 | -8 | -9 | -10 | -11 | -13 | -15 |
Tab. 21 Střední hodnoty f [Hz] pásem 1/3 oktávy v rozsahu zvukoizolačního pásma a hodnoty SK [dB] směrné křivky pro kročejový zvuk
| č. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| f [Hz] | 100 | 125 | 160 | 200 | 250 | 315 | 400 | 500 | 630 | 800 | 1 000 | 1 250 | 1 600 | 2 000 | 2 500 | 3 150 |
| SK [dB] | 62 | 62 | 62 | 62 | 62 | 62 | 61 | 60 | 59 | 58 | 57 | 54 | 51 | 48 | 45 | 42 |
LITERATURA
[1] Zákon č. 258/2000 Sb., o ochraně veřejného zdraví a o změně některých souvisejících předpisů, ve znění pozdějších předpisů.
[2] Nařízení vlády č. 272/2011 Sb., o ochraně zdraví před nepříznivými účinky hluku a vibrací, se změnami: č. 317/2016 Sb., č. 241/2018 Sb.
[3] Vyhláška č. 268/2009 Sb., o technických požadavcích na stavby, ve znění pozdějších předpisů
[4] ČSN 73 0525:1998 Akustika – Projektování v oboru prostorové akustiky – všeobecné zásady. Praha: ČNI.
[5] ČSN 73 0527:2005 Akustika – Projektování v oboru prostorové akustiky – Prostory pro kulturní účely – Prostory ve školách – Prostory pro veřejné účely. Praha: ČNI.
[6] ČSN 73 0532:2020 Akustika – Ochrana proti hluku v budovách a posuzování akustických vlastností stavebních konstrukcí a výrobků – Požadavky. Praha: Úřad pro technickou normalizaci, metrologii a státní zkušebnictví, 2020.
[7] ARDILLON, M. J. Acoustique des espace fonctionnelle. Paris: Caniers du CSTB, No.127/1972.
[8] BERANEK, L. L. Noise reduction, McGraw-Hill Book Company. Inc. New York, Toronto, London 1960.
[9] BERANEK, L. L. Snižování hluku. Praha: SNTL, 1965.
[10] BINKO, J. KAŠPAR, I. Fyzika stavebního inženýra. Praha: SNTL, 1983.
[11] CONARD, J. HEMOND, JR. Engineering acoustics and noise kontrol. Prentice – Hall 1983.
[12] ČECHURA, J. Stavební fyzika 10 – akustika stavební konstrukcí. Praha: ČVUT, 1997.
[13] ČECHURA, J. WEIGLOVÁ, J. Stavební akustika a denní osvětlení. Praha: ČVUT, 1987.
[14] GINN, K. B. Architectural Acoustics. Bruel a Kjaer 1978.
[15] HALAHYJA, M. a kol. Stavebná tepelná technika, akustika a osvetlenie. Bratislava: Alfa, 1985.
[16] HAVRÁNEK, J. Hluk a zdraví. Praha: Avicenum, 1990.
[17] CHALUPOVÁ, V. Životní prostředí. Praha: ČVUT, 1985.
[18] KAŇKA, J. Akustika v architektuře. Praha: ČVUT, 1994.
[19] KAŇKA, J. Hluk osobních a nákladních vozidel v dopravním proudu. sborník 36. Akustické konference, Kouty u Ledče n./Sáz. květen 2000.
[20] KAŇKA, J. Stavební fyzika 1 Akustika budov. Praha: ČVUT, 2007.
[21] KAŇKA, J. Stavební fyzika 1. Praha: ČVUT, 2003.
[22] KAŇKA, J. SVOBODA, Z. Stavební fyzika 31. Praha: ČVUT, 2004.
[23] KAŇKA, J. Akustika stavebních objektů. Brno: ERA, 2009.
[24] LIBERKO, M. a kol. Novela metodiky pro výpočet hluku silniční dopravy, Hluk v životním prostředí. Ministerstvo životního prostředí, edice PLANETA 2/2005.
[25] MAEKAWA, Z. LORD, P. Environmental and Architectural Acoustics. London: E & FN Spon 1994.
[26] MAEKAWA, Z. Metodi simplificati per la previsione dell isolamento acustico ottenebile da barriere di vario tipo, Rivista italiana di acustica,1987.
[27] MEJSTŘÍK, J. Tuhé těleso na pružném podkladu. Bratislava: ALFA, 1968.
[28] MELLER, M. STĚNIČKA, J. Podklady pro navrhování a posuzování průmyslových staveb, díl 3 – stavební akustika. Praha: VÚPS, 1985.
[29] MOURIC, K. Stavební akustika. Praha: ČVUT, 1974.
[30] NĚMEC, J, RANSDORF, J. ŠNÉDRLE, M. Hluk a jeho snižování v technické praxi. Praha: SNTL, 1970.
[31] NOVÁČEK, J. Vzduchová neprůzvučnost mezimístnostmi v závislosti na akustických vlastnostech stavebních prvků. ČVUT, Praha: ČVUT, 2008.
[32] STROUHAL, Č. Akustika. Praha: JČM. 1902.
[33] ČSN EN ISO 717-1:2013 Akustika – Hodnocení zvukové izolace stavebních konstrukcí a v budovách – Část 1: Vzduchová neprůzvučnost
[34] ČSN EN ISO 717-2:2013 Akustika – Hodnocení zvukové izolace stavebních konstrukcí a v budovách – Část 2: Kročejová neprůzvučnost
[35] Zákon č. 89/2012 Sb., občanský zákoník, se změnami: zákon č. 460/2016 Sb., zákon č. 303/2017 Sb.
[36] ČSN ISO 9613-1:1995 Akustika. Útlum při šíření zvuku ve venkovním prostoru. Část 1: Výpočet pohlcování zvuku v atmosféře