ČESKÁ KOMORA AUTORIZOVANÝCH INŽENÝRŮ A TECHNIKŮ ČINNÝCH VE VÝSTAVBĚ
Rada pro podporu rozvoje profese ČKAIT
Autoři: doc. Ing. Tomáš Matuška, Ph.D.
Stav: kontrola 2018, vydání 2012
Anotace:
Pomůcka přibližuje problematiku solárních tepelných soustav a jejich využití pro ohřev vody a vytápění. Zabývá se sluneční energií, jejím původem, šířením, geometrií a měřením veličin slunečního záření. Popisuje konstrukce, druhy a funkce solárních kolektorů a zásobníků tepla, jejich zkoušení a systémy certifikace. Uvádí zásady pro navrhování a zapojování soustav. V kapitole 10 uvádí klimatické údaje pro navrhování solárních soustav.
OBSAH
1 SLUNEČNÍ ENERGIE
1.1 ÚVOD
1.1.1 Slunce
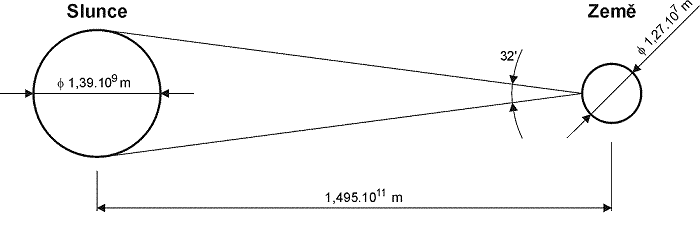
Země je součástí planetární soustavy, jejímž středem je Slunce. Slunce je nám nejbližší a nejdůležitější hvězdou. Je trvalým zdrojem veškeré energie pro naši planetu. Slunce má tvar koule o průměru 1,39×109 m, tj. 109 násobně větším než je průměr Země. Od Země je Slunce vzdáleno v průměru 1,5×1011 m. Hmotnost Slunce je 2×1030 kg. Slunce je 330 000násobně hmotnější než Země a tvoří přibližně 99,9 % hmotnosti celé sluneční soustavy.
1.1.2 Zdroj energie
Slunce se skládá převážně z atomárního vodíku (70 %), helia (28 %) a z nepatrného množství ostatních prvků periodické soustavy (2 %). Všechny prvky jsou ve hmotě Slunce obsaženy ve skupenství plasmy. Zdrojem energie Slunce je termonukleární reakce (jaderná syntéza, fúze), probíhající v centrální oblasti Slunce. Fúzí v jádru Slunce dochází ke kontinuální přeměně vodíku na helium. Přeměna probíhá při teplotách desítek mil. K a tlacích desítek miliard MPa za stavu, při němž jsou všechny atomy zcela ionizovány. Jádro atomu vodíku má za těchto podmínek podstatně vyšší hmotnost a ztrácí svůj záporně nabitý obal elektronů, které narážejí rychlostí okolo 1 000 km/s na jiné atomy vodíku. Do reakce vstupují čtyři protony vodíku, spojují se a vytvářejí jedno jádro helia. Každou sekundu se takto přemění 564×109 kg vodíku na 560×109 kg helia. Hmotnost vzniklého jádra helia je totiž menší, než hmotnost čtyř protonů vodíku vstupujících do reakce. Rozdíl hmoty se při reakci přemění na energii podle vztahu
(1.1)
a ta ve formě vysoce energetických rentgenových a gamma fotonů proniká směrem k povrchu.
Obr. 1.1 Schematický řez
Na obr. 1.1 je znázorněn řez Sluncem. Centrální oblast (jádro), ve které probíhá jaderná fúze, zasahuje do cca 23 % poloměru Slunce. V oblasti mezi 23 % a 70 % poloměru se nachází tzv. radiační zóna, s velmi vysokou hustotou a teplotou postupně klesající až na 130 000 K. Rentgenové fotony se průchodem radiační zónou přeměňují na energeticky „chudší“ fotony. Konvekční zóna mezi radiační zónou a povrchem Slunce má hustotu již výrazně nižší; hlavním způsobem přenosu energie je konvekce. Nositel energie záření – foton – se z jádra Slunce „prodere“ na vnější povrch zhruba za milion let. Vnějším viditelným obalem Slunce (fotosférou) je energie vyzařována do kosmického prostoru. Celkový tok vyzařované energie je 3,85×1026 W. Hustota zářivého toku energie na povrchu Slunce je 6×107 W/m2. Podle množství helia, které až dosud vzniklo, lze stáří Slunce odhadnout na 5 miliard let. Předpokládá se, že jaderná fúze bude pokračovat ještě dalších 5 až 10 miliard let.
1.1.3 Spektrální charakter slunečního záření
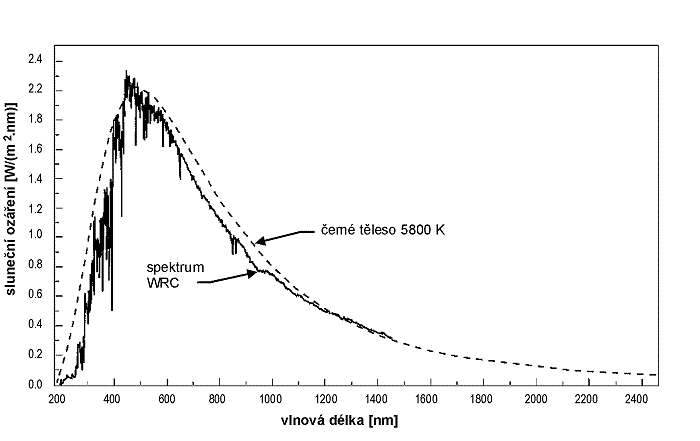
Slunce si lze zjednodušeně představit jako absolutně černé těleso s povrchovou teplotou okolo 5 800 K. Spektrální hustotu zářivého toku absolutně černého tělesa popisuje Planckův zákon
(1.2)
kde je
h … Planckova konstanta, h = 6,6256.10-34 J.s
k … Boltzmannova konstanta, k = 1,3805.10-23 J/K
c … rychlost světla ve vakuu, c = 2,9979.108 m/s
T … povrchová absolutní teplota tělesa v K, pro Slunce T = 5 800 K
Obr. 1.2 Spektrální charakteristika zářivého toku sluneční energie na hranicích zemské atmosféry
Sluneční záření zahrnuje vlnové délky od 10-10 m (rentgenové a ultrafialové záření) až do několika metrů (rádiové záření). Spektrální charakteristika zářivého toku sluneční energie je uvedena na obr. 1.2. Největší část sluneční energie však připadá na vlnové délky 0,2 až 3,0 μm. Mezi vlnovými délkami 0,2 až 0,4 μm se nachází ultrafialové záření typu UVC (0,2 až 0,28 μm, životu nebezpečné), UVB 0,28 až 0,32 μm) a neškodné UVA (nad 0,32 μm). Vlnové délky viditelného záření jsou 0,4 až 0,75 μm. Nad hodnotou 0,75 μm se nachází infračervené záření, zhruba do hodnoty 5 μm se označuje jako blízké infračervené záření. V ultrafialové oblasti se přenáší cca 9 % energie slunečního záření, ve viditelné 41 % a v blízce infračervené celých 50 %.
Vlnovou délku maxima vyzařování ëmax lze odvodit z Planckova zákona z vyhledání lokálního extrému funkce. Vztah mezi teplotou tělesa a vlnovou délkou maxima vyzařování pak udává Wienův posouvací zákon
(1.3)
Wienův zákon konstatuje, že vlnová délka maxima je nepřímo úměrná termodynamické teplotě tělesa. S klesající teplotou klesá jednak maximum hustoty zářivého toku (mohutnost vyzařování), a zároveň se maximum posouvá směrem do oblasti větších vlnových délek. Pro teplotu 5 800 K se vlnová délka maxima pohybuje okolo 0,5 μm (žlutá barva). Pro běžné teploty v aplikacích, např. v solárních kolektorech, okolo 100 °C se vlnová délka maxima posouvá k hodnotám okolo 8 μm. Toho se využívá např. v oblasti spektrálně selektivních povrchů absorbérů solárních kolektorů.
1.2 ŠÍŘENÍ SLUNEČNÍ ENERGIE
Sluneční záření na cestě k Zemi není ničím pohlcováno a přichází na hranici atmosféry s nezměněnou spektrální charakteristikou, avšak při značně zmenšené hustotě zářivého toku tím, že výkon se s rostoucí vzdáleností rozptýlí na větší plochu. Z celkového výkonu vyzařovaného Sluncem dopadá na vnější povrch atmosféry Země jen přibližně půl miliardtina výkonu Slunce, tj. asi 1,7×1017 W. Podobně nepatrná část je zachycena ostatními planetami. Zbývající tok záření, tzn. téměř celý tok vyzařované sluneční energie, uniká do mezihvězdného a mezigalaktického prostoru.
Obr. 1.3 Základní geometrické charakteristiky postavení Země a Slunce
Země obíhá okolo Slunce po eliptické oběžné dráze a Slunce je v jednom z ohnisek této elipsy. Vzdálenost Země od Slunce je proto během roku proměnlivá, mění se zhruba o ±1,7 %. Střední roční hodnota hustoty zářivého toku sluneční energie, dopadající na jednotku plochy kolmou ke směru šíření záření na vnější povrch zemské atmosféry při střední vzdálenosti Slunce od Země, se nazývá sluneční konstanta. Její hodnota naposledy přijatá v roce 1981 Světovou meteorologickou organizací (WMO) je Gsc = 1 367 W/m2 s nepřesností v řádu 1 %.
Obr. 1.4 Změna toku slunečního záření dopadajícího na vnější povrch atmosféry během roku
Vzhledem k proměnlivé vzdálenosti Země – Slunce se hodnota hustoty zářivého toku sluneční energie vně atmosféry během roku také mění, a to o ±3 %. Proměnlivost hustoty slunečního zářivého toku během roku se řídí vztahem
(1.4)
kde je
n … pořadí dne v roce.
Graficky je tato závislost znázorněna na obr. 1.4.
Poznámka:
V zimě je Slunce k Zemi blíž než v létě a vnější povrch atmosféry přijímá více slunečního záření než v zimě. Nicméně, nízká úroveň slunečního záření v zimním období (v Evropě) je způsobena odklonem Země vlivem precesního pohybu (viz deklinace) a tedy nižším úhlem dopadu slunečních paprsků, které překonávají větší hmotu atmosféry a více se pohltí, a dále samozřejmě zvýšenou oblačností v zimě.
1.3 PRŮCHOD SLUNEČNÍHO ZÁŘENÍ ATMOSFÉROU
1.3.1 Změna spektra
Sluneční záření dopadající na Zemi vstupuje do atmosféry ve výšce zhruba 1 000 km od zemského povrchu. Atmosféra se skládá převážně z dusíku a kyslíku. Ve výškách nad 60 km pohlcují tyto atmosférické plyny sluneční ultrafialové a rentgenové záření a ionizují se (ionosféra). Níže, ve výškách 20 až 30 km, se nachází vrstva s velkým obsahem ozónu, ozonosféra. Zde se pohlcuje zbývající část životu nebezpečného ultrafialového (UVC) záření. V nejnižších vrstvách atmosféry (v troposféře) dochází k pohlcování slunečního záření vodní párou, CO2, prachem a kapkami vody v mracích.
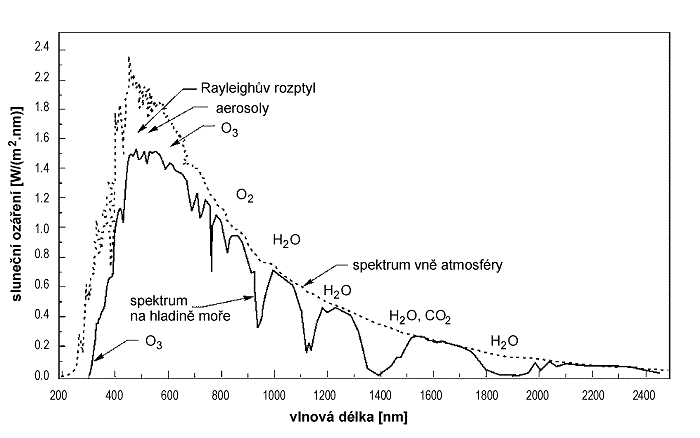
Obr. 1.5 Spektrální charakteristika zářivého toku sluneční energie procházejícího zemskou atmosférou
Na obr. 1.5 je kromě spektrální charakteristiky slunečního záření na vnějším povrchu atmosféry (AM0) znázorněna spektrální charakteristika po průchodu atmosférou kolmo na zemský povrch (AM1). Ze spektrální charakteristiky na zemském povrchu je patrné především odfiltrování UVC záření a významné pohlcení záření vodní párou v atmosféře. Na zemský povrch dopadá sluneční záření s významným energetickým obsahem v oblasti vlnových délek od 0,3 do 3,0 μm.
1.3.2 Roční bilance
V průměrné roční bilanci se z celkového toku energie slunečního záření ze Slunce zpět do vesmíru odrazí od mraků, částeček prachu a zemského povrchu zhruba 34 %. V atmosféře se pohltí okolo 19 %. Zbývající část sluneční energie je pohlcena zemským povrchem (47 %). Záření pohlcené zemským povrchem se mění v teplo, které je vyzařováno z povrchu Země jako infračervené záření (14 %). Infračervené záření je pohlcováno v atmosféře víceatomovými plyny, což vede k trvalému zvýšení teploty zemského povrchu (skleníkový efekt). Značné množství energie dopadající na rozsáhlé plochy oceánů se spotřebuje na vypařování vody (23 %). Vodní pára je proudy vzduchu vynášena nahoru, kde v chladnějších vrstvách atmosféry kondenzuje, předává své skupenské teplo okolnímu vzduchu a ve formě srážek přichází zpět na zemský povrch (vodní koloběh). Zbytek slunečního záření pohlceného zemským povrchem (10 %) je odveden konvekcí. Vzduch zahřátý od povrchu Země stoupá nahoru a na jeho místo proudí těžší chladný vzduch, čímž vznikají větry. Nepatrné množství sluneční energie dopadající na Zemi (asi 1 ‰) připadá na biologické reakce probíhající v biosféře. Energie slunečního záření je tak nepřímo podstatou i všech ostatních obnovitelných zdrojů energie (energie prostředí, vodní energie, větrná energie, energie biomasy), s výjimkou energie geotermální a slapové.
1.4 GEOMETRIE SLUNEČNÍHO ZÁŘENÍ
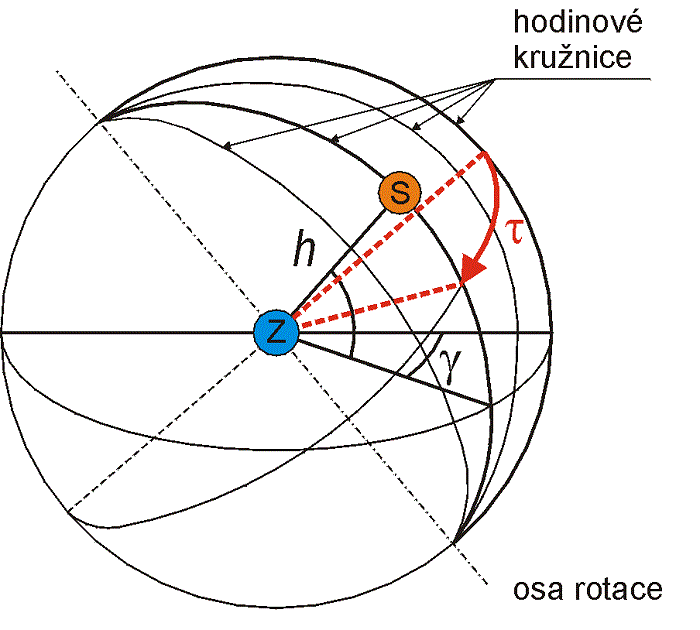
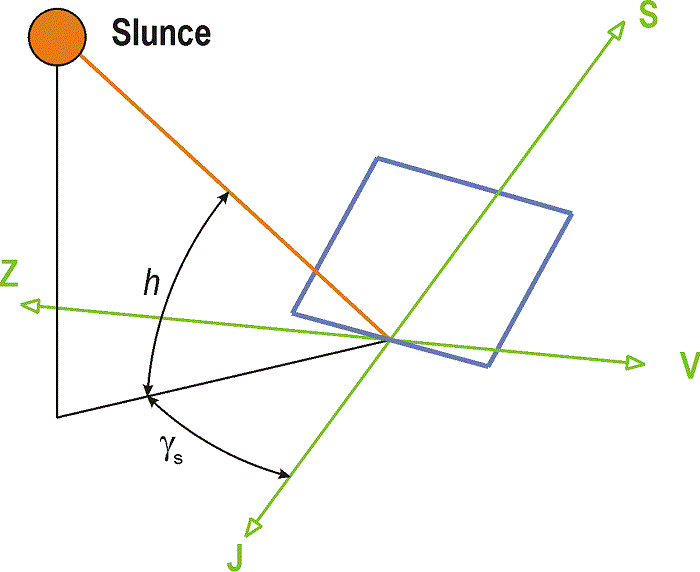
Výkon a energie slunečního záření dopadajícího na obecnou plochu je ovlivněna faktory, které lze změnit (zeměpisná šířka místa instalace, orientace plochy vůči světovým stranám – azimut plochy, sklon plochy vůči vodorovné rovině) a které nelze změnit, tj. zdánlivý pohyb Slunce vůči Zemi, který vnímáme jako čas. Ze zdánlivého pohybu Slunce po obloze vyplývá řada geometrických charakteristik, které jsou souhrnně znázorněny na obr. 1.6.
Obr. 1.6 Geometrické charakteristiky pohybu Slunce vůči jímací ploše
1.4.1 Zeměpisná šířka
Zeměpisná šířka φ daného místa je úhel, který svírá rovina rovníku s přímkou, procházející středem Země a příslušným místem na povrchu Země. Pro ČR se hodnota zeměpisné šířky pohybuje od cca 49° (jižní Čechy) do 51° severní šířky (Šluknovský výběžek). Konvence znamének je: severně od rovníku (+), jižně od rovníku (-).
1.4.2 Azimut plochy
Azimut plochy γ je úhel mezi průmětem normály plochy do vodorovné roviny a lokálním poledníkem, tj. jihem. Konvence znamének je: jih (0°), na východ záporné hodnoty, na západ kladné hodnoty.
Poznámka:
Definice se odlišuje od běžného chápání azimutu jako úhlové odchylky od severu.
Obr. 1.7 Azimut a sklon plochy
1.4.3 Sklon plochy
Úhel sklonu plochy β je úhel mezi vodorovnou rovinou a rovinou uvažované plochy. Sklon vodorovné plochy je 0°, sklon svislé plochy je 90°.
1.4.4 Deklinace
Deklinace δ je úhlem náklonu zemské osy vlivem precesního pohybu během rotace a oběhu Země kolem Slunce. Úhel náklonu se během roku mění od -23,45° při zimním slunovratu (maximální odklon od Slunce) přes 0° při jarní a podzimní rovnodennosti do +23,45° při letním slunovratu (maximální příklon ke Slunci).
Obr. 1.8 Definice deklinace
Další definice deklinace vycházejí z obr. 1.8:
- úhel, který svírá spojnice středů Země a Slunce s rovinou zemského rovníku;
- zeměpisná šířka místa, kde v daný den ve 12 h (poledne) je Slunce kolmo nad obzorem.
Deklinaci lze stanovit z různých vztahů, buď podle vztahu
(1.5)
kde je
D … pořadí dne v měsíci;
M … pořadí měsíce v roce,
nebo podle vztahu
(1.6)
kde je
n … pořadí dne v roce.
1.4.5 Sluneční čas
Každé časové pásmo má standardní čas vztažen k místnímu referenčnímu poledníku. Na zeměkouli se rozlišuje 24 časových pásem po 1 hodině, referenční poledníky jsou odstupňovány po 15° (360°/24). Standardní čas je v podstatě smluvní čas, který „souhlasí“ se zdánlivým pohybem Slunce po obloze pouze v případě, že pozorovatel stojí na referenčním poledníku. Čím dále je pozorovatel v rámci časového pásma od referenčního poledníku, tím více se čas na jeho hodinkách rozchází se zdánlivým pohybem Slunce a odchylka může teoreticky být až 30 minut (na hranici časového pásma).
Středoevropský čas je vztažen k poledníku 15° východní délky, který v ČR prochází například Jindřichovým Hradcem. Zatímco v Jindřichově Hradci bude sluneční poledne tedy přesně ve 12 hodin standardního času, v Brně (16,6° východní délky) sluneční poledne nastane již v 11:53 a v Košicích (21,2° východní délky) již v 11:35. V Praze (14,4° východní délky) sluneční poledne nastane až 2 minuty po dvanácté.
Převod standardního času na sluneční čas využívá kromě konstantní korekce přepočtem na místní poledník z referenčního (4 minuty na 1°) ještě korekci E, zohledňující proměnlivost rotace Země během oběhu okolo Slunce. Korekce E je vyjádřena vztahem
(1.7)
kde
(1.8)
kde je
n … pořadí dne v roce.
Sluneční čas ST stanoví ze vztahu
(1.9)
Časová odchylka E způsobená nerovnoměrnou rotací Země může být v určitých částech roku relativně významná, kdy dosahuje až hodnot ±15 minut. Grafické znázornění odchylky E je uvedeno na obr. 1.9.
Obr. 1.9 Průběh odchylky slunečního času od standardního vlivem nerovnoměrné rotace Země
1.4.6 Sluneční časový úhel
Sluneční časový úhel τ je úhel zdánlivého posunu Slunce z východu na západ nad místními poledníky vlivem rotace Země vztažený ke slunečnímu poledni. Z předpokladu, že Země se otočí jednou kolem své osy (360°) za 24 hodin, vyplývá, že 1 hodině odpovídá 15°.
Sluneční časový úhel se tedy stanoví ze slunečního času ST jako
(1.10)
kde platí konvence znamének: před polednem záporné hodnoty a po poledni kladné hodnoty.
Obr. 1.10 Sluneční časový úhel
Převod standardního času na sluneční čas je uveden v předchozí kapitole.
1.4.7 Výška Slunce
Výška Slunce h je úhel sevřený spojnicí plochy a Slunce s vodorovnou rovinou (viz obr. 1.11). Výška Slunce se stanoví ze vztahu
(1.11)
Doplňkový úhel výšky Slunce do 90° je zenitový úhel θz neboli úhel sevřený spojnicí pozorovatele a Slunce a svislicí (vertikálou). Zenitový úhel θz se tedy určí jako
(1.12)
Obr. 1.11 Znázornění výšky a azimutu Slunce
Z výšky Slunce nebo zenitového úhlu lze určit poměrnou vzdálenost, kterou sluneční záření v atmosféře urazí při daném úhlu vůči vzdálenosti, kterou by urazilo, kdyby Slunce bylo v zenitu (nejkratší trasa). Vzdálenost zde reprezentuje hmotu atmosféry, kterou sluneční záření musí projít. Poměr se nazývá air mass (vzduchová hmota) nebo AM a stanoví se ze vztahu
(1.13)
Pro různé hodnoty AM odpovídající hodnotám zenitového úhlu jsou standardizovány spektrální charakteristiky slunečního záření:
AM0 … mimozemské sluneční záření
AM1 … Slunce je v zenitu, zenitový úhel = 0°
AM1,5 … zenitový úhel = 48°
AM2 … zenitový úhel = 60°
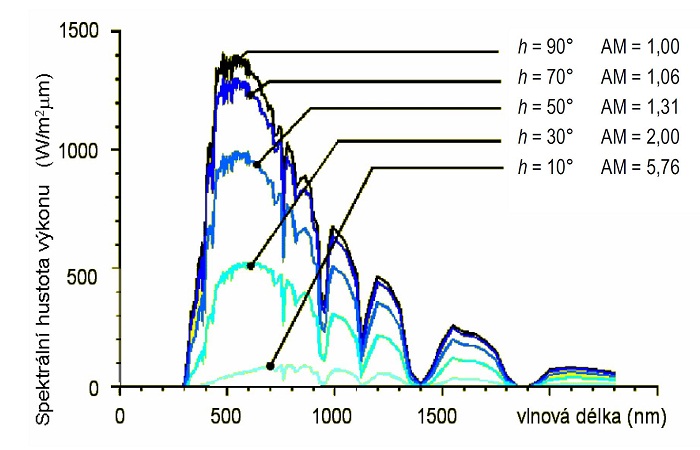
Čím vyšší hodnota AM a tedy větší hmota, kterou sluneční záření prochází, tím více absorpce se ve spektru projeví. Na obr. 1.12 je uvedeno porovnání spektrálních charakteristik slunečního záření pro různé hodnoty vzduchové hmoty.
Obr. 1.12 Spektrální charakteristika hustoty slunečního zářivého toku pro různé hodnoty AM
1.4.8 Azimut Slunce
Azimut Slunce γs je úhel mezi průmětem spojnice plochy a Slunce do vodorovné roviny a jižním směrem (viz obr. 1.11). Konvence znamének je stejná jako u azimutu plochy: na západ kladné hodnoty, na východ záporné hodnoty. Azimut Slunce se stanoví podle vztahu
(1.14)
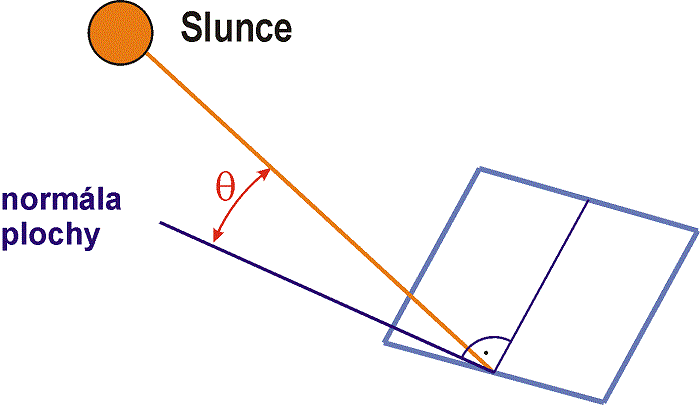
1.4.9 Úhel dopadu
Úhel dopadu slunečního záření θ na obecnou plochu je úhel mezi spojnicí plochy a Slunce a normálou plochy (viz obr. 1.13). Stanoví se podle vztahu
(1.15)
Obr. 1.13 Úhel dopadu slunečního záření na obecnou plochu
1.5 TEORETICKÝ VÝPOČET SLUNEČNÍHO ZÁŘENÍ
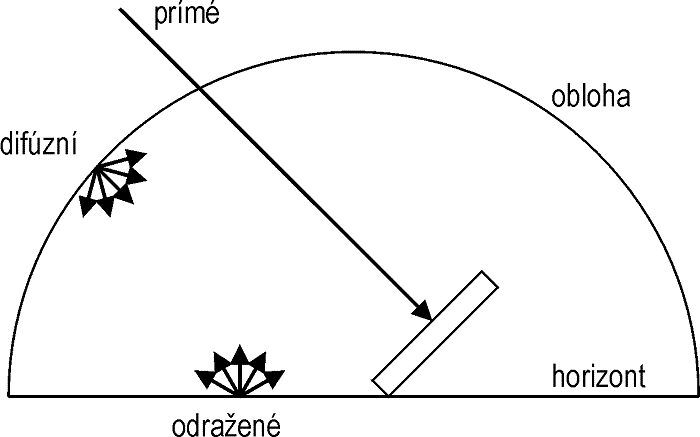
1.5.1 Přímé a difuzní záření
Na vnější povrch atmosféry dopadá sluneční záření v nerozptýlené formě a lze si ho představit jako paprsky přicházející přímo ze slunečního kotouče. Průchodem atmosférou dochází k rozptylu na molekulách plynů, částicích prachu, krystalcích ledu či kapičkách vody. Část zářivého toku pak z oblohy přichází ve formě rozptýleného, tzv. difuzního slunečního záření, které nemá směrový charakter (všesměrové – izotropické, značí se indexem „d“), a část ve formě přímého slunečního záření bez rozptylu v atmosféře s výrazně směrovým charakterem (značí se indexem „b“). Kromě přímého a difuzního záření se (v závislosti na odrazivosti okolních ploch) může uplatnit i odražené sluneční záření (r), které má zpravidla charakter difuzního slunečního záření, vzhledem k obecně převažujícím difuzně odrážejícím povrchům. I za jasného dne je podíl difuzního záření okolo 10 %.
1.5.2 Veličiny a značení
Při výpočtech je nutné rozlišovat mezi výkonovou hustotou slunečního zářivého toku, tzv. slunečním ozářením G [W/m2] a hustotou sluneční zářivé energie, tzv. dávkou slunečního ozáření H [kWh/m2]. Sluneční ozáření je zářivý výkon procházející jednotkou plochy. Dávka slunečního ozáření H je úhrnem zářivého toku za určitý časový úsek, jak je naznačeno ve vztahu
(1.16)
Poznámka:
Pro sluneční ozáření G se ve starší literatuře uvádí termín intenzita dopadajícího slunečního záření se značením I. Termín intenzita je však zpravidla vyhrazen směrové (úhlové) charakteristice hustoty zářivého toku ve W/m2.sr. Pro dávku slunečního ozáření H se ve starší literatuře uvádí termín množství dopadající sluneční energie se značením Q.
1.5.3 Součinitel znečištění
Teoreticky možné přímé sluneční ozáření na plochu kolmou ke směru paprsků (normálové) Gbn prošlé atmosférou lze stanovit z hodnoty slunečního ozáření na vnějším povrchu atmosféry podle vztahu
(1.17)
kde je
Gon … normálové sluneční ozáření na vnějším povrchu atmosféry, ve W/m2
Z … součinitel znečištění atmosféry (bezrozměrný), závislý na dané oblasti (hory, venkov, město, průmyslová oblast)
ε … činitel závislý na výšce Slunce a nadmořské výšce (bezrozměrný)
Součinitel znečištění atmosféry Z udává, kolikrát by atmosféra musela být hmotnější, aby měla stejnou propustnost pro sluneční záření, jako má uvažovaná znečištěná atmosféra v dané oblasti. Je tedy parametrem definujícím snížení toku slunečního záření průchodem atmosférou. Součinitel znečištění lze stanovit z dlouhodobých měření jako
(1.18)
kde je
Gb0 … přímé sluneční ozáření při průchodu zcela čistým vzduchem (Z = 1), ve W/m2.
(1.19)
kde je
h … výška Slunce
Lv … nadmořská výška daného místa, v m
Tab. 1 Hodnoty součinitele znečištění Z pro různé typy oblastí během roku
| Měsíc | Průměrné měsíční hodnoty součinitele Z pro oblasti s rozdílnou čistotou ovzduší | |||
| horské oblasti | venkov | města | průmyslové oblasti | |
| I. | 1,5 | 2,1 | 3,1 | 4,1 |
| II. | 1,6 | 2,2 | 3,2 | 4,3 |
| III. | 1,8 | 2,5 | 3,5 | 4,7 |
| IV. | 1,9 | 2,9 | 4,0 | 5,3 |
| V. | 2,0 | 3,2 | 4,2 | 5,5 |
| VI. | 2,3 | 3,4 | 4,3 | 5,7 |
| VII. | 2,3 | 3,5 | 4,4 | 5,8 |
| VIII. | 2,3 | 3,3 | 4,3 | 5,7 |
| IX. | 2,1 | 2,9 | 4,0 | 5,3 |
| X. | 1,8 | 2,6 | 3,6 | 4,9 |
| XI. | 1,6 | 2,3 | 3,3 | 4,5 |
| XII. | 1,5 | 2,2 | 3,1 | 4,2 |
| roční průměr | 1,9 | 2,75 | 3,75 | 5,0 |
Součinitel znečištění Z je tabelován v tab. 1. Jeho hodnoty se pohybují běžně od 2 do 6 (i více). Zjednodušeně lze aplikovat charakteristické hodnoty součinitele znečištění následovně:
- horské oblasti … Z = 2;
- venkov … Z = 3;
- města … Z = 4;
- průmyslové oblasti … Z = 5 a více.
1.5.4 Sluneční ozáření na obecnou plochu
Při teoretickém výpočtu celkového slunečního ozáření na obecně orientovanou a skloněnou plochu se stanoví odděleně přímé sluneční ozáření, difuzní sluneční ozáření z oblohy a odražené sluneční ozáření od terénu podle
(1.20)
Obr. 1.14 Znázornění složek slunečního záření
Přímé sluneční ozáření na uvažovanou plochu GbT [W/m2] je dáno přímým normálovým ozářením a úhlem dopadu θ paprsků podle vztahu
(1.21)
kde je
θ … úhel dopadu slunečního záření, stanovený z geometrie slunečního záření.
Difuzní sluneční ozáření z oblohy na uvažovanou plochu GdT [W/m2] se stanoví jako rozptýlené všesměrové (izotropické) záření přicházející z prostorové výseče oblohy, kterou plocha „vidí“ podle vztahu
(1.22)
kde je
Gd … difuzní sluneční ozáření vodorovné roviny, ve W/m2;
β … sklon kolektoru.
Sluneční ozáření odražené na uvažovanou plochu od vodorovné roviny (terénu) se stanoví ze vztahu
(1.23)
kde je
Gd … difuzní sluneční ozáření vodorovné roviny dopadající z oblohy (hemisféry), ve W/m2
Gb … přímé sluneční ozáření vodorovné roviny, ve W/m2
ρg … odrazivost vodorovné roviny (albedo), zpravidla se uvažuje ρgg = 0,2
β … sklon kolektoru
Odrazivost terénu (albedo) je poměr mezi odraženou a dopadlou hustotou slunečního zářivého toku. Hodnoty albeda se pro běžnou vegetaci pohybují mezi 0,15 a 0,25, nicméně v případě čerstvého sněhu může hodnota dosahovat až 0,90. Naproti tomu tmavé povrchy vykazují odrazivost nízkou pod 0,10.
Přímé sluneční ozáření na vodorovnou rovinu se stanoví z geometrie jako
(1.24)
Difuzní sluneční ozáření na vodorovnou rovinu se stanoví ze zjednodušeného předpokladu, že třetina slunečního záření ztraceného v atmosféře dopadá na vodorovnou rovinu (sinh) jako difuzní sluneční ozáření
(1.25)
1.5.5 Teoretická denní dávka slunečního ozáření
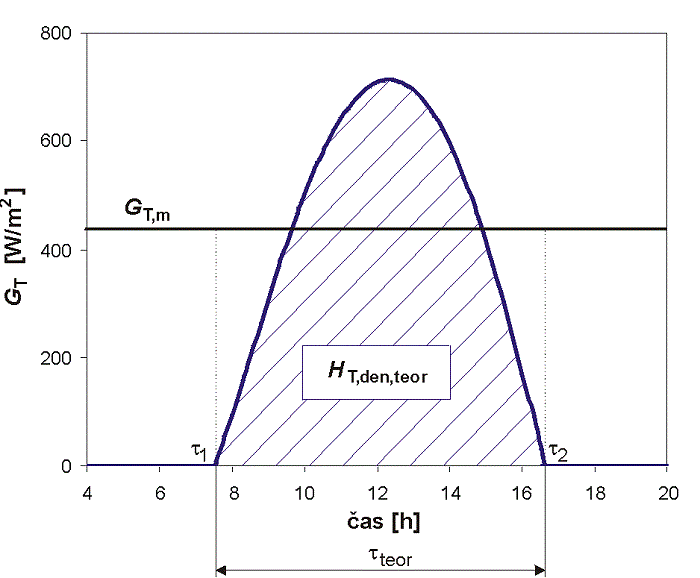
Teoreticky možná denní dávka celkového slunečního ozáření (množství dopadající energie) HT,den,teor [MJ/(m2·den), kWh/(m2·den)] se stanoví integrací teoreticky stanoveného celkového slunečního ozáření GT na uvažovanou plochu od východu τ1 do západu Slunce τ2, tedy za dobu teoretické doby slunečního svitu τteor podle
(1.26)
Obr. 1.15 Teoretický průběh celkového slunečního ozáření
Teoretická denní dávka celkového slunečního ozáření HT,den,teor dopadá na osluněnou plochu jen v jasných slunečných dnech. Tabelované hodnoty teoretické dávky slunečního ozáření v jednotlivých měsících jsou uvedeny pro oblasti s různým součinitelem znečištění v příloze A (kapitola 10). Pro tvorbu tabulkových hodnot se zpravidla stanoví hodnota pro referenční 21. den v měsíci a všechny ostatní dny v měsíci se uvažují jako identické.
Během reálného dne se však střídá jasná obloha s oblohou zataženou mraky, kdy dopadá pouze difuzní záření. Teoretická denní dávka difuzního ozáření se stanoví podobně jako teoretická celková integrací.
(1.27)
Tabelované hodnoty denní dávky difuzního slunečního ozáření v jednotlivých měsících jsou uvedeny pro oblasti s různým stupněm znečištění v příloze B (kapitola 10).
Z teoretické dávky slunečního ozáření HT,den,teor je možné vypočítat střední denní hodnotu slunečního ozáření GT,m [W/m2] dané plochy vydělením teoretickou dobou slunečního svitu τteor podle rovnice
(1.28)
Střední denní hodnoty slunečního ozáření GT,m jsou uvedeny v příloze C (kapitola 10). Střední hodnota slunečního ozáření GT,m je důležitou veličinou ve výpočtech střední denní účinnosti solárních kolektorů při navrhování jejich plochy a bilancování zisků solární soustavy.
1.5.6 Doba slunečního svitu
Východ a západ Slunce nastává při nulové výšce Slunce (h = 0). Z dosazení této podmínky do rovnice (1.11)
(1.29)
vyplývá matematické vyjádření časového úhlu východu (nebo západu) Slunce τ1,2
(1.30)
Dobu mezi východem a západem Slunce, tzv. teoretickou dobu slunečního svitu τteor, lze potom určit jako
(1.31)
pro kterýkoli den v roce.
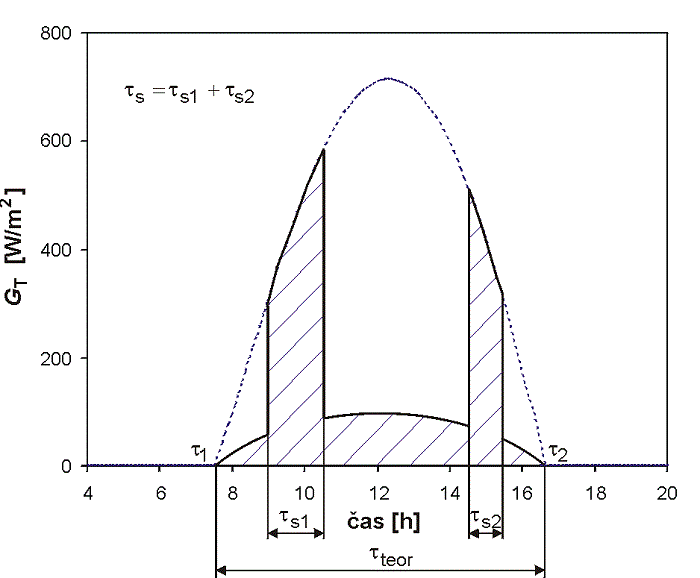
Obr. 1.16 Teoretická a skutečná doba slunečního svitu
Pro praktické výpočty dávky slunečního ozáření v reálných dnech s běžnou oblačností je nutné znát skutečnou dobu slunečního svitu τskut. Ta je definována jako doba, kdy je k dispozici přímé sluneční ozáření (je vidět sluneční kotouč) a jeho hodnota je větší než 120 W/m2 (viz obr. 1.16). V ČR ji měřením zjišťuje ČHMÚ a hodnoty pro jednotlivé měsíce ve vybraných lokalitách bývají zpřístupněny veřejnosti. Příklad měsíčních hodnot je uveden v tab. 2 pro různá města. Ze skutečné doby slunečního svitu lze potom vyjádřit tzv. poměrnou dobu slunečního svitu jako
(1.32)
Hodnoty poměrné doby slunečního svitu pro některá místa ČR a SR jsou uvedeny v příloze D (kapitola 10).
Tab. 2 Orientační hodnoty skutečné doby slunečního svitu pro vybraná města
| Měsíc | Praha | České Budějovice | Hradec Králové | Brno |
| I. | 53 | 46 | 47 | 46 |
| II. | 90 | 82 | 77 | 88 |
| III. | 157 | 136 | 149 | 142 |
| IV. | 187 | 164 | 185 | 163 |
| V. | 247 | 207 | 241 | 232 |
| VI. | 266 | 226 | 249 | 258 |
| VII. | 266 | 238 | 252 | 270 |
| VIII. | 238 | 219 | 233 | 230 |
| IX. | 190 | 174 | 188 | 179 |
| X. | 117 | 108 | 115 | 116 |
| XI. | 53 | 55 | 48 | 56 |
| XII. | 35 | 36 | 42 | 30 |
| roční suma | 1 899 | 1 691 | 1 826 | 1 810 |
1.5.7 Skutečná denní dávka slunečního ozáření
Skutečná denní dávka slunečního ozáření HT,den [kWh/(m2·den)] na obecnou plochu se stanoví ze vztahu
(1.33)
kde je
τr … poměrná doba slunečního svitu, viz příloha D (kapitola 10)
HT,den, teor … teoretická celková denní dávka slunečního ozáření, hodnoty pro různé sklony a orientace jsou uvedeny pro jednotlivé měsíce v příloze A (kapitola 10)
HT,den,dif … teoretická difuzní denní dávka slunečního ozáření, hodnoty pro různé sklony jsou uvedeny pro jednotlivé měsíce v příloze B (kapitola 10)
1.6 MĚŘENÍ VELIČIN SLUNEČNÍHO ZÁŘENÍ
Pro měření slunečního ozáření se používají dva základní typy přístrojů. Pyrheliometr (někdy nazýván aktinometr) je přístroj využívající kolimované čidlo pro měření slunečního ozáření přicházejícího přímo ze Slunce a malé části oblohy okolo (přímé sluneční ozáření) při kolmém úhlu dopadu. Pyranometer (někdy nazýván solarimetr) je přístroj pro měření celkového hemisférického ozáření (přímého a difuzního dohromady), obvykle na vodorovnou rovinu. Pokud je pyranometer stíněn od vlivu přímého záření, je možné s ním měřit difuzní složku slunečního ozáření.
1.6.1 Měření přímého slunečního ozáření – pyrheliometr
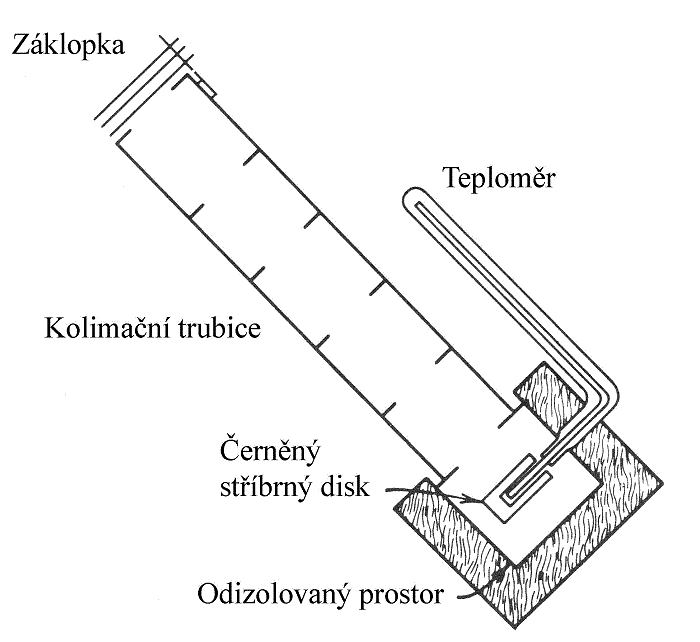
Pyrheliometry jsou normálovými přístroji (etalony) pro měření slunečního ozáření, podle kterých se kalibrují ostatní přístroje. Jako etalony druhého stupně se využívají dva základní typy, Abbotův pyrheliometr se stříbrným diskem a Angstromův kompenzační pyrheliometr. Princip pyrheliometru je možné vysvětlit na původním Abbotově pyrheliometru se stříbrným diskem (1905). U Abbotova pyrheliometru slouží stříbrný disk (průměr 38 mm, tloušťka 7 mm) jako absorbér slunečního záření. Strana disku vystavená slunečnímu záření je načerněna, pata přesného rtuťového teploměru je vložena v otvoru na straně disku v dobrém kontaktu s diskem. Stříbrný disk je pružně uložen na drátkách na konci kolimační trubice se zorným úhlem 5,7° (čidlo – disk – vidí 0,13 % hemisféry). Disk je instalován v měděném válci, vloženém v dřevěném válcovém pouzdru s izolací (viz obr. 1.17). Záklopka (clona) střídavě vpouští a stíní záření v pravidelných intervalech, z odpovídajících změn měřené teploty disku se stanoví množství pohlceného záření.V Angstromově kompenzačním pyrheliometru jsou uspořádány dva černěné manganinové pásky tak, že jeden je může být vystaven slunečnímu záření na patě kolimační trubice odklopením clony. Oba pásky mají možnost elektrického ohřevu a jsou vybaveny termočlánkem. Při měření je jeden pásek stíněn, druhý vystaven záření a elektrický proud prochází stíněným páskem pro dosažení stejné teploty jako u exponovaného pásku. Při nulovém teplotním rozdílu se množství elektrické energie dodané do stíněného pásku rovná sluneční energii pohlcené exponovaným páskem, která je dána plochou a pohltivostí pásku. Pro měření se využívá střídání obou trubic (exponovaná se zastíní, stíněná je vystavena záření). Tím se kompenzují rozdíly způsobené okrajovými vlivy a nerovnoměrností elektrického vyhřívání pásků.
Obr. 1.17 Abbotův pyrheliometr se stříbrným diskem
Jako sekundární etalony pro kalibraci přístrojů pro měření v terénu a v provozu se v současné době využívají dva typy pyrheliometrů: Eppley Normal Incidence Pyrheliometr (USA) a Kipp&Zonen aktinometr (Evropa). Eppley NIP má na konci kolimační trubice načerněné čidlo, které se skládá z několika membrán – sériových termočlánků. Tak je zajištěna teplotní kompenzace a snížena citlivost vůči změnám okolní teploty. Zorný úhel přístroje je 5,7°. Kipp&Zonen aktinometr je založen na Linke-Feussnerově konstrukci a využívá 40 násobný termočlánek konstantan-manganin s „teplými“ spoji ohřívanými slunečním zářením a studeným spoji v dobrém kontaktu s pouzdrem (viz obr. 1.18 a obr. 1.19). Tepelná setrvačnost pouzdra je o řád vyšší než „teplých“ termočlánků a při vystavení slunečnímu záření se na „teplých“ termočláncích prudce zvýší teplota nad hodnotu studených. Dosažený rozdíl teplot je měřítkem slunečního ozáření.
Obr. 1.18 Moderní typ pyrheliometru CHP1 (2008)
Obr. 1.19 Moderní typ pyrheliometru CHP1 (2008)
1.6.2 Měření celkového slunečního ozáření – pyranometr
Pyranometry jsou přístroje pro měření celkového slunečního ozáření (přímé a difuzní) především na vodorovnou rovinu a jsou nejčastěji používanými přístroji pro měření slunečního ozáření. Čidla těchto přístrojů musí mít odezvu nezávislou na vlnové délce v celém solárním spektru od 0,3 do 3 μm a na úhlu dopadu slunečního záření. Čidla jsou často kryta jedním nebo dvěma polokulovými kryty pro zabránění vlivu dlouhovlnného záření a ochlazování čidla účinky větru, případně vedením do okolního prostředí. Dvojitý kryt zabezpečuje vysokou těsnost přístroje vůči atmosférickým vlivům. Kryty musí mít rovnoměrnou tloušťku, aby nezpůsobovaly nerovnoměrnou distribuci slunečního ozáření na čidlo.
Segmentový pyranometr má čidlo složené ze 6 nebo 12 tenkých měděných radiálních segmentů (viz obr. 1.20), střídavě černých a bílých. V každém segmentu je několik termočlánků (chromel-konstantan), dohromady zpravidla několik desítek termočlánkových spojů. Černé segmenty čidla jsou opatřeny vysoce pohltivou černí, bílé segmenty nátěrem, který vykazuje téměř dokonalý odraz slunečního záření. Při vystavení slunečnímu záření dochází k teplotnímu rozdílu mezi černými a bílými segmenty. Teplotní rozdíl je přímo úměrný slunečnímu ozáření a není závislý na teplotě okolí. Segmentové pyranometry se používají především v USA.

Obr. 1.20 Segmentový pyranometr (Eppley)
Obr. 1.21 Terčíkový pyranometr (Kipp&Zonen)
Obr. 1.22 Terčíkový pyranometr (Kipp&Zonen)
V Evropě jsou běžnější terčíkové pyranometry, využívající tzv. Mollův termočlánek pro měření teplotního rozdílu mezi černým povrchem čidla a hmotným tělem přístroje (viz obr. 1.21 a obr. 1.22). Termočlánková sestava je kryta jednoduchou nebo dvojitou skleněnou kupolí, sloužící k ochraně proti atmosférickým vlivům.
Při měření pyranometry při jiných sklonech než vodorovných je nutné si uvědomit, že nakloněním pyranometru se mění podmínky volného proudění uvnitř skleněné kupole s čidlem a přenos tepla z termočlánku na kryt a jiné části zařízení. Je nutné proto uvažovat korekci na sklon pyranometru (zpravidla 1–2 %). Pyranometry jsou obvykle kalibrovány etalonovými pyrheliometry, nebo sekundárními etalonovými pyranometry.

Obr. 1.23 Polovodičový snímač slunečního ozáření
Obr. 1.24 Polovodičový snímač slunečního ozáření
Obr. 1.25 Polovodičový snímač slunečního ozáření
Existují i další druhy čidel slunečního ozáření, např. s bimetalovými elementy ohřívanými slunečním zářením s přenosem mechanického pohybu na zapisovač, nebo pyranometry založené na polovodičových (fotovoltaických) čidlech (viz obr. 1.23–25). Oba druhy však mají řádově nižší přesnost měření. U fotovoltaických snímačů je hlavní nevýhodou jejich spektrálně omezená citlivost na dopadající sluneční záření (viz obr. 1.26), která neumožňuje je použít pro měření s dostatečnou spolehlivostí.
Obr. 1.26 Spektrální odezva základních typů čidel slunečního záření pro různé vlnové délky
1.6.3 Měření difuzního slunečního ozáření
Měření difuzního slunečního ozáření se provádí pyranometry se stíněním čidla přístroje před přímou složkou záření. Obvykle se používá stínicí prstenec z černě eloxovaného hliníku o průměru cca 60 cm a šířce 7,5 cm (viz obr. 1.27 až obr. 1.29). Prstenec umožňuje kontinuální měření difuzní složky během dne bez neustálého přestavování. Přestavuje se pouze při změně deklinace (jednou za několik dní). Používá se při synchronizovaném měření s druhým nestíněným pyranometrem, z rozdílu naměřených hodnot se potom stanovuje velikost přímé složky slunečního záření.

Obr. 1.27 Měření difuzního záření (stínicí prstenec)

Obr. 1.28 Měření difuzního záření (stínicí prstenec)
Obr. 1.29 Měření difuzního záření (stínicí disk)
1.6.4 Měření doby trvání slunečního svitu
Důležitou veličinou v dlouhodobém sledování solárních dat je doba trvání slunečního svitu, po kterou je sluneční kotouč viditelný (doba přímého slunečního ozáření). Jak již bylo uvedeno v předchozích kapitolách, jde o dobu, kdy je tok přímého slunečního záření dopadajícího na plochu kolmou ke směru šíření větší nebo roven 120 W/m2. Doba trvání slunečního svitu se vyjadřuje v hodinách a desetinách hodiny a patří k základním klimatickým prvkům. Závisí nejen na astronomické délce dne, ale také na výskytu oblačnosti nebo mlh, případně na překážkách v okolí místa pozorování. Doba trvání slunečního svitu nepopisuje energii slunečního záření, ale umožňuje charakterizovat sluneční záření nepřímo.

Obr. 1.30 Campbell-Stokesův slunoměr
Obr. 1.31 Záznamy slunoměru (heliogramy)
Pro stanovení doby slunečního svitu se používají různé typy přístrojů. Campbell-Stokesův slunoměr (heliograf, viz obr. 1.30) je velmi starým přístrojem (již více než 100letá tradice). Používá skleněnou pevnou kouli o průměru cca 10 cm jako čočku, která vytváří obraz slunečního kotouče na protilehlém povrchu koule soustředěnými slunečními paprsky. Registrační pásek z tenkého ztuženého papíru je instalován na příslušnou část koule a solární obraz vypálí stopu na papír, kdykoliv je přímá složka záření vyšší než kritická hodnota. Stopa je vypalována po délce pásku během dne tak, jak se pohybuje ohnisko čočky s pohybem Slunce po obloze. Délka vypálené stopy na záznamu slunoměru (heliogramu) udává dobu trvání slunečního svitu. Heliogramy se vyčíslují s přesností na desetinu hodiny. Na obr. 1.31 jsou zobrazeny záznamy slunoměru. Horní vzorek záznamu bez jakékoli vypálené stopy byl v zapisovači během zcela zataženého dne. Další vzorek byl použit během převážně zataženého dne, kdy sluneční paprsky pouze občas (řádově minuty) dopadly na kouli zapisovače. Třetí byl pořízen během dne s rozptýlenými mraky a poslední dolní pro zcela jasný den s nepřerušenou dobou slunečního svitu. Přístroj samozřejmě není výrazně přesný z důvodu nízké odezvy na nízké hladiny ozáření v ranních a pozdních večerních hodinách a vzhledem k možné závislosti délky stopy na místní vlhkosti.
Mezi elektronické typy slunoměrů patří v ČR používaný slunoměr na bázi bimetalických senzorů mechanicky spínajících el. obvod. Senzory jsou tvořeny 6 bimetalickými pásky, zahřívanými a deformovanými přímým slunečním zářením. Používané jsou také štěrbinové slunoměry, u kterých proniká přímé záření štěrbinou (štěrbinami) a postupně ozařuje fotodiody přímým zářením.
1.6.5 Měření odraženého slunečního záření – albedometr
Albedometr se využívá pro měření odrazivosti obecného povrchu (albedo), nejčastěji zemského terénu. Skládá se ze dvou pyranometrů, z nichž jeden přijímá celkové sluneční ozáření dopadající na daný povrch a druhý je natočen čelem vůči povrchu a přijímá pouze z něj odražené záření. Údaje z obou pyranometrů jsou zaznamenávány a albedo se určí jako poměr ozáření odraženého a dopadajícího. Jelikož obě čidla měří pouze sluneční ozáření (0,3–3,0 μm), nejsou ovlivněna dlouhovlnným pozemským zářením (tepelné osálání).

Obr. 1.32 Albedometr segmentový

Obr. 1.33 Albedometr terčíkový
1.7 SLUNEČNÍ ENERGIE V ČR
1.7.1 Roční úhrny
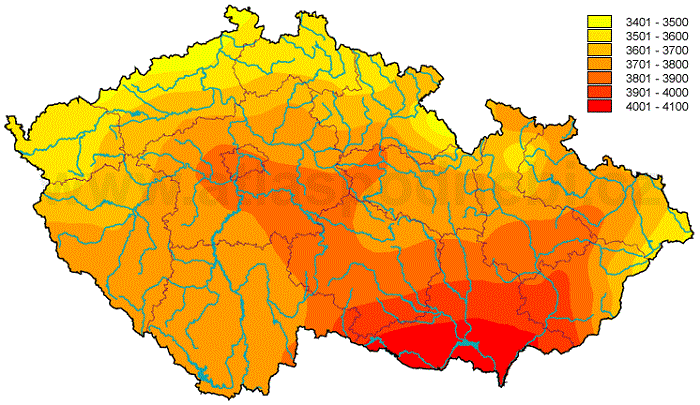
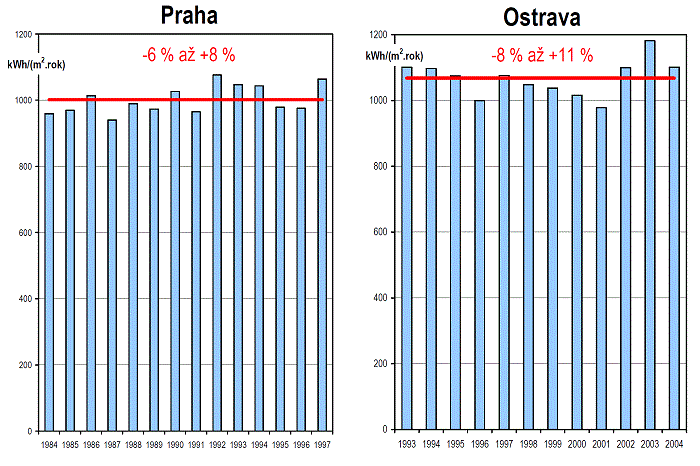
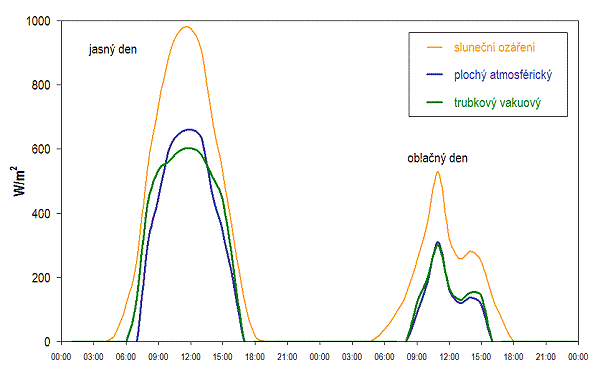
Roční úhrny sluneční energie dopadající na vodorovnou rovinu v ČR se podle různých zdrojů údajů (měření, teoretický výpočet) pohybují mezi 1 000 až 1 200 kWh/(m2·rok), obdobné hodnoty lze uvažovat i pro optimálně orientované a skloněné plochy. Sluneční energie dopadající na fasády (90°) dosahuje zhruba 70 % hodnoty při optimálním sklonu. Na obr. 1.34 je znázorněna mapa dávek slunečního ozáření pro celou ČR, ze které jsou patrné rozdíly mezi jižní částí Moravy a severní částí Čech. Nicméně rozdíly jsou zhruba ±10 % od průměrné hodnoty pro celé území. Podobné hodnoty slunečního ozáření se vyskytují na většině území sousedního Německa (s výjimkou jeho jižní části). Naproti tomu v sousedním Rakousku odpovídají nejnižší dávky slunečního ozáření našim nejvyšším. Nejvyšší roční úhrny slunečního ozáření v Rakousku dosahují hodnot 1 800 až 2 000 kWh/m2. Z toho důvodu je vhodné v oblasti využití sluneční energie přebírat zkušenosti spíše z Německa, kde se díky obdobným podmínkám instalují stejné druhy solárních soustav se stejnými druhy kolektorů a stejnými ročními přínosy. V Rakousku se prakticky neinstalují trubkové vakuové kolektory – tvoří zhruba 1 % trhu oproti ČR a Německu, kde trubkové kolektory zaujímají 15 až 20 % trhu. Přínosy solárních soustav v Rakousku jsou s ohledem na množství dopadající sluneční energie adekvátně vyšší než v ČR a Německu.
Obr. 1.34 Roční dávky slunečního záření na vodorovnou plochu v ČR v MJ/(m2·rok), zdroj: ČHMU
Na obr. 1.35 jsou porovnány naměřené roční dávky slunečního ozáření pro různé reálné roky ve dvou městech (Praha, Ostrava). Z porovnání je patrné, že meziročně se dopadající sluneční energie nemění více než o ±10 %. Díky tomuto malému kolísání je možné zaručit každoročně stálé přínosy solární soustavy, bez obav z možné proměnlivosti počasí.
Obr. 1.35 Porovnání naměření dávek slunečního ozáření v různých letech
Poměr mezi sluneční energií dopadající jako přímé a difuzní sluneční záření je v podmínkách ČR zhruba 50 : 50 %. Z toho důvodu se v ČR příliš neprosazují koncentrační (soustřeďující) solární kolektory, které využívají pouze přímou složku slunečního záření. Skutečná doba trvání slunečního svitu se pohybuje mezi hodnotami 1 400 až 1 900 hodin (viz obr. 1.36).
Obr. 1.36 Roční doba slunečního svitu v ČR v hodinách, zdroj: ČHMU
1.7.2 Optimální orientace a sklon plochy
Dopadlá sluneční energie na plochu za určitý časový úsek je závislá na orientaci a sklonu plochy. Optimální orientace plochy kolektorů je z hlediska roční dopadající sluneční energie jižní. Při odchylce azimutu plochy od jižního směru do 45° (jihovýchod, jihozápad) se roční úhrn dopadající energie nemění o více než 10 %, nicméně u solárních tepelných kolektorů jsou zisky příznivější při orientaci jihozápad vzhledem k vyšším odpoledním teplotám vzduchu (menší tepelné ztráty). Při orientaci na východ či západ dochází již k významnému poklesu dopadající energie o více než 20 % a tomu odpovídají i nižší zisky (viz obr. 1.37).
Obr. 1.37 Roční úhrny energie slunečního záření v závislosti na orientaci a sklonu plochy
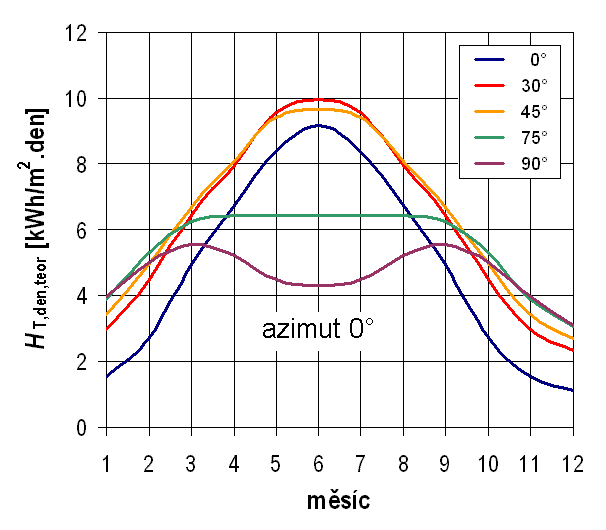
Zatímco optimální sklon kolektorové plochy s ohledem maximální výtěžnost (nejvyšší úhrn dopadlé energie za rok) je okolo 35°, při zohlednění celoroční využitelnosti sluneční energie je to 40 až 50°. Pro aplikace, u kterých se provoz přepokládá sezónní, se sklon přizpůsobuje danému období. Pro letní využití (bazény, koupaliště) je vhodné volit sklon 10 až 30°, naopak při snaze o významné pokrytí potřeby tepla pro vytápění bez letního využití energie se sklon kolektorů volí 70 až 90°. Na obr. 1.37 je znázorněna výše teoretických denních úhrnů energie slunečního záření za jasného dne během roku pro různě skloněné plochy. Pro vyšší sklony je patrný relativně vyrovnaný profil denní dopadlé sluneční energie během roku. Na druhou stranu je počet takových jasných dnů v zimě výrazně nižší než v letním období.
Obr. 1.38 Vliv sklonu plochy na teoretickou denní dávku slunečního ozáření v průběhu roku – azimut 0°
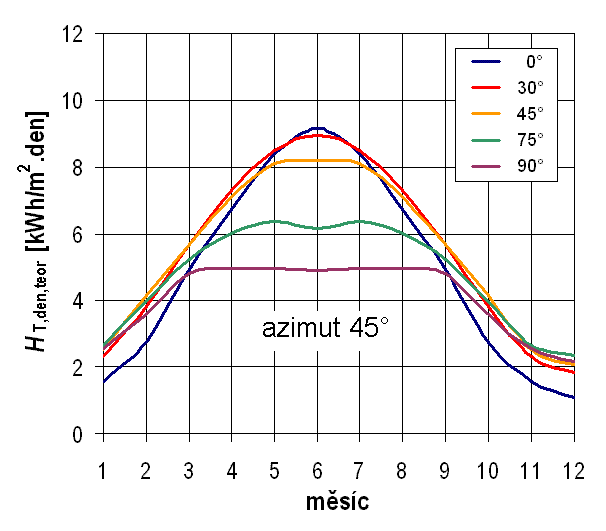
Obr. 1.39 Vliv sklonu plochy na teoretickou denní dávku slunečního ozáření v průběhu roku – azimut 45°
V tab. 3 jsou uvedeny typické hodnoty celkového slunečního ozáření pro různé stavy oblačnosti. Vysoké úrovně slunečního ozáření nejsou podmíněny ročním obdobím, ale zejména oblačností (jasno) a sklonem přijímající plochy. Proto při jasném zimním dnu lze v poledne při kolmém úhlu dopadu slunečního záření naměřit úroveň 1 000 W/m2. Naměření hodnot významně přesahujících úroveň 1 000 W/m2 zpravidla naznačuje významnou složku odraženého slunečního záření.
Tab. 3 Hodnoty celkového slunečního ozáření
| G = Gb + Gd | poměr Gd/G | |
| jasná obloha | 800–1 000 W/m2 | 10–20 % |
| lehce zataženo | 400–700 W/m2 | podle oblačnosti |
| silně zataženo | 100–300 W/m2 | 100 % |
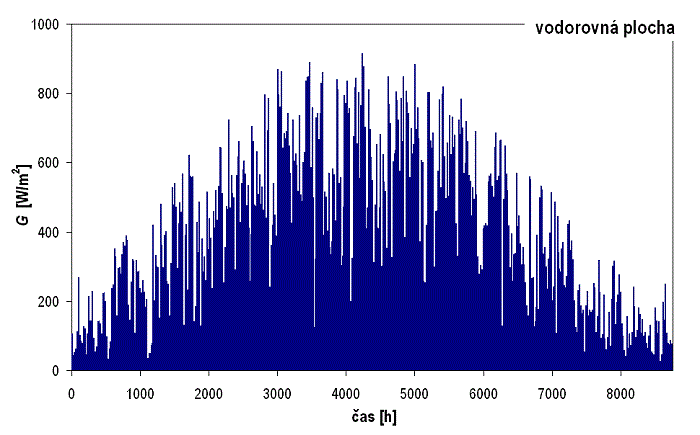
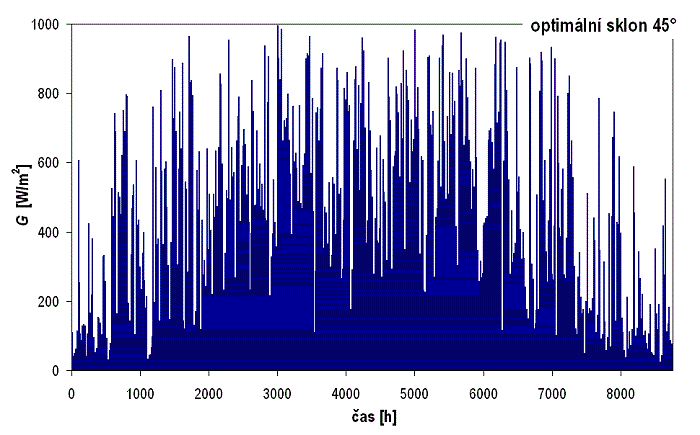
Obr. 1.40 Roční průběh slunečního ozáření na různě skloněné jižní plochy – vodorovná plocha
Obr. 1.41 Roční průběh slunečního ozáření na různě skloněné jižní plochy – optimální sklon 45°
Na obr. 1.40 a obr. 1.41 jsou znázorněny průběhy slunečního ozáření během typického meteorologického roku (Praha) na vodorovnou plochu a plochu skloněnou pod úhlem 45° (optimální sklon). Je patrné, že zvýšením sklonu plochy dochází k výhodnější poloze s ohledem na úhel dopadu slunečního záření a úrovně slunečního ozáření plochy se zvláště v zimním a přechodovém období významně zvýší.
V tab. 4 jsou uvedeny typické hodnoty denních úhrnů energie slunečního záření v různých obdobích roku při zcela jasném dni. Výrazně nižší hodnoty v zimním období jsou dány především kratší dobou slunečního svitu a zvýšenou oblačností.
Tab. 4 Sluneční energie dopadající během roku
| max. dávka ozáření v létě | 8 kWh/(m2·den) |
| max. dávka ozáření v zimě | 3 kWh/(m2·den) |
| max. dávka ozáření v přechodovém období | 5 kWh/(m2·den) |
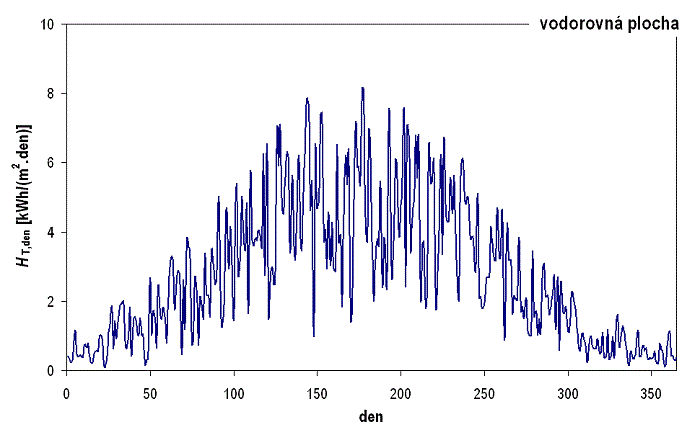
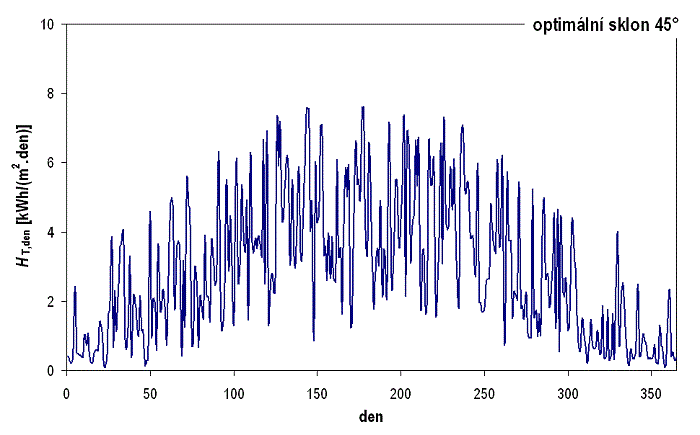
Na obr. 1.42 a obr. 1.43 jsou uvedeny průběhy denních úhrnů dopadající sluneční energie pro typický meteorologický rok (Praha) na vodorovnou plochu a plochu skloněnou pod úhlem 45° (optimální sklon). Z porovnání průběhů je opět patrný vliv zvýšení sklonu na významné zvýšení denních úhrnů v zimním a přechodovém období, zatímco v letním období jsou úhrny pro obě plochy srovnatelné.
Obr. 1.42 Roční průběh denních úhrnů slunečního ozáření na různě skloněné jižní plochy – vodorovná plocha
Obr. 1.43 Roční průběh denních úhrnů slunečního ozáření na různě skloněné jižní plochy – optimální sklon 45°
1.8 LITERATURA
[1] DUFFIE, J., A., BECKMAN, W., A., Solar enginnering of thermal processes. 3. vydání. Wiley: 2006, ISBN 13-978-0-471-69867-8.
[2] CIHELKA, J.: Solární tepelná technika, Nakladatelství T. Malina. Praha: 1994.
[3] MATUŠKA, T., Sešit projektanta č. 1 – Solární tepelné soustavy, Společnost pro techniku prostředí, 2009. ISBN 978-80-02-02186-5.
[4] MATUŠKA, T., Názvoslovný výkladový slovník z oboru Solární tepelná technika, příloha časopisu Vytápění, větrání, instalace, č. 5, STP: 2009. ISBN 978-80-02-02177-3.
[5] Meteonorm, Global Meteorological Database for Engineers, Planners and Education, dostupný z www.meteonorm.com
[6] Photovoltaic Geographical Information System (PVGIS), http://re.jrc.ec.europa.eu/pvgis
[7] Český hydrometeorologický ústav, Odbor klimatologie, Informace o klimatu.
[8] MATUŠKA, T., Experimentální metody v technice prostředí, Skriptum ČVUT v Praze. Praha: 2005.
2 SOLÁRNÍ KOLEKTORY
2.1 PRINCIP
Přeměna energie slunečního záření v tepelnou energii, fototermální přeměna, je jednou z nejjednodušších cest, jak využít sluneční záření. Fototermální přeměna spočívá v absorpci slunečního záření na povrchu tuhých látek a kapalin, kdy se energie fotonů mění v teplo (pohyb molekul). Základním prvkem kolektoru je tedy absorpční plocha, která se jímáním slunečního záření ohřívá. Tepelná energie pak může být z absorpčního povrchu odváděna různými teplonosnými látkami, nejčastěji kapalinami (voda, nemrznoucí směs), které proudí v kanálkové struktuře, spojené s absorpčním povrchem. Nejčastější podobou je trubkový registr.
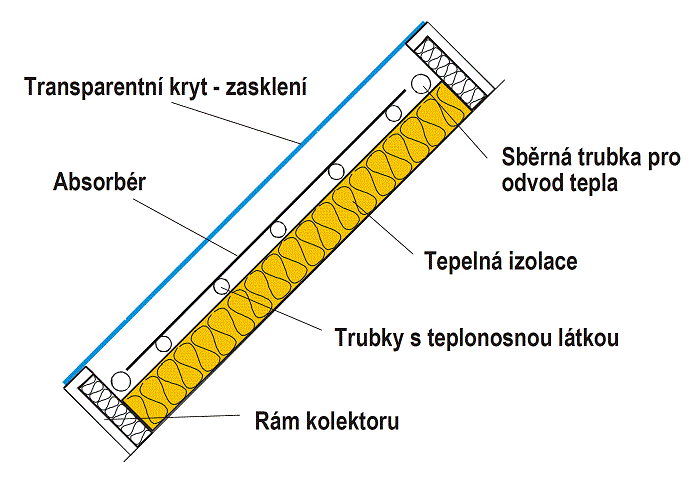
Obr. 2.1 Základní součásti solárního tepelného kolektoru (plochý)
Pro snížení tepelných ztrát z absorbéru se využívá na přední straně kolektoru zasklení, propouštějící sluneční záření. Zasklení omezuje jednak tepelné ztráty sáláním, neboť je nepropustné vůči dlouhovlnnému záření, a zároveň vytváří před absorbérem vzduchovou vrstvu, která vytváří tepelný odpor mezi absorbérem a okolním prostředím. Na zadní straně a bočních stranách absorbéru, které nepřijímají sluneční záření, se ztrátám tepla zabraňuje neprůhlednou tepelnou izolací, uchycenou v rámu (skříni) kolektoru. Následující text se věnuje zejména kapalinovým solárním kolektorům, které v aplikacích v oblasti solární tepelné techniky na trhu převažují.
2.2 KONSTRUKCE SOLÁRNÍHO KOLEKTORU
Solární tepelný kolektor je zařízení určené k pohlcení slunečního záření a jeho přeměně na tepelnou energii, která je předávána teplonosné látce, protékající kolektorem. Užívání termínu „panel“ se potlačuje, aby se předešlo nežádoucím záměnám s fotovoltaickými panely. Solární kolektor je sestaven z dílčích prvků, které mohou svými parametry významně ovlivňovat jeho výkon a energetické zisky.
2.2.1 Zasklení
Zasklení slouží především pro snížení tepelných ztrát absorbéru. Jednoduché zasklení je nezbytné pro zajištění dostatečné účinnosti přeměny slunečního záření na teplo při provozu solárních kolektorů v teplotních úrovních více než 10 K nad teplotou okolí. V případě teplotních rozdílů mezi kolektorem a okolím nad 80 K je nutné použít násobná zasklení, nebo průhledné izolační struktury.
Zasklení ale snižuje množství slunečního záření, dopadajícího na absorbér odrazem na jednotlivých fázových rozhraní (materiál zasklení-vzduch, nejčastěji sklo-vzduch) a pohlcením ve vlastním materiálu zasklení. Nutnou podmínkou efektivního využití sluneční energie je tedy dostatečná propustnost zasklení v oblasti vlnových délek slunečního záření (0,3 až 3,0 μm).
Pro omezení optických ztrát, pohlcením záření v materiálu zasklení, se využívá skel s velmi nízkým obsahem oxidu železa (nízkoželezité sklo, solární sklo), u kterých se pohlcení slunečního záření v materiálu podílí na optické ztrátě méně než 1 %. Na obr. 2.2 jsou uvedeny spektrální charakteristiky propustnosti běžného skla a solárního skla v oblasti slunečního záření.
Obr. 2.2 Spektrální charakteristika běžného a solárního nízkoželezitého jednoduchého zasklení
U nejčastějšího jednoduchého zasklení způsobují optické ztráty odrazem na obou površích (vnitřní, vnější) okolo 8 % ztráty propustnosti slunečního záření při normálovém úhlu dopadu. Optické ztráty odrazem jsou dány rozdílem mezi indexem lomu materiálu zasklení (sklo n = 1,52) a okolního prostředí (vzduch n = 1). Ztráty odrazem lze snížit aplikací vrstev materiálu s velmi nízkým indexem lomu, tzv. antireflexními povlaky. Jako antireflexní vrstvy se nejčastěji používají porézní tenkovrstvé povlaky na bázi SiO2 nebo TiO2 s definovaným indexem lomu (n < 1,3) a tloušťkou (okolo 100 nm). Antireflexní povlaky mohou zlepšit propustnost slunečního záření zasklením o cca 4 až 5 % (při normálovém úhlu dopadu), pokud jsou aplikovány na obou površích jednoduchého zasklení. Důležitým požadavkem je odolnost antireflexních povlaků proti vnějším vlivům a otěru z důvodu zachování dlouhodobé stability optických vlastností zasklení.
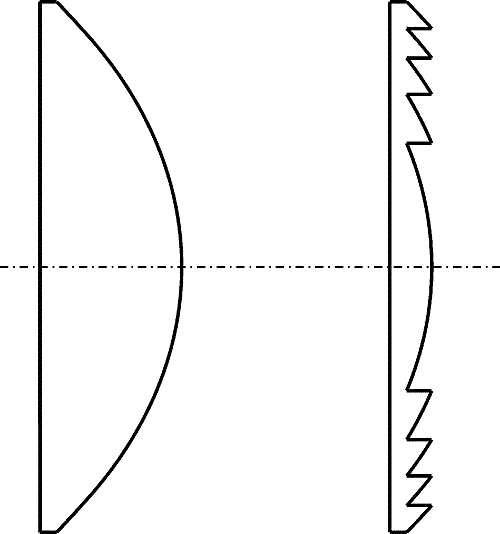
Se zvyšováním úhlu dopadu slunečních paprsků na zasklení rostou ztráty odrazem, propustnost slunečního záření zasklením mírně klesá až do úhlu cca 50° a potom se prudce snižuje až na nulovou hodnotu při úhlu dopadu 90° (viz obr. 2.3). Pro zvýšení propustnosti v oblasti vyšších úhlů dopadu se používají prizmatická zasklení, nejčastěji s pyramidovými vzory na vnitřní straně zasklení. Textura prizmatického zasklení funguje jako optický rastr, který láme sluneční paprsky přicházející pod vysokými úhly do energeticky výhodnějšího směru na absorbér. Tímto posouvají náhlý pokles křivky propustnosti zasklení do oblasti vyšších úhlů dopadu. Dopad použití prizmatického zasklení na účinnost kolektorů však není vysoký, pohybuje se okolo 1 %. Používání prizmatických zasklení má především praktické důvody, např. přes něj není dobře vidět na absorbér kolektoru pro jeho matný vzhled a tudíž nejsou patrné výrobní vady a nedostatky absorbéru.
Obr. 2.3 Závislost propustnosti slunečního záření zasklení na úhlu dopadu
2.2.2 Absorpční plocha, absorbér
Absorbér slouží k přímé přeměně slunečního záření na teplo, pohlcením na povrchu s vhodnými optickými vlastnostmi (výrazně pohltivý v oblasti vlnových délek slunečního záření). Pohlcením slunečního záření se absorbér zahřívá, zvyšuje svoji teplotu vůči okolnímu prostředí. Pro omezení tepelných ztrát ohřátého absorpčního povrchu sáláním je nutné zajistit nízkou emisivitu povrchu v oblasti infračerveného záření. Absorpční povrchy, které účinně pohlcují sluneční záření (oblast vlnových délek 0,3 až 3,0 μm, index SOL) a minimálně vyzařují tepelné záření (oblast vlnových délek > 3,0 μm, infračervené záření, index IR), se nazývají spektrálně selektivní a jsou využívány ve většině solárních tepelných kolektorů pro celoročně provozované solární soustavy.
Spektrálně selektivní absorbér vykazuje v oblasti slunečního krátkovlnného záření nízkou odrazivost (ideálně ρSOL = 0), resp. vysokou pohltivost či emisivitu (ideálně αSOL = εSOL = 1, prakticky 0,90 až 0,95) a v oblasti infračerveného dlouhovlnného záření vysokou odrazivost (ideálně ρIR = 1), resp. co nejnižší pohltivost či emisivitu (ideálně αIR = εIR = 0, , prakticky 0,05 až 0,15), viz obr. 2.4. Kvalita selektivního povrchu se odvíjí od vysoké hodnoty poměru pohltivosti v oblasti slunečního záření k emisivitě v oblasti infračerveného záření αSOL / εIR (selektivní poměr, selektivita povrchu). Běžné selektivní povrchy dosahují selektivity 10 až 20.
Selektivní povrchy se mohou vyrábět různými technologickými postupy – chemicky, elektrochemicky (galvanicky), napařováním (PVD), naprašováním, apod. Většina komerčních produktů je v současné době založena na keramicko-kovových vícevrstvých povlacích (cermet: ceramic – metal). Vlastní povlak se skládá z několika dielektrických vrstev s postupně nižším obsahem a velikostí částic kovu od podkladu směrem k vnějšímu povrchu. Poslední vrstva (pouze dielektrikum) slouží jako antireflexní povlak pro snížení odrazivosti slunečního záření a zároveň jako ochrana proti setření povrchu neopatrnou manipulací s absorbérem. Sluneční záření se pohlcuje na částicích kovu s vysokou pohltivostí rozptýlených v dielektriku, zatímco tepelné záření se odráží od podkladu (substrátu) s vysokou odrazivostí (nízkou emisivitou). Tloušťky cermetových selektivních povlaků zpravidla nepřesahují 300 nm. Povlaky jsou ohebné a někdy díky svrchní antireflexní horní vrstvě i omyvatelné. Hodnoty deklarované výrobci jsou pro pohltivost 0,95 a pro emisivitu 0,05. Menší podíl na trhu zaujímají galvanické povlaky vyráběné elektrochemicky. Tyto povlaky jsou však citlivé na manipulaci a snadno se mechanicky poškodí otěrem. Jejich pohltivost se pohybuje od 0,92 do 0,96 a emisivita od 0,08 do 0,16.
Obr. 2.4 Princip selektivního povrchu absorbéru solárního kolektoru
Absorbér může být vyroben jako celoplošný, nebo ve formě jednotlivých lamel. Pro odvod tepla z povrchu absorbéru se využívají v zásadě tři konfigurace chladičů:
- trubkový registr – sítí trubek přímo protéká teplonosná kapalina, která odvádí teplo z okolí spoje s absorbérem;
- plně průtočná struktura – teplonosná kapalina v kontaktu s celou plochou absorbéru;
- výparník tepelné trubice – vypařující se pracovní látka stoupá do kondenzační části, kde předává teplo do kapalinového okruhu.
Nejčastějším konstrukčním provedením absorbéru je tradiční typ „lamela-trubka“ (viz obr. 2.5), kdy je absorpční plocha spojena s trubkou tepelně vodivým spojem. Konstrukce se používá jak v plochých, tak trubkových solárních kolektorech. Účinnost odvodu tepla z absorbéru je dána:
- tepelným odporem mezi místem pohlcení slunečního záření (absorpční plochou) a místem odvodu tepla (spoj s trubkou). Závisí tedy na tloušťce a tepelné vodivosti absorpční plochy a vzdálenosti mezi jednotlivými místy odvodu tepla;
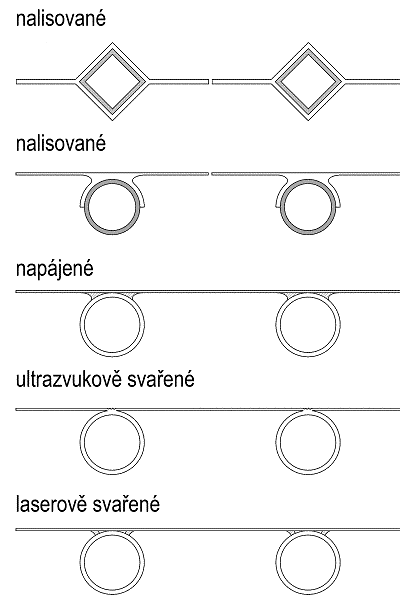
- tepelným odporem spoje – závisí na geometrii a provedení spoje. Zda jde o výlisek z jednoho materiálu, svařený spoj, spájený spoj, nalisovaný spoj, naklapnutý spoj či pouze nepevný spoj dotykem absorbéru a trubky (velmi neúčinné);
- tepelným odporem stěny trubky – zanedbatelný vzhledem k vysoké tepelné vodivosti trubky a malé tloušťce stěny trubky;
- tepelný odporem vůči přestupu tepla z vnitřního povrchu stěny trubky do pracovní látky. Teplonosné kapaliny (přímo protékaný absorbér) konvekcí nebo změnou skupenství vypařující se kapaliny (tepelná trubice).
Pro zajištění vysoké účinnosti odvodu tepla z povrchu absorbéru se využívají absorbéry z kovů s vysokou tepelnou vodivostí, u nichž je potom možné použít malé tloušťky absorbéru 0,2 (měď) až 0,3 mm (hliník) a větší rozteče trubkového registru 100 až 150 mm pro úsporu materiálu trubek. V případě použití plastových absorbérů s velmi nízkou tepelnou vodivostí je nutné použít větší tloušťku absorpčního povrchu (několik mm) a řádově menší rozteče (řádově mm, často trubky či kanály těsně vedle sebe), viz obr. 2.6.
Pro dosažení kvalitního odvodu tepla z absorpčního povrchu do teplonosné látky díky vysoké tepelné propustnosti spoje mezi absorbérem a trubkovým registrem se používají lisované nebo svařované spoje. Stále v menší míře se vyskytují technologicky náročné a pracné pájené spoje. Lisování a laserové svařování umožňuje navíc i spojování dvou nejpoužívanějších nesourodých materiálů – hliníkového absorbéru a měděné trubky registru.
Obr. 2.5 Konstrukční řešení kovových absorbérů
Obr. 2.6 Konstrukční řešení plastových absorbérů
2.2.3 Trubkový registr
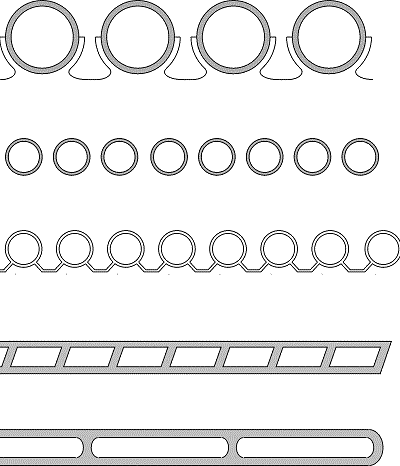
Trubkový registr solárního kolektoru je více či méně složitá síť potrubí ve tvaru meandru, lyry nebo U smyček a jejich sériově nebo paralelně zapojených kombinací (viz obr. 2.7). Hydraulika trubkového registru se řídí použitými průměry rozvodných a sběrných trubek a spojovacích trubek odvádějících teplo z absorpční plochy kolektoru a jejich hydraulickým zapojením. Pokud jsou tlakové ztráty třením ve spojovacích trubkách výrazně vyšší než místní tlakové ztráty odbočením a spojením spojovacích trubek s rozvodnou a sběrnou trubkou a než vlastní ztráty třením v rozvodné a sběrné trubce, potom je možné předpokládat, že trubkový registr kolektoru je hydraulicky vyvážen a průtok teplonosné kapaliny, rovnoměrně rozdělený do spojovacích trubek, zajišťuje rovnoměrný odvod tepla z absorbéru. V případě hydraulicky nevyváženého kolektoru však může docházet ke špatnému zatékání do některých spojovacích trubek. Vlivem podprůtoku se taková oblast přehřívá, snižuje se odvod tepla z povrchu absorbéru a klesá účinnost využití sluneční energie v kolektoru.
U solárního kolektoru s rostoucím průtokem teplonosné kapaliny roste na jedné straně přestup tepla do kapaliny, a tedy i částečně účinnost solárního kolektoru (platí pouze omezeně), na druhé straně však roste významně jeho tlaková ztráta. Hydraulika solárních kolektorů a návrh konstrukce absorbéru pro maloplošné a velkoplošné solární kolektory proto vždy vyžadují určitou optimalizaci těchto dvou protichůdných požadavků.
Vlastní hydrauliku trubkového registru jednotlivých kolektorů je nutné zohlednit i při vzájemném spojování solárních kolektorů do větších polí. Rozvodná a sběrná trubka, procházející kolektorem, umožňuje spolehlivé zatékání kapaliny do lamel pouze do určité hodnoty průtoku. Spojováním kolektorů paralelně, tedy vedle sebe, se zvyšuje návrhový průtok kapaliny rozvodnou a sběrnou trubkou, zatímco průtok jednotlivými spojovacími trubkami by měl zůstávat stejný. S rostoucím průtokem roste výrazně rychlost a tedy tlakové ztráty třením a místními odpory v rozvodné a sběrné trubce. Okrajové části (krajní kolektory v poli) mohou potom vykazovat výrazné podprůtoky, případně opačný směr proudění. To vede k přehřívání okrajových částí kolektorů a kolektorových polí a snížení jejich účinnosti.
Dobré zatékání teplonosné kapaliny v kolektorovém poli je zajištěno především u serpentinového absorbéru (S), který má sice z uvedených konfigurací největší tlakovou ztrátu (cca 10 kPa pro 1 kolektor), nicméně v případě zapojení více kolektorů do pole se tlaková ztráta již nezvyšuje a zároveň je zajištěno rovnoměrné zatékání do kolektorů vzhledem k vysoké hydraulické stabilitě zapojení. Takových kolektorů je možné bez problémů zapojit paralelně až 10 kusů. U konfigurace typu Z a T se maximální možný počet kolektorů zapojených do jednoho pole s ohledem na zatékání typicky pohybuje okolo 6 kusů. Konfigurace absorbérů typu U a M jsou pro zapojování do větších kolektorových polí s více než 3 kolektory nevhodné, neboť sériové zapojení výrazně zvyšuje tlakové ztráty celého pole (nad 50 kPa), pokud nemá jít cíleně o provoz s nízkým průtokem.
Obr. 2.7 Hydraulické konfigurace trubkových registrů solárních kolektorů
2.2.4 Skříň kolektoru
Skříň kolektoru vytváří vnější obal solárního kolektoru a chrání vnitřní prostor před vnějšími nepříznivými vlivy. Zvláštní úpravy pro snížení emisivity vnějšího povrchu skříně nejsou nutné, neboť nemají významný vliv na snížení tepelné ztráty (převažuje konvekce vlivem větru). Pouze u plochých vakuových kolektorů, které neobsahují na zadní straně neprůteplivou tepelnou izolaci (tepelnou izolací je plyn o sníženém tlaku uvnitř skříně), má vliv na jeho tepelnou ztrátu i emisivita vnitřního povrchu skříně.
Skříň kolektoru je v podstatě nosnou konstrukcí, ke které jsou uchyceny ostatní části kolektoru (zasklení, absorbér s trubkovým registrem, tepelná izolace). Je vyrobena buď jako výlisek, nebo je složena z profilů a podle potřeby vyplněna tepelnou izolací. Lisovaná skříň kolektoru je těsná a vnitřní části kolektoru jsou chráněny před možnou degradací vlivem vlhkosti. Skříň kolektoru, skládaná z profilů, těsná není, je proto obvykle opatřena větracími otvory pro odvod vlhkosti a zamezení rosení na zasklení kolektoru.
Tepelná izolace použitá pro minimalizaci tepelné ztráty boční a zadní stranou kolektorové skříně musí být odolná proti extrémním teplotám, které se v kolektoru mohou vyskytnout při stavu bez odběru tepla. V běžných solárních kolektorech se maximální teploty v kontaktu s izolací mohou pohybovat od 140 °C (ploché) do 250 °C (trubkové vakuové). Jako tepelná izolace se proto používá minerální (kamenná, skelná) vlna nebo polyuretanová pěna.
2.3 DRUHY SOLÁRNÍCH KOLEKTORŮ
Pro naprostou většinu aplikací se využívají solární kolektory, ve kterých je používána kapalina jako teplonosná látka (voda, nemrznoucí směs vody a propylenglykolu). Kapalinové kolektory mají absorbér zpravidla tvořený trubkami, protékanými teplonosnou kapalinou, která odvádí teplo z povrchu absorbéru. Okrajově jsou využívány kolektory vzduchové pro předehřev čerstvého vzduchu pro větrání, nebo oběhového vzduchu pro cirkulační vytápění (teplovzdušné, sálavé – hypokaustické).
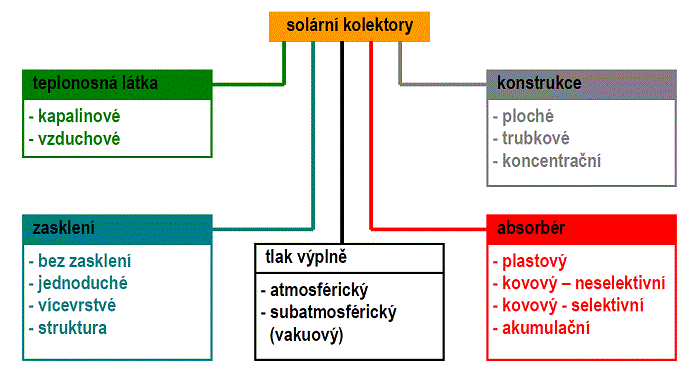
Solární kapalinové kolektory lze rozdělit podle řady hledisek (viz obr. 2.8). Z uvedeného rozdělení vyplývají konstrukční kombinace, s nimiž je možné se v praxi setkat:
- plochý nekrytý kolektor – zpravidla plastová rohož bez zasklení nejčastěji využívaná pro sezónní ohřev bazénové vody o nízké teplotní úrovni;
- plochý neselektivní kolektor – zasklený deskový kolektor s kovovým absorbérem se spektrálně neselektivním povlakem (např. černým pohltivým nátěrem) – určený pro sezónní předehřev vody při nízké teplotní úrovni;
- plochý selektivní kolektor – zasklený deskový kolektor s kovovým absorbérem se spektrálně selektivním povlakem – určený pro celoroční ohřev vody a vytápění;
- plochý vakuový kolektor – deskový kolektor s kovovým absorbérem se spektrálně selektivním povlakem a tlakem uvnitř kolektoru nižším (absolutní tlak cca 1 až 10 kPa) než atmosférický tlak v okolí kolektoru – určený pro celoroční ohřev vody a vytápění, případně průmyslové aplikace s provozními teplotami okolo 100 °C;
- trubkový vakuový kolektor – kolektor s plochým nebo válcovým selektivním absorbérem umístěným ve vakuované (absolutní tlak < 10-3 Pa) skleněné trubce, s variantami předávání tepla do teplonosné látky: přímo protékaný registr, nebo tepelná trubice, určená pro kombinované soustavy pro vytápění či průmyslové vysokoteplotní aplikace (provozní teploty nad 100 °C);
- soustřeďující (koncentrační) kolektor – obecně kolektor, ve kterém jsou použita zrcadla (reflektory), čočky (refraktory) nebo další optické prvky k usměrnění a soustředění přímého slunečního záření na absorbér.
Obr. 2.8 Rozdělení solárních kolektorů
Podle statistiky z roku 2010 jsou nejčastějšími typy kolektorů na trhu v ČR ploché atmosférické selektivní kolektory, kterých bylo nainstalováno cca 74 tis. m2. Trubkové vakuové kolektory tvoří cca 20 % trhu zasklených kolektorů (okolo 18 tis. m2). Nezanedbatelnou součástí trhu jsou také nezasklené kolektory ve formě bazénových rohoží s roční instalovanou plochou cca 50 tis. m2. Koncentračních kolektorů se ročně instaluje pouze okolo 100 m2.
2.3.1 Nekryté (nezasklené) kolektory
Absence krytu (zasklení) zlepšuje optické vlastnosti kolektoru, protože odpadají ztráty odrazem na zasklení, nicméně na druhé straně kolektor vykazuje vysoké tepelné ztráty. Zatímco u zasklených kolektorů vzduchová mezera mezi krytem a absorbérem snižuje tepelné ztráty absorbéru (sáláním, konvekcí), u nezasklených jsou výkon a účinnost kolektoru výrazně ovlivňovány okolním prostředím (teplota okolí, teplota oblohy, rychlost větru). Zvláště se zvyšující se rychlostí větru výrazně rostou tepelné ztráty a účinnost kolektoru prudce klesá.
Obr. 2.9 Bazénový absorbér (plastová rohož)
Obr. 2.10 Bazénový absorbér (plastová rohož)
Nekryté absorbéry se vyrábějí zpravidla z plastu odolného vůči UV záření (EPDM) a jsou vzhledem ke své účinnosti vhodné především k nízkoteplotnímu ohřevu vody pro bazény.
2.3.2 Ploché atmosférické kolektory
Ploché solární kolektory se obecně vyznačují plochým zasklením a zpravidla i plochým absorbérem. Základní schema plochého solárního kolektoru je uvedeno na obr. 2.11. Současným standardem jsou ploché kolektory se selektivním povrchem absorbéru, typy s neselektivním povrchem se objevují pouze okrajově u menších výrobních společností jako levné kolektory pro sezónní aplikace.
Obr. 2.11 Schematický řez plochým solárním kolektorem
Obr. 2.12 Možnost integrace solárního kolektoru do fasády budovy
Ploché kolektory nacházejí uplatnění v oblasti integrace do obálky budov (náhrada části střechy či fasády). Konstrukční integrace solárních kolektorů přináší architektonicky přijatelné řešení, vyšší účinnost kolektoru při kontaktní instalaci s izolační vrstvou obálky, možnost využití zimních pasivních zisků a snížení tepelné ztráty pláště budovy a v případě integrace do fasády (viz obr. 2.12) i snížení period extrémních stagnačních podmínek v letním období.
Pro řešení kolektorových polí velkých solárních soustav se čím dál více uplatňují ploché velkoplošné kolektory s plochou od 4 do 10 m2 (viz obr. 2.13). Absorbéry takových kolektorů jsou tvořeny podélnými lamelami zapojenými do ležatého trubkového registru. Zasklení kolektorů je s ohledem na kompenzaci tepelné roztažnosti děleno do menších ploch. Montáž kolektorového pole z velkoplošných modulů je výrazně rychlejší vzhledem k omezenému počtu prováděných spojů. Na jednoho montážního pracovníka a den je možné nainstalovat cca 50 m2 velkoplošných kolektorů oproti 20 m2 maloplošným.
Obr. 2.13 Velkoplošný solární kolektor o ploše 10 m2, zdroj: Propuls Solar
2.3.3 Ploché vakuové kolektory
Ploché vakuové kolektory využívají sníženého tlaku v prostoru skříně kolektoru k zajištění celkově nízké tepelné ztráty kolektoru omezením volného proudění vzduchu mezi absorbérem a zasklením nebo zadní stěnou kolektoru (kolektorová skříň neobsahuje izolaci). Rám kolektoru musí být velmi těsný, proto je tvořen výliskem (bezešvou vanou), který je v přední části uzavřen tabulí solárního skla, napojenou speciálním tepelně odolným těsněním. Aby sklo neprasklo působením vnějšího atmosférického tlaku nebo nárazem předmětů, je vyztuženo rastrově uspořádanými nerezovými podpůrnými elementy. Jak je zřejmé z obr. 2.14, podpůrné elementy nesmí být v tepelném kontaktu s absorbérem, aby se vyloučily tepelné mosty.
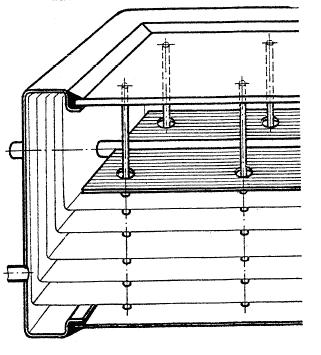
Obr. 2.14 Konstrukce nízkotlakého (vakuového) plochého kolektoru z 80. let
Obr. 2.15 Konstrukce nízkotlakého (vakuového) – současný výrobek, zdroj: Thermosolar
Důležitým aspektem plochých vakuových kolektorů je zajištění těsnosti vnitřního prostoru a možnosti opětovně vakuovat kolektor. Protože ploché vakuové kolektory jsou běžně provozovány za podmínek nízkého vakua (absolutní tlak uvnitř skříně od 1 do 10 kPa), není v podstatě problém udržet tlak v těchto mezích. Kolektor je konstruován ze samotěsnicích částí, které se podtlakem více svírají a utěsňují. Vana kolektoru je vybavena ventilem pro připojení k vývěvě, pokud je nutné vnitřní prostor znovu evakuovat. Součástí instalace kolektoru je manometr pro indikaci ztráty vakua a nárůstu tlaku v kolektoru. Zbytkový vzduch může být nahrazen vzácným plynem kryptonem (argonem) s nižší tepelnou vodivostí.
2.3.4 Trubkové vakuové kolektory
Trubkové vakuové solární kolektory jsou obecně kolektory s válcovým zasklením, u kterých je prostor mezi absorbérem a zasklením vakuován na extrémně nízký tlak (pod 10-3 Pa). Vysoké vakuum vlivem téměř dokonalé absence molekul plynů minimalizuje přenos tepla vedením a konvekcí ve vakuovém prostoru a přenos tepla mezi absorbérem a zasklením způsobuje především sálání. Pro vyloučení výskytu zbytkových plynů ve vakuovém prostoru trubky se používají tzv. „getry“ využívající baryum, které pohlcuje molekuly plynů. Při výrobě je po evakuaci vnitřního prostoru getrová vložka indukčně zahřáta na vysokou teplotu, baryum se odpaří a usadí na dně skleněné trubky jako stříbrně zbarvená vrstva. Getr i nadále aktivně pohlcuje molekuly plynů, které se do vakuovaného prostoru mohou dostat během provozu (např. uvolňováním z absorpčního povrchu), a udržuje tak dlouhodobou stabilitu vakua. Pokud se obálka vakuované trubky poruší a do vnitřního prostoru vakuové trubky se dostane větší množství vzduchu, getrová usazenina změní při reakci s plyny významně barvu – zhnědne, zbělá, zprůhlední apod. – a tím indikuje porušení vakua, viz obr. 2.16.
Obr. 2.16 Držák getru ve vakuové trubce (vlevo) a příklad zbarvení getrové usazeniny (stříbrná = vakuum, mléčná = atmosférický tlak)
Trubkové vakuové kolektory dosahují kombinací vakuové izolace a nízkoemisivního povrchu absorbéru extrémně nízkých tepelných ztrát i při vysokých rozdílech teplot mezi absorbérem a okolním prostředím. Trubkové vakuové kolektory tak umožňují využití slunečního záření i při vysokých provozních teplotách, např. v oblasti průmyslového a technologického tepla nebo solárního chlazení.
Termín trubkový vakuový kolektor je relativně široký pojem, který zahrnuje velké množství různých konstrukčních provedení. Pro potřebu základní klasifikace se odlišují dvě konstrukce:
- trubkové kolektory s jednostěnnou trubkou – „evropský“ typ, původně vyráběný v Evropě;
- trubkové kolektory s dvojstěnnou trubkou (Sydney) – „čínský“ typ, převážně vyráběný v Číně.
Podle konstrukčního uspořádání odvodu tepla lze rozdělit oba konstrukční druhy na další poddruhy:
- přímo protékané – absorbér je vodivě spojen s potrubím přímo protékaným teplonosnou kapalinou (koncentrické potrubí, potrubí ve tvaru U-smyčky = U-registr);
- s tepelnou trubicí – absorbér je vodivě spojen s výparníkem, kde se vypařuje pracovní látka;
- suché napojení – kondenzátor uchycený v pouzdru omývaném teplonosnou kapalinou;
- mokré napojení – kondenzátor přímo omývaný teplonosnou kapalinou.
Řada trubkových vakuových kolektorů využívá pro přenos tepla mezi povrchem absorbéru a teplonosnou kapalinou tzv. tepelných trubic. Princip tepelné trubice je relativně dobře známý. Pracovní látka se přívodem tepla vypařuje ve výparníkové části vodivě spojené s absorbérem, pára samovolně stoupá trubicí do kondenzační části, kde se sráží na kapalné skupenství a kapalina stéká zpět do výparníkové části. Změnou skupenství se dosahuje intenzivního přestupu tepla uvnitř tepelné trubice. Pro zajištění správné funkce běžné tepelné trubice je nutné zajistit její sklon minimálně 20–25°, aby se kondenzát mohl samovolně vrátit zpět do výparníku. Na trhu se již objevují i provedení bez takového omezení. U vakuových solárních kolektorů se jako tepelná trubice používá měděná trubka, jejíž výparníková část má průměr 8 až 12 mm, kondenzační část má zpravidla větší průměr cca 18 až 20 mm, pro zajištění dostatečné teplosměnné plochy pro předání tepla do teplonosné kapaliny. Uvnitř tepelné trubice se jako pracovní látka používá buď čistá voda (případně se zvláštními aditivy), nebo líh, obojí při určitém tlaku (podtlaku).
Trubkové kolektory s jednostěnnou trubkou
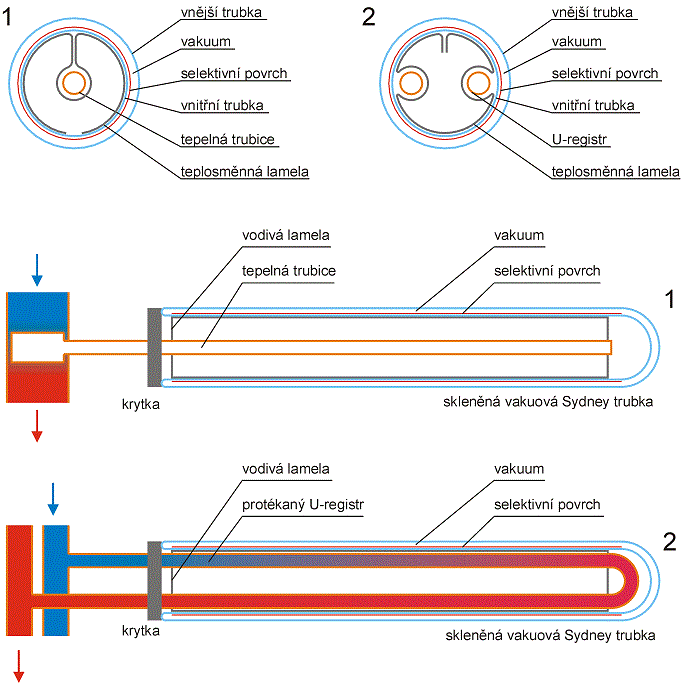
Tradiční typ trubkových vakuových kolektorů využívá jednostěnné uzavřené skleněné trubky, ve které je umístěna plochá lamela absorbéru se selektivním povrchem (viz obr. 2.17). Odvod tepla z absorbéru je zajišťován tepelnou trubicí, přímo protékaným U-registrem, nebo přímo protékaným koncentrickým potrubím. Vnitřní prostor skleněné trubky je vakuován na tlak pod 1 mPa.
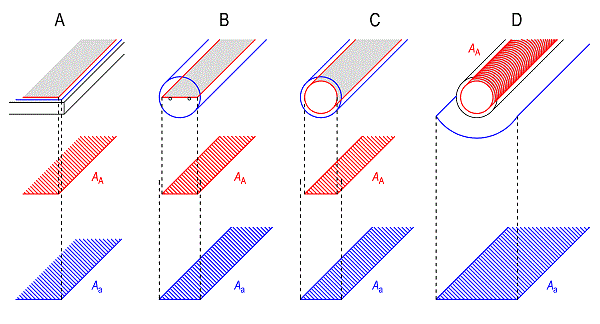
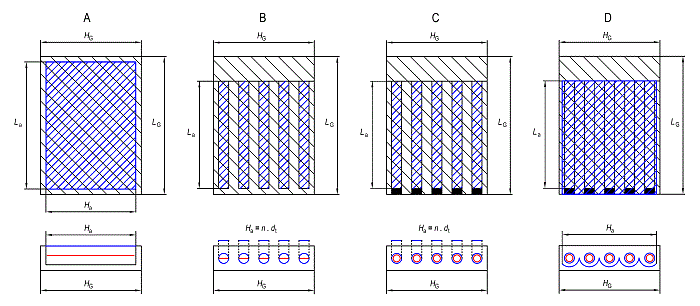
Obr. 2.17 Příčný řez a podélný řez jednostěnným trubkovým vakuovým kolektorem s tepelnou trubicí (1) a s přímo protékaným U-registrem (2)
Jednostěnné trubky se vyrábějí v průměrech od 40 do 150 mm z boritokřemičitého skla s vysokou pevností a odolností vůči teplotním změnám a gradientům. Kvalitní jednostěnné trubky jsou dostupné s antireflexním povlakem pro zvýšení propustnosti slunečního záření (až 94 %). Kolektory s jednostěnnou trubkou a plochým absorbérem mají velmi dobrý přestup tepla z absorbéru do teplonosné látky zajištěný především ultrazvukovým nebo laserovým navařením absorbéru na teplosměnné potrubí (výparník tepelné trubice, přímo protékané potrubí).
Obr. 2.18 Praktické provedení jednostěnného vakuového trubkového kolektoru s přímo protékaným koncentrickým potrubím, zdroj: Viessmann
Obr. 2.19 Praktické provedení jednostěnného vakuového trubkového kolektoru s tepelnou trubicí, zdroj: Viessmann
U trubkových kolektorů s jednostěnnou trubkou je pro funkci zcela zásadní zajištění dokonalého těsnění prostupu tepelné trubice či protékaného potrubí skleněnou vakuovou trubkou (těsnění spoje kov-sklo). Řešení spolehlivého těsnění spočívá v použití slitin niklu a železa, které vykazují stejný součinitel tepelné roztažnosti jako použité boritokřemičité sklo. Tyto dnes již klasické kolektory jsou na vysoké technické úrovni, pracují s vysokou účinností, nicméně pro většinu aplikací jde o investičně velmi náročné řešení.
Trubkové kolektory s dvoustěnnou skleněnou trubkou
V posledním desetiletí se na českém a evropském trhu objevují vakuové kolektory s tzv. Sydney trubkou, vyvinutou na základě spolupráce mezi Sydney University a Tsinghua University v 80. letech. Sydney trubka je válcová dvojstěnná koncentrická celoskleněná trubka, obdobná Dewarově nádobě – termosce, kde vnitřní skleněná trubka slouží jako válcový absorbér k zachycování slunečního záření a přeměnu na teplo, vnější krycí trubka slouží jako zasklení k ochraně před atmosférickými vlivy. Meziprostor mezi oběma skleněnými trubkami je vakuován na 1 mPa, vnější povrch vnitřní absorpční trubky je opatřen selektivním absorpčním povrchem.
Podobně jako jednostěnné trubkové kolektory, jsou i trubkové Sydney kolektory konstrukčně řešeny s přímo protékaným trubkovým registrem nebo s tepelnou trubicí (viz obr. 2.20). Kritickým místem Sydney kolektorů je přenos tepla z vnitřního povrchu vnitřní absorpční trubky do teplonosné kapaliny, tedy především na povrch potrubí přímo protékaného U-registru nebo na povrch výparníku tepelné trubice. K tomu slouží teplosměnná vodivá lamela z hliníku nebo mědi, která by měla vykazovat co nejvodivější kontakt jak s vnitřním povrchem absorpční trubky, tak s potrubím pro odvod tepla (U-registr, tepelná trubice). Toho není vždy docíleno a špatný přenos tepla z absorpčního povrchu do teplonosné kapaliny se projevuje negativně na celkové účinnosti kolektoru. Na druhé straně, oproti konstrukčnímu uspořádání kolektorů s jednostěnnými vakuovanými skleněnými trubkami s absorbérem ve tvaru plochých lamel, odpadá u kolektorů se Sydney trubkou problém utěsnění vakua a prostupů potrubí, což vede k jejich nižší ceně.
Sydney trubky se vyrábějí z boritokřemičitého skla s nízkou tepelnou roztažností a jako spektrálně selektivní povrch na absorpční skleněné trubce se používá keramicko-kovový vícevrstvý povlak na bázi nitridu hliníku (Al-N-Al). Typické rozměry v současné době vyráběných Sydney trubek jsou v podstatě dva: 58 / 47 mm nebo 47 / 37 mm s tloušťkami zasklení 1,6 až 1,8 mm, vyráběné běžně v délkách od 1 do 2 m. Naprostá většina Sydney trubek se vyrábí v Číně, z nichž část je využita přímo k výrobě solárních trubkových kolektorů (převážně s tepelnou trubicí) a část se dováží dalším výrobcům trubkových kolektorů po celém světě.
Obr. 2.20 Příčný řez a podélný řez trubkovým vakuovým Sydney kolektorem s přímo protékaným U-registrem (1) a s tepelnou trubicí (2)
Obr. 2.21 U-registr z měděného potrubí s hliníkovou lamelou, zdroj: OPC
Obr. 2.22 Vlastní vakuová skleněná Sydney trubka, zdroj: OPC
2.3.5 Koncentrační kolektory
Koncentrační (soustřeďující) kolektory využívají koncentrace přímého slunečního záření odrazem od zrcadel nebo lomem čočkami do ohniska, v němž je umístěn absorbér o výrazně menší ploše než je vlastní plocha apertury (nízké tepelné ztráty). Poměr mezi velikostí apertury a absorbéru určuje stupeň koncentrace. Podle tvaru ohniska se rozlišují koncentrační kolektory s lineárním ohniskem (parabolický reflektor, Winstonův kolektor, kolektor s lineární Fresnellovou čočkou) nebo bodovým ohniskem (paraboloidní reflektor, fasetové reflektory, heliostaty). Pro účinné použití koncentračních kolektorů je základní podmínkou dostatek přímého slunečního záření během roku a navádění buď apertury nebo absorbéru podle zákonů geometrie slunečního záření.
Obr. 2.23 Koncentrační kolektor s lineárním ohniskem – Fresnellův koncentrátor
Obr. 2.24 Koncentrační kolektor s lineárním ohniskem – parabolický koncentrátor
Solárními kolektory s vysokými koncentračními poměry je možné dosáhnout vysokých teplot při minimalizaci tepelných ztrát (minimální absorpční plocha, použití vakuových trubek). Pro průmyslové aplikace s teplotami 100 až 300 °C se využívá kolektorů s koncentračním poměrem 10 až 40.
Obr. 2.25 Kolektor s bodovým ohniskem – solární tepelná elektrárna s heliostaty a centrální věží
Obr. 2.26 Kolektor s bodovým ohniskem – paraboloidní reflektor se Stirlingovým motorem v ohnisku
Koncentrační kolektory s Fresnellovou lineární čočkou
Lineární Fresnellova čočka představuje v principu tradiční válcovou čočku s lineárním ohniskem avšak „komprimovanou“ do deskového tvaru odstraněním hmoty, která se nepodílí na lomu (viz obr. 2.27). Koncentrací přímého slunečního záření na lineární absorbér protékaný teplonosnou kapalinou lze vytvořit solární kolektor. Koncentrační poměr Fresnellovy čočky se pohybuje okolo hodnoty 5, integrace čočky do zasklívacího systému obálky budovy (okno) umožňuje spojit pasivní a aktivní prvek pro využití slunečního záření do jediného zařízení. Koncentrací přímého záření na absorbér se snižuje tepelná zátěž prostoru, do kterého pak vstupuje pouze difuzní složka zajišťující přirozené osvětlení. Kapalinu ohřátou v absorbéru je možné využít například pro přípravu teplé vody.
Obr. 2.27 Fresnellova čočka, zdroj: ENKI
Obr. 2.28 Kolektor s lineární Fresnellovou čočkou, zdroj: ENKI
Koncentrační trubkové kolektory
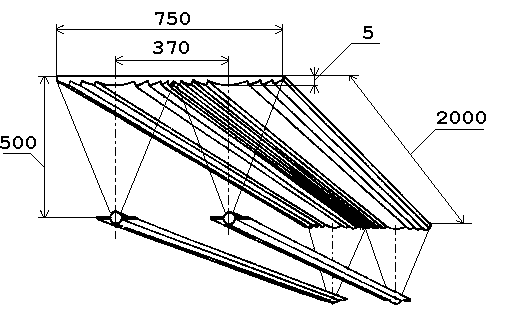
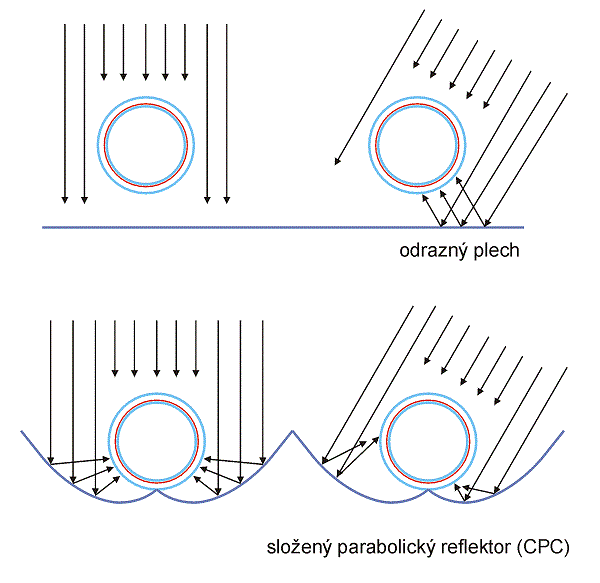
Vzhledem k válcovému tvaru absorbéru se trubkové vakuové Sydney kolektory často vybavují odraznými zrcadly (reflektory) s opticky více či méně propracovaným tvarem pro zvýšení množství dopadající energie na absorbér, viz obr. 2.29. Mezi koncentrační kolektory nejsou běžně zařazovány vzhledem k nízkému koncentračnímu poměru. Levnější typy trubkových Sydney kolektorů využívají jednoduché ploché difuzní reflektory umístěné za trubkami. Vyššího účinku lze docílit reflektory s vhodně tvarovaným povrchem (parabolické koncentrátory).
Obr. 2.29 Použití reflektorů pro zvýšení aktivní plochy trubkového kolektoru
Použití reflektorů na jedné straně snižuje počet použitých trubek v kolektoru (levnější řešení) a zvětšuje aktivní plochu kolektoru (výkon/m2 zastavěné plochy), na druhé straně v určitých zeměpisných oblastech může být použití reflektorů problematické s ohledem na zachycování sněhové pokrývky a tvorbu ledu, která může vést k destrukci skleněných vakuových trubek kolektoru.
2.4 PARAMETRY A CHARAKTERISTIKY SOLÁRNÍCH KOLEKTORŮ
Pro komplexní popis tepelného chování solárního kolektoru pro navrhování a hodnocení solárních soustav je nutné znát jeho charakteristické parametry a jejich závislost na provozních a klimatických podmínkách:
- tepelná účinnost η – indikuje, jak kolektor pohlcuje záření a ztrácí teplo, určuje jeho okamžitý tepelný výkon Q‚k při daných klimatických a provozních podmínkách;
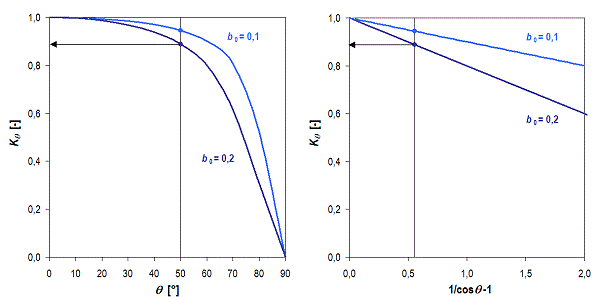
- modifikátor úhlu dopadu Kθ – určuje vliv úhlu dopadu slunečního záření na účinnost a výkon solárního kolektoru, někdy se označuje jako optická charakteristika kolektoru;
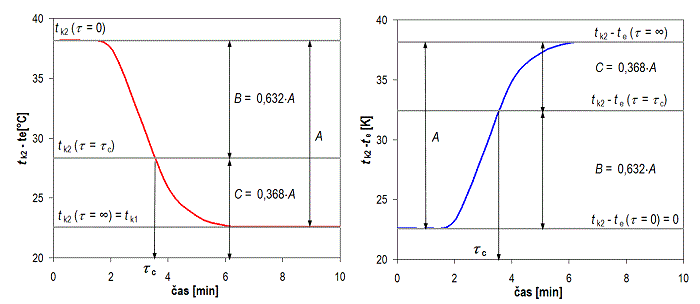
- časová konstanta τ a tepelná kapacita C – určuje vliv tepelné setrvačnosti hmot kolektoru na jeho okamžitý výkon.
2.4.1 Teoretické vyjádření účinnosti
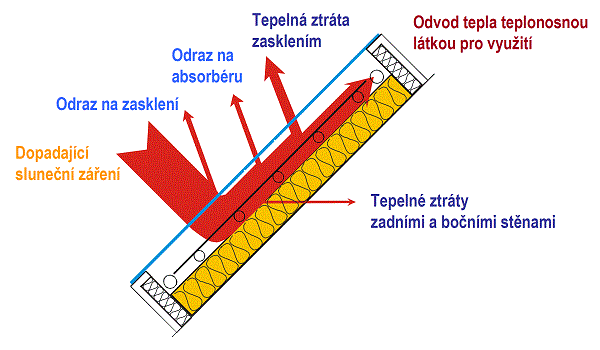
Funkci solárního tepelného kolektoru lze popsat obecnou energetickou rovnováhou (viz obr. 2.30). Solární kolektor přijímá sluneční záření, které je částečně odraženo od zasklení a absorbéru a zbytek se pohlcuje na povrchu absorbéru a mění v teplo. Část tepla z pohlceného záření se odvádí teplonosnou kapalinou, část odchází zpět do okolního prostředí ve formě tepelných ztrát a část tepla se akumuluje v těle kolektoru. Energetickou bilanci kolektoru lze popsat diferenciální rovnicí
(2.1)
kde je
dQ/dt … časová změna tepelného obsahu kolektoru a teplonosné kapaliny uvnitř absorbéru, ve W;
Q‚s … sluneční ozáření jímací plochy kolektoru, ve W;
Q‚z,o … optické ztráty kolektoru, ve W;
Q‚z,t … tepelné ztráty kolektoru, ve W;
Q‚k … tepelný výkon solárního kolektoru, ve W.
Obr. 2.30 Schematické znázornění energetické bilance kolektoru
Akumulační člen v rovnici bilance je ovlivňován slunečním ozářením, změnou teploty a rychlosti proudění teplonosné kapaliny na vstupu do kolektoru. V řadě případů je nutný pro popis chování solárního kolektoru za reálných proměnlivých podmínek (počítačové modelování, kolektory s vysokou tepelnou kapacitou). Nicméně pro naprostou většinu technických výpočtů lze vycházet z bilance v ustáleném stavu. Využitelný tepelný výkon solárního kolektoru lze potom zapsat jako
(2.2)
Dopadající výkon slunečního záření se stanoví ze vztahu
(2.3)
kde je
G … sluneční ozáření kolektoru, ve W/m2;
Ak … vztažná plocha solárního kolektoru, v m2. Za vztažnou přední plochu kolektoru je možné uvažovat plochu apertury, absorbéru či obrysovou plochu kolektoru, viz kapitola 2.4.2.
Optické ztráty kolektoru lze vyjádřit ze vztahu
(2.4)
kde je
τ … propustnost slunečního záření zasklení solárního kolektoru, bezrozměrná;
α … pohltivost slunečního záření absorbéru, bezrozměrná.
Tepelné ztráty kolektoru se stanoví jako součet tepelných ztrát z absorbéru přední stranou (plocha Ak), zadní stranou (plocha Ak) a boční stranou (plocha Ab) kolektoru
(2.5)
kde je
Up … součinitel prostupu tepla přední stranou kolektoru, ve W/(m2·K);
Uz … součinitel prostupu tepla zadní stranou kolektoru, ve W/(m2·K);
Ub … součinitel prostupu tepla bočními stranami kolektoru, ve W/(m2·K);
tabs … střední teplota povrchu absorbéru, ve °C;
te … teplota okolního vzduchu, ve °C.
Po dosazení rovnic (2.3) až (2.5) do rovnice (2.2) lze získat rovnici využitelného výkonu solárního kolektoru vyjádřenou v závislosti na povrchové teplotě absorbéru
(2.6)
Účinnost solárního kolektoru ηk je za ustálených podmínek definována jako poměr výkonu odváděného z kolektoru k „příkonu“ slunečního záření dopadajícího na kolektor
(2.7)
kde je
τα … optická účinnost kolektoru (bezrozměrná);
U … součinitel prostupu tepla kolektoru, ve W/(m2·K);
střední redukovaný teplotní spád mezi povrchem absorbéru a okolím, v m2·K/W.
Obr. 2.31 Křivka účinnosti solárního kolektoru s vyznačením optických a tepelných ztrát
Z grafu na obr. 2.31 je patrné, že s nárůstem teploty hrají u kolektorů obecně dominantní roli tepelné ztráty z kolektoru do okolí, při vyšších teplotách rostou tepelné ztráty sáláním se 4. mocninou rozdílu teplot (zakřivení průběhu křivky účinnosti). Rovnicí (2.7) je účinnost kolektoru vyjádřena pouze na základě fyzikálních vlastností částí kolektoru vně absorbéru, tzn. bez zohlednění vlivu použitého materiálu, konstrukce a geometrie absorbéru, vlivu průtoku teplonosné kapaliny atd. Vyjádření účinnosti kolektoru jako funkce střední teploty povrchu absorbéru tabs je však problematické, neboť teplota absorbéru zpravidla není známa a lze ji obtížně změřit bez demontáže zasklení kolektoru. Ve starší literatuře je teplota absorbéru tabs nesprávně slučována se střední teplotou teplonosné kapaliny tm. Měřením povrchových teplot lze prakticky ukázat, že mezi povrchem absorbéru (střední teplotou) a teplonosnou kapalinou je teplotní spád řádově jednotky (velmi vodivé, plnoprůtočné absorbéry) až desítky K (konfigurace lamela-trubka).
Pro vyjádření kvality přenosu tepla z povrchu absorbéru do teplonosné kapaliny se využívá bezrozměrného účinnostního součinitele kolektoru F‚, který ve své podstatě stanovuje poměr mezi dvěma tepelnými odpory, ve jmenovateli je obsažen odpor proti přenosu tepla z kapaliny do okolního vzduchu, v čitateli je odpor proti přenosu tepla z povrchu absorbéru do okolního vzduchu. Účinnostní součinitel kolektoru je pro danou konstrukci absorbéru konstantní a lze jej analyticky vypočítat. Je závislý na geometrii absorbéru (průměr trubek registru, rozteč trubek registru, tloušťka absorbéru), na tepelných vlastnostech absorbéru (tepelná vodivost absorbéru, trubek registru a spoje trubek s absorbérem) a přestupu tepla v trubkách registru (laminární, turbulentní). Přestup tepla z povrchu absorbéru do teplonosné kapaliny zohledněný účinnostním součinitelem je znázorněn na obr. 2.32. Zavedení účinnostního součinitele kolektoru F‚ umožňuje rovnici účinnosti solárního kolektoru vyjádřit v závislosti na střední teplotě teplonosné kapaliny tm tak, jak to odpovídá evropské praxi, ve tvaru
(2.8)
kde je
F‚ τα … účinnost při nulových tepelných ztrátách, někdy nepřesně nazývaná optická účinnost;
střední redukovaný teplotní spád mezi kapalinou a okolím, v m2·K/W.
Obr. 2.32 Energetická bilance kolektoru, včetně vedení tepla absorbérem a přestupu do teplonosné kapaliny
Z účinnostního součinitele kolektoru F‚ vyplývají důležité zásady návrhu konstrukce kolektoru, zejména absorbéru. Se zmenšováním rozteče trubek registru a tedy zmenšováním šířky lamely absorbéru se zvyšuje účinnostní součinitel kolektoru, stejně jako se zvětšující se tloušťkou absorbéru a zvyšující se tepelnou vodivostí materiálu absorbéru a trubky. Praktické omezení tloušťky absorbéru na hodnoty max. 0,5 mm vyplývá ze snahy o minimalizaci spotřeby materiálu a zároveň udržení nízké tepelné setrvačnosti kolektoru. Nicméně na trhu v ČR existují i kolektory s válcovanými hlliníkovými absorbéry o tloušťce cca 2 mm, které mají velmi vysokou hodnotou průsečíku s osou účinnosti F‚ τα (až 0,83).
Americké normy vyjadřují křivku účinnosti v závislosti na teplotě kapaliny vstupující do kolektoru tk1. Rovnice účinnosti má tvar
(2.9)
kde je
FR … tepelný přenosový součinitel kolektoru (bezrozměrný).
Tepelný přenosový součinitel kolektoru FR vztahuje energii dodanou solárním kolektorem (okamžitý využitelný tepelný zisk) k energii, která by byla dodána za předpokladu, že by teplota celého absorbéru byla rovna vstupní teplotě teplonosné kapaliny. Svým významem je tak ekvivalentní účinnosti tepelného výměníku, definované jako poměr okamžitého přeneseného tepelného výkonu k maximálnímu možnému tepelnému výkonu. V solárním kolektoru dochází k maximálnímu možnému využitelnému výkonu v případě, že celý kolektor je na teplotě rovné teplotě vstupující kapaliny.
Tepelný přenosový součinitel kolektoru FR je závislý na průtoku a na vlastnostech teplonosné kapaliny (hustota, tepelná kapacita). Zvyšováním průtoku kapaliny v kolektoru se snižuje teplotní spád na kolektoru (rozdíl mezi výstupem a vstupem), střední teplota v kolektoru se přibližuje teplotě na vstupu a přenosový součinitel kolektoru roste.
Na obr. 2.33 jsou graficky znázorněny křivky účinnosti, stanovené v závislosti ke střední teplotě povrchu absorbéru, střední teplotě teplonosné kapaliny a ke vstupní teplotě teplonosné kapaliny. Z grafu je patrné, že se tvar křivek liší v závislosti na způsobu vyjádření. To je nutné si uvědomit například při přebírání parametrů křivek účinnosti solárních kolektorů z amerických zkušebních laboratoří a certifikačních programů.
Obr. 2.33 Porovnání křivek účinnosti jediného kolektoru v závislosti na různě vyjádřeném středním redukovaném teplotním spádu
Na obr. 2.34 je zobrazeno vyjádření účinnosti solárního kolektoru v závislosti pouze na teplotním rozdílu mezi teplonosnou kapalinou a okolím. Jednotlivé křivky pak odpovídají různým hladinám slunečního ozáření G. Z grafu je patrné, že při nízkých úrovních slunečního ozáření klesá účinnost kolektoru výrazně dolů. Čím nižší je tepelná ztráta kolektoru, tím je pokles účinnosti s klesajícím ozářením nižší.
Obr. 2.34 Závislost účinnosti solárního kolektoru na rozdílu teplot při různém slunečním ozáření
2.4.2 Vztažná plocha solárního kolektoru
Účinnost solárního kolektoru musí být vždy uváděna společně s označením plochy kolektoru Ak, ke které byla vztažena. Lze rozlišit celkem tři plochy, ke kterým je možné vztáhnout výkon nebo účinnost solárního kolektoru:
- plocha absorbéru AA – plocha, na níž dochází cíleně k přeměně slunečního záření v teplo;
- plocha apertury Aa – plocha průmětu otvoru (zasklení), kterým vstupuje do kolektoru nesoustředěné sluneční záření;
- celková obrysová (hrubá) plocha AG – plocha průmětu celkového obrysu solárního kolektoru.
Podle současné evropské zkušební normy ČSN EN 12975 je možné účinnost vztáhnout buď k ploše absorbéru AA, nebo k ploše apertury Aa. Plochy absorbéru a plochy apertury pro různé druhy kolektorů jsou definovány na obr. 2.35. Nejmenší plochou je zpravidla plocha absorpční, nicméně je problematické ji změřit bez rozebrání, případně rozbití kolektoru. U plochých kolektorů a jednostěnných trubkových kolektorů s plochým absorbérem je absorpční plochou průmět absorpčního povrchu, připevněného na trubkový registr. U trubkových kolektorů s válcovým absorbérem je nutné rozlišit, zda jde o:
- kolektor bez reflektoru – absorpční plochou je plocha průmětu válcového absorbéru (dA·L);
- kolektor s reflektorem – absorpční plochou je povrch válce absorbéru (π·dA·L).
Plochou apertury plochého kolektoru je plocha propustné části jeho zasklení. U trubkového kolektoru bez reflektoru (jednostěnný, dvojstěnný Sydney) je plochou apertury průmět vnější krycí trubky. U trubkového Sydney kolektoru s reflektorem je aperturou kolektoru plocha průmětu reflektoru. Apertura kolektoru se měří snadno, neboť je zvnějšku přístupná a obecně je považována za referenční plochu kolektoru. Na její velikosti závisí množství kolektorem využitelného záření a tepelné ztráty kolektoru (80 až 90 % tepelných ztrát odchází z kolektoru zasklením) v případě, že apertura je současně i zasklením, nikoli reflektorem.
Obr. 2.35 Definice plochy apertury a absorbéru solárních kolektorů: A) plochý; B) trubkový s plochým absorbérem; C) trubkový s válcovým absorbérem; D) trubkový s válcovým absorbérem a reflektorem
Protože plocha absorbéru je zpravidla menší než plocha apertury, leží v grafickém porovnání křivka účinnosti vztažená k absorbéru vždy výše než křivka účinnosti vztažená k apertuře. Naopak nejníže leží křivka účinnosti vztažená k obrysové ploše kolektoru. Dodavatelé solárních kolektorů proto uvádějí z marketingových důvodů především křivku účinnosti vztaženou k ploše absorbéru. Evropské normy a certifikační systémy (např. Solar Keymark, Modrý anděl aj.) používají jako vztažnou plochu pro solární kolektory zásadně plochu apertury.
Obr. 2.36 Definice plochy apertury a obrysové plochy solárních kolektorů: A) plochý; B) trubkový s plochým absorbérem; C) trubkový s válcovým absorbérem; D) trubkový s válcovým absorbérem a reflektorem
Vztažení křivky účinnosti k ploše apertury kolektoru je vhodné z hlediska porovnání vlastností dvou kolektorů, různé konstrukce a kvality provedení, nicméně nevhodné z hlediska rozhodování o potenciálu kolektoru pro danou aplikaci či pro porovnání kolektorů s různými účinnými plochami. Investora by při analýze potenciálu využití sluneční energie na konkrétním místě instalace mělo zajímat hodnocení účinnosti kolektoru vztažené k obrysové ploše kolektoru AG, tedy ke skutečné ploše, kterou kolektor zaujímá v prostoru (na střeše, na terénu apod.).
Obr. 2.37 Porovnání křivek účinnosti jednotlivých typů solárních kolektorů vztažených k ploše apertury (tučně) a k obrysové ploše (tence); křivky vyneseny v závislosti na rozdílu teplot při ozáření 800 W/m2
Na obr. 2.36 jsou porovnány rozdíly mezi plochou apertury a hrubou plochou různých druhů kolektorů. Zejména trubkové kolektory bez reflektoru vykazují výrazný podíl neúčinné plochy na celkové ploše zastavěné kolektorem na střeše (cca 40 %), zvláště v porovnání s plochými kolektory (cca 10 %). V případě, kdy je prostor pro instalaci solárních kolektorů omezený, pak může dojít k situaci, že na dané ploše lze plochými kolektory zajistit vyšší výkony a celkové zisky než s trubkovými kolektory bez reflektoru právě díky výrazně větší využitelné aktivní ploše.
Porovnání mezi křivkou účinnosti vztaženou k ploše apertury a vztaženou k hrubé ploše je uvedeno na obr. 2.37. Je patrné, že vztažením k větší ploše bude křivka účinnosti podle hrubé plochy v grafu ležet níže než křivka podle apertury. Pro ploché kolektory rozdíl není příliš významný, avšak u trubkových kolektorů jsou rozdíly značné.
2.4.3 Experimentální stanovení výkonu a účinnosti
Měření výkonu solárních kapalinových kolektorů a stanovení jejich účinnosti se věnuje evropská zkušební norma přijatá do české normalizace jako ČSN EN 12975-2:2006. Udává zkušební metody a výpočtové postupy pro určení ustáleného tepelného výkonu ve venkovním prostředí při přirozeném slunečním záření a přirozeném či simulovaném větru a ve vnitřním prostředí při simulovaném záření a větru. Dále norma poskytuje zkušební metody a výpočtové postupy pro určení výkonových parametrů solárních kolektorů za proměnlivých podmínek počasí (kvazidynamická zkouška výkonu). Norma není použitelná na kolektory s vestavěným zásobníkem. Pro zkoušení kolektorů zhotovovaných na zakázku, např. vestavby do střechy, je nutné použít zkušební moduly stejné konstrukce.
Venkovní zkouška ustáleného tepelného výkonu probíhá za jasného dne (ozáření G > 700 W/m2) v období okolo slunečního poledne tak, aby sluneční záření dopadalo na referenční rovinu kolektoru kolmo s odchylkou cca do 20°. Pro minimalizaci ovlivnění výsledků zkoušky proměnlivostí proudění vzduchu okolo kolektoru je předepsáno zajištění minimální rychlosti proudění vzduchu w > 3 m/s (ventilátory na zkušební stolici). Kolektor je zkoušen v rozsahu provozních teplot pro minimálně 4 různé vstupní teploty. Jedna ze vstupních teplot je zvolena tak, aby střední teplota teplonosné kapaliny byla v blízkosti teploty okolního vzduchu pro stanovení účinnosti při nulových ztrátách kolektoru (optická účinnost). Teplonosnou kapalinou při zkoušce je zásadně voda. Další podrobnosti o experimentálním stanovení účinnosti solárního kolektoru jako okrajové podmínky nebo zapojení měřicí tratě, jsou uvedeny v příslušné normě.
Obr. 2.38 Proložení experimentálně zjištěných bodů účinnosti
Při experimentálním stanovení účinnosti solárního kolektoru zkouškou tepelného výkonu solárního kolektoru se vychází z definice účinnosti
(2.10)
kde je
M‚ … hmotnostní průtok teplonosné kapaliny solárním kolektorem, v kg/s;
c … měrná tepelná kapacita teplonosné kapaliny, v J/(kg·K);
tk1 … teplota teplonosné kapaliny na vstupu do kolektoru, ve °C;
tk2 … teplota teplonosné kapaliny na výstupu z kolektoru, ve °C.
Stanovenými hodnotami účinnosti v závislosti na středním redukovaném teplotním spádu (rozdílu mezi střední teplotou teplonosné kapaliny v kolektoru tm a teplotou okolí te poděleném slunečním ozářením G) se proloží regresní křivka 2. řádu (parabola)
(2.11)
a po úpravě
(2.12)
kde je
η0 … účinnost solárního kolektoru při nulovém teplotním spádu mezi střední teplotou teplonosné kapaliny tm a okolím te (nulové tepelné ztráty), zjednodušeně označována jako optická účinnost;
a1 … lineární součinitel tepelné ztráty kolektoru, v W/(m2·K);
a2 … kvadratický součinitel tepelné ztráty kolektoru, ve W/(m2·K2);
střední redukovaný teplotní spád mezi kapalinou a okolím, v m2·K/W.
Rovnice (2.12) je v podstatě experimentálním vyjádřením teoreticky odvozené rovnice (2.8). Člen vyjadřující průsečík křivky s osou účinnosti je „optická“ účinnost a z porovnání lze odvodit
(2.13)
Efektivní součinitel prostupu tepla kolektorem lze stanovit z porovnání jako
(2.14)
Střední teplota teplonosné kapaliny se stanoví jednoduše jako průměr ze vstupní a výstupní teploty
(2.15)
Křivka účinnosti solárních kolektorů je nezbytná pro navrhování a hodnocení solárních soustav. Součinitele (konstanty) křivky účinnosti daného kolektoru spolu s plochou, ke které byla vztažena, by měl poskytnout výrobce nebo dodavatel kolektoru, popřípadě zkušebna nebo příslušný certifikační orgán jako součást zkušebního protokolu a osvědčení o certifikaci. Pokud protokol není k dispozici, nelze podat informaci o výkonu, účinnosti ani potenciálních energetických přínosech kolektoru.
2.4.4 Uvádění účinnosti kolektoru
Jak již bylo uvedeno, účinnost kolektoru je charakterizována křivkou ve tvaru paraboly. Zásadně nelze uvádět jedinou hodnotu účinnosti solárního kolektoru bez uvedení okrajových podmínek, při kterých byla stanovena (teplota teplonosné kapaliny tm, teplota venkovního vzduchu te a sluneční ozáření G). Někteří výrobci uvádějí pouze hodnotu maximální účinnosti η0 – průsečík s osou účinnosti, tzv. účinnost při nulových tepelných ztrátách, kdy střední teplota teplonosné kapaliny v kolektoru tm je rovna teplotě okolí te, a nedochází tedy k tepelným ztrátám z kolektoru do okolí. V běžných aplikacích se této hodnoty při provozu prakticky nedosahuje, neboť to znamená zajistit na vstupu do kolektoru v každém případě teplotu nižší než je teplota okolního vzduchu. Kolektor v tomto případě získává teplo nejen ze slunečního záření, ale také z okolního vzduchu (chová se jako velmi špatný výměník vzduch-voda). Taková „informace“ o účinnosti kolektoru má sama o sobě spornou vypovídající hodnotu, neříká nic o tepelně technických vlastnostech kolektoru, ani o reálné provozní účinnosti kolektoru. Průsečík je zjednodušeně nazýván optickou účinností, neboť v zásadě vypovídá o optických vlastnostech kolektoru (propustnost zasklení, pohltivost absorbéru), nicméně významný vliv na tuto hodnotu mají také geometrické a tepelné vlastnosti absorbéru a kvalita jeho provedení (účinnostní součinitel kolektoru, viz kapitola 2.4.1). Snížení hodnoty η0, ať již nízkou propustností zasklení, nekvalitním povrchem absorbéru či špatným kontaktem absorbéru s chladicím trubkovým registrem, posouvá celou křivku účinnosti k nízkým hodnotám.
Popis křivky účinnosti je však možné zjednodušit tak, že se uvedou alespoň oba krajní body křivky, tj. průsečík s osou x (redukovaný teplotní spád při nulové účinnosti) a y (účinnost při nulových ztrátách), mezi kterými lze orientačně interpolovat celou křivku (viz obr. 2.39). Průsečík s osou x, kdy kolektor má účinnost a výkon rovné nule, neboť energie pohlcená absorbérem se vyrovná tepelným ztrátám, se nazývá bod stagnace (chodu naprázdno, bez odběru tepla, klidový stav). Z hodnoty redukovaného teplotního spádu v bodu průsečíku [(tm – te)/G]η=0 lze potom stanovit maximální teplotu v kolektoru při daných klimatických podmínkách.
Obr. 2.39 Zjednodušené uvádění účinnosti kolektoru
Nicméně, aby bylo přece jen možné porovnat kvalitu solárních kolektorů pouze jedinou hodnotou účinnosti, je možné orientačně použít její hodnotu vyjádřenou pro střední redukovaný teplotní spád 0,05 m2·K/W, tzn. například při podmínkách (tm – te) = 40 K a G = 800 W/m2. Hodnota účinnosti η0,05, uváděná i ve zkušebních protokolech některých zkušeben, dává náhled na průměrnou provozní účinnost solárního kolektoru v jeho nejčastější aplikaci – solární přípravě teplé vody.
2.4.5 Uvádění výkonu kolektoru
Výkon solárních kolektorů, resp. solární soustavy, narozdíl od tradičních zdrojů energie je silně ovlivněn klimatickými podmínkami (venkovní teplota te, sluneční ozáření G) a provozními podmínkami (teplota v kolektorech tm), a je proto nutné jej stanovit a uvádět za jasně definovaných okrajových podmínek.
Výkon solárního kolektoru se na základě výsledků zkoušky při kolmém úhlu dopadu slunečního záření stanoví ze vztahu
(2.16)
kde je
ηk … účinnost kolektoru při daných provozních a klimatických podmínkách, vztažená k referenční ploše;
G … sluneční ozáření na kolektor, ve W/m2;
Ak … referenční plocha kolektoru, v m2.
Při stanovení výkonu kolektoru se tedy vychází z křivky účinnosti (od výrobce) a po úpravě vztahu (2.16) lze psát
(2.17)
Obr. 2.40 Křivka tepelného výkonu solárního kolektoru
Křivka výkonu solárního kolektoru se uvádí při G = 1000 W/m2 v závislosti na rozdílu teplot mezi kapalinou a okolním vzduchem. Křivka jednoznačně definuje výkon celého solárního kolektoru při daných provozních podmínkách. Uvádění křivky výkonu solárního kolektoru má tu výhodu, že oproti křivkám účinnosti je vyjádřena pro celý kolektor bez vlivu volby vztažné plochy (absorbér, apertura, obrysová plocha). Na druhé straně výkonovými křivkami nelze porovnat kvalitu dvou různě velkých kolektorů.
Podobně jako u fotovoltaických zařízení vznikla i v oblasti solárních tepelných kolektorů časem potřeba uvádět instalovaný výkon kolektorů nebo soustav. Dokument Evropské federace průmyslových společností v oblasti solární tepelné techniky (ESTIF) definuje okrajové podmínky pro stanovení instalovaného výkonu:
G = 1 000 W/m2, te = 20 °C, tm = 50 °C pro zasklené kolektory;
G = 1 000 W/m2, te = 20 °C, tm = 30 °C, w = 1,5 m/s pro nezasklené kolektory.
Instalovaný výkon je určen bez ohledu na sklon či orientaci kolektoru; předpokládá se kolmý dopad paprsků na aperturu kolektoru, podobně jako např. u biomasy je jmenovitý výkon kotle stanoven pro referenční palivo.
S ohledem na výsledky pro typické solární kolektory se pro potřeby přepočtu instalované plochy solárních kolektorů na instalovaný výkon používá ve statistikách zjednodušeně hodnota 0,7 kW/m2 plochy apertury kolektoru. Přepočet se v současné době používá v rámci národních (Ministerstvo průmyslu a obchodu) a mezinárodních (ESTIF) statistických zjišťování instalovaného tepelného výkonu solárních soustav.
Maximální či špičkový výkon kolektoru se stanovuje pro navrhování pojistných a zabezpečovacích zařízení solárních soustav. Norma ČSN EN 12975-2 definuje špičkový výkon solárního kolektoru jako jeden z výsledků zkoušky výkonu uváděných v protokolu. Stanoví se na základě zkoušky v ustáleném stavu podle vztahu
(2.18)
Hodnota slunečního ozáření G se uvažuje 1 000 W/m2. Podobně jako u uvádění hodnoty η0 kolektoru, pro praktické energetické zhodnocení solárního kolektoru nemá hodnota špičkového výkonu význam, neboť nevypovídá o výkonu dosahovaném za běžných podmínek provozu.
2.4.6 Křivky účinnosti různých typů kolektorů
Na současném trhu v České republice jsou dostupné různé typy solárních tepelných kolektorů o různé kvalitě. V tab. 2.1 jsou uvedeny typické konstanty různých konstrukčních druhů solárních kolektorů. V grafu na obr. 2.41 jsou pak znázorněny typické křivky účinnosti základních druhů solárních kolektorů, vyjádřené v závislosti na teplotním spádu pro hodnotu slunečního ozáření 800 W/m2. V grafu jsou zároveň vyznačeny typické rozsahy provozních teplotních rozdílů mezi střední teplotou kapaliny a okolním vzduchem v základních aplikacích.
Nezasklené kolektory se vyznačují vysokou optickou účinností, na druhé straně vysokými tepelnými ztrátami, výrazně ovlivněnými rychlostí proudění okolního vzduchu (větru). Naproti tomu u kvalitních solárních kolektorů s nízkými tepelnými ztrátami (selektivní absorbér, vakuový kolektor) klesá účinnost s rostoucím teplotním spádem velmi pomalu.
Ze srovnání křivek vyplývají některé zásady použití solárních kolektorů v daných aplikacích. Pro sezónní ohřev bazénové vody nemá smysl používat drahé trubkové vakuové Sydney kolektory, vykazující v nízkoteplotních hladinách dokonce nižší účinnost než levné nezasklené kolektory. V oblasti přípravy teplé vody a vytápění jsou trubkové vakuové kolektory a atmosférické ploché kolektory z hlediska účinnosti vztažené k ploše apertury srovnatelné. Pro průmyslové aplikace s vysokými provozními teplotami jsou nutné kolektory s velmi nízkou tepelnou ztrátou (trubkové vakuové, případně kvalitní koncentrační kolektory).
Obr. 2.41 Křivky účinnosti nejběžnějších typů solárních kolektorů
Tab. 2.1 Typické křivky účinnosti nejběžnějších druhů solárních kolektorů
| Typ kolektoru | η0 | a1 | a2 |
| – | W/m2K | W/(m2K2) | |
| Nezasklený | 0,85 | 20 | – |
| Plochý neselektivní | 0,75 | 6,5 | 0,030 |
| Plochý selektivní | 0,78 | 4,2 | 0,015 |
| Trubkový vakuový jednostěnný | 0,75 | 1,5 | 0,008 |
| Trubkový vakuový dvojstěnný (Sydney) | 0,65 | 1,5 | 0,005 |
2.4.7 Optická charakteristika – modifikátor úhlu dopadu
Rovnice křivek účinnosti a výkonu vycházejí z výsledků zkoušek tepelného chování solárního kolektoru v ustáleném stavu za definovaných podmínek: jasný den s výraznou přímou složkou slunečního záření a kolmý úhel dopadu slunečního záření na rovinu kolektoru. Takové podmínky však v běžném provozu solárního kolektoru nejsou časté, úhel dopadu slunečních paprsků na kolektory je obecně různý vlivem proměnlivé geometrie slunečního záření během dne a roku a podíl přímého záření je proměnlivý a závislý na oblačnosti. Křivka účinnosti, resp. výkonu solárního kolektoru, pro komplexní charakterizaci jeho výkonnosti proto nestačí. Vzhledem k tomu, že propustnost slunečního záření zasklení kolektoru, pohltivost absorpčního povrchu či odrazivost reflektoru jsou parametry závislé na úhlu dopadu slunečního záření, je nutné doplnit křivku účinnosti závislostí vyjadřující změnu optické účinnosti kolektoru s úhlem dopadu slunečního záření oproti kolmému úhlu dopadu. Takovou závislostí je křivka modifikátoru úhlu dopadu Kq, někdy označovaného také IAM (z angl. zkratky Incidence Angle Modifier). Závislost optické účinnosti na úhlu dopadu slunečního záření θ se u různých typů kolektorů obecně liší. Modifikátor úhlu dopadu je definován jako poměr
(2.19)
kde je
η0(θ) … optická účinnost při obecném úhlu dopadu θ;
η0(0°) … optická účinnost při kolmém úhlu dopadu (θ = 0°).
Ploché solární kolektory (ploché zasklení, plochý absorbér) mají optické vlastnosti v obou hlavních rovinách (příčné: východ-západ, podélné: jih-sever) symetrické. Prakticky tedy není důležité, ze které strany sluneční záření dopadá na kolektor, pouze hodnota úhlu dopadu θ. Průběh modifikátoru úhlu dopadu má charakteristický tvar uvedený na obr. 2.42, který lze aproximovat rovnicí
(2.20)
kde je
b0 … součinitel modifikátoru úhlu dopadu (kladná hodnota).
Přímková závislost modifikátoru na souřadnici (1/cosθ – 1) umožňuje z hodnoty modifikátoru pro jediný úhel dopadu (např. č = 50°) vypočítat součinitel b0 a získat tak rovnici křivky. Na obr. 2.42 jsou zobrazeny dvě závislosti modifikátoru úhlu dopadu, mezi kterými se pohybuje naprostá většina plochých solárních kolektorů (čiré sklo, prizmatické sklo, antireflexní sklo, dvojité sklo).
Obr. 2.42 Tvar křivky modifikátoru úhlu dopadu pro ploché solární kolektory v souřadnici θ [o] a souřadnici 1/cosθ – 1
Pro solární kolektory, které mají nesymetrickou optickou charakteristiku, např. trubkové vakuové kolektory nebo koncentrační kolektory s reflektory, se hodnoty Kθ vyhodnocují odděleně v rovině:
- podélné jako Kθ,L = Kθ(θL,0);
- příčné jako Kθ,T = Kθ(0,čT).
a výsledná závislost modifikátoru na obecném úhlu dopadu č se stanoví jako součin modifikátorů určených pro úhly dopadu v jednotlivých rovinách
(2.21)
Na obr. 2.43 je uvedena geometrie úhlů dopadu v hlavních rovinách pro jednu trubku trubkového kolektoru. Úhly čL a čT jsou průměty úhlu dopadu č do hlavních rovin a platí pro ně vztah
(2.22)
Obr. 2.43 Geometrie trubkového kolektoru a úhlů dopadu slunečního záření v hlavních rovinách
Modifikátor úhlu dopadu se experimentálně vyhodnocuje v souladu s ČSN EN 12975-2 a výsledkem je tabulka hodnot, příp. křivka v závislosti na úhlu dopadu θ. Pro určení modifikátoru se vyhodnocují hodnoty účinnosti při nulových tepelných ztrátách η0, tj. při střední teplotě kapaliny v kolektoru blízké teplotě okolního vzduchu, při různých úhlech dopadu. U plochých solárních kolektorů se kromě normálové hodnoty η0 pro kolmý dopad získané ze zkoušky výkonu určuje pouze hodnota η0 pro úhel dopadu θ = 50° a v souladu se vztahy (2.19) a (2.20) se z přímkové závislosti vypočítá součinitel b0 pro stanovení celé křivky modifikátoru. V protokolech o zkoušce plochých solárních kolektorů se proto uvádí pouze hodnota modifikátoru K50.
Obr. 2.44 Typické tvary charakteristik modifikátoru úhlu dopadu pro ploché kolektory a trubkové kolektory s plochým absorbérem
Obr. 2.45 Typické tvary charakteristik modifikátoru úhlu dopadu pro trubkové kolektory s válcovým absorbérem bez reflektoru (vlevo) a s reflektorem (vpravo)
U trubkových vakuových solárních kolektorů je nutné podrobné stanovení hodnot modifikátoru v příčné rovině (pro úhly dopadu θT nejlépe po 10°). V podélné rovině má křivka modifikátoru trubkového kolektoru stejný tvar jako u plochých kolektorů (viz řez podélnou rovinou na obr. 2.43, který je geometricky stejný jako u plochého kolektoru) a postačuje stanovit pouze η0 při θL = 50°.
Na obr. 2.44 jsou uvedeny typické průběhy křivky modifikátoru úhlu dopadu pro plochý kolektor (ploché zasklení, plochý absorbér) a trubkový solární kolektor s plochým absorbérem. Na obr. 2.45 jsou uvedeny typické průběhy křivky modifikátoru úhlu dopadu pro trubkové solární kolektory s válcovým absorbérem bez reflektoru a s reflektorem. Zvýšení hodnot modifikátoru v oblasti úhlů 50 až 60° je u různých konstrukcí kolektoru (různý průměr trubek, vzdálenost trubek, …) různé a pohybuje se od hodnoty 1,2 až do 1,6. U trubkových kolektorů s reflektorem se pro různé konstrukce může tvar křivky příčného modifikátoru Kθ,T pohybovat mezi oběma variantami (viz obr. 2.45).
Hodnoty modifikátoru úhlu dopadu Kθ je nutné vždy uvažovat v souvislosti:
- s referenční rovinou solárního kolektoru, na které uvažujeme (nebo přímo měříme) dopadající sluneční záření. U solárních kolektorů s válcovým absorbérem na referenční rovinu v odpoledních hodinách sice dopadá pod velkým úhlem již nízká hladina slunečního ozáření (nízká hodnota příkonu slunečního záření), nicméně na skutečnou plochu válcového absorbéru jde o přibližně stejnou hodnotu (podobnou hodnotu výkonu) jako v poledne. Proto pro vyšší úhly dopadu může hodnota modifikátoru narůst na hodnoty vyšší než 1,0;
- s hodnotou η0 pro kolmý úhel dopadu slunečního záření, kterou modifikátor koriguje pro jiné úhly dopadu. Solární kolektor s vysokým nárůstem hodnoty Kθ,T při vyšších úhlech dopadu, avšak nízkou hodnotou η0 nemusí vykazovat celoročně vyšší zisky než kolektor s nízkým nárůstem Kθ,T a vysokou η0. Je právě časté, že vysoká maxima hodnot Kθ,T souvisejí s nízkými hodnotami η0.
Obr. 2.46 Porovnání průběhu výkonu kolektoru s plochým a válcovým absorbérem (tm = 40 °C)
Křivka modifikátoru úhlu dopadu popisuje závislost účinnosti při nulových tepelných ztrátách η0 na úhlu dopadu směrově závislé přímé složky slunečního záření. Pro difuzní sluneční záření, které má homogenní směrovou charakteristiku (rovnoměrná intenzita záření ve všech směrech, izotropické záření), je nutné stanovit modifikátor Kη,d experimentálně kvazidynamickou metodou zkoušky podle ČSN EN 12975, nebo integračním výpočtem z křivky modifikátoru v očekávaném rozsahu úhlů dopadu (všech možných směrů). Rozsah úhlů dopadu závisí na sklonu solárního kolektoru â, který udává, z jaké poměrné části polokoule oblohy (hemisféry) solární kolektor přijímá sluneční ozáření.
Charakteristika modifikátoru úhlu dopadu se používá především v počítačových simulacích solárních soustav. Modifikátor Kθ umožňuje zohlednit vyšší zisky některých typů solárních kolektorů s trubkovým absorbérem v dopoledních a odpoledních hodinách oproti kolektorům s plochým absorbérem. Na obr. 2.46 jsou znázorněny průběhy měrného výkonu plochého atmosférického kolektoru a trubkového vakuového kolektoru s válcovým absorbérem a typickou charakteristikou účinnosti. Trubkový vakuový kolektor těží nejen z optických vlastností válcové plochy apertury a absorbéru, ale také z vyšší „citlivosti“ na nízké hladiny slunečního ozáření vlivem výrazně nižších tepelných ztrát. Nicméně tyto výhody mohou být „kompenzovány“ často výrazně nižší hodnotou η0(0°) a nižším výkonem v okolí poledne oproti plochému kolektoru.
2.4.8 Tepelná setrvačnost kolektoru
Tepelná setrvačnost solárního kolektoru ovlivňuje jeho okamžitý výkon při proměnlivých podmínkách a může mít určitý vliv na využití solárních zisků zvláště ve středoevropských klimatických podmínkách. Tepelnou setrvačnost solárního kolektoru je možné vyjádřit různými způsoby, nejčastěji určením jeho tepelné kapacity nebo časové konstanty.
Tepelná kapacita
Kolektor může být obvykle uvažován jako kombinace hmot, z nichž každá má rozdílnou teplotu. Je-li kolektor v provozu, každá jeho součást reaguje rozdílně na změnu provozních podmínek, takže je účelné uvažovat účinnou tepelnou kapacitu pro celý kolektor. Účinná tepelná kapacita však závisí na provozních podmínkách a není konstantní hodnotou.
Výpočtově je možné účinnou tepelnou kapacitu solárního kolektoru v J/K zjednodušeně stanovit jako součet tepelných kapacit jednotlivých součástí kolektoru (sklo, absorbér, obsah kapaliny, izolace) s ohledem na jejich celkový vliv podle vztahu
(2.23)
kde je
pi … váhový součinitel pro i-tou součást kolektoru;
mi … hmotnost i-té součásti kolektoru, v kg;
ci … měrná tepelná kapacita i-té součásti kolektoru, v J/(kg·K).
Tab. 2.2 Hodnoty váhových součinitelů pro určení tepelné kapacity kolektorů
| Součásti kolektoru | pi |
| Absorbér | 1,0 |
| Tepelná izolace | 0,5 |
| Teplonosná kapalina | 1,0 |
| Vnější zasklení | 0,01·a1 |
| Druhé zasklení | 0,2·a1 |
| Třetí zasklení | 0,3·a1 |
Hodnoty váhových součinitelů pro jednotlivé části solárního kolektoru jsou uvedeny v tab. 2.2. Váhový součinitel pi (hodnoty mezi 0 a 1) respektuje skutečnost, že určité díly se jen částečně podílejí na tepelné setrvačnosti kolektoru. Součinitel a1 uvedený v tab. 2.2 je hodnota lineárního součinitele tepelné ztráty kolektoru, která se získá jako jedna z konstant křivky účinnosti vyhodnocení v rámci zkoušky tepelného výkonu solárního kolektoru.
Zatímco hodnoty tepelné kapacity plochých solárních kolektorů a jednostěnných trubkových vakuových kolektorů vztažené na plochu apertury Ce/Aa se pohybují řádově mezi 2 a 5 kJ/(m2·K), u trubkových Sydney kolektorů jsou hodnoty několikanásobně vyšší, mezi 10 až 40 kJ/(m2·K).
Časová konstanta kolektoru
Časová konstanta vyjadřuje tepelnou setrvačnost kolektoru jako rychlost odezvy na změnu podmínek vlivem tepelné kapacity jeho částí. Je definována jako čas potřebný ke změně teploty teplonosné látky na výstupu z kolektoru o 63.2 % z celkové hodnoty teplotní změny z původní teploty na novou ustálenou hodnotu po skokové změně dopadajícího slunečního záření či vstupní teploty.
Obr. 2.47 Stanovení časové konstanty při chladnutí kolektoru (vlevo) a při ohřívání kolektoru (vpravo)
Časová konstanta závisí na provozních podmínkách, především na průtoku teplonosné kapaliny kolektorem. Hodnoty časové konstanty běžných solárních kolektorů se pohybují řádově v minutách a je tedy možné jejich chování pro výpočty solárních soustav s výhodou popisovat stacionárními modely.
Časová konstanta se stanovuje experimentálně za ustálených podmínek s konstantní vstupní teplotou teplonosné látky tk1 blízkou teplotě okolí te. Solární kolektor je náhle zastíněn od dopadajícího slunečního záření a je sledován pokles výstupní teploty jako funkce času, nebo naopak stíněný kolektor v ustáleném stavu je náhle vystaven slunečnímu záření a sledován je nárůst výstupní teploty na novou ustálenou hodnotu. Časová konstanta kolektoru τc je potom čas, při němž je dosaženo rovnosti
při chladnutí kolektoru
(2.24)
případně
při ohřívání kolektoru
(2.25)
kde je
tk2(τ = 0) … výstupní teplota na výstupu z kolektoru v době začátku zkoušky (zakrytí nebo odkrytí kolektoru), ve °C;
tk2(τ = τc) … výstupní teplota v čase τc, ve °C;
tk2(τ = ∞) … nová ustálená teplota na výstupu z kolektoru, ve °C.
2.4.9 Výkonnost solárních kolektorů
Výkonnost solárních kolektorů je možné definovat jako schopnost kolektoru produkovat energetický zisk za stanovených podmínek. S ohledem na očekávání uživatelů solárních soustav je vhodné hodnotit celoroční měrný tepelný zisk za typických místních klimatických a provozních podmínek. Pro hodnocení výkonnosti solárních kolektorů existuje řada přístupů, které hodnotí celoroční produkci tepla z kolektoru simulačním výpočtem s využitím křivky účinnosti, křivky modifikátoru úhlu dopadu kolektoru, popřípadě tepelné kapacity jako vstupních údajů a databáze hodinových klimatických údajů (sluneční ozáření G, venkovní teplota te). Mezi základní přístupy patří:
- solární kolektor zapojený do přesně definované solární soustavy s daným solárním pokrytím, např. model pro určení minimálního zisku kolektoru v solární soustavě pro přípravu teplé vody se 40% pokrytím pro udělení známky Modrý anděl (Německo) nebo simulační výpočet zkušebny SPF Rapperswil (Švýcarsko) ve třech typických aplikacích s definovaným solárním pokrytím: solární předehřev teplé vody (25 %), solární příprava teplé vody (60 %), kombinovaná soustava pro přípravu teplé vody a vytápění (25 %);
- solární kolektor nezapojený do solární soustavy, avšak s definovanou a celoročně stálou provozní teplotou: simulační výpočet zkušebny SP Boras (Švédsko) pro provozní teploty 25 °C, 50 °C, 75 °C, nebo stanovení křivky měrných teoretických zisků v simulačním modelu VYKON_SK Solární laboratoře ČVUT v Praze, který je dále podrobněji popsán.
Simulační model VYKON_SK hodnotí výkonnost (roční teoretické zisky kolektoru) jako parametr vlastní solárnímu kolektoru bez ohledu na provedení zbytku solární soustavy a bez ohledu na využitelnost produkovaných zisků v závislosti na podmínkách odběru tepla aplikace. Program na základě parametrů kolektoru stanovuje pro každou hodinu teoreticky dostupný měrný výkon solárního kolektoru v závislosti na úhlu dopadu slunečního záření a na klimatických podmínkách pro celoročně konstantní teplotu tm podle vztahu
(2.26)
Pro vyhodnocení celoročního teoreticky dostupného energetického zisku solárního kolektoru jsou kladné hodinové energetické zisky sečteny a záporné nejsou uvažovány. Vstupními údaji pro simulační model VYKON_SK jsou:
- konstanty křivky účinnosti solárního kolektoru η0, a1 a a2 stanovené zkouškou v souladu s ČSN EN 12975;
- hodnoty modifikátoru úhlu dopadu solárního kolektoru stanovené pro obě hlavní roviny (podélná, příčná) v rozsahu 0° až 90° v rozlišení po 10° v souladu s ČSN EN 12975;
- hodinové klimatické údaje: celkové sluneční ozáření na horizontální rovinu G, teplota venkovního vzduchu te (databáze typického meteorologického roku TMY pro Prahu);
- uvažovaný sklon a orientace solárního kolektoru.
Výpočet je v programu proveden postupně pro střední teploty kapaliny v kolektoru 10 až 120 °C v rozlišení po 10 K. Z výsledků je vynesena křivka výkonnosti kolektoru v závislosti na provozní teplotě (viz obr. 2.48).
Výpočet simulačním modelem VYKON_SK lze použít především pro srovnání:
- výkonnosti daného kolektoru pro různé orientace a sklony;
- výkonnosti různých kolektorů při daném sklonu a orientaci.
pro zvolenou očekávanou provozní teplotu kapaliny tm v solárních kolektorech, např. 40 °C nebo celý rozsah provozních teplot.
Obr. 2.48 Křivky výkonnosti kolektoru v závislosti na provozní teplotě pro různé orientace
V grafu na obr. 2.49 jsou porovnány roční měrné zisky uvedených solárních kolektorů pro střední teplotu kapaliny v kolektorech 40 °C jako výstup z výpočtu v modelu VYKON_SK. Tepelné zisky solárních kolektorů jsou jednak vztaženy k ploše apertury (aby bylo možné srovnávat obdobné konstrukce mezi sebou) a jednak k obrysové ploše (srovnání tepelného zisku ze skutečně zabrané plochy na střeše).
Jako referenční solární kolektor byl zvolen běžný plochý atmosférický kolektor PK3. Z porovnání výkonnosti kolektorů vztažené k ploše apertury vyplývá, že v případě běžných aplikací s provozní teplotou tm = 40 °C produkují kvalitní trubkové vakuové kolektory bez reflektoru ročně o cca 20 až 30 % více energie než běžné ploché kolektory, nicméně méně kvalitní kolektory stejného typu mohou vykazovat stejný, případně i o 30 % menší zisk. Trubkové kolektory s reflektorem vykazují v porovnání výsledky lepší. Vzhledem ke spolehlivé kvalitě trubkových kolektorů s plochým absorbérem lze předpokládat, že jejich o 30 % vyšší výkonnost oproti plochým kolektorům platí pro tento konstrukční typ obecně.
Odlišná je situace v případě vztažení výkonnosti solárních kolektorů k obrysové ploše při zjišťování energetického potenciálu dostupné plochy na střeše. Rozdíly mezi referenčním plochým kolektorem a trubkovými vakuovými kolektory obecně nejsou již tak výrazné (okolo 10 % u kvalitních trubkových kolektorů). Navíc, zvláště trubkové kolektory typu Sydney bez reflektoru mohou vykazovat vzhledem k vysokému podílu neúčinné plochy (až 40 %) výrazně nižší výkonnost (některé varianty i o více než 30 %) než referenční plochý kolektor.
Poměry se výrazně změní při vysokých provozních teplotách využitelných například pro solární chlazení, viz obr. 2.50. Neselektivní plochý kolektor vykazuje zcela zanedbatelný zisk. Oproti plochému atmosférickému kolektoru vykazují kvalitní trubkové vakuové kolektory více než 50% přínos i při vztažení zisků k hrubé ploše kolektoru. Stejně tak ovšem platí, že méně kvalitní trubkové kolektory dostupné na trhu ani při této vysoké teplotě výkonnosti plochého kolektoru nedosáhnou.
Obr. 2.49 Roční měrné zisky srovnávaných solárních kolektorů podle apertury (modrý levý sloupec) a podle obrysové plochy (šedý pravý sloupec)
Obr. 2.50 Roční měrné zisky srovnávaných solárních kolektorů podle apertury (modrý levý sloupec) a podle obrysové plochy (šedý pravý sloupec)
Z výše uvedeného vyplývá v první řadě výrazná variabilita energetické kvality různých trubkových vakuových kolektorů s válcovým absorbérem a její dopad na potenciální tepelné zisky trubkových solárních kolektorů, které v řadě případů mohou být lepší než u plochých kolektorů, ale v řadě případů dostupných na trhu také výrazně horší. Při srovnávání energetické kvality solárních kolektorů nelze paušálně označit určitý konstrukční druh za více či méně ziskový v porovnání s jinými bez znalosti základních parametrů kolektoru (křivka účinnosti a křivka modifikátoru) pro konkrétní případy a konkrétní účel hodnocení (provozní teplota, hodnocení podle typu referenční plochy).
2.5 ZKOUŠENÍ A CERTIFIKACE SOLÁRNÍCH KOLEKTORŮ
2.5.1 Normy
V české a evropské normalizaci existují pro solární tepelné kolektory dvě normy, týkající se kapalinových solárních kolektorů, které vycházejí z původnějších norem ISO 9806 pro zkoušení zasklených a nezasklených kapalinových kolektorů:
ČSN EN 12975-1:2011 (73 0301) Tepelné solární soustavy a součásti – Solární kolektory – Část 1: Všeobecné požadavky, která určuje požadavky na odolnost (včetně mechanické pevnosti), spolehlivost a bezpečnost kapalinových tepelných solárních kolektorů. Rovněž obsahuje návody k hodnocení shody s těmito požadavky. ČSN EN 12975-2:2006 (73 0301) Tepelné solární soustavy a součásti – Solární kolektory – Část 2: Zkušební metody, která detailně popisuje zkušební metody a podmínky, za kterých jsou solární kolektory zkoušeny.
Norma je určena pro ploché i trubkové kolektory. Je v zásadě použitelná pro soustřeďující kolektory, od nenatáčivých nezobrazujících koncentrátorů jako jsou složené parabolické koncentrátory (CPC) po vysoce soustřeďující natáčivé konstrukce. Norma není určena pro kolektory s vestavěným zásobníkem tepla.
Mezi zkoušky solárních kolektorů požadované podle EN 12975 patří zkoušky:
a) vnitřní přetlak v absorbéru;
b) odolnost proti vysokým teplotám;
c) vystavení vlivům prostředí;
d) vnější tepelný ráz;
e) vnitřní tepelný ráz;
f) odolnost proti dešti (jen pro zasklené kolektory);
g) mechanické zatížení;
h) tepelný výkon;
i) odolnost proti mrazu (nepovinná, pouze pro mrazuvzdorné kolektory);
j) odolnost proti nárazu (nepovinná).
Zatímco zkoušky a) až g) jsou mechanické zkoušky odolnosti a bezpečnosti, zkouška h) hodnotí účinnost solárního kolektoru při různých okrajových podmínkách. Nicméně současná legislativa nenařizuje, aby solární kolektor vstupující na trh splnil požadavky zkušební normy. Výrobce solárních kolektorů tedy nemusí mít kolektory vyzkoušeny podle výše uvedených zkoušek. Nemusí uvádět ve svých podkladech ani výkonové parametry kolektoru (křivku účinnosti solárního kolektoru), ačkoli jsou základem výpočtů pro návrh a hodnocení solárních soustav.
2.5.2 Zkoušky spolehlivosti
Norma EN 12975-1 určuje požadavky na odolnost (včetně mechanické pevnosti), spolehlivost a bezpečnost kapalinových tepelných solárních kolektorů. Rovněž obsahuje návody k hodnocení shody s těmito požadavky. Norma EN 12975-2 pak určuje metody spolehlivostních zkoušek.
Vnitřní přetlak v absorbéru
Absorbér solárního kolektoru je zkoušen pro posouzení rozsahu, ve kterém odolává tlakům předpokládaným v provozu. Anorganické absorbéry (zpravidla kovové) jsou tlakově zkoušeny při okolní teplotě v rozmezí 5 °C až 30 °C. Organické absorbéry jsou zkoušeny při zvýšené teplotě, protože tlaková odolnost absorbéru z organických materiálů může být nepříznivě ovlivněna zvyšující se teplotou. Zkušební teplota se u organických absorbérů rovná maximální teplotě, kterou může absorbér dosáhnout za klidových podmínek (stagnační teplota).
Zkušební tlak je 1,5 násobkem nejvyššího pracovního tlaku kolektoru určeného výrobcem. U neorganických absorbérů se zkušební tlak udržuje po dobu 15 minut, u organických se postupně zvyšuje po 20 kPa s prodlením 5 minut na každé tlakové úrovni. Zkušební tlak je udržován nejméně po dobu 1 hodiny.
Solární kolektor se poté zkontroluje na netěsnosti, vydutí a zkroucení. Výsledky prohlídky musí být zaznamenány. Podrobný popis podmínek zkoušky je uveden v normě.
Vystavení vysokým teplotám
Účelem této zkoušky je rychlé hodnocení, zda kolektor odolává vysokým úrovním slunečního ozáření bez poškození, jako jsou prasknutí nebo zhroucení krytu, roztavení absorbéru (z plastu) nebo významné úsady na krytu kolektoru, způsobené zplynováním materiálu kolektoru. Nenaplněný, avšak uzavřený kolektor se zkouší ve vnějším prostředí nebo v simulátoru slunečního ozáření za definovaných klimatických podmínek: sluneční ozáření G > 1 000 W/m2, venkovní teplota te = 20 až 40 °C a rychlost proudění okolního vzduchu w < 1 m/s.
Solární kolektor se poté zkontroluje na degradaci, smrštění, zplynování materiálu a zkroucení. Výsledky prohlídky se zaznamenají spolu s průměrnými hodnotami klimatických podmínek. Zkouška se často spojuje s určením klidové (stagnační) teploty. Podrobný popis podmínek zkoušky je uveden v normě.
Vystavení vlivům prostředí
Zkouška vystavení vnějším vlivům poskytuje zkušební postup s nízkými náklady za provozních podmínek, které pravděpodobně nastanou při skutečném provozu a které naznačují, že kolektor vyhoví dalším spolehlivostním zkouškám, dávajícím pravděpodobnější opakovatelné výsledky.
Nenaplněný uzavřený kolektor se při zkoušce vystaví vlivům venkovního prostředí nejméně po dobu 30 dnů, v nichž je dosažena denní dávka slunečního ozáření H > 14 MJ/m2. Dny nemusejí následovat nepřetržitě po sobě. Dále je vystaven pod dobu alespoň 30 hodin podmínkám: úroveň slunečního ozáření G > 850 W/m2 a teplota okolního vzduchu te > 10 °C. Tyto hodiny by se měly skládat z úseků nejméně 30 minut dlouhých.
Solární kolektor se poté zkontroluje na poškození a degradaci. Výsledky prohlídky se zaznamenají spolu s klimatickými údaji v průběhu zkoušky. Zkoušku lze kombinovat se zkouškou odolnosti vnějším a vnitřním tepelným rázům (zkouší se dvakrát během prvních a posledních 10 z 30 hodin). Podrobný popis podmínek zkoušky je uveden v normě.
Vnější tepelný ráz
Solární kolektory mohou být občas vystaveny v horkých slunečných dnech náhlým přívalům deště, které způsobují prudký vnější tepelný ráz. Tato zkouška se zaměřuje na hodnocení schopnosti kolektoru odolávat takovým tepelným rázům bez poškození.
Solární kolektor je udržován pod vysokou úrovní slunečního ozáření G > 850 W/m2 ve venkovním prostředí nebo v simulátoru a při teplotě okolí te > 10 °C po dobu 1 hodiny před započetím vodního skrápění. Poté je kolektor chlazen vodním proudem o teplotě nižší než 25 °C s průtokem 0,03 až 0,05 kg/(s·m2) apertury kolektoru po dobu 15 minut. Kolektor se podrobí celkem dvěma vnějším tepelným rázům.
Solární kolektor se poté zkontroluje na jakékoli praskliny, zkroucení, kondenzaci, průnik vody nebo ztrátu vakua. Výsledky prohlídky se zaznamenají společně s klimatickými údaji a zkušebními podmínkami (teplota a průtok skrápějící vody). Podrobný popis podmínek zkoušky je uveden v normě.
Vnitřní tepelný ráz
Zkouška je zaměřena na hodnocení schopnosti solárního kolektoru odolat tepelným rázům způsobených náhlým vstupem chladné teplonosné kapaliny v horkých slunečných dnech bez poškození. Taková situace může v provozu nastat například po období odstávky při uvádění do chodu, kdy se kolektor nachází při své klidové teplotě.
Nenaplněný kolektor se při zkoušce udržuje pod vysokou úrovní slunečního ozáření G > 850 W/m2 ve venkovním prostředí nebo v simulátoru a při teplotě okolí te > 10 °C po dobu 1 hodiny před ochlazením teplonosnou kapalinou, která je poté dodávána po dobu nejméně 5 minut, dokud teplota absorbéru nepoklesne pod 50 °C. Teplonosná kapalina musí mít teplotu nižší než 25 °C. Doporučený průtok kapaliny je nejméně 0,02 kg/(s·m2) apertury kolektoru (pokud není výrobcem stanoveno jinak). Kolektor se podrobí celkem dvěma vnitřním tepelným rázům.
Solární kolektor se poté zkontroluje na jakékoli praskliny, zkroucení, deformace, průnik vody nebo ztrátu vakua. Výsledky prohlídky se zaznamenají společně s klimatickými údaji a zkušebními podmínkami (teplota a průtok teplonosné kapaliny). Podrobný popis podmínek zkoušky je uveden v normě.
Průnik deště
Zkouška je použitelná pouze pro zasklené solární kolektory a slouží ke zhodnocení rozsahu, ve kterém jsou zasklené kolektory odolné proti průniku deště. Kolektory nesmí dovolit průnik buď volně padajícího, nebo pohybujícího se deště. Kolektory mohou mít větrací otvory nebo odvodňovací otvory, ty však nesmí dovolit průnik proudícího deště.
Solární kolektor je při zkoušce skrápěn na exponovaných stranách s použitím rozprašovacích trysek nebo sprch vodou o teplotě nižší než 30 °C o průtoku větším než 0,05 kg/(s·m2) sprchované plochy, zatímco absorbér v kolektoru je udržován v teplém stavu (nejméně 50 °C). Zkouška trvá 4 hodiny. Průnik vody do kolektoru se stanoví kontrolou (prohlédnutím výskytu vodních kapek, kondenzace na krycím sklu nebo ostatních viditelných známek vody) a některou z normou předepsaných metod:
- vážením kolektoru;
- měřením absolutní vlhkosti ve vzduchové mezeře mezi absorbérem a zasklením;
- měřením úrovně kondenzace na krycím sklu.
Solární kolektor se poté zkontroluje na průnik vody. Výsledky prohlídky, tj. rozsah průniku vody a místa, kde voda pronikla, se zaznamenají. Podrobný popis podmínek zkoušky je uveden v normě.
Mechanické zatížení
Zkouška je zaměřena na zhodnocení rozsahu, ve kterém transparentní kryt solárního kolektoru je schopen odolat kladnému tlakovému zatížení od účinků větru a sněhu.
Na vodorovně umístěný kolektor se do rámu v postupných krocích přidává materiál (sypký materiál – štěrk, voda, jiné prostředky, např. tlak vzduchu), kterým se vyvozuje stejnoměrné zatížení na kryt. Zkušební tlak se zvyšuje po největších krocích 250 Pa, dokud se neprojeví vada, nebo až na hodnotu stanovenou výrobcem. Zkušební tlak je nejméně 1 kPa. Závadou může být rozlámání krytu, také deformace skříně kolektoru nebo úchytů. Podrobný popis podmínek zkoušky je uveden v normě.
Obr. 2.51 Zkouška průniku deště, zdroj ITW, ISE/ESTIF
Obr. 2.52 Zkouška mechanického zatížení, zdroj ITW, ISE/ESTIF
Vystavení mrazu
Zkouška je zaměřena na hodnocení rozsahu, v jakém vodní solární kolektory, prohlášené za mrazuvzdorné, odolávají mrazu a cyklům zmrazování/rozmrazování (například drain-back kolektory). Zkouška není určena pro solární kolektory; v jejich montážním návodu je jasně stanoveno, že smí být používány jedině s nemrznoucí kapalinou.
Solární kolektory se zkouší na mrazuvzdornost:
- při plnění vodou – kolektor se naplní vodou o pracovním tlaku a cyklicky se zmrazuje na -20 ± 2 °C (po dobu 30 minut) a rozmrazuje při 10 °C (po dobu 30 minut), celkem ve třech cyklech zmrazování/rozmrazování;
- při vypouštění vody – kolektor využívající vypouštění k ochraně před zamrznutím je naplněn vodou, udržován při pracovním tlaku po dobu 10 minut a potom vypuštěn spoužitím přístrojů instalovaných výrobcem. Poté se provede cyklické zmrazování/rozmrazování.
Počet provedených cyklů se zaznamená. Kolektor se poté zkontroluje na netěsnosti, poškození, zkroucení a deformace. Výsledky prohlídky jsou zaznamenány spolu s teplotami absorbéru, dosaženými při teplotních cyklech a časy, po které byl kolektor podroben zkušebním teplotám. Podrobný popis podmínek zkoušky je uveden v normě.
Vystavení nárazu (krupobití)
Zkouška je zaměřena na hodnocení rozsahu, ve kterém solární kolektor může odolat účinkům těžkých nárazů způsobených kroupami. Kroupy jsou ve zkoušce nahrazeny ocelovými nebo ledovými kuličkami.
Ocelová kulička o hmotnosti 150 g se pouští na vodorovný kolektor pádem nebo na skloněný kolektor kyvadlem 10krát z první zkušební výšky (0,4 m), dále 10krát z druhé zkušební výšky (0,6 m) atd. Postup se opakuje z výšek po 0,2 m, dokud není dosažena největší zkušební výška 2 m. Zkouška je ukončena, jestliže kolektor utrpí nějaké poškození nebo jestliže kolektor odolá nárazu 10 ocelových kuliček z největší zkušební výšky. Metoda neodpovídá přesně fyzikálnímu účinku krup, protože se neuvažuje deformační energie pohlcená částicemi ledu.
Ledové kuličky o průměru 25 mm, vyrobené ve formách v mrazicím zařízení (-10 °C), vyhovující velikostí, hmotností a bez prasklin se umístí do zásobníku (teplota -4 °C) a ponechají se tam nejméně 1 hodinu před použitím. Ze spouštěcího zařízení se ledová kulička odpaluje na kryt kolektoru 10krát; zkouška je ukončena, jestliže kolektor utrpí nějaké poškození, nebo jestliže kolektor odolá nárazu 10 ledových kuliček. Metoda je svou podstatou blíže skutečnosti a je upřednostňována.
Solární kolektor se poté zkontroluje na poškození. Výsledky prohlídky se zaznamenají spolu s výškou, ze které byly spouštěny ocelové kuličky, byly-li použity, a počet nárazů, který způsobil poškození. Podrobný popis podmínek zkoušky je uveden v normě.
2.5.3 Značka CE
Právní předpisy nenařizují, aby solární kolektor jako výrobek vstupující na trh splnil požadavky normy. Normy pro solární kolektory nejsou zatím v Evropě harmonizované, nelze tedy vyhlásit shodu solárního kolektoru s technickými požadavky normy a nelze označit solární kolektor značkou CE. V normalizace se v současné době očekává změna v souvislosti s plánovaným sjednocením normy EN 12975 a ISO 9806.

Obr. 2.53 Značka CE
Ani v oblasti působnosti evropské směrnice 27/93/EC o tlakových zařízeních (PED) nelze běžné solární kolektory označit značkou CE vzhledem k jejich velmi malému objemu (součin tlaku a objemu p·V < 50 bar·litr), s výjimkou některých velkoplošných kolektorů. Solární kolektor je sice podle pravidel směrnice prohlášen za tlakové zařízení, avšak nespadající do její kompetence. Na druhé straně neoprávněné označení solárního kolektoru CE značkou může být postiženo sankcí ze strany České obchodní inspekce podle zákona č. 22/1997 Sb.
Ve snaze pomoci zákazníkům v orientaci v nepřeberném množství nabízených druhů a typů solárních kolektorů a soustav a pro zvýšení jejich důvěry v instalace solárních soustav se proto objevují různé dobrovolné certifikační systémy, které umožňují zhodnotit kvalitu provedení kolektorů z hlediska trvanlivosti nebo energetické výkonnosti (účinnost, zisky), případně komplexně zhodnotit vliv solárního kolektoru na životní prostředí.
2.5.4 Solar Keymark
Nejznámějším certifikačním systémem v oblasti solárních kolektorů je Solar Keymark. Značka Solar Keymark je systém dobrovolné certifikace třetí stranou, zavedený Evropskou komisí pro normalizaci (CEN) ve spolupráci s Evropskou federací pro průmysl solární tepelné techniky (ESTIF). Solar Keymark je jednou z oficiálních značek certifikačního systému CEN (systém Keymark), kterou se konstatuje splnění požadavků evropských norem.

Obr. 2.54 Logo
Solar Keymark v současné době pokrývá především dvě oblasti:
- solární tepelné kolektory definované podle EN 12975;
- průmyslové vyráběné solární tepelné soustavy definované podle EN 12976.
Značka Solar Keymark zákazníkovi jednoduše sděluje, že takto označený solární kolektor nebo soustava splňuje požadavky příslušných evropských norem, tedy prošel všemi zkouškami v souladu s uvedenými normami. Ve své podstatě Solar Keymark znamená poskytnutí informace o funkční kvalitě kolektoru nebo soustavy a informace o jejich účinnosti pro projektanta, ochranu koncového zákazníka před nekvalitním produktem a obchodní nástroj pro výrobce nebo dodavatele. Pro koncového zákazníka je Solar Keymark určitou zárukou, že funkční vlastnosti zakoupeného kolektoru a jeho deklarovaná účinnost se během doby použití významně nezmění. Značka však neznamená, že certifikovaný kolektor je vysoce výkonný výrobek se špičkovými energetickými parametry. Značka pouze poskytuje informaci, že deklarovanou křivku účinnosti budou mít všechny kolektory z výrobní řady (reprodukovatelnost vlastností), ne pouze zkoušený kolektor. Na obr. 2.55 a obr. 2.56 jsou uvedeny křivky účinnosti vybraných plochých a trubkových kolektorů certifikovaných v rámci systému Solar Keymark a je patrné, že certifikát mají i kolektory s vysokými optickými a tepelnými ztrátami.
Obr. 2.55 Výkonové parametry plochých solárních kolektorů certifikovaných značkou Solar Keymark
Obr. 2.56 Výkonové parametry trubkových solárních kolektorů certifikovaných značkou Solar Keymark
Postup a pravidla
Žadatel (výrobce) kontaktuje certifikační orgán, akreditovaný a zmocněný Certifikačním výborem CEN pro udělování značky Solar Keymark. Společně s certifikačním orgánem je vybrána zkušební laboratoř a inspekční orgán. Zkušební laboratoř musí splňovat podmínky pro komplexní zkoušky v rámci Solar Keymark a je schválena certifikačním orgánem. Zmocněných zkušeben je v současné době okolo 30, z toho některé jsou i mimo Evropu (např. USA, Austrálie nebo Čína).
Na solárním kolektoru, jehož vzorek je náhodně vybrán přímo z výroby nebo skladu výrobce, se provedou počáteční, tzv. vstupní zkoušky. Vzorky vybírá inspektor, identifikuje podle výrobních čísel a buď je sám odveze, nebo je označí, zapečetí a nechá dopravit do zkušební laboratoře. Zároveň výrobce prokazuje systém řízení jakosti podle norem řady EN ISO 9000. Certifikačnímu orgánu musí výrobce dodat jednoznačnou výrobní dokumentaci ke zkoušenému zařízení. V případě konstrukčně stejných kolektorů, odlišujících se pouze rozměry (délka, šířka), se vybírá pouze nejmenší a největší vzorek kolektoru. Největší vzorek se podrobí všem zkouškám, nejmenší pouze zkoušce tepelného výkonu, neboť malý rozměr je z energetického hlediska nejnevýhodnější. U kolektorů stavěných na zakázku a sestavovaných přímo na místě instalace musí výrobce prokázat shodu zkušebního modulu s obvyklou výrobou a dodat podrobný popis použitých prvků. Pokud se na certifikovaném kolektoru provedou změny, je nutné upozornit certifikační orgán a ten na základě rozsahu změn stanoví, zda je potřeba provést znovu vstupní zkoušky, nebo pouze dílčí.
Certifikace
Solar Keymark může být vystaven pouze zplnomocněným certifikačním orgánem poté, co byl solární kolektor (solární kolektor, solární soustava) odzkoušen akreditovanou zkušební laboratoří. Pokud výrobce má zaveden systém řízení jakosti a jeho kolektor nebo soustava splňují kvalitativní požadavky EN 12975 nebo EN 12976, je výrobku udělena značka Solar Keymark. Značku je možné uvádět v podkladech a na výrobcích. Podle pravidel značky se každoročně kontroluje dokumentace systému řízení jakosti a každé dva roky inspektor ze zkušební laboratoře vykoná fyzickou prohlídku výroby a shodu výkresové dokumentace s vyráběným kolektorem. V případě pochyb může nařídit opakovanou zkoušku kolektoru. Tu ostatně může vyvolat kdokoli, od nespokojeného zákazníka až po konkurenta na trhu. Aby byla opakovaná zkouška úspěšná, musí prokázat shodu výkonových parametrů do 10 % a opětovné splnění kvalitativních požadavků na solární kolektor (spolehlivostní zkoušky). V případě úspěšné certifikace hradí náklady vyvolavatel zkoušky, v případě neúspěšné certifikace hradí náklady výrobce a značka Solar Keymark je navíc výrobku odebrána.
Z postupu a pravidel udělování certifikátu Solar Keymark je zřejmé, že systém je zaměřen na kontrolu kvality solárních kolektorů, resp. průmyslové vyráběných solárních soustav. V současné době (2011) je certifikováno přes 1 500 typů solárních kolektorů. Značkou Solar Keymark je označeno zhruba 2/3 z prodaných solárních kolektorů v Evropě. Solar Keymark je uznávanou evropskou i mezinárodní značkou, která je v některých zemích podmínkou udělení dotací na solární kolektory (Německo, Švédsko Slovensko, aj.).
Důvodem zavedení značky Solar Keymark je snaha, aby výrobci (exportéři) nemuseli opakovaně zkoušet a certifikovat výrobky podle národních certifikačních programů jednotlivých států. Zavedení značky Solar Keymark jim přináší úsporu nákladů na zkoušení (pouze jedna zkouška). Na druhé straně je certifikační proces natolik finančně náročný, že pro menší výrobce solárních kolektorů je prakticky nedostupný.
2.5.5 Modrý anděl (RAL-UZ 73)
Modrý anděl (Der Blaue Engel) je známá ekologická známka, udělovaná německou Spolkovou agenturou pro životní prostředí výrobkům splňujícím základní kritéria definovaná asociací RAL. V případě solárních kolektorů se jí označují takové výrobky, které umožňují produkcí energie významně uspořit konvenční zdroje energie (fosilní, jaderné) a s její spotřebou svázané emise škodlivin.

Obr. 2.57 Logo
Kromě splnění ekologických požadavků směrnice na kolektor je podmínkou pro udělení značky dosažení kritéria minimálního měrného ročního tepelného zisku kolektorů (nikoli solární soustavy) qk = 525 kWh/(m2·rok) v přesně definované referenční solární soustavě s určeným solárním pokrytím 40 % za klimatických podmínek lokality Würzburg. Referenční solární soustava a provozní podmínky pro výpočet kritéria roční produkce energie jsou definovány v tab. 2.3. Odchylky vstupních hodnot modelu od stanovených podmínek se povolují pouze, pokud snižují roční produkci tepla solárním kolektorem. Výpočet může provádět každá autorizovaná zkušební instituce s využitím jakéhokoliv simulačního programu, který byl uzpůsoben pro simulaci referenční solární soustavy na základě referenčního modelu v programu TRNSYS, schváleného alespoň dvěma nezávislými autorizovanými zkušebními institucemi.
Je dobré si v této souvislosti uvědomit, že stanovená hodnota zisku kolektorů platí pouze a jen pro tuto soustavu. Pro běžnou projekční praxi nemá význam, neboť 99,9 % projektovaných solárních soustav pracuje s odlišnými provozními podmínkami. Stanovená hodnota je pouze ukazatelem energetické kvality kolektoru. V Německu je Modrý anděl jednou z podmínek pro udělení dotační podpory na solární kolektory. Postup směrnice pro výpočet minimálního měrného tepelného zisku solárního kolektoru převzal zkušební ústav TSU Piešťany (Slovensko) v návaznosti na kritérium pro udělení dotace v rámci slovenského programu podpory solárních instalací. Výpočet se provádí pro klimatické údaje lokality Piešťany.
Tab. 2.3 Parametry referenční solární soustavy a provozní podmínky RAL-UZ 73
| Lokalita | Würzburg, 49,8° severní šířky |
| Počasí | TMY nebo ekvivalentní klimatická databáze |
| Orientace kolektoru | jižní, sklon kolektoru podle stupně šířky |
| Plocha kolektoru | musí zaručit 40% pokrytí potřeby tepla (výsledek výpočtu mezi 39,5 a 40,5 %) |
| Parametry kolektoru | podle DIN nebo ISO na základě zkoušky autorizovanou zkušební institucí |
| Referenční plocha | podle DIN 4757-4 |
| Činitel úhlové korekce | podle měření v rámci DIN 4757-4, nebo podle uznaného výpočetního modelu |
| Hmotnostní průtok kolektorem | zkušební průtok kolektorem nebo 50 l/(h·m2), u kolektorů určených pro low-flow provoz lze použít průtoků nižších |
| Teplonosná látka | podle zkušebních podmínek, nebo 30% směs propylenglykolu s vodou |
| Řízení čerpadla | spínání čerpadla při rozdílu teplot ΔT = 2 K mezi výstupem kolektoru a teplotou zásobníku v oblasti teplosměnné plochy |
| Potrubní rozvod | přívodní a zpětné potrubí vedené vnitřním a vnějším prostředím: 7,5 m každé, DN 16 s 25 mm tepelné izolace (λ = 0,04 W/mK). Ztráty se stanovují vůči vnitřní, resp. venkovní teplotě |
| Výměník tepla | vnořený tepelný výměník z hladkých trubek s UA = 400 W/K (±15 %) při 42 °C / 40 °C (vstupní teplota / teplota zásobníku) |
| Zásobník | objem: 300 l; tepelná ztráta: 2,2 W/K; poměr výška/průměr: 2,5; pohotovostní část 135 l na 47 °C |
| Teplota studené vody | 10 °C |
| Vnitřní teplota | 15 °C |
| Referenční odběr | 200 l/den při 45 °C, (pokud je teplota zásobníku > 45 °C, přimíchává se studená voda pro dosažení 45 °C; odběr odpovídá 2950 kWh/rok ±10 kWh/rok), odběrový průtok 10 l/min podle ISO 9459-5 |
| Odběrový profil | v 7.00 ráno a v 7.00 večer se odebere 40 % a v poledne 20 % denního odběru teplé vody |
2.6 LITERATURA
[1] BUFKA, A., Solární kolektory – Výsledky statistického zjišťování pro roky 2004-2010. MPO: 2011.
[2] DUFFIE, J., A., BECKMAN, W., A., Solar enginnering of thermal processes. 3. vydání. Wiley: 2006, ISBN 13-978-0-471-69867-8.
[3] JIRKA, V., Skleněné rastry pro stavebnictví a architekturu – využití v modulárním skleníku v Třeboni, ČVUT v Praze. ISBN 978-80-01-04288-5. 2009.
[4] MATUŠKA, T., Aktivní solární tepelné systémy – 1. část Teoretické vztahy, Vytápění, větrání, instalace. Roč. 12, č. 2, s. 64-67. 2003.
[5] ČSN EN 12975-1 Tepelné solární soustavy a součásti – Solární kolektory – Část 1: Všeobecné požadavky. ČNI: 2006.
[6] ČSN EN 12975-2 Tepelné solární soustavy a součásti – Solární kolektory – Část 2: Zkušební metody. ČNI: listopad 2006.
[7] MATUŠKA, T., Aktivní solární tepelné systémy – 2. část Experimentální měření, Vytápění, větrání, instalace. 2003, roč. 12, č. 3, s. 102-105.
[8] Converting solar thermal collector are into installed capacity, dokument European Solar Thermal Industry Federation, dostupný na www.estif.org
[9] MATUŠKA, T., Nástroj pro hodnocení výkonnosti solárních kolektorů VYKON_SK, dostupné na http://solab.fs.cvut.cz
[10] Pressure equipment directive 97/23/EC, Guideline 2/23. 2006.
[11] CE-marking related to Pressure Equipment Directive (PED), dokument ESTIF, dostupný z www.estif.org/solarkeymark/ce-solarcollectors_ped.php. 2007
[12] Solar Keymark – CEN Keymark Scheme for Solar Thermal Products, dostupné z www.estif.org/solarkeymark
[13] Solar Keymark Collector Database, August 2009, dostupné z www.estif.org/solarkeymark
[14] RAL-UZ 73: Basic Criteria for Award of the Environmental Label „Der Blaue Engel“, Solar Collectors, březen 2009, dostupné z www.blauer-engel.de
3 ZÁSOBNÍKY TEPLA
Většina soustav pro využití obnovitelných zdrojů tepla (solární tepelné soustavy, tepelná čerpadla, zdroje na spalování biomasy) vyžadují pro efektivní provoz akumulaci energie. U solárních soustav je požadavek na akumulaci dán především nestálým přísunem sluneční energie pro pokrytí nepravidelné potřeby tepla během dne a během roku. K uchování tepelných zisků solární soustavy z určitého časového úseku do jiného slouží právě zásobníky tepla. Zásobníky tepla hrají v solární technice významnou roli, často se o nich hovoří jako o centrálním prvku solární soustavy a proto je jim věnována zvláštní kapitola. Z praxe vyplývá poznatek, že solární soustava se sebelepším solárním kolektorem v kombinaci s nevhodně navrženým zásobníkem bude vykazovat nízké celkové zisky a neumožní vysoké pokrytí potřeby tepla. Konstrukci a výběru zásobníku tepla pro danou solární soustavu by proto měla být věnována zvýšená pozornost.
Základními kritérii pro výběr zásobníků tepla jsou:
- hustota akumulace (kapacita) – ovlivňuje velikost zařízení, preferuje se co nejvyšší hustota akumulace, tedy co nejmenší zásobníkem zastavěný objem v prostoru;
- účinnost akumulace – ovlivňuje účinnost solární tepelné soustavy a stupeň pokrytí potřeby tepla, nejedná se pouze o ztráty tepla ze zásobníku, ale i o ztráty využitelnosti teplotní úrovně naakumulované tepelné energie, tj. o energetické ztráty;
- cena – v praxi jedno z nejdůležitějších kritérií a současně jeden z hlavních důvodů, proč se jiné než vodní zásobníky na trhu zatím příliš neprosazují;
- životnost – je dána provozními podmínkami, u různých principů akumulace je životnost dána jinými vlivy, např. u ocelových vodních zásobníků je životnost ovlivněna především korozí a minerálními usazeninami, u PCM zásobníků druhem použité akumulační látky a její odolností vůči cyklické změně skupenství, apod.;
- bezpečnost – správný návrh s ohledem na přípustné tlaky a teploty;
- ekologie – předpokládá se použití netoxických akumulačních látek odbouratelných v přírodě, recyklovatelných materiálů pláště zásobníků, apod.
3.1 PRINCIPY AKUMULACE TEPLA
Teplo (tepelnou energii) je možné akumulovat různými způsoby a podle druhu akumulační látky a využití fyzikálních dějů lze rozlišit čtyři následující principy:
- akumulace s využitím citelného tepla – využívá se tepelné kapacity látek v daném rozsahu teplot, akumulovaná energie závisí přímo úměrně na rozdílu mezi počáteční a konečnou teplotou, hustota akumulace se pohybuje mezi 100 až 300 MJ/m3;
- akumulace s využitím skupenského tepla – využívá se skupenského (latentního) tepla tání-tuhnutí a tepelné kapacity látky (citelné teplo látky v pevném a kapalném stavu), hustota akumulace se pohybuje mezi 200 až 500 MJ/m3;
- akumulace s využitím sorpčního tepla – využívá akumulace vodní páry pohlcením v tuhé (adsorpce) nebo kapalné (absorpce) látce, teplo se ze zásobníku uvolňuje při sorpci, tepelná energie se dodává pro regeneraci sorpčního zásobníku (uvolnění vodní páry), hustota akumulace se může pohybovat mezi 500 až 1 000 MJ/m3;
- akumulace s využitím chemických reakcí – využívá se vratných chemických reakcí vhodných látek, které jsou doprovázeny jímáním/uvolňováním tepla, předpokládaná hustota akumulace až 3 000 MJ/m3.
Na obr. 3.1 je uvedeno přehledné rozdělení solárních zásobníků podle jednotlivých principů s uvedením konkrétních používaných akumulačních látek. Naprostá většina komerčně dostupných zásobníků tepla v oblasti solární tepelné techniky pracuje na principu akumulace citelného tepla, malá část využívá změny skupenství akumulační látky. Zásobníky s využitím sorpce a chemických reakcí, někdy společně označované jako termochemické zásobníky, jsou zatím ve fázi výzkumu a vývoje.
Obr. 3.1 Rozdělení solárních zásobníků tepla podle principu akumulace tepla
Podle časových požadavků na akumulaci je možné zásobníky rozdělit na:
- krátkodobé zásobníky – denní či vícedenní zásobníky, využívané především pro akumulaci tepla ze dne do noci, případně ze dne na den;
- dlouhodobé zásobníky – zásobníky tepla, které dlouhodobě (řádově měsíce) uchovávají solární zisky pro využití v jiném ročním období.
3.1.1 Akumulace citelného tepla
Akumulace s využitím citelného tepla využívá tepelné kapacity pracovní akumulační látky. Jímání (uvolňování) tepla je provázeno změnou teploty pracovní látky (ohřevem nebo ochlazením). Matematicky lze akumulaci citelného tepla Q v Joulech popsat rovnicí
(3.1)
kde je
V … objem pracovní látky, v m3;
ρ … hustota pracovní látky, v kg/m3;
c … měrná tepelná kapacita pracovní látky, v J/(kg.K);
t1,2 … teploty na počátku a na konci jímání/uvolňování tepla, ve °C.
Vhodnou pracovní látkou je látka s vysokou tepelnou kapacitou, tedy součinem hustoty a měrné tepelné kapacity ρ·c v J/(m3·K). Nejlépe těmto podmínkám vyhovuje voda (viz tab. 3.1), která je navíc dostupná, levná, trvanlivá a ekologická. Dále se používá pevných látek, např. beton pro akumulaci tepla/chladu v konstrukcích budov, kamenivo nebo štěrk často i v kombinaci s vodou pro zvýšení akumulační schopnosti.
Tab. 3.1 Vlastnosti pracovních látek pro akumulaci v oblasti citelného tepla
| Pracovní látka | Měrná tepelná kapacita [J/(kg·K)] | Hustota [kg/m3] | Objemová tepelná kapacita [MJ/(m3·K)] | Hustota akumulace pro Δt = 60 K [MJ/m3] |
| voda | 4 187 | 998 | 4,2 | 251 |
| vzduch | 1 010 | 1,2 | 0,0 | 0 |
| štěrk | 750 | 1 650 | 1,2 | 74 |
| beton | 1 020 | 2 300 | 2,3 | 141 |
| cihla | 900 | 1 800 | 1,6 | 97 |
| dřevo | 2 510 | 600 | 1,5 | 90 |
| železo | 440 | 7 850 | 3,5 | 207 |
Výhodou použití pevných látek je především vyšší rozsah provozních teplot a často jednodušší konstrukce akumulátoru. Obecnou nevýhodou akumulátorů citelného tepla je relativně nízká hustota akumulace vedoucí k velkým objemům zásobníků, a navíc změna teploty v průběhu ukládání a jímání tepla s ohledem na využitelnost. Názorně je porovnání tří základních akumulačních látek ještě uvedeno na obr. 3.2.
Obr. 3.2 Akumulace citelného tepla do různých látek o objemu 1 m3 pro δt = 40 K
3.1.2 Akumulace skupenského tepla
Změna skupenství látky (pevná látka ↔ kapalina, kapalina ↔ plyn) je provázená uvolněním, resp. jímáním skupenského tepla, někdy nazývaného též latentní teplo neboli skryté, kdy při jímání či uvolňování tepla nepozorujeme výraznou změnu teploty látky. Pro akumulaci tepelné energie v běžných aplikacích je využitelná pouze změna skupenství mezi pevnou látkou a kapalinou (tání – tuhnutí), protože změna skupenství kapalina – plyn (vypařování – srážení) není prakticky vhodná pro akumulaci energie vzhledem k velké změně objemu akumulační látky a s tím spojeným vysokým nárůstem tlaku. Matematicky lze akumulaci tepla s využitím změny skupenství při tání / tuhnutí pracovní látky zapsat
(3.2)
kde je
V … objem pracovní látky, v m3;
ρp,k … hustota pracovní látky v pevném (kapalném) skupenství, v kg/m3;
cp,k … měrná tepelná kapacita pracovní látky v pevném (kapalném) skupenství, v J/(kg·K);
lt … skupenské teplo tání/tuhnutí, v J/kg;
t1,2 … teploty na počátku (1) a na konci (2) jímání/uvolňování tepla, ve °C;
tt … teplota tání/tuhnutí, ve °C.
Akumulace tepla s využitím změny skupenství látek vzhledem k jímání a uvolňování energeticky významného skupenského tepla za přibližně stálých teplotních podmínek (viz obr. 3.3) může poskytnout výraznou akumulační kapacitu oproti akumulaci citelného tepla, především pokud teplotní rozsah akumulace je vymezen okolo teploty změny skupenství. Se zvyšujícím se rozdílem mezi počáteční a konečnou teplotou akumulace tato výhoda klesá.
Obr. 3.3 Porovnání průběhu teplot při akumulaci citelného tepla a akumulaci se změnou skupenství
Výběrem vhodných látek se změnou skupenství ve vhodném teplotním rozmezí a způsobem jejich použití lze akumulaci optimalizovat. Výhodou akumulace se změnou skupenství jsou při vhodném použití menší tepelné ztráty díky téměř izotermní akumulaci. Zatímco zcela čisté látky tají / tuhnou při stálé teplotě, směsi látek mění skupenství v určitém rozsahu teplot. Většina látek navíc projevuje určitou hysterezi, tzn. vykazují odlišnou teplotu tání od teploty tuhnutí.
Látky vhodné pro akumulaci tepla se změnou skupenství (Phase Change Materials, PCM) by se měly vyznačovat především vysokou hodnotou skupenského tepla tání lt v kJ/kg nebo kJ/m3, vysokou tepelnou vodivostí a bodem tání tt, ležícím ve vhodném rozsahu pro danou aplikaci (u solárních soustav 35 až 70 °C, nejčastěji okolo 65 °C). Z hlediska praktického použití by PCM měly být chemicky stálé, levné, netoxické a nekorozivní. Důležitá je také stabilita vlastností při dlouhodobém cyklickém použití. U některých látek může při cyklickém zatížení táním-tuhnutím docházet k rozkladu a postupnému snižování hodnot skupenského tepla.
Obr. 3.4 Porovnání akumulační kapacity látek se změnou skupenství a vody vztažené k jejich hmotnosti (vlevo) a objemu (vpravo)
Rozlišují se dva základní typy látek se změnou skupenství vhodné pro dané teplotní podmínky solárních soustav:
3.1.2.1 Organické látky
Komerční (technické) parafiny a vosky jsou levné s hodnotami skupenského tepla tání mezi 90 až 200 MJ/m3 a velkým rozsahem možných teplot tání (od 30 do 70 °C) v podstatě definovatelnými na požádání. Vyznačují se chemickou netečností a minimálním sklonem k podchlazování. Nicméně vosky a parafíny mají nízkou tepelnou vodivost zpravidla okolo 0,2 W/(m·K) a je nutné je kombinovat s kovovými matricemi, lamelami a výplňovými strukturami pro zvýšení vodivosti a přestupu tepla do pracovní látky.
Vhodnými kandidáty pro zásobníky se změnou skupenství jsou také mastné kyseliny, např. palmitová nebo stearová. Teploty tání kyselin leží také v rozsahu od 30 do 65 °C.
3.1.2.2 Anorganické látky
Vhodnými pracovními látkami jsou také hydratované soli pro jejich vysokou hodnotu skupenského tepla tání v objemovém vyjádření od 180 do 350 MJ/m3, relativně vysokou tepelnou vodivost okolo 0,5 W/(m·K) a nízkou cenu srovnatelnou s parafiny. Nejznámější je Glauberova sůl neboli síran sodný (Na2SO4·10·H2O) s teplotou tání 32,4 °C, která je jednou z nejlevnějších látek pro akumulaci se změnou skupenství. Jako další materiály jsou předmětem výzkumu hydratovaná sůl kyseliny octové (CH3COONa·3H2O) s teplotou tání 58 °C. Použití solí v zásobnících je však omezeno vzhledem k problémům se zvýšenou korozivitou, s podchlazováním a dlouhodobě se také snižuje jejich akumulační hustota. Tyto překážky lze překonat zatím pouze za cenu snížení tepelně-akumulačních parametrů vlastní látky.
Na obr. 3.4 jsou zobrazeny vztahy mezi akumulovaným teplem a teplotou pro různé látky se změnou skupenství pro využití v solární tepelné technice s ohledem na požadovanou teplotu změny skupenství (60 °C). Je patrné, že při vztažení tepla akumulovaného v látce k její hmotnosti (vlevo), jsou PCM látky z hlediska akumulační schopnosti téměř srovnatelné. Nicméně, pro praktické účely se požaduje informace o objemové náročnosti akumulátoru, tzn. kolik zabere místa v prostoru a proto je nutné vztahovat využitelné teplo akumulace k objemu akumulační látky (vpravo). Potom jsou patrné významné rozdíly v hustotě akumulace mezi organickými (parafíny) a anorganickými (soli) látkami.
3.1.3 Akumulace s využitím sorpce
Sorpční akumulační systémy využívají fyzikálního jevu absorpce (v kapalné látce) nebo adsorpce (v tuhé látce). Lze rozlišit dva systémy:
- otevřený, viz obr. 3.5;
- uzavřený, viz obr. 3.6.
V otevřeném adsorpčním systému dochází k výměně vodní páry a tepla mezi přiváděným vzduchem a adsorbentem v podobě lože s tuhým desikantem. V režimu desorpce vstupuje teplý vzduch, ohřátý např. solárním teplem, do lože a vypuzuje z něj vodní páru. Vzduch nasycený vodní párou je odváděn z lože do okolí. V režimu adsorpce se vzduch nejprve zvlhčí, např. v adiabatické pračce, a ochlazený vstupuje do lože vysušeného po desorpci, desikant adsorbuje vodní páru ze vzduchu a uvolňuje se sorpční teplo. Vysušený a ohřátý vzduch odchází z lože pro předání tepla v navazující aplikaci.
Obr. 3.5 Princip otevřeného cyklu s tuhým sorbentem
Podobně v otevřeném absorpčním systému dochází k výměně páry mezi přiváděným vzduchem a absorbentem, kterým je kapalný hygroskopický roztok a výše popsaný proces probíhá analogicky.
Energie, která je akumulována v systému, je sorpční teplo přiváděné ze solárních kolektorů pro desorpci akumulační látky a teplo odváděné pro využití uvolněné sorpcí vodní páry v látce – sorbentu. Akumulace tepla je dosaženo oddělením procesu desorpce (nabíjení zásobníku) od procesu sorpce (vybíjení zásobníku). Po vysušení sorbentu může v tomto „nabitém“ stavu zásobník zůstat bez tepelných ztrát až do doby, kdy je spuštěn proces adsorpce nebo absorpce.
Uzavřený systém využívá stejného jevu, avšak pro přenos vodní páry nevyužívá vzduchu. Podobně jako otevřené systémy i uzavřené systémy pracují buď s tuhým adsorbentem nebo kapalným absorbentem. Celý systém je vakuován a oddělen od vnějšího prostředí (uzavřen). Do sorbentu je teplo přiváděno a z něj odváděno přes výměníky tepla. Podobně do vody je teplo pro její odpaření přiváděno výparníkem a odváděno kondenzátorem pro zkapalnění. Během desorpce je do sorbentu přiváděno teplo z vysokopotenciálního zdroje (solární kolektory), sorbent se vysušuje, uvolňuje se z něj vodní pára a ta kondenzuje v kondenzátoru, který je současně chlazen (odvod nízkopotenciálního tepla, např. do okolního prostředí). V časovém úseku akumulace je suchý sorbent oddělen od kapalné pracovní látky. V opačném režimu sorpce se do výparníku přivádí nízkopotenciální teplo z okolního prostředí pro odpaření vodní páry za nízkého tlaku. Ta se přivádí do sorbentu, pohlcuje se v něm a ze sorbentu je odváděno sorpční teplo (vysokopotenciální o využitelné teplotní hladině). Občas se takové systémy nazývají chemická tepelná čerpadla. Účinnost celého systému a hustota akumulace je značně závislá na efektivitě přenosu tepla do sorbentu a do vodní páry a přenosu vodní páry mezi výparníkem/kondenzátorem a sorbentem, tedy na kvalitě sdílení tepla do těchto látek výměníky.
Obr. 3.6 Princip uzavřeného cyklu s tuhým sorbentem
Jako tuhé sorbenty se využívají mikroporézní a mezoporézní materiály, např. silikagely, zeolity, aj. Nevýhodou jsou vysoké potřebné teploty pro jejich desorpci. Pro využití v solární technice jsou proto hledány nové materiály na bázi aluminosilikátů nebo aluminofosfátových molekulárních sít, např. AlPO4, které mají hustotu akumulace obdobnou jako zeolity. Mezi kapalnými sorbenty se nejvíce používá LiCl v kombinaci s vodou jako sorbátem (pracovní látkou). V současné době v oblasti akumulace s využitím sorpce probíhá intenzivní výzkum. Byla realizována řada demonstračních projektů, nicméně sorpční technologie je zatím velmi drahá vzhledem k vysokým investičním nákladům a ve srovnání s konvenčními způsoby akumulace stále ekonomicky nedostupná. Zajímavé se jeví především hybridní kombinace vytápění a chlazení nebo chlazení a odvlhčování, kde lze využít i další funkce než pouze akumulaci energie.
3.1.4 Akumulace s využitím chemických reakcí
Pro akumulaci energie je možné využít také vratných chemických reakcí, kdy v jednom směru jde o reakci endotermickou spojenou s jímáním a akumulací tepla a v opačném směru o reakci exotermickou s uvolněním tepla. Princip lze zapsat rovnicí
(3.3)
kde přivedením reakčního tepla ΔH lze sloučeninu AB rozložit na dvě samostatné látky A a B. Produkty reakce A a B musí být snadno separovatelné a nepodléhat dalším reakcím. Složky AB a A jsou zpravidla v pevném nebo kapalném skupenství, B je zpravidla plyn. Množství akumulovaného tepla je dáno
(3.4)
kde je
ar … reagující podíl látky;
m … hmotnost látky, v kg;
ΔH … reakční teplo, v J/kg.
Akumulace s využitím chemických reakcí je vysoce energetický proces a hustoty akumulace se pohybují od 1 000 do 3 000 MJ/m3. Produkty reakce mohou být skladovány při pokojové teplotě (bez ztrát, bez nutnosti tepelné izolace, citelné teplo je nepoměrně menší vzhledem k reakčnímu). V praxi jde především o rozklad hydridů kovů, oxidů kovů, peroxidů, aj., avšak pro solární tepelnou techniku za relativně vysokých teplot. V tab. 3.2 jsou uvedeny některé dvojice látek spolu s jejich vlastnostmi. Látky s endotermní reakcí ve vhodné teplotní úrovni do 100 °C jsou zatím ve stádiu základního výzkumu. Akumulace s využitím vratných chemických reakcí je navíc provázena řadou problémů, zejména se stabilitou, reverzibilitou, životností, tlaky v reaktoru, korozí a toxicitou.
Tab. 3.2 – Látky pro akumulaci s využitím reakčního tepla
| Reakce materiálů | Hustota akumulace [GJ/m3] | Teplota reakce [°C] | ||
| AB ↔ A + B | ||||
| MgSO4·7H2O | MgSO4 | H2O | 2,8 | 122 |
| FeCO3 | FeO | CO2 | 2,6 | 180 |
| Fe(OH)2 | FeO | H2O | 2,2 | 150 |
| CaSO4·2H2O | CaSO4 | H2O | 1,4 | 89 |
3.2 VODNÍ ZÁSOBNÍKY TEPLA
Mezi nejběžnější a nejpoužívanější zásobníky tepla pro solární kapalinové soustavy patří vodní zásobníky. Voda má oproti jiným materiálům řadu výhod: je dostupná, levná, netoxická, nehořlavá a má výborné přenosové vlastnosti a vysokou tepelnou kapacitu. K jejím nevýhodám patří omezený rozsah teplot použití: pod 0 °C tuhnutí se změnou objemu, nad 100 °C vypařování s výraznou změnou objemu a dále relativně malé povrchové napětí podporující úniky netěsnostmi a korozivita.
3.2.1 Druhy zásobníků
Naprostou většinu vodních zásobníků solárních soustav tvoří denní a vícedenní zásobníky tepla. Podle počtu teplosměnných ploch lze rozlišit vodní zásobníky tepla:
- bez teplosměnné plochy – akumulační nádrže;
- s 1 teplosměnnou plochou – monovalentní zásobníky;
- se 2 teplosměnnými plochami – bivalentní zásobníky;
- s více teplosměnnými plochami – multivalentní zásobníky.
Obr. 3.7 Druhy zásobníků tepla podle teplosměnné plochy
Akumulační nádrže se používají především u velkoplošných solárních soustav, kde se pro přenos výkonu solárních kolektorů do zásobníku tepla využívá externích výměníků tepla.
Monovalentní zásobníky se využívají jako čistě solární zásobníky, kde jedinou teplosměnnou plochou umístěnou uvnitř zásobníku se předává teplo ze solárního okruhu. U přípravy teplé vody jde především o dodatečnou instalaci solární soustavy pro solární předehřev vody. Zásobník je zapojen před stávající ohřívač vody, který zajišťuje dohřev. Při použití monovalentních solárních zásobníků u kombinovaných solárních soustav pro přípravu teplé vody a vytápění se dohřev otopné vody a příprava teplé vody řeší externím výměníkem vně zásobníku.
Bivalentní zásobníky se dvěma teplosměnnými plochami se používají jako kompaktní zásobníky, kde spodní výměník je určen pro přenos tepla ze solárního okruhu, horní výměník zajišťuje dohřev v horní části zásobníku dodatkovým zdrojem tepla. Pokud je dodatkovým zdrojem tepla elektrická energie, je místo horního výměníku instalována v zásobníku elektrická otopná vložka. Jde o vhodné řešení především do novostaveb s omezeným prostorem pro instalaci samostatného dohřívacího zásobníku.
Podle tlaku vody v zásobníku lze rozlišit:
- tlakové zásobníky;
- netlakové (beztlaké) zásobníky.
Tlakové zásobníky jsou konstrukčně navrženy a vyrobeny pro provoz za tlaků běžných ve vodovodním rozvodu (zásobníky teplé vody, 0,6 až 1 MPa) nebo v otopné soustavě (zásobníky tepla, 250 až 300 kPa). Sériová produkce zásobníků ve výrobním závodě pod konkrétní obchodní značkou zpravidla zajišťuje kvalitu provedení především s ohledem na tlakovou odolnost spojů. V případě velkých objemů nad 2 m3 se tlakové zásobníky instalují již ve fázi hrubé stavby nebo se potřebný akumulační objem rozdělí na větší počet zásobníků o menším objemu. Pro udržení tlaku v přípustných mezích při objemových změnách vlivem teplotní roztažnosti vody vyžadují tlakové vodní zásobníky expanzní nádobu. Objem expanzní nádoby je nezbytné stanovit výpočtem na základě údajů o celkovém objemu a tlakových poměrech v síti.
Beztlaké zásobníky tepla se používají zvláště u větších objemů nebo u rekonstrukcí, kde je potřeba umístit velkoobjemový zásobník ve špatně dostupných prostorech a je nutné jej sestavit na místě. Otevřená nádoba s volnou hladinou vody v kontaktu s okolním vzduchem je vystavena menšímu tlakovému namáhání (pouze hydrostatický tlak). Z toho vyplývají menší nároky na stěny zásobníků a možnost použití lehkých a levnějších materiálů např. plastů, sklolaminátu, apod. Výroba na místě však klade požadavky na přísnou kontrolu provedené práce. U beztlakých zásobníků tepla odpadá expanzní nádoba, změna objemu vodní náplně vlivem teploty se v zásobníku projeví změnou výšky volné hladiny. Na druhé straně, z důvodu styku vodního objemu s okolním vzduchem je nutné beztlaký zásobník vůči soustavě přípravy teplé vody nebo otopné soustavě oddělit dalším výměníkem, což snižuje využitelnou teplotu naakumulovaného tepla ze solární soustavy.
Podle účelu použití lze rozlišit:
- zásobníky teplé vody;
- zásobníky otopné vody.
Zásobníky teplé vody (TV) slouží k akumulaci tepla přímo do připravované teplé vody a podléhají hygienickým požadavkům na pitnou vodu. Zásobník musí být na vnitřní straně ve styku s vodou opatřen povrchovou úpravou s hygienickým atestem a vysokou trvanlivostí nebo být vyroben z nerezové oceli. Zatímco běžné smaltované zásobníky se cenově příliš neliší od neupravených ocelových nádrží, nerezové zásobníky jsou více než dvojnásobně dražší.
Zásobníky otopné vody (OV) se využívají především v kombinovaných soustavách pro přípravu TV a vytápění. Buď jsou provozovány odděleně od přípravy TV z důvodu výrazně odlišné teplotní úrovně nebo se s přípravou TV kombinují – kombinované zásobníky tepla. Pro akumulaci tepla do otopné vody se využívá levných ocelových nádrží bez vnitřní úpravy.
Kombinované zásobníky se používají ve snaze uspořit místo pro instalaci sdružením akumulačního objemu pro otopnou vodu s přípravou teplé vody. Principiálně se používají dvě konstrukce uvedené na obr. 3.8 – buď příprava teplé vody průtokovým způsobem v trubkovém výměníku nebo v zásobníku TV vloženém do objemu zásobníku otopné vody. Nevýhodou je teplotní spád nutný na výměníku pro zajištění požadované teploty TV a tedy vyšší teplota objemu otopné vody v zásobníku a vyšší tepelné ztráty. Pro přenesení výkonu potřebného k ohřevu běžného odběru 10 l/min (cca 20 kW) je nutná velká teplosměnná plocha průtočného výměníku či vnitřního plovoucího zásobníku TV. Zatímco v případě trubkového výměníku lze při dostatečném teplotním spádu a objemu zásobníku tepla připravit relativně velké objemy teplé vody, zásobníky typu „nádrž v nádrži“ jsou vhodné spíše pro menší potřeby teplé vody odpovídající pouze jeho objemu, neboť okamžitý předávaný výkon teplosměnné plochy je relativně malý (malá plocha, nízký přestup tepla vlivem volné konvekce na obou stranách teplosměnné plochy).
Obr. 3.8 Zásobník tepla s průtokovou přípravou TV trubkovým výměníkem (vlevo) a zásobník typu nádrž TV v nádrži OV (vpravo)
3.3 PODMÍNKY ÚČINNÉ AKUMULACE TEPLA
Na obr. 3.9 je uveden příklad dvou zásobníků teplé vody o objemu 300 l. Uživatel požaduje 150 l teplé vody o teplotě 50 °C, přičemž teplota přiváděné studené vody je 10 °C. U prvního zásobníku je horní část zásobníku (150 l) ohřáta na 50 °C a dolní část zásobníku zůstává na teplotě 10 °C, zatímco druhý zásobník je celý nahřátý na 30 °C (zcela promíchán). Do obou zásobníků bylo dodáno stejné množství tepla. Uživatel prvního zásobníku je spokojen, protože má k dispozici požadované množství vody o požadované teplotě. Uživatel druhého spokojen není, neboť odběr požadovaného množství vody ze zásobníku musí být dohříván dodatkovým zdrojem tepla. Jedna soustava tak pracuje správně (100% pokrytí potřeby tepla) a druhá špatně, přestože mají ostatní prvky stejné. Důvodem je odlišné rozvrstvení objemu zásobníku podle teploty (stratifikace), resp. hustoty pracovní látky, zde vody.
Pro správnou funkci zásobníku tepla je nutné nejen vrstvení objemu podle teploty vytvořit, ale také udržet. To znamená zamezit promíchávání vrstev akumulační látky o různé teplotě. Již z uvedeného příkladu je zřejmé, že kvalita teplotního vrstvení objemu v zásobníku bude ovlivňovat provozní parametry celé solární soustavy, její solární pokrytí i účinnost. Teplotní vrstvení je ovlivňováno především způsobem přívodu a odběru pracovní látky zásobníku. Druhým faktorem ovlivňujícím zásadně účinnost akumulace tepla jsou tepelné ztráty pláštěm zásobníku, zahrnující tepelné mosty a úniky vlivem nesprávně provedených potrubních přípojek.
Pro přirozené udržení teplotního vrstvení objemu zásobníku vlivem vztlakových sil se zásadně používají stojaté štíhlé zásobníky s poměrem výšky k průměru nad hodnotou 2,0, u kterých dochází k přirozenému teplotnímu rozvrstvení objemu a jeho snadnému udržení vlivem vztlakových sil. Ležaté solární zásobníky nejsou z důvodu omezeného rozvrstvení pro soustavy s nuceným oběhem vhodné a používají se pouze pro samotížné solární soustavy, nejčastěji jako jeden kompaktní celek s kolektorem pro sezónní ohřev.
Obr. 3.9 Rozdíl mezi stratifikovaným a promíchaným zásobníkem z hlediska využitelné energie
3.3.1 Přívod a odběr tepla
Způsob nabíjení a vybíjení zásobníku má rozhodující vliv na teplotní vrstvení. Na příkladech kombinace různého způsobu přívodu a odběru pracovní látky zásobníku je možné poukázat na výhody a nevýhody současné praxe.
Nejběžnějším řešením je zásobník s nepřímým nabíjením a přímým vybíjením (viz obr. 3.10). Teplo ze solárního okruhu je do zásobníku přiváděno přes vnitřní teplosměnnou plochu umístěnou v dolní nejchladnější části zásobníku pro zajištění dobré účinnosti kolektoru a maximálního využití akumulačního objemu zásobníku. Při nabíjení zásobníku voda ohřátá v blízkosti vnějšího povrchu vnitřního výměníku stoupá volným prouděním vzhůru a vytváří konvekční proudy, které částečně promíchávají zásobník. Při vybíjení se z horní části zásobníku odebírá teplá voda a do spodní části se přivádí studená (vybíjení po vrstvách). Tento způsob nabíjení a vybíjení je běžný u maloplošných solárních soustav pro přípravu teplé vody.
Obr. 3.10 Zásobník s nepřímým nabíjením a přímým vybíjením
Dalším způsobem je zásobník s přímým nabíjením a nepřímým vybíjením (viz obr. 3.11), kdy z vnějšku zásobníku, např. z externího deskového výměníku, je přiváděna teplá voda do horní části zásobníku a z dolní části je odebírána chladná. Nabíjení lze výhodně realizovat bez promíchání zásobníku, např. s použitím externího výměníku a řízeného přívodu ohřáté vody do vrstev o podobné teplotě (řízené vrstvení). Naproti tomu odběr tepla je realizován přes vnitřní tepelný výměník v horní části zásobníku. Umístění trubkového výměníku do horní části kombinovaného zásobníku tepla vede při vybíjení odběrem tepla k silnému promíchávání vrstev padající ochlazenou vodou v zásobníku (sestupné konvekční proudy) a vyrovnávání vertikálního teplotního profilu (degradace teplotního vrstvení).
Řešení vybíjecího výměníku hraje zásadní roli pro udržení teplotního rozvrstvení zásobníku. Trubkový průtočný výměník pro přípravu TV je nezbytné umístit po celé výšce zásobníku (odspodu nahoru), aby přiváděná studená voda ohřívaná přes teplosměnnou plochu výměníku vychlazovala především dolní část objemu zásobníku vyhrazenou solárním kolektorům a v horní části zásobníku docházelo již jen k dohřevu na požadovanou výstupní teplotu. Tímto způsobem je možné dosáhnout dostatečného teplotního rozvrstvení i vysokých zisků z kolektorů a používá se především u kombinovaných solárních soustav pro přípravu teplé vody (ve vnitřním výměníku) a vytápění (otopná voda je pracovní látka zásobníku).
Obr. 3.11 Zásobník s přímým nabíjením a nepřímým vybíjením
Zásobník tepla s nepřímým nabíjením a nepřímým vybíjením (viz obr. 3.12) je realizován dvěma výměníky (přívod a odběr tepla). Jde o nejběžněji využívané zapojení v oblasti jednoduchých kombinovaných solárních soustav. Z hlediska vrstvení tepla je zapojení nejméně účinné, neboť může docházet k promíchávání objemu zásobníku jak při nabíjení tak při vybíjení zásobníku. Proto je nutné zajistit vhodné podmínky pro dosažení vrstvení, např. dvěma nabíjecími výměníky (dolní, horní) nebo již zmíněný trubkový výměník pro průtočnou přípravu TV instalovaný po celé výšce zásobníku. Potom lze udržet účinnost akumulace na dostatečné úrovni.
Obr. 3.12 Zásobník s nepřímým nabíjením a vybíjením
Zásobník tepla s přímým nabíjením a vybíjením (viz obr. 3.13) představuje koncepčně nejvhodnější případ. Nabíjení i vybíjení se odehrává po jednotlivých vrstvách (pístový efekt). Do solárního okruhu je přiváděna stále chladná voda až do úplného nabití zásobníku (menší tepelné ztráty okruhu). Přímé nabíjení horní části při proměnlivých podmínkách slunečního záření je možné docílit proměnlivým průtokem solární soustavou (regulace na konstantní výstupní teplotu, např. 60 °C) případně v kombinaci s prvky pro řízené vrstvení. Přímé vybíjení zásobníku lze řešit externím výměníkem tepla v kombinaci s proměnlivým průtokem pro dostatečné vychlazení vratné vody do zásobníku, např. hydraulické skupiny pro průtočnou přípravu TV – tzv. „fresh water“ skupiny.
Obr. 3.13 Zásobník s přímým nabíjením a vybíjením
U kombinovaných zásobníků tepla je nutné při návrhu zapojení zdrojů a odběrů tepla rozlišit hlavní předpokládané teplotní zóny objemu zásobníku. Na obr. 3.14 je v levé části zobrazena zdrojová strana zásobníku tepla, v pravé části odběrová strana. Teplo přivedené z kolektorového okruhu se přivádí do spodní (jednoduché výměníky) až horní části (stratifikační prvky, horní solární výměník) objemu zásobníku tepla. V závislosti na druhu a výkonu dodatkového zdroje tepla je horní čtvrtina (plynový kotel, elektrická vložka) až polovina (kotel na dřevo) zásobníku tepla vyhrazena dohřevu na požadovanou teplotu pro přípravu teplé vody (65 °C). Přípojka vratné větve dodatkového zdroje tepla vymezuje solární akumulační objem neovlivněný jiným zdrojem tepla než solárními kolektory. Do spodní části zásobníku může být přípojka vratné vody dodatkového zdroje napojena pouze v případě, kdy nabíjení objemu horní části zásobníku dodatkovým zdrojem je řízeno podle teplotního čidla umístěného v horní polovině. Potom solární objem zásobníku vymezuje poloha takového řídicího čidla.
Jak již bylo uvedeno dříve, na odběrové straně je nutné dbát na dostatečné vychlazení spodní (solární) části zásobníku tepla vloženou teplosměnnou plochou (viz obr. 3.14) nebo přívodem vychlazené vody z externího výměníku. Prostřední část objemu zásobníku je vyhrazena především vodě v teplotní úrovni vhodné pro otopnou soustavu. Poloha objemu by měla zohledňovat teplotní úroveň v otopné soustavě (zpravidla nízkoteplotní vytápění), velikost objemu by měla být úměrná průtoku v otopné soustavě. Vratná větev z otopné soustavy je napojena zhruba ve třetině zásobníku, aby vratná voda mohla být na jedné straně předehřáta solárními zisky ze solárního objemu zásobníku, na druhé straně – aby nevhodně neohřívala vychlazený objem vyhrazený solárním kolektorům – by vratná větev nikdy neměla být napojena do spodní části zásobníku, pokud není na vratné větvi v zásobníku použit stratifikační prvek. Výstup otopné vody přiváděné do otopné soustavy by měl být umístěn nad připojením vratné vody dodatkového zdroje tepla, aby bylo umožněno v případě nedostatku solárních zisků otopnou vodu dodatkovým zdrojem dohřívat. Horní část (třetina až čtvrtina) objemu zásobníku tepla je vyhrazena pohotovostnímu dohřevu teplé vody a je trvale udržována na dostatečně vysoké teplotě. Je zcela nevhodné z této části odebírat otopnou vodu pro přívod do nízkoteplotní otopné soustavy (nutné směšování, degradace docílených teplot).
Obr. 3.14 Hlavní teplotní zóny v kombinovaném zásobníku tepla a napojení zdrojů a odběrů
3.3.2 Vodní zásobníky tepla s řízeným teplotním vrstvením
V oblasti vodních zásobníků (tlakové, netlakové) se v poslední době začínají i na tuzemském trhu objevovat tzv. stratifikační zásobníky. Využívají se především ve velkých solárních soustavách, nicméně se lze čím dál více s nimi setkat i v menších objemech pro rodinné domy. Teplotní stratifikací se rozumí vrstvení objemu zásobníku podle teploty řízeným ukládáním tepla do vrstev o stejné nebo podobné teplotě. Princip je zjednodušeně znázorněn na obr. 3.15.
Pokud je při slunečných podmínkách na výstupu z výměníku solárního okruhu k dispozici tepelná energie o dostatečně vysoké teplotě odpovídající například teplotě v horní vrstvě zásobníku, přivádí se voda z výměníku do této vrstvy (viz obr. 3.15 vlevo). Pokud je vlivem snížené úrovně slunečního záření k dispozici teplota nižší, přivádí se chladnější voda z výměníku do odpovídající chladnější vrstvy níže v zásobníku (viz obr. 3.15 vpravo). Výsledkem je takové rozvrstvení objemu zásobníku, kdy v horní části zásobníku je teplota výrazně vyšší než ve spodní části. Kvalitní stratifikační zásobníky, oproti běžným zásobníkům bez řízeného vrstvení, umožňují dodávat teplo o požadované teplotě (bez potřeby dohřevu) do odběrového okruhu již během náběhu zásobníku tepla, což zvyšuje pokrytí potřeby tepla solární soustavou. Navíc spodní část zásobníku zůstává chladná až do úplného nabití zásobníku a na vstupu do solárních kolektorů se udržuje během nabíjení zásobníku nízká teplota, což zaručuje vysokou účinnost. Použití stratifikačního zásobníku je zásadně výhodné u solárních soustav s nízkým průtokem teplonosné kapaliny (tzv. „low flow“ soustavy) a vysokým ohřátím teplonosné kapaliny (> 30 K), u kterých je možné na výstupu z kolektoru docílit vysokých teplot, při zachování nízkých teplot na vstupu.
Obr. 3.15 Zjednodušený princip řízeného vrstvení zásobníku u solární soustavy
Pro zásobníky tepla s řízeným vrstvením se používají různé způsoby jak dosáhnout teplotního vrstvení při nabíjení zásobníku, některé z nich jsou uvedeny na obr. 3.16. První způsob (vlevo) je řízení vrstvení ventily ovládanými na základě porovnávání teploty v dané vrstvě zásobníku a teploty přiváděné vody z výměníku tepla. Přívodní potrubí s ventily do zásobníku je nutné navrhovat na nízkou vstupní rychlost a konstrukčně řešit tak, aby přiváděný proud nenarušil teplotní rozvrstvení objemu zásobníku. Řešení je náročné na osazení čidly, ventily a vlastní regulaci nabíjení.
Obr. 3.16 Různé způsoby řízeného teplotního vrstvení
Jednodušším způsobem bez nároku na regulaci a elektrickou energii jsou samočinné trubkové stratifikační vestavby, které pracují na základě rozdílu hustot mezi přiváděnou vodou z výměníku a vrstvami akumulačního zásobníku. Voda o hustotě € při teplotě T je přiváděna vždy pod vrstvu, která má nejblíže nižší hustotu (nejbližší teplejší vrstva). Trubkové vestavby (obr. 3.16 uprostřed) jsou levné prvky, zpravidla z plastového PVC potrubí. Odbočky se vybavují velmi lehkými zpětnými klapkami, které zabraňují snížení teploty přiváděné teplé vody přisáváním vody z dolní chladnější části zásobníku (viz obr. 3.17). Speciální talířové vestavby (obr. 3.16 vpravo) mají tento problém vyřešen vlastní konstrukcí (přirozená gravitační zpětná klapka). U trubkových vestaveb je důležité udržet nízkou rychlost v přiváděcím potrubí pod 0,1 m/s, aby nebylo teplotní rozvrstvení narušeno účinkem kinetické energie proudu přiváděné vody.
Obr. 3.17 Ukázka jednoduchých stratifikačních vestaveb z odpadních PVC trubek
Stejně důležité jako zajištění teplotního rozvrstvení při přívodu tepla je udržení vrstvení objemu při odběru tepla. Pro přívod vratné vody s proměnlivou teplotou z otopné soustavy je možné použít obdobných stratifikačních vestaveb. Vratná voda z výměníku přípravy teplé vody je buď dostatečně vychlazena použitím elektronicky řízeného vybíjecího čerpadla (regulace průtoku podle odběru TV) a není potřeba stratifikační vestavba, nebo v případě neřízeného čerpadla je nezbytné stratifikační zařízení použít. Podobně je to s cirkulací teplé vody, pokud je použita. Na obr. 3.18 jsou uvedené možnosti zobrazeny.
Obr. 3.18 Zásobník teplota s vrstvením při nabíjení (SOL) a vybíjení (OV, řízené čerpadlo TV)
3.3.3 Tepelné ztráty zásobníků
Zásobníky tepla by měly být dostatečně tepelně izolovány pro zamezení ztrátám tepla a degradaci teplotního vrstvení. Tepelná izolace by měla být dostatečná především v horní části zásobníku, která je provozována častěji na vyšší teplotě než spodní část, zvláště v případě bivalentních zásobníků s neustálým dohřevem v horní části. Tepelná izolace zásobníku tepla by měla být souvislá po celém povrchu zásobníku, včetně dna a měla by tvořit dokonale přilnavý plášť. Netěsnosti ve formě vzduchových mezer, zvláště v případech odnímatelné izolace, mohou způsobit tepelné ztráty a ochlazování zásobníku prouděním vzduchu mezi izolačním pláštěm a zásobníkem.
Tepelná ztráta zásobníku ve W se stanoví podle vztahu
(3.5)
kde je
U·A … měrná tepelná ztráta pláštěm zásobníku, ve W/K;
taku,m … střední teplota objemu v zásobníku, ve °C;
tok,m … střední teplota okolí zásobníku, ve °C.
Měrnou tepelnou ztrátu pláštěm zásobníku lze teoreticky stanovit z dílčích součinitelů prostupu tepla stěny Us, dolního dna Ud a horního víka Uh a příslušných vztažných povrchů podle vztahu
(3.6)
Jednotlivé součinitele prostupu tepla lze stanovit zjednodušeně s uvažováním stěn zásobníku jako plochých (nikoli válcových) s minimální odchylkou ve výpočtu a s uvažováním přibližně plochého horního víka a dolního dna podle vztahu
(3.7)
kde je
siz … tloušťka tepelné izolace pláště (stěny, dna nebo horního víka), v m;
λiz … tepelná vodivost příslušné izolace, ve W/(m·K);
sw … tloušťka stěny zásobníku, v m;
λw … tepelná vodivost materiálu stěn zásobníku, ve W/(m·K);
hi … součinitel přestupu tepla na vnitřním povrchu stěny zásobníku (v kapalině), ve W/(m2·K);
he … součinitel přestupu tepla na vnějším povrchu tepelné izolace (okolní vzduch), ve W/(m2·K).
Pro praktické výpočty je možné zanedbat tepelný odpor vlastního materiálu stěn zásobníku, stejně jako součinitel přestupu tepla na vnitřním povrchu v kapalině (výrazně vyšší než na vnějším povrchu).
Vztažné povrchy částí pláště zásobníku se pro teoretický výpočet uvažují pro střední rozměry zásobníku včetně tepelné izolace (viz obr. 3.19 zcela vpravo) jako
(3.8)
(3.9)
Uvažováním vnitřního povrchu (pod izolací, průměr D a výška H) by nebyly zohledněny tepelné mosty na hranách pláště, uvažováním vnějšího povrchu (průměr D + 2 · siz, výška H + 2 · siz) by byla tepelná ztráta nadhodnocena. Stanovením vztažných povrchů v souladu s (3.8) a (3.9) a součinitele prostupu tepla zjednodušeně podle (3.7) je nepřesnost stanovení měrné tepelné ztráty U.A zanedbáním válcového tvaru zásobníku a izolace do 1 %.
Obr. 3.19 Vztažné rozměry pro stanovení pláště zásobníku
Teoretické stanovení měrné tepelné ztráty U·A výpočtem však přináší řadu praktických problémů, především obtížné zahrnutí nerovnoměrnosti tepelné izolace, nepřesnost stanovení skutečného vztažného rozměru a tedy vztažných povrchů pláště, zohlednění tepelných mostů v izolaci, včetně připojovacích nátrubků, apod.
Upřednostňuje se proto experimentální stanovení denní pohotovostní ztráty tepla Q24 v kWh/den při definovaných teplotách uvnitř zásobníku (taku,m = 65 °C) a vně zásobníku (tok,m = 20 °C) podle standardizovaného postupu. Pro solární zásobníky jsou k dispozici přímo normy ČSN EN 12977-3 [4] (solární ohřívače vody) a prEN 12977-4 [5] (solární kombinované zásobníky). Pro stanovení pohotovostní ztráty tepla elektrických nebo nepřímo ohřívaných ohřívačů vody platí např. ČSN EN 60379 [6] nebo ČSN EN 12897 [7]. Denní pohotovostní ztráta tepla odpovídá velikosti (objemu) zásobníku. Někdy se také uvádí jako měrná pohotovostní ztráta tepla q24 vztažená k objemu zásobníku a vyjádřená v kWh/(l·den).
Z laboratorně stanovené pohotovostní ztráty tepla lze potom stanovit měrnou tepelnou ztrátu ve W/K
(3.10)
Měrná tepelná ztráta je komplexním parametrem charakterizujícím tepelnou ztrátu zásobníku a lze z ní určit ztráty tepla zásobníku při skutečných provozních podmínkách.
V požadavcích zahraničních předpisů [8, 9] nebo norem [10,11] na maximální pohotovostní ztrátu tepla zásobníků je vždy požadovaná velikost pohotovostní ztráty tepla svázána s objemem zásobníku. Pro vyjádření závislosti se uvádí různé varianty obecného vztahu
(3.11)
kde zpravidla n < 1, podle druhu zásobníků (nepřímo ohřívaný, elektricky ohřívaný, přímo plynem ohřívaný). Některé normy určené pro hodnocení technických soustav budov v rámci hodnocení energetické náročnosti budov, např. DIN V 18599-8:2007 [12], uvádí hodnoty pro vztah (3.11) i pro různé stáří zásobníků. Podobně je souvislost mezi měrnou tepelnou ztrátou solárního zásobníku a jeho objemem vyjádřena např. v normě ČSN EN 12977-3 [4] obecným vztahem
(3.12)
Platí tedy, že s rostoucím objemem zásobníku denní pohotovostní ztráta tepla Q24 roste, na druhé straně měrná pohotovostní ztráta tepla klesá. Prakticky to znamená, že s rostoucím objemem zásobníku roste požadovaná tloušťka izolace. Čím menší je zásobník, tím je požadavek na tloušťku izolace měkčí. Bohužel, česká legislativa takovou souvislost v současné době nezohledňuje. Platná vyhláška [13] předepisuje úroveň tloušťky tepelné izolace zásobníků oproti běžným normovým standardům velmi přísně a bez zohlednění objemu zásobníků:
- zásobníky teplé vody – požadovaná tloušťka 100 mm při λiz = 0,045 W/(m·K) nebo adekvátní;
- zásobníky tepla – požadovaná tloušťka 100 mm při λiz = 0,04 W/(m·K) nebo U ≤ 0,3 W/(m2·K);
- dlouhodobé zásobníky tepla – požadavek na provedení optimalizačního výpočtu.
Zvláště pro malé objemy jsou vyhláškou požadované tepelné izolace o tloušťce 100 mm těžko realizovatelné (a proto v praxi nerealizované). V zahraničních předpisech [8, 9] je pro běžné velikosti zásobníků od 100 do 1 000 l oproti české legislativě požadována méně než poloviční tloušťka tepelné izolace (od 40 do 50 mm), tloušťka izolace 100 mm odpovídá objemům řádově jednotky až desítky m3.
Obr. 3.20 Měrná pohotovostní ztráta tepla podle různých norem a předpisů
Obdobná situace vyplývá i z české vyhlášky pro elektrické ohřívače vody podle [14] pro potřeby štítkování elektrospotřebičů. V tab. 3.3 jsou uvedeny hodnoty měrné denní pohotovostní ztráty tepla q24 [Wh/(l·den)] vztažené k objemu ohřívače pro jednotlivé třídy energetické náročnosti. Oproti normě ČSN EN 15332 [11], která také definuje kategorie A až G v závislosti na objemu, uvedená česká vyhláška toto nezohledňuje. Navíc, při porovnání s požadavky zmíněných předpisů a norem (viz obr. 3.20) je patrné, že do třídy A podle [14] mohou spadat pouze velké solární zásobníky s objemem nad 600 l. Pro malé objemy je principiálně nemožné se do třídy A dostat. Např. pro zásobník o objemu 100 l s průměrem 440 mm by tloušťka tepelné izolace s vodivostí 0,04 W/(m·K) musela být alespoň 130 mm, což je prakticky i ekonomicky nerealizovatelné.
Tab. 3.3 Hodnoty měrné denní ztráty tepla elektrických zásobníkových ohřívačů pro jednotlivé třídy energetické účinnosti [14]
| Třída energetické účinnosti | A | B | C | D | E | F | G |
| Denní měrná ztráta tepla q24 [Wh/(l·den)] | < 5 | 5–7 | 7–9 | 9–11 | 11–13 | 13–15 | >15 |
S ohledem na problematický stav požadavků české legislativy na tepelnou izolaci zásobníků lze proto pro návrh minimální tloušťky izolace solárního zásobníku doporučit hodnoty vyplývající z požadavků již ze zmíněné normy ČSN EN 15450 (navrhování soustav s tepelnými čerpadly). Přepočtené minimální tloušťky odpovídající tepelné vodivosti použitého materiálu izolace jsou vyneseny v grafu na obr. 3.21 v závislosti na objemu solárního zásobníku.
Obr. 3.21 Doporučené minimální tloušťky tepelné izolace solárních zásobníků
Tepelně izolační materiály vhodné pro solární zásobníky tepla / teplé vody jsou uvedeny v tab. 3.4 společně s typickými vlastnostmi. Kromě tepelné vodivosti je důležitým praktickým aspektem i způsob aplikace izolace na zásobník. Zatímco měkké polyuretanové pěny a polyesterová vlákna (plsť) jsou pružné a snadno přilnou k válcovému povrchu zásobníku, u panelů z polystyrenu a melaminové pryskyřice je nutné řasení (drážky), aby je bylo možné ohnout do válcového tvaru bez zlomení.
Tab. 3.4 Hlavní používané tepelně izolační materiály pro solární zásobníky
| Materiál | Maximální teplota [°C] | Tepelná vodivost při 10 °C [W/m·K] | Třída hořlavosti | Dostupné tloušťky [cm] |
| plsť z polyesterového vlákna | 110–120 | 0,035–0,040 | B2 | do 10 |
| měkká polyuretanová pěna | 110 | 0,040–0,042 | B2 | do 15 |
| tvrdá polyuretanová pěna | 130 | 0,025 | B3 | do 10 |
| pěna z melaminové pryskyřice | 150 | 0,035 | B2 | do 10 |
| skelná vlna | 150 | 0,037 | A1 | do 12 |
| kamenná vlna | 500 | 0,040 | A2 | do 15 |
Pro zajištění kvalitního zaizolování zásobníku je nutné neopomenout izolaci spodní části (izolační prstence, usazení zásobníku na tuhou nosnou izolaci, apod.) a horní části (izolační víko) a také izolační záklopky pro nepřipojené nátrubky.
3.3.4 Připojovací potrubí zásobníků
Způsob připojení potrubí přívodu a odběru otopné nebo studené/teplé vody ze zásobníku může výrazně ovlivnit jednak vrstvení zásobníku a jednak jeho tepelné ztráty. Často jednoduchým konstrukčním řešením připojení potrubí k zásobníku tepla je možné tyto vlivy eliminovat.
Pro zamezení míchání objemu zásobníku přívodem studené vody při současném odběru teplé se využívají hydraulické brzdy – přepážky, které zbrzdí proud studené vody vstupující do zásobníku. Obdobnou funkci zajišťuje vhodný tangenciální přívod vstupního potrubí do zásobníku, kdy vstupující proud je zbrzděn o stěny v dolní části zásobníku. Další možností je připojení studené vody potrubím a přírubou o dostatečné světlosti zaručující pokles rychlosti na vstupu do zásobníku při maximálním průtoku pod 0,1 m/s.
Obr. 3.22 Odběr teplé vody ze zásobníku a přívod studené vody (A – špatně, B,C – dobře)
U řady zásobníků je teplá voda odebírána v horní části a potrubí je vedeno nesprávně shora do zásobníku. Při takovém řešení odběru dochází k postupnému chladnutí teplé vody, která zůstává v odběrném potrubí. Ochlazená těžší voda klesá potrubím dolů do horní části zásobníku a vytlačuje do potrubí lehčí teplejší vodu (viz obr. 3.22A). Dochází tak k přirozenému proudění ve výstupní trubce, což může způsobit degradaci teplotní úrovně a rozvrstvení v horní části zásobníku ochlazenou vodou a tepelné ztráty tímto způsobem mohou činit až 15 % [2] z celkové ztráty tepla zásobníku.
Podobný jev je možné zaznamenat i u vodorovných rozvodů. Teplonosná kapalina se přirozeným prouděním dostává do připojovacích potrubí rozvodů k zásobníku, kde se ochlazuje a stejným potrubím ve spodní polovině jeho průřezu se vrací zpět do zásobníku. Řešením je vést odběr teplé vody z horní části vnitřním objemem zásobníku a vyústit jej níže (viz obr. 3.22B,C), případně vést odběr z horní části do strany tepelnou izolací zásobníku s ohybem potrubí o 180° (sifon) nebo vést odběr šikmo dolů tepelnou izolací zásobníku (viz obr. 3.23). Taková řešení zajišťují přirozenou zpětnou klapku, kdy voda ochlazená v potrubí vně zásobníku je těžší než teplá voda uvnitř a nemůže překonat výškový rozdíl (působící vztlak).
Obr. 3.23 Vhodná řešení připojení přívodů a odběrů teplonosné látky (teplé vody) k zásobníku
3.4 NAVRHOVÁNÍ SOLÁRNÍCH ZÁSOBNÍKŮ
3.4.1 Návrh objemu
Návrh objemu solárních zásobníků závisí na požadované aplikaci a navrhovaném solárním pokrytí, velikosti kolektorové plochy, maximální dovolené teplotě v zásobníku, odběrovém profilu, hydraulickém zapojení soustavy a případných dalších zdrojích tepla ať už obnovitelných či neobnovitelných, které ve větší či menší míře akumulační objem vyžadují. Často se pro návrh objemu zásobníku využívá zkušeností s provozní funkcí a uvádí se měrné hodnoty objemu vztažené na plochu apertury instalovaných solárních kolektorů. Zatímco pro účely krátkodobé akumulace se lze setkat s hodnotou 50 až 70 l/m2 solárních kolektorů, u solárních soustav se sezónní akumulací se v závislosti na návrhovém pokrytí měrné hodnoty objemu pohybují řádové okolo m3/m2 solárních kolektorů. U velkých solárních soustav je nezbytné funkci navrženého objemu solárního zásobníku ověřit v dalším stupni projektu simulačním výpočtem.
Obr. 3.24 Křivky solárního pokrytí pro různé okrajové podmínky solární soustavy k přípravě teplé vody
V grafu na obr. 3.24 jsou uvedeny křivky solárního pokrytí v závislosti na zvolené měrné hodnotě objemu zásobníku pro různé návrhové podmínky solární soustavy, např. různý typ kolektoru (kvalitní plochý, kvalitní trubkový), různou úroveň odběru teplé vody (4 osoby se 160 l/den, 2 osoby s 80 l/den), různou maximální dovolenou teplotou v zásobníku (tmax = 65 °C a tmax = 80 °C) a různě dlouhé rozvody primárního okruhu solárních kolektorů. Plocha kolektorů byla v analýze uvažována shodná pro všechny případy a počítačovou simulací s hodinovým krokem bylo zjišťováno docílené solární pokrytí potřeby teplé vody při použití různě velkého objemu solárního zásobníku (tl. izolace 50 mm).
Z grafu je patrné, že vyznačený rozsah 50 až 70 l/m2 zahrnuje ve všech případech maximum solárního pokrytí potřeby tepla. Křivky solárního pokrytí jsou relativně ploché a nedoporučuje se proto zbytečně zásobník tepla navrhovat příliš velký. Na druhé straně je patrné, že při nízkých měrných hodnotách pod 40 l/m2 se solární pokrytí začíná významně snižovat.
3.4.2 Počet zásobníků
U solárních zásobníků s velkým objemem v řádu několika m3 je problematické zajistit dopravu zásobníku do místa instalace, zvláště v případě rekonstrukce a umístění v suterénu bytového domu. Celkový akumulační objem je potom nezbytné rozdělit do několika zásobníků, což usnadňuje manipulaci a umístění, avšak zvyšuje tepelné ztráty vzhledem k nevýhodnému poměru povrchu pláště k objemu zásobníků. Zatímco při rozdělení celkového objemu do dvou zásobníků se celkové tepelné ztráty zvýší pouze o čtvrtinu, při rozdělení do 4 zásobníků je to již o 60 % a při rozdělení do 10 zásobníků na více než dvojnásobek (viz tab. 3.5).
Tab. 3.5 Nárůst tepelné ztráty zásobníku při rozdělení do většího počtu zásobníků se stejným objemem
| Počet zásobníků | 1 | 2 | 3 | 4 | 6 | 10 |
| Tepelná ztráta [%] | 100 | 126 | 144 | 159 | 182 | 215 |
3.5 LITERATURA
[1] MATUŠKA, T., Sešit projektanta – Solární tepelné soustavy, STP 2009. ISBN: 978-80-02-02186-5.
[2] Planning and Installing Solar Thermal Systems – a guide for installers, architects and engineers. James&James/Earthscan 2005. ISBN 1-84407-125-1.
[3] HADORN, J.-CH., Thermal energy storage for solar and low energy buildings, IEA-SHC 2005, ISBN: 84-8409-877-X.
[4] ČSN EN 12977-3:2009 Tepelné solární soustavy a součásti – Soustavy stavěné na zakázku – Část 3: Metody zkoušení parametrů solárních zásobníků pro ohřev vody, ČNI 2009.
[5] prEN 12977-4:2011 Thermal solar systems and components – Custom built systems Part 4: Performance test methods for solar combistores – Tepelné solární soustavy a součásti – Soustavy stavěné na zakázku – Část 4: Metody zkoušení parametrů solárních kombinovaných zásobníků, CEN 2011.
[6] ČSN EN 60379 Metody měření funkce elektrických akumulačních ohřívačů vody pro domácnost a podobné účely, ČNI 2004.
[7] ČSN EN 12897 Zásobování vodou – Nepřímo ohřívané uzavřené zásobníkové ohřívače vody, ČNI 2007
[8] DIN V 4753-8 Water heaters and water heating installations for drinking water and for service water – Part 8: Thermal insulation for water heaters with nominal capacity up to 1000 l – requirements and testing EnEV – Energieeinsparverordnung, DIN 2002.
[9] Energieverordnung 730.01 (Švýcarská energetická vyhláška), stav k 2011.
[10] ČSN EN 15450 Tepelné soustavy v budovách – Navrhování tepelných soustav s tepelnými čerpadly, ČNI 2011.
[11] ČSN EN 15332 Kotle pro ústřední vytápění – Stanovení energetické náročnosti zásobníků na teplou vodu, ČNI 2008.
[12] DIN V 18599-8:2007 Energy efficiency of buildings – Calculation of the energy needs, delivered energy and primary energy for heating, cooling, ventilation, domestic hot water and lighting – Part 8: Energy need and delivered energy for domestic hot water systems, DIN 2007.
[13] Vyhláška č. 193/2007 Sb., kterou se stanoví podrobnosti účinnosti užití energie při rozvodu tepelné energie a vnitřním rozvodu tepelné energie a chladu.
[14] Příloha č. 7 – Elektrické ohřívače vody, k vyhlášce č. 442/2004 Sb., kterou se stanoví podrobnosti označování energetických spotřebičů energetickými štítky a zpracování technické dokumentace, jakož i minimální účinnost užití energie pro elektrické spotřebiče uváděné na trh.
4 SOLÁRNÍ TEPELNÉ SOUSTAVY
Solární tepelné soustavy pro energetické zásobování budov s využitím sluneční energie mají poměrně velký aplikační potenciál. Solární teplo je využitelné v podstatě v jakékoli aplikaci, která teplo potřebuje. Nicméně je vždy nutné mít na paměti, že vzhledem k dostupnosti slunečního záření během roku je solární teplo v naprosté většině aplikací ve funkci „spořiče“ energie či paliva, nikoli hlavního zdroje tepla. Z aktivních (nuceně poháněných) solárních soustav jsou v podmínkách ČR v naprosté většině využívány soustavy s kapalinovými solárními kolektory. Kapalinové soustavy jsou univerzálně využitelné, v ČR mají dlouhodobou tradici a nespočet úspěšných instalací.
Solární kapalinové soustavy lze klasifikovat podle různých hledisek.
Podle aplikace (spotřebiče):
- předehřev teplé vody;
- příprava teplé vody;
- kombinovaná (sdružená) příprava teplé vody a vytápění;
- ohřev bazénové vody;
- solární chlazení a klimatizace;
- průmyslové aplikace.
Podle velikosti kolektorové plochy lze rozlišit:
- malé solární soustavy – maloplošné (do 20 m2);
- střední solární soustavy – středněplošné (od 20 m2 do 200 m2);
- velké solární soustavy – velkoplošné (nad 200 m2).
Jako maloplošné je možné označit solární soustavy do 20 m2, které vzhledem ke svému výkonu zpravidla ještě nevyžadují externí deskový výměník tepla, a k přenesení výkonu kolektorového pole postačuje trubkový výměník uvnitř zásobníku. Rozdělení podle plochy je však nejednotné; často se jako velkoplošné soustavy označují i soustavy s více než 50 m2 kolektorové plochy.
Podle měrného průtoku teplonosné kapaliny kolektory se navrhují solární soustavy:
- Soustavy s nízkým průtokem – „low flow“ soustavy, 10 až 15 l/(h·m2) se navrhují především pro velkoplošné soustavy z důvodu úspory nákladů na potrubí a izolace a dále obecně v kombinaci se stratifikačními zásobníky. Při nízkém průtoku dochází k ohřátí teplonosné kapaliny v kolektorech o cca 30 až 50 K a využitelná teplota pro aplikaci je k dispozici již po jediném průchodu kapaliny kolektorem. V horní části zásobníku je i při nízké úrovni slunečního záření k dispozici část objemu o dostatečně vysoké teplotě, použitelná pro okamžitou spotřebu bez nutnosti dodatkového ohřevu (zvýšení solárního podílu oproti „high flow“ soustavě). V dolní části zásobníku se až do konečného nabití udržuje nízká teplota, která vstupuje do kolektoru. Účinnost kolektoru, i přes vyšší výstupní teplotu, se tedy nezhoršuje. Podmínkou je však použití zásobníků s řízeným teplotním vrstvením, jinak se výhody „low flow“ provozu znehodnocují.
- Soustavy s vysokým průtokem – „high flow“ soustavy, 50 až 75 l/(h·m2) jsou běžné především u maloplošných soustav pro rodinné domy. Vlivem vysokého průtoku dochází k ohřátí teplonosné kapaliny o 6 až 10 K. Zásobník nevyužívá výrazného vrstvení teplot a je nabíjen postupně celý objem současně (pomalý nárůst teploty v celém zásobníku).
- Soustavy s proměnným průtokem – „matched flow“ se používají v kombinaci s pokročilou regulační strategií, která optimalizuje průtok solární soustavou pro dosažení vysokého solárního pokrytí a vyšší využitelnosti solárního tepla. Regulační strategie s proměnným průtokem je součástí i regulátorů maloplošných solárních soustav se dvěma solárními výměníky (horní, dolní). Otáčky oběhového čerpadla jsou řízeny tak, aby na výstupu z kolektoru byla dostatečně využitelná teplota („low flow“ režim), např. 60 °C, kterou je nabíjena horní část zásobníku tepla. Pokud soustava nedosahuje využitelné teploty, přechází soustava do „high flow“ režimu a teplo je ukládáno do spodní části zásobníku.
Podle konstrukce:
- soustavy uzavřené (naprostá většina soustav);
- Soustavy s vyprazdňováním, tzv. drain-back soustavy, pracují jako otevřené soustavy. V době mimo provoz jsou kolektory a potrubí primárního okruhu bez teplonosné kapaliny (vody) a jsou vyplněny vzduchem. V případě ohřátí kolektorů na dostatečně využitelnou teplotu se zapíná oběhové čerpadlo a vytlačuje vodu do kolektorů (nutný vysoký výtlak oběhového čerpadla, úměrný rozdílu výšek v solární soustavě). Po zaplavení primárního okruhu se čerpadlo přepne na nižší otáčky a hradí pouze tlakové ztráty okruhu. Při poklesu rozdílu teplot mezi kolektory a zásobníkem pod nastavenou hodnotu se čerpadlo vypíná a voda stéká do sběrné nádrže. Ačkoli soustavy s vyprazdňováním nejsou v ČR příliš rozšířené, přinášejí oproti kapalinovým soustavám řadu výhod. Zpravidla není nutné použití nemrznoucí kapaliny, teplonosnou kapalinou je voda. Nicméně v řadě případů nevhodných konfigurací potrubního rozvodu pro odvedení kapaliny do sběrné nádrže se i ve vyprazdňovacích soustavách nemrznoucí kapalina používá, platí však, že v době mimo provoz jsou kolektory bez kapaliny. Odpadají tedy problémy s možnou tvorbou páry v kolektorech v případě stagnace, kdy solární kolektory přijímají sluneční záření, ale oběhové čerpadlo je vypnuto z důvodu splnění poptávky po teple (zásobník na max. teplotě), nebo z důvodu výpadku el. energie. Na druhé straně je nutné, aby byl primární okruh vhodně vyspádován pro dokonalé vyprázdnění kolektorů a trubek.
4.1 SOLÁRNÍ SOUSTAVY PRO OHŘEV BAZÉNOVÉ VODY
Ohřev bazénové vody je jednou z nejpříznivějších aplikací solárních soustav, jednak z důvodů časové korelace mezi poptávkou po tepla (otevřené venkovní bazény využívané především v létě) a jednak z důvodu nízké požadované teploty (do 30 °C).
Schémata zapojení solárních soustav pro bazény jsou jednoduchá: bazénová voda buď protéká přímo solárními kolektory (bazénové absorbéry pro sezónní použití), nebo je použit výměník tepla (celoroční ohřev bazénové vody). Zásobníkem tepla a zároveň jeho spotřebičem je vlastní bazén.
4.1.1 Solární soustavy pro otevřené venkovní bazény
Provozní doba venkovních otevřených bazénů se omezuje na letní sezónu. Teplonosnou kapalinou protékající kolektory proto může být bazénová voda. Jako kolektory se s výhodou používají levné nezasklené plastové absorbéry z EPDM nebo PP, které jsou z hlediska účinnosti v letním období postačující, a navíc jsou odolné vůči působení dezinfekčních přísad do bazénové vody (oproti kovovým kolektorům).
Schéma zapojení solární soustavy pro přímý ohřev bazénové vody je uvedeno na obr. 4.1 ve dvou variantách. U bazénů, kde filtrační čerpadlo běží celou provozní dobu, se kolektorové pole zapojuje na společnou větev filtrace (za filtr ve směru průtoku). Bazénové čerpadlo musí být navrženo i na překonání tlakové ztráty kolektorů. Případný dohřev bazénové vody, pokud je požadován, se instaluje až za kolektory. Snímá se teplota v potrubí na výstupu z bazénu a teplota v kolektorech a na základě teplotního rozdílu se trojcestným ventilem buď přimíchává teplá voda z kolektorů, nebo se do okruhu kolektorů přepne celý průtok. V době, kdy jsou solární kolektory mimo provoz, má voda ze solárních kolektorů snahu odtéci (pokud jsou instalovány výše než bazén), ale trojcestný ventil, případně druhý instalovaný dvojcestný tomu zabraňuje.
V případě periodického běhu filtrace může solární regulátor podle potřeby spínat filtrační čerpadlo v době provozu solárních kolektorů. To však vzhledem k vysokým elektrickým příkonům filtračních čerpadel může vyvolat zvýšenou spotřebu elektrické energie pro pohon solární soustavy.
Obr. 4.1 Sezónní solární soustava pro ohřev bazénové vody
U bazénů, kde filtrační čerpadlo neběží celou dobu provozu, ale pouze v určitých periodách, se pole solárních kolektorů připojuje samostatnou větví s vlastním oběhovým čerpadlem s předřazeným jemným filtrem. Teplá voda z kolektorů se pouze přímíchává do proudu bazénové vody (při chodu filtračního čerpadla), nebo se ohřívá menší průtok vody nasávané z bazénu.
4.1.2 Solární soustavy pro kryté vnitřní bazény
U krytých bazénů se předpokládá celoroční provoz, a tedy i dohřev dodatkovým zdrojem tepla. Solární kolektory se volí běžné zasklené se selektivním povrchem. Teplonosnou kapalinou protékající kolektory je nemrznoucí směs. Solární okruh je tak oddělen od bazénové vody výměníkem tepla (trubkový nerezový výměník), předřazeným před výměník dohřevu (viz obr. 4.2). Zapojení sekundárního bazénového okruhu je analogické se zapojením u otevřených bazénů. Ohřev bazénové vody solární soustavou je zapojen buď do okruhu filtračního čerpadla, nebo paralelně (provoz i mimo periody filtrace).
Obr. 4.2 Solární soustava pro celoroční ohřev bazénové vody v krytých bazénech
4.2 SOLÁRNÍ SOUSTAVY PRO PŘÍPRAVU TEPLÉ VODY
Solární soustavy pro přípravu teplé vody (TV) mají dobrou využitelnost díky relativně rovnoměrnému profilu potřeby tepla na TV v průběhu roku. Příprava teplé vody v budovách tvoří významnou část energetické potřeby a v případě zavádění úspor v budovách je využití sluneční energie pro snížení energetické náročnosti přípravy teplé vody logickým krokem po omezení tepelných ztrát prostupem (zateplování budov) a větráním (využití rekuperace tepla).
Solární soustavy pro přípravu teplé vody jsou kromě obytných budov vhodné pro využití v terciárním sektoru, např. pro ústavy sociální péče, domovy důchodců, hotely, sportovní centra apod., kde je vysoká spotřeba teplé vody celoročně nebo se špičkami odběru v letním období. Vždy platí, že případnou rekonstrukci stávající přípravy teplé vody je nutné provést před nebo v průběhu instalace solární soustavy. Je nutné nejprve snížit spotřebu tepla na přípravu teplé vody a teprve potom uvažovat o realizaci solární soustavy. V opačném případě bude solární soustava zbytečně předimenzovaná a její provoz bude nehospodárný.
4.2.1 Maloplošné solární soustavy pro přípravu teplé vody (rodinné domy)
Maloplošné solární soustavy pro přípravu teplé vody jsou zpravidla standardním řešením (průmyslově vyráběné a dodávané komplety), nejčastěji aplikovaným v rodinných domech. Vzhledem k běžné potřebě teplé vody 30 až 50 l/den·os jde o solární soustavy s plochou kolektorů 4 až 8 m2 se zásobníkem teplé vody o objemu 200 až 400 l. Používají se solární soustavy ve variantě s předehřívacím zásobníkem, nebo solární soustavy ve variantě s bivalentním zásobníkem. Malé soustavy se vyznačují především jednoduchou regulací na základě rozdílu teplot mezi kolektorem a zásobníkem teplé vody. Provoz malých solárních soustav využívá zpravidla vysokého průtoku teplonosné kapaliny (high-flow, 50 až 70 l/h·m2 plochy kolektorů), při kterém dochází ke zvýšení teploty teplonosné látky v kolektoru o 7 až 10 K. Malé zvýšení teploty je výhodné z hlediska provozu kolektoru při vysoké účinnosti při použití standardních zásobníků tepla (bez řízené stratifikace). Zásobník se nahřívá pomalu a postupně, bez výrazných rozdílů teplot mezi horní a dolní částí.
Obr. 4.3 Schéma solární soustavy pro přípravu TV s předřazeným monovalentním solárním zásobníkem a s bivalentním zásobníkem
Solární soustavy s předehřívacím zásobníkem
Zjednodušené schéma solární soustavy ve variantě s předehřívacím zásobníkem je uvedeno na obr. 4.3 (vlevo). Monovalentní solární zásobník zajišťuje předehřev vody solárním výměníkem v dolní části. Výstup ze solárního zásobníku je přiveden do dohřívacího zásobníkového nebo průtokového ohřívače. Pokud teplá voda na výstupu zásobníkového ohřívače nedosahuje požadované teploty, dohřívá se dodatkovým zdrojem tepla. Solární soustavy s předehřívacím zásobníkem jsou vhodné především při rekonstrukcích, kdy je předehřívací zásobník předřazen stávající přípravě teplé vody.
Solární soustavy s bivalentním zásobníkem
Bivalentní zásobník obsahuje v dolní části solární výměník a v horní části dodatkový zdroj tepla (dohřívací teplovodní výměník tepla, elektrická topná vložka). Dodatkový zdroj tepla udržuje horní pohotovostní část zásobníku na požadované teplotě vody (např. 60 °C). Schéma solární soustavy ve variantě s bivalentním zásobníkem je uvedeno na obr. 4.3 (vpravo). Výhodou koncepce je kompaktní provedení zásobníku, malé požadavky na prostor (důležité zvláště v novostavbách), na druhou stranu v zásobníku dochází k částečnému ovlivnění spodní části zásobníku dohřevem.
4.2.2 Velkoplošné solární soustavy pro přípravu teplé vody
Solární soustavy s plochou kolektorů nad 20 m2 nacházejí uplatnění v bytových domech, hotelech, nemocnicích, ústavech sociální péče, sportovních zařízeních apod. Na rozdíl od maloplošných soustav v rodinných domech většinou představují vzhledem k různorodosti aplikací originální řešení z hlediska zapojení zdroje tepla a odběrového okruhu. Přesto je možné orientačně ukázat některá variantní řešení zapojení velkoplošných solárních soustav a vysvětlit na nich základní zásady.
Pro velkoplošné soustavy je vhodný provoz s nízkým průtokem teplonosné látky („low flow“, 10 až 15 l/(h·m2) kolektorové plochy). Z nízkých průtoků vyplývají menší tlakové ztráty, menší potřebné výkony oběhových čerpadel, menší průměry potrubí a díky menším povrchům potrubí i nižší tepelné ztráty. Použití menšího množství materiálu vede k nižším měrným investičním nákladům na soustavu. Podmínkou úsporného provozu je doplnění low-flow soustav zásobníky s řízeným teplotním vrstvením, u kterých nedochází k teplotnímu promíchávání akumulačního objemu. Potom je v horní části k dispozici objem dostatečně nahřáté vody pro využití, zatímco v dolní části se udržuje chladná voda až do úplného nabití zásobníku.
Velkoplošné solární soustavy vyžadují pro účinné přenesení tepelného výkonu z primárního okruhu do zásobníku deskový výměník. Deskový výměník se používá v některých zapojeních i na sekundární straně zásobníku, především tam, kde je využito netlakových zásobníků (oddělení teplé vody od vody, která je ve styku se vzduchem), zásobníků otopné vody nebo pro účely průtokové přípravy teplé vody jako eliminace problémů legionelly.
Solární soustava s centrálním bivalentním zásobníkem TV
Nejjednodušší zapojení velkoplošné solární soustavy pro přípravu TV s jediným centrálním stratifikačním zásobníkem TV je zobrazeno na obr. 4.4. Solární soustavy s jedním zásobníkem jsou vhodné především do novostaveb, u kterých se předem počítá s umístěním velkého zásobníku. Nevýhodou je velký objem centrálního zásobníku, kdy je nutné přihlížet k požadavku ochrany proti legionelle (periodický ohřev objemu zásobníku na 60 °C), z čehož vyplývají dodatečné tepelné ztráty centrálního zásobníku. Solární okruh je zapojen přes deskový výměník do centrálního tlakového zásobníku, stejně jako dodatkový zdroj tepla pro dohřev vody v horní části; v případě potřeby umožňuje prohřát celý objem solárního zásobníku jako ochrana proti legionelle.
Obr. 4.4 Solární soustava s jedním centrálním stratifikačním zásobníkem teplé vody
Solární soustavy se solárním vyrovnávacím zásobníkem teplé vody
Jako velmi efektivní a nákladům příznivé se ukázaly solární soustavy se dvěma zásobníky – solárním vyrovnávacím a dohřívacím pohotovostním. U těchto variant soustav je pohotovostní zásobník teplé vody navržen s malým objemem a slouží jen k pokrytí špičkové potřeby. Získaná solární energie je ukládána do velkoobjemového tlakového nebo netlakového vyrovnávacího zásobníku a v případě odběru teplé vody je do pohotovostního automaticky přečerpávána. V solárním vyrovnávacím zásobníku, který slouží jako akumulátor solárního tepla, se využívá řízeného teplotního vrstvení buď řízeným přívodem do různých výškových úrovní zásobníku, nebo s použitím stratifikačních vestaveb. V zapojení s pohotovostním zásobníkem je zajištěna ochrana proti legionelle jednak vzhledem k malému objemu zásobníku teplé vody a jednak kvůli neustálému udržování dohřevem na 60 °C.
Obr. 4.5 Solární soustava pro přípravu TV s tlakovým vyrovnávacím a pohotovostním zásobníkem
Na obr. 4.5 je zobrazena solární soustava s tlakovým vyrovnávacím zásobníkem a malým pohotovostním zásobníkem, doplněným dodatkovým zdrojem tepla pro pohotovostní dohřev vody. Teplotní vrstvení v solárním zásobníku je zajišťováno jednoduchým přepínáním mezi dvěma teplotními zónami (horní, dolní). Cirkulace teplé vody je zavedena jak do vyrovnávacího zásobníku (pokud teplota dostačuje k ohřevu), tak do horní části pohotovostního zásobníku (pokud teplota ve vyrovnávacím zásobníku je nižší než teplota cirkulace). Přepínání trojcestného ventilu zajišťuje jednoduchý diferenční regulátor.
Solární soustava s více solárními zásobníky teplé vody
Zapojení solární soustavy s několika solárními vyrovnávacími zásobníky je zvláště vhodné pro rekonstrukce. Rozdělení potřebného akumulačního objemu do více zásobníků zohledňuje jejich maximální velikost pro transport. Vyrovnávací zásobníky mohou být zapojeny paralelně (viz obr. 4.6) nebo sériově (viz obr. 4.7). Pro lepší využití sluneční energie je sekundární okruh zapojen do zásobníků ve dvou teplotních úrovních v objemu vyrovnávacích zásobníků (podpora stratifikace). Provoz je řízen na základě porovnávání teploty v horní a dolní částí zásobníků a teploty na výstupu z deskového výměníku (otevírání ventilů regulátorem). Řešení umožní částečné teplotní vrstvení, především udržovat v horní části zásobníků pohotovostní objem teplé vody pro využití (zvýšení solárního pokrytí). Zatímco u paralelního zapojení zásobníků jsou oba zásobníky nabíjeny současně a vykazují stejné teploty, v případě sériového zapojení vyrovnávacích zásobníků lze dosáhnout lepšího teplotního rozvrstvení do celkem 4 teplotních zón. Koncová zóna před výstupem do dohřívacího okruhu je nejteplejší, naopak zóna, do které je napojen přívod studené vody, je nejchladnější.
V obou zapojeních je realizováno zapojení cirkulace do solárních zásobníků, aby bylo možné tepelné ztráty cirkulací pokrýt solárními zisky. Zapojení cirkulace pouze do dohřívacího pohotovostního zásobníku by omezilo využití solárních zisků pro krytí tepelných ztrát rozvodu teplé vody a cirkulace.
V primárním okruhu solárních soustav je zapojen směšovací ventil pro náběh teplonosné kapaliny na provozní teplotu bez degradace teplot v zásobníku vlivem vychladlého primárního okruhu (u rozsáhlých vedení primárního okruhu).
Obr. 4.6 Solární soustava s dvěma paralelně řazenými vyrovnávacími zásobníky a pohotovostním zásobníkem
Nevýhodou soustav s více vyrovnávacími zásobníky jsou zvýšené tepelné ztráty vzhledem k nevýhodnému poměru povrchu pláště k objemu zásobníků. Zatímco při rozdělení celkového objemu vyrovnávacího objemu do dvou zásobníků se celkové tepelné ztráty zvýší pouze o 15 %, při rozdělení do 4 zásobníků je to již o 36 % a při rozdělení do 10 zásobníků o 76 %.
Obr. 4.7 Solární soustava s dvěma sériově řazenými vyrovnávacími zásobníky a pohotovostním zásobníkem
Solární soustava se zásobníky otopné vody (tepla)
Stále více se pro řešení velkoplošných solárních soustav pro přípravu teplé vody využívá akumulace solárních zisků do běžných ocelových zásobníků tepla a ohřev vody se realizuje deskovým výměníkem v čistě průtokovém zapojení nebo s maloobjemovou špičkovou akumulací předřazenými dohřívacímu stupni. Na obr. 4.8 je zobrazeno schéma solární soustavy s tlakovým solárním vyrovnávacím a pohotovostním zásobníkem. Dodatkový zdroj tepla dohřívá pracovní kapalinu (otopnou vodu) v horní části solárního bivalentního zásobníku. Dohřev ve velkoobjemovém vyrovnávacím zásobníku však způsobuje výraznější tepelné ztráty a je používán stále méně. Teplo se do pohotovostního zásobníku předává přes deskový výměník. Zpětné potrubí vychlazené otopné vody je zapojeno do stratifikační vestavby, aby v případě proměnlivého vychlazení vlivem odběru při použití čerpadla bez řízení otáček nebylo narušeno teplotní vrstvení. Cirkulace teplé vody je zapojena pouze do pohotovostního zásobníku.
Obr. 4.8 Solární soustava pro přípravu TV se zdrojem tepla ve vyrovnávacím zásobníku
Při použití zásobníků otopné vody jako mezistupně mezi primárním solárním okruhem a přípravou teplé vody je z hlediska tepelných ztrát výhodnější předřadit solární vyrovnávací zásobník dohřívacímu pohotovostnímu.
Na obr. 4.9 je uvedeno sériové zapojení dvou zásobníků tepla s průtokovým ohřevem přes stanici s vysoce výkonným deskovým výměníkem a čerpadlem řízeným na maximální vychlazení vratné vody do solárního zásobníku. Průtokový ohřev vody poskytuje výhodu vysokého vychlazení vyrovnávacího zásobníku během jeho vybíjení, na druhé straně klade nároky na vysoký tepelný výkon výměníku, měřicí a regulační techniku (rychlá reakce čidel průtoku, teploty, umístění čidel, regulace průtoku – čerpadla, zohlednění setrvačnosti). V praxi tyto soustavy zřídkakdy pracují bezchybně. Zásadně se doporučuje použít sériově vyráběných průtokových „vybíjecích“ stanic, předem konfigurovaných výrobcem.
Obr. 4.9 Solární soustava pro přípravu TV se solárními zásobníky otopné vody a průtokovou stanicí
Solární soustavy s beztlakým vyrovnávacím zásobníkem
Možností jak zachovat kompaktní objem akumulačního solárního zásobníku a zároveň realizovat ho v těžko přístupných prostorech jsou netlakové (beztlaké) zásobníky tepla. Netlakové zásobníky svařené na místě instalace, často zpevněné rozpěrami pro zvýšení tuhosti a pevnosti, mohou být vyrobeny s použitím menšího množství materiálu (levněji) než klasické tlakové zásobníky. Schémata solárních soustav s vyrovnávacím a pohotovostním zásobníkem jsou uvedena na obr. 4.10 a 4.11.
Pro nabíjení objemu zásobníku se výhodně využívá jednoduchých stratifikačních vestaveb. Vlastní příprava teplé vody je od solárního vyrovnávacího zásobníku oddělena výměníkem tepla podobně jako u zásobníků otopné vody, a to buď výkonnou průtokovou stanicí (viz obr. 4.10) nebo kombinací výměníku a předehřívacího zásobníku (viz obr. 4.11).
V zapojení podle schématu na obr. 4.10 je vratná netlaková voda napojena na stratifikační vestavbu (případ neregulovaného oběhového čerpadla). Cirkulace teplé vody není zapojena do solárního předehřevu a tepelné ztráty cirkulací a rozvodem teplé vody tedy nejsou kryty solárním teplem.
Ve schématu na obr. 4.11 slouží předehřívací zásobník jako pohotovostní zásobník solárního tepla na straně teplé vody. Instalace předehřívacího zásobníku snižuje potřebný výkon výměníku a nutnost rychlé regulace. Nabíjecí předehřívacího zásobníku je řízeno na základě rozdílu teplot mezi předehřívacím a solárním zásobníkem. Pokud je teplota cirkulace teplé vody menší než teplota v předehřívacím zásobníku, je do něj zavedena.
Obr. 4.10 Solární soustava pro přípravu TV s netlakovým vyrovnávacím a tlakovým pohotovostním zásobníkem (průtočný solární předehřev)
Obr. 4.11 Solární soustava pro přípravu TV s netlakovým vyrovnávacím a tlakovým pohotovostním zásobníkem (zásobníkový předehřev sluneční energií)
4.3 SOLÁRNÍ SOUSTAVY PRO PŘÍPRAVU TEPLÉ VODY A VYTÁPĚNÍ
Se snižováním potřeby tepla na vytápění budov nacházejí stále větší uplatnění solární soustavy sdružující přípravu teplé vody a vytápění, tzv. kombinované solární soustavy. Nižší tepelné ztráty budov vedou k nižším teplotám otopné vody (nízkoteplotní vytápění) a umožňují využití sluneční energie zvláště v přechodovém období i pro vytápění.
Potřeba tepla na vytápění budov se během roku časově rozchází se špičkami dostupných solárních zisků. V otopném období se proto dosáhne vždy jen částečného pokrytí. Ekonomicky přijatelné jsou hodnoty mezi 15 a 30 % celkové roční potřeby tepla pro přípravu teplé vody a vytápění. Hodnota požadovaného solárního pokrytí ovlivňuje návrh zařízení a musí být jasně stanovena.
Základními předpoklady úspěšného návrhu solárních kombinovaných soustav jsou:
dostatečná tepelná izolace domu a kvalitní okna – nízkoenergetický nebo pasivní standard budov; nízkoteplotní otopná soustava s návrhovou teplotou otopné vody do 45 °C – podlahové vytápění, vhodná otopná tělesa; vhodná návaznost na ostatní zdroje tepla a technologie v budově, včetně regulace; sklon kolektoru od 45° až 90°, jižní orientace kolektoru v nezastíněném prostranství; možnost využít letní přebytky solární soustavy (bazén, sušení, akumulace).
U solárních soustav dimenzovaných pro vytápění je nutné vždy uvažovat o smysluplném využití letních přebytků tepla (soustava je předimenzovaná vůči letní potřebě teplé vody), případně jakým způsobem zamezit stagnačním podmínkám v soustavě (maření zisků, vývin páry v kolektorech). Solární kolektory pro solární kombinované soustavy je proto vhodné instalovat se sklonem nad 45°, případně je integrovat do fasády budovy. Dochází tak k rovnoměrnému profilu tepelných zisků, letní přebytečné a nevyužitelné zisky klesají a zimní zisky mírně narostou díky příznivějšímu úhlu dopadu slunečních paprsků, případně vlivem odrazivosti od okolního terénu či sněhové pokrývky.
4.3.1 Maloplošné solární kombinované soustavy (rodinné domy)
Maloplošnou solární kombinovanou soustavu lze pořídit jako průmyslově vyrobenou a dodávanou stavebnici v kompaktním provedení s optimalizovanými prvky nebo častěji jako soustavu dodanou na objednávku, vyznačující se různým stupněm originality v závislosti na požadované funkci a využívaných zdrojích tepla.
U maloplošných kombinovaných soustav v rodinných domech lze často výrazné letní přebytky odvést do bazénu či jiného spotřebiče tepla, čímž se eliminuje problém stagnace a vývinu páry v kolektorech. Tam, kde není možné se letním přebytkům tepla vyhnout, je vhodné zbytečně plochu kolektorů nepředimenzovávat (menší solární pokrytí potřeby tepla na vytápění) a zajistit opatření vůči extrémním podmínkám stagnace.
Solární kombinovaná soustava se dvěma zásobníky
Solární soustava využívá dvou oddělených zásobníků pro teplou vodu a pro otopnou vodu. Podle zvolené strategie řízení solární soustava nabíjí buď přednostně zásobník teplé vody (cílová teplota 60 °C) a v případě přebytečných zisků zásobník otopné vody (cílová teplota: ekvitermní teplota otopné vody 30 až 45 °C), nebo přednostně vždy chladnější zásobník (maximalizace solárních zisků). Výhodné je strategie střídat během roku podle potřeby. Dodatkový zdroj tepla dohřívá podle potřeby oba zásobníky (viz obr. 4.12). Podle velikosti soustavy se používají v solárním okruhu buď trubkové vnitřní výměníky, nebo vnější deskové výměníky.
Obr. 4.12 Solární soustava se dvěma zásobníky s dodatkovým zdrojem pro oba zásobníky
Nevýhodou soustav se dvěma zásobníky mohou být zvýšené tepelné ztráty vlivem většího povrchu a také nároky na prostor či potrubní rozvody ve strojovně. Výhodou zapojení je oddělení „vysokoteplotní“ přípravy TV od nízkoteplotní otopné vody pro zvýšení účinnosti solárních kolektorů. Vlastní zásobník otopné vody je také výhodný pro provoz běžných plynových kotlů, které jsou v případě rodinných nízkoenergetických a pasivních domů výrazně předimenzované. Tepelná ztráta domů o běžné velikosti je po většinu otopného období menší než 1 kW (pasivní rodinný dům) či nebo než 2,5 kW (nízkoenergetický rodinný dům), zatímco běžný plynový kotel má výkon okolo 12 kW a více. Při použití takových kotlů je potom výhodné jeho hydraulické oddělení od otopné soustavy právě zásobníkem tepla, který umožňuje akumulovat přebytečné teplo. Eliminuje se tak cyklování kotle a související zvýšená spotřeba paliva, snížená účinnost a především vysoké emise.
Solární kombinovaná soustava s jedním centrálním zásobníkem
V oblasti maloplošných solárních kombinovaných soustav nabyly v posledních letech značně na významu různé varianty s jediným centrálním (integrovaným) zásobníkem tepla. Příprava teplé vody v centrálním zásobníku tepla je realizována ve vestavěném zásobníku (systém „nádrž v nádrži“), nebo průtokově (vnější deskový výměník, vnitřní trubkový výměník). Pro dosažení vysokých solárních zisků hraje u solárních kombinovaných soustav s centrálním zásobníkem významnou roli schopnost teplotního rozvrstvení objemu zásobníku. Horní pohotovostní část zásobníku se udržuje na teplotě 45 až 65 °C v dostatečném objemu pro potřeby přípravy teplé vody v požadovaném množství. Střední část je využívána pro účely vytápění (30 až 50 °C). Spodní nabíjecí část je nejchladnější (vychlazená od předehřevu studené vody) a je do ní zaveden buď vnitřní trubkový výměník, nebo spodní část vestavěné nádrže. Vzhledem k tomu, že objem zásobníku tvoří otopná voda, nejsou zde výrazné hygienické požadavky na zásobník, což zlevňuje pořizovací náklady.
Pokročilým řešením centrálních zásobníků otopné vody jsou zásobníky se stratifikačními vestavbami, které se v poslední době objevují i v aplikacích pro rodinné domy. Stratifikační vestavby se zde používají jak pro přívod tepla ze solárního okruhu, tak pro přívod vracející se otopné vody. V souvislosti se snahou o maximální integraci zařízení a snížení montážní práce (snížení chyb zapojení) se objevují komplexní řešení centrálních zásobníků tepla s integrovanými dodatkovými zdroji tepla do vlastní konstrukce zásobníku (elektrické vložky, plynové hořáky, hořáky na pelety se zásobníkem), viz obr. 4.14. Nespornou výhodou centrálního zásobníku jsou menší nároky na prostor, nižší tepelné ztráty, jednoduchost instalace (prefabrikované řešení napojení rozvodů).
Obr. 4.13 Zapojení solárního kombinovaného zásobníku
Obr. 4.14 Solární kombinovaná soustava s vysokým stupněm integrace prvků
4.3.2 Velkoplošné solární kombinované soustavy
Velkoplošné kombinované solární soustavy pro přípravu teplé vody a vytápění nejsou tak častým řešením jako soustavy čistě pro přípravu teplé vody. Varianty zapojení soustav jsou obdobné, solární okruh nabíjí solární vyrovnávací zásobník tepla s otopnou vodou a z ní je teplo předáváno pro přípravu teplé vody přes teplosměnnou plochu. Protože se jedná o velkoplošné soustavy, je nezbytné použít výkonné deskové výměníky tepla. Odlišnosti od maloplošných soustav spočívají především v zapojení sekundární části (okruh spotřeby).
Solární kombinovaná soustava s centrální přípravou teplé vody
V případě menších staveb je možné přípravu teplé vody řešit centrálně (průtokově, zásobníkovým způsobem) a v rámci bytového domu je navržen 3-trubkový (2 potrubí pro vytápění, 1 potrubí teplá voda), případně 4-trubkový rozvod (+ cirkulace teplé vody), viz obr. 4.15. Výhodou je možnost různé teplotní úrovně rozvodu otopné soustavy (nízkoteplotní vytápění) a rozvodu teplé vody (50 až 60 °C). Na druhé straně může 4-trubkový rozvod vykazovat příliš vysoké tepelné ztráty, zvláště u dlouhých vedení.
Obr. 4.15 Solární kombinovaná soustava pro bytové domy s centrální přípravou teplé vody (průtočná příprava teplé vody) a 4-trubkovým rozvodem
Kombinované solární soustavy s místní přípravou teplé vody
U rozsáhlých staveb (řadové domy) s malou hustotou odběru energie, kde by tepelné ztráty dlouhých rozvodů mohly negativně ovlivnit energetickou bilanci solární kombinované soustavy, je vhodné řešit zapojení sekundární části 2-trubkovým rozvodem (2 potrubí otopné vody). V jednotlivých připojených bytech nebo stavbách jsou instalovány bytové (domovní) předávací stanice. Příprava teplé vody je místní (decentrální). Na obr. 4.16 je zobrazeno zapojení kombinované solární soustavy pro bytový dům s 2-trubkovou sítí a různými možnostmi zapojení přípravy teplé vody v bytech. Teplá voda je připravována v souladu s přísnými hygienickými požadavky průtokově nebo v malých zásobnících bez rizika množení legionelly. Nízké teploty vratné vody pod 30 °C snižují tepelné ztráty rozvodu na minimum a zajišťují účinný provoz solární soustavy.
Pro relativně vysoké náklady, způsobené použitím lokálních zásobníků při vyšších odběrových hustotách (konvenční stavby pro více rodin), se ukazuje z hlediska nákladů příznivější alternativou průtočná příprava bez zásobníku. V posledních letech se v zahraničí pro výstavbu bytových domů s více rodinami prosadily ve spojení se solárními kombinovanými soustavami tlakově závislé bytové předávací stanice, kdy je 2-trubkovým rozvodem přivedena otopná voda v budově až k jednotlivým bytům. V bytové předávací stanici je připravována teplá voda (deskový výměník tepla) a regulována otopná voda pro vytápění (ekvitermní, individuální regulace). Byty jsou opatřeny vlastním měřením spotřeby tepla. Velikost prostoru pro umístění bytové předávací stanice je srovnatelná nebo menší než kterýkoli jiný zdroj tepla (plynový kotel, elektrokotel). Bytové stanice se dodávají v nástěnném provedení. Náklady na bytové předávací stanice, včetně měření tepla, však mohou být hlavní překážkou většího rozšíření dvojtrubkového konceptu v podmínkách ČR.
Obr. 4.16 Solární kombinovaná soustava s 2-trubkovým rozvodem a třemi variantami decentrální přípravy teplé vody
Na obr. 4.17 je kombinovaná solární soustava s dvojtrubkovým rozvodem s objemem solárního zásobníku tepla rozděleným do dvou sériově zapojených a dodatkovým zdrojem tepla zapojeným do okruhu přívodní otopné vody přes termohydraulický rozdělovač (THR).
Obr. 4.17 Kombinovaná solární soustava se dvěma solárními vyrovnávacími zásobníky a dohřevem centrálního rozvodu přes termohydraulický rozdělovač
4.4 HYDRAULICKÁ ZAPOJENÍ SOLÁRNÍCH SOUSTAV
Hydraulická zapojení solárních soustav pro přípravu teplé vody, případně vytápění v kombinaci s dodatkovým zdrojem tepla jsou velmi rozmanitá. Většinou se jedná o zařízení s vodním zásobníkem tepla, který je nezbytnou podmínkou pro provoz solárních soustav (vyrovnání nesoučasnosti dodávky a odběru tepla). V následujícím textu je přehled různých způsobů zapojení primárních a sekundárních okruhů solárních soustav.
4.4.1 Primární okruh – okruh solárních kolektorů
Hydraulické zapojení primárního okruhu závisí na několika hlediscích:
- plocha kolektorového pole;
- počet kolektorových polí;
- délce venkovních rozvodů;
- typ odběru (zásobník tepla – stratifikační, nestratifikační, bazén, tepelný výměník aj.);
- počet připojených odběrů.
Nabíjení akumulačního zásobníku solární soustavou je možné realizovat různými způsoby, uvedenými na obr. 4.18. Pro maloplošné soustavy pro rodinné domy je ve většině případů postačující použití vnitřního výměníku v dolní části zásobníku (viz obr. 4.18a), případně v dolní a horní části pro zvýšení využití tepla (viz obr. 4.18b). Pro pokročilé řízení teplotního vrstvení lze použít výměník umístěný ve spodní části stratifikačního válce (viz obr. 4.18c). Schopnost vnitřního vestavěného výměníku předat výkon kolektorového pole do zásobníku tepla by měl určit projektant. Výpočtu výměníků se věnuje samostatná kapitola. Výrobce nebo dodavatel by měl výkon nebo alespoň teplosměnnou plochu výměníku uvádět ve svých podkladech.
Obr. 4.18 Zapojení primárního okruhu solární soustavy s vnitřními výměníky
Pro střední a velké soustavy (plocha kolektorů > 20 m2, výkon cca do 10 kW) je vhodné použití výkonnějšího deskového výměníku umístěného vně zásobníku tepla (viz obr. 4.19). V sekundárním okruhu vnějšího výměníku je nutné použít oběhové čerpadlo. U přípravy teplé vody je nutné zohlednit, že neupravené vodě musí odpovídat typ čerpadla a v případě výskytu minerálních látek použít rozebiratelný výměník. Stav výměníku je nutné pravidelně kontrolovat, zda nedochází k jeho zanášení vodním kamenem, případně jej v pravidelných intervalech čistit. U kombinovaných solárních soustav je na sekundární straně upravená otopná voda.
U speciálně konstruovaných typů výměníků je možné použít na sekundární straně gravitační oběh (viz obr. 4.19c). Podmínkou je umístění výměníku dostatečně pod úrovní zásobníku, aby vztlakové síly mohly vyvolat a udržet přirozený oběh. Průtok výměníkem na sekundární straně se automaticky přizpůsobuje teplotní úrovni kolektorů (vyšší teplota, vyšší vztlak, vyšší průtok).
Obr. 4.19 Zapojení primárního okruhu solární soustavy s vnějšími výměníky
Pokud jsou venkovní rozvody příliš dlouhé, dochází při nízkých venkovních teplotách k prochladnutí celého objemu potrubí. Aby se při rozběhu, kdy je v kolektorech již ohřátá teplonosná kapalina, v potrubí je však ještě studená, nevychlazoval zásobník tepla, je nutné objem primárního okruhu před vstupem do výměníku zahřát na požadovanou teplotu. V těchto případech je vhodné použití tzv. obtoku (viz obr. 4.20a), kdy po sepnutí oběhového čerpadla se obtokovým trojcestným ventilem zkratuje přívod do výměníku a teplo z kolektorů ohřívá nejprve objem primárního okruhu. Teprve po dosažení dostatečné teploty kapaliny před vstupem do výměníku se ventil přepne a sepne se i čerpadlo sekundárního okruhu. Nejvhodnější umístění obtokového ventilu je co nejblíže zásobníku tepla. Při použití vnějšího deskového výměníku místo trubkového vnitřního se zároveň jedná o protimrazovou ochranu výměníku. V případě podnulových teplot nemrznoucí kapaliny ve venkovním potrubí by při absenci obtoku mohlo po spuštění oběhového čerpadla dojít k zamrznutí vody na sekundární straně výměníku.
Obr. 4.20 Zapojení obtoku (a), regulace výměníku (b) a různým způsobem provozovaných kolektorových polí (východ, západ)
V některých aplikacích může být potřebné řídit výkon soustavy na sekundární straně výměníku (viz obr. 4.20b). Z hlediska orientace kolektorového pole může dojít k případům, kdy není na jedné části střechy (či jiné instalační plochy) dostatek místa pro potřebný počet kolektorů. Kolektorové pole je rozděleno na více částí. V případě shodné orientace může být použito jedno společné oběhové čerpadlo. Pokud však mají části kolektorového pole jinou orientaci a jejich provozní doba a teplotní úroveň je obecně různá, je nutné pro každou část kolektorového pole instalovat vlastní oběhové čerpadlo a regulací solární soustavy zajistit samostatné spínání jednotlivých částí (viz obr. 4.20c).
V některých případech, kdy je teplo ze solární soustavy využíváno ve více odběrech (teplá voda, vytápění, ohřev bazénu aj.), může být na několik okruhů rozdělen již primární okruh solární soustavy (viz obr. 4.21). Provoz jednotlivých okruhů je potom možné realizovat buď trojcestnými přepínacími ventily (viz obr. 4.21a), dvojcestnými ventily (viz obr. 4.21b) nebo samostatnými oběhovými čerpadly (viz obr. 4.21c). U spotřebičů (okruhů) s velmi rozdílnou tlakovou ztrátou je výhodné zapojení se samostatnými oběhovými čerpadly. Oběhová čerpadla se potom navrhnou individuálně na každý okruh podle hydraulických poměrů (průtok, tlaková ztráta).
Obr. 4.21 Rozdělení primárního okruhu do jednotlivých odběrů
4.4.2 Zapojení dodatkového zdroje tepla
Stejně jako u kolektorové části solární soustavy je i u zapojení dodatkového zdroje tepla několik možností. Konkrétní zapojení závisí na řadě hledisek:
- ohřívaná teplonosná látka – teplá voda, otopná voda, bazénová voda;
- typ dodatkového zdroje – kotel, průtokový dohřev, předávací stanice, el. topná vložka aj.;
- způsob instalace – monovalentní, bivalentní, multivalentní zásobník tepla;
- způsob napojení zdroje – vnitřní výměník, vnější výměník, přímé napojení.
Při dohřevu teplé vody je nutné zdroj tepla (otopná voda) oddělit buď vestavěným výměníkem (viz obr. 4.22a, f), nebo externím výměníkem (viz obr. 4.22b). Je také možné použít průtokový dohřev v kotli (obr. 4.22d). Průtokový ohřívač musí umožnit modulaci v širokém rozsahu výkonu pro udržení požadované konstantní výstupní teploty.
V případě elektrického dohřevu nezáleží (viz obr. 4.22e), zda je připravována teplá voda nebo otopná voda. U solárních kombinovaných soustav se zásobníkem otopné vody není nutné dodatkový zdroj tepla oddělovat (viz obr. 4.22c).
Obr. 4.22 – Zapojení dodatkového zdroje tepla
V některých případech je zdroj oddělen od zásobníku výměníkem nikoliv z hygienických důvodů, ale z důvodů různé tlakové odolnosti jednotlivých součástí. Například řada teplovodních krbových vložek má max. přípustný tlak 0,15 MPa, a pokud je nutné ve zbytku otopné soustavy udržovat tlak vyšší, je nutné takový zdroj tlakově oddělit.
Na obr. 4.22f je zobrazena instalace dvou zásobníků teplé vody (solární vyrovnávací, dohřívací pohotovostní). Do pohotovostního je zapojen dodatkový zdroj tepla, který udržuje požadovanou teplotu teplé vody. Pokud není zaručen během dne dostatečný odběr teplé vody tak, aby se předehřátá voda dostala ze solárního zásobníku tepla do pohotovostního, je možné akumulované solární zisky z vyrovnávacího zásobníku do pohotovostního přečerpat. Pokud je teplota ve vyrovnávacím zásobníku tepla vyšší než v pohotovostním, sepne se přečerpávací čerpadlo.
4.4.3 Zapojení odběru tepla
Zatímco u solárních soustav pro přípravu teplé vody je odběr teplé vody ze zásobníku řešen běžným způsobem (viz obr. 4.23a), hydraulické zapojení odběru teplé vody používané v solárních kombinovaných soustavách může být provedeno v řadě různých variant (viz obr. 4.23). U odběru teplé vody ze solárních zásobníků je nutné vždy na výstupu osadit termostatický ventil jako ochranu proti opaření.
Nevhodné promíchávání objemu zásobníku tepla vlivem padajících chladných proudů z odběrového výměníku (např. při variantě viz obr. 4.23b) může být potlačeno vhodným zapojením průtočného výměníku teplé vody v zásobníku (viz obr. 4.23c-e), nebo použitím vestavěného zásobníku teplé vody v celé výšce zásobníku tepla (viz obr. 4.23f, g). Je nutné však zdůraznit, že vestavěný zásobník teplé vody má velmi omezený výkon a po nárazovém vyčerpání jeho obsahu je třeba vyčkat relativně dlouhou dobu na jeho opětovné nabití (volná konvekce na obou stranách teplosměnné plochy).
Pokročilým řešením pro předání vysokých výkonů v průtokovém ohřevu je instalace deskového výměníku přípravy teplé vody ve spojení se stratifikační vestavbou, která přivádí v závislosti na odběru teplé vody různě vychlazenou otopnou vodu zpět do zásobníku bez degradace teplotního vrstvení. Takové řešení nevyžaduje řízení otáček čerpadla. Energeticky výhodnější možností je použít řízení otáček čerpadla na základě teploty na vstupu do solárního zásobníku, aby bylo v každé provozní situaci dosaženo maximálního vychlazení vratné vody. Potom není stratifikační vestavba v zásobníku nezbytná.
Obr. 4.23 Variantní zapojení odběru tepla (příprava teplé vody)
4.4.4 Zapojení cirkulace teplé vody
Dalším hlediskem jak pro výběr zásobníku tepla, tak následně pro hydraulické zapojení odběru tepla je možnost zapojení cirkulace. Pokud je systém přípravy teplé vody vybaven cirkulací, je třeba pečlivě uvážit, kam bude tato cirkulace zapojena. Pro solární soustavy pouze s přípravou teplé vody jsou možnosti uvedeny na obr. 4.24. Především ve velkoplošných soustavách pro přípravu teplé vody se používá rozdělení cirkulace mezi solární vyrovnávací zásobník teplé vody a pohotovostní dohřívací zásobník podle teplotních poměrů. Pokud je v horní části solárního zásobníku dostatečná teplota pro ohřev cirkulace, trojcestný ventil přesměruje cirkulaci na ohřev solárními zisky. Cirkulace přepojená do solárního zásobníku tak zároveň plní funkci přečerpávacího čerpadla.
Obr. 4.24 Zapojení cirkulace u solárních zásobníků teplé vody
U solárních kombinovaných soustav se zásobníkem otopné vody a vestavěnou přípravou teplé vody je možnost využití cirkulace vázaná na typ zásobníku. Zásobník tepla s jedním vestavěným výměníkem pro přípravu teplé vody není pro zaústění cirkulace příliš vhodný. Pokud je v horní části (viz obr. 4.25a), k narušení teplotního vrstvení nedojde, pokud je však průběžný po celé výšce (obr. 4.25d), dochází vlivem průtoku cirkulace k ohřívání spodní části akumulační nádoby. Potom je lepší zvolit dělený průtočný výměník (dolní, horní) a cirkulaci napojit do spojky mezi oběma výměníky (viz obr. 4.25c). Výhodné jsou z hlediska připojení cirkulace vestavěné zásobníky teplé vody (viz obr. 4.25b).
Obr. 4.25 Zapojení cirkulace u zásobníku tepla solárních kombinovaných soustav
4.5 ENERGETICKÉ PARAMETRY SOLÁRNÍCH SOUSTAV
Energetické charakteristiky solárních soustav a efektivitu jejich provozu lze vyjádřit několika základními parametry. Základem jsou skutečně využité (využitelné) tepelné zisky solární soustavy a vlastní spotřeba tepla v aplikaci, kterou má solární soustava pokrýt. Parametry slouží jako podklad k energetickému (úspora energie), ekologickému (úspora emisí) a ekonomickému (návratnost) hodnocení solárních tepelných soustav.
4.5.1 Využité tepelné zisky solární soustavy
Za využité tepelné zisky solární soustavy Qss,u [kWh/rok, GJ/rok] jsou považovány ty, které soustava včetně zahrnutí všech svých ztrát dodá pro krytí potřeby tepla v dané aplikaci (příprava teplé vody, vytápění, ohřev bazénové vody). Tepelné zisky solární soustavy je vhodné v optimálním případě stanovit na skutečné hranici mezi vlastní solární soustavou a danou aplikací (viz obr. 4.26). Stanovení solárních zisků pouze kolektorového pole, resp. kolektorového okruhu před vstupem do solárního zásobníku nezohledňuje tepelné ztráty kolektorového okruhu Qz,ko, resp. solárního zásobníku Qz,sz a může nadhodnocovat reálné přínosy solární soustavy do dané aplikace. V řadě případů však s ohledem na jednoduchost a spolehlivost měření se zisky solární soustavy stanovují jako teplo Qk, dodané z kolektorového okruhu do solárního zásobníku. Při výpočtovém hodnocení je navíc nutné stanovit využitelnost teoreticky dostupných solárních zisků pro pokrytí potřeby tepla. Přebytky tepla (zisky překračující potřebu) nelze započítat jako využité.
Využité solární zisky nejsou závislé pouze na kvalitě navržených komponent (kolektor, zásobník), na tepelných ztrátách soustavy (rozvod potrubí, solární zásobník) a na orientaci a sklonu solárních kolektorů, ale především na návrhu plochy solárních kolektorů vzhledem k potřebě tepla, tzn. využitelnosti tepelných zisků kolektorů pro krytí potřeby tepla.
Obr. 4.26 Zjednodušené schéma solární soustavy pro přípravu TV a její energetická bilance
4.5.2 Roční úspora energie
Samotné využité solární zisky nemusí mít o skutečné úspoře instalací solární soustavy dostatečnou vypovídající schopnost. Vyšší přínos instalací solárních soustav je patrný především tam, kde svými zisky uspoří produkci tepla zdrojem s nízkou provozní účinností, např. předimenzovaný a cyklující kotel spalující fosilní palivo (plyn), svázaný s vysokou spotřebou paliva a produkcí emisí. Pro stanovení úspory paliva, resp. úspory primární energie instalací solární soustavy je proto nezbytné předně určit provozní účinnost nahrazovaného zdroje tepla. Na druhé straně, pokud má solární soustava nahradit účinný kotel na spalování biomasy, který má relativně nízký negativní dopad na životní prostředí, bude taková instalace vykazovat nízké snížení spotřeby primárních paliv a emise znečišťujících látek.
Roční úspora energie instalací solární soustavy vychází z ročních celkových zisků jako
(4.1)
kde je
ηnz … provozní účinnost nahrazovaného zdroje tepla.
4.5.3 Dodatková energie
Dodatkový zdroj tepla slouží pro dohřev v solární soustavě v případě, že energie produkovaná solární soustavou nedokáže pokrýt potřebu tepla. Při výpočtovém hodnocení se dodatková energie Qd stanoví jako rozdíl mezi předpokládanou potřebou tepla a využitými tepelnými zisky solární soustavy v dané aplikaci. Při provozním měření a hodnocení solárních soustav se dodatková energie měří, neboť skutečná spotřeba tepla Qp,c není známa. Stanovit celkovou potřebu tepla dané aplikace Qp,c provozním měření je nerealizovatelné vzhledem k praktické nemožnosti stanovit tepelné ztráty aplikace měřením. Proto se vyhodnocuje jako součet naměřených hodnot tepla dodaného solární soustavou a dodatkovým zdrojem energie podle vztahu
(4.2)
Z dodatkové energie se stanovuje provozní spotřeba konvenční energie dodatkového zdroje tepla a provozní náklady při známé ceně konvenční energie.
4.5.4 Měrné využité tepelné zisky solární soustavy
Měrné využité tepelné zisky solární soustavy qss,u v kWh/(m2·rok), tzn. celkové roční zisky vztažené k instalované účinné ploše solárního kolektoru Ak (zpravidla ploše apertury) podle vztahu
(4.3)
jsou ve své podstatě ekonomickým parametrem. Roční měrný zisk, resp. úsporu z 1 m2 instalované plochy kolektorů lze porovnat s měrnými investičními náklady na pořízení solární soustavy pro rychlý náhled na ekonomické parametry.
Poznámka:
Velikost a tedy cena prvků solárních soustav souvisí s velikostí instalované plochy solárních kolektorů (výkon, průtok): zásobník tepla (od potřeby tepla, na kterou je navržena plocha kolektorů), výměník tepla (přenáší výkon kolektorů, daný jejich plochou), světlost (dimenze) potrubí (průtok kolektory, daný jejich plochou, výkonem), tepelná izolace potrubí (tloušťka je dána světlostí potrubí), oběhové čerpadlo (průtok, tlaková ztráta související se světlostí potrubí), expanzní nádoba (odvíjí se od světlosti potrubí a počtu kolektorů).
Měrné tepelné zisky qss,u jsou nejčastěji hodnoceným kritériem energetické kvality solárních soustav. Pro ekonomicky navrhované solární soustavy by se měrné zisky měly pohybovat nad minimálními doporučenými hodnotami, uvedenými v tab. 4.1.
Tab. 4.1 Minimální doporučené hodnoty měrných zisků solární soustavy
| Solární soustava | Rodinné domy | Bytové domy |
| Příprava teplé vody | 350 kWh/(m2·rok) | 400 kWh/(m2·rok) |
| Příprava teplé vody a vytápění | 280 kWh/(m2·rok) | 350 kWh/(m2·rok) |
| Ohřev bazénové vody | Sezónní využití | Celoroční využití |
| 350 kWh/(m2·rok) | 500 kWh/(m2·rok) |
4.5.5 Solární pokrytí, solární podíl f
Solární pokrytí (měsíční, roční) je obecně poměr mezi celkovými využitými zisky solární soustavy Qss,u a celkovou potřebou tepla (včetně ztrát) dané aplikace Qp,c
(4.4)
V případě provozního měření dodatkové energie Qd se solární podíl vyhodnotí podle vztahu
(4.5)
V grafu na obr. 4.27 jsou pro orientační příklad solární přípravy teplé vody uvedeny závislosti solárního pokrytí f a ročních měrných využitých zisků qss,u na poměru instalované plochy solárních kolektorů Ak k denní potřebě teplé vody VTV. Z grafu je patrná obecná zákonitost, že s instalovanou plochou kolektorů solární pokrytí sice roste, nicméně od určité hodnoty (okolo 50 až 60 %) je nárůst již velmi pozvolný. S rostoucím solárním pokrytím na druhé straně klesají měrné solární zisky z kolektorů, protože nárůst pokrytí potřeby tepla je doprovázen zvýšením průměrné provozní teploty v solární soustavě, nárůstem provozních tepelných ztrát, souvisejícím poklesem účinnosti solárních kolektorů a zejména snížením využitelnosti solárních zisků v letním období (viz obr. 4.28).
Obr. 4.27 Souvislost mezi instalovanou plochou solárních kolektorů, solárním pokrytím a měrnými využitými zisky solární soustavy pro přípravu teplé vody (orientační příklad)
Obr. 4.28 Průběh teoreticky využitelných tepelných zisků a skutečně využitých zisků solární soustavy pro přípravu teplé vody při různém solárním pokrytí (orientační příklad)
Obr. 4.29 (a, b, c) Souvislost mezi měrnými solárními zisky a solárním pokrytím při různém dimenzování plochy solárních kolektorů pro solární přípravu teplé vody (orientační příklady)
Na obr. 4.29 je znázorněna analýza vlivu instalované plochy při dané potřebě teplé vody na solární pokrytí a měrné zisky. Jako referenční případ je uvažována solární soustava s pokrytím 60 % a měrnými solárními zisky okolo 400 kWh/m2·rok. Instalovaná plocha kolektorů je cca 2,5 m2 / 100 l připravované teplé vody. Snížením instalované plochy kolektorů na polovinu se solární pokrytí sníží na 40 %, nicméně měrné zisky vzrostou až na 570 kWh/m2·rok. Zvýšením instalované plochy solárních kolektorů o polovinu se solární pokrytí zvýší oproti referenčnímu případu pouze o 5 %, neboť výrazně narostou především letní nevyužitelné přebytky energie (viz obr. 4.29). Na druhé straně výrazně poklesnou měrné tepelné zisky solární soustavy na neekonomickou hodnotu 300 kWh/m2·rok. V zásadě tedy platí, že pro běžné aplikace bez výrazných spotřebičů letních přebytků energie z kolektorů jsou solární pokrytí a měrné tepelné zisky solární soustavy v protikladu.
4.5.6 Provozní účinnost solární soustavy
Vzhledem k nestejným klimatickým podmínkám a různým úrovním dopadající sluneční energie se bude v různých lokalitách a v různých letech hodnota využitých tepelných zisků solární soustavy lišit. Na obr. 4.30 jsou uvedeny měrné zisky solární soustavy pro přípravu teplé vody stanovené pro různé reálné roky (1984-1997) a pro dva druhy statisticky zpracovaných klimatických let (referenční klimatický rok, typický meteorologický rok).
Obr. 4.30 Měrné zisky solární soustavy v různých letech
Vztažením využitých tepelných zisků Qss,u ke sluneční energii Qs dopadlé v místě instalace na plochu kolektorů se stanoví celková účinnost solární soustavy
(4.6)
Účinnost solární soustavy charakterizuje energetickou kvalitu solární tepelné soustavy bez ohledu na klimatické podmínky. Účinnost soustavy je závislá jak na kvalitě použitých prvků (kolektor, zásobník, výměník, tepelné izolace, regulace, hydraulické zapojení), tak na dimenzování plochy kolektorů vůči potřebě tepla. Na obr. 4.31 je graficky uveden vztah mezi měrnými ročními využitými zisky solární soustavy a ročním úhrnem slunečního záření. Směrnice přímky je účinnost soustavy, pro jednotlivé případy se odchyluje řádově v procentech. U maloplošných solárních soustav se celková účinnost solární soustavy pohybuje okolo 35 % (podle typického dimenzování), u velkoplošných soustav nad 45 %.
Obr. 4.31 Závislost ročních měrných zisků na úhrnu slunečního záření
4.5.7 Spotřeba pomocné energie soustavy
Pro stanovení celkové energetické bilance solární soustavy je nezbytné hodnotit také spotřebu pomocné elektrické energie na provoz solární soustavy. Zatímco u samotížných solárních soustav je spotřeba pomocné energie nulová, u solárních soustav s nuceným oběhem je zapotřebí dodat elektrickou energii na pohon oběhových čerpadel, ovládaných ventilů, regulaci aj. Pomocná elektrická energie je důležitá pro vyhodnocení reálných přínosů solární soustavy s ohledem na vyjádření skutečných úspor primární energie a emisí znečišťujících látek. Spotřeba pomocné el. energie se stanoví z elektrického příkonu solární soustavy a doby běhu jednotlivých elektrických zařízení. Výpočet je možné zjednodušit na stanovení příkonu oběhových čerpadel v pracovním návrhovém bodě a uvažováním doby jejich běhu jako rovné skutečné době slunečního svitu (1400 až 1800 h/rok). Potom se spotřeba pomocné elektrické energie Qpom [kWh/rok] stanoví podle vztahu
(4.7)
kde je
Pč … příkon oběhových čerpadel, ve W.
U maloplošných solárních soustav s běžnými oběhovými čerpadly se poměr pomocné el. energie k tepelným zisků soustavy může pohybovat až do 4 %, u velkoplošných soustav vzhledem k velké ploše a vysoké absolutní hodnotě tepelných zisků se pohybuje do 1 %.
Nízkou spotřebu pomocné elektrické energie je možné docílit energeticky především návrhem hydrauliky solární soustavy a použitím úsporných oběhových čerpadel (např. s permanentními magnety).
4.6 LITERATURA
[1] DUFFIE, J. A., BECKMAN, W. A. Solar enginnering of thermal processes. 3. vydání. Wiley 2006, ISBN 13-978-0-471-69867-8.
[2] LADENER, H., SPÄTE, F. Solární zařízení, Grada Publishing 2003, Praha, ISBN 80-247-0362-9.
[3] REMMERS, K. H.: Velká solární zařízení, ERA group, 2007, ISBN 978-80-7366-110-6.
[4] PEUSER, F. A., REMMERS, K.-H., SCHNAUSS, M. Solar thermal systems. James&James, Solarpraxis AG. ISBN 1-902916-39-5.
[5] PEUSER, F.A., REMMERS, K.H., SCHNAUSS, M. Langzeiterfahrung Solarthermie, Solarpraxis Supernova A.G., Berlin, 2001, ISBN 3-934595-01-4.
[6] Planning and Installing Solar Thermal Systems – a guide for installers, architects and engineers. James&James/Earthscan 2005. ISBN 1-84407-125-1.
[7] WEISS, W. et al. Solar Heating Systems for Houses: A Design Handbook for Solar Combisystems. Earthscan Publications Ltd. (June 2004), ISBN 978-1902916460.
[8] MATUŠKA, T. Názvoslovný výkladový slovník z oboru Solární tepelná technika, příloha časopisu Vytápění, větrání, instalace, č. 5, STP 2009. ISBN 978-80-02-02177-3, březen 2009.
5 NAVRHOVÁNÍ SOLÁRNÍCH SOUSTAV
Navrhováním solárních soustav se obecně rozumí určení plochy a počtu solárních kolektorů. Návrh plochy a počtu solárních kolektorů je základním předstupněm k dalšímu navrhování. Z navržené plochy solárních kolektorů se odvíjí návrh všech ostatních prvků a často také hydraulické zapojení soustavy. Následující kapitoly se věnují návrhu tří základních a nejrozšířenějších typů solárních soustav v ČR pro aplikace:
- příprava teplé vody;
- příprava teplé vody a vytápění (kombinované soustavy);
- ohřev bazénové vody.
Při návrhu se nejprve určuje potřeba tepla v dané aplikaci, kterou je možné pokrýt solárními zisky. Dále se určí teoretické zisky 1 m2 solárních kolektorů v uvažovaném období (referenční den v návrhovém měsíci), ve kterém je požadavek na pokrytí celé (100 %) nebo částečné potřeby tepla. Z porovnání se určí potřebná plocha solárních kolektorů.
5.1 POTŘEBA TEPLA
Prvním krokem při návrhu plochy kolektorů dané solární soustavy je stanovení potřeby tepla v dané aplikaci měřením nebo výpočtem. Pokud je potřeba tepla známá z dlouhodobých a věrohodných měření (celoroční) na patě stavby, jeho uvažované části nebo na patě vlastní aplikace, použije se tato hodnota místo výpočtu uvedeného v následujících kapitolách 5.1.1 až 5.1.3. Častějším případem je situace, kdy k dispozici měřené hodnoty nejsou a potřebu tepla je nutné stanovit spolehlivým výpočtem s reálnými hodnotami, vycházejícími z dlouhodobé zkušenosti či relevantních norem.
Před vlastním návrhem a instalací solární soustavy je vhodné provést nejprve úsporná opatření v dané aplikaci. Omezení potřeby tepla vede ke:
- snížení nároků na investiční náklady solární soustavy (kolektor, zásobník);
- omezení provozních problémů, způsobených předimenzováním v případě nasazení úsporných opatření v budoucnosti;
- snížení rizika neekonomicky předimenzované plochy kolektorů, případně velikosti zásobníku, nízkých měrných zisků solární soustavy.
Provedení úsporných opatření a pečlivá analýza potřeby tepla v předinvestiční fázi je zcela zásadní pro správný návrh soustavy (plocha kolektorů, objem zásobníku) a dosažení očekávaných energetických přínosů.
5.1.1 Potřeba tepla na přípravu teplé vody
Využití sluneční energie pro přípravu teplé vody má vysoký potenciál vzhledem k relativně rovnoměrnému průběhu potřeby teplé vody během roku (např. obytné budovy, hotely, sportovní zařízení) a možnosti dosažení dobrých ekonomických parametrů. Aby byla instalace solární soustavy pro přípravu teplé vody efektivní, je nutné ještě před vlastním návrhem solární soustavy v první řadě omezit spotřebu teplé vody a tepla na její přípravu úspornými opatřeními, např.:
- úspornými výtokovými armaturami;
- minimalizací délky rozvodů teplé vody;
- omezením tepelných ztrát rozvodů teplé vody a cirkulace;
- omezením běhu cirkulace na nezbytně nutnou dobu, případně využitím řízení cirkulace na základě teplotních čidel;
- u dlouhých a rozvětvených tras rozvodů teplé vody a cirkulace je nutné jejich hydraulické vyvážení, aj.
Návrh solární soustavy pro bytový dům musí vycházet z reálné potřeby tepla na přípravu teplé vody. Celková potřeba tepla na přípravu teplé vody Qp,TV [kWh/den] v návrhovém měsíci se výpočtem stanovuje jako potřeba tepla na ohřev vody, včetně zahrnutí tepelných ztrát vlastní soustavy přípravy teplé vody (související pouze s přípravou TV), které je možné pokrýt solárními zisky.
Potřeba tepla na ohřev vody
Potřeba tepla na ohřev vody je dána vztahem
(5.1)
kde je
VTV,den … průměrná denní potřeba teplé vody, v m3/den;
ρ … hustota vody, v kg/m3;
c … měrná tepelná kapacita vody, v J/(kg·K);
tSV … teplota studené vody, ve °C;
tTV … teplota teplé vody, ve °C.
Tab. 5.1 Měrná denní potřeba teplé vody při teplotním spádu 60/15 °C
| Typ budovy | Typ spotřeby | m.j. | VTV,mj,den [l/mj·den] |
| Obytné budovy | Nízký standard | os | 10–20 |
| Střední standard | os | 20–40 | |
| Vysoký standard | os | 40–80 | |
| Nízké (letní) vytížení | 0,75 x VTV | ||
| Nemocnice | Nízké (letní) vytížení | os | 30–35 |
| Zbylá část roku | os | 30–60 | |
| Domovy důchodců | Nízké (letní) vytížení | os | 30–35 |
| Zbylá část roku | os | 30–60 | |
| Studentské domovy, koleje | Nízké (letní) vytížení | os | 20–25 |
| Zbylá část roku | os | 25–50 | |
| Školy | Nízké (letní) vytížení | os | 0 |
| Zbylá část roku | os | 5–10 | |
| Hostince, restaurace | Nízký standard | místo | 5 |
| Střední standard | místo | 15 | |
| Vysoký standard | místo | 30 | |
| Ubytovací zařízení** | Nízký standard | lůžko | 20 |
| Střední standard | lůžko | 35 | |
| Vysoký standard | lůžko | 70 | |
| Sportovní zařízení*** | Nízký standard | sprcha | 30 |
| Střední standard | sprcha | 60 | |
| Vysoký standard | sprcha | 100 |
Potřeba teplé vody se stanoví podle tab. 5.1. Potřeba teplé vody souvisí s teplotní úrovní. Směrné hodnoty jsou zpravidla uváděny pro teplotu studené vody 15 °C a teplotu teplé vody 60 °C. V případě, že je teplá voda připravována za jiných teplotních podmínek, než při kterých jsou známy denní odběry, použije se vztah (5.1) se zjištěnými potřebami teplé vody a příslušnými teplotami (studená voda, teplá voda).
Tab. 5.2 Měrná denní potřeba teplé vody při různých teplotních úrovních
| Typ spotřeby | 60 °C | 45 °C | Tepelná energie |
| Nízký standard | 10 až 20 l/os·den | 15 až 30 l/os·den | 0,5 až 1,0 kWh/os·den |
| Střední standard | 20 až 40 l/os·den | 30 až 60 l/os·den | 1,0 až 2,1 kWh/os·den |
| Vysoký standard | 40 až 80 l/os·den | 60 až 120 l/os·den | 2,1 až 4,2 kWh/os·den |
K určení potřeby teplé vody pro návrh a bilancování solární soustavy pro přípravu teplé vody nelze použít hodnot z normy ČSN 06 0320, určené pro návrh konvenčních zařízení pro přípravu teplé vody [1]. Návrhové hodnoty uvedené v normě jsou určeny pro návrh zdroje teplé vody a její bezpečné zajištění v dané budově a jsou ze své podstaty výrazně vyšší než běžně dosahované (cca dvojnásobné). Pro orientaci jsou níže uvedeny hodnoty pro typické aplikace podle uvedené normy:
bytové stavby: potřeba teplé vody 82 l/os·den (60/15 °C), odpovídající denní potřebě tepla QTV = 4,3 kWh/os·den, administrativa: potřeba teplé vody 25 l/os·den (60/15 °C), odpovídající denní potřebě tepla QTV = 1,3 kWh/os·den,
Reálné údaje o potřebě teplé vody lze najít v ČSN EN 15316-3-1 [2] nebo ve směrnici VDI 2067 [3], ze kterých vychází hodnoty uvedené v tab. 5.1. Praktická měření dokládají podobné hodnoty spotřeby teplé vody a vykazují rozdíly denní spotřeby při různém životním standardu, stáří, povolání osob, ročním období atd.
Průzkum spotřeby energií v domácnostech ENERGO 2004, jehož cílem bylo získání údajů o parametrech, vybavenosti, energetické náročnosti a nákladech na provoz bytu, resp. domácnosti, mimo jiné vyhodnotil měrnou potřebu tepla pro přípravu teplé vody v ČR ve výši 8,4 GJ/byt·rok (včetně zahrnutí tepelných ztrát) [4]. Při uvažování průměrné obsazenosti bytů v ČR v rámci průzkumu 2,5 osob/byt lze jednoduše odhadnout průměrnou ekvivalentní spotřebu TV okolo 49 l/os·den (60 / 15 °C), ve které již jsou zahrnuty tepelné ztráty přípravy TV. Při porovnání s hodnotami v tab. 5.1 je patrné, že průměrná hodnota čisté spotřeby TV v ČR (beze ztrát při přípravě a v rozvodu) se pohybuje spíše v nízkém a středním standardu.
Pro stanovení reálných hodnot potřeby teplé vody během roku podle tab. 5.1 je nezbytné uvažovat reálnou obsazenost budov, případně roční profil potřeby tepla na přípravu TV, který může mít významný vliv na návrh nebo hodnocení solární soustavy. Typickým příkladem je průběh spotřeby teplé vody v bytových domech během roku s letním poklesem.
Obr. 5.1 Průběh spotřeby teplé vody a teploty studené vody vstupující do přípravy TV v bytovém domě v Praze-Stodůlkách
Na obr. 5.1 je zobrazen průběh spotřeby teplé vody v bytovém domě v Praze-Stodůlkách. Z grafu je patrný pokles odběru teplé vody v letním období červen-srpen, typický pro bytové domy. V létě dochází obecně k poklesu spotřeby tepla na přípravu teplé vody o zhruba 25 až 30 % oproti ročnímu průměru vlivem:
- školních prázdnin a dovolených uživatelů;
- vyšších teplot studené vody v letním období, až o 15 K (viz obr. 5.1);
- různého chování uživatelů v různých obdobích (v letním období převažuje osvěžující sprchování, v zimním období spíše horká lázeň).
V uvedeném případě bytového domu klesá v létě celková potřeba tepla na přípravu teplé vody vlivem poklesu odběru a nárůstu teploty studené vody dokonce o 40 % oproti ročnímu průměru.
Měření spotřeby teplé vody
Pro stanovení spotřeby tepla na přípravu teplé vody je u stávajících budov vhodné vycházet z dlouhodobých a věrohodných měření (následující pořadí označuje vhodnost):
- dodaného tepla (celoroční měření, průběh během roku) na patě budovy, jeho uvažované části nebo na patě vlastního zásobníku teplé vody (např. dohřívací okruh plynového kotle), včetně cirkulace, pokud je instalována;
- spotřebovaného množství teplé vody při znalosti teploty studené vody na vstupu do ohřívačů a nastavené teploty ohřívačů (skutečná teplotní úroveň připravované teplé vody);
- nárazového měření spotřeby teplé vody (např. týdenní měření průběhu spotřeby) v různých obdobích roku (přechod léto – podzim);
- měření energie spotřebované zdrojem tepla pro přípravu TV, např. spotřeby plynu; zvláště u spalovacích zařízení však může být problematické odhadnout reálnou provozní účinnost pro stanovení skutečné spotřeby tepla, kterou má krýt solární soustava.
Měření spotřeby tepla může být součástí vlastního okruhu přípravy teplé vody, nebo může být dodatečně nainstalováno (příložné ultrazvukové průtokoměry, alespoň příložná teplotní čidla) pro účely odhadu reálné spotřeby. Na obr. 5.2 je znázorněno umístění čidel (průtokoměry, teplotní čidla) pro správné stanovení reálné spotřeby tepla. Pro stanovení skutečného odběru teplé vody nelze umístit průtokoměr na patu rozvodu studené vody (P1 měří celkový odběr vody, P2 měří odběr studené vody i pro jiné účely než ohřev), na vstup ani výstup zásobníku (P4 a P5 měří průtok odebrané vody pro ohřev včetně průtoku cirkulací). Spotřeba tepla na ohřev studené vody se stanoví z množství odebrané teplé vody (P3) při rozdílu teplot mezi studenou a teplou vodou. Teplotu studené vody je nezbytné měřit před smícháním s cirkulující teplou vodou a za případným předehřevem zdrojem tepla s vyšší prioritou použití (nenahrazovaným zdrojem tepla) než má solární soustava, např. zpětné získávání tepla z odpadní vody pro předehřev studené. Teplota teplé vody se měří buď ve výstupním potrubí ze zásobníku teplé vody, nebo v jeho horní části. Tepelné ztráty cirkulací se stanoví z množství cirkulující vody (P6) při rozdílu teplot mezi teplou vodou a cirkulující vodou vstupující zpět do ohřevu.
Obr. 5.2 Měření spotřeby tepla na přípravu teplé vody
Pokud není k dispozici záznam dlouhodobého měření odběru teplé vody nebo tepla na její přípravu, není zpravidla možné při praktickém návrhu solární soustavy dlouhodobé (roční) měření realizovat. V budově se proto osadí krátkodobé měření odběru v určitém úseku roku, kdy je to možné, a průběh odběru se uvažuje na základě typického profilu, včetně letního poklesu. Na základě střední hodnoty denního odběru naměřeného v konkrétní části roku se provede korekce na letní období. Příklad normalizovaného průběhu pro bytový dům je uveden na obr. 5.3. Z měření provedeného ve 12. až 17. týdnu byla stanovena denní spotřeba 3 m3 teplé vody. Hodnota korekce pro uvedené období měření je 1,44 a průměrná letní spotřeba teplé vody bude tedy 2,1 m3/den. Podobně lze postupovat u přepočtu mezi jakýmikoli úseky roku.
Obr. 5.3 Normalizovaný průběh spotřeby teplé vody vzhledem k letnímu poklesu [5]
Tepelné ztráty přípravy teplé vody
Tepelné ztráty přípravy teplé vody Qz,TV jsou dány tepelnými ztrátami vlastní přípravy teplé vody (např. pohotovostního dohřívacího zásobníku teplé vody, průtokového ohřívače apod.), rozvodu teplé vody a rozvodu cirkulace, pokud je použita. Podrobný výpočet tepelných ztrát přípravy teplé vody stanovuje ČSN EN 15316-3-2 (rozvody TV a CV) [6] a ČSN EN 15316-3-3 (příprava, zásobníky) [7].
Pokud by shromáždění požadovaných parametrů pro výpočet tepelných ztrát bylo příliš složité a nákladné, je možné zjednodušeně použít paušální přirážku z na tepelné ztráty přípravy teplé vody na základě tab. 5.3. Není neobvyklé, že celkové hodnoty přirážky z pro rodinné domy s celodenní cirkulací mohou dosáhnout až 100 %, v případě centrální přípravy teplé vody pro rozlehlé sídliště může hodnota přirážky vlivem cirkulace dosáhnout až 500 % (pětinásobek čisté potřeby tepla na přípravu teplé vody). Ve velmi nepříznivých případech, kdy je velký zásobník dohřívaný na vysokou teplotu s nízkým odběrem teplé vody, se lze v praxi setkat i hodnotami okolo 1 000 %. Odhad celkové přirážky z na tepelné ztráty zásobníku a rozvodů přípravy TV tedy z velké míry závisí na místních podmínkách a zkušenosti posuzovatele.
Tab. 5.3 Přirážka na tepelné ztráty přípravy teplé vody [8]
| Typ přípravy TV | z |
| Lokální průtokový ohřev | 0,00 |
| Centrální zásobníkový ohřev bez cirkulace | 0,15 |
| Centrální zásobníkový ohřev s řízenou cirkulací | 0,30 |
| Centrální zásobníkový ohřev s neřízenou cirkulací | 1,00 |
| CZT, příprava TV s meziobjektovými přípojkami, TV, CV | > 2,00 |
Pro výpočet předpokládané spotřeby tepla jako výchozí hodnoty pro návrh solární soustavy je nezbytné uvažovat pouze tu část tepelných ztrát, kterou je možné solárními zisky pokrýt. Například pokud tepelné ztráty cirkulace v předpokládaném zapojení solární soustavy mají být kryty pouze konvenčním dohřevem, nemohou být započítány pro návrh plochy solárních kolektorů.
Celková potřeba tepla na přípravu TV
Celková denní potřeba tepla na přípravu teplé vody Qp,c [kWh/den] při návrh nebo bilancování solární soustavy pro přípravu teplé vody je potom
(5.2)
5.1.2 Potřeba tepla na vytápění
Pro navrhování a bilancování kombinovaných solárních soustav pro přípravu teplé vody a vytápění se kromě celkové potřeby tepla na přípravu teplé vody (viz 5.1.1) stanoví potřeba tepla na vytápění QVYT [kWh/měs] v jednotlivých měsících, resp. pro navrhování plochy se stanoví QVYT [kWh/den] v referenčním dnu návrhového měsíce. Podobně jako u přípravy teplé vody platí, že základním předpokladem realizace solárních kombinovaných soustav je nízká potřeba tepla na vytápění (nízkoenergetické domy, nízkoteplotní otopné soustavy), tedy provedení úsporných opatření (zateplení, výměna oken, mechanické větrání se zpětným získáváním tepla) před návrhem a realizací solární soustavy.
Výpočet podle ČSN EN ISO 13790
Denní, resp. měsíční potřeba tepla na vytápění QVYT se stanovuje v souladu s ČSN EN ISO 13790 [9]. Pro získání reálných hodnot potřeby tepla u domů s nízkou potřebou tepla se využijí okrajové podmínky v souladu s TNI 73 0329 [10] a TNI 73 0330 [11]. Norma kromě výpočtu vlastní energetické ztráty prostupem a větráním zahrnuje výpočet solárních zisků okny, vnitřních tepelných zisků, vliv akumulace tepla do vnitřních částí konstrukcí na využití tepelných zisků (včetně stanovení časové konstanty stavby), případně příspěvků od nestandardních solárních stavebních prvků (Trombeho stěna, solární skleník apod.). Výpočet potřeby tepla se provádí pro jednotlivé měsíce, denní potřeba tepla se získá z měsíčních hodnot prostým podělením počtem dní příslušného měsíce. Metodika je velmi detailní ve výpočtu a výsledky vykazují relativně dobrou shodu s dynamickými simulačními metodami (při použití stejných klimatických dat). Nevýhodou je potřeba rozsáhlého množství informací, především o zasklení (nejen tepelné, ale i optické vlastnosti), o stínění oken (výpočet stínění přesahy a markýzami), vlastnostech materiálů všech konstrukcí (hustota, tepelná kapacita).
Zjednodušená denostupňová metoda
Výpočet potřeby tepla na vytápění podle ČSN EN ISO 13790 je pracný a především náročný na vstupní údaje. Časová náročnost výpočtu je neúměrná vlivu přesnosti stanovení potřeby na výsledky návrhu plochy solárních kolektorů nebo bilance tepelných zisků solární soustavy. Pokud nejsou k dispozici výsledky podle ČSN EN ISO 13790 z předchozího energetického hodnocení budovy (v rámci EPBD), je možné pro návrhové výpočty použít zjednodušenou a relativně známou denostupňovou metodu přibližného stanovení potřeby tepla na vytápění v určitém období (den, měsíc) z hodnoty návrhové tepelné ztráty budovy, uvedené v projektové dokumentaci vytápění. Denní potřeba tepla na vytápění se stanoví ze vztahu
(5.3)
kde je
Q‚Z … návrhová tepelná ztráta budovy, v kW;
tiv … výpočtová vnitřní teplota v daném měsíci, ve °C;
tip … střední vnitřní teplota v daném měsíci, ve °C;
tev … výpočtová venkovní teplota, ve °C;
tep … střední venkovní teplota v daném měsíci, ve °C;
ε … korekční součinitel podle tab. 5.4, který zahrnuje snížení potřeby tepla vlivem účinky regulace, přerušovaného vytápění, mj. také vlivem vnitřních a solárních zisků.
Tab. 5.4 Korekční součinitel e pro denostupňovou metodu [8]
| Energetická náročnost budovy (vytápění) | ε | |
| Běžný standard | Tepelné vlastnosti konstrukcí vyhláškou požadované | 0,75 |
| Nízkoenergetický standard | Vyhláškou doporučené tepelné vlastnosti konstrukcí | 0,60 |
| Pasivní standard | Tepelné vlastnosti konstrukcí nad rámec vyhláškou doporučených hodnot | 0,50 |
Další postupy
Pokud je k dispozici z energetického hodnocení budovy pouze celková roční potřeba tepla na vytápění QVYT v kWh/rok nebo měrná roční potřeba tepla na vytápění qVYT v kWh/(m2·rok) spolu se vztažnou podlahovou plochou Ap, lze zjednodušeně hodnoty potřeby tepla na vytápění pro jednotlivé měsíce odhadnout podle středních měsíčních venkovních teplot v otopném období. Otopné období se zjednodušeně uvažuje od září do května.
Pozn.: Z praxe je známá skutečnost, že především v oblasti pasivních domů je otopné období zkráceno o cca 2-3 měsíce a je tedy možné okrajové měsíce (září a květen) do bilance nezahrnovat.
Potřeba tepla na vytápění v j-tém měsíci se stanoví jako
(5.4)
Pro stanovení denní potřeby tepla v referenčním dnu měsíce pro návrh plochy solárních kolektorů se měsíční potřeba tepla vydělí počtem dnů v měsíci.
Tepelné ztráty otopné soustavy
Tepelné ztráty otopné soustavy Qz,VYT jsou dány tepelnými ztrátami vlastního ohřevu otopné vody (např. v zásobníku otopné vody), rozvodu otopné vody, který nepřispívá k vytápění (nevytápěnými místnostmi), a také setrvačností otopné soustavy spolu s nevhodně pracující regulací, způsobující přetápění prostoru a zvýšení odběru tepla. Podrobný výpočet tepelných ztrát otopných soustav stanovují ČSN EN 15316-2-1 (sdílení tepla) [12] a ČSN EN 15316-2-3 (rozvody tepla pro vytápění) [13].
Solární kombinované soustavy zpravidla využívají centrálního zásobníku otopné vody, do kterého je přiváděn tepelný zisk ze solárních kolektorů a teplo z dodatkového zdroje energie, odebírána otopná voda pro vytápění a ve vestavěném průtočném výměníku nebo zásobníku je připravována teplá voda. Nelze proto jednoznačně odlišit jaká část tepelných ztrát jde na vrub přípravě teplé vody, jaká vytápění a jaká solární soustavě.
S ohledem na použití přirážky z pro stanovení potřeby tepla na přípravu TV se ke stanovené potřebě tepla na vytápění QVYT připočítají tepelné ztráty spojené s provozem zásobníku tepla pro vytápění paušálně přirážkou v = 5 %, které může solární soustava hradit. Zpětně využitelné tepelné ztráty rozvodů otopné vody přispívají k vytápění a jsou v podstatě zahrnuty ve výpočtu potřeby tepla jako tepelné zisky.
Celková potřeba tepla na vytápění
Celková denní nebo měsíční potřeba tepla na vytápění, včetně tepelných ztrát otopné soustavy, se stanoví
(5.5)
kde je
QVYT … potřeba tepla na vytápění prostoru budovy v jednotlivých měsících nebo pro referenční dny, v kWh/měs nebo kWh/den;
v … přirážka na tepelné ztráty otopné soustavy.
Celková potřeba tepla na přípravu teplé vody a vytápění Qp,c [kWh/měs nebo kWh/den] pro návrh nebo bilancování solární kombinované soustavy se potom stanoví jako
(5.6)
5.1.3 Potřeba tepla na ohřev bazénové vody
Ohřev bazénové vody je energeticky náročný a využití sluneční energie je relativně jednoduché a levné. Základním předpokladem realizace a následného provozu solárních soustav je zakrývání vodní hladiny bazénu v době mimo provoz pro omezení značných tepelných ztrát odparem z vodní hladiny. Špičky dávek sluneční energie se navíc zpravidla shodují s dobou využití bazénů. Nízká teplota bazénové vody zaručuje vysoké zisky i při použití levných solárních kolektorů.
Dimenzování plochy solárních kolektorů pro ohřev bazénové vody a jejich bilancování silně ovlivňuje druh bazénu (venkovní, vnitřní), požadované parametry bazénové vody a způsob omezování tepelných ztrát bazénu (zakrývání). U venkovních otevřených bazénů se uvažuje návrhová teplota bazénové vody tw = 18 až 25 °C a provoz v letním období (od května do září). Sluneční záření dopadající na vodní hladinu se zahrnuje do energetické bilance. U venkovních sezónních bazénů je možné využít nezasklené solární kolektory (plastové rohože) s optimálním sklonem 15° až 30°. U vnitřních krytých bazénů se uvažuje vyšší návrhová teplota bazénové vody tw = 25 až 28 °C a zpravidla celoroční provoz, který vyžaduje použití zasklených solárních kolektorů s optimálním sklonem 30° až 50°. Nízké teploty bazénové vody znamenají vysokou účinnost solárních kolektorů a vysoké tepelné zisky. Teploty není výhodné příliš zvyšovat, neboť
- roste potřeba tepla;
- bazén přestává být osvěžující;
- studie prokázaly, že kolísání teploty bazénové vody s venkovní teplotou nemá zvláštní vliv na kolísání návštěvnosti bazénu (u venkovních bazénů).
Při ohřívání vody v bazénech je potřeba dodávat teplo pro:
- krytí tepelných ztrát přestupem z vodní hladiny (sálání, proudění, vypařování);
- krytí tepelných ztrát prostupem tepla stěnami bazénu (pod úrovní vodní hladiny);
- ohřívání přiváděné čisté vody (náhrada ztrát vody – vystříkání, vynášení na tělech plavců, voda pro praní filtrů).
Tepelná ztráta prostupem stěnami bazénu je většinou velmi malá a proti tepelné ztrátě přestupem z vodní hladiny ji lze většinou zanedbat. Rozložení tepelných ztrát venkovního otevřeného bazénu vypadá zhruba následovně:
- konvekcí do okolí 10 až 20 %;
- zářením vůči obloze 5 až 20 %;
- vypařováním z vodní hladiny 50 až 80 %;
- vedením do stěn bazénu 2 až 5 %.
Před vlastním návrhem plochy solárních kolektorů je vhodné zajistit opatření pro snížení tepelných ztrát. Zakrýváním hladiny během provozních přestávek plastovými fóliemi s plováky lze eliminovat přestup tepla vypařováním a částečně snížit i přestup tepla sáláním a konvekcí. Celkově lze zakrýváním vodní hladiny snížit tepelné ztráty o cca 50 %. U vnitřních bazénů má zakrývání vodní hladiny ještě další významný dopad, a to snížení produkce vlhkosti v interiéru (menší potřeba odvlhčení, nižší riziko poruch stavebních konstrukcí). Zakrývací fólie musí být odolná vůči UV záření (především u venkovních bazénů). U velkých veřejných bazénů je ekonomicky problematické zakrývání hladiny zajistit, často vychází levněji zvýšit plochu solárních kolektorů.
Kromě tepelných ztrát se do energetické bilance potřeby tepla bazénu promítají také tepelné zisky, jejichž zdrojem může být přímo dopadající sluneční záření (u venkovních bazénů), teplo uvolněné z oběhových čerpadel či teplo předávané plavci (100 až 250 W/os). Nejvýznamnější z výše uvedených jsou tepelné zisky pohlcením slunečního záření dopadajícího na vodní hladinu. Výpočet energie zachycené osluněnou vodní hladinou je obdobný jako u slunečních kolektorů. Uvažuje se pouze stálá absorpce slunečního záření vodou ηa = 0,85 (ztráty odrazem od hladiny 15 %), neboť tepelné ztráty bazénu do okolí jsou již zahrnuty v tepelné ztrátě přestupem z vodní hladiny.
Tepelná ztráta bazénu
Výpočet potřeby tepla u bazénů vychází z tepelné ztráty bazénu během jeho provozu a mimo provoz (dodávka tepla udržuje požadovanou teplotu bazénové vody) a z potřeby přiváděné čisté (studené) vody pro doplňování bazénu [8]. Výpočtový postup rozlišuje mezi bazény vnitřními (krytými) a venkovními (nekrytými), které jsou provozovány za odlišných podmínek, ovlivňujících tepelnou ztrátu. Pro výpočet se použije okrajových provozních podmínek, definovaných v tab. 5.5. Pokud jsou k dispozici reálné provozní podmínky, použijí se pro výpočet.
Tab. 5.5 Provozní podmínky bazénů
| Typ bazénu | tw [°C] | p„d(tw) [Pa] | tv [°C] | ϕv [%] | pd(tv) [Pa] |
| Vnitřní – v provozu | 28 | 3781 | 30 | 65 | 2759 |
| Vnitřní – mimo provoz | 24 | 2985 | 20 | 65 | 1521 |
| Vnější – v provozu | 24 | 2985 | = te,s | 50 | výpočet podle (5.7), (5.8) |
| Vnější – mimo provoz | 20 | 2339 | = te,n | 50 | výpočet podle (5.7), (5.8) |
Parciální tlak syté vodní páry p‚d v Pa se pro danou teplotu vzduchu t ve °C stanoví podle vztahu
(5.7)
Parciální tlak vodní páry pd v Pa ve vzduchu se stanoví z relativní vlhkosti vzduchu j a tlaku syté vodní páry p‚d v Pa pro příslušnou teplotu vzduchu
(5.8)
Denní potřeba tepla v kWh/den na krytí tepelné ztráty vnitřního (krytého) bazénu vypařováním (přenos hmoty) a přestupem tepla z hladiny bazénu v době provozu a mimo provoz bazénu se stanoví ze vztahu
(5.9)
kde je
τp … denní provozní doba bazénu; pokud není doba provozu známa, uvažuje se τp = 12 h/den;
βp … součinitel přenosu hmoty vypařováním pro vnitřní bazény v době provozu, uvažuje se jednotně βp = 1,6×10-4 kg/(h·m2·Pa) [14];
βn … součinitel přenosu hmoty vypařováním pro vnitřní bazény v době mimo provoz, pro zakrývaný bazén se uvažuje jednotně βn = 0 kg/(h·m2·Pa); pro nezakrývaný βn = βp;
Ab … plocha vodní hladiny bazénu, v m2;
tw,p … teplota bazénové vody v době provozu bazénu (viz tab. 5.5), ve °C;
tw,n … teplota bazénové vody v době mimo provoz bazénu (viz tab. 5.5), ve °C;
tv,p … vnitřní teplota v bazénové místnosti v době provozu bazénu (viz tab. 5.5), ve °C;
tv,n … vnitřní teplota v bazénové místnosti v době mimo provoz bazénu (viz tab. 5.5), ve °C;
p„d(tw) … tlak syté vodní páry v blízkosti hladiny bazénu při teplotě vzduchu rovné teplotě bazénové vody tw, v Pa;
pd(tv) … tlak vodní páry v okolním vzduchu při teplotě tv a vlhkosti ϕv, v Pa;
lw … výparné teplo vody, lw = 2,5×106 J/kg;
hi … součinitel přestupu tepla mezi okolním prostředím a hladinou bazénu sáláním a prouděním, uvažuje se hi = 10 W/(m2·K) pro vnitřní bazény.
Poznámka:
V případě použití tepelněizolačního zakrytí použitého pro snížení tepelné ztráty bazénu se místo součinitele přestupu tepla hi po dobu mimo provoz použije odpovídající hodnota součinitele prostupu tepla zakrytí U ve W/(m2·K).
Ve výpočtu se předpokládá udržování různé teploty bazénové vody tw v době provozu a mimo provoz a různá teplota vzduchu tv bazénové místnosti v době provozu a mimo provoz.
V době provozu bazénu dochází k tepelné ztrátě vypařováním z vodní hladiny bazénu a k tepelnému zisku přestupem sáláním a volným prouděním z okolního vzduchu do bazénu, v době mimo provoz dochází k tepelné ztrátě sáláním a volným prouděním z bazénu do okolí (zakrývaný bazén).
Denní potřeba tepla v kWh/den na krytí tepelné ztráty venkovního (nekrytého) bazénu vypařováním (přenos hmoty) a přestupem tepla z hladiny bazénu v době provozu a mimo provoz bazénu, částečně kompenzovaná přímými tepelnými zisky ze slunečního záření dopadlým a pohlceným na hladině bazénu, se stanoví ze vztahu
(5.10)
kde je
τs … denní teoretická doba slunečního svitu, v h/den;
τp … denní provozní doba bazénu (zjednodušeně uvažován pouze v době slunečního svitu), stanoví se jako τp = τs, v h/den;
βp … součinitel přenosu hmoty pro venkovní bazény v době provozu, uvažuje se jednotně βp = 2,9×10-4 kg/(h·m2·Pa) [14];
βn … součinitel přenosu hmoty pro venkovní bazény v době mimo provoz, pro zakrývaný bazén se uvažuje jednotně βn = 0 kg/(h·m2·Pa); pro nezakrývaný βn = βp;
Ab … plocha vodní hladiny bazénu, v m2;
tw,p … požadovaná teplota bazénové vody v době provozu bazénu (viz tab. 5.5), ve °C;
tw,n … teplota bazénové vody v době mimo provoz bazénu (viz tab. 5.5), ve °C;
te,s … střední teplota venkovního vzduchu v době slunečního svitu (den), ve °C; pro jednotlivé měsíce se stanoví podle přílohy E;
te,n … střední teplota venkovního vzduchu v době mimo sluneční svit (noc), ve °C; pro jednotlivé měsíce se stanoví z průměrné denní teploty te,p a teploty v době slunečního svitu te,s jak
(5.11)
p„d(tw) … tlak syté vodní páry v blízkosti hladiny bazénu při teplotě vzduchu rovné teplotě bazénové vody tw, v Pa;
pd(te) … tlak vodní páry v okolním vzduchu při venkovní teplotě a vlhkosti v příslušné části dne (viz tab. 5.5), v Pa;
lw … výparné teplo vody, lw = 2,5×106 J/kg;
he … součinitel přestupu tepla mezi okolním prostředím a hladinou bazénu sáláním a prouděním, uvažuje se he = 15 W/(m2·K) pro venkovní bazény;
Hden … energie slunečního záření dopadající na volnou hladinu bazénu, stanovená pro vodorovnou plochu s využitím tabulek v kapitole 10, v kWh/(m2·den).
Ve výpočtu se předpokládá udržování různé teploty bazénové vody tw v době provozu a mimo provoz a různá teplota okolního venkovního vzduchu te během provozu v době slunečního svitu a mimo provoz v noci. V době provozu přispívá tepelným ziskem sluneční energie pohlcená na vodní hladině s účinností 85 %.
Ohřev doplňované vody
Denní potřeba tepla v kWh/den na ohřev doplňované studené vody
(5.12)
kde je
kd … denní počet návštěvníků;
VSV,os … měrná potřeba přiváděné čisté vody na návštěvníka bazénu, v m3/os; množství ředicí vody se uvažuje jednotně 30 l/os, pokud není stanoveno jinak;
ρ … hustota vody, v kg/m3;
c … měrná tepelná kapacita vody, v J/(kg·K);
tSV … teplota studené vody, uvažuje se celoročně tSV = 15 °C;
tw … teplota bazénové vody, ve °C.
Pokud není známý denní počet návštěvníků bazénu k, stanoví se přibližně jako 20% využití měsíční kapacity bazénu. Hodinová kapacita bazénu kb je dána vztahy
(5.13)
Denní počet návštěvníků se potom stanoví ze vztahu
(5.14)
Celková potřeba tepla na ohřev bazénu
Celková denní potřeba tepla na ohřev bazénové vody Qp,BV v kWh/den pro návrh bazénové solární tepelné soustavy je
(5.15)
Tepelné ztráty bazénu jsou zahrnuty ve výpočtu potřeby tepla. Tepelné ztráty rozvodů jsou oproti tepelným ztrátám z vodní hladiny bazénu zanedbatelné.
5.2 NÁVRH PLOCHY SOLÁRNÍCH KOLEKTORŮ
Základním parametrem solární soustavy, ať jde o čistě přípravu teplé vody nebo komplikovanou vícespotřebičovou aplikaci, je velikost plochy a konkrétní typ solárních kolektorů. Typ solárního kolektoru je často vybrán již v rané fázi návrhu, plochu kolektorů je možné spočítat na základě výběru typu solárního kolektoru od konkrétního výrobce.
5.2.1 Obecný postup
Návrh plochy solárních kolektorů vychází ze stanovené denní potřeby tepla v dané aplikaci a ze zvolených rozhodovacích kritérií a podmínek. Ty mohou být různé:
- dosažení vysokých využitých měrných zisků solární soustavy qss,u a dobrých ekonomických parametrů solární soustavy (ekonomický přístup) – snaha o eliminaci letních přebytků, návrh plochy vychází z potřeby tepla v letním období;
- dosažení vysokého nahrazení primárních paliv (ekologický přístup) – snaha o dosažení vysoké úspory, tzn. vysokého solárního pokrytí f;
- požadované solární pokrytí f – např. optimalizace pokrytí v bytových domech s ohledem na zamezení letnímu přehřívání;
- respektování omezujících podmínek struktury budovy – maximální velikost střechy, možný sklon kolektorů, architektonické souvislosti.
Návrh plochy solárních kolektorů v dané aplikaci se provádí pro referenční den v návrhovém období, ve kterém je požadováno celkové nebo částečné (zvolené) pokrytí potřeby tepla solární soustavou. Celková potřeba tepla Qp,c v dané aplikaci se pro referenční den stanoví podle kapitoly 5.1. Dopadající sluneční energie na kolektory o uvažovaném sklonu a orientaci – denní dávka slunečního ozáření HT,den se stanoví 5 s využitím tabulek v kapitole 10. Ze střední účinnosti solárního kolektoru ηk během referenčního dne se stanoví denní měrný tepelný zisk kolektorů qk,u z 1 m2 kolektoru a porovnáním s požadovanou potřebou tepla, kterou je třeba solární soustavou pokrýt, se stanoví plocha solárních kolektorů.
Stanovení plochy kolektorů vychází z jednotného zjednodušeného bilančního postupu [8], který je aplikován i na stanovení ročních zisků solární soustavy v kapitole 7. Okrajové podmínky výpočtů – návrhové hodnoty teplot v kolektorech a srážky ze solárních zisků vlivem tepelných ztrát jsou použity v obou případech (návrh, bilancování) stejné.
Počet solárních kolektorů se stanoví prostým vydělením vypočtené celkové plochy plochou jednoho kolektoru a výsledek se zaokrouhlí na celé číslo. U malých soustav do 5 kolektorů, kdy zaokrouhlení může činit desítky procent celkové plochy, je nutné uvážit, zda zaokrouhlovat směrem nahoru (pokud je zajištěno využití vzniklých přebytků), nebo směrem dolů. U větších solárních soustav, kde se plocha 1 kolektoru pohybuje v řádech jednotek procent celkové plochy a méně, se konečný počet kolektorů může řídit celým násobkem požadovaného počtu kolektorů, zapojených v jedné řadě kolektorového pole (podle dispozice na střeše nebo fasádě).
Denní dávka slunečního ozáření
Podrobný postup stanovení sluneční energie dopadající na obecně orientovanou a skloněnou plochu je uveden v kapitole 1. V kapitole 10 jsou pro zjednodušení výpočtů tabelovány pro různé oblasti (horské oblasti, venkov, města, průmyslové oblasti) hodnoty teoretické denní dávky celkového slunečního ozáření HT,den,teor v kWh/(m2·den). V kapitole 10 jsou dále tabelovány difuzní dávky slunečního ozáření HT,den,dif v kWh/(m2·den) v různých orientacích a sklonech kolektoru, poměrné doby slunečního svitu τr pro vybraná města v ČR a SROV. Denní dávka slunečního ozáření HT,den dopadající na kolektor se stanoví
(5.16)
Účinnost solárního kolektoru
Střední účinnost solárního kolektoru během dne se stanoví z rovnice křivky účinnosti
(5.17)
kde je
GT,m … střední denní sluneční ozáření uvažované plochy solárních kolektorů; pro různé sklony a orientace plochy kolektorů v různých oblastech (horské oblasti, venkov, města, průmyslové oblasti) se v jednotlivých měsících stanoví podle kapitoly 10, ve W/m2;
tk,m … průměrná teplota teplonosné kapaliny v solárních kolektorech v průběhu dne, ve °C; hodnota se zjednodušeně uvažuje celoročně konstantní a stanoví se podle typu aplikace z tab. 5.6;
te,s … průměrná venkovní teplota v době slunečního svitu, ve °C (hodnoty v jednotlivých měsících se určí podle kapitoly 10).
Parametry (konstanty) rovnice křivky účinnosti solárního kolektoru, tzn. hodnota účinnosti při nulových ztrátách η0, lineární součinitel tepelné ztráty a1 v W/(m2·K) a kvadratický součinitel tepelné ztráty kolektoru a2 v W/(m2·K2), vztažené k ploše apertury solárního kolektoru Ak, se získají od výrobce nebo dodavatele navrženého kolektoru.
Tab. 5.6 Průměrná teplota v solárních kolektorech [8]
| Typ aplikace | tk,m [°C] |
| Ohřev bazénové vody (venkovní bazén) | 30 |
| Ohřev bazénové vody (vnitřní bazén) | 35 |
| Předehřev teplé vody, pokrytí < 35 % | 35 |
| Příprava teplé vody, 35 % < pokrytí < 70 % | 40 |
| Příprava teplé vody, pokrytí > 70 % | 50 |
| Příprava teplé vody a vytápění, pokrytí < 25 % | 50 |
| Příprava teplé vody a vytápění, pokrytí > 25 % | 60 |
Návrhové hodnoty teplot v kolektorech jsou průměrné denní, vycházející z reálných podmínek provozu. Nejsou zohledněny rozdíly mezi jednotlivými měsíci.
Denní teoretické zisky solárních kolektorů
Teoreticky využitelný tepelný zisk solárních kolektorů za den vztažený na 1 m2 plochy apertury je dán vztahem
(5.18)
kde je
p … hodnota srážky z tepelných zisků solárních kolektorů vlivem tepelných ztrát solární soustavy (rozvody, solární zásobník); pro typické případy jsou hodnoty uvedeny v tab. 5.7.
Tepelné ztráty solární soustavy Qss,z v kWh/den se skládají z tepelných ztrát rozvodů (uvažovány pouze v době běhu solární soustavy, pokud se zanedbají dynamické jevy chladnutí a ohřívání) a tepelných ztrát solárních zásobníků (uvažovány celodenně, 24 h) a je možné je stanovit s použitím výpočtových vztahů např. podle ČSN EN 12241 [15]. Nicméně, jelikož srážka p je definovaná jako
(5.19)
nelze ji teoreticky stanovit bez znalosti hledané plochy solárních kolektorů. Při vlastním stanovení tepelných ztrát solární soustavy (bez použití paušální srážky z tab. 5.7) je proto nezbytné výpočet plochy solárních kolektorů provést iteračním způsobem, např. v tabulkovém procesoru.
Tab. 5.7 Srážka z tepelných zisků solárních kolektorů vlivem tepelných ztrát [8]
| Typ solární soustavy | p |
| Bazén, ohřev bazénové vody | 0,01 |
| Příprava teplé vody, do 10 m2 | 0,20 |
| Příprava teplé vody, od 10 do 50 m2 | 0,10 |
| Příprava teplé vody, od 50 do 200 m2 | 0,05 |
| Příprava teplé vody, nad 200 m2 | 0,03 |
| Příprava teplé vody a vytápění, do 10 m2 | 0,30 |
| Příprava teplé vody a vytápění, od 10 do 50 m2 | 0,20 |
| Příprava teplé vody a vytápění, od 50 do 200 m2 | 0,10 |
| Příprava teplé vody a vytápění, nad 200 m2 | 0,06 |
Plocha solárních kolektorů
Návrh plochy solárních kolektorů spočívá v porovnání denní potřeby tepla Qp,c v dané aplikaci a využitelných tepelných zisků kolektoru Qk,u, které v referenčním dnu návrhového měsíce kryjí potřebu tepla nebo její určenou část danou požadovaným denním solárním pokrytím f
(5.20)
Stanovená plocha solárních kolektorů je plochou apertury, neboť k ní je vztažena křivka účinnosti použitá ve výpočtu.
5.2.2 Stanovení plochy kolektorů pro přípravu TV
Rodinné domy
Solární soustavy pro celoroční přípravu teplé vody v rodinných domech se navrhují na měsíce duben a září (stanoví se průměr), není-li určeno jinak. Střední teplota teplonosné látky v kolektoru se volí 40 °C. Z výsledných hodnot plochy kolektoru určených pro oba měsíce se stanoví průměr. Při volbě větší kolektorové plochy než je výpočet je vhodné zajistit smysluplné využití letních přebytků, které může ekonomicky zvýhodnit instalaci solární soustavy:
- ohřev bazénové vody;
- sušení palivového dřeva;
- sušení zahradních rostlin či plodin.
jinak jsou disponibilní solární zisky mařeny (stagnace, var teplonosné kapaliny atd.).
Návrh zajišťuje solární pokrytí potřeby tepla na přípravy teplé vody zhruba ze 60 %. V provozu to znamená téměř plné pokrytí potřeby teplé vody v letním období solární soustavou.
Bytové domy
U návrhu solárních soustav pro přípravu teplé vody v bytových domech je zásadní omezující podmínkou skutečnost, že bytové domy nemají k dispozici v letním období žádný „spotřebič tepla“ pro využití letních přebytků. Návrh solární soustavy se tak omezuje na krytí letní potřeby tepla. Předimenzované solární soustavy pro bytové domy mohou vést k provozním problémům spojeným v letním období se stagnací (var teplonosné látky v kolektorech, pronikání přehřáté páry do rozvodů, nebezpečí poškození i prvků vzdálených od kolektorového pole) a ke snížení měrných využitých tepelných zisků solární soustavy, které jsou u bytových domů více zohledňovány z důvodu sledování ekonomických parametrů instalace.
Solární soustavy pro přípravu teplé vody v bytových domech se proto navrhují pro měsíc červenec. Je nutné samozřejmě zohlednit letní útlum potřeby tepla na přípravu teplé vody. Střední teplota v solárním kolektoru se opět volí 40 °C. Návrh zajišťuje minimalizaci letních nevyužitelných přebytků energie a celoroční solární pokrytí potřeby tepla na přípravu teplé vody okolo 40 až 50 %.
5.2.3 Stanovení plochy kolektorů pro přípravu TV a vytápění
Snahou u kombinovaných soustav je využít sluneční energii kromě přípravy teplé vody i pro pokrytí tepelných ztrát domu, a to zvláště v přechodovém období (nízká tepelná ztráta, dostatek slunečního záření). Potřebná plocha solárních kolektorů je teoreticky přímo závislá na potřebě tepla pro vytápění budovy a požadované hodnotě solárního pokrytí. Potřeba tepla na vytápění budov se časově rozchází se špičkami dostupných solárních zisků. V otopném období se proto dosáhne vždy jen částečného pokrytí; zpravidla ekonomicky přijatelné jsou hodnoty mezi 15 a 35 % roční potřeby tepla pro přípravu teplé vody a vytápění. Tato hodnota pokrytí ovlivňuje dimenzování zařízení a musí být jasně stanovena.
Solární kombinované soustavy pro přípravu teplé vody a vytápění se navrhují na pokrytí celkové potřeby tepla (teplá voda, vytápění) v okrajových měsících přechodového období: měsíce květen a září (stanoví se průměr). Nejčastějším řešením kombinovaných solárních soustav je zapojení s centrálním zásobníkem otopné vody, který zajišťuje i přípravu teplé vody (ve vnitřním nebo vnějším tepelném výměníku). Střední teplota teplonosné látky v kolektoru se volí 50 °C. Vyšší teplotní úrovně jsou dány nutností udržovat v části zásobníku dostatečnou teplotu pro vytápění v zimním období, předimenzovanou plochou kolektorů pro letní období (přebytky tepla) a větším objemem centrálního zásobníku než u samostatné přípravy teplé vody (větší akumulace, menší vychlazování zásobníku v létě).
U solárních soustav navržených pro částečné vytápění je nutné uvažovat o využití letních přebytků tepla, případně jakým způsobem zamezit stagnačním podmínkám v soustavě (maření zisků, vývin páry v kolektorech). Solární kolektory pro kombinované soustavy přípravy teplé vody a vytápění s vyšším solárním pokrytím je vhodné instalovat s vyšším sklonem (60 až 75°), případně je integrovat do fasády budovy (90°). Takové řešení vede k rovnoměrnému profilu tepelných zisků, letní přebytečné a nevyužitelné zisky klesají a zimní zisky mírně narostou (vlivem příznivějšího úhlu dopadu slunečních paprsků, vlivem odrazivosti sněhové pokrývky).
5.2.4 Stanovení plochy solárních kolektorů pro ohřev bazénové vody
Návrh plochy se provádí podle obecného postupu pro referenční den v návrhovém měsíci, ve kterém je požadavek na pokrytí potřeby tepla sluneční energií. Střední teplota teplonosné látky v kolektoru se volí tk,m = 30 až 35 °C podle druhu bazénu (venkovní, vnitřní).
Je-li solární soustava navrhována pro venkovní bazén, přípravu teplé vody anebo podporu vytápění, je třeba potřebné plochy kolektorů pro ohřev bazénové vody a přípravu teplé vody sečíst. Nepřičítá se plocha kolektorů pro vytápění. V létě dodává solární soustava teplo pro venkovní bazén, v zimě pro vytápění. Teplá voda je připravována po celý rok.
LITERATURA
[1] ČSN 06 0320 Ohřívání užitkové vody – Navrhování a projektování. ČNI, 1998.
[2] ČSN EN 15316-3-1 Tepelné soustavy v budovách – Výpočtová metoda pro stanovení energetických potřeb a účinností soustavy – Část 3-1: Soustavy teplé vody, charakteristiky potřeb (požadavky na odběr vody), ČNI, 2008.
[3] Richtlinie VDI 2067, Blatt 4 – Berechnung der Kosten von Wärmeversorgungsanlagen; Warmwasserversorgung, 1982.
[4] Průzkum ENERGO 2004 – Informace o šetření spotřeby paliv a energie v domácnostech, Český statistický úřad, 2005, dostupné na http://www.czso.cz
[5] Remmers, K. H.: Velká solární zařízení – Návrh, provoz, realizace, Era 2008.
[6] ČSN EN 15316-3-2 Tepelné soustavy v budovách – Výpočtová metoda pro stanovení energetických potřeb a účinností soustavy – Část 3-2: Soustavy teplé vody, rozvody, ČNI, 2008.
[7] ČSN EN 15316-3-3 Tepelné soustavy v budovách – Výpočtová metoda pro stanovení energetických potřeb a účinností soustavy – Část 3-3: Soustavy teplé vody, příprava, ČNI, 2008.
[8] TNI 73 0302 Energetické hodnocení solárních tepelných soustav – Zjednodušený výpočtový postup, ÚNMZ 2009.
[9] ČSN EN ISO 13790 Energetická náročnost budov – Výpočet potřeby energie na vytápění a chlazení, ÚNMZ 2008.
[10] TNI 73 0329 Zjednodušené výpočtové hodnocení a klasifikace obytných budov s velmi nízkou potřebou tepla na vytápění – Rodinné domy, ÚNMZ, 2009.
[11] TNI 73 0330 Zjednodušené výpočtové hodnocení a klasifikace obytných budov s velmi nízkou potřebou tepla na vytápění – Bytové domy, ÚNMZ, 2009.
[12] ČSN EN 15316-2-1 Tepelné soustavy v budovách – Výpočtová metoda pro stanovení potřeby energie a účinností soustavy – Část 2-1: Sdílení tepla pro vytápění, ČNI, 2008.
[13] ČSN EN 15316-2-3 Tepelné soustavy v budovách – Výpočtová metoda pro stanovení energetických potřeb a účinností soustavy – Část 2-3: Rozvody tepla pro vytápění, ČNI, 2008.
[14] Chyský, J., Hemzal, K. a kol.: Technický průvodce – Větrání a klimatizace. Bolit B-press Brno, 1993.
[15] ČSN EN ISO 12241 Tepelně izolační výrobky pro zařízení budov a průmyslové instalace – Pravidla výpočtu, ÚNMZ 2009.
6 PRVKY SOLÁRNÍCH SOUSTAV A JEJICH NÁVRH
Projektování solární soustavy kromě návrhu potřebné plochy kolektorů a jejich typu obnáší samozřejmě i návrh jejích jednotlivých funkčních součástí – prvků. Na obr. 6.1 je uvedeno schéma jednoduché solární soustavy pro přípravu teplé vody s vyznačením všech prvků důležitých pro její provoz.
Obr. 6.1 Schéma solární soustavy pro přípravu teplé vody s vyznačením jednotlivých prvků
Jde především o:
- solární kolektor;
- zásobník tepla;
- teplonosná kapalina;
- potrubí, tepelné izolace potrubí;
- výměníky tepla (VT);
- oběhové čerpadlo (Č);
- zpětná klapka (ZK);
- pojistný ventil (PV);
- expanzní nádoba (EN);
- odvzdušňovací ventil (AOV);
- regulátor (R);
- uzavírací armatury (KK);
- vypouštěcí a napouštěcí armatury (VK);
- termostatický směšovací ventil (TSV);
- regulační ventil (RV);
- teploměry (T), teplotní čidla;
- manometry (M), průtokoměry (P).
Projektování prvků solárních soustav se vzhledem k výrazným odlišnostem v chování zdroje tepla (kolektorů), především z hlediska jeho výkonové a teplotní stability, obecně liší od projektování klasických tepelných soustav, ačkoli řada prvků je obdobná a liší se pouze teplotní a tlakovou odolností. Návrh většiny prvků vychází z určené plochy solárních kolektorů a zohledňuje extrémní provozní stavy solární soustavy, tzv. stagnaci neboli klidový stav bez odběru tepla při současném příjmu slunečního záření kolektory.
6.1 STAGNAČNÍ CHOVÁNÍ SOLÁRNÍCH SOUSTAV
Solární soustavy s vyšším celoročním podílem pokrytí potřeby tepla sluneční energií vykazují především v letním období přebytky tepla oproti vlastní potřebě dané aplikace. Tato situace vyskytuje u solárních soustav pro přípravu teplé vody s pokrytím nad 50 %, zvláště pak u solárních kombinovaných soustav pro přípravu teplé vody a vytápění, vyznačujících se předimenzovanou plochou solárních kolektorů vůči letní potřebě tepla. Stav, kdy při dopadajícím sluneční záření na kolektor se teplo z kolektoru neodvádí (regulátor nesepne oběhové čerpadlo, neboť není potřeba dodávat teplo, např. zásobník je nahřátý na maximální provozní teplotu), se nazývá stagnace. V solárním kolektoru se při stagnaci dosahuje rovnováhy mezi tepelnými ztrátami kolektoru a zářivým tokem pohlceným absorbérem a kolektor má nulovou účinnost a výkon. Teplota kolektoru pak dosahuje maximální hodnoty při daných klimatických podmínkách. Při dostatečné úrovni slunečního záření pak může být stagnace spojena s varem teplonosné kapaliny a pronikáním páry do rozvodu solární soustavy.
Stagnace však může nastat i při výpadku elektrické energie, poruše oběhového čerpadla nebo při prostém nežádoucím uzavření některého v hlavních uzávěrů rozvodu solární soustavy. Nicméně na rozdíl od těchto nežádoucích jevů je provozní stagnace běžnou součástí provozu solární soustavy a je třeba s ní při projektování prvků počítat.
6.1.1 Stagnační teplota
Základním parametrem pro charakterizaci stagnačních podmínek v kolektoru je tzv. stagnační teplota tstg – ustálená teplota kolektoru přijímajícího sluneční záření bez odvodu tepla, někdy také označována jako klidová teplota kolektoru. Stagnační teplotu lze měřit nebo stanovit výpočtem z křivky účinnosti solárního kolektoru pro dané okrajové podmínky. Za referenční okrajové podmínky se smluvně uvažují teplota okolního vzduchu te = 30 °C a sluneční ozáření G = 1000 W/m2. Extrémní hodnoty zajišťují, že maximální stagnační teplota je pokládána za maximální možnou teplotu v kolektoru během provozu. Stagnační teplota se měří v kolektoru nezapojeném do soustavy („na sucho“), nicméně uzavřeného z důvodu eliminace volného proudění uvnitř absorbéru a ochlazování kolektoru.
Stagnační teplota je rovná střední teplotě teplonosné kapaliny, stejně jako střední teplotě povrchu absorbéru, v bodě nulové účinnosti kolektoru. Stagnační teplota se vypočítá z hodnoty průsečíku křivky účinnosti (naměřené zkušebnou) s osou (tm – te)/G, tedy z hodnoty redukovaného teplotního spádu při η = 0
(6.1)
Obr. 6.2 Stanovení stagnační teploty z průsečíku křivky účinnosti
Hodnotu redukovaného teplotního spádu při η = 0 lze určit buď prostým odečtením z grafu účinnosti (viz obr. 6.2), nebo vyhledáním průsečíků jako kladného kořene kvadratického polynomu (paraboly) popisujícího křivku účinnosti
(6.2)
Průsečík s osou (tm – te)/G (kořen) se pak stanoví
(6.3)
V tab. 6.1 jsou uvedeny typické hodnoty stagnačních teplot pro různé typy solárních kolektorů. Výrobce kolektoru samozřejmě musí volbu materiálu částí kolektoru z hlediska odolnosti přizpůsobit očekávaným stagnačním teplotám.
Tab. 6.1 Orientační hodnoty stagnační teploty různých typů solárních kolektorů
| Typ kolektoru | tstg [°C] |
| Nezasklený kolektor | 65 |
| Zasklený neselektivní kolektor | 100 |
| Zasklený selektivní kolektor | 180 |
| Trubkový jednostěnný vakuový kolektor | 300 |
| Trubkový vakuový Sydney kolektor | 250 |
6.1.2 Stagnační chování kolektoru
Procesy odehrávající se při stagnaci v solárním kolektoru a soustavě lze obecně rozdělit do několika fází, znázorněných na obr. 6.3. Kapalina se vlivem zvýšené teploty nejprve roztahuje (fáze 1), při dosažení bodu varu se začínají objevovat první bubliny, tvoří se sytá pára, která vytlačuje kapalinu z kolektorů (fáze 2). Zbylá kapalina v kolektoru se dále odpařuje a kolektor je vyplňován sytou párou teplonosné látky (fáze 3). Tato fáze přeměny skupenství teplonosné látky se vyznačuje vysokým odvodem tepla z kolektoru do okolí a vlivem postupného pronikání páry i do rozvodů soustavy. Další přehřívání kolektoru vysušuje kolektor a objem páry v soustavě může dokonce klesnout (částečně se stáhnout do kolektoru), přestože příjem energie slunečního záření trvá (fáze 4). Tento stav může být stabilní po dlouhou dobu. Poklesem dopadajícího slunečního ozáření klesá teplota v kolektoru pod bod varu, teplonosná látka ve formě páry kondenzuje a kapalina opět vyplní kolektor (fáze 5).
Největší zátěž soustavy probíhá ve fázi 2 a 3. Objem kapaliny, která na konci fáze 2 zůstane v kolektoru, určuje délku a intenzitu následující fáze 3. Vypařování zbylé kapaliny udržuje kolektor na bodu varu po dlouhou dobu a vznikající velké objemy páry mohou pronikat do soustavy, předávat teplo a zatěžovat i prvky umístěné daleko od kolektorů. Na konci fáze 3 po ukončení vypařování dosahuje kolektor své maximální (stagnační) teploty a do soustavy se již teplo neuvolňuje.
Na průběh stagnace v solární soustavě má zásadní vliv schopnost kolektoru vyprázdnit svůj objem teplonosné kapaliny při začátku fáze 2. Čím více teplonosné kapaliny se drží v kolektoru, tím více páry vzniká. Na obr. 6.3 je porovnán průběh stagnace pro stejnou soustavu a stejné kolektory lišící se pouze různou vyprazdňovací schopností [1]. Hodnota tlaku odpovídá množství produkované páry a tedy potenciálnímu riziku zasažení dalších prvků solární soustavy teplotou varu, která běžně může dosahovat hodnot nad 130 °C. V příkladech na obr. 6.3 tlak 3,2 bar odpovídá množství páry, které vyplní pouze objem kolektorů (nešíří se do soustavy), vyšší tlaky odpovídají stavu, kdy pára proniká do vzdálenějších částí soustavy a zatěžuje prvky jako čerpadlo, výměník, průtokoměr, kalorimetr atd. Tyto prvky pak mohou být zatíženy teplotami přesahujícími výrobcem doporučené hodnoty, a tak může dojít k předčasnému zestárnutí, poškození nebo zničení soustavy.
Obr. 6.3 Průběh stagnace v soustavě při použití kolektorů s různou vyprazdňovací schopností [1]
6.1.3 Ochrana proti problémům se stagnací
Problémům s důsledky stagnace je možné se zpravidla vyhnout již ve fázi návrhu solární soustavy, a to správnou volbou, návrhem a umístěním prvků, které zabrání vlastní produkci páry, případně jejímu proniknutí k ostatním prvkům soustavy.
Vyprazdňovací schopnost kolektorů
Schopnost kolektorů a kolektorových polí vytlačit kapalnou fázi při vzniku páry je závislá na jejich hydraulickém zapojení a určuje četnost, hladinu a dobu trvání kritické tepelné zátěže solární soustavy a jejích prvků. Dobrá vyprazdňovací schopnost znamená, že hydraulické zapojení absorbéru kolektoru (viz obr. 6.4 – horní řada) umožňuje při přeměně zlomku objemu teplonosné kapaliny v páru ve fázi 2 vytlačení zbylého objemu teplonosné kapaliny z kolektoru. Tím nevzniká další pára, která by mohla pronikat do soustavy, a ta je chráněna před kritickou zátěží. Špatná vyprazdňovací schopnost se vyznačuje omezeným vytlačením kapaliny z kolektoru (viz obr. 6.4 – dolní řada) zapojení absorbéru vytváří „pytel“ teplonosné kapaliny, který nelze z kolektoru vytlačit (lokální zvýšení tlaku nepřevýší hydrostatickou výšku sloupce kapaliny), ale pouze odvést ve formě páry. To vede k velkému množství produkované páry a energie, které je při stagnaci přenášeno párou do soustavy, přeměně části obsahu potrubí soustavy v páru a k rozsáhlým oblastem v rozvodech soustavy vyplněným sytou párou. Možnou ochranou proti výrazné tvorbě páry u nevhodně zapojených absorbérů může být často jednoduchá změna montážní polohy kolektoru, např. u trubkových vakuových solárních kolektorů s protékaným U-registrem pootočením kolektoru o 90°, nebo ještě lépe umístěním rozvodných potrubí dolů (pootočení o 180° – naráží na problém řádného odvzdušnění).
Obr. 6.4 Kolektory s dobrou (nahoře) a špatnou (dole) vyprazdňovací schopností z hlediska tvorby páry při stagnaci [2]
Poloha zpětné klapky
Vyprazdňování kolektorů závisí výrazně také na poloze zpětné klapky vzhledem k tlakové expanzní nádobě v soustavě. Pokud je sestava prvků na přívodním potrubí do kolektorů zapojena podle obr. 6.5 (vpravo), potom je vyprazdňování kolektoru omezeno pouze horním vývodem. Vzniká velké množství páry i u solárních kolektorů s vhodným hydraulickým zapojením z hlediska vyprazdňování, pára se dostane daleko do soustavy a po kondenzaci např. na výměníku teprve do expanzní nádoby. Na druhou stranu, přívodní potrubí do kolektoru zůstává vyplněné kapalinou až ke kolektoru díky nevhodné poloze zpětné klapky.
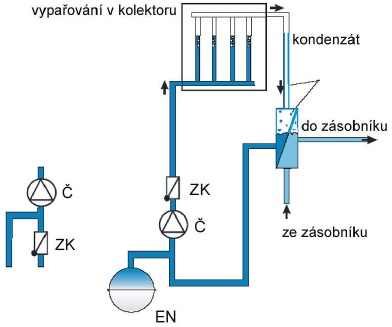
Obr. 6.5 Správné (vlevo) a špatné (vpravo) umístění zpětné klapky v solární soustavě [2]
Podmínky pro dobré vyprázdnění kolektorů v případě stagnace se dosáhnou změnou polohy zpětné klapky vzhledem k expanzní nádobě podle obr. 6.5 (vlevo). Při tomto uspořádání prvků může být obsah kolektorů vytlačen do expanzní nádoby především přívodním potrubím kolektoru, a objem zbylé kapaliny produkující páru v kolektoru je minimální. Pára se šíří do soustavy oběma cestami, což sníží navíc riziko proniknutí páry daleko od kolektoru a zasažení prvků ve strojovně.
Návrh expanzní nádoby
Správné dimenzování expanzní nádoby může předejít problémům se ztrátou teplonosné kapaliny pojistným ventilem. Velikost expanzní nádoby by měla respektovat tvorbu páry v kolektorech při stagnaci, objemové změny s tím spojené a zejména vytlačení objemu kapaliny z kolektorů. Potom nedochází k výraznému nárůstu tlaku v soustavě a reakci pojistného ventilu při běžných stagnačních podmínkách. Více o návrhu expanzní nádoby v kapitole 6.8.3.
Volba teplonosné látky
Běžné teplonosné látky na bázi nemrznoucích směsí glykolu a vody s inhibitory koroze mohou při dlouhodobém působení vysokých teplot (nad 130 °C) podléhat degradaci, vylučování pevných látek, vzniku kyselin, zvýšení korozivity teplonosné kapaliny, „cuckovatění“ apod. U kolektorů a soustav s dobrou vyprazdňovací schopností dochází k působení nepříznivé tepelné zátěže pouze na zlomek objemu teplonosné kapaliny a jen krátkodobě. U kolektorů a soustav se špatnou vyprazdňovací schopností je celý objem kapaliny zadržené v kolektorech vystaven kritickým podmínkám po delší dobu. To může mít za následek nejdříve odpařování vodního obsahu nemrznoucí směsi (oddělená destilace), nárůst koncentrace glykolu a inhibitorů ve zbytkovém objemu kapaliny v kolektorech až do vysokých hodnot s bodem varu 210 °C (čistý glykol při běžných stagnačních tlacích). Potom např. u plochých kolektorů s teplotou stagnace 160 až 180 °C nemusí dojít k úplnému odpaření glykolové složky nemrznoucí směsi, nicméně celý objem je vystaven dlouhodobé tepelné zátěži, což může mít za následek jeho rychlou degradaci. U vakuových kolektorů s teplotami stagnace nad 250 °C dochází k odpaření glykolu a tvorbě pevných usazenin v potrubí (vyloučené inhibitory), které mají omezenou zpětnou rozpustnost při následné kondenzaci po skončení stagnace. Pro solární soustavy, u kterých je předpoklad zvýšené četnosti výskytu extrémních stagnačních podmínek, se tedy doporučuje použití kvalitních nemrznoucích směsí, odolávajících vysokým teplotám bez degradace, a dále nemrznoucích směsí s kapalnými inhibitory koroze, odpařitelnými a zpětně smísitelnými s teplonosnou látkou.
Sklon kolektorů
Omezení stagnačních podmínek je možné také realizovat zvýšením sklonu kolektorů, který v letním období zajišťuje nižší příjem slunečního záření oproti optimálnímu sklonu 45° (pro celoroční použití). U kombinovaných soustav pro vytápění s vysokým solárním pokrytím je proto výhodná integrace kolektorů do fasády (90°). Z hlediska provozních parametrů se dosahuje stejných zisků a pokrytí jako u kombinované soustavy s kolektory na střeše se sklonem 45°. Integrací kolektoru do fasády sice dochází na jedné straně ke zvýšení účinnosti kolektoru a tedy k nárůstu teoreticky dosažitelné stagnační teploty, na druhé straně se výrazně sníží provozní četnost výskytu stagnačních podmínek a jejich úroveň (tvorba páry) v letním období.
6.2 TEPLONOSNÁ KAPALINA
Pro přenos tepla v aktivních solárních soustavách z místa zdroje (kolektorů) do místa spotřeby (zpravidla akumulační zásobník) se využívá různých teplonosných látek, nejčastěji kapaliny (kapalinové solární soustavy) nebo vzduchu (vzduchové solární soustavy), velmi vzácně pevných látek (sypký písek). Pro celoroční použití kapalinových solárních soustav je pak nejrozšířenější použití nemrznoucí směsi s ohledem na ochranu soustavy v zimním období před poškozením mrazem. Nemrznoucím směsím je proto v kapitole věnováno nejvíce prostoru.
Teplonosná kapalina musí splňovat řadu požadavků pro zajištění dlouhodobě bezproblémového provozu solárních soustav:
- nízký bod tuhnutí (nejlépe kolem -25 až -30 °C);
- dobré tepelněfyzikální vlastnosti (tepelná kapacita, viskozita), co nejvíce podobné vodě;
- nehořlavost;
- ochrana proti korozi;
- kompatibilita s těsnicími materiály;
- ekologické aspekty (netoxická, biologicky rozložitelná);
- dlouhodobá stálost vlastností – teplotní odolnost;
- rozumná cena.
6.2.1 Voda
Voda je netoxická, nehořlavá a levná. Je ideální teplonosnou látkou z hlediska vysoké tepelné kapacity, tepelné vodivosti a nízké viskozity. Bohužel, voda má nízký bod varu a především vysoký bod tuhnutí, což ji předurčuje pro použití pouze v sezónních solárních soustavách s letním provozem. Voda může způsobovat korozi, pokud její pH (hladina kyselosti-zásaditosti) klesne pod neutrální hodnotu 7, a dále samozřejmě při nevhodné kombinaci faktorů jako obsah kyslíku, teplota, koncentrace dalších rozpuštěných chemických látek či elektrochemický potenciál přítomných kovů. V případě použití vody s vysokým obsahem minerálů (tvrdá voda) může docházet k vylučování minerálních usazenin při vyšších teplotách v kolektorech (zarůstání).
6.2.2 Glykolové nemrznoucí směsi
Vodní směsi propylenglykolu nebo etylenglykolu jsou nejčastěji používanými teplonosnými látkami v solárních soustavách. Etylenglykol je však vysoce jedovatý a měl by být používán pouze v takových soustavách, kde je primární okruh oddělen od pitné vody alespoň dvěma teplosměnnými plochami, např. kombinované solární soustavy. V současné době se od jeho použití upouští a upřednostňuje se směs netoxického propylenglykolu a vody s potřebnými inhibitory koroze. Korozivita směsi propylenglykol-voda je totiž významně vyšší než u čisté vody nebo čistého glykolu, je nepřímo úměrná koncentraci glykolu. Inhibitory, rozpuštěné v kapalině, umožňují zamezit korozi vytvořením tenké ochranné vrstvy na povrchu kovů. Zatímco solární soustavy obsahují různé materiály (měď, bronz, ocel, litina), v současné době není k dispozici univerzální inhibitor; problém se zpravidla řeší kombinací několika různých (organických, anorganických) inhibitorů s ochranným potenciálem pro specifický kov.
Nemrznoucí směsi propylenglykolu a vody mají sklon ke stárnutí vlivem vysokých teplot při stagnačních podmínkách v kolektorech. Při nárůstu teploty nad bod varu směsi dochází k tvorbě bublinek páry a vypařování kapaliny. U dobře navržených kolektorů a soustav dochází k přeměně v páru pouze u malého množství směsi, vznikající pára vytlačí ostatní kapalinu z kolektorů do míst o nižší teplotě (vytlačený objem by měla pohltit expanzní nádoba). Rozpuštěné inhibitory (pevné neodpařitelné látky) se mohou vylučovat na stěnách. Při ochlazení kolektoru kapalina zpětně kondenzuje a zaplavuje kolektor. Aby nedocházelo k postupnému vyloučení inhibitorů na stěny potrubí v kolektorech a tím k degradaci jak teplonosné látky, tak kolektorů, měla by být kvalitní teplonosná látka schopná zpětně rozpustit vyloučené inhibitory. Postupující degradace teplonosné látky se projevuje změnou barvy (tmavnutí kapaliny), pomalu se snižující hodnotou pH a tvorbou pevných látek na stěnách potrubí kolektorů (vylučování inhibitorů). U propylenglykolu dochází k rozkladu v důsledku oxidačních reakcí, tvoří se kyseliny, a při opakovaném přehřívání dochází k poklesu pH kapaliny pod hodnotu 7 (měla by se pohybovat nad touto hodnotou). Rychlost degradace propylenglykolu je přímo úměrná teplotním stresům a obsahu kyslíku. Proto se doporučuje vždy sledovat hodnotu pH, bod tuhnutí a koncentraci inhibitorů pro včasnou výměnu a ochranu solárního okruhu před zvýšenou korozí.
Glykolové směsi se zpravidla používají v objemovém ředění 40–50 % glykolu podle požadované teploty tuhnutí (zpravidla od výrobce namíchány na teplotu tuhnutí okolo -30 °C). Takové směsi se oproti vodě vyznačují zhruba o 25 % nižší tepelnou kapacitou a obecně vyšší kinematickou viskozitou (při 20 °C až 6x vyšší než u vody) s její výraznou teplotní závislostí (při 80 °C pouze cca 2x vyšší než u vody). V současné době jsou k dispozici jednak klasicky inhibitované glykolové směsi pro použití v plochých kolektorech (stagnační teploty pod 200 °C) a jednak pokročilé směsi s kapalnými inhibitory, umožňující použití v trubkových vakuových kolektorech (stagnační teploty do 300 °C). Přehled používaných glykolových směsí uvádí tab. 6.2.
Tab. 6.2 Vybrané teplonosné látky na bázi směsi glykolových směsí dostupné na trhu
| Teplonosná látka | Složení | Výrobce | tt [°C] |
| Solaren EKO | propylenglykol (1,2 propandiol) s inhibitory | Velvana, a.s. | -31 |
| Kolektor P Super | monopropylenglykol (1,2 propandiol) s inhibitory | Agrimex, s.r.o., Třebíč | -30 |
| Tyfocor L | propylenglykol (1,2 propandiol) s inhibitory | Tyforop Chemie, GmbH | -50 |
| Tyfocor LS | propylenglykol (1,2 propandiol) s inhibitory | Tyforop Chemie, GmbH | -28 |
| Antifrogen N | monoetylenglykol | ||
| (1,2 etandiol) s inhibitory | Gerling, Holz & CO Handels, GmbH | -70 | |
| Antifrogen SOL | propylenglykol s inhibitory | Gerling, Holz & CO Handels, GmbH | -34 |
Znalost tepelněfyzikálních vlastností glykolových vodních nemrznoucích směsí je nutná pro stanovení tlakových ztrát v potrubí (viskozita, hustota), předávaného výkonu solární soustavy (měrná tepelná kapacita, hustota), návrhu expanzních nádob (hustota, součinitel objemové roztažnosti) atd. Tabelární hodnoty je možné získat buď přímo od výrobce (zpravidla pro vybrané teploty), nebo z různých publikovaných obecných tabulek a atlasů glykolových teplonosných látek, např. [3, 4]. V současné době při použití výpočetní techniky jsou vhodnější modely jednotlivých vlastností v podobě výpočtových polynomů, ze kterých je možné hodnotu určité vlastnosti stanovit v závislosti na teplotě a koncentraci směsi. Níže jsou uvedeny obecné tvary polynomů a v tab. 6.3 a 6.4 příslušné konstanty vlastností etylenglykolových a propyleglykolových vodních směsí [5].
Termodynamickou teplotu tuhnutí Tt [K] lze stanovit z rovnice
(6.4)
kde je
ξ … hmotnostní koncentrace glykolu v roztoku [-].
Hustotu, tepelnou vodivost a měrnou tepelnou kapacitu lze vypočítat podle obecné rovnice, kde daná vlastnost je reprezentována členem Px
(6.5)
Podobná obecná rovnice je použitelná pro dynamickou iskozitu a Prandtlovo číslo
(6.6)
Tab. 6.3 Parametry matematických modelů pro vlastnosti vodních směsí etylenglykolu [5]
| Parametr A | ρ [kg/m3] | cp [kJ/(kg·K)] | λ [W/(m.K)] | μ [Pa·s] | Pr [-] | Tt [K] |
| 0 | – | – | – | – | – | 1,0 |
| 1 | 658,49825 | 5,36449 | 0,83818 | -4,63024 | 3,96951 | -0,06982 |
| 2 | -54,81501 | 0,78863 | -1,37620 | -2,14817 | 0,70076 | -0,35780 |
| 3 | 664,71643 | -2,59001 | -0,07629 | -12,70106 | -12,98045 | – |
| 4 | 232,72605 | -2,73187 | 1,07720 | 5,40536 | 2,64789 | – |
| 5 | -322,61661 | 1,43759 | -0,20174 | 10,98990 | 11,58900 | – |
Tab. 6.4 Parametry matematických modelů pro vlastnosti vodních směsí propylenglykolu [5]
| Parametr A | ρ [kg/m3] | cp [kJ/(kg·K)] | λ [W/(m·K)] | μ [Pa·s] | Pr [-] | Tt [K] |
| 0 | – | – | – | – | – | 1,0 |
| 1 | 508,41109 | 4,47642 | 1,18886 | -1,02798 | 6,66139 | -0,03736 |
| 2 | -182,40820 | 0,60863 | -1,49110 | -10,03298 | -6,99440 | -0,40050 |
| 3 | 965,76507 | -0,71497 | -0,69682 | -19,93497 | -18,55114 | – |
| 4 | 280,29104 | -1,93855 | 1,13633 | 14,65802 | 12,04640 | – |
| 5 | -472,22510 | 0,47873 | 0,06735 | 14,62050 | 14,47735 | – |
6.2.3 Alkoholy
Teplonosné látky jako metanol či etanol se častěji než u kolektorů používají v primárních okruzích tepelných čerpadel s ohledem na nízký bod tuhnutí. Tepelná kapacita je výrazně nižší než u vody (téměř o 40 %) a pro použití jako teplonosné látky v okruzích solárních soustav je nevýhodný také nízký bod varu (metanol 64 °C, etanol 78 °C). Metanol a etanol jsou těkavé a toxické látky.
6.2.4 Silikonové oleje
Teplonosné látky na bázi silikonových olejů mají velmi nízký bod tuhnutí a velmi vysoký bod varu. Nejsou korozivní a mají vysokou životnost. Na druhou stranu se vyznačují vysokou viskozitou a nízkou tepelnou kapacitou (poloviční než u vody), což vede k vyšší spotřebě energie pro pohon oběhových čerpadel (vyšší průtok, vyšší tlakové ztráty). Silikonové oleje jsou také vzlínavé, snadno unikají z uzavřeného okruhu mikroskopickými netěsnostmi. Jejich použití se omezuje pro vysokoteplotní aplikace a soustřeďující kolektory s vysokým koncentračním poměrem.
6.2.5 Vliv kapaliny na účinnost kolektoru
Při zkouškách tepelného výkonu solárních kolektorů podle [6] se používá jako teplonosná látka voda, z důvodu jejích neměnných vlastností a potřeby porovnatelnosti naměřených výsledků. Vzhledem k tomu, že nemrznoucí směs má jiné tepelněfyzikální vlastnosti (nižší měrná tepelná kapacita, tepelná vodivost, vyšší viskozita), naskýtá se otázka, jak se změní účinnost solárního kolektoru při použití např. nemrznoucí směsi místo čisté vody. Na obr. 6.6 jsou porovnány standardní křivky účinnosti solárního kolektoru při použití různých teplonosných látek (voda, směs propylenglykolu a vody, etanol a silikonový olej). Z grafů je zřejmé, že zatímco u běžné nemrznoucí směsi se účinnost kolektoru snižuje v řádu 1 %, u etanolu a silikonového oleje jde o cca 5 %.
Obr. 6.6 Křivky účinnosti solárního kolektoru s různými teplonosnými látkami
6.2.6 Vliv kapaliny na hydrauliku solární soustavy
Pro hydrauliku soustavy jsou určujícími vlastnostmi viskozita a hustota teplonosné látky. Viskozita u nemrznoucích směsí na bázi glykolů vykazuje výraznou závislost na teplotě, s rostoucí teplotou klesá (viz obr. 6.7). Způsob výpočtu tlakových ztrát třením v soustavách s nemrznoucí směsí na bázi glykolů je uveden například v [3]. Tabelované hodnoty měrné třecí ztráty R [Pa/m] je možné pro propylenglykol nalézt v literatuře [4].
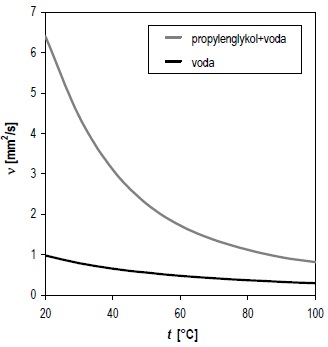
Obr. 6.7 Závislost kinematické viskozity teplonosných kapalin na teplotě

Obr. 6.8 Porovnání tlakových spádů potrubí di = 20 mm pro různé teplonosné kapaliny
Na obr. 6.8 je porovnána tlaková ztráta 1 m ocelového a měděného potrubí (vnitřní průměr 20 mm) v závislosti na průtoku teplonosné kapaliny (voda, vodní směs propylenglykolu Solaren při 20 °C). Rozsah průtoků odpovídá běžným návrhovým rychlostem v potrubí do 0,8 m/s. U propylenglykolové vodní směsi je vlivem vysoké viskozity pro běžné průtoky v potrubí laminární proudění, tlaková ztráta tedy nezávisí na drsnosti potrubí (pouze na Reynoldsově čísle) a závislost tlakové ztráty třením na průtoku je proto lineární a pro oba typy potrubí stejná. Z hlediska tlakových ztrát tedy není u nemrznoucích směsí při běžném použití v solárních soustavách rozhodující, zda se použije potrubí hydraulicky drsné nebo hladké.
6.3 POTRUBÍ
Rozvody potrubí solárních tepelných soustav spojují zdroj tepla (kolektor) s místem akumulace a spotřeby (zásobník). Základním požadavkem na potrubí je především jejich funkčnost a životnost. Návrh materiálu potrubí rozvodů solárních kapalinových soustav musí odpovídat druhu a použití soustavy. Potrubí musí být odolné v první řadě teplonosné kapalině, zvláštní pozornost je nutné věnovat v případě použití nestandardních kapalin, a dále musí vyhovovat teplotním a tlakovým poměrům v solární soustavě.
Dalším, ač často zanedbávaným, požadavkem je hydraulická (energetická) náročnost navržené potrubní sítě. Světlost potrubí je vhodné pro danou aplikaci optimalizovat s ohledem na spotřebu elektrické energie pro pohon soustavy (čerpací práce).
6.3.1 Materiály
Plastové potrubí je možné použít zejména u nízkoteplotních solárních soustav s nezasklenými kolektory pro sezónní (letní) ohřev bazénové vody, kde teploty stěží překročí 60 °C i v případě stagnace. Plastové potrubí používané přímo v solárních kolektorech obsahuje uhlíkové částice z důvodu ochrany proti UV záření a pro zajištění dobré pohltivosti. Pro kolektory se nejčastěji používají materiály na bázi polypropylenu, EPDM nebo polyesteru. Pro potrubí lze použít běžný síťovaný polyetylen (obdobně jako vodovodní instalace), chráněný proti UV záření, nebo obdobné materiály jako pro plastové kolektory.
Obr. 6.9 Používané materiály pro potrubí solárních soustav: měď, nerezová ocel (vlnovec)
U solárních soustav s pokročilými selektivními kolektory pro celoroční využití sluneční energie je nutné navrhovat potrubí kovové (měd, ocel), neboť potrubí primárního okruhu takových solárních soustav musí být odolné teplotám okolo 180 °C (ploché atmosférické kolektory se selektivní vrstvou), případně 250 °C (trubkové vakuové kolektory) a tlakům do 1 MPa. Pro takové podmínky je vyloučené použití plastových trubek z hlediska teplotního a mechanického namáhání. Nejpoužívanějším materiálem jsou měděné trubky, které umožňují rychlou montáž (pájení, lisování, svěrné). Výhodou je použití stejného materiálu jako pro registry v kolektorech a tudíž nulový elektrochemický potenciál (omezení rizika koroze). Použití ocelových trubek je principiálně možné, nicméně montáž je pracnější a zdlouhavá (svařování, ohýbání, řezání závitů). Ocelové trubky se používají především u velkých solárních soustav, kde měděné potrubí ve velkých světlostech (nad 28 mm) je velmi drahé. Nevhodné jsou pozinkované ocelové trubky vzhledem ke korozivním reakcím zinku s nemrznoucí směsí na bázi glykolů.
U jednoduchých solárních soustav jsou pro propojení kolektoru a zásobníku k dispozici pružné nerezové vlnovcové trubky s převlečnými maticemi. Vlnovcové potrubí je vhodné z hlediska usnadnění montáže kolen a ohybů, které lze jednoduše vytvarovat.
Stranou od tradičních instalačních trubek jsou k dispozici kompaktní potrubní systémy, sdružující přívodní a zpětné potrubí (měď, nerez), tepelnou izolaci a elektrické vedení mezi regulátorem a čidlem teploty v kolektoru.
Obr. 6.10 Kompaktní potrubní systém s tepelnou izolací a kabeláží
6.3.2 Spojování potrubí
Pro spojování nejčastěji používaných měděných rozvodů s mosaznými a bronzovými fitinkami se v minulosti osvědčilo měkké kapilární pájení (při 270 °C) pro ploché kolektory a tvrdé kapilární pájení (nad 450 °C, zpravidla při 600 až 800 °C) u vysokoteplotních trubkových kolektorů. Přestože teplotní odolnost měkkého pájení (např. pájka S-Sn97Cu3, S-Sn97Ag3) je deklarovaná pro trvalé teploty do 110 °C při tlaku 1,6 MPa, je velmi častým způsobem spojování potrubí u většiny solárních soustav. Provozní teploty pro tvrdou pájku (např. L-Ag2P) jsou vyšší (nad 110 °C, tlaky 1,6 MPa).
Obr. 6.11 Nejčastěji používané spoje potrubí v solárních soustavách (pájené – vlevo, lisované – vpravo)
Stále rozšířenějším způsobem rychlého spojování měděných trubek se v poslední době stávají lisované nerozebíratelné spoje (lisovací měděné tvarovky s O-kroužky z EPDM). Přestože jde o materiálově dražší způsob spojování než pájení, převažuje výhoda rychlosti a menší pracnosti montáže. Při provádění těchto mechanických spojů nejsou ostatní prvky soustavy během montáže tepelně namáhány a na stavbě nevzniká požární riziko. Vzhledem k omezení montáže pájením nebo svařováním je takové řešení vhodné např. pro solární soustavy instalované ve dřevostavbách. Použití rozebíratelných svěrných spojů (svěrný prstenec okolo trubky nebo vnější objímka se šrouby) se omezuje na teplotně namáhané připojení kolektorů k potrubnímu rozvodu.
6.3.3 Vedení potrubí
Při kladení rozvodů potrubí je nutné věnovat pozornost tepelné roztažnosti potrubí a zohlednit délkovou dilataci promyšleným vedením a správným umístěním pevných bodů, kluzných uložení a dilatačních prvků. Na každých 10 až 15 m vedení rozvodů by měl být umístěn dilatační prvek (smyčky, ohyby, kompenzátory), aby se zabránilo škodám a případným netěsnostem, vzniklým vnitřním pnutím. U plastových potrubí je nutné zohlednit vyšší míru dilatací.
Vratné (teplejší) potrubí od kolektorů je vhodné vést co nejkratší trasou. Tichelmannova smyčka pro rovnoměrné zatékání do více kolektorových polí se proto provádí zásadně na přívodním (chladnějším) potrubí do kolektorů. Délka potrubí vedeného venkovním prostředím by měla být minimalizována (drahá izolace odolná UV záření, tepelné ztráty). Potrubí ke kolektorům je možné vést stávajícími komíny, větracími šachtami nebo drážkami ve zdi. Otevřené šachty je třeba vhodně utěsnit, aby nedocházelo k vyšším tepelným ztrátám přirozeným prouděním vzduchu kolem potrubí. Vedení potrubí by mělo zohledňovat řádně odvzdušnění a snadné vypouštění celé soustavy. Kovová potrubí by měla být připojena na uzemnění domu.
Všechny části solární soustavy musí být pečlivě a bezpečně utěsněny proti úniku teplonosné kapaliny. Má-li být soustava provozována s nemrznoucí směsí na bázi glykolu, musí být všechny prvky (i elastická těsnění ventilových sedel, membrány v expanzních nádobách atd.) z materiálu odolného glykolu a teplotám alespoň nad 120 °C. Tvarovky a armatury se proto nejčastěji vyrábějí z mědi, mosazi nebo bronzu.
6.3.4 Návrh světlosti potrubí
Navrhování potrubí okruhů solárních tepelných kapalinových soustav výrazně závisí na způsobu jejich provozu, daným hodnotou měrného průtoku kolektorovým polem. V zásadě rozeznáváme soustavy s vysokým průtokem 50–70 l/(h·m2) kolektorové plochy (high-flow, většinou maloplošné soustavy pro rodinné domy s běžnými zásobníky tepla) nebo s nízkým průtokem 10–15 l/(h·m2) kolektorové plochy (low-flow, zpravidla větší soustavy, zásobník tepla se stratifikací). Nižší průtok samozřejmě vede k nižším světlostem potrubí a menším tloušťkám tepelných izolací. Návrh světlosti potrubí solárních soustav se provádí stejným způsobem jako u běžných tepelných soustav, například metodou ekonomické rychlosti proudění (do od 0,3 do 0,6 m/s).
Dalším významným parametrem, který může ovlivnit hydrauliku soustavy a tedy i návrh světlosti potrubí, je druh teplonosné kapaliny, respektive její viskozita, na které závisejí tlakové ztráty třením.
Návrh světlosti potrubí primárního kolektorového okruhu by měl zohlednit také parametry kolektorů, které ovlivňují jejich stagnační chování, jako je objem kolektorů a kvalita vyprazdňování kolektorů. Jako základní pravidlo platí, že objem přívodního Vp a zpětného potrubí Vz ke kolektorům by měl být minimálně polovina objemu kolektorů Vk
(6.7)
Objem potrubí tvoří nárazníkový objem proti šíření páry potrubím do technické místnosti k teplotně méně odolným prvkům soustavy. U velkých soustav, kde ekonomicky odůvodnitelný objem potrubí nemusí být dostatečný, se používá nárazníková nádrž (předloha) předřazená expanzní nádobě na té straně primárního okruhu, která je příznivější vůči vyprázdnění kolektorů (zpravidla chladná).
6.4 TEPELNÁ IZOLACE POTRUBÍ
Základním požadavkem na tepelné izolace je jejich životnost (odolnost vůči teplotám, degradaci, atmosférickým vlivům atd.) a nízká tepelná vodivost. Tloušťku izolace je vhodné pro danou aplikaci optimalizovat s ohledem na tepelné ztráty, ovlivňující konečné zisky a celkovou funkčnost solární soustavy.
Zatímco potrubí nízkoteplotních sezónně provozovaných solárních soustav pro ohřev bazénové vody se zpravidla tepelně neizolují, v celoročně provozovaných solárních soustavách pro přípravu teplé vody a případně přitápění je nutné potrubí opatřit tepelnou izolací, aby tepelné ztráty z potrubí do okolí podstatně nesnižovaly celkovou účinnost solární soustavy.
6.4.1 Materiály
Tepelná izolace by měla být odolná minimálně vůči teplotám nad 150 °C, u venkovních rozvodů je navíc nutná ochrana proti UV záření a nenavlhavost. Nejčastěji se používají tepelné izolace na bázi EPDM s uzavřenou strukturou (odolné vlhkosti), minerální vlna kašírovaná hliníkovou síťovou fólií, případně izolace opláštěné hliníkovým plechem kvůli ochraně před vlhkostí, UV zářením a poškozením způsobeným ptáky či hlodavci.
6.4.2 Návrh tloušťky izolace
Při návrhu tloušťky tepelné izolace rozvodů solárních soustav se lze řídit vyhláškou [7] určenou obecně pro tepelné soustavy. Vyhláška stanovuje minimální požadovaný součinitel prostupu tepla U [W/(m·K)] pro různé rozsahy světlosti potrubí (viz tab. 6.5), případně možnost stanovení tloušťky izolace optimalizačním výpočtem. U rozvodů z měděného a plastového potrubí se tloušťka tepelné izolace stanovuje ze součinitele U, zvoleného podle vnějšího průměru potrubí nejbližšího vnějšímu potrubí řady DN.
Součinitel prostupu tepla U z teplonosné látky izolací potrubí do okolí se stanoví podle vztahu
(6.8)
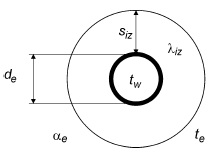
kde je
λiz … tepelná vodivost izolace, ve W/(m·K);
de … vnější průměr potrubí (vnitřní průměr izolace), v m;
siz … tloušťka tepelné izolace, v m;
αe … součinitel přestupu tepla na vnějším povrchu tepelné izolace, ve W/(m2·K).
Tepelný odpor vůči prostupu tepla vodivou trubkou a tepelný odpor vůči přestupu tepla z vnitřního povrchu trubky do proudící teplonosné látky se ve vztahu pro praktické výpočty zanedbává.
Tab. 6.5 Určující hodnoty součinitelů prostupu tepla vztažených na jednotku délky potrubí u vnitřních rozvodů podle [7]
| DN | 10 až 15 | 20 až 32 | 40 až 65 | 80 až 125 | 150 až 200 |
| U [W/(m·K)] | 0,15 | 0,18 | 0,27 | 0,34 | 0,40 |
Evropská norma pro průmyslově vyráběné solární soustavy [8] doporučuje navrhovat tloušťku izolace 20 mm pro potrubí do vnějšího průměru 22, tloušťku 30 mm pro potrubí s vnějším průměrem 28 až 42 mm, a pro větší dimenze potrubí dodržet tloušťku izolace stejnou jako vnitřní průměr potrubí, přičemž tepelná vodivost materiálu izolace je uvažována λ ≤ 0,040 W/(m·K).
6.4.3 Provedení izolací
Důležité je izolovat celý potrubní rozvod, včetně fitinek, ventilů, zásobníkových vstupů a výstupů. Uchycení potrubí do třmenů je vhodné umístit až na tepelnou izolaci potrubí, aby se nevytvářely zbytečné tepelné mosty.
6.5 TLAKOVÉ ZTRÁTY SOUSTAVY
V převážné většině solárních soustav navrhovaných v České republice se využívá nuceného oběhu teplonosné kapaliny pro přenos tepelné energie ze solárního kolektoru do místa spotřeby (zásobníku tepla), který zajišťují oběhová čerpadla. Čerpadla překonávají tlakové ztráty celého okruhu solární soustavy, které jsou závislé na dílčích hydraulických charakteristikách jednotlivých prvků (solární kolektor, výměník tepla, potrubí aj.). Výpočet tlakových ztrát okruhů solární soustavy a návrh oběhových čerpadel je obdobný jako u otopných soustav. Zásadní rozdíly ve výpočtu spočívají v uvažované teplonosné kapalině, která má nižší tepelnou kapacitu než voda (je zapotřebí vyšší průtok pro přenesení stejného výkonu), vyšší viskozitu (vyšší třecí ztráty) a výraznou závislost viskozity na teplotě (v teplotním rozsahu 20 až 80 °C se mění od 6 do 1 mm2/s). Vlastnosti teplonosné kapaliny se navíc mohou měnit stupněm ředění. Pro výpočet fyzikálních vlastností nemrznoucích směsí se použijí vztahy uvedené v kapitole 6.2. V tab. 6.6 jsou porovnány vlastnosti různých používaných teplonosných kapalin (při teplotě 20 °C), potřebné k hydraulickému výpočtu.
Tab. 6.6 Fyzikální vlastnosti vody a glykolových směsí s vodou
| Teplonosná kapalina | tt [°C] | ρ20°C [kg/m3] | ρ80°C [kg/m3] | ν20°C [m2/s] | ν80°C [m2/s] | c20°C [J/(kg·K)] | c80°C [J/(kg·K)] |
| Voda | 0 | 998 | 973 | 1,0·10-6 | 4,7·10-6 | 4181 | 4196 |
| Etylenglykol + voda | -20 | 1058 | 1026 | 2,7·10-6 | 7,8·10-7 | 3549 | 3731 |
| Propylenglykol + voda | -20 | 1028 | 986 | 3,7·10-6 | 7,2·10-7 | 3771 | 3871 |
| Propylenglykol + voda | -30 | 1036 | 989 | 5,3·10-6 | 8,1·10-7 | 3651 | 3782 |
6.5.1 Tlakové ztráty potrubní sítě
Pro ucelený pohled na hydrauliku solárních soustav jsou níže uvedeny základní vztahy pro stanovení tlakových ztrát třením Δpλ a místními odpory Δpξ. Výpočet tlakové ztráty třením v potrubí vychází ze základního vztahu
(6.9)
kde je
w … rychlost proudění teplonosné látky v potrubí, v m/s;
ρ … hustota teplonosné látky, v kg/m3;
d … vnitřní průměr potrubí, v m;
l … délka potrubí, v m;
λ … součinitel třecí ztráty (bezrozměrný).
Pro oblast laminárního proudění (Re < 2 300) se součinitel třecí ztráty potrubí o kruhovém průřezu stanoví ze vztahu
(6.10)
Součinitel třecí ztráty v laminární oblasti není závislý na drsnosti potrubí, pouze na Reynoldsově čísle
(6.11)
kde je
ν … kinematická viskozita teplonosné kapaliny, v m2/s.
Pro turbulentní oblast (Re > 5 000) se součinitel třecí ztráty stanoví iteračním výpočtem podle obecného Colebrookova vztahu
(6.12)
kde je
k … absolutní drsnost potrubí, v m.
Pro výpočty je možné použít směrných hodnot drsnosti: ocelové potrubí k = 0,10 až 0,15 mm (nové 0,05 až 0,1 mm, mírně orezavělé 0,15 až 0,20 mm), měděné potrubí k = 0,01 mm, plastové potrubí k = 0 mm (hydraulicky hladké).
Za předpokladu hydraulicky hladkého potrubí (měděné, plastové potrubí) je možné použít Blasiova zjednodušeného vztahu
(6.13)
Za předpokladu použití nemrznoucí směsi propylenglykolu s teplotou tuhnutí -30 °C a návrhové rychlosti proudění kapaliny v potrubí do 0,6 m/s se solární soustavy z hlediska hydrauliky pohybují v oblasti laminárního proudění. V určitých aplikacích (vyšší ředění nemrznoucí směsi vodou, vyšší provozní teploty) se však může proudění dostat do tzv. přechodové oblasti mezi laminárním a turbulentním režimem (2 300 < Re < 5 000). Proudění v této oblasti je značně nestabilní a nelze tedy jednoznačně určit ani součinitele třecí ztráty jako funkci Re. Na výměnících tepla může přechodová oblast způsobit nestabilitu nejen tlakové ztráty, ale i přenášeného výkonu (nutná kontrola Re při výpočtu). Pokud se nelze přechodové oblasti vhodným návrhem světlosti potrubí či nominálního průtoku vyhnout (doporučeno kvůli stabilitě přenášeného výkonu solárních kolektorů), je nutné počítat tlakové třecí ztráty podle vztahů pro turbulentní oblast (vyšší tlakové ztráty, výpočet na straně bezpečnosti).
Další možností je použití tabelovaných hodnot měrné třecí ztráty R [Pa/m] pro daný vnitřní průměr potrubí a rychlost proudění uvažované teplonosné látky podle vztahu
(6.14)
Tabelované hodnoty měrné třecí ztráty R je možné nalézt v literatuře pro vodu [9] a propylenglykol s obchodním názvem Solaren [4].
Tlaková ztráta místními odpory se stanoví podle vztahu
(6.15)
kde je
ξ … součinitel místní tlakové ztráty (bezrozměrný).
Zatímco hodnoty součinitelů místní tlakové ztráty ξ běžných prvků (T-kus, koleno, kohout aj.) jsou známy v turbulentní automodelní oblasti jako konstantní hodnoty v závislosti na průtoku, hodnoty ξ v laminární oblasti známy nejsou, nejsou konstantními hodnotami (závislost na Re), a navíc jsou vždy vyšší než turbulentní oblasti. Pro zohlednění místních tlakových ztrát se proto doporučuje počítat s přirážkou cca 50 % oproti stanoveným s běžnými tabulkovými hodnotami ξ.
6.5.2 Tlakové ztráty solárních kolektorů
Solární kolektor je z hydraulického hlediska více či méně složitá síť potrubí ve tvaru lyry, serpentiny nebo meandru a jejich sériově nebo paralelně zapojených kombinací (viz obr. 6.12). Hydraulika vlastních kolektorů se řídí použitými průměry rozvodných a sběrných trubek a spojovacích trubek odvádějících teplo z absorpční plochy kolektoru (celoplošný absorbér, lamely) a jejich hydraulickým zapojením. Pokud jsou tlakové ztráty třením ve spojovacích trubkách výrazně vyšší než místní tlakové ztráty odbočením a spojením spojovacích trubek s rozvodnou a sběrnou trubkou (mění se podél rozvodné a sběrné trubky podle poměru průtoků v jednotlivých směrech) a vlastní ztráty třením v rozvodné a sběrné trubce, potom je možné předpokládat, že trubkový registr kolektoru je hydraulicky vyvážený a průtok, rovnoměrně rozdělený do spojovacích trubek, zajišťuje rovnoměrný odvod tepla z kolektoru. V případě hydraulicky nevyváženého kolektoru (krátké spojovací trubky s nízkou tlakovou ztrátou) však může docházet ke špatnému zatékání do některých spojovacích trubek a vlivem podprůtoku se daná oblast přehřívá a snižuje tak odvod tepla z povrchu absorbéru.
Obr. 6.12 Hydraulické konfigurace plochých absorbérů solárních kolektorů
Obdobná úvaha platí i pro vzájemné paralelní spojování běžných solárních kolektorů. Vhodně dimenzovaná (s nízkou rychlostí) rozvodná a sběrná trubka procházející kolektorem umožňuje spolehlivé zatékání do lamel až do určité hodnoty průtoku. Spojováním kolektorů paralelně „vedle sebe“ se zvyšuje návrhový průtok rozvodnou a sběrnou trubkou, zatímco návrhový průtok jednotlivými spojovacími trubkami by měl zůstávat stejný. S rostoucím průtokem roste výrazně rychlost a tedy tlakové ztráty třením a místními odpory v rozvodné a sběrné trubce. Okrajové části (krajní kolektory) mohou potom vykazovat výrazné podprůtoky, případně opačný směr proudění. To vede k přehřívání okrajových částí kolektorů a kolektorových polí, snížení účinnosti a využitelných solárních zisků.
Ačkoli serpentinový absorbér (S) má z uvedených konfigurací největší tlakovou ztrátu (pro 1 kolektor, viz obr. 6.13), v případě zapojení více kolektorů do pole se tlaková ztráta již nezvyšuje a je zároveň zajištěno rovnoměrné zatékání do jednotlivých kolektorů, vzhledem k tlakové ztrátě serpentiny. Naopak konfigurace absorbérů typu U a M jsou pro zapojování do větších kolektorových polí (> 3 kolektory) nevhodné, neboť sériové zapojení výrazně zvyšuje tlakové ztráty celého pole, pokud nemá jít cíleně low-flow režim (s nízkým průtokem).
Obr. 6.13 Hydraulické charakteristiky kolektorů s různým uspořádáním absorbéru [10]
S – serpentinový (Cu10x1), M – meandrový (Cu12x1), Z – lyrový (paralelní Cu8x0,6), T – trubkový kolektor (paralelní Cu10x1)
6.6 OBĚHOVÁ ČERPADLA
Oběhové čerpadlo je hybným prvkem solární soustavy, překonává tlakové ztráty potrubní sítě a dopravuje teplonosnou kapalinu mezi kolektorem a zásobníkem tepla.
6.6.1 Typy a charakteristiky
Oběhová čerpadla je možné principiálně rozdělit na hydrostatická a hydrodynamická. V obecném případě čerpání kapalin je celková energie Y [J/kg] 1 kg čerpané kapaliny definována Bernoulliho rovnicí
(6.16)
U hydrostatických čerpadel převažuje potenciální energie (g·H + p/ρ) a rychlostní energie (c2/2) je zanedbatelná, u hydrodynamických čerpadel jsou potenciální a rychlostní energie rovnocenné. Mezi hydrostatická čerpadla, která se vyznačují tvrdou (strmou) charakteristikou, patří např. zubová čerpadla. Tvrdá charakteristika způsobuje nezávislost průtoku na tlakových ztrátách potrubní sítě, což umožňuje přesné nastavení a udržení konstantního průtoku (pracovního bodu) v solární soustavě i při výrazné závislosti tlakové ztráty na teplotě vlivem viskozity nemrznoucí směsi.
Častěji se používají hydrodynamická čerpadla, běžná v otopných soustavách (bezucpávková mokroběžná oběhová čerpadla s přepínáním otáček). V současné době se vyrábí v provedení vhodném pro použití s nemrznoucí směsí (kataforézní povlak), při zvýšených teplotách (do 110 °C) a především jsou cenově přijatelná. Ke zvýšení odolnosti oběhových čerpadel se důležité součásti těchto čerpadel vyrábějí z korozivzdorné oceli nebo kompozitů zesílených skleněnými vlákny. Hydrodynamická čerpadla mají měkkou charakteristiku s výraznou funkční vazbou mezi průtokem a výtlakem kapaliny. Zvyšování tlakové ztráty v potrubní síti u nich vede ke snižování průtoku.
Obr. 6.14 Charakteristiky oběhových čerpadel
Na obr. 6.14 je uvedeno porovnání tvaru charakteristik obou typů čerpadel (hydrodynamické, hydrostatické) spolu s charakteristikou potrubní sítě pro propylenglykol + voda při 20 °C a 80 °C (výrazně odlišné viskozity). Z grafu je patrné, že při použití hydrostatického čerpadla se docílí téměř konstantního průtoku i při změně tvaru charakteristiky potrubní sítě solární soustavy vlivem teploty. Při použití běžného hydrodynamického čerpadla dochází k výraznější změně průtoku (až o 30 %).
V instalacích, kde není k dispozici střídavé napájecí napětí, je možné použít oběhová čerpadla na stejnosměrný proud. Konstrukce těchto čerpadel vychází z běžných verzí pro střídavý proud, nabízí tedy i stejné aplikační možnosti. Odlišnosti jsou ve statoru a rotoru (motor výše uvedeného oběhového čerpadla má zabudovanou ochranu proti přepětí do 32 V). Výhodná je potom kombinace s využitím fotovoltaických modulů pro pohon solární soustavy, kdy se předpokládá, že v době potřeby čerpací práce je k dispozici zároveň elektrický proud z FV modulů.
U oběhových čerpadel je nutno zabránit působení kondenzace vodních par ve statoru, resp. svorkovnici čerpadla. Taková situace může nastat při provozu solární soustavy v chladnější části roku, kdy je nemrznoucí směs v potrubí od kolektoru vychlazená na nízkou teplotu, nicméně vlastní kolektor se zahřeje na provozní teplotu a regulátor sepne čerpadlo. Tam, kde taková situace hrozí, např. dlouhé rozvody venkovním prostředím, je buď nutné zajistit, aby teplota čerpané kapaliny byla vyšší než je teplota okolí, nebo je nutné zvolit takový typ čerpadla, který obsahuje konstrukční opatření eliminující tento nepříznivý jev (drenážní otvory, zesílené statorové vinutí).
Pro solární soustavy, kde je požadavek na přizpůsobení průtoku provozním podmínkám, např. konstantní teplota na výstupu z kolektorů, se využívají otáčkově regulovaná oběhová čerpadla. Změna otáček má za následek
přímo úměrnou změnu průtoku
změnu dopravní výšky s druhou mocninou
změnu příkonu s třetí mocninou
kde je
V … průtok, v m3/h;
H … dopravní výška, v m;
P … elektrický příkon, v W;
n … otáčky, v ot/min.
6.6.2 Účinnost čerpadla a spotřeba čerpací práce
Při výběru oběhového čerpadla by měl pracovní bod solární soustavy (V‚; Δp) ležet v oblasti maximální účinnosti čerpadla. Křivky účinnosti běžně výrobci čerpadel neuvádějí (pouze naznačují optimální bod či oblast), projektant si je však případně může dopočítat z křivek příkonu čerpadla. Celková účinnost čerpadla, včetně elektromotoru, se stanoví jako
(6.17)
kde je
ΔY … rozdíl měrné energie kapaliny mezi sáním a výtlakem, v J/kg;
Δp … rozdíl tlaku mezi sáním a výtlakem (dopravní tlak čerpadla), v Pa;
V‚ … průtok čerpadlem, v m3/s;
ρ … hustota čerpané kapaliny, v kg/m3;
Pč … hydraulický výkon čerpadla, ve W;
Pe … elektrický příkon čerpadla, ve W.
Poznámka:
Výrobci oběhových čerpadel používají místo dopravního tlaku Δp [Pa] dopravní výšku H [m], průtok V‚ [m3/s nebo m3/h] označují Q, což je v tepelné technice zavedené označení pro teplo.
Stávající oběhová čerpadla pracují s velmi nízkou účinností, zvláště u malých čerpadel je účinnost nedostatečná (5-15 %). Nabízí se zde široké pole potenciálních úspor elektrické energie přechodem na oběhová čerpadla. Na obr. 6.15 jsou porovnány průběhy účinnosti oběhového čerpadla pro malé a velké průtoky v různých stupních otáček.
Obr. 6.15 Porovnání účinnosti výkonnostně odlišných oběhových čerpadel
Výrobci čerpadel uvádějí charakteristiky čerpadel pro vodu při kinematické viskozitě v = 1·10-6 m2/s. Při čerpání kapalin s vyšší viskozitou se však u hydrodynamických čerpadel charakteristika obecně mění (klesá výtlak) vlivem vyšších tlakových ztrát v čerpadle. Charakteristiku lze přepočítat na kapalinu s jinou viskozitou přes měrné otáčky čerpadla a přepočtovými součiniteli pro průtok, dispoziční tlak a účinnost [11]. U hydrostatických čerpadel vlivem malého vlivu rychlostní energie k posunu charakteristiky nedochází.
Při čerpání nemrznoucích směsí s viskozitou do 10·10-6 m2/s jsou v běžných solárních soustavách změny charakteristiky hydrodynamického čerpadla zanedbatelné, významná je však změna účinnosti a příkonu oběhového čerpadla. Na obr. 6.16 je uvedena charakteristika oběhového čerpadla pro vodu (černě) a pro nemrznoucí směs s viskozitou 6·10-6 m2/s (šedě). Hydraulická charakteristika je pro obě kapaliny v podstatě totožná, křivka účinnosti vykazuje v bodě optima absolutní rozdíl cca 5 % poměrově téměř 15 %. Vlivem čerpání viskoznější kapaliny se tedy účinnost zhorší o 15 % oproti čerpání vody (zvýší se spotřeba elektrické energie).
Často se pro maloplošné solární soustavy používají tzv. instalační jednotky, obsahující potřebné armatury, teploměry, pojistná zařízení a oběhové čerpadlo. Instalační jednotky se používají pro široký rozsah velikosti solárních soustav. Čerpadlo je proto navržené (podobně jako u plynových kotlů), aby „utáhlo“ i tu největší soustavu v daném rozsahu. Je nutné ověřit, zda čerpadlo instalační jednotky je svými parametry pro danou potrubní síť solární soustavy vhodné, a případně jej nechat vyměnit za menší, aby nedocházelo ke zbytečně vysoké spotřebě pomocné elektrické energie v provozu.
Obr. 6.16 Charakteristiky čerpadla pro vodu (černé) a přepočtené pro směs propylenglykol-voda (šedé)
6.7 VÝMĚNÍKY TEPLA
Pro přenos tepla získaného solárními kolektory a dopravovaného teplonosnou kapalinou solárního okruhu do dané aplikace (jiné pracovní látky) se využívá výměníků tepla. Obecně je možné rozlišit podle pozice výměníku vnitřní a vnější výměníky tepla.
6.7.1 Tepelný výkon výměníku
Základním vztahem pro výpočet tepelného výkonu Q‚ [W] výměníku tepla je rovnice
(6.18)
kde je
U … součinitel prostupu tepla výměníku, ve W/(m2·K);
A … přestupní plocha výměníku, v m2;
Δtm … střední (logaritmický) teplotní rozdíl, v K.
Součinitel prostupu tepla U závisí na hydraulických poměrech (typ teplonosné kapaliny, rychlost proudění, teplota, režim proudění kapalin na obou stranách teplosměnné plochy výměníku tepla. Zároveň pro tepelný výkon přenášený z kapaliny primárního (ohřívajícího) okruhu do kapaliny sekundárního (ohřívaného) okruhu platí za předpokladu zanedbání tepelných ztrát výměníku rovnice
(6.19)
kde je
M‚ … hmotnostní průtok kapalin (primární, sekundární strana), v kg/s;
c … měrná tepelná kapacita, v J/(kg·K);
t/1 … teplota ohřívající teplonosné kapaliny na vstupu do výměníku, ve °C;
t//1 … teplota ohřívající teplonosné kapaliny na výstupu z výměníku, ve °C;
t/2 … teplota ohřívané teplonosné kapaliny na vstupu do výměníku, ve °C;
t//2 … teplota ohřívané teplonosné kapaliny na výstupu z výměníku, ve °C.
Střední teplotní rozdíl Δtm se stanoví jako
(6.20)
kde je
ΔtI a ΔtII … pro protiproudý a souproudý výměník definovány v grafech na obr. 6.17.
Obr. 6.17 Průběh teplot na souproudém a protiproudém výměníku
Tepelná účinnost výměníku η je definovaná jako podíl výkonu na jedné nebo druhé straně k maximálně dosažitelnému výkonu
(6.21)
kde
(6.22)
jako rozdíl vstupních teplot na obou stranách výměníku.
Účinnost výměníku a tedy i jeho výkon závisí značně na znečištění teplosměnné plochy, např. vodním kamenem. Návrh výměníku solární soustavy je vždy určitou optimalizací mezi jeho cenou a účinností. Snahou je dosáhnout na výměníku co největšího vychlazení teplonosné kapaliny kolektorového okruhu, neboť je tím zajištěna nízká teplota na vstupu do kolektoru a tedy vyšší účinnost kolektoru (vyšší tepelné zisky kolektoru). Pro dosažení dostatečně vysokých solárních zisků je vhodné, aby se tepelná účinnost výměníků pohybovala nad hranicí 75 %, resp. střední teplotní spád na výměníku byl menší než 8 K.
6.7.2 Vnitřní výměníky tepla
Jako vnitřní výměníky tepla, tzn. tepelné výměníky uvnitř zásobníků tepla a akumulačních nádob, se používají hladké trubky, vlnovce nebo žebrované trubky (s rozšířenou teplosměnnou plochou žebry). Vlnovce a žebrované plochy jsou výhodné z hlediska větší přestupní plochy, která je na 1 m délky trubky k dispozici. Výměníky z hladkých trubek se instalují do zásobníků zpravidla ve výrobě, zatímco výměníky ze žebrovaných trubek mohou být vzhledem ke svému kompaktnímu tvaru instalovány do zásobníků na místě prostřednictvím přírub a těsnění (viz obr. 6.18). Připojení potrubí externího okruhu k výměníku by mělo respektovat požadavek na stratifikaci, tedy do horní přípojky teplejší kapalina, do spodní chladnější. U vnitřních výměníků se nejedná jednoznačně o protiproudé nebo souproudé uspořádání, ale spíše křížové, které nelze jednoduše hodnotit a navrhnout bez pokročilých výpočetních nástrojů.
Součinitel prostupu tepla u vnitřních výměníků se pohybuje na nízké hodnotě mezi 120 až 300 W/(m2·K) vzhledem k laminárnímu proudění na primární straně (nemrznoucí směs) a volné konvekci na sekundární straně uvnitř zásobníku.
Obr. 6.18 Trubkové vnitřní výměníky tepla (hladká trubka – vlevo, žebrovaná trubka – vpravo)
6.7.3 Vnější výměníky tepla
Vnější výměníky se vyrábějí jako deskové nebo trubkové výměníky, kde obě teplonosné kapaliny zpravidla výhodně proudí v protiproudém uspořádání. Vnější výměníky jsou tepelně izolovány. Jejich součinitel prostupu tepla je výrazně vyšší než u vnitřních výměníků, pohybuje se od 500 do 3500 W/(m2·K) vzhledem ke spíše vyvinutému turbulentnímu proudění na obou stranách, a je možné jimi přenášet výrazně vyšší výkony.
Obr. 6.19 Vnější výměníky tepla (trubkový – vlevo, deskový – vpravo)
Především deskové výměníky mají malé stavební rozměry vzhledem k přenášenému výkonu. Jsou složeny z tenkých desek (nejčastěji nerezový plech), které mají předlisované kanály na zvýšení turbulence kapaliny, jsou mezi sebou spojeny a vytvářejí síť sudých a lichých kanálů. V sudých protéká jedna kapalina (např. nemrznoucí směs), která předává teplo a ochlazuje se, v lichých protéká druhá kapalina (např. pitná voda), která odebírá teplo a ohřívá se (viz obr. 6.19). Spojení desek může být pevné bez těsnění (pájené nebo svažované výměníky), nebo rozebíratelné s těsněním (desky jsou sešroubovány mezi 2 nosnými deskami). Počtem desek lze ovlivnit velikost teplosměnné plochy výměníku a tím jeho výkon.
Různým profilováním kanálků, kterými proudí teplonosné kapaliny, a rozdílnou průchodností těchto kanálků je možné maximalizovat výkon výměníku při určené maximální tlakové ztrátě výměníku. Kombinací H-desek (vysoký součinitel přestupu tepla, ale vyšší hydraulický odpor) a L-desek (nízký součinitel přestupu tepla, ale nižší hydraulický odpor) a rozdílnou hloubkou prolisů výměníkových desek je možné vedle „čistých“ H nebo L-kanálků také sestavit asymetrické proudové kanálky, což umožňuje optimální dimenzování rozdílných hydraulických poměrů.
6.7.4 Výpočet výměníků
Pro výpočet výměníků se doporučuje použít pokročilých programů, které umožňují zadávat různé sady okrajových podmínek (vstupů), vybírat z dostupných typů výměníků a teplonosných kapalin a optimalizovat návrh výměníku pro danou aplikaci. Pro návrh výměníku je nutné předem jasně definovat okrajové podmínky návrhového stavu solární soustavy pro dodávku tepla.
Při definování podmínek je vhodné začít na sekundární straně nejnižší teplotou kapaliny t/2, kterou je potřeba ohřát ve výměníku, např. teplota studené vody 15 °C na vstupu do výměníku (stav na začátku nabíjení zásobníku).
Základní okrajovou podmínkou na primární straně je objemový nebo hmotnostní průtok v kolektorovém okruhu M‚1. U malých soustav se využívá vysokého měrného objemového průtoku 50 až 70 l/(h·m2), u velkých soustav se využívá nízkého objemového průtoku 10 až 15 l/(h·m2). Druhou okrajovou podmínkou je požadovaná teplota na vstupu do solárních kolektorů tk1 = t//1, kterou v případě velkých soustav je vhodné udržet na co nejnižší úrovni (do 5 K nad vstupní teplotou sekundární strany t/2, neboť přímo ovlivňuje účinnost solárních kolektorů ηk.
Poslední podmínku, kterou je nutné zadat, je přenášený výkon z kolektorů Q‚k nebo teplotu na výstupu z kolektorů tk2 = t/1 (zároveň teplota na vstupu do výměníku). Obě veličiny jsou však navzájem závislé. Výkon kolektorového pole je dán vztahem
(6.23)
kde je
Ak … plocha apertury kolektoru, v m2;
G … sluneční ozáření na kolektor, ve W/m2; pro výpočet výměníku je vhodné uvažovat s hodnotou 1 000 W/m2, aby zajistil přenesení maximálního výkonu kolektorového pole;
η0 … účinnost solárního kolektoru při nulovém teplotním spádu mezi střední teplotou teplonosné kapaliny tm a teplotou okolního vzduchu te;
a1 … lineární součinitel tepelné ztráty kolektoru, ve W/(m2·K);
a2 … kvadratický součinitel tepelné ztráty kolektoru (vyjadřuje zvýšení tepelných ztrát vlivem sálání, závislé na rozdílu 4. mocnin teplot), ve W/(m2·K2);
tm … střední teplota teplonosné kapaliny v kolektoru, ve °C; dána jako průměr ze vstupní a výstupní teploty kolektoru tk1 a tk2;
te … teplota okolí, pro výpočet výkonu kolektorového pole je možné uvažovat s teplotou 20 °C.
Obr. 6.20 Veličiny pro návrh výměníku tepla
Jednou z možností je zvolit přibližně požadovanou teplotu na výstupu ze sekundární strany výměníku t//2 a výstupní teplotu z kolektoru tk2 = t/1 v oblasti teplot požadovaných na sekundární straně (např. 55 až 65 °C) a stanovit předběžně výkon kolektorové plochy Q‚k, který vstupuje do výpočtu jako okrajová podmínka výměníku. Z výpočtu je následně stanovena teplota na výstupu z kolektoru obecně jiná než původně zvolená. Je tedy nutné přepočítat zpětně výkon kolektorové plochy a znovu zadat do výpočtu výměníku. Druhým výsledkem výpočtu je průtok na sekundární straně, zajišťující dosažení požadovaného rozdílu teplot kapaliny na sekundáru M‚2. Tímto postupem jsou navrženy výměníky tepla s dostatečně nízkým Δtm (dostatečně velkou plochou A) v závislosti na zvolených teplotních rozdílech mezi „teplými“ a „studenými“ stranami výměníku.
Cílem návrhu je zajistit, aby zvolený tepelný výměník byl schopen přenést výkon kolektorového pole a zároveň umožnil dostatečné vychlazení teplonosné kapaliny na vstupu do kolektorů.
6.8 POJISTNÁ A ZABEZPEČOVACÍ ZAŘÍZENÍ
Solární soustavy, podobně jako ostatní tepelné soustavy, musí být vybaveny pojistnými a zabezpečovacími zařízeními. U uzavřených solárních soustav jde především o pojistný ventil a expanzní nádobu. Pro jejich návrh a instalaci v solárních soustavách v české normalizaci neexistují samostatné normy; je možné pouze analogicky přejímat metodiku návrhu podle topenářských norem, ovšem s ohledem na provozní specifika solárních soustav.
6.8.1 Tlakové poměry v solární soustavě
Solární soustava je provozována v rozmezí od plnicího tlaku p0 při stavu „za studena“ při minimální provozní teplotě, zpravidla teplotě plnění soustavy t0 = 10 až 20 °C do maximálního provozního tlaku pe „za tepla“ při maximální provozní teplotě soustavy tmax = 90 až 130 °C. Plnicí tlak (počáteční) je dán hydrostatickým tlakem sloupce teplonosné kapaliny nad místem připojení expanzní nádoby a minimálním tlakem pd, požadovaným v nejvyšším místě soustavy (zpravidla horní část kolektorů)
(6.24)
kde je
hs … výška sloupce teplonosné látky nad místem připojení EN, v m;
pd … minimální tlak v nejvyšším místě solární soustavy, v Pa.
Poznámka:
Pro přetlak ve shodě s normami používám termín tlak. Pokud je v textu míněn absolutní tlak (přetlak + atmosférický tlak), je to výslovně uvedeno.
Minimální tlak pd se zpravidla volí v rozsahu od 20 kPa (minimální hodnota) do 150 kPa podle druhu provozu soustavy. Pokud se jedná o soustavy, u kterých je nutné zajistit provoz při vysokých teplotách bez varu teplonosné kapaliny, musí být již plnicí tlak nastaven na odpovídající hodnoty. Například při předpokládaném provozu s propylenglykolem při 150 °C musí být tlak v kolektorech nad hodnotou 300 kPa (absolutní tlak 400 kPa). Pokud solární soustava nebude provozována nad 90 °C, je možné volit minimální doporučenou hodnotu.
Maximální provozní tlak pe [kPa] se odvozuje od maximálního dovoleného tlaku v soustavě (otevírací tlak pojistného ventilu). Maximální provozní tlak se volí cca 50 kPa pod hodnotou otevíracího tlaku pojistného ventilu pPV, případně jako
(6.25)
Velikost rozsahu provozních tlaků pe – po ovlivňuje výrazně návrh expanzní nádoby: čím menší je provozní rozsah, tím větší nádoba musí být navržena pro udržení tlaku v daných mezích.
Hodnota provozního tlaku je také úzce svázána s druhem teplonosné kapaliny v soustavě. Pokud bude v solární soustavě teplonosná kapalina, která vykazuje degradaci při vysokých teplotách např. nad 120 °C, je vhodné udržovat maximální provozní tlak pod hodnotou tlaku odpovídajícího teplotě bodu varu teplonosné látky 120 °C (viz obr. 6.21). V případě, že teplota v kolektorech přesáhne teplotu bodu varu látky, dojde k varu a teplota teplonosné látky v kolektorech se dále nezvyšuje. U kolektorů s dobrým vyprazdňováním se odpaří pouze zlomek teplonosné látky a zbytek objemu kolektorů je vytlačen do přívodního a zpětného potrubí (chráněn před přímým tepelným zatížením). Tento předpoklad však závisí jednak na schopnosti expanzní nádoby pohltit vytlačený objem z kolektorů a jednak na vyprazdňovací schopnosti kolektorů a s ní spojeným stagnačním chováním soustavy. V případě teplonosné kapaliny odolné velmi vysokým teplotám je možné, s ohledem na tlakovou odolnost prvků v soustavě, volit vysoké provozní tlaky a tak eliminovat změnu skupenství (var) při stagnačních podmínkách a pronikání páry do rozvodů solární soustavy.
Obr. 6.21 Závislost teploty varu teplonosné kapaliny na absolutním tlaku v soustavě
6.8.2 Pojistný ventil
Pojistný ventil je zařízení, které chrání primární okruh solární soustavy proti nedovolenému tlaku. Otevírací přetlak pojistného ventilu pPV se nastavuje na 300 až 600 kPa, určuje maximální tlak v soustavě s ohledem na tlakovou odolnost nejslabšího prvku solární soustavy (zpravidla výměník nebo kolektor), určuje tlakový stupeň expanzní nádoby a nepřímo i její velikost.
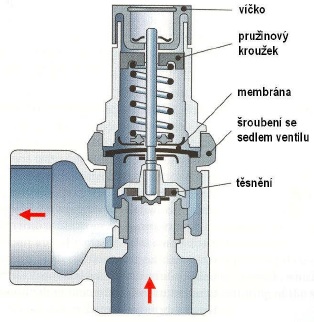
Obr. 6.22 Pojistný ventil (řez)
Jelikož každý zdroj musí být vybaven neuzavíratelně připojeným pojistným zařízením [12], platí, že v potrubí mezi kolektory a pojistným ventilem (pojistný úsek) nesmí být zařazeny žádné uzavírací prvky. Pokud se kolektorové pole skládá z více uzavíratelných či odpojitelných sekcí, musí být každá sekce vybavena samostatným pojistným ventilem (viz obr. 6.23).
V souladu s EN 12828 tlaková ztráta úseku mezi zdrojem tepla (kolektorem) a pojistným ventilem by neměla překročit 3 % hodnoty otevíracího přetlaku pojistného ventilu [12].
Obr. 6.23 Dělené pole solárních kolektorů a umístění pojistných ventilů
Pojistný ventil by měl odolat extrémním teplotním podmínkám dosažitelným v soustavě, zvláště nejvyšší teplotě, která se může vyskytnout, tj. stagnační teplotě. Pojistný ventil by měl být také odolný teplonosné kapalině. Zároveň s pojistným ventilem by měl být instalován i tlakoměr a teploměr.
Průřez pojistného ventilu musí být dimenzován tak, aby umožnil odvod největšího průtoku páry, který může nastat. Pojistný ventil se navrhuje tak, že celý tepelný výkon kolektorů (podobně jako u teplovodních kotlů) se přepočte na množství syté páry při požadovaném otevíracím tlaku pojistného ventilu a velikost pojistného ventilu se stanoví podle jeho charakteristik (průřez sedla, výtokový součinitel) na toto množství. Lze vycházet z postupu podle [13]. Průtočný průřez sedla ventilu v [mm2] se stanoví jako
(6.26)
kde pojistný výkon Qp [kW] je špičkový výkon kolektorového pole, αv [-] je výtokový součinitel pojistného ventilu, a hodnota K [kW/mm2] se stanoví podle tab. 6.7 (pozn. autora: hodnoty jsou pro sytou vodní páru, pro směs propylenglykolu nejsou k dispozici). Z řady pojistných ventilů se podle jejich charakteristik vybere takový, který podmínku splňuje.
Tab. 6.7 Tabulka hodnot K pro vodu
| p [kPa] | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 | 600 | 700 |
| K [kW/mm2] | 0,50 | 0,67 | 0,82 | 0,97 | 1,12 | 1,26 | 1,55 | 1,83 | 2,10 | 2,37 |
S ohledem na uvedenou problematiku s umístěním pojistných ventilů se doporučuje při umístění ventilů daleko od kolektorů volit větší dimenzi pojistného ventilu.
Průměr pojistného potrubí se stanoví ze vztahu
(6.27)
Pojistné potrubí by mělo být instalováno takovým způsobem, že v něm nedochází k akumulaci nečistot či k zarůstání vodním kamenem. Odvodní potrubí by mělo být uspořádáno tak, aby unikající teplonosná kapalina nebo pára nepředstavovala riziko pro uživatele (opaření), zařízení nebo materiály. Odtok pojistného ventilu by měl být zaústěn do uzavřené kovové nádoby dostatečného objemu, aby pojmula objem primárního okruhu. Zachycená teplonosná kapalina může tak být po odstranění příčiny otevření pojistného ventilu znovu použita v soustavě. Nedoporučuje se zaústit odtok pojistného ventilu do kanalizace s ohledem na možné provozní ztráty teplonosné kapaliny. Na pojistném ani odvodním potrubí nesmí být uzavírací armatura. Funkce pojistného ventilu musí být pravidelně kontrolována.
6.8.3 Expanzní nádoba
Solární soustava musí být vybavena expanzním zařízením, které umožňuje změny objemu teplonosné kapaliny vlivem tepelné objemové roztažnosti bez nedovoleného zvýšení tlaku a zbytečných ztrát kapaliny způsobených otevřením pojistného ventilu, a to ani v případě stagnace (maximální teploty, tvorba páry v kolektorech). V současné době je většina solárních soustav provozována jako uzavřené (omezení přístupu vzduchu do soustavy) a jen velmi malá část jako otevřené (drain-back). Zatímco u uzavřených solárních soustav je nutné použití tlakových expanzních nádob s membránou, u otevřených soustav se roztažnost teplonosné látky projevuje zvýšením hladiny v otevřeném zásobníku.
Obr. 6.24 Tlaková expanzní nádoba – tvar membrány v různých provozních stavech
Tlaková expanzní nádoba je kovová nádoba, uprostřed rozdělená pružnou membránou, oddělující dvě látky: teplonosnou kapalinu solárního okruhu a stlačený plyn (dusík, případně vzduch). Plynová náplň je z výroby nastavena na počáteční tlak. Oproti expanzním nádobám pro otopné soustavy je u solárních soustav důležitá odolnost membrány vůči působení glykolu a vysokým teplotám a tlakům; zpravidla se používá nitrilová membrána nebo membrána z EPDM. Expanzní nádoby určené pro solární soustavy se proto od běžných provedení liší barevně (často provedení v bílé barvě).
Teplonosná látka se zahříváním při provozu solární soustavy roztahuje a vyplňuje postupně objem expanzní nádoby. Při stagnaci, kdy teplota v kolektoru a přilehlém potrubí může dosáhnout vysokých teplot, se teplonosná kapalina v kolektorech vaří (bod varu je závislý na tlaku v soustavě), pára vytlačuje zbylý objem kapaliny z kolektorů, případně proniká do rozvodů. Při poklesu teploty v kolektorech pára teplonosné kapaliny kondenzuje a vytlačená teplonosná kapalina se vrací zpět do kolektorů.
Expanzní nádoba solárních soustav musí být proto dimenzována na zajištění minimálního objemu teplonosné látky v nádobě ve studeném stavu Vs (1 až 10 % celkového objemu soustavy V, minimálně však 2 litry), na změnu objemu teplonosné látky v soustavě ze studeného stavu daného minimální teplotou (t0 = 10 °C) do ohřátí na maximální provozní teplotu (podle druhu provozu tmax = 90 až 130 °C), a dále na vytlačení celého objemu teplonosné kapaliny z kolektorů při možném vývinu páry. Minimální objem expanzní nádoby se tedy stanoví jako
(6.28)
kde je
β … součinitel objemové roztažnosti teplonosné látky určený pro daný provozní teplotní rozsah (např. Δt = 130 – 10 = 120 K odpovídá pro propylenglykol β = 0,1),
Vk … objem solárních kolektorů, v l; v případě solárních kolektorů se špatným vyprazdňováním a výraznou produkcí páry (trubicové) je vhodné zahrnout do Vk i objem přívodního a zpětného potrubí.
Skutečná velikost expanzní nádoby se získá vydělením minimálního objemu tzv. stupněm využití expanzní nádoby, stanoveným jako
(6.29)
kde je
pe … maximální provozní tlak soustavy, v kPa;
p0 … minimální provozní tlak soustavy (plnicí tlak), v kPa;
pb … atmosférický tlak (100 kPa).
Objem expanzní nádoby se stanoví ze vztahu
(6.30)
Zatímco hodnoty součinitele objemové roztažnosti jsou pro vodu běžně známy [13], pro nemrznoucí teplonosné kapaliny je často obtížné je od jejich výrobců získat. Pro praktický výpočet lze při znalosti změny hustoty nemrznoucí kapaliny s teplotou (viz vztahy v kapitole 7.2.2) použít pro jakýkoli provozní rozsah teplot následující vztah
(6.31)
kde je
v(t) … měrný objem teplonosné látky při teplotě t, v m3/kg;
ρ(t) … hustota teplonosné kapaliny při teplotě t, v kg/m3.
Na obr. 6.25 jsou zobrazeny závislosti součinitele objemové roztažnosti β na provozním rozdílu teplot Δt = tmax – t0 pro různé typy teplonosných kapalin s vyznačením běžného návrhového bodu (Δt = 120 K).
Obr. 6.25 Závislost poměrného zvětšení objemu teplonosných kapalin na teplotním rozdílu
Expanzní nádoba se připojuje do rozvodu primárního okruhu expanzním potrubím přes uzavírací armaturu (kulový kohout) nejlépe s ochranou proti uzavření a s vypouštěcím ventilkem, z důvodu možné revize (tlakové zařízení) a kontroly tlaku v nádobě. Průměr expanzního potrubí dv [mm] se stanoví podle vztahu
(6.32)
Expanzní nádoba může být teoreticky umístěna kdekoliv v solární soustavě. S výhodou se umísťuje na studené straně primáního okruhu kvůli nižšímu tepelnému namáhání, z hlediska tlakových poměrů na sání oběhového čerpadla (soustava vždy v přetlaku). Umístění zpětné klapky vůči expanzní nádobě by mělo respektovat řádné vyprazdňování kolektorů v případě stagnačních podmínek.
Dále je vhodné, aby expanzní nádoba byla instalována v takové poloze, při které nedochází k jejímu zavzdušňování (viz obr. 6.26), případně tepelnému namáhání.
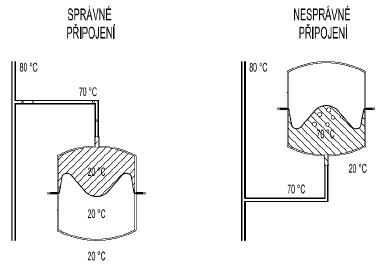
Obr. 6.26 Správné a nesprávné připojení expanzní nádoby
Expanzní nádoba musí být odborně nainstalována, včetně seřízení hodnoty předtlaku náplně v plynové části nádoby, který je přednastaven z výroby. Předtlak plynu v expanzní nádobě se stanoví z plnicího tlaku p0 [kPa] podle vztahu
(6.33)
Nastavení předtlaku pv se provádí plynovým ventilkem (upouštění, tlakování hustilkou). Nejméně jednou za rok by měla být provedena vnější kontrola, spojená s kontrolou plnicího tlaku.
U velkoplošných solárních soustav a soustav, u nichž lze předpokládat zvýšené doby stagnace, je třeba zapojit do expanzního potrubí předřazenou nádobu k ochraně expanzní nádoby i ostatních prvků před příliš vysokými teplotami a před pronikáním páry. Objem předřazené nádoby se dimenzuje na 50 až 100 % objemu pole kolektorů Vk.
6.9 ODPLYŇOVACÍ ZAŘÍZENÍ
Po instalaci a napuštění solární soustavy teplonosnou kapalinou je nutné ze soustavy odstranit zbytkové plyny (vzduch) nerozpuštěné i rozpuštěné v kapalině. Kromě hlukových projevů (bublání, šum) způsobuje přítomnost kyslíku zvýšenou náchylnost soustavy ke korozi, ke kavitaci, omezení chlazení motoru čerpadel a snížení přenosových vlastností kapaliny (nižší výkon). Větší množství vzduchu v soustavě může způsobit selhání oběhu, což kromě stagnačních podmínek na kolektorech (zatímco v zásobníku jsou nízké teploty) může způsobit i přehřátí a poškození čerpadla.
Odvzdušňovací zařízení se využívají především pro odvzdušnění soustavy při plnění teplonosnou kapalinou a pro postupné odstranění plynů v kapalině při zahájení provozu soustavy, kdy se rozpuštěné plyny uvolňují při zahřívání teplonosné látky. Odvzdušňovací zařízení se instalují na nejvyšší místa solárního okruhu na výstupu z kolektorů. V těchto místech je vhodné zajistit nízkou rychlost teplonosné látky (místní rozšíření potrubí) pro usnadnění odvodu bublinek plynů.
Pro odstraňování nerozpuštěných plynů (bublinky) se používají automatické odvzdušnovací ventily s ručním uzavíráním, nebo jednoduché ruční odvzdušnovací ventily. Po naplnění soustavy a odvzdušnění se automatické ventily odpojí (uzavře se ruční ventil) a jsou odstaveny. Při provozu s automatickým odvzdušněním by mohlo docházet k únikům nemrznoucí teplonosné kapaliny v obdobích se stagnací, kdy se v kolektoru tvoří pára, která by automaticky odvzdušňovacím ventilem unikala. Po každé stagnaci by pak bylo nutné doplňovat teplonosnou kapalinu do soustavy. Odvzdušňovací zařízení, včetně uzavíracího kohoutu, musí být odolné teplotám min. 150 °C (plováčky z ušlechtilé oceli).
Obr. 6.27 Zapojení odvzdušňovacího ventilu (vlevo nahoře – nevhodné, vlevo dole – vhodné, vpravo – optimální)
Automatické kontinuální odlučovače plynů se používají pro odstranění rozpuštěných plynů v kapalině. Instalují se v místech, kde nemůže dojít k průniku páry teplonosné kapaliny (strojovna). Používají se především u velkých solárních soustav, kde je větší objem teplonosné kapaliny a může hrozit i vyšší riziko netěsností (více spojů). Umístění kontinuálního odplyňovače je dáno jeho funkcí: rozpustnost plynů v kapalině klesá s rostoucí teplotou a klesajícím tlakem. Odplyňovače se proto instalují do míst s nejvyšší teplotou (výstup z kolektorů) a zároveň nejnižším tlakem (sání oběhového čerpadla s ohledem na polohu expanzní nádoby).

Obr. 6.28 Automatický odplyňovač Spirovent
Ke správnému odvzdušnění solární soustavy dále přispívá:
- vhodné spádování jak solárních kolektorů, tak potrubí soustavy;
- vhodná rychlost napouštění solární soustavy, aby se vzduch dostal do horních částí soustavy s odvzdušněním;
- vizuální kontrola na plovákových průtokoměrech.
6.10 REGULACE
Elektronická regulace je důležitým prvkem solární soustavy. Řídí bezobslužný automatický provoz. Existuje široká škála regulátorů od jednoduchých jednookruhových diferenčních regulátorů po komplexní víceokruhové digitální regulátory s mnoha dodatkovými funkcemi.
6.10.1 Analogové regulátory
Nejjednoduššími solárními regulátory jsou analogové diferenciální regulátory bez displeje. Mají možnost připojení dvou teplotních čidel (Pt100 nebo Pt1000). Jedno čidlo je určené pro solární kolektor a druhé pro spotřebič (zásobník, bazén). Jediný nastavitelný parametr je spínací teplotní rozdíl mezi čidly (spínací diference), který se nastavuje v závislosti na aplikaci a provozních parametrech od 5 do 20 K. Pokud je naměřený teplotní rozdíl vyšší než nastavený, regulátor zapne oběhové čerpadlo (výstupní spínací relé), pokud naměřený teplotní rozdíl klesne pod požadovanou hodnotu o pevně danou teplotní hysterezi (zpravidla nelze u jednoduchých regulátorů nastavit), regulátor čerpadlo vypne. Nastavení spínacího teplotního rozdílu je možné šroubovákem na nastavitelném odporu (trimru). Provoz oběhového čerpadla je signalizován svítící diodou.
I tyto jednoduché regulátory mohou mít integrované servisní funkce, např. trvalé sepnutí oběhového čerpadla, nebo ochranné funkce, např. vychlazování zásobníku při překročení teploty v zásobníku nad určenou teplotu (např. 70 °C) v noční době přes kolektory. Nespornou výhodou těchto regulátorů je bezesporu jejich nízká cena. Naopak nevýhodou je absence zobrazení aktuálních hodnot měřených veličin a indikace alarmů.

Obr. 6.29 Analogový regulátor
6.10.2 Digitální regulátory
Základní digitální regulátory mají možnost připojení 4 teplotních čidel a mají 2 výstupní relé. Pokročilejší mají až 10 teplotních čidel a 6 relé (mechanická, polovodičová), možnost připojení až dvou pulzních vstupů od průtokoměru a proudového vstupu od čidla slunečního záření. Regulátor umožňuje nastavení a zobrazení jednotlivých parametrů a veličin na digitálním displeji. Pokročilé typy zobrazují i zjednodušená schémata zapojení solárních soustav, podle kterých pracuje regulátor. Základní nastavitelné parametry jsou spínací diference (5 až 20 K), vypínací diference (0 až 5 K), omezení maximální teploty spotřebiče (při které regulátor vypíná čerpadlo, např. u zásobníku 60 až 90 °C), maximální teplota kolektoru pro ochranu prvků v solárním okruhu (okolo 130 °C), minimální teplota kolektoru pro zamezení častému spínání oběhového čerpadla atd.
Obr. 6.30 Digitální regulátory a hydraulická skupina s integrovaným regulátorem
Digitální regulátory umožňují nastavovat pokročilé ochranné funkce a funkce, které mohou zvýšit energetické přínosy solární soustavy. Některé z těchto funkcí jsou popsány dále v textu. Při servisním nebo kontrolním zásahu je možné manuálně nastavit provozní režim regulátoru, tzn. jednotlivá výstupní relé trvale zapnout nebo vypnout. Pro lepší povědomí uživatele o chování a přínosu solární soustavy jsou k dispozici funkce jako počítadlo provozních hodin jednotlivých výstupních relé.
Digitální regulátory mohou být integrovány do hydraulických skupin. Přispívají tak ke snížení časové náročnosti montáže solárních soustav. Hydraulické skupiny jsou vhodné nejen pro úsporu místa při instalaci, ale především kvůli tomu, že obsahují důležité komponenty pro správnou funkci solární soustavy. Vývoj směřuje stále více k právě takovým integracím. V hydraulických skupinách jsou pak navíc umístěny prvky, díky kterým regulátor snímá například tlak nebo průtok.
6.10.3 Základní regulační funkce a zapojení
Vlastních regulačních algoritmů digitálních regulátorů a možností zapojení regulované solární soustavy je nepřeberné množství. V následujícím textu jsou vybrána některá základní a nejpoužívanější zapojení.
Solární soustava s jedním spotřebičem
Nejjednodušším zapojením s využitím jediného výstupního relé (R1) pro jedno čerpadlo a dvou teplotních čidel (S1, S2) lze realizovat jednoduchou solární soustavu (viz obr. 6.31 vlevo). Využitím třetího čidla (S3) a druhého výstupního relé (R2) je možné ovládat solárním regulátorem i dodatkový zdroj tepla (viz obr. 6.31 vpravo) na základě nastavení požadované teploty na čidle S3.
Obr. 6.31 Regulační okruh solární soustavy s jedním spotřebičem
Solární soustava se dvěma spotřebiči
V případě požadavku na stratifikaci v solárním zásobníku se dvěma výměníky lze využít čidla S2 a S3 jako čidla v různých úrovních zásobníku (viz obr. 6.32 vlevo) a relé R2 pro ovládání trojcestného ventilu. Jde v zásadě o stejné zapojení jako u dvou spotřebičů – zásobníků (viz obr. 6.32 vpravo). Identické schéma lze použít, pokud namísto trojcestného ventilu a jediného oběhového čerpadla jsou instalována samostatně spínaná oběhová čerpadla, což je vhodné například u solárních soustav v kombinaci s bazénem provozovaným s jiným průtokem a hydraulickými podmínkami.
U solární soustavy se dvěma spotřebiči, např. teplá voda a bazén, dovolují regulátory zvolit logiku jejich ohřevu. Nejjednodušším způsobem je nezávislý ohřev podle priority. Ve chvíli, kdy je splněn požadavek v prvním spotřebiči (teplá voda), přepne se třícestný ventil do druhého (bazén). Výhodnějším z hlediska využitelnosti solárních zisků je střídavý ohřev. Pokud nelze do spotřebiče 1 (s vyšší prioritou) dodávat teplo z kolektorů, přepne regulátor do spotřebiče 2 (s nižší prioritou). Nicméně, teplo je do spotřebiče 2 dodáváno pouze po určený časový úsek. Po uplynutí této doby regulátor zastaví chod soustavy a sleduje teplotu na výstupu ze solárních kolektorů, resp. její nárůst. Pokud je nárůst teploty dostatečný pro využití k dodávce tepla do spotřebiče 1, přepne se soustava do něho. Pokud není teplota dostatečná, regulátor pokračuje v dodávce tepla do spotřebiče 2. Stejná logika se používá i při použití zásobníku s více výměníky, kde se využívá možnosti prioritně ohřívat vrchní část zásobníku.
Obr. 6.32 Regulační okruh solární soustavy se dvěma spotřebiči
Veškeré ochranné funkce soustavy a kolektorů jsou vztaženy k prioritnímu spotřebiči 1. To je nutné zohlednit především při navrhování ohřevu bazénu jako prioritního spotřebiče 1. Pro bazénové rozvody se používají komponenty a potrubí, které neodolávají teplotám, kterých se může v kritických podmínkách dosáhnout.
Obr. 6.33 Příklad zapojení solární soustavy s předehřevem zpátečky vytápění
Solární soustava s podporou vytápění
Solární regulátory mají i funkce, které mohou pomoci při integraci solární soustavy s kombinovaným zásobníkem tepla do otopné soustavy budovy. Podle zapojení dle obr. 6.33 je zásobník tepla osazen dvěma teplotními čidly. Jedním ve spodní části, k němuž se bude vztahovat diference pro sepnutí oběhového čerpadla solárního okruhu. Druhé teplotní čidlo bude v horní části zásobníku tepla. Na vratném potrubí otopné soustavy je umístěno další teplotní čidlo. V situaci, kdy v horní části zásobníku tepla bude k dispozici vyšší teplota než ve vratném potrubí, přepne ovládaný třícestný ventil do polohy, kdy bude zpátečka otopné vody předehřívána ze solárního kombinovaného zásobníku.
Složité solární soustavy
Pro využití většího počtu již zmíněných regulačních funkcí lze použít regulátory s rozšířeným počtem vstupů a výstupů. Regulátory tak mohou řídit velmi složité soustavy, kombinující přípravu teplé vody, přitápění, ohřev bazénu a vytápění celé budovy spolu s pokročilým řízením předáváním zisků tepla z kolektorů.
Na obr. 6.34 je zobrazeno zapojení komplexní solární soustavy pro přípravu teplé vody a vytápění. Primární kolektorový okruh je zapojen do dvou solárních výměníků tepla a je řízen podle střídavé priority (ohřev horní části za příhodných podmínek, jinak ohřev dolní části zásobníku), viz výše. Teplá voda se předehřívá průtočným způsobem v trubkovém výměníku, vestavěném v kombinovaném zásobníku tepla v celé jeho výšce. Dohřev zajišťuje pohotovostní zásobník tepla, který je součástí plynového kotle. Ohřev otopné vody pro vytápění je řešen jednak jako předehřev zpátečky a jednak jako plnohodnotný zdroj tepla pro otopnou soustavu (přechodové období). Pokud je v zásobníku tepla nedostatečná teplota, zpátečka otopné soustavy jde do plynového kotle, kde se dohřívá na ekvitermní teplotu ( ondenzační kotel s modulovaným výkonem) pro vytápění. Pokud je v zásobníku teplota vyšší než teplota vratné vody, je možné buď pouze předehřát zpátečku, nebo odstavit plynový kotel a ekvitermním řízením zabudovaným v regulátoru lze řídit směšovací ventil pro dosažení požadované teploty.
Pokročilé regulátory mohou řídit dohřev v horní části bivalentních zásobníků (termostat), případně funkci dohřevu omezit na určité časové úseky a nastavit na základě profilu odběru teplé vody. Podobně je možné zpravidla regulátorem solární soustavy řídit i cirkulaci teplé vody. Komplexní regulátory solárních soustav umožňují měření tepla dodaného solární soustavou či řízení otáček oběhového čerpadla vybaveného frekvenčním měničem (provoz na konstantní výstupní teplotu z kolektorů).
Obr. 6.34 Příklad zapojení solární soustavy se stratifikačním zásobníkem a směšovaným okruhem otopné soustavy
6.10.4 Pokročilé regulační funkce
Regulátory se pro vyšší přínos ze solární soustavy doplňují různými pokročilými funkcemi, které slouží k zefektivnění chodu soustavy.
Funkce trubkového kolektoru
U trubkových vakuových kolektorů bývá problematické měřit teplotu absorbéru, teplotní čidlo je často pouze vnořeno do rozvodné trubky. Volbou funkce trubkového kolektoru na regulátoru je možné automaticky spouštět na krátké časové úseky oběhové čerpadlo a na základě chování teploty na výstupu z kolektorů zjistit, zda je kolektor schopen dodávat energii.
Regulace otáček
Při proměnlivém slunečním záření je různý optimální průtok kolektorovým polem. Optimálního průtoku je možné dosáhnout změnou otáček oběhového čerpadla. Této změny je možné dosáhnout několika způsoby. Nejjednodušší a nejlevnější způsob je použití polovodičového relé, konkrétně triodového spínače střídavého proudu (triaku). Toto relé může přímo spínat a regulovat výkon obyčejných oběhových čerpadel. Další možností je použít oběhová čerpadla s integrovanou elektronickou regulací. Tato možnost je jistě méně energeticky náročná na provoz oběhového čerpadla, ale je nepoměrně dražší oproti použití obyčejného čerpadla řízeného polovodičovým relé. Vlastní funkce na zvýšení nebo snížení průtoku je závislá na teplotní diferenci mezi kolektorovým polem a spotřebičem, nebo na intenzitě slunečního záření.
Řízený obtok
Pokud je potrubí od kolektorového pole ke spotřebiči velmi dlouhé nebo jeho delší část prochází nevytápěnými prostory, používá se před spotřebičem řízený obtok, tzv. bypass. Při sepnutí oběhového čerpadla v zimním období vlivem ohřátí čidla v kolektoru je primární okruh zkratován obtokem (trojcestný ventil), viz obr. 6.35. Objem potrubní sítě se postupně nahřívá na provozní teplotu. Pokud se teplota před trojcestným ventilem zvýší nad teplotu sekundární strany o požadovaný teplotní rozdíl, trojcestný ventil se přestaví pro přívod tepla do solární výměníku. Funkce zabrání nežádoucímu vychlazování zásobníku a cyklování solární soustavy při rozběhu.
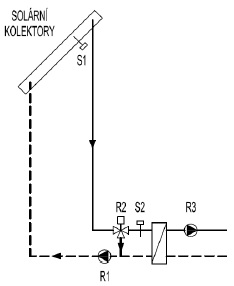
Obr. 6.35 Řízený obtok (Bypass)
Další vlastnosti regulátorů
Možnost připojení dvou průtokoměrů s impulsním výstupem umožňuje kontrolu dodaného tepla i u složitějších soustav. Z dalších periferií stojí za zmínku možnost připojení čidla reagujícího na sluneční záření, nebo možnost komunikace s počítačem. Tyto regulátory poskytují pro nevyužité výstupní relé možnost sestavit funkční bloky podobně jako u volně programovatelných regulátorů. Znamená to, že lze definovat podmínky, za kterých dojde k sepnutí příslušného relé. Podmínkami mohou být například dosažení určité teploty, diference mezi dvěma teplotními čidly a určený časový okamžik.
6.11 ZPĚTNÁ KLAPKA
Zpětná klapka je do primárního kolektorového okruhu montována vždy, když je akumulační nádoba níže než kolektorové pole (většina soustav s nuceným oběhem). Jejím úkolem je zabránit zpětné cirkulaci teplonosné kapaliny, která může nastat v případě, kdy zásobník má vyšší teplotu než kolektory, např. v noci.
Obr. 6.36 Funkce solární soustavy bez zpětné klapky: vlevo – nabíjení zásobníku během dne, vpravo – samotížná cirkulace – vychlazování zásobníku během noci
Ohřátá teplonosná kapalina ve výměníku by stoupala vlivem přirozeného vztlaku do kolektorů, kde by byla vychlazována a klesala by zpět kolektorovým okruhem do výměníku (viz obr. 6.36). Teplo odebrané ze zásobníku je potom odváděno jako tepelná ztráta z kolektoru. Samovolná cirkulace může způsobit nejen maření solárních zisků soustavy, ale v nepříznivých případech i ztrátu energie z dohřívacího zdroje tepla, který spotřebič (bivalentní zásobník) udržuje na provozní teplotě.
V každém okruhu solární soustavy, který má oběhové čerpadlo, je vhodné instalovat zpětnou klapku. Nedochází tak ani k vzájemnému přetlačování okruhů, kdy v provozu je soustava řízena zapínáním a vypínáním jednotlivých čerpadel.
6.12 TERMOSTATICKÝ SMĚSOVACÍ VENTIL
U solárních soustav pro přípravu teplé vody je běžné, že v letním období může teplota vody v zásobníku překročit běžnou hodnotu 50 °C. Horní hranici teploty v zásobníku je možné nastavit až na 90 °C pro vyšší využití akumulačního objemu. Proto se doporučuje instalovat termostatický směšovací ventil jako ochranu před opařením vysokou teplotou teplé vody na výtoku z kohoutku. Termostatický ventil obsahuje tepelně roztažný člen (vosková patrona), který svou konstrukcí zajišťuje automatické otevírání a uzavírání vstupu studené vody do proudu teplé od zásobníku tak, aby teplota výstupní vody po smíšení nepřekračovala nastavenou požadovanou hodnotu. Ventil zároveň slouží k centrálnímu nastavení teploty teplé vody.
6.13 NOSNÉ KONSTRUKCE
Nosné konstrukce pro kolektory zajišťují jejich uchycení ke konstrukci budovy, případně na terén. Možné varianty umístění kolektorů jsou uvedeny na obr. 6.37. Nejčastěji se solární kolektory umísťují na šikmé nebo ploché střechy.

Obr. 6.37 Umísťování kolektorů na budově
6.13.1 Šikmé střechy
Konstrukce pro uchycení kolektorů nad vhodně skloněné a orientované šikmé střechy se v podstatě skládají z háků uchycovaných na konstrukci střechy (zpravidla krokve) a profilů uzpůsobených k uchycení kolektorů (úchytky). Pro různé typy krytin jsou k dispozici různé typy háků. Někteří výrobci střešních krytin dodávají speciální kovové držáky, plně kompatibilní se střešní krytinou (součást krytiny). Doporučuje se vždy vyžádat si od statika posouzení střechy z hlediska nosnosti. Kolektory uchycované nad krytinou zvýší zatížení střechy o cca 25 kg/m2.
Pokročilým uchycením kolektorové plochy na šikmou střechu je její integrace do střešní krytiny. Řada dodavatelů má dispozici typizované systémy pro integraci dodávaných solárních kolektorů, včetně oplechování. Kolektor v případě integrace nahrazuje střešní krytinu a vlastní zatížení střechy se může i snížit, neboť měrná hmotnost nahrazovaných např. betonových tašek je okolo 40 kg/m2.
6.13.2 Ploché střechy
Konstrukce pro ploché střechy sestávají ze stojanů, uchycených buď k vlastní střeše nebo jiné konstrukci budovy, anebo položených na pochozí části střechy a dostatečně zatížených.
Při uchycení nosné konstrukce kolektorů do nosné konstrukce ploché střechy musí být zajištěna těsnost průchodů patek jak tepelnou izolací, tak hydroizolací proti průniku vody. Je nutné pečlivě řešit i detaily s vlivem na tepelné mosty. Z hlediska montáže jde o řešení značně náročné na požadavky na stavbu.
Dalším, nepříliš rozšířeným způsobem je uchycení nosné konstrukce k atikám střechy. Zde je nutné především vyřešit kluzné uložení nosných profilů na jedné z atik, aby nedošlo k jejich narušení vlivem tepelné roztažnosti profilů. Řešení je opět náročné na koordinaci se stavební profesí.
Preferovaným způsobem bezpečně eliminujícím zásahy do vlastní stavby jsou nosné konstrukce, volně stojící na ploché střeše. Pro zajištění stability i při vysokých rychlostech větru musí být stojany zatíženy, např. betonovými bloky, patky jsou kotveny do tvárnic položených na střeše. Na patky jsou pak přichyceny vlastní konstrukce pro kolektory. Někteří dodavatelé dodávají stojany z betonových prefabrikátů, které slouží jako stojan i jako vlastní zátěž.
U plochých střech je nutné udržet určité rozestupy mezi jednotlivými kolektorovými řadami pro omezení vzájemného stínění během roku. Obecně platí: čím menší sklon kolektorů a nižší kolektory, tím menší potřebná vzdálenost mezi řadami. Potřebnou vzdálenost ovlivňuje období a denní doba (výška Slunce nad obzorem h), pro které je požadavek zajistit nestíněné kolektory. Pro stanovení potřebné vzdálenosti mezi kolektorovými řadami x [m] je možné použít vztah
(6.34)
kde je
α … sklon kolektorů;
h … výška Slunce (nad obzorem);
L … výška kolektoru, v m.
Geometrické charakteristiky jsou znázorněny v grafu na obr. 6.38. Grafické znázornění vztahu (6.34) ukazuje charakteristické souvislosti mezi sklonem kolektorů, výškou Slunce nad obzorem, výškou kolektorového pole (výškový rozměr v rovině kolektoru) a potřebnou vzdáleností. Pro celoročně provozované solární soustavy se doporučuje vzdálenost mezi řadami x stanovit pro poledne v zimním období (výška Slunce okolo 21° v podmínkách ČR). Jak vyplývá z obr. 6.38, pro takové podmínky je nutné zajistit rozestup mezi kolektory x pro sklon 45° ve výši zhruba dvojnásobku výšky uvažovaného kolektoru.
Obr. 6.38 Grafické znázornění poměru rozestupu kolektorových polí k výšce kolektoru v závislosti na sklonu kolektoru β a uvažované výšce Slunce (hodnota 20° odpovídá zhruba poledni o zimním slunovratu)
LITERATURA
[1] Hausner, R., Fink, Ch.: Stagnation Behaviour of Thermal Solar Systems. Sborník konference ISES Eurosun 2000, Copenhagen.
[2] Weiss, W. et al.: Solar Heating Systems for Houses: A Design Handbook for Solar Combisystems. Earthscan Publications Ltd. (June 2004), ISBN 978-1902916460
[3] Hemzal, K., Lerl, Z.: Větrání, vytápění, instalace, roč. 15, č. 3. Společnost pro techniku prostředí Praha 2006.
[4] Kramoliš, P., Vrtek, M.: Tabulky pro stanovení hydraulické ztráty třením v kruhovém potrubí a hydraulické ztráty místními odpory při proudění teplonosné kapaliny SOLAREN. Technické vydavatelství Praha, 2004. ISBN 80-803261-1-0
[5] Conde, M.: Thermophysical properties of brines – Models, Conde Engineering, http://www.mrc-eng.com , Zurich 2002.
[6] ČSN EN 12975 – Tepelné solární soustavy a součásti – Solární kolektory – Část 2: Zkušební metody. ČNI, listopad 2006.
[7] Vyhláška č. 193/2007 Sb., kterou se stanoví podrobnosti účinnosti užití energie při rozvodu tepelné energie a vnitřním rozvodu tepelné energie a chladu.
[8] ČSN EN 12976-2 Tepelné solární soustavy a součásti – Soustavy průmyslově vyráběné – Část 2: Zkušební metody, ČNI 2006.
[9] Laboutka, K., Suchánek, T.: Výpočtové tabulky pro vytápění (sešit projektanta č. 9). Společnost pro techniku prostředí, Praha 2001.
[10] Matuška, T.: Projekt IGS ČVUT 2005 č. CTU 0511412. Optimalizace solárního kolektoru pro kombinované soustavy vytápění a chlazení. ČVUT 2005.
[11] Bláha, J., Brada, K.: Příručka čerpací techniky. Vydavatelství ČVUT, Praha 1997.
[12] ČSN EN 12828 – Tepelné soustavy v budovách – Navrhování teplovodních tepelných soustav,CNI 2005.
[13] ČSN 06 0830 Tepelné soustavy v budovách – Zabezpečovací zařízení, ČNI 2006.
7 VÝPOČTOVÉ BILANCOVÁNÍ SOLÁRNÍCH SOUSTAV
Jako podklad k energetickému, ekologickému a ekonomickému hodnocení nerealizovaných solárních tepelných soustav slouží vyhodnocení energetických přínosů dané instalace výpočtem. Energetické přínosy solárních soustav nejsou závislé pouze na kvalitě navržených komponent (kolektor, zásobník), ale především na návrhu plochy solárních kolektorů vzhledem k potřebě tepla, resp. na požadovaném pokrytí potřeby tepla, na tepelných ztrátách soustavy (potrubí, solární zásobník) a samozřejmě na orientaci a sklonu solárních kolektorů.
7.1 ZJEDNODUŠENÁ BILANČNÍ METODA (TNI 73 0302)
Podstatou bilanční metody je stanovení skutečně využitých zisků na základě porovnání využitelných tepelných zisků solární soustavy a potřeby tepla, která má být kryta. Jedná se o zjednodušený výpočtový postup energetické bilance základních typů solárních tepelných soustav za stanovených okrajových podmínek, který je standardizován v TNI 73 0302 [1]. Zjednodušený postup není detailním výpočtem energetických přínosů solární tepelné soustavy „co nejblíže skutečnosti“, kdy je zapotřebí používat klimatické údaje, včetně parametrů stínění z místa instalace, podrobné parametry a vlastnosti solární soustavy, detailní parametry prvků a jejich hydraulické zapojení, informace o způsobu provozu solární soustavy, a kdy může být potřebné použití jiného podrobnějšího výpočtu, například dynamické simulace soustavy. Zjednodušený výpočtový postup je určen ke stanovení přibližných energetických zisků a je použitelný pro ruční výpočet či výpočet pomocí běžného tabulkového procesoru.
Výsledkem výpočtu jsou základní parametry solární tepelné soustavy:
- celkové roční využitelné tepelné zisky solární soustavy Qss,u;
- měrné roční využitelné tepelné zisky solární soustavy qss,u;
- solární pokrytí potřeby tepla solární soustavou f.
na základě kterých je možné stanovit celkovou úsporu primární energie a svázaných emisí škodlivých látek nebo ekonomické parametry.
7.1.1 Princip výpočtu a nutná zjednodušení
Výpočtový postup pro stanovení energetických zisků solárních tepelných soustav je založen na bilanci potřeby tepla v dané aplikaci, včetně tepelných ztrát, tepla dodaného solárními kolektory, tepelných ztrát solární soustavy a využitelnosti solárního tepla v dané aplikaci. Výpočtový postup je určen pro základní druhy solárních soustav:
- solární soustavy pro přípravu teplé vody;
- kombinované solární soustavy pro přípravu teplé vody a vytápění;
- solární soustavy pro ohřev bazénové vody.
Výpočet založený na energetické bilanci využitelných měsíčních tepelných zisků solárních tepelných soustav je fyzikálně zřetelný, nicméně je do značné míry zjednodušený, řada vlivů se při výpočtu paušalizuje:
- střední teplota v kolektorech je v celém roce konstantní hodnota – neuvažuje se vliv poměru mezi tepelnými zisky instalované plochy kolektorů, velikostí zásobníku a odběrem tepla;
- tepelné ztráty solární soustavy se zahrnují paušální srážkou ze zisků – neuvažuje se vliv různé úrovně tepelné izolace solárního zásobníku a rozvodů, předpokládá se kvalitní izolační standard;
- vliv modifikátoru je paušálně zjednodušen v korekci celkových zisků kolektoru z důvodu snížení náročnosti na získání vstupních údajů pro výpočet.
a proto metoda udává pouze přibližné výsledky. Okrajovými podmínkami výpočtu jsou jednotné údaje o provozních parametrech soustav a jednotné klimatické údaje (teplota, vlhkost, sluneční ozáření, dávka slunečního ozáření) bez ohledu na skutečné místní podmínky instalace. Pouze v odůvodněných případech se připouští použití jiných hodnot provozních parametrů, které musí být výslovně uvedeny. Výpočet nezohledňuje velikost akumulačního zásobníku a neumožňuje tedy vyhodnotit soustavy s extrémně malou nebo velkou plochou kolektorů. Platnost výsledků se omezuje zhruba na rozsah solárního pokrytí 30 až 75 %. V žádném případě výpočtový postup nemůže nahradit detailní výpočetní metodiky či výpočty v pokročilých simulačních programech s časovým krokem 1 hodina a kratším, zohledňující dynamické chování solárních soustav a využívající validované simulační modely prvků soustavy (kolektor, zásobník, výměník, atd.), viz kapitola 7.2.
Zjednodušený výpočtový postup využívá základní údaje o solárním kolektoru podle ČSN EN 12975-2 [2], tzn. konstanty křivky účinnosti h0, a1 a a2, který by měl mít každý výrobce a dodavatel k dispozici, a plochu apertury kolektoru Aa, ke které je křivka účinnosti vztažena.
7.1.2 Potřeba tepla
Základním krokem při bilancování využitých (využitelných) tepelných zisků solární tepelné soustavy je stanovení vlastní potřeby tepla v dané aplikaci. Pokud je známa spotřeba tepla v dané aplikaci z dlouhodobých věrohodných měření (celoroční údaje, včetně tepelných ztrát), s výhodou se použije. V opačném případě se potřeba tepla v dané aplikaci vypočte podle postupů uvedených v části 5.1.
7.1.3 Dopadlá sluneční energie
Podrobný postup stanovení množství sluneční energie dopadající na obecně orientovanou a skloněnou plochu je uveden v části 1. V části 10 v příloze A jsou pro zjednodušení výpočtů tabelovány pro různé oblasti (horské oblasti, venkov, města, průmyslové oblasti) hodnoty teoretické denní dávky celkového slunečního ozáření HT,den,teor [kWh/(m2·den)]. V části 10 příloze B jsou tabelovány difuzní dávky slunečního ozáření HT,den,dif [kWh/(m2·den)] v různých orientacích a sklonech kolektoru. V příloze D jsou tabelovány poměrné doby slunečního svitu τr pro vybraná města v ČR a SR. Denní dávka slunečního ozáření HT,den dopadající na kolektor se stanoví
(7.1)
7.1.4 Účinnost solárního kolektoru
Střední denní účinnost solárního kolektoru se stanoví z rovnice křivky účinnosti
(7.2)
kde je
GT,m … střední denní sluneční ozáření uvažované plochy solárních kolektorů; pro různé sklony a orientace plochy kolektorů v různých oblastech (horské oblasti, venkov, města, průmyslové oblasti) se v jednotlivých měsících stanoví podle přílohy C, ve W/m2;
tk,m … průměrná teplota teplonosné kapaliny v solárních kolektorech v průběhu dne, ve °C; hodnota se uvažuje celoročně konstantní a stanoví se podle druhu aplikace z tab. 7.1;
te,s … průměrná venkovní teplota v době slunečního svitu, ve °C (hodnoty v jednotlivých měsících se stanoví podle přílohy E).
Parametry (konstanty) rovnice křivky účinnosti solárního kolektoru, tzn. hodnota účinnosti při nulových ztrátách η0, lineární součinitel tepelné ztráty a1 ve W/(m2·K) a kvadratický součinitel tepelné ztráty kolektoru a2 ve W/(m2·K2), vztažené k ploše apertury solárního kolektoru Aa, se získají od výrobce nebo dodavatele navrženého kolektoru.
Tab. 7.1 – Střední denní teplota v solárních kolektorech [1]
| Typ aplikace | tk,m [°C] |
| Ohřev bazénové vody (venkovní bazén) | 30 |
| Ohřev bazénové vody (vnitřní bazén) | 35 |
| Předehřev teplé vody, pokrytí < 35 % | 35 |
| Příprava teplé vody, 35 % < pokrytí < 70 % | 40 |
| Příprava teplé vody, pokrytí > 70 % | 50 |
| Příprava teplé vody a vytápění, pokrytí < 25 % | 50 |
| Příprava teplé vody a vytápění, pokrytí > 25 % | 60 |
Střední teploty v kolektorech podle tab. 7.1 jsou pro bilancování zisků uvažovány zjednodušeně jako celoroční průměrné hodnoty v dané aplikaci při zvoleném dimenzování solární soustavy.
7.1.5 Teoreticky využitelné zisky solárních kolektorů
Teoretický měsíční využitelný tepelný zisk ze solárních kolektorů Qk,u v kWh/měs je dán vztahem
(7.3)
kde je
ηk … střední denní (měsíční) účinnost solárního kolektoru;
HT,den … skutečná denní dávka slunečního ozáření, v kWh/(m2·den);
Aa … plocha apertury solárních kolektorů, v m2;
n … počet dní v měsíci;
p … hodnota srážky z tepelných zisků solárních kolektorů vlivem tepelných ztrát solární soustavy (rozvody, solární zásobník); pro typické případy jsou hodnoty uvedeny v tab. 7.2.
Tab. 7.2 – Srážka z tepelných zisků solárních kolektorů vlivem tepelných ztrát [1]
| Typ solární soustavy | p |
| Bazén, ohřev bazénové vody | 0,01 |
| Příprava teplé vody, do 10 m2 | 0,20 |
| Příprava teplé vody, od 10 do 50 m2 | 0,10 |
| Příprava teplé vody, od 50 do 200 m2 | 0,05 |
| Příprava teplé vody, nad 200 m2 | 0,03 |
| Příprava teplé vody a vytápění, do 10 m2 | 0,30 |
| Příprava teplé vody a vytápění, od 10 do 50 m2 | 0,20 |
| Příprava teplé vody a vytápění, od 50 do 200 m2 | 0,10 |
| Příprava teplé vody a vytápění, nad 200 m2 | 0,06 |
Hodnota konstanty 0,9 ve vztahu (7.3) vychází ze střední roční hodnoty modifikátoru úhlu dopadu solárního kolektoru. Modifikátor úhlu dopadu Kθ (IAM) solárních kolektorů je dán konkrétní konstrukcí kolektoru (plochý, trubkový s plochým absorbérem, trubkový s válcovým absorbérem) a jejím provedením. Pro různé typy se pohybuje se mezi hodnotami 0,8 až 1,0. Nelze však obecně říci, že všechny trubkové kolektory s válcovým absorbérem mají vždy vyšší hodnoty Kθ než ploché, vždy záleží na konkrétním tvaru reflektoru a konkrétním zasklení (velké rozdíly u Sydney kolektorů). Z výše uvedených důvodů byla zjednodušeně stanovena paušální hodnota korekce solárních zisků vlivem geometrie slunečního záření právě na hodnotu 0,9.
Při podrobnějším výpočtu, např. s hodinovým krokem, je možné uvažovat s křivkou modifikátoru pro daný typ kolektoru, pokud je k dispozici v protokolu o zkoušce. Nicméně snahou zjednodušeného výpočtu solárních zisků je omezení potřebných vstupních údajů na minimální možnou míru. Výpočet je určený pro široké použití; pouze menšina dodavatelů solárních kolektorů je schopna poskytnout křivku modifikátoru (většinou solární kolektory s označením Solar Keymark) a jen malé procento z nich má představu co modifikátor IAM znamená.
7.1.6 Využité tepelné zisky solární soustavy
Využité zisky solární soustavy Qss,u [kWh/měs] pokrývající měsíční potřebu tepla v dané aplikaci se vyjádří jako průnik celkové potřeby tepla a teoreticky využitelných tepelných zisků solárních kolektorů. Matematicky vyjádřeno, jde o stanovení minimální hodnoty z teoretických tepelných zisků solárních kolektorů a celkové potřeby tepla v jednotlivých měsících
(7.4)
Celkové roční využité tepelné zisky solární soustavy v kWh/rok se stanoví jako součet měsíčních hodnot. Ze stanovených ročních využitelných zisků je možné určit měrné roční využité tepelné zisky jako
(7.5)
Měrné roční využité zisky solární tepelné soustavy qss,u v kWh/(m2·rok) se používají jako ukazatel pro posouzení úspory energie, emisí či provozních nákladů z 1 m2 apertury instalovaných solárních kolektorů.
Solární pokrytí f v %, tj. procentní pokrytí potřeby tepla v dané aplikaci využitelnými tepelnými zisky solární soustavy v daném období, se stanoví výpočtem, např. z měsíčních a ročních hodnot využitých tepelných zisků solární soustavy Qss,u podle vztahu
(7.6)
7.1.7 Program Bilance SS
Z metody TNI 73 0302 vycházejí výpočetní programy řady Bilance SS v tabulkovém procesoru Excel, které jsou koncipovány jako jednoduché nástroje pro projektanty a auditory pro snadné navrhování plochy solárních kolektorů a bilancování energetických přínosů solárních tepelných soustav pro přípravu teplé vody, vytápění nebo ohřev bazénové vody.
Program ve verzi 5.6 [3] zachovává postup i zdrojová data podle TNI 73 0302 a je možné jej použít pro potřeby hodnocení v souladu s TNI (např. v rámci dotačních programů).
Na zadávacím listu programu (viz obr. 7.1) se vkládají údaje potřebné pro výpočet potřeby tepla a solárních zisků. Potřeba teplé vody se zadává jako denní množství o teplotě studené přiváděné vody a požadované teplotě teplé vody, včetně informace o možném snížení spotřeby teplé vody v letním období (podle TNI). Volí se způsob přípravy teplé vody pro zohlednění provozních tepelných ztrát ve výpočtu.
Obr. 7.1 Zadávací list programu Bilance SS_5.6
Ing. Tomáš Matuška, PhD; Ing. Bořivoj Šourek (2009-2010)
V souladu s TNI 73 0302
Zpracování tohoto programu bylo podpořeno z výzkumného záměru Technika prostředí – MSM6840770011
Pro stanovení potřeby tepla na vytápění program umožňuje zadat buď okrajové podmínky pro výpočet denostupňovou metodou, nebo přímo měsíční hodnoty potřeby tepla pro vytápění, získané výpočtem v souladu s ČSN EN 13 790. Stejně tak program umožňuje zadat okrajové podmínky provozu bazénu, vnitřního i vnějšího, pokud se liší od definovaných v TNI (metodika připouští).
Pro solární kolektor se zadává plocha apertury a počet kusů kolektorů, jejich sklon a orientace. Křivka účinnosti solárního kolektoru se zadává konstantami η0, a1 a a2, vztaženými k ploše apertury kolektoru. Definuje se typ solární soustavy pro zohlednění tepelných ztrát soustavy.
Výstupem programu je kromě celkové potřeby tepla Qp,c roční využitý energetický zisk soustavy Qss,u, měrný energetický zisk soustavy qss,u a solární pokrytí potřeby tepla f. Grafické znázornění bilance umožňuje náhled na funkci a využitelnost solárních zisků soustavy během roku (viz obr. 7.2).
Obr. 7.2 List výsledků výpočtu programu Bilance SS_5.6
Ing. Tomáš Matuška, PhD; Ing. Bořivoj Šourek (2009-2010)
V souladu s TNI 73 0302
Zpracování tohoto programu bylo podpořeno z výzkumného záměru Technika prostředí – MSM6840770011
7.2 BILANCOVÁNÍ SOLÁRNÍCH SOUSTAV S VYUŽITÍM POČÍTAČOVÝCH SIMULACÍ
Měsíční bilance uvedená ve zjednodušeném výpočetním postupu má díky svým zjednodušením řadu nevýhod a zanedbává vliv řady provozně důležitých parametrů na skutečné energetické přínosy solární soustavy (zisky). Pokud existuje potřeba podrobněji hodnotit solární soustavy s uvažováním například vlivu objemu zásobníku, účinnosti konkrétního použitého výměníku, průtoku teplonosné kapaliny, stratifikace v zásobníku, odběrové křivky apod., je nezbytné použít některý z dostupných simulačních nástrojů. Takovým případem může být například smlouva o garantovaných solárních, kdy je nutné již při přípravě projektové dokumentace s vysokým stupněm jistoty stanovit budoucí zisky navržené solární soustavy, za které se dodavatel zaručí.
Matematické modelování s využitím komplexních moderních simulačních nástrojů umožňuje, pokud má uživatel dostatečnou zkušenost, snadné a poměrně přesné stanovení zisků s ohledem na okrajové podmínky s využitím databází klimatických údajů statisticky typických roků. Počítačové simulace umožňují optimalizaci solárních soustav pro daný konkrétní případ. Optimalizací se rozumí v první řadě maximalizace využitelných energetických zisků a minimalizace vstupu jiných neobnovitelných energií (spotřeba pomocné energie na pohon, spotřeba energie dodatkového zdroje tepla apod.).
Simulační programy zohledňují dynamické chování jednotlivých prvků od solárních kolektorů s časovou konstantou v řádu minut, po obytné budovy s časovou konstantou v řádu dnů. Simulační výpočet se provádí s hodinovým a kratším krokem, podle možností daného programu.
Z hlediska konceptu simulačních programů je možné je rozdělit na systémové, které využívají předdefinovanou solární soustavu z hlediska hydraulického schématu, použitelných prvků soustavy a parametrů vlastního výpočtu, a na modulární, u kterých uživatel musí složit solární soustavu z jednotlivých modelů prvků (podprogramů, výpočtových rutin, vlastních programů) jako jsou kolektory, zásobníky, čerpadla, potrubí, regulace, výměníky, kotle aj., a nastavit potřebné parametry vlastního matematického výpočtu.
7.2.1 Systémové simulační programy
Programy založené na předdefinovaných zapojeních solárních soustav umožňují uživateli vybrat vždy z určitého omezeného počtu konfigurací. Zadáním parametrů jednotlivých prvků nebo jejich výběrem z produktové řady umožňují detailní návrh a hodnocení dané (zjednodušené) solární soustavy s dostatečnou přesností, a přitom zůstávají relativně přátelské pro uživatele. Umožňují některé detailní studie solárních soustav. Jsou vhodné pro návrh a hodnocení solárních soustav jak pro rodinné domy, tak pro bytové domy jako pomůcka při navrhování.
Dostupných je několik takových programů založených na předdefinovaných zapojeních soustav. Jako příklad lze uvést následující programy Polysun nebo T-Sol, které jsou k dispozici i v českém jazyce. Oba je relativně jednoduché používat a umožňují volbu řady proměnných. Základní instalace obsahují poměrně rozsáhlé klimatické databáze pro velké množství lokalit, včetně ČR.
7.2.2 Modulární programy
Modulární programy jsou založené na modelech jednotlivých prvků a umožňují navzájem je propojovat v libovolné konfiguraci, která je následně simulována. Nevýhodou je časová náročnost výpočtů, neboť systém musí být schopný řešit jakoukoliv kombinaci prvků. Flexibilita však přináší i další problém pro uživatele – sledovat, co vše je součástí soustavy a zajistit, že všechny hodnoty v jednotlivých modelech prvků jsou takové, jaké mají opravdu být. Je velmi snadné vnést do modelu celé soustavy systémovou chybu.
Jako modulární programy slouží pokročilé verze zmíněných programů Polysun a T-Sol. Dále však existuje řada univerzálních programů (řešičů), založených buď přímo na vytvořených prvcích solárních soustav (modelech), nebo na obecných diferenciálních rovnicích, matematicky popisujících fyzikální podstatu prvku. Tyto programy mohou být v principu využity pro simulaci solární soustavy, nicméně vyžadují programátorské schopnosti převést fyzikální realitu do simulačního prostředí. Společným jmenovatelem takových nástrojů je uživatelsky nepřístupné prostředí a často omezená dostupnost funkčních modelů prvků. Jedním z nejpoužívanějších pokročilých simulačních programů je TRNSYS, který se používá již více než 25 let a je v komunitě využívající simulace solárních soustav základní simulační platformou. Z dalších je možné jmenovat INSEL, nebo prostředí Matlab Simulink.
Detailní simulační programy vyžadují detailní znalosti jak fyzikální podstaty simulovaného problému, tak vlastního programu. Jsou určeny převážně pro vývoj a výzkum v oblasti solárních soustav. Některé simulační programy (TRNSYS) však umožňují na základě detailního modelu vytvářet jednodušší nástroje, které mohou být nezávisle na zdrojovém simulačním programu používány (jednoúčelové programy se vstupním a výstupním rozhraním).
7.2.3 Program Polysun
Program Polysun [4] je vyvíjen od roku 1992 v Institut für Solartechnik SPF Rapperswil (Švýcarsko). Umožňuje simulaci solárních soustav pro přípravu teplé vody, solárních kombinovaných soustav či soustav technologických. Obsahuje velmi obsáhlou databázi solárních kolektorů, které byly přímo ve výzkumném ústavu zkoušeny (s funkcí aktualizace databáze), nicméně umožňuje i zadání vlastních parametrů solárního kolektoru. Polysun obsahuje klimatické databáze pro více než 6300 lokací z celého světa, včetně ČR. Klimatické údaje však není možné importovat z externích databází.
V programu Polysun 4 Light lze používat pouze předdefinované varianty zapojení solárních soustav, nicméně program umožňuje volbu některých parametrů u jednotlivých prvků; ovládání je intuitivní a lze jej zvládnout v řádu minut.
U verze Polysun 4 Professional je možné používat vlastní prvky (zařízení) v předdefinovaných variantách zapojení.
Obr. 7.3 Příklad složení solární soustavy pro přípravu TV a přitápění z připravených prvků v programu Polysun 4
Obr. 7.4 Příklad grafického výstupu (vizualizace simulace, sumární výsledky) v programu Polysun 4
Vlastní zapojení soustavy lze tvořit pouze ve verzi Polysun 4 Designer. Tato programová verze je koncipována jako modulární, kdy je možné jednotlivé prvky (moduly) skládat do požadované solární soustavy. V databázi je množství připravených modulů s prakticky využitelnými parametry, které lze měnit. K dispozici je také modul pro simulaci budovy, včetně geometrie budovy, izolace, oken apod. Program lze využít pro řešení komplexních solárních soustav i s prvky jako jsou tepelná čerpadla.
Program Polysun je kompletně přeložen do češtiny a je relativně rozšířený i mezi českými projektanty a dodavateli solárních kolektorů a soustav. Řada výrobců hlavních prvků solárních soustav (kolektory, zásobníky) dodává parametry svých výrobků do modulů programu, případně má k dispozici „firemní“ verze programu Polysun, kde lze vybírat pouze z firemních prvků.
7.2.4 Program T*Sol
Program T-Sol [5] je vyvíjen od roku 1993 v Dr. Valentin EnergieSoftware GmbH (Německo). Program je k dispozici v několika variantách.
Obr. 7.5 Schéma simulované solární soustavy v program T-Sol
Program T*Sol Expres obsahuje pouze 5 předdefinovaných variant zapojení solárních soustav pro přípravu teplé vody. Je vhodný pro širokou veřejnost, pro výuku nebo pro základní výpočty energetických bilancí jednoduchých solárních soustav pro přípravu TV. Program obsahuje klimatické databáze ze 650 míst v celé Evropě.
Obr. 7.6 Výběr varianty zapojení solární soustavy v programu T*Sol
T*Sol Professional a T*Sol Expert umožňuje vybírat z množství předdefinovaných variant zapojení a u jednotlivých prvků upravovat jejich parametry. Umožňuje jak hodinové simulace (Professional), tak simulace se 6minutovým krokem (Expert). Součástí programů je i ekonomická či emisní analýza zvolené solární soustavy. Program T*Sol Expert umožňuje parametrické analýzy pro optimalizaci prvků a provozních parametrů solární soustavy, import experimentálních dat, současné porovnávání dvou variant návrhu aj. Grafický výstup výsledků je přehledný a umožňuje poměrně snadno procházet výsledky po dnech týdnech či měsících. Program má několik jazykových variant – němčinu, angličtinu, španělštinu, francouzštinu a italštinu. Program pracuje s 2000 klimatických databází (Meteosyn).
Obr. 7.7 Příklad grafického výstupu v programu T*Sol
7.3 LITERATURA
[1] TNI 73 0302 Energetické hodnocení solárních tepelných soustav – Zjednodušený výpočtový postup. ÚNMZ 2009.
[2] ČSN EN 12975-2 Tepelné solární soustavy a součásti – Solární kolektory – Část 2: Zkušební metoda, která detailně popisuje zkušební metody a podmínky, za kterých jsou solární kolektory zkoušeny. ČNI 2006.
[3] Šourek, B., Matuška, T.: Program BilanceSS_5.1, dostupný na http://users.fs.cvut.cz/~matustom
[4] Polysun 4, Institut für Solartechnik SPF, Švýcarsko, dostupné z http://www.solarenergy.ch
[5] T*Sol, Dr. Valentin EnergieSoftware GmbH, Německo, dostupné z http://www.tsol.de
8 MĚŘENÍ A PROVOZNÍ VYHODNOCOVÁNÍ SOLÁRNÍCH SOUSTAV
Investor či provozovatel zpravidla požaduje spolehlivou a zároveň jednoduchou kontrolu funkce nainstalované solární soustavy. To se neobejde bez instalace čidel, monitorovacího a vyhodnocovacího systému. Nejspolehlivějším údajem o správnosti funkce solární soustavy je vyhodnocení dosaženého přínosu (solární zisky soustavy pro danou aplikaci), ze kterého je možné vyhodnotit skutečnou ekonomiku provozu. Na druhé straně využití měřicí a vyhodnocovací techniky znamená investice do čidel a monitorovacího systému (snímání a ukládání dat), zpracování měřených údajů a interpretace z hlediska funkce solární soustavy a dosažených přínosů.
Provozní měření na solárních tepelných soustavách jsou velmi významná vzhledem ke skutečnosti, že oproti standardním zkušebním metodám v laboratoři za jasně definovaných „ideálních“ podmínek poskytují informaci o chování solární soustavy jako celku v reálných podmínkách v průběhu určitého časového období. Ve výsledném tepelném zisku stanoveném z experimentálně zjištěných údajů z provozu soustavy je zahrnuta vlastní interakce mezi zdrojem tepla (solární kolektory), přenosovou soustavou (výměníky, potrubí, zásobníky), spotřebičem (příprava teplé vody, otopná soustava, ohřev bazénové vody) a dalšími faktory, např. provozní a regulační strategie (nastavení regulačních parametrů soustav), tepelné ztráty, údržba aj. Je zřejmé, že vysoce účinný solární kolektor, který je zapojen ve špatně navržené soustavě s neefektivními prvky nebo je „pouze“ špatně udržovaný a provozovaný, bude vykazovat nízký zisk.
Poznámka:
Příkladem může být kvalitní solární kolektor, jehož plocha je předimenzovaná oproti potřebě tepla vlastní aplikace, zatímco výměník tepla je výkonově poddimenzovaný, a navíc jsou potrubí solární soustavy a zásobník opatřeny nedostatečnou tepelnou izolací. Taková solární soustava bude pracovat za vysokých teplot na solárním kolektoru (tedy nízkou účinností) a vysokými tepelnými ztrátami (degradace tepelných zisků).
Provozní měření je možné využít pro prosté stanovení přínosu instalací solárních soustav provozovatelům (jednoduché měřicí zařízení), nebo pro detailní analýzy solárních soustav (složitější monitorovací systém, měření teplot a průtoků v různých částech soustavy, možnost identifikace slabých míst návrhu, zkoumání chování zdroje tepla za reálných podmínek apod.). Požadavky na přístrojové vybavení a dobu trvání měření odpovídají požadovanému typu informace. Podle složitosti soustav, jejich investiční náročnosti a požadovaného stupně informace lze rozlišit:
- základní měření – energie dodaná solární soustavou (solární zisk) a elektrická energie spotřebovaná na pohon soustavy v měsíčním (ročním) rozlišení;
- pokročilé měření – energie dodaná solární soustavou, energie dodaná neobnovitelným zdrojem tepla (stanovení pokrytí) a elektrická energie spotřebovaná na pohon soustavy v měsíčním rozlišení;
- komplexní monitoring – kromě detailního snímání energetických toků také ukládání teplot a průtoků v různých částech solární soustavy pro zpětnou analýzu provozního chování a optimalizaci funkce soustavy.
8.1 HODNOCENÉ PARAMETRY SOLÁRNÍCH SOUSTAV
8.1.1 Teplota
Základním monitorovaným provozním parametrem solárních soustav je teplota, jednak v kolektorech, jednak v zásobnících. Často však ke zhodnocení správné funkce soustavy nestačí pouze údaj o teplotě kolektorů či zásobníku, neboť taková informace může být zavádějící. Vysoké teploty na kolektorech, vychvalované uživateli „jak jim systém jede“, zpravidla nemusí automaticky znamenat vysoké zisky soustavy ani správné dimenzování plochy kolektorů. Naopak, mohou vypovídat o špatné funkci solární soustavy, např. o podprůtocích kolektorovým okruhem, zavzdušněné soustavě, nedostatečném odběru tepla, zaneseném výměníku apod.
Měření teplot na výměníku primárního okruhu solární soustavy může poskytnout informaci o správnosti návrhu velikosti výměníku, zda je vychlazování teplonosné kapaliny v primárním okruhu dostatečné. Porovnání teplot na výstupu z kolektoru a na vstupu do výměníku tepla ukazuje na kvalitu izolace rozvodů primárního okruhu. Z měření teplot v různých výškách zásobníku tepla lze usoudit na chování zásobníku z hlediska teplotního vrstvení jeho objemu, nebo z hlediska jeho tepelných ztrát.
8.1.2 Využité tepelné zisky solární soustavy a dodatková energie
Aby bylo možné zhodnotit přínosy solární soustavy (nahrazení konvenční energie), je nutné stanovit z měření solární zisky soustavy Qss,u využité pro krytí potřeby tepla v dané aplikaci. Na obr. 8.1 je zobrazena solární soustava pro přípravu teplé vody s předehřívacím (vyrovnávacím) solárním zásobníkem a dohřívacím (pohotovostním) zásobníkem, ohřívaným nahrazovaným (dodatkovým) zdrojem tepla. Na jejím příkladu je možné objasnit, kde je nutné měřit solární zisky, aby bylo možné správně vyhodnotit reálné přínosy solární soustavy.
Pro správné vyhodnocení přínosu solární soustavy je třeba si nejprve stanovit hranice mezi vlastní aplikací, např. přípravou teplé vody, a vlastní solární soustavou. Na obr. 8.1 je to zřetelně hranice č. 3, která odděluje vlastní přípravu TV v pohotovostním zásobníku a předřazenou solární soustavu. Skutečné tepelné zisky solární soustavy je nutné měřit právě na této hranici a tedy Qss,u = Qk,u3. Solární soustava se tepelnými zisky ze solárních kolektorů snaží krýt jednak celkovou potřebu tepla aplikace Qp,c:
- vlastní potřebu tepla aplikace Qp;
- tepelné ztráty rozvodů aplikace Qr,z3;
- tepelné ztráty pohotovostního zásobníku Qz,aku2.
a vlastní tepelné ztráty solární soustavy:
- tepelné ztráty rozvodu primárního okruhu Qz,r1;
- tepelné ztráty solárního zásobníku Qz,aku1.
Skutečné solární zisky není vhodné vyhodnocovat v primárním okruhu před solárním zásobníkem tepla (hranice č. 2) jako Qk,u2, neboť v sobě nezahrnují sobě tepelné ztráty zásobníku Qz,aku1 a jeho exergetické charakteristiky (např. vliv výhodného teplotního vrstvení na zvýšení solárního pokrytí aplikace). Na druhou stranu, tepelné ztráty solárního zásobníku se v běžném případě nepodílejí na celkových tepelných ztrátách více než 10 %. Měření solárních zisků Qk,u1 na výstupu z kolektorového pole (hranice č. 1) je nutné se vyhnout, neboť nezahrnuje nezanedbatelné tepelné ztráty v potrubí solární soustavy.
Obecná teoretická definice solárních zisků soustavy je celkem jasná: jde o zisky, které dodá solární soustava pro krytí potřeby tepla v dané aplikaci, a je možné ji stanovit jako rozdíl mezi celkovou potřebou tepla aplikace (včetně tepelných ztrát) a teplem dodaným ze dodatkového (nahrazovaného) zdroje
(8.1)
Čistou potřebu tepla Qp lze sice jednoduše změřit (např. odběr teplé vody při dané teplotě studené a odebírané teplé vody) stejně jako dodanou energii Qd (elektroměr, plynoměr), tepelné ztráty se však jednoduše nezměří. Pro určení skutečného přínosu solární soustavy je tedy nutné vyhodnocovat solární zisky Qss,u měřením.
Skutečné solární pokrytí pokrytí potřeby tepla dané aplikace solárními zisky soustavy se stanoví jako
(8.2)
Aby bylo možné stanovit jednoduše pokrytí potřeby tepla aplikace tepelnými zisky solární soustavy, je nutné měřit dodatkovou energii Qd dodanou konvenčním (nahrazovaným) zdrojem. Měření dodatkové energie je zpravidla součástí tepelné soustavy nahrazovaného zdroje tepla s ohledem na fakturaci za odebrané teplo (nebo obecně energii v palivu).
Obr. 8.1 – Hranice vyhodnocení tepelných zisků solární soustavy (1 – špatně, 2- lépe, 3 – správně)
Způsob měření dodatkové energie a přístroje se volí podle druhu zdroje energie: plynový kotel (kalorimetrické měření nebo plynoměr), přímý ohřev plynovým hořákem (plynoměr), elektrický kotel nebo vložka (kalorimetr nebo elektroměr) nebo jiný teplovodní zdroj tepla, např. CZT (kalorimetr).
Měření solárního tepla dodaného do různých míst solární soustavy (na různé hranice) může odhalit špatnou funkci hlavních částí soustavy, např. špatné teplotní vrstvení vlivem nevhodné konstrukce zásobníku, vysoké tepelné ztráty solárního zásobníku, případně potrubního okruhu, nevhodně nastavené parametry v regulátoru solární soustavy. Identifikace slabých míst solární soustavy je však složitý proces a vyžaduje pokročilou měřicí techniku.
8.1.3 Účinnost solární soustavy
Pokud je k dispozici měření dopadlé sluneční energie HT ve kWh/m2 na solární kolektory (v rovině kolektorů), lze vyhodnotit za určité časové období také provozní účinnost celé solární soustavy jako
(8.3)
kde je
Aa … plocha apertury kolektorů v m2
8.2 MĚŘENÍ A VYHODNOCOVÁNÍ VELEČIN
8.2.1 Měření teplot
Měření teplot v solárních soustavách je důležité pro řízení samotného provozu tepelné soustavy, kontrolu funkce a pro vyhodnocování dodaných tepelných zisků. Použití nevhodných čidel může narušit nebo zcela zastavit provoz solární soustavy či nesprávně vypovídat o celkovém provozu soustavy. Náklady na kvalitní teplotní čidla jsou nízké ve srovnání se ztrátami, ke kterým může později dojít při výskytu provozních problémů.
Teplotní čidla
Pro měření teplot v primárních nebo sekundárních okruzích solárních soustav se v naprosté většině používají odporová teplotní čidla, založená na platinovém odporovém drátku o referenčním elektrickém odporu, stanoveném pro 0 °C: 100 Ω(Pt100), 500 Ω(Pt500) nebo 1000 Ω(Pt1000). Platinová odporová čidla mohou být provozována za teplot od -200 °C do 850 °C, nicméně jednotlivé typy a provedení se liší podle provozní teploty a přesnosti (třída A, B).
Pro měření tepla dodaného solární soustavou, kdy je nutné měřit přesně rozdíl teplot, jsou vhodná tzv. párová teplotní čidla ocejchovaná vůči sobě v třídě A, pro zajištění minimální odchylky. Vzájemná odchylka teplotních čidel pro běžné teplotní rozdíly 3 až 10 K by neměla být vyšší než ± 0,05 K. Pro přesná měření je vhodné použít na delší vzdálenosti (např. nad 20 m) čtyřvodičové zapojení teplotních čidel pro kompenzaci vlivu elektrického odporu přívodních vodičů. Z hlediska kontroly funkce tepelných soustav postačuje kvalita v třídě B ve dvojvodičovém zapojení. Teplotní čidla s vyšším elektrickým odporem jsou oproti Pt100 výhodnější v tom, že při stejné teplotní změně je změna odporu 5násobně (Pt500) až 10násobně (Pt1000) vyšší, tzn. při kratších vzdálenostech je možné je i pro přesné měření připojovat pouze dvojvodičově.
Vysoká teplotní odolnost předurčuje platinová čidla pro použití v solárních kolektorech s vysokými stagnačními teplotami (kvalitní ploché kolektory, vakuové kolektory). Obal čidla musí zaručit vysokou odolnost proti pronikání vlhkosti k čidlu a odolat vysokým teplotám. Pro elektrickou izolaci vodičů čidel se používá silikon nebo teflon, namísto běžného PVC. Takové izolace odolají bezpečně do 230 °C.
Umísťování teplotních čidel
Teplotní čidla mohou být v provedení pro instalaci do jímek nebo méně často v bezjímkovém provedení. Umísťování čidel do jímek je výhodné z hlediska snadné výměny čidla, na druhé straně je nutné zajistit dlouhodobě tepelně vodivý kontakt mezi čidlem a jímkou (nejlépe kombinace těsná jímka – vodivá pasta). Jímka by neměla být masivní a měla by být z tepelně vodivého materiálu s nízkou tepelnou kapacitou pro zajištění rychlé reakce teplotního čidla na změnu teploty. V současné době jsou na trhu k dispozici měděné tenkostěnné jímky, které by měly být spolu s tenkostěnnými nerezovými upřednostňovány před běžnými silnostěnnými ocelovými jímkami, mj. také s ohledem na menší sklon ke korozi. Bezjímkové provedení čidel vede k rychlejší reakci, zajištění dokonalého kontaktu čidla s měřenou kapalinou, nicméně jejich případná výměna je spojena s vypuštěním části solární soustavy.
Obr. 8.2 – Nesprávné a správné umístění čidla / jímky v potrubí
Jímky nebo bezjímková čidla se do potrubí umísťují tak, aby je kapalina obtékala, nejlépe protiproudým způsobem (čidlo rozráží proud kapaliny, viz obr. 8.2). Je důležité, aby čidlo nebo jímka byly dostatečně dlouhé a zasahovaly do proudící kapaliny. Vhodná je instalace především do ohybů a kolen potrubí.
Přestože lze při zajištění správného tvaru, trvale vodivého dotyku (pasta) a dostatečného odstínění od okolí (tepelná izolace) dosáhnout určité přesnosti (± 0,5 K), nedoporučuje se měřit teplotu kapaliny kontaktním teplotním čidlem přiloženým k trubce, vzhledem k převážně laminárnímu charakteru proudění v potrubí solární soustavy. Takové čidlo měří teplotu kapaliny u stěny, a ne reprezentativní teplotu proudící kapaliny v celém průřezu. Kontaktní způsob měření není vhodný pro účely vyhodnocování solárních zisků soustavy, nicméně je postačující pro kontrolu funkce soustavy.
Teplotní čidlo kolektorového pole by mělo být vždy v dostatečně tepelně vodivém kontaktu s nejteplejší částí kolektoru (horní sběrací trubka, okraj absorbéru) nebo kolektorového pole (poslední kolektor v sérii). Čidlo (nebo jímka) by tedy mělo být vnořeno dostatečně daleko do horní sběrací trubky (nutný dlouhý stonek nebo jímka), nebo vsunuto do speciálně zhotovené jímky pro čidlo v kontaktu s absorbérem (připájené, přivařené, velmi záleží na kvalitě spoje a kolektoru, tepelném styku čidla a jímky).
Je nutné se vyvarovat instalací příliš krátkých teplotních čidel nezasahujících do sběrné trubky kolektoru, nebo dokonce instalovaných sice ve výstupním potrubí, ale mimo kolektor, navíc v tepelně neizolovaném T-kusu. To má za následek příliš nízké teploty snímané na kolektoru a opožděné sepnutí solární soustavy regulátorem a s tím související nižší provozní úspory.
Podobně správné umístění teplotního čidla pro nabíjení zásobníku do jeho spodní nejchladnější části zaručuje účinnou funkci solární soustavy. Řada výrobců v současné době dává přednost kontaktnímu snímání teploty zásobníku na vnějším povrchu jeho pláště s ohledem na minimalizaci potenciálních defektů (vadný svar v návarku, těsnění čidla / jímky).
8.2.2 Měření průtoku
Hodnotu průtoku solární soustavou je nutné často znát jednak pro zprovoznění soustavy a nastavení jejích jmenovitých parametrů, a dále především pro vyhodnocení tepla dodaného do aplikace. U primárních okruhů solárních soustav se vzhledem k výrazné závislosti viskozity nemrznoucích směsí propyleglykol-voda na teplotě mohou v provozu měnit tlakové ztráty soustavy a při pevně nastaveném výkonu oběhových čerpadel tak může průtok okruhem kolísat (až o 30 %).
Obecné požadavky na průtokoměry
Průtokoměry použité v solární soustavě musí odpovídat jejich použití, tedy zejména umožnit dlouhodobé měření s uvažovanou kapalinou (voda, nemrznoucí směs). Rozsah měřených průtoků musí odpovídat provozním podmínkám pro udržení nejistoty měření v přijatelných mezích. Průtokoměry by měly být dostatečně přesné a citlivé. Citlivost průtokoměru (pulzní číslo) může hrát svou roli především při měření dodaného tepla. Pulzní číslo průtokoměru by mělo odpovídat měřenému průtoku a době trvání průtoku. Například u solárních soustav je možné považovat jako dostatečné takové pulzní číslo, které umožní zápis alespoň 1 pulzu za 1 minutu (nejkratší uvažovaný čas běhu solární soustavy) při hodnotě měřeného průtoku.
V solárních soustavách je nutné zohlednit teplotní odolnost průtokoměrů s ohledem jejich umístění v solární soustavě. Podobně jako teplotní čidla, musí být i průtokoměry odolné provozním teplotám alespoň do 120 °C, případně umístěny v takovém místě solární soustavy, kde nehrozí extrémní zatížení nevhodnými teplotami.
Při navrhování oběhových čerpadel je třeba zohlednit případné vnesené tlakové ztráty instalovaných průtokoměrů. Některé průtokoměry vyžadují uklidňující délky na vstupu, u jiných je nutné zajistit filtry proti zanesení.
Plovákové průtokoměry
Pro nastavení a kontrolu průtoku jsou u solárních soustav rozšířené jednoduché plovákové průtokoměry, které tvoří součást kompaktních čerpadlových skupin (viz obr. 8.3). Plovák se pohybuje ve svislé, nahoru se rozšiřující, kuželové trubici. Průtočný průřez je dán mezerou mezi plovákem a trubicí, tlakový spád pak hmotností plováku a jeho průřezem. V rovnovážné poloze se gravitační síla redukovaná o vztlak rovná síle způsobené tlakovým rozdílem mezi spodní a horní částí plováku. Plovák se při daném průtoku tedy ustálí v takové poloze, aby v mezeře mezi plovákem a stěnou trubice byl stále stejný tlakový spád. Výška, do které plovák vystoupí, je tak úměrná průtoku. Poloha plováku se odečítá na stupnici nanesené na trubici. Stupnice je zpravidla ocejchovaná v jednotkách průtoku (např. v l/min). Pro zajištění kompaktního tvaru a zkrácení délky trubice je u provozních plovákových průtokoměrů použita pružina, působící na plovák proti pohybu kapaliny.
Obr. 8.3 Plovákové průtokoměry pro nastavení a kontrolu průtoku v solární soustavě
Měření průtoku běžnými plovákovými průtokoměry je orientační vzhledem k relativně hrubé stupnici a nesnadno specifikovatelnému vlivu teploty kapaliny na polohu plováku. Změna teploty má vliv na změnu viskozity měřené tekutiny (změna odporu třením), změnu její hustoty (změna vztlaku), na změnu velikosti štěrbiny vlivem rozdílné teplotní roztažnosti materiálu plováku a trubice, případně na vlastnosti pružiny.
Plovákový průtokoměr používaný v čerpadlových skupinách solárních soustav slouží kromě nastavení požadovaného průtoku také jako zpětná klapka. Teplotní odolnost běžných typů plovákových průtokoměrů se pohybuje okolo 130 °C. U speciálních typů určených přímo pro solární soustavy (viz obr. 8.3, vpravo) je plovák umístěn v obtoku a není vystaven extrémním podmínkám. Pouze v případě potřeby měřit průtok se protékající kapalina přepustí obtokem. Teplotní odolnost takového průtokoměru je okolo 180 °C.
Rychlostní (mechanické) průtokoměry
U rychlostních měřidel proudící tekutina působí na soustavu lopatek oběžného kola, které roztáčí. Otáčky kola se přenášejí na počítadlo, nebo se snímají bezdotykově a elektronicky vyhodnocují (čítačem). Tato měřidla udávají celkový proteklý objem, nikoli okamžitý průtok. Přístroje s axiálním nebo radiálním vstupem tekutiny na oběžné kolo se nazývají turbínové průtokoměry, přístroje s tečným vstupem se nazývají lopatkové průtokoměry. U dobře provedených přístrojů je nad spodní mezí (3 – 5 % rozsahu) lineární závislost mezi průtokem a otáčkami oběžného kola. Na takovém principu pracují např. běžné vodoměry s mechanickým počítadlem, používané k měření spotřeby vody. Usměrněný proud vody je tečně naváděn na oběžné kolo, otáčející se ve válcové komůrce. Údaj do počítadla je převáděn magnetickou spojkou.
Vzhledem k nízké ceně jsou rychlostní lopatkové nebo turbínové průtokoměry (viz obr. 8.4) často používané pro měření průtoku i v solárních soustavách. Rychlostní průtokoměry však obsahují pohyblivé části, které se časem opotřebovávají, jejich přesnost se může postupně zhoršovat a po určité době je nutné je vyměnit, opravit či znovu ocejchovat. Nečistoty v teplonosné kapalině mohou způsobit jejich poruchu. Nevýhodou rychlostních průtokoměrů, podobně jako plovákových, je také jejich trvalá provozní tlaková ztráta, způsobená hydraulickým odporem roztáčeného členu, která má za následek zvýšenou provozní spotřebu pomocné elektrické energie měřené solární soustavy. Tento typ průtokoměrů vyžaduje instalaci jemného filtru pro snížení rizika poruchy.
Obr. 8.4 Lopatkový a turbínový průtokoměr
Ultrazvukové průtokoměry
Principem ultrazvukových (ultrasonických) průtokoměrů je vektorové skládání rychlosti tekutiny a rychlosti šíření zvukové (ultrazvukové) vlny. Dvě stanice, jedna pro generování a jedna pro registraci ultrazvuku, jsou zabudovány buď šikmo napříč potrubím (diagonálně proti sobě), na stejné straně (využití odrazu ultrazvuku), nebo jsou použity pro snímání ultrazvuku dvě stanice za sebou (dvoustopé provedení). Z rychlosti šíření signálu je možné při známém průřezu určit průtok kapaliny. Ultrazvukové průtokoměry jsou vhodné k měření průtoku vodivých i nevodivých kapalin. Podmínkou správného měření je dodržet výrobcem požadované délky rovných úseků potrubí před průtokoměrem a za ním, kvůli ustálení rychlostního profilu. Kromě průtokoměrů zabudovaných do potrubí se používají i průtokoměry s příložnými stanicemi, které se instalují na vnější povrch potrubí (kontaktní pasta), viz obr. 8.5. Jejich přesnost závisí na správné montáži, správném zadání parametrů potrubí a měřené kapaliny podle skutečnosti a na správném nastavení vzdálenosti stanic.
Obr. 8.5 Ultrazvukový průtokoměr: princip, provedení do potrubí, provedení příložné
Ultrazvukové průtokoměry nejsou závislé na vodivosti kapaliny a lze je použít i na znečištěné, nemrznoucí nebo špatně vodivé kapaliny. Jejich výhodou je velký rozsah měřených průtoků, vysoká přesnost měření, dlouhodobá stabilita a zanedbatelná tlaková ztráta. Nevýhodou je nutnost uklidňovací délky potrubí, což je problematické zajistit zvláště v případě dodatečné instalace průtokoměru.
Indukční průtokoměry
V magneticko-indukčním průtokoměru proudí kapalina v magnetickém poli vytvořeném mezi póly magnetu. Obsahuje-li kapalina ionty, jsou vychylovány ve směru kolmém k siločárám magnetického pole. Pokud jsou v těchto místech elektrody, shromáždí se na nich náboje, které vytvoří elektrické pole. Snímané indukované napětí je úměrné rychlosti proudění kapaliny. Indukční průtokoměry vyžadují minimální elektrickou vodivost kapaliny 5 μS/cm.
Indukční průtokoměry jsou vhodné pro měření vody s předepsanou elektrickou vodivostí, jejich přesnost je závislá na kvalitě vody. Pro měření průtoku nemrznoucích směsí jsou indukční průtokoměry (kalibrované vždy pro vodu) nevhodné vzhledem k odlišným elektrickým vlastnostem nemrznoucích kapalin od vlastností vody. Indukční průtokoměry, podobně jako ultrazvukové, vyžadují uklidňující délku potrubí před a za průtokoměrem (okolo 50 mm).
8.2.3 Měření tepla
Dodané (a měřené) teplo ze zdroje tepla (solární soustavy, dodatkového zdroje) nebo odebrané do aplikace se stanoví ze vztahu
(8.5)
kde je
V … průtok teplonosné kapaliny soustavou, m3/s;
ρ … hustota teplonosné kapaliny, v kg/m3;
c … měrná tepelná kapacita teplonosné kapaliny, v J/(kg·K);
ts2 … výstupní teplota teplonosné kapaliny přiváděné ze zdroje tepla do tepelné soustavy, ve °C;
ts1 … vstupní teplota vychlazené teplonosné kapaliny přiváděné z tepelné soustavy do zdroje tepla, ve °C;
τ … časový úsek měření, v s;
V … objem teplonosné kapaliny proteklé na časový úsek.
Z výše uvedeného vyplývá, že pro měření a vyhodnocení tepla je nutné použít průtokoměr a dvě teplotní čidla spolu se znalostí termofyzikálních vlastností teplonosné kapaliny. Pokud je to možné, mělo by měření a vyhodnocování dodaného tepla být umístěno v takové části tepelné soustavy, kde se výrazně nemění průtok (stabilita měření, přesnost měření). Pro zajištění dostatečné přesnosti měření rozdílu teplot Δt je nutné použití párovaných teplotních čidel. Důležitá je také měřená hodnota rozdílu teplot, která by měla být vyšší než 2 K. Tomu musí samozřejmě odpovídat nastavení průtoku v měřeném okruhu.
Orientační měření tepla
U jednoduchých regulátorů solárních tepelných soustav je možné realizovat bez nadnákladů orientační měření dodaného tepla na základě měření teploty na kolektoru a v dolní části zásobníku (čidla instalována primárně pro účely regulace Δt), pevně zadané hodnoty průtoku, např. nastavené na plovákovém průtokoměru při spuštění soustavy, a údaje o chodu čerpadla (0 nebo 1). Takové stanovení dodaného tepla je značně nepřesné a může být velmi zavádějící, jednak z hlediska měření irelevantních teplot a jednak z důvodu možného kolísání průtoku v solární soustavě.
Kompaktní kalorimetry
Přímé měření dodaného tepla k tomu určenými měřidly (kalorimetry) je možné využít, pokud je teplonosnou kapalinou voda, např. sekundární okruhy solárních soustav s deskovými výměníky. Kalorimetry jsou dodávány v kompaktní konstrukci nebo v provedení s integrační jednotkou a jsou cejchovány pro vodu, často včetně entalpické korekce na změnu termofyzikálních vlastností vody s teplotou. Vlastní výpočet předané tepelné energie ze změřeného průtoku a teplotního rozdílu zajišťuje integrační jednotka, která umožňuje i vyhodnocení minimálních a maximálních teplot, proteklého množství kapaliny atd.
V případě použití nemrznoucích směsí v primárních okruzích solárních soustav nelze kalorimetry přímo použít jednak kvůli termofyzikálním vlastnostem nemrznoucích kapalin obecně odlišným od vody, jednak kvůli závislosti vlastností na směšovacím poměru směsí (různě naředěné nemrznoucí směsi).
Obr. 8.6 – Závislost objemové tepelné kapacity různých teplonosných kapalin
Na obr. 8.6 jsou znázorněny závislosti objemové tepelné kapacity (ρ·c) vody a různě naředěných vodních směsí etylenglykolu a propylenglykolu. Z grafu je zřejmá výrazná odlišnost objemové kapacity nemrznoucích směsí od vody. Zatímco u směsi etylenglykol-voda je odlišný i trend teplotní závislosti tepelné kapacity (s rostoucí teplotou roste), u běžně používaného propylenglykolu je trend změny objemové tepelné kapacity s teplotou obdobný (klesá) jako u vody i při různých poměrech ředění. Při znalosti poměru ředění a přibližné střední teploty nemrznoucí teplonosné kapaliny v průběhu vyhodnocovaného období je možné nepřímo použít pro měření dodaného tepla kalorimetru cejchovaného pro vodu a skutečně dodané teplo vyhodnotit přepočtem pomocí korekčního faktoru, který je dán poměrem objemových tepelných kapacit nemrznoucí směsi a vody. Závislost korekčního faktoru pro vodní směs propylenglykolu na různém stupni ředění pro různé střední provozní teploty (různé typy aplikací) je graficky znázorněna na obr. 8.7 a tabelárně uvedena v tab. 8.1. Korekční faktory pro teplotu tm = 40 °C lze použít pro běžné solární soustavy, hodnoty korekčního faktoru pro střední provozní teplotu teplotu tm = 80 °C platí pro soustavy solárního chlazení. Pro konkrétní soustavy je nutné zohlednit reálnou střední provozní teplotu a stanovit příslušné korekční faktory. Je patrné, že v širokém rozsahu teplot jsou korekční faktory pro dané ředění prakticky stejné, např. pro nejběžnější ředění 50/50 % je korekční faktor 0,91.
Tab. 8.1 – Závislost korekčního faktoru pro různé ředění a střední provozní teploty vodní směsi propylenglykolu
| tt [°C] | poměr ředění | tm = 30 °C | tm = 40 °C | tm = 50 °C | tm = 60 °C | tm = 80 °C |
| -22 | 0,40 | 0,927 | 0,929 | 0,930 | 0,931 | 0,932 |
| -27 | 0,45 | 0,917 | 0,919 | 0,920 | 0,921 | 0,923 |
| -32 | 0,50 | 0,906 | 0,908 | 0,910 | 0,912 | 0,914 |
Výhoda použití běžného kompaktního kalorimetru cejchovaného pro vodu spočívá ve vlastní přesnosti teplotních čidel (párově cejchovány) a možnosti automatického ukládání měsíčních naměřených hodnot do paměti (odečet 1x ročně). Dále je výhodné využití entalpické korekce i přesto, že je teplotní závislost objemové tepelné kapacity směsi propylenglykol-voda je obecně odlišná než u čisté vody. Nicméně závislost má alespoň stejný trend a s klesajícím podílem propylenglykolu se přibližuje závislosti vlastností vody.
Použití kompaktních kalorimetrů s uvedenou korekcí je výhodné pro maloplošné soustavy, neboť jde o finančně výrazně levnější řešení (do 6000 Kč) než při použití průtokoměru, párově cejchovaných čidel a měřicího regulátoru soustavy nebo samostatného dataloggeru se záznamem do paměti (měřicí ústředny).
Obr. 8.7 Závislost korekčního faktoru pro různé ředění a různé provozní teploty vodní směsi propylenglykolu
Regulátory pro měření dodaného tepla
Pro reálné měření dodaného tepla jsou uzpůsobeny vyšší generace solárních regulátorů renomovaných výrobců, které jednak umožňují zapojit více teplotních čidel (přívodní, zpětné potrubí), jednak snímat pulzní výstup odpovídajícího průtokoměru. Na základě zadaného typu nemrznoucí teplonosné kapaliny a poměru jejího ředění s vodou pak vnitřní program regulátoru stanoví výpočtem dodanou tepelnou energii. Pro správné měření je nutné mít spárovaná teplotní čidla, případně provést korekci. To však řada regulátorů neumožňuje, což může nakonec vést k nesprávnému vyhodnocení zisků solární soustavy. Nejjednodušší regulátory zpravidla načítají údaje o dodané energii a ukazují pouze současný stav, tj. energii dodanou od spuštění do současnosti (podobně jako např. elektroměry). Pokročilé typy regulátorů již obsahují paměť s možností záznamu měřených hodnot, případně grafickou vizualizaci po jednotlivých dnech, viz obr. 8.8.
Obr. 8.8 Vizualizace denních zisků na displeji regulátoru
Pokročilý monitoring solárních soustav
Pokročilé přesné měření předpokládá použití nezávislého systému monitorování (průtokoměr, teplotní čidla, datalogger, webserver a internetová aplikace pro zobrazení měřených údajů), umožňujícího v nastavitelném časovém kroku odečítat dodanou energii s ohledem na vlastnosti teplonosné kapaliny, ukládat údaje a vyhodnocovat jednotlivá období (dny, týdny, měsíce), případně pravidelně zveřejňovat vybrané údaje na přidělené internetové stránce (online monitoring, vyhodnocené úspory, datové reporty). Cena závisí na složitosti systému měření, zpravidla se pohybuje v řádech desetitisíců. Použití monitoringu se předpokládá především pro velkoplošné solární soustavy s vysokými investičními náklady.
8.2.4 Měření průtoku a spotřeby plynu
V případě plynového hořáku pracujícího přímo do akumulačního zásobníku nebo průtokového plynového ohřívače je nutné měřit spotřebu zemního plynu plynoměrem a odečítat ji v pravidelných intervalech, nebo využít plynoměrů s pulzním výstupem pro zpracování měřicí ústřednou (dataloggerem).
Obr. 8.9 Plynoměr s pulzním výstupem
8.2.5 Měření elektrické energie
V solárních soustavách se měří elektrická energie:
- předaná do tepelné soustavy jako energie dodatkového zdroje tepla (elektrokotel, elektrické otopné těleso v zásobníku);
- zajišťující funkci solární soustavy (pomocná energie: oběhová čerpadla, regulátor).
Spotřeba elektrického dodatkového zdroje tepla solární soustavy, podobně jako neelektrického, se vyhodnocuje pro stanovení skutečného podílu solárních zisků na celkové spotřebě tepla v soustavě.
Měření pomocné energie by mělo zahrnovat měření veškeré elektrické energie spotřebovávané vlastní solární soustavou, tedy spotřeby elektrické energie pro prvky výhradně související s instalací solární soustavy (nikoliv se stávající přípravou teplé vody nebo vytápění). Jedná se především o oběhová čerpadla, regulátor solární soustavy, elektricky ovládané ventily aj., které je pak vhodné sdružit pod jeden přívod elektrické energie a opatřit jediným jednofázovým elektroměrem. Zobrazovanou hodnotu spotřebované elektrické energie je vhodné zapisovat v definované periodě (např. jednou za rok, jednou za měsíc v referenční den), nebo v případě možnosti napojit na monitorovací systém.
Elektrická energie, tj. práce elektrického proudu, se měří elektroměry. Pro měření spotřeby elektrické energie ve střídavých jednofázových i trojfázových sítích se používají:
- indukční elektroměry;
- elektronické impulzní elektroměry.
Indukční elektroměry
Indukční elektroměry jsou založeny na otáčení kovového kotouče vyvolané magnetickým polem proudové a napěťové cívky. Magnetické toky vytvářejí podobně jako v jednofázovém indukčním motoru točivé magnetické pole, které otáčí kotoučem, jímž protékají vířivé proudy. Točivý moment je úměrný proudu v proudové cívce, tedy v měřené síti odběratele elektrické energie. Otáčející se kotouč pohání bubínkové mechanické počítadlo s takovým (šnekovým) převodem, že údaj na počítadle odpovídá spotřebě elektrické energie v kWh, viz obr. 8.10.
Obr. 8.10 Indukční elektroměr s mechanickým počítadlem
Elektronické elektroměry
U elektronických impulzních elektroměrů se využívá elektronického wattmetru (měří se vnitřní pulzy generované polovodičovým relé úměrně měřené energii). Konstanta elektroměru se udává v impulzech na 1 kWh. Přístroje mají mnoho funkcí, například měření maximální spotřeby, vícesazbové měření, ukládání časového odběrového diagramu do paměti, komunikace s počítačem či datová komunikace po rozvodné síti. Elektronické elektroměry jsou zpravidla vybaveny LCD displejem (viz obr. 8.11) nebo mechanickým číselníkem (dražší provedení).
Obr. 8.11 Elektronický elektroměr s displejem
Zapojení elektronických elektroměrů je vhodné provést do rozvaděče na DIN lištu. Galvanicky oddělený pulzní výstup umožňuje externí měření spotřeby elektrické energie (svorky S0). Pulzní číslo odpovídá odebíranému elektrickému příkonu (elektroměry s možností nastavení pulzního čísla).
8.2.6 Měření slunečního ozáření
Pro účely vyhodnocování celkové účinnosti a stupně využití sluneční energie solárními soustavami je nutné znát celkovou sluneční energii, dopadající na kolektory během roku. Měření sluneční energie se provádí tzv. pyranometry (někdy nesprávně označovanými jako solarimetry). Pyranometry jsou přístroje pro měření celkového slunečního ozáření (přímé, difuzní a odražené) nejčastěji na vodorovnou plochu (v meteorologii), nebo na obecně skloněnou v rovině kolektorů (pro vyhodnocování solárních soustav). Pro přesné měření musí mít čidla těchto přístrojů odezvu nezávislou na vlnové délce v celém solárním spektru od 0,3 do 3,0 mm a na úhlu dopadu slunečního záření.
Vzhledem k pořizovacím nákladům na kvalitní pyranometry se měření slunečního ozáření uplatňuje pouze u velkoplošných solárních soustav.
Termočlánkové (teplotní) pyranometry
V současné době existují dva nejužívanější koncepty čidel, které vyhodnocují sluneční ozáření na základě rozdílu teplot:
- mezi dvěma různě pohltivými povrchy (bílý a černý) vystavenými slunečnímu záření – segmentové, hvězdicové;
- mezi načerněným povrchem a okolní teplotou – terčíkové.
Čidla jsou často kryta jedním nebo dvěma polokulovými kryty pro zabránění vlivu dlouhovlnného záření a ochlazování čidla účinky větru, případně vedením do okolního prostředí. Dvojitý kryt zabezpečuje také vysokou těsnost přístroje vůči atmosférickým vlivům. Kryty musí mít rovnoměrnou tloušťku, aby nezpůsobovaly nerovnoměrnou distribuci slunečního záření na čidlo.
Především v USA je rozšířený tzv. segmentový pyranometr, který má čidlo složené ze 12 tenkých měděných radiálních segmentů (viz obr. 8.12), střídavě černých a bílých. V každém segmentu je 6 termočlánků (chromel-konstantan), tzn. dohromady 72 termočlánkových spojů. Černé segmenty čidla jsou opatřeny vysoce pohltivou černí, bílé segmenty nátěrem, který vykazuje téměř dokonalý odraz slunečního záření. Při vystavení slunečnímu záření dochází k teplotnímu rozdílu mezi černými a bílými segmenty. Teplotní rozdíl je přímo úměrný slunečnímu ozáření a není závislý na teplotě okolí.
Na obdobném principu pracuje čidlo, skládající se ze dvou soustředných stříbrných prstenců. Vnější prstenec je povlakován oxidem hořčíku, který má vysokou odrazivost pro záření v solárním spektru, na vnitřní prstenec je nanesena optická čerň s velmi vysokou pohltivostí slunečního záření. Teplotní rozdíl mezi prstenci je snímán termočlánkem a je měřítkem pohlceného sluneční záření. Kruhová symetrie čidla minimalizuje vlivy azimutového úhlu na odezvu přístroje. Čidlo je zakryto jednoduchou skleněnou kupolí. Přístroj obsahuje teplotní kompenzaci (-20 až +40 °C).

Obr. 8.12 Segmentový pyranometr
V Evropě jsou běžnější Moll-Gorczynskiho (terčíkové) pyranometry (viz obr. 8.13), využívající Mollův termočlánek pro měření teplotního rozdílu mezi černým povrchem čidla a tělem přístroje. Tělo přístroje si udržuje rovnoměrnou teplotu okolí bez výrazných výkyvů vlivem náhodných teplejších (nebo chladnějších) proudů. Jelikož na teplotě těla přístroje závisí výsledný údaj čidla, je nutné tělo chránit před osáláním slunečním zářením krytem. Samotný černý pohltivý terč čidla s termočlánkovou sestavou je kryt jednoduchou (méně přesné, levnější) nebo dvojitou skleněnou kupolí, sloužící k ochraně proti atmosférickým vlivům. Při měření pyranometry při jiných sklonech než vodorovných je nutné si uvědomit, že nakloněním pyranometru se mění podmínky volného proudění uvnitř skleněné kupole s čidlem a přenos tepla z termočlánku na kryt a jiné části zařízení. Pro přesné měření je proto nutné uvažovat korekci na sklon pyranometru (zpravidla 1-2 %).
Obr. 8.13 Moll-Gorczynskiho terčíkový pyranometr
Polovodičové snímače
Vzhledem k vysokým cenám kvalitních pyranometrů na bázi sériových termočlánků (nad 20 tisíc Kč) se hledají levnější čidla s dostatečnou přesností (do 2 tisíc Kč). Takovými kandidáty jsou zpravidla pyranometry pracující s polovodičovými snímači (fotodiody, fototranzistory, fotovoltaické články), viz obr. 8.14.
Obr. 8.14 Polovodičové snímače slunečního záření
U fotovoltaických čidel je z hlediska přesnosti měření a použitelnosti pro vyhodnocování hlavní nevýhodou jejich odlišná spektrální odezva od rozložení solárního spektra (viz obr. 8.15). Pokud by spektrální charakteristika slunečního záření byla stálá, bylo by možné kalibrací tento jev odstínit. Nicméně, spektrální rozložení slunečního záření se mění, a to především v závislosti na oblačnosti a obsahu vodní páry v ovzduší, což vede ke zvýšené nejistotě měření slunečního záření. Levná čidla navíc mají ochranné kryty zpravidla z plastů (plexisklo), které mohou vést k problémům s dlouhodobou životností (otěr, změna propustnosti) či přesností výroby krytu (konstantní tloušťka, tvar). Na druhé straně odezva fotovoltaických čidel na sluneční záření je v zásadě konstantní a lineární. Teplotní závislost čidla je relativně malá.
Obr. 8.15 Spektrální odezva základních typů čidel slunečního záření pro různé vlnové délky
8.3 SOLÁRNÍ SOUSTAVY PRO PŘÍPRAVU TEPLÉ VODY DO 20 M2
Z hlediska principu měření je nutné solární soustavy pro přípravu teplé vody rozdělit podle druhu zapojení na soustavy s předehřívacím zásobníkem (monovalentním, pouze výměník solárního okruhu) a s centrálním zásobníkem (bivalentním, výměník solárního okruhu a okruhu doplňkového zdroje tepla).
8.3.1 Solární soustavy pro přípravu TV s předřazeným zásobníkem
U solární soustavy s předřazeným solárním zásobníkem konvenční přípravě teplé vody (zásobníkový, průtokový dohřev) je solární soustava jasně oddělená od vlastní přípravy teplé vody (viz obr. 8.16). Vyhodnocení tepelné energie dodané solární soustavou se zajišťuje přesným měřením na okruhu předehřevu teplé vody před vstupem do dohřívacího zásobníku nebo průtokového ohřívače běžným měřičem tepla (kalorimetrem) cejchovaným a použitelným pro vodu, včetně korekce na její teplotu (entalpická korekce). Teplotní čidla snímají teplotu studené vody a předehřáté vody na výstupu z předřazeného solárního zásobníku. Měřené dodané teplo zahrnuje všechny tepelné ztráty související s instalací solární soustavy. Pozornost je nutné věnovat volbě návrhového průtoku měřiče tepla, která by měla zohlednit předpokládanou úroveň průtoků. Volbou příliš vysokého jmenovitého průtoku QN měřiče tepla oproti odběrovým průtokům studené vody do ohřívačů dochází ke snížené přesnosti měření.
Obr. 8.16 Schéma měření na solární soustavě pro přípravu TV s předřazeným zásobníkem
8.3.2 Solární soustavy pro přípravu TV s bivalentním zásobníkem
U zapojení solární soustavy s bivalentním zásobníkem, ve kterém je v jeho horní části teplá voda dohřívána doplňkovým zdrojem tepla na požadovanou teplotu, je možné teplo dodané solární soustavou měřit pouze na primárním okruhu s nemrznoucí směsí (viz obr. 8.17). Část tepelných ztrát centrálního zásobníku, odpovídající instalaci solární soustavy, tedy z principu není zahrnuta do měřených hodnot solárních zisků. Vyhodnocování dodané energie na primárním okruhu solární soustavy musí zohledňovat tepelnou kapacitu a hustotu nemrznoucí směsi obecně odlišné od vlastností vody, navíc významně závislé na poměru ředění a teplotě. Pro měření dodaného tepla ze solární soustavy je možné využít pokročilých solárních regulátorů, vybavených teplotními čidly a průtokoměrem.
Obr. 8.17 Schéma měření na solární soustavě pro přípravu TV s bivalentním zásobníkem
8.4 KOMBINOVANÉ SOLÁRNÍ SOUSTAVY PRO PŘÍPRAVU TV A VYTÁPĚNÍ DO 20 M2
Naprostá většina kombinovaných solárních soustav je realizována s kombinovaným zásobníkem otopné vody (OV, určené k vytápění) s vestavěnou teplosměnnou plochou pro předehřev teplé vody (průtokový trubkový výměník, vestavěný zásobník TV). Z hlediska provozního vyhodnocování je vhodné odlišit soustavy s předehřevem teplé a otopné vody v předřazeném zásobníku před doplňkovým zdrojem tepla od soustav s dohřevem teplé a otopné vody v centrálním zásobníku s vestavěným doplňkovým zdrojem tepla.
8.4.1 Kombinované solární soustavy s předřazeným zásobníkem
Podobně jako u solární soustavy pro předehřev teplé vody je možné u kombinované soustavy s předřazeným zásobníkem stanovit měřením na vodních okruzích (předehřátá TV a OV) celkové dodané teplo solární soustavou, včetně zahrnutí tepelných ztrát souvisejících s její instalací (tepelné ztráty potrubního rozvodu, předřazeného solárního zásobníku tepla).
Pro efektivní funkci solární soustavy a pro vyhodnocení skutečných přínosů solární soustavy je nutné správné zapojení a regulace solární soustavy. Dodatkový zdroj tepla nesmí dodávat žádným způsobem teplo do předřazeného zásobníku. V případě, že by dodatkový zdroj přes vratné potrubí otopné soustavy dodával teplo do předřazeného zásobníku a zvyšoval jeho teplotu, potom se nejedná o kombinovanou soustavu s předřazeným zásobníkem. Trojcestný ventil (viz schéma na obr. 8.18) slouží k přepínání mezi odběrem tepla z předřazeného zásobníku nebo z dodatkového zdroje tepla.
Vyhodnocení tepelné energie dodané solární soustavou se zajišťuje přesným měřením dvěma měřiči tepla cejchovanými pro vodu s odpovídajícími parametry (měřený průtok, teplotní rozdíl). U měření tepla dodaného do otopné soustavy je nutné při volbě měřiče tepla zohlednit průtok otopnou soustavou (proměnlivý, konstantní) a měřený rozdíl teplot (proměnlivý, závislý na období).
Obr. 8.18 Schéma měření na solární kombinované soustavě s předřazeným zásobníkem
8.4.2 Kombinované solární soustavy s kombinovaným zásobníkem
V zapojení kombinované solární soustavy s kombinovaným zásobníkem, ve kterém je v jeho horní části teplá voda dohřívána doplňkovým zdrojem tepla na požadovanou teplotu a ve střední části je udržována otopná voda na požadované ekvitermní teplotě, je možné dodané teplo solární soustavou měřit opět v podstatě pouze na primárním okruhu s nemrznoucí směsí – podobně jako u solární soustavy pro přípravu teplé vody; část tepelných ztrát kombinovaného zásobníku, odpovídající instalaci solární soustavy, z principu není zahrnuta do měřených hodnot solárních zisků. Vyhodnocování dodané energie na primárním okruhu solární soustavy se řeší příslušným zařízením (viz obr. 8.19).
Obr. 8.19 Schéma měření na solární kombinované soustavě s kombinovaným zásobníkem
8.5 VELKOPLOŠNÉ SOLÁRNÍ SOUSTAVY
Pod pojmem velkoplošné solární soustavy se rozumí soustavy s výrazně většími instalovanými plochami solárních kolektorů, např. solární soustavy pro bytové domy, hotely, zdravotnická zařízení (nemocnice, kliniky), sportovní centra, veřejné budovy (studentské koleje, internáty atd.), průmyslové aplikace apod. Vzhledem k výrazně vyšším očekávaným absolutním energetickým a emisním úsporám než u maloplošných soustav (do 20 m2) je zde význam provozního sledování daleko větší, neboť nevhodným návrhem, instalací nebo provozem solární soustavy dochází k výrazným energetickým, ekologickým a ekonomickým ztrátám.
Například realizace velkoplošných solárních soustav pro bytové domy v ČR jsou teprve v počátečním stadiu, není k dispozici téměř žádná zkušenost z navrhování a provozování takových solárních soustav (nepočítáme-li nestandardní domy s pečovatelskou službou, domovy důchodců a podobná zařízení). Proto je zásadně zapotřebí dlouhodobého provozního sledování takových realizovaných soustav, vyhodnocení a uveřejnění výsledků energetických přínosů pro odbornou veřejnost.
Z hlediska finanční náročnosti provozního sledování a vyhodnocování velkoplošných solárních soustav je vhodné je rozdělit na soustavy s plochou solárních kolektorů do 200 m2 a nad 200 m2. Zatímco investičně levnější soustavy je nutné osadit odpovídajícím pokročilým provozním měřením energetických toků, u investičně náročných je možné uvažovat o komplexním provozním sledování chování soustavy s možností identifikace případných provozních problémů a nejslabších prvků realizované soustavy (optimalizace).
8.5.1 Solární soustavy pro přípravu teplé vody do 200 m2
Pro velkoplošné soustavy pro přípravu teplé vody obecně se v primárním okruhu předpokládá použití odděleného solárního akumulačního zásobníku (zásobníků), napájených z vnějšího deskového solárního výměníku. Výstup předehřáté teplé vody napájí pohotovostní (dohřívací) zásobník s doplňkovým zdrojem tepla. Tepelné zisky dodané solární soustavou se měří běžným cejchovaným měřičem tepla (kalorimetrem) na vstupu do pohotovostního zásobníku. Měření tepelných zisků autonomními kalorimetry je jednoduché a levné. Kalorimetry cejchované pro vodu jsou běžně dostupné na trhu, a umožňují ukládání souhrnných hodnot za kalendářní měsíc do paměti (odečet jednou za rok vyvoláním historie údajů).
Obr. 8.20 Schéma měření na solární soustavě pro přípravu teplé vody (bez cirkulace) s jednoduchým meřicím systémem na bázi svou kalorimetrů (P1-T1-T2: solární zisky, P2-T3-T4: celková potřeba tepla, P3-T5-T6 doplňkový zdroj tepla)
Vzhledem k velikosti solární soustavy a její investiční náročnosti se dále měří dodatková energie na dohřev teplé vody (kalorimetr, plynoměr, elektroměr), aby bylo možné stanovit solární pokrytí. Samozřejmé je měření pomocné energie pro pohon soustavy (oběhová čerpadla primárního solárního okruhu a sekundárního okruhu, regulace), viz obr. 8.20.
8.5.2 Solární soustavy s plochou kolektorů nad 200 m2
U velmi rozsáhlých soustav se nabízí možnost monitorování více parametrů (sluneční záření, potřeba tepla stavby pro vytápění a přípravu teplé vody, účinnost akumulace, atd.), viz obr. 8.21.
Měřené parametry:
- spotřeba teplé vody, spotřeba tepla na přípravu teplé vody (odběr): průtok, teploty;
- tepelné ztráty cirkulace (průtok, teploty);
- celkové dodané energie dodatkovým zdrojem tepla: průtok, teploty;
- dopadlé sluneční energie (účinnost soustavy): ozáření (pyranometr);
- pomocné elektrické energie na pohon celé soustavy: elektroměr;
- měření doby běhu solární soustavy (z průtokoměru);
- teploty v primárním okruhu, teploty v sekundárním okruhu (účinnost výměníku);
- teploty v horní, střední a dolní části solárního zásobníku;
- teplota ve střední části pohotovostního zásobníku.
Obr. 8.21 Schéma měření na solární soustavě pro přípravu teplé vody (bez cirkulace) s komplexním meřicím systémem
Měření dodané energie se realizuje samostatnými průtokoměry a teplotními čidly. Všechny měřicí přístroje a čidla jsou zapojeny do měřicí ústředny, která naměřené údaje vyhodnocuje (výpočet veličin a charakteristických parametrů) a ukládá do paměti. Ukládání se provádí v časovém intervalu 1 min (a méně). Uložené údaje mohou sloužit pro pozdější případnou kontrolu funkce soustavy a analýzu provozních problémů. Za určité časové období (měsíc, rok) ústředna automaticky vyhodnocuje využitelné solární zisky, množství dodatkové energie, solární pokrytí, účinnost soustavy za dané časové období.
9 EKONOMIKA SOLÁRNÍCH SOUSTAV
Ekonomické parametry solárních soustav jsou předmětem řady více či méně čísly podložených diskuzí, neboť výsledky ekonomických analýz vždy výrazně závisejí na kvalitě vstupních údajů. Pro vlastní ekonomické zhodnocení solárních soustav je nutné určit řadu parametrů, které ekonomickou výhodnost instalace solární soustavy významně ovlivňují:
- investiční náklady solární soustavy;
- provozní náklady;
- energetické zisky solární soustavy;
- úspora energie instalací solární soustavy;
- diskontní sazba (míra ceny investovaného kapitálu);
- místní cena energie a její předpokládaný růst.
9.1 INVESTIČNÍ NÁKLADY
Do investičních nákladů na instalaci solární soustavy se započítávají všechny výdaje spojené s instalací solární soustavy, od ceny studie, projektu, materiálu, dopravy a montáže po nezbytné stavební úpravy, které instalace solární soustavy vyvolá. Právě stavební úpravy (kotvení nosných konstrukcí k plášti budovy, zajištění hydroizolací, úpravy pro strojovnu apod.) mohou investici do solární soustavy, zvláště u stávajících budov, významně zvýšit. Tyto nadnáklady jsou místně specifické a obtížně postižitelné statisticky. Na druhé straně do nákladů na solární soustavu se nemohou započítávat náklady sice časově související s instalací solární soustavy, ale vynucené vlastní nezbytnou rekonstrukcí budovy (např. střechy). Optimální je spojení instalace solární soustavy s rekonstrukcí rozvodů teplé vody, změnou otopné soustavy nebo výměnou zdroje tepla.
Obr. 9.1 Rozdělení investičních nákladů na solární soustavu, zpracováno podle konkrétních realizací
Investiční náklady na instalaci solární soustavy jsou silně závislé na instalované ploše a typu solárních kolektorů, neboť velikost a tedy i cena prvků solární soustavy souvisí s velikostí navržené plochy solárních kolektorů:
- objem solárního zásobníku tepla se odvíjí od plochy kolektorů, slouží k akumulaci zisků z kolektorů;
- výměník tepla přenáší tepelný výkon solárních kolektorů, daný jejich plochou;
- světlost potrubí je dána průtokem kolektory na základě celkového výkonu (plochy) kolektorů;
- tloušťka tepelné izolace potrubí je dána světlostí potrubí;
- oběhové čerpadlo je určeno na základě průtoku a tlakové ztráty, související se světlostí potrubí;
- objem expanzní nádoby primárního okruhu se odvíjí se od objemu potrubí a instalovaných kolektorů;
- rozměry a počet nosných konstrukcí na kolektory je dán rozměrem a počtem kolektorů.
Obecně platí, že čím větší je solární soustava, tím nižší jsou měrné investiční náklady na solární soustavu vztažené na 1 m2 instalované plochy solárního kolektoru, a tím více celkové náklady závisejí na ceně solárního kolektoru. Na obr. 9.1 je uvedeno typické rozdělení nákladů na solární soustavu pro různě velké soustavy s plochými solárními kolektory. Zatímco u malých soustav tvoří kolektory 30 až 40 % ceny instalace a měrné náklady se pohybují 25 až 30 tisíc Kč/m2, u větších solárních soustav nad 50 m2 je podíl kolektorů téměř 50 % a náklady mohou v ideálním případě klesnout až na cca 15 až 20 tisíc Kč/m2. V případě použití trubkových vakuových solárních kolektorů lze očekávat náklady na solární soustavu o 25 až 50 % vyšší při stejné instalované ploše kolektorů.
9.1.1 Solární kolektory
Cena solárních kolektorů vztažená na m2 apertury významně ovlivňuje celkovou cenu investice. Ploché solární kolektory v průměru vykazují nižší měrnou cenu (poloviční až třetinová) oproti trubkovým vakuovým kolektorům s plochým, resp. válcovým absorbérem (Sydney) bez reflektoru nebo s reflektorem. Na obr. 9.2 jsou uvedeny měrné ceny (bez DPH) různých typů solárních kolektorů vztažené k ploše apertury.
Obr. 9.2 Cena solárních kolektorů různých konstrukčních typů (bez DPH) vztažená k 1 m2 apertury
9.1.2 Solární zásobníky
Další významnou položkou v nákladech na solární soustavu jsou solární zásobníky a jejich příslušenství (izolace, expanze, jímky, čidla). Cena zásobníků se liší podle účelu použití (zásobníky teplé vody, zásobníky otopné vody), vnitřní povrchové úpravy (bez úpravy, smalt), případně použitého materiálu (uhlíková ocel, nerezová ocel). Na obr. 9.3 jsou uvedeny ceny solárních akumulačních zásobníků bez výměníků tepla (nádrže) a průměrné měrné ceny, vztažené na objem zásobníku.
Obr. 9.3 Měrná cena zásobníků teplé vody a zásobníků otopné vody (včetně tepelné izolace)
Z grafu je patrné, že nízkonákladové řešení solární soustavy pro přípravu teplé vody dává přednost smaltovaným zásobníkům teplé vody před trvanlivějšími, avšak výrazně dražšími nerezovými. U velkých soustav je určitým kompromisem provedení solární přípravy teplé vody s vyrovnávacími zásobníky tepla (uhlíková ocel), ze kterých je teplo předáváno do pohotovostního nerezového zásobníku teplé vody přes výměník.
V případě rodinných domů existuje na trhu nepřehledné množství vyráběných typů solárních zásobníků teplé vody a kombinovaných zásobníků s velmi odlišnými měrnými cenami, navíc i významně závislými na objemu či na vystrojení zásobníku.
9.1.3 Potrubí
V nákladech na solární soustavu může významnou roli hrát i cena potrubí a tepelné izolace. Světlost potrubí hlavní větve primárního okruhu je dána velikostí kolektorové plochy, návrhem průtoku (nízký průtok, vysoký průtok) a hydraulickým návrhem (např. snaha o minimalizaci tlakových ztrát). Cena potrubí je výrazně dána jeho světlostí. Na obr. 9.4 jsou uvedeny měrné ceny měděného a ocelového potrubí pro různé světlosti. Je patrné, že u měděného potrubí cena od rozměru 42×1,5 mm začíná strmě růst. Proto se u větších světlostí primárního okruhu solárních soustav měděné potrubí nahrazuje ocelovým. Pracnější montáž je kompenzována nižší cenou potrubí.
Pro snížení investice do potrubí se velkoplošné solární soustavy projektují jako soustavy s nízkým průtokem (low-flow, 10 až 20 l/h·m2) a vysokým ohřátím teplonosné kapaliny v kolektoru (nad 30 K). Solární „low-flow“ soustava však zároveň předpokládá pokročilý systém řízeného nabíjení více zásobníků podle teploty, která je k dispozici na výstupu z kolektoru, nebo řízeného teplotního vrstvení objemu uvnitř zásobníků samočinnými stratifikačními vestavbami či kombinaci obou přístupů.
Obr. 9.4 Porovnání měrných cen měděného a ocelového potrubí
9.1.4 Tepelná izolace
Na světlosti potrubí závisí tloušťka tepelné izolace. Pro potrubí solárních soustav se obecně doporučuje tloušťka izolace rovná průměru potrubí, což zároveň přibližně odpovídá požadavkům vyhlášky [1] na instalaci tepelné izolace rozvodů tepelných soustav obecně. Na základě analýzy hospodárné tloušťky tepelné izolace je však možné stanovit hodnoty jiné (menší).
Obr. 9.5 Porovnání měrných cen tepelných izolací
Na obr. 9.5 jsou uvedeny ceny používaných tepelných izolací pro primární okruh solárních soustav na bázi EPDM (uzavřená nenasákavá struktura, UV odolná, tmax = 175 °C) a minerální vlny (otevřená struktura, kašírovaná Al, tmax = 280 °C). I když cena minerální izolace je především pro větší světlosti potrubí velmi příznivá, je nutné v případě venkovních instalací počítat s použitím plechového opláštění izolace jako ochrany před atmosférickými vlivy (vlhkost, vítr). Použití hliníkového oplechování zvyšuje cenu rozvodu o cca 100 Kč/m.
9.1.5 Sazba daně z přidané hodnoty
Pro investiční náklady v případě dodávky instalace solárních soustav na klíč ve stavbách pro sociální bydlení lze uvažovat podle zákona o DPH [2] sníženou sazbu 10 %. Do definice staveb pro sociální bydlení spadají
- rodinné domy s podlahovou plochou menší než 350 m2;
- bytové domy s byty s celkovou podlahovou plochou menší než 120 m2.
Sníženou sazbu DPH lze proto uvažovat v naprosté většině instalací solárních soustav v běžných domech.
9.2 DOTAČNÍ PODPORA
Investiční náklady na instalaci solární soustavy mohou být významně sníženy veřejnými podporami, buď ve formě:
- paušálního příspěvku na bytovou jednotku (byt, dům);
- na m2 kolektorové plochy;
- nebo ve formě procenta z investičních nákladů.
Paušální podpora sleduje především maximalizaci solárního pokrytí, tzn. za daný finanční objem dotace se očekává co největší zisk energie a úspora primárních paliv (např. dříve národní program podpor nebo dotační program Zelená úsporám). Procentní podpora, kde dotace tvoří poměrnou částku z celkových uznatelných investičních nákladů, sleduje i ekonomické parametry podpořené solární soustavy jako je investiční náročnost uspořené energie nebo úspory emisí, tzn. zda jsou finanční prostředky dotace vynakládány efektivně (např. Operační program Životní prostředí).
9.3 PROVOZNÍ NÁKLADY
Finanční prostředky vynakládané na zajištění funkce solární soustavy působí proti úsporám poskytovaným solární soustavou. Patří mezi ně především náklady na pomocnou energii pro pohon solární soustavy, servisní náklady na obsluhu a údržbu zařízení, případné opravy, náklady na pojištění apod. Obecně opět platí, že čím větší je solární soustava, tím menší jsou poměrné provozní náklady vztažené k dosaženému zisku nebo kolektorové ploše.
9.3.1 Náklady na pomocnou energii
Náklady spojené se spotřebou pomocné elektrické energie pro pohon solární soustavy (spotřeba čerpadel, regulace aj.) závisejí na velikosti solární soustavy a ceně elektrické energie. Spotřeba pomocné elektrické energie se u rodinných domů pohybuje mezi 3 a 5 % využitého tepelného zisku solární soustavy, zatímco u větších solárních soustav klesá pod 1 %.
9.3.2 Náklady na servis
Roční servisní náklady na údržbu a opravy je možné odhadnout ve výši 0,3 až 0,5 % z investičních nákladů na pořízení soustavy (bez dotace) [3]. Procento je nižší než u konvenčních zdrojů energie, neboť opotřebení solární soustavy za běžných provozních podmínek je nižší. Čím větší je solární soustava, tím je možné uvažovat procento nižší. Údržba se skládá především z vizuální kontroly, kde náklady jsou z velké části spojené s dopravou. Výměna solární kapaliny se provádí cca po 8 až 10 letech, výměna oběhových čerpadel po cca 10 letech, výměna zásobníků po cca 15 letech.
9.4 CENA ENERGIE A JEJÍ PŘEDPOKLÁDANÝ RŮST
Cena nahrazované energie zásadně ovlivňuje ekonomiku solární soustavy a je nezbytné vycházet z konkrétní místní situace, konkrétní ceny za teplo dodávané nahrazovaným zdrojem tepla pro daný účel. V grafu na obr. 9.6 jsou uvedeny ceny různých energonositelů pro domácnosti v letech 2005 až 2012.
Současná cena elektrické energie pro domácnosti (D45d, rok 2012) se v nízkém tarifu pohybuje okolo 2,5 Kč/kWh vč. DPH (včetně distribuce, příplatku na OZE apod.). Do ceny elektrické energie pro výpočet návratnosti se nezapočítávají stálé poplatky za instalovaný jistič, neboť úsporou spotřeby energie instalací solární soustavy se nijak nemění. Růst cen elektrické energie pro domácnosti za poslední roky je cca 12 %. V grafu jsou na obr. 9.6 uvedeny ceny pro domácnosti v sazbě přímotopného vytápění (D45d, 20 h nízký tarif, Pražská energetika) [4].
Cena energie zemního plynu se během roku mění (čtvrtletně); cena k lednu 2009 se pro běžný odběr do 9,45 MWh/rok (vytápění zemním plynem) pohybovala na úrovni okolo 1,4 Kč/kWh vč. DPH. Stálý měsíční plat se pro ekonomické hodnocení do ceny energie zemního plynu nezapočítává. Přestože koncem roku 2009 došlo k výraznému poklesu (až na ceny okolo 1,1 Kč/kWh), lze uvažovat průměrný růst ceny energie zemního plynu u různých dodavatelů v posledních letech cca 9 %. V grafu na obr. 9.6 jsou uvedeny ceny pro domácnosti vytápěné zemním plynem (Pražská plynárenská) [4].
Ceny dálkového tepla dodávaného konečným spotřebitelům v rámci systémů centralizovaného zásobování teplem (CZT) se v roce 2009 pohybovaly mezi 450 až 700 Kč/GJ (1,6 až 2,5 Kč/kWh) vč. DPH v závislosti na palivové základně a konkrétní lokalitě. Růst cen tepla z CZT se v letech 2005-2009 (ceny z pozdějších let nemá autor k dispozici) pohybuje na úrovni 7 % (uhlí) až 10 % (ostatní paliva, např. plyn) [5], nicméně lze předpokládat obdobný trend. V grafu na obr. 9.6 jsou uvedeny ceny na úrovni předávací stanice (kotelny) v domě.
Obr. 9.6 Trend růstu cen energie v ČR pro vybrané energonositele (k lednu uvedeného roku)
V časovém horizontu životnosti solární soustavy (20 a více let) nelze cenu konvenční energie seriózně předpovědět. To je nutné mít na paměti při jakýchkoli ekonomických výpočtech návratnosti.
9.5 ČASOVÁ HODNOTA INVESTICE
Pro reálnější odhad skutečných ekonomických přínosů realizace solárních soustav se zohledňuje časová hodnota investovaných finančních prostředků použitím předpokládané diskontní míry. Diskontní míra vyjadřuje výnosovou míru, se kterou je možné počítat ve srovnatelně rizikových investičních alternativách jako je investice do solární soustavy (velmi jistá, každoročně přibližně stálý zisk). Diskontování zohledňuje časovou hodnotu peněz, převádí budoucí hodnotu investice na současnou. Jako diskontní míru lze uvažovat například úrokovou míru (zhodnocení finančních prostředků uložením v bance, nebo úrok úvěru při nutné půjčce od banky). Pro obecné hodnocení projektů energetických úspor se běžně používá zpravidla diskontní míra okolo 5 %, u podnikatelských záměrů (firem) se používá hodnota průměrných nákladů na kapitál (požadovaný výnos, podniková diskontní míra). V případě soukromníků (majitelé domů, bytů apod.) vždy záleží na konkrétní situaci. Pokud má investor své finanční prostředky na účtu v bance s úrokem 1 %, je nutné počítat s diskontní mírou těchto prostředků 1 %. Pokud si na investici musí naopak od banky půjčit, diskontní mírou bude roční procentní sazba nákladů (RPSN), zohledňující všechny náklady spojené s půjčkou.
9.6 EKONOMICKÉ EXTERNALITY
Obtížně kvantifikovatelný při posuzování ekonomických parametrů solárních soustav je vliv produkce energie z tradičních paliv na zdraví obyvatel a životní prostředí spojené s nadnáklady na zdravotní péči a sanaci ekologických škod (těžba a spotřeba paliv). Výrazná nejistota leží také v předpovědi nákladů na konvenční energetické zdroje v budoucnosti, která souvisí s riziky výroby energie, těžby fosilních paliv, hrozeb a případných řešení ozbrojených konfliktů souvisejících s přístupem ke zdrojům energie. Postihnout tyto externality a zahrnout je do reálné ceny konvenčních paliv je velmi obtížné. Řada evropských států zpoplatňuje fosilní paliva formou ekologických daní. V Evropě se výhledově počítá se zavedením tzv. „uhlíkové“ daně.
9.7 NÁVRATNOST VLOŽENÝCH INVESTIC
Při ekonomických analýzách investic do solárních soustav se podobně jako u jiných opatření na úsporu energie hodnotí prostá doba návratnosti a diskontovaná doba návratnosti.
9.7.1 Prostá návratnost
Prostá doba návratnosti τp nezohledňuje skutečnou časovou hodnotu peněz a peněžní toky za dobu návratnosti; proto je její vypovídací schopnost omezená, zkresluje pohled na efektivnost investice a slouží jen jako pomocné orientační kritérium pro investiční rozhodování. Prostá návratnost určuje, za jak dlouho pokryjí nediskontované úspory energie instalací solární soustavy její investiční náklady.
(9.1)
kde je
IN … investiční náklady na solární soustavu, v Kč;
RU … roční úspora nákladů instalací solární soustavy, někdy označovaná jako CF (cash flow), v Kč/rok.
9.7.2 Reálná (diskontovaná) návratnost
Uvažováním výnosové míry alternativní investiční příležitosti a předpokládaného tempa růstu ceny nahrazované energie v budoucnosti lze získat dobu návratnosti o lepší vypovídací schopnosti než má prostá návratnost. Reálná doba návratnosti τd je definována jako doba (konkrétní rok), kdy skutečný výnos pokryje počáteční investici podle podmínky
(9.2)
kde je
IN … investiční náklady na solární soustavu, v Kč;
RU … roční úspora nákladů instalací solární soustavy, v Kč/rok.
p … tempo růstu ceny konvenční energie;
r … diskontní (výnosová) míra;
t … doba, v letech.
Na obr. 9.7 je grafickým způsobem porovnán výpočet návratnosti s různými variantami okrajových podmínek pro stanovení reálné doby návratnosti solární soustavy. V případě stejného tempa růstu cen energie jako je diskontní míra, jde o prostou návratnost. Pokud se předpokládá tempo růstu cen energie vyšší než diskontní míra, reálná doba návratnosti se oproti prosté zkracuje. Pokud jsou počáteční investiční náklady významně sníženy dotací, nemá již časová hodnota investice příliš vysoký vliv na dobu návratnosti, odchylky pro různé varianty se pohybují řádově v měsících.
Obr. 9.7 Vliv okrajových podmínek faktoru času při výpočtu ekonomické návratnosti
9.8 CENA SOLÁRNÍHO TEPLA
Posouzení reálné návratnosti spoléhá na řadu předpokladů, zejména špatně odhadnutelného budoucího tempa růstu ceny nahrazované energie, zvláště pokud je časovým horizontem životnost solární soustavy (25 až 30 let). Alternativní metodou ekonomického zhodnocení je výpočet ceny tepla dodávaného solární soustavou v časovém horizontu předpokládané životnosti z anuit investičních a provozních nákladů solární soustavy a z energetických zisků solární soustavy. Metoda anuit přepočítává neperiodické a periodické náklady do periodických konstantních plateb. Metoda umožňuje navíc sčítat různé druhy nákladů vzniklých v různých periodách životnosti solární soustavy, transformovaných faktorem anuity do průměrných nákladů v průběhu sledovaného časového období τ (životnost solárních kolektorů).
Obecně může být metoda anuit relativně komplexní metodou, zohledňující řadu faktorů jako jsou změny provozních nákladů na provoz, obsluhu a údržbu s časem. Níže je uveden zjednodušený výpočet zohledňující podrobněji především anuity jednotlivých investic, včetně oprav a údržby solární soustavy, s různou životností τi, a konstantní provozní náklady PN spojené se spotřebou energie pro pohon solární soustavy.
Cena solárního tepla se stanoví ze vztahu
(9.3)
kde je
τ … sledované časové období (životnost solárních kolektorů);
INi … investiční náklady na i-tý prvek solární soustavy s danou životností τi, v Kč;
a(τi) … anuitní faktor určený pro životnost daného prvku τi;
PN … roční provozní náklady pro pohon soustavy, v Kč/rok;
Qu … úspora energie vlivem provozu solární soustavy, energetický přínos solární soustavy, v kWh/rok.
Anuitní faktor i-tého prvku se stanoví ze vztahu
(9.4)
kde je
r … diskontní míra.
Při výpočtu ceny solárního tepla se investiční náklady na jednotlivé prvky rozdělí podle jejich předpokládané životnosti τi (viz tab. 9.1). Součet ročních anuit nákladů na solární soustavu po dobu životnosti (30 let) je potom dán vztahem
(9.5)
Tab. 9.1 Doba životnosti hlavních nákladových prvků solární soustavy a anuitní faktor
| Ozn. | Materiálové položky | ti | a(5 %, τi) |
| IN1 | Solární kolektory, potrubí, izolace, nosné konstrukce, montáž | 30 let | 0,065 |
| IN2 | Solární zásobníky | 15 let | 0,096 |
| IN3 | Oběhová čerpadla, teplonosná kapalina | 10 let | 0,130 |
| IN4 | Náklad na významnější údržbu | 5 let | 0,231 |
Cena elektrické energie cel a její zvýšení v budoucnosti má na ekonomické parametry solární soustavy u bytového domu zpravidla marginální vliv. Cena solárního tepla v Kč/kWh je potom
(9.6)
kde je
Qss,u … využité tepelné zisky solární soustavy, v kWh/rok;
hnz … účinnost zdroje tepla nahrazovaného solární soustavou.
Vypočtená cena solárního tepla je cena energie dodávané ze solární soustavy (cena úspory) a předpokládá se stálá po celou dobu životnosti solární soustavy, tzn. nezvyšuje se v čase. Poskytuje tak garanci ceny solárního tepla oproti rostoucím cenám konvenčních energií v budoucnosti.
Základem pro správné ekonomické zhodnocení solární soustavy jsou především správné informace o vstupních okrajových podmínkách výpočtu, zejména o celkových investičních nákladech a očekávaných finančních výnosech (energetické zisky, změny v ceně energie, diskontní míra). Častou chybou je podcenění nákladů souvisejících s instalací solární soustavy (stavební úpravy), které mohou významně zhoršit ekonomické parametry a nadhodnocení skutečné provozní účinnosti nahrazovaných zdrojů tepla hnz, zejména v případě kotlů pro spalování fosilních paliv. Na druhé straně mezi faktory papírově zlepšujícími ekonomiku solárních soustav se lze setkat s nerealisticky nadhodnocenými zisky solárních soustav.
9.9 EKONOMICKÉ SMLUVNÍ NÁSTROJE
Solární tepelné soustavy v současné době představují investičně náročné opatření pro snížení energetické náročnosti budov s návratností okolo 10 až 15 let, bez využití dotací. Vysoké náklady a mezi veřejností stále ještě rozšířené vnímání solárních zařízení jako ne zcela zavedené technologie, navíc náchylné k poruše nebo neefektivnímu provozu, mohou případné zájemce odradit. Ve snaze překonat nedůvěru potenciálního vlastníka domu a poskytnout mu přidanou hodnotu se na trhu solární tepelné techniky objevují různé typy smluvních nástrojů, z nichž profitují dodavatelé energie i vlastníci domů. V prvé řadě to je metoda EPC aplikovaná na solární soustavy a dále systém garance solárních zisků. Smluvní nástroje mají za cíl zainteresovat dodavatele solární soustavy na kvalitě návrhu, realizace a provozu, zajistit vhodné ekonomické parametry a posílit záruky dosažení úspor. Poskytování garance úspory a souvisejících komplexních služeb se postupně může stát významnou „přidanou“ hodnotou k nabídce v rámci výběrových řízení, ve kterých je bohužel tak často zohledňována pouze výše investičních nákladů. Obě varianty jsou uplatnitelné především v oblasti velkoplošných instalací solárních soustav.
9.9.1 Solární EPC
Vzhledem k vysoké počáteční investici do solární soustavy může být pro potenciální investory zajímavá realizace solární soustavy metodou EPC (Energy Performance Contracting). Principem je, že realizaci solární soustavy zajišťuje společnost poskytující energetické služby se zárukou (Energy Services COmpany – ESCO) na své náklady, na klíč a bez investice zákazníka. Poskytovatelem služeb mohou být energetické společnosti, dodavatelé energie, asociace aj. Investice, úroky a náklady na služby ESCO splácí zákazník společnosti až z prokazatelně dosažené úspory v provozních nákladech a po dobu sjednanou smluvně.
Energetické služby, které zákazník společnosti ESCO splácí, představují:
- návrh opatření na úsporu nákladů na energie;
- financování celého projektu;
- výstavbu „na klíč“ a zprovoznění zařízení;
- kontrolu výkonnosti a údržbu zařízení po dobu splácení projektu (tj. trvání smlouvy o energetických službách);
- měření a vyhodnocování dosažených výsledků.
Zákazník garantuje, že po dobu trvání smlouvy bude uvažovat se stejnými provozními náklady na energie jako „před projektem“ a rozdíl vzniklý úsporami bude používat ke splácení všech nákladů projektu. Na druhé straně ESCO garantuje, že pokud nebude dosažena očekávaná úspora, zákazník není povinen „doplácet“ za nedosaženou úsporu, tzn. ESCO bude mít nižší příjem ze splátek.
Splácení projektu se děje výhradně na základě dosažených úspor energie. Riziko investice a odpovědnost za dohled, obsluhu a údržbu solární soustavy přebírá ESCO. ESCO se samozřejmě snaží o optimální provoz solární soustavy, protože dosažený zisk snižuje její provozní náklady a umožňuje zákazníkovi splácet.
Výhodami metody EPC jsou především:
- dosažení úspor nákladů na energie bez nutnosti vynaložit vlastní finanční zdroje na realizaci nezbytných úsporných opatření;
- smluvní záruka ESCO za dosažené finanční výsledky projektu;
- ESCO je jediným smluvním partnerem při realizaci projektu – dodávka a montáž projektu „na klíč“;
- ESCO má stejný zájem jako zákazník – minimalizace pořizovacích (investičních) i budoucích provozních nákladů, protože obojí jsou spláceny z dosažených úspor nákladů na energii;
- zákazník má reálnou možnost dodatečných příjmů, pokud budou úspory ještě větší, než bylo původně předpokládáno, protože ESCO „se stará“ ve vlastním zájmu o minimalizaci provozních nákladů.
EPC v oblasti solárních soustav do obytných budov zatím není ani v Evropě příliš rozšířený vzhledem k jejich době návratnosti bez dotace nad 10 let, zatímco běžný horizont trvání smluv o energetických službách se pohybuje mezi 5 a 10 lety.
9.9.2 Garantované solární zisky
Koncept garantovaných solárních zisků (Guaranteed Solar Results – GSR) má s metodou EPC společnou snahu zajistit realizací solární soustavy co nejvyšší úsporu, případně garantovat minimální úsporu. Specializovaná společnost, případně konsorcium firem se smluvně zavazuje docílit realizací solární soustavy minimální zisk za definovaných podmínek odběru tepla, a má tedy stejný zájem jako zákazník. V případě nedosažení smluvní úrovně musí realizační firma na své náklady vylepšit soustavu, nebo rozdíl v zisku kompenzovat.
To samozřejmě nutí firmy, aby v nabídkách na solární soustavu v rámci výběrového řízení uváděly realistické hodnoty dosažitelných úspor, neboť je potom v provozu musí zaručit. Na rozdíl od EPC, u systému garantovaných zisků leží břemeno investice na vlastníkovi domu, pokud není smluvně dohodnuto jinak. Garantovaný solární zisk je na jedné straně smlouvou, která vyjadřuje zájem dodavatelských a montážních firem odvést svou práci co nejlépe a zaručit se za ni, na druhé straně je ve své podstatě pojistnou smlouvou pro investora, zahrnující všechna rizika. Smlouva zbavuje investora také starosti o údržbu solární soustavy a její opravy, neboť je v zájmu dodavatele zajistit co nejefektivnější provoz. Smlouva o zaručených solárních ziscích mezi investorem a dodavatelem obsahuje především:
- smluvní období (zpravidla 5 let);
- technický popis solární soustavy (snaha o co nejjednodušší soustavu);
- monitorovací systém;
- projektovou dokumentaci a klimatické podmínky;
- očekávaná roční produkce energie v solární soustavě = solární přínos;
- podmínky finanční kompenzace.
Koncept garantovaných solárních zisků je aplikován především na střední a velkoplošné instalace solární přípravy teplé vody, např. v bytových domech vzhledem ke snadno ověřitelným okrajovým podmínkám provozu. Cílový smluvní solární přínos (v kWh/rok) je definován na základě místního klimatu (především dostupnost sluneční energie), orientace a sklonu kolektorů a předpokládaných provozních podmínek v dané aplikaci. Garantované solární zisky nejsou rigidní konstantou, ale jsou aktualizovány na základě skutečných měsíčních spotřeb teplé vody v daném místě. Pro každý měsíc platí následující podmínky:
- pokud je reálná spotřeba teplé vody (při definované teplotní úrovni) vyšší než původně odhadovaná spotřeba, cílový solární přínos je stanoven z původně odhadované spotřeby;
- pokud je reálná spotřeba teplé vody v rozmezí 50 až 100 % původně odhadované spotřeby, cílový solární přínos je přepočítán na reálnou spotřebu (snížen);
- pokud je reálná spotřeba teplé vody nižší než 50 % původně odhadované spotřeby, měsíc není pro záruku uvažován.
Pravidla garantovaných solárních zisků tak ve své podstatě odráží dvě základní zásady u solárních soustav pro přípravu teplé vody:
1. se snižující se spotřebou teplé vody při dané ploše kolektorů se snižují solární zisky – soustava se stává předimenzovanou, pracuje za vyšších provozních teplot a vykazuje vyšší podíl nevyužitelných přebytků tepla. Pokud se tedy v provozu sníží z jakéhokoli důvodu spotřeba teplé vody, změní se tím projektovaný předpoklad (zhorší se podmínky úsporného provozu solární soustavy), za který nemohou být projektant ani montážní firma penalizováni, a pro výpočet garance je nutný přepočet zisků podle skutečných podmínek;
2. v projektové dokumentaci je nutné velmi pečlivě a přesně stanovit skutečnou spotřebu teplé vody, resp. tepla na její přípravu a vhodně navrhnout solární soustavu, jinak instalace nedosáhne požadovaných přínosů. Dalším krokem je správně vyhodnotit reálné přínosy solární soustavy. Pokud dodavatel nesprávně stanoví (nadhodnotí) tepelné zisky soustavy, vystavuje se riziku, že uvedené hodnoty zisků na reálné soustavě s uvedeným pokrytím ve skutečném provozu nenaměří a bude nakonec muset doplatit investorovi rozdíl mezi předpokladem auditu a skutečností.
Instalace je nainstalována a vybavena monitoringem, který měsíc po měsíci zaznamenává a vyhodnocuje dodané solární zisky, spotřebu teplé vody a spotřebu dodatkové energie. Monitoring je dostupný pro všechny zúčastněné strany. Výhodné jsou vzdálené monitorovací systémy s webovým rozhraním, tzv. telemonitoring. S náklady na monitoring je nutné počítat už v přípravné fázi, nicméně u solárních soustav s plochou nad 200 m2 není monitoring významnou nákladovou položkou. Po prvním roce provozu (verifikační fáze) jsou přínosy soustavy vyhodnoceny a instalace musí prokázat schopnost dodat zaručený zisk. Pokud daná soustava dodala alespoň 90 % smluvně zaručené energie, měření a sledování pokračuje po dobu následujících 4 let pro potvrzení stability dodávky zisků s ohledem na klimatické podmínky (prokazovací fáze). Pokud solární soustava nedosahuje požadavku, musí technický tým opravit soustavu, nebo zlepšit její provozní podmínky na vlastní náklady, aby splnila závazné cíle.
Na konci celého smluvního období, pokud je dosaženo předpokládaných zisků a instalace osvědčila správnou funkci, je dodavatel uvolněn ze smlouvy a za solární soustavu je nadále zodpovědný pouze investor. Pokud ani po uplynutí celého smluvního období nedokáže soustava dodat garantované solární zisky, musí garant investorovi uhradit „odškodné“ – kompenzaci za nedodané zisky. Kompenzací se rozumí poměrná část z investičních nákladů úměrná nedodaným ziskům podle vztahu
V podmínkách finanční kompenzace může být zahrnuto osvobození od kompenzací v případech živelních pohrom, výpadku síťového napájení delšího než určitý časový úsek, nestandardní poruchy čidel, regulace, oběhového čerpadla nebo z dlouhodobého hlediska extrémně nízké úrovně slunečního záření.
Některé typy jednoduchých smluv kalkulují s fixní hodnotou garantovaného solárního zisku pro zjednodušení smluvních závazků a jejich administrace. Jako kritérium se používá hodnota minimálního měrného ročního zisku solární soustavy vztaženého k ploše apertury solárních kolektorů. V Rakousku se pro solární přípravu teplé vody v bytových domech používá běžně hodnota 350 kWh/(m2·rok) jako minimální reálný solární přínos.
Kromě zvýšené kvality instalace velkoplošných solárních soustav a důvěry investora v předpokládanou dobu návratnosti má koncept řadu dalších souvisejících výhod:
- garantovaný energetický přínos a kvalita provedení soustavy vede investora k přijetí sice delší, avšak smluvně zaručené doby návratnosti;
- smlouva o garantovaných solárních ziscích poskytuje transparentní a automatickou záruku skutečného snížení CO2, ne pouze na stránkách energetických auditů a odborných posudků;
- aplikace garance povede k vyšším požadavkům na výrobky a instalace a podporuje jejich rozvoj;
- u monitorované solární soustavy lze velmi rychle identifikovat nesprávnou funkci díky okamžité zpětné vazbě a zajistit nápravu bez výrazných ztrát na dodávce tepla;
- projektant je motivován navrhnout a vyhodnotit solární soustavu kvalitně za použití pokročilých metod návrhu;
- v rámci výběrového řízení musí dodavatel technologie optimalizovat nabídku tak, aby na jedné straně udržel nízkou cenu solární soustavy (solárního tepla) a na druhé straně vysoký zisk, za který se může zaručit. Jednoznačná výhoda pro investora, který si z nabídek vybírá, je zřejmá.
I v zemích s rozvinutým solárním trhem se smluvní garance solárních zisků zatím týká pouze omezeného množství velkoplošných instalací. Nicméně v základním dokumentu Evropské technologické platformy pro solární tepelnou techniku se předpokládá, že do roku 2030 bude garantovaný solární zisk standardem nejen pro velkoplošné aplikace, ale i pro malé solární soustavy s plochou pod 20 m2, kde se v současné době soustředí nejvýznamnější část instalovaného výkonu solárních tepelných soustav. Postupným zaváděním záruk za produkci tepla solární soustavou do širší praxe se bude zvyšovat tlak na kvalitu dodaných prvků a montáže, stejně jako na nabídku komplexních služeb, zahrnujících i provozování a údržbu solární soustavy. Zatímco spolehliví dodavatelé koncept GSR vítají, očekává se zároveň, že solární soustavy nízké kvality postupně zmizí z trhu.
LITERATURA
[1] Vyhláška č. 193/2007 Sb., kterou se stanoví podrobnosti účinnosti užití energie při rozvodu tepelné energie a vnitřním rozvodu tepelné energie a chladu
[2] Zákon č. 235/2004 Sb., o dani z přidané hodnoty.
[3] Remmers, K., H.: Velká solární zařízení, Era 2007.
[4] Historický přehled vývoje cen, http://www.tzb-info.cz/t.py?t=1&i=3
[5] Blažíček, J: Vyhodnocení cen tepelné energie k roku 2008, http://www.tzb-info.cz/t.py?t=2&i=6152&h=3
[6] Berner, J.: Guaranteed solar yield, Sun and Wind Energy, roč. 2008, č. 1, str. 46-50.
10 KLIMATICKÉ ÚDAJE PRO NAVRHOVÁNÍ
Příloha A – Teoretické denní dávky celkového slunečního ozáření HT,den,teor
| Úhel sklonu plochy β | Teoretická denní dávka celkového slunečního ozáření HT,den,teor [kWh/(m2·den)] pro charakteristickou oblast hory (Z = 2) | |||||||||||
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | |
| Azimutový úhel osluněné plochy γ = ± 0° (orientace na jih) | ||||||||||||
| 0 | 1,87 | 3,04 | 5,11 | 7,31 | 9,08 | 9,65 | 9,25 | 7,77 | 5,77 | 3,69 | 2,20 | 1,54 |
| 15 | 3,26 | 4,53 | 6,46 | 8,27 | 9,55 | 9,86 | 9,59 | 8,52 | 6,95 | 5,12 | 3,60 | 2,85 |
| 30 | 4,44 | 5,74 | 7,42 | 8,75 | 9,51 | 9,59 | 9,44 | 8,79 | 7,72 | 6,24 | 4,78 | 3,98 |
| 45 | 5,35 | 6,59 | 7,93 | 8,73 | 8,97 | 8,83 | 8,80 | 8,57 | 8,03 | 6,97 | 5,67 | 4,86 |
| 60 | 5,91 | 7,03 | 7,96 | 8,20 | 7,96 | 7,63 | 7,71 | 7,87 | 7,86 | 7,28 | 6,19 | 5,44 |
| 75 | 6,10 | 7,03 | 7,50 | 7,20 | 6,54 | 6,10 | 6,25 | 6,74 | 7,22 | 7,13 | 6,32 | 5,66 |
| 90 | 5,89 | 6,58 | 6,59 | 5,80 | 4,85 | 4,36 | 4,56 | 5,27 | 6,16 | 6,54 | 6,04 | 5,51 |
| Azimutový úhel osluněné plochy γ = ± 15° | ||||||||||||
| 15 | 3,21 | 4,47 | 6,41 | 8,23 | 9,53 | 9,86 | 9,58 | 8,49 | 6,91 | 5,06 | 3,55 | 2,80 |
| 30 | 4,35 | 5,63 | 7,33 | 8,71 | 9,50 | 9,59 | 9,43 | 8,76 | 7,65 | 6,14 | 4,69 | 3,89 |
| 45 | 5,22 | 6,45 | 7,81 | 8,69 | 8,98 | 8,85 | 8,81 | 8,54 | 7,94 | 6,83 | 5,53 | 4,74 |
| 60 | 5,75 | 6,85 | 7,82 | 8,17 | 8,00 | 7,70 | 7,76 | 7,87 | 7,76 | 7,11 | 6,02 | 5,28 |
| 75 | 5,91 | 6,83 | 7,36 | 7,21 | 6,64 | 6,21 | 6,35 | 6,78 | 7,13 | 6,94 | 6,13 | 5,48 |
| 90 | 5,70 | 6,37 | 6,45 | 5,86 | 5,01 | 4,52 | 4,71 | 5,36 | 6,09 | 6,34 | 5,85 | 5,33 |
| Azimutový úhel osluněné plochy γ = ± 30° | ||||||||||||
| 15 | 3,07 | 4,32 | 6,27 | 8,14 | 9,48 | 9,83 | 9,54 | 8,41 | 6,79 | 4,92 | 3,40 | 2,67 |
| 30 | 4,07 | 5,34 | 7,08 | 8,56 | 9,45 | 9,58 | 9,40 | 8,64 | 7,43 | 5,86 | 4,40 | 3,63 |
| 45 | 4,82 | 6,03 | 7,49 | 8,53 | 8,99 | 8,91 | 8,84 | 8,44 | 7,67 | 6,44 | 5,13 | 4,37 |
| 60 | 5,27 | 6,35 | 7,46 | 8,06 | 8,10 | 7,85 | 7,88 | 7,82 | 7,48 | 6,64 | 5,53 | 4,83 |
| 75 | 5,38 | 6,27 | 6,99 | 7,17 | 6,86 | 6,49 | 6,59 | 6,82 | 6,87 | 6,43 | 5,59 | 4,98 |
| 90 | 5,14 | 5,80 | 6,13 | 5,94 | 5,38 | 4,95 | 5,10 | 5,53 | 5,90 | 5,84 | 5,29 | 4,81 |
| Azimutový úhel osluněné plochy γ = ± 45° | ||||||||||||
| 15 | 2,84 | 4,08 | 6,05 | 7,97 | 9,39 | 9,77 | 9,47 | 8,28 | 6,59 | 4,68 | 3,18 | 2,45 |
| 30 | 3,64 | 4,89 | 6,70 | 8,30 | 9,35 | 9,53 | 9,32 | 8,44 | 7,10 | 5,43 | 3,97 | 3,22 |
| 45 | 4,22 | 5,42 | 6,99 | 8,25 | 8,93 | 8,93 | 8,81 | 8,23 | 7,26 | 5,88 | 4,53 | 3,79 |
| 60 | 4,54 | 5,63 | 6,92 | 7,81 | 8,14 | 8,00 | 7,96 | 7,67 | 7,04 | 5,98 | 4,81 | 4,12 |
| 75 | 4,57 | 5,50 | 6,47 | 7,01 | 7,05 | 6,79 | 6,82 | 6,77 | 6,48 | 5,75 | 4,79 | 4,19 |
| 90 | 4,31 | 5,04 | 5,69 | 5,92 | 5,73 | 5,42 | 5,49 | 5,62 | 5,60 | 5,19 | 4,48 | 4,00 |
| Azimutový úhel osluněné plochy γ = ± 60° | ||||||||||||
| 15 | 2,56 | 3,77 | 5,76 | 7,76 | 9,26 | 9,69 | 9,36 | 8,09 | 6,33 | 4,39 | 2,89 | 2,18 |
| 30 | 3,12 | 4,34 | 6,20 | 7,94 | 9,15 | 9,42 | 9,17 | 8,14 | 6,66 | 4,90 | 3,44 | 2,72 |
| 45 | 3,50 | 4,69 | 6,37 | 7,83 | 8,75 | 8,86 | 8,68 | 7,91 | 6,71 | 5,18 | 3,81 | 3,10 |
| 60 | 3,69 | 4,79 | 6,24 | 7,41 | 8,05 | 8,03 | 7,92 | 7,38 | 6,47 | 5,20 | 3,97 | 3,30 |
| 75 | 3,66 | 4,62 | 5,82 | 6,70 | 7,08 | 6,97 | 6,91 | 6,57 | 5,95 | 4,95 | 3,90 | 3,30 |
| 90 | 3,41 | 4,21 | 5,13 | 5,74 | 5,92 | 5,74 | 5,73 | 5,56 | 5,18 | 4,45 | 3,61 | 3,10 |
| Azimutový úhel osluněné plochy γ = ± 75° | ||||||||||||
| 15 | 2,24 | 3,42 | 5,43 | 7,49 | 9,10 | 9,57 | 9,22 | 7,87 | 6,03 | 4,04 | 2,56 | 1,88 |
| 30 | 2,54 | 3,72 | 5,62 | 7,49 | 8,87 | 9,23 | 8,93 | 7,76 | 6,13 | 4,30 | 2,86 | 2,17 |
| 45 | 2,74 | 3,89 | 5,64 | 7,29 | 8,44 | 8,67 | 8,43 | 7,46 | 6,06 | 4,41 | 3,05 | 2,38 |
| 60 | 2,82 | 3,89 | 5,45 | 6,87 | 7,79 | 7,91 | 7,72 | 6,94 | 5,78 | 4,35 | 3,10 | 2,46 |
| 75 | 2,75 | 3,71 | 5,06 | 6,22 | 6,92 | 6,95 | 6,82 | 6,22 | 5,30 | 4,10 | 2,99 | 2,42 |
| 90 | 2,53 | 3,36 | 4,48 | 5,39 | 5,90 | 5,86 | 5,77 | 5,33 | 4,64 | 3,68 | 2,74 | 2,25 |
| Azimutový úhel osluněné plochy γ = ± 90° | ||||||||||||
| 15 | 1,90 | 3,04 | 5,06 | 7,19 | 8,90 | 9,44 | 9,06 | 7,62 | 5,69 | 3,67 | 2,21 | 1,57 |
| 30 | 1,96 | 3,07 | 4,97 | 6,95 | 8,51 | 8,97 | 8,62 | 7,31 | 5,54 | 3,65 | 2,26 | 1,63 |
| 45 | 2,00 | 3,06 | 4,83 | 6,63 | 7,99 | 8,35 | 8,05 | 6,89 | 5,32 | 3,60 | 2,29 | 1,68 |
| 60 | 1,99 | 2,99 | 4,59 | 6,18 | 7,35 | 7,60 | 7,35 | 6,36 | 5,00 | 3,47 | 2,26 | 1,68 |
| 75 | 1,91 | 2,81 | 4,23 | 5,59 | 6,56 | 6,72 | 6,52 | 5,70 | 4,55 | 3,23 | 2,15 | 1,62 |
| 90 | 1,75 | 2,54 | 3,74 | 4,88 | 5,65 | 5,74 | 5,58 | 4,93 | 4,00 | 2,89 | 1,95 | 1,49 |
| Úhel sklonu plochy β | Teoretická denní dávka celkového slunečního ozáření HT,den,teor [kWh/(m2·den)] pro charakteristickou oblast venkov (Z = 3) | |||||||||||
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | |
| Azimutový úhel osluněné plochy γ = ± 0° (orientace na jih) | ||||||||||||
| 0 | 1,70 | 2,81 | 4,74 | 6,67 | 8,22 | 8,84 | 8,40 | 7,13 | 5,34 | 3,36 | 1,98 | 1,37 |
| 15 | 2,84 | 4,08 | 5,92 | 7,51 | 8,66 | 9,07 | 8,74 | 7,80 | 6,37 | 4,54 | 3,11 | 2,39 |
| 30 | 3,81 | 5,10 | 6,75 | 7,92 | 8,64 | 8,84 | 8,62 | 8,04 | 7,03 | 5,46 | 4,06 | 3,27 |
| 45 | 4,54 | 5,82 | 7,18 | 7,89 | 8,16 | 8,17 | 8,05 | 7,83 | 7,28 | 6,05 | 4,76 | 3,94 |
| 60 | 4,99 | 6,17 | 7,18 | 7,40 | 7,26 | 7,10 | 7,09 | 7,20 | 7,11 | 6,27 | 5,17 | 4,37 |
| 75 | 5,12 | 6,15 | 6,75 | 6,51 | 6,01 | 5,71 | 5,79 | 6,18 | 6,52 | 6,12 | 5,25 | 4,53 |
| 90 | 4,93 | 5,74 | 5,92 | 5,26 | 4,50 | 4,14 | 4,27 | 4,86 | 5,56 | 5,59 | 5,00 | 4,39 |
| Azimutový úhel osluněné plochy γ = ± 15° | ||||||||||||
| 15 | 2,80 | 4,03 | 5,88 | 7,48 | 8,64 | 9,06 | 8,72 | 7,77 | 6,33 | 4,49 | 3,07 | 2,35 |
| 30 | 3,73 | 5,01 | 6,67 | 7,87 | 8,62 | 8,84 | 8,60 | 8,00 | 6,96 | 5,37 | 3,98 | 3,20 |
| 45 | 4,43 | 5,69 | 7,07 | 7,83 | 8,15 | 8,18 | 8,05 | 7,79 | 7,19 | 5,93 | 4,65 | 3,85 |
| 60 | 4,85 | 6,02 | 7,05 | 7,36 | 7,28 | 7,14 | 7,11 | 7,18 | 7,01 | 6,13 | 5,03 | 4,25 |
| 75 | 4,97 | 5,98 | 6,62 | 6,49 | 6,07 | 5,79 | 5,85 | 6,19 | 6,42 | 5,96 | 5,10 | 4,39 |
| 90 | 4,77 | 5,56 | 5,79 | 5,28 | 4,61 | 4,27 | 4,39 | 4,91 | 5,48 | 5,43 | 4,85 | 4,25 |
| Azimutový úhel osluněné plochy γ = ± 30° | ||||||||||||
| 15 | 2,68 | 3,90 | 5,75 | 7,38 | 8,58 | 9,02 | 8,68 | 7,70 | 6,22 | 4,37 | 2,96 | 2,25 |
| 30 | 3,50 | 4,76 | 6,44 | 7,72 | 8,55 | 8,80 | 8,55 | 7,88 | 6,76 | 5,14 | 3,76 | 2,99 |
| 45 | 4,11 | 5,33 | 6,77 | 7,66 | 8,11 | 8,19 | 8,03 | 7,67 | 6,94 | 5,60 | 4,33 | 3,56 |
| 60 | 4,46 | 5,58 | 6,71 | 7,21 | 7,30 | 7,23 | 7,16 | 7,09 | 6,74 | 5,73 | 4,64 | 3,90 |
| 75 | 4,53 | 5,49 | 6,27 | 6,39 | 6,19 | 5,99 | 6,00 | 6,17 | 6,17 | 5,53 | 4,66 | 4,00 |
| 90 | 4,32 | 5,07 | 5,48 | 5,29 | 4,86 | 4,59 | 4,66 | 5,00 | 5,28 | 4,99 | 4,39 | 3,85 |
| Azimutový úhel osluněné plochy γ = ± 45° | ||||||||||||
| 15 | 2,50 | 3,69 | 5,56 | 7,24 | 8,49 | 8,96 | 8,60 | 7,57 | 6,04 | 4,17 | 2,77 | 2,08 |
| 30 | 3,14 | 4,37 | 6,09 | 7,48 | 8,42 | 8,73 | 8,44 | 7,68 | 6,46 | 4,77 | 3,40 | 2,67 |
| 45 | 3,61 | 4,80 | 6,32 | 7,38 | 8,00 | 8,16 | 7,95 | 7,45 | 6,55 | 5,11 | 3,84 | 3,10 |
| 60 | 3,85 | 4,95 | 6,21 | 6,94 | 7,26 | 7,28 | 7,16 | 6,90 | 6,32 | 5,16 | 4,04 | 3,35 |
| 75 | 3,85 | 4,81 | 5,78 | 6,19 | 6,26 | 6,17 | 6,11 | 6,07 | 5,78 | 4,93 | 4,00 | 3,38 |
| 90 | 3,62 | 4,39 | 5,05 | 5,20 | 5,07 | 4,92 | 4,91 | 5,02 | 4,97 | 4,42 | 3,72 | 3,21 |
| Azimutový úhel osluněné plochy γ = ± 60° | ||||||||||||
| 15 | 2,26 | 3,42 | 5,30 | 7,04 | 8,37 | 8,87 | 8,49 | 7,41 | 5,81 | 3,92 | 2,53 | 1,87 |
| 30 | 2,71 | 3,89 | 5,65 | 7,14 | 8,21 | 8,59 | 8,27 | 7,40 | 6,06 | 4,32 | 2,97 | 2,27 |
| 45 | 3,00 | 4,16 | 5,75 | 6,98 | 7,79 | 8,04 | 7,79 | 7,13 | 6,05 | 4,52 | 3,24 | 2,55 |
| 60 | 3,13 | 4,21 | 5,59 | 6,55 | 7,11 | 7,25 | 7,05 | 6,60 | 5,79 | 4,49 | 3,34 | 2,69 |
| 75 | 3,09 | 4,04 | 5,18 | 5,87 | 6,21 | 6,25 | 6,11 | 5,84 | 5,29 | 4,24 | 3,25 | 2,67 |
| 90 | 2,86 | 3,66 | 4,54 | 4,99 | 5,15 | 5,12 | 5,04 | 4,91 | 4,57 | 3,78 | 2,99 | 2,49 |
| Azimutový úhel osluněné plochy γ = ± 75° | ||||||||||||
| 15 | 1,99 | 3,12 | 5,00 | 6,80 | 8,21 | 8,76 | 8,36 | 7,20 | 5,54 | 3,63 | 2,26 | 1,63 |
| 30 | 2,22 | 3,35 | 5,12 | 6,73 | 7,95 | 8,40 | 8,04 | 7,05 | 5,58 | 3,81 | 2,48 | 1,84 |
| 45 | 2,37 | 3,46 | 5,09 | 6,49 | 7,48 | 7,83 | 7,53 | 6,71 | 5,46 | 3,85 | 2,61 | 1,97 |
| 60 | 2,40 | 3,42 | 4,88 | 6,04 | 6,83 | 7,08 | 6,83 | 6,19 | 5,17 | 3,75 | 2,62 | 2,02 |
| 75 | 2,32 | 3,24 | 4,49 | 5,42 | 6,01 | 6,17 | 5,97 | 5,50 | 4,70 | 3,50 | 2,50 | 1,96 |
| 90 | 2,12 | 2,91 | 3,94 | 4,65 | 5,07 | 5,16 | 5,01 | 4,67 | 4,08 | 3,11 | 2,27 | 1,80 |
| Azimutový úhel osluněné plochy γ = ± 90° | ||||||||||||
| 15 | 1,71 | 2,79 | 4,68 | 6,54 | 8,03 | 8,63 | 8,21 | 6,98 | 5,25 | 3,32 | 1,98 | 1,38 |
| 30 | 1,74 | 2,78 | 4,55 | 6,26 | 7,61 | 8,14 | 7,75 | 6,64 | 5,06 | 3,26 | 1,99 | 1,40 |
| 45 | 1,75 | 2,74 | 4,37 | 5,90 | 7,07 | 7,51 | 7,16 | 6,20 | 4,81 | 3,17 | 1,98 | 1,42 |
| 60 | 1,71 | 2,64 | 4,11 | 5,43 | 6,41 | 6,77 | 6,47 | 5,66 | 4,47 | 3,01 | 1,92 | 1,40 |
| 75 | 1,62 | 2,46 | 3,75 | 4,86 | 5,65 | 5,93 | 5,67 | 5,02 | 4,03 | 2,77 | 1,80 | 1,33 |
| 90 | 1,47 | 2,20 | 3,29 | 4,19 | 4,82 | 5,02 | 4,81 | 4,30 | 3,51 | 2,45 | 1,63 | 1,21 |
| Úhel sklonu plochy β | Teoretická denní dávka celkového slunečního ozáření HT,den,teor [kWh/(m2·den)] pro charakteristickou oblast město (Z = 4) | |||||||||||
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | |
| Azimutový úhel osluněné plochy γ = ± 0° (orientace na jih) | ||||||||||||
| 0 | 1,48 | 2,49 | 4,30 | 6,09 | 7,62 | 8,27 | 7,86 | 6,60 | 4,84 | 3,02 | 1,74 | 1,20 |
| 15 | 2,30 | 3,47 | 5,27 | 6,80 | 8,02 | 8,51 | 8,18 | 7,18 | 5,69 | 3,96 | 2,58 | 1,95 |
| 30 | 3,00 | 4,25 | 5,95 | 7,15 | 8,01 | 8,31 | 8,08 | 7,39 | 6,23 | 4,68 | 3,28 | 2,58 |
| 45 | 3,52 | 4,79 | 6,28 | 7,10 | 7,57 | 7,69 | 7,56 | 7,19 | 6,41 | 5,13 | 3,78 | 3,07 |
| 60 | 3,82 | 5,04 | 6,25 | 6,66 | 6,76 | 6,71 | 6,67 | 6,61 | 6,24 | 5,28 | 4,06 | 3,37 |
| 75 | 3,89 | 4,98 | 5,86 | 5,86 | 5,62 | 5,43 | 5,48 | 5,69 | 5,71 | 5,12 | 4,10 | 3,46 |
| 90 | 3,72 | 4,63 | 5,13 | 4,75 | 4,24 | 3,97 | 4,08 | 4,50 | 4,87 | 4,66 | 3,88 | 3,34 |
| Azimutový úhel osluněné plochy γ = ± 15° | ||||||||||||
| 15 | 2,28 | 3,44 | 5,24 | 6,78 | 8,00 | 8,49 | 8,17 | 7,16 | 5,66 | 3,92 | 2,55 | 1,92 |
| 30 | 2,94 | 4,19 | 5,88 | 7,10 | 7,98 | 8,29 | 8,06 | 7,35 | 6,17 | 4,61 | 3,22 | 2,53 |
| 45 | 3,44 | 4,69 | 6,19 | 7,04 | 7,56 | 7,69 | 7,55 | 7,15 | 6,33 | 5,03 | 3,70 | 2,99 |
| 60 | 3,72 | 4,92 | 6,14 | 6,61 | 6,76 | 6,73 | 6,68 | 6,58 | 6,15 | 5,16 | 3,96 | 3,28 |
| 75 | 3,78 | 4,85 | 5,74 | 5,82 | 5,65 | 5,49 | 5,52 | 5,68 | 5,62 | 4,99 | 3,98 | 3,36 |
| 90 | 3,61 | 4,49 | 5,01 | 4,75 | 4,33 | 4,08 | 4,17 | 4,53 | 4,79 | 4,52 | 3,76 | 3,23 |
| Azimutový úhel osluněné plochy γ = ± 30° | ||||||||||||
| 15 | 2,19 | 3,33 | 5,13 | 6,69 | 7,95 | 8,46 | 8,12 | 7,09 | 5,57 | 3,82 | 2,46 | 1,84 |
| 30 | 2,78 | 3,99 | 5,69 | 6,96 | 7,90 | 8,25 | 8,00 | 7,23 | 6,00 | 4,42 | 3,05 | 2,38 |
| 45 | 3,20 | 4,41 | 5,92 | 6,87 | 7,49 | 7,68 | 7,51 | 7,02 | 6,11 | 4,76 | 3,46 | 2,78 |
| 60 | 3,43 | 4,57 | 5,83 | 6,44 | 6,74 | 6,78 | 6,70 | 6,47 | 5,89 | 4,84 | 3,67 | 3,02 |
| 75 | 3,46 | 4,47 | 5,42 | 5,70 | 5,72 | 5,63 | 5,62 | 5,63 | 5,37 | 4,63 | 3,65 | 3,07 |
| 90 | 3,28 | 4,10 | 4,72 | 4,70 | 4,50 | 4,33 | 4,38 | 4,56 | 4,58 | 4,17 | 3,42 | 2,93 |
| Azimutový úhel osluněné plochy γ = ± 45° | ||||||||||||
| 15 | 2,05 | 3,17 | 4,97 | 6,56 | 7,86 | 8,39 | 8,05 | 6,98 | 5,42 | 3,66 | 2,32 | 1,72 |
| 30 | 2,51 | 3,68 | 5,38 | 6,74 | 7,77 | 8,16 | 7,88 | 7,04 | 5,73 | 4,12 | 2,78 | 2,14 |
| 45 | 2,83 | 3,98 | 5,53 | 6,60 | 7,36 | 7,62 | 7,41 | 6,80 | 5,77 | 4,36 | 3,09 | 2,45 |
| 60 | 2,98 | 4,07 | 5,39 | 6,18 | 6,66 | 6,79 | 6,66 | 6,27 | 5,52 | 4,36 | 3,21 | 2,61 |
| 75 | 2,96 | 3,92 | 4,98 | 5,48 | 5,73 | 5,75 | 5,68 | 5,49 | 5,02 | 4,13 | 3,15 | 2,61 |
| 90 | 2,77 | 3,55 | 4,33 | 4,58 | 4,63 | 4,58 | 4,56 | 4,53 | 4,29 | 3,68 | 2,91 | 2,46 |
| Azimutový úhel osluněné plochy γ = ± 60° | ||||||||||||
| 15 | 1,88 | 2,96 | 4,75 | 6,39 | 7,74 | 8,30 | 7,94 | 6,83 | 5,22 | 3,46 | 2,15 | 1,56 |
| 30 | 2,19 | 3,29 | 5,00 | 6,44 | 7,57 | 8,02 | 7,72 | 6,79 | 5,38 | 3,75 | 2,45 | 1,85 |
| 45 | 2,38 | 3,47 | 5,04 | 6,24 | 7,15 | 7,48 | 7,24 | 6,50 | 5,33 | 3,87 | 2,63 | 2,04 |
| 60 | 2,45 | 3,47 | 4,85 | 5,81 | 6,49 | 6,72 | 6,53 | 5,98 | 5,05 | 3,80 | 2,67 | 2,11 |
| 75 | 2,38 | 3,29 | 4,45 | 5,17 | 5,64 | 5,77 | 5,64 | 5,27 | 4,57 | 3,55 | 2,57 | 2,07 |
| 90 | 2,19 | 2,96 | 3,87 | 4,37 | 4,66 | 4,72 | 4,63 | 4,41 | 3,93 | 3,14 | 2,34 | 1,92 |
| Azimutový úhel osluněné plochy γ = ± 75° | ||||||||||||
| 15 | 1,68 | 2,72 | 4,50 | 6,18 | 7,60 | 8,20 | 7,82 | 6,65 | 4,99 | 3,22 | 1,94 | 1,38 |
| 30 | 1,83 | 2,86 | 4,55 | 6,07 | 7,32 | 7,83 | 7,50 | 6,47 | 4,98 | 3,33 | 2,08 | 1,52 |
| 45 | 1,90 | 2,91 | 4,47 | 5,80 | 6,85 | 7,27 | 6,98 | 6,12 | 4,82 | 3,32 | 2,14 | 1,60 |
| 60 | 1,90 | 2,84 | 4,24 | 5,35 | 6,21 | 6,54 | 6,30 | 5,60 | 4,51 | 3,19 | 2,11 | 1,61 |
| 75 | 1,81 | 2,65 | 3,86 | 4,76 | 5,43 | 5,67 | 5,48 | 4,94 | 4,06 | 2,95 | 1,99 | 1,54 |
| 90 | 1,63 | 2,36 | 3,36 | 4,05 | 4,55 | 4,72 | 4,58 | 4,17 | 3,49 | 2,59 | 1,79 | 1,40 |
| Azimutový úhel osluněné plochy γ = ± 90° | ||||||||||||
| 15 | 1,47 | 2,46 | 4,23 | 5,96 | 7,44 | 8,07 | 7,68 | 6,45 | 4,75 | 2,97 | 1,73 | 1,19 |
| 30 | 1,46 | 2,41 | 4,07 | 5,66 | 7,02 | 7,59 | 7,23 | 6,11 | 4,54 | 2,88 | 1,70 | 1,19 |
| 45 | 1,44 | 2,34 | 3,86 | 5,28 | 6,47 | 6,97 | 6,64 | 5,66 | 4,27 | 2,76 | 1,66 | 1,18 |
| 60 | 1,38 | 2,22 | 3,59 | 4,81 | 5,82 | 6,24 | 5,96 | 5,12 | 3,92 | 2,59 | 1,59 | 1,14 |
| 75 | 1,29 | 2,03 | 3,23 | 4,26 | 5,09 | 5,43 | 5,19 | 4,51 | 3,50 | 2,35 | 1,46 | 1,06 |
| 90 | 1,15 | 1,80 | 2,81 | 3,65 | 4,31 | 4,57 | 4,38 | 3,83 | 3,01 | 2,06 | 1,30 | 0,95 |
| Úhel sklonu plochy β | Teoretická denní dávka celkového slunečního ozáření HT,den,teor [kWh/(m2·den)] pro charakteristickou oblast průmysl (Z = 5) | |||||||||||
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | |
| Azimutový úhel osluněné plochy γ = ± 0° (orientace na jih) | ||||||||||||
| 0 | 1,32 | 2,22 | 3,88 | 5,53 | 6,96 | 7,53 | 7,16 | 5,98 | 4,37 | 2,67 | 1,53 | 1,05 |
| 15 | 1,92 | 2,97 | 4,65 | 6,12 | 7,32 | 7,75 | 7,44 | 6,47 | 5,05 | 3,38 | 2,12 | 1,56 |
| 30 | 2,42 | 3,55 | 5,18 | 6,39 | 7,30 | 7,58 | 7,35 | 6,62 | 5,47 | 3,90 | 2,61 | 2,00 |
| 45 | 2,78 | 3,94 | 5,42 | 6,32 | 6,91 | 7,04 | 6,90 | 6,43 | 5,59 | 4,22 | 2,95 | 2,32 |
| 60 | 2,99 | 4,10 | 5,36 | 5,92 | 6,18 | 6,17 | 6,11 | 5,92 | 5,41 | 4,30 | 3,12 | 2,51 |
| 75 | 3,02 | 4,02 | 5,00 | 5,22 | 5,17 | 5,04 | 5,05 | 5,11 | 4,94 | 4,13 | 3,11 | 2,55 |
| 90 | 2,87 | 3,72 | 4,37 | 4,25 | 3,95 | 3,74 | 3,81 | 4,07 | 4,21 | 3,74 | 2,93 | 2,44 |
| Azimutový úhel osluněné plochy γ = ± 15° | ||||||||||||
| 15 | 1,90 | 2,94 | 4,62 | 6,10 | 7,30 | 7,74 | 7,43 | 6,45 | 5,03 | 3,35 | 2,10 | 1,55 |
| 30 | 2,38 | 3,50 | 5,12 | 6,35 | 7,27 | 7,57 | 7,33 | 6,59 | 5,42 | 3,85 | 2,57 | 1,96 |
| 45 | 2,73 | 3,86 | 5,34 | 6,27 | 6,89 | 7,03 | 6,88 | 6,39 | 5,52 | 4,15 | 2,89 | 2,27 |
| 60 | 2,92 | 4,01 | 5,26 | 5,87 | 6,17 | 6,18 | 6,11 | 5,88 | 5,33 | 4,21 | 3,05 | 2,44 |
| 75 | 2,94 | 3,92 | 4,90 | 5,17 | 5,19 | 5,08 | 5,08 | 5,09 | 4,86 | 4,04 | 3,03 | 2,48 |
| 90 | 2,78 | 3,61 | 4,27 | 4,23 | 4,01 | 3,82 | 3,88 | 4,07 | 4,14 | 3,64 | 2,85 | 2,37 |
| Azimutový úhel osluněné plochy γ = ± 30° | ||||||||||||
| 15 | 1,83 | 2,86 | 4,54 | 6,02 | 7,25 | 7,70 | 7,39 | 6,38 | 4,95 | 3,28 | 2,04 | 1,49 |
| 30 | 2,26 | 3,35 | 4,96 | 6,22 | 7,20 | 7,51 | 7,27 | 6,48 | 5,27 | 3,71 | 2,45 | 1,86 |
| 45 | 2,55 | 3,65 | 5,12 | 6,11 | 6,81 | 7,00 | 6,82 | 6,27 | 5,33 | 3,94 | 2,72 | 2,12 |
| 60 | 2,70 | 3,74 | 5,01 | 5,71 | 6,13 | 6,19 | 6,09 | 5,76 | 5,11 | 3,96 | 2,84 | 2,26 |
| 75 | 2,70 | 3,63 | 4,63 | 5,04 | 5,20 | 5,16 | 5,12 | 5,01 | 4,64 | 3,76 | 2,80 | 2,28 |
| 90 | 2,54 | 3,31 | 4,01 | 4,16 | 4,11 | 4,00 | 4,01 | 4,06 | 3,94 | 3,36 | 2,60 | 2,16 |
| Azimutový úhel osluněné plochy γ = ± 45° | ||||||||||||
| 15 | 1,73 | 2,73 | 4,40 | 5,91 | 7,17 | 7,64 | 7,32 | 6,29 | 4,83 | 3,16 | 1,94 | 1,41 |
| 30 | 2,06 | 3,11 | 4,71 | 6,03 | 7,07 | 7,42 | 7,15 | 6,31 | 5,05 | 3,48 | 2,25 | 1,69 |
| 45 | 2,28 | 3,32 | 4,79 | 5,87 | 6,67 | 6,91 | 6,71 | 6,06 | 5,04 | 3,63 | 2,45 | 1,89 |
| 60 | 2,37 | 3,35 | 4,63 | 5,46 | 6,02 | 6,16 | 6,01 | 5,57 | 4,79 | 3,59 | 2,51 | 1,98 |
| 75 | 2,33 | 3,20 | 4,25 | 4,82 | 5,17 | 5,21 | 5,12 | 4,86 | 4,32 | 3,37 | 2,44 | 1,96 |
| 90 | 2,16 | 2,88 | 3,67 | 4,02 | 4,18 | 4,16 | 4,12 | 4,00 | 3,68 | 2,98 | 2,23 | 1,83 |
| Azimutový úhel osluněné plochy γ = ± 60° | ||||||||||||
| 15 | 1,60 | 2,57 | 4,23 | 5,76 | 7,06 | 7,56 | 7,22 | 6,16 | 4,67 | 3,00 | 1,81 | 1,30 |
| 30 | 1,82 | 2,81 | 4,39 | 5,77 | 6,88 | 7,29 | 7,00 | 6,09 | 4,76 | 3,19 | 2,01 | 1,48 |
| 45 | 1,94 | 2,91 | 4,38 | 5,55 | 6,47 | 6,77 | 6,53 | 5,79 | 4,67 | 3,24 | 2,12 | 1,60 |
| 60 | 1,97 | 2,87 | 4,17 | 5,13 | 5,84 | 6,05 | 5,87 | 5,30 | 4,39 | 3,15 | 2,12 | 1,63 |
| 75 | 1,89 | 2,70 | 3,80 | 4,53 | 5,05 | 5,19 | 5,05 | 4,64 | 3,94 | 2,91 | 2,01 | 1,58 |
| 90 | 1,72 | 2,40 | 3,28 | 3,81 | 4,16 | 4,23 | 4,14 | 3,86 | 3,36 | 2,55 | 1,81 | 1,44 |
| Azimutový úhel osluněné plochy γ = ± 75° | ||||||||||||
| 15 | 1,46 | 2,39 | 4,02 | 5,59 | 6,94 | 7,46 | 7,11 | 6,01 | 4,48 | 2,82 | 1,66 | 1,17 |
| 30 | 1,55 | 2,47 | 4,03 | 5,46 | 6,66 | 7,11 | 6,80 | 5,81 | 4,43 | 2,87 | 1,74 | 1,25 |
| 45 | 1,58 | 2,47 | 3,91 | 5,16 | 6,19 | 6,56 | 6,30 | 5,46 | 4,25 | 2,82 | 1,76 | 1,29 |
| 60 | 1,55 | 2,37 | 3,66 | 4,73 | 5,58 | 5,87 | 5,65 | 4,96 | 3,93 | 2,67 | 1,70 | 1,27 |
| 75 | 1,46 | 2,19 | 3,30 | 4,17 | 4,85 | 5,06 | 4,88 | 4,34 | 3,51 | 2,44 | 1,58 | 1,19 |
| 90 | 1,30 | 1,93 | 2,85 | 3,53 | 4,04 | 4,19 | 4,06 | 3,65 | 3,00 | 2,12 | 1,40 | 1,07 |
| Azimutový úhel osluněné plochy γ = ± 90° | ||||||||||||
| 15 | 1,30 | 2,19 | 3,80 | 5,40 | 6,79 | 7,35 | 6,99 | 5,84 | 4,28 | 2,63 | 1,51 | 1,04 |
| 30 | 1,28 | 2,12 | 3,63 | 5,11 | 6,39 | 6,89 | 6,56 | 5,51 | 4,07 | 2,52 | 1,47 | 1,02 |
| 45 | 1,23 | 2,02 | 3,41 | 4,73 | 5,86 | 6,29 | 5,99 | 5,07 | 3,79 | 2,39 | 1,41 | 0,99 |
| 60 | 1,17 | 1,89 | 3,13 | 4,27 | 5,23 | 5,59 | 5,34 | 4,55 | 3,45 | 2,20 | 1,32 | 0,94 |
| 75 | 1,07 | 1,71 | 2,79 | 3,75 | 4,55 | 4,83 | 4,62 | 3,97 | 3,05 | 1,98 | 1,20 | 0,86 |
| 90 | 0,94 | 1,50 | 2,40 | 3,18 | 3,82 | 4,04 | 3,87 | 3,35 | 2,60 | 1,71 | 1,05 | 0,76 |
Příloha B – Teoretické denní dávky difuzního slunečního ozáření HT,den,dif
| Úhel sklonu plochy β | Teoretická denní dávka difuzního slunečního ozáření HT,den,dif [kWh/(m2·den)] | |||||||||||
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | |
| Charakteristická oblast hory (Z = 2) | ||||||||||||
| 0 | 0,29 | 0,41 | 0,60 | 0,77 | 0,93 | 1,10 | 1,07 | 0,96 | 0,74 | 0,50 | 0,34 | 0,26 |
| 15 | 0,30 | 0,41 | 0,61 | 0,78 | 0,94 | 1,12 | 1,08 | 0,97 | 0,75 | 0,51 | 0,34 | 0,26 |
| 30 | 0,30 | 0,42 | 0,63 | 0,82 | 0,98 | 1,16 | 1,12 | 1,00 | 0,77 | 0,52 | 0,35 | 0,27 |
| 45 | 0,31 | 0,44 | 0,66 | 0,87 | 1,06 | 1,22 | 1,18 | 1,04 | 0,80 | 0,54 | 0,36 | 0,27 |
| 60 | 0,31 | 0,46 | 0,71 | 0,94 | 1,15 | 1,31 | 1,26 | 1,11 | 0,84 | 0,56 | 0,37 | 0,27 |
| 75 | 0,32 | 0,48 | 0,76 | 1,03 | 1,25 | 1,41 | 1,36 | 1,18 | 0,89 | 0,59 | 0,38 | 0,28 |
| 90 | 0,33 | 0,51 | 0,81 | 1,11 | 1,37 | 1,51 | 1,46 | 1,25 | 0,95 | 0,62 | 0,39 | 0,28 |
| Charakteristická oblast venkov (Z = 3) | ||||||||||||
| 0 | 0,38 | 0,52 | 0,78 | 1,08 | 1,35 | 1,50 | 1,48 | 1,27 | 0,95 | 0,67 | 0,45 | 0,35 |
| 15 | 0,38 | 0,52 | 0,78 | 1,09 | 1,35 | 1,50 | 1,49 | 1,27 | 0,95 | 0,67 | 0,45 | 0,34 |
| 30 | 0,37 | 0,52 | 0,79 | 1,10 | 1,37 | 1,51 | 1,50 | 1,28 | 0,96 | 0,67 | 0,44 | 0,34 |
| 45 | 0,37 | 0,53 | 0,80 | 1,12 | 1,39 | 1,54 | 1,51 | 1,29 | 0,97 | 0,67 | 0,44 | 0,34 |
| 60 | 0,37 | 0,53 | 0,82 | 1,14 | 1,42 | 1,56 | 1,53 | 1,31 | 0,98 | 0,67 | 0,43 | 0,33 |
| 75 | 0,36 | 0,54 | 0,84 | 1,17 | 1,46 | 1,60 | 1,56 | 1,32 | 0,99 | 0,67 | 0,43 | 0,32 |
| 90 | 0,36 | 0,54 | 0,86 | 1,21 | 1,49 | 1,63 | 1,58 | 1,34 | 1,01 | 0,67 | 0,42 | 0,31 |
| Charakteristická oblast město (Z = 4) | ||||||||||||
| 0 | 0,49 | 0,68 | 0,99 | 1,37 | 1,64 | 1,77 | 1,75 | 1,53 | 1,19 | 0,83 | 0,56 | 0,43 |
| 15 | 0,48 | 0,67 | 0,99 | 1,36 | 1,64 | 1,77 | 1,74 | 1,52 | 1,19 | 0,83 | 0,56 | 0,43 |
| 30 | 0,47 | 0,66 | 0,99 | 1,36 | 1,63 | 1,76 | 1,74 | 1,51 | 1,18 | 0,82 | 0,55 | 0,42 |
| 45 | 0,46 | 0,65 | 0,97 | 1,34 | 1,62 | 1,75 | 1,72 | 1,50 | 1,16 | 0,80 | 0,53 | 0,40 |
| 60 | 0,44 | 0,63 | 0,96 | 1,33 | 1,61 | 1,74 | 1,70 | 1,48 | 1,14 | 0,78 | 0,51 | 0,38 |
| 75 | 0,42 | 0,61 | 0,94 | 1,31 | 1,60 | 1,73 | 1,68 | 1,45 | 1,11 | 0,75 | 0,48 | 0,36 |
| 90 | 0,39 | 0,59 | 0,93 | 1,29 | 1,58 | 1,71 | 1,66 | 1,42 | 1,08 | 0,72 | 0,46 | 0,33 |
| Charakteristická oblast průmysl (Z = 5) | ||||||||||||
| 0 | 0,57 | 0,81 | 1,20 | 1,64 | 1,96 | 2,13 | 2,09 | 1,83 | 1,43 | 1,01 | 0,67 | 0,50 |
| 15 | 0,56 | 0,80 | 1,20 | 1,63 | 1,95 | 2,12 | 2,08 | 1,82 | 1,42 | 1,00 | 0,67 | 0,50 |
| 30 | 0,55 | 0,78 | 1,17 | 1,60 | 1,92 | 2,09 | 2,05 | 1,79 | 1,39 | 0,97 | 0,65 | 0,48 |
| 45 | 0,52 | 0,75 | 1,14 | 1,56 | 1,88 | 2,04 | 2,00 | 1,74 | 1,35 | 0,94 | 0,62 | 0,46 |
| 60 | 0,49 | 0,72 | 1,10 | 1,51 | 1,82 | 1,98 | 1,93 | 1,67 | 1,29 | 0,89 | 0,58 | 0,43 |
| 75 | 0,45 | 0,67 | 1,04 | 1,44 | 1,75 | 1,90 | 1,85 | 1,60 | 1,23 | 0,83 | 0,54 | 0,40 |
| 90 | 0,42 | 0,63 | 0,99 | 1,37 | 1,68 | 1,82 | 1,76 | 1,51 | 1,15 | 0,77 | 0,49 | 0,36 |
Příloha C – Střední hodnota slunečního ozáření GT,m
| Úhel sklonu plochy β | Střední hodnota slunečního ozáření GT,m [W/m2] pro charakteristickou oblast hory (Z = 2) | |||||||||||
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | |
| Azimutový úhel osluněné plochy γ = ± 0° (orientace na jih) | ||||||||||||
| 0 | 223 | 311 | 436 | 538 | 596 | 601 | 591 | 546 | 465 | 352 | 248 | 194 |
| 15 | 387 | 463 | 551 | 608 | 626 | 614 | 613 | 598 | 559 | 488 | 406 | 358 |
| 30 | 528 | 587 | 633 | 644 | 624 | 597 | 603 | 618 | 622 | 595 | 540 | 501 |
| 45 | 636 | 674 | 676 | 642 | 589 | 549 | 562 | 602 | 647 | 665 | 640 | 612 |
| 60 | 703 | 719 | 679 | 603 | 522 | 475 | 493 | 553 | 633 | 694 | 699 | 684 |
| 75 | 725 | 718 | 640 | 529 | 429 | 379 | 400 | 474 | 581 | 680 | 713 | 712 |
| 90 | 700 | 673 | 562 | 426 | 318 | 271 | 291 | 370 | 496 | 623 | 682 | 693 |
| Azimutový úhel osluněné plochy γ = ± 15° | ||||||||||||
| 15 | 382 | 457 | 546 | 606 | 625 | 613 | 612 | 596 | 556 | 483 | 401 | 353 |
| 30 | 517 | 576 | 625 | 640 | 623 | 597 | 603 | 615 | 616 | 585 | 529 | 490 |
| 45 | 620 | 659 | 666 | 639 | 589 | 551 | 563 | 600 | 639 | 651 | 624 | 596 |
| 60 | 683 | 701 | 667 | 601 | 525 | 479 | 496 | 553 | 625 | 677 | 680 | 665 |
| 75 | 703 | 698 | 627 | 530 | 435 | 386 | 406 | 476 | 574 | 661 | 692 | 690 |
| 90 | 677 | 651 | 550 | 431 | 328 | 281 | 301 | 377 | 490 | 604 | 661 | 671 |
| Azimutový úhel osluněné plochy γ = ± 30° | ||||||||||||
| 15 | 365 | 441 | 535 | 599 | 622 | 611 | 610 | 591 | 546 | 469 | 384 | 336 |
| 30 | 484 | 546 | 604 | 630 | 620 | 596 | 601 | 607 | 599 | 558 | 497 | 457 |
| 45 | 573 | 616 | 638 | 628 | 590 | 554 | 565 | 593 | 618 | 614 | 579 | 550 |
| 60 | 626 | 649 | 636 | 593 | 531 | 489 | 503 | 549 | 602 | 633 | 625 | 608 |
| 75 | 639 | 641 | 596 | 528 | 450 | 404 | 421 | 479 | 553 | 613 | 631 | 627 |
| 90 | 612 | 593 | 523 | 437 | 353 | 308 | 326 | 389 | 475 | 557 | 597 | 605 |
| Azimutový úhel osluněné plochy γ = ± 45° | ||||||||||||
| 15 | 338 | 417 | 516 | 587 | 616 | 608 | 605 | 582 | 531 | 447 | 359 | 309 |
| 30 | 433 | 500 | 571 | 611 | 613 | 593 | 595 | 593 | 572 | 518 | 448 | 405 |
| 45 | 502 | 554 | 596 | 607 | 586 | 556 | 563 | 579 | 584 | 560 | 511 | 477 |
| 60 | 539 | 575 | 590 | 575 | 534 | 498 | 509 | 539 | 567 | 571 | 543 | 519 |
| 75 | 543 | 562 | 552 | 516 | 462 | 423 | 436 | 476 | 521 | 548 | 541 | 528 |
| 90 | 513 | 515 | 485 | 435 | 376 | 337 | 351 | 395 | 451 | 495 | 506 | 503 |
| Azimutový úhel osluněné plochy γ = ± 60° | ||||||||||||
| 15 | 304 | 386 | 492 | 571 | 608 | 603 | 598 | 569 | 510 | 418 | 326 | 275 |
| 30 | 370 | 443 | 529 | 584 | 600 | 586 | 586 | 572 | 536 | 467 | 389 | 342 |
| 45 | 416 | 479 | 543 | 576 | 574 | 552 | 555 | 556 | 540 | 494 | 430 | 390 |
| 60 | 438 | 489 | 532 | 545 | 528 | 500 | 506 | 518 | 521 | 496 | 448 | 415 |
| 75 | 435 | 473 | 496 | 493 | 464 | 433 | 442 | 462 | 479 | 472 | 440 | 415 |
| 90 | 405 | 431 | 438 | 422 | 388 | 357 | 366 | 391 | 417 | 425 | 407 | 391 |
| Azimutový úhel osluněné plochy γ = ± 75° | ||||||||||||
| 15 | 266 | 350 | 463 | 551 | 597 | 596 | 589 | 553 | 485 | 386 | 289 | 237 |
| 30 | 302 | 380 | 479 | 551 | 582 | 574 | 571 | 545 | 493 | 410 | 323 | 274 |
| 45 | 326 | 397 | 481 | 536 | 554 | 540 | 539 | 524 | 488 | 421 | 344 | 299 |
| 60 | 335 | 397 | 465 | 505 | 511 | 492 | 493 | 488 | 466 | 415 | 350 | 310 |
| 75 | 326 | 379 | 432 | 458 | 454 | 432 | 435 | 437 | 427 | 391 | 338 | 304 |
| 90 | 301 | 344 | 382 | 397 | 387 | 364 | 368 | 375 | 373 | 350 | 310 | 283 |
| Azimutový úhel osluněné plochy γ = ± 90° | ||||||||||||
| 15 | 226 | 311 | 431 | 529 | 584 | 587 | 579 | 535 | 458 | 350 | 250 | 197 |
| 30 | 233 | 314 | 424 | 511 | 558 | 558 | 551 | 513 | 446 | 348 | 255 | 205 |
| 45 | 238 | 313 | 412 | 487 | 524 | 519 | 514 | 484 | 428 | 343 | 258 | 212 |
| 60 | 237 | 305 | 391 | 454 | 482 | 473 | 469 | 447 | 402 | 331 | 255 | 212 |
| 75 | 227 | 287 | 360 | 411 | 430 | 418 | 416 | 400 | 367 | 308 | 242 | 204 |
| 90 | 208 | 259 | 319 | 359 | 371 | 357 | 357 | 346 | 322 | 275 | 221 | 188 |
| Úhel sklonu plochy β | Střední hodnota slunečního ozáření GT,m [W/m2] pro charakteristickou oblast venkov (Z = 3) | |||||||||||
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | |
| Azimutový úhel osluněné plochy γ = ± 0° (orientace na jih) | ||||||||||||
| 0 | 203 | 287 | 404 | 491 | 539 | 550 | 537 | 501 | 430 | 320 | 224 | 172 |
| 15 | 338 | 417 | 505 | 552 | 568 | 565 | 558 | 548 | 512 | 433 | 352 | 300 |
| 30 | 453 | 522 | 576 | 583 | 567 | 550 | 551 | 565 | 566 | 520 | 459 | 411 |
| 45 | 540 | 595 | 612 | 580 | 535 | 508 | 515 | 550 | 586 | 577 | 538 | 496 |
| 60 | 593 | 631 | 612 | 545 | 476 | 442 | 453 | 506 | 572 | 598 | 583 | 551 |
| 75 | 609 | 628 | 576 | 479 | 394 | 356 | 370 | 434 | 525 | 583 | 593 | 570 |
| 90 | 586 | 587 | 505 | 387 | 295 | 257 | 273 | 341 | 448 | 533 | 565 | 553 |
| Azimutový úhel osluněné plochy γ = ± 15° | ||||||||||||
| 15 | 333 | 412 | 501 | 550 | 567 | 564 | 557 | 546 | 509 | 429 | 347 | 296 |
| 30 | 443 | 512 | 569 | 579 | 565 | 550 | 550 | 562 | 560 | 512 | 450 | 402 |
| 45 | 527 | 582 | 603 | 576 | 535 | 509 | 514 | 548 | 579 | 565 | 525 | 484 |
| 60 | 577 | 615 | 601 | 541 | 478 | 444 | 454 | 504 | 564 | 584 | 568 | 535 |
| 75 | 591 | 611 | 564 | 477 | 398 | 361 | 374 | 435 | 517 | 568 | 576 | 553 |
| 90 | 567 | 568 | 494 | 389 | 303 | 266 | 280 | 345 | 441 | 517 | 547 | 536 |
| Azimutový úhel osluněné plochy γ = ± 30° | ||||||||||||
| 15 | 319 | 398 | 490 | 543 | 563 | 562 | 554 | 541 | 501 | 417 | 334 | 283 |
| 30 | 416 | 486 | 549 | 568 | 561 | 548 | 546 | 554 | 544 | 490 | 424 | 377 |
| 45 | 488 | 545 | 577 | 564 | 532 | 510 | 513 | 539 | 559 | 534 | 489 | 448 |
| 60 | 530 | 571 | 572 | 530 | 479 | 450 | 457 | 498 | 542 | 547 | 524 | 491 |
| 75 | 538 | 561 | 535 | 470 | 406 | 373 | 383 | 434 | 496 | 527 | 526 | 503 |
| 90 | 513 | 518 | 467 | 389 | 319 | 285 | 298 | 351 | 425 | 476 | 496 | 484 |
| Azimutový úhel osluněné plochy γ = ± 45° | ||||||||||||
| 15 | 297 | 377 | 474 | 532 | 557 | 558 | 549 | 532 | 486 | 398 | 313 | 262 |
| 30 | 374 | 447 | 520 | 550 | 552 | 543 | 539 | 540 | 520 | 455 | 384 | 336 |
| 45 | 429 | 491 | 539 | 543 | 525 | 508 | 508 | 524 | 528 | 487 | 433 | 391 |
| 60 | 457 | 506 | 530 | 511 | 476 | 453 | 457 | 485 | 509 | 492 | 456 | 421 |
| 75 | 458 | 492 | 493 | 456 | 410 | 384 | 391 | 426 | 465 | 470 | 452 | 426 |
| 90 | 431 | 449 | 431 | 382 | 333 | 306 | 314 | 352 | 400 | 421 | 420 | 404 |
| Azimutový úhel osluněné plochy γ = ± 60° | ||||||||||||
| 15 | 269 | 350 | 452 | 518 | 549 | 552 | 543 | 520 | 468 | 374 | 286 | 235 |
| 30 | 322 | 397 | 481 | 526 | 539 | 535 | 529 | 520 | 488 | 412 | 335 | 286 |
| 45 | 357 | 425 | 490 | 514 | 511 | 500 | 498 | 501 | 487 | 431 | 366 | 321 |
| 60 | 373 | 430 | 477 | 482 | 466 | 451 | 451 | 464 | 466 | 428 | 377 | 338 |
| 75 | 367 | 413 | 441 | 432 | 407 | 389 | 391 | 411 | 426 | 404 | 367 | 336 |
| 90 | 340 | 374 | 387 | 367 | 338 | 319 | 322 | 345 | 368 | 360 | 337 | 313 |
| Azimutový úhel osluněné plochy γ = ± 75° | ||||||||||||
| 15 | 237 | 319 | 427 | 500 | 539 | 545 | 534 | 506 | 446 | 346 | 256 | 205 |
| 30 | 264 | 342 | 437 | 495 | 521 | 523 | 514 | 495 | 450 | 363 | 280 | 231 |
| 45 | 281 | 353 | 434 | 477 | 491 | 487 | 481 | 472 | 440 | 367 | 294 | 248 |
| 60 | 286 | 350 | 416 | 445 | 448 | 440 | 436 | 435 | 416 | 358 | 295 | 254 |
| 75 | 276 | 331 | 383 | 399 | 394 | 384 | 381 | 386 | 378 | 334 | 283 | 246 |
| 90 | 253 | 298 | 336 | 342 | 332 | 321 | 320 | 328 | 328 | 297 | 257 | 227 |
| Azimutový úhel osluněné plochy γ = ± 90° | ||||||||||||
| 15 | 203 | 286 | 399 | 481 | 527 | 537 | 524 | 490 | 422 | 316 | 224 | 173 |
| 30 | 206 | 284 | 388 | 461 | 499 | 507 | 495 | 467 | 407 | 311 | 225 | 177 |
| 45 | 208 | 280 | 373 | 434 | 464 | 467 | 458 | 436 | 387 | 302 | 224 | 179 |
| 60 | 204 | 270 | 351 | 399 | 421 | 421 | 413 | 398 | 360 | 287 | 217 | 176 |
| 75 | 193 | 252 | 320 | 357 | 371 | 369 | 362 | 353 | 325 | 264 | 204 | 167 |
| 90 | 175 | 225 | 281 | 308 | 316 | 312 | 307 | 302 | 283 | 234 | 183 | 152 |
| Úhel sklonu plochy β | Střední hodnota slunečního ozáření GT,m [W/m2] pro charakteristickou oblast město (Z = 4) | |||||||||||
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | |
| Azimutový úhel osluněné plochy γ = ± 0° (orientace na jih) | ||||||||||||
| 0 | 176 | 255 | 367 | 448 | 500 | 515 | 502 | 463 | 390 | 288 | 197 | 151 |
| 15 | 274 | 355 | 450 | 501 | 526 | 529 | 523 | 505 | 458 | 377 | 292 | 245 |
| 30 | 357 | 435 | 507 | 526 | 525 | 517 | 516 | 519 | 501 | 446 | 370 | 325 |
| 45 | 418 | 489 | 536 | 522 | 497 | 479 | 483 | 505 | 516 | 489 | 427 | 386 |
| 60 | 454 | 515 | 533 | 490 | 443 | 417 | 426 | 465 | 502 | 503 | 459 | 424 |
| 75 | 462 | 509 | 500 | 431 | 368 | 338 | 350 | 400 | 460 | 488 | 462 | 435 |
| 90 | 442 | 473 | 437 | 350 | 278 | 247 | 260 | 316 | 392 | 444 | 438 | 420 |
| Azimutový úhel osluněné plochy γ = ± 15° | ||||||||||||
| 15 | 271 | 351 | 447 | 499 | 525 | 529 | 522 | 503 | 456 | 374 | 288 | 241 |
| 30 | 350 | 428 | 501 | 522 | 524 | 516 | 515 | 516 | 497 | 439 | 364 | 319 |
| 45 | 408 | 480 | 528 | 518 | 496 | 479 | 482 | 502 | 510 | 480 | 418 | 377 |
| 60 | 442 | 503 | 523 | 486 | 443 | 419 | 427 | 462 | 495 | 492 | 447 | 412 |
| 75 | 449 | 496 | 489 | 428 | 371 | 342 | 353 | 399 | 452 | 476 | 450 | 423 |
| 90 | 429 | 459 | 427 | 350 | 284 | 254 | 266 | 318 | 386 | 431 | 425 | 407 |
| Azimutový úhel osluněné plochy γ = ± 30° | ||||||||||||
| 15 | 260 | 341 | 438 | 493 | 521 | 526 | 519 | 498 | 448 | 364 | 278 | 232 |
| 30 | 330 | 407 | 485 | 512 | 518 | 513 | 511 | 508 | 483 | 421 | 344 | 300 |
| 45 | 380 | 451 | 505 | 506 | 491 | 478 | 480 | 493 | 492 | 454 | 391 | 350 |
| 60 | 408 | 468 | 498 | 474 | 442 | 422 | 428 | 455 | 475 | 461 | 414 | 380 |
| 75 | 411 | 457 | 462 | 419 | 375 | 350 | 359 | 395 | 432 | 442 | 412 | 386 |
| 90 | 389 | 419 | 403 | 346 | 295 | 270 | 280 | 321 | 369 | 397 | 386 | 369 |
| Azimutový úhel osluněné plochy γ = ± 45° | ||||||||||||
| 15 | 244 | 324 | 423 | 483 | 516 | 522 | 514 | 490 | 436 | 349 | 262 | 216 |
| 30 | 299 | 376 | 459 | 496 | 510 | 508 | 504 | 495 | 461 | 393 | 314 | 270 |
| 45 | 337 | 407 | 472 | 486 | 483 | 474 | 473 | 478 | 464 | 416 | 348 | 308 |
| 60 | 355 | 416 | 460 | 454 | 437 | 423 | 425 | 441 | 445 | 416 | 363 | 328 |
| 75 | 352 | 401 | 425 | 403 | 376 | 358 | 363 | 386 | 404 | 394 | 356 | 329 |
| 90 | 329 | 363 | 369 | 337 | 304 | 285 | 291 | 318 | 345 | 351 | 329 | 310 |
| Azimutový úhel osluněné plochy γ = ± 60° | ||||||||||||
| 15 | 223 | 302 | 405 | 470 | 508 | 517 | 507 | 480 | 420 | 330 | 242 | 196 |
| 30 | 260 | 337 | 426 | 473 | 497 | 499 | 493 | 477 | 434 | 357 | 277 | 232 |
| 45 | 283 | 355 | 429 | 459 | 469 | 466 | 462 | 457 | 429 | 369 | 297 | 256 |
| 60 | 291 | 355 | 414 | 427 | 426 | 418 | 417 | 420 | 407 | 362 | 302 | 266 |
| 75 | 283 | 337 | 380 | 380 | 370 | 359 | 360 | 370 | 368 | 339 | 291 | 261 |
| 90 | 260 | 302 | 330 | 321 | 306 | 294 | 296 | 310 | 316 | 300 | 265 | 242 |
| Azimutový úhel osluněné plochy γ = ± 75° | ||||||||||||
| 15 | 200 | 278 | 384 | 455 | 498 | 510 | 499 | 467 | 402 | 307 | 219 | 174 |
| 30 | 217 | 293 | 388 | 447 | 480 | 487 | 479 | 454 | 401 | 317 | 235 | 191 |
| 45 | 226 | 297 | 381 | 426 | 449 | 452 | 446 | 430 | 388 | 317 | 242 | 201 |
| 60 | 226 | 290 | 361 | 394 | 407 | 407 | 402 | 393 | 363 | 305 | 239 | 202 |
| 75 | 215 | 271 | 329 | 350 | 356 | 353 | 350 | 347 | 327 | 281 | 225 | 193 |
| 90 | 194 | 241 | 286 | 298 | 299 | 294 | 292 | 293 | 281 | 247 | 202 | 176 |
| Azimutový úhel osluněné plochy γ = ± 90° | ||||||||||||
| 15 | 175 | 252 | 360 | 438 | 488 | 502 | 490 | 453 | 382 | 283 | 195 | 150 |
| 30 | 174 | 247 | 347 | 417 | 460 | 473 | 462 | 429 | 365 | 275 | 192 | 150 |
| 45 | 171 | 239 | 330 | 388 | 424 | 433 | 424 | 397 | 343 | 263 | 188 | 149 |
| 60 | 165 | 226 | 306 | 354 | 382 | 388 | 381 | 360 | 316 | 246 | 179 | 144 |
| 75 | 153 | 208 | 276 | 314 | 334 | 338 | 332 | 317 | 282 | 224 | 165 | 134 |
| 90 | 137 | 184 | 240 | 268 | 283 | 284 | 280 | 269 | 243 | 196 | 147 | 120 |
| Úhel sklonu plochy β | Střední hodnota slunečního ozáření GT,m [W/m2] pro charakteristickou oblast průmysl (Z = 5) | |||||||||||
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | |
| Azimutový úhel osluněné plochy γ = ± 0° (orientace na jih) | ||||||||||||
| 0 | 156 | 227 | 331 | 407 | 457 | 469 | 457 | 420 | 352 | 255 | 173 | 132 |
| 15 | 228 | 303 | 397 | 450 | 480 | 482 | 476 | 454 | 407 | 322 | 240 | 197 |
| 30 | 288 | 363 | 441 | 470 | 479 | 472 | 470 | 465 | 440 | 372 | 295 | 251 |
| 45 | 331 | 403 | 462 | 465 | 453 | 438 | 441 | 452 | 450 | 402 | 333 | 292 |
| 60 | 355 | 419 | 457 | 436 | 406 | 384 | 390 | 416 | 435 | 410 | 352 | 315 |
| 75 | 359 | 411 | 426 | 384 | 339 | 314 | 323 | 359 | 398 | 394 | 352 | 321 |
| 90 | 341 | 380 | 373 | 313 | 259 | 233 | 244 | 286 | 339 | 357 | 331 | 307 |
| Azimutový úhel osluněné plochy γ = ± 15° | ||||||||||||
| 15 | 226 | 300 | 394 | 448 | 479 | 482 | 475 | 453 | 405 | 320 | 237 | 195 |
| 30 | 283 | 358 | 437 | 467 | 477 | 471 | 468 | 463 | 436 | 367 | 290 | 247 |
| 45 | 324 | 395 | 455 | 461 | 452 | 438 | 439 | 449 | 444 | 395 | 326 | 285 |
| 60 | 347 | 410 | 449 | 432 | 405 | 385 | 390 | 413 | 429 | 401 | 344 | 308 |
| 75 | 349 | 401 | 418 | 380 | 340 | 316 | 324 | 357 | 391 | 385 | 343 | 312 |
| 90 | 331 | 369 | 364 | 311 | 263 | 238 | 248 | 286 | 333 | 347 | 321 | 298 |
| Azimutový úhel osluněné plochy γ = ± 30° | ||||||||||||
| 15 | 218 | 292 | 387 | 443 | 476 | 479 | 472 | 449 | 398 | 312 | 230 | 188 |
| 30 | 268 | 342 | 423 | 458 | 472 | 468 | 464 | 455 | 425 | 353 | 276 | 234 |
| 45 | 303 | 373 | 437 | 450 | 447 | 435 | 436 | 440 | 429 | 376 | 307 | 267 |
| 60 | 321 | 383 | 427 | 420 | 402 | 385 | 389 | 405 | 411 | 377 | 320 | 285 |
| 75 | 321 | 371 | 395 | 371 | 341 | 321 | 327 | 352 | 373 | 359 | 316 | 287 |
| 90 | 302 | 338 | 342 | 306 | 270 | 249 | 256 | 286 | 318 | 321 | 294 | 272 |
| Azimutový úhel osluněné plochy γ = ± 45° | ||||||||||||
| 15 | 206 | 279 | 375 | 435 | 470 | 475 | 467 | 442 | 388 | 301 | 219 | 177 |
| 30 | 245 | 318 | 402 | 443 | 463 | 462 | 457 | 443 | 407 | 332 | 254 | 213 |
| 45 | 271 | 339 | 408 | 432 | 438 | 430 | 429 | 426 | 405 | 346 | 276 | 238 |
| 60 | 282 | 342 | 395 | 402 | 395 | 383 | 384 | 391 | 385 | 342 | 284 | 249 |
| 75 | 277 | 327 | 362 | 355 | 339 | 324 | 327 | 341 | 348 | 321 | 275 | 247 |
| 90 | 257 | 294 | 313 | 296 | 274 | 259 | 263 | 281 | 296 | 284 | 252 | 231 |
| Azimutový úhel osluněné plochy γ = ± 60° | ||||||||||||
| 15 | 191 | 263 | 360 | 424 | 463 | 470 | 461 | 433 | 376 | 286 | 204 | 163 |
| 30 | 216 | 287 | 375 | 424 | 452 | 453 | 447 | 428 | 383 | 304 | 227 | 187 |
| 45 | 231 | 297 | 373 | 408 | 424 | 421 | 417 | 407 | 376 | 309 | 239 | 201 |
| 60 | 234 | 294 | 356 | 377 | 383 | 377 | 375 | 372 | 353 | 300 | 239 | 205 |
| 75 | 225 | 276 | 324 | 334 | 332 | 323 | 323 | 326 | 317 | 277 | 227 | 198 |
| 90 | 205 | 246 | 279 | 280 | 273 | 263 | 264 | 271 | 271 | 243 | 205 | 182 |
| Azimutový úhel osluněné plochy γ = ± 75° | ||||||||||||
| 15 | 173 | 244 | 343 | 411 | 455 | 464 | 454 | 422 | 361 | 269 | 188 | 147 |
| 30 | 184 | 252 | 343 | 401 | 437 | 442 | 434 | 408 | 357 | 273 | 197 | 158 |
| 45 | 188 | 252 | 333 | 380 | 406 | 408 | 402 | 383 | 342 | 269 | 198 | 162 |
| 60 | 184 | 243 | 312 | 348 | 366 | 365 | 361 | 348 | 317 | 255 | 192 | 159 |
| 75 | 173 | 224 | 282 | 307 | 318 | 315 | 312 | 305 | 282 | 232 | 179 | 150 |
| 90 | 155 | 197 | 243 | 260 | 265 | 261 | 259 | 256 | 241 | 202 | 159 | 135 |
| Azimutový úhel osluněné plochy γ = ± 90° | ||||||||||||
| 15 | 155 | 223 | 324 | 397 | 446 | 457 | 446 | 410 | 344 | 250 | 170 | 131 |
| 30 | 152 | 217 | 310 | 376 | 419 | 429 | 419 | 387 | 327 | 241 | 166 | 129 |
| 45 | 147 | 207 | 291 | 348 | 384 | 391 | 383 | 356 | 305 | 227 | 159 | 125 |
| 60 | 139 | 193 | 267 | 314 | 343 | 348 | 341 | 320 | 277 | 210 | 149 | 118 |
| 75 | 127 | 175 | 238 | 276 | 298 | 301 | 295 | 279 | 245 | 188 | 135 | 108 |
| 90 | 112 | 153 | 205 | 234 | 251 | 252 | 247 | 236 | 210 | 163 | 119 | 96 |
Poznámka:
Přílohy týkající se slunečního záření byly vypracovány ing. Bořivojem Šourkem na základě teoretických vztahů (viz kapitola 1) pro dopadající tok slunečního záření během roku na zeměpisnou šířku 50°.
Příloha D – Poměrná doba slunečního svitu τr
| Místo | Poměrná doba slunečního svitu τr | |||||||||||
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | |
| Praha | 0,21 | 0,32 | 0,42 | 0,45 | 0,51 | 0,54 | 0,55 | 0,55 | 0,53 | 0,37 | 0,21 | 0,14 |
| České Bud. | 0,18 | 0,29 | 0,37 | 0,39 | 0,43 | 0,46 | 0,49 | 0,51 | 0,48 | 0,34 | 0,22 | 0,15 |
| Hradec K. | 0,18 | 0,27 | 0,40 | 0,44 | 0,50 | 0,51 | 0,52 | 0,54 | 0,52 | 0,37 | 0,19 | 0,17 |
| Brno | 0,18 | 0,31 | 0,38 | 0,39 | 0,48 | 0,53 | 0,56 | 0,53 | 0,50 | 0,37 | 0,23 | 0,12 |
| Bratislava | 0,25 | 0,35 | 0,46 | 0,50 | 0,56 | 0,59 | 0,66 | 0,66 | 0,63 | 0,47 | 0,25 | 0,20 |
| Košice | 0,26 | 0,31 | 0,42 | 0,46 | 0,53 | 0,54 | 0,58 | 0,59 | 0,57 | 0,47 | 0,27 | 0,23 |
Příloha E – Střední venkovní teploty te,s a te,p
| Místo | Střední teplota v době slunečního svitu te,s v jednotlivých měsících [°C] | |||||||||||
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | |
| Praha | 2,2 | 3,4 | 6,5 | 12,1 | 16,6 | 20,6 | 22,5 | 22,6 | 19,4 | 13,8 | 7,3 | 3,5 |
| České Bud. | 1,7 | 2,4 | 6,2 | 10,7 | 15,8 | 18,6 | 20,8 | 20,6 | 17,4 | 12,1 | 6,9 | 3,3 |
| Hradec K. | 1,6 | 2,4 | 6,0 | 10,7 | 15,9 | 18,9 | 20,7 | 20,8 | 18,0 | 12,7 | 7,2 | 3,3 |
| Brno | 1,7 | 2,8 | 7,0 | 12,0 | 17,2 | 20,2 | 22,1 | 21,8 | 18,5 | 13,1 | 7,7 | 3,5 |
| Bratislava | 2,1 | 3,6 | 8,5 | 13,4 | 18,5 | 21,6 | 23,5 | 23,6 | 20,5 | 14,7 | 8,5 | 4,2 |
| Košice | 0,1 | 1,7 | 6,6 | 12,1 | 16,3 | 20,5 | 22,4 | 22,2 | 18,7 | 13,1 | 7,5 | 2,8 |
| Místo | Střední teplota te,p v jednotlivých měsících [°C] | |||||||||||
| I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | |
| Praha | -1,5 | 0,0 | 3,2 | 8,8 | 13,6 | 17,3 | 19,2 | 18,6 | 14,9 | 9,4 | 3,2 | -0,2 |
| České Bud. | -2,0 | -0,9 | 3,0 | 7,4 | 12,7 | 15,7 | 17,5 | 16,6 | 12,9 | 7,7 | 2,8 | -0,4 |
| Hradec K. | -2,1 | -1,0 | 2,7 | 7,4 | 12,8 | 15,6 | 17,4 | 16,8 | 13,5 | 8,3 | 3,1 | -0,4 |
| Brno | -2,0 | -0,6 | 3,7 | 8,7 | 14,1 | 16,9 | 18,8 | 17,8 | 14,0 | 8,7 | 3,6 | -0,2 |
| Bratislava | -1,6 | 0,2 | 5,2 | 10,1 | 15,4 | 18,3 | 20,2 | 19,6 | 16,0 | 10,3 | 4,4 | 0,5 |
| Košice | -3,6 | -1,7 | 3,3 | 8,8 | 14,3 | 17,2 | 19,1 | 18,2 | 14,2 | 8,7 | 3,4 | -0,9 |