Autoři: Ing. Jiří Lahodný, Ph.D., Ing. Petra Poláková
Stav: kontrola 2022, vydání 2019
Anotace:
Příklad výpočtu zatížení reklamního pylonu větrem.
OBSAH
ÚVOD
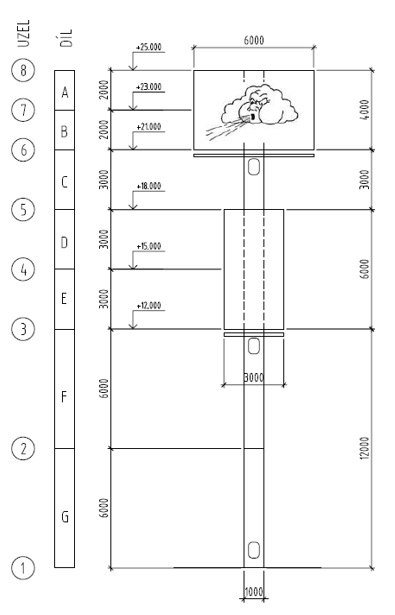
Pylon o celkové výšce 25 m je tvořen ocelovou rourou o průměru 1 000 m. Tloušťka stěny je v dolní části do výšky 12 m rovna 16 mm, v horní části 12 mm. Na pylonu jsou ve dvou výškových úrovních umístěny obdélníkové reklamní panely o rozměrech 6 x 4 a 3 x 6 m, viz obr. 1.1. Žebřík a kabely jsou umístěny uvnitř roury. Konstrukce je vetknuta do betonového základu.
Zatížení větrem je stanoveno pro II. větrnou oblast (základní rychlost větru 25 m/s). Pylon je umístěn v předměstském terénu (kategorie terénu III podle ČSN EN 1991-1-4 ed. 2 [1]) ve vzdálenosti cca 5 km od hranice města a otevřeného terénu (kategorie II). Odezva konstrukce na zatížení větrem je vypočtena podle normy ČSN EN 1991-1-4 ed. 2 [1]. Součinitel konstrukce cscd je určen podrobným postupem podle Přílohy B [1]. Vzhledem k typu konstrukce se pro stanovení celkové odezvy a pro zatřídění spolehlivosti použijí rovněž normy pro navrhování komínů a stožárů ČSN EN 1993-3-2 [2] a ČSN EN 1993-3-1 [3].
Obr. 1.1 Schéma konstrukce – čelní pohled.
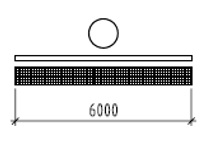
Obr. 1.2 Pohled shora
1 VLASTNOSTI HLAVNÍ NOSNÉ KONSTRUKCE
Průřezové charakteristiky hlavní nosné roury jsou uvedeny v tab. 2.1, vlastní tíha roury v tab. 2.2.
Tab. 2.1 Průřezové charakteristiky
| Díl | Modul pružnosti | Průměr roury, resp. šířka prutu | Tloušťka stěny | Průřezová plocha | Moment setrvačnosti | Elastický modul průřezu | Plastický modul průřezu |
| E | di | ti | Ap,i | Iy,i | Wel,i | Wpl,i | |
| [MPa] | [mm] | [mm] | [mm2] | [mm4] | [mm3] | [mm3] | |
| A-E | 210 000 | 1 000,0 | 12,0 | 37 247 | 4,545E+09 | 9,091E+06 | 1,171E+07 |
| F-G | 210 000 | 1 000,0 | 16,0 | 49 461 | 5,988E+09 | 1,198E+07 | 1,549E+07 |
Tab. 2.2 Hmotnost jednotlivých panelů
| Díl | Výška panelu | Čistá hmotnost na bm | Přídavek hmotnosti | Přídavek hmotnosti | Celková hmotnost na bm |
| hi | gnw | gnw,t | |||
| [m] | [kg/m] | [%] | [kg/m] | [kg/m] | |
| A-E | 2,000 | 292,39 | 0 | 0,00 | 292,39 |
| F-G | 6,000 | 388,27 | 0 | 0,00 | 388,27 |
U paty pylonu a v úrovni obou reklamních panelů jsou umístěny vyztužené výstupní otvory. Tuhost roury v místě vyztužených otvorů je přibližně shodná s tuhostí roury mimo otvor. Vliv rozdílné tuhosti je v tomto případě možno zanedbat.
Konstrukce je vyrobena z materiálu S235. Roura o průměru 1 000 mm je tvarována za studena.
2 ZATÍŽENÍ
2.1 TŘÍDA SPOLEHLIVOSTI A DÍLČÍ SOUČINITELE ZATÍŽENÍ
Dílčí součinitele zatížení a třída spolehlivosti konstrukce je určena podle normy ČSN EN 1993-3-2 [2], která se vztahuje kromě komínů rovněž na ocelové válcové prvky vetknutých stožárů (viz čl. 1.1 [2]). Podle Přílohy A [2] je konstrukce zařazena do třídy spolehlivosti 2.
Dílčí součinitele zatížení podle Přílohy A [2] jsou
Tab. 3.1 Dílčí součinitele zatížení
| Typ účinku | Stálá zatížení | Proměnná zatížení |
| γG | γQ | |
| Nepříznivý | 1,1 | 1,4 |
| Příznivý | 1,0 | 0,0 |
| Mimořádná situace | 1,0 | 1,0 |
2.2 KOMBINACE ZATÍŽENÍ
Konstrukce je zatížena stálým zatížením, dále větrem a případně námrazou a sněhem. Zatížení sněhem není pro tuto konstrukci s ohledem na velmi malou půdorysnou plochu uvažováno. Kombinace zatížení námrazou a větrem je uvažována v souladu s čl. 2.3.3.5 [2] podle C.6 [3].
Obecně má být pro návrh konstrukce použito 6 kombinací zatížení:
- Nepříznivý, resp. příznivý účinek stálých zatížení + maximální vítr působící na nenamrzlou konstrukci (kombinace značené COM1, resp. COM2):
\begin{gathered}
\gamma_\text{G} \space G_\text{k} + \gamma_\text{w} \space Q_\text{w}
\end{gathered}- Nepříznivý, resp. příznivý účinek stálých zatížení + dominantní námraza a příslušný vítr (kombinace COM3, resp. COM4):
\begin{gathered}
\gamma_\text{G} \space G_\text{k} + \gamma_\text{ice} \space Q_\text{k,ice} + \gamma_\text{W} \space k \space \psi_\text{w} \space Q_\text{k,w}
\end{gathered}- Nepříznivý, resp. příznivý účinek stálých zatížení + dominantní vítr a příslušná námraza (kombinace COM5, resp. COM6):
\begin{gathered}
\gamma_\text{G} \space G_\text{k} + \gamma_\text{W} \space k \space Q_\text{k,w} + \gamma_\text{ice} \space \psi_\text{ice} \space Q_\text{k,ice}
\end{gathered}kde součinitel k je definován v ČSN ISO 12494 [6] v závislosti na třídě námrazy a hodnoty součinitelů kombinace jsou ψw = 0,5 a ψice = 0,0 podle Národní přílohy, čl. NA 2.34 [3].
Protože součinitel kombinace ψice je roven 0, nejsou kombinace s dominantním větrem a příslušnou námrazou rozhodující a není je třeba v ČR uvažovat.
Dílčí a kombinační součinitele jsou pro příslušnou třídu spolehlivosti zrekapitulovány v tab. 3.2:
Tab. 3.2 Kombinace zatížení, dílčí a kombinační součinitele
| Kombinace zatížení | Stálé zatížení | Námraza | Vítr | ||||
| Dílčí souč. | Dílčí souč. | Souč. komb. | Námraza | Dílčí souč. | Souč. komb. | Aerodynamický odpor | |
| γG | γQ,i | ψice | γQ,w | ψw | |||
| COM1 | 1,1 | bez námrazy | 1,4 | 1,0 | pro max. vítr | ||
| COM2 | 1,0 | bez námrazy | 1,4 | 1,0 | pro max. vítr | ||
| COM3 | 1,1 | 1,4 | 1,0 | dominantní | 1,4 | 0,5 | pro příslušný vítr |
| COM4 | 1,0 | 1,0 | 1,0 | dominantní | 1,4 | 0,5 | pro příslušný vítr |
| COM5 | 1,1 | 1,4 | 0,0 | příslušná | 1,4 | 1,0 | pro dominantní vítr |
| COM6 | 1,0 | 1,0 | 0,0 | příslušná | 1,4 | 1,0 | pro dominantní vítr |
2.3 SVISLÁ ZATÍŽENÍ
2.3.1 Stálé zatížení
Vlastní tíha konstrukce
Hmotnost roury je uvedena v kapitole 2, tab. 2.2.
Roura je stykována přes vnitřní příruby. Hmotnost styků je započítána hodnotou 170 kg ve výškách 6 m, 12 m a 18 m.
Ostatní stálé zatížení
Pro výstup na konstrukci je uvnitř roury instalován žebřík o hmotnosti 12 kg/m. Hmotnost kabelů vedených uvnitř roury je 15 kg/m.
Reklamní panely jsou tvořeny plochými obdélníkovými deskami uloženými na roštu z ocelových prvků. Celková hmotnost horního panelu včetně podpůrné konstrukce, styků a výztuh roury je 5 t, dolního panelu 3,75 t.
V dolní úrovni panelů jsou obslužné lávky a osvětlení. Celková hmotnost horní lávky včetně pochozího roštu, styků, výztuh roury a také hmotnosti dvířek a výztuh roury v místě otvoru činí 270 kg. Hmotnost dolní lávky + výztuh otvoru roury je 160 kg.
2.3.2 Zatížení námrazou
Zatížení námrazou se stanoví podle normy ČSN ISO 12494 [6]. Uvažuje se, že pylon je umístěn v námrazové oblasti R3. Hmotnost námrazy je mk = 1,6 kg/m. Součinitel k pro snížení tlaku větru (podle tab. 27 [6]) je k = 0,50.
Vzhledem k redukci zatížení větrem při kombinaci větru a námrazy podle čl. C.6 a NA 2.34 ČSN EN 1993-3-1 [3] je zřejmé, že kombinace zatížení větrem s námrazou nebude pro návrh hlavní nosné konstrukce rozhodující. Zatížení námrazou není proto v tomto příkladu vyčísleno.
2.4 VODOROVNÉ ZATÍŽENÍ – VÍTR
Zatížení větrem je stanoveno podle ČSN EN 1991-1-4 ed 2 [1].
2.4.1 Větrná oblast a základní rychlost větru
viz čl. 4.2 [1]
Větrná oblast:
\begin{gathered}
\text{II}
\end{gathered}Výchozí základní rychlost větru:
\begin{gathered}
v_\text{b,0}=25{,}0\space\text{m/s}
\end{gathered}Součinitel směry větru:
\begin{gathered}
c_\text{dir}=1{,}0
\end{gathered}Součinitel ročního období:
\begin{gathered}
c_\text{season}=1{,}0
\end{gathered}Základní rychlost větru (pro střední dobu návratu 50 let):
\begin{gathered}
v_\text{b}=c_\text{dir}\cdot c_\text{season}\cdot v_\text{b,0}=25{,}0\space\text{m/s}
\end{gathered}2.4.2 Kategorie terénu
viz čl. 4.3.2 a A.2 [1]
Konstrukce je umístěna v terénu kategorie III, ale ve vzdálenosti cca 5 km od hranice s terénem kategorie II. Přechod mezi kategoriemi drsnosti terénu je zohledněn podle čl. A.2 [1]. Podle národní přílohy má být použit postup 2. V tab. A.1 [1] je uvedena minimální vzdálenost stavby od přechodu mezi kategoriemi terénu, při které je možné uvažovat vyšší parametry drsnosti terénu. Pro přechod mezi kategoriemi II a III a výšku stavby 25 m je tato vzdálenost rovna 8,5 km, viz tab. A.1 [1]. Podmínka pro použití kategorie terénu III není splněna a pro výpočet bude uvažován vzdálenější terén kategorie II.
Kategorie terénu:
\begin{gathered}
\text{II}
\end{gathered}Parametr drsnosti terénu:
\begin{gathered}
z_0=0{,}05\space\text{m}
\end{gathered}Minimální výška:
\begin{gathered}
z_\text{min}=2{,}00\space\text{m}
\end{gathered}Parametr drsnosti pro kategorii terénu II:
\begin{gathered}
z_\text{0,II}=0{,}05\space\text{m}
\end{gathered}Součinitel terénu:
\begin{gathered}
k_\text{r} = 0{,}19 \cdot \bigg( \frac{z_0}{z_\text{0,II}} \bigg)^{0{,}07} = 0{,}19
\end{gathered}2.4.3 Střední rychlost větru, maximální dynamický tlak
viz čl. 4.3, 4.4 a 4.5 [1]
Doba integrace pro stanovení střední rychlosti větru:
\begin{gathered}
T=600\space\text{s}\space\text{(10 minut)}
\end{gathered}Součinitel turbulence:
\begin{gathered}
k_\text{I}=1{,}00
\end{gathered}Měrná hmotnost vzduchu:
\begin{gathered}
\rho=1{,}25\space\text{kg/m}^3
\end{gathered}Základní dynamický tlak větru:
\begin{gathered}
q_\text{b} = \frac{1}{2} \cdot \rho \cdot v_\text{b}^2 = 0{,}39 \space \text{kN/m}^2
\end{gathered}Tab. 3.3 Střední rychlost větru, intenzita turbulence a maximální dynamický tlak
| Díl | Součinitel drsnosti terénu | Součinitel orografie | Střední rychlost větru | Intenzita turbulence | Maximální dynamický tlak |
| cr(z) | c0(z) | vm(z) | Iv(z) | qp(z) | |
| [m/s] | [kN/m2] | ||||
| A | 1,181 | 1,000 | 29,5 | 0,161 | 1,158 |
| B | 1,165 | 1,000 | 29,1 | 0,163 | 1,135 |
| C | 1,148 | 1,000 | 28,7 | 0,166 | 1,111 |
| D | 1,118 | 1,000 | 28,0 | 0,170 | 1,070 |
| E | 1,084 | 1,000 | 27,1 | 0,175 | 1,022 |
| F | 1,041 | 1,000 | 26,0 | 0,182 | 0,965 |
| G | 0,910 | 1,000 | 22,7 | 0,209 | 0,796 |
kde součinitel drsnosti terénu se vypočte jako
\begin{gathered}
c_\text{r}(z) = k_\text{r} \cdot \ln \bigg(\frac{z}{z_0}\bigg),
\end{gathered}střední rychlost větru
\begin{gathered}
v_\text{m}(z) = c_\text{r}(z) \cdot c_0(z)\cdot v_\text{b},
\end{gathered}intenzita turbulence
\begin{gathered}
I_\text{v}(z) = \frac{k_\text{I}}{c_0(z)\cdot \ln \Bigg(\dfrac{z}{z_0}\Bigg)},
\end{gathered}a maximální dynamický tlak
\begin{gathered}
q_\text{p}(z) = [1 + 7 \cdot I_\text{v}(z)] \cdot \frac{1}{2} \cdot \rho \cdot v_\text{m}^2(z).
\end{gathered}2.4.4 Aerodynamický odpor
2.4.4.1 Aerodynamický odpor hlavní roury
viz čl. 7.9 [1]
Tvarový součinitel (součinitel síly) se určí jako
\begin{gathered}
c_\text{f} = c_\text{f,0} \cdot \psi_\lambda
\end{gathered}kde cf,0 značí tvarový součinitel (součinitel síly) pro válce bez vlivu proudění kolem volných konců. Je stanoven podle obr. 7.28 [1]. Součinitel koncového efektu značený ψλ se určí podle čl. 7.13 [1].
Poznámka:
V normách [2, 3] a [1] je použito rozdílné názvosloví. Součinitel síly je v normách [2, 3] nazýván tvarovým součinitelem, význam je ovšem shodný. V dalším textu je tato veličina označována jako tvarový součinitel.
Součinitel koncového efektu ψλ je závislý na efektivní štíhlosti λ. Pro směr větru kolmý na panely se efektivní štíhlost určí pro jednotlivé úseky roury mezi reklamními panely.
Úsek C … podle tab. 7.16, řádku č. 4 [1] (šířka panelu = 3 m < 2,5 ∙ b = 2,5 ∙ 1 = 2,5 m) pro výšku I = 3,00 m, šířku b = 1,00 m, l < 15 m:
\begin{gathered}
\lambda=\text{max}(I/b{;}70)=\text{max}(3/1{;}70)=70
\end{gathered}Úsek F-G … podle tab. 7.16, řádku č. 4 [1] (šířka panelu = 3 m > 2,5 ∙ b = 2,5 ∙ 1 = 2,5 m) pro výšku I = 12,00 m, šířku b = 1,00 m, l < 15 m:
\begin{gathered}
\lambda=\text{max}(I/b{;}70)=\text{max}(12/1{;}70)=70
\end{gathered}Součinitel koncového efektu je pro oba úseky ψλ = 0,92 (podle obr. 7.36 [1] pro součinitel plnosti φ = 1.0).
Roura je zinkovaná, ekvivalentní drsnost povrchu k = 0,2 mm (podle tab. 7.13 [1]).
Tvarové součinitele a aerodynamický odpor roury jsou vypočteny v tab. 3.4.
Tab. 3.4 Rovnoměrná návětrná plocha a tvarový součinitel konstrukce
| Díl | Max. rychlost větru | Průměr roury | Reynoldsovo číslo | Ekvivalentní drsnost povrchu | Tvarový součinitel bez vlivu proudění kolem volných konců | Součinitel koncového efektu | Tvarový součinitel | Součinitel stínění konstrukce | Celková návětrná plocha včetně tvarového souč. a součinitele stínění | Šířka konstrukce včetně příslušenství |
| vmax(z) | b | Re | k | cf,0 | ψλ | cf | η | cf ∙ b ∙ η | b‚ | |
| [m/s] | [mm] | [m/s] | [mm] | [m2/m‘] | [m] | |||||
| A | 43,0 | 1 000,0 | 2,87E+06 | 0,20 | 0,789 | – | – | 0,00 | 0 | 6,0 |
| B | 42,6 | 1 000,0 | 2,84E+06 | 0,20 | 0,789 | – | – | 0,00 | 0 | 6,0 |
| C | 42,2 | 1 000,0 | 2,81E+06 | 0,20 | 0,788 | 0,92 | 0,725 | 1,00 | 0,725 | 1,0 |
| D | 41,4 | 1 000,0 | 2,76E+06 | 0,20 | 0,787 | – | – | 0,00 | 0 | 3,0 |
| E | 40,4 | 1 000,0 | 2,70E+06 | 0,20 | 0,786 | – | – | 0,00 | 0 | 3,0 |
| F | 39,3 | 1 000,0 | 2,62E+06 | 0,20 | 0,784 | 0,92 | 0,721 | 1,00 | 0,721 | 1,0 |
| G | 35,7 | 1 000,0 | 2,38E+06 | 0,20 | 0,778 | 0,92 | 0,716 | 1,00 | 0,716 | 1,0 |
kde maximální rychlost větru je určena jako
\begin{gathered}
v_\text{max}(z)=\sqrt{2 \cdot q_\text{p}(z)/ \rho},
\end{gathered}Reynoldsovo číslo
\begin{gathered}
Re = \frac{b \cdot v_\text{max}(z)}{v},
\end{gathered}kde v značí kinematickou viskozitu vzduchu uvažovaná hodnotou v = 15 ∙ 10-6 m2/s (podle [1]).
Protože panely jsou umístěny v těsné blízkosti roury, uvažuje se plné zastínění zakrytých částí roury a zatížení větrem na nich nepůsobí.
2.4.4.2 Aerodynamický odpor panelů a ostatního příslušenství
viz čl. 7.4.3 [1]
Referenční návětrná plocha horního panelu je Aref,h = 6,0 ∙ 4,0 = 24,0 m2, dolního panelu Aref,d = 3,0 ∙ 6,0 = 18,0 m2. Tvarový součinitel panelů je uvažován podle čl. 7.4.3 [1] hodnotou 1,8.
Lávky jsou vyrobeny z ocelových profilů typu UPE a úhelníků, na kterých je uložen podlahový rošt. Lávky nejsou opatřeny zábradlím. Výška konstrukce lávek je 150 mm.
Návětrná plocha horní lávky je 6,0 ∙ 0,15 = 0,9 m2. Příslušný tvarový součinitel je podle čl. 7.7 určen jako
cf = cf,0 ∙ ψλ = 2,0 ∙ 0,92 = 1,84 pro λ = min(2 ∙ l/b; 70) = min(2 ∙ 6,0/0,15; 70) = 70 (podle čl. 7.13 [1]).
Návětrná plocha dolní lávky je 3,0 ∙ 0,15 = 0,45 m2. Příslušný tvarový součinitel je
cf = cf,0 ∙ ψλ = 2,0 ∙ 0,85 = 1,70 pro λ = min(2 ∙ l/b; 70) = min(2 ∙ 3,0/0,15; 70) = 40
Celková návětrná plocha světel je uvažována hodnotou 0,6 m2 shodně pro oba panely, tvarový součinitel hodnotou 1,4.
Plechy v místě otvorů, prvky pro výstup na lávku a další prvky se uvažují celkovou návětrnou plochou 0,5 m2 a tvarovým součinitelem 1,4.
Celková návětrná plocha v úrovni +21 m je součtem 0,9 + 0,6 + 0,5 = 2,00 m2. Tvarový součinitel příslušný této ploše je roven (0,9 ∙ 1,84 + 0,6 ∙ 1,4 + 0,5 ∙ 1,4) / (0,9 + 0,6 + 0,5) = 1,60.
Celková návětrná plocha v úrovni +12 m je součtem 0,45 + 0,6 + 0,5 = 1,55 m2. Tvarový součinitel příslušný této ploše je roven (0,45 ∙ 1,70 + 0,6 ∙ 1,4 + 0,5 ∙ 1,4) / (0,45 + 0,6 + 0,5) = 1,49.
Přehled osamělých příslušenství je zpracován v tab. 3.5.
Tab. 3.5 Návětrné plochy a tvarové součinitele osamělých příslušenství
| Příslušenství | Výška | Návětrná plocha | Tvarový součinitel | Součinitel stínění | Celková návětrná plochavčetně tvarového součinitele a součinitele stínění |
| AA | cf | η | cf ∙ AA ∙ η | ||
| [m] | [m2] | [m2] | |||
| Reklamní panel 1 | 23,0 | 24,00 | 1,80 | 1,00 | 43,2 |
| Horní lávka | 21,0 | 2,00 | 1,60 | 1,00 | 3,2 |
| Reklamní panel 2 | 15,0 | 18,00 | 1,80 | 1,00 | 32,4 |
| Dolní lávka | 12,0 | 1,55 | 1,49 | 1,00 | 2,3 |
3 ANALÝZA KONSTRUKCE
3.1 MODÁLNÍ ANALÝZA A ÚTLUM
Jsou určeny modální charakteristiky konstrukce, zejména vlastní tvary a frekvence kmitání konstrukce. První tři vlastní frekvence jsou uvedeny v tab. 4.1. Vlastní tvary jsou vykresleny na obr. 4.1. Pořadnice prvního vlastního tvaru jsou uvedeny v tab. 4.2.
Tab. 4.1 Vlastní frekvence
| Číslo vlastní frekvence | Vlastní frekvence [Hz] |
| 1 | 0,93 |
| 2 | 6,11 |
| 3 | 21,48 |

Obr. 4.1 Vlastní tvary kmitání č. 1 (modře), č. 2 (červeně) a č. 3 (zeleně)
Tab. 4.2 Pořadnice prvního vlastního tvaru, hmotnost a návětrná plocha konstrukce rozpočítaná do uzlů
| Číslo uzlu | Výška uzlu | Střední rychlost větru | Hmotnost v uzlu | Celková návětrná plocha | Pořadnice základního vlastního tvaru kmitání |
| m | cf ∙ Aref ∙ η | Φ1 | |||
| [m] | [m/s] | [kg] | [m2] | ||
| 8 | 25,0 | 29,5 | 319 | 0,000 | 12,060 |
| 7 | 23,0 | 29,1 | 639 | 43,200 | 10,670 |
| 6 | 21,0 | 28,7 | 798 | 4,288 | 9,283 |
| 5 | 18,0 | 28,0 | 958 | 1,088 | 7,250 |
| 4 | 15,0 | 27,1 | 958 | 32,400 | 5,335 |
| 3 | 12,0 | 26,0 | 1725 | 4,473 | 3,619 |
| 2 | 6,0 | 22,7 | 2492 | 4,310 | 1,019 |
| 1 | 0,0 | 22,7 | 1246 | 2,147 | 0,000 |
Útlum
Celkový útlum je stanoven podle článku F.5 [1] jako součet konstrukčního, aerodynamického útlumu a útlumu od zvláštních zařízení. Logaritmický dekrement konstrukčního útlumu je určen pro první tvar kmitání podle tab. F.2 [1]. Logaritmický dekrement aerodynamického útlumu se určuje podle odstavce (3), F.5 [1].
Poznámka:
Vzorce F.16, resp. F.18 [1] pro stanovení aerodynamického útlumu jsou platné pro konstantní tvarový součinitel po výšce věže, resp. rovněž pro konstantní šířku konstrukce. V případě řady konstrukcí včetně tohoto pylonu se tvarový součinitel po výšce výrazně liší. Pro výpočet logaritmického dekrementu aerodynamického útlumu byl proto použit přesnější vzorec, odvozený z [7]:
\begin{gathered}
\delta_\text{a,i} = \frac{\rho \cdot \int\limits_H c_\text{f}(z) \cdot A_\text{ref}(z)\cdot v_\text{m}(z) \cdot \phi_\text{i}(z)^2 \cdot dz}{2 \cdot n_\text{i} \cdot \int\limits_H m(z) \cdot \phi_\text{i}(z)^2 \cdot dz}
\end{gathered}kde Aref(z), resp. m(z), je celková návětrná plocha, resp. hmotnost, příslušná uzlu ve výšce z, cf(z) je tvarový součinitel a Φi(z) pořadnice i-tého tvaru kmitání kmitání v uzlu ve výšce z, ni značí i-tou vlastní frekvenci a ρ měrnou hmotnost vzduchu.
Na konstrukci nejsou umístěna žádná zařízení zvyšující útlum konstrukce. Logaritmický dekrement útlumu od zvláštních zařízení je roven nule. Jednotlivé dekrementy a celkový dekrement útlumu je uveden v tab. 4.3.
Tab. 4.3 Logaritmický dekrement útlumu pro první (základní) vlastní tvar
| Číslo vlastní frekvence | Konstrukční útlum | Útlum od zvláštních zařízení | Aerodynamický útlum | Celkový logaritmický dekrement útlumu |
| ϭs | ϭd | ϭa | ϭ | |
| 1 | 0,012 | 0,000 | 0,122 | 0,134 |
3.2 STANOVENÍ ZATÍŽENÍ VĚTREM
Odezva na zatížení větrem je stanovena kvazistatickým výpočtem podle [1]. Součinitel konstrukce cscd je určen podle přílohy B [1].
Poznámka:
Postup podle normy [1] lze použít v případech, kdy konstrukce odpovídá jednomu z obecných tvarů na obr. 6.1 [1] a pokud je významné kmitání pouze v jednom základním tvaru kmitání. Tvar kmitání má mít po výšce konstantní znaménko. Jestliže tyto podmínky nejsou splněny, je třeba použít některou z přesnějších metod, např. spektrální analýzu. K těmto metodám normy ČSN EN neposkytují žádný návod. Normy [1, 2] bohužel neuvádí ani přesněji definovaná kritéria, podle kterých by bylo možné předem zjistit, kdy je postup bezpečný a kdy už nikoli.
Odezva na zatížení větrem je dále vypočtena podle [1]. Výsledky budou pro informaci porovnány s výsledky spektrální analýzy.
3.2.1 Součinitel konstrukce cscd
viz 6.3 [1]
Referenční výška pro stanovení součinitele konstrukce cscd:
zs = 23,00 m (viz obr. 6.1 c [1])
Součinitel orografie v referenční výšce:
c0(zs) = 1,00
Intenzita turbulence v referenční výšce:
\begin{gathered}
I_\text{v}(z_\text{s}) = \frac{k_\text{I}}{c_0(z_\text{s}) \cdot \ln \Bigg(\dfrac{z_\text{s}}{z_0} \Bigg)} = \frac{1}{1{,}0 \cdot \ln \Bigg( \dfrac{23}{0{,}05} \Bigg)} = 0{,}163
\end{gathered}Střední rychlost větru v referenční výšce:
\begin{gathered}
v_\text{m}(z_s) = k_\text{r} \cdot \ln \Bigg(\frac{z_\text{s}}{z_0}\Bigg) \cdot c_0(z_\text{s})\cdot v_\text{b} = 0{,}19 \cdot \ln \Bigg( \frac{23}{0{,}05} \Bigg) \cdot 1{,}0 \cdot 25 = 29{,}12 \text{ m/s}
\end{gathered}Turbulence větru
viz B.1 [1]
Referenční výška:
zt = 200 m
Lt = 300 m
Referenční měřítko délky:
\begin{gathered}
\alpha = 0{,}67 + 0{,}05 \cdot \ln(z_0) = 0{,}67+ 0{,}05 \cdot \ln(0{,}05) = 0{,}52
\end{gathered}Měřítko délky turbulence:
\begin{gathered}
L(z_\text{s}) = L_t \cdot \Bigg( \frac{z_\text{s}}{z_\text{t}} \Bigg)^\alpha = 300 \Bigg(\frac{23}{200}\Bigg)^{0{,}52} = 97{,}4 \text{ m}
\end{gathered}Vlastní frekvence:
n1 = 0,93 Hz
Bezrozměrná vlastní frekvence:
\begin{gathered}
f_\text{L}(n_1,z_\text{s}) = \frac{n_1 \cdot L}{v_\text{m}} = \frac{0{,}93 \cdot 97{,}4}{29{,}1} = 3{,}11
\end{gathered}Bezrozměrná výkonová spektrální hustota rychlosti větru:
\begin{gathered}
S_\text{L}(n_1,z_\text{s}) = \frac{6{,}8 \cdot f_\text{L}}{(1+10{,}2 \cdot f_\text{L})^{5/3}} = \frac{6{,}8 \cdot 3{,}11}{(1+10{,}2 \cdot 3{,}11)^{5/3}} = 0{,}063
\end{gathered}Součinitel konstrukce
Součinitel odezvy pozadí, podle B.2 (2) [1]:
\begin{gathered}
B^2 = \frac{1}{1+0{,}9 \Bigg(\dfrac{b+h}{L(z_\text{s})}\Bigg)^{0{,}63}} = \frac{1}{1+0{,}9 \Bigg(\dfrac{2{,}28+25}{97{,}4}\Bigg)^{0{,}63}} = 0{,}712
\end{gathered}kde b značí šířku konstrukce. Je dosazena průměrná šířka konstrukce včetně příslušenství.
Rezonanční část odezvy, podle B.2 (5) [1]:
\begin{gathered}
R^2 = \frac{\pi^2}{2 \cdot \delta} \cdot S_\text{L} (z_\text{s} \cdot n_\text{1,x}) \cdot R_\text{h}(\eta_\text{h}) \cdot R_\text{b}(\eta_\text{b})
\end{gathered}kde
\begin{gathered}
\eta_\text{h} = \frac{4{,}6 \cdot h}{L(z_\text{s})} \cdot f_\text{L}(z_\text{s} \cdot n_\text{1,x}) = \frac{4{,}6 \cdot 25}{97{,}4} \cdot3{,}11 = 3{,}672
\end{gathered}\begin{gathered}
\eta_\text{b} = \frac{4{,}6 \cdot b}{L(z_\text{s})} \cdot f_\text{L}(z_\text{s} \cdot n_\text{1,x}) = \frac{4{,}6 \cdot 2{,}28}{97{,}4} \cdot3{,}11 = 0{,}335
\end{gathered}\begin{gathered}
R_\text{h} = \frac{1}{\eta_\text{h}} - \frac{1}{2 \cdot \eta_\text{h}^2} \cdot(1-e^{-2\eta_\text{h}}) = \frac{1}{3{,}672} - \frac{1}{2 \cdot 3{,}672^2} \cdot ( 1-e^{-23{,}672}) = 0{,}235
\end{gathered}\begin{gathered}
R_\text{b} = \frac{1}{\eta_\text{b}} - \frac{1}{2 \cdot \eta_\text{b}^2} \cdot(1-e^{-2\eta_\text{b}}) = \frac{1}{0{,}335} - \frac{1}{2 \cdot 0{,}335^2} \cdot ( 1-e^{-20{,}335}) = 0{,}810
\end{gathered}\begin{gathered}
R^2 = \frac{\pi^2}{2 \cdot 0{,}134} \cdot 0{,}063 \cdot 0{,}235 \cdot 0{,}810 = 0{,}443
\end{gathered}Frekvence přechodů s kladnou směrnicí, podle B.2 (4) [1]:
\begin{gathered}
v = n_\text{1,x} \cdot \sqrt{\frac{R^2}{B^2 + R^2}} = 0{,}93 \cdot \sqrt{\frac{0{,}443}{0{,}712 + 0{,}443}} = 0{,}576 \text{ Hz}
\end{gathered}Součinitel maximální hodnoty, podle B.2 (3) [1]:
\begin{gathered}
k_\text{p} = \sqrt{2 \cdot \ln (v \cdot T)} + \frac{0{,}6}{\sqrt{2 \cdot \ln (v \cdot T)}} = \sqrt{2 \cdot \ln (0{,}576 \cdot 600)} + \frac{0{,}6}{\sqrt{2 \cdot \ln (0{,}576 \cdot 600)}} = 3{,}595
\end{gathered}Součinitel konstrukce cscd, podle čl. 6.3.1 [1]:
\begin{gathered}
c_\text{s}c_\text{d} = \frac{1 + 2 \cdot k_\text{p} \cdot I_\text{v}(z_\text{s}) \cdot \sqrt{B^2 + R^2} }{1 + 7 \cdot I_\text{v}(z_\text{s})} = \frac{1 + 2 \cdot 3{,}595 \cdot 0{,}163 \cdot \sqrt{0{,}712 + 0{,}443} }{1 + 7 \cdot 0{,}163} = 1{,}055
\end{gathered}3.2.2 Zatížení větrem
viz čl. 5.3 [1]
Rovnoměrné zatížení větrem je určeno jako fw = cscd · qp(ze) · cf · bref · η
Tab. 4.5 Rovnoměrné zatížení větrem na konstrukci – charakteristické hodnoty
| Díl | Maximální dynamický tlak větru | Celková návětrná plocha včetněsoučinitele síly a součinitele stínění | Spojité zatížení od větru |
| qp(z) | cf ∙ bref ∙ η | fw | |
| [kN/m2] | [m2/m‘] | [kN/m] | |
| A | 1,158 | 0 | 0 |
| B | 1,135 | 0 | 0 |
| C | 1,111 | 0,725 | 0,850 |
| D | 1,070 | 0 | 0 |
| E | 1,022 | 0 | 0 |
| F | 0,965 | 0,721 | 0,734 |
| G | 0,796 | 0,716 | 0,601 |
Osamělé zatížení větrem je vypočteno jako Fw = cscd · qp(ze) · cf · Aref · η
Tab. 4.6 Osamělé zatížení větrem – charakteristické hodnoty
| Příslušenství | Výška | Maximální dynamickýtlak větru | Celková návětrná plocha včetněsoučinitele síly a součinitele stínění | Osamělé síly od větru |
| qp(z) | cf ∙ Aref ∙ η | Fw | ||
| [m] | [kN/m2] | [m2] | [kN] | |
| Reklamní panel 1 | 23,0 | 1,135 | 43,2 | 51,73 |
| Horní lávka | 21,0 | 1,111 | 3,2 | 3,75 |
| Reklamní panel 2 | 15,0 | 1,022 | 32,4 | 34,93 |
| Dolní lávka | 12,0 | 0,965 | 2,3 | 2,34 |
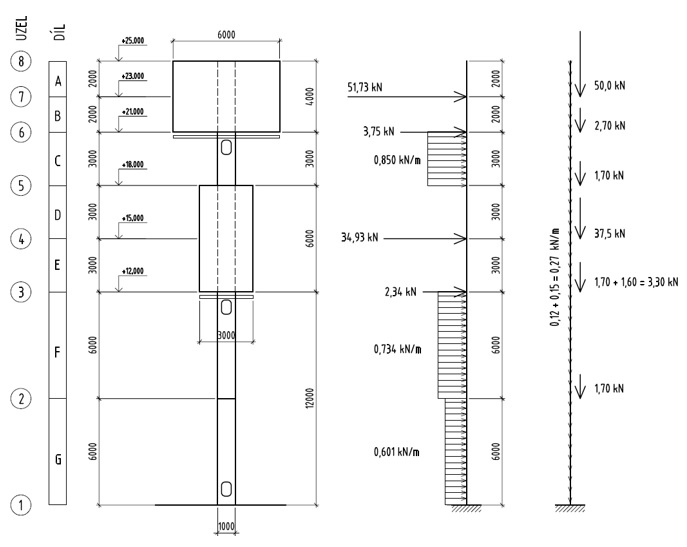
Obr. 4.2 Schéma zatížení
Poznámka:
Na obrázku 4.2 není zobrazeno zatížení vlastní tíhou. Osamělá břemena byla v tomto případě zadána do osy roury (excentricita byla zanedbána).
3.3 ÚČINKY DRUHÉHO ŘÁDU
Protože roura je proměnného průřezu a přenáší proměnnou osovou sílu je pro její posouzení vhodné použít nelineární výpočet namísto zjednodušeného posudku pro ohyb a tlak prutů stálého průřezu podle normy ČSN EN 1993-1-1 ed. 2 [4].
Imperfekce pro mezní stav únosnosti je uvažována jakou součet ekvivalentní imperfekce ve tvaru počátečního naklonění a ekvivalentní imperfekce ve tvaru počátečního prohnutí.
Počáteční naklonění je určeno podle čl. 5.2.2 [2] podle vzorce pro výchylku vrcholu:
\begin{gathered}
\Delta = \frac{h}{500} \sqrt{1 + \frac{50}{h}} = \frac{25}{500} \sqrt{1 + \frac{50}{25}} = 0{,}087 \text{ m}
\end{gathered}Imperfekce ve tvaru počátečního prohnutí jsou určeny podle čl. 5.3.2 (3) [4] pro křivku vzpěrné pevnosti „c“ a plasticitní analýzu jako e0/L = 1/150. Tvar vybočení je uvažován pro dvojnásobek výšky konstrukce. Maximální hodnota prohnutí činí e0,max = 1/150 ∙ L = 1/150 ∙ 2 ∙ h = 1/150 ∙ 2 ∙ 25 = 0,33 m.
Pro mezní stav použitelnosti se předpokládá, že počáteční geometrie konstrukce odpovídá montážním tolerancím. Montážní tolerance jsou určeny podle tab. D.1.14, ČSN EN 1090-2+A1 [5]. Uvažuje se naklonění konstrukce s výchylkou vrcholu
Δ = h/1 000 = 25/1 000 = 0,025 m.
Celkový počáteční tvar konstrukce je uveden v tab. 4.7:
Tab. 4.7 Imperfekce stožáru
| Značení | Výška [m] | Pořadnice imperfektního tvaru [mm] | |||
| Imperfekce ve tvaru počátečního naklonění | Imperfekce ve tvaru počátečního prohnutí | Celková počáteční imperfekce pro MSÚ | Celková počáteční imperfekce pro MSP | ||
| A | 25,000 | 87 | 333 | 420 | 25 |
| B | 23,000 | 80 | 282 | 362 | 23 |
| C | 21,000 | 73 | 235 | 308 | 21 |
| D | 18,000 | 62 | 173 | 235 | 18 |
| E | 15,000 | 52 | 120 | 172 | 15 |
| F | 12,000 | 42 | 77 | 118 | 12 |
| G | 6,000 | 21 | 19 | 40 | 6 |
3.4 VÝSLEDNÉ DEFORMACE A VNITŘNÍ SÍLY
Odezva konstrukce na stálá zatížení i na zatížení větrem byla určena statickým nelineárním výpočtem. Maximální hodnoty deformací jsou uvedeny v tab. 4.8, maximální vnitřní síly v tab. 4.9.
Tab. 4.8 Maximální hodnoty deformací (charakteristické hodnoty) pro posouzení MSP
| Uzel | Výška | Vodorovné posunutí | Natočení |
| [m] | [mm] | [deg] | |
| 8 | 25,0 | 290 | 0,95 |
| 7 | 23,0 | 257 | 0,95 |
| 6 | 21,0 | 224 | 0,94 |
| 5 | 18,0 | 175 | 0,91 |
| 4 | 15,0 | 130 | 0,84 |
| 3 | 12,0 | 88 | 0,73 |
| 2 | 6,0 | 25 | 0,45 |
| 1 | 0,0 | 0 | 0,00 |
Tab. 4.9 Maximální hodnoty vnitřních sil (návrhové hodnoty) pro posouzení MSÚ
| Uzel | Výška | Ohybový moment | Posouvající síla | Normálová síla |
| [m] | [kNm] | [kN] | [kN] | |
| 8 | 25,0 | 0 | 0 | 0 |
| 7 | 23,0 | 0 | 0 | 7 |
| 6 | 21,0 | 151 | 75 | 69 |
| 5 | 18,0 | 398 | 84 | 83 |
| 4 | 15,0 | 652 | 84 | 95 |
| 3 | 12,0 | 1 055 | 135 | 147 |
| 2 | 6,0 | 1 897 | 143 | 178 |
| 1 | 0,0 | 2 761 | 147 | 207 |
4 POSOUZENÍ KONSTRUKCE
Dílčí součinitele materiálu se mají pro návrh roury uvažovat podle [2] jako
γM0 = 1,00
γM1 = 1,10
γM2 = 1,25
4.1 POSOUZENÍ ÚNOSNOSTI KONSTRUKCE
Účelem příkladu nebylo posuzovat kompletně celou konstrukci. Jako příklad je proveden pouze posudek roury ve výšce 12 m a v patě konstrukce.
Nejsou provedeny posudky v místě vyztužených otvorů. Pro analýzu se předpokládalo, že těžiště průřezu v místě vyztužených otvorů leží přibližně v ose roury a že přídavné momenty lze zanedbat.
Dále nejsou provedeny posudky styků, pomocných konstrukcí lávek a panelů a základu.
Postupuje se standardně podle příslušných norem pro navrhování ocelových konstrukcí, resp. základů.
Posouzení roury mimo otvory
Průřezové charakteristiky viz tab. 2.1.
Díly A-E
Profil: TR 1000×12, ocel S235
d/t = 83,3 … třída průřezu 3
Únosnost ve smyku:
\begin{gathered}
V_\text{pl,Rd} = \frac{A_\text{v} \cdot f_\text{y}}{\sqrt{3} \cdot \gamma_\text{M0} } = \frac{23\space712 \cdot 235}{\sqrt{3} \cdot 1{,}0} \cdot 10^{-3} = 3\space217 \text{ kN}
\end{gathered}Únosnost ve ohybu:
\begin{gathered}
M_\text{c,Rd} = \frac{W_\text{el} \cdot f_\text{y}}{ \gamma_\text{M1} } = \frac{9\space090\space903 \cdot 235}{ 1{,}10 } \cdot 10^{-6} = 1\space942 \text{ kN}
\end{gathered}Únosnost v tlaku:
\begin{gathered}
N_\text{Rd} = \frac{A \cdot f_\text{y}}{ \gamma_\text{M1} } = \frac{37\space247 \cdot 235}{ 1{,}10 } \cdot 10^{-3} = 7\space957 \text{ kN}
\end{gathered}Posouzení smyku:
\begin{gathered}
V_\text{Ed} = 135 \text{ kN} \le 0{,}5 \cdot V_\text{pl,Rd} = 0{,}5 \cdot 3\space217 = 1\space608 \text{ kN ... vyhovuje}
\end{gathered}Kombinace ohybu a osové síly:
\begin{gathered}
\frac{N_\text{Ed}}{N_\text{Rd}} + \frac{M_\text{Ed}}{M_\text{c,Rd}} = \frac{147}{7\space957} + \frac{1\space055}{1\space942} = 0{,}56 \le 1{,}0 \text{ ... vyhovuje}
\end{gathered}Díly F, G
Profil: TR 1000×16, ocel S235
d/t = 62,5 … třída průřezu 2
Únosnost ve smyku:
\begin{gathered}
V_\text{pl,Rd} = \frac{A_\text{v} \cdot f_\text{v}}{\sqrt{3} \cdot \gamma_\text{M0}} = \frac{31\space488 \cdot 235}{\sqrt{3} \cdot 1{,}0} \cdot 10^{-3} = 4\space272 \text{ kN}
\end{gathered}Únosnost ve ohybu:
\begin{gathered}
M_\text{c,Rd} = \frac{W_\text{pl} \cdot f_\text{y}}{\gamma_\text{M1}} = \frac{1\space549\space3461 \cdot 235}{1{,}10} \cdot 10^{-6} = 3\space310 \text{ kNm}
\end{gathered}Únosnost v tlaku:
\begin{gathered}
N_\text{b,y,Rd} = \frac{A \cdot f_\text{y}}{\gamma_\text{M1}} = \frac{49\space461 \cdot 235}{1{,}10} \cdot 10^{-3} = 10\space567 \text{ kN}
\end{gathered}Posouzení smyku:
\begin{gathered}
V_\text{Ed} = 147 \text{ kN} \le 0{,}5 \cdot V_\text{pl,Rd} = 0{,}5 \cdot 4\space272 = 2\space136 \text{ kN ... vyhovuje}
\end{gathered}Kombinace ohybu a osové síly:
\begin{gathered}
\frac{N_\text{Ed}}{N_\text{Rd}} + \frac{M_\text{Ed}}{M_\text{c,Rd}} = \frac{207}{10\space567} + \frac{2\space761}{3\space310} = 0{,}85 \le 1{,}0 \text{ ... vyhovuje}
\end{gathered}4.2 POSOUZENÍ DEFORMACÍ
Maximální vodorovná deformace vrcholu je 290 mm, což je 1/86 výšky. Doporučená maximální deformace podle normy [2] činí 1/50 výšky, tj. 500 mm. Konstrukce vyhovuje v mezním stavu použitelnosti.
5 POROVNÁNÍ S VÝSLEDKY SPEKTRÁLNÍ ANALÝZY
Pro porovnání byla stanovena odezva konstrukce spektrální analýzou. Výkonová spektrální hustota rychlosti větru a parametry koherenční funkce byly uvažovány podle [1]. Do výpočtu byly zahrnuty první 3 vlastní tvary kmitání.
Maximální hodnoty deformací jsou uvedeny v tab. 6.1, maximální vnitřní síly v tab. 6.2.
Tab. 6.1 Maximální hodnoty deformací (charakteristické hodnoty) a porovnání s výsledky v tab. 4.8
| Uzel | Výška | Vodorovné posunutí | Natočení |
| [m] | [mm] | [deg] | |
| 8 | 25,0 | 308 (106%) | 1,01 (106%) |
| 7 | 23,0 | 273 (106%) | 1,01 (106%) |
| 6 | 21,0 | 238 (106%) | 1,01 (107%) |
| 5 | 18,0 | 186 (106%) | 0,97 (107%) |
| 4 | 15,0 | 137 (105%) | 0,89 (106%) |
| 3 | 12,0 | 93 (105%) | 0,78 (107%) |
| 2 | 6,0 | 26 (104%) | 0,47 (104%) |
| 1 | 0,0 | 0 | 0,00 |
Tab. 6.2 Maximální hodnoty vnitřních sil (návrhové hodnoty) a porovnání s výsledky v tab. 4.9
| Uzel | Výška | Ohybový moment | Posouvající síla | Normálová síla |
| [m] | [kNm] | [kN] | [kN] | |
| 8 | 25,0 | 1 | 3 | 0 |
| 7 | 23,0 | 5 | 3 | 7 |
| 6 | 21,0 | 171 (113%) | 81 (108%) | 69 |
| 5 | 18,0 | 444 (112%) | 92 (110%) | 83 |
| 4 | 15,0 | 737 (113%) | 98 (117%) | 95 |
| 3 | 12,0 | 1 145 (109%) | 139 (103%) | 147 |
| 2 | 6,0 | 2 008 (106%) | 149 (104%) | 178 |
| 1 | 0,0 | 2 907 (105%) | 152 (103%) | 207 |
Hodnoty odezvy určené přesnějším postupem jsou v tomto případě větší až o cca 13% (pro ohybové momenty). Je zřejmé, že analyzovaná konstrukce je již (mírně) za hranicí použitelnosti postupu stanovení odezvy podle [1].
Poznámka:
Pro porovnání byl určen součinitel konstrukce cscd rovněž podle přílohy C [1], přestože v ČR je třeba používat přílohu B. Příloha C umožňuje zvolit tvar kmitání pro základní vlastní frekvenci (konstantní, lineární, parabolický nebo sinusový) a zohlednit ho při výpočtu. Hodnota součinitele konstrukce určeného podle přílohy C [1] je 1,108. Poměr mezi výsledky spektrální analýzy a zjednodušeného postupu by byl pro tuto hodnotu cscd o 5% menší. Deformace konstrukce a vnitřní síly v patě stožáru by dosahovaly velmi dobré shody. Příloha C může být pro obdobné konstrukce vhodnější než příloha B používaná pro běžné stavby. Ovšem kromě posunu hodnot výsledků (maximálně však do cca 5%) vlivem zohlednění tvaru kmitání, ani tento postup neumožňuje započítat vyšší tvary kmitání.
6 ZÁVĚR
Příklad popisuje výpočet odezvy konstrukce na zatížení větrem podle norem ČSN EN. Tento postup se použije pro většinu konstrukcí. Upozorňuje se na skutečnost, že pro velmi štíhlé konstrukce je nezbytné použít přesnější postupy.
7 LITERATURA, NORMY
[1] ČSN EN 1991-1-4 ed. 2 Eurokód 1: Zatížení stavebních konstrukcí – Část 1-4: Obecná zatížení – Zatížení větrem, 04/2013
[2] ČSN EN 1993-3-2 Eurokód 3: Navrhování ocelových konstrukcí – Část 3-2: Stožáry a komíny – Komíny, 09/2008
[3] ČSN EN 1993-3-1 Eurokód 3: Navrhování ocelových konstrukcí – Část 3-1: Stožáry a komíny – Stožáry, 09/2008
[4] ČSN EN 1993-1-1 ed. 2 Eurokód 3: Navrhování ocelových konstrukcí – Část 1-1: Obecná pravidla a pravidlo pro pozemní stavby, 07/2011
[5] ČSN EN 1090-2+A1 Provádění ocelových konstrukcí a hliníkových konstrukcí – Část 2: Technické požadavky na ocelové konstrukce, 01/2012
[6] ČSN ISO 12494 Zatížení konstrukcí námrazou, 12/2018
[7] Madugula, M.K.S. et al.: Dynamic Response of Lattice Towers and Guyed Masts, ASCE 2002