Autoři: Ing. Jiří Lahodný, Ph.D., Ing. Petra Poláková
Stav: kontrola 2022, vydání 2019
Anotace:
Příklad výpočtu zatížení technologického mostu větrem.
OBSAH
ÚVOD
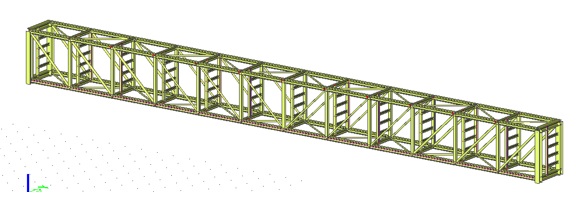
Technologický most délky 31,7 m je tvořen příhradovou konstrukcí z válcovaných profilů HEA, HEB, IPE a trubek. Konstrukce je opláštěna. Most je uložen jako prostý nosník na dvou oddělených budovách.
Zatížení větrem je stanoveno pro II. větrnou oblast (základní rychlost větru 25 m/s), kategorii terénu II podle ČSN EN 1991-1-4 ed. 2 [1]. Součinitel konstrukce cscd je určen podrobným postupem podle Přílohy B [1].
Výpočet vlastních tvarů a frekvencí je proveden pomocí programu SCIA Engineer.
Obr. 1.1 Schéma konstrukce
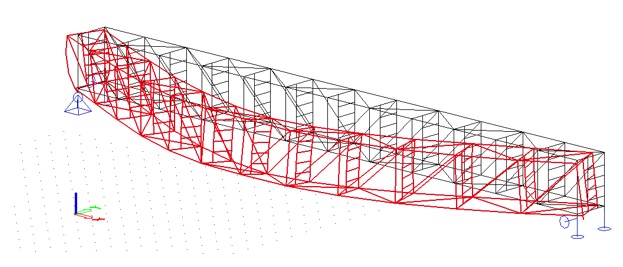
Obr. 1.2 Statické schéma a podepření – boční pohled
Obr. 1.3 Půdorys, vodorovné ztužidlo a schéma uvolnění posunů v kloubových podporách
Obr. 1.4 Schéma nosné konstrukce – axonometrie
1 ZATÍŽENÍ
1.1 SVISLÁ ZATÍŽENÍ
1.1.1 Stálé zatížení
Vlastní tíha konstrukce je počítána pomocí programu SCIA. S přídavkem na styčníky její hodnota na běžný metr mostu činí … 4,05 kN/m.
Ostatní stálé zatížení (lávka, opláštění) … 3,0 kN/m.
1.1.2 Užitné zatížení
Maximální tíha nesených technologií se uvažuje … 22 kN/m.
1.1.3 Zatížení sněhem
Zatížení sněhem podle ČSN EN 1991-1-3 ed. 2 [2].
Sněhová oblast:
\begin{gathered}
\text{I}
\end{gathered}Charakteristická hodnota zatížení sněhem na zemi:
\begin{gathered}
s_\text{k}=0{,}70\space\text{kN/m}^2
\end{gathered}Součinitel expozice:
\begin{gathered}
C_\text{e}=0{,}80
\end{gathered}Tepelný součinitel:
\begin{gathered}
C_\text{t}=1{,}00
\end{gathered}Tvarový součinitel zatížení sněhem:
\begin{gathered}
\mu=0{,}80
\end{gathered}Zatížení sněhem:
\begin{gathered}
s=0{,}45\space\text{kN/m}^2
\end{gathered}Zatížení sněhem na běžný metr mostu (šířka mostu 2,2 m):
\begin{gathered}
s_n = 0{,}45 \cdot 2{,}2 = 1{,}0 \space\text{kN/m}
\end{gathered}Součinitel kombinace pro zatížení sněhem (podle tab. A1.1, ČSN EN 1990 ed. 2 [3]):
\begin{gathered}
\psi_\text{0,s}=0{,}50
\end{gathered}1.2 VODOROVNÉ ZATÍŽENÍ – VÍTR
Zatížení větrem podle ČSN EN 1991-1-4 ed. 2 [1].
1.2.1 Větrná oblast a základní rychlost větru
Větrná oblast a základní rychlost větru podle čl. 4.2 [1]
Větrná oblast:
\begin{gathered}
\text{II}
\end{gathered}Výchozí základní rychlost větru:
\begin{gathered}
v_\text{b,0}=25{,}\space\text{m/s}
\end{gathered}Součinitel směru větru:
\begin{gathered}
c_\text{dir}=1{,}0
\end{gathered}Součinitel ročního období:
\begin{gathered}
c_\text{season}=1{,}0
\end{gathered}Základní rychlost větru (pro střední dobu návratu 50 let):
\begin{gathered}
v_\text{b}=c_\text{dir}\cdot c_\text{season}\cdot v_\text{b,0}=25{,}0\space\text{m/s}
\end{gathered}1.2.2 Kategorie terénu
podle čl. 4.3.2 a A.1 [1]
Kategorie terénu:
\begin{gathered}
\text{II}
\end{gathered}Parametr drsnosti terénu:
\begin{gathered}
z_0=0{,}05\space\text{m}
\end{gathered}Minimální výška:
\begin{gathered}
z_\text{min}=2{,}00\space\text{m}
\end{gathered}Parametr drsnosti pro kategorii terénu II:
\begin{gathered}
z_\text{0,II}=0{,}05\space\text{m}
\end{gathered}Součinitel terénu:
\begin{gathered}
k_\text{r}= 0{,}19\cdot\Bigg(\frac{z_0}{z_\text{{0,II}}}\Bigg)^{0{,}07} = 0{,}19
\end{gathered}1.2.3 Střední rychlost větru, maximální dynamický tlak
podle čl. 4.3, 4.4 a 4.5 [1]
Referenční výška:
\begin{gathered}
z=28\space\text{m}
\end{gathered}Doba integrace pro stanovení střední rychlosti větru:
\begin{gathered}
T=600\space\text{s}
\end{gathered}Součinitel turbulence:
\begin{gathered}
k_\text{I}=1{,}00
\end{gathered}Měrná hmotnost vzduchu:
\begin{gathered}
\rho=1{,}25\space\text{kg/m}^3
\end{gathered}Základní dynamický tlak větru:
\begin{gathered}
q_\text{b}=\frac{1}{2}\cdot\rho\cdot v_\text{b}^2=0{,}39\space\text{kN/m}^2
\end{gathered}
Součinitel drsnosti terénu:
\begin{gathered}
c_\text{r}=k_\text{r}\cdot\ln\Bigg(\frac{z}{z_0}\Bigg)=0{,}19\cdot\ln\Bigg(\frac{28}{0{,}05}\Bigg)=1{,}202
\end{gathered}
Součinitel orografie:
\begin{gathered}
c_0=1{,}0
\end{gathered}
Střední rychlost větru:
\begin{gathered}
v_\text{m}(z)=c_\text{r}\cdot c_0\cdot v_\text{b}=1{,}202\cdot1\cdot25=30{,}05\space\text{m/s}
\end{gathered}
Intenzita turbulence:
\begin{gathered}
I_\text{v}(z)=\frac{k_\text{I}}{c_0\cdot\ln\bigg(\frac{z}{z_0}\bigg)}=\frac{1{,}0}{1{,}0\cdot\ln\bigg(\frac{28}{0{,}05}\bigg)}=0{,}158
\end{gathered}
Maximální dynamický tlak větru:
\begin{gathered}
q_\text{p}(z)=[1+7\cdot I_\text{v}]\cdot\frac{1}{2}\cdot\rho\cdot v_\text{m}^2=[1+7+0{,}158]\cdot\frac{1}{2}\cdot1{,}25\cdot30{,}05^2=1{,}189\space\text{kN/m}^2
\end{gathered}
1.2.4 Aerodynamický odpor
podle čl. 7.6 a 7.13 [1]
Kinematická viskozita vzduchu:
\begin{gathered}
v=15\cdot10^{-6}\space\text{m}^2\text{/s}
\end{gathered}Efektivní štíhlost
Délka
\begin{gathered}
I=31{,}7\space\text{m}
\end{gathered}Výška
\begin{gathered}
b=3{,}00\space\text{m}
\end{gathered}Efektivní štíhlost:
\begin{gathered}
\lambda=9{,}1\space(\text{podle tab. 7.16, řádku č. 4, určeno interpolací})
\end{gathered}Součinitel koncového efektu:
\begin{gathered}
\psi_\lambda=0{,}69\space(\text{podle obr. 7.36 [1] pro součinitel plnosti}\space\varphi=1{,}0)
\end{gathered}Poznámka:
Součinitel koncového efektu zohledňuje vliv proudění větru kolem volných konců konstrukce na snížení jejího aerodynamického odporu. Součinitel nabývá podle [1] hodnoty 0,69, přestože je konstrukce ohraničena budovami a volné konce nemá. Za pozornost jistě stojí, že podle národní přílohy Velké Británie má být v tomto případě součinitel koncového efektu uvažován rovný 1,0 (naopak národní příloha Německa ponechává kap. 7.13 [1] beze změny). Součinitel koncového efektu se neuplatňuje rovněž v případě mostů, na které se vztahuje kap. 8.3.1 [1] (mimo stavební stavy u konzolové montáže, letmé betonáže apod.).
Součinitel koncového efektu je dále uvažován bezpečně hodnotou:
\begin{gathered}
\psi_\lambda=1{,}0
\end{gathered}Součinitel síly
Součinitel síly bez vlivu koncových efektů (podle obr. 7.23 [1]) pro d/b = 2,2 / 3,0 = 0,73):
\begin{gathered}
c_\text{f,0}=2{,}37
\end{gathered}Redukční součinitel pro průřezy se zaoblenými rohy (podle obr. 7.24 [1] pro r = 0):
\begin{gathered}
\psi_\text{r}=1{,}0
\end{gathered}Součinitel síly:
\begin{gathered}
c_\text{f}=c_\text{f,0}\cdot\psi_\text{r}\cdot\psi_\lambda=2{,}37\cdot1{,}0\cdot1{,}0=2{,}37
\end{gathered}Návětrná plocha celkem:
\begin{gathered}
A_\text{ref}=b\cdot I=3\cdot31{,}7=95{,}1\space\text{m}^2
\end{gathered}Aerodynamický odpor konstrukce celkem:
\begin{gathered}
c_\text{f}\cdot A_\text{ref}=2{,}37\cdot95{,}1=225{,}39\space\text{m}^2
\end{gathered}2 ANALÝZA KONSTRUKCE
2.1 MODÁLNÍ ANALÝZA A ÚTLUM
Vlastní frekvence a tvary kmitání byly spočteny pomocí statického software pro kombinaci hmot odpovídající charakteristickým hodnotám celkového stálého zatížení, užitného technologického zatížení a zatížení sněhem. Stálé a užitné technologické zatížení je započítáno plnou hodnotou. Zatížení sněhem bylo redukováno součinitelem kombinace ψ0,s = 0,50 (viz 2.1.3).
Základní vlastní frekvence kmitání pro kmitání ve směru větru je 1,70 Hz. Příslušný vlastní tvar je vykreslen na obr. 3.1 a jeho pořadnice na obr. 3.2. Jedná se o první vlastní tvar kmitání ve vodorovném směru.
Obr. 3.1a Základní vlastní tvar kmitání ve směru větru – axonometrie
Obr. 3.1b Základní vlastní tvar kmitání ve směru větru – pohled shora (vlevo), čelní pohled (vpravo)
Obr. 3.2 Pořadnice základního vlastního tvaru kmitání pro kmitání ve směru větru (jsou uvedeny průměrné hodnoty po výšce), schéma číslování bodů
Útlum
Celkový logaritmický dekrement útlumu je stanoven podle článku F.5 [1] jako součet konstrukčního, aerodynamického útlumu a útlumu od zvláštních zařízení. Logaritmický dekrement konstrukčního útlumu pro první tvar kmitání je uvažován hodnotou ds = 0,03 (podle tab. F.2 [1], pro ocelové mosty s vysokopevnostními šrouby). Logaritmický dekrement útlumu od zvláštních zařízení se v tomto případě neuplatní.
Logaritmický dekrement aerodynamického útlumu je určen podle odstavce (3), F.5 [1].
Vzhledem ke skutečnosti, že pořadnice základního tvaru kmitání jsou po výšce konstrukce přibližně konstantní, je logaritmický dekrement aerodynamického útlumu vypočten pro průměrné hodnoty vztažené k podélné ose konstrukce. Délky příslušné jednotlivým uzlům dy jsou znázorněny na obr. 3.2. Výška příslušná uzlům se uvažuje konstantně dz = 3 m.
Tab. 3.1 Veličiny pro výpočet aerodynamického útlumu konstrukce
| Číslo uzlu | Délka příslušná uzlu | Hmotnost na jednotku návětrné plochy | Pořadnice základního vlastního tvar kmitání | m · φ2 · dydz | φ2 · dydz |
| dy | μ | φ | |||
| [m] | [kg/m2] | ||||
| 1 | 1,258 | 985 | 0,2 | 149 | 0,15 |
| 2 | 2,591 | 985 | 1,3 | 12 940 | 13,14 |
| 3 | 2,667 | 985 | 2,5 | 49 257 | 50,01 |
| 4 | 2,667 | 985 | 3,6 | 102 139 | 103,69 |
| 5 | 2,667 | 985 | 4,5 | 159 593 | 162,02 |
| 6 | 2,667 | 985 | 5,2 | 213 105 | 216,35 |
| 7 | 2,667 | 985 | 5,4 | 229 813 | 233,31 |
| 8 | 2,667 | 985 | 5,2 | 213 105 | 216,35 |
| 9 | 2,667 | 985 | 4,8 | 181 581 | 184,34 |
| 10 | 2,667 | 985 | 3,9 | 119 872 | 121,70 |
| 11 | 2,667 | 985 | 2,8 | 61 788 | 62,73 |
| 12 | 2,591 | 985 | 1,5 | 17 227 | 17,49 |
| 13 | 1,258 | 985 | 0,2 | 149 | 0,15 |
| Suma: | 31,700 | 1 360 717 | 1 381 |
Hmotnost na jednotku délky je určena jako součet
m = 405 kg/m (vlastní tíha) + 300 kg/m (ostatní stálé) + 2 200 kg/m (technologie) + 0,5 ∙ 100 kg/m (0,5 ∙ sníh) = 2 955 kg/m
Hmotnost na jednotku návětrné plochy konstrukce (pro výšku konstrukce 3 m):
\begin{gathered}
\mu=2\space955/3=985\space\text{kg/m}^2
\end{gathered}Ekvivalentní hmotnost na jednotku návětrné plochy konstrukce
\begin{gathered}
\mu_\text{e}=\frac{\int\limits_0^\text{h}\int\limits_0^\text{b}\mu(y{,}z)\cdot\varPhi_1^2(y{,}z)\cdot dydz}{\int\limits_0^\text{h}\int\limits_0^\text{b}\varPhi_1^2(y{,}z)\cdot dydz}=\frac{1\space360\space717}{1\space381}=985\space\text{kg/m}^2
\end{gathered}Logaritmický dekrement aerodynamického útlumu je určen jako
\begin{gathered}
\delta_\text{a}=\frac{\rho\cdot c_\text{f}\cdot v_\text{m}(z_\text{s})}{2\cdot n_1\cdot\mu_\text{e}}=\frac{1{,}25\cdot2{,}37\cdot29{,}80}{2\cdot1{,}70\cdot985}=0{,}026
\end{gathered}Celkový logaritmický dekrement útlumu je
\begin{gathered}
\delta=\delta_\text{s}\cdot\delta_\text{a}\cdot\delta_\text{d}=0{,}03+0{,}026+0=0{,}056
\end{gathered}2.2 STANOVENÍ ODEZVY NA ZATÍŽENÍ VĚTREM
Odezva na zatížení větrem je stanovena kvazistatickým výpočtem podle [1]. Součinitel konstrukce cscd je určen podle přílohy B [1].
2.2.1 Součinitel konstrukce cscd
podle 6.3 [1]
Referenční výška pro stanovení součinitele konstrukce cscd:
\begin{gathered}
z_\text{s}=26{,}50\space\text{m}\space(\text{viz obr. 6.1 b [1]})
\end{gathered}Součinitel orografie v referenční výšce:
\begin{gathered}
c_0(z_\text{s})=1{,}00
\end{gathered}Intenzita turbulence v referenční výšce:
\begin{gathered}
I_\text{v}(z_\text{s})=\frac{k_\text{I}}{c_0\cdot\ln\bigg(\frac{z_\text{s}}{z_0}\bigg)}=\frac{1}{1\cdot\ln\bigg(\frac{26{,}5}{0{,}05}\bigg)}=0{,}159
\end{gathered}Střední rychlost větru v referenční výšce:
\begin{gathered}
v_\text{m}(z_\text{s})=k_\text{r}\cdot\ln\bigg(\frac{z_\text{s}}{z_0}\bigg)\cdot c_0\cdot v_\text{b}=0{,}19\cdot\ln\bigg(\frac{26{,}5}{0{,}05}\bigg)\cdot1\cdot25=29{,}80\space\text{m/s}
\end{gathered}Turbulence větru
podle B.1 [1]
Referenční výška:
\begin{gathered}
z_\text{t}=200\space\text{m}
\end{gathered}Referenční měřítko:
\begin{gathered}
L_\text{t}=300\space\text{m}
\end{gathered}\begin{gathered}
\alpha=0{,}67+0{,}05\cdot\ln(z_0)=0{,}67+0{,}05\cdot\ln(0{,}05)=0{,}52
\end{gathered}Měřítko délky turbulence:
\begin{gathered}
L(z_\text{s})+L_\text{t}\cdot\bigg(\frac{z_\text{s}}{z_\text{t}}\bigg)^\alpha=300\cdot\bigg(\frac{26{,}5}{200}\bigg)^{0{,}52}=104{,}875\space\text{m}
\end{gathered}Základní vlastní frekvence:
\begin{gathered}
n_{1,\text{x}}=1{,}70\space\text{Hz}
\end{gathered}Bezrozměrná vlastní frekvence:
\begin{gathered}
f_\text{L}(z_\text{s}{,}n_{1,\text{x}})=\frac{n_{1,\text{x}}\cdot L(z_\text{s})}{v_\text{m}(z_\text{s})}=\frac{1{,}70\cdot104{,}875}{29{,}80}=5{,}983
\end{gathered}Bezrozměrná výkonová spektrální hustota rychlosti větru:
\begin{gathered}
S_\text{L}(z_\text{s}{,}n_{1,\text{x}})=\frac{6{,}8\cdot f_\text{L}(z_\text{s}{,}n_{1,\text{x}})}{(1+10{,}2\cdot f_\text{L}(z_\text{s}{,}n_{1,\text{x}}))^{5/3}}=\frac{6{,}8\cdot5{,}983}{(1+10{,}2\cdot5{,}983)^{5/3}}=0{,}042
\end{gathered}Součinitel konstrukce
Součinitel odezvy pozadí (zvaný též součinitel základní části odezvy), podle B.2 (2) [1]:
\begin{gathered}
B^2=\frac{1}{1+0{,}9\cdot\bigg(\frac{b+h}{L(z_\text{s})}\bigg)^{0{,}63}}=\frac{1}{1+0{,}9\cdot\bigg(\frac{31{,}7+3}{104{,}875}\bigg)^{0{,}63}}=0{,}69
\end{gathered}Veličiny b a h odpovídají obr. 6.1 [1].
Rezonanční část odezvy, podle B.2 (5) [1]:
\begin{gathered}
R^2=\frac{\pi^2}{2\cdot\delta}\cdot S_\text{L}(z_\text{s}{,}n_{1,\text{x}})\cdot R_\text{h}(\eta_\text{h})\cdot R_\text{b}(\eta_\text{b})
\end{gathered}kde
\begin{gathered}
\eta_\text{h}=\frac{4{,}6\cdot h}{L(z_\text{s})}\cdot f_\text{L}(z_\text{s}{,}n_{1,\text{x}})=\frac{4{,}6\cdot3}{104{,}875}\cdot5{,}983=0{,}787
\end{gathered}\begin{gathered}
\eta_\text{b}=\frac{4{,}6\cdot b}{L(z_\text{s})}\cdot f_\text{L}(z_\text{s}{,}n_{1,\text{x}})=\frac{4{,}6\cdot31{,}7}{104{,}875}\cdot5{,}983=8{,}319
\end{gathered}\begin{gathered}
R_\text{h}=\frac{1}{\eta_\text{h}}-\frac{1}{2\cdot\eta_\text{h}^2}\cdot(1-e^{-2\eta_\text{h}})=\frac{1}{0{,}787}-\frac{1}{2\cdot0{,}787^2}\cdot(1-e^{-2\cdot0{,}787})=0{,}631
\end{gathered}\begin{gathered}
R_\text{b}=\frac{1}{\eta_\text{b}}-\frac{1}{2\cdot\eta_\text{b}^2}\cdot(1-e^{-2\eta_\text{b}})=\frac{1}{8{,}319}-\frac{1}{2\cdot8{,}319^2}\cdot(1-e^{-2\cdot8{,}319})=0{,}113
\end{gathered}\begin{gathered}
R^2=\frac{\pi^2}{2\cdot0{,}056}\cdot0{,}042\cdot0{,}631\cdot0{,}113=0{,}264
\end{gathered}Frekvence přechodů s kladnou směrnicí, podle B.2 (4) [1]:
\begin{gathered}
v=n_{1,\text{x}}\cdot\sqrt\frac{R^2}{B^2+R^2}=1{,}70\cdot\sqrt\frac{0{,}264}{0{,}69+0{,}264}=0{,}894\space\text{Hz}
\end{gathered}Součinitel maximální hodnoty, podle B.2 (3) [1]:
\begin{gathered}
k_\text{p}=\sqrt{2\cdot\ln(b\cdot T)}+\frac{0{,}6}{\sqrt{2\cdot\ln(b\cdot T)}}=\sqrt{2\cdot\ln(0{,}894\cdot600)}+\frac{0{,}6}{\sqrt{2\cdot\ln(0{,}894\cdot600)}}=3{,}714
\end{gathered}Součinitel konstrukce cscd, podle čl. 6.3.1 [1]:
\begin{gathered}
c_\text{s}c_\text{d}=\frac{1+2\cdot k_\text{p}\cdot I_\text{v}(z_\text{s})\cdot\sqrt{B^2+R^2}}{1+7\cdot I_\text{v}(z_\text{s})}=\frac{1+2\cdot3{,}714\cdot0{,}159\cdot\sqrt{0{,}69+0{,}263}}{1+7\cdot0{,}159}=1{,}02
\end{gathered}Poznámka:
Podle národní přílohy ČR se má pro výpočet součinitele konstrukce použít Příloha B [1]. Pro informaci a porovnání uvádíme, že hodnota součinitele konstrukce spočtená podle Příloha C [1], ve které může být zvolen sinusový tvar kmitání odpovídající kmitání mostů, by činila 1,04. Shoda výsledků obou postupů je v tomto případě velmi dobrá.
2.2.2 Zatížení větrem
podle čl. 5.3 [1]
Celkové zatížení
Zatížení větrem na jednotku délky:
\begin{gathered}
f_\text{w}=c_\text{s}c_\text{d}\cdot q_\text{p}(z_\text{e})\cdot c_\text{f}\cdot b=1{,}02\cdot1{,}189\cdot2{,}37\cdot3{,}0=8{,}62\space\text{kN/bm}
\end{gathered}Toto zatížení má být použito pro návrh nosné konstrukce mostu jako celku.
Lokální zatížení
Opláštění a prvky, na které je uloženo (tj. svislice nebo pasy), mají navíc odolat místnímu tlaku, resp. vztlaku větru. Hodnoty součinitelů vnějšího tlaku nejsou pro tento případ v normě [1] uvedeny. Je patrné, že v případě použití součinitelů cpe,1 podle kap. 7.2.2 [1] pro návětrnou a závětrnou svislou stěnu, nedosáhne součet těchto součinitelů ani celkového tvarového součinitele cf o hodnotě 2,37.
Součinitel vnějšího tlaku cpe,1 pro návětrnou stěnu (oblast D) je roven 1,0. Součinitel cpe,1 pro závětrnou stěnu (oblast E) je vyčíslen pro poměr h/d = 1,5 / 2,2 = 0,68, kde h je poloviční výška konstrukce (zjednodušeně uvážíme, že se proud vzduchu rovnoměrně dělí pod a nad konstrukci). Součinitel vnějšího tlaku cpe,1 pro závětrnou stěnu je roven – 0,41 (určeno interpolací z tab. 7.1 [1] pro oblast E). Součet součinitelů návětrné a závětrné stěny je 1,0 + 0,41 = 1,41, což je významně menší než 2,37.
Součinitele vnějších tlaků na stěny konstrukce doporučujeme uvažovat hodnotami 1,0 pro návětrnou stěnu a -1,37 pro stěnu závětrnou (tak, aby výsledná hodnota zatížení odpovídala celkovému tvarovému součiniteli cf = 2,37).
Pro vnější tlak na střeše a podlaze mostu je přibližně uvažován součinitel vnějšího tlaku pro ploché střechy podle kap. 7.2.3 [1] pro poloviční výšku konstrukce:
e = min(b;2h) = min (31,7;2∙1.5) = 3 m
oblast G … šířka e/10 = 0,3 m … cpe,1 = -2,0
oblast H … cpe,1 = -1,2
oblast F se neuvažuje, protože střecha mostu nemá volný roh.
Výše vedené součinitele vnějších lokálních tlaků byly určeny přibližně na základě zjednodušené představy o působení větru. V případě potřeby přesnějšího určení lokálních účinků, je nezbytné provést numerickou simulaci proudění vzduchu, případně zkoušku ve větrném tunelu.
Poznámka:
Pro porovnání uvádíme, že podle původní normy ČSN 730035 [4] byla hodnota tvarového součinitele 0,8 pro návětrnou stěnu a -1,2 pro stěnu závětrnou. Součinitel pro horní a dolní vodorovnou plochu byl -1,5, viz tab. 20, poř. č. 13 [4]. V normě [4] byl tento případ uveden.
Lokální tlaky větru na jednotlivé plochy budou určeny podle vzorce (s ohledem na kap. 5.3 (3) [1])
\begin{gathered}
w_\text{e}=c_\text{s}c_\text{d}\cdot q_\text{p}(z_\text{e})\cdot c_\text{pe,1}=1{,}02\cdot1{,}189\cdot c_\text{pe,1}\space\text{kN/m}^2.
\end{gathered}Pro návrh lehkých prvků opláštění lze uvažovat (viz kap. 5.2 (1) [1])
\begin{gathered}
w_\text{e}=q_\text{p}(z_\text{e})\cdot c_\text{pe,1}=1{,}189\cdot c_\text{pe,1}\space\text{kN/m}^2.
\end{gathered}2.2.3 Odezva na zatížení větrem a celková odezva
Odezva na zatížení větrem je stanovena statickým výpočtem pro zatížení uvedené v předchozím odstavci.
Kombinace zatížení se volí podle normy [3], stejně jako dílčí součinitele zatížení a kombinační součinitele. Použije se tab. A.1.2 (B) – Návrhové hodnoty zatížení pro STR/GEO (soubor B), [3].
Předmětem tohoto příkladu je postup stanovení odezvy na zatížení větrem. Výpis jednotlivých vnitřních sil a deformací od zatížení větrem ani od ostatních zatížení a jejich kombinací zde není uveden. Rovněž posudky prvků konstrukce nejsou provedeny, neboť přesahují účel tohoto příkladu.
3 LITERATURA, NORMY
[1] ČSN EN 1991-1-4 ed. 2 Eurokód 1: Zatížení stavebních konstrukcí – Část 1-4: Obecná zatížení – Zatížení větrem, 04/2013
[2] ČSN EN 1991-1-3 ed. 2 Eurokód 1: Zatížení stavebních konstrukcí – Část 1-3: Obecná zatížení – Zatížení sněhem, 06/2013
[3] ČSN EN 1990 ed. 2 Eurokód: Zásady navrhování konstrukcí, 05/2015
[4] ČSN 730035 Zatížení stavebních konstrukcí, 1986 (neplatná)