ČESKÁ KOMORA AUTORIZOVANÝCH INŽENÝRŮ A TECHNIKŮ ČINNÝCH VE VÝSTAVBĚ
Rada pro podporu rozvoje profese ČKAIT
Autoři: Ing. Jiří Šmejkal, CSc., prof. Ing. Jaroslav Procházka, CSc.
Stav: kontrola 2022, vydání 2015
Anotace:
V dnešní praxi se navrhují železobetonové konstrukce podle evropské normy ČSN EN 1992–1-1:2006. Často se vytvářejí komplexní prostorové modely celých konstrukcí. Při navrhování výztuže však prostorový model nedokáže vystihnout skutečné chování v jednotlivých konstrukčních detailech zvláště proto, že nebývá splněna Bernoulliova podmínka zachování rovinnosti průřezu po deformaci. Proto se vyztužení konstrukční detailů (poruchových oblastí nebo též oblastí nespojitosti) musí provádět následně zvlášť metodami lokální analýzy. Nejznámější metoda pro lokální analýzu je metoda náhradní příhradoviny. V základní normě ČSN EN 1992-1-1:2006 se uvádí pouze obecné zásady pro navrhování a posuzování konstrukcí, nejsou však zde podrobně definovány postupy návrhu poruchových oblastí. Problematika poruchových oblastí je podrobně specifikována v odborné, obvykle zahraniční literatuře. Proto jsou v pomůcce uvedeny základní i alternativní postupy pro návrh nejběžnějších poruchových oblastí.
Metoda náhradní příhradoviny je přibližná inženýrská metoda, která umožňuje bezpečný návrh poruchové oblasti poměrně jednoduchými prostředky.
OBSAH
1 ANALÝZA KONSTRUKCE
Při analýze konstrukce jako celku je důležitá idealizace konstrukce, tj. volba výpočetního modelu. Jednotlivé prvky konstrukce lze idealizovat prvky prutovými (pomocí jejich střednice), prvky plošnými (pomocí jejich rovinné nebo zakřivené střednicové plochy). Při tvorbě modelu konstrukce jako celku tyto prvky vzájemně spojujeme a vytváříme globální model nosné konstrukce. Tento model může být jednorozměrný, dvojrozměrný, popřípadě trojrozměrný.
Při tvorbě globálního modelu je velmi důležitá volba vhodného spojení mezi prvky v uzlových bodech a výběr podmínek podepření. Spojení prvků a podepření prvků se pohybují mezi dvěma limitními stavy, které lze zjednodušeně označit jako prosté podepření a vetknutí. U monolitických železobetonových konstrukcí obvykle uvažujeme vetknutí mezi jednotlivými konstrukčními prvky. U prefabrikovaných konstrukcí se většinou snažíme s přihlédnutím k jednoduchosti realizace o kloubové připojení (pevný nebo posuvný kloub). Pokud uvažujeme vetknutí konce prvku, je nutné, aby uložení neumožňovalo pootočení. Pokud v reálné konstrukci nelze nulové pootočení zajistit, přesune se příslušná část ohybového momentu z vetknutí do pole. Při nerespektování chování reálné konstrukce by mohlo být vyztužení prvku nedostatečné. Pro modelování vzájemného spojení konstrukce s podpěrami je nutné uvážit, zda je vhodné vazbu modelovat, nebo ji naopak zanedbat, a pak její vliv pokrýt vloženou přídavnou výztuží.
Při celkové analýze konstrukce lze stanovit rozdělení vnitřních sil, napětí, deformací a reakcí konstrukce. Celková analýza je obvykle nutná pro stanovení, popřípadě ověření rozměrů a výztuže, celkové tuhosti a prostorové stability konstrukce. Pro jednotlivé konstrukční detaily a dílčí oblasti je nutná navazující lokální analýza.
Při řešení globálního i lokálního modelu konstrukce je důležitá kromě idealizace geometrie i uvažovaná idealizace chování konstrukce. Chování konstrukce lze v zásadě idealizovat následovně:
- lineárně pružné chování;
- lineárně pružné chování s omezenou redistribucí;
- plastické chování;
- nelineární chování.
Lineárně pružná analýza prvků je založena na teorii pružnosti, lze ji použít jak v mezních stavech únosnosti, tak v mezních stavech použitelnosti. Při lineárně pružné analýze se předpokládá:
- průřezy nejsou porušeny trhlinami;
- závislost napětí a poměrného přetvoření je lineární;
- moduly pružnosti mají průměrné hodnoty.
Pro stanovení účinků teplotních deformací, sedání podpor a smršťování v mezních stavech únosnosti, lze předpokládat redukované tuhosti odpovídající průřezům s trhlinami bez uvažování tahového zpevnění, avšak s přihlédnutím k účinkům dotvarování. V mezních stavech použitelnosti má být uvažován postupný vývoj trhlin.
Při lineárně pružné analýze s omezenou redistribucí se uvažuje vliv případné možné redistribuce silových účinků. Lineární analýzu s omezenou redistribucí lze použít při analýze nosných prvků při ověřování mezních stavů únosnosti, kde silové účinky stanovené lineárně pružnou analýzou lze redistribuovat za předpokladu, že výsledné rozdělení silových účinků zůstane v rovnováze s působícím zatížením. Redistribuce se nemá používat v případech, pokud nelze spolehlivě určit schopnost plastických pootočení.
Metody založené na plastické analýze mohou být použity pouze při ověřování v mezních stavech únosnosti. Pro vytvoření předpokládaného mechanismu porušení musí být dostatečná duktilita kritických oblastí (duktilita prvku je schopnost plastického přetvoření charakterizovaného nevratnými deformacemi a disipací energie). Plastická analýza má být založena buď na metodě se spodním ohraničením (statická metoda), nebo na metodě s horním ohraničením (kinematická metoda).
Účinky předcházejících zatížení lze obecně při plastické analýze zanedbat a předpokládat monotónní nárůst intenzity zatížení.
1.1 IDEALIZACE KONSTRUKCE
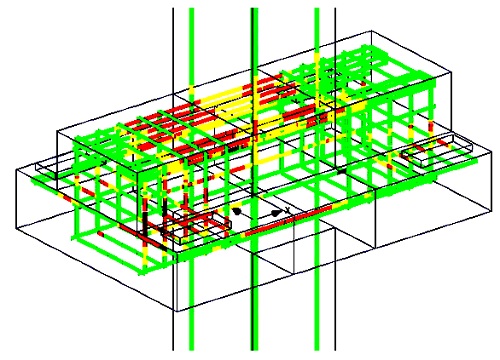
V současné době se pro celkovou analýzu nosného systému používají dvourozměrné, popřípadě třírozměrné modely konstrukce. Většinou ve výpočtech používáme dvourozměrné modely, pokud však požadujeme vystihnout prostorové chování konstrukce jako celku, používáme třírozměrné modely.
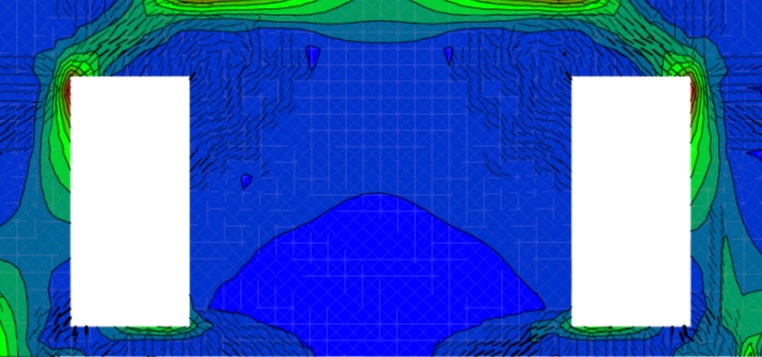
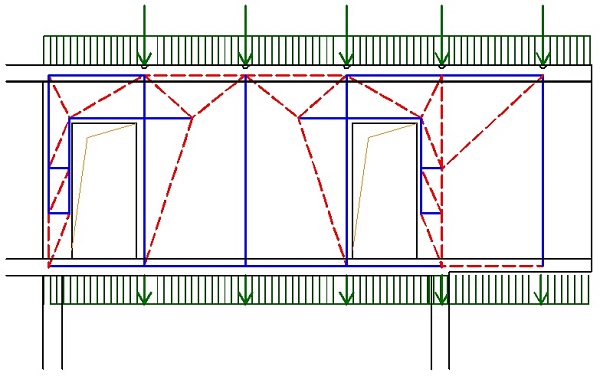
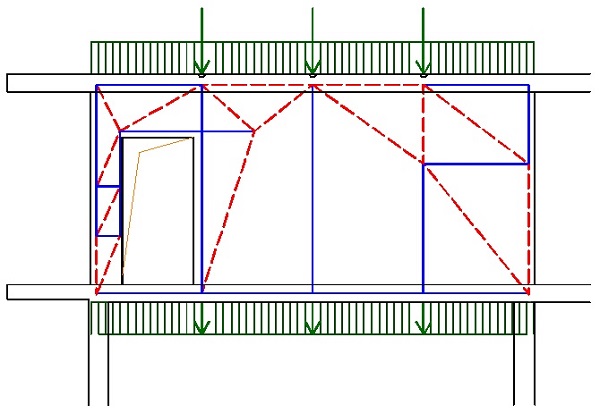
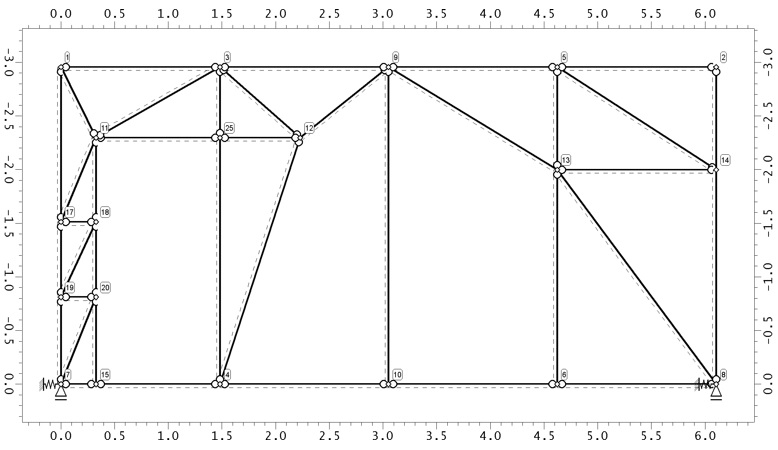
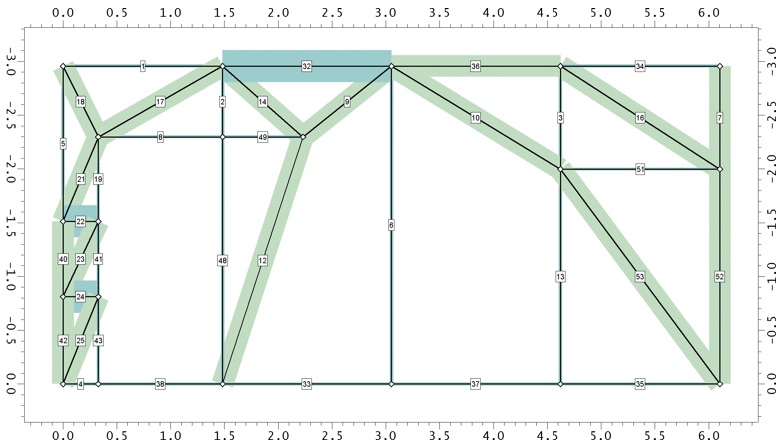
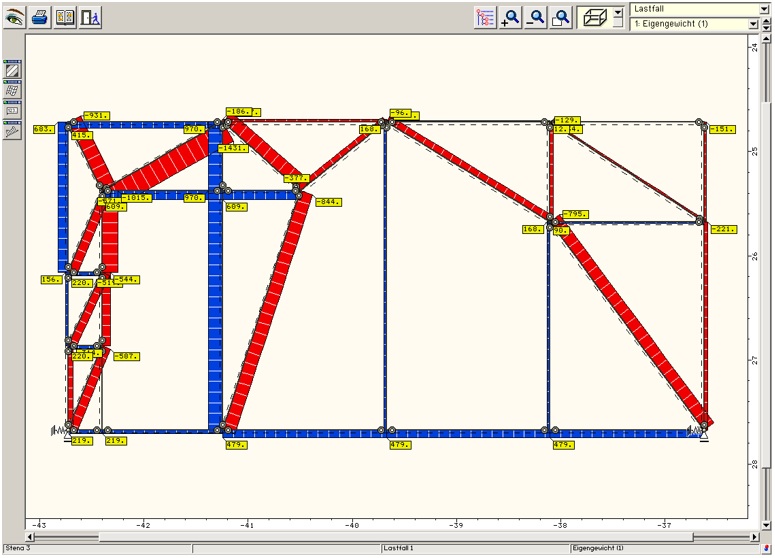
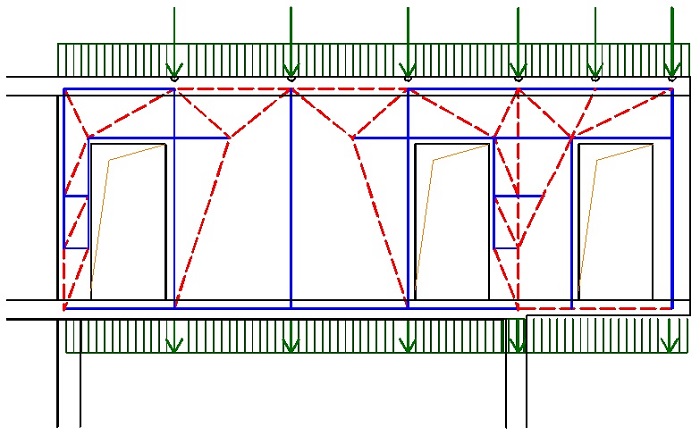
Při globální analýze vycházíme z předpokladu zachování rovinnosti průřezů před a po přetvoření. Tento předpoklad však neplatí ve všech oblastech modelované konstrukce. Proto nosné železobetonové konstrukce rozdělujeme na oblastí B a D – viz obr. 1.1.
Obr. 1.1 Poruchové oblasti – rozdělení konstrukce na B a D oblasti
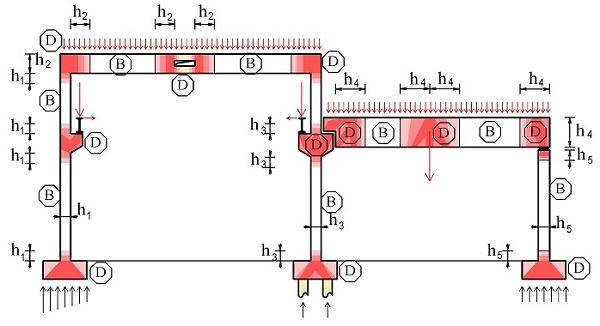
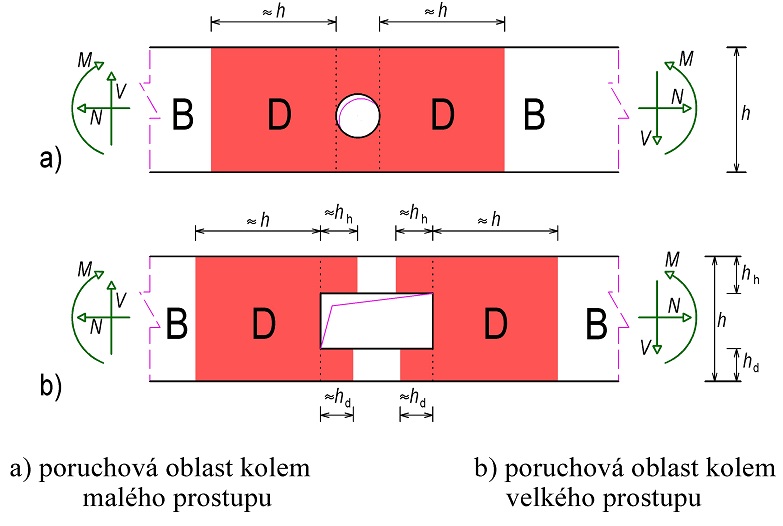
Oblasti B (někdy nazývané Bernoulliovy někdy nosníkové oblasti) představují části konstrukce, kde platí předpoklad zachování rovinnosti průřezu podle Bernoulliovy hypotézy. V těchto částech konstrukce lze poměrně jednoduchým výpočtem získat věrohodné výsledky chování konstrukce. Oblasti D jsou oblasti s diskontinuitami (tzv. poruchové oblasti). Jedná se o oblasti, kde nelze předpokládat lineární rozdělení poměrného přetvoření po průřezu. Jedná se například o oblasti (obr. 1.2), ve kterých působí lokální zatížení, nebo se mění náhle rozměr průřezu, a podobně. Podle hypotézy St. Venanta lokální porucha vymizí ve vzdálenosti rovné výšce přilehlého průřezu.
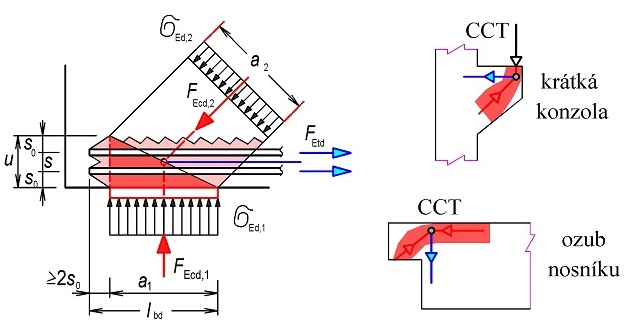
Obr. 1.2 Příklady poruchových oblastí (D oblastí)
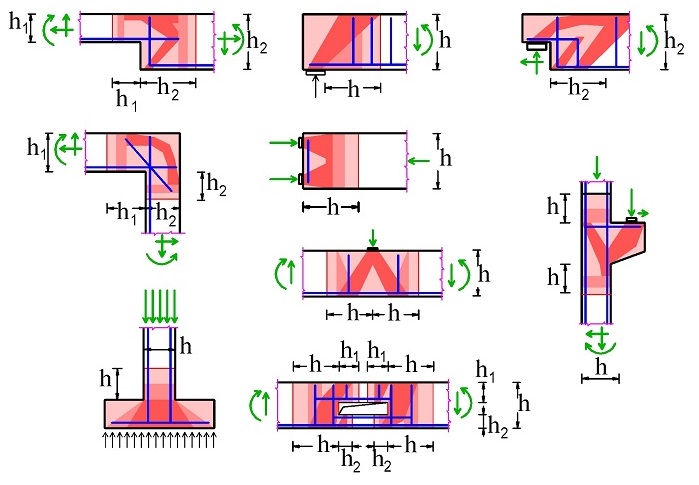
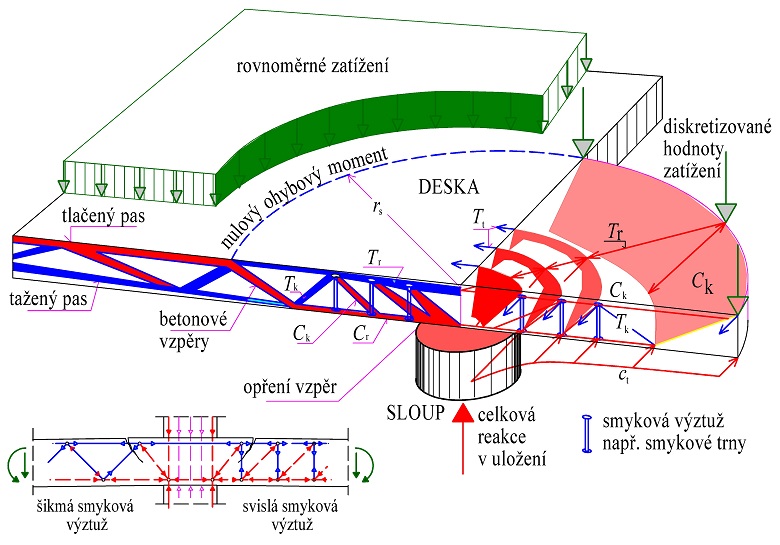
Při návrhu výztuže v mezních stavech únosnosti v poruchových oblastech se používají modely náhradní příhradoviny (obr 1.3). Tyto modely lze použít i pro prvky, u nichž je předpokládáno lineární rozdělení poměrného přetvoření po průřezu. Při posuzování mezních stavů použitelnosti lze rovněž použít modely náhradní příhradoviny, pokud je však zaručena přibližná kompatibilita prutových modelů (zvláště poloha a směr důležitých tlakových diagonál a poloha a směr výztuže – táhel).
Obr. 1.3 Příklady modelů náhradní příhradoviny
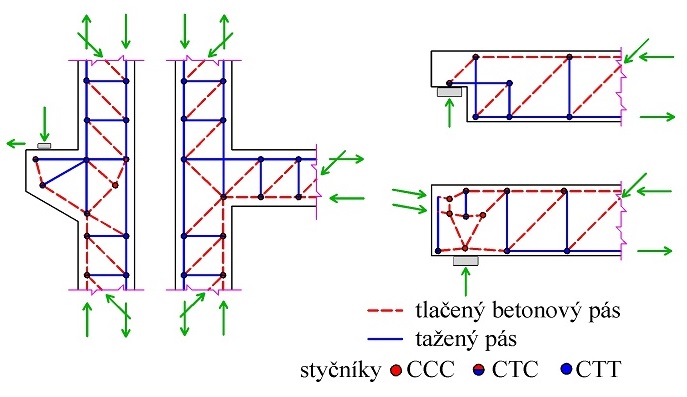
Modely náhradní příhradoviny (strut and tie models obr 1.3) se skládají z tlačených prutů, tažených prutů (přenášení pouze normálovou sílu) a spojovacích uzlů – styčníků. Síly v prvcích prutového systému – náhradní příhradoviny se stanovují z podmínky zachování rovnováhy s působícím zatížením. Poloha a směr táhel modelu náhradní příhradoviny má souhlasit s odpovídající výztuží.
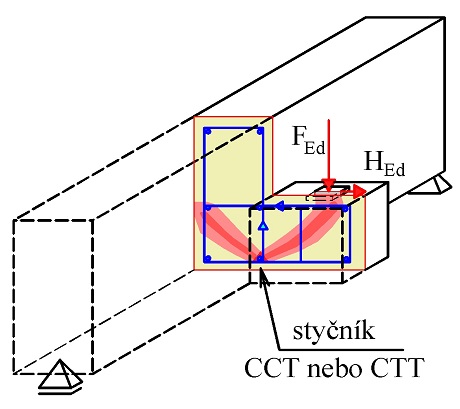
Styčníky jsou oblasti, ve kterých jsou transformovány síly mezi tlačenými prvky, z tlačených prvků do tažených prvků nebo také do reakcí (obr. 1.3). Styčníky jsou klasifikovány podle působících sil. Ve styčníku s označením CCC působí nejméně tři tlakové betonové pásy – vzpěry. Ve styčníku s označením CTC působí nejméně dva tlakové betonové pásy a jeden tažený pás představovaný výztuží. Ve styčníku CTT působí nejméně jeden tlakový betonový pás a nejméně dva tažené pásy působící v různých směrech.
1.2 TLAČENÉ PRUTY – BETONOVÉ VZPĚRY (Struts)
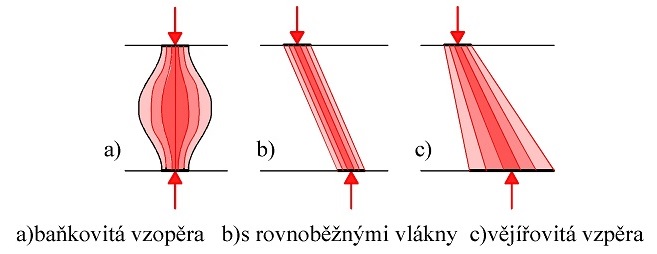
Tlačené pruty jsou základním stavebním prvkem modelů náhradní příhradoviny při analýze poruchových oblastí. Tlačené pruty mohou mít různý tvar (obr. 1.4). Rozlišujeme základní tři typy betonových vzpěr podle změny jejich šířky po délce [7]. Tlačené pruty přenášejí pouze osový tlak. Příklady tlačených prutů jsou na obr. 1.5.
Obr. 1.4 Základní tvary betonových vzpěr
Obr. 1.5 Příklady betonových vzpěr
U betonových diagonál se napětí se stanoví podle vztahu:
\begin{gathered}
\sigma_\text{c}=\frac{N_\text{c}}{d_\text{c}\cdot b}
\end{gathered}(1.1)
kde je
Nc … normálová síla v tlačené diagonále;
dc … tloušťka tlačené diagonály;
b … šířka tlačené diagonály.
Tlačené betonové pruty náhradní příhradoviny se v [1] rozlišují podle působícího příčného napětí. Uvažují se tlačené pruty s působícím příčným tlakovým napětím, bez působícího příčného napětí a s příčným tahovým napětím. Návrhové napětí na mezi únosnosti pro tlačené betonové pruty v oblasti s příčným tlakovým napětím, nebo bez příčného tlakového napětí, se stanoví ze vztahu 1.2 (obr 1.6a):
\begin{gathered}
S_\text{Rd,max}=f_\text{cd}
\end{gathered}(1.2)
V oblastech s víceosým tlakem lze předpokládat vyšší návrhovou pevnost.
Návrhové napětí na mezi únosnosti pro betonové tlačené pruty v oblastech s trhlinami je nutné redukovat. Pokud se nepoužije přesnější výpočet, lze návrhovou pevnost uvažovat podle vztahu (1.3) (obr 1.6b):
\begin{gathered}
\sigma_\text{Rd,max}=0{,}6\cdot\nu'\cdot f_\text{cd}
\end{gathered}(1.3)
\begin{gathered}
\text{kde}\space\space\nu'\space\space\text{lze vyjádřit}\space\space\nu'=1-f_\text{ck}{/}250{.}\text{ Hodnota}\space\space f_\text{ck}\space\space\text{je v MPa.}
\end{gathered}(1.4)
Obr. 1.6 Betonové vzpěry z hlediska působení příčného napětí
Pokud není betonová diagonála po celé délce namáhána příčným tlakovým napětím (viz obr. 1.6a) je nutné zvážit velikost vznikajících příčných tahů v tlačených betonových diagonálách, které jsou schematicky zobrazeny na obr. 1.7.
Obr. 1.7 Příčné tahové síly v tlakovém poli vzpěry
Příčnou tahovou sílu tlačené betonové diagonály stanovíme podle následujících vztahů (1.5) a (1.6). Tahová síla T působí ve čtvrtinách oblasti s úplnou nespojitostí (obr. 1.7b). Staticky nutná výztuž, která má odolávat příčným tahovým silám T v betonových vzpěrách, může být rozptýlena po příslušné délce oblasti nespojitosti.
a) Pro částečně nespojité oblasti, kde b ≤ H/2 a bef = b podle obr. 1.7a:
\begin{gathered}
T=\frac{1}{4}\frac{b-a}{b}F
\end{gathered}(1.5)
b) Pro úplně nespojité oblasti, kde b > H/2 a bef = 0,5H + 0,65a, h = H/2 podle obr. 1.7b:
\begin{gathered}
T=\frac{1}{4}\Bigg(1-0{,}7\frac{a}{h}\Bigg)F
\end{gathered}(1.6)
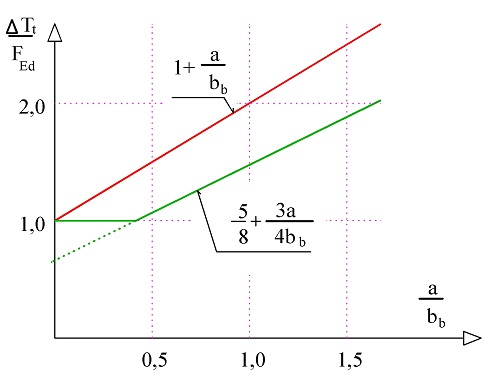
Vztahy vycházejí ze závěrů experimentů uvedených v [7]. V jiných předpisech lze nalézt i vztah:
\begin{gathered}
T=\frac{1}{4}\Bigg(1-0{,}7\frac{a}{H}\Bigg)F
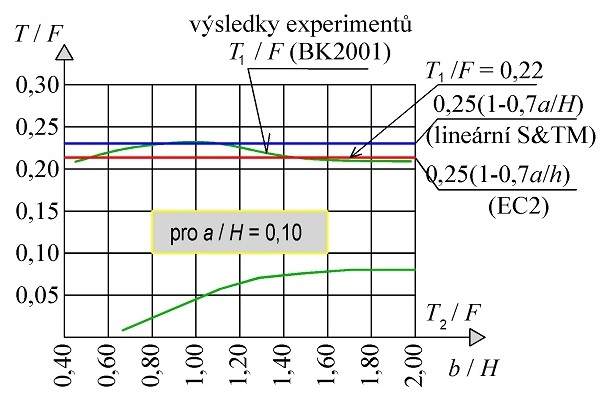
\end{gathered}[22], který představuje lineární řešení poruchové oblasti tlačené betonové vzpěry podle obr. 1.7c. Tento vztah dává větší příčné tahy; v konstrukcích pozemních staveb jsou rozdíly mezi vztahy do 10 % (obr. 1.8 a obr. 1.9).
Obr. 1.8 Závislost vznikajícího příčného tahu na tlakové síle Fc v betonové vzpěře a geometrii oblasti (a, H)
Obr. 1.9 Závislost vznikajícího příčného tahu T na tlakové síle Fc a geometrii oblasti (a, H)
Pro konstrukce pozemních staveb, nebo jiné drobné konstrukce, lze stanovit sílu představující vznikající příčné tahy podle následujícího vztahu:
\begin{gathered}
T\le0{,}22F
\end{gathered}(1.7)
Příčnou tahovou sílu může přenést beton, pokud jsou tahová napětí menší než 0,5fctd. Pokud jsou tahová napětí v rozmezí 0,5fctd až fctd, musí být oblast minimálně vyztužena konstrukční výztuží podle [1]. Při větších tahových napětích musí veškeré tahy přenést navržená výztuž.
Při tvorbě modelu náhradní příhradoviny lze využít skutečnosti, že diagonální betonové vzpěry jsou obecně rovnoběžné s očekávaným průběhem trhlin v betonu daného prvku. Vzpěry by neměly křižovat trhliny, jinak by model náhradní příhradoviny neodpovídal skutečnému chování betonu a výztuže v oblasti.
Únosnost betonové vzpěry s trhlinami (rovnoběžnými s podélnou osou vzpěry) je definována vztahem (1.3). Uvedené však platí pro alespoň konstrukčně vyztužené oblasti. Pokud není oblast s betonovou vzpěrou ve směru působení příčných tahů alespoň konstrukčně vyztužena, musí veškeré příčné tahy převzít beton. V tomto případě se doporučuje omezit únosnost tlačené betonové vzpěry na 60 % únosnosti vycházející ze vztahu (1.3).
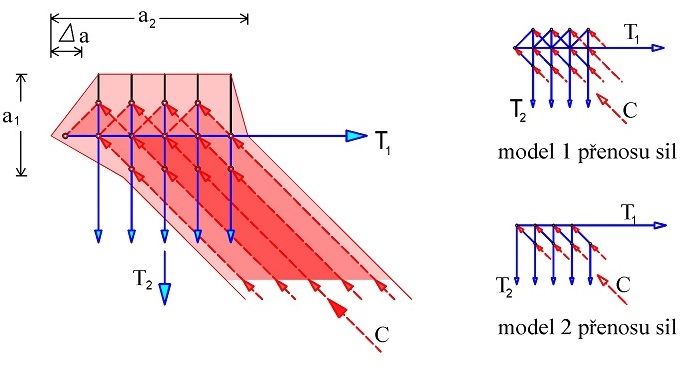
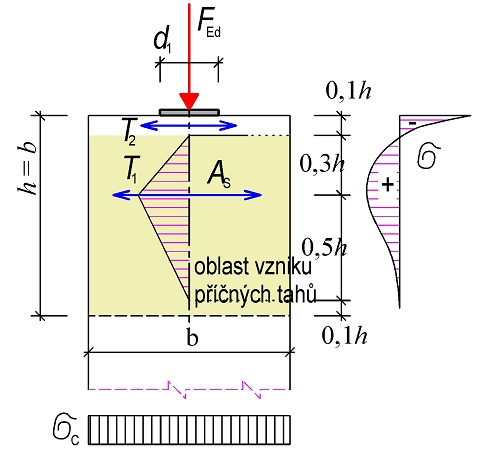
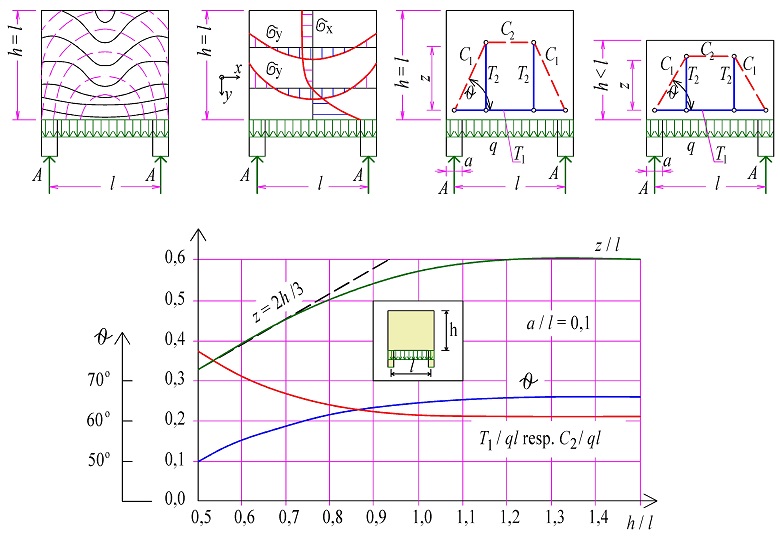
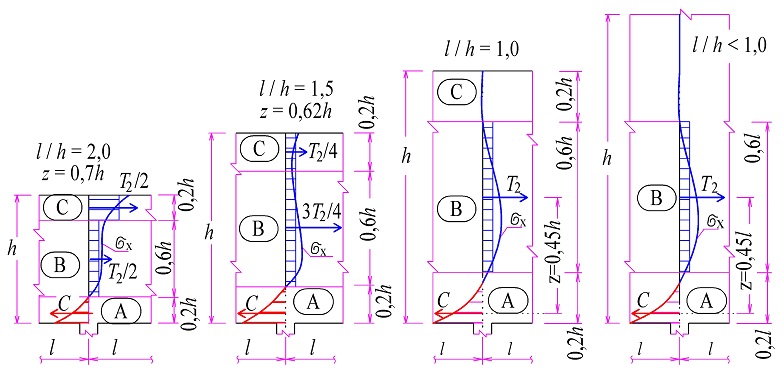
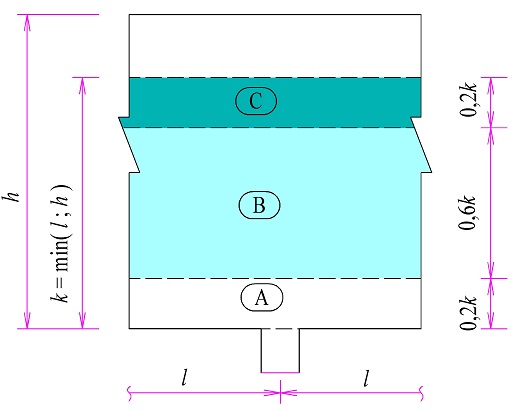
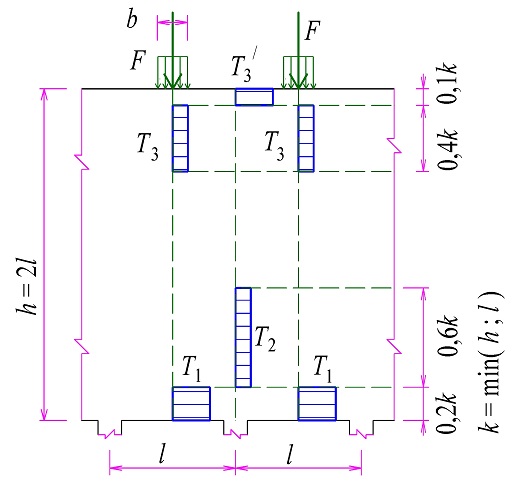
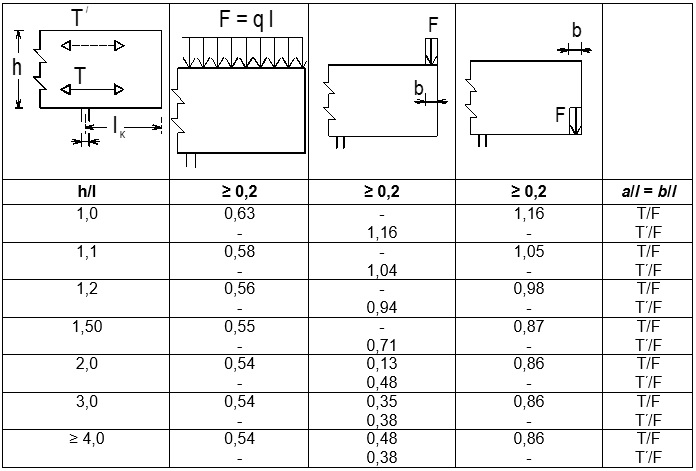
Při zatížení osamělým břemenem vzniká při horním líci oblast s tahy T2 – viz obr. 2.1. Velikost tahů lze zjednodušeně uvažovat hodnotou T2 ≈ 0,10F.
1.2.1 Příklady tlačených vzpěr
Příklady tlačených prutů jsou na obr. 1.5. U betonových diagonál se napětí stanoví podle vztahu:
\begin{gathered}
\sigma_\text{c}=\frac{N_\text{c}}{d_\text{c}\cdot b}
\end{gathered}kde je
Nc … normálová síla v tlačené diagonále;
dc … tloušťka tlačené diagonály;
b … šířka tlačené diagonály.
Pro prvky s rovnoběžnými tlačenými betonovými vlákny podle (obr. 1.5), lze napětí v šikmé betonové vzpěře vyjádřit vztahem:
\begin{gathered}
\sigma_\text{c}=\frac{q}{b\cdot\sin^2\theta}
\end{gathered}Pro vzpěry s vějířovitými tlačenými vlákny lze napětí vyjádřit podle vztahu:
\begin{gathered}
\sigma_\text{c}=\frac{q_\text{h}\cdot e}{b\cdot\sin^2\theta_1\cdot e'}\cong\frac{q_\text{h}}{b\cdot\sin^2\theta_1}
\end{gathered}kde je
e … tloušťka betonové vzpěry měřená v ose horního tlačeného pasu modelu náhradní příhradoviny;
e´ … tloušťka betonové vzpěry v dolním líci horního tlačeného pasu;
qh … koncentrované zatížení (například pod ložiskem nebo styčnou deskou) působící na tloušťce e betonové vzpěry v kN/m;
b … šířka vzpěry (obvykle šířka nosníku);
θ1 … úhel sklonu tlakové diagonály (betonové vzpěry).
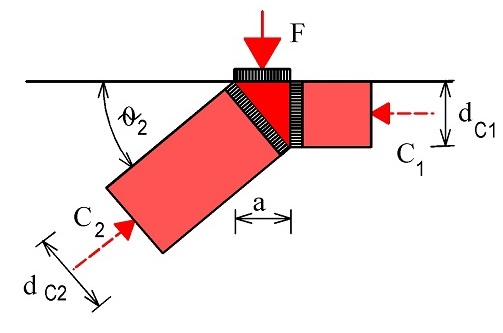
Příklad stanovení šířky šikmé betonové vzpěry podle obr. 1.11
\begin{gathered}
d_\text{c2}=a\cdot\sin\theta_2+d\cdot\cos\theta_2
\end{gathered}1.2.2 Odvození vztahů pro částečnou a plně nespojitou oblast
Síla F působící na délce a se rozloží do dvou shodných částí F1 = F/2. Síly působí ve vzdálenosti a/2. Při částečně nespojité oblasti (pro oblast D) platí b ≤ H/2, h = b, bef = b podle obr. 1.7. Svislá délka šikmé vzpěry je b/2. Tlak vzpěr se rozloží na šířku b. Pro sklon tlačené diagonály podle modelu náhradní příhradoviny platí:
\begin{gathered}
\cot\theta=\frac{(0{,}5b-0{,}5a)/2}{0{,}5b}=\frac{b-a}{2b}
\end{gathered}Po dosazení zatížení F vyjádříme tahovou sílu T podle vztahu:
\begin{gathered}
T=F_1\cot\theta=\frac{1}{4}\frac{b-a}{b}F\text{, viz vztah (1.7).}
\end{gathered}Pro úplnou nespojitost platí b > h = 0,5H a bef = 0,5H + 0,65a podle obr. 1.7c:
\begin{gathered}
\cot\theta=\frac{0{,}5\cdot b_\text{eff}}{0{,}5h}\frac{(0{,}5\cdot(0{,}5H+0{,}65a)-0{,}5a)/2}{0{,}25H}=\frac{(0{,}25H+0{,}325a-0{,}5a)}{0{,}5\cdot0{,}25H}\\
\\
\cot\theta=\frac{(0{,}5h-0{,}175a)}{0{,}5\cdot0{,}5h}=\frac{1}{2}\bigg(1-0{,}35\frac{a}{h}\bigg)\\
\\
T=F_1\cot\theta=\frac{1}{4}\bigg(1-0{,}35\frac{a}{h}\bigg)F=\frac{1}{4}\bigg(1-0{,}7\frac{a}{H}\bigg)F
\end{gathered}Podle závěrů experimentů prof. Schlaicha [7] je přesnější řešení podle vztahu:
\begin{gathered}
T=\frac{1}{4}\bigg(1-0{,}7\frac{a}{H}\bigg)^2F=\frac{F}{4}\bigg(1-1{,}4\frac{a}{H}+0{,}49\frac{a^2}{H^2}\bigg)
\end{gathered}kde člen:
\begin{gathered}
0{,}49\frac{a^2}{H^2}
\end{gathered}lze vůči ostatním členům v předchozím výrazu zanedbat. Zanedbání je ve prospěch bezpečnosti (vychází větší tah).
Po úpravě dostaneme výraz uváděný v normě ČSN EN 1992-1-1 [1] viz (1.8):
\begin{gathered}
T=\frac{1}{4}\bigg(1-0{,}7\frac{a}{h}\bigg)F
\end{gathered}Z obr. 1.8 a obr. 1.9 je patrné, že pro konstrukce pozemních staveb lze provést zjednodušení. Podle obr. 1.8 lze přibližnou hodnotu příčného tahu definovat jako T ≈ 0,22 F. To platí pro oblasti, kde šířka a vzpěry (v místě opření vzpěry ve styčníku) je poměrně malá ve srovnání s délkou vzpěry H. Hodnota poměru a/H = 0,10 představuje u konstrukcí pozemních staveb obvykle maximální hodnotu. Podle obr. 1.9 hodnota vznikajících příčných tahů klesá s rostoucím poměrem a/H. Pokud se betonová vzpěra výrazně nerozšiřuje a ≈ bef, nejsou vznikající příčné tahy velké [7]. Pro konstrukce pozemních staveb, nebo jiné drobné konstrukce, lze vztah zjednodušit:
\begin{gathered}
T\le0{,}22F
\end{gathered}1.3 TAŽNÉ PRVKY – TÁHLA (Ties)
Táhlo v modelu náhradní příhradoviny představuje výztuž. Táhlo může být tvořeno i několika vrstvami výztužných prutů. Šířka táhla se stanoví tak, že ke krajním prutům se připočítá tloušťka betonové krycí vrstvy, nebo polovina vzdálenosti mezi další výztuží. Výztuž musí být vždy odpovídajícím způsobem zakotvena ve styčníku. Při návrhu táhla se uvažuje dosažení meze kluzu výztuže v táhle před tlakovým porušením betonové vzpěry. Tahové síly v betonu se až na výjimky zanedbávají (betonová táhla jsou někdy uvažována například u rámových rohů, ozubů desek a podobně).
Při návrhu táhla je nutné vždy zohlednit jeho skutečnou šířku. Obvykle se uvažuje celá teoretická šířka táhla. Obvykle není vhodné zkoncentrovat táhlo pouze do místa teoretické osy táhla podle modelu náhradní příhradoviny, protože model představuje pouze náhradu skutečného přenosu vnitřních sil v oblasti. Koncetrovaná táhla se uvažují u líce změn průřezů nebo prostupů, v ostatních případech se výztuž táhla rovnoměrně rozděluje po celé šířce táhla. Šířku táhla můžeme stanovit podle ČSN EN 1992-1-1:2006 hodnotou 2,5 ∙ (h – d).
1.4 STYČNÍKY (Joints)
Styčníky v modelech náhradní příhradoviny představují oblasti styku táhel a vzpěr. Styčníky jsou betonové. Všechny síly působící ve styčníku musí být v rovnováze. Styčníky uvažujeme ve spojích prutů náhradní příhradoviny, v místech působení soustředěných zatížení, v podporách a v ohybech výztužných prutů.
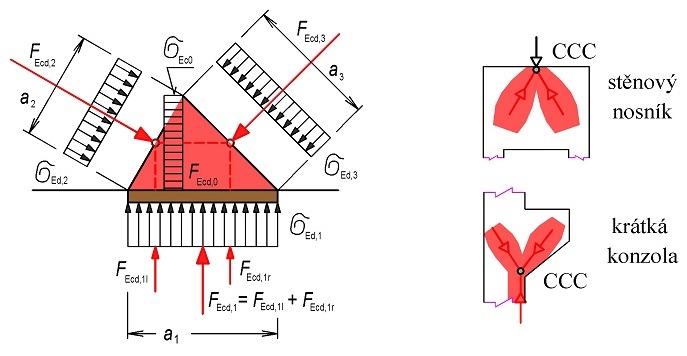
Obr. 1.10 Styčník s tlačenými diagonálami CCC
Obr. 1.11 Příklad styčníku CCC
Při posouzení styčníku je rozhodující stanovení jeho velikosti. U styčníku s tlačenými diagonálami (vícerým tlakem) vycházíme z předpokladu, že ve styčníku je dosaženo únosnosti betonu v tlaku (CCC – obr. 1.10). Dále se předpokládá stejné napětí v celé oblasti styčníku (Mohrovy kružnice). Oblast styčníku se nazývá hydrostatická uzlová – styčníková zóna. U styčníku s táhly (CTC a CTT) je velikost styčníku dána délkou táhla, na které se síla z táhla přenese do styčníku – ostatních prutů soustavy. Tím se rozšiřuje oblast styčníku (ve srovnání s CCC); nazýváme ji rozšířená styčníková zóna. Na obr. 1.12 je oblast hydrostatické uzlové zóny zobrazena tmavší barvou a rozšířená uzlová oblast označené světlejší barvou. Rozšířená uzlová zóna je tvořena oblastí s tlakovým napětím od betonových vzpěr a od reakce. Tlakové napětí napomáhá přenosu sil z jedné vzpěry do druhé nebo do táhla představovaného výztuží.
Obr. 1.12 Styčník s tlačenými diagonálami a táhlem v jednom směru CTC
Protože beton je jen omezeně plasticky deformovatelný, systém vnitřních sil musí být stanoven tak, aby v žádné části oblasti nebyla překročena mezní deformace. Pro stanovení optimálního modelu náhradní příhradoviny je nejlepší vycházet z pružné analýzy oblasti nejlépe pomocí MKP. Ze stanovených pružných vnitřních sil je potom možné vykonstruovat model náhradní příhradoviny. Do modelu je nutno vhodně zakomponovat vyztužení prvku – táhla. Betonové vzpěry u nepřímého uložení se musí opírat o zakotvenou výztuž táhla. Obvykle výztuž táhla obepíná smyčkou styčník CTC nebo CTT.
Ze zkušeností se ukazuje, že není nutné přesně sledovat pružný tok vnitřních sil v mezním stavu únosnosti. Nejjednodušším příkladem je příhradový model pro návrh smykové výztuže, který připouští uvažovat základní sklon tlačeného betonového pásu pod úhlem 45° až 63° od neutrální osy.
Návrhové hodnoty pro tlaková napětí na mezi únosnosti ve styčnících lze určit následovně:
a) Styčníky s tlakovými silami (CCC), ve kterých nejsou kotvena táhla podle [1] – obr. 1.10:
\begin{gathered}
\sigma_\text{Rd,max}=1{,}0\cdot \nu'\cdot f_\text{cd}
\end{gathered}(1.8)
kde je
σRd, max … maximální napětí, které může působit na hranách styčníku a ν‚ je dáno vztahem (1.4).
b) Styčníky s tlakovými i tahovými silami s táhly kotvenými v jednom směru podle (CTC) a podle [1] – obr. 1.12:
\begin{gathered}
\sigma_\text{Rd,max}=0{,}85\cdot\nu'\cdot f_\text{cd}
\end{gathered}(1.9)
kde je
σRd, max … maximální napětí a ν‚ viz vztah (1.4).
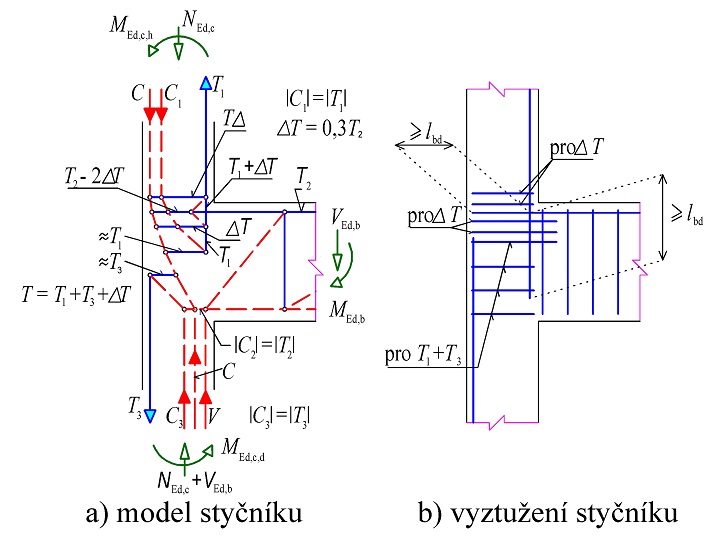
Typickým představitelem styčníku CTC je místo uložení nosníku. Idealizovaný model styčníku je na obr. 1.12.
Obr. 1.13 Příklady styčníků CTC
c) Styčníky s tlakovými i tahovými silami a táhly kotvenými ve více směrech (CTT) podle [1].
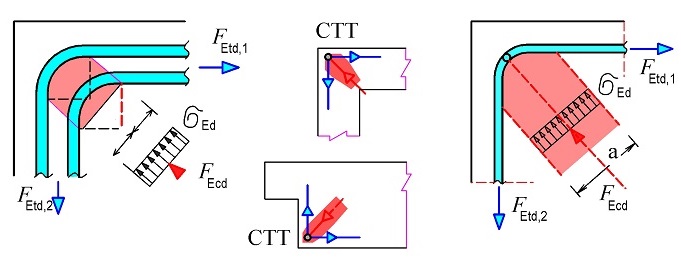
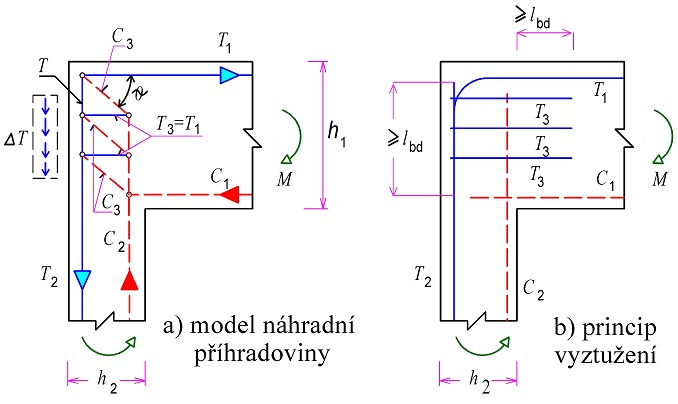
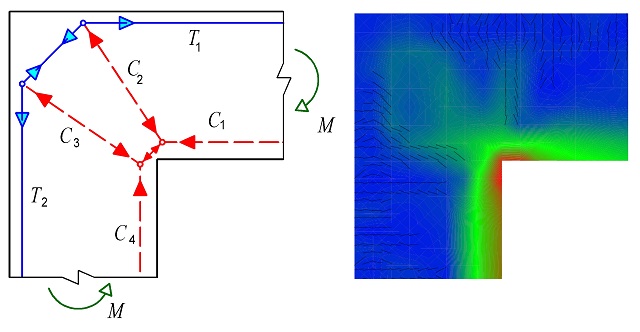
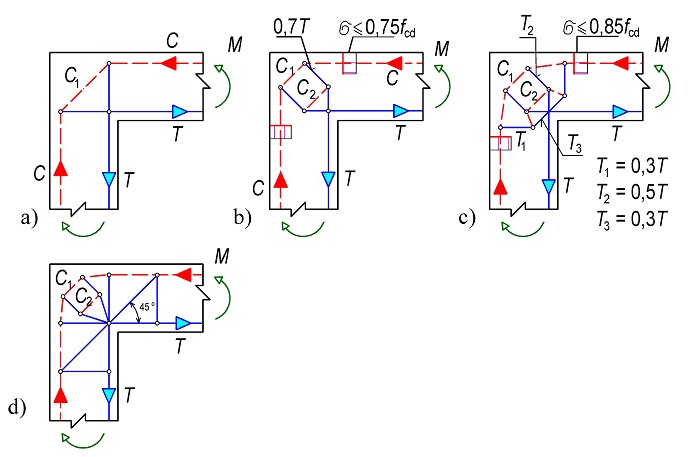
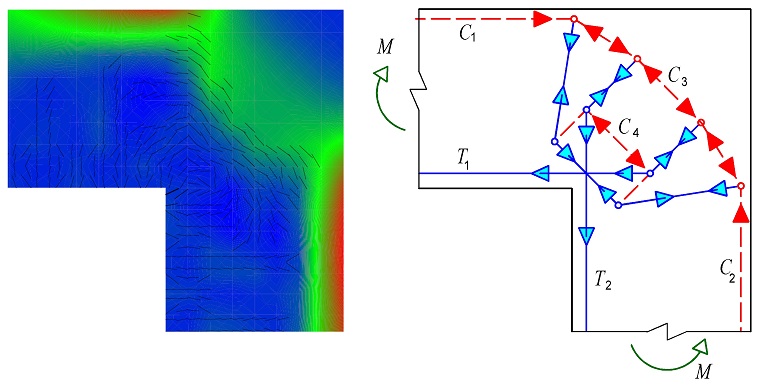
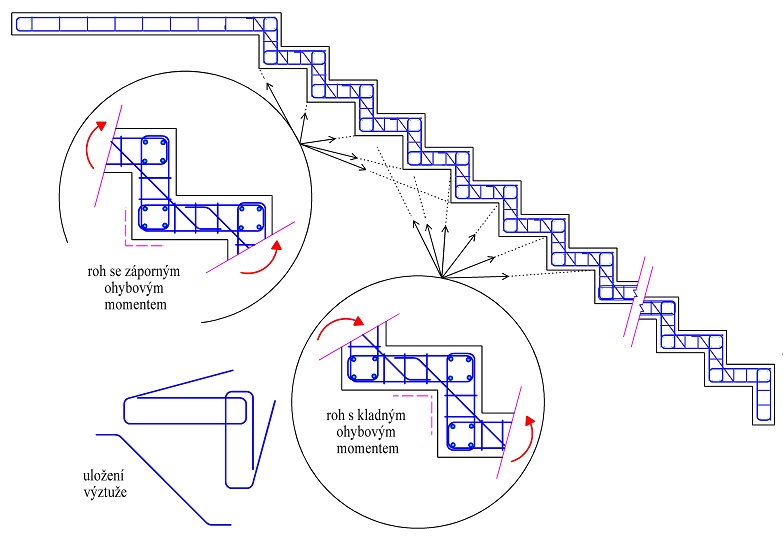
Nejčastěji se vyskytuje styčník CTT v rámových rozích (obr. 1.14) se záporným působením ohybového momentu [31]. Napětí σRd, max se stanoví podle vztahu:
\begin{gathered}
\sigma_\text{Rd,max}=0{,}75\cdot\nu'\cdot f_\text{cd}
\end{gathered}(1.10)
kde ν‚ viz vztah (1.4).
Obr. 1.14 Styčník s minimálně jednou tlačenou diagonálou a táhly ve dvou směrech CTT
Obr. 1.15 Příklad styčníku CTT
Hodnotu návrhového tlakového napětí lze zvýšit o 10 %, pokud je splněna alespoň jedna z následujících podmínek podle [1]:
- je zaručen trojosý tlak;
- všechny úhly mezi tlačenými pruty a táhly jsou ≥ 55;
- výztuž je umístěna v několika vrstvách;
- pohyb styčníku je spolehlivě omezen uspořádáním v uložení nebo třením.
Pokud je známé rozdělení tlaků do všech tří směrů u trojose tlačených styčníků, zvětšené návrhové napětí se omezuje maximálním napětím podle vztahu:
\begin{gathered}
\sigma_\text{Rd,max}\le3{,}0\cdot\nu'\cdot f_\text{cd}
\end{gathered}(1.11)
kde ν‚ viz vztah (1.4).
1.4.1 Příklady řešení styčníků
Typickým představitelem styčníku CCT je místo uložení nosníku. Idealizovaný model styčníku je na obr. 1.12. Pokud výztuž není jen v jedné vrstvě, je vhodné uvažovat postupný přenos sil do táhla – viz obr. 1.13. Pro nepřímé uložení je nutné uvažovat opření vzpěry ve styčníku do oblasti uzavřené táhlem – třmínky. Tím se nám výrazně posouvá poloha styčníku od líce prvku.
V obr. 1.13a [16] lze stanovit napětí v šikmé betonové vzpěře šířky b podle vztahu:
\begin{gathered}
\sigma_\text{c}=\frac{A}{b\cdot\sin\theta_1\cdot(a_1\cdot\sin\theta_1+u\cdot\sin\theta_1)}
\end{gathered}Pokud budeme uvažovat postupný přenos namáhání do táhla podle obr. 1.13b [16], napětí v betonové vzpěře se vyjádří podle vztahu:
\begin{gathered}
\sigma_\text{c}=\frac{A}{b\cdot a_1\sin^2\theta_1}
\end{gathered}Při vějířovité betonové vzpěře podle obr. 1.13ac [16], je namáhání v místě styku vzpěry a táhla:
\begin{gathered}
\sigma_\text{c}=\frac{A}{b\cdot\sin^2\theta_1\cdot[a_1+0{,}5u(\cot\theta-\cot\theta_2)]}
\end{gathered}Pokud se uvažuje postupný přenos sil do táhla podle obr. 1.13b a obr. 1.13c, dochází k prodloužení styčníku o délku ø. Toto prodloužení přispívá k délce, na které se musí táhlo dostatečně zakotvit. Při parabolickém tvaru hranice styčníku lze délku x stanovit:
\begin{gathered}
x=\frac{1}{4}\Bigg(\frac{a_2}{\cos\theta_1}+u\cdot\tan\theta_1-a_1\Bigg)
\end{gathered}pro zakotvení táhla je k dispozici délka l = a1 + 0,5x – c
kde je
a1 … celková šířka tlačeného betonového pásu;
a2 … šířka šikmé betonové;
u … šířka táhla;
c … betonová krycí vrstva prutů táhla;
θ1 … úhel střednice betonové vzpěry;
θ2, θ … viz obr. 1.17 – úhly okrajů vějířovité vzpěry na okraji styčníku;
x … posun okraje styčníku – viz obr. 1.13.
Styčníky CTT
Na obr. 1.15 je podrobný model pro přenos sil z táhla reprezentovaného třmínky do tlačené betonové vzpěry. Pro přenos můžeme použít model z obr. 1.15. Část tlakové síly vzpěry je opřena přímo do táhla a zbylá část se opírá až za táhlem a vytváří podružnou tlačenou vzpěru opírající se o táhlo z druhé strany. To se projeví prodloužením kotevní délky táhla o Δa (obr. 1.15). Délka prodloužení kotevní délky je závislá především na úhlu sklonu vzpěry. Pokud posuneme styčník níže, lze použít druhý model podle obr. 1.14. Tím však dostaneme excentricitu v modelu náhradní příhradoviny – styčník se prodlužuje ve směru působící síly.
Kotvení výztuže (táhel) ve styčnících s tlakovými a tahovými silami uvažujeme od okraje styčníku. Například při kotvení nad podporou začíná kotvení u vnitřního líce podpory. Pro kotevní délku táhla je k dispozici celá délka styčníku. Zakotvení výztuže lze provést i za styčníkem.
1.4.2 Příklady řešení nejčastějších styčníků
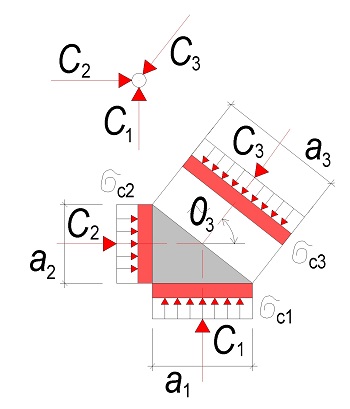
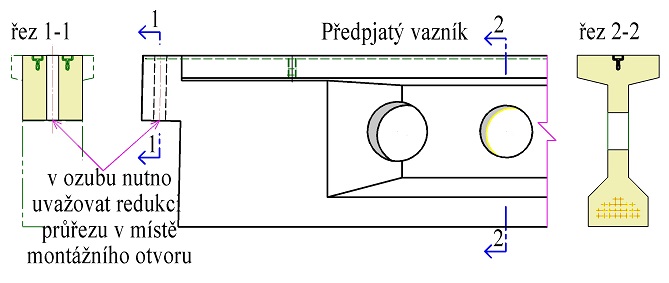
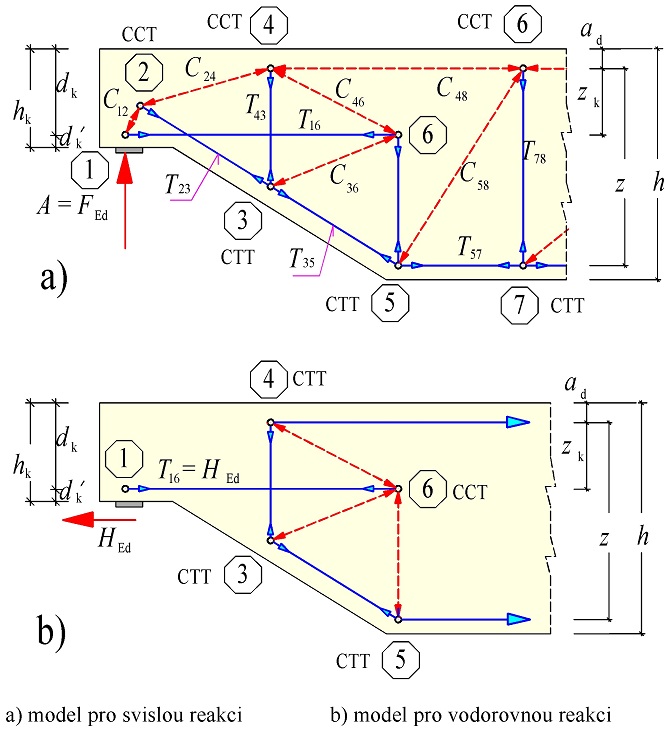
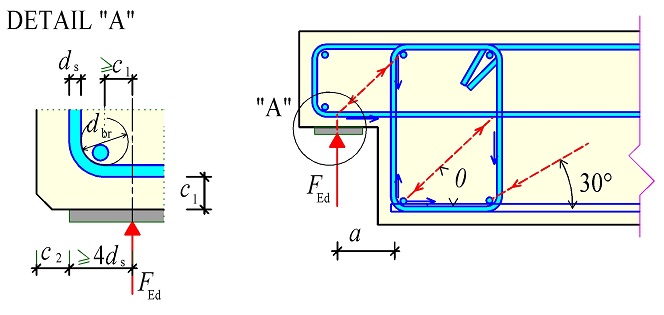
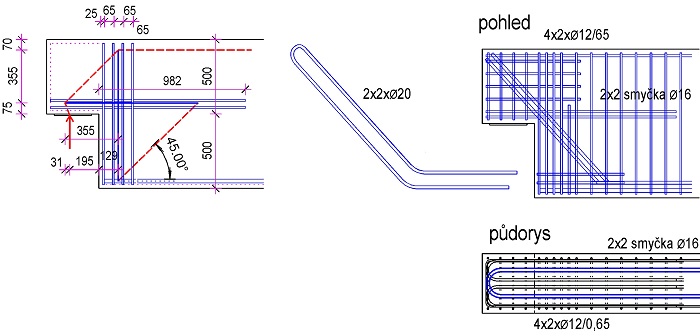
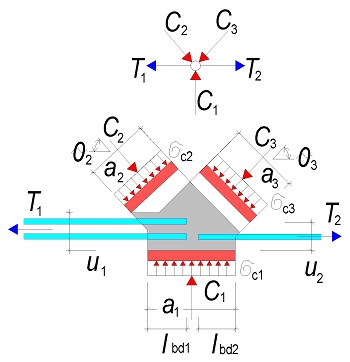
Koncové uložení předepnutých nosníků
Posouzení
\begin{gathered}
\sigma_\text{c1}=\frac{C_1}{a_1\cdot b}\le\sigma_\text{Rd,max}\\\\
\sigma_\text{c2}=\frac{C_2}{a_2\cdot b}\le\sigma_\text{Rd,max}\\\\
\sigma_\text{c3}\le\sigma_\text{Rd,max}
\end{gathered}Napětí σc3 lze vypočítat
\begin{gathered}
\sigma_\text{c3}=\frac{C_3}{a_3\cdot b}\space\text{ s }\space a_3=a_1\sin\theta_3+a_2\sin\theta_3
\end{gathered}nebo
\begin{gathered}
\sigma_\text{C3}=\frac{\sigma_1^2+\sigma_2^2\cdot(a_2/a_1)^2}{\sigma_1+\sigma_2\cdot(a_2/a_1)^2}
\end{gathered}nebo
\begin{gathered}
\sigma_\text{c3}=\frac{C_1}{(a_1\sin^2\theta_3+a_2\sin\theta_3\cdot\cos\theta_3)\cdot b}
\end{gathered}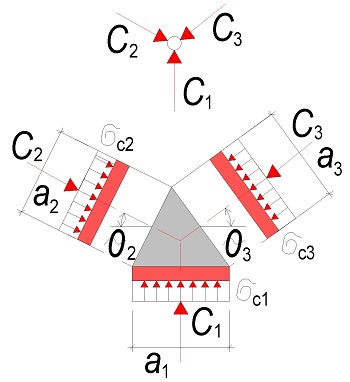
Je dána geometrie a1 a sklon tlačených diagonál θ2 a θ3
Hydrostatická zóna
\begin{gathered}
\sigma_\text{c0}=\sigma_\text{c1}=\sigma_\text{c2}=\sigma_\text{c3}\le\sigma_\text{Rd,max}
\end{gathered}Například osamělé břemeno, uložení stěny, uložení konzoly
\begin{gathered}
a_0=\frac{a_1}{\tan\theta_2+\tan\theta_3}\\\\
\sigma_\text{c1}=\frac{C_1}{a_1\cdot b}\le\sigma_\text{Rd,max}
\end{gathered}Napětí ve styčníku
\begin{gathered}
\sigma_\text{c0}=\frac{C_0}{a_0\cdot b}\le\sigma_\text{Rd,max}
\end{gathered}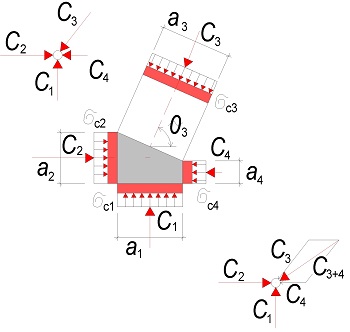
Je dána geometrie a1 a sklon tlačené diagonály θ3.
Hodnota a2 se stanoví z únosnosti vzpěry v tlaku
\begin{gathered}
a_\text{c}=\frac{C_2}{\sigma_\text{Rd,max}\cdot b}
\end{gathered}Posouzení
\begin{gathered}
\sigma_\text{c1}=\frac{C_1}{a_1\cdot b}\le\sigma_\text{Rd,max}\\\\
\sigma_\text{c2}=\frac{C_2}{a_2\cdot b}\le\sigma_\text{Rd,max}
\end{gathered}Posouzení napětí σc3 a σc4 vyplývají z rovnováhy ve styčníku
Je doporučeno síly C3 a C4 složit a řešit jako předchozí styčník

Příkladem je vnitřní podpěra stěnového nosníku
Je doporučeno síly C2 a C3 a C4 a C5 složit a řešit jako styčník CCT se třemi betonovými vzpěrami

Styčník CTC
Délka styčníku je dána kotevní délkou táhla
Nutná konstrukční příčná výztuž

Styčník CTC
Délka styčníku je dána kotevní délkou táhla
Nutná konstrukční příčná výztuž


Styčník CTC
Délka styčníku je dána kotevní délkou táhla
Nutná konstrukční příčná výztuž
Styčník CTC
Délka styčníku je dána kotevní délkou táhla
Nutná konstrukční příčná výztuž
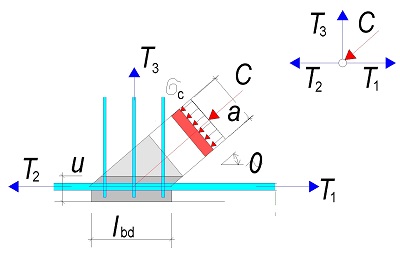

Styčník CTT
Délka styčníku je dána kotevní délkou táhla
Nutná konstrukční příčná výztuž
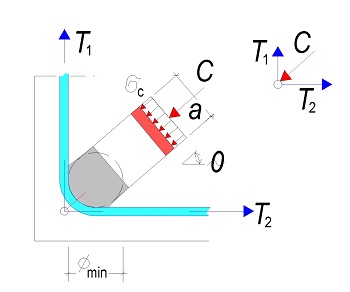
Styčník CTT
Délka styčníku je dána kotevní délkou táhla
Nutná konstrukční příčná výztuž

Styčník CTT
Délka styčníku je dána kotevní délkou táhla
Nutná konstrukční příčná výztuž
1.5 TVORBA MODELŮ NÁHRADNÍ PŘÍHRADOVINY
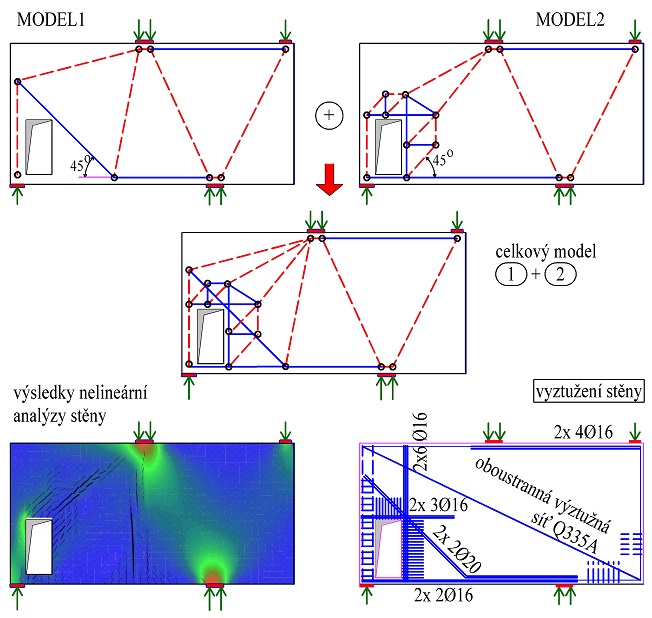
Tvorba modelů náhradní příhradoviny bývá často založena také na empirických zkušenostech, popřípadě na podrobném nelineárním modelování D-oblastí. Pro zjednodušení jsou základní pravidla uvedena v normě [1] a další literatuře například v [8], [13], [16], [18], [20] atd. Předpokládá se, že tlakové síly přenáší betonové vzpěry a tahové síly přenáší betonářská výztuž. Základy modelování D-oblastí vycházejí z výzkumných prací prof. Schlaicha publikovaných v roce 1984 [38]. Postupně byla pak tato metoda rozvíjena a ověřena řadou experimentů. Podrobněji je o tvorbě modelů pojednáno v následujících kapitolách.
Při tvorbě modelu náhradní příhradoviny se doporučuje postupovat následovně:
- nalézt reakce v modelované části konstrukce;
- přechod D-oblasti do B-oblasti musí být plynulý bez jakýchkoliv skokových změn;
- rozdělení zatížení a nalezení vnitřních sil – působící napětí nahradit výslednicemi, nahradit asymetrická napětí dvojicí sil, definovat model náhradní příhradoviny soustavou vzpěr a táhel. Při definování jednotlivých prvků je nutné vždy zvážit polohu skutečného vyztužení sledované části konstrukce, včetně zakotvení výztuže v oblasti styčníků.
Předpoklady pro řešení modelů náhradní příhradoviny
- v táhlech je dosaženo meze kluzu výztuže před vyčerpáním pevnosti betonových vzpěr;
- síly ve vzpěrách a táhlech jsou jen osové;
- tahové síly v betonu jsou většinou zanedbány (kromě soudržnosti, ta musí být vždy uvažována);
- ve všech styčnících musí být zajištěna rovnováha;
- výztuž táhel se plně aktivuje po vzniku trhlin v betonu;
- k redistribuci vnitřních sil dochází především po vzniku trhlin v betonové části průřezu;
- vzpěry jsou obvykle rovnoběžné s očekávaným směrem trhlin vznikajících v důsledku příčných tahových sil v tlačené betonové části průřezu.
Pro omezení šířky trhlin D-oblastí je nutné
- při povrchu oblasti vložit minimálně konstrukční ortogonální výztuž s plochou nejméně As ≥ 0,003Ac při obou površích;
- maximální vzdálenost výztužných prutů má být menší než 250 mm.
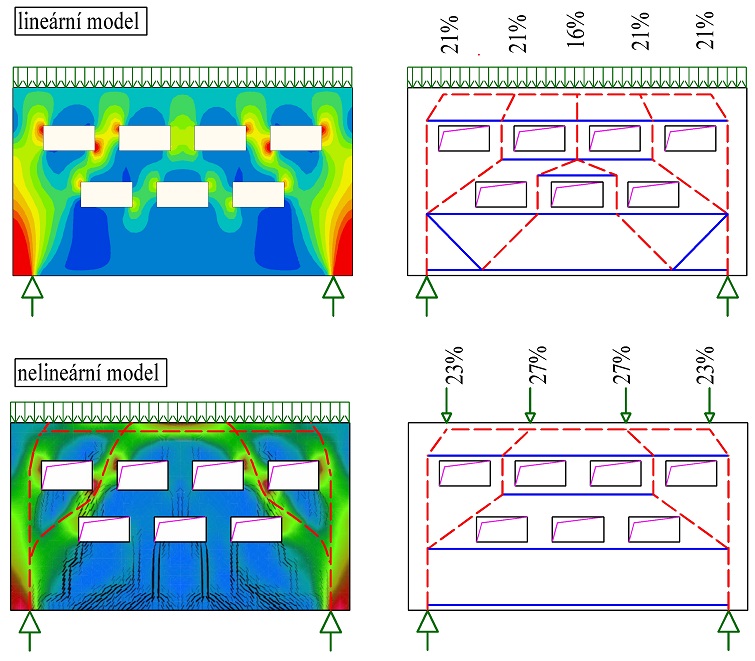
Je nutné si uvědomit, že modely náhradní příhradoviny jsou tzv. inženýrské modely, které poměrně jednoduchým způsobem umožňují provést bezpečný návrh poruchové oblasti. Při řešení oblasti nelineárními metodami, dostaneme přesnější řešení, které je však výrazně náročnější. Přesné nelineární řešení se liší od modelů náhradní příhradoviny především v tom, že uvažuje tah v betonové části průřezu do vzniku trhliny.
2 JEDNODUCHÉ MODELY
2.1 LOKÁLNÍ PŮSOBENÍ OSAMĚLÉHO BŘEMENE
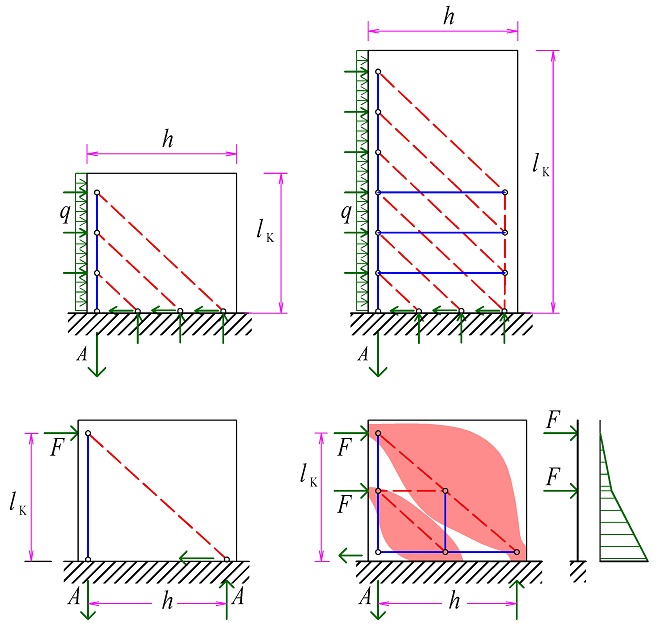
Působí-li na povrch betonového prvku jedno nebo více soustředěných zatížení vznikají v přilehlé betonové oblasti tahová a tlaková napětí. Největší tahové napětí vzniká pod soustředěným břemenem blízkosti povrchu, kde lze připustit jen velmi úzké trhlinky, neboť by se změnila napjatost celé roznášecí oblasti. Hlavně však by to mohlo ovlivnit místa těsně pod soustředěným břemenem, kde by se snížila pevnost betonu v tlaku, neboť by se omezil vliv víceosé napjatosti. Při vnesení břemen do prvku vzniká typická poruchová oblast, kde se musí dbát hlavně na to, aby výztuž přenesla tahové síly vznikající často blízko u povrchu. Proto se při návrhu výztuže vychází jednak z napjatosti roznášecí oblasti, která leží přímo pod soustředěným břemenem, jednak z napjatosti poruchové oblasti, jejíž rozměry jsou závislé na rozměrech prvku (lze předpokládat, že tato lokální porucha vymizí ve vzdálenosti rovné většímu rozměru průřezu). Při zjednodušeném řešení lze vycházet z příhradových modelů, kde pomocí rozkladu sil, lze stanovit výztuž v této poruchové oblasti.
Působí-li na povrch betonového prvku na styčné ploše Ac0 soustředěné zatížení vyvozené návrhovou tlakovou silou FEd a, není-li splněna podmínka (2.1), pak je třeba posoudit roznášecí oblast z hlediska možného porušení:
\begin{gathered}
|F_\text{Ed}|\le A_\text{c0}\cdot f_\text{cd}
\end{gathered}(2.1)
kde je
Fed … tlaková síla;
fcd … návrhová pevnost betonu v tlaku;
Ac0 …zatížená plocha.
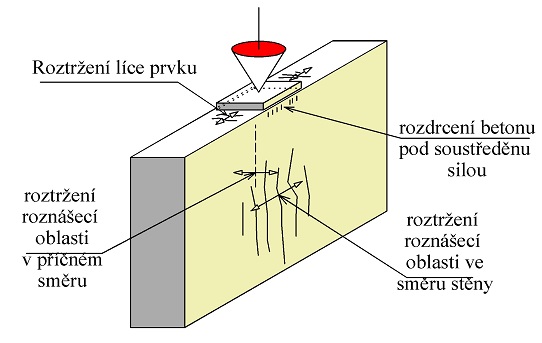
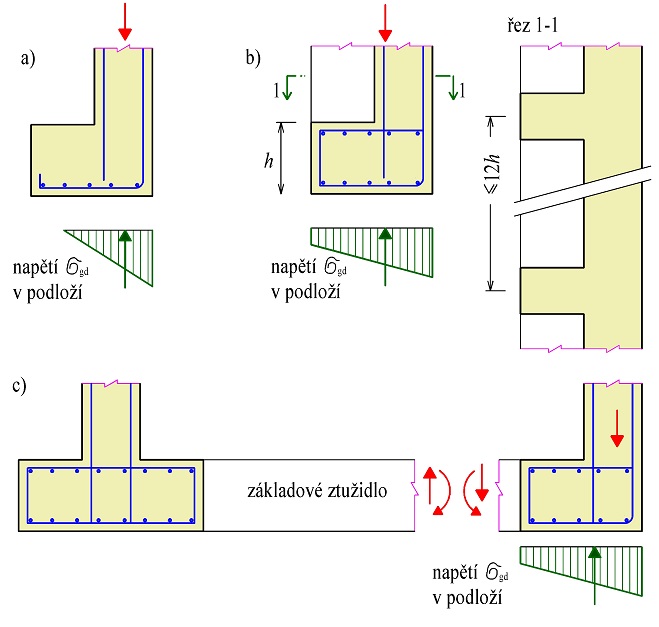
Při působení osamělého břemene na betonový prvek může dojít k následujícím porušením (viz obr. 2.1):
- Při působení soustředěného tlakového zatížení FEd na povrchu betonového prvku může dojít k rozdrcení betonu ve styčné spáře mezi dosedací plochou břemene a betonem. Tento stav většinou nepostihují modely náhradní příhradoviny, způsob řešení je uveden na následujících stránkách nebo podrobněji v [40].
- Ze styčné plochy se tlakové napětí roznáší do prvku na tzv. roznášecí plochu, jejíž těžiště se nalézá na přímce zatížení (těžiště styčné a roznášecí plochy se nalézají na společné normále k povrchu prvku). Oblast mezi zatíženou plochou a roznášecí plochou nazýváme roznášecí oblastí. Při roznášení tlakového napětí betonem může dojít k roztržení roznášecí oblasti v důsledku příčných tahů v betonu.
Poznámka:
Roztržení roznášecí oblasti je nutné uvažovat v obou směrech – v příčném a v podélném směru viz obr. 2.1. Pokud má v příčném směru roznášecí oblast konstantní šířku, lze u železobetonových konstrukcí běžných pozemních staveb zjednodušeně uvažovat příčné tahy hodnotou 0,25FEd.
- Pokud tlakové napětí se má roznést do průřezu prvku, kde je napětí rozděleno lineárně, a jehož těžiště neleží na přímce zatížení, pak vzniká u tohoto prvku poruchová oblast, ve které mohou vznikat tahová a tlaková napětí. Lze předpokládat, že tato lokální porucha vymizí ve vzdálenosti rovné většímu rozměru průřezu (srovnej – délka poruchové oblasti). Pokud však na celém povrchu působí řada břemen přibližně stejné velikosti, je tato vzdálenost menší. Pro vyšetření těchto oblastí lze použít modely náhradní příhradoviny.
- Při působení osamělého břemene na líc prvku vznikají obvykle u povrchu tahové síly, které mohou způsobit roztržení líce prvku a je třeba přenést je výztuží. Pro stanovení velikosti těchto sil viz obr. 2.1. Zjednodušeně lze uvažovat u železobetonových konstrukcí běžných pozemních staveb velikost vznikající tahové síly hodnotou 0,1FEd.
Obr. 2.1 Působení osamělého břemene – možné způsoby porušení prvku
Posouzení rozdrcení betonu pod soustředěnou silou
U místně zatížených ploch soustředěnou silou FEd se musí posoudit únosnost v betonu v tlaku, aby nedošlo k jeho rozdrcení (obr. 2.2). Únosnost v soustředěném tlaku lze vyjádřit vtahem:
\begin{gathered}
F_\text{Rdu}=A_\text{c0}\cdot f_\text{cd}\sqrt{(A_\text{c1}/A_\text{c0})}\le3{,}0\cdot f_\text{cd}\cdot A_\text{c0}
\end{gathered}(2.2)
kde je
Ac0 … zatížená plocha;
Ac1 … největší návrhová roznášecí plocha podobného tvaru jako Ac0 se středem v přímce zatížení.
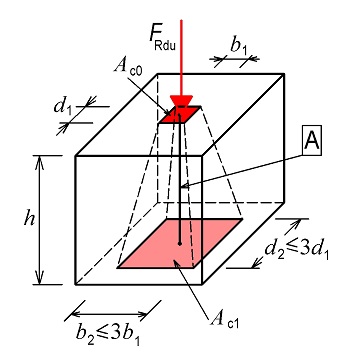
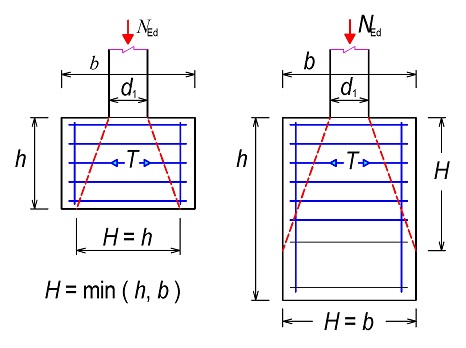
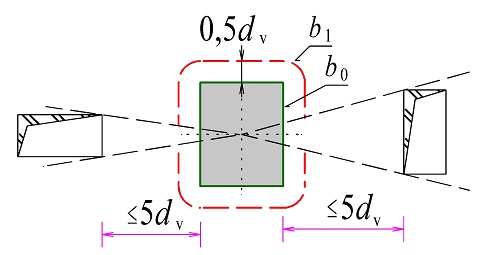
Obr. 2.2 Návrh roznášení zatížené plochy Aco podle [1] při h ≥ (b2 – b1) a současně h ≥ (d2 – d1)
Posouzení podle vztahu (2.2) platí za podmínek
- zatížení je rovnoměrně rozděleno na ploše Ac0;
- plochy Ac0 a Ac1 jsou tvarově (geometricky) podobné;
- jejich těžiště leží na společné normále obou ploch;
- rozměr roznášecí plochy v každém vyšetřovaném hlavním směru, rovnoběžném s osou roznášecí plochy, je roven nejmenší z těchto hodnot (obr. 2.2 a obr. 2.3):
\begin{gathered}
b_2\le3b_1;\space b_2\le b_1+2a_1;\space b_2\le b_1+h
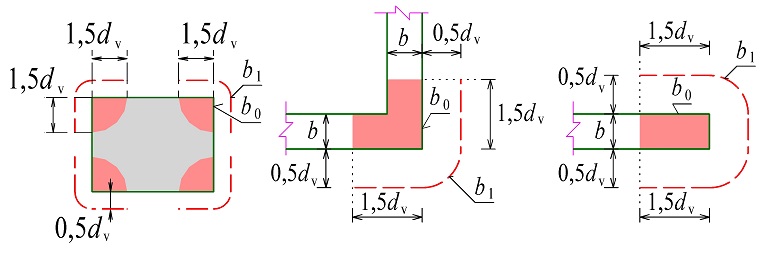
\end{gathered}Obr. 2.3 Schéma stanovení roznášecí plochy
- výška roznášecí oblasti ve vyšetřovaném směru je rovna nejmenší z těchto hodnot (obr. 2.3):
\begin{gathered}
h\le2b_1;\space h\le2a_1;\space h\le h_\text{d}
\end{gathered}kde je
b1 … rozměr styčné plochy;
b2 … rozměr roznášecí plochy;
a1 … zdálenost styčné plochy od nejbližšího okraje prvku;
hd … výška roznášecí oblasti;
h … tloušťka prvku.
Při více zatěžovacích plochách se nesmí plochy Ac1 překrývat.
Příklady vyztužení oblastí jsou na obr. 2.4.
Obr. 2.4 Příklady vyztužení oblasti pod osamělým břemenem
Roztržení roznášecí oblasti podle [40]
Maximální tahové napětí betonu na povrchu prvku σct, max v roznášecí oblasti se vypočte takto:
- pro obdélníkovou roznášecí plochu pro každý z obou na sebe kolmých hlavních směrů ze vztahu:
\begin{gathered}
\sigma_\text{ct,max}=\frac{|F_\text{Ed}|}{b_{21}b_{22}}(0{,}60-0{,}44\beta-0{,}16\beta_\text{p}^4)
\end{gathered}s omezením
\begin{gathered}
\sigma_\text{ct,max}\le0{,}44\frac{|F_\text{Ed}|}{b_{21}b_{22}}
\end{gathered}(2.3)
- pro kruhovou roznášecí plochu:
\begin{gathered}
\sigma_\text{ct,max}=1{,}3\frac{|F_\text{Ed}|}{b_2^2}[0{,}44(1-\beta)+0{,}40(1-\beta)^4]
\end{gathered}s omezením
\begin{gathered}
\sigma_\text{ct,max}\le0{,}56\frac{|F_\text{Ed}|}{b_2^2}
\end{gathered}(2.4)
kde je
FEd … soustředěná tlaková síla od návrhového zatížení;
β … poměr stanovený:
- při obdélníkové roznášecí ploše pro směr 1, popř. směr 2 ze vztahu:
\begin{gathered}
\beta=b_{11}/b_{21},\space\text{ popř. }\space\beta=b_{12}/b_{22}
\end{gathered}- při kruhové roznášecí ploše;
\begin{gathered}
\beta=b_1/b_2
\end{gathered}βp … doplňkový poměr b stanovený pro směr kolmý na směr vyšetřovaný (při obdélníkové zatěžovací ploše);
b11, b12 … rozměry obdélníkové styčné plochy;
b21, b22 … rozměry obdélníkové roznášecí plochy;
b1 … průměr kruhové styčné plochy;
b2 … průměr kružnice určující roznášecí plochu Ad stanovenou při rozdrcení betonu soustředěnou silou.
Jestliže je splněna podmínka (u obdélníkové roznášecí oblasti v obou směrech):
\begin{gathered}
\sigma_\text{ct,max}\le0{,}4\cdot f_\text{ctd}
\end{gathered}(2.5)
není třeba v roznášecí oblasti dimenzovat výztuž proti roztržení roznášecí oblasti. Jinak je třeba pro příčné tahy navrhnout výztuž proti roztržení roznášení oblasti. Pro stanovení příčné tahové síly lze využít vztahu uvedeného normě ČSN EN 1992-1-1:2006 [1] (viz kap. 1)
\begin{gathered}
T=\frac{1}{4}(1-0{,}7\frac{b_1}{h_\text{d}})F_\text{Ed}
\end{gathered}kde za výšku roznášecí oblasti při návrhu výztuže na roztržení se považuje větší z výšek hd určených pro oba vyšetřované hlavní směry roznášecí oblasti.
Při návrhu příčné výztuže lze uvažovat, přihlížíme-li k limitní šířce trhlin v betonu wlim, napětí ve výztuži:
\begin{gathered}
\sigma_\text{s,lim}=\frac{8\cdot10^6w_\text{lim}}{2\space000\cdot(d_\text{s})^{\frac{1}{3}}}\space\text{ s omezením }\space0{,}5f_\text{yd}\le\sigma_\text{s,lim}\le f_\text{yd}
\end{gathered}(2.6)
kde je
σs, lim … napětí ve výztuži v MPa;
wlim … limitní šířce trhlin v mm;
ds … průměr výztužného prutu v mm;
fyd … návrhová mez kluzu betonářské výztuže.
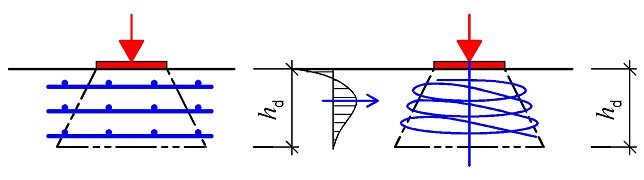
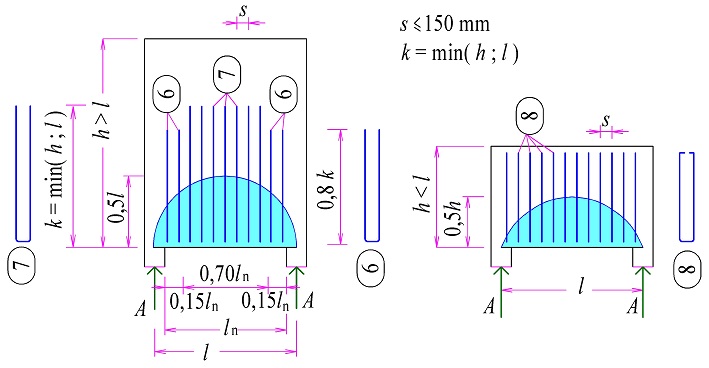
Příčná výztuž se v roznášecí oblasti rozmístí podle schématu na obr. 2.4. Výztuž musí být rozmístěna na výšku rovnou větší z výšek hd pro oba vyšetřované hlavní tvary roznášecí oblasti. Tvar a koncová úprava výztuže musí zajistit její kotvení za lícem roznášecí plochy. V každém směru vrstvy výztuže musí být nejméně dvě vložky, přičemž vzdálenost vložek ve vrstvě smí být nejvýše 150 mm a vzdálenost jednotlivých vrstev nesmí být větší než 150 mm. Příčné tahy lze vyšetřit rovněž modely náhradní příhradoviny viz obr. 2.5.
Obr. 2.5 Základní modely náhradní příhradoviny pro stanovení příčných tahů v roznášecí oblasti
Pokud na prvek působí několik soustředěných sil, lze příčnou výztuž, stanovenou pro některou roznášecí oblast, využít i pro další oblasti.
Pokud je vyztužení roznášecí oblasti nosnou výztuží nutné pouze v jednom z vyšetřovaných směrů, musí být výztuž navržená pro tento směr opatřena rozdělovací výztuží o průřezové ploše nejméně 25 % průřezové plochy navržené výztuže.
Má-li roznášecí plocha tvar kruhu o průměru b1, nebo obdélníku, jehož strany splňují podmínku:
\begin{gathered}
0{,}85b_{21}\le b_{22}\le b_{21}
\end{gathered}lze příčnou výztuž v roznášecí oblasti uspořádat ve tvaru jedné nebo několika šroubovic, přičemž nejmenší šroubovice musí mít průměr 200 mm a největší maximálně o 20 % větší, než je průměr, nebo menší rozměr roznášecí plochy (příčná výztuž pod kotvami předpínacích kabelů bývá často součástí dodávky kotev).
Porušení roztržením líce prvku
Na obr. 2.6 jsou principy vyztužení líce prvku proti případnému roztržení. Navržená výztuž musí vždy splňovat konstrukční zásady.
Obr. 2.6 Doporučené uspořádání výztuže proti porušení líce prvku při působení osamělého břemene
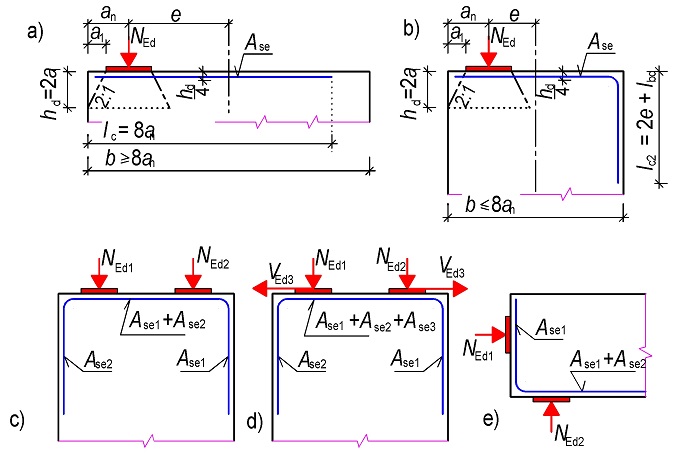
Při excentrickém působení soustředěné tlakové síly na povrchu betonu předpokládáme, že napětí se roznese lineárně ve vzdálenosti rovné šířce prvku b. Oblast roznosu je typickou poruchovou oblastí, kterou můžeme řešit náhradní příhradovou analogií.
Působí-li soustředěná tlaková síla excentricky na prvek s výstředností e > 0,1b, kde b je šířka prvku, musí se do líce prvku navrhnout doplňková výztuž, neboť poblíž tohoto líce vznikají tahová napětí. Pokud se nepočítá přesněji, lze podle [40] navrhnout doplňkovou výztuž.
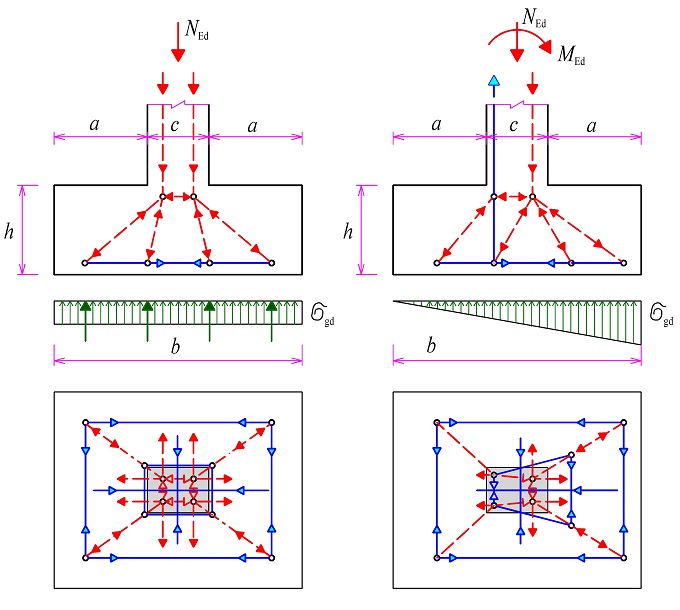
Na následujících obrázcích obr. 2.7, obr. 2.8, obr. 2.9, obr. 2.10, obr. 2.11, obr. 2.12 jsou příklady působení osamělého břemene, průběhy napětí pod břemenem a modely náhradní příhradoviny. Zároveň jsou uvedeny vztahy pro zjednodušený návrh oblasti. Navržená výztuž podle níže uvedených vztahů musí vždy splňovat konstrukční zásady.
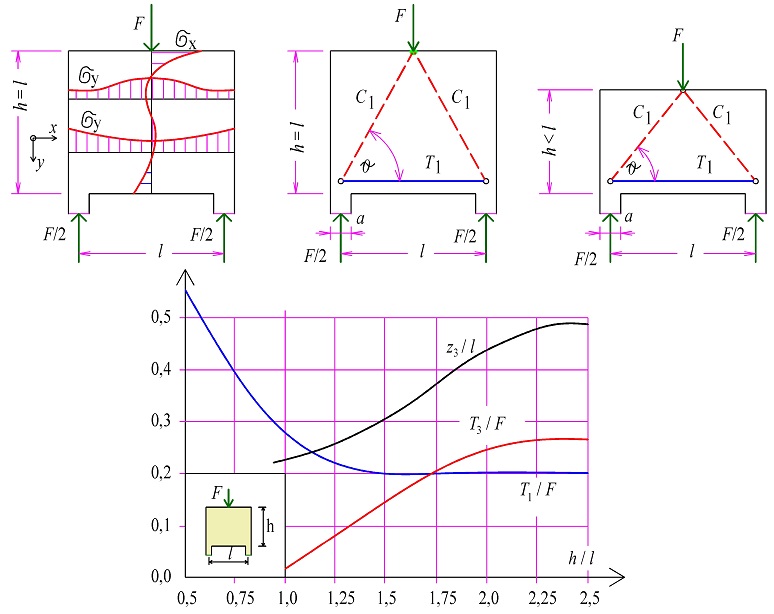
Obr. 2.7 Působení osamělého břemene na horním líci vysoké stěny
Obr. 2.8 Působení osamělého břemene na horním líci nízké stěny a závislost vnitřních sil na poměru šířky zatěžovací oblasti a k šířce stěny b
Obr. 2.9 Model náhradní příhradoviny pro působení osamělého břemene na okraji na horním líci stěny
Obr. 2.10 Zjednodušené stanovení příčných tahových sil pro osamělé břemeno v ose stěny
Obr. 2.11 Zjednodušené stanovení příčných tahových sil pro osamělé břemeno u kraje stěny
Obr. 2.12 Příklady vyztužení základového pasu na skalním podloží
V oblastech s částečnou nespojitostí se řeší podle modelu, znázorněném na obr. 2.7 a dalších, zatížení stěny osamělým břemenem. V modelu jsou stanovena táhla uvnitř D-oblasti a rovině stěny. Při návrhu výztuže D-oblasti se musí navíc zohlednit vznik tahů při horním líci stěny – tzv. roztržení líce oblasti a zohlednit i příčné tahy působící ve směru tloušťky stěny. Při horním líci lze zjednodušeně uvažovat výztuž, která přenese sílu 0,1F. Výztuž se umístí při horním líci v obou směrech. Ve směru tloušťky není v uvedených případech prostor k rozšíření betonových vzpěr, protože stěna je štíhlá a šířka a a b jsou stejné. Proto ve směru tloušťky navrhujeme konstrukčně výztuž na sílu 0,25F. Výztuž se umístí ve směru tloušťky ve stejné oblasti jako výztuž táhla T1 podle následujících obr. 2.9, obr. 2.10 a obr. 2.11.
Příčný tah při centrickém zatížení stěny podle obr. 2.10 lze konzervativně stanovit podle následujících vztahů (viz [2], popř. DAfStB 240):
\begin{gathered}
T_1=0{,}25\bigg(1-\frac{d_1}{b}\bigg)F_\text{Ed}
\end{gathered}(2.7)
T2 ≈ 0,1FEd konstrukční vyztužení, proti roztržení líce prvku (označení tahů podle [2]).
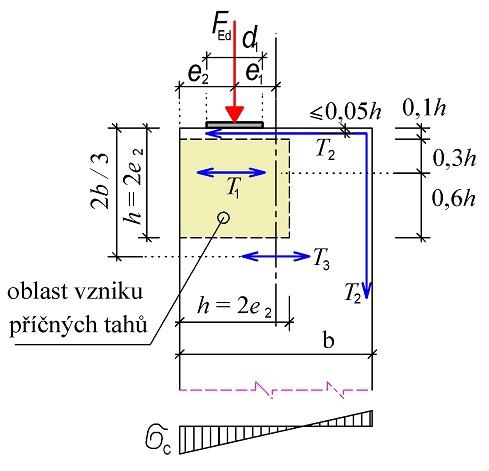
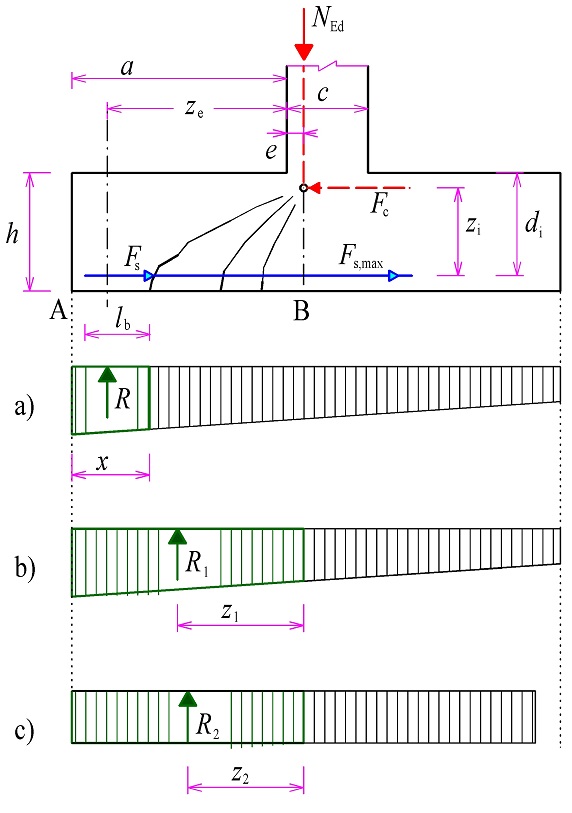
Příčný tah při excentrickém zatížení stěny podle obr. 2.11 lze konzervativně stanovit podle následujících vztahů (viz [2] popř. DAfStB 240):
\begin{gathered}
T_1=0{,}25\bigg(1-\frac{d_1}{h}\bigg)F_\text{Ed}\ge0{,}1F_\text{Ed}
\end{gathered}(2.8)
\begin{gathered}
T_2=0{,}25\bigg(\frac{e_1}{b}-\frac{1}{6}\bigg)F_\text{Ed}\ge0{,}1F_\text{Ed}
\end{gathered}(2.9)
\begin{gathered}
T_3\approx0{,}3T_2
\end{gathered}(2.10)
(označení tahů podle [2]).
2.2 ZATÍŽENÍ OSAMĚLÝM BŘEMENEM V BLÍZKOSTI ULOŽENÍ
Při zatížení osamělým břemenem v blízkosti uložení (obr. 2.13 a obr. 2.14) se předpokládá, že se zatížení přenáší přímo do podpory šikmou betonovou vzpěrou a při zvětšující se vzdálenosti břemene od podpory, ještě pak prostřednictvím přilehlých betonových diagonál (obr. 2.14). Do vzdálenosti břemene od podpory rovné účinné výšce průřezu lze předpokládat pouze jednu diagonální vzpěru. Při návrhu podle jedné (hlavní) betonové vzpěry je nutné navrhnout výztuž na vznikající příčné tahy. Pokud se při návrhu bude uvažovat rozdělení zatížení do přímé diagonály a vložené příhrady (označena 2 na obrázku obr. 2.14b), potom se navrhne svislá výztuž na tu část zatížení, která je vynášená vloženou příhradovinou. Předpokládané roznášení tlaků a umístění táhel je na obr. 2.14.
Obr. 2.13 Osamělé břemeno v blízkosti podpory
Obr. 2.14 Osamělé břemeno v blízkosti krajní podpory
2.2.1 Návrh s vloženou příhradovinou podle [1]
Působí-li osamělé břemeno na horním líci ve vzdálenosti av od osy uložení (av je vzdálenost mezi lícem uložení a lícem zatěžovací plochy (obr. 2.14)), lze navrhnout svislou výztuž na redukovanou posouvající sílu β·VEd. Redukci působící posouvající síly lze provést pro vzdálenost av, pro niž platí:
\begin{gathered}
0{,}5d\le a_\text{v}\le2d
\end{gathered}(2.11)
kde je
d … účinná výška průřezu.
Součinitel β má hodnotu:
\begin{gathered}
\beta=a_\text{v}/2d
\end{gathered}(2.12)
Pro vzdálenosti av ≤ 0,5d, se uvažuje minimální posouvající síla v hodnotě 0,25VEd. Přitom musí být pro posouvající sílu VEd vypočtenou bez redukce součinitelem b splněna následující podmínka:
\begin{gathered}
V_\text{Ed}\le0{,}5\cdot b_\text{w}\cdot d\cdot\nu\cdot f_\text{cd}
\end{gathered}(2.13)
kde je
bw … nejmenší šířka průřezu mezi tlačeným a taženým pásem;
ν … redukční součinitel pevnosti betonu při porušení smykem ν = 0,6 (1 – fck/250).
U prvků vyžadující návrh smykové výztuže, musí být navíc plněna podmínka pro redukovanou posouvající sílu:
\begin{gathered}
V_\text{Ed}\le A_\text{sw}\cdot f_\text{ywd}\cdot\sin\alpha
\end{gathered}(2.14)
kde je
Asw∙fywd … únosnost smykové výztuže protínající šikmou smykovou trhlinu mezi zatíženými oblastmi a α je sklon smykové výztuže. Smyková výztuž se však má umístit pouze ve střední části délky 0,75av. Redukce posouvající síly je možná, pokud je podélná výztuž dostatečně zakotvena v uložení.
2.2.2 Návrh s vloženou příhradovinou podle [8] a [7]
Nosníky s osamělým břemenem v blízkosti uložení a na krátkých konzolách mohou být alternativně navrženy podle modelů náhradní příhradoviny. Při vzdálenosti osamělého břemene do hodnoty av ≤ d/2 se předpokládá, že se zatížení přenáší přímo (na obr. 2.14 označeno 1). Pro vzdálenější působiště osamělé síly od místa uložení se na přenosu zatížení podílejí obě soustavy 1 a 2 podle obr. 2.14. Pro vzdálenosti av ≥ 2d veškeré zatížení přenáší soustava označená 2 na obr. 2.14. Svislá výztuž pro vynášení svislého zatížení soustavy 2 je účinná pouze v oblasti 0,75av podle [1] nebo aw = 0,85a – z/4 podle [7] a [8]. Tato svislá výztuž se navrhuje na redukovanou na svislou sílu:
\begin{gathered}
F_2=\frac{2}{3}\cdot\bigg(\frac{a}{z}-\frac{1}{2}\bigg)\cdot F
\end{gathered}(2.15)
Při návrhu svislé výztuže je nutné zbývající část oblasti konstrukčně vyztužit svislými třmínky a vodorovnou výztuží pro zachycení příčných tahů vznikajících v tlačených betonových vzpěrách obou soustav 1 a 2 náhradní příhradoviny.
2.2.3 Návrh s hlavní diagonálou podle [24]
Pokud se uvažuje pouze jedna hlavní diagonála do sklonu θ ≤ 45°, je nutné navrhnout výztuž na příčné tahy. Hodnotu příčného tahu můžeme zjednodušeně uvažovat hodnotou 0,22F. Celková svislá síla z příčných tahů je potom:
\begin{gathered}
F_\text{v}=2\cdot0{,}22\cdot\cos\theta
\end{gathered}(2.16)
a vodorovná síla je
\begin{gathered}
F_\text{h}=2\cdot0{,}22\cdot\sin\theta
\end{gathered}(2.17)
Při návrhu podle metody hlavní diagonály se navrhuje i vodorovná výztuž, která u předchozích metod není zohledněna. Sklon diagonály θ ≤ 45° odpovídá délce poruchové oblasti podle Saint Venantovy podmínky – viz kap. 1.
2.3 ZMĚNA PRŮŘEZU
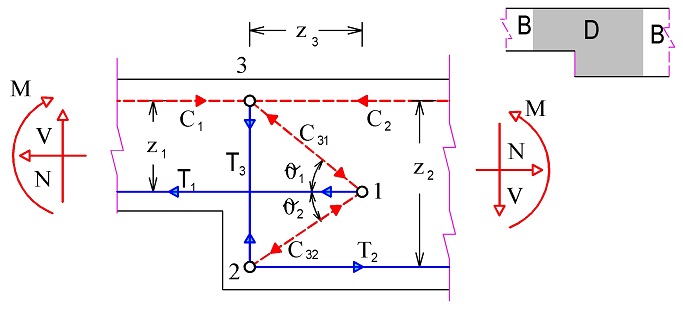
Při náhlé změně výšky průřezu vznikají v průřezu sekundární vnitřní síly – tahy a tlaky. Jejich působení je pro kladné momenty schematicky zobrazeno na obr. 2.15. Pro záporné momenty je rozdělení na D- a B-oblasti zobrazeno na obr. 2.16.
Obr. 2.15 Změna průřezu – dolní tažená vlákna
Obr. 2.16 Změna průřezu – dolní tlačená vlákna
Vztahy pro řešení oblasti lze odvodit za předpokladu, že tah při spodním líci se přenáší mezi táhly T1 a T2 pod úhlem θ2 = 45° (cot θ2 = 1). Obdobný předpoklad je i v případě tlaku při spodním líci pro tlačené prvky C1 a C2.
Vzdálenost z3 se stanoví ze vzdáleností
\begin{gathered}
z_1\space\text{ a }\space z_2-z_1{...}z_3=(z_2-z_1)\cdot\cot\theta_2=(z_2-z_1)
\end{gathered}(2.18)
Síla v táhle T3 stanovíme z podmínky rovnováhy ve svislém směru v uzlech 3 a 2 dostaneme rovnice:
\begin{gathered}
C_{31}=-\frac{T_3}{\sin\theta_1}\space\text{ a }\space C_{32}-\frac{T_3}{\sin\theta_2}
\end{gathered}Z podmínky rovnováhy ve styčníku 1 ve vodorovném směru dostaneme:
C31∙cos θ1 + C32∙cos θ2 = T1, po dosazení výše uvedených vztahů:
\begin{gathered}
\frac{T_3}{\sin\theta_1}\cdot\cos\theta_1+\frac{T_3}{\sin\theta_2}\cdot\cos\theta_2=T_1\\\\
T_3(\cot\theta_1+\cot\theta_2)=T_1\\\\
\text{Přitom }\space\cot\theta_1=\frac{z_3}{z_1}\space\text{ a }\space\cot\theta_2=\frac{z_3}{(z_2-z_1)}=1\\\\
T_3\cdot\bigg(\frac{z_3}{z_1}+1\bigg)=T_3\cdot\bigg(\frac{z_2-z_1}{z_1}+1\bigg)=T_1\\\\
T_3=T_1\cdot\frac{z_1}{z_2}
\end{gathered}(2.19)
Táhlo T1 musí být dostatečně zakotveno za styčníkem 1.
U tlačeného dolního okraje dostaneme obdobným postupem
\begin{gathered}
T_3=-C_1\cdot\frac{z_1}{z_2}
\end{gathered}(2.20)
V literatuře [16] je uveden jiný přístup definující vzdálenost z3 jako geometrický průměr ramen vnitřních sil před a po změně průřezu. Odvození předpokládá průměrný sklon tlačené diagonály cca 33°. Vzdálenost stanovíme podle vztahu:
\begin{gathered}
z_3=1{,}5\sqrt{(z_1\cdot(z_2-z_1))}
\end{gathered}Tah v táhle T3 (při změně výška průřezu v tažených vláknech) stanovíme z rovnováhy ve vodorovném směru ve styčníku 1 a z rovnováhy ve svislém směru ve styčnících 2 a 3. V táhle T3 vzniká síla (obr. 2.15):
\begin{gathered}
T_3=T_1\frac{z_1(z_2-z_1)}{z_2\cdot z_3}
\end{gathered}(2.21)
Tah v táhle T3 (při změně výška průřezu v tlačených vláknech) stanovíme z rovnováhy ve vodorovném směru ve styčníku 1 a z rovnováhy ve svislém směru ve styčnících 2 a 3. V táhle T3 vzniká síla (obr. 2.16):
\begin{gathered}
T_3=-C_1\cdot\frac{z_1(z_2-z_1)}{z_2\cdot z_3}
\end{gathered}(2.22)
Při návrhu výztuže je třeba si uvědomit, že při změně výšky průřezu s dolními tlačenými vlákny je staticky nutná tažená třmínková výztuž vzdálena od líce ozubu. Její těžiště je ve vzdálenosti z3 od líce změny výšky průřezu.
2.4 NEPŘÍMÉ ULOŽENÍ
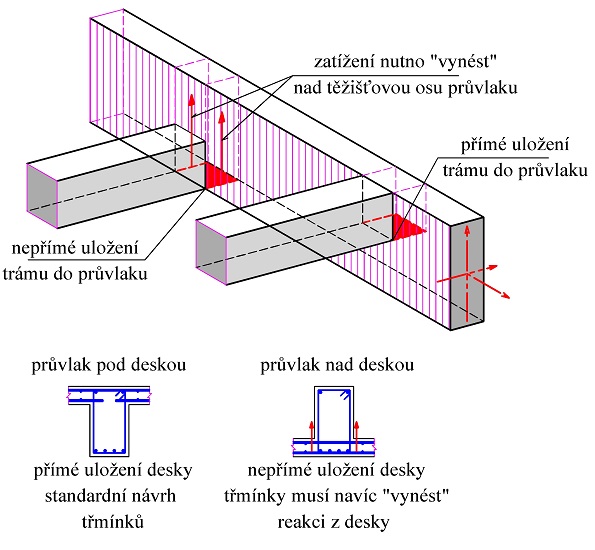
Nepřímé uložení je uložení, při kterém se reakce z vynášeného prvku vnáší pod těžišťovou osou vynášecího prvku. Reakce z vynášeného prvku se musí výztuží vynést k hornímu líci vynášecího prvku, viz obr. 2.17. (Je tam tedy navíc například třmínková výztuž pro vynesení reakce z vynášeného prvku – trámu k hornímu líci průvlaku). Pro návrh výztuže oblasti s nepřímým uložením můžeme postupovat rovněž podle modelů náhradní příhradoviny.
Obr. 2.17 Přímé a nepřímé uložení – příklady
2.5 PŘÍKLADY
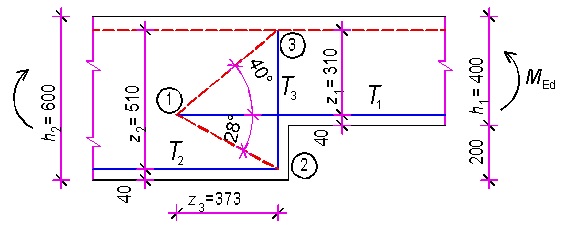
2.5.1 Změna výšky průřezu
Obr. 2.18 Změna výšky průřezu s taženým dolním lícem
Materiály
Beton C35/45:
\begin{gathered}
f\text{cd}=23{,}3\text{ MPa};\space\nu'=(1-f_\text{ck}/250)=0{,}86;\space f_\text{ctd}=1{,}47\text{ MPa}
\end{gathered}Styčník s táhlem CCT:
\begin{gathered}
\sigma_\text{Rd,max}=0{,}85\cdot\nu'\cdot f_\text{cd}=17{,}06\text{ MPa}
\end{gathered}Výztuž B500B:
\begin{gathered}
f_\text{yd}=\frac{f_\text{yk}}{\gamma_\text{s}}=435\text{ MPa};\space\varepsilon_\text{yd}=\frac{f_\text{yd}}{E_\text{s}}=\frac{435}{200}=2{,}175\space‰
\end{gathered}Ramena vnitřních sil podle obrázku, vzdálenost z3 – styčník 3:
\begin{gathered}
z_3=1{,}5\sqrt{(z_1\cdot(z_2-z_1))}=1{,}5\cdot\sqrt{0{,}31\cdot0{,}2}=0{,}373
\end{gathered}Rozhodující vnitřní síla – ohybový moment v místě změny průřezu je MEd = 300 kNm
\begin{gathered}
T_1=M_\text{Ed}/z_1=300/0{,}31=967{,}7\text{ kN};\space T_2=M_\text{Ed}/z_2=300/0{,}51=588{,}3\text{ kN}
\end{gathered}Táhlo u líce změny průřezu:
\begin{gathered}
T_3=T_1\frac{z_1\cdot(z_2-z_1)}{z_2\cdot z_6}=588{,}3\frac{0{,}31\cdot(0{,}51-0{,}31)}{0{,}31\cdot0{,}373}=315{,}4
\end{gathered}Návrh výztuže táhla ve formě třmínků
As = 315 400/435 = 7 25,1 mm2…→ 4 x 2ø12 – navíc 4 třmínky o průměru 12 mm při líci změny výšky průřezu.
Výztuž táhla T1 je As = 967 700/435 = 2 224,6 mm2…→ 5 x ø25 (2454 mm2).
Výztuž táhla T2 je As = 588 300/435 = 1 352,4 mm2…→ 5 x ø20 (1571 mm2) vzhledem ke komplikovanějšímu zakotvení volíme menší průřez prutů výztuže.
Táhlo T1 je nutné kotvit za styčníkem 1 v délce lbd,rqd:
\begin{gathered}
l_\text{b,rqd}=\frac{\phi}{4}\cdot\frac{\sigma_\text{sd}}{f_\text{bd}}=\frac{20\cdot435\cdot(2\space224{,}6/2\space454)}{4\cdot3{,}3}=598\text{ mm}
\end{gathered}Minimální délka táhla T1 je 598 + 373 = 971 mm (měřeno od svislice 2–3)
\begin{gathered}
f_\text{bd}=2{,}25\cdot\eta_1\cdot\eta_2\cdot f_\text{ctd}=3{,}3\text{ MPa}
\end{gathered}Táhlo T2 je nutné kotvit za styčníkem 2 v délce lbd,rqd, vzhledem k požadované kotevní délce se prut vyhne k hornímu líci (při horním líci se uvažují špatné podmínky soudržnosti, proto je nutné zde kotevní délku prodloužit).
\begin{gathered}
l_\text{b,rqd}=\frac{\phi}{4}\cdot\frac{\sigma_\text{sd}}{f_\text{bd}}=\frac{20\cdot435\cdot(1\space352{,}4/1\space571)}{4\cdot2{,}31}=811\text{ mm}
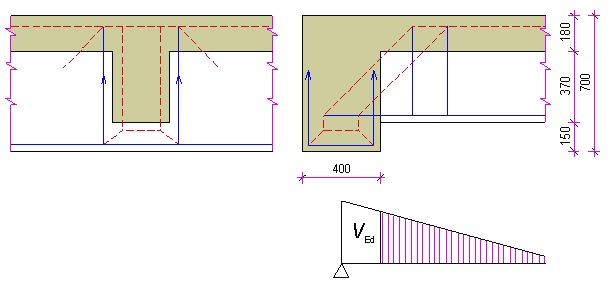
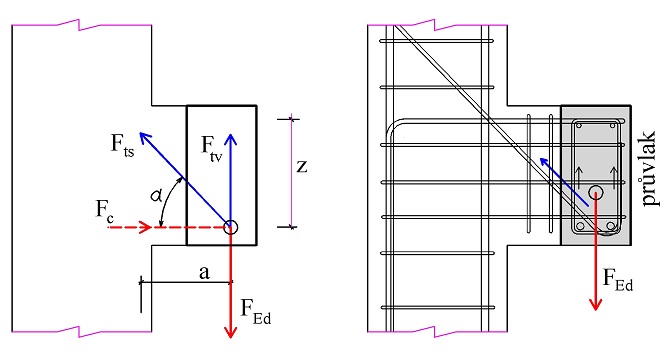
\end{gathered}2.5.2 Nepřímé uložení trámu
Příklad nepřímého uložení trámu do průvlaku podle obr. 2.20.
Materiály
Beton C35/45:
\begin{gathered}
f_\text{cd}=23{,}3\text{ MPa};\space\nu'=(1-f_\text{ck}/250)=0{,}8
\end{gathered}Styčník s táhlem CCT:
\begin{gathered}
\sigma_\text{Rd,max}=0{,}85\cdot\nu'\cdot f_\text{cd}=22{,}7\text{ MPa}
\end{gathered}Výztuž B500B:
\begin{gathered}
f_\text{yd}=\frac{f_\text{yk}}{\gamma_\text{s}}=\frac{500}{1{,}15}=435\text{ MPa};\space\varepsilon_\text{yd}=\frac{f_\text{yd}}{E_\text{s}}=\frac{435}{200}=2{,}175\space‰
\end{gathered}Obr. 2.19 Nepřímé uložení trámu do průvlaku
Rozhodující reakce z nepřímo uloženého trámu je 100 kN.
Třmínky pro vynesení reakce 100 kN … As = 100 000/435 = 229,9 mm2.
Navrženy dva dvoustřižné třmínky o průměru 10 mm (314 mm2) po obou stranách stropního trámu. Třmínky musí být navíc přidány ke standardně navržené třmínkové výztuži průvlaku.
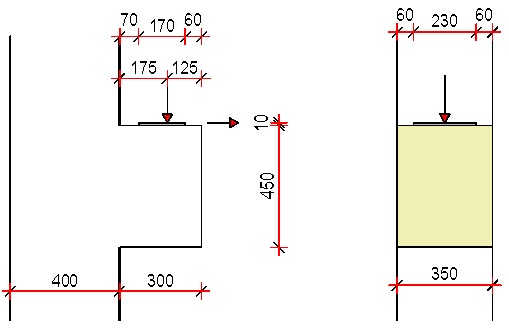
2.5.3 Lokální zatížení – příklad 1
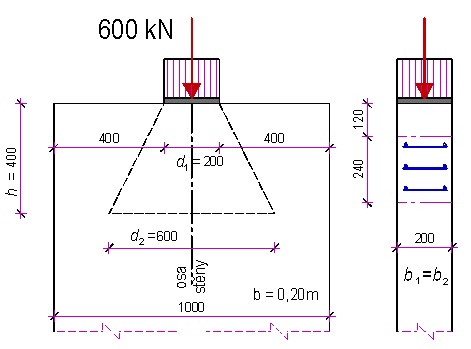
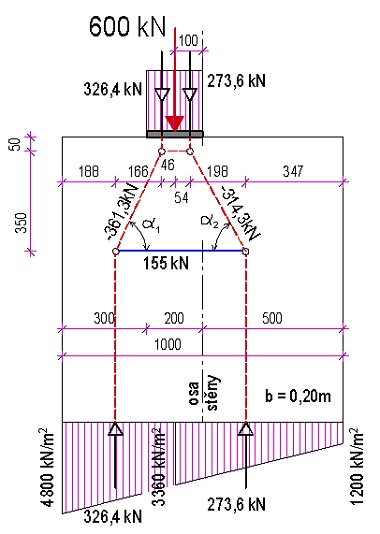
Navrhněte výztuž na přenesení příčných tahů
Lokální zatížení 600 kN při horním líci stěny. Stěna je široká 0,20 m, pro prvek je z betonu třídy C25/30. Betonářská výztuž B500A, betonová krycí vrstva 30 mm.
Obr. 2.20
Styčná plocha – soustředěný tlak:
\begin{gathered}
d_2\le3d_1=3\cdot200=600\text{ mm}\space\text{ a }\space b_2=b_1=200\text{ mm,}\space f_\text{cd}=30/1{,}5=20\text{ MPa}\\\\
A_\text{c1}=b_2\cdot d_2=0{,}2\cdot0{,}6=0{,}12\text{ m}^2
\end{gathered}Výška oblasti s příčnými tahy h:
\begin{gathered}
h\ge(d_2-d_1)=(600-200)=400\text{ mm}
\end{gathered}Plocha styčné desky je
\begin{gathered}
A_\text{c0}=b_1\cdot d_1=0{,}2\cdot0{,}2=0{,}04\text{ m}^2
\end{gathered}Únosnost v soustředěném tlaku:
\begin{gathered}
F_\text{Rdu}=A_\text{c0}f_\text{cd}\cdot\sqrt{\frac{A_\text{c1}}{A_\text{c0}}}=0{,}04\cdot20\cdot\sqrt{0{,}12/0{,}04}=1{,}386\text{ MN}=1\space386\text{ kN}\\\\
F_\text{Rdu}<3\cdot f_\text{cd}\cdot A_\text{c0}=3\cdot20\cdot0{,}04=2{,}4\text{ MN}=2\space400\text{ kN}\\\\
F_\text{Ed}=600\text{ kN}< F_\text{Rdu}=1\space386\text{ kN}{....}\text{vyhovuje}
\end{gathered}Příčný tah podle vztahu (1.7) z kapitoly 1 (uvažujeme částečnou nespojitost – oblast D):
\begin{gathered}
T=\frac{1}{4}\bigg(\frac{d_2-d_1)}{d_2}\bigg)\cdot F_\text{Ed}=\frac{1}{4}\bigg(\frac{0{,}6-0{,}2}{0{,}6}\bigg)\cdot600=100\text{ kN}
\end{gathered}Minimální výztuž na příčné tahy (betonářská výztuž B500A):
\begin{gathered}
A_\text{s}=\frac{100}{435\space000}=0{,}00023\text{ m}^2,\space\text{ což představuje }\space3\text{\o}8
\end{gathered}2.5.4 Lokální zatížení – příklad 2
Lokální zatížení 600 kN při horním líci stěny. Stěna je široká 0,20 m, pro prvek je z betonu třídy C25/30. Betonářská výztuž B500A, betonová krycí vrstva 30 mm.
\begin{gathered}
e_1=400\text{ mm}\space\space\text{a}\space\space e_2=600\text{ mm}
\end{gathered}Navrhněte výztuž na přenesení příčných tahů

Obr. 2.21
Stanovení modelu náhradní příhradoviny pro výpočet staticky nutné výztuže pro přenesení vznikajících příčných tahů.
Nejprve určíme průběh napětí v nosníkové části (B) průřezu:
\begin{gathered}
\sigma_1=\frac{F_\text{Ed}}{b\cdot h}\bigg(1+\frac{6\cdot e}{h}\bigg)\space\space\text{a}\space\space\sigma_2=\frac{F_\text{Ed}}{b\cdot h}\bigg(1-\frac{6\cdot e}{h}\bigg)\\\\
\sigma_1=\frac{600}{0{,}2\cdot1{,}0}\bigg(1+\frac{6\cdot0{,}10}{1{,}0}\bigg)=4\space800\text{ kNm}^2\space\text{ a }\space\sigma_2=\frac{600}{0{,}2\cdot1{,}0}\bigg(1-\frac{6\cdot0{,}10}{1{,}0}\bigg)=1\space200\text{ kNm}^2\\\\
\sigma=\frac{(\sigma_1-\sigma_2)\cdot e_2}{h}+\sigma_2\\\\
F_1=\frac{(\sigma_1+\sigma)}{2}\cdot e_1\cdot b\space\space\text{a}\space\space F_2=\frac{(\sigma+\sigma_1)}{2}\cdot e_2\cdot b
\end{gathered}Nutná posouzení:
- soustředěný tlak;
- roztržení líce prvku pod břemenem;
- roztržení roznášecí oblasti – příčné tahy.
Obr. 2.22
Hodnota napětí pod působištěm:
\begin{gathered}
\sigma=(4\space800-1\space200)/1\cdot0{,}6+1\space200=3\space360\text{ kNm}^2
\end{gathered}Obrazec napětí rozdělíme hodnotou 3 360 kNm2 na dvě části a stanovíme výslednice sil každé části:
\begin{gathered}
F_1=(4\space800+3\space360)/2\cdot0{,}4\cdot0{,}2=326{,}4\text{ kN}
\end{gathered}a
\begin{gathered}
F_2=(1\space200+3\space360)/2\cdot0{,}6\cdot{,}2=273{,}6\text{ kN}
\end{gathered}Pro výslednice stanovíme jejich působiště. Zatížení rozdělíme podle výslednic na dvě síly (stejné hodnoty jako výslednice). Jejich působiště stanovíme z momentové rovnováhy (k působišti zatížení).
\begin{gathered}
273{,}6/600\cdot0{,}10=0{,}0456\text{ m}\\\\
326{,}4/600\cdot0{,}10=0{,}0544\text{ m}
\end{gathered}Oblast roznesení zatížení podle obr. 2.2.
h ≥ (d2 – d1) ≥ (600 – 200) ≥ 400 mm. Budeme uvažovat výšku h = 400 mm.
Obr. 2.23 Příklad excentricky zatížené stěny – průběhy napětí
Příčné tahy působí ve vzdálenosti a/4 + b/2 = 0,2/4 + 0,8/2 = 0,45 m od horního líce. První tlačená vzpěra je ve vzdálenosti a/4 = 0,2/4 = 0,05 m. Tím je stanovena geometrie modelu náhradní příhradoviny.
Sklon vzpěr je
\begin{gathered}
\alpha_1=\text{arctan}(0{,}4/0{,}166)=64{,}6\degree\space\text{ a }\space\alpha_2=\text{arctan}(0{,}4/0{,}198)=60{,}5\degree
\end{gathered}Tlakové síly ve vzpěrách jsou
\begin{gathered}
C_1=\frac{326{,}4}{\sin\alpha_1}=361{,}3\text{ kN}\space\text{ a }\space C_2=\frac{273{,}6}{\sin\alpha_2}=314{,}3\text{ kN}
\end{gathered}Příčný tah je
\begin{gathered}
T_1=T_2=C_1\cdot\cos\alpha_1=155\text{ kN}
\end{gathered}Odtud staticky nutná plocha výztuže zachycující příčné tahy:
\begin{gathered}
A_\text{S}=155\cdot10^{-3}/435=0{,}00036\text{ m}^2
\end{gathered}Navrhneme nejméně 5ø10.
Zjednodušeně můžeme vyjít rovnou ze vztahu (1.7) podle [1]:
\begin{gathered}
T=\frac{1}{4}\bigg(\frac{d_2-d_1}{d_2}\bigg)\cdot F_\text{Ed}=\frac{1}{4}\bigg(\frac{0{,}6-0{,}2}{0{,}6}\bigg)\cdot600=100\text{ kN}
\end{gathered}Vzhledem k excentricitě zatížení není použití vztahu vhodné. Hodnota je pouze informativní. Totéž platí i o následujícím výpočtu pomocí vztahu (2.1). Pro dosazení – celá oblast D je vysoká d = 2h
\begin{gathered}
T_1=0{,}25\bigg(1-\frac{d_1}{d}\bigg)\cdot F_\text{Ed}=0{,}25(1-0{,}2/0{,}8)\cdot600=112{,}5\text{ kN}
\end{gathered}ostatní tahové složky (T2) se pokryjí konstrukční výztuží.
2.5.5 Lokální zatížení – příklad 3
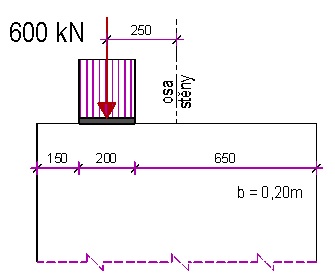
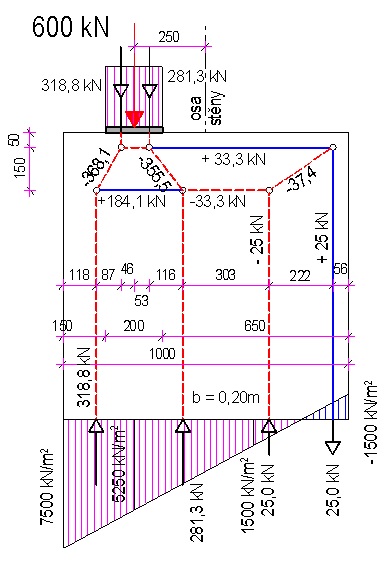
Obr. 2.24 Příklad excentricky zatížené stěny – velká excentricita
Lokální zatížení 600 kN při horním líci stěny. Stěna je široká 0,20 m, pro prvek je z betonu třídy C25/30. Betonářská výztuž B500A, betonová krycí vrstva 30 mm.
Navrhněte výztuž na přenesení příčných tahů.
Model náhradní příhradoviny
Nejprve určíme průběhy napětí v nosníkové části (B) průřezu:
\begin{gathered}
\sigma=\frac{600}{0{,}2\cdot1{,}0}\bigg(1+\frac{6\cdot0{,}25}{1{,}0}\bigg)=7\space500\text{ kNm}^2\space\\\text{a}\\
\sigma=\frac{600}{0{,}2\cdot1{,}0}\bigg(1-\frac{6\cdot0{,}25}{1{,}0}\bigg)=1\space500\text{ kNm}^2
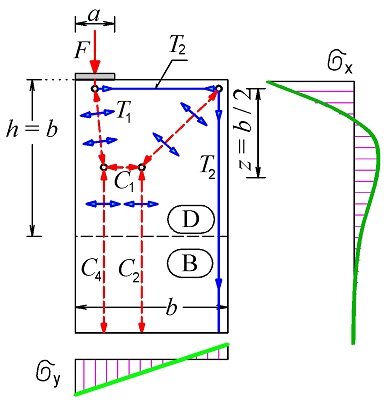
\end{gathered}Obr. 2.25 Příklad excentricky zatížené stěny – průběhy napětí
Obr. 2.26
Hodnota napětí pod působištěm síly:
\begin{gathered}
\sigma=7\space500-(7\space500+1\space500)/1\cdot0{,}25=5\space250\text{ kNm}^2
\end{gathered}Obrazec napětí rozdělíme hodnotou 5 250 kNm2, 1 500 kNm2 0 kNm2 na čtyři části a stanovíme výslednice sil každé části. Nulové napětí je ve vzdálenosti 0,167 m od vzdálenějšího líce.
\begin{gathered}
(7\space500+5\space250)/2\cdot0{,}25\cdot0{,}2=318{,}8\text{ kN}\\\\
(5\space250+1\space500)/2\cdot0{,}417\cdot0{,}2=218{,}3\text{ kN}\\\text{ a}\\
1\space500/2\cdot0{,}167\cdot0{,}2=25\text{ kN}
\end{gathered}Pro výslednice stanovíme jejich působiště. Zatížení rozdělíme podle výslednic na dvě síly (stejné hodnoty jako výslednice). Jejich působiště stanovíme z momentové rovnováhy k působišti zatížení.
\begin{gathered}
318{,}8/600\cdot0{,}10=0{,}053\text{ m}\\\\
281{,}3/600\cdot0{,}10=0{,}047\text{ m}
\end{gathered}Výška oblasti roznášející zatížení podle obr. 2.14
\begin{gathered}
h=2\cdot e_2=500\text{ mm}
\end{gathered}Příčné tahy působí podle ve vzdálenosti h ∙ (0,1 + 0,3) = 0,20 od horního líce. První tlačená vzpěra je ve vzdálenosti 0,5 ∙ 0,1 = 0,05 m. Tím je stanovena geometrie modelu náhradní příhradoviny.
Sklon vzpěr je
\begin{gathered}
\alpha_1=\text{arctan}(0{,}15/0{,}087)=60\degree;\space\alpha_2=\text{arctan}(0{,}15/0{,}116)=52{,}3\degree\space\text{ a }\space\alpha_3=\text{arctan}(0{,}15/0{,}222)=34\degree
\end{gathered}Tlakové síly ve vzpěrách jsou
\begin{gathered}
C_1=\frac{-318{,}8}{\sin\alpha_1}=-368{,}1\text{ kN}\space\space\text{a}\space\space C_2=\frac{-281{,}3}{\sin\alpha_2}=-355{,}5\text{ kN}
\end{gathered}Příčný tah je
\begin{gathered}
T_1=-C_1\cdot\cos\alpha_1=184{,}1\text{ kN},\space C_3=184{,}1-(-C_2\cdot\cos\alpha_2)=-33{,}3\text{ kN}\\\\
C_4=33{,}3\cdot\cos34\degree+25\cdot\cos(90\degree-34\degree)=-37{,}4\text{ kN}
\end{gathered}Odtud staticky nutná plocha výztuže zachycující příčné tahy:
\begin{gathered}
\text{táhlo }\space T_1\cdot A_\text{s}=184\cdot10^{-3}/435=0{,}000423\text{ m}^2{...}\text{navrhneme nejméně }6\phi10\\\\
\text{táhlo }\space T_2\cdot A_\text{s}=33{,}3\cdot10^{-3}/435=0{,}000077\text{ m}^2{...}\text{navrhneme nejméně }2\phi
\end{gathered}Příčný tah při excentrickém zatížení stěny lze zjednodušeně stanovit podle vztahů (2.8) až (2.10):
\begin{gathered}
T_1=0{,}25\cdot\bigg(1-\frac{d_1}{h}\bigg)\cdot F_\text{Ed}=0{,}25\cdot(1-0{,}4)\cdot600=90\text{ kN}\\\\
T_2=0{,}25\cdot\bigg(\frac{e_1}{b}-\frac{1}{6}\bigg)\cdot F_\text{Ed}=T_2=0{,}25\cdot\bigg(\frac{0{,}25}{1}-\frac{1}{6}\bigg)\cdot600=12{,}5\text{ kN}\cdot T_2\ge0{,}1\cdot F_\text{Ed}=60\text{ kN}\text{ (rozhoduje konstrukční vyztužení)}\\\\
\text{a}\space\space T_3=0{,}3\cdot T_2=20\text{ kN}\text{ (rozhoduje konstrukční vyztužení)}
\end{gathered}3 KONZOLY
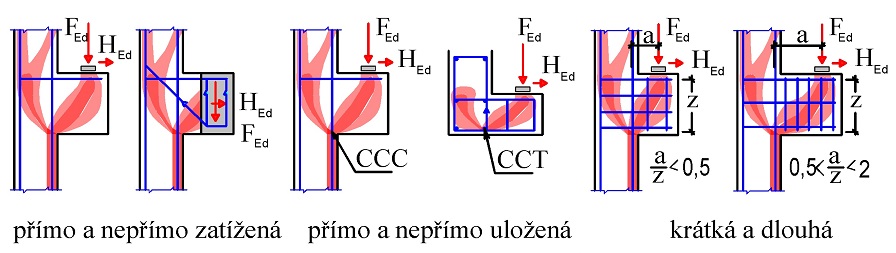
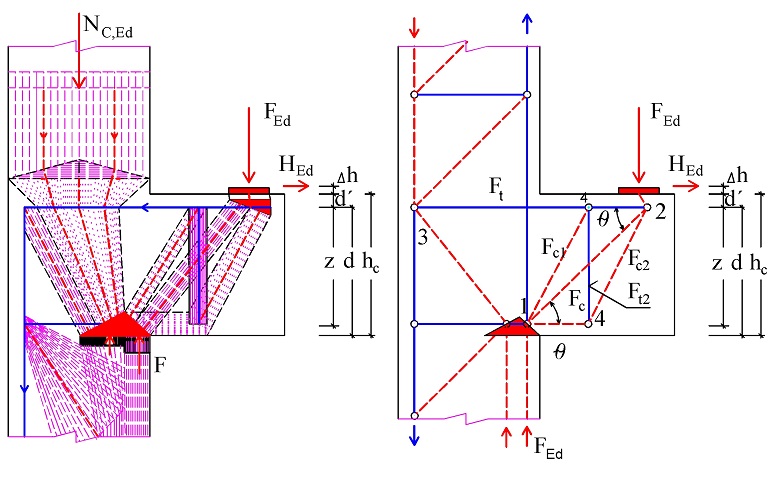
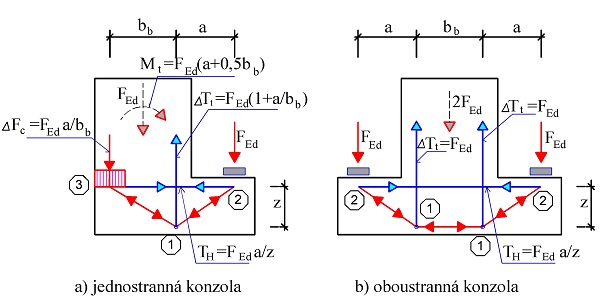
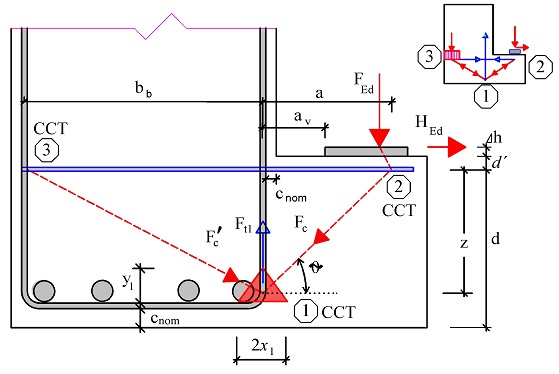
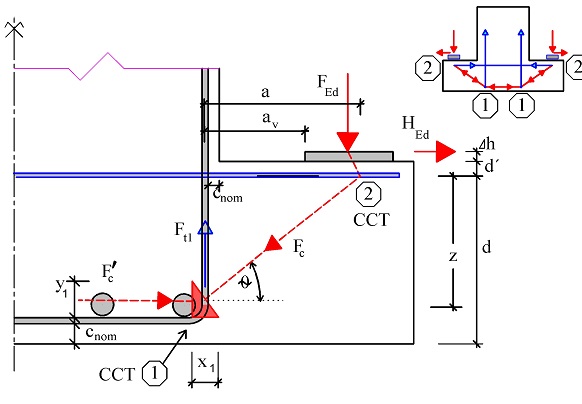
Návrh konzol je častý problém, zejména u prefabrikovaných konstrukcí. K jejich návrhu byla vypracována řada uveřejněných postupů zejména v [7], [8], [13] a [18]. Návrhové modely vycházejí z principů modelování poruchových oblastí pomocí náhradní příhradoviny. Z hlediska zatížení mohou být konzoly přímo nebo nepřímo zatížené (obr. 3.1a,b), z hlediska napojení na konstrukci přímo a nepřímo uložené (obr. 3.1c,d) a z hlediska jejich poměrného vyložení a/z konzoly mohou být krátké při a/z ≤ 0,5 nebo dlouhé při 0,5 < a/z ≤ 2,0, kde a je rameno vnější síly FEd, z je rameno vnitřních sil (obr. 3.1e,f). Pokud je a/z > 2,0, řešíme konzolu jako nosník a oblast jeho uložení řešíme jako rámový roh.
Obr. 3.1 Základní typy konzol
3.1 TYPY KONZOL A METODY NÁVRHU
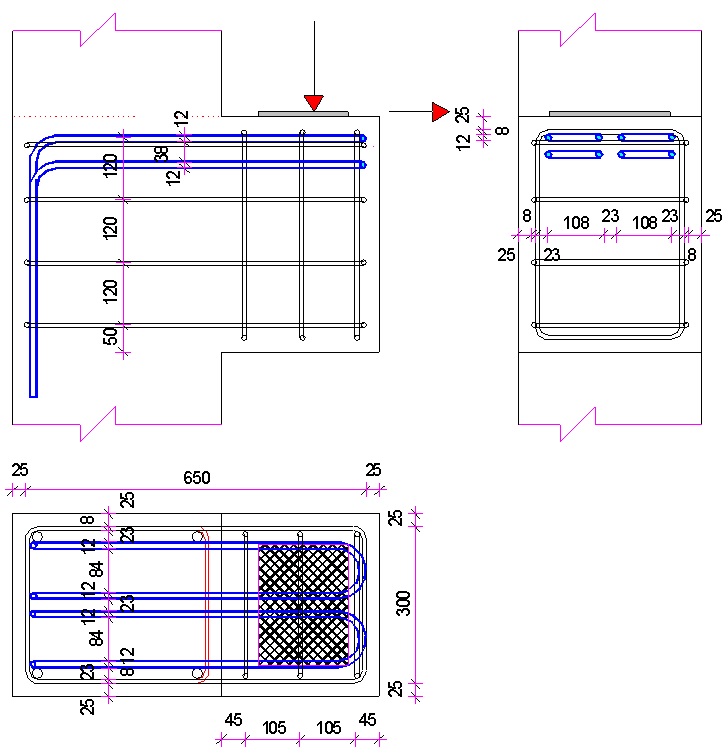
Konzoly na sloupech představují z hlediska bezpečnosti a spolehlivosti celé konstrukce velmi významný prvek (např. haly apod.). Proto je nutné jejich návrhu věnovat maximální pozornost. Na dokumentaci pro konzoly je nutné uvádět všechny závazné parametry a předpoklady, které jsou při návrhu použity. Velmi vhodné je například uvádět nejen tloušťku betonové krycí vrstvy, ale i maximální toleranci v uložení rozhodující výztuže – maximální betonovou krycí vrstvu v souladu s ČSN EN ISO 3766:2004. Výkresy stavebních konstrukcí – Kreslení výztuže do betonu. Pro správný návrh je dobré znát i např. výrobní postup prefabrikátu s konzolou (podmínky soudržnosti pro dostatečné zakotvení výztuže konzoly apod.). Při návrhu konzoly je nutné po dokončení výpočtu a nakreslení výztuže ověřit předpokládanou geometrii modelu náhradní příhradoviny. Vzhledem k tomu, že se při prvním návrhu dají obtížně odhadnout všechny veličiny, které ovlivňují geometrii modelu, bývá obvykle nutné provést nové posouzení s upřesněnou geometrií modelu.
Při návrhu konzoly je velmi důležité rozlišovat místo působení zatížení. Principiálně jsou dvě možnosti způsobu zatížení. Prvním je přímé zatížení, u kterého zatížení působí na horním povrchu konzoly; u přímo uložené konzoly se pak zatížení přenáší přímo do sloupu obr. 3.1a. Druhým způsobem je nepřímé zatížení obr. 3.1b. U nepřímo zatížených konzol přímo uložených se např. část zatížení přenáší svislou taženou výztuží k hornímu líci konzoly a zbývající část přímo šikmou výztuží do sloupu. Zatížení přenesené svislou výztuží k hornímu líci konzoly se pak dále přenáší do sloupu jako u krátkých nebo dlouhých konzol přímo zatížených.
Při návrhu konzoly je nutné uvážit polohu zatížení vyvolanou nepřesnostmi při montáži a výrobě. Nepřesnosti polohy zatížení FEd musí být uváženy při stanovení působiště, tj. při stanovení vzdálenosti a. Obvykle zvětšujeme excentricitu zatížení o cca 20 mm.
Pro přenos zatížení z konzoly do sloupu je důležitý poměr ramen vnější síly a a vnitřních sil z. Vzhledem k tomu, že při začátku návrhu nejsou známé délky ramen vnitřních a vnějších sil, některé předpisy uvádějí jiná rozhraní mezi krátkou a dlouhou konzolou. Rozhraní mezi krátkou a dlouhou konzolou je zvolená konvence experimenty ověřená. Tato konvence je důležitá především pro stanovení svislé a vodorovné výztuže. Hranice mezi krátkou a dlouhou konzolou není u všech předpisů stejná. V ČSN EN 1992-1-1:2006 [1] je rozhraní pro krátkou konzolu uvažováno hodnotou ac/z0 ≤ 0,5, kde ac je vzdálenost břemene od líce sloupu FEd a z0 je průsečík tlačené diagonály s okrajem podporovaného prvku. Jedná se v podstatně o poměr ramen vnějších a vnitřních sil a/z. Pokud platí a/z ≤ 0,5, hovoříme o krátké konzole a zatížení se přenáší přímo šikmou diagonálou do sloupu. Pokud platí 0,5 < a/z ≤ 2,0, jedná se o dlouhou konzolu a zatížení se přenáší nejen hlavní diagonálou, ale i vloženou příhradovinou.
3.2 PŘÍMO ZATÍŽENÉ KONZOLY
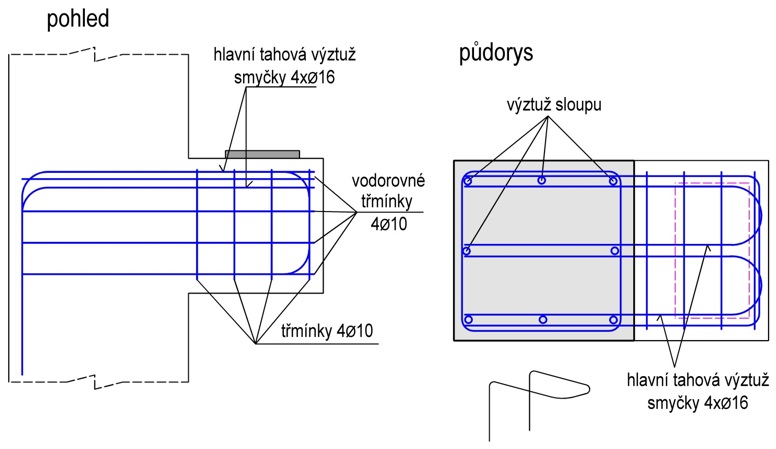
Geometrie přímo zatížené a přímo uložené konzoly je na obr. 3.2a. Zatížení z konzoly se přenáší hlavní tlačenou betonovou diagonálou do styčníku při okraji sloupu a tahovou vodorovnou výztuží přímo do sloupu. V předpisech [2], [7], [8] a [13] je předepsáno uvažovat u každé konzoly minimální vodorovnou sílu HEd = 0,20 FEd.
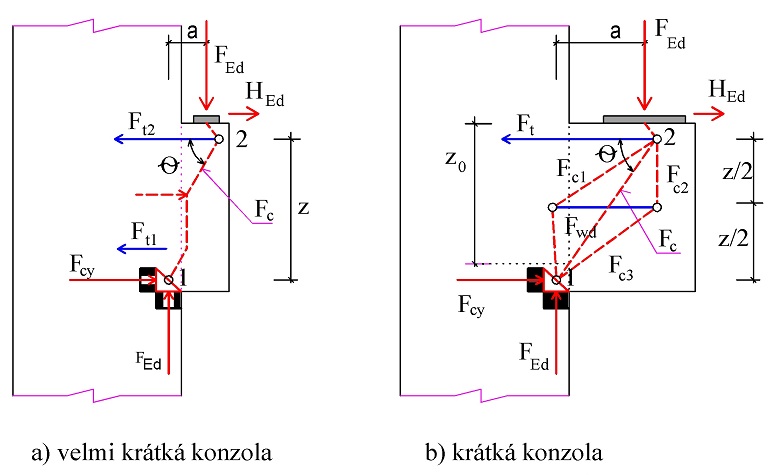
Obr. 3.2 Nejčastější typy modelů náhradní příhradoviny
V ČSN EN 1992-1-1:2006 [1] není tato vodorovná síla blíže specifikována a záleží tedy na uvážení statika, jaké síly bude při návrhu uvažovat. Doporučuje se však uvažovat minimální hodnotu vodorovné síly HEd = 0,2FEd. Vliv vodorovné síly HEd se projevuje především ve zvětšeném množství hlavní tahové výztuže. Dále se doporučuje počítat s excentricitou e zatížení FEd, která může vzniknout jako důsledek výrobních tolerancí a montážních tolerancí.
3.2.1 Postup návrhu konzoly – základní výpočetní postup
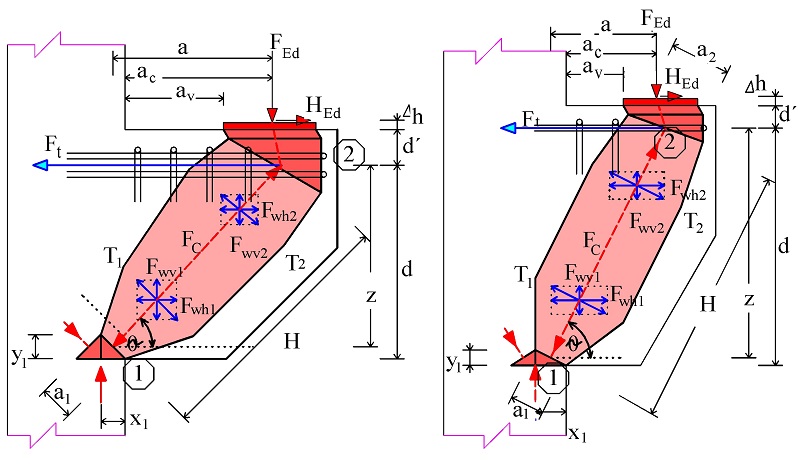
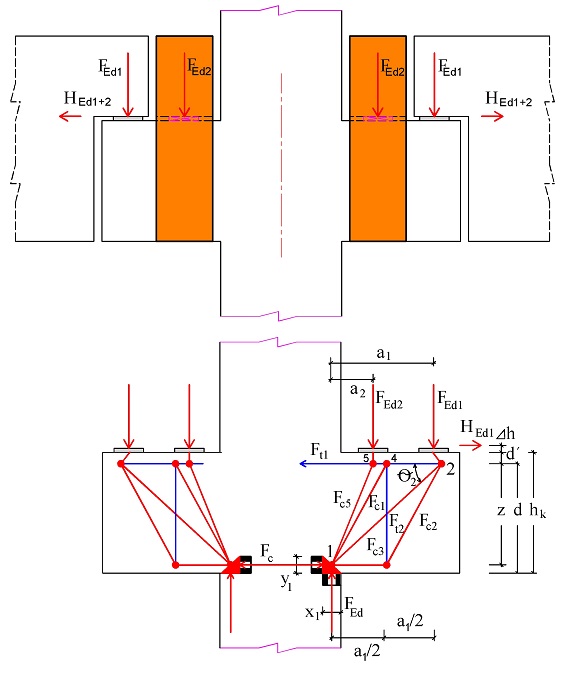
Postup řešení poruchové oblasti konzoly podle ČSN EN 1992-1-1:2006 [1], podle metody hlavní diagonály a podle DAfStB 525 [20] a podle K. H. Reinecka [8] vychází z rovnováhy sil ve styčnících 1 a 2 (obr. 3.3, obr. 3.4 a obr. 3.5). Z podmínky rovnováhy ve styčníku 1 (obr. 3.6) ve svislém směru stanovíme šířku tlačené oblasti x1 od kraje sloupu. Z momentové rovnováhy ve styčníku 1 stanovíme výšku tlačené oblasti y1. V dalším stanovíme rameno vnitřních sil z a rameno vnějších sil a. Z jejich poměru dopočteme sklon tlačené diagonály θ. Hlavní tahovou sílu stanovíme z rovnováhy ve vodorovném směru ve styčníku 2, z rovnováhy ve svislém směru stanovíme pak tlakovou sílu v betonové diagonále.
Obr. 3.3 Základní model náhradní příhradoviny
Obr. 3.4 Modely náhradní příhradoviny pro krátké konzoly podle ČSN EN 1992-1-1
Obr. 3.5 Modely náhradní příhradoviny pro dlouhé konzoly (konzoly s velkým vyložením)
Obr. 3.6 Řešení styčníku 1 modelu náhradní příhradoviny
3.2.1.1 Základní výpočetní postup – stanovení hlavní tahové výztuže a hlavní diagonály – odvození
- Šířka tlačené oblasti ve sloupu se stanoví z rovnováhy svislých sil ve styčníku 1 (obr. 3.6).
Rovnováha svislých sil je FEd = x1 ∙ b ∙ σRd,max . Odtud vyjádříme x1:
\begin{gathered}
x_1=\frac{F_\text{Ed}}{\sigma_\text{Rd,max}\cdot b}
\end{gathered}(3.1)
Styčník 1: U přímo uložené konzoly se jedná o styčník CCC (obr. 1.10). Únosnost betonu v tlaku σRd,max je definována vztahem (1.10), b je šířka konzoly.
Rameno vnější síly (obr. 3.6):
\begin{gathered}
a=a_\text{c}+0{,}5x_1+\frac{H_\text{Ed}}{F_\text{Ed}}(d'+\Delta h)
\end{gathered}(3.2)
- Výška y1 tlačené oblasti ve styčníku 1 se stanoví z momentové rovnováhy ke styčníku 1, kterou lze vyjádřit:
\begin{gathered}
F_\text{t}\cdot z-F_\text{Ed}\cdot a-H_\text{Ed}\cdot(z+d'+\Delta h)=0
\end{gathered}Předpokládá se maximální namáhání ve styčníku 1 rovnému σRd,max (viz rovnice 3.1). Z rovnováhy ve vodorovném směru určíme sílu F:
\begin{gathered}
F_\text{t}-H_\text{Ed}=y_1\cdot b\cdot\sigma_\text{Rd,max}
\end{gathered}Po úpravě dostaneme rovnici:
\begin{gathered}
(y_1\cdot b\cdot\sigma_\text{Rd,max}+H_\text{Ed})\cdot z-F_\text{Ed}\cdot a-H_\text{Ed}\cdot(z+d'+\Delta h)=0\\\\
y_1\cdot b\cdot\sigma_\text{Rd,max}\cdot z/F_\text{Ed}+H_\text{Ed}\cdot z/F_\text{Ed}-a-H_\text{Ed}\cdot(z+d'+\Delta h)/F_\text{Ed}=0\\\\
y_1\cdot z/x_1+H_\text{Ed}\cdot z/F_\text{Ed}-a-H_\text{Ed}\cdot(z+d'+\Delta h)/F_\text{Ed}=0
\end{gathered}Za rameno vnitřních sil dosadíme z = d – 0,5 ∙ y1
\begin{gathered}
y1\cdot(d-0{,}5\cdot y_1/x_1+H_\text{Ed}\cdot(d-0{,}5\cdot y_1)/F_\text{Ed}-H_\text{Ed}((d-0{,}5\cdot y_1)+d'+\Delta h)/F_\text{Ed}-a=0
\end{gathered}a dostaneme kvadratickou rovnici pro y1 ve tvaru
\begin{gathered}
y_1^2/(2x_1)-y_1\cdot d/x_1+H_\text{Ed}(d'+\Delta h)/F_\text{Ed}+a=0
\end{gathered}Upravíme vynásobením 2x1
\begin{gathered}
y_1^2-2y_1\cdot d+2x_1\cdot(H_\text{Ed}(d'+\Delta h)/F_\text{Ed}+a)=0
\end{gathered}a jejím řešením je vztah pro výšku styčníku 1
\begin{gathered}
y_1=d-\sqrt{d^2-2x_1(a+H_\text{Ed}/F_\text{Ed}(d'+\Delta h))}
\end{gathered}(3.3)
- Rameno vnitřních sil (viz obr. 3.3)
\begin{gathered}
z=d-0{,}5y_1
\end{gathered}(3.4)
- Tahovou sílu při horním líci konzoly určíme z momentové rovnováhy ve styčníku 1 (obr. 3.7)
\begin{gathered}
F_\text{t}\cdot z-H_\text{Ed}(z+d'+\Delta h)-F_\text{Ed}\cdot a=0\\\\
\text{odtud}\space\space F_\text{t}=F_\text{Ed}\cdot\frac{a}{z}+H_\text{Ed}(1+(d'+\Delta h)/z)\\\\
\text{nebo}\space\space F_\text{t}=F_\text{Ed}\cdot\cot\theta+H_\text{Ed}(1+(d'+\Delta h)/z)
\end{gathered}(3.5)
Obr. 3.7 Řešení styčníku 2 modelu náhradní příhradoviny
- Hlavní tahová výztuž:
\begin{gathered}
A_\text{s,main}=F_\text{t}/f_\text{yd}
\end{gathered}(3.6)
Navrhneme výztuž a ověříme předpoklady pro tahovou výztuž (průměr, počet vrstev, vzdálenost od horního líce). Po upřesnění musíme model náhradní příhradoviny překontrolovat a případně přepočítat s upřesněnou geometrií. Důležité je překontrolování zakotvení hlavní tahové výztuže pod ložiskem – styčnou deskou a ve sloupu (pozor kotevní délku ve sloupu uvažujeme až při vzdálenějším líci, nikoliv od přilehlého líce sloupu).
- Síla v betonové diagonální vzpěře
\begin{gathered}
F_\text{c}=F_\text{Ed}/\sin\theta
\end{gathered}(3.7)
kde sin θ = z/H podle obr. 3.3. Délka betonové vzpěry H:
\begin{gathered}
H=\sqrt{a^2+z^2}
\end{gathered}Únosnost betonové vzpěry se uvažuje podle vztahu σRd,max = 0,6 ∙ ν’fcd (viz kap. 1).
- Napětí v betonu pod styčnou deskou:
\begin{gathered}
\sigma_\text{c}=\frac{F_\text{Ed}}{A_\text{desky}};\space\Tau=\frac{H_\text{Ed}}{A_\text{desky}}
\end{gathered}(3.8)
Hodnoty napětí v tlaku σc a T je nutné srovnat s hodnotami únosnosti materiálu ložiska a s únosností betonu v tlaku pod ložiskem.
Pro vysoké (velmi krátké – obr. 3.4a) konzoly s úhlem θ ≥ 63,5° uvažujeme ve výpočtu vnitřních sil s úhlem θ = 63,5°. V místě průniku tlačené diagonály s rovinou vnějšího líce sloupu (vzdálenost z0 podle [1]) se předpokládá částečné opření (vložený styčník 3). Dále je zatížení přenášeno svisle do dalšího vloženého styčníku 4, kde nastává odklon pod stejným úhlem θ = 63,5° do místa uložení – styčníku 1. U krátkých a velmi krátkých konzol je nutná především vodorovná konstrukční výztuž pro zachycení příčných tahů vznikajících v betonové vzpěře.
Návrh dlouhé konzoly zůstává v principu stejný jako návrh krátké konzoly. Navíc oproti návrhu krátké konzoly je nutné se soustředit na návrh svislých třmínků v oblasti mezi lícem sloupu a vnitřním lícem styčné – ložiskové desky. Rozhodující pro posouzení svislé výztuže je u většiny postupů opět poměr ramene vnějších sil a a vnitřních sil z. Pro dlouhé konzoly a/z ≥ 0,5 se předpokládá částečné vynášení svislého zatížení nepřímo – vloženou příhradovinou.
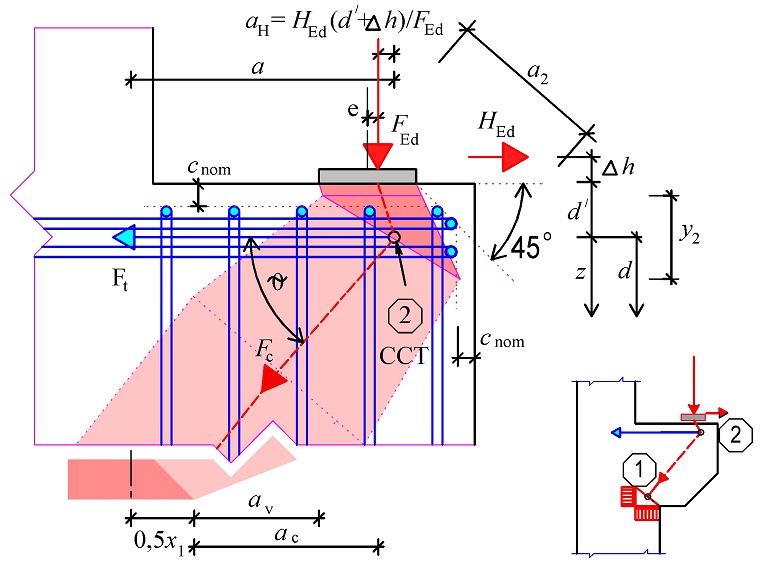
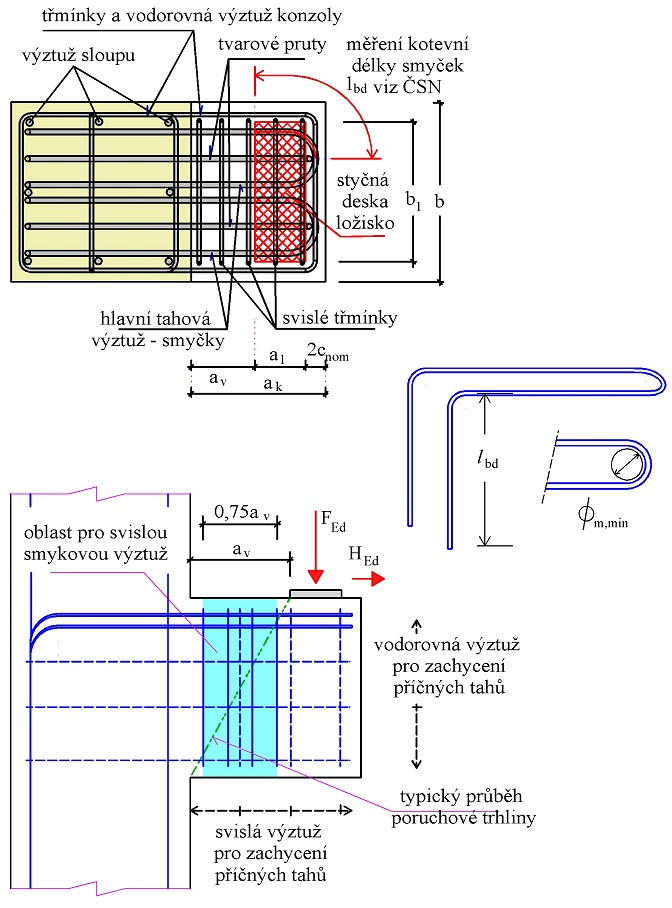
3.2.2 Postup návrhu konzoly podle ČSN EN 1992-1-1:2006, příloha J
Podle přílohy J [1] lze navrhovat krátké konzoly, pro které platí ac < z0 Hodnota z0 je v normě [1] naznačena v obrázku J5 (viz obr. 3.8) jako svislá vzdálenost mezi styčníkem 2 a průnikem tlakové diagonály s okrajem sloupu. Skon tlačené diagonály je v [1] omezen vztahem 1,0 ≤ tan θ ≤ 2,5, poměr ac/z0 vyjadřuje podle cot θ:
\begin{gathered}
\frac{a}{z}=\cot\theta=\frac{a_\text{c}}{z_0}
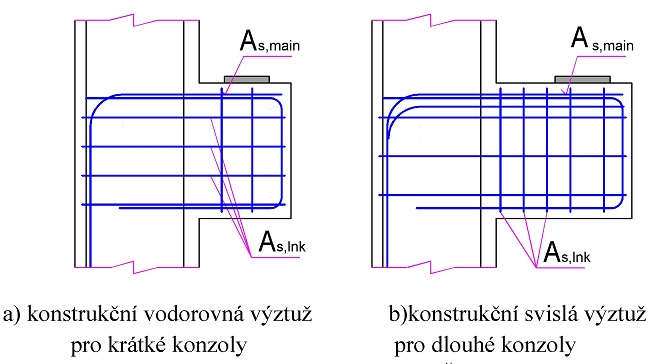
\end{gathered}Obr. 3.8 Krátká konzola podle ČSN EN 1992-1-1 příloha J
Návrh hlavní tahové výztuže konzoly se provede podle postupu uvedeného v kap. 3.2.1.1. Po té se pro krátké konzoly s ac < 0,5hc kromě výše uvedené hlavní výztuže navrhnou uzavřené vodorovné třmínky s průřezovou plochou nejméně 25 % plochy hlavní tahové výztuže. Pro dlouhé konzoly s ac < 0,5hc a FEd > VRd,c (podle [1] kap. 6.2.2) se navrhnou přídavné uzavřené svislé třmínky s průřezovou plochou As,lnk ≥ 0,5 FEd/fyd.
Hlavní tahová výztuž musí být řádně zakotvena na obou koncích. Kotevní délku ve sloupu je vhodné bezpečně uvažovat od styčníku 3. Kotevní délka při horním líci konzoly se uvažuje od vnitřního líce styčné (zatěžovací) desky. Při bezpečném tlakovém namáhání v horní části sloupu, lze uvažovat kladné působení tlakového namáhání na stanovení kotevní délky vodorovné výztuže. U kotevní délky pod styčnou deskou lze do návrhu kotevní délky započítat kladný vliv tlaku od zatížení FEd.
Při tlakovém namáhání betonové diagonály vznikají příčné tahy. Pro návrh výztuže na zachycení příčných sil lze též použít model uvedený na obr. 2.14 a vodorovnou sílu Fwd stanovit podle doporučení MC90 ze vztahu:
\begin{gathered}
F_\text{wd}=(2\frac{a}{z}-1)\cdot F_\text{cy}/(3+\frac{F_\text{Ed}}{F_\text{cy}})
\end{gathered}(3.9)
kde je
Fcy … vodorovná reakce ve styčníku 1.
Odtud se stanoví staticky nutná plocha vodorovné výztuže:
\begin{gathered}
A_\text{sw}=A_\text{s,link}=F_\text{wd}/f_\text{yd}\ge0{,}25A_\text{s,main}
\end{gathered}(3.10)
kde je
As,main … průřezová plocha hlavní tahové výztuže konzoly.
Ve styčníku 2 (CTC) je nutné překontrolovat dostatečné zakotvení hlavní tahové výztuže. V tlačené diagonále je síla Fc podle vztahu (3.7). Velikost plochy, o kterou se betonová vzpěra opírá:
\begin{gathered}
A_\text{c}=\sqrt{x_1^2+y_1^2}\cdot b
\end{gathered}Odtud tlakové namáhání v betonové vzpěře:
\begin{gathered}
\sigma_\text{c}=F_\text{c}/A_\text{c}\le\sigma
\end{gathered}(3.11)
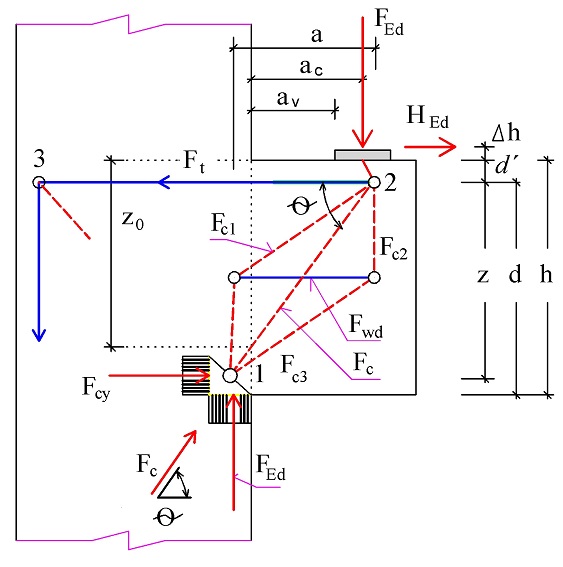
3.2.3 Postup návrhu konzoly podle metody hlavní diagonály [24]
V návaznosti na postup uvedený v kap. 3.2.1.1. se navrhnou svislé a vodorovné třmínky na příčné tahové síly vznikající v betonové vzpěře. Velikost příčných tahů je definována vztahem (1.8) v souladu s [1]. U konstrukcí pozemních staveb lze vznikající příčné tahy zjednodušit na hodnotu 0,22F. Síla v betonové diagonální vzpěře je podle vztahu (3.7) Fc = FEd/sin θ, podle obr. 3.9.
Obr. 3.9 Krátká i dlouhá konzola řešená metodou hlavní diagonály
- Svislá tahová síla vznikající v betonové vzpěře:
\begin{gathered}
F_\text{wv}=F_\text{wv1}+F_\text{wv2}
\end{gathered}(3.12)
\begin{gathered}
F_\text{wv1}=T_1\cdot\cos\theta=\kappa_1F_\text{c}\cdot\cos\theta=\kappa_1F_\text{Ed}\cdot\cot\theta
\end{gathered}(3.13)
a
\begin{gathered}
F_\text{wv2}=T_2\cdot\cos\theta=\kappa_2F_\text{c}\cdot\cos\theta=\kappa_2F_\text{Ed}\cot\theta
\end{gathered}(3.14)
Při zjednodušení κ1 ≈ κ2 ≈ 0,22 dostaneme
\begin{gathered}
F_\text{wv}=0{,}44\cdot\cot\theta\cdot F_\text{Ed}
\end{gathered}(3.15)
- Vodorovná tahová síla vznikající v betonové vzpěře
\begin{gathered}
F_\text{wh}=F_\text{wh1}+F_\text{wh2}
\end{gathered}(3.16)
\begin{gathered}
F_\text{wh1}=T_1\cdot\sin\theta=\kappa_1F_\text{c}\sin\theta=\kappa_1F_\text{Ed}=\kappa_1\frac{F_\text{t}}{\cot\theta}
\end{gathered}(3.17)
a
\begin{gathered}
F_\text{wh2}=T_2\cdot\sin\theta=\kappa_2F_\text{c}\sin\theta=\kappa_2F_\text{Ed}=\kappa_2\frac{F_\text{t}}{\cot\theta}
\end{gathered}(3.18)
Při zjednodušení κ1 ≈ κ2 ≈ 0,22 dostaneme
\begin{gathered}
F_\text{wh}=0{,}44\cdot F_\text{Ed}=0{,}44\frac{F_\text{t}}{\cot\theta}
\end{gathered}(3.19)
Metoda hlavní diagonály podstatně zjednodušuje komplikované modely náhradní příhradoviny poruchových oblasti.
Při návrhu modelu D-oblasti je důležité doplnit konstrukční výztuž v celé oblasti a zejména v částech betonových vzpěr. Pro její návrh existuje řada kritérií, která jsou často rozporuplná a velmi odlišná. Při aplikaci metody hlavní diagonály se důsledně navrhne výztuž na příčné tahy vznikající v tlačených betonových diagonálách.
3.2.4 Principy vyztužení konzoly
U krátkých konzol je nutné konstrukční vyztužení především vodorovnou výztuží, u dlouhých konzol je nutné především vyztužení svislými třmínky (obr. 3.10). Pro vyztužení konzoly platí následující zásady:
- navrhnout maximálně dvě vrstvy horní tahové výztuže (obr. 3.11), při větším počtu se výrazně zmenšuje rameno vnitřních sil;
- volit větší průměr vnitřního zakřivení smyček hlavní tahové výztuže (obr. 3.11), viz [1];
- minimálně dva podélné vodorovné třmínky menšího průměru (obvykle 6 až 10 mm), plocha těchto třmínků u krátkých konzol by měla být větší než 25 % [1] hlavní tahové výztuže. Přitom vodorovné třmínky jsou umístěny obvykle jako třmínky sloupu první od vnějšího líce prvku;
- minimálně tři svislé třmínky menšího průměru (obvykle 6 až 10 mm), u dlouhých konzol by měly svislé třmínky přenést minimálně sílu 0,5FEd [1]. Svislé třmínky jsou obvykle umístěny jako druhé od líce sloupu v úrovni s podélnou výztuží sloupu obr. 3.11, obr. 3.10;
- používat betonářskou výztuž tažnosti třídy B (vysoká tažnost) [1];
- zhustit třmínky sloupu pod a nad konzolou, podélnou výztuž sloupu nestykovat v oblasti napojení konzoly na sloup;
- lze použít i speciální výztuž pro konzoly při respektování stavebně technického osvědčení a národní přílohy ČSN EN 1992-1-1:2006 [1];
- styčná – roznášecí plocha desky nesmí přesahovat obrys výztuže konzoly při uvažování roznášení zatížení pod úhlem 45° (obr. 3.12). Jedinou výjimkou jsou konzolové pásy, které jsou málo zatížené – viz konzolové pásy. Velmi důležité je překontrolování polohy styčné desky při použití svislých smyček (obvykle nikoliv v objektech pozemních staveb). Bližší viz ČSN EN 1992-1-1:2006 [1].
Poznámka:
u konzol se zešikmeným okrajem nemusíme zešikmení uvažovat, pokud zešikmení nezasahuje do tlačené diagonály (při uvažování rozšíření diagonály bef = 0,5H + 0,6a; pozor – zde a je šířka tlačené diagonály u styčníku 1 nebo 2 – viz obr. 3.3).
Model napojení konzoly na sloup je na obr. 3.13. Model rozložení vertikálního zatížení do dvou soustav u konzol s velkým vyložením je na obr. 3.5.
Obr. 3.10 Principy vyztužení konzol podle ČSN EN 1992-1-1
Obr. 3.11 Principy vyztužení konzol
Obr. 3.12 Umístění ložiska na konzole
Obr. 3.13 Přenos zatížení z konzoly do sloupu – model náhradní příhradoviny a schéma hlavních tlakových napětí
3.2.5 Další metody návrhu konzol
3.2.5.1 Posouzení konzoly podle DAfStB 525 [20]
Posouzení podle DAfStb 525 [20] (v návaznosti na DAfStB 425) vychází z modelu příhradové analogie podle [2]. Metoda zavádí jinou podmínku maximálního zatížení konzoly. Pro maximální posouvající sílu na konzole platí:
\begin{gathered}
V_\text{Ed}=F_\text{Ed}\le V_\text{Rd,max}=0{,}5v\cdot b\cdot f_\text{cd}
\end{gathered}(3.20)
kde v ≥ (0,7 – fck/200) ≥ 0,5
- Hlavní tahová síla Ft se stanoví podle vztahu:
\begin{gathered}
F_\text{t}=F_\text{Ed}\frac{a_\text{c}}{z_0}+H_\text{Ed}\frac{a_\text{H}+z_0}{z_0}
\end{gathered}(3.21)
kde je
aH … vzdálenost působiště vodorovné síly od těžiště hlavní tažené výztuže (měřeno ve svislém směru);
z0 … poloha tlačeného pasu, která se vyjádří podle z0 = d(1 – 0,4VEd/VRd,max), přičemž musí platit ac/z0 ≥ 0,40.
- Pro krátkou konzolu ac < 0,5hc a pokud platí FEd > 0,3VRd,max se navrhnou uzavřené vodorovné třmínky o minimální ploše rovné 50 % plochy hlavní tahové výztuže.
- Pro dlouhou konzolu ac ≥ 0,5hc a pokud platí FEd ≥ VRd,ct se navrhnout uzavřené svislé třmínky na přenos celkové síly Fwd = 0,7FEd, kde VRd,ct se stanoví jako podle [1] s použitím německých národních parametrů nebo přímo podle [2].
3.2.5.2 Posouzení konzoly podle K. H. Reinecka [8]
Metoda posouzení konzoly podle prof. K. H. Reinecka (viz obr. 3.4 a obr. 3.5) odpovídá metodě náhradní příhradoviny ve smyslu ČSN EN 1992-1-1:2006 [1]. Ve výpočtu jsou uvažovány pouze jiné únosnosti betonu v tlačených pásech, které vyplývají z národních parametrů pro soustavu norem DIN (Německo). Postupuje se podle kap. 3.2.1.1. Odlišnosti jsou především ve stanovení vodorovné a svislé třmínkové výztuže (viz obr. 3.4 a obr. 3.5). Dále všechny předpisy, které vycházejí z DIN 1045-1, požadují minimální vodorovnou sílu v uložení rovnou HEd = 0,2 ∙ FEd.
Nejprve se určí velikost tlačené oblasti x1 z následující rovnice:
\begin{gathered}
x_1=\frac{F_\text{Ed}}{\sigma_\text{c}\cdot b}
\end{gathered}(3.22)
kde je
\begin{gathered}
\sigma_\text{c}=\chi\cdot f_\text{cd}\space\space\text{a}\space\space f_\text{cd}=0{,}85\cdot f_\text{ck}/\gamma_\text{c}
\end{gathered}χ … součinitel využití betonu v tlaku, který je závislý na třídě betonu:
- χ = 0,95 pro fck ≤ 50 MPa
- χ = (1,05 – fck/500) pro fck > 50 MPa
Základní styčník je umístěn ve vzdálenosti x1/2 od vnějšího líce sloupu. Horní tahová výztuž je umístěna d‘ od horního líce konzoly.
Vzdálenost a se určí ze vztahu:
\begin{gathered}
a=a_\text{c}+0{,}5x_1+\frac{H_\text{Ed}}{F_\text{Ed}}(d'+\Delta h)
\end{gathered}(3.23)
kde je
Δh … svislá vzdálenost působiště vodorovné síly od horního líce konzoly.
Pro určení výšky tlačené oblasti na kraji sloupu vyjdeme z momentové výminky rovnováhy a silové výminky rovnováhy ve styčníku 1.
\begin{gathered}
F_\text{Ed}\cdot a+H_\text{Ed}(z+d')-F_\text{t}\cdot z=0
\end{gathered}(3.24)
\begin{gathered}
F_\text{x}=F_\text{Ed}=0{,}5x_1\cdot\sigma_\text{c}\cdot b\space\space\text{a}\space\space F_\text{y}=F_\text{t}=0{,}5y_1\cdot\sigma_\text{c}\cdot b
\end{gathered}(3.25)
Odtud dostaneme výšku tlačené oblasti:
\begin{gathered}
y_1=d-\sqrt{d^2-2x_1(a+H_\text{Ed}/F_\text{Ed}\cdot(d'+\Delta h))}
\end{gathered}(3.26)
Po stanovení výšky tlačené oblasti je nutné překontrolovat její maximální velikost pro zajištění dostatečné duktility konstrukce. Musí být splněna následující podmínka:
\begin{gathered}
y_1/(1-f_\text{ck}/250)\le0{,}4d
\end{gathered}(3.27)
Rameno vnitřních sil se vypočte ze vztahu:
\begin{gathered}
z=d-y_1/2
\end{gathered}(3.28)
Sklon tlačené betonové diagonály stanovíme:
\begin{gathered}
\cot\theta=\frac{x_1}{y_1}=\frac{a}{z}
\end{gathered}(3.29)
Tahová síla při horním líci konzoly:
\begin{gathered}
F_\text{t}=F_\text{Ed}\cot\theta+H_\text{Ed}
\end{gathered}(3.30)
Hlavní tahovou výztuž konzoly stanovíme ze vztahu:
\begin{gathered}
A_\text{s}=F_\text{t}/f_\text{yd}
\end{gathered}(3.31)
U této výztuže je nutné překontrolovat zakotvení ve styčníku 2, obvykle se výztuž navrhuje ve smyčkách. Alternativně lze vyřešit zakotvení výztuže za styčníkem 2 pomocí kotevních desek, nebo kotevních spojek. Jako hlavní tahovou výztuž lze navrhnout i trny s kovanými hlavicemi, u nichž je zakotvení řešeno kovanou hlavicí. Pro návrh trnů s kovanými hlavicemi je nutné postupovat podle příslušného stavebně technického osvědčení například Z-15.6-204 (Německo).
V zakotvení hlavní tahové výztuže jsou v DIN 1045-1[2] některé odlišnosti oproti ČSN EN 1992-1-1:2006 [1], které je nutné zohlednit při návrhu.
Maximální výška tlačené oblasti musí splňovat navíc podmínku dostatečné duktility konstrukce, která je vyjádřena výrazem:
\begin{gathered}
2y_1/d<0{,}4
\end{gathered}(3.32)
Pro krátké konzoly (a ≤ 0,5z) lze vyjádřit vznikající vodorovnou sílu podle vztahu:
\begin{gathered}
F_\text{wh}\ge0{,}20F_\text{t}
\end{gathered}(3.33)
Pro dlouhé konzoly (0,5z > a ≥ 2z) se tahová síla ve svislých třmínkách vyjádří ze vztahu:
\begin{gathered}
F_\text{wv}=\frac{2}{3}(\cot\theta-\frac{1}{2})\cdot F_\text{Ed}
\end{gathered}(3.34)
3.2.5.3 Posouzení konzoly podle BetonKalender 2009 [13] a DIN 1045-1 [2]
Podle této metody se rozlišují konzoly na krátké ac ≤ hc, dlouhé 0,5hc < ac ≤ hc a velmi dlouhé hc < ac ≤ 1,5hc. U delších konzol ac > 1,5hc se navrhuje podle běžné nosníkové teorie na ohybový moment, posouvající a normálovou sílu. Metoda vychází z příhradové analogie jako předchozí metoda podle DAfStB 525. Pro krátké a dlouhé konzoly se doporučuje redukovat únosnost ve styčníku 1 na 0,75fcd a pro velmi dlouhé konzoly na hodnotu 0,95fcd. Navíc se doporučuje ponechat i u prefabrikovaných konzol součinitel materiálu pro beton γc = 1,50. Z důvodu dostatečné duktility konstrukce konzoly je omezena výška tlačené oblasti na 0,45d pro betony do třídy C50/60 (včetně) a pro betony vyšších tříd je omezena výška tlačené oblasti na 0,35d. Minimální tahová síla pro návrh hlavní tahové výztuže je omezena podmínkou Ft ≥ 0,4FEd. Současně však dovoluje zanedbat vlastní tíhu konzoly, jako nevýznamné zatížení.
Metoda eliminuje problematický skokový přechod mezi nutnou vodorovnou výztuží pro krátké konzoly a nutnou svislou výztuží pro dlouhé konzoly vztahem pro svislou výztuž:
\begin{gathered}
A_\text{sw,v}\ge\beta\cdot F_\text{Ed}/f_\text{yd}
\end{gathered}(3.35)
kde pro součinitel β platí:
\begin{gathered}
0\le\beta=2a_\text{c}/h_\text{c}-1\le1{,}0
\end{gathered}(3.36)
a vztahem pro vodorovnou výztuž:
\begin{gathered}
A_\text{sw,h}\ge(1-\beta)\cdot0{,}30A_\text{s,main}
\end{gathered}(3.37)
kde je
As,main … průřezová plocha hlavní tahová výztuž konzoly.
Množství konstrukční svislé a vodorovné výztuže se podle výše uvedených předpisů uvedených v kap. 3. odlišuje. Je doporučeno:
- navrhnout minimálně dva podélné vodorovné třmínky menšího průměru (obvykle 6 až 10 mm), plocha těchto třmínků u krátkých konzol by měla být větší než 50 % [8] hlavní tahové výztuže. Přitom vodorovné třmínky jsou umístěny obvykle jako třmínky sloupu první od vnějšího líce prvku;
- navrhnout minimálně tři svislé třmínky menšího průměru (obvykle 6 až 10 mm), u dlouhých konzol by měly svislé třmínky přenést minimálně sílu 0,7FEd [8] až 1,0FEd [13]. Svislé třmínky jsou obvykle umístěny jako druhé od líce sloupu v úrovni s podélnou výztuží sloupu – viz obr. 3.11 a obr. 3.12.
3.3 KONZOLOVÝ NOSNÍK
Konzolové nosníky mají vyložení větší než 2hc. Podle Saint Venantova předpokladu je délka poruchové oblasti přibližně rovná výšce oblasti. Při zatížení osamělým břemenem vzniká jedna poruchová oblast přímo pod břemenem a druhá oblast v místě uložení. Obě oblasti na sebe navazují a jejich maximální délka je 2hc. Pro delší nosníky, jak 2hc se oblast B mezi poruchovými oblastmi D řeší běžnými metodami založenými na teorii nosníků. Napojení nosníku na sloup se řeší jako rámový roh viz [31].
3.4 NEPŘÍMO ZATÍŽENÉ KONZOLY
Nepřímo zatížené konzoly jsou konzoly zatížené při spodním líci (nepřímé uložení – viz kap. 2.4. Jedná se například o monolitický nosník vynášený konzolou, nosník tedy tvoří část konzoly sloupu – viz obr. 3.14. Při řešení nepřímo zatížených konzol se předpokládá, že část zatížení se přenáší svislou taženou výztuží k hornímu líci konzoly a zbývající část přímo šikmou výztuží do sloupu. Zatížení přenesené svislou výztuží k hornímu líci konzoly se dále přenáší do sloupu jako u přímo zatížených konzol.
Obr. 3.14 Nepřímo zatížené konzoly
Svislá tahová výztuž:
\begin{gathered}
F_\text{tv}=F_\text{Ed}\cdot\chi
\end{gathered}(3.38)
Šikmá výztuž:
\begin{gathered}
F_\text{ts}=F_\text{Ed}(1-\chi)/\sin\alpha
\end{gathered}(3.39)
Tlaková síla:
\begin{gathered}
F_\text{c}=F_\text{Ed}(1-\chi)/\cot\alpha
\end{gathered}(3.40)
kde je
α … úhel sklonu šikmé výztuže;
χ … součinitel rozložení tahu do šikmé a svislé části tahové výztuže.
Vznikající tlakovou sílu Fc nutno zahrnout do řešení styčníku 1 (viz předcházející kapitoly). Tahovou sílu Ftv vynese svislá výztuž k hornímu líci konzoly a s jejími účinky dále počítáme jako u přímo zatížené konzoly viz kap. 3.2. Šikmou tahovou sílu Fts vynáší šikmá výztuž přímo do sloupu, kde je nutné ji dostatečně zakotvit (kotvíme na kotevní délku při odvráceném líci sloupu). Rozdělení tahových sil na svislou a šikmou složku závisí především na možnostech vyztužení oblasti, šikmá výztuž je účinnější, ale komplikuje vyztužení oblasti, proto se doporučuje využívat spíše vynesení svislou tahovou silou Fts k hornímu líci konzoly a šikmou výztuž konstrukčně doplnit podle možností vyztužení oblasti. Výztuž konzoly je nutné umístit tak, aby nebyla v kolizi s průběžnou výztuží sloupu a výztuží vynášeného nosníku viz obr. 3.14. Umístění výztuže vždy určuje geometrii modelu náhradní příhradoviny – určuje polohu táhel.
3.5 VLIV NEPŘESNOSTÍ PŘI VÝROBĚ A MONTÁŽI PRVKU S KONZOLAMI
Při návrhu konzol a ozubů je nutné zohlednit výrobní a montážní tolerance. I při dodržení přípustných tolerancí při výrobě prvků a při velmi pečlivé montáži může být rameno vnějších sil působících na konzole odlišné od hodnoty uvažované ve statickém výpočtu. Mezi výrobní tolerance prvku musíme uvažovat i nepřesnost v uložení výztuže. Poloha výztuže ovlivňuje i geometrii použitého modelu náhradní příhradoviny [28].
Pro lokalizaci místa uložení je doporučeno použít úložné prvky například neoprénová či jiná ložiska. Při malých zatíženích lze použít i maltové lože. Ložiska koncentrují zatížení do styčné plochy, která musí být dostatečně vzdálena od hrany prvku, aby nedošlo k ulomení jeho hrany. Pod ložiskem uvažujeme rovnoměrné roznesení zatížení.
Obr. 3.15 Konzola s ozubem – minimální rozměry a tolerance vyztužení vodorovnými smyčkami
Obr. 3.16 Konzola s ozubem – minimální rozměry a tolerance vyztužení svislými smyčkami
Délku uložení a (obr. 3.15 a obr. 3.16) lze vyjádřit následovně:
\begin{gathered}
a\ge a_1+d_2+d_3+\Delta d
\end{gathered}(3.41)
kde je
a … délka uložení;
σEd … napětí v betonu pod ložiskem σEd = FEd/(a1 · b1),
a1 … základní (čistá) délka ložiska, pro kterou platí a1 = FEd/(b1 · fRd), ne však menší jak hodnota uvedená v tab. 3.1 podle [1], [4], [3] a [10];
FEd … návrhová hodnota reakce v uložení;
b1 … šířka ložiska, pokud je b1 ≤ 600 mm a prvek je uložen do maltového lože nebo na neoprénové či jiné ložisko, lze uvažovat rovnoměrné roznesení v příčném směru;
fRd … návrhová hodnota pevnosti v uložení:
- fRd = 0,4fcd pro suché uložení bez ložiska nebo malty;
- fRd = fbed ≤ 0,85fcd pro všechny ostatní případy.
fcd … návrhová pevnost betonu v tlaku, uvažuje se menší z hodnot konzoly a ozubu;
fbed … návrhová pevnost materiálu ložiska;
d2 … vzdálenost ložiska ke kraji podporujícího prvku pro redukci odštěpení prvku:
- při vyztužení vodorovnými smyčkami (obr. 3.15) platí d2 > a2 ≥ c1 + c2;
- při vyztužení se svisle kotvenou výztuží (obr. 3.16) platí d2 > a2 + r2 ≥ c1 + c2 + r2.
roznášení v betonové krycí vrstvě je uvažováno pod úhlem 45°;
c1, c2 … betonové krytí výztuže podporujícího prvku;
a2 … předpokládaná minimální neúčinná vzdálenost k vnějšímu líci podporujícího prvku, hodnota a2 podle [1] a [10] je v tab. 3.2;
d3 … vzdálenost ložiska ke kraji podporovaného prvku pro redukci odštěpení prvku:
- při vyztužení vodorovnými smyčkami platí d3 > a3 ≥ c3 + c4;
- při vyztužení se svisle kotvenou výztuží platí d3 > a3 + r3 ≥ c3 + c4 + r3.
c3, c4 … betonové krytí výztuže podporovaného prvku;
a3 … předpokládaná minimální neúčinná vzdálenost k vnějšímu líci podporovaného prvku, hodnota a3 podle [1] a [10] je v tab. 3.3;
Δd … celková mezní odchylka uložení, která lze vyjádřit ;
\begin{gathered}
\Delta d=\sqrt{\Delta a_2^2+\Delta a_3^2}
\end{gathered}Δa2 … mezní odchylka pro světlé vzdálenosti mezi podporujícími prvky – viz tab. 3.4;
Δa3 … mezní odchylka délky podporovaného prvku Δa3 = ln/2 500;
ln … délka podporovaného prefabrikátu – prvku;
r2, r3 … jsou vnitřní poloměry zakřivení výztuže ve svislém směru podpírajícího a podporovaného prvku, význam uvedených a dalších veličin je patrný také z obr. 3.17.
Obr. 3.17 Montážní tolerance prefabrikovaných prvků
Pro jednotlivé prostě uložené prefabrikáty bez možnosti redistribuce je doporučeno délku ramena vnější síly a zvětšit o 20 mm. Pokud se použijí posuvná ložiska, je nutné délku uložení příslušně upravit podle délky předpokládaného posunu.
Při výrobě prvků dochází k nepřesnostem. Podle [4] a [5] je výrobní délková tolerance tyčových prvků:
\begin{gathered}
\Delta L=\pm(10+L/1\space000)\le\pm40\text{ mm}
\end{gathered}(3.42)
kde je
L … délka prefabrikátu.
Pro průřezové rozměry velikostí odpovídajících konzole a ozubu je návrhová odchylka rozměru ±15 mm. Návrhová odchylka v poloze výztuže je +15 mm a -10 mm [3]. Při montáži sloupů rovněž dochází k nepřesnostem. Přípustné odchylky v uložení prvků jsou definovány v [3] a [4]. Poloha sloupu ve vodorovném směru má návrhovou odchylku ±25 mm (obr. 3.17). Návrhová odchylka délky volného prostoru mezi sloupy, a tím i mezi líci konzol je větší z hodnot L/600 a ±25 mm (obr. 3.17). Návrhová odchylka svislosti sloupů je větší z hodnot ±H/300 a ±15 mm. Pro vodorovné dílce platí vodorovná odchylka od osy ±25 mm a prostor mezi prvky – větší z hodnot ±L/500 a ±15 mm, maximálně 40 mm.
Poloha osy ložiska má toleranci Δ vůči okraji prvku podle [3]. Hodnota Δ je větší z hodnot ±l /20 a ±15 mm podle obr. 3.17 (kde l je délka od okraje prvku – v obr. 3.17 označeno l0 (u ozubu nosníku) resp. lk (u konzoly)). Ve většině případů ozubů a konzol v pozemním stavitelství bude rozhodovat hodnota tolerance Δ = ±15 mm. Polohu osy ložiska potřebujeme při výpočtu konzoly a ozubu, v obou případech budeme uvažovat nepříznivější hodnotu, tedy posun osy k okraji prvku. Příklady velkých tolerancí jsou na obr. 3.18 a obr. 3.19.
Změnu návrhového modelu D-oblastí mohou ovlivnit i odchylky v poloze výztuže a rozměrové odchylky průřezů jednotlivých oblastí. Pro analýzu uvedených odchylek chybí dostatečné soubory měření a v době návrhu oblastí nebudou většinou k dispozici. Pro to je vhodné posunout při návrhu oblasti působiště síly nebo reakce o 1/6 a1 k vnějšímu líci ložiska.
Tab. 3.1 Minimální šířka ložiska a1 v [mm]
| Typ uložení | Poměr σEd/fcd | |||
| ≤ 0,15 | 0,15 ÷ 0,40 | > 0,4 | ||
| Liniové uložení (desky) | 25 | 30 | 40 | |
| Soustředěná podpora | žebrové stropy a vaznice | 55 | 70 | 80 |
| nosníky | 90 | 110 | 140 | |
Tab. 3.2 Minimální délka a2 v [mm] od kraje podporující konstrukce
| Materiál podporující konstrukce | Poměr σEd/fcd | |||
| ≤ 0,15 | 0,15 ÷ 0,40 | > 0,4 | ||
| Železobetonová konstrukce třídy ≥ C30/37 | liniové uložení | 5 | 10 | 15 |
| soustředěná podpora | 10 | 15 | 25 | |
| Prostý beton a železobeton třídy < C30/37 | liniové uložení | 10 | 15 | 25 |
| soustředěná podpora | 20 | 25 | 35 | |
Tab. 3.3 Minimální délka a3 v [mm] od kraje podporované konstrukce
| Způsob vyztužení styčníku | Způsob uložení | |
| Liniové uložení | Soustředěná podpora | |
| Spojitá výztuž nad vnitřní podporou | 0 | 0 |
| Rovná výztuž nebo vodorovné smyčky ukončené za ložiskem | 5 | 15 mm nejméně však cnom |
| Svislé výztužné smyčky | 15 | cnom + vnitřní poloměr smyčky (r2 nebo r3) |
Tab. 3.4 Mezní hodnota Da2 v [mm] světlé vzdálenosti mezi líci podpěr
| Materiál podporující konstrukce | Δa2 |
| Ocel a prefabrikovaný železobeton | 10 ≤ L/1200 ≤ 30 mm |
| Zdivo a monolitický železobeton | 15 ≤ L/1200 + 5 ≤ 40 mm |
| kde L je rozpětí v [m] mezi podpěrami | |
Obr. 3.18 Příliš velké tolerance v uložení nosníků na konzolách
Obr. 3.19 Velká tolerance v uložení předpjatého nosníku a posun těžiště opření
3.6 SPECIÁLNÍ VÝZTUŽ PRO KONZOLY
Použití speciální tahové výztuže ve formě trnů s kovanými hlavicemi (viz obr. 3.20) je možné pouze v souladu s příslušným stavebně technickým osvědčením například Z-15.6-204 z 2. 11. 2007. Metoda vychází z modelu příhradové analogie podle DAfStb 425. Návrh nosného systému konzoly se sloupem je nutné provádět podle jednoho předpisu například podle ČSN EN 1992-1-1:2006 [1]. Při použití smykových trnů je nutné v návrhu zohlednit rozdíly v návrhových postupech a v národních parametrech. Řešení může být výhodné pro sloupy s dodatečně betonovanými konzolami.
Pro maximální posouvající sílu na konzole platí:
\begin{gathered}
V_\text{Ed}=F_\text{Ed}\le V_\text{Rdmax}=0{,}5\cdot v_\text{DIN}\cdot b\cdot z\cdot f_\text{cd}
\end{gathered}(3.43)
kde
\begin{gathered}
v_\text{DIN}\ge(0{,}7-f_\text{ck}/200)\ge0{,}5
\end{gathered}V návrhové pevnosti betonu v tlaku se neuvažuje součinitel acc. Návrhová pevnost se vyjádří podle vztahu
\begin{gathered}
F_\text{cd}=f_\text{ck}/\gamma_\text{c}
\end{gathered}Součinitel acc, který zohledňuje dlouhodobé účinky na pevnost betonu v tlaku a nepříznivé účinky vyplývající ze způsobu zatěžování, je již obsažen v hodnotě VRd,max
Rameno vnitřních sil z odhadneme hodnotou z = 0,9d.
V dalším kroku se stanoví hlavní tahová síla Ft.
\begin{gathered}
F_\text{t}=F_\text{Ed}\frac{a_\text{c}}{z_0}+H_\text{Ed}\frac{a_\text{H}+z_0}{z_0}
\end{gathered}(3.44)
kde je
aH … vzdálenost působiště vodorovné síly od těžiště hlavní tažené výztuže (měřeno ve svislém směru);
z0 … poloha tlačeného pasu, která se vyjádří podle vztahu
\begin{gathered}
z_0=d(1-0{,}4\cdot V_\text{Ed}/V_\text{Rd,max})
\end{gathered}Obr. 3.20 Příklad speciální výztuže v konzolách
Dále je nutné splnit podmínku ac/z0 ≥ 0,40 pro monolitické konzoly a podmínku ac/z0 ≥ 1,00 pro konzoly s pracovní spárou mezi sloupem a konzolou. Pracovní spára musí splňovat svým povrchem podmínky stavebně technického osvědčení Z-15,6-204.
Staticky nutná plocha hlavní tahové výztuže ve formě trnů s kovanými hlavami (např. HSC Halfen) se vypočte podle vztahu:
\begin{gathered}
A_\text{s}=F_\text{t}/f_\text{yd}
\end{gathered}(3.45)
Pro zajištění příčného tahu v oblasti zakotvení hlavic trnů je nutno vložit svislý uzavřený třmínek za hlavici trnu. Třmínek musí obepínat všechny trny. Průměr třmínku je stanoven jako 40 % průměru trnu. Další svislá výztuž se navrhuje stejně jako v metodě podle DAfStB 525 [8] – viz předchozí kapitoly. Vodorovná výztuž se obvykle neuvažuje, proto nemůže být únosnost stejná jako u monoliticky prováděných konzol.
3.7 PŘÍKLADY
3.7.1 Krátká konzola
Navrhněte výztuž konzoly prefabrikovaného sloupu zatížené FEd = 300 kN a vodorovnou silou HEd = 0,2 · 300 = 60 kN. Konzola je z betonu třídy C40/50, betonářská výztuž B500B, betonová krycí vrstva 20 mm. Tvar konzoly je definován obr. 3.21. Z hlediska výrobních a montážních nepřesností uvažována excentricita v uložení 20 mm (celkem).
Obr. 3.21
Materiály
Beton C40/50:
\begin{gathered}
f_\text{cd}=26{,}7\text{ MPa};\space f_\text{ctd}=1{,}67\text{ MPa};\space f_\text{bd}=3{,}75\text{ MPa};\space v'=(1-f_\text{ck}/250)=0{,}84
\end{gathered}Styčník s tlakovými silami CCC:
\begin{gathered}
\sigma_\text{Rd,max}=1{,}0\cdot v'f_\text{cd}=22{,}4\text{ MPa}
\end{gathered}Styčník s táhlem CCT:
\begin{gathered}
\sigma_\text{Rd,max}=0{,}85\cdot v'f_\text{cd}=19{,}04\text{ MPa}
\end{gathered}Betonová vzpěra se vznikem trhlin:
\begin{gathered}
\sigma_\text{Rd,max}=0{,}6\cdot v'f_\text{cd}=13{,}44\text{ MPa}
\end{gathered}Výztuž B500B:
\begin{gathered}
f_\text{yd}=\frac{f_\text{yk}}{\gamma_\text{s}}=\frac{500}{1{,}15}=435\text{ MPa};\space\varepsilon_\text{yd}=\frac{f_\text{yd}}{E_\text{s}}=\frac{435}{200}=2{,}175\space‰
\end{gathered}LOŽISKO ESZ Typ 200, t = 10 mm
\begin{gathered}
\sigma_\text{cd}=\frac{300\cdot10^{-3}}{0{,}17\cdot0{,}23}=7{,}67\text{ MPa}
\end{gathered}Návrh hlavní tahové výztuže
Předpokládáme dvě vrstvy výztuže, vzdálenost těžiště hlavní tahové výztuže od horního líce konzoly odhadneme na d‘ = 56 mm.
Účinná výška průřezu je:
\begin{gathered}
d=h_\text{c}-d'=0{,}45-0{,}056=0{,}394\text{ m}
\end{gathered}Šířka tlačené oblasti x1 je:
\begin{gathered}
x_1=\frac{F_\text{Ed}}{b\cdot\sigma_\text{Rd,max}}=\frac{0{,}300}{0{,}35\cdot22{,}4}=0{,}038\text{ m}
\end{gathered}Rameno vnější síly:
\begin{gathered}
a=a_\text{c}+0{,}5x_1+\frac{H_\text{Ed}}{F_\text{Ed}}(d'+0{,}01)=0{,}175+0{,}019+0{,}2\cdot0{,}066=0{,}207\text{ m}
\end{gathered}Výška tlačené oblasti y1 je:
\begin{gathered}
y_1=d-\sqrt{d^2-2\cdot x_1\cdot(a+H_\text{Ed}/F_\text{Ed}\cdot(d'+\Delta h))}\\\\
y_1=0{,}394-\sqrt{0{,}394^2-2\cdot0{,}038(0{,}207+0{,}2(0{,}066)}=0{,}022\text{ m}
\end{gathered}Rameno vnitřních sil:
\begin{gathered}
z=d-0{,}5y_1=0{,}394-0{,}022/2=0{,}383\text{ m}
\end{gathered}Úhel sklonu tlačené diagonály je
\begin{gathered}
\cot\theta=a/z=0{,}207/0{,}383=0{,}541\to\theta=61{,}6\degree
\end{gathered}Vodorovná tahová síla:
\begin{gathered}
F_\text{t}=F_\text{Ed}\cdot\frac{a}{z}+H_\text{Ed}=300\cdot0{,}541+60=222{,}4\text{ kN}
\end{gathered}Hlavní tahová výztuž při horním líci konzoly je:
\begin{gathered}
A_\text{s}=\frac{222400}{435}=512\text{ mm}^2
\end{gathered}Navrhneme dvě smyčky ø12 mm ve dvou vrstvách (celkem 8 profilů) As = 905 mm2
Zakotvení v uzlu 2, rozhodující výztuž ve formě dvou smyček o průřezu ø12 mm
Základní kotevní délka výztužného prutu je:
\begin{gathered}
l_\text{b,req}=\frac{\phi}{4}\cdot\frac{\sigma_\text{sd}}{f_\text{bd}}=\frac{12\cdot435\cdot(512/905)}{4\cdot3{,}75}=197\text{ mm}
\end{gathered}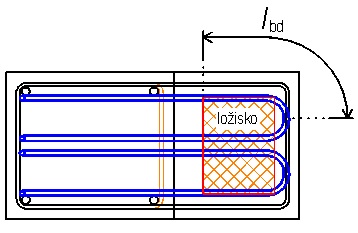
Obr. 3.22
Návrhová kotevní délka výztužných prutů ø12 mm je
\begin{gathered}
l_\text{bd}=\alpha_1\cdot\alpha_2\cdot\alpha_3\cdot\alpha_4\cdot\alpha_5\cdot l_\text{b,req}=0{,}7\cdot197=138\text{ mm}\ge l_\text{b,min}
\end{gathered}kde je
lb,min … minimální kotevní délka;
lb,min ≥ max [0,3 · lb,rqd; 10 · ø; 100 mm].
Pro smyčku je třeba překontrolovat minimální vnitřní průměr zakřivení prutu podle [1]. Kontrola je nutná provést jak u krajní, tak i u vnitřní smyčky, aby nedošlo k podrcení betonu ve smyčce. Z toho vyjde minimální vzdálenost smyček od sebe.
V jedné větvi smyčky je tah:
\begin{gathered}
F_\text{bt}=0{,}000113\cdot435\space000\cdot\frac{512}{905}=27{,}8\text{ kN}\\\\
\phi_\text{m,min}=\frac{F_\text{bt}}{f_\text{cd}}\cdot\bigg(\frac{1}{a_\text{b}}+\frac{1}{2\phi}\bigg)=\frac{27{,}8\cdot10^{-3}}{26{,}7}\bigg(\frac{1}{0{,}034}+\frac{1}{0{,}024}\bigg)=74\text{ mm}
\end{gathered}kde je
ab … vzdálenost osy prutu od líce prvku 20 + 8 + 6 = 34
popřípadě poloviční vzdálenost mezi smyčkami 25 mm, øm,min = 85 mm
Obr. 3.23
Vnitřní průměr zakřivení smyčky z profilu ø12 mm navrhneme 84 mm (7ø). Kotevní délka prutu od kraje styčné desky je délka osy čtvrtiny kruhu 75 mm a rovné části pod styčnou deskou 143 mm – celkem 218 mm, zakotvení výztužné smyčky vyhovuje. Jako hlavní tahovou výztuž navrhneme dvě smyčky z průměru 12 mm nad sebou.
Zakotvení hlavní tahové výztuže za vnitřním styčníkem ve sloupu (uvažujeme špatné podmínky soudržnosti)
\begin{gathered}
f_\text{bd}=3{,}75\cdot0{,}7=2{,}63\text{ MPa}\\\\
l_\text{b,rqd}=\frac{\phi}{4}\cdot\frac{\sigma_\text{sd}}{f_\text{bd}}=\frac{12\cdot435\cdot(512/905)}{4\cdot2{,}63}=280\text{ mm}
\end{gathered}
Obr. 3.24
Posouzení tlačené betonové diagonály
V tlačené diagonále je síla:
\begin{gathered}
F_\text{c}=F_\text{Ed}/\sin\theta=\frac{300}{\sin\theta}=341\text{ kN}
\end{gathered}délka diagonály je:
\begin{gathered}
H=\sqrt{a^2+z^2}=436\text{ mm}
\end{gathered}Sklon diagonály dle předchozího výpočtu je θ = 61,6°. Šířka diagonály se stanoví podle vztahu (1.8) pro úplně nespojité oblasti:
\begin{gathered}
b_\text{ef}=0{,}5\cdot H+0{,}65\cdot a=0{,}5H+0{,}65\cdot\sqrt{x_1^2+y_1^2}=0{,}246\text{ m}
\end{gathered}Poznámka:
ve vzorci a je šířka betonové vzpěry na hranici styčníku nikoliv rameno vnější síly – viz kap. 1 vztah (1.8)
Šířka tlačené diagonály 350 mm. V tlačené diagonále je napětí:
\begin{gathered}
\sigma_\text{c}=0{,}341/(0{,}246\cdot0{,}35)=3{,}96\le0{,}6\cdot v'f_\text{cd}=13{,}44\text{ MPa}
\end{gathered}Napětí v tlačené diagonále vyhovuje.
Návrh svislé a vodorovné výztuže
Pro návrh vodorovné a svislé výztuže se vychází ze sklonu tlačené diagonály nebo z poměru vyložení konzoly k její výšce. Podle EC2 [1] je kritérium pro krátkou konzolu ac/hc = 0,175/0,45 = 0,389 ≤ 0,5, jedná se o krátkou konzolu.
Vyztužení podle konstrukčních kritérií:
- minimálně dva vodorovné třmínky o průměru 6 až 8 mm, plocha třmínků u krátkých konzol by měla být nejméně 25 % hlavní tahové výztuže. Tedy Aswh = 0,25 · 512 = 128 mm2 … návrh 4 dvoustřižné třmínky ø8 Aswh = 402 mm2;
- doporučeno minimálně tři svislé třmínky o průměru 6 až 8 mm, navrženy konstrukčně 3 třmínky ø6 mm Avwv = 170 mm2.
Přesnější určení vodorovné a svislé výztuže podle metody hlavní diagonály – vztuž pro zachycení příčných tahů vznikajících v betonové vzpěře:
V tlačené diagonále je síla Fc = 341 kN, délka diagonály je 436 mm. Příčný tah v tlačené diagonále při použití zjednodušení:
\begin{gathered}
T=2\cdot0{,}22\cdot F_\text{c}=2\cdot0{,}22\cdot341=150\text{ kN}
\end{gathered}Příčný tah je nutno rozložit do svislého a vodorovného směru.
Plocha vodorovné výztuže:
\begin{gathered}
A_\text{swh}=\frac{T\cdot\sin\theta}{f_\text{yd}}=A_\text{swh}=\frac{150\space000\cdot\sin61{,}6\degree}{435}=303\text{ mm}^2
\end{gathered}Plocha svislé výztuže:
\begin{gathered}
A_\text{swh}=\frac{T\cdot\cos\theta}{f_\text{yd}}=A_\text{swh}=\frac{150\space000\cdot\cos61{,}6\degree}{435}=164\text{ mm}^2
\end{gathered}Výše navržená výztuže vyhovuje.
Výztuž konzoly je na obr. 3.25.
Přesnějším vyjádřením příčných tahů podle vztahu 1.6 obr. 1.7b dostaneme nižší hodnoty příčné konstrukční výztuže.
Napětí v betonu pod ložiskem:
\begin{gathered}
\sigma=0{,}300/(0{,}18\cdot0{,}20)=8{,}33\text{ MPa}
\end{gathered}a
\begin{gathered}
\tau=0{,}060/(0{,}18\cdot0{,}20)=1{,}67\text{ MPa}
\end{gathered}Napětí pod ložiskem vyhovuje.
Obr. 3.25
3.7.2 Dlouhá konzola
Navrhněte výztuž konzoly prefabrikovaného sloupu zatížené FEd = 500 kN a vodorovnou silou HEd = 100 kN. Konzola je z betonu třídy C50/60, betonářská výztuž B500B, betonová krycí vrstva 25 mm (třmínků). Montážní a výrobní tolerance je uvažována hodnotou 20 mm (celkem).
Obr. 3.26 Příklad konzoly 2
Materiály
Beton C50/60:
\begin{gathered}
f_\text{cd}=33{,}3\text{ MPa};\space f_\text{ctd}=1{,}93\text{ MPa};\space f_\text{bd}=4{,}26\text{ MPa};\space v'=(1-f_\text{ck}/250)=0{,}8
\end{gathered}
Styčník s tlakovými silami CCC:
\begin{gathered}
\sigma_\text{Rd,max}=1{,}0\cdot v'f_\text{cd}=26{,}7\text{ MPa}
\end{gathered}Styčník s táhlem CTC:
\begin{gathered}
\sigma_\text{Rd,max}=0{,}85\cdot v'f_\text{cd}=22{,}7\text{ MPa}
\end{gathered}Betonová vzpěra se vznikem trhlin:
\begin{gathered}
\sigma_\text{Rd,max}=0{,}6\cdot v'f_\text{cd}=16{,}0\text{ MPa}
\end{gathered}Výztuž B500B:
\begin{gathered}
f_\text{yd}=\frac{f_\text{yk}}{\gamma_\text{s}}=\frac{500}{1{,}15}=435\text{ MPa};\space\varepsilon_\text{yd}=\frac{f_\text{yd}}{E_\text{s}}=\frac{435}{200}=2{,}175\space‰
\end{gathered}Ložisko ESZ Typ 200, t = 10 mm
\begin{gathered}
\sigma_\text{cd}=\frac{500\cdot10^{-3}}{0{,}20\cdot0{,}30}=8{,}33\text{ MPa}
\end{gathered}Návrh hlavní tahové výztuže
Předpokládáme dvě vrstvy výztuže, těžiště výztuže odhadneme na d‘ = 60 mm
Účinná výška průřezu je
\begin{gathered}
d=h_\text{c}-d'=0{,}40-0{,}06=0{,}34\text{ m}
\end{gathered}Šířka tlačené oblasti x1:
\begin{gathered}
x_1=\frac{F_\text{Ed}}{b\cdot\sigma_\text{Rd,max}}=\frac{500\cdot10^{-3}}{0{,}4\cdot26{,}7}=0{,}047\text{ m}
\end{gathered}Rameno vnější síly:
\begin{gathered}
a=a_\text{c}+0{,}5x_1+\frac{H_\text{Ed}}{F_\text{Ed}}(d'+0{,}01)=0{,}22+0{,}0235+0{,}2\cdot0{,}07=0{,}258\text{ m}
\end{gathered}Výška tlačené oblasti y1:
\begin{gathered}
y_1=d-\sqrt{d^2-2\cdot x_1\cdot(a+H_\text{Ed}/F_\text{Ed}\cdot(d'+\Delta h))}\\\\
y_1=0{,}34-\sqrt{0{,}34^2-2\cdot0{,}047(0{,}258+0{,}2(0{,}07)}=0{,}04\text{ m}
\end{gathered}Rameno vnitřních sil:
\begin{gathered}
z=d-0{,}5y_1=0{,}34-0{,}04/2=0{,}32\text{ m}
\end{gathered}Úhel sklonu tlačené diagonály:
\begin{gathered}
\cot\theta=a/z=0{,}258/0{,}32=0{,}806\to\theta=51{,}1\degree
\end{gathered}Vodorovná tahová síla:
\begin{gathered}
F_\text{t}=F_\text{Ed}\cdot\frac{a}{z}+H_\text{Ed}=500\cdot0{,}802+100=501{,}2\text{ kN}
\end{gathered}Hlavní tahová výztuž při horním líci konzoly:
\begin{gathered}
A_\text{s}=\frac{501\space200}{435}=1\space153\text{ mm}^2
\end{gathered}Navrhneme čtyři smyčky Æ16 mm As = 1 608 mm2
Zakotvení v uzlu 2 (pod styčnou deskou – ložiskem)
Základní kotevní délka výztužného prutu je:
\begin{gathered}
l_\text{b,rqd}=\frac{\phi}{4}\cdot\frac{\sigma_\text{sd}}{f_\text{bd}}=\frac{16\cdot435\cdot1\space153/1\space608}{4\cdot4{,}26}=292\text{ mm}
\end{gathered}
Obr. 3.27
Návrhová kotevní délka výztužných prutů Æ16 mm:
\begin{gathered}
l_\text{bd}=\alpha_1\cdot\alpha_2\cdot\alpha_3\cdot\alpha_4\cdot\alpha_5\cdot l_\text{b,rqd}=0{,}7\cdot292=205\text{ mm}\ge l_\text{b,min}
\end{gathered}kde je
lb,min … minimální kotevní délka;
lb,min ≥ max [0,3 · lb,rqd; 10 · ø; 100 mm].
Pro smyčku je třeba překontrolovat minimální vnitřní průměr zakřivení prutu. Kontrola je nutná provést jak u krajní, tak i u vnitřní smyčky, aby nedošlo k podrcení betonu ve smyčce. Z toho vyjde minimální vzdálenost smyček od sebe.
V jedné větvi smyčky je tah:
\begin{gathered}
F_\text{bt}=0{,}000201\cdot435\space000\cdot1\space153/1\space608=62{,}7\text{ kN}\\\\
\phi_\text{m,min}=\frac{F_\text{bt}}{f_\text{cd}}\cdot\bigg(\frac{1}{a_\text{b}}+\frac{1}{2\phi}\bigg)=\frac{62{,}7}{33{,}3}\bigg(\frac{1}{0{,}041}+\frac{1}{0{,}032}\bigg)=105\text{ mm}
\end{gathered}kde je
ab … vzdálenost osy prutu od líce prvku 25 + 8 + 8 = 41 mm,
popřípadě poloviční vzdálenost mezi smyčkami minimálně 35 mm (nutno upřesnit model náhradní příhradoviny – viz počáteční předpoklad vzdálenosti vrstev 60 mm).

Obr. 3.28
Vnitřní průměr zakřivení smyčky z profilu ø16 mm navrhneme 7ds = 112 mm. Kotevní délka prutu od kraje styčné desky je délka osy čtvrtiny kruhu výztuže 101 + 136 = 237 mm, zakotvení výztužné smyčky vyhovuje.
Zakotvení hlavní tahové výztuže za vnitřním styčníkem ve sloupu (uvažujeme špatné podmínky soudržnosti):
\begin{gathered}
l_\text{b,rqd}=\frac{\phi}{4}\cdot\frac{\sigma_\text{sd}}{f_\text{bd}}=\frac{16\cdot435\cdot(1\space153/1\space608)}{4\cdot3{,}05}=409\text{ mm}
\end{gathered}
Obr. 3.29
V tlačené diagonále je síla:
\begin{gathered}
F_\text{c}=F_\text{Ed}/\sin\theta=\frac{500}{\sin\theta}=641\text{ kN}
\end{gathered}Sklon tlačené diagonály – viz výše θ = 51,1
Délka diagonály:
\begin{gathered}
H=\sqrt{a^2+z^2}=411\text{ mm}
\end{gathered}Šířka diagonály:
\begin{gathered}
b_\text{ef}=0{,}5\cdot H+0{,}65\cdot a=0{,}5H+0{,}65\cdot\sqrt{x_1^2+y_1^2}=0{,}245\text{ m}
\end{gathered}Poznámka:
ve vzorci a je šířka betonové vzpěry na hranici styčníku nikoliv rameno vnější síly – viz kap. 1 vztah (1.8).
Průřez tlačené diagonály 0,098 m2.
V tlačené diagonále je napětí:
\begin{gathered}
\sigma_\text{c}=0{,}641/(0{,}245\cdot0{,}4)=6{,}54\le0{,}6\cdot v'f_\text{cd}=16{,}0\text{ MPa}
\end{gathered}Napětí v tlačené diagonále vyhovuje.
Návrh svislé a vodorovné výztuže
Pro návrh vodorovné a svislé výztuže se vychází ze sklonu tlačené diagonály nebo z poměru vyložení konzoly k její výšce.
Podle sklonu tlačené diagonály a/z = cot θ ≥ 0,5 se jedná o konzolu dlouhou. Podle EC2 [1] je též ac/hc = 0,22/0,40 = 0,55 ≥ 0,5.
Vyztužení podle konstrukčních kritérií:
Doporučeny minimálně dva vodorovné třmínky o průměru 6 až 8 mm;
Minimálně tři svislé třmínky o průměru 6 až 8 mm, u dlouhých konzol by měly svislé třmínky přenést minimálně sílu 0,5 FEd. Tedy Aswv = 0,5 · 500 000/435 = 575 mm2 návrh 4 dvojstřižné třmínky ø10 = 628 mm2.
Přesnější vyjádření podle metody hlavní diagonály:
V tlačené diagonále je síla Fc = 641,1 kN, délka diagonály je 411 mm. Příčný tah v tlačené diagonále při použití zjednodušení:
\begin{gathered}
T=2\cdot0{,}22\cdot F_\text{c}=2\cdot0{,}22\cdot641{,}1=282\text{ kN}
\end{gathered}Příčný tah je nutno rozložit do svislého a vodorovného směru.
Plocha vodorovné výztuže:
\begin{gathered}
A_\text{swh}=\frac{T\cdot\sin\theta}{f_\text{yd}}=A_\text{swh}=\frac{282\space000\cdot\sin51{,}3\degree}{435}=506\text{ mm}^2
\end{gathered}Navrženy 4 dvojstřižné třmínky ø10 As = 628 mm2.
Plocha svislé výztuže:
\begin{gathered}
A_\text{swh}=\frac{T\cdot\cos\theta}{f_\text{yd}}=A_\text{swh}=\frac{282\space000\cdot\cos51{,}3\degree}{435}=405\text{ mm}^2
\end{gathered}Navrženy 4 dvojstřižné třmínky ø10 As = 628 mm2.
Přesnějším vyjádřením příčných tahů podle vztahu 1.6 obr. 1.7b dostaneme nižší hodnoty příčné konstrukční výztuže.
Výztuž konzoly je znázorněna na obr. 3.30.
Napětí pod ložiskem:
\begin{gathered}
\sigma=0{,}500/(0{,}20\cdot0{,}30)=8{,}33\text{ MPa}
\end{gathered}a
\begin{gathered}
\tau=0{,}10/(0{,}20\cdot0{,}30)=1{,}67\text{ MPa}
\end{gathered}Napětí pod ložiskem vyhovuje.
Obr. 3.30
4 NEPŘÍMO ULOŽENÉ KONZOLY (ZAVĚŠENÉ KONZOLY)
4.1 NEPŘÍMO ULOŽENÉ KONZOLY – ZAVĚŠENÉ KONZOLY
Nepřímo uložené konzoly (zavěšené konzoly) jsou z hlediska návrhu složitější než přímo uložené. Nepřímo uložené konzoly mohou být umístěny například při spodním líci trámů (obr. 4.1) nebo mohou být průběžné (obr. 4.9) nebo vícenásobné (obr. 4.10). Způsob uložení zavěšené konzoly velmi zásadním způsobem mění geometrii modelu náhradní příhradoviny. Na obr. 4.2) jsou zobrazeny nejčastější případy, kdy těžiště opření tlačené diagonály se uvažuje v těžišti třmínkové výztuže obepínající podélnou výztuž podporujícího prvku. Zatížení konzoly se přenáší hlavní tlačenou betonovou diagonálou do styčníku 1, který je oproti přímo uložené konzole posunut do oblasti podélné výztuže podporujícího prvku viz obr. 4.3 a obr. 4.4. Na obr. 4.2 je rozebrán jen vliv svislých zatížení. Pro návrh konzoly je nutné uvažovat i vodorovné zatížení v hodnotě minimálně HEd = 0,2FEd. Viz následující obr. 4.3 a obr. 4.4.
Obr. 4.1 Příklad nepřímé (zavěšené) konzoly
Obr. 4.2 Modely náhradní příhradoviny pro nepřímé (zavěšené) konzoly bez vlivu vodorovné síly
Obr. 4.3 Řešení styčníku 1 modelu náhradní příhradoviny pro jednostrannou nepřímou (zavěšenou) konzolu
Obr. 4.4 Řešení styčníku 1 modelu náhradní příhradoviny pro oboustrannou nepřímou (zavěšenou) konzolu
Ve styčníku 1 se setkávají dvě betonové vzpěry a jedno táhlo. Jedná se o styčník CTC [1], ve kterém se uvažuje pevnost betonu porušeného trhlinami. Táhlo představují přilehlé větve třmínků, které vynášejí zatížení k hornímu líci podporujícího prvku (proto se někdy uvádí termín zavěšená konzola místo nepřímo uložené konzoly). Třmínky podporujícího prvku tedy musí přenést nejen tahy od posouvající síly a kroucení podporujícího prvku, ale navíc i tah ze styčníku 1 odpovídající zatížení na konzole. Posunutím styčníku 1 do oblasti za třmínkovou výztuž podporujícího prvku se výrazně zkracuje rameno vnitřních sil a prodlužuje rameno vnější síly.
Umístění styčníku 1 vychází z předpokladu zakotvení tažené větve třmínku pomocí podélné krajní výztuže podporujícího prvku [28]. Vzhledem k opření tlakové diagonály lze bezpečně předpokládat, že styčník CTC je umístěn blízko těžiště krajní podélné výztuže podporujícího prvku (obr. 4.3 a obr. 4.4). Pokud je podporující prvek namáhán ohybem a v místě uložení konzoly dojde k rozvoji trhlin v oblasti tažené podélné výztuže, doporučuje se redukovat pevnosti betonu v místě styčníku 1. Pro nepřímo uložené konzoly uvažujeme styčník 1 typu CTC (obr. 1.12) (popřípadě CTT (obr. 1.15) pokud je konzola na nosníku s taženým spodním okrajem). Styčník uvažujeme nad třmínkovou výztuží nosníku, účinná výška d je tak snížena o betonovou krycí vrstvu a průměr třmínkové výztuže nosníku. Účinná výška konzoly je d = h – d‘ – cnom + øsw,nosnik, účinnou výšku stanovíme obvyklým způsobem, je třeba odhadnout těžiště tažené výztuže při horním líci. Obvykle se uvažuje jedna vrstva výztuže. Vzdálenost těžiště výztuže od horního líce je d‘.
d'=c_\text{nom}+\phi_\text{sw}+0{,}6\phiNosníky s nepřímo uloženou konzolou mají nejčastěji tvar L-průřezu nebo obráceného T-průřezu (v místě konzoly). U těchto podporujících nosníků se musí vynášet zatížení z konzoly k hornímu líci nosníku (jedná se o nepřímé uložení – viz kap. 2.4). U oboustranných konzol se symetrickým zatížením se obvykle vynášející výztuž v krajních větvích třmínku u konzoly stanoví z celkového svislého zatížení konzol (při každé straně ΔTt = –FEd) a přidává se ke standardní smykové výztuži. U jednostranných konzol nebo u nesymetricky zatížených konzol lze stanovit přírůstek tahu ve svislých třmínkách v místě konzoly (obr. 4.2) podle:
\begin{gathered}
\Delta T_\text{t}=-F_\text{Ed}(1+\frac{a}{b_\text{b}})\space \Delta F_\text{c}=F_\text{Ed}\frac{a}{b_\text{b}}
\end{gathered}(4.1)
kde je
ΔTt … přírůstek tahové síly v přilehlé větvi svislého třmínku od zatížení konzoly;
A … rameno vnější síly FEd;
bb … osová vzdálenost větví svislých třmínků.
Uvedená hodnota vychází z momentové rovnováhy vodorovného řezu celým prvkem v úrovni horního líce konzoly k těžišti vzdálenější větve třmínku. Odtud stanovíme tlakovou sílu ΔFc působící na opačné straně průřezu, než je konzola (obr. 4.2). Podle [36] je vztah (4.1) pro více vyložené konzoly (pro které platí a/bb ≥ 0,5) velmi konzervativní a lze jej upravit na vztah:
\begin{gathered}
\Delta T_\text{t}=-F_\text{Ed}(\frac{5}{8}+\frac{3a}{4b_\text{b}})
\end{gathered}(4.2)
Vztah (4.1) je sice konzervativní ale je optimální, pokud je výška konzoly výrazně menší, než je celková výška průřezu podporujícího prvku, a pokud pro vyložení konzoly platí a/bb ≥ 0,5. Do hodnoty vyložení konzoly a/bb ≤ 0,5 lze uvažovat ΔTt = –FEd, při větším vyložení konzoly, síla v krajní větvi třmínku narůstá. Srovnání obou vztahů je na obr. 4.5 (převzato z [10] a [36]). Pro konzolové pásy se však doporučuje užívat konzervativní vztah (4.1).
Obr. 4.5 Přírůstek tahové síly v krajní větvi třmenu v závislosti na poměrném vyložení konzoly
Základní model pro návrh nepřímo uložené konzoly je na obr. 4.2a, b. Návrh vnitřních sil u nepřímo uložené konzoly vychází obdobně jako u přímo uložených konzol [27] z podmínky rovnováhy ve styčníku 1 ve svislém směru (obr. 4.3 a obr. 4.4). Odtud stanovíme šířku tlačené oblasti x1 v ose krajní větve třmínku a nad těžištěm krajní podélné výztuže podporujícího prvku. Z momentové rovnováhy ve styčníku 1 stanovíme výšku tlačené oblasti y1. V dalším stanovíme rameno vnitřních sil z a rameno vnějších sil a. Z jejich poměru dopočteme sklon tlačené diagonály θ. Hlavní tahovou sílu stanovíme z rovnováhy ve vodorovném směru ve styčníku 2, z rovnováhy ve svislém směru stanovíme pak tlakovou sílu v betonové diagonále. Jako u dlouhé konzoly je nutné navrhnout svislé třmínky v oblasti mezi lícem podporujícího prvku a vnitřním lícem styčné – ložiskové desky. Při návrhu použijeme vztahy uvedené u přímo uložené konzoly (kap. 3). Obdobně jako u přímo uložené konzoly je doporučeno uvažovat s vodorovnou silou minimální velikosti HEd = 0,20 FEd.
Nepřímo uložená konzola představuje rámový roh s kladným působením ohybového momentu. Při návrhu rámových rohů se doporučuje vkládat šikmou výztuž, která je účinnější na redukci vznikající poruchové trhliny než soustava ortogonální výztuže. Stejný princip můžeme použít i při vyztužování nepřímo uložených konzol. Model náhradní příhradoviny je na obr. 4.6. Šikmá tahová výztuž vynáší zatížení konzoly do oblasti blízké těžišti průřezu podporujícího nosníku. Tento model náhradní příhradoviny je však kinematický a není schopen přenášet žádná vodorovná zatížení. Proto se kombinuje s modelem na obr. 4.2. Model zobrazený na obr. 4.6 nelze použít pro přenos celého zatížení (maximálně lze uvažovat přenos 50 % celkového zatížení). Pokud použijeme kombinovaný model, je obtížné stanovit, jakou část zatížení přenáší model podle obr. 4.2 a jakou část model podle obr. 4.6. Reálné rozdělení zatížení vyplývá z poměru tuhostí jednotlivých modelů, které jsou obtížně stanovitelné. Proto lze použít podle [10] zjednodušení a navrhnout bezpečné vyztužení obou modelů na 60 % celkového svislého zatížení. Vodorovné zatížení je nutné přiřadit pouze k modelu podle obr. 4.2. Velmi důležité je překontrolovat dostatečné zakotvení tahové výztuže v příslušném styčníku. Při horním líci navrhujeme tahovou výztuž ve formě smyček a při návrhu kotvení lze využit kladný vliv tlaku pod styčnou deskou. Pro zakotvení šikmé výztuže je v rohu konzoly velmi málo prostoru a běžné kotvení smyčkami nevyhovuje – viz obr. 4.6. Obvykle je nutné řešit zakotvení šikmé tahové výztuže kotevními spojkami nebo přivařenou kotevní deskou. Pokud v návrhu nevyužijeme únosnost šikmé tahové výztuže vzhledem ke krátké délce na zakotvení, je vhodné alespoň vkládat konstrukční šikmé pruty ve formě smyček.
Obr. 4.6 Model náhradní příhradoviny nepřímo uložené konzoly se šikmým táhlem
V praxi při návrhu zavěšených konzol se často používal i jiný model (obr. 4.7) podle [37]. Model vychází z předpokládaného průběhu poruchové trhliny. Předpokládá se, že poruchová trhlina vychází z taženého rohu konzoly a směruje šikmo ke spodnímu líci podporujícího prvku. Sklon trhliny lze uvažovat v souladu s [1] hodnotou 45°, maximálně však do poloviny šířky podporujícího trámu. Při experimentech bylo zjištěno, že poloha poruchové trhliny je obvykle posunuta směrem k vnitřní hraně styčné desky, předpokládaná poloha však dává nepříznivější výsledky, a proto se takto uvažuje. Šikmá trhlina oddělí z celkového prvku část konzoly, kterou předpokládáme dokonale tuhou.
Obr. 4.7 Model pro návrh nepřímo uložené konzoly – metoda poruchové trhliny
Při návrhu vyjdeme ze svislé síly v krajní větvi třmínku, z rovnováhy ve svislém směru vyplývá Ft = FEd. Dále odhadneme ohybový moment působící ve styčníku 2:
\begin{gathered}
M_\text{Ed}=F_\text{Ed}\cdot a_\text{v}\cdot H_\text{Ed}\cdot(h_\text{k}+\Delta h)
\end{gathered}(4.3)
kde je
FT … tahová síla v hlavní tažené výztuži;
B … šířka konzoly nebo šířka oblasti na které se roznáší zatížení konzoly;
HEd … vodorovné zatížení konzoly.
Rameno vnitřních sil uvažujeme přibližně
\begin{gathered}
z_\text{k}=h_\text{k}-d'-0{,}4x_\text{k}
\end{gathered}(4.4)
kde výška tlačené oblasti xk:
\begin{gathered}
x_\text{k}=\frac{M_\text{Ed}}{0{,}8b\cdot f_\text{cd}}
\end{gathered}(4.5)
kde je
fcd … návrhová pevnost betonu prvku.
Upřesněný ohybový moment působící ve styčníku 2:
\begin{gathered}
F_\text{t}\cdot z_\text{k}=F_\text{Ed}\cdot a_\text{k}\cdot H_\text{Ed}(z_\text{k}\cdot d'+\Delta h)
\end{gathered}(4.6)
Odtud Ft = MEd/Zk. Upřesní se xk a postup se opakuje.
Uvedený postup modelu s poruchovou trhlinou nepřináší ve srovnání s metodou náhradní příhradoviny žádné výhody. Naopak tento model je založen na Bernoulliho hypotéze zachování rovinnosti deformovaného průřezu, která není splněna, protože se jedná o poruchovou oblast. Model předpokládá odtrhávanou část konzoly jako tuhé těleso, což také neodpovídá skutečnosti. Stanovené vnitřní síly v modelu s trhlinou jsou mírně menší, protože uvažovaná ramena vnitřních sil jsou větší než v modelu náhradní příhradoviny. Model náhradní příhradoviny představuje rovněž velké zjednodušení skutečnosti. Jedná se o zjednodušené řešení poruchové oblasti, které je na straně bezpečnosti. Pro přesná řešení poruchových oblastí je nutné použít software, umožňující nelineární výpočty a modelování výztuže podle skutečného návrhu prvku. Takový software je například program ATENA.
Při jednostranně zatížených konzolách vznikají v podporujících prvcích – průvlacích nebo trámech krouticí momenty. Krouticí momenty lze zredukovat pomocí speciálních zakotvení podle obr. 4.8. Při návrhu je vždy nutné uvedené zakotvení posoudit a posoudit prvek na všechny montážní stavy, při kterých ke kroucení bude docházet, pokud nebude prvek vhodně montážně podepřen. Příklady z obr. 4.8 redukují kroucení podporujícího prvku pouze v konečném stavu, nikoliv při montáži. Mezi konzoly a ozuby je třeba vždy vkládat podložky, které především vymezují polohu zatížení na jednotlivých prvcích – konzolách a ozubech a které zabraňují odštěpování hran prvků.
Obr. 4.8 Způsoby redukce kroucení průvlaku s jednostrannou konzolou
U nepřímo uložených konzol platí stejné zásady vyztužení jako u přímo uložených konzol.
Poznámka:
u nepřímo uložených konzol je nutné vždy posoudit vliv konzoly na vynášející nosník. Jedná se především o kroucení – nutno posoudit kroucení i během montážních stavů, ne jenom v konečném stavu smontované konstrukce. Dále je nutné, jako u všech nepřímo zatížených prvků, vynést svislé zatížení k hornímu líci prvku.
4.2 PRŮBĚŽNÉ KONZOLY A SMYKOVĚ NEVYZTUŽENÉ KONZOLY
Nepřímo uložené průběžné konzoly se užívají pro uložení deskových prvků s ozubem, jako jsou například schodišťová ramena, vložená desková dilatační pole a podobně (obr. 4.9). Průběžné konzoly u desek obvykle nemají smykovou výztuž jako konzoly a místo vodorovných výztužných smyček se konzola vyztužuje pouze svislými třmínky. Průběžné konzoly bývají méně zatížené. Pokud je napětí pod styčnou deskou menší než σ ≤ 0,08 fck, může být styčná deska posunuta blíže k okraji než u klasické konzoly. Její umístění je omezeno minimální vzdáleností jejího okraje od hrany konzoly a minimální vzdáleností působiště zatížení od středu ohybu svislého třmínku – viz obr. 4.9. Pokud uvažujeme roznášení v betonové krycí vrstvě pod 45°, tlačená betonová diagonála zasahuje až k líci konzoly a není ovinuta výztuží jako u klasických konzol. Předpokládá se tedy, že příčná tahová napětí v betonu nepřekročí hodnotu 0,5fctd (50 % návrhové pevnosti betonu v tahu). Z tohoto důvodu také není nutné navrhovat svislou a vodorovnou třmínkovou výztuž vlastního konzolového pásu, pro kterou není v běžných konzolových pásech dostatečné místo.
Obr. 4. 9 Konzolový pás – spojitá nepřímo uložená konzola, platí pro napětí pod styčnou deskou δ ≤ 0,08fck
Při návrhu průběžné konzoly je nutné, jako u klasické konzoly, navrhnout taženou výztuž při horním líci a překontrolovat únosnost tlačené betonové diagonály s tím, že vznikající příčné tahy musí spolehlivě přenést beton v tahu. Styčník 1 uvažujeme obdobně jako u nepřímo uložených konzol. Vzhledem k obvykle menšímu namáhání než u klasických konzol lze styčník 1 uvažovat tak, že jeho dolní líc je v úrovni dolního líce výztuže. Z polohy styčníku 1 vyplývá geometrie modelu a sklon tlačené betonové vzpěry θ. Postup je stejný jako u nepřímo uložených konzol. Šířku b uvažujeme buď v délce 1 m, nebo ve skutečné délce, např. u konzolových pásů pro uložení schodišťových ramen.
4.3 VÍCENÁSOBNÉ KONZOLY
Vícenásobné konzoly jsou konzoly, na kterých je uloženo více prvků – průvlaků, vazníků nebo trámů (obr. 4.10). Konzoly jsou zatíženy více silami v různých působištích. Pokud jsou těžiště zatížení v podélné ose konzoly a nedochází ke kroucení konzoly, lze použít upravené modely náhradní příhradoviny (obr. 4.10). Pro návrh vícenásobných konzol nesymetricky zatížených (dochází i ke kroucení konzoly) je možné využít pouze speciální software na nelineární prostorové výpočty – například ATENA 3D (obr. 4.13, obr. 4.14). Pokud podobný software při návrhu vícenásobné prostorově zatížené konzoly není dostupný, použijeme pro návrh vícenásobný model náhradní příhradoviny, popřípadě soustavu modelů náhradní příhradoviny na sebe navazující. Pro každé zatížení sestavíme zvláštní model náhradní příhradoviny. Společná místa, jako je například opření konzoly do sloupu – styčník 1 nebo hlavní tahová výztuž, musíme řešit společně pro všechny modely.
Obr. 4.10 Příklad vícenásobné konzoly
Pro vícenásobnou konzolu je model náhradní příhradoviny na obr. 4.10. Model náhradní příhradoviny je navržen podle předpisu [8]. Při návrhu se nejprve stanoví výška tlačené oblasti x1 podle vztahu:
\begin{gathered}
x_1=\frac{F_\text{Ed1}}{b\cdot\sigma_\text{Rd,max}}+\frac{F_\text{Ed2}}{b\cdot\sigma_\text{Rd,max}}
\end{gathered}(4.7)
kde je
b … šířka konzoly,
FEd1, FEd2 … svislá zatížení konzoly.
Obdobně jako u jednoduché konzoly stanovíme ramena vnějších sil a1 a a2. Hlavní tahovou sílu stanovíme z momentové podmínky a silové podmínky ve svislém směru ve styčníku 1 a dopočteme výšku tlačené oblasti.
U konzoly zatížené více silami je nutné vždy překontrolovat kroucení konzoly při nesymetrickém zatížení. Výztuž zachycující krouticí účinky se musí přidat k navržené výztuži konzoly v souladu s pravidly ČSN EN 1992-1-1:2006.
U prostorově zatížených vícenásobných konzol se postupuje obdobně. Zatížení rozložíme do základních směrů a řešíme každou oblast zvlášť. Zatížení se směrem k podporujícím prvkům sčítají. U konzoly zatížené více silami je nutné vždy překontrolovat kroucení konzoly při nesymetrickém zatížení. Výztuž zachycující krouticí účinky se musí přidat k navržené výztuži podporující konstrukce. Dále je nutné u složených konzol uvažovat všechny zatěžovací stavy včetně všech montážních zatěžovacích stavů.
4.4 PŘÍKLADY
4.4.1 Příklad průběžné konzoly
Navrhněte výztuž konzoly průvlaku zatížené FEd = 20 kN a vodorovnou silou HEd = 4 kN. Průvlak včetně konzoly je z betonu třídy C25/30, betonářská výztuž B500B, betonová krycí vrstva cnom = 20 mm. Rozměry jsou definovány na obr. 4.11. Šířka konzoly je 1,0 m, délka ložiska je 0,90 m, tloušťka ložiska 5 mm. Montážní a výrobní tolerance je uvažována hodnotou +/-5 mm. Svislé třmínky a smyčky jsou profilu 8 mm.
Materiály
Beton C25/30:
\begin{gathered}
f_\text{cd}=16{,}7\text{ MPa};\space\alpha_\text{cc}=1{,}0;\space\varepsilon_\text{cu3}=3{,}5\space‰;\space\eta=1{,}0{,}\lambda=0{,}8;\space v'=(1-f_\text{ck}/250)=0{,}9
\end{gathered}Styčník se dvěma táhly CTT:
\begin{gathered}
\sigma_\text{Rd,max}=0{,}75\cdot v'f_\text{cd}=11{,}3\text{ MPa}
\end{gathered}Betonová vzpěra se vznikem trhlin:
\begin{gathered}
\sigma_\text{Rd,max}=0{,}6\cdot v'f_\text{cd}=9{,}0\text{ MPa}
\end{gathered}Výztuž B500B:
\begin{gathered}
f_\text{yd}=\frac{f_\text{yk}}{\gamma_\text{s}}=\frac{500}{1{,}15}=435\text { MPa}\\\\
y_\text{yd}=\frac{f_\text{yd}}{E_\text{s}}=\frac{435}{200}=2{,}175\space‰
\end{gathered}Obr. 4.11 Příklad nepřímo uloženého (zavěšeného) konzolového pásu
Návrh hlavní tahové výztuže
Předpokládáme jednu vrstvu výztuže, těžiště výztuže odhadneme na d‘ = 24 mm.
Účinná výška průřezu konzoly
\begin{gathered}
d=0{,}120-0{,}024=0{,}096\text{ m}
\end{gathered}Návrh pomocí modelu náhradní příhradoviny. Vzhledem k malému zatížení průběžného deskové konzoly se uvažuje dolní líc styčníku 1 úrovni dolního líce výztuže – dolní větve třmínku (20 mm od dolního líce).
Šířka tlačené oblasti x1:
\begin{gathered}
x_1=\frac{F_\text{Ed}}{b\cdot\sigma_\text{Rd,max}}=\frac{20\cdot10^{-3}}{1{,}0\cdot11{,}3}=0{,}018\text{ m}
\end{gathered}Rameno vnější síly:
\begin{gathered}
a=a_\text{v}+\frac{H_\text{Ed}}{F_\text{Ed}}(d'+\Delta h)=0{,}07+0{,}024+0{,}2\cdot(0{,}024+0{,}005)=0{,}100\text{ m}
\end{gathered}Výška tlačené oblasti y1:
\begin{gathered}
y_1=d-\sqrt{d^2-2\cdot x_1\cdot(a+H_\text{Ed}/F_\text{Ed}\cdot(d'+\Delta h))}\\\\
y_1=0{,}096-\sqrt{0{,}096^2-2\cdot0{,}018(0{,}10+0{,}2(0{,}024+0{,}005))}=0{,}0224\text{ m}
\end{gathered}Rameno vnitřních sil:
\begin{gathered}
z=d-y_1\cdot0{,}5-0{,}2=0{,}096-0{,}010-0{,}20=0{,}065\text{ m}
\end{gathered}Úhel sklonu tlačené diagonály je
\begin{gathered}
\cot\theta=a/z=0{,}1/0{,}065=1{,}54\to\theta=33\degree
\end{gathered}Vodorovná tahová síla:
\begin{gathered}
F_\text{t}=F_\text{Ed}\cdot\frac{a}{z}+H_\text{Ed}=20\cdot1{,}54+4=34{,}8\text{ kN}
\end{gathered}Hlavní tahová výztuž při horním líci konzoly je As = 34 800/435 = 80 mm2.
\begin{gathered}
A_\text{s}=34\space800/435=80\text{ mm}^2
\end{gathered}Navrhneme pět smyček ø6 mm As = 141 mm2 (svislých smyček).
Zakotvení za vzdálenější větví svislého třmínku.
Základní kotevní délka výztužného prutu:
\begin{gathered}
l_\text{b,rqd}=\frac{\varphi}{4}\cdot\frac{\sigma_\text{sd}}{f_\text{bd}}=\frac{6\cdot435\cdot90/141}{4\cdot2{,}7}=154{,}3\text{ mm}
\end{gathered}Návrhová kotevní délka výztužných prutů ø6 mm:
\begin{gathered}
l_\text{bd}=\alpha_1\cdot\alpha_2\cdot\alpha_3\cdot\alpha_4\cdot\alpha_5\cdot l_\text{b,rqd}=154{,}3\text{ mm}
\end{gathered}Síla v betonové diagonále je
\begin{gathered}
F_\text{c}=F_\text{Ed}/\sin\theta=20/0{,}545=36{,}7\text{ kN}
\end{gathered}Betonová diagonála má délku:
\begin{gathered}
H=\sqrt{a^2+z^2}=119\text{ mm}
\end{gathered}Šířka diagonály:
\begin{gathered}
b_\text{ef}=0{,}5\cdot H+0{,}65\cdot a=0{,}5H+0{,}65\cdot\sqrt{x_1^2+y_1^2}=0{,}09\text{ m}
\end{gathered}Poznámka:
ve vzorci a je šířka betonové vzpěry na hranici styčníku nikoliv rameno.
Šířka diagonály je 1,0 m (viz zadání). Napětí v betonové diagonále je
\begin{gathered}
\sigma_\text{c}=41\cdot10^{-3}/(1\cdot0{,}09)=0{,}46\text{ MPa}\le0{,}4_{\sigma_\text{Rd,max}}
\end{gathered}Není nutné ani konstrukční vyztužení na vznik příčných tahů v tlačené diagonále, tahy převezme beton.
4.4.2 Příklad vícenásobné konzoly
Obr. 4.12 Tvar vícenásobné prostorově zatížené konzoly
Obr. 4.13 Výsledky nelineární prostorové analýzy konzoly – trhliny a napětí v betonové části konzoly
Obr. 4.14 Výsledky nelineární prostorové analýzy konzoly – napětí ve výztuži konzoly

Obr. 4.15 Svázaná výztuž jednostranné prostorové konzoly (příliš hustá výztuž pro dobré dobetonování, geometrie prvku by na dané namáhání měla být upravena)
5 OZUBY NOSNÍKŮ A DESEK
S návrhem ozubů u nosníků a desek se velmi často setkáváme u prefabrikovaných konstrukcí. Pomocí ozubů ukládáme prefabrikované nosníky na konzoly s tím, že spodní líce obou prvků jsou obvykle ve stejné úrovni. Obdobné je to i u prefabrikovaných desek, ukládaných na ozuby průběžných konzol. Velmi častým případem je uložení schodišťového ramene pomocí deskového ozubu na deskovou konzolu podesty.
K návrhu ozubů využíváme především modely náhradní příhradoviny. Jsou to rovněž poruchové oblasti (D-oblasti). Ozuby na nosnících jsou principiálně stejné poruchové oblasti jako nepřímo uložené konzoly (viz kap. 4 nebo [29], pokud se na ně podíváme obráceně). Nepřímé uložení ozubem chápeme jako napojení na vlastní plnou část průvlaku, vazníku nebo desky (je to tedy obrácená nepřímo uložená konzola).
5.1 TYPY OZUBŮ A METODY NÁVRHU
Ozuby jsou na nosníkových nebo deskových prvcích. V první části jsou řešeny ozuby na nosnících. Pro jejich výpočet se nejčastěji používají dva modely náhradní příhradoviny – pro snazší orientaci jsou modely v následujícím textu označeny písmeny A a B. Model A má za lícem ozubu koncentrovanou svislou třmínkovou výztuž a při spodním líci ozubu koncentrované vodorovné táhlo (obr. 5.1), zatímco hlavním nosným prvkem modelu B (obr. 5.2) je šikmé táhlo. Nejčastějším návrhovým modelem oblasti ozubu je kombinovaný model A a B. Odborným odhadem rozdělíme namáhání ozubu na část přenášenou příhradovinou modelu A a část přenášenou příhradovinou modelu B. Po navržení konkrétního vyztužení je vhodné původní předpoklad o rozdělení do modelů A a B ověřit, případně zpřesnit.
Obr. 5.1 Ozub nosníku – model A
Obr. 5.2 Ozub nosníku – model B
Modely náhradní příhradoviny nejsou blíže specifikované v základní normě ČSN EN 1992-1-1:2006 [1] (viz obr. 5.3). Jejich podrobný rozbor je dostupný především v zahraniční literatuře (viz např. [7], [10] a [20]). Modely byly ověřeny četnými experimenty i nelineárními výpočty. Konkrétní modely náhradní příhradoviny oblasti ozubu vycházejí především z geometrie prvku a z jeho vyztužení. Proto návrh náhradní příhradoviny obvykle provádíme ve dvou a více krocích. V prvním kroku odhadneme výztuž a dopočteme síly v táhlech a vzpěrách. Ve druhém kroku upřesníme model náhradní příhradoviny podle dimenzování táhel a vzpěr a novým výpočtem upřesníme vnitřní síly.
Obr. 5.3
V normě ČSN EN 1992-1-1:2006 [1] (viz obr. 5.3) není předepsána (jen graficky naznačena) minimální vodorovná reakce, na kterou má být ozub navržen. Přesto se doporučuje při návrhu počítat s minimální vodorovnou silou v hodnotě 20 % svislé reakce, pokud nám z výpočtu objektu nevyjde vodorovná síla větší. Přitom model B nemůže přenášet žádné vodorovné zatížení, a proto veškeré vodorovné zatížení přisuzujeme modelu A.
Poznámka:
někdy se v literatuře uvádí samostatný model C jen pro přenos vodorovných účinků zatížení, obr. 5.4.
Norma [1] rovněž nepředepisuje uvažování běžných výrobních a montážních tolerancí (bližší viz kap. 3). Přesto je zřejmé, že žádné prvky nelze vyrobit a smontovat zcela přesně. Proto je rovněž doporučeno uvažovat se zvětšenou excentricitou reakce v místě uložení prvku.
Další zjednodušení je v definici zatížení. Při řešení poruchové oblasti ozubu uvažujeme reakci v uložení ozubu a v celé oblasti neredukujeme posouvající sílu (uvažujeme, že v oblasti nepůsobí žádné zatížení). Reakce v uložení je tak shodná s posouvající silou na nosníku za poruchovou oblastí kolem ozubu.
Obr. 5.4 Ozub nosníku – model A – vodorovná reakce model náhradní příhradovniny
5.1.1 Model A
Pro model A se obvykle uvažuje model náhradní příhradoviny podle obr. 5.1. Pro představu o chování ozubu vyztuženého především svislými třmínky a vodorovným táhlem, viz obr. 5.5a a obr. 5.5b, kde jsou zobrazeny výsledky nelineárního výpočtu příkladu ozubu. Z obrázků je patrno, že trhliny vznikají především ve směru betonové vzpěry, třmínková výztuž není na vznikající trhliny kolmá, není tedy maximálně účinná. Při větším počtu třmínků za lícem ozubu se zvětšuje rameno reakce A, což vede k velkému množství staticky nutné výztuže. Tlakové vzpěry z nelineárního výpočtu odpovídají modelu náhradní příhradoviny.
Nevýhodou modelu A (obr. 5.1) je tedy velké množství svislé tahové výztuže ve formě třmínků hned za lícem ozubu.
Poznámka:
je nutné překontrolovat dostatečné zakotvení třmínků háky, nepostačuje jen dodržet délku háků podle konstrukčních zásad ČSN EN 1992-1-1:2006 [1].
Svislá výztuž (obvykle ve formě třmínků) není optimálně skloněna ke vznikající poruchové trhlině a je tak méně účinná na její rozvoj. Velké množství výztuže také posouvá styčník 2 dále do vlastního průvlaku a tím prodlužuje rameno vnější síly – reakce v uložení ozubu. Předností modelu A je především možnost přenosu vodorovné síly v uložení (obr. 5.1).

Obr. 5.5a

Obr. 5.5b
Model pro přenos vodorovné síly
Pro přenos vodorovné síly uvažujeme model náhradní příhradoviny podle modelu A. Na rozdíl od modelu A je zde doplněna vzpěra ΔC24 – viz obr. 5.4. V okamžiku vyčerpání únosnosti však uvedenou vzpěrou prochází poruchová trhlina (trhlina kolmá na vzpěru je v rozporu se vzpěrou, proto nelze s ní uvažovat v modelech náhradní příhradoviny). Proto tento model uvažujeme pouze pro přenos vodorovné síly. Pro svislé účinky uvažujeme přenos sil podle modelu A – viz obr. 5.1. Model přenosu vodorovné síly je někdy v literatuře označován jako model C.
5.1.2 Model B
Model B (obr. 5.2) má optimální umístění šikmé výztuže takřka kolmo na směr rozvoje trhlin u rohu ozubu. Šikmá výztuž je nejúčinnější pro přenos zatížení z průvlaku do ozubu. Pro představu o chování ozubu vyztuženého především šikmým táhlem viz obr. 5.6a a obr. 5.6b, kde jsou zobrazeny výsledky nelineárního výpočtu příkladu ozubu. Z obrázků je patrno, že šikmá výztuž je takřka kolmá (dané geometrií ozubu a sklonu táhla) na vznikající trhliny, je tedy maximálně účinná. Vznikají však i velké vodorovné trhliny pod ozubem, jejich vliv model B nepostihuje. Velkou nevýhodou modelu B však je, že nemůže přenášet případné vodorovné síly působící ozubu průvlaku (kinematický model náhradní příhradoviny). Pokud uvažujeme na konzolách sloupů minimální vodorovnou sílu v hodnotě 0,2FEd, stejná síla by se měla uvažovat pro druhou stranu uložení – pro ozuby na průvlacích. Z toho vyplývá, že varianta B nemůže být nikdy použita samostatně, ale pouze v kombinaci s variantou A. Další nevýhodou této varianty B je rovněž malý prostor pro zakotvení šikmé tahové výztuže v horním rohu ozubu. Šikmou výztuž navrhujeme obvykle pomocí smyček, nebo jednotlivých prutů zakotvených pomocí přivařených desek.
Poznámka:
svařování pouze v souladu s ČSN EN ISO 17660-1:2007.
Pokud navrhneme zakončení šikmé tahové výztuže ve tvaru smyček a je nutné navrhnout smyčky ve více vrstvách, bude kotevní oblast větší, což může vést ke změně modelu příhradové analogie. Vznikne totiž další vložený styčník CTT, který bude vyžadovat další vodorovnou a svislou výztuž (viz obr. 5.7).
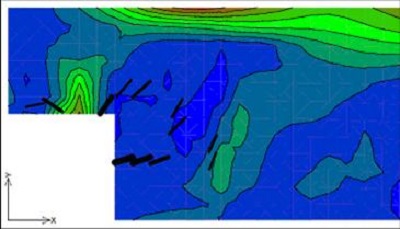
Obr. 5.6a
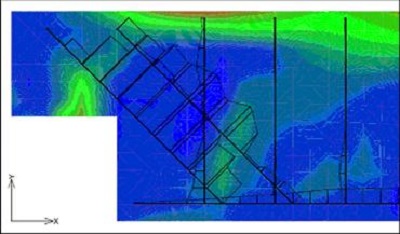
Obr. 5.6b
Obr. 5.7 Ozub nosníku – model B* – upravený model příhradoviny
5.1.3 Kombinovaný model A+B
Při návrhu ozubu průvlaku je optimální vytvořit model kombinací obou uvedených modelů A a B (viz obr. 5.8). Rozdělení zatížení ozubu do dvou soustav náhradní příhradoviny lze provést přesně na základě poměru jejich tuhostí. V době zpracování návrhu výztuže ozubu však neznáme staticky nutné vyztužení ozubu a nejsme schopni tak stanovit tuhosti jednotlivých modelů. Pro nalezení optimálního řešení by bylo nutné provádět poměrně komplikovaný iterační postup. V současné době je optimálním a doporučeným postupem každý model navrhnout na 55 % celkového zatížení s tím, že vodorovné zatížení se celé přisoudí modelu A (viz [10]). Tím, že navrhujeme výztuž na 110 % celkového svislého zatížení, vzniká rezerva 10 %, která se využije na pokrytí rozdílných tuhostí obou modelů, protože tužší model z obou bude přenášet větší část zatížení než poddajnější model. Znovu je třeba připomenout, že model B nelze nikdy použít samostatně. Model A lze použít samostatně, a pokud bychom jej navrhli jako samostatný, doporučuje se vkládat konstrukční šikmou výztuž pro redukci rozvoje poruchové trhliny.
Obr. 5.8 Ozub nosníku – kombinovaný model A+B
Ozub průvlaku je nutné navrhovat současně s konzolou, na kterou se nosník s ozubem uloží. Geometrie ozubu a konzoly si musí odpovídat, obě oblasti musí být také spolehlivě vyztuženy. Při návrhu je nutné dořešit i velikost spár mezi jednotlivými prefabrikáty, které vycházejí z reálných výrobních a montážních tolerancí. Velikost spár je rovněž závislá na použitém ložisku. Malé spáry mohou vést k porušení hran prefabrikátů, velké spáry zbytečně zvětšují namáhání ozubů. Postup stanovení tolerancí, umístění a velikosti ložisek a další byly uvedeny v kap. 3. Dále je vhodné umístit svislé zatížení – reakci s excentricitou e (viz kap. 3), bližší – viz [28]. V tomto bodě se liší umístění reakce na konzole a na ozubu, tolerance se u obou oblastí uvažují v jiném směru (viz obr. 3.17).
Na začátku návrhu ozubu (kombinovaný model viz obr. 5.8) přiřadíme každému modelu 55 % zatížení – reakce (A* = 0,55A). V rámci optimalizace výztuže je vhodné po dopočtení tuhostí rozdělení upravit s tím, že část přenášená modelem B nesmí nikdy být větší než 70 % celkového zatížení.
Poznámka:
pokud jsou v modelech náhradní příhradoviny uvažovány současně silové účinky od obou modelů, pak jsou rozlišeny horním indexem (1) pro síly prvního modelu A a indexem (2) pro síly druhého modelu B.
Nejprve navrhneme ložisko a překontrolujeme napětí v betonu pod styčnou deskou. Návrhová mez únosnosti betonu v tlaku odpovídá styčníku CTC.
Poznámka:
návrh ložiska není součástí této publikace – podrobněji viz ČSN EN 1337-1.
\begin{gathered}
\sigma_\text{c}=\frac{F_\text{Ed}}{A_\text{desky}};\space\Tau=\frac{H_\text{Ed}}{A_\text{desky}}
\end{gathered}(5.1)
Parametry pro omezení napětí pod ložiskem – styčnou deskou a umístění ložiska u okraje prvku byly uvedeny v kap. 3.
5.2 NÁVRHOVÝ MODEL A
Model náhradní příhradoviny modelu A je uveden na obr. 5.1 a 5.9. Jednotlivé styčníky jsou detailně zobrazeny na obr. 5.10 (geometrie styčníku 1 (CTC) a 2 (CTT)) a obr. 5.11 (geometrie styčníku 3 (CTT), 4 (CTT) a 5 (CTT)). Model A je obdobný jako nepřímo uložená konzola (obrácená – viz obr. 4.8). Proto můžeme použít všechny vztahy pro návrh výztuže odvozené u konzol. Přenos vodorovné síly uvažujeme podle modelu na obr. 5.4, tedy jako pro změnu průřezu (kap. 2, obr. 2.15) a účinky vodorovného zatížení zahrnujeme do modelu A. Pro zjednodušení uvažujeme sklon vzpěry ΔC34 hodnotou θ = 45°. Ve svislém táhle vznikne síla.
Poznámka:
označujeme jako přírůstek síly, konečná hodnota tahové síly bude součtem tahové síly od vertikálního zatížení – reakce A a vodorovného zatížení – reakce H.
\begin{gathered}
\Delta T_{23}=H_\text{Ed}\cdot\frac{z_\text{k}}{z}
\end{gathered}kde proměnné – viz obr. 5.4 a obr. 2.15, (odvození vztahu viz kap. 2).
U modelu A podle obr. 5.1 lze jednoduše stanovit síly v táhlech a vzpěrách z podmínek rovnováhy ve styčnících obdobně jako u konzol (viz kap. 3 a kap. 4).
Obr. 5.9 Ozub nosníku – model A – svislá reakce – model náhradní příhradoviny
Obr. 5.10 Ozub nosníku – model A – řešení styčníků 1 a 2
Obr. 5.11 Ozub nosníku – model A – řešení styčníků 3 a 4
Výpočetní postup
- Stanovíme množství svislé tahové výztuže u líce ozubu (viz obr. 5.10). Za předpokladu, že T23 = A + ΔT23 obdržíme staticky nutnou plochu výztuže táhla:
\begin{gathered}
A_\text{s}=T_{23}/f_\text{yd}
\end{gathered}(5.2)
a navrhneme vyztužení třmínky (šířka táhla je označena x2). V těžišti třmínků bude styčník 2 vzdálený Δa od líce betonu (prvku) – viz obr. 5.10. Obdobně jako u nepřímo uložených konzol předpokládáme styčník 2 v oblasti uzavřené svislými třmeny (viz kap. 4). Svislé třmínky se obvykle navrhují z průřezů max.12 (lze připustit i profil 14 mm) v osových vzdálenostech cca 50 mm. Pro zvýšení jejich účinnosti lze třmínky mírně sklonit směrem k ozubu [10]. Toto však pak pochopitelně ovlivní i geometrii modelu (a komplikuje výrobu výztuže). Počet profilů táhla by neměl být velký, raději volíme větší střižnost třmínků; větší profily (fsw ≥ 16 mm) nejsou vhodné. Pozor také na dostatečné zakotvení třmínků – nutno zakotvit za styčníkem na rozdíl od běžných třmínků, což obvykle představuje delší háky). Šířku styčníku označíme x2. Svislá poloha styčníku 2 (obr. 5.10) je jako u nepřímo uložených konzol uvažována uvnitř třmínků táhla T23, ve vzdálenosti od líce ad = c + fsw + 0,5 ∙ y2. Hodnotu c + fsw označíme Δy.
- Výztuž táhla T14 při dolním líci ozubu uvažujeme nejprve ve dvou vrstvách jako u konzol:
\begin{gathered}
d_\text{k}'=c+\phi_\text{sw}+(1+0{,}6)\cdot\phi
\end{gathered}Poznámka:
více vrstev výrazně snižuje rameno vnitřních sil. Mezi jednotlivými vrstvami je nutné dodržet vzdálenosti stanovené při určování vnitřního zakřivení smyček, minimální vzdálenost jednotlivých vrstev bývá cca 50 mm.
Účinná výška ozubu:
\begin{gathered}
d_\text{k}'=h_\text{k}-d_\text{k}'=h_\text{k}-(c_\text{nom}+\phi_\text{sw}+0{,}5\cdot\phi+0{,}05/2)
\end{gathered}(Osová vzdálenost vrstev tahové výztuže je uvažována 50 mm).
- Rameno vnitřních sil je:
\begin{gathered}
z_\text{k}=d_\text{k}-\Delta y-0{,}5\cdot y_2=d_\text{k}-a_\text{d}
\end{gathered}- Rameno vnějších sil – reakce A:
\begin{gathered}
a_\text{c}+c_\text{nom}+0{,}5\cdot x_2+H_\text{Ed}/F_\text{Ed}(d_\text{k}'+\Delta h)
\end{gathered}- Stanovíme rameno a reakce A:
\begin{gathered}
a=ac+\Delta a+a_\text{H}
\end{gathered}(5.3)
kde je
Δa … vodorovná vzdálenost těžiště navržených třmínků (táhla T23) od bočního líce prvku: Δa = cnom + 0,5 ∙ x2. Do hodnoty ac doporučeno započítat vliv ∆ ≈ 15…25 mm (podle kap. 3) nepřesnosti výroby a montáže prvku podle ČSN EN 13760:2004;
aH … zohledňuje působení vodorovné síly:
\begin{gathered}
a_\text{H}=\frac{H_\text{Ed}}{A}(d_\text{k}'+\Delta h)
\end{gathered}(5.4)
- Odhadneme rameno vnitřních sil ozubu
\begin{gathered}
z_\text{k}=h_\text{k}-d_\text{k}'-a_\text{d}
\end{gathered}(5.5)
Hodnota dk představuje vzdálenost mezi dolním lícem ozubu a těžištěm tahové výztuže T14. Na začátku výpočtu musíme odhadnout průměr výztuže, tloušťku betonové krycí vrstvy výztuže, počet vrstev výztuže a výšku tlačené oblasti ad. Po stanovení síly v táhle je nutné tyto předpoklady překontrolovat a případně upravit.
- Stanovíme sklon první vzpěry:
\begin{gathered}
\theta_1=\text{arctan}(z_\text{k}/a)
\end{gathered}(5.6)
- Stanovíme sílu v první vzpěře:
\begin{gathered}
C_{12}=A/\sin\cdot\theta_1
\end{gathered}(5.7)
- Tlaková síla při horním líci ozubu:
\begin{gathered}
C_{26}=C_{12}\cdot\cos\theta_1
\end{gathered}(5.8)
- Výška tlačeného pásu při horním líci (ve styčníku 2 – viz obr. 5.10) se stanoví z momentové rovnováhy ke styčníku 2, kterou lze vyjádřit:
\begin{gathered}
F_{14}\cdot z_\text{k}-H_\text{Ed}\cdot(z_\text{k}+d_\text{k}'+\Delta h)-F_\text{Ed}\cdot a=0
\end{gathered}- Rovnici upravíme na tvar:
\begin{gathered}
F_{14}\cdot z_\text{k}/F_\text{Ed}-H_\text{Ed}\cdot(z_\text{k}+d_\text{k}'+\Delta h)/F_\text{Ed}-a=0
\end{gathered}Předpokládá se napětí ve styčníku σRd,max (pozor, styčník CTC)
Z rovnováhy ve vodorovném směru určíme sílu F14 (b je šířka ozubu):
\begin{gathered}
F_{14}-H_\text{Ed}=y_2\cdot b\cdot\sigma_\text{Rd,max}
\end{gathered}a šířka x2 je na rozdíl od konzoly dána šířkou táhla T23.
Po úpravě dostaneme rovnici:
\begin{gathered}
z_\text{k}/F_\text{Ed}\cdot(F_{14}-H_\text{Ed})+H_\text{Ed}\cdot(d_\text{k}{'}+\Delta h)/F_\text{Ed}-a=0\\\\
z_\text{k}/F_\text{Ed}\cdot(y_2\cdot b\cdot\sigma_\text{Rd,max})+H_\text{Ed}\cdot(d_\text{k}{'}+\Delta h)/F_\text{Ed}-a=0
\end{gathered}Za rameno vnitřních sil dosadíme
\begin{gathered}
z_\text{k}=d_\text{k}-\Delta y-0{,}5\cdot y_2\\\\
(d_\text{k}-\Delta y-0{,}5\cdot y_2)\cdot(y_2\cdot b\cdot\sigma_\text{Rd,max})+H_\text{Ed}\cdot(d_\text{k}'+\Delta h)-a\cdot F_\text{Ed}=0\\\\
-y_2^2\cdot(y_2\cdot b\cdot\sigma_\text{Rd,max})+y_2\cdot(d_\text{k}-\Delta y)\cdot(b\cdot\sigma_\text{Rd,max})+H_\text{Ed}\cdot(d_\text{k}'+\Delta h)-a\cdot F_\text{Ed}=0\\\\
0{,}5y_2^2-y_2\cdot(d_\text{k}-\Delta y)+F_\text{Ed}\cdot(-H_\text{Ed}/F_\text{Ed}\cdot(d_\text{k}'+\Delta y)+a)/(b\cdot\sigma_\text{Rd,max})=0
\end{gathered}Označíme jako pomocnou proměnnou X výraz:
\begin{gathered}
X=(a-H_\text{Ed}/F_\text{Ed}\cdot(d_\text{k}'+\Delta h))\cdot F_\text{Ed}/(b\cdot\sigma_\text{Rd,max})\\\\
0{,}5y_2^2-y_2\cdot(d_\text{k}+\Delta y)+X=0
\end{gathered}Řešením kvadratické rovnice je vztah pro výšku styčníku 2:
\begin{gathered}
y_2=(d_\text{k}-\Delta y)-\sqrt{(d_\text{k}-\Delta y)^2-4\cdot0{,}5\cdot X}
\end{gathered}(5.9)
- Upřesníme těžiště horního tlačeného pásu:
\begin{gathered}
a_\text{d}=c_\text{nom}+\phi_\text{st}+0{,}5\cdot y_2
\end{gathered}(5.10)
kde ϕst je průměr svislých třmínků u ozubu a cnom je tloušťka betonové krycí vrstvy třmínků.
- Tím je daná geometrie modelu A, překontrolujeme rameno vnitřních sil a sílu v první vzpěře podle vztahů (5.6) až (5.7).
- Stanovíme sílu v táhle T14:
\begin{gathered}
T_{14}=\frac{A\cdot a+H_\text{Ed}(z_\text{k}+d_\text{k}'+\Delta h)}{z_\text{k}}
\end{gathered}(5.11)
Hlavní tahová výztuž se stanoví (výztuž táhla)
\begin{gathered}
A_\text{s14}=T_{14}/f_\text{yd}
\end{gathered}Táhlo T14 provádíme obvykle ve tvaru vložených smyček ve dvou až maximálně třech vrstvách. Počet vrstev tahové výztuže opět významně ovlivňuje geometrii modelu – zmenšuje rameno vnitřních sil zk (obr. 5.10). Pokud jsme při prvním návrhu neodhadli počet vrstev tahové výztuže, je nutné opět přepočítat předchozí vztahy (5.4) až (5.11).
Poznámka:
vzdálenosti jednotlivých vrstev ovlivňují minimální průměr vnitřního zakřivení smyček, proto je nutné polohu jednotlivých vrstev upřesnit spolu s definováním minimálního poloměru vnitřního zakřivení.
Minimální průměr vnitřního zakřivení smyčky táhla se stanoví podle vztahu:
\begin{gathered}
\phi_\text{m,min}=\frac{F_\text{bt}}{f_\text{cd}}\cdot\bigg(\frac{1}{a_\text{b}}+\frac{1}{2\phi}\bigg)
\end{gathered}(5.12)
kde je
Fbt … síla v jedné větvi smyčky, která je třeba zakotvit;
ab … poloviční osová vzdálenost mezi jednotlivými vrstvami výztuže nebo vzdálenost osy prutu smyčky od líce prvku;
ø … průměr prutu smyčky.
Obr. 5.12 Rozšíření styčníkové oblasti 3
Obr. 5.13 Ozub nosníku
- Překontrolujeme zakotvení výztuže táhla T14 ve formě smyček ve styčníku 1. Obdobně jako u konzoly je nutné překontrolovat vnitřní poloměr zakřivení smyček podle vztahu 8.1, uvedeného v ČSN EN 1992-1-1:2006 [1], aby nemohlo dojít k drcení betonu uvnitř smyček.
Poznámka:
je nutné překontrolovat nejen krajní smyčku u líce, ale i další vnitřní smyčky.
Dále překontrolujeme zakotvení táhla za styčníkem 4 (obr. 5.11 a obr. 5.12) – rovných prutů obvykle ve špatných podmínkách soudržnosti [1]. Polohu styčníku 4 stanovíme z geometrie modelu podle obr. 5.1, obr. 5.11 a obr. 5.12 a obr. 5.13.
- Překontrolujeme zakotvení táhla T23. Třmínky musí být v tlačené části nosníku (ve styčníku 2 podle obr. 5.10) zakotveny v souladu s ČSN EN 1992-1-1:2006 [1].
Poznámka:
obvykle jsou zakotveny přesahem větví třmínku, zakotvení háky podle běžných konstrukčních zásad není dostatečné.
- Překontrolujeme zakotvení hlavní tahové výztuže nosníku ve styčníku 3 [1] – viz obr. 5.11. Pokud by nebyla dostatečná kotevní délka l3 daná geometrií styčníku 3:
\begin{gathered}
T_{23}'=\frac{l_3}{l_\text{bd}}T_{23}\space\space\text{a}\space\space T_{35}'=\frac{l_3}{l_\text{bd}}T_{35}
\end{gathered}doplníme v obou směrech výztuž na síly viz obr. 5.12.
kde je
l3 … šířku táhla T23 ve styčníku 3. Stanovení šířky táhla bylo vysvětleno v kap. 2;
lbd … návrhová kotevní délka hlavní tahové výztuže ve styčníku 3.
- Stanovíme výztuž v táhle T45 a T67
\begin{gathered}
T_{45}=T_{23}=T_{67}
\end{gathered}(5.13)
Z modelu náhradní příhradoviny na obr. 5.1 je patrno, že síly v uvedených táhlech jsou stejné (zanedbáváme tak průběh vnějšího zatížení, což je ve prospěch bezpečnosti). Šířku táhla T45 stanovíme jako součet polovičních vodorovných vzdáleností styčníků 3 a 5 a styčníků 5 a 7.
- Sklon tlačené diagonály θ … cot θ1= a/zk
Poznámka:
sklon tlačené diagonály je nejoptimálnější kolem 45°. Sklon je však definován geometrií oblasti a jejím vyztužení.
- Síla v betonové diagonální vzpěře
\begin{gathered}
F_{14}=F_\text{Ed}/\sin\theta
\end{gathered}Délka betonové vzpěry H je H=\sqrt{a^2+z_\text{k}^2} (označení podle kap. 1 a [1]).
Únosnost betonové vzpěry se uvažuje podle vztahu
\begin{gathered}
\sigma_\text{Rd,max}=0{,}6\cdot v'f_\text{cd}
\end{gathered}Obr. 5.14 Příčné tahy v tlačené diagonále
- V betonové vzpěře C12 (obr. 5.13 a obr. 5.14) vznikají příčné tahy, na které je nutné navrhnout konstrukční výztuž svislou a vodorovnou.
Uvažujeme buď zjednodušení příčných tahů T = 0,22F12, nebo přesněji skutečné
příčné tahy podle vzorce:
\begin{gathered}
T=\frac{1}{4}\bigg(1-0{,}7\frac{a}{h}\bigg)F_{12}
\end{gathered}(pozor – zde a je šířka tlačené diagonály u styčníku 1 nebo 2. a h = H/2 je poloviční délka tlačené diagonály, označení je podle ČSN EN 1992-1-1:2006 [1])
Jako šířku tlačené diagonály u styčníku 1 uvažujeme
\begin{gathered}
a=\sqrt{(x_1^2+y_1^2)}
\end{gathered}obdobně u styčníku 2 se uvažuje a = la ∙ sin θ1. (la je délka ložiska – styčné desky).
- Vodorovný příčný tah v betonové vzpěře (viz obr. 5.13 a obr. 5.14):
\begin{gathered}
T_\text{wh}=2T\cdot\sin\theta_1=0{,}44F_{12}\sin\theta_1=0{,}44F_\text{Ed}
\end{gathered}Přitom je nutné dodržet u krátkých konzol ve smyslu ČSN EN 1992-1-1:2006 minimální plochu vodorovné konstrukční výztuže 0,25Amain. To doplníme do předchozího vztahu
\begin{gathered}
T_\text{wh}=0{,}44F_\text{Ed}\ge0{,}25\cdot F_{14}\space\space\text{pokud}\space\space a\le0{,}5z_\text{k}
\end{gathered}- Svislý příčný tah v betonové vzpěře (viz obr. 5.13 a obr. 5.14):
\begin{gathered}
T_\text{wv}=2T\cdot\cos\theta_1=0{,}44F_\text{c}\cos\theta_1=0{,}44F_\text{Ed}\cdot\cos\theta_1
\end{gathered}Přitom je nutné dodržet u dlouhých konzol ve smyslu ČSN EN 1992-1-1:2006 minimální plochu svislé konstrukční výztuže Aswv ≥ 0,5 ∙ FEd/fywd. To doplníme do předchozího vztahu:
\begin{gathered}
T_\text{wv}=2T\cdot\cos\theta_1=0{,}44F_c\cos\theta_1=0{,}44F_\text{Ed}\cdot\cot\theta_1\ge0{,}5F_\text{Ed},\space\space\text{pokud}\space\space a\ge0{,}5z_\text{k}
\end{gathered}- Přesnějším výpočtem příčných tahů dostaneme (viz obr. 5.13 a obr. 5.14) příznivější hodnoty z hlediska vyztužení:
Vyjdeme ze vzorce T=\frac{1}{4}\bigg(1-0{,}7\frac{a}{h}\bigg)F_{12} (pozor – zde a je šířka tlačené diagonály u styčníku 1 nebo 2, a h je poloviční délka tlačené diagonály, označení je podle ČSN EN 1992-1-1:2006). Jako šířku tlačené diagonály u styčníku 1 uvažujeme a=\sqrt{(x_1^2+y_1^2)} obdobně u styčníku 2 se uvažuje a = la ∙ sin θ. (la je délka ložiska – styčné desky). Délka diagonály je h=\sqrt{(a^2+z^2)} (a je rameno vnějších sil a z je rameno vnitřních sil). Dosazením dostaneme skutečné příčné tahy v betonové vzpěře. Rozložení příčných tahů do vodorovného a svislého směru provedeme obdobně jako u zjednodušeného výpočtu.
- Ke stanovení konstrukčního vyztužení ozubu platí stejné konstrukční zásady vyztužení jako pro konzoly, viz kap. 3 a kap. 4. Konstrukční vyztužení ozubu – viz také obr. 5.12.
Poznámky k vyztužení:
Z modelu náhradní příhradoviny (obr. 5.1) vyplývá, že táhla T23, T45 a T67 jsou stejně namáhána, rovněž stejná je staticky nutná plocha výztuže třmínků. Táhla se liší svojí šířkou (obr. 5.1). Vodorovné táhlo T14 se musí dostatečně zakotvit ve styčníku 1 (smyčkami) a za styčníkem 4 (obvykle špatné podmínky soudržnosti). Hlavní tahová výztuž nosníku se musí zakotvit ve styčníku 3, pro zakotvení lze použít dodatečnou smyčkou výztuž ve druhé (a popřípadě další) vrstvě (viz obr. 5.11 a obr. 5.12). Stejná tlaková síla jako v C12 je i ve vzpěře C34. Všechny tlačené vzpěry nutno vyztužit na vznikající příčné tahy, minimálně však podle konstrukčních zásad – viz obr. 5.14.
5.3 NÁVRHOVÝ MODEL B
Model náhradní příhradoviny modelu B je na obr. 5.2 a obr. 5.15.
- Stanovíme sklon šikmé výztuže θ2. Optimální sklon je kolmý na poruchovou trhlinu, sklon je dán geometrií navržené výztuže a vlastní poruchové oblasti. Na začátku můžeme vycházet ze sklonu 45°, po navržení výztuže sklon upřesníme a posouzení opakujeme se skutečným sklonem táhla T23 (obr. 5.2 a obr. 5.15). Síla v táhle T23:
\begin{gathered}
T_{23}=A/\sin\theta_2
\end{gathered}(5.14)
- Překontrolujeme zakotvení táhla ve styčníku 2 (obr. 5.2). Šikmou výztuž navrhujeme obvykle ve tvaru smyček, nebo šikmého prutu, kotveného nahoře pomocí kotevní desky. Táhlo zakotvíme na druhé straně přesahem s hlavní tahovou výztuží nosníku. U zakotvení ve styčníku 2 je nutné překontrolovat velikost minimálního průměru zakřivení výztužné vložky podle vztahu (5.12) a vzdálenosti prutů (smyček), pokud je výztuž šikmého táhla ve více vrstvách. Vzdálenost prutů musí splňovat konstrukční zásady podle [1] a vztah (5.12).
- Ověříme únosnost betonových vzpěr C12 a C24 při uvažování styčníku CTC:
\begin{gathered}
C_{12}=A\space\space\text{a}\space\space C_{24}=C_{12}\cdot\cot\theta_2
\end{gathered}(5.15)
Velmi častým problémem u modelu B je zakotvení šikmé výztuže (táhlo T23) v horním rohu ozubu (viz obr. 5.2). Pokud je kotevní délka prutu (obvykle ve formě smyčky) nedostatečná, můžeme využít následující řešení:
- Zakotvit šikmé pruty kotevními spojkami nebo přivařenými kotevními destičkami.
- Zvětšit plochu výztuže tažených šikmých prutů. Tím se sníží využití výztuže a zkrátí se potřebná kotevní délka.
- Zvýšit třídu betonu, tím se výrazně zkrátí potřebná kotevní délka.
- Změnit návrhový model, např. podle obr. 5.7.
- Vytvořením kombinovaného modelu A a B (viz následující kapitola).
Všechny tlačené vzpěry nutno vyztužit na vznikající příčné tahy, minimálně však podle konstrukčních zásad – viz obr. 5.14 a obr. 5.16. Postup stanovení příčných tahů je stejný jako u modelu A – viz předchozí kapitola. Konstrukční zásady vyztužení jsou opět obdobné jako u modelu A – bližší viz obr. 5.17.
Obr. 5.15 Ozub nosníku – model B – model náhradní příhradoviny
Obr. 5.16 Ozub nosníku – model B – příčné tahy ve vzpěrách
Obr. 5.17 Principy vyztužení ozubů
5.4 KOMBINOVANÝ MODEL A + B
Vzhledem k tomu, že nelze použít model B samostatně, je nutné jej kombinovat s modelem A – viz obr. 5.8. Obvykle se rozdělí svislá zatížení do dvou částí cca 55 % a na každou část se navrhne výztuž oblasti. Při kombinovaném modelu je nutné v některých styčnících uvažovat současně namáhání od obou modelů. Přiřazení 55 % zatížení každému modelu neznamená předimenzování konstrukce. Totiž celkové zatížení se rozdělí do obou modelů podle poměru jejich tuhostí. Tuhosti jsou obtížně definovatelné zvláště na začátku výpočtu. Po dokončení výpočtu lze vyjádřením poměru tuhostí jednotlivých dílčích modelů optimalizovat rozdělení zatížení a tím optimalizovat vyztužení oblasti. Vodorovné zatížení se přiřadí pouze k modelu A. V návrhových postupech označíme reakci A jako reakci A*. Ve styčnících, kde se setkávají vzpěry obou modelů, je nutné současně uvažovat síly z obou modelů. V následujícím návrhovém postupu jsou označeny síly z modelu A horním indexem (1) a síly z modelu B horním indexem (2).
Návrhový postup kombinovaného modelu A + B
- Tlaková síla při horním líci ozubu pro stanovení výšky styčníku 2(1), viz obr. 5.8
\begin{gathered}
C^{(1)+(2)}=C_{12}^{(1)}\cdot\cos\theta_1+C_{24}^{(2)}
\end{gathered}(5.16)
je součtem tlakových sil v betonových vzpěrách obou modelů A a B.
- Výška tlačeného pásu při horním líci (ve styčníku 2(1))
\begin{gathered}
y_2=C^{(1)+(2)}/(\sigma_\text{Rd,max}\cdot b)
\end{gathered}(5.17)
kde je
σRd,max … návrhová únosnost betonu v tlaku ve styčníku CTC (viz kap. 1);
b … šířka ozubu.
V ostatních krocích je postup stejný s postupem pro jednotlivé modely A a B. Konstrukční výztuž na zachycení příčných tahů vznikajících v betonových diagonálách je doporučeno řešit společně pro oba modely – viz obr. 5.17.
Poznámka k návrhu ozubů:
při návrhu ozubů na prefabrikovaných prvcích je nutné uvažovat s montážním otvorem pro fixování průvlaku po montáži. Obvykle se po montáži do otvoru osadí tyč kotvená do konzoly. Tyč se zalívá zálivkovým betonem, ale plnou soudržnost mezi prefabrikátem a zálivkou nelze zaručit; proto je vhodné plochu montážního otvoru neuvažovat při návrhu výztuže ozubu (šířku ozubu tedy redukovat o velikost montážního otvoru) – viz obr. 5.18.
Obr. 5.18 Ozuby nosníků s montážními prostupy
5.5 PRINCIPY VYZTUŽENÍ OZUBŮ NOSNÍKŮ
Ozuby průvlaků a desek obdobně jako konzoly představují z hlediska bezpečnosti a spolehlivosti konstrukce velmi významný prvek. Proto je nutné jejich návrhu věnovat maximální pozornost. Na dokumentaci pro ozuby je nutné uvádět všechny závazné parametry a předpoklady, které jsou při návrhu použity. Velmi vhodné je například uvádět nejen tloušťku betonové krycí vrstvy výztuže, ale i maximální toleranci v uložení rozhodující výztuže – maximální tloušťky betonové krycí vrstvy. Pro správný návrh je dobré znát i výrobní postup realizace prefabrikátu s ozubem.
Při návrhu ozubu je nutné po dokončení výpočtu a nakreslení výztuže ověřit předpokládanou geometrii modelu náhradní příhradoviny. Vzhledem k tomu, že se při prvním návrhu dá velmi špatně dostatečně přesně odhadnout všechny veličiny, které ovlivňují geometrii modelu, je obvykle nutné provést nové posouzení s upřesněnou geometrií modelu. Pro návrh ozubů by měla být vždy používána výztuž s vysokou duktilitou – třídy B nebo C.
Po návrhu výztuže táhel je nutné překontrolovat vznikají příčné tahy v betonových vzpěrách. Na příčné tahy je nutné navrhnou příslušnou ortogonální výztuž. Příčné tahy se musí překontrolovat u všech betonových vzpěr – viz obr. 5.13, obr. 5.16 a obr. 5.8.
Pro ozuby platí stejné konstrukční zásady jako pro nepřímo uložené konzoly – viz kap. 4. Principy vyztužení ozubů jsou na obr. 5.17.
Příklady výztuže ozubu při kombinovaném modelu návrhu viz obr. 5.19, obr. 5.20 a obr. 5.21.
Obr. 5.19
Obr. 5.20
Obr. 5.21
5.6 OZUBY NA NOSNÍCÍCH S NÁBĚHY
Pokud je například nutné vést instalace v blízkosti sloupů nad spodním lícem vazníků, lze navrhnout ozub vazníku s náběhem. Model náhradní příhradoviny je na obr. 5.22 V první části na obr. 5.22a je uveden model pro vynášení svislé síly a na obr. 5.22b je model pro přenos vodorovné síly. Největším problémem je dostatečné zakotvení šikmého táhla T23 ve styčníku 2 a vodorovného táhla ve styčníku 1. Vzhledem ke geometrii ozubu je dostatečné zakotvení řešitelné například pomocí přivařených kotevní destiček (pro svařování betonářské výztuže platí ČSN EN ISO 17660-1:2007). Uvedené řešení je velmi citlivé na realizaci a návrh těchto prvků vyžaduje značné zkušenosti v oblasti prefabrikovaných konstrukcí.
Obr. 5.22 Ozuby nosníků s náběhy – modely náhradní příhradoviny
5.7 OZUBY DESEK A SMYKOVĚ NEVYZTUŽENÉ OZUBY
Prefabrikovaná schodišťová ramena se nejčastěji ukládají svými ozuby na průběžné konzoly podest. Obdobně lze ukládat i výměny mezi prefabrikovanými stropními deskami. Ozuby desek (obr. 5.23 a obr. 5.24) odpovídají průběžným nepřímo uloženým konzolám, které byly analyzovány v kap. 4.
Obr. 5.23 Průběžný ozub deskové konstrukce – model náhradní příhradoviny
Obr. 5.24 Návrh řešení průběžného deskového ozubu
Ozuby desek obvykle nemívají smykovou výztuž. To je možné jen tehdy, pokud veškeré zatížení vyvozené smykem přebírá tlakové a tahové napětí v betonu. Vzhledem k velikosti ozubu nelze umístit ložisko dostatečně daleko od kraje prvku [27]. Při napětí pod styčnou deskou do hodnoty σ ≤ 0,08 fck může být styčná deska – ložisko posunuto blíže k okraji než u klasického ozubu (obr. 5.24). Její umístění je omezeno minimální vzdáleností jejího okraje od hrany konzoly a minimální vzdáleností působiště zatížení od vnitřního poloměru ohybu svislého třmínku. Pokud uvažujeme roznášení v betonové krycí vrstvě pod 45°, tlačená betonová diagonála zasahuje až k líci ozubu a nemusí být plně ovinuta výztuží jako u ozubů na nosnících. Předpokládá se tedy, že příčná tahová napětí v betonu nepřekročí pevnost betonu v tahu. Z tohoto důvodu také není nutné navrhovat přídavnou svislou a vodorovnou třmínkovou výztuž do průběžného ozubu.
Při návrhu průběžného ozubu je nutné navrhnout taženou výztuž při dolním líci a překontrolovat únosnost tlačené betonové diagonály s tím, že vznikající příčné tahy musí spolehlivě přenést beton v tahu. Styčník 2 (obr. 5.24), vzhledem k malému namáhání, lze uvažovat již od líce prvku s tím, že táhlo ve formě třmínku musí být ve styčníku dostatečně zakotveno. Z polohy styčníku 2 vyplývá geometrie modelu a sklon první tlačené betonové diagonály θ. Pro smykově nevyztužené části lze uvažovat sklon druhé tlačené diagonály θ = 45° a dalších betonových diagonál θ = 30° (oblast B). Při vyztužení oblasti je třeba pamatovat na to, že tato výztuž ovlivňuje sklon tlačené betonové diagonály. Návrh odpovídá průběžné, nepřímo uložené konzole, viz kap. 4.
5.7.1 Návrh podle ČSN EN 1992-1-1:2006 [1]
Podle článku 10.9.4.6. normy ČSN EN 1992-1-1:2006 [1] lze navrhovat ozuby nosníků pomocí modelů náhradní příhradoviny. Norma definuje dva alternativní modely a jejich vyztužení. Norma připouští kombinaci modelů, nic bližšího dále není uvedeno. Modely jsou na obr. 5.3.
V levé části obr. 5.3 model náhradní příhradoviny odpovídá modelu A podle obr. 5.1. Druhý model odpovídá modelu B podle obr. 5.9. U modelu A nutno pamatovat na přenos vodorovných sil.
5.8 SPECIÁLNÍ VÝZTUŽ OZUBŮ
Výztuž ozubů prefabrikovaných prvků je poměrně složitá a vyžaduje velmi pečlivé provedení. Pro zjednodušení někdy komplikovaného vyztužení je možné použít speciální ozuby od firmy PEIKKO nebo PFEIFER. Jedná se principiálně o dva typy ozubů. První typ (PEIKKO) řeší namáhání ozubu ocelovým svařencem, který se zabuduje do prvku s příslušnou staticky nutnou a konstrukční výztuží.
Druhým typem je ocelový ozub PFEIFER, který řeší únosnost vlastního ozubu ocelovým HEA nosníkem (obr. 5.25 a obr. 5.26 a obr. 5.27). Svislou tahovou výztuž nahrazuje přivařeným výztužným prutem většího průměru, který je při spodním líci opatřen přivařenou kotevní deskou. To výrazně zjednodušuje vyztužení kraje prefabrikovaného prvku u ozubu.
Obr. 5.25 Speciální zabudované prvky pro řešení ozubů nosníků

Obr. 5.26
Obr. 5.27
5.9 PŘÍKLADY NÁVRHU A VYZTUŽENÍ OZUBŮ
5.9.1 Ozub průvlaku 1
Navrhněte výztuž ozubu průvlaku (podle obr. 5.28) z betonu C50/60 s betonářskou výztuží B500B, betonová krycí vrstva třmínků 25 mm. Průřez průvlaku v poli je 1000 x 400 mm, ozub má rozměry 400 x 350 x 500 mm, průvlak má rozpětí 6,4 m, modulová síť je 7,20 m. Průvlak je zatížen rovnoměrným zatížením 160 kN/m. Reakce průvlaku je 576 kN, průvlak je při dolním líci vyztužen 6 x ø25 a při horním líci 2x ø14, těžiště horní výztuže je 50 mm od horního líce průvlaku. Horizontální síla není zadána, předpokládáme HEd = 0,2A =116 kN. Roznášecí deska 300 x 250 mm. Vzhledem k nepřesnostem výroby a montáže je uvažována tolerance 20 mm.
Předpokládáme rozdělení namáhání do dvou modelů náhradní příhradoviny v poměru 55 % pro model A (317 kN) a 55 % pro model B (317 kN). Zvýšené zatížení vyrovnává rozdílné tuhosti jednotlivých modelů.
Obr. 5.28 Příklad ozubu nosníku
Materiály
Beton C50/60:
\begin{gathered}
f_\text{cd}=33{,}3\text{ MPa};\space\alpha_\text{cc}=1{,}0;\space\varepsilon_\text{cu3}=3{,}5\space‰;\space\eta=1{,}0;\space\lambda=0{,}8;\space v'=(1-f_\text{ck}/250)=0{,}8
\end{gathered}Styčník s táhlem CTC:
\begin{gathered}
\sigma_\text{Rd,max}=0{,}85\cdot v'f_\text{cd}=22{,}7\text{ MPa}
\end{gathered}Styčník s více táhly CTT:
\begin{gathered}
\sigma_\text{Rd,max}=0{,}75\cdot v'f_\text{cd}=20{,}0\text{ MPa}
\end{gathered}Betonová vzpěra se vznikem trhlin:
\begin{gathered}
\sigma_\text{Rd,max}=0{,}6\cdot v'f_\text{cd}=16{,}0\text{ MPa}
\end{gathered}Výztuž B500B:
\begin{gathered}
f_\text{yd}=\frac{f_\text{yk}}{\gamma_\text{s}}=\frac{500}{1{,}15}=435\text{ MPa}
\end{gathered}5.9.1.1 Návrh výztuže modelu A (včetně vodorovného zatížení)
Účinky vodorovné síly ΔT23 ≈ 116 · hk/h = 116 · 0,5 = 58 kN. V táhle T23 je síla 317 + 58 = 375 kN, staticky nutná plocha výztuže je As = 375 000/435 = 862 mm2.
Navrhneme 4 dvoustřižné třmínky ø12 mm po 65 mm (As = 905 mm2) x2 = 195.
Těžiště táhla od líce ozubu:
\begin{gathered}
\Delta a=25+98+6=129\text{ mm}
\end{gathered}Vzdálenost reakce od líce ozubu:
\begin{gathered}
a_\text{c}=175+20=195\text{ mm}
\end{gathered}V ozubu předpokládáme dvě vrstvy hlavní tahové výztuže z prutů o průměru 16 mm. Vrstvy výztuže uvažujeme po 60 mm (osově).
Těžiště styčníku od dolního líce:
\begin{gathered}
25+12+16/2+60/2=75\text{ mm }(d_\text{k}')
\end{gathered}Rameno a reakce A bude (vodorovná vzdálenost styčníku 1 a 2):
\begin{gathered}
a=a_\text{c}+\Delta a+H_\text{Ed}/A\cdot(d'_\text{k}+\Delta h)=195+129+116/317\cdot(75+10)=355\text{ mm}
\end{gathered}Stanovíme polohu styčníku 2:
\begin{gathered}
X=(H_\text{Ed}/F_\text{Ed}\cdot(d'_\text{k}+\Delta h)-a)\cdot F_\text{Ed}/(b\cdot\sigma_\text{Rd,max})=(355-116/317\cdot(75+10))\cdot317/(400\cdot22{,}7\cdot10^{-3})=11\space308
\end{gathered}Řešením kvadratické rovnice je vztah pro výšku styčníku 2:
\begin{gathered}
y_2=(d_\text{k}-\Delta y)\sqrt{(d_\text{k}-\Delta y)^2-2\cdot X}\\\\
y_2=(500-75-25-12)\sqrt{(388)^2-2\cdot11308}=30{,}3\text{ mm}
\end{gathered}Posuneme styčník 2 ještě o vliv modelu
\begin{gathered}
\text{B}-y_2^{(2)}=317/(400\cdot22{,}7\cdot10^{-3})=34{,}9\\\\
a_\text{d}=c_\text{nom}+\Delta y+y_2/2+y_2^{(2)}=25+12+30{,}3/2+34{,}9/2=69{,}6\text{ mm}
\end{gathered}Dále stanovíme rameno vnitřních sil ozubu:
\begin{gathered}
z_\text{k}=h_\text{k}-a_\text{d}-d_\text{k}'=500-69{,}6-75=355{,}4\text{ mm}
\end{gathered}Dále pak sklon tlačené diagonály C21 je
\begin{gathered}
\theta_1=\text{arccot}(a/z_\text{k})=\text{arccot}(355/355{,}4)\to45{,}0\degree
\end{gathered} Tlaková síla v betonové vzpěře je
\begin{gathered}
C_{12}=A/\sin\theta_1=317/\sin45{,}0\degree=448{,}3\text{ kN}
\end{gathered}Nyní stanovíme sílu v táhle T14:
\begin{gathered}
T_{14}=\frac{A\cdot a+H_\text{Ed}(z_\text{k}+d_\text{k}'+\Delta h)}{z_\text{k}}=\frac{317\cdot0{,}355+116\cdot(0{,}3554+0{,}075+0{,}01)}{0{,}3554}=460{,}4\text{ kN}
\end{gathered}Jako výztuž táhla T14 navrhneme smyčky z průměru ø16 mm. Staticky nutná plocha táhla je 460 400/435 = 1 059 mm2. To představuje nejméně čtyři smyčky ø16 umístěné uvnitř tažených třmínků ø12 mm. Skutečná plocha výztuže táhla je 1 609 mm2. Při šířce průřezu b = 400 mm a betonovém krytí 25 mm je prostor pro smyčky 400 – 2 · 25 – 2 · 12 = 326 mm. Smyčky mohou být umístěny vždy dvě vedle sebe. Budou tak dvě vrstvy výztuže. Výztuž bude využita z 66 %.
Dále překontrolujeme dostatečné zakotvení smyček.
Základní kotevní délka výztužného prutu:
\begin{gathered}
l_\text{bd,rqd}=\frac{\phi}{4}\cdot\frac{\sigma_\text{sd}}{f_\text{bd}}=\frac{16}{4}\cdot\frac{0{,}66\cdot435}{4{,}35}=264\text{ mm}
\end{gathered}Návrhová kotevní délka pro smyčku:
\begin{gathered}
l_\text{bd}=\alpha_1\cdot\alpha_2\cdot\alpha_3\cdot\alpha_4\cdot\alpha_5\cdot l_\text{bd,rqd}=0{,}7\cdot264=185\text{ mm}\ge l_\text{b,min}
\end{gathered}kde je
lb,min … minimální kotevní délka lb,min ≥ max [0,3 ∙ lb,rqd; 10 ∙ ø; 100 mm].
Pro smyčku je třeba překontrolovat minimální průměr zakřivení prutu ø=16 mm.
Pro krajní smyčku:
\begin{gathered}
a_\text{b}=25+12+8=45\text{ mm}\\\\
\phi_\text{m,min}=\frac{F_\text{bt}}{f_\text{cd}}\cdot\bigg(\frac{1}{a_\text{b}}+\frac{1}{2\phi}\bigg)=\frac{0{,}66\cdot87{,}4}{33\space300}\bigg(\frac{1}{0{,}045}+\frac{1}{0{,}032}\bigg)=0{,}093\text{ mm}
\end{gathered}Pro vnitřní smyčku:
\begin{gathered}
a_\text{b}=60/2=30\text{ mm}\\\\
\phi_\text{m,min}=\frac{F_\text{bt}}{f_\text{cd}}\cdot\bigg(\frac{1}{a_\text{b}}+\frac{1}{2\phi}\bigg)=\frac{0{,}66\cdot87{,}4}{33\space300}\bigg(\frac{1}{0{,}030}+\frac{1}{0{,}032}\bigg)=0{,}112\text{ mm}
\end{gathered}Při průměru zakřivení 112 mm (7ø) je délka osy čtvrtiny kruhu výztuže 100,5 mm. Zakotvení výztuže uvažujeme od líce roznášecí desky, k dispozici pro zakotvení prutu je tedy délka 250 mm, započítáme-li čtvrtinu délky smyčky, dostaneme délku zakotvení 287 mm, zakotvení výztužné smyčky ø16 vyhovuje. Na druhém konci ve styčníku 4 bude zakotven rovný prut ø16. Poloha styčníku 4 je ve vzdálenosti z4 od styčníku 2.
\begin{gathered}
z_4=(z-z_\text{k})\cot\theta_1=(0{,}9\cdot950-355{,}4)\cot45\degree=500\text{ mm}
\end{gathered}Základní kotevní délka bude jiná vzhledem k poloze výztuže:
\begin{gathered}
l_\text{bd,rqd}=\frac{\phi}{4}\cdot\frac{\sigma_\text{sd}}{f_\text{bd}}=\frac{16}{4}\cdot\frac{0{,}66\cdot435}{3{,}05}=377\text{ mm}
\end{gathered}Návrhová kotevní délka:
\begin{gathered}
l_\text{bd}=\alpha_1\cdot\alpha_2\cdot\alpha_3\cdot\alpha_4\cdot\alpha_5\cdot l_\text{bd,rqd}=1{,}0\cdot377=377\text{ mm}\ge l_\text{b,min}
\end{gathered}Smyčky z ø16 je nutné protáhnout nejméně 129 + 476 + 377 = 982 mm od vnitřního líce ozubu.
V táhle T23 je podle modelu náhradní příhradoviny síla rovna reakci A v uložení průvlaku a reakci z vodorovného zatížení ΔT23. V první tlačené vzpěře je síla 375/sin 45° = 530,3 kN.
Svislou a vodorovnou výztuž ozubu (na vznikající příčné tahy) navrhneme po dopočtení modelu B – druhé části.
Dále je nutné posoudit zakotvení hlavní tahové výztuže průvlaku 6ø25. Výztuž je umístěna v jedné vrstvě při spodním líci. Jedná se o nepřímé uložení výztuže. Z modelu náhradní příhradoviny vyplývá, že tahová síla ve výztuži je 460,4 kN (T35 = T14). Výztužné vložky jsou využity ze 36 %.
Základní kotevní délka výztužného prutu:
\begin{gathered}
l_\text{bd,rqd}=\frac{\phi}{4}\cdot\frac{\sigma_\text{sd}}{f_\text{bd}}=\frac{25}{4}\cdot\frac{0{,}36\cdot435}{4{,}35}=255\text{ mm}\space\space\text{a}\space\space l_\text{b,min}=250\text{ mm}
\end{gathered}Návrhová kotevní délka:
\begin{gathered}
l_\text{bd}=\alpha_1\cdot\alpha_2\cdot\alpha_3\cdot\alpha_4\cdot\alpha_5\cdot l_\text{bd,rqd}=1{,}0\cdot225=225\text{ mm}\ge l_\text{bd}=l_\text{b,min}=250\text{ mm}
\end{gathered}Výztužné vložky jsou uloženy ve třmínkách v délce 195 mm. Kotvení je nutné posílit, optimálním řešením je doplnění příložných smyček v dalších vrstvách dolní výztuže Vodorovné příložky nutno navrhnout na sílu T35‚:
\begin{gathered}
T_{35}'=T_{35}\frac{l_\text{bd}-l_\text{bd,exist}}{l_\text{bd}}=460{,}4\frac{250-195}{250}=101{,}3\text{ kN}\space\space\text{navrhneme}\space\space4\text{x}\phi10
\end{gathered}A svislé příložky nutno navrhnout na sílu T‘23, kterou vyjádříme jako:
\begin{gathered}
T_{23}'=T_{23}\frac{l_\text{bd}-l_\text{bd,exist}}{l_\text{bd}}=375\frac{250-195}{250}=82{,}5\text{ kN}\space\space\text{navrhneme}\space\space4\text{x}\phi10
\end{gathered}5.9.1.2 Návrh výztuže druhého modelu B
Sklon šikmé výztuže je dán geometrií modelu, z geometrie vyplývá klon θ2 = 48. Síla v šikmém táhle je
\begin{gathered}
T_{23}=317/\sin48\degree=426{,}7\text{ kN}
\end{gathered}Navrhneme šikmou výztuž z profilů ø22 mm. Staticky plocha výztuže je
\begin{gathered}
426\space700/435=981\text{ mm}^2
\end{gathered}Navrhneme smyčky z 4 x ø20. Skutečná nutná plocha výztuže 4 x ø20 je 1 257 mm2. Využití prutů táhla je 78 %.
Překontrolujeme zakotvení smyčkami:
\begin{gathered}
l_\text{bd,rqd}=\frac{\phi}{4}\cdot\frac{\sigma_\text{sd}}{f_\text{bd}}=\frac{20}{4}\cdot\frac{0{,}78\cdot435}{4{,}35}=390\text{ mm}
\end{gathered}Základní kotevní deska:
\begin{gathered}
l_\text{bd}=\alpha_1\cdot\alpha_2\cdot\alpha_3\cdot\alpha_4\cdot\alpha_5\cdot l_\text{bd,rqd}=0{,}7\cdot390=273\text{ mm}\ge l_\text{b,min}
\end{gathered}Je nutné překontrolovat průměr vnitřního zakřivení u smyčky. Smyčky jsou osově vzdáleny 80 mm.
\begin{gathered}
\phi_\text{m,min}=\frac{F_\text{bt}}{f_\text{cd}}\cdot\bigg(\frac{1}{a_\text{b}}+\frac{1}{2\phi}\bigg)=\frac{0{,}78\cdot136{,}6}{33\space300}\bigg(\frac{1}{0{,}040}+\frac{1}{0{,}040}\bigg)=0{,}160
\end{gathered}Pro zakotvení je k dispozici délka 200/sin 48° = 269 mm. Při uvažování vnitřní průměr zakřivení 160 mm. K dispozici je délka 269 – 100 + 141 = 310 mm. Kotevní délka prutu se smyčkami vyhovuje.
Konstrukční svislá a vodorovná výztuž ozubu
V tlačené diagonále první části modelu je tlaková síla C12 = 375 kN. Vznikající příčné tahy jsou T = 2 ∙ 0,22 ∙ 375 = 165 kN. Síla T se rozloží do vodorovného TH a svislého směru TV.
Ke každému směru připočteme účinky z druhého modelu B.
\begin{gathered}
T_\text{H}=165\cdot\sin45\degree+2\cdot0{,}22\cdot317=256\text{ kN}\to4\text{x}2\phi10\\\\
T_\text{V}=165\cdot\cos45\degree+2\cdot0{,}22\cdot317=256\text{ kN}\to4\text{x}2\phi10
\end{gathered}Ozub na průvlaku je podobný obrácené nepřímo uložené konzole. Pro konstrukční výztuž lze použít i kritéria minimálního vyztužení z konzol. Každý ozub by měl být vyztužen nejméně dvěma vodorovnými smyčkami s plochou 25 % hlavní tahové výztuže (pro krátké ozuby ac/hc ≤ 0,5) a neméně třemi svislými třmínky s únosností nejméně 0,5A (pro ozuby s velkým vyložením).
Konstrukční vodorovná výztuž by měla mít plochu nejméně 0,25 ∙ 1 059 = 265 mm2. To představuje nejméně 2 smyčky ø12. Navrženy jsou 4 smyčky – navržená výztuž vyhovuje.
Výztuž je zobrazena na obr. 5.29.
Obr. 5.29 Vyztužení ozubu
5.9.2 Ozub průvlaku 2
5.9.2.1 Návrh stejného ozubu s vyztužením pouze podle modelu A
Zatížení a geometrie a materiály jsou shodná s předchozím příkladem viz obr. 5.28.
Účinky vodorovné síly:
\begin{gathered}
\Delta T_{23}\approx116\cdot h_\text{k}/h=116\cdot0{,}5=58\text{ kN}
\end{gathered}V táhle T23 je síla:
\begin{gathered}
576+58=634\text{ kN}
\end{gathered}Staticky nutná plocha výztuže:
\begin{gathered}
A\text{s}=634\space000/435=1\space458\text{ mm}^2
\end{gathered}Navrhneme z osmi dvoustřižných třmínků ø12 mm po 50 mm (As = 1 810 mm2).
Těžiště táhla od líce ozubu:
\begin{gathered}
25+175+6=206\text{ mm}
\end{gathered}Vzdálenost reakce od líce ozubu:
\begin{gathered}
175+20=195\text{ mm}
\end{gathered}Předpokládáme čtyři vrstvy hlavní tahové výztuže z prutů o průměru 16 mm a vzdálenost vrstev osově je 60 mm.
Poznámka:
pro tři vrstvy nevyjde průměr vnitřního zakřivení tak, aby bylo možné umístit v každé vrstvě výztuže dvě smyčky vedle sebe.
Těžiště styčníku od dolního líce:
\begin{gathered}
25+12+16/2+90=135\text{ mm}
\end{gathered}Rameno a reakce A bude (vodorovná vzdálenost styčníku 1 a 2):
\begin{gathered}
a=195+206+116/576\cdot135=428\text{ mm}
\end{gathered}Stanovíme výšku styčníku 2:
\begin{gathered}
X=(H_\text{Ed}/F_\text{Ed}\cdot(d'_\text{k}+\Delta h)-a)\cdot F_\text{Ed}/(b\cdot\sigma_\text{Rd,max})=(428-116/576\cdot(135+10))\cdot576/(400\cdot22{,}7\cdot10^{-3})=25\space311
\end{gathered}Řešením kvadratické rovnice je vztah pro výšku styčníku 2:
\begin{gathered}
y_2=(d_\text{k}-\Delta y)\sqrt{(d_\text{k}-\Delta y)^2-2\cdot X}\\\\
y_2=(500-135-25-12)\sqrt{(365-37)^2-2\cdot25\space311}=89\text{ mm}
\end{gathered}Stanovíme polohu styčníku 2 – těžiště styčníku je od horního líce vzdálenost:
\begin{gathered}
a_\text{d}=25+12+y_2/2=25+12+89/2=25+12+44{,}5=81{,}5\text{ mm}
\end{gathered}Dále stanovíme rameno vnitřních sil ozubu
\begin{gathered}
z_\text{k}=500-135-81{,}5=284\text{ mm}
\end{gathered}Dále pak sklon tlačené diagonály C21:
\begin{gathered}
\theta_1=\text{arccot}(428/284)=33{,}6\degree
\end{gathered}Tlaková síla v betonové vzpěře je
\begin{gathered}
C_{12}=A/\sin\theta_1=576/\sin33{,}6\degree=1\space041\text{ kN}\\\\
C_{26}=1\space041\cos34\degree=863\text{ kN}
\end{gathered}Nyní stanovíme sílu v táhle T14:
\begin{gathered}
T_{14}=\frac{A\cdot a+H_\text{Ed}(z_\text{k}+d_\text{k}'+\Delta h)}{z_\text{k}}=\frac{576\cdot0{,}428+116\cdot(0{,}284+0{,}135+0{,}01)}{0{,}284}=1\space043\text{ kN}
\end{gathered}Jako výztuž táhla T14 navrhneme smyčky z průměru ø16 mm. Staticky nutná plocha táhla je 1 043 000/435 = 2 398 mm2. To představuje nejméně osm smyček ø16 umístěné uvnitř tažených třmínků ø12 mm (4 vrstvy). Skutečná plocha výztuže táhla je 3216 mm2. Při šířce průřezu b = 400 mm a betonovém krytí 25 mm je prostor pro smyčky 400 – 2 ∙ 25 – 2 ∙ 12 = 326 mm. Smyčky mohou být umístěny vždy dvě vedle sebe. Výztuž bude využita z 74 %.
Dále překontrolujeme dostatečné zakotvení smyček.
Základní kotevní délka výztužného prutu:
\begin{gathered}
l_\text{bd,rqd}=\frac{\phi}{4}\cdot\frac{\sigma_\text{sd}}{f_\text{bd}}=\frac{16}{4}\cdot\frac{0{,}74\cdot435}{4{,}35}=296\text{ mm}
\end{gathered}Návrhová kotevní délka:
\begin{gathered}
l_\text{bd}=\alpha_1\cdot\alpha_2\cdot\alpha_3\cdot\alpha_4\cdot\alpha_5\cdot l_\text{bd,rqd}=0{,}7\cdot296=207\text{ mm}\ge l_\text{b,min}
\end{gathered}kde je
lb,min … minimální kotevní délka lb,min ≥ max [0,3 lb,rqd; 10 ∙ ø; 100 mm].
Pro smyčku je třeba překontrolovat minimální poloměr zakřivení prutu.
Pro krajní smyčku:
\begin{gathered}
\phi_\text{m,min}=\frac{F_\text{bt}}{f_\text{cd}}\cdot\bigg(\frac{1}{a_\text{b}}+\frac{1}{2\phi}\bigg)=\frac{0{,}74\cdot87{,}4}{33\space333}\bigg(\frac{1}{0{,}045}+\frac{1}{0{,}032}\bigg)=0{,}104\text{ mm}
\end{gathered}Pro vnitřní smyčku:
\begin{gathered}
\phi_\text{m,min}=\frac{F_\text{bt}}{f_\text{cd}}\cdot\bigg(\frac{1}{a_\text{b}}+\frac{1}{2\phi}\bigg)=\frac{0{,}74\cdot87{,}4}{33\space333}\bigg(\frac{1}{0{,}03}+\frac{1}{0{,}032}\bigg)=0{,}125\text{ mm}
\end{gathered}Při průměru zakřivení 125 mm je délka osy čtvrtiny kruhu výztuže 110 mm. Zakotvení výztuže uvažujeme od líce roznášecí desky, k dispozici pro zakotvení prutu je tedy délka 250 mm, započítáme-li čtvrtinu délky smyčky, dostaneme délku zakotvení 281 mm, zakotvení výztužné smyčky ø16 vyhovuje.
Poznámka:
smyčky budou široké 125 + 32 = 157 mm, mezi líci smyček zůstane mezera 326 – 2 ∙ 157 = 12 mm ≤ 1,2 ∙ 16 = 19,2 mm, prostor mezi smyčkami je nedostatečný.
Na druhém konci ve styčníku 4 bude zakotven rovný prut ø16. Poloha styčníku 4 je ve vzdálenosti z4 od styčníku 2.
\begin{gathered}
z_4=(z-z_\text{k})\cot\theta_1=(0{,}9\cdot950-284)\cot34\degree=847\text{ mm}
\end{gathered}Základní kotevní délka bude jiná vzhledem k poloze výztuže:
\begin{gathered}
l_\text{bd,rqd}=\frac{\phi}{4}\cdot\frac{\sigma_\text{sd}}{f_\text{bd}}=\frac{16}{4}\cdot\frac{0{,}74\cdot435}{3{,}05}=422\text{ mm}
\end{gathered}Návrhová kotevní délka:
\begin{gathered}
l_\text{bd}=\alpha_1\cdot\alpha_2\cdot\alpha_3\cdot\alpha_4\cdot\alpha_5\cdot l_\text{bd,rqd}=422\text{ mm}\ge l_\text{b,min}
\end{gathered}Smyčky z ø16 je nutné protáhnout nejméně 206 + 847 + 422 = 1 475 mm od vnitřního líce ozubu.
V první tlačené vzpěře je síla 1 041 kN.
Konstrukční svislá a vodorovná výztuž ozubu
V tlačené diagonále je tlaková síla 1 041 kN.
C12 = 1041 kN. Vznikající příčné tahy jsou T = 2 ∙ 0,22 ∙ 1041 = 458 kN. Síla T se rozloží do vodorovného TH a svislého směru TV.
\begin{gathered}
T_\text{H}=458\cdot\sin34\degree=256\text{ kN}\to3\text{x}2\phi12\\\\
T_\text{V}=458\cdot\cos34\degree=380\text{ kN}\to A_\text{sV}=380\space000/435=874\text{ mm}\to4\text{x}2\phi12
\end{gathered}Výztuž je zobrazena na obr. 5.30.
Druhé řešení ozubu jen pomocí modelu A je nevhodné, protože vyžaduje velké množství tahové výztuže ve formě smyček při spodním líci. Kombinovaný model A+B dává optimální řešení výztuže oblasti.
Obr. 5.30 Vyztužení ozubu
6 OTVORY V NOSNÍCÍCH
S prostupy v nosnících se velmi často setkáváme jak u monolitických, tak u prefabrikovaných železobetonových konstrukcí. Prostupy se většinou provádějí pro snadnější vedení instalací (obr. 6.1 až obr. 6.2). Prostup v nosníku ovlivňuje průběh vnitřních sil v jeho okolí. Z hlediska návrhu nosníku můžeme prostupy rozdělit na malé a velké. U malých prostupů zůstává v jeho blízkém okolí přibližně v platnosti Bernoulliova hypotéza zachování rovinnosti průřezu po deformaci nosníku a lze vytvořit běžný příhradový model nosníku s přihlédnutím k poloze prostupu. Zpravidla se jedná o kruhové prostupy. Pokud je prostup nevhodně umístěn nebo je velký, neplatí zde už Bernolliova hypotéza o zachování rovinnosti průřezu. Prostup výrazně ovlivňuje rozdělení vnitřních sil v oblasti prostupu a je nutné vytvořit modely náhradní příhradoviny v D-oblastech před a za prostupem a v horním a dolním pasu kolem prostupu. Pro všechny prostupy platí podmínka plynulého přechodu modelů náhradní příhradoviny do sousedních částí prvku. Velikost poruchové oblasti lze odhadnout na základě Saint Venantovy hypotézy, podle které je délka poruchové oblasti přibližně rovna výšce prvku (obr. 6.3).
Obr. 6.1
Obr. 6.2
Obr. 6.3 Poruchové oblasti kolem prostupu v nosníku
V normě ČSN EN 1992-1-1 [1] nejsou k řešení prostupů bližší pravidla. Při návrhu prostupů v nosnících lze vyjít z předpisů DAfStB 459 [16], DAfStB 525 [20], BetonKalender 2001 [7], BetonKalender 2005 [8], BetonKalender 2009 [10] a podobně. Německé předpisy sice vycházejí z DIN 1045-1 [2], ale vycházejí ze stejných zásad tvorby modelů náhradní příhradoviny jako jsou uvedeny v [1]. Následné posouzení jednotlivých prvků modelu jako jsou styčníky, tlačené a tažené pruty je nutné provést v souladu s ČSN EN 1992-1-1 [1]. Postup návrhu je přiblížen v následujících odstavcích.
Prostupy s přilehlými částmi jsou oblasti, které velmi často rozhodujícím způsobem ovlivňují chování prvků. Prostupům se často nevěnuje dostatečná pozornost, což může vést k nedostatečné únosnosti celého prvku. Kolem prostupů je nutné umístit nosnou výztuž podle závěrů výpočtu a konstrukční výztuž podle zásad uvedených v [1]. V rozích prostupů, ze kterých se šíří poruchové trhliny, je nutné vkládat konstrukční šikmou výztuž, která podstatně zvyšuje duktilitu celé oblasti. Při návrhu oblasti nosníku s prostupem je nutné po dokončení výpočtu a nakreslení výztuže ověřit předpokládanou geometrii modelu náhradní příhradoviny.
6.1 MALÉ KRUHOVÉ PROSTUPY
Nejčastějším případem prostupu v nosníku je malý kruhový otvor. Maximální velikost otvoru závisí na jeho umístění po výšce profilu (obr. 6.2). Maximální možnou velikost otvoru lze také ovlivnit nakloněním třmínků. Správné naklonění třmínků nosníku je v praxi problematické a u monolitických konstrukcí se nedoporučuje. Běžným případem je použití svislých třmínků, které jsou uvažovány v následujících návrhových postupech. Při návrhu D-oblasti je nutné vycházet z rozhodujících vnitřních sil (MEd,VEd event. NEd), které působí v oblasti prostupu. Dále je nutné definovat oblast před a za prostupem s přihlédnutím k umístění prostupu.
Oblast před prostupem je u líce prostupu, ve kterém je posouvající síla v absolutní hodnotě menší než absolutní hodnota posouvající síly za prostupem (obr. 6.4). Polohu oblasti za prostupem ovlivňuje tlačená betonová diagonála, umístěná nad nebo pod prostupem (obr. 6.4). Rozhodující posouvající síla pro návrh svislého táhla Ft1 bude ta, která působí před prostupem. Pro návrh betonové vzpěry a svislého táhla Ft2 se uvažují vnitřní síly, které působí v řezu ve středu délky betonové vzpěry. V oblasti před prostupem vzniká táhlo Ft1 s koncentrovanou třmínkovou výztuží v šířce e1 Za prostupem není táhlo bezprostředně u prostupu, ale koncentrované třmínky začínají v oblasti odsunuté o e2 – 2r od líce prostupu v závislosti na geometrii diagonální vzpěry (r je poloměr kruhového prostupu). Táhlo za prostupem Ft2 předpokládáme rovněž v šířce e1. Šikmá betonová vzpěra se opírá do oblasti uzavřené třmínky. Při horním líci nosníku se jedná o styčník CTC a při spodním líci nosníku o styčník CTT. Velikost styčníků a zakotvení táhel bylo uvedeno v kap. 1 nebo [26]. Obdobně jako u všech poruchových oblastí vznikají v betonové vzpěře příčné tahy – viz kap. 1, které je nutné vykrýt svislými třmínky a vodorovnými příložkami. Kolem prostupu je nutné konstrukčně doplnit i šikmé příložky, které redukují rozvoj diagonálních trhlin v tažených částech prostupu. Z modelu náhradní příhradoviny (obr. 6.4) vyplývá optimální umístění otvoru přímo nad dolním taženým pasem, nebo pod horním tlačeným pasem při návrhu svislých třmínků a ve středu výšky při použití šikmých třmínků (obr. 6.5 a obr. 6.6). Alternativně k modelu uvedenému na obr. 6.7 se někdy používá model podle obr. 6.7 a obr. 6.8, který však nepopisuje dostatečně příčné tahy.
Obr. 6.4 Základní model náhradní příhradoviny pro malý kruhový postup
Obr. 6.5 Modely náhradní příhradoviny po více malých kruhových prostupů
Obr. 6.6 Model náhradní příhradoviny pro malý kruhový postup ve středu výšky nosníku
Obr. 6.7 Alternativní model náhradní přihradoviny pro malý kruhový prostup
Obr. 6.8 Alternativní model náhradní příhradoviny pro malý kruhový prostup s rozšířenou vzpěrou
Pro návrh D-oblasti v okolí malého kruhového prostupu vyjdeme z geometrie průřezu nosníku a z velikosti kruhového prostupu o poloměru r. Předpokládáme nosník o celkové výšce h, výšce horního pasu nad prostupem hh a výšce dolního pasu pod prostupem hd. Dále známe rameno vnitřních sil z v místě před prostupem (obr. 6.4). Při návrhu postupujeme následovně:
- Nejprve stanovíme výztuž v táhle před prostupem a šířku táhla e1. Plocha výztuže As1 se stanoví
\begin{gathered}
A_\text{s1}=\frac{F_\text{t1}}{f_\text{ywd}}=\frac{|V_\text{Ed1}|}{f_\text{ywd}}
\end{gathered}(6.1)
kde je
fywd … návrhová pevnost smykové výztuže – třmínků;
VEd1 … návrhová posouvající síla, působící v líci před prostupem.
Při návrhu výztuže stanovíme průřez třmínků, jejich počet a vzdálenost, dále pak stanovíme šířku táhla e1. Šířka táhla je rovna vzdálenosti vnějších líců třmínků táhla.
- Z geometrie oblasti stanovíme úhel θ podle detailu na obr. 6.4. Úhel θ sklonu tlačené betonové diagonály stanovíme ze vztahu:
\begin{gathered}
\theta=90\degree-(\alpha_1+\alpha_2)
\end{gathered}(6.2)
kde je
α1 a α2 … pomocné úhly, které stanovíme z následujících vztahů:
\begin{gathered}
\alpha_1=\text{arctg}\bigg(\frac{e_1+r}{h_\text{h}-0{,}4x+r}\bigg)\\\\
\alpha_2=\text{arcsin}\Bigg(\frac{r}{\sqrt{(e_1+r)^2+(h_\text{h}-0{,}4x+r)^2}}\Bigg)
\end{gathered}kde je
x … výška tlačené oblasti v průřezu (před prostupem).
Přitom je třeba dodržet omezení sklonu tlačené diagonály podle normy [1]
\begin{gathered}
21{,}8\degree\le\theta\le45\degree
\end{gathered}Nutné je dodržet i omezení výšky tlačené oblasti.
- Pomocí úhlu sklonu α stanovíme šířku betonové vzpěry c1:
\begin{gathered}
c_1=e_1\cdot\sin\theta
\end{gathered}(6.3)
- Ověříme napětí v betonové vzpěře – viz kap. 1.2
\begin{gathered}
\sigma_\text{c}=\frac{|V_\text{Ed1}|}{b\cdot c_1\cdot\sin\theta}\le\sigma_\text{Rd,max}
\end{gathered}(6.4)
kde je
b … rozhodující šířka nosníku;
σRd,max … návrhové napětí na mezi únosnosti tlačené betonové vzpěry při vzniku příčných trhlin (vztah 6.56N [1]);
VEd1 … návrhová posouvající síla, působící v řezu před prostupem.
- V taženém spodním pasu bude působit síla Ft :
\begin{gathered}
F_\text{t}=\frac{M_\text{Ed2}+N_\text{Ed2}\cdot z_1}{z}+\frac{|V_\text{Ed2}|}{\tan\theta}+N_\text{Ed2}
\end{gathered}(6.5)
kde je
z1 … vzdálenost těžiště tažené výztuže k těžišti průřezu;
MEd2 … návrhový ohybový moment v řezu ve středu délky betonové vzpěry;
NEd2 … návrhová normálová síla, působící v řezu ve středu délky betonové vzpěry v těžišti nosníku (kladné znaménko je u tahu);
VEd2 … návrhová posouvající síla, působící v řezu za prostupem.
- V tlačeném horním pasu bude působit síla Fc. Rozhodující vnitřní síly jsou stejné jako u vzorce (6.5).
\begin{gathered}
F_\text{c}=\frac{-M_\text{Ed2}-N_\text{Ed2}\cdot z_1}{z}-|V_\text{Ed}|\cdot\cot\theta
\end{gathered}(6.6)
- Překontrolujeme únosnost v horním a spodním pasu a geometrii modelu náhradní příhradoviny. Při změně geometrie je nutné opakovat výpočet.
- V dalším kroku navrhneme výztuž, zachycující vznikající příčné tahy v betonové vzpěře. Navrhneme ortogonální výztuž. Pro návrh výztuže použijeme principy uvedené v kap. 1. Vzhledem k tomu, že se předpokládá vznik příčného tahu především ve čtvrtinách délky betonové vzpěry, je nutné vložit svislé třmínky a vodorovné příložky i do horní části nosníku nad prostupem.
- Pro spolehlivý přenos sil ve styčnících je nutné překontrolovat zakotvení třmínků, působících jako táhla v oblasti styčníku – bližší viz kap. 1.
Pro první posouzení vhodnosti kruhového prostupu lze použít diagramy na následujících grafech (obr. 6.9). Na obrázcích představuje vztažná posouvající síla v‘Ed hodnotu podle vztahu:
\begin{gathered}
v'_\text{Ed}=|V_\text{Ed}|/(b\cdot z\cdot v'\cdot f_\text{cd})
\end{gathered}(6.7)
kde kromě již výše uvedených proměnných je hodnota v‘= 1 – fck/250 podle [1]. Hodnoty odečtené z grafu jsou pouze informativní.
a) hd/z = 0,10
b) hd/z = 0,25
Obr. 6.9 Maximální informativní velikost malého kruhového prostupu v nosníku v závislosti na výšce dolního pasu
6.2 NĚKOLIK MALÝCH KRUHOVÝCH PROSTUPŮ
Pokud kruhové prostupy jsou v takové vzdálenosti, že oblasti diskontinuity se nepřekrývají, lze oblast kolem každého prostupu posuzovat samostatně. Například u prvního nosníku uvedeného na obr. 6.10 a zůstala oblast B mezi oblastí D u prostupu a oblastí D v místě uložení nosníku. U nosníku na obr. 6.10b, ale obě D-oblasti (u otvoru a v místě uložení nosníku) na sebe přímo navazují; model náhradní příhradoviny je zde ovlivněn navazujícími D- oblastmi. Pokud se oblast D s kruhovým prostupem posune ještě více k místu uložení (nosník na obr. 6.10c), obě D-oblasti splynou.
Při návrhu modelu náhradní příhradoviny podle obr. 6.4 vzniká nad betonovou diagonální vzpěrou prostor pro druhý kruhový prostup (obr. 6.5). Při vhodném umístění druhého prostupu se model náhradní příhradoviny příliš nezmění. Dále pokud takováto dvojice kruhových prostupů bude od druhé dvojice prostupů dostatečně vzdálena (s ≥ z ∙ cot θ), lze postupovat při návrhu D-oblastí jako u jednotlivých dvojic prostupů (obr. 6.5). Pokud však budou dvojice prostupů vzájemně blíže (z ∙ cot θ > s ≥ e1), musí se při návrhu D-oblasti vytvořit pro obě dvojice prostupů společný model náhradní příhradoviny (obr. 6.5).
Pokud se kruhový prostup posouvá do středu průřezu, je výhodné v této oblasti použít šikmé třmínky. Odpovídající modely náhradní příhradoviny jsou na obr. 6.6 a obr. 6.11. Na obrázku obr. 6.6 je model pro samostatný prostup a na druhém obr. 6.11 je model náhradní příhradoviny pro řadu prostupů. Systém šikmých třmínků je nutné doplnit další ortogonální výztuží pro zachycení příčných tahů, vznikajících v betonových vzpěrách. Na obr. 6.12 je zobrazeno uspořádání výztuže v oblasti dvou kruhových prostupů železobetonového střešního vazníku.
Obr. 6.10 Modely náhradní příhradoviny pro konec nosníku s malým kruhovým prostupem
Obr. 6.11 Model náhradní příhradoviny pro více malých kruhových prostupů v středu výšky nosníku
Obr. 6.12
Pro výpočet poruchové oblasti nosníku v okolí prostupů je výhodné použít nelineární analýzu, například program ATENA 2D (obr. 6.13 a obr. 6.14). Nelineární analýzy oblastí s kruhovými prostupy dokládají poměrně dobrou shodu s teoretickým modelem náhradní příhradoviny. U nelineárních metod je nutné uvážit působení betonu v tahu, se kterým se podle ČSN EN 1992-1-1 [1] v mezním stavu únosnosti nepočítá.
Obr. 6.13 Nelineární řešení oblasti s malým prostupem s naznačeným modelem náhradní příhradoviny
Obr. 6.14 Nelineární řešení oblasti s malými kruhovými prostupy s naznačeným modelem náhradní příhradoviny
6.3 VELKÉ PROSTUPY V NOSNÍKU
U velkých prostupů v nosníku dochází k deplanaci příčného průřezu a neplatí Bernoulliova hypotéza. Kolem velkého prostupu vznikají poruchové D-oblasti, které řešíme pomocí náhradní příhradoviny (obr. 6.3 a obr. 6.15). Na rozdíl od řešení malých prostupů nelze vytvořit jeden univerzální model náhradní příhradoviny. Modely jsou závislé nejen na geometrii prostupu, nosníku a možnostech vyztužení oblasti, ale i na zatěžovací kombinaci (model A – viz dále). Ohraničení oblastí D kolem prostupu vychází opět ze Saint Venantova principu. Předpokládá se, že vzniká poruchová oblast před a za prostupem v délce rovné výšce průřezu od líce prostupu, která dále pokračuje do jednotlivých pasů na délku rovnou výškám jednotlivých pasů (obr. 6.3b).
Obr. 6.15 Poruchová oblast kolem velkého obdélníkového prostupu
Vnitřní část horního a dolního pasu se uvažuje jako standardní nosníková B-oblast. Pro výpočet D-oblastí kolem velkého prostupu byla vytvořena řada modelů náhradní příhradoviny. Při jejich sestavování se vychází z rozdělení vnitřních sil na vnitřní síly vzniklé z vnějšího zatížení (primární) a vnitřní síly (sekundární – druhotné) vzniklé ze změny průřezu. Působící ohybový moment se primárně rozdělí do dvojice sil, působící v těžištích horního a dolního pasu. V místě vetknutí pasů do plného průřezu vznikají druhotné vnitřní síly. Vetknutí pasů se analyzuje modelem náhradní příhradoviny. Tak vzniká poměrně komplikovaný komplexní model náhradní příhradoviny. V literatuře jsou nejčastěji publikovány tři modely náhradní příhradoviny A, B a zjednodušený model podle DAfStB 459 [16]. Nejčastěji se používá zjednodušený model podle [16]. Modely A a B jsou přesnější, ale při řešení oblasti výrazně náročnější. Přínosem modelů A a B je, kromě přesnějšího popisu chování oblasti, i úspora výztuže ve srovnání se zjednodušeným modelem. Modely nejsou navrženy pro prostupy, které jsou ve středu rozpětí nosníků se symetrickým zatížením. V tomto případě lze využít pro modelování oblasti redukci dolního pasu na táhlo a horního na tlačený pás. Při tvorbě modelu náhradní příhradoviny podle [16] se vychází z analogie s Vierendeelovým nosníkem. Nosné prvky kolem prostupu se uvažují jako obdélníkový rám s nekonečně tuhými stojkami (navazují na celý průřez nosníku). Horní příčel tvoří horní pas nosníku nad prostupem a dolní příčel tvoří dolní pas nosníku pod prostupem. V následujících vztazích jsou veličiny horního pasu označeny indexem h a veličiny dolního pasu označeny indexem d. Nelineární řešení nosníky s velkým prostupem je na obr. 6.16.
Obr. 6.16 Příklad nelineárního řešení poruchové oblasti kolem velkého obdélníkového prostupu
Návrh výztuže příčlí se provádí podle nosníkové teorie – oblast B. Nosníky horního a dolního pasu jsou nepřímo uložené do masivní části průřezu (u samostatných prostupů) – viz [28]. U nepřímého uložení je nutné také uvažovat zvětšení maximální tahové síly v dolním pasu o hodnotu 0,5VEd·cot θ podle vztahu (6.18) ČSN EN 1992-1-1 [1]. Posouzení horního tlačeného pasu lze provést na maximální ohybový moment v místě vetknutí, což je to na straně bezpečnosti. Poruchovou oblast horního pasu v místě uložení není nutné samostatně posuzovat, rozhodující pro návrh je tlačená betonová diagonála pasu. V taženém dolním pasu je vhodné volit sklon tlačené diagonály θd = 45°. Pokud je tažený pas nízký, je optimální vůbec nepředpokládat přenos posouvající síly, pas se tak redukuje na táhlo [7].
6.4 ROZDĚLENÍ VNITŘNÍCH SIL KOLEM PROSTUPU
Pro návrh velkého prostupu je nutné nejprve rozdělit vnitřní síly v oblasti prostupu do horního a dolního pasu. Z celkového modelu prvku stanovíme vnitřní síly v místě prostupu bez ohledu na prostup v nosníku metodami lineární analýzy. Uvedené zjednodušení umožňuje i ČSN EN 1992-1-1 [1]. V praxi se běžně řeší prostupy až po dokončení celkové analýzy konstrukce, protože dříve nejsou k nim podklady. Uvedeným zjednodušením není nutné opravovat celkovou analýzu konstrukce při upřesnění prostupů.
Pro zjednodušení se neuvažuje s působením zatížení přímo ani na horním, ani na dolním pasu. Na dolním pasu zatížení obvykle nepůsobí, prostupem prochází technologie, která se o dolní pas neopírá. Na horním pasu naopak takřka vždy působí zatížení. Jeho vliv na průběh momentů v horním pasu se obvykle zanedbává. Pokud by vliv zatížení na průběh momentů v horním pasu nebyl zanedbatelný (například při působení většího osamělého břemene apod.), je nutné upravit příslušně model náhradní příhradoviny (viz obr. 6.17).
Obr. 6.17 Příklady průběhu ohybového momentu na idealizovaném rámu kolem velkého prostupu
Rozdělení vnitřních sil do horního a dolního pasu je nutné pro návrh výztuže obou pasů a pro celkový návrh oblasti zjednodušeným modelem podle DAfStB 459 [16]. U přesnějších modelů A a B se rozdělení vnitřních sil neužívá.
6.4.1 Rozdělení posouvajících sil
Na rozdělení posouvajících sil do horního a dolního pasu není jednotný názor. Problém spočívá ve změně únosnosti průřezu při působení normálové síly. Při taženém průřezu únosnost betonové části průřezu klesá o cca 15 % normálového napětí, které působí v průřezu, a naopak při tlačeném průřezu únosnost přibližně o stejnou hodnotu roste. Dolní pas u prostupu je většinou tažen a často porušen trhlinami po celé výšce. Únosnost dolního pasu je výrazně nižší a v literatuře se uvádí, že dolní pas přenáší pouze 10 % až 20 % celkové posouvající síly [16]. Vliv rozdělení posouvajících sil nemá na konečný návrh oblasti rozhodující vliv. V praxi se používají podle [16] následující metody rozdělení:
- Rozdělení posouvajících sil v poměru momentů setrvačnosti. Rozdělení vychází z lineárně pružného řešení rámu bez vlivu smykových deformací a bez vlivu změny únosnosti průřezu vlivem normálových sil:
\begin{gathered}
V_\text{Ed,h}=V_\text{Ed}\frac{I_\text{h}}{I_\text{h}+I_\text{d}}\space\space\text{a}\space\space V_\text{Ed,d}=V_\text{Ed}\frac{I_\text{d}}{I_\text{h}+I_\text{d}}
\end{gathered}(6.8)
kde je
Ih a Id … monety setrvačnosti horního, resp. dolního pasu;
VEd … rozhodující posouvající síla z celkové analýzy prvku.
- Rozdělení posouvajících sil na základě parametrických studií:
\begin{gathered}
V_\text{Ed,d}=V_\text{Ed}\frac{\sqrt{A_\text{d}I_\text{d}}}{\sqrt{A_\text{h}I_\text{h}}+\sqrt{A_\text{d}I_\text{d}}}\space\space\text{a}\space\space V_\text{Ed,h}=V_\text{Ed}-V_\text{Ed,d}
\end{gathered}(6.9)
- Upravené rozdělení posouvajících sil v poměru upravených momentů setrvačnosti:
\begin{gathered}
V_\text{Ed,h}=V_\text{Ed}\frac{I_\text{h}}{I_\text{h,zvt}+I_\text{d,red}}\space\space\text{a}\space\space V_\text{Ed,d}=V_\text{Ed}\frac{I_\text{d}}{I_\text{h,zvt}+I_\text{d,red}}
\end{gathered}(6.10)
kde je
Id,red … redukovaný moment setrvačnosti dolního pasu porušeného trhlinami;
Ih,zvt … zvětšený moment setrvačnosti tlačeného horního pasu.
Úpravu únosností můžeme stanovit ze změny únosnosti průřezu při tahové a tlakové normálové síle podle vztahu (6.2) z ČSN EN 1992-1-1 [1]. Únosnost horního nebo dolního pasu stanovíme s vlivem normálové síly. Poměrem mezi změněnou únosností a únosností bez normálového napětí potom upravíme moment setrvačnosti průřezu dolního nebo horního pasu. Pro velmi štíhlé dolní pasy lze zredukovat dolní pas na tažený prvek a neuvažovat s přenosem posouvající síly. Tento princip lze využít jako zjednodušení při výpočtu mezních stavů použitelnosti.
6.4.2 Rozdělení normálových sil
Normálové síly se rozdělí do horního a horního pasu v závislosti vzdáleností těžišť jednotlivých pasů od těžiště otvoru, viz obr. 6.18 (tlaková normálová síla je záporná, tahová normálová síla kladná). Rozdělení vychází z podmínky rovnováhy ve vodorovném směru a z momentové podmínky k působišti celkové normálové síly:
\begin{gathered}
N_\text{Ed}=N_\text{Ed,hN}+N_\text{Ed,hN}\space\space\text{a}\space\space0=N_\text{Ed,hN}\cdot z_\text{hN}+N_\text{Ed,dN}\cdot z_\text{dN}\\\\
N_\text{Ed,dN}=N_\text{Ed}\frac{z_\text{dN}}{z_\text{dN}+z_\text{hN}}\space\space\text{a}\space\space N_\text{Ed,hN}=N_\text{Ed}\frac{z_\text{hN}}{z_\text{dN}+z_\text{hN}}
\end{gathered}(6.11)
Obr. 6.18 Rozdělení normálových sil do horního a dolního pasu kolem velkého prostupu – podrobný model
Obr. 6.19 Rozdělení normálových sil do horního a dolního pasu zjednodušený model
Normálová síla NEd se před prostupem rozdělí na část odpovídající hornímu pasu NEd,h a část odpovídající dolnímu pasu NEd,dN. Pro model náhradní příhradoviny musíme definovat vzdálenost prutů TN a CN – viz obr. 6.18 a obr. 6.19. Vzdálenost mezi tahovou a tlakovou silou označujeme zCT a lze ji stanovit podle vztahu:
\begin{gathered}
z_\text{CT}\approx0{,}6(z_\text{dN}+z_\text{hN})
\end{gathered}(6.12)
Tahová síla TN při okraji otvoru je rovna:
\begin{gathered}
T_\text{N}=N_\text{Ed,hN}\cdot\frac{z_\text{hN}}{z_\text{CT}}=N_\text{Ed,dN}\cdot\frac{z_\text{dN}}{z_\text{CT}}
\end{gathered}Po dosazení dostaneme:
\begin{gathered}
T_\text{N}=N_\text{Ed,hN}\cdot\frac{z_\text{hN}}{0{,}6\cdot(z_\text{dN}+z_\text{hN})}=N_\text{Ed,dN}\cdot\frac{z_\text{dN}}{0{,}6\cdot(z_\text{dN}+z_\text{hN})}
\end{gathered}(6.13)
Pro modely, u kterých normálová síla není hlavním namáháním prvku, lze rameno dvojice sil zCT převzít shodně s dílčími modely pro posouvající sílu a ohybový moment – viz modely A, B a zjednodušený model.
Pokud je prostup umístěn excentricky nebo pokud je normálová síla excentrická, vznikají v horním a dolním pasu různá namáhání, a tím i různá přetvoření, která vedou k natočení průřezu (obr. 6.18). Úhel natočení lze odhadnout podle vztahu:
\begin{gathered}
\Delta\phi=\frac{I_\text{ot}N_\text{Ed,N}}{E_\text{c}\cdot(z_\text{dN}+z_\text{hN})^2}\cdot\bigg(\frac{z_\text{dN}}{A_\text{h}}-\frac{z_\text{hN}}{A_\text{d}}\bigg)
\end{gathered}(6.14)
kde je
Ec … modul pružnosti betonu;
Ad, Ah … plocha průřezu dolního (horního) pasu.
Pro zjednodušení se neuvažuje s působením zatížení přímo na horním ani na dolním pasu. Pokud na oba pasy nepůsobí zatížení, lze uvažovat průběh ohybových momentů lineární (obr. 6.15). Pro rozdělení momentů je rozhodující stanovit bod s nulovým momentem. Jako první přiblížení lze umístit nulový bod do poloviny rozpětí horního pasu. To však vede k podhodnocenému ohybovému momentu při návrhu výztuže obou pasů.
Pro stanovení polohy x nulového bodu lze použít následující postupy:
- Pro poměr hot/h ≤ 0,5 platí:
\begin{gathered}
\frac{x}{I_\text{ot}}=\frac{1}{2}-\frac{M_\text{Ed}}{37\cdot V_\text{Ed}\cdot I_\text{ot}}\bigg[\frac{\text{max}(h_\text{h}{;}h_\text{d})}{\text{min}(h_\text{h}{;}h_\text{d})}\bigg]^3
\end{gathered}(6.15)
- a pro hot/h ≥ 0,5 platí:
\begin{gathered}
\frac{x}{I_\text{ot}}=\frac{1}{2}-\frac{M_\text{Ed}}{5\cdot V_\text{Ed}\cdot I_\text{ot}}\bigg[\frac{\text{min}(h_\text{h}{;}h_\text{d})}{\text{max}(h_\text{h}{;}h_\text{d})}\bigg]^3
\end{gathered}(6.16)
kde je
VEd a MEd … vnitřní síly na kraji prostupu.
- Poloha nulového bodu x se stanoví ze vztahu:
\begin{gathered}
x=I_\text{ot}\cdot\bigg(\frac{1}{2}-\bigg(\frac{M_\text{Ed}}{V_\text{Ed}\cdot I_\text{ot}}+\frac{1}{2}\bigg)\cdot w\bigg)
\end{gathered}(6.17)
kde součinitel W se stanoví podle vztahu:
\begin{gathered}
w=\frac{\frac{I_\text{h}}{A_\text{h}}+\frac{I_\text{h}}{A_\text{d}}+\frac{I_\text{h}^2}{I_\text{d}A_\text{h}}+\frac{I_\text{h}^2}{I_\text{d}A_\text{d}}}{z_\text{ot}^2\frac{I_\text{h}}{I_\text{d}}+\bigg(\frac{I_\text{h}}{A_\text{h}}+\frac{I_\text{h}}{A_\text{d}}+\frac{I_\text{h}^2}{I_\text{d}A_\text{h}}+\frac{I_\text{h}^2}{I_\text{d}A_\text{d}}\bigg)}
\end{gathered}(6.18)
kde je
Ih,d … momenty setrvačnosti horního, resp. dolního pasu;
Ah,d … průřezové plochy horního, resp. dolního pasu;
zot … vzdálenost mezi těžištěm horního a dolního pasu.
Pro zjednodušení stanovení nulového bodu lze použít grafů, uvedených na obr. 6.20. Graf je sestaven pro rovnoměrné zatížení prostého nosníku za předpokladu, že nad prostupem není žádné zatížení (viz podmínky metody).
Obr. 6.20 Rozdělení ohybových momentů horního a dolního pasu kolem velkého prostupu (druhotné ohybové momenty)
Pokud je známa poloha nulového bodu x, lze rozdělit vnitřní síly bez řešení staticky neurčitého rámu. Pokud označíme za rozhodující vnitřní síly na celkovém prvku MEd a VEd hodnoty odpovídající poloze nulového bodu x v rámci prostupu, pak lze primární vnitřní síly stanovit podle následujících vztahů.
Návrhové ohybové momenty horního a dolního pasu v líci prostupu:
\begin{gathered}
M_\text{Ed,h}=\text{max}[V_\text{Ed,h}\cdot x;V_\text{Ed,h}\cdot(I_\text{ot}-x)]\space\space\text{a}\space\space M_\text{Ed,d}=\text{max}[V_\text{Ed,h}\cdot x;V_\text{Ed,h}\cdot(I_\text{ot}-x)]
\end{gathered}(6.19)
Návrhové normálové síly z nahrazení momentu MEd dvojicí vnitřních sil:
\begin{gathered}
N_\text{Ed,h}=-\frac{M_\text{Ed}}{z_\text{dN}+z_\text{hN}}\space\space\text{a}\space\space N_\text{Ed,h}=\frac{M_\text{Ed}}{z_\text{dN}+z_\text{hN}}
\end{gathered}(6.20)
Všechny modely (A, B a zjednodušený model podle DAfStB 459 [16]) dávají před a za prostupem ve třmíncích tahové síly větší než odpovídající tahové síly při řešení B-oblasti, za předpokladu, že by nosník neměl v daném místě prostup (důležité kritérium pro ověření výsledků). Soustředěná třmínková výztuž není umístěna jen bezprostředně u líce prostupu, ale také v určité vzdálenosti od líce. To je nutné mít na paměti při stanovení kotevní délky podélných příložek kolem prostupu. Příložky nemohou být protaženy za líc prostupu jen na kotevní délku, to je naprosto nedostatečné. Příložky u tažených rohů musí být protaženy až do příslušných styčníků a tam teprve zakotveny. Pokud se nepoužijí zjednodušené modely náhradní příhradoviny a vytvoří model náhradní příhradoviny přímo pro daný nosník s prostupem obr. 6.21, je nutné v taženém dolním pásu pod otvorem zohlednit obvykle výrazně menší únosnost dolního pasu z důvodu tahu.
Obr. 6.21 Příklady modelů náhradní příhradoviny pro nosník s velkým prostupem
6.5 MODEL A PRO NÁVRH OBLASTI KOLEM PROSTUPU
Model A vychází z předpokladu, že tahové a tlakové síly z horního a dolního pasu ovlivňují tvar krajních tlačených diagonál C2 a C12 (obr. 6.22a,b a obr. 6.23a,b ). Tahová síla z horního pasu A1 způsobí v tlačené vzpěře C2 její vychýlení (styčník 4 – obr. 6.22a,b a obr. 6.23b). Jedná se o kinematický model náhradní příhradoviny, což představuje pro každou zatěžovací kombinaci vytvoření samostatného modelu. Pro zajištění univerzálnosti použití modelu jsou použity součinitele κ1 a κ2. Součinitele κ1 a κ2 se zvolí podle geometrie prostupu a nosníku, podle únosnosti betonu v tlaku a podle možnosti vyztužení dané oblasti. Součinitele se volí obvykle v rozsahu 0,5 < κ1 < 2,0 a 0,5 < κ2 < 2,0. Malé hodnoty součinitelů vedou na malé oblasti zakotvení výztuže pasů kolem prostupu a k velké koncentraci tahové výztuže bezprostředně před a za prostupem. Rozdílné polohy těžiště horního a dolního pasu mezi B-oblastí nosníku a horního a dolního pasu kolem prostupu jsou zohledněny úhlem γ1 a γ2 podle obr. 6.22a,b a obr. 6.23b.
Obr. 6.22 Podrobný model A pro oblast velkého prostupu – záporná posouvající síla
Obr. 6.23 Podrobný model A pro oblast velkého prostupu – kladná posouvající síla
Model A vychází z obdobného rozdělení vnitřních sil jako u změny průřezu (viz kap. 2). Z modelu je také patrno, že zakotvení vodorovného táhla A1 je až za styčníkem 4, nikoliv za lícem prostupu. Styčník 4 také určuje polohu druhé oblasti se soustředěnou svislou tahovou výztuží T1. Pro tahovou sílu T1 také platí T1 > T2. Z toho vyplývá, že koncentrovaná tahová výztuž ve formě třmínků není hned za lícem prostupu. Totéž platí nejen před prostupem, ale i za prostupem (obr. 6.23), kde platí T‘2 > T‘1. Podrobný návrh modelu A náhradní příhradoviny pro oblast nosníku s velkým prostupem je proveden v publikaci [16].
Stanovení vnitřních sil kolem prostupu vychází z výpočtu rámu. Sklon tlačených diagonál θh a θd se stanoví z poměru normálových a posouvajících sil. Při tvorbě modelu lze předpokládat, že sklon tlačených diagonál je mimo krajní diagonální vzpěry shodný. Krajní vzpěra se odchyluje na vzdálenosti κ1 ∙ zh ∙ cos θh do oblasti před otvorem. Na této vzdálenosti musí veškerou posouvající sílu přenést třmínky. Část posouvající síly připadající na dolní pás se přenese přímo do dolního pasu na vzdálenosti zd ∙ cos θd podle obr. 6.22. Součinitele κ1, κ2 slouží především k větší flexibilitě modelu. Součinitele κ1 a κ2 se zvolí podle geometrie prostupu a nosníku a podle únosnosti betonu v tlaku a podle možnosti vyztužení oblasti. Součinitele se volí obvykle v rozsahu 0,5 < κ1 < 2,0 a 0,5 < κ2 < 1,0.
6.5.1 Základní vztahy modelu A náhradní příhradoviny
Pro návrh předpokládáme, že jsou známé následující veličiny:
- z – rameno vnitřních sil nosníku a ramena vnitřních sil dolní zd a horního pasu zh;
- hd – výška dolního pasu nosníku pod prostupem;
- hh – výška dolního pasu nosníku nad prostupem;
- θ – sklon tlačených betonových diagonál v oblasti B pro daný nosník;
- θh – sklon tlačných diagonál v horním pasu a θd – sklon tlačných v dolním pasu;
- κ1 – součinitel pro šířku táhla přiléhajícího k prostupu.
Dále se předpokládají již rozdělené vnitřní síly do horního a dolního pasu.
Horní pas nad prostupem
- Redukovaný sklon první šikmé vzpěry:
\begin{gathered}
\theta_\text{hR}=\text{arctan}\bigg(\frac{2\cdot\tan\theta_\text{h}}{\kappa_1+1}\bigg)
\end{gathered}(6.21)
- Tlaková síla v horní pasu:
\begin{gathered}
G_2=\frac{-M_\text{Ed,h}+N_\text{Ed,h}z_\text{hN}}{z_\text{h}}+\frac{|V_\text{Ed,h}|}{2\cdot\tan\theta_\text{h}}
\end{gathered}(6.22)
- Tahová síla při dolním líci horního pasu nad prostupem:
\begin{gathered}
A_1=\frac{|V_\text{Ed,h}|}{\tan\theta_\text{hR}}-G_2+N_\text{Ed,h}
\end{gathered}(6.23)
- Tlaková síla v první šikmé betonové vzpěře:
\begin{gathered}
C_5=\frac{-|V_\text{Ed,h}|}{\sin\theta_\text{hR}}
\end{gathered}(6.24)
- Tahová síla T3 pro návrh třmínkové výztuže horního pasu:
\begin{gathered}
T_3=|V_\text{Ed,h}|
\end{gathered}(6.25)
Dolní pas pod prostupem
- Tlaková síla při horním líci dolního pasu A2:
\begin{gathered}
A_2=\frac{-M_\text{Ed,d}+N_\text{Ed,d}z_\text{dN}}{z_\text{d}}+\frac{|V_\text{Ed,d}|}{2\cdot\tan\theta_\text{d}}
\end{gathered}(6.26)
- První tlačená betonová vzpěra dolního pasu:
\begin{gathered}
C_6=\frac{-|V_\text{Ed,d}|}{\sin\theta_\text{d}}
\end{gathered}(6.27)
- Tahová síla T4 pro návrh třmínkové výztuže dolního pasu:
\begin{gathered}
T_4=|V_\text{Ed,h}|
\end{gathered}(6.28)
Síly dolního a horního pasu při přechodu z B-oblasti na D-oblast:
\begin{gathered}
G_\text{h}=-\frac{1}{z}\bigg[M_\text{Ed}-V_\text{Ed}\bigg(\frac{1}{2}\kappa_2z\cdot\cot\theta+\kappa_1z_\text{h}\cdot\cot\theta_\text{h}\bigg)-N_\text{Ed}z_\text{Nh}\bigg]
\end{gathered}(6.29)
\begin{gathered}
G_\text{d}=-G_\text{h}+N_\text{Ed}+|V_\text{Ed}|\cot\theta
\end{gathered}(6.30)
Oblast před prostupem
- Odklon horního a dolního pasu:
\begin{gathered}
\gamma_1=\text{arctan}\bigg(\frac{2(z_\text{hG}-z_\text{h})}{\kappa_2z\cdot\cot\theta+\kappa_1z_\text{h}\cdot\cot\theta_\text{h}}\bigg)\text{(dolní pas)}
\end{gathered}(6.31)
\begin{gathered}
\gamma_2=\text{arctan}\bigg(\frac{2(z_\text{dG}-z_\text{d})}{\kappa_2z\cdot\cot\theta+\kappa_1z_\text{h}\cdot\cot\theta_\text{h}}\bigg)\text{(horní pas)}
\end{gathered}(6.32)
- Síly v hlavních prvcích náhradní příhradoviny oblasti D před prostupem:
\begin{gathered}
C_1=\frac{G_2-|V_\text{Ed,h}|\cot\theta_\text{hR}}{\cos\gamma_1}
\end{gathered}(6.33)
\begin{gathered}
T_2=G_1\sin\gamma_1+|V_\text{Ed,h}|
\end{gathered}(6.34)
\begin{gathered}
C_3=\frac{G_\text{d}-|V_\text{Ed,d}|\cot\theta}{\cos\gamma_2}
\end{gathered}(6.35)
\begin{gathered}
T_1=-G_3\sin\gamma_2+|V_\text{Ed}|
\end{gathered}(6.36)
- Úhly sklonu osové síly jednotlivých prvků modelu náhradní příhradoviny:
\begin{gathered}
\alpha_1=\text{arctan}\bigg(\frac{T_1+G_1\sin\gamma_1}{G_\text{h}-G_1\cos\gamma_1}\bigg)
\end{gathered}(6.37)
\begin{gathered}
C_1=\frac{T_1+G_1\sin\gamma_1}{\sin\alpha_1}
\end{gathered}(6.38)
\begin{gathered}
\alpha_1=\text{arctan}\bigg(\frac{-\sin\alpha_2}{A_1/C_1+\cos\alpha_2}\bigg)
\end{gathered}(6.39)
\begin{gathered}
C_2=C_1\frac{\sin\alpha_1}{\sin\alpha_2}
\end{gathered}(6.40)
\begin{gathered}
\alpha_3=\text{arccot}\bigg[\frac{-C_2\cos\alpha_2+A_2-|V_\text{Ed,h}|/(2z_\text{d})(z_\text{d}\cdot\cot\theta_\text{d}+\kappa_1z_\text{h}\cdot\cot\theta_\text{h})}{(T_2-G_3\sin\gamma_2+|V_\text{Ed,u}|)}\bigg]
\end{gathered}(6.41)
\begin{gathered}
\alpha_4=\text{arccot}\bigg[\frac{1}{\tan\alpha_3}+\frac{1}{2z_\text{d}}(z_\text{d}\cdot\cot\theta_\text{d}+\kappa_1z_\text{h}\cdot\cot\theta_\text{h})\bigg]
\end{gathered}(6.42)
\begin{gathered}
C_4=-\frac{|V_\text{Ed,d}|}{\sin\alpha_4}
\end{gathered}(6.43)
\begin{gathered}
C_3=-\frac{T_2-G_3\sin\gamma_2}{\sin\alpha_3}
\end{gathered}(6.44)
\begin{gathered}
G_4=G_3\cos\gamma_2+C_3\cos\alpha_3
\end{gathered}(6.45)
\begin{gathered}
G_5=G_4+C_4\cos\alpha_4
\end{gathered}(6.46)
- Napětí v šikmé betonové vzpěře:
\begin{gathered}
\sigma_\text{c}=\frac{-|V_\text{Ed}|}{b\cdot\kappa_2z\cdot\cot\theta\cdot\sin^2\theta}=\frac{-|V_\text{Ed}|}{b\cdot \kappa_2z\cdot\cos\theta\cdot\sin\theta}
\end{gathered}(6.47)
- Šířka pasů a napětí v betonu v místech odklonu vzpěr:
e_1=0{,}5z[2\cot\theta-\cot\theta(1+\kappa_2)](6.48)
\begin{gathered}
\theta_1=\text{arctan}\bigg(\frac{2\tan\theta}{1+\kappa_1}\bigg)
\end{gathered}(6.49)
\begin{gathered}
\theta_2=\text{arctan}\bigg(\frac{z_\text{hG}}{z_\text{hG}\cot\theta_1-e_1}\bigg)
\end{gathered}(6.50)
- Horní bod – možné polohy bodu odklonu – platí maximální hodnota z níže uvedených vztahů:
\begin{gathered}
L_\text{xh}=\kappa_1z_\text{h}\cot\theta_\text{h}+\kappa_2z_\text{h}\cot\theta_\text{h}+e_1-z_\text{hG}\cot\theta_1
\end{gathered}(6.51)
\begin{gathered}
L_\text{xh}=\kappa_2z\cot\theta-2z_\text{hG}(\cot\alpha_1+\cot\theta_2)
\end{gathered}(6.52)
\begin{gathered}
L_\text{xh}=2(\kappa_1z_\text{h}\cot\theta_\text{h}+z_\text{hG}\cot\alpha_1)+\kappa_2z\cot\theta
\end{gathered}(6.53)
- Napětí v betonové vzpěře:
\begin{gathered}
\sigma_\text{c}=C_2/(b\cdot L_\text{xh}\sin\alpha_2)\le v\cdot f_\text{cd}
\end{gathered}(6.54)
- Horní bod – možné polohy bodu odklonu – platí maximální hodnota z níže uvedených vztahů:
\begin{gathered}
L_\text{xd}=\kappa_1z_\text{h}\cot\theta_\text{h}+z_\text{d}\cot\theta_1
\end{gathered}(6.55)
\begin{gathered}
L_\text{xd}=2z_\text{d}(\cot\alpha_4-0{,}5\cot\theta_\text{d})
\end{gathered}(6.56)
\begin{gathered}
L_\text{xd}=2(0{,}5\kappa_1\cdot z_\text{h}\cot\theta_\text{h}+z_\text{d}\cot\theta_1-z_\text{d}\cot\alpha_3)
\end{gathered}(6.57)
- Napětí v betonové vzpěře:
\begin{gathered}
\sigma_\text{c}=C_2/(b\cdot L_\text{xd}\sin\alpha_2+h_\text{A}\cos\alpha_2)\le v\cdot f_\text{cd}
\end{gathered}kde je
hA … výška tlačeného pasu A2.
Obdobně se postupuje pro model A s kladnou posouvající sílou podle obr. 6.22b a obr. 6.23b.
6.6 MODEL B PRO NÁVRH OBLASTI KOLEM PROSTUPU
Model B (obr. 6.24) je flexibilnější než model A, není nutné pro každou zatěžovací kombinaci vytvářet nový model. Na druhou stranu předepsaná geometrie modelu náhradní příhradoviny není univerzální a může vést až k nevhodnému řešení oblasti. Při velkých záporných momentech při kraji prostupu je problematické nalézt odpovídající model náhradní příhradoviny.
Obr. 6.24 Podrobný model B pro oblast velkého prostupu – záporná posouvající síla
Model B vychází z obdobného rozdělení vnitřních sil jako u ozubu nosníku (viz kap. 4). Síla A1 (obr. 6.24) je zakotvena ve styčníku 3, kde se rozloží do betonové vzpěry C3 a táhla T1. Celková svislá tahová síla se v oblasti styčníku 3 skládá z T1 a T3. Na tuto sílu navrhujeme svislé třmínky. Jejich maximum opět není bezprostředně za lícem prostupu. Totéž platí i pro oblast za prostupem jako u modelu A.
Podrobný návrh modelu B náhradní příhradoviny pro oblast nosníku s velkým prostupem je proveden v publikaci [16].
6.6.1 Základní vztahy modelu B náhradní příhradoviny
Pro návrh předpokládáme, že jsou známé následující veličiny:
- z – rameno vnitřních sil nosníku a ramena vnitřních sil dolní zd a horního pasu zh;
- hd – výška dolního pasu nosníku pod prostupem a hh a nad prostupem;
- θ – sklon tlačených betonových diagonál v oblasti B pro daný nosník;
- θh – sklon tlačných diagonál v horním pasu a θd – sklon tlačných v dolním pasu;
- κ1 – součinitel pro šířku táhla T2 a κ2 – součinitel pro šířku táhla T1.
Dále se předpokládají již rozdělené vnitřní síly do horního a dolního pasu.
Horní pas nad prostupem
- Redukovaný sklon první šikmé vzpěry:
\begin{gathered}
\theta_\text{hR}=\text{arctan}\bigg(\frac{2\cdot\tan\theta_\text{h}}{\kappa_1+1}\bigg)
\end{gathered}(6.58)
- Tlaková síla v horním pasu:
\begin{gathered}
G_2=\frac{-M_\text{Ed,h}+N_\text{Ed,h}z_\text{hN}}{z_\text{h}}+\frac{|V_\text{Ed,h}|}{2\cdot\tan\theta_\text{h}}
\end{gathered}(6.59)
- Tahová síla při dolním líci horního pasu nad prostupem:
\begin{gathered}
A_1=\frac{|V_\text{Ed,h}|}{\tan\theta_\text{hR}}-G_2+N_\text{Ed,h}
\end{gathered}(6.60)
- Tlaková síla v první šikmé betonové vzpěře:
\begin{gathered}
C_8=\frac{-|V_\text{Ed,h}|}{\sin\theta_\text{hR}}
\end{gathered}(6.61)
Dolní pas pod prostupem
- Tlaková síla při horním líci dolního pasu A2:
\begin{gathered}
A_2=\frac{-M_\text{Ed,d}+N_\text{Ed,d}z_\text{dN}}{z_\text{d}}+\frac{|V_\text{Ed,d}|}{2\cdot\tan\theta_\text{d}}
\end{gathered}(6.62)
- První tlačená betonová vzpěra:
\begin{gathered}
C_5=\frac{-|V_\text{Ed,d}|}{\sin\theta_\text{d}}-A_2
\end{gathered}(6.63)
\begin{gathered}
C_7=-|V_\text{Ed,d}|/\sin\theta_\text{d}
\end{gathered}(6.64)
Síly dolního a horního pasu při přechodu z B-oblasti na D-oblast:
\begin{gathered}
G_\text{h}=-\frac{1}{z}\bigg[M_\text{Ed}-V_\text{Ed}\bigg(\frac{1}{2}\kappa_2z_\text{h}\cdot\cot\theta_\text{h}+\kappa_1z_\text{h}\cdot\cot\theta_\text{h}\bigg)- N_\text{Ed}z_\text{Nh}\bigg]
\end{gathered}(6.65)
\begin{gathered}
G_\text{d}=-G_\text{h}+N_\text{Ed}+|V_\text{Ed}|\cot\theta
\end{gathered}(6.66)
\begin{gathered}
C_1=\frac{-|V_\text{Ed,d}|}{\sin\theta}
\end{gathered}(6.67)
Oblast před prostupem
- Geometrie:
\begin{gathered}
e_1=\frac{1}{2}(z\cdot\cot\theta-\kappa_2\cdot z_\text{h}\cot\theta_\text{h})
\end{gathered}(6.68)
\begin{gathered}
\theta_1=\text{arctan}\bigg(\frac{2z}{z\cdot\cot\theta+\kappa_2\cdot z_\text{h}\cot\theta_\text{h}}\bigg)
\end{gathered}(6.69)
\begin{gathered}
L_\text{x,d}=z_\text{hG}\cot\theta_1+\kappa_1\cdot z_\text{h}\cot\theta_\text{h}\space\space\text{a}\space\space\text{L}_\text{x,h}=\kappa_2\cdot z_\text{h}\cot\theta_\text{h}
\end{gathered}(6.70)
přitom musí být splněna podmínka:
\begin{gathered}
L_\text{x,h}\le(\kappa_1+\kappa_2)\cdot z_\text{h}\cot\theta_\text{h}
\end{gathered}(6.71)
- Odklon horního a dolního pasu:
\begin{gathered}
\gamma_1=\text{arctan}\bigg(\frac{2(z_\text{hG}-z_\text{h})}{(\kappa_2+\kappa_1)z_\text{h}\cdot\cot\theta_\text{h}}\bigg)
\end{gathered}(6.72)
\begin{gathered}
\gamma_2=\text{arctan}\bigg(\frac{2(z_\text{dG}-z_\text{d})}{(\kappa_2+\kappa_1)z_\text{h}\cdot\cot\theta_\text{h}}\bigg)
\end{gathered}(6.73)
\begin{gathered}
\alpha_1=\text{arctan}\bigg(\frac{2(z_\text{hG}-z_\text{ot})}{(\kappa_2+\kappa_1)\cdot z_\text{h}\cot\theta_\text{h}-z_\text{dG}\cot\theta_1}\bigg)
\end{gathered}(6.74)
\begin{gathered}
\alpha_2=\text{arctan}\bigg(\frac{2\cdot z_\text{ot}}{(\kappa_2+\kappa_1)\cdot z_\text{h}\cot\theta_\text{h}-z_\text{dG}\cot\theta_1}\bigg)
\end{gathered}(6.75)
\begin{gathered}
\alpha_3=\text{arctan}\bigg(\frac{2\cdot z_\text{d}}{z_\text{dG}\cot\theta_1}\bigg)
\end{gathered}(6.76)
\begin{gathered}
\alpha_4=\text{arctan}\bigg(\frac{2\cdot z_\text{d}}{L_\text{x,d}+z_\text{d}\cot\theta_\text{d}}\bigg)
\end{gathered}(6.77)
\begin{gathered}
\alpha_5=\text{arctan}\bigg(\frac{2\cdot z_\text{dG}}{(\kappa_2+\kappa_1)\cdot z_\text{h}\cot\theta_\text{h}-z_\text{dG}\cot\theta_1}\bigg)
\end{gathered}(6.78)
- Síly v hlavních prvcích náhradní příhradoviny oblasti D:
\begin{gathered}
G_1=\frac{G_2+C_8\cot\theta_\text{hR}}{\cos\gamma_1}=\frac{G_2-|V_\text{Ed,h}|\cot\theta_\text{hR}}{\cos\gamma_1}
\end{gathered}(6.79)
\begin{gathered}
T_2=G_1\sin\gamma_1-C_8\sin\theta_\text{hR}=G_1\sin\gamma_1+|V_\text{Ed,d}|
\end{gathered}(6.80)
\begin{gathered}
C_2=\frac{G_\text{hd}-G_1\cos\gamma_1}{\cos\alpha_1}
\end{gathered}(6.81)
\begin{gathered}
T_3=-C_2\sin\alpha_1-G_1\sin\gamma_1
\end{gathered}(6.82)
\begin{gathered}
C_3=-\frac{A_1}{\cos\alpha_2}
\end{gathered}(6.83)
\begin{gathered}
T_1=-C_3\sin\alpha_2=A_1\sin\alpha_2
\end{gathered}(6.84)
\begin{gathered}
C_6=-\frac{|V_\text{Ed,d}|}{\sin\alpha_4}
\end{gathered}(6.85)
\begin{gathered}
C_4=G_5-C_6\cos\alpha_4=G_5+\frac{|V_\text{Ed,d}|}{\tan\alpha_4}
\end{gathered}(6.86)
\begin{gathered}
G_3=-\frac{G_4+T_2\cot\alpha_3}{\cos\gamma_2(1+\tan\gamma_2/\tan\alpha_3)}
\end{gathered}(6.87)
\begin{gathered}
G_5=-\frac{G_4+T_2\cot\alpha_3}{\sin\alpha_3}
\end{gathered}(6.88)
\begin{gathered}
C_4=-\frac{C_1\sin\theta+G_3\sin\gamma_2+T_3+T_1}{\sin\alpha_5}
\end{gathered}(6.89)
\begin{gathered}
\alpha_{1{,}2}=\text{arctan}\bigg(\frac{C_2\sin\alpha_1+C_3\sin\alpha_2}{C_2\cos\alpha_1+C_3\cos\alpha_2}\bigg)
\end{gathered}(6.90)
\begin{gathered}
C_{2{,}3}=\frac{C_2\sin\alpha_1+C_3\sin\alpha_2}{\sin\alpha_3}
\end{gathered}(6.91)
- Napětí v betonových vzpěrách:
\begin{gathered}
\text{Ve výšce A}_1:\sigma_\text{c{,}2{,}3{,}h}=\frac{C_{2{,}3}}{b\cdot L_\text{x,h}\sin\alpha_{1{,}2}}
\end{gathered}(6.92)
\begin{gathered}
\text{Ve výšce A}_2:\sigma_\text{c{,}2{,}3{,}d}=\frac{C_{2{,}3}}{b\cdot L_\text{x,d}\sin\alpha_{1{,}2}}
\end{gathered}(6.93)
\begin{gathered}
\text{Ve vzpěře dole}:\sigma_\text{c{,}1}=\frac{C_1}{b\cdot\kappa_2\cdot z_\text{h}\cdot\cot\theta_\text{h}\cdot\sin\theta}=\frac{-|V_\text{Ed}|}{b\cdot\kappa_2\cdot z_\text{h}\cdot\cot\theta_\text{h}\cdot\sin^2\theta}
\end{gathered}(6.94)
6.7 ZJEDNODUŠENÝ MODEL PRO OBLAST KOLEM PROSTUPŮ
Pro běžnou praxi jsou modely A a B velmi složité. V publikaci [16] DAfStB 459 je navržen zjednodušený postup pro stanovení rozhodujících vnitřních sil v D-oblasti před a za prostupem. Pro zjednodušení jsou síly opatřeny dolním indexem h a d podle toho, zda se jedná o horní nebo dolní pas. Výpočet vychází z rozdělení modelu podle vnitřních sil. Účinky působení normálových sil jsou označeny indexem N, posouvajících sil indexem V a ohybových momentů indexem M.
Pro zjednodušený postup výpočtu jsou vnitřní síly rozděleny do primárních účinků ohybového momentu a posouvající síly (obr. 6.25, obr. 6.26a a obr. 6.26b) a sekundárních účinků z vetknutí pasů do plné části průřezu (obr. 6.27, obr. 6.28a a obr. 6.28b). Zjednodušený postup je navržen pro samostatné velké prostupy, které nejsou ve středu rozpětí nosníku.
Modely pro primární a sekundární účinky jsou složeny a výsledky jsou zjednodušeny do následujících přehledů. Označení jednotlivých sil a jejich polohy jsou patrny z obr. 6.29 pro zápornou posouvající sílu a z obr. 6.30 pro kladnou posouvající sílu.
Obr. 6.25 Model náhradní příhradoviny pro přenos ohybového momentu a posouvající síly kolem velkého prostupu
Obr. 6.26 Modely náhradní příhradoviny pro přenos posouvající síly v dolním a horním pasu
Obr. 6.27 Modely náhradní příhradoviny podle DAfStB 459 pro přenos druhotných momentů
Obr. 6.28 Modely náhradní příhradoviny pro druhotné ohybové momenty v dolním a horním pasu
Obr. 6.29 Zjednodušený model pro oblast velkého prostupu – záporná posouvající síla
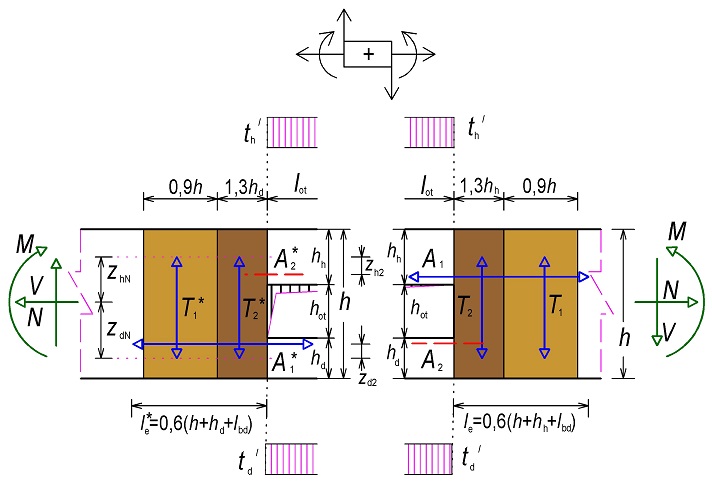
Obr. 6.30 Zjednodušený model pro oblast velkého prostupu – kladná posouvající síla
6.7.1 Výpočetní postup pro velký prostup a zápornou posouvající sílu
Šířka táhel
Kolem prostupu vzniknou táhla T1 a T2, popřípadě T‘1 a T‘2. Šířka táhel záleží na sklonu tlačených diagonál v celém nosníku, v horním a dolním pasu. Šířku lze stanovit následně uvedeným postupem.
O šířkách táhla u prostupu rozhoduje poloha taženého rohu prostupu. Pokud je u dolního pasu, pak rozhoduje výška dolního pasu, a pokud je u horního pasu, rozhoduje o šířce výška horního pasu.
První táhlo před prostupem je široké 1,3hd. V dolním pasu se uvažuje sklon tlačených diagonál cot θd = 1, protože dolní pas je namáhán tahem. V horním pasu se uvažuje sklon tlačených diagonál cot θ ≤ 2,0 a v celém nosníku se uvažuje obvykle sklon tlačených diagonál cot θ ≤ 2,5. Druhé táhlo před prostupem se uvažuje v šířce 0,9h (tedy přibližně d – účinná výška celého průřezu). Vzdálenost táhel se uvažuje hodnotou:
\begin{gathered}
\frac{1}{2}(\kappa\cdot z\cdot\cot\theta+z_\text{d}\cdot\cot\theta_\text{d})
\end{gathered}(6.95)
Za prostupem má první táhlo šířku 1,3hh a vzdálenost táhel:
\begin{gathered}
\frac{1}{2}(\kappa\cdot z\cdot\cot\theta+z_\text{h}\cdot\cot\theta_\text{h})
\end{gathered}(6.96)
Součinitel κ se obvykle uvažuje hodntou κ ≈ 0,70.
Síly v horním A1 a dolním pasu A2
\begin{gathered}
A_1=\frac{-M_\text{Ed,h}-N_\text{Ed,h}\cdot z_\text{h2}}{z_\text{h}}+\frac{|V_\text{Ed.h}|}{\tan\theta_\text{h}}
\end{gathered}(6.97)
\begin{gathered}
A_2=\frac{M_\text{Ed,d}-N_\text{Ed,d}\cdot z_\text{h2}}{z_\text{d}}+\frac{|V_\text{Ed.d}|}{\tan\theta_\text{d}}
\end{gathered}(6.98)
\begin{gathered}
T_\text{h}'=\frac{|V_\text{Ed,h}|}{z_\text{h}\cdot\cot\theta_\text{h}}\space\space\text{a}\space\space T_\text{d}'=\frac{|V_\text{Ed,d}|}{z_\text{d}\cdot\cot\theta_\text{d}}
\end{gathered}(6.99)
Normálová síla vyvolá v táhle T2N a T1N následující sílu:
\begin{gathered}
T_\text{2N}=-N_\text{Ed}\cdot\frac{z_\text{dN}}{(z_\text{dN}+z_\text{hN})}\cdot\frac{z_\text{hN}}{(0{,}9h+1{,}3h_\text{h})}=-N_\text{Ed}\cdot\frac{z_\text{hN}}{(z_\text{dN}+z_\text{hN})}\cdot\frac{z_\text{dN}}{(0{,}9h+1{,}3h_\text{h})}\\\\
T_\text{1N}=N_\text{Ed}\cdot\frac{z_\text{dN}}{(z_\text{dN}+z_\text{hN})}\cdot\frac{z_\text{hN}}{(0{,}9h+1{,}3h_\text{h})}=N_\text{Ed}\cdot\frac{z_\text{hN}}{(z_\text{dN}+z_\text{hN})}\cdot\frac{z_\text{dN}}{(0{,}9h+1{,}3h_\text{h})}
\end{gathered}Svislé táhlo T1
\begin{gathered}
T_1=T_\text{1v}+T_\text{1M}+T_\text{1N}
\end{gathered}(6.100)
kde
\begin{gathered}
T_\text{1M}=\frac{1{,}3A_1\cdot h_\text{d}\cdot h_\text{h}+1{,}6A_2\cdot h_\text{d}(0{,}8h_\text{h}+1{,}1h_\text{ot})}{0{,}7h^2+h_\text{h}\cdot h}\ge0
\end{gathered}(6.101)
\begin{gathered}
T_\text{1v}=|V_\text{Ed}|
\end{gathered}(6.102)
Svislé táhlo T2
\begin{gathered}
T_2=T_\text{2v}+T_\text{2M}+T_\text{2N}
\end{gathered}(6.103)
kde
\begin{gathered}
T_\text{2M}=\frac{1{,}3A_2\cdot h_\text{d}\cdot h_\text{h}+1{,}6A_1\cdot h_\text{h}(0{,}8h_\text{d}+1{,}1h_\text{ot})}{0{,}7h^2+h_\text{h}\cdot h}
\end{gathered}(6.104)
\begin{gathered}
T_\text{2v}=|V_\text{Ed,h}|
\end{gathered}(6.105)
6.7.2 Výpočetní postup pro velký prostup s kladnou posouvající silou obr. 6.30
Šířku táhel a jejich polohu stanovíme stejně jako v předchozím případu velkého prostupu se zápornou posouvající silou.
Síly v horním A1* a dolním pasu A2*
\begin{gathered}
A_2^*=\frac{M_\text{Ed,h}+N_\text{Ed,h}\cdot z_\text{h2}}{z_\text{h}}+\frac{|V_\text{Ed,h}|}{\tan\theta_\text{h}}
\end{gathered}(6.106)
\begin{gathered}
A_1^*=\frac{-M_\text{Ed,d}-N_\text{Ed,d}\cdot z_\text{d2}}{z_\text{d}}+\frac{|V_\text{Ed,d}|}{\tan\theta_\text{d}}
\end{gathered}(6.107)
\begin{gathered}
T_\text{h}'=\frac{|V_\text{Ed,h}|}{z_\text{h}\cdot\cot\theta_\text{h}}\space\space\text{a}\space\space T_\text{d}'=\frac{|V_\text{Ed,d}|}{z_\text{d}\cdot\cot\theta_\text{d}}
\end{gathered}(6.108)
Svislé táhlo T1
\begin{gathered}
T_1^*=T_\text{1v}^*+T_\text{1M}^*+T_\text{1N}^*
\end{gathered}(6.109)
kde
\begin{gathered}
T_\text{1M}^*=\frac{1{,}3A_1\cdot h_\text{d}\cdot h_\text{h}+1{,}6A_2\cdot h_\text{d}(0{,}8h_\text{h}+1{,}1h_\text{ot})}{0{,}7h^2+h_\text{h}\cdot h}\ge0
\end{gathered}(6.110)
\begin{gathered}
T_\text{1N}^*=N\frac{z_\text{hN}z_\text{dN}}{(z_\text{dN}+z_\text{hN})(0{,}9h+1{,}3h_\text{d})}\space\space\text{a}\space\space T_\text{1v}^*=|V_\text{Ed}|
\end{gathered}(6.111)
Svislé táhlo T2
\begin{gathered}
T_2^*=T_\text{2v}^*+T_\text{2M}^*+T_\text{2N}^*
\end{gathered}(6.112)
kde
\begin{gathered}
T_\text{2M}^*=\frac{1{,}3A_2\cdot h_\text{d}\cdot h_\text{h}+1{,}6A_1\cdot h_\text{h}(0{,}8h_\text{d}+1{,}1h_\text{ot})}{0{,}7h^2+h_\text{h}\cdot h}\ge0
\end{gathered}(6.113)
\begin{gathered}
T_\text{2N}^*=-N\frac{z_\text{hN}z_\text{dN}}{(z_\text{dN}+z_\text{hN})(0{,}9h+1{,}3h_\text{d})}\space\space\text{a}\space\space T_\text{2v}^*=|V_\text{Ed,d}|
\end{gathered}(6.114)
6.8 PRINCIPY VYZTUŽENÍ OBLASTI V OKOLÍ VELKÝCH PROSTUPŮ
Příklad řešení velkého prostupu nosníku nelineární analýzou programem ATENA 2D je na obr. 6.16. Při srovnání je patrná dobrá shoda s předpokládaným průběhem tlačených diagonál a trhlin. Nelineární metody výpočtu uvažují tahové napětí v betonu, se kterými v mezním stavu únosnosti obvykle neuvažujeme. Tím je pochopitelně ovlivněn přenos sil z tlačených betonových vzpěr do tažené výztuže. Při konzervativním přístupu metodami náhradní příhradoviny neuvažujeme s tahem v betonu; přenos mezi vzpěrou a táhlem se ve styčníku předpokládá soudržností a zajišťuje se ovinutím celé oblasti výztuží – viz [6]. Tím se poloha styčníku posouvá do středu nosníku ve srovnání s nelineární analýzou. Při nelineární analýze je do přenosu síly mezi vzpěrou a táhlem zapojen beton v tahu, který vzhledem k relativně velkému objemu ve srovnání s výztuží významně ovlivňuje geometrii modelu oblasti. Nelineární metody tedy mohou přinést úspory ve stanovení množství výztuže oblasti. Na druhou stranu nejsou současné předpisy připraveny na spolehlivé a dlouhodobé využití betonu v tahu v mezním stavu únosnosti. Při návrhu oblasti pomocí nelineární analýzy je nutné postupovat iteračně. Množství, tvar a polohu výztuže je nutné postupně optimalizovat. Neoptimalizované použití nelineární analýzy při návrhu výztuže může vést až k výraznému podhodnocení výztuže v dané oblasti [12].
6.9 PŘÍKLADY NÁVRHU A VYZTUŽENÍ OBLASTÍ KOLEM PROSTUPŮ
6.9.1 Příklad kruhového prostupu v nosníku
V průvlaku T-průřezu navrhněte výztuž v oblasti kruhového prostupu o průměru 2r = 300 mm. Průvlak má celkovou výšku 1 000 mm, tloušťka desky horní příruby je 200 mm, šířka horní příruby 600 mm, šířka stojiny je 200 mm, dolní výztuž průvlaku je 3ø28. V místě prostupu působí ohybový moment MEd = 500 kNm a posouvající síla VEd = -250 kN. Průvlak je navržen z betonu třídy C40/50, betonářská výztuž B500B, betonová krycí vrstva 25 mm (třmínků).
Materiály
Beton C40/50:
\begin{gathered}
f_\text{cd}=26{,}67\text{ MPa};\space\alpha_\text{cc}=1{,}0;\space\varepsilon_\text{cu3}=3{,}5\space‰;\space\eta=1{,}0;\space\lambda=0{,}8;\space v'=(1-f_\text{ck}/250)=0{,}84
\end{gathered}Styčník s táhlem CCT:
\begin{gathered}
\sigma_\text{Rd,max}=0{,}85v'\cdot f_\text{cd}=19{,}04\text{ MPa}
\end{gathered}Vzpěra s příčnými tahy:
\begin{gathered}
\sigma_\text{Rd,max}=0{,}6v'\cdot f_\text{cd}=0{,}6\cdot0{,}84\cdot26{,}67=13{,}44\text{ MPa}
\end{gathered}Výztuž B500B:
\begin{gathered}
f_\text{yd}=\frac{f_\text{yk}}{\gamma_\text{s}}=\frac{500}{1{,}15}=435\text{ MPa};\space\varepsilon_\text{yd}=\frac{f_\text{yd}}{E_\text{s}}=\frac{435}{200}=2{,}175\space‰
\end{gathered}Geometrie
Obr. 6.31 Geometrie oblasti s malým kruhovým prostupem – příklad (naznačené třmínky jsou pro nosníkovou B oblast nosníku)
\begin{gathered}
3\phi28\to A_\text{s}=1\space847\text{ mm}^2
\end{gathered}Návrh výztuže oblasti
Nejprve stanovíme výztuž v táhle před a za prostupem a šířku svislého táhla e1. Plocha výztuže As1 se stanoví:
\begin{gathered}
A_\text{s1}=\frac{F_\text{t1}}{f_\text{ywd}}=\frac{|V_\text{Ed}|}{f_\text{ywd}}=\frac{0{,}250}{435}=0{,}000575\text{ m}^2\to3\text{x}\space\text{třmen}\space2\phi12\text{ mm}\space\text{po}\space\space0{,}05\text{ m }(A_\text{s1}=679\text{ mm}^2)
\end{gathered}Šířka táhla Ft1 je
\begin{gathered}
e_1=2\cdot0{,}05+2\cdot0{,}025=0{,}15\text{ m}
\end{gathered}Výška tlačené oblasti (nosníkové části B)
\begin{gathered}
x=\frac{0{,}001847\cdot435}{0{,}8\cdot0{,}60\cdot26{,}67}=0{,}0628\text{ m}
\end{gathered}rameno vnitřních sil je
\begin{gathered}
z=1{,}0-0{,}025-0{,}012-0{,}028/2-0{,}4\cdot0{,}0628=0{,}924\text{ m}
\end{gathered}Z geometrie oblasti stanovíme úhel θ podle obrázku. Úhel θ sklonu tlačené betonové diagonály stanovíme ze vztahu:
\begin{gathered}
\theta=90\degree-(\theta_1-\theta_2)
\end{gathered}kde θ1 a θ2 jsou pomocné úhly, které stanovíme z následujících vztahů.
Obr. 6.32 Geometrie oblasti nad prostupem
\begin{gathered}
\alpha_1=\text{arctg}\bigg(\frac{e_1+r}{h_\text{h}-0{,}4x+r}\bigg)=\text{arctg}\bigg(\frac{0{,}15+0{,}15}{0{,}6-0{,}4\cdot0{,}0628+0{,}15}\bigg)=22{,}5\degree\\\\
\alpha_2=\text{arcsin}\bigg(\frac{r}{\sqrt{(e_1+r)^2+(h_\text{h}-0{,}4x+r)^2}}\bigg)=\text{arcsin}\bigg(\frac{0{,}15}{\sqrt{0{,}30^2+0{,}725^2}}\bigg)=11{,}0\degree\\\\
\theta=90\degree-(\theta_1+\theta_2)=90-(22{,}5+11)=56{,}5\degree
\end{gathered}Přitom je třeba dodržet omezení sklonu tlačené diagonály 21,8° ≤ α.
Pomocí úhlu sklonu α stanovíme šířku betonové vzpěry c1.
\begin{gathered}
c_1=e_1\cdot\sin\theta=0{,}15\sin56{,}5\degree=0{,}125\text{ m}
\end{gathered}Ověříme napětí v betonové vzpěře:
\begin{gathered}
\sigma_\text{c}=\frac{|V_\text{Ed}|}{b\cdot c_1\cdot\sin\theta}=\frac{0{,}25}{0{,}25\cdot0{,}125\cdot\sin56{,}5\degree}=0{,}96\text{ MPa}\le\sigma_\text{Rd,max}=13{,}44\text{ MPa}
\end{gathered}V taženém spodním pasu bude působit síla Ft:
\begin{gathered}
F_\text{t}=\frac{M_\text{Ed}+N_\text{Ed2}\cdot z_1}{z}+\frac{|V_\text{Ed}|}{\tan\theta}+N_\text{Ed}=\frac{500}{0{,}924}+\frac{250}{1{,}51}=706\text{ kN}
\end{gathered}Staticky nutná plocha výztuže v dolním pasu
\begin{gathered}
A_\text{s}=706\space700/435=1\space624{,}6\text{ mm}^2
\end{gathered}Navržená výztuž na ohybový moment 3ø28 (1 847mm2) vyhovuje.
V tlačeném horním pasu bude působit síla Fc:
\begin{gathered}
F_\text{c}=-\frac{M_\text{Ed}+N_\text{Ed}\cdot z_1}{z}+\frac{|V_\text{Ed}|}{\tan\theta}=-706{,}7\text{ kN}
\end{gathered}Síla v betonové vzpěře:
\begin{gathered}
F_\text{C1}=\frac{|V_\text{Ed}|}{\tan\theta}=\frac{250}{\sin56{,}5\degree}=300\text{ kN}
\end{gathered}V dalším kroku navrhneme výztuž zachycující vznikající příčné tahy v betonové vzpěře obdobně jako u jiných poruchových oblastí. Vzhledem k tomu, že se předpokládá vznik příčného tahu především ve čtvrtinách betonové vzpěry, je nutné vložit svislé třmínky a vodorovné příložky i do horního pasu nosníku nad prostupem.
Půdorysná celková délka tlačené betonové diagonály:
\begin{gathered}
e_1+e_2=z/\tan\theta=0{,}926/1{,}5108=0{,}613\text{ m}
\end{gathered}Délka horní části tlačené betonové diagonály:
\begin{gathered}
H_\text{H}=r/\tan\alpha_2=0{,}15/\tan11{,}0\degree=0{,}772\text{ m}
\end{gathered}Šířka vzpěry ve styčníku:
\begin{gathered}
a=0{,}15\cdot\sin56{,}5\degree=0{,}125\text{ m}
\end{gathered}Vznikající příčné tahy
\begin{gathered}
2T=2\cdot F_\text{c1}\cdot(1-0{,}7\cdot a/h)/4=2\cdot300\cdot(1-0{,}7\cdot0{,}125/0{,}386)/4=116\text{ kN}
\end{gathered}Svislé třmínky nad otvorem:
\begin{gathered}
A_\text{sV}=2T\cdot\sin\theta/f_\text{yd}=116\cdot\sin56{,}5\degree/435\space000=0{,}000222\text{ m}^2
\end{gathered}navržen 1x třmen ø12 (226 mm2).
Vodorovná výztuž nad otvorem:
\begin{gathered}
A_\text{sH}=2T\cdot\cos\theta/f_\text{yd}=116\cdot\cos56{,}5\degree/435\space000=0{,}000147\text{ m}^2
\end{gathered}navržen 2x třmen ø10 (314 mm2).
Délka dolní části tlačené betonové diagonály je 1,111 – 0,772 = 0,339 m, vznikající příčné tahy:
\begin{gathered}
2T=2\cdot F_\text{c1}\cdot(1-0{,}7\cdot a/h)/4=2\cdot300\cdot(1-0{,}7\cdot0{,}125/0{,}17)/4=72{,}8\text{ kN}
\end{gathered}Svislé třmínky za otvorem:
\begin{gathered}
A_\text{sV}=2T\cdot\sin\alpha/f_\text{yd}=72{,}8\cdot\sin56{,}5\degree/435\space000=0{,}00014\text{ m}^2
\end{gathered}navržen 1x třmen ø12 (226 mm2).
Vodorovná výztuž nad otvorem:
\begin{gathered}
A_\text{sH}=2T\cdot\cos\alpha/f_\text{yd}=72{,}8\cdot\cos56{,}5/435\space000=0{,}000092\text{ m}^2
\end{gathered}navrženy 2xø10 (314 mm2).
Obr. 6.33 Návrh vyztužení oblasti kolem malého kruhového prostupu
6.9.2 Příklad velkého prostupu 1
Průvlak T-průřezu s celkovou výškou 1,0 m, tloušťka desky 200 mm a šířkou horní příruby 600 mm, šířka stojiny je 300 mm. Ve více namáhaném okraji prostupu je namáhání ohybovým momentem MEd = 300 kNm a posouvající silou VEd = 300 kN. Průvlak je vyroben z betonu C40/50, použitá betonářská výztuž B500B, rameno vnitřních sil z = 0,90 m. V průvlaku je obdélníkový prostup podle obr. 6.34. Dolní výztuž průvlaku je 4ø28, betonové krytí třmínků je 25 mm.
Rozhodující vnitřní síly pro návrh oblasti jsou obvykle uvažovány v místě nulového momentu na horním (dolním) pasu. Pro zjednodušení se předpokládá, že na horní pas nepůsobí nad prostupem žádné zatížení. Vzhledem k tomu, že na začátku výpočtu není známa poloha nulového momentu na pasech, vychází se z vnitřních sil na více namáhaném okraji prostupu. Rozhodující ohybový moment se upraví po dopočtení polohy nulového bodu.
Materiály
Beton C40/50:
\begin{gathered}
f_\text{cd}=26{,}67\text{ MPa};\space\alpha_\text{cc}=1{,}0;\space\varepsilon_\text{cu3}=3{,}5\space‰;\space\eta=1{,}0;\space\lambda=0{,}8;\space v'=(1-f_\text{ck}/250)=0{,}84
\end{gathered}Styčník s táhlem CCT:
\begin{gathered}
\sigma_\text{Rd,max}=0{,}85v'\cdot f_\text{cd}=19{,}04\text{ MPa}
\end{gathered}Vzpěra s příčnými tahy:
\begin{gathered}
\sigma_\text{Rd,max}=0{,}6v'\cdot f_\text{cd}=0{,}6\cdot0{,}84\cdot26{,}67=13{,}44\text{ MPa}
\end{gathered}Výztuž B500B:
\begin{gathered}
f_\text{yd}=\frac{f_\text{yk}}{\gamma_\text{s}}=\frac{500}{1{,}15}=435\text{ MPa};\space\varepsilon_\text{yd}=\frac{f_\text{yd}}{E_\text{s}}=\frac{435}{200}=2{,}175\space‰
\end{gathered}Geometrie oblasti
Obr. 6.34 Geometrie oblasti s prostupem
Návrh výztuže
Rozdělení ohybového momentu a posouvajících sil do horního a dolního pasu. Pro zjednodušení budeme předpokládat, že rameno vnitřních sil celého průvlaku je z = 0,9h = 0,9 m a ramena vnitřních sil jednotlivých pasů jsou zd= 0,8 ∙ hd = 0,8 ∙ 0,25 = 0,20 m, zd= 0,8 ∙ hd = 0,8 ∙ 0,35 = 0,28m. Ramena normálových sil v jednotlivých pasech zdN = 0,5zd = 0,10 m a zhN = 0,5zh = 0,14 m. Vzdálenost mezi těžištěm horního a dolního pasu je zot = 1,0 – 2 ∙ 0,025 – 0,10 – 0,14 = 0,71 m. V dolním pasu budeme předpokládat sklon tlačené diagonály θd = 45° a horního pasu θh = 30°.
\begin{gathered}
A_\text{h}=0{,}165\text{ m}^2,\space A_\text{d}=0{,}075\text{ m}^2,\space I_\text{h}=0{,}001504\text{ m}^4\space\space\text{a}\space\space I_\text{d}=0{,}000391\text{ m}^4
\end{gathered}Rozdělení vnitřních sil do dolního a horního pasu
Nejprve rozdělíme posouvající sílu do dolního a horního pasu:
\begin{gathered}
V_\text{Ed,d}=V_\text{Ed}\frac{\sqrt{A_\text{d}I_\text{d}}}{\sqrt{A_\text{h}I_\text{h}}+\sqrt{A_\text{d}I_\text{d}}}=0{,}256\cdot V_\text{Ed}=76{,}8\text{ kN}\space\space\text{a}\space\space V_\text{Ed,h}=V_\text{Ed}-V_\text{Ed,d}=223{,}2\text{ kN}
\end{gathered}Dále stanovíme nulový bod x (vzdálenost od okraje prostupu) horního pasu pomocí zjednodušeného vztahu.
Pro poměr hot/h = 0,40 ≤ 0,5 platí vztah:
\begin{gathered}
x=\bigg(\frac{1}{2}-\frac{M_\text{Ed}}{37\cdot|V_\text{Ed}|\cdot I_\text{ot}}\bigg[\frac{\text{max}(h_\text{h}{;}h_\text{d})}{\text{min}(h_\text{h}{;}h_\text{d})}\bigg]^3\bigg)\cdot I_\text{ot}=\bigg(\frac{1}{2}-\frac{300}{37\cdot300\cdot0{,}8}\bigg[\frac{0{,}350}{0{,}250}\bigg]^3\bigg)\cdot0{,}8=0{,}33\text{ m}
\end{gathered}Návrhové ohybové momenty horního a dolního pasu v místě vetknutí:
\begin{gathered}
M_\text{Ed,h}=\text{max}[V_\text{Ed,h}\cdot x;V_\text{Ed,h}\cdot(I_\text{ot}-x)]=\text{max}[223{,}2\cdot0{,}33{;}223{,}2\cdot(0{,}8-0{,}33)]=105\text{ kN}\\\\
M_\text{Ed,d}=\text{max}[V_\text{Ed,d}\cdot x;V_\text{Ed,d}\cdot(I_\text{ot}-x)]=\text{max}[76{,}8\cdot0{,}33{;}76{,}8\cdot(0{,}8-0{,}33)]=36{,}1\text{ kN}
\end{gathered}Návrhové normálové síly z nahrazení momentu MEd dvojicí vnitřních sil:
\begin{gathered}
N_\text{Ed,h}=-\frac{M_\text{Ed}}{z_\text{ot}}=\frac{300}{0{,}71}=-422{,}5\text{ kN}\space\space\text{a}\space\space N_\text{Ed}=\frac{M_\text{Ed}}{z_\text{ot}}=\frac{300}{0{,}71}=422{,}5\text{ kN}
\end{gathered}V horním i dolním pasu navrhneme výztuž standardním postupem podle ČSN EN 1992-1-1 jako u B – oblastí.
Stanovení sil v jednotlivých táhlech a vzpěrách
Síly v horním A1 a dolním pasu A2
\begin{gathered}
A_1=\frac{-M_\text{Ed,h}-N_\text{Ed,h}\cdot z_\text{hN}}{z_\text{h}}+\frac{|V_\text{Ed,h}|}{\tan\theta_\text{h}}=\frac{105+422{,}5\cdot0{,}14}{0{,}28}+\frac{223{,}2}{0{,}577}=184\text{ kN}\\\\
A_2=\frac{M_\text{Ed,d}+N_\text{Ed,d}\cdot z_\text{dN}}{z_\text{d}}+\frac{|V_\text{Ed,d}|}{\tan\theta_\text{d}}=\frac{36{,}1+422{,}5\cdot0{,}10}{0{,}20}+\frac{76{,}8}{1{,}0}=391{,}8\text{ kN}\\\\
T_\text{h}'=\frac{|223{,}2|}{0{,}28\cdot1{,}73}=460{,}8\text{ kN}\space\space\text{a}\space\space T_\text{d}'=\frac{|76{,}8|}{0{,}20\cdot1{,}0}=384\text{ kN}
\end{gathered}Svislé táhlo T1
\begin{gathered}
T_1=T_\text{1V}+T_\text{1M}+T_\text{1N}\\
\text{kde}\\
T_\text{1M}=-\frac{1{,}3A_1\cdot h_\text{h}\cdot h_\text{d}+1{,}6A_2\cdot h_\text{d}(0{,}8h_\text{h}+1{,}1h_\text{ot})}{0{,}7h^2+h_\text{h}\cdot h}=\frac{1{,}3\cdot184\cdot0{,}35\cdot0{,}25+1{,}6\cdot392\cdot0{,}25\cdot(0{,}8\cdot0{,}35+1{,}1\cdot0{,}4)}{0{,}7\cdot1^2+0{,}35\cdot1}=127{,}5\text{ kN}\\\\
T_\text{1N}=N\frac{z_\text{hN}z_\text{dN}}{(z_\text{dN}+z_\text{hN})(0{,}9h+1{,}3h_\text{h})}=0\space\space\text{a}\space\space T_\text{1v}=|V_\text{Ed,d}|=300\text{ kN}\\\\
T_1=T_\text{1V}+T_\text{1M}+T_\text{1N}=300+127{,}5+0=427{,}5\text{ kN}
\end{gathered}Svislé táhlo T2
\begin{gathered}
T_2=T_\text{2V}+T_\text{2M}+T_\text{2N}=223{,}2+105{,}3+0=328{,}5\text{ kN}\\
\text{kde}\\
T_\text{2M}=\frac{1{,}3A_2\cdot h_\text{h}\cdot h_\text{d}+1{,}6A_1\cdot h_\text{h}(0{,}8h_\text{d}+1{,}1h_\text{ot})}{0{,}7h^2+h_\text{h}\cdot h}=\frac{1{,}3\cdot392\cdot0{,}35\cdot0{,}25+1{,}6\cdot184\cdot0{,}35\cdot(0{,}8\cdot0{,}25+1{,}1\cdot0{,}4)}{0{,}7\cdot1^2+0{,}35\cdot1}=105{,}3\text{ kN}\\\\
T_\text{2N}=-N\frac{z_\text{hN}z_\text{dN}}{(z_\text{dN}+z_\text{hN})(0{,}9h+1{,}3h_\text{h})}=0\space\space\text{a}\space\space T_\text{2v}=|V_\text{Ed,h}|=223{,}2\text{ kN}
\end{gathered}Návrh výztuže táhel
- Na táhlo A1 navrhneme výztuž
\begin{gathered}
A_1/f_\text{yd}=184\cdot10^{-3}/435=0{,}000423\text{ m}^2
\end{gathered}navrhneme výztuž 3ø16…As1 = 0,000603 m2.
Délka přesahu táhla A1 od hrany prostupu le:
\begin{gathered}
l_\text{bd}=\frac{\phi}{4}\cdot\frac{\sigma_\text{s}}{f_\text{bd}}=\frac{16}{4}\cdot\frac{435\cdot423/603}{2{,}63}=464\text{ mm}\\\\
l_\text{e}=0{,}6\cdot(h+h_\text{h}+l_\text{bd})=0{,}6\cdot(1+0{,}35+0{,}47)=1{,}092\text{ m}
\end{gathered}- Na táhlo A2 navrhneme výztuž
\begin{gathered}
A_2/f_\text{yd}=392\cdot10^{-3}/435=0{,}000901\text{ m}^2
\end{gathered}navrhneme výztuž 3ø20…As2 = 0,000942 m2.
- Na táhlo T1 navrhneme výztuž
\begin{gathered}
T_1/f_\text{yd}=427{,}5\cdot10^{-3}/435=0{,}000983\text{ m}^2{....}5\text{x}2\phi12
\end{gathered}šířka táhla T1 je 0,9h = 0,90 m.
- Na táhlo T2 navrhneme výztuž
\begin{gathered}
T_2/f_\text{yd}=328{,}5\cdot10^{-3}/435=0{,}000755\text{ m}^2{....}4\text{x}2\phi12
\end{gathered}šířka táhla T2 je 1,3hh = 0,455 m.
Obr. 6.35 Návrh výztuže oblasti
6.9.3 Příklad velkého prostupu 2
Průvlak obdélníkového průřezu s výškou 1,0 m a šířkou 0,30 m, MEd = 300 kNm, VEd = 330 kN, beton C35/45, betonářská výztuž B500, geometrie poruchové oblasti viz obr. 6.36
Obr. 6.36 Příklad 2 velkého prostupu
Pro výpočet je nutné definovat následující parametry:
- úhly sklonu betonových vzpěr θ = 30°, θd = 45°, θh = 30°, předpoklad cot θ = 1,73;
- rameno vnitřních sil v průvlaku z = 0,85·h = 0,85 m, hot = 0,40 m;
- ramena vnitřních sil v horní a dolním pasu kolem otvoru:
\begin{gathered}
z_\text{d}=0{,}8\cdot h_\text{d}=0{,}20\text{ m}\\\\
z_\text{h}=0{,}8\cdot h_\text{h}=0{,}28\text{ m},\space z_\text{dN}=0{,}5\cdot z_\text{d}=0{,}10\text{ m},\space z_\text{hN}=0{,}5\cdot z_\text{h}=0{,}14\text{ m}\\\\
z_\text{ot}=z_\text{dN}+z_\text{hN}+h_\text{ot}=0{,}64.\space\space\text{Součinitel}\space\space\kappa=0{,}70,\space\text{tahové a tlakové složky ze změny polohy horního a dolního pasu se zanedbají.}
\end{gathered}- Rozdělení posouvající síly do horního a dolního pasu podle vztahu (6.9):
\begin{gathered}
A_\text{d}=0{,}075\text{ m}^2,\space A_\text{h}=0{,}105\text{ m}^2,\space I_\text{d}=0{,}000391\text{ m}^4\space\text{a}\space I_\text{h}=0{,}001072\text{ m}^4\\\\
\sqrt{A_\text{d}\cdot I_\text{d}}/(\sqrt{A_\text{d}\cdot I_\text{d}}+\sqrt{A_\text{h}\cdot I_\text{h}})=0{,}338,V_\text{Ed,d}=300\cdot0{,}338=101{,}4\text{ kN}\\\\
V_\text{Ed,h}=300-101{,}4=198{,}6\text{ kN}
\end{gathered}- Stanovení nulového bodu x ohybových momentů podle vztahu (6.15):
\begin{gathered}
h_\text{ot}/h=0{,}4\le0{,}5,\frac{x}{I_\text{ot}}=\frac{1}{2}-\frac{M_\text{Ed}}{37\cdot V_\text{Ed}\cdot I_\text{ot}}\bigg[\frac{\text{max}(h_\text{d}{;}h_\text{h})}{\text{min}(h_\text{d}{;}h_\text{h})}\bigg]^3\\
\text{po dosazení}\\
\frac{x}{0{,}8}=\frac{1}{2}-\frac{300}{37\cdot300\cdot0{,}8}\cdot\bigg[\frac{0{,}35}{0{,}25}\bigg]^3=0{,}41\to x=0{,}41\cdot0{,}8=0{,}33\text{ m}
\end{gathered}- Návrhové ohybové momenty horního a dolního pasu v místě vetknutí:
\begin{gathered}
M_\text{Ed,h}=\text{max}[V_\text{Ed,h}\cdot x{;}V_\text{Ed,h}\cdot(I_\text{ot}-x)]=\text{max}[198{,}6\cdot0{,}33{;}198{,}6\cdot(0{,}8-0{,}33)]=93{,}3\text{ kN}\\\\
M_\text{Ed,d}=\text{max}[V_\text{Ed,d}\cdot x{;}V_\text{Ed,d}\cdot(I_\text{ot}-x)]=\text{max}[101{,}4\cdot0{,}33{;}101{,}4\cdot(0{,}8-0{,}33)]=47{,}7\text{ kN}
\end{gathered}- Návrhové normálové síly z nahrazení momentu MEd dvojicí vnitřních sil:
\begin{gathered}
N_\text{Ed,h}=-\frac{M_\text{Ed}}{z_\text{ot}}=\frac{300}{0{,}64}=-468{,}8\text{ kN}\space\space\text{a}\space\space N_\text{Ed}=\frac{M_\text{Ed}}{z_\text{ot}}=\frac{300}{0{,}64}=468{,}8\text{ kN}
\end{gathered}V horním i dolním pasu navrhneme výztuž standardním postupem podle ČSN EN 1992-1-1 jako u B- oblastí (nosníkové oblasti s výše uvedenými sklony tlačených diagonál).
Stanovení sil v jednotlivých táhlech a vzpěrách (obr. 6.29)
Síly v horním A1 a dolním pasu A2:
\begin{gathered}
A_1=\frac{-M_\text{Ed,h}-N_\text{Ed,h}\cdot z_\text{hN}}{z_\text{h}}+\frac{|V_\text{Ed,h}|}{\tan\theta_\text{h}}=\frac{-93{,}3+468{,}8\cdot0{,}14}{0{,}28}+\frac{198{,}6}{0{,}577}=245{,}7\text{ kN}\\\\
A_2=\frac{M_\text{Ed,d}+N_\text{Ed,d}\cdot z_\text{dN}}{z_\text{d}}+\frac{|V_\text{Ed,d}|}{\tan\theta_\text{d}}=\frac{47{,}7+468{,}8\cdot0{,}10}{0{,}20}+\frac{101{,}4}{1{,}0}=574{,}3\text{ kN}\\\\
T_\text{h}'=\frac{|198{,}6|}{0{,}28\cdot1{,}73}=409{,}5\text{ kN}\space\space\text{a}\space\space T_\text{d}'=\frac{|101{,}4|}{0{,}20\cdot1{,}0}=507\text{ kN}
\end{gathered}Svislé táhlo T1
\begin{gathered}
T_1=T_\text{1V}+T_\text{1M}+T_\text{1N}=300+184{,}1+0=484{,}1\text{ kN}\\
\text{kde}\\
T_\text{1M}=\frac{1{,}3A_1\cdot h_\text{h}\cdot h_\text{d}+1{,}6A_2\cdot h_\text{d}(0{,}8h_\text{h}+1{,}1h_\text{ot})}{0{,}7h^2+h_\text{h}\cdot h}=\frac{1{,}3\cdot245{,}7\cdot0{,}35\cdot0{,}25+1{,}6\cdot574{,}3\cdot0{,}25\cdot(0{,}8\cdot0{,}35+1{,}1\cdot0{,}4)}{0{,}7\cdot1^2+0{,}35\cdot1}=184{,}1\text{ kN}\\\\
T_\text{1N}=N\frac{z_\text{hN}z_\text{dN}}{(z_\text{dN}+z_\text{hN})(0{,}9h+1{,}3h_\text{h})}=0\space\space\text{a}\space\space T_\text{1v}=|V_\text{Ed,d}|=300\text{ kN}
\end{gathered}Svislé táhlo T2
\begin{gathered}
T_2=T_\text{2V}+T_\text{2M}+T_\text{2N}=198{,}6+146{,}1+0=344{,}7\text{ kN}\\
\text{kde}\\
T_\text{2M}=\frac{1{,}3A_2\cdot h_\text{h}\cdot h_\text{d}+1{,}6A_1\cdot h_\text{h}(0{,}8h_\text{d}+1{,}1h_\text{ot})}{0{,}7h^2+h_\text{h}\cdot h}=\frac{1{,}3\cdot574{,}3\cdot0{,}35\cdot0{,}25+1{,}6\cdot245{,}7\cdot0{,}35\cdot(0{,}8\cdot0{,}25+1{,}1\cdot0{,}4)}{0{,}7\cdot1^2+0{,}35\cdot1}=146{,}1\text{ kN}\\\\
T_\text{2N}=-N\frac{z_\text{hN}z_\text{dN}}{(z_\text{dN}+z_\text{hN})(0{,}9h+1{,}3h_\text{h})}=0\space\space\text{a}\space\space T_\text{2v}=|V_\text{Ed,h}|=198{,}6\text{ kN}
\end{gathered}Návrh výztuže táhel
Na táhlo A1 navrhneme výztuž
\begin{gathered}
A_1/f_\text{yd}=245{,}7\cdot10^{-3}/435=0{,}000565\text{ m}^2
\end{gathered}navrhneme výztuž 3ø16…As1 = 0,000603 m2
Délka přesahu táhla A1 od hrany prostupu je le:
\begin{gathered}
l_\text{bd}=\frac{\phi}{4}\cdot\frac{\sigma_\text{s}}{f_\text{bd}}=\frac{16}{4}\cdot\frac{435\cdot565/603}{2{,}31}=705\text{ mm}\\\\
l_\text{e}=0{,}6\cdot(h+h_\text{h}+l_\text{bd})=0{,}6\cdot(1+0{,}35+0{,}71)=1{,}24\text{ m}
\end{gathered}- Na táhlo A2 navrhneme výztuž
\begin{gathered}
A_2/f_\text{yd}=547{,}3\cdot10^{-3}/435=0{,}001258\text{ m}^2
\end{gathered}navrhneme výztuž 4ø20…As2 = 0,001257 m2
- Na táhlo T1 navrhneme výztuž
\begin{gathered}
T_1/f_\text{yd}=484{,}1\cdot10^{-3}/435=0{,}001129\text{ m}^2{....}5\text{x}2\phi12
\end{gathered}šířka táhla T1 je 0,9h = 0,90 m,
- Na táhlo T2 navrhneme výztuž
\begin{gathered}
T_2/f_\text{yd}=344{,}7\cdot10^{-3}/435=0{,}00792\text{ m}^2{....}4\text{x}2\phi12
\end{gathered}šířka táhla T2 je 1,3hh = 0,455 m.
Obr. 6.37 Vyztužení oblasti kolem velkého prostupu
7 RÁMOVÉ ROHY
Rámové rohy jsou nejčastější poruchové oblasti monolitických železobetonových konstrukcí. Jedná se například o spojení mezi průvlakem a sloupem, mezi základovou deskou a stěnou, mezi stěnami nádrží, mezi stěnami komunikačních šachet a podobně. V prefabrikovaných konstrukcích jsou rámové rohy například u zalomených schodišťových ramen (obr. 7.1) a obecně ve všech zalomených prefabrikátech. V rámových rozích neplatí Bernoulliova hypotéza zachování rovinnosti průřezu po deformaci. Pro návrh oblasti používáme modely náhradní příhradoviny.
Obr. 7.1
Z hlediska působení vnitřních sil rozlišujeme rámové rohy s kladným a záporným působením ohybového momentu. Záporný ohybový moment rámový roh uzavírá – vnější líc prvku je tažen a vnitřní líc tlačen (obr. 7.2). Kladný ohybový moment rámový roh rozevírá (obr. 7.3). Vnitřní líc rohu je tažen a vnější líc je tlačen. Velikost poruchové oblasti lze odhadnout na základě Saint Venantovy hypotézy, podle které je délka poruchové oblasti přibližně rovna výšce prvku.
Obr. 7.2 Rámový roh se záporným ohybovým momentem
Obr. 7.3 Rámový roh s kladným ohybovým momentem – způsoby vyztužení
V normě ČSN EN 1992-1-1 [1] jsou v příloze J zobrazeny základní modely náhradní příhradoviny. Podrobnější pravidla pro návrh rámových rohů jsou v předpisu DAfStB 525 [20] a BetonKalender 2001 [7]. Německé předpisy sice vycházejí z DIN 1045-1 [2] v oblasti tvorby modelů náhradní příhradoviny, ale jsou zde uvedena stejná pravidla jako v [1]. Následné posouzení jednotlivých prvků modelu, jako jsou styčníky, tlačené a tažené pruty, je nutné provést v souladu s ČSN EN 1992-1-1 [1].
Modely náhradní příhradoviny vycházejí z možností vyztužení této oblasti a průběhu tlakových napětí v betonové části průřezu. Při návrhu jednotlivých prvků náhradní příhradoviny se vychází z jednotlivých únosností výztuže a betonu. Přitom je nutné u táhel vždy překontrolovat dostatečné zakotvení táhla ve styčníku a navrhnout vždy výztuž na přenesení vznikajících příčných tahů v betonových vzpěrách (viz kap. 1). Pro zjednodušení lze uvažovat, že v betonové vzpěře vznikají příčné tahové síly o velikosti cca 0,22Fc, které působí kolmo na podélnou osu vzpěry vždy ve čtvrtinách délky vzpěry (Fc je tlaková síla v betonové vzpěře – podrobněji viz [24]). Dále jsou uvedeny nejčastější modely jednotlivých typů rámových rohů s kritérii pro jejich vyztužení. Návrhové postupy pro styčníky a pruty modelů náhradní příhradoviny jsou podrobně rozebrány v předcházejících kapitolách.
7.1 RÁMOVÉ ROHY SE ZÁPORNÝM PŮSOBENÍM OHYBOVÉHO MOMENTU
Při působení záporného ohybového momentu vzniká při vnějším líci rohu tah, který je přenášen hlavní výztuží. Tahová výztuž v rohu mění směr, a přitom vznikají diagonální betonové vzpěry. Průběh hlavních napětí v rámovém rohu je na obr. 7.2a, b. Základní model náhradní příhradoviny je na obr. 7.2c. Model lze použít, pokud se výška průřezu sloupu h2 a příčle h1 od sebe výrazně neliší (2/3 < h2/h1 < 3/2).
Při vyčerpání únosnosti správně vyztuženého průřezu může dojít k následujícím poruchám:
- vyčerpání únosnosti tahové výztuže;
- porušení betonu v tlaku;
- porušení kotevní oblasti výztuže příčnými trhlinami;
- odštěpením povrchové betonové vrstvy.
Tahová výztuž musí být navržena s dostatečným poloměrem vnitřního zakřivení, aby se zabránilo otlačení betonu pod zakřivením výztuže a vzniku příčných tahů, které jsou nebezpečné, zejména pokud je výztuž umístěna poblíž líce betonu. Základní příklady vyztužení jsou na obr. 7.4. U rámového rohu je obvykle nutné řešit i stykování výztuže v pracovní spáře, které bývá pod dolním lícem příčle. U rohu rámové konstrukce je zásada, že ohnutá výztuž ze sloupu může být využita pro přenášení záporného ohybového momentu v příčli – průvlaku, ale nesmí zasahovat z výrobních důvodů příliš daleko od vnitřního líce sloupu. Výztuž z příčle – průvlaku nemůže zasahovat příliš do sloupu (jen na úroveň pracovní spáry), a proto bývá využita jen k přenesení záporného ohybového momentu průvlaku. Zápornou výztuž průvlaku proto kotvíme za úhlopříčkou rámového rohu. Při stykování tahové výztuže přesahem je vhodné podél stykované výztuže doplnit příčnou výztuž podle [1]. Pro napojení hlavní výztuže rohu lze použít i mechanické spojky výztuže [10].
Obr. 7.4 Rámový roh se záporným ohybovým momentem – způsoby vyztužení
Vyztužení smyčkami podle obr. 7.5d se používá především v rozích železobetonových stěn. Pokud jsou výšky příčle h1 a průřezu sloupu h2 přibližně stejné (2/3 < h2/h1 < 3/2), není nutné podle [1] posouzení třmínkové výztuže; pokud je ohnuta veškerá horní tahová výztuž průvlaku kolem rohu s dostatečným poloměrem ohybu a pokud má výztuž u líce betonu dostatečnou betonovou krycí vrstvu. Vyztužení podle obr. 7.4b a obr. 7.4c je vhodné pro mechanický stupeň vyztužení příčle ω =0,2 až 0,25 a pevnostní třídu betonu C25/30 a vyšší (mechanický stupeň vyztužení je ω = (Asfyd)/(Acfcd). Vyztužení podle obr. 7.4d je vhodné pro napojení stropní desky na železobetonovou stěnu. Spojení je vhodné pro stupeň příčle vyztužení podélnou výztuží ρL ≤ 0,4 % s průměrem podélné výztuže øL ≤ d/20 (d je účinná výška průřezu desky).
Obr. 7.5 Rámový roh se záporným ohybovým momentem – způsoby vyztužení
Obr. 7.6 Rámový roh se záporným ohybovým momentem srovnání nelineárního výpočtu s modelem náhradní příhradoviny
Pro návrh oblasti je možné také využít nelineární analýzu. Na obr. 7.6 je srovnání nelineární analýzy (programem ATENA 2D) s běžným modelem náhradní příhradoviny. Pokud je výška příčle h1 větší než výška průřezu sloupu h2 (h2/h1 ≤ 2/3), je nutné upravit model náhradní příhradoviny v souladu s obr. 7.5. Pro sklon tlačené betonové diagonály θ platí omezení 0,4 ≤ tan θ ≤ 1,0. Kotevní délka táhla T2 podle obr. 7.5a [1] má být navržena minimálně na sílu ∆T = T2 – T1.
Změna směru hlavní tahové výztuže vyvolává kolmo k rovině rámu tahové síly v betonu. Tyto síly jsou nebezpečné u ohybů blízko povrchu betonu, mohou způsobit odštěpení betonu. Velikost příčných tahových sil závisí především na poloměru ohybu hlavní tahové výztuže. Pokud je uvažován konstrukčně minimální poloměr ohybu tahové výztuže, musí být příčné tahové síly zachyceny příčnou výztuží (třmínky) ve vzdálenostech cca 5ds (ds je průmět výztužného prutu hlavní tahové výztuže). Proto je vhodné ohýbat hlavní tahovou výztuž s větším vnitřním průměrem øm. Doporučená hodnota průměru hlavní tahové výztuže podle [7] je øm ≥ 10ds a betonová krycí vrstva 3 až 5ds. Uvnitř rámového rohu se někdy provádí drobné zešikmení rohu, které částečně redukuje špičku tlakového napětí.
U rámových rohů s T průřezy nebo u komůrkových průřezů je nutné vždy při návrhu oblasti uvažovat způsob přenosu vnitřních sil mezi stojinou průřezu a tlačenou nebo taženou pásnicí průřezu, kde se poruchová oblast rohu zvětšuje – blíže viz [7]. Pro modelování přenosu sil z pásnic do stojiny průřezu používáme také náhradní příhradovinu.
Příklad nesprávného řešení rámového rohu je na obr. 7.7. Z obrázku je patrné chybné uložení výztuže rámového rohu, jehož důsledkem je nedostatečná únosnost rámového rohu.
Obr. 7.7
7.2 RÁMOVÉ ROHY S KLADNÝM PŮSOBENÍM OHYBOVÉHO MOMENTU
Kladný ohybový moment otevírá rámový roh. Vnitřní líc rohu je tažen, vnější líc rohu je tlačen. Průběh hlavních napětí v rámovém rohu je na obr. 7.3. Při zatížení rámového rohu kladným momentem vzniká prakticky nezávisle na množství výztuže v průřezu první trhlina, která vychází přímo z rámového rohu a má diagonální směr (trhlina a, viz obr. 7.3). Vzniku trhliny nelze zabránit vložením výztuže. Výztuž totiž musí splňovat požadavky na tloušťku betonové krycí vrstvy podle [1] a první trhlina vzniká právě v betonové krycí vrstvě. Další rozvoj trhliny a a následně vznik dalších trhlin je již závislý na vyztužení D-oblasti. Při malém nebo nesprávném vyztužení oblasti navazuje na trhlinu a šikmá poruchová trhlina b, která má velmi progresivní rozvoj a vede k porušení oblasti. Pokud se vhodným umístěním výztuže potlačí vznik trhliny b, vznikne v tlačené části průřezu poruchová trhlina c. Trhlina c (obr. 7.3) způsobí oddělení tlačené části průřezu. Tím se zmenší rameno vnitřních sil (sníží únosnost průřezu) a dochází k porušení této oblasti. Ovinutím vzpěry třmínky (C1, C2 na obr. 7.9) se oslabí vliv trhliny c. K oddělení části tlačeného betonu může pak dojít v betonové krycí vrstvě a v betonu mezi výztuží. Vhodným umístěním výztuže a jejím dostatečným množstvím lze rámový roh vyztužit tak, že porucha nastane vně D-oblasti. Proto, aby bylo možné průřez vyztužit, musí být rámový roh dostatečně robustní. O využití tahové výztuže při vnitřním líci rohu prakticky vždy rozhoduje její možné zakotvení v tlačené části průřezu. U subtilních konstrukcí je dostatečné zakotvení tahové výztuže velmi problematicky proveditelné. K zakotvení této výztuže lze s výhodou použít i přivařené kotevní desky nebo desky speciální.
Obr. 7.8 Rámový roh s kladným ohybovým momentem Modely náhradní příhradoviny podle úrovně namáhání
Dále uvedené modely náhradní příhradoviny rámových rohů vycházejí z předpokladu, že výšky průřezu před a za rámovým rohem jsou přibližně stejné. Na obr. 7.8 jsou nejčastější modely náhradní příhradoviny poruchové oblasti rámového rohu. Nejjednodušší model na obr. 7.8a je vhodný pouze pro málo zatížené a robustní konstrukce. Při vyšším využití rámového rohu je možné dostatečné zakotvení tahové výztuže při vnitřním líci jen pomocí přivařených kotevních desek, nebo pomocí mechanických kotevních spojek [25]. Zpřesněním modelu rámového rohu je možné více využít beton v tlačené vzpěře. Pro model na obr. 7.8b je maximální namáhání v betonové vzpěře 0,75fcd. Pro přesnější modely na obr. 7.8c, d, které zároveň představují optimální modely oblasti, je maximální namáhání betonové vzpěry 0,85fcd. Vyšší namáhání v betonové vzpěře je možné pouze, pokud je výška tlačené oblasti x průřezu před rámovým rohem omezena vztahem x ≤ d/4. Na obr. 7.8c jsou stanoveny i velikosti vznikajících příčných tahů T1 až T3. Na obr. 7.9 je srovnání nelineární analýzy rámového rohu s kladným působením s modelem náhradní příhradoviny.
Obr. 7.9 Rámový roh s kladným ohybovým momentem srovnání nelineárního výpočtu s modelem náhradní příhradoviny
Na obr. 7.10 jsou příklady vyztužení oblasti. Největším problémem při vyztužování oblasti je možnost dostatečného zakotvení tažené výztuže při vnitřním líci rohu. Tahovou výztuž je třeba zakotvit v tlačeném betonovém pásu při vnějším líci. Výška tlačeného pásu je relativně malá pro dostatečné zakotvení výztuže. Proto se rámové rohy vyztužují smyčkami výztuže při taženém líci rohu ve tvaru podle obr. 7.10a a obr. 7.10e. Smyčky kolmé na tažený líc rohu podle obr. 7.10c, d jsou vhodné spíše pro vyztužení rohů stěn. Smyčka podle obr. 7.10c je však složitější z hlediska přesnosti výroby. Ve vyztužení rámových rohů má velký vliv na únosnost šikmá výztuž, která nejúčinněji zabraňuje dalšímu rozvoji prvotní poruchové trhliny a (obr. 7.3).
Obr. 7.10 Rámový roh s kladným ohybovým momentem – způsoby vyztužení
Rámové rohy jsou i ve spojení stěn např. nádrží, ale vzhledem k menšímu namáhání a stěnovému působení obvykle zde nevznikají poruchové trhliny.
Z porovnání vyztužení rámových rohů na obr. 7.11 vyplývá, že je možné vyztužit rámový roh tak, aby k vyčerpání únosnosti průřezu došlo mimo poruchovou oblast rohu. Na obr. 7.11 je porovnána únosnost získaná z experimentů (převzato z [39]) rámového MRu a vypočítaná únosnost rámového rohu MRd (únosnost je stanovena jako pro stejně vyztuženou B-oblast) v závislosti na způsobu vyztužení rámového rohu. V grafu na svislé ose je vynesen poměr η = MRu/MRd, na vodorovné ose pak procento vyztužení ρ průřezu příčle rámového rohu. Z obr. 7.11 je patrné, že se zvyšujícím se vyztužením se u všech modelů snižuje skutečná únosnost průřezu MRu ve srovnání s návrhovou únosností MRd. Šikmá výztuž (model A) umožňuje plnohodnotné navržení výztuže rámového rohu (do mechanického stupně vyztužení příčle \omega=\frac{A_\text{s}f_\text{yd}}{A_\text{c}f_\text{cd}}\le0{,}2 podle [20]). Místo šikmé výztuže je možné doplnit k tahové výztuži příložky o ploše rovné 50 % staticky nutné tahové výztuže. Pokud pro (geometrický) stupeň vyztužení příčle platí ρ ≤ 0,4 %, není nutné posilovat smyčkové vyztužení rohu podle obr. 7.11d příložkami nebo šikmou výztuží (model B). Model vyztužení G má takřka třetinovou únosnost vzhledem k nedostatečnému zakotvení tahové výztuže a v průřezu zcela chybí výztuž zabraňující vzniku poruchové trhliny b a c podle obr. 7.3c. V typech vyztužení E, F a G není žádná výztuž zachycující vznikající příčné tahy v betonové vzpěře. Proto dochází po vzniku první trhliny k velmi rychlému porušení celého průřezu. Průřez nemá dostatečnou duktilitu.
Obr. 7.11 Srovnání vypočtené a experimentem stanovené únosnosti rámových rohů s kladným ohybovým momentem
U rámových rohů je vhodné vždy navrhnout výztuž pro zachycení příčných tahů v betonové vzpěře ve formě 3 až 4 smyček, nebo použít vícestřižné třmínky (např. obr. 7.10a, b, e). Při posuzování betonové vzpěry je možné započítat pouze průřez betonové vzpěry, který je ovinut výztuží. V betonové vzpěře při vnějším líci nemůže být započtena betonová krycí vrstva do celkové plochy vzpěry, protože při větším namáhání může dojít k jejímu odtržení. Přesněji by se neměla uvažovat krycí vrstva, včetně tloušťky betonu v úrovni příčné výztuže.
U rámových rohů s kladným ohybovým momentem je hlavní tahová výztuž při vnitřním líci rohu. Při vyčerpání únosnosti průřezu může dojít k následujícím poruchám:
- vyčerpání únosnosti tahové výztuže;
- porušení betonu v tlaku v důsledku příčného tahu;
- porušení betonu v tlaku odtržením krycí vrstvy výztuže;
- porušení kotevní oblasti tažené výztuže.
Předcházející modely vycházely z předpokladu, že výšky průřezu před a za rámovým rohem jsou přibližně stejné. Pokud je výška průřezu příčle výrazně větší než výška průřezu sloupu, potom je nutné upravit model náhradní příhradoviny podle obr. 7.12. Spolu s tím je nutné doplnit výztuž podle principů zobrazených na obr. 7.12c.
Obr. 7.12 Rámový roh s kladným ohybovým momentem, Rohy s větší výškou příčle než sloupu, Model náhradní příhradoviny a princip vyztužení
Rámové rohy nemusí mít pravý úhel. Podle obr. 7.13 rozeznáváme rámové rohy pravoúhlé, tupé a ostré. Ostré rámové rohy jsou například u zalomených schodišťových ramen (prefabrikovaných, ale i monolitických). Tupé rámové rohy jsou méně časté. Optimální vyztužení tupého rámového rohu je na obr. 7.14a, odpovídající model oblasti na obr. 7.14b. Pokud není prostor k vytvoření smyček, je možné vyztužit podle obr. 7.14c. Tento způsob vyztužení je však možný pouze pro velmi málo namáhané rámové rohy, protože diagonální tah v rohu přebírá beton (tečkovaně vyznačeno v modelu na obr. 7.14d). Zvláštní pozornost vyžaduje případ, kde kromě momentu působí ještě normálová tahová síla.
Obr. 7.13 Označení rámových rohů
Obr. 7.14 Tupé rámové rohy s kladným ohybovým momentem
Obdobná situace je i u ostrých rámových rohů (obr. 7.15). U ostrého rámového rohu vyztužení podle obr. 7.15a (běžné u zalomených schodišťových ramen), přenáší diagonální tah v rohu beton (na rozdíl od běžných předpokladů tvorby modelů poruchových oblastí, kde nepředpokládáme působení betonu v tahu). Únosnost rámového rohu je velmi omezena únosností tažené betonové diagonály. Poruchová trhlina má průběh jako trhlina b na obr. 7.3. Pokud vložíme do rohu třmínek, únosnost rohu se výrazně nezvýší. Poruchová trhlina se přesouvá do polohy c podle obr. 7.3 a výrazně zmenšuje výšku průřezu. Optimálním vyztužením je zakotvení tahové výztuže smyčkami a vložením šikmé výztuže podle obr. 7.15c.
Obr. 7.15 Ostré rámové rohy s kladným ohybovým momentem
7.3 RÁMOVÉ STYČNÍKY
Rámové styčníky představují obvykle napojení průvlaků (vodorovných trámových prvků) na sloupy (svislé nosné prvky). Spojení je namáháno normálovou silou, posouvající silou a ohybovým momentem. Navíc ve styku bývá pracovní spára. Pokud je nosný systém ztužen rámy, styčníky – rámové rohy musí přenést veškerá vodorovná a stabilitní zatížení. Pokud jsou rámové rohy ve ztuženém nosném systému, nepřenášejí vodorovné účinky zatížení a podílejí se jen na přenášení účinků vertikálních zatížení. Rámové rohy bývají často hodně namáhané, a přitom jsou svým způsobem slabým místem konstrukce. Je nutné si uvědomit, že vlivem trhlin v tažených částech rámového rohu dochází často k výraznému přerozdělení momentů a zvětšení tak momentů v přilehlých polích průvlaků – rámových příčlí. To je zvlášť důležité při rámově ztužených nosných systémech, nebo například u komor sil, kde je třeba navrhnout výztuže ve stěně u obou povrchů. Na obr. 7.16a, b jsou příklady rámů ve ztužených nosných systémech (tedy bez vlivu vodorovného zatížení). Na obr. 7.16c je zobrazen průběh momentů na ztužujícím rámu s vlivem vodorovných účinků zatížení. V průbězích ohybových momentů jsou zobrazeny maximální a minimální hodnoty z výpočtu.
Obr. 7.16 Příklad rámové konstrukce
Na obr. 7.16c je patrna změna tažených vláken u sloupového prvku. To znamená, že rámové styčníky (jako např. všechny prvky s vlivem stability) je nutné vyšetřovat pro všechny rozhodující návrhové kombinace zatížení, nikoliv jen pro výsledné obálky vnitřních sil. Pro některé návrhové kombinace zatížení může být nutné vytvořit jiný model náhradní příhradoviny.
7.3.1 Rámový styčník – sloup se spojitou příčlí
Rámové rohy jsou ve spojení sloupu a příčle. Na obr. 7.17 jsou uvedeny modely náhradní příhradoviny pro spojitou rámovou příčel, spojenou se sloupem při různých kombinacích vnitřních sil. K modelu je schematicky nakresleno doporučené vyztužení oblasti. Pokud je styk sloupu s příčlí celý tlačený (obr. 7.17a), postačuje zakotvit výztuž sloupu na kotevní délku v průřezu příčle. Pro zakotvení pozitivně působí tlačená oblast přilehlé příčle. Pokud ve styku sloupu a příčle vznikají tahy, je nutné upravit model náhradní příhradoviny podle obr. 7.17b až obr. 7.17d. Pro zakotvení tažené výztuže sloupu bývá výška průřezu nedostatečná a je nutné zakotvit výztuž smyčkou nebo ohybem obr. 7.17c, d, případně lze použít přivařených kotevních desek nebo speciálních mechanických kotevních spojek [25]. Při ohybu tažené výztuže vznikají příčné tahy, které je nutné zachytit třmínky příčle – doplněním třmínků i do oblasti přímo nad sloupem. Při velkém momentovém namáhání styku sloupu s příčlí (obr. 7.17d) je možné dostatečné zakotvení výztuže ohnutím výztuže do tažené příčle při jejím horním líci.
Poznámka:
Pokud ve styčníku mohou vzniknout ohybové trhliny, nelze dimenzovat výztuž příčle na ohybový moment redukovaný do líce podpory.
Obr. 7.17 Styčník sloupu s průběžnou rámovou příčlí modely a principy vyztužení
7.3.2 Rámový styčník průběžného sloupu s příčlí
Pro rámové styčníky krajních průběžných sloupů obecně platí, že tlačená a tažená oblast sloupu se pod styčníkem mění (obr. 7.18a, obr. 7.19). Změna vyvolává vodorovné tahy ve střední části výšky příčle (označené T). Vzniklé tahy je nutné zakotvit v oblasti, kde je zároveň kotvena tahová výztuž příčle. Podrobnější model na obr. 7.19 lépe dokládá vznik tažené oblasti přibližně ve středu výšky příčle. Vodorovná výztuž navržená na vzniklé tahy T zároveň musí přenést i vznikající příčné tahy z tlačené betonové diagonály C. Podle obr. 7.18a v rámovém rohu působí posouvající síla Vjh. Při posouzení únosnosti průřezů se obdobně jako u nosníkových průřezu rozlišuje průřez bez třmínkové (smykové) výztuže a s třmínkovou výztuží [20].
- Únosnost styčníku bez třmínkové výztuže podle [20] (deskové a stěnové rohy):
\begin{gathered}
V_\text{j,cd}=1{,}4\bigg(1{,}2-0{,}3\frac{h_\text{b}}{h_\text{c}}\bigg)b_\text{eff}h_\text{c}f_\text{cd}^{1/4}
\end{gathered}(7.1)
- Únosnost styčníku se třmínkovou výztuží podle [20]:
\begin{gathered}
V_\text{j,Rd}=V_\text{j,cd}+0{,}4A_\text{sj,eff}f_\text{yd}\le2V_\text{j,cd}\space\space\text{a současně}\space\space V_\text{j,Rd}\le\gamma_\text{N}0{,}25f_\text{cd}b_\text{eff}h_\text{c}
\end{gathered}(7.2)
kde je
hc, bc … výška, šířka průřezu sloupu;
hb, bb … výška, šířka průřezu nosníku – příčle;
Asj,eff … plocha vodorovných třmínků v oblasti mezi tlačenou oblastí příčle a horním lícem styčníku;
NEd,c … návrhová hodnota normálové síly ve sloupu v rámovém rohu;
beff … efektivní šířka styčníku beff = (bc+bb)/2 ≤ bc;
γN … vliv normálové síly ve sloupu a štíhlosti styčníku γN = γN1 ∙ γN2.
\begin{gathered}
\gamma_\text{N1}=1{,}5\bigg(1-0{,}8\frac{N_\text{Ed,c}}{A_\text{c,c}\cdot f_\text{ck}}\bigg)\le1{,}0\space\space\text{a}\space\space\gamma_\text{N2}=1{,}9-0{,}6h_\text{b}/h_\text{c}\le1{,}0
\end{gathered}(7.3)
Doporučené vyztužení je na obr. 7.18c.
Obr. 7.18 Rohový styčník sloupu a rámové příčle
Obr. 7.19 Rohový styčník sloupu s rámovou příčlí vyšší výšky
7.3.3 Rámový styčník – průběžný sloup se spojitou příčlí
Pro rámové styčníky s průběžnou příčlí i průběžným sloupem jsou modely náhradní příhradoviny znázorněné na obr. 7.20. Navržená výztuž podle obr. 7.20a není vhodná. Výztužné pruty sloupu jsou kotveny přímo v oblasti rámového rohu. V diagonálách styčníku se koncentrují velké síly, zvětšené o síly ze zakotvení podélné výztuže. Taženou diagonální výztuž je velmi obtížné dostatečně zakotvit. Možným řešením je ohnout podélnou taženou výztuž sloupu do příčle podle obr. 7.18b. Lépe je protáhnout výztuž sloupu styčníkem a kotvit ji až za oblastí rámového rohu obr. 7.18c. Návrh příložek výztuže příčle a sloupu podle [2] je na obr. 7.18c.
Pro rámové rohy nejsou v ČSN EN 1992-1-1 [1] další pravidla. Podrobnější pravidla pro vyztužení sloupů lze najít v DAfStB 525 [20].
Obr. 7.20 Styčník průběžného sloupu s průběžnou rámovou příčlí modely a principy vyztužení
U rámových styčníků vnitřních sloupů ztužených nosných systémů, kde veškeré vodorovné zatížení přebírají ztužující systémy, lze rámové působení zanedbat (zanedbat přenos ohybového momentu z příčle do sloupu – uvažovat kloubové uložené příčle na sloupu), pokud pro sousední pole příčlí platí poměr 0,5 < l0,1/l0,2 < 2,0 (podle [20]). U ostatních styčníků, kde pro poměr výšky průřezů sloupu a příčlí platí 1,0 ≤ hb/hc ≤ 1,5, je nutné posoudit únosnost podle vztahu:
\begin{gathered}
V_\text{jh}=(|M_\text{b,1}|+|M_\text{b,2}|)/z_\text{b}-|V_\text{c}|\le\gamma_\text{N}0{,}25f_\text{cd}b_\text{eff}h_\text{c}
\end{gathered}(7.4)
kde je
Mnos,1, Mnos,2 … jsou antisymetrické ohybové momenty příčlí 1 a 2;
beff … šířka sloupu v úrovni styčníku;
γN … vliv normálové síly ve sloupu a štíhlosti styčníku.
\begin{gathered}
\gamma_\text{N1}=1{,}5\bigg(1-0{,}8\frac{N_\text{Ed,c}}{A_\text{c,c}\cdot f_\text{ck}}\bigg)\le1{,}0
\end{gathered}Pro rámové styčníky platí následující doporučení:
- podélná výztuž sloupu musí být přímá a procházet spojitě celou oblastí;
- u nosných neztužených rámových soustav je doporučeno zvýšit plochu podélné výztuže sloupu v D-oblasti. Takto doplněná výztuž musí být dostatečně zakotvena za D-oblastí.
V příčlích a ve sloupech je nutné v oblasti délky většího rozměru sloupu doplnit příčnou třmínkovou výztuž ve vzdálenostech 0,6násobku vzdálenosti třmínků ve sloupech, pokud není v důsledku stykování výztuže ve sloupu požadována oblast větší.
7.3.4 Zalomené nosníky
Zalomené nosníky, desky se používají například pro schodišťová ramena, viz obr. 7.21. Po celé délce zalomené desky schodišťového ramene jsou rámové rohy s kladným i záporným působením ohybového momentu. Poruchové oblasti rámových rohů bezprostředně na sebe navazují. Vyztužení oblasti je možné pouze na sebe navazujícími třmínky a šikmou výztuží. (obr. 7.21). Estetický tvar prefabrikátu schodišťové desky je vykoupen velmi komplikovanou a náročnou výztuží.
Obr. 7.21 Příklad řešení rámových roh
7.4 PRINCIPY VYZTUŽENÍ RÁMOVÝCH ROHŮ
Rámové rohy a styčníky rámů jsou oblasti, které velmi často rozhodujícím způsobem ovlivňují chování celých konstrukcí, proto je nutné věnovat návrhu poruchových oblastí rámových rohů dostatečnou pozornost. V oblasti rámového rohu a rámových styčníků je nutné umístit nosnou a konstrukční výztuž, odpovídající modelu náhradní příhradoviny. Ve všech navazujících prvcích (sloupech a příčlích) je vhodné doplnit konstrukční výztuž v oblasti přechodu poruchové oblasti a běžné nosníkové (sloupové) oblasti. Ve všech rozích s kladným ohybovým momentem je doporučeno vkládat šikmou výztuž k omezení vznikající poruchové trhliny a k posílení duktility oblasti.
Při návrhu konstrukce s rámovými rohy je vhodné uvažovat s možným přerozdělením ohybových momentů. Vlivem trhlinami oslabeného průřezu rámového rohu dochází k nárůstu ohybového momentu v přilehlém poli. Tento nárůst momentů v přilehlém poli může být přibližně až 30 % [7]. Zároveň je třeba mít na paměti, že pokud ve styčníku vzniknou trhliny, není možné redukovat ohybové momenty k líci podpory.
Při návrhu poruchové oblasti rámového rohu je také nutné po dokončení výpočtu a nakreslení výztuže ověřit předpokládanou geometrii modelu náhradní příhradoviny.
8 STĚNOVÉ KONSTRUKCE
Stěnové nosníky jsou vysoké nosníky, pro něž trojnásobek výšky h průřezu je větší než rozpětí nosníku l (3h ≥ l). V odborné literatuře se někdy uvádí hranice mezi nosníkem a stěnovým nosníkem od poměru 2,0 (2,0 pro prosté stěnové nosníky a 2,5 pro spojité stěnové nosníky) pro zatížení osamělými břemeny až po 5,0 (5h ≥ l) pro zatížení rovnoměrným spojitým zatížením. U stěnových nosníků neplatí Bernouliova hypotéza o zachování rovinnosti průřezu po deformaci, která je základním předpokladem při řešení nosníků jako jednorozměrných prvků. Stěnové nosníky jsou dvourozměrné prvky. Na obr. 8.1 je schematicky zobrazen rozdíl v průběhu napětí mezi nosníkem (l/h >> 2) a stěnovým nosníkem o různých výškách průřezu. U nosníku dochází k zakřivenému průběhu vodorovných napětí σx již při poměru h/l = 0,4 až 0,5.
Stěnové nosníky jsou dnes častými konstrukcemi v pozemních stavbách, kdy nad volnou dispozici např. garážových prostor navazuje stěnový nosný systém vyšších podlaží. Se stěnovými nosníky se setkáme v průmyslových stavbách a v mostních konstrukcích.
Obr. 8.1 Nosník a stěnový nosník – průběhy napětí
Charakteristické vlastnosti stěnových nosníků
- Průběh napětí v tahu je po celé délce rozpětí přibližně stejný, tzn. hodnota tahového napětí ve spodních vláknech průřezu ve středu rozpětí se jen velmi málo liší od hodnoty u podpory obr. 8.2.
- Maximální hodnota tahového napětí průřezu je značně rozdílná od maximální hodnoty tlakového napětí.
- Vzhledem k chování železobetonu je celý stěnový nosník poruchovou D-oblastí (obr. 8.2).
- U stěnových nosníků nelze zanedbat smykové deformace.
Obr. 8.2 Stěnový nosník – lineární a nelineární model
Stěnové nosníky jsou moderní nosné prvky i v pozemních stavbách. Pro jejich návrh je vhodné použít modely náhradní příhradoviny. Pro stěnové konstrukce s konstantní tloušťkou stěny a bez větších otvorů lze použít zjednodušené vzorce přímo pro návrh jednotlivých prvků modelu náhradní příhradoviny. Pro složitější stěnové nosníky s proměnnou tloušťkou oblasti, se ztužujícími okraji nebo s většími otvory je nutno vytvořit speciální model náhradní příhradoviny za pomoci výsledků lineárně pružného 2D výpočtu metodou konečných prvků. Stěnové nosníky lze řešit i nelineární metodou konečných prvků, u nelineárního řešení je nutné vždy kontrolovat mezní stav použitelnosti. Stěžejním místem návrhu stěnových nosníků je vždy řešení táhel, jejich zakotvení a řešení styčníků. Každý stěnový nosník musí být při obou lících vyztužen minimálně konstrukční výztuží, včetně příčných spon. Principy vyztužení stěnového nosníku jsou na obr. 8.3.
Obr. 8.3 Stěnový nosník – principy vyztužení
8.1 MODELOVÁNÍ STĚNOVÝCH KONSTRUKCÍ
Stěnový nosník je rovinný prvek. Pro jeho řešení máme k dispozici lineární a nelineární metody založené na FEM a metodu náhradní příhradoviny. Podle normy [2] a [19] lze provést výpočet podle plasticity pro stěny bez nutnosti posoudit dostatečnou rotační kapacitu průřezu i pro výztuž s duktilitou A. V ČSN EN 1992-1-1 [1] není k výpočtu stěn podle teorie plasticity uvedeno nic bližšího. Stěnovým nosníkům je věnován např. předpis [18] a [7]. Na obr. 8.2 je znázorněn rozdíl mezi lineárně pružným modelem a nelineárním modelem stěnového nosníku (prostý nosník). Při nelineárním modelu se v důsledku vzniku trhlin posunuje tlačená část k hornímu okraji nosníku a zvětšuje se rameno vnitřních sil z. Tím se zmenšuje staticky nutná dolní tahová výztuž. Na druhé straně snižováním množství tahové výztuže roste šířka trhlin. Proto je doporučeno při modelování oblasti vycházet spíše z lineárních modelů. Lineární 2D modely stěnových nosníků slouží obvykle jako podklad pro tvorbu modelů náhradní příhradoviny. Na základě průběhu hlavních napětí lze odvodit optimální model náhradní příhradoviny. U všech modelů musí být vždy splněna stejná podmínka celkové rovnováhy nosníku. Z modelů náhradní příhradoviny je patrné, že táhlo, představující dolní taženou výztuž, je plně využito po celé délce mezi styčníky nad podporami. Proto musí být veškerá spodní výztuž stěn vždy na celé rozpětí a zakotvena nad podporou. Spodní výztuž stěny umísťujeme do výšky 0,1k až 0,20k (k je menší z rozměrů stěny – výšky h a rozpětí l), nikoli tedy jen při spodním líci, což odpovídá průběhu tahových napětí. Redukuje se tímto také šířka trhlin. Principy vyztužení prostě uloženého stěnového nosníku jsou na obr. 8.3. U podpor se přidává svislá a vodorovná výztuž (položky 3 a 4 na obr. 8.3) s ohledem na rozptyl sil (příčné tahy) v tlačených prutech směřujících k podporám. U stěnových nosníků je nutné vždy překontrolovat také podmínky maximálního napětí ve styčné spáře s podporující konstrukcí.
U stěnových nosníků s konstantní tloušťkou stěny a bez velkých otvorů není nutné posuzovat napětí v tlačených betonových vzpěrách, protože pro návrh jsou rozhodující styčníky, táhla a zakotvení táhel ve styčnících.
8.2 JEDNODUCHÉ STĚNOVÉ KONSTRUKCE
8.2.1 Prostý stěnový nosník přímo zatížený
Přímo zatížený nosník je zatížený při horním líci. Průběh napětí v prostém stěnovém nosníku je na obr. 8.4. Trajektorie tlakových napětí probíhají strmě k podporám, tahové trajektorie jsou k nim kolmé, nejsou tedy příliš skloněny směrem k podporám jako u běžných nosníků. Proto vznikají především svislé trhliny. Nebezpečí porušení vzniká především u podpor, kde zakotvení výztuže a velký podporový tlak vyvozuje velké místní namáhání (proto je nutné tyto oblasti patřičně vyztužit viz obr. 8.4). Průběh vodorovných napětí σx je v celém rozpětí prakticky stejný. Průběh svislých napětí σy se po výšce mění v závislosti na poloze a charakteru zatížení (zatížení na dolním nebo při horním povrchu). Přibližně lze stanovit hlavní tahovou sílu v poli pomocí analogie s nosníkem při redukovaném ramenu vnitřních sil. Tahovou sílu T v poli lze vyjádřit vztahem:
\begin{gathered}
T=M_\text{Ed}/z
\end{gathered}(8.1)
kde je
MEd … ohybový moment stanovený na nosníkové analogii;
z … rameno vnitřních sil.
\begin{gathered}
z=0{,}3h(3-h/l)\space\text{ pro }\space0{,}5\le h/l\le1{,}0
\end{gathered}(8.2)
\begin{gathered}
\text{a}\space\space z=0{,}6l\space\space\text{pro}\space\space h/l>1{,}0
\end{gathered}(8.3)
kde je
l … rozpětí stěnového nosníku;
h … celková výška průřezu stěnového nosníku.
Obr. 8.4 Prostý stěnový nosník přímo zatížený rovnoměrným zatížením
Uvedené hodnoty odpovídají lineárnímu modelu podle obr. 8.2 a obr. 8.4. Na obr. 8.4 je zobrazena velikost vnitřních sil v táhlech a vzpěrách v závislosti na poměru výšky průřezu h k rozpětí l. Při poměru h/l ≥ 1 lze uvažovat rameno vnitřních sil z = 0,6l a sklon tlačených diagonál θ ≈ 68,5°. V horním tlačeném pasu je napětí v betonu v tlaku rovno 0,35q/b (při výšce tlačené oblasti 0,6l), přitom při horním líci je v úrovni zatížení svislé tlakové napětí q/b. Napětí v betonové vzpěře C2 není tedy pro návrh rozhodující. Pro návrh oblasti je rozhodující síla v táhle T při spodním líci, včetně jejího zakotvení ve styčnících nad podporou a řešení styčníků. Přesnější vyjádření vnitřních sil je v tab. 8.1.
8.2.2 Prostý stěnový nosník zatížený osamělým břemenem
Průběh napětí ve stěnovém nosníku zatíženém osamělým břemenem je na obr. 8.5. Průběh vodorovných napětí σx se po délce rozpětí mění především v horních vláknech. Pro stěnový nosník jsou modely náhradní příhradoviny na obr. 8.5. Pro velmi vysoké nosníky lze v části výšky průřezu uvažovat oblast B – viz obr. 8.6 (podle Saint Venantovy hypotézy je délka poruchové oblasti rovna výšce průřezu). Závislost velikosti vnitřních sil na zatěžovací síle a poměru výšky průřezu k rozpětím je na obr. 8.5. Tahová síla T1 při spodních vláknech průřezu je pro nosníky s poměrem h/l ≥ 1,5 rovna 0,2F. Přesnější vyjádření vnitřních sil je v tab. 8.1.
Obr. 8.5 Prostý stěnový nosník přímo zatížený osamělým břemenem
Obr. 8.6 Prostý vysoký stěnový nosník přímo zatížený osamělým břemenem
8.2.3 Prostý stěnový nosník nepřímo zatížený
Při zatížení působícím u dolního okraje tlakové trajektorie vytvářejí klenbu opřenou v podporách (obr. 8.7), přičemž zatížení je do určité míry zavěšeno na této klenbě. Tahové trajektorie při spodním povrchu jsou skoro vodorovné, vytvářejí táhlo klenby. U nepřímo zatíženého stěnového nosníku je nutné zatížení vynést táhly T2 do styčníku tlačených vzpěr C1 a C2 (obr. 8.7). U nepřímo zatíženého stěnového nosníku se mění na rozdíl od přímo zatíženého nosníku především průběh svislých napětí σy. Pro výpočet vnitřních sil v táhlech modelu náhradní příhradoviny lze použít stejných vztahů (8.1) až (8.3) jako u přímo zatíženého stěnového nosníku. Sílu v táhle T2 stanovíme ze zatížení působícího při spodním líci nosníku. Na obr. 8.7 je zobrazena závislost velikosti vnitřních sil v táhlech a vzpěrách na poměru výšky průřezu h k rozpětí l. Při poměru h/l ≥ 1 lze uvažovat také rameno vnitřních sil z = 0,6l a sklon tlačených diagonál θ ≈ 66,5°. Skon tlačených diagonál je tedy mírně ovlivněn polohou zatížení stěnového nosníku. Výztuž vynášející zatížení při spodním líci musí tvořit třmínky obepínající hlavní výztuž. Třmínky se navrhují na sílu odpovídající celkovému zatížení při spodním líci (T2 = 0,5ql). Přesnější vyjádření vnitřních sil je v tab. 8.1. Model stěnového nosníku s přímým a nepřímým zatížením je na obr. 8.8.
Obr. 8.7 Prostý stěnový nosník přímo zatížený osamělým břemenem
Obr. 8.8 Prostý stěnový nosník přímo i nepřímo zatížený
Pokud se uvažuje pouze zatížení vlastní tíhou stěnového nosníku, potom je nutné vždy navrhnout táhlo T2 na vlastní tíhu, odpovídající minimálně tmavé ploše podle obr. 8.9. U vysokých stěnových nosníků plocha odpovídá půlkruhu s poloměrem 0,5l a u nižších nosníků parabolické ploše s vrcholem v 0,5h.
Obr. 8.9 Principy vyztužení nepřímo zatíženého prostého nosníku
8.2.4 Prostý stěnový nosník nepřímo zatížený osamělým břemenem
Pokud stěnový nosník vynáší druhý stěnový nosník, uvažuje se působení reakce z vynášeného stěnového nosníku při spodním líci hlavního stěnového nosníku (obr. 8.10). Nepřímé zatížení silou můžeme vynést svislými třmínky (obepínajícími hlavní výztuž – model 1) v maximálním počtu 6 kusů. Pro větší zatížení je nutné doplnit šikmou výztuž. Přitom model 2 náhradní příhradoviny může vynášet jen 50 % celkového zatížení (nemůže být použit pro přenos celého zatížení – kinematický model obdobě jako u ozubů nosníků). U šikmé výztuže je nutné dodržet maximální poloměr zakřivení prutu podle kap. 8.3 ČSN EN 1992-1-1 [1]. U zavěšeného nosníku je nutné doplnit ortogonální výztuž podle obr. 8.10. Šikmá výztuž je nutná především pro větší reakce. Při návrhu výztuže dolního konce zavěšené stěny je nutné vycházet především z modelu náhradní příhradoviny zavěšené stěny.
Obr. 8.10 Principy vyztužení styku stěnových nosníků
Tab. 8.1 Výsledné tahové síly T prostého stěnového nosníku pro různá zatížení a různé výšky
8.3 SPOJITÉ STĚNOVÉ KONSTRUKCE
8.3.1 Spojitý stěnový nosník
U spojitých stěnových nosníků jsou výsledné vnitřní síly závislé na způsobu uložení nosníku – na reakcích (obr. 8.11). Pokud není k dispozici lineárně pružný 2D výpočet stěny, lze pro stanovení reakcí použít prutovou analogii spojitého nosníku. Pokud je nosník vysoký (platí h/l > 1), je však nutné redukovat jeho výšku na hodnotu h = l (viz obr. 8.12).
Obr. 8.11 Spojitý stěnový nosník – model náhradní příhradoviny
Obr. 8.12 Spojitý stěnový nosník – průběh napětí nad podporou v závislosti nad výškou stěnového nosníku
Pro spojitý stěnový nosník lze stanovit hlavní tahové síly v poli T1 a nad podporou T2 pomocí analogie se spojitým nosníkem při redukovaném ramenu vnitřních sil:
\begin{gathered}
T_1=M_\text{Ed,1}/z_1\space\space\text{a}\space\space T_2=M_\text{Ed,2}/z_2
\end{gathered}(8.4)
kde je
MEd1 (MEd2) … ohybový moment v poli (nad podporou) stanovený na nosníkové analogii;
z1 a z2 … ramena vnitřních sil.
- pro krajní pole nebo pro spojitý nosník o dvou polích:
\begin{gathered}
z_1=z_2=0{,}5h(1{,}9-h/l)\space\space\text{pro}\space\space0{,}4\le h/l\le1{,}0
\end{gathered}(8.5)
\begin{gathered}
\text{a}\space\space z_1=z_2=0{,}45l\space\space\text{pro}\space\space h/l>1{,}0
\end{gathered}(8.6)
- pro vnitřní pole spojitého nosníku o více polích:
\begin{gathered}
z_1=z_2=0{,}5h(1{,}8-h/l)\space\space\text{pro}\space\space0{,}3\le h/l\le1{,}0
\end{gathered}(8.7)
\begin{gathered}
\text{a}\space\space z_1=z_2=0{,}4l\space\space\text{pro}\space\space h/l>1{,}0
\end{gathered}(8.8)
kde je
l … rozpětí příslušného pole stěnového nosníku;
h … celková výška průřezu stěnového nosníku.
Uvedené hodnoty odpovídají zjednodušenému lineárnímu modelu podle obr. 8.11. Na obr. 8.12 jsou zobrazeny průběhy vodorovných normálových napětí σx v závislosti na poměru výšky nosníku k rozpětí. Z obr. 8.12 je zřejmá poloha tažených vláken nad vnitřní podpěrou pro různě vysoké stěnové nosníky. Pro nosníky s poměrem l/h < 1 není tažená oblast nad podporou v horních vláknech průřezu, ale v části 0,2l ÷ 0,8l výšky průřezu. Pro zjednodušení se výztuž spojitých stěnových nosníků nad vnitřní podporou (při 0,5 ≥ l/h > 1) rozděluje do dvou pruhů B a C (obr. 8.13) podle [9]. Pruh B je vysoký 0,6k a pruh C 0,2k (hodnota k je menší z rozměrů výšky a rozpětí jednoho pole spojitého stěnového nosníku).
Obr. 8.13 Spojitý stěnový nosník – oblasti pro výztuž nad podporou
Výztuž se do pruhů rozdělí následovně:
- do pruhu B
\begin{gathered}
A_2^B=\frac{1}{2}\bigg(3-\frac{l}{h}\bigg)A_2
\end{gathered}(8.9)
- do pruhu C
\begin{gathered}
A_2^C=\frac{1}{2}\bigg(\frac{l}{h}-1\bigg)A_2
\end{gathered}(8.10)
Pro stěnové nosníky s výškou větší než rozpětí (l/h ≤ 1) se výztuž umísťuje jen do pruhu B o výšce 0,6k.
Polovina výztuže nad podporou musí proběhnout přilehlými poli, druhou polovinou výztuže lze zakotvit ve vzdálenosti 0,4k od líce podpory.
Na obr. 8.14 je schéma rozdělení hlavní tahové výztuže nad vnitřní podporou spojitého stěnového nosníku s poměrem výšky a rozpětí l/h = 2. Jedná se o stěnový nosník zatížení osamělými silami, proto je nutné v horní části průřezu v poli doplnit výztuž táhla T3 a nad podporou táhla T‘3. Hodnoty tahových sil T3 lze stanovit podle obr. 8.6 nebo zjednodušeně uvažovat hodnotou T3 = 0,25F a T‘3 = 0,10F. Přesné řešení je v ČSN EN 1992-1-1 [1].
Obr. 8.14 Spojitý stěnový nosník – oblasti pro vyztužení
Pokud je spojitý stěnový nosník zatížen břemeny F nad podporami, je nutné navrhnout pod působištěm břemen výztuž vzdorující příčným tahům. Výztuž se navrhuje na sílu 0,25F (obr. 8.15). Do plochy výztuže lze započítat hlavní výztuž, pokud není nad podporou stykována. Výztuž se umístí do dvou pruhů E a D podle obr. 8.15. Na příčné tahy nutno doplnit v této oblasti i spony, tedy výztuž kolmou na střednici stěny.
Obr. 8.15 Spojitý stěnový nosník zatížený osamělými břemeny – oblasti pro vyztužení
Spojité stěnové nosníky je nutné vyztužit také s ohledem na šířku trhlin, vznikajících při smršťování nebo jiných objemových změnách. Z těchto důvodů musí být příslušně vyztužen i tlačený okraj spojitého stěnového nosníku. Veškeré objemové změny jsou velmi důležitým zatěžovacím stavem při návrhu spojitých stěnových nosníků.
Přesnější výsledky pro spojité nosníky jsou v tab. 8.2 a tab. 8.3.
Tab. 8.2 Výsledné tahové síly T spojitého stěnového nosníku o dvou polích
8.3.2 Stěnový nosník s konzolou
Průběh napětí v překonzolovaném stěnovém nosníku je na obr. 8.16. Průběh vodorovných napětí σx nad podporou je obdobný jako u vnitřních podpor spojitého stěnového nosníku obr. 8.12. Přibližně lze stanovit hlavní tahovou sílu ve vetknutí pomocí analogie s nosníkem při redukovaném ramenu vnitřních sil. Tahovou sílu T2 ve vetknutí stanovíme:
\begin{gathered}
T_2=M_\text{Ed}/z_2
\end{gathered}(8.11)
kde je
MEd … ohybový moment stanovený na nosníkové analogii;
z2 … rameno vnitřních sil
\begin{gathered}
z_2=0{,}65l_\text{k}+0{,}10h\space\space\text{pro}\space\space1{,}0\le h/l_\text{k}\le2{,}0
\end{gathered}(8.12)
\begin{gathered}
\text{a}\space\space z_2=0{,}85l_\text{k}\space\space\text{pro}\space\space h/l_\text{k}>2{,}0
\end{gathered}(8.13)
lK vyložení konzolového nosníku;
h celková výška průřezu stěnového nosníku.
Obr. 8.16 Konzolový stěnový nosník průběhy napětí v závislosti na výšce nosníku
Pro konzolové nosníky s poměrem l/h < 0,33 není tažená oblast nad podporou v horních vláknech průřezu, ale v části 0,3lK ÷ 1,7lK výšky průřezu. Přesnější vyjádření vnitřních sil je v tab. 8.4.
Tab. 8.3 Výsledné tahové síly T spojitého stěnového nosníku o více polích
Tab. 8.4 Stěnový konzolový nosník
8.4 SMYKOVÉ STĚNY
Pro zajištění prostorové stability objektů se využívají smykové stěny. Jedná se o stěnové nosníky obvykle vetknuté do základových konstrukcí, které procházejí celým objektem. Smykové stěny lze také modelovat pomocí náhradní příhradoviny. Modely pro rovnoměrné vodorovné zatížení i zatížení osamělými břemeny jsou na obr. 8.17. Vnitřní síly v táhlech a vzpěrách lze stanovit z okrajových podmínek – z reakcí v uložení smykové stěny. Smyková stěna je obvykle uvažována jako konzola spojitě vetknutá do základů nebo diskrétně kloubově uložená. Pokud jsou jednotlivé smykové stěny spojeny do komplikovanějších statických soustav, je nutné nejprve vyřešení celé soustavy (globální analýza objektu) a následně pak podrobná analýza jednotlivých smykových stěn (lokální analýza). Smykovou stěnu, obdobně jako stěnový nosník, uvažujeme celou jako poruchovou D-oblast [26], [7] a [14].
Při výpočtu prostorové stability objektu se vodorovná síla přenáší ve své rovině dostatečně tuhou stropní deskou. Pro návrh přenosu vodorovného zatížení stropní deskou do svislých ztužujících prvků můžeme postupovat jako u stěnových nosníků – rovinných prvků, zatížených ve střednicové rovině. Účinky vodorovného zatížení je nutné zahrnout do návrhu průřezu stropní konstrukce.
Obr. 8.17 Smyková stěna jako konzolový stěnový nosník
8.5 PRINCIPY VYZTUŽENÍ STĚNOVÝCH NOSNÍKŮ
Stěnové nosníky je nutné při každém povrchu opatřit ortogonální výztužnou sítí s minimální průřezovou plochou As,dbmin = 0,001Ac nejméně však 150 mm2/m, v každém směru. Osová vzdálenost sousedních výztužných prutů nemá překročit dvojnásobek tloušťky stěnového nosníku, maximálně však 300 mm.
Dolní výztuž, představující táhlo v příhradovém modelu stěnového nosníku, musí být řádně zakotvena ve styčnících nad podporami. Pro zakotvení výztuže lze použít háků (vodorovně položených), příložných smyček nebo kotevních spojek, pokud není ve styčníku dostatečný prostor pro rovnou kotevní délku ldb. Pro výpočet kotevní délky dolní výztuže nad podporou lze uvažovat s redukovanou tahovou silou 0,8T1. Veškerá hlavní tahová výztuž v poli musí být dotažena za líc uložení, a to nejen u prostého stěnového nosníku, ale i u spojitého stěnového nosníku. Nad vnitřní podporou při spodním líci spojitých stěnových nosníků je možné umístit však pouze rovné pruty s příslušným stykováním přesahem obvykle ve druhé vrstvě výztuže. V krajních podporách se doporučuje posílit zakotvení hlavní tahové výztuže vodorovnými smyčkami. Hlavní tahovou výztuž pole je nutné rovnoměrně rozdělit po výšce ν = 0,25h – 0,05l ≤ 0,2l podle [33] nebo 0,1k až 0,2k [7]. Tahová výztuž se neumísťuje jen při spodním líci proto, aby se redukovala šířka trhlin. U stěnových nosníků zatížených při spodním okraji se musí navrhnout svislá tahová výztuž pro vynášení nepřímého zatížení stěny (včetně vlastní tíhy stěny) podle obr. 8.9, výztuž musí být dostatečně zakotvena v tlačeném pasu při horním líci stěny.
U stěnových nosníků je nutné vždy překontrolovat mezní stav použitelnosti – obvykle šířku trhlin a případně doplnit výztuž pro omezení šířky trhlin.
Stěnové nosníky jsou uvažovány celé jako poruchové oblasti. Ve všech tlačených betonových vzpěrách vznikají příčné tahy. Na ně je nutné navrhnout konstrukční výztuž. Vzhledem k tomu, že betonové vzpěry bývají šikmé, je nutné výztuž příčných tahů rozdělit do vodorovného a svislého směru. Příčné tahy v betonových vzpěrách lze v konstrukcích pozemních staveb uvažovat hodnotou 0,22 % až 0,25 % tlakové síly podle [24]. Příčné tahy působí především ve čtvrtinách délky vzpěry, výztuž lze však rovnoměrně rozdělit po celé délce vzpěry. Příčné tahy však působí i ve směru kolmém na střednicovou rovinu stěnového nosníku. Proto je nutné doplnit také příčnou výztuž ve formě například spon. Pokud se takto využijí spony, nejedná se tedy o konstrukční výztuž pro zajištění polohy výztuže, ale o nosnou výztuž, u které záleží na přesné poloze a množství (nutno uvést ve výkresové dokumentaci).
8.6 STĚNOVÉ NOSNÍKY S OTVORY
Stěnové nosníky jsou častým nosným prvkem v konstrukcích pozemních staveb. Vzhledem k dispozičním požadavkům jsou však oslabeny otvory pro dveře, okna nebo instalace. Při návrhu výztuže stěnového nosníku nelze vycházet z výše uvedených vztahů a je nutné vytvořit pro každou stěnu zvláštní model příhradové analogie. Tvorbu modelů nelze jednoduše zobecnit, a tím usnadnit návrh příslušné výztuže stěny. Na obr. 8.18 a obr. 8.19 je zobrazen postup při návrhu stěny prolomené otvory. Zároveň je na obrázcích srovnání mezi lineárním a nelineárním výpočtem pomocí MKP.
Obr. 8.18 Příklad řešení stěnového nosníku
Obr. 8.19 Příklad řešení stěnového nosníku
Na obr. 8.18 je řešen překonzolovaný stěnový nosník se dveřním otvorem. Návrhový model náhradní příhradoviny je řešen jako kombinace modelu 1 a modelu 2. U obou modelů se využívá podobnost s ozubem na nosníku [8]. Ze srovnání návrhového modelu s nelineárním výpočtem (Atena2D) vyplývá, že dominantní vliv na návrh výztuže má model 1. Ve spodní části obr. 8.18 je návrh vyztužení stěnového nosníku.
Na obr. 8.19 je řešen prostý stěnový nosník s řadou prostupů. V části a) jsou zobrazeny výsledky lineární analýzy oblasti a z ní odvozený model náhradní příhradoviny. V části b) jsou zobrazeny výsledky nelineární analýzy (Atena2D) a z ní odvozený model náhradní příhradoviny. Při nelineární analýze došlo k přerozdělení vnitřních sil v betonových vzpěrách mezi otvory. Vlivem porušení dolní části stěny trhlinami se vnitřní tlakové síly přerozdělily do krajních částí stěnového nosníku a střední vzpěra prakticky vymizela. Druhý model b) přináší větší únosnost stěnového nosníku, na druhou stranu zároveň však způsobuje větší trhliny ve spodní části.
Obecné řešení stěnových nosníků s prostupy není možné. Pro návrh modelu náhradní příhradoviny lze vyjít z lineárně pružného 2D řešení oblasti – z průběhu hlavních napětí. V požadovaných průřezech je nutné integrovat příslušná normálová napětí a stanovit tak sílu v odpovídající betonové vzpěře. Tímto způsobem se vytvoří dostatečně vhodný model náhradní příhradoviny pro řešení oblasti. Pro posouzení skutečné mezní únosnosti oblasti je nutné použít nelineární analýzu s již definovanou polohou nosné výztuže. Při nelineární analýze je nutné vždy kontrolovat mezní stav použitelnosti – obvykle šířku trhlin.
8.7 STĚNOVÉ KONSTRUKCE – PŘÍKLADY
Obr. 8.20 Příčný řez 1-1
Předpoklady výpočtu
Příčné rámy – stěny po modulové vzdálenosti 6,0 m – zatěžovací šířka.
Stěny tloušťky 200 mm, celková délka stěny 6,30 m, diskretizace zatížení 6,30/4 = 1,575 → 1,60 m.
Tab. 8.5
| Deska | Stálé zatížení | Proměnné zatížené |
| Střešní deska | 2,0 + 6,25 kN/m2 | 2,0 kN/m2 |
| Deska v úrovni 1 | 2,0 + 6,25 kN/m2 | 2,0 kN/m2 |
| Deska v úrovni 0 | 2,0 + 6,25 kN/m2 | 2,0 kN/m2 |
Obr. 8.21 Příčný řez 2-2
Tab. 8.6
| Zatěžovací síly po 1,60 m | Stálé zatížení | Proměnné zatížené |
| Horní líc | 246 kN | 58 kN |
| Dolní líc | 140 kN | 28 kN |
8.7.1 Stěna 1
Obr. 8.22 Model náhradní příhradoviny, stěna 1, h = 200, C25/30
Obr. 8.23 Model náhradní příhradoviny – očíslování styčníků
Obr. 8.24 Souřadnice jednotlivých styčníků
Obr. 8.25 Očíslování prutů
Obr. 8.26 Celkové zatížení stěny
Obr. 8.27 Průběh normálových sil na prutech
Obr. 8.28 Detail prutů v horním rohu
Obr. 8.29 Detail vnitřní sil v levém dolním rohu
Obr. 8.30 Návrh výztuže v tažených prutech
Tab. 8.7 Návrh výztuže táhel
| Osová síla | síla | As | navržená výztuž | |
| táhlo | průměr | kusů | ||
| 1 | 415 | 0,000954 | 20 | 4 |
| 2 | 971 | 0,002233 | 20 | 8 |
| 3 | 896 | 0,002061 | 20 | 7 |
| 4 | 219 | 0,000504 | 12 | 5 |
| 5 | 683 | 0,001571 | 20 | 5 |
| 6 | 168 | 0,000386 | 12 | 4 |
| 7 | 859 | 0,001976 | 20 | 7 |
| 8 | 609 | 0,001401 | 20 | 5 |
| 11 | 501 | 0,001152 | 20 | 4 |
| 22 | 220 | 0,000506 | 12 | 5 |
| 24 | 220 | 0,000506 | 12 | 5 |
| 28 | 244 | 0,000561 | 12 | 5 |
| 30 | 246 | 0,000566 | 12 | 6 |
| 33 | 480 | 0,001104 | 20 | 4 |
| 34 | 500 | 0,001150 | 20 | 4 |
| 35 | 243 | 0,000559 | 12 | 5 |
| 36 | 186 | 0,000428 | 12 | 4 |
| 37 | 480 | 0,001104 | 20 | 4 |
| 38 | 249 | 0,000573 | 12 | 6 |
| 39 | 243 | 0,000559 | 12 | 5 |
| 40 | 156 | 0,000359 | 12 | 4 |
| 44 | 272 | 0,000626 | 12 | 6 |
| 48 | 971 | 0,002233 | 20 | 8 |
| 49 | 609 | 0,001401 | 20 | 5 |
| 50 | 896 | 0,002061 | 20 | 7 |
| 51 | 501 | 0,001152 | 20 | 4 |
Posouzení betonových vzpěr a návrh výztuže na příčné tahy (úplná nespojitost, tahová síla ve čtvrtinách délky vzpěry):
\begin{gathered}
T=0{,}25(1-0{,}7a/h)F_\text{ed}{........}T_\text{Max}=0{,}25F_\text{Ed}\\\\
T=\frac{1}{4}\bigg(1-0{,}7\cdot\frac{a}{h}\bigg)\cdot F_\text{Ed}
\end{gathered}Tab. 8.8
| Osová síla | síla | min. šířka b | příčný tah T | As | navržená výztuž | |
| vzpěra | průměr | kusů | ||||
| 9 | 378 | 0,210 | 94,5 | 0,000217 | 12 | 2 |
| 10 | 378 | 0,210 | 94,5 | 0,000217 | 12 | 2 |
| 12 | 844 | 0,469 | 211 | 0,000485 | 12 | 5 |
| 13 | 765 | 0,425 | 191,25 | 0,000440 | 12 | 4 |
| 14 | 857 | 0,476 | 214,25 | 0,000493 | 12 | 5 |
| 15 | 744 | 0,413 | 186 | 0,000428 | 12 | 4 |
| 17 | 1431 | 0,795 | 357,75 | 0,000823 | 12 | 8 |
| 18 | 1431 | 0,795 | 357,75 | 0,000823 | 12 | 8 |
| 19 | 932 | 0,518 | 233 | 0,000536 | 12 | 5 |
| 20 | 1015 | 0,564 | 253,75 | 0,000584 | 12 | 6 |
| 21 | 1130 | 0,628 | 282,5 | 0,000650 | 12 | 6 |
| 23 | 1131 | 0,628 | 282,75 | 0,000650 | 12 | 6 |
| 25 | 519 | 0,288 | 129,75 | 0,000298 | 12 | 3 |
| 26 | 1128 | 0,627 | 282 | 0,000649 | 12 | 6 |
| 27 | 636 | 0,353 | 159 | 0,000366 | 12 | 4 |
| 28 | 578 | 0,321 | 144,5 | 0,000332 | 12 | 3 |
| 31 | 654 | 0,363 | 163,5 | 0,000376 | 12 | 4 |
| 32 | 186 | 0,103 | 46,5 | 0,000107 | 12 | 1 |
| 41 | 544 | 0,302 | 136 | 0,000313 | 12 | 3 |
| 42 | 315 | 0,175 | 78,75 | 0,000181 | 12 | 2 |
| 45 | 607 | 0,337 | 151,75 | 0,000349 | 12 | 4 |
Obr. 8.31 Schéma vyztužení stěny
8.7.2 Stěna 2
Obr. 8.32 Stěna 2, h = 200, C25/30
Obr. 8.33 Model konstrukce – očíslování styčníků
Obr. 8.34 Model náhradní příhradoviny – souřadnice styčníků
Obr. 8.35 Model náhradní příhradoviny – očíslování prutů
Obr. 8.36 Celkové zatížení stěny
Obr. 8.37 Průběh normálových sil na prutech
Obr. 8.38 Detail levého horního rohu – normálové síly
Obr. 8.39 Pravý horní roh – průběh normálových sil
Obr. 8.40 Styčník nad pravou podporou – průběh normálových sil
Obr. 8.41 Stěna 2, h = 200, C25/30
Tab. 8.9
| Osová síla | síla | As | navržená výztuž | |
| táhlo | průměr | kusů | ||
| 1 | 375 | 0,000862 | 20 | 3 |
| 2 | 848 | 0,001950 | 20 | 7 |
| 3 | 872 | 0,002006 | 20 | 7 |
| 4 | 200 | 0,000460 | 12 | 5 |
| 5 | 603 | 0,001387 | 20 | 5 |
| 6 | 168 | 0,000386 | 12 | 4 |
| 7 | 598 | 0,001375 | 20 | 5 |
| 8 | 567 | 0,001304 | 20 | 5 |
| 11 | 329 | 0,000757 | 20 | 3 |
| 22 | 200 | 0,000460 | 12 | 5 |
| 24 | 200 | 0,000460 | 12 | 5 |
| 28 | 292 | 0,000672 | 12 | 6 |
| 30 | 192 | 0,000442 | 12 | 4 |
| 33 | 421 | 0,000968 | 20 | 4 |
| 34 | 824 | 0,001895 | 20 | 7 |
| 35 | 192 | 0,000442 | 12 | 4 |
| 37 | 421 | 0,000968 | 20 | 4 |
| 38 | 200 | 0,000460 | 12 | 5 |
| 39 | 192 | 0,000442 | 12 | 4 |
| 40 | 123 | 0,000283 | 12 | 3 |
| 45 | 123 | 0,000283 | 12 | 3 |
| 48 | 849 | 0,001953 | 20 | 7 |
| 49 | 568 | 0,001306 | 20 | 5 |
| 50 | 871 | 0,002003 | 20 | 7 |
| 51 | 329 | 0,000757 | 20 | 3 |
| 52 | 378 | 0,000869 | 20 | 3 |
| 54 | 218 | 0,000501 | 12 | 5 |
Tab. 8.10
| Osová síla | síla | min. šířka b | příčný tah T | As | navržená výztuž | |
| vzpěra | průměr | kusů | ||||
| 9 | 286 | 0,159 | 71,5 | 0,000164 | 12 | 2 |
| 10 | 470 | 0,261 | 117,5 | 0,000270 | 12 | 3 |
| 12 | 716 | 0,398 | 179 | 0,000412 | 12 | 4 |
| 13 | 740 | 0,411 | 185 | 0,000425 | 12 | 4 |
| 14 | 760 | 0,422 | 190 | 0,000437 | 12 | 4 |
| 15 | 621 | 0,345 | 155,25 | 0,000357 | 12 | 4 |
| 16 | 1548 | 0,860 | 387 | 0,000890 | 12 | 8 |
| 17 | 1315 | 0,731 | 328,75 | 0,000756 | 12 | 7 |
| 18 | 842 | 0,468 | 210,5 | 0,000484 | 12 | 5 |
| 19 | 925 | 0,514 | 231,25 | 0,000532 | 12 | 5 |
| 20 | 292 | 0,162 | 73 | 0,000168 | 12 | 2 |
| 21 | 521 | 0,289 | 130,25 | 0,000300 | 12 | 3 |
| 23 | 473 | 0,263 | 118,25 | 0,000272 | 12 | 3 |
| 25 | 535 | 0,297 | 133,75 | 0,000308 | 12 | 3 |
| 26 | 1006 | 0,559 | 251,5 | 0,000578 | 12 | 6 |
| 27 | 1489 | 0,827 | 372,25 | 0,000856 | 12 | 8 |
| 29 | 457 | 0,254 | 114,25 | 0,000263 | 12 | 3 |
| 32 | 198 | 0,110 | 49,5 | 0,000114 | 12 | 2 |
| 36 | 55 | 0,031 | 13,75 | 0,000032 | 12 | 1 |
| 41 | 496 | 0,276 | 124 | 0,000285 | 12 | 3 |
| 42 | 306 | 0,170 | 76,5 | 0,000176 | 12 | 2 |
| 44 | 1147 | 0,637 | 286,75 | 0,000660 | 12 | 6 |
| 46 | 1560 | 0,867 | 390 | 0,000897 | 12 | 8 |
| 55 | 528 | 0,293 | 132 | 0,000304 | 12 | 3 |
8.7.3 Stěna 3
Obr. 8.42 Stěna 3, h = 200, C25/30
Obr. 8.43 Model náhradní příhradoviny – očíslování styčníků
Obr. 8.44 Model náhradní příhradoviny – souřadnice styčníků
Obr. 8.45 Model náhradní příhradoviny – očíslování prutů
Obr. 8.46 Celkové zatížení stěny
Obr. 8.47 Průběh normálových sil
Obr. 8.48 Pravý horní roh – průběh normálových sil
Obr. 8.49
Tab. 8.11
| Osová síla | síla | As | navržená výztuž | |
| táhlo | průměr | kusů | ||
| 1 | 415 | 0,000954 | 20 | 4 |
| 2 | 970 | 0,002231 | 20 | 8 |
| 4 | 219 | 0,000504 | 12 | 5 |
| 5 | 683 | 0,001571 | 20 | 5 |
| 6 | 168 | 0,000386 | 20 | 2 |
| 8 | 609 | 0,001401 | 20 | 5 |
| 13 | 168 | 0,000386 | 12 | 4 |
| 22 | 220 | 0,000506 | 12 | 5 |
| 24 | 220 | 0,000506 | 12 | 5 |
| 33 | 480 | 0,001104 | 20 | 4 |
| 34 | 13 | 0,000030 | 12 | 1 |
| 35 | 480 | 0,001104 | 20 | 4 |
| 37 | 480 | 0,001104 | 20 | 4 |
| 38 | 219 | 0,000504 | 12 | 5 |
| 40 | 156 | 0,000359 | 12 | 4 |
| 48 | 970 | 0,002231 | 20 | 8 |
| 49 | 609 | 0,001401 | 20 | 5 |
| 51 | 91 | 0,000209 | 12 | 2 |
Tab. 8.12
| Osová síla | síla | min. šířka b | příčný tah T | As | navržená výztuž | |
| vzpěra | průměr | kusů | ||||
| 3 | 234 | 0,130 | 58,5 | 0,000135 | 12 | 2 |
| 7 | 151 | 0,084 | 37,75 | 0,000087 | 12 | 1 |
| 9 | 378 | 0,210 | 94,5 | 0,000217 | 12 | 2 |
| 10 | 451 | 0,251 | 112,75 | 0,000259 | 12 | 3 |
| 12 | 844 | 0,469 | 211 | 0,000485 | 12 | 5 |
| 14 | 857 | 0,476 | 214,25 | 0,000493 | 12 | 5 |
| 15 | 130 | 0,072 | 32,5 | 0,000075 | 12 | 1 |
| 17 | 1431 | 0,795 | 357,75 | 0,000823 | 12 | 8 |
| 18 | 932 | 0,518 | 233 | 0,000536 | 12 | 5 |
| 19 | 1015 | 0,564 | 253,75 | 0,000584 | 12 | 6 |
| 21 | 572 | 0,318 | 143 | 0,000329 | 12 | 3 |
| 23 | 519 | 0,288 | 129,75 | 0,000298 | 12 | 3 |
| 25 | 588 | 0,327 | 147 | 0,000338 | 12 | 3 |
| 32 | 186 | 0,103 | 46,5 | 0,000107 | 12 | 1 |
| 36 | 97 | 0,054 | 24,25 | 0,000056 | 12 | 1 |
| 41 | 545 | 0,303 | 136,25 | 0,000313 | 12 | 3 |
| 42 | 315 | 0,175 | 78,75 | 0,000181 | 12 | 2 |
| 52 | 222 | 0,123 | 55,5 | 0,000128 | 12 | 2 |
| 53 | 796 | 0,442 | 199 | 0,000458 | 12 | 5 |
8.7.4 Stěna 4
Obr. 8.50 Stěna 4, h = 200, C25/30
Obr. 8.51 Model náhradní příhradoviny – očíslování styčníků
Obr. 8.52 Model náhradní příhradoviny – souřadnice styčníků
Obr. 8.53 Model náhradní příhradoviny – očíslování prutů
Obr. 8.54 Celkové zatížení
Obr. 8.55 Celkový model – průběh normálových sil
Obr. 8.56 Průběh normálových sil v levé části modelu
Obr. 8.57 Normálové síly pravá část – konzola
Obr. 8.58 Normálové síly v oblasti nad pravou podporou
Tab. 8.13
| Osová síla | síla | As | navržená výztuž | |
| táhlo | průměr | kusů | ||
| 1 | 312 | 0,000718 | 20 | 3 |
| 2 | 647 | 0,001488 | 20 | 5 |
| 3 | 781 | 0,001796 | 20 | 6 |
| 4 | 168 | 0,000386 | 12 | 4 |
| 5 | 475 | 0,001092 | 20 | 4 |
| 6 | 152 | 0,000350 | 12 | 4 |
| 7 | 659 | 0,001516 | 20 | 5 |
| 8 | 491 | 0,001129 | 20 | 4 |
| 11 | 68 | 0,000156 | 12 | 2 |
| 22 | 168 | 0,000386 | 12 | 4 |
| 24 | 168 | 0,000386 | 12 | 4 |
| 28 | 342 | 0,000787 | 20 | 3 |
| 30 | 124 | 0,000285 | 12 | 3 |
| 33 | 329 | 0,000757 | 12 | 7 |
| 34 | 1237 | 0,002845 | 20 | 10 |
| 35 | 124 | 0,000285 | 12 | 3 |
| 36 | 118 | 0,000271 | 12 | 3 |
| 37 | 329 | 0,000757 | 12 | 7 |
| 38 | 168 | 0,000386 | 12 | 4 |
| 39 | 124 | 0,000285 | 12 | 3 |
| 40 | 72 | 0,000166 | 12 | 2 |
| 48 | 647 | 0,001488 | 20 | 5 |
| 49 | 492 | 0,001132 | 20 | 4 |
| 50 | 781 | 0,001796 | 20 | 6 |
| 51 | 68 | 0,000156 | 12 | 2 |
| 52 | 596 | 0,001371 | 20 | 5 |
| 56 | 170 | 0,000391 | 12 | 4 |
| 61 | 80 | 0,000184 | 12 | 2 |
| 62 | 336 | 0,000773 | 20 | 3 |
| 64 | 659 | 0,001516 | 20 | 5 |
| 67 | 135 | 0,000310 | 12 | 3 |
| 72 | 215 | 0,000494 | 12 | 5 |
Tab. 8.14
| Osová síla | síla | min. šířka b | příčný tah T | As | navržená výztuž | |
| vzpěra | průměr | kusů | ||||
| 9 | 156 | 0,087 | 39 | 0,000090 | 12 | 1 |
| 10 | 573 | 0,318 | 143,25 | 0,000329 | 12 | 3 |
| 12 | 521 | 0,289 | 130,25 | 0,000300 | 12 | 3 |
| 13 | 662 | 0,368 | 165,5 | 0,000381 | 12 | 4 |
| 14 | 603 | 0,335 | 150,75 | 0,000347 | 12 | 4 |
| 15 | 412 | 0,229 | 103 | 0,000237 | 12 | 3 |
| 16 | 1642 | 0,912 | 410,5 | 0,000944 | 12 | 9 |
| 17 | 1117 | 0,621 | 279,25 | 0,000642 | 12 | 6 |
| 18 | 699 | 0,388 | 174,75 | 0,000402 | 12 | 4 |
| 19 | 776 | 0,431 | 194 | 0,000446 | 12 | 4 |
| 20 | 1044 | 0,580 | 261 | 0,000600 | 12 | 6 |
| 21 | 437 | 0,243 | 109,25 | 0,000251 | 12 | 3 |
| 23 | 397 | 0,221 | 99,25 | 0,000228 | 12 | 3 |
| 25 | 449 | 0,249 | 112,25 | 0,000258 | 12 | 3 |
| 26 | 1178 | 0,654 | 294,5 | 0,000677 | 12 | 6 |
| 27 | 893 | 0,496 | 223,25 | 0,000513 | 12 | 5 |
| 29 | 811 | 0,451 | 202,75 | 0,000466 | 12 | 5 |
| 31 | 333 | 0,185 | 83,25 | 0,000191 | 12 | 2 |
| 32 | 208 | 0,116 | 52 | 0,000120 | 12 | 2 |
| 41 | 416 | 0,231 | 104 | 0,000239 | 12 | 3 |
| 42 | 288 | 0,160 | 72 | 0,000166 | 12 | 2 |
| 44 | 166 | 0,092 | 41,5 | 0,000095 | 12 | 1 |
| 46 | 1404 | 0,780 | 351 | 0,000807 | 12 | 8 |
| 55 | 497 | 0,276 | 124,25 | 0,000286 | 12 | 3 |
| 57 | 555 | 0,308 | 138,75 | 0,000319 | 12 | 3 |
| 59 | 549 | 0,305 | 137,25 | 0,000316 | 12 | 3 |
| 64 | 659 | 0,366 | 164,75 | 0,000379 | 12 | 4 |
| 65 | 497 | 0,276 | 124,25 | 0,000286 | 12 | 3 |
| 66 | 459 | 0,255 | 114,75 | 0,000264 | 12 | 3 |
| 69 | 399 | 0,222 | 99,75 | 0,000229 | 12 | 3 |
| 71 | 336 | 0,187 | 84 | 0,000193 | 12 | 2 |
Obr. 8.59
9 PRVKY NAMÁHANÉ SMYKEM
9.1 ŠIKMÁ POSOUVAJÍCÍ SÍLA
Při působení posouvající síly ve dvou směrech (obr. 9.1) lze provést rozklad síly do svislého a vodorovného směru a posuzovat smykovou výztuž v každém směru odděleně. Výsledný návrh smykové výztuže však neodpovídá skutečnosti, smyková výztuž je podhodnocena. Podhodnocení smykové výztuže nastává proto, že ve výztuži, ve druhém směru vznikají tahy z opření tlakové betonové vzpěry. Tyto tahy je nutné při návrhu zohlednit, řešíme to zvětšením tahové síly ve smykové výztuži součinitelem k1 a zredukováním únosnosti betonové tlačené diagonály součinitelem k2. Metodika vychází z publikace [41].
Obr. 9.1 Působení šikmé posouvající síly na obdélníkový průřez
Součinitele k1 a k2 lze vyjádřit ze vztahů:
\begin{gathered}
k_1=1+\Bigg[\frac{2}{\sqrt{(b/h)^2+1}}-1\Bigg]\cdot\alpha_\text{v}^{1/2}\space\text{a}\space k_2=1+\frac{2}{3}\cdot\alpha_\text{v}^{1/2}
\end{gathered}(9.1)
kde
αv vyjadřuje poměr posouvající sil:
\begin{gathered}
\alpha_\text{v}=\frac{|V_\text{Edy}|}{|V_\text{Edz}|}\cdot\frac{h}{b}\le1\space\text{(pro}\space b/h\le1)
\end{gathered}(9.2)
kde je
k1 … součinitel vyjadřující zvětšení tahové síly ve smykové výztuži s omezením 1 ≤ k1 < 2;
k2 … součinitel vyjadřující redukci únosnosti betonové tlačené diagonály s omezení 1 ≤ k2 < 1,67;
VEdy a VEdz … složky posouvající síly VEd ve směrech y a z.
Čím je větší sklon posouvající síly VEd od svislice, tím narůstá staticky nutné množství výztuže ve srovnání s rozložením do jednotlivých směrů.
Posouzení
Posouzení smykové výztuže:
\begin{gathered}
V_\text{Ed}=\sqrt{(V_\text{Ed,y}^2+V_\text{Ed,z}^2)}\le V_\text{Rd,s}
\end{gathered}(9.3)
a posouzení betonové vzpěry:
\begin{gathered}
V_\text{Ed}=\sqrt{(V_\text{Ed,y}^2+V_\text{Ed,z}^2)}\le V_\text{Rd,max}
\end{gathered}(9.4)
kde
\begin{gathered}
V_\text{Rd,s}=\frac{A_\text{sw}}{s_\text{w}}f_\text{yd}z\cdot\cot\theta\cdot\frac{1}{k_1}\space\text{je únosnost smykové výtuže}
\end{gathered}(9.5)
a
\begin{gathered}
V_\text{Rd,max}=\frac{b_\text{w}\cdot z\cdot v\cdot f_\text{cd}}{\cot\theta+\tan\theta}\cdot\frac{1}{k_2}\space\text{je únosnost šikmé betonové vzpěry}
\end{gathered}(9.6)
Pro šikmou posouvající sílu je doporučeno zvýšení minimální plochy smykové výztuže podle následujícího vztahu:
\begin{gathered}
\frac{A_\text{sw}}{s_\text{w}}\le\rho_\text{w,min}\cdot b_\text{w}\cdot k_1
\end{gathered}(9.7)
kde je
ρw,min … minimální stupeň smykového vyztužení podle EC2.
9.2 SMYKOVÁ VÝZTUŽ KRUHOVÉHO PRŮŘEZU
Posouzení se provede podle následujících rovnic (Metodika vychází z publikace [41])
VEd ≤ VRd,s … posouzení únosnosti smykové výztuže;
VEd ≤ VRd,max … posouzení únosnost tlačené betonové diagonály.
Jednotlivé únosnosti se stanoví podle vztahu:
\begin{gathered}
V_\text{Rd,s}=\alpha_\text{k}\cdot\frac{A_\text{sw}}{s_\text{w}}\cdot f_\text{yd}\cdot\cot\theta
\end{gathered}(9.8)
a
\begin{gathered}
V_\text{Rd,max}=\frac{\alpha_\text{k}\cdot D\cdot z\cdot\alpha_\text{c}\cdot f_\text{cd}}{\cot\theta+\tan\theta}0
\end{gathered}(9.9)
kde je
αk … součinitel spolupůsobení, jeho hodnota se pohybuje v rozmezí 0,715 až 0,785, konzervativně lze uvažovat αk ≈ 0,72 (bližší viz [9]);
αc … redukční součinitel tlačené betonové vzpěry, uvažuje se hodnotou αc = 0,75;
z … rameno vnitřních sil;
D … průměr průřezu;
θ … sklon tlačené betonové diagonály;
VRd,c … únosnost smykově nevyztuženého průřezu s uvažováním bw = 0,9D.
Pro kruhový průřez (obr. 9.2) je doporučeno zvýšení minimální plochy smykové výztuže podle následujícího vztahu:
\begin{gathered}
\frac{A_\text{sw}}{s_\text{w}}\ge\rho_\text{w,min}\cdot b_\text{w}\cdot\frac{1}{1/\alpha_\text{k}}=\rho_\text{w,min}\cdot b_\text{w}\cdot\alpha_\text{k}
\end{gathered}(9.10)
kde je
ρw,min … minimální stupeň smykového vyztužení podle EC2 [1].
Obr. 9.2 Působení posouvající síly na kruhový průřez
10 PROTLAČENÍ STROPNÍCH DESEK
Protlačení je smykové porušení deskového prvku v oblasti soustředěných břemen nebo reakcí v lokálních podporách. Pro porušení protlačením je typická poměrně malá plocha, na které se přenáší zatížení z desky do svislých nosných konstrukcí – sloupů či stěn. Tuto plochu nazýváme styčnou (úložnou, zatěžovanou) plochou Aload. Oblast přenášení zatížení z desky na styčnou plochu nazýváme poruchovou oblastí (D-oblast) desky. Tuto oblast namáhanou protlačením lze modelovat náhradní příhradovinou podle obr. 10.1. Model náhradní příhradoviny je závislý na způsobu vyztužení oblasti [26]. V obr. 10.2 jsou modely náhradní příhradoviny podle EC2[1]. Modely vycházejí z předpokládaného mechanismu poškození. Při protlačení vzniká kuželovitá poruchová plocha, která se promítá do taženého líce desky poruchovou trhlinou ve vzdálenosti přibližně 2d (d je průměrná účinná výška stropní desky) od styčné plochy obr. 10.3 a obr. 10.4.
Obr. 10.1 Mechanismus protlačení deskovou konstrukcí
Obr. 10.2 Model náhradní příhradoviny podle EN 1992-1-1
Obr. 10.3 Výztuž proti progresivnímu kolapsu
Obr. 10.4 Oblast namáhaná protlačením kontrolované obvody
Při návrhu desky na protlačení se uvažuje prostorová náhradní příhradovina podle obr. 10.1. Z mechanismu poškození (obr. 10.3) vyplývá i nutnost dostatečného zakotvení horní tahová výztuž až za smykovou trhlinou a nutnost dolní výztuže pro zabrání progresivního kolapsu konstrukce.
Mezní stav protlačení se posuzuje podle ČSN EN 1992-1-1 [1], kde návrh pro tuto oblast vychází z modelu náhradní příhradoviny (obr. 10.2). V současné době se často navrhují smykové trny jako smyková výztuž této oblasti, přitom návrh smykových trnů se provádí podle metodiky ETA [45], která uvažuje náhradní příhradovinu odlišně od ČSN EN 1992-1-1 [1]. V kapitole je provedeno srovnání uvedených metodik a upozorněno na rozdíly v návrhu oblasti. V závěru je uvedena metodika MC2010.
Protlačení u základových konstrukcích je v kap. 11.
10.1 PROTLAČENÍ STROPNÍCH DESEK
Protlačení deskových konstrukcí vzniká v okolí lokálních podpěr, na koncích nosných stěn, popřípadě v rozích stěn. Obdobné je to i u základových desek, popřípadě základových patek. Při výpočtech konstrukcí pomocí MKP se jedná obvykle o singulární body řešení. Proto je nutné věnovat velkou pozornost i modelování. Protlačení na rozdíl od běžného smykového namáhání má sbíhající tlačené betonové diagonály.
Při návrhu mezní únosnosti desky v protlačení se vychází z tzv. kontrolovaných obvodů (viz obr. 10.4 a obr. 10.5), které závisí především na tvaru styčné plochy a vzdáleností 2d od styčné plochy nebo od poslední účinné smykové výztuže (účinná smyková výztuž je smyková výztuž dostatečně zakotvená na obou stranách poruchové plochy). Ve výpočtu se uvažuje průměrná účinná výška deskového prvku. Při použití ocelové hlavice, při nedostatečně dlouhé smykové výztuži nebo při nadbetonování sloupu (obr. 10.6), je nutné účinnou délku příslušně zkrátit. Kritická smyková trhlina (kuželová plocha protlačení) je při taženém líci deskového prvku podle EC2 ve vzdálenosti 2d od líce styčné plochy (sklon smykové plochy je ϴ = 26,6°). Smyková výztuž (zpravidla svislá) se umísťuje nejčastěji soustředně k těžišti styčné plochy (pravidla pro svislou smykovou výztuž viz obr. 10.7). Vzhledem k možnostem zakotvení svislé smykové výztuže se uvažuje s účinnou délkou pro vyztužení 1,5d (ve vnitřní části vzdálenosti 2d, kde lze zajistit dostatečné zakotvení smykové výztuže před a za smykovou trhlinou) V této vzdálenosti je nutné umístit nejméně dvě svislice smykové výztuže, svislice ležící blízko kontrolovaného obvodu nebo základního obvodu u0 nelze řádně zakotvit, a proto je nelze zahrnout do únosnosti. Při mezním stavu protlačení se uvažuje se spolupůsobením betonu při přenosu tahů v rozsahu do 75 % celkové únosnosti bez smykové výztuže.
Obr. 10.5 Základní kontrolované obvody
Obr. 10.6 Rozhodující účinná výška desky v oblasti protlačení
Obr. 10.7 Principy vyztužení oblasti protlačení svislou smykovou výztuží
V kontrolovaném průřezu působí při vnějším zatížení VEd smykové napětí podle vztahu:
\begin{gathered}
V_\text{Ed}=\beta\frac{V_\text{Ed}}{u_\text{i}\cdot d}\end{gathered}(10.1)
kde je
d … průměrná účinná výška průřezu d = (dy + dz)/2 ;
dxy, dyz … účinná výška v kontrolovaném průřezu ve směru y a z;
ui … délka uvažovaného kontrolovaného obvodu;
β … součinitel vyjadřující vliv excentricity působící síly vůči těžišti styčné plochy.
U ztužených konstrukcí (prostorová stabilita nezávisí na rámovém působení sloupů a stropní desky), a pokud se rozpětí sousedních polí neliší více než o 25 % kratšího rozpětí, lze přibližně stanovit součinitel β podle obr. 10.8. Pokud nejsou uvedené podmínky splněny, je nutné stanovit součinitel β přesněji podle ČSN EN 1992-1-1 [1].
Obr. 10.8 Součinitel β pro vyjádření excentrického zatížení sloupů pravidelného nosného systému
Při návrhu prvku na protlačení se postupuje následovně (obr. 10.4 a obr. 10.7):
- Stanoví se vRd,c – návrhová únosnost prvku v protlačení bez smykové výztuže a překontroluje se, zda je nutná smyková výztuž v oblasti prvního kontrolovaného obvodu u1 ležícího v určité vzdálenosti od líce styčné plochy. Při splnění podmínky vEd ≤ vRd,c smyková výztuž není nutná. Veškeré tahy v oblasti namáhané protlačením přenese beton.
- Pokud vEd > vRd,c stanoví se vRd,max – maximální návrhová únosnost prvku ve smyku ve stavu drcení betonových vzpěr. Smyková únosnost tlačených diagonál se posuzuje v líci styčné plochy – kontrolovaný obvod u0. Pokud není únosnost tlačených betonových diagonál dostatečná vEd > vRd,max, je nutné změnit geometrii oblasti nebo zvolit vyšší třídu betonu.
- Navrhne se smyková výztuž, stanoví se staticky nutná plocha smykové výztuže.
- Stanoví se poslední kontrolovaný obvod uout, ve kterém již není nutná smyková výztuž. Od posledního kontrolovaného obvodu má být podle ČSN EN 1992-1-1 [1], vzdálenosti 1,5d (ve směru ke styčné ploše).
- Stanoví se počet řad (obvykle prstenců) smykové výztuže při respektování konstrukčních pravidel pro vzdálenosti smykové výztuže. Maximální radiální vzdálenost smykové výztuže je 0,75d (d je průměrná účinná výška průřezu desky).
- Současně je nutné kontrolovat, zda navržená smyková výztuž vyhovuje konstrukčním zásadám pro vyztužení oblasti.
U lokálně podepřených stropních desek jsou obvykle rozhodujícím kritériem pro návrh tloušťky desky průhyb v poli a protlačení v okolí lokálních podpor. Minimální tloušťka smykově vyztužené desky je 200 mm. Při použití smykových trnů podle ETA [45] lze navrhnout smykově vyztuženou desku o tloušťce nejméně 180 mm. Část zatížení z desky se přenáší přímo do styčné plochy (např. sloupu). U běžných deskových konstrukcí se toto zanedbává. U základových konstrukcí část zatížení přenášená přímo do základové spáry je významná, proto při výpočtu smykového namáhání v kontrolovaném průřezu musíme toto respektovat (viz kap. 11 Základové konstrukce).
Do posouzení lze uvažovat pouze tu tahovou výztuž, která je dostatečně zakotvená za prvním kontrolovaným obvodem nevyžadujícím smykovou výztuž (obr. 10.4 a obr. 10.7).
Celková staticky nutná plocha výztuže, která musí být umístěna v délce 1,5d (ve vnitřní části úseku při uvažované vzdálenosti kritické smykové trhliny 2d od líce styčné plochy z důvodu jejího dostatečného zakotvení na obou stranách smykové trhliny – viz obr. 10.7). Její celková plocha lze vyjádřit vztahem:
\begin{gathered}
\sum A_\text{ss}=\frac{A_\text{sw}\cdot\sin\alpha}{s_\text{r}}\cdot1{,}5d
\end{gathered}(10.2)
kde je
Asw … plocha smykové výztuže v jednom obvodu (prstenci) okolo styčné plochy;
sr … radiální vzdálenost obvodů smykové výztuže;
α … sklon smykové výztuže.
Pokud by byla styčná (zatěžovaná) plocha velká ve srovnání s účinnou výškou deskového prvku, je nutné ji redukovat, protože přenos smykového namáhání se realizuje především v rozích styčné plochy. Principy redukce kontrolovaného obvodu velkých styčných ploch jsou na obr. 10.5. Délky uvažovaných kontrolovaných průřezů se uvažují podle následujících vztahů:
\begin{gathered}
b_1=\text{min}(b{;}3d)\space\space\text{a}\space\space a_1=\text{min}(a{;}2b{;}6d-b_1)
\end{gathered}(10.3)
kde je
d … účinná výška průřezu;
a … delší strana průřezu sloupu;
b … kratší strana průřezu sloupu.
Kontrolovaný obvod se vždy zmenšuje, pokud jsou ve vzdálenosti menší nebo rovné, než 6d od líce styčné plochy umístěny prostupy podle obr. 10.9. Pokud je okraj desky ve vzdálenosti menší než vzdálenosti 6d od styčné plochy, mění se tvar a délka průběh kontrolovaných obvodů podle obr. 10.10.Pro průběh kontrolovaného obvodu je rozhodující minimální délka obvodu stanovena jednak u okraje desky a bez vlivu okraje desky, popřípadě s vlivem okraje desky jako velkého prostupu. Pokud se smykové plochy (a tím i kontrolované obvody) u blízkých sloupů překrývají, uvažuje se jeden společný kontrolovaný obvod.
Obr. 10.9 Vliv prostupů v blízkosti zatěžované plochy
Obr. 10.10 Základní kontrolované obvody sloupů při okraji desky
10.2 PROTLAČENÍ STROPNÍCH DESEK PODLE ČSN EN 1992-1-1 [1]
Únosnost ve smyku při protlačení se posoudí v základním kontrolovaném obvodu. Návrhová únosnost betonového průřezu bez smykové výztuže se stanoví podle vztahu:
\begin{gathered}
V_\text{Rd,c}=C_\text{Rd,c}k\cdot(100\rho_\text{l}f_\text{ck})^{1/3}+k_\text{l}\sigma_\text{cp}\ge(v_\text{min}+k_\text{l}\sigma_\text{cp})
\end{gathered}(10.4)
kde je
fck … charakteristická pevnost betonu v tlaku v MPa;
k … součinitel zohledňující tloušťku desky
\begin{gathered}
k=1+\sqrt{\frac{200}{d}\le2{,}0}d\space\text{je v mm.}
\end{gathered}(10.5)
\begin{gathered}
\rho_\text{l}=\sqrt{\rho_\text{ly}+\rho_\text{lz}}\le0{,}02
\end{gathered}(10.6)
ρly ρlz … se vztahují k tahové výztuži ve směrech y a z, dostatečně zakotvené za posuzovaným kontrolovaným průřezem, šířka desky se ve výpočtu uvažuje rovná tloušťce sloupu plus 3d po každé straně sloupu;
σcp … normálové napětí v betonu (MPa, tlak > 0) v kritickém průřezu σcp = (σcy + σcz)/2;
σcy, σcz … jsou normálová napětí v kritickém průřezu ve směru os y a z:
\begin{gathered}
\sigma_\text{c,y}=\frac{N_\text{Ed,y}}{A_\text{cy}}\space\space\text{a}\space\space\sigma_\text{c,z}=\frac{N_\text{Ed,z}}{A_\text{cz}}
\end{gathered}(10.7)
NEdy, NEdz … jsou normálové síly v celé šířce pole desky pro střední sloupy a normálové síly působící v kontrolovaném průřezu pro okrajové sloupy; síla může být vyvolána zatížením nebo předpětím;
Aci … průřezové plochy betonu v kritickém řezu podle NEdi.
\begin{gathered}
v_\text{min}=0{,}035\cdot k^{3/2}\cdot f_\text{ck}^{1/2}
\end{gathered}(10.8)
\begin{gathered}
C_\text{Rd,c}=1{,}8/\gamma_\text{c}\space\space\text{a}\space\space k_1=0{,}10
\end{gathered}Maximální návrhová únosnost je dána výrazem – viz změna 2 normy ČSN EN 1992-1-1 [1]. Kontroluje se v líci styčné plochy viz obr. 10.7 (kontrolovaný obvod u0).
\begin{gathered}
v_\text{Rd,max}=0{,}4v\cdot f_\text{cd}
\end{gathered}(10.9)
kde je
fcd … návrhová hodnota pevnosti betonu v tlaku v MPa;
ν … redukční součinitel pevnosti betonu při porušení smykem podle vztahu
\begin{gathered}
v=0{,}6\cdot(1-f_\text{ck}/250)
\end{gathered}(10.10)
Vztah (10.9) vychází z modelu náhradní příhradoviny podle obr. 10.2. Vyjadřuje maximální únosnost tlačené betonové diagonály v líci styčné plochy. Při omezení maximální únosnosti podle vztahu (10.9) není vyjádřen vliv smykové výztuže v průřezu. Experimentálně bylo prokázáno, že při velkém množství smykové výztuže v průřezu ji nelze spolehlivě zakotvit a je tak nedostatečně účinná. Proto se omezuje únosnost smykové výztuže podle vztahu (10.11). Maximální únosnost je definovaná kmax – násobkem návrhové únosnosti na protlačení bez smykové výztuže stanovené v prvním kontrolovaném obvodu u1 (ve vzdálenosti 2d od líce styčné plochy), tedy:
\begin{gathered}
\beta V_\text{Ed}\le V_\text{Rd,max}=k_\text{max}\cdot v_\text{Rd,c}\cdot u_1\cdot d\space\space\text{resp.}\space\space v_\text{Ed,1}=\beta V_\text{Ed}/(u_1d)\le k_\text{max}\cdot v_\text{Rd,c}
\end{gathered}(10.11)
příp.
\begin{gathered}
v_\text{Rd,cs}=0{,}75v_\text{Rd,c}+1{,}5(d/s_\text{r})A_\text{sw}f_\text{ywd,ef}(1/(u_1d))\sin\alpha\le k_\text{max}\cdot v_\text{Rd,c}
\end{gathered}kde je
vRd,c … návrhová únosnost betonového průřezu bez smykové výztuže viz vztah (10.4);
kmax … součinitel maximální únosnosti, jehož hodnota závisí na typu smykové výztuže a způsobu jejího zakotvení.
Pro třmínkovou výztuž dostatečně zakotvenou v úrovni spodní i horní výztuže (obr. 10.11) se uvažuje součinitel kmax hodnotou:
- kmax=1,45 pro účinnou výšku desky d ≤ 200 mm;
- kmax=1,70 pro účinnou výšku desky d ≥ 700 mm.
mezilehlé hodnoty lze interpolovat.
Pro smykové kozlíky je kmax=1,35.
Pro smykové trny, lišty a smykovou příhradovou výztuž lze uvažovat vyšší hodnoty, ale tato speciální smyková patentovaná smyková výztuž má být navrhována podle příslušných evropských technických doporučení (viz čl. 6.45.5(6) [1]). Vyšší hodnoty únosnosti vycházejí z řady ověřovacích zkoušek a jsou podmíněny řadou dalších podmínek odlišných od standardních podmínek uvedených v ETA [45] a ETA [44]. Použití třmínků podle článku 8.5 [1] je nevhodné z hlediska jejich nedostatečného zakotvení. Pro jejich případné použití je nutné upravit délky přesahů, popřípadě háků tak, aby smyková výztuž byla dostatečně zakotvena v úrovni horní i spodní výztuže (jednu vrstvu výztuž musí obepínat).

Obr. 10.11
Návrhová únosnost prvního kontrolovaného obvodu se smykovou výztuží se stanoví podle vztahu:
\begin{gathered}
v_\text{Rd,cs}=0{,}75v_\text{Rd,c}+1{,}5(d/s_\text{r})A_\text{sw}f_\text{ywd,ef}(1/(u_1d))\sin\alpha\le k_\text{max}\cdot v_\text{Rd,c}
\end{gathered}(10.12)
kde je
Asw … plocha smykové výztuže na jednom obvodu okolo sloupu v mm2;
sr … radiální vzdálenost obvodů smykové výztuže v mm;
fywd,ef … účinná návrhová pevnost smykové výztuže na protlačení podle vztahu:
\begin{gathered}
f_\text{ywd,eff}=250+0{,}25d\le f_\text{ywd}\text{[MPa]}
\end{gathered}(10.13)
kde je
d … průměrná účinná výška ve směrech y a z v mm;
u1 … délka prvního kontrolovaného obvodu v mm;
α … úhel, který svírá smyková výztuž s rovinou desky.
Pokud je smyková výztuž tvořena ohyby (kozlíky – viz obr. 10.12) v jedné řadě, pak poměr d/sr lze ve vztahu (10.12) nahradit hodnotou 0,67.
Obr. 10.12 Principy vyztužení smykovými kozlíky
Kontrolovaný průřez uout, ve kterém se již smyková výztuž není staticky nutná, se stanoví ze vztahu:
\begin{gathered}
v_\text{Ed}=\beta\frac{V_\text{Ed}}{u_\text{out}\cdot d}\le v_\text{Rd,c}
\end{gathered}(10.14)
odkud
\begin{gathered}
u_\text{out}\ge\beta V_\text{Ed}/(v_\text{Rd,c}\cdot d)
\end{gathered}(10.15)
Nejvzdálenější obvod smykové výztuže má být lze umístit ve vzdálenosti maximálně 1,5d od posledního kontrolovaného obvodu uout (obr. 10.4 a obr. 10.7).
Třmínková smyková výztuž musí obepínat alespoň jednu vrstvu dolní a horní výztuže. Pokud je zajištěno spolehlivé zakotvení betonářské smykové výztuže na protlačení – viz obr. 10.11 (např. smykové spony, svařované žebříčky, smykové trny) lze použít i vyšších hodnot součinitele kmax.
Výztuž proti progresivnímu kolapsu
Podle obr. 10.3 je nutné umístit při spodním tlačeném lící stropní desky nad sloupy výztuže proti progresivnímu kolapsu. Výztuž má zabránit pádu stropní desky po překonání únosnosti v protlačení. Porušená stropní deska má zůstat zavěšená na této výztuži tak, aby nezatížila níže položenou stropní desku. Výztuž se má navrhnout na sílu FEd,x = FEd,y = VEd, které je rovná reakci stropní desky ve sloupu. Výztuž se navrhne v obou směrech, musí být v oblasti sloupu spojitá. Výztuž se umístí v šířce do 2d od líce sloupu na obě strany.
V [1] jsou požadovány u vnitřních sloupů pouze 2 výztužné pruty v každém směru spojitě uložené při spodním líci ve směru sloupových pruhů. Podrobnější definice výztuže proti progresivnímu kolapsu je v ČSN 73 1201 [51].
Konstrukční uspořádání výztuže
Konstrukční uspořádání výztuže na protlačení je definováno na obr. 10.7 a obr. 10.13 až obr. 10.15. Svislá smyková výztuž má být umístěna ve vzdálenosti větší něž 0,3d od líce styčné plochy (do vzdálenosti 0,3d prakticky nejde účinně zakotvit smykovou výztuž pod poruchovou trhlinou), ale ne současně větší než 0,5d (při uvažování styčníku nad sloupem podle obr. 10.2 je sklon první tlačené diagonály větší jak 45°). V celé smykově vyztužené oblasti nemá v radiálním směru překročit vzdálenost svislé smykové výztuže 0,75d (to odpovídá sklonu tlačené diagonály přibližně 45°, pokud dolní styčník CCT [28] se uvažuje v těžišti zakotveného táhla – smykové výztuže). U prvního kontrolovaného obvodu nemá překročit tangenciální vzdálenost s2 ≤ 1,5d (obr. 10.7) smykové výztuže a vně prvního kontrolního obvodu vzdálenost s2 ≤ 2d. V radiálním směru musí být nejméně dvě větve smykové výztuže v oblasti kontrolovaného obvodu, a v oblasti každého dalšího kontrolovaného obvodu, který se uvažuje od poslední spolehlivě zakotvené smykové výztuže, musí být rovněž nejméně dvě větve smykové výztuže.
Obr. 10.13 Principy vyztužení smykovou výztuží ortogonální smykové mřížky
Obr. 10.14 Principy vyztužení oblasti protlačení u konce stěny
Obr. 10.15 Principy vyztužení oblasti protlačení u rohu stěny
Svislá smyková výztuž musí být zakotvena co možná nejblíže k líci desky. Výztuž musí obepínat alespoň jednu vrstvu tahové výztuže při horním líci a při spodním líci jednu vrstvu konstrukční výztuže nebo výztuže proti progresivní havárii (obr. 10.11). Podle konstrukčních pravidel uvedených v ČSN EN 1992-1-1 [1] je nutné zhustit tahovou výztuž nad podporou podle paragrafu 9.4. Pokud je smyková výztuž nutná, potom plocha větve třmínku (nebo ekvivalentu) Asw,min je dána vztahem:
\begin{gathered}
A_\text{sw,min}\cdot(1{,}5\cdot\sin\alpha+\cos\alpha)/(s_\text{r}\cdot s_\text{t})\ge0{,}08\cdot\sqrt{f_\text{ck}/f_\text{yk}}
\end{gathered}(10.16)
kde je
α … úhel, který svírá smyková výztuž s nosnou výztuží;
sr … osová vzdálenost spon (svislých větví třmínků) v radiálním směru;
st … osová vzdálenost spon (svislých větví třmínků) v tangenciálním směru.
Pokud se použijí ohyby (smykové kozlíky, obr. 10.12) jako smyková výztuž, lze je umístit pouze v jedné řadě, přitom ohyby mají mít sklon α = 30° ([1]). Při návrhu je nutné rovněž posouzení kontrolovaného obvodu bez smykové výztuže jako u svislé smykové výztuže.
10.2.1 Vliv nesymetrického zatížení styčné plochy – součinitel β
Součinitel β, vystihující přesněji vliv ohybového momentu MEd působícího v rovině kolmé na osu y nebo z na styčnou plochu, lze při uvažování rovnoměrného rozdělení posouvající síly po obvodě základního kritického průřezu, stanovit ze vztahu:
\begin{gathered}
\beta=1+k\frac{M_\text{Ed}}{V_\text{Ed}}\frac{u_1}{W_1}
\end{gathered}(10.17)
kde je
u1 … délka základního kontrolovaného průřezu;
k … součinitel závislý na poměru rozměrů styčné plochy c1 a c2. Jeho hodnota vyjadřuje poměrnou část ohybového momentu působícího na styčné ploše, která je přenášena posouvajícími silami (zbývající část se přenáší převážně normálovými silami); jeho hodnota je v tab. 10.1;
W1 … modul, který odpovídá rozdělení smyku podle obr. 10.16 je funkcí základního kontrolovaného obvodu u1:
\begin{gathered}
W_1=\int\limits_0^{u_1}|e|dl
\end{gathered}(10.18)
kde je
dl … diferenciál délky obvodu u1;
e … vzdálenost diferenciálů délky dl od osy kolem které otáčí moment MEd.
Tab. 10.1 Hodnoty součinitele k pro obdélníkové zatěžované plochy.
| c1/c2 | ≤ 0,5 | 1,0 | 2,0 | ≥ 3,0 |
| k | 0,45 | 0,60 | 0,70 | 0,80 |
Mezilehlé hodnoty součinitele k z tab. 10.1 lze interpolovat. Pro kruhový průřez platí k = 0,6.
Pro základní kontrolovaný obvod vnitřního obdélníkového sloupu je průřezový modul
\begin{gathered}
W_1=\frac{c_1^2}{2}+c_1c_2+4c_2d+16d^2+2\pi dc_1
\end{gathered}(10.19)
kde je
c1 … rozměr styčné plochy ve směru rovnoběžném s rovinou působícího ohybového momentu MEd;
c2 … rozměr styčné plochy ve směru kolmém k rovině působícího momentu MEd.
Pro základní kontrolovaný obvod vnitřního kruhového sloupu je součinitel β:
\begin{gathered}
\beta=1+0{,}6\pi\frac{e}{D+4d}
\end{gathered}(10.20)
kde je
e … výstřednost působící síly;
D … průměr kruhového sloupu.
Pro základní kontrolovaný obvod vnitřního obdélníkového sloupu s momenty působícími ve dvou směrech lze stanovit přibližnou hodnotu β ze vztahu:
\begin{gathered}
\beta=1+1{,}8\sqrt{\Bigg[\bigg(\frac{e_\text{y}}{c_\text{z}}\bigg)^2+\bigg(\frac{e_\text{z}}{c_\text{y}}\bigg)^2\Bigg]}
\end{gathered}(10.21)
kde jsou
ey, (ez) … výstřednosti MEd/ VEd ve směru osy y a z;
cy, (cz) … rozměry kontrolovaného obvodu ve směru osy y a z.
Pro přesnější vyjádření součinitele β viz [9] a obr. 10.17. Excentricitu zatížení lze vyjádřit také redukcí kontrolovaného obvodu viz obr. 10.18.
Obr. 10.16 Vliv ohybových momentů v kontrolované obvodu pro vnitřní sloup
Obr. 10.17 Vliv ohybových momentů v kontrolovaném obvodu pro krajní sloup
Obr. 10.18 Vliv ohybových momentů redukovaný kontrolované obvody pro krajní a rohový sloup
10.2.2 Vliv okraje v blízkosti styčné plochy
U okrajových sloupů, kde ohybový moment působí v rovině kolmé k okraji desky směrem do interiéru (výstřednost je kolmá na okraj desky) a ohybový moment ve druhém směru nepůsobí, se uvažuje rovnoměrné rozdělení posouvajících sil podél obvodu redukovaného základního kritického průřezu ured,1 ured,1. Součinitel β se stanoví ze vztahu:
\begin{gathered}
\beta=\frac{u_1}{u_\text{red,1}}+k\frac{u_1}{W_1}e_\text{par}
\end{gathered}(10.22)
kde je
u1 … základní kontrolovaný obvod;
ured,1 … redukovaný základní kontrolovaný obvodu;
epar … výstřednost rovnoběžná s okrajem desky vyplývající z momentu k ose kolmé na okraj desky.
Pro obdélníkový průřez podle ČSN EN 1992-1-1 [1] platí:
\begin{gathered}
W_1=\frac{c_2^2}{4}+c_1c_2+4c_1d+8d^2+\pi dc_2
\end{gathered}(10.23)
Pro rohový sloup, pokud výstřednost směřuje k vnitřním sloupům, se předpokládá, že síla při protlačení se rovnoměrně rozdělí podél redukovaného kontrolovaného obvodu ured,1, který se stanoví podle obr. 10.10, obr. 10.17 a obr. 10.18. Hodnotu součinitele β lze uvažovat ze vztahu:
\begin{gathered}
\beta=\frac{u_1}{u_\text{red,1}}
\end{gathered}(10.24)
10.2.3 Vliv konce a rohu stěny
Délka kontrolovaných obvodů vychází z principů na obr. 10.5. Namáhání se koncentruje ve vnějším rohu stěny nebo na konci stěny. Pokud desková konstrukce podepřená stěnovým pilířem, protlačení vzniká na koncích stěnového pilíře, střední část stěnového pilíře je namáhána smykem. Je nutné posoudit jak koncové části namáhané protlačením, tak i střední část namáhanou smykem. Principy vyztužení konce stěny svislou smykovou výztuží jsou na obr. 10.14 a principy vyztužení vnějšího rohu stěny jsou na obr. 10.15.
10.2.4 Minimální množství tahové výztuže v oblastech namáhaných protlačením
Aby bylo možné použít pro návrh a posouzení metodiku podle ČSN EN 1992-1-1 [1] je nutné oblast vyztužit dostatečným množstvím tahové výztuže. Minimální tahovou výztuže je nutné umístit podle obr. 10.19. Tahová výztuž musí být navržena na minimální ohybové momenty mEdx a mEdy v oblastech styků mezi deskou a sloupem podle tab. 10.2. Pokud není počítáno přesněji, lze splnit podmínku:
\begin{gathered}
m_\text{Ex}(\text{popř.}\space\space m_\text{Ey})\ge\eta\cdot V_\text{Ed}
\end{gathered}(10.25)
kde η je momentový součinitel podle tab. 10.2 a ohybové momenty mEdx a mEdy ve stycích mezi deskou a sloupem při mimostředném namáhání a účinné šířky přenášející tyto momenty.
Obr. 10.19 Minimální vyztužení tahovou výztuží nad sloupy
Tab. 10.2 Hodnoty momentového součinitele η
| Poloha sloupu | Pro mEdx | Pro mEdy | ||||
| horní výztuž | dolní výztuž | účinná šířka | horní výztuž | dolní výztuž | účinná šířka | |
| Vnitřní sloup | -0,125 | 0 | 0,3ly | -0,125 | 0 | 0,3 lx |
| Okrajový sloup (okraj rovnoběžný s osou x) | -0,25 | 0 | 0,15 ly | -0,125 | 0,125 | na 1 m |
| Okrajový sloup (okraj rovnoběžný s osou y) | -0,125 | 0,125 | na 1 m+ | -0,25 | 0 | 0,15 lx |
| Rohový sloup | -0,50 | 0,50 | na 1 m | -0,50 | 0,50 | na 1 m |
10.3 PROTLAČENÍ STROPNÍCH DESEK SE SMYKOVÝMI TRNY
Při protlačení deskových konstrukcí se dnes nejčastěji navrhují smykové trny, popřípadě smykové lišty. Jedná se o speciální patentované výrobky (obr. 10.20, obr. 10.21 a obr. 10.22). Jejich zabudování je poměrně jednoduché a lze je vložit i dodatečně do již vytvořené horní a dolní nezabetonované výztuže desky. Jejich kontrola a případná oprava jsou jednoduché. Navíc je možné přenést touto smykovou výztuž větší zatížení z důvodu jejího dobrého zakotvení v úrovni horní a dolní výztuže. To je vykoupeno vyšší cenou prvků. Při návrhu této patentované výztuže je však nutné postupovat podle metodik výrobců. Z pohledu ČSN EN 1992-1-1 [1] se uvádí v článku 6.4.5(5) „Pokud jsou použity patentované výrobky jako smyková výztuž, má se vRd,cs stanovit zkouškami podle příslušného evropského technického schválení“. To znamená, že smykové trny, lišty, smyková příhradová výztuž by neměla být posuzována podle obecné metodiky uvedené v normě [1], protože nelze využít některých jejich speciálních vlastností (vyšší únosnost výztuže, lepší zakotvení v úrovni horní a dolní výztuže deskového prvku a podobně). Závěry zkoušek smykových trnů Halfen na mezní stav protlačení jsou na obr. 10.20, obr. 10.21 a obr. 10.22. Metodiky výrobců zohledňují všechny výhody speciální smykové výztuže, což se promítá do vyšší celkové únosnosti průřezu na protlačení. Pokud bychom použili standardní postup návrhu podle normy [1], nedosáhli bychom požadované spolehlivosti návrhu a při případných sporech by výrobce patentované výztuže odmítl převzít záruku za takovýto návrh. Specializované návrhové postupy jsou navíc obvykle zajištěny specializovaným, volně dostupným a pravidelně aktualizovaným návrhovým software. Jednotlivé postupy rozhodně nelze kombinovat nebo přejímat hodnoty součinitelů, příp. jednotlivých únosností. Srovnání jednotlivých přístupů je dobře patrno z následujícího příkladu. Příklady použití smykových trnů jsou na obr. 10.20, obr. 10.21 a obr. 10.22.

Obr. 10.20

Obr. 10.21
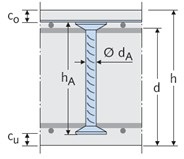
Obr. 10.22
Praktické příklady použití smykových trnů jsou na obr. 10.23, obr. 10.24, obr. 10.25 a obr. 10.26.

Obr. 10.23
Obr. 10.24
Obr. 10.25
Obr. 10.26
Návrh smykových trnů podle ETA [45] respektuje všechny zásady normy EN 1990. Vychází ze zatížení podle EN 1991 a z návrhových kombinací EN 1990. Respektuje všechny principy návrhu protlačení podle EN 1992-1-1 [1]. V předpisu se vychází ze závěrů řady experimentů (obr. 10.27, obr. 10.28 a obr. 10.29) a lze tak zvýšit únosnost prvního kontrolovaného obvodu až kmax = 1,96 oproti smykově nevyztuženému průřezu. Vzdálenosti kontrolovaných obvodů 2d a posledního kontrolovaného obvodu 1,5d jsou stejné jako v normě ČSN EN 1992-1-1 [1]. Stejně se uvažuje vliv otvorů a okrajů desky.
Poznámka:
V předpisu ETA [45] se nekontroluje maximální únosnost tlačené betonové diagonály VRd,max, proto je doporučeno vždy kontrolovat maximální únosnost podle vztahu (10.9) i při výpočtu podle předpisu ETA[45].
Obr. 10.27
Obr. 10.28
Obr. 10.29
Všechna stavebně technická osvědčení většiny výrobců smykových trnů mají stejnou nebo velmi podobnou metodiku návrhu i konstrukční zásady. Oblast deskového prvku namáhaná protlačením je rozdělena do dvou oblastí C a D. Oblast C je do vzdálenosti 1,125 od líce styčné plochy a oblast D navazuje na oblast C a představuje zbývající smykově vyztuženou oblast desky (viz obr. 10.30).
Obr. 10.30 Principy vyztužení oblasti protlačení smykovými trny podle ETA
Návrhový postup podle evropského certifikátu ETA (např. [45]) vychází tradičně označených oblastí „C“ a „D“ (viz obr. 10.30) namáhaných na protlačení. Oblast „C“ je oblast bezprostředně související se styčnou plochou, je dlouhá 1,125d od líce styčné plochy a smyková výztuž v této oblasti musí přenést veškeré namáhání (bez spolupůsobení betonu). V této oblasti musí být nejméně 2 trny v paprsku od styčné plochy (nc ≥ 2). První musí být ve vzdálenosti 0,35d až 0,5d od kraje styčné plochy a druhý do vzdálenosti 1,125d. Pro silnější desky s účinnou výšku d ≥ 0.50 m musí být nejméně 3 smykové trny, pokud platí VEd ≥ 0,85VRd,max. V tangenciálním směru nesmí vzdálenost smykových trnů překročit 1,7d ve vzdálenosti 1,0d od kraje styčné plochy. Na oblast „C“ navazuje oblast „D“. V oblasti „D“ je maximální tangenciální vzdálenost smykových trnů 3,5d a v radiálním směru 0,75d. Pro silnější desky se v radiálním směru redukuje vzdálenost mezi smykovými trny podle vztahu:
\begin{gathered}
s_\text{w,d}=\frac{3d\cdot m_\text{D}}{2\cdot n_\text{C}\cdot m_\text{C}}\le0{,}75d
\end{gathered}(10.26)
kde je
mC … počet smykových trnů v „C“ v tangenciálním směru – paralelně s okrajem styčné plochy;
mD … počet smykových trnů v „D“ v tangenciálním směru – paralelně s okrajem styčné plochy;
nC … počet smykových trnů v „C“ v radiálním směru – kolmo na okraj styčné plochy.
V posledním kontrolovaném obvodu se upravuje součinitel excentrického zatížení styčné plochy β na hodnotu βred. Hodnota se stanoví ze vztahu:
\begin{gathered}
\beta_\text{red}=K_\beta\cdot\beta\ge1{,}10
\end{gathered}(10.27)
Tab. 10.3 Součinitel Kβ pro stavení součinitele βred
Pozice styčné plochy / sloupu
\begin{gathered}
\text{Součinitel}\space K_\beta
\end{gathered}Vnitřní sloup
\begin{gathered}
K_\beta=1{,}0
\end{gathered}Sloup u okraje
\begin{gathered}
K_\beta=\frac{1}{1{,}2+(\beta/20)\cdot(l_\text{s}/d)}
\end{gathered}Sloup v rohu
\begin{gathered}
K_\beta=\frac{1}{1{,}2+(\beta/15)\cdot(l_\text{s}/d)}
\end{gathered}Roh stěny
\begin{gathered}
K_\beta=1{,}0
\end{gathered}Konec stěny
\begin{gathered}
K_\beta=1{,}0
\end{gathered}Principiální rozdíly návrhu podle ETA [54] a ČSN EN 1992-1-1 [1]
(viz 10.7 a obr. 10.30)
- Maximální obvod 2(a + b) ≤ 12d.
- Minimální tloušťka desky při použití smykových trnů je 180 mm (v normě [1] je 200 mm).
- Doplňující omezení maximálního Uvažuje se plná návrhová únosnost smykové výztuže fyd = 435 MPa (v normě [1] je redukovaná účinná únosnost fywd,ef = 250 + 0,25 d ≤ fywd [MPa]).
- Vyztužení \rho_\text{l}=\sqrt{\rho_\text{ly}\cdot\rho_\text{lz}}\le0{,}5f_\text{cd}/f_\text{yd}.
- CRd,c = 1,8/yc pro u0/d ≥ 4 a CRd,c = 1,8/yc (0,1u0/d + 0,6) ≥ 0,15/yc pro u0/d < 4, ale lze uvažovat i standardní hodnoty. CRd,c = 1,5 pro blokové základové patky.
- Je doporučena jiná hodnota součinitele β ≥ 1,10 pro vnitřní sloupy (v normě [1] je 1,15). Upřesnění vlivu excentrického zatížení se provádí podle standardního postupu uvedeného v normě [1].
- Oblast protlačení je rozdělena na dvě části. Oblast „C“ přímo souvisí se zatěžovanou plochou (například sloupem) a její hranice je ve vzdálenosti 1,125d. Zbylá část smykově vyztužené oblasti je označena „D“.
- V oblasti „C“ se uvažuje, že veškeré zatížení přenáší pouze smyková výztuž (nejvýznamnější rozdíl od standardního postupu normy [1]).
Staticky nutná plocha smykových trnů:
\begin{gathered}
A_\text{s,req}=V_\text{Ed}\cdot\beta\cdot\eta/f_\text{yd}
\end{gathered}(10.28)
kde η = 1,0 pro d ≤ 200 mm a η = 1,6 pro d ≥ 800 mm (mezilehlé hodnoty lze interpolovat).
Posouzení
\begin{gathered}
V_\text{Rd,sy}=m_\text{C}\cdot n_\text{C}\cdot A_\text{Anker}\cdot f_\text{yd}/\eta\ge V_\text{Ed}\cdot\beta
\end{gathered}(10.29)
kde je
AAnker … průřezová plocha dříku smykového trnu;
mc … počet smykových trnů v prstenci v oblasti „C“ (obr. 10.30);
nc … počet smykových trnů v radiálním směru v oblasti „C“.
- Maximální únosnost průřezu je pro desky VRd,max = 1,96 ∙ VRd,c a pro základové patky VRd,max = 1,50 ∙ VRd,c.
- Konstrukční zásady podle ETA [54] jsou jiné (obr. 10.30). Maximální vzdálenost trnů v tangenciálním směru je 1,75d v obvodu ve vzdálenosti do 1,0d od líce styčné plochy. Maximální vzdálenost v posledním smykově vyztuženém obvodu je 3,5d v tangenciálním směru v nejvzdálenějším smykově vyztuženém obvodu. Radiálně je nutné umístit nejméně 2 trny do 1,125d od líce sloupu (případně 3 trny pro silnější více namáhané desky). V radiálním směru ve v obou předpisech stejná maximální vzdálenost 0,75d.
Pokud se navrhují smykové trny jako smyková výztuž na protlačení pro spřažené stropní desky (obr. 10.26), je nutné navíc k výše uvedenému postupu posoudit smyk v pracovní spáře mezi prefabrikátem a monolitickou částí konstrukce. Posouzení se provádí standardním způsobem podle ETA [54] nebo EC2 [1]. Při posouzení je doporučené uvažovat vodorovnou pracovní spáru s hladkým povrchem.
10.4 PROTLAČENÍ STROPNÍCH DESEK SE SPECIÁLNÍ PŘÍHRADOVOU VÝZTUŽÍ
Jako smykovou výztuž na mezní stav protlačení lze použít i příhradovou výztuž (obr. 10.31, obr. 10.32 a obr. 10.33), vyrobenou v souladu s ETA [44]. Jedná se o příhradovou výztuž se skloněnými diagonálami o průměru 9 mm, dolní pas příhradové výztuže tvoří dva pruty o průměru 7 mm a horní pas prut o průměru 10 mm (betonářská výztuž BSt 500G) – viz obr. 10.31, obr. 10.32 a obr. 10.33. Posouzení speciální příhradové výztuže vychází z metodiky uvedené v ETA [44] a doplněné pro použití příhradové výztuže. Příhradová výztuž navržená pro oblast C musí procházet celou oblastí D.
Obr. 10.31
Obr. 10.32

Obr. 10.33
Návrhový postup pro speciální příhradovou výztuž podle ETA [44] umožňuje využít smykovou výztuž pro zvýšení únosnosti v prvním kontrolovaném průřezu o vyšší hodnotu, než je uvedeno u smykových trnů. Maximální únosnost je:
\begin{gathered}
V_\text{Ed,1}=\beta V_\text{Ed}/(u_1d)\le k_\text{max}\cdot V_\text{Rd,c}
\end{gathered}(10.30)
kde kmax = 2,09.
S tím, že v oblasti „C“ je nutné posoudit únosnost smykové výztuže podle vztahu:
\begin{gathered}
\beta\cdot V_\text{Ed}\le V_\text{Rd,sy}=\frac{f_\text{yk}}{\gamma_\text{s}\cdot\eta}\cdot\sum(A_\text{sy}\cdot\sin\alpha_\text{i})
\end{gathered}(10.31)
kde η = 1,0 pro β ∙ VEd/VRd,c = 1,8 a η = 1,5 pro β ∙ VEd/VRd,c = 2,09
Ostatní parametry jsou stejné, jak u smykových trnů (délka oblasti, součinitel βred apod.) Konstrukční zásady jsou rozdílné vzhledem k charakteru smykové výztuže – viz obr. 10.34).
Obr. 10.34 Principy vyztužení oblasti protlačení příhradovou výztuží podle ETA
Poznámka:
i v návrhovém postupu pro speciální příhradovou výztuž je doporučeno kontrolovat maximální únosnost tlačené diagonály VRd,max podle [1].
10.5 POSOUZENÍ STROPNÍCH DESEK PROTI PROTLAČENÍ S OCELOVÝMI HLAVICEMI
Připojení desky ke sloupu může být navrženo buď bez smykové výztuže na protlačení nebo s jejím použitím. Za smykovou výztuž na protlačení lze považovat i tuhé výztužné vložky – ocelové skrytí hlavice. Ocelové skryté hlavice jsou hlavice umístěné v konstrukci tak, že je zachována rovinnost obou povrchů desky v okolí lokálního podporujícího prvku. Ocelové hlavice z hlediska namáhání deskového prvku posouvají poruchovou trhlinu. Kontrolované obvody se uvažují od vnějšího líce ocelové hlavice (obr. 10.35). Přitom je nutné uvážit případné snížení účinné výšky desky – viz obr. 10.6.
Obr. 10.35 Ocelová hlavice – základní kontrolovaný obvod
Ocelová skrytá manžetová hlavice – svařená manžeta (obr. 10.36) slouží ke zvětšení obvodu lokálního podporujícího prvku z hlediska protlačení.
Obr. 10.36 Nejčastější typ ocelové roštové hlavice
Ocelová skrytá roštová hlavice (obr. 10.37) – ocelový svařovaný rošt je z ramen navzájem k sobě kolmých; každé rameno je tvořeno jedním nebo dvěma obvykle válcovanými profily; hlavice musí být nad lokálně podporujícím prvkem spojitá. Tato hlavice slouží ke zvětšení obvodu lokálně podporujícího prvku z hlediska mezního stavu protlačení a podílí se na přenášení ohybových momentů a posouvajících sil v místech napojení desky na lokální podporující prvek.
Obr. 10.37 Nejčastější typy ocelových roštových hlavic
Ocelové skryté hlavice se uplatňují především u vnitřních podpor, u kterých jsou účinky desky zhruba souměrné ke svislé ose podporujícího prvku. Vlastní konstrukce ocelové skryté hlavice se navrhuje podle řady norem ČSN EN 1993 (průřezy, svarové spoje apod.).
U skryté manžetové hlavice se kontrolované průřezy stanoví podle ČSN EN 1992-1-1 s tím, že za okraj podporujícího prvku se považuje obrys manžetové hlavice a tloušťka desky se uvažuje jen nad lícem dolní pásnice manžety (obr. 10.6). U skryté roštové a žebrové hlavice je základní kontrolovaný průřez ve vzdálenosti 0,75 délky světlého vyložení ramene, popř. žebra. Přitom základní kontrolovaný průřez nemá být vzdálen od líce podporujícího prvku víc než 2d v částech, kde se posouvající síla přenáší přímo do podporujícího prvku. Ostatní parametry při návrhu mezního stavu protlačení se uvažují podle ČSN EN 1992-1-1 (viz obr. 10.35 a obr. 10.38).
Obr. 10.38 Základní kontrolovaný obvod – roštové ocelové hlavice
Skryté roštové a žebrové hlavice mohou zvětšit základní kontrolovaný průřez ucr,a maximálně na 1,25-ti násobek základního kritického průřezu u1 uvažovaného u stejného podporujícího prvku avšak bez použití skryté ocelové hlavice (kritický průřez u1 – viz ČSN EN 1992-1-1 kap. 6.4).
Ocelové skryté hlavice se musí konstrukčně uspořádat tak, aby se v místě uložení desky na lokální podporující prvek dala umístit svislá výztuž do podporujícího prvku a vodorovná výztuž do desky a aby bylo možné vyplnit řádně všechny dutiny zhutněným betonem. U ocelové manžetové hlavice je nutno pamatovat na její ochranu před účinky požáru. U ocelových skrytých roštových hlavic se uspořádají prvky do dvou navzájem kolmých směrů. Při vyložení jednoho prvku po každé straně pravoúhelníkové úložné plochy se prvek umístí do osy úložné plochy; při vyložení dvou prvků se prvky umístí do třetin délky stran úložné plochy. V místě křížení prvků se navrhnou svařované styky tak, aby byly splněny předpoklady konzolového působení prvků. U ocelových skrytých roštových hlavic se uspořádají prvky do dvou navzájem kolmých směrů. Při vyložení jednoho prvku po každé straně pravoúhelníkové úložné plochy se prvek umístí do osy úložné plochy; při vyložení dvou prvků se prvky umístí do třetin délky stran úložné plochy. V místě křížení prvků se navrhnou svařované styky tak, aby byly splněny předpoklady konzolového působení prvků. Nad skrytými ocelovými roštovými a žebrovými hlavicemi musí probíhat nepřerušeně betonářská výztuž. U žebrových hlavic v případě použití kruhových výztužných prutů zachycujících tangenciální ohybové momenty, musí být tyto prvky přichyceny svarem nebo sponami k žebrům hlavice (svařovaná pouze v souladu s ČSN EN ISO 17660-1); v případě použití křižujících se přímých prutů musí být tyto pruty zavedeny za koncem jejich působení do tlačené části betonu, případně zahnuty ke spodnímu okraji desky a tam zakotveny tak, aby nemohly být vytrženy z betonu účinkem tangenciálních momentů.
10.6 PROTLAČENÍ STROPNÍCH DESEK PODLE MC 2010 [46]
Podle metodiky Model Code 2010 [46] je kontrolní obvod b0 ve vzdálenosti 0,5dv (dv je průměrná účinná výška deskového prvku) viz obr. 10.39 a obr. 10.40. Pro rohy a konce stěn se uvažuje délka oblasti 1,5dv (obr. 10.23).
Obr. 10.39 Posouzení oblasti protlačení podle MC2010
Obr. 10.40 Základní kontrolovaný obvod podle MC2010
Při posouzení protlačení musí být splněna podmínka pro posouvající síly (na rozdíl od předchozích předpisů nikoliv napětí jako v EC2 [1] nebo síly vztažené na 1 m kontrolovaného obvodu jako v DIN 1045-1 [2]):
\begin{gathered}
V_\text{Ed}\le V_\text{Rd}
\end{gathered}(10.32)
kde VEd je návrhová posouvající síla vypočtená jakou součet všech návrhových posouvajících sil působících v základním kontrolním obvodu podle obr. 10.40.
Zatěžovací účinky, které se stanoví stejně jako podle ČSN EN 1990 a navazujících norem. Vliv ohybového namáhání styku je na rozdíl od předpisů EC2 [1], DIN 1045-1 [2] a ETA [44], [45] řešeno redukcí kontrolovaného obvodu součinitelem ke. Součinitel ke představuje část ohybového momentu přenášeného z desky do sloupu smykem.
Na rozdíl od návrhového postupu EC2 [1] a DIN 1045-1 [2], kdy se vlivem excentricity zatížení zvětšuje součinitelem β zatěžující síla VEd, u návrhu podle MC 2010 [46] se vlivem excentrického zatížení redukuje délka kontrolovaného obvodu součinitelem ke. Součinitel ke zohledňuje část ohybového momentu přenášeného z desky do sloupu smykem. Pro ztužené nosné systémy s pravidelným půdorysem (sousední rozpětí se neliší více než 25 % kratšího rozpětí) lze použít součinitel ke z tab. 10.4. Přesněji lze součinitel ke lze vyjádřit podle vztahu:
\begin{gathered}
k_\text{e}=\frac{1}{1+e/b}
\end{gathered}(10.33)
kde je
e = │MEd/VEd│ … excentricita působící zatížení;
b … průměr kruhu o stejné ploše jako styčná plocha.
Tab. 10.4 Součinitel ke vlivu excentrického zatížení styčné plochy
| Součinitel ke | Umístění sloupu |
| 0,90 | Vnitřní sloup |
| 0,70 | Sloup u okraje |
| 0,65 | Sloup v rohu desky |
Oblast protlačení je ovlivněna prostupy do vzdálenosti 5dv od líce styčné plochy (viz obr. 10.41). Pokud je styčná plocha velká ve srovnání s účinnou výškou deskového prvku (viz obr. 10.42), uvažuje se kontrolovaný obvod pouze v délce 3,0dv kolem každého rohu styčné plochy. Délka kontrolovaného obvodu se redukuje o část ovlivněnou prostupy.
Obr. 10.41 Základní kontrolovaný obvod – vliv prostupů
Obr. 10.42 Základní kontrolovaný obvod konce a rohu stěny a velké styčné plochy podle MC2010
Únosnost v protlačení je definována následující rovnicí:
\begin{gathered}
V_\text{Rd}=V_\text{Rd,c}+V_\text{Rd,s}
\end{gathered}(10.34)
kde je
VRd,c … smyková únosnost betonu, která se stanoví podle vztahu:
\begin{gathered}
V_\text{Rd,c}=k_\Psi\frac{\sqrt{f_\text{ck}}}{\gamma_\text{c}}\cdot b_0\cdot d_\text{v}\end{gathered}(10.35)
fck … cylindrická pevnost betonu v tlaku v MPa;
kψ … součinitel závisející na deformační kapacitě (pootočení) deskového prvku v oblasti styčné plochy, součinitel lze stanovit podle následujícího vztahu. Součinitel v sobě zahrnuje rozměrový efekt a vliv vyztužení průřezu tahovou výztuží.
\begin{gathered}
k_\Psi=\frac{1}{1{,}5+0{,}6\Psi\cdot d_\text{v}\cdot k_\text{dg}}\le0{,}6
\end{gathered}(10.36)
kdg … součinitel velikosti maximálního zrna kameniva, kdg = 48/(16 + dg) ≥ 1,15 (dg je velikost zrna kameniva v [mm]);
ψ … úhel natočení deskového prvku v oblasti styčné plochy vně poruchové smykové plochy – viz obr. 10.3;
bo … délka základního kontrolovaného obvodu podle obr. 10.40 až obr. 10.42, včetně redukce z vlivu excentrického zatížení (ke) a z vlivu blízkých prostupů;
dv … průměrná účinná výška deskového prvku – ve vztahu (10.33) dosazujeme výšku v [mm];
VRd,s … únosnost smykové výztuže, která se stanoví podle vztahu:
\begin{gathered}
V_\text{Rd,s}=\sum A_\text{sw}k_\text{e}\sigma_\text{sd}\sin\alpha
\end{gathered}(10.37)
kde je
ΣAsw … celková plocha smykové výztuže dostatečně zakotvené, která prochází potenciální poruchovou plochou (kuželová plocha pod úhlem 45°) v oblasti ohraničené vzdáleností od 0,35dv až po dv od líce styčné plochy;
α … úhel mezi smykovou výztuží a rovinou deskového prvku;
σsd … napětí ve smykové výztuži, které lze uvažovat podle vzorce:
\begin{gathered}
\sigma_\text{sd}=\frac{E_\text{s}\Psi}{6}f_\text{ywd}
\end{gathered}(10.38)
fywd … návrhová pevnost smykové výztuže;
Es … modul pružnosti smykové výztuže.
Pro stanovení natočení deskového prvku za poruchovou trhlinou lze v MC2010 [46] použít 3 základní úrovně přesnosti výpočtu:
- Úroveň I – pro pravidelné desky navržené pomocí lineárně pružné analýzy bez významné redistribuce vnitřních sil (např. metodou náhradních rámů):
\begin{gathered}
\Psi=1{,}5\cdot\frac{r_\text{s}}{d_\text{v}}\cdot\frac{f_\text{yd}}{E_\text{s}}
\end{gathered}(10.39)
kde rs je vzdálenost místa nulového momentu v radiálním směru od osy sloupu (viz obr. 10.39). Hodnotu rs lze stanovit pro pravidelná rozpětí (s poměrem rozpětí ve směru x a y 0,5 ≤ Lx/Ly ≤ 2 a pro horizontálně ztužený nosný systém) přibližně podle vztahu:
\begin{gathered}
r_\text{s}=0{,}22L_\text{x}\space\space\text{nebo}\space\space r_\text{s}=0{,}22L_\text{y}
\end{gathered}(10.40)
Provádíme-li návrh podle této úrovně, se nezohledňuje se vliv vyztužení průřezu, proto je vhodné postupovat podle následující návrhové úrovně II:
- Úroveň II – pro pravidelné desky navržené pomocí lineárně pružné analýzy s využitím významné redistribuce vnitřních sil (např. metodou náhradních rámů):
\begin{gathered}
\Psi=1{,}5\cdot\frac{r_\text{s}}{d_\text{v}}\cdot\frac{f_\text{yd}}{E_\text{s}}\cdot\bigg(\frac{m_\text{Sd}}{m_\text{Rd}}\bigg)^{1{,}5}
\end{gathered}(10.41)
kde je
mSd … průměrný ohybový moment v podporovém pruhu – uvažován na jednotku délky:
- pro vnitřní sloupy mSd = VEd/8;
- pro sloupy u okraje mSd = VEd/4 pro směr rovnoběžný s okrajem a mSd = VEd/8 pro výztuž kolmou k okraji;
- pro rohové sloupy mSd = VEd/2 v každém směru.
mRd … návrhová únosnost v ohybu v podporovém pruhu;
rs … lze uvažovat stejně jako v úrovni I – vzdálenost místa nulového momentu v radiálním směru od osy sloupu.
- Úroveň III – přesnější výpočet. Pokud se při výpočtu rs desky použije lineárně pružný model MKP (MKP – rovinný nebo prostorový výpočet metodou konečných prvků, výpočet bez vlivu trhlin) a pokud je mSd stanoveno jako průměrná hodnota ohybového momentu ve sloupovém pruhu na základě lineárně pružného modelu MKP (bez vlivu trhlin):
\begin{gathered}
\Psi=1{,}2\cdot\frac{r_\text{s}}{d_\text{v}}\cdot\frac{f_\text{yd}}{E_\text{s}}\cdot\bigg(\frac{m_\text{Sd}}{m_\text{Rd}}\bigg)^{1{,}5}
\end{gathered}(10.42)
- Úroveň IV – nejpřesnější výpočet. Výpočet předpokládá nelineární analýzu MKP se zahrnutím vlivu trhlin, vlivu zpevnění tažené výztuže (a jiných nelineárních vlivů na chování železobetonové deskové konstrukce) – bližší viz MC2010 [46].
Maximální únosnost v protlačení s příčnou smykovou výztuží představuje porušení tlačených betonových diagonál a lze vyjádřit
\begin{gathered}
V_\text{Rd,max}=k_\text{sys}k_\Psi\frac{\sqrt{f_\text{ck}}}{\gamma_\text{c}}\cdot b_0\cdot d_\text{v}\le\frac{\sqrt{f_\text{ck}}}{\gamma_\text{c}}\cdot b_0\cdot d_\text{v}
\end{gathered}(10.43)
kde je
ksys … součinitel účinnosti smykové výztuže, pokud nejsou bližší data, lze uvažovat hodnotou ksys = 2. Přesnější hodnoty lze získat z experimentů;
kψ … součinitel stanovený pro smykově nevyztuženou oblast.
Vztah (10.35) omezuje smykovou únosnosti na maximálně dvojnásobek smykové únosnosti nevyztuženého průřezu na líci styčné plochy b0.
Pro zajištění dostatečné deformační kapacity průřezu je nutné, aby smyková výztuž, pokud je nutná, přenesla více než 50 % celkového zatížení (VRd,s ≥ 0,5VEd).
Pro zajištění konstrukce proti progresivnímu kolapsu je nutné navrhnou výztuž podle MC2010 [46], obdobně jako u výše uvedených předpisů.
10.7 Příklady
10.7.1 Navrhněte výztuž na protlačení stropní desky
Tloušťka desky h = 250 mm, rozměry průřezu sloupu jsou 0,30 x 0,30 m, betonová krycí vrstva 25 mm, horní tahová výztuž v obou směrech je navržena z prutů ø14 mm/100 mm (As = 2545 mm2/m), posouvající síla VEd = 800 kN, vliv excentrického zatížení – vnitřní sloup – β = 1,15 (pravidelný půdorys, ztužená konstrukce). Stropní deska je z betonu C30/37, betonářská výztuž B500A/B.
Obr. 10.43
Účinná výška – směr x:
\begin{gathered}
d_\text{x}=250-25-7=218\text{ mm}=0{,}218\text{ m}
\end{gathered}Účinná výška – směr y:
\begin{gathered}
d_\text{y}=250-25-14-7=204\text{ mm}=0{,}204\text{ m}
\end{gathered}\begin{gathered}
d=\frac{d_\text{x}+d_\text{y}}{2}=\frac{218+204}{2}=211\text{ mm};\space2\cdot d=2\cdot0{,}211=0{,}422\text{ m}\\\\
\rho_\text{lx}=\frac{A_\text{s}}{d_\text{x}\cdot b}=\frac{2545}{218\cdot1000}=0{,}0117;\space\rho_\text{ly}=\frac{2545}{204\cdot1000}=0{,}0125\\\\
\rho_\text{l}=\sqrt{\rho_\text{lx}\cdot\rho_\text{ly}}=\sqrt{0{,}0117\cdot0{,}0125}=0{,}0121
\end{gathered}Kontrolovaný obvod
\begin{gathered}
u_0=4\cdot0{,}30=1{,}20\text{ m}
\end{gathered}Kontrolovaný obvod
\begin{gathered}
u_1=1{,}2+2\cdot3{,}14\cdot2\cdot0{,}211=3{,}85\text{ m}
\end{gathered}\begin{gathered}
V_\text{Ed,0}=\frac{\beta\cdot V_\text{Ed}}{u_0\cdot d}=\frac{1{,}15\cdot0{,}800}{1{,}2\cdot211}=3{,}633\text{ MPa}
\end{gathered}Posouzení betonové tlačené diagonály:
\begin{gathered}
V_\text{Rd,max}=0{,}4\cdot v\cdot f_\text{cd}=0{,}4\cdot0{,}6\cdot(1-30/250)\cdot30=6{,}336\text{ MPa}\\\\
V_\text{Ed,0}=3{,}633\text{ MPa}< V_\text{Rd,max}=6{,}336\text{ MPa}
\end{gathered}Posouzení prvního kontrolovaného průřezu:
\begin{gathered}
V_\text{Ed,1}=\frac{\beta\cdot V_\text{Ed}}{u_1\cdot d}=\frac{1{,}15\cdot0{,}800}{3{,}85\cdot 211}=1{,}133\text{ MPa}\\\\
k=1+\sqrt{200/d}=1+\sqrt{200/211}=1{,}973<2{,}0\\\\
v_\text{Rd,c}=\frac{C_\text{Rd,c}}{\gamma_\text{c}}\cdot k\cdot(100\cdot\rho_\text{l}f_\text{ck})^{1/3}\\\\
v_\text{Rd,c}=C_\text{Rd,c}k\cdot(100\rho_\text{l}f_\text{ck})^{1/3}\\\\
v_\text{Rd,c}=\frac{0{,}18}{1{,}5}\cdot1{,}973\cdot(100\cdot0{,}0121\cdot30)^{1/3}=0{,}784\text{ MPa}\\\\
v_\text{Ed,1}=1{,}133\text{ MPa}> v_\text{Rd,c}=0{,}784\text{ MPa}\to\text{výztuž na protlační je nutná}.
\end{gathered}Únosnost smykové výztuže (B500B):
\begin{gathered}
f_\text{ywd,eff}=250+0{,}25d\le f_\text{ywd}\\\\
f_\text{ywd,eff}=250+0{,}25\cdot211=302{,}75\text{ MPa}<435\text{ MPa}
\end{gathered}Návrh smykové výztuže (dobře zakotvené svislé pruty ø8 mm.
Omezení únosnosti v prvním kontrolovaném obvodu:
\begin{gathered}
k_\text{max}=1{,}51(\text{interpolací}),\space V_\text{Ed,1}=1{,}133\text{ MPa}< k_\text{max}\cdot V_\text{Rd,c}=1{,}51\cdot0{,}784=1{,}184\text{ MPa}
\end{gathered}Obvod uout, u kterého již smykovou výztuž není nutná:
\begin{gathered}
u_\text{out}=\frac{\beta\cdot V_\text{Ed}}{v_\text{Rd,c}\cdot d}=\frac{1{,}15\cdot0{,}800}{0{,}784\cdot0{,}211}=5{,}56\text{ m}=1{,}12+2\pi\text{r}_\text{out}
\end{gathered}⇒ rout = 0,695 m. Od toho obvodu je poslední smyková výztuž ve vzdálenosti 1,5d (0,3165 m). Smykově vyztužená oblast je tedy dlouhá nejméně 0,695 – 0,3165 = 0,3785 m.
Z konstrukčních zásad – první prut ve vzdálenosti 100 mm (do 0,5d), následující po 150 mm (do 0,75d). Celkem 3 pruty (0,1 + 0,15 + 0,15 = 0,40 m) v radiálním směru. Ve druhém směru platí maximální vzdálenost smykové výztuže 2d a vzdálenost 1,5d v prvním kontrolovaném obvodu. Z prvního kontrolovaného obvodu 2,77(1,5∙d) = 8,8→9.
Z obvodu v místě nejvzdálenější smykové výztuže je minimální počet smykových prutů 3,72/(2 ∙ 0,211) = 8,82→9. Z konstrukčních zásad (symetrická konstrukce) se navrhne 12 paprsků smykové výztuže (Asw = 603 mm2). Únosnost smykově vyztuženého průřezu:
\begin{gathered}
V_\text{Rd,cs}=0{,}75\cdot0{,}784+1{,}5(0{,}211/0{,}15)\cdot603\cdot10^{-6}\cdot302{,}75(1/(3{,}85\cdot0{,}211)\cdot1=0{,}589+0{,}474=1{,}062\text{ MPa}>1{,}15\cdot0{,}8=0{,}92\text{ MPa}
\end{gathered}Navrená smyková výztuž ø8 mm ve dvanácti radiálních paprscích vždy se třemi pruty vyhovuje.
Kontrola minima smykové výztuže:
\begin{gathered}
\rho_\text{sw}=\frac{1{,}5\cdot A_\text{sw1}}{s_\text{r}\cdot s_\text{t}}=\frac{1{,}5\cdot603}{150\cdot230}=0{,}026\ge\rho_\text{sw,min}\\\\
\rho_\text{sw,min}=0{,}08\cdot\sqrt{f_\text{ck}}/f_\text{yk}=0{,}08\cdot\sqrt{30}/500=0{,}00088\space\text{vyhovuje}
\end{gathered}10.7.2 Navrhněte výztuž na protlačení stropní desky podle metodiky ETA
Tloušťka desky h = 250 mm, rozměry průřezu sloupu jsou 0,30 x 0,30 m, betonová krycí vrstva 25 mm, horní tahová výztuž v obou směrech je navržena z prutů ø14 mm/100 mm (As = 2 545 mm2/m), posouvající síla VEd = 800 kN, vliv excentrického zatížení – vnitřní sloup – β = 1,15 (pravidelný půdorys, ztužená konstrukce). Stropní deska je z betonu C30/37, betonářská výztuž B500A/B.

Obr. 10.44
Účinná výška – směr x:
\begin{gathered}
d_\text{x}=250-25-7=218\text{ mm}=0{,}218\text{ m}
\end{gathered}Účinná výška – směr y:
\begin{gathered}
d_\text{y}=250-25-14-7=204\text{ mm}=0{,}204\text{ m}
\end{gathered}\begin{gathered}
d=\frac{d_\text{x}+d_\text{y}}{2}=\frac{218+204}{2}=211\text{ mm};\space2\cdot d=2\cdot0{,}211=0{,}422\text{ m}\\\\
\rho_\text{lx}=\frac{A_\text{s}}{d_\text{x}\cdot b}=\frac{2545}{218\cdot1\space000}=0{,}0117;\space\rho_\text{ly}=\frac{2545}{204\cdot1\space000}=0{,}0125\\\\
\rho_\text{l}=\sqrt{\rho_\text{lx}\cdot\rho_\text{ly}}=\sqrt{0{,}0117\cdot0{,}0125}=0{,}0121
\end{gathered}Kontrolovaný obvod
\begin{gathered}
u_0=4\cdot0{,}30=1{,}20\text{ m}
\end{gathered}Kontrolovaný obvod
\begin{gathered}
u_1=1{,}2+2\cdot3{,}14\cdot2\cdot0{,}211=3{,}85\text{ m}
\end{gathered}\begin{gathered}
V_\text{Ed,0}=\frac{\beta\cdot V_\text{Ed}}{u_0\cdot d}=\frac{1{,}15\cdot0{,}800}{1{,}2\cdot211}=3{,}633\text{ MPa}
\end{gathered}Posouzení betonové tlačené diagonály:
\begin{gathered}
V_\text{Rd,max}=0{,}4\cdot v\cdot f_\text{cd}=0{,}4\cdot0{,}6\cdot(1-30/250)\cdot30=6{,}336\text{ MPa}\\\\
V_\text{Ed,0}=3{,}633\text{MPa}< V_\text{Rd,max}=6{,}336\text{ MPa}
\end{gathered}Posouzení prvního kontrolovaného průřezu:
\begin{gathered}
V_\text{Ed,1}=\frac{\beta\cdot V_\text{Ed}}{u_1\cdot d}=\frac{1{,}15\cdot0{,}800}{3{,}85\cdot 211}=1{,}133\text{ MPa}\\\\
k=1+\sqrt{200/d}=1+\sqrt{200/211}=1{,}973<2{,}0\\\\
V_\text{Rd,c}=C_\text{Rd,c}k\cdot(100\rho_\text{l}f_\text{ck})^{1/3}\\\\
V_\text{Rd,c}=\frac{0{,}18}{1{,}5}\cdot1{,}973\cdot(100\cdot0{,}0121\cdot30)^{1/3}=0{,}784\text{ MPa}\\\\
V_\text{Ed,1}=1{,}133\text{ MPa}> v_\text{Rd,c}=0{,}784\text{ MPa}\to\text{výztuž na protlační je nutná}.
\end{gathered}Únosnost smykové výztuže (B500B).
\begin{gathered}
f_\text{ywd,eff}=f_\text{ywd}=435\text{ MPa}
\end{gathered}Návrh smykové výztuže v oblasti „C“ (oblast „C“ je do vzdálenosti 1,125d od líce sloupu. V této oblasti přenáší veškeré zatížení smykové trny.) Z konstrukčních zásad – první prut ve vzdálenosti 75 mm (do 0,35 až 0,5d), následující po 150 mm (do 0,75d). Celkem 2 trny v radiálním směru. Ve druhém směru platí maximální vzdálenost trnů 1,75d v obvodu ve vzdálenosti d od sloupu. Obvod 1,2 + 2 ∙ 0,211 ∙ π = 2,53m, minimální počet trnů 2,53/(1,75d) = 6,85→8 radiálních paprsků. V oblasti „C“ je 8 ∙ 2 = 16 trnů. Minimální plocha smykového trnu:
\begin{gathered}
A_\text{s1}=1{,}15\cdot800\cdot1{,}03/435\space000/16=0{,}000136\text{ m}^2\to\text{trny}\phi14\text{ mm}
\end{gathered}(η = 1,03 )
Únosnost trnů v oblasti „C“:
\begin{gathered}
V_\text{Rd}=0{,}002464\cdot435\space000=1\space072\ge1{,}15\cdot800\text{ kN}
\end{gathered}Délku smykově vyztužené oblasti ls stanovíme ze vztahu:
\begin{gathered}
V_\text{Ed,out}=\beta_\text{red}\cdot V_\text{Ed}/(u_\text{out}\cdot d)=1{,}1\cdot800/(u_\text{out}\cdot0{,}211)\le784\text{ kPa}\\\\
u_\text{out}=5{,}32\text{ m},u_\text{out}=4\cdot a+2\pi\cdot(l_\text{s}+1{,}5d)
\end{gathered}minimální ls = (5,32 – 1,2)/(2π) – 1,5d = 0,339 m, to představuje nejméně 3 trny.
Skutečná délka smykově vyztužené oblasti ls je tedy
\begin{gathered}
l_\text{s}=(0{,}35+(3-1)\cdot0{,}75)\cdot d=0{,}390\text{ m}
\end{gathered}Poslední kontrolovaný obvod
\begin{gathered}
u_\text{out}=1{,}2+(0{}39+1{,}5\cdot d)\cdot2\cdot\pi=5{,}64\text{ m}
\end{gathered}Posouzení:
\begin{gathered}
V_\text{Ed,out}=\beta_\text{red}\cdot V_\text{Ed}/(u_\text{out}\cdot d)=1{,}1\cdot800/(5{,}64\cdot0{,}211)=739\le784\text{ kPa}
\end{gathered}Ověření konstrukčních zásad v oblasti „D“: obvod s posledním trnem 3,65 m, počet trnů 8, vzdálenost mezi trny 0,456 m, maximální vzdálenost je 3,5d = 0,739 m, vyhovuje.
Při splnění konstrukčních zásad ETA není nutné posuzovat další kontrolované obvody.
Obr. 10.45
Obr. 10.46
10.7.3 Navrhněte výztuž na protlačení stropní desky podle metodiky ETA
Stropní deska o průměrné účinné výšce d = 230 mm je uložena na vnitřním sloupu o průřezu 400 x 400 mm (jedná se o ztuženou konstrukci, sloupy se nepodílejí na přenosu vodorovných zatížení). Stropní deska je navržena z betonu C25/30 XC1, betonová krycí vrstva 30 mm, vyztužení nad sloupem je tvořeno profily ø20 po 120 mm v obou směrech, betonářská výztuž B500B. Zatížení přenášené z desky do sloupu je VEd = 930 kN.
Průměrný stupeň vyztužení ρ = 0,0114
Vliv rozměru desky
\begin{gathered}
k=1+\sqrt{200/d}=1{,}93\le2{,}0
\end{gathered}Kontrolované obvody – obvod u0 = 1,60 m, kontrolovaný obvod u1= 1,60 + 4 ∙ πd = 4,49 m, součinitel excentrického zatížení β = 1,15 (podle ETA β = 1,1).
Smykové napětí na líci styčné plochy.
\begin{gathered}
V_\text{Ed,0}=\beta\cdot V_\text{Ed}/(u_0\cdot d)=2{,}91\text{ MPa}\le V_\text{Rd,max}
\end{gathered}Maximální únosnost první tlačené diagonály.
\begin{gathered}
V_\text{Rd,max}=0{,}4v\cdot f_\text{cd}=3{,}6\text{ MPa}\space(v=0{,}6[1-f_\text{ck}/250]=0{,}54)
\end{gathered}Smykové napětí v prvním kontrolovaném obvodu.
\begin{gathered}
V_\text{Ed,1}=\beta\cdot V_\text{Ed}/(u_1\cdot d)=1{,}04\text{ MPa}
\end{gathered}Únosnost nevyztuženého průřezu
\begin{gathered}
V_\text{Rd,c}=C_\text{Rd,c}k\cdot(100\rho_\text{l}f_\text{ck})^{1/3}\ge v_\text{min}\space\space\text{při}\space\space C_\text{Rd,c}=0{,}18/\gamma c\space\space\text{a}\space\space\gamma c=1{,}5\space\text{platí}:\\\\
V_\text{Rd,c}=0{,}12\cdot1{,}93\cdot(100\cdot0{,}0114\cdot25)^{1/3}=0{,}707\text{ MPa}\ge V_\text{min}\\\\
V_\text{min}=0{,}035\cdot1{,}93^{3/2}\cdot25^{1/2}=0{,}469\text{ MPa}
\end{gathered}Návrh smykových trnů v oblasti „C“ podle ETA
Maximální únosnost.
\begin{gathered}
V_\text{Rd,max}=1{,}96\cdot V_\text{Rd,c}=1{,}96\cdot0{,}707=1{,}387\text{ MPa}\ge V_\text{Ed1}\space\text{vyhovuje}
\end{gathered}Staticky nutná plocha smykových trnů (v celé oblasti „C“):
\begin{gathered}
A_\text{s,req}=V_\text{Ed}\cdot\beta\cdot\eta/f_\text{yd}=930\cdot1{,}15\cdot1{,}03/435\space000=2{,}53\cdot10^{-3}\text{ m}^2\space(\eta=1{,}03)
\end{gathered}Minimální počet trnů z konstrukční podmínky (z maximální vzdálenosti smykových trnů v obvodu do vzdálenosti d od líce sloupu – viz výše) (1,6 + 2πd)/(1,75d) = 3,045/0,403 = 7,6.
Minimální počet trnů po obvodu je 8 a radiálně 2 – celkem 16 trnů.
25,3 ∙ 10-4/16 = 1,58 ∙ 10-4 – minimální průměr trnů 16 mm As1 = 2,01 ∙ 10-4 m2.
Navrženo uspořádání trnů o průměru 16 mm v osmi radiálních paprscích. Celkem 16 smykových trnů.
Posouzení
\begin{gathered}
V_\text{Rd,sy}=8\cdot2\cdot2{,}01\cdot10^{-4}\cdot435\space000/1{,}03=1\space358{,}2\text{ kN}\ge930\cdot1{,}15=1\space069{,}5\text{ kN}
\end{gathered}Návrh smykových trnů v oblasti „D“ podle ETA:
Délka smykově vyztužené oblasti ls ze vztahu:
\begin{gathered}
u_\text{out}=2(a+b)+2\pi\cdot(l_\text{s}+1{,}5d)\\\\
V_\text{Ed,out}=\beta_\text{Red}\cdot V_\text{Ed}/(u_\text{out}\cdot d)=1{,}1\cdot930/(u_\text{out}\cdot0{,}23)\le707\text{ kPa}
\end{gathered}uout = 6,58 m, minimální ls = (6,58 – 1,6)/(2π) – 1,5d = 0,448, to představuje nejméně 4 trny.
Skutečná délka smykově vyztužené oblasti ls je tedy
\begin{gathered}
l_\text{s}=(0{,}35+(4-1)\cdot0{,}75)\cdot d=0{,}598\text{ m}
\end{gathered}Poslední kontrolovaný obvod
\begin{gathered}
u_\text{out}=1{,}6+(0{,}598+15{,}5\cdot d)\cdot2\cdot\pi=7{,}53\text{ m}
\end{gathered}Posouzení
\begin{gathered}
V_\text{Ed,out}=\beta_\text{Red}\cdot V_\text{Ed}/(u_\text{out}\cdot d)=1{,}1\cdot930/(7{,}53\cdot0{,}23)=590{,}7\le707\text{ kPa}
\end{gathered}Vyhovuje
Ověření konstrukčních zásad v oblasti „D“: obvod s posledním trnem 5,36 m, počet trnů 8, vzdálenost mezi trny 0,669 m, maximální vzdálenost je 3,5d = 0,805 m, vyhovuje.
Při splnění konstrukčních zásad ETA není nutné posuzovat další kontrolované obvody.
Obr. 10.47
Obr. 10.48
10.7.4 Navrhněte výztuž na protlačení stropní desky podle ČSN EN 1992-1-1
Stropní deska o průměrné účinné výšce d = 210 mm je uložena na vnitřním sloupu o průřezu 400 x 400 mm (jedná se o ztuženou konstrukci, sloupy se nepodílejí na přenosu vodorovných zatížení). Stropní deska je navržena z betonu C35/45 XC1, betonová krycí vrstva 30 mm, vyztužení nad sloupem je tvořeno profily ø20 po 150 mm v obou směrech, betonářská výztuž B500B. Zatížení přenášené z desky do sloupu je VEd = 800 kN.
Průměrný stupeň vyztužení ρ = 0,01
Vliv rozměru desky
\begin{gathered}
k=1+\sqrt{200/d}=1{,}98\le2{,}0
\end{gathered}Kontrolované obvody – obvod u0 = 1,60 m, kontrolovaný obvod u1 = 1,60 + 4 ∙ πd = 4,24 m, součinitel excentrického zatížení β = 1,15.
Smykové napětí na líci styčné plochy:
\begin{gathered}
V_\text{Ed,0}=\beta\cdot V_\text{Ed}/(u_0\cdot d)=2{,}74\text{ MPa}\le V_\text{Rd,max}
\end{gathered}Maximální únosnost první tlačené diagonály:
\begin{gathered}
V_\text{Rd,max}=0{,}4v\cdot f_\text{cd}=4{,}82\text{ MPa}\cdot(v=0{,}6[1-f_\text{ck}/250]=0{,}516)
\end{gathered}Smykové napětí v prvním kontrolovaném obvodu:
\begin{gathered}
V_\text{Ed,1}=\beta\cdot V_\text{Ed}/(u_1\cdot d)=1{,}033\text{ MPa}
\end{gathered}Únosnost nevyztuženého průřezu
\begin{gathered}
V_\text{Rd,c}=C_\text{Rd,c}k\cdot(100\rho_\text{l}f\text{ck})^{1/3}\ge V_\text{min}\\\\
\text{Při}\space\space C_\text{Rd,c}=0{,}18/\gamma c\space\space\text{a}\space\space\gamma c=1{,}5\space\space\text{platí}\space\space V_\text{Rd,c}=0{,}12\cdot1{,}98\cdot(100\cdot0{,}01\cdot35)^{1/3}=0{,}777\text{ MPa}\ge V_\text{min}\\\\
V_\text{min}=0{,}035\cdot1{,}98^{3/2}\cdot35^{1/2}=0{,}577\text{ MPa}
\end{gathered}Smyková výztuž nutná.
Návrh smykových prvků v prvním kontrolovaném obvodu:
\begin{gathered}
V_\text{Rd,max}=k_\text{max}\cdot V_\text{Rd,c}=1{,}47\cdot0{,}777=1{,}085\text{ MPa}>1{,}033\text{ MPa}\space\text{vyhovuje}
\end{gathered}Podle konstrukčních zásad je maximální vzdálenost mezi smykovými prvky 1,5d v oblasti prvního kontrolovaného obvodu. Druhý smykový prvek je 1,25d od líce sloupu, jejich obvod je 3,41m. Minimální počet smykových prvků je n = 3,41/(1,5d) = 10.
Z důvodu symetrie zvolíme 12 paprsků. Účinná návrhová pevnost smykové výztuže:
\begin{gathered}
f_\text{ywd,eff}=250+0{,}25\cdot230=307{,}5\text{ MPa}\\\\
V_\text{Rd,cs}=0{,}75\cdot0{,}777+2\cdot A_\text{sw}307{,}5\cdot(1/(4{,}24\cdot0{,}21))
\end{gathered}Staticky nutná plocha smykové výztuže v jednom obvodu kolem sloupu:
\begin{gathered}
A_\text{sw}=(1{,}033-0{,}75\cdot0{,}777)\cdot1{,}123/(2\cdot307{,}5)=8{,}22\cdot10^{-4}\text{ m}^2
\end{gathered}Při dvanácti paprscích postačuje profil 10 mm, celková plocha smykové výztuže v jednom obvodu je Asw = 942 mm2.
Únosnost v prvním kontrolovaném obvodu je
\begin{gathered}
V_\text{Rd,cs}=0{,}75\cdot0{,}777+2\cdot9{,}42\cdot10^{-4}\cdot307{,}5\cdot(1/(4{,}24\cdot0{,}21))=1{,}233\text{ MPa}\ge V_\text{Ed1}=1{,}033\text{ MPa}
\end{gathered}Únosnost vyhovuje.
Poslední kontrolovaný obvod – bez smykové výztuže
\begin{gathered}
V_\text{Ed,1}=\beta\cdot V_\text{Ed}/(u_\text{out}\cdot d)=777\text{ kPa}\to u_\text{out}=\beta\cdot V_\text{Ed}/(V_\text{Rd,c}\cdot d)=5{,}64\text{ m}\\\\
l_\text{s}=(u_\text{out}-u_0)/(2\pi)-1{,}5d=0{,}325\text{ m}
\end{gathered}Délka smykově vyztužené oblasti je 0,327 m.
První smykový prvek umístíme 0,3d až 0,5d od líce styčné plochy ve vzdálenosti 0,10 m. Další prvky po vzdálenostech 0,75d = 0,158 m. Skutečná délka smykově vyztužené oblasti je
Uspořádáme smykové prvky následovně: 0,1 + 2 ∙ 0,158 = 0,416 m, vyhovují 3 smykové prvky v paprsku.
Posouzení posledního kontrolovaného obvodu
\begin{gathered}
u_\text{out}=1{,}6+2\cdot(0{,}416+0{,}315)\cdot\pi=6{,}19\text{ m}\\\\
V_\text{Ed,out}=\beta\cdot V_\text{Ed}/(u_\text{out}\cdot d)=1{,}15\cdot800/(6{,}19\cdot,0{,}21)=707{,}7\text{ kPa}\le777\text{ kPa}
\end{gathered}Konstrukčně počet smykových prvků v posledním vyztuženém obvodu (1,6 + 2 ∙ 0,416 ∙ π)/(2 ∙ 0,416 ∙ π)/(2d) = 7,83→dvanáct paprsků vyhovuje.
Minimální množství smykové výztuže v prvním obvodu 12 ∙ 2 ∙ ø10 = 0,001884 m2.
\begin{gathered}
\sum A_\text{sw}\ge(0{,}08\sqrt{f_\text{ck}})/f_\text{yk}=9{,}5\cdot10^{-4}\text{ m}^2
\end{gathered}Celkový počet větví smykové výztuže:
\begin{gathered}
4\cdot12=48\space\text{trnů}\space\phi10\space\text{výšky}\space\space225\text{ mm}
\end{gathered}10.7.5 Příklad návrhu protlačení smykových trnů podle ETA a EC2
Pro srovnání je zpracován návrhu smykové výztuže podle standardní metodiky ČSN EN 1992-1-1 [1] a podle evropského certifikátu ETA [45]. Stropní deska o účinné výšce d = 230 mm je uložena na vnitřním sloupu o průřezu 400×400 mm (jedná se o ztuženou konstrukci, sloupy se nepodílejí na přenosu vodorovných zatížení). Stropní deska je navržena z betonu C25/30 XC1, betonová krycí vrstva 30 mm, vyztužení nad sloupem je tvořeno profily ø20 po 120 mm v obou směrech, betonářská výztuž B500B. Zatížení přenášené z desky do sloupu je VEd = 930 kN.
Oba postupy mají řadu společných parametrů a postupů vycházejících z metodiky ČSN EN 1992-1-1 [1].
Společné parametry:
- Průměrný stupeň vyztužení ρ = 0,0114;
- vliv rozměru desky
\begin{gathered}
k=1+\sqrt{200/d}=1{,}93\le2{,}0
\end{gathered}- kontrolované obvody – obvod u0 = 1,60m, kontrolovaný obvod u1 = 1,60 + 4 ∙ πd = 4,49 m, součinitel excentrického zatížení β = 1,15 (podle ETA [45] β = 1,1);
- smykové napětí na líci styčné plochy
\begin{gathered}
V_\text{Ed,0}=\beta\cdot V_\text{Ed}/(u_0\cdot d)=2{,}91\text{ MPa}\le V_\text{Rd,max}
\end{gathered}- maximální únosnost první tlačené diagonály
\begin{gathered}
V_\text{Rd,max}=0{,}4v\cdot f_\text{cd}=3{,}6\text{ MPa}\\\\
\text{kde}\space\space v=0{,}6[1-f_\text{ck}/250]=0{,}54
\end{gathered}- smykové napětí v prvním kontrolovaném obvodu
\begin{gathered}
V_\text{Ed,1}=\beta\cdot V_\text{Ed}/(u_1\cdot d)=1{,}04\text{ MPa}
\end{gathered}- únosnost nevyztuženého průřezu
\begin{gathered}
V_\text{Rd,c}=C_\text{Rd,c}k\cdot(100\rho_\text{l}f_\text{ck})^{1/3}\ge V_\text{min}\\\\
\text{při}\space\space C_\text{Rd,c}=0{,}18/\gamma c\space\space\text{a}\space\space\gamma c=1{,}5\space\space\text{obdržíme}\space\space V_\text{Rd,c}=0{,}12\cdot1{,}93\cdot(100\cdot0{,}01114\cdot25)^{1/3}=0{,}777\text{ MPa}\ge V_\text{min}\\\\
V_\text{min}=0{,}035\cdot1{,}93^{3/2}\cdot25^{1/2}=0{,}469\text{ MPa}
\end{gathered}Návrh smykových trnů v oblasti „C“ podle ETA [45]:
Maximální únosnost.
\begin{gathered}
V_\text{Rd,max}=1{,}96\cdot V_\text{Rd,c}=1{,}96\cdot0{,}707=1{,}387\text{ MPa}\ge V_\text{Ed1}\space\text{vyhovuje}
\end{gathered}Staticky nutná plocha smykových trnů (v celé oblasti „C“):
\begin{gathered}
A_\text{s,req}=V_\text{Ed}\cdot\beta\cdot\eta/f_\text{yd}=930\cdot1{,}15\cdot1{,}03/435\space000=2{,}53\cdot10^{-3}\text{ m}^2\space(\eta=1{,}03)
\end{gathered}Minimální počet trnů z konstrukční podmínky (z maximální vzdálenosti smykových trnů v obvodu do vzdálenosti d od líce sloupu – viz výše).
\begin{gathered}
(1{,}6+2\pi d)/(1{,}75d)=3{,}045/0{,}403=7{,}6
\end{gathered}Minimální počet trnů po obvodu je 8 a radiálně 2 – celkem 16 trnů.
25,3 ∙ 10-4/16 = 1,58 ∙ 10-4 – minimální průměr trnů 16 mm As1 = 2,01 ∙ 10-4m2
Navrženo uspořádání trnů o průměru 16 mm v osmi radiálních paprscích. Celkem 16 smykových trnů. Alternativně je možné navrhnout 9 paprsků s trny o průměru 14 mm, nebo 12 paprsků s trny o průměru 12 mm a 16 paprsků s trny o průměru 10 mm.
Posouzení
\begin{gathered}
V_\text{Rd,sy}=8\cdot2\cdot2{,}01\cdot10^{-4}\cdot435\space000/1{,}03=1\space358{,}2\text{ kN}\ge930\cdot1{,}15=1\space069{,}5\text{ kN}
\end{gathered}Návrh smykových trnů v oblasti „D“ podle ETA [45]:
Délka smykově vyztužené oblasti ls ze vztahu:
\begin{gathered}
u_\text{out}=2(a+b)+2\pi\cdot(l_\text{s}+1{,}5d)\\\\
V_\text{Ed,out}=\beta_\text{Red}\cdot V_\text{Ed}/(u_\text{out}\cdot d)=1{,}1\cdot930/(u_\text{out}\cdot0{,}23)\le707\text{ kPa}
\end{gathered}uout = 6,58m, minimální ls = (6,58 – 1,6)/(2π) – 1,5d = 0,448, to představuje nejméně 4 trny.
Skutečná délka smykově vyztužené oblasti ls je tedy.
\begin{gathered}
(0{,}35+(4-1)\cdot0{,}75)\cdot d=0{,}598\text{ m}
\end{gathered}Poslední kontrolovaný obvod
\begin{gathered}
u_\text{out}=1{,}6+(0{,}598+1{,}5\cdot d)\cdot2\cdot\pi=7{,}53\text{ m}
\end{gathered}Posouzení
\begin{gathered}
V_\text{Ed,out}=\beta_\text{Red}\cdot V_\text{Ed}/(u_\text{out}\cdot d)=1{,}1\cdot930/(7{,}53\cdot0{,}23)=590{,}7\le707\text{ kPa}
\end{gathered}Vyhovuje
Ověření konstrukčních zásad v oblasti „D“: obvod s posledním trnem 5,36 m, počet trnů 8, vzdálenost mezi trny 0,669 m, maximální vzdálenost je 3,5d = 0,805 m, vyhovuje.
Při splnění konstrukčních zásad ETA není nutné posuzovat další kontrolované obvody.
Celkový počet smykových trnů:
\begin{gathered}
4\cdot8=32\text{ trnů }\phi16\text{ výšky }\space225\text{ mm}
\end{gathered}Poslední kontrolovaný obvod je od osy sloupu 0,943 m, minimální délka horní výztuže je 2,29 m + 2 ∙ ldb.
Při použití trnů o průměru 12 mm by bylo celkem 24 trnů v oblasti „C“ a při použití trnů o průměru 10 mm by bylo celkem 34. Takto velké počty trnů v oblasti „C“ nejsou vhodné z hlediska provádění. Celkový počet trnů v oblasti namáhané protlačením je uveden v tab. 1.
Standardní návrh smykové výztuže podle normy ČSN EN 1992-1-1 [1]
Návrh smykových trnů v prvním kontrolovaném obvodu:
Maximální únosnost (pokud nesprávně budeme uvažovat zvýšenou únosnost prvního kontrolovaného průřezu jako u ETA [45]):
\begin{gathered}
V_\text{Rd,max}=1{,}96\cdot V_\text{Rd,c}=1{,}96\cdot0{,}707=1{,}385\text{ MPa}\space\space\text{vyhovuje, smyková výzruž je nutná}
\end{gathered}Podle konstrukčních zásad je maximální vzdálenost mezi smykovými prvky 1,5d v oblasti prvního kontrolovaného obvodu. Druhý smykový prvek je 1,25d od líce sloupu, jejich obvod je 3,41m. Minimální počet smykových prvků je n = 3,41/(1,5d) = 10.
Účinná návrhová pevnost smykové výztuže:
\begin{gathered}
f_\text{ywd,eff}=250+0{,}25\cdot230=307{,}5\text{ MPa}\\\\
V_\text{Rd,cs}=0{,}75\cdot0{,}707+2\cdot A_\text{sw}307{,}5\cdot(1/(4{,}49\cdot0{,}23))
\end{gathered}Staticky nutná plocha smykové výztuže v jednom obvodu kolem sloupu:
\begin{gathered}
A_\text{sw}=(1{,}0695-0{,}75\cdot0{,}707)\cdot1{,}033/(2\cdot307{,}5)=9{,}06\cdot10^{-4}\text{ m}^2
\end{gathered}Při deseti paprscích postačuje profil 12 mm, celková plocha smykové výztuže v jednom obvodu je Asw = 1 131 mm2.
Únosnost v prvním kontrolovaném obvodu je:
\begin{gathered}
V_\text{Rd,cs}=0{,}75\cdot0{,}707+2\cdot11{,}31\cdot10^{-4}\cdot307{,}5\cdot(1/(4{,}49\cdot0{,}23))=1{,}204\text{ MPa}\ge V_\text{Ed1}=1{,}04\text{ MPa}
\end{gathered}Únosnost vyhovuje.
Délka posledního kontrolovaného obvodu bez smykové výztuže je stejná u obou postupů.
Délka smykově vyztužené oblasti je 0,522 m (viz předchozí výpočet).
První trn umístíme 0,3d až 0,5d od líce styčné plochy ve vzdálenosti 0,10 m.
Další trny po vzdálenostech 0,75d = 0,173 m.
Skutečná délka smykově vyztužené oblasti je
Uspořádáme trny následovně: 0,1 + 3 ∙ 0,173 = 0,619 m, vyhovují 4 trny v paprsku.
Posouzení posledního kontrolovaného obvodu
\begin{gathered}
u_\text{out}=1{,}6+2\cdot(0{,}619+0{,}345)\cdot\pi=7{,}66\text{ m}\\\\
V_\text{Ed,out}=\beta\cdot V_\text{Ed}/(u_\text{out}\cdot d)=1{,}15\cdot1\space000/(7{,}66\cdot,0{,}23)=652{,}7\text{kPa}\le707\text{ kPa}
\end{gathered}Konstrukčně počet trnů v posledním vyztuženém obvodu 5,49/(2d) = 11,9→12
Musíme změnit počet radiálních paprsků výztuže na 12 a můžeme i zmenšit průměr
smykového trnu na 10 mm (Asw = 942 mm2 ≥ 906 mm2).
Minimální množství smykové výztuže v prvním obvodu 12 ∙ 2 ∙ ø10 = 0,001884 m2.
\begin{gathered}
\sum A_\text{sw}\ge0{,}08\sqrt{f_\text{ck}}/f_\text{yk}=8\cdot10^{-4}\text{ m}^2
\end{gathered}Celkový počet smykových trnů:
\begin{gathered}
4\cdot12=48\space\text{trnů}\space\phi10\space\text{výšky}\space\space225\text{ mm}
\end{gathered}10.7.6 Závěry srovnání
Podle EC2 [1] je celkově jinak umístěná výztuž menšího průměru v dokonce menším počtu. Z toho vyplývá, že není dosažena stejná úroveň spolehlivosti jako u ETA [45], proto není možné zvyšovat maximální únosnost v prvním kontrolovaném obvodu podle ETA [45] oproti normou definované hodnotě (jak bylo uvažováno v příkladu). Příklad nelze zobecňovat, v daném příkladu jsou výsledky na nebezpečné straně. V metodice ETA [45] jsou navíc upřesněny případy silných deskových konstrukcí, základových konstrukcí a doporučena redukce únosnosti v prvním kontrolovaném obvodu bez smykové výztuže. Zvýšení únosnosti smykově vyztuženého průřezu je umožněno především tím, že zakotvení smykových trnů s rozkovanou hlavou (na trojnásobný průměr oproti dříku) je výrazně lepší než u běžné smykové výztuže. Uvedené však musí být doplněno konstrukčními a návrhovými pravidly definovanými v ETA [45]. Především návrhovým předpokladem, že v prvním kontrolovaném obvodu je veškeré zatížení přenášeno pouze smykovou výztuží bez započítání části přenášené betonem.
Tab. 10.5 Celkový počet smykových trnů
| Umístění | ø10 | ø12 | ø14 | ø16 | |
| ETA | První kontrolovaný obvod | 32 | 24 | 18 | 16 |
| Zbylé obvody | 32 | 24 | 18 | 16 | |
| celkem | 64 | 48 | 36 | 32 | |
| ČSN EN 1992-1-1 | První kontrolovaný obvod | 24 | – | – | – |
| Zbylé obvody | 24 | – | – | – | |
| celkem | 48 | *) | *) | *) | |
| *) Rozhodují konstrukční zásady, počet trnů by byl stejný | |||||
11 METODA NÁHRADNÍ PŘÍHRADOVINY V ZÁKLADOVÝCH KONSTRUKCÍCH
Základové konstrukce se navrhují především z geotechnického hlediska v souladu s ČSN EN 1997-1 [47]. Následně je nutné ověřit základové konstrukce z hlediska únosnosti použitého materiálu, ze kterého budou realizovány. Norma ČSN EN 1992-1-1 [1] uvádí základní informace, týkající se doporučených postupů pro návrh některých typů betonových základů, včetně interakce nadzákladové konstrukce, základu a podloží. Interakce základové půdy, základu a nadzákladové konstrukce je blíže popsána v [48]. Pro účely návrhu lze obvykle uvažovat čtyři úrovně výpočtu:
- úroveň 0 – předpokládá se lineární rozdělení kontaktního napětí v základové spáře; případné rozdílné sedání je nevýznamné (masivní a dostatečně tuhé základové konstrukce);
- úroveň 1 – kontaktní napětí v základové spáře se stanoví s přihlédnutím k poměrné tuhosti základu a podloží; životnost konstrukce nesmí být ovlivněna deformací podloží; konstrukční systém musí být dostatečně duktilní;
- úroveň 2 – nutno uvažovat vliv deformace základu na nadzákladové konstrukce; z deformací základu vyplývá přerozdělení sil v nadzákladové konstrukci; pokud je přerozdělení sil velké (nad 10 %), nutno postupovat iteračně – úroveň 3;
- úroveň 3 – iteračním postupem stanovit skutečné chování systému nadzákladové konstrukce, základ a podloží.
Kapitola se zabývá základovými konstrukcemi z hlediska únosnosti použitého materiálu – betonu, železobetonu. Základové konstrukce bývají masivní železobetonové konstrukce, u kterých často nebývá splněna Bernoulliova podmínka zachování rovinnosti průřezu po přetvoření. Základové konstrukce lze řešit metodami náhradní příhradoviny. Nejběžnějšími základovými konstrukcemi jsou základové blokové patky, patky s prohlubněmi (kalichové patky) a základové pasy. Modely náhradní příhradoviny lze použít i pro návrh hlavic pilot (někdy uváděních jako převázky pilot).
11.1 ZÁKLADOVÉ PASY
Základové pasy se navrhují především pod nosnými stěnami [48]. Pokud je méně únosné podloží a základové patky vycházejí příliš velké, nebo pokud je nutné posílit prostorovou tuhost systému, např. v poddolovaném území nebo v seismické oblasti, navrhují se i pod nosnými sloupy. Namáhání základových pasů závisí na tuhosti nezákladových konstrukcí. Pokud jsou nadzákladové konstrukce tuhé a jsou spojité (vysoké nosné stěny), jsou základové pasy namáhány především v příčném směru. Pokud jsou nadzákaldové konstrukce poddajné nebo nespojité, jsou základové pasy namáhány i v podélném směru.
Základový pás z prostého nebo slabě vyztuženého betonu může být navržen pouze pod průběžnou nosnou stěnou (i cihelnou), která není namáhána ohybem v podélném směru. Zároveň musí být nevyztužený základový pas dostatečně vysoký, aby veškerá tahová namáhání přenesl beton. V ostatních případech navrhujeme železobetonové základové pásy.
Obr. 11.1 Základový pas z nevyztuženého betonu
Obr. 11.2 Základový pas z nevyztuženého betonu – rozměry
Pokud jsou základové pasy nevyztužené v příčném směru, veškeré tahy při spodním líci musí přenést beton. Pro návrh nevyztužených základů lze s výhodou použít náhradní příhradovinu s tím, že na rozdíl od jiných poruchových oblastí je táhlo betonové. Model je na obr. 11.1 a obr. 11.2. Aby nebyla překročena návrhová mez pevnosti betonu v tahu při spodním líci, je nutné, aby byl základový pas dostatečně vysoký. Pro výšku nevyztuženého základového pasu platí vztah podle [1]:
\begin{gathered}
h_\text{f}\ge1{,}176a\cdot\sqrt{(3\cdot\sigma_\text{gd}/f_\text{ctd,pl}})
\end{gathered}(11.1)
kde je
a … vzdálenost mezi lícem stěny a okrajem pasu – vyložení od líce sloupu;
σgd … návrhová hodnota v tlaku v základové spáře;
fctd,pl … návrhová hodnota pevnosti betonu v tahu podle [1];
\begin{gathered}
f_\text{ctd,pl}=\alpha_\text{ct,pl}\cdot f_\text{ctk{,}0{,}05}/\gamma c
\end{gathered}αct,pl … součinitel pevnosti betonu v tahu podle čl. 12.3.1 [1].
Ze vztahu (11.1) je zřejmé, že pro méně únosná podloží, může být rozšíření základů menší (obr. 11.2). Pro zjednodušení lze použít vztah z [1]:
\begin{gathered}
h_\text{f}\ge2a
\end{gathered}(11.2)
Vztah (11.2) je konzervativní a odpovídá úhlu roznášení θ = 63°. Výpočtem podle (11.1) se dostanou příznivější hodnoty. Velký vliv ve vztahu (11.1) má způsob realizace základových konstrukcí. Pokud výrobce nezaručí pevnost betonu v tahu průkazními zkouškami a nejsou při návrhu výstižně stanoveny účinky nepřímých zatížení od objemových změn betonové konstrukce, platí pro součinitel αct,pl = 0,60. Tato situace je velmi častá u běžných menších staveb. Pokud je pevnost betonu v tahu zaručena průkazními zkouškami, lze uvažovat αct,pl = 0,80.
Podle vztahu (11.1) je rozhodující ohybový moment MEd pro návrh nevyztuženého pasu nebo patky ve vzdálenosti 0,176 a od vnitřního líce stěny nebo sloupu [45]. Posun odpovídá poloze styčníku 1 jako na obrácené konzole [27]. Šířku styčníku můžeme stanovit přesně analogicky ke konzole ze svislého zatížení NEd/2 a únosnosti ve styčníku CCC (σ Rd,max = v‘fcd). Přesnější výpočet se uplatní u příčně vyztuženého základového pasu. Při dodržení vtahu (11.1) není nutné posuzovat únosnost betonu v tahu při spodním líci základového pasu. Posouzení na vznikající tahy musíme provést, pokud je základ na velmi únosném – skalním položí (pro všechna podloží, s únosnosti σgd = ≥ 5 MPa). Podle [1] při založení na skalním podloží vznikají v pasu příčné tahy T, na které je nutno navrhnout výztuž (obr. 11.3):
\begin{gathered}
T=0{,}25(1-c/H)N_\text{Ed}
\end{gathered}(11.3)
kde je
H … menší z hodnot b (šířka pasu při spodním líci) a hf (výška pasu).
Obr. 11.3 Základové patky a pasy na skalním podloží
Tahy podle vztahu (11.3) odpovídají příčným tahům v betonových vzpěrách [24].
Pro velké základové pasy je možné základ po výšce odstupňovat [45] (obr. 11.4). Kdysi navrhované zešikmení horního líce základových pasů není vhodné, protože v místě největšího namáhání základu může být beton nedostatečně zhutněn. V místě uložení stěny je nutné překontrolovat napětí ve styčné spáře (blíže – viz patky).
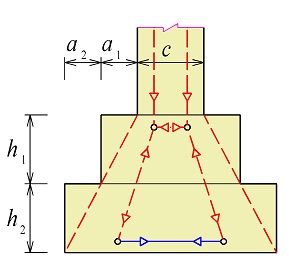
Obr. 11.4 Vícestupňový základový pas z nevyztuženého betonu
Vyztužené základové pasy v příčném směru lze posuzovat jako obrácené konzoly nebo jako konzolové nosníky (v závisti na štíhlosti, navrhování konzol viz [27]). Výhodné je vytvořit model náhradní příhradoviny (obr. 11.5 a obr. 11.6). Geometrie modelu je dána umístěním výztuže (a způsobem namáhání). I kotvení tahové výztuže závisí na způsobu namáhání. Podle obr. 11.6a při namáhání převážně ohybovým momentem, je nutné kotvit tahovou výztuž sloupu až při spodním líci. Pokud je namáhání ohybovým momentem malé, lze uvažovat počátek kotvení výztuže sloupu podle obr. 11.6b. Tahovou sílu při spodním líci patky je nutné dostatečně zakotvit v krajním styčníku, a proto se zakončuje výztuž hákem nebo se vytahuje až do tlačené části průřezu. Základový pas lze vyztužit i rovnými výztužnými sítěmi (bez koncových háků), pokud je zakotvení přivařenými pruty sítě dostatečné. U základových konstrukcí je napětí v podloží tedy zatížení překonzolované části základu velmi velké ve srovnání s běžnými konzolami [27]. To může vyvolat prudké změny v napětí ve výztuži táhla, které mohou vést až k porušení soudržnosti mezi výztuží a betonem a k odštěpování betonu. Proto se doporučuje nepoužívat pruty velkých průměrů a zvětšit betonového krytí (pro betonáž na zemině musí být betonové krytí nejméně 75 mm a při betonáži na podkladní beton nejméně 40 mm [1]).
Obr. 11.5 Excentricky zatížený základový pas
Obr. 11.6 Excentricky zatížení základový pas – principy vyztužení
Pro základový pas pod průběžnou nosnou stěnou je rozhodující příčné vyztužení při spodním líci (obr. 11.6). Při rovnoměrném podloží v podélném směru postačuje obvykle slabé vyztužení obvykle 20 % příčné výztuže (asy = 0,2 asx). Pokud je nerovnoměrné podloží nebo je objekt v poddolovaném území je nutné doplnit i nosnou podélnou výztuž při spodním líci případně i při horním líci. Její posouzení záleží kromě geotechnických podmínek i na tom, zda základ a stěna spolupůsobí (stěnový efekt) nebo zda vyzděná stěna dostatečně roznáší zatížení v podélném směru [48].
Výztuž při horním líci je nutno také doplnit, pokud základový pas není po celé délce spojitě (se stejnou intenzitou zatížení) zatížen stěnou, stěna je například prolomena většími prostupy. Potom základový pas tvoří nosník zatížený reakcí podloží a je nutná výztuž i při horním líci základového pasu. Podélná výztuž základového pasu je rozhodující, pokud je základový pas navržen pod sloupy (lokálně zatížený nosník na pružném podloží, záleží na tuhosti nadzákladových konstrukcí [48]).
Pokud je zatížení základového pasu excentrické, například z důvodu zemního tlaku nebo jednostranného přitížení zeminou, potom tvoří stěna se základem rámový roh (viz kap. 7), který musí být odpovídajícím způsobem vyztužen (viz obr. 11.5 a obr. 11.7). Excentrické základy jsou například na hraně pozemku nebo u dilatací (obr. 11.8). Optimálním řešením je posílení krouceného základového pasu podle možností v malých vzdálenostech ztužujícím příčnými stěnami nebo pilíři (viz obr. 11.8b). Základový pas musí být potom vyztužen na kroucení nebo na přenos excentrické síly. Jednostranně vyložený základový pas lze posílit i příčnými základovými ztužidly [45] (obr. 11.8c).
Obr. 11.7 Přenos ohybového momentu ze sloupu do patky – rámový roh
Obr. 11.8 Excentricky zatížený základový pas a základové ztužidlo
11.2 ZÁKLADOVÉ PATKY
Základové patky se obvykle navrhují pod sloupy. Většinou bývají vyztužené při spodním líci, mohu být však i nevyztužené nebo vyztužené při obou površích podle způsobu namáhání.
Při centricky zatížených základových patkách na rovnoměrném podloží může dojít následujícím porušením:
- ohybové porušení způsobené dosažením pevnosti kluzu ve výztuži nebo tahu v betonu u nevyztužených nebo slabě vyztužených patek;
- porušení patky protlačením;
- porušení soudržnosti mezi výztuží a betonem v kotevních oblastech;
- porušení betonu v tlaku (podrcení) pod uložením sloupu.
Přenos zatížení ze sloupu do podloží v základové patce lze modelovat betonovými vzpěrami a táhly. U blokových patek (platí b ≤ ci + 2di obr., 11.9) se předpokládá tuhý základ oproti poddajnému podlaží s koncentrací napětí podloží v krajních částech patky. Proto se uvažuje roznášení zatížení ze sloupu především do rohových oblastí základu. U větších patek (poddajnější konstrukce – deskové patky – b ≥ ci + 2di) je roznášení po spodním líci patky rovnoměrnější nebo naopak koncentrované ve střední části patky. Roznesení zatížení vyvolá pod uložením sloupu vodorovné tlakové síly (obvykle v obou směrech) a při spodním líci základu vodorovné tahové síly. Je nutné zkontrolovat koncentraci tlaků v betonu pod styčnou spárou mezi sloupem od zatížení sloupem a od prostorového ohybu patky. To často vede k poruchám patek podrcením betonu pod styčnou spárou. Velmi často bývají také sloupy navrženy z výrazně lepší třídy betonu než základové patky, což není vhodné řešení.
Při excentricky zatíženém základu obdobně jako u rámových konstrukcí se tahová síla ze sloupu stáčí při spodním líci základu a vzniká tak rámový roh s negativním působením ohybového momentu (viz kap. 7) (viz obr. 11.7).
Obr. 11.9 Bloková základová patka
11.2.1 Nevyztužené základové patky
Také základové patky pod sloupy mohou být nevyztužené, pokud jsou dostatečně vysoké. Patkový základ z prostého betonu se chová jako tlustá deska, u které převládá stěnové, popř. prostorové namáhání a pro případný vznik trhlin, a tudíž i dosažení meze únosnosti je rozhodující hlavní napětí betonu v tahu. V mezním stavu únosnosti se přenáší tlaková síla NEd tlačenými pruty (vzpěrami) do spodní části základu. Únosnost vzpěr v podstatě závisí na vznikajících příčných tazích. Tahové napětí vzrůstá se zmenšujícím se sklonem betonové vzpěry. Pro zajištění dostatečné únosnosti musí být omezen sklon betonových vzpěr. Z výsledků experimentů byl odvozen vztah (11.1) pro minimální výšku základové patky obdobně jako u nevyztuženého základového pasu s tím, že je nutné posoudit patku v obou směrech. Pro velké základové patky je možné základ odstupňovat po výšce obdobně jako u základových pasů (obr. 11.4).
11.2.2 Vyztužené základové patky
U vyztužené základové patky (obr. 11.9 a obr. 11.10) tahovou sílu přenáší výztuž. Obdobně jako u základových pasů se může při návrhu tahové výztuže postupovat jako u obrácených konzol. Posouzení patky podle teorie desek není zcela v souladu s předpoklady zachování rovinnosti průřezu. Proto pro návrh a posouzení tahové výztuže patek se používají modely náhradní příhradoviny (viz [52]). Pro posouzení ohybu je rozhodující ohybový moment v líci sloupu, který lze vyjádřit:
\begin{gathered}
\text{max}M_\text{Ed}=N_\text{Ed}\frac{b_\text{i}}{8}(1-\frac{c_\text{i}}{b_\text{i}})^2
\end{gathered}(11.4)
kde je
NEd … normálová síla ve sloupu;
bi … šířka patky ve vyšetřovaném směru;
ci … šířka sloupu ve vyšetřovaném směru.
Obr. 11.10 Excentricky zatížená základová patka
Při namáhání základové patky normálovou silou NEd a ohybovým momentem MEd se může uvažovat buď lichoběžníkové rozdělení napětí v základové spáře (obr. 11.10 a obr. 11.11) nebo zjednodušeně rovnoměrné rozdělení (obr. 11.11) na části základové plochy (těžiště plochy musí být shodné s působištěm síly NEd). Tahovou sílu ve výztuži a kotvení lze stanovit z podmínek rovnováhy při současném uvážení účinků šikmých trhlin (obr. 11.11b, a, c):
\begin{gathered}
F_\text{s}=R_1\frac{z_1}{z_\text{i}}\space\text{a}\space F_\text{s}=R_2\frac{z_2}{z_\text{i}}
\end{gathered}(11.5)
kde jsou
R1, R2 … výslednice kontaktních tlakových napětí v základové spáře na délce (a+e);
z1, z2 … ramena vnějších sil R1 R2 a zi rameno vnitřních sil.
Obr. 11.11 Vyztužení základové patky
Ramena vnitřních sil mohou být stanovena za předpokladu e = 0,15c a z = 0,9d. Navržená výztuž musí splňovat podmínky minimálního vyztužení [1].
Obdobně se postupuje při stanovení tahové síly Fs, která musí být v místě x dostatečně zakotvena ve stejné vzdálenosti x od okraje základu (dostatečně zakotvena za šikmou trhlinou, obr. 11.11a):
\begin{gathered}
F_\text{s}=R\frac{z_\text{e}}{z_\text{i}}
\end{gathered}(11.6)
kde je
R … výslednice kontaktních tlakových napětí v základové spáře na délce x;
ze … rameno vnější síly R a zi je rameno vnitřních sil.
Pro zakotvení výztuže je k dispozici délka lb. Pokud tato délka není dostatečná, je nutné pruty ohnout nahoru, přivařit k příčné výztuži (pozor svařování pouze v souladu s ČSN EN ISO 17 660-1 a ČSN EN ISO 17 660-2), nebo opatřit mechanickou kotvou. Pro rovné pruty je obvykle nejkritičtější délka xmin = h/2. Pro jiné druhy kotvení mohou být kritické větší hodnoty x. U blokových patek (platí b ≤ ci + 2di, obr. 11.9) nejsou dostatečné koncové háky u dolní tahové výztuže pro zakotvení, protože celou svojí výškou leží v oblasti trhlin. Tahovou výztuž je nutné zakotvit až v tlačené oblasti patky. Při použití větších průměrů výztuže může dokonce docházet k odštěpování betonu.
Při návrhu tahové výztuže je nutné uvažovat posun tahové síly v souladu s ČSN EN 1992-1-1 [1] hodnotou ai ≈ d (obr. 11.12). Pro blokové základové patky (platí b ≤ ci + 2di) lze tahovou výztuž umístit rovnoměrně po celé ploše základu. Tahovou výztuž je však nutné zakotvit až v tlačené oblasti průřezu nebo ji zakotvit prostřednictvím přivařených příčných prutů nebo mechanických spojek. U větších patek (pro které platí b > ci + 2di ), je nutné tahovou výztuž koncentrovat ve střední části patky podle procentuálního vyjádření na obr. 11.12 podle [2].
Obr. 11.12 Principy vyztužení základové patky – podrobný návrh výztuže
Obr. 11.13 Principy vyztužení základové patky – zjednodušený návrh výztuže
Jednodušší rozdělení výztuže lze provést podle následujících principů (obr. 11.13):
- hlavní výztuž rovnoběžná s delší stranou se rozdělí rovnoměrně po šířce kratší strany;
- výztuž rovnoběžná s kratší stranou se rozdělí tak, aby ve vnitřním pásu šířky lA byla umístěna výztuž o průřezové ploše AsA:
\begin{gathered}
A_\text{sA}=\frac{2l_\text{A}}{b_\text{i}+l_\text{A}}A_\text{si}
\end{gathered}(11.7)
kde je
Asi … průřezová plocha výztuže stanovená pro směr rovnoběžný s kratší stranou půdorysu;
lA … šířka pásma se zesílenou výztuží lA = min (bj; ci + 2h);
bi … delší strana půdorysu patky;
bj … kratší strana půdorysu patky;
ci … šířka sloupu ve směru rovnoběžném s delší stranou patky;
h … celková výška patky.
- tahovou výztuž se doporučuje dovést až k okraji patky a tam zakotvit minimálně s koncovou úpravou pravoúhlý hák.
11.2.3 Excentricita zatížení
Při excentrickém zatížení vzniká kromě normálové síly i ohybový moment. Se zvyšující se excentricitou výrazně klesá únosnost patky v mezním stavu protlačení (viz obr. 11.14). Pro návrh základu namáhaného osovým tlakem a ohybovým momentem, lze výztuž navrhnout odděleně pro působení osového tlaku a ohybového momentu. Část výztuže přenášející ohybový moment je obvykle uvažuje na náhradním nosníku podle obr. 11.7. Šířka náhradního nosníku se uvažuje b1 = ci + di. Výztuž se potom umístí do střední části uvedeného nosníku v šířce cca 0,5b1. Náhradní nosník tvoří se sloupem rámový roh s negativním působením ohybového moment (viz kap. 7). Pro zmenšení excentricity zatížení lze navrhnout ztužující nosníky [52].
Obr. 11.14 Vliv excentrického zatížení patky na její únosnost
11.3 PROTLAČENÍ ZÁKLADOVÝCH KONSTRUKCÍ
Šikmé smykové trhliny vznikají podstatně dříve, než je dosaženo poruchového zatížení (obr. 11.15). První smykové trhliny lze očekávat kolem 50 % poruchového zatížení základové patky bez smykové výztuže. Při navržení smykové výztuže lze zvýšit poruchové zatížení. Optimální je navrhnout ohyby pod 45°, protože křižují trhlinu pod úhlem cca 90° a jsou tak nejúčinnější. Pro dosažení dostatečného zakotvení je vhodné používat pruty menších průřezů. Použití třmínků je omezeno na jejich přesné umístění. Část třmínku před a za poruchovou trhlinou musí zůstat dostatečně zakotvena. Ze zkušeností (viz [52]) lze uvažovat se zvýšením únosnosti smykově vyztužené patky v mezním stavu protlačení o cca 25 % oproti nevyztužené patce. Z výsledků experimentů nebývá mezní stav protlačení rozhodující pro návrh vhodně navržené základové patky.
Obr. 11.15 Posouzení protlačení základové patky – iterační postup stanovení rozhodujícího kontrolovaného obvodu
Při excentrickém zatížení s rostoucí excentricitou poměrně velmi rychle klesá únosnost v mezním stavu protlačení – viz obr. 11.14. Podle ČSN EN 1992-1-1 [1] lze zjednodušeně posoudit patku na zvýšené zatížení součinitelem jako u krajových sloupů desek. Velké snížení únosnosti v mezním stavu protlačení lze vysvětlit pomocí obr. 11.16. Správné stanovení součinitele β (součinitel zvětšující zatížení, které odpovídá vlivu excentricity u pravidelných deskových konstrukcí namáhaných na protlačení) je velmi obtížné. Vliv excentrického zatížení lze vyjádřit pomocí postupu uvedeného v normě [1] nebo v kap. 10 této publikace nebo pomocí sektorového modelu (obr. 11.16). Pro posouzení mezního stavu protlačení pomocí sektorového modelu uvažujeme pouze nejvíce zatíženou část patky ohraničené spojnicemi středu patky a rohů viz obr. 11.16. Zatížení se uvažuje pouze z vyšrafované plochy a kontrolní obvod je rovněž omezen výše uvedenými spojnicemi. Posouzení se tak provede pouze v nejvíce namáhané části a stejná smyková výztuž se konstrukčně umístí po celém kontrolovaném obvodu.
Obr. 11.16 Posouzení protlačení základové patky – sektorový model
\begin{gathered}
v_\text{Ed,i}=\frac{V_\text{Ed,X}}{u_\text{i,X}d}\le v_\text{Rd,c}
\end{gathered}(11.8)
kde je
VEd,X … síla odpovídající zatížení (reakce z podloží) z vyšrafované plochy na obr. 11.16;
ui,X … část kontrolovaného průřezu vymezená spojnicemi ze středu patky do jejích rohů podle obr. 11.16.
Na obr. 11.16 jsou také zobrazeny rozhodující ohybové momenty pro dimenzování dolní tahové výztuže excentrické zatížení základové patky.
11.3.1 Únosnost ve smyku při protlačení desek a základů sloupů bez smykové výztuže
Únosnost ve smyku při protlačení se posoudí v základním kontrolovaném průřezu. Návrhová únosnost se stanoví podle vztahu:
\begin{gathered}
v_\text{Rd,c}=\frac{0{,}18}{\gamma c}k\cdot(100\rho_\text{l}f_\text{ck})^{\frac{1}{3}}+k_1\sigma_\text{cp}\ge(v_\text{min}+k_1\sigma_\text{cp})
\end{gathered}(11.9)
kde je
fck … charakteristická pevnost betonu v MPa;
k … součinitel zohledňující tloušťku desky
\begin{gathered}
k=1+\sqrt{\frac{200}{d}}\le2{,}0,d\space\text{je v mm}
\end{gathered}(11.10)
\begin{gathered}
\rho_\text{l}=\sqrt{\rho_\text{ly}\cdot\rho_\text{lz}}\le0{,}02
\end{gathered}(11.11)
kde je
ρly∙ρlz … se vztahují k soudržné výztuži ve směrech y a z a dostatečně zakotvených za posuzovaným kontrolním průřezem, šířka desky se ve výpočtu uvažuje rovná tloušťce sloupu plus 3d po každé straně sloupu;
σcp … normálové napětí v betonu v kritickém průřezu σcp = (σcy, + σcz )/2;
σcy, σcz … jsou normálová napětí v kritickém průřezu ve směru os y a z.
\begin{gathered}
\sigma_\text{c,y}=\frac{N_\text{Ed,y}}{A_\text{cy}}\space\text{ a }\space \sigma_\text{c,z}=\frac{N_\text{Ed,z}}{A_\text{cz}}
\end{gathered}(11.12)
kde jsou
NEdy, NEdz … normálové síly v celé šířce pole desky pro střední sloupy a normálové síly působící v kontrolovaném průřezu pro okrajové sloupy; síla může být vyvolána zatížením nebo předpětím;
Acy a Acz … průřezové plochy betonu v kritickém řezu podle NEd.
\begin{gathered}
v_\text{min}=0{,}035\cdot k^{3/2}\cdot f_\text{ck}^{1/2}
\end{gathered}(11.13)
Únosnost ve smyku základů sloupů při protlačení se má ověřit na kontrolovaných obvodech ve vzdálenostech do 2d od líce sloupu – viz obr. 11.17. Při řešení je třeba nalézt kritický obvod na protlačení, u kterého se nejvíce přiblíží smykové napětí od návrhového zatížení vEd k ekvivalentní smykové pevnosti tohoto průřezu vRd. Iterační postup je zobrazen na obr. 11.18.
Obr. 11.17 Posouzení protlačení základové patky – zjednodušený postup
Obr. 11.18
Na zvoleném kontrolovaném obvodu ui se stanoví smykové napětí v protlačení vEdi ze vztahu:
\begin{gathered}
v_\text{Edi}=\frac{V_\text{Ed,red}}{u_\text{i}\cdot d}=\frac{V_\text{Ed}-\Delta V_\text{Edi}}{u_\text{i}\cdot d}=\frac{V_\text{Ed}\cdot\bigg(1-\frac{A_\text{i}}{A_\text{b}}\bigg)}{u_\text{i}\cdot d}
\end{gathered}(11.14)
kde je
Ai … plocha základu uvnitř kontrolovaného obvodu;
Ab … plocha celé základové patky;
VEd,red … redukované zatížení – zatížení přispívá zatížení uvnitř kontrolovaného obvodu k únosnosti a lze jej tedy odečíst podle následujícího vztahu:
\begin{gathered}
V_\text{Ed,red}=V_\text{Ed}-\Delta V_\text{Ed}
\end{gathered}(11.15)
VEd … působící posouvající síla;
ΔVEd … výslednice zatížení působících uvnitř kontrolovaného průřezu – tlak podloží.
Ekvivalentní smykovou pevnost betonu ve zvoleném kontrolovaném průřezu lze určit ze vztahu:
\begin{gathered}
v_\text{Rdi}=C_\text{Rd,c}k(100\rho_\text{l}f_\text{ck})^{1/3}(2d/a_\text{i})\ge v_\text{min}(2d/a_\text{i})
\end{gathered}(11.16)
kde hodnoty d a ρl se uvažují průměrnými hodnotami (vztah 11.11).
S přihlédnutím k tomu, že musí být ai < 2 d, lze vztah (11.13) upravit do tvaru:
\begin{gathered}
v_\text{Rd,i}=v_\text{Rd,c}(2d/a_\text{i})\ge v_\text{Rd,c}
\end{gathered}(11.17)
kde
\begin{gathered}
v_\text{Rd,c}=C_\text{Rd,c}k(100\rho_\text{l}f_\text{ck})^{1/3}\ge v_\text{min}
\end{gathered}(11.18)
Kritický průřez na protlačení bude ve vzdálenosti ai = acrit , při které bude rozdíl (vRdi – vEdi) minimální.
Pro excentrickou sílu platí:
\begin{gathered}
v_\text{Ed}=\frac{V_\text{Ed,red}}{ud}\bigg[1+k\frac{M_\text{Ed}u}{V_\text{Ed,red}W}\bigg]
\end{gathered}(11.19)
11.3.2 Únosnost ve smyku při protlačení desek a základů sloupů se smykovou výztuží
Pokud není splněn vztah vEdi ≤ vRdc, je nutná smyková výztuž. Nejprve ověříme, zda není překročena maximální únosnost ve smyku při protlačení na obvodu sloupu podle vztahu (11.20), kde vRd,max stanovíme ze vztahu:
\begin{gathered}
v_\text{Ed}=\frac{\beta V_\text{Ed}}{u_\text{o}\cdot d}\le v_\text{Rd,max}=0{,}4\cdot v\cdot f_\text{ck}
\end{gathered}(11.20)
kde je
uo … pro vnitřní sloup délka obvodu sloupu;
pro krajový sloup uo = c2 +3d ≤ c2 +2c1;
pro rohový sloup uo = 3d ≤ c1 +c2;
ν … v = 0,6 (1 – fck/250), kde fck je v MPa.
Únosnost se stanoví podle vztahu:
\begin{gathered}
v_\text{Rd,cs}=0{,}75\cdot v_\text{Rd,c}+1{,}5(d/s_\text{r})\cdot A_\text{sw}f_\text{ywd,ef}(1/(u_1d)\sin\alpha\le k_\text{max}\cdot v_\text{Rd,c}
\end{gathered}(11.21)
kde je
Asw … plocha smykové výztuže na jednom obvodu okolo sloupu v mm2;
sr … radiální vzdálenost obvodů smykové výztuže v mm;
fywd,ef … účinná návrhová pevnost smykové výztuže na protlačení podle vztahu:
\begin{gathered}
f_\text{ywd,eff}=250+0{,}25d\le f_\text{ywd}[\text{MPa}]
\end{gathered}(11.22)
d … průměrná účinná výška v ortogonálních směrech;
α … úhel, který svírá smyková výztuž s rovinou desky;
kmax … součinitel maximální únosnosti, jehož hodnota závisí na typu smykové výztuže a způsobu jejího zakotvení.
Pro smykovou výztuž spolehlivě zakotvenou v úrovni horní i dolní výztuže a svařované smykové mřížky dostatečně zakotvené v úrovni výztuže při obou lících základové konstrukce lze uvažovat součinitel kmax =1,50.
Pro smykové trny, lišty a smykovou příhradovou výztuž lze uvažovat vyšší hodnoty kmax, ale tato speciální smyková patentovaná smyková výztuž má být navrhována podle příslušných evropských technických doporučení (viz čl. 6.45.5(6) [1]). Vyšší hodnoty únosnosti vycházejí z řady ověřovacích zkoušek a jsou podmíněny řadou dalších podmínek odlišných od standardních podmínek uvedených v [1]. Použití třmínků podle článku 8.5 [1] je nevhodné z hlediska jejich nedostatečného zakotvení.
Pokud je smyková výztuž tvořena kozlíky v jedné řadě, pak poměr d/sr lze ve vztahu (11.21) nahradit hodnotou 0,67.
Kontrolovaný průřez uout, ve kterém se již smyková výztuž není staticky nutná se stanoví ze vztahu:
\begin{gathered}
u_\text{out}=\beta V_\text{Ed}l(v_\text{Rd,c}\cdot d)
\end{gathered}(11.23)
Nejvzdálenější obvod smykové výztuže lze umístit maximálně ve vzdálenosti 1,5d od kontrolovaného obvodu uout.
11.4 ZÁKLADOVÉ PATKY S PROHLUBNÍ (KALICHOVÉ PATKY)
Pro zakotvení prefabrikovaných sloupů se obvykle navrhují patky s prohlubní. Prohlubně mohou být přímou součástí základového bloku (bloková patka s prohlubní – viz obr. 11.19), nebo mohou být částečně popřípadě úplně vybetonovány nad patkou (obr. 11.20 a obr. 11.21). Návrh vlastní patky lze obvykle provést podle výše uvedených zásad. Posouzení a návrh stěn prohlubně se provádí podle toho, zda je nebo není zajištěno dostatečné spolupůsobení sloupu se stěnami prohlubně. Pro dostatečné zakotvení sloupu do patky s prohlubní je nutná také dostatečné tloušťka stěn prohlubně (pokud jsou nad vlastní patkou). Tloušťka stěn je dostatečná, pokud platí podmínka:
\begin{gathered}
d_\text{k}\ge(c_\text{x}+c_\text{y}+4a_\text{k})/6\space\text{ nebo }\space d_\text{k}\ge0{,}5_\text{max}(c_\text{x}{;}c_\text{y})
\end{gathered}(11.24)
Obr. 11.19 Excentricky zatížená patka s prohlubní model náhradní příhradoviny
Obr. 11.20 Excentricky zatížená patka s prohlubní, prohlubeň i sloup s dostatečně zdrsněnými povrchy model náhradní příhradoviny
Obr. 11.21 Excentricky zatížená patka s prohlubní, prohlubeň i sloup s nedostatečně zdrsněnými povrchy model náhradní příhradoviny
U kónických stěn prohlubně s malým zešikmením (do 10 %) lze uvažovat jako rozhodující rozměry stěn prohlubně hodnoty v poloviční výšce prohlubně.
Spolupůsobení stěn prohlubně se sloupem je dostatečné, pokud jsou splněny všechny následující podmínky:
- hloubka prohlubně je dostatečná I ≥ 1,5max(cx;cy), přitom minimální hloubka prohlubně je 500 mm a pokud je excentricita zatížení větší než 2,5 (e/c > 2,5), je nutné hloubku prohlubně zvětšit v poměru e/(2,5c) (cx, resp. cy, podle vyšetřovaného směru);
- dostatečné zazubení vnitřního líce stěn prohlubně a líce sloupu, hloubka zazubení je nejméně 15 mm a šířka ozubů (vzdálenost mezi ozuby) je menší než čtyřnásobek jejich hloubky, minimálně však 15 mm;
- šířka spáry ak mezi sloupem a vnitřním lícem stěn prohlubně je větší než 50 – 70 mm;
- pevnost zálivkového betonu je nejméně C20/25, pro silně vyztužené sloupy (ρc ≥ 4% ) pak nejméně C30/37.
Pokud nejsou splněny výše uvedené podmínky, je nutno přenos sil posoudit podle ČSN EN 1992-1-1 [1] jako patku s prohlubní a s hladkými stěnami (obr. 11.21). Pokud jsou podmínky splněny, je možné posoudit patku s prohlubní jako monolitickou. Modely náhradní příhradoviny jsou na obr. 11.19 a obr. 11.20 (pro splněné výše uvedené podmínky). Při mezním stavu protlačení je nutné provést posouzení v montážním stavu, kdy vzdoruje zatížení pouze dolní deska pod kalichem, a v konečném stavu, kdy vzdoruje celá patka (obr. 11.20).
Pokud není zajištěn dostatečný přenos sil spárou mezi sloupem a vnitřním lícem stěn prohlubně, je nutné postupovat podle obr. 11.21 (pro zjednodušení označíme tyto stěny za „hladké“). U hladkých stěn se síly ze sloupu do patky přenášejí třením. Při použití tohoto modelu musí být sloup zapuštěn do prohlubně nejméně I ≥ 1,2h. Součinitel tření nemá být větší než μ ≤ 0,3.
Při návrhu je nutné se zaměřit na tyto problémy:
- konstrukční uspořádání výztuže pro přenesení síly F1 v horní části stěn prohlubně;
- přenesení síly F1 podél bočních stěn do základu;
- kotvení hlavní tahové výztuže ve sloupu a ve stěnách prohlubně;
- únosnost v protlačení desky pod sloupem, kde může být uvažováno spolupůsobení dobetonovávky pod prefabrikovaným sloupem.
Nedostatečně zdrsnělé stěny prohlubně a sloupu jsou velmi nevhodné při velkých excentricitách. U blokových patek s prohlubní musí být kontaktní plochy vždy dostatečně zdrsněné.
Pro návrh a posouzení výztuže stěn prohlubně jsou rozhodující vnější síly působící při horním líci prohlubně (obr. 11.20 a obr. 11.21).
Vodorovné třmínky prohlubně (kalichu)
Pro návrh nebo posouzení vodorovných třmínků kalichu můžeme použít následujících vztahů (podle [52]):
- velká excentricita vnějších sil e/c ≥ 0,67
- pro hladké stěny kalichu:
\begin{gathered}
T_\text{H}=0{,}53(T_\text{c}+2H_\text{Ed}+|N_\text{Ed}|)
\end{gathered}(11.25)
- pro profilované stěny prohlubně:
\begin{gathered}
T_\text{H}=0{,}42(T_\text{c}+2H_\text{Ed}+|N_\text{Ed}|)
\end{gathered}(11.26)
- malá excentricita vnějších sil
- pro hladké stěny prohlubně e/c < 0,67:
\begin{gathered}
T_\text{H}=(0{,}276+0{,}883\frac{e}{c})\cdot|N_\text{Ed}|\ge0{,}3|N_\text{Ed}|
\end{gathered}(11.27)
- pro kónické stěny prohlubně je minimální síla:
\begin{gathered}
T_\text{H}\ge0{,}35|N_\text{Ed}|
\end{gathered}(11.28)
- pro profilované stěny prohlubně:
\begin{gathered}
T_\text{H}=(0{,}276+0{,}641\frac{e}{c})\cdot|N_\text{Ed}|\ge0{,}4|N_\text{Ed}|
\end{gathered}(11.29)
kde je
TH … vodorovná síla pro návrh vodorovných třmínků ve stěnách prohlubně;
e … excentricita vnějšího zatížení e = MEd/NEd;
c … šířka sloupu v posuzovaném směru;
Tc … tahová síla ve výztuži sloupu;
HEd … vodorovná síla sloupu v úrovni horního líce prohlubně;
NEd … osová síla sloupu.
Posouzení se provede odděleně pro oba směry x a y. Rozhodující pro návrh a posouzení výztuže jsou maximální hodnoty z obou směrů. V každém případě je nutné dodržet minimální množství výztuže v hodnotě 0,3 %.
Vodorovné třmínky prohlubně se rovnoměrně rozdělí po výšce s tím, že při horním líci se doplní třmínek v poloviční vzdálenosti.
Svislé třmínky prohlubně (kalichu)
Při posouzení svislých třmínků vycházíme z průřezových charakteristik stěn prohlubně jako uzavřeného profilu s otvorem. Rozhodující jsou rozměry v dolním líci prohlubně. Síla Tv pro návrh svislých třmínků se stanovuje pro jednu čtvrtinu obvodu prohlubně. Výztuž se navrhne konstrukčně podle nejnepříznivější kombinace symetricky i v ostatních čtvrtinách obvodu.
- U prohlubní zapuštěných do základových bloků (obr. 11.19) se svislé třmínky navrhují na sílu:
\begin{gathered}
T_\text{V}=T_\text{c}\cdot\frac{a}{a+z}
\end{gathered}(11.30)
- U prohlubní vystupujících nad blok základový (částečně nebo zcela) se svislé třmínky posuzují na svislou sílu zvětšenou o vliv vodorovného zatížení při horním líci prohlubně:
\begin{gathered}
T_\text{V}=T_\text{c}\cdot\frac{a}{a+z}+H_\text{Ed}\cdot\frac{a_\text{w}}{a_\text{t}}
\end{gathered}(11.31)
kde kromě výše uvedených proměnných jsou
TV … svislá síla pro návrh svislých třmínků ve stěnách prohlubně;
aw … vzdálenost podle obr. 11.20 mezi výztuží a osou protilehlé stěny prohlubně;
at … vzdálenost podle obr. 11.20 mezi vodorovnou výztuží a dolním lícem prohlubně.
Příklad vyztužení kalichové patky se zdrsněnýmí líci stěn prohlubně a sloupu je na obr. 11.22.
Obr. 11.22 Excentricky zatížená patka s prohlubní, prohlubeň i sloup s dostatečně zdrsněnými povrchy princip vyztužení
Mezní stav protlačení
Podle přenosu zatížení mezi stěnami prohlubně a sloupem se odlišuje návrh na mezní stav protlačení. Pokud zdrsněná spára zajistí dostatečný přenos zatížení, lze při posouzení mezního stavu protlačení uvažovat celou patku jako monolitickou. Při mezním stavu protlačení je nutné provést posouzení v montážním stavu, kdy vzdoruje zatížení pouze dolní deska pod prohlubní, a v konečném stavu, kdy vzdoruje celá patka (obr. 11.20). Pokud nelze zajistit dostatečný přenos zatížení spárou mezi sloupem a stěnami prohlubně, je nutné uvažovat ve výpočtu pouze část desky pod kalichem (obr. 11.21).
Prohlubně v hlavicích pilot
V současné době se navrhují i prohlubně přímo v rozšířených hlavicích pilot. Pro návrh prohlubně platí výše uvedené vztahy. Svislá tahová síla působící ve výztuži sloupu se převádí do podélné výztuže pilot. Problém je obvykle s umístěním podélné výztuže pilot (v kruhu) oproti ortogonální výztuži prohlubně. Obvykle je nutné vkládat další výztuž, která zprostředkuje přenos tahových sil. Velmi pečlivě je nutné zajistit dostatečné zakotvení tahové výztuže ve styčnících. Celá oblast přenosu tahové síly musí být ovinuta třmínky.
11.5 HLAVICE PILOT
Pro přenos zatížení ze sloupu nebo pilíře do skupiny pilot se navrhují hlavice pilot. Jedná se většinou o silné desky, které obvykle nezachovávají rovinnost průřezu po deformaci. Jedná se o D-oblasti. Hlavice musí být dostatečně silná, aby betonové vzpěry, které přenášejí zatížení ze sloupu do pilot, byly skloněny více jak 45° od vodorovné roviny (obr. 11.23 až obr. 11.24). Mezi betonovými vzpěrami pak vznikají vodorovná táhla, která je nutné pečlivě zakotvit v oblasti nad pilotou.
- návrh pomocí náhradní příhradoviny
Patky uložené na pilotách navrhujeme pomocí náhradní příhradoviny např. podle [18]. Zatížení ze sloupu je vynášeno plochou klenbou do jednotlivých pilot. Při uložení sloupu půdorysně mezi pilotami, je nutno navíc k dolní tahové výztuž navrhnout smykovou výztuž na vynášení zatížení, aby nedošlo k rozvoji trhlin jako u nepřímého uložení. Při návrhu je nutné se soustředit na posouzení jednotlivých vzpěr a zakotvení výztuž táhel ve styčnících nad pilotami.
- návrh pomocí kritického řezu
Návrh patky podle starších předpisů vycházel z definování kritického průřezu. Kritický průřez se uvažoval ve vzdálenosti a2 od osy vnější piloty podle. V kritickém průřezu je nutné posoudit dostatečnou únosnost patky ve smyku a v ohybu – viz obr. 11.25.
Obr. 11.23 Hlavice dvou pilot – model náhradní příhradoviny a princip vyztužení
Obr. 11.24 Hlavice čtyř pilot pod koncem nosné stěny – model náhradní příhradoviny
Obr. 11.25 Kritický průřez pro smyk u patek uložených na pilotách
Obr. 11.26 Hlavice tří pilot – model náhradní příhradoviny a princip vyztužení
Obr. 11.27 Hlavice čtyř pilot – model náhradní příhradoviny a princip vyztužení – varianta A
Obr. 11.28 Hlavice čtyř pilot – model náhradní příhradoviny a princip vyztužení – varianta B
Obr. 11.29 Hlavice čtyř pilot pod stěnovým pilířem – model náhradní příhradoviny
V [52] se uvádí vhodná tloušťka hlavice pilot. Tab. 11.1 platí pro hlavice s maximálním počtem šesti pilot.
Tab. 11.1 Doporučená tloušťka hlavice pilot v mm
| Průměr piloty v mm | 300 | 350 | 400 | 450 | 500 | 550 | 600 | 750 |
| Tloušťka převázky | 700 | 800 | 900 | 1 000 | 1 100 | 1 200 | 1 400 | 1 800 |
Na obr. 11.23 je zobrazena hlavice dvojice pilot. Podle modelu náhradní příhradoviny je ve vzpěrách síla:
\begin{gathered}
C=0{,}5\text{ N}/\sin\theta
\end{gathered}(11.32)
a v táhle:
\begin{gathered}
T=C\cdot\cos\theta=0{,}5N\cot\theta
\end{gathered}(11.33)
kde je
θ … sklon tlačených betonových diagonál.
Táhla z betonářské výztuže jsou v kotevních oblastech silně stlačena tak, že často postačuje kotevní délka rovného prutu bez koncové úpravy – háků. Pokud je nutné větší množství výztuže, je lépe ji umístit ve více vrstvách, než ji ukládat půdorysně vedle piloty (mimo styčník). Při velkém vyztužení oblasti se navíc doporučuje doplnit obepínající třmínky v kotevní oblasti táhla. Zakotvení výztuže se uvažuje až od středu pilot. Minimální plocha ortogonální výztuže při spodním a horním líci je 0,0013bh v každém směru. Minimální průměr výztužných prutů je 12 mm a maximální rozteč prutů je 250 mm. Piloty musí být při Hlavice je nutné posoudit na únosnost ve smyku. Posuzovaný průřez prochází okrajem pilot (20 % průměru piloty od vnitřního líce piloty). Únosnost ve smyku průřezu lze zvýšit poměrem 2d/av (av je vzdálenost posuzovaného průřezu k líci sloupu) v šířce rovné trojnásobku průměru piloty (symetricky vůči ose piloty). Obdobný je postup při posouzení mezního stavu protlačení. Mezní stav protlačení by měl být posuzován, pokud je vzdálenost jednotlivých pilot větší než trojnásobek jejich průměru. Kontrolní obvod pro posouzení protlačení prochází vnitřními líci pilot – viz následující obr. 11.23 až obr. 11.24.
Model náhradní příhradoviny na obr. 11.23 je jednoduchý. Celou oblast je nutno navíc konstrukčně vyztužit svislými třmínky a vodorovnou výztuží, která zachytí příčné tahy v betonových vzpěrách. Pokud budeme uvažovat zjednodušenou hodnotu vznikajícího příčného tahu podle [24] hodnotou:
\begin{gathered}
T_\rho=0{,}22C
\end{gathered}(11. 34)
Lze poměrně jednoduše stanovit minimální plochu svislé a vodorovné výztuže.
Svislé třmínky navrhneme na sílu (pro každou vzpěru):
\begin{gathered}
T_\text{sv}=2T_\rho\cos\theta=0{,}44\cdot0{,}5\text{ N}\cdot\cot\theta=0{,}22\text{ N}\cot\theta
\end{gathered}(11.35)
Vodorovné pruty navrhneme na sílu (pro každou vzpěru):
\begin{gathered}
T_\text{sH}=2T_\rho\sin\theta=0{,}44\cdot0{,}5\text{ N}=0{,}22\text{ N}
\end{gathered}(11.36)
Navržené množství výztuže musí splňovat kritéria minima vyztužení pro poruchové oblasti – viz [18]. Navržená výztuž se rovnoměrně rozdělí po délce betonové vzpěry. Příklad konstrukčního vyztužení hlavice dvojice pilot je na obr. 11.23.
Pokud by nebylo možné dodržet dostatečně strmé betonové vzpěry, pak by bylo nutné upravit model náhradní příhradoviny jako u dlouhé konzoly vložením svislých táhel – viz kap. 3. Vložená svislá táhla je nutné navrhnout na každé straně na sílu 0,5N.
Hlavice pro trojici pilot
Na obr. 11.26 je hlavice tří pilot. Pro návrh lze vytvořit obdobný model náhradní příhradoviny jako u dvojice pilot. Axonometrie základního modelu je rovněž na obr. 11.26. Pro vyztužení oblasti platí stejné principy jako u hlavice pro dvojici pilot.
Pro pouze osově zatížený sloup ve středu pravidelné hlavice tvaru rovnostranného trojúhelníku lze síly v prvcích náhradní příhradoviny vyjádřit následovně:
Tlaková síla v betonových vzpěrách:
\begin{gathered}
C_1=C_2=C_3=0{,}33\text{ N}/\sin\theta
\end{gathered}(11.37)
Síla v táhlech je
\begin{gathered}
T_1=T_2=T_3=(0{,}33\text{ N}/\cos\theta)/(2\cos30\degree)\approx0{,}2\text{ N}/\cos\theta
\end{gathered}(11.38)
Na příčné tahy v betonových vzpěrách navrhneme konstrukční svislou a vodorovnou výztuž obdobně jako u předchozí hlavice.
Svislé třmínky navrhneme na sílu (pro každou vzpěru):
\begin{gathered}
T_\text{sv}=2T_\rho\cos\theta=0{,}44\cdot0{,}33\text{ N}\cdot\cot\theta=0{,}15\text{ N}\cot\theta
\end{gathered}(11.39)
Vodorovné pruty navrhneme na sílu (pro každou vzpěru):
\begin{gathered}
T_\text{sH}=2T_\rho\sin\theta=0{,}44\cdot0{,}33\text{ N}=0{,}15\text{ N}
\end{gathered}(11.40)
Navržené množství výztuže musí splňovat kritéria minima vyztužení pro poruchové oblasti – viz [18]. Navržená výztuž se rovnoměrně rozdělí po délce betonové vzpěry.
U složitěji zatížených hlavic s nepravidelnou geometrií je nutné vyřešit obecnou náhradní příhradovou soustavu.
Hlavice pro čtveřici pilot
Na obr. 11.27 a obr. 11.28 je hlavice čtveřice pilot. Pro návrh oblasti jsou k dispozici dva modely. První je na obr. 11.27 a druhý na obr. 11.28. Podle prvního modelu analogicky k předchozím modelům se zatížení přenáší přímo betonovými vzpěrami do pilot. Ortogonální táhla modelu však nepostačují k přenesení vznikajících tahů v diagonálním směru – ve směru vzpěr. Při vyztužení oblasti je tedy nutné k obvodovým táhlům doplnit ještě diagonální táhla nebo doplnit poměrné hustou ortogonální výztuž po celém spodním líci.
Model náhradní příhradoviny na obr. 11.28 je komplikovanější. Zatížení ze sloupu se přenáší v nejkratším směru do obvodových skrytých trámů, které příslušnou část zatížení potom roznášejí do pilot. Obvodové trámy jsou tak nepřímo zatíženy a musí být opatřeny tahovou výztuží, která vynáší zatížení k hornímu líci. Odtud je potom betonovými vzpěrami rozneseno přímo do pilot. Model je natolik komplikovaný, že nebude zcela odpovídat chování konstrukce. Na druhou stranu model dává návod na dobré vyztužení oblasti. Model lépe odpovídá skutečnému ortogonálnímu charakteru vyztužení oblasti než model podle obr. 11.27. Skutečné chování konstrukce bude nejspíš kombinací obou uvedených modelů.
Pro pouze osově zatížený sloup ve středu pravidelné hlavice tvaru čtverce lze síly v prvcích náhradní příhradoviny prvního modelu (obr. 11.27) vyjádřit následovně.
Tlaková síla v betonových vzpěrách:
\begin{gathered}
C_1=C_2=C_3=C_4=0{,}25\text{ N}/\sin\theta
\end{gathered}(11.41)
Síla v táhlech je
\begin{gathered}
T_1=T_2=T_3=T_4=(0{,}25\text{ N}/\cos\theta)/(\cos45\degree)\approx0{,}18\text{ N}/\cos\theta
\end{gathered}(11.42)
Obvodové táhlo je však málo účinné a je nutné doplnit diagonální táhla na sílu:
\begin{gathered}
T=0{,}25\text{ N}/\cos\theta
\end{gathered}(11.43)
Na příčné tahy v betonových vzpěrách navrhneme konstrukční svislou a vodorovnou výztuž obdobně jako u předchozí hlavice.
Svislé třmínky navrhneme na sílu (pro každou vzpěru):
\begin{gathered}
T_\text{sv}=2T_\rho\cos\theta=0{,}44\cdot0{,}25\text{ N}\cdot\cot\theta=0{,}11\text{ N}\cot\theta
\end{gathered}(11.44)
Vodorovné pruty navrhneme na sílu (pro každou vzpěru):
\begin{gathered}
T_\text{sH}=2T_\rho\sin\theta=0{,}44\cdot0{,}25\text{ N}=0{,}11\text{ N}
\end{gathered}(11.45)
Navržené množství výztuže musí splňovat kritéria minima vyztužení pro poruchové oblasti – viz [7]. Navržená výztuž se rovnoměrně rozdělí po délce betonové vzpěry. Při návrhu podle modelu na obr. 11.28 je nutné doplnit tažené třmínky na celkovou sílu odpovídající zatížení sloupu a místo diagonálních táhel se táhla uloží ortogonálně.
U složitěji zatížených hlavic s nepravidelnou geometrií je nutné vyřešit obecnou náhradní příhradovou soustavu.
Další příklady hlavic
Na obr. 11.29 a obr. 11.24 jsou další příklady hlavic pilot. Pro dané konstrukce lze vytvořit model náhradní příhradoviny podle principů uvedených v předchozích modelech.
Konstrukční zásady vyztužení patky nad pilotách
Dolní výztuž musí být vždy dotažena až nad piloty. Pro návrh kotevní délky lze uvažovat redukci síly ve výztuži na 80 % obdobně jako u stěnových konstrukcí (viz kap. 8). Navíc musí být v patce doplněna konstrukční výztuž:
- na vznikající příčné tahy v betonových vzpěrách;
- při horním líci o průřezové ploše nejméně 10 % hlavní tahové výztuže;
- při svislých površích vodorovné uzavřené vložky a uzavřenými třmínky s tím, že průřezová plocha jednotlivých prutů má být nejméně (kde B je šířka patky a t je vzdálenost mezi výztužnými pruty).
U patek uložených na několika pilotách lze hlavní tahovou výztuž uspořádat v pásech umístěných osově nad pilotami. V každém případě je třeba zajistit dostatečné kotvení výztuže vně obvodových pilot, a to tak, aby výztuž probíhající nad pilotou přenášela vně piloty 0,8násobek maximální síly v pilotě. Do této výztuže lze zahrnout pouze pruty, které jsou plně kotveny za rovinou procházející osou piloty a kolmou na spojnici středu piloty s těžištěm půdorysu patky.
11.6 PŘÍKLAD PROTLAČENÍ ZÁKLADOVÉ PATKY
Obr. 11.30 Příklad základové patky
Plocha základové patky:
\begin{gathered}
A_\text{b}=5{,}0^2=25\text{ m}^2
\end{gathered}průměrná účinná výška patky:
\begin{gathered}
d=1\text{ m},k=1+\sqrt{200/1\space000}=1{,}45
\end{gathered}průměrný stupeň vyztužení:
\begin{gathered}
\rho_\text{l}=0{,}005\to100\cdot\rho_\text{l}=0{,}5\%
\end{gathered}charakteristická pevnost betonu v tlaku:
\begin{gathered}
f_\text{ck}=25\text{ MPa},C_\text{Rd,c}=0{,}12
\end{gathered}\begin{gathered}
v_\text{min}=0{,}035\cdot k^{3/2}\cdot f_\text{ck}^{1/2}=0{,}035\cdot1{,}45^{3/2}\cdot25^{1/2}=0{,}305\text{ MPa}\\\\
v_\text{Rd,c}=C_\text{Rd,c}k(100\rho_\text{l}f_\text{ck})^{1/3}=0{,}12\cdot1{,}45(0{,}5\cdot25)^{1/3}=0{,}404\text{ MPa}\ge v_\text{min}
\end{gathered}Pro rychlé nalezení hodnoty acrit je možné použít přibližného odhadu této hodnoty pomocí grafu na obr. 11.18. Orientačně lze s využitím tohoto grafu též základovou patku posoudit. Navržené rozměry patky vyhovují, pokud pro parametry c/d, l/c vyjde poměr VEd/(vRc,d ∙ d2) menší než mezní hodnota podle obr. 11.18c. Po dosazení platí: c/d = 0,5; l/c = 10;
\begin{gathered}
V_\text{Ed}/(v_\text{Rd,c}d^2)=19{,}8\le21
\end{gathered}Z grafu na obr. 11.18b lze pak odhadnout pro stejné parametry přibližný poměr acrit/d. Po dosazení:
\begin{gathered}
a_\text{crit}/d\cong0{,}7\to a_\text{crit}\cong0{,}7\cdot1{,}0=0{,}7\text{ m}
\end{gathered}Pro stanovení přesné hodnoty acrit je však nutné použít iterační výpočet podle následujícího příkladu pro volené hodnoty ai.
Pro obvod zvoleného kontrolovaného průřezu ui (0):
\begin{gathered}
u_\text{i}=4\cdot c+2\cdot\pi\cdot a_\text{i}=4\cdot0{,}5+2\cdot3{,}14\cdot a_\text{i}=2+6{,}28a_\text{i}
\end{gathered}a plochu uvnitř kontrolovaného obvodu:
\begin{gathered}
A_\text{i}=c^2+4\cdot c\cdot a_\text{i}+\pi\cdot a_\text{i}^2=0{,}5^2+4\cdot0{,}5\cdot a_\text{i}+3{,}14\cdot a_\text{i}^2=0{,}25+2a_\text{i}+3{,}14a_\text{i}^2
\end{gathered}Pak se určí hodnoty vEdi a vRdi a jejich rozdíl (vRdi – vEdi); po dosazení bude:
\begin{gathered}
v_\text{Edi}=\frac{V_\text{Ed}\cdot\bigg(1-\frac{A_\text{i}}{A_\text{b}}\bigg)}{u_\text{i}\cdot d}=\frac{8{,}0\bigg(1-\frac{A_\text{i}}{25}\bigg)}{u_\text{i}\cdot10}\\\\
v_\text{Rd,i}=v_\text{Rd,c}(2\cdot d/a_\text{i})=0{,}404\cdot2{,}0/a_\text{i}=0{,}808/a_\text{i}
\end{gathered}Pro minimální hodnotu (vRdi – vEdi) je ai = acrit.
Hodnotu acrit hledáme v okolí hodnoty 0,7m. V tab. 11.2 stanovíme pro ai = 0,6m; 0,7m; 0,8m; 0,9m a 1,0m s použitím výše uvedených vztahů určíme hodnoty ui, Ai, vEd,i, vRd,i a hodnotu rozdílu (vRdi – vEdi). Hodnoty rozdílů (vRdi – vEdi) jsou graficky vyneseny v závislosti na hodnotě ai v obr. 11.31. Z tohoto obrázku je zřejmé, že minimální rozdíl (vRdi – vEdi) bude pro hodnotu ai = acrit = 0,88m.
Tab. 11.2 Hodnoty ai; ui, Ai, vEd,i, vRd,i, (vRdi – vEdi)
| ai [m] | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 |
| ui [m] | 5,768 | 6,396 | 7,024 | 7,652 | 8,280 |
| Ai [m2] | 2,580 | 3,188 | 3,859 | 4,593 | 5,390 |
| vEd,i [MPa] | 1,243 | 1,091 | 0,963 | 0,853 | 0,758 |
| VRd,i [MPa] | 1,347 | 1,154 | 1,010 | 0,898 | 0,808 |
| (vRdi – vEdi)[MPa] | 0,103 | 0,063 | 0,047 | 0,045 | 0,050 |
Obr. 11.31 Iterační proces graficky
Pro ai = acrit = 0,88 m stanovíme:
\begin{gathered}
u_\text{crit}=2+6{,}28\cdot0{,}88=7{,}52\text{ m},\space A_\text{crit}=4{,}44\text{ m}^2\\\\
v_\text{Ed,crit}=8(1-4{,}44/25)/7{,}52=0{,}875\text{ MPa},\space v_\text{Rd.crit}=0{,}404(2/0{,}88)=0{,}918\text{ MPa}\\\\
v_\text{Rd,crit}=0{,}918\ge v_\text{Ed,crit}=0{,}875\text{ MPa}
\end{gathered}Navržená základová patka bez smykové výztuže na protlačení vyhovuje, poněvadž je současně splněna podmínka spolehlivosti.
Z obr. 11.31 je zřejmé, že v poměrně široké oblasti (0,80 až 1,00) jsou rozdíly (vRdi – vEdi) velmi malé. Z toho plyne, že stanovení ai se nemusí provádět tak podrobně; postačí hodnoty z tab. 8.4 pro ai = 0,9 m.
12 Literatura
[1] ČSN EN 1992-1-1:2006. Navrhování betonových konstrukcí – Část 1-1: Obecná pravidla a pravidla pro pozemní stavby. Praha: ČNI.
[2] DIN 1045-1:2008-08. Tragwerke aus Beton, Stahlbeton und Spannbeton – Teil 1: Bemessung und Konstruktion. Berlin: DIN Deutsches Institut für Normung s. V., Beuth Verlag GmbH.
[3] ČSN EN 13 670:2003. Provádění betonových konstrukcí – Změna Z1. Praha: ČNI.
[4] ČSN EN 73 0205:1995. Geometrická přesnost ve výstavbě. Navrhování geometrické přesnosti. Praha: ČNI.
[5] ČSN EN 13 369:2005. Společná ustanovení pro betonové prefabrikáty – Změna: A1. Praha: ČNI.
[6] Practitioners’guide to finite element modellinh od freinforced concrete structures. Bulletin 45. FIB. 2008.
[7] SCHLAICH, J., SCHÄFER, K. Konstruieren im Stahlbetonbau. BetonKalender 2001. Ernst&Sohn, A Wiley Company, 2001.
[8] REINECK, K., H. Modellierung der D-Bereiche von Fertigteilen. BetonKalender 2005. Ernst&Sohn, A Wiley Company, 2005.
[9] ZILCH, K., ZEHETMAIER, G. Bemessung im Konstruktiven Batonbau. Nach DIN 1045-1 und EN 1992-1-1. Springer-Verlag Berlin Heidelberg, 2010.
[10] BACHMANN, H., STEINLE, A., HAHN, V. Bauen mit Betonfertigteilen im Hochabu. BetonKalender 2009. Ernst & Sohn, A Wiley Company, 2009.
[11] ROMECH, G. Anwendung der Finite-Elemente-Methode in Betonbau. Ernst&Sohn, 2007.
[12] Stabwerkmodelle, Institut für Tragkonstruktionen – Betonbau / TU Wien, März 2007 – Klg/RP.
[13] STENZEL, G., FINGERLOOS, F. Konstruktion und Bemessung von Details nach DIN 1045-1. BetonKalender 2007. Ernst & Sohn, Wiley Company, 2007.
[14] GRASSER, E., THIELEN, G. Hilfsmittel zur Berechnung der Schnitgrössen und Formänderungen von Stahbetontragwerken nach DIN 1045. DAfStB 240. Berlin: Beuth Verlag GmbH. 3. überarbeitete Auflage, 1991.
[15] KORDINA, K. Bemesungshilfmittel zu Eurocode4 2. Teil 1. Planung von Stahl-und Spannbetontragwerken. DAfStB 425. Berlin: Beuth Verlag GmbH. 3. überarbeitete Auflage, 1997.
[16] HOTTMANN U., SCHÄFER K. Bemesung von Stahlbetonbalken und Wandscheiben mit Öffnungen. DAfStB 459. Berlin: Beuth Verlag GmbH, 1996.
[17] PREGARTNER T. Bemessung von Befestigungen in Beton. Einfuehrung mit Beispielen. Weilerbach: Ernst&Sohn Verlag für Architektur und technische Wissenschaft GmbH&Co. KG. 2009.
[18] SCHÄFER, K., SUNDERMANN, W. Tragfähigkeit von Druckstreiben und Knoten in D-Bereichen. DAfStB 478. Berlin: Beuth Verlag GmbH, 1997.
[19] KORDINA, K., TEUTSCH, M., WEGENER, E. Trag- und Verformungsverhalten von Rahmenknmoten. DAfStB 486. Berlin: Beuth Verlag GmbH, 1998.
[20] Erläuterung zu DIN 1045-1. DAfStB 525. Berlin: Beuth Verlag GmbH, 2003.
[21] HEGGER, J., ROESER, W. Die Bemessung und Konstruktion von Rahmenknoten. Grundlagen und Beispiele gemäss DIN1045-1. DAfStB 532. Berlin: Beuth Verlag GmbH, 2002.
[22] GORIS, A., SCHNEIDER, K., J. Bautabellen für Ingenieure. 19. Auflage 2010, Köln: Werner Verlag, Wolters Kluwer Deutschland GmbH, 2008.
[23] RUSSWURM, D., FABRITIUS, E. Bewehren von Stahlbeton- Tragwerke nach DIN 1045-1. Düsseldorf: Institut für Stahlbetonbewehrung e.V., 2007.
[24] ŠMEJKAL, J., PROCHÁZKA, J. Discontinuity regions design experiences with strut-and-tie models according to EN 1992-1-1. Design of concrete structures using EN 1992-1-1. Workshop CTU Prague 2010.
[25] PROCHÁZKA, J., ŠMEJKAL, J. Betonářská výztuž – Trendy výroby a spojování. Praha: Nakladatelství ČVUT, 2008.
[26] ŠMEJKAL, J., PROCHÁZKA, J. Navrhování s použitím modelů náhradní příhradoviny. Beton TKS, 5/2009.
[27] ŠMEJKAL, J., PROCHÁZKA, J. Navrhování konzol s použitím modelů náhradní příhradoviny. Beton TKS, 6/2009.
[28] ŠMEJKAL, J., PROCHÁZKA, J. Navrhování nepřímo uložených a složených konzol s použitím modelů náhradní příhradoviny. Beton TKS, 1/2010.
[29] ŠMEJKAL, J., PROCHÁZKA, J. Navrhování ozubů nosníků a desek s použitím modelů náhradní příhradoviny. Beton TKS, 2/2010.
[30] ŠMEJKAL, J., PROCHÁZKA, J. Navrhování prostupů nosníků s použitím modelů náhradní příhradoviny. Beton TKS, 3/2010.
[31] ŠMEJKAL, J., PROCHÁZKA, J. Navrhování rámových rohů s použitím modelů náhradní příhradoviny. Beton TKS, 5/2010.
[32] ŠMEJKAL, J., PROCHÁZKA, J. Navrhování stěnových nosníků s použitím modelů náhradní příhradoviny. Beton TKS, 6/2010.
[33] PROCHÁZKA, J. Betonové konstrukce. Předpjatý beton. Konstrukce pozemních staveb a inženýrských staveb. Praha: Ediční středisko ČVUT, 1990.
[34] PROCHÁZKA, J., ŠTĚPÁNEK, P., KRÁTKÝ, J., KOHOUTKOVÁ, A., VAŠKOVÁ, J. Navrhování betonových konstrukcí I. Praha: ČBS Servis, s.r.o., 2009.
[35] NILSSON, J., H., E. Reinforced concrete corners and joints subjected to bending moment. Nation Swedish Building Research. Document D7, 1973.
[36] GRAUBNER C., A. Zur Bemessung von Stahlbetonbalken bei unsymetrischer Belastung aus Konsolenbänder. Bauingenieur 59. Spinger-Verlag, 1984.
[37] PAUL, J., A KOL.: Navrhování betonových konstrukcí podle ČSN 731201. Praha: SNTL 1968.
[38] SCHLAICH, J., SCHÄFER, K. Konstruieren im Stahlbetonbau. BetonKalender 1984. Ernst&Sohn, 1984.
[39] FOERSTER, S., MAEKAWA, K., VECCHIO, F. Practitioners’guide to finite element modelling of reinforced concrete structures. Bulletin 45, FIB. Stuttgart: Sprint-Digital-Druck.
[40] ČSN 73 1201:1988. Praha: Vydavatelství úřadu pro normalizaci a měření, 1986.
[41] MARK, P., A KOL. Sondernaspekte zur Schubbemessung nach DIN 1045-1 und EC2. BetonKalender 2008. Ernst &Sohn A Wiley Company, 2008.
[42] FEIX, J., HÄUSLER, F., WALKNER, R. Necesary amendments to the rules for punching design according to EN 1992-1-1. In Design of concrete structures and bridges using eurocodes. 2nd international workshop 2011, Bratislava.
[43] ŠMEJKAL, J., PROCHÁZKA, J., HANZLOVÁ, H. Navrhování na mezní stav porušení protlačením. Beton TKS, 5/2011 a Beton TKS, 6/2011.
[44] ETA-13-0521 Filigran-Durchstanzbewehrung.II.. European technical approval Filigran Trägersysteme GmbH& Co.KG., 13. 6. 2013.
[45] ETA-12/0454 Punching reinforcement. European technical approval Halfen GmbH. 18. 12. 2012.
[46] Model code 2010, fib Bulletin 55, First komplete draft, DCC Dokument Kompetence Center Siegmar Kästl e.K. Germany.
[47] ČSN EN 1997-1:2006. Navrhování geotechnických konstrukcí – Část 1: Obecná pravidla. Praha: ČNI.
[48] PROCHÁZKA, J., KOHOUTKOVÁ, A. Zavádění EN 1992-1-1: „Navrhování betonových konstrukcí“ do praxe – Základy. Beton TKS, 5/2004.
[49] ŠTEFAN, R. Řešení příhradových modelů D-oblastí s postupným vylučováním méně namáhaných prvků. Praha: Odborná společnost pro vědu, výzkum a poradenství ČSSI, 2009.
[50] TUAN HGO, D. Punching sear resistence of high-stregth concrete slab. Department of Civil Engineering, Tuh University of Melbourne, Parkville, Victoria, Australia, 2001.
[51] HEGGER, J., BEUTEL, R., KERKENI, N. Gutachten zur Durchstanzemessung von Halfen HDB-Anker nach ČSN 73 1201. Langenfeld: Halfen GmbH& Co. KG, 2003.
[52] DAfStB Heft 411: Untersuchungen über das Tragverhalten von Kächerfundamenten. Berlin: Beuth Verlag GmbH, 1990.
[53] ČSN EN 1997-1:2006. Eurokód 7: Navrhování geotechnických konstrukcí – Část 1: Obecná pravidla. Praha: ČNI.
[54] SIBURG, C., HEGGER, J. Punching of flat slabs – comparison of models. Fib Symposium PRAGUE 2011.
[55] Zulassung Z-15.1-217. Deutsches Institut für Bautechnik, 2009.
[56] MUTTONI, A., GUANDALINI, S. Kommentar zum Durchstanzen nach Norm SIA 262. Ecole Polytechnice Fédérale de Lausanne. 2006. http|.//is-beton.epfl.ch/Public.
[57] ČSN 73 1201:2010. Navrhování betonových konstrukcí pozemních staveb. Praha: Úřad pro technickou normalizaci, metrologii a státní zkušebnictví.
[58] Stabwerkmodelle, Institut für Tragkonstruktionen – Betonbau / TU Wien, März 2007 – Klg/RP.