ČESKÁ KOMORA AUTORIZOVANÝCH INŽENÝRŮ A TECHNIKŮ ČINNÝCH VE VÝSTAVBĚ
Rada pro podporu rozvoje profese ČKAIT
Autoři: doc. Ing. Jan Masopust, CSc.
Stav: aktualizace 2021, vydání tiskem 2018
Anotace:
Pomůcka byla vydána tištěnou formou v roce 2018 a elektronickou formou byla zveřejněna v roce 2021 jako aktualizace. Je rozdělena do sedmi kapitol: stavební jámy, jejich účel, druhy, metody a technologie pažicích konstrukcí; kotvení stavební konstrukce, druhy horninových kotev; zásady provádění injektovaných horninových kotev s příkladem; navrhování pažených stavebních jam; posouzení pažicích konstrukcí statickým výpočtem; opěrné zdi jejich druhy a navrhování s příkladem; zásady odvodňování stavebních jam; monitoring pažicích konstrukcí, metody, návrh a vyhodnocení monitoringu.
Obsah
ÚVOD
Předložená pomůcka navazuje na TP 1.9.5 s názvem: Navrhování základových konstrukcí a zabývá se dalšími rozsáhlými součástmi zakládání staveb – návrhem a realizací stavebních jam, odvodňováním základové půdy, monitoringem pažicích konstrukcí, opěrnými zdmi, ochraně základové půdy před účinky agresivního prostředí a zlepšováním vlastností základové půdy. Tím je v podstatě vyčerpána hlavní náplň zakládání staveb, a to zejména z hlediska praktického přístupu k této problematice.
Do oblasti speciálního zakládání staveb náleží tedy roubení stavebních jam, jež má rozsáhlé využití zejména v městské zástavbě, neboť si dnes již těžko umíme představit pozemní stavbu bez hlubokého suterénu, pro jehož výstavbu je vytvoření stavební jámy nutné. S ohledem na nedostatek prostoru přichází prakticky vždy návrh stavební jámy roubené, tj. jámy se svislými stěnami opatřenými pažením a příslušnými prvky stabilizačními, což jsou zejména kotvy a rozpěry. Roubené konstrukce stavebních jam jsou velmi rozdílné jednak s ohledem na návrh konstrukčních prvků a také s ohledem na dobu, po níž jsou tyto konstrukce ve funkci. V zásadě se rozlišuje roubení na dočasné, kde jeho funkce končí po 2 letech a na trvalé. Je snahou, aby dočasné roubené konstrukce byly alespoň z části demontovatelné, naopak v případě konstrukcí trvalých jejich návrh přizpůsoben nejen funkci pažení, ale trvalé funkci obvodových zdí suterénu. V městské zástavbě bývají problémy s čerpáním podzemní vody, které je vždy drahé a často obtížně proveditelné. Proto je častou snahou vytvářet pažicí konstrukce vodotěsné a vetknout je do nepropustných vrstev základové půdy tak, aby se omezil přítok podzemní vody. Pažicí konstrukce se navrhují vždy na základě statického výpočtu, přičemž se stále častěji při jejich návrhu uplatňuje observační metoda, jejíž nedílnou součástí je monitoring chování pažicích konstrukcí, jež je rovněž dostatečně podrobně probrán. Příslušná kapitola se pak zabývá ochranou základových konstrukcí před účinky agresivního prostředí, přičemž agresivita prostředí, zvláště pak podzemní vody může významně ovlivnit jak návrh, tak zejména provádění a cenu příslušné konstrukce.
Poslední kapitola obsahuje základní pojmy a metody z oblasti zlepšování vlastností základové půdy, přičemž probrány jsou hlavně klasické postupy. Tyto metody se neustále rozvíjejí a není tedy v možnostech této pomůcky podat jejich vyčerpávající přehled. Stručně jsou rovněž probrány opěrné stěny, jež také náleží ke geotechnickým konstrukcím. Nejrozsáhlejší část pomůcky je věnována stavebním jámám, tj. metodám jejich výstavby, návrhu a posouzení spolu s nejužívanějšími výpočetními postupy a odkazy na komerčně i jinak dostupná programová vybavení. Na způsoby posuzování stavebních jam statickým výpočtem potom volně navazuje kapitola věnovaná odvodňování základové půdy, zvláště pak stavebních jam. Samostatná kapitola je věnována ochraně základových konstrukcí před účinky agresivního prostředí, jež souvisí s životností staveb. Jsou především popsány reálné možnosti ochrany typických základových prvků a konstrukcí před účinky agresivní podzemní vody. Poslední kapitola se zabývá některými metodami zlepšování vlastností základové půdy. Tato problematika je velmi obsáhlá a zasahuje samozřejmě i do jiných oborů stavebnictví (silniční a železniční stavitelství apod.).
Jak již bylo uvedeno v předmluvě k TP 1.9.5 Navrhování základových konstrukcí, pokrok v zakládání staveb je spjat především s rozvojem nových technologií, podmíněných jak vývojem v oblasti strojů a zařízení, tak zvláště potřebami stavebnictví, kdy jsou zastavovány pozemky se stále komplikovanějšími geotechnickými poměry spolu s často mimořádnými nároky navrhovaných staveb, zejména deformačními. Aby bylo možné nové technologie dostatečně rozvinout a uplatnit, je vytvářen tlak na hlubší poznávání fyzikálních principů v geotechnice, přičemž do popředí se dostávají metody matematického modelování. Nelze však opomenout tu skutečnost, že zakládání staveb řeší především konkrétní praktické úlohy, tj. musí umožnit návrh a realizaci geotechnických konstrukcí na konkrétním staveništi v reálném čase a s reálnými prostředky. Proto zůstává inženýrský přístup k řešení problémů a běžných úloh v zakládání staveb stále nejčastěji využívaný, nicméně budoucnost oboru zřejmě spočívá v kritické syntéze obou přístupů. Pokud má být vzájemná symbióza obou přístupů přínosná, je třeba mít vždy na mysli, že oba přístupy slouží především pro potřeby stavebnictví a konečným produktem je bezpečný, spolehlivý a ekonomický základ (stavba), nikoliv průzkum, návrh či projekt, jež jsou pouze prostředky k dosažení popsaného cíle.
1 STAVEBNÍ JÁMY
1.1 ÚČEL STAVEBNÍCH JAM
Stavební jámy jsou výkopy sloužící pro spolehlivé založení stavby a výstavbu podzemních prostor objektu. Různě hluboké stavební jámy se provádějí prakticky ve všech případech plošných základů, ale velmi často i v případech, kdy objekty jsou zakládány hlubinně. Při výstavbě objektů pozemního stavitelství, tj. zvláště budov bytových a občanských, je dnes téměř pravidlem návrh suterénních prostor těchto objektů, jež jsou budovány ve stavebních jámách. Stavební jámy mohou být hloubeny jak v zeminách suchých, tak i částečně, nebo zcela pod hladinou podzemní vody, v oblastech nezastavěných i v územích se stávající zástavbou. Rovněž tak objekty inženýrského a vodního stavitelství, jako jsou mosty, hloubené tunely, hloubené stanice podzemních drah, nábřežní zdi, jezy a přehrady bývají zakládány ve stavebních jámách, hloubených především za účelem dosažení únosné základové půdy, nebo i ochrany základů před výmoly apod. Podzemní inženýrské sítě se ukládají většinou do rýh vytvořených výkopy, jejichž zajištění spadá do oblasti prací speciálního zakládání staveb. Při ražbě štol, kolektorů a jiných drobných podzemních staveb je třeba vybudovat v předstihu těžní a přístupové šachty, jejichž roubení se rovněž týká popisované problematiky.
Vedle ražených podzemních prostor, při jejichž výstavbě nedochází k odstranění nadloží, jsou velmi častým typem i podzemní prostory prováděné ve stavebních jamách. Stavební jámy objektů pozemního i dopravního charakteru mohou být značně hluboké a plošně rozlehlé, velmi často jsou hloubeny v husté okolní zástavbě. Nelze proto ve většině případů použít jámy svahované, které jsou prostorově velmi náročné, nýbrž se uplatní především jámy roubené.
1.2 DRUHY STAVEBNÍCH JAM
Volba technologie provádění stavební jámy je závislá na celé řadě faktorů, jejichž důležitost není stejná a může být v různých případech proměnlivá. Je třeba vycházet především z účelu jejího použití, geologických a hydrogeologických poměrů staveniště, z charakteru jejího okolí (zástavba, komunikace, inženýrské sítě apod.) i z charakteru vlastní stavby.
Rozeznáváme následující základní typy stavebních jam, které se často vzájemně kombinují:
- svahované jámy, které jsou bočně omezené svahy provedenými ve sklonu zajišťujícím jejich obvykle dočasnou stabilitu;
- těsněné jámy se používají pro zakládání v propustných zeminách hluboko pod hladinou podzemní vody, kdy vznikají problémy s vodou přitékající do stavební jámy jejím dnem. Těsné pažicí stěny nelze vždy zavázat do nepropustné zemní vrstvy, a proto se musí v řadě případů vybudovat kompletní těsnicí vana, která podstatně sníží průsaky do prostoru stavební jámy;
- jímkové jámy, (jímky) jsou stavební jámy budované přímo ve vodě, nejčastěji pro vytvoření základů vodních a mostních staveb;
- roubené jámy, po obvodě omezené pažicími stěnami s doplňujícími podporovými konstrukcemi, zajišťujícími dočasnou nebo i trvalou stabilitu jámy. Současně užívaná terminologie dává přednost označení pažené jámy, které bude také v dalším textu používáno.
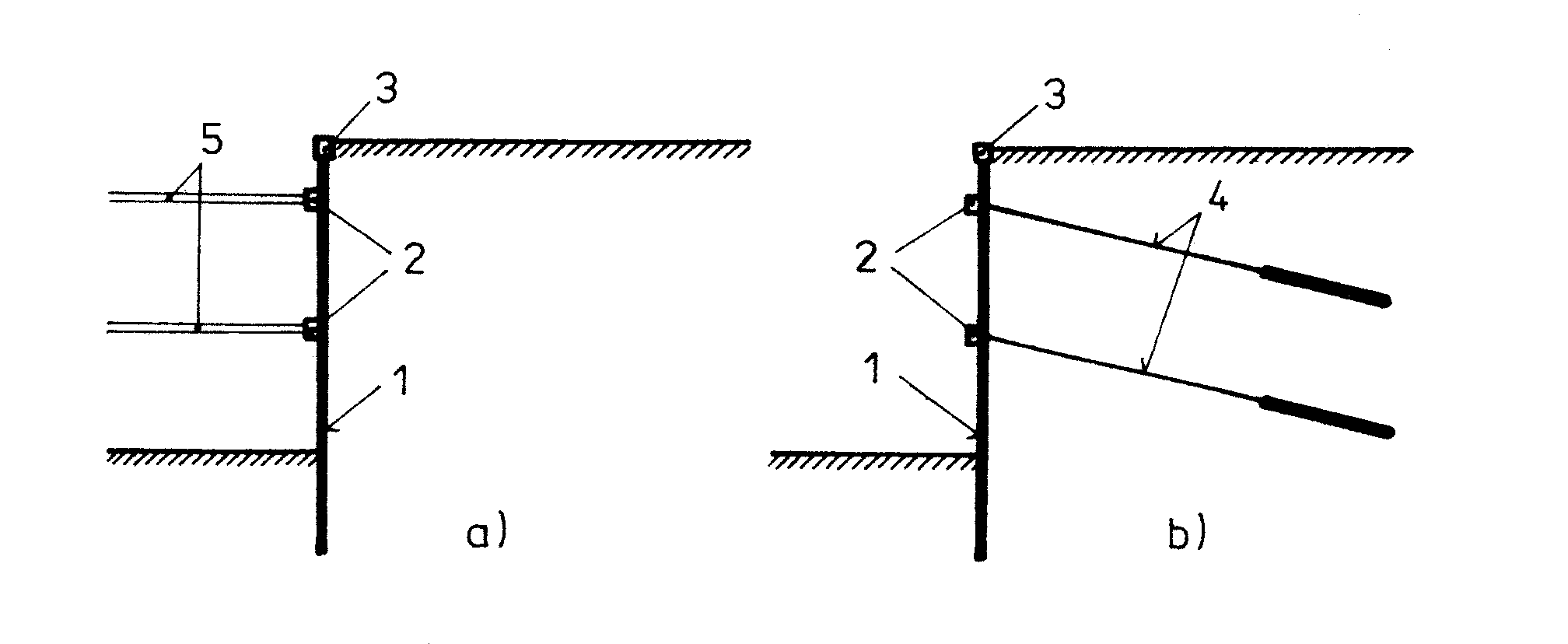
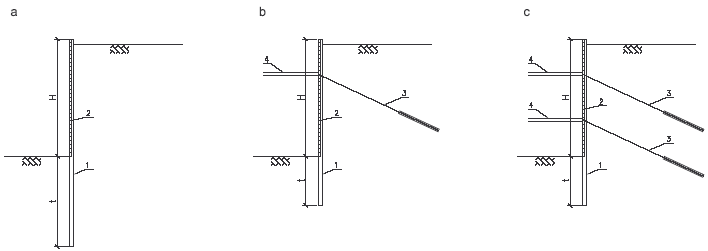
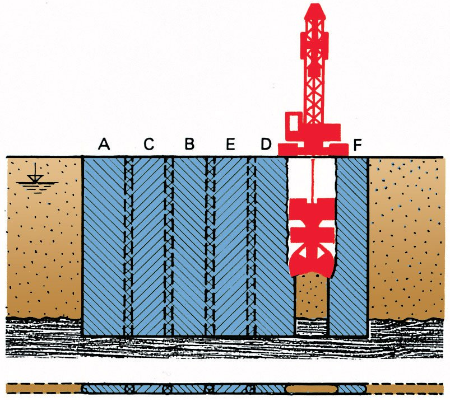
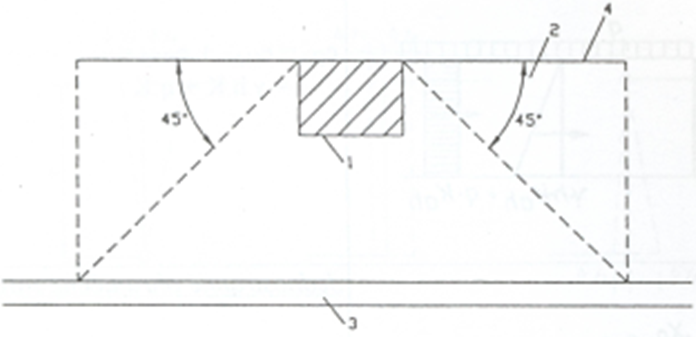
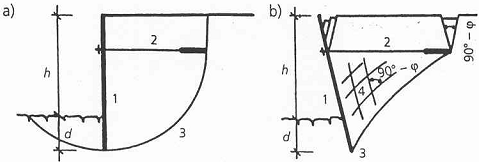
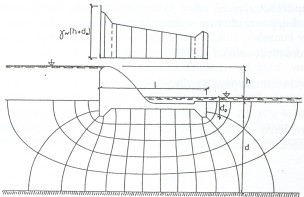
Konstrukce pažené jámy se skládá obvykle ze tří základních typů konstrukčních prvků, z nichž každý má odlišnou funkci v celkové konstrukci, (obr. 1):
- pažení;
- roznášecí prahy (převázky), v případě potřeby také horní ztužující věnec;
- podpěrné konstrukce (rozpěry nebo kotvy).
Obr. 1 Hlavní části konstrukce pažené stavební jámy, a) rozepřené pažení, b) kotvené pažení; 1 – pažicí stěna, 2 – roznášecí prahy, 3 – horní věnec, 4 – kotvy, 5 – rozpěry
Pažení je ta část konstrukce pažené jámy, která bezprostředně přiléhá k hornině a zajišťuje spolu s dalšími prvky bezpečnost stěn jámy nejen proti celkovému sesutí, ale i proti erozi, vypadávání menších objemů horniny a u nepropustných pažení i proti pronikání podzemní vody. Pažení jámy uplatňuje svou nosnou schopnost především ve vodorovném směru, v některých případech i ve směru svislém.
Roznášecí prahy, (převázky) jsou vodorovné nebo mírně skloněné nosníky, které přiléhají k pažení a umožňují roznesení velkých soustředěných sil z podpor na větší plochu pažení. Roznášecí prahy jsou obvykle ze strany jámy připojené k pažení, což jsou tzv. převázky vnější, v některých případech je účelné vybudovat je ve formě vyztužených nosníků uvnitř pažicí konstrukce, čímž vzniknou tzv. převázky vnitřní, (zapuštěné). Převázky se zhotovují v jedné nebo více výškových úrovních. Vedle podstatné statické funkce plní též funkci ztužení celého konstrukčního systému pažené jámy a zajišťují vyrovnávání deformací dílčích částí pažicí konstrukce.
Podpěrné konstrukce jsou prvky konstrukce pažené jámy, jimiž se realizují reakce horninových a dalších tlaků působících na pažení. Podle charakteru sil, které vznikají v podpěrných konstrukcích působením tlaků na pažení, rozeznáváme podpěrné konstrukce:
- rozpěrné, jimiž se tlakové reakční síly přenášejí rozpěrami buď do protilehlého pažení, nebo do horninového prostředí dna jámy, případně do vnitřní bárky;
- kotvené, u nichž jsou reakční síly realizovány tahovými silami v kotvách a přeneseny do horninového prostředí za pažením.
Konstrukce pažené stavební jámy může být navržena v různých variantách a kombinacích uvedených tří základních prvků, přičemž některé prvky mohou někdy chybět. Konstrukce pažené jámy může být např. tvořena jen pažicí stěnou vetknutou do podloží dna jámy, nebo naopak může být u jam ve skalních horninách zredukována pouze na kotevní prvky.
Dočasné rozpěrné konstrukce jsou tvořeny většinou ocelovými rourami, nebo válcovanými nosníky a obyčejně se neaktivuji, tzn., že se do nich příslušná osová síla předem nevnáší, ta vzniká až v souvislosti s deformací pažení. Při velkých rozpětím mohou být tvořeny ocelovou příhradovou konstrukcí a/nebo mohou být podepřeny. Rozpěrné konstrukce je také možné v pažené jámě účelně kombinovat po výšce nebo půdorysně s kotvením.
Trvalé rozpěrné konstrukce se během výstavby začleňují do konstrukce podpovrchového objektu většinou ve formě definitivních stropů, které bývají železobetonové, řidčeji ocelové. Vedle deskových železobetonových konstrukcí se používají i trámové stropy, při větších rozpětích případně s průvlaky. Jako vnitřní podpory, pokud jsou potřebné, se používají vrtané širokoprofilové piloty nebo prvky podzemních stěn. Do nich spadá i metoda „top and down“ (něm. „Deckelbauweise“), kdy po zhotovení konstrukčních stěn a prvního stropu možno realizovat současně výstavbu podzemní i nadzemní části objektu. To umožňuje zkrátit dobu výstavby a ve stísněných podmínkách využít strop nad prvním podzemním podlaží jako součást zařízení staveniště. Zemní práce v překryté podpovrchové části objektu podstatně méně zatěžují životní prostředí okolí.
Kotvení je velmi frekventovanou metodou speciálního zakládání, která umožňuje přenos značných tahových sil ze stavební konstrukce do horninového prostředí, případně slouží ke stabilizaci zemního či horninového masivu samostatnými předepnutými horninovými kotvami. Používají se tudíž nejen jako podpory u pažení stavebních jam, ale též pro zajištění stability zemních svahů včetně sanace svahů sesutých, pro stabilizaci skalních stěn v zářezech a odřezech, pro stabilizaci tunelových portálů a stěn podzemních kaveren, pro zajištění stavebních konstrukcí proti vyplavání působením vztlaku, případně proti posunutí či překlopení. O kotvení stavebních konstrukcí pojednává podrobněji kap. 4. 8 části A.
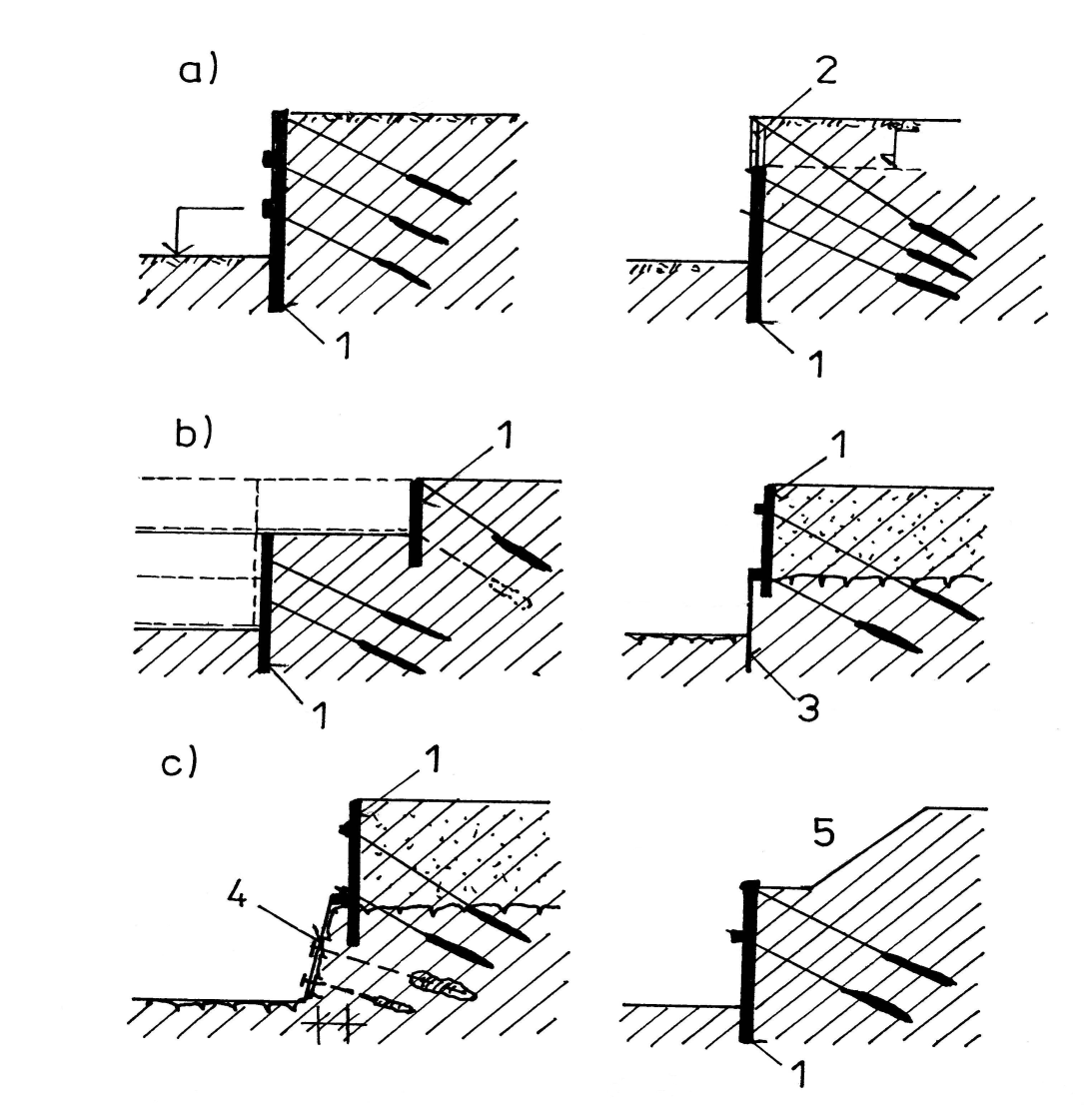
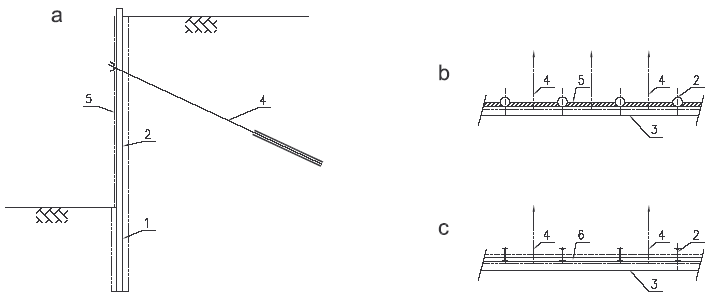
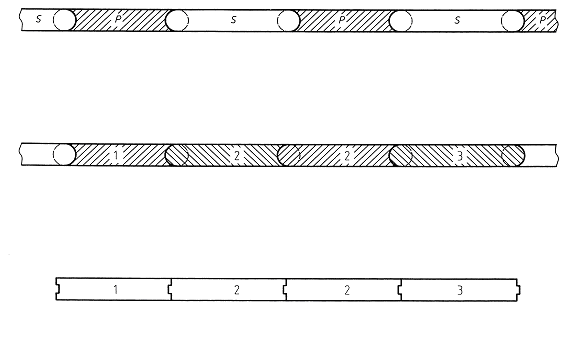
Základní varianty uspořádání příčného řezu pažicích konstrukcí jsou, (obr. 2):
- stavební jáma je pažená na celou výšku;
- stavební jáma je pažená jen zčásti (kombinované zajištění jámy);
- stavební jáma s kotveným svahem.
Pažicí stěna na celou výšku jámy bývá po výšce technologicky a konstrukčně homogenní, což je nejběžnější uspořádání, nebo se může typ pažení po výšce měnit. Odstupňované zajištění po výšce pažené stavební jámy se navrhuje v případě dispozičních nároků, vyžadujících výrazné půdorysné rozšíření horního podzemního podlaží přes obrys spodních podlaží (vstupy, podchody, vestibuly, přístupové rampy v definitivním stadiu, sjízdné rampy ve stavebním stadiu), nebo v případě návrhu relativně měkkého pažení pro velkou volnou výšku, kdy deformace pažicí konstrukce by byly nepřijatelné.
Kombinované zajištění stavební jámy je kombinací pažení a svahování, což je umožněno jednak geotechnickými podmínkami, jednak dostatkem místa pro horní svahování. Svahované stěny se často zajišťují hřebíkováním, popř. kotvami přes vodorovné prahy.
Stavební jáma s kotveným svahem má své uplatnění v pevnějších prostředích a v prostorově méně náročných podmínkách, kdy je umožněno určité rozšíření výkopů svahováním.
Z hlediska délky provozního působení rozeznáváme pažení dočasná a trvalá. Tato jejich funkce úzce souvisí se způsobem začlenění pažení do definitivního podpovrchového objektu.
Dočasná pažení plní svou stavební a statickou funkci jen po dobu výstavby. U dočasných pažení je třeba technicky a ekonomicky zvážit možnost a vhodnost odstranění, resp. znovuzískání některých konstrukčních prvků pro opakované použití. Za dočasné pažení jsou považovány konstrukce s životností do 2 let. Je třeba upozornit, že tato časová hranice je nastavena legislativně a obvykle po uplynutí této doby nenese projektant a zhotovitel dočasného pažení zodpovědnost za jeho stavební stav.
Pažení trvalá jsou ta, u nichž stavební i statická funkce trvá po celou dobu životnosti vlastního objektu. Trvalá pažení jsou buď částečně, nebo celá definitivním stavebním prvkem a začleňují se do konečného objektu jako jeho konstrukční součást. Musí proto vyhovovat požadavkům na pažení i na konečnou funkci objektu.
Obr. 2 Typy příčného uspořádání pažené stavební jámy: a) pažení na plnou výšku jámy, b) odstupňované pažení, c) kombinované zajištění; 1 – podzemní stěna, 2 – snáze demontovatelné pažení, 3 – mikrozáporové pažení, 4 – hřebíkování, 5 – svahovaná jáma
Výkopy pro šachty, rýhy a stavební jámy se hloubí v různých druzích zemin i hornin a s ohledem na vlastnosti základových půd a na okolní zástavbu, lze výkopy navrhnout:
- svahované;
- pažené.
1.3 SVAHOVANÉ STAVEBNÍ JÁMY
Svahované stavební jámy se navrhují tam, kde je dostatek místa pro vytvoření co nejstrmějších svahů, jež ovšem vyhovují z hlediska požadované stability. Jedná se tedy vesměs o stavební jámy dočasné, sloužící pro výstavbu suterénu stavebních objektů, popř. pro podzemní stavby hloubené (z povrchu). V městské zástavbě mají svahované stavební jámy nepatrný význam, neboť pro jejich vytvoření není většinou dostatek místa. Je však třeba vždy tuto variantu uvážit zejména proto, že bývají ekonomičtější. Relativně častý bývá případ částečně svahované jámy, kde svahování se navrhne na té straně, kde je to z hlediska prostorového možné. V případě hlubokých stavebních jam se zvažují možnosti svahovaného předvýkopu s pokračováním paženou jámou, nebo naopak paženého předvýkopu s následným svahováním. Druhý případ se používá v takových geotechnických podmínkách, kdy svrchu jsou zeminy a níže pak horniny poloskalní, či skalní, kde lze vytvořit poměrně strmé stěny zajištěné např. hřebíkováním či kotvením.
Svahované stavební jámy se navrhují jak v suchých, tak i zvodnělých zeminách a v poloskalních či skalních horninách. Ve zvodnělých zeminách je součástí návrhu i odvodnění stavebních jam, které se provádí buď povrchové, nebo hloubkové. Rozměry dna stavební jámy jsou dány potřebami budoucí stavby, tedy jejím půdorysným tvarem. Dno stavební jámy bývá však zvětšeno o šířku potřebnou jak pro vytvoření bednění, tak i pro obvodový odvodňovací rigol, který je nutný i v suché zemině pro odvod srážkové vody. Sklony svahů stavební jámy mají rozhodující vliv na kubaturu výkopů, a tudíž na cenu zemních prací. Volí se tedy co nejstrmější, a to zejména s ohledem na dobu funkce stavební jámy, roční období, klimatické vlivy a podmínky okolní zástavby. U svahů s výškou do 6 až 8 m v jednoduchých geotechnických poměrech a v suchém prostředí nebývá třeba stabilitních výpočtů a lze přibližně vycházet z tab. 1 a 2. V těchto tabulkách jsou rovněž uvedeny doporučené sklony svahů trvalých. U nich je však třeba vždy počítat s návrhem ochranných opatření z hlediska klimatických vlivů a dešťové eroze, (pokryv vhodnou geotextilií, hydroosev, vysázení vegetace a pod). Podrobněji se o tom pojednává v silničním stavitelství. U vyšších svahů, ve složitých geotechnických podmínkách a u zvodnělých svahů je třeba stabilitních výpočtů, stručně uvedených v následující kap. 1.3.1.
Při hloubení stavebních jam je třeba postupovat opatrně zejména v oblasti budoucího dna stavební jámy tak, aby nedošlo k výraznému poškození základové půdy a snížení její únosnosti. Samostatnou kapitolou je problém odvodňování stavebních jam a ochrana před prolomením dna stavební jámy. Strojní hloubení v zeminách, zejména jemnozrnných, má být ukončeno v úrovni 0,50 m nad budoucí základovou spárou a vlastní dotěžení má pokračovat ručně, nebo pomocí malé mechanizace. Důležitá je okamžitá ochrana základové spáry podkladním betonem, jehož minimální tloušťka musí činit nejméně 0,10 m, neboť požadovaná přesnost dotěžení bývá ± 50 mm. V některých případech, zvláště náročných staveb a složitých geotechnických podmínek (3. GK) se požaduje přebírka základové spáry geotechnikem. Je třeba odhalit základovou spáru pouze v tom rozsahu, který bude v jedné směně zakryt (podkladním betonem) a vzápětí bude zde vybudován vlastní základ.
Tab. 1 Stabilní sklony svahů v nezvodnělýchx) horninách a hrubozrnných zeminách
| Hornina (zemina) | Sklon svahu | |
| dočasného | trvaléhoxx) | |
| skalní horniny nezvětralé (R1, R2) | 10 : 1 | 8 : 1 |
| skalní horniny R3 nezvětralé, navětralé R1, R2 | 5 : 1 | 3 : 1 |
| poloskalní horniny nezvětralé R4, R5 | 3 : 1 | 2 : 1 |
| poloskalní horniny navětralé až zvětralé R4, R5 | 2 : 1 až 1 : 1 | 1,5 : 1 |
| balvanitý štěrk | 1 : 1 | 1 : 1,25 |
| písčitý štěrk | 1 : 1,25 | 1 : 1,5 |
| hrubý písek | 1 : 1,5 | 1 : 1,75 |
| jemný písek | 1 : 1,75 | 1 : 2 |
| x) sklon dočasného svahu v hrubozrnných zeminách s vyvěrající podzemní vodou je 2x plošší xx) v trvalých svahů bývá potřebný stabilitní výpočet a současně zvláštní opatření proti erozi |
||
Tab. 2 Stabilní sklony svahů v nezvodnělých jemnozrnných zeminách
| Zemina | Výška svahu [m] | Trvalý sklon svahux) |
| jílovitý silt | 0–3 3–6 6–9 |
1 : 1,25 1 : 1,60 1 : 1,75 |
| písčitý silt | 0–3 3–6 6–9 |
1 : 1,25 1 : 1,25 1 : 1,40 |
| jíl | 0–3 3–6 6–9 |
1 : 1,25 1 : 1,25 1 : 1,40 |
| spraš | 0–6 | 2,5 : 1,0 |
| x) u trvalých svahů je třeba navrhnout zvláštní ochranná opatření z hlediska klimatických vlivů a eroze | ||
V některých případech je požadováno položení tzv. konsolidační vrstvy tvořené hutněným štěrkem v tloušťce 0,2–0,3 m. Je ovšem nutné vždy zvážit, nezpůsobí-li se tím více škody, např. spočívá-li štěrk na jemnozrnné zemině či poloskalní hornině typu jílovců, prachovců apod., může vrstva štěrku způsobit její zvodnění, změnu konzistence a ztrátu únosnosti. V případě základové půdy tvořené hrubozrnnými zeminami lze strojně vytěžit až na základovou spáru, neboť příslušná zemina se před položením podkladního betonu upravuje hutněním, jehož míra je kontrolována příslušnými polními geotechnickými zkouškami. V těchto případech je třeba vždy uvážit typ a dosah příslušného hutnícího mechanizmu s ohledem na požadovanou kvalitu základové půdy. Zůstane-li základová spára v jemnozrnných zeminách delší dobu nezakrytá a je-li pouze pocházena, či pojížděna malou (ruční) mechanizací, měla by být před výstavbou základů odstraněna vrstva v tloušťce 0,20 m (a nahrazena např. hubeným betonem). Pokud základová spára přezimuje, (což je ovšem velká technologická závada), musí se počítat s promrznutím a s nepříznivou změnou vlastností až na hloubku 0,80 m. Zakládá-li se ve skalních horninách, jež se lámou pomocí trhavin, skončí se s touto technologií těžby na úrovni nejméně 1,0 m nad základovou spárou. Další dolamování má probíhat ručně, pomocí malé mechanizace, nebo i pomocí malých (usměrněných) náloží. Vždy však záleží na druhu skalní horniny, sklonu vrstev a charakteru puklin. Ochrana a úprava základové spáry v horninách je významná zejména v případě velkých vodních staveb, kde se základová spára důkladně zkoumá, velké trhliny se vyplňují maltou, oslabené oblasti se odtěží a plombují betonem a pukliny se injektují po provedení vodních tlakových zkoušek.
1.3.1 Posouzení stability svahovaných stavebních jam
V případě stavebních jam, (tedy i dočasných) hlubokých přes 6–8 m je třeba navržený sklon jámy posoudit stabilitním výpočtem. Přitom je třeba uvědomit si, že „přesnost“ výpočtu není zdaleka tak ovlivněna zvoleným výpočetním modelem, tedy použitou metodikou výpočtu, jako volbou vstupních, tzv. stabilitních parametrů základové půdy. Jde tedy o objemovou tíhu v přirozeném uložení γ [kN·m-3], úhel vnitřního tření φ a soudržnost c [kPa]. Stabilita svahů zářezů (tedy stavebních jam) se pochopitelně řeší v efektivních smykových parametrech (φef, cef). Stabilitní výpočet je řešením 1. mezního stavu – porušení, k němuž je třeba použít návrhové hodnoty zatížení, únosnosti a pevnosti základové půdy, a tudíž dílčí součinitele podle ČSN EN 1997-1. Ve smyslu doporučení České geotechnické společnosti je k ověření mezních stavů (STR) a (GEO) celkové stabilitu svahů vhodné použití návrhového přístupu NP3, jehož schéma je:
\begin{gathered}
(A1^*\space\text{nebo}\space A2^+)\space„+“\space M2\space„+“\space R3
\end{gathered}(1)
kde je:
A1, A2 … dílčí koeficienty pro zatížení γF podle tab. 3, přičemž A1* se použije na zatížení konstrukce, A2+ na zatížení geotechnické;
M2 … dílčí koeficienty na parametry základové půdy γM podle tab. 4;
R3 … dílčí koeficient odolnosti svahů a celkové stability podle tab. 5.
Tab. 3 Dílčí součinitelé zatížení γF nebo účinků zatížení γE
| Zatížení | Značka | Soubor | ||
| A1 | A2 | |||
| stálé | nepříznivé | γG | 1,35 | 1,0 |
| příznivé | 1,0 | 1,0 | ||
| proměnné | nepříznivé | γQ | 1,5 | 1,3 |
| příznivé | 0 | 0 | ||
Tab. 4 Dílčí součinitelé parametrů zemin γM
| Parametr zeminy | Značka | Soubor | |
| M1 | M2 | ||
| úhel vnitřního tření a) | γφ´ | 1,0 | 1,25 |
| efektivní soudržnost | γc´ | 1,0 | 1,25 |
| neodvodněná smyková pevnost | γcu | 1,0 | 1,4 |
| pevnost v prostém tlaku | γqu | 1,0 | 1,4 |
| objemová tíha | γγ | 1,0 | 1,0 |
| a) Tento součinitel se použije na tg φ´ | |||
Tab. 5 Dílčí součinitelé odolnosti γR svahů a celkové stability
| Únosnost | Značka | Soubor | ||
| R1 | R2 | R3 | ||
| odolnost základové půdy | γR;e | 1,0 | 1,1 | 1,0 |
Pro orientační výpočty obyčejně vystačíme s typickými charakteristickými velikostmi (uvedenými jakožto velikosti normové např. v ČSN EN 1997-1), které budou převedeny na velikosti návrhové podle vztahu (1) a tab. 3, 4 a 5. V případě hlubokých a náročných stavebních jam se neobejdeme bez laboratorních, či polních zkoušek a z nich odvozených vlastností základových půd.
Stabilitu svahu řešíme především metodou mezní rovnováhy, tedy řešíme rovnováhu sil podél uvažované smykové plochy, která by vznikla v okamžiku ztráty této rovnováhy. Míru stability vyjadřujeme nejčastěji stupněm stability F, který je v podstatě definován poměrem sil pasivních (jež brání vzniku sesuvu) k silám aktivním, které sesuv vyvolávají. Tvar smykových ploch, na nichž řešíme stabilitu svahu výkopu, závisí především na charakteru základové půdy. V hrubozrnných zeminách je tedy smyková plocha rovinná a z hlediska mezní rovnováhy svahu s jednotným sklonem α, je pasivní silou tření T´, jež z Coulombova zákona je dáno součinem normálové síly N a součinitele tření, jež je dán velikostí tg φef, tedy N = G · cos α a T´= N · tg φef = G · cos α · tg φef. Aktivní silou je pak složka T = G · sin α, přičemž G je v obou případech tíha jednotkového objemu zeminy, tudíž např. γ. Potom stupeň stability svahu je dán:
\begin{gathered}
F=\frac{T'}{T}=\frac{(\tg\varphi_\text{ef})}{(\tg\alpha)}
\end{gathered}(2)
Pro případy dočasných svahů lze připustit Fmin = 1,1, tudíž tg α ≤ (tg φef) / 1,1
V zeminách jemnozrnných se smyková plocha vlivem koheze zakřivuje a může mít různý tvar, přičemž nejčastěji předpokládáme smykovou plochu válcovou, jež je v řezu tvořena kruhovým obloukem. V tomto případě k silám pasivním přistoupí i soudržnost zeminy na smykové ploše. Pro vlastní posouzení stability využíváme většinou tzv. proužkovou metodu (někdy zvanou metoda Pettersonova), kdy řešíme obyčejně příčný řez, resp. tloušťku svahu 1,0 m. Statické schéma je na obr. 3. Smyková plocha je tvořena kruhovým obloukem se středem O, zemní masív nad smykovou plochou je rozdělen na svislé proužky jednotné šířky b a výšky (v těžišti proužku) h. Tíha každého proužku se na smykové ploše rozkládá do síly normálné N a tangenciální T. K pasivním silám (N · tg φef) přistupuje koheze cef, jež působí na části smykové plochy 1 · Δl. Pro stanovení stupně stability využíváme pouze momentovou podmínku rovnováhy sil na smykové ploše ke středu otáčení O, tudíž stupeň stability bude dán:
\begin{gathered}
F=\frac{M_\text{pasivních\space sil}}{M_\text{aktivních\space sil}}=\frac{(\sum N\cdot\tg\varphi_\text{ef}+c_\text{ef}\cdot\sum\Delta l\cdot0{,}8)}{\sum T}
\end{gathered}(3)
Působení koheze uvažujeme pouze na 80 % délky smykové plochy, neboť v koruně svahu mohou vznikat trhliny. Pokud se smyková plocha při patě svahu výrazně zakřivuje, mohou působit příslušné síly T obráceným směrem a přispívat tedy k bezpečnosti (ty se projeví záporným znaménkem v části jmenovatele). Zvolená smyková plocha, jež je dána středem O a poloměrem R ovšem nemusí být ta, na níž je stupeň stability F minimální. K jejímu vyhledání poslouží většinou komerčně poskytované programy, jichž je na trhu dostatek, nebo i různé dříve publikované nomogramy.
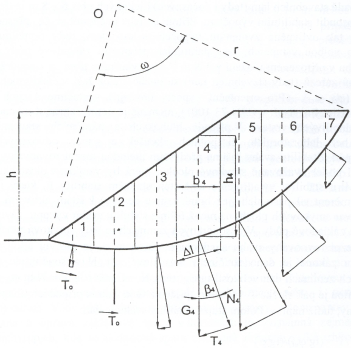
Obr. 3 Pettersonovo řešení stability suchého svahu v jemnozrnných zeminách
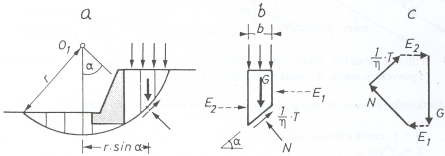
Teoreticky přesnější model poskytuje řešení podle Bishopa (obr. 4), jež uvažuje uzavřený složkový obrazec vnitřních sil na každém proužku, tzn., že počítá též s vodorovnými silami E1, E2 na styku proužků. Platí základní vztah pro stanovení pasivní síly:
\begin{gathered}
T=N\cdot\tg\varphi_\text{ef}+c_\text{ef}\cdot\Delta l
\end{gathered}(4)
Z rovnováhy svislých sil ve složkovém obrázku vyplývá, že:
\begin{gathered}
G-N\cdot \cos\alpha-\frac{1}{F}\cdot T\cdot\sin\alpha=0
\end{gathered}(5)
Po dosazení vztahu (4) do rovnice (5) můžeme psát:
\begin{gathered}
G-N\cdot\alpha-N\cdot\frac{1}{F}\cdot\sin\alpha\cdot\tg\varphi_\text{ef}-c_\text{ef}\cdot\Delta l\cdot\frac{1}{F}\cdot\sin\alpha=0,\space\text{tudíž:}\\\\
N=\frac{(G-c_\text{ef}\cdot\Delta l\cdot\frac{1}{F}\cdot\sin\alpha)}{(\frac{1}{F}\cdot\sin\alpha\cdot\tg\varphi_\text{ef}+\cos\alpha)}\\\\
T=\frac{(G\cdot\tg\varphi_\text{ef}+c_\text{ef}\cdot b)}{(\frac{1}{F}\cdot\sin\alpha\cdot\tg\varphi_\text{ef}+\cos\alpha)},\space\space\text{neboť}\space\space b=1\cdot\cos\alpha\space\text{a tudíž stupeň stability}\\\\
F=\frac{M_\text{pasivních sil}}{M_\text{aktivních sil}}=\frac{\sum T\cdot r}{\sum G\cdot a+\sum M_\text{P}}=\frac{\sum[\frac{(G\cdot\tg\varphi_\text{ef}+c_\text{ef}\cdot b)}{(\frac{1}{F}\cdot\sin\alpha\cdot\tg\varphi_\text{ef}+\cos\alpha)}]\cdot R}{(\sum G\cdot R\cdot\sin\alpha+\sum M_\text{P})}
\end{gathered}(6)
kde je:
∑MP … moment event. vnějších sil ke středu otáčení O a = r · sin α
Obr. 4 Bishopovo řešení stability suchého svahu v soudržných zeminách, a – statické schéma, b – síly na proužku, c – složkový obrazec
Tento výpočet byl různými autory, (např. Franke, Spencer) upřesňován z hlediska skutečné velikosti sil E1, E2 a jejich sklonu δ od vodorovné, vliv na stupeň stability F je ovšem minimální.
Stabilita svahu ve skalních horninách je ovlivněna především sklonem vrstev, resp. systému jejich diskontinuit a pevnostními charakteristikami horninového masívu, zejména pak těmi, jimiž je charakterizována pevnost na diskontinuitách. Nebezpečné jsou zejména svahy v sedimentárních horninách, jejichž vrstvy zapadají z hory a vrstevní spáry jsou vyplněny zeminou s pevnostními parametry φ, c. Některá řešení těchto svahů jsou uvedena v [1].
1.3.2 Filtrační stabilita svahů stavebních jam
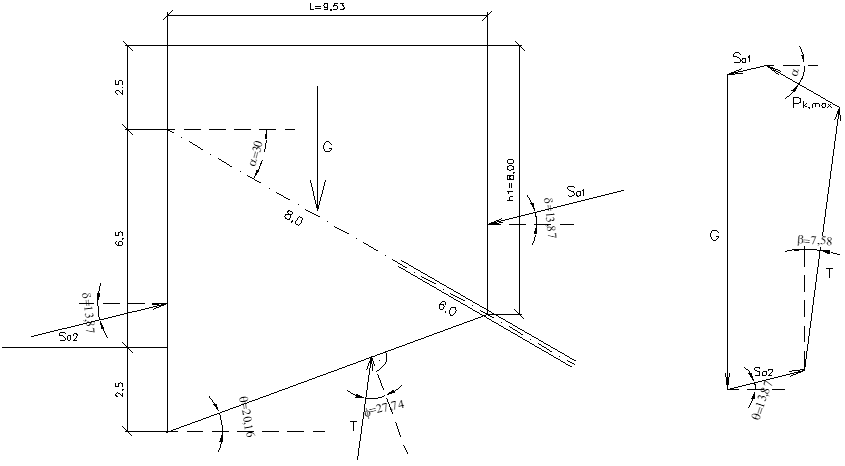
Při hloubení stavební jámy v hrubozrnné, zvodnělé zemině vytéká podzemní voda ze svahu do jámy a působí na zeminu proudovým tlakem, který může ohrozit stabilitu svahu jámy. Ve stejnozrnné zemině může dojít ke ztekucení, v zemině nestejnozrnné hrozí sufoze, tj. vyplavování jemnozrnných části ze skeletu zeminy. Aby k těmto jevům nedošlo, musí být sklony svahů přizpůsobeny a hloubení musí postupovat pomalu, resp. v součinnosti s povrchovým odvodňováním tak, aby voda stačila ze svahu vytéct a vytvořila tak proudnici, na níž je gradient přípustné velikosti. Proudí-li podzemní voda rovnoběžně se svahem, lze stanovit maximální přípustný sklon svahu α podle obr. 5. Jednotková tíha zeminy G´ pod vodou je určena velikostí objemové tíhy zeminy pod vodou γ´, kde:
\begin{gathered}
\gamma´=(1-n)\cdot(\gamma_\text{s}-\gamma_\text{w})
\end{gathered}(7)
kde je:
n … pórovitost zeminy [%];
γs … měrná tíha zrn zeminy (jež je prakticky u všech zemin stejná a činí 26,5 – 27,5 kN·m3);
γw … objemová tíha vody (10 kN·m-3).
Obr. 5 Filtrační stabilita svahu v nesoudržné zemině: a – voda proudí rovnoběžně s povrchem svahu, b – voda proudí šikmo k povrchu
Tíhu jednotkového objemu zeminy pod vodou lze potom rozložit do síly normálné:
\begin{gathered}
N=\gamma´\cdot\cos\alpha\space\text{a tangenciální}\\\\
T=\gamma´\cdot\sin\alpha
\end{gathered}Proudový tlak vody j proudící rovnoběžně svahem:
\begin{gathered}
j=\gamma_\text{w}\cdot i
\end{gathered}(8)
kde je:
i … hydraulický spád definovaný poměrem rozdílu výšek hladin Δh ku délce dráhy Δl, tudíž i = sin α. Mezní rovnováha nastane, bude-li poměr sil působících sesuv k silám způsobujícím tření roven 1, tedy:
\begin{gathered}
\frac{(N\cdot\tg\varphi_\text{ef})}{(T+j)}=1,\space\text{resp.}\space\frac{(\gamma´\cdot\cos\alpha)}{(\gamma´\cdot\sin\alpha+\gamma_\text{w}\cdot\sin\alpha)}=\tg\varphi_\text{ef},\space\text{neboli}\\\\
\tg\varphi_\text{ef}\ge(\frac{(\gamma´+\gamma_\text{w})}{\gamma´})\cdot\tg\alpha
\end{gathered}(9)
dosadíme-li přibližně γ´ ≅ 10 kN·m-3, obdržíme podmínku pro filtračně stabilní sklon svahu
\begin{gathered}
\tg\alpha\le\frac{1}{2}\cdot\tg\varphi_\text{ef},\space\text{tudíž rovněž přibližně lze psát}\space\alpha\le\frac{\varphi_\text{ef}}{2}
\end{gathered}Proudí-li podzemní voda svahem pod úhlem β < α, potom platí následující podmínka filtrační stability:
\begin{gathered}
\tg\varphi_\text{ef}\ge\frac{(\gamma´\cdot\sin\alpha+\gamma_\text{w}\cdot\sin\beta\cdot\cos(\alpha-\beta))}{(\gamma´\cdot\cos\alpha-\gamma_\text{w}\cdot\sin\beta\cdot\sin(\alpha-\beta))}
\end{gathered}(10)
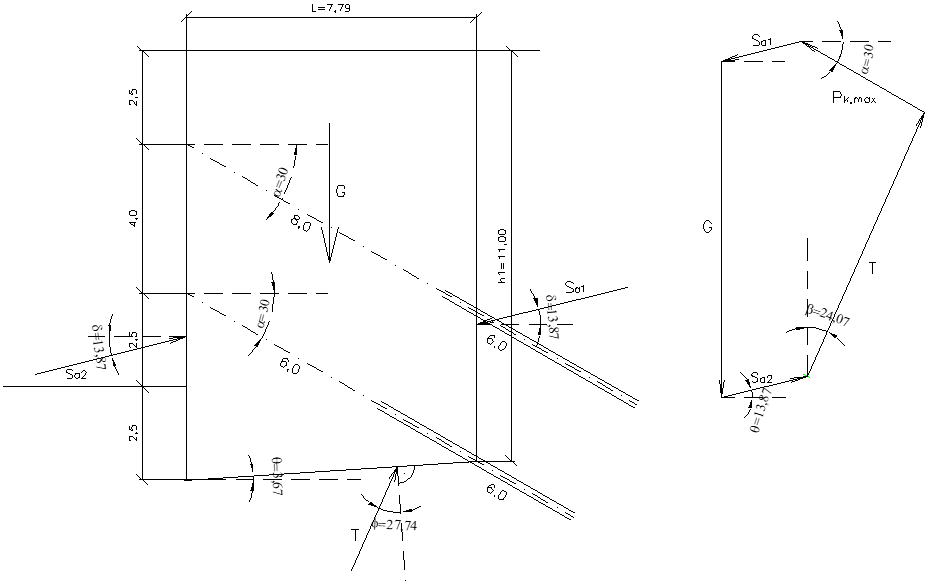
V jemnozrnné zvodnělé zemině za předpokladu válcové smykové plochy s poloměrem R a středem O bude filtrační stabilita dána vztahy podle obr. 6.
Obr. 6 Filtrační stabilita svahu ve zvodnělé soudržné zemině: a – statické schéma, b – znázornění sil působících na typický proužek zeminy, c – složkový obrázek
Ze schématu na obr. 6b vyplývají následující velikosti sil:
- tíha zeminy nad vodou
\begin{gathered}
G=\gamma\cdot h\cdot b
\end{gathered}- tíha zeminy pod vodou
\begin{gathered}
G´=\gamma\cdot h´\cdot b
\end{gathered}- tíha vody
\begin{gathered}
G_\text{w}=\gamma_\text{w}\cdot h´\cdot b
\end{gathered}- svislá složka vztlaku
\begin{gathered}
U_\text{v}=\gamma_\text{w}\cdot h´\cdot b
\end{gathered}- svislá složka normálné síly
\begin{gathered}
N_\text{v}=N\cdot\cos\alpha
\end{gathered}- svislá složka tření včetně
\begin{gathered}
\frac{F1}{F}\cdot T_\text{v}=\frac{1}{F}\cdot T\cdot\sin\alpha
\end{gathered}Ze složkového obrázku vyplývá, že:
\begin{gathered}
G+G´+G_\text{w}-U_\text{v}-N\cdot\cos\alpha-\frac{1}{F}\cdot T\cdot\sin\alpha=0
\end{gathered}po úpravě (Gw = Uv) a po dosazení do rovnice
\begin{gathered}
T=N\cdot\tg\varphi_\text{ef}+c_\text{ef}\cdot\Delta l\space\text{a}\space b=\Delta l\cdot\cos\alpha\space\text{obdržíme velikosti sil:}\\\\
N=\frac{(G+G´-c\cdot\Delta l\cdot\frac{1}{F}\cdot\sin\alpha)}{(\frac{1}{F}\cdot\sin\alpha\cdot\tg\varphi_\text{ef}+\cos\alpha)}\\\\
T=\frac{((G+G´)\cdot\tg\varphi_\text{ef}+c_\text{ef}\cdot b)}{(\frac{1}{F}\cdot\sin\alpha\cdot\tg\varphi_\text{ef}+\cos\alpha)}
\end{gathered}Stupeň stability svahu je pak dán rovnicí:
\begin{gathered}
F=\frac{\sum[\frac{((G+G´)\cdot\tg\varphi_\text{ef}+c_\text{ef}\cdot b)}{(\frac{1}{F}\cdot\sin\alpha\cdot\tg\varphi_\text{ef}+\cos\alpha)}]}{\sum[(G+G´)\cdot\sin\alpha+\sum G_\text{w}\cdot\sin\alpha]}
\end{gathered}(11)
1.3.3 Deformace dna stavební jámy
Při vyhloubení stavební jámy, (svahované, či roubené), dojde k výrazné změně napjatosti v zemním masívu, jež je způsobena především odstraněním tíhy vyhloubené zeminy, změnou režimu podzemních vod a ostatními vlivy. Změna napjatosti vyvolá deformace, které se projeví zejména zvednutím dna stavební jámy. Mechanizmus těchto deformací a jejich fyzikální podstata je zřejmá, prognóza je však problematická. Měření deformací je rovněž problematické především v důsledku obtížného stanovení nultého měření, tedy výchozí měřické základny. Mechanizmus zvedání dna je jasný za předpokladu zemního tělesa jako pružného kontinua. Tento předpoklad však pro zeminy, zvláště jemnozrnné, není zcela výstižný. V souvislosti s těžením zeminy dochází k odlehčování dna, jež by se mělo projevit okamžitou deformací způsobenou pouze smykovým napětím, tj. příčným roztažením za konstantního objemu. Následovat by mělo konsolidační zvedání způsobené okamžitou změnou napětí a jejím vlivem na pórové tlaky, kdy teoreticky dochází k sání. To je však málo pravděpodobné, a proto prognóza konsolidačního zvedání dna rovněž není výstižná. Pokud v průběhu výkopových prací dojde ke změně režimu a proudění podzemní vody, má tato skutečnost významný vliv na deformace. Snížení hladiny podzemní vody vede k zvýšení efektivního napětí, neboť pomíjí vztlak. Proto je nutné do modelu, z něhož počítáme deformace, veškeré vlivy vhodným způsobem zavést. Pro výpočet zvedání dna je zapotřebí získat representativní velikosti modulů deformace základové půdy (z triaxiálu) při vhodně modelované dráze napětí, jež odpovídá odlehčování a změnám proudového tlaku. Pro dlouhodobé prognózy, jež pro klasické stavební jámy, které jsou vzápětí zastavěny, nemají praktický význam, bylo by nutné též stanovení koeficientu konsolidace Cv získaného dlouhodobými zkouškami. Jakékoliv matematické modelování (např. MKP), nezahrnuje-li výše uvedené vstupy nemá význam, neboť není schopno postihnout skutečný mechanizmus tohoto jevu v reálném zemním prostředí.
Na straně druhé, plošné základy na dně hluboké stavební jámy sedají méně než plošné základy umístěné na povrchu. Mechanizmus je zřejmý ze statického schématu pro výpočet sedání, kdy tzv. strukturní pevnost roste s hloubkou, a tudíž hloubka deformační zóny se zmenšuje, a rovněž tak klesá velikost napětí (σz – m · σor), jež sedání plošného základu způsobuje. Počáteční nadzvednutí základu velmi rychle vymizí v souvislosti s rostoucí tíhou stavěné konstrukce, přičemž je zřejmé, že čas výstavby pracuje správným směrem.
1.4 METODY A TECHNOLOGIE PROVÁDĚNÍ PAŽICÍCH KONSTRUKCÍ
Jde o zabezpečení svislých nebo výrazně strmých stěn výkopů, které se skládá z pažení a stabilizace pažení, což může být rozepření nebo kotvení, popř. kombinace těchto metod. Jinou metodu představuje hřebíkování, jež zajišťuje svislý, či strmý svah v určitých základových půdách na základě poněkud odlišného mechanizmu.
V hrubozrnných zeminách je nutné pažit vždy, (prakticky od hloubky 0,80 m), v jemnozrnných zeminách pak od hloubky 1,50 m, rovněž tak v horninách poloskalních. Ve skalních horninách závisí potřeba pažení především na vlastnostech horninového masívu.
Stavební rýhy se paží zvláště v zástavbě, a to z titulu nedostatku místa pro svahování. Stavební šachty se paží vždy. Stavební jámy v extravilánu, zvláště hluboké s hl. přes 6–8 m se rovněž většinou paží, neboť to i v případech dostatku prostoru nebývá dražší. Je však vhodné ekonomické srovnání obou alternativ. V městské zástavbě se stavební jámy paží vždy, nicméně se většinou volí taková konstrukce, které po dobu výstavby jámy paží její stěny a následně zároveň vytváří suterénní zdi. Navíc u těchto konstrukcí přistupují často problémy s podchycováním sousedních, vesměs mělčeji založených objektů. Dalším typickým aspektem stavebních jam v městské zástavbě je snaha o co největší využití půdorysu podzemí, což vytváří tlak na návrh štíhlých pažicích konstrukcí přimknutých co nejtěsněji ke stávající zástavbě.
1.4.1 Pažení rýh
Stavební rýhy se paží pažením příložným, zátažným, nebo hnaným. Pro výstavbu hlubokých stavebních rýh, (např. pro hloubené úseky podzemních staveb), se požívá též pažení záporové, výjimečně pak i pilotové stěny. Je-li potřeba stavební rýhu těsnit, navrhují se štětové stěny, většinou dočasné.
Vodorovné příložné pažení
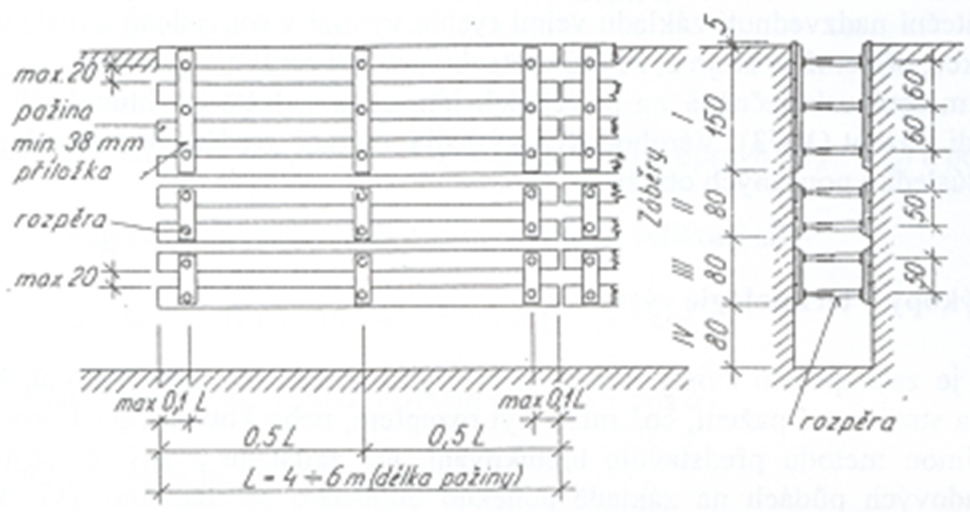
Používá se hojně pro pažení rýh kopaných ručně nebo s malou mechanizací v suché zemině, jako jsou písčité štěrky, písčité hlíny apod. Pažení podle obr. 7 se skládá:
- z vodorovných pažin, (fošny tl. 38–65 mm, výjimečně i ocelových pažiny UNION), jež jsou kladeny buď na sraz, (hrubozrnná zemina), nebo i s mezerami (jemnozrnná zemina), délka pažin je 3–5 m;
- ze svislých převázek z hranolů nebo polštářů tl. 80–100 mm, kladených ve vzdálenostech 1,5–2,5 m;
- vodorovných rozpěr z dřevěných kuláčů průměru 100–200 mm, výjimečně z ocelových trubek kladených mezi převázky ve svislých vzdálenostech do 1,0 m.
Obr. 7 Stavební rýha pažená vodorovným příložným pažením [1]
Svislé příložné pažení
Používá se v suché jemnozrnné zemině, jež umožní provést dočasný výkop bez okamžitého pažení na větší výšku, (přes 1,5 m). Toto pažení se skládá z následujících prvků (obr. 8):
- svislých pažin z fošen, popř. i ocelových pažin UNION, jež se kladou obyčejně s mezerami šířky 0,2–0,4 m, pokud možno na celou výšku vyhloubené rýhy;
- vodorovných převázek, nebo podélníků, jež mohou být tvořeny dřevěnými polštáři tl. 120–160 mm, typické jsou však ocelové z válcovaných nosníků I, nebo U kladené ve svislých vzdálenostech po 0,8–1,5 m;
- vodorovných rozpěr z ocelových trubek, (vesměs teleskopických, spojovaných na závlačky, nebo i šroubovacích).
Svislé příložné pažení stavebních rýh bývá nahrazováno komunálním pažením, jež patří k běžné výbavě stavebních firem zabývajících se zemními a vodohospodářskými pracemi. To se skládá ze dvou svisle kladených ocelových desek vyztužených rámy a spojených dvěma dvojicemi ocelových teleskopických rozpěr, které jsou buď šroubovací, nebo hydraulicky ovládané. Hloubící mechanizmus, (většinou bagr s hydraulickým pohonem), vyhloubí jistý úsek rýhy a ihned do něj osadí toto komunální pažení, které aktivuje pomocí teleskopických rozpěr. Běžné díl pažení má délku 4,0 m a výšku 1,0 nebo 1,5 m a lze jím pažit rýhu šířky do 2,5 m. Díly lze skládat i nad sebe.
Místo dřevěných pažit se používají pažiny ocelové, jež jsou u nás dodávány pod názvem UNION, (obr. 9). Jsou lisovány z plechu tl. 5 mm v délkách 2,0, 3,0 a 4,0 m. Jejich hmotnost je 12,9 kg/m, resp. 52,7 kg/m2, průřezová plocha A = 0,00672 m2/m a modul odporu W = 0,0000304 m3/m. Ze statického hlediska nahrazují tyto ocelové pažiny dřevěné fošny o tloušťce asi 60 mm.
Obr. 8 Stavební rýha roubená svislým příložným pažením [1]
Obr. 9 Ocelové pažiny UNION
Svislé zátažné pažení
Toto pažení lze použít v málo soudržných jemnozrnných i hrubozrnných nezvodnělých zeminách, jež nesnesou obnažení na větší výšku či plochu. Pažení podle obr. 10 se skládá z těchto prvků:
- svislých pažin (vesměs ocelových – UNION, výjimečně i dřevěných fošen), jež se straží již na začátku výkopu za vodorovný rám, upevňují se dřevěnými klíny a vyčnívají nad terén a s postupujícím výkopem se uvolňují (odklínují) a spustí na dno výkopu;
- vodorovných ocelových rámů z válcovaných profilů I, nebo U, kladených ve svislém směru po asi 1,5 až 2,0 m;
- vodorovných rozpěr z ocelových trubek (vesměs teleskopických, spojovaných na závlačky, nebo i šroubovacích).
Obr. 10 Svislé zátažné pažení pro roubení stavební rýhy [1]
Hnané pažení
Jedná se o nejtěžší pažení vhodné pro nesoudržné a zvodnělé základové půdy. Výstavba tohoto pažení vyžaduje značný díl ruční práce, a proto se nahrazuje dočasnými štětovými stěnami tam, kde je možné beranit, vibrovat či zatlačovat. Pro drobné stavby se však stále používá klasického hnaného pažení (obr. 11), které se skládá z následujících prvků:
- ocelových pažin, které se zatloukají mírně šikmo před postupujícím výkopem a paží jej již v době hloubení;
- příslušných dřevěných, nebo spíše ocelových rámů, jež se stavějí s postupujícím výkopem v takových svislých roztečích, které jsou umožněny délkami hnaných pažin.
Obr. 11 Hnané pažení [1]
1.4.2 Pažení šachet
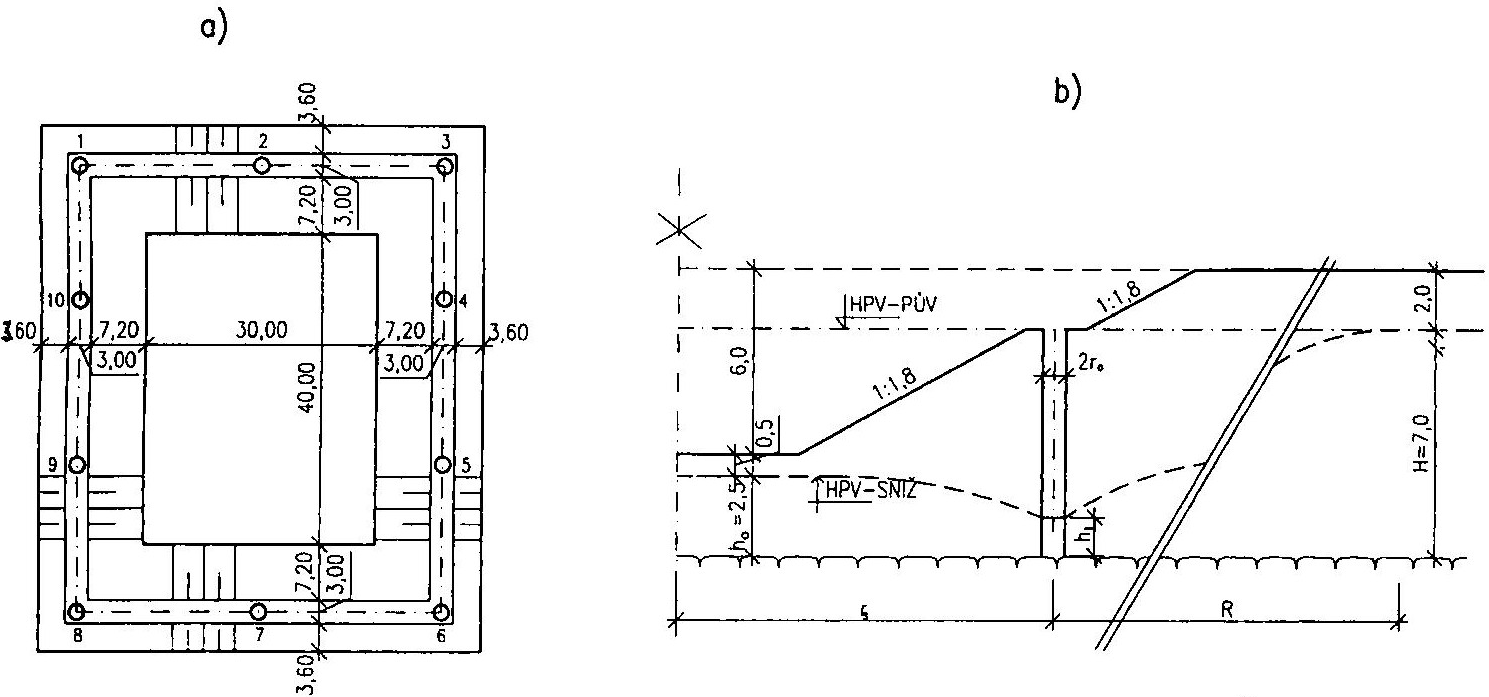
Za stavební šachtu se považuje svislé dílo půdorysné plochy přes 2,75 m2 a teoreticky neomezené hloubky. Se vzrůstající hloubkou však ve smyslu příslušných báňských předpisů přibývá požadavků na výstroj šachty a tím i na její profil. Především je třeba oddělit těžní a lezní oddělení a v případě výskytu podzemní vody vytvořit i strojní oddělení pro čerpání vody a osvětlení. Mělké stavební, jakož i průzkumné šachty min. půdorysného rozměru 1,2 x 1,8 m lze pažit jak příložným, tak i zátažným pažením. Výjimečně lze použít i pažení hnaného. V souvislosti s výstavbou ražených štol nebo i kolektorů v městské zástavbě se hloubí stavební šachty větších půdorysných rozměrů, jež slouží jak pro dopravu materiálu do raženého díla, tak i pro nasazení stavebních mechanizmů potřebných pro tyto práce. Pro pažení těchto stavebních šachet se využívá většinou záporového pažení, mikrozáporových stěn a stěn pilotových. Společným problémem těchto konstrukcí bývá požadavek na co největší světlý příčný profil umožňující spouštění dostatečně veliké vany pro dopravu rubaniny a ostatního materiálu, jakož i stavebních mechanizmů. Tento požadavek komplikuje návrh pažené konstrukce, jež vyžaduje mohutně dimenzované převázky ve formě rámů bez vnitřních rozpěr. Ty lze navrhovat většinou pouze jako rohové, jež zkrátí délku vodorovného nosníku a umožní jeho dimenzování v přijatelných mezích.
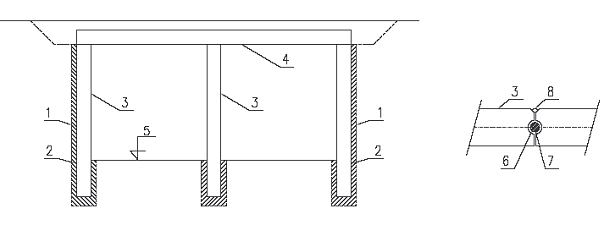
S výhodou se pro tuto výstavbu využívá kruhových šachet z převrtávaných pilotových stěn, neboť jejich namáhání je příznivé z titulu roznosu radiálního vodorovného napětí, které se přenáší jako obvodová tlaková síla do pilot. Příklad takového konstrukce je na obr. 12 a 13. Jiný příklad mikrozáporového pažení obdélníkové těžní šachty je na obr. 14 a 15 Svislé prvky jsou tvořeny ocelovými válcovanými profily HEB č. 140 vkládanými do vrtů ø 250 mm vyplněných cementovou zálivkou. Pažiny Union jsou vkládány mezi příruby těchto mikrozápor. Vodorovná rámy jsou z válcovaných profilů a v rozích jsou rozepřeny ocelovými rourami.
Obr. 12 Pažení kruhové šachty z převrtávaných pilot, půdorys
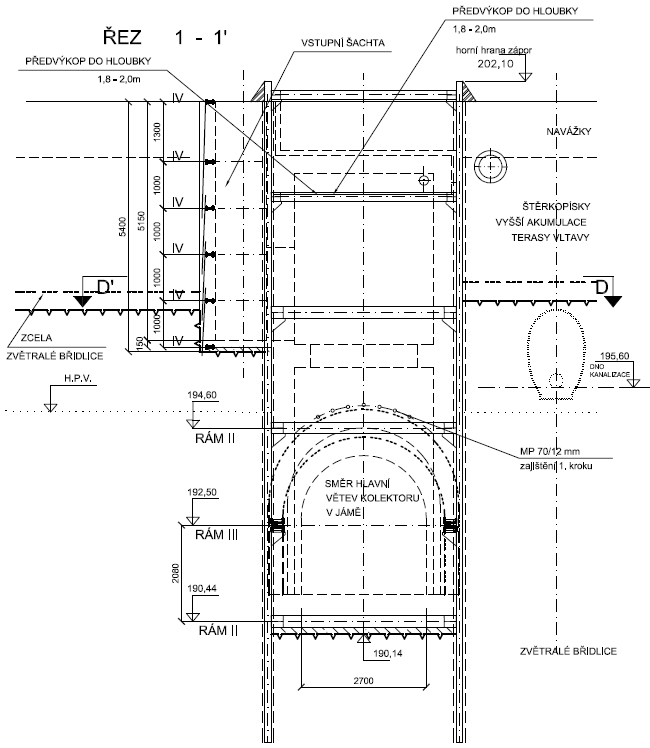
Obr. 13 Pažení kruhové šachty z převrtávaných pilot, řez
Obr. 14 Pažení obdélníkové těžní šachty pomocí rozepřených mikrozáporových stěn, půdorys
Obr. 15 Pažení obdélníkové těžní šachty pomocí rozepřených mikrozáporových stěn, řez
1.4.3 Pažení stavebních jam
Stavební jámy, zvláště v městské zástavbě, bývají vždy pažené, neboť pro svahování není dostatek místa a pozemky bývají drahé. Rovněž tak v extravilánech bývají stavební jámy, zvláště hluboké paženy, neboť to mnohdy vychází levněji a rychleji. V těchto případech je vždy na místě ekonomické srovnání. Pažení stavebních jam je buď dočasné, kdy přebírá pažicí funkci pouze do doby výstavby suterenních částí stavby a následně je buď zlikvidováno, nebo zůstane v zemi např. jako ztracené bednění, avšak ztratí svoji původní funkci, kterou přebere konstrukce suterénu stavbu. Pažení stavebních jam však může být i trvalé, kdy jednak umožní výkop stavební jámy, jednak vytvoří definitivní konstrukci suterenních obvodových zdí, jež jsou schopny trvale přenášet příslušná zatížení. Druhý způsob je z hlediska vlastního pažení dražší, neboť použité konstrukce jsou trvalého charakteru, nicméně z hlediska celkové ceny může vyjít tato konstrukce hospodárněji. Rovněž je vhodné ekonomické srovnání. Lze konstatovat, že trvalé konstrukce převládají.
Výstavba stavebních jam v městské zástavbě zahrnuje soubor specifických geotechnických problémů, na jejichž řešení se podílejí inženýrští geologové, projektanti – geotechnici a specializované firmy zabývající se speciálními metodami zakládání staveb, jež disponují osvědčenými i moderními technologiemi z tohoto oboru. Prudký rozvoj výstavby obchodních, prodejních i společenských center, jakož i podzemních garáží ve městech lze v České republice zaznamenat zvláště po roce 1990, kdy např. v Praze došlo k postupné a systematické zástavbě prakticky všech významnějších proluk a stavebních parcel v centru města. Za posledních asi 20 let bylo v Praze realizováno více než 80 stavebních jam s půdorysnou plochou 300–3 000 m2, s hloubkou od 6 do 18 m a to převážně v historické zástavbě, nebo v jejím těsném okolí. V ostatních velkých městech, jako je Brno, Ostrava, Olomouc, Plzeň, Hradec Králové apod., je tempo výstavby poněkud pomalejší. Lze ovšem předpokládat, že postupně i zde dojde k zástavbě, která vyvolá potřebu realizace hlubokých stavebních jam.
V souvislosti s návrhem a realizací stavebních jam ve městech je třeba řešit zejména následující problémy:
a) v průběhu provádění průzkumných a přípravných prací:
- svízelné získávání údajů o stávající a historické zástavbě parcely, kdy archivní výkresová dokumentace často není k dispozici, nebo je nepřesná a nevěrohodná;
- je snaha investorů omezit průzkumné práce na minimum a od prováděcí firmy se vyžaduje převzetí rizika vyplývajícího z nedostatečného geotechnického průzkumu, což je nepřípustné a zejména v poslední době se daří toto riziko přenášet na investora jakožto majitele dotčeného pozemku;
- úplná absence, nebo nedostatečné provedení stavebně – historického průzkumu, jež má za následek různá „překvapení“ v průběhu výstavby stavební jámy;
- snaha o minimalizaci pasportizace sousedních objektů, což má za následek nejasnosti v případě odpovědnosti dodavatele za eventuální následné poruchy na sousední zástavbě;
- snaha investora o maximální využití podzemních prostor na úkor tuhosti a bezpečnosti pažicí konstrukce.
b) v průběhu projektování:
- navrhovat úsporné pažicí konstrukce ve stísněných podmínkách;
- navrhovat podchytávání a zesilování stávající, vesměs cihelné, nebo smíšené zástavby mělce založené bez potřebného vodorovného ztužení;
- vyrovnat se s vlivem snižování hladiny podzemní vody na okolní zástavbu;
- vyrovnat se s vlivem vztlaku podzemní vody na podlahu suterénu;
- vyrovnat se s vlivem agresivity prostředí a podzemních vod;
- navrhovat vodotěsné pažicí konstrukce;
- navrhnout úsporný a účinný monitorovací systém pro sledování deformací stavební jámy a sousední zástavby;
- respektovat orgány ochrany památek.
c) v průběhu realizace:
- poradit si s inženýrskými sítěmi, jejichž průběh je často nejasný a jež jsou mnohdy ve špatném stavu;
- vypořádat se s vlivem dynamických účinků, (zejména vibrací), na stávající zástavbu při realizaci prací speciálního zakládání staveb;
- řešit problematiku obtížné přístupnosti stavenišť nacházejících se např. na dvorních parcelách, a to nejen pro techniku zabezpečující pažení stavebních jam, ale i pro následující zemní práce;
- vyrovnat se s častým přerušováním prací vyplývajícím např. z dodatečného archeologického průzkumu.
Návrh konstrukce pažení stavebních jam závisí především na následujících faktorech:
- na inženýrskogeologických a hydrogeologických poměrech na staveništi, jež bývají velmi pestré a vesměs složité; na pevnostních a deformačních vlastnostech základové půdy, na charakteru navážky a násypů, na eventuální existenci stávajících, nebo i předpokládaných podzemních prostor na staveništi, nebo v jeho těsné blízkosti;
- na půdorysných rozměrech stavební jámy a možnostech přístupu pro stavební stroje a mechanizmy;
- na reliéfu terénu, na hloubce stavební jámy a na hloubce základových spár sousední zástavby;
- na charakteru a stavebním stavu sousední zástavby, na stupni prozkoumanosti této zástavby;
- na velikosti využitelného prostoru pro vytvoření pažicí konstrukce;
- na požadavku na charakter této konstrukce (pouze pažicí – dočasná, nebo trvalá);
- na požadavku na vodotěsnost pažicí konstrukce, popř. požadavku na využití této konstrukce jako ztracené bednění, na požadavku na rovinnost této konstrukce využité např. jako podklad pod svislou izolaci;
- na požadavku na likvidaci pažicí konstrukce, nebo jejích prvků, (zápor, pažin, kotev);
- na požadavku na tuhost pažicí konstrukce s ohledem na její přípustné deformace a deformace vyvolané výkopem na sousední zástavbu.
V průběhu posledních cca 25 let se pro pažení stavebních jam v České republice využívá především následujících prvků a metod:
- záporové pažení (kotvené i rozepřené, zcela výjimečně volně stojící), které je typickou konstrukcí pažení dočasného. Využíváno je vesměs zápor vkládaných do vrtů a pode dnem stavební jámy zabetonovaných, (Mnichovská varianta), dále dřevěných pažin, ocelových převázek a dočasných tyčových a pramencových kotev. Výjimečně tam, kde je to proveditelné, lze zápory i beranit či vibrovat, (pažení Berlínské). Záporové pažení se u nás na rozdíl od celého světa provádí většinou bez pracovního prostoru, kdy se jeho povrch někdy opatřuje omítkou, jež slouží jako podklad pod svislou izolaci. Takto provedené pažení nelze po skončení jeho funkce likvidovat, zůstává trvale v zemi a jeho využití není ekonomické. Tam, kde je to nutné, využívá se ztracených hlav kotev, popřípadě zapuštěných převázek, jež umožní vytvoření hladkého líce pažení. Ve světě a výjimečně i u nás se záporové pažení provádí s pracovním prostorem, což umožní jeho likvidaci (kromě kotev) po skončení jeho funkce;
- podzemní stěny většinou monolitické, sloužící vesměs jako stěny konstrukční v tl. 0,40 m, 0,60 m a výjimečně i 0,80 m, kotvené dočasnými i trvalými pramencovými kotvami. Pro výrobu podzemních stěn se využívá vesměs hydraulických drapáků, výjimečně pak hydrofréz. Byly vyvinuty detaily napojení základové desky i stropů do těchto podzemních stěn, jakož i těsnění jejich pracovních spár. Největší využití podzemních stěn je při výstavbě podzemních garáží, kde se jejich povrch neopatřuje žádnou další úpravou;
- pilotové stěny volně stojící, tangenciální a převrtávané jsou rovněž konstrukcemi trvalými. Využívají se stále častěji, zvláště pak jako stěny převrtávané, neboť jsou cenově srovnatelné se stěnami podzemní a jejich bezprostřední výhodou je relativně čistá technologie provádění bez využití pažicí suspenze. Nevýhodou je pak větší možnost vzniku netěsností zvláště v komplikovaných geotechnických podmínkách;
- mikrozáporové pažení je trvalá konstrukce, která spolu se stříkaným betonem a kotvením vytváří prostorově úsporné svislé stěny stavebních jam často s hladkým povrchem, připravené pro svislou izolaci. Zvláště v zástavbě historických městských proluk se jedná o typickou pažicí konstrukci sloužící současně pro podchycení stávající, mělce založené sousední zástavby. S ohledem na dimenze použitých prvků jde však o konstrukce relativně měkké – neformovatelné a současně velice drahé, proto jejich návrh a využití je třeba vždy důkladně promyslet;
- trysková injektáž, využívaná vesměs jako konstrukce trvalá pro podchytávání stávajících stavebních konstrukcí mělčeji založených, dále pro vytváření vodotěsných stěn stavebních jam menšího rozsahu i pro těsnění dna stavebních jam. Často se prvky tryskové injektáže kombinují s mikrozáporovým pažením;
- štětové stěny, které slouží jako těsnicí konstrukce pažení v souvislosti s dlouhodobou ochranou proti podzemní vodě, např. jako součást protipovodňového opatření. Pro pažení stavebních jam se u nás prakticky nevyužívají, a to zejména s ohledem na komplikace s dynamickými účinky během jejich instalace a dále s ohledem na jejich cenu;
- hřebíkovaný svah se využívá jako dočasné pažení výkopu v nezastavěném terénu v základové půdě tvořené vesměs poloskalními horninami, popř. jemnozrnnými zeminami;
- alternativní technologie, jako je např. provádění vmíchávaných sloupů nevyztužených či vyztužených a jiné, jež mají pouze lokální význam a není zapotřebí se jimi zabývat.
Statický výpočet pažicích konstrukcí je základním nástrojem pro posouzení technické správnosti a předpokladem jejich hospodárného a současně bezpečného návrhu. Zásady statického posouzení pažicích konstrukcí jsou obsaženy v ČSN EN 1997-1, kap. 9. Vychází se z teorie mezních stavů, přičemž rozhodující je vesměs mezní stav použitelnosti, a to z hlediska přípustných deformací pažicí konstrukce a okolní zástavby. Ve vlastním statickém výpočtu se posuzují následující návrhové situace:
- vliv jednotlivých stavebních stádií výstavby stavební jámy, tj. zvláště v případě kotvených, nebo rozpíraných stavebních jam podrobný výpočet deformací pro jednotlivá stavební stádia;
- vliv eventuálního kolísání hladiny podzemní vody;
- vliv případného proudového tlaku podzemní vody;
- vliv přitížení od sousední zástavby, provozu a změny zatížení na povrchu nebo v podzemí;
- vliv přitížení základové půdy z hlediska předpětí v kotvách;
- vliv dodatečných výkopů ve stavební jámě, nebo i za rubem pažicí konstrukce.
Kromě toho je v případě konstrukcí kotvených posuzována celkové stabilita pažicí konstrukce, a to jak vnitřní, tak i vnější.
Dimenzování jednotlivých prvků pažicích konstrukcí (zápor, mikrozápor, pilot, podzemních stěn, kotev, rozpěr, převázek apod.) vychází rovněž z teorie mezních stavů, přičemž zde je rozhodující 1. mezní stv (porušení). Za účelem získání potřebných návrhových velikostí vnitřních sil pro jejich dimenzování se postupuje dvojím způsobem:
- provede se statický výpočet pro návrhové velikosti zatížení a z něj se stanoví návrhové velikosti vnitřních sil pro dimenzování;
- vychází se z velikostí vnitřních sil charakteristických vypočtených v rozhodující fázi statického výpočtu podle 2. mezního stavu (použitelnosti) a tyto charakteristické hodnoty se přibližně převedou na velikosti návrhové (vynásobením globálním součinitelem, který bývá obvykle roven 1,4).
První způsob je pochopitelně teoreticky správnější, je však pracný a z hlediska praktického s přihlédnutím na „bezpečnost“ dimenzí prvků pažicí konstrukce je přijatelný a dostatečně spolehlivý způsob druhý.
1.4.3.1 Hřebíkování
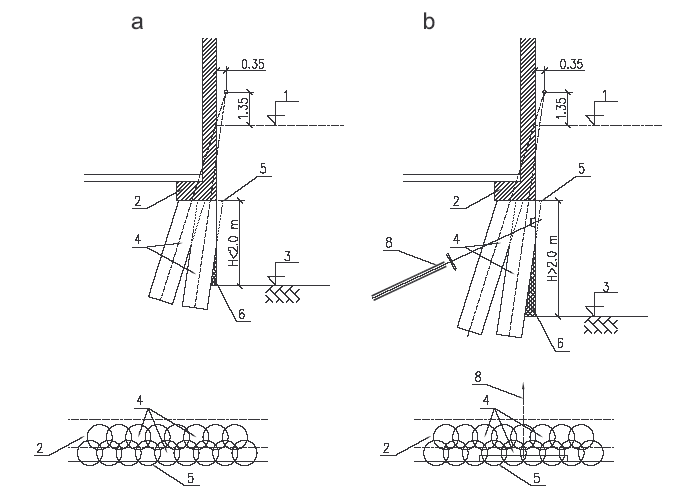
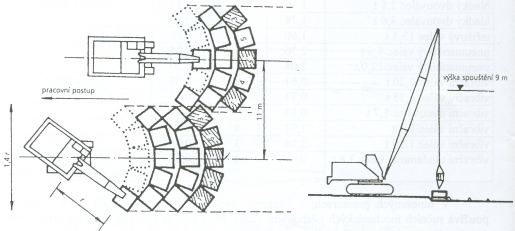
Hřebíkování základové půdy je metodou zlepšení jejích vlastností, zvláště pak smykové pevnosti pomocí kombinace jejího vyztužení a vytvoření odolného pokrytí povrchu svahu za účelem vytvoření jakési tížné kompaktní zdi, která vytvoří stabilní svah výkopu. Tato metoda byla poprvé použita ve Francii při vytvoření zárubní zdi zářezu železniční trati u Versailles v poloskalních horninách v roce 1974. V podstatě se jedná o dočasné zajištění svahu svislého, nebo strmého výkopu, neboť konstrukce hřebíků a krytu povrchu zářezu nevyhovují zejména z hlediska trvanlivosti. Metoda hřebíkování cílevědomě využívá přirozené deformace zemního tělesa po provedení výkopu či odkopu svahu k přirozenému aktivování výztužných prvků – hřebíků. Jejich aktivace, tj. vnesení síly do hřebíků spolu s omezením, resp. řízením deformací povrchu stěny pomocí krytu zvolené pevnosti účinně zabraňuje tvoření trhlin zejména v oblasti podél povrchu svahu. Aby mohly být síly do jednotlivých úrovní hřebíků účinně vneseny, musí se výstavba hřebíkovaného svahu provádět po etapách, přičemž všechny předepsané operace, (instalace hřebíků, provedení vrstvy stříkaného betonu po event. předchozím odvodnění), této technologie musí proběhnout komplexně v každé etapě, jak je znázorněno na obr. 16.
Obr. 16 Schéma pracovního postupu provádění hřebíkovaného svahu
Hřebíky se realizují většinou „mokrým procesem“, tzn., že do předem připraveného maloprofilového vrtu (průměr 90–150 mm) navržené délky a sklonu se do cementové zálivky osadí hřebík většinou z betonářské oceli (øR 20–32 mm, popř. i 2 ø R 20–25 mm). Pouze zcela výjimečně se používá kvalitnějších ocelí (např. tyčí GEWI ø 26,5 až 32 mm), neboť jsou dražší a nejsou využitelné. Mají však výhodu nalisovaných závitů, což umožní jednoduchý spoj přes plechovou podložku a matici.
Používá se cementová zálivka c : v = 2,2 : 1 jako v případě mikropilot, nebo kotev [5]. Injektáž těchto hřebíků nemá význam, naopak následná injektáž hřebíků vložených „na sucho“ do vrtů nemusí zajistit dokonalý kontakt mezi cementovou suspenzí, hřebíkem a okolní základovou půdou.
Je třeba uvědomit si, že hřebíky jsou podél celé své délky opatřeny zálivkou a na rozdíl od kotev neumožňují předepnutí, neboť nemají žádnou volnou délku, na níž by mohlo být realizováno protažení, tudíž i vnesení předpínací síly. Hřebíky tedy spolupůsobí s okolní základovou půdou podobně jako mikropiloty ve své kořenové délce – podél celého hřebíku je aktivováno smykové napětí, jehož velikost roste s deformací mezi pláštěm vrtu vyplněného cementovou maltou a okolní základovou půdou. Dostoupí-li tato deformace jisté velikosti, smykové napětí již neroste a ustálí se na jisté velikosti reziduální. Je třeba si znovu uvědomit významný rozdíl mezi hřebíkem a zemní, či horninovou kotvou, neboť zvláště v oblasti podzemního stavitelství často dochází k matení pojmů a záměně obou prvků. Hřebíky se tedy vkládají do vrtů s cementovou zálivkou bez jakékoliv úpravy jejich povrchu, tudíž z hlediska jejich životnosti se jedná o jednoduchou protikorozní ochranu výztuže, jež je přijatelná pro konstrukce dočasné (s dobou životnosti 2 roky). Zde platí jasná analogie se zemními kotvami (viz ČSN EN 1537 Provádění speciálních geotechnických prací – Horninové kotvy). Aby bylo zajištěno předepsané krytí výztuže cementovou maltou, používá se centrátorů z umělé hmoty, jež se v roztečích cca 2–3 m navlékají na výztuž. Pokud bychom uvažovali s hřebíkováním jakožto konstrukcí trvalou, musely by být hřebíky opatřeny dvojitou antikorozní ochranou, což by vesměs znamenalo jejich povlečení ohebnou vrubovanou trubkou z měkčeného PVC nebo PE se zainjektováním mezikruží vhodnou hmotou (viz vzpomenutá norma týkající se zemních kotev). Tato úprava by se však týkala pouze vlastních hřebíků a problém trvalého použití stříkaného betonu vystaveného povětrnostním vlivům by zůstal nevyřešen. Rovněž by bylo potřebné řešit nelehký problém odvodnění rubu stříkaného betonu, aby se tato konstrukce dala považovat za úpravu trvalou.
Hřebíky lze realizovat i suchou cestou, a to zvláště v poloskalních či skalních horninách, kde se využívá např. systému „split-set“, kde hřebík je tvořen podélně rozříznutou trubkou, která svojí deformací zajistí spolupůsobení s okolní zeminou. Tento způsob se ovšem používá ojediněle, neboť je drahý.
Hřebík vyčnívá z povrchu svahu na vhodnou délku a upraví se zakotvením do krytu tvořeném ze stříkaného betonu. Teoreticky lze sice provádět i hřebíky s hlavou nekotvenou, to je však nevýhodné z hlediska jejich účinnosti. Zakotvení se provádí několika způsoby, z nichž dva jsou na obr. 17 a 18.
Správný postup při zajišťování svahu výkopu hřebíkováním:
- předvýkop na 1. etáž, přičemž maximální hloubka předvýkopu se stanoví buď ze zkušeností, nebo i výpočtem;
- realizace hřebíků 1. úrovně;
- event. položení provizorního odvodnění v rubu stříkaného betonu, položení výztužné sítě a realizace stříkaného betonu na 1. etáží;
- předvýkop na 2. etáž, protažení provizorního odvodnění;
- provedení hřebíků 2. etáže;
- výztužná síť a stříkaný beton 2. etáže;
- takto se postupuje až do úrovně definitivního výkopu.
Obr. 17 Zakotvení hlavy hřebíku s přivařenou ocelovou deskou do krytu ze stříkaného betonu: 1 – hřebík, 2 – výztužná svařovaná síť, 3 – stříkaný beton, 4 – ocelová přivařená deska
Obr. 18 Zakotvení hlavy hřebíku s ohnutým koncem do krytu ze stříkaného betonu: 1 – hřebík, 2 – výztužná svařovaná síť, 3 – stříkaný beton
Zcela výjimečně lze provádět nejprve stříkané betony (s event. rubovým odvodněním) a vzápětí pak hřebíky, jejichž hlavy jsou opatřeny ocelovou roznášecí deskou, jež je k povrchu stříkaného betonu aktivována pomocí matice na hlavy hřebíku našroubované.
Odvodnění rubu stříkaného betonu lze doporučit v každém případě, zvláště u dočasných hřebíkovaných svahů, jež slouží delší dobu (samozřejmě nejvýše do 2 let). Používají se nejčastěji ohebné perforované drenážní PE, PVC trubky Js 40–80 mm, jež se pokládají do rýh ve spádnici svahu, provizorně se uchycují pomocí háků z betonářské oceli ø 6–8 mm a proti zanesení otvorů stříkaným betonem se chrání položením pásu vhodné geotextilie. Osová vzdálenost těchto odvodňovacích trubek se volí 2–4 m. Výjimečně lze pooužít i nopové fólie, její účinnost je všakl omezena následným provedením stříkaného betonu.
Je třeba znovu zdůraznit, že v případě hřebíkování musí být dodrženy všechny konstrukční zásady, jakož i správný technologický postup. Např. zcela nevhodné bývá dočasné zajištění strmých svahů v poloskalních horninách pouze stříkaným betonem, kdy cílem bývá jakási „ochrana“ před větráním hornin. Stříkaný beton se v tomto případě obyčejně zřítí, pokud se za jeho nepropustným rubem vystaví srážková, nebo puklinová voda a výsledek je horší, než kdyby svah zůstal obnažen, popř. pokryt pouze geomříží.
1.4.3.2 Záporové pažení
Záporové pažení náleží mezi nejvíce používané metody zajištění dočasných svislých výkopů stavebních jam a hlubokých rýh. Je známo již přes 100 let a v průběhu této doby zaznamenalo mnoho variant, i když princip zůstává stejný. Záporové pažení (obr. 19) se skládá z následujících prvků:
- zápor (obyčejně ocelových nosníků I, H, 2xU), což jsou svislé nosné prvky;
- pažin (většinou dřevěných hranolů, výjimečně i fošen, polštářů, kuláčů, ocelových pažin typu Union, betonových prefabrikátů a stříkaného betonu s výztužnou sítí);
- stabilizačních prvků, což jsou buď rozpěry, (šikmé i vodorovné, většinou ocelové, výjimečně dřevěné), nebo dočasné kotvy, (tyčové či pramencové);
- převázek, jež umožňují ekonomické uspořádání stabilizačních prvků, tj. rozpěr či kotev;
- dalších prvků či úprav, což může být rubové odvodnění, úprava povrchu pažení, zavětrování v ploše pažení, těsnění tohoto pažení pod hladinou podzemní vody.
Záporové pažení ve své klasické podobě je vždy konstrukce dočasná, neboť jeho životnost je právními předpisy omezena na 2 roky. To ovšem neznamená, že záporové pažení musí být vždy po skončení své životnosti odstraněno. V zásadě rozeznáváme 2 případy:
- záporové pažení s pracovním prostorem, (obr. 19a), které bývá od stavby realizované v zapažené jámě či rýze dostatečně odsazeno, (minimální pracovní prostor je 0,80 m; do něj se nepočítá případné místní zúžení např. v oblasti převázek) a po skončení své funkce bývá odstraněno, přičemž většinu jeho prvků lze použít opakovaně;
- záporové pažení bez pracovního prostoru použité jako ztracené bednění (obr. 19b), jež je tedy naopak přisazeno k rubu suterénní části stavby; zde bývá požadavek na rovinnost pažení bez jakýchkoliv výstupků tak, aby jeho povrch mohl sloužit např. jako podklad pro svislou izolaci. Toto pažení obyčejně zůstává v zemi (až na horní část, která bývá do hloubky cca 1,5 m, dodatečně odstraněna z rýhy hloubené vně již vybudované stavby).
Vlastní záporové pažení se realizuje jako:
- volně stojící (nekotvené, nerozepřené), obr. 20a, pokud jeho volná výška je dostatečně malá, (asi do 3,5–4,0 m) a pokud nehrozí nebezpečí z titulu jeho značných deformací v hlavě na okolní zástavbu;
- jednonásobně rozepřené, či kotvené (v jedné úrovni), obr. 20b, při volné výšce pažení od cca 3,5 do 7,0 m;
- vícenásobně rozepřené či kotvené (ve více úrovních), obr. 20c s ohledem na relativně malou tuhost záporového pažení se nedoporučuje kotvení či rozpírání ve více jak třech úrovních, což odpovídá volné výšce do asi 12,0 m.
Pokud je třeba pažit vyšší výkopy, doporučuje se realizace odstupňovaného pažení s bermami, kde bývají rozpěrné trámy obyčejně betonové.
Obr. 19 Schéma záporového pažení: a – pažení s pracovním prostorem, b – pažení bez pracovního prostoru: 1 – zápora, 2 – pažiny, 3 – předsazená převázka, 4 – kotva, 5 – skrytá (utopená) převázka, 6 – event. povrchová úprava pažin (omítka apod.)
Záporové pažení bylo významně využito např. při stavbě podzemní dráhy (U-Bahn a S-Bahn) v Berlíně – odtud jeho původně používaný název „Berlínské pažení“, což je překlad německého termínu „Berliner Verbau“. S ohledem na dobu výstavby, a zvláště geotechnické podmínky v Berlíně, (jemné písky a silty), byly zápory beraněny. Dřevěné pažiny byly mezi zápory klínovány dřevěnými klíny a zápory byly v rýze rozpírány ocelovými rozpěrami. Jelikož toto pažení není nepropustné, byla podzemní voda čerpána studněmi realizovanými jak v rýze, tak i vně rýhy. S ohledem na relativně strmé depresní kužele v těchto zeminách bylo čerpání úspěšné beze škod na sousední zástavbě. Na staveništích, kde beranění nebylo možné, a to jak z důvodu geotechnických poměrů, tak i dynamických účinků beranění na sousední zástavbu, byly zápory vkládány do vrtů a v části pode dnem jámy byly zabetonovány hubeným betonem, cementovou či vápennou stabilizací, popř. pouze zasypány mokrým pískem. Takto se postupně vyprofilovala tzv. Mnichovská, či Hamburská varianta tohoto pažení, jež je v geotechnických podmínkách České republiky nejvíce využívána. Jsou známy i další varianty tohoto pažení jako je Heidelberská podle patentu č. 2830264 a Essenská, ty však mají pouze omezený význam.
Zápory se navrhují obyčejně v osové vzdálenosti od 1,0 do 3,0 m, přičemž zcela nejtypičtější jsou osové vzdálenosti kolem 2,0 m. Ty lze poměrně snadno optimalizovat podle cenového kritéria. Používá se profilů I č. 300–450, IPE č. 300–450, HEB č. 240–340 a dvojice U profilů č. 260–300. V tomto případě se oba U profily obrácené k sobě stojinami ve vzdálenosti 120–200 mm spojují oboustranně navařenou pásovinou 100/10 po asi 2,0 m. Ocelové nosníky slabších průřezů se používají pro mikrozáporové pažení. V tab. 6 je přehled nejvíce používaných ocelových nosníků pro zápory.
Obr. 20 Druhy záporového pažení: a) volně stojící, b) jednonásobně kotvené, či rozepřené, c) vícenásobně kotvené či rozepřené; H – volná výška, t – vetknutí zápor pod dno jámy; 1 – zápora, 2 – pažiny, 3 – kotva, 4 – rozpěra
Zápory (s výjimkou dvojic U nosníků) lze beranit či vibrovat, a to ve vhodných základových půdách, kde je tato technologie reálná a dynamické účinky z toho vznikající jsou přijatelné jak z hlediska ochrany životního prostředí, tak i z hlediska event. vlivu na sousední objekty. Na městských staveništích se však zápory vesměs vkládají do vrtů. Jejich průměr se volí podle použitých zápor od 400 do 650 mm, nejtypičtější jsou průměry vrtů 630 mm, které umožňují jistý posun zápor při jejich osazování za účelem dosažení přesné polohy. Zápory se obyčejně osazují jeřábem, po vycentrování se opřou o dno vrtu a u jeho ústí se poloha zajistí klíny, či jiným vhodným způsobem. Vetknutá část zápor, jež by neměla být kratší než 1,5 m, (bez ohledu na statické posouzení), bývá ve vrtu stabilizována hubeným betonem (C8/10, cementovou či vápennou stabilizací). Dodržení správného technologického postupu betonáže kořenové části zápory je obtížné zvláště v případě zvodněných vrtů, kdy není dostatek místa pro použití licí roury. V těchto případech se vcelku osvědčila poněkud kuriózní metoda, při níž je do vrtu nejprve vhozen pytel cementu, dále je zapuštěna zápora a zbylá část kořenové délky je volně zasypána suchým hubeným betonem. Vrt v části nade dnem jámy se obyčejně zasype vyvrtanou zeminou bez hutnění, z níž je separována velmi hrubá frakce, (přes 60 mm).
Tab. 6 Průřezové charakteristiky ocelových nosníků používaných jako zápory
| Průřez | H [mm] | B [mm] | Hmotnost [kg/m] | A [mm2] | Ix [mm4] | Wx [mm3] | ix [mm] |
| I 300 | 300 | 125 | 54,2 | 6,91 | 98,0 | 653,0 | 119 |
| I 320 | 320 | 131 | 61,1 | 7,78 | 125,1 | 782,0 | 127 |
| I 340 | 340 | 137 | 68,1 | 8,68 | 157,0 | 923,0 | 135 |
| I 360 | 360 | 143 | 76,2 | 9,71 | 196,1 | 1 090,0 | 142 |
| I 400 | 400 | 155 | 92,6 | 11,80 | 292,1 | 1 460,0 | 157 |
| HE 240B | 240 | 240 | 83,2 | 10,6 | 113,0 | 938,0 | 103 |
| HE 260B | 260 | 260 | 93,0 | 11,8 | 149,0 | 1 150,0 | 112 |
| HE 280B | 280 | 280 | 103,0 | 13,1 | 193,0 | 1 380,0 | 121 |
| HE 300B | 300 | 300 | 117,0 | 14,9 | 252,0 | 1 680,0 | 130 |
| HE 320B | 320 | 300 | 127,0 | 16,1 | 308,0 | 1 930,0 | 138 |
| HE 340B | 340 | 300 | 134,0 | 17,1 | 367,0 | 2 160,0 | 146 |
| 2xU 260 | 260 | 901) | 75,8 | 9,66 | 96,4 | 742,0 | 99,9 |
| 2xU 300 | 300 | 1001) | 92,4 | 11,76 | 160,6 | 1 070,0 | 117,0 |
| násobitel | – | – | – | 103 | 106 | 103 | – |
| 1) šířka pouze jedné příruby | |||||||
Při hloubení výkopu je třeba, aby se zabránilo nadměrnému těžení zeminy za záporami. Po provedení výkopu na vhodnou hloubku, jež závisí především na charakteru základové půdy, se ihned osazuje výdřeva. V zásadě se vždy dřeví za příruby zápor, přičemž v horní etáži se pažiny zasouvají shora. Délka zasunutí pažiny za přírubu zápory by měla být nejméně 1/5 šířky příruby. Ihned po osazení jedné či několika málo pažin se prostor za rubem pažin zasype vhodnou zeminou, nejlépe hlinitým pískem a ručně, (palicí) se zhutní ve vrstvách tloušťky do 0,1 m. Této pracovní fázi je třeba věnovat mimořádnou pozornost, neboť významně rozhoduje o následném chování záporového pažení. V následující fázi se buď podle geometrického tvaru navrženého pažení realizují stabilizační prvky, (rozpěry, kotvy a převázky – v případě rozepřeného či kotveného pažení), nebo se pokračuje s výdřevou, (v případě pažení volně stojícího) a výdřeva pažení se provádí po příslušné stabilizaci. Výdřevu následujících fází pažení již nelze zasouvat shora, musí být ukládána z líce pažení, což znamená, že úprava délky pažin musí být prováděna na místě. Opět je krajně důležité zaplňování prostoru za rubem výdřevy vhodnou zhutněnou zeminou. Toho nelze pochopitelně docílit v případě poslední pažiny, kdy není místo pro zasýpání. V některých případech se navrhuje zaplňování rubu pažin cementovou stabilizací. Je vždy třeba snažit se o minimalizaci vzniklých „kaveren“ za rubem pažení. Výdřeva se v případě pažení s pracovním prostorem klínuje pomocí dřevěných klínů proti přírubám zápor, čímž se zemina za rubem pažení aktivuje a deformace pažicí stěny se minimalizují. Doporučuje se nakonec zajistit klíny pomocí svislých latí, jež jsou na povrch pažení přibity. Klíny se nepoužívají v případě pažení, jež slouží jako ztracené bednění. Zde bývá naopak požadavek na zcela rovný líc pažení, jehož povrch se často opatřuje i omítkou se zednickou úpravou povrchu. Pažiny v tomto případě jsou vždy hraněné (hranoly tl. 60–120 mm, výjimečně i fošny tl. nejméně 60 mm – podle statického posouzení). V ostatních případech není požadavek na rovinnost povrchu pažení až tak přísný a lze použít i nehraněné pažiny, jako jsou polštáře, či dokonce kuláče. V tomto případě je třeba správně stanovit jejich průměr, neboť minimální tloušťka výdřevy bývá ve statickém posudku udána pro obdélníkový průřez, resp. pro průřez výšky 1,0 m.
Záporové pažení je v obvyklé své formě konstrukce vodopropustná; nenavrhuje se tedy obyčejně jako konstrukce těsnicí. Tak, jak se zpřísňují požadavky na jeho rovinný a hladký líc, realizují se obyčejně pažiny hraněné, jež působením vlhkosti či podzemní vody za jeho rubem nabobtnají a pažení se stává prakticky vodotěsným, s čímž však často jeho statický návrh nepočítá. Je známo několik havárií tohoto pažení, kdy z titulu požadavku na jeho hladký líc vzniklo nakonec pažení vodotěsné, jež však pro účinky hydrostatického tlaku nebylo navrženo.
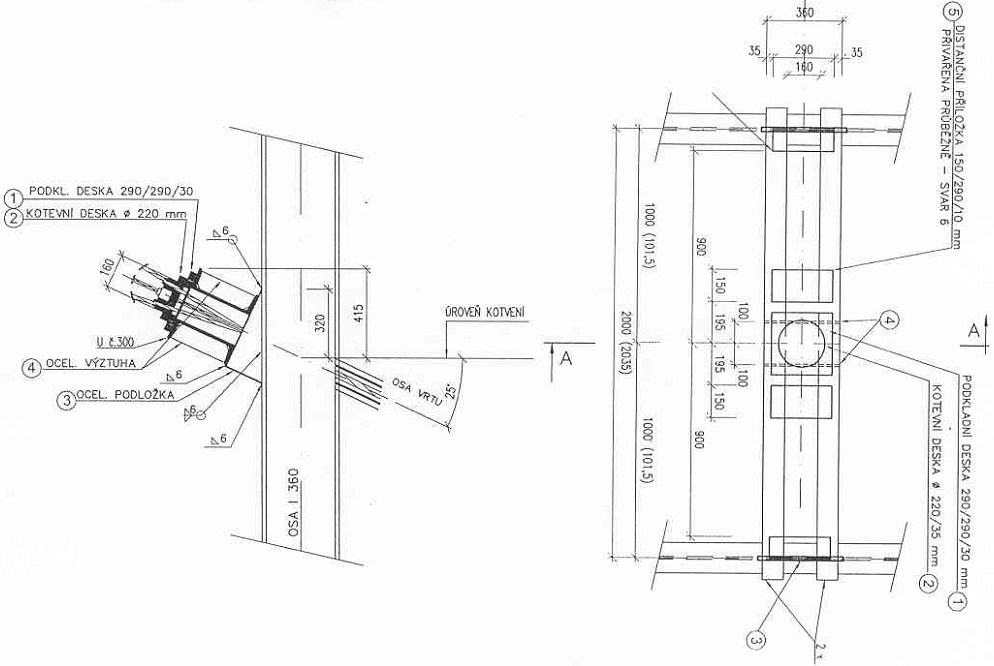
Stabilizační prvky jsou buď rozpěry, nebo kotvy. Rozpěry lze výjimečně navrhovat jako šikmé, opřené patou např. o vybudovaný základ, nebo vodorovné, kdy v nepříliš širokých jámách či rýhách jde o vzájemné rozepření. Rozpěry nebývají předepnuty, musí být však alespoň aktivovány. S tím je třeba počítat při stanovení deformací pažicí konstrukce. Nerozepírá se pochopitelně každá zápora, nýbrž se navrhují ocelové převázky a zápory se rozepírají ve větších roztečích. Typický je návrh převázek vždy ob 2 zápory a rozpěr také. Tím se vyhneme problémům při podkládání převázek z titulu jejich nepřesného osazení. To je rovněž zcela typické pro případ kotvení, jež se navrhuje v širokých stavebních jámách, kde je požadavek na volný prostor v jámě. Převázky nevadí v případě pažení s pracovním prostorem, který sice místně zužují, to však bývá přípustné. Používá se tzv. předsazených převázek obyčejně z dvojic U profilů (2x U č. 240–300), v případě potřeby i z dvojic I profilů, obr. 21. Převázky se vhodně natáčejí podle sklonu kotvy, či rozepření a osazují se na kozlíky z plechu tl. 10–20 mm přivařených k záporám.
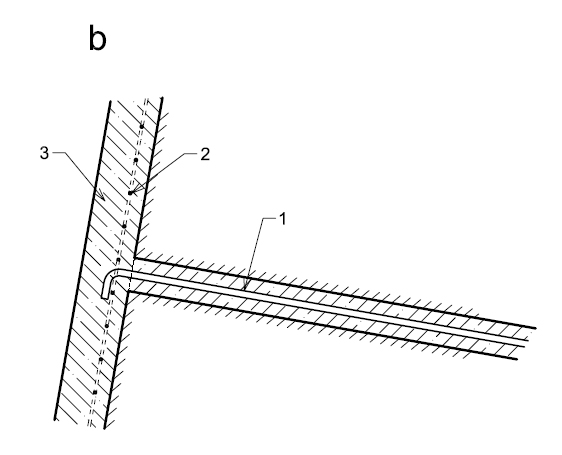
Obr. 21 Detail předsazené kotevní převázky
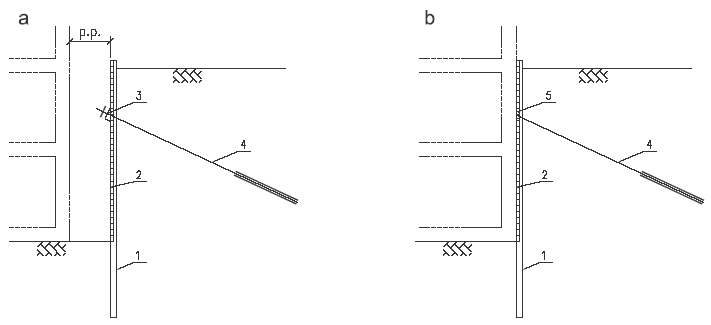
V případě záporového pažení bez pracovního prostoru nebývá návrh předsazených převázek přijatelný, pokud se nepodaří umístit je vhodně tak, aby postupně budovaná stavba převzala vodorovné síly pomocí příslušných stropů a převázky mohly být, (postupně od spodu likvidovány po deaktivaci kotev). To však bývá pouze výjimečně možné a nezbývá, než použit jiné řešení:
- zápory z dvojic U profilů, kde lze kotvy umístit mezi stojiny a hlavy kotev „zapustit“ tak, aby nevyčnívaly, znamená to však pochopitelně kotvit každou záporu, obr. 22;
- navrhnout tzv. „zapuštěné převázky“ umístěné mezi stojiny zápor, jež se však obtížně montují. Někdy se používá zesílených profilů Larsen IIIn, obr. 23.
Obr. 22 Kotvení zápor tvořených dvojicí U – profilů
Obr. 23 Detail zapuštěné (ztracené) převázky ze zesíleného profilu Larssen
Záporové pažení s pracovním prostorem lze po skončení své funkce zlikvidovat. Pracovní postup je následující:
- po položení obvodové drenáže mezi stavbou a pažením se vyrabují pažiny ode dna stavební jámy na výšku kolem 1,0 m a prostor mezi stavbou a základovou půdou se zasype vhodnou zeminou, která se po vrstvách hutní;
- takto se postupuje až k úrovni převázky, popř. až k povrchu pažení;
- pokud je pažení kotvené přes převázku, kotva se deaktivuje a převázka se demontuje a vytáhne, (kotva se v základové půdě ponechá);
- po likvidaci všech pažin a zásypu rýhy na celou výšku se zápory vytáhnou; používá se při tom speciálního zařízení na principu obráceného beranu, kterým se zápora uvolní a povytáhne, návazně se použije mobilního jeřábu.
V některých případech vzniká problém s „ponechanými“ kotvami v základové půdě. Jde vesměs o problém umělý, nemající nic společného s technickou stránkou věci, neboť dočasné kotvy v zemi nepředstavují prakticky žádnou překážku i pro následnou výstavbu. V některých případech je uplatňován požadavek na zákaz dočasných kotev, přičemž tento požadavek má za cíl zejména zabránit nežádoucí výstavbě navrhované stavební jámy.
1.4.3.3 Mikrozáporové stěny
Mikrozáporové stěny představují určitou alternativu k záporovému pažení. Mikrozáporové, nebo též Janovské stěny se navrhují tam, kde z jakýchkoliv důvodů není dostatek místa a prostoru pro klasické pažení záporové, které je vždy levnější. Jde tedy v prvé řadě o stísněné prostory, kde není dostatek šířky pro jiný druh pažení, nebo kam nemohou potřebné stavební mechanizmy zajet, (úzké dvorní proluky, sklepy apod.). V druhé řadě jde o staveniště, kde provádění klasických zápor, (ražených, či vkládaných do velkoprůměrových vrtů) není možné např. z titulu nevrtatelných překážek v navážkách a podobně. Tyto stěny na rozdíl od stěn záporových vždy zůstávají v zemi a provádějí se většinou jako konstrukce bez pracovního prostoru, tj. jako ztracené bednění. Přesto se však téměř vždy jedná o konstrukce dočasné, které nejsou určeny pro trvalý přenos příslušných zatížení, a to jednak z důvodů své nedostatečné trvanlivosti, (ohrožení tenkých ocelových prvků korozí), jednak z důvodů malé ohybové tuhosti. Skládají se z následujících prvků:
- mikrozápor, což jsou buď ocelové trouby, (profilu např. 108/16–191/10 mm), nebo profily HEB (např. HE 100 B až HE 160 B), přičemž mikrozápory se vesměs vkládají do maloprofilových vrtů realizovaných jako bezjádrové, jež jsou opatřeny cementovou zálivkou, popř. i cementovou maltou;
- pažin, které jsou výjimečně tvořeny fošnami tl. nejméně 40 mm, spíše pak ocelovými pažinami typu UNION, nebo stříkaným betonem s výztužnou sítí – to zvláště v případě výkopů v poloskalních a event. skalních horninách;
- rozpěrného, nebo kotevního systému sestávajícího z převázek a dočasných tyčových, či pramencových kotev;
- dočasného rubového odvodnění stříkaného betonu, podobně, jako v případě hřebíkovaných svahů.
Mikrozáporové stěny, (obr. 24) jsou konstrukce poměrně měkké – deformovatelné a s tím je třeba počítat při jejich návrhu. Mikrozápory se navrhují v osových vzdálenostech od 0,6 do 1,5 m a lze je umístit v minimální vzdálenosti (např. 0,20–0,30 m) od stávající konstrukce. Je-li dostatek místa, (hlavně výšky) ukládají se mikrozápory do vrtů vyplněných zálivkou nebo maltou vcelku. Potom lze s výhodou využít válcovaných profilů, které jsou ekonomičtější. Není-li dostatek místa, musí se mikrozápory spojovat. V tom případě jsou nejvhodnější ocelové trouby, které se spojují např. přes závitovaný spojník. Trubky však představují profil nejméně vhodný pro ohybová zatížení a s tím je třeba při jejich návrhu počítat.
S ohledem na malou tuhost mikrozáporových stěn stoupá potřeba jejich podepření, které je dáno především kotvením. Kotví se vždy přes převázky, jež bývají většinou ocelové. Tyto převázky představují značný problém při dodržení požadavku na hladký líc pažení. Využívá se často profilů Larsen, které lze „zapustit“ do mikrozápor HEB 160, do menších válcovaných profilů, avšak do ocelových trub nikoliv. Předsazené převázky znamenají pak vždy nutnost rozšíření tohoto pažení nejméně o 150–200 mm. Výjimečně se využívá železobetonových převázek, a to hlavně ve formě hlavových trámů.
Obr. 24 Schéma mikrozáporového pažení: a – charakteristický řez, b – půdorys – trubní mikrozápory, c – půdorys – mikrozápory HEB; 1 – vrt vyplněný cementovou zálivkou, 2 – mikrozápora, 3 – převázka (např. Larssen), 4 – kotva, 5 – stříkaný beton, 6 – pažiny (např. UNION)
Dočasné kotvy se volí jak tyčové, (Dywidag ø 26,5 mm, 32 mm), tak i pramencové (2xLpp, 3xLpp). Častá potřeba kotvení mikrozáporových stěn po jejich výšce tyto konstrukce jednak zdražuje, jednak prodlužuje dobu jejich výstavby, neboť je třeba počítat s technologickými přestávkami na tuhnutí zálivky a injektáže apod. Výjimečně lze v poloskalních a skalních horninách používat ocelových hřebíků, které nejsou předpjaté. To je však třeba příslušně zohlednit ve statickém výpočtu.
Pro mikrozáporové stěny je typické použití vyztuženého stříkaného betonu za účelem pažení mezi jednotlivými záporami. To se navrhuje vždy v případě poloskalních a skalních hornin a jemnozrnných zemin pevné konzistence. V hrubozrnných zeminách a navážkách je však použití stříkaného betonu riskantní, nebo zcela nemožné, a to z titulu možnosti náhlého kolapsu výkopu nebo potřeby zřizování malých hloubkových záběrů. Využívá se tedy klasických pažin, a to buď ve formě fošen min. tlustých 40 mm, nebo spíše ocelových pažin UNION, které jsou z hlediska své ohybové únosnosti rovnocenné s dřevěnými fošnami tl. 60 mm. V případě mikrozápor tvořených ocelovými troubami se využívá úhelníků přivařených k trubce tak, aby bylo možné osadit pažiny.
1.4.3.4 Pilotové stěny
Pilotové stěny představují vesměs trvalou pažicí konstrukci, nebo konstrukci zárubních zdí. Jsou tvořeny zpravidla jednou řadou pravidelně, výjimečně i nepravidelně rozmístěných vrtaných pilot, jež jsou namáhány na ohyb, resp. mimostředný tlak. Přesto, že kruhový železobetonový průřez je nejméně výhodným tvarem pro ohybové namáhání, je rozšíření pilotových stěn značné. To je dáno především těmito důvody:
- vrtání je poměrně progresivní a účinná technologie;
- jsou k dispozici výkonné stroje;
- vrty se paží vesměs ocelovými, (spojovatelnými) pažnicemi, přičemž odpadá problém s pažicí suspenzí, jejím čištěním, transportem, skladováním a likvidací;
- pilotové stěny lze velmi dobře tvarově přizpůsobit požadavkům stavby.
Pilotové stěny v mnoha případech plní dvojí účel (např. pažicí a konstrukční, nebo konstrukční a sanační), což je dáno tou skutečností, že se jedná vesměs o konstrukce trvalé. Pilotové stěny se konstruují pouze z pilot typu „replacement“, tj. z pilot vrtaných, ostatní typy pilot, (displacement) se pro tyto konstrukce nehodí. V závislosti na vzájemné osové vzdálenosti pilot a s ohledem na jejich průměr d rozeznáváme:
- pilotové stěny s velkou osovou vzdáleností pilot (a > d), obr. 25a;
- pilotové stěny tangenciální (a ~ d), obr. 25b;
- pilotové stěny převrtávané (a < d), obr. 25c.
Obr. 25 Příklady pilotových stěn: a – s velkou osovou vzdáleností pilot, b – tangenciální pilotová stěna, c – převrtávaná pilotová stěna, p – primární pilota, s – sekundární pilota, 1 – stříkaný beton, 2 – odvodnění
Podle volné výšky rozeznáváme pilotové stěny:
- volně stojící (nekotvené, nerozepřené);
- kotvené (výjimečně i rozepřené) v jedné, či více úrovních.
Provádění pilotových stěn, jakož i kontrola a supervize nad jejich prováděním se řídí ustanovením evropské normy ČSN EN 1536+A1 Provádění speciálních geotechnických prací – Vrtané piloty.
Volně stojící pilotové stěny lze navrhovat pro volnou výšku H < 5–6 m, přičemž pochopitelně s rostoucí výškou H roste jak vodorovná deformace těchto stěn, tak i požadavek na hloubku jejich vetknutí pode dno výkopu. Pro větší volné výšky se pilotové stěny kotví.
Pilotové stěny s velkou osovou vzdáleností pilot jsou typickou trvalou konstrukcí zárubních zdí v případě silničních a železničních odřezů nebo rýh v soudržných zeminách, nebo i poloskalních horninách. Mezery mezi pilotami, jež se volí v šířce (0,5 – 1,0) · d, výjimečně i větší, jsou vyplněny plochými klenbičkami z vyztuženého stříkaného betonu s odvodněním jeho rubu. To se realizuje pomocí perforovaných ohebných PE hadic. Pro jejich kotvení se využívá vesměs železobetonových převázek, a to jak hlavových, (trám v hlavách pilot), tak i předsazených (v jedné, či více úrovních pod hlavami pilot). Převázky jsou vždy průběžné, nicméně dilatované na úseky délky asi do 20 m. Výhodou těchto převázek je jejich značná a volitelná tuhost, jež dovolí šetřit na kotvách, nevýhodou relativně komplikovaná stavba a zdržení z titulu jejich zrání). Hlavové převázky jsou s pilotami spojeny výztuží vyčnívající z hlav pilot, předsazené převázky je třeba s pilotami řádně spojit (obr. 26). Kotvy bývají v obou případech umístěny v nikách vytvořených v převázkách s kontaktní plochou kolmou na směr a sklon kotev. Takto navrhované pilotové stěny se buď ponechávají v popsaném tvaru, nebo se opatřují pohledovou konstrukcí budovanou většinou z žb. prefabrikátů, nebo i umělých hmot.
Obr. 26 Pilotová stěna s velkou osovou vzdáleností pilot využitá jako zárubní zeď s obkladem
Tangenciální pilotové stěny se navrhují zřídka. Jejich hlavní výhodou je ta skutečnost, že není třeba budovat předsazené převázky, neboť kotvy lze umístit do mezer vždy mezi dvojice pilot. Pochopitelně každá pilota je vyztužená a stěna není vodotěsná. Lze ji opatřit povrchovou úpravou např. ze stříkaného betonu.
Převrtávané pilotové stěny představují velice rozšířenou konstrukci průběžných (vodotěsných) stěn, jež značně konkurují průběžným stěnám podzemním, a to zvláště z toho důvodu, že při jejich výrobě odpadá nutnost pažení pomocí pažicí suspenze. Stěna se skládá z pilot primárních, jež se realizují s jistým časovým předstihem a vyplněny jsou prostým (nevyztuženým) betonem. Tyto primární piloty nejsou nosné z hlediska ohybových namáhání a nemusí zasahovat na vypočtenou hloubku pod dno stavební jámy. Jejich hlavní funkcí je těsnění, resp. pomoc při vytvoření souvislé stěny. Po jisté časové prodlevě, je-li beton primárních pilot již tuhý (nikoliv však tvrdý), tedy, je-li pevnost betonu dostatečná, nikoliv však taková, aby tvořila překážku pro převrtání, přistupuje se k realizaci pilot sekundárních.
Výsledná osová vzdálenost převrtávaných pilot a v řadě závisí na jejich průměru d, volné výšce stěny H a na geotechnických poměrech na staveništi a bývá kolem 0,8 · d. Tak např. pro vrtané piloty ø 630 mm je typická vzdálenost a = 500 mm, pro d = 750 mm pak a = 600 mm a pro d = 880 mm a = 700 – 740 mm. Sekundární piloty jsou nosné, železobetonové a jsou vetknuty na vypočtenou délku pode dno stavební jámy nebo výkopu. Při provádění převrtávané pilotové stěny je třeba dodržet polohu i svislost pilot tak, aby výsledná stěna byla souvislá. Za tím účelem se na úrovni pracovní plošiny připraví šablona pro piloty, jež nahrazuje vodící zídky v případě podzemních stěn, její zhotovení je však komplikovanější. Vodící šablona by měla mít výšku nejméně 0,80 m a měla by co nejvěrněji kopírovat půdorys převrtávaných pilot. Do připravené rýhy šířky větší o cca 0,5–0,6 m, než je průměr pilot se přesně osadí svařenec z ocelových trub a segmentů, které se potáhnou pryží tl. 10 mm. Průměr otvorů je o 20 mm větší, než je průměr příslušné pažnice při provádění pilot. Takto připravená šablona se obetonuje betonem kvality nejméně C16/20, popř. se do boků vloží výztuž ve formě svařované sítě (obr. 27). Obyčejně se šablona připravuje z 5 ks trub, resp. segmentů a používá se opakovaně. Po zatvrdnutí betonu šablony se provádí vrty pro piloty, které se vrtají pomocí spojovatelé pažnice, jež se do zeminy rotuje buď pomocí teleskopu, nebo i pomocí dopažovacího zařízení. Z pažnic se zemina vybírá příslušným nástrojem (šapou, spirálem), přičemž se pata pažnice nepodvrtává. Tuhost spojovatelných pažnic (tl. 40 mm) zajišťuje spolu s vodící šablonou polohu i svislost jednotlivých pilot s pilotové stěny jako celku. Jedná se však o práci náročnou jak na technologii provádění, tak i na organizaci, neboť beton primárních pilot tuhne a tvrdne bez ohledu na event. překážky a přerušení, což může vést ke komplikacím.
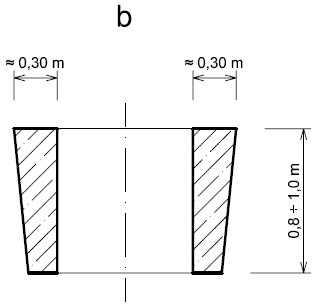
Obr. 27 Vodící šablona pro převrtávanou pilotovou stěnu, půdorys a řez
Pokud je třeba převrtávanou pilotovou stěnu kotvit, využívá se k tomu primárních pilot, skrz něž se provádějí vrty pro kotvy a do nichž se přímo osazují kotevní hlavy. Výhodou je, že odpadnou převázky, nevýhodou pak jasně stanovený počet kotev, které nemusí být ekonomicky využité.
Převrtávané pilotové stěny se všeobecně považují za konstrukce vodotěsné, jež jsou schopny být namáhány hydrostatickým tlakem. Pokud jsou piloty vetknuty do nepropustného podloží, lze tuto pilotovou stěnu považovat za těsnicí konstrukci. Převrtávané pilotové stěny se kromě běžného využití ve formě trvalých konstrukcí suterénu staveb různých půdorysných tvarů využívají s výhodou pro vytváření trvalého pažení kruhových šachet. Pomocí převrtávaných pilot lze vytvořit prakticky dokonalý kruh o průměru i kolem 5–6 m, což je zcela minimální průměr např. pro těžní šachty kolektorů apod. Statická výhoda je jasná – radiální vodorovné napětí p v hloubce z vyvolá pouze normálovou sílu v pilotách (N = p · R, kde R je poloměr kruhové šachty) a není třeba zvláštních podpor. Je ovšem nutné kontrolovat velikost tlaku v betonu pilot tak, aby nedošlo k příčným tahům v betonu primárních (nevyztužených) pilot, a to s ohledem na velikost kontaktní plochy převrtané pilot při zohlednění tolerancí ve sklonu pilot a jejich půdorysném umístění. Z převrtaných pilotových stěn byly realizovány i šachty eliptického průřezu. V těchto případech ovšem vznikají již v rovinných řezech ohybové momenty, na něž je třeba průřezy navrhnout a posoudit. V některých případech postačí vnitřní ostění z vyztuženého stříkaného betonu, jindy se nevyhneme návrhu železobetonových rámů. Na obr. 28 je příklad takovéto šachty nekruhového půdorysu, kdy tento tvar vznikl v důsledku stísněných podmínek v poloze inženýrských sítí. Při realizaci byla využita tzv. observační metoda návrhu a pomocí geotechnického monitoringu byly sledovány deformace pilotové stěny. V případě, že by tyto deformace přestoupily přípustné velikosti, byl připraven návrh provedení příslušného železobetonového rámu, jež by pilotovou stěnu vyztužil. Monitoring ovšem prokázal, že skutečně naměřené deformace byly prakticky nulové a eliptický tvar převrtávané pilotové stěny mohl zůstat bez vyztužení pomocí převázek.
Obr. 28 Příklad eliptické šachty v převrtávaných pilotových stěnách: a – půdorys šachty, b – řez šachtou
V 80. letech minulého století byly v Německu vyvinuty vrtné soupravy pro realizaci pilot VDW (německá zkratka „vor der Wand“ – před stěnou). Vrtné soupravy umožňují přisunout osu pilot velmi těsně ke stávající (nadzemní) stěně, tj. na vzdálenost až 300 mm, zatímco klasické vrtné soupravu z titulu konstrukce hydromotoru mají tuto vzdálenost nejméně 650 mm. Tak lze provádět převrtávané pilotové stěny např. z pažených pilot ø 420 mm (v osových vzdálenostech pilot cca 350 mm), jež umožňují zvětšit prostor ve stavební jámě prováděné např. v městské proluce na maximum. Jedná se ovšem o relativně měkké piloty velmi náchylné na přesnost provádění, kde i jejich vodotěsnost je silně ohrožena.
1.4.3.5 Podzemní stěny
Podzemní, nebo též Milánské stěny jsou liniové konstrukce trvalého zajištění vesměs svislých výkopů stavebních jam a rýh. Z hlediska účelu se dělí na podzemní stěny:
- těsnicí;
- pažicí;
- konstrukční.
Těsnicí podzemní stěny byly prvními, které byly realizovány již kolem roku 1950. Mají vytvořit souvislou stěnu zabraňující průsaku vody pod vodním dílem, přítoku vody do stavební jámy a infiltraci vody z řeky na přilehlé území. Často se využívají při ochraně životního prostředí, kde zabraňují kontaminaci do širšího okolí, a to v případě různých (chemických) skládek, na území chemických provozů, letišť, skladů pohonných hmot apod. Výplň těsnicích podzemních stěn je tvořena materiálem, jež je především dostatečně vodotěsný, jde tedy vesměs o jílocementovou suspenzi různého složení, výjimečně i o prostý beton. Tyto stěny nejsou obnažené, tudíž nejsou namáhány ohybem a požadavek na pevnost výplně není významný. Zhusta se k jejich výrobě používá tzv. samotvrdnoucí suspenze, která plní dvojí účel:
- v průběhu těžby paží rýhu;
- následně v rýze zůstává a po čase ztuhne a získá požadované vlastnosti, což je především vodotěsnost daná příslušnou velikostí koeficientu filtrace k [m·s-1] a též příslušná velikost pevnosti (v prostém tlaku) σf [MPa].
Vlastní receptura pažicí a těsnicí suspenze bývá „know-how“ zhotovitele, je však na bázi bentonitu, cementu a plnidel, popř. popílků a vysokopecní strusky. V některých případech se vyžaduje jistá odolnost proti chemickým polutantům, což znamená použití speciálních přísad, (např. mletých zeolitů a pod). Schématický technologický postup výroby těsnicí podzemní stěny je na obr. 29.
Podzemní stěny navržené čistě k pažicím účelům (jako dočasné) se dnes již prakticky nepoužívají, neboť jejich železobetonová výplň je schopna i dlouhodobě odolávat vnějšímu zatížení. Proto se v současné době využívá železobetonových podzemních stěn konstrukčních, jež rovněž plní dvojí účel:
- v průběhu výstavby stavební jámy či rýhy paží její svislé stěny;
- vytvářejí zároveň definitivní obvodové stěny suterénu, a to často bez jakékoliv významné úpravy dané např. přibetonováním.
Obr. 29 Postup výroby těsnicí podzemní stěny, (převzato z podkladu firmy Soletanche)
Železobetonové (betonové) podzemní stěny konstrukční se podle charakteru výplně dělí dále na:
- monolitické, na místě betonované, kde výplň tvoří transportbeton, kterým se betonuje vesměs pod pažicí suspenzi;
- prefabrikované, kde jejich výplň tvoří napřed vyrobené železobetonové prefabrikáty, jež jsou osazovány do rýh vyplněných většinou samotvrdnoucí suspenzí.
Monolitické podzemní stěny převažují, neboť jsou levnější a rychlejší. Jistou nevýhodou je samozřejmě nerovný povrch po odtěžení, neboť se v podstatě jedná o odlitek rýhy vytvořené v základové půdě. Proto se v případě konstrukčních podzemních stěn vyžaduje často úprava jejich povrchu, která se provádí buď frézováním, (pomocí speciálních rotačních fréz), nebo naopak stříkaným betonem, resp. kombinací obou technologií. Podzemní stěny představují vodotěsné konstrukce schopné odolávat hydrostatickému tlaku. Za tím účelem se jednotlivé lamely podzemních stěn navzájem těsní pomocí umělohmotného těsnění (tzv. „water-stop“), která se osazují do koutových pažnic, a to buď v jedné, či dvou vrstvách. V současné době se pro výrobu podzemních stěn využívá v podstatě následujících technologií daných využitím příslušných strojních zařízení:
- hydraulické drapáky (vedené, resp. i řiditelné);
- hydrofrézy.
Provádění podzemních stěn, jakož i kontrola nad prováděním a příslušná supervize jsou stanoveny evropskou normou ČSN EN 1538+A1 Provádění speciálních geotechnických prací – Podzemní stěny. Tvar a pojmenování lamely podzemní stěny je na obr. 30.
Obr. 30 Lamela podzemní stěny: 1– tloušťka stěny, 2 – vodorovná délka stěny, 3 – šířka armokoše, 4 – délka lamely, 5 – úroveň pracovní plošiny, 6 – úroveň betonáže, 7– vodící zídky, 8 – konečná úroveň čistého betonu, 9 – délka armokoše, 10 – armokoš, 11 – hloubka těžby, 12 – zaoblení styčných spar, (lanové drapáky)
Stručný technologický postup provádění:
- přípravné práce, jež spočívají ve vytvoření dostatečně únosné pracovní plošiny a vodících zídek, jež jsou betonové, oboustranné, obyčejně slabě vyztužené svařovanými sítěmi, jejich hloubka je nejméně 0,80 m, typicky pak 1,0–1,5 m a tloušťka 0,2–0,3 m. Vnitřní světlost je o 50–100 mm větší, než je šířka příslušného drapáku či frézy. Takto provedené zídky se na určitou vzdálenost zahradí a napustí pažicí suspenzí, v ostatních místech se buď rozepřou kulatinou, či zasypou zeminou;
- zahájí se těžba; typické tloušťky podzemních stěn jsou 400, 600, 800 a 1000 mm. V případě hydraulických drapáků je jejich délka 2,50–2,80 m a hloubí se lamely buď jednozáběrové, (stále primární), nebo trojzáběrové, (2 primární a jedna sekundární, jež vždy odstraní hrázku vytvořenou po hloubení dvou jednozáběrových lamel);
- po vyhloubení příslušné lamely se rýha vyčistí od napadané zeminy a zkontroluje se kvalita pažicí suspenze, zvláště její písčitost [5]. Osadí se koutové pažnice. Ty jsou výjimečně tvořeny ocelovými troubami příslušného průměru, (rovného tloušťce lamely), nebo spíše plochými průřezy s navlečenými „water-stopy“;
- osadí se výztuž podzemní stěny ve formě armokoše. Ten se skládá z podélných a příčných nosných prutů, ale i ze spojovací a diagonální výztuže, jež zajišťuje tuhost armokoše. Armokoš se osazuje, pokud je to možné, zásadně vcelku, spojování armokošů je komplikované. Armokoše jsou vybaveny distančními kolečky (betonovými, plastovými) za účelem dodržení předepsaného krytí výztuže;
- neprodleně, (max. do 2 hodin po přečištění pažicí suspenze) se zahájí betonáž. Betonuje se pomocí sypákových rour pod suspenzi. Při šířce lamely 2,50–2,80 m se použije 1 sypáková roura, pro 3záběrovou lamelu šířky 6,5 m se použijí 2 sypákové roury. Betonuje se transportbetonem, kde požadavky na kvalitu betonu jsou dány ČSN EN 1538+A1. V průběhu betonáže se sleduje plynulost stoupání jeho hladiny v betonované lamele (olovnicí) a pažicí suspenze se odčerpává, přečišťuje a skladuje pro event. nové použití. Poslední vrstva suspenze, jež přišla do bezprostředního styku s betonem se likviduje;
- hlavy podzemních stěn se obyčejně přebetonují, pokud jsou v úrovni pracovní plošiny, beton se nechá přelít a odstraní se. Po jisté době, když dojde k zatuhnutí betonu se koutové pažnice vytahují.
Technologický postup výroby monolitické podzemní stěny prováděné zejména hydraulickým drapákem je schématicky znázorněn na obr. 31. Příklady různých typů lamel a jejich spojů jsou na obr. 32.
Obr. 31 Schéma technologie provádění monolitických podzemních stěn
Prefabrikované podzemní stěny se navrhují pro trvalé konstrukce zárubních zdí, popř. i hloubených tunelů. Jejich výhoda spočívá v dokonalé pohledové úpravě lícní plochy a možnostech dosažení naprosto přesné polohy jednotlivých panelů. Nevýhoda je dána relativně vysokou cenou, jež souvisí s výrobou a zejména transportem těchto panelů. Vlastní rozměry panelů jsou dány nejen statickým posouzením, ale též jejich hmotností, jež souvisí s použitými zvedacími mechanizmy na stavbě. Zvláštnost technologického postupu prefabrikovaných podzemních stěn spočívá v tom, že se hloubí rýha o šířce obyčejně o 200–300 mm širší, než jsou panely. Ta se hloubí pomocí jednozáběrových, či trojzáběrových lamel, které se paží obyčejně samotvrdnoucí suspenzí, která na rozdíl od suspenze použité pro stěny těsnicí má jistý časový nárůst pevnosti, jež bývá větší než v případě stěn těsnicích, (na úkor např. vodotěsnosti). Do vyčištěné rýhy pod suspenzí se vkládají železobetonové panely a kontroluje se jejich poloha i svislost. Panely se neopírají o dno rýhy, vyvěšují se pomocí vodících zídek. Jistý problém spočívá v napojování jednotlivých panelů. Na dně jsou panely jednostranně opatřeny ocelovým „nosem“ s čepem, jež slouží pro ukotvení následného panelu a znemožní vybočení následného panelu jakýmkoliv směrem. U horního povrchu se panely fixují na vodících zídkách. Do půlkruhových drážek ve styku obou sousedních panelů se vloží hadice z umělé hmoty, jež se po zatvrdnutí suspenze zainjektuje vhodným materiálem, čímž dojde k utěsnění spár mezi jednotlivými panely. Z lícní strany se panely obyčejně natírají separačním nátěrem, (např. na bázi želatiny), za účelem snadného odstranění samotvrdnoucí suspenze v průběhu výkopu, obr. 33.
Obr. 32 Příklady různých typů lamel a pracovních spár: P – primární, S – sekundární, 1 – počáteční, 2 – mezilehlý, 3 – zavírací
Obr. 33 Podzemní stěna prefabrikovaná: a. schématický řez; b. detail styku lamel (panelů), 1 – rýha pro PS, 2 – samotvrdnoucí suspenze, 3 – prefa PS (panel), 4 – stropní deska, 5 – výkop, 6 – těsnicí hadice z měkčeného PVC, 7 – injektáž samotvrdnoucí suspenzí, 8 – zatmelení spáry
Při použití hydrofrézy, (obr. 34) je zapotřebí nejprve vyhloubit rýhu drapákem pod ochranou pažicí suspenze do hl. nejméně 3,50–5,0 m tak, aby další postup hloubení hydrofrézou byl možný. Ta zeminu nenabírá, nýbrž ji drtí dvěma frézami tvaru ozubených kol s vyměnitelnými nástroji a vrtnou drť spolu s pažicí suspenzí vysává mohutným čerpadlem, jež pro první nasátí potřebuje právě tuto minimální výšku hladiny suspenze. Ta následně putuje potrubím na čístící stanici, kde se na vibrosítech zbavuje hrubších částic základové půdy a proces čištění je pak dokončen na hydrocyklonu. Vyčištěná, popř. regenerovaná pažicí suspenze je pak znovu čerpána do rýhy. Pomocí hydrofrézy lze realizovat monolitické železobetonové lamely podzemních stěn podobně jako je tomu v případě hydraulických drapáků, tedy např. třízáběrové lamely s těsnicími pásy (water-stopy). Obvyklejší je však takový postup, při němž se realizují běžné jednozáběrové lamely (primární, vč. výztuže) a ty jsou po určité časové prodlevě částečně přefrézovány lamelami sekundárními (rovněž nakonec vyztuženými).
Obr. 34 Hydrofréza
1.4.3.6 Konstrukce z tryskové injektáže
Konstrukce z tryskové injektáže se skládají z jednotlivých prvků tryskové injektáže, (sloupů nebo lamel) a popřípadě z dalších prvků speciálního zakládání staveb, (kotev, mikropilot, stříkaného betonu) a slouží buď pro podchycování, nebo zesilování stávajících základů, nebo pro vytváření těsnicích a pažicích stěn, výjimečně pak i jako základové konstrukce novostaveb. Z hlediska využití těchto konstrukcí pro návrh roubení stavebních jam vzniká problém v souvislosti s relativně malou ohybovou únosností těchto prvků, které nelze jednoduše vyztužit. Požadovaná ohybová únosnost je pak získána buď dostatečnou tloušťkou této konstrukce tak, aby v průřezu nevznikala tahová napětí, nebo spolupůsobením s dalšími prvky, (např. mikropilotami) tak, že přebírají tahová napětí. Stěny ze sloupů tryskové injektáže však mohou dobře plnit funkci těsnicí, a proto se používají pro těsnění určitých úseků záporového pažení, popř. pilotových stěn volně stojících či tangenciálních ve zvodnělých partiích základové půdy, (obr. 35).
Obr. 35 Těsnění pažicích konstrukcí pomocí sloupů z tryskové injektáže: a – těsnění záporového pažení, b – těsnění pilotové stěny; 1 – zápora, 2 – hladina podzemní, vody, 3 – nepropustná zemina, 4 – kotva, 5 – sloupy tryskové injektáže, 6 – kotevní, převázka, 7 – vrtaná pilota, 8 – stříkaný beton
V případě pažení stavebních jam navazujících na stávající zástavbu vzniká požadavek na co největší zábor pozemku. V těchto případech je třeba řešit souběžně dva úkoly:
- podchytit stávající, obyčejně mělčeji založenou zástavbu;
- zajistit zapažení svislé stěny stavební jámy pod stávajícími základy.
Pokud jsou geotechnické poměry příznivé pro umožnění technologie tryskové injektáže, uplatní se v těchto případech nejlépe konstrukce z překrývajících se sloupů tryskové injektáže. Je-li hloubka od základové spáry stávajících základů po dno stavební jámy malá, (asi do 2,0 m), vyhoví příslušnému namáhání pouze jednoduchá řada sloupů. Při zvětšující se hloubce je třeba počítat s kotvením, které podchycující a pažicí konstrukci stabilizuje a umožní její příznivé namáhání. Takto vytvořená pažicí konstrukce je samozřejmě dočasná do doby výstavby suterénu, pro nějž slouží jako ztracené bednění. Proto i kotvy bývají dočasné a převázky jsou navrhovány z úpalků profilů Larssen zapuštěných do vybouraných nik ve sloupech tryskové injektáže. V průběhu těžby stavební jámy se přečnívající sloupy odbourají, naopak ve spodní části bývá zapotřebí klíny dobetonovat. Pokud se takto vytvořená stěna využije jako podklad pod svislou izolaci opatří se většinou vrstvou stříkaného betonu s výztužnou sítí a zednickou úpravou povrchu, obr. 36.
V případě větších hloubek pažení (např. přes 4,0 m) bývá nutné kotvit ve více úrovních, popřípadě kombinovat stěnu ze sloupů tryskové injektáže se stěnou mikrozáporovou. Dalším důvodem je pak i změna geotechnických podmínek, kdy se přechází do soudržných zemin, nebo do poloskalních hornin, v nichž je technologie tryskové injektáže nevhodná, nebo neekonomická, obr. 37.
Obr. 36 Pažicí konstrukce z překrývajících se sloupů tryskové injektáže: a – při volné výšce H < 2,0 m – volně stojící, b – při volné výšce H > 2,0 m – kotvená; 1–pracovní plošina, 2 – podchycovaný základ, 3 – dno stavební jámy, 4 – sloupy tryskové injektáže, 5 – odbouraná část, 6 – dobetonováno (stříkaný beton), 7 – zapuštěná ocelová převázka (úpalek Larssen), 8 – dočasná kotva
1.4.3.7 Těsnicí konstrukce a jímky
Pro vytvoření stavební jámy pod hladinou vody se kromě některých výše popsaných konstrukcí využívá zejména jímek, jež jsou nutné tehdy, zakládá-li se pod hladinou volné vody, (v řece, rybníku, jezeru). Jímky jsou tedy dočasné konstrukce, které ohrazují stavební jámu při zakládání ve vodě. Jímky se dělí zejména podle materiálu, z něhož se staví na jímky hrázové, (zemina), dřevěné, ocelové a betonové, dále podle výšky vzdutí, složení dna, rozměrů jámy a doby trvání jímky. Podrobné údaje o konstrukci, stavbě a výpočtu různých druhů jímek uvádí Bažant [1] a Smoltczyk [12]. My se pro stručnost omezíme pouze na jímky hrázové a ocelové.
Obr. 37 Kombinované pažení – sloupy tryskové injektáže s mikrozáporovou stěnou kotvenou
Hrázové jímky (obr. 38) jsou tvořeny zemní hrází sypanou do volné vody, obyčejně stojící, či jen málo proudící, přičemž jejich stabilita je zajištěna pouze touto zeminou a jejími vlastnostmi. Používají se zejména na nepropustném podloží nebo na skále. Sklon návodního svahu bývá pochopitelně strmější, než je sklon vzdušného svahu, který je třeba v průběhu čerpání jímky upravit a neustále monitorovat, popř. utěsňovat tak, aby se zabránilo významnějším průsakům. Hrázové jímky bývají ekonomické při vzdutí do asi 3 m. Často se používají jako pomocná konstrukce pro vytvoření ocelové jímky jednoduché, nebo i zdvojené tehdy, nelze-li štětovnice razit z vody, V tom případě se potom zemina z prostoru uvnitř jímky odstraní.
Obr. 38 Hrázové jímky, [1]: a – část sypána z lodi, zbytek z jámy, b – neopevněná hráz, c – opevněná jímka v proudící vodě, d – návodní těsnění
Tam, kde je to technologicky možné, používají se jímky ocelové ražené, jednoduché, jež vyhoví pro vzdutí do asi 8–10 m, které jsou většinou rozpírané, obr. 40. V našich podmínkách se používají ocelové štětovnice typu Larssen (obr. 39), jejichž typické rozměry a vlastnosti jsou v tab. 7. Ve světě, zvláště v přímořských zemích se ovšem využívá i jiných typů ocelových štětovnic, jejichž přehled uvádí Smoltczyk [12].
Obr. 39 Ocelové štětovnice typu Larssen
Tab. 7 Ocelové štětovnice typu Larssen nejčastěji užívané v České republice
| Označení | Rozměry průřezu | Pro 1 bm stěny | Hmotnosti | |||||
| b [mm] | h [mm] | t [mm] | t1 [mm] | A [m2] | W [m3] | 1 bm [kg] | 1 m2 [kg] | |
| IIn | 400 | 270 | 9,5 | 7,5 | 0,0156 | 0,0011 | 48,8 | 122,0 |
| IIIn | 400 | 290 | 13,0 | 8,5 | 0,0198 | 0,0016 | 62,0 | 155,0 |
| IVn | 400 | 360 | 14,8 | 10,0 | 0,0236 | 0,0022 | 74,0 | 185,0 |
| 22 | 500 | 340 | 10,0 | 10,0 | 0,0155 | 0,0013 | ||
Obr. 40 Ocelová jímka ze štětovnic Larssen, rozepřená
Není-li možné štětovnice zarazit na potřebnou hloubku pode dno řeky, např. z titulu skalního podloží, navrhují se ocelové jímky nasazené, které jsou rovněž dvojité, neboť odolávají příslušnému hydrostatickému tlaku svojí tíhou, obr. 41, 42.
Požadavky na vodotěsnost pažicích a těsnicích konstrukcí stavebních jam se mnohdy značně liší a to posuzují-li se z pohledu investora, uživatele stavby, nebo projektanta a event. zhotovitele této konstrukce. To se týká zejména konstrukcí trvalých – betonových. Tak např. ve Francii nebývají na vodotěsnost konstrukčních monolitických podzemních stěn vytvářejících obvodové zdi podzemních garáží tak přísné požadavky, jistý velmi omezený průsak bývá připuštěn a prosakující voda bývá odvedena obvodovým žlabem vyplněným např. keramzitem, nebo kačírkem. Vychází se z faktu, že v zimě automobily „přinesou“ do těchto prostor tolik sněhu, který zde roztaje, že jeho množství často převyšuje event. průsaky. Současně pak požadavek na „absulutní“ vodotěsnost je natolik nákladný, že se prostě nevyplatí. U nás zatím ovšem často vládne mínění, že vodotěsná konstrukce musí mít absolutní nepropustnost. Podstatnou roli při tom hraje:
- druh pažicí a těsnicí konstrukce;
- účel, pro nějž byla tato konstrukce navržena;
- tlak podzemní vody.
Obr. 41 Nasazená dvojitá ocelová jímka kolem mostního pilíře v řece, řez
Obr. 42 Nasazená dvojitá ocelová jímka kolem mostního pilíře v řece, půdorys
Za účelem určitého sjednocení názorů a stanovisek zúčastněných stran výstavby těchto konstrukcí vydal v roce 1999 Rakouský betonářský svaz směrnici nazvanou: „Wasseundurchlässige Betonbauwerke – Weisse Wannen“, jež byla v roce 2007 přejata Českou betonářskou společností ČSSI a vydána ve formě technických pravidel ČBS 02: Bílé vany – Vodotěsné betonové konstrukce. Tento předpis obsahuje zejména zatřídění požadavků na vodotěsnost, jež je součástí tab. 8. Na ní navazuje tabulka, jež se týká tříd železobetonových bedněných konstrukcí a požadavků na jejich návrh a provádění. Ta však není pro konstrukce speciálního zakládání staveb příliš vhodná a použitelná. Konečně následující tab. 9 rozděluje tlaky vody do 5 tříd. Ukazuje se, že zejména tab. 8, popisující kvalitativní požadavky na jednotlivé konstrukce vystavené dlouhodobému působení vodního tlaku je použitelná i pro betonové prvky a konstrukce speciálního zakládání staveb a poskytuje zejména investorům vodítko pro usměrnění a reálnost svých požadavků.
Tab. 8 Třídy požadavků na vodotěsnost betonových konstrukcí
| Třída | Popis | Popis lícní plochy | Posouzení vlhkosti a průsaku | Přípustné Projevy vlhkosti | Příklady |
| A0 | zcela suché | Žádné vizuální projevy vlhkosti | – | – | sklady pro zboží s mimořádnýmí požadavky |
| A1 | suché (dlouho- době) | Vizuálně jednot– livé omezené projevy vlhkosti změna barvy | při stěru suchou rukou nezůstane na ruce mokrá stopa | 1% pohledové plochy smí prosakovat | garáže s vysokými požadavky na vlhkost, sklepy |
| A2 | mírně vlhké | vizuálně zjistitelná lesklá místa | při stěru suchou rukou zůstane na ruce mokrá stopa | 1% pohledové plochy smí prosakovat | garáže, technické prostory, kotelny, kolektory, tunely |
| A3 | vlhké | kapající voda s vytvářením mokrých ploch | Skapávající množství vody je měřitelné (např. v nádobách) | průsak do 0,2 l/hod na 1 bm podzemní stěny nebo 0,01 l/hod na m2 | garáže s násl. opatřením, jako např. obvodové drážky |
| A4 | mokré | jednotlivá proté-kající místa | protékající množství vody je dobře měřitelné | průsak do 2,0 l/hod na 1 bm podzemní stěny nebo 1,0 l/hod na m2 | – |
Tab. 9 Třídy pro vodní tlak
| Třída vodního tlaku | Popis |
| W0 | vodní sloupec 0,0–1,0 m |
| W1 | vodní sloupec 1,0–5,0 m |
| W2 | vodní sloupec 5,0–10,0 m |
| W3 | vodní sloupec 10,0–20,0 m |
| W4 | vodní sloupec > 20,0 m |
2 NAVRHOVÁNÍ PAŽENÝCH STAVEBNÍCH JAM
2.1 PODKLADY PRO NÁVRH
Pro návrh a posouzení návrhu pažení stavebních jam jsou zapotřebí následující podklady:
A. Podklady geotechnické
Jsou základními a získáváme je na základě zadaného a provedeného inženýrsko-geologického průzkumu. Ten financuje většinou investor, výsledky průzkumu jsou tedy jeho majetkem a on za ně nese příslušnou zodpovědnost. Aby byl průzkum použitelný a současně hospodárný, je velice vhodné, aby se jeho plánování zúčastnil i geotechnik – statik, tj. budoucí navrhovatel geotechnických konstrukcí. Zkušený geotechnik většinou dokáže odhadnout již ve stádiu přípravných prací metodu, resp. metody zajištění stavební jámy, jež by přicházely v úvahu a těm potom přizpůsobit požadavky na geotechnický průzkum. Jádrem každého průzkumu je realizace průzkumných sond, tj. většinou jádrových vrtů, výjimečně i kopaných sond a v některých případech polních geotechnických zkoušek. Plánování těchto prací by měla předcházet geologická rešerše, kdy si zkušený inženýrský geolog jednak na základě svých znalostí, ale zejména pak na základě inženýrsko-geologických map a archivních průzkumných děl z Geofondu učiní základní obraz o geotechnických poměrech na lokalitě a s nimi seznámí geotechnika – statika. Samozřejmě, že na základě této rešerše nelze určit detaily, např. přesnou hloubku skalního podloží, hladinu podzemní vody, ale i konzistence a ulehlosti zemin, jak i mocnost navážky apod. Lze však hovořit o globálních poměrech a odhadnout, zda lze očekávat podloží v rozumné hloubce a o jaké podloží půjde, jaké typy základových půd budou vytvářet pokryvné útvary apod. Tuto rešerši nelze v žádném případě zaměňovat za řádný geotechnický průzkum, neboť to může být velmi kontraproduktivní.
Na základě rešerše, nebo zkušenosti se plánuje geotechnický průzkum, (podrobný, či doplňkový). Ten by měl vycházet ze znalosti:
- základních geotechnických poměrů na lokalitě;
- rozsahu a hloubce stavební jámy;
- okolní zástavby;
- očekávaných poměrů hydrogeologických.
Základem budou vždy klasické technické práce spočívající v provedení a vyhodnocení, (odborném popisu) jádrových vrtů zasahujících vždy pod budoucí dno stavební jámy. Je jisté, že výsledky tohoto průzkumu neslouží pouze pro pažení stavebních jam, ale současné i pro zakládání objektů ve stavební jámě budovaných. Množství vrtů nelze nijak specifikovat, neboť závisí na tom, zdali se jedná spíše o poměry monotónní, nebo naopak lze očekávat v rámci staveniště velké změny, co do rozsahu i hloubek. Nicméně většinou platí, že lépe je méně vrtů dostatečně dlouhých než naopak mnoho krátkých vrtů, k čemuž mají průzkumné firmy sklon. Velice důležitý je základní geotechnický popis vč. zatřídění podle (dnes již neplatné, nicméně stále využívané) ČSN EN 1997-1, (třídy R, G, S, F) a to jak na základě subjektivních kritérií, tak i podle upřesnění na základě indexových zkoušek, (zrnitost, konzistenční meze), popř. v poloskalních a skalních horninách na základě velikosti prosté tlakové pevnosti. Tento průzkum může být doplněn i polními zkouškami, tedy statickou, výjimečně i dynamickou penetrací, ale pouze za účelem upřesnění jistých kvalitativních faktorů, (ulehlost, konzistence). V žádném případě nesmějí být tyto zkoušky jako jediné, a to zejména v případě složitých geotechnických poměrů. Samostatnou kapitolu vytvářejí laboratorní zkoušky mechaniky zemin. Jak je v následujících kapitolách popsáno, pro posouzení navržených pažicích konstrukcí statickým výpočtem, což je prakticky jediná používaná metoda, je třeba znát zejména velikosti stabilitních parametrů, (γ – objemová tíha v přirozeném uložení, φ – úhel vnitřního tření, c – soudržnost) příslušných vrstev základové půdy. Tyto parametry lze nejlépe získat na základě laboratorních zkoušek neporušených vzorků zemin, je tedy zcela na místě, aby průzkum tyto zkoušky plánoval. Nesmí to však být na úkor dostatečného počtu a metráže průzkumných vrtů. Samotná sbírka výsledků laboratoře mechaniky zemin je z praktického hlediska skoro bezcenná, pokud není zhodnocena zkušeným geotechnikem, který stanoví jednotlivé geotechnické typy a jim příslušné parametry přiřadí nikoliv mechanicky, (např. na základě jednoduchého statistického zpracování výsledků), ale se znalostí hlubších souvislostí. Výsledkem geotechnického průzkumu je soubor hodnot odvozených, přičemž charakteristickou velikost příslušného parametru určuje projektant, jenž je za ní zodpovědný.
B. Podklady stavební
Jde jednak o podklady o plánované stavbě, jednak o podklady o stávající zástavbě. Investor by měl znát stavební záměr a být si vědom všech souvislostí. Tak např. požadavek na maximální využití suterénních prostor staveniště v městské zástavbě, (v proluce), vede k riskantnímu podchycování sousedních objektů, a tudíž k zvýšené ceně konstrukcí. Požadavek na maximální využití podzemní části parcely vede i k požadavkům na mnohem důkladnější průzkum stavební, a to formou kopaných sond realizovaných podél zdí stávající zástavby. Tomu je třeba věnovat velkou pozornost, neboť se často stává, že některé starší domy neměly prakticky žádné samostatné základy a založeny byly na pasech náležejících demolovanému objektu místo, něhož se staví nový objekt se suterénem. Potom existuje významné riziko vyplývající z neznalosti základové spáry domu sousedního se všemi negativními důsledky.
Poměrně častý je požadavek sousedů, kteří ve snaze zabránit výstavbě nesouhlasí např. s kotvením pažicích konstrukcí, kdy by kotvy zasahovaly pod jejich pozemky. Tento technicky nesmyslný požadavek vede k návrhu rozpírané pažicí konstrukce, která zejména v případě rozsáhlých stavebních jam je jednak ekonomicky nevýhodná, současně pak značně riskantní, neboť rozpěry se prakticky nedají aktivovat, resp. jde o velice náročný technologický postup. Stavebník, (investor) by si měl být tohoto rizika vědom a včas (v předstihu) učinit příslušná opatření v tom smyslu, aby kotvení bylo povoleno.
C. Pasportizace
Součástí stavebních podkladů by měla být i pasportizace sousední zástavby, pokud existuje. Má se skládat z podrobných zákresů, (po patrech, či i místnostech s jednoznačným označením místností), dále z fotodokumentace a event. i videozáznamu. Zprávu o pasportizaci je dobré nechat podepsat majitelem nemovitosti, nebo jejím správcem, popř. mu jeden výtisk předat. Pokud soused odmítne přístup do své nemovitosti, je třeba o tom pořídit zápis předem a na něj se později odvolat.
D. Podklady o inženýrských sítích
Tvoří samostatnou a velmi problematickou skupinu potřebných podkladů. Hlavní problém spočívá ve dvou aspektech:
- podklady jsou obtížně získatelné;
- podklady, pokud existují, jsou krajně nevěrohodné.
Z hlediska pažicích konstrukcí se jedná o konstrukce svislé, realizované z pracovní plošiny, přičemž pod jejich navrhovaným půdorysem se může vyskytovat určitá překážka. To bývá často řešeno návrhem předvýkopu do určité hloubky (např. 1,0 m) a zjištění průběhu této překážky, osazení průchodek, nebo zřízení vodících zídek nebo šablon. Větší problémy jsou s návrhem kotev ve vztahu k stávajícím inženýrským sítím. Naštěstí kotvy bývají uloženy dosti hluboko, tudíž jde vesměs „pouze“ o event. střet s kanalizací, neboť ostatní sítě jako el. vedení, slaboproud, voda a plyn bývají vedeny mělčeji.
2.2 ZATÍŽENÍ PAŽICÍCH KONSTRUKCÍ
Posouzení navržených pažicích konstrukcí se provádí zásadně statickým výpočtem, přičemž se podle ČSN EN 1997-1 vychází z mezních stavů 1. skupiny, při jejichž překročení dochází k úplné a trvalé ztrátě způsobilosti konstrukce a také z mezních stavů 2. skupiny (použitelnosti), jejichž překročení omezuje, případně i vylučuje obvyklé užívání konstrukce, nebo zkracuje dobu životnosti konstrukce vzhledem k době předpokládané. Jejich analýza vede vesměs ke stanovení deformací pažicích konstrukcí, které jsou obvykle rozhodující pro jejich návrh.
Pažicí konstrukce jsou jak dočasné, tak i trvalé. Za dočasné pokládáme ty, jejichž funkčnost je ohraničena dobou 2 let přesto, že to automaticky neznamená, že po 2 letech zkolabují. Přesto však po skončení této doby se na jejich funkci nevztahuje záruka, což bývá výslovně uvedeno jednak v realizační projektové dokumentaci a jednak v příslušné Smlouvě o dílo. Trvalé pažicí konstrukce mají obdobnou dobu životnosti jako kterékoliv konstrukce stavební. Dočasnost či trvalost pažicí konstrukce je často dána i jejím druhem, kdy např. záporové pažení je typickou konstrukcí dočasnou, rovněž tak pažení mikrozáporové, jež přesto, že zůstává trvale v zemi, nebývá navrhováno pro trvalý přenos zatížení. Rovněž tak hřebíkování svahů je typicky dočasnou konstrukcí, což souvisí s neexistující sekundární ochranou hřebíků a nedokonalým odvodněním. Naopak pilotové stěny a zejména pak stěny podzemní bývají v současné době navrhovány jako konstrukce trvalé, což se projevuje zejména při návrhu trvalého kotvení. V případě štětových stěn jsou obě alternativy přijatelné.
Pro statické posouzení pažicích konstrukcí je třeba vytvořit výpočetní model – statické schéma pro výpočet. Do něj se potom zavede zatížení, jež je tvořeno:
- zemními tlaky;
- přírůstky zemních tlaků od ostatního stálého i nahodilého zatížení;
- vlivy podzemní a event. i volné vody;
- dalším vnějším zatížením.
Ve smyslu ČSN EN 1997-1 se zatížení dělí podle doby trvání a podle změn velikosti, polohy nebo smyslu na zatížení:
- stálá;
- nahodilá (pohyblivá);
- dlouhodobá;
- krátkodobá;
- mimořádná.
Za stálá zatížení se považují:
- tíhy nosné konstrukce a všech jejich trvalých částí;
- trvale působící tlaky zemin, sypkých hmot a kapalin;
- účinky předpětí konstrukce.
Za nahodilá se považují zatížení:
- užitná;
- klimatická;
- od vynucených přetvoření;
- montážní.
U typických pažicích konstrukcí bude tedy zatížení zemním tlakem, zatížení hydrostatické i hydrodynamické, jakož i tíha konstrukce a všech jejich trvalých součástí zatížením stálým, přírůstky zemních tlaků budou pak podle svého charakteru jak zatížením stálým, tak i nahodilým.
2.2.1 Zemní tlaky
Zemním nebo horninovým tlakem nazýváme síly, kterými na sebe navzájem působí zemina, (hornina) a stavební konstrukce, (pažicí, opěrná, zárubní apod.). Velikost zemního tlaku závisí na vlastnostech základové půdy – na jejích stabilitních parametrech, (objemové tíze γ, úhlu vnitřního tření – φ a soudržnosti – c), na druhu konstrukce, její tuhosti a uložení v základové půdě, tedy především na velikosti posunu, potočení či jiného přetvoření zatížené části konstrukce. V závislosti na velikosti této deformace může nabýt zemní tlak jakékoliv velikosti mezi dvěma hodnotami mezními, kterými jsou aktivní a pasivní zemní tlak. Všechny tyto mezilehlé hodnoty kromě zemního tlaku v klidu lze stanovit pouze přibližně, obr. 43.
Zemní tlak v klidu
Vodorovné napětí působící na svislý rub zatěžované konstrukce, která se nedeformuje se stanoví:
\begin{gathered}
\sigma_\text{r}=K_\text{r}\cdot\sigma_\text{z}
\end{gathered}(12)
kde je:
σz … svislé (geostatické) napětí v hloubce z;
Kr … součinitel zemního tlaku v klidu.
Velikost tohoto součinitele vyplývá za předpokladu základové půdy jakožto pružného poloprostoru z rozšířeného Hookeova zákona:
\begin{gathered}
K_\text{r}=\frac{\nu}{(1-v)}
\end{gathered}(13)
kde je:
ν … Poissonovo číslo základové půdy.
Pro praktické výpočty se využívá zejména empirické Jákyho formule:
\begin{gathered}
K_\text{r}=1-\sin\varphi_\text{c}
\end{gathered}(14)
kde je
φc … náhradní úhel vnitřního tření základové půdy:
pro hrubozrnné zeminy, kde cef = 0 je φc = φeb;
pro jemnozrnné zeminy, kde cef ≠ 0 se φc stanoví opatrně podle obr. 44.
Výslednice zemního tlaku v klidu Sr působící na svislý rub konstrukce zatížené na plnou výšku h:
\begin{gathered}
S_\text{r}=\frac{1}{2}\cdot\gamma\cdot h^2\cdot K_\text{r}
\end{gathered}(15)
Tato síla působí kolmo na svislou rubovou stěnu v těžišti zatěžovacího obrazce, má tedy vodorovný směr. Napětí při zemním tlaku v klidu σr v hloubce z pod vodorovným povrchem terénu působící na šikmou stěnu odkloněnou od svislice o úhel α se vypočte:
\begin{gathered}
\sigma_\text{r}=\sigma_\text{z}\cdot(\sin^2\alpha+K_\text{r}^2\cdot\cos^2\alpha)^\frac{1}{2}
\end{gathered}(16)
přičemž úhel odklonu výslednice od normály ke stěně δ je:
\begin{gathered}
\tg\delta=\frac{((1-K_\text{r})\cdot\tg\alpha)}{(K_\text{r}+\tg^2\alpha)}
\end{gathered}(17)
a normálová a tangenciální složka tohoto napětí:
\begin{gathered}
\sigma_\text{n}=\sigma_\text{z}\cdot(\sin^2\alpha+K_\text{r}\cdot\cos^2\alpha);\space\tau=\sigma_\text{z}\cdot(1-K_\text{r})\cdot\sin\alpha\cdot\cos\alpha
\end{gathered}(18)
Výslednice zemního tlaku:
\begin{gathered}
S_\text{r}=\frac{1}{2}\cdot\gamma\cdot h^2\cdot(K_\text{r}^2+\tg^2\alpha)^\frac{1}{2}
\end{gathered}(19)
Je-li terén šikmý (β ≤ φ), potom napětí při zemním tlaku v klidu:
\begin{gathered}
\sigma_\text{r}=\frac{(\sigma_\text{z}\cdot K_\text{r}\cdot\sin\varphi\cdot\cos\beta)}{(\sin\varphi-\sin^2\beta)}
\end{gathered}(20)
Obr. 43 Závislost velikosti zemních tlaků na deformaci konstrukce: a) velikost zemního tlaku, b) směr deformace konstrukce
Obr. 44 Stanovení náhradního úhlu vnitřního tření φc pro jemnozrnné zeminy
Aktivní zemní tlak – hrubozrnné zeminy
Napětí při aktivním zemním tlaku σa v hloubce z působící na rubu zatížené konstrukce je:
\begin{gathered}
\sigma_\text{a}=\sigma_\text{z}\cdot K_\text{a}
\end{gathered}(21)
kde je:
Ka … součinitel aktivního zemního tlaku:
\begin{gathered}
K_\text{a}=\frac{(\cos^2(\varphi-\alpha))}{\cos^2\alpha}\cdot\cos(\alpha+\delta)\cdot[1+(\frac{((\sin(\varphi+\delta)\cdot\sin(\varphi-\beta))}{((\cos(\alpha+\delta)\cdot\cos(\alpha-\beta))})^\frac{1}{2}]^2
\end{gathered}(22)
Vodorovná a svislá složka napětí při aktivním zemním tlaku jsou pak dány:
\begin{gathered}
\sigma_\text{ax}=\sigma_\text{a}\cdot\cos(\alpha+\delta);\space\sigma_\text{az}=\sigma_\text{a}\cdot\sin(\alpha+\delta)
\end{gathered}(23)
a kritická smyková plocha, po níž dochází k usmyknutí sypké zeminy svírá s vodorovnou úhel θ, pro nějž platí:
\begin{gathered}
\theta=\varphi+\varepsilon
\end{gathered}kde je:
\begin{gathered}
\cotg\varepsilon=\tg(\varphi-\alpha)+\frac{1}{(\cos(\varphi-\alpha))}\cdot[\frac{(\sin(\varphi+\alpha)\cdot\cos(\alpha-\beta))}{(\sin(\varphi-\beta)\cdot\cos(\varphi-\delta))}]^\frac{1}{2}
\end{gathered}Je-li terén za rubem vodorovný, (β = 0), pažicí konstrukce je svislá, α = 0) a zanedbáme-li tření mezi zeminou a rubem konstrukce, (δ = 0), vychází známý vzorec:
\begin{gathered}
K_\text{a}=\tg^2(45\degree-\frac{\varphi}{2})
\end{gathered}(25)
Výslednice aktivního zemního tlaku se pak stanoví ze vztahu:
\begin{gathered}
S_\text{a}=\frac{1}{2}\cdot\gamma\cdot h^2\cdot K_\text{a}
\end{gathered}(26)
Aktivní zemní tlak – jemnozrnné zeminy
Rozeznáváme 3 charakteristické typy jemnozrnných zemin pro účely stanovení velikosti aktivního zemního tlaku:
a) nekonzolidované jemnozrnné zeminy plně nasycené vodou, u nichž proces konzolidace nastane v době, kdy zatěžují konstrukci a u nichž je smyková pevnost charakterizována: φu = 0, cu ≠ 0. V tomto případě lze pro napětí při aktivním zemním tlaku psát:
\begin{gathered}
\sigma_\text{a}=\gamma\cdot z-2\cdot c_\text{u}\cdot(1+\frac{a}{c_\text{u}})^\frac{1}{2}
\end{gathered}(27)
kde je:
a … přilnavost (adheze) zeminy ke konstrukci, jež se vyjadřuje a = (0,2 – 0,8) · cu.
Z rovnice (27) vyplývá, že pro hloubku (0 < z < hc) je vodorovné napětí záporné, resp. nulové, tudíž vzorec platí pro hloubku z > hc, kde:
\begin{gathered}
h_\text{c}=2\cdot\frac{c_\text{u}}{\gamma}\cdot(1+\frac{a}{c_\text{u}})^\frac{1}{2}\\\\
\text{a pro}\space\space z\lt h_\text{c}\space\space\text{je}\space\space\sigma_\text{a}=0
\end{gathered}(28)
b) normálně konzolidované jemnozrnné zeminy charakterizované φef ≠ 0, cef ≠ 0, kde napětí při aktivním zemním tlaku lze vypočítat ze vztahu:
\begin{gathered}
\sigma_\text{a}=\gamma\cdot z\cdot K_\text{a}-2\cdot c_\text{ef}\cdot(K_\text{a})^\frac{1}{2}
\end{gathered}(29)
vzorec platí pro z > hc, kde:
\begin{gathered}
h_\text{c}=2\cdot \frac{c_\text{ef}}{\gamma}\cdot(\frac{1}{K_\text{a}})^\frac{1}{2}\\\\
\text{pro}\space\space z\lt h_\text{c}\space\space\text{je}\space\space\sigma_\text{a}=0
\end{gathered}(30)
c) překonzolidované jemnozrnné zeminy, jež při poklesu napjatosti ztrácejí svojí smykovou pevnost; v tomto případě je třeba postupovat individuálně – vesměs podle b) s příslušně redukovanými smykovými parametry φef, cef.
Pasivní zemní tlak – hrubozrnné zeminy
Napětí při pasivním zemním tlaku nesoudržných zeminy v hloubce z lze vypočítat:
\begin{gathered}
\sigma_\text{p}=\sigma_\text{z}\cdot K_\text{p}\cdot\psi
\end{gathered}(31)
kde je:
Kp … součinitel pasivního zemního tlaku pro δ = –φ, podle tab. 10;
ψ … zmenšovací součinitel pro |δ| < φ podle tab. 11;
(v obou tabulkách lze lineárně interpolovat).
Výslednice pasivního zemního tlaku je pak dána:
\begin{gathered}
S_\text{p}=\frac{1}{2}\cdot\gamma\cdot h^2\cdot K_\text{p}\cdot\psi
\end{gathered}(32)
Tab. 10 Součinitelé pasivního zemního tlaku Kp
| α | φ | Kp pro β | |||||||||
| 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | |||
| -20 | 10 | 1,36 | 1,58 | 1,70 | |||||||
| 15 | 1,68 | 1,97 | 2,20 | 2,38 | |||||||
| 20 | 2,13 | 2,52 | 2,92 | 3,22 | 3,51 | ||||||
| 25 | 2,78 | 3,34 | 3,99 | 4,60 | 5,29 | 5,57 | |||||
| 30 | 3,78 | 4,61 | 5,56 | 6,61 | 7,84 | 9,12 | 9,77 | ||||
| 35 | 5,36 | 6,69 | 8,26 | 10,10 | 12,20 | 14,80 | 17,40 | 19,00 | |||
| 40 | 8,07 | 10,40 | 12,00 | 16,50 | 20,00 | 25,50 | 36,50 | 37,80 | 42,20 | ||
| -10 | 10 | 1,52 | 1,72 | 1,83 | |||||||
| 15 | 1,95 | 2,23 | 2,57 | 2,66 | |||||||
| 20 | 2,57 | 2,98 | 3,42 | 3,75 | 4,09 | ||||||
| 25 | 3,50 | 4,14 | 4,90 | 5,62 | 6,45 | 6,81 | |||||
| 30 | 4,98 | 6,01 | 7,19 | 8,51 | 10,10 | 11,70 | 12,60 | ||||
| 35 | 7,47 | 9,24 | 11,30 | 13,80 | 16,70 | 20,10 | 23,70 | 26,00 | |||
| 40 | 12,00 | 15,40 | 19,40 | 24,10 | 29,80 | 37,10 | 53,20 | 55,10 | 61,60 | ||
| 0 | 10 | 1,64 | 1,81 | 1,93 | |||||||
| 15 | 2,19 | 2,46 | 2,73 | 2,91 | |||||||
| 20 | 3,01 | 3,44 | 3,91 | 4,42 | 4,66 | ||||||
| 25 | 4,29 | 5,02 | 5,81 | 6,72 | 7,71 | 8,16 | |||||
| 30 | 6,42 | 7,69 | 9,13 | 10,80 | 12,70 | 14,80 | 15,90 | ||||
| 35 | 10,20 | 12,60 | 15,30 | 18,60 | 22,30 | 26,90 | 31,70 | 34,90 | |||
| 40 | 17,50 | 22,30 | 28,00 | 34,80 | 42,90 | 53,30 | 76,40 | 79,10 | 88,70 | ||
| +10 | 10 | 1,73 | 1,87 | 1,98 | |||||||
| 15 | 2,40 | 2,65 | 2,93 | 3,12 | |||||||
| 20 | 3,45 | 3,90 | 4,40 | 4,96 | 5,23 | ||||||
| 25 | 5,17 | 5,99 | 6,90 | 7,95 | 9,11 | 9,67 | |||||
| 30 | 8,17 | 9,69 | 11,40 | 13,50 | 15,90 | 18,50 | 19,90 | ||||
| 35 | 13,80 | 16,90 | 20,50 | 24,80 | 29,80 | 35,80 | 42,30 | 46,60 | |||
| 40 | 25,50 | 32,20 | 40,40 | 49,90 | 61,70 | 76,40 | 110,00 | 113,00 | 127,00 | ||
| +20 | 10 | 1,78 | 1,89 | 2,01 | |||||||
| 15 | 2,58 | 2,82 | 3,11 | 3,30 | |||||||
| 20 | 3,90 | 4,38 | 4,92 | 5,53 | 5,83 | ||||||
| 25 | 6,18 | 7,12 | 8,17 | 9,39 | 10,70 | 11,40 | |||||
| 30 | 10,40 | 12,30 | 14,40 | 16,90 | 20,00 | 23,20 | 25,00 | ||||
| 35 | 18,70 | 22,80 | 27,60 | 33,30 | 40,00 | 48,00 | 56,80 | 62,50 | |||
| 40 | 37,20 | 46,90 | 58,60 | 72,50 | 89,30 | 111,00 | 158,00 | 164,00 | 185,00 | ||
Tab. 11 Zmenšovací součinitel ψ pro δ < φ
| φ | δ / φ | |||||
| 1,0 | 0,8 | 0,6 | 0,4 | 0,2 | 0,0 | |
| 10 | 1,00 | 0,989 | 0,962 | 0,929 | 0,898 | 0,864 |
| 15 | 1,00 | 0,979 | 0,934 | 0,881 | 0,830 | 0,775 |
| 20 | 1,00 | 0,968 | 0,901 | 0,824 | 0,752 | 0,678 |
| 25 | 1,00 | 0,954 | 0,860 | 0,759 | 0,666 | 0,574 |
| 30 | 1,00 | 0,937 | 0,811 | 0,686 | 0,574 | 0,467 |
| 35 | 1,00 | 0,916 | 0,752 | 0,603 | 0,475 | 0,362 |
| 40 | 1,00 | 0,886 | 0,682 | 0,512 | 0,375 | 0,262 |
Pasivní zemní tlak – jemnozrnné zeminy
V případě suchých, nebo částečně nasycených jemnozrnných zemin, jejichž smyková pevnost je dána efektivními parametry, lze napětí při pasivním zemním tlaku spočítat ze vztahu:
\begin{gathered}
\sigma_\text{p}=\sigma_\text{z}\cdot K_\text{p}\cdot\psi+2\cdot c_\text{ef}\cdot(K_\text{p}\cdot\psi)^\frac{1}{2}
\end{gathered}(33)
a výslednice pasivního zemního tlaku bude:
\begin{gathered}
S_\text{p}=\frac{1}{2}\cdot h^2\cdot(K_\text{p}\cdot\psi)+2\cdot c_\text{ef}\cdot h\cdot(K_\text{p}\cdot\psi)^\frac{1}{2}
\end{gathered}(34)
Pasivní zemní tlak na konstrukce omezené šířky
Jde o typický případ záporových a mikrozáporových stěn a též pilotových stěn volně stojících s velkou osovou vzdáleností pilot, kde pode dnem stavební jámy vzdoruje pasivní zemní tlak ovšem na omezenou šířku konstrukce b. V tomto případě se buď počítá se šířkou b danou průměrem vrtu pro záporu (mikrozáporu), nebo se použije empirických vztahů podle ČSN 73 0037. V případě jemnozrnných zemin charakterizovaných: φef < 30° a cef ≠ 0 lze výslednici pasivního zemního tlaku stanovit:
\begin{gathered}
S_\text{pb}=\min(S_\text{pb1},S_\text{pb2})
\end{gathered}kde jsou:
\begin{gathered}
S_\text{pb1}=\eta\cdot c_\text{ef}\cdot b\cdot d\\\\
S_\text{pb2}=2\cdot c_\text{ef}\cdot b\cdot d\cdot(1+\frac{L}{d})
\end{gathered}(35)
podle označení podle obr. 45. Součinitel η se stanoví z grafu na obr. 46. Výslednice Spb je ve výšce 0,47d od paty pažicí konstrukce. Platnost vzorců (35) je omezena podmínkou: L / b ≥ (L / b)cr, přičemž kritické velikosti lze odečíst z grafu na obr. 47. Je-li L / b < (L / b)cr, využije se výše uvedených vzorců pro rovinný problém.
Obr. 45 Pasivní zemní tlak na konstrukce omezené šířky
Obr. 46 Graf pro stanovení velikosti součinitele η
V případě, že φ ≥ 30°, potom výslednice pasivního zemního tlaku na konstrukci šířky b a výšky d se stanoví:
\begin{gathered}
S_\text{pb}=\frac{1}{2}\cdot\gamma\cdot\omega_\text{r}\cdot d^3+2\cdot c_\text{ef}\cdot\omega_\text{k}\cdot d^2
\end{gathered}(36)
kde je:
ωr … podle grafu na obr. 47;
ωk … podle grafu na obr. 48.
Působiště výslednice Spb je ve výšce 0,3d nad patou pažicí konstrukce pro posouzení podle I. skupiny mezního stavu, resp. ve výšce 0,4d nad patou v případě posouzení podle II. skupiny mezního stavu. Vzorec (36) platí pro b ≥ 0,3d a L ≥ d. Pokud tyto nerovnosti nejsou splněny, je třeba posoudit řešení rovinného problému a jako směrodatné vzít nižší hodnoty Sp.
Obr. 47 Graf pro určení součinitele ωr
Obr. 48 Graf pro určení součinitele ωk
2.2.2 Přírůstky zemních tlaků od ostatního stálého i nahodilého zatížení
Stálé i nahodilé zatížení za rubem pažicí konstrukce (v libovolné hloubce) má vliv na přírůstky příslušných zemních tlaků, (v klidu, aktivních a even. i pasívních). Náhradní zatížení povrchu terénu za silniční vozidla a stavební stroje o celkové hmotnosti do 24 t se uvažuje jako celoplošné neohraničené zatížení povrchu za rubem stěny o charakteristické velikosti p = 10 kPa, obr. 49a, přičemž musí být dodržena vzdálenost vozidla od pažicí konstrukce y ≥ 3,0 m. Je-li tato vzdálenost menší, (y = 0,6 – 3,0 m), doporučuje se zvýšit zatížení v pásu širokém 3,0 m na následující velikosti, (obr. 49b):
- při vzdálenosti y > 2,0 m … p1 = 20 kPa;
- při vzdálenosti y > 1,0 m … p1 = 30 kPa;
- při vzdálenosti y > 0,6 m … p1 = 40 kPa.
Při hmotnosti vozidel a strojů převyšující 24 t, zvýší se příslušná charakteristická ztížení p, p1 na:
- 1,2 – násobek při hmotnosti vozidel 30 t;
- 1,9 – násobek při hmotnosti vozidel 45 t;
- 2,5 – násobek při hmotnosti vozidel 60 t.
Pokud se za rubem stěny pohybují pásové bagry nebo jeřáby, je třeba dodržet minimální vzdálenost pásů 0,6 m za rubem pažicí konstrukce a účinek zatížení lze nahradit zatížením pásovým p2 o šířce 1,50 m podle obr. 50c a to o charakteristické velikosti:
- p2 = 30 kPa při hmotnosti stroje do 10 t;
- p2 = 60 kPa při hmotnosti stroje do 30 t;
- p2 = 90 kPa při hmotnosti stroje do 50 t.
Obr. 49 Schéma náhradního zatížení povrchu terénu za rubem pažicí konstrukce
Účinky osamělých břemen je třeba vyšetřit individuálně za předpokladu půdorysného roznášení podle obr. 50. Pro městskou hromadnou dopravu, (tramvaj), lze počítat s plošným neohraničeným zatížením p = 10 kPa, pokud je dodržena vzdálenost okraje tramvajového svršku od rubu pažicí konstrukce 0,6 m. Přitížení od železniční dopravy opět za předpokladu min. vzdálenosti okraje železničního svršku od rubu pažicí konstrukce 0,6 m se stanoví podle obr. 51 a činí ve směru podélném 20 kPa v celé délce, přičemž v libovolném místě se na délku 6,4 m zvýší na 39 kPa, v příčném směru se podélné zatížení roznáší na šířku 4,0 m.
Veškeré zde uvedené velikosti náhradního plošného zatížení jsou velikostmi charakteristickými. Při posuzování pažicí konstrukce z hlediska mezního stavu únosnosti je třeba upravit je na velikosti návrhové (ve smyslu ČSN EN 1997-1). Náhradní zatížení od dopravy jsou zatížením nahodilým, (pohyblivým).
Obr. 50 Půdorysné roznášení osamělých břemen: 1 – osamělé břemeno, 2 – půdorysné roznášení zatížení pod úhlem 45°, 3 – pažicí konstrukce, 4 – náhradní přímkové zatížení
Obr. 51 Náhradní zatížení od železniční dopravy: a – v podélném směru, b – v příčném směru
Veškeré zde uvedené velikosti náhradního plošného zatížení jsou velikostmi charakteristickými. Při posuzování pažicí konstrukce z hlediska mezního stavu únosnosti je třeba upravit je na velikosti návrhové (ve smyslu ČSN EN 1997-1). Náhradní zatížení od dopravy jsou zatížením nahodilým, (pohyblivým).
Zatížení od sousedních staveb a konstrukcí, (např. zatížení v základové spáře sousedních objektů) se uvažuje skutečnou hodnotou v příslušné hloubce a vzdálenosti od pažicí konstrukce, přičemž se jedná vesměs o zatížení stálé. Hloubkový roznos zatížení, tj. přírůstek zatížení je pro jeho nejpoužívanější druhy uveden na obr. 52. Je počítáno s homogenní zeminou za rubem pažicí konstrukce výšky h charakterizovanou objemovou tíhou v přirozeném uložení γ a s náhradním úhlem vnitřního tření podle obr. 45, tj. za předpokladu c = 0. Příslušné velikosti náhradního zatížení jsou označeny q [kPa] a příslušný koeficient zemního tlaku je obecně označen K, (bez ohledu na to, jedná-li se o zemní tlak v klidu, o zemní tlak aktivní, či jakkoliv zvýšený zemný tlak aktivní). Vyšetřována je vždy vodorovná složka napětí e při příslušném zemním tlaku.
Pro nejjednodušší a současně nejtypičtější případy vodorovného terénu a svislého rubu pažicí konstrukce platí, že ϑa = 45° + φ / 2.
2.2.3 Zemní tlaky na pažení
Rozdělení zemního tlaku podél pažicí konstrukce charakterizuje obrazec napětí, který je závislý na tuhosti této konstrukce a charakteru deformace. Je-li zamezeno jakémukoliv přetvoření konstrukce a zeminy, působí zemní tlak v klidu, jehož výslednice je kolmá na rub této konstrukce, (δ = 0), neboť na jejím rubu nevzniká tření. V případě dostatečně tuhé pažicí konstrukce, která se deformuje pouze pootočením a/nebo posunem jsou typické obrazce rozdělení zemního tlaku aktivního a pasivního po výšce na obr. 53 a příslušné velikosti deformací potřebných k mobilizaci těchto tlaků jsou v tab. 12.
Tab. 12 Deformace tuhé pažicí konstrukce potřebné k mobilizaci zemních tlaků
| Zemní tlak | Nesoudržná zemina | Relativní velikosti deformace pažicí konstrukce Δy / h nutné pro dosažení velikosti zemního tlaku | ||
| Základní typ deformace | Naklonění kolem paty | Vodorovný posun | Naklonění kolem hlavy | |
| aktivní Sa | kyprá | 0,004–0,005 | 0,002–0,003 | 0,008–0,01 |
| aktivní Sa | ulehlá | 0,001–0,002 | 0,0005–0,001 | 0,002–0,004 |
| pasivní Sp | kyprá | 0,3 | 0,1 | 0,15 |
| pasivní 0,5 Sp | kyprá | 0,04 | 0,005 | 0,01 |
| pasivní Sp | ulehlá | 0,1 | 0,05 | 0,05 |
| pasivní 0,5 Sp | kyprá | 0,025 | 0,005 | 0,005 |
Obr. 52 Průběh vodorovného napětí s hloubkou od přitížení za rubem pažicí konstrukce
Vlivem pootočení, posunů a průhybů pažicích konstrukcí dochází tedy k změně původního lineárního rozdělení napětí při zemním tlaku, tedy k redistribuci zatížení pažicí konstrukce zemním tlakem. Příklad redistribuce původního, (trojúhelníkového) rozdělení napětí při zemním tlaku v případě jednonásobně kotvené, nebo i rozepřené pažicí konstrukce je na obr. 54. V případě vícenásobně kotvených a rozepřených pažicích konstrukcí lze rozdělení napětí od zemního tlaku stanovit pouze velmi přibližně, např. jak je uvedeno na obr. 55. Při střídajících se vrstvách hrubozrnných a jemnozrnných zemin je třeba provést řešení pažicí konstrukce jednak na zatížení s reálnými smykovými parametry v jednotlivých vrstvách, jednak na zatížení tzv. minimálním dimenzačním tlakem. Ten se určí tak, že ve vrstvách jemnozrnných zemin se velikost tlaků na hranicích vrstvy vypočte se součinitelem Ka,min = 0,20, jako pro zeminu hrubozrnnou. Pro dimenzování konstrukce je směrodatný zatěžovací obrazec, který vyvodí nepříznivější vnitřní síly (obr. 56). Podrobněji je o doporučených způsobech rozdělení zemního tlaku v klidu, tlaků aktivního a pasivního na pažicí konstrukce pojednáno např. v ČSN 73 0037.
Obr. 53 Základní případy deformace tuhé pažicí konstrukce a odpovídající obrazce rozdělení zemních tlaků (v případě hrubozrnných zemin)
Obr. 54 Redistribuce aktivního tlaku u jedenkrát podepřených stěn: a) klasický trojúhelník, b) trojúhelník s vrcholem v úrovni kotvy, c) parabola, d) obdélník
Obr. 55 Doporučené tlakové obrazce pro vícenásobně podepřené stěny: a) hrubozrnné zeminy, b) jemnozrnné zeminy
Obr. 56 Tlak na pažicí stěnu ve vrstevnatém prostředí
2.2.4 Účinky podzemní vody
Účinky podzemní vody se na zatížení pažicích konstrukcí projevují:
- změnou geotechnických vlastností základové půdy;
- hydrostatickým tlakem;
- proudovým tlakem.
Podzemní voda ovlivňuje zejména objemovou tíhu základové půdy a v případě jemnozrnných zemin může mít vliv na velikost smykové pevnosti. Objemová tíha propustných, (zejména hrubozrnných) zemin pod vodou je dána vztahem:
\begin{gathered}
\gamma_\text{su}=(1-n)\cdot(\gamma_\text{s}-\gamma_\text{w})
\end{gathered}(37)
objemová tíha málo propustných zemin nasycených vodou, (zejména jemnozrnných) je dána:
\begin{gathered}
\gamma_\text{sat}=(1-n)\cdot\gamma_\text{s}+S_\text{r}\cdot n\cdot\gamma_\text{w}
\end{gathered}(38)
kde je:
n … pórovitost zeminy;
γs … měrná tíha zrn zeminy, (průměrně 27 kN·m-3);
γw … objemová tíha vody, (10 kN·m3);
Sr … stupeň nasycení (pro plně saturovanou zeminu Sr = 1,0).
Hydrostatický tlak se uplatňuje jak v případě propustných, tak i nepropustných zemin, neboť z titulu deformace pažicí konstrukce nelze vyloučit vznik příslušného vodního sloupce za rubem stěny. Je-li však pata stěny vetknuta do nepropustného, resp. málo propustného prostředí, (s koef. filtrace k < 10-7 až 10-8 m·s-1), předpokládá se obyčejně, že podzemní voda pod patou pažicí konstrukce neproudí a vzniká pouze hydrostatický tlak s napětím:
\begin{gathered}
\sigma_\text{w}=\gamma_\text{w}\cdot h_\text{w}
\end{gathered}(39)
jež působí kolmo na rub pažicí konstrukce s výslednicí:
\begin{gathered}
S_\text{w1}=\frac{1}{2}\cdot\gamma_\text{w}\cdot h_\text{w}^2
\end{gathered}(40)
Pokud je pažicí konstrukce pode dnem výkopu rovněž ve zvodnělé základové půdě, bude se výsledný zatěžovací obrazec skládat ze dvou částí – horní trojúhelníkové a spodní obdélníkové, jak vyplývá z obr. 57a, podle vztahu:
\begin{gathered}
S_\text{w2}=\gamma_\text{w}\cdot h_\text{w}\cdot d_\text{pr}
\end{gathered}(41)
V případě pažicí konstrukce vetknuté do propustné základové půdy vzniká pod patou proudění, které jednak ovlivňuje velikost hydrostatického tlaku, jednak je příčinou vzniku tzv. proudového tlaku j. V důsledku ztrát vzniklých prouděním podzemní vody v okolí paty pažicí konstrukce předpokládáme, že napětí při hydrostatickém tlaku klesá k nule, (obr. 58b), tudíž:
\begin{gathered}
S_\text{w2}=\frac{1}{2\gamma_\text{w}}\cdot h_\text{w}\cdot d
\end{gathered}(42)
(Původní německá norma DIN 4085 ovšem předpokládala u paty stěny tzv. zbytkový tlak o velikosti 0,3 · γw · hw).
V případě proudění podzemní vody pod patou pažicí konstrukce ovšem vzniká také proudový tlak podle vztahu:
\begin{gathered}
j=\gamma_\text{w}\cdot i
\end{gathered}(43)
kde je:
i … hydraulický spád, jež je bezrozměrný, tudíž platí, že j = kN·m-3, tedy proudový tlak má fyzikální rozměr objemové tíhy.
Na rubové straně konstrukce proudí voda směrem dolů, tudíž zvyšuje objemovou tíhu zeminy podle vztahu:
\begin{gathered}
\gamma_\text{ef,a}=\gamma_\text{su}+\gamma_\text{w}\cdot i
\end{gathered}(44)
na lícní straně proudí voda vzhůru, tudíž snižuje objemovou tíhu zeminy:
\begin{gathered}
\gamma_\text{ef,p}=\gamma_\text{su}-\gamma_\text{w}\cdot i
\end{gathered}(45)
Aplikujeme-li tyto vztahy na příklad znázorněný na obr. 57b, získáme:
\begin{gathered}
\gamma_\text{ef,a}=\gamma_\text{su}+\gamma_\text{w}\cdot\frac{h_\text{w}}{(h_\text{w}+2d)};&&\gamma_\text{ef,p}=\gamma_\text{su}-\gamma_\text{w}\cdot\frac{h_\text{w}}{(h_\text{w}+2d)}
\end{gathered}(46)
Je tedy podle rovnice (45) zřejmé, že při dostatečně velikém hydraulickém spádu i může dojít k vzniku „beztížného“ stavu v zemině, který se nazývá hydraulickým prolomením dna. Ten vzniká teoreticky při tzv. kritickém spádu:
\begin{gathered}
i_\text{cr}=\frac{\gamma_\text{su}}{\gamma_\text{w}}=1{,}0
\end{gathered}(47)
Prakticky to ale znamená, že lze připustit podstatně menší velikost hydraulického spádu, a to v případě malých stavebních jam, (zejména jímek) imax = 0,5, v případě velmi hlubokých jímek a dlouhodobého proudění podzemní vody pak imax = 0,3 – 0,4.
Obr. 57 Tlak podzemní vody na pažení: a) pata pažicí stěny je vetknuta do nepropustné zeminy, b) pata pažicí konstrukce se nachází v propustné zemině
2.3 POSOUZENÍ PAŽICÍCH KONSTRUKCÍ STATICKÝM VÝPOČTEM
Statický výpočet představuje základní metodu pro posouzení návrhu pažicí konstrukce. Ve smyslu EC 7-1, kap. 9 je výpočet založen na teorii mezních stavů. V případě jakékoliv pažicí konstrukce je třeba posoudit následující mezní stavy:
- 1) ztrátu celkové stability;
- 2) porušení konstrukčního prvku, (zápora, pilota, podzemní stěna, kotva, převázka, pažina, apod.) a spojení mezi nimi;
- 3) kombinace porušení v základové půdě a v konstrukčním prvku;
- 4) porušení nadzdvižením a vnější erozí;
- 5) deformace pažicí konstrukce, jež mohou vést k jejímu kolapsu, nebo mohou ovlivnit použitelnost pažicí konstrukce a konstrukcí nacházejících se v jejím sousedství, (stavby, inženýrské sítě, komunikace apod.);
- 6) nepřijatelný průsak vody pažicí konstrukcí;
- 7) nepřijatelný transport částic zeminy pažicí konstrukcí, (sufoze);
- 8) nepřijatelná změna v režimu podzemních vod.
Stav ad 1) se vyšetřuje zejména u konstrukcí kotvených, a to jak pomocí zemních kotev, tak i táhel s kotevními prvky např. typu „deadmen“. Stavy ad 2) a 3) souvisí s dimenzováním jednotlivých prvků pažicích stěn, jež by mělo probíhat pro 1. mezní stav porušení ve smyslu porušení typu STR. Stav ad 4) a zejména ad 5) souvisí s deformací pažicí konstrukce, která se jeví jako rozhodujícím stavem pro skutečný návrh pažicích konstrukcí. Stavy ad 6), 7) a 8) jsou zajímavé u konstrukcí těsnicích. Je tedy zřejmé, že výpočet pažicích konstrukcí by měl vycházet z mezního stavu použitelnosti, tj. z 2. mezního stavu, a to zejména v případě záporového pažení, pilotových a podzemních stěn, vnější a vnitřní stabilita pažicích konstrukcí by měla být posouzena ve smyslu zásad mezního stavu porušení, tj. 1. mezní stav. Příklady mezních stavů ztráty stability pažicích konstrukcí jsou na obr. 58 a 59.
Návrh konstrukce pažení stavebních jam závisí především:
- na inženýrskogeologických a hydrogeologických poměrech na staveništi, na pevnostních a deformačních vlastnostech základové půdy, na charakteru navážky a násypů, na eventuální existenci stávajících, nebo i předpokládaných podzemních prostor na staveništi, nebo v jeho těsné blízkosti;
- na půdorysných rozměrech stavební jámy a možnostech přístupu pro stavební stroje a mechanizmy;
- na reliéfu terénu, na hloubce stavební jámy a na hloubce základových spár sousední zástavby;
- na charakteru a stavebním stavu sousední zástavby, na stupni prozkoumanosti této zástavby;
- na velikosti využitelného prostoru pro vytvoření pažicí konstrukce;
- na požadavku na charakter této konstrukce (pouze pažicí – dočasná, nebo trvalá);
- na požadavku na vodotěsnost pažicí konstrukce, popř. požadavku na využití této konstrukce jako ztracené bednění, na požadavku na rovinnost této konstrukce využité např. jako podklad pod svislou izolaci;
- na požadavku na likvidaci pažicí konstrukce, nebo jejích prvků (zápor, pažin, kotev);
- na požadavku na tuhost pažicí konstrukce s ohledem na její přípustné deformace a deformace vyvolané výkopem na sousední zástavbu.
Obr. 58 Příklady mezních stavů ztráty stability pažicích konstrukcí: a, b – celková stabilita kotvených konstrukcí; c, d, e, f – ztráta stability pootočením pažicí konstrukce, g – ztráta stability porušením ve svislém směru; h, i, j, k, l, m – konstrukční porušení
Obr. 59 Příklady mezních stavů ztráty stability pažicích konstrukcí: n, o, p – ztráta stability vytažením kotvy
2.3.1 Hřebíkované svahy
Pro posouzení hřebíkovaného svahu je třeba sestavit geotechnický výpočetní model, přičemž jeho statické schéma odpovídá quazihomogenní gravitační opěrné zdi. Zavádí se následující předpoklady:
1) podmínka excentricity výslednice sil v průřezu: pro provozní stav hřebíkované stěny je nutné dodržet zásadu, aby v průřezu nevzniklo tahové napětí, musí tedy platit:
\begin{gathered}
e_\text{max}=\frac{M}{A_\text{V}}\le\frac{L}{6}
\end{gathered}(48)
kde je:
L … tloušťka vyztužené stěny, (tj. v podstatě délka hřebíků l);
M … moment vnějších sil k ose průřezu;
AV … plocha průřezu.
2) podmínka bezpečnosti proti usmyknutí ve vodorovném řezu:
\begin{gathered}
\frac{\tau}{\sigma}\le\frac{\tg\varphi}{s_1}
\end{gathered}(49)
kde je:
τ … průměrné smykové napětí od vodorovných sil v posuzovaném průřezu;
σ … průměrné normálové napětí v posuzovaném průřezu;
s1 … předepsaný stupeň bezpečnosti;
φ … úhel vnitřního tření zeminy.
3) podmínka týkající se návrhu a dimenzování hřebíků, tj. zachycení tlaku zeminy na rubu stříkaného betonu:
\begin{gathered}
K_\text{n}\le K_\text{a}=\tg^2\cdot(45-\frac{\varphi}{2})\\\\
K_\text{n}\cong0{,}85K_\text{a}
\end{gathered}(50)
Hřebíky se navrhují v síti s vodorovným rozponem b a svislou vzdáleností v, přičemž platí, že b · v < 6 m2, obvykle b i v = 1,5 – 2,5 m. Pro předběžný návrh lze použít francouzských nomogramů, (Clouterre) podle obr. 60, kde pro stabilitní parametry svahu: γ, φef, cef a poměr L / H je uvedena doporučená hustota hřebíkování d podle vztahu:
\begin{gathered}
D=\frac{T}{(\gamma\cdot b\cdot v)}
\end{gathered}(51)
přičemž
\begin{gathered}
T=\pi\cdot D\cdot l\cdot\tau_\text{s}
\end{gathered}(52)
kde je:
D … průměr vrtu pro hřebík;
l … délka hřebíku;
τs … smykové napětí na styku vrt – zemina, (pro písky a štěrky 0,1–0,3 MPa, pro jíly to jsou zhruba poloviční velikosti, pro poloskalní horniny až dvojnásobné velikosti).
Obr. 60 Nomogramy pro předběžný návrh hustoty hřebíků
Posouzení hřebíkovaného svahu
Vycházíme ze statického schéma na obr. 61.
1. Návrhová délka hřebíků: (tloušťka stěny v libovolné hloubce z)
\begin{gathered}
l\ge z\cdot(K_\text{a})^\frac{1}{2}=z\cdot\tg(45-\frac{\varphi}{2})\space\text{a zároveň}\\\\
l\ge s_1\cdot z\cdot\frac{\tg^2(45-\frac{\varphi}{2})}{(2\cdot\tg\varphi)}
\end{gathered}(53)
2. Výška etáže
\begin{gathered}
h_\text{lim}=\frac{(4c\cdot\sin\omega\cdot\cos\varphi)}{(\gamma\cdot(1-\cos(\omega-\varphi)))}-\frac{2p}{\gamma}
\end{gathered}(54)
kde je:
p … zatížení terénu nad zářezem
3. Zemní tlak
Vodorovná složka aktivní síly:
\begin{gathered}
S_\text{ahc}=0{,}5\gamma\cdot z^2\cdot K_\text{ah}-2c\cdot K_\text{ahc}+\frac{2c^2}{\gamma}\cdot\frac{K_\text{ahc}^2}{K_\text{ah}}
\end{gathered}(55)
Kah viz rovnice (22)
\begin{gathered}
K_\text{ahc}=\frac{[\cos\varphi\cdot\cos\beta\cdot\cos(\delta+\alpha)\cdot(1+\tg\alpha\cdot\tg\beta)]}{(1+\sin(\varphi+\delta+\alpha+\beta))}
\end{gathered}(56)
Svislá složka aktivní síly:
\begin{gathered}
S_\text{avc}=S_\text{ahc}\cdot\tg(\delta-\alpha)
\end{gathered}(57)
Výslednice aktivního tlaku:
\begin{gathered}
S_\text{ac}=\frac{S_\text{ahc}}{\cos(\delta-\alpha)}\space\text{jež působí pod úhlem}\space(\delta–\alpha)\space\text{k vodorovné}
\end{gathered}(58)
K libovolnému bodu P střednice prohřebované zóny působí síla Sahc na rameni ah a síla Savc na rameni av:
\begin{gathered}
a_\text{h}=\frac{z_1}{3};\space\space a_\text{v}=\frac{b}{2}+\frac{z_1}{3}\cdot\tg\alpha
\end{gathered}(59)
Výška z1 na níž působí zemní tlak:
\begin{gathered}
z_1=z-h_\text{c}=z-\frac{2c}{\gamma}\cdot\frac{K_\text{ahc}}{K_\text{ah}}
\end{gathered}(60)
4. Tíha tělesa
Tíha prohřebovaného tělesa 1, 2, 3, 4:
\begin{gathered}
G=\gamma\cdot z\cdot\frac{L}{\cos\alpha}
\end{gathered}(61)
Obr. 61 Statické schéma pro výpočet hřebíkovaného svahu
Vnější stabilita konstrukce
Posouzení proti překlopení
\begin{gathered}
s_1\cdot e\le\frac{L}{2},\space\space\text{neboli}\space\space e\le\frac{L}{3},\space\space\text{když}\space\space s_1=1{,}5,\space\space\text{tedy}\space\space e=\frac{(S_\text{ahc}\cdot a_\text{h}-S_\text{avc}\cdot a_\text{v})}{(G\cdot\cos\alpha+S_\text{ac}\cdot\sin\delta)}\le\frac{L}{3}
\end{gathered}(62)
Posouzení proti usmyknutí
\begin{gathered}
\tau_\text{m}\le\sigma_\text{m}\cdot\tg\varphi+c,
\end{gathered}kde je:
\begin{gathered}
\tau_\text{m}=S_\text{ac}\cdot\frac{\cos\delta}{L}
\end{gathered}(63)
\begin{gathered}
\sigma_\text{m}=\frac{(S_\text{ac}\cdot\sin\delta+G\cdot\cos\alpha)}{L}
\end{gathered}(64)
Posouzení únosnosti v základové spáře
\begin{gathered}
\sigma=\frac{V_\text{d}}{A_\text{ef}}=\frac{(S_\text{ac}\cdot\sin\delta+G\cdot\cos\alpha)}{(L-2e)}\le R_\text{du}\space\text{(vše na 1 bm šířky svahu)}
\end{gathered}(65)
Vnější stabilitu na smykové ploše je třeba prokázat na ploše procházející vně hřebíkované oblasti. Používá se známých postupů z řešení stability svahů, (viz kap. 1.2).
Vnitřní stabilita konstrukce
Návrh a posouzení hřebíků
Pro dimenzování je rozhodující dolní hřebík v hloubce zH, jež přenáší zatížení z plochy: b (šířka) a v (výška). Pro nezatížený povrch platí:
\begin{gathered}
z_\text{H}=h-\frac{v}{2};&&\sigma_\text{az}=K_\text{n}\cdot\gamma\cdot z_\text{H}
\end{gathered}(66)
Síla v hřebíku:
\begin{gathered}
F_\text{H}=b\cdot v\cdot K_\text{n}\cdot\gamma\cdot z_\text{H}
\end{gathered}(67)
Celkový počet hřebíků n musí být takový, aby hřebíky po výšce svahu přenesly sílu:
\begin{gathered}
S_\text{ac,per}=\frac{S_\text{ahc}}{\cos\alpha}
\end{gathered}(68)
Návrh a posouzení betonového krytu – stříkaného betonu
Betonový kryt se posoudí na ohyb, (spojitý nosník) a na protlačení skrz stříkaný beton.
Posouzení na možných smykových plochách:
- a) ve stádiu výstavby;
- b) v konečném stádiu.
Obr. 62a Příklady posouzení stability na vnitřních smykových plochách: a – během výstavby hřebíkované stěny
Obr. 62b Příklady posouzení stability na vnitřních smykových plochách: b – v konečném stádiu
2.3.2 Prutové modely na tuhých podporách s předem stanoveným zatížením, příklady 1 a 2
Jedná se o klasické postupy výpočtu pažicích konstrukcí, které jsou použitelné zejména pro stanovení velikostí vnitřních sil a dimenzování prvků pažicí konstrukce. Pro odhad jejích deformací však nejsou vhodné. Princip tohoto řešení bude stručně vysvětlen pro pochopení a správnou aplikaci programového řešení, jež naprosto převládá a pro analýzu získaných výsledků. Ke klasickým postupům patří zejména tzv. Blumova metoda, která umožňuje jednoduché výpočty nepodepřených a jedenkrát podepřených pažicích konstrukcí, neboť jde o případy staticky určité, (obr. 63 a, b, c) a dále též výpočty vícekrát podepřených pažicích konstrukcí, které jsou převedeny na výpočet spojitého nosníku, (obr. 63 d).
Obr. 63 Statické typy pažicích konstrukcí: a) vetknutí do dna, b) kotvení s volným uloženímpaty, c) kotvení s vetnutím paty, d) vícenásobné podepření
Princip tohoto řešení pro nekotvenou a nerozepřenou pažicí konstrukci je patrný z obr. 64, přičemž se počítá s trojúhelníkovým rozdělením zatížení od zemních tlaků.
Obr. 64 Statické schéma pro nepodepřenou pažicí konstrukci: a) průběh zatížení, b) průběhy momentů; 1 – obecná základní čára momentové plochy, 2 – čára pro volné uložení v patě, 3 – čára pro vetnutí v patě, 4 – moment od kotvy pod vrcholem stěny, 5 – průběh momentu na stěně pouze vetknuté do dna, jinak nepodepřené
Pomocí tří statických rovnic rovnováhy vypočteme neznámé veličiny:
- potřebnou hloubku vetknutí pažicí konstrukce pode dno jámy dp, (pomocí momentové podmínky rovnováhy k bodu C);
- potřebné prodloužení vetknutí Δdp tak, aby byla splněna silová podmínka rovnováhy ve vodorovném směru;
- pomocí silové podmínky rovnováhy ve směru svislém stanovíme velikost potřené síly přenášené patou pažicí konstrukce, popř. též třením v jejím vetknutí, přičemž zde je třeba zajistit 1,5násobnou bezpečnost.
Vlastní pažicí konstrukce se dimenzuje na mimostředný tlak, přičemž maximální moment je pode dnem stavební jámy v hloubce, v níž je posouvající síla nulová. Při tomto výpočtu je třeba zejména zohlednit:
- charakter pažicí konstrukce, a to pro správnou volbu velikosti zatížení v oblasti pode dnem stavební jámy, přičemž pro souvislé pažicí konstrukce, (např. podzemní a štětové stěny) se počítá s pruhem B = 1,0 m, pro konstrukce nesouvislé (např. záporové pažení, pilotové stěny) se počítá s výrazně zmenšenou zatěžovací šířkou;
- velikosti působících zemních tlaků ve vztahu k očekávaným, resp. přípustným deformacím pažicí konstrukce. V žádném případě nelze např. kombinovat plnou velikost zemního tlaku aktivního s plnou velikostí tlaku pasivního. Počítá se s tzv. zvýšeným aktivním zemním tlakem např.:
\begin{gathered}
S_\text{a,zv}=S_\text{a}+k_1\cdot(S_0-S_\text{a})
\end{gathered}a sníženým pasivním zemním tlakem
\begin{gathered}
S_\text{p,sn}=S_\text{p}-k_2\cdot(S_\text{p}-S_0)
\end{gathered}kde k1, k2 = 0,33 – 0,66; ve vztahu k přípustným velikostem deformací lze navrhnout i jiné vztahy pro velikost Sa,zv, Sp,sn.
V případě jednonásobně podepřené (kotvené, či rozepřené) pažicí konstrukce, (podle obr. 65) se postupuje obdobně s tím, že bod otáčení se volí v bodě K, (k němu je vztažena momentová podmínka rovnováhy) a neznámými jsou jednak hloubka vetknutí (d + Δd), jednak síla Fk, (síla v kotvě po příslušném přepočtu s ohledem na její sklon, popř. síla v rozepření). K tomu výpočtu slouží podmínka rovnováhy ve směru vodorovném. Podmínku rovnováhy ve směru svislém využijeme obdobně jako v předchozím případě.
Obr. 65 Jednoduše podepřené stěna vetknutá v patě: a) rozdělení tlaků, b) ohybové momenty, c) náhradní nosníky
V případě záporového pažení a pilotových stěn s velkou roztečí pilot nebo zápor B > d, budou opět aktivní síly působící do úrovně dna stavební jámy počítány na celou šířku B (osová vzdálenost zápor, nebo pilot), kdežto ostatní aktivní a pasivní síly pode dnem stavební jámy budou působit na šířku d, popř. pouze na šířku příruby zápor zejména v případě zápor beraněných či vibrovaných. K těmto pasivním silám přistupují ovšem další síly Rk, jež působí ve svislých rovinách vedených okrajem zápor či pilot. Podél každé zápory či piloty jsou to potom síly dvě o shodné velikosti. Ty lze stanovit za předpokladu vzniku smykové plochy procházející patou pažicí konstrukce pod úhlem 45 – φ / 2 od vodorovné (obr. 66). Tím je vymezen svislý trojúhelník KLM o výšce t a základně a = t · tg(45 + φ / 2). Tření ve dvou svislých rovinách KLM podél vetknuté části zápory či piloty je dáno:
\begin{gathered}
2R_\text{k}=E_\text{s}\cdot\tg\varphi
\end{gathered}(69)
kde je:
\begin{gathered}
E_\text{s}=A_\text{(KLM)}\cdot\gamma\cdot\frac{t}{3}=\gamma\cdot\frac{t^3}{6}\cdot\tg(45+\frac{\varphi}{2})
\end{gathered}(70)
Tyto síly se potom výrazně uplatní při sestavení podmínek rovnováhy.
Obr. 66 Definice třecích sil Rk
Smykové síly Rk samozřejmě nevznikají v případě podzemních stěn a štětových stěn, jakož i převrtávaných stěn pilotových, zde ovšem pasivní síly působí na stejnou šířku jako síly aktivní (obyčejně se počítá s šířkou B = 1,0 m).
Přibližné řešení vícenásobně podepřených pažicích konstrukcí lze provést aplikací metody náhradních nosníků podle obr. 67. Horní náhradní nosník je tvořen spojitým nosníkem s podporami v místech zakotvení, spodní náhradní nosník je stejný jako v předchozím případě. Na horním spojitém nosníku se určí všechny podporové a mezipodporové momenty, spodní prostý nosník umožňuje určit hloubku vetknutí z podmínky, že výslednice uvažovaného pasivního tlaku by měla být větší než 1,5násobek spodní reakce spojitého nosníku.
Obr. 67 Přibližné řešení vícenásobně kotvené konstrukce: a) při vetknutí stěny v patě, b) při volném uložení paty
Příklad 1
Výpočet pilotové stěny trvalé z vrtaných pilot ø 630 mm v osových vzdálenostech B = 0,90 m pro volnou výšku H = 3,20 m podle statického schéma na obr. 68. Stěna je v homogenní zemině s charakteristickými hodnotami: γk = 18,5 kN/m3, φef,k = 33°, cef,k = 0, přitížení za rubem p = 8,0 kN/m2.
Obr. 68 Statické schéma pro výpočet nekotvené a nerozepřené pilotové stěny
Řešení:
a) zemní tlaky
- koeficient zemního tlaku v klidu:
\begin{gathered}
K_\text{r}=1-\sin33=0{,}455
\end{gathered}- koeficient zemního tlaku aktivního:
\begin{gathered}
K_\text{a}=\tg^2(45-\frac{33}{2})0{,}295
\end{gathered}- koeficient zemního tlaku pasivního:
\begin{gathered}
K_\text{p}=\tg^2(45+\frac{33}{2})=3{,}392
\end{gathered}- koeficient zvýšeného aktivního zemního tlaku:
\begin{gathered}
K_\text{a,zv}=0{,}5\cdot(0{,}455+0{,}295)=0{,}375
\end{gathered}- koeficient sníženého pasivního zemního tlaku:
\begin{gathered}
K_\text{p,sn}=0{,}5\cdot(0{,}455+3{,}392)=1{,}923
\end{gathered}b) velikosti vodorovných napětí ze zemních tlaků, (δ = φef / 2 = 16,5°)
- v hlavě stěny:
\begin{gathered}
e_0=p\cdot K_\text{a,zv}=8{,}0\cdot0{,}375\cdot\cos16{,}5=2{,}88\space\text{kPa}
\end{gathered}- ve dně jámy:
\begin{gathered}
e_1=18{,}5\cdot3{,}20\cdot0{,}375\cdot\cos16{,}5=21{,}29\space\text{kPa}
\end{gathered}- výpočet hloubky u:
\begin{gathered}
(2{,}88+21{,}29)-18{,}5u\cdot1{,}923\cdot\cos16{,}5=0\space....\space u=0{,}71\space\text{m}
\end{gathered}- ve dně jámy:
\begin{gathered}
e_\text{t}=24{,}17\cdot\frac{(t-0{,}71)}{0{,}71}=34{,}04t-24{,}17
\end{gathered}c) vodorovné síly
\begin{gathered}
S_\text{1h}=2{,}88\cdot3{,}20\cdot0{,}90=8{,}29\space\text{kN}&&\text{rameno k bodu O:}\space s_1=1{,}60+t\\\\
S_\text{2h}=21{,}29\cdot\frac{3{,}20}{2}\cdot0{,}90=30{,}66\space\text{kN}&&\text{rameno k bodu O:}\space s_2=1{,}07+t\\\\
S_\text{3h}=24{,}17\cdot0{,}71\cdot\frac{0{,}63}{2}=5{,}41\space\text{kN}&&\text{rameno k bodu O:}\space s_3=t-0{,}24
\end{gathered}(volíme vzdorující šířku piloty v pasivní oblasti rovnou d = 0,63 m)
\begin{gathered}
S_\text{ph}=(34{,}04t-24{,}17)\cdot(t-0{,}71)\cdot\frac{0{,}63}{2}=10{,}72t^2-10{,}19t+1{,}83&&\text{rameno k bodu O:}\space s_\text{p}=t-\frac{0{,}71}{3}=t-0{,}24
\end{gathered}d) momentová podmínka rovnováhy k bodu O
\begin{gathered}
S_\text{1h}\cdot s_1+S_\text{2h}\cdot s_2+S_\text{3h}\cdot s_3-S_\text{ph}\cdot s_\text{p}=0\\\\
8{,}29\cdot(1{,}60+t)+30{,}66\cdot(1{,}07+t)+5{,}41\cdot(t-0{,}24)-(10{,}72t^2-10{,}19t+1{,}83)\cdot(t-0{,}24)=0\space......\space t^3-1{,}188t^2-3{,}739t-3{,}739t-4{,}217=0\space......\space t=3{,}00\space\text{m}\\\\
S_\text{ph}=128{,}88\space\text{kN}
\end{gathered}e) součtová podmínka ve vodorovném směru
\begin{gathered}
Q=-S_\text{1h}-S_\text{3h}-S_\text{3h}+S_\text{ph}=84{,}52\space\text{kN}
\end{gathered}- napětí
\begin{gathered}
\sigma_\text{p, sn}=3{,}0\cdot18{,}5\cdot1{,}923=106{,}72\space\text{kPa}
\end{gathered}- prodloužení vetknutí
\begin{gathered}
\Delta t=\frac{84{,}52}{(0{,}63\cdot106{,}72)}=1{,}26\space\text{m}
\end{gathered}- celková délka vetknutí
\begin{gathered}
t_\text{celk}=3{,}0+1{,}26=4{,}26\space\text{m}
\end{gathered}f) výpočet hloubky z´, pro níž je posouvající síla nulová
\begin{gathered}
S_\text{ah}=8{,}29+30{,}66+5{,}51=44{,}36\space\text{kN}\\\\
\sigma_\text{z}=18{,}5\cdot1{,}923z´=35{,}58z´\space......\space44{,}36-35{,}58z´=0\space......\space z´=1{,}25\space\text{m}\\\\
z=1{,}25+0{,}71=1{,}96\space\text{m pode dnem výkopu}
\end{gathered}g) maximální moment v hloubce z
\begin{gathered}
M_\text{max}=8{,}29\cdot3{,}56+30{,}66\cdot3{,}03+5{,}41\cdot1{,}72-70{,}35\cdot\frac{1{,}25^2}{6}=123{,}81\space \text{kNm}
\end{gathered}h) normálová síla v hloubce z
\begin{gathered}
N=(8{,}29+30{,}66+5{,}41)\cdot\tg16{,}5+3{,}14\cdot\frac{0{,}63^2}{4}\cdot(3{,}2+1{,}96)\cdot25=53{,}33\space\text{kN (tlak)}
\end{gathered}Vlastní dimenzování průřezu vrtané piloty ø 630 mm bude provedeno podle 1. mezního stavu pro návrhové velikosti vnitřních sil:
\begin{gathered}
N_\text{d}=1{,}4\cdot53{,}33=74{,}66\space\text{kN},&&M_\text{d}=1{,}4\cdot123{,}81=173{,}33\space\text{kNm}
\end{gathered}Poznámka:
Navržená pilotová stěn z příkladu na obr. 68 vyšla staticky jako konstrukce na hranici výhodnosti, a to zejména s ohledem na vypočtenou délku vetknutí t = 4,26 m a rovněž vodorovná deformace v hlavě pilotové stěny bude značná; ekonomicky výhodněji by zřejmě vyšla stěna kotvená, jež umožní snížit jak potřebnou hloubku vetknutí, tak i vodorovnou deformaci pilotové stěny.
Příklad 2:
Stanovte hloubku vetknutí, sílu v kotvě a průběh vnitřních sil na záporové stěně při zadání na obr. 69. Pažicí konstrukce je v hlinitém písku s velikostí charakteristických parametrů: γ =19,0 kN·m-3, φ = 28°, c = 5 kPa, rovnoměrné přitížení rubu pažení p = 10,0 kPa.
Řešení
a) volíme zápory I 425 osově po B = 1,80 m zabetonované ve vrtech ø 630 mm, kotvy dočasné 3xLp15,7 mm po 3,60 m, L = 5,0 + 6,0 = 11,0 m, sklon od vodorovné α = 25°, pažiny dřevěné, výpočet bude proveden pro charakteristické hodnoty zatížení,
b) zatížení zemním tlakem
- koeficient zemního tlaku v klidu:
\begin{gathered}
K_0=1-\sin28=0{,}53
\end{gathered}- koeficient aktivního zemního tlaku:
\begin{gathered}
K_\text{a}=\tg^2(45-\frac{28}{2})=0{,}36
\end{gathered}- koeficient pasivního zemního tlaku:
\begin{gathered}
K_\text{p}=\tg^2(45+\frac{28}{2})=2{,}77
\end{gathered}c) pažení se nachází v zástavbě, nelze připustit větší deformace, tudíž:
- koeficient zemního tlaku ze strany aktivní:
\begin{gathered}
K_\text{a,zv}=0{,}36+0{,}5\cdot(0{,}53-0{,}36)=0{,}45
\end{gathered}- koeficient zemního tlaku ze strany pasivní:
\begin{gathered}
K_\text{p,sn}=2{,}77-0{,}5\cdot(2{,}77-0{,}53)=1{,}65
\end{gathered}Obr. 69 Zadání k příkladu 2, statické schéma 1x kotvené záporové stěny
d) zatížení zemním tlakem
- koeficient zemního tlaku v klidu:
\begin{gathered}
K_0=1-\sin28=0{,}53
\end{gathered}- koeficient aktivního zemního tlaku:
\begin{gathered}
K_\text{a}=\tg^2(45-\frac{28}{2})=0{,}36
\end{gathered}- koeficient pasivního zemního tlaku: Kp = tg2(45 + 28 / 2) = 2,77.
\begin{gathered}
K_\text{p}=\tg^2(45+\frac{28}{2})=2{,}{77}
\end{gathered}e) pažení se nachází v zástavbě, nelze připustit větší deformace, tudíž:
- koeficient zemního tlaku ze strany aktivní:
\begin{gathered}
K_\text{a,zv}=0{,}36+0{,}5\cdot(0{,}53-0{,}36)=0{,}45
\end{gathered}- koeficient zemního tlaku ze strany pasivní:
\begin{gathered}
K_\text{p,sn}=2{,}77-0{,}5\cdot(2{,}77-0{,}53)=1{,}65
\end{gathered}f) napětí a síly:
\begin{gathered}
\sigma_\text{a,0}=10\cdot0{,}45=4{,}5\space\text{kPa};&\sigma_\text{a,1}=4{,}5+5{,}5\cdot19{,}0\cdot0{,}45=51{,}53\space\text{kPa};&\sigma_\text{a,2}=51{,}53+19{,}0t\cdot0{,}45=51{,}53+8{,}55t;\space\sigma_\text{p}=19{,}0t\cdot1{,}65=31{,}35t\\\\
S_\text{a,1}=1{,}8\cdot5{,}5\cdot4{,}5=44{,}55\space\text{kN};&S_\text{a1,h}=44{,}55\cdot\cos14=43{,}23\space\text{kN};&S_\text{a1,v}=44{,}55\cdot\sin14=10{,}78\space\text{kN}\\\\
S_\text{a,2}=1{,}8\cdot5{,}5\cdot\frac{(51{,}53-4{,}50)}{2}=232{,}80\space\text{kN};&S_\text{a2,h}=232{,}80\cdot\cos14=225{,}88\space\text{kN};&S_\text{a2,v}=232{,}80\cdot\sin14=56{,}32\space\text{kN}\\\\
S_\text{a,3}=0{,}63t\cdot51{,}53=32{,}46t\space\text{kN};&S_\text{a3,h}=32{,}46t\cdot\cos14=31{,}50t\space\text{kN};&S_\text{a3, v}=32{,}46t\cdot\sin14=7{,}85t\space\text{kN}\\\\
S_\text{a,4}=0{,}63t\cdot\frac{8{,}55t}{2}=2{,}69t^2\space\text{kN};&S_\text{a4,h}=2{,}69t^2\cdot\cos14=2{,}61t^2\space\text{kN};&S_\text{a4,v}=2{,}69t^2\cdot\sin14=0{,}65t^2\space\text{kN}\\\\
S_\text{p}=0{,}63t\cdot\frac{31{,}35t}{2}=9{,}88t^2\space\text{kN};&S_\text{p,h}=9{,}88t^2\cdot\cos14=9{,}59t^2\space\text{kN};&S_\text{p,v}=2{,}39t^2\space\text{kN}
\end{gathered}- tření ve svislé rovině KLM podél stěny vrtu:
\begin{gathered}
R_\text{k}=E_\text{s}\cdot\tg\varphi,\space\text{kde}\space E_\text{s}=\gamma\cdot\frac{t^3}{6}\cdot\tg(45+\frac{\varphi}{2}),\space\text{tedy}:\\\\
E_\text{s}=\frac{19{,}0t^3}{6}\cdot\tg59=5{,}27t^3\space\text{kN};&R_\text{k}=5{,}27t^3\cdot\tg28=2{,}80t^3
\end{gathered}g) momentová podmínka k působišti kotvy (výpočet délky vetknutí t):
\begin{gathered}
S_\text{a1,h}\cdot0{,}75+S_\text{a2,h}\cdot2{,}16+S_\text{a3,h}\cdot(4{,}0+0{,}5t)+S_\text{a4,h}\cdot(4{,}0+0{,}67t)-S_\text{p}\cdot(4{,}0+0{,}67t)-2R_\text{k}\cdot(4{,}0+0{,}33t)=0\\\\
43{,}23\cdot1{,}25+225{,}88\cdot2{,}17+31{,}5t\cdot(4{,}0+0{,}5t)-6{,}98t^2\cdot(4{,}0+0{,}67t)-5{,}60t^3\cdot(4{,}0+0{,}33t)=0\\\\
t^4+14{,}48t^3+6{,}51t^2-67{,}38t-291{,}02=0;\space......\space t=2{,}90\space\text{m}
\end{gathered}h) podmínka vodorovných sil (velikost vodorovné síly v místě kotvení Ah):
\begin{gathered}
S_\text{a1,h}+S_\text{a2,h}+S_\text{a3,h}+S_\text{a4,h}-S_\text{p}-2R_\text{k}-A_\text{h}=0\\\\
43{,}23+225{,}88+91{,}35+21{,}95-80{,}65-136{,}58=A_\text{h}\space......\space A_\text{h}=165{,}18\space\text{kN}
\end{gathered}i) síla v kotvě:
\begin{gathered}
A_\text{k}=2\cdot\frac{165{,}18}{\cos25}=364{,}51\space\text{kN},\space\text{volíme kotevní sílu}\space A_\text{k, skut}=380\space\text{kN}
\end{gathered}j) podmínka rovnováhy ve svislém směru (posouzení svislé únosnosti zápory):
\begin{gathered}
S_\text{a1,v}+S_\text{a2,v}+S_\text{a3,v}+S_\text{a4,v}+\frac{A_\text{k}}{2}\sin25-R=0\\\\
R=10{,}78+56{,}32+22{,}76+5{,}46-20{,}10+80{,}29=155{,}51\space\text{kN}
\end{gathered}(na tuto sílu je třeba posoudit svislou únosnost kořene zápory)
k) vnitřní síly (ohybové momenty):
- moment v úrovni kotvení:
\begin{gathered}
M_1=-1{,}8\cdot(4{,}50\cdot\frac{1{,}5^2}{2}+19{,}0\cdot0{,}45\cdot\frac{1{,}5^2}{6})=-14{,}88\space\text{kNm}
\end{gathered}- nulová posouvající síla v hloubce z:
\begin{gathered}
1{,}8\cdot(4{,}5z+19{,}0\cdot\frac{0{,}45z^2}{2})-165{,}18=0;&z^2+1{,}053z-20{,}39=0;\space......\space z=4{,}02\space\text{m}
\end{gathered}- maximální moment je v hloubce z = 4,02 m:
\begin{gathered}
M_\text{max}=165{,}18\cdot2{,}52-1{,}8\cdot(4{,}5\cdot\frac{4{,}02^2}{2}+19{,}0\cdot0{,}45\cdot\frac{4{,}02^2}{6})=309{,}35\space\text{kNm}
\end{gathered}l) posouzení zápor I300 (ocel 37,3 …. A = 0,0132 m2, W = 0,00174 m3):
\begin{gathered}
\sigma=0{,}19\cdot\frac{\sin25}{0{,}0132}+\frac{0{,}309}{0{,}00174}=183{,}67\space\text{MPa}\space\implies\space\text{vyhovuje}
\end{gathered}m) návrh a posouzení pažin – volíme pažiny dřevěné tl. 120 mm (W = 0,0024 m3/m):
- max. napětí
\begin{gathered}
\sigma=(10{,}0+19{,}0\cdot5{,}5\cdot0{,}45)=57{,}05\space\text{kPa}
\end{gathered}- moment na prostém nosníku:
\begin{gathered}
M=\frac{1}{8}\cdot57{,}05\cdot(1{,}8-0{,}1)^2=20{,}61\space\text{kNm/m}\\\\
\sigma=\frac{0{,}0206}{0{,}0024}=8{,}58\space\text{MPa}\space\implies\space\text{vyhovuje}
\end{gathered}2.3.3 Nosník na pružném podkladě, metoda závislých tlaků, příklad 3
Metoda vznikla v roce 1978 v projektovém závodu 07 Vodních staveb jako program pro kalkulátor Hewlett-Packard. Ve větším rozsahu byla metoda závislých tlaků, (dále jen MZT) poprvé použita v návrhu zajištění stavební jámy pro dostavbu ND v roce 1978, tehdy byla i publikována. Později se výrazně rozšířila, takže v současné době používají název a princip výpočtu i jiné firmy, např. programy GEO firmy Fine.
Vycházíme ze základního poznatku, že velikost a rozdělení zemního tlaku závisí především na deformaci pažicí konstrukce a základové půdy. Je-li k dispozici diagram vyjadřující tuto závislost, můžeme pro libovolný bod pažicí konstrukce stanovit velikost napětí při příslušném zemním tlaku. Na základě této zobecněné závislosti lze z výchozího zatížení, kterým může být např. zemní tlak v klidu, u něhož je výchozí deformace nulová, stanovit iteračním postupem konečné rozdělení zemního tlaku, jež odpovídá měnícímu se přetvoření pažicí konstrukce v průběhu její výstavby. Úvaha o diskretizaci velikosti napětí při zemních tlacích v závislosti na přetvoření je základem metod metody závislých tlaků. Obyčejně se postupuje dvěma způsoby.
V prvém případě jde o řešení diferenciální rovnice ohybové čáry nosníku, jež má tvar:
\begin{gathered}
(EI)\cdot\frac{d^4y}{(dz)^4}=\sigma_\text{y, z}
\end{gathered}(71)
kde je:
σ(y,z) … napětí od zemního tlaku v hloubce z, jež závisí na velikosti vodorovné deformace y podle obr. 70;
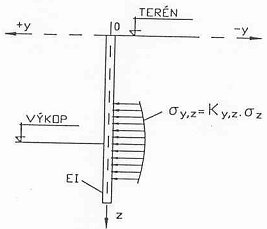
Obr. 70 Statické schéma pro výpočet ohebné pažicí konstrukce
Jelikož je vodorovné napětí funkcí jak hloubky z, tak i vodorovného posunu y, lze psát:
\begin{gathered}
\sigma_\text{(y,z)}=K_\text{(y,z)}\cdot\sigma_\text{z,(z)}
\end{gathered}(72)
nebo obecněji:
\begin{gathered}
\sigma_\text{(y,z)}=K_\text{(y,z)}\cdot(\sigma_\text{z}+\frac{c}{\tg\varphi})-\frac{c}{\tg\varphi}
\end{gathered}(73)
kde je:
K(y,z) … součinitel zemního tlaku v hloubce z, jehož velikost závisí na velikosti a smyslu vodorovné deformace y.
Pro velikost K(y,z) platí, (podle obr. 43):
\begin{gathered}
K_\text{a,(z)}\le K_\text{(y,z)}\le K_\text {p,(z)}\space\text{a}\space K_\text{(0,z)}=K_\text{r,(z)}
\end{gathered}(74)
Funkce vyjadřující velikost součinitele zemního tlaku K(y,z) musí být logicky spojitá, bez lokálních extrémů v intervalu (Ka, Kp) a nesmí mít svislou tečnu v tomto intervalu. Těmto požadavků zřejmě nejlépe vyhovuje křivka skládající se ze dvou větví hyperbol se společným bodem i tečnou v bodě y = 0 a s vodorovnými asymptotami, jež vyjadřující velikost Ka, Kp podle obr. 71.
Obr. 71 Příklad funkce K(y,z) složené ze dvou větví hyperbol
Dále je třeba stanovit velikost posunu ya, pro který klesne tlak v klidu např. na 101 % aktivního tlaku, čímž je funkce K(y,z) jednoznačně určena. Diferenciální rovnici (71), jež je obecně nelineární, lze převést na diferenciální rovnici lineární rozvojem do dvou členů Taylorovy řady a tuto linearizovanou diferenciální rovnici lze řešit metodou sítí neboli převést na soustavu lineárních rovnic.
Druhá metoda směřující ke stejnému cíli využívá Winklerovský model podloží a řeší ohybovou čáru nosníku konečné délky na pružném podkladě, (obdobně, jako je to s výpočtem příčně zatížených pilot nebo podzemních stěn). Výpočetní schéma je na obr. 72.
Je třeba stanovit jednotlivé síly:
\begin{gathered}
P_\text{i}=k_\text{hi}\cdot b\cdot z\cdot y_\text{i}
\end{gathered}(75)
kde je:
khi … součinitel vodorovné reakce podloží v bodě i [kN·m-3];
b … uvažovaná šířka konstrukce;
z … délka dílku konstrukce;
y … vodorovná deformace bodu i.
Nelineární závislost velikosti zemních tlaků na posunu pažicí konstrukce, (vyznačenou na obr. 43) lze přibližně nahradit trilineární závislostí podle obr. 73. Velikosti mezních deformací ya, yp potom budou:
\begin{gathered}
y_\text{a}=\frac{(\sigma_\text{a}-\sigma_\text{r})}{k_\text{h}}\\\\
y_\text{p}=\frac{(\sigma_\text{p}-\sigma_\text{r})}{k_\text{h}}
\end{gathered}(76)
kde je:
σa, σr, σp … velikosti napětí při zemním tlaku aktivním, klidovém a pasivním v příslušném bodě.
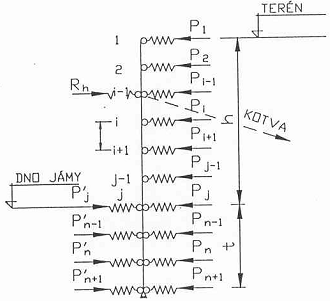
Obr. 72 Výpočetní schéma Winklerovského modelu ohebné pažicí konstrukce
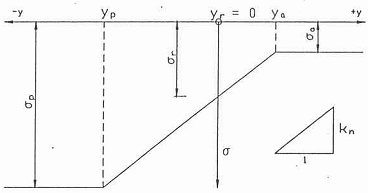
Obr. 73 Závislost velikosti napětí při zemním tlaku na deformaci
V intervalu (ya, yp) se tedy zemina chová pružně podle Winklerovy hypotézy, tzn., že platí lineární závislost mezi velikostí napětí při zemním tlaku a deformací, přičemž konstantou úměrnosti je součinitel vodorovné deformace základové půdy kh. Ten lze stanovit postupem uvedeným např. ve skriptech Zakládání staveb 1. Mimo tento interval se zemina chová dokonale plasticky, tzn., že velikost napětí při příslušném zemním tlaku zůstává konstantní a nezávisí již na posunu. Lze tedy psát:
pro:
\begin{gathered}
y\in(y_\text{a},\space y_\text{p})&P=P_\text{r}+k_\text{h}\cdot b\cdot z\cdot y=P_\text{r}+C\cdot y\\\\
y\ge y_\text{a}&P=P_\text{a}\\\\
y\le y_\text{p}&P=P_\text{p}
\end{gathered}(77)
Vlastní výpočet probíhá v iteračních cyklech, přičemž v prvém cyklu je konstrukce zatížena zemním tlakem v klidu, všechny pružné podpory jsou ve funkci a spočítá se deformace konstrukce, obr. 74. V případě, že v některé z oblastí dojde k překročení ya, resp. yp, je místo pružné podpory dosazena síla Pa, resp. Pp, odpovídající plné velikosti napětí při aktivním, resp. pasivním zemním tlaku a výpočet se opakuje. Současně ovšem musí být splněny rovnice rovnováhy, tj. součet všech vodorovných sil je nulový a momentová podmínka rovnováhy – např. k patě pažicí konstrukce. Pro kotvy, resp. i pro rozpěry lze zadat též pracovní diagram, tj. závislost síly R(y) na deformaci. Tento postup výpočtu se aplikuje na libovolné stádium výstavby pažicí konstrukce.
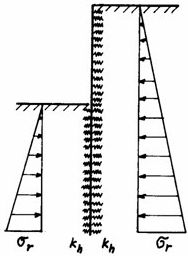
Schéma konstrukce před první iterací
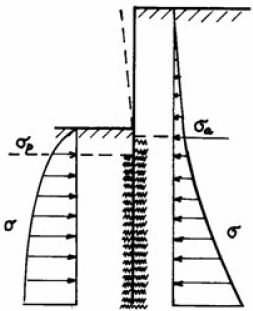
Schéma konstrukce během iterace
Obr. 74 Rozdělení zatížení po délce konstrukce, (Manuál GEO5)
Důležitým vstupním parametrem pro výpočet podle tohoto druhého způsobu je tedy velikost koeficientu kh, který udává strmost střední části bilineární závislosti z grafu na obr. 73. Tento parametr lze odhadnout s ohledem na volnou výšku pažicí konstrukce a její obecné chování, nebo je nutné přímo zadat velikost modulu horizontální stlačitelnosti pro jednotlivé vrstvy základové půdy (Winklerův model). Parametr je specifický zejména tím, že nevyjadřuje pouze vlastnost základové půdy, ale také závislost na velikosti zatěžované plochy. To znamená, že v rámci geotechnického průzkumu tento parametr nelze jednoznačně stanovit, resp. odvodit např. ze zkoušek základové půdy. Proto se do výpočtu nejčastěji používají hodnoty či korelace odvozené z literatury anebo na základě zkušeností. Podle manuálu programu GEO5 firmy Fine lze vybrat z těchto možností:
- a) průběhem, (zadává se průběh modulu horizontální stlačitelnosti podloží kh);
- b) podle Schmitta – v závislosti na ohybové tuhosti konstrukce (EI) a edometrickém modulu zeminy (Eoed);
- c) podle Ménarda – na základě presiometrický modulu zeminy (Epres), geometrického parametru „a“ a reologického parametru „α“;
- d) podle Chadeissona – na základě ohybové tuhosti konstrukce (EI) a smykových parametrů zeminy (ϕ´ a c´), objemové tíhy zeminy (γ) a tzv. součinitelu vlivu koheze (Ap);
- e) iterací z přetvárných charakteristik zemin – modulu přetvárnosti (Edef), koeficientu strukturní pevnosti (m).
Podrobnější informace, resp. vztahy pro výpočet parametru kh lze nalézt v manuálu programu GEO5.
Příklad 3
Stanovení průběhu vnitřních sil, sil kotevních a deformací 2x kotvené PS s maximální hloubkou výkopu H = 9,0 m. Veškeré vstupní parametry základové půdy, tvaru pažicí konstrukce, kotev a vnějšího zatížení jsou patrné z obr. 75.
Řešení:
Volíme PS tlustou 0,60 m, celková volná výška pažení H = 9,0 m, kotvy jsou dočasné ve dvou úrovních: 1. úroveň -3,50 m, 2. úroveň -6,70 m. Výpočet bude proveden pro 2. mezní stav použitelnosti, vstupní parametry základové půdy jsou hodnotami charakteristickými. Pro výpočet bude použit interaktivní program MZT 2003 (autor Ing. P. Hurych), přičemž pažicí konstrukce bude počítána pro následujících 5 stavebních stavů:
- 0. předvýkop 0,5 m pod úroveň 1. kotvy, tj. na hloubku H = 3,5 m, obr. 75;
- 1. předvýkop na H = 3,5 m, zřízení a aktivace 1. kotevní úrovně, kotvy 4 x Lp 15,7 mm, půdorysně po 4,0 m, dl. kotev 8,0 + 6,0 = 14,0 m, kotevní síla P = 400 kN, obr. 76;
- 2. předvýkop 0,5 m pod úroveň 2. kotvy, tj. na hloubku H = 7,2 m, obr. 77;
- 3. předvýkop na H = 7,2 m, zřízení a aktivace 2. kotevní úrovně na kótě -6,70 m, kotvy 6 x Lp 15,7 mm, půdorysně po 4,0 m, dl. kotev 6,0 + 6,0 = 12,0 m, kotevní síla P = 600 kN, obr. 78;
- 4. definitivní výkop na konečnou hloubku H = 9,0 m, obr. 79.
Výsledky výpočtu jsou na obr. 75 až 79.
Obr. 75 Zadání příkladu č. 3; výsledky výpočtu 1. fáze výstavby
Obr. 76 Výsledky výpočtu 2. fáze výstavby
Obr. 77 Výsledky výpočtu 3. fáze výstavby
Obr. 78 Výsledky výpočtu 4. fáze výstavby
Obr. 79 Výsledky výpočtu 5. fáze výstavby
Komentář k výsledkům:
Shrnutí výsledků:
Tab. 13 Deformace pažicí konstrukce
| Fáze výstavby deformace v bodě | 0. fáze u [mm] |
1. fáze u [mm] |
2. fáze u [mm] |
3. fáze u [mm] |
4. fáze u [mm] |
| hlava PS | 12,22 | 11,51 | 22,99 | 23,50 | 21,63 |
| v úrovni 1. kotvy | – | 7,25 | 19,50 | 20,10 | 20,41 |
| v úrovni 2. kotvy | – | – | – | 15,95 | 19,37 |
| v úrovni dna jámyx) | 7,15 | 6,35 | 14,85 | 15,25 | 18,70 |
| x) dno jámy je úroveň výkopu odpovídající příslušné fázi výstavby/výpočtu | |||||
Tab. 14 Síly v kotvách
| Fáze výstavby síla v kotvě | 0. fáze P [kN] |
1. fáze P [kN] |
2. fáze P [kN] |
3. fáze P [kN] |
4. fáze P [kN] |
| v 1. kotvě | – | 400 | 572 | 572 | 586 |
| v 2. kotvě | – | – | – | 600 | 766 |
Tab. 15 Ohybové mementy
| Fáze výstavby vel. M, poloha z | 0. fáze | 1. fáze | 2. fáze | 3. fáze | 4. fáze |
| moment Mmax [kNm] | –107,50 | –91,50 | 193,40 | 160,50 | 171,70 |
| v hloubce z [m] | 6,70 | 7,10 | 5,75 | 5,25 | 8,10 |
2.3.4 Numerické metody
Numerické metody se staly standardním nástrojem geotechnického inženýrství především pro předpověď deformací konstrukce během její výstavby a jejího využití. Pro posouzení mezního stavu použitelnosti, (2. mezní stav), jsou numerické metody pro tvarově složitější konstrukce v komplikovaných geotechnických podmínkách často jedinou možností jejich statického posouzení. Umožňují dále stanovit velikosti deformací nejen na vlastní pažicí konstrukci, ale teoreticky kdekoliv v jejím sousedství, což je významné zejména pro odhad deformací sousední zástavby, inženýrských sítí a ostatních konstrukcí.
Význam těchto metod roste však i při prokazování mezního stavu porušení, (1. mezní stav). Rozvoj numerických metod a jejich použití v návrhové praxi souvisí s intenzivním výzkumem na poli geomechaniky, k němuž přispěl zejména výzkum nových konstitutivních vztahů a postupů řešení pro nelineární soustavy rovnic, jehož výsledky byly implementovány do řady komerčních programů. I přesto je zřejmé, že numerické metody jsou v geotechnice daleko méně rozšířeny ve srovnání s ostatními obory inženýrského stavitelství, (ocelové, betonové konstrukce). Jedním ze zřejmých a hlavních důvodu je skutečnost, že zemina jakožto součást konstrukce je materiál vytvořený přírodou na rozdíl od většiny ostatních stavebních materiálů, které jsou vyráběny kontrolovaným procesem. Další významnou skutečností je i vysoká prostorová variabilita horninového prostředí, a to jak po stránce vlastností, tak i geometrie, (vrstevnatost, plochy diskontinuit apod.). Vlastnosti základových půd získáváme na základě geotechnického průzkumu, jehož možnosti jsou ovšem omezené co do rozsahu i kvality, což souvisí např. s technikou odběru „neporušených“ vzorků zemin pro laboratorní zkoušky a s možnosti polních geotechnických měření. Rozsah průzkumu pak může ovlivnit míru nejistoty, kterou jsou zatíženy jednotlivé parametry, ale nemůže tuto nejistotu vyloučit. To je ostatně uvedeno i v Eurokódu 7, v čl. 2.4.1(2):
„Má se vzít na zřetel, že znalost základových poměrů závisí na rozsahu a kvalitě geotechnického průzkumu. Taková znalost a kontrola prací je pro splnění základních požadavků obvykle mnohem důležitější, než je přesnost výpočetních modelů a dílčích součinitelů.“
V této kapitole budou tedy stručně ukázány možnosti a hranice numerických metod ve vztahu k pažicím konstrukcí, a to z hlediska současného stupně poznání a praktických výpočtů. Je však třeba uvědomit si, že tyto metody procházejí rychlým vývojem.
Speciální aspekty numerického modelování v geomechanice
Chování zemin je téměř výhradně nelineární, což značně komplikuje jeho popis. Další skutečností je nehomogenita a anizotropie základových půd. To vše je důvodem pro sestavení velice komplexních konstitutivních modelů, které se pokoušejí o popis chování zemin. Specifika numerického modelování v geomechanice oproti jiným disciplínám jsou dále stručně uvedena:
a) Velikost modelované oblasti
Horninové prostředí, které je součástí geotechnické konstrukce, je teoreticky neomezené. Zřejmé je, že od určité vzdálenosti je vzájemné ovlivňování horninového prostředí a pažicí konstrukce zanedbatelné. Proto si lze při vytváření modelu problém zjednodušit na analýzu v omezené oblasti. Ze zkušeností z numerického modelování mohou být stanovena pravidla pro velikost modelované oblasti, jak pro stavební jámy doporučuje např. Meissner, (2002) podle obr. 80. Ve speciálních případech, např. za odvodněných podmínek musí být modelovaná oblast podstatně větší, aby se vyloučil vliv okraje modelu na výsledky.
b) Vliv počáteční napjatosti
Důležitým krokem pro modelování geotechnických úloh je definování počáteční napjatosti. Na ni má rozhodující vliv geologická minulost daného území. Počáteční napjatost, vystihující historii materiálu, počítáme ze znalosti míry překonsolidace anebo maximálního svislého zatížení, které působilo na horninový masív v minulosti. Kromě této počáteční napjatosti je nutné zohlednit změnu napjatosti způsobenou lidskou činností, (např. přitížení od okolních objektů).
Obr. 80 Doporučená velikost modelované oblasti, (podle Meissnera, 2002)
c) Vliv vícefázového systému
Zemina je třífázový systém, který se skládá z pevných částic, vody a vzduchu. Proto i celkové, (totální) napětí se skládá z více složek. V případě plně nasycených zemin jde o efektivní napětí a pórové tlaky. Úlohy dočasných pažicích konstrukcí v jemnozrnných zeminách můžeme někdy s výhodou řešit jako neodvodněné, přičemž se lze rozhodnout, zda úlohu budeme řešit v totálních napětích při použití neodvodněné pevnosti nebo v efektivních napětích za použití neodvodněné pevnosti nebo odvodněné pevnosti. Při řešení za neodvodněného stavu v efektivních napětích a efektivních parametrech pevnosti je výsledná pevnost materiálu závislá na použitém konstitutivním vztahu, zejména pak na objemovém chování během smýkání. Proto je zde volba vhodného konstitutivního modelu velmi důležitá. Pro ověření vhodnosti daného konstitutivního modelu je možno využít numerických metod, pomocí nichž lze nasimulovat průběh laboratorních zkoušek, (např. triaxiální zkoušky) a posléze porovnat experimentální data s výsledky numerické simulace pro různé konstitutivní modely, jde o tzv. kalibraci modelu.
d) Modelování jednotlivých fází výstavby
Vzhledem k materiálové nelinearitě není možné použít princip superpozice. Musíme tedy zachytit postupnou výstavbu konstrukce v jednotlivých krocích. To je třeba mít na paměti i při tvorbě geometrie, protože je nutné modelovat nejen výsledný stav konstrukce, ale i všechny fáze průběhu výstavby.
e) Interakce zeminy a konstrukce
K modelování kontaktu mezi konstrukcí a zeminou se běžně používají tzv. přechodových prvků (interface elements). Pomocí nich je možné upravit pevnost na modelovaném rozhraní. V některých případech se ukazuje, že parametry definující chování těchto přechodových prvků mají velký vliv na výsledky. Proto se doporučuje provést parametrickou studii k vyhodnocení vlivu těchto hodnot na výsledky, a to zejména v těch případech, kdy uživatel programu nemá dostatek zkušeností se stanovením velikostí příslušných parametrů. Další vlastností těchto přechodových prvků je rovnoměrnější rozložení modelových napětí působících na model konstrukce a často i snížení závislosti na velikosti sítě zejména pro úlohy, při kterých se příslušná napětí již blíží porušení.
f) Výběr konstitutivního modelu
Na rozdíl od jiných inženýrských úloh máme v geotechnice k dispozici velkou nabídku možných konstitutivních modelů. V praxi oblíbený lineárně elastický – ideálně plastický model s Mohr-Coulombovou podmínkou porušení je dostatečný k modelování porušení konstrukce, ale pro predikci deformací konstrukce je zjevně nevhodný, protože až do okamžiku porušení předpovídá lineárně elastické chování, které není realistické. Výběr konstitutivního modelu tedy závisí hlavně na typu zeminy, typu geotechnické úlohy a účelu ke kterému má výpočet sloužit.
g) Modelování pažicích konstrukcí
Stavební jámy jsou často velké stavební objekty, jejichž geometrický tvar se v směru pažení příliš nemění, a proto může být modelování často zjednodušeno na úlohu rovinné deformace. Takové zjednodušení znamená, že např. kotvy a rozpěry nejsou modelovány jako prvky působící jednotlivě v prostoru, ale jsou zjednodušeny na liniové podpory, což je pro popis globálního chování konstrukce dostatečně výstižné. V případě složitého půdorysného tvaru stavební jámy, kdy se očekává, že prostorové efekty budou mít značný vliv na výsledek, je nutné uvážit, zda není třeba vytvořit 3D model řešené úlohy.
Základní pravidla pro velikost modelované oblasti jsou zmíněna v bodě a). Ve speciálních případech, kterými jsou např. modelování stavební jámy ve svahu, modelování proudění podzemní vody nebo modelování za neodvodněných podmínek, musí být příslušná oblast podstatně větší, abychom vyloučili vliv okraje modelu na výsledky.
V případě symetrické úlohy nebo v případě, kdy protilehlé strany stavební jámy jsou vzdáleny natolik, že nedochází k jejich vzájemnému ovlivňování, je možné modelovat pouze polovinu stavební jámy. Při generování sítě musejí být patřičně zjemněny oblasti velkých gradientů napětí. Jde zejména o oblast za pažicí stěnou, pod patou stěny, dále o pasivní zónu před patou stěny a o oblast kořenové části zemních kotev. Jednotlivé konstrukční prvky musí být patřičně namodelovány zejména z hlediska jejich osové a ohybové tuhosti, které musí odpovídat skutečnosti. Při úlohách rovinné deformace, kdy se počítá s pruhem délky 1,0 m, musí modelované tuhosti odpovídat této délce stěny. Pokud se nachází v modelované oblasti zástavba, je správné zohlednit ji v závislosti na tuhosti konstrukčního systému. Pokud je její tuhost malá, postačí nahradit ji odpovídajícím plošným zatížením.
Konstitutivní modely
Pro numerické modelování je k dispozici celá řada konstitutivních modelů popisujících chování zemin a lze očekávat, že tento výběr se bude nadále rozšiřovat. Konstitutivní modely můžeme na základě popisu chování zemin rozdělit do několika skupin:
- lineárně pružný-ideálně plastický model, (Mohr-Coulomb model);
- další elasto-plastické modely, (cam-clay model – Roscoe, Burland, 1968; hardening soil model – Schanz et al., 1999; small strain hardening soil model – Benz, 2007);
- elasto-plastické modely s kinematickým zpevněním, (např. 3-SKH – Stallebrass, Taylor, 1997);
- hypoplastické modely, (hypoplastický model pro písky – von Wolffersdorff, 1996, hypoplastický model pro jemnozrnné zeminy – Mašín, 2005).
Je tedy k dispozici celá řada konstitutivních modelů. Projektanti se však často uchylují k jednodušším materiálovým modelům, které mají omezenou platnost predikce chování zemin. Hlavním příčinou tohoto stavu je potřeba speciálních parametrů zemin jakožto vstupních údajů pro vyšší modely, a tudíž nutnost použití speciálních zkoušek mechaniky zemin. Jednoznačně lze tedy konstatovat, že čím vyšší, složitější a pro konkrétní typ základové půdy výstižnější model, tím větší potřeba speciálních parametrů základové půdy, z nichž některé lze jen obtížně stanovit v laboratoři mechaniky zemin. Bohužel praktické využití těchto modelů pro konkrétní úlohy pažení stavebních jam je mizivé, neboť v praxi není dostatek času ani prostředků pro získání těchto věrohodných vstupních parametrů.
Lineárně pružný-ideálně plastický model
Z hlediska současné technické praxe je u nás asi nejpoužívanějším konstitutivním modelem. Nejčastěji se setkáváme s názvem Mohr-Coulombův model, (MC), poněvadž plocha plasticity je dána Mohr-Coulombovou podmínkou porušení. Samotný model je popsán pěti parametry (φ, c, E, ν, ψ), které (kromě úhlu dilatance ψ) bývají k dispozici po provedení standardních zkoušek mechaniky zemin. Asi největším nedostatkem modelu je nemožnost rozlišení tuhosti při prvotním zatížení a tuhosti při odtížení. Při použití tohoto modelu získáváme nerealistické zvedání dna stavební jámy a povrchu za stavební jámou. Pro účely přesnější predikce deformací konstrukce nelze tento model doporučit.
Elasto-plastické modely se zpevněním
Izotropní modely této skupiny zavádí rozdílnou podmínku pro plasticitu a porušení. Mezi tyto modely se řadí např. i tzv. hardening soil model – HS, který je u nás rovněž dobře znám a používán. Tento model zohledňuje:
- tuhost zeminy závislou na napětí;
- deviátorové a objemové zpevnění, (obr. 81);
- hyperbolickou závislost mezi deviátorovým napětím a osovým přetvořením při triaxiální zkoušce, (obr. 81);
- rozlišení tuhostí pro prvotní zatížení a odtížení, resp. další zatížení;
- Mohr-Coulombova podmínku porušení.
Více informací o tomto konstitučním vztahu lze nalézt v manuálech programu, (např. Plaxis).
Pro co nejvýstižnější modelování chování pažicích konstrukcí, je vhodné použít konstitutivní model, který je schopen popsat zvýšenou tuhost zeminy při malých smykových přetvořeních, např. 10-4 ÷ 10-3 m, (Atkinson, 1991). Toto rozšíření je implementována v modelu small-strain hardening model – HSS. Uvedené modely jsou podstatně vhodnější pro řešení pažicích konstrukcí než modely první skupiny, neboť pro deformace dávají věrohodnější výsledky.
Dalším velmi rozšířený model s izotropním zpevněním je model cam-clay. V komerčních programových vybaveních se v současné době v cizině nejvíce používá tzv. modified cam clay, který se od základního modelu liší odlišnou plochou plasticity. Jiným zástupcem této skupiny je model 3-SKH (three-surface kinematic hardening model), který byl vyvinut při City University v Londýně. V České republice se tento model v technické praxi nepoužívá a dá se říct, že v ní není asi vůbec znám. Příčinou toho bude zřejmě jeho složitost, a to nejen po stránce matematické, ale především z hlediska potřeby definování 10 vstupních materiálových parametrů.
Hypoplastické modely
V posledních letech se začínají uplatňovat modely vycházející z teorie hypoplasticity, jejichž podstata spočívá v tom, že není potřeba dělit přetvoření na pružná a plastická a není ani potřeba definovat podmínky plasticity a tím pádem je možné používat jednodušší matematickou formulaci rovnice pro konstitutivní vztah. Hypoplastické modely jsou vytvořeny jak pro hrubozrnné, tak i pro jemnozrnné zeminy. Hypoplastický model pro jemnozrnné zeminy vychází z principu kritických stavů, resp. z cam clay modelu. Základní model vyžaduje obdobně jako velmi populární cam – cay model pět materiálových parametrů. Tento materiálový model je samozřejmě dále modifikován.
Odvodněné a neodvodněné podmínky
Pro případ zemin, ve kterých dochází dostatečně rychle k disipaci pórových tlaků vzhledem k délce trvání stavby, tak že vzniklé pórové tlaky nemají vliv na chování konstrukce, využíváme odvodněný „drained“ výpočet. Pokud pórové tlaky mají vliv na chování konstrukce, pak je situace komplikovanější. V případě, kdy je zaručeno, že disipace pórových tlaků bude minimální během užívání konstrukce, je možné provést výpočet za neodvodněných „undrained“ podmínek. Pro tento výpočet se principielně nabízejí tři varianty výpočtu, které jsou proveditelné ve většině softwarů využívající MKP:
Metoda A
- analýza s rozlišením efektivních a pórových tlaků;
- typ materiálu: „undrained“;
- použití efektivních parametrů pevnosti cef, φef, ψef;
- použití efektivních deformačních parametrů Eef, νef.
Metoda B
- analýza s rozlišením efektivních a pórových tlaků;
- typ materiálu: „undrained“;
- použití totálních parametrů pevnosti cu, φu = 0°, ψ = 0°;
- použití efektivních deformačních parametrů Eef, νef.
Metoda C
- analýza v totálních napětích, (bez rozlišení efektivních a pórových tlaků);
- typ materiálu: „drained“;
- použití totálních parametrů pevnosti cu, φu = 0°, ψ = 0°;
- použití totálních deformačních parametrů Eu, νu ≈ 0,5.
Typ materiálu „drained“ neumožňuje generovat přebytečné pórové tlaky, zatímco typ „undrained“ předpokládá plné nasycení zeminy a umožňuje výpočet přebytečných pórových tlaků a zároveň automaticky přidává tuhost vody k efektivní tuhosti zeminy.
Metoda A je nejvhodnější metodou řešení konstrukcí za neodvodněných podmínek, protože nejlépe popisuje fyzikální podstatu problému. Jako jediná umožňuje využít všech rysů pokročilých konstitutivních modelů a uvažovat nárůst pevnosti při případné konsolidaci. Je však bezpodmínečně nutné zkontrolovat, zda použité efektivní parametry pevnosti predikují správné parametry neodvodněné pevnosti, protože predikovaná efektivní dráha napětí se může lišit od skutečné. Tento fakt byl jedním z pochybení při katastrofě při výstavbě hluboké stavební jámy pro metro v Singaporu, známé jako Nicoll Highway Colapse.
Metoda B je často používanou metodou pro řešení neodvodněných podmínek, protože hodnota neodvodněné pevnosti cu bývá často udána v geologickém průzkumu.
Metodu C nelze obecně pro řešení neodvodněných podmínek doporučit, protože ztrácíme informaci o efektivních napětích a vzniklých pórových tlacích.
V případě že disipace pórových tlaků během výstavby není zanedbatelná, potom je správné zabývat se konsolidací během jednotlivých fází hloubení stavební jámy. Výpočet by měl probíhat v následujících krocích:
- 1) výpočet efektivních napětí a pórových tlaků za předpokladu neodvodněných podmínek pro danou fázi výkopu;
- 2) konsolidace po dobu technologické přestávky v dané fázi výkopu;
- 3) opakování postupu pro další fáze výkopu;
- 4) po dosažení finální hloubky, další konsolidace až po úplné vymizení přebytečných pórových tlaků, pokud je tento stav pro konstrukci relevantní.
Zohlednění režimu podzemní vody
Během výstavby pažicí konstrukce dochází často k ovlivnění režimu podzemní vody, nejčastěji pak ke snížení hladiny podzemní vody ve stavební jámě. Tato změna režimu podzemní vody musí být zachycena i v numerickém modelu. Pro modelování snížení hladiny podzemní vody je možno užít několika postupů. V případě, kdy je konstrukce zavázána do vrstvy, jejíž propustnost je řádově nižší než propustnosti ostatních vrstev, tudíž lze tuto vrstvu základové půdy považovat za dostatečně nepropustnou, je možné využít hydrostatické rozložení uvnitř i vně pažicí konstrukce (metoda 1). Při takovém rozložení nám vznikne skok v pórovém napětí u paty konstrukce, resp. rozdíl hydrostatických tlaků na aktivní a pasivní straně, který se následně interpoluje ve vztahu k tloušťce pažicí konstrukce. V případech, kdy jsou propustnosti jednotlivých vrstev řádově podobné, je nejvhodnější provést výpočet stacionárního proudění podzemní vody, pomocí nějž spočteme pórové tlaky v modelované oblasti. Rozložení proudového tlaku plynoucí z řešení úlohy pomocí MKP je znázorněno na obr. 82. Výpočet lze provést pomocí mnoha metod, přičemž je nutné znát koeficient filtrace základové půdy k, jehož přesnější odhad je však bez příslušných zkoušek nemožný, (viz kap. 2). Proto se často používá zjednodušené rozložení pórového tlaku, které předpokládá interpolaci pórového napětí na pasívní straně pažicí konstrukce, (metoda 2). Srovnání těchto přístupů je znázorněno na obr. 82. Při rigorózním modelování režimu podzemní vody je automaticky uvážen hydraulický spád a tím i mezní stav hydraulického prolomení dna stavební jámy.
Obr. 82 Rozložení pórových tlaků kolem pažicí konstrukce
Modelování stěn
Pro modelování stěn můžeme využít prutových, resp. deskových prvků, (2D/3D), jejichž hlavní výhoda spočívá v přímém znázornění vnitřních sil v daném prvku. Nevýhodou prvků je jejich nulová tloušťka, která může vést k problémům při přenosu svislé síly do podloží. Tato síla je přenášena bodově a vznikají tedy velké koncentrace napětí, které mohu vést k numerickým obtížím. Problém se dá částečně obejít vymodelováním krátkého prutu u paty stěny, který zajistí přenos svisle síly. Dále můžeme použít plošných, resp. objemových prvků, pomocí nichž vymodelujeme skutečné rozměry konstrukce. Tohoto přístupu se využívá převážně pro masivnější pažicí systémy, jako jsou např. pilotové stěny, podzemní stěny, stěny z tryskové injektáže. Pro modelování deformací stěny nám většinou postačí lineárně elastický model pro popis chování stěny. Pokud je cílem modelování porušení konstrukce, (mezní stavy porušení), je nutné použít modely, které umožní zplastizování konstrukce. Většinou se pak používá lineárně elastický ideálně plastický model. Speciální otázkou je modelování kontaktu mezi stěnou a zeminou. V případě, že není k dispozici dostatečná zkušenost uživatele, doporučuje se parametrická studie ke zhodnocení vlivu použitých kontaktních prvků.
Modelování kotev a hřebíků
Kotvu můžeme z hlediska silového působení rozdělit na volnou délku kotvy a na délku kořenovou. Pro modelování volné délky používáme prvky, které jsou pružinou o definované tuhosti. Pružina je spojena s ostatními prvky modelu pouze na svém začátku a konci. Mezi těmito body je pružina volně pohyblivá. Pro modelování kořenové délky kotev, příp. hřebíků, můžeme využít membránových prvků, které mají osovou tuhost a nulovou ohybovou tuhost. Tyto prvky jsou po celé své délce spojeny s okolím, (zeminou) a tím umožňují plynulé vnesení kotevní síly do zeminy. Pokud nejsou membránové prvky k dispozici, je možné použít řetězec krátkých prutových prvků navzájem spojených kloubem, pro vyloučení ohybové pevnosti. Ve 2D modelu modelujeme místo osamělých kotev náhradní průběžnou stěnu. Takové zjednodušení je často přijatelné převážně pro modelování deformací konstrukce, ale je zřejmé, že takto nelze namodelovat např. vytržení kotvy. Praktická ukázka namodelované kotvy spolu s posouzení stability kotevního systému pro dílčí kotevní úrovně je na obr. 83. Porovnáme-li tento výstup s obr. 84, který je běžně využíván pro výpočet vnitřní stability pažicí konstrukce, vidíme poměrně dobrou shodu v simulaci mechanismu porušení.
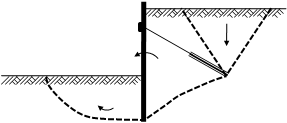
Obr. 84 Stabilita kotevního systému EC7
Modelování jednotlivých fází výstavby
Výhodou numerického modelování je možnost sledovat chování pažicí konstrukce během dílčích fází hloubení, (ostatně to umožňuje v kap. 2.3.3 popisované metoda závislých tlaků také). Je to tedy paralela s předchozí možností modelovat celý postup výstavby, ale v komplexnějším pojetí, resp. s možností získání informací o napětí a deformacích v sousedství pažicí konstrukce. Během hloubení a instalování stabilizačních prvků je možné sledovat zvolené parametry, které jsou významné. V případě geotechnických konstrukcí je nutné definovat primární stav napjatosti.
2.3.5 Vnější a vnitřní stabilita kotvených pažicích konstrukcí, příklad 4
V předchozích kapitolách bylo pojednáno o výpočtu pažicích konstrukcí z hlediska stanovení velikosti vnitřních sil potřebných pro dimenzování prvků, jež jsou součástí těchto konstrukcí. Kromě toho je však třeba posoudit jejich vnější a vnitřní stabilitu.
Pro posouzení vnější stability platí schémata uvedená na obr. 58 a to zejména ad a) až f), názorně pak pro nejtypičtější případ kotvené pažicí konstrukce na obr. 85a. Postupuje se obyčejně klasickým způsobem známým z výpočtů stupně stability svahů, jež jsou stručně uvedeny v kap. 1.2.
Představa o mechanizmu vzniku porušení z hlediska vnitřní stability kotvené pažicí konstrukce je složitější a názorně je uvedena na obr. 85b. Vychází se z předpokladu, že síla v kotvě odtrhne horninový klín mezi pažicí stěnou a kořenem kotvy, dojde k vyklonění stěny směrem do jámy a k plošnému porušení dílčími smykovými plochami.
Obr. 85 Stabilita kotvené pažicí konstrukce: a – mechanizmus pro stanovení vnější stability, b – mechanizmus pro stanovení vnitřní stability; 1 – pažicí stěna, 2 – kotva, 3 – smyková plocha, 4 – dílčí smykové plochy
Na základě posouzení vnitřní stability se kontroluje navržená délka kotev a kotevní síla Pk. Statické schéma pro posouzení vnitřní stability kotvené pažicí konstrukce je na obr. 86. Předpokládá se, že se stěna otočí kolem bodu b jako celek, přičemž bod b leží v patě stěny, je-li umožněn vodorovný posun této paty. V opačném případě se bod b umisťuje do úrovně, v níž je součet vodorovných sil pode dnem stavební jámy nulový. Smyková plocha probíhá z bodu b do bodu c, jež je umístěn do středu kotevní délky k a dále pokračuje svisle do bodu e na terénu. Na klín abce působí soustava následujících vnějších sil:
- G je tíha klínu, do níž se započítá vnější zatížení za rubem stěny p pouze tehdy, je-li úhel θ > φ; současně je třeba vzít v úvahu event. zmenšenou tíhu zeminy pod vodou;
- Sa1 je aktivní zemní tlak na svislou stěnu ce;
- Sa je aktivní zemní tlak na pažicí stěnu ab;
- T je reakce na smykové ploše bc odkloněná od normály o úhel φ;
- Pk,max je maximální možná kotevní síla, jež je schopna zaručit stabilitu.
Obr. 86 Vnitřní stabilita kotvené pažicí konstrukce: a – jednonásobně kotvená stěna, b – vícenásobně kotvená stěna
Výpočet lze provést graficky, (uzavřením složkového obrazce pro neznámé velikosti sil T, Pk,max avšak jejich známé směry a rovněž známé síly G, Sa, Sa1), nebo početně pomocí podmínek rovnováhy ve vodorovném a svislém směru. Platí, (za označení úhlů δ, který vyjadřuje odklon výslednice aktivního zemního tlaku Sa, Sa1 od vodorovné, ω je sklon kotvy od vodorovné, β = φ – θ:
\begin{gathered}
S_\text{a1,v}+G-S_\text{a,v}-T_\text{v}-P_\text{k,max,v}=0\\\\
S_\text{a,h}+T_\text{h}-P_\text{k, max,h}-S_\text{a1,h}=0
\end{gathered}(78)
Dále platí:
\begin{gathered}
T_\text{v}=T\cdot\cos\beta&T_\text{h}=T\cdot\sin\beta\\\\
P_\text{k,max,h}=P_\text{k,max}\cdot\sin\omega&P_\text{k,max,h}=P_\text{k,max}\cdot\cos\omega
\end{gathered}(79)
Po dosazení a úpravě získáme pro velikost maximální kotevní síly Pk,max vztah:
\begin{gathered}
P_\text{k,max}=\frac{[G\cdot\sin\beta-(S_\text{a1}-S_\text{a})\cdot(\sin\delta\cdot\sin\beta-\cos\delta\cdot\cos\beta)]}{(\sin\omega\cdot\sin\beta+\cos\omega\cdot\cos\beta)}
\end{gathered}(80)
Požaduje se, aby síla Pk,max byla alespoň 1,5násobkem kotevní síly Pk, tedy stupeň vnitřní stability:
\begin{gathered}
\eta=\frac{P_\text{k,max}}{P_\text{k}}\ge1{,}5
\end{gathered}(81)
V případě vícenásobně kotvených pažicích konstrukcí se postupuje obdobně, (obr. 86b). Nejprve se vyšetří stabilita horní řady kotev pro smykovou plochu bcd (resp. bce) bez uplatnění síly v 2. kotvě, (Pk2) a stanoví se stupeň stability:
\begin{gathered}
\eta^{(bcd)}=\frac{P^{(bcd)}_\text{k,max}}{P_\text{k1}}\ge1{,}5
\end{gathered}(82)
Dále se vyšetří stabilita na smykové ploše bfg (resp. bfh) z rovnováhy na zemním klínu abfh, na nějž působí obě kotevní síly Pk1 a Pk2, musí platit:
\begin{gathered}
\eta^{(bfg)}=\frac{P^{(bfg)}_\text{k,max}}{(P_\text{k1}+P_\text{k2})}\ge1{,}5
\end{gathered}(83)
Příklad 4
Stanovení vnitřní stability pažicí konstrukce podle obr. 87, kontrola navržené délky kotev
Řešení:
Nejprve vyšetříme rovnováhu pro případ 1. kotvy. Vycházíme ze statického schéma na obr. 88:
- výpočet provedeme pro šířku B = 1,0 m
- průměrná objemová tíha zeminy v případě zemního klínu:
\begin{gathered}
\gamma=\frac{(1{,}5\cdot19{,}0+2{,}5\cdot20{,}0+1{,}5\cdot19{,}5+1{,}5\cdot11{,}5+2{,}5\cdot21{,}5+2{,}5\cdot22{,}5)}{11{,}5}=19{,}6\space\text{kN}\cdot\text{m}^{-3}
\end{gathered}- průměrná velikost úhlu vnitřního tření:
\begin{gathered}
\varphi=\frac{(1{,}0\cdot20+2{,}5\cdot25+3{,}0\cdot33+2{,}5\cdot25+2{,}5\cdot30)}{11{,}5}=27{,}74\degree;\\\\
\delta=\frac{\varphi}{2}=13{,}87\degree
\end{gathered}(soudržnost zanedbáváme)
- geometrické údaje:
\begin{gathered}
h_1=2{,}5+11{,}0\cdot\sin30=8{,}00\space\text{m};&L=11{,}0\cdot\cos30=9{,}53\space\text{m}\\\\
\tg\theta=\frac{(11{,}5-8{,}00)}{9{,}53}=0{,}3673\implies\theta=20{,}16\degree,&\beta=\varphi-\theta=7{,}58\degree
\end{gathered}síly:
\begin{gathered}
G=1{,}0\cdot19{,}6\cdot(11{,}5\cdot9{,}53-9{,}53\cdot3{,}0\cdot0{,}5)=1867{,}88\space\text{kN}\\\\
S_\text{a1}=0{,}5\cdot19{,}6\cdot1{,}0\cdot8{,}0^2\cdot\tg^2(45-\frac{27{,}74}{2})=228{,}78\space\text{kN}\\\\
S_\text{a2}=0{,}5\cdot19{,}6\cdot1{,}0\cdot11{,}5^2\cdot\tg^2(45-\frac{27{,}74}{2})=472{,}75\space\text{kN}
\end{gathered}Obr. 87 Zadání k příkladu 4 – pažicí konstrukce
Obr. 88 Statické schéma pro výpočet vnitřní stability – 1. kotva
Maximální síla v 1. kotvě:
\begin{gathered}
P_\text{k,max}=\frac{[G\cdot\sin\beta-(S_\text{a1}-S_\text{a})\cdot(\sin\delta\cdot\sin\beta-\cos\delta\cdot\cos\beta)]}{(\sin\omega\cdot\sin\beta+\cos\omega\cdot\cos\beta)}=512{,}21\space\text{kN}
\end{gathered}- stupeň bezpečnosti
\begin{gathered}
\eta=\frac{512{,}21}{(\frac{441}{4})}=4{,}65\gt1{,}5\implies\space\text{vyhovuje}
\end{gathered}Vyšetření rovnováhy pro případ 2. kotvy, resp. celé kotvené konstrukce podle obr. 89.
- výpočet provedeme pro šířku B = 1,00 m (osová vzdálenost spodních kotev);
- geometrické údaje:
\begin{gathered}
h_1=6{,}5+9{,}0\cdot\sin30=11{,}00\space\text{m};&L=9{,}0\cdot\cos30=7{,}79\space\text{m}\\\\
\tg\theta=\frac{(11{,}5-11{,}0)}{7{,}79}=0{,}0641\implies\theta=3{,}67\degree,&\beta=\varphi-\theta=24{,}07\degree
\end{gathered}síly:
\begin{gathered}
G=1{,}0\cdot19{,}6\cdot(11{,}5\cdot7{,}79-7{,}79\cdot0{,}5\cdot0{,}5)=1794{,}04\space\text{kN}\\\\
S_\text{a1}=0{,}5\cdot19{,}6\cdot1{,}0\cdot11{,}0^2\cdot\tg^2(45-\frac{27{,}74}{2})=432{,}53\space\text{kN}\\\\
S_\text{a2}=0{,}5\cdot19{,}6\cdot1{,}0\cdot11{,}5^2\cdot\tg^2(45-\frac{27{,}74}{2})=472{,}75\space\text{kN}
\end{gathered}Maximální síla v 2. kotvě:
\begin{gathered}
P_\text{k,max}=\frac{[G\cdot\sin\beta-(S_\text{a1}-S_\text{a})\cdot(\sin\delta\cdot\sin\beta-\cos\delta\cdot\cos\beta)]}{(\sin\omega\cdot\sin\beta+\cos\omega\cdot\cos\beta)}=771{,}10\space\text{kN}
\end{gathered}- stupeň bezpečnosti:
\begin{gathered}
\eta=\frac{950{,}50}{(\frac{441}{2}+380)}=1{,}58\gt1{,}5\implies\space\text{vyhovuje}
\end{gathered}Obr. 89 Statické schéma pro výpočet vnitřní stability – 2. kotva
Stanovení stupně vnější stability kotvené konstrukce pomocí MKP je výhodné, neboť mechanizmus porušení je automatickým výsledkem výpočtu. Nejčastěji se využívá metody zvané „phi-c reduction“, kdy dochází k postupnému zmenšování parametrů pevnosti, (úhlu vnitřního tření zeminy a koheze), dokud nedojde k porušení. Systém před porušením se nachází v plastickém stavu, kde deformace již nehrají žádnou roli, proto se často při určování stupně stability používají lineárně elastické ideálně plastické modely s Mohr-Coulombovou podmínkou porušení. Je však možné použít i jiných podmínek porušení, jako např. Hoek-Brown nebo Matsuoka-Nakai. Pro kvantifikování stupně bezpečnosti se převážně používá definice bezpečnosti podle Felleniuse, tj.:
\begin{gathered}
F=\frac{\tg\varphi_0}{\tg\varphi_\text{red}}=\frac{c_0}{c_\text{ed}}
\end{gathered}(84)
kde je:
φ0 a c0 … vstupní parametry pevnosti;
φred a cred … pevnosti, při kterých dojde k porušení.
Výsledný stupeň bezpečnosti závisí na kvalitě použité sítě a stupni tvarové funkce podstatně více než např. vypočtené deformace při analýze konstrukce za provozních podmínek. Výsledky níže prezentovaného příkladu ilustrují výstupy, které je možné obdržet z metody postupné redukce vstupních parametrů. Zdeformovaná síť naznačuje mechanismus porušení. Světlé pásy indikují zóny, kde dochází ke koncentracím smykových napětí, tedy smykové plochy. Uvedený příklad názorně ilustruje rozdíl mezi pažicí stěnou modelovanou elastickým prvkem (obr. 90) a pažicí stěnou modelovanou lineárně elastickým ideálně plastickým prvkem (obr. 91). Vidíme, že omezením maximálního ohybového momentu, který může stěna přenést, dojde k vytvoření plastického kloubu ve stěně a tím je umožněn vznik zcela jiného mechanismu porušení konstrukce. Tak dojde i ke snížení stupně bezpečnosti. Uvedený příklad ilustruje jednu z hlavních výhod MKP, kdy mechanismus porušení je výstupem analýzy a nemusí být předpokládán, jak je tomu u většiny jiných metod.
Obr. 90 Deformace konstrukce a smyková přetvoření při porušení; pažicí stěna – elastický prvek, výsledný stupeň bezpečnosti F = 2,02
Obr. 91 Deformace konstrukce a smyková přetvoření při porušení; pažicí stěna – lineárně elastický ideálně plastický prvek, výsledný Stupeň bezpečnosti F = 1,75
3 ODVODŇOVÁNÍ ZÁKLADOVÉ PŮDY
3.1 DRUHY VODY V ZÁKLADOVÉ PŮDĚ
Podzemní voda je voda vyskytující se pod povrchem terénu. Jejím zdrojem jsou jednak srážky, jednak průsak z vodotečí, nádrží, jezer a moří. Jde tedy o vodu gravitační, která je pod vlivem zemské přitažlivosti, jež se dělí na vodu:
- volnou, která souvisle vyplňuje póry v základové půdě pod hladinou podzemní vody;
- kapilární, která pod vlivem povrchového napětí vzlíná v pórech (a kapilárách) v zemině nad hladinu podzemní vody.
Kromě toho je v zemině voda vázaná, jež vytváří na povrchu částic zeminy difúzní obal z orientovaných molekul vody. Podle velikosti elektromolekulárních sil se tato voda dělí na:
- pevně vázanou, (adsorbovanou);
- slabě vázanou, (obalovou, osmotickou).
Součástí krystalické mřížky minerálů je voda strukturální, jež může být:
- chemicky vázaná, (v podobě iontů H+, OH–);
- krystalická, jež si zachovává molekulární formu H2O.
Strukturální voda nemá na mechanické vlastnosti zemin žádný vliv a lze ji z minerálů odstranit pouze zahřátím na vysoké teploty. Vázaná voda má rozhodující vliv na vlastnosti jemnozrnných zemin, neboť ovlivňuje rozhodujícím způsobem jejich základní vlastnosti jako jsou soudržnost a plasticitu. Na vlastnosti nesoudržných zemin nemá vázaná voda praktický vliv.
Kapilární voda vzlíná vlivem povrchového napětí, jež je σ ≅ 7,4 · 10-2 N·m-1, (při teplotě 10° C). Molekuly stěny kapiláry přitahují vodu, která v dostatečně dlouhé kapiláře vystoupí na výšku hk, kdy je tíha vody v rovnováze s výslednicí povrchového napětí s po obvodu trubice:
\begin{gathered}
h_\text{k}=\frac{2\sigma}{(\gamma_\text{w}\cdot r)}
\end{gathered}(85)
kde je:
r … poloměr příslušné kapiláry.
Průměr pórů v zeminách není konstantní, a proto kapilární výška hk značně kolísá. Póry zeminy nad hladinou kapilární vody jsou v rozsahu kapilární výšky plně nasyceny vodou, jež se označuje jako voda podepřená. V tab. 16 jsou typické kapilární výšku pro některé zeminy.
Tab. 16 Kapilární výšky některých druhů základových půd
| Zemina | Kapilární výška hk [m] | Odpovídající průměr kapiláry 2 r [μm] |
| jemnozrnný písek sprašová hlína jílovitá hlína jíl |
0,1–0,5 2–5 10–30 > 50 |
300–60 16–6 3–1 < 0,6 |
Volná voda zaplňuje souvisle póry zeminy pod hladinou podzemní vody, jejíž úroveň se zjišťuje v rámci geotechnického průzkumu. Přitom je třeba rozlišovat naraženou hladinu podzemní vody, (pro případ konkrétního průzkumného díla a konkrétního času) a ustálenou hladinu podzemní vody, jež bývá pro další úvahy rozhodující. Ta může být ovlivněna i případnou napjatostí podzemní vody způsobenou např. existencí artéského stropu, (nepropustné vrstvy) apod. Proudění vody v zemině je způsobeno gravitací, přičemž voda proudí ve směru hydraulického spádu. Její pohyb však není obyčejně pravidelný, neboť voda prosakuje složitým systémem vzájemně více, či méně propojených kanálků, kdy částice vody při průsaku mění směr i rychlost, což nelze matematicky jednoduše vyjádřit. V praxi se potom používá filtrační (průsaková) rychlost proudění podzemní vody v, jež je definována:
\begin{gathered}
v=\frac{q}{A}
\end{gathered}(86)
kde je:
q … množství prosáklé vody;
A … příčná plocha k průsaku, (kolmá na vektor hydraulického spádu).
Skutečná rychlost vody v pórech vsk je ovšem podstatně větší a závisí zejména na pórovitosti zeminy n. Pokud by se jednalo o relativně pomalý pohyb vody v trubici, mluvíme o laminárním proudění. Čím je pohyb rychlejší a dráha zakřivenější, tím více dochází k víření vody a pohyb se mění na turbulentní. Hranice je dána kritickou hodnotou Reynoldsova čísla Recr podle vztahu:
\begin{gathered}
Re=v\cdot\frac{d}{\nu}
\end{gathered}(87)
kde je:
v … rychlost vody [m·s-1];
d … účinný průměr póru [m];
ν … kinematická viskozita vody [m2·s-1].
Pro hrubozrnné písky a štěrky je Recr = 3 – 10. V jemnozrnných zeminách a v píscích je pohyb vody vždy laminární, pouze v hrubých štěrcích přechází v pohyb turbulentní. Rychlost proudění vody v základové půdě v se řídí Darcyho zákonem:
\begin{gathered}
v=k\cdot i
\end{gathered}(88)
kde je:
k … koeficient filtrace základové půdy [m·s1], (někdy nesprávně nazýván jako součinitel propustnosti); jeho orientační velikosti jsou uvedeny v tab. 17;
i … hydraulický spád, (sklon, gradient), jež je definován jako poměr rozdílu hladin dvou bodů na proudnici Δh ku délce průsaku Δl, tedy:
\begin{gathered}
i=\frac{\Delta h}{\Delta l}
\end{gathered}(89)
U jemnozrnných zemin může proudění nastat teprve po překonání odporu částic vázané vody v pórech, tj. po překonání počátečního gradientu ior, potom lze Darcyho zákon upravit na tvar:
\begin{gathered}
v=k\cdot(i-i_\text{or})
\end{gathered}(90)
přičemž v případě jílů může dosáhnout počáteční gradient až ior = 10.
Tab. 17 Orientační velikosti koeficientu filtrace k pro vybrané typy zemin
| Zemina | k [m·s1] |
| štěrk a písčitý štěrk jemnozrnný písek jílovitý písek a spraš hlína, silt jíl |
10-1–10-4 10-3–10-6 10-5–10-8 10-6–10-9 10-8–10-10 |
3.2 POHYB VODY V ZÁKLADOVÉ PŮDĚ
Pro jakékoliv výpočty a úvahy týkající se pohybu vody v zemině je třeba znát hydrogeologické poměry na staveništi, tj. úroveň hladiny podzemní vody, směr jejího proudění, vlastnosti jednotlivých vrstev základové půdy, tj. zejména velikost koeficientu filtrace a event. úroveň nepropustného podloží.
3.2.1 Koeficient filtrace a metody jeho stanovení
Propustnost základové půdy lze stanovit in situ, v laboratoři, popř. nepřímou metodou ve vztahu k základním indexovým vlastnostem této zeminy. Nejlepší způsob je přímé stanovení v poli tzv. čerpací zkouškou, jde však samozřejmě o metodu nejdražší. Zkouška však zahrnuje poměrně velký objem zeminy a výsledek není tak ovlivněn bodovým odběrem, jež je typický pro stanovení laboratorní. Nejlevnější a současně nejméně věrohodné je odvození velikosti koeficientu filtrace nepřímými metodami z ostatních vlastností základové půdy (z křivky zrnitosti, z charakteristických průměrů zrn a z pórovitosti).
Čerpací zkouška
Využívá se tzv. hydrologického kříže v jehož středu je studna, jež má být dokonalá, tzn., že je vetknuta do nepropustného podloží a přítok do ní je zprostředkován pouze jejím pláštěm, na němž je osazena perforovaná zárubnice. Ta bývá obklopena tzv. obráceným filtrem, tj. kačírkem různé zrnitosti, jímž je vyplněno mezikruží mezi pažnicí, (jež přijde po obsypu vytáhnout) a zárubnicí. Průměr zárubnice by měl být alespoň 400 mm. Ze studny se čerpá konstantní množství vody Q, při němž dojde ke konstantnímu snížení hladiny vody o velikost s, tedy původní výška vody, (nad nepropustným podložím) H bude snížena na velikost h0. Kolem čerpací studny jsou rozmístěny tzv. pozorovací vrty, (pégly) ve dvou na sebe kolmých směrech, v nichž se měří příslušné snížení hladiny vody hi v závislosti na vzdálenostech od studny ri. Vzdálenost 1. péglu se volí asi r1 = H / 2, druhého r2 = 2 r1, atd. Tím se zajistí dobrá možnost pro stanovení skutečného poloměru deprese R (obr. 92). Vlastní výpočet přítoku vody do dokonalé studny, jež je základem všech následných hydrologických výpočtů vychází z předpokladu, že rozdělení rychlosti proudění podzemní vody po výšce je rovnoměrné, tudíž je třeba aby depresní kužel byl dostatečně plochý a snížení ve studni s nebylo větší než asi H / 4. Pláštěm studny protéká množství vody:
\begin{gathered}
q=2\pi\cdot r\cdot h\cdot v=2\pi\cdot r\cdot h\cdot k\cdot i=2\pi\cdot r\cdot h\cdot k\cdot\frac{dh}{dl}=2\pi\cdot r\cdot h\cdot k\cdot\frac{dh}{dr}
\end{gathered}(91)
neboť pro malé spáry hladin můžeme psát: dl ≅ dr
Platí tedy:
\begin{gathered}
\frac{q}{(\pi\cdot k)}\cdot\frac{r}{r}=2\cdot h\cdot dh,\space\text{neboli}\space \frac{q}{(\pi\cdot k)}\cdot\frac{\int dr}{r}=2\cdot\int h\cdot dh
\end{gathered}(92)
po integraci:
\begin{gathered}
h^2=\frac{q}{(\pi\cdot k)}\cdot ln\cdot(r)+\text{C}
\end{gathered}(93)
integrační konstantu C určíme z okrajových podmínek: pro r = r0 je h = h0, tedy:
\begin{gathered}
\text{C}=h_0^2-\frac{q}{(\pi\cdot k)}\cdot ln\cdot(r_0)
\end{gathered}(94)
a po dosazení do rovnice (93) a náhradě q = Q pro r = R a h = H získáme:
\begin{gathered}
H^2-h_0^2=\frac{Q}{(\pi\cdot k)}\cdot(ln\cdot(R)-ln\cdot(r_0))=\frac{Q}{(\pi\cdot k)}\cdot ln\cdot(\frac{R}{r_0})
\end{gathered}(95)
tedy konečně:
\begin{gathered}
Q=\pi\cdot k\cdot\frac{(H^2-h_0^2)}{ln}\cdot(\frac{R}{r_0})
\end{gathered}(96)
což je základní vzorec pro přítok vody do dokonalé studny. Velikost koeficientu filtrace pak při změřených a známých velikostech (H, h0, R, r0, Q) vypočteme:
\begin{gathered}
k=Q\cdot ln\cdot\frac{(\frac{Q}{r_0})}{(\pi\cdot(H^2-h_0^2))}
\end{gathered}(97)
Obr. 92 Princip čerpací zkoušky
Stanovení koeficientu filtrace v laboratoři
Zkoušky se provádí na neporušených vzorcích zemin, a to buď na přístroji s konstantním spádem, nebo s proměnným spádem. Princip zkoušky s konstantním hydraulickým spádem je znázorněn na obr. 93. Voda se ke vzorku průřezové plochy A a výšky l přivádí spodem a prosakuje svislým směrem a odtéká do odměrné nádoby, kde se měří prosáklé množství Q za dobu t. Lze potom psát:
\begin{gathered}
Q=A\cdot v\cdot t=A\cdot k\cdot i\cdot t=A\cdot k\cdot\frac{h}{l}\cdot t,\space\text{tedy}\space k=Q\cdot\frac{l}{(A\cdot h\cdot t)}
\end{gathered}(98)

Obr. 93 Princip propustoměru s konstantním hydraulickým spádem
Zkouška s proměnným spádem se provádí v přístroji, jehož princip je na obr. 94. V rouře je vzorek zeminy průřezové plochy A a výšky l. Roura je na začátku zkoušky naplněna vodou (výška h0), na konci zkoušky se hladina vody sníží na hodnotu h1 (za čas t).
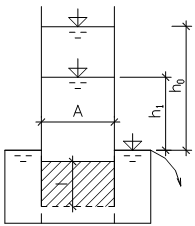
Obr. 94 Princip propustoměru s proměnným hydraulickým spádem
Za diferenciál času dt proteče zeminou voda o objemu
\begin{gathered}
dQ=-A\cdot dh=A\cdot v=A\cdot k\cdot\frac{h}{l}\cdot dt
\end{gathered}tedy:
\begin{gathered}
\frac{-\intop\limits^{h1\space t}_{h0\space0}dh}{h}=\frac{k}{1}\cdot\int dt,\space\text{tedy}\space ln\cdot(\frac{h_0}{h_1})=\frac{k}{l}\cdot t\space\text{a potom}\space k=\frac{l}{t}\cdot ln\cdot(\frac{h_0}{h_1})
\end{gathered}(99)
Nepřímé metody k určení koeficientu filtrace
Informativní údaje lze získat z křivky zrnitosti zeminy, jež je základní laboratorní zkouškou potřebnou pro zatřídění zeminy do příslušné klasifikace. Na obr. 95 je graf vyjadřující granulometrické složení zeminy s příslušnými poli, jímž jsou přiřazeny typické velikosti koeficientu filtrace k, pole jsou oddělena empirickými křivkami.
Obr. 95 Graf pro přibližné stanovení koeficientu filtrace základové půdy na základě jejího zrnitostního rozboru
Jiné, níže uvedené empirické vzorce a přibližné metody vycházejí z charakteristického průměru zrn zeminy a event. z čísla pórovitosti:
Hanzen (1893)
\begin{gathered}
k\cong1{,}16\cdot10^4\cdot d_{10}^2\space[\text{m}\cdot\text{s}^{-1}]
\end{gathered}(100)
kde je:
d10 … průměr zrn [m] odpovídající propadu na sítě v množství 10 %
Jáky (1944)
\begin{gathered}
k\cong10^4\cdot d_\text{m}^2\space[\text{m}\cdot\text{s}^{-1}]
\end{gathered}(101)
kde je:
dm … průměr zrn [m] vyskytující se s největší frekvencí
Cassagrande (1948)
\begin{gathered}
k\cong1{,}4\cdot k_{0{,}85}\cdot e^2\space[\text{m}\cdot\text{s}^{-1}]
\end{gathered}(102)
kde je:
k0,85 … koeficient filtrace při čísle pórovitosti e = 0,85
Terzaghi (1955)
\begin{gathered}
k\cong2\cdot10^4\cdot d_\text{e}^2\cdot e^2\space[\text{m}\cdot\text{s}^{-1}]
\end{gathered}(103)
kde je:
de … efektivní průměr zrn [m]
e … číslo pórovitosti.
3.2.2 Proudový tlak
Pojmem proudový tlak označujeme objemovou sílu j [kN·m-3] působící na částice zeminy při průsaku vody základovou půdou. Proudový tlak tedy nezávisí na rychlosti proudění (daném v podstatě velikosti koeficientu filtrace k), ale na hydraulickém spádu i podle vztahu:
\begin{gathered}
j=\gamma_\text{w}\cdot i
\end{gathered}(104)
Pokud voda prosakuje svisle dolů, (ve směru gravitace), zvětšuje objemovou tíhu zeminy podle vztahu daném rovnicí (44), naopak prosakuje-li voda svisle vzhůru, zmenšuje proudový tlak tíhu zeminy podle vztahu (45). Z tohoto vztahu vyplývá možnost tzv. ztekucení zeminy (fluidizace), kdy zrna zeminy se ve vodě vznáší, neboť jejich efektivní tíha je nulová. Dochází tedy k prolomení základové půdy. Hydraulický sklon, při němž k tomuto jevu dochází označujeme za kritický:
i_\text{cr}=\frac{\gamma_\text{su}}{\gamma_\text{w}}\cong1{,}0(105)
S proudovým tlakem se musí počítat zejména při posuzování stability dna těsněných jímek, kde při nedostatečně dlouhém vetknutí např. štětovnic hrozí právě prolomení dna. Kritickým místem je právě dno výkopu těsně u stěny. Uvažujeme-li pouze dráhu vodní částice těsně podél stěny při výšce vody h a hloubce vetknutí pode dno t vychází kritický hydraulický spád:
\begin{gathered}
i_\text{cr}=\frac{h}{2t}\cong1{,}0;\implies t_\text{min}\cong\frac{h}{2}
\end{gathered}(106)
Pokud uvažujeme obdobný případ podle obr. 96, vychází:
\begin{gathered}
i_\text{cr}=\frac{(h+D)}{(D+2t)}\cong1{,}0;\implies t_\text{min}\cong\frac{h}{2}
\end{gathered}(107)
Tato řešení jsou ovšem velmi zjednodušená a přibližná, neboť vycházejí pouze z přímé dráhy vodní částice. Pod patou stěny se však směr proudění obrací, a proto je třeba vycházet z celkového řešení proudové sítě. Tímto přesnějším řešením dostáváme vztah pro tmin:
\begin{gathered}
t_\text{min}=\frac{h}{\pi}\cong\frac{h}{3}
\end{gathered}(108)
Obr. 96 Stěna jímky – označení pro stanovení minimální délky vetknutí
V případě písků, zvláště jemnozrnných, dochází vlivem proudění podzemní vody k unášení jednotlivých zrn a k jejich vyplavování – sufozi, což z dlouhodobějšího hlediska vede k výraznému oslabení struktury zeminy a změně jejich vlastností. Negativním jevem doprovázejícím sufozi je též zanášení, (kolmatace) filtrů čerpacích studní. Příkladem je zakládání žb. obilního sila v jemnozrnných zeminách pod hladinou podzemní vody podle obr. 97. Silo bylo založeno plošně na základové desce, jež byla izolována. Projektant se chtěl vyhnout event. problémům s nedokonalou izolací a navrhl kolem objektu soustavu čerpacích studní s plovákovým systémem, jež udržovaly trvale hladinu podzemní vody pod základovou spárou. V průběhu času však vlivem sufoze došlo ke kolmataci studní a depresní křivka se stala strmější, což mělo za následek zvýšení hladiny podzemní vody ve střední části základové desky a první drobné průsaky. Byly tedy vyhloubeny náhradní studny a celý jev se opakoval. Sufoze však značně postoupila a došlo ke změně vlastností základové půdy, (modulu deformace) a silo sedalo a naklonilo se. Navíc vlivem kolmatovaných studní a prasklin v základové desce docházelo již k výraznějším průsakům podzemní vody do suterenních prostor. Sanace je mimořádně náročná, jak technicky, tak zejména finančně.
Obr. 97 Příklad sufoze v případě čerpání podzemní vody při plošném zakládání pod hladinou podzemní vody: S – soustava čerpacích studní, 1 – normální hladina podzemní, 2 – snížená hladina podzemní vody u nekolmatovaných studní, 3 – depresní křivka u kolmatovaných studní
3.2.3 Proudové sítě
Voda se při průsaku zeminou pohybuje ve směru maximálního gradientu. Pokud obecný, (prostorový) pohyb vody základovou půdou omezíme na rovinné proudění, (ve svislé rovině řezu), zjednodušíme tím značně celé řešení. Proudí-li tedy voda v homogenním, izotropním prostředí z hydraulického hlediska charakterizovaném koeficientem filtrace k, můžeme pro toto proudění psát tzv. Laplaceovu rovnici (v rovině x, y):
\begin{gathered}
\frac{\partial^2\phi}{\partial_\text{x}^2}+\frac{\partial^2\phi}{\partial_\text{y}^2}=\Delta\phi=0
\end{gathered}(109)
Řešením této rovnice je tvar tzv. proudové sítě v souřadném systému x, y. Křivky vytvořené spojením míst o stejném gradientu jsou tzv. ekvipotenciály, přičemž maximální hydraulický sklon působí ve směru nejkratší spojnice mezi sousedními ekvipotenciálami – jedná se o tzv. proudnice, jež jsou samozřejmě kolmé na ekvipotenciály. Pro praktická řešení je nejvhodnější, aby proudová síť byla pravidelná, tzn. aby poměr změny gradientu ke změně proudové funkce v libovolném poli proudové sítě byl stejný. Výsledkem je tzv. čtvercová proudová síť, kdy střední vzdálenost ekvipotenciál je stejná jako střední vzdálenost proudnic; (lze tedy do každého pole vepsat kružnici). Nejjednodušší proudová síť pro případ vetknuté štětové stěny je na obr. 98a. Čtvercová síť je složena ze zakřivených (deformovaných) čtverců, jejichž tečny v rozích jsou na sebe kolmé a středy vepsaných kružnic jsou umístěny na zakřivených úhlopříčkách, jejichž tečny jsou rovněž na sebe kolmé. Označíme-li počet ekvipotenciálních pásů n, pak rozdíl mezi dvěma ekvipotenciálami je:
\begin{gathered}
\Delta h=\frac{h}{n}\space\text{a hydraulický sklon}\space i=\frac{\Delta h}{\Delta l}
\end{gathered}(110)
kde je:
Δl … šířka ekvipotenciálního pásu, (vzdálenost ekvipotenciál).
Čím jsou ekvipotenciály blíže u sebe, tím je hydraulický spád i větší a větší je jak rychlost proudění, (v = k · i), tak i proudový tlak, (j = γw · i). Jak vyplývá z obr. 98a, je hydraulický spád i proměnný, přičemž největší je u paty stěny, kde může dosáhnout i velikosti i > icr, což může znamenat lokální porušení základové půdy.
Obr. 98 Stanovení hydrodynamického tlaku: a – proudová síť, b – hydrostatický a hydrodynamický tlak na obě strany štětovnice, c – výsledné schéma z obr. b
Pomocí proudové sítě lze dostatečně přesně stanovit průsak vody pod stěnou. Označíme-li počet proudových pásů m, pak při ustáleném proudění je průsakové množství ΔQ v každém pásu stejné. Celkový průsak na délku 1 bm stěny je pak:
\begin{gathered}
Q=m\cdot\Delta Q=m\cdot k\cdot(\frac{\Delta h}{\Delta l})\cdot\Delta l=m\cdot k\cdot(\frac{h}{n})=(\frac{m}{n})\cdot k\cdot h
\end{gathered}(111)
Pomocí proudové sítě lze též stanovit rozdělení hydrodynamického tlaku podél stěny, neboť rozdíl tlaku mezi dvěma ekvipotenciálami je:
\begin{gathered}
\gamma_\text{w}\cdot\Delta h=\gamma_\text{w}\cdot(\frac{h}{n})
\end{gathered}(112)
Jednoduchý příklad štětové stěny v propustném prostředí je na obr. 98b, kde čárkovaně je vyznačen průběh hydrostatického tlaku na obě strany štětovnice a plně pak hydrodynamický tlak, jež je z obou stran u paty stejný. Na obr. 98c je potom vykreslen výsledný tlak – čárkovaně hydrostatický, plně definitivní hydrodynamický. Tím lze vysvětlit řešení uvedené na obr. 57b dané rovnicemi (44), resp. (45).
Příklad složitější proudové sítě pod jezovou konstrukcí je na obr. 99, kde je rovněž uveden průběh vztlaku podél základové spáry jezu.
Obr. 99 Proudová síť jezové konstrukce a stanovení vztlaku
3.3 ZPŮSOBY ODVODŇOVÁNÍ ZÁKLADOVÉ PŮDY
Při zakládání pod hladinu podzemní vody je nutné základovou spáru odvodnit, tzn. vyčerpat podzemní vodu nejen z vytěženého prostoru, ale zčásti i pod základovou spáru. Odvodnění stavebních jam se provádí buď povrchově, obr. 100, nebo hloubkově, obr. 101.
Při povrchovém odvodnění se voda odčerpává postupně s hloubením, (pod úroveň původní hladiny podzemní vody). Voda se odvádí postupně hloubenými svahovanými příkopy do sběrných jímek, (studní), z nichž se čerpá. Povrchové odvodnění se provádí ponejvíce v případě nehlubokých svahovaných jam v relativně stabilních zeminách, (štěrcích, píscích a v horninách poloskalních a skalních), neboť svahy prosakující voda snižuje významně jejich stabilitu.
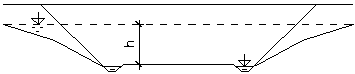
Obr. 100 Povrchové odvodnění stavebních jam
V případě hloubkového, (podpovrchového) odvodnění se voda čerpá systémem studní a jáma se hloubí až po snížení podzemní vody. Rozměry studní, jejich počet a čerpané množství vody se stanoví většinou orientačním výpočtem. Velikosti studní závisí na druhu základové půdy, (její propustnosti) a na čerpaném množství. V silně propustných zeminách se navrhuje menší počet studní větších průměrů, neboť dosah depresní křivky je značný. Naopak v málo propustných zeminách postačí menší průměr studní, jejich počet musí však být značný, neboť depresní křivka je strmá a dosah deprese malý. Voda se čerpá buď ponornými čerpadly, jež jsou umístěny ve studni vybavené obyčejně plovákovým systémem s automatickým udržováním zvolené hladiny, nebo odstředivými čerpadly, umístěnými na povrchu s příslušným rozvodem a sacími koši v jednotlivých studních. V tomto případě lze však počítat se sací výškou kolem 6–7 m, neboť vodu vytlačuje atmosférický tlak rovný přibližně 100 kPa, čemuž odpovídá teoretická hydrostatická výška 10 m.
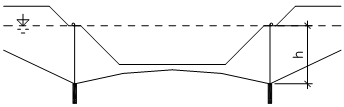
Obr. 101 Hloubkové odvodnění stavebních jam
V případě zvodnělých písků s koeficientem filtrace k = 10-4 až 10-5 m·s-1 se používá vakuové hloubkové odvodňování čerpacími jehlami.
3.3.1 Návrh povrchového odvodnění, příklad 5
Povrchové odvodnění bývá levnější, vyžaduje však dostatek prostoru v okolí stavební jámy, neboť sklony svahů jsou plošší. Vycházíme z předpokladu, že stavební jáma se nachází ve zvodnělém prostředí charakterizovaném koeficientem filtrace k a v jisté hloubce H pod hladinou podzemní vody, jež je větší, než je hloubka stavební jámy, existuje nepropustné podloží. Z hydraulického hlediska se tedy jedná o případ tzv. nedokonalé, (neúplné) studny, kde přítok vody nastává jednak pláštěm, (svahu stavební jámy), jednak dnem studny, (jámy). Gravitační přítok do úplné studny, (zapuštěné do nepropustného podloží) byl odvozen v kap. 2.2.1 (rovnice 96). Jde-li o artézkou vodu s přetlakovou výškou (H – t), viz obr. 102a, je přítok do této studně dán vztahem:
\begin{gathered}
Q=2\pi\cdot k\cdot t\cdot\frac{(H-h_0)}{ln}\cdot(\frac{R}{r})
\end{gathered}(113)
Jde-li o stavební rýhu délku l ve zvodni s klidnou hladinou podzemní vody (obr. 102b), je jednostranný přítok:
\begin{gathered}
Q=k\cdot(H^2-h_0)^2\cdot\frac{ln}{2R}
\end{gathered}(114)
a konečně v případě stavební rýhy s artézkou hladinou vody (obr. 102c) je jednostranný přítok:
\begin{gathered}
Q=k\cdot t\cdot(H-h_0)\cdot\frac{ln}{R}
\end{gathered}(115)
Obr. 102 Znázornění přítoku vody do studny a rýhy: a – artézký přítok do úplné studny, B – gravitační přítok do úplné rýhy, c – artézký přítok do úplné rýhy
Jde-li o stavební rýhu délku l ve zvodni s klidnou hladinou podzemní vody (obr. 103b), je jednostranný přítok:
\begin{gathered}
Q=k\cdot(H^2-h_0)^2\cdot\frac{l}{2R}
\end{gathered}(114)
a konečně v případě stavební rýhy s artézkou hladinou vody (obr. 103c) je jednostranný přítok:
\begin{gathered}
Q=k\cdot t\cdot(H-h_0)\cdot\frac{l}{R}
\end{gathered}(115)
Dosah snížení, (depresní křivky), lze určit pouze přibližně pomocí empirických vzorců:
- podle Sichardta
\begin{gathered}
R=3\space000\cdot(H-h_0)\cdot(k)^{\frac{1}{2}}
\end{gathered}(116)
- podle Kusakina
\begin{gathered}
R=575\cdot(H-h_0)\cdot(k\cdot H)^{\frac{1}{2}}
\end{gathered}(117)
Vypočtené velikosti R ze vzorců (116) a (117) se mohou lišit až o 100 %, pro další úvahy se obyčejně uvažuje s menší velikostí R, což odpovídá vesměs vztahu (117).
Pokud je v blízkosti úplné studny přímkový zdroj vody, (vodoteč, nádrž, jezero apod.) ve vzdálenosti L, potom se v případě, že R > 2L, dosazuje do vzorců pro výpočet přítoku (96) a (113) dosazuje R = 2L a do vzorců (114) a (115) se dosadí R = L v případě, že R > L.
Přítok vody do stavební jámy při povrchovém odvodnění se stanoví přibližně jako přítok vody do neúplné studny o poloměru rs, jež je rovnoplochá se stavební jámou o ploše A, (podle obr. 103):
\begin{gathered}
r_\text{s}=(\frac{A}{\pi})^\frac{1}{2}
\end{gathered}(118)
Dosah snížení podzemní vody R se obvykle měří od tohoto poloměru, tedy vzorec pro gravitační přítok stěnami (96) se upraví na tvar:
\begin{gathered}
Q_1=\pi\cdot k\cdot\frac{(H^2-h_0)^2}{ln}\cdot(\frac{(r_\text{s}+)}{r_\text{s}})
\end{gathered}(119)
Přítok vody dnem jámy se stanoví obyčejně podle empirického vzorce:
\begin{gathered}
Q_2=\pi\cdot k\cdot2\cdot(H-h_0)\cdot\frac{r_\text{s}}{[\frac{\pi}{2}+2\cdot\arcsin h\cdot(\frac{r_\text{s}}{(h_0+(h_0^2+r_\text{s}^2)^\frac{1}{2}})+0{,}515\cdot\frac{r_\text{s}}{h_0}\cdot ln\cdot(\frac{(r_\text{s}+R)}{4}\cdot h_0)]}
\end{gathered}(120)
přičemž celkový přítok je:
\begin{gathered}
Q=Q_1+Q_2
\end{gathered}(121)
Obr. 103 Schéma pro povrchové odvodnění
Příklad 5
Stanovte přítok vody do stavební jámy půdorysných rozměrů dna 30 x 45 m podle obr. 104 pro případ povrchového odvodnění. Jáma je hloubena ve štěrku o mocnosti 8,0 m s jílovým nepropustným podložím. Hloubka jámy je 5,0 m, hladina podzemní vody v hloubce 1,5 m pod terénem. Písčitý štěrk má koeficient filtrace k = 5 · 10-4 m·s-1.
Obr. 104 Schéma pro výpočet povrchového odvodnění z příkladu 5: a – půdorys stavební jámy, b – charakteristický řez
Řešení:
1. Návrh sklonů svahů stavební jámy:
- předpokládáme efektivní úhel vnitřního tření štěrků φef = 36°, tedy nad vodou bude sklon
\begin{gathered}
\tg\beta=\frac{(\tg\varphi)}{1{,}1}=0{,}66,&\text{tedy sklon bude asi}\space1:1{,}5
\end{gathered}pod vodou bude sklon 2x plošší, tedy asi 1 : 3
2. Rozměry fiktivní studně:
- jednostranné rozšíření nad vodou (voda bude snížena z titulu deprese nejméně o 1,0 m)
\begin{gathered}
1\cdot1{,}5+2{,}5\cdot3{,}0=9{,}0\space\text{m}
\end{gathered}- fiktivní rozměry a plocha jámy v úrovni hladiny podzemní vody:
\begin{gathered}
A=(30{,}0+2\cdot9{,}0)\cdot(45{,}0+2\cdot9{,}0)=48{,}0\cdot63{,}0=3\space024{,}0\space\text{m}^2
\end{gathered}- poloměr náhradní studny:
\begin{gathered}
r_\text{s}=(\frac{3\space024}{\pi})^{\frac{1}{2}}=31{,}0\space\text{m}
\end{gathered}3. Zbylé údaje – viz obr. 104:
\begin{gathered}
H=6{,}50\space\text{m};&h_0=2{,}50\space\text{m},\space(\text{snížení volíme}\space0{,}5\space\text{m pode dnem jámy})
\end{gathered}4. dosah snížení:
- podle Sicharta
\begin{gathered}
R=3\space000\cdot(6{,}5-2{,}5)\cdot(5\cdot10^{-4})^{\frac{1}{2}}=268{,}3\space\text{m}
\end{gathered}- podle Kusakina
\begin{gathered}
R=575\cdot(6{,}5-2{,}5)\cdot(6{,}5\cdot5\cdot10^{-4})^{\frac{1}{2}}=131{,}1\space\text{m, (volíme tuto velikost)}
\end{gathered}5. Přítok vody svahy jámy:
\begin{gathered}
Q_1=\pi\cdot5\cdot10^{-4}\cdot\frac{(6{,}5^2-2{,}5^2)}{\ln}\cdot(\frac{(31{,}0+131{,}1)}{31})=0{,}0342\space\text{m}^3\cdot\text{s}^{-1}
\end{gathered}6. Přítok vody dnem:
\begin{gathered}
Q_2=\pi\cdot5\cdot10^{-4}\cdot2\cdot(6{,}5-2{,}5)\cdot\frac{31{,}0}{[\frac{\pi}{2}+2\cdot\arcsin h\cdot(\frac{31{,}0}{(2{,}5+(2{,}5^2+31{,}0^2)^{\frac{1}{2}}})+0{,}515\cdot\frac{31{,}0}{2{,}5}\cdot\ln\cdot(\frac{(31{,}0+185{,}4)}{(4\cdot2{,}5)})]}=0{,}0170\space\text{m}^3\cdot\text{s}^{-1}
\end{gathered}7. Celkový přítok:
\begin{gathered}
Q=0{,}0342+0{,}0170=0{,}0512\space\text{m}^3\cdot\text{s}^{-1}=184{,}3\space\text{m}^3/\text{hod}=4423\space\text{m}^3/\text{den}
\end{gathered}Podzemní vodu lze vypouštět do vodního toku, pokud není k dispozici, není navržené povrchové odvodnění reálné pro množství čerpané vody.
3.3.2 Návrh hloubkového odvodnění, příklad 6
Při hloubkovém odvodnění se kolem stavební jámy realizuje řada studní, v nichž se předem čerpá podzemní voda a vytvoří se tak příslušná deprese a stavební jáma se hloubí již v suchu. Vlastní odvodnění se stanoví za předpokladu, že přítok do stavební jámy je přítokem do dokonalé studny, (pouze pláštěm), za níž se pokládá fiktivní rovnoplochá studna daná rozměry obvodu jámy podél studní.
Příklad 6
Stanovte přítok vody do stavební jámy půdorysných rozměrů dna 30 x 40 m hluboké 6,0 m v prostředí písků s koeficientem filtrace k = 5 · 10-4 m·s-1 podle obr. 105. Mocnost písků je 9,0 m, hladina podzemní voda je v hloubce 2,0 m pod terénem. Nepropustné podloží je tvořeno křídovým slínovcem.
Obr. 105 Schéma pro výpočet podpovrchového odvodnění z příkladu 6: a – půdorys stavební jámy, b – charakteristický řez
Řešení:
1. sklon stavů stavební jámy:
- předpokládáme efektivní úhel vnitřního tření písků φef = 32°, potom dočasný sklon:
\begin{gathered}
\tg\beta=\frac{(\tg32)}{1{,}1}=0{,}568,\space\text{tj.}\space1:76,\space\text{volíme}\space1:1{,}8\space\text{v celém rozsahu jámy}
\end{gathered}2. umístění studní a geometrické charakteristiky:
- studně umístíme na lavici šířky 3,0 m v úrovni původní hladiny podzemní vody ve vzdálenosti 1,5 m od hrany svahu, tedy:
- jednostranné rozšíření jámy (po osu studní):
\begin{gathered}
4\cdot1{,}8+1{,}5=8{,}7\space\text{m}
\end{gathered}- rozměry fiktivní plochy:
\begin{gathered}
30{,}0+2\cdot8{,}7=47{,}4\space\text{m};&40{,}0+2\cdot8{,}7=57{,}4\space\text{m}
\end{gathered}- hloubka původní hladiny podzemní vody
\begin{gathered}
H=9{,}0-2{,}0=7{,}0\space\text{m}
\end{gathered}- požadované snížení pode dno jámy je 0,5 m, tedy
\begin{gathered}
h_0=3{,}0-0{,}5=2{,}5\space\text{m}
\end{gathered}3. výpočet potřebných údajů:
- náhradní plocha
\begin{gathered}
A=47{,}4\cdot57{,}4=2\space720{,}76\space\text{m}^2
\end{gathered}- poloměr náhradní studny
\begin{gathered}
r_\text{s}=(\frac{2\space720{,}76}{p})^{\frac{1}{2}}=29{,}44\space\text{m}
\end{gathered}- dosah snížení podle Sichardta
\begin{gathered}
R=3\space000\cdot(7{,}0-2{,}5)\cdot(5\cdot10^{-4})^{\frac{1}{2}}=301{,}9\space\text{m}
\end{gathered}- dosah snížení podle Kusakina
\begin{gathered}
R=575\cdot(7{,}0-2{,}5)\cdot(5\cdot7{,}0\cdot10^{-4})^{\frac{1}{2}}=153{,}07\space\text{m (použijeme)}
\end{gathered}4. celkový přítok do stavební jámy:
\begin{gathered}
Q=\pi\cdot5\cdot10^{-4}\cdot\frac{(7{,}0^2-2{,}5^2)}{\ln}\cdot(\frac{153{,}07+29{,}44)}{29{,}44})=0{,}0368\space\text{m}^3\cdot\text{s}^{-1}=37\space\text{l}\cdot\text{s}^{-1}
\end{gathered}5. návrh studní:
- obvod stavební jámy (v ose studní) je:
\begin{gathered}
2\cdot(47{,}4+57{,}4)=209{,}6\space\text{m}
\end{gathered}- volíme 10 studní (rozmístění podle obr. 105)
- každá studna bude čerpat
\begin{gathered}
Q_\text{s}=\frac{37{,}0}{10}=3{,}7\space\text{l}\cdot\text{s}^{-1}
\end{gathered}- kapacita jedné studny
\begin{gathered}
Q_\text{c}=2\text{p}\cdot r_0\cdot h_1\cdot v_\text{p}
\end{gathered}kde je:
r0 … poloměr studny (zárubnice);
h1 … vtoková výška pláště studny:
\begin{gathered}
(h_1=h_0-1{,}5=1{,}0\space\text{m});
\end{gathered}vp … mezní přípustná rychlost proudění, podle Sichardta vp = (k)1/2 / 15 = 0,0015 m·s-1;
\begin{gathered}
v_\text{p}=\frac{(k)^{\frac{1}{2}}}{15}=0{,}0015\space\text{m}\cdot\text{s}^{-1};
\end{gathered}- min. poloměr studny bude tedy
\begin{gathered}
r_0=\frac{Q_\text{s}}{(2_\text{p}\cdot h_1\cdot v_\text{p})}=\frac{0{,}0037}{(2_\text{p}\cdot1{,}0\cdot0{,}0015)}=0{,}392\space\text{m};
\end{gathered}- volíme tedy 10 studní se zárubnicí o průměru 800 mm.
3.3.3 Vakuové odvodnění
Při hloubkovém odvodňování v píscích se s výhodou využívá vakuového odvodňování pomocí tzv. jehlofiltrů, což jsou ocelové perforované trubky průměru do 100 mm opatřené kulovým ventilem a jednoduchou filtrační mřížkou. Ty se obyčejně do základové půdy vplachují proudem vody. Jejich osová vzdálenost bývá kolem 2–3 m. Napojeny jsou na sběrné potrubí, v němž se vytvoří podtlak. Schéma tohoto odvodňování je na obr. 106.
Přítok vody do stavební jámy při tomto způsobu odvodnění lze spočítat pomocí vzorce:
\begin{gathered}
Q=\pi\cdot k\cdot\frac{(H^2+2\cdot m\cdot h_0-3\cdot h_0^2)}{\ln(\frac{(R+r_\text{s})}{r_\text{s}})}
\end{gathered}(122)
\begin{gathered}
m=\frac{(p_0-p)}{\gamma_\text{w}}
\end{gathered}(123)
kde je:
p0 … vnější atmosférický tlak;
p … podtlak vyvozený vakuem v čerpací jehle (sběrném potrubí).
Obr. 106 Vakuové odvodnění pomocí čerpacích jehel: 1 – čerpací jehla, 2 – koncovka čerpací jehly, 3 – sběrné potrubí
4 MONITORING PAŽÍCÍCH KONSTRUKCÍ
Monitoring, neboli sledování chování a odezvy pažicích konstrukcí je nedílnou součástí projektu na všech významnějších stavbách. Jde o soubor činností, tedy zejména měření a vyhodnocování výsledků měření za účelem:
- ověření platnosti předpokladů, nebo i výsledků statických výpočtů navržených pažicích konstrukcí;
- ověření předpokládaného chování konstrukce z dlouhodobého hlediska, tj. po skončení její výstavby a event. po celou dobu její životnosti.
Monitoring geotechnických konstrukcí a speciálně pak konstrukcí pažicích je zejména v případě složitých geotechnických poměrů a náročných staveb v podstatě jedinou možností, jak a zejména kdy, (tj. včas) získat o chování konstrukce věrohodné údaje. Je tedy významným pilířem observační metody, která je jednou z metod doporučených Eurokódem 7, (ČSN EN 1997-1) pro návrh a posuzování geotechnických konstrukcí. Monitoring různých pažicích a opěrných konstrukcí se liší v detailech, nicméně sestává vždy z následujících kroků a opatření:
- návrh, (projekt) monitoringu, který se zpracuje ve stádiu realizační projektové dokumentace, a to jednak na základě zkušeností, jednak podle výsledků statického výpočtu podporovaného znalostí geotechnických poměrů na staveništi, podmínkami vlastního staveniště a požadavky na chování navrhované konstrukce;
- realizace přípravných opatření pro monitoring, jež sestává v osazení geodetických bodů, osazení a stabilizování bodů pro měření deformetry a extenzometry, osazení inklinometrických pažnic do prvků a konstrukcí speciálního zakládání staveb, osazení dynamometrů pro měření změny sil v kotvách a rozpěrách, tenzometrů pro zjišťování změn napětí v jednotlivých prvcích a event. i piezometrů pro zjišťování změn pórových tlaků v základové půdě; v případě stavebních jam se obvykle počítá s osazováním dalších geodetických bodů v průběhu hloubení stavební jámy;
- vlastní měření na jednotlivých zařízeních v čase podle předem stanoveného plánu s možností jeho operativní změny podle naměřených skutečností, (např. ve vztahu k varovným stavům);
- okamžité vyhodnocení jednotlivých záznamů a vhodné znázornění a archivování výsledků;
- doporučení pro další postup prací.
Návrh monitoringu vypracuje projektant – geotechnik, a to zejména na základě výsledků svého posouzení pažicích konstrukcí. Ten by měl vycházet z analýzy konstrukce, tj. ze statického výpočtu, matematického modelování, popř. i z experimentů a na jejich základě určit místa pro monitoring a jeho druh tak, aby výsledky byly nejen věrohodné, ale i dostatečně ilustrativní a vypovídající. V současné době, kdy je k dispozici rozsáhlá škála měřických a zkušebních metod, není velkým problémem shromáždit ohromné množství údajů, nicméně jejich interpretace je potom obtížná, časově náročná, a tudíž často kontraproduktivní. Nelze sice předložit jednoznačný recept na rozsah monitoringu, neboť ten závisí především na zkušenostech navrhovatele, lze však uvést určité zásady:
- nejdůležitější je prosté geodetické sledování vybraných (a významných) bodů dostatečně stabilizovaných na pažicí konstrukci; body by měly být měřeny totální stanicí s dostatečnou přesností, která je řádově v mm (např. ± 1–2 mm);
- inklinometrická měření ve svislých prvcích pažení, tj. umístěná na záporách, v pilotách pilotové stěny, popř. podzemní stěny jsou velice užitečná ovšem pouze tehdy, jsou-li navázána na geodetická měření; inklinometry nemá smysl přikládat k mikrozáporám, a to z titulu malé ohybové tuhosti této konstrukce, jež se potom může projevit chybami ve výsledcích měření, rovněž tak osazení inklinometrů do pažicích stěn z tryskové injektáže, popř. stěn z prvků „mixed in place“ nemá praktický význam;
- tenzometrická měření napětí v prvcích jsou s ohledem na jejich „přesnost“ přijatelná pouze pro měření významných změn normálných napětí, tudíž v podstatě pro prvky namáhané tlakem, což vesměs není případ pažicích konstrukcí, a tedy možnost tenzometrického měření změny průběhu napětí v průřezu, (např. při ohybovém namáhání) není reálná;
- rovněž tak umisťování tlakoměrných podušek v základových prvcích, nebo dokonce mimo pažicí konstrukci v základové půdě za účelem měření změn napětí je bezpředmětné, neboť je zatíženo výraznými chybami, které nelze odhadnout ani ovlivnit;
- dynamometrická měření změn tlakových či tahových sil, (v kotvách, popř. rozpěrách) jsou reálná a mají své významné místo v monitoringu pažicích konstrukcí; jsou v podstatě jedinou možností, jak tyto síly sledovat;
- měření změn pórových tlaků pomocí piezometrů je možné, nicméně však pro praktické výsledky málo vhodné, a proto se v případě pažicích konstrukcí nepoužívá;
- samostatnou kapitolou jsou geofyzikální metody; snad žádná jiná oblast geotechnického průzkumu nedisponuje takovou škálou různých měření, jako je užitá geofyzika a současně v žádné jiné oblasti geotechniky více neplatí tak komplikovaný vztah mezi naměřenými hodnotami a jejich interpretací; lze tedy konstatovat, že naprostá většina geofyzikálních metod nenalézá uplatnění v monitoringu pažicích konstrukcí snad s jednou výjimkou, kterou tvoří georadar.
Body pro geodetické, (dnes již vesměs 3D) sledování je třeba volit vhodně tam, kde jednak mají nejlepší vypovídací schopnost a kde nebudou v průběhu výstavby zničeny ne snad nepozorností, (k tomu může dojít vždy), ale v důsledku jistých stavebních postupů, kdy dojde např. k odstranění, nebo zakrytí některých prvků, či k odtěžení základové půdy a současně, kde příslušná měření budou dostatečně spolehlivá. Je vždy vhodné spolupracovat se zkušeným geodetem. Není např. zcela ideální osadit měřické body do hlav zápor, popř. pilot nebo podzemních stěn, lépe je stabilizovat je poněkud níže, kde jsou lépe chráněny. Velmi vhodné je osazovat měřické body do převázek, zejména železobetonových. V případě dočasných ocelových převázek je třeba vždy uvážit druh a funkci spoje mezi svislým prvkem a převázkou. Měřické body je třeba navrhovat do vhodných systémů a ne nahodile. Tak např. je správné stanovit určité řezy pažicí konstrukcí a ty plně, (po výšce) instrumentovat, nikoliv osadit velké množství bodů nahodile po ploše pažení. Výsledkem je potom všeobecný zmatek a nikoliv tendence, která je mnohdy důležitější než rozsáhlý soubor osamělých měření, který lze jen těžko zpracovat, uvážíme-li rovněž „nepřesnosti“ z titulu měření, změn teplot apod.
Velice významná je stabilizace totální stanice a základní měření. Příkladem může být výstavba jedné stavební jámy v Praze, kde monitoring vykazoval značné deformace pažicích konstrukcí ovšem bez jakékoliv tendence a logiky – pažení se deformovalo jak směrem do jámy, tak i směrem do základové půdy. Po kontrole bylo zjištěno, že základní měření bylo vztaženo k dosti vzdálené věži kostela, která ve větru vykazovala takové výchylky, že bylo obtížné je vůbec sledovat. Výsledky takového měření jsou ovšem zcela bezcenné.
Krajně důležitá je stabilizace výchozích měřických bodů a to dlouhodobá, neboť nedostatečnou stabilizací lze znehodnotit všechna měření. Příkladem může být monitoring chování rozsáhlé zárubní zdi ve formě kotvené pilotové stěny na D8 budované v oblasti výsypky s volnou výškou dosahující až 17,0 m, kdy se na monitoring deformací velmi spoléhalo. V průběhu výstavby však došlo k poškození výchozích měřických bodů a veškeré deformace svislých prvků musely být sledovány pouze pomocí inklinometrů. Ty však nebyly navázány na měření geodetická a výsledky byly málo spolehlivé.
Příklad úspěšného inklinometrického měření vodorovných deformací pilotové stěny zajišťující cca 30 m vysoký portál tunelu je na obr. 107.
Obr. 107 Inklinometrická měření při výstavbě tunelu Komořany na raženém portálu
V průběhu výstavby pažicí konstrukce a v době její funkce je třeba kontrolovat velikosti předpínacích sil v kotvách. To je důležité zejména z hlediska ubezpečení o případné rezervě kotevních sil, resp. o nutnosti změnit systém kotvení v průběhu výstavby, nebo životnosti konstrukce. V současné době se používá prakticky pouze dynamometrů s odporovými tenzometry, kterými se měří změna elektrického odporu proudu procházejícího tenzometry. Ten se mění v závislosti na deformaci tenzometru. Uvedený vztah je kalibrován a přepočtem lze získat změnu mechanického napětí a z ní pak přes plochu změnu kotevní síly. Původní mechanické dynamometry, (vyráběné vesměs z dělových hlavní) se dnes již nepoužívají. Vhodné jsou rovněž strunové dynamometry, pracující na podobném principu jako tenzometry přehradní, tj. měří se změna kmitočtu rozkmitané struny. Kmitočet je závislý na délce struny a odtud lze, (z Hookova zákova) získat z poměrné deformace velikost napětí, a tudíž i kotevní síly. Oba typy tenzometrů jsou relativně vysoce citlivé a reagují okamžitě. Nicméně je třeba reálně posoudit skutečné změny kotevních sil v čase, a hlavně pak tendenci těchto změn. Je třeba uvědomit si, že změny řádu desítek kN většinou neznamenají vůbec nic a jde o nepřesnost měření, popř. i vliv teploty, (oslunění a pod). Tak jako u všech těchto polních měření není problém něco naměřit, problém je správná interpretace výsledků. Na obr. 108 je příklad dynamometrického měření sil na kotvách záporové stěny kotvené ve 3 úrovních.
Obr. 108 Příklad monitoringu velikosti kotevních sil v dočasných kotvách záporového pažení kotveného ve 3 úrovních
5 OPĚRNÉ ZDI
5.1 DRUHY OPĚRNÝCH ZDÍ
Podle kap. 9 – Opěrné konstrukce evropské normy ČSN EN 1997-1 se z hlediska návrhu opěrných konstrukcí rozlišují následující 3 typy:
- a) gravitační zdi, jež bývají kamenné, z prostého nebo vyztuženého betonu, přičemž sama tíha zdi, event. vč. stabilizující tíhy spolupůsobící zeminy hrají významnou roli v podpírání zadržovaného materiálu; příkladem jsou gravitační zdi konstantní nebo proměnné tloušťky plošně založené, úhlové železobetonové zdi atd.;
- b) vetknuté stěny, jež jsou relativně tenké stěny ocelové, železobetonové, složené z oceli a dřeva, (např. záporové stěny), podporované kotvami nebo rozpěrami a/nebo pasivním zemním tlakem, přičemž jejich ohybová únosnost hraje významnou roli při podpoře zadržovaného materiálu na rozdíl od tíhy těchto zdí, jež není významná; příkladem jsou štětové stěny, podzemní a pilotové stěny, záporové pažení atd., tedy konstrukce, o nichž je pojednáno v kapitole 1;
- c) složené opěrné konstrukce, jež se skládají z kombinace obou výše jmenovaných s využitím dalších prvků a konstrukcí speciálního zakládání staveb; těchto konstrukcí je mnoho druhů, za příklad slouží dvojité štětové stěny jímek, zemní konstrukce vyztužené táhly nebo geomřížemi, hřebíkování svahů či jakkoli jinak složené konstrukce.
Uvedené dělení opěrných konstrukcí jeví snahu o komplexnosti, není vyčerpávající, je však dostatečné pro účely jejich návrhu. V běžné praxi se však většinou výše uvedené vetknuté stěny a složené opěrné konstrukce řadí spíše ke konstrukcím pažicím, jež jsou realizovány vesměs metodami speciálního zakládání staveb a za gravitační zdi se podle platné ČSN 73 0037 Zemní tlak na stavební konstrukce považují:
- opěrné zdi, jež jsou stavební konstrukce, které zajišťují stabilitu násypu a jsou obvykle vybudovány v přestihu před sypáním a hutněním zemního tělesa za jejich rubem;
- zárubní zdi, které jsou stavební konstrukcí přistavenou ke svahu horniny/zeminy v přirozeném uložení, jehož stabilitu pak zajišťují.
Zatímco podle tohoto běžně používaného dělení jsou opěrné zdi nejčastěji budovány ve výkopu či v odřezu, který může být dočasně zajištěn jistým druhem pažení a prvky speciálního zakládání staveb se při jejich výstavbě mohou využít buď pro jejich zakládání nebo pro zajištění jejich stability, zárubní zdi bývající často budovány jakožto konstrukce speciálního zakládání staveb. Kromě toho jsou v některých případech uváděny i zdi obkladní,které se svým charakterem blíží zdem zárubním avšak nejsou určeny pro přenášení zemního tlaku, slouží v podstatě pouze k ochraně zemního/horninového masívu před větráním a ostatním poškozením. Je třeba ihned v úvodu poznamenat, že zejména zdi historické byly často budovány jako zdi obkladní a jsou-li dnes posouzeny běžnými statickými metodami, je vesměs konstatováno, že nevyhovují.
S ohledem na tu skutečnost, že problematika vetknutých stěn a zčásti i složených opěrných konstrukcí byla probrána v předchozím textu, budeme se v této kapitole zabývat pouze zdmi gravitačními, plošně založenými, nebo i hlubinně založenými, ačkoliv ty podle poněkud nezvyklého rozdělení z EC 7-1 spadají již do konstrukcí složených.
5.2 NÁVRHOVÁNÍ GRAVITAČNÍCH OPĚRNÝCH ZDÍ, PŘÍKLADY 7,8
Pro návrh a posouzení gravitačních opěrných zdí platí zásady mezních stavů, přičemž se musí uvažovat s následujícími:
- ztrátou celkové stability, (1. mezní stav);
- porušením konstrukčního prvku – stěna, styk mezi jednotlivými prvky, (1. mezní stav);
- kombinací porušení v základové půdě a v konstrukčním prvku, (1. mezní stav);
- porušení únosnosti základové půdy, (1. mezní stav);
- porušení smykem v základové spáře, (1. mezní stav);
- porušení nakloněním zdi, (2. mezní stav);
- porušení vztlakem, (1. mezní stav) a vnitřní erozí;
- pohybem opěrné konstrukce, který může být příčinou kolapsu nebo může ovlivnit efektivní užívání konstrukce, popř. sousedních konstrukcí nebo inž. sítí, (2. mezní stav);
- nepřijatelným průsakem stěnou nebo pod stěnou;
- nepřijatelným transportem částic zeminy skrz stěnu nebo pod stěnou;
- nepřijatelnou změnou režimu podzemní vody.
Zatížení gravitačních opěrných zdí je tvořeno:
- vlastní tíhou konstrukce zdi a zásypových materiálů;
- zemními tlaky stanovenými s ohledem na možný pohyb opěrné zdi;
- přírůstky zemního tlaku od ostatního stálého a užitného zatížení;
- účinky vody a podzemní vody, (změnou mechanických parametrů základové půdy, tlakem hydrostatickým a event. i hydrodynamickým);
- silami vln a ledu, (pokud to přichází v úvahu);
- kolizními silami, (např. od dopravy, silami působícími na zábradlí atd., pokud to přichází v úvahu);
- vlivem teploty.
Ve všech těchto případech je třeba důkladně zvážit, je-li konkrétní účinek zatížením stálým, nebo pohyblivých, a to zejména s ohledem na statické posouzení podle mezního stavu porušení tak, aby mohl být pro příslušný návrhový přístup vybrán správný dílčí koeficient zatížení typu A.
Při volbě velikosti zatížení zemním tlakem se musí zvážit možný relativní pohyb stěny a základové půdy. Pokud tento pohyb nenastane, je třeba počítat se zemním tlakem v klidu, jehož výslednice v případě vodorovného povrchu terénu působí kolmo na svislou stěnu. Pokud terén za rubem stěny stoupá pod úhlem β, má výslednice směr rovnoběžný s povrchem terénu a součinitel zemního tlaku v klidu (viz rov. 14) se změní na:
\begin{gathered}
K_{\text{r},\beta}=K_\text{r}\cdot(1+\sin\beta)
\end{gathered}(124)
V základové půdě za opěrnou konstrukcí se uvažuje se zemním tlakem v klidu, pokud je relativní pohyb konstrukce menší než 5 · 10-4 · H, kde H je výška opěrné konstrukce. Pokud je relativní pohyb omezen a nesplňuje podmínky pro dosažení aktivního zemního tlaku, musí se počítat s mezilehlými hodnotami. Zvláštní pozornost je třeba věnovat velikosti pasivního zemního tlaku, s jehož plnou hodnotou nelze prakticky počítat nikdy.
Při určení velikosti zemních tlaků je třeba vzít v úvahu účinky ev. zhutňování zásypu za rubem konstrukce, resp. naopak při návrhu zhutňování je třeba vyhnout se nadměrným dodatečným zemním tlakům vyvolaným právě tímto zhutňováním.
Při určení velikosti působícího hydrostatického tlaku je třeba vždy zvážit možnou úroveň hladiny podzemní vody za rubem stěny s ohledem na drenážní účinek, a to i v případě zemin se střední nebo i nízkou propustností, (silty i jíly).
Návrh gravitačních opěrných zdí se musí posoudit proti dosažení mezního stavu porušení, (1. mezní stav) a to pro návrhové situace, které tomuto stavu odpovídají za použití návrhových zatížení nebo účinků zatížení a návrhové únosnosti, přičemž rozhodující bývá porušení typu GEO, popř. i STR (obr. 109). Pro zeminy jemnozrnné se musí počítat jak s krátkodobou, tak i dlouhodobou únosností. Opěrné zdi, na které působí rozdílné tlaky vody, (s ohledem na různé úrovně jejich hladin před a za zdí) se musí ověřit na bezpečnost proti porušení v důsledku hydraulického vztlaku (UPL) a event. i sufoze (HYD).
Návrh gravitačních opěrných zdí se musí rovněž ověřit v mezním stavu použitelnosti, přičemž se pro příslušné výpočty, (sedání, deformací) použije charakteristických hodnot zatížení.
Obr. 109 Příklady mezních stavů porušení základů gravitačních opěrných zdí
Příklad 7
Posouzení masivní betonové opěrné zdi podle obr. 110. Zemina tvořící zásyp za rubem má charakteristické velikosti stabilitních parametrů: γ1,k = 18,5 kN·m-3, φ1,k,ef = 25°, c1,k,ef = 5 kPa, zemina tvořící základovou půdu je pevný jíl F6 s parametry: γ2,k = 20,5 kN·m-3, φ2,k,ef = 20°, c2,k,ef = 10 kPa, c2,ku = 45 kPa; s hladinou podzemní vody není počítáno. Terén za rubem stěny je vodorovný a je zatížen rovnoměrným charakteristickým zatížením pk = 5,0 kN/m2.
Řešení:
Bude posouzen mezní stav porušení podle NP1 (tj. NP1a, 1b) a podle NP2 pro porušení typu GEO. Při výpočtu působících sil bude postupováno podle ČSN 73 0037 Zemní tlak na stavební konstrukce a to pro případ masivní opěrné zdi, kdy je umožněna její malá deformace a její hlavní zatížení bude tzv. zvýšeným aktivním zemním tlakem podle vztahu Sa,zv = 0,5 · Sr + 0,5 · Sa.
1. NP1a: A1„+“M1„+“R1
a) tíhy zdi, (prostý beton γb, k = 23,0 kN/m3)
\begin{gathered}
G_\text{1,k}=1{,}8\cdot0{,}8\cdot23{,}0=33{,}12\space\text{kN/m}&&G_\text{1,d}=1{,}35\cdot33{,}12=44{,}71\space\text{kN/m}\\\\
G_\text{2,k}=\frac{(0{,}8+0{,}5)}{2}\cdot2{,}7\cdot23{,}0=40{,}37\space\text{kN/m}&&G_\text{2,d}=1{,}35\cdot40{,}37=54{,}49\space\text{kN/m}
\end{gathered}Obr. 110 Masivní betonová opěrná zeď – zadání k příkladu 7
b) zemní tlak
- náhradní úhel vnitřního tření (podle postupu z obr. 45):
\begin{gathered}
\sigma_\text{n}=18{,}5\cdot\frac{3{,}50}{3}=21{,}58\space\text{kPa},&\tau_\text{n}=5{,}0+21{,}58\cdot\tg25=15{,}06\space\text{kPa};\\\\
\tg\varphi_\text{n}=\frac{15{,}06}{21{,}58}=0{,}698\space....\space\varphi_\text{n}=35\degree,&\delta=\frac{\varphi_\text{n}}{2}=17{,}5\degree
\end{gathered}- součinitel
\begin{gathered}
K_\text{r}=1-\sin\varphi_\text{n}=0{,}426
\end{gathered}- součinitel
\begin{gathered}
K_\text{a}=\tg^2(45-\frac{\varphi_\text{n}}{2})=0{,}271
\end{gathered}- součinitel
\begin{gathered}
K_\text{a,zv}=0{,}5\cdot0{,}426+0{,}5\cdot0{,}271=0{,}348
\end{gathered}- zemní tlak od rovnoměrného zatížení p:
\begin{gathered}
S_\text{0,k}=p_\text{k}\cdot K_\text{a, zv}\cdot3{,}50=6{,}09\space\text{kN/m}&&S_\text{0,d}=1{,}5\cdot6{,}09=9{,}14\space\text{kN/m}\\\\
S_\text{0,kh}=S_\text{0,k}\cdot\cos\delta=5{,}81\space\text{kN/m}&&S_\text{0,kh}=1{,}5\cdot5{,}81=8{,}71\space\text{kN/m}\\\\
S_\text{0,kv}=S_\text{0,k}\cdot\sin\delta=1{,}83\space\text{kN/m}&&S_\text{0,kv}=1{,}5\cdot1{,}83=2{,}75\space\text{kN/m}
\end{gathered}- zemní tlak od zeminy za rubem:
\begin{gathered}
S_\text{1,k}=0{,}5\cdot18{,}5\cdot3{,}5^2\cdot K_\text{a,zv}=39{,}43\space\text{kN/m}&&S_\text{1,d}=1{,}35\cdot39{,}43=53{,}23\space\text{kN/m}\\\\
S_\text{1,kh}=S_\text{1,k}\cdot\cos\delta=37{,}61\space\text{kN/m}&&S_\text{0,kh}=1{,}35\cdot37{,}61=50{,}77\space\text{kN/m}\\\\
S_\text{1,kv}=S_\text{1,k}\cdot\sin\delta=11{,}86\space\text{kN/m}&&S_\text{0,kv}=1{,}35\cdot11{,}86=16{,}00\space\text{kN/m}
\end{gathered}c) návrhové velikosti zatěžovacích sil v těžišti základové spáry T:
- svislá síla:
\begin{gathered}
N_\text{d}=40{,}37+54{,}49+2{,}75+16{,}00=113{,}61\space\text{kN/m}
\end{gathered}- vodorovná síla:
\begin{gathered}
H_\text{d}=8{,}71+50{,}77=59{,}48\space\text{kN/m}
\end{gathered}- moment:
\begin{gathered}
M_\text{d}=-54{,}49\cdot(0{,}90-0{,}33)+8{,}71\cdot\frac{3{,}5}{2}+50{,}77\cdot\frac{3{,}5}{3}-(2{,}75+16{,}00)\cdot0{,}9=26{,}54\space\text{kNm/m}
\end{gathered}d) excentricita síly v základové spáře, napětí v základové spáře:
- excentricita
\begin{gathered}
e=\frac{26{,}54}{113{,}61}=0{,}233\space\text{m}\lt\frac{1{,}80}{3}=01{,}60\space\text{m}\implies\text{vyhovuje}
\end{gathered}- napětí v základové spáře
\begin{gathered}
\sigma_\text{d}=\frac{113{,}61}{(1{,}0\cdot(1{,}80-2\cdot0{,}233))}=85{,}16\space\text{kPa}
\end{gathered}e) krátkodobá návrhová únosnost základové spáry, (jemnozrnné zeminy – neodvodněné podmínky):
- hloubka založení D = 1,0 m, efektivní tlak nadloží
\begin{gathered}
q´=18{,}5\cdot1{,}0=18{,}5\space\text{kPa};&c_\text{u}=45\space\text{kPa}
\end{gathered}- součinitel tvaru základu:
\begin{gathered}
s_\text{c}=1+0{,}2\cdot(\frac{B_\text{ef}}{L})=1+0{,}2\cdot(\frac{1{,}334}{10{,}0})=1{,}03,
\end{gathered}(předpokládáme dilatační úseky v délce L = 10,0 m)
- součinitel šikmosti:
\begin{gathered}
i_\text{c}=0{,}5\cdot(1+(1-\frac{H_\text{d}}{(A_\text{ef}\cdot c_\text{u})})^\frac{1}{2})=0{,}55
\end{gathered}\begin{gathered}
R_\text{d}=(\pi+2)\cdot c_\text{u}\cdot s_\text{c}\cdot i_\text{c}+q=149{,}53\space\text{kPa};
\end{gathered}součinitel typu R1 pro únosnost γR, v = 1,0
\begin{gathered}
R_\text{d}=\frac{149{,}53}{1{,}0}=149{,}53\space\text{kPa}\gt85{,}16\space\text{kPa}\implies\text{vyhovuje}
\end{gathered}- vodorovná návrhová únosnost v základové spáře:
\begin{gathered}
R_\text{h,d}=1{,}334\cdot45=60{,}03\space\text{kN/m};
\end{gathered}součinitel pro R1 γR,h = 1,0
\begin{gathered}
R_\text{h,d}=\frac{60{,}03}{1{,}0}=60{,}03\space\text{kN/m}\gt59{,}48\implies\text{vyhovuje}
\end{gathered}f) dlouhodobá návrhová únosnost základové spáry (pro odvodněné podmínky):
- součinitelé únosnosti:
\begin{gathered}
N_\text{q}=e^{1{,}143}\cdot\tg^2(45+\frac{20}{2})=6{,}37;\\\\
N_\text{c}=5{,}37\cdot\cotg20=14{,}75;\\\\
N_\gamma=25{,}37\cdot\tg20=3{,}91
\end{gathered}- součinitelé tvaru základu:
\begin{gathered}
s_\text{q}=1+\frac{1{,}334}{10}\cdot\sin20=1{,}05;\\\\
s_\gamma=1-0{,}3\cdot\frac{1{,}334}{10}=0{,}96;\\\\
s_\text{c}=\frac{(1{,}05\cdot6{,}37-1)}{(6{,}37-1)}=1{,}06
\end{gathered}- součinitelé šikmosti zatížení:
\begin{gathered}
m_\text{B}=\frac{(2+\frac{1{,}334}{10})}{(1+\frac{1{,}334}{10})}=1{,}882\\\\
i_\text{q}=(1-\frac{59{,}48}{(113{,}61+1{,}334\cdot10{,}0\cdot\cotg20)})^{1{,}882}=0{,}39\\\\
i_\gamma=(1-\frac{59{,}48}{(113{,}61+1{,}334\cdot10{,}0\cdot\cotg20)})^{2{,}882}=0{,}23\\\\
i_\text{c}=0{,}39-\frac{(1-0{,}39)}{(14{,}75\cdot\tg20)}=0{,}28\\\\
R_\text{d}=10{,}0\cdot14{,}75\cdot1{,}06\cdot0{,}28+18{,}5\cdot6{,}37\cdot1{,}05\cdot0{,}39+0{,}5\cdot20{,}5\cdot\frac{1{,}334}{2}\cdot0{,}96\cdot0{,}23=43{,}75+48{,}26+1{,}51=93{,}53\space\text{kPa}\gt85{,}16\space\text{kPa}\implies\text{vyhovuje}\\\\
R_\text{h, d}=1\space113{,}61\cdot\tg20+1{,}334\cdot10=54{,}69\space\text{kN}\lt59{,}48\space\text{kN}\implies\text{mírně nevyhovuje}
\end{gathered}(je třeba buď základovou spáru zvětšit, např. na B = 2,0 m, nebo provést úpravu v základové spáře – např. ozubem).
2. NP1b: A2„+“M2„+“R1
a) tíhy zdi, (prostý beton γb, k = 23,0 kN/m3)
\begin{gathered}
G_\text{1, k}=1{,}8\cdot0{,}8\cdot23{,}0=33{,}12\space\text{kN/m}&G_\text{1, d}=1{,}0\cdot33{,}12=33{,}12\space\text{kN/m}\\\\
G_\text{2, k}=\frac{(0{,}8+0{,}5)}{2}\cdot2{,}7\cdot23{,}0=40{,}37\space\text{kN/m}&G_\text{2, d}=1{,}0\cdot40{,}37=40{,}37\space\text{kN/m}
\end{gathered}b) zemní tlak
- náhradní úhel vnitřního tření
\begin{gathered}
\varphi_\text{n,k}=35\degree,(\frac{\tg35}{1{,}25})=0{,}560\space...\space\varphi_\text{n,d}=29{,}2\degree,\space delta=14{,}6\degree
\end{gathered}- součinitel
\begin{gathered}
K_\text{r}=1-\sin\varphi_\text{n}=0{,}512
\end{gathered}- součinitel
\begin{gathered}
K_\text{a}=\tg^2(45-\frac{\varphi_\text{n}}{2})=0{,}344
\end{gathered}- součinitel
\begin{gathered}
K_\text{a,zv}=0{,}5\cdot0{,}512+0{,}5\cdot0{,}344=0{,}428
\end{gathered}- zemní tlak od rovnoměrného zatížení p:
\begin{gathered}
S_\text{0,k}=p_\text{k}\cdot K_\text{a,zv}\cdot3{,}50=7{,}49\space\text{kN/m}&&S_\text{0,d}=1{,}3\cdot7{,}49=9{,}74\space\text{kN/m}\\\\
S_\text{0,kh}=S_\text{0,k}\cdot\cos\delta=7{,}25\space\text{kN/m}&&S_\text{0,kh}=1{,}3\cdot7{,}25=9{,}42\space\text{kN/m}\\\\
S_\text{0,kv}=S_\text{0,k}\cdot\sin\delta=1{,}89\space\text{kN/m}&&S_\text{0,kv}=1{,}3\cdot1{,}89=2{,}46\space\text{kN/m}
\end{gathered}- zemní tlak od zeminy za rubem:
\begin{gathered}
S_\text{1,k}=0{,}5\cdot18{,}5\cdot3{,}5^2\cdot K_\text{a,zv}=48{,}49\space\text{kN/m}&&S_\text{1,d}=48{,}49\space\text{kN/m}\\\\
S_\text{1,kh}=S_\text{1,k}\cdot\cos\delta=46{,}93\space\text{kN/m}&&S_\text{0,kh}=46{,}93\space\text{kN/m}\\\\
S_\text{1,kv}=S_\text{1,k}\cdot\sin\delta=12{,}22\space\text{kN/m}&&S_\text{0,kv}=12{,}22\space\text{kN/m}
\end{gathered}c) návrhové velikosti zatěžovacích sil v těžišti základové spáry T:
- svislá síla:
\begin{gathered}
N_\text{d}=33{,}12+40{,}37+2{,}46+12{,}22=88{,}17\space\text{kN/m}
\end{gathered}- vodorovná síla:
\begin{gathered}
H_\text{d}=9{,}42+46{,}93=56{,}35\space\text{kN/m}
\end{gathered}- moment:
\begin{gathered}
M_\text{d}=-40{,}37\cdot(0{,}90-0{,}33)+9{,}42\cdot\frac{3{,}5}{2}+46{,}93\cdot\frac{3{,}35}{3}-(2{,}46+12{,}22)\cdot0{,}9=35{,}01\space\text{kNm/m}
\end{gathered}d) excentricita síly v zákl. spáře, napětí v základové spáře:
- excentricita
\begin{gathered}
e=\frac{35{,}01}{88{,}17}=0{,}397\space\text{m}\lt\frac{1{,}80}{3}=0{,}60\space\text{m}\implies\text{vyhovuje}
\end{gathered}- napětí v základové spáře
\begin{gathered}
\sigma_\text{d}=\frac{88{,}17}{(1{,}0\cdot(1{,}80-2\cdot0{,}397))}=88{,}17\space\text{kPa}
\end{gathered}e) krátkodobá návrhová únosnost základové spáry, (jemnozrnné zeminy – neodvodněné podmínky):
- hloubka založení D = 1,0 m, efektivní tlak nadloží
\begin{gathered}
q´=18{,}5\cdot1{,}0=18{,}5\space\text{kPa};\\\\
c_\text{u,d}=\frac{45{,}0}{1{,}4}=32{,}14\space\text{kPa},
\end{gathered}(koeficient pro M2 a cu …. γcu = 1,4),
- součinitel tvaru základu:
\begin{gathered}
s_\text{c}=1+0{,}2\cdot(\frac{B_\text{ef}}{L})=1+0{,}2\cdot(\frac{1{,}0}{10{,}0})=1{,}02
\end{gathered}- součinitel šikmosti:
\begin{gathered}
i_\text{c}=0{,}5\cdot(1+(1-\frac{H_\text{d}}{(A_\text{ef}\cdot c_\text{u})})^{\frac{1}{2}})\implies\text{nevyhovuje, neboť}\space A_\text{ef}\cdot c_\text{u,d}\lt H_\text{d},\space\text{volíme}\space i_\text{c}=0{,}50
\end{gathered}\begin{gathered}
R_\text{d}=(\pi+2)\cdot c_\text{u,d}\cdot s_\text{c}\cdot i_\text{b}+q=149{,}53\space\text{kPa};
\end{gathered}součinitel typu R1 pro únosnost γR,v = 1,0
\begin{gathered}
R_\text{d}=\frac{149{,}53}{1{,}0}=102{,}75\space\text{kPa}\gt88{,}17\space\text{kPa}\implies\text{vyhovuje}
\end{gathered}- vodorovná návrhová únosnost v základové spáře:
\begin{gathered}
R_\text{h,d}=1{,}00\cdot32{,}14=32{,}14\space\text{kN/m},
\end{gathered}součinitel pro R1 γR,h = 1,0
\begin{gathered}
R_\text{h,d}=\frac{32{,}14}{1{,}0}=32{,}14\space\text{kN/m}\lt56{,}35\space\text{kN/m}\implies\text{nevyhovuje}
\end{gathered}f) dlouhodobá návrhová únosnost základové spáry (pro odvodněné podmínky):
\begin{gathered}
\frac{(\tg20)}{1{,}25}=0{,}291\space....\space\varphi_\text{ef}=16{,}22\degree,&c_\text{ef}=\frac{10{,}0}{1{,}25}=8{,}0\space\text{kPa}
\end{gathered}- součinitelé únosnosti:
\begin{gathered}
N_\text{q}=e^{0{,}913}\cdot\tg^2(45+\frac{16{,}22}{2})=4{,}45;\\\\
N_\text{c}=3{,}45\cdot\cotg16{,}22=11{,}86;\\\\
N_\gamma=2\cdot3{,}45\cdot\tg16{,}22=2{,}00
\end{gathered}- součinitelé tvaru základu:
\begin{gathered}
s_\text{q}=1+\frac{1{,}0}{10}\cdot\sin16{,}22=1{,}03;\\\\
s_\gamma=1-0{,}3\cdot\frac{1{,}0}{10}=0{,}97;\\\\
s_\text{c}=\frac{(1{,}03\cdot4{,}45-1)}{(4{,}45-1)}=1{,}04
\end{gathered}- součinitelé šikmosti zatížení:
\begin{gathered}
m_\text{B}=\frac{(2+\frac{1{,}0}{10})}{(1+\frac{1{,}0}{10})}=1{,}909\\\\
i_\text{q}=(1-\frac{56{,}35}{(88{,}17+1{,}00\cdot8{,}0\cdot\cotg16{,}22)})^{1{,}909}=0{,}28\\\\
i_\gamma=(1-\frac{56{,}35}{(88{,}17+1{,}00\cdot8{,}0\cdot\cotg16{,}22)})^{2{,}909}=0{,}14\\\\
i_\text{c}=0{,}28-\frac{(1-0{,}285)}{(11{,}86\cdot\tg16{,}22)}=0{,}07\\\\
R_\text{d}=8{,}0\cdot11{,}86\cdot1{,}04\cdot0{,}07+18{,}5\cdot4{,}45\cdot1{,}03\cdot0{,}28+0{,}5\cdot20{,}5\cdot\frac{1{,}00}{2}\cdot0{,}97\cdot0{,}14=6{,}91+23{,}74+0{,}70=31{,}35\space\text{kPa}\lt88{,}17\space\text{kPa}\implies\text{nevyhovuje}\\\\
R_\text{h, d}=88{,}17\cdot\tg16{,}22+1{,}00\cdot8{,}0=33{,}65\space\text{kN}\lt56{,}35\space\text{kN}\implies\text{nevyhovuje}
\end{gathered}(je třeba základovou spáru zvětšit, volíme na B = 2,0 m)
3. NP2: A1“+“M1“+“R2
Volíme základový pas o šířce B = 2,00 m
a) tíhy zdi, (prostý beton γb,k = 23,0 kN/m3)
\begin{gathered}
G_\text{1,k}=2{,}0\cdot0{,}8\cdot23{,}0=36{,}80\space\text{kN/m}&&G_\text{1,d}=1{,}35\cdot36{,}80=49{,}68\space\text{kN/m}\\\\
G_\text{2,k}=\frac{(0{,}8+0{,}5)}{2}\cdot2{,}7\cdot23{,}0=40{,}37\space\text{kN/m}&&G_\text{2,d}=1{,}35\cdot40{,}37=54{,}49\space\text{kN/m}
\end{gathered}b) zemní tlak
- náhradní úhel vnitřního tření
\begin{gathered}
\varphi_\text{n}=35\degree,\space\delta=\frac{\varphi_\text{n}}{2}=17{,}5\degree,\space c_\text{ef}=0
\end{gathered}- součinitel
\begin{gathered}
K_\text{r}=1-\sin\varphi_\text{n}=0{,}426
\end{gathered}- součinitel
\begin{gathered}
K_\text{a}=\tg^2(45-\frac{\varphi_\text{n}}{2})=0{,}271
\end{gathered}- součinitel
\begin{gathered}
K_\text{a,zv}=0{,}5\cdot0{,}426+0{,}5\cdot0{,}271=0{,}348
\end{gathered}- zemní tlak od rovnoměrného zatížení p:
\begin{gathered}
S_\text{0,k}=p_\text{k}\cdot K_\text{a,zv}\cdot3{,}50=6{,}09\space\text{kN/m}&&S_\text{0,d}=1{,}5\cdot6{,}09=9{,}14\space\text{kN/m}\\\\
S_\text{0,kh}=S_\text{0,k}\cdot\cos\delta=5{,}81\space\text{kN/m}&&S_\text{0,kh}=1{,}5\cdot5{,}81=8{,}71\space\text{kN/m}\\\\
S_\text{0,kv}=S_\text{0,k}\cdot\sin\delta=1{,}83\space\text{kN/m}&&S_\text{0,kv}=1{,}5\cdot1{,}83=2{,}75\space\text{kN/m}
\end{gathered}- zemní tlak od zeminy za rubem:
\begin{gathered}
S_\text{1,k}=0{,}5\cdot18{,}5\cdot3{,}5^2\cdot K_\text{a,zv}=39{,}43\space\text{kN/m}&&S_\text{0,d}=1{,}5\cdot6{,}09=9{,}14\space\text{kN/m}\\\\
S_\text{1,kh}=S_\text{1,k}\cdot\cos\delta=37{,}61\space\text{kN/m}&&S_\text{0,kh}=1{,}35\cdot37{,}61=50{,}77\space\text{kN/m}\\\\
S_\text{1,kv}=S_\text{1,k}\cdot\sin\delta=11{,}86\space\text{kN/m}&&S_\text{0,kv}=1{,}35\cdot11{,}86=16{,}00\space\text{kN/m}
\end{gathered}c) návrhové velikosti zatěžovacích sil v těžišti základové spáry T:
- svislá síla:
\begin{gathered}
N_\text{d}=49{,}68+54{,}49+2{,}75+16{,}00=122{,}92\space\text{kN/m}
\end{gathered}- vodorovná síla:
\begin{gathered}
H_\text{d}=8{,}71+50{,}77=59{,}48\space\text{kN/m}
\end{gathered}- moment:
\begin{gathered}
M_\text{d}=-54{,}49\cdot(1{,}00-0{,}33)+8{,}71\cdot\frac{3{,}5}{2}+50{,}77\cdot\frac{3{,}5}{3}-(2{,}75+16{,}00)\cdot1{,}0=19{,}38\space\text{kNm/m}
\end{gathered}d) excentricita síly v základové spáře, napětí v základové spáře:
- excentricita
\begin{gathered}
e=\frac{19{,}38}{122{,}92}=0{,}158\space\text{m}\lt\frac{2{,}00}{3}=0{,}67\space\text{m}\implies\text{vyhovuje}
\end{gathered}- napětí v základové spáře
\begin{gathered}
\sigma_\text{d}=\frac{122{,}92}{(1{,}0\cdot(2{,}00-2\cdot0{,}158))}=72{,}99\space\text{kPa}
\end{gathered}e) krátkodobá návrhová únosnost základové spáry, (jemnozrnné zeminy – neodvodněné podmínky):
- hloubka založení D = 1,0 m, efektivní tlak nadloží
\begin{gathered}
q´=18{,}5\cdot1{,}0=18{,}5\space\text{kPa};\\\\
c_\text{u}=45\space\text{kPa}
\end{gathered}- součinitel tvaru základu:
\begin{gathered}
s_\text{c}=1+0{,}2\cdot(\frac{B_\text{ef}}{L})=1+0{,}2\cdot(\frac{1{,}68}{10{,}0})=1{,}03
\end{gathered}- součinitel šikmosti:
\begin{gathered}
i_\text{c}=0{,}5\cdot(1+(1-\frac{H_\text{d}}{(A_\text{ef}\cdot c_\text{u})^{\frac{1}{2}}})=1{,}16
\end{gathered}\begin{gathered}
R_\text{d}=(\pi+2)\cdot c_\text{u}\cdot s_\text{c}\cdot i_\text{c}+q=294{,}85\space\text{kPa}
\end{gathered}součinitel typu R1 pro únosnost γR,v = 1,4
\begin{gathered}
R_\text{d}=\frac{294{,}85}{1{,}4}=210{,}60\space\text{kPa}\gt72{,}99\space\text{kPa}\implies\text{vyhovuje}
\end{gathered}- vodorovná návrhová únosnost v základové spáře:
\begin{gathered}
R_\text{h,d}=1{,}68\cdot45=75{,}60\space\text{kN/m}
\end{gathered}součinitel typu pro R1 γR,h = 1,1
\begin{gathered}
R_\text{h,d}=\frac{75{,}60}{1{,}1}=68{,}72\space\text{kN/m}\gt59{,}48\space\text{kN/m}\implies\text{vyhovuje}
\end{gathered}f) dlouhodobá návrhová únosnost základové spáry (pro odvodněné podmínky):
- součinitelé únosnosti:
\begin{gathered}
N_\text{q}=e^{1{,}143}\cdot\tg^2(45+\frac{20}{2})=6{,}37;\\\\
N_\text{c}=5{,}37\cdot\cotg20=14{,}75;\\\\
N_\gamma=2\cdot5{,}37\cdot\tg20=3{,}91
\end{gathered}- součinitelé tvaru základu:
\begin{gathered}
s_\text{q}=1+\frac{1{,}68}{10}\cdot\sin20=1{,}06;\\\\
s_\gamma=1-0{,}3\cdot\frac{1{,}68}{10}=0{,}95;\\\\
s_\text{c}=\frac{(1{,}06\cdot6{,}37-1)}{(6{,}37-1)}=1{,}07
\end{gathered}- součinitelé šikmosti zatížení:
\begin{gathered}
m_\text{B}=\frac{(2+\frac{1{,}68}{10})}{(1+\frac{1{,}68}{10})}=1{,}856\\\\
i_\text{q}=(1-\frac{59{,}48}{(122{,}92+1{,}68\cdot10{,}0\cdot\cotg20)})^{1{,}856}=0{,}44\\\\
i\gamma=(1-\frac{59{,}48}{(122{,}92+1{,}68\cdot10{,}0\cdot\cotg20)})^{2{,}856}=0{,}29\\\\
i_\text{c}=0{,}44-\frac{(1-0{,}44)}{(14{,}75\cdot\tg20)}=0{,}34\\\\
R_\text{d}=10{,}0\cdot14{,}75\cdot1{,}07\cdot0{,}34+18{,}5\cdot6{,}37\cdot1{,}06\cdot0{,}44+0{,}5\cdot20{,}5\cdot3{,}91\cdot1{,}68\cdot0{,}95\cdot0{,}29=53{,}66+54{,}96+18{,}55=127{,}17\space\text{kPa, součinitel pro R2 ... }\gamma_\text{r,v}=1{,}4\\\\
R_\text{d}=\frac{127{,}17}{1{,}4}=90{,}84\space\text{kPa}\gt72{,}99\space\text{kPa}\implies\text{vyhovuje}\\\\
R_\text{h,d}=122{,}92\cdot\tg20+1{,}68\cdot10=61{,}55\space\text{kN, součinitel pro R2 ... }\gamma_\text{R,h}=1{,}1\\\\
R_\text{h,d}=\frac{61{,}55}{1{,}1}=55{,}95\space\text{kN}\lt59{,}48\space\text{kN}\implies\text{mírně nevyhovuje}
\end{gathered}(je vhodné provést úpravu v základové spáře – např. ozubem)
g) kontrola velikosti napětí v průřezu 1-1:
- tíha zdi:
\begin{gathered}
G_\text{2,d}=1{,}35\cdot40{,}37=54{,}49\space\text{kN/m}
\end{gathered}- zemní tlak od pasu:
\begin{gathered}
S_\text{0,d}=5{,}0\cdot1{,}5\cdot2{,}7\cdot0{,}348=7{,}05\space\text{kN/m},\\\\
S_\text{0,dh}=6{,}72\space\text{kN/m},\\\\
S_\text{0,dv}=2{,}12\space\text{kN/m}
\end{gathered}- zemní tlak od zásypu:
\begin{gathered}
S_\text{1,d}=18{,}5\cdot1{,}35\cdot\frac{2{,}7^2}{2}\cdot0{,}348=31{,}68\space\text{kN/m},\\\\
S_\text{1,dh}=30{,}21\space\text{kN/m},\\\\
S_\text{1,dv}=9{,}53\space\text{KNm/m}
\end{gathered}- síly v těžišti průřezu 1-1 (o šířce N = 0,80 m);
\begin{gathered}
N_\text{d}=54{,}49+2{,}12+9{,}53=66{,}14\space\text{kN/m},\\\\
H_\text{d}=6{,}72+30{,}21=36{,}93\space\text{kN/m},\\\\
M_\text{d}=-54{,}49\cdot(0{,}4-0{,}33)+6{,}72\cdot\frac{2{,}7}{2}+30{,}21\cdot\frac{2{,}7}{3}-(2{,}12+9{,}53)\cdot0{,}4=27{,}78\space\text{kNm/m}
\end{gathered}- excentricita v průřezu:
\begin{gathered}
e_1=\frac{27{,}78}{66{,}14}=0{,}42\space\text{m}\gt\frac{0{,}8}{3}=0{,}27\space\text{m}
\end{gathered}průřez z prostého betonu nevyhovuje, je třeba průřez příslušně vyztužit v tažené oblasti.
Příklad 8
Posouzení železobetonové úhlové opěrné zdi podle obr. 111. Zemina tvořící zásyp za rubem má char. velikosti stabilitních parametrů: γ1,k = 17,5 kN·m-3, φ1,k,ef = 28°, c1,k,ef = 0, zemina tvořící základovou půdu je písek S3 s parametry: γ2,k = 19,0 kN·m-3, φ2,k,ef = 30°, c2,k,ef = 0, s hladinou podzemní vody není počítáno. Terén za rubem stěny je ve sklonu β = 20°, za rubem je zatížení kolovým vozidlem o celkové tíze Fk = 800 kN, jež se rozkládá na plochu 3,8 x 6,0 m podle obr. 111.
Obr. 111 Úhlová opěrná železobetonová zeď – zadání k příkladu 8
Řešení
Bude posouzen mezní stav porušení podle NP1 (tj. NP1a, 1b) a podle NP2 pro porušení typu GEO. Při výpočtu působících sil bude postupováno podle ČSN 73 0037 Zemní tlak na stavební konstrukce, a to pro případ úhlové zdi, kdy je umožněna příslušná deformace navržené opěrné zdi pro vznik aktivního zemního tlaku.
1) NP1a: A1“+“M1“+“R1
a) tvar zatěžovacího obrazce:
\begin{gathered}
\sin^2\alpha=\frac{(\sin(\varphi_1-\beta)\cdot\cos(\alpha+\varphi_1))}{(2\tg\varphi_1\cdot\cos(\alpha-\beta)}\space ....\space\alpha=17{,}6\degree\\\\
\theta_\text{as}=90-\alpha=72{,}4\degree\\\\
\theta_a=\alpha+\varphi_1=45{,}6\degree
\end{gathered}b) charakteristické tíhy zdi a zemního klínu (na šířku B = 1,0 m):
\begin{gathered}
G_\text{1,k}=3{,}0\cdot0{,}4\cdot25=30{,}0\space\text{kNP/m}\\\\
G_\text{2,k}=3{,}6\cdot0{,}4\cdot25=36{,}0\space\text{kN/m}\\\\
G_3=17{,}5\cdot(0{,}88\cdot3{,}6+0{,}88\cdot\frac{0{,}32}{2}+1{,}21\cdot\frac{3{,}92}{2})=99{,}41\space\text{kN/m}
\end{gathered}c) aktivní zemní tlak (charakteristické velikosti na šířku B = 1,0 m):
- součinitel
\begin{gathered}
K_a=\cos^2\varphi_1/\cos\delta_1/[1+(\frac{((\sin(\varphi_1+\delta_1)\sin(\varphi_1-\beta))}{(\cos\delta_1\cdot\cos\beta)})^\frac{1}{2}]^2=0{,}461
\end{gathered}(pro horní vrstvu)
\begin{gathered}
S_\text{a1,k}=17{,}5\cdot\frac{4{,}1^2}{2}\cdot0{,}461=67{,}80\text{kN/m};\\\\
S_\text{a1h,k}=S_\text{a1,k}\cdot\cos\theta_\text{a}=47{,}44\space\text{kN/m};\\\\
S_\text{a1v,k}=S_\text{a1,k}\cdot\sin\theta_\text{a}=48{,}44\space\text{kN/m}
\end{gathered}- součinitel
\begin{gathered}
K_\text{a}=\tg^2(45-\frac{\varphi_2}{2})=0{,}333
\end{gathered}pro spodní vrstvu
\begin{gathered}
S_\text{a2,k}=19{,}0\cdot\frac{0{,}4^2}{2}\cdot0{,}333=0{,}51\space\text{kN/m};\\\\
S_\text{a2h,k}=S_\text{a2,k}\cdot\cos\delta_2=0{,}49\space\text{kN/m};\\\\
S_\text{a2v,k}=S_\text{a2,k}\cdot\sin\delta_2=0{,}12\space\text{kN/m}
\end{gathered}d) vnější zatížení F, (charakteristická velikost):
- pomocný úhel:
\begin{gathered}
\cotg\varepsilon=\tg\varphi_1+(\frac{1}{\cos\varphi_1})\cdot(\frac{(\sin(\varphi_1+\delta_1)\cdot\cos\beta)}{(\sin(\varphi_1-\beta)\cdot\cos\delta_1)})^\frac{1}{2}\varepsilon=22{,}3\degree,\\\\
\theta=\varphi+\varepsilon=28+22{,}3=50{,}3\degree
\end{gathered}- pomocné pořadnice od vrcholu zdi:
\begin{gathered}
\tg28\degree=\frac{v_1}{0{,}5},&&v_1=0{,}27,&&a_1=0{,}27-0{,}18=0{,}09\space\text{m}\\\\
\tg50{,}3\degree=\frac{v_2}{4{,}3},&&v_2=5{,}18,&&a_2=5{,}18-1{,}57=3{,}60\space\text{m}\\\\
h_\text{f}=3{,}60-0{,}09=3{,}51\space\text{m}
\end{gathered}- součinitel zemního tlaku
\begin{gathered}
K_\text{af}=\frac{\sin(\theta-\varphi_2)}{\cos(\theta-\varphi_2-\delta_2)}=0{,}38
\end{gathered}- náhradní zatížení
\begin{gathered}
f_a=\frac{800}{(3{,}8\cdot6{,}0)}=35{,}08\space\text{kN/m}^2
\end{gathered}- silový přírůstek:
\begin{gathered}
\Delta S_\text{a}=f_\text{a}\cdot B\cdot K_\text{af}=35{,}08\cdot3{,}8\cdot0{,}38=50{,}66\space\text{kN/m}
\end{gathered}- horní pořadnice:
\begin{gathered}
\Delta\sigma_\text{fs}=\frac{\Delta S_\text{a}}{h_\text{f}}\cdot(1+\frac{a}{(a+b)})=16{,}11\space\text{kN/m}
\end{gathered}- spodní pořadnice:
\begin{gathered}
\Delta\sigma_\text{fi}=\frac{\Delta S_\text{a}}{h_\text{f}}\cdot(1-\frac{a}{(a+b)})=12{,}75\space\text{kN/m}
\end{gathered}e) návrhové velikosti zatěžovacích sil (A1: γG = 1,35 – stálé zatížení, γQ = 1,5 – proměnné zatížení)
- svislé síly:
\begin{gathered}
N_\text{d}=1{,}35\cdot(30{,}0+36{,}0+99{,}41+48{,}44+0{,}13)=288{,}87\space\text{kN/m}
\end{gathered}- vodorovné síly:
\begin{gathered}
H_\text{d}=1{,}35\cdot(47{,}44+0{,}49)+1{,}5\cdot50{,}66=140{,}70\space\text{kN/m}
\end{gathered}- moment ke středu základové spáry:
\begin{gathered}
M_\text{d}=1{,}35\cdot(36{,}0\cdot0{,}9+0{,}88\cdot3{,}6\cdot17{,}5\cdot0{,}26+0{,}88\cdot\frac{0{,}32}{2}\cdot17{,}5\cdot0{,}11-3{,}92\cdot\frac{1{,}21}{2}\cdot17{,}5\cdot0{,}69+47{,}44\cdot1{,}71-48{,}44\cdot1{,}08+0{,}49\cdot0{,}13-0{,}13\cdot1{,}5)+1{,}5\cdot(12{,}75\cdot3{,}51\cdot2{,}15+3{,}36\cdot\frac{3{,}51}{2}\cdot2{,}74)=232{,}18\space\text{kNm/m}
\end{gathered}f) excentricita síly v základové spáře, napětí v základové spáře:
- excentricita
\begin{gathered}
e=\frac{232{,}18}{288{,}87}=0{,}80\space\text{m}\lt\frac{3{,}0}{3}=1{,}0\space\text{m}\implies\text{vyhovuje}
\end{gathered}- napětí v základové spáře
\begin{gathered}
\sigma_\text{d}=\frac{288{,}87}{(1{,}0\cdot(3{,}0-2\cdot0{,}8))}=206{,}33\space\text{kPa}
\end{gathered}g) návrhová únosnost základové spáry (hrubozrnné zeminy – odvodněné podmínky):
- hloubka založení D = 1,0 m, efektivní tlak nadloží
\begin{gathered}
q´=19{,}0\cdot1{,}0=19{,}0\space\text{kPa};&&\varphi=30\degree;&&c=0
\end{gathered}- součinitelé únosnosti:
\begin{gathered}
N_\text{q}=e^{\pi\cdot\tg\varphi}\cdot\tg^2(45+\frac{\varphi}{2})=18{,}38;\\\\
N_\gamma=2\cdot(N_\text{q}-1)\cdot\tg\varphi=20{,}07
\end{gathered}- součinitelé tvaru základu:
\begin{gathered}
s_\text{q}=1+\frac{1{,}4}{1{,}0}\cdot\sin30=1{,}7;&&s_\gamma=0{,}7
\end{gathered}- součinitelé šikmosti:
\begin{gathered}
m_\text{B}=\frac{(2+\frac{1{,}4}{1{,}0})}{(1+\frac{1{,}4}{1{,}0})}=1{,}42\\\\
i_\text{q}=(1-\frac{140{,}7}{288{,}87})^{1{,}42}=0{,}38;\\\\
i_\gamma=(1-\frac{140{,}7}{288{,}87})^{2{,}42}=0{,}20
\end{gathered}\begin{gathered}
R_\text{d}=19{,}0\cdot20{,}07\cdot1{,}7\cdot0{,}38+0{,}5\cdot19{,}0\cdot1{,}4\cdot20{,}07\cdot0{,}7\cdot0{,}20=283{,}71\space\text{kPa}\gt206{,}33\implies\text{vyhovuje}
\end{gathered}h) vodorovná návrhová únosnost v základové spáře:
\begin{gathered}
R_\text{h,d}=288{,}87\cdot\tg30=166{,}67\space\text{kN/m}\lt140{,}701\implies\text{vyhovuje}
\end{gathered}2) NP1b: A2“+“M2“+“R1
a) součinitelé pro M2
\begin{gathered}
\gamma_\varphi=1{,}1:&&\varphi_\text{1,d}=25{,}8\degree;&&\varphi_\text{2,d}=27{,}7\degree
\end{gathered}b) tvar zatěžovacího obrazce:
\begin{gathered}
\sin^2\alpha=\frac{(\sin(\varphi_1-\beta)\cdot\cos(\alpha+\varphi_1))}{(2\cdot\tg\varphi_1\cdot\cos(\alpha-\beta)}\space....\space\alpha=16{,}2\degree;&\theta_\text{as}=90-\alpha=73{,}8\degree\\\\
\theta_\text{a}=\alpha+\varphi_1=42{,}0\degree
\end{gathered}c) charakteristické tíhy zdi a zemního klínu (na šířku b = 1,0 m):
\begin{gathered}
G_\text{1k}=3{,}0\cdot0{,}4\cdot25=30{,}0\space\text{kN/m}\\\\
G_\text{2k}=3{,}6\cdot0{,}4\cdot25=36{,}0\space\text{kN/m}\\\\
G_3=17{,}5\cdot(1{,}05\cdot3{,}6+1{,}05\cdot\frac{0{,}38}{2}+1{,}15\cdot\frac{3{,}98}{2})=109{,}69\space\text{kN/m}
\end{gathered}d) aktivní zemní tlak (charakteristické velikosti na šířku b = 1,0 m):
- součinitel
\begin{gathered}
K_a=\cos^2\varphi_1/\cos\delta_1/[1+(\frac{(\sin(\varphi_1+\delta_1)\cdot\sin(\varphi_1-\beta))}{(\cos\delta_1\cdot\cos\beta)})^\frac{1}{2}]^2=0{,}521
\end{gathered}(pro horí vrstvu)
\begin{gathered}
S_\text{a1,k}=17{,}5\cdot\frac{4{,}14^2}{2}\cdot0{,}521=78{,}14\space\text{kN/m};\\\\
S_\text{a1h,k}=S_\text{a1,k}\cdot\cos\theta_\text{a}=58{,}06\space\text{kN/m};\\\\
S_\text{a1v,k}=S_\text{a1,k}\cdot\sin\theta_\text{a}=52{,}30\space\text{kN/m}
\end{gathered}- součinitel
\begin{gathered}
K_\text{a}=\tg^2(45-\frac{\varphi_2}{2})=0{,}365
\end{gathered}(pro spodní vrstvu)
\begin{gathered}
S_\text{a2,k}=19{,}0\cdot\frac{0{,}4^2}{2}\cdot0{,}365=0{,}55\space\text{kN/m};\\\\
S_\text{a2h,k}=S_\text{a2,k}\cdot\cos\delta_2=0{,}53\space\text{kN/m};\\\\
S_\text{a2v,k}=S_\text{a2,k}\cdot\sin\delta_2=0{,}15\space\text{kN/m}
\end{gathered}e) vnější zatížení F (charakteristická velikost):
- pomocný úhel:
\begin{gathered}
\cotg\varepsilon=\tg\varphi_1+(\frac{1}{\cos\varphi_1})\cdot(\frac{(\sin(\varphi_1+\delta_1)\cdot\cos\beta)}{(\sin(\varphi_1-\beta)\cdot\cos\delta_1)})^\frac{1}{2}\varepsilon=17{,}4\degree\\\\
\theta=\varphi+\varepsilon=25{,}8+17{,}4=43{,}2\degree
\end{gathered}- pomocné pořadnice od vrcholu zdi:
\begin{gathered}
\tg25{,}7\degree=\frac{v_1}{0{,}5}&&v_1=0{,}24&&a_1=0{,}24-0{,}1=0{,}06\space\text{m}\\\\
\tg43{,}2\degree=\frac{v_2}{4{,}3}&&v_2=4{,}04&&a_2=4{,}04-1{,}57=2{,}47\space\text{m}\\\\
h_\text{f}=2{,}47-0{,}06=2{,}41\space\text{m}
\end{gathered}- součinitel zemního tlaku
\begin{gathered}
K_\text{af}=\frac{\sin(\theta-\varphi_2)}{\cos(\theta-\varphi_2-\delta_2)}=0{,}27
\end{gathered}- náhradní zatížení
\begin{gathered}
f_\text{a}=\frac{800}{(3{,}8\cdot6{,}0)}=35{,}08\space\text{kN/m}^2
\end{gathered}- silový přírůstek:
\begin{gathered}
\Delta S_\text{a}=f_\text{a}\cdot B\cdot K_\text{af}=35{,}08\cdot3{,}8\cdot0{,}27=35{,}99\space\text{kN/m}
\end{gathered}- horní pořadnice:
\begin{gathered}
\Delta\sigma_\text{fs}=\frac{\Delta S_\text{a}}{h_\text{f}}\cdot(1+\frac{a}{(a+b)})=16{,}67\space\text{kN/m}
\end{gathered}- spodní pořadnice:
\begin{gathered}
\Delta\sigma_\text{fi}=\frac{\Delta S_\text{a}}{h_\text{f}}\cdot(1-\frac{a}{(a+b)})=13{,}20\space\text{kN/m}
\end{gathered}f) návrhové velikosti zatěžovacích sil (A2: γG = 1,0 – stálé zatížení, γQ = 1,3 – proměnné zatížení):
- svislé síly:
\begin{gathered}
N_\text{d}=1{,}0\cdot(30{,}0+36{,}0+109{,}69+52{,}30+0{,}15)=228{,}14\space\text{kN/m}
\end{gathered}- vodorovné síly:
\begin{gathered}
H_\text{d}=1{,}0\cdot(58{,}06+0{,}53)+1{,}3\cdot35{,}99=105{,}38\space\text{kN/m}
\end{gathered}- moment ke středu základové spáry:
\begin{gathered}
M_\text{d}=1{,}0\cdot(36{,}0\cdot0{,}9+1{,}05\cdot3{,}6\cdot17{,}5\cdot0{,}18+1{,}05\cdot\frac{0{,}38}{2}\cdot17{,}5\cdot0{,}0-3{,}98\cdot\frac{1{,}15}{2}\cdot17{,}5\cdot0{,}73+58{,}06\cdot1{,}73-52{,}30\cdot1{,}11+0{,}53\cdot0{,}13-0{,}15\cdot1{,}5)+1{,}3\cdot(13{,}20\cdot2{,}41\cdot2{,}74+3{,}47\cdot\frac{2{,}41}{2}\cdot3{,}14)=187{,}68\space\text{kNm/m}
\end{gathered}g) excentricita síly v základové spáře, napětí v základové spáře:
- excentricita
\begin{gathered}
e=\frac{187{,}68}{228{,}14}=0{,}82\space\text{m}\lt\frac{3{,}0}{3}=1{,}0\space\text{m}\implies\text{vyhovuje}
\end{gathered}- napětí v základové spáře
\begin{gathered}
\sigma_\text{d}=\frac{228{,}14}{(1{,}0\cdot(3{,}0-2\cdot0{,}82))}=167{,}75\space\text{kPa}
\end{gathered}h) návrhová únosnost základové spáry, (hrubozrnnézeminy – odvodněné podmínky):
- hloubka založení D = 1,0 m, efektivní tlak nadloží
\begin{gathered}
q´=19{,}0\cdot1{,}0=19{,}0\space\text{kPa};&&\varphi=27{,}7\degree,&&c=0
\end{gathered}- součinitelé únosnosti:
\begin{gathered}
N_\text{q}=e^{\pi\cdot\tg\varphi}\cdot\tg^2(45+\frac{\varphi}{2})=14{,}23;\\\\
N_\gamma=2\cdot(N_\text{q}-1)\cdot\tg\varphi=13{,}89
\end{gathered}- součinitelé tvaru základu:
\begin{gathered}
s_\text{q}=1+\frac{1{,}36}{1{,}0}\cdot\sin30=1{,}68;&&s_\gamma=0{,}07
\end{gathered}- součinitelé šikmosti:
\begin{gathered}
m_\text{B}=\frac{(2+\frac{1{,}36}{1{,}0})}{(1+\frac{1{,}36}{1{,}0})}=1{,}42\\\\
i_\text{q}=(1-\frac{105{,}38}{228{,}14})^{1{,}42}=0{,}41;\\\\
i_\gamma=(1-\frac{105{,}38}{228{,}14})^{2{,}42}=0{,}22
\end{gathered}\begin{gathered}
R_\text{d}=19{,}0\cdot14{,}23\cdot1{,}68\cdot0{,}41+0{,}5\cdot19{,}0\cdot1{,}36\cdot13{,}89\cdot0{,}7\cdot0{,}22=213{,}86\space\text{kPa}\gt167{,}75\implies\text{vyhovuje}
\end{gathered}i) vodorovná návrhová únosnost v základové spáře:
\begin{gathered}
R_\text{h,d}=228{,}14\cdot\tg27{,}7=119{,}77\space\text{kN/m}\lt105{,}38\implies\text{vyhovuje}
\end{gathered}3) NP2: A1“+“M1“+“R2
a) tvar zatěžovacího obrazce:
\begin{gathered}
\sin^2\alpha=\frac{(\sin(\varphi_1-\beta)\cdot\cos(\alpha+\varphi_1))}{(2\cdot\tg\varphi_1\cdot\cos(\alpha-\beta)}\space....\space\alpha=17{,}6\degree;\\\\
\theta_\text{as}=90-\alpha=72{,}4\degree
\end{gathered}\begin{gathered}
\theta_\text{a}=\alpha+\varphi_1=45{,}6\degree
\end{gathered}b) charakteristické tíhy zdi a zemního klínu (na šířku b = 1,0 m):
\begin{gathered}
G_\text{1k}=3{,}0\cdot0{,}4\cdot25=30{,}0\space\text{kN/m}\\\\
G_\text{2k}=3{,}6\cdot0{,}4\cdot25=36{,}0\space\text{kN/m}\\\\
G_3=17{,}5\cdot(0{,}88\cdot3{,}6+0{,}88\cdot\frac{0{,}32}{2}+1{,}21\cdot\frac{3{,}92}{2})=99{,}41\space\text{kN/m}
\end{gathered}c) aktivní zemní tlak (charakteristické velikosti na šířku b = 1,0 m):
- součinitel
\begin{gathered}
K_\text{a}=\cos^2\varphi_1/\cos\delta_1/[1+(\frac{((\sin(\varphi_1+\delta_1)\cdot\sin(\varphi_1-\beta))}{(\cos\delta_1\cdot\cos\beta)})^\frac{1}{2}]^2=0{,}461
\end{gathered}(pro horní vrstvu)
\begin{gathered}
S_\text{s1,k}=17{,}5\cdot\frac{4{,}1^2}{2}\cdot0{,}461=67{,}80\space\text{kN/m};\\\\
S_\text{a1h,k}=S_\text{a1,k}\cdot\cos\theta_\text{a}=47{,}44\space\text{kN/m};\\\\
S_\text{a1v,k}=S_\text{a1,k}\cdot\sin\theta_\text{a}=48{,}44\space\text{kN/m}
\end{gathered}- součinitel
\begin{gathered}
K_a=\tg^2(45-\frac{\varphi_2}{2})=0{,}333
\end{gathered}(pro spodní vrstvu)
\begin{gathered}
S_\text{a2,k}=19{,}0\cdot\frac{0{,}4^2}{2}\cdot0{,}333=0{,}51\space\text{kN/m};\\\\
S_\text{a2h,k}=S_\text{a2,k}\cdot\cos\delta_2=0{,}49\space\text{kN/m};\\\\
S_\text{a2v,k}=S_\text{a2,k}\cdot\sin\delta_2=0{,}13\space\text{kN/m}
\end{gathered}d) vnější zatížení F (charakteristická velikost):
- pomocný úhel:
\begin{gathered}
\cotg\varepsilon=\tg\varphi_1+(\frac{1}{\cos\delta_1})\cdot(\frac{(\sin(\varphi_1+\delta_1)\cdot\cos\beta)}{(\sin(\varphi_1-\beta)\cdot\cos\delta_1)})^\frac{1}{2}\varepsilon=22{,}3\degree,\\\\
\theta=\varphi+\varepsilon=28+22{,}3=50{,}3\degree
\end{gathered}- pomocné pořadnice od vrcholu zdi:
\begin{gathered}
\tg28\degree=\frac{v_1}{0{,}5},&&v_1=0{,}27,&&a_1=0{,}27-0{,}18=0{,}09\space\text{m}\\\\
\tg50{,}3\degree=\frac{v_2}{4{,}3},&&v_2=5{,}18,&&a_2=5{,}18-1{,}57=3{,}60\space\text{m}\\\\
h_\text{f}=3{,}60-0{,}09=3{,}51\space\text{m}
\end{gathered}- součinitel zemního tlaku
\begin{gathered}
K_\text{af}=\frac{\sin(\theta-\varphi_2)}{\cos(\theta-\varphi_2-\delta_2)}=0{,}38
\end{gathered}- náhradní zatížení
\begin{gathered}
f_\text{a}=\frac{800}{(3{,}8\cdot6{,}0)}=35{,}08\space\text{kN/m}^2
\end{gathered}- silový přírůstek:
\begin{gathered}
\Delta S_\text{a}=f_\text{a}\cdot B\cdot K_\text{af}=35{,}08\cdot3{,}8\cdot0{,}38=50{,}66\space\text{kN/m}
\end{gathered}- horní pořadnice:
\begin{gathered}
\Delta\sigma_\text{fs}=\frac{\Delta S_\text{a}}{h_\text{f}}\cdot(1+\frac{a}{(a+b)})=16{,}11\space\text{kN/m}
\end{gathered}- spodní pořadnice:
\begin{gathered}
\Delta\sigma_\text{fi}=\frac{\Delta S_\text{a}}{h_\text{f}}\cdot(1-\frac{a}{(a+b)})=12{,}75\space\text{kN/m}
\end{gathered}e) návrhové velikosti zatěžovacích sil (A1: γG = 1,35 – stálé zatížení, γQ = 1,5 – proměnné zatížení)
- svislé síly:
\begin{gathered}
N_\text{d}=1{,}35\cdot(30{,}0+36{,}0+99{,}41+48{,}44+0{,}13)=288{,}87\space\text{kN/m}
\end{gathered}- vodorovné síly:
\begin{gathered}
H_\text{d}=1{,}35\cdot(47{,}44+0{,}49)+1{,}5\cdot50{,}66=140{,}70\space\text{kN/m}
\end{gathered}- moment ke středu základové spáry:
\begin{gathered}
M_\text{d}=1{,}35\cdot(36{,}0\cdot0{,}9+0{,}88\cdot3{,}6\cdot17{,}5\cdot0{,}26+0{,}88\cdot\frac{0{,}32}{2}\cdot17{,}5\cdot0{,}11-3{,}92\cdot\frac{1{,}21}{2}\cdot17{,}5\cdot0{,}69+47{,}44\cdot1{,}71-48{,}44\cdot1{,}08+0{,}49\cdot0{,}13-0{,}13\cdot1{,}5)+1{,}5\cdot(12{,}75\cdot3{,}51\cdot2{,}15+3{,}36\cdot\frac{3{,}51}{2}\cdot2{,}74)=232{,}18\space\text{kNm/m}
\end{gathered}f) excentricita síly v základové spáře, napětí v základové spáře:
- excentricita:
\begin{gathered}
e=\frac{232{,}18}{288{,}87}=0{,}80\space\text{m}\lt\frac{3{,}0}{3}=1{,}0\space\text{m}\implies\text{vyhovuje}
\end{gathered}- napětí v základové spáře:
\begin{gathered}
\sigma_\text{d}=\frac{288{,}87}{(1{,}0\cdot(3{,}0-2\cdot0{,}8))}=206{,}33\space\text{kPa}
\end{gathered}g) návrhová únosnost základové spáry (hrubozrnné zeminy – odvodněné podmínky), pro R2 je dílčí koeficient pro únosnost γR,v = 1,4 a pri usmyknutí γR,h = 1,1:
- hloubka založení D = 1,0 m, efektivní tlak nadloží
\begin{gathered}
q´=19{,}0\cdot1{,}0=19{,}0\space\text{kPa};&&\varphi=30\degree;&&c=0
\end{gathered}- součinitel únosnosti:
\begin{gathered}
N_\text{q}=e^{\pi\tg\varphi}\cdot\tg^2(45+\frac{\varphi}{2})=18{,}38;\\\\
N_\gamma=2\cdot(N_\text{q}-1)\cdot\tg\varphi=20{,}07
\end{gathered}- součinitelé tvaru základu:
\begin{gathered}
s_\text{q}=1+\frac{1{,}4}{1{,}0}\cdot\sin30=1{,}7;&&s_\gamma=0{,}7
\end{gathered}- součinitelé šikmosti:
\begin{gathered}
m_\text{B}=\frac{(2+\frac{1{,}4}{1{,}0})}{(1+\frac{1{,}4}{1{,}0})}=1{,}42;\\\\
i_\text{q}=(1-\frac{140{,}7}{288{,}87})^{1{,}42}=0{,}38;\\\\
i_\gamma=(1-\frac{140{,}7}{288{,}87})^{2{,}42}=0{,}20;
\end{gathered}\begin{gathered}
R_\text{d}=\frac{(19{,}0\cdot20{,}07\cdot1{,}7\cdot0{,}38+0{,}5\cdot19{,}0\cdot1{,}4\cdot20{,}07\cdot0{,}7\cdot0{,}20)}{1{,}4}=202{,}65\space\text{kPA}\\\\
202{,}65\space\text{kPa}\lt206{,}33\implies\text{mírně nevyhovuje}
\end{gathered}bylo by nutné poněkud zvětšit šířku základové spáry
h) vodorovná návrhová únosnost v základové spáře:
\begin{gathered}
R_\text{h,d}=\frac{(288{,}87\cdot\tg30)}{1{,}1}=151{,}52\space\text{kN/m}\\\\
151{,}52\space\text{kN/m}\lt140{,}70\space\text{kN/m}\implies\text{vyhovuje}
\end{gathered}4. Deformace opěrné zdi (mezní stav použitelnosti)
(není započítáno se zatížením pohyblivým)
a) charakteristické tíhy zdi a zemního klínu (na šířku b = 1,0 m):
\begin{gathered}
G_\text{1k}=3{,}0\cdot0{,}4\cdot25=30{,}0\space\text{kN/m}\\\\
G_\text{2k}=3{,}6\cdot0{,}4\cdot25=36{,}0\space\text{kN/m}\\\\
G_3=17{,}5\cdot(0{,}88\cdot3{,}6+0{,}88\cdot\frac{0{,}32}{2}+1{,}21\cdot\frac{3{,}92}{2})=99{,}41\space\text{kN/m}
\end{gathered}b) aktivní zemní tlak (charakteristické velikosti na šířku b = 1,0 m):
\begin{gathered}
S_\text{a1,k}=17{,}5\cdot\frac{4{,}1^2}{2}\cdot0{,}461=67{,}80\space\text{kN/m};\\\\
S_\text{a1h,k}=S_\text{a1,k}\cdot\cos\theta_\text{a}=47{,}44\space\text{kN/m};\\\\
S_\text{a1v,k}=S_\text{a1,k}\cdot\sin\theta_\text{a}=48{,}44\space\text{kN/m}
\end{gathered}- součinitel
\begin{gathered}
K_\text{a}=\tg^2(45-\frac{\varphi_2}{2})=0{,}333
\end{gathered}(pro spodní vrstvu)
\begin{gathered}
S_\text{a2,k}=19{,}0\cdot\frac{0{,}4^2}{2}\cdot0{,}333=0{,}51\space\text{kN/m};\\\\
S_\text{a2h,k}=S_\text{a2,k}\cdot\cos\delta_2=0{,}49\space\text{kN/m};\\\\
S_\text{a2v,k}=S_\text{a2,k}\cdot\sin\delta_2=0{,}13\space\text{kN/m}
\end{gathered}c) charakteristické velikosti zatěžovacích sil:
- svislé síly:
\begin{gathered}
N_\text{k}=30{,}0+36{,}0+99{,}41+48{,}44+0{,}13=213{,}98\space\text{kN/m}
\end{gathered}- vodorovné síly:
\begin{gathered}
H_\text{k}=47{,}44+0{,}49=47{,}93\space\text{kN/m}
\end{gathered}- moment ke středu základové spáry:
\begin{gathered}
M_\text{k}=36{,}0\cdot0{,}9+0{,}88\cdot3{,}6\cdot17{,}5\cdot0{,}26+0{,}88\cdot\frac{0{,}32}{2}\cdot17{,}5\cdot0{,}11-3{,}92\cdot\frac{1{,}21}{2}\cdot17{,}5\cdot0{,}69+47{,}44\cdot1{,}71-48{,}44\cdot1{,}08+0{,}49\cdot0{,}13-0{,}13\cdot1{,}5=47{,}12\space\text{kNm/m}
\end{gathered}d) svislé napětí v základové spáře:
\begin{gathered}
\sigma_1=\frac{213{,}98}{3{,}0}+47{,}12\cdot\frac{6}{3{,}0^2}=102{,}74\space\text{kPa};\\\\
\sigma_1=\frac{213{,}98}{3{,}0}-47{,}12\cdot\frac{6}{3{,}0^2}=39{,}89\space\text{kPa}
\end{gathered}- původní geostatické napětí v základové spáře:
\begin{gathered}
\sigma_\text{or,0}=19{,}0\cdot1{,}0=19{,}0\space\text{kPa}
\end{gathered}- napětí konstantní:
\begin{gathered}
\sigma_\text{a}=39{,}89-19{,}0=20{,}89\space\text{kPa}
\end{gathered}- napětí trojúhelníkové:
\begin{gathered}
\sigma_\text{b}=102{,}74-39{,}89-19{,}0=43{,}85\space\text{kPa}
\end{gathered}e) deformační vlastnosti základové půdy a tuhosti základu:
\begin{gathered}
E_\text{def}=14{,}0\space\text{MPA},&&v=0{,}30;&&\beta=0{,}74;&&E_\text{oed}=15{,}73\space\text{MPA}
\end{gathered}\begin{gathered}
k=(\frac{26\space500}{14{,}0})\cdot(\frac{0{,}4}{3{,}0})^3=4{,}48\gt1\implies\text{základ je tuhý}
\end{gathered}f) výpočet konečného sedání bude součtem sedání tuhého základu pod charakteristickým bodem pro zatížení konstantní σa = 20,89 kPa a zatížení trojúhelníkové s pořadnicí σb = 43,85 kPa; (podrobněji viz např. Navrhování základových konstrukcí), vlastní výpočet bude sestaven do tab. 18.
Tab. 18 Výpočet sedání základu úhlové opěrné zdi z příkladu 8
| Číslo vrstvy | Mocnost hi [m] | zi [m] | D/zi | κ1 | zc/zi | κ2 | Zri = κ1 · κ2 · zi | σor,i [kPa] | 0,2 · σor,i [kPa] |
| 1 | 0,5 | 0,25 | 4,00 | 1,82 | 32,0 | 1,0 | 0,45 | 27,55 | 5,51 |
| 2 | 0,5 | 0,75 | 1,33 | 1,55 | 10,66 | 1,0 | 1,16 | 41,04 | 8,20 |
| 3 | 0,5 | 1,25 | 0,80 | 1,40 | 6,40 | 1,0 | 1,75 | 52,25 | 10,45 |
| 4 | 1,0 | 2,00 | 0,50 | 1,30 | 4,00 | 1,0 | 2,60 | 68,40 | 13,68 |
| 5 | 1,0 | 3,00 | 0,33 | 1,19 | 2,66 | 0,97 | 3,46 | 84,74 | 16,95 |
| 6 | 1,0 | 4,00 | 0,25 | 1,12 | 2,00 | 0,95 | 4,26 | 99,94 | 19,98 |
Pokračování tab. 18
| Sedání pro konstantní napětí σa = 20,89 kPa | Sedání pod nezatíženou hranou | ||||||||
| Číslo vrstvy | zi/B | I2 | σzi [kPa] | σzi – 0,2 · σor,i | Eoed,i [MPa] | si [mm] | IA,1 | σzi – 0,2 · σor,i | sA,i [mm] |
| 1 | 0,150 | 0,90 | 18,80 | 13,29 | 15,73 | 0,42 | 0,020 | -3,75 | – |
| 2 | 0,387 | 0,68 | 14,21 | 6,00 | 15,73 | 0,19 | 0,057 | -3,20 | – |
| 3 | 0,583 | 0,59 | 12,33 | 1,88 | 15,73 | 0,06 | 0,070 | -4,31 | – |
| 4 | 0,867 | 0,50 | 10,45 | -3,23 | 15,73 | – | 0,079 | -6,75 | – |
| 5 | 1,153 | 0,43 | 8,98 | – | 15,73 | – | 0,080 | – | – |
| 6 | 1,420 | 0,36 | 7,52 | – | 15,73 | – | 0,073 | – | – |
| Sedání pod charakteristickým bodem | 0,67 mm | Sedání pod bodem A | 0 mm | ||||||
pokračování tab. 18
| Sedání pod zatíženou hranou | |||||
| Číslo vrstvy | zi/B | IB,1 | σzi – 0,2 · σor,i | Eoed,i [MPa] | sB,i [mm] |
| 1 | 0,150 | 0,248 | 16,24 | 15,73 | 0,52 |
| 2 | 0,387 | 0,238 | 12,67 | 15,73 | 0,40 |
| 3 | 0,583 | 0,228 | 9,55 | 15,73 | 0,30 |
| 4 | 0,867 | 0,212 | 6,18 | 15,73 | 0,39 |
| 5 | 1,153 | 0,192 | -0,11 | 15,73 | – |
| 6 | 1,420 | 0,165 | – | 15,73 | – |
| Sedání pod bodem B | 1,61 mm | ||||
Komentář k výsledkům
- navržený tvar základového pasu (B = 3,0 m) vyhoví pro NP1a, b mezního stavu porušení, jež je v ČR doporučen pro posouzení opěrných konstrukcí, mírně nevyhovuje (98,2 %) pro NP2, kdy by bylo nutné zvětšit šířku základové spáry na B = 3,1 m;
- sedání základové patky na hraně A:
\begin{gathered}
s_\text{A}=0{,}67\space\text{mm}
\end{gathered}- sedání základové patky na hraně B:
\begin{gathered}
s_\text{B}=0{,}67+1{,}61=2{,}28\space\text{mm}
\end{gathered}- průměrné sedání základové patky:
\begin{gathered}
s=\frac{(2{,}28+0{,}67)}{2}=1{,}48\space\text{mm}\implies\text{jistě vyhoví}
\end{gathered}- naklonění základové patky:
\begin{gathered}
\frac{\Delta s}{B}=\frac{(2{,}28-0{,}67)}{3\space000}=0{,}00054\implies\text{vyhobí}
\end{gathered}- posun hlavy opěrné zdi:
\begin{gathered}
u=0{,}00054\cdot3\space600=1{,}94\space\text{mm}\gt1{,}80\space\text{mm}
\end{gathered}- naklonění pro vznik aktivního zemního tlaku: u = 5 · 10-4 · 3 600 = 1,80 mm, zavedení zatížení aktivním zemním tlakem bylo oprávněné.
6 OCHRANA ZÁKLADOVÝCH KONSTRUKCÍ ÚČINKY AGRESIVNÍHO PROSTŘEDÍ
Hlubinné základy přicházejí do styku s přírodním prostředím, které může významně ovlivnit dobu jejich životnosti. Jedná se zejména o různé látky obsažené v podzemní vodě, jež mohou být původu jak přírodního, tak i umělého, což obyčejně souvisí se znečištěním životního prostředí. Z hlediska materiálu základových konstrukcí jde především o beton, jak prostý, tak i vyztužený, popř. o cementovou maltu, nebo cementový kámen v zatvrdlé cementové suspenzi. Výjimečně se též jedná o ocel, popř. i o dřevo. Naprostá většina prvků a konstrukcí speciálního zakládání staveb je však tvořena betonem, na nějž může dlouhodobě působit okolní geotechnické prostředí a způsobit tak jeho poškození, korozi a ztrátu požadovaných vlastností. Je tedy krajně důležité již v rámci geotechnického průzkumu stanovit vlastnosti tohoto prostředí ve vztahu k jeho agresivním účinkům. Přesto, že se někdy hovoří o agresivitě základové půdy, rozhodující význam má agresivita podzemních vod, tedy jak výluh agresivních látek ve vodě, tak i přímý průsak agresivních vod do základové půdy. Zatímco prvý případ bývá původu přírodního, druhý pak zejména umělého, související s lidskou činností. Na základě průzkumem zjištěného stupně agresivity prostředí, jeho druhu a možnosti kolísání v čase je třeba navrhnout příslušnou ochranu základových konstrukcí hlubinných základů, a to zejména trvalých. Jedná se o mimořádně důležitý aspekt návrhu speciálního zakládání staveb, jež může vést ve svých důsledcích k výraznému zdražení zakládání stavby, nebo i dokonce k změně zakládání, popř. i umístění stavby.
3.1 CHEMIZMUS PODZEMNÍCH VOD
Podzemní vody mají různou genezi, nicméně převážná jejich část má původ v infiltraci srážkových vod. Jejich chemizmus přírodního původu je dán především charakterem geologického prostředí. Podzemní vody s obsahem minerálních látek do 1 g/litr jsou vody prosté, s vyšším obsahem jsou pak mineralizované, a to buď slabě, (1–3 g/litr), středně, (3–10 g/litr) nebo silně, (10–50 g/litr), při ještě vyšší koncentraci jde o solanky.
Významnou chemickou charakteristikou vody je její celková tvrdost, daná obsahem vápníku a hořčíku. Pokud je jejich obsah tvořen kyselým uhličitanem vápenatým, popř. hořečnatým, jde o tzv. přechodnou tvrdost. Je-li naopak vázán ve formě chloridů a síranů, způsobuje trvalou tvrdost vody. Ta je obyčejně měřena tzv. německými stupni, (1° něm. odpovídá 10 mg CaO, nebo 7,1 mg MgO v 1 litru vody, popř. jejich příslušnou kombinací). Podle toho rozeznáváme vody:
- velmi měkké, (0–4° něm.);
- měkké, (4–8° něm.);
- středně tvrdé, (8–12° něm.);
- dosti tvrdé, (12–18° něm.);
- tvrdé, (18–25° něm.);
- velmi tvrdé, (25–50° něm.);
- mimořádně tvrdé, (přes 50° něm.).
V současné době se původní klasifikace podle stupňů něm. nepoužívá a nahrazuje se ukazatelem tvrdosti vyjádřeným v mmol/litr.
Pro bližší chemickou charakteristiku vody existuje řada postupů a klasifikačních metod, jež hodnotí zastoupení a vztahy charakteristických iontů. Nejrozšířenější je klasifikace podle Ch. Palmera, jež spočívá v rozdělení základních disociovaných iontů do 5 skupin:
- silné kationty K+, Na+, Li+ – skupina a;
- slabé kationty Ca2+, Mg2+ – skupina e;
- velmi slabé kationty, tvořené ionty těžkých kovů a volného H+ – skupina m;
- silné anionty Cl–, SO42-, I–, Br– – skupina S;
- slabé anionty CO32-, HCO32-, OH– – skupina A.
Podle poměru iontů se pak dělí vody do 5 tříd:
- S + a = první salinita S1;
- S + e = druhá salinita S2;
- S + m = třetí salinita S3;
- A + a = první alkalita A1;
- A + e = druhá alkalita A2.
Z hlediska ochrany základových prvků proti působící podzemní vodě nás zajímají především podzemní vody agresivní, a to jak na beton, (resp. na jeho nejdůležitější složku – cement), tak na ocel, (železo). Útočnost podzemní vody může být:
- vyluhovací, (charakterizovaná dočasnou tvrdostí v mmol/litr);
- kyselostní, (stanovená na základě acidity podzemní vody, resp. neutralizační kapacity, jejímž ukazatelem je pH – faktor);
- síranová, (jejímž ukazatelem je množství aniontů SO42- v mg/litr);
- uhličitá, (vyjádřená množstvím agresivního CO2 na Ca, popř. na Fe v mg/litr);
- hořečnatá, (vyjádřená množstvím Mg2+ v mg/litr).
Tyto agresivity bývají většinou přírodního původu, (např. síranová agresivita v puklinových podzemních vodách v ordovických břidlicích, jejíž původ je v rozpouštění vylouženého pyritu na puklinách, nebo agresivní CO2 v mineralizovaných vodách v Karlových Varech). Agresivita však může být způsobena i různými polutanty pronikajícími do základové půdy vlivem lidské činnosti, (odkaliště, výsypky apod.). Kromě toho existuje řada agresivních chemikálií anorganických i organických, jež se dostávají do podzemních vod v souvislosti s průmyslovou a zemědělskou činností, (oleje, cukry, tuky, fenoly apod.); jejich chemické působení na beton není ještě často dokonale známo.
6.2 STUPNĚ VLIVU PROSTŘEDÍ
Aby bylo možné posoudit konkrétní vliv příslušné agresivity na beton, popř. na ocel základové konstrukce, byly již v minulosti vytvářeny různé klasifikace agresivního prostředí. Příkladem může být tabulka č. 22 původní ČSN 73 1001 z roku 1967, jež byla vztažena ke třem typům hydrogeologického prostředí, (málo propustné, středně propustné a propustné, resp. proudící voda v propustném prostředí). Údaje obsažené v této tabulce byly velmi přísné a více než 30letá praxe ukázala, že hodnocení bylo příliš pesimistické. To bylo dokumentováno zejména srovnáním s cizími předpisy, jež se zabývaly problematikou hodnocení útočnosti podzemních vod, (viz např. tab. 19). Ta platila pro stojící, či málo proudící podzemní vody, jež přicházejí ve velkém množství do styku s betonem základových konstrukcí. Při kombinované útočnosti, (např. vysoký obsah síranových iontů a současně nízký pH-faktor), nebo v případě silně proudící vody ve vysoce propustném prostředí, (s koeficientem filtrace k > 10-3 · s-1), se stupeň agresivity zvětšuje o jeden, naopak, jedná-li se o malý výskyt vody, jež se prakticky nepohybuje, (např. v málo propustném prostředí s k < 10-5 · s-1), se stupeň o jeden snižuje. Na základě poznatků z 36 zemí světa o hodnocení útočnosti a působení agresivity na beton základových konstrukcí, zejména pak v případě betonovaných pilot a podzemních stěn, byly sestaveny zásady ochranných opatření proti této agresivitě, uvedené v tab. 20–22.
Tab. 19 Klasifikace agresivity prostředí podle DIN 1045, 1048, 4030 (SRN), podle Concrete Manual (USA) a B · R · E. Digest No · 174, C · P. 110, Part 1 a C · P · 2004 (GB)
| Stupeň agresivity | Limity agresivity | |||||
| SO42- [mg·l-1] | CO2x) [mg·l-1] | pH | ||||
| zanedbatelný | 200 | 350 | 150 | 15 | > 6,5 | 9,0–6,0 |
| slabý | 600 | 1400 | 1500 | 15–30 | 6,5–5,5 | 6,0–5,0 |
| silný | 3 000 | 6 000 | 10 000 | 30–60 | 5,5–4,5 | 5,0–3,5 |
| velmi silný | 3 000 | 6 000 | 10 000 | 60 | < 4,5 | < 3,5 |
| země | SRN | GB | USA | SRN | SRN, USA | GB |
| x) Limity pro agresivní CO2 udává DIN 4030, ostatní předpisy zahrnují uhličité vody mezi vody kyselé a limitují pouze pH-faktor | ||||||
Tab. 20 Opatření používané pro ochranu hlubinných základů na místě betonovaných, [Bartholomew, 1979]
| Druh opatření | Agresivita | |||
| zanedbatelná | slabá | silná | velmi silná | |
| hutný nepropustný beton | ano | ano | ano | ano |
| portlandský cement | ano | ano | ne | ne |
| síranovzdorný cement | ne | ano | ano | ano |
| speciální cement (např. pucolánový) | ne | ano | ano | ano |
| určení min. vodního součinitele | ano | ano | ano | ano |
| speciální kamenivo | ne | v kyselém prostředí lze použít vápencové kamenivo | ||
| zvětšení krytí (tloušťky prvku) | ne | někdy | někdy | ne |
| Použití sekundární ochrany: | ||||
|
ne | ne | ne | ano |
|
ne | ne | ne | ano |
|
ne | ne | ne | ano |
Tab. 21 Minimální obsah cementu [kg·m-3] a maximální vodní součinitel v/c pro výrobu na místě betonovaných, (vrtaných) pilot v agresivním prostředí
| Technologie provádění | Množství cementu, vodní součinitel | ||
| Běžné podmínky | Slabá agresivita | Silná agresivita | |
| nepažené vrty nebo pažení ocelovou pažnicí | 300–450 0,50–0,55 |
350–450 0,48–0,50 |
380–500 0,45–0,50 |
| pažení jílovou pažicí suspenzí | 350–450 0,50–0,60 |
350–450 0,48–0,50 |
400–500 0,43–0,45 |
V tab. 20 je zhodnocena účinnost nejvíce používaných opatření pro snížení vlivu agresivity prostředí, (zejména podzemní vody) na hlubinné základy na místě betonované. Ukazuje se, že speciální ochranu, (sekundární), vyžaduje pouze velmi silná agresivita. V tab. 21 jsou uvedeny minimální obsahy cementu a velikosti vodního součinitele. Tabulka je platná pro nejvíce užívaný směsný cement CEM II/B-S. Odolnost jednotlivých druhů cementů v agresivním prostředí uvádí tab. 22.
V současné době platná klasifikace stupňů vlivu prostředí je stanovena evropskou normou ČSN EN 206+A2: Beton – Specifikace, vlastnosti, výroba a shoda. V zásadě se rozeznávají následující stupně vlivu prostředí, (tab. 23). Mezní hodnoty pro posouzení stupňů chemického působení prostředí jsou v tab. 24.
Tab. 22 Odolnost cementů vůči agresivnímu prostředí
| Druh cementu | Odolnost vůči chemickému prostředí | ||
| sírany | nízký pH-faktor | nízká tvrdost | |
| portlandský (CEM I) | nízká | nízká | nízká |
| struskoportlandský (CEM II) | střední | střední – vysoká | nízká |
| síranovzdorný | vysoká | nízká | nízká |
| pucolánový | vysoká | střední | střední |
Tab. 23 Stupně vlivu prostředí, (upraveno podle tabulky 1 ČSN EN 206+A2)
| Označení stupně | Popis prostředí | Příklady výskytu prostředí |
| 1. Bez nebezpečí koroze nebo narušení | ||
| X0 | platí pro nevyztužený beton ve velmi suchém prostředí | chráněné betonové konstrukce např. uvnitř budov; pro prvky hlubinného zakládání nepřichází v úvahu |
| 2. Koroze vlivem karbonatace | ||
| XC1 | suché nebo stále mokré prostředí | beton trvale pod vodou (neagresivní) |
| XC2 | mokré, občas suché | většina základových konstrukcí |
| XC3 | středně mokré, vlhké | platí pro základové konstrukce |
| XC4 | střídavě mokré a suché | většinou se netýká základů |
| 3. Koroze vlivem chloridů, ne však z mořské vody | ||
| XD1 | středně mokré, vlhké | většinou se netýká základů |
| XD2 | mokré, občas suché | většinou se netýká základů |
| XD3 | střídavě mokré a suché | většinou se netýká základů |
| 4. Koroze vlivem chloridů z mořské vody | ||
| XS1 | vystavení slanému vzduchu, ne v přímém styku s mořskou vodou | např. štětové stěny nábřežních zdí |
| XS2 | trvale ponořeny ve vodě | hlubinné základy v moři |
| XS3 | smáčené a ostřikované přílivem | speciální základové konstrukce nábřežních zdi, off-shore konstrukce apod. |
| 5. Střídavé působení mrazu a rozmrazování (mrazové cykly) s rozmrazovacími prostředky nebo bez nich | ||
| XF1 | mírné nasycení vodou bez rozmrazovacích prostředků | pilotové a podzemní stěny jako trvalé konstrukce |
| XF2 | mírné nasycení vodou s rozmrazovacími prostředky | většinou se netýká konstrukcí speciálního zakládání staveb |
| XF3 | značně nasycen vodou bez rozmrazovacích prostředků | pilotové a podzemní stěny jako trvalé konstrukce |
| XF4 | značně nasycen vodou s rozmrazovacími prostředky | většinou se netýká konstrukcí speciálního zakládání staveb |
| 6. Chemické působení | ||
| XA1 | slabě agresivní chemické prostředí | týká se zejména prvků a konstrukcí speciálního zakládání staveb |
| XA2 | středně agresivní chemické prostředí | týká se zejména prvků a konstrukcí speciálního zakládání staveb |
| XA3 | silně agresivní chemické prostředí | týká se zejména prvků a konstrukcí speciálního zakládání staveb |
Útočnost podzemní vody se hodnotí na základě chemických rozborů a na základě hydrogeologických poměrů na staveništi. Toto hodnocení je třeba provést vždy komplexně a přihlédnout jak k vlivům zhoršujícím, (soustředěné účinky, možnost kontaminace z blízkých chemických provozů, rychlost pohybu vody a její výměna, tlak vody, její teplota, možnost současného působení mrazu), tak i k vlivům zlepšujícím, (dlouhodobé snížení hladiny podzemní vody, nízká propustnost prostředí, neproudící podzemní voda apod).
Tab. 24 Mezní hodnoty pro stupně chemického působení podzemní vody a zemního prostředí
| Chemická charakteristika | Referenční zkušební metoda | XA1 | XA2 | XA3 |
| Podzemní voda | ||||
| síranová SO42 [mg·l-1] | EN 196-2 | 200–600 | 600–3 000 | 3 000–6 000 |
| kyselostní pH-faktor | ISO 4316 | 6,5–5,5 | 5,5–4,5 | 4,5–4,0 |
| uhličitá CO2 agresivní na Ca [mg·l-1] | EN 13577 | 15–40 | 40–100 | 100–nasycení |
| amoniak NH [mg·l-1] | ISO 7150-1 | 15–30 | 30–60 | 60–100 |
| hořečnatá Mg2+ [mg·l-1] | ISO 7980 | 300–1 000 | 1 000–3 000 | 3 000–nasycení |
| Zemina | ||||
| shíranová SO42- [mg · kg-1]a) celkem | EN 196-2b) | 2 000–3 000c) | 3 000c)–12 000 | 12 000–24 000 |
| kyselost [ml·kg] | DIN 4030-2 | > 200 Baumann-Gully | v praxi se nepoužívá | |
| a) V případě jílovitých zemin s koeficientem filtrace k < 10-5 m·s-1 se zařadí do nižšího stupně. b) Jde o výluh SO42, kyselinu chlorovodíkovou; na základě zkušeností lze použít i vodní výluh. c) Mezní hodnotu 3 000 mg/kg je nutné zmenšit na 2 000 mg/kg v případě nebezpečí hromadění síranových iontů v betonu při střídavém vysoušení a zvlhčování nebo v důsledku kapilárního sání. |
||||
| Klasifikace chemického prostředí platí pro podzemní vodu a zeminu při teplotě +5 až +25° C a pro velmi mírné proudění vody blížící se nehybnému stavu. Pro odstupňování je určující nejvyšší hodnota jednotlivých chemických charakteristik. Pokud dvě nebo více chemických charakteristik jsou stejného stupně, pak je nutné použít nejblíže vyšší stupeň, pokud se pomocí zvláštní studie neprokáže, že to není nutné. |
||||
Konkrétní chemizmus podzemní vody se stanovuje vesměs na základě tzv. zkrácených chemických rozborů na vzorcích podzemní vody odebíraných v rámci geotechnického průzkumu přímo ve vrtaných, popř. kopaných sondách, ve studních, nebo i vodotečích. O technice odběru a vzorkování podzemní vody pojednává např. publikace bývalého VÚIS Bratislava – Odběr a analýza podzemních vod, 1981. Rozlišují se především jednorázové odběry, jež poskytnou obraz o aktuálním stavu a dále řadové odběry, jež poskytnou obraz o změnách chemizmu v čase a mají tedy mnohem větší vypovídací schopnost. Pro správné posouzení agresivity podzemní vody bývá směrodatná analýza vody proudící ve vodonosné vrstvě, ne pak analýza povrchové vody, jež může být různě ovlivněna. Při odběru vzorku podzemní vody z vrtu je třeba vodu po jistou dobu čerpat a teprve potom odebrat vzorek.
V podstatě lze konstatovat, že se vždy vyplatí více správných odběrů a příslušných analýz, z nichž lze provést statistické hodnocení agresivity než osamocené odběry, neboť event. závěr o střední, nebo i vysoké agresivitě vede vždy k výraznému zvýšení investičních nákladů na zakládání staveb, pokud nevede přímo ke změně metody zakládání, nebo i opuštění staveniště. Současná praxe v geotechnickém průzkumu je bohužel velmi nedobrá, neboť spolupráce mezi zpracovatelem průzkumu, jež poskytuje významné podklady pro projekt a následnou realizaci a projektantem speciálního zakládání buď vůbec neexistuje, nebo je na velmi nízké úrovni. Zpracovatel průzkumu často odebere vzorek vody při návštěvě lokality, vozí jej několik dní v autě a příležitostně jej předá laboratoři. Ti provedou rutinní chemickou analýzu bez jakékoliv znalosti souvislostí a zpracovatel průzkumu opíše jejich závěr, který velmi často zařazuje vzorek vody do stupně XA2, nebo i XA3 a na základě osamělého odběru je potom hodnocena agresivita podzemní vody na celém staveništi. Navíc, zejména v případě uhličité agresivity, je její stupeň hodnocen tzv. výpočtem, což je zkouška zcela neprůkazná, neboť obyčejně při ní nejsou splněny příslušné předpoklady pro její použití. V zásadě platí, že by vždy uhličitá agresivita měla být posuzována Heyerovou, (mramorovou) zkouškou, jejíž výsledky jsou průkazné, přičemž odběr vzorků vody pro tuto zkoušku je poměrně náročný. V případě agresivity síranové je to nepoměrně jednodušší. V žádném případě nelze agresivitu podzemních vod na staveništi seriózně hodnotit na základě jednoho, nebo dvou náhodně odebraných vzorků vody.
6.3 NEJDŮLEŽITĚJŠÍ DRUHY CHEMICKÉ KOROZE
6.3.1 Agresivita síranová
Síranová koroze je důsledkem vázání síranových iontů SO42- z vodního prostředí s některými složkami zatvrdlé cementové kaše, při němž vznikají málo rozpustné krystalické novotvary s objemem až 5x větším. Tím se vysvětluje expanzní charakter síranové koroze, nazývané též cementovým bacilem, která postupuje tak, že v první fázi beton získává paradoxně větší pevnost v důsledku vyplňování pórů těmito expandujícími krystaly, v další fází však v důsledku dalšího rozpínání vznikají trhliny, až se jeho struktura zcela rozpadne. Rychlost vázání síranových iontů z agresivní vody závisí nejen na jejich koncentraci, ale též na druhu použitého cementu, jeho množství, vodním součiniteli a na technologii zpracování betonu. Zatímco klasický portlandský cement (CEM I) je málo odolný, vyšší odolnost vykazují směsné cementy CEM II A-S, s obsahem strusky 6–20 %, nebo CEM II B-S, s obsahem strusky 21–35 %. Podstatně vyšší odolnost mají cementy se sníženým obsahem trikalciumaluminátu C3A ve slínku, jež se nazývají síranovzdorné. Určitý význam mají též vysokopecní cementy CEM II/A, B, C, jež jsou však méně používané. Významný vliv mají příměsi, a to zejména elektrárenský popílek, křemičitý úlet a mletý zeolit, které však již náleží k primárním opatřením pro ochranu základových konstrukcí před agresivitou prostředí.
6.3.2 Agresivita uhličitá
Uhličitá agresivita je v porovnání s agresivitou síranovou horší a to zejména z hlediska možností primární ochrany základových konstrukcí z betonu, (cementu), neboť ta svojí podstatou napadá přímo základní vlastnost cementu – schopnost hydratace, tuhnutí a tvrdnutí. Agresivní oxid uhličitý CO2 z vody reaguje na cementovou kaši v betonu tak, že se váže s volným hydroxidem vápenatým Ca(OH)2 a v prvním stadiu vzniká málo rozpustný uhličitan vápenatý:
\begin{gathered}
\text{CO}_2+\text{Ca(OH)}_2\to\text{CaCO}_3+\text{H}_2\text{O}
\end{gathered}Tento proces však pokračuje a působením dalšího agresivního CO2 se mění nerozpustný uhličitan vápenatý na vysoce rozpustný kyselý uhličitan vápenatý Ca(HCO3)2, který se vlivem proudící podzemní vody z betonu vyplavuje a beton se postupně rozpadá na kamenivo, neboť mu ubývá pojivo:
\begin{gathered}
\text{CaCO}_3+\text{CO}_2+\text{H}_2\text{O}\to\text{Ca(HCO}_3)_2
\end{gathered}Je zřejmé, že možnosti primární ochrany proti této agresivitě jsou silně omezené, neboť – jak již bylo uvedeno – tato agresivita napadá samu podstatu cementu jako stavební hmoty. V zásadě jde o návrh speciální receptury betonové směsi s přísadami, (elektrárenský popílek, křemičitý úlet, mleté zeolity a železný prášek, neboť agresivní CO2 se ochotně váže s hydroxidy železa). Jistou možností je i pokus o úpravu chemizmu podzemní vody clonou z vrtů vyplněných vápencovou drtí tak, aby uvedená reakce proběhla na této cloně, a nikoliv v betonu základového prvku. Je zřejmé, že v neproudícím prostředí je tato agresivita méně nebezpečná, neboť nemůže dojít k vyplavování pojiva, a tudíž kolem základového prvku vznikne sice narušený beton, porucha však nepostupuje hlouběji.
6.4 MOŽNOSTI OCHRANY PRVKŮ A KONSTRUKCÍ HLUBINNÝCH ZÁKLADŮ
Hlubinné základy přicházejí do styku s podzemní vodou velice často, neboť právě přítomnost podzemní vody ovlivňuje významně volbu metody zakládání. Co se týče chemizmu této vody a jejího vlivu na životnost základových konstrukcí, hodnotí se podle platné ČSN EN 206+A2 (tab. 21), neboť hlubinné základy jsou vesměs tvořeny betonem, železobetonem, nebo cementovou maltou či suspenzí, přičemž pro všechny tyto stavební materiály je toto hodnocení adekvátní. Pokud by se jednalo o speciální kontaminaci látkami, jež nejsou obvyklé, a tudíž nejsou a tab. 21 obsaženy, je třeba postupovat individuálně a problém konzultovat s odborníky na stavební chemii.
Je tedy zřejmé, že rozhodující je posouzení vlivu agresivního prostředí na beton a podobné hmoty, jež jsou založeny na hydrataci základního pojiva – cementu. Navíc prvky a konstrukce speciálního zakládání staveb díky technologickým požadavkům na jejich realizaci mají rovněž specifické požadavky na vlastnosti betonů, které se často významně liší od požadavků na beton nadzemních konstrukcí betonovaných vesměs do bednění, kde je beton zpracováván klasickým způsobem, zejména vibrací. To je ostatně důvod pro určitou kritiku normy EN 206+A2, neboť ta se samozřejmě týká zejména těchto betonů, (z hlediska objemů výroby) a nikoliv speciálně betonů pro hlubinné základy. Jelikož je tato problematika vážná, připravuje se dodatek k uvedené normě EN 206+A2, jež bude řešit právě příslušná specifika betonů pro prvky a konstrukce speciálního zakládání staveb.
Opatření na ochranu hlubinných základů před účinky agresivního prostředí, (zejména podzemní vody) lze rozdělit do dvou skupin:
- primární ochrana, jež spočívá zejména v návrhu či úpravě receptury betonu, v návrhu přísad a konzistence betonu, v úpravě technologie provádění příslušné konstrukce, v konstrukčních úpravách příslušného základového prvku a ve snaze o úpravu chemizmu podzemní vody;
- sekundární ochrana, jež spočívá ve významném omezení, či zábraně styku agresivní podzemní vody s prvkem či konstrukcí hlubinného zakládání staveb.
6.4.1 Požadavky na beton hlubinných základů
Jde zejména o hlubinné základy na místě betonované, což v našich podmínkách představují vrtané piloty a podzemní stěny, nebo jejich lamely. Ražené, na místě betonované piloty, (typu Franki), mají díky speciální technologii výroby podstatně odlišné požadavky na beton, který se ostatně vesměs vyrábí na staveništi a nejedná se tudíž o klasický transportbeton, pro nějž právě platí zmiňovaná EN 206+A2. Beton Franki pilot je, pokud se nejedná o případ nedostatečné hydratace, vesměs podstatně odolnější vůči agresivnímu prostředí a to jak z hlediska síranové, či uhličité agresivity a to zejména díky svému „absolutnímu“ zpracování ražením, neboť výsledný beton je, resp. měl by být prakticky nepropustný.
Norma ČSN EN 206+A2 udává doporučené mezní hodnoty pro složení a vlastnosti betonu na základě stupňů vlivu prostředí. Výňatek z této tabulky týkající se chemicky agresivního prostředí je v tab. 25. Z ní je např. patrné, že v případě nízké a střední agresivity (XA1, XA2) je minimální pevnostní třída betonu C30/37 a v případě vysoké agresivity (XA3) pak dokonce C35/45. Současně je udán i maximální vodní součinitel v/c, jež postupně klesá z 0,55 na 0,45 a minimální obsah cementu, jež je však podstatně nižší než obsah, jež udávají příslušné prováděcí normy ČSN EN 1536+A1: Provádění speciálních geotechnických prací – Vrtané piloty a ČSN EN 1538+A1: Provádění speciálních geotechnických prací – Podzemní stěny. Tyto obě normy jsou samozřejmě z hlediska návrhu recepturu betonu pro piloty a podzemní stěny nadřazeny uvedené normě EN 206+A2 a jsou pro obsah cementu, resp. jemných částí závazné. Toto množství se potom, bez ohledu na výslednou pevnostní třídu betonu řídí zejména technologií betonáže a to:
- v případě vrtaných pilot, (výjimečně i lamel podzemních stěn) betonovaných do sucha je to nejméně 325 kg/m3, konzistence je S3 nebo S4;
- v případě vrtaných pilot s lamel podzemních stěn betonovaných pod vodu nebo pod pažicí suspenzi je to nejméně 375 kg/m3, konzistence je S4 nebo S5;
- v případě podzemních stěn je to nejméně 400 kg/m3 cementu a konzistence S4, S5, neboť ty se vždy betonují pod pažicí suspenzi.
Obě speciální normy, (EN 1536+A1 a EN 1538+A1) předepisují rovněž max. zrno použitého kameniva, jež nesmí být větší než 32 mm, resp. ¼ světlé vzdálenosti mezi výztužnými pruty v železobetonovém průřezu.
Tab. 25 Doporučené mezní hodnoty pro složení a vlastnosti betonu v chemicky agresivním prostředí
| Stupeň vlivu prostředí – chemicky agresivní prostředí | |||
| Vlastnost betonu, požadavek na složení | XA1 | XA2 | XA3 |
| Maximální vodní součinitel v/c | 0,55 | 0,50 | 0,45 |
| Minimální pevnostní třída | C30/37 | C30/37 | C35/45 |
| Minimální obsah cementu [kg·m-3] | 300 | 320 | 360 |
| Jiné požadavky | síranovzdorný cement x) | ||
| x) Pokud je stupeň vlivu prostředí XA2, XA3 vyvolán síranovou agresivitou (SO42-), je nutné použít síranovzdorný cement. Je-li cement klasifikován s ohledem na síranovzdornost, potom pro prostředí XA2 (a případně i pro XA1) se použije mírně nebo vysoce síranovzdorný cement, pro prostředí XA3 potom pouze vysoce síranovzdorný cement | |||
Z tab. 25 a požadavků na beton prvků speciálního zakládání staveb vyplývá, že se tento beton dosti liší od výroby betonu na běžné betonárce a ta tedy musí svoji výrobu pro betonáž prvků speciálního zakládání staveb příslušně přizpůsobit. Jaké jsou tedy rozhodující technologické požadavky na beton speciálních základů:
- beton musí být především dobře zpracovatelný, a to bez jakéhokoliv použití vibrace, propichování či jiných metod, jež jsou výslovně zakázány; ukládání betonu litím sypákovými rourami, popř. čerpáním betonážním čerpadlem vyžaduje konzistenci S4–S5, resp. dokonce F4–F5;
- beton musí být dostatečně homogenní, nesmí se roztřiďovat, nesmí v něm po jeho uložení sedat větší kamenivo a nesmí se roztřiďovat;
- beton musí být samozhutnitelný;
- beton musí být po dostatečně dlouhou dobu mobilní, tzn., že počátek tuhnutí musí být oddálen a to nejméně na 4 hodiny, popř. i více, neboť zejména dlouhé vrtané piloty, (30–40 i více metrů) a rozsáhlé lamely podzemních stěn se betonují 4–6 hodin.
Uvedených vlastností betonu lze dosáhnout speciálním složením betonu a rozumným nakládáním s požadavkem na pevnostní třídu betonu. Je třeba uvědomit si, že požadavek pevnostní třídy v příslušné tabulce ČSN EN 206+A2 byl dán spíše snahou o příslušnou vodotěsnost, jež se dnes již speciálně neudává a je vázána na příslušnou třídu betonu. Na straně druhé však výsledná pevnost betonu daná jeho třídou C30/37, resp. C35/45 není ve skutečnosti požadována z hlediska statického působení těchto základových prvků, resp. je z hlediska statického výpočtu zcela přehnaná a irelevantní. Současně pak i požadavek na rychlý náběh této pevnosti, (28 – denní pevnost) je v případě speciálních základů vesměs přehnaný a zbytečný. Výsledkem jistých kompromisů mezi požadavky normy ČSN EN 206+A2 a skutečnými požadavky na technologii provádění speciálních základů jsou tzv. samozhutnitelné betony, (SCC) s přísadou polykarboxylátových plastifikátorů. Ty jsou ovšem stále ve vývoji a při jejich návrhu je třeba postupovat opatrně. V současné době se používají tzv. snadnozhutnitelné betony, (SHB), jež jsou jistým vývojovým stádiem betonů SCC. Jsou rovněž velmi citlivé na množství záměsové a technologické vody, jejíž nadbytečný objem má za následek segregaci kameniva se všemi nepříjemnými důsledky spočívajícími v prokazování kvality výsledného betonu. Značně také pomáhá redukce požadavku na nárůst výsledné pevnosti betonu, kdy se výsledná pevnost požaduje nikoliv po 28 dnech, ale po 90 dnech.
6.4.2 Primární ochrana
Primární ochrana betonu hlubinných základů spočívá zejména v návrhu či úpravě receptury betonu, v návrhu přísad a konzistence betonu, v úpravě technologie provádění příslušné konstrukce, v konstrukčních úpravách příslušného základového prvku a ve snaze o úpravu chemizmu podzemní vody. Přísady do betonu zmírňující vliv agresivity podzemní vody jsou:
- elektrárenský popílek, jež váže volný hydroxid vápenatý, jež se uvolňuje při hydrataci cementu a vytvářejí se tak odolnější a stabilnější sloučeniny;
- vysokopecní struska jemně mletá, zásaditá, jež je součástí směsných cementů CEM II/A-S, CEM II/B-S a jež tvoří až 95 % obsahu ve vysokopecních cementech CEM III/A, CEM III/B a CEM III/C;
- křemičitý úlet s vysokým obsahem amorfního oxidu křemičitého s extrémně malými částicemi, (0,1–0,2 mm) a ohromným měrným povrchem, (1,5 – 3,0) · 104 m2/kg;
- mletý zeolit, což je pucolánová příměs zvyšující významně odolnost cementového kamene;
- železité příměsi ve formě jednak litinových pilin, jednak železných prášků, jež ochraňují cementový kámen zejména před stykem s kyselým prostředím tím, že vytvářejí koloidní gelové kalciumferohydráty, jež jsou chemicky odolné;
- provzdušňovací přísady, jež v betonu, (cementovém kameni) vytvářejí velké množství vzájemně oddělených a rovnoměrně rozptýlených pórů o velikosti 50–200 mm; tím že nejsou vzájemně propojeny ruší se efekt kapilárního sání betonu, což výrazně zmenšuje možnost pohybu agresivní vody betonovým prvkem;
- plastifikační přísady, jejichž hlavní význam spočívá v možnosti snížení vodního součinitele betonu při zachování požadované zpracovatelnosti.
Elektrárenský popílek je tím kvalitnější, čím je jemnější, (např. z elektrostatických odlučovačů). Současně by neměl obsahovat více než 5 % spalitelných látek. Má se používat jako příměs zejména do portlandských cementů v množství do 30 % množství cementu. Významný je zejména z hlediska síranové agresivity.
Vysokopecní struska je rovněž použitelná zejména z hlediska síranové agresivity, kdy zvyšuje odolnost betonu až trojnásobně.
Křemičitý úlet je velmi významným pomocníkem jak při síranové agresivitě, tak zejména při agresivitě tvořené chloridem hořečnatým. S ohledem na velký měrný povrch vyžaduje vyšší dávkování vody a rovněž použití superplastifikátorů. Jeho cena ovšem výrazně překračuje cenu cementu, a proto se používá zejména pro přípravu cementových suspenzí, (pro mikropiloty, kotvy apod.).
Mletý zeolit je perspektivní přísada jak pro ochranu proti síranové agresivitě, tak i zčásti proti agresivitě uhličité. Jeho cena je zhruba srovnatelná s cenou cementu a mletý zeolit se rovněž používá zejména pro přípravu suspenzí. Rozsáhlé jeho použití je známé např. při přípravě samotvrdnoucí suspenze do těsnicích podzemních stěn, jež utěsnily skládku nebezpečného chemického odpadu u Spolany Neratovice.
Železné příměsi, (piliny i prášek) jsou rovněž velmi účinnou přísadou v případě jak síranové, tak zejména uhličité agresivity. Jejich chemické působení je známé, hlavní problém jejich využití je však technologický. Jde o to docílit jejich dostatečné a zejména rovnoměrné rozptýlení v cementovém kameni, nebo v betonu, což s ohledem na jejich měrnou hmotnost, (převyšující cca 2–3 x hmotnost ostatních agregátů) je problematické, zvláště při použití litinových pilin. Přesto byla tato přísada několikrát použita, příkladem jsou třeba základové mikropiloty použité při stavbě nové lanovky na Petřín, (rok 1975).
Pokud byla na staveništi zjištěna nízká síranová agresivita XA1, doporučuje se používat pro přípravu betonu směsných cementů, (CEM II), popř. přísady jako elektrárenský popílek a jemně mletá vysokopecní struska. V případě síranové agresivity střední XA2 je doporučeno již použití síranovzdorných cementů. Pokud se jedná o vysokou síranovou agresivitu XA3 je nutný síranovzdorný cement a přísady jako křemičitý úlet a mletý zeolit. V případě nízké agresivity uhličité jsou to směsné cementy a mletý zeolit, při střední uhličité agresivitě pak navíc železité příměsi a v případě vysoké uhličité agresivity je již doporučena sekundární ochrana, je-li vůbec reálná.
Zvláštní způsob primární ochrany spočívá ve vytváření clon, jejichž cílem má být úprava chemizmu podzemní vody před jejím stykem se základovou konstrukcí. Jde zejména o případy uhličité agresivity, kdy kolem základů je vytvořena clona z vrtů vyplněných vápencovou nebo dolomitovou drtí. Ta má obsahovat alespoň 80 % CaCO3 + MgCO3. Účinnost této metody, jež byla použita např. při zakládání několika mostů v Ostravě, je třeba kontrolovat odběry vzorků podzemní vody před a za clonou.
6.4.3 Sekundární ochrana
Účelem sekundární ochrany je zabránění styku agresivní podzemní vody se základovým prvkem či konstrukcí. Jde tedy v podstatě o izolaci základového prvku vhodným obalem. Je zřejmé, že metody této ochrany a zejména její možnosti se budou významně lišit podle druhů základových prvků speciálního zakládání staveb. Návrh sekundární ochrany je reálný v případě pilot, a to jak ražených, tak i vrtaných. Sekundární ochrana není reálná v případě podzemních stěn. Možnosti sekundární ochrany v případě mikropilot jsou silně omezené. V případě kotev je sekundární ochrana v podstatě součástí všech trvalých kotev. Hřebíky se obyčejně nepoužívají jako konstrukce trvalé, tudíž potřeba sekundární ochrany není aktuální. Pokud by tento požadavek nastal, jde o případ analogický s trvalými kotvami. Sloupy a lamely tryskové injektáže, popř. klasickou injektáž pochopitelně nelze opatřit sekundární ochranou.
Nejvýznamnější uplatnění sekundární ochrany je tedy v případě pilot, zvláště vrtaných, jež – jak již bylo několikrát zmíněno – jsou nejrozšířenějšími prvky speciálního zakládání staveb. Sekundární ochrana prošla v případě těchto prvků rozsáhlým vývojem, který lze dokumentovat na příkladu rozsáhlého staveniště FN v Hradci Králové. Tento areál se nachází pod soutokem Labe s Orlicí v široké údolní nivě, kde skalní podloží v hl. kolem 11,0 m pod terénem je tvořeno křídovými slínovci svrchu na hl. asi 1,0 m zvětralými, (R5/R6), níže pak navětralými (R4). Nadloží je tvořeno mohutnou terasou tvořenou štěrky a písky o mocnosti 8–9 m s poříční podzemní vodou v hloubce kolem 2,5–3,0 m pod terénem. Nadloží tvoří pak povodňové hlíny písčité, zbytky navážky a humózní hlíny. Pleistocenní terasa ovšem obsahuje vrstvy, resp. čočky tzv. hnilokalů, což jsou zbytky původních slepých ramen Labe a Orlice, kde vlivem rozkladu humózních sedimentů pohřbených v okolní základové půdě vzniká CO2, jež sytí okolní podzemní vodu a způsobuje tak její uhličitou agresivitu jež kolísá od cca 25 do 65 mg CO2 agresivního na Ca (na litr vody).
V areálu této nemocnice byla kolem roku 1972 plánována výstavba chirurgického bloku, což byl osmipodlažní ocelový skelet s podzemním podlažím pod hladinou podzemní vody, jež byl založen hlubinně na vrtaných pilotách, resp. jejich skupinách spojených v hlavách základovými patkami pro 2, 3 a 4 piloty. Ty byly na základě znaleckého posudku Stavebního ústavu ČVUT v Praze opatřeny sekundární ochranou spočívající v ponechání ocelové roury profilu 820 mm obalené dehtovanou jutou a zasahující do nepropustného podloží. Pata piloty byla potom vetknuta na délku asi 1,5 m do nepropustných slínovců – bez ochrany. Detail této úpravy včetně kotvení sloupů ocelové konstrukce je na obr. 112.
Obr. 112 Detail kotvení sloupů OK a návaznost pilot na izolovanou desku: 1 – monolitická deska, 2, 4 – betonová mazanina, 3, 5 – izolace, 6 – podkladní beton, 7 – štěrkový podsyp
Na základě výsledků statických zatěžovacích zkoušek pilot opatřených touto izolací bylo zjištěno, že došlo k redukci tření na plášti o 70 % ve srovnání s neizolovanými pilotami, což je pochopitelně další cenový dopad této sekundární ochrany.
Ocelové roury opatřené další povlakovou izolací představují pochopitelně nejdokonalejší sekundární ochranu, jsou však mimořádně drahé, a tudíž v dnešní době již prakticky nepoužitelnéx). V 80. letech bylo potom v areálu této nemocnice zakládáno několik dalších objektů, (ubytovna sester, laboratoř apod.), kdy bylo rovněž nutné využít sekundární ochranu. Navržena byla povlaková izolace z fólie PVC, jež je pochopitelně cenově dostupná. Při provádění vrtů pro piloty skrz zvodnělé štěrky bylo nutné pažit. Použilo se ocelových spojovatelných pažnic a armokoš pilot byl opatřen „pytlem“ bez dna z fólie PVC tloušťky 1,1 mm. Po vybetonování piloty a vytažení pažnic ovšem došlo k „svléknutí“ fólie PVC a zničení této ochrany. Mechanizmus tohoto jevu je jasný – vlivem tlaku čerstvého betonu dojde k přitisknutí fólie k vnitřní stěně pažnice a následnému vytažení. Po několika pokusech bylo zřejmé, že k zabránění tohoto jevu by bylo nutné naplnit pažnici betonem pouze na výšku h = d / (2 · f), kde f je koeficient tření mezi fólií a stěnou pažnice, jehož konkrétní velikost závisí zejména na drsnosti pažnice, (jejím znečištění betonem apod.) a pohybuje se kolem 0,3–0,5.
Betonáž pilot touto technologií by tedy byla natolik náročná, že není prakticky použitelná. Je-li nutné dřík piloty zapažené ocelovou pažnicí opatřit ochrannou fólií s PVC, (PE), obalí se armokoš piloty nejprve pletivem B-systému, (pletivo z drátu 1,25 mm s oky 4/4 až 5/5 mm) a přes toto pletivo se navlékne fólie svařená do válce, (bez dna) a upevní se vhodnými úvazky a jako celek se zapustí do vrtu. Po betonáží je odpažení možné bez poškození fólie, neboť B-systém zabrání protečení většího množství betonu a tím přitisknutí fólie ke stěně vrtu. Dochází však také k redukci tření na plášti pilot asi o 40 % v závislosti na druhu základové půdy.
Konečně koncem 90. let byl v areálu FN v Hradci Králové zakládán onkologický pavilon, kde byla využita sekundární ochrana pilot spočívající ve zvětšení staticky nutného průměru pilot o 200 mm, příslušného zvětšení krytí výztuže a použití superplastifikovaného betonu se sníženým vodním součinitelem. Byl použit směsný cement, (typu CEM II/B-S) v množství 400 kg/m3 a v / c = 0,50.
Fólie, jakožto sekundární ochrana vrtaných pilot se však používá i nadále. V případě nepažených vrtů bylo při výstavbě panelových domů na sídlišti Lhotka-Libuš použito tenké fólie tl. 0,15–0,20 mm tak, že pytel bez dna byl shozen do vrtu a jeho okraj byl u ohlubně vrtu provizorně upevněn. Betonováno bylo usměrňovací rourou přímo do tohoto pytle a po vybetonování byla hlava opatřena zapíchanou spojovací výztuží. Redukce plášťového tření byla v tomto případě zanedbatelná, (10–20 %). Otázkou ovšem zůstává o jak účinnou ochranu se ve skutečnosti jednalo, neboť kontrola její neporušenosti nebyla žádná.
Pro zamezení výše popsaného nepříznivého efektu tření mezi fólií a pažnicí bylo při zakládání mostu v Prostějově použito pažení vrtů pomocí pažicí suspenze. Při následné betonáži do vrtů opatřených fólií PVC nedošlo k setření filtračního koláče a únosnost pilot na plášti byla tudíž nepatrná. Je tedy zřejmé, že se nejedná o správný technologický postup. Následná rekonstrukce těchto pilot byla mimořádně náročná.
Sekundární ochrana ražených pilot je reálná, i když obtížná. Jak bylo popsáno ve skriptech Zakládání staveb 1, v ČR přicházejí v úvahu prakticky pouze piloty typu Franki, na nichž byla technologie sekundární ochrany pomocí fólie PVC již odzkoušena. Po vyformování paty, kterou pochopitelně nelze chránit se osadí armokoš s navlečenou fólií tl. nejméně 1,1 mm. Dochází k pozvolnému plnění betonem a pozvolnému povytahování pažnice, což je případ analogický s případem již výše popsaným. Pochopitelně možnost hutnění dříku je omezena. Na druhou stranu je třeba uvědomit si, že beton pilot Franki je natolik zhutněný, že je prakticky nepropustný, a tudíž i vysoce odolný, zvláště počítáme-li se zvětšeným krytím.
poznámka:
x) Podobné konstrukce bylo však použito též při zakládání železniční estakády v Jirkově u Chomutova v roce 1978 rovněž v prostředí se silně agresivní podzemní vodou v uhelných slojích.
V případě trubních mikropilot je návrh sekundární ochrany problematický a komplikovaný, a to zejména štíhlostí těchto prvků a obecným nedostatek tloušťky ochranné vrstvy. Norma ČSN EN 14199 udává sice požadavky na minimální krytí nosné výztuže ve vztahu k agresivnímu prostředí, jedná se však o nezaručené hodnoty. V zásadě jde o to, že vlastní výztužnou trubku sice lze chránit dostatečně např. ochrannými nátěry i povlakem, (např. Epoxydehtem), přesto ovšem styk s agresivním prostředím jde přes zálivku, (a injektáž), kterou lze chránit pouze primárně příslušnými přísadami. Je zřejmé, že pro vysoce agresivní prostředí se mikropiloty jakožto základové prvky nehodí.
7 ZLEPŠOVÁNÍ VLASTNOSTÍ ZÁKLADOVÉ PŮDY
Hlavními důvody pro zlepšování základových půd jsou:
- redukce deformací základové půdy, (absolutní, relativní a sedání v čase – primární konsolidace);
- zvýšení únosnosti základové půdy, (plošné – homogenizace, bodové – analogie s hlubinnými základy);
- snížení propustnosti základové půdy;
- změna dynamické odezvy;
- snížení rizika vyplavování jemných částic, (sufoze).
Při zakládání staveb však absolutně převládá první jmenovaný důvod. V zásadě lze hlavní způsoby zlepšování vlastností základových půd pro účely zakládání staveb rozdělit následovně:
- A. Výměna základové půdy:
- a) podsypy;
- b) plomby;
- c) štěrkové polštáře;
- B. Hloubkové hutnění:
- a) hloubková vibrace, (vibroflotace);
- b) použití trhavin;
- c) dynamická konsolidace;
- d) zhutňování pomocí pilot typu displacement;
- C. Předkonzolidace:
- a) předběžbé předtížení;
- aa) násypem;
- ab) vodními nádržemi;
- ac) pod tlakem, (vakuace);
- b) svislé drenáže;
- ba) pískové, (a štěrkové);
- bb) pásové, (svislé drény, geodrény);
- c) elektroosmóza;
- a) předběžbé předtížení;
- D. Injektování:
- a) injektáže silikátovými suspenzemi;
- b) injektáže chemické;
- c) trysková injektáž;
- E. Stabilizace základových půd:
- a) hloubková stabilizace;
- aa)vmíchávané pilíře vápenné a cementové;
- b) plošná stabilizace;
- ba) stabilizované násypy;
- bb) zásypy stabilizovanou zeminou;
- c) termální stabilizace;
- ca) zmrazování zemin;
- cb) vypalování zemin;
- a) hloubková stabilizace;
- F. Vytužování zemin:
- a) štěrkové pilíře;
- b) geotextilie;
- c) geosyntetiky.
V rámci této kapitoly se nebudeme zabývat klasickým zhutňováním zemin využívaným zejména při stavbě násypů a úpravě podloží v silničním a železničním stavitelství, jakož i některými speciálními metodami, které nemají v ČR praktické využití, nebo jsou uplatněny velmi sporadicky, (termální stabilizace, elektroosmóza, některými druhy předkonzolidace). Rovněž se nebudeme zabývat metodami vyztužováním zemin pomocí geotextilií a geosyntetik, neboť se jedná o kapitolu značně obsáhlou a odkazujeme zde na příslušnou literaturu, zejména firemní. Naopak některé metody související s injektováním zemin byly již uvedeny v TP 1.9.5 Navrhování základových konstrukcí.
Pokud hovoříme o zlepšování vlastností základových půd, máme na mysli většinou zeminy, neboť v případě hornin obyčejně není třeba zlepšení realizovat; (výjimkou je injektáž za účelem snížení propustnosti). Základní metody zlepšování vlastností zemin jsou potom uvedeny v tab. 26.
Tab. 26 Základní metody zlepšování základových půd tvořených zeminami
| Způsob zlepšení | Zeminy soudržné | Zeminy nesoudržné |
| hutnění | statické zatížení s urychlením nebo bez urychlení konsolidace | dynamické hloubkové zhutňování (vibroflotace) |
| hnjektáž stabilizace | stabilizace, chemické nebo termické úpravy | injektáž klasická injektáž trysková |
| vyztužování | štěrkové pilíře vápenné pilíře | vyztužená zemina |
7.1 ŠTĚRKOVÉ POLŠTÁŘE
Účelem návrhu štěrkových polštářů je náhrada nevhodné zeminy pod celým rozsahem příslušného plošného základu. Za nevhodnou zeminu pokládáme zejména zeminu stlačitelnou s nepříznivými deformačními vlastnostmi, jde tedy vesměs o snížení velikosti sedání. Výjimečně na zcela neúnosných zeminách jde též o zvýšení únosnosti v základové spáře. Štěrkové polštáře se budují zejména pod základovými patkami a základovými pasy nad hladinou podzemní vody. Jejich tloušťka může dosahovat i několik metrů, ukazuje se však, že ekonomické jsou při tloušťce do 1,5–2,0 m. Štěrkové polštáře se nebudují pod základovými deskami, zde se nahrazují plošně stabilizovanou zeminou. Tloušťka polštáře se volí obyčejně tak, aby napětí na styku polštáře s původní zeminou nepřekročilo její návrhovou únosnost, (při započtení tíhy polštáře). Vlastní plošný základ se pak navrhuje pro stabilitní parametry materiálu štěrkového polštáře a to vždy, je-li jeho tloušťka rovna alespoň 1/3 šířky základu. Šířka polštáře se volí s ohledem na předpokládaný úhel roznosu b = 30°, tedy:
\begin{gathered}
B_\text{p}=B+2\cdot h_\text{p}\cdot\tg\beta\cong B+1{,}15\cdot h_\text{p}
\end{gathered}(125)
kde je:
Bp … šířka polštáře;
B … šířka plošného základu;
hp … tloušťka polštáře.
Výpočtem je třeba zkontrolovat, zda napětí na styku štěrkový polštář – původní základová půda je v přípustných mezích, tzn., nepřesahuje návrhovou únosnost původní základové půdy. Rozhodující však bývá posouzení sedání, při němž se výrazně projeví vysoký modul deformace, (resp. oedometrický modul) materiálu zhutněného polštáře.
Jak již název napovídá, roznášecí polštáře se budují ze štěrku a písku, přičemž rozhodující je vhodná křivka zrnitosti, jež musí být plynulá. Štěrk a písek by tedy měl obsahovat jisté množství jemnozrnných zemin, jejich max. obsah by měl být:
- do 15 % v hrubozrnných štěrcích;
- do 10 % ve štěrcích s příměsí písku;
- do 8 % v píscích.
Štěrkové polštáře se budují tak, že do připraveného výkopu se sype vhodný materiál, který se urovnává a hutní ve vrstvách tloušťky podle použitého hutnícího prostředku. Vhodné jsou malé a střední vibrační válce, kde tloušťka vrstvy by neměla přesáhnout 0,2–0,3 m. Efektivní bývá dynamické hutnění pomocí úderů železobetonové desky rozměrů asi 1,2 x 1,2 m o hmotnosti kolem 2,0 t, jež padá volným pádem z výšky 3–4 m.
Kvalitu zhutněného štěrkového polštáře je třeba před stavbou plošných základů ověřit. K tomu účelu se využívá statické zatěžovací zkoušky tuhou, (ocelovou) deskou o ploše 1 000 cm2 (průměru 0,357 m), která se zatláčí statickou silou, (obyčejně proti nápravě zemích stroje, nákladního auta apod.) a měří se deformace podloží. K vyhodnocení se využívá tzv. upraveného Schleicherova vzorce popodle původní ČSN 73 6190: Statická zatěžovací zkouška podloží a podkladních vrstev vozovek podle rovnice:
\begin{gathered}
E_0=\frac{\pi}{2}\cdot(1-\mu^2)\cdot p\cdot\frac{r}{f_\text{tot}}
\end{gathered}(126)
kde je:
μ … Poissonovo číslo zkoušeného prostředí x);
p … tlak zatěžovací desky na zeminu, jež pro zkoušky podloží vozovek činí 0,05–0,35 MPa, pro zkoušku základové půdy může dosahovat až 1,0 MPa;
r … poloměr zatěžovací desky (0,1785 m);
ftot … průměrné celkové zatlačení desky při příslušném tlaku p.
- x) Doporučené velikosti Poissonova čísla μ jsou:
- štěrky a balvanité štěrky – μ = 0,15
- písky – 0,20
- písky hlinité – 0,25
- hlíny písčité a prachovité – 0,30–0,35
- jíl s malou až střední plasticitou – 0,35 – 0,37
- jíl s vysokou plasticitou – 0,40
Výsledný modul deformace by neměl být menší než 60 MPa, výjimkou nejsou dosažené moduly deformace 100–200 MPa.
Výjimečně se k dosažení rovnoměrného sedání rozsáhlých objektů využívá tzv. vyrovnávacích polštářů, když část objektu se nachází v prostředí velmi únosných a prakticky nestlačitelných základových půd, (hornin) a zbylá část objektu naopak v prostředí stlačitelných zemin (obr. 113a). Jde tedy v podstatě o obrácený úkol, kdy je třeba zabezpečit jisté sedání základů na nestlačitelných horninách, jež by odpovídalo sedání na stlačitelné základové půdě.
Horniny se tedy na jistou hloubku odstraní a nahradí vyrovnávacím polštářem tvořeným většinou hlinitým pískem (obr. 113b). Tloušťku stlačitelného polštáře h lze určit analogicky k oedometrické zkoušce zeminy tvořené vyrovnávacím polštářem, neboť sedání s vrstvy zeminy h bude přímo úměrné sedání szk vrstvy zeminy při oedometrické zkoušce hzk.
Při oedometrické zkoušce zatížíme zeminu napětím szk = sd, (provozním napětím odpovídajícím kontaktnímu napětí pod plošným základem) a stanovíme oedometrický modul:
\begin{gathered}
E_\text{oed}=\sigma_\text{zk}\cdot\frac{h_\text{zk}}{s_\text{zk}}
\end{gathered}(127)
Potřebnou tloušťku vyrovnávacího polštáře lze pro zvolené sedání s vypočítat ze vztahu:
\begin{gathered}
h=E_\text{oed}\cdot\frac{s}{\sigma_\text{d}}
\end{gathered}(128)
Obr. 113 Schéma použití vyrovnávacího polštáře (podle Turčeka): a) před úpravou, b) po úpravě
7.2 HUTNĚNÍ A DYNAMICKÁ KONSOLIDACE
Účelem zhutňování je úprava vlastností zemin v přirozeném uložení, nebo sypaných materiálů při budování zemních konstrukcí. Při hutnění dochází ke zvýšení smykové pevnosti zemin, zvýšení deformačních modulů, (snížení stlačitelnosti) a snížení propustnosti, (snížení velikosti koeficientu filtrace). Pomineme-li problematiku silničního a železničního stavitelství, jakož i budování hrází a sypaných přehrad ve vodním stavitelství, kde technologie hutnění hrají spolu s výběrem vhodného materiálu rozhodující roli, potom v zakládání staveb se hutnění uplatňuje zejména při úpravě základové spáry pod plošnými základy, (hlavně pod rozsáhlými základovými deskami) a pod zatíženými podlahami, (např. skladových a výrobních objektů). Účinnost zhutňování závisí na použitých zhutňovacích prostředcích a na volbě technologie zhutňování. Účinné formy zhutňování jsou:
a) pro hrubozrnné zeminy:
- přitížení (násypem);
- válcování vibračními válci;
- ubíjení;
- dynamická konsolidace;
- hloubková vibrace (vibroflotace).
b) pro jemnozrnné zeminy:
- přitížení násypem;
- válcování;
- dynamická konsolidace;
- štěrkové pilíře.
Přitížení, a to zvláště násypem je jedna z nejstarších metod zhutňování, které probíhá přirozeným způsobem působením, (statického) napětí v základové půdě. Jeho výhodou je relativně dokonalé a rovnoměrné zhutnění, nevýhodou je doba potřebná ke konsolidaci a cena vyplývající z potřeby značných zemních prací. V dnešní době má jen omezené uplatnění, např. při budování silničních násypů na nevhodné základové půdě, (dálnice D8 v oblasti severočeských výsypek hnědouhelných dolů), v zakládání staveb se neuplatňuje vůbec. Součástí této metody je budování drénů za účelem rychlejšího vyrovnávání pórových tlaků, a to v zeminách jemnozrnných. Princip přitěžování základové půdy násypem je patrný z obr. 114. Budování projektovaného násypu je znázorněno čarou 1. Sedání základové půdy pod tímto násypem je dáno čarou 3, přičemž je zřetelné, že sedání pokračuje relativně plynule až do výsledného času t100, tedy doby potřebné k dokonalé primární konsolidaci. Pokud využijeme nadnásypu 2, (přitížení nadnásypem) po dobu ts, bude sedání podloží dáno křivkou 4. Je zřejmé, že po odstranění nadnásypu již nedojde k dalšímu sedání podloží. Obrázek současně ukazuje, po jak dlouhou dobu je třeba s nadnásypem uvažovat: ta je dána sedáním, jež musí být větší než sedání vypočtené bez přitížení nadnásypem.
Obr. 114 Sedání násypu v čase: 1 – násyp, 2 – nadnásyp, 3 – sedání násypu, 4 – sedání násypu s nadnásypem
Zhutňování základové půdy válcováním je základní metodou vhodnou jak pro zeminy hrubozrnné, u nichž se využívá kombinace válcování s vibrováním, tak pro zeminy jemnozrnné, kde se válcuje bez vibrací. Válcování je vhodné v případě větších ploch, (pod základovými deskami, pod podlahami apod.). V případě základových pasů či patek nelze obyčejně použít výkonnou techniku a musíme se spokojit s malou mechanizací, jež je obyčejně méně účinná a vyžaduje speciální technologii. Válcování současně nelze použít v těsné blízkosti staveb, neboť by mohlo způsobit jejich poruchy.
Válcovací stroje jsou v zásadě dvojího typu: tažené a samohybné. Podle účinků se dělí na statické a vibrační, u nichž je statický účinek násoben přídavnou vibrací. Vlastní povrch válců je hladký, ježkový, mřížový a pneumatikový. Hmotnost válců se pohybuje od 2,0 do 12,0 t, (v případě pneumatikových až 50 t) a na ní zejména závisí účinek zhutňování co se týče hloubky. Na základě následujících empirických vztahů lze stanovit optimální tloušťku zhutňované vrstvy h0 [m] podle použitých válců:
- pro jemnozrnné zeminy:
\begin{gathered}
h_0=0{,}028\cdot(G\cdot\frac{r}{b})^\frac{1}{2}
\end{gathered}(129)
- pro nesoudržné zeminy:
\begin{gathered}
h_0=0{,}038\cdot(G\cdot\frac{r}{b})^\frac{1}{2}
\end{gathered}(130)
kde je:
G … tíha válce [kN];
r … poloměr válce [m];
b … šířka válce [m}.
Počet pojezdů válce pro zhutnění příslušné vrstvy tloušťky h0 bývá v jemnozrnných zeminách 9–16, v hrubozrnných zeminách pak 7–10. V případě vibračních válců se počet pojezdů snižuje asi o 30–40 % a účinnost z hlediska tloušťky zhutňované vrstvy se zvyšuje až o 50 %. Základní parametry některých typických válců jsou v tab. 27.
Tab. 27 Základní parametry zhutňovacích válců
| Typ válce | Šířka [m] | Počet pojezdů | Výška h0 [m] | Vhodnost pro zeminy |
| hladký dvouválec 2,8 t | 1,30 | 8 | 0,13 | většina zemin |
| hladký dvouválec 8,0 t | 1,78 | 4 | 0,15 | -„- |
| mřížový válec 13,5 t | 1,60 | 7 | 0,20 | -„- |
| pneumatikový válec 4,6 t | 2,36 | 3 | 0,15 | -„- |
| pneumatikový válec 12,0 t | 2,08 | 4 | 0,20 | -„- |
| vibrační válec 0,20 t | 0,61 | 8 | 0,08 | hrubozrnné |
| vibrační válec 0,35 t | 0,71 | 12 | 0,15 | -„- |
| vibrační dvouválec 1,7 t | 0,84 | 4 | 0,11 | -„- |
| vibrační válec 8,5 t | 1,91 | 4 | 0,30 | -„- |
| vibrační válec 12,0 t | 2,08 | 3 | 0,30 | -„- |
| vibrační tandemový válec 3,8 t | 0,99 | 4 | 0,18 | většina zemin kromě stejnozrnných písků |
V omezených prostorech, v blízkosti objektů a pro zpětné zásypy rýh apod. se používá ručních mechanických pěchovadel, (žab), které působí převážně dynamickými účinky, (v případě dieselového pohonu), resp. vibračními účinky, (v případě elektrického pohonu). Některé používané typy pěchovadel jsou uvedeny v tab. 28.
Tab. 28 Základní parametry pěchovade
| Typ pěchovadla | Šířka, plocha | Počet pojezdů | Výška h0 [m] | Vhodnost pro zeminy |
| vibrační deska 200 kg | 0,38 m | 3 | 0,15 | hrubozrnné |
| vibrační deska 450 kg | 0,61 m | 8–12 | 0,15 | -„- |
| vibrační deska 700 kg | 0,61 m | 2 | 0,15 | -„- |
| vibrační deska 2000 kg | 0,86 m | 2–3 | 0,30 | -„- |
| žába 10 kg | 0,05 m2 | 12 úderů | 0,15 | většina zemin |
| žába 100 kg | 0,43 m2 | 6 úderů | 0,30 | -„- |
| pěchovací deska 600 kg | 0,09 m2 | 2 údery | 0,60 | -„- |
| vibroúderové pěchovadlo 55 kg | 0,28 m2 | 3 | 0,10 | -„- |
| vibroúderové pěchovadlo 100 kg | 0,40 m2 | 3 | 0,20 | -„- |
Dynamická konsolidace spočívá ve zhutňování zemin pádem závaží z výšky, přičemž uplatnění má zejména na odlehlých staveništích bez blízké zástavby, neboť dynamické účinky jsou velké. Běžně se používá závaží o hmotnosti 12–20 t, jež padá volným pádem z výšky 10–20 m. Jsou však známy případy použití extrémních závaží o hmotnosti 200 t padajících z výšky až 40 m, (Francie, Hong – Kong). Technologický postup dynamické konsolidace je znázorněn na obr. 115. Deska, obyčejně ocelová, je zavěšena na výložníku jeřábu, jenž je opatřen buď vypouštěcími kleštěmi, nebo speciální brzdou uvolněného lana. V prvém případě jde o jednoduchou úpravu, práce je však zdržována potřebou neustálého připínání desky. Druhý případ je technicky složitější, avšak výkonnější. Pro vlastní technologický postup dynamického zhutňování je třeba připravit podrobný plán dopadů desky, přičemž na jedno místo deska dopadá vícekrát, ovšem s časovým odstupem. Ten je nutný zejména v případě jemnozrnných zemin, kdy je třeba delších časových odstupů. Účinek zhutnění jde především svislým směrem a roznos do stran bývá až o 50 % menší, než je tomu v případě statického hutnění.
Obr. 115 Technologický postup dynamické konsolidace
V ČR bylo dynamické konsolidace použito několikrát, a to jak úspěšně, tak i neúspěšně. Příkladem prvého je hutnění skládky chemického odpadu na lokalitě Spolana Neratovice, kde v souvislosti s enkapsulací této skládky bylo třeba přesypanou skládku homogenizovat a zhutnit. Bylo použito desky o hmotnosti 22 t, jež padala z výšky 10 m, počet úderů na jedno místo byl 3–5. Jiným příkladem je zakládání sila v cementárně Radotín, kde byl dynamicky zhutněn násyp z hlušiny vápencové drti. Naopak neúspěšný byl případ dynamické konsolidace výsypkových materiálů – jílů a zvětralých jílovců na Ervěnickém koridoru v severních Čechách, kde se použilo 10 t desky padající z výšky 7,5 m. Důsledkem tohoto zhutňování bylo významné zplastizování jílů a zvětšování jejich objemu, požadované konsolidace tedy dosaženo nebylo.
Účinky zhutňování je třeba kontrolovat. Kontrolu lze provádět následujícími metodami:
- a) stanovením předepsané míry zhutnění Proctorovou zkouškou;
- b) stanovením rovnovážné objemové tíhy zeminy;
- c) stanovením relativní ulehlosti zeminy;
- d) stanovením modulu deformace, (statickou zatěžovací zkouškou tuhou deskou);
- e) penetračními zkouškami, (statickými i dynamickými);
- f) ev. geofyzikálními metodami.
Nejběžnějším kritériem zhutnění je standardní zkouška Proctorova, (PS), jejíž provedení je schématicky vyznačeno na obr. 116a. Připravená zemina určité vlhkosti w se zhutňuje ve válci průměru 0,10 m ve 3 vrstvách vždy 25 údery normového pěchovadla, (tíhy 25 N padajícího z výšky 0,30 m) na celkovou výšku vrstvy 0,12 m. Přitom se vyloučí štěrky s velikostí zrna přes 20 mm. Stanoví se objemová hmotnost r [g·cm3] a zkouška se opakuje pro jinou vlhkost w. Výsledkem je graf z obr. 116b, udávající vztah mezi objemovou hmotností, (suché zeminy) rd a optimální vlhkostí wpr. Obvykle se požaduje zhutnění na 90–98 % podle Proctor – standard, (PS).
Obr. 116 Zkouška Proctor – standard: a – princip zkoušky, b – stanovení optimální vlhkosti
Rovnovážná objemová tíha zeminy odpovídá její tíze při zkonsolidovaném stavu, tzn., že rovnovážná objemová tíha zeminy γdk odpovídá zkonsolidované zemině zatížené příslušným napětím σk. Ke stanovení γdk se využívá oedometrické zkoušky zeminy, kdy vzorek je postupně zatěžován po stupních cca 10 kPa a zcela odlehčován až po dosažení napětí odpovídajícího zkoumaným podmínkám. Na tomto základě lze pro každý typ zeminy stanovit velikost γdk v závislosti na působícím napětí σ.
7.3 HLOUBKOVÉ ZHUTŇOVÁNÍ
Hloubkové zhutňování znamená využití mechanické energie v základových půdách do potřebné hloubky přesahující běžný dosah povrchového hutnění za účelem zvýšení hustoty, (objemové hmotnosti) základové půdy a/nebo snížení její propustnosti, tedy obecně za účelem zlepšení vlastností základové půdy. Máme tedy na mysli využití takových metod, jež umožní zhutňování zemin v hloubkách, kam povrchové hutnění již nedosáhne, (např. přes 5 m až do 30 m i více) a naopak, hloubkové hutnění není účinné ve vrstvě těsně pod povrchem, (do hloubky 0,6–1,0 m). Hloubkové hutnění může být dosaženo dynamickým nebo statickým zatížením nebo jejich kombinací. Použití statického zatížení, (např. přitěžovacími násypy) je typické pro jemnozrnné zeminy. Účinnost jejich zhutnění však významně souvisí s jejich propustností, jež ovlivňuje rychlost jejich konsolidace. Proto součástí hutnění jemnozrnných zemin bývá návrh urychlení jejich konsolidace, což je především otázka budování tzv. svislých drénů, jež ovlivňují proces konsolidace a dále štěrkových pilířů, které kromě urychlení konsolidace současně zlepšují deformační parametry základových půd. V hrubozrnných zeminách je základní metodou hloubkového hutnění vibrační zhutňování, tzv. vibroflotace. Provádění štěrkových pilířů a vibroflotace náleží mezi základní metody hloubkového zlepšování základových půd, a to nejen v zakládání staveb, ale i v silničním a železničním stavitelství:
a) štěrkové pilíře jsou prvky hlubinného zakládání staveb typu „displacement“, při jejichž provádění se v základové půdě vibrací, beraněním, nebo předrážením vytvoří otvor, který se vzápětí zaplní vhodným materiálem, (převážně štěrkem, ale i recyklátem) a ten se příslušně zhutní;
b) vibroflotace je metoda zhutňování hrubozrnných zemin, zvláště kyprých písků, účinkem vibrací bez jakéhokoliv přidávání dalšího materiálu; zhutňování je dosahováno pomocí vibrační jehly, jež penetruje základovou půdu vlastní tíhou, nebo za přítlaku, popřípadě s podporou vzduchového či vodního paprsku, (vplachování).
Za štěrkové pilíře obyčejně nepovažujeme prvky typu „non-displacement“, jež vznikají např. vrtáním (a odstraněním vyvrtané zeminy) a její náhradou propustnou zeminou, (štěrkem a pískem) bez náležitého hutnění. Jde vesměs o tzv. pískové drény, které sice urychlují konsolidaci, ale nedosahují příznivého efektu štěrkových pilířů, při jejichž budování je zemina roztlačena do stran i směrem dolů a dochází tak k jejímu hutnění.
První doložené použití předchůdců štěrkových pilířů pochází z Francie z konce 18. století, kdy do měkké základové půdy byl zatloukán štěrk pro zlepšení základové půdy pro zakládání vojenských objektů. Vibroflotace pak souvisí s vynálezem ponorného vibrátoru z roku 1928, (firma PTC, Francie), přičemž první kontrakt na zhutňování písků vibroflotací obdržela v Berlíně firma Johann Keller v roce 1930. Značný rozvoj vibroflotace souvisí s obnovou válkou zničených měst v Evropě v 50. letech minulého století. Vibroflotace a provádění štěrkových pilířů je rozšířeno hlavně v Belgii, Holandsku, severním Německu, Polsku a na Ukrajině, tedy v zemích, kde se vyskytují mohutné vrstvy neulehlých nebo málo ulehlých písků a mohutné vrstvy měkkých soudržných zemin. Do výroby štěrkových pilířů razantně zasáhla technologie předrážení známá z výroby pilot Franki. Postupem doby se tedy ustálily v celém světe dvě základní metody výroby štěrkových pilířů, tj. vibroražení, (označované často jako metoda Keller, podle firmy, která tuto metodu mnoho desetiletí úspěšně realizuje) a předrážení, (označované jako metoda Franki), rovněž podle známé nadnárodní firmy, přičemž dochází vesměs z komerčních důvodů ke sporům týkajícím se výhod a nevýhod a účinnosti obou metod.
Na obr. 117 jsou uvedeny přibližné hranice využitelnosti obou výše uvedených metod hloubkového zlepšování základových půd v zeminách, (podle jejich křivky zrnitosti). Je tedy zřejmé, že hlavní doménou vibroflotace jsou písky, (neulehlé, nebo málo ulehlé) a rovněž tak i štěrky, zatímco štěrkové pilíře má smysl provádět zejména v zeminách jemnozrnných. Je zřejmé, že realizace štěrkových pilířů v píscích a štěrcích postrádá významu. Současně je třeba uvědomit si i rozsah využitelnosti těchto prvků. Tak např. štěrkové pilíře nemá smysl provádět v zeminách pevné konsistence, popř. v poloskalních horninách, neboť míra jejich využití je nepatrná, pokud vůbec existuje. Bohužel v konkurenčním boji o zakázku některých specializovaných firem dochází k podobným excesům, jejichž příkladem bylo zakládání obchodního domu v Praze 8 v prostředí zvětralých břidlic, (tř. vesměs R5) na štěrkových pilířích za účelem zlepšení těchto základových půd. Skupiny štěrkových pilířů byly spojeny základovými patkami, jež přenášejí napětí do základové půdy a štěrkové pilíře zde byly navrženy v podstatě zbytečně. Jsou však i příklady opačné, a to zejména v případě plošného zlepšování základových půd, např. pod podlahami průmyslových a skladovacích objektů, kdy ve snaze co nejvíce ušetřit je volena tak řídká síť těchto prvků, že nedochází k potřebnému plošnému zlepšení a podlaha sedá.
Obr. 117 Přibližné vymezení vibroflotace a štěrkových pilířů z hlediska druhů zemin
7.3.1 Vibroflotace
Princi provádění vibroflotace, tj. hloubkového hutnění hrubozrnných zemin pomocí vibrace bez přídavku dalšího materiálu je na obr. 118. Zařízení podle obr. 119 se skládá z tzv. vibrační jehly délky 5–8 m, průměru kolem 0,30–0,50 m se špicí opatřenou křídly k zabránění reakční rotace této jehly vlivem vibrování. Vlastní tělo jehly je opatřeno hydromotorem, (výjimečně i elektromotorem), který pohání vodorovný excentr, jež způsobuje vodorovné vibrace. Tělo jehly je dále opatřeno průběžnými otvory s tryskami pro přívod stlačeného vzduchu nebo vody ke špici vibrátoru. Tato média usnadňují vnikání jehly do základové půdy. Jehla je potom zavěšena na výložníku jeřábu a vedou k ní jak hydraulické hadice, tak i hadicový přívod médií. Hmotnost jehly je 2,0–3,0 t a dosažená odstředivá síla je 160–450 kN, přičemž amplituda vibrace dosahuje 40–80 mm. Hloubkový dosah je běžně do 30 m, může být i větší. Problém je pak zejména v rychlosti a možnosti penetrace základovou půdou, zvláště, je-li již okolí zhutněno nebo obsahuje-li základové půda kameny nebo balvany.
Vibroflotační vpichy se provádějí z připravené pláně v pravidelné, nebo i nepravidelné plošné síti, tj. např. ve vrcholech rovnostranných trojúhelníků nebo čtverců. Délka strany závisí potom na druhu základové půdy, na její relativní ulehlosti ID, na požadovaném stupni zhutnění, (tj. na požadovaném výsledném ID) a samozřejmě i na druhu použitého vibroflotačního zařízení a pohybuje se od cca 1,0 do nejvýše 2,5 m.
Při spuštění vibrátoru klesá vibrační jehla do zeminy vlastní tíhou často za pomoci proudu stlačeného vzduchu nebo vody tryskající z oblasti špice. V bezprostřední blízkosti jehly dochází ke ztekucení zeminy. Když vibrátor klesne na předpokládanou hloubku, začíná vlastní proces zhutňování, a to již bez přívodu podpůrných médií. Vliv hutnění je obyčejně ihned patrný na povrchu, kde se vytváří typický depresní kužel. Současně lze na pohonné jednotce pozorovat a monitorovat zvyšující se spotřebu energie při vytahování jehly. Rychlost vytahování se řídí právě spotřebou, resp. dosažením jisté energie, jež je úměrná dosaženému stupni zhutnění.
Obr. 118 Schéma pracovního postupu při provádění vibroflotace
Účinnost zhutňování vibroflotací se kontroluje, a to nejlépe pomocí statické, nebo i dynamické penetrace. Před prováděním vibroflotace se realizuje základní pole penetračních sond, které se vhodně zaznamená a po provedení vibroflotace se penetrace opakují, přičemž se zjišťuje nárůst odporů, (v případě statické penetrace), popř. nárůst počtu úderů, (v případě dynamické penetrace). Toto srovnání vyjadřuje nejen míru zhutnění, ale též její rovnoměrnost a na základě těchto výsledků lze vibroflotaci doplnit, je-li to potřebné.
Příkladem realizace takové vibroflotace je stavba železničního podjezdu pod tratí ČD na jižní Moravě, obr. 120. Pro vybudování podjezdu bylo zapotřebí vyhloubit stavební jámu půdorysných rozměrů asi 10 x 22 m, jejíž dno zasahovalo až 3,0 m pod hladinu podzemní vody, přičemž niveleta silnice v ose podjezdu zasahovala 2,0 m pod souvislou hladinu podzemní vody. Základovou půdu tvořily jemnozrnné až prachovité písky o mocnosti přesahující 25 m s nepravidelnými čočkami prachovitých zemin. Průměrná velikost koeficientu filtrace byla k = 5 · 10-5 m·s-1. Na základě čerpacích pokusů byl ověřen poloměr depresního kužele, jež byl stanoven R = 250 m při snížení hladiny podzemní vody o 3,0 m, což bylo s ohledem na sousední zástavbu již nepřípustné. Úkolem bylo tedy vybudovat jednak stavební jámu bez čerpání podzemní vody a jednak připravit podmínky pro výstavbu komunikace s niveletou trvale 2,0 m pod hladinou podzemní vody. Jáma byla půdorysně ohrazena štětovou stěnou, a to kromě úseků pod vybudovaným podjezdem, kde bylo využito stěn ze sloupů tryskové injektáže. Tyto konstrukce však nezasahovaly do nepropustného podloží a v případě čerpání by nastal rozhodující přítok dnem této jámy o ploše cca 2 200 m2. Byla tedy navržena plošná vibroflotace za účelem snížení propustnosti písků, a to v síti vpichů se stranou délky 2,0 m do hloubky 3,0 m pode dno budoucí stavební jámy. Účinnost vibroflotace byla kontrolována sondami dynamické penetrace před a po vibroflotaci, přičemž nárůst úderů dosahoval 70–160 %, průměrně 98 %. Zjištěný koeficient filtrace základové půdy po vibroflotaci byl snížen o 1,5–2 řády na hodnotu k = x · 10-7 m·s-1. Přesto bylo dno jámy po vyhloubení, (bez čerpání) betonováno pod vodou vrstvou betonu tloušťky odpovídající příslušnému vztlaku podzemní vody a silnice pod podjezdem byla úspěšně dokončena.
Obr. 119 Zařízení používané při vibroflotaci
Obr. 120 Půdorysné schéma stavební jámy pro výstavbu podjezdu pod tratí ČD
7.3.2 Štěrkové pilíře
Štěrkové pilíře se provádějí v jemnozrnných zeminách a jejich hlavním posláním je zvýšení únosnosti základové půdy, a to zejména cestou zvýšení průměrné velikosti modulu deformace. Jsou to výztužné prvky, jejichž tuhost je mnohonásobně větší než tuhost okolní základové půdy. Vzhledem k tomu, že se vyrábějí jako štěrkové, působí současně jako svislé drény a urychlují tak konsolidaci základové půdy. Mechanizmus jejich statického působení je významně odlišný od mechanizmu únosnosti pilot, proto je nevhodné používat názvy štěrkové, nebo dokonce štěrkopískové piloty. Na rozdíl od pilot, které přenášejí vnější zatížení do okolní základové půdy třením na plášti a napětím na patě, přenos zatížení štěrkovými pilíři je závislý na schopnosti okolní zeminy vzdorovat boulení těchto prvků zatížených na horní podstatě příslušným tlakovým napětím sc. Přesto se mnohdy na štěrkové pilíře pohlíží dvěma poněkud rozdílnými způsoby:
- jako na základové prvky schopné přenášet osové, (tlakové) zatížení, kdy se navrhují v relativně omezených skupinách, (zcela výjimečně i jako osamělé), pod základovými pasy i patkami;
- jako na plošné, (resp. spíše prostorové) zlepšení vlastností základové půdy, tj. zvýšení průměrné velikosti modulu deformace Edef a urychlení konsolidace.
Zejména v druhém případě, jež je typičtější, musí být síť těchto prvků dostatečně hustá tak, aby zlepšení základové půdy bylo rovněž dostatečné a zejména rovnoměrné. Experimentálně bylo prokázáno, že deformace základové půdy vyztužené štěrkovými pilíři pod tuhým plošným základem je rovnoměrná, což znamená, že napětí v základové spáře je úměrné koncentraci napětí na štěrkové pilíře sc a zeminu ss. Tento koncentrační poměr n = sc / ss je základním návrhovým parametrem štěrkových pilířů závislým na mnoha okolnostech včetně poměru plochy pilířů Ac k ploše zlepšené základové půdy A. Zkoušky, (laboratorní i polní) prokázaly, že koncentrační poměr n = 3 – 5, zcela výjimečně je větší a to ve velkých hloubkách a ve zcela měkkých jílech. Pokud bychom základovou půdu pokládali za pružný poloprostor, potom by koncentrační poměr n = Ec / Es odpovídal poměrům modulů deformace materiálu štěrkových pilířů a okolní zeminy.
Štěrkové pilíře se v jemnozrnné základové půdě provádějí různými způsoby, přičemž rozeznáváme zejména:
- a) vibrační metodu, (vibro-lance, Rüttelstopfverfahren):
- b) metodu předrážení štěrkové pilíře typu Franki, (obr. 123).
Obr. 121 Schéma provádění štěrkových pilířů vibrační metodou bez plnění ke špici
Obr. 122 Schéma provádění štěrkových pilířů vibrační metodou s plněním ke špici
Metoda ad aa) je vhodná v případě relativně krátkých štěrkových pilířů v dobře penetrovatelné základové půdě a v zásadě při plošné realizaci těchto prvků. Využívá se vibrační jehly, (jako v případě vibroflotace) a pomocného média vzduchového. Voda se nepoužívá, neboť by výrazně zhoršila vlastnosti okolní zeminy. Po vytvoření otvoru, jež je v jemnozrnné zemině dočasně stabilní se jehla povytáhne a přisýpá se štěrk s pískem, který se postupně hutní vibrační jehlou. Takto se postupuje až k terénu, přičemž poslední vrstva mocnosti cca 0,6 m již není dostatečně zhutněna, proto se obyčejně volí jako štěrková vrstva, která se nakonec zhutní, (vibračními válci). Rychlost a tím i efektivita provádění těchto pilířů závisí především na rychlosti penetrace základovou půdou. Ta zejména v případě delších pilířů, (přes 8–10 m) nebývá dostatečná, proto se někdy používá krátkých předvrtů průměru 0,3–0,4 m, které penetraci usnadňují, snižují však hutnící efekt.
Metoda Franki, (ad b) je známa z železobetonových pilot (viz část 1). Místo suchého betonu se k formování dříku používá drceného štěrku frakce 8–32 mm, který lze ražením zhutnit na takovou míru, že modul deformace Ec = 150 – 200 MPa. To však obyčejně není třeba, neboť toho nelze využít. Nicméně lze ražením docílit průměry pilířů až dvojnásobné s ohledem na průměr razící roury.
Jak již bylo zmíněno, existuje značná rivalita mezi oběma způsoby, (vibračním a Franki), přičemž otázka by nikdy neměla být položena ve smyslu rozhodnutí, která z nich je lepší, neboť obě metody mají jistě dostatečné uplatnění. Aniž bychom vyčerpali všechny aspekty, můžeme konstatovat, že vibrační metoda je obvykle produktivnější, (co se týče množství pilířů za určitou časovou jednotku, např. směnu), zatímco metoda Franki bývá účinnější z hlediska dosaženého efektu. Dynamické účinky při vibrační metodě, (např. na okolní zástavbu) bývají příznivější než dynamické účinky u metody Franki. Schopnost „prorazit“ možné překážky v násypech a navážkách má výraznější metoda Franki, v případě vibrační metody je třeba použít pomocných metod, (provrtání a pod). Takto bychom mohli s výčtem výhod a nevýhod postupovat dále, není to však účelné.
Obr. 123 Schéma provádění štěrkových pilířů předrážením, (metoda Franki)
Rozsah smysluplného použití štěrkových pilířů je dán zejména původními vlastnostmi základové půdy. Pokud se jedná o jemnozrnné zeminy, jež lze charakterizovat neodvodněnou kohezí cu, potom:
- v případě, že neodvodněná koheze základové půdy bude zhruba v rozmezí 15 kPa < cu < 60 – 80 kPa, jsou štěrkové pilíře vhodné;
- v případě, že cu < 15 kPa, jsou štěrkové pilíře nevhodné, neboť zlepšení již není reálné, ani efektivní;
- v případě, že cu > 60 – 80 kPa je použití štěrkových pilířů nehospodárné, neboť dosažitelná míra zlepšení základové půdy není adekvátní rozsahu a množství štěrkových pilířů.
Kromě toho se štěrkové pilíře provádějí úspěšně v přemístěných zeminách charakteru navážek apod. Příkladem může být výstavba halových skladovacích objektů na předměstí Londýna, kde základovou půdu tvoří navážka stará již několik set let tvořená odpadem a zejména sutí po požárech a bouračkách. Zde se staví přízemní železobetonové montované haly, nebo i haly ocelové a základová půda se plošně zlepšuje štěrkovými pilíři délky 5–8 m, přičemž jako výplňový materiál je používán vesměs betonový recyklát ze sousedních bouraných objektů. Pod podlahou haly je síť pilířů s délkou strany cca 1,5–2,0 m, pod základovými patkami je potom pilířů tolik, kolik se tam prakticky vejde.
7.3.3 Návrh štěrkových pilířů, příklady 9–12
Návrh štěrkových pilířů je podřízen dvěma následujícím přístupům, z nichž každý vychází z podobného mechanizmu přenosu zatížení pilíři do základové půdy:
- štěrkové pilíře se pokládají za osově nosné prvky, (pro svislé tlakové zatížení), jež přenášejí zatížení do hlubších vrstev základové půdy obdobně jako jiné prvky hlubinného zakládání;
- štěrkové pilíře se považují za prvky zlepšující zejména deformační vlastnosti základové půdy a jsou tedy navrhovány v rozsáhlých skupinách (plošné, resp. prostorové působení).
Ve skutečnosti však neexistuje striktní hranice mezi oběma přístupy, neboť mechanizmus porušování štěrkových pilířů je dán zejména vlastnostmi okolní základové půdy a dále geometrickým tvarem pilíře, jak vyplývá z obr. 124.
Obr. 124 Mechanizmus porušení štěrkových pilířů: 1, 2 – dlouhý pilíř ve vrstevnaté zemině, 3 – krátký pilíř, a – velmi měkká zemina, b – měkká zemina, c – tuhé podloží
Jedná-li se o dlouhý štěrkový pilíř v měkké zemině zasahující do pevné vrstvy základové půdy (1), potom se při zatížení poruší v oblasti těsně pod hlavou, přičemž toto porušení je svým mechanizmem podobné mezní únosnosti plošných základů: pod hlavou pilíře se vytvoří (Rankinův) klín zcela ulehlé zeminy na jehož vrcholu vzniknou smykové plochy, podle nichž se okolní zemina vytlačí do stran a vzhůru.
Dlouhý pilíř uložený ve vrstevnaté zemině, kdy jedna z vrstev je výrazně „měkčí“ než vrstvy okolní (2) se deformuje podobně jako vzorek zeminy v triaxiálním přístroji, kde o porušení rozhoduje zejména pevnost okolní zeminy; jde o typické „soudečkové“ porušení.
Jde-li o velmi krátký pilíř v měkké zemině nezasahující do tužší vrstvy, jeho deformace se blíží deformaci tuhého tělesa, které se do této vrstvy „zaboří“.
a) Osamělé štěrkové pilíře
V případě osamělých štěrkových pilířů, popř. malých skupin těchto pilířů, lze na ně nahlížet jako na vertikálně nosné prvky, jejichž osová tlaková únosnost závisí zejména na pevnosti okolní základové půdy. Gibson a Anderson (1961) odvodili vztah mezi maximálním laterálním napětím σL působícím na štěrkový pilíř a napětím vodorovným σr, kterým pilíř působí na okolní zeminu v elastoplastickém médiu charakterizovaném modulem deformace Edef, Poissonovým číslem ν a totální pevností zeminy cu:
\begin{gathered}
\sigma_\text{L}=\sigma_\text{r}+c\cdot[1+\frac{(\log E)}{(2\cdot c\cdot(1+v))}]
\end{gathered}(131)
Tento vztah lze pro většinu zemin zjednodušit na výraz:
\begin{gathered}
\sigma_\text{L}=\sigma´_\text{r}+4\cdot c_\text{u}-u_0
\end{gathered}(132)
kde je
σr´ … efektivní vodorovné napětí;
cu … neodvodněná koheze;
u0 … tlak vody v pórech, který je v případě štěrkových pilířů roven 0.
Příslušné svislé napětí je podle Mohrova předpokladu dáno:
\begin{gathered}
\sigma_\text{v}´=\sigma_\text{r}´\cdot\frac{(1+\sin\varphi)}{(1-\sin\varphi)}=\sigma_\text{r}´\cdot\tg^2(45+\frac{\varphi}{2})=K_\text{p}\cdot\sigma_\text{r}´,\space\text{tedy}
\end{gathered}(133)
\begin{gathered}
\sigma_\text{v}´=K_\text{p}\cdot(\sigma_\text{r0}+4\cdot c_\text{u})
\end{gathered}(134)
kde je:
σr0 … svislé napětí v hloubce hkrit, tedy σr0 = γ · hkrit
φ … úhel vnitřního tření materiálu pilíře, (s ohledem na hutnění se volí φ = 38 – 42°);
γ … objemová tíha okolní základové půdy.
Kritická hloubka hkrit, v níž dojde k usmyknutí pilíře, závisí samozřejmě na pevnosti okolní zeminy (cu). V případě homogenní zeminy je pak obyčejně podle obr. 125a dána vztahem:
\begin{gathered}
h_\text{krit}=h_0+\frac{d}{2}\cdot\tg(45+\frac{\varphi}{2})
\end{gathered}(135)
kde je:
h0 … tloušťka homogenizační vrstvy zhutněného štěrku nad hlavami štěrkových pilířů, (pokud je navržena);
d … průměr štěrkového pilíře.
Ve snaze zvýšit σr0 a tím i σv´, provádí se v některých případech horní část štěrkového pilíře na výšku h1 z betonu, nebo se horní část pilíře injektuje cementovou maltou (obr. 125b), potom:
\begin{gathered}
h_\text{krit}=h_1+\frac{d}{2}\cdot(45+\frac{\varphi}{2})
\end{gathered}(136)
Maximální přípustná síla na pilíř průměru d bude pak:
\begin{gathered}
Q=A_\text{s}\cdot\frac{\sigma_\text{v}´}{\gamma_\text{s}}
\end{gathered}(137)
kde je:
γs … součinitel spolehlivosti, jehož doporučená velikost je 2,0, (v Anglii, kde je použití štěrkových pilířů velmi rozšířené, je bráno obyčejně γs = 2,5).
Autor prováděl v roce 2 000 statické zatěžovací zkoušky na štěrkových pilířích d = 500 mm délky kolem 5,0 m formovaných jako předrážené – metodou Franki. Okolní základová půda byla tvořena jílovitou hlínou tuhé až pevné konzistence, jejichž pevnost byla charakterizována hodnotou totální koheze cu = 70 – 80 kPa. Sestava zatěžovací zkoušky je na obr. 126, její výsledky pak na obr. 127. Po provedení zkoušky a stanovení kritické síly Qkrit byl štěrkový pilíř opatrně odkopán za účelem zjištění kritické hloubky, která byla potvrzena podle výše uvedených vztahů.
Obr. 125 Stanovení kritické hloubky v případě osamělého štěrkového pilíře: a) – pilíř s homogenizační vrstvou, b) – pilíř s betonovou částí dříku
Pokud stanovíme početně ze zadaných veličin kritickou sílu, získáme:
\begin{gathered}
h_\text{krit}=0{,}25\cdot\tg(45+20)=0{,}54\space\text{m}\\\\
K_\text{p}=\tg^2(45+\frac{40}{2})=4{,}60\\\\
\sigma_\text{v}´=4{,}60\cdot(20\cdot0{,}54+4\cdot75)=1429{,}7\space\text{kPa}\\\\
Q_\text{krit}=\pi\cdot\frac{0{,}50^2}{4}\cdot1429{,}7=280{,}5\space\text{kN}\approx275\space\text{kN (zjištěno při zkoušce)}
\end{gathered}Obr. 126 Sestava statické zatěžovací zkoušky osamělého štěrkového pilíře
Obr. 127 Průběh statické zatěžovací zkoušky štěrkového pilíře
b) Skupiny štěrkových pilířů
Skupiny štěrkových pilířů se obvykle navrhují rovnoměrné v pravidelné trojúhelníkové nebo čtvercové síti. Mezi pilíři ve skupině vznikají potom tzv. buňky, (cells), jež mají v rovinném řezu tvar šestiúhelníka nebo čtverce a vyznačují se tím, že na jejich obvodu je nulová radiální deformace. Definuje se tzv. ekvivalentní průměr náhradní buňky De podle obr. 128, který je:
- pro trojúhelníkovou síť
\begin{gathered}
D_\text{e}=1{,}05\cdot s
\end{gathered}- pro čtvercovou síť
\begin{gathered}
D_\text{e}=1{,}13\cdot s
\end{gathered}kde je:
s … osová vzdálenost pilířů ve skupině.
Dalším parametrem je poměr plochy pilíře As a náhradní buňky A, přičemž za náhradní buňku se považuje rovnoplochý kruh a poměr plochy okolní zeminy v buňce Ac a náhradní buňky A:
\begin{gathered}
a_\text{s}=\frac{A_\text{s}}{A}=C_1\cdot(\frac{D}{s})^2
\end{gathered}(138)
kde je:
\begin{gathered}
C_1=\frac{\pi}{(2\cdot3^\frac{1}{2})}\approx0{,}907\text{ – pro trojúhelníkovou síť}\\\\
C_1=\frac{\pi}{4}\approx0{,}785\text{ – pro čtvercovousíť}
\end{gathered}a dále:
\begin{gathered}
a_\text{c}=\frac{(A-A_\text{s})}{A}=1-a_\text{s}
\end{gathered}(139)
Obr. 128 Definice ekvivalentních průměrů náhradní buňky: a) – trojúhelníková síť, b) – čtvercová síť
Základním návrhovým parametrem je tzv, koncentrační poměr n = σs / σc, tj. poměr mezi svislým napětím σs, které přenáší štěrkový pilíř a napětím σc, které přenáší okolní základová půda v rozsahu příslušné buňky. Laboratorní i polní zkoušky prokázaly, že tento poměr je vesměs v rozmezí n = 3 – 5. Teoreticky, za předpokladu pružného poloprostoru je n = Es / Ec, (dán velikostí poměru modulů pružnosti). Průměrné napětí σ na povrchu základové půdy vyztužené skupinou štěrkových pilířů bude tedy:
\begin{gathered}
\sigma=\sigma_\text{s}\cdot a_\text{s}+\sigma_\text{c}\cdot(1-a_\text{s})
\end{gathered}(140)
a dále:
\begin{gathered}
\sigma_\text{c}=\frac{\sigma}{[1+(n-1)\cdot a_\text{s}]}=\mu_\text{c}\cdot\sigma
\end{gathered}(141)
\begin{gathered}
\sigma_\text{s}=n\cdot\frac{\sigma}{[1+(n-1)\cdot a_\text{s}]}=\mu_\text{s}\cdot\sigma
\end{gathered}(142)
Vztah mezi svislým napětím σ1 a vodorovným napětím σ3 je dán rovnicí (132), přičemž v jemnozrnné zemině, jejíž pevnost lze charakterizovat totální pevností: φu = 0, cu bude:
\begin{gathered}
\sigma_3=9\cdot c_\text{u}
\end{gathered}(143)
a v jemnozrnné zemině, jejíž pevnost je charakterizována efektivními smykovými parametry: φef, cef bude velikost s3 dána vztahem (130), tedy:
\begin{gathered}
\sigma_3=\sigma_\text{p}+c_\text{ef}\cdot[1+\log(\frac{E_\text{def}}{(2\cdot c_\text{ef}\cdot(1-\nu)})]
\end{gathered}(144)
kde je:
σp … původní vodorovné napětí.
Celkové svislé napětí:
\begin{gathered}
\sigma_\text{c}=\sigma_3\cdot K_\text{p}\le5\cdot c_\text{u}\text{ (maximální přípustné napětí v okolí štěrkového pilíře)}
\end{gathered}(145)
c) Zvýšení deformačních charakteristik základové půdy
Jedním z hlavních cílů zlepšování vlastností základové půdy pomocí skupin štěrkových pilířů je zlepšení jejich deformačních charakteristik. Chování zeminy vyztužené štěrkovými pilíři např. pod násypovým tělesem lze charakterizovat dvěma základními aspekty:
- ve střední části zatěžované plochy vyztužené zeminy je převládající deformace svislá; tu lze zjednodušeně popsat pomocí parametru β:
\begin{gathered}
\beta=\frac{\text{(sedání vyztužené zeminy)}}{\text{(sedání nevyztužené zeminy)}}
\end{gathered}- podél obvodu zatěžované plochy jsou významné obě deformace, tj. jak svislá, tak i vodorovná, která může dosahovat přibližně stejné velikosti; je tedy třeba posoudit stabilitu podloží násypu s ohledem na možný vznik smykové plochy.
Velikost součinitele β lze stanovit různými postupy – empirickými, analytickými a na základě měření získaného na stavbách. Všechny tyto metody využívají dvou podstatných vstupních parametrů, kterými jsou poměr koncentrace napětí n a koeficient poměru ploch as·
Jednoduchý vzorec založený na předpokladu stejného sedání štěrkového pilíře a zeminy publikoval Aboshi (1979):
\begin{gathered}
\beta=\frac{1}{(1+(n-1)\cdot a_\text{s})}
\end{gathered}(146)
K jedním z nejznámějších analytických řešení náleží výpočet podle Priebeho, (1976), který předpokládá, že nad nekonečně velkým pravidelným rastrem štěrkových pilířů leží tuhý základ vyvozující rovnoměrné zatížení na jejich povrchu. Základová půda je považována za izotropní materiál, přičemž paty štěrkových pilířů leží v konečné hloubce na dostatečně únosném podloží. Velikost součinitele zlepšení deformačních vlastností základové půdy β vychází potom z řešení rozšíření válcového tělesa obklopeného pružným poloprostorem podle obr. 129, jež je:
\begin{gathered}
\Delta d_1=\Delta\sigma_\text{h}\cdot(1-\nu)\cdot\frac{d_1}{E}\cdot[(1-2\cdot\nu)\cdot\frac{(1-\frac{d_1^2}{d_2^2})}{(1-2\cdot\nu+\frac{d_1^2}{d_2^2})}]
\end{gathered}(147)
kde je:
\begin{gathered}
\Delta\sigma_\text{h}=q\cdot K_\text{a}-\sigma_\text{v,z}
\end{gathered}(148)
rozdíl vodorovného tlaku pilíře na zeminu (q · Ka) a tlaku zeminy na pilíř, (σv,z = σh,z – předpoklad);
Ka … součinitel aktivního zemního tlaku;
\begin{gathered}
(K_\text{a}=\tg^2(45\degree-\frac{\varphi}{2}))
\end{gathered}E … modul (pružnosti) základové půdy;
d1 … průměr štěrkového pilíře;
d2 … průměr zemního válce, (náhradní buňky);
ν … Poissonovo číslo základové půdy.
Obr. 129 Schéma štěrkového pilíře v pružném poloprostoru
Nahradíme-li modul pružnosti E modulem oedometrickým Eoed podle vztahu:
\begin{gathered}
E=(1-2\cdot\frac{\nu^2}{(1-\nu)})\cdot E_\text{eod}
\end{gathered}(149)
a zavedeme-li místo poměru kvadrátů průměrů poměr ploch:
\begin{gathered}
\frac{d_1^2}{d_2^2}=\frac{A_\text{s}}{A}=a_\text{s}
\end{gathered}(viz rovnice 137), potom získáme:
\begin{gathered}
\Delta d_1=\Delta\sigma_\text{h}\cdot\frac{d_1}{E_\text{oed}}\cdot f(\nu,\space a_\text{s})
\end{gathered}(150)
kde je:
\begin{gathered}
f(\nu,a_\text{s})=\frac{[(1-\nu)^2\cdot(1-2\cdot\nu)\cdot(1-a_\text{s})]}{[(1-\nu-2\cdot\nu^2)\cdot(1-2\cdot\nu+a_\text{s})]}
\end{gathered}(151)
Předpokládáme dále, že v průběhu zatěžování nemění štěrkový pilíř svůj objem, tudíž bude radiálnímu rozšíření Δd1 odpovídat axiální zkrácení čili sednutí pilíře sc podle vztahu:
\begin{gathered}
s_\text{c}=2h\cdot\frac{\Delta d_1}{d_1}=2\Delta\sigma_\text{h}\cdot f(\nu,a_\text{s})\cdot\frac{h}{E_\text{oed}}
\end{gathered}(152)
kde je:
h … hloubka, (délka) štěrkového pilíře.
Sednutí základové půdy za předpokladu nekonečně velkého tuhého základu lze vyjádřit vztahem:
\begin{gathered}
s_\text{z}=\sigma_\text{h,z}\cdot\frac{h}{E_\text{eod}}
\end{gathered}(153)
Jelikož platí rovnost sc = sz, bude:
\begin{gathered}
\sigma_\text{h,z}=2\Delta\sigma_\text{h}\cdot f(\nu,a_\text{s})
\end{gathered}(154)
Poměr svislých napětí ve štěrkovém pilíři a základové půdě bude:
\begin{gathered}
\frac{\sigma_\text{v,c}}{\sigma_\text{v,z}}=\frac{(0{,}5+f(\nu,a_\text{s}))}{(K_\text{a}+f(\nu,a_\text{s}))}
\end{gathered}(155)
Pro celkové zatížení povrchu zlepšené zeminy bude platit:
\begin{gathered}
A\cdot q=A_\text{c}\cdot\sigma_\text{v,c}+A_\text{s}\cdot\sigma_\text{v,z}
\end{gathered}(156)
tedy:
\begin{gathered}
\frac{q}{\sigma_\text{v,z}}=1+a_\text{s}\cdot[\frac{\frac{1}{2}+f(\nu,a_\text{s}))}{(K_\text{a}\cdot f(\nu,a_\text{s})}]
\end{gathered}(157)
Již dříve definovaný poměr β bude potom:
\begin{gathered}
\beta=\frac{s}{s_\text{z}}=\frac{q}{\sigma_\text{v,z}}=\frac{1}{k}
\end{gathered}(158)
kde je:
k … stupeň zlepšení zeminy štěrkovými pilíři, jež lze vyjádřit rovnicí:
\begin{gathered}
k=1+a_\text{s}\cdot[\frac{(\frac{1}{2}+f(\nu,a_\text{s}))}{(K_\text{a}\cdot f(\nu,a_\text{s}))}-1]
\end{gathered}(159)
Na obr. 130 je příklad stupně zlepšení základové půdy pro případ, že její Poissonovo číslo ν = 0,35 a štěrk pilíře má různou pevnost danou velikostí úhlu vnitřního tření φ v intervalu 35° až 45°. Ukazuje se, že pro typickou osovou vzdálenost pilířů danou poměrem s / D = 1,75 až 2,5 je poměr zlepšení k = 3,9 – 2,1, přičemž velikost 3,9 lze považovat již za mírně nadsazenou. Rovněž tak je zřejmé, že při osové vzdálenosti pilířů s / D ≥ 3,0 je poměr zlepšení již zanedbatelný (pod cca 1,5). Velikosti stupně zlepšení jsou také v tab. 26.
Obr. 130 Vztah mezi poměrem s / D a koeficientem zlepšení základové půdy k pro štěrkové pilíře charakterizované velikostí φ v zemině s ν = 0,35
Tab. 29 Číselné velikosti stupně zlepšení základové půdy s ν = 0,35 štěrkovými pilíři o pevnosti dané velikostí úhlu vnitřního tření φ v trojúhelníkovém rastru daném poměrem s / D
| Poměr s / D | Stupeň zlepšení k pro φ = | ||
| 35° | 40° | 45° | |
| 1,5 | 4,883 | 5,950 | 7,351 |
| 1,75 | 3,274 | 3,914 | 4,755 |
| 2,0 | 2,520 | 2,955 | 3,526 |
| 2,25 | 2,098 | 2,416 | 2,834 |
| 2,5 | 1,836 | 2,080 | 2,400 |
| 2,75 | 1,659 | 1,854 | 2,108 |
| 3,0 | 1,525 | 1,678 | 1,883 |
Příklad 9
Stanovte maximální mocnost H násypu na podloží zlepšeném rozsáhlou skupinovou štěrkových pilířů podle obr. 131.
Obr. 131 Zadání k příkladu 9: a) – půdorysné uspořádání skupiny štěrkových pilířů, b) – řez skupinou štěrkových pilířů
Řešení:
- a) vstupní údaje:
- volíme rozteč pilířů s = 2,3 m, průměr pilířů D = 0,80 m (systém vibro-lance)
- délka pilířů L = 5,0 m (vetknutí do podložních štěrků t = 0,5 m)
- materiál štěrkových pilířů – hutněný štěrk: φs = 40°
- základová půda – měkký jíl: φu = 0, cu = 20 kPa
b) výpočet:
- trojúhelníková síť1
\begin{gathered}
a_\text{s}=0{,}907\cdot(\frac{0{,}8}{2{,}3})^2=0{,}11
\end{gathered}- průměr ekvivalentní buňky
\begin{gathered}
D_\text{e}=1{,}05\cdot2{,}3=2{,}415\space\text{m}\\\\
A_\text{s}=\pi\cdot\frac{0{,}8^2}{4}=0{,}502\space\text{m}^2\\\\
A=\pi\cdot\frac{2{,}415^2}{4}=4{,}578\space\text{m}^2\\\\
\sigma_3=9\cdot20=180{,}0\space\text{kPa}\\\\
K_\text{p}=\tg^2(45+\frac{40}{2})=4{,}60\\\\
\sigma_1=K_\text{p}\cdot\sigma_3=4{,}60\cdot180{,}0=828{,}0\space\text{kPa}=\sigma_\text{c}
\end{gathered}- (maximální napětí způsobující porušení pilíře)
- maximální napětí přenášené jílem s
\begin{gathered}
c_\text{u}=20{,}0\space\text{kPa}&&\sigma=5\cdot c_\text{u}=5\cdot20{,}0=100\space\text{kPa}
\end{gathered}- koncentrační poměr n = 3, (zvoleno ze zkušenosti)
\begin{gathered}
\mu_\text{s}=\frac{n}{[1+(n-1)\cdot a_\text{s}]}=\frac{3}{(1+2\cdot0{,}11)}=2{,}459\\\\
\mu_\text{c}=\frac{1}{[1+(n-1)\cdot a_\text{s}]}=\frac{1}{(1+2\cdot0{,}11)}=0{,}819\\\\
\sigma_\text{c}\le\mu_\text{c}\cdot\sigma=\mu_\text{c}\cdot\frac{\sigma_\text{c}}{\mu_\text{s}}=0{,}819\cdot\frac{828}{2{,}459}=275{,}77\space\text{kPa}\ge100\space\text{kPa}
\end{gathered}- (maximální napětí je větší, než max. přípustné napětí u jílů 5 · cu, proto platí menší hodnota)
- maximální síla přenášená fiktivní buňkou
\begin{gathered}
P_\text{c}=\sigma_\text{s}\cdot A_\text{s}+\sigma_\text{c}\cdot(A-A_\text{s})=28{,}0\cdot0{,}502+100\cdot(4{,}578-0{,}502)=823{,}25\space\text{kN}
\end{gathered}- volíme součinitel spolehlivosti γs = 2,0, tedy
\begin{gathered}
P=\frac{823{,}25}{2{,}0}=411{,}63\space\text{kN}
\end{gathered}- přípustná výška násypu, (s předpokládanou objemovou tíhou γ = 18,0 kN·m-3) bude dána vztahem: P = γ · H · A, tedy
\begin{gathered}
H=\frac{P}{(\gamma\cdot A)}=\frac{411{,}63}{(18{,}0\cdot4{,}578)}=5{,}00\space\text{m}
\end{gathered}Příklad 10
Stanovte poměr zlepšení základové půdy tvořené měkkými jíly s ν = 0,40 pomocí štěrkových pilířů průměru D = 0,60 m v osových vzdálenostech s = 1,50 m v pravidelném rastru 1) rovnostranných trojúhelníků, 2) čtverců. Štěrkové pilíře jsou prováděny ražením, (metoda Franki) a jejich pevnost je vyjádřena φ = 42°.
Řešení:
1) síť pravidelných trojúhelníků podle rovnice (136) je
\begin{gathered}
a_\text{s}=0{,}907\cdot(\frac{D}{s})^2=0{,}145
\end{gathered}- funkce
\begin{gathered}
f(n,a_\text{s})=(1-0{,}4)^2\cdot(1-2\cdot0{,}4)\cdot\frac{(1-0{,}145)}{((1-0{,}4-2\cdot0{,}4^2)\cdot(1-2\cdot0{,}4+0{,}145))}=0{,}637
\end{gathered}- koeficient aktivního zemního tlaku
\begin{gathered}
K_\text{a}=\tg^2(45-\frac{42}{2})=0{,}198
\end{gathered}- poměr zlepšení
\begin{gathered}
k=1+0{,}145\cdot[\frac{(0{,}5+0{,}637)}{(0{,}198\cdot0{,}637)}-1]=2{,}162
\end{gathered}2) čtvercová síť podle rov. (137) je
\begin{gathered}
a_\text{s}=0{,}785\cdot(\frac{D}{s})^2=0{,}126
\end{gathered}- funkce
\begin{gathered}
f(n,a_\text{s})=(1-0{,}4)^2\cdot(1-2\cdot0{,}4)\cdot\frac{(1-0{,}126)}{((1-0{,}4-2\cdot0{,}4^2)\cdot(1-2\cdot0{,}4+0{,}126))}=0{,}689
\end{gathered}- koeficient aktivního zemního tlaku
\begin{gathered}
K_\text{a}=\tg^2(45-\frac{42}{2})=0{,}198
\end{gathered}- poměr zlepšení
\begin{gathered}
k=1+0{,}126\cdot[\frac{(0{,}5+0{,}680)}{(0{,}198\cdot0{,}689)}-1]=1{,}972
\end{gathered}stanovení náhradních stabilitních parametrů základové půdy vyztužené štěrkovými pilíři:
- platí koncepce ekvivalentní buňky o průměru De se štěrkovým pilířem průměru D v ose této buňky, povrch buňky je zatížen průměrnou velikostí napětí σ;
- stabilitní parametry štěrkového pilíře jsou: γs, φs, cs = 0;
- stabilitní parametry okolní (nezlepšené) zeminy jsou: γc, φc, cc;
- náhradní objemová tíha vyztužené zeminy
\begin{gathered}
\gamma_\text{n}=(1-a_\text{s})\cdot\gamma_\text{c}+a_\text{s}\cdot\gamma_\text{s}
\end{gathered}- náhradní soudržnost vyztužené zeminy
\begin{gathered}
c_\text{n}=(1-a_\text{s})\cdot c_\text{c}
\end{gathered}- náhradní úhel vnitřního tření vyztužené zeminy:
\begin{gathered}
\tg\varphi_\text{n}=\frac{((1-a_\text{s})\cdot\tg\varphi_\text{s}+n_\text{n}\cdot a_\text{s}\cdot\tg\varphi_\text{s})}{(1+a_\text{s}\cdot(n_\text{n}-1))}
\end{gathered}- prochází-li vyztuženou zeminou smyková plocha pod úhlem α, (od vodorovné) bude:
- nn = 1 + (n – 1) · cos α (kde n je koncentrační poměr);
- svislé napětí na smykové ploše v pilíři
\begin{gathered}
\sigma_\text{s}=\gamma_\text{s}\cdot z+\sigma\cdot\mu_\text{s}
\end{gathered}- smykové napětí na smykové ploše v pilíři
\begin{gathered}
\tau_\text{s}=(\sigma\cdot\cos\alpha)\cdot\tg\varphi_\text{s}
\end{gathered}- průměrné smykové napětí na smykové ploše procházející celou náhradní buňkou,
\begin{gathered}
\tau_\text{n}=(1-a_\text{s})\cdot\tau_\text{c}+a_\text{s}\cdot\tau_\text{s}\cdot\cos\alpha
\end{gathered}- kde τc je smykové napětí v původní zemině.
Příklad 11
Stanovte únosnost základové patky založené na skupině štěrkových pilířů podle obr. 132.
Řešení
- geometrické charakteristiky:
- pilíře 10 ks, D = 0,75 m, H = 7,0 m, s = 2,5 m;
- patka B = 5,0 m, L = 7,5 m, t = 1,0 m;
- mechanické vlastnosti základové půdy a štěrkových pilířů:
- pilíře: φs = 42°;
- zeminy: γc = 18,5 kN·m-3, φc = 0, cc = 25 kPa.
Obr. 132 Zadání k příkladu 11 – únosnost základové patky podepřené skupinou štěrkových pilířů
a) základní vztahy:
\begin{gathered}
A_\text{s}=\pi\cdot\frac{0{,}75^2}{4}\cdot10=4{,}416\space\text{m}^2\\\\
A=5{,}0\cdot7{,}5=37{,}5\space\text{m}^2\\\\
a_\text{s}=\frac{4{,}416}{37{,}5}=0{,}1178
\end{gathered}- koncentrační faktor volíme n = 2
\begin{gathered}
\mu_\text{s}=\frac{2}{(1+(2-1)\cdot0{,}1178)}=1{,}789\\\\
\mu_\text{c}=\frac{1}{(1+(2-1)\cdot0{,}1178)}=0{,}895\\\\
\tg\varphi_\text{n}=1{,}789\cdot0{,}1178\cdot\tg42\degree=0{,}1898,\space\text{tedy}\space\varphi_\text{n}=10{,}75\degree\\\\
c_\text{n}=25\cdot(1-0{,}1178)=22{,}06\space\text{kPa}
\end{gathered}b) stanovení napětí σ3, σ1 a únosnosti P – předpoklad tuhý základ:
- úhel smykové plochy
\begin{gathered}
\beta=45\degree+\frac{\varphi_\text{n}}{2}=45+\frac{10{,}75}{2}=50{,}375\degree
\end{gathered}- vodorovné napětí
\begin{gathered}
\sigma_3=\gamma_\text{c}\cdot\frac{L}{2}\cdot\tg\beta=18{,}5\cdot\frac{7{,}5}{2}\cdot\tg50{,}375=83{,}78\space\text{kPa}
\end{gathered}- napětí
\begin{gathered}
\sigma_1=\sigma_\text{celk}=\sigma_3\cdot\tg^2\beta+2\cdot c_\text{n}\cdot\tg\beta=83{,}78\cdot1{,}459+2\cdot22{,}06\cdot1{,}208=175{,}53\space\text{kPa}
\end{gathered}- svislá síla přenášená patkou (součinitel bezpečnosti volíme s = 2,0)
\begin{gathered}
P=37{,}5\cdot\frac{175{,}53}{2{,}0}=3\space291\space\text{kN}
\end{gathered}- napětí ve štěrkových pilířích
\begin{gathered}
\sigma_\text{s}=\mu_\text{s}\cdot\sigma=1{,}759\cdot\frac{175{,}53}{2{,}0}=157{,}0\space\text{kPa}
\end{gathered}- napětí v okolním jílu
\begin{gathered}
\sigma_\text{c}=\mu_\text{c}\cdot\sigma=0{,}895\cdot\frac{175{,}53}{2{,}0}=78{,}6\space\text{kPa}
\end{gathered}c) stanovení napětí σ3, σ1 a únosnosti P – předpoklad poddajný základ
- náhradní průměr kruhu
\begin{gathered}
B´=(4\cdot\frac{37{,}5}{\pi})\frac{1}{2}=6{,}91\space\text{m}
\end{gathered}- původní izotropní napětí pod smykovou plochou, (K0 = 0,6)
\begin{gathered}
q=\frac{(\sigma_1+2\cdot\sigma_3)}{3}=\sigma_1\cdot\frac{(1+2\cdot K_0)}{3}=\frac{(18{,}5\cdot(1{,}0+\frac{6{,}61}{2})\cdot(1+2\cdot0{,}6))}{3}=60{,}44\space\text{kPa}
\end{gathered}- koeficient tuhosti patky
\begin{gathered}
I_\text{r}=\frac{E_\text{def}}{(2\cdot(1+\nu)\cdot(c_\text{c}+q\cdot\tg\varphi_\text{c}))}=11\cdot\frac{25}{(2{,}9\cdot25)}=3{,}793\\\\
F´_\text{c}=\ln\cdot I_\text{r}+1=2{,}333;&&F´_\text{q}=1{,}0\\\\
\sigma_3=c_\text{c}\cdot F´_\text{q}+q\cdot F´_\text{q}=25\cdot2{,}333+60{,}44=118{,}77\space\text{kPa}\\\\
\sigma_1=\sigma_\text{celk}=118{,}77\cdot1{,}459+2\cdot22{,}06\cdot1{,}208=226{,}58\space\text{kPa}
\end{gathered}- únosnost základu (s = 2,0)
\begin{gathered}
P=37{,}5\cdot\frac{226{,}58}{2{,}0}=4\space249\space\text{kN}
\end{gathered}- napětí ve štěrkových pilířích
\begin{gathered}
\sigma_\text{s}=\mu_\text{s}\cdot\sigma=1{,}789\cdot\frac{226{,}58}{2{,}0}=202{,}7\space\text{kPa}
\end{gathered}- napětí v okolním jílu
\begin{gathered}
\sigma_\text{c}=\mu_\text{c}\cdot\sigma=0{,}895\cdot\frac{226{,}58}{2{,}0}=101{,}4\space\text{kPa}
\end{gathered}Příklad 12
Stanovte velikost konsolidačního sedání podloží násypu z příkladu 9 a rovněž časový průběh primární konsolidace podloží násypu zlepšeného štěrkovými pilíři.
Řešení:
1) doplnění zadání:
- v podloží násypu je H2 = 0,60 m mocná drenážní vrstva štěrku, (γ = 17,5 kN·m-3), nad ním je násyp mocnosti H1 = 4,4 m, (γ = 18,5 kN·m-3);
- základová půda – jíl je zcela zvodnělá: (měrná tíha γs = 27,5 kN·m-3, číslo pórovitosti e = 1,3, koeficient stlačitelnosti Cc = 0,5;
- koeficient konsolidace jílu Cv = 4 · 10-3 m2·den-1 (tj. 0,463 cm2·sec-1);
- předpoklad, že horizontální propustnost bude 3xvětší než propustnost vertikální, tj. poměr koeficientů filtrace kh / kv = 3;
- předpokládáme, že štěrkové pilíře jsou i v patách uloženy v propustné zemině, tj. voda může drénovat oběma směry (N = 2);
- koeficient konsolidace pro horizontální směr Cvh = Cv · (kh / kv) = 12 · 10-3 m2·den-1;
- volíme trojúhelníkovou síť štěrkových pilířů D = 0,8 m s De = 2,415 m a mocností stlačitelné vrstvy L = 4,5 m;
- redukovaný průměr drenáže – volíme D´= D / 5 = 0,8 / 5 = 0,16 m.
2) původní geostatické napětí v polovině mocnosti stlačitelné vrstvy jílu:
- pórovitost
\begin{gathered}
n=\frac{e_0}{(1+e_0)}=0{,}565=56{,}5\space\%
\end{gathered}- objemová tíha jílu pod vodou
\begin{gathered}
\gamma´=(1-n)\cdot(\gamma_\text{s}-\gamma_\text{w})=(1-0{,}565)\cdot(27{,}5-10{,}0)=7{,}61\space\text{kN}\cdot\text{m}^{-3}
\end{gathered}- geostatické napětí v houbce
\begin{gathered}
z=\frac{L}{2}=2{,}25\space\text{m},&&\sigma_0=\gamma´\cdot z=7{,}61\cdot2{,}25=17{,}12\space\text{kPa}
\end{gathered}3) konsolidační sedání st stlačitelné vrstvy zeminy o mocnosti H = 4,5 m:
- zatížení na povrchu zlepšené zeminy
\begin{gathered}
p=4{,}4\cdot18{,}0+0{,}6\cdot17{,}5=89{,}7\space\text{kPa}
\end{gathered}- sedání
\begin{gathered}
s_\text{t}=\frac{C_\text{c}}{(1+e_0)}\cdot\log(\frac{(\sigma_0+p)}{\sigma_0})=\frac{0{,}5}{2{,}3}\cdot\log6{,}239=0{,}173\space\text{m}=173\space\text{mm}
\end{gathered}4) stanovení stupně konsolidace za doby t = 60 dní, obr. 133, 134:
- poměr
\begin{gathered}
n´=\frac{D_\text{e}}{D´}=\frac{2{,}415}{0{,}16}=15{,}09
\end{gathered}- bezrozměrný faktor
\begin{gathered}
T_\text{z}=C_\text{v}\cdot\frac{t}{(\frac{L}{N})^2}=4\cdot10^{-3}\cdot\frac{60}{(\frac{4{,}5}{2})^2}=0{,}047
\end{gathered}- bezrozměrný faktor
\begin{gathered}
T_\text{r}=C_\text{vh}\cdot\frac{t}{D_\text{e}^2}=12\cdot10^{-3}\cdot\frac{60}{2{,}415^2}=0{,}123
\end{gathered}- z grafu na obr. 133 pro
\begin{gathered}
T_\text{z}=0{,}047&&U_\text{z}=0{,}18
\end{gathered}- z grafu na obr. 134 pro
\begin{gathered}
T_\text{r}=0{,}123\space\text{a}\space n´=15&&U_\text{r}=0{,}78
\end{gathered}- stupeň konsolidace
\begin{gathered}
U=1-(1-U_\text{z})\cdot(1-U_\text{r})=1-(1-0{,}18)\cdot(1-0{,}78)=0{,}897=81\%
\end{gathered}- za dobu 2 měsíce (60 dní) bude sednutí násypu činit
\begin{gathered}
s_{60}=U\cdot s_\text{t}=0{,}81\cdot173=140\space\text{mm}
\end{gathered}Obr. 133 Graf pro stanovení stupně konsolidace Uz ve vertikálním směru
Obr. 134 Graf pro stanovení stupně konsolidace Ur v radiálním směru
8 PŘÍLOHY
8.1 SEZNAM SOUVICEJÍCÍCH ČSN
| Označení | Název |
| ČSN 73 0020 | Terminologie spolehlivosti stavebních konstrukcí a základových půd |
| ČSN ISO 2394 | Obecné zásady spolehlivosti konstrukcí |
| ČSN EN 1990 | Zásady navrhování konstrukcí |
| ČSN EN 1991 – (1 až 7) | Zatížení konstrukcí |
| ČSN EN 1992-1-1 | Navrhování betonových konstrukcí – Část 1-1: Obecná pravidla a pravidla pro pozemní stavby |
| ČSN EN 1992-2 | Navrhování betonových konstrukcí – Část 2: Betonové mosty a konstrukční zásady |
| ČSN EN 1993-1-1 | Navrhování ocelových konstrukcí – Část 1-1: Obecná pravidla a pravidla pro pozemní stavby |
| ČSN EN 1993-2 | Navrhování ocelových konstrukcí – Část 2: Ocelové mosty |
| ČSN EN 1996-1-1+A1 | Navrhování zděných konstrukcí – Část 1-1: Obecná pravidla pro vyztužené a nevyztužené zděné konstrukce |
| ČSN EN 1997-1 | Navrhování geotechnických konstrukcí – Část 1: Obecná pravidla |
| ČSN EN 1997-2 | Navrhování geotechnických konstrukcí – Část 2: Průzkum a zkoušení základové půdy |
| ČSN EN 1998-1 | Navrhování konstrukcí odolných proti zemětřesení – Část 1: Obecná pravidla, seizmická zatížení a pravidla pro pozemní stavby |
| ČSN EN 1998-2 | Navrhování konstrukcí odolných proti zemětřesení – Část 2: Mosty |
| ČSN EN 1998-3 | Navrhování konstrukcí odolných proti zemětřesení – Část 3: Hodnocení a zesilování pozemních staveb |
| ČSN EN 1536+A1 | Provádění speciálních geotechnických prací – Vrtané piloty |
| ČSN EN 1537 | Provádění speciálních geotechnických prací – Horninové kotvy |
| ČSN EN 1538+A1 | Provádění speciálních geotechnických prací – Podzemní stěny |
| ČSN EN 12063 | Provádění speciálních geotechnických prací – Štětové stěny |
| ČSN EN 12699 | Provádění speciálních geotechnických prací – Ražené piloty |
| ČSN EN 12715 | Provádění speciálních geotechnických prací – Injektáže |
| ČSN EN 12716 | Provádění speciálních geotechnických prací – Trysková injektáž |
| ČSN EN 14199 | Provádění speciálních geotechnických prací – Mikropiloty |
| ČSN EN 14475 | Provádění speciálních geotechnických prací – Vyztužené zemní konstrukce |
| ČSN EN 14490 | Provádění speciálních geotechnických prací – Hřebíkování zemin |
| ČSN EN 14679 | Provádění speciálních geotechnických prací – Hloubkové zlepšování zemin |
| ČSN EN 14731 | Provádění speciálních geotechnických prací – Hloubkové zhutňování zemin vibrováním |
| ČSN EN 15237 | Provádění speciálních geotechnických prací – Svislé drény |
| ČSN 73 0037 | Zemní tlak na stavební konstrukce |
| ČSN 73 0039 | Navrhování objektů na poddolovaném území – Základní ustanovení |
| ČSN 73 0040 | Zatížení stavebních konstrukcí technickou seismicitou a jejich odezva |
| ČSN 73 0601 | Ochrana staveb proti radonu z podloží |
8.2 LITERATURA
[1] BAŽANT, Z. Metody zakládání staveb. Praha: Academia, 1973, 592 s.
[2] FINE spol. s r. o. Geo5_user_guide_cs.pdf, ver. 5.8, www.fine.cz, 2008
[3] HURYCH, P. Některé problémy výpočtu pažení hlubokých stavebních jam. Sborník konference Automatizácia projektovania. Vysoké Tatry, 1979.
[4] MASOPUST, J. Vrtané piloty. Praha: Čeněk a Ježek, 1994, 263 s.
[5] MASOPUST, J. Zakládání staveb 1. Praha: Nakladatelství ČVUT, 2012, 163 s.
[6] MASOPUST, J. Zakládání staveb 2. Praha: Nakladatelství ČVUT, 2017, 190 s.
[7] MASOPUST, J. a kol. Rizika prací speciálního zakládání staveb. Praha: Informační centrum ČKAIT, s. r. o. 2011, 136 s.
[8] MEISSNER, H. Empfelungen des Arbeitskreises 1.6 „Numerik in der Geotechnik“. Geotechnik 25, 2002, Abschintt 3, Baugruben, s. 44 – 56.
[9] Software pro geotechnickou analýzu PLAXIS. Netherlands: Delft, 2006.
[10] ROZSYPAL, A. Kontrolní sledování a rizika v geotechnice. Bratislava: JAGA, 2001, 198 s.
[11] ROZSYPAL, A. Inženýrské stavby řízení rizik. Bratislava: JAGA, 2008, 174 s.
[12] SMOLTCZYK, U. a kol. Grundbau Taschenbuch, 3. Auflage, Teil 2. Berlin: Verlag W. Ernst u. Sohn, 1982, 995 s.
[13] TURČEK, P. a kol. Zakládání staveb. Bratislava: JAGA, 2005, 302 s.
[14] VERFEL, J. Injektování hornin a výstavba podzemních stěn. Bratislava: MÚS Bradlo, 1992, 511 s.