ČESKÁ KOMORA AUTORIZOVANÝCH INŽENÝRŮ A TECHNIKŮ ČINNÝCH VE VÝSTAVBĚ
Rada pro podporu rozvoje profese ČKAIT
Autoři: doc. Ing. Karel Lorenz, CSc.
Stav: kontrola 2022, vydání 2014
Anotace:
Pomůcka je určena především pro projektanty pozemních staveb. Záměrem bylo poskytnout souhrnnou pomůcku pro navrhování konstrukcí, která usnadní provedení architektonického a konstrukčního návrhu tím, že umožní předběžný návrh dimenzí nosných konstrukcí za použití relativně jednoduchých pravidel, empirických vzorců popř. dalších nestandardních metod. Předpokládá se, že uživatel pomůcky má základní znalosti o nosných konstrukcích, o jejich uspořádání a statickém působení.
OBSAH
PŘEDMLUVA
Předložená publikace je určena především pro projektanty pozemních staveb. Záměrem autora bylo poskytnout souhrnnou příručku pro navrhování konstrukcí, která usnadní provedení architektonického a konstrukčního návrhu tím, že umožní předběžný návrh dimenzí nosných konstrukcí za použití relativně jednoduchých pravidel, empirických vzorců, popř. dalších nestandardních metod. Předpokládá se, že uživatel příručky má základní znalosti o nosných konstrukcích, o jejich upořádání a statickém působení.
Při použití příručky je nutné vycházet vždy z konkrétních podmínek, ve kterých konstrukce působí, a splnit okrajové podmínky, za kterých návrh platí. V textu nebo na obrázcích uváděné rozměry konstrukcí je nutno chápat jako směrné, proto je vždy nutno přihlédnout ke konkrétním podmínkám a rozměrové hodnoty v konečném návrhu staticky ověřit. V příručce nejsou uvedeny podklady pro návrh podrobností konstrukce, styků, uložení apod., což je rovněž předmětem statického a konstrukčního řešení.
Publikace je rozdělena do čtrnácti kapitol – konstrukční zásady, vícepodlažní stavby, výškové budovy, halové stavby a zastřešení na velká rozpětí, výkopy, opěrné zdi a seznam literatury. V příloze je pak uveden výtah statických veličin a přehled některých vzorců, rovněž potřebných pro návrh konstrukce. Vzhledem k uvádění empirických vztahů je třeba použít odpovídající jednotky veličin. Pro snazší orientaci jsou v některých partiích uvedeny konkrétní příklady, aby měl čtenář kontrolu reálnosti návrhu.
Autor považuje za svou milou povinnost poděkovat recenzentům Ing. Miloši Horákovi a Dr. Ing. Tomášovi Novotnému, za jejich cenné rady a připomínky k rukopisu. Dále bych rád požádal čtenáře či uživatele o laskavé sdělení případných poznámek a připomínek k obsahu a zaměření publikace i rozsahu jednotlivých kapitol, které by bylo možné uplatnit při dalším vydání.
1 Konstrukční zásady
V této kapitole jsou uvedeny některé všeobecné zásady a pravidla, která se používají při návrhu nosných konstrukcí, Jedná se o volbu materiálu, prostorové uspořádání z hlediska rozmístění nosných prvků, prostorové tuhosti objektu a velikosti dilatačních celků.
1.1 Materiály v nosných konstrukcích
Pro nosné konstrukce pozemních staveb jsou základními materiálovými variantami:
- zdivo;
- železový beton;
- předpjatý beton;
- dřevo;
- ocel;
- hliníkové slitiny;
- plastické hmoty;
- sklo.
Zpravidla se hmoty kombinují – zdivo s ocelí a železovým či prostým betonem, popřípadě ocelí apod.
Zásadně jsou všechny uvedené stavební hmoty vhodné pro každý stavební záměr – za určitých předpokladů a podmínek mají jednotlivé stavební hmoty své klady a zápory, které mohou být pro volbu předmětné konstrukce rozhodující.
Dřevěné konstrukce
a) výhody
- přizpůsobitelné každému půdorysu;
- jednoduchá možnost stavby, snadná demontáž;
- znovu použitelné po demontáži;
- jednoduché a lehké pro výrobu, jednoduché spoje, jednoduchá montáž;
- pro malou vlastní hmotnost možná výroba velkých dílců, proto jednoduchý transport a montáž pomocí lehkého jeřábu či ručně;
- malé základy díky malé vlastní tíze;
- výhodná pevnost téměř shodná pro tlak, tah i ohyb;
- výhodné stavebně fyzikální vlastnosti – dobrá tepelná izolace, malá tepelná roztažnost, a proto není nutná dilatace;
- psychologicky příjemné pro obývání;
- esteticky vhodné;
- nekoroduje, životnost se prodlužuje konstruktivním řešením a chemickým ošetřením;
- dobrá možnost kombinace se zdivem a ocelí.
b) nevýhody
- výškové omezení do dvou nadzemních podlaží (mimo sklep a využívané podkroví) z požárních důvodů;
- rozpětí nosníků jsou omezena zejména díky průhybu, pokud je dána maximální konstrukční výška stropu;
- nevhodné pro příliš velká zatížení vzhledem k mechanickým vlastnostem dřeva;
- anizotropie – rozdílné materiálové vlastnosti dřeva v různých směrech;
- pro nosnou konstrukci především tyčové prvky;
- objemové změny vlivem vlhkosti;
- riziko napadení dřevokaznými houbami a hmyzem;
- hořlavost dřeva vyžadující ochranu proti požáru.
Zděné konstrukce
a) výhody
- díky malé stavební jednotce velmi dobrá tvarovatelnost konstrukce;
- hospodárnost, malá potřeba technického vybavení a malé nároky na jeřáby;
- dobrý přenos tlakových sil stěnami a pilíři, vodorovné síly je vhodné přenášet stěnovým prvky;
- jednoduchá výstavba i rozebrání, ještě jednodušší bourání;
- odolnost proti ohni velmi dobrá i bez omítky a obkladů, poškození ohněm malá a opravitelná;
- příznivé stavebně-fyzikální vlastnosti, tepelně izolační schopnosti zejména u děrovaných a dutých cihel, velká tepelná jímavost u plných cihel, smršťování a roztahování velmi malé, malá tepelná roztažnost, a proto možné velké vzdálenosti dilatačních spár;
- odolné proti povětrnosti, vyžadující minimum údržby (mimo omítku);
- architektonicky a psychologicky působí „lidsky“;
- dobře se kombinuje se dřevem, ocelí i betonem.
b) nevýhody
- malá únosnost zdiva v tahu, a proto je vhodné jen pro převážně tlačené prvky (stěny, pilíře, klenby), proti tahovým napětím je možno vyztužit, případně předepnout;
- střední úroveň pevnosti neumožňuje příliš vysoké budovy;
- citlivé na dynamické účinky – exploze, zemětřesení, technická seismicita způsobují trhliny;
- omítané zdivo vyžaduje údržbu;
- zdění je závislé na počasí;
- rozměrové tolerance přinášejí problémy dalším profesím.
Ocelové konstrukce
a) výhody
- přesná a čistá výroba, rychlá montáž, možno bezprostředně pokračovat s kompletací;
- krátké lhůty výstavby nezávislé na počasí a ročním období;
- flexibilní dispozice díky velkým vzdálenostem mezi sloupy;
- možnost rozšíření a přestavby bez velkých technických problémů;
- nepatrné náklady na demontáž, možnost opakovaného použití, zbytková hodnota šrotu;
- vysoká pevnost v tahu, tlaku i ohybu, malé rozměry prvků při velkých rozpětích a velkém počtu podlaží;
- malá vlastní tíha konstrukce a z toho vyplývající malé nároky na zdvihací prostředky a základy konstrukce;
- možnost vedení instalací v relativně velkých mezistropech;
- jednoduché připojení fasády, dělicích příček i zavěšeného podhledu;
- konstrukce působí lehce a elegantně;
- lze dobře kombinovat se dřevem, zdivem, betonem i sklem.
b) nevýhody
- potřeba trvalé údržby a ochrany proti korozi;
- ocel sice nehoří, ale vysoké teploty ovlivňují mechanické vlastnosti, to vyžaduje ochranu proti požáru, například obklady apod.;
- velká protažení vlivem teploty, nutno řešit dilatacemi;
- náročné na návrh konstrukce a jejích detailů;
- výroba vyžaduje specializované firmy.
Železobetonové konstrukce
a) výhody
- téměř neomezené možnosti tvarování a uspořádání (skelety, skořepiny, nádrže, věže, stožáry, bunkry);
- velká pevnost betonu v tlaku v kombinaci s výztuží také v tahu a ohybu, což lze ovlivnit volbou materiálu ve velkém rozsahu;
- i další vlastnosti lze naprogramovat, jako je vodonepropustnost, chemická odolnost, tepelně-technické vlastnosti (lehčený beton), propustnost záření;
- velká životnost, malé náklady na údržbu;
- jako konstrukční materiál nehoří, netaví se, nepředstavuje žádné požární zatížení, po požáru jsou zpravidla konstrukce dobře opravitelné;
- velká tepelná jímavost při změnách teploty;
- konstrukčně příznivé – stropní desky tvoří současně vodorovné vyztužení, schodišťové stěny a výtahové šachty tvoří současně ztužující elementy;
- dobře se kombinuje s ocelí a zdivem.
b) nevýhody
- „ambulantní“ výroba;
- výroba je závislá na počasí;
- beton tvoří bez dalších opatření tepelný most;
- ochrana proti elektrickému poli a patogenním zónám není dosud pro beton známá;
- bourání, rozšiřování, popř. zesilování je obtížnější;
- architektonicky sporné, hovoří se o sklonu k šedivému „brutalismu“.
1.2 Optimální rozpony
Tab. 1.1 Ekonomicky optimální modulové osnovy pro skeletové stavby
| Železobeton | < 6 x 6 m |
| Ocel nebo železobeton | 6 x 6 – 10 x 10 m |
| Ocel | > 10 x 10 m |

Obr. 1.1 Schéma modulové osnovy pro skeletové stavby
Tab. 1.2 Ekonomicky optimální rozpony stropů
| Trapézové plechy | < 5 m |
| Železobeton | < 6 m |
| Železobeton nebo ocel s trámy a průvlaky | 6–12 m |
| Ocel s trámy a průvlaky | > 12 m |

Obr. 1.2 Schéma rozpětí stropů
1.3 Prostorová tuhost a vyztužení
Prostorovou tuhostí nazýváme schopnost stavební konstrukce odolávat zatížení, které působí obecným směrem. Síla obecného směru vzniká kombinací svislých účinků vlastní tíhy konstrukce, užitného zatížení apod., a vodorovného zatížení reprezentovaného zejména účinky větru, ale i vodorovných složek užitného zatížení atd.
Ztužení ve vodorovných rovinách zpravidla tvoří stropní či střešní konstrukce, které u patrových objektů jsou dostatečně tuhé ve své rovině, takže jsou schopné přenést účinky zatížení na ztužující konstrukci (monolitické stropy nebo panelové stropy se zálivkovou výztuží apod.) U halových staveb se tuhost střešní roviny zajišťuje větrovými ztužidly (zavětrováním ve střešní rovině).
Svislé ztužující konstrukce jsou uvedeny v následujícím přehledu:
- vetknuté sloupy především u halových jednopodlažních popř. dvoupodlažních staveb musí být dostatečně zakotvené do základů. Na účinky vodorovného zatížení sloupy působí staticky jako konzoly vetknuté buď v obou směrech, nebo mohou být v jednom směru uložené kloubově (především u dřeva a oceli). V zásadě je možné vetknuté sloupy navrhnout ze všech materiálů pro různé konstrukční výšky. Vetknuté sloupy neomezují dispoziční řešení a umožňují maximální flexibilitu.

Obr. 1.3 Schéma vetknutého sloupu
- příhradová zavětrování jsou typická pro dřevěné a ocelové skelety a halové stavby. Zajišťují tuhost konstrukce pouze ve své rovině, kolmo ke své rovině jsou měkké. Staticky jsou velmi výhodné s ohledem na přenos účinků osovými silami v jednotlivých prutech a díky velké tuhosti. Průřezy prutů jsou relativně malé, ale po architektonické stránce zavětrování omezuje dispoziční řešení.
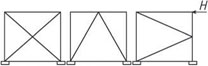
Obr. 1.4 Schéma příhradového zavětrování
- rámy jsou možné u všech typů staveb a jsou architektonicky a provozně velmi výhodné. V halách jsou časté dvoukloubové rámy různých provedení, u vícepodlažních budov patrové rámy, které vzniknou tuhým spojením sloupů s průvlaky. Typickým materiálem pro rámy je železobeton. Patrové rámy je možné použít do velké výšky objektu.

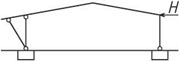
Obr. 1.5 Statická schémata rámů
- stěny jsou možné u všech druhů staveb; u obytných a provozních budov mohou tvořit výztužné stěny štíty, dělicí příčky (mezibytové apod.), schodišťové stěny a stěny u výtahů probíhající po celé výšce objektu. Staticky působí jako konzoly vetnuté do základů, jejich tuhost je závislá především na šířce stěny. Mohou být plné nebo s otvory.
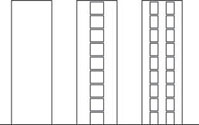
Obr. 1.6 Výztužné stěny
- monolitická jádra vznikají propojením stěn ohraničujících komunikační prostory. Od pěti podlaží je hospodárné použití posuvného bednění. Umožňují vyztužit budovu do velké výšky.
Výztužná konstrukce může plnit svou funkci podle uspořádání, buď v jedné rovině (příhradové zavětrování, rovinný rám, stěna) s minimální tuhostí ve směru kolmém k této rovině, nebo zajistí prostorovou tuhost ve všech směrech (monolitické jádro, sloup vetknutý ve všech směrech, prostorový rám).
Pro zajištění prostorové tuhosti objektu musí být, za předpokladu tuhých stropů či střešní roviny, konstrukce ztužena alespoň ve třech svislých rovinách, které se neprotínají ve společné přímce (průsečnici). Tím je zamezeno jak posunutí stropních desek ve vodorovné rovině (od podélných a vodorovných účinků větru), tak pootočení (nakroucení) stavby.
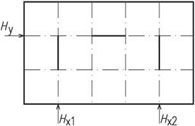
Obr. 1.7 Půdorysné rozmístění ztužujících konstrukcí – síly H musí být v rovnováze se vnějším vodorovným zatížením
Příklad 1.1
Navrhněte ztužení rohového objektu s vyztužením ve třech svislých rovinách, půdorys:
a)
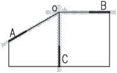
Vyztužení, která se však protínají v jedné průsečnici – zamezí posunutí stropních desek, ale kolem bodu „O“ může dojít k pootočení – vyztužení je nedostatečné,
b)
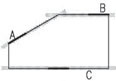
dostatečné vyztužení objektu podle výše uvedených pravidel – je zamezeno posunutí i pootočení stropních desek.
1.4 Dilatace
Konstrukce je nutné dělit na dilatační úseky z důvodů:
- délkových změn způsobených tepelnou roztažností materiálu a kolísáním teplot v průběhu dne a celého roku;
- smršťování a bobtnání materiálu způsobeného změnami vlhkosti;
- různého zatížení částí stavby způsobeného rozdíly ve výšce objektu či rozdílného využití;
- různého sedání vlivem nestejnorodých základových poměrů;
- při přístavbách.
Podle příčiny se dilatace navrhuje pro předpokládaný vzájemný posun ve svislém směru, například pro různé sedání, nebo ve vodorovném směru z důvodů objemových změn materiálu konstrukce, způsobených například smršťováním betonu, tepelnou roztažností apod. Podle toho je možno navrhnout způsob dilatace:
- zdvojením nosné konstrukce (sloupů, průvlaků);
- vloženým polem s možností výškového pohybu;
- vytvořením styků s možností vodorovného posunu (kluzné uložení stropů apod.).
Jednotlivé dilatační celky je nutné z hlediska prostorové tuhosti zkoumat odděleně a každou část samostatně vyztužit.
Velikosti dilatačních celků pro jednotlivé konstrukční materiály jsou předepsány v některých normách, nebo se musí konstrukce na účinek například smršťování betonu posoudit. Při kombinaci různých materiálů je nutné vzít v úvahu nejnepříznivější z hodnot. Návrhu dilatačních celků z důvodů rozdíleného zatížení, nestejnorodých základových poměrů či různých výšek stavby se úseky volí podle konkrétních podmínek.
Velikost dilatačního úseku závisí také na uspořádání ztužujících prvků stavby. Například největší délky dilatačních celků s ohledem na tepelnou roztažnost jsou u ocelových konstrukcí, pokud je konstrukce uspořádána tak, že konstrukce může volně dilatovat od středu k oběma koncům. Pokud ztužující konstrukce brání volné dilataci, zmenšuje se délka dilatačního úseku za účelem omezení velikosti silových účinků od zabráněné dilatace.
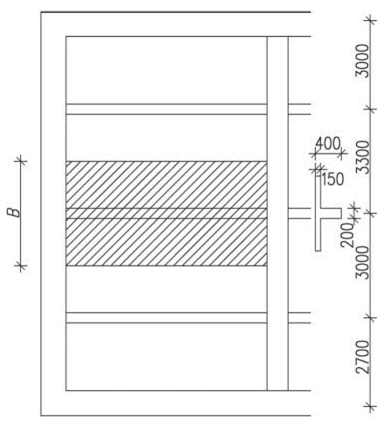
Podle ČSN EN 1992-1-1 lze u železobetonových konstrukcí zanedbat účinky teploty a smršťování, pokud je dodržena maximální vzdálenost dilatačních spár djoint = 30 m. Pro prefabrikované konstrukce mohou být vzdálenosti spár větší, protože část smršťování a dotvarování proběhla před montáží. V normě ČSN 73 1201 jsou uvedeny doplňující články, mimo jiné i rozměry dilatačních celků podle následujících tabulek:
Tab. 1.3 Maximální délky dilatačních úseků ℓdil,1 [m] pro budovy a haly podle ČSN 73 1201
| Řádek | Druh konstrukce | Maximální délka ℓdil,1 [m] při nosné konstrukci | ||||
| monolitické | montované | |||||
| chráněné1)2) | nechráněné | chráněné1)2) | nechráněné | |||
| 1 | Skeletové konstrukce se ztužujícími prvky3) | uprostřed dilatačního celku4) | 54 | 36 | 60 | 42 |
| 2 | na jednom konci dilatačního celku | 42 | 27 | 45 | 30 | |
| 3 | v mezilehlé poloze | viz ČSN 73 1201 | ||||
| 4 | na obou koncích dilatačního celku | 33 | 21 | 36 | 27 | |
| 5 | na dvou a více místech dilatačního celku | viz ČSN 73 1201 | ||||
| 6 | Stěnové konstrukce s nosnými obvodovými stěnami | třívrstvými nebo dvouvrstvými | 515) | 33 | 545) | 46 |
| 7 | jednovrstvými z lehkých betonů, samonosnými nebo nosnými | – | 39 | – | 45 | |
| 1) Skeletová konstrukce se považuje za chráněnou, jestliže její nosné obvodové prvky (sloupy, průvlaky, stěny, stropní desky nad nejvyšším podlažím, popř. střešní desky) jsou chráněny před účinky teplotních změn tepelnou izolací odpovídající požadavkům norem tepelně technických vlastností stavebních konstrukcí a budov. 2) Stěnová konstrukce se považuje za chráněnou, jestliže je nosná vrstva vícevrstvé stěny opatřena z vnější strany tepelnou izolací odpovídající požadavkům norem uvedeným v předchozí vysvětlivce. 3) Ztužujícím prvkem je např. samostatná stěna, stěny schodiště, stěny výtahové šachty. Předpokládá se, že ztužující prvek brání volné dilataci pouze v rovině střednicové plochy stěn, které je tvoří. 4) Hodnoty také platí pro skeletovou konstrukci bez ztužujících prvků. 5) Délky platí také pro konstrukce s obvodovými stěnami nenosnými, tj. se stěnami podporovanými (nesenými), pokud nenosné obvodové stěny, popř. zavěšené lehké dílce zajišťují tepelnou izolaci vnitřní nosné konstrukce. |
||||||
Tab. 1.4 Největší délky dilatačních celků ℓdil [m] u konstrukcí z prostého a slabě vyztuženého betonu podle ČSN 73 1201
| Řádek | Druh nosné konstrukce | Maximální délky dilatačních celků ℓdil [m] při nosné konstrukci | ||
| chráněné | nechráněné | |||
| 1 | Monolitická konstrukce | bez pomocné výztuže | 22 | 12 |
| 2 | s pomocnou výztuží | 30 | 24 | |
| 3 | Montovaná konstrukce | 42 | 30 | |
Tab. 1.5 Doporučené maximální délky dilatačních celků ℓdil [m] nenosných betonových součástí stavebních objektů
| Řádek | Druh konstrukce | Doporučené maximální délky dilatačních úseků ℓdil [m] u konstrukce | |||
| monolitické | montované | ||||
| 1 | Atiky, římsy na volném prostranství | z prostého betonu | 3 | – | |
| 2 | ze železobetonu | 6 | 12 | ||
| 3 | Podlahy střech, teras, balkonů apod. | nechráněné tepelnou izolací | na zdivu | 6 | 9 |
| 4 | na betonu | 9 | 12 | ||
| 5 | chráněné tepelnou izolací | na zdivu | 9 | 12 | |
| 6 | na betonu | 18 | 24 | ||
| 7 | Ochranné vnější vrstvy třívrstvých obvodových stěn při spojení s vnitřní stěnou | ve spoji dokonale poddajnými ve smyku | – | – | 7,2 |
| 8 | ve spoji nedokonale poddajnými ve smyku (např. betonovými žebry) | – | – | 4,2 | |
| 9 | Podlahy z prostého betonu v budovách a halách | nevytápěných při tloušťce podlahy | 140 – 180 m | 4,5 | – |
| 10 | 200 – 240 mm | 6 | – | ||
| 11 | vytápěných při tloušťce podlahy | 140 – 240 mm | 18 | – | |
Tab. 1.6 Největší doporučené vodorovné vzdálenosti ℓm mezi svislými dilatačními spárami u nevyztužených nenosných zděných stěn podle ČSN EN 1996-2
| Typ zdiva | ℓm [m] |
| Zdivo z pálených zdicích prvků | 12 |
| Zdivo z vápenopískových zdicích prvků | 8 |
| Zdivo z betonu a umělého kamene | 6 |
| Zdivo z autoklávovaného pórobetonu | 6 |
| Zdivo z přírodního kamene | 12 |
Tab. 1.7 Doporučené mezní vzdálenosti dilatačních spár ve zdivu podle již neplatné ČSN 73 1101
| Zdivo | Mezní vzdálenosti mezi dilatačními spárami ℓm [m] pro zdivo na maltu pevnostní značky | ||
| 15,0; 10,0 a 5,0 | 2,5 a 1,0 | 0,4 | |
| Z cihlářských výrobků | 60 | 90 | 120 |
| Z vápenopískových cihel a z dílců z obyčejného a lehkého betonu | 45 | 60 | 80 |
| Z dílců z pórobetonu | 24 | 24 | 24 |
Tab. 1.8 Mezní hodnoty dilatačních úseků pro ocelové konstrukce podle zrušené ČSN 73 1401:1995
| Konstrukce | Vzdálenost [m] | |||
| a | b | L | ||
| Chráněná | ve vytápěné budově | 50 | 95 | 230 |
| v nevytápěné budově a v teplých provozech | 50 | 75 | 200 | |
| Nechráněná (venkovní) | 30 | 50 | 130 | |
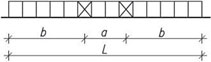
Obr. 1.8 Schéma dilatačních úseků ocelových konstrukcí
2 Střechy
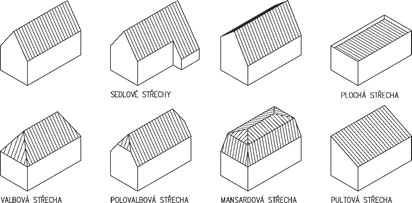
Nosná konstrukce střech závisí především na tvaru zastřešení, zatížení vlastní tíhou střešního pláště, nahodilým zatížením sněhem a větrem. U střech s větším sklonem se zpravidla navrhují krovy, nejčastěji dřevěné. Při větších rozponech nebo neobvyklých tvarech může být krov podepřen ocelovými prvky (nosníky na větší rozpětí, rámy apod.). Zpravidla uspořádání vychází ze základních soustav – krokevní, hambalkové, vaznicové nebo vlašské, které jsou uvedeny dále. Pro nosné konstrukce plochých střech se používají systémy obdobné jako u stropů.
Obr. 2.1 Tvary střech
Tab. 2.1 Doporučené sklony střešních krytin skládaných bez doplňkového izolačního opatření
| Krytina | Druh krytiny | Nejmenší sklon | |
| α [°] | S [%] | ||
| Tašková keramická | dvojitá z hladkých tašek na řídké nebo husté laťování | 30 | 58 |
| tažené jednodrážkové tašky | 35 | 70 | |
| ražené drážkové tašky se spojitou vodní drážkou | 22 | 40 | |
| ražené drážkové tašky s přerušovanou vodní drážkou | 30 | 58 | |
| prejzy a háky (kůrky a korýtka | 40 | 84 | |
| vlnovky (esovky) holandky | 35 | 70 | |
| Betonová | tašky profilované drážkované | 22 | 40 |
| betonové tašky obyčejné | 30 | 58 | |
| Vláknocementová | vlnitá (vlnovky) | 10 | 18 |
| šablony jednoduché | 30 | 58 | |
| šablony dvojité | 25 | 47 | |
| Břidlicová | jednoduchá z přírodní břidlice | 30 | 58 |
| dvojitá z přírodní břidlice | 25 | 47 | |
| Plechová | plechová šablony | 30 | 58 |
| vlnitý plech | 15 | 27 | |
| ohýbané profily | 8 | 14 | |
| hladká na lišty nebo drážky | 7 | 12 | |
| Šindelová | jednoduchá | 40 | 84 |
| dvojitá | 35 | 70 | |
| Došková | sláma, rákos | 45 | 100 |
| Z plastů | skelné lamináty, PVC | 15 | 27 |
| Hydroizolační pásy | jednoduchá na hladko | 10 | 18 |
| jednoduchá na trojboké lišty | 10 | 18 | |
| dvojitá na hladko | 2 | 3 | |
| křemílková | 2 | 3 | |
| Lepenková | jednoduchá na hladko | 10 | 18 |
| asfaltové šindele | 18 | 32 | |
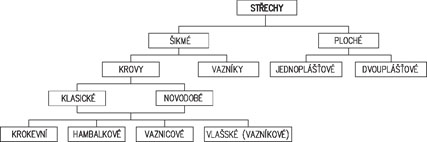
Obr. 2.2 Schéma konstrukčních typů střech
2.1 Zatížení
Hodnoty zatížení jsou uváděny v kN/m2 podle druhu zatížení:
- svisle na plochu střechy (vlastní tíha);
- svisle na půdorysnou plochu (sníh);
- kolmo k ploše střechy (vítr).
Tab. 2.2 Vlastní tíha
| Druh zatížení | Charakteristická hodnota zatížení q [kN/m2] |
| Krytina tašková a laťování | |
|
0,55 |
|
0,75 |
|
0,85 |
| Krytina prejzová | 1,00 |
| Krytina plechová s bedněním | 0,20 |
| Krytina lepenková s bedněním | 0,35 |
| Vláknocementové šablony | |
|
0,25 |
|
0,40 |
| Třívrstvá živičná krytina bez podkladu | 0,25 |
| Krokve či vaznice | 0,15 |
| Zateplení půdy | 0,10 |
| Sádrokartonový pohled s roštem | 0,25 |
Vlastní tíha nosných konstrukcí střechy jako jsou panely, železobetonové desky apod. jsou uvedeny v kap. 2.2.1.
Tab. 2.3 Užitné zatížení
| Kategorie | Stanovené použití | Charakteristická hodnota zatížení | ||
| q [kN/m2] | Q [kN] | |||
| H | střechy nepřístupné | střechy nepřístupné s výjimkou běžné údržby a oprav | 0,75 | 1,0 |
| I | střechy přístupné | střechy pochůzné, s využíváním podle kategorií A–D | podle způsobu využívání podle kategorií A–D, viz tab. 3.8 |
|
| K | střechy přístupné pro zvláštní provoz – například plochy pro přistávání vrtulníků | |||
| třída vrtulníku | startovací zatížení vrtulníku Q [kN] |
startovací zatížení Qk [kN] |
rozměry zatěžovací plochy [m · m] |
|
| HC-1 HC-2 |
Q ≤ 20 20 ≤ Q ≤ 60 |
Qk = 20 Qk = 60 |
0,2 · 0,2 0,3 · 0,3 |
|
Zatížení od střešních zahrad na plochých střechách – skladba vegetace, substrát, ochrana proti prorůstání kořenů, drenážní a filtrační vrstva, vodotěsná a tepelná izolace, parotěsná zábrana. Podle druhu vegetace jsou orientační hodnoty uvedeny v tab. 2.4.
Tab. 2.4 Zatížení od střešních zahrad
| Druh vegetace | Výška vzrůstu [mm] | Konstrukční výška [mm] | Charakteristická hodnota zatížení q [kN/m2] | |
| Extenzívně ozeleněné střechy | mechové pokryvy | 10–30 | 25–50 | 0,3–0,4 |
| trávníkové pokryvy | 50–100 | 50–100 | 0,4–0,8 | |
| extenzivní trávníky | 100–200 | 50–100 | 0,4–0,8 | |
| travnaté koberce | 100–250 | 80–140 | 0,8–1,2 | |
| trávníky horského typu (bylinné) | 100–300 | 100–150 | 1,0–1,45 | |
| Intenzívně ozeleněné střechy | sucho snášející zahrádka (půda, zakrslé keře) | 150–600 | 160–200 | ≈ 2,50 |
| trvalky, drobné keře | 150–800 | ≈ 250 | 2,0–3,0 | |
| středně velké keře | < 1 500 | ≈ 300 | 3,0–3,5 | |
| velké keře | < 6 000 | 400–450 | 4,0–5,0 | |
| malé stromky | < 10 000 | > 400 + pahorky | > 5,0 + vlastní tíha | |
2.1.1 Zatížení sněhem
Způsob stanovení zatížení sněhem je dán normou ČSN EN 1991-1-3. Postup je takový, že se podle zeměpisné polohy určí sněhová oblast podle mapy na obr. 2.3 a každé sněhové oblasti přináleží charakteristická hodnota zatížení sněhem na zemi sk v tab. 2.6, jejíž překročení je dáno s určitou statistickou zárukou. Tato hodnota se dále upraví pomocí součinitelů, které zohledňují tvar střechy, sklon, drsnost, tepelné vlastnosti, možnost tvoření návějí, vliv okolního terénu a vzdálenost sousedních staveb na charakteristickou hodnotu zatížení sněhem na střeše, která je dána zatížením na metr čtvereční půdorysné plochy střechy. Uvažují se základní dvě situace zatížení nenavátým sněhem a navátým sněhem.
Pro trvalé a dočasné návrhové situace je charakteristická hodnota zatížení sněhem na střeše určena vztahem
\begin{gathered}
s=\mu\cdot C_\text{e}\cdot C_\text{t}\cdot s_\text{k}
\end{gathered}kde je
μ … tvarový součinitel podle tvaru střechy, viz tab. 2.8,
Ce … součinitel expozice podle okolí stavby, viz tab. 2.7,
Ct … tepelný součinitel závislý na tepelné prostupnosti střechy, běžně Ct = 1,0.
Tab. 2.5 Tíha sněhu
| Typ sněhu | Objemová tíha ρ [kN/m3] |
| Čerstvý suchý sníh | 1,0 |
| Ulehlý (několik hodin nebo dnů po napadnutí) | 2,0 |
| Starý (několik týdnů nebo měsíců po napadnutí | 2,5–3,5 |
| Mokrý | 4,0 |
Tab. 2.6 Sněhové oblasti na území České republiky
| Oblast | Charakteristická hodnota sk [kN/m2] | Označení v mapě |
| I. | 0,70 | |
| II. | 1,00 | |
| III. | 1,50 | |
| IV. | 2,00 | |
| V. | 2,50 | |
| VI. | 3,00 | |
| VII. | 4,00 | |
| VIII. | >4,00*) | |
| *) Charakteristickou hodnotu určí příslušná pobočka Českého hydrometeorologického ústavu | ||
Skutečné zatížení sněhem závisí na tvaru a sklonu střechy, její drsnosti, tepelných vlastnostech, možnosti tvoření závějí, okolním terénu a vzdálenosti sousedních staveb, podrobně viz ČSN EN 1991-1-3.
Obr. 2.3 Mapa sněhových oblastí České republiky
Tab. 2.7 Doporučené hodnoty součinitele Ce pro různé typy krajiny
| Typ krajiny | Ce | |
| otevřená | rovná plocha bez překážek, otevřená do všech stran, nechráněná nebo jen málo chráněná terénem, vyššími budovami nebo stromy | 0,8 |
| normální | plochy, kde nedochází na stavbách k výraznému přemístění sněhu kvůli okolnímu terénu, jiným stavbám nebo stromům | 1,0 |
| chráněná | plochy, kde je uvažovaná stavba výrazně nižší než okolní terén nebo je stavba obklopena vysokými stromy a/nebo vyššími stavbami | 1,2 |
Pro jednoduché tvary pultových a sedlových střech, kde není bráněno sesouvání sněhu, se zatížení uvažuje do sklonu 60°. Tvarový součinitel lze určit v závislost na úhlu podle následujícího grafu v tab. 2.8. Na dalším obr. 2.4 jsou příklady uspořádání zatížení nenavátým a navátým sněhem.
Tab. 2.8 Tvarový součinitel zatížení sněhem
| sklon střechy α | 0° ≤ α ≤ 30° | 30° < α < 60° | α < 60° |
| m1 | 0,8 | 0,8(60 – α) / 30 | 0 |
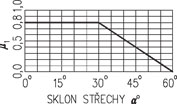

Obr. 2.4 Uspořádání zatížení sněhem a) pultová střecha, nenavátý sníh, b) sedlová střecha, nenavátý sníh, c) sedlová střecha s navátým sněhem
Příklad 2.1
Stanovte zatížení sněhem s na sedlové střeše objektu v normální krajině v okolí Tábora, sklon střechy je 45°.
| Okolí Tábora – II. sněhová oblast | sk = 1,0 kN/m2 |
| Normální krajina | Ce = 1,0 |
| Zateplené podkroví | Ct = 1,0 |
| Sklon střechy α = 45° | m1 = 0,4 |
| Charakteristická hodnota zatížení na střeše | s = 0,4 kN/m2 |

2.1.2 Zatížení větrem
Stanovení účinku větru na stavební konstrukce podle normy ČSN EN 1991-1-4 je poměrně složité a vyžaduje stanovení řady dílčích parametrů. Hodnoty tlaku větru v následující tabulce Beaufortovy stupnice mohou posloužit pouze k představě, jakých velikostí může tlak větru nabývat.
Tab. 2.9 Beaufortova stupnice větru
| Beaufortův stupeň [°Bf] | Označení | Znaky | Rychlost v [m/s] | Tlak větru w [kN/m2] |
| 0 | Bezvětří | kouř stoupá kolmo vzhůru, listy se nepohybují | 0,0–0,2 | 0,000 |
| 1 | Vánek | směr větru poznatelný podle kouře, neúčinkuje na větrnou korouhev | 0,3–1,5 | ≤ 0,001 |
| 2 | Slabý vítr | je cítit na tváři, listy stromů šelestí, korouhev se začíná pohybovat | 1,6–3,3 | ≤ 0,007 |
| 3 | Mírný vítr | listy stromů a větvičky v trvalém pohybu, vítr napíná praporky | 3,4–5,4 | ≤ 0,020 |
| 4 | Dosti čerstvý vítr | vítr zdvíhá prach a kousky papíru, pohybuje slabšími větvemi | 5,5–7,9 | ≤ 0,040 |
| 5 | Čerstvý vítr | listnaté keře se začínají hýbat, na stojatých vlnách se tvoří menší vlny se zpěněnými hřebeny | 8,0–10,7 | ≤ 0,070 |
| 6 | Silný vítr | vítr pohybuje silnějšími větvemi, telegrafní dráty sviští, obtížné je použití deštníku | 10,8–13,8 | ≤ 0,120 |
| 7 | Prudký vítr | vítr pohybuje celými stromy, chůze proti větru je obtížná | 13,9–17,1 | ≤ 0,180 |
| 8 | Bouřlivý vítr | vítr ulamuje větve, chůze proti větru je obtížná | 17,2–20,7 | ≤ 0,270 |
| 9 | Vichřice | menší škody na stavbách (vítr strhává komíny a tašky) | 20,8–24,4 | ≤ 0,370 |
| 10 | Silná vichřice | vyskytuje se na pevnině zřídka, velké škody | 24,5–28,4 | ≤ 0,500 |
| 11 | Mohutná vichřice | vyskytuje se velmi zřídka, rozsáhlá zpustošení | 28,5–32,6 | ≤ 0,670 |
| 12 | Orkán | ničivé účinky | 32,7–36,9 | ≤ 0,850 |
| 13 | Orkán | ničivé účinky | 37,0–41,4 | ≤ 1,070 |
| 14 | Orkán | ničivé účinky | 41,5–46,1 | ≤ 1,330 |
| 15 | Orkán | ničivé účinky | 46,2–50,9 | ≤ 1,620 |
| 16 | Orkán | ničivé účinky | 51,0–56,0 | ≤ 1,960 |
| 17 | Orkán | ničivé účinky | ≥ 56,1 | > 1,960 |
| *) Tlak větru w [kN/m2] = rychlost2/1600 | ||||
V následujícím textu je uveden zjednodušený postup pro stanovení účinku větru pro jednoduché pozemní stavby. Základním údajem pro stanovení účinku větru je jeho základní výchozí rychlost. Ta je stanovena pro určitou geografickou polohu v České republice podle mapy na obr. 2.5 pro jednotlivé větrné oblasti v tab. 2.10. Je to desetiminutová střední rychlost s roční pravděpodobností překročení p = 0,02 ve výšce 10 m nad plochým terénem. Tato hodnota se v České republice v běžných případech považuje za základní rychlost větru nb.
Základní dynamický tlak větru qb ve výšce 10 m nad terénem lze přepočítat pomocí vztahu
\begin{gathered}
q_\text{b}=0{,}5\rho\cdot n_\text{b}^2\space[\text{N/m}^2]
\end{gathered}kde je
ρ = 1,25 kg/m3 … měrná hmotnost vzduchu – hodnoty qb pro jednotlivé větrné oblasti jsou uvedené v tab. 2.10.
Tab. 2.10 Větrné oblasti na území České republiky
| Oblast | Výchozí základní rychlost větru vb,0 [m/s] | Základní dynamický tlak větru qb [kN/m2] | Označení v mapě |
| I. | 22,5 | 0,316 | |
| II. | 25,0 | 0,391 | |
| III. | 27,5 | 0,473 | |
| IV. | 30,0 | 0,563 | |
| V. | 36,0 *) | 0,810 | |
| *) Charakteristickou hodnotu určí příslušná pobočka Českého hydrometeorologického ústavu | |||
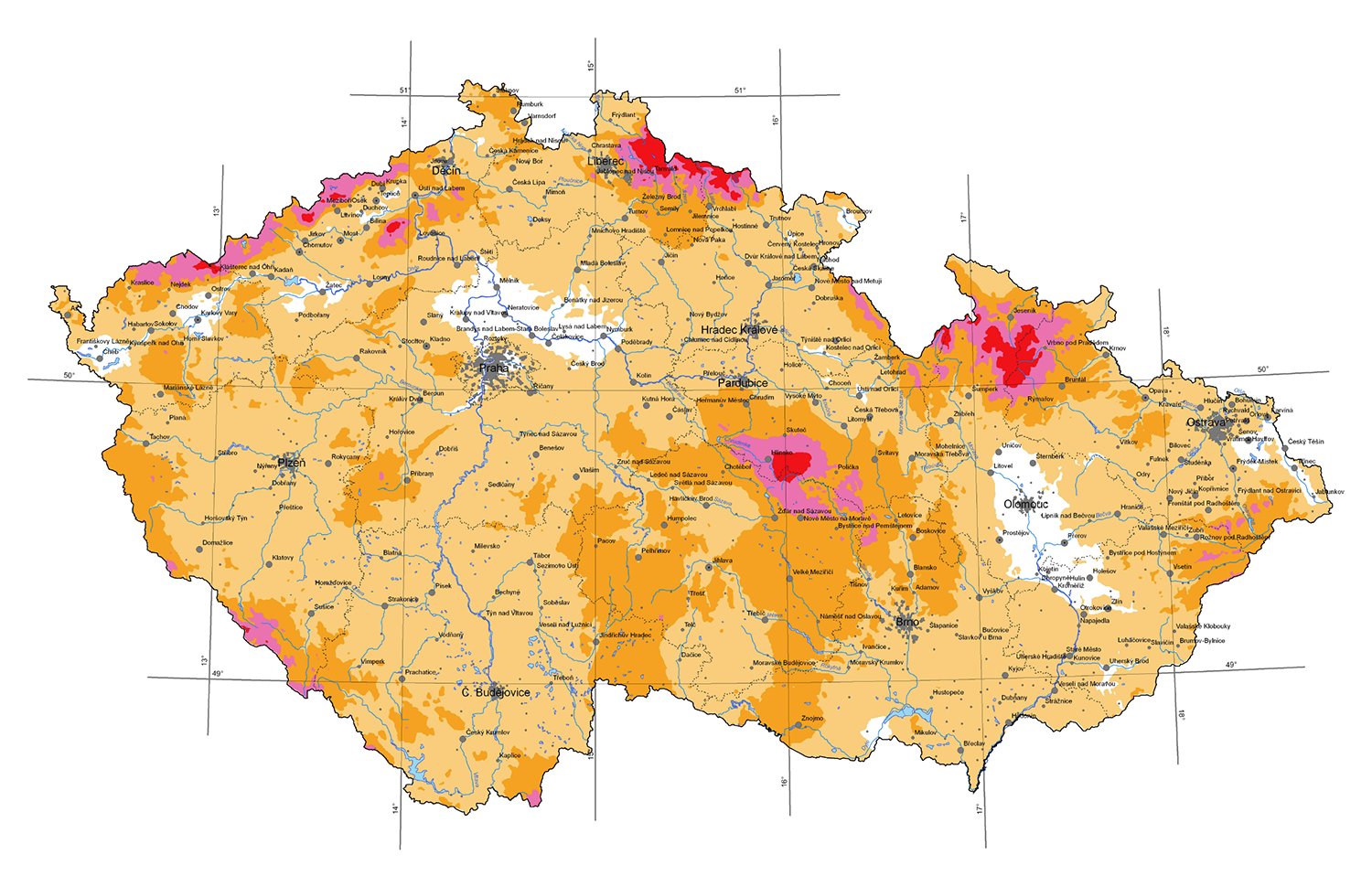
Obr. 2.5 Mapa větrných oblastí na území České republiky
Dalšími faktory, které ovlivňují zatížení větrem, je tvar a drsnost terénu v okolí stavby. Okolní terénní útvary jako kopce, hřebeny, terénní zlomy (tzv. orografie) výrazně ovlivňují proudění vzduchu. Vzhledem ke složitosti problému je v dalším popisu vliv orografie zanedbán a předpokládáme rovinatý terén.
Pro určení vlivu drsnosti terénu se rozlišují kategorie terénu podle následující tab. 2.11.
Tab. 2.11 Kategorie terénu a jejich parametry
| Kategorie terénu | zmin[m] | |
| 0 | Moře a pobřežní oblasti vystavené otevřenému moři | 1 |
| I | Jezera a vodorovné oblasti se zanedbatelnou vegetací a bez překážek | 1 |
| II | Oblasti s nízkou vegetací jako je tráva a s izolovanými překážkami jako (stromy, budovy), jejichž vzdálenost je větší než 20násobek jejich výšky | 2 |
| III | Oblasti rovnoměrně pokryté vegetací nebo budovami nebo s izolovanými překážkami, jejichž vzdálenost je maximálně 20násobek výšky překážek (jako jsou vesnice, předměstský terén, souvislý les) | 5 |
| IV | Oblasti, ve kterých je nejméně 15 % povrchu pokrytu pozemními stavbami, jejichž průměrná výška je větší než 15 m | 10 |
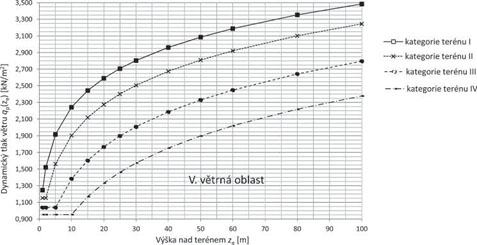
Referenční výška nad terénem ze, ve které se zjišťuje účinek větru, se uvažuje v intervalu zmin ≤ ze ≤ 200 m – viz tab. 2.10. Maximální dynamický tlak qp(ze) v referenční výšce ze lze stanovit z grafu na následujícím obr. 2.6 pro jednotlivé větrné oblasti a kategorie terénu, pokud se neuplatňuje vliv orografie terénu.
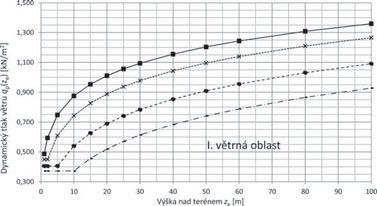
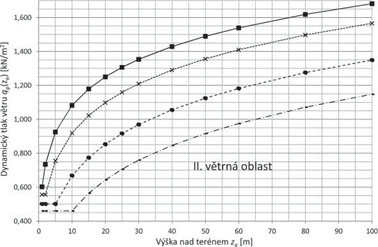
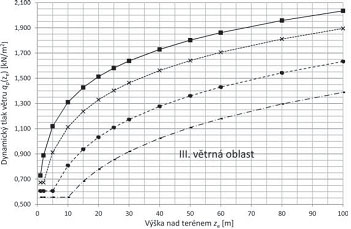
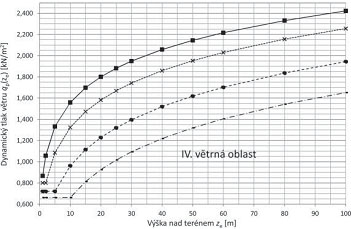
Obr. 2.6 Maximální dynamický tlak větru qp(ze) ve výšce ze nad terénem
Příklad 2.2
Určete hodnotu maximálního dynamického tlaku větru v Kutné Hoře ve výšce 20 m nad terénem bez vlivu orografie.
| Kutná Hora – II. větrná oblast | |
| základní rychlost větru | vb,0 = 25 m/s |
| základní dynamický tlak větru | qb = 0,391 kN/m2 |
| Historické centrum kategorie terénu III | |
| Maximální dynamický tlak větru | qp(20) = 0,85 kN/m2 |
Zatížení větrem se uvažuje jako tlak nebo sání kolmo na uvažovanou plochu střechy nebo fasády, případně jako tření proudu vzduchu o danou plochu ve směru této plochy. Pro určení účinku větru (tlaku a sání) na konkrétním místě jednoduchých objektů závisí na několika okolnostech:
- na výšce místa nad terénem (zohledňuje se pomocí referenční výšky ze);
- sklonu plochy vůči působení větru (svislé plochy (fasády), šikmé plochy (střechy), vodorovné plochy (ploché střechy);
- objemovém uspořádání objektu (vzájemné vztahy délky, šířky a výšky);
- velikosti referenční plochy (lokální účinek větru na relativně malé ploše může být větší než na plochu velkou).
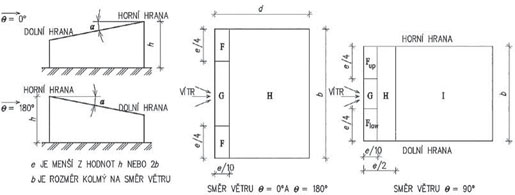
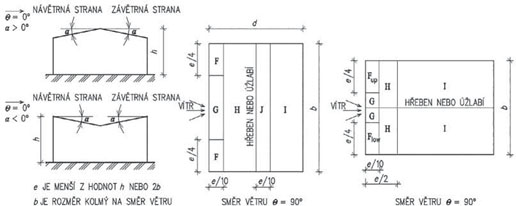
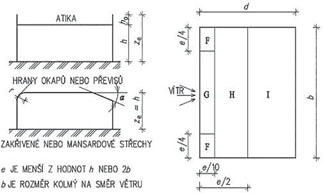
V následujících tab. 2.12 – 2.15 jsou uvedeny součinitele vnějšího tlaku na ploché, pultové a sedlové střechy a pro úplnost též na svislé fasády tvarově jednoduchých budov. Účinek větru v daném místě pláště budovy se určí jako součin maximálního dynamického tlaku větru qp(ze) pro referenční výšku ze a součinitele vnějšího tlaku cpe. Vysvětlení jednotlivých parametrů pro určení tvarového součinitele je jednak patrné ze schémat k jednotlivým tabulkám, případně je ve vysvětlivkách. Pro jednotlivé oblasti vnější plochy stavby jsou tvarové součinitele uvedeny ve dvou hodnotách – cpe,10 a cpe,1. První z hodnot cpe,10 platí pro referenční plochy o velikosti 10 m2 a větší. Tato hodnota je menší než hodnota druhá cpe,1, platící pro referenční plochu do 1 m2 včetně. Pokud je referenční plocha v intervalu od 1 do 10 m2, součinitel se lineárně interpoluje.
Pro další tvary střech, jako je střecha valbová, šedová, střechy vícelodních hal, válcová střecha a kupole je nutné součinitele vnějšího tlaku vyhledat v normě ČSN EN 1991-1-4.
Tab. 2.12 Součinitele vnějšího tlaku pro ploché střechy
| Typ střechy | Oblasti | ||||||||
| F | G | H | I | ||||||
| cpe,10 | cpe,1 | cpe,10 | cpe,1 | cpe,10 | cpe,1 | cpe,10 | cpe,1 | ||
| Ostré hrany | -1,8 | -2,5 | -1,2 | -2,0 | -0,7 | -1,2 | +0,2 | ||
| -0,2 | |||||||||
| S atikou | hp/h = 0,025 | -1,6 | -2,2 | -1,1 | -1,8 | -0,7 | -1,2 | +0,2 | |
| -0,2 | |||||||||
| hp/h = 0,05 | -1,4 | -2,0 | -0,9 | -1,6 | -0,7 | -1,2 | +0,2 | ||
| -0,2 | |||||||||
| hp/h = 0,10 | -1,2 | -1,8 | -0,8 | -1,4 | -0,7 | -1,2 | +0,2 | ||
| -0,2 | |||||||||
| Zakřivené hrany | r/h = 0,05 | -1,0 | -1,5 | -1,2 | -1,8 | -0,4 | +0,2 | ||
| -0,2 | |||||||||
| r/h = 0,10 | -0,7 | -1,2 | -0,8 | -1,4 | -0,3 | +0,2 | |||
| -0,2 | |||||||||
| r/h = 0,20 | -0,5 | -0,8 | *0,5 | -0,8 | -0,3 | +0,2 | |||
| -0,2 | |||||||||
| Mansardové hrany | α = 30° | -1,0 | -1,5 | -1,0 | -1,5 | -0,3 | +0,2 | ||
| -0,2 | |||||||||
| α = 45° | -1,2 | -1,8 | -1,3 | -1,8 | -0,4 | +0,2 | |||
| -0,2 | |||||||||
| α = 60° | -1,3 | -1,9 | -1,3 | -1,9 | -0,5 | +0,2 | |||
| -0,2 | |||||||||
|
Poznámky: |
|||||||||
Tab. 2.13 Součinitele vnějšího tlaku pro pultové střechy
| Oblast | Úhel sklonu α | 5° | 15° | 30° | 45° | 60° | 75° | |||||
| pro směr větru θ = 0° | F | cpe,10 | -1,7 | +0,0 | -0,9 | +0,2 | -0,5 | +0,7 | -0,0 | +0,7 | +0,7 | +0,8 |
| cpe,1 | -2,5 | -2,0 | -1,5 | |||||||||
| G | cpe,10 | -1,2 | +0,0 | -0,8 | +0,2 | -0,5 | +0,7 | -0,0 | +0,7 | +0,7 | +0,8 | |
| cpe,1 | -2,0 | -1,5 | -1,5 | |||||||||
| H | cpe,10 | -0,6 | +0,0 | -0,3 | +0,2 | -0,2 | +0,4 | -0,0 | +0,7 | +0,7 | +0,8 | |
| cpe,1 | -1,2 | |||||||||||
| pro směr větru θ = 180° | F | cpe,10 | -2,3 | -2,5 | -1,1 | -0,6 | -0,5 | -0,5 | ||||
| cpe,1 | -2,5 | -2,8 | -2,3 | -1,3 | -1,0 | -1,0 | ||||||
| G | cpe,10 | -1,3 | -1,3 | -0,8 | -0,5 | -0,5 | -0,5 | |||||
| cpe,1 | -2,0 | -2,0 | -1,5 | |||||||||
| H | cpe,10 | -0,8 | -0,9 | -0,8 | -0,7 | -0,5 | -0,5 | |||||
| cpe,1 | -1,2 | -1,2 | ||||||||||
| pro směr větru θ = 90° | Fup | cpe,10 | -2,1 | -2,4 | -2,1 | -1,5 | -1,2 | -1,2 | ||||
| cpe,1 | -2,6 | -2,9 | -2,9 | -2,4 | -2,0 | -2,0 | ||||||
| Flow | cpe,10 | -2,1 | -1,6 | -1,3 | -1,3 | -1,2 | -1,2 | |||||
| cpe,1 | -2,4 | -2,4 | -2,0 | -2,0 | -2,0 | -2,0 | ||||||
| G | cpe,10 | -1,8 | -1,9 | -1,5 | -1,4 | -1,2 | -1,2 | |||||
| cpe,1 | -2,0 | -2,5 | -2,0 | -2,0 | -2,0 | -2,0 | ||||||
| H | cpe,10 | -0,6 | -0,8 | -1,0 | -1,0 | -1,0 | -1,0 | |||||
| cpe,1 | -1,2 | -1,2 | -1,3 | -1,3 | -1,3 | -1,3 | ||||||
| I | cpe,10 | -0,5 | -0,7 | -0,8 | -0,9 | -0,7 | -0,5 | |||||
| cpe,1 | -1,2 | -1,2 | -1,2 | -1,2 | ||||||||
|
Poznámka 1: |
||||||||||||
Tab. 2.14 Součinitele vnějšího tlaku pro sedlové střechy
| Úhel sklonu α | -45° | -30° | -15° | -5° | 5° | 15° | 30° | 45° | 60° | 75° | |||||||
| pro směr větru θ = 0° | F | cpe,10 | -0,6 | -1,1 | -2,5 | -2,3 | -1,7 | +0,0 | -0,9 | +0,2 | -0,5 | +0,7 | +0,0 | +0,7 | +0,7 | +0,8 | |
| cpe,1 | -2,0 | -2,8 | -2,5 | -2,5 | -2,0 | -1,5 | |||||||||||
| G | cpe,10 | -0,6 | -0,8 | -1,3 | -1,2 | -1,2 | +0,0 | -0,8 | +0,2 | -0,5 | +0,7 | +0,0 | +0,7 | +0,7 | +0,8 | ||
| cpe,1 | -1,5 | -2,0 | -2,0 | -2,0 | -1,5 | -1,5 | |||||||||||
| H | cpe,10 | -0,8 | -0,8 | -0,9 | -0,8 | -0,6 | +0,0 | -0,3 | +0,2 | -0,2 | +0,4 | +0,0 | +0,6 | +0,7 | +0,8 | ||
| cpe,1 | -1,2 | -1,2 | -1,2 | ||||||||||||||
| I | cpe,10 | -0,7 | -0,6 | -0,5 | +0,2 | -0,6 | -0,6 | -0,4 | +0,0 | -0,4 | +0,0 | -0,2 | +0,0 | -0,2 | -0,2 | ||
| cpe,1 | |||||||||||||||||
| J | cpe,10 | -1,0 | -0,8 | -0,7 | +0,2 | -0,6 | +0,2 | -0,6 | -1,0 | +0,0 | -0,5 | +0,0 | -0,3 | +0,0 | -0,3 | -0,3 | |
| cpe,1 | -1,5 | -1,4 | -1,2 | -1,5 | +0,0 | ||||||||||||
| pro směr větru θ = 90° | F | cpe,10 | -1,4 | -1,5 | -1,9 | -1,8 | -1,6 | -1,3 | -1,1 | -1,1 | -1,1 | -1,1 | |||||
| cpe,1 | -2,0 | -2,1 | -2,5 | -2,5 | -2,2 | -2,0 | -1,5 | -1,5 | -1,5 | -1,5 | |||||||
| G | cpe,10 | -1,2 | -1,2 | -1,2 | -1,2 | -1,3 | -1,3 | -1,4 | -1,4 | -1,2 | -1,2 | ||||||
| cpe,1 | -2,0 | -2,0 | -2,0 | -2,0 | -2,0 | -2,0 | -2,0 | -2,0 | -2,0 | -2,0 | |||||||
| H | cpe,10 | -1,0 | -1,0 | -0,8 | -0,7 | -0,7 | -0,6 | -0,8 | -0,9 | -0,8 | -0,8 | ||||||
| cpe,1 | -1,3 | -1,3 | -1,2 | -1,2 | -1,2 | -1,2 | -1,2 | -1,2 | -1,0 | -1,0 | |||||||
| I | cpe,10 | -0,9 | -0,9 | -0,8 | -0,6 | -0,6 | -0,5 | -0,5 | -0,5 | -0,5 | -0,5 | ||||||
| cpe,1 | -1,2 | -1,2 | -1,2 | -1,2 | |||||||||||||
|
Poznámka 1: |
|||||||||||||||||
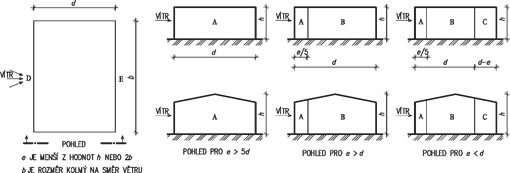
Tab. 2.15 Součinitele vnějšího tlaku pro svislé stěny pozemních staveb s pravoúhlým půdorysem
Příklad 2.3
Určete rozložení tlaku větru na vnější plášť jednoduchého objektu se sedlovou střechou, umístěného v Plzni v rovinatém terénu otevřené krajiny. Rozměry jsou patrné ze schématu.
| Plzeň – II. větrná oblast – obr. 2.5 a tab. 2.10 | |
| základní rychlost větru | vb,0 = 25 m/s |
| základní dynamický tlak větru | qb = 0,391 kN/m2 |
| Rovinatý terén, v nízké zástavbě kategorie terénu III – viz tab. 2.11 | |
| Maximální dynamický tlak větru | |
| výška nad terénem h ≈ 10 m – viz obr. 2.6 | qp(10) ≈ 0,67 kN/m2 |
2.2 Konstrukční typy krovů
Krov je nosná konstrukce šikmé střechy (sklon 10–45°) a strmé střechy (sklon > 45°). Přenáší zatížení vlastní hmotností a hmotností střešního pláště, účinky zatížení sněhem a větrem na svislé nosné konstrukce.
Krokevní soustava
Jednotlivé krokve se opírají v patě o pozednice nebo jsou zakotveny do vazného trámu a vzájemně se opírají ve hřebeni. Přenášejí ohybový moment a normálovou sílu, případná vrcholová vaznice má funkci pouze při montáži a pro celkové spolupůsobení jednotlivých vazeb.
Sklon střechy α = 25–50°.
Při rozpětí L < 12 m (hospodárné L ≤ 8 m) se navrhují krokve z řeziva, při větších rozpětích lepené nosníky apod. lamelové, skříňové, příhradové.
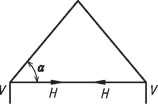
Obr. 2.7 Schéma krokevní soustavy
Výhody: hospodárné při větším sklonu; volný půdní prostor; krov nezatěžuje stropní konstrukci.
Nevýhody: nutné zakotvení každého páru krokví; nelze navrhnout valba, šířka vikýře maximálně dvojnásobek vzdálenosti krokví; vodorovné zatížení nadezdívky.
Hambalková soustava
Pro zmenšení rozpětí krokví je vložený hambalek v každém páru krokví (popřípadě více hambalků v patrech), která rozpírá krokve pro svislé zatížení – hambalek je tlačený prvek. Pro vodorovné zatížení působí pouze neposuvné hambalky, zajištěné např. zavětrováním v rovině hambalků.
Sklon střechy α = 25–60°
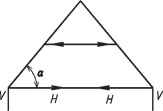
Obr. 2.8 Schéma hambalkové soustavy
Výhody: stejné jako krokevní soustava; jednoduchá půdní vestavba; výhodnější při větších sklonech; možnost většího rozponu.
Nevýhody: obtížné řešení valby; problematické nad lomených půdorysem (např. ve tvaru písmene L a T); složitější vazba; obtížná výměna vadných částí krovu.
Vaznicová soustava
Krokve leží na vodorovných vaznicích a jsou namáhány jen ohybem.
Sklon střechy α = 12–30° – krov bez vzpěr, vodorovné účinky od větru se přenáší přímo na pozednice.
Sklon střechy α = 20–50° – krov se vzpěrami, které vyztužují vazbu ve vodorovném směru.
Plné vazby se vzpěrami a sloupky se navrhují ve vzdálenostech do 4 m.
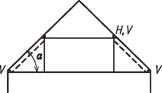
Obr. 2.9 Schéma vaznicové soustavy
Výhody: při vazbě se vzpěrami nejsou vodorovné účinky na pozednice; dobře řešitelná je nadezdívka; hospodárnější jsou nižší sklony střechy; dobře se konstruují vikýře i větších rozměrů; jednodušší výměna vadných krokví; výhodné pro valbu; jednodušší výroba a montáž krovu.
Nevýhody: větší spotřeba řeziva při větších sklonech; podpory v půdním prostoru omezují využitelnost podkroví; přenos zatížení krovu na stropní konstrukci (při absenci vazných trámů).
Vlašská soustava
Tato soustava vznikla ve středozemní oblasti pro střechy s menším sklonem. V našich oblastech se používala pro velká rozpětí jako josu jízdárny, taneční a divadelní sály apod. Základním prvkem jsou plné vazby tvořící vazníky ve vzdálenostech po 4–5 m. Plné vazby mohou tvořit v tradičním provedení věšadla, jako variantu lze navrhnout příhradové vazníky.
Tzv. vlašské krokve (vazničky) jsou orientovány rovnoběžně s hřebenem střechy a jsou umístěny ve vzdálenostech po cca 0,8–1 m. Pro krytinu, vyžadující vodorovné laťování, umísťují se po spádu na vlašské krokve další latě.
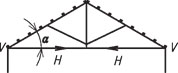
Obr. 2.10 Schéma vlašské soustavy
Výhody: soustava je vhodná pro sedlové střechy malého sklonu a je úsporná.
Nevýhody: plné vazby omezují využití podkroví.
2.3 Krokevní soustava
Přibližná vzorce pro rozměry krokví za předpokladů:
- vlastní tíha g = 65 kN/m2 plochy střechy;
- výška do 20 m nad terénem;
- II. sněhová oblast;
- rozpětí 7,0–10,0 m;
- sklon α = 20–50°.
Bez půdní vestavby
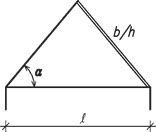
Obr. 2.11 Schéma krokevní soustavy bez půdní vestavby
Krokve
\begin{gathered}
\alpha=20{-}30\degree
\end{gathered}\begin{gathered}
\end{gathered}\begin{gathered}
\alpha=30{-}50\degree
\end{gathered}\begin{gathered}
h=20\ell+20\space[\text{mm}]
\end{gathered}\begin{gathered}
b=0{,}1e\ge70\space[\text{mm}]
\end{gathered}\begin{gathered}
h=20\ell+30+(\alpha-30\degree)\space[\text{mm}]
\end{gathered}\begin{gathered}
b=0{,}1e\ge70\space[\text{mm}]
\end{gathered}kde je
ℓ … rozpětí střechy [m],
e … osová vzdálenost krokví [mm].
Příklad 2.4
Navrhněte rozměry krokví

a)
\begin{gathered}
\alpha=25\degree,\space\ell=6{,}0\space\text{m},\space e=700\space\text{mm}
\end{gathered}\begin{gathered}
h=20\cdot6{,}0+20=120+20=140\space\text{mm}
\end{gathered}\begin{gathered}
b=0{,}1\cdot700=70\space\text{mm}
\end{gathered}\begin{gathered}
\end{gathered}\begin{gathered}
\end{gathered}\begin{gathered}
\text{profil}\space70/140\space\text{mm}
\end{gathered}b)
\begin{gathered}
\alpha=45\degree,\space\ell=8{,}0\space\text{m},\space e=800\space\text{mm}
\end{gathered}\begin{gathered}
h=20\cdot8{,}0+30+(45-30)=205\space\text{mm}
\end{gathered}\begin{gathered}
b=0{,}1\cdot800=80\space\text{mm}
\end{gathered}\begin{gathered}
\end{gathered}\begin{gathered}
\end{gathered}\begin{gathered}
\text{profil}\space80/210\space\text{mm}
\end{gathered}S půdní vestavbou
Krokevní soustava se používá s půdní vestavbou zpravidla zřídka, v tomto případě se výška krokve zvětší o 10–20 mm při stejné šířce krokve.
2.4 Hambalková soustava
2.4.1 Nepohyblivý hambalek
Platí za následujících předpokladů:
- v rovině hambalků je tuhá rovina (zavětrování, tuhý podhled podkroví);
- tato rovina je zakotvena do štítových a schodišťových stěn;
- vzdálenost zakotvení je rovna maximálně dvojnásobku délky hambalku.
Bez půdní vestavby
Předpoklady:
- rozpětí ℓ = 7,0–14,0 m;
- vlastní tíha g = 65 kN/m2 plochy střechy;
- zatížení hambalků v = 1,00 kN/m2;
- výška do 20 m nad terénem;
- II. sněhová oblast.
a) návrh krokve
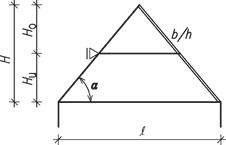
b) návrh hambalku
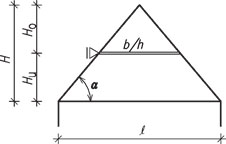
Obr. 2.12 Schéma hambalkové soustavy bez půdní vestavby
Krokve
\begin{gathered}
\alpha\le35\degree
\end{gathered}\begin{gathered}
\end{gathered}\begin{gathered}
\alpha=30{-}55\degree
\end{gathered}\begin{gathered}
h=15\ell\space[\text{mm}]
\end{gathered}\begin{gathered}
b=0{,}1e\space[\text{mm}]
\end{gathered}\begin{gathered}
h=16\ell+(\alpha-35\degree)\space[\text{mm}]
\end{gathered}\begin{gathered}
b=0{,}1e\space[\text{mm}]
\end{gathered}kde je
ℓ … rozpětí střechy [m],
e … osová vzdálenost krokví [mm].
Hambalky
\begin{gathered}
H_\text{U}\approx2/3H
\end{gathered}\begin{gathered}
\end{gathered}\begin{gathered}
H_\text{U}\approx H_0
\end{gathered}\begin{gathered}
h=10\ell+60\space[\text{mm}]
\end{gathered}\begin{gathered}
b=0{,}1e-10\ge70\space[\text{mm}]
\end{gathered}\begin{gathered}
h=10\ell+80\space[\text{mm}]
\end{gathered}\begin{gathered}
b=2\cdot0{,}1e-10\space[\text{mm}]
\end{gathered}Hambalky se zpravidla navrhují zdvojené, u starých krovů bývají jednoduché, začepované do krokví. Je-li prostor nad hambalkem průchozí H0 > 2 m, zvětší se výška průřezu hambalku o cca 30 %.
Příklad 2.5
\begin{gathered}
\alpha=45\degree,\space\ell=10{,}0\space\text{m},\space e=800\space\text{mm},\space H_\text{U}\approx H_0
\end{gathered}Krokev
\begin{gathered}
h=16\cdot10{,}50+(45-35)=178\space\text{mm}
\end{gathered}\begin{gathered}
b=0{,}1\cdot800=80\space\text{mm}
\end{gathered}\begin{gathered}
\end{gathered}\begin{gathered}
\text{profil}\space80/180\space[\text{mm}]
\end{gathered}Hambalek
\begin{gathered}
h=10\cdot10{,}50+80=185\space\text{mm}
\end{gathered}\begin{gathered}
b=2{,}0\cdot0{,}1\cdot800-10=150\space\text{mm}
\end{gathered}\begin{gathered}
\end{gathered}\begin{gathered}
\text{profil}\space150/185\space\space\text{nebo}\space\space2\text{ x }80/185\space[\text{mm}]
\end{gathered}S půdní vestavbou
a) návrh krokve

b) návrh hambalku
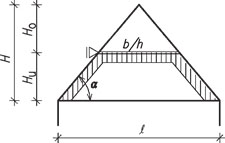
Obr. 2.13 Schéma hambalkové soustavy s půdní vestavbou
Krokve
\begin{gathered}
\alpha\le35\degree
\end{gathered}\begin{gathered}
\end{gathered}\begin{gathered}
\alpha=\gt35\degree
\end{gathered}\begin{gathered}
h=16{,}5\ell\space[\text{mm}]
\end{gathered}\begin{gathered}
b=0{,}1e-10\ge70\space[\text{mm}]
\end{gathered}\begin{gathered}
h=17{,}5\ell+2(\alpha-35\degree)\space[\text{mm}]
\end{gathered}\begin{gathered}
b=0{,}1e-10\ge70\space[\text{mm}]
\end{gathered}kde je
ℓ … rozpětí střechy [m],
e … osová vzdálenost krokví [mm].
Hambalky
\begin{gathered}
H_\text{U}\approx2/3H
\end{gathered}\begin{gathered}
\end{gathered}\begin{gathered}
H_\text{U}\approx H_0
\end{gathered}\begin{gathered}
h=10\ell+60\space[\text{mm}]
\end{gathered}\begin{gathered}
b=0{,}1e-10\ge70\space[\text{mm}]
\end{gathered}\begin{gathered}
h=10\ell+80\space[\text{mm}]
\end{gathered}\begin{gathered}
b=2\cdot0{,}1e-10\space[\text{mm}]
\end{gathered}Příklad 2.6
Navrhněte rozměry krokve a hambalku
\begin{gathered}
\alpha=50\degree,\space\ell=10{,}0\space\text{m},\space e=800\space\text{mm},\space H_\text{U}\approx2/3H
\end{gathered}Krokev
\begin{gathered}
h=17{,}5\cdot10+(50-35)=205\space\text{mm}
\end{gathered}\begin{gathered}
b=0{,}1\cdot800-10=70\space\text{mm}
\end{gathered}\begin{gathered}
\end{gathered}\begin{gathered}
\text{profil}\space70/210\space[\text{mm}]
\end{gathered}Hambalek
\begin{gathered}
h=10\cdot10+60=160\space\text{mm}
\end{gathered}\begin{gathered}
b=2\cdot0{,}1\cdot800-10=150\space\text{mm}
\end{gathered}\begin{gathered}
\end{gathered}\begin{gathered}
\text{profil}\space150/160\space\space\text{nebo}\space\space2\text{ x }75/160\space[\text{mm}]
\end{gathered}2.4.2 Pohyblivý hambalek
V rovině hambalků není krov vyztužen, na nesouměrné zatížení hambalek zajišťuje pouze stejný průhyb krokví. Pro vítr působí krokev na celou její délku.
Bez půdní vestavby
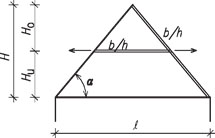
Obr. 2.14 Schéma hambalkové soustavy bez půdní vestavby
Krokve
\begin{gathered}
\alpha\le35\degree
\end{gathered}\begin{gathered}
\end{gathered}\begin{gathered}
\alpha=\gt35\degree
\end{gathered}\begin{gathered}
h=15\ell+30\space[\text{mm}]
\end{gathered}\begin{gathered}
b=0{,}1e-10\space[\text{mm}]
\end{gathered}\begin{gathered}
h=15\ell+40+2(\alpha-35\degree)\space[\text{mm}]
\end{gathered}\begin{gathered}
b=0{,}1e-10\space[\text{mm}]
\end{gathered}kde je
ℓ … rozpětí střechy [m],
e … osová vzdálenost krokví [mm].
S půdní vestavbou
Krokve se zvětší cca o 10–20 mm.
Hambalky
\begin{gathered}
H_\text{U}\approx2/3H
\end{gathered}\begin{gathered}
\end{gathered}\begin{gathered}
H_\text{U}\approx H_0
\end{gathered}\begin{gathered}
h=10\ell+60\space[\text{mm}]
\end{gathered}\begin{gathered}
b=0{,}1e-10\ge70\space[\text{mm}]
\end{gathered}\begin{gathered}
h=10\ell+80\space[\text{mm}]
\end{gathered}\begin{gathered}
b=2\cdot0{,}1e-10\space[\text{mm}]
\end{gathered}Hambalky se navrhují zpravidla zdvojené.
2.4.3 Rozměry ostatních dílů
Tab. 2.16 Vzdálenosti krokví pro použitý profil latí a daný sklon střechy
| Průřez latí [mm] | Sklon střechy α | ||
| < 30° | 30–45° | 45–60° | |
| 24/48 | 700 | 800 | 900 |
| 35/50 | 800 | 900 | 1 000 |
| 40/60 | 900 | 1 000 | 1 000 |
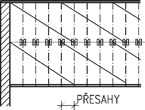
Obr. 2.15 Zavětrování v rovině střechy
h/b = 30/50–40/60 [mm] pro malé rozpony
h/b = 30/80–40/100 [mm] pro větší rozpony
Tab. 2.17 Spotřeba dřeva pro rozpětí krovu ℓ [m]
| Spotřeba dřeva v m3/100 m2 půdorysné plochy | Sklon střechy α | Spotřeba řeziva [m3/100 m2] |
| Střešní latě | 35–50° | 0,96–1,25 |
| Krokevní soustava | 25–45° | 0,2ℓ–0,4ℓ |
| Hambalková soustava bez tesařských spojů | 25–45° | 0,2ℓ–0,4ℓ |
Tab. 2.18 Spotřeba dřeva při tradičním provedení s tesařskými spoji
| Rozpětí ℓ [m] | 8,0–12,5 |
| Hranoly [m3] | 2,2–2,7 |
| Fošny [m3] | 1,8–2,4 |
2.5 Vaznicová soustava
2.5.1 Rozměry prvků
Krokve za následujících předpokladů:
- vlastní tíha g = 0,65 kN/m2;
- výška do 20 m nad terénem;
- II. sněhová oblast;
- řezivo C24, průhyb 1/200ℓ.
Bez půdní vestavby

Obr. 2.16 Schéma vaznicové soustavy bez půdní vestavby
\begin{gathered}
\alpha\le30\degree
\end{gathered}\begin{gathered}
\end{gathered}\begin{gathered}
\alpha=\gt30\degree
\end{gathered}\begin{gathered}
\end{gathered}\begin{gathered}
h=40\ell\space[\text{mm}]
\end{gathered}\begin{gathered}
b=0{,}1e\space[\text{mm}]
\end{gathered}\begin{gathered}
h=40\ell+2(\alpha-30\degree)\space[\text{mm}]
\end{gathered}\begin{gathered}
b=0{,}1e-10\space[\text{mm}]
\end{gathered}kde je
ℓ … vodorovný průmět rozpětí krokví [m] (viz obr. 2.16),
e … vzdálenost krokví [mm].
Příklad 2.7
Navrhněte rozměry krokví
\begin{gathered}
\alpha=40\degree,\space\ell=3{,}5\space\text{m},\space e=700\space\text{mm}
\end{gathered}\begin{gathered}
h=40\cdot3{,}5+2(40-30)=160\space\text{mm}
\end{gathered}\begin{gathered}
b=0{,}1\cdot700=70\space\text{mm}
\end{gathered}\begin{gathered}
\end{gathered}\begin{gathered}
\end{gathered}\begin{gathered}
\text{profil}\space70/160\space\text{mm}
\end{gathered}S půdní vestavbou
Výška krokví stejná jako bez vestavby
\begin{gathered}
b=0{,}1e+20\le70\space[\text{mm}]
\end{gathered}Nárožníky pro valbovou střechu
\begin{gathered}
h_\text{nar}=1{,}5h_\text{normal}\space[\text{mm}]
\end{gathered}\begin{gathered}
b_\text{nar}=b_\text{normal}+20\space[\text{mm}]
\end{gathered}Pozednice volba rozměrů je z konstrukčních důvodů
\begin{gathered}
b/h=120/100{-}180/140\space[\text{mm}]
\end{gathered}Vaznice
- Vrcholová vaznice je namáhána jen svislými silami, zároveň proti vodorovným silám se vzájemně podepírají krokve.
- Mezilehlé vaznice jsou namáhány svislými i vodorovnými silami. Pro hospodárnější návrh je vhodné v rovině umístit zavětrování tvořené kleštinami a vloženými diagonálami a síly přenést do schodišťových a štítových stěn, popřípadě tuhost roviny zajistit vodorovným bedněním.
V případě použití pásků lze redukovat rozpětí vaznice.
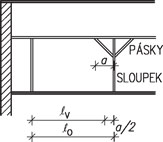
Obr. 2.17 Schéma vaznicové soustavy s půdní vestavbou v podélném směru
\begin{gathered}
\ell_\text{v}=\ell_0-\frac{a}{2}
\end{gathered}Předpoklady:
- rozpětí vaznic ℓv = 3,0–6,0 m;
- zatěžovací šířka vaznic B = 2,0–5,0 m;
- vlastní tíha střechy 0,65 kN/m2;
- výška do 20 m nad terénem, vaznice vítr nepřenáší;
- na úrovni vaznic není zatížená podlaha;
- II. sněhová oblast.
Bez půdní vestavby
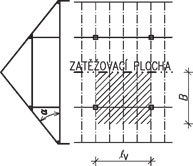
Obr. 2.18 Schéma zatěžované plochy vaznicové soustavy
\begin{gathered}
\alpha=25{-}55\degree
\end{gathered}\begin{gathered}
h=40(\ell_\text{v}+B/2)+20\space[\text{mm}]
\end{gathered}\begin{gathered}
b=25(\ell_\text{v}+B/2)+10\space[\text{mm}]
\end{gathered}Příklad 2.8
Navrhněte rozměry vaznice
\begin{gathered}
\ell_\text{v}=4{,}5\space\text{m},\space B=3{,}5\space\text{m},\space\alpha=40\degree
\end{gathered}\begin{gathered}
h=40(4{,}5+3{,}0/2)+20=260\space\text{mm}
\end{gathered}\begin{gathered}
b=25\cdot6{,}00+10=160\space\text{mm}
\end{gathered}\begin{gathered}
\end{gathered}\begin{gathered}
\end{gathered}\begin{gathered}
\text{profil}\space160/260\space\text{mm}
\end{gathered}Zatížení vlastní tíhou zateplení a podhledu, bez užitného zatížení na strop vestavby.
S půdní vestavbou
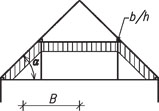
Obr. 2.19 Schéma vaznicové soustavy s půdní vestavbou
\begin{gathered}
h=40(\ell_\text{v}+3/4B)+20\space[\text{mm}]\\\\
b=25(\ell_\text{v}+3/4B)+10\space[\text{mm}]
\end{gathered}Sloupky – obvyklé průřezy v závislosti na zatěžovací ploše a vzpěrné délce
\begin{gathered}
\begin{split}b/h=
&100/200\space\space\space120/120\space\space\space100/140\space\space\space120/140\space[\text{mm}]\\\\
&140/140\space\space\space120/160\space\space\space140/160\space\space\space120/180\space[\text{mm}]
\end{split}
\end{gathered}\begin{gathered}
b=\sqrt{100\frac{S}{c}}+15\ell_\text{ef}\space[\text{mm}]
\end{gathered}kde je
S … osová síla ve sloupku [kN],
ℓef … vzpěrná délka sloupku [m],
c = b/h … poměr stran průřezu sloupku.
Příklad 2.9
Navrhněte rozměry sloupku
\begin{gathered}
S=40{,}0\space\text{kN},\space\ell_\text{ef}=3{,}0\space\text{m},\space c=1\space\text{(čtverec)}\\\\
b=\sqrt{100\frac{40}{\ell}}+15\cdot3{,}0=108{,}2\space\text{mm}
\end{gathered}profil 120/120 mm
Tab. 2.19 Spotřeba dřeva
| Spotřeba dřeva v m3/100 m2 půdorysné plochy | Sklon střechy α | Spotřeba latí | |
| Střešní latě | 35–50° | 3,0–4,5 | |
| Profily na vazby | jednoduchá soustava | 2,5–3,5 | |
| krov se vzpěrami | 3,0–4,5 | ||
2.5.2 Tradiční empirické vzorce
Podle literatury [4] se uvádějí následující rozměry a empirické vztahy pro části vaznicových krovů, běžné krovové dřevo podle provedených vazeb do 22 metrů.
Tab. 2.20 Empirické profily vaznicových krovů
| Označení | Krov prostý do 5 m | Stolice stojatá a věšadlo pro rozpon ℓ [m] | |||
| 5–10 | 10–14 | 14–18 | 18–22 | ||
| Krokve po 1 m | 100/120 | 100/140 | 120/140 | 120/140 | 120/140 |
| Vaznice | |||||
|
140/160 | 160/180 | – | – | – |
|
140/160 | 160/180 | – | – | – |
|
140/160 | 150/180 | – | – | – |
| Pásek | 100/130 | 100/130 | 130/150 | 130/180 | 130/210 |
| Sloupek | 160/160 | 160/160 | 160/180 | 180/180 | 180/180 |
| Rozpěra | – | – | 160/180 | 180/180 | 180/180 |
| Pozednice | 120/150 | 120/150 | 160/160 | 180/180 | 180/180 |
| Kleště 2x | – | 80/160 | 80/160 | 100/160 | 100/180 |
| Vazný trám | 160/210 | 160/210 | 160/210 | 180/240 | 180/240 |
Rozměry jsou platné pro obvyklou tíhu dvojité taškové krytiny, jestliže se krokve podporují na vzdálenost 4,5–5,0 m, stejnou vzdálenost mají od sebe i plné vazby.
2.6 Vazníková (vlašská) soustava
Konstrukce krovů vlašské soustavy patří mezi nejstarší a byly používány již ve starém Římě pro střechy s malým sklonem (v = 1/5–1/4 rozpětí), to je α = 21,8–26,5°. Mohou se používat nad jednoduchými půdorysy větších rozponů s tvarem střechy sedlové nebo pultové. Střešní konstrukce této soustavy se vyznačují jednoduchostí a menší spotřebou dřeva. Princip podpírání vodorovných krokví byl přejat do novodobých střešních konstrukcí, ve kterých jsou věšadlové vazníky nahrazeny vazníky příhradovými nebo plnostěnnými.
2.6.1 Vlašské krokve
Vlašské krokve (vazničky) se u této soustavy umísťují rovnoběžně s okapovou hranou, jejich rozpětí se pohybuje 4–5 m, vzájemné vzdálenosti krokví jsou obvykle mezi 0,8–1,0 m. Krokve se kladou na vzpěry (horní pasy) vazníků, které se zapouštějí do krokví (vazniček) na hloubku 20 mm. Proti pootočení se vazničky mohou zapřít špalíky (zvanými pachole) přibitými na vzpěry. Běžné krokve jsou obdélníkového průřezu, hřebenová krokev má pětiúhelníkový průřez a okapová lichoběžníkový. Bednění pro krytinu 25 mm tloušťky se přibíjí na krokve ve směru spádu střechy.
Profily vlašských krokví za předpokladů:
- vlastní tíha střešního pláště g = 0,75 kN/m2 (těžká krytina);
- vlastní tíha střešního pláště g = 0,30 kN/m2 (lehká krytina);
- nezateplená střecha (mimo samonosný pohled zavěšený přímo na vazníky);
- výška do 20 m nad terénem;
- II. sněhová oblast;
- řezivo C24, průhyb 1/200ℓ;
- krokve působí jako prosté nosníky.
Tab. 2.21 Profily vlašských krokví pro těžkou krytinu
| Rozpětí ℓ [m] | ||||||||
| 4,0 | 4,2 | 4,4 | 4,6 | 4,8 | 5,0 | 5,2 | ||
| Odstup krokví a [m] | 0,8 | 120/140 | 100/160 | 120/160 | 130/160 | 100/180 | 120/180 | 130/180 |
| 0,9 | 120/150 | 110/160 | 120/160 | 140/160 | 110/180 | 130/180 | 140/180 | |
| 1,0 | 120/150 | 120/160 | 140/160 | 120/180 | 120/180 | 140/180 | 160/180 | |
Tab. 2.22 Profily vlašských krokví pro lehkou krytinu
| Rozpětí ℓ [m] | ||||||||
| 4,0 | 4,2 | 4,4 | 4,6 | 4,8 | 5,0 | 5,2 | ||
| Odstup krokví a [m] | 0,8 | 120/120 | 100/140 | 100/140 | 120/140 | 120/150 | 120/150 | 120/160 |
| 0,9 | 120/130 | 100/140 | 110/140 | 130/140 | 120/150 | 120/160 | 130/160 | |
| 1,0 | 120/130 | 120/140 | 120/140 | 120/150 | 120/160 | 120/160 | 140/160 | |
2.6.2 Vazníky
Nosnou konstrukcí vazníků – plných vazeb – jsou věšadla z hranolů, jejichž tvar a profily se řídí rozpětím, v klasickém provedení mají zpravidla trojúhelníkový tvar. V pozdějším období se používaly i kombinace dřevěných prvků s ocelovými táhly popřípadě i litinovými vzpěrami. Plné vazby (vazníky) se osazují ve vzdálenostech 4–5 m a jejich profily a spoje se navrhují na základě statického výpočtu. Na obr. 2.20 jsou uvedeny pro orientaci profily pro vazník na rozpětí 9 m.
V podélném směru jsou vazníky vzájemně vyztuženy ondřejovými kříži případně i jiným tvarem zavětrování. Zavětrování se čepuje buď ve svislé rovině do věšáků, nebo v šikmé rovině do obrysových vzpěr vazníků. Při velkých rozpětích se důležitý spoj hlavní vzpěry s vazným trámem u nosné zdi ještě vyztuží podpůrným krátkým sedlem, které je pomocí hmoždíků s ním spojeno.
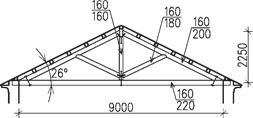
Obr. 2.20 Schéma vazníkové soustavy
2.7 Ploché střechy
Z hlediska nosné konstrukce je plochá střecha obdobná stropu v běžném podlaží a liší se pouze velikostí zatížení, viz kap. 3.
3 Stropy
- Stropní konstrukce se skládají z nosné stropní desky, ze stropních nosníků, průvlaků, podlahy a podhledu. Tab. 3.1 uvádí orientační tloušťky jednotlivých částí stropů.
- Při rozhodování o volbě stropní nosné konstrukce bereme mimo jiné zřetel na její rozpětí. Každému druhu stropní konstrukce odpovídá doporučený rozsah rozpětí, ve kterém je vhodné konstrukci navrhovat. Tento rozsah je pouze doporučený, a proto nelze vyloučit návrh konstrukce mimo něj.
Tab. 3.1 Orientační hodnoty tloušťky stropní konstrukce
| Prvky stropní konstrukce | Tloušťka h | ||
| min. [mm] | max. [mm] | ||
| Podlaha | nášlapná vrstva (linoleum, PVC, koberec, dlažba) | 5 | 60 |
| betonová mazanina | 30 | 45 | |
| kročejový útlum, tepelná izolace | 20 | 30 | |
| vyrovnávací vrstva | 10 | 15 | |
| celkem | 35 | 150 | |
| Nosná konstrukce | do 1,5 m rozpětí | 70 | 150 |
| do 3,0 m rozpětí | 100 | 250 | |
| do 6,0 m rozpětí | 150 | 350 | |
| nad 6,0 m rozpětí | 200 | 400 | |
| celkem | 70 | 400 | |
| Podhled | omítka včetně případného rákosu nebo pletiva | 15 | 20 |
| podhledové desky na nosnou konstrukci nebo | |||
| podhledový rošt | 50 | 100 | |
| zavěšený podhled | 50 | 100 | |
| celkem | 15 | 100 | |
| Podlaha, nosná konstrukce a podhled celkem | min. [mm] | max. [mm] | |
| Rozpětí stropní konstrukce do 1,5 m | podlaha | 35 | 100 |
| celkem | 120 | 350 | |
| Rozpětí stropní konstrukce do 3,0 m | podlaha | 35 | 100 |
| celkem | 150 | 450 | |
| Rozpětí stropní konstrukce do 6,0 m | podlaha | 35 | 100 |
| celkem | 200 | 550 | |
| Rozpětí stropní konstrukce nad 6,0 m | podlaha | 35 | 100 |
| celkem | 250 | 600 | |
Tab. 3.2 Doporučená rozpětí stropů
| Specifikace podle konstrukce materiálu | Druh stropu | Tloušťka nosné stropní konstrukce h [mm] | Doporučené rozpětí ℓ [m] |
| Dřevěné stropy | dřevěný strop trámový, povalový, fošnový, vídeňský | 250–500 | 3–5,5 |
| Keramické stropy | polomontované stropy z nosníků a keramických vložek | 210–290 | 1,5–8,0 |
| keramické panely | 230 | 1,25–7,0 | |
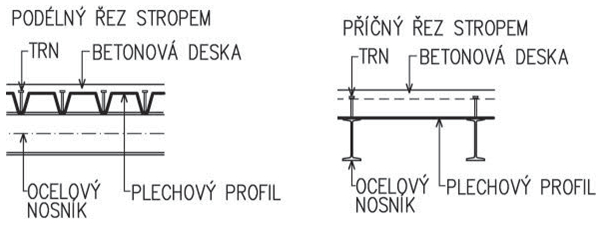
| Spřažené stropy | spřažená ocelobetonová konstrukce – ocelové nosníky + trapézové plechy + železobetonová deska |
250–550 | 3,0–7,5 |
| Železobetonové stropy | jednosměrně pnutá plná železobetonová deska | 50–250 | < 3,5 |
| jednosměrně pnutá vylehčená železobetonová deska (např. podélnými otvory) | 65–250 | 0,6–6,6 | |
| obousměrně pnutá plná železobetonová deska | 100–300 | 3,0–7,2 | |
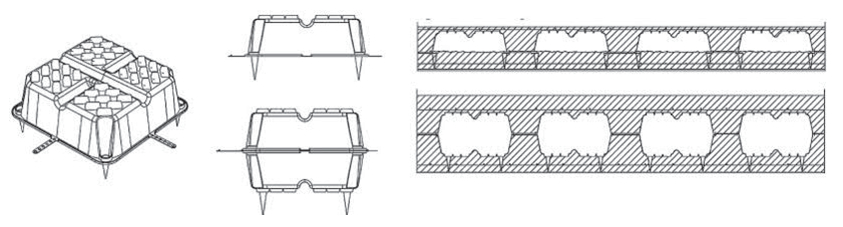
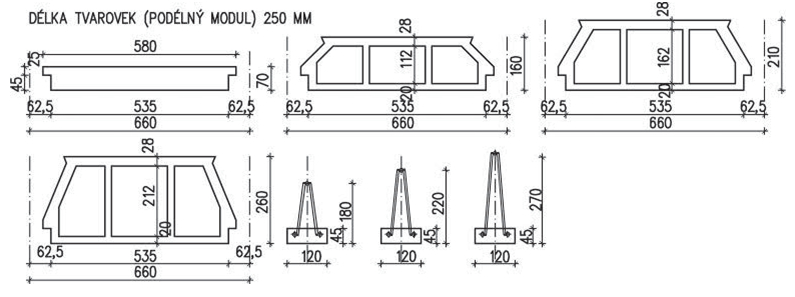
| žebrová deska (s dutými tvarovkami v jednom směru) | 150–400 | 4,0–12,0 | |
| roštová deska (s dutými tvarovkami v obou směrech) | 150–450 | 6,0–12,0 | |
| hřibový strop | 150–350 | 4,0–10,0 | |
| Stropy z předpjatého betonu | předpjaté stropní panely | 250–300 | 2,0–12,0 |
Tab. 3.3 Minimální tloušťky stropních konstrukcí [mm]
| Stropy z keramických panelů | 215 |
| Polomontované keramické stropy s vložkami Miako | 210 |
| Jednosměrně pnuté železobetonové desky | |
|
50 |
|
60 |
|
70 |
| Hřibové stropy | 160 |
| Bezhřibové bodově podepřené desky bez deskového zesílení | 160 |
| Bezhřibové desky s deskovým zesílením | 120 |
3.1 ZATÍŽENÍ
U zatížení stropů podle požadavku ČSN EN 1990 se stanovují charakteristické hodnoty zatížení, které se používají při výpočtu podle mezního stavu použitelnosti, tj. především průhybů, a návrhové hodnoty zatížení, používané při posuzování konstrukce podle mezního stavu únosnosti. Hodnoty návrhových hodnot zatížení se vypočítají tak, že charakteristické hodnoty se přenásobí součiniteli spolehlivosti zatížení, které pro většinu případů jsou větší než 1, pouze při posouzení rovnováhy, popř. u stabilitních problémů mohou být menší než 1. Pro zatížení stálé je součinitel spolehlivosti γf = 1,35, pro nahodilé zatížení γf = 1,5.
Zatížení stropů se skládá ze součtu stálého zatížení (například podlahou s podkladem, vlastní tíha stropní nosné konstrukce) a zatížení nahodilého (podle účelu místnosti).
Vlastní tíha
Vlastní tíhu stropu spolu s podlahou, příčkami a zabudovaným nábytkem označujeme jako zatížení stálé. Při výpočtu zatížení předpokládáme určitou skladbu podlah a určitou tloušťku nosné konstrukce, jestliže potom výpočtem zjistíme, že tloušťka nosné konstrukce bude jiná, zatížení již nepřepočítáváme. Pro potřebu vyčíslení hodnot stálého zatížení je uvedena tab. 3.4 objemových hmotností nejčastěji používaných materiálů.
Tab. 3.4 Hmotnosti vybraných materiálů
| Materiál | Objemová hmotnost ρ [kg/m3] |
| Měkké dřevo | |
|
500–650 |
| Tvrdé dřevo | |
|
700–800 |
| Dřevovláknité desky tvrdé | 1 000 |
| Dřevovláknité desky měkké | 300 |
| Překližky | 400–650 |
| Desky OSB | 600–680 |
| Desky Cetris | 1 150–1 450 |
| Stavební ocel | 7 850 |
| Litina, zinek, válcované výrobky | 7 200 |
| Hliník, hliníkové slitiny | 2 700–2 800 |
| Vyvřelé horniny | |
|
2 600–3 000 |
|
1 800 |
| Přeměněné horniny | |
| břidlice, mramor, serpentin, rula | 2 600–2 900 |
| Sedimentované horniny | |
|
2 500–2 800 |
|
2 400 |
| Lehčené cihly | 900–1 500 |
| Cihly pálené plné | 1 800 |
| Vápenopískové cihly | 2 000 |
| Tvárnice porobetonové | 600–650 |
| Příčkovky | 1 100 |
| Malty | 1 500–1 900 |
| Beton obyčejný | 2 200–2 400 |
| Železobeton | 2 500 |
| Sklobeton | 2 600 |
| Anhydrid | 2 100 |
| Desky korkové | 350 |
| Silikork | 700 |
| Pilinové podlahové desky | 1 000 |
| Dlažba dřevěná špalíková | 1 100 |
| Dlažba kameninová, cementová, teraco | 2 200–2 300 |
| Mazanina z korkové drti | 500 |
| Mazanina xylolitová | 1 800 |
| Lehčené betony | 300–1 200 |
| Kovral, Jekor | 1 200 |
| Fibrex | 70–110 |
| Sádrokarton | 1 200 |
| Polystyren | 40 |
| Rohože z minerální vlny | 100–200 |
Příklad 3.1
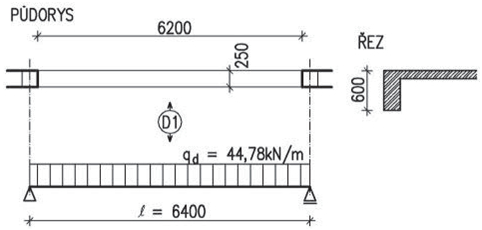
Zjistěte návrhovou hodnotu stálého zatížení stropní konstrukce, která má skladbu podle schématu.
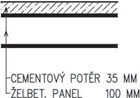
Cementový potěr
\begin{gathered}
0{,}035\cdot23=0{,}81\space\text{kN/m}^2
\end{gathered}Železobetonový panel
\begin{gathered}
0{,}1\cdot25=2{,}50\space\text{kN/m}^2
\end{gathered}Celkem charakteristická hodnota zatížení
\begin{gathered}
3{,}31\space\text{kN/m}^2
\end{gathered}Součinitel spolehlivosti zatížení
\begin{gathered}
\gamma_\text{f}=1{,}35
\end{gathered}Celkem návrhová hodnota stálého zatížení
\begin{gathered}
1{,}35\cdot3{,}31=4{,}47\space\text{kN/m}^2
\end{gathered}Tab. 3.5 Návrhové hodnoty zatížení od vlastní tíhy železobetonové desky pro ρ = 25 kN/m3, γf = 1,35
| Tloušťka [mm] | 50 | 60 | 70 | 80 | 90 | 100 | 120 | 150 | 180 | 200 | 250 | 300 | 350 |
| Zatížení [kN/m2] | 1,69 | 2,03 | 2,36 | 2,70 | 3,04 | 3,38 | 4,05 | 5,06 | 6,08 | 6,75 | 8,44 | 10,13 | 11,82 |
Poznámka:
V tabulce lze lineárně interpolovat.
Pro nosné konstrukce z lehkého betonu získáme zatížení vlastní tíhou, vynásobíme-li uvedené hodnoty pro železobetonovou desku součinitelem z tab. 3.6.
Tab. 3.6 Hodnoty součinitele zatížení pro lehký beton
| Součinitel | Objemová hmotnost lehkého betonu ρ [kg/m3] |
| 0,2–0,8 | 500–2 000 |
Poznámka:
V tabulce lze lineárně interpolovat.
Pro plechobetonové desky můžeme použít tabulkových hodnot pro železobetonové desky. V následující tab. 3.7 můžeme nalézt návrhové hodnoty zatížení od vlastní tíhy podlah.
Tab. 3.7 Návrhové hodnoty zatížení od vlastní tíhy podlah
| Typ | Náčrt | Skladba podlahy | Tloušťka vrstvy h1 [mm] | Objem. tíha ρ [kN/m3] | Charakter. hodnota gk [kN/m2] | Návrhová hodnota gd [kN/m2] |
| Pro bytovou a občanskou výstavbu | 1 |
podlahový povlak PVC | 2 | 12 | 0,024 | 0,032 |
| podložka | 2 | 7 | 0,014 | 0,019 | ||
| cementový potěr | 31 | 22 | 0,682 | 0,921 | ||
| celkové zatížení podlahou | 0,720 | 0,972 | ||||
| 2 |
podlahový povlak PVC | 4 | 12 | 0,024 | 0,032 | |
| cementový potěr | 31 | 22 | 0,682 | 0,921 | ||
| lepenka | zanedbatelná | – | – | – | ||
| zvukoizolační vrstva | 10 | 5 | 0,050 | 0,068 | ||
| celkové zatížení podlahou | 0,756 | 1,021 | ||||
| 3 |
textilní podlah. povlak | 5 | 1 | 0,005 | 0,007 | |
| disperzní lepidlo | zanedbatelná | – | – | – | ||
| betonová mazanina | 44 | 22 | 0,968 | 1,307 | ||
| celkové zatížení podlahou | 0,973 | 1,304 | ||||
| 4 |
textilní podlah povlak | 5 | 1 | 0,005 | 0,007 | |
| disperzní lepidlo | zanedbatelná | – | – | – | ||
| betonová mazanina | 37 | 22 | 0,814 | 1,099 | ||
| lepenka | zanedbatelná | – | – | – | ||
| polystyrén | 30 | 1 | 0,03 | 0,041 | ||
| celkové zatížení podlahou | 0,849 | 1,147 | ||||
5 |
podlahová stěrka | 3 | 20 | 0,03 | 0,041 | |
| vyrovnávací stěrka | 2 | 20 | 0,02 | 0,027 | ||
| cementový potěr | 18 | 22 | 0,396 | 0,535 | ||
| betonová mazanina | 40 | 22 | 0,88 | 1,188 | ||
| lepenka | zanedbatelná | – | – | – | ||
| zvuková izolace | 10 | 10 | 0,1 | 0,135 | ||
| celkové zatížení podlahou | 1,426 | 1,925 | ||||
| Pro byt., obč., prům. i zeměděl. výstavbu | 6 |
keramická dlažba | 8 | 22 | 0,176 | 0,238 |
| maltové lože | 20 | 19 | 0,38 | 0,513 | ||
| betonová mazanina | 42 | 22 | 0,924 | 1,247 | ||
| vodorovná izolace | zanedbatelná | – | – | – | ||
| celkové zatížení podlahou | 1,480 | 1,998 | ||||
| 7 |
keramická dlažba | 8 | 12 | 0,096 | 0,129 | |
| maltové lože | 18 | 19 | 0,342 | 0,462 | ||
| betonová mazanina | 24 | 22 | 0,528 | 0,713 | ||
| celkové zatížení podlahou | 0,966 | 1,304 | ||||
| Pro bytovou a občanskou výstavbu | 8 |
kamenné desky (žula, mramor) | 40 | 28 | 1,120 | 1,512 |
| maltové lože | 20 | 19 | 0,380 | 0,513 | ||
| betonová mazanina | 40 | 22 | 0,88 | 1,188 | ||
| celkové zatížení podlahou | 2,38 | 3,213 | ||||
| 9 |
vlysy | 19 | 7 | 0,133 | 0,180 | |
| asfaltový tmel | zanedbatelná | – | – | – | ||
| dřevovlák. deska měk. | 12 | 3 | 0,036 | 0,049 | ||
| vyrovnávací stěrka | 3 | 20 | 0,060 | 0,081 | ||
| celkové zatížení podlahou | 0,229 | 0,309 | ||||
10 |
vlysy | 19 | 7 | 0,133 | 0,180 | |
| asfaltový tmel | zanedbatelná | – | – | – | ||
| betonová mazanina | 42 | 22 | 0,924 | 1,247 | ||
| asfaltová lepenka | zanedbatelná | – | – | – | ||
| zvuková izolace | 10 | 10 | 0,100 | 0,135 | ||
| celkové zatížení podlahou | 1,157 | 1,562 | ||||
11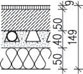 |
lamelová podlaha | 9 | 9 | 0,108 | 0,146 | |
| anhydrit | 50 | 21 | 1,050 | 1,418 | ||
| podlahové topení | 40 | – | 0,200 | 0,200 | ||
| tepelná izolace | 50 | 1,5 | 0,075 | 0,101 | ||
| celkové zatížení podlahou | 1,433 | 1,935 | ||||
| Pro průmyslovou výstavbu | 12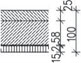 |
cementový potěr | 25 | 22 | 0,550 | 0,743 |
| betonová mazanina | 58 | 22 | 1,276 | 1,723 | ||
| lepenka | zanedbatelná | – | – | – | ||
| zvuková izolace | 15 | 15 | 0,225 | 0,304 | ||
| celkové zatížení podlahou | 2,051 | 2,768 | ||||
Poznámka:
Zatížení obdobné skladby podlahy určíme porovnáním s uvedenými příklady. Zatížení podlahou, která se výrazně liší, určíme z objemových hmotností a tlouštěk vrstev.
Užitné zatížení
Užitné zatížení se stanoví podle určení příslušné plochy, které se zařazují do kategorie podle ČSN EN 1991-1-1, viz následující tab. 3.8. Ke kategoriím jsou přiřazeny charakteristické hodnoty užitného zatížení, a to jednak rovnoměrné spojité zatížení, jednak osamělé břemeno – viz tab. 3.8, 3.9.
Tab. 3.8 Kategorie užitného zatížení podle ČSN EN 1991-1-1
| Kategorie | Stanovené použití | Příklad |
| A | Obytné plochy a plochy pro domácí činnosti | místnosti obytných budov a domů, lůžkové pokoje a čekárny v nemocnicích, ložnice hotelů a ubytoven, kuchyně a toalety |
| B | Kancelářské plochy | |
| C | Plochy, kde může docházek ke shromažďování lidí (kromě ploch uvedených v kategoriích A, B a D) | C1: plochy se stoly atd., například ve školách, kavárnách, restauracích, jídelnách, čítárnách, recepcích C2: plochy se zabudovanými sedadly, např. plochy v kostelech, divadlech a kinech, v konferenčních sálech, přednáškových a zasedacích místnostech, nádražních a jiných čekárnách C3: plochy bez překážek pro pohyb osob, např. plochy v muzeích, ve výstavních síních a přístupové plochy ve veřejných a administrativních budovách, hotelích, nemocnicích, železničních halách C4: plochy určené k pohybovým aktivitám, např. taneční sály, tělocvičny, jeviště apod. C5: plochy, kde může dojít k vysoké koncentraci lidí, např. budovy pro veřejné akce jako koncertní síně, sportovní haly včetně tribun, terasy a přístupové plochy, železniční nástupiště |
| D | Obchodní plochy | D1: plochy v malých obchodech D2: plochy v obchodních domech |
| E | Plochy pro skladování a průmyslovou činnost | E1: plochy, kde může dojít k hromadění zboží, včetně přístupových ploch, plochy pro skladování, včetně knih a dalších dokumentů E2: průmyslová činnost |
| F | Dopravní a parkovací plochy pro lehká vozidla (celková tíha ≤ 30 kN a s nejvýše 8 sedadly kromě řidiče) | garáže, parkovací plochy a parkovací garáže |
| G | Dopravní a parkovací plochy pro středně těžká vozidla (30 kN < celková tíha vozidla ≤ 160 kN, na dvě nápravy) | přístupové cesty, zásobovací oblasti, přístupové zóny pro požární mobilní techniku (≤ 160 kN celkové tíhy vozidla) |
| H | Střechy nepřístupné | střechy nepřístupné s výjimkou běžné údržby a oprav |
| I | Střechy přístupné | střechy pochůzné, obytné terasy, plochy určené k pozorováním, popř. ke sportovním či kulturním akcím |
| K | Střechy přístupné pro zvláštní provoz | například plochy pro přistávání vrtulníků |
Tab. 3.9 Kategorie zatěžovacích ploch
| Kategorie zatěžovaných ploch | gk [kN/m2] | Qk [kN] | |
| Kategorie A | |||
|
1,5 | 2,0 | |
|
3,0 | 2,0 | |
|
3,0 | 2,0 | |
| Kategorie B | 2,5 | 4,0 | |
| Kategorie C | |||
|
3,0 | 3,0 | |
|
4,0 | 4,0 | |
|
5,0 | 4,0 | |
|
5,0 | 7,5 | |
|
5,0 | 4,0 | |
| Kategorie D | |||
|
5,0 | 5,0 | |
|
5,0 | 7,0 | |
| Kategorie E | |||
|
7,5 | 7,0 | |
|
zatížení podle technologických specifikací v souladu se způsobem využívání | ||
| Kategorie F | 2,5 | 20,0 | |
| Kategorie G | 5,0 | 120,0 | |
| Kategorie H | 0,75 | 1,0 | |
| Kategorie I | podle způsobu využívání podle kategorií A až D | ||
| Kategorie K | |||
| Třída vrtulníku | Startovací zatížení vrtulníku Q [kN] | Startovací zatížení Qk [kN] | Rozměry zatěžovací plochy [m] |
| HC-1 HC-2 |
Q ≤ 20 20 ≤ Q ≤ 60 |
20 60 |
0,2 x 0,2 0,3 x 0,3 |
Příklad 3.2
Zjistěte návrhovou hodnotu zatížení stropní konstrukce administrativní budovy. Skladba podlahy tab. 3.7 podlaha č. 4, nosná konstrukce je železobetonová deska tloušťky 150 mm.
Zatížení stálé
návrhová hodnota zatížení
podlaha
\begin{gathered}
1{,}15\space\text{kN/m}^2
\end{gathered}stropní deska
\begin{gathered}
5{,}06\space\text{kN/m}^2
\end{gathered}stále celkem
\begin{gathered}
6{,}21\space\text{kN/m}^2
\end{gathered}Zatížení nahodilé
\begin{gathered}
1{,}5\cdot2{,}5=3{,}75\space\text{kN/m}^2
\end{gathered}Zatížení konstrukce celkem
\begin{gathered}
9{,}96\space\text{kN/m}^2
\end{gathered}Příklad 3.3
Zjistěte zatížení stropní konstrukce pod tělocvičnou, skladba podlahy je patrná ze schématu, nosná konstrukce je železobetonová deska tloušťky 220 mm. Stanovte charakteristickou a návrhovou hodnotu zatížení.
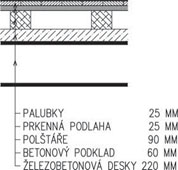
Zatížení stálé
palubky
\begin{gathered}
0{,}025\cdot6=0{,}15\space\text{kN/m}^2
\end{gathered}prkenná podlaha
\begin{gathered}
0{,}025\cdot5=0{,}13\space\text{kN/m}^2
\end{gathered}prkenné polštáře – srovnané tl. 30 mm
\begin{gathered}
0{,}03\cdot5=0{,}15\space\text{kN/m}^2
\end{gathered}betonový podklad
\begin{gathered}
0{,}06\cdot23=1{,}38\space\text{kN/m}^2
\end{gathered}železobetonová deska
\begin{gathered}
0{,}22\cdot25=5{,}50\space\text{kN/m}^2
\end{gathered}Stálé celkem
\begin{gathered}
7{,}31\space\text{kN/m}^2
\end{gathered}Zatížení užitné
\begin{gathered}
5{,}00\space\text{kN/m}^2
\end{gathered}Zatížení celkem
Charakteristická hodnota
\begin{gathered}
7{,}31+5{,}00=12{,}31\space\text{kN/m}^2
\end{gathered}Návrhová hodnota
\begin{gathered}
1{,}35\cdot7{,}31+1{,}5\cdot5{,}00=17{,}36\space\text{kN/m}^2
\end{gathered}3.3 Železobetonové stropy monolitické
Tloušťku železobetonových nepředpjatých desek mohou určovat vymezující štíhlostní kritéria, která jsou ve tvaru:
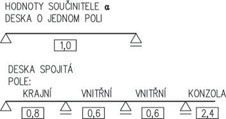
Obr. 3.1 Prostá a spojitá železobetonová deska
\begin{gathered}
1.\space h_\text{e}=\ell_\text{i}/35\space[\text{mm}]\\\\
2.\space h_\text{e}=\ell_\text{i}^2/1500\space000\space[\text{mm}]
\end{gathered}kde je
ℓi = α · ℓ [mm] … α koeficient podle obr. 3.1.
Tloušťka desky … hd + 20 mm.
Příklad 3.4
Navrhněte tloušťku železobetonové spojité desky.
Rozpětí desky ℓ = 4,2 m, spojitá deska α = 0,8
\begin{gathered}
\ell_\text{i}=0{,}8\cdot4{,}2=3{,}36\space\text{m}\\\\
1.\space h_\text{e}=\ell_\text{i}/35=3\space360/35=96\space\text{mm},\space h_\text{d}=96+20=116\space\text{mm}\\\\
2.\space h_\text{e}-\ell_\text{i}^2/150\space000=3{,}362/150\space000=75\space\text{mm},\space h_\text{d}=75+20=95\space\text{mm}
\end{gathered}Navržená tloušťka desky je 120 mm, podmínka minimální tloušťky desky je splněna.
Jednosměrně pnuté desky
Tab. 3.10 Jednosměrně pnuté desky
| Prvek | Nákres | Tloušťka hd [mm] | Rozpětí ℓ [m] | Poměr ℓ/hd [–] | |
| Jednosměrně pnutá deska |
|
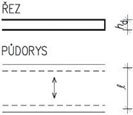 |
100–250 | 2,0–7,0 | 22–32 |
| 125–200 | 5,0–9,0 | 38–45 | |||
Jednosměrně pnuté desky jsou hospodárné na rozpětí zhruba do 3 metrů. Nejsou vyloučeny desky s větším rozpětím, ale je třeba upozornit na to, že v těchto případech bývá výhodnější volit jinou stropní konstrukci

Obr. 3.2 Půdorys stropu s poměrem b : ℓ < 1 : 2
Pro beton C20/25
\begin{gathered}
h_\text{d}=0{,}026\ell+20\space[\text{mm}]
\end{gathered}Pro beton C25/30
\begin{gathered}
h_\text{d}=0{,}020\ell+20\space[\text{mm}]
\end{gathered}Jestliže je deska spojitá o více než o dvou polích, může se zmenšit její tloušťka o 20 %.
Příklad 3.5
Navrhněte tloušťku železobetonové spojité desky o třech polích.
Rozpětí desky je 3,5 m, deska je z betonu C25/30.
Tloušťka desky je:
\begin{gathered}
h_\text{d}=0{,}026\cdot3\space500+20=111\space\text{mm}
\end{gathered}s přihlédnutím ke štíhlosti
\begin{gathered}
\ell=3\space500\cdot0{,}8=2\space800\space\text{mm}
\end{gathered}\begin{gathered}
1)\space h_\text{e}2\space800/35=80\space\text{mm}\\\\
2)\space h_\text{e}=2\space800^2/150\space000=52\space\text{mm}\\\\
h_\text{d}=80+20=100\space\text{mm}
\end{gathered}Navržená tloušťka desky je 100 mm.
Tab. 3.11 Tloušťka desky [mm] pro procento vyztužení μ = 0,5 %
| Moment M [kNm] | C20/25 B420B | C20/25 B500B | C25/30 B420B | C25/30 B500B | C30/37 B420B | C30/37 B500B | C35/45 B420B | C35/45 B500B |
| do 2 | 54 | 52 | 53 | 51 | 53 | 51 | 53 | 51 |
| 4 | 67 | 64 | 67 | 63 | 66 | 63 | 66 | 62 |
| 6 | 78 | 74 | 77 | 73 | 76 | 72 | 76 | 72 |
| 8 | 87 | 82 | 86 | 81 | 85 | 80 | 85 | 80 |
| 10 | 94 | 89 | 94 | 88 | 93 | 87 | 93 | 87 |
| 12 | 102 | 96 | 101 | 95 | 100 | 94 | 100 | 93 |
| 14 | 108 | 102 | 107 | 101 | 107 | 100 | 106 | 99 |
| 16 | 114 | 107 | 113 | 106 | 113 | 105 | 112 | 105 |
| 18 | 120 | 113 | 119 | 112 | 119 | 111 | 118 | 110 |
| 20 | 126 | 118 | 125 | 117 | 124 | 116 | 124 | 115 |
| 22 | 131 | 123 | 130 | 121 | 129 | 121 | 129 | 120 |
| 24 | 136 | 127 | 135 | 126 | 134 | 125 | 134 | 124 |
| 26 | 141 | 132 | 140 | 130 | 139 | 129 | 138 | 129 |
| 28 | 145 | 136 | 144 | 135 | 143 | 134 | 143 | 133 |
| 30 | 150 | 140 | 149 | 139 | 148 | 138 | 147 | 137 |
| 32 | 154 | 144 | 153 | 143 | 152 | 142 | 152 | 141 |
| 34 | 158 | 148 | 157 | 146 | 156 | 145 | 156 | 145 |
| 36 | 162 | 152 | 161 | 150 | 160 | 149 | 160 | 148 |
| 38 | 166 | 155 | 165 | 154 | 164 | 153 | 164 | 152 |
| 40 | 170 | 159 | 169 | 157 | 168 | 156 | 167 | 156 |
| 42 | 174 | 162 | 173 | 161 | 172 | 160 | 171 | 159 |
| 44 | 178 | 166 | 176 | 164 | 175 | 163 | 175 | 162 |
| 46 | 181 | 169 | 180 | 167 | 179 | 166 | 178 | 166 |
| 48 | 185 | 172 | 183 | 171 | 182 | 169 | 182 | 169 |
| 50 | 188 | 175 | 187 | 174 | 186 | 173 | 185 | 172 |
| 52 | 192 | 179 | 190 | 177 | 189 | 176 | 188 | 175 |
| 54 | 193 | 180 | 192 | 178 | 191 | 177 | 190 | 176 |
| 56 | 198 | 185 | 197 | 183 | 196 | 182 | 195 | 181 |
| 58 | 201 | 188 | 200 | 186 | 199 | 185 | 198 | 184 |
| 60 | 205 | 190 | 203 | 189 | 202 | 187 | 201 | 187 |
| 62 | 208 | 193 | 206 | 191 | 205 | 190 | 204 | 189 |
| 64 | 211 | 196 | 209 | 194 | 208 | 193 | 207 | 192 |
| 66 | 214 | 199 | 212 | 197 | 211 | 196 | 210 | 195 |
| 68 | 217 | 202 | 215 | 200 | 214 | 198 | 213 | 198 |
Poznámka:
Doporučuje se tloušťky desky zaokrouhlit na následující hodnoty: 50, 60, 70, 80, 100, 120, 150, 180, 200, 220, 250, 300 mm.
Tab. 3.12 Železobetonové a železobetovnové předpjaté desky
| Prvek | Nákres | Tloušťka hd [mm] | Rozpětí ℓ [m] | Poměr ℓ/hd [–] | |
| Jednosměrně pnutá žebrová deska |
|
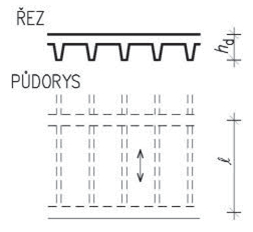 |
225–600 | 4,0–12,0 | 18–26 |
|
300–450 | 10,0–18,0 | 30–38 | ||
| Jednosměrně pnutá deska s trámy |
|
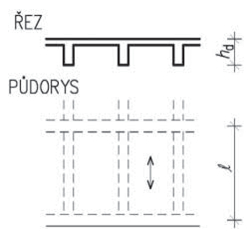 |
150–300 | 3,0–7,0 | 20–25 |
| Deska pnutá v obou směrech |
|
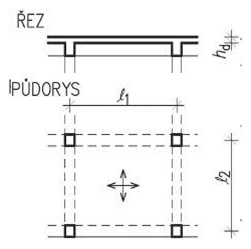 |
100–250 | 3,0–11,0 | 28–35 |
| Kazetová deska pnutá v obou směrech |
|
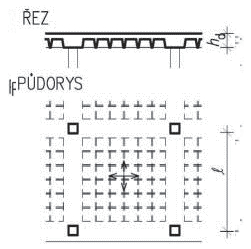 |
350–650 | 6,0–15,0 | 18–24 |
|
450–650 | 9,0–22,0 | 25–32 | ||
Oboustranně pnuté železobetonové desky
Obousměrně pnuté železobetonové desky se používají nad půdorysem čtvercovým nebo obdélným s poměrem stran do poměru 1 : 2.
Obousměrně pnuté desky jsou nejhospodárnější na rozpětí od 3 do 6 m. Rozpětí v jednom směru se označí ℓx a ve druhém směru ℓy.
U běžných deskových konstrukcí může na sebe navazovat několik desek a podle toho, jestli se jedná o desku vnitřní nebo krajovou rozlišujeme uspořádání podle tab. 3.13. Zdvojená čára označuje, že deska je vetknutá, to znamená například do jiného, dostatečně tuhého nosného prvku, nebo následuje další deska.
Tloušťku spojité desky lze určit z dalších empirických vzorců.
Součinitel
\begin{gathered}
K=\ell_\text{x}\cdot\ell_\text{v}\space[\text{m}^2]
\end{gathered}Poměrný moment
\begin{gathered}
M=10K/m\space[\text{kNm}]
\end{gathered}Momentový faktor pro volně uložené desky
\begin{gathered}
m=27-5e
\end{gathered}Momentový faktor pro spojité desky
\begin{gathered}
m=9+3n
\end{gathered}kde je
e = ℓx / ℓy,
n … součinitel podle tab. 3.13.
Potřebná účinná výška je:
- pro beton C20/25
\begin{gathered}
\ell_\text{e}=22\sqrt{M}\space[\text{mm}]
\end{gathered}- pro beton C25/30
\begin{gathered}
\ell_\text{e}=19\sqrt{M}\space[\text{mm}]
\end{gathered}- pro beton C30/37
\begin{gathered}
\ell_\text{e}=16\sqrt{M}\space[\text{mm}]
\end{gathered}Tloušťka desky
\begin{gathered}
h_\text{d}=h_\text{e}+20\space[\text{mm}]
\end{gathered}Tab. 3.13 Součinitel n
| Popis | n | Schéma |
| Deska volně uložená po všech čtyrech stranách | 0 |  |
| Deska spojitá přes jednu libovolnou hranu | 1 |  |
| Deska spojitá přes dvě libovolné hrany | 2 |  |
| Deska spojitá přes tři libovolné hrany | 3 |  |
| Deska spojitá přes všechny čtyři hrany | 4 |  |
Příklad 3.6
Určete tloušťku desky při použití betonu C20/25, podle půdorysu na schématu.
V zadaném půdorysu se vybere deska s největším rozpětím 6 x 6 m.

\begin{gathered}
e=\ell_\text{x}/\ell_\text{y}=6/6=1{,}0
\end{gathered}\begin{gathered}
K=\ell_\text{x}\cdot\ell_\text{y}=6{,}0\cdot6{,}0=36{,}0\space\text{m}^2
\end{gathered}Momentový faktor (deska spojitá typu 2)
\begin{gathered}
m=9+3\cdot2=15
\end{gathered}Poměrný moment
\begin{gathered}
M=10K/m=10\cdot36/15=24\space\text{kNm}
\end{gathered}Účinná výška
\begin{gathered}
h_\text{e}=22\sqrt{24}=107{,}8\space\text{mm}
\end{gathered}Tloušťka desky
\begin{gathered}
h=107{,}8+20=127{,}8\space\text{mm}
\end{gathered}S přihlédnutím ke štíhlosti
\begin{gathered}
\ell_\text{i}=0{,}8\cdot6{,}0=4{,}8\space\text{m}
\end{gathered}\begin{gathered}
h_\text{e}=4\space800/35=137{,}1\space\text{mm}
\end{gathered}\begin{gathered}
h_\text{e}=4\space800^2/150\space000=153{,}6\space\text{mm}
\end{gathered}\begin{gathered}
h_\text{d}=153{,}6+20=173{,}6\space\text{mm}
\end{gathered}Je navržena deska tloušťky
\begin{gathered}
h_\text{d}=180\space\text{mm}.
\end{gathered}Bodově podepřené desky
Tab. 3.14 Bodově podepřené desky
| Prvek | Nákres | Tloušťka hd [mm] | Rozpětí ℓ [m] | Poměr ℓ/hd [–] |
| Bodově podepřená deska bez zesílení | 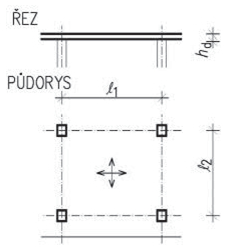 |
160–300 | 4–8 | 28–36 |
|
||||
|
200–350 | 9–10 | 35–48 | |
| Bodově podepřená deska se zesílením | 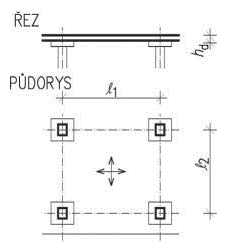 |
120–300 | 5–10 | 28–36 |
|
||||
|
200–350 | 12–14 | 35–48 |
Bodově podepřené desky jsou v současné době velmi oblíbenou konstrukcí hlavně díky rovnosti podhledu a jednoduchosti bednění.
Bodově podepřené desky mohou být konstruovány jako:
- bez deskového zesílení – sloup přímo podepírá stropní desku, minimální tloušťka desky je 160 mm;
- s deskovým zesílením – v místě napojení sloupu na desku je stropní deska zesílena, minimální tloušťka je 120 mm.
Obr. 3.3 Bodově podepřená deska: a) bez deskového zesílení, b) s deskovým zesílením
Tloušťku bodově podepřené desky lze orientačně stanovit ze vzorce
\begin{gathered}
h=\frac{1{,}1\ell}{34{,}8}\space[\text{m}]
\end{gathered}kde je
ℓ … maximální rozpětí mezi sloupy [m].
Příklad 3.7
Vypočítejte tloušťku bodově podepřené desky, jejíž půdorys je skelet o 3 x 3 polích podle schématu.
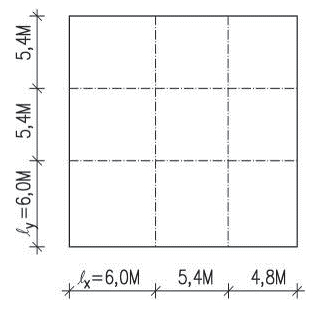
\begin{gathered}
h_\text{d}=\frac{1{,}1\cdot6}{34{,}8}=0{,}189\space\text{m}
\end{gathered}Vypočítaná tloušťka desky 0,189 m se zaokrouhlí směrem nahoru na 0,2 m. Požadavek minimální desky tj. 0,16 m je splněn.
Desky vylehčené
Vylehčená deska s kazetovými tvarovkami z recyklovaného plastu U-boot. Výšky tvarovek jsou ve dvou velikostech – 160 a 240 mm. Ukládají se buď dnem vzhůru v jedné vrstvě, nebo spojené do uzavřených krabic, tím se docílí výšky 160, 240, 320, 400 a 480 mm. Podle statických nároků lze volit tloušťku betonu pod a nad tvarovkami a šířku žeber. Vynecháním tvarovek mohou vzniknout lokální zesílení desky, např. jako hlavice deskových stropů nebo jako průvlaky.
Obr. 3.4 Vylehčené desky s kazetovými tvarovkami z recyklovaného plastu U-boot
Tab. 3.15 Čtvercový půdorys rozpětí ℓ x ℓ m, pro nahodilé zatížení 3,5 kN/m2
| Rozpětí ℓ [m] | Tloušťka desky H [mm] | Deska spodní s1 [mm] | Deska horní s2 [mm] | Výška tvarovek U‑boot h [mm] | Šířka žebra b [mm] | Poměr H/ℓ [–] |
| 5 | 250 | 50 | 40 | 160 | 120 | 1/20 |
| 6 | 285 | 50 | 75 | 160 | 120 | 1/21 |
| 7 | 320 | 100 | 60 | 160 | 120 | 1/22 |
| 8 | 355 | 100 | 95 | 160 | 120 | 1/22,5 |
| 9 | 390 | 100 | 130 | 160 | 120 | 1/23 |
| 10 | 425 | 50 | 55 | 320 | 120 | 1/23,5 |
| 11 | 460 | 50 | 90 | 320 | 120 | 1/24 |
| 12 | 495 | 100 | 75 | 320 | 120 | 1/24 |
| 13 | 530 | 100 | 110 | 320 | 120 | 1/24,5 |
| 14 | 565 | 100 | 145 | 320 | 120 | 1/24,8 |
| 15 | 600 | 100 | 180 | 320 | 120 | 1/25 |
3.3 ŽELEZOBETONOVÉ STROPY NOSNÍKOVÉ (VLOŽKOVÉ, POLOMONTOVANÉ)
Nosníkové stropy jsou stropy, ve kterých nosným prvkem jsou předem vyrobené nosníky, vložky a betonová část je vyrobená na místě. Výhodné jsou tyto stropy především proto, že je lze sestavovat ručně a nevyžadují bednění (kromě omezeného liniového podepření nosníku po dobu tvrdnutí betonu u stropů většího rozpětí). Únosnost stropu je závislá na únosnosti a vzdálenosti nosníků, na výšce tvarovek, a na výšce betonové vrstvy nad tvarovkami. Nosníky mohou být buď nepředpjaté, nebo předem předpjaté; vložky pak betonové tvarovky plné, s dutinami nebo pórobetonové. Vzhledem k poměrně značnému rozšíření v současné době jsou v této kapitole uvedeny zjednodušené statické tabulky, sestavené z konkrétních firemních podkladů. Při detailním návrhu, kdy je nutné zohlednit v kladečském výkresu například polohu příček, prostupy, průvlaky, výměny u schodiště, nebo dodržení výrobního postupu apod., je třeba použít přímo firemní příručky.
Obr. 3.5 Nepředpjaté nosníky s betonovými vložkami
Nepředpjaté nosníky s betonovými vložkami
Systém stropní konstrukce BSK vyrábí např. firma Betonové stavby Group s. r. o. Klatovy (www.betonstavby.cz). Betonové nosníky jsou vyztužené prostorovou výztuží a používají se buď jednoduché po 660 mm, anebo zdvojené (dva vedle sebe) po 780 mm. Rozměry základních prvků jsou uvedeny na obr. 3.5. Stropy se navrhují o celkové výšce 200, 220, 250, 270, 300, 320 a 350 mm. V tab. 3.16–3.29 jsou uvedena zatížení jednak gk,1 + gk,2 + qk jako charakteristická, a gd,1 + gd,2 + qd jako návrhová hodnota celkového zatížení stropu od vlastní tíhy nosné konstrukce, skladby podlahy včetně příček a užitného zatížení.
Tab. 3.16 Nosníky BSK PLUS – nosníky jednoduché, tloušťka stropu 200 mm
| BSK PLUS (nosníky jednoduché) tloušťka stropu h = 200 mm, nadbetonávka h1 = 40 mm, vložky výšky H2 = 160 mm, vlastní tíha gk,1 = 2,88 kN/m2 | ||||||
| Délka nosníku L [mm] | Maximální světlá délka ℓs,max (uložení 100 mm) | Průměrná světlá délka ℓs,prům (uložení 150 mm) | ||||
| světlá délka ℓs,max [mm] | zatížení [kN/m2] | světlá délka ℓs,prům [mm] | zatížení [kN/m2] | |||
| gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | |||
| 1600 | 1400 | 37,24 | 28,65 | 1300 | 43,60 | – |
| 1800 | 1600 | 27,77 | 21,36 | 1500 | 32,02 | – |
| 2000 | 1800 | 21,27 | 16,36 | 1700 | 24,14 | – |
| 2200 | 2000 | 16,62 | 12,78 | 1900 | 18,76 | – |
| 2400 | 2200 | 13,19 | 9,68 | 2100 | 14,87 | – |
| 2600 | 2400 | 10,57 | 8,13 | 2300 | 11,79 | – |
| 2800 | 2600 | 8,54 | 6,36 | 2500 | 9,49 | – |
| 3000 | 2800 | 6,93 | 5,33 | 2700 | 7,68 | 5,91 |
| 3200 | 3000 | 5,63 | 4,29 | 2900 | 6,24 | 4,80 |
| 3400 | 3200 | 4,61 | 3,55 | 3100 | 5,10 | 3,92 |
| 3600 | 3400 | 5,68 | 4,32 | 3300 | 6,20 | 4,77 |
| 3800 | 3600 | 4,74 | 3,65 | 3500 | 5,20 | 4,00 |
| 4000 | 3800 | 5,44 | 4,15 | 3700 | 5,89 | 4,53 |
| 4200 | 4000 | 4,62 | 3,55 | 3900 | 5,02 | 3,86 |
| 4400 | 4200 | 6,13 | 4,64 | 4100 | 6,57 | 5,05 |
| 4600 | 4400 | 5,33 | 4,10 | 1300 | 5,73 | 4,41 |
| 4800 | 4600 | 4,62 | 3,56 | 4500 | 4,98 | 3,83 |
| 5000 | 4800 | 4,25 | 3,27 | 4700 | 4,90 | 3,77 |
| 5200 | 5000 | – | 3,60 | 4900 | – | 4,07 |
| 5400 | 5200 | – | 3,28 | 5100 | – | 3,71 |
| 5600 | 5400 | – | 3,25 | 5300 | – | 3,70 |
| 5800 | 5600 | – | 3,05 | 5500 | – | 3,45 |
| 5900 | 5700 | – | 3,12 | 5700 | – | 3,57 |
| 6000 | 5800 | – | 3,26 | 2900 | – | 3,67 |
| 6200 | 6000 | – | 3,07 | 6100 | – | 3,51 |
| 6400 | 6200 | – | 2,93 | 6300 | – | 3,34 |
| 6600 | 6400 | – | 2,79 | 6500 | – | 3,16 |
Tab. 3.17 Nosníky BSK PLUS – nosníky zdvojené, tloušťka stropu 200 mm
| BSK PLUS (nosníky zdvojené) tloušťka stropu h = 200 mm, nadbetonávka h1 = 40 mm, vložky výšky H2 = 160 mm, vlastní tíha gk,1 = 3,21 kN/m2 | ||||||
| Délka nosníku L [mm] | Maximální světlá délka ℓs,max (uložení 100 mm) | Průměrná světlá délka ℓs,prům (uložení 150 mm) | ||||
| světlá délka ℓs,max [mm] | zatížení [kN/m2] | světlá délka ℓs,prům [mm] | zatížení [kN/m2] | |||
| gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | |||
| 1600 | 1400 | 63,40 | – | 1300 | 74,20 | – |
| 1800 | 1600 | 48,19 | – | 1500 | 53,35 | – |
| 2000 | 1800 | 37,35 | – | 1700 | 42,19 | – |
| 2200 | 2000 | 29,60 | – | 1900 | 33,19 | – |
| 2400 | 2200 | 23,85 | – | 2100 | 26,69 | – |
| 2600 | 2400 | 19,52 | – | 2300 | 21,52 | – |
| 2800 | 2600 | 16,10 | – | 2500 | 17,69 | – |
| 3000 | 2800 | 13,40 | – | 2700 | 14,89 | – |
| 3200 | 3000 | 11,22 | – | 2900 | 12,27 | – |
| 3400 | 3200 | 9,52 | 7,32 | 3100 | 10,35 | 7,96 |
| 3600 | 3400 | 11,25 | 8,65 | 3300 | 12,12 | 9,32 |
| 3800 | 3600 | 9,72 | 7,48 | 3500 | 10,46 | 8,05 |
| 4000 | 3800 | 10,81 | 8,32 | 3700 | 11,56 | 8,89 |
| 4200 | 4000 | 9,45 | 7,27 | 3900 | 10,11 | 7,78 |
| 4400 | 4200 | 11,85 | 9,12 | 4100 | 12,61 | 9,70 |
| 4600 | 4400 | 1054 | 8,11 | 1300 | 11,19 | 8,61 |
| 4800 | 4600 | 9,39 | 7,22 | 4500 | 9,96 | 7,66 |
| 5000 | 4800 | 9,29 | 7,14 | 4700 | 9,81 | 7,54 |
| 5200 | 5000 | 10,50 | 8,08 | 4900 | 11,29 | 8,66 |
| 5400 | 5200 | – | 7,46 | 5100 | – | 8,22 |
| 5600 | 5400 | – | 7,64 | 5300 | – | 8,36 |
| 5800 | 5600 | – | 7,04 | 5500 | – | 7,71 |
| 5900 | 5700 | – | 7,21 | 5700 | – | 7,89 |
| 6000 | 5800 | – | 7,46 | 2900 | – | 8,16 |
| 6200 | 6000 | – | 7,10 | 6100 | – | 7,76 |
| 6400 | 6200 | – | 6,80 | 6300 | – | 7,42 |
| 6600 | 6400 | – | 6,52 | 6500 | – | 7,11 |
Tab. 3.18 Nosníky BSK PLUS – nosníky jednoduché, tloušťka stropu 220 mm
| BSK PLUS (nosníky jednoduché) tloušťka stropu h = 220 mm, nadbetonávka h1 = 60 mm, vložky výšky H2 = 160 mm, vlastní tíha gk,1 = 3,34 kN/m2 | ||||||
| Délka nosníku L [mm] | Maximální světlá délka ℓs,max (uložení 100 mm) | Průměrná světlá délka ℓs,prům (uložení 150 mm) | ||||
| světlá délka ℓs,max [mm] | zatížení [kN/m2] | světlá délka ℓs,prům [mm] | zatížení [kN/m2] | |||
| gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | |||
| 1600 | 1400 | 41,67 | 32,05 | 1300 | 48,77 | – |
| 1800 | 1600 | 31,03 | 23,87 | 1500 | 35,76 | – |
| 2000 | 1800 | 23,75 | 18,27 | 1700 | 26,90 | – |
| 2200 | 2000 | 18,53 | 14,25 | 1900 | 20,31 | – |
| 2400 | 2200 | 14,69 | 10,76 | 2100 | 16,56 | – |
| 2600 | 2400 | 11,74 | 9,03 | 2300 | 13,11 | – |
| 2800 | 2600 | 9,47 | 7,03 | 2500 | 10,55 | – |
| 3000 | 2800 | 7,66 | 5,89 | 2700 | 8,52 | 6,55 |
| 3200 | 3000 | 6,20 | 4,70 | 2900 | 6,89 | 5,30 |
| 3400 | 3200 | 5,06 | 3,89 | 3100 | 5,61 | 4,32 |
| 3600 | 3400 | 6,26 | 4,74 | 3300 | 6,85 | 5,27 |
| 3800 | 3600 | 5,22 | 4,02 | 3500 | 5,73 | 4,41 |
| 4000 | 3800 | 6,00 | 4,56 | 3700 | 6,52 | 5,02 |
| 4200 | 4000 | 5,10 | 3,92 | 3900 | 5,53 | 4,25 |
| 4400 | 4200 | 6,79 | 5,12 | 4100 | 7,28 | 5,60 |
| 4600 | 4400 | 5,89 | 4,53 | 1300 | 6,33 | 4,87 |
| 4800 | 4600 | 5,10 | 3,92 | 4500 | 5,49 | 4,22 |
| 5000 | 4800 | 5,06 | 3,89 | 4700 | 5,43 | 4,17 |
| 5200 | 5000 | 6,10 | 4,69 | 4900 | 6,54 | 5,03 |
| 5400 | 5200 | – | 4,20 | 5100 | – | 4,78 |
| 5600 | 5400 | – | 4,24 | 5300 | – | 4,91 |
| 5800 | 5600 | – | 3,92 | 5500 | – | 4,45 |
| 5900 | 5700 | – | 4,05 | 5700 | – | 4,59 |
| 6000 | 5800 | – | 4,26 | 2900 | – | 4,83 |
| 6200 | 6000 | – | 4,04 | 6100 | – | 4,57 |
| 6400 | 6200 | – | 3,84 | 6300 | – | 4,36 |
| 6600 | 6400 | – | 3,69 | 6500 | – | 4,17 |
Tab. 3.19 Nosníky BSK PLUS – nosníky zdvojené, tloušťka stropu 220 mm
| BSK PLUS (nosníky zdvojené) tloušťka stropu h = 220 mm, nadbetonávka h1 = 60 mm, vložky výšky H2 = 160 mm, vlastní tíha gk,1 = 3,67 kN/m2 | ||||||
| Délka nosníku L [mm] | Maximální světlá délka ℓs,max (uložení 100 mm) | Průměrná světlá délka ℓs,prům (uložení 150 mm) | ||||
| světlá délka ℓs,max [mm] | zatížení [kN/m2] | světlá délka ℓs,prům [mm] | zatížení [kN/m2] | |||
| gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | |||
| 1600 | 1400 | 71,69 | – | 1300 | 83,40 | – |
| 1800 | 1600 | 54,02 | – | 1500 | 62,19 | – |
| 2000 | 1800 | 41,85 | – | 1700 | 47,52 | – |
| 2200 | 2000 | 33,19 | – | 1900 | 37,19 | – |
| 2400 | 2200 | 26,77 | – | 2100 | 29,86 | – |
| 2600 | 2400 | 21,85 | – | 2300 | 24,19 | – |
| 2800 | 2600 | 18,03 | – | 2500 | 19,85 | – |
| 3000 | 2800 | 14,34 | – | 2700 | 16,44 | – |
| 3200 | 3000 | 12,55 | – | 2900 | 13,72 | – |
| 3400 | 3200 | 10,64 | 8,18 | 3100 | 11,56 | 8,89 |
| 3600 | 3400 | 12,60 | 9,69 | 3300 | 13,56 | 10,43 |
| 3800 | 3600 | 10,87 | 8,36 | 3500 | 11,69 | 8,99 |
| 4000 | 3800 | 12,12 | 9,32 | 3700 | 12,97 | 9,98 |
| 4200 | 4000 | 10,60 | 8,15 | 3900 | 11,35 | 8,73 |
| 4400 | 4200 | 13,32 | 10,25 | 4100 | 14,15 | 10,88 |
| 4600 | 4400 | 11,84 | 9,11 | 1300 | 12,56 | 9,66 |
| 4800 | 4600 | 10,54 | 8,11 | 4500 | 11,17 | 8,59 |
| 5000 | 4800 | 10,42 | 8,02 | 4700 | 11,04 | 8,49 |
| 5200 | 5000 | 12,11 | 9,31 | 4900 | 12,74 | 9,80 |
| 5400 | 5200 | 12,18 | 9,37 | 5100 | 12,97 | 9,96 |
| 5600 | 5400 | – | 9,56 | 5300 | – | 10,49 |
| 5800 | 5600 | – | 8,89 | 5500 | – | 9,70 |
| 5900 | 5700 | – | 9,12 | 5700 | – | 9,96 |
| 6000 | 5800 | – | 9,46 | 2900 | – | 10,31 |
| 6200 | 6000 | – | 9,08 | 6100 | – | 9,87 |
| 6400 | 6200 | – | 8,75 | 6300 | – | 9,50 |
| 6600 | 6400 | – | 8,45 | 6500 | – | 9,18 |
Tab. 3.20 Nosníky BSK STANDARD – nosníky jednoduché, tloušťka stropu 250 mm
| BSK STANDARD (nosníky jednoduché) tloušťka stropu h = 250 mm, nadbetonávka h1 = 40 mm, vložky výšky H2 = 210 mm, vlastní tíha gk,1 = 3,26 kN/m2 | ||||||
| Délka nosníku L [mm] | Maximální světlá délka ℓs,max (uložení 100 mm) | Průměrná světlá délka ℓs,prům (uložení 150 mm) | ||||
| světlá délka ℓs,max [mm] | zatížení [kN/m2] | světlá délka ℓs,prům [mm] | zatížení [kN/m2] | |||
| gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | |||
| 1600 | 1400 | 49,16 | – | 1300 | 57,60 | – |
| 1800 | 1600 | 36,85 | – | 1500 | 42,26 | – |
| 2000 | 1800 | 28,38 | – | 1700 | 32,22 | – |
| 2200 | 2000 | 22,27 | – | 1900 | 25,12 | – |
| 2400 | 2200 | 17,80 | 12,98 | 2100 | 20,00 | – |
| 2600 | 2400 | 14,37 | 11,05 | 2300 | 15,99 | – |
| 2800 | 2600 | 11,73 | 8,64 | 2500 | 12,98 | – |
| 3000 | 2800 | 9,61 | 7,39 | 2700 | 10,63 | – |
| 3200 | 3000 | 7,91 | 5,92 | 2900 | 8,72 | – |
| 3400 | 3200 | 6,57 | 5,05 | 3100 | 7,23 | 5,56 |
| 3600 | 3400 | 7,99 | 5,97 | 3300 | 8,68 | 6,68 |
| 3800 | 3600 | 6,77 | 5,21 | 3500 | 7,36 | 5,66 |
| 4000 | 3800 | 7,69 | 5,77 | 3700 | 8,31 | 6,39 |
| 4200 | 4000 | 6,63 | 5,10 | 3900 | 7,18 | 5,52 |
| 4400 | 4200 | 8,64 | 6,43 | 4100 | 9,23 | 70,10 |
| 4600 | 4400 | 7,58 | 5,83 | 4300 | 8,06 | 6,22 |
| 4800 | 4600 | 6,65 | 5,12 | 4500 | 7,12 | 5,48 |
| 5000 | 4800 | 6,61 | 5,08 | 4700 | 7,07 | 5,44 |
| 5200 | 5000 | 5,84 | 4,49 | 4900 | 6,24 | 4,80 |
| 5400 | 5200 | 5,16 | 3,89 | 5100 | 5,50 | 4,23 |
| 5600 | 5400 | 4,53 | 3,48 | 5300 | 4,84 | 3,72 |
| 5800 | 5600 | 5,61 | 4,21 | 5500 | 5,94 | 4,57 |
| 5900 | 5700 | – | 3,76 | 5700 | – | 3,98 |
| 6200 | 6000 | – | 3,07 | 5900 | – | 3,44 |
| 6400 | 6200 | – | 3,00 | 6100 | – | 3,37 |
| 6600 | 6400 | – | 3,10 | 6300 | – | 3,50 |
| 6700 | 6500 | – | 3,16 | 6400 | – | 3,54 |
| 6800 | 6600 | – | 3,20 | 6500 | – | 3,58 |
| 6900 | 6700 | – | 2,73 | 6600 | – | 3,06 |
| 7000 | 6800 | – | 2,81 | 6700 | – | 3,16 |
| 7200 | 7000 | – | 2,70 | 6900 | – | 3,04 |
| 7400 | 7200 | – | 2,30 | 7100 | – | 2,88 |
Tab. 3.21 Nosníky BSK STANDARD – nosníky zdvojené, tloušťka stropu 250 mm
| BSK STANDARD (nosníky zdvojené) tloušťka stropu h = 250 mm, nadbetonávka h1 = 50 mm, vložky výšky H2 = 210 mm, vlastní tíha gk,1 = 3,72 kN/m2 | ||||||
| Délka nosníku L [mm] | Maximální světlá délka ℓs,max (uložení 100 mm) | Průměrná světlá délka ℓs,prům (uložení 150 mm) | ||||
| světlá délka ℓs,max [mm] | zatížení [kN/m2] | světlá délka ℓs,prům [mm] | zatížení [kN/m2] | |||
| gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | |||
| 1600 | 1400 | 83,35 | – | 1300 | 98,69 | – |
| 1800 | 1600 | 63,69 | – | 1500 | 73,02 | – |
| 2000 | 1800 | 49,52 | – | 1700 | 56,02 | – |
| 2200 | 2000 | 39,35 | – | 1900 | 44,02 | – |
| 2400 | 2200 | 31,85 | – | 2100 | 35,52 | – |
| 2600 | 2400 | 26,03 | – | 2300 | 28,69 | – |
| 2800 | 2600 | 21,69 | – | 2500 | 23,74 | – |
| 3000 | 2800 | 18,11 | – | 2700 | 13,79 | – |
| 3200 | 3000 | 15,27 | – | 2900 | 16,62 | – |
| 3400 | 3200 | 13,02 | – | 3100 | 14,11 | – |
| 3600 | 3400 | 15,32 | – | 3300 | 16,47 | – |
| 3800 | 3600 | 13,32 | – | 3500 | 14,29 | – |
| 4000 | 3800 | 14,80 | – | 3700 | 15,81 | – |
| 4200 | 4000 | 13,03 | – | 3900 | 13,89 | – |
| 4400 | 4200 | 16,27 | – | 4100 | 17,24 | – |
| 4600 | 4400 | 14,52 | – | 4300 | 15,36 | – |
| 4800 | 4600 | 12,99 | 9,99 | 4500 | 13,72 | 10,55 |
| 5000 | 4800 | 12,89 | 9,92 | 4700 | 12,22 | 10,46 |
| 5200 | 5000 | 11,61 | 8,93 | 4900 | 11,02 | 9,40 |
| 5400 | 5200 | 10,46 | 8,05 | 5100 | 9,93 | 8,48 |
| 5600 | 5400 | 9,44 | 7,26 | 5300 | 11,69 | 7,64 |
| 5800 | 5600 | 11,14 | 8,57 | 5500 | 10,64 | 8,99 |
| 6000 | 5800 | 10,12 | 7,78 | 5900 | 9,67 | 8,18 |
| 6200 | 6000 | 9,02 | 6,94 | 6100 | 9,37 | 7,44 |
| 6400 | 6200 | 8,61 | 6,62 | 6300 | – | 7,21 |
| 6600 | 6400 | – | 6,94 | 6500 | – | 7,54 |
| 6700 | 6500 | – | 7,10 | 6400 | – | 7,71 |
| 6800 | 6600 | – | 7,07 | 6500 | – | 7,66 |
| 6900 | 6700 | – | 6,44 | 6600 | – | 7,02 |
| 7000 | 6800 | – | 6,71 | 6700 | – | 7,31 |
| 7200 | 7000 | – | 6,44 | 6900 | – | 7,01 |
| 7400 | 7200 | – | 8,47 | 7100 | – | 6,72 |
Tab. 3.22 Nosníky BSK STANDARD – nosníky jednoduché, tloušťka stropu 270 mm
| BSK STANDARD (nosníky jednoduché) tloušťka stropu h = 270 mm, nadbetonávka h1 = 60 mm, vložky výšky H2 = 210 mm, vlastní tíha gk,1 = 3,72 kN/m2 | ||||||
| Délka nosníku L [mm] | Maximální světlá délka ℓs,max (uložení 100 mm) | Průměrná světlá délka ℓs,prům (uložení 150 mm) | ||||
| světlá délka ℓs,max [mm] | zatížení [kN/m2] | světlá délka ℓs,prům [mm] | zatížení [kN/m2] | |||
| gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | |||
| 1600 | 1400 | 53,69 | – | 1300 | 62,75 | – |
| 1800 | 1600 | 40,20 | – | 1500 | 46,01 | – |
| 2000 | 1800 | 30,88 | – | 1700 | 34,98 | – |
| 2200 | 2000 | 24,24 | – | 1900 | 27,30 | – |
| 2400 | 2200 | 19,38 | 14,06 | 2100 | 21,58 | – |
| 2600 | 2400 | 15,57 | 11,98 | 2300 | 17,35 | – |
| 2800 | 2600 | 12,68 | 9,30 | 2500 | 14,02 | – |
| 3000 | 2800 | 10,36 | 7,97 | 2700 | 11,46 | – |
| 3200 | 3000 | 8,51 | 6,33 | 2900 | 9,37 | – |
| 3400 | 3200 | 7,03 | 5,41 | 3100 | 7,73 | 5,95 |
| 3600 | 3400 | 8,56 | 6,38 | 3300 | 9,31 | 7,18 |
| 3800 | 3600 | 7,26 | 5,58 | 3500 | 7,89 | 6,07 |
| 4000 | 3800 | 8,29 | 6,17 | 3700 | 8,92 | 6,86 |
| 4200 | 4000 | 7,11 | 5,47 | 3900 | 7,68 | 5,91 |
| 4400 | 4200 | 9,29 | 6,91 | 4100 | 9,93 | 7,64 |
| 4600 | 4400 | 8,13 | 6,25 | 4300 | 8,70 | 6,69 |
| 4800 | 4600 | 7,15 | 5,50 | 4500 | 7,64 | 5,88 |
| 5000 | 4800 | 7,11 | 5,47 | 4700 | 7,58 | 5,83 |
| 5200 | 5000 | 6,26 | 4,82 | 4900 | 6,67 | 5,13 |
| 5400 | 5200 | 5,48 | 4,18 | 5100 | 5,88 | 4,51 |
| 5600 | 5400 | 4,82 | 3,71 | 5300 | 5,14 | 3,95 |
| 5800 | 5600 | 5,99 | 4,54 | 5500 | 6,36 | 4,89 |
| 5900 | 5700 | 5,33 | 4,10 | 5700 | 5,67 | 4,36 |
| 6200 | 6000 | 4,74 | 3,65 | 5900 | 5,03 | 3,97 |
| 6400 | 6200 | 5,02 | 3,86 | 6100 | 5,34 | 4,11 |
| 6600 | 6400 | – | 3,98 | 6300 | – | 4,26 |
| 6700 | 6500 | – | 4,02 | 6400 | – | 4,33 |
| 6800 | 6600 | – | 4,08 | 6500 | – | 4,41 |
| 6900 | 6700 | – | 3,61 | 6600 | – | 4,08 |
| 7000 | 6800 | – | 4,11 | 6700 | – | 4,18 |
| 7200 | 7000 | – | 3,66 | 6900 | – | 4,03 |
| 7400 | 7200 | – | 4,01 | 7100 | – | 3,91 |
Tab. 3.23 Nosníky BSK STANDARD – nosníky zdvojené, tloušťka stropu 270 mm
| BSK STANDARD (nosníky zdvojené) tloušťka stropu h = 270 mm, nadbetonávka h1 = 60 mm, vložky výšky H2 = 210 mm, vlastní tíha gk,1 = 4,19 kN/m2 | ||||||
| Délka nosníku L [mm] | Maximální světlá délka ℓs,max (uložení 100 mm) | Průměrná světlá délka ℓs,prům (uložení 150 mm) | ||||
| světlá délka ℓs,max [mm] | zatížení [kN/m2] | světlá délka ℓs,prům [mm] | zatížení [kN/m2] | |||
| gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | |||
| 1600 | 1400 | 91,69 | – | 1300 | 107,50 | – |
| 1800 | 1600 | 69,85 | – | 1500 | 80,02 | – |
| 2000 | 1800 | 54,02 | – | 1700 | 60,86 | – |
| 2200 | 2000 | 43,02 | – | 1900 | 48,03 | – |
| 2400 | 2200 | 34,69 | – | 2100 | 38,69 | – |
| 2600 | 2400 | 28,36 | – | 2300 | 31,36 | – |
| 2800 | 2600 | 23,52 | – | 2500 | 25,86 | – |
| 3000 | 2800 | 19,69 | – | 2700 | 21,53 | – |
| 3200 | 3000 | 16,52 | – | 2900 | 18,09 | – |
| 3400 | 3200 | 14,19 | – | 3100 | 15,32 | – |
| 3600 | 3400 | 16,53 | – | 3300 | 17,92 | – |
| 3800 | 3600 | 14,06 | – | 3500 | 15,53 | – |
| 4000 | 3800 | 16,14 | – | 3700 | 17,22 | – |
| 4200 | 4000 | 14,19 | – | 3900 | 15,13 | – |
| 4400 | 4200 | 17,69 | – | 4100 | 18,81 | – |
| 4600 | 4400 | 15,84 | – | 4300 | 16,76 | – |
| 4800 | 4600 | 14,17 | – | 4500 | 14,96 | – |
| 5000 | 4800 | 14,06 | 10,82 | 4700 | 14,84 | 11,42 |
| 5200 | 5000 | 12,64 | 9,72 | 4900 | 13,32 | 10,25 |
| 5400 | 5200 | 11,39 | 8,76 | 5100 | 11,99 | 9,22 |
| 5600 | 5400 | 10,27 | 7,90 | 5300 | 10,81 | 8,32 |
| 5800 | 5600 | 12,16 | 9,35 | 5500 | 12,74 | 9,80 |
| 6000 | 5800 | 11,06 | 8,51 | 5900 | 11,59 | 8,92 |
| 6200 | 6000 | 10,08 | 7,75 | 6100 | 10,54 | 8,11 |
| 6400 | 6200 | 10,52 | 8,09 | 6300 | 10,99 | 8,45 |
| 6600 | 6400 | 11,12 | 8,55 | 6500 | 12,06 | 9,28 |
| 6700 | 6500 | – | 8,60 | 6400 | – | 9,36 |
| 6800 | 6600 | – | 8,11 | 6500 | – | 8,84 |
| 6900 | 6700 | – | 7,74 | 6600 | – | 8,40 |
| 7000 | 6800 | – | 8,08 | 6700 | – | 8,76 |
| 7200 | 7000 | – | 7,78 | 6900 | – | 8,44 |
| 7400 | 7200 | – | 7,52 | 7100 | – | 8,15 |
Tab. 3.24 Nosníky BSK MAX – nosníky jednoduché, tloušťka stropu 300 mm
| BSK MAX (nosníky jednoduché) tloušťka stropu h = 300 mm, nadbetonávka h1 = 40 mm, vložky výšky H2 = 260 mm, vlastní tíha gk,1 = 3,66 kN/m2 | ||||||
| Délka nosníku L [mm] | Maximální světlá délka ℓs,max (uložení 100 mm) | Průměrná světlá délka ℓs,prům (uložení 150 mm) | ||||
| světlá délka ℓs,max [mm] | zatížení [kN/m2] | světlá délka ℓs,prům [mm] | zatížení [kN/m2] | |||
| gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | |||
| 1600 | 1400 | 61,17 | – | 1300 | 70,50 | – |
| 1800 | 1600 | 45,81 | – | 1500 | 52,77 | – |
| 2000 | 1800 | 35,37 | – | 1700 | 40,26 | – |
| 2200 | 2000 | 27,98 | – | 1900 | 31,50 | – |
| 2400 | 2200 | 22,43 | – | 2100 | 25,10 | – |
| 2600 | 2400 | 18,21 | – | 2300 | 20,17 | – |
| 2800 | 2600 | 14,92 | – | 2500 | 16,47 | – |
| 3000 | 2800 | 12,30 | – | 2700 | 13,54 | – |
| 3200 | 3000 | 10,20 | – | 2900 | 11,21 | – |
| 3400 | 3200 | 8,58 | – | 3100 | 9,36 | – |
| 3600 | 3400 | 10,30 | – | 3300 | 11,14 | – |
| 3800 | 3600 | 8,82 | – | 3500 | 9,53 | – |
| 4000 | 3800 | 9,96 | – | 3700 | 11,72 | – |
| 4200 | 4000 | 8,66 | – | 3900 | 9,30 | – |
| 4400 | 4200 | 11,14 | – | 4100 | 11,86 | – |
| 4600 | 4400 | 9,84 | – | 4300 | 10,47 | – |
| 4800 | 4600 | 8,70 | – | 4500 | 9,24 | – |
| 5000 | 4800 | 8,65 | – | 4700 | 9,20 | – |
| 5200 | 5000 | 7,69 | 5,92 | 4900 | 8,18 | 6,29 |
| 5400 | 5200 | 6,83 | 5,25 | 5100 | 7,26 | 5,58 |
| 5600 | 5400 | 6,08 | 4,68 | 5300 | 6,45 | 4,96 |
| 5800 | 5600 | 7,42 | 5,72 | 5500 | 7,84 | 6,03 |
| 6000 | 5800 | 6,67 | 5,13 | 5700 | 7,05 | 5,42 |
| 6200 | 6000 | 5,98 | 4,60 | 2900 | 6,33 | 4,87 |
| 6400 | 6200 | 6,34 | 4,88 | 6100 | 6,68 | 5,14 |
| 6600 | 6400 | 5,71 | 4,39 | 6300 | 6,01 | 4,62 |
| 6800 | 6600 | 5,16 | 3,97 | 6500 | 5,42 | 4,17 |
| 7000 | 6800 | – | 3,00 | 6700 | – | 3,21 |
| 7200 | 7000 | – | 3,12 | 6900 | – | 3,44 |
| 7400 | 7200 | – | 3,00 | 7100 | – | 3,18 |
| 7500 | 7300 | – | 3,07 | 7200 | – | 3,37 |
| 7600 | 7400 | – | 3,23 | 7300 | – | 3,61 |
| 7800 | 7600 | – | 3,14 | 7500 | – | 3,50 |
| 8000 | 7800 | – | 3,07 | 7700 | – | 3,43 |
| 8200 | 8000 | – | 3,00 | 7900 | – | 3,36 |
Tab. 3.25 Nosníky BSK MAX – nosníky zdvojené, tloušťka stropu 300 mm
| BSK MAX (nosníky zdvojené) tloušťka stropu h = 300 mm, nadbetonávka h1 = 40 mm, vložky výšky H2 = 260 mm, vlastní tíha gk,1 = 4,25 kN/m2 | ||||||
| Délka nosníku L [mm] | Maximální světlá délka ℓs,max (uložení 100 mm) | Průměrná světlá délka ℓs,prům (uložení 150 mm) | ||||
| světlá délka ℓs,max [mm] | zatížení [kN/m2] | světlá délka ℓs,prům [mm] | zatížení [kN/m2] | |||
| gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | |||
| 1600 | 1400 | 61,17 | – | 1300 | 70,50 | – |
| 1800 | 1600 | 45,81 | – | 1500 | 52,77 | – |
| 2000 | 1800 | 35,37 | – | 1700 | 40,26 | – |
| 2200 | 2000 | 27,98 | – | 1900 | 31,50 | – |
| 2400 | 2200 | 22,43 | – | 2100 | 25,10 | – |
| 2600 | 2400 | 18,21 | – | 2300 | 20,17 | – |
| 2800 | 2600 | 14,92 | – | 2500 | 16,47 | – |
| 3000 | 2800 | 12,30 | – | 2700 | 13,54 | – |
| 3200 | 3000 | 10,20 | – | 2900 | 11,21 | – |
| 3400 | 3200 | 8,56 | – | 3100 | 9,38 | – |
| 3600 | 3400 | 10,30 | – | 3300 | 11,14 | – |
| 3800 | 3600 | 8,82 | – | 3500 | 9,53 | – |
| 4000 | 3800 | 9,96 | – | 3700 | 11,72 | – |
| 4200 | 4000 | 8,66 | – | 3900 | 9,30 | – |
| 4400 | 4200 | 11,14 | – | 4100 | 11,86 | – |
| 4600 | 4400 | 9,84 | – | 4300 | 10,47 | – |
| 4800 | 4600 | 8,70 | – | 4500 | 9,24 | – |
| 5000 | 4800 | 8,66 | – | 4700 | 9,20 | – |
| 5200 | 5000 | 7,69 | 5,92 | 4900 | 8,18 | 6,29 |
| 5400 | 5200 | 6,83 | 5,25 | 5100 | 7,26 | 5,58 |
| 5600 | 5400 | 6,08 | 4,68 | 5300 | 6,45 | 4,96 |
| 5800 | 5600 | 7,42 | 5,72 | 5500 | 7,84 | 6,03 |
| 6000 | 5800 | 6,67 | 5,13 | 5700 | 7,05 | 5,42 |
| 6200 | 6000 | 5,98 | 4,60 | 2900 | 6,33 | 4,87 |
| 6400 | 6200 | 6,34 | 4,88 | 6100 | 6,68 | 5,14 |
| 6600 | 6400 | 5,71 | 4,39 | 6300 | 6,01 | 4,62 |
| 6800 | 6600 | 5,16 | 3,97 | 6500 | 5,42 | 4,17 |
| 7000 | 6800 | – | 3,00 | 6700 | – | 3,21 |
| 7200 | 7000 | – | 3,12 | 6900 | – | 3,44 |
| 7400 | 7200 | – | 3,00 | 7100 | – | 3,18 |
| 7500 | 7300 | – | 3,07 | 7200 | – | 3,37 |
| 7600 | 7400 | – | 3,23 | 7300 | – | 3,61 |
| 7800 | 7600 | – | 3,14 | 7500 | – | 3,50 |
| 8000 | 7800 | – | 3,07 | 7700 | – | 3,43 |
| 8200 | 8000 | – | 3,00 | 7900 | – | 3,36 |
Tab. 3.26 Nosníky BSK MAX – nosníky jednoduché, tloušťka stropu 320 mm
| BSK MAX (nosníky jednoduché) tloušťka stropu h = 320 mm, nadbetonávka h1 = 60 mm, vložky výšky H2 = 260 mm, vlastní tíha gk,1 = 4,12 kN/m2 | ||||||
| Délka nosníku L [mm] | Maximální světlá délka ℓs,max (uložení 100 mm) | Průměrná světlá délka ℓs,prům (uložení 150 mm) | ||||
| světlá délka ℓs,max [mm] | zatížení [kN/m2] | světlá délka ℓs,prům [mm] | zatížení [kN/m2] | |||
| gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | |||
| 1600 | 1400 | 65,71 | – | 1300 | 76,40 | – |
| 1800 | 1600 | 49,36 | – | 1500 | 56,71 | – |
| 2000 | 1800 | 38,03 | – | 1700 | 43,12 | – |
| 2200 | 2000 | 29,96 | – | 1900 | 33,66 | – |
| 2400 | 2200 | 23,95 | – | 2100 | 26,87 | – |
| 2600 | 2400 | 19,42 | – | 2300 | 21,46 | – |
| 2800 | 2600 | 15,85 | – | 2500 | 17,51 | – |
| 3000 | 2800 | 13,06 | – | 2700 | 14,38 | – |
| 3200 | 3000 | 10,79 | – | 2900 | 11,86 | – |
| 3400 | 3200 | 9,02 | – | 3100 | 9,87 | – |
| 3600 | 3400 | 10,87 | – | 3300 | 11,80 | – |
| 3800 | 3600 | 9,29 | – | 3500 | 10,05 | – |
| 4000 | 3800 | 10,55 | – | 3700 | 11,35 | – |
| 4200 | 4000 | 9,14 | – | 3900 | 9,83 | – |
| 4400 | 4200 | 11,81 | – | 4100 | 12,60 | – |
| 4600 | 4400 | 10,40 | – | 4300 | 11,08 | – |
| 4800 | 4600 | 9,18 | – | 4500 | 9,77 | – |
| 5000 | 4800 | 9,16 | – | 4700 | 9,71 | – |
| 5200 | 5000 | 8,11 | 6,24 | 4900 | 8,61 | 6,62 |
| 5400 | 5200 | 9,19 | 5,53 | 5100 | 7,63 | 5,87 |
| 5600 | 5400 | 6,36 | 4,89 | 5300 | 6,76 | 5,20 |
| 5800 | 5600 | 7,80 | 6,00 | 5500 | 8,26 | 6,35 |
| 6000 | 5800 | 7,01 | 5,39 | 5700 | 7,39 | 5,68 |
| 6200 | 6000 | 6,26 | 4,82 | 2900 | 6,60 | 5,08 |
| 6400 | 6200 | 6,65 | 5,12 | 6100 | 7,00 | 5,38 |
| 6600 | 6400 | 5,96 | 4,58 | 6300 | 6,31 | 4,85 |
| 6800 | 6600 | 5,36 | 4,13 | 6500 | 5,67 | 4,36 |
| 7000 | 6800 | 4,81 | 3,70 | 6700 | 5,08 | 3,90 |
| 7200 | 7000 | – | 3,91 | 6900 | – | 4,28 |
| 7400 | 7200 | – | 3,78 | 7100 | – | 3,99 |
| 7500 | 7300 | – | 3,89 | 7200 | – | 4,22 |
| 7600 | 7400 | – | 4,09 | 7300 | – | 4,53 |
| 7800 | 7600 | – | 4,00 | 7500 | – | 4,43 |
| 8000 | 7800 | – | 3,94 | 7700 | – | 4,37 |
| 8200 | 8000 | – | 3,89 | 7900 | – | 4,31 |
Tab. 3.27 Nosníky BSK MAX – nosníky zdvojené, tloušťka stropu 320 mm
| BSK MAX (nosníky zdvojené) tloušťka stropu h = 320 mm, nadbetonávka h1 = 60 mm, vložky výšky H2 = 260 mm, vlastní tíha gk,1 = 4,72 kN/m2 | ||||||
| Délka nosníku L [mm] | Maximální světlá délka ℓs,max (uložení 100 mm) | Průměrná světlá délka ℓs,prům (uložení 150 mm) | ||||
| světlá délka ℓs,max [mm] | zatížení [kN/m2] | světlá délka ℓs,prům [mm] | zatížení [kN/m2] | |||
| gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | |||
| 1600 | 1400 | 111,69 | – | 1300 | 131,00 | – |
| 1800 | 1600 | 85,02 | – | 1500 | 97,69 | – |
| 2000 | 1800 | 66,35 | – | 1700 | 75,02 | – |
| 2200 | 2000 | 52,69 | – | 1900 | 59,02 | – |
| 2400 | 2200 | 42,77 | – | 2100 | 47,89 | – |
| 2600 | 2400 | 35,10 | – | 2300 | 38,69 | – |
| 2800 | 2600 | 29,19 | – | 2500 | 32,02 | – |
| 3000 | 2800 | 24,49 | – | 2700 | 26,69 | – |
| 3200 | 3000 | 20,64 | – | 2900 | 22,46 | – |
| 3400 | 3200 | 17,67 | – | 3100 | 19,09 | – |
| 3600 | 3400 | 20,77 | – | 3300 | 22,29 | – |
| 3800 | 3600 | 18,09 | – | 3500 | 19,38 | – |
| 4000 | 3800 | 20,14 | – | 3700 | 21,49 | – |
| 4200 | 4000 | 17,77 | – | 3900 | 18,91 | – |
| 4400 | 4200 | 22,19 | – | 4100 | 23,47 | – |
| 4600 | 4400 | 19,77 | – | 4300 | 20,84 | – |
| 4800 | 4600 | 17,77 | – | 4500 | 18,76 | – |
| 5000 | 4800 | 17,69 | – | 4700 | 18,64 | – |
| 5200 | 5000 | 15,96 | 12,28 | 4900 | 16,79 | 12,92 |
| 5400 | 5200 | 14,42 | 11,09 | 5100 | 15,17 | 11,67 |
| 5600 | 5400 | 13,04 | 10,02 | 5300 | 13,71 | 10,55 |
| 5800 | 5600 | 11,79 | 9,07 | 5500 | 12,39 | 9,53 |
| 6000 | 5800 | 14,02 | 10,78 | 5700 | 14,69 | 11,30 |
| 6200 | 6000 | 12,81 | 9,85 | 2900 | 13,41 | 10,32 |
| 6400 | 6200 | 13,41 | 10,32 | 6100 | 14,01 | 10,78 |
| 6600 | 6400 | 12,31 | 9,47 | 6300 | 12,84 | 9,88 |
| 6800 | 6600 | 11,29 | 8,68 | 6500 | 11,77 | 9,06 |
| 7000 | 6800 | 10,36 | 7,97 | 6700 | 10,81 | 8,31 |
| 7200 | 7000 | – | 8,59 | 6900 | 12,05 | 9,27 |
| 7400 | 7200 | – | 8,16 | 7100 | – | 8,81 |
| 7500 | 7300 | – | 8,48 | 7200 | – | 9,15 |
| 7600 | 7400 | – | 8,90 | 7300 | – | 9,58 |
| 7800 | 7600 | – | 8,92 | 7500 | – | 9,39 |
| 8000 | 7800 | – | 8,59 | 7700 | – | 9,24 |
| 8200 | 8000 | – | 8,47 | 7900 | – | 9,12 |
Tab. 3.28 Nosníky BSK MAX MAX – nosníky jednoduché, tloušťka stropu 350 mm
| BSK MAX MAX (nosníky jednoduché) tloušťka stropu h = 3500 mm, nadbetonávka h1 = 90 mm, vložky výšky H2 = 260 mm, vlastní tíha gk,1 = 4,81 kN/m2 | ||||||
| Délka nosníku L [mm] | Maximální světlá délka ℓs,max (uložení 100 mm) | Průměrná světlá délka ℓs,prům (uložení 150 mm) | ||||
| světlá délka ℓs,max [mm] | zatížení [kN/m2] | světlá délka ℓs,prům [mm] | zatížení [kN/m2] | |||
| gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | |||
| 6600 | 6400 | 6,39 | – | 6300 | 6,76 | – |
| 6800 | 6600 | 5,72 | – | 6500 | 6,05 | – |
| 7000 | 6800 | 5,10 | – | 6700 | 5,40 | – |
| 7200 | 7000 | 5,92 | – | 6900 | 6,39 | – |
| 7400 | 7200 | 6,13 | 4,71 | 7100 | 6,60 | 5,08 |
| 7500 | 7300 | 6,61 | 5,08 | 7200 | 7,27 | 5,59 |
| 7600 | 7400 | 7,15 | 5,50 | 7300 | 7,85 | 6,04 |
| 7800 | 7600 | 7,03 | 5,41 | 7500 | 7,72 | 5,94 |
| 8000 | 7800 | 6,96 | 5,37 | 7700 | 7,67 | 5,90 |
| 8200 | 8000 | 6,88 | 5,29 | 7900 | 7,57 | 5,82 |
| 8400 | 8200 | – | 4,41 | 8100 | – | 4,84 |
| 8600 | 8400 | – | 3,56 | 8300 | – | 3,97 |
| 8800 | 8600 | – | 2,88 | 8500 | – | 3,26 |
Tab. 3.29 Nosníky BSK MAX MAX – nosníky zdvojené, tloušťka stropu 350 mm
| BSK MAX MAX (nosníky zdvojené) tloušťka stropu h = 350 mm, nadbetonávka h1 = 90 mm, vložky výšky H2 = 260 mm, vlastní tíha gk,1 = 5,42 kN/m2 | ||||||
| Délka nosníku L [mm] | Maximální světlá délka ℓs,max (uložení 100 mm) | Průměrná světlá délka ℓs,prům (uložení 150 mm) | ||||
| světlá délka ℓs,max [mm] | zatížení [kN/m2] | světlá délka ℓs,prům [mm] | zatížení [kN/m2] | |||
| gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | gd,1 + gd,2 + qd | gk,1 + gk,2 + qk | |||
| 6600 | 6400 | 13,51 | – | 6300 | 14,11 | – |
| 6800 | 6600 | 12,37 | – | 6500 | 12,92 | – |
| 7000 | 6800 | 11,34 | – | 6700 | 11,83 | – |
| 7200 | 7000 | 12,89 | – | 6900 | 13,44 | – |
| 7400 | 7200 | 13,19 | 10,15 | 7100 | 13,76 | 10,58 |
| 7500 | 7300 | 14,19 | 10,91 | 7200 | 14,79 | 11,38 |
| 7600 | 7400 | 15,37 | 11,82 | 7300 | 16,03 | 12,33 |
| 7800 | 7600 | 15,17 | 11,67 | 7500 | 16,26 | 12,52 |
| 8000 | 7800 | 15,02 | 11,55 | 7700 | 16,16 | 12,43 |
| 8200 | 8000 | 14,85 | 11,42 | 7900 | 16,02 | 12,32 |
| 8400 | 8200 | – | 10,03 | 8100 | – | 10,76 |
| 8600 | 8400 | – | 8,71 | 8300 | – | 9,35 |
| 8800 | 8600 | – | 7,51 | 8500 | – | 8,09 |
| 9000 | 8800 | – | 6,43 | 8700 | – | 6,94 |
| 9200 | 9000 | – | 5,42 | 8900 | – | 5,90 |
| 9400 | 9200 | – | 4,49 | 9100 | – | 4,95 |
| 9600 | 9400 | – | 3,67 | 9300 | – | 4,07 |
Příklad 3.8
Vypočítejte zatížení na stropní konstrukci.
Světlé rozpětí stropní konstrukce v administrativní budově je 5,1 m, skladba podlahy číslo 4 podle tab. 3.7.
Zatížení
charakteristické
návrhové
Vlastní tíha stropu
3,67
\begin{gathered}
3{,}65\cdot1{,}35=4{,}95\space\text{kN/m}^2
\end{gathered}Podlaha
0,85
\begin{gathered}
1{,}15\space\text{kN/m}^2
\end{gathered}Nahodilé
2,50
\begin{gathered}
2{,}5\cdot1{,}5=3{,}75\space\text{kN/m}^2
\end{gathered}Zatížení celkem
7,02
\begin{gathered}
9{,}85\space\text{kN/m}^2
\end{gathered}Je zvolen strop BSK PLUS se zdvojenými nosníky o tloušťce 220 mm, a výškou vložek 160 mm. V tab. 3.16–3.29, který má při úložné délce 150 mm a světlém rozpětí hodnoty mezního zatížení v charakteristické hodnotě gk,1 + gk,2 + qk = 9,66 > 7,02 kN/m2, a v návrhové hodnotě gd,1 + gd,2 + qd = 12,97 > 9,85 kN/m2.
Předpjaté nosníky s betonovými vložkami
Vložkový strop systému NORD firmy CZ NORD s.r.o. (www.cznord.cz) se skládá z přepjatých nosníků, podle vyztužení označených NPN132 až NPN139, umístěných v osových vzdálenostech 590 mm, Vložky kladené mezi nosníky jsou jednak plné, výšky 70 mm, jednak dutinové, výšky 120, 160, 200 a 250 mm. Statické schéma nosníků je buď prostý, nebo, po vložení horní výztuže, spojitý nosník.
Obr. 3.6 Vložky systému NORD
Následující tab. 3.30–3.31 uvádějí maximální světlosti místností pro stálé zatížení gk,2 bez vlastní tíhy stropu a užitné zatížení qk.
Tab. 3.30 Maximální světlosti místnosti pro stálé zatížení gk,2 bez vlastní tíhy stropu a užitné zatížení qk
| Typ nosníku | Maximální světlá délka ℓs,max [m] | ||||||
| výška tvarovek H1 + výška nabetonávky h2 [mm] | |||||||
| 120 + 50 | 160 + 40 | 160 + 50 | 200 + 40 | 200 + 50 | 250 + 50 | 250 + 60 | |
| NPN132 | 3,58 | 3,70 | 3,70 | 3,70 | 3,70 | 3,70 | – |
| NPN133 | 4,42 | 4,50 | 4,50 | 4,50 | 4,50 | 4,50 | – |
| NPN134 | 4,99 | 5,00 | 5,00 | 5,00 | 5,00 | 5,00 | – |
| NPN135 | 5,04 | 5,67 | 5,84 | 5,90 | 5,90 | 5,90 | 5,90 |
| NPN136 | 5,09 | 5,72 | 5,90 | 6,49 | 6,65 | 6,90 | 6,89 |
| NPN139 | 5,15 | 5,79 | 5,97 | 6,57 | 6,74 | 7,53 | 7,67 |
| 2NPN135 | 5,67 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 |
| 2NPN136 | 5,73 | 6,42 | 6,62 | 6,90 | 6,90 | 6,90 | 6,90 |
| 2NPN139 | 5,80 | 6,48 | 6,69 | 7,33 | 7,53 | 8,42 | 8,59 |
| Typ nosníku | Maximální světlá délka ℓs,max [m] | ||||||
| výška tvarovek H1 + výška nabetonávky h2 [mm] | |||||||
| 120 + 50 | 160 + 40 | 160 + 50 | 200 + 40 | 200 + 50 | 250 + 50 | 250 + 60 | |
| NPN132 | 3,41 | 3,69 | 3,70 | 3,70 | 3,70 | 3,70 | – |
| NPN133 | 4,22 | 4,50 | 4,50 | 4,50 | 4,50 | 4,50 | – |
| NPN134 | 4,79 | 5,00 | 5,00 | 5,00 | 5,00 | 5,00 | – |
| NPN135 | 4,92 | 5,54 | 5,71 | 5,90 | 5,90 | 5,90 | 5,90 |
| NPN136 | 4,97 | 5,60 | 5,76 | 6,35 | 6,51 | 6,76 | 6,64 |
| NPN139 | 5,03 | 5,66 | 5,84 | 6,43 | 6,60 | 7,39 | 7,53 |
| 2NPN135 | 5,54 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 |
| 2NPN136 | 5,59 | 6,27 | 6,48 | 6,90 | 6,90 | 6,90 | 6,90 |
| 2NPN139 | 5,66 | 6,33 | 6,54 | 7,17 | 7,38 | 8,26 | 8,44 |
| Typ nosníku | Maximální světlá délka ℓs,max [m] | ||||||
| výška tvarovek H1 + výška nabetonávky h2 [mm] | |||||||
| 120 + 50 | 160 + 40 | 160 + 50 | 200 + 40 | 200 + 50 | 250 + 50 | 250 + 60 | |
| NPN132 | 3,27 | 3,54 | 3,58 | 3,70 | 3,70 | 3,70 | – |
| NPN133 | 4,04 | 4,39 | 4,44 | 4,50 | 4,50 | 4,50 | – |
| NPN134 | 4,59 | 5,00 | 5,00 | 5,00 | 5,00 | 5,00 | – |
| NPN135 | 4,71 | 5,35 | 5,52 | 5,90 | 5,90 | 5,90 | 5,90 |
| NPN136 | 4,76 | 5,39 | 5,57 | 6,13 | 6,29 | 6,51 | 6,41 |
| NPN139 | 4,84 | 5,46 | 5,64 | 6,22 | 6,38 | 7,17 | 7,29 |
| 2NPN135 | 5,33 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 |
| 2NPN136 | 5,38 | 6,04 | 6,25 | 6,86 | 6,90 | 6,90 | 6,90 |
| 2NPN139 | 5,45 | 6,11 | 6,32 | 6,93 | 7,14 | 8,02 | 8,19 |
| Typ nosníku | Maximální světlá délka ℓs,max [m] | ||||||
| výška tvarovek H1 + výška nabetonávky h2 [mm] | |||||||
| 120 + 50 | 160 + 40 | 160 + 50 | 200 + 40 | 200 + 50 | 250 + 50 | 250 + 60 | |
| NPN132 | 3,14 | 3,41 | 3,45 | 3,70 | 3,70 | 3,70 | – |
| NPN133 | 3,88 | 4,22 | 4,28 | 4,50 | 4,50 | 4,50 | – |
| NPN134 | 4,42 | 4,82 | 4,89 | 5,00 | 5,00 | 5,00 | – |
| NPN135 | 4,54 | 5,18 | 5,29 | 5,71 | 5,80 | 5,90 | 5,90 |
| NPN136 | 4,59 | 5,22 | 5,39 | 5,90 | 6,11 | 6,28 | 6,20 |
| NPN139 | 4,65 | 5,29 | 5,46 | 6,03 | 6,20 | 6,95 | 7,12 |
| 2NPN135 | 5,16 | 5,80 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 |
| 2NPN136 | 5,20 | 5,85 | 6,06 | 6,66 | 6,85 | 6,90 | 6,90 |
| 2NPN139 | 5,27 | 5,91 | 6,12 | 6,72 | 6,93 | 7,80 | 7,98 |
| Typ nosníku | Maximální světlá délka ℓs,max [m] | ||||||
| výška tvarovek H1 + výška nabetonávky h2 [mm] | |||||||
| 120 + 50 | 160 + 40 | 160 + 50 | 200 + 40 | 200 + 50 | 250 + 50 | 250 + 60 | |
| NPN132 | 3,03 | 3,29 | 3,34 | 3,57 | 3,61 | 3,70 | – |
| NPN133 | 3,74 | 4,07 | 4,13 | 4,43 | 4,47 | 4,50 | – |
| NPN134 | 4,26 | 4,65 | 4,73 | 5,00 | 5,00 | 5,00 | – |
| NPN135 | 4,39 | 5,03 | 5,15 | 5,55 | 5,62 | 5,90 | 5,90 |
| NPN136 | 4,43 | 5,08 | 5,24 | 5,74 | 5,94 | 6,07 | 6,00 |
| NPN139 | 4,50 | 5,14 | 5,31 | 5,79 | 6,03 | 6,81 | 6,95 |
| 2NPN135 | 5,01 | 5,64 | 5,83 | 5,90 | 5,90 | 5,90 | 5,90 |
| 2NPN136 | 5,05 | 5,69 | 5,89 | 6,47 | 6,67 | 6,90 | 6,90 |
| 2NPN139 | 5,12 | 5,75 | 5,95 | 6,54 | 6,74 | 7,61 | 7,79 |
| Typ nosníku | Maximální světlá délka ℓs,max [m] | ||||||
| výška tvarovek H1 + výška nabetonávky h2 [mm] | |||||||
| 120 + 50 | 160 + 40 | 160 + 50 | 200 + 40 | 200 + 50 | 250 + 50 | 250 + 60 | |
| NPN132 | 2,99 | 3,25 | 3,30 | 3,53 | 3,57 | 3,70 | – |
| NPN133 | 3,70 | 4,03 | 4,09 | 4,38 | 4,42 | 4,50 | – |
| NPN134 | 4,21 | 4,60 | 4,67 | 5,00 | 5,00 | 5,00 | – |
| NPN135 | 4,47 | 5,01 | 5,10 | 5,49 | 5,56 | 5,90 | 5,90 |
| NPN136 | 4,47 | 5,16 | 5,30 | 5,91 | 5,91 | 6,00 | 5,94 |
| NPN139 | 4,67 | 5,31 | 5,48 | 6,05 | 6,21 | 6,99 | 6,73 |
| 2NPN135 | 5,18 | 5,82 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 |
| 2NPN136 | 5,23 | 5,88 | 6,08 | 6,68 | 6,87 | 6,90 | 6,90 |
| 2NPN139 | 5,30 | 5,94 | 6,14 | 6,75 | 6,95 | 7,81 | 8,00 |
| Typ nosníku | Maximální světlá délka ℓs,max [m] | ||||||
| výška tvarovek H1 + výška nabetonávky h2 [mm] | |||||||
| 120 + 50 | 160 + 40 | 160 + 50 | 200 + 40 | 200 + 50 | 250 + 50 | 250 + 60 | |
| NPN132 | 2,72 | 2,97 | 3,02 | 3,24 | 3,27 | 3,50 | – |
| NPN133 | 3,36 | 3,67 | 3,74 | 4,01 | 4,06 | 4,34 | – |
| NPN134 | 3,82 | 4,20 | 4,28 | 4,60 | 4,66 | 5,00 | – |
| NPN135 | 3,82 | 4,48 | 4,56 | 5,04 | 5,11 | 5,46 | 5,43 |
| NPN136 | – | 4,48 | 4,63 | 5,22 | 5,25 | 5,46 | 5,43 |
| NPN139 | 4,24 | 4,89 | 5,01 | 5,55 | 5,75 | 6,16 | 6,65 |
| 2NPN135 | 4,74 | 5,36 | 5,56 | 5,90 | 5,90 | 5,90 | 5,90 |
| 2NPN136 | 4,78 | 5,41 | 5,61 | 6,17 | 6,36 | 6,90 | 6,90 |
| 2NPN139 | 4,86 | 5,47 | 5,67 | 6,24 | 6,44 | 7,29 | 7,44 |
| Typ nosníku | Maximální světlá délka ℓs,max [m] | ||||||
| výška tvarovek H1 + výška nabetonávky h2 [mm] | |||||||
| 120 + 50 | 160 + 40 | 160 + 50 | 200 + 40 | 200 + 50 | 250 + 50 | 250 + 60 | |
| NPN132 | 2,57 | 2,81 | 2,86 | 3,07 | 3,11 | 3,34 | – |
| NPN133 | 3,19 | 3,48 | 3,55 | 3,81 | 3,86 | 4,15 | – |
| NPN134 | 3,48 | 3,98 | 4,06 | 4,37 | 4,43 | 4,77 | – |
| NPN135 | – | 4,12 | 4,21 | 4,77 | 4,80 | 5,02 | 5,14 |
| NPN136 | – | 4,12 | 4,21 | 4,77 | 4,80 | 5,16 | 5,14 |
| NPN139 | 3,99 | 4,44 | 4,55 | 5,27 | 5,36 | 6,26 | 6,40 |
| 2NPN135 | 4,50 | 5,13 | 5,33 | 5,86 | 5,90 | 5,90 | 5,90 |
| 2NPN136 | 4,54 | 5,17 | 5,37 | 5,91 | 6,10 | 6,90 | 6,90 |
| 2NPN139 | 4,61 | 5,23 | 5,43 | 5,98 | 6,17 | 7,01 | 7,18 |
| Typ nosníku | Maximální světlá délka ℓs,max [m] | ||||||
| výška tvarovek H1 + výška nabetonávky h2 [mm] | |||||||
| 120 + 50 | 160 + 40 | 160 + 50 | 200 + 40 | 200 + 50 | 250 + 50 | 250 + 60 | |
| NPN132 | 2,54 | 2,78 | 2,83 | 3,04 | 3,08 | 3,31 | – |
| NPN133 | 3,15 | 3,45 | 3,51 | 3,77 | 3,82 | 4,11 | – |
| NPN134 | 3,58 | 3,94 | 4,01 | 4,33 | 4,33 | 4,72 | – |
| NPN135 | – | 4,05 | 4,14 | 4,69 | 4,73 | 4,96 | 5,08 |
| NPN136 | – | 4,09 | 4,14 | 4,69 | 4,73 | 5,09 | 5,08 |
| NPN139 | – | 4,35 | 4,46 | 5,16 | 5,26 | 6,33 | 6,37 |
| 2NPN135 | 4,69 | 5,31 | 5,51 | 5,90 | 5,90 | 5,90 | 5,90 |
| 2NPN136 | 4,73 | 5,36 | 5,56 | 6,11 | 6,30 | 6,90 | 6,90 |
| 2NPN139 | 4,80 | 5,42 | 5,62 | 6,18 | 6,38 | 7,22 | 7,39 |
| Typ nosníku | Maximální světlá délka ℓs,max [m] | ||||||
| výška tvarovek H1 + výška nabetonávky h2 [mm] | |||||||
| 120 + 50 | 160 + 40 | 160 + 50 | 200 + 40 | 200 + 50 | 250 + 50 | 250 + 60 | |
| NPN132 | 2,42 | 2,65 | 2,70 | 2,91 | 2,95 | 3,17 | – |
| NPN133 | 3,00 | 3,29 | 3,35 | 3,55 | 3,66 | 3,94 | – |
| NPN134 | – | 3,74 | 3,83 | 4,13 | 4,20 | 4,53 | – |
| NPN135 | – | – | 3,86 | 4,39 | 4,44 | 4,71 | 4,83 |
| NPN136 | – | – | – | 4,39 | 4,44 | 4,71 | 4,83 |
| NPN139 | – | 3,99 | 4,10 | 4,75 | 4,85 | 5,84 | 5,96 |
| 2NPN135 | 4,45 | 5,09 | 5,28 | 5,76 | 5,86 | 5,90 | 5,90 |
| 2NPN136 | 4,48 | 5,13 | 5,32 | 5,86 | 6,04 | 6,85 | 6,90 |
| 2NPN139 | 4,56 | 5,18 | 5,38 | 5,92 | 6,12 | 6,95 | 7,12 |
Tab. 3.31 Maximální světlosti místnosti pro stálé zatížení bez vlastní tíhy stropu g2 a užitné zatížení q, spojité nosníky o poměru rozpětí přilehlých polí 0,8 ≤ ℓ1 / ℓ2 ≤ 1,25
| Typ nosníku | Maximální světlá délka ℓs,max [m] | ||||||
| výška tvarovek H1 + výška nabetonávky h2 [mm] | |||||||
| 120 + 50 | 160 + 40 | 160 + 50 | 200 + 40 | 200 + 50 | 250 + 50 | 250 + 60 | |
| NPN132 | 3,70 | 3,70 | 3,70 | 3,70 | 3,70 | 3,70 | – |
| NPN133 | 4,50 | 4,50 | 4,50 | 4,50 | 4,50 | 4,50 | – |
| NPN134 | 5,00 | 5,00 | 5,00 | 5,00 | 5,00 | 5,00 | – |
| NPN135 | 5,40 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 |
| NPN136 | 5,46 | 6,15 | 6,33 | 6,90 | 6,90 | 6,89 | 6,89 |
| NPN139 | 5,53 | 6,22 | 6,41 | 7,06 | 7,24 | 8,11 | 7,85 |
| 2NPN135 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 |
| 2NPN136 | 6,16 | 6,90 | 6,90 | 6,90 | 6,90 | 6,90 | 6,90 |
| 2NPN139 | 6,24 | 6,97 | 7,19 | 7,88 | 8,11 | 9,07 | 9,19 |
| Typ nosníku | Maximální světlá délka ℓs,max [m] | ||||||
| výška tvarovek H1 + výška nabetonávky h2 [mm] | |||||||
| 120 + 50 | 160 + 40 | 160 + 50 | 200 + 40 | 200 + 50 | 250 + 50 | 250 + 60 | |
| NPN132 | 3,70 | 3,70 | 3,70 | 3,70 | 3,70 | 3,70 | – |
| NPN133 | 4,50 | 4,50 | 4,50 | 4,50 | 4,50 | 4,50 | – |
| NPN134 | 5,00 | 5,00 | 5,00 | 5,00 | 5,00 | 5,00 | – |
| NPN135 | 5,28 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 |
| NPN136 | 5,33 | 6,01 | 6,20 | 6,83 | 6,84 | 6,76 | 6,64 |
| NPN139 | 5,40 | 6,08 | 6,27 | 6,92 | 7,10 | 7,96 | 7,56 |
| 2NPN135 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 |
| 2NPN136 | 6,01 | 6,75 | 6,90 | 6,90 | 6,90 | 6,90 | 6,90 |
| 2NPN139 | 6,09 | 6,81 | 7,04 | 7,22 | 7,94 | 8,90 | 9,09 |
| Typ nosníku | Maximální světlá délka ℓs,max [m] | ||||||
| výška tvarovek H1 + výška nabetonávky h2 [mm] | |||||||
| 120 + 50 | 160 + 40 | 160 + 50 | 200 + 40 | 200 + 50 | 250 + 50 | 250 + 60 | |
| NPN132 | 3,61 | 3,70 | 3,70 | 3,70 | 3,70 | 3,70 | – |
| NPN133 | 4,46 | 4,50 | 4,50 | 4,50 | 4,50 | 4,50 | – |
| NPN134 | 5,00 | 5,00 | 5,00 | 5,00 | 5,00 | 5,00 | – |
| NPN135 | 5,09 | 5,75 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 |
| NPN136 | 5,14 | 5,80 | 5,99 | 6,60 | 6,55 | 6,51 | 6,41 |
| NPN139 | 5,20 | 5,87 | 6,06 | 6,68 | 6,87 | 7,72 | 7,29 |
| 2NPN135 | 5,73 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 |
| 2NPN136 | 5,79 | 6,51 | 6,73 | 6,90 | 6,90 | 6,90 | 6,90 |
| 2NPN139 | 5,87 | 6,57 | 6,80 | 7,46 | 7,69 | 8,64 | 8,83 |
| Typ nosníku | Maximální světlá délka ℓs,max [m] | ||||||
| výška tvarovek H1 + výška nabetonávky h2 [mm] | |||||||
| 120 + 50 | 160 + 40 | 160 + 50 | 200 + 40 | 200 + 50 | 250 + 50 | 250 + 60 | |
| NPN132 | 3,48 | 3,70 | 3,70 | 3,70 | 3,70 | 3,70 | – |
| NPN133 | 4,30 | 4,50 | 4,50 | 4,50 | 4,50 | 4,50 | – |
| NPN134 | 4,89 | 5,00 | 5,00 | 5,00 | 5,00 | 5,00 | – |
| NPN135 | 4,89 | 5,57 | 5,68 | 5,90 | 5,90 | 5,90 | 5,90 |
| NPN136 | 4,89 | 5,62 | 5,68 | 6,29 | 6,26 | 6,28 | 6,20 |
| NPN139 | 5,04 | 5,68 | 5,88 | 6,49 | 6,67 | 7,51 | 7,04 |
| 2NPN135 | 5,55 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 |
| 2NPN136 | 5,60 | 6,30 | 6,53 | 6,90 | 6,90 | 6,90 | 6,90 |
| 2NPN139 | 5,68 | 6,37 | 6,59 | 7,24 | 7,46 | 8,42 | 8,61 |
| Typ nosníku | Maximální světlá délka ℓs,max [m] | ||||||
| výška tvarovek H1 + výška nabetonávky h2 [mm] | |||||||
| 120 + 50 | 160 + 40 | 160 + 50 | 200 + 40 | 200 + 50 | 250 + 50 | 250 + 60 | |
| NPN132 | 3,37 | 3,66 | 3,70 | 3,70 | 3,70 | 3,70 | – |
| NPN133 | 4,16 | 4,50 | 4,50 | 4,50 | 4,50 | 4,50 | – |
| NPN134 | 4,60 | 5,00 | 5,00 | 5,00 | 5,00 | 5,00 | – |
| NPN135 | 4,60 | 5,33 | 5,39 | 5,90 | 5,90 | 5,90 | 5,90 |
| NPN136 | 4,60 | 5,33 | 5,39 | 6,00 | 5,99 | 6,07 | 6,00 |
| NPN139 | 4,89 | 5,53 | 5,71 | 6,31 | 6,49 | 7,33 | 7,29 |
| 2NPN135 | 5,39 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 |
| 2NPN136 | 5,44 | 6,12 | 6,34 | 6,90 | 6,90 | 6,90 | 6,90 |
| 2NPN139 | 5,51 | 6,19 | 6,41 | 7,05 | 7,27 | 8,21 | 8,40 |
| Typ nosníku | Maximální světlá délka ℓs,max [m] | ||||||
| výška tvarovek H1 + výška nabetonávky h2 [mm] | |||||||
| 120 + 50 | 160 + 40 | 160 + 50 | 200 + 40 | 200 + 50 | 250 + 50 | 250 + 60 | |
| NPN132 | 3,20 | 3,49 | 3,55 | 3,70 | 3,70 | 3,70 | – |
| NPN133 | 3,96 | 4,32 | 4,39 | 4,50 | 4,50 | 4,50 | – |
| NPN134 | 4,50 | 4,93 | 5,00 | 5,00 | 5,00 | 5,00 | – |
| NPN135 | 4,51 | 5,23 | 5,30 | 5,90 | 5,90 | 5,90 | 5,90 |
| NPN136 | 4,51 | 5,23 | 5,30 | 5,91 | 5,91 | 6,00 | 5,94 |
| NPN139 | 5,03 | 5,67 | 5,86 | 6,46 | 6,65 | 7,36 | 6,73 |
| 2NPN135 | 5,54 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 |
| 2NPN136 | 5,59 | 6,29 | 6,51 | 6,90 | 6,90 | 6,90 | 6,90 |
| 2NPN139 | 5,66 | 6,35 | 6,58 | 7,22 | 7,45 | 8,39 | 8,58 |
| Typ nosníku | Maximální světlá délka ℓs,max [m] | ||||||
| výška tvarovek H1 + výška nabetonávky h2 [mm] | |||||||
| 120 + 50 | 160 + 40 | 160 + 50 | 200 + 40 | 200 + 50 | 250 + 50 | 250 + 60 | |
| NPN132 | 2,95 | 3,22 | 3,28 | 3,52 | 3,57 | 3,70 | – |
| NPN133 | 3,65 | 3,99 | 4,06 | 4,37 | 4,42 | 4,50 | – |
| NPN134 | 3,84 | 4,53 | 4,63 | 5,00 | 5,00 | 5,00 | – |
| NPN135 | 3,84 | 4,53 | 4,63 | 5,22 | 5,25 | 5,46 | 5,43 |
| NPN136 | – | 4,53 | 4,63 | 5,22 | 5,25 | 5,46 | 5,43 |
| NPN139 | 4,59 | 4,89 | 5,06 | 5,99 | 6,16 | 6,16 | 6,14 |
| 2NPN135 | 5,10 | 5,74 | 5,90 | 5,90 | 5,90 | 5,90 | 5,90 |
| 2NPN136 | 5,14 | 5,80 | 6,01 | 6,62 | 6,83 | 6,90 | 6,90 |
| 2NPN139 | 5,21 | 5,86 | 6,08 | 6,69 | 6,90 | 7,83 | 8,01 |
| Typ nosníku | Maximální světlá délka ℓs,max [m] | ||||||
| výška tvarovek H1 + výška nabetonávky h2 [mm] | |||||||
| 120 + 50 | 160 + 40 | 160 + 50 | 200 + 40 | 200 + 50 | 250 + 50 | 250 + 60 | |
| NPN132 | 2,81 | 3,07 | 3,13 | 3,37 | 3,41 | 3,68 | – |
| NPN133 | 3,48 | 3,81 | 3,88 | 4,17 | 4,23 | 4,50 | – |
| NPN134 | 3,50 | 4,16 | 4,27 | 4,79 | 4,86 | 5,00 | – |
| NPN135 | – | 4,16 | 4,27 | 4,85 | 4,89 | 5,16 | 5,14 |
| NPN136 | – | 4,16 | 4,27 | 4,85 | 4,89 | 5,16 | 5,14 |
| NPN139 | 3,99 | 4,44 | 4,55 | 5,27 | 5,36 | 5,65 | 5,64 |
| 2NPN135 | 4,87 | 5,50 | 5,71 | 5,90 | 5,90 | 5,90 | 5,90 |
| 2NPN136 | 4,92 | 5,55 | 5,76 | 6,35 | 6,55 | 6,90 | 6,90 |
| 2NPN139 | 4,98 | 5,61 | 5,82 | 6,42 | 6,63 | 7,53 | 7,72 |
| Typ nosníku | Maximální světlá délka ℓs,max [m] | ||||||
| výška tvarovek H1 + výška nabetonávky h2 [mm] | |||||||
| 120 + 50 | 160 + 40 | 160 + 50 | 200 + 40 | 200 + 50 | 250 + 50 | 250 + 60 | |
| NPN132 | 2,68 | 2,93 | 2,99 | 3,22 | 3,27 | 3,53 | – |
| NPN133 | 3,31 | 3,63 | 3,71 | 3,99 | 4,05 | 4,37 | – |
| NPN134 | 3,44 | 4,09 | 4,20 | 4,57 | 4,65 | 5,00 | – |
| NPN135 | – | 4,09 | 4,20 | 4,77 | 4,82 | 5,09 | 5,08 |
| NPN136 | – | 4,09 | 4,20 | 4,77 | 4,82 | 5,09 | 5,08 |
| NPN139 | – | 4,35 | 4,46 | 5,16 | 5,26 | 5,58 | 5,57 |
| 2NPN135 | 5,02 | 5,66 | 5,86 | 5,90 | 5,90 | 5,90 | 5,90 |
| 2NPN136 | 5,07 | 5,71 | 5,93 | 6,53 | 6,71 | 6,90 | 6,90 |
| 2NPN139 | 5,13 | 5,77 | 5,99 | 6,59 | 6,81 | 7,22 | 7,91 |
| Typ nosníku | Maximální světlá délka ℓs,max [m] | ||||||
| výška tvarovek H1 + výška nabetonávky h2 [mm] | |||||||
| 120 + 50 | 160 + 40 | 160 + 50 | 200 + 40 | 200 + 50 | 250 + 50 | 250 + 60 | |
| NPN132 | 2,57 | 2,82 | 2,88 | 3,10 | 3,15 | 3,40 | – |
| NPN133 | 3,15 | 3,49 | 3,57 | 3,84 | 3,90 | 4,22 | – |
| NPN134 | – | 3,79 | 3,90 | 4,39 | 4,,48 | 4,83 | – |
| NPN135 | – | – | 3,90 | 4,40 | 4,52 | 4,83 | 4,83 |
| NPN136 | – | – | 3,90 | 4,40 | 4,52 | 4,83 | 4,83 |
| NPN139 | – | 3,99 | 4,10 | 4,75 | 4,85 | 5,29 | 5,30 |
| 2NPN135 | 4,79 | 5,43 | 5,62 | 5,90 | 5,90 | 5,90 | 5,90 |
| 2NPN136 | 4,84 | 5,47 | 5,62 | 6,26 | 6,46 | 6,90 | 6,90 |
| 2NPN139 | 4,91 | 5,18 | 5,38 | 6,33 | 6,50 | 7,43 | 7,61 |
Příklad 3.9
Navrhněte nosníky stropní konstrukce.
Světlé rozpětí stropní konstrukce v obytné budově je 5,1 m, skladba podlahy číslo 8 podle tab. 3.7.
Podlaha
2,38
2,50 kN/m2
Nahodilé
1,5
1,50 kN/m2
Předpokládá se působení stropních nosníků jako prostých nosníků a v odpovídající tab. 3.30 jsou vyhovující kombinace nosníků 2 NPN135, výšky tvarovek 120 mm a tloušťky nadbetonávky 50 mm nebo NPN135, výšky tvarovek 160 mm a tloušťky nabetonávky 40 mm.
Nepředpjaté nosníky s pórobetonovými vložkami
Firma Xella CZ s.r.o. dodává systém stropní konstrukce pod označením YTONG. ve variantách Ekonom, Klasik a Komfort. Nosné železobetonové nosníky mají prostorovou výztuž a umísťují se do vzdáleností po 680 mm. Mezi nosníky se vkládají vložky s pórobetonu a strop se po přiložení přídatné výztuže zabetonuje buď s nadbetonováním, nebo se vyplňují pouze žebra. Systém je vhodný jednak na stropy ale i pro šikmé střechy. Základní prvky systému jsou patrné z obr. 3.7.
V tab. 3.32–3.34 jsou uvedeny charakteristické hodnoty zatížení od skladby podlahy, popř. příček gk,2, kterými je možné zatížit stropní konstrukci při hodnotě užitného zatížení 1,5 kN/m2 bez uvažování vlastní tíhy stropu gk,1, která jsou uvedena v záhlaví tab. 3.32. Ve čtyřech sloupcích jsou uvedeny pro určité uspořádání konstrukce hodnoty, při kterých by bylo dosaženo mezního průhybu 1/250 nebo 1/350 rozpětí, vyčerpána únosnost v ohybu nebo smyku – konkrétně je nutné vybrat hodnotu nejnižší.
Obr. 3.7 Stropní tvarovky Xella
Tab. 3.32 Ytong Klasik 200 + 50 (50 mm nadbetonávka)
| Ytong Klasik 200 + 50 (50 mm nadbetonávka), vlastní tíha stropu gk,1 = 3,29 kN/m2, ostatní stálé zatížení gk,2, užitné zatížení qk = 1,5 kN/m2 | ||||||
| Délka nosníku L [mm] | Maximální světlá délka ℓs [mm] | Charakteristická hodnota ostatního stálého zatížení gk,2 [kN/m2] při splnění kritéria | Nadvýšení [mm] | |||
| průhyb w ≤ 1/250 ℓ [mm] | průhyb w ≤ 1/350 ℓ [mm] | moment M ≤ MRd [kNm] | posouvající síla V ≤ VRd [kN] | |||
| 1000 | 700 | – | – | 132,66 | 24,93 | – |
| 1200 | 900 | – | – | 86,02 | 19,23 | – |
| 1400 | 1100 | 220,00 | 125,71 | 59,79 | 15,36 | – |
| 1600 | 1300 | 127,60 | 72,91 | 43,45 | 112,56 | – |
| 1800 | 1500 | 72,60 | 41,49 | 32,52 | 10,44 | – |
| 2000 | 1700 | 54,27 | 31,01 | 24,91 | 8,77 | – |
| 2200 | 1900 | 45,10 | 25,77 | 19,40 | 7,43 | – |
| 2400 | 2100 | 33,00 | 18,86 | 15,30 | 6,33 | – |
| 2600 | 2300 | 26,95 | 15,40 | 12,13 | 5,41 | – |
| 2800 | 2500 | 11,10 | 6,35 | 9,65 | 4,63 | – |
| 3000 | 2700 | 8,09 | 4,62 | 7,67 | 3,95 | – |
| 3200 | 2900 | 5,59 | 3,20 | 6,07 | 3,37 | – |
| 3400 | 3100 | 4,40 | 2,51 | 40,75 | 2,86 | – |
| 3600 | 3300 | 3,57 | 2,04 | 3,66 | 2,40 | – |
| 3800 | 3500 | 4,23 | 2,42 | 6,43 | 8,96 | – |
| 4000 | 3700 | 3,46 | 1,98 | 5,28 | 8,24 | – |
| 4200 | 3900 | 2,92 | 1,67 | 4,29 | 7,58 | – |
| 4400 | 4100 | 2,48 | 1,42 | 3,44 | 6,99 | – |
| 4600 | 4300 | 2,74 | 1,57 | 2,71 | 6,46 | 5 |
| 4800 | 4500 | 2,65 | 1,51 | 2,92 | 5,97 | 5 |
| 5000 | 4700 | 2,66 | 1,52 | 3,46 | 5,51 | 5 |
| 5200 | 4900 | 2,32 | 1,33 | 2,81 | 5,10 | 5 |
| 5400 | 5100 | 2,43 | 1,39 | 2,23 | 4,72 | 10 |
| 5600 | 5300 | 2,45 | 1,40 | 2,79 | 4,36 | 10 |
| 5800 | 5500 | 2,51 | 1,43 | 2,25 | 4,03 | 15 |
| 6000 | 5700 | 2,27 | 1,30 | 3,06 | 3,72 | 10 |
| 6200 | 5900 | 2,32 | 1,32 | 2,54 | 3,44 | 15 |
| 6400 | 6100 | 2,45 | 1,40 | 3,50 | 3,17 | 15 |
| 6600 | 6300 | 2,20 | 1,26 | 2,98 | 2,92 | 15 |
| 6800 | 6500 | 2,28 | 1,30 | 3,84 | 2,68 | 15 |
| 7000 | 6700 | 2,30 | 1,32 | 3,34 | 2,46 | 20 |
| 7200 | 6900 | 2,30 | 1,32 | 2,87 | 2,25 | 25 |
| 7400 | 7100 | 2,28 | 1,30 | 2,45 | 2,05 | 30 |
| 7600 | 7300 | 2,10 | 1,20 | 2,05 | 1,86 | 35 |
Tab. 3.33 Ytong Komfort 200 + 0 (bez nadbetonávky)
| Ytong Komfort 200 + 0 (bez nadbetonávky), vlastní tíha stropu gk,1 = 2,23 kN/m2, ostatní stálé zatížení gk,2, užitné zatížení qk = 1,5 kN/m2 | ||||||
| Délka nosníku L [mm] | Maximální světlá délka ℓs [mm] | Charakteristická hodnota ostatního stálého zatížení gk,2 [kN/m2] při splnění kritéria | Nadvýšení [mm] | |||
| průhyb w ≤ 1/250 ℓ [mm] | průhyb w ≤ 1/350 ℓ [mm] | moment M ≤ MRd [kNm] | posouvající síla V ≤ VRd [kN] | |||
| 1000 | 700 | – | – | 37,11 | 39,93 | – |
| 1200 | 900 | 42,00 | 24,00 | 29,30 | 31,58 | – |
| 1400 | 1100 | 50,00 | 28,57 | 23,98 | 25,90 | – |
| 1600 | 1300 | 29,00 | 16,57 | 20,14 | 21,79 | – |
| 1800 | 1500 | 22,00 | 12,57 | 17,22 | 18,68 | – |
| 2000 | 1700 | 14,80 | 8,46 | 14,94 | 16,24 | – |
| 2200 | 1900 | 10,25 | 5,86 | 13,10 | 14,27 | – |
| 2400 | 2100 | 7,50 | 4,27 | 11,59 | 12,66 | – |
| 2600 | 2300 | 3,92 | 2,24 | 10,33 | 11,30 | – |
| 2800 | 2500 | 2,65 | 1,51 | 9,25 | 10,16 | – |
| 3000 | 2700 | 2,04 | 1,16 | 8,33 | 9,17 | – |
| 3200 | 2900 | 1,61 | 0,92 | 7,53 | 8,31 | – |
| 3400 | 3100 | 1,26 | 0,72 | 6,82 | 7,56 | – |
| 3600 | 3300 | 1,04 | 0,59 | 6,20 | 6,90 | – |
| 3800 | 3500 | 1,19 | 0,68 | 5,65 | 6,30 | – |
| 4000 | 3700 | 1,00 | 0,57 | 5,15 | 5,77 | – |
| 4200 | 3900 | 1,11 | 0,63 | 4,71 | 5,30 | 5 |
| 4400 | 4100 | 1,16 | 0,66 | 4,30 | 4,86 | 10 |
| 4600 | 4300 | 1,17 | 0,67 | 3,93 | 4,47 | 15 |
| 4800 | 4500 | 1,10 | 0,63 | 3,59 | 4,11 | 15 |
| 5000 | 4700 | 1,06 | 0,61 | 3,29 | 3,78 | 15 |
| 5200 | 4900 | 1,05 | 0,60 | 3,00 | 3,48 | 20 |
| 5400 | 5100 | 0,86 | 0,49 | 2,74 | 3,19 | 25 |
| 5600 | 5300 | 0,83 | 0,48 | 2,49 | 2,93 | 25 |
| 5800 | 5500 | 0,81 | 0,46 | 2,27 | 2,69 | 30 |
| 6000 | 5700 | 0,81 | 0,46 | 2,06 | 2,47 | 30 |
| 6200 | 5900 | 0,85 | 0,49 | 1,86 | 2,26 | 40 |
| 6400 | 6100 | 0,86 | 0,49 | 1,68 | 2,06 | 40 |
| 6600 | 6300 | 0,82 | 0,47 | 1,50 | 1,87 | 45 |
| 6800 | 6500 | 0,64 | 0,36 | 1,34 | 1,70 | 45 |
Tab. 3.34 Ytong Komfort 250 + 0 (bez nadbetonávky)
| Ytong Komfort 250 + 0 (bez nadbetonávky), vlastní tíha stropu gk,1 = 2,97 kN/m2, ostatní stálé zatížení gk,2, užitné zatížení qk = 1,5 kN/m2 | ||||||
| Délka nosníku L [mm] | Maximální světlá délka ℓs [mm] | Charakteristická hodnota ostatního stálého zatížení gk,2 [kN/m2] při splnění kritéria | Nadvýšení [mm] | |||
| průhyb w ≤ 1/250 ℓ [mm] | průhyb w ≤ 1/350 ℓ [mm] | moment M ≤ MRd [kNm] | posouvající síla V ≤ VRd [kN] | |||
| 1000 | 700 | – | – | 127,90 | 25,10 | – |
| 1200 | 900 | – | – | 82,20 | 19,40 | – |
| 1400 | 1100 | 150,00 | 69,12 | 56,66 | 15,58 | – |
| 1600 | 1300 | 87,00 | 40,09 | 40,91 | 12,79 | – |
| 1800 | 1500 | 49,50 | 22,81 | 30,54 | 10,68 | – |
| 2000 | 1700 | 27,75 | 12,79 | 23,35 | 9,02 | – |
| 2200 | 1900 | 24,60 | 11,34 | 18,15 | 7,69 | – |
| 2400 | 2100 | 16,88 | 7,78 | 14,28 | 6,59 | – |
| 2600 | 2300 | 9,80 | 4,52 | 11,32 | 5,68 | – |
| 2800 | 2500 | 6,36 | 2,93 | 9,00 | 4,90 | – |
| 3000 | 2700 | 4,38 | 2,02 | 7,15 | 4,23 | – |
| 3200 | 2900 | 3,45 | 1,59 | 5,66 | 3,65 | – |
| 3400 | 3100 | 2,75 | 1,27 | 4,43 | 3,14 | – |
| 3600 | 3300 | 2,18 | 1,00 | 3,41 | 2,69 | – |
| 3800 | 3500 | 2,49 | 1,15 | 5,44 | 2,29 | – |
| 4000 | 3700 | 2,08 | 0,96 | 4,42 | 1,93 | – |
| 4200 | 3900 | 1,77 | 0,82 | 3,55 | 1,60 | – |
| 4400 | 4100 | 1,52 | 0,70 | 2,80 | 7,26 | – |
| 4600 | 4300 | 1,68 | 0,78 | 2,14 | 6,72 | 5 |
| 4800 | 4500 | 1,60 | 0,74 | 2,25 | 6,23 | 5 |
| 5000 | 4700 | 1,57 | 0,72 | 2,62 | 5,78 | 5 |
| 5200 | 4900 | 1,65 | 0,76 | 2,05 | 5,37 | 10 |
| 5400 | 5100 | 1,68 | 0,77 | 1,55 | 4,99 | 15 |
| 5600 | 5300 | 1,65 | 0,76 | 1,95 | 4,64 | 15 |
| 5800 | 5500 | 1,65 | 0,76 | 1,49 | 4,31 | 20 |
| 6000 | 5700 | 1,66 | 0,77 | 2,07 | 4,00 | 20 |
| 6200 | 5900 | 1,48 | 0,68 | 1,63 | 3,72 | 20 |
| 6400 | 6100 | 1,51 | 0,69 | 2,28 | 3,45 | 20 |
| 6600 | 6300 | 1,50 | 0,69 | 1,85 | 3,20 | 25 |
| 6800 | 6500 | 1,64 | 0,76 | 1,92 | 2,96 | 30 |
| 7000 | 6700 | 1,61 | 0,74 | 1,54 | 2,74 | 35 |
Příklad 3.10
Navrhněte strop z tvarovek YTONG.
Světlé rozpětí stropní konstrukce v obytné budově je 5,1 m, skladba podlahy číslo 10 podle tab. 3.7.
Zatížení
Charakteristické
Podlaha
1,157 kN/m2
Je zvoleno provedení stropu Ytong Komfort 250 + 0 a podle tab. 3.32–3.34 se zjistí, že pro světlost 5 100 mm a mezní průhyb w = 1/250ℓs odpovídá nejmenší hodnota přídatného zatížení od podlahy kritériu překročení únosnosti na ohyb, kdy g2,k = 1,55 > 1,157 kN/m2.
Pro daný účel vyhovuje strop Ytong Komfort 250 + 0.
3.4 ŽELEZOBETONOVÉ STROPY MONTOVANÉ
Železobetonovými montovanými stropy rozumíme stropy montované ze železobetonových panelů. Pro různá rozpětí stropů se vyrábějí různé panely. Délky a šířky těchto panelů, s výjimkou panelů na velká rozpětí, jsou nejčastěji v násobcích 300 mm. Tloušťky panelů jsou v závislosti na rozpětí.
Hlavní výhoda železobetonových montovaných stropů je v tom, že zrychlují dobu výstavby, nevýhoda je ta, že je lze použít jen pro určitá rozpětí.
Návrh železobetonových montovaných panelů lze provést tak, že se vypočítá charakteristická hodnota zatížení působící na strop, kromě vlastní tíhy, a ta se porovná s přípustnou hodnotou charakteristického zatížení gk,2 + qk.
V tab. 3.35–3.42 jsou uvedeny některé v současnosti vyráběné stropní panely a desky. Pro menší rozpětí se používají stropní desky plné PZD nebo stropní desky dutinové nepředpjaté, pro rozpětí větší se používají dutinové panely, např. SPIROLL.
Tab. 3.35 Stropní desky PZD firmy Rieder Beton s.r.o.
| Označení | Rozměry prvku [mm] | Informativní hmotnost m [kg] | Uložení min. 100 mm | Uložení opt. 140 mm | Zatížení gk,2 + qk [kN/m2] | ||
| délka L | šířka B | výška H | světlá délka ℓs,min [mm] | světlá délka ℓs,opt [mm] | |||
| PZD 001/Ji | 2080 | 590 | 140 | 397 | 1900 | 1800 | 6,64 |
| PZD 002/Ji | 2080 | 1190 | 140 | 814 | 8,72 | ||
| PZD 003/Ji | 2080 | 1790 | 140 | 1237 | 8,68 | ||
| PZD 004/Ji | 2080 | 2390 | 140 | 1648 | 8,67 | ||
| PZD 005/Ji | 2080 | 590 | 140+ | 387 | 11,37 | ||
| PZD 006/Ji | 2080 | 1190 | 140+ | 814 | 9,70 | ||
| PZD 007/Ji | 2080 | 1790 | 140+ | 1237 | 9,14 | ||
| PZD 008/Ji | 2080 | 2390 | 140+ | 1648 | 8,09 | ||
| PZD 009/Ji | 2380 | 590 | 140 | 454 | 2200 | 2100 | 3,86 |
| PZD 010/Ji | 2380 | 1190 | 140 | 932 | 5,43 | ||
| PZD 011/Ji | 2380 | 1790 | 140 | 1410 | 5,40 | ||
| PZD 012/Ji | 2380 | 2390 | 140 | 1887 | 5,00 | ||
| PZD 013/Ji | 2380 | 590 | 140+ | 454 | 7,43 | ||
| PZD 014/Ji | 2380 | 1190 | 140+ | 932 | 6,17 | ||
| PZD 015/Ji | 2380 | 1790 | 140+ | 1410 | 5,75 | ||
| PZD 016/Ji | 2380 | 2390 | 140+ | 1887 | 5,00 | ||
| PZD 017/Ji | 2680 | 590 | 140 | 511 | 2500 | 2400 | 4,76 |
| PZD 018/Ji | 2680 | 1190 | 140 | 1049 | 3,79 | ||
| PZD 019/Ji | 2680 | 1790 | 140 | 1589 | 3,47 | ||
| PZD 020/Ji | 2680 | 2390 | 140 | 2126 | 2,85 | ||
| PZD 021/Ji | 2680 | 590 | 140+ | 511 | 7,10 | ||
| PZD 022/Ji | 2680 | 1190 | 140+ | 1049 | 7,10 | ||
| PZD 023/Ji | 2680 | 1790 | 140+ | 1589 | 7,13 | ||
| PZD 024/Ji | 2680 | 2390 | 140+ | 2126 | 7,12 | ||
| PZD 025/Ji | 2980 | 590 | 140 | 569 | 2800 | 2700 | 4,00 |
| PZD 026/Ji | 2980 | 1190 | 140 | 1167 | 3,98 | ||
| PZD 027/Ji | 2980 | 1790 | 140 | 1766 | 3,95 | ||
| PZD 028/Ji | 2980 | 2390 | 140 | 2365 | 3,95 | ||
| PZD 029/Ji | 2980 | 590 | 140+ | 569 | 7,20 | ||
| PZD 030/Ji | 2980 | 1190 | 140+ | 1467 | 7,30 | ||
| PZD 031/Ji | 2980 | 1790 | 140+ | 1766 | 7,30 | ||
| PZD 032/Ji | 2980 | 2390 | 140+ | 2365 | 7,30 | ||
| PZD 033/Ji | 3280 | 590 | 140 | 626 | 3100 | 3000 | 3,85 |
| PZD 034/Ji | 3280 | 1190 | 140 | 1285 | 3,85 | ||
| PZD 035/Ji | 3280 | 1790 | 140 | 1948 | 3,86 | ||
| PZD 036/Ji | 3280 | 2390 | 140 | 2604 | 3,85 | ||
| PZD 037/Ji | 3280 | 590 | 140+ | 626 | 5,50 | ||
| PZD 038/Ji | 3280 | 1190 | 140+ | 1285 | 5,50 | ||
| PZD 039/Ji | 3280 | 1790 | 140+ | 1945 | 5,00 | ||
| PZD 040/Ji | 3280 | 2390 | 140+ | 2604 | 5,15 | ||
| PZD 041/Ji | 3580 | 590 | 140 | 684 | 3400 | 3300 | 2,85 |
| PZD 042/Ji | 3580 | 1190 | 140 | 1403 | 2,87 | ||
| PZD 043/Ji | 3580 | 1790 | 140 | 2123 | 2,95 | ||
| PZD 044/Ji | 3580 | 2390 | 140 | 2842 | 2,63 | ||
| PZD 045/Ji | 3580 | 590 | 140+ | 684 | 5,10 | ||
| PZD 046/Ji | 3580 | 1190 | 140+ | 1403 | 5,60 | ||
| PZD 047/Ji | 3580 | 1790 | 140+ | 2123 | 5,00 | ||
| PZD 048/Ji | 3580 | 2390 | 140+ | 2842 | 5,20 | ||
| PZD 101/Ji | 3880 | 590 | 185 | 1012 | 3700 | 3600 | 3,00 |
| PZD 102/Ji | 3880 | 1190 | 185 | 2005 | 2,95 | ||
| PZD 103/Ji | 3880 | 590 | 185+ | 1012 | 5,60 | ||
| PZD 104/Ji | 3880 | 1190 | 185+ | 2005 | 5,56 | ||
| PZD 105/Ji | 4180 | 590 | 185 | 1090 | 4000 | 3900 | 3,12 |
| PZD 106/Ji | 4180 | 1190 | 185 | 2250 | 3,08 | ||
| PZD 107/Ji | 4180 | 590 | 185+ | 1090 | 5,25 | ||
| PZD 108/Ji | 4180 | 1190 | 185+ | 2250 | 5,34 | ||
| PZD 109/Ji | 4480 | 590 | 185 | 1168 | 4300 | 4200 | 3,00 |
| PZD 110/Ji | 4480 | 1190 | 185 | 2418 | 3,00 | ||
| PZD 111/Ji | 4480 | 590 | 185+ | 1168 | 6,52 | ||
| PZD 112/Ji | 4480 | 1190 | 185+ | 2418 | 5,70 | ||
| PZD 113/Ji | 4780 | 590 | 185 | 1241 | 4600 | 4500 | 2,67 |
| PZD 114/Ji | 4780 | 1190 | 185 | 2573 | 2,70 | ||
| PZD 115/Ji | 4780 | 590 | 185+ | 1241 | 5,74 | ||
| PZD 116/Ji | 4780 | 1190 | 185+ | 2573 | 5,03 | ||
| PZD 117/Ji | 5080 | 590 | 185 | 1318 | 4900 | 4800 | 3,48 |
| PZD 118/Ji | 5080 | 1190 | 185 | 2734 | 2,90 | ||
| PZD 119/Ji | 5080 | 590 | 185+ | 1318 | 5,02 | ||
| PZD 120/Ji | 5080 | 1190 | 185+ | 2734 | 5,04 | ||
| PZD 121/Ji | 5380 | 590 | 185 | 1403 | 5200 | 5100 | 2,51 |
| PZD 122/Ji | 5380 | 1190 | 185 | 2896 | 2,53 | ||
| PZD 201/Ji | 3880 | 2390 | 185 | 4242 | 3700 | 3600 | 2,95 |
| PZD 202/Ji | 3880 | 2390 | 185+ | 4242 | 5,56 | ||
| PZD 203/Ji | 4180 | 2390 | 185 | 4570 | 4000 | 3900 | 3,08 |
| PZD 204/Ji | 4180 | 2390 | 185+ | 4570 | 5,25 | ||
| PZD 205/Ji | 4480 | 2390 | 185 | 4898 | 4300 | 4200 | 3,00 |
| PZD 206/Ji | 4480 | 2390 | 185+ | 4898 | 5,70 | ||
| PZD 207/Ji | 4780 | 2390 | 185 | 5226 | 4600 | 4500 | 2,67 |
| PZD 208/Ji | 4780 | 2390 | 185+ | 5226 | 5,03 | ||
| PZD 209/Ji | 5080 | 2390 | 185 | 5553 | 4900 | 4800 | 2,90 |
| PZD 210/Ji | 5080 | 2390 | 185+ | 5553 | 5,00 | ||
| PZD 211/Ji | 5880 | 2390 | 185 | 5881 | 5700 | 5600 | 2,50 |
Tab. 3.36 Desky PZD firmy Prefa Plchovice
| Označení | Rozměry [mm] | Informativní hmotnost m [kg] | Uložení 125 mm | Zatížení gk,2 + qk [kN/m2] | ||
| délka L | šířka B | výška H | světlá délka ℓs [mm] | |||
| PZD 9/10 – 30/60 | 590 | 290 | 65 | 28 | 460 | 2,2 |
| PZD 10/10 – 30/75 | 740 | 290 | 65 | 35 | 610 | 1,97 |
| PZD 11/10 – 30/91 | 890 | 290 | 65 | 40 | 760 | 1,91 |
| PZD 12/10 – 30/105 | 1040 | 290 | 65 | 48 | 910 | 1,91 |
| PZD 244 – 30/90 | 890 | 290 | 80 | 43 | 600 | 1,91 |
| PZD 244 – 30/120 | 1190 | 290 | 80 | 58 | 900 | 1,91 |
| PZD 244 – 30/150 | 1490 | 290 | 80 | 73 | 1200 | 1,91 |
| PZD 244 – 30/180 | 1790 | 290 | 80 | 87 | 1500 | 1,91 |
| PZD 244 – 30/210 | 2090 | 290 | 80 | 102 | 1800 | 1,91 |
| PZD 238 – 30/240 | 2390 | 290 | 80 | 147 | 2100 | 1,91 |
| PZD 238 – 30/270 | 2690 | 290 | 100 | 188 | 2400 | 1,91 |
| PZD 238 – 30/300 | 2990 | 290 | 100 | 209 | 2700 | 1,91 |
| PZD 238 – 30/330 | 3290 | 290 | 100 | 230 | 3000 | 1,91 |
| PZD 180 SE | 1760 | 600 | 200 | 398 | 1400 | 50 |
| PZD 240 SE | 2365 | 600 | 200 | 540 | 2000 | 50 |
| PZD 180 OB – pozink | 1760 | 575 | 200 | 398 | 1400 | 50 |
| PZD 240 OB – pozink | 2360 | 575 | 200 | 540 | 2000 | 50 |
V tab. 3.37–3.42 jsou stropní panely z předpjatého betonu, uváděné pod jménem SPIROLL. V tabulkách je uváděna charakteristická hodnota rovnoměrného zatížení qk [kN/m2], pro které lze panely použít mimo účinek vlastní tíhy panelu a podlahy o vlastní tíze do 1,5 [kN/m2]. Pro stanovení světlé vzdálenosti mezi podporami panelů se od celkové délky panely odečte minimálně 2 · 150 = 300 mm na jejich uložení.
U označení panelů PPD se uvádí délka panelu v centimetrech, za lomítkem trojčíslí znamená součet tloušťky panelu v milimetrech a počtu prvků výztuže (PPD 600/169).
Charakteristické hodnoty rovnoměrného zatížení [kN/mm2] stropních panelů SPIROLL firmy Prefa Brno a.s. (www.prefa.cz) tab. 3.37–3.42.
Tab. 3.37 Stropní panely SPIROLL H = 160 mm
| Předpjaté stropní panely, výška H = 160 mm | |||||||||||||
| Značka | Délka panelu L [m] | ||||||||||||
| 2,00 | 2,50 | 3,00 | 3,50 | 4,00 | 4,50 | 5,00 | 5,50 | 6,00 | 6,50 | 7,00 | 7,50 | 8,00 | |
| PPD../165 | 26,65 | 22,12 | 17,39 | 12,79 | 8,89 | 6,25 | 4,37 | 2,99 | 1,95 | 1,14 | 0,50 | – | – |
| PPD../167 | 38,34 | 28,45 | 21,26 | 16,04 | 11,37 | 8,20 | 5,95 | 4,29 | 3,04 | 2,07 | 1,30 | 0,69 | 0,18 |
| PPD../169 | 39,90 | 27,75 | 20,68 | 15,55 | 11,00 | 7,91 | 5,71 | 4,10 | 2,88 | 1,93 | 1,19 | 0,57 | – |
| PPD../171 | 44,01 | 32,22 | 24,55 | 18,78 | 13,46 | 9,85 | 7,28 | 5,40 | 3,97 | 2,86 | 1,99 | 1,28 | 0,69 |
Tab. 3.38 Stropní panely SPIROLL H = 200 mm
| Předpjaté stropní panely, výška H = 200 mm | |||||||||||||||||
| Značka | Délka panelu L [m] | ||||||||||||||||
| 3,00 | 3,50 | 4,00 | 4,50 | 5,00 | 5,50 | 6,00 | 6,50 | 7,00 | 7,50 | 8,00 | 8,50 | 9,00 | 9,50 | 10,00 | 10,50 | 11,00 | |
| PPD../205 | 26,03 | 19,41 | 13,86 | 10,10 | 7,45 | 5,50 | 4,03 | 2,89 | 1,99 | 1,27 | 0,68 | 0,19 | – | – | – | – | – |
| PPD../207 | 30,19 | 24,22 | 17,51 | 12,97 | 9,76 | 7,41 | 5,63 | 4,25 | 3,17 | 2,30 | 1,58 | 1,00 | 0,48 | 0,07 | – | – | – |
| PPD../209 | 31,83 | 23,94 | 17,30 | 12,80 | 9,63 | 7,30 | 5,54 | 4,12 | 3,10 | 2,24 | 1,52 | 0,92 | 0,43 | 0,00 | – | – | – |
| PPD../219 | 36,52 | 30,13 | 25,58 | 20,60 | 15,92 | 12,48 | 9,89 | 7,88 | 6,29 | 5,02 | 3,98 | 3,13 | 2,41 | 1,79 | 1,25 | 0,79 | 0,39 |
Tab. 3.39 Stropní panely SPIROLL H = 250 mm
| Předpjaté stropní panely, výška H = 250 mm | ||||||||||||||||||||
| Značka | Délka panelu L [m] | |||||||||||||||||||
| 4,00 | 4,50 | 5,00 | 5,50 | 6,00 | 6,50 | 7,00 | 7,50 | 8,00 | 8,50 | 9,00 | 9,50 | 10,00 | 10,50 | 11,00 | 11,50 | 12,00 | 12,50 | 13,00 | 13,50 | |
| PPD../254 | 25,23 | 19,67 | 14,97 | 11,53 | 8,92 | 6,91 | 5,32 | 4,05 | 3,01 | 2,15 | 1,42 | 0,80 | 0,27 | – | – | – | – | – | – | – |
| PPD../256 | 33,11 | 26,24 | 20,27 | 15,89 | 12,58 | 10,02 | 8,01 | 6,38 | 5,06 | 3,97 | 3,06 | 2,29 | 1,63 | 1,07 | 0,58 | 0,15 | – | – | – | – |
| PPD../258 | 40,70 | 32,55 | 25,36 | 20,08 | 16,10 | 13,02 | 10,59 | 8,63 | 7,04 | 5,72 | 4,62 | 3,70 | 2,90 | 2,23 | 1,64 | 1,13 | 0,68 | – | – | – |
| PPD../250 | 39,77 | 31,84 | 24,79 | 19,61 | 15,71 | 12,69 | 10,30 | 8,38 | 6,82 | 5,53 | 4,45 | 3,54 | 2,77 | 2,10 | 1,53 | 1,03 | 0,59 | 0,20 | – | – |
| PPD../252 | 47,14 | 37,96 | 29,72 | 23,68 | 19,11 | 15,58 | 12,80 | 1056 | 8,74 | 7,23 | 5,97 | 4,91 | 4,00 | 3,22 | 2,55 | 1,96 | 1,45 | 1,00 | 0,60 | 0,24 |
Tab. 3.40 Stropní panely SPIROLL H = 265 mm
| Předpjaté stropní panely, výška H = 265 mm | |||||||||||||||||||||||
| Značka | Délka panelu L [m] | ||||||||||||||||||||||
| 3,00 | 3,50 | 4,00 | 4,50 | 5,00 | 5,50 | 6,00 | 6,50 | 7,00 | 7,50 | 8,00 | 8,50 | 9,00 | 9,50 | 10,00 | 10,50 | 11,00 | 11,50 | 12,00 | 12,50 | 13,00 | 13,50 | 14,00 | |
| PPD../264 | 39,81 | 34,16 | 27,48 | 21,71 | 16,62 | 13,90 | 10,08 | 7,90 | 6,19 | 4,80 | 3,69 | 2,75 | 1,95 | 1,28 | 0,71 | 0,22 | – | – | – | – | – | – | – |
| PPD../266 | 52,03 | 42,23 | 35,49 | 29,05 | 22,55 | 17,78 | 14,17 | 11,38 | 9,19 | 7,42 | 5,98 | 4,79 | 3,79 | 2,95 | 2,22 | 1,59 | 1,04 | 0,56 | 0,14 | – | – | – | – |
| PPD../268 | 53,24 | 43,40 | 36,63 | 31,30 | 27,05 | 22,48 | 18,12 | 14,74 | 12,08 | 9,94 | 8,19 | 6,75 | 5,55 | 4,53 | 3,67 | 2,92 | 2,26 | 1,67 | 1,16 | 0,71 | 0,31 | – | – |
| PPD../270 | 54,61 | 44,74 | 37,94 | 32,49 | 27,63 | 21,97 | 17,69 | 14,38 | 11,77 | 9,67 | 7,96 | 6,54 | 5,36 | 4,33 | 3,45 | 2,70 | 2,05 | 1,48 | 0,99 | 0,57 | 0,01 | – | – |
| PPD../272 | 55,76 | 45,84 | 39,01 | 33,45 | 28,94 | 25,39 | 21,63 | 17,73 | 14,66 | 12,18 | 10,17 | 8,50 | 7,11 | 5,94 | 4,94 | 4,04 | 3,27 | 2,60 | 2,01 | 1,49 | 1,04 | 0,64 | 0,05 |
Tab. 3.41 Stropní panely SPIROLL H = 320 mm
| Předpjaté stropní panely, výška H = 320 mm | |||||||||||||||||||||||||
| Značka | Délka panelu L [m] | ||||||||||||||||||||||||
| 4,00 | 4,50 | 5,00 | 5,50 | 6,00 | 6,50 | 7,00 | 7,50 | 8,00 | 8,50 | 9,00 | 9,50 | 10,00 | 10,50 | 11,00 | 11,50 | 12,00 | 12,50 | 13,00 | 13,50 | 14,00 | 14,50 | 15,00 | 15,50 | 16,00 | |
| PPD../326 | 48,38 | 38,40 | 30,00 | 23,85 | 19,20 | 15,60 | 12,75 | 1048 | 8,62 | 7,09 | 5,80 | 4,72 | 3,80 | 2,99 | 2,28 | 1,67 | 1,13 | 0,65 | 0,23 | – | – | – | – | – | – |
| PPD../320 | 49,98 | 42,65 | 36,85 | 30,13 | 24,46 | 20,08 | 16,62 | 13,84 | 11,57 | 9,70 | 8,14 | 6,81 | 5,69 | 4,72 | 3,89 | 3,16 | 2,50 | 1,91 | 1,39 | 0,93 | 0,52 | 0,16 | – | – | – |
| PPD../332 | 51,44 | 43,97 | 38,01 | 33,36 | 29,43 | 24,30 | 20,25 | 17,00 | 14,35 | 12,16 | 10,33 | 8,79 | 7,48 | 6,35 | 5,37 | 4,52 | 3,77 | 3,11 | 2,50 | 1,96 | 1,47 | 1,04 | 0,65 | 0,30 | – |
| PPD../335 | 52,23 | 44,69 | 38,64 | 33,92 | 30,13 | 25,51 | 21,29 | 17,90 | 15,14 | 12,86 | 10,96 | 9,35 | 7,98 | 6,80 | 5,78 | 4,90 | 4,12 | 3,44 | 2,83 | 2,29 | 1,81 | 1,38 | 0,99 | 0,63 | 0,32 |
Tab. 3.42 Stropní panely SPIROLL H = 400 mm
| Předpjaté stropní panely, výška H = 400 mm | |||||||||||||||||||||||||
| Značka | Délka panelu L [m] | ||||||||||||||||||||||||
| 4,00 | 4,50 | 5,00 | 5,50 | 6,00 | 6,50 | 7,00 | 7,50 | 8,00 | 8,50 | 9,00 | 9,50 | 10,00 | 10,50 | 11,00 | 11,50 | 12,00 | 12,50 | 13,00 | 13,50 | 14,00 | 14,50 | 15,00 | 15,50 | 16,00 | |
| PPD../410 | 69,62 | 59,14 | 49,93 | 40,18 | 32,82 | 27,12 | 22,63 | 19,02 | 16,07 | 13,64 | 11,61 | 9,90 | 8,44 | 7,18 | 6,10 | 5,15 | 4,32 | 3,59 | 2,93 | 2,33 | 1,80 | 1,32 | 0,88 | 0,49 | 0,14 |
| PPD../412 | 71,70 | 61,00 | 52,59 | 46,09 | 39,31 | 32,64 | 27,38 | 23,15 | 19,71 | 16,86 | 14,48 | 12,47 | 10,76 | 9,30 | 8,03 | 6,92 | 5,95 | 5,10 | 4,34 | 3,67 | 3,05 | 2,49 | 1,97 | 1,51 | 1,09 |
| PPD../414 | 72,99 | 62,14 | 53,59 | 46,94 | 41,70 | 35,33 | 29,70 | 25,17 | 21,46 | 18,43 | 15,88 | 13,73 | 11,90 | 10,32 | 8,96 | 7,78 | 6,74 | 5,83 | 5,02 | 4,29 | 3,65 | 3,05 | 2,50 | 2,01 | 1,56 |
| PPD../416 | 76,26 | 65,59 | 56,60 | 49,65 | 44,11 | 39,32 | 33,12 | 28,15 | 24,10 | 20,75 | 17,95 | 15,59 | 13,58 | 11,85 | 10,35 | 9,05 | 7,91 | 6,91 | 6,02 | 5,22 | 4,48 | 3,82 | 3,22 | 2,68 | 2,19 |
Příklad 3.11
Navrhněte železobetonové stropní panely nepředpjaté pro obytnou budovu. Světlá vzdálenost nosných stěn je 4,8 m, stálé zatížení podlahou se uvažuje 1,5 kN/m2.
Zatížení
Stálé mimo vlastní tíhu panelu
1,5 kN/m2
Nahodilé
1,5 kN/m2
Celkem
3,0 kN/m2
V tab. 3.35 únosností panelů se vyhledá nejprve panel pro odpovídající rozpětí a potom z nabízejících se možností vybere takový panel, jehož qk je větší než vypočítané zatížení.
Vybere se PZD 120/Ji – 5080/1190/185+, jehož gk,2 + qk = 5,04 kNm2 > 3,00 kNm2.
Tab. 3.43 Předpjaté panely tvaru TT
| Prvek | Nákres | Tloušťka Hd [mm] | Rozpět L [m] | Poměr L/Hd [–] |
| Předpjaté panely ve tvaru TT | 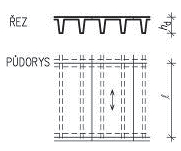 |
350–800 | 9–18 | 20–30 |
3.5 KERAMICKÉ STROPY
Keramické stropy se skládají z keramických stropních tvarovek, z betonářské výztuže a betonu. Keramické stropy působí ve velké většině případů jako prosté nosníky.
Podle statického působení a provádění se dělí na:
- nosníkové (vložkové, polomontované);
- stropní keramické panely a povaly.
3.6 NOSNÍKOVÉ STROPY (POLOMONTOVANÉ)
Nosníkové stropy jsou takové stropy ve kterých nosným prvkem jsou předem vyrobené nosníky, keramické vložky a betonová část, vyrobená na místě a jsou obdobnou polomontovaných stropů popsaných v kap. 3.3. Výhodou těchto stropů je především to, že je lze sestavovat ručně a nevyžadují bednění (kromě omezeného liniového podepření po dobu tvrdnutí betonu u stropů většího rozpětí) Únosnost stropu je závislá na únosnosti a vzdálenosti nosníků, na výšce tvarovky a výšce betonové vrstvy nad tvarovkami.
U keramických nosníkových stropů se nejčastěji používají tvarovky MIAKO pro osovou vzdálenost nosníků 500 a 625 mm. Výška tvarovek je 120, 190 a 230 mm.
Šířka nosníků je 140 mm a jejich výška je 190 mm a jsou vždy několika typů podle velikosti zabudované výztuže.
Obr. 3.8 Tvarovky MIAKO
V tab. 3.44 jsou uvedeny hodnoty maximálního stálého a užitného zatížení (bez vlastní tíhy nosné části stropní konstrukce pro jednotlivá uspořádání stropů Porotherm firmy Wienerberger Cihlářský průmysl a. s. Dalším nejrozšířenějším systémem jsou stropy Heluz, které jsou uspořádáním i z hlediska únosnosti podobné.
Tab. 3.44 POT nosníky pro vložky MIAKO výšky stropu h = 210 mm
| Charakteristiky stropů výšky h = 210 mm po zmonolitnění, vložky MIAKO výšky H1 = 150 mm, nadbetonávka h2 = 60 mm, vzdálenost nosníků 625 mm, vlastní tíha stropu gk,1 = 3,14 kN/m2 | ||||||||||
| Typ nosníku | Délka nosníku L [mm] | Světlá délka místnosti ℓs [mm] | Beton C20/25 | Beton C25/30 | ||||||
| zatížení gk,2 + qk [kN/m2] | zatížení gd,2 + qd [kN/m2] | moment Mrd [kNm] | posouvající síla Vrd [kN] | zatížení gk,2 + qk [kN/m2] | zatížení gd,2 + qd [kN/m2] | moment Mrd [kNm] | posouvající síla Vrd [kN] | |||
| POT 175/902 | 1750 | 1500 | rozhoduje mezní stav únosnosti | 15,17 | 6,89 | 9,51 | rozhoduje mezní stav únosnosti | 16,62 | 6,91 | 10,25 |
| POT 200/902 | 2000 | 1750 | 12,67 | 6,89 | 9,51 | 13,92 | 6,91 | 10,25 | ||
| POT 225/902 | 2250 | 2000 | 10,76 | 6,89 | 9,51 | 11,87 | 6,91 | 10,25 | ||
| POT 250/902 | 2500 | 2250 | 9,26 | 6,89 | 9,51 | 10,25 | 6,91 | 10,25 | ||
| POT 275/902 | 2750 | 2500 | 8,03 | 6,89 | 9,51 | 8,93 | 6,91 | 10,25 | ||
| POT 300/902 | 3000 | 2750 | 8,67 | 10,61 | 11,00 | 8,61 | 10,66 | 11,85 | ||
| POT 325/902 | 3250 | 3000 | 7,69 | 10,61 | 11,00 | 8,56 | 10,66 | 11,85 | ||
| POT 350/902 | 3500 | 3250 | 6,85 | 10,61 | 11,00 | 7,66 | 10,66 | 11,85 | ||
| POT 375/902 | 3750 | 3500 | 6,14 | 10,61 | 11,00 | 6,81 | 10,66 | 11,85 | ||
| POT 400/902 | 4000 | 3750 | 6,63 | 15,03 | 12,37 | 7,42 | 15,13 | 13,33 | ||
| POT 425/902 | 4250 | 4000 | 6,01 | 15,03 | 12,37 | 6,75 | 15,13 | 13,33 | ||
| POT 450/902 | 4500 | 4250 | 5,74 | 16,87 | 12,88 | 6,57 | 17,00 | 13,88 | ||
| POT 475/902 | 4750 | 4500 | 5,57 | 18,27 | 13,25 | 6,28 | 18,42 | 14,27 | ||
| POT 500/902 | 5000 | 4750 | 5,38 | 20,03 | 13,68 | 6,08 | 20,22 | 14,73 | ||
| POT 525/902 | 5250 | 5000 | 5,24 | 22,15 | 14,16 | 5,56 | 22,39 | 14,81 | ||
| POT 550/902 | 5500 | 5250 | 4,83 | 22,15 | 14,16 | 5,22 | 22,39 | 14,81 | ||
| POT 575/902 | 5750 | 5500 | 2,96 | 4,46 | 22,15 | 14,16 | 3,18 | 4,83 | 22,39 | 14,81 |
| POT 600/902 | 6000 | 5750 | 2,37 | rozhoduje průhyb | 24,59 | 14,25 | 2,58 | rozhoduje průhyb | 24,89 | 14,70 |
| POT 625/902 | 6250 | 6000 | 1,65 | 24,59 | 14,25 | 1,83 | 24,89 | 14,70 | ||
Tab. 3.45 POT nosníky pro vložky MIAKO výšky stropu h = 250 mm
| Charakteristiky stropů výšky h = 250 mm po zmonolitnění, vložky MIAKO výšky H1 = 190 mm, nadbetonávka h2 = 60 mm, vzdálenost nosníků 625 mm, vlastní tíha stropu gk,1 = 3,42 kN/m2 | ||||||||||
| Typ nosníku | Délka nosníku L [mm] | Světlá délka místnosti ℓs [mm] | Beton C20/25 | Beton C25/30 | ||||||
| zatížení gk,2 + qk [kN/m2] | zatížení gd,2 + qd [kN/m2] | moment Mrd [kNm] | posouvající síla Vrd [kN] | zatížení gk,2 + qk [kN/m2] | zatížení gd,2 + qd [kN/m2] | moment Mrd [kNm] | posouvající síla Vrd [kN] | |||
| POT 175/902 | 1750 | 1500 | rozhoduje mezní stav únosnosti | 17,23 | 8,48 | 10,70 | rozhoduje mezní stav únosnosti | 18,85 | 8,50 | 11,53 |
| POT 200/902 | 2000 | 1750 | 14,41 | 8,48 | 10,70 | 15,82 | 8,50 | 11,53 | ||
| POT 225/902 | 2250 | 2000 | 12,27 | 8,48 | 10,70 | 13,51 | 8,50 | 11,53 | ||
| POT 250/902 | 2500 | 2250 | 10,58 | 8,48 | 10,70 | 11,69 | 8,50 | 11,53 | ||
| POT 275/902 | 2750 | 2500 | 9,20 | 8,48 | 10,70 | 10,21 | 8,50 | 11,53 | ||
| POT 300/902 | 3000 | 2750 | 9,94 | 13,09 | 12,39 | 11,00 | 13,15 | 13,35 | ||
| POT 325/902 | 3250 | 3000 | 8,84 | 13,09 | 12,39 | 9,82 | 13,15 | 13,35 | ||
| POT 350/902 | 3500 | 3250 | 7,90 | 13,09 | 12,39 | 8,80 | 13,15 | 13,35 | ||
| POT 375/902 | 3750 | 3500 | 7,09 | 13,09 | 12,39 | 7,93 | 13,15 | 13,35 | ||
| POT 400/902 | 4000 | 3750 | 7,67 | 18,61 | 13,96 | 8,56 | 18,71 | 15,04 | ||
| POT 425/902 | 4250 | 4000 | 6,97 | 18,61 | 13,96 | 7,81 | 18,71 | 15,04 | ||
| POT 450/902 | 4500 | 4250 | 6,77 | 20,89 | 14,53 | 7,59 | 21,02 | 15,66 | ||
| POT 475/902 | 4750 | 4500 | 6,47 | 22,64 | 14,94 | 7,27 | 22,79 | 16,10 | ||
| POT 500/902 | 5000 | 4750 | 6,26 | 24,85 | 15,43 | 7,04 | 25,04 | 16,62 | ||
| POT 525/902 | 5250 | 5000 | 6,10 | 27,51 | 15,99 | 6,87 | 27,75 | 17,22 | ||
| POT 550/902 | 5500 | 5250 | 5,64 | 27,51 | 15,99 | 6,37 | 27,75 | 17,22 | ||
| POT 575/902 | 5750 | 5500 | 5,22 | 27,51 | 15,99 | 5,92 | 27,75 | 17,22 | ||
| POT 600/902 | 6000 | 5750 | 5,15 | 30,60 | 16,99 | 5,85 | 30,90 | 17,87 | ||
| POT 625/902 | 6250 | 6000 | 4,78 | 30,60 | 16,59 | 5,45 | 30,90 | 17,87 | ||
| POT 650/902 | 6500 | 6250 | 2,88 | 30,60 | 16,59 | 3,12 | 30,90 | 17,87 | ||
| POT 675/902 | 6750 | 6500 | 2,45 | 34,10 | 20,03 | 2,67 | 34,47 | 18,54 | ||
| POT 700/902 | 7000 | 6750 | 2,06 | 37,97 | 19,83 | 2,23 | 38,45 | 25,10 | ||
| POT 725/902 | 7250 | 7000 | 1,44 | 37,97 | 19,83 | 1,62 | 38,45 | 25,10 | ||
Tab. 3.46 POT nosníky pro vložky MIAKO výšky stropu h = 290 mm
| Charakteristiky stropů výšky h = 290 mm po zmonolitnění, vložky MIAKO výšky H1 = 230 mm, nadbetonávka h2 = 60 mm, vzdálenost nosníků 625 mm, vlastní tíha stropu gk,1 = 3,84 kN/m2 | ||||||||||
| Typ nosníku | Délka nosníku L [mm] | Světlá délka místnosti ℓs [mm] | Beton C20/25 | Beton C25/30 | ||||||
| zatížení gk,2 + qk [kN/m2] | zatížení gd,2 + qd [kN/m2] | moment Mrd [kN/m2] | posouvající síla Vrd [kN] | zatížení gk,2 + qk [kN/m2] | zatížení gd,2 + qd [kN/m2] | moment Mrd [kN/m2] | posouvající síla Vrd [kN] | |||
| POT 175/902 | 1750 | 1500 | rozhoduje mezní stav únosnosti | 18,38 | 10,07 | 11,50 | rozhoduje mezní stav únosnosti | 20,13 | 10,09 | 12,39 |
| POT 200/902 | 2000 | 1750 | 15,35 | 10,07 | 11,50 | 16,87 | 10,09 | 12,39 | ||
| POT 225/902 | 2250 | 2000 | 13,05 | 10,07 | 11,50 | 14,38 | 10,09 | 12,39 | ||
| POT 250/902 | 2500 | 2250 | 11,23 | 10,07 | 11,57 | 12,42 | 10,09 | 12,39 | ||
| POT 275/902 | 2750 | 2500 | 9,75 | 10,07 | 11,57 | 10,83 | 10,09 | 12,39 | ||
| POT 300/902 | 3000 | 2750 | 10,55 | 15,58 | 13,33 | 11,69 | 15,63 | 14,36 | ||
| POT 325/902 | 3250 | 3000 | 9,36 | 15,58 | 13,33 | 10,42 | 15,63 | 14,36 | ||
| POT 350/902 | 3500 | 3250 | 8,35 | 15,58 | 13,33 | 9,32 | 15,63 | 14,36 | ||
| POT 375/902 | 3750 | 3500 | 7,48 | 15,58 | 13,33 | 8,39 | 15,63 | 14,36 | ||
| POT 400/902 | 4000 | 3750 | 8,11 | 22,18 | 15,02 | 9,07 | 22,29 | 16,18 | ||
| POT 425/902 | 4250 | 4000 | 7,36 | 22,18 | 15,02 | 8,26 | 22,29 | 16,18 | ||
| POT 450/902 | 4500 | 4250 | 7,14 | 24,91 | 15,63 | 8,02 | 25,05 | 16,84 | ||
| POT 475/902 | 4750 | 4500 | 6,82 | 27,01 | 16,07 | 7,68 | 27,16 | 17,31 | ||
| POT 500/902 | 5000 | 4750 | 6,59 | 29,67 | 16,60 | 7,43 | 29,86 | 17,88 | ||
| POT 525/902 | 5250 | 5000 | 6,43 | 32,88 | 17,20 | 7,26 | 33,11 | 18,53 | ||
| POT 550/902 | 5500 | 5250 | 5,93 | 32,88 | 17,20 | 6,72 | 33,11 | 18,53 | ||
| POT 575/902 | 5750 | 5500 | 5,47 | 32,88 | 17,20 | 6,23 | 33,11 | 18,53 | ||
| POT 600/902 | 6000 | 5750 | 5,40 | 36,61 | 17,85 | 6,15 | 36,91 | 19,23 | ||
| POT 625/902 | 6250 | 6000 | 5,01 | 36,61 | 17,85 | 5,73 | 36,91 | 19,23 | ||
| POT 650/902 | 6500 | 6250 | 4,63 | 36,61 | 17,85 | 5,32 | 36,91 | 19,23 | ||
| POT 675/902 | 6750 | 6500 | 4,62 | 40,83 | 18,54 | 5,32 | 41,23 | 19,97 | ||
| POT 700/902 | 7000 | 6750 | 4,53 | 45,57 | 19,26 | 5,32 | 46,05 | 20,75 | ||
| POT 725/902 | 7250 | 7000 | 4,31 | 45,57 | 19,26 | 4,98 | 46,05 | 20,75 | ||
| POT 750/902 | 7500 | 7250 | 2,80 | 4,02 | 45,57 | 19,26 | 3,05 | 4,66 | 46,05 | 20,75 |
| POT 775/902 | 7750 | 7500 | 2,62 | 3,85 | 50,74 | 19,54 | 2,86 | rozhoduje průhyb | 51,34 | 21,04 |
| POT 800/902 | 8000 | 7750 | 1,98 | rozhoduje průhyb | 50,74 | 19,54 | 2,19 | 51,34 | 21,04 | |
| POT 825/902 | 8250 | 8000 | 1,41 | 50,74 | 19,54 | 1,60 | 51,34 | 21,04 | ||
Tab. 3.47 POT nosníky pro vložky MIAKO výšky stropu h = 210 mm
| Charakteristiky stropů výšky h = 210 mm po zmonolitnění, vložky MIAKO výšky H1 = 150 mm, nadbetonávka h2 = 60 mm, vzdálenost nosníků 625 mm, vlastní tíha stropu gk,1 = 3,84 kN/m2 | ||||||||||
| Typ nosníku | Délka nosníku L [mm] | Světlá délka místnosti ℓs [mm] | Beton C20/25 | Beton C25/30 | ||||||
| zatížení gk,2 + qk [kN/m2] | zatížení gd,2 + qd [kN/m2] | moment Mrd [kN/m2] | posouvající síla Vrd [kN] | zatížení gk,2 + qk [kN/m2] | zatížení gd,2 + qd [kN/m2] | moment Mrd [kN/m2] | posouvající síla Vrd [kN] | |||
| POT 175/902 | 1750 | 1500 | rozhoduje mezní stav únosnosti | 19,71 | 6,86 | 5,91 | rozhoduje mezní stav únosnosti | 21,52 | 6,89 | 10,25 |
| POT 200/902 | 2000 | 1750 | 16,59 | 6,86 | 5,91 | 18,15 | 6,89 | 10,25 | ||
| POT 225/902 | 2250 | 2000 | 14,20 | 6,86 | 5,91 | 15,59 | 6,89 | 10,25 | ||
| POT 250/902 | 2500 | 2250 | 12,32 | 6,86 | 5,91 | 13,56 | 6,89 | 10,25 | ||
| POT 275/902 | 2750 | 2500 | 10,79 | 6,86 | 5,91 | 11,91 | 6,89 | 10,25 | ||
| POT 300/902 | 3000 | 2750 | 11,58 | 10,55 | 11,00 | 12,76 | 10,61 | 11,85 | ||
| POT 325/902 | 3250 | 3000 | 10,36 | 10,55 | 11,00 | 11,45 | 10,61 | 11,85 | ||
| POT 350/902 | 3500 | 3250 | 9,32 | 10,55 | 11,00 | 10,32 | 10,61 | 11,85 | ||
| POT 375/902 | 3750 | 3500 | 8,42 | 10,55 | 11,00 | 9,21 | 10,61 | 11,85 | ||
| POT 400/902 | 4000 | 3750 | 9,04 | 15,03 | 12,37 | 10,03 | 15,03 | 13,33 | ||
| POT 425/902 | 4250 | 4000 | 8,27 | 16,87 | 12,37 | 9,19 | 15,03 | 13,33 | ||
| POT 450/902 | 4500 | 4250 | 8,05 | 15,03 | 12,88 | 8,96 | 16,87 | 13,88 | ||
| POT 475/902 | 4750 | 4500 | 7,72 | 18,27 | 13,25 | 8,60 | 18,27 | 14,27 | ||
| POT 500/902 | 5000 | 4750 | 7,48 | 20,03 | 13,68 | 8,35 | 20,03 | 14,73 | ||
| POT 525/902 | 5250 | 5000 | 7,31 | 22,15 | 14,16 | 7,69 | 22,15 | 14,65 | ||
| POT 550/902 | 5500 | 5250 | 4,58 | 6,79 | 22,15 | 14,16 | 4,88 | 7,16 | 22,15 | 14,65 |
| POT 575/902 | 5750 | 5500 | 3,48 | rozhoduje průhyb | 22,15 | 14,16 | 3,73 | rozhoduje průhyb | 22,15 | 14,65 |
| POT 600/902 | 6000 | 5750 | 2,83 | 24,59 | 14,25 | 3,06 | 24,59 | 14,52 | ||
| POT 625/902 | 6250 | 6000 | 2,03 | 24,59 | 14,25 | 2,23 | 24,59 | 14,52 | ||
Tab. 3.48 POT nosníky pro vložky MIAKO výšky stropu h = 250 mm
| Charakteristiky stropů výšky h = 250 mm po zmonolitnění, vložky MIAKO výšky H1 = 190 mm, nadbetonávka h2 = 60 mm, vzdálenost nosníků 500 mm, vlastní tíha stropu gk,1 = 3,60 kN/m2 | ||||||||||
| Typ nosníku | Délka nosníku L [mm] | Světlá délka místnosti ℓs [mm] | Beton C20/25 | Beton C25/30 | ||||||
| zatížení gk,2 + qk [kN/m2] | zatížení gd,2 + qd [kN/m2] | moment Mrd [kN/m2] | posouvající síla Vrd [kN] | zatížení gk,2 + qk [kN/m2] | zatížení gd,2 + qd [kN/m2] | moment Mrd [kN/m2] | posouvající síla Vrd [kN] | |||
| POT 175/902 | 1750 | 1500 | rozhoduje mezní stav únosnosti | 22,28 | 8,45 | 10,70 | rozhoduje mezní stav únosnosti | 24,32 | 8,48 | 11,53 |
| POT 200/902 | 2000 | 1750 | 18,77 | 8,45 | 10,70 | 20,53 | 8,48 | 11,53 | ||
| POT 225/902 | 2250 | 2000 | 16,09 | 8,45 | 10,70 | 17,64 | 8,48 | 11,53 | ||
| POT 250/902 | 2500 | 2250 | 13,97 | 8,45 | 10,70 | 15,36 | 8,48 | 11,53 | ||
| POT 275/902 | 2750 | 2500 | 12,25 | 8,45 | 10,70 | 13,51 | 8,48 | 11,53 | ||
| POT 300/902 | 3000 | 2750 | 13,17 | 13,03 | 12,39 | 14,50 | 13,09 | 13,35 | ||
| POT 325/902 | 3250 | 3000 | 11,80 | 13,03 | 12,39 | 13,02 | 13,09 | 13,35 | ||
| POT 350/902 | 3500 | 3250 | 10,62 | 13,03 | 12,39 | 11,75 | 13,09 | 13,35 | ||
| POT 375/902 | 3750 | 3500 | 9,61 | 13,03 | 12,39 | 10,67 | 13,09 | 13,35 | ||
| POT 400/902 | 4000 | 3750 | 10,34 | 18,47 | 13,96 | 11,45 | 18,61 | 15,04 | ||
| POT 425/902 | 4250 | 4000 | 9,46 | 18,47 | 13,96 | 10,51 | 18,61 | 15,04 | ||
| POT 450/902 | 4500 | 4250 | 9,21 | 20,72 | 14,53 | 10,24 | 20,89 | 15,66 | ||
| POT 475/902 | 4750 | 4500 | 8,84 | 22,44 | 14,94 | 9,84 | 22,64 | 16,10 | ||
| POT 500/902 | 5000 | 4750 | 8,57 | 24,61 | 15,43 | 9,55 | 24,85 | 16,62 | ||
| POT 525/902 | 5250 | 5000 | 8,38 | 27,22 | 15,99 | 9,34 | 27,71 | 17,22 | ||
| POT 550/902 | 5500 | 5250 | 7,80 | 27,22 | 15,99 | 8,72 | 27,71 | 17,22 | ||
| POT 575/902 | 5750 | 5500 | 7,27 | 27,22 | 15,99 | 8,15 | 27,71 | 17,22 | ||
| POT 600/902 | 6000 | 5750 | 7,19 | 30,23 | 16,59 | 8,06 | 30,60 | 17,87 | ||
| POT 625/902 | 6250 | 6000 | 4,50 | 6,73 | 30,23 | 16,59 | 4,81 | rozhoduje průhyb | 30,60 | 17,87 |
| POT 650/902 | 6500 | 6250 | 3,49 | rozhoduje průhyb | 30,23 | 16,59 | 3,76 | 30,60 | 17,87 | |
| POT 675/902 | 6750 | 6500 | 3,14 | 33,63 | 19,75 | 3,39 | 34,10 | 25,04 | ||
| POT 700/902 | 7000 | 6750 | 2,86 | 37,38 | 19,52 | 3,10 | 37,97 | 24,78 | ||
| POT 725/902 | 7250 | 7000 | 2,13 | 37,38 | 19,52 | 2,34 | 37,97 | 24,78 | ||
Tab. 3.49 POT nosníky pro vložky MIAKO výšky stropu h = 290 mm
| Charakteristiky stropů výšky h = 290 mm po zmonolitnění, vložky MIAKO výšky H1 = 230 mm, nadbetonávka h2 = 60 mm, vzdálenost nosníků 500 mm, vlastní tíha stropu gk,1 = 4,06 kN/m2 | ||||||||||
| Typ nosníku | Délka nosníku L [mm] | Světlá délka místnosti ℓs [mm] | Beton C20/25 | Beton C25/30 | ||||||
| zatížení gk,2 + qk [kN/m2] | zatížení gd,2 + qd [kN/m2] | moment Mrd [kN/m2] | posouvající síla Vrd [kN] | zatížení gk,2 + qk [kN/m2] | zatížení gd,2 + qd [kN/m2] | moment Mrd [kN/m2] | posouvající síla Vrd [kN] | |||
| POT 175/902 | 1750 | 1500 | rozhoduje mezní stav únosnosti | 23,74 | 10,04 | 11,50 | rozhoduje mezní stav únosnosti | 25,93 | 10,07 | 12,39 |
| POT 200/902 | 2000 | 1750 | 19,86 | 10,04 | 11,50 | 21,85 | 10,07 | 12,39 | ||
| POT 225/902 | 2250 | 2000 | 17,08 | 10,04 | 11,50 | 18,75 | 10,07 | 12,39 | ||
| POT 250/902 | 2500 | 2250 | 14,80 | 10,04 | 11,50 | 16,30 | 10,07 | 12,39 | ||
| POT 275/902 | 2750 | 2500 | 13,76 | 10,04 | 11,50 | 14,31 | 10,07 | 12,39 | ||
| POT 300/902 | 3000 | 2750 | 13,95 | 15,51 | 13,33 | 15,38 | 15,58 | 14,36 | ||
| POT 325/902 | 3250 | 3000 | 12,47 | 15,51 | 13,33 | 13,79 | 15,58 | 14,36 | ||
| POT 350/902 | 3500 | 3250 | 11,21 | 15,51 | 13,33 | 12,43 | 15,58 | 14,36 | ||
| POT 375/902 | 3750 | 3500 | 10,12 | 15,51 | 13,33 | 11,26 | 15,58 | 14,36 | ||
| POT 400/902 | 4000 | 3750 | 10,91 | 22,05 | 15,02 | 12,11 | 22,18 | 16,18 | ||
| POT 425/902 | 4250 | 4000 | 9,97 | 22,05 | 15,02 | 11,09 | 22,18 | 16,18 | ||
| POT 450/902 | 4500 | 4250 | 9,69 | 24,75 | 15,63 | 10,80 | 24,91 | 16,84 | ||
| POT 475/902 | 4750 | 4500 | 9,29 | 26,81 | 16,07 | 10,37 | 27,01 | 17,31 | ||
| POT 500/902 | 5000 | 4750 | 9,01 | 29,43 | 16,60 | 10,06 | 29,67 | 17,88 | ||
| POT 525/902 | 5250 | 5000 | 8,80 | 32,58 | 17,20 | 9,84 | 32,88 | 18,53 | ||
| POT 550/902 | 5500 | 5250 | 8,18 | 32,58 | 17,20 | 9,17 | 32,88 | 18,53 | ||
| POT 575/902 | 5750 | 5500 | 7,61 | 32,58 | 17,20 | 8,55 | 32,88 | 18,53 | ||
| POT 600/902 | 6000 | 5750 | 7,52 | 36,24 | 17,85 | 8,46 | 36,61 | 19,23 | ||
| POT 625/902 | 6250 | 6000 | 7,03 | 36,24 | 17,85 | 7,93 | 36,61 | 19,23 | ||
| POT 650/902 | 6500 | 6250 | 6,56 | 36,24 | 17,85 | 7,43 | 36,61 | 19,23 | ||
| POT 675/902 | 6750 | 6500 | 6,55 | 40,38 | 18,54 | 7,41 | 40,85 | 19,97 | ||
| POT 700/902 | 7000 | 6750 | 6,55 | 44,98 | 19,26 | 7,42 | 45,57 | 20,75 | ||
| POT 725/902 | 7250 | 7000 | 6,16 | 44,98 | 19,26 | 5,06 | 6,99 | 45,57 | 20,75 | |
| POT 750/902 | 7500 | 7250 | 3,79 | rozhoduje průhyb | 44,98 | 19,26 | 4,09 | rozhoduje průhyb | 45,57 | 20,75 |
| POT 775/902 | 7750 | 7500 | 3,57 | 49,99 | 19,54 | 3,85 | 50,74 | 21,04 | ||
| POT 800/902 | 8000 | 7750 | 2,80 | 49,99 | 19,54 | 3,05 | 50,74 | 21,04 | ||
| POT 825/902 | 8250 | 8000 | 2,12 | 49,99 | 19,54 | 2,35 | 50,74 | 21,04 | ||
Příklad 3.12
Navrhněte strop Porotherm, světlé rozpětí stropní konstrukce v administrativní budově je 5,1 m, skladba podlahy číslo 8 podle tab. 3.7.
Zatížení
charakteristické
návrhové
Podlahou
2,38
\begin{gathered}
3{,}21\space\text{kN/m}^2
\end{gathered}Nahodilé
2,50
\begin{gathered}
2{,}5\cdot1{,}5=3{,}75\space\text{kN/m}^2
\end{gathered}Zatížení celkem
4,88
\begin{gathered}
6{,}69\space\text{kN/m}^2
\end{gathered}Zvolí se tloušťku stropu 250 mm, osové vzdálenosti nosníků 500 mm a beton C20/25. V tab. 3.48 se nalezne pro nosník POT 550/902 při světlosti místnosti 5 250 mm, přípustná charakteristická hodnota přidaného zatížení gk,2 + qk nerozhoduje a návrhová hodnota gd,2 + pqd = 7,80 > 6,96 kN/m2.
Pro daný účel vyhovuje strop Porotherm s nosníky POT 550/902 po 500 mm s vložkami MIAKO 19/50 s betonem C20/25 na dobetonování stropu.
3.7 KERAMICKÉ PANELY A POVALY
Zatížení jsou charakteristické hodnoty zatížení bez vlastní hmotnosti prvku.
Tab. 3.50 Stropní keramické panely z tvarovek CST-HELUZ šířky 1200 mm
| Označení | Rozměry [mm] | Informativní hmotnost m [kg] | Uložení 125 mm | ||||
| délka L | šířka B | výška H | světlé rozpětí ℓs [m] | zatížení gk,2 + qk [kN/m2] | zatížení gd,2 + qd [kN/m2] | ||
| HELUZ 1500/1200/230 | 1500 | 1200 | 230 | 640 | 1,25 | 20,00 | 27,23 |
| HELUZ 1750/1200/230 | 1750 | 1200 | 230 | 740 | 1,50 | 20,00 | 27,23 |
| HELUZ 2000/1200/230 | 2000 | 1200 | 230 | 850 | 1,75 | 18,80 | 25,61 |
| HELUZ 2250/1200/230 | 2250 | 1200 | 230 | 960 | 2,00 | 13,80 | 18,86 |
| HELUZ 2500/1200/230 | 2500 | 1200 | 230 | 1060 | 2,25 | 10,30 | 14,13 |
| HELUZ 2750/1200/230 | 2750 | 1200 | 230 | 1170 | 2,50 | 7,80 | 10,76 |
| HELUZ 3000/1200/230 | 3000 | 1200 | 230 | 1280 | 2,75 | 5,80 | 8,06 |
| HELUZ 3250/1200/230 | 3250 | 1200 | 230 | 1380 | 3,00 | 4,30 | 6,03 |
| HELUZ 3500/1200/230 | 3500 | 1200 | 230 | 1490 | 3,25 | 5,10 | 7,11 |
| HELUZ 3750/1200/230 | 3750 | 1200 | 230 | 1600 | 3,50 | 5,60 | 7,79 |
| HELUZ 4000/1200/230 | 4000 | 1200 | 230 | 1700 | 3,75 | 4,40 | 6,17 |
| HELUZ 4250/1200/230 | 4250 | 1200 | 230 | 1810 | 4,00 | 4,90 | 6,84 |
| HELUZ 4500/1200/230 | 4500 | 1200 | 230 | 1920 | 4,25 | 5,30 | 7,38 |
| HELUZ 4750/1200/230 | 4750 | 1200 | 230 | 2020 | 4,50 | 4,30 | 6,03 |
| HELUZ 5000/1200/230 | 5000 | 1200 | 230 | 2130 | 4,75 | 4,80 | 6,71 |
| HELUZ 5250/1200/230 | 5250 | 1200 | 230 | 2240 | 5,00 | 5,60 | 7,79 |
| HELUZ 5500/1200/230 | 5500 | 1200 | 230 | 2340 | 5,25 | 5,30 | 7,38 |
| HELUZ 5750/1200/230 | 5750 | 1200 | 230 | 2450 | 5,50 | 5,40 | 7,52 |
| HELUZ 6000/1200/230 | 6000 | 1200 | 230 | 2650 | 5,75 | 5,30 | 7,38 |
| HELUZ 6250/1200/230 | 6250 | 1200 | 230 | 2660 | 6,00 | 5,20 | 7,25 |
| HELUZ 6500/1200/230 | 6500 | 1200 | 230 | 2770 | 6,25 | 4,50 | 6,30 |
| HELUZ 6750/1200/230 | 6750 | 1200 | 230 | 2880 | 6,50 | 4,00 | 5,63 |
| HELUZ 7000/1200/230 | 7000 | 1200 | 230 | 2990 | 6,75 | 3,40 | 4,82 |
| HELUZ 7250/1200/230 | 7250 | 1200 | 230 | 3090 | 7,00 | 3,00 | 4,28 |
Tab. 3.51 Stropní keramické panely z tvarovek CST-HELUZ šířky 600 mm
| Označení | Rozměry [mm] | Informativní hmotnost m [kg] | Uložení 125 mm | ||||
| délka L | šířka B | výška H | světlé rozpětí ℓs [m] | zatížení gk,2 + qk [kN/m2] | zatížení gd,2 + qd [kN/m2] | ||
| HELUZ 1500/600/230 | 1500 | 600 | 230 | 470 | 1,25 | 20,00 | 27,23 |
| HELUZ 1750/600/230 | 1750 | 600 | 230 | 550 | 1,50 | 20,00 | 27,23 |
| HELUZ 2000/600/230 | 2000 | 600 | 230 | 630 | 1,75 | 18,70 | 25,47 |
| HELUZ 2250/600/230 | 2250 | 600 | 230 | 710 | 2,00 | 13,70 | 18,72 |
| HELUZ 2500/600/230 | 2500 | 600 | 230 | 790 | 2,25 | 10,20 | 14,00 |
| HELUZ 2750/600/230 | 2750 | 600 | 230 | 870 | 2,50 | 7,60 | 10,49 |
| HELUZ 3000/600/230 | 3000 | 600 | 230 | 950 | 2,75 | 5,70 | 7,92 |
| HELUZ 3250/600/230 | 3250 | 600 | 230 | 1020 | 3,00 | 8,60 | 11,84 |
| HELUZ 3500/600/230 | 3500 | 600 | 230 | 1100 | 3,25 | 6,80 | 9,41 |
| HELUZ 3750/600/230 | 3750 | 600 | 230 | 1180 | 3,50 | 5,40 | 7,52 |
| HELUZ 4000/600/230 | 4000 | 600 | 230 | 1260 | 3,75 | 7,60 | 10,49 |
| HELUZ 4250/600/230 | 4250 | 600 | 230 | 1340 | 4,00 | 6,20 | 8,60 |
| HELUZ 4500/600/230 | 4500 | 600 | 230 | 1420 | 4,25 | 5,10 | 7,11 |
| HELUZ 4750/600/230 | 4750 | 600 | 230 | 1500 | 4,50 | 6,80 | 9,41 |
| HELUZ 5000/600/230 | 5000 | 600 | 230 | 1580 | 4,75 | 5,70 | 7,92 |
| HELUZ 5250/600/230 | 5250 | 600 | 230 | 1660 | 5,00 | 6,00 | 8,33 |
| HELUZ 5500/600/230 | 5500 | 600 | 230 | 1740 | 5,25 | 6,10 | 8,46 |
| HELUZ 5750/600/230 | 5750 | 600 | 230 | 1810 | 5,50 | 5,20 | 7,25 |
| HELUZ 6000/600/230 | 6000 | 600 | 230 | 1890 | 5,75 | 5,20 | 7,25 |
| HELUZ 6250/600/230 | 6250 | 600 | 230 | 1970 | 6,00 | 5,10 | 7,11 |
| HELUZ 6500/600/230 | 6500 | 600 | 230 | 2050 | 6,25 | 4,40 | 6,17 |
| HELUZ 6750/600/230 | 6750 | 600 | 230 | 2130 | 6,50 | 3,80 | 5,36 |
| HELUZ 7000/600/230 | 7000 | 600 | 230 | 2210 | 6,75 | 3,30 | 4,68 |
| HELUZ 7250/600/230 | 7250 | 600 | 230 | 2290 | 7,00 | 2,80 | 4,01 |
Tab. 3.52 Keramické panely RIEDER
| Označení | Rozměry [mm] | Informativní hmotnost m [kg] | Uložení 125 mm | |||
| délka L | šířka B | výška H | světlé rozpětí ℓs [m] | zatížení gk,2 + qk [kN/m2] | ||
| POD 001/Ji | 3580 | 590 | 215 | 740 | 3,350 | 6,50 |
| POD 002/Ji | 3580 | 590 | 215+ | 740 | 3,350 | 10,70 |
| POD 003/Ji | 3580 | 1190 | 215 | 1274 | 3,350 | 6,45 |
| POD 004/Ji | 3580 | 1190 | 215+ | 1274 | 3,350 | 6,10 |
| POD 005/Ji | 3880 | 590 | 215 | 797 | 3,350 | 5,85 |
| POD 006/Ji | 3880 | 590 | 215+ | 797 | 3,350 | 8,15 |
| POD 007/Ji | 3880 | 1190 | 215 | 1136 | 3,350 | 4,80 |
| POD 008/Ji | 3880 | 1190 | 215+ | 1363 | 3,350 | 7,46 |
| POD 009/Ji | 4180 | 590 | 215 | 854 | 3,950 | 7,56 |
| POD 010/Ji | 4180 | 590 | 215+ | 854 | 3,950 | 7,52 |
| POD 011/Ji | 4180 | 1190 | 215 | 1450 | 3,950 | 4,55 |
| POD 012/Ji | 4180 | 1190 | 215+ | 1450 | 3,950 | 6,34 |
| POD 013/Ji | 4480 | 590 | 215 | 911 | 4,250 | 4,55 |
| POD 014/Ji | 4480 | 590 | 215+ | 911 | 4,250 | 6,32 |
| POD 015/Ji | 4480 | 1190 | 215 | 1538 | 4,250 | 3,55 |
| POD 016/Ji | 4480 | 1190 | 215+ | 1538 | 4,250 | 5,20 |
| POD 017/Ji | 4780 | 590 | 215 | 968 | 4,550 | 3,83 |
| POD 018/Ji | 4780 | 590 | 215+ | 968 | 4,550 | 5,11 |
| POD 019/Ji | 4780 | 1190 | 215 | 1626 | 4,550 | 2,62 |
| POD 020/Ji | 4780 | 1190 | 215+ | 1626 | 4,550 | 5,09 |
| POD 021/Ji | 5080 | 590 | 215 | 1025 | 4,850 | 2,55 |
| POD 022/Ji | 5080 | 590 | 215+ | 1025 | 4,850 | 5,06 |
| POD 123/Ji | 5080 | 1190 | 215 | 1714 | 4,850 | 2,51 |
| POD 124/Ji | 5080 | 1190 | 215+ | 1714 | 4,850 | 5,05 |
| POD 125/Ji | 5380 | 590 | 245 | 1298 | 5,150 | 3,50 |
| POD 126/Ji | 5380 | 590 | 245+ | 1298 | 5,150 | 5,00 |
| POD 127/Ji | 5380 | 1190 | 245 | 2620 | 5,150 | 2,80 |
| POD 128/Ji | 5380 | 1190 | 245+ | 2620 | 5,150 | 5,00 |
| POD 129/Ji | 5680 | 590 | 245 | 1371 | 5,450 | 2,80 |
| POD 130/Ji | 5680 | 590 | 245+ | 1371 | 5,450 | 5,00 |
| POD 131/Ji | 5680 | 1190 | 245 | 2766 | 5,450 | 2,50 |
| POD 132/Ji | 5680 | 1190 | 245+ | 2766 | 5,450 | 5,00 |
| POD 133/Ji | 5980 | 590 | 245 | 1444 | 5,750 | 2,50 |
| POD 134/Ji | 5980 | 590 | 245+ | 1444 | 5,750 | 5,00 |
| POD 135/Ji | 5980 | 1190 | 245 | 2912 | 5,750 | 2,50 |
| POD 136/Ji | 5980 | 1190 | 245+ | 2912 | 5,750 | 5,00 |
| POD 137/Ji | 6280 | 590 | 245 | 1516 | 6,050 | 2,50 |
| POD 138/Ji | 6280 | 1190 | 245 | 3057 | 6,050 | 2,50 |
Příklad 3.13
Vyberte panel při světlosti stropní konstrukce 5,75 m a zatížení 5,0 kN/m2.
Těmto hodnotám odpovídá panel POD 134/Ji – 5980/1190/245+.
3.8 OCELOVÉ STROPY
Mezi ocelové stropy můžeme řadit takové stropy, jejichž nosným prvkem je ocelový plech. Pro konstrukce zastropení se používají buď plechy profilované (trapézové), nebo plechy rovné, nejčastěji s výstupky na lícové straně (žebrované, s oválnými či kruhovými výstupky apod.). Pro konstrukce zastropení se používají trapézové plechy různých výrobců, například trapézové plechy VSŽ (Východoslovenské železárny), plechy TR (Kovové profily spol. s. r. o.) – viz tab. 14.12. Nosným prvkem pro tyto plechy bývají nejčastěji ocelové válcované profily.
Tab. 3.53 VSŽ plechy
| Prvek | Nákres | Výška hd [mm] | Rozpětí ℓ [m] | Poměr ℓ/hd [–] |
| Za studena tvarované trapézové plechy | 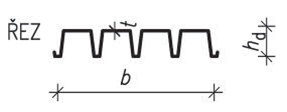 |
25–150 | 2–6 | 40–70 |
Tab. 3.54 Základní charakteristiky vybraných trapézových plechů
| Profil | Rozměry B x H x T [mm] | Výrobní délka L [m] | Hmotnost m [kg/m3] | Moment setrvačnosti Iy [mm4] | Průřezový modul Wy [mm3] | Součinitel K [–] |
| 12101 | 600 x 80 x 0,8 | 3–12 | 11,42 | 138,54 | 29,80 | 3340 |
| 12102 | 600 x 80 x 1,0 | 3–12 | 14,28 | 169,40 | 36,10 | 4040 |
| 12103 | 600 x 80 x 1,3 | 3–12 | 28,38 | 214,20 | 46,60 | 5241 |
| 12104 | 600 x 80 x 1,5 | 3–12 | 21,40 | 249,52 | 55,01 | 6161 |
| 12105 | 600 x 80 x 1,8 | 3–12 | 25,65 | 289,51 | 63,76 | 7141 |
| 13001 | 300 x 150 x 1,0 | 6–12 | 17,00 | 550,00 | 61,15 | 6848 |
| 13002 | 300 x 150 x 1,3 | 6–12 | 22,10 | 724,00 | 79,01 | 8849 |
| 13003 | 300 x 150 x 1,5 | 6–12 | 25,50 | 844,00 | 91,45 | 10242 |
| 13004 | 300 x 150 x 1,8 | 6–12 | 30,60 | 1080,00 | 108,40 | 12140 |
| 13005 | 300 x 150 x 2,0 | 6–12 | 34,00 | 1128,00 | 120,80 | 13529 |
| Násobitel | – | – | – | 104 | 103 | – |
Přípustnou charakteristickou hodnotu zatížení qk,dov, kterým lze profilované plech zatížit, můžeme stanovit podle následujícího vztahu
\begin{gathered}
q_\text{k,dov}=0{,}01K/L^2\space[\text{kN/m}^2]
\end{gathered}kde je
L … rozpětí plechu [m],
K … součinitel, uvedený v tab. 3.54,
qk,dov … přípustná charakteristická hodnota zatížení [kN/m2].
Příklad 3.14
Zjistěte zatížení, kterým lze zatížit profilovaný plech, je-li jeho rozpětí 4,8 m.
Je zvolen plech 12 104.
Zatížení qk,dov = 0,01 · 6 161 / 4,82 = 2,67 kN/m2.
Žebrované plechy
Žebrované plechy se kladou na podlahové nosníky (válcované profily) s mezerou 10 mm a přivaří se na ně průběžnými svary (vetknutí plechů sníží průhyb plechů).
V následující tab. 3.55 jsou uvedena možná rozpětí v metrech v závislosti na zatížení a tloušťce plechu za předpokladu průhybu 1/200 rozpětí.
Tab. 3.55 Přípustná rozpětí žebrovaných plechů
| Charakteristická hodnota zatížení qk,dov [kN/m2] | Přípustné rozpětí ℓdov [m] | ||||
| tloušťka plechu t [mm] | |||||
| 4 | 5 | 6 | 8 | 10 | |
| 3,0 | 0,86 | 1,07 | 1,28 | 1,68 | 2,07 |
| 4,0 | 0,79 | 0,98 | 1,17 | 1,55 | 1,91 |
| 5,0 | 0,74 | 0,92 | 1,11 | 1,45 | 1,79 |
| 6,0 | 0,69 | 0,87 | 1,04 | 1,37 | 1,70 |
| 7,0 | 0,66 | 0,83 | 0,99 | 1,31 | 1,62 |
| 8,0 | 0,63 | 0,79 | 0,95 | 1,26 | 1,56 |
| 9,0 | 0,61 | 0,76 | 0,91 | 1,21 | 1,51 |
| 10,0 | 0,59 | 0,74 | 0,88 | 1,17 | 1,46 |
Příklad 3.15
Zjistěte přípustné rozpětí pro plech tloušťky 6 mm, je-li zatížení 5,5 kN/m2.
V tabulce budeme interpolovat mezi hodnotami rozpětí pro zatížení 5 a 6 kN/m2, to je mezi hodnotami 1,11 a 1,04.
Přípustné rozpětí ℓdov = (1,11 + 1,04) / 2 = 1,08 m.
3.9 SPRAŽENÉ STROPY
Tab. 3.56 Spřažený strop
| Prvek | Nákres | Tloušťka hd [mm] | Rozpětí ℓ [m] | Poměr ℓ/hd |
| Spřažený strop |  |
200–1000 | 5–15 | 20–25 |
Spřaženými stropy rozumíme spřaženou ocelobetonovou konstrukci, která se skládá z ocelových nosníků IPN, přes které je položeno trapézový profilovaný plech, tvořící bednění pro železobetonovou desku. Železobetonová deska je spojena s ocelovým nosníkem prvky spřažení, čímž napomáhá hospodárnějšímu využití konstrukce. Železobetonová deska se navrhuje jako spojitá deska, pnutá přes ocelové nosníky.
Příklad 3.16
Navrhněte spřažený ocelobetonový strop v administrativní budově, kde rozpětí ocelových nosníků je 5,7 m. Skladbu podlahy číslo 11 zvolte podle tab. 3.7, osovou vzdálenost ocelových nosníků volte 1,5 m.
Zatížení (návrhové hodnoty)
Stálé
Podlaha
\begin{gathered}
1{,}94\space\text{kN/mm}^2
\end{gathered}Železobetonová deska 70 mm
\begin{gathered}
1{,}75\cdot1{,}35=2{,}36\space\text{kN/mm}^2
\end{gathered}Stálé celkem
\begin{gathered}
4{,}30\space\text{kN/mm}^2
\end{gathered}Nahodilé
\begin{gathered}
2{,}5\cdot1{,}5=3{,}75\space\text{kN/mm}^2
\end{gathered}Zatížení celkem
\begin{gathered}
8{,}05\space\text{kN/mm}^2
\end{gathered}Železobetonová deska se navrhne podle zásad minimálních tlouštěk desky, tj. 70 mm.
Ocelový nosník.
Zatížení od desky
\begin{gathered}
8{,}05\cdot1{,}5=12{,}08\space\text{kN/m}
\end{gathered}Vlastní tíha I 2450
\begin{gathered}
0{,}362\cdot1{,}35=0{,}26\space\text{kN/m}
\end{gathered}Celkem
\begin{gathered}
12{,}38\space\text{kN/m}
\end{gathered}Pro jednoduchost návrhu použijeme tab. 4.2 ocelových nosníků uvedenou v kap. 4.3. Pro rozpětí 5,7 m vybereme řádek 6,0 m a pro zatížení 12,38 kN/m vybereme mezi sloupci pro 10,0 a 20,0 kN/m profil stropnice IPN 240.
3.10 DŘEVENÉ STROPY
Dřevěné stropy se pro svoje nesporné výhody v současnosti opět stále více používají. Při jejich návrhu můžeme vycházet z empirických vzorců v závislosti na rozpětí: (vzorce předpokládají osovou vzdálenost trámů 0,65–0,75 m).
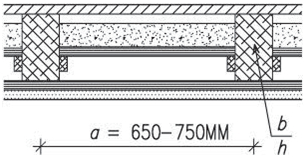
Obr. 3.9 Řez dřevěným stropem se spuštěným záklopem
\begin{gathered}
h=130+20\ell\space[\text{mm}]
\end{gathered}kde je
ℓ … světlost [m],
b … 0,6h [mm].
Za zmínku stojí pravidla, podle kterých v dřívějších dobách navrhovali nosné trámy dřevěných stropů staří tesaři.
\begin{gathered}
h=160+20\ell\space[\text{mm}]\\\\
b=5/7h
\end{gathered}Jestliže bylo zatížení q = 5,0 kN/m2 a osová vzdálenost trámů a = 0,85 m,
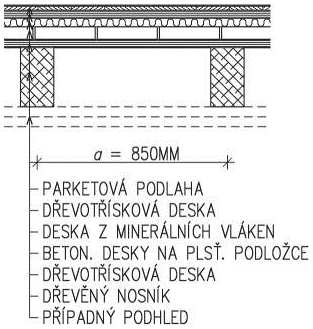
Obr. 3.10 Řez dřevěným stropem
\begin{gathered}
h=110+30\ell\space[\text{mm}]
\end{gathered}kde je
ℓ … rozpětí [m],
h … výška trámu [m],
b … šířka trámu [m].
Empirické vzorce, které berou v úvahu průhyb 1/300ℓ
h = ℓ/16 [m] pro návrhovou pevnost dřeva fd > 12 MPa,
h = ℓ/20 [m] pro návrhovou pevnost dřeva fd > 9 MPa.
Vzorce platí pro rovnoměrné spojité zatížení, ne pro zatížení osamělými břemeny.
Příklad 3.17
Navrhněte rozměry stropního dřevěného trámu, při světlé osové vzdálenosti mezi stěnami 4,6 m a osová vzdálenosti trámů 0,7 m.
\begin{gathered}
h=130+20\cdot4{,}6=222\space\text{mm}\\\\
b=0{,}6\cdot0{,}222=133{,}2\space\text{mm}
\end{gathered}Při uvážení průhybu
\begin{gathered}
h=4{,}6/20=0{,}23\space\text{m}=230\space\text{mm}\\\\
b=0{,}6\cdot230=138\space\text{mm}
\end{gathered}Je zvolen průřez 140/240 mm.
Pro přesnější návrh lze použít vzorců, které berou v úvahu nejen rozpětí, ale i zatížení a osovou vzdálenost trámů. Vypočítají se nutné hodnoty průřezového modulu Wy,nut a momentu setrvačnosti Iy, nut
\begin{gathered}
W_\text{y,nut}=14q_\text{d}\cdot a\cdot\ell^2\cdot10^3\space[\text{mm}^3]\\\\
I_\text{y,nut}=33W_\text{y}\cdot\ell\space[\text{mm}^4]
\end{gathered}kde je
qd … návrhová hodnota zatížení [kN/m],
a … osová vzdálenost trámů [m],
ℓ … rozpětí [m].
Příklad 3.18
Navrhněte a posuďte rozměry stropního trámu, při světlosti mezi stěnami 5,0 m, zatížení 5,5 kN/m2 a osové vzdálenosti trámů 0,9 m.
\begin{gathered}
W_\text{y,nut}=14\cdot5{,}5\cdot0{,}9\cdot5{,}0^2\cdot10^3=1\space732\cdot10^3\space\text{mm}^3\\\\
I_\text{y,nut}=33\cdot5{,}0\cdot1\space732\cdot10^3=285{,}78\cdot10^6\space\text{mm}^4
\end{gathered}Je navržen průřez 160/280 mm.
\begin{gathered}
W_\text{y}=1/6\text{b}\cdot h^2=1/6\cdot160\cdot280^2=2\space090\cdot10^3\gt W_\text{y,nut}=1\space732\cdot10^3\space\text{mm}^3\\\\
I_\text{y}=1/12\text{b}\cdot h^3=1/12\cdot160\cdot280^2=292{,}69\cdot10^6\gt I_\text{y,nut}=285{,}78\cdot10^6\space\text{mm}^4
\end{gathered}Navržený průřez vyhovuje.
3.11 KLENBY A OBLOUKY
Klenby do ocelových nosníků
Nosnými prvky v tomto stropu jsou jednak ocelové stropní nosníky (nejčastěji válcovaného průřezu) a potom klenba v polích mezi nosníky.
Vzepětí klenby se doporučuje volit nejméně 0,1 m. Tloušťku klenby lze určit ze vztahu
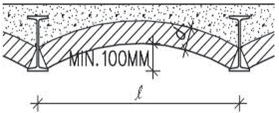
Obr. 3.11 Klenba do ocelových nosníků
\begin{gathered}
d=\frac{\ell^2\cdot q_\text{d}}{0{,}4f_\text{d}}
\end{gathered}kde je
ℓ … rozpětí klenby [m],
qd … zatížení [kN/m2],
fd … návrhová pevnost cihel klenby [MPa],
d … tloušťka klenby [mm].
Příklad 3.19
Navrhněte tloušťku klenby při zatížení 9,5 kN/m2, rozpětí 2,1 m a návrhová pevnost cihel klenby 0,9 MPa.
\begin{gathered}
d=\frac{2{,}1^2\cdot9{,}5}{0{,}4\cdot0{,}9}=116{,}3\space\text{mm}
\end{gathered}Navržená tloušťka klenby na půl cihly klasického formátu je 140 mm.
V tab. 3.54 a 3.57 jsou podle uvedeného vzorce vyčíslena největší možná rozpětí, uvažujeme-li návrhovou pevnost cihel klenby 1,2 MPa.
Tab. 3.56 Tloušťka klenby ½ cihly
| Tloušťka klenby ½ cihly | zatížení qd [kN/m2] | 7,50 | 8,00 | 9,00 | 10,00 | 12,50 | 15,00 | 20,00 |
| rozpětí ℓ [m] | 2,99 | 2,90 | 2,73 | 2,59 | 2,32 | 2,11 | 1,83 |
Tab. 3.57 Tloušťka klenby 1 cihla
| Tloušťka klenby 1 cihla | zatížení qd [kN/m2] | 15,00 | 17,50 | 20,00 | 25,00 | 30,00 |
| rozpětí ℓ [m] | 3,05 | 2,82 | 2,64 | 2,36 | 2,15 |
Ocelové nosníky nesoucí klenby je možné posoudit podle tabulek pro únosnost ocelových nosníků.
Valené klenby a oblouky
Pro stanovení dimenzí kleneb můžeme použít následujících, velmi přibližných vzorců.
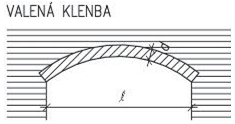
Tab. 3.58 Valené klenby
| ℓ | 3,0 m | 4,0 m | 5,0 m |
| d | ½ cihly | vrchol – ½ cihly pata – 1 cihla |
1 cihla |
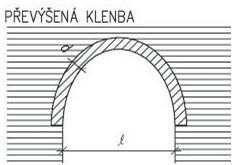
Tab. 3.59 Převýšené oblouky
| ℓ | 2,0 m | 3,5 m | 5,5 m | 8,0 m |
| d | 1 cihla | 1 ½ cihly | 2–2 ½ cihly | 2 ½–3 cihly |
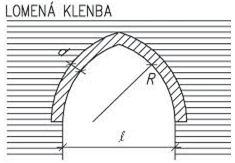
Obr. 3.12 Klenby
Tab. 3.60 Lomené oblouky
| ℓ | 2,0 m | 3,5 m | 5,5 m | 8,0 m |
| d | ½ cihly | 1 cihla | 1 ½ cihly | 2 cihly |
4 TRÁMY A PRŮVLAKY
Rozměry nosníků (trámů, průvlaků, příčlí) jsou závislé na materiálu, ze kterého jsou zhotoveny (dřevo, ocel, železobeton, předpjatý beton), na tvaru příčného řezu, na zatížení, na rozpětí a na statickém schématu nosníku.
4.1 ZATÍŽENÍ
Zatížení na trámy a průvlaky se pro potřeby jejich návrhu udává většinou jako zatížené spojité v kN/m.
4.1.1 Zatížení na trámy (stropnice)
Trámy (stropnice) nejčastěji slouží jako podpora pro deskovou konstrukci, například stropní nebo střešní, a jsou také touto konstrukcí zatíženy. Pro výpočet zatížení působícího na trám je důležité určit zatěžovací šířku B, ze které se přenáší zatížení z desky do trámu.
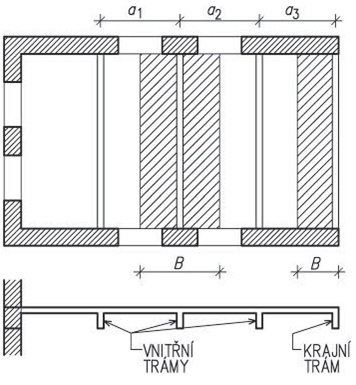
Obr. 4.1 Uspořádání trámového stropu
Zatěžovací šířka B, pro vnitřní trám je
\begin{gathered}
B=(a_1+a_2)/2\space[\text{m}]
\end{gathered}kde je
a1 … vzdálenost trámů vlevo od vyšetřovaného trámu [m],
a2 … vzdálenost trámů vpravo do vyšetřovaného trámu [m].
Zatěžovací šířka B, pro kraj ní trám je
\begin{gathered}
B=a_3/2\space[\text{m}]
\end{gathered}kde je
a3 … vzdálenost k sousednímu trámu [m].
Zatížení na trám se určí tak, že plošné zatížení na desku se vynásobí zatěžovací šířkou a přičte se zatížení vlastní tíhou trámu.
Příklad 4.1
Zjistěte návrhovou hodnotu zatížení na trám vyznačený na obrázku. Jedná se administrativní budovu. Skladba stropní konstrukce odpovídá číslu skladbě 4 v tab. 3.7, nosná železobetonová deska je tloušťky 150 mm.
V př. 3.2 je vypočítáno plošné zatížení stropní desky 9,96 kN/m2.
Zatěžovací šířka trámu je
\begin{gathered}
B=(3{,}0+3{,}3)/2=3{,}15\space\text{m}
\end{gathered}Návrhové zatížení na trám je:
- od stropní desky
\begin{gathered}
9{,}96\cdot3{,}15=31{,}37\space\text{kN/m}
\end{gathered}- vlastní tíha trámu
\begin{gathered}
25\cdot0{,}2\cdot0{,}4\cdot1{,}35=2{,}70\space\text{kN/m}
\end{gathered}Zatížení na trám celkem
\begin{gathered}
34{,}07\space\text{kN/m}
\end{gathered}4.1.2 Zatížení na průvlak
Průvlak má obvykle větší rozměry než trám. Může se použít jako podpora pro stropní desku na větší rozpětí. V tomto případě se zatížení určí stejně jako u trámu s tím, že zatěžovací šířka se určí jako polovina vzdálenosti nosných prvků desky.
Průvlak může tvořit také podporu pro trámy. V tom případě trámy působí na průvlak jako osamělá břemena z odpovídající zatěžovací šířky. Účinek osamělých břemen je možno rozpočítat na spojité rovnoměrné zatížení a připočítá se vlastní tíha průvlaku.
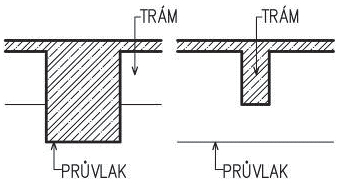
Obr. 4.2 Obvyklý poměr rozměrů trámu a průvlaku
Příklad 4.2
Vypočítejte zatížení na průvlak za předpokladu, že trámy stropu z příkl. 4.1 jsou podpírány průvlakem podle schématu.
Zatěžovací šířka trámu T1
\begin{gathered}
B=(3{,}3+3{,}0)/2=3{,}15\space\text{m}
\end{gathered}Zatížení
\begin{gathered}
9{,}96\cdot3{,}15+0{,}20\cdot0{,}4\cdot25\cdot1{,}35=34{,}07\space\text{kN/m}
\end{gathered}Zatěžovací šířka trámu T2 je jako T1
Zatěžovací šířka trám T3
\begin{gathered}
B=(2{,}7+3{,}0)/2=2{,}85\space\text{m}
\end{gathered}Zatížení
\begin{gathered}
9{,}96\cdot2{,}85+0{,}20\cdot0{,}4\cdot25\cdot1{,}35=31{,}09\space\text{kN/m}
\end{gathered}Zatěžovací šířka pro průvlaky je
\begin{gathered}
B=(5{,}1+4{,}2)/2=4{,}65\space\text{m}
\end{gathered}Zatížení od trámů na průvlak:
- od trámu T1
\begin{gathered}
34{,}07\cdot4{,}65=158{,}44\space\text{kN}
\end{gathered}- od trámu T2
\begin{gathered}
34{,}07\cdot4{,}65=158{,}44\space\text{kN}
\end{gathered}- od trámu T3
\begin{gathered}
31{,}09\cdot4{,}65=144{,}55\space\text{kN}
\end{gathered}Zatížení spojité od vlastní tíhy průvlaku:
\begin{gathered}
0{,}3\cdot0{,}6\cdot25\cdot1{,}35=6{,}08\space\text{kN/m}
\end{gathered}Osamělá břemena se rozpočítají na spojité rovnoměrné zatížení (sečtou se všechna břemena a dělíme se rozpětím průvlaku)
Zatížení od osamělých břemen
\begin{gathered}
(2\cdot158{,}44+144{,}55)/12=38{,}45\space\text{kN/m}
\end{gathered}Vlastní tíha
\begin{gathered}
6{,}08\space\text{kN/m}^2
\end{gathered}Zatížení průvlaku celkem
\begin{gathered}
44{,}53\space\text{kN/m}^2
\end{gathered}Průvlak, popř. trám lze provádět například jako nosník pod zdí. V tom případě se zatížení vypočítá jako součet zatížení tíhy zdiva nad průvlakem a vlastní tíhy průvlaku.
Příklad 4.3
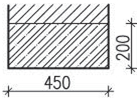
Zatížení stěnou
\begin{gathered}
0{,}45\cdot3{,}3\cdot18\cdot1{,}35=36{,}09\space\text{kN/m}
\end{gathered}Vlastní tíha nosníku
\begin{gathered}
0{,}45\cdot0{,}20\cdot25\cdot1{,}35=3{,}04\space\text{kN/m}
\end{gathered}Zatížení celkem
\begin{gathered}
39{,}13\space\text{kN/m}
\end{gathered}4.1.3 Statické veličiny
Největší ohybový moment prostého nosníku nebo spojitého nosníku o dvou polích, zatížený spojitým rovnoměrným zatížení je
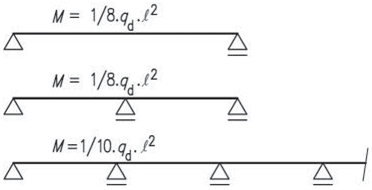
Obr. 4.3 Prostý nosník, spojitý nosník o dvou a více polích
\begin{gathered}
M=f_\text{d}\cdot\ell^2/8\space[\text{kNm}]
\end{gathered}kde je
ℓ … rozpětí [m],
fd … návrhová hodnota spojitého zatížení [kN/m].
Maximální ohybový moment spojitého nosníku o třech a více polích, zatíženého spojitým rovnoměrným zatížením je přibližně
\begin{gathered}
M=f_\text{d}\cdot\ell^2/10\space[\text{kNm}]
\end{gathered}Jestliže se rozpětí spojitého nosníku liší vzájemně do přibližně 20 %, vypočítám ohybový moment z aritmetického průměru rozpětí.
Poznámka:
Vzorce pro jiná zatížen a jiné podepření nosníku jsou v tab. 14.1.
4.2 DŘEVENÉ TRÁMY A PRŮVLAKY
Přibližné vzorce pro návrh rozměrů dřevěného úzkého trámu jsou následující.
Obr. 4.3 Profily dřevěných trámů
Pro návrh úzkého trámu
\begin{gathered}
h_\text{nut}=50\sqrt{M}\space[\text{mm}],\space b=0{,}5h\space[\text{mm}]
\end{gathered}a pro návrh širokého trámu
\begin{gathered}
h_\text{nut}=65\sqrt{M}\space[\text{mm}],\space b=0{,}7\space[\text{mm}]
\end{gathered}kde je
M … ohybový moment [kNm].
Napětí ve dřevěném průřezu se předpokládá 10 MPa.
U dřevěných nosníku je nutné vyšetřovat průhyb, který by neměl překročit hodnotu 1/300 rozpětí. V závislosti na průhybu lze určit nutnou výšku nosníku hnut jako
\begin{gathered}
h_\text{nut}=\frac{\ell}{16}\space[\text{mm}]
\end{gathered}kde je
ℓ … rozpětí trámu [mm].
Příklad 4.4
Navrhněte dřevěný trám, jehož rozpětí je 4,5 m a zatížení 8,4 kN/m.
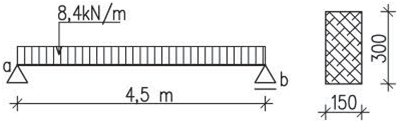
\begin{gathered}
M=8{,}4\cdot4{,}5^2/8=21{,}26\space\text{kNm}
\end{gathered}Úzký nosník
\begin{gathered}
h_\text{nut}=50\cdot\sqrt{21{,}26}=230{,}6\space\text{mm}
\end{gathered}Z podmínky průhybu
\begin{gathered}
h_\text{nut}=4\space500/16=281{,}25\space\text{mm}
\end{gathered}Navrhujeme výšku nosníku h = 300 mm
Šířka
\begin{gathered}
b=0{,}5\cdot300=150\space\text{mm}
\end{gathered}Je zvolen průřez
\begin{gathered}
150/300\space\text{mm}
\end{gathered}Pro některá zatížení a rozpětí lze velikosti profilů z řeziva pevnosti C24 vyhledat přímo z tab. 4.1 (uvedeny jsou vždy dvě hodnoty). O velikosti profilů rozhoduje omezení průhybu, uvažovaného 1/300 ℓ.
Tab. 4.1 Návrhové dřevěné profily trámů pevnosti C24
| Rozpětí ℓ [m] | Návrhová hodnota zatížení qd [kN/m] | |||||||
| 2,0 | 4,0 | 6,0 | 8,0 | 10,0 | 12,0 | 14,0 | 16,0 | |
| 3,00 | 60/180 80/160 |
100/180 80/200 |
100/200 80/220 |
120/220 100/240 |
140/220 120/240 |
180/220 120/260 |
200/220 140/260 |
200/240 140/280 |
| 3,50 | 80/180 60/200 |
100/200 80/200 |
120/220 100/240 |
160/220 140/240 |
200/220 140/260 |
200/240 140/280 |
220/240 160/280 |
220/260 160/300 |
| 4,00 | 100/180 80/200 |
120/220 100/240 |
130/240 120/260 |
180/240 140/260 |
220/240 160/280 |
220/260 160/300 |
260/260 220/280 |
250/280 220/300 |
| 4,50 | 120/200 80/220 |
160/220 120/240 |
180/240 160/260 |
200/260 160/280 |
240/260 170/300 |
240/280 200/300 |
280/280 240/300 |
– 280/300 |
| 5,00 | 120/220 100/240 |
160/240 140/260 |
200/260 160/280 |
200/280 250/260 |
220/300 270/280 |
– 260/300 |
– 300/300 |
– – |
| 5,50 | 140/220 120/240 |
180/260 140/280 |
220/280 180/300 |
230/300 – |
– 290/300 |
– – |
– – |
– – |
| 6,00 | 160/240 120/260 |
230/260 150/300 |
280/280 230/300 |
300/300 – |
– – |
– – |
– – |
– – |
Příčný řez dřevěného plného nosníku nelze volit libovolně veliký. Největší rozměr, který lze běžně navrhnout je 300/360 mm, ale snažíme se navrhovat průřez do 200/260 mm. Při větších rozměrech se navrhují průřezy spojované – lepené KVH, lamelové, trámové rošty apod.
4.3 OCELOVÉ TRÁMY A PRŮVLAKY
Ocelové trámy a průvlaky mají díky svým výhodám (vzhledem ke své hmotnosti vysoká únosnost) široké použití, např. různé typy průvlaků, nosníky pod nosné stěny, nosníky jako podpory pro stropní desku. Staticky působí nejčastěji jako prosté nosníky. Ocelové trámy a průvlaky se navrhují následovně.
Zatížení na trám nebo průvlak se stanoví podle kap. 4.1 ze zatěžovací šířky, která na trám nebo průvlak působí. K zatížení se přičte vlastní tíha nosníku, která se zjistí z tab. 14.2–14.11 válcovaných nosníků. Vlastní návrh ocelového trámu nebo průvlaku se může provést dvěma způsoby.
Návrh ocelových trámů výpočtem
Při výpočtu se prokazuje, zda ocelové nosníky vyhoví podle mezních stavů únosnosti (na napětí) i použitelnosti (na průhyb). Podle napětí se navrhují všechny nosníky stejně.
\begin{gathered}
W_\text{nut}=\frac{M_\text{d}}{f_\text{d}}\space[\text{mm}^3]
\end{gathered}kde je
M … ohybový moment na nosníku [Nmm],
fd … návrhová hodnota pevnosti oceli.
V tab. 14.2–14.11 se vyhledá profil, jehož Wy > Wnut. Posouzení na průhyb se liší podle toho, zda se jedná o stropnici nebo průvlak.
Stropnice
Maximální průhyb
\begin{gathered}
w_\text{lim}=\frac{\ell}{250}\space[\text{mm}]
\end{gathered}Průvlak
Maximální průhyb
\begin{gathered}
w_\text{lim}=\frac{\ell}{400}\space[\text{mm}]
\end{gathered}kde je
ℓ … rozpětí [mm].
Jak pro stropnici tak průvlak platí
\begin{gathered}
I_\text{nut}=4{,}28\cdot10^{-8}\cdot\frac{q_\text{d}\cdot\ell^4}{w_\text{lim}}\space[\text{mm}^4]
\end{gathered}kde je
ℓ … rozpětí [mm],
qd … zatížení [kN/m],
wlim … mezní průhyb [mm].
V tab. 14.2 se vyhledá profil, pro který je Iz > Inut.
Pro správný návrh ocelového trámu nebo průvlaku je nutné splnit obě kritéria W (průřezový modul) a I (moment setrvačnosti).
Poznámka:
Uvedený vzorec výpočtu průhybu je upraven tak, že lze do něho dosazovat návrhovou hodnotu zatížení, tj. přibližně γf = 1,45 (qd = qk · γf).
Příklad 4.5
Navrhněte stropní trám (stropnici) školní budovy na rozpětí 6,6 m. Osová vzdálenost stropnic je 2,4 m, přes stropnice jsou položeny železobetonové panely PZD 238-30/240 o tloušťce 80 mm a na panelech je podlaha, jejíž skladby odpovídá skladbě číslo 2 v tab. 3.7.
Zatížení
Stálé:
- podlaha (tab. 3.7)
\begin{gathered}
1{,}02\space\text{kN/m}^2
\end{gathered}- železobetonový panel (tab. 3.4)
\begin{gathered}
1{,}47/2{,}39/0{,}29\cdot1{,}35=2{,}76\space\text{kN/m}^2
\end{gathered}Stálé celkem
\begin{gathered}
3{,}78\space\text{kN/m}^2
\end{gathered}Užitné (kategorie C1) (tab. 3.8)
\begin{gathered}
3{,}0\cdot1{,}5=4{,}5\space\text{kN/m}^2
\end{gathered}Zatížení celkem
\begin{gathered}
8{,}28\space\text{kN/m}^2
\end{gathered}Zatížení na stropnici:
- od desky
\begin{gathered}
8{,}28\cdot2{,}4=19{,}78\space\text{kN/m}
\end{gathered}- vlastní tíha (IPN300)
\begin{gathered}
0{,}542\cdot1{,}35=0{,}73\space\text{kN/m}
\end{gathered}Celkem
\begin{gathered}
20{,}60\space\text{kN/m}
\end{gathered}\begin{gathered}
M=20{,}60\cdot6{,}6^2/8=112{,}19\space\text{kNm}
\end{gathered}\begin{gathered}
W_\text{nut}=112{,}19\cdot10^6/210=534\space225\space\text{mm}^3=534{,}2\cdot10^3\space\text{mm}^3
\end{gathered}\begin{gathered}
w_\text{lim}=6\space600/250=26{,}4\space\text{mm}
\end{gathered}\begin{gathered}
I_\text{nut}=4{,}28\cdot10^{-8}\cdot20{,}60\cdot6\space600^4/26{,}4=6\space336\space986\space932\space\text{mm}^4=63{,}37\cdot10^6\space\text{mm}^4
\end{gathered}Je navržen IPN280
\begin{gathered}
I_\text{y}=75{,}8\cdot10^6\space\text{mm}^4\gt I_\text{nut}=63{,}37\cdot10^6\space\text{mm}^4
\end{gathered}\begin{gathered}
W_\text{y}=541\cdot10^3\space\text{mm}^3\gt I_\text{nut}=534{,}2\cdot10^3\space\text{mm}^3
\end{gathered}Návrh ocelových trámů a průvlaků použitím vypracovaných tabulek
Pro rychlejší a jednodušší stanovování profilů ocelových nosníků byla vypracována tab. 4.2, ve které se přímo v závislosti na rozpětí a zatížení vyhledávají profily.
Tab. 4.2 Návrh stropních nosníků IPN, UPN a HEB
| Rozpětí ℓ [m] | Ocelové stropní nosníky IPN, UPN a HEB | |||||||||||||||
| návrhová hodnota zatížení qd [kN/m] | ||||||||||||||||
| 10,0 | 20,0 | 30,0 | 40,0 | 50,0 | 60,0 | 70,0 | 80,0 | |||||||||
| stropnice | průvlak | stropnice | průvlak | stropnice | průvlak | stropnice | průvlak | stropnice | průvlak | stropnice | průvlak | stropnice | průvlak | stropnice | průvlak | |
| 2,0 | IPN100 2 IPN80 – – |
IPN100 2 IPN80 – – |
IPN120 3 IPN80 – – |
IPN120 2 IPN100 4 IPN80 – |
IPN140 2 IPN100 4 IPN80 – |
IPN140 2 IPN120 3 IPN100 – |
2 IPN140 2 IPN120 3 IPN100 – |
IPN160 2 IPN140 2 IPN120 – |
2 IPN140 2 IPN120 4 IPN100 – |
IPN 160 2 IPN140 2 IPN120 – |
IPN180 2 IPN140 3 IPN120 4 IPN100 |
IPN180 2 IPN140 3 IPN120 – |
IPN180 2 IPN140 3 IPN120 – |
IPN180 2 IPN140 3 IPN120 – |
2 IPN160 3 IPN140 4 IPN120 – |
IPN180 2 IPN160 3 IPN140 4 IPN120 |
| UPN80 2 UPN65 |
UPN100 2 UPN80 |
UPN120 UPN80 |
UPN120 2 UPN100 |
2 UPN120 2 UPN100 |
UPN140 2 UPN120 |
UPN140 2 UPN100 |
UPN140 2 UPN120 |
UPN160 2 UPN140 |
UPN160 2 UPN140 |
UPN160 2 UPN140 |
UPN160 2 UPN140 |
UPN180 2 UPN140 |
UPN180 2 UPN140 |
UPN200 2 UPN140 |
UPN200 2 UPN140 |
|
| HE100B | HE100B | HE100B | HE100B | HE100B | HE100B | HE100B | HE120B | HE100B | HE120B | HE120B | HE120B | HE140B | HE140B | HE140B | HE160B | |
| 3,0 | IPN140 IPN120 2 IPN100 – |
IPN140 2 IPN120 3 IPN100 – |
IPN160 2 IPN140 2 IPN120 – |
IPN160 2 IPN140 3 IPN120 – |
IPN180 2 U140 3 IPN120 – |
IPN180 2 IPN160 3 IPN140 – |
IPN200 2 IPN160 3 IPN140 – |
IPN200 2 IPN160 4 IPN120 – |
IPN220 2 IPN180 3 IPN140 – |
IPN220 2 IPN180 3 IPN160 – |
IPN240 2 IPN180 3 IPN160 4 IPN140 |
IPN240 2 IPN180 3 IPN160 – |
2 IPN200 3 IPN180 3 IPN160 – |
IPN240 2 IPN200 3 IPN180 4 IPN160 |
IPN260 2 IPN200 3 IPN180 – |
IPN260 2 IPN200 3 IPN180 – |
| UPN 120 2 UPN100 |
UPN140 2 UPN120 |
UPN160 2 UPN120 |
UPN160 2 UPN140 |
UPN180 2 UPN140 |
UPN200 2 UPN160 |
UPN200 2 UPN160 |
UPN200 2 UPN160 |
UPN220 2 UPN180 |
UPN220 2 UPN180 |
UPN240 2 UPN180 |
UPN240 2 UPN200 |
UPN260 2 UPN200 |
UPN260 2 UPN200 |
UPN280 2 UPN200 |
UPN280 2 UPN200 |
|
| HE100B | HE120B | HE120B | HE140B | HE120B | HE140B | HE140B | HE160B | HE140B | HE160B | HE160B | HE160B | HE180B | HE180B | HE180B | HE180B | |
| 4,0 | IPN160 2 IPN140 3 IPN120 – |
IPN180 2 IPN140 3 IPN140 4 IPN120 |
IPN200 2 IPN160 3 IPN140 – |
IPN220 3 IPN160 2 IPN180 – |
IPN220 2 IPN180 3 IPN160 – |
IPN240 2 IPN200 3 IPN180 – |
IPN240 2 IPN200 3 IPN160 – |
IPN260 2 IPN200 3 IPN180 – |
IPN260 2 IPN200 3 IPN180 – |
IPN260 2 IPN220 3 IPN200 – |
IPN280 2 IPN220 3 IPN200 4 IPN180 |
IPN280 2 IPN240 3 IPN220 4 IPN200 |
IPN300 2 IPN240 3 IPN200 4 IPN180 |
IPN300 2 IPN240 3 IPN220 – |
IPN320 2 IPN240 3 IPN220 4 IPN220 |
IPN320 2 IPN260 3 IPN220 4 IPN220 |
| UPN160 2 UPN120 |
UPN180 2 UPN140 |
UPN200 2 UPN160 |
UPN220 2 UPN180 |
UPN240 2 UPN200 |
UPN240 2 UPN200 |
UPN260 2 UPN200 |
UPN260 2 UPN220 |
UPN280 2 UPN220 |
UPN280 2 UPN220 |
UPN300 2 UPN240 |
UPN300 2 UPN240 |
– 2 UPN240 |
– 2 UPN260 |
– 2 UPN260 |
– 2 UPN260 |
|
| HE120B | HE140B | HE140B | HE160B | HE160B | HE180B | HE180B | HE200B | HE180B | HE200B | HE200B | HE220B | HE220B | HE220B | HE220B | HE240B | |
| 5,0 | IPN200 2 IPN60 3 IPN140 |
IPN200 2 IPN80 3 IPN160 |
IPN220 2 IPN180 3 IPN160 4 IPN160 |
IPN240 2 IPN200 3 IPN180 4 IPN180 |
IPN260 2 IPN220 3 IPN200 4 IPN180 |
IPN280 2 IPN240 3 IPN240 4 IPN200 |
IPN280 2 IPN220 3 IPN200 4 IPN180 |
IPN300 2 IPN240 3 IPN220 4 IPN200 |
IPN300 2 IPN240 3 IPN220 4 IPN200 |
IPN320 2 IPN260 3 IPN240 4 IPN220 |
IPN320 2 IPN260 3 IPN220 4 IPN200 |
IPN340 2 IPN280 3 IPN240 4 IPN240 |
IPN340 2 IPN280 3 IPN240 4 IPN220 |
IPN340 2 IPN280 3 IPN260 4 IPN240 |
IPN360 2 IPN280 3 IPN240 4 IPN220 |
IPN360 2 IPN300 3 IPN260 4 IPN240 |
| UPN200 2 UPN160 |
UPN220 2 UPN180 |
UPN240 2 UPN200 |
UPN260 2 UPN220 |
UPN280 2 UPN220 |
UPN280 2 UPN240 |
UPN300 2 UPN240 |
– 2 UPN260 |
– 2 UPN260 |
– 2 UPN280 |
– 2 UPN280 |
– 2 UPN300 |
– 2 UPN300 |
– 2 UPN300 |
– 2 UPN300 |
– – |
|
| HE140B | HE160B | HE180B | HE200B | HE200B | HE220B | HE220B | HE240B | HE220B | HE240B | HE240B | HE260B | HE240B | HE260B | HE260B | HE280B | |
| 6,0 | IPN220 2 IPN180 3 IPN160 4 IPN140 |
IPN240 2 IPN200 3 IPN180 4 IPN160 |
IPN260 2 IPN220 3 IPN200 4 IPN180 |
IPN280 2 IPN240 3 IPN220 4 IPN200 |
IPN300 2 IPN240 3 IPN220 4 IPN200 |
IPN320 2 IPN260 3 IPN240 4 IPN220 |
IPN320 2 IPN260 3 IPN220 4 IPN220 |
IPN340 2 IPN280 3 IPN260 4 IPN240 |
IPN360 2 IPN280 3 IPN240 4 IPN220 |
IPN360 2 IPN300 3 IPN280 4 IPN260 |
IPN380 2 IPN300 3 IPN260 4 IPN240 |
IPN380 2 IPN320 3 IPN280 4 IPN260 |
IPN400 2 IPN320 3 IPN280 4 IPN240 |
IPN400 2 IPN340 3 IPN300 4 IPN280 |
IPN450 2 IPN320 3 IPN280 4 IPN260 |
IPN450 2 IPN340 3 IPN300 4 IPN280 |
| UPN220 2 UPN180 |
UPN240 2 UPN200 |
UPN280 2 UPN220 |
UPN300 2 UPN260 |
– 2 UPN240 |
– 2 UPN280 |
– 2 UPN280 |
– 2 UPN300 |
– – |
– – |
– – |
– – |
– – |
– – |
– – |
– – |
|
| HE160B | HE180B | HE200B | HE220B | HE220B | HE240B | HE240B | HE260B | HE260B | HE280B | HE260B | HE300B | HE280B | HE320B | HE300B | HE320B | |
| 7,0 | IPN240 2 IPN200 3 IPN80 4 IPN160 |
IPN260 2 IPN220 3 IPN200 4 IPN180 |
IPN280 2 IPN240 3 IPN220 4 IPN200 |
IPN320 2 IPN280 3 IPN240 4 IPN220 |
IPN320 2 IPN260 3 IPN240 4 IPN240 |
IPN360 2 IPN300 3 IPN260 4 IPN260 |
IPN360 2 IPN280 3 IPN260 4 IPN240 |
IPN380 2 IPN320 3 IPN300 4 IPN260 |
IPN400 2 IPN300 3 IPN280 4 IPN260 |
IPN400 2 IPN340 3 IPN300 4 IPN280 |
IPN450 2 IPN320 3 IPN280 4 IPN260 |
IPN450 2 IPN360 3 IPN320 4 IPN300 |
IPN450 2 IPN340 3 IPN300 4 IPN280 |
IPN450 2 IPN380 3 IPN340 4 IPN320 |
IPN500 2 IPN360 3 IPN320 4 IPN280 |
IPN500 2 IPN380 3 IPN340 4 IPN320 |
| UPN240 2 UPN200 |
UPN280 2 UPN240 |
UPN300 2 UPN240 |
– 2 UPN280 |
– 2 UPN280 |
– – |
– 2 I300 |
– – |
– – |
– – |
– – |
– – |
– – |
– – |
– – |
– – |
|
| HE180B | HE220B | HE220 | HE260 | HE240 | HE280 | HE260 | HE300 | HE280 | HE320 | HE300 | HE340 | HE320 | HE360 | HE340 | HE400 | |
| 8,0 | IPN260 2 IPN220 3 IPN200 4 IPN180 |
IPN300 2 IPN260 3 IPN220 4 IPN200 |
IPN320 2 IPN260 3 IPN240 4 IPN220 |
IPN360 2 IPN300 3 IPN260 4 IPN260 |
IPN360 2 IPN300 3 IPN260 4 IPN240 |
IPN400 2 IPN340 3 IPN300 4 IPN280 |
IPN400 2 IPN320 3 IPN280 4 IPN260 |
IPN450 2 IPN360 3 IPN320 4 IPN300 |
IPN400 2 IPN340 3 IPN300 4 IPN280 |
IPN450 2 IPN380 3 IPN340 4 IPN320 |
IPN450 2 IPN360 3 IPN320 4 IPN300 |
IPN500 2 IPN400 3 IPN360 4 IPN340 |
IPN450 2 IPN380 3 IPN340 4 IPN300 |
IPN500 2 IPN450 3 IPN400 4 IPN340 |
IPN500 2 IPN400 3 IPN340 4 IPN320 |
– 2 IPN450 3 IPN380 4 IPN360 |
| UPN280 2 UPN220 |
– 2 UPN260 |
– 2 UPN280 |
– – |
– – |
– – |
– – |
– – |
– – |
– – |
– – |
– – |
– – |
– – |
– – |
– – |
|
| HE200B | HE240B | HE240B | HE280B | HE280 | HE320B | HE300B | HE340B | HE320B | HE360B | HE340B | HE400B | HE360B | HE450B | HE400B | HE450B | |
| 9,0 | IPN300 2 IPN240 3 IPN220 4 IPN200 |
IPN320 2 IPN280 3 IPN240 4 IPN240 |
IPN340 2 IPN300 3 IPN260 4 IPN240 |
IPN400 2 IPN320 3 IPN300 4 IPN280 |
IPN400 2 IPN320 3 IPN300 4 IPN280 |
IPN450 2 IPN360 3 IPN320 4 IPN300 |
IPN450 2 IPN340 3 IPN320 4 IPN300 |
IPN500 2 IPN400 3 IPN360 4 IPN320 |
IPN450 2 IPN360 3 IPN340 4 IPN300 |
IPN500 2 IPN450 3 IPN380 4 IPN340 |
IPN500 2 IPN380 3 IPN340 4 IPN320 |
– 2 IPN450 3 IPN400 4 IPN360 |
IPN500 2 IPN450 3 IPN360 4 IPN340 |
– 2 IPN450 3 IPN400 4 IPN380 |
– 2 IPN450 3 IPN360 4 IPN340 |
– 2 IPN500 3 IPN400 4 IPN380 |
| 2 UPN260 | 2 UPN300 | – | – | – | – | – | – | – | – | – | – | – | – | – | – | |
| HE220B | HE260B | HE280B | HE280B | HE300B | HE340B | HE340B | HE400B | HE350B | HE450B | HE400B | HE500B | HE450B | HE550B | HE450B | HE550B | |
| 10,0 | IPN320 2 IPN260 3 IPN240 4 IPN220 |
IPN360 2 IPN300 3 IPN260 4 IPN240 |
IPN380 2 IPN320 3 IPN280 4 IPN260 |
IPN450 2 IPN360 3 IPN320 4 IPN300 |
IPN450 2 IPN360 3 IPN320 4 IPN300 |
IPN500 2 IPN400 3 IPN360 4 IPN340 |
IPN500 2 IPN380 3 IPN340 4 IPN320 |
– 2 IPN450 3 IPN380 4 IPN360 |
IPN500 2 IPN400 3 IPN360 4 IPN340 |
– 2 IPN450 3 IPN400 4 IPN380 |
– 2 IPN450 3 IPN380 4 IPN360 |
– 2 IPN500 3 IPN450 4 IPN400 |
– 2 IPN450 3 IPN400 4 IPN360 |
– 2 IPN500 3 IPN450 4 IPN450 |
– 2 IPN500 3 IPN400 4 IPN380 |
– – 3 IPN450 4 IPN450 |
| 2 UPN280 | – | – | – | – | – | – | – | – | – | – | – | – | – | – | – | |
| HE240B | HE280B | HE300B | HE300B | HE340B | HE400B | HE360B | HE450B | HE400B | HE500B | HE450B | HE550B | HE500B | HE550B | HE500B | HE600B | |
Příklad 4.6
Navrhněte ocelový trám (stropnici) použitím tab. 4.2, je-li zatížení na stropnici včetně vlastní tíhy 16,727 kN/m a rozpětí stropnice 6,6 m.
V tabulce se interpoluje mezi rozpětím 6 a 7 m, působící zatížení se zaokrouhlí ze 16,727 na 20 kN/m. Rozpětí 6 m odpovídá IPN260, rozpětí 7 m odpovídá IPN280. Rozpětí 6,6 m je přibližně uprostřed mezi 6 a 7 m, ale zatížení bylo zaokrouhleno nahoru, proto se volí profil IPN260.
Tab. 4.3 Prolamovaný ocelový nosník
| Prvek | Nákres | Rozpětí ℓ [m] | Poměr ℓ/hd |
| Prolamovaný ocelový nosník |  |
6–18 | 10–18 |
4.4 ŽELEZOBETONOVÉ TRÁMY A PRŮVLAKY
Tab. 4.4 Železobetonové trámy a průvlaky
| Prvek | Nákres | Tloušťka hd [mm] | Rozpětí ℓ [m] | Poměr ℓ/hd |
| Trámy a průvlaky L a T |  |
|||
|
300–700 | 4–7 | 14–20 | |
|
300–850 | 8–24 | 20–30 | |
| Deskové trámy nebo průvlaky | 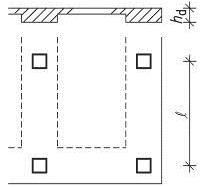 |
|||
|
300–650 | 5–12 | 16–22 | |
|
350–500 | 9–15 | 22–32 |
Železobetonové trámy a průvlaky lze používat jako prvky stropů, jako roznášecí nosníky, například pod nosné zdi, jako podpory pod stropní konstrukce apod.
Železobetonové trámy a průvlaky dělíme podle technologie výroby:
- monolitické;
- prefabrikované.
Monolitické trámy a průvlaky
Monolitické trámy a průvlaky se díky svým výhodám používají poměrně často. Lze je navrhovat buď jako prosté nosníky o jednom poli, jako spojité nosníky o více polích, nebo jako vetknuté nosníky do železobetonových stěn. Pro železový beton jsou výhodnější nosníky spojité nebo vetknuté, neboť vhodným vyztužením nosníku lze oproti nosníku prostému zmenšit průřez.
Prefabrikované trámy a průvlaky
Prefabrikované trámy a průvlaky se používají poměrně méně často z toho důvodu, že výztuž, která je použita v trámu nebo v průvlaku musí být dimenzována na určité zatížení a to je závislé na zatěžovací šířce, ze které se zatížení přenáší na trám. Zatěžovací šířky mohou být v praktických případech podstatně rozlišné. Známy jsou prefabrikované průvlaky jako součást montovaných skeletů, dále staveništní prefabrikáty nebo prefabrikáty vyrobené v panelárně „na míru“ pro konkrétní stavbu.
Používané průřezy
Železobetonové trámy a průvlaky bývají nejčastěji obdélníkového průřezu buď klasického tvaru, kdy šířka je menší než výška, nebo jako deskové průvlaky, kdy šířka průvlaku je větší než jeho výška. Na trám nebo průvlak může navazovat stropní deska, tzn. „T“ průřez. T průřez díky spolupůsobení se železobetonovou deskou má vyšší únosnost než obdélníkový průřez. Pro potřeby předběžného návrhu je ale možné s touto rezervou nepočítat.
Poznámka:
Kromě železobetonových trámů a průvlaků lze uvažovat ještě předpjaté trámy a průvlaky, které je možno navrhovat na větší rozpětí a vyšší zatížení.
Postup při navrhování podle tabulek
Zatížení na nosník se vypočítá podle kap. 4.1 Zatížení. Dále zjistíme, zda se jedná o nosník prostě podepřený, vetknutý nebo nosník spojitý a podle toho se zjistí z kap. 4.1.3 Statické veličiny hodnotu ohybového momentu. Pro některé specifičtější případy lze hodnotu ohybového momentu zjistit z tabulek v závěru publikace. Dále se použijí tab. 4.5–4.7, ve kterých lze pro zvolený průřez b/h a procento vyztužení nalézt odpovídající návrhovou hodnotu momentu únosnosti a dvě hodnoty rozpětí ℓ, pro které jsou splněny podmínky vymezující štíhlosti (poměr rozpětí k účinné výšce průřezu) při jednak prostém uložení nosníku (menší hodnota), jednak pro vnitřní pole spojitého nosníku (větší hodnota).
Poznámka:
Tabulky byly vypracovány pro jednostranně vyztužené průřezy z betonu C25/30 s výztuží B500B (10 505) a procentem vyztužení 0,5 %, 1,0 %, 1,5 % a u průvlaků 2,0 %.
Příklad 4.7
Použití tabulek – vyberte z tabulky stropní trám průřezu 100/250 mm (neuvažovaný jako T průřez, z čehož plyne případná rezerva), při stupni vyztužení 1 % má moment únosnosti 19,28 kNm a jako vnitřní pole spojitého nosníku při rozpětí 2,43 m splňuje podmínku vymezující štíhlosti a nemusí být posuzován na průhyb (rozpětí 1,62 m by odpovídalo prostému uložení nosníku).
| Průřez b/h[mm] | 100/250 | ||
| Procento vyztužení ρ [%] | 0,50 | 10,53 | 2,03 |
| 3,05 | |||
| 1,00 | 19,28 | 1,62 | |
| 2,43 | |||
| 1,50 | 26,26 | 1,48 | |
| 2,22 | |||
Tab. 4.5 Návrhové hodnoty momentu únosnosti pro trámy
| Návrhové hodnoty momentu únosnosti MRd [kNm] a rozpětí ℓ [m], odpovídající vymezující štíhlosti pro trámy | |||||||||||||||||||||
| Průřez b/h [mm] | 50/150 | 50/200 | 50/250 | 50/300 | 50/350 | – | – | – | – | – | |||||||||||
| Procento vyztužení ρ [%] | 0,5 | 1,63 | 2,03 | 3,19 | 2,95 | 5,26 | 3,88 | 7,84 | 4,80 | 10,93 | 5,72 | – | – | – | – | – | – | – | – | – | |
| 3,05 | 4,43 | 5,82 | 7,20 | 8,59 | – | – | – | – | |||||||||||||
| 1,0 | 2,95 | 1,62 | 5,82 | 2,36 | 9,64 | 3,09 | 14,40 | 3,83 | 20,11 | 4,56 | – | – | – | – | – | – | – | – | – | ||
| 2,43 | 3,53 | 4,64 | 5,74 | 6,85 | – | – | – | – | |||||||||||||
| 1,5 | 3,94 | 1,48 | 7,88 | 2,16 | 13,13 | 2,83 | 19,69 | 3,50 | 27,56 | 4,18 | – | – | – | – | – | – | – | – | – | ||
| 2,22 | 3,23 | 4,24 | 5,26 | 6,27 | – | – | – | – | |||||||||||||
| Průřez b/h [mm] | 100/150 | 100/200 | 100/250 | 100/300 | 100/350 | 100/400 | 100/450 | 100/500 | – | – | |||||||||||
| Procento vyztužení ρ [%] | 0,5 | 3,27 | 2,03 | 6,39 | 2,95 | 10,53 | 3,88 | 15,68 | 4,80 | 21,85 | 5,72 | 29,04 | 6,65 | 37,24 | 7,57 | 46,46 | 8,49 | – | – | – | – |
| 3,05 | 4,43 | 5,82 | 7,20 | 8,59 | 9,97 | 11,36 | 12,74 | – | – | ||||||||||||
| 1,0 | 5,90 | 1,62 | 11,64 | 2,36 | 19,28 | 3,09 | 28,81 | 3,83 | 40,23 | 4,56 | 53,53 | 5,30 | 68,73 | 6,04 | 85,82 | 6,77 | – | – | – | – | |
| 2,43 | 3,53 | 4,64 | 5,74 | 6,85 | 7,95 | 9,05 | 10,16 | – | – | ||||||||||||
| 1,5 | 7,89 | 1,48 | 15,77 | 2,16 | 26,26 | 2,83 | 39,39 | 3,50 | 55,13 | 4,18 | 73,50 | 4,85 | 94,49 | 5,53 | 118,10 | 6,20 | – | – | – | – | |
| 2,22 | 3,23 | 4,24 | 5,26 | 6,27 | 7,28 | 8,29 | 9,30 | – | – | ||||||||||||
| Průřez b/h [mm] | 150/150 | 150/200 | 150/250 | 150/300 | 150/350 | 150/400 | 150/450 | 150/500 | 150/550 | 150/600 | |||||||||||
| Procento vyztužení ρ [%] | 0,50 | 4,90 | 2,03 | 9,58 | 2,95 | 15,79 | 3,88 | 23,52 | 4,80 | 32,78 | 5,72 | 43,55 | 6,65 | 55,86 | 7,57 | 69,68 | 8,49 | 85,03 | 9,42 | 101,91 | 10,34 |
| 3,05 | 4,43 | 5,82 | 7,20 | 8,59 | 9,97 | 11,36 | 12,74 | 14,13 | 15,51 | ||||||||||||
| 1,00 | 8,85 | 1,62 | 17,47 | 2,36 | 28,92 | 3,09 | 43,21 | 3,83 | 60,34 | 4,56 | 80,30 | 5,30 | 103,10 | 6,04 | 128,73 | 6,77 | 157,20 | 7,51 | 188,51 | 8,25 | |
| 2,43 | 3,53 | 4,64 | 5,74 | 6,85 | 7,95 | 9,05 | 10,16 | 11,26 | 12,37 | ||||||||||||
| 1,50 | 11,83 | 1,48 | 23,65 | 2,16 | 39,40 | 2,83 | 59,08 | 3,50 | 82,69 | 4,18 | 110,25 | 4,85 | 141,73 | 5,53 | 177,15 | 6,20 | 216,50 | 6,87 | 259,79 | 7,55 | |
| 2,22 | 3,23 | 3,68 | 5,26 | 6,27 | 7,28 | 8,29 | 9,30 | 10,31 | 11,32 | ||||||||||||
| Průřez b/h [mm] | – | 200/200 | 200/250 | 200/300 | 200/350 | 200/400 | 200/450 | 200/500 | 200/550 | 200/600 | |||||||||||
| Procento vyztužení ρ [%] | 0,50 | – | – | 12,78 | 2,95 | 21,05 | 3,88 | 31,36 | 4,80 | 43,70 | 5,72 | 58,07 | 6,65 | 74,48 | 7,57 | 92,91 | 8,49 | 113,38 | 9,42 | 135,88 | 10,34 |
| – | 4,43 | 5,82 | 7,20 | 8,59 | 9,97 | 11,36 | 12,74 | 14,13 | 15,51 | ||||||||||||
| 1,00 | – | – | 23,29 | 2,36 | 38,56 | 3,09 | 57,26 | 3,83 | 80,45 | 4,56 | 107,07 | 5,30 | 137,47 | 6,04 | 171,64 | 6,77 | 209,60 | 7,51 | 251,34 | 8,25 | |
| – | 3,53 | 4,64 | 5,74 | 6,85 | 7,95 | 9,05 | 10,16 | 11,26 | 12,37 | ||||||||||||
| 1,50 | – | – | 31,53 | 2,16 | 52,53 | 2,83 | 78,77 | 3,50 | 110,26 | 4,18 | 146,99 | 4,85 | 188,97 | 5,53 | 236,20 | 6,20 | 288,67 | 6,87 | 345,39 | 7,55 | |
| 3,23 | 3,68 | 5,26 | 6,27 | 7,28 | 8,29 | 9,30 | 10,31 | 11,32 | |||||||||||||
| Průřez b/h [mm] | – | – | 250/250 | 250/300 | 250/350 | 250/400 | 250/450 | 250/500 | 250/550 | 250/600 | |||||||||||
| Procento vyztužení ρ [%] | 0,50 | – | – | – | – | 26,32 | 3,88 | 39,20 | 4,80 | 54,63 | 5,72 | 72,59 | 6,65 | 93,09 | 7,57 | 116,14 | 8,49 | 141,72 | 9,42 | 169,85 | 10,34 |
| – | – | 5,82 | 7,20 | 8,59 | 9,97 | 11,36 | 12,74 | 14,13 | 15,51 | ||||||||||||
| 1,00 | – | – | – | – | 48,20 | 3,09 | 72,02 | 3,83 | 100,57 | 4,56 | 133,84 | 5,30 | 171,83 | 6,04 | 214,56 | 6,77 | 262,00 | 7,51 | 314,18 | 8,25 | |
| – | – | 4,64 | 5,74 | 6,85 | 7,95 | 9,05 | 10,16 | 11,26 | 12,37 | ||||||||||||
| 1,50 | – | – | – | – | 65,66 | 2,83 | 98,46 | 3,50 | 137,82 | 4,18 | 183,74 | 4,85 | 236,22 | 5,53 | 295,25 | 6,20 | 360,84 | 6,87 | 432,99 | 7,55 | |
| – | – | 3,68 | 5,26 | 6,27 | 7,28 | 8,29 | 9,30 | 10,31 | 11,32 | ||||||||||||
| Průřez b/h [mm] | – | – | – | 300/300 | 300/350 | 300/400 | 300/450 | 300/500 | 300/550 | 300/600 | |||||||||||
| Procento vyztužení ρ [%] | 0,50 | – | – | – | – | – | – | 47,04 | 4,80 | 65,55 | 5,72 | 87,11 | 6,65 | 111,71 | 7,57 | 139,37 | 8,49 | 170,07 | 9,42 | 203,82 | 10,34 |
| – | – | – | 7,20 | 8,59 | 9,97 | 11,36 | 12,74 | 14,13 | 15,51 | ||||||||||||
| 1,00 | – | – | – | – | – | – | 86,43 | 3,83 | 120,68 | 4,56 | 160,60 | 5,30 | 206,20 | 6,04 | 257,47 | 6,77 | 314,40 | 7,51 | 377,01 | 8,25 | |
| – | – | – | 5,74 | 6,85 | 7,95 | 9,05 | 10,16 | 11,26 | 12,37 | ||||||||||||
| 1,50 | – | – | – | – | – | – | 118,16 | 3,50 | 165,39 | 4,18 | 220,49 | 4,85 | 283,46 | 5,53 | 354,30 | 6,20 | 433,01 | 6,87 | 519,58 | 7,55 | |
| – | – | – | 5,26 | 6,27 | 7,28 | 8,29 | 9,30 | 10,31 | 11,32 | ||||||||||||
Tab. 4.6 Návrhová hodnota momentu únosnosti pro deskové průvlaky
| Návrhová hodnota momentu únosnosti MRd [kNm] a rozpětí ℓ [m], odpovídající vymezující štíhlosti pro deskové průvlaky | |||||||||||||||||||
| Průřez b/h mm | 250/250 | 300/250 | 350/250 | 400/250 | 450/250 | – | – | – | – | ||||||||||
| Procento vyztužení ρ [%] | 0,5 | 26,32 | 3,88 | 31,58 | 3,88 | 36,84 | 3,88 | 43,11 | 3,88 | 47,37 | 3,88 | – | – | – | – | – | – | – | – |
| 5,82 | 5,82 | 5,82 | 5,82 | 5,82 | – | – | – | – | |||||||||||
| 1,0 | 48,20 | 3,09 | 57,84 | 3,09 | 67,49 | 3,09 | 77,13 | 3,09 | 86,77 | 3,09 | – | – | – | – | – | – | – | – | |
| 4,64 | 4,64 | 4,64 | 4,64 | 4,64 | – | – | – | – | |||||||||||
| 1,5 | 65,66 | 2,83 | 78,79 | 2,83 | 91,92 | 2,83 | 105,06 | 2,83 | 118,19 | 2,83 | – | – | – | – | – | – | – | – | |
| 4,24 | 4,24 | 4,24 | 4,24 | 4,24 | – | – | – | – | |||||||||||
| Průřez b/h mm | 300/300 | 350/300 | 400/300 | 450/300 | 500/300 | 550/300 | 600/300 | – | – | ||||||||||
| Procento vyztužení ρ [%] | 0,5 | 47,04 | 4,80 | 54,88 | 4,80 | 62,72 | 4,80 | 70,56 | 4,80 | 78,40 | 4,80 | 86,24 | 4,80 | 94,08 | 4,80 | – | – | – | – |
| 7,20 | 7,20 | 7,20 | 7,20 | 7,20 | 7,20 | 7,20 | – | – | |||||||||||
| 1,0 | 86,43 | 3,83 | 110,83 | 3,83 | 115,24 | 3,83 | 129,64 | 3,83 | 144,05 | 3,83 | 158,45 | 3,83 | 172,85 | 3,83 | – | – | – | – | |
| 5,74 | 5,74 | 5,74 | 5,74 | 5,74 | 5,74 | 5,74 | – | – | |||||||||||
| 1,5 | 118,16 | 3,50 | 137,85 | 3,50 | 157,54 | 3,50 | 177,24 | 3,50 | 196,93 | 3,50 | 216,62 | 3,50 | 236,31 | 3,50 | – | – | – | – | |
| 5,26 | 5,26 | 5,26 | 5,26 | 5,26 | 5,26 | 5,26 | – | – | |||||||||||
| Průřez b/h mm | 350/350 | 400/350 | 450/350 | 500/350 | 550/350 | 600/350 | 650/350 | 700/350 | 750/350 | ||||||||||
| Procento vyztužení ρ [%] | 0,50 | 76,48 | 5,72 | 87,4 | 5,72 | 98,33 | 5,72 | 109,25 | 5,72 | 120,18 | 5,72 | 131,1 | 5,72 | 142,03 | 5,72 | 152,95 | 5,72 | 163,88 | 5,72 |
| 8,59 | 8,59 | 8,59 | 8,59 | 8,59 | 8,59 | 8,59 | 8,59 | 8,59 | |||||||||||
| 1,00 | 140,79 | 4,56 | 160,91 | 4,56 | 181,02 | 4,56 | 201,13 | 4,56 | 221,25 | 4,56 | 241,36 | 4,56 | 261,47 | 4,56 | 281,59 | 4,56 | 301,70 | 4,56 | |
| 6,85 | 6,85 | 6,85 | 6,85 | 6,85 | 6,85 | 6,85 | 6,85 | 6,85 | |||||||||||
| 1,50 | 192,95 | 4,18 | 220,52 | 4,18 | 248,08 | 4,18 | 275,65 | 4,18 | 303,21 | 4,18 | 330,78 | 4,18 | 358,34 | 4,18 | 385,91 | 4,18 | 413,47 | 4,18 | |
| 6,27 | 6,27 | 6,27 | 6,27 | 6,27 | 6,27 | 6,27 | 6,27 | 6,27 | |||||||||||
| Průřez b/h mm | 400/400 | 450/400 | 500/400 | 550/400 | 600/400 | 650/400 | 700/400 | 750/400 | 800/400 | ||||||||||
| Procento vyztužení ρ [%] | 0,50 | 116,14 | 6,65 | 130,66 | 6,65 | 145,18 | 6,65 | 159,70 | 6,65 | 174,22 | 6,65 | 188,73 | 6,65 | 203,25 | 6,65 | 217,77 | 6,65 | 232,29 | 6,65 |
| 9,97 | 9,97 | 9,97 | 9,97 | 9,97 | 9,97 | 9,97 | 9,97 | 9,97 | |||||||||||
| 1,00 | 214,14 | 5,30 | 240,91 | 5,30 | 267,67 | 5,30 | 294,44 | 5,30 | 321,21 | 5,30 | 347,98 | 5,30 | 374,74 | 5,30 | 401,51 | 5,30 | 428,28 | 5,30 | |
| 7,95 | 7,95 | 7,95 | 7,95 | 7,95 | 7,95 | 7,95 | 7,95 | 7,95 | |||||||||||
| 1,50 | 293,99 | 4,85 | 330,74 | 4,85 | 367,49 | 4,85 | 404,23 | 4,85 | 440,98 | 4,85 | 477,73 | 4,85 | 514,48 | 4,85 | 551,23 | 4,85 | 587,98 | 4,85 | |
| 7,28 | 7,28 | 7,28 | 7,28 | 7,28 | 7,28 | 7,28 | 7,28 | 7,28 | |||||||||||
| Průřez b/h mm | 450/450 | 500/450 | 550/450 | 600/450 | 650/450 | 700/450 | 750/450 | 800/450 | 850/450 | ||||||||||
| Procento vyztužení ρ [%] | 0,50 | 167,57 | 7,57 | 186,19 | 7,57 | 204,81 | 7,57 | 223,43 | 7,57 | 242,05 | 7,57 | 260,66 | 7,57 | 279,28 | 7,57 | 297,90 | 7,57 | 316,52 | 7,57 |
| 11,36 | 11,36 | 11,36 | 11,36 | 11,36 | 11,36 | 11,36 | 11,36 | ||||||||||||
| 1,00 | 309,30 | 6,04 | 343,67 | 6,04 | 378,03 | 6,04 | 412,40 | 6,04 | 446,77 | 6,04 | 481,13 | 6,04 | 515,50 | 6,04 | 549,87 | 6,04 | 584,23 | 6,04 | |
| 9,05 | 9,05 | 9,05 | 9,05 | 9,05 | 9,05 | 9,05 | 9,05 | ||||||||||||
| 1,50 | 425,19 | 5,53 | 472,44 | 5,53 | 519,68 | 5,53 | 566,92 | 5,53 | 614,17 | 5,53 | 661,41 | 5,53 | 708,65 | 5,53 | 755,90 | 5,53 | 803,14 | 5,53 | |
| 8,29 | 8,29 | 8,29 | 8,29 | 8,29 | 8,29 | 8,29 | 8,29 | ||||||||||||
| Průřez b/h mm | 500/500 | 550/500 | 600/500 | 650/500 | 700/500 | 750/500 | 800/500 | – | 850/500 | ||||||||||
| Procento vyztužení ρ [%] | 0,50 | 232,28 | 8,49 | 255,51 | 8,49 | 278,73 | 8,49 | 301,96 | 8,49 | 325,19 | 8,49 | 348,42 | 8,49 | 371,64 | 8,49 | 394,87 | 8,49 | 418,10 | 8,49 |
| 12,74 | 12,74 | 12,74 | 12,74 | 12,74 | 12,74 | 12,74 | 12,74 | 12,74 | |||||||||||
| 1,00 | 429,11 | 6,77 | 472,02 | 6,77 | 514,93 | 6,77 | 557,84 | 6,77 | 600,75 | 6,77 | 643,67 | 6,77 | 686,58 | 6,77 | 729,49 | 6,77 | 772,40 | 6,77 | |
| 10,16 | 10,16 | 10,16 | 10,16 | 10,16 | 10,16 | 10,16 | 10,16 | 10,16 | |||||||||||
| 1,50 | 590,50 | 6,20 | 649,55 | 6,20 | 708,60 | 6,20 | 767,65 | 6,20 | 826,70 | 6,20 | 885,75 | 6,20 | 944,80 | 6,20 | 1003,85 | 6,20 | 1062,90 | 6,20 | |
| 9,30 | 9,30 | 9,30 | 9,30 | 9,30 | 9,30 | 9,30 | 9,30 | 9,30 | |||||||||||
Tab. 4.7 Návrhová hodnota momentu únosnosti pro vysoké průvlaky
| Návrhová hodnota momentu únosnosti MRd [kNm] a rozpětí ℓ [m], odpovídající vymezující štíhlosti pro vysoké průvlaky | |||||||||||||||||||
| Průřez b/h [mm] | 250/300 | 250/350 | 250/400 | 250/450 | 250/500 | 250/550 | 250/600 | 250/650 | 250/700 | ||||||||||
| Procento vyztužení ρ [%] | 0,50 | 39,20 | 4,80 | 54,63 | 5,72 | 72,59 | 6,65 | 93,09 | 7,57 | 116,14 | 8,49 | 141,72 | 9,42 | 168,85 | 10,34 | 200,51 | 11,26 | 233,72 | 12,19 |
| 7,20 | 8,59 | 9,97 | 11,36 | 12,74 | 14,13 | 15,51 | 16,90 | 18,28 | |||||||||||
| 1,00 | 72,20 | 3,83 | 100,57 | 4,56 | 133,84 | 5,30 | 171,83 | 6,04 | 214,56 | 6,77 | 262,00 | 7,51 | 314,18 | 8,25 | 371,08 | 8,98 | 433,70 | 9,72 | |
| 5,74 | 6,85 | 7,95 | 9,05 | 10,16 | 11,26 | 12,37 | 13,47 | 14,58 | |||||||||||
| 1,50 | 98,46 | 3,50 | 137,82 | 4,18 | 183,74 | 4,85 | 236,22 | 5,53 | 295,25 | 6,20 | 360,84 | 6,87 | 432,99 | 7,55 | 511,69 | 8,22 | 596,95 | 8,89 | |
| 5,26 | 6,27 | 7,28 | 8,29 | 9,30 | 10,31 | 11,32 | 12,33 | 13,34 | |||||||||||
| 2,00 | 118,53 | 3,34 | 166,40 | 3,98 | 222,31 | 4,63 | 286,25 | 5,27 | 358,22 | 5,91 | 438,23 | 6,55 | 526,28 | 7,20 | 622,35 | 7,84 | 726,47 | 8,48 | |
| 5,01 | 5,98 | 6,94 | 7,90 | 8,87 | 9,83 | 10,80 | 11,76 | 12,72 | |||||||||||
| Průřez b/h [mm] | 300/350 | 300/400 | 300/450 | 300/500 | 300/550 | 300/600 | 300/650 | 300/700 | 300/750 | ||||||||||
| Procento vyztužení ρ [%] | 0,5 | 65,55 | 5,72 | 87,11 | 6,65 | 111,71 | 7,57 | 138,37 | 8,49 | 170,07 | 9,42 | 203,82 | 10,34 | 240,62 | 11,26 | 280,46 | 12,19 | 323,36 | 13,11 |
| 8,59 | 9,97 | 11,35 | 12,74 | 14,13 | 15,51 | 16,90 | 18,28 | 19,67 | |||||||||||
| 1,0 | 120,68 | 4,56 | 161,60 | 5,30 | 206,20 | 6,04 | 257,47 | 6,77 | 314,40 | 7,51 | 377,01 | 8,25 | 445,29 | 8,98 | 519,24 | 9,72 | 598,87 | 10,45 | |
| 6,85 | 7,95 | 9,05 | 10,16 | 11,26 | 12,37 | 13,47 | 14,58 | 15,68 | |||||||||||
| 1,5 | 159,39 | 4,18 | 220,49 | 4,85 | 283,46 | 5,53 | 354,30 | 6,20 | 433,01 | 6,87 | 519,58 | 7,55 | 614,03 | 8,22 | 716,34 | 8,89 | 826,52 | 9,57 | |
| 6,27 | 7,28 | 8,29 | 9,30 | 10,31 | 11,32 | 12,33 | 13,34 | 14,35 | |||||||||||
| 2,0 | 199,68 | 3,96 | 266,77 | 7,63 | 343,50 | 5,27 | 429,87 | 5,91 | 525,88 | 6,55 | 631,53 | 7,20 | 746,22 | 7,84 | 871,76 | 8,48 | 1006,23 | 9,12 | |
| 5,98 | 6,94 | 7,90 | 8,87 | 9,83 | 10,80 | 11,76 | 12,72 | 13,69 | |||||||||||
| Průřez b/h [mm] | 350/400 | 350/450 | 350/500 | 350/550 | 350/600 | 350/650 | 350/700 | 350/750 | 350/800 | ||||||||||
| Procento vyztužení ρ [%] | 0,5 | 101,63 | 6,65 | 130,33 | 7,57 | 162,59 | 8,49 | 198,41 | 9,42 | 237,79 | 10,34 | 280,72 | 11,26 | 327,21 | 12,19 | 377,25 | 13,11 | 430,85 | 14,03 |
| 9,97 | 11,35 | 12,74 | 14,13 | 15,51 | 16,90 | 18,28 | 19,67 | 21,05 | |||||||||||
| 1,0 | 187,37 | 5,30 | 240,57 | 6,04 | 300,38 | 6,77 | 366,81 | 7,51 | 439,85 | 8,25 | 519,51 | 8,98 | 605,78 | 9,72 | 698,68 | 10,45 | 798,19 | 11,19 | |
| 7,95 | 9,05 | 10,16 | 11,26 | 12,37 | 13,47 | 14,58 | 15,68 | 16,78 | |||||||||||
| 1,5 | 257,24 | 4,85 | 330,71 | 5,53 | 413,35 | 6,20 | 505,18 | 6,87 | 606,18 | 7,55 | 716,37 | 8,22 | 835,73 | 8,89 | 964,28 | 9,57 | 1102,00 | 10,24 | |
| 7,28 | 8,29 | 9,30 | 10,31 | 11,32 | 12,33 | 13,34 | 14,35 | 15,36 | |||||||||||
| 2,0 | 311,23 | 7,63 | 400,75 | 5,27 | 501,51 | 5,91 | 613,53 | 6,55 | 736,79 | 7,20 | 871,29 | 7,84 | 1017,05 | 8,48 | 1174,05 | 9,12 | 1342,31 | 9,77 | |
| 6,94 | 7,90 | 8,87 | 9,83 | 10,80 | 11,76 | 12,72 | 13,69 | 14,65 | |||||||||||
| Průřez b/h [mm] | 400/450 | 400/500 | 400/550 | 400/600 | 400/650 | 400/700 | 400/750 | 400/800 | 400/850 | ||||||||||
| Procento vyztužení ρ [%] | 0,5 | 148,95 | 7,57 | 185,82 | 8,49 | 226,76 | 9,42 | 271,76 | 10,34 | 320,82 | 11,26 | 373,95 | 12,19 | 431,14 | 13,11 | 492,40 | 14,03 | 557,72 | 14,96 |
| 11,35 | 12,74 | 14,13 | 15,51 | 16,90 | 18,28 | 19,67 | 21,05 | 22,44 | |||||||||||
| 1,0 | 274,92 | 6,04 | 343,29 | 6,77 | 419,21 | 7,51 | 502,68 | 8,25 | 593,72 | 8,98 | 692,33 | 9,72 | 798,49 | 10,45 | 912,21 | 11,19 | 1033,50 | 11,93 | |
| 9,05 | 10,16 | 11,26 | 12,37 | 13,47 | 14,58 | 15,68 | 16,78 | 17,89 | |||||||||||
| 1,5 | 377,95 | 5,53 | 472,40 | 6,20 | 577,34 | 6,87 | 692,78 | 7,55 | 818,71 | 8,22 | 955,12 | 8,89 | 1102,03 | 9,57 | 1259,43 | 10,24 | 1427,33 | 10,92 | |
| 8,29 | 9,30 | 10,31 | 11,32 | 12,33 | 13,34 | 14,35 | 15,36 | 16,37 | |||||||||||
| 2,0 | 458,00 | 5,27 | 573,16 | 5,91 | 701,17 | 6,55 | 842,04 | 7,20 | 995,77 | 7,84 | 1162,34 | 8,48 | 1341,78 | 9,12 | 1534,06 | 9,77 | 1739,21 | 10,41 | |
| 7,90 | 8,87 | 9,83 | 10,80 | 11,76 | 12,72 | 13,69 | 14,65 | 15,61 | |||||||||||
| Průřez b/h [mm] | 450/500 | 450/550 | 450/600 | 450/650 | 450/700 | 450/750 | 450/800 | 450/850 | 450/900 | ||||||||||
| Procento vyztužení ρ [%] | 0,5 | 209,50 | 8,49 | 255,10 | 9,42 | 305,73 | 10,34 | 360,93 | 11,26 | 420,69 | 12,19 | 485,04 | 13,11 | 553,95 | 14,03 | 627,44 | 14,96 | 705,50 | 15,88 |
| 12,74 | 14,13 | 15,51 | 16,90 | 18,28 | 19,67 | 21,05 | 22,44 | 23,82 | |||||||||||
| 1,0 | 386,20 | 6,77 | 471,61 | 7,51 | 562,52 | 8,25 | 667,94 | 8,98 | 448,87 | 9,72 | 898,30 | 10,45 | 1026,24 | 11,19 | 1162,68 | 11,93 | 1307,64 | 12,66 | |
| 10,16 | 11,26 | 12,37 | 13,47 | 14,58 | 15,68 | 16,78 | 17,89 | 18,99 | |||||||||||
| 1,5 | 531,45 | 6,20 | 649,51 | 6,87 | 779,38 | 7,55 | 921,04 | 8,22 | 1074,51 | 8,89 | 1239,79 | 9,57 | 1416,86 | 10,24 | 1605,74 | 10,92 | 1806,42 | 11,59 | |
| 9,30 | 10,31 | 11,32 | 12,33 | 13,34 | 14,35 | 15,36 | 16,37 | 17,38 | |||||||||||
| 2,0 | 644,80 | 5,91 | 788,80 | 6,55 | 947,30 | 7,20 | 1120,24 | 7,84 | 1307,64 | 8,48 | 1509,50 | 9,12 | 1724,82 | 9,77 | 1956,61 | 10,41 | 2201,85 | 11,05 | |
| 8,87 | 9,83 | 10,80 | 11,76 | 12,72 | 13,69 | 14,65 | 15,61 | 16,58 | |||||||||||
| Průřez b/h [mm] | 500/550 | 500/600 | 500/650 | 500/700 | 500/750 | 500/800 | 500/850 | 500/900 | 500/950 | ||||||||||
| Procento vyztužení ρ [%] | 0,5 | 283,45 | 9,42 | 339,70 | 10,34 | 401,03 | 11,26 | 467,44 | 12,19 | 538,93 | 13,11 | 615,50 | 14,03 | 697,15 | 14,96 | 738,88 | 15,88 | 875,70 | 16,80 |
| 14,13 | 15,51 | 16,90 | 18,28 | 19,67 | 21,05 | 22,44 | 23,82 | 25,21 | |||||||||||
| 1,0 | 524,01 | 7,51 | 628,36 | 8,25 | 742,16 | 8,98 | 865,41 | 9,72 | 998,11 | 10,45 | 1140,26 | 11,19 | 1291,87 | 11,93 | 1452,93 | 12,66 | 1623,44 | 13,40 | |
| 11,26 | 12,37 | 13,47 | 14,58 | 15,68 | 16,78 | 17,89 | 18,99 | 20,10 | |||||||||||
| 1,5 | 721,68 | 6,87 | 865,97 | 7,55 | 1023,38 | 8,22 | 1193,90 | 8,89 | 1377,54 | 9,57 | 1574,29 | 10,24 | 1784,16 | 10,92 | 2007,14 | 11,59 | 2243,23 | 12,26 | |
| 10,31 | 11,32 | 12,33 | 13,34 | 14,35 | 15,36 | 16,37 | 17,38 | 18,39 | |||||||||||
| 2,0 | 876,47 | 6,55 | 1052,55 | 7,20 | 1244,71 | 7,84 | 1452,93 | 8,48 | 1677,22 | 9,12 | 1917,58 | 9,77 | 2174,01 | 10,41 | 2446,50 | 11,05 | 2735,07 | 11,70 | |
| 9,83 | 10,80 | 11,76 | 12,72 | 13,69 | 14,65 | 15,61 | 16,58 | 17,54 | |||||||||||
| Průřez b/h [mm] | 550/600 | 550/650 | 550/700 | 550/750 | 550/800 | 550/850 | 550/900 | 550/950 | 550/1000 | ||||||||||
| Procento vyztužení ρ [%] | 0,5 | 373,67 | 10,34 | 441,13 | 11,26 | 514,18 | 12,19 | 592,82 | 13,11 | 677,05 | 14,03 | 766,87 | 14,96 | 862,27 | 15,88 | 962,27 | 16,80 | 1067,85 | 17,73 |
| 15,51 | 16,90 | 18,28 | 19,67 | 21,05 | 22,44 | 23,82 | 25,21 | 26,59 | |||||||||||
| 1,0 | 691,19 | 8,25 | 816,37 | 8,98 | 951,95 | 9,72 | 1097,92 | 10,45 | 1254,29 | 11,19 | 1421,06 | 11,93 | 1598,22 | 12,66 | 1785,78 | 13,40 | 1983,74 | 14,13 | |
| 12,37 | 13,47 | 14,58 | 15,68 | 16,78 | 17,89 | 18,99 | 20,10 | 21,90 | |||||||||||
| 1,5 | 952,57 | 7,55 | 1125,72 | 8,22 | 1313,29 | 8,89 | 1515,29 | 9,57 | 1731,72 | 10,24 | 1962,57 | 10,92 | 2207,85 | 11,59 | 2467,55 | 12,26 | 2741,68 | 12,94 | |
| 11,32 | 12,33 | 13,34 | 14,35 | 15,36 | 16,37 | 17,38 | 18,39 | 19,41 | |||||||||||
| 2,0 | 1157,81 | 7,20 | 1369,18 | 7,84 | 1598,22 | 8,48 | 1844,94 | 9,12 | 2109,34 | 9,77 | 2391,41 | 10,41 | 2691,15 | 11,05 | 3008,57 | 11,70 | 3343,67 | 12,34 | |
| 10,80 | 11,76 | 12,72 | 13,69 | 14,65 | 15,61 | 16,58 | 17,54 | 18,51 | |||||||||||
| Průřez b/h [mm] | 600/650 | 600/700 | 600/750 | 600/800 | 600/850 | 600/900 | 600/950 | 600/1000 | 600/1050 | ||||||||||
| Procento vyztužení ρ [%] | 0,5 | 481,23 | 11,26 | 560,93 | 12,19 | 646,72 | 13,11 | 739,60 | 14,03 | 836,58 | 14,96 | 940,66 | 15,88 | 1050,84 | 16,80 | 1167,11 | 17,73 | 1289,48 | 18,65 |
| 16,90 | 18,28 | 19,67 | 21,05 | 22,44 | 23,82 | 25,21 | 26,59 | 27,98 | |||||||||||
| 1,0 | 890,59 | 8,98 | 1038,49 | 9,72 | 1197,73 | 10,45 | 1368,32 | 11,19 | 1550,25 | 11,93 | 1743,52 | 12,66 | 1948,13 | 13,40 | 2164,08 | 14,13 | 2391,38 | 14,87 | |
| 13,47 | 14,58 | 15,68 | 16,78 | 17,89 | 18,99 | 20,10 | 21,90 | 22,31 | |||||||||||
| 1,5 | 1228,06 | 8,22 | 1432,68 | 8,89 | 1653,05 | 9,57 | 1889,15 | 10,24 | 2140,99 | 10,92 | 2408,56 | 11,59 | 2691,88 | 12,26 | 2990,93 | 12,94 | 3305,71 | 13,61 | |
| 12,33 | 13,34 | 14,35 | 15,36 | 16,37 | 17,38 | 18,39 | 19,41 | 20,42 | |||||||||||
| 2,0 | 1493,65 | 7,84 | 1743,52 | 8,48 | 2012,87 | 9,12 | 2301,10 | 9,77 | 2608,81 | 10,41 | 2935,80 | 11,05 | 3282,08 | 11,70 | 3647,64 | 12,34 | 4032,48 | 12,98 | |
| 11,76 | 12,72 | 13,69 | 14,65 | 15,61 | 16,58 | 17,54 | 18,51 | 19,47 | |||||||||||
Příklad 4.8
Navrhněte trámový strop nad půdorysem uvedeným na schématu. Jedná se o prodejní objekt. Skladbu podlahy uvažujte podle tab. 3.7, skladba č. 8.
Návrhové hodnoty zatížení na 1 m2 stropu
Stálé:
- podlaha
\begin{gathered}
3{,}21\space\text{kN/m}^2
\end{gathered}- železobetonová deska tl. 80 mm
\begin{gathered}
0{,}080\cdot25\cdot1{,}35=2{,}70\space\text{kN/m}^2
\end{gathered}Stálé celkem
\begin{gathered}
5{,}91\space\text{kN/m}^2
\end{gathered}Užitné – obchodní plochy D2
\begin{gathered}
7{,}5\space\text{kN/m}^2
\end{gathered}Zatížení celkem
\begin{gathered}
13{,}41\space\text{kN/m}^2
\end{gathered}Trám
Zatížení na trám:
- od desky
\begin{gathered}
13{,}41\cdot1{,}2=16{,}09\space\text{kN/m}
\end{gathered}- vlastní tíha
\begin{gathered}
0{,}2\cdot0{,}4\cdot25\cdot1{,}35=2{,}70\space\text{kN/m}
\end{gathered}Celkem
\begin{gathered}
q_\text{d}=18{,}79\space\text{kN/m}
\end{gathered}Trámy působí jako spojité nosníky o dvou polích, ohybový moment vypočítáme jako
\begin{gathered}
M=q_\text{d}\cdot\ell^2/8=18{,}79\cdot4{,}5^2/8=47{,}57\space\text{kNm}.
\end{gathered}Hodnotu vypočítaného momentu zaokrouhlíme na 50 kNm a v tabulkách rozměrů železobetonových trámů vyhledáme, že dané hodnotě odpovídá například průřez 200/400 mm při procentu vyztužení 0,5 %, Při výpočtu zatížení jsme předpokládali průřez 200/400 mm, zatížení se nepřepočítává.
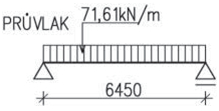
Průvlak
Reakce od trámů
prostření reakce B = 1,25q · ℓ
\begin{gathered}
1{,}25\cdot18{,}79\cdot4{,}5=105{,}69\space\text{kN}
\end{gathered}Rozpočítano na spojité zatížení
\begin{gathered}
105{,}69\cdot4/6{,}45=65{,}54\space\text{kN/m}
\end{gathered}vlastní tíha
\begin{gathered}
0{,}3\cdot0{,}6\cdot25\cdot1{,}35=6{,}07\space\text{kN/m}
\end{gathered}Celkem
\begin{gathered}
q_\text{d}=71{,}61\space\text{kN/m}
\end{gathered}Průvlak působí jako prostý nosník
\begin{gathered}
M=q_\text{d}\cdot\ell^2/8=71{,}61\cdot6{,}45^2/8=372{,}39\space\text{kNm}.
\end{gathered}Pro vypočítanou hodnotu momentu se vyhledá v tab. 4.7 odpovídající průřez 350/550 mm při procentu vyztužení 1 %. Rozpětí, odpovídající vymezující štíhlosti je 7,51 m, což je větší než naše rozpětí 6,45 m.
Příklad 4.9
Navrhněte železobetonový žebírkový strop v hotelové budově, ve které je nosná konstrukce uspořádána do příčného stěnového systému. Žebírka uvažujte obdélníkového průřezu, která budou při provádění bedněna plechovými vyjímatelnými tvarovkami, podkládanými na rovinné bednění. Podlahu uvažujte podle tab. 3.7, skladba č. 4.
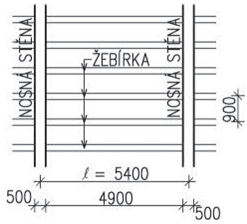
Návrhové hodnoty zatížení na 1 m2 stropu
Stálé:
- podlaha
\begin{gathered}
1{,}15\space\text{kN/m}^2
\end{gathered}- železobetonová deska tl. 70 mm
\begin{gathered}
0{,}070\cdot25\cdot1{,}35=2{,}36\space\text{kN/m}^2
\end{gathered}- podhled SDK s roštem
\begin{gathered}
(0{,}015\cdot12+0{,}1)\cdot1{,}35=0{,}38\space\text{kN/m}^2
\end{gathered}Stálé celkem
\begin{gathered}
3{,}89\space\text{kN/m}^2
\end{gathered}Užitné
\begin{gathered}
1{,}5\cdot1{,}5=2{,}25\space\text{kN/m}^2
\end{gathered}Zatížení celkem
\begin{gathered}
6{,}14\space\text{kN/m}^2
\end{gathered}Zatížení na žebírko:
- od stropu
\begin{gathered}
6{,}14\cdot0{,}9=5{,}52\space\text{kN/m}
\end{gathered}- vlastní tíha
\begin{gathered}
0{,}15\cdot0{,}3\cdot25\cdot1{,}35=1{,}52\space\text{kN/m}
\end{gathered}Celkem
\begin{gathered}
q_\text{d}=7{,}04\space\text{kN/m}
\end{gathered}Žebírka působí jako spojité nosníky o více polích, ohybový moment vypočítáme jako
\begin{gathered}
M=q_\text{d}\cdot\ell^2/10=7{,}04\cdot5{,}4^2/10=20{,}53\space\text{kNm}.
\end{gathered}Podle hodnoty vypočítaného momentu 20,53 kNm se vyhledá v tab. 4.5 průřez 100/350 mm při procentu vyztužení 0,5 %. Rozpětí, odpovídající vymezující štíhlosti tj. 8,59 m je větší než rozpětí 5,4 m.
Příklad 4.10
V jednom z pavilonů mateřské školy proveďte návrh průvlaků. Přes průvlaky je pnuta železobetonová deska na rozpětí 3 m, tloušťka desky je 120 mm. Vnější nosný plášť je zděný, uvnitř objektu jsou nosné sloupy, jejich umístění je patrné ze schématu. Průvlak navrhněte jako skrytý s výškou nepřesahující 300 mm. Podlahu uvažujte podle tab. 3.7, skladba č. 2.
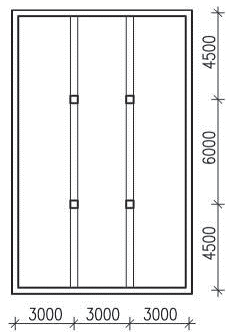
Návrhové hodnoty zatížení na 1 m2 stropu
Stálé:
- podlaha
\begin{gathered}
1{,}02\space\text{kN/m}^2
\end{gathered}- železobetonová deska tl. 120 mm
\begin{gathered}
0{,}120\cdot25\cdot1{,}35=4{,}05\space\text{kN/m}^2
\end{gathered}- podhled (podle údajů výrobce)
\begin{gathered}
0{,}90\space\text{kN/m}^2
\end{gathered}Stálé celkem
\begin{gathered}
5{,}97\space\text{kN/m}^2
\end{gathered}Užitné
\begin{gathered}
1{,}5\cdot1{,}5=2{,}25\space\text{kN/m}^2
\end{gathered}Zatížení celkem
\begin{gathered}
8{,}22\space\text{kN/m}^2
\end{gathered}Zatížení na průvlak:
- od stropu
\begin{gathered}
8{,}22\cdot3{,}0=24{,}66\space\text{kN/m}
\end{gathered}- vlastní tíha
\begin{gathered}
0{,}50\cdot0{,}30\cdot25\cdot1{,}35=5{,}06\space\text{kN/m}
\end{gathered}Celkem
\begin{gathered}
q_\text{d}=29{,}72\space\text{kN/m}
\end{gathered}Průvlaky působí jako spojité nosníky o třech polích, ohybový moment se vypočítá jako
\begin{gathered}
M=q_\text{d}\cdot\ell^2/10=29{,}72\cdot((4{,}5+6{,}0)/2)^2/10=81{,}915\space\text{kNm}.
\end{gathered}Podle hodnoty vypočítaného momentu 81,915 kNm se vyhledá v tab. 4.6 průřez 500/300 mm při procentu vyztužení 0,5 %. Rozpětí, odpovídající vymezující štíhlosti pro vnitřní pole spojitého nosníku, tj. 7,2 m je větší než naše rozpětí 6,0 m, překročení návrhové únosnosti o cca 4 % bude zajištěno větším procentem vyztužení.
5 PŘEKLADY
Překlady se používají nad dveřními, okenními popř. jinými otvory a slouží k přenosu zatížení působícího nad otvorem do zdiva kolem otvoru.
5.1 ZATÍŽENÍ
Zatížení na překlad se skládá jednak ze zatížení zdivem, které je nad překladem a vlastní tíhy překladu, jednak ze zatížení stropní konstrukce, která může být uložena do zdiva nad překladem.

Obr. 5.1 Rozložené zatížení
5.1.1 Zatížení pouze nadezděným zdivem
Vlivem vazby zdiva předpokládáme, že překlad zatěžuje pouze trojúhelník zdiva vyznačený na obrázku. Zatížení trojúhelníkové převedeme na rovnoměrné spojité zatížení o velikosti
\begin{gathered}
q_\text{k}=\frac{1{,}73\ell_\text{s}}{4}\cdot g\space[\text{kN/m}]
\end{gathered}kde je
ℓs … světlost otvoru [m],
g … návrhovová hodnota vlastní tíhy stěny [kN/m2].
Tento případ nastává tehdy, jestliže nad překladem nejsou uloženy stropy.
Příklad 5.1
Vypočítejte zatížení na překlad nad otvorem o světlosti ℓs = 1,8 m v cihelné zdi z plných pálených cihel tloušťky t = 450 mm. Předpokládejte, že překlad budou tvořit dva profily IPN 120.
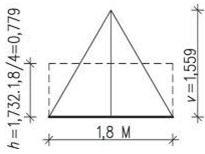
Zatížení od zdiva
\begin{gathered}
q_\text{k}=(1{,}73\cdot1{,}8/4)\cdot0{,}45\cdot18\cdot1{,}35=8{,}51\space\text{kN/m}
\end{gathered}2 IPN 120 vlastní tíha
\begin{gathered}
2\cdot0{,}111\cdot1{,}35=0{,}30\space\text{kN/m}
\end{gathered}Zatížení celkem
\begin{gathered}
8{,}81\space\text{kN/m}
\end{gathered}5.1.2 Zatížení překladu do stropů, které jsou nad ním uloženy
Jestliže jsou nad překladem uloženy stropy, je překlad kromě nadezdění zatížen reakcí od stropu.
Příklad 5.2
Vypočítejte zatížení na překlad nad otvorem o světlosti ℓs = 1,5 m. Bezprostředně nad překladem jsou uloženy stropní panely, jejichž rozpětí ℓ = 4,2 m. Plošné celkové návrhové zatížení stropu je g = 8,5 kN/m2.
Zatěžovací šířka, ze které se na překlad přenáší zatížení stropu je 4,2 / 2 = 2,1 m.
Zatížení stropu
\begin{gathered}
8{,}5\cdot2{,}10=17{,}85\space\text{kN/m}
\end{gathered}Vlastní tíha
\begin{gathered}
0{,}2\cdot0{,}25\cdot25\cdot1{,}35=1{,}69\space\text{kN/m}
\end{gathered}Nadezdívka
\begin{gathered}
1{,}73\cdot1{,}5/4\cdot0{,}25\cdot18\cdot1{,}35=3{,}94\space\text{kN/m}
\end{gathered}Zatížení celkem
\begin{gathered}
23{,}48\space\text{kN/m}
\end{gathered}5.2 PREFABRIKOVANÉ PŘEKLADY
5.2.1 Překlady betonové
Prefabrikované překlady jsou v současné době jedny z nejpoužívanějších překladů. Mezi jejich největší výhody patří rychlá montáž. Základní rozměry překladů jsou v násobcích zdicích prvků, sestavením jednotlivých prefabrikátů lze vytvořit překlad nad libovolnou tloušťkou stěny.
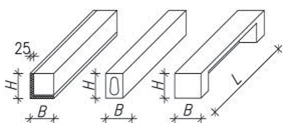
Obr. 5.2 Překlady betonové
Překlady RTP mají na vnější straně vrstvu z desky z dřevěné vlny a cementu (například heraklit). Tyto překlady se používají pro vnější stěny.
Jelikož jsou překlady vyztuženy na zatížení působící shora, nesmějí se zabudovávat otočené o 90° nebo 180°.
Prefabrikované překlady se posuzují tak, že se vypočítá charakteristické hodnota zatížení působící na překlad vyjma vlastní tíhy překladu a porovná se s přípustným zatížením překladu. V současné době se vyrábí překlady uvedené v tab. 5.1–5.4.
Příklad 5.3
Posuďte železobetonový prefabrikovaný překlad nad otvorem světlosti ℓs = 2,4 m. Překlad je uložen na obvodové zdi tloušťky t = 450 mm z plných cihel. Stropy jsou uloženy rovnoběžně s překladem, a tudíž překlad nezatěžují
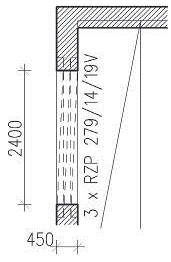
Zatížení
Nadezdívka
\begin{gathered}
(1{,}73\cdot2{,}4/4)\cdot0{,}45\cdot18=8{,}408\space\text{kN/m}
\end{gathered}Překlad je tvořen z následujících prefabrikátů tab. 5.4
3 x RZP 279/14/19V
Hodnoty přípustných hodnot charakteristického zatížení:
RZP 279/14/19V
\begin{gathered}
3\cdot4{,}5=13{,}50\space\text{kN/m}
\end{gathered}Celkem
\begin{gathered}
13{,}50\space\text{kN/m}
\end{gathered}Únosnost složeného překladu je 13,50 kN/m > 8,408 kN/m.
Tab. 5.1 Překlady výšky 240 mm P – plné, V – vylehčené
| Značka | Rozměry [mm] | Hmotnost [kg] | Zatížení qk [kN/m] | Posouvající síla Vud [kN] | Moment Mud [kNm] | Mezní moment při limitním průhybu Mlim [kNm] | Maximální průhyb w [mm] | Délka uložení [mm] | ||
| délka L | šířka B | výška H | ||||||||
| RZP119/7/24P | 1190 | 70 | 240 | 42 | 11,0 | 5,6 | 2,95 | 2,36 | 0,1 | 140 |
| RZP149/7/24P | 1490 | 70 | 240 | 54 | 11,0 | 7,7 | 4,82 | 3,87 | 1,1 | 140 |
| RZP179/7/24P | 1790 | 70 | 240 | 64 | 11,0 | 9,9 | 7,10 | 5,69 | 2,7 | 140 |
| RZP209/7/24P | 2090 | 70 | 240 | 74 | 11,0 | 12,0 | 9,70 | 7,78 | 4,9 | 140 |
| RZP239/7/24P | 2390 | 70 | 240 | 86 | 11,0 | 13,4 | 10,33 | 8,28 | 8,7 | 190 |
| RZP269/7/24P | 2690 | 70 | 240 | 97 | 11,0 | 15,5 | 13,08 | 10,48 | 12,0 | 190 |
| RZP299/7/24P | 2990 | 70 | 240 | 108 | 11,0 | 17,7 | 15,89 | 12,16 | 14,0 | 190 |
| RZP329/7/24P | 3290 | 70 | 240 | 118 | 11,0 | 19,8 | 17,60 | 13,53 | 15,5 | 190 |
| RZP119/12/24V | 1190 | 115 | 240 | 55 | 17,2 | 8,4 | 5,13 | 4,29 | 0,1 | 140 |
| RZP149/12/24V | 1490 | 115 | 240 | 64 | 17,2 | 11,5 | 8,90 | 7,43 | 0,8 | 140 |
| RZP179/12/24V | 1790 | 115 | 240 | 82 | 17,2 | 14,7 | 15,00 | 12,53 | 2,1 | 140 |
| RZP209/12/24V | 2090 | 115 | 240 | 93 | 17,2 | 17,9 | 15,00 | 12,53 | 5,0 | 140 |
| RZP239/12/24V | 2390 | 115 | 240 | 112 | 17,2 | 20,0 | 20,07 | 16,77 | 6,7 | 190 |
| RZP269/12/24V | 2690 | 115 | 240 | 117 | 17,2 | 23,3 | 25,34 | 21,16 | 9,3 | 190 |
| RZP119/14/24V | 1190 | 140 | 240 | 61,5 | 21,6 | 10,5 | 5,15 | 4,31 | 0,1 | 140 |
| RZP149/14/24V | 1490 | 140 | 240 | 74,1 | 21,6 | 14,5 | 10,80 | 9,02 | 1,1 | 140 |
| RZP179/14/24V | 1790 | 140 | 240 | 87,6 | 21,6 | 18,4 | 15,40 | 12,87 | 2,6 | 140 |
| RZP209/14/24V | 2090 | 140 | 240 | 103,3 | 21,6 | 22,4 | 20,07 | 17,29 | 4,7 | 140 |
| RZP239/14/24V | 2390 | 140 | 240 | 131,8 | 21,6 | 25,1 | 20,07 | 17,29 | 8,2 | 190 |
| RZP269/14/24V | 2690 | 140 | 240 | 134,2 | 21,6 | 29,1 | 26,45 | 22,10 | 11,5 | 190 |
| qk – charakteristická hodnota zatížení bez vlastní tíhy překladu, Vud – návrhová hodnota únosnosti pro posouvající sílu, Mud – návrhová hodnota momentu únosnosti. |
||||||||||
Tab. 5.2 Překlady výšky 140 mm V – vylehčené
| Značka | Rozměry [mm] | Hmotnost [kg] | Zatížení qk [kN/m] | Posouvající síla Vud [kN] | Moment Mud [kNm] | Mezní moment při limitním průhybu Mlim [kNm] | Maximální průhyb w [mm] | Délka uložení [mm] | ||
| délka L | šířka B | výška H | ||||||||
| RZP89/14/14V | 890 | 140 | 140 | 33 | 4,07 | 6,4 | 2,13 | 1,72 | 0,0 | 140 |
| RZP119/14/14V | 1190 | 140 | 140 | 41 | 4,07 | 6,4 | 2,13 | 1,72 | 0,1 | 140 |
| RZP149/14/14V | 1490 | 140 | 140 | 55 | 4,07 | 6,4 | 2,13 | 1,72 | 0,3 | 140 |
| RZP179/14/14V | 1790 | 140 | 140 | 67 | 4,07 | 6,8 | 2,91 | 2,35 | 1,8 | 140 |
| RZP209/14/14V | 2090 | 140 | 140 | 76 | 4,07 | 7,6 | 4,08 | 3,87 | 4,3 | 140 |
| RZP239/14/14V | 2390 | 140 | 140 | 86 | 4,07 | 7,6 | 4,08 | 3,87 | 9,7 | 140 |
| RZP254/14/14V | 2540 | 140 | 140 | 93 | 4,07 | 7,6 | 4,08 | 3,41 | 12,0 | 140 |
| RZP284/14/14V | 2840 | 140 | 140 | 104 | 4,07 | 8,3 | 7,01 | 4,30 | 13,5 | 140 |
| qk – charakteristická hodnota zatížení bez vlastní tíhy překladu, Vud – návrhová hodnota únosnosti pro posouvající sílu, Mud – návrhová hodnota momentu únosnosti. |
||||||||||
Tab. 5.3 Překlady výšky 220 mm V – vylehčené
| Značka | Rozměry [mm] | Hmotnost [kg] | Zatížení qk [kN/m] | Posouvající síla Vud [kN] | Moment Mud [kNm] | Mezní moment při limitním průhybu Mlim [kNm] | Maximální průhyb w [mm] | Délka uložení [mm] | ||
| délka L | šířka B | výška H | ||||||||
| RZP119/14/22V | 1190 | 140 | 215 | 73 | 17,20 | 8,9 | 3,18 | 3,67 | 0,1 | 140 |
| RZP149/14/22V | 1490 | 140 | 215 | 89 | 17,20 | 12,2 | 7,87 | 5,74 | 1,2 | 140 |
| RZP179/14/22V | 1790 | 140 | 215 | 109 | 17,20 | 15,6 | 9,32 | 8,74 | 4,0 | 140 |
| RZP239/14/22V | 2390 | 140 | 215 | 146 | 17,20 | 21,2 | 17,86 | 14,41 | 8,7 | 190 |
| RZP254/14/22V | 2540 | 140 | 215 | 157 | 17,20 | 22,8 | 22,79 | 14,32 | 9,2 | 190 |
| RZP284/14/22V | 2840 | 140 | 215 | 178 | 17,20 | 26,2 | 27,87 | 17,19 | 12,0 | 190 |
| qk – charakteristická hodnota zatížení bez vlastní tíhy překladu, Vud – návrhová hodnota únosnosti pro posouvající sílu, Mud – návrhová hodnota momentu únosnosti. |
||||||||||
Tab. 5.4 Překlady výšky 190 mm P – plné, V – vylehčené
| Značka | Rozměry [mm] | Hmotnost [kg] | Zatížení qk [kN/m] | Posouvající síla Vud [kN] | Moment Mud [kNm] | Mezní moment při limitním průhybu Mlim [kNm] | Maximální průhyb w [mm] | Délka uložení [mm] | ||
| délka L | šířka B | výška H | ||||||||
| RZP119/12/19V | 1190 | 115 | 190 | 59 | 3,50 | 7,2 | 3,06 | 2,48 | 0,0 | 140 |
| RZP149/12/19V | 1490 | 115 | 190 | 73 | 3,50 | 7,2 | 3,06 | 2,48 | 0,1 | 140 |
| RZP179/12/19V | 1790 | 115 | 190 | 87 | 3,50 | 7,2 | 3,06 | 2,48 | 0,3 | 140 |
| RZP209/12/19V | 2090 | 115 | 190 | 104 | 3,50 | 7,2 | 3,06 | 2,48 | 0,5 | 140 |
| RZP239/14/19V | 2390 | 115 | 190 | 118 | 3,50 | 7,6 | 4,20 | 3,41 | 2,0 | 140 |
| RZP269/14/19V | 2690 | 115 | 190 | 132 | 3,50 | 7,6 | 4,20 | 3,41 | 5,8 | 140 |
| RZP299/14/19V | 2990 | 115 | 190 | 146 | 3,50 | 8,4 | 6,99 | 5,67 | 7,7 | 140 |
| RZP119/14/19V | 1190 | 140 | 190 | 63 | 4,50 | 8,6 | 4,32 | 3,49 | 0,1 | 140 |
| RZP159/14/19V | 1590 | 140 | 190 | 84 | 4,50 | 8,6 | 4,32 | 3,49 | 0,2 | 140 |
| RZP199/14/19V | 1990 | 140 | 190 | 105 | 4,50 | 8,6 | 4,32 | 3,49 | 0,5 | 140 |
| RZP239/14/19V | 2390 | 140 | 190 | 127 | 4,50 | 9,5 | 7,15 | 5,78 | 3,3 | 140 |
| RZP279/14/19V | 2790 | 140 | 190 | 148 | 4,50 | 10,3 | 10,58 | 8,55 | 6,7 | 140 |
| RZP319/14/19V | 3190 | 140 | 190 | 169 | 4,50 | 10,3 | 10,58 | 8,55 | 13,8 | 140 |
| RZP119/14/19P | 1190 | 240 | 190 | 128 | 24,38 | 12,4 | 5,89 | 4,93 | 0,1 | 140 |
| RZP149/14/19P | 1490 | 240 | 190 | 161 | 24,38 | 17,0 | 10,56 | 8,84 | 1,0 | 140 |
| RZP179/14/19P | 1790 | 240 | 190 | 195 | 24,38 | 21,6 | 14,38 | 12,41 | 3,2 | 140 |
| RZP199/14/19P | 1990 | 240 | 190 | 217 | 24,38 | 24,6 | 14,80 | 12,41 | 0,6 | 140 |
| RZP239/14/19P | 2790 | 240 | 190 | 260 | 24,38 | 29,3 | 24,74 | 20,70 | 9,4 | 140 |
| RZP269/14/19P | 3190 | 240 | 190 | 295 | 24,38 | 33,9 | 34,88 | 29,18 | 11,8 | 140 |
| RZP299/14/19P | 3190 | 240 | 190 | 327 | 24,38 | 38,5 | 43,54 | 36,44 | 13,4 | 140 |
| RZP319/14/19P | 3190 | 240 | 190 | 351 | 24,38 | 41,6 | 43,72 | 33,55 | 15,0 | 140 |
| qk – charakteristická hodnota zatížení bez vlastní tíhy překladu, Vud – návrhová hodnota únosnosti pro posouvající sílu, Mud – návrhová hodnota momentu únosnosti. |
||||||||||
Tab. 5.5 Překlady s tepelnou izolací P – plné
| Značka | RTP119/14/14P | RTP149/14/14P | RTP179/14/14P | |
| Rozměry [mm] | délka L | 1190,0 | 1490,0 | 1790,0 |
| šířka B | 140,0 | 140,0 | 140,0 | |
| výška H | 140,0 | 140,0 | 140,0 | |
| Hmotnost [kg] | 35,0 | 47,0 | 55,0 | |
| Zatížení qk [kN/m] | 4,07 | 4,07 | 4,07 | |
| Posouvající síla Vud [kN] | 8,3 | 8,3 | 9,0 | |
| Moment Mud [kNm] | 2,03 | 2,03 | 2,03 | |
| Mezní moment při limitním průhybu Mlim [kNm] | 1,64 | 2,64 | 2,73 | |
| Maximální průhyb w [mm] | 0,2 | 2,2 | 5,0 | |
| Délka uložení [mm] | 140,0 | 140,0 | 140,0 | |
| qk – charakteristická hodnota zatížení bez vlastní tíhy překladu, Vud – návrhová hodnota únosnosti pro posouvající sílu, Mud – návrhová hodnota momentu únosnosti. |
||||
5.3 KERAMICKÉ PŘEKLADY
5.3.1 Překlady samonosné (vysoké)
Keramické překlady se používají zejména v cihelném zdivu, neboť potom spolu se zdicím materiálem tvoří jednolitý podklad pro omítku.
Tab. 5.6 Technické údaje keramických překladů (Porotherm překlady KP 7, Heluz 23,8)
| Délka L [mm] | Délka uložení [mm] | Světlá délka ℓs [mm] | Posouvající síla Vud [kN] | Moment Mud [kNm] | Zatížení gd pro počet překladů | |||
| 1 kus | 2 kusy | 3 kusy | 4 kusy | |||||
| 1000 | 125 | 750 | 14,7 | 1,62 | 14,9 | 29,7 | 44,6 | 59,4 |
| 1250 | 1000 | 14,5 | 3,06 | 12,7 | 25,4 | 38,1 | 50,8 | |
| 1500 | 1250 | 14,5 | 3,06 | 11,2 | 22,4 | 33,7 | 44,9 | |
| 1750 | 1500 | 14,4 | 4,84 | 10,1 | 20,2 | 30,3 | 40,4 | |
| 2000 | 200 | 1600 | 14,3 | 4,84 | 12,3 | 24,6 | 36,9 | 49,2 |
| 2250 | 1850 | 14,2 | 5,81 | 12,2 | 24,4 | 36,6 | 48,8 | |
| 2500 | 250 | 2000 | 14,2 | 5,81 | 10,1 | 20,3 | 30,4 | 40,6 |
| 2750 | 2250 | 14,2 | 7,83 | 8,2 | 16,4 | 24,7 | 32,9 | |
| 3000 | 2500 | 14,2 | 7,83 | 6,8 | 13,6 | 20,3 | 27,1 | |
| 3025 | 2750 | 14,2 | 7,83 | 5,6 | 11,3 | 16,9 | 22,5 | |
| 3500 | 3000 | 14,2 | 7,83 | 4,7 | 9,4 | 14,2 | 18,9 | |
| qd – maximální hodnota spojitého rovnoměrného zatížení bez vlastní tíhy překladu [kN/m], Vud – maximální hodnota posouvající síly na jeden překlad od návrhového zatížení [kN], Mud – maximální hodnota ohybového momentu na jeden překlad od návrhového zatížení [kNm]. Hmotnost překladu 35 kg/m. |
||||||||
Keramické překlady se vyrábí z keramických tvarovek. Nejpoužívanější jsou keramické tvarovky ve tvaru U. Tvarovky se položí vedle sebe naležato, uloží se výztuž, korýtko se zabetonuje a vznikne prefabrikát. Překlady mají šířku 70 mm, výšku 238 mm a zabudovávají se na výšku. Délka překladu je v násobcích délky tvarovky tj. 250 mm. Překlady vysoké 238 mm působí samostatně, v únosnosti není započítáno spolupůsobení zdiva.
Příklad 5.4
Navrhněte překlad v cihelné stěně tloušťky t = 450 mm je otvor světlosti ℓs = 1,6 m. Překlad není zatížen stropní konstrukcí.
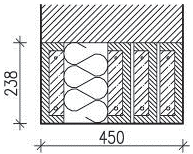
Zatížení nadložním zdivem – návrhová hodnota
\begin{gathered}
(1{,}73\cdot1{,}6/4)\cdot0{,}45\cdot18\cdot1{,}35=7{,}567\space\text{kN/m}
\end{gathered}Vlastní hmotnost překladu (čtyři překlady délky 2,00 m)
\begin{gathered}
4\cdot0{,}35\cdot1{,}35=1{,}890\space\text{kN/m}
\end{gathered}Celkem
\begin{gathered}
9{,}457\space\text{kN/m}
\end{gathered}Jsou navrženy čtyři nosníky Porotherm překlad KP 7-2000 vyhovují s velkou rezervou.
\begin{gathered}
q_\text{d}=49{,}2\gg9{,}45\space\text{kN/m}
\end{gathered}5.3.2 Překlady spřažené (nízké)
Keramické překlady se používají zejména v cihelném zdivu, neboť potom spolu se zdicím materiálem tvoří jednolitý podklad pro omítku.
Keramické překlady ploché se vyrábí z keramických tvarovek tvaru U o šířkách 115 a 145 mm – viz obr. 5.3. Překlady se používají buď jako nenosné v příčkách, nebo jako nosné, pokud jsou dostatečně zakotveny v podporách a je zajištěno jejich spolupůsobení se zdivem nebo věncem, umístěným nad překladem (únosnosti nosných překladů jsou uvedeny v tab. 5.7 a 5.8, jako qud,2).
Obr. 5.3 Spřažené překlady
Tab. 5.7 Technické údaje keramických překladů, pro návrh jsou rozhodující tučně vyznačené hodnoty qud,1, qud,2 (Porotherm překlady KP 11,5)
| Délka L [mm] | Minimální délka uložení [mm] | Světlá délka ℓs [mm] | Zatížení | Průhyb wd, [mm] | |||
| qud,M [kN/m] | qud,V [kN/m] | qud,1 [kN/m] | qud,2 [kN/m] | ||||
| 750 | 115 | 500 | 93,9 | 125,3 | 72,8 | 145,3 | 1,6 |
| 1000 | 750 | 49,5 | 39,1 | 39,1 | 75,8 | 2,2 | |
| 1250 | 1000 | 29,1 | 17,9 | 17,9 | 33,4 | 2,8 | |
| 1500 | 1250 | 19,5 | 11,6 | 11,6 | 20,8 | 3,5 | |
| 1750 | 1500 | 13,9 | 8,6 | 8,6 | 14,8 | 4,1 | |
| 2000 | 1600 | 10,5 | 6,8 | 6,8 | 11,2 | 4,7 | |
| 2250 | 1850 | 8,2 | 5,7 | 5,7 | 8,9 | 5,3 | |
| 2500 | 2000 | 6,5 | 4,8 | 4,8 | 7,3 | 6,0 | |
| 2750 | 2250 | 5,3 | 4,2 | 4,2 | 6,0 | 6,6 | |
| 3000 | 2500 | 4,5 | 3,7 | 3,7 | 5,1 | 7,2 | |
Tab. 5.8 Technické údaje keramických překladů, pro návrh jsou rozhodující tučně vyznačené hodnoty qud,1, qud,2 (Porotherm překlady KP 14,5)
| Délka L [mm] | Minimální délka uložení [mm] | Světlá délka ℓs [mm] | Zatížení | Průhyb wd, [mm] | |||
| qud,M [kN/m] | qud,V [kN/m] | qud,1 [kN/m] | qud,2 [kN/m] | ||||
| 750 | 115 | 500 | 118,4 | 139,7 | 72,8 | 142,7 | 1,6 |
| 1000 | 750 | 62,4 | 49,0 | 48,6 | 94,3 | 2,2 | |
| 1250 | 1000 | 36,7 | 22,6 | 22,6 | 42,3 | 2,8 | |
| 1500 | 1250 | 24,6 | 14,6 | 14,6 | 26,3 | 3,5 | |
| 1750 | 1500 | 17,6 | 10,8 | 10,8 | 18,7 | 4,1 | |
| 2000 | 1600 | 13,2 | 8,6 | 8,6 | 14,3 | 4,7 | |
| 2250 | 1850 | 10,3 | 7,1 | 7,1 | 11,3 | 5,3 | |
| 2500 | 2000 | 8,2 | 6,1 | 6,1 | 9,3 | 6,0 | |
| 2750 | 2250 | 6,7 | 5,3 | 5,3 | 7,7 | 6,6 | |
| 3000 | 2500 | 5,6 | 4,7 | 4,7 | 6,5 | 7,2 | |
| qud,M – návrhová hodnota zatížení jednoho překladu včetně vlastní tíhy překladu a s ním spřažené nadezdívky a nadbetonováni při vyčerpání únosnosti v ohybu [kN/m], qud,V – návrhová hodnota zatížení jednoho překladu včetně vlastní tíhy překladu a s ním spřažené nadezdívky a nadbetonováni při vyčerpání únosnosti ve smyku [kN/m], qud,1 – maximální hodnota návrhového zatížení jednoho překladu včetně vlastní tíhy překladu a s ním spřažené nadezdívky a nadbetonováni [kN/m], qud,2 – maximální hodnota návrhového zatížení sestavy dvojice překladů bez vlastní tíhy překladu a s ním spřažené nadezdívky a nadbetonováni [kN/m], wd, – průbyb při maximální hodnotě návrhového zatížení [mm]. |
|||||||
5.4 MONOLITICKÉ PŘEKLADY
Monolitické překlady se nejčastěji používají v těch případech, kde nelze používat prefabrikované (například otvor je větší než vyráběný sortiment, překlad působí jako spojitý nosník apod.). Monolitické překlady mohou být ale v některých případech díky své technologii nevýhodné (například monolitický překlad pod montovanými stropy).
Zatížení na překlad se stanoví podle kap. 5.1 a dále se navrhuje jako betonový nosník při stanovení momentů podle kap. 4.1.3 a při stanovení rozměrů podle kap. 4.4.
Příklad 5.5
Navrhněte železobetonový monolitický překlad nad dva okenní otvory o šířce 2 100 mm v tloušťce zdi 300 mm, mezi kterými je pilíř 300 x 300 mm. Nad překladem jsou uloženy monolitické stropy o rozpětí 4,2 m, Návrhová hodnota celkového zatížení stropu je 9,8 kN/m2.
Zatížení:
- od stropu
\begin{gathered}
4{,}2/2\cdot9{,}8=20{,}58\space\text{kN/m}
\end{gathered}- vlastní tíha
\begin{gathered}
0{,}2\cdot0{,}3\cdot25\cdot1{,}35=2{,}03\space\text{kN/m}
\end{gathered}- nadložním zdivem
\begin{gathered}
(1{,}73\cdot2{,}1/4)\cdot0{,}3\cdot18\cdot1{,}35=6{,}62\space\text{kN/m}
\end{gathered}Celkem
\begin{gathered}
q_\text{d}=29{,}23\space\text{kN/m}
\end{gathered}Okenní otvory budou působit jako spojitý nosník. Rozpětí tohoto nosníku se stanoví následovně. V místě pilíře bude teoretická podpora ve středu pilíře, v místě navazující zdi bude teoretická podpora asi 100 mm od líce zdi. Rozpětí nosníku bude
\begin{gathered}
\ell=2{,}1+0{,}15+0{,}1=2{,}35\space\text{m}
\end{gathered}Ohybový moment se vypočítá podle kap. 4.1.3 jako
\begin{gathered}
M=f_\text{d}\cdot\ell^2/8=29{,}23\cdot2{,}352^2/8=20{,}17\space\text{kNm}.
\end{gathered}V kap. 4.4 Železobetonové trámy a průvlaky v tab. 4.5–4.7 se vyhledají rozměry železobetonového průřezu.
Vypočítanému ohybovému momentu a šířce stěny odpovídá průřez 300/250 mm.
Příklad 5.6
Navrhněte železobetonový překlad nad prosklenou stěnou. Překlad bude v šířce zdi 250 mm, světlost otvoru bude 6,2 mm. Bezprostředně nad překladem jsou uloženy stropy o světlosti 7,2 m. Nad stropem je pochozí terasa, takže překlad není zatížen nadložím zdivem. Návrhovou hodnotu celkového zatížení stropu uvažujte 11,5 kN/m2.
Zatížení:
- od stropu
\begin{gathered}
(7{,}2/2)\cdot11{,}5=41{,}40\space\text{kN/m}
\end{gathered}- vlastní hmotnost
\begin{gathered}
0{,}4\cdot0{,}25\cdot25\cdot1{,}35=3{,}38\space\text{kN/m}
\end{gathered}Celkem
\begin{gathered}
q_\text{d}=44{,}78\space\text{kN/m}
\end{gathered}Nosník bude prostě uložen na zdivu. Uložení nosníku předpokládáme 2,5 % světlosti na každou stranu, tj.
\begin{gathered}
6{,}2\cdot2{,}5/100=0{,}155\space\text{m na každou stranu}
\end{gathered}se zaokrouhlí na 0,2 m. Rozpětí nosníku potom bude světlá délka plus polovina uložení z každé strany, tj.
\begin{gathered}
6{,}2+2\cdot0{,}2\cdot0{,}5=6{,}2+0{,}2=6{,}4\space\text{m}.
\end{gathered}Moment prostého nosníku se určí podle kap. 4.1.3 jako
\begin{gathered}
M=f_\text{d}\cdot\ell^2/8=44{,}78\cdot6{,}4^2/8=229{,}25\space\text{kNm}.
\end{gathered}V tab. 4.5–4.7 se vyhledá k momentu odpovídající průřez, který je pro danou šířku otvoru 250/600 mm s procentem vyztužení 1,00 %.
5.5 OCELOVÉ PŘEKLADY
Ocelové překlady jsou oblíbené a často používané díky svým výhodám, kterými jsou vysoká únosnost, výhodná možnost použití při rekonstrukcích, rychlý technologický proces atd. Jako materiálu se používají za tepla válcované profily, a to nejčastěji profily IPN.
Zatížení na překlad se stanoví podle kap. 5.1, nosník se navrhuje jako ocelový. Návrh se může provést buď přímým výpočtem podle kap. 4.3, nebo se použije pro návrh tab. 4.2.
Pro překlady platí následující podmínka průhybu
Obr. 5.4 Ocelové překlady z válcovaných profilů IPN a UPN
\begin{gathered}
f_\text{lim}=\frac{\ell}{600}
\end{gathered}kde je
ℓ … rozpětí v mm
Tab. 5.9 Za předpokladu splnění jak kritéria únosnosti, tak kritéria průhybu překladů byla vypracována následující tabulka.
| Rozpětí ℓ [m] | Návrhová hodnota celkového zatížení qd [kN/m] | |||||||
| 10,0 | 20,0 | 30,0 | 40,0 | 50,0 | 60,0 | 70,0 | 80,0 | |
| 1,00 | IPN 80 – – |
IPN 80 – – |
IPN 100 2 IPN 80 – |
IPN 100 2 IPN 80 – |
IPN 100 2 IPN 80 – |
IPN 120 2 IPN 100 3 IPN 80 |
IPN 120 2 IPN 100 3 IPN 80 |
IPN 120 2 IPN 100 3 IPN 80 |
| 2,00 | IPN 120 2 IPN 100 – 4 IPN 80 |
IPN 140 2 IPN 120 3 IPN100 – |
IPN 160 2 IPN140 3 IPN120 – |
IPN 180 2 IPN140 – 4 IPN120 |
IPN 180 2 IPN160 3 IPN 140 4 IPN120 |
IPN 200 2 IPN160 3 IPN 140 – |
IPN 200 2 IPN 160 – 4 IPN140 |
IPN 200 2 IPN 180 3 IPN 160 4 IPN 140 |
| 3,00 | IPN 160 2 IPN140 3 IPN120 – |
IPN 200 2 IPN 160 3 IPN 140 – |
IPN 220 2 IPN 180 3 IPN160 – |
IPN 240 2 IPN 200 3 IPN 180 4 IPN 160 |
IPN 240 2 IPN 200 3 IPN 180 – |
IPN 260 2 IPN 220 3 IPN 200 4 IPN 180 |
IPN 280 2 IPN 220 3 IPN 200 – |
IPN 280 2 IPN 240 3 IPN 220 4 IPN 200 |
| 4,00 | IPN 200 2 IPN 180 3 IPN 160 4 IPN 140 |
IPN 240 2 IPN 200 3 IPN 180 – |
IPN 280 2 IPN 220 3 IPN 200 – |
IPN 300 2 IPN 240 3 IPN 220 4 IPN 200 |
IPN 320 2 IPN 260 3 IPN 240 4 IPN 220 |
IPN 320 2 IPN 280 3 IPN 240 4 IPN 220 |
IPN 340 2 IPN 280 3 IPN 260 4 IPN 240 |
IPN 360 2 IPN 300 3 IPN 260 4 IPN 240 |
| 5,00 | IPN 240 2 IPN 200 3 IPN 120 – |
IPN 300 2 IPN 240 3 IPN 220 4 IPN 200 |
IPN 320 2 IPN 280 3 IPN 240 4 IPN 220 |
IPN 340 2 IPN 300 3 IPN 260 4 IPN 240 |
IPN 360 2 IPN 300 3 IPN 280 4 IPN 260 |
IPN 380 2 IPN 320 3 IPN 300 4 IPN 280 |
IPN 400 2 IPN 340 3 IPN 300 4 IPN 280 |
IPN 450 2 IPN 340 3 IPN 320 4 IPN 300 |
| 6,00 | IPN 280 2 IPN 240 3 IPN 220 4 IPN 200 |
IPN 340 2 IPN 280 3 IPN 260 4 IPN 240 |
IPN 380 2 IPN 320 3 IPN 280 4 IPN 260 |
IPN 400 2 IPN 340 3 IPN 300 4 IPN 280 |
IPN 450 2 IPN 360 3 IPN 320 4 IPN 300 |
IPN 450 2 IPN 380 3 IPN 340 4 IPN 320 |
IPN 500 2 IPN 380 3 IPN 340 4 IPN 320 |
IPN 500 2 IPN 400 3 IPN 360 4 IPN 340 |
| 7,00 | IPN 320 2 IPN 260 3 IPN 240 4 IPN 220 |
IPN 380 2 IPN 320 3 IPN 280 4 IPN 260 |
IPN 450 2 IPN 360 3 IPN 320 4 IPN 300 |
IPN 450 2 IPN 380 3 IPN 340 4 IPN 320 |
IPN 500 2 IPN 400 3 IPN 360 4 IPN 340 |
IPN 500 2 IPN 450 3 IPN 380 4 IPN 360 |
– 2 IPN 450 3 IPN 400 4 IPN 360 |
– 2 IPN 450 3 IPN 400 4 IPN 380 |
| 8,00 | IPN 360 2 IPN 300 3 IPN 260 4 IPN 240 |
IPN 450 2 IPN 360 3 IPN 320 4 IPN 300 |
IPN 500 2 IPN 380 3 IPN 360 4 IPN 320 |
IPN 500 2 IPN 450 3 IPN 380 4 IPN 360 |
– 2 IPN 450 3 IPN 400 4 IPN 380 |
– 2 IPN 500 3 IPN 450 4 IPN 380 |
– 2 IPN 500 3 IPN 450 4 IPN 400 |
– 2 IPN 500 3 IPN 450 |
| 9,00 | IPN 380 2 IPN 320 3 IPN 280 4 IPN 260 |
IPN 450 2 IPN 380 3 IPN 340 4 IPN 320 |
IPN 500 2 IPN 450 3 IPN 380 4 IPN 360 |
– 2 IPN 450 – 4 IPN 380 |
– 2 IPN 500 3 IPN 450 4 IPN 400 |
– 2 IPN 500 3 IPN 450 – |
– – 3 IPN 500 4 IPN 450 |
– – 3 IPN 500 4 IPN 450 |
Příklad 5.7
Navrhněte ocelový překlad nad okenní otvor o světlé délce ℓs = 3,3 m (rozpětí cca 3,5 m) ve zdi tloušťky t = 300 mm. Nad překladem jsou uloženy montované stropní panely o rozpětí ℓ = 6 m. Návrhové hodnota celkového zatížení stropu je 9,4 kN/m2.
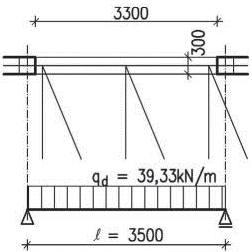
Zatížení:
- od stropu
\begin{gathered}
(6/2)\cdot9{,}4=28{,}20\space\text{kN/m}
\end{gathered}- vlastní tíha překladu (3 IPN 160)
\begin{gathered}
3\cdot0{,}18\cdot1{,}35=0{,}73\space\text{kN/m}
\end{gathered}- nadezdění
\begin{gathered}
(1{,}73\cdot3{,}3/4)\cdot0{,}3\cdot18\cdot1{,}35=10{,}40\space\text{kN/m}
\end{gathered}Celkem
\begin{gathered}
39{,}33\space\text{kN/m}^2
\end{gathered}Zatížení 39,33 kN/m se zaokrouhlí na 40 kN/m a v tab. 5.9 se interpoluje pro rozpětí 3,5 m, tj. mezi 3,0 a 4,0 m, a to mezi profily 3 IPN 180 a 3 IPN 220 (počet profilů se volí podle šířky stěny). Výsledek interpolace ležící mezi těmito hodnotami odpovídá 3 IPN 200.
5.6 ZDĚNÉ PŘEKLADY
Zděné překlady se v dnešní době uplatňují nejvíce v režném zdivu. Zděné překlady mohou být:
- rovné;
- obloukové.
Rovné překlady
Maximální rozpětí jsou uvedena v tab. 5.10 v závislosti na šířce překladu.

Obr. 5.5 Překlad zděný rovný
Tab. 5.10 Maximální rozpětí v závislosti na tloušťce zdiva
| Tloušťka zdiva t [mm] | Maximální rozpětí ℓ [m] |
| 250 | 0,80–0,90 |
| 375 | 1,20–1,30 |
Oblouky
Provádějí se s nadvýšením
\begin{gathered}
f=1/6\space\space\text{až}\space\space1/12
\end{gathered}Maximální rozpětí lze získat ze vztahu

Obr. 5.6 Překlad zděný obloukový
\begin{gathered}
\ell_\text{max}=\sqrt{\frac{0{,}4}{3}}+\frac{b_0+h\cdot R_\text{d}}{f_\text{d}}\space[\text{m}]
\end{gathered}kde je
b0 … šířka překladu [mm],
h … výška překladu [mm],
Rd … návrhova pevnost zdiva překladu [MPa]
\begin{gathered}
(R_\text{d}=1{,}5-2{,}5\space\text{MPa}),
\end{gathered}fd … zatížení překladu [kN/m].
Příklad 5.8
Zjistěte maximální světlost otvoru, je-li překlad navržen v tloušťce t = 450 mm a výšce h = 150 mm. Působící zatížení je fd = 35 kN/m a návrhová pevnost zdiva předpokládáme Rd = 1,5 MPa.
\begin{gathered}
\ell_\text{max}=\sqrt{\frac{0{,}4}{3}}+\frac{450+150\cdot1{,}5}{35}=1{,}6\space\text{m}
\end{gathered}Maximální světlá délka překladu je 1 600 mm.
6 SCHODIŠTĚ
Schodiště slouží k propojení jednotlivých podlaží nebo výškových rozdílů.
Schodiště jsou:
- jednoramenné;
- víceramenné;
- točité.
6.1 VŠEOBECNÉ ÚDAJE O SCHODIŠTÍCH
Tab. 6.1 Minimální šířka ramene
| Rodinné domy do dvou podlaží | 800–900 mm |
| Ostatní běžné stavby (bytové, občanské) | 1 100 mm |
| Vícepodlažní stavby | 1 200 mm |
| Podřadná, málo používaná schodiště | 550 mm |
Poznámka:
Při schodišťovém rameni širším než 2 750 mm se doporučuje rozdělit je mezilehlým zábradlím s madlem (požární bezpečnost).
Tab. 6.2 Minimální šířka podesty
| Mezipodesta | šířka ramene |
| Podlažní podesta | šířka ramene (lépe zvětšit o 100–200 mm) |
| Výtah na podestě | 1 600 mm |
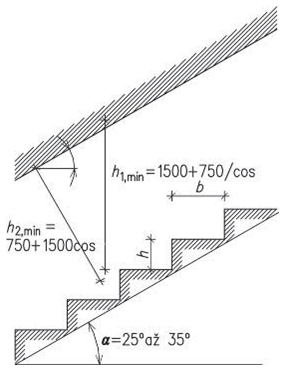
Obr. 6.1 Minimální světlá podchodná výška
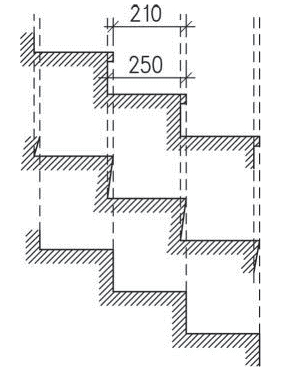
Obr. 6.2 Šířka stupně
Tab. 6.3 Minimální světlá podchodná výška
| Pomocná schodiště v rodinných domech | h1 = 2 100 mm |
| Uvnitř bytů | h2 = 1 900 mm |
| V ostatních případech (viz obr. 6.1) | h1,min, h2,min |
Pro běžná schodiště se sklonem 25°–35° s výškou stupňů 150–180 mm platí vztah odvozený z průměrné délky kroku dospělého člověka (cca 630 mm)
\begin{gathered}
b+2h=630\space[\text{mm}]
\end{gathered}Zvláště výhodný poměr b/h = 290/170 [mm].
\begin{gathered}
B_\text{min}=210\space\text{mm}
\end{gathered}schodišťový stupeň,
\begin{gathered}
b=250\space\text{mm}
\end{gathered}šířka stupnice (viz obr. 6.2).
Tab. 6.4 Výška zábradlí
| Obecně na schodišťových ramenech | 900 mm |
| Na podestách | 1 000 mm |
| Při schodišťovém zrcadle větším než 250 mm od devátého podlaží výše (včetně) | 1 100 mm |
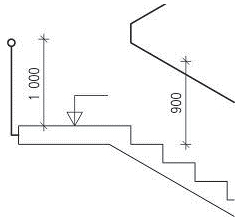
Obr. 6.3 Výšky schodišťového zábradlí
Zatížení
Tab. 6.5 Charakteristické hodnoty rovnoměrných zatížení podest, schodišťových ramen a mezipodest podle kategorie zatěžovacích ploch viz kap. 3.1.
| Kategorie zatěžovacích ploch | Spojité zatížení na plochu půdorysu qk [kN/m2] | Soustředěné břemeno Qk [kN] | |
| Kategorie A | 3,0 | 2,0 | |
| Kategorie B | 2,5 | 4,0 | |
| Kategorie C | C1 | 3,0 | 3,0 |
| C2 | 4,0 | 4,0 | |
| C3 | 5,0 | 4,0 | |
| C4 | 5,0 | 7,0 | |
| C5 | 5,0 | 4,5 | |
| Kategorie D | D1 | 5,0 | 5,0 |
| D2 | 5,0 | 7,0 | |
Na schodištích v obytných objektech (rodinných domech, vilách apod.), která jsou vytvořená z jednotlivých, vzájemně nespolupůsobích stupňů, je vhodné uvažovat charakteristické hodnoty soustředěného užitného zatížení velikosti na každém úseku běžné délky stupně (na schodištích vytvořených z jednotlivých stupňů, které spolu nespolupůsobí při přenášení zatížení) – viz obr. 6.4.
\begin{gathered}
F_1=F_2=2{,}0\space\text{kN}
\end{gathered}F2 se neuplatní při x < 400 mm
Tab. 6.6 Charakteristické hodnoty vodorovných rovnoměrných zatížení zábradlí na 1 m délky madla
| Kategorie zatěžovacích ploch | qk [kN/m2] |
| Kategorie A (obytné budovy, hotely, školky, zdravot. zařízení) | 0,5 |
| Kategorie B a C1 (školy, restaurace, čítárny) | 1,0 |
| Kategorie C2–C4 a D (divadla, nádraží, obchodní domy) | 1,0 |
| Kategorie C5 (velká koncentrace lidí – sportovní haly apod.) | 5,0 |
| Kategorie E (skladování, průmyslová činnost) | min. 2,0 kN/m2 |
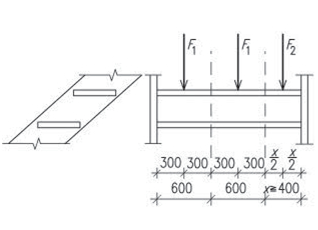
Obr. 6.4 Schéma zatížení jednotlivého stupně

Obr. 6.5 Zatížení na madlo zábradlí
6.2 DŘEVĚNÁ SCHODIŠTĚ
Dřevěná schodiště se uplatní jen v obytných budovách do dvou nadzemních podlaží. Materiál z prvotřídního dřeva borového, modřínového, dubového (zejména na stupnice). Méně vhodné je dřevo smrkové a jedlové. Lze použít i lepených prvků.
6.2.1 Schodiště schodnicová
Nejčastěji přímočaré jedno nebo dvouramenné, vyjímečně křivočaré, šířka ramene (délka stupně) 800–1 200 mm.
6.2.1.1 Schodnice postranní
Tab. 6.7 Rozměry stupně
| Šířka stupnice | 280–340 mm |
| Výška stupně | 160–200 mm |
Tloušťka t stupnice je závislá na vzdálenosti podpůrných schodnic viz tab. 6.8.
Tab. 6.8 Přibližné hodnoty schodnice
| Délka ℓ [mm] | Tloušťka t [mm] |
| 800 | 38 |
| 900, 1 000 | 45 |
| 1 100 | 50 |
| 1 200 | 60 |
Při větších šířkách ramene se stupnice podporují ještě třetí, střední (vyříznutou) schodnicí.
Podstupnice (spojené se stupnicemi obvykle na pero a drážku), navrhují-li se, mají tloušťku 18 nebo 24 mm.
Schodnice se zasouvanými stupnicemi do drážek – šířka ramene 1,00 m Při dvouramenném schodišti
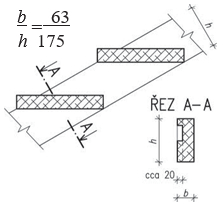
Obr. 6.6 Schodnice se zasouvanými stupnicemi do drážek
Schodnice se začepovanými stupnicemi – šířka ramene < 1,2 m
Při dvouramenném schodišti a délce ramene ≤ 3,50 m
\begin{gathered}
\frac{b}{h}=\frac{63}{300}
\end{gathered}Při dvouramenném schodišti a délce ramene ≤ 4,00 m
\begin{gathered}
\frac{b}{h}=\frac{75}{300}
\end{gathered}Při jednoramenném schodišti a délce ramene ≤ 4,50 m
\begin{gathered}
\frac{b}{h}=\frac{100}{300}
\end{gathered}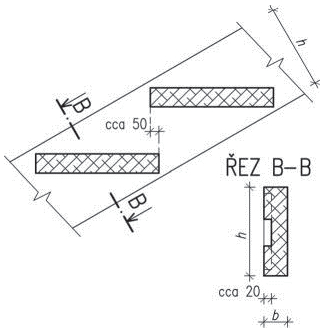
Obr. 6.7 Schodnice se začepovanými stupnicemi
Poznámka:
Výška h = 300 mm je voleno z konstrukčních důvodů, staticky by vyhověl i nižší průřez od h ≥ 250 mm.
Schodnice s nasazenými stupnicemi (shora vyříznuté schodnice) – šířka ramene < 1,0 m
Při jednoramenném schodišti a délce ramene ≤ 4,50 m
\begin{gathered}
\frac{b}{h}=\frac{75}{275}\space\space\text{popř.}\space\space\frac{100}{250}
\end{gathered}Při dvouramenném schodišti a délce ramene ≤ 2,00 m
\begin{gathered}
\frac{b}{h}=\frac{50}{160}
\end{gathered}Při dvouramenném schodišti a délce ramene ≤ 2,50 m
\begin{gathered}
\frac{b}{h}=\frac{75}{160}
\end{gathered}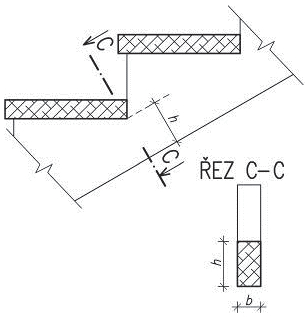
Obr. 6.8 Schodnice s nasazenými stupnicemi
Podestové nosníky
\begin{gathered}
\frac{b}{h}=\frac{160}{220}\space\space\text{až}\space\space\frac{180}{250}
\end{gathered}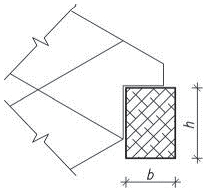
Obr. 6.9 Podestový nosník
6.2.1.2 Schodnice střední
Jednotlivé stupně (stupnice) musí být ohybově tuze spojeny se schodnicí (například šroubováním). Při dimenzování schodnice nutno pamatovat na účinek krouticího momentu, vyvolaného jednostranným zatížením stupnice. Hodí se jen na malá rozpětí. Délka stupně (stupnice) by neměla přesáhnout 1,00 m.
Při jednoramenném schodišti
\begin{gathered}
\frac{b}{h}=\frac{180}{250}
\end{gathered}Při dvouramenném schodišti
\begin{gathered}
\frac{b}{h}=\frac{120}{180},\space\space\text{až}\space\space\frac{100}{200}
\end{gathered}t ≥ 40 mm (odvislé od vyložení stupnice)

Obr. 6.10 Schodnice střední
6.2.1.3 Schodiště vřetenová
Vřetenová schodiště mohou být celá zhotovená ze dřeva (jednotlivé stupně jsou vykonzolované z vřetene z kulatiny) obvykle na výšku podlaží. Při doplnění vnější šroubovicovou lepenou dřevěnou schodnicí, do níž jsou stupně zapuštěny, lze realizovat schodiště i přes dvě podlaží.
Jednotlivé stupně mohou být navlečeny s případnými distančními objímkami na ocelovou trubku a následně sepnuty.
Tab. 6.9 Doporučené rozměry vřetenového schodiště
| Šířka ramene ŠR | 600–900 mm |
| Průměr vřetene d | 160–200 mm |
| Tloušťka stupňů t při volném uložení | min. 60 mm |
| Šířka stupně v místě výstupní čáry b | 215–270 mm |
| Výška stupně h | 180–210 mm |
| Průměr schodiště D | max. 2 000 mm |
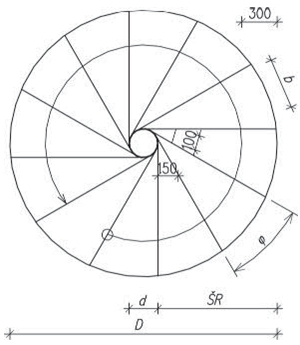
Obr. 6.11 Vřetenové schodiště
Návrh průměru vřetene:
- obecně d=2\Big(\frac{100}{\sin\varphi}-150\Big) [mm];
- z jednoho kusu na výšku podlaží d=\frac{D}{9}\ge160 [mm];
- při sepnutí jednotlivých stupňů v jeden celek d=\frac{D}{7{,}2}\ge180 [mm];
- stupně z jehličnatého dřeva d=\frac{D}{6{,}4}\ge180 [mm].
Poznámka:
Minimální průměr vřetene je závislý na nutné nášlapné šířce 100 mm ve vzdálenosti 150 mm od vřetene a od případného oslabení (vřetene) připojením stupňů.
6.3 OCELOVÁ SCHODIŠTĚ
Ocelová schodiště se mohou uplatnit ve všech druzích budov, nutno však respektovat příslušné protipožární předpisy.
Materiál: ocel S235
Válcované profily:
- tyče UPN, IPN, L;
- trubky bezešvé, čtyřhranné popř. uzavřené obdélníkové profily;
- hladký plech.
6.3.1 Schodnicová schodiště
Nejčastěji přímočaré jedno nebo víceramenné, popř. křivočaré (vřetenové, točité apod.). Níže uvedené prvky odpovídají užitnému zatížení qk ≤ 5 kN/m2, není-li uvedeno jinak.
6.3.1.1 Schodnice postranní
Při konstrukční výšce podlaží 3 m, délce ramene (půdorysně) ℓ ≤ 2,5 m a jeho šířce 1,00 m.

Obr. 6.12 Schodnice postranní ℓ ≤ 2,5 m
2 UPN140
popř. ohýbaný plech 2 x 60/170/3 až 5 [mm]
Při zalomených schodnicích se zahrnutím částí podesty
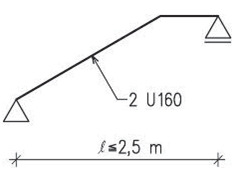
Obr. 6.13 postranní zalomená schodnice
2 UPN160
Při délce ramena (půdorysně) ℓ = 2,65 m a jeho šířce 1,5 m
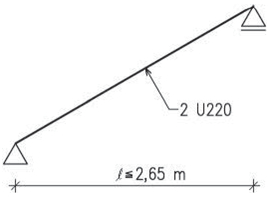
Obr. 6.14 Schodnice postranní ℓ = 2,5 m
2 UPN220
Podestový nosník u dvouramenných schodnicových schodišť
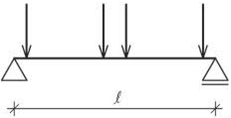
Obr. 6.15 Rozložení sil u podestového nosníku
při rozpětí ℓ = 2,4 m
2 UPN160
při rozpětí ℓ = 3,7 m
2 UPN220
6.3.1.2 Schodnice střední
Schodnice přímá – půdorysná délka 4,65 m
konstrukční výška podlaží 2,9 m, šířka ramene 1,1 m
užitné zatížení qk = 3 kN/m2, dřevěné stupně (stupnice) tloušťky min. 40 mm

Obr. 6.16 Schodnice střední
Schodnice 2 UPN140
6.3.1.3 Schodiště točivá s nosnými schodnicemi
Dvě krajní šroubovicové schodnice, mezi které jsou navařeny stupnice z ocelového plechu nebo z ocelových válcovaných úhelníků.
Tab 6.10 Informativní rozměry schodnic
| Užitné zatížení qk [kN/m2] | Výška podlaží [m] | Poloměr schodiště | Rozměry schodnic | ||
| vnější [m] | vnitřní [m] | vnější [mm] | vnitřní [mm] | ||
| 3,00 | 4,25 | 2,00 | 0,50 | 10/300 | 10/250 |
| 4,50 | 1,90 | 0,50 | 10/300 | 10/300 | |
| 2,75 | 1,28 | 0,31 | 6/250 | 6/200 | |
| 5,00 | 4,50 | 1,70 | 0,50 | 20/280 | 20/280 |
| 4,00 | 2.50 | 1,00 | 30/330 | 30/350 | |
| 3,00 | 1,65 | 0,50 | 18/255 | 18/255 | |
| 3,50 | 2,50 | 1,05 | 25/330 | 25/330 | |
6.3.2 Schodiště vřetenová
6.3.2.1 Vřeteno – ocelová trubka
Vřeteno (ocelová trubka) vodorovně opřeno v úrovni podest.
Stupně lze realizovat z vytvarovaného konglomerovaného kamene, ocelových plechů, ocelových rámů s dřevěnými stupnicemi, lepených dřevěných schodů, železobetonových dílců. Tloušťka t = 40–60 mm.
Průměr ocelových trubek lze směrně navrhnout podle následující tab 6.11
Tab 6.11 Směrný návrh průměru ocelových trubek
| Pro užitná zatížení qk [kN/m2] | Počet podlaží | Výška podlaží [m] | Průměr schodiště D [m] | Ocelová trubka | |
| vnější průměr d [mm] | tloušťka stěny t [mm] | ||||
| 3,00 | 1 | 3,00 | 1,30 | 108 | 4 |
| 2,00 | 83 | 5 | |||
| 2 | 3,50 | 1,60 | 133 | 4 | |
| 60 | 7 | ||||
| ≤ 3 | 2,75 | 1,60 | 89 | 4 | |
| 108 | 4 | ||||
| 133 | 4 | ||||
| 152 | 7 | ||||
| 5,00 | 2 | 3,50 | 1,40 | 133 | 4 |
| 6 | 3,40 | 1,20 | 168 | 8 | |
6.3.2.2 Spínavé vřeteno – předpjatá ocelová trubka
Spínání (předpětí) je docíleno centrálním šroubem. Vykonzolované ocelové stupně jsou přivařené k vřetenu.
Průměr schodiště
\begin{gathered}
D=1{,}40{-}2{,}15\space\text{m}
\end{gathered}Užitné zatížení
\begin{gathered}
q_\text{k}=3{,}00\space\text{kN/m}^2
\end{gathered}Ocelová trubka
- vnější průměr d = 3,00 mm;
- tloušťka stěny t = 7 mm;
- předpínací síla 160 kN;
- šroub M20 – objímkový styk.
6.4 SCHODIŠTĚ ŽELEZOBETONOVÁ
V tomto odstavci jsou prezentována jen monolitická schodiště (kromě vřetenových, sestavených z dílců), a to jenom jednodušší konstrukční systémy.
Montovaná schodiště z dílců (ramena, podesty, nosníky, stěny apod.) jsou obvykle součástí příslušného montovaného, většinou unifikovaného systému, nejsou obsahem publikace.
6.4.1 Schody konzolové
Deska jednostranně vetknutá do nosné schodišťové stěny (staticky působí jako konzola) – stupně jsou nabetonované, kamenné nebo prefabrikované.
\begin{gathered}
h=\frac{1}{10}\ell\space\space\text{obvykle}\space\space h=80{-}120\space\text{mm}
\end{gathered}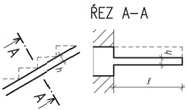
Obr. 6.17 Schodnicová deska jednostranně vetknutá
6.4.2 Schody oboustranně podporované
Schodišťové rameno je podporováno v příčném směru schodišťovou stěnou nebo schodnicí, popř. schodnicemi (deska působí jako deska částečně vetknutá do schodnice).
\begin{gathered}
h_1=\frac{1}{25}\ell_1\space\space\text{obvykle}\space\space h_1=50{-}80\space\text{mm}
\end{gathered}Schodnice (šikmé nosníky) – staticky působí jako prosté nosníky, popř. částečně vetknuté do podestových nosníků.
\begin{gathered}
h_2=\frac{1}{10}\ell_2\space\space\text{obvykle}\space\space h_2=300{-}400\space\text{mm}
\end{gathered}\begin{gathered}
b_2=\Big(\frac{1}{2}\space\text{až}\space\frac{2}{3}\Big)\ell_2\space\space\text{obvykle}\space\space b_2=150{-}250\space\text{mm}
\end{gathered}kde je
ℓ … půdorysná délka schodnice.
Obr. 6.18 Schodnicová deska částečně vetknutá do stěny nebo schodnice
6.4.3 Schody deskové
6.4.3.1 Deska podporovaná podestovými nosníky
Prostý nosník tloušťky
\begin{gathered}
h_1=120{-}160\space\text{mm}
\end{gathered}Spojitý nosník, navazuje-li výztuž z šikmé desky (ramene) na podestové desky tloušťky
\begin{gathered}
h_1=90{-}120\space\text{mm}
\end{gathered}Podestový nosník tloušťky \frac{b_\text{w}}{h_2}=\frac{150}{200}\space\text{až}\space\frac{150}{300}\space\text{mm}
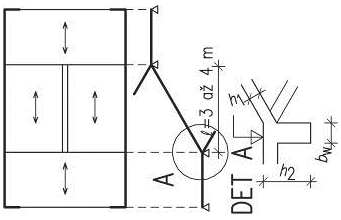
Obr. 6.19 Schodnicová deska podporovaná podestovými trámy
6.4.3.2 Deska jednou zalomená s podeskovým nosníkem
Tloušťka desky a podesty h ≥ 120 mm
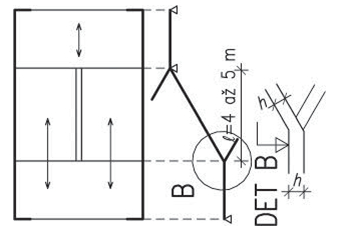
Obr. 6.20 Schodnicová deska jednou zalomená s podestovým nosníkem
6.4.3.3 Deska dvakrát zalomená bez podestových nosníků
Tloušťka desky a podesty h ≥ 200 mm
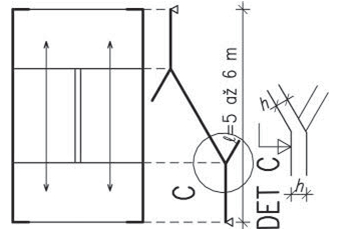
Obr. 6.21 Schodnicová deska dvakrát zalomená bez podestových nosníků
6.4.3.4 Deska se skrytými podestovými nosníky
Podpory se předpokládají přibližně ve vzdálenosti 1/3 šířka podesty od místa zalomení
Tloušťka desky h1 = 100–140 mm
Tloušťka podesty h2 = 120–160 mm
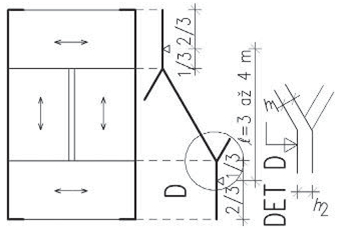
Obr. 6.22 Schodnicová deska se skrytými podestovými nosníky
6.4.3.5 Visutá (vykrakorcovaná) zalomená deska
Tloušťka ramene i mezipodesty je stejná. Musí být zajištěna kontinuita v úrovních stropů, popř. vetknutí do stropní tabule.
Tloušťka desky a podesty h = 170–210 [mm]
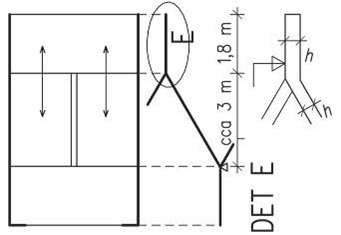
Obr. 6.23 Schodnicová zalomená deska
6.4.3.6 Točité deskové schody
Uložení (podpory) v úrovních stropních konstrukcí. Obecně nelze stanovit rozměry průřezů prvků, řešení vyžaduje individuální přístup od případu k případu.
Směrná hodnota tloušťky desky ramene h při některých daných parametrech je:
- s velkým zrcadlem
- konstrukční výška podlaží
\begin{gathered}
H\le3{,}5\space\text{m}
\end{gathered}- poloměr
\begin{gathered}
r_1=3{,}0\space\text{m}
\end{gathered}- užitné zatížení
\begin{gathered}
q_\text{k}\le5\space\text{kN/m}^2
\end{gathered}- tloušťka desky
\begin{gathered}
h=150{-}180\space\text{mm}
\end{gathered}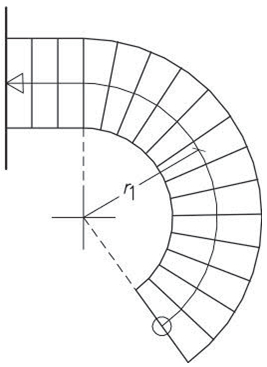
Obr. 6.24 Točité deskové schody s velkým zrcadlem
- s malým zrcadlem
- konstrukční výška podlaží
\begin{gathered}
H\le3{,}5\space\text{m}
\end{gathered}- poloměr
\begin{gathered}
r_2=0{,}5\space\text{m},\space r_3=1{,}2\space\text{m}
\end{gathered}- užitné zatížení
\begin{gathered}
q_\text{k}\le3\space\text{kN/m}^2
\end{gathered}- tloušťka desky
\begin{gathered}
h=140{-}160\space\text{mm}
\end{gathered}- užitné zatížení
\begin{gathered}
q_\text{k}\le5\space\text{kN/m}^2
\end{gathered}- tloušťka desky
\begin{gathered}
h=150{-}180\space\text{mm}
\end{gathered}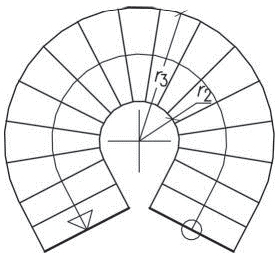
Obr. 6.25 Točité deskové schody s malým zrcadlem
6.4.4 Schodiště vřetenové
Předvyrobené železobetonové podestové desky a stupně s nebo bez podstupnic včetně vřetenové objímky se navlečou a svary přistehují na ocelovou trubku (TR 133/4, popř. TR 152/4,5), která je zakotvena do betonového základu. I vícepodlažní provedení je možné.
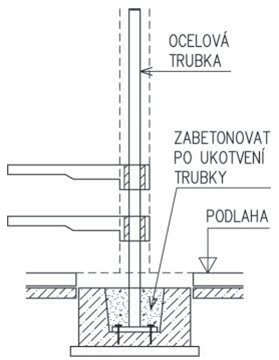
Obr. 6.26 Vřetenové schodiště
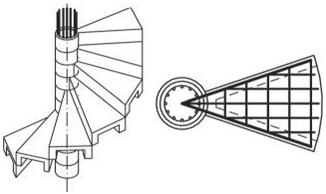
Poznámka:
Vodicí ocelovou trubku lze nahradit železobetonovým monolitickým kruhovým sloupem. Složitější technologie provádění – postupná betonáž vyztuženého jádra viz obr. 6.26.
Tab. 6.12 Vřetenová schodiště od firmy Gimmler (Německo)
| Vřeteno průměru1) d [mm] | Šířka ramene (vyložení) [mm] | Průměr schodiště D [mm] |
| 250 | 800–1 000 | 1 850–2 250 |
| 300 | 1 000–1 400 | 2 300–3 100 |
| 350 | 2 350–3 150 | |
| 500 | 850–1 500 | 2 200–3 500 |
| 1) Použitá ocelová trubka Ø 140 mm | ||
6.4.5 Šikmé trámy
Tab. 6.13 Největší dovolené sklony šikmých ramp
| u vnitřních ramp | 1 : 6 (16,6 % nebo α = 9° 27´) |
| u vnějších ramp, pro L ≤ 3 m | 1 : 8 (12,5 % nebo α = 7° 8´) |
| u vnějších ramp, pro L ≥ 3 m | 1 : 12 (8,3 % nebo α = 4° 45´) |
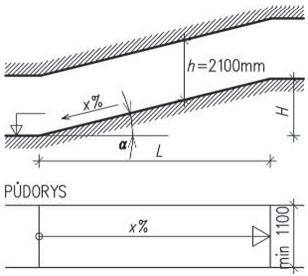
Obr. 6.27 Šikmé rampy
Poznámka:
Na volných stranách musí být šikmá rampa opatřena zábradlím.
6.4.6 Pohyblivé schody
Rozměrové hodnoty viz obr. 6.27.
Půdorysná délka ramene a
- při stoupání α = 30°
\begin{gathered}
a=1{,}73H\space[\text{mm}]
\end{gathered}- při stoupání α = 35°
\begin{gathered}
a=1{,}73H\space[\text{mm}]
\end{gathered}Celková délka eskalátoru ℓ
\begin{gathered}
\ell=a+2\space100+2\space340=a+4\space400\space[\text{mm}]
\end{gathered}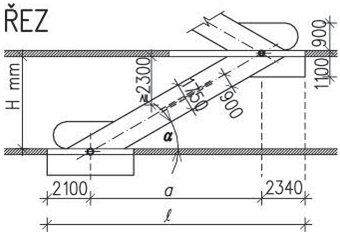
Obr. 6.28 Pohyblivé schody
Šířka prostupů ve stropech
délka stupňů
600 mm
800 mm
1 000 mm
b = 1 300 mm
b = 1 500 mm
b = 1 700 mm
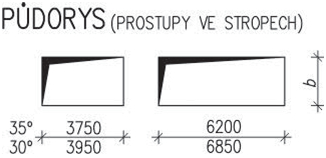
Obr. 6.29 Velikost prostupů ve stropech pro pohyblivé schody
Podporové reakce (při délce stupňů 800 mm)
- stoupání α = 30°
\begin{gathered}
R_\text{sup}=R_\text{inf}=(3+H)\cdot10\space[\text{kN}]
\end{gathered}- stoupání α = 35°
\begin{gathered}
R_\text{sup}=R_\text{inf}=(2{,}5+H)\cdot10\space[\text{kN}]
\end{gathered}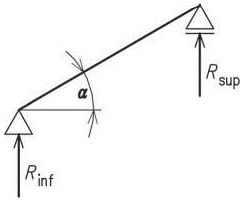
Obr. 6.30 Podporové reakce
Poznámka:
Výška H se dosazuje při stanovení podporových reakcí v m. Při délce stupňů 600 mm se snižují výše vypočtené reakce o 10 %. Při délce stupňů 1 000 mm se zvyšují výše vypočtené reakce o 10 %.
7 ZDĚNÉ KONSTRUKCE
Charakteristickými vlastnostmi zdiva je relativně vysoká únosnost v tlaku a nízká únosnost v tahu a smyku. Z toho plynou nároky na prostorové uspořádání s ohledem na vyztužení objektu proti vodorovným silám, což se současně projeví i na vzpěrných délkách jednotlivých prvků.
7.1 KONSTRUKČNÍ SYSTÉM
U staveb obytných, občanských a jim podobných je obvyklá vzdálenost mezi nosnými stěnami okolo 6 m a konstrukční výška podlaží nepřesahuje zpravidla 3,6 m. Nejběžnější případ nosného systému tohoto charakteru budov je kombinace zděných stěn s monolitickými, popř. prefabrikovanými zmonolitněnými stropy až do výšky 10 nadzemních podlaží.
Systém podélných stěn (podélný systém) se hodí zejména pro budovy s průběžnými nebo dělitelnými prostorami, jako jsou školy, administrativní budovy apod. Podélné nosné zdi oddělují jednotlivé trakty vnější případně střední – obvykle se navrhují dva a tři trakty. Stropy jsou orientovány příčně. U obytných budov se rozpon obvodového traktu pohybuje v rozmezí 4–6 m, u budov občanských 6–8 m. Při více traktech se často střední stěna nahrazuje cihelnými pilíři se spojitým průvlakem. Prostorová tuhost se nejlépe zajistí vložením ztužujících stěn zpravidla ve štítech, u schodiště apod., stropní konstrukce musí zajistit přenos vodorovného zatížení na ztužující konstrukci (nepoddajná soustava). V opačném případě, bez ztužujících stěn či tuhých stropů se jedná o méně výhodnou soustavu pružnou.
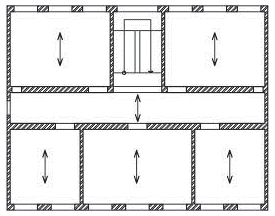
Obr. 7.1 Systém podélných stěn
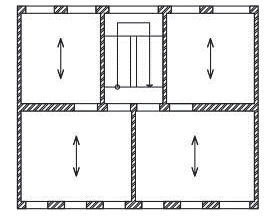
Systém příčných stěn (příčný systém) je vhodný pro objekty jako jsou obytné budovy, lůžkové části hotelů a nemocnic apod., které nevyžadují velké průběžné prostory ani variabilní dispozici. Příčné stěny mají pouze nosnou funkci, odpadá tepelně izolační funkce a stěny mohou být tenčí popř. z kvalitnějšího zdiva. Obvodové zdivo je pak nenosné, výplňové, kam je možné umístit velké okenní otvory či obvodovou stěnu zcela vynechat. Účinky větru, které působí na podélnou fasádu, přenese obvodové zdivo buď do stropů, nebo při malých vzdálenostech příčných stěn do stropů a příčných stěn současně. Prostorová tuhost v podélném směru se nejlépe zajistí podélně orientovanou ztužující stěnou. Příčné stěny přenesou účinky zatížení do základů. Stropní konstrukce jsou orientovány podélně – vzdálenost příčných stěn určuje jejich rozpětí. Systém nosných stěn mohou tvořit:
- příčné stěny s malými rozestupy (3 000, 3 600, 4 200 mm);
- příčné stěny s velkými rozestupy (5 400–6 000 mm);
- příčné stěny s kombinovanými rozestupy.
Účelnou kombinací rozponů lze dosáhnout výhodného půdorysného dispozičního řešení
Obr. 7.2 Systém příčných stěn
Krabicová konstrukce vznikne kombinací nosných a ztužujících stěn vzájemně propojených tuhými stropy, kde se jednotlivé prvky nemohou nezávisle přetvořovat a vzájemně spolupůsobí.
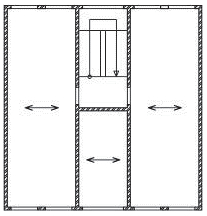
Obr. 7.3 Systém krabicové konstrukce
Polokrabicová konstrukce má například z dispozičních důvodů nahrazeny některé příčné stěny sloupy či zděnými pilíři a příčně orientovanými průvlaky.
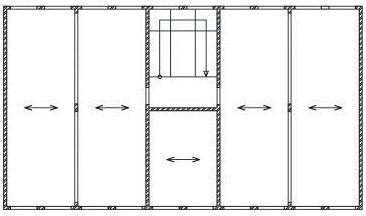
Obr. 7.4 Systém polokrabicové konstrukce
Obousměrný systém vznikne kombinací příčného a podélného systému – nosné stěny jsou orientovány v obou směrech a veškeré svislé síly se podílí na stabilitě polohy objektu jako celku ať působí vítr v podélném či příčném směru. Systém je výhodný zejména tehdy, jestliže se jeho půdorys blíží čtverci. Nejúčinnější je varianta sklípkového (buňkového) systému, kdy se maximum stěn vzájemně podporuje a spolupůsobí.
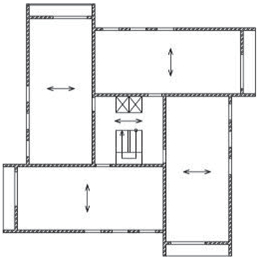
Obr. 7.5 Obousměrný systém
7.2 NOSNÉ STĚNY A PILÍŘE
Typickými zděnými prvky jsou stěny a pilíře z prostého, vyztuženého případně předpjatého zdiva, namáhané převážně tlakem.
Tab. 7.1 Přehled zděných stěn a pilířů
| Prvek | Nákres | Typická výška hw [m] | Poměr h/t [–] |
| Zděné stěny | 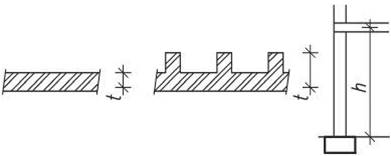 |
1–5 | 18–22 |
| Zděné pilíře | 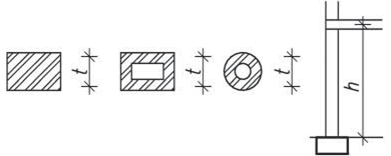 |
1–4 | 15–20 |
| Vyztužené a předpjaté zděné stěny a pilíře | 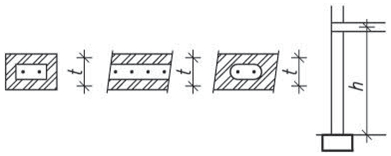 |
1–4 | 20–35 |
7.2.1 Omezení štíhlosti
Prvním omezením pro volbu rozměrů podle ČSN EN 1996-1-1 jsou mezní poměry výšky a tloušťky stěn a pilířů bez ohledu na jejich únosnost. Poměr účinné výšky stěny hef a účinné výšky průřezu tef se označuje jako štíhlost stěny. Štíhlost zděné stěny, zatížené převážně svislým zatížením, nesmí překročit 27.
Vzpěrná výška stěny
Stanovení vzpěrné výšky stěny závisí na její skutečné výšce a dále na způsobu podepření. Jedná se jednak o vodorovné podepření, zpravidla stropy nebo střechou na spodním a horním konci stěny, nebo o svislé podepření napojením příčných stěn. Napojení musí být staticky účinné na tah i tlak prostřednictvím vazby, spon apod. Ztužující stěna musí být dostatečně tuhá, což znamená, že její tloušťka musí být alespoň třetinou tloušťky podporované stěny a její délka musí být větší než pětina světlé výšky podlaží. Pokud jsou ve ztužující stěně otvory, jejich rozměry nesmí překročit jisté meze – podrobněji viz ČSN EN 1996-1-1.
Pokud jsou svislé ztužující konstrukce od sebe příliš vzdálené (délka podporované stěny ℓ ≥ 30tef při dvou ztužených okrajích nebo ℓ ≥ 15tef při jednom ztužujícím okraji), uvažuje se pouze podepření podle vodorovných okrajů.
Vzpěrná délka stěny se určí podle vztahu
\begin{gathered}
h_\text{ef}=\rho_\text{n}\cdot h
\end{gathered}kde je
hef … vzpěrná výška stěny [m];
ρn … součinitel podle okrajových podmínek má hodnoty ρ2, ρ3 a ρ4;
h … světlá výška podlaží [m].
U stěny oboustranně ve stejné výšce podepřené železobetonovým stropem nebo střechou nebo u stěny jednostranně podepřené železobetonovým stropem, uloženým alespoň na délku 2/3ts a výstřednost výslednice na horním konci stěny je menší než 1/4ts.
\begin{gathered}
\rho_2=0{,}75
\end{gathered}Pokud nejsou výše uvedené podmínky splněny, nebo je stěna bočně oboustranně podepřena dřevěným stropem nebo střechou případně je podepřená jednostranně podepřena dřevěným stropem uloženým na délku nejméně 2/3hs a 85 mm
\begin{gathered}
\rho_2=1{,}00
\end{gathered}U stěny podepřené v hlavě, patě a podél jednoho svislého okraje (druhý okraj volný), platí při h ≤ 3,5ℓ
\begin{gathered}
\rho_3=\frac{1}{1+\Big[\frac{\rho_2\cdot h}{3\ell}\Big]^2}\cdot\rho_2
\end{gathered}popř. při h > 3,5ℓ
\begin{gathered}
\rho_3=\frac{1{,}5\ell}{h}\ge0{,}3
\end{gathered}U stěny podepřené v hlavě, patě a podél obou svislých okrajů, platí při h ≤ 1,15ℓ
\begin{gathered}
\rho_4=\frac{1}{1+\Big[\frac{\rho_2\cdot h}{\ell}\Big]^2}\cdot\rho_2
\end{gathered}popř. při h > 1,15ℓ
\begin{gathered}
\rho_3=\frac{0{,}5\ell}{h}
\end{gathered}Účinná tloušťka stěny
Účinná tloušťka stěny tef je rovna skutečné tloušťce ts u stěn jednovrstvých, jednovrstvých s lícovou vrstvou, stěn s obvodovými pruhy malty, stěn dvouvrstvých s dvouvrstvých s vyplněnou mezerou.
\begin{gathered}
t_\text{ef}=t_\text{s}\space[\text{m}]
\end{gathered}U stěny s výztužnými pilíři se podle uspořádání pilířů určí účinná tloušťky stěny tef vynásobením skutečné tloušťky skutečné stěny ts součinitelem ρ1 podle tab. 7.2.
\begin{gathered}
t_\text{ef}=\rho_1\cdot t_\text{s}\space[\text{m}]
\end{gathered}
Obr. 7.6 Zděná stěna vyztužená pilíři
Tab. 7.2 Tloušťky vyztužujících pilířů zděných stěn
| Poměr osové vzdálenosti pilířů k jejich šířce ℓp/tp [–] | Poměr tloušťky pilíře k tloušťce stěny tp/ts [–] | ||
| 1 | 2 | 3 | |
| 6 | 1,0 | 1,4 | 2,0 |
| 10 | 1,0 | 1,2 | 1,4 |
| 20 | 1,0 | 1,0 | 1,0 |
| Mezilehlé hodnoty se lineárně interpolují | |||
U dutinových stěn se dvěma vrstvami spojeními stěnovými sponami se pro výpočet štíhlosti určí účinná tloušťka stěny podle vztahu
\begin{gathered}
\ell_\text{ef}=\sqrt[3]{k_\text{tef}\cdot t^3_1+t_2^3}
\end{gathered}kde je
t1 … tloušťka vnější nebo nezatížené vrstvy [m];
t2 … tloušťka vnitřní nebo zatížené vrstvy [m];
ktef = E1/E2 … poměr modulů pružnosti zdiva stěny a pilířů, pokud jsou odlišné.
7.2.2 Únosnost stěn
Únosnost stěn na vzpěrný tlak závisí na pevnostní značce zdicích prvků, pevnosti malty, rozměrech průřezu a vzpěrné délce, resp. štíhlosti prvku.
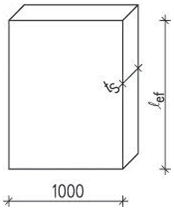
Obr. 7.7 Schéma stěny
Mimo únosnost nesmí být překročen mezní poměr tloušťky a výšky stěny (štíhlost).
V následující tab. 7.2 jsou uvedeny únosnosti Nm,Rd pro jednotkovou délku stěny uprostřed její výšky pro různé tloušťky a vzpěrné délky 1,5–6,0 m. V oddílech tabulky jsou hodnoty pro určité druhy zdiva při různých pevnostech zdicích prvků a malt s uvedením příslušné návrhové pevnosti fd zdiva. Při větších výškách nejsou uvedeny hodnoty únosnosti, pokud je štíhlost stěny hef / tef > 27.
Únosnost je stanovena bez vlivu vodorovného zatížení (například větrem u obvodových stěn).
Tab. 7.2 Únosnost stěny Nm,Rd namáhané vzpěrným tlakem [kN/m]
| Pálené zdicí prvky plné klasického formátu, P5, malta M1,0, fd = 0,44 [MPa] | |||||||||
| tef [mm] | vzpěrná délka hef [m] | ||||||||
| 1,5 | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 | 4,5 | 5,0 | 6,0 | |
| 150 | 55,80 | 51,92 | 47,12 | 41,72 | 35,77 | 29,07 | – | – | – |
| 300 | 118,67 | 116,98 | 114,61 | 111,59 | 107,98 | 103,84 | 99,23 | 94,25 | 88,96 |
| 450 | 179,44 | 178,60 | 177,28 | 175,48 | 173,21 | 170,51 | 167,39 | 163,87 | 159,98 |
| 600 | 239,67 | 239,26 | 238,48 | 237,33 | 235,83 | 233,97 | 231,76 | 229,22 | 226,36 |
| 750 | 299,67 | 299,52 | 299,07 | 298,33 | 297,29 | 295,97 | 294,35 | 292,46 | 290,29 |
| Pálené zdicí prvky plné klasického formátu P10, malta M5,0, fd = 1,17 [MPa] | |||||||||
| 150 | 146,90 | 136,69 | 124,07 | 109,85 | 94,17 | 76,54 | – | – | – |
| 300 | 312,42 | 307,99 | 301,74 | 293,79 | 284,28 | 273,37 | 261,26 | 248,13 | 234,21 |
| 450 | 472,43 | 470,22 | 466,73 | 461,99 | 456,03 | 448,92 | 440,69 | 431,42 | 421,19 |
| 600 | 630,98 | 629,91 | 627,86 | 624,84 | 620,88 | 615,98 | 610,18 | 603,49 | 595,95 |
| 750 | 788,95 | 788,56 | 787,39 | 785,43 | 782,71 | 779,21 | 774,97 | 769,98 | 764,26 |
| Pálené zdicí prvky plné klasického formátu P20, malta M10,0, fd = 2,34 [MPa] | |||||||||
| 150 | 293,79 | 273,37 | 248,13 | 219,70 | 188,34 | 153,08 | – | – | – |
| 300 | 624,84 | 615,98 | 603,49 | 587,59 | 568,56 | 546,75 | 522,52 | 496,27 | 468,42 |
| 450 | 944,86 | 940,44 | 933,46 | 923,97 | 912,07 | 897,83 | 881,38 | 862,85 | 842,38 |
| 600 | 1261,97 | 1259,82 | 1255,72 | 1249,69 | 1241,76 | 1231,97 | 1220,35 | 1206,98 | 1191,89 |
| 750 | 1577,90 | 1577,12 | 1574,77 | 1570,86 | 1565,41 | 1558,43 | 1549,93 | 1539,96 | 1528,52 |
| Pálené zdicí prvky příčně děrované CDm P10, malta M5,0, fd = 1,21 [MPa] | |||||||||
| 125 | 121,76 | 109,37 | 94,79 | 78,18 | 60,18 | 43,87 | 30,13 | 19,40 | 11,63 |
| 250 | 267,49 | 261,57 | 253,51 | 243,51 | 231,83 | 218,74 | 204,55 | 189,58 | 174,14 |
| 375 | 406,65 | 403,43 | 398,65 | 392,36 | 384,64 | 375,58 | 365,27 | 353,84 | 341,41 |
| 500 | 544,02 | 542,20 | 539,17 | 534,97 | 529,62 | 523,15 | 515,60 | 507,03 | 497,48 |
| Pálené zdicí prvky příčně děrované Porotherm P10, malta M5,0, fd = 1,25 [MPa] | |||||||||
| 140 | 145,15 | 133,48 | 119,29 | 103,62 | 85,39 | – | – | – | – |
| 175 | 188,20 | 178,83 | 166,85 | 152,85 | 137,50 | 121,08 | 102,02 | 83,73 | – |
| 240 | 265,46 | 258,99 | 250,25 | 239,46 | 226,93 | 212,98 | 197,95 | 182,21 | 165,50 |
| 300 | 335,20 | 330,45 | 323,74 | 315,21 | 305,01 | 293,31 | 280,31 | 266,22 | 251,29 |
| 365 | 409,90 | 406,41 | 401,26 | 394,52 | 386,26 | 376,60 | 365,64 | 353,51 | 340,36 |
| 400 | 449,91 | 446,93 | 442,43 | 436,44 | 429,03 | 420,28 | 410,27 | 399,11 | 386,89 |
| 425 | 478,41 | 475,76 | 471,65 | 466,14 | 459,27 | 451,10 | 441,71 | 431,17 | 419,59 |
| 440 | 495,49 | 493,01 | 489,13 | 483,88 | 477,30 | 469,46 | 460,41 | 450,24 | 439,02 |
| 500 | 563,68 | 561,80 | 558,66 | 554,31 | 548,76 | 542,06 | 534,24 | 525,35 | 515,47 |
| Pálené zdicí prvky příčně děrované Porotherm P15, malta M10,0, fd = 2,05 [MPa] | |||||||||
| 140 | 237,35 | 218,26 | 195,07 | 169,44 | 139,63 | – | – | – | – |
| 175 | 307,75 | 292,42 | 272,83 | 249,95 | 224,84 | 197,98 | 166,83 | 136,91 | – |
| 240 | 434,08 | 423,51 | 409,21 | 391,57 | 371,08 | 348,27 | 323,70 | 297,96 | 270,62 |
| 300 | 548,12 | 540,35 | 529,39 | 515,44 | 498,75 | 479,61 | 458,36 | 435,33 | 410,90 |
| 365 | 670,28 | 664,57 | 656,15 | 645,12 | 631,62 | 615,82 | 597,90 | 578,07 | 556,56 |
| 400 | 735,69 | 730,83 | 723,46 | 713,67 | 701,56 | 687,25 | 670,88 | 652,62 | 632,65 |
| 425 | 782,31 | 777,96 | 771,25 | 762,23 | 751,00 | 737,64 | 722,28 | 705,06 | 686,12 |
| 440 | 810,24 | 806,18 | 799,83 | 791,24 | 780,48 | 767,66 | 752,87 | 736,23 | 717,89 |
| 500 | 921,74 | 918,65 | 913,53 | 906,41 | 897,34 | 886,37 | 873,59 | 859,06 | 842,89 |
| Pórobetonové zdicí prvky (Ytong) s tenkými spárami P2, fd = 0,70 [MPa] | |||||||||
| 200 | 121,34 | 116,84 | 110,96 | 103,90 | 95,95 | 87,38 | 78,46 | – | – |
| 250 | 154,10 | 150,70 | 146,05 | 140,29 | 133,56 | 126,02 | 117,84 | 109,22 | 100,32 |
| 300 | 186,38 | 183,73 | 180,01 | 175,26 | 169,59 | 163,08 | 155,86 | 148,03 | 139,72 |
| 375 | 234,28 | 232,42 | 229,67 | 226,05 | 221,60 | 216,38 | 210,44 | 203,85 | 196,69 |
| Pórobetonové zdicí prvky (Ytong) s tenkými spárami P4, fd = 1,08 [MPa] | |||||||||
| 200 | 188,58 | 181,60 | 172,45 | 161,49 | 149,13 | 135,80 | 121,95 | – | – |
| 250 | 239,51 | 234,22 | 227,00 | 218,05 | 207,58 | 195,86 | 183,16 | 169,75 | 155,93 |
| 300 | 289,67 | 285,56 | 279,77 | 272,40 | 263,58 | 253,47 | 242,23 | 230,07 | 217,16 |
| 375 | 364,12 | 361,24 | 356,96 | 351,33 | 344,41 | 336,30 | 327,07 | 316,84 | 305,70 |
| Pórobetonové zdicí prvky (Ytong) s tenkými spárami P6, fd = 1,57 [MPa] | |||||||||
| 200 | 273,35 | 263,23 | 249,97 | 234,08 | 216,16 | 196,84 | 176,76 | – | – |
| 250 | 347,17 | 339,49 | 329,03 | 316,06 | 300,89 | 283,90 | 265,48 | 246,05 | 226,01 |
| 300 | 419,88 | 413,92 | 405,53 | 394,84 | 382,06 | 367,40 | 351,12 | 333,48 | 314,76 |
| 375 | 527,79 | 523,61 | 517,40 | 509,24 | 499,22 | 487,46 | 474,09 | 459,25 | 443,11 |
7.2.3 Únosnost pilířů
Únosnost pilířů se stanoví pomocí tab. 7.2 použitím únosnosti Nm,Rd pro tef odpovídající menšímu rozměru pilíře a přenásobením druhým rozměrem pilíře bp v metrech.
\begin{gathered}
N_\text{m,Rd,p}=N_\text{m,Rd}\cdot b_\text{p}\space[\text{kN}]
\end{gathered}7.2.4 Omezení štíhlosti z hlediska použitelnosti
Bez ohledu na to, že stěna splňuje kritéria mezního stavu únosnosti, musí s ohledem na mezní stav použitelnosti splnit omezení štíhlosti podle grafů na obr. 7.8–7.10. Platí pro jednovrstvou stěnu nebo zděnou vrstvu dutinové stěny o minimální tloušťce 100 mm.
Obr. 7.8 Omezení štíhlosti jednovrstvé stěny z hlediska použitelnosti, podepřené podél všech čtyř stran
Obr. 7.9 Omezení štíhlosti jednovrstvé stěny z hlediska použitelnosti, podepřené podél tří stran s volnou jednou svislou stranou
Obr. 7.10 Omezení štíhlosti jednovrstvé stěny z hlediska použitelnosti, podepřené podél tří stran s volnou horní stranou
8 SLOUPY
Svislé podepření stropních, popř. střešních konstrukcí může být realizováno stěnami, sloupy popřípadě jejich kombinací. Výhodou sloupů jsou malé rozměry a menší omezení dispozice objektu. Velikost průřezu sloupů je dána jednak pevností použitého materiálu, jednak jejich štíhlostí, která nepříznivě ovlivňuje vzpěrnou pevnost sloupů. Průřez sloupů může též významně ovlivnit to, že kromě osové síly může být namáhán na ohyb.
Tab. 8.1 Přehled sloupů
| Prvek | Nákres | Typická výška h [m] | Poměr h/d [–] | |
| Dřevěný | sloup z řeziva | 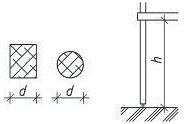 |
2–4 | 15–30 |
| lamelové průřezy sloupů | 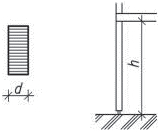 |
2–4 | 15–30 | |
| žebra v panelech | 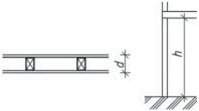 |
2–4 | 20–35 | |
| Ocelový | válcovaný otevřený profil | 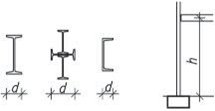 |
||
|
2–8 | 20–25 | ||
|
2–4 | 17–18 | ||
| válcovaný uzavřený profil | 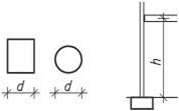 |
|||
|
2–8 | 20–25 | ||
|
2–4 | 17–28 | ||
| členěný průřez | 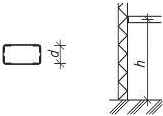 |
4–10 | 20–25 | |
| spřažený průřez | 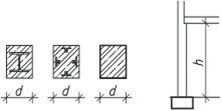 |
4–10 | 6–15 | |
| žebrový panel | 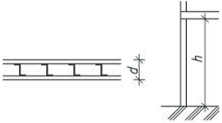 |
2–8 | 15–50 | |
| závěs z vysokopevnostní oceli | 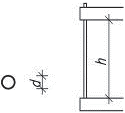 |
1–40 | – | |
| Železobetonový | monolitický sloup | 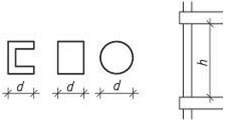 |
||
|
2–8 | 12–18 | ||
|
2–4 | 6–15 | ||
| monolitická stěna | 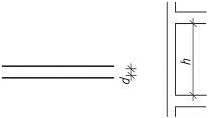 |
2–4 | 18–25 | |
| stěna z mezerovitého betonu | 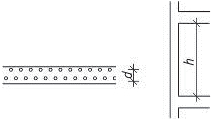 |
2–3 | 10–15 | |
| prefabrikované sloupy | 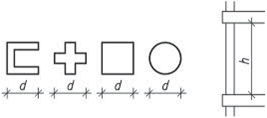 |
|||
|
2–8 | 10–15 | ||
|
2–4 | 8–15 | ||
| prefabrikovaný stěnový nosný panel | 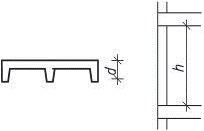 |
2–4 | 20–25 | |
| prefabrikovaný stěnový žebrový panel | 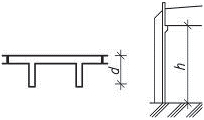 |
4–8 | 15–25 | |
| předpjatý sloup | 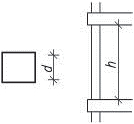 |
|||
|
4–8 | 15–25 | ||
|
2–4 | 10–20 | ||
| předpjatý závěs | 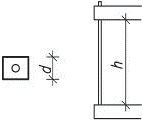 |
1–40 | 100–150 | |
8.1 DŘEVENÉ SLOUPY
Únosnost dřevěných tlačených prvků závisí na druhu dřeva (jeho třídě pevnosti, délce trvání zatížení a vlhkostním režimu), velikosti průřezu a vzpěrné délce prutu. Běžně se navrhují průřezy čtvercové, vhodné zejména při stejných vzpěrných délkách ve směru obou hlavních os setrvačnosti. Kruhový průřez se může uplatnit jako provizorní opěra, součást lešení apod.

Obr. 8.1 Průřezy dřevěných sloupů
Omezení štíhlosti
Podle dnes již neplatné ČSN 73 1701 byly omezeny štíhlosti tlačených prvků bez ohledu na jejich únosnost podle tab. 8.2, uvedené hodnoty lze použít jako doporučené.
Tab. 8.2 Doporučené mezní štíhlostní poměry dřevěných sloupů
| Konstrukční prvky | Mezní štíhlostní poměr λ = ℓef /i pro konstrukce | ||
| trvalé | dočasné | ||
| Sloupy a podporové stojky | 120 | 150 | |
| Tlačené části vazníků apod. | celistvé | 150 | 175 |
| složené a členěné | 175 | 200 | |
| Ztužidla a jejich části | 200 | 225 | |
Únonost sloupů
Tab. 8.3 Únosnost dřevěných sloupů čtvercového a kruhového profilu v [kN]
| Rozměr d [mm] | Profil | Vzpěrná délka ℓef [m] | ||||||||
| 2,0 | 2,5 | 3,0 | 3,5 | 4,0 | 4,5 | 5,0 | 6,0 | 7,0 | ||
| 100 | ■ | 57,49 | 40,25 | 29,11 | 21,89 | – | – | – | – | – |
| ● | 36,13 | 24,52 | 17,53 | – | – | – | – | – | – | |
| 120 | ■ | 103,85 | 77,95 | 57,96 | 44,13 | 34,53 | – | – | – | – |
| ● | 68,62 | 48,60 | 35,31 | 26,60 | – | – | – | – | – | |
| 140 | ■ | 160,73 | 130,91 | 101,63 | 78,89 | 62,34 | 50,27 | – | – | – |
| ● | 112,18 | 84,63 | 63,07 | 48,06 | 37,62 | – | – | – | – | |
| 160 | ■ | 225,39 | 196,20 | 160,84 | 128,52 | 103,04 | 83,76 | 69,16 | – | – |
| ● | 163,76 | 132,63 | 102,59 | 79,50 | 62,77 | 50,60 | – | – | – | |
| 180 | ■ | 297,50 | 270,43 | 233,66 | 193,83 | 158,64 | 130,41 | 108,39 | 77,69 | – |
| ● | 221,47 | 190,54 | 154,40 | 122,55 | 97,91 | 79,44 | 65,52 | – | – | |
| 200 | ■ | 377,41 | 352,17 | 316,89 | 273,57 | 229,96 | 191,98 | 161,00 | 116,45 | 87,56 |
| ● | 284,99 | 255,87 | 217,39 | 177,94 | 144,51 | 118,29 | 98,08 | 70,11 | – | |
| 220 | ■ | 465,41 | 441,36 | 408,30 | 365,08 | 316,25 | 269,28 | 228,54 | 167,30 | 126,49 |
| ● | 354,54 | 327,28 | 289,39 | 245,20 | 203,39 | 168,47 | 140,64 | 101,25 | – | |
| 240 | ■ | 561,70 | 538,27 | 507,13 | 465,81 | 415,39 | 361,89 | 311,81 | 231,84 | 176,50 |
| ● | 430,35 | 404,49 | 368,45 | 322,78 | 274,50 | 230,83 | 194,42 | 141,23 | 106,41 | |
Poznámka:
Předpoklady: pevnostní třída řeziva C24 (SI), fc,0,k = 24 MPa, kmod = 0,7 (třída provozu 1, třída trvání zatížení dlouhodobé zatížení), dílčí součinitel materiálu γM = 1,3, štíhlost λ ≤ 120.
8.2 OCELOVÉ SLOUPY
Volba profilu závisí na vzpěrných délkách. Při stejných vzpěrných délkách v obou směrech jsou vhodné trubkové profily, čtvercové trubky, HEB popřípadě profily složené ze dvou U nebo L profilů.
Pro prvky namáhané vzpěrným tlakem, kdy se uplatní výrazněji součinitel vzpěrnosti, není vhodné volit ocel vyšší pevnosti.
Doporučené mezní štíhlosti
Podobně jako u dřeva není štíhlost ocelových prvků omezena, doporučuje se použít omezení podle dnes již neplatné normy ČSN 73 1401.
Tab. 8.4 Doporučené mezní štíhlosti ocelových prvků
| Pruty | Mezní štíhlost λ = ℓef/i |
| Příhradových nosníků a sloupy budov | 180 |
| Ztužidel namáhaných větrem a brzdnými silami, výplňové pruty sloupů, klopení nosníků | 200 |
| Ztužidel zajišťujících vzpěrné délky jiných prutů a jiné přímo nezatížené pruty, prvky v montážním stádiu | 250 |
Tab. 8.5 Návrhové hodnoty únosnosti ocelových sloupů (v nevybarvených polích mají pruty štíhlost λ ≤ 180, v šedých polích 180 < λ ≤ 200 a v černých 200 < λ ≤ 250)
| Profil | Vzpěrná délka ℓef [m] | |||||||||
| Výška H | Profil | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 | 4,5 | 5,0 | 6,0 | 7,0 |
| 100 | IPN | 52,62 | 35,10 | – | – | – | – | – | – | – |
| IPE | 66,13 | 44,64 | 31,98 | – | – | – | – | – | – | |
| HEB | 388,54 | 311,72 | 247,39 | 197,57 | 159,96 | 131,51 | 109,75 | 79,47 | – | |
| HEA | 314,72 | 251,86 | 199,52 | 159,15 | 128,75 | 105,80 | 88,26 | 63,88 | – | |
| 2 UPN | 510,21 | 455,82 | 399,39 | 344,72 | 295,24 | 252,60 | 216,86 | 162,83 | 125,72 | |
| 120 | IPN | 89,91 | 60,65 | 43,43 | – | – | – | – | – | – |
| IPE | 137,93 | 172,41 | 206,90 | 241,38 | – | – | – | – | – | |
| HEB | 580,98 | 494,04 | 411,32 | 339,76 | 281,38 | 234,93 | 198,18 | 145,49 | 110,86 | |
| HEA | 428,92 | 363,38 | 301,49 | 248,38 | 205,32 | 171,21 | 144,30 | 105,82 | 80,57 | |
| 2 UPN | 670,52 | 611,54 | 549,06 | 485,75 | 425,19 | 370,17 | 322,06 | 246,13 | 192,02 | |
| 140 | IPN | 141,40 | 96,71 | 69,71 | – | – | – | – | – | – |
| IPE | 166,223 | 117,01 | 85,49 | 64,83 | 50,72 | – | – | – | – | |
| HEB | 796,65 | 701,81 | 610,84 | 521,85 | 443,22 | 376,82 | 322,01 | 240,33 | 184,90 | |
| HEA | 577,30 | 508,82 | 439,16 | 373,78 | 316,51 | 268,50 | 229,08 | 170,62 | 131,11 | |
| 2 UPN | 827,18 | 764,09 | 696,90 | 627,29 | 558,32 | 493,22 | 434,22 | 337,32 | 265,79 | |
| 160 | IPN | 210,47 | 146,38 | 106,35 | 80,39 | – | – | – | – | – |
| IPE | 236,97 | 171,22 | 126,68 | 96,71 | 75,98 | 61,16 | – | – | – | |
| HEB | 1057,07 | 958,15 | 853,87 | 749,53 | 651,39 | 563,78 | 488,27 | 370,85 | 288,27 | |
| HEA | 750,53 | 678,21 | 602,19 | 526,62 | 456,14 | 393,73 | 340,29 | 257,74 | 200,02 | |
| 2 UPN | 997,91 | 931,98 | 861,84 | 788,23 | 713,28 | 639,97 | 571,04 | 452,48 | 360,99 | |
| 180 | IPN | 297,68 | 211,18 | 154,87 | 117,68 | 92,19 | – | – | – | – |
| IPE | 321,54 | 240,10 | 180,61 | 139,12 | 109,87 | 88,75 | 73,09 | – | – | |
| HEB | 1322,43 | 1220,98 | 1112,93 | 1001,06 | 890,38 | 786,06 | 691,67 | 536,92 | 422,86 | |
| HEA | 914,39 | 842,98 | 766,96 | 688,43 | 611,05 | 538,45 | 473,06 | 366,42 | 288,19 | |
| 2 UPN | 1187,40 | 1117,99 | 1044,53 | 967,06 | 886,94 | 806,56 | 728,66 | 588,85 | 475,98 | |
| 200 | IPN | 402,11 | 291,85 | 216,40 | 165,40 | 130,03 | 104,73 | – | – | – |
| IPE | 420,90 | 324,40 | 248,34 | 193,10 | 153,37 | 124,33 | 102,64 | – | – | |
| HEB | 1627,29 | 1521,20 | 1408,39 | 1289,89 | 1169,01 | 1050,40 | 938,49 | 745,15 | 595,27 | |
| HEA | 1115,84 | 1041,06 | 961,50 | 878,05 | 793,30 | 710,66 | 633,23 | 500,71 | 398,92 | |
| 2 UPN | 1388,65 | 1316,06 | 1239,74 | 1159,29 | 1075,37 | 989,67 | 904,60 | 745,75 | 611,43 | |
| 220 | IPN | 525,51 | 391,13 | 293,72 | 226,03 | 178,42 | 144,08 | 118,63 | – | – |
| IPE | 539,64 | 432,63 | 339,53 | 267,76 | 214,43 | 174,74 | 144,77 | 103,69 | – | |
| HEB | 1940,28 | 1830,90 | 1715,34 | 1593,43 | 1466,98 | 1339,27 | 1214,50 | 987,63 | 801,81 | |
| HEA | 1366,60 | 1287,93 | 1204,72 | 116,96 | 1026,07 | 934,62 | 845,69 | 685,21 | 554,87 | |
| 2 UPN | 1633,65 | 1555,61 | 147,08 | 1388,36 | 1298,65 | 1206,12 | 1112,79 | 933,18 | 775,18 | |
| 240 | IPN | 665,73 | 508,82 | 387,64 | 300,63 | 238,40 | 193,07 | 159,29 | – | – |
| IPE | 670,31 | 554,57 | 445,51 | 356,35 | 287,80 | 235,77 | 196,02 | 141,01 | – | |
| HEB | 2299,95 | 2184,82 | 2064,14 | 1937,05 | 1804,22 | 1667,87 | 1531,41 | 1272,79 | 1049,96 | |
| HEA | 1662,01 | 1577,27 | 1488,33 | 1394,63 | 1296,76 | 1196,51 | 1096,51 | 908,18 | 747,21 | |
| 2 UPN | 1869,29 | 1787,34 | 1702,29 | 1613,22 | 1519,98 | 1423,23 | 1324,47 | 1129,42 | 951,17 | |
| 260 | IPN | 813,60 | 635,50 | 490,40 | 383,02 | 305,00 | 247,66 | 204,69 | – | – |
| HEB | 2598,36 | 2481,49 | 2359,93 | 2232,48 | 2099,03 | 1960,76 | 1820,06 | 1544,25 | 1295,04 | |
| HEA | 1907,17 | 1819,97 | 1729,18 | 1633,90 | 1534,15 | 1430,90 | 1326,07 | 1121,56 | 938,10 | |
| 2 UPN | 2155,06 | 2067,36 | 1976,85 | 1882,49 | 1783,84 | 1681,20 | 1575,63 | 1363,13 | 1162,67 | |
| 270 | IPE | 842,13 | 725,93 | 604,87 | 496,07 | 406,95 | 336,69 | 281,76 | 204,28 | 154,24 |
| 280 | IPN | 972,70 | 774,85 | 605,49 | 476,31 | 380,87 | 310,09 | 256,74 | 183,75 | – |
| HEB | 2920,64 | 2801,18 | 2677,85 | 2549,23 | 2414,75 | 2274,84 | 2131,02 | 1841,83 | 1569,59 | |
| HEA | 2165,28 | 2075,43 | 1982,55 | 1885,61 | 1784,21 | 1678,76 | 1570,49 | 1353,57 | 1150,60 | |
| 2 UPN | 2401,97 | 2310,37 | 2216,31 | 2118,67 | 2016,82 | 1910,78 | 1801,23 | 1577,66 | 1361,23 | |
| 300 | IPN | 1139,03 | 923,16 | 730,10 | 578,39 | 464,44 | 379,11 | 314,44 | 225,53 | – |
| IPE | 1035,07 | 920,02 | 792,24 | 667,18 | 557,32 | 466,60 | 393,56 | 288,00 | 218,57 | |
| HEB | 3357,35 | 3231,27 | 3101,96 | 2967,87 | 2828,09 | 2682,56 | 2532,12 | 2224,19 | 1924,37 | |
| HEA | 2519,12 | 2423,12 | 2324,54 | 2222,21 | 2115,48 | 2004,35 | 1889,55 | 1655,22 | 1428,32 | |
| 2 UPN | 2663,55 | 2567,76 | 2469,83 | 2368,58 | 2263,25 | 2153,64 | 2040,15 | 1806,20 | 1574,93 | |
Tab. 8.6 Návrhová únosnost ocelových trubek (výběr) v [kN], ocel S 235, fk = 235 [MPa]
| Profil | Vzpěrná délka ℓef [m] | |||||||||
| průměr | stěna | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 | 4,5 | 5,0 | 6,0 | 7,0 |
| 38 | 4 | 24,44 | 16,69 | 12,05 | – | – | – | – | – | – |
| 51 | 4 | 55,34 | 39,60 | 29,32 | 22,45 | 17,69 | – | – | – | – |
| 70 | 4 | 115,59 | 90,44 | 70,54 | 55,71 | 44,79 | 36,65 | 30,48 | – | – |
| 5,6 | 154,48 | 120,01 | 93,16 | 73,37 | 58,87 | 48,12 | 39,98 | – | – | |
| 89 | 4 | 180,68 | 152,91 | 126,75 | 104,35 | 86,21 | 71,87 | 60,55 | 44,39 | 33,80 |
| 7 | 298,69 | 250,32 | 205,68 | 168,23 | 138,37 | 115,00 | 96,69 | 70,68 | 53,72 | |
| 114 | 4 | 265,13 | 238,60 | 210,84 | 183,49 | 158,25 | 136,14 | 117,36 | 88,59 | 68,61 |
| 7 | 446,67 | 399,94 | 351,33 | 303,99 | 260,89 | 223,57 | 192,17 | 144,51 | 111,68 | |
| 133 | 5 | 406,09 | 374,48 | 340,82 | 306,04 | 271,74 | 239,54 | 210,51 | 163,12 | 128,32 |
| 8 | 406,09 | 374,48 | 340,82 | 306,04 | 271,74 | 239,54 | 210,51 | 163,12 | 128,32 | |
| 168 | 5 | 549,58 | 519,95 | 488,73 | 455,80 | 421,52 | 386,66 | 352,27 | 288,76 | 235,77 |
| 10 | 1058,64 | 999,07 | 936,14 | 869,77 | 800,88 | 731,30 | 663,29 | 539,56 | 438,14 | |
| 219 | 6 | 903,85 | 869,65 | 834,56 | 798,14 | 760,18 | 720,65 | 679,79 | 596,29 | 515,22 |
| 10 | 1474,04 | 1416,99 | 1358,35 | 1297,42 | 1233,82 | 1167,60 | 1099,26 | 960,16 | 826,27 | |
Tab. 8.7 Návrhová únosnost ocelových bezešvých čtvercových trubek (výběr) [kN], ocel S 235, fk = 235 [MPa]
| Profil | Vzpěrná délka ℓef [m] | |||||||||
| obrys | stěna | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 | 4,5 | 5,0 | 6,0 | 7,0 |
| 60/60 | 4 | 141,74 | 109,30 | 82,64 | 63,48 | 49,94 | 40,18 | 32,98 | – | – |
| 80/80 | 5 | 285,61 | 252,36 | 211,77 | 172,53 | 140,06 | 114,74 | 95,22 | 68,18 | – |
| 100/100 | 6 | 459,43 | 430,32 | 391,52 | 344,19 | 294,67 | 249,44 | 211,19 | 154,47 | 116,83 |
| 120/120 | 8 | 885,20 | 845,65 | 794,65 | 729,63 | 652,80 | 572,06 | 495,92 | 372,15 | 284,88 |
| 150/150 | 8 | 789,37 | 774,67 | 758,45 | 740,10 | 718,90 | 694,09 | 665,00 | 593,32 | 510,05 |
| 180/180 | 8 | 1055,52 | 1038,50 | 1020,13 | 999,87 | 977,06 | 951,00 | 920,94 | 846,50 | 753,83 |
| 200/200 | 10 | 1675,53 | 1647,40 | 1616,86 | 1582,93 | 1544,47 | 1500,21 | 1448,88 | 1321,58 | 1165,45 |
| 250/250 | 12,5 | 1761,41 | 1739,90 | 1717,46 | 1693,68 | 1668,10 | 1640,21 | 1609,45 | 1536,77 | 1445,25 |
Tab. 8.8 Návrhová únosnost ocelových bezešvých obdélníkových trubek (výběr) v [kN], ocel S 235, fk = 235 [MPa]
| Profil | Vzpěrná délka ℓef [m] | |||||||||
| obrys | stěna | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 | 4,5 | 5,0 | 6,0 | 7,0 |
| 60/40 | 4 | 68,89 | 46,91 | 33,61 | 25,17 | – | – | – | – | – |
| 90/50 | 5 | 175,77 | 127,47 | 93,69 | 71,02 | 55,47 | 44,45 | – | – | – |
| 120/80 | 6 | 435,85 | 390,28 | 332,80 | 274,42 | 224,36 | 184,54 | 153,53 | 110,22 | 82,62 |
| 140/100 | 8 | 717,39 | 674,06 | 616,42 | 545,34 | 469,52 | 399,00 | 338,67 | 248,36 | 188,09 |
| 160/100 | 8 | 788,44 | 742,87 | 682,39 | 607,19 | 525,55 | 448,33 | 381,49 | 280,49 | 212,68 |
| 200/150 | 8 | 1160,23 | 1131,70 | 1098,65 | 1059,26 | 1011,63 | 954,38 | 887,78 | 739,32 | 599,13 |
| 250/150 | 10 | 1644,97 | 1605,30 | 1559,51 | 1505,15 | 1439,58 | 1360,81 | 1268,89 | 1061,87 | 863,44 |
| 300/200 | 10 | 2145,50 | 2112,11 | 2076,26 | 2036,91 | 1992,92 | 1942,95 | 1885,62 | 1744,06 | 1566,04 |
8.3 ŽELEZOBETONOVÉ SLOUPY
Pro potřeby návrhu železobetonových, dostředně tlačených sloupů byly vypracovány tab. 8.9–8.11 pro různé typy průřezů. Tabulky byly zpracovány pro beton pevnostní třídy C25/30 a ocel B500B. Pro každou sílu jsou k dispozici dvě hodnoty: velikost průřezu a délka sloupu. Délka sloupu je vypočítána pro štíhlost λ = 35. Sloup daného průřezu lze navrhnout i pro větší délku, ale potom je třeba vzít v úvahu jeho štíhlost.
Tab. 8.9 Návrhová únosnost čtvercových železobetonových sloupů Nud [kN]
| Průřez b/h [mm] | 200/200 | 250/250 | 300/300 | 350/350 | 400/400 | 450/450 | 500/500 | 550/550 | 600/600 | |
| Procento vyztužení | ρ = 1 % | 700 | 1100 | 1590 | 2160 | 2830 | 3580 | 4420 | 5340 | 6360 |
| ρ = 2 % | 880 | 1370 | 1980 | 2690 | 3520 | 4460 | 5500 | 6660 | 7930 | |
| ρ = 4 % | 1220 | 1920 | 2760 | 3760 | 4910 | 6220 | 7680 | 9290 | 11060 | |
| Délka při štíhlosti λ = 35 | 2000 | 2500 | 3000 | 3500 | 4000 | 4500 | 5000 | 5500 | 6000 | |
Tab. 8.10 Návrhová únosnost obdelníkových železobetonových sloupů Nud [kN]
| Průřez b/h [mm] | 200/250 | 200/300 | 200/350 | 200/400 | 200/450 | 200/500 | 200/550 | 200/600 | 200/650 | |
| Procento vyztužení | ρ = 1 % | 880 | 1060 | 1230 | 1410 | 1590 | 1760 | 1940 | 2120 | 2300 |
| ρ = 2 % | 1100 | 1320 | 1540 | 1760 | 1980 | 2200 | 2420 | 2640 | 2860 | |
| ρ = 4 % | 1530 | 1840 | 2150 | 2450 | 2760 | 3070 | 3380 | 3680 | 3990 | |
| Délka při štíhlosti λ = 35 | 2000 | 2000 | 2000 | 2000 | 2000 | 2000 | 2000 | 2000 | 2000 | |
| Průřez b/h [mm] | – | 250/300 | 250/350 | 250/400 | 250/450 | 250/500 | 250/550 | 250/600 | 250/650 | |
| Procento vyztužení | ρ = 1 % | – | 1320 | 1540 | 1770 | 1990 | 2210 | 2430 | 2650 | 2870 |
| ρ = 2 % | – | 1650 | 1920 | 2200 | 2480 | 2750 | 3030 | 3300 | 3580 | |
| ρ = 4 % | – | 2300 | 2680 | 3070 | 3450 | 3840 | 4220 | 4600 | 4990 | |
| Délka při štíhlosti λ = 35 | – | 2500 | 2500 | 2500 | 2500 | 2500 | 2500 | 2500 | 2500 | |
| Průřez b/h [mm] | – | – | 300/350 | 300/400 | 300/450 | 300/500 | 300/550 | 300/600 | 300/650 | |
| Procento vyztužení | ρ = 1 % | – | – | 3000 | 3000 | 3000 | 3000 | 3000 | 3000 | 3000 |
| ρ = 2 % | – | – | 1850 | 2120 | 2380 | 2650 | 2910 | 3180 | 3440 | |
| ρ = 4 % | – | – | 2310 | 2640 | 2970 | 3300 | 3634 | 3960 | 4290 | |
| Délka při štíhlosti λ = 35 | – | – | 3220 | 3680 | 4140 | 4600 | 5070 | 5530 | 5990 | |
| Průřez b/h [mm] | – | – | – | 350/400 | 350/450 | 350/500 | 350/550 | 350/600 | 350/650 | |
| Procento vyztužení | ρ = 1 % | – | – | – | 2470 | 2780 | 3090 | 3400 | 3710 | 4020 |
| ρ = 2 % | – | – | – | 3080 | 3470 | 3850 | 4240 | 4620 | 5010 | |
| ρ = 4 % | – | – | – | 4300 | 4840 | 5370 | 5910 | 6450 | 6990 | |
| Délka při štíhlosti λ = 35 | – | – | – | 3500 | 3500 | 3500 | 3500 | 3500 | 3500 | |
| Průřez b/h [mm] | – | – | – | – | 400/450 | 400/500 | 400/550 | 400/600 | 400/650 | |
| Procento vyztužení | ρ = 1 % | – | – | – | – | 3180 | 3530 | 3890 | 4240 | 4590 |
| ρ = 2 % | – | – | – | – | 3960 | 4400 | 4840 | 5280 | 2720 | |
| ρ = 4 % | – | – | – | – | 5530 | 6140 | 6760 | 7370 | 7990 | |
| Délka při štíhlosti λ = 35 | – | – | – | – | 4000 | 4000 | 4000 | 4000 | 4000 | |
| Průřez b/h [mm] | – | – | – | – | – | 450/500 | 450/550 | 450/600 | 450/650 | |
| Procento vyztužení | ρ = 1 % | – | – | – | – | – | 3980 | 4370 | 4770 | 5170 |
| ρ = 2 % | – | – | – | – | – | 4950 | 5450 | 5940 | 6440 | |
| ρ = 4 % | – | – | – | – | – | 6910 | 7600 | 8290 | 8980 | |
| Délka při štíhlosti λ = 35 | – | – | – | – | – | 4500 | 4500 | 4500 | 4500 | |
| Průřez b/h [mm] | – | – | – | – | – | – | 500/550 | 500/600 | 500/650 | |
| Procento vyztužení | ρ = 1 % | – | – | – | – | – | – | 4862 | 5300 | 5740 |
| ρ = 2 % | – | – | – | – | – | – | 6060 | 6600 | 7160 | |
| ρ = 4 % | – | – | – | – | – | – | 8450 | 9210 | 9980 | |
| Délka při štíhlosti λ = 35 | – | – | – | – | – | – | 5000 | 5000 | 5000 | |
Tab. 8.11 Návrhová hodnota únosnosti kruhových železobetonových sloupů Nud [kN]
| Průměr d [mm] | 200 | 250 | 300 | 350 | 400 | 450 | 500 | 550 | 600 | |
| Procento vyztužení | ρ = 1 % | 550 | 860 | 1250 | 1700 | 2220 | 2810 | 3470 | 4200 | 5000 |
| ρ = 2 % | 690 | 1080 | 1550 | 2100 | 2760 | 3500 | 4320 | 5230 | 6230 | |
| ρ = 4 % | 960 | 1500 | 2170 | 2950 | 3860 | 4880 | 6030 | 7300 | 8680 | |
| Délka při štíhlosti λ = 35 | 1750 | 2190 | 2630 | 3060 | 3500 | 3900 | 4375 | 4800 | 5250 | |
Příklad 8.1
Navrhněte čtvercový nebo kruhový sloup, na který působí v dostředném tlaku normálová síla Nd = 1 400 kN. Délka sloupu je 2,9 m.
V tab. 8.9 pro čtvercový průřez a pro procento vyztužení ρ = 2 % (obvyklé vyztužení sloupů) vyhledáme pro nejbližší vyšší hodnotu únosnosti 1 980 kN čtvercový sloup 300/300 mm a zkontroluje se štíhlost: délka navrhovaného sloupu je 2,9 m < 3,0 m, což je délka, která odpovídá štíhlosti λ = 35.
Obdobně v tab. 8.11 pro kruhové průřezy se ověří únosnost pro průměr 300 mm (1 550 > 1 400 kN), s ohledem na dodržení štíhlosti ale zvolí se průměr 350 mm (2 100 > 1 400 kN; 2,9 m < 3,060 m).
9 VÝŠKOVÉ BUDOVY
Se vzrůstající výškou objektu roste důležitost zajištění prostorové tuhosti – stabilizačního podsystému. Jeho účinnost závisí na konstrukčním řešení, uspořádání a rozměrech (poměru šířky ztužujících prvků k výšce budovy).
Tab. 9.1 Konstrukční systémy
| Základní prvky | Uspořádání stabilizačního podsystému | ||
| z jednotlivých oddělených vazeb | prostorové uspořádání | ||
| otevřené | uzavřené | ||
| Pruty (skelety) |
|
otevřený prutový systém
|
uzavřený prutový systém
|
| Stěny |
|
otevřený stěnový systém
|
uzavřený stěnový systém
|
| Zobrazení |  |
 |
 |
Gravitační podsystém tvoří prvky, které se podílí na přenosu gravitačních sil působících na konstrukci. Se stabilizačním systémem úzce souvisí – gravitační síly (vlastní tíha budovy) působí proti převržení objektu. Proto je vhodné uspořádání konstrukčního systému tak, aby se co nejvíce gravitačních sil přeneslo do stabilizačního podsystému a tím zvýšilo jeho účinnost. Princip je patrný z momentové výminky znázorněné na obr. 9.1.
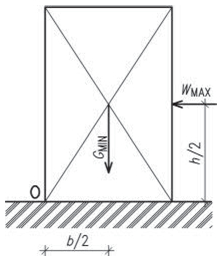
Obr. 9.1 Schéma momentové výminky k bodu O
\begin{gathered}
G_\text{min}\cdot b/2\ge V_\text{max}\cdot h/2
\end{gathered}Tab. 9.2 Přehled vybraných konstrukčních systémů
| Nosná konstrukce | Nákres | Počet podlaží | Poměr H/V | |
| Zděné | zděné stěny a železobetonové stropy |  |
5–25 | 1,5–3,5 |
| Železobetonové | patrové monolitické rámy | 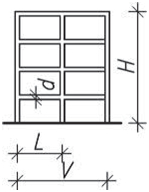 |
5–15 | 1–5 |
| monolitické stěny s tuhými rámy | 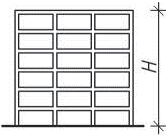 |
10–55 | 4–5 | |
| rámové komůrky a jádra |  |
40–65 | 6–7 | |
| jádro se zavěšenými stropy nebo polotuhými rámy |  |
10–30 | 8–12 | |
| Ocelové | patrové tuhé rámy | 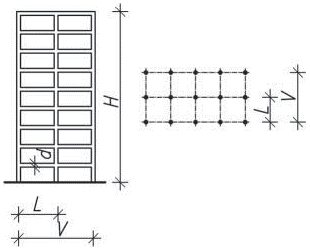 |
< 24 | 4–5 |
| zavětrování s měkkými vazbami | 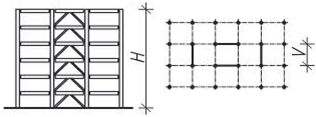 |
5–20 | 6–8 | |
| zavětrování s tuhými rámy | 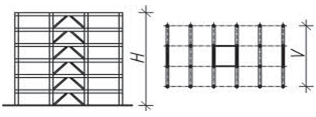 |
10–40 | 3–4 | |
| zavětrování s propojenými sloupy |  |
40–60 | 5–7 | |
| rámová komůrka | 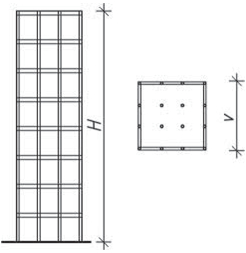 |
30–80 | 5–7 | |
| příhradová komůrka | 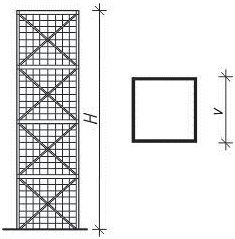 |
60–110 | 5–7 | |
Jádrový systém je možný v několika variantách, které se především liší způsobem přenosu gravitačních sil – stabilizačním podsystémem je ve všech případech jádro.
Obr. 9.2 Varianty jádrových systémů
Tubusový systém je nejúčinnější, neboť stabilizační konstrukce, rozmístěná po obvodě stavby, má maximální rozměry. Celková efektivnost je ovlivněna:
- konstrukčním řešením (příhradový, nebo rámový tubus);
- uspořádáním (systém s vnitřními sloupy, se svazkem tubusů a s tubusem bez vnitřních podpor).
Možnosti jednotlivých systémů jsou srovnány v následující tab. 9.3.
Tab. 9.3 Srovnání konstrukčních systémů
| H/B | H [m] | Počet podlaží |  |
 |
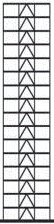 |
 |
 |
 |
 |
 |
 |
| 8 | 480 | 120 | |||||||||
| 7 | 440 | 110 | |||||||||
| 400 | 100 | ||||||||||
| 6 | |||||||||||
| 360 | 90 | ||||||||||
| 5 | 320 | 80 | |||||||||
| 280 | 70 | ||||||||||
| 4 | |||||||||||
| 240 | 60 | ||||||||||
| 3 | 200 | 50 | |||||||||
| 160 | 40 | ||||||||||
| 2 | |||||||||||
| 120 | 30 | ||||||||||
| 1 | 80 | 20 | |||||||||
| 40 | 10 | ||||||||||
| 0 | |||||||||||
| Půdorys |  |
 |
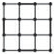 |
 |
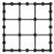 |
 |
 |
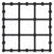 |
 |
||
| polotuhé rámy | rámy | přihradová ztužidla | vnějsí rámy | přihrad. komůrka s vnitř. rámy | rámová komurka | svazek komůrek | příhrad. komůrka | ||||
10 HALOVÉ OBJEKTY A ZASTŘEŠENÍ NA VELKÁ ROZPĚTÍ
U halových objektů se podstatným problémem stává překlenutí velkého rozpětí. Předpokladem úspěšného návrhu je zpravidla minimalizování vlastní hmotnosti konstrukce, pokud tato není využita jako balast pro stabilizaci tvaru nebo k zajištění konstrukce proti sání větru. Při návrhu je velmi důležité podle zvoleného statického systému rezervovat dostatečný prostor pro konstrukci. U ohýbaných konstrukcí je to výška trámu, u tlačených konstrukcí vzepětí a u tažených konstrukcí průvěs. Pokud nejsou dodrženy doporučené poměry, jednak narůstají vnitřní síly v prvcích systému, jednak se zmenšuje celková tuhost.
10.1 STATICKÉ SYSTÉMY
Tab. 10.1 Statické systémy podle namáhání
| Namáhání hlavního nosného systému | Prostorové uspořádání | Statický systém | Schéma | Charakteristické průřezy |
| Ohyb | rovinné konstrukce |
|
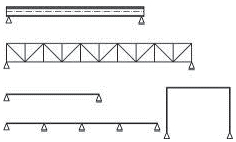 |
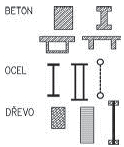 |
| prostorové konstrukce |
|
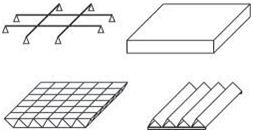 |
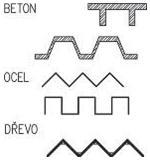 |
|
| Tlak | rovinné konstrukce |
|
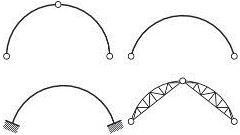 |
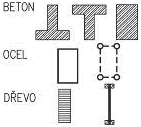 |
| prostorové konstrukce |
|
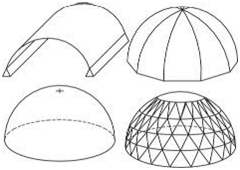 |
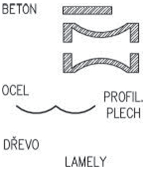 |
|
| Tah | rovinné konstrukce |
|
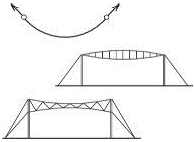 |
 |
| prostorové konstrukce |
|
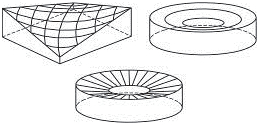 |
 |
Halové objekty můžeme rozdělovat podle různých hledisek. Podle použitého materiálu dělíme haly na:
- železobetonové;
- ocelové;
- dřevěné;
- kombinované.
10.2 ŽELEZOBETONOVÉ HALY
Tab. 10.2 Typy železobetonových hal
| Prvek | Nákres | Tloušťka h [mm] | Rozpětí ℓ [m] | Poměr ℓ/h |
| Jednoduchý jednopodlažní rám | 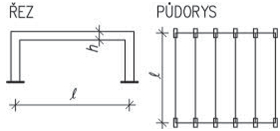 |
– | 12–24 | 22–30 |
| Oblouk | 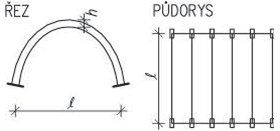 |
– | 15–60 | 28–40 |
| Železobetonové převrácené hyperbolické paraboloidy (deštníky) | 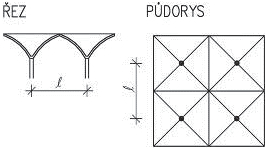 |
75–100 | 9–15 | 120–200 |
| Železobetonové hyperbolicko parabolické skořepiny | 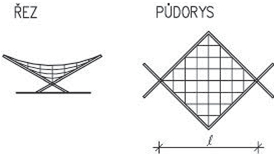 |
75–100 | 15–55 | 200–450 |
| Kupole, báně | 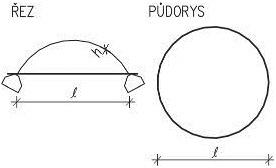 |
75–300 | 15–120 | 300–450 |
| Železobetonové lomenice |  |
75–125 | 9–36 | 40–50 |
| Železobetonové dlouhé válcové skořepiny | 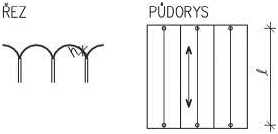 |
75–100 | 25–40 | 50–65 |
| Železobetonové šikmé rošty | 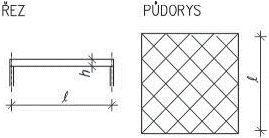 |
300–700 | 10–20 | 25–35 |
Podle technologie mohou být železobetonové haly prefabrikované, pro obvyklý provoz a dispozici, např. průmyslové haly apod., nebo mohou být monolitické, které se kromě průmyslových hal používají také v méně typických případech – haly sportovních stadionů, výstavní haly, kulturní sály apod. Podle technologických požadavků provozu u průmyslových a některých zemědělských hal rozeznáváme halové objekty s podvěsnou dopravou (jeřáb uchycen do střešního nosného pláště) a halové objekty s mostovými jeřáby (jeřábová dráha uložena na sloupech, nejčastěji na krátkých konzolách). Z hlediska konstrukčně statického rozeznáváme halové systémy trámové (rámové), obloukové, deskové a skořepinové.
Konstrukce založené na ohybu
Železobetonové trámové konstrukce lze obecně dělit na systémy vazníkové a systémy bezvazníkové.
Vazníkovým systémem označujeme příčný nosný konstrukční systém, který se skládá z příčných rámů s různým stupněm statické neurčitosti, orientovaných ve směru rozpětí lodí a který přenáší zatížení ze střešních konstrukcí (trámů, desek apod.) do základových konstrukcí.
Bezvazníkovým systémem označujeme podélný nosný konstrukční systém. Na podélné rámy se ukládá vlastní střešní konstrukce o délce rovné rozpětí lodí (např. TT panely).
Rámové systémy monolitické
Některé typy železobetonových monolitických hal s uvedením jejich přípustného rozpětí a rozměry jednotlivých prvků jsou uvedeny na následujících obrázcích.
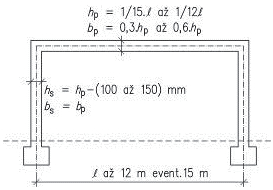
Obr. 10.1 Železobetonové rámové systémy
Vazníkové systémy montované
V současné době se montované železobetonové haly používají častěji než monolitické, což je způsobeno jednoduchostí konstrukčního uspořádání. Skutečně vystačíme s několika málo druhy prefabrikovaných dílců a malá výška konstrukce dovoluje snadnou montáž. Montované haly mohou být vyrobeny ze železobetonu nebo předem předpjatého betonu.
10.3 OCELOVÉ HALY
Tab. 10.4 Konstrukční systémy ocelových hal
| Prvek | Nákres | Rozpětí ℓ [m] | Poměr ℓ/h (ℓ/f) |
| Vlnitý oblouk | 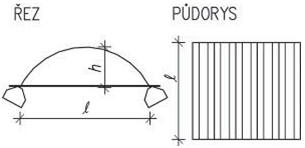 |
30–45 | 5–6 |
| Hala ze zavěšených nosníků | 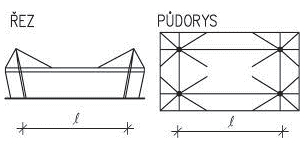 |
60–150 | 5–10 |
| Lanová zavěšená hala | 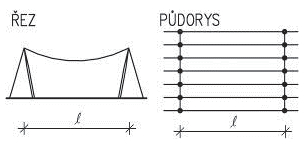 |
50–180 | 8–15 |
| Hala se síťovými lany a s tuhým zastřešením | 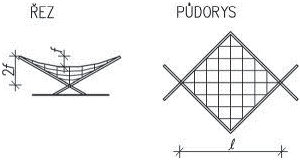 |
30–180 | 6–12 |
| Kupole z mřížoviny | 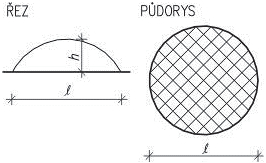 |
15–100 | 5–7 |
| Lomenice | 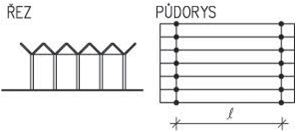 |
9–30 | 10–20 |
| Dvouvrstvá hyperbolicko parabolická skořepina | 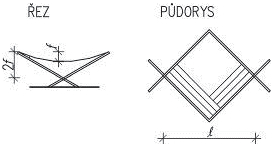 |
9–30 | 6–12 |
| Nafukovací membrána z korozivzdorné oceli | 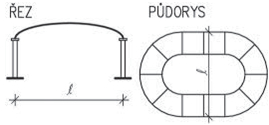 |
80–300 | 25–30 |
| Jednopodlažní rám | 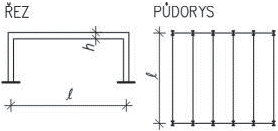 |
9–60 | 35–40 |
| Oblouk | 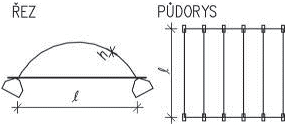 |
60–150 | 40–50 |
| Hala s příhradovým vazníkem |  |
6–40 | 12–20 |
| Prostorová příhradová deska | 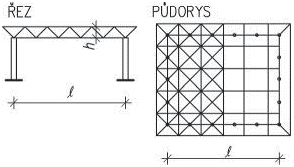 |
30–150 | 15–30 |
| Prostorová příhradovina ve tvaru oblouku | 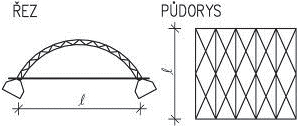 |
20–200 | 55–60 |
Ocelové haly pro průmyslovou nebo zemědělskou výrobu
Typické ocelové haly pro průmyslovou výstavbu se skládají z vaznic, vazníků, průvlaků, sloupů a zavětrování.
Vaznice přenášejí zatížení ze střešního pláště na vazníky. Jejich řešení a uspořádání závisí kromě zatížení především na rozpětí podle tab. 10.5.
Tab. 10.5 Způsoby uložení vaznic
| Rozpětí ℓ [m] | ||||
| 6 | 9 | 12 | ||
| Provedení | válcovaný profil | |||
| prostý nosník | ||||
 |
||||
| prolamovaný nosník | ||||
| prostý nosník | ||||
| příhradový nosník | 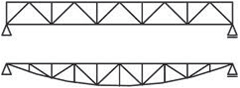 |
|||
| prostý nosník | ||||
Vazníky jsou určeny požadovaným rozpětím haly a tvarem střechy. Plnostěnné svařované vazníky se navrhují do rozpětí 12–15 m, výška svařovaného profilu přibližně 1/15 rozpětí. Příhradové vazníky se navrhují od 15 m rozpětí. Výška příhradového vazníku se volí přibližně 1/10 rozpětí. Příhradové vazníky se nejčastěji navrhují buď úhelníkové, nebo trubkové. Jak plnostěnné tak příhradové vazníky mohou být předpjaté.
Průvlaky se použijí u hal, pokud vzdálenost vazníků je menší než vzdálenost sloupů. Mezilehlé vazníky jsou podepřeny průvlaky většinou příhradového provedení. Výška průvlaku se navrhuje rovna výšce čel vazníků.
Sloupy mohou být buď vetknuty do základů a tak zajišťovat tuhost objektu v příčném směru, nebo mohou být tuze spojeny s vazníkem a tvořit rámovou vazbu. V obou případech jsou sloupy buď příhradové, nebo plnostěnné. Plnostěnný sloup se navrhuje do šířky 1,2–1,5 m.
Zavětrování a ztužidla jsou montována z jednotlivých prutů buď trubkového profilu, nebo profilů IPN, UPN nebo úhelníků. Tato ztužidla mají různou funkci – svislá ztužidla mezi vazníky (v čelech a uvnitř rozpětí) zajišťují svislou polohu vazníků, zavětrování ve střešní rovině ztužuje střešní desku a přenáší vodorovné zatížení od větru na tuhé vazby.
Některé firmy vyrábějí typizované ocelové haly, jejichž použití může zjednodušit a urychlit jak proces výstavby, tak projektovou přípravu.
Ocelové příhradové desky
Příhradové desky jsou relativně tenké, jejich tloušťka se navrhuje 1/20–1/25 kratšího rozpětí. Prostorové působení deskové příhradoviny se nejlépe uplatní, pokud je její půdorysný tvar blízký čtverci a deska je uložena po obvodě ať spojitě nebo řadami sloupů.
10.4 DŘEVĚNÉ HALY
Tab. 10.6 Konstrukční systémy rámových dřevěných hal
| Prvek | Nákres | Rozpětí ℓ [m] | Poměr ℓ/h |
| Dřevěný lepený rám | 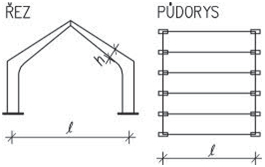 |
12–35 | 30–50 |
| Dřevěný lepený rám složený z nosníků a stojek | 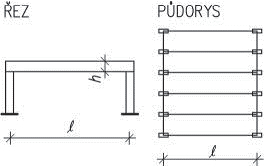 |
4–30 | 18–22 |
| Portálový rám z překližky | 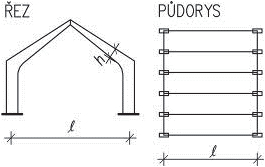 |
9–45 | 20–40 |
| Lepený oblouk | 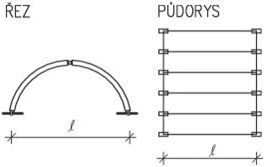 |
15–100 | 30–50 |
Hlavní nosnou konstrukci hal mohou tvořit buď vazníky, nebo rámy. Vazníky se mohou ukládat na podpůrnou konstrukci z jiného materiálu – ocelové, popř. betonové sloupy, nebo betonové či zděné stěny. Svislá konstrukce se řeší tak, aby byla schopná samostatně přenášet účinky větru – sloupy jsou vetknuté, popř. v podélném směru zavětrované, stěna, pokud je tenká, se vyztužuje pilířky apod.
Dřevěné vazníky se běžně používají do rozpětí 24–30 m, pro větší rozpětí jsou výhodnější obloukové konstrukce. Rozteče vazníků se volí v rozmezí 3,6; 4,2; 4,8 a 6,0 m podle druhu pláště. Pro větší rozpětí od 40 m se doporučují rozteče 9–12 m. Stejně i rámové vazby se umísťují ve vzdálenosti 3,6–6,0 m.
Ohýbané prvky probraných dřevěných konstrukcí mají většinou výrazný nepoměr ohybových tuhostí vůči hlavním osám setrvačnosti. Dále většina spojů prvků bývá kloubová, a proto celá soustava bednění, krokví, vaznic, vazníků, popř. rámů není schopna přenášet libovolný směr zatížení. Proto je třeba doplnit ztužidla jednak ve střeše samotné, popř. u rámů ještě ve směru kolmém k jejich rovině.
Tab. 10.7 Dřevěné vazníky
| Provedení | Obrázek | Rozpětí ℓ [m] | Výška h [m] | Vzdálenost vazeb [m] | |
| Sbíjené | 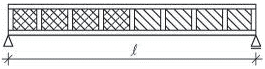 |
7,5–20 | ℓ/8–ℓ/12 | – | |
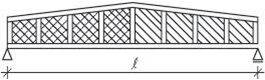 |
7,5–20 | ℓ/8–ℓ/10 | – | ||
 |
6–12 | ℓ/8–ℓ/10 | – | ||
| Lepené | lamelové | 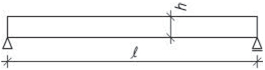 |
10–30 | ℓ/17 | – |
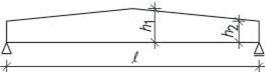 |
10–30 | h1 = ℓ/16 h2 = ℓ/30 |
3,6–9 | ||
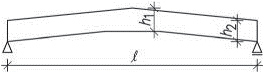 |
10–30 | h1 = ℓ/16 h2 = ℓ/30 |
3,6–9 | ||
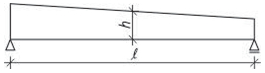 |
10–30 | ℓ/16 | – | ||
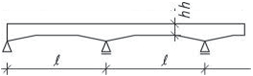 |
10–25 | ℓ/20 | – | ||
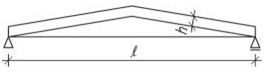 |
15–50 | ℓ/40 | – | ||
 |
15–40 | ℓ/36 | 4,2–7 | ||
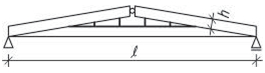 |
15–40 | ℓ/36 | 4,2–7 | ||
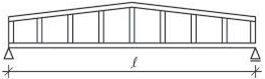 |
6–15 | ℓ/8–ℓ/12 | – | ||
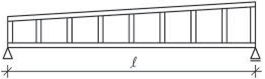 |
6–15 | ℓ/8–ℓ/12 | – | ||
 |
4–8 | ℓ/20–ℓ/30 | – | ||
| Příhradové | 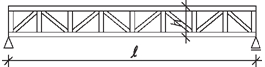 |
10–30 | ℓ/10 | – | |
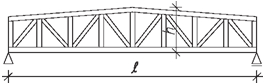 |
24–30 | ℓ/6–ℓ/7 | – | ||
 |
12–18 | ℓ/6 | – | ||
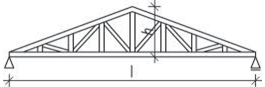 |
21–30 | ℓ/5 | – | ||
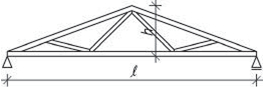 |
12–24 | ℓ/5–ℓ/7 | – | ||
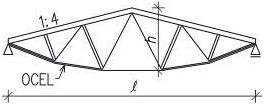 |
30–100 | ℓ/8 | – | ||
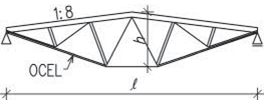 |
30–100 | ℓ/8 | – | ||
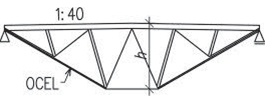 |
30–100 | ℓ/8 | – | ||
Tab. 10.8 Dřevěné rámy
| Provedení | Obrázek | Rozpětí ℓ [m] | Výška h [m] | Vzdálenost vazeb [m] |
| Lepené lamelové | 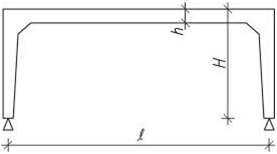 |
15–30 | ℓ/23 | ℓ/3–ℓ/40 |
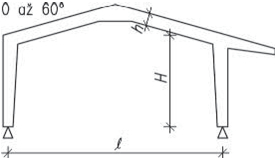 |
15–50 | ℓ/25 | – | |
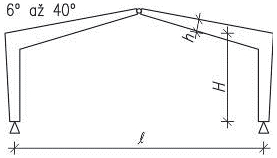 |
15–60 | ℓ/26 | ℓ/4–ℓ/6 | |
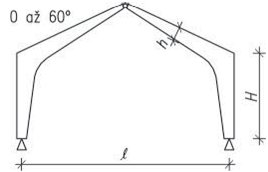 |
15–50 | ℓ/26 | – | |
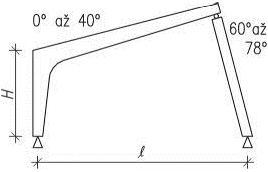 |
15–40 | ℓ/20 | – | |
| Sbíjené | 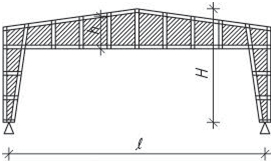 |
10–18 | ℓ/10–ℓ/8 | ℓ/2–ℓ/3 |
| Skříňové | 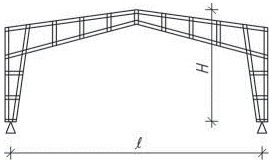 |
15–30 | – | ℓ/3–ℓ |
| Příhradové | 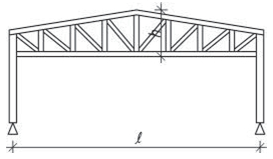 |
10–25 | ℓ/10 | – |
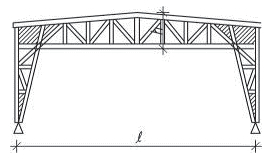 |
10–18 | ℓ/10–ℓ/9 | – | |
 |
15–30 | ℓ/15 | – |
10.5 ZDĚNÉ HALY
Tab. 10.9 Konstrukční systémy zděných hal
| Provedení | Obrázek | Rozpětí ℓ [m] | Tloušťka h [mm] | Poměr ℓ/h |
| Zděné skořepiny | 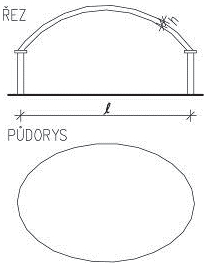 |
6–15 | 75–125 | 80–120 |
| Zděné oblouky | 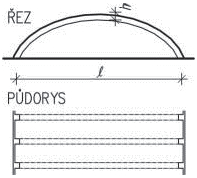 |
8–50 | 70–600 | 30–60 |
| Zděné klenby, kupole a báně | 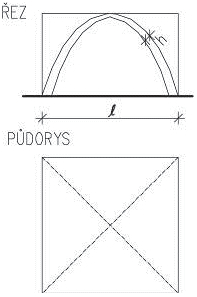 |
5–40 | 75–300 | 30–80 |
10.6 HALY Z PLASTŮ
Tab. 10.10 Konstrukční systémy hal z plastů
| Provedení | Obrázek | Rozpětí ℓ [m] | Poznámka |
| Kupole, báně z tvarovaných panelů | 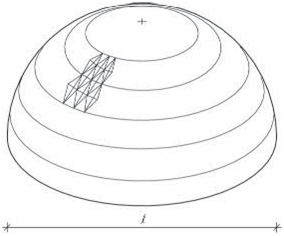 |
4–20 | Kupole mohou mít buď pravoúhlý, nebo kruhový půdorys |
| Lomenice z tvarovaných desek |  |
5–20 | Vyrobí se spojením 2–3 typů tvarovaných desek |
10.7 HALY Z TKANIN A FOLIÍ
Tab. 10.11 Konstrukční systémy z tkanin a folií
| Provedení | Obrázek | Rozpětí ℓ [m] | Poloměr zakřivení [m] |
| Tkaninový stan |  |
9–18 | 25–35 |
| Lanový vyztužený stan |  |
18–60 | 80–100 |
| Síť z předpjaté oceli s tkaninovým překrytím | 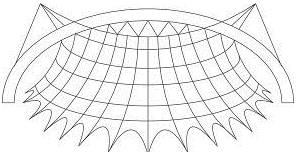 |
25–100 | 100–300 |
| Lany podepřená nafukovací (přetlaková) hala |  |
90–180 | 80–100 |
| Nafukovací (přetlaková) hala | 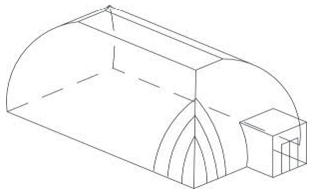 |
15–45 | Povrch membrány má mít tvar kupole a je předpjatý v každém bodě |
| Pneumatický rám (přetlaková žebra) |  |
6–18 | K dosažení potřebné nosnosti a tuhosti je nutný vysoký přetlak v žebrech |
11 ZAKLÁDÁNÍ STAVEB
Způsob založení stavby je závislý na druhu základové půdy (základových poměrech), na zatížení a na konstrukčním uspořádání objektu. Základová konstrukce a základová půda tvoří jeden neoddělitelný celek.
Základové konstrukce lze rozdělit na plošné (patky, pasy, rošty, desky), hlubinné (piloty, studny, kesony) a na speciální (pracovní pažení stavebních jam, konstrukční a těsnící podzemní stěny, skříňové základy apod.).
11.1 ZÁKLADY PLOŠNÉ
Plošné základové konstrukce zprostředkovávají přenos zatížení stavby do základové půdy v bezprostředním okolí konstrukce. Konstrukčním materiálem je zpravidla prostý, vyztužený nebo výjimečně předpjatý beton. Plošné základy jsou nejrozšířenějším způsobem zakládání staveb.
Při navrhování plošných základů se postupuje podle složitosti základových poměrů, podle náročnosti konstrukcí a podle stupně projektové přípravy.
Podle složitosti rozeznáváme základové poměry:
- jednoduché (základové půda se v rozsahu stavebního objektu podstatně nemění, jednotlivé vrstvy mají přibližně stejnou mocnost a jsou uloženy vodorovně, podzemní voda neovlivňuje návrh konstrukce objektu);
- složité (základová půda se v rozsahu stavebního objektu podstatně mění nebo vykazuje nepříznivé vlastnosti např. malou únosnost, podzemní voda se nepříznivě uplatňuje při navrhování objektu.
Podle náročnosti se rozlišují stavební konstrukce:
- nenáročné které nejsou citlivé na rozdíly v nerovnoměrném sedání, patří sem většina nízkých objektů do dvou podlaží – rodinné domy, garáže, zařízení staveniště apod.;
- náročné jsou všechny ostatní stavební objekty.
Rozlišují se tři geotechnické kategorie podle kombinace složitosti základových poměrů a náročnosti stavebního objektu.
Podle zásad 1. geotechnické kategorie se postupuje:
- při předběžných hodnoceních staveniště;
- při předprojektové přípravě;
- při definitivním návrhu, kdy je možno užít těchto zásad u nenáročných stavebních objektů v jednoduchých základových poměrech. Napětí v základové spáře získané z charakteristických hodnot zatížení se srovnávají s hodnotami tabulkové návrhové pevnosti zeminy Rdt – viz tab. 11.1–11.3.
Podle zásad 2. geotechnické kategorie se postupuje:
- při definitivním návrhu:
- nenáročné konstrukce ve složitých základových poměrech;
- náročné konstrukce v jednoduchých základových poměrech.
Používají se směrné nebo místní charakteristické hodnoty vlastností základové půdy. Podle zásad 3. geotechnické kategorie se postupuje:
- při definitivním návrhu náročných konstrukcí ve složitých základových poměrech. Do výpočtu vstupují charakteristické hodnoty vlastností základové půdy stanovené zkouškami.
U 2. a 3. geotechnické kategorie se srovnávají účinky extrémních hodnot návrhového zatížení s návrhovou únosností základové půdy Rd. Při výpočtu sedání se však uplatní charakteristické hodnoty zatížení.
Z hlediska technologického se základové konstrukce z prostého betonu provádějí zpravidla přímo do výkopu, pokud vlastnosti zeminy umožní jeho dočasně dostatečně stabilní tvar. Popřípadě je možné použít betonové tvárnice ztraceného bednění, část základu se vybetonuje do výkopu, na druhou část se použijí tvárnice a základ se slabě vyztuží. Železobetonové základy se bední, pro bednění je nutné zvětšit výkop.
Zatížení na základovou konstrukci se stanoví statickým výpočtem. Při posouzení únosnosti základové půdy lze předběžně určit vlastní tíhu základu (např. základový pas pod stěnou, základová patka) jako 10 % normálové síly působící na základ.
11.1.1 Únosnost a přetvoření základové půdy
Návrhová únosnost základové půdy závisí na jejích mechanických a fyzikálních vlastnostech, na její homogenitě, izotropii, na rozměrech, tvaru, hloubce, tuhosti základové konstrukce, mimostřednosti a šikmosti zatížení a na hladině podzemní vody.
Hodnoty tabulkové charakteristické únosnosti základové půdy Rdt jsou uvedeny v následujících tab. 11.1–11.3 a platí pro 1. geotechnikou kategorii (nenáročné stavby v jednoduchých základových poměrech, u nichž se výpočet sedání neprovádí. Pro 2. a 3. geotechnickou kategorii je nutné důsledně postupovat podle teorie mezních stavů.
Tab. 11.1 Návrhová hodnota únosnosti Rdt pro jednozrnné zeminy
| Zemina | Hloubka založení [m] | Šířka základu [m] | Tabulková návrhová hodnota únosnosti Rdt [Mpa] | ||||
| druh | třída | konzistence | |||||
| měkká | tuhá | pevná | tvrdá | ||||
| Jemnozrnné (hlíny, jíly) | F1 | 0,8–1,5 | ≤ 3 | 0,11 | 0,200 | 0,300 | 0,50 |
| F2 | 0,10 | 0,175 | 0,275 | 0,45 | |||
| F3 | 0,10 | 0,175 | 0,275 | 0,45 | |||
| F4 | 0,08 | 0,150 | 0,250 | 0,40 | |||
| F5 | 0,07 | 0,150 | 0,250 | 0,40 | |||
| F6 | 0,05 | 0,100 | 0,200 | 0,35 | |||
| F7 | 0,05 | 0,100 | 0,200 | 0,35 | |||
| F8 | 0,04 | 0,080 | 0,160 | 0,30 | |||
Tab. 11.2 Návrhová hodnota únosnosti Rdt pro písčité a štěrkovité zaminy
| Zemina | Hloubka založení [m] | Tabulková návrhová hodnota únosnosti Rdt [Mpa] | ||||
| druh | třída | šířka základu b [m] | ||||
| 0,5 | 1,0 | 3,0 | 6,0 | |||
| Písčité | S1 | 1,0 | 0,300 | 0,500 | 0,800 | 0,600 |
| S2 | 0,250 | 0,350 | 0,600 | 0,500 | ||
| S3 | 0,225 | 0,275 | 0,400 | 0,325 | ||
| S4 | 0,175 | 0,225 | 0,300 | 0,250 | ||
| S5 | 0,125 | 0,175 | 0,175 | 0,175 | ||
| Štěrkovité | G1 | 0,500 | 0,800 | 1,000 | 0,800 | |
| G2 | 0,400 | 0,650 | 0,850 | 0,650 | ||
| G3 | 0,300 | 0,450 | 0,700 | 0,500 | ||
| G4 | 0,250 | 0,300 | 0,400 | 0,300 | ||
| G5 | 0,175 | 0,200 | 0,250 | 0,200 | ||
Poznámka:
U zemin tříd S a G při hloubce založení větší než 1 m, lze tabulkové hodnoty únosnosti zvětšit o 2,5 násobek tíhy zeminy ležící mezi hloubkou založení a hloubkou 1 m. U zemin třídy F se únosnost zvětší o tíhu zeminy ležící mezi hloubkou 1,5 m a hloubkou založení. Pokud se hladina podzemní vody nachází základovou spárou v hloubce, rovnající se šířce základu anebo menší, zmenšují se tabulkové hodnoty o 30 %. Nalézá-li se v hloubce poloviny šířky základu pod základovou spárou únosnější, lze zvětšit tabulkové hodnoty o 20 %.
Příklad 11.1
Zjistěte výslednou (upravenou) tabulkovou návrhovou únosnost Rdt,výsl pro základový pas (pod stěnou) šířky b = 2,00 m, je-li objemová hmotnost zeminy třídy S2 γ = 2 000 kg/m3.
Interpolací se stanoví z tab. 11.2 výchozí tabulková únosnost.
\begin{gathered}
R_\text{dt}=(0{,}35+0{,}60)/2=0{,}475\space\text{MPa}
\end{gathered}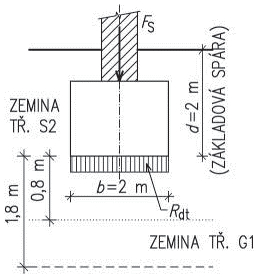
Výsledná návrhová únosnost (zvětšení o 2,5 násobek tíhy zeminy ležící mezi hloubkou založení (2 m) a hloubkou 1 m, zvětšení o 20 % vyplývající z únosnější zeminy v hloubce 0,8 m pod základovou spárou a níže, snížení o 30 %, plynoucí z přítomnosti podzemní vody – hladina 1,8 m < 2 m pod základovou spárou).
\begin{gathered}
R_\text{dt,výsl}=1{,}\cdot20{,}7[R_\text{dt}+2{,}5\cdot\gamma\cdot(D-1\space000)]=0{,}84[0{,}475+2{,}5\cdot20\cdot10^{-6}\cdot1\space000)]=0{,}441\space\text{MPa}
\end{gathered}Tab. 11.3 Zatřídění skalních hornin podle pevnosti
| Zatřídění skalních hornin podle pevnosti | Únosnost Rdt [MPa] | ||||
| třída | pevnost [MPa] | střední hustota diskontinuit [mm] | |||
| velmi malá až malá 600 | střední až velká 600–60 | velmi velká až extrémně velká 60 | |||
| R1 | > 150 | velmi vysoká | 8,00 | 4,00 | 2,50 |
| R2 | 150–50 | vysoká | 4,00 | 2,00 | 1,20 |
| R3 | 50–15 | střední | 1,60 | 0,80 | 0,50 |
| R4 | 15–5 | nízká | 0,80 | 0,40 | 0,25 |
| R5 | 5–0,5 | velmi nízká | 0,60 | 0,30 | 0,20 |
| R6 | 1,5–0,5 | extrémně nízká | 0,40 | 0,25 | 0,15 |
Poznámka:
Tabulková návrhová únosnost základové půdy Rdt má orientační význam a odpovídá dřívějšímu pojmu „odvozené normové namáhání“.
Mezní stav použitelnosti (přetvoření, sednutí staveb) se pro 1. geotechnickou kategorii neposuzuje. Pro 2. a 3. geotechnickou kategorii se pro výpočet sednutí použijí charakteristické hodnoty přetvárných charakteristik vlastností základové půdy.
Tabulkové hodnoty návrhových únosností Rdt jsou sestaveny s ohledem na obě skupiny mezních stavů (únosnosti a použitelnosti). Návrhová únosnost Rd roste přibližně lineárně s šířkou základu, naopak zatížení spáry σd potřebné k dosažení určité konstantní hodnoty sedání klesá se šířkou základu – viz obr. 11.1.
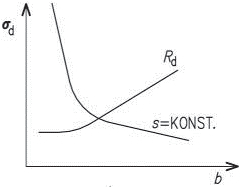
Obr. 11.1 Závislost dosažení mezních stavů únosnosti a použitelnoti (sedání) plošného základu na jeho šířce
Z průběhu obou mezních stavů je patrné, že u úzkých základů rozhoduje mezní stav únosnosti, u širokých základů mezní stav použitelnosti. V tabulkách se toto omezení projevuje u nesoudržných zemin (písčitých a štěrkovitých), kde tabulkové hodnoty únosnosti pro šířku b = 6 m jsou menší než pro b = 3 m. U soudržných zemin (jemnozrnných) jsou tabulkové hodnoty únosnosti do šířky základu b = 3 m konstantní, neboť vliv šířky základu b na únosnost je malý a sedání od zatížení Rdt také.
11.1.2 Klimatické vlivy
Z hlediska promrzání se stanoví nejmenší hloubka založení pod upraveným povrchem území u definitivních staveb:
- pod zámrznou hloubkou, 0,800 m u hlinitopísčitých a písčitohlinitých půd;
- 1,000 m u jílovitých půd;
- 1,400 m u smrštitelných jílů;
- 0,500 m u skalních hornin;
- 1,600 m u jemnozrnných zemin F6 a F7, které mohou namrzat;
- 0,450 m pod vnitřními stěnami;
- nejméně 0,4 m u provizorních konstrukcí a u základů prokazatelně chráněných proti promrzání;
- hloubku založení je třeba zvětšit v oblastech s mrazovým indexem větším než 625 (součin mrazových dnů v souvislém období a průměrné záporné teploty příslušné těmto mrazovým dnům).
Z hlediska vysychání základové půdy se stanoví u zemin třídy F7 a F8 (hlíny a jíly s vysokou až extrémně vysokou plasticitou) nejmenší hloubky založení 1,6 m pod upraveným povrchem území.
V průběhu výstavby je třeba základovou půdu chránit proti nepříznivým klimatickým účinkům a proti porušení proudovým tlakem podzemní vody nebo zaplavení základové spáry.
11.1.3 Základový pas
Používá se pod stěnami (zdmi) u stěnových konstrukčních systémů staveb. Pro 1. geotechnickou kategorii u betonových a železobetonových, dostředně zatížených pasů, se nutná šířka b stanoví z tabulkové návrhové únosnosti základové spáry Rdt – viz tab. 11.1–11.3, nutná výška h se určí pomocí roznášecího úhlu α = 60° (viz obr. 11.2 a 11.3), který je odvislý od návrhové pevnosti betonu v tahu a únosnosti základové půdy.
Základové pasy se navrhují obvykle z prostého betonu pevnostních tříd C8/10–C12/15 popřípadě C16/20. Rozměry základů zaokrouhlujeme na 50 mm. Platí rovněž pro základové patky – viz kap. 11.1.4.
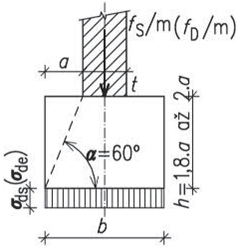
Obr. 11.2 Základový pas z prostého betonu
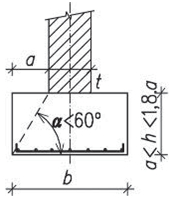
Obr.11.3 Základový pas ze železobetonu
Hloubka založení
Základová spára pod zámrznou hloubkou (viz kap. 11.1.4)
šířka pasu
\begin{gathered}
b=1{,}1\cdot f_\text{s}/R_\text{dt}\space[\text{m}]
\end{gathered}výška pasu
\begin{gathered}
h=(1{,}8-2)\cdot\alpha\space[\text{m}]
\end{gathered}Při roznášecím úhlu α < 60° nutno pas vyztužit a použít beton minimální třídy C20/25 (hlavní nosná výztuž se umístí při spodním povrchu a je orientována kolmo na směr stěny).
Poznámka:
Výraz pro předběžné stanovení šířky pasu, popř. výšky pasu, lze použít i pro 2. a 3. geotechnikou kategorii, zaměníme-li fs za fd a Rdt za Rd (fs/fd je účinek od charakteristických/návrhových hodnot zatížení, Rd/Rdt je návrhová/tabulková únosnost základové půdy, σds/σde je kontaktní napětí v základové spáře od charakteristických/návrhových hodnot zatížení).
Příklad 11.2
Navrhněte základový pas fk = 200 kN/m, hloubka založení 1 m, zemina písčitá S4 Rdt = 0,224 MPa (při předpokládané šířce pasu b = 1,0 m), tloušťka stěny t = 0,3 m, beton C16/20.
\begin{gathered}
b\ge1{,}1\cdot f_\text{s}/R_\text{dt}=1{,}1\cdot200/0{,}225\cdot10^3=0{,}98\space\text{m}\\\\
h\ge 1{,}8a=1{,}8\cdot(0{,}98-0{,}3)/2=0{,}612\space\text{m}
\end{gathered}Navržený základový pas b/h = 1,00/0,65 m
11.1.4 Základové patky
Základové patky jsou nejčastěji používanými základovými prvky u sloupových konstrukčních systémů staveb. Navrhují se pokud možno v půdorysném tvaru čtverce popř. obdélníka až do poměru stran 3 : 5, výjimečně ve tvaru kruhu. Z hlediska hospodárnosti a postupu výstavby jsou patky výhodné do největšího rozměru rovnému polovině osové vzdálenosti sloupů. Podmínkou pro zakládání na patkách je pokud možno stejnorodá základová zemina o zhruba stejné mocnosti a menší stlačitelnosti. Při návrhu konstrukčního systému stavby je výhodné přihlédnout k tomu, aby zatížení přenesené od patek nebylo příliš rozdílné jak z důvodů výrobních, tak i pro stejné stlačení zeminy.
Patky z prostého betonu
Navrhují se podle tvaru jako jednostupňové, popř. vícestupňové. Výška patky je závislá na návrhové hodnotě pevnosti betonu v tahu (popř. napětí v šikmém tahu) a na únosnosti základové půdy. Roznášecí úhel lze předpokládat α = 60°. Použijí se třídy betonu C8/10 až C12/15, popř. C16/20 viz kap. 11.1.3.
Obr. 11.4 Patka z prostého betonu
Patky železobetonové
Pro nejčastěji se vyskytující čtvercový základ, při dostředném zatížení, přibližně platí
\begin{gathered}
b=\ell\ge\sqrt{1{,}1F_\text{s}/R_\text{dt}}
\end{gathered}kde je
b … šířka patky [m],
ℓ … délka patky [m].
Viz též poznámku v kap. 11.1.3
\begin{gathered}
h\ge1{,}8\cdot a
\end{gathered}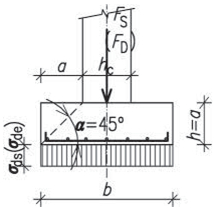
Obr. 11.5 Patka ze železobetonu
Doporučuje se navrhnout patky konstantní výšky h, pokud možno čtvercového půdorysu b = ℓ, s dvousměrnou ortogonální výztuží a z betonu pevnostní třídy C20/25.
Při návrhu půdorysných rozměrů se postupuje stejně jako u patek z prostého betonu (pro čtvercový půdorys b = ℓ platí výraz z kap. 11.1.4).
Výška patky bez smykové výztuže
\begin{gathered}
h=a
\end{gathered}\begin{gathered}
\alpha=45\degree
\end{gathered}výška patky se smykovou výztuží
\begin{gathered}
a/2\lt h\lt a
\end{gathered}\begin{gathered}
\alpha=30{-}45\degree
\end{gathered}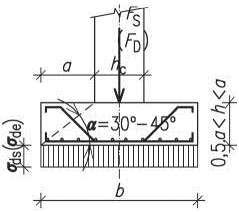
Obr. 11.6 Železobetonová patka se smykovou výztuží
Poznámka:
Při mimostředném tlaku mohou nastat dva případy:
- Základová patka je kromě normálovou silou namáhána střídavě působícími ohybovými momenty opačných znamének přibližně stejných velikostí, pak navrhujeme rozšířenou patku symetrickou (jako při dostředném tlaku).
- Základová patka je kromě normálové síly namáhána konstantním momentem jednoho znaménka, pak rozšiřujeme patku ve směru výstřednosti nesouměrně tak, aby těžiště základové spáry se přibližně krylo s působištěm středu tlaku (v kolmém směru se patra rozšiřuje souměrně) viz obr. 11.7.
Obr. 11.7 Patka zatížená excentrickými tlaky
11.1.5 Základové pasy a rošty
Vyjdou-li nutné plochy základů v základové spáře pod sloupy příliš veliké (např. v méně únosných zeminách), je úsporné upravit pro celou řadu sloupů společný vyztužený základová pas. Založení sloupů na pasech lze též dosáhnout stejnoměrnějšího sedání objektu. Vyložením konců pasů můžeme dosáhnout příznivého průběhu momentů (viz obr. 11.8).
Základové pasy se s výhodou mohou použít i v zeminách únosnějších v oblastech seizmických a v poddolovaných územích.
Nejběžnějším průřezovým tvarem je obdélník nebo obrácený T průřez.
Pokud nevystačíme se základovými pasy orientovanými jednosměrně (např. menší únosnost základové půdy), lze použít roštu, vznikajícího vzájemným křížením podélných a příčných železobetonových pasů. Konstrukční úprava je obdobná jako u pasů jednosměrných.
Obr. 11.8 Základový pas
11.1.6 Základové desky
Nevystačíme-li se základovými rošty, je-li třeba využít pro základovou spáru celého půdorysu stavby (např. málo únosná základová půda), navrhujeme základové desky. Rovněž při zakládání objektu pod hladinou podzemní vody, kdy je třeba jej založit v uzavřené vodotěsné vaně, uplatní se základová deska s bočními stěnami.
Základové desky pod nosnými stěnami mívají konstantní tloušťku 0,25–1,40 m u staveb pozemních a tloušťku až 5,00 m u výškových a inženýrských staveb (těžký průmysl, vodní stavby apod.).
Základové desky pod osamělými břemeny lze navrhnout podle velikosti silových účinků na ně působících jako desky hřibové (se skrytými či viditelnými hlavicemi), jako desky spojené se dvěma systémy navzájem se křižujících pasů (křížem vyztužené desky po obvodě upnuté do pasů), popř. jako desky tvořící součást základové skříně (krabice).
Hrubý odhad tloušťky základové desky h v závislosti na počtu podlaží n objektu udává vztah
\begin{gathered}
h=(0{,}08\space\text{až}\space0{,}1)n\space[\text{m}]
\end{gathered}
Obr. 11.9
Příklad 11.3
Stanovte předběžně tloušťku h základové desky 14 podlažní budovy:
\begin{gathered}
h=(0{,}08\space\text{až}\space0{,}10)\cdot14=1{,}12\space\text{až}\space1{,}40\space\text{m}
\end{gathered}11.2 ZÁKLADY HLUBINNÉ
Hlubinné základové konstrukce přenášejí zatížení z objektu (stavby) do základové půdy prostřednictvím hlubinných prvků (zpravidla pilot, ale též pilířů, studen, kesonů i podzemních stěn – pilotových, milánských).
11.2.1 Pilotové základy
Pilotou se přenáší zatížení do základové půdy odporem na patě a v plášti. Pilota je buď na celou délku, nebo na značnou část délky zapuštěna do základové půdy, čehož se dosáhne buď vháněním hotové piloty (dřevěné, betonové, ocelové) nebo zhotovením piloty na místě (in situ) do vyhloubeného otvoru (výplň z betonu) – viz obr. 11.10.
Obr. 11.10 Pilotované základy
Piloty mohou být namáhány tlakem, tahem a výjimečně ohybem.
Piloty dělíme na maloprůměrové d = 0,20–0,60 m, u nichž se uplatní technologie beranění, předrážení a vrtání při d ≥ 0,25 m, velkoprůměrové d = 0,61–1,50 m, které se téměř výhradně provádějí vrtnou technologií, a na mikropiloty d = 0,19–0,15 m, které se realizují vrtnou technologií a jsou vyztužené ocelovými trubkami.
Nejmenší osová vzdálenost je u maloprůměrových pilot 2,5d [m], u velkoprůměrových je zpravidla 1,5d [m], minimálně však d + 0,5 [m]. U pilot předrážených pilot je nejmenší osová vzdálenost 3,5d [m]. Jinak se osová vzdálenost pilot stanoví s ohledem na statické působení pilot a technologii jejich provádění.
Pilotové základy se navrhují podle mezních stavů, tj. únosnost se srovnává s extrémními hodnotami návrhových zatížení a sedání s hodnotami charakteristických zatížení.
Únosnost pilot se skládá z únosnosti její paty a z únosnosti pláště piloty. Výsledná únosnost je závislá na parametrech zeminy, rozměrech piloty, materiálu piloty, způsobu jejího zabudování do zeminy a charakteru zatížení.
Pro navrhování lze s výhodou použít tabulkových únosností (Uv,tab ve svislém směru [kN], Uh,tab ve vodorovném směru [kN]), piloty nebo skupin pilot jak pro extrémní návrhové zatížení svislé Vd [kN], tak vodorovné Hd [kN], uvedené v tab. 11.4–11.11, přičemž musí platit
\begin{gathered}
V_\text{d}\le U_\text{v,tab},\space H_\text{d}\le U_\text{h,tab}
\end{gathered}Poznámka:
Piloty podporují plošné základy. Spojení pilot se základem provádíme obnažením výztuže hlavy piloty, kterou zabetonujeme do plošného základu. Piloty (pokud jsou vyztuženy), se vyztužují jako sloupy.
Tab. 11.4 Svislá tabulková únosnost Uv,tab pilot beraněných
| Délka piloty [m] | Průměr piloty d [m] | Únosnost piloty Uv,tab [kN]1) |
| 3–5 | 0,25 | 150 |
| 0,30 | 200 | |
| 0,35 | 250 | |
| 0,40 | 350 | |
| 0,50 | 450 | |
| > 5–10 | 0,30 | 350 |
| 0,35 | 400 | |
| 0,40 | 500 | |
| 0,50 | 600 | |
| 1) Hodnoty platí za předpokladu, že u vháněných pilot železobetonových, z předpjatého betonu a kovových se tíha beranu rovná přibližně hmotnosti piloty, u dřevěných jejímu dvojnásobku, dále pak že u vibroberaněných pilot úderná síla nepřekročila tíhu piloty. Pokud pata vháněných pilot zasáhne do vodou nasycených písků, je nutno po přestávce několika hodin opakovat poslední fázi beranění nebo vibroberanění s měřením vniků. Platí rovněž za předpokladu, že pilota je ukončena v horninách třídy R1 až R5 (skalní masiv). | ||
Tab. 11.5 Svislá tabulková únosnost Uv,tab pilot vrtaných v horninách třídy R1–R3 (skalní masiv)
| Délka vetknutí piloty ℓf v hornině třídy R1–R3 (skalní masiv) [m] | Únosnost Uv,tab [kN] pilot v horninách třídy R1–R3 (skalní masiv) pro průměr pilot d [m] | ||||||
| 0,30 | 0,40 | 0,50 | 0,60 | 1,0 | 1,3 | 1,50 | |
| 0–0,5 | 200 | 380 | 600 | 850 | 2300 | 4000 | 6000 |
| 1,5 | 300 | 500 | 720 | 1000 | 2500 | 4300 | 6000 |
Tab. 11.6 Svislá tabulková únosnost Uv,tab pilot vrtaných v horninách třídy R4 až R6 (skalní masiv)
| Délka vetknutí piloty ℓf v hornině třídy R4–R6 (skalní masiv) [m] | Únosnost Uv,tab [kN] pilot v horninách třídy R4–R6 (skalní masiv) pro průměr pilot d [m] | ||||||
| 0,30 | 0,40 | 0,50 | 0,60 | 1,0 | 1,3 | 1,50 | |
| 0–0,5 | 100 | 200 | 300 | 430 | 1000 | 1600 | 2000 |
| 1,5 | 150 | 300 | 400 | 580 | 1250 | 1900 | 2200 |
| 3,0 | 200 | 400 | 500 | 730 | 1500 | 2200 | 2600 |
Tab. 11.7 Svislá tabulková únosnost Uv,tab pilot vrtaných v zeminách třídy G1–G4 (štěrkopísek)
| Délka vetknutí piloty ℓf [m] | Únosnost pilot Uv,tab [kN] v zeminách třídy G1–G4 (štěrkopísek) pro průměry pilot d [m] | ||||||||||||||||||||
| 0,30 | 0,33 | 0,50 | 0,60 | 1,00 | 1,30 | 1,50 | |||||||||||||||
| při relativní ulehlosti ID1) | |||||||||||||||||||||
| 0,33 | 0,67 | 1,00 | 0,33 | 0,67 | 1,00 | 0,33 | 0,67 | 1,00 | 0,33 | 0,67 | 1,00 | 0,33 | 0,67 | 1,00 | 0,33 | 0,67 | 1,00 | 0,33 | 0,67 | 1,00 | |
| 1–1,5 | 35 | 70 | 200 | 60 | 120 | 400 | 100 | 200 | 600 | 140 | 280 | 850 | 400 | 800 | 2300 | 650 | 1300 | 3900 | 820 | 1600 | 5000 |
| 3 | 89 | 160 | 380 | 110 | 230 | 610 | 160 | 330 | 870 | 220 | 430 | 1150 | 520 | 1050 | 2800 | 800 | 1600 | 4500 | 1000 | 2000 | 5600 |
| 5 | 110 | 220 | 500 | 150 | 330 | 750 | 220 | 420 | 1060 | 280 | 550 | 1400 | 630 | 1300 | 3200 | 950 | 1900 | 5000 | 1100 | 2300 | 6300 |
| 10 | 180 | 370 | 800 | 240 | 500 | 1100 | 320 | 650 | 1500 | 420 | 840 | 2000 | 840 | 1700 | 4000 | 1200 | 2400 | 6200 | 1450 | 3050 | 8000 |
| 1) ID = 0,33–0,67 zeminy středně ulehlé ID > 0,67 zeminy ulehlé |
|||||||||||||||||||||
Tab. 11.8 Svislá tabulková únosnost Uv,tab pilot vrtaných v zeminách třídy S1–S4 (štěrkopísek)
| Délka vetknutí piloty ℓf [m] | Únosnost pilot Uv,tab [kN] v zeminách třídy S1–S4 (štěrkopísek) pro průměry pilot d [m] | ||||||||||||||||||||
| 0,30 | 0,33 | 0,50 | 0,60 | 1,00 | 1,30 | 1,50 | |||||||||||||||
| při relativní ulehlosti ID1) | |||||||||||||||||||||
| 0,33 | 0,67 | 1,00 | 0,33 | 0,67 | 1,00 | 0,33 | 0,67 | 1,00 | 0,33 | 0,67 | 1,00 | 0,33 | 0,67 | 1,00 | 0,33 | 0,67 | 1,00 | 0,33 | 0,67 | 1,00 | |
| 1–1,5 | 20 | 50 | 175 | 40 | 80 | 300 | 60 | 120 | 500 | 85 | 170 | 700 | 240 | 480 | 1900 | 400 | 800 | 3300 | 520 | 900 | 4200 |
| 3 | 35 | 110 | 275 | 60 | 170 | 450 | 85 | 235 | 680 | 120 | 300 | 920 | 300 | 700 | 2300 | 460 | 1100 | 3800 | 580 | 1300 | 4800 |
| 5 | 50 | 160 | 370 | 75 | 240 | 550 | 100 | 320 | 820 | 140 | 400 | 1100 | 340 | 870 | 2500 | 500 | 1300 | 4150 | 650 | 1600 | 5300 |
| 10 | 70 | 280 | 570 | 100 | 400 | 800 | 140 | 520 | 1100 | 190 | 650 | 1500 | 400 | 1200 | 3000 | 600 | 1800 | 5000 | 750 | 2200 | 6500 |
| 1) ID = 0,33–0,67 zeminy středně ulehlé ID > 0,67 zeminy ulehlé |
|||||||||||||||||||||
Tab. 11.9 Svislá tabulková únosnost Uv,tab pilot vrtaných v zeminách třídy F1–F61) (jemnozrnné,), R7 (skalní masiv) a G6 (štěrkovité)
| Délka vetknutí piloty ℓf [m] | Únosnost pilot Uv,tab [kN] v zeminách třídy F1–F6, R7 a G6 pro průměry pilot d [m] | ||||||||||||||||||||
| 0,30 | 0,40 | 0,50 | 0,60 | 1,00 | 1,30 | 1,50 | |||||||||||||||
| při indexu konzistence IC2) | |||||||||||||||||||||
| 0,50 | 1,00 | >1,50 | 0,50 | 1,00 | >1,50 | 0,50 | 1,00 | >1,50 | 0,50 | 1,00 | >1,50 | 0,50 | 1,00 | >1,50 | 0,50 | 1,00 | >1,50 | 0,50 | 1,00 | >1,50 | |
| 1–1,5 | 25 | 60 | 120 | 45 | 100 | 200 | 60 | 150 | 300 | 80 | 220 | 430 | 230 | 630 | 1000 | 400 | 1000 | 1600 | 500 | 1250 | 2000 |
| 3 | 60 | 130 | 240 | 95 | 190 | 380 | 130 | 260 | 520 | 170 | 350 | 710 | 370 | 860 | 1500 | 580 | 1300 | 2200 | 700 | 1600 | 2700 |
| 5 | 90 | 180 | 340 | 130 | 260 | 520 | 170 | 350 | 700 | 220 | 450 | 900 | 460 | 1050 | 1850 | 700 | 1500 | 2650 | 820 | 1800 | 3400 |
| 10 | 160 | 320 | 580 | 210 | 420 | 840 | 260 | 550 | 1100 | 330 | 680 | 1350 | 700 | 1430 | 2600 | 1000 | 2000 | 3600 | 1200 | 2400 | 4200 |
| 2) IC = 0,50 až 1,00 konzistence tuhá IC > 1,00 konzistence pevná |
|||||||||||||||||||||
Tab. 11.10 Vodorovná tabulková únosnost Uh,tab pilot beraněných
| Druh materiálu piloty | Vodorovná tabulková únosnost beraněných pilot Uh,tab [kN] pro průměr pilot d [m] | ||
| 0,30 | 0,35 | 0,40 | |
| Dřevěná | 20 | 25 | 30 |
| Železobetonová | 30 | 35 | 40 |
Tab. 11.11 Vodorovná tabulková únosnost Uh,tab pilot vrtaných
| Třída zeminy | Délka vetknutí piloty ℓf [m] | Vodorovná tabulková únosnost Uh,tab [kN] pilot vrtaných pro průměry d [m] | ||||||
| 0,30 | 0,40 | 0,50 | 0,60 | 1,00 | 1,30 | 1,50 | ||
| G, S (štěrkovité a písčité) | 5 | 90 | 110 | 140 | 170 | 280 | 360 | 400 |
| 10 | 140 | 180 | 200 | 280 | 450 | 560 | 650 | |
| F (jemnozrnné) | 5 | 60 | 80 | 100 | 120 | 200 | 250 | 300 |
| 10 | 120 | 150 | 190 | 360 | 360 | 450 | 550 | |
Tab. 11.12 Svislá tabulková únosnost Uv,tab mikropilot
| Druh zeminy | Tření na plášti [kN/m2] | Průměr mikropiloty d [mm] | ||
| 150 | 200 | 250 | ||
| [kN] | ||||
| Štěrkovitá | 200–250 | 300–(400) | 400–(550) | 550–(650) |
| Písčitá | 150 | 150 | 300 | 400 |
| Jemnozrnná (soudržná zemina) | 100 | 100 | 200 | 250 |
| Přípustná síla na dřík mikropiloty | 310 | 550 | 750 | |
|
Poznámka: |
||||
Celkové sedání pilot s je součtem sedání pod patami (špičkami) pilot sz a stlačením vlastního tělesa piloty sp Pro úplnost (přehled) jsou v tab. 11.13 uvedeny limitní hodnoty sednutí pro různé druhy staveb, které uvádí a jsou též aplikované při posouzení pilotových základů.
11.2.2 Mikropilotové základy
Mikropiloty, nazývané též kořenové piloty, jsou v podstatě piloty velmi malého průměru, prováděné velmi hustě nebo ve skupinách pod základy nebo v jejich těsném okolí. Mikropiloty se provádí vrtáním zapaženého nebo nezapaženého vrtu, který je vyplněn aktivovanou cementovou směsí, vystrojen silnostěnnou trubkou. V kořenové části je trubka manžetová s obturátory, ve volné části je trubka hladká (nejčastěji jsou používány průměry 70/10, 89/10, 108/16 mm). Asi po 24 hodinách od osazení trubky do zálivky ve vrtu se provádí injektáž kořenové části mikropiloty, rozšířený do okolí zeminy – viz obr. 11.11. Při injektáži se postupuje po 0,5 metrových krocích a sleduje se tlak a množství injektované cementové směsi. Vrtné soupravy jsou malé a lehké, takže se hodí zejména pro sanace, např. v podzemních prostorách stávajících budov. Vzhledem k malému průměru těchto pilot hodí se též k provrtání stávajícího zdiva a plošných základů (nevyztužených pasů).
Obvyklý postup při provádění mikropilot:
- vyhloubení vrtu;
- vyplnění vrtu cementovou zálivkou;
- zapuštění mikropiloty;
- injektování kořenové části – obvykle pomocí dvojitého obturátoru.
Mikropilota dosahuje značné únosnosti, která se zjišťuje buď z plášťového účinku nebo zatěžovací zkouškou. Např. Ribicky uvádí tyto provozní hodnoty zatížení v kN na vyztuženou mikropilotu (při zapuštění mikropiloty do základové zeminy 6 m, použitím součinitele bezpečnosti s = 1,75 a betonu ≥ B 35 – viz tab. 11.12.
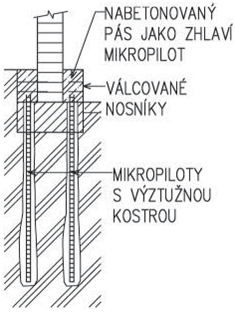
Obr. 11.11 Mikropilotový základ
11.2.3 Trysková injektáž
Trysková injektáž slouží ke zlepšování pevnosti základových půd a snižování jejich propustnosti. Podstatou technologie je injektáž z vrtu do okolní zeminy, prováděná vysokým tlakem. 30–55 MPa s použitím cementových a jílocementových směsí. Tímto způsobem se mohou zpevňovat zeminy různé zrnitosti od jílů po balvanité štěrky. V zemině se na požadovanou hloubku vyvrtá maloprofilový vrt. Trysková injektáž pak probíhá během vytahování vrtného soutyčí z vrtu. Pokud se při vytahování vrtné soutyčí neotáčí, vzniká rovinný prvek – stěna, pokud se vrtná kolona otáčí vzniká pilíř, což že nejčastější případ.
Technologie tryskové injektáže má dvě základní metody:
- metoda M 1 – (jednofázová) zemina je rozrušována a zároveň injektována paprskem injekční směsi do vzdálenosti 400–1 400 mm;
- metoda M 2 – (dvourázová, vzduchová) zemina je rozrušována a zároveň injektována paprskem injekční směsi, usměrněným proudem stlačeného vzduchu. Injektáž může zasáhnout do vzdálenosti 1 200–2 200 mm.
Tryskovou injektáž lze aplikovat v mnoha rozličných variantách, samostatně nebo v kombinaci s ostatními metodami speciálního zakládání při nové výstavbě, ale především při sanacích podzákladí rekonstruovaných budov, například:
- konsolidace stlačitelných zemin;
- zastavení deformací podzákladí vlivem nevhodného nebo poddimenzovaného založení;
- zvyšování únosnosti stávajících základů pro plánované přitížení rekonstruovaných staveb;
- pažení stavebních jam;
- zpevňování klenby nad budoucím výrubem tunelů;
- zpevnění klenby a boků budoucího tunelu svislými prvky při malé výšce nadloží;
- pažení šachet;
- zpevnění zeminy před patou prefabrikované podzemní stěny;
- ochrana založení mostů před vymíláním;
- přerušení smykové plochy sesuvů;
- kořeny kotev ve složitých geologických poměrech;
- podzemní těsnicí stěny ze vzájemně se překrývajících injektážních pilířů. Výhody tryskové injektáže:
- tryskovou injektáží lze zpevňovat zeminy i středně pevné horniny;
- promísení zeminy se směsí se provádí přímo ve vrtu;
- k podchycení základů stačí vyvrtat maloprofilový vrt a trysková injektáž se pak provede až pod základy a není tedy nutné zajišťovat jejich vzájemné propojení;
- rychlost celého procesu – pilíř je vytvrzen již za přibližně 24 hodin;
- tryskovou injektáž lze využít i v omezeném (i vnitřním) prostoru.
11.3 OMEZENÍ DEFORMACE ZÁKLADOVÝCH KONSTRUKCÍ
Základové konstrukce musí splňovat kritéria mezních stavů použitelnosti, kdy se posuzuje sedání základové konstrukce. Přípustné deformace jsou stanoveny jednak s ohledem na charakter stavebního objektu, jednak s ohledem na způsob sedání – viz tab. 11.13. Sedání stavby vzniká přirozeným stlačováním základové půdy, přičemž nemusí být překročena kritéria mezního stavu únosnosti.
Narušení stavby může způsobit především nerovnoměrné sedání, které vznikají:
- nestejnorodou stlačitelností základové půdy;
- nestejnorodým složením základové půdy;
- různou mocností vrstev;
- nerovnoměrným zatížením základové konstrukce.
Celkové svislé sednutí stavby nemusí přímo způsobit narušení nosné konstrukce. Při nerovnoměrném sedání (rozdílný relativní průhyb, úhlové přetvoření) vznikají v nosné konstrukci přidatná namáhání tím větší, čím je konstrukce tužší, staticky více neurčitá. Tato namáhání mohou způsobit narušení prvků, která se nejčástěji projeví vznikem trhlin.
Zamezit nežádoucím deformacím lze tuhou základovou konstrukcí, např. základovou deskou, krabicovou konstrukcí apod.
Sednutí ovlivňují přístavby budov, vždy je vhodné přístavby důsledně oddělit svislou spárou po celé výšce budovy. Při malé vzdálenosti základů se základy vzájemně ovlivňují. Důsledkem je nerovnoměrné sedání stejně zatížených a stejně dimenzovaných základů.
Tab. 11.13 Mezní hodnoty sednutí stavby
| Druh stavby | Konečné celkové průměrné sednutí sm,lim | Nerovnoměrné sednutí | ||||||
| hodnota [mm] | druh | hodnota | ||||||
Budovy a konstrukce
|
120 | ∆s/LT | 0,003 | |||||
| ∆s/L | 0,006 | |||||||
| Konstrukce | ||||||||
|
100 | ∆s/L | 0,005 | |||||
|
60 | ∆s/L | 0,002 | |||||
|
80 | ∆s/L | 0,003 | |||||
| Vícepodlažní skeletové budovy | ||||||||
|
60 | ∆s/L | 0,0015 | |||||
|
70 | ∆s/L | 0,0025 | |||||
| Vícepodlažní skeletové budovy | ||||||||
|
80 | ∆s/LT | 0,0015 | |||||
|
60 | ∆s/L | 0,0015 | |||||
|
200 | ∆s/b | 0,003 | |||||
|
200 | ∆s/b | 0,005 | |||||
|
100 | ∆s/b | 0,002 | |||||
| Jeřábové dráhy | 50 | ∆s/L | 0,0015 | |||||
| relativní průhyb ∆s/LT | úhlové přetvoření ∆s/L | naklonění ∆s/b | ||||||
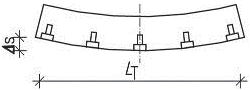 |
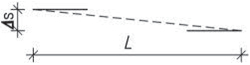 |
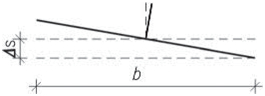 |
||||||
12 STAVEBNÍ JÁMY
Většina staveb je budována jako podsklepená, z čehož vyplývá, že není prováděna z upraveného terénu ale ze snížené úrovně stavební jámy. Stavební rámu lze koncipovat tak, že po ukončení stavebních prací a odstranění jejího vystrojení zaniká (např. svahované jámy, jámy pažené provizorním způsobem apod.), nebo je její vystrojení trvalé a stává se součástí stavby (např. podzemní stěny). Provizorní pažení a podzemní stěny se navrhují podle metody mezních stavu, výpočet musí být proveden nebo ověřen vždy statikem nebo geotechnikem.
12.1 SVAHOVÉ JÁMY
Pro prostorovou náročnost v běžné zástavbě je použití svahovaných stavebních jam omezené, mohou se však uplatnit v plném rozsahu u staveb budovaných jako solitéry (ve volné krajině nebo dostatečně vzdálené od okolní zástavby). Problémem bývá otázka stability svahu a úroveň hladiny podzemní vody, kterou, hrozí-li zaplavení jámy, nutno trvale a účinně odvádět (drenážemi popř. i čerpadly). V tab. 12.1 jsou uvedeny některé jednoduché případy návrhu svahovaných jam v závislosti na druhu zeminy (horniny).
Tab. 12.1 Přehled svahovaných jam
| Náčrtek | Maximální úhel sklonu svahu | Požadované parametry |
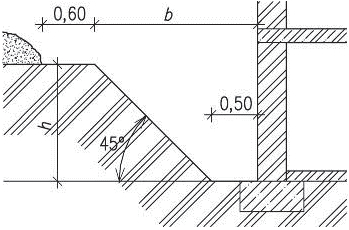 |
45° |
b = h + 0,5 [m] |
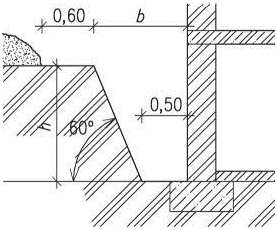 |
60° |
b = h + 0,5 [m] |
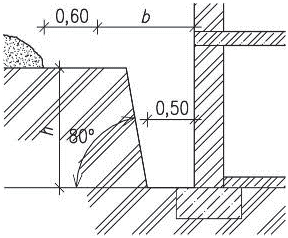 |
80° |
b = 0,18h + 0,5 [m] |
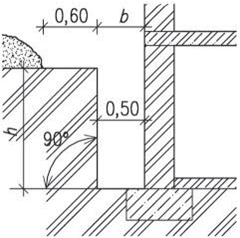 |
90° |
b = 0,5 [m] |
12.2 ROUBENÉ PAŽENÍ
Roubené pažení v klasickém slova smyslu se používá dnes již jen zřídka, důvodem není jen vysoká cena dřeva a náročnost tesařských prací, ale také malá uvolněnost pro realizaci stavby. Stále se však dosti často používá u rýh a stavebních jam, prováděných v zástavbě pro inženýrské sítě.
12.2.1 Vodorovné a svislé příložné pažení rýh
V níže uvedených tab. 12.2 a 12.3 jsou uvedeny nutné tloušťky pažin v závislosti na rozměrových hodnotách (výška jámy (rýhy), délkové a průřezové rozměry dřevěných nosných prvků apod.), použitelné pro téměř všechny druhy zemin.
Poznámka:
Místo dřevěných pažin se mohou použít ocelové pažnice (tenkostěnné otevřené profily ploché s oblými výztuhami) s minimálním průřezovým modulem Wy ≥ 50 · 103 mm3/m. U záporového pažení lze použít válcovaných ocelových nosníků, rozepřených masivními rozpěrami rovněž ocelovými. Jako pažin lze použít betonových deskových dílců.
Tab.12.2 Vodorovné příložné pažení
| Rozměrové hodnoty | Tloušťka pažin [mm] | |||||
| 50 | 60 | 70 | ||||
| Výška rýhy (stěny) h [m] | 3,00 | 3,00 | 4,00 | 5,00 | 5,00 | |
| Maximální vodorovná podpůrná vzdálenost pažin [m] | ||||||
|
1,90 | 2,10 | 2,00 | 1,90 | 2,10 | |
|
0,50 | 0,50 | 0,50 | 0,50 | 0,50 | |
| Maximální svislá podpůrná vzdálenost převázek [m] | ||||||
|
80/160 | 0,70 | 0,70 | 0,65 | 0,60 | 0,60 |
| 120/150 | 1,10 | 1,10 | 1,00 | 0,90 | 0,90 | |
|
80/160 | 0,60 | 0,60 | 0,55 | 0,50 | 0,50 |
| 120/160 | 0,80 | 0,80 | 0,75 | 0,70 | 0,70 | |
| Maximální vzpěrná délka rozpěr sk [m] | ||||||
|
1,65 | 1,55 | 1,50 | 1,45 | 1,35 | |
|
1,95 | 1,85 | 1,80 | 1,75 | 1,65 | |
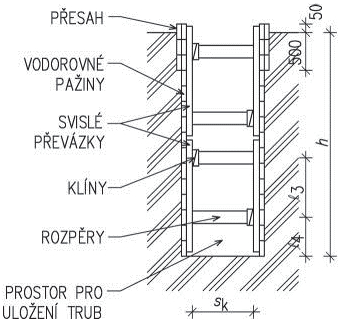
Obr.12.1 Vodorovné příložné pažení
Tab. 12.3 Svislé příložné pažení
| Rozměrové hodnoty | Tloušťka pažin [mm] | |||||
| 50 | 60 | 70 | ||||
| Výška rýhy (stěny) h [m] | 3,00 | 3,00 | 4,00 | 5,00 | 5,00 | |
| Maximální svislá podpůrná vzdálenost pažin ℓ1 [m] | ||||||
|
1,80 | 2,00 | 1,90 | 1,80 | 2,00 | |
|
0,50 | 0,60 | 0,60 | 0,60 | 0,70 | |
| Maximální vodorovná podpůrná vzdálenost převázek [m] | ||||||
|
160/160 | 1,60 | 1,50 | 1,40 | 1,30 | 1,20 |
| 200/200 | 2,30 | 2,30 | 2,00 | 1,80 | 1,70 | |
|
160/160 | 0,80 | 0,75 | 0,70 | 0,65 | 0,60 |
| 200/200 | 1,15 | 1,10 | 1,00 | 0,90 | 0,85 | |
| Maxmání vzpěrná délka rozpěr sk [m] | ||||||
|
1,70 | 1,65 | 1,50 | 1,30 | 1,25 | |
|
1,90 | 1,85 | 1,65 | 1,45 | 1,40 | |
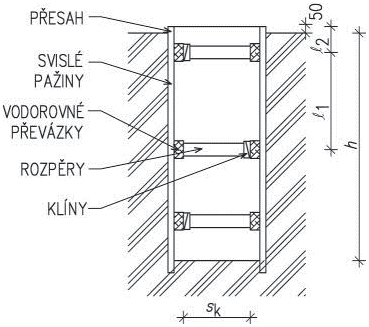
Obr. 12.2 Svislé příložné pažení
12.3 ŠTĚTOVÉ STĚNY
Štětové stěny jsou svislé stěnové konstrukce z ocelových štětovnic vetknutých do podloží. Štětové stěny jsou prováděny beraněním štětovnic spojených vodotěsnými zámky. Hloubka, do které lze tyto stěny realizovat je omezena pouze technickými podmínkami beranění.
U nás se používají štětovnice systému Larsen (viz tab. 12.4). Používají se stěny nerozepřené a) při h ≤ 4 m, rozepřené, b) nebo kotvené, c) při h ≤ 4–12 m v jedné etáži, h ≤ 12–17 m ve dvou etážích.
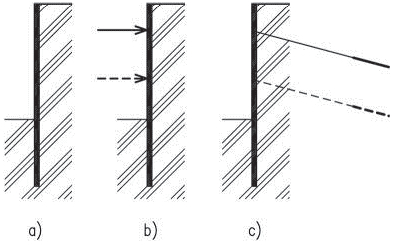
Obr. 12.3 Štětové stěny vetknuté, rozepřené a kotvené
Tab. 12.4 Tabulka štětovnic Larsen (Arcelor Mittal) – U Sekce
| Profil | Rozměry [mm] | Hmotnost | Moment setrvačnosti Iy [104 mm4/m] | Průřezový modul Wy [103 mm3/m] | ||||
| b | h | t | s | kusu [kg/m] | stěny [kg/m2] | |||
| AU 14 | 750 | 408 | 10,0 | 8,3 | 77,9 | 103,8 | 28680 | 1405 |
| AU 16 | 750 | 411 | 11,5 | 9,3 | 86,3 | 115,0 | 32850 | 1600 |
| AU 18 | 750 | 441 | 10,5 | 9,1 | 88,5 | 118,0 | 39300 | 1780 |
| AU 20 | 750 | 444 | 12,0 | 10,0 | 96,9 | 129,2 | 44440 | 2000 |
| AU 23 | 750 | 447 | 13,0 | 9,5 | 102,1 | 136,1 | 50700 | 2270 |
| AU 25 | 750 | 450 | 14,5 | 10,2 | 110,4 | 147,2 | 56240 | 2500 |
| PU 12 | 600 | 360 | 9,8 | 9,0 | 66,1 | 110,1 | 21600 | 1200 |
| PU 12-10/10 | 600 | 360 | 10,0 | 10,0 | 69,6 | 116,0 | 22580 | 1255 |
| PU 18-1 | 600 | 430 | 10,2 | 8,4 | 72,6 | 121,0 | 35950 | 1670 |
| PU 18 | 600 | 430 | 11,2 | 9,0 | 76,9 | 128,2 | 38650 | 1800 |
| PU 18+1 | 600 | 430 | 12,2 | 9,5 | 81,1 | 136,2 | 41320 | 1920 |
| PU 22-1 | 600 | 450 | 11,1 | 9,0 | 81,9 | 136,5 | 46380 | 2060 |
| PU 22 | 600 | 450 | 12,1 | 9,5 | 86,1 | 143,6 | 49460 | 2200 |
| PU 22+1 | 600 | 450 | 13,1 | 10,0 | 90,4 | 150,7 | 52510 | 2335 |
| PU 28-1 | 600 | 452 | 14,2 | 9,7 | 97,4 | 162,3 | 60580 | 2680 |
| PU 28 | 600 | 454 | 15,2 | 10,1 | 101,8 | 169,6 | 64460 | 2840 |
| PU 28+1 | 600 | 456 | 16,2 | 10,5 | 106,2 | 177,1 | 68380 | 3000 |
| PU 32-1 | 600 | 452 | 18,5 | 10,6 | 109,9 | 183,2 | 69210 | 3065 |
| PU 32 | 600 | 452 | 19,5 | 11,0 | 114,1 | 190,2 | 72320 | 3200 |
| PU 32+1 | 600 | 452 | 20,5 | 11,4 | 118,4 | 197,3 | 75410 | 3340 |
| GU 6N | 600 | 309 | 6,0 | 6,0 | 41,9 | 69,9 | 9670 | 625 |
| GU 7N | 600 | 310 | 6,5 | 6,4 | 44,1 | 73,5 | 10450 | 675 |
| GU 7S | 600 | 311 | 7,2 | 6,9 | 46,3 | 77,1 | 11540 | 740 |
| GU 7HWS | 600 | 312 | 7,3 | 6,9 | 47,4 | 79,1 | 11620 | 745 |
| GU 8N | 600 | 312 | 7,5 | 7,1 | 48,5 | 80,9 | 12010 | 770 |
| GU 8S | 600 | 313 | 8,0 | 7,5 | 50,8 | 84,6 | 12800 | 820 |
| GU 13N | 600 | 418 | 9,0 | 7,4 | 59,9 | 99,8 | 26590 | 1270 |
| GU 14N | 600 | 420 | 10,0 | 8,0 | 64,3 | 107,1 | 29410 | 1400 |
| GU 15N | 600 | 422 | 11,0 | 8,6 | 68,7 | 114,5 | 32260 | 1530 |
| GU 16N | 600 | 430 | 10,2 | 8,4 | 72,6 | 121,0 | 35950 | 1670 |
| GU 18N | 600 | 430 | 11,2 | 9,0 | 76,9 | 128,2 | 38650 | 1800 |
| GU 20N | 600 | 430 | 12,2 | 9,5 | 81,1 | 135,2 | 41320 | 1920 |
| GU 21N | 600 | 450 | 11,1 | 9,0 | 81,9 | 136,5 | 46380 | 2060 |
| GU 22N | 600 | 450 | 12,1 | 9,5 | 86,1 | 143,6 | 49460 | 2200 |
| GU 23N | 600 | 450 | 13,1 | 10,0 | 90,4 | 150,7 | 52510 | 2335 |
| GU 27N | 600 | 452 | 14,2 | 9,7 | 97,4 | 162,3 | 60580 | 2680 |
| GU 28N | 600 | 454 | 15,2 | 10,1 | 101,8 | 169,6 | 64460 | 2840 |
| GU 30N | 600 | 456 | 16,2 | 10,5 | 106,2 | 177,1 | 68380 | 3000 |
| GU 31N | 600 | 452 | 18,5 | 10,6 | 109,9 | 183,2 | 69210 | 3065 |
| GU 32N | 600 | 452 | 19,5 | 11,0 | 114,1 | 190,2 | 72320 | 3200 |
| GU 33N | 600 | 452 | 20,5 | 11,4 | 118,4 | 197,3 | 75410 | 3340 |
| GU 16-400 | 400 | 290 | 12,7 | 9,4 | 62,0 | 154,9 | 22580 | 1560 |
| GU 18-400 | 400 | 292 | 15,0 | 9,7 | 69,3 | 173,3 | 26090 | 1785 |
Nákres |
||||||||
Tab. 12.5 Tabulka štětovnic Larsen (Arcelor Mittal) – Z Sekce
| Profil | Rozměry [mm] | Hmotnost | Moment setrvačnosti Iy [104 mm4/m] | Průřezový modul Wy [103 mm3/m] | ||||
| b | h | t | s | kusu [kg/m] | stěny [kg/m2] | |||
| AZ 12-770 | 770 | 344 | 8,5 | 8,5 | 72,6 | 94,3 | 21430 | 1245 |
| AZ 13-770 | 770 | 344 | 9,0 | 9,0 | 76,1 | 98,8 | 22360 | 1300 |
| AZ 14-770 | 770 | 345 | 9,5 | 9,5 | 79,5 | 103,2 | 23300 | 1355 |
| AZ 14-770-10/10 | 770 | 345 | 10,0 | 10,0 | 82,9 | 107,7 | 24240 | 1405 |
| AZ 12-700 | 700 | 314 | 8,5 | 8,5 | 67,7 | 96,7 | 18880 | 1205 |
| AZ 13-700 | 700 | 315 | 9,5 | 9,5 | 74,0 | 105,7 | 20450 | 1305 |
| AZ 13-700-10/10 | 700 | 316 | 10,0 | 10,0 | 77,2 | 110,2 | 21370 | 1355 |
| AZ 14-700 | 700 | 316 | 10,5 | 10,5 | 80,3 | 114,7 | 22190 | 1405 |
| AZ 17-700 | 700 | 420 | 8,5 | 8,5 | 73,1 | 104,4 | 36230 | 1730 |
| AZ 18-700 | 700 | 420 | 9,0 | 9,0 | 76,5 | 109,3 | 37800 | 1800 |
| AZ 19-700 | 700 | 421 | 9,5 | 9,5 | 80,0 | 114,3 | 39380 | 1870 |
| AZ 20-700 | 700 | 421 | 10,0 | 10,0 | 83,5 | 119,3 | 40960 | 1945 |
| AZ 24-700 | 700 | 459 | 11,2 | 11,2 | 95,7 | 136,7 | 55820 | 2430 |
| AZ 26-700 | 700 | 460 | 12,2 | 12,2 | 102,9 | 146,9 | 59720 | 2600 |
| AZ 28-700 | 700 | 461 | 13,2 | 13,2 | 110,0 | 157,2 | 63620 | 2760 |
| AZ 24-700N | 700 | 459 | 12,5 | 9,0 | 89,7 | 128,2 | 55890 | 2435 |
| AZ 26-700N | 700 | 460 | 13,5 | 10,0 | 96,9 | 138,5 | 59790 | 2600 |
| AZ 28-700N | 700 | 461 | 14,5 | 11,0 | 104,1 | 148,7 | 63700 | 2765 |
| AZ 36-700N | 700 | 499 | 15,0 | 11,2 | 118,6 | 169,5 | 89610 | 3590 |
| AZ 38-700N | 700 | 500 | 16,0 | 12,2 | 126,4 | 180,6 | 94840 | 3795 |
| AZ 40-700N | 700 | 501 | 17,0 | 13,2 | 134,2 | 191,7 | 100080 | 3995 |
| AZ 42-700N | 700 | 499 | 18,0 | 14,0 | 142,1 | 203,1 | 104930 | 4205 |
| AZ 44-700N | 700 | 500 | 19,0 | 15,0 | 149,9 | 214,2 | 110150 | 4405 |
| AZ 46-700N | 700 | 501 | 20,0 | 16,0 | 157,7 | 225,3 | 115370 | 4605 |
| AZ 18 | 630 | 380 | 9,5 | 9,5 | 74,4 | 118,1 | 34200 | 1800 |
| AZ 18-10/10 | 630 | 381 | 10,0 | 10,0 | 77,8 | 123,4 | 35540 | 1870 |
| AZ 26 | 630 | 427 | 13,0 | 12,2 | 97,8 | 155,2 | 55510 | 2600 |
| AZ 46 | 580 | 481 | 18,0 | 14,0 | 132,6 | 228,6 | 110450 | 4595 |
| AZ 48 | 580 | 482 | 19,0 | 15,0 | 138,6 | 240,6 | 115670 | 4800 |
| AZ 50 | 580 | 483 | 20,0 | 16,0 | 146,7 | 252,9 | 121060 | 5015 |
Nákres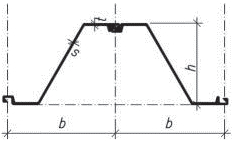 |
||||||||
12.3.1 Nerozepřené (nekotvené) stěny
Tyto stěny navrhujeme do maximální výše h = 4,00 m z důvodů ekonomických, se zvětšováním výšky rychle stoupá namáhání ohybovým momentem a požadovaná délka d vetknutí do podloží.
Působí-li nahodilé zatížení p, počítáme s náhradní výškou viz obr. 12.4.
\begin{gathered}
h'=h+\Delta h,\space\text{přičemž}\space \Delta h=p/\gamma
\end{gathered}kde je
γ … objemová tíha zeminy
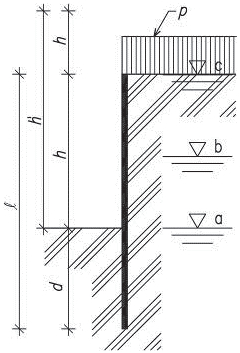
Obr. 12.4 Základní polohy úrovně hladiny podzemní vody
Podzemní voda působící na štětovou stěnu ovlivňuje příslušný ohybový moment a hloubku vetknutí d.
Tab. 12.6 Délka vetknutí nerozepřených štětových stěn
Pro rychlý orientační návrh stěny lze použít pomocných hodnot závislých na druhu často se vyskytujících se zemin a na výšce podzemní vody (tři polohy: a) bez účinku vody, b) hladina vody v úrovni 0,5h, c) hladina vody v úrovni h – viz obr. 12.4) uvedených v následující tabulce.
| Zemina | Objemová tíha γ [kN/m3] | Podzemní voda | Ohybový moment Ms,max [kNm/m] | Délka vetknutí d [m] | |
| hladina ode dna jámy | případ | ||||
| Spraše, Jíly | 18 | 0 | a | 2,4h3 | 1,35h |
| 0,5h | b | 4,0h3 | 1,70h | ||
| 1,0h | c | 8,8h3 | 2,22h | ||
| Písek kyprý | 18 | 0 | a | 1,7h3 | 1,00h |
| 0,5h | b | 3,0h3 | 1,22h | ||
| 1,0h | c | 6,8h3 | 1,70h | ||
| Písek středně ulehlý | 19 | 0 | a | 1,4h3 | 0,83h |
| 0,5h | b | 2,4h3 | 1,05h | ||
| 1,0h | c | 5,7h3 | 1,42h | ||
|
Poznámka: |
|||||
Příklad 12.1
Navrhněte vetknutou nerozepřenou štětovnicovou stěnu. Zemina kyprý písek, g = 18 kN/m2, nahodilé zatížení p = 10 kN/m2, výška stěny h = 3,00 m, hladina podzemní vody přibližně 0,5h (ode dna jámy)
\begin{gathered}
\Delta h=p/\gamma=10/18=0{,}55\space\text{m},\space h'=3{,}55\space\text{m}\\\\
M_\text{s,max}=3\cdot3{,}55^3=134{,}22\space\text{kNm}\\\\
d=1{,}22\cdot3{,}55=4{,}35\space\text{m}\\\\
\ell=d+h=4{,}35+3{,}00=7{,}35\space\text{m (délka štětovnic)}
\end{gathered}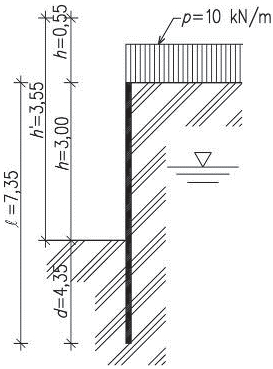
Vzhledem k tomu, že při výpočtu se vycházelo z charakteristických hodnot zatížení, je nutno uvažovat redukovanou pevnost oceli zavedením součinitele s = 1,5, takže
\begin{gathered}
\sigma_\text{s}=R/s=210/1{,}5=140\space\text{MPa}\\\\
W_\text{y}=\frac{M_\text{s,max}}{\sigma_\text{s}}=\frac{134{,}22}{140\cdot10^3}=0{,}96\cdot10^{-3}\space\text{m}^3/\text{m}=960\cdot10^3\space\text{mm}^3/\text{m}
\end{gathered}tomu odpovídá profil štětovnice GU 13N, Wy = 1270 · 103 mm3/m (viz tab. 12.4 a 12.5).
12.3.2 Kotvené stěny
Kotvení je konstrukce, přenášející síly od tlaku zeminy a vody působící na pažicí stěnu do základové půdy vně stavební jámy. Kotva, složená z táhla a vlastního kotevního prvku (například injektovaného kořene), bývá přepjatá a může být umístěna, podle výšky jámy, i v několika úrovních. Sklon šikmého kotvení bývá α = 15°–30°.
V běžných případech lze předběžně navrhnout kotvení v jedné úrovni (etáži) při nahodilém zatížení p ≤ 20 kN/m2, sklonu šikmé vrtané kotvy s injektovaným kořenem od vodorovné α = 20° podle vztahů:
a) zemina nesoudržná při φ = 30°, δ = 0°
- vodorovná síla v úrovni kotvy (p ≤ 20 kN/m2)
\begin{gathered}
F_\text{h}\cong80+35(h-4)\space[\text{kN/m}]
\end{gathered}- vodorovná síla v úrovni kotvy, nepůsobí-li nahodilé zatížení (v = 0 kN/m2)
\begin{gathered}
F_\text{h}\cong60+35(h-4)\space[\text{kN/m}]
\end{gathered}- síla ve směru kotvy při jejím sklonu α = 20° od vodorovné
\begin{gathered}
F_\text{k}\cong\cos\alpha\cdot F_\text{h}=1{,}06F_\text{h}\space[\text{kN/m}]
\end{gathered}- délka kotvy (včetně táhla)
\begin{gathered}
\ell_\text{k}\cong5+1{,}25(h-4)+0{,}4h\space[\text{m}]\\\\
\ell_\text{h}\cong\cos\alpha\cdot\ell_\text{k}=0{,}94\ell_\text{k}\space[\text{m}]
\end{gathered}Příklad 12.2
Navrhněte kotvení kotvené stěny v nesoudržné zemině.
Výška h = 7,00 m, p = 15 kN/m2
\begin{gathered}
F_\text{h}=80+35\cdot(7-4)=185\space\text{kN/m}\\\\
F_\text{k}=1{,}06\cdot185=196\space\text{kN/m}
\end{gathered}umístíme-li kotvy v půdorysné vzdálenosti 2,5 m od sebe, vychází 2,5 Fk = 2,5 · 196 = 490 kN tahové síly (při charakteristických hodnotách zatížení), na kterou se navrhuje ocelová tyč, svazek patentovaných drátů nebo ocelový pramenec.
\begin{gathered}
\ell_\text{k}=5+1{,}25\cdot(7-4)+0{,}4\cdot7=11{,}55\space\text{m (délka kotvení viz schéma)}\\\\
\ell_\text{h}=0{,}84\cdot11{,}55=10{,}86\space\text{m (půdorysná délka namáhané oblasti)}
\end{gathered}b) zemina soudržná při φ = 25°, d = 0
- vodorovná síla v kotvě (p ≤ 20 kN/m2)
\begin{gathered}
F_\text{h}\cong100+40\cdot(h-4)\space[\text{kN/m}]
\end{gathered}- vodorovná síla v kotvě, nepůsobí-li nahodilé zatížení (p = 0 kN/m2)
\begin{gathered}
F_\text{h}\cong80+40\cdot(h-4)\space[\text{kN/m}]
\end{gathered}- vodorovná síla při jejím sklonu a = 20° od vodorovné
\begin{gathered}
F_\text{k}\cong1{,}06F_\text{h}=1{,}06F_\text{h}\space\space\text{popř.}\space\space1{,}06F'_\text{h}\space[\text{kN/m}]
\end{gathered}- délka kotvy (včetně táhla)
\begin{gathered}
\ell_\text{k}=6+1{,}4\cdot(h-4)+0{,}4h\space[\text{m}]\\\\
\ell_\text{h}=0{,}94\ell_\text{k}\space[\text{m}]
\end{gathered}Příklad 12.3
Navrhněte kotvení kotvené stěny v soudržné zemině.
Výška h = 7,00 m, p = 15 kNm/m2 (ponecháno stejné jako u předcházejícího příkladu)
\begin{gathered}
F_\text{h}=100+40\cdot(7-4)=220\space\text{kN/m}\\\\
F_\text{k}=1{,}06\cdot220=233{,}2\space\text{kN/m}\\\\
\ell_\text{k}=6+1{,}4\cdot(7-4)+0{,}4\cdot7=13\space\text{m (délka kotvení)}\\\\
\ell_\text{h}=0{,}94\cdot13=12{,}20\space\text{m (půdorysná délka namáhané oblasti)}
\end{gathered}12.3.3 Podzemní stěny
Podzemní stěny patří mezi moderní technologie a navrhují se obvykle buď jako pilotové nebo tzv. milánské stěny.
Pilotové stěny jsou u nás nejrozšířenější. Stěny jsou vytvářeny z velkoprůměrových pilot d ≥ 0,60 m, vyšší pilotové stěny bývají přikotvovány obdobně jako štětové stěny, někdy i v patě, nevyplatí-li se jinak nutné vetknutí do podloží. Tyto stěny je možno využít i jako součást stavby, popř. lze na ně uložit celou vrchní stavbu – pak je nutno stěny dimenzovat na definitivní přenos jak svislého (od budovy), tak vodorovného zatížení (od zemního tlaku). U vysokých stěn se pak rozepřou tuhými stropy podzemní části stavby. Přikotvování se obvykle nepokládá za definitivní způsob zajištění z důvodu přerezavění i obetonovaných táhel například vlivem bludných proudů. Půdorysná vzdálenost kotvení bývá cca 2,5 m.
Milánské stěny jsou ploché stěnové prvky tloušťky cca 0,60 m, jejichž rýhy (obvykle lamelové technologie) jsou prováděny drapáky, vlečnými korečky nebo sací mi vrtáky, paženy jílovými suspenzemi a následně po osazení výztužného koše směrem ode dna vybetonované. U vysokých stěn se provádí kotvení obdobným způsobem jako u pilotových stěn s optimální vzdáleností okolo 2,5 m (půdorysně). Založení nadzemní části stavby na tyto stěny není příliš vhodné.
Poznámka:
Podle německých zkušeností je přibližná cenová relace podzemních stěn následující:
- milánské stěny 100 %;
- pilotové stěny 80 %;
- štětové stěny 80 %.
Při požadavku vodotěsnosti konstrukce se posunují výše uvedená procenta ve prospěch milánských stěn.
Mikrozápory
Mikrozápory jsou štíhlé nosné prvky pažicí, zpevňující a stabilizující konstrukce, přenášející především ohybová namáhání. Princip a podmínky pro realizaci mikrozáporového pažení jsou obdobné jako pro záporové pažení. Nahrazují zápory hnaného záporového pažení v případech, kdy z hlediska prostorového uspořádání je nutno otevřít co největší prostor v dané zástavbě, především ve stísněných místních prolukách pro svislé pažení stěn stavebních jam, kde tato konstrukce nejlépe odpovídá potřebám záboru pozemku.
Mikrozáporové pažení tvoří následující prvky: mikrozápory, pažiny, případně pažiny lze nahradit stříkaným betonem, a převázky rozepřené ocelovou konstrukcí nebo kotvené horninovými kotvami. Mikrozáporové pažení se navrhuje. Výztuž mikrozápor tvoří buď silnostěnné ocelové trubky profilu Ø 108/16 mm, popřípadě i větší, nebo je s výhodou použito širokopřírubových válcovaných nosníků (např. HEB), jejichž velikost je omezena průměrem vrtu. Rozhodujícím kritériem pro výběr výztuže je poměr únosnosti v ohybu k vlastní hmotnosti a k její ceně. Pažení mezi mikrozáporami je tvořeno buď výdřevou nebo ocelovými pažinami. V případě dřevěných pažin je nutné provést zpětný zásyp zeminou za rub záporového pažení, čímž je pažící konstrukce aktivována. Velmi často je prostor mezi mikrozáporami vyplněn vrstvou stříkaného betonu s výztužnou sítí. S ohledem na relativní malou ohybovou tuhost této konstrukce je třeba mikrozáporové stěny kotvit nebo rozpírat. Kotevní síly se na mikrozápory přenášejí převázkami, které se navrhují v různých výškových úrovních z oceli nebo železobetonu. O umístění převázek a jejich konstrukci rozhodují místní podmínky, statické charakteristiky a podmínky budoucích konstrukcí. Z konstrukčního hlediska platí, že vzdálenost vrtů by měla dosahovat maximálně 3 Ø vrtu. U mikrozápor se na rozdíl od mikropilot zpravidla neinjektuje jejich kořen.
Při statickém výpočtu kotvené mikrozáporové stěny je třeba posoudit:
- ocelové mikrozápory;
- převázku;
- kotvy.
Při posuzování výztužných ocelových trubek se obvykle neuvažuje spolupůsobení cementové zálivky.
Trysková injektáž
Zapažení stavební jámy lze realizovat též tryskovou injektáží. Vzledem k tomu, že při tého technologii nelze vkládat do vrtů výztuž, musí být pažicí konstrukce vůči hloubce stavební jámy dostatečně robustní, aby se dostatečně uplatnila její vlastní hmotnost (podobně jako u gravitačních opěrných stěn).
Popis technologie tryskové injektáže je v kap. 11.2.3.
13 OPĚRNÉ STĚNY
Opěrné stěny slouží k zajištění zeminy při změně úrovně terénu, je-li úrovně terénu, je-li přechod pod větším úhlem než je přirozený úhel zeminy.
Podle statického působení se rozlišují:
- stěny obkladní;
- stěny zárubní;
- stěny opěrné.
Obr. 13.1 Opěrné stěny a) gravitační, b) úhelníkové, c) žebrové, d) kotvené
13.1 ODKLADNÍ STĚNY
Účelem obkladní zdi je ochrana svahu proti účinkům povětrnosti – svah má stabilní sklon větší nebo stejný jako je přirozený svah. Materiálem obkladní stěny může být prostý nebo železový beton, prefabrikáty, popř. zdivo. Betonová obkladní stěna se navrhuje o tloušťce 300–400 mm v koruně, v patě obkladní stěny se tloušťka zvětšuje na
\begin{gathered}
h_\text{d}=0{,}1H\space\space\text{až}\space\space h_\text{d}=(0{,}30+0{,}1H)\space[\text{m}]
\end{gathered}kde je
H … výška stěny [m].
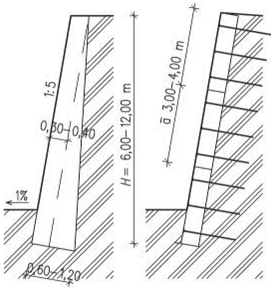
Obr. 13.2 Obkladní opěrné stěny
Příklad 13.1
Navrhněte tloušťku obkladní stěny v patě.
Výška stěny H = 9,00 m, tloušťka v koruně d0 = 0,4 m,
Tloušťka v patě d = 0,1 · 9,0 = 0,9 m až d = (0,30 + 0,1 · 9,0) = 1,2 m.
13.2 GRAVITAČNÍ STĚNY
U gravitačních stěn se využívá jejich vlastní tíhy proti převržení zemním tlakem. Hloubka založení se volí v závislosti na:
- geologických poměrech (0,2 m pod lícem únosné zeminy);
- klimatických poměrech – v nezámrzné hloubce (minimálně 0,8 m, na horách 1,2 m);
- úrovni podzemní vody.
Opěrná stěna se nejčastěji skládá ze základu a dříku – tvar podle obr. 13.3. Staticky se posuzuje:
- překlopení kolem bodu o;
- posunutí v základové spáře;
- napětí v základové spáře;
- spojení mezi základem a dříkem.
Materiál – prostý beton nižší pevnosti, beton proložený kameny, zdivo.
Obr. 13.3 Gravitační opěrná stěna
Rozměry podle Bellina – platí pro H ≤ 5 m, sklon předního líce 1 : 10 až 1 : 5
Šířka v koruně
\begin{gathered}
H\le2\space\text{m}\space\space d_0=0{,}3{-}0{,}5\space\text{m},\\\\
H\gt2\space\text{m}\space\space d_0=0{,}5{-}1{,}0\space\text{m}.
\end{gathered}Šířka v patě du se určí v závislosti na hloubce H [m] podle následujících vzorců za předpokladu, že na výše položené úrovni nepůsobí zatížení (např. nahodilé)
- pro vlhkou zeminu
\begin{gathered}
d_\text{u}=(0{,}4H+0{,}015H^2)\space[\text{m}]
\end{gathered}- pro suchou zeminu
\begin{gathered}
d_\text{u}=(0{,}3H+0{,}01H^2)\space[\text{m}]
\end{gathered}
Obr. 13.4 Gravitační opěrná stěna podle Bellina
Příklad 13.2
Navrhnětě šířku paty gravitační opěrné stěny podle Bellina. Hloubka H = 4,0 m
Šířka paty ve vlhké zemině
\begin{gathered}
d_\text{u}=0{,}4\cdot4{,}0+0{,}015\cdot4{,}0^2=1{,}84\space\text{m}
\end{gathered}Šířka paty v suché zemině
\begin{gathered}
d_\text{u}=0{,}3\cdot4{,}0+0{,}01\cdot4{,}0^2=1{,}36\space\text{m}
\end{gathered}Rozměry podle Graßhoffa – sklon předního líce 1:5 Šířka v koruně
\begin{gathered}
d_0\ge0{,}3\space[\text{m}]
\end{gathered}Šířka v patě du
- písčité zeminy φ = 35°, γ = 18,0 kN/m3
\begin{gathered}
d_\text{u}=(0{,}25{-}0{,}30)H\space[\text{m}]
\end{gathered}- soudržné zeminy φ = 25°, γ = 22,0 kN/m3
\begin{gathered}
d_\text{u}=(0{,}35{-}0{,}40)H\space[\text{m}]
\end{gathered}Příklad 13.3
Navrhněte šířku paty gravitační stěny podle Graßhoffa. Hloubka H = 4,0 m
Šířka paty ve písčité zemině
\begin{gathered}
d_\text{u}=(0{,}25{-}0{,}30)\cdot4{,}0=1{,}0{-}1{,}2\space\text{m}
\end{gathered}Šířka paty ve soudržné zemině
\begin{gathered}
d_\text{u}=(0{,}35{-}0{,}40)\cdot4{,}0=1{,}4{-}1{,}6\space\text{m}
\end{gathered}Zatížení na horním povrchu terénu se zahrne zvětšením hloubky H o hodnotu
\begin{gathered}
\delta_\text{H}=p/\gamma\space[\text{m}]
\end{gathered}kde je
p … zatížení povrchu terénu [kN/m2],
γ … objemová tíha zeminy [kN/m3].
do výše uvedených vzorců se pak dosadí
\begin{gathered}
H'=H+\delta_\text{H}
\end{gathered}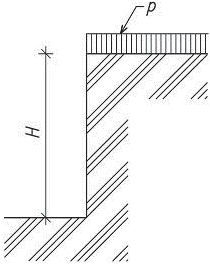
Obr. 13.5 Zatížení na horním povrchu terénu
Příklad 13.4
Určete zvětšení výšky terénního schodu při uvážení zatížení na jeho horní úrovni.
\begin{gathered}
p=5{,}0\space\text{kN/m}^2\space\space\gamma=22\space\text{kN/m}^3\\\\
\delta_\text{H}=5{,}00/0{,}22=0{,}23\space\text{m}
\end{gathered}Stěny z vyztuženého zdiva
Stěny jsou ze zdiva z dutých tvarovek vyplněných železobetonem, nebo zdivo je kombinováno s železovým betonem, vybetonovaným do kapes (drážek) ve zdivu.
Typické výšky
\begin{gathered}
H=1{,}0{-}6{,}0\space\text{m}
\end{gathered}Šířka stěny
\begin{gathered}
d=H/10{-}H/15\space[\text{m}]
\end{gathered}Šířka základu
\begin{gathered}
B=H/2{-}2H/3\space[\text{m}]
\end{gathered}Obr. 13.6 Stěna z vyztuženého zdiva
Gabiony – stěny z klecí či košů se štěrkem – drátová kostra potažená pletivem nebo konstrukce ze svařovaných sítí vyplněná hrubým kamenivem. Tato konstrukce je zpravidla hospodárnější než jiné typy opěrných stěn.
Typické výšky
\begin{gathered}
H=1{,}0{-}3{,}0\space\text{m}
\end{gathered}Šířka stěny
\begin{gathered}
d=H{-}H/2\space[\text{m}]
\end{gathered}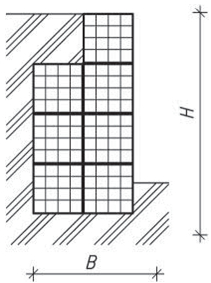
Obr. 13.7 Gabionová stěna
13.3 ÚHELNÍKOVÉ STĚNY
Navrhují se ze železového betonu do výšky přibližně 4,0 m, při větší výšce se navrhují stěny žebrové. Stabilita je zajištěna vyložením základové desky, na kterou působí svisle tlak zeminy. Proti případnému posunutí v základové spáře se navrhuje jednak její naklonění, jednak zazubení.
Obr. 13.8 Úhelníková stěna
U stěny se staticky posuzuje:
- překlopení kolem bodu o (viz obr. 13.8);
- posunutí v základové spáře;
- namáhání zeminy v základové spáře;
- ohyb popř. smyk ve stěně a základové desce.
Rozměry:
- není-li horní povrch terénu zatížen p = 0
\begin{gathered}
b=H\cdot\sqrt{\frac{K_\text{a}}{1+4\cdot n}}\space[\text{m}]
\end{gathered}- při zatížení povrchu horního terénu p uvažujeme zvětšení hloubky založení o
\begin{gathered}
\delta_\text{H}=p/\gamma
\end{gathered}kde je
p … zatížení povrchu terénu [kN/m2],
γ … objemová tíha zeminy [kN/m3].
\begin{gathered}
b=\sqrt{\frac{H\cdot(H+3\cdot\delta_\text{H})K_\text{a}}{1+4n}}\space[\text{m}]
\end{gathered}Součinitel
\begin{gathered}
K_\text{a}=\tg^2(45\degree-\varphi/2)
\end{gathered}kde je
φ … úhel vnitřního tření zeminy [°].
Tab. 13.1 Orientační charakteristiky zeminy pro určení aktivního tlaku
| Zemina | Úhel vnitřního tření φ [°] | Součinitel aktivního tlaku Ka [–] | Objemová hmotnost γ [kN/m3] |
| mateční hornina | 25° | 0,41 | 18 |
| vlhký písek, štěrk | 30° | 0,33 | 18 |
| jíl, hlína do 4 m | 25° | 0,41 | 21 |
| jíl, hlína pod 4 m | 20° | 0,49 | 20 |
Předsazení základové desky b1 = n · b, pak
\begin{gathered}
B=(1+n)b\space[\text{m}]
\end{gathered}Předsazení se volí od b1 = 0 při malé výšce H do b1 = 0,5b, kdy vyjde celková šířka B nejmenší.
Obr. 13.9 Rozměry úhelníkové stěny
Příklad 13.5
Navrhněte úhelníkovou stěnu v nesoudržné zemině.
výška h = 3,5 m, zatížení p = 5,0 kN/m2, předsazení b1 = 0,25 · b, n = 0,25
\begin{gathered}
\delta_\text{H}=5{,}0/18=0{,}28\space\text{m}\\\\
b=\sqrt{\frac{0{,}33\cdot3{,}5\cdot(3{,}5+3{,}0\cdot0{,}28)}{1+4\cdot0{,}25}}=1{,}58\approx1{,}6\space\text{m}\\\\
B=1{,}25\cdot1{,}6=2{,}0\space[\text{m}],\space b_1=0{,}4\space\text{m}
\end{gathered}- bez zatížení v
\begin{gathered}
b=3{,}5\cdot\sqrt{\frac{3{,}3}{1+4\cdot0{,}25}}=1{,}42\approx1{,}4\space\text{m}\\\\
B=1{,}25\cdot1{,}4=1{,}77\approx1{,}75\space[\text{m}],\space b_1=0{,}35\space\text{m}
\end{gathered}- bez zatížení v a předsazení b1
\begin{gathered}
B=b=3{,}5\cdot\sqrt{0{,}33}=2{,}01\approx2{,}0\space\text{m}
\end{gathered}Ohybový moment v patě stěny při výšce h
Nesoudržné zeminy
\begin{gathered}
M=h^3+h\space[\text{kNm/m}]
\end{gathered}Soudržné zeminy
\begin{gathered}
M=1{,}5\cdot(h^3+h)\space[\text{kNm/m}]
\end{gathered}Tloušťka stěny v patě stěny
\begin{gathered}
d=\sqrt{1\space000M}\space[\text{mm}]
\end{gathered}Příklad 13.6
Navrhněte tloušťku stěny v její patě.
h = 3,0 m, soudržná zemina
\begin{gathered}
M=1{,}5\cdot(3{,}0^3+3{,}0)=45\space\text{kNm/m}\\\\
d=\sqrt{1\space000\cdot45}=212\space\text{mm}
\end{gathered}Navržená tloušťka je 250 mm.
13.4 DESKOVÁ STĚNA NA ŽEBRECH
Navrhují se pro větší výšky H = 4,0–8,0 m.
Stěna mezi žebry:
- křížem vyztužená deska h1/ℓ ≤ 1,6–2,0
\begin{gathered}
h_\text{d}\ge(h_1+\ell)/70\space[\text{m}]
\end{gathered}- jednosměrně pnutá desky h2/ℓ > 2,0
\begin{gathered}
h_\text{d}\ge\ell/25\space[\text{m}]
\end{gathered}Příčná žebra – osová vzdálenost a1 = 2,0–4,0 m
- tloušťka žeber br = 0,3–0,5 m;
- šířka žeber podle vyložení základové desky viz obr. 13.10.
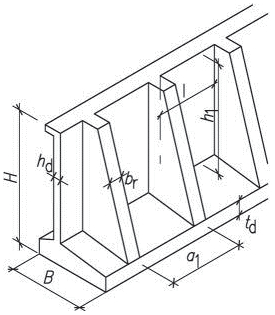
Obr. 13.10 Desková stěna na žebrech
Podélný nosník v koruně stěny může být nahrazen deskovým prvkem.
Základová spára šířky b1, b a B se volí stejně jako u úhelníkové stěny, tloušťka desky td = 0,5–0,8 m při výšce H = 4,0–8,0 m.
Dilatační spáry se umísťují po 20–30 m.
Příklad 13.7
Navrhněte deskovou stěnu na žebrech. Rozdíl výšek terénu 6,0 m, hloubka založení 1,0 m, zatížení povrchu terénu p = 5,0 kN/m2, štěrkovitá zemina
\begin{gathered}
H=7{,}0\space\text{m}\\\\
\delta_\text{H}=5{,}0/18=2{,}777=2{,}8\space\text{m}
\end{gathered}vyložení b1 = 0,5 · b, n = 0,5
\begin{gathered}
b=\sqrt{\frac{0{,}33\cdot7{,}0\cdot(7{,}0+3\cdot0{,}29)}{1+3\cdot0{,}5}}=2{,}457=2{,}5\space\text{m}\\\\
B=1{,}5\cdot2{,}5=3{,}75\space\text{m},\space b_1=1{,}25\space\text{m}
\end{gathered}tloušťka základové desky td = 0,7 m
vzdálenost žeber 3,0 m
tloušťka stěny 0,4 m
\begin{gathered}
h_1/\ell=(7{,}0-0{,}7)/(3{,}0-0{,}4)=2{,}42\space\text{m}
\end{gathered}jednosměrně pnutá deska
\begin{gathered}
h_\text{d}=(3{,}0-0{,}40)/25=0{,}104=0{,}11\space\text{m}
\end{gathered}13.5 PALISÁDA
Pro dětská hřiště, zahradní úpravy apod. lze navrhnout z hloubkově impregnovaných kruhových výřezů palisádovou opěrnou stěna o rozměrech uvedených v tab. 13.2 za předpokladu rovinného navazujícího terénu a užitného charakteristického zatížení terénu do 5 kN/m2.
Tab. 13.2 Empirické vztahy pro návrh palisády
| Rozdíl úrovní terénu h [m] | 0,50 | 0,85 | 1,20 | 1,50 | 1,80 |
| Zapuštění t [m] | 0,50 | 0,55 | 0,80 | 1,00 | 1,20 |
| Min. průměr d [m] | 0,08 | 0,08 | 0,08 | 0,10 | 1,12 |
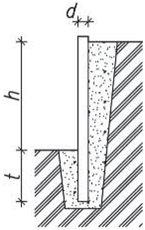
Obr. 13.11 Palisáda
13.6 VYZTUŽENÁ ZEMINA
K zajištění výškového rozdílu terénu zejména u dopravních staveb apod. se používá k vyztužení zeminy buď mřížovina z oceli, geosyntetika případně geotextílie.
S ocelovou nebo geosyntetickou výztuží se tyto konstrukce navrhují ve skladbě:
- výplňová zemina, která se ukládá ve vrstvách do 350 mm a hutní se;
- z ocelové výztuže (pletiva, mřížoviny), žárově pozinkované, průřez podle statického výpočtu (oka 50/50–150/150 mm, průměr 4–5 mm) nebo z ocelových pozinkovaných profilovaných plechů.

Obr. 13.12 Vyztužená zemina ocelovou nebo geosyntetickou výztuží
Vodorovné účinky zeminy se přenášejí výztuží a třením ve výplňové zemině.
Šířka vyztuženého tělesa:
\begin{gathered}
b\ge(0{,}7\space\text{až}\space0{,}8)\cdot h\space[\text{m}]
\end{gathered}Do výškového rozdílu 4 m jsou opěrné stěny levnější, nad 4 m činí úspory
při h = 6 m
20 %
při h = 10 m
35 %
Hloubka zapuštění
při vodorovném terénu
\begin{gathered}
t\ge0{,}1h\space[\text{m}]
\end{gathered}při sklonitém terénu
\begin{gathered}
t\ge0{,}2h\space[\text{m}]
\end{gathered}Vyztužení geotextilií se navrhuje pro zemní tělesa s omezenou životností. K vyztužení se používá vysokopevnostní netkané textilie.

Obr. 13.13 Vyztužená zemina geotextilií
Při vodorovném povrchu terénu a úhlu vnitřního tření φ ≥ 25°
\begin{gathered}
b=5/6h+1{,}5\space[\text{m}]\\\\
t_\text{min}=0{,}1h\space[\text{m}]
\end{gathered}Příklad 13.8
Navrhněte hloubku zapuštění vyztužené zeminy geotextílií.
výška h = 4 m
\begin{gathered}
b=5/6h\cdot4+1{,}5=4{,}8\space\text{m}\\\\
t_\text{min}\ge0{,}1\cdot4=0{,}4\space\text{m}
\end{gathered}14 PŘÍLOHY
Tab. 14.1 Ohybové momenty, posouvající síly a průhyby na nosnících ℓ
| Nákres | Ohybové momenty | Posouvající síly | Průhyb |
| Prostý nosník | |||
 |
M_1=\frac{1}{2}q\cdot c\cdot d\\M_\text{s}=\frac{1}{8}q\cdot\ell^2 | V_\text{ab}=\frac{1}{2}q\cdot\ell\\ V_\text{ba}=-\frac{1}{2}q\cdot\ell | w_\text{s}=\frac{5}{384}\cdot\frac{q\cdot\ell^4}{E\cdot I} |
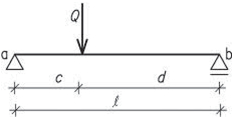 |
M_1=\frac{1}{\ell}Q\cdot c\cdot d | V_\text{ab}=\frac{1}{\ell}Q\cdot d\\ V_\text{ba}=-\frac{1}{\ell}Q\cdot c | c\le\ell/2\\ w_\text{s}=\frac{Q\cdot c}{48E\cdot I}(3\ell^2-4c^2)\\ c\ge\ell/2\\ w_\text{s}=\frac{Q\cdot d}{48E\cdot I}(3\ell^2-4d^2) |
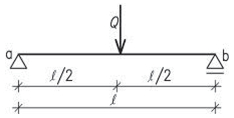 |
M_\text{s}=\frac{1}{4}Q\cdot\ell | V_\text{ab}=-V_\text{ba}=\frac{1}{2}Q | w_\text{s}=\frac{1}{48}\cdot\frac{Q\cdot\ell^3}{E\cdot I} |
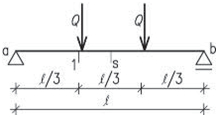 |
M_1=M_\text{s}=M_2=\frac{1}{3}Q\cdot\ell | V_\text{ab}=-V_\text{ba}=Q | w_\text{s}=\frac{23}{648}\cdot\frac{Q\cdot\ell^3}{E\cdot I} |
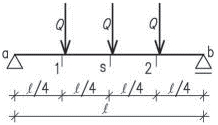 |
M_1=M_2=\frac{3}{8}Q\cdot\ell\\ M_\text{s}=\frac{1}{2}Q\cdot\ell | V_\text{a1}=-V_\text{b2}=1{,}5Q\\ V_\text{1s}=-V_\text{s2}=0{,}5Q | w_\text{s}=\frac{19}{384}\cdot\frac{Q\cdot\ell^3}{E\cdot I} |
 |
M_\text{max}=\frac{1}{9\sqrt{3}}q\cdot\ell^2 | V_\text{ab}=\frac{1}{3}q\cdot\ell\\ V_\text{ba}=\frac{1}{6}q\cdot\ell | w_\text{max}=0{,}00625\frac{q\cdot\ell^4}{E\cdot I} |
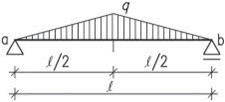 |
M_\text{max}=\frac{1}{12}q\cdot\ell^2 | V_\text{ab}=-V_\text{ba}=\frac{1}{4}q\cdot\ell | w_\text{s}=\frac{1}{120}\cdot\frac{q\cdot\ell^4}{E\cdot I} |
| Jednostranně vetknutý nosník | |||
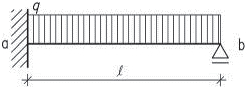 |
M_\text{ab}=-\frac{1}{8}q\cdot\ell^2 | V_\text{ab}=\frac{5}{8}q\cdot\ell\\ V_\text{ba}=-\frac{3}{8}q\cdot\ell | w_\text{s}=\frac{2}{384}\cdot\frac{q\cdot\ell^4}{E\cdot I} |
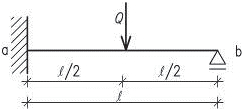 |
M_\text{ab}=-\frac{3}{16}Q\cdot\ell | V_\text{ab}=\frac{11}{16}Q\\ V_\text{ab}=-\frac{5}{16}Q | w_\text{s}=\frac{7}{768}\cdot\frac{Q\cdot\ell^3}{E\cdot I} |
| Oboustranně vetknutý nosník | |||
 |
M_\text{ab}=M_\text{ab}=-\frac{1}{12}q\cdot\ell^2\\ M_\text{s}=\frac{1}{24}q\cdot\ell^2 | V_\text{ab}=-V_\text{ba}=\frac{1}{2}q\cdot\ell | w_text{s}=\frac{1}{384}\cdot\frac{q\dot\ell^4}{E\cdot I} |
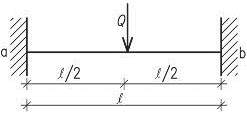 |
M_\text{ab}=M_\text{ba}=-\frac{1}{8}Q\cdot\ell\\ M_\text{s}=\frac{1}{8}Q\cdot\ell | V_\text{ab}=-V_\text{ba}=\frac{1}{2}Q | w_\text{s}=\frac{1}{192}\cdot\frac{Q\cdot\ell^3}{E\cdot I} |
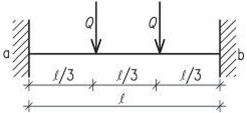 |
M_\text{ab}=M_\text{ba}=-\frac{2}{9}Q\cdot\ell | V_\text{ab}=-V_\text{ba}=Q | w_\text{s}=\frac{5}{648}\cdot\frac{Q\cdot\ell^3}{E\cdot I} |
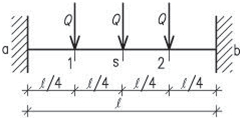 |
M_\text{ab}=M_\text{ba}=-\frac{5}{16}Q\cdot\ell | V_\text{ab}=-V_\text{ba}=1{,}5Q | w_\text{s}=\frac{1}{96}\cdot\frac{Q\cdot\ell^3}{E\cdot I} |
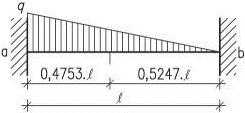 |
M_\text{ab}=-\frac{1}{20}q\cdot\ell^2\\ M_\text{ba}=-\frac{1}{30}q\cdot\ell^2 | V_\text{ab}=\frac{7}{20}q\cdot\ell\\ V_\text{ba}=-\frac{3}{20}q\cdot\ell | w_\text{s}=0{,}001308\frac{q\dot\ell^4}{E\cdot I} |
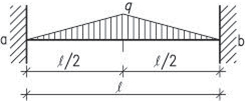 |
M_\text{ab}=M_\text{ba}=-\frac{5}{96}q\cdot\ell^2 | V_\text{ab}=-V_\text{ba}=\frac{1}{4}q\cdot\ell | w_\text{s}=\frac{7}{3\space840}\cdot\frac{q\cdot\ell^4}{E\cdot I} |
| Konzola | |||
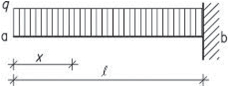 |
M_\text{x}=-\frac{1}{2}q\cdot x^2\\ M_\text{b}=\frac{1}{2}q\cdot\ell^2 | V_\text{x}=-q\cdot x\\ V_\text{b}=-q\cdot I | w_\text{a}=\frac{1}{8}\cdot\frac{q\cdot\ell^4}{E\cdot I} |
 |
M_\text{x}=-Q\cdot x\\ M_\text{b}=-Q\cdot\ell | V_\text{x}=-Q\\ V_\text{b}=-Q | w_\text{a}=\frac{1}{3}\cdot\frac{Q\cdot\ell^3}{E\cdot I} |
Tab. 14.2 Válcované IPN nosníky DIN 1025-1, ČSN 42 5550
A – plocha průřezu
I – moment setrvačnosti
t – tloušťka stěny
W – průřezový modul
i – poloměr setrvačnosti
m – hmotnost
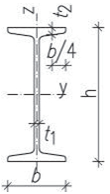
| Označení průřezu IPN | Jmenovité rozměry | m | A | Iy | Wy | iy | Iz | Wz | iz | |||
| h | b | t1 | t2 | |||||||||
| [mm] | [kg/m] | 103 [mm2] | 106 [mm4] | 103 [mm3] | [mm] | 106 [mm4] | 103 [mm3] | [mm] | ||||
| 80 | 80 | 42 | 3,9 | 5,9 | 5,94 | 0,757 | 0,777 | 19,4 | 32,0 | 0,0628 | 2,99 | 9,11 |
| 100 | 100 | 50 | 4,5 | 6,8 | 8,34 | 1,06 | 1,70 | 34,1 | 40,0 | 0,122 | 4,86 | 10,7 |
| 120 | 120 | 58 | 5,1 | 7,7 | 11,1 | 1,42 | 3,27 | 54,5 | 48,0 | 0,214 | 7,38 | 12,3 |
| 140 | 140 | 66 | 5,7 | 8,6 | 14,3 | 1,82 | 5,72 | 81,8 | 56,0 | 0,351 | 10,6 | 13,9 |
| 160 | 160 | 74 | 6,3 | 9,5 | 17,9 | 2,28 | 9,34 | 117 | 64,0 | 0,546 | 14,8 | 15,5 |
| 180 | 180 | 82 | 6,9 | 10,4 | 21,9 | 2,79 | 14,4 | 160 | 72,0 | 0,812 | 19,8 | 17,1 |
| 200 | 200 | 90 | 7,5 | 11,3 | 26,2 | 3,34 | 21,4 | 214 | 80,0 | 1,16 | 25,9 | 18,7 |
| 220 | 220 | 98 | 8,1 | 12,2 | 31,0 | 3,95 | 30,5 | 278 | 87,9 | 1,62 | 33,1 | 20,3 |
| 240 | 240 | 106 | 8,7 | 13,1 | 36,2 | 4,61 | 42,4 | 353 | 95,9 | 2,20 | 41,5 | 21,9 |
| 260 | 260 | 113 | 9,4 | 14,1 | 41,9 | 5,33 | 57,3 | 441 | 104 | 2,87 | 50,9 | 23,2 |
| 280 | 280 | 119 | 10,1 | 15,2 | 47,9 | 6,10 | 75,8 | 541 | 111 | 3,63 | 61,0 | 24,4 |
| 300 | 300 | 125 | 10,8 | 16,2 | 54,2 | 6,90 | 97,9 | 652 | 119 | 4,49 | 71,9 | 25,5 |
| 320 | 320 | 131 | 11,5 | 17,3 | 61,0 | 7,77 | 125 | 781 | 127 | 5,54 | 84,6 | 26,7 |
| 340 | 340 | 137 | 12,2 | 18,3 | 68,0 | 8,67 | 157 | 922 | 134 | 6,72 | 98,1 | 27,8 |
| 360 | 360 | 143 | 13,0 | 19,5 | 76,1 | 9,70 | 196 | 1090 | 142 | 8,17 | 114 | 29,0 |
| 380 | 380 | 149 | 13,7 | 20,5 | 84,0 | 10,70 | 240 | 1260 | 150 | 9,72 | 131 | 30,2 |
| 400 | 400 | 155 | 14,4 | 21,6 | 92,3 | 11,8 | 291 | 1460 | 157 | 11,4 | 148 | 31,2 |
| 450 | 450 | 170 | 16,2 | 24,3 | 115,0 | 14,7 | 457 | 2030 | 176 | 16,9 | 199 | 33,9 |
| 500 | 500 | 185 | 18,0 | 27,0 | 140,0 | 17,9 | 683 | 2730 | 195 | 24,0 | 260 | 36,7 |
Tab. 14.3 Válcované IPE nosníky DIN 1025-5, ČSN 42 5553
A – plocha průřezu
I – moment setrvačnosti
t – tloušťka stěny
W – průřezový modul
i – poloměr setrvačnosti
m – hmotnost
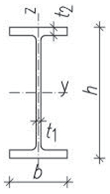
| Označení průřezu IPN | Jmenovité rozměry | m | A | Iy | Wy | iy | Iz | Wz | iz | |||
| h | b | t1 | t2 | |||||||||
| [mm] | [kg/m] | 103 [mm2] | 106 [mm4] | 103 [mm3] | [mm] | 106 [mm4] | 103 [mm3] | [mm] | ||||
| 80 | 80 | 46 | 3,8 | 5,2 | 6,0 | 0,764 | 0,801 | 20,0 | 32,4 | 0,0849 | 3,69 | 10,5 |
| 100 | 100 | 55 | 4,1 | 5,7 | 8,1 | 1,03 | 1,71 | 34,2 | 40,7 | 0,159 | 5,79 | 12,4 |
| 120 | 120 | 64 | 4,4 | 6,3 | 10,4 | 1,32 | 3,18 | 53,0 | 49,0 | 0,277 | 8,65 | 14,5 |
| 140 | 140 | 73 | 4,7 | 6,9 | 12,9 | 1,64 | 5,41 | 77,3 | 57,4 | 0,449 | 12,3 | 16,5 |
| 160 | 160 | 82 | 5,0 | 7,4 | 15,8 | 2,01 | 8,69 | 109 | 65,8 | 0,683 | 16,7 | 18,4 |
| 180 | 180 | 91 | 5,3 | 8,0 | 18,8 | 2,39 | 13,2 | 146 | 74,2 | 1,01 | 22,2 | 20,5 |
| 200 | 200 | 100 | 5,6 | 8,5 | 22,4 | 2,85 | 19,4 | 194 | 82,6 | 1,42 | 28,5 | 22,4 |
| 220 | 220 | 110 | 5,9 | 9,2 | 26,2 | 3,34 | 27,7 | 252 | 91,1 | 2,05 | 37,3 | 24,8 |
| 240 | 240 | 120 | 6,2 | 9,8 | 30,7 | 3,91 | 38,9 | 324 | 99,7 | 2,84 | 47,3 | 26,9 |
| 270 | 270 | 135 | 6,6 | 10,2 | 36,1 | 4,59 | 57,9 | 429 | 112 | 4,20 | 62,2 | 30,2 |
| 300 | 300 | 150 | 7,1 | 10,7 | 42,2 | 5,38 | 83,6 | 557 | 125 | 6,04 | 80,5 | 33,5 |
| 330 | 330 | 160 | 7,5 | 11,5 | 49,1 | 6,26 | 117,7 | 713 | 137 | 7,88 | 98,5 | 35,5 |
| 360 | 360 | 170 | 8,0 | 12,7 | 57,1 | 7,27 | 162,7 | 904 | 150 | 10,40 | 123 | 37,9 |
| 400 | 400 | 180 | 8,6 | 13,5 | 66,3 | 8,45 | 231,3 | 1160 | 165 | 13,2 | 146 | 39,5 |
| 450 | 450 | 190 | 9,4 | 14,6 | 77,6 | 9,88 | 337,4 | 1500 | 185 | 16,8 | 176 | 41,2 |
| 500 | 500 | 200 | 10,2 | 16,0 | 90,7 | 11,6 | 482,0 | 1930 | 204 | 21,4 | 214 | 43,1 |
| 550 | 550 | 210 | 11,1 | 17,2 | 106,0 | 13,4 | 671,2 | 2240 | 223 | 26,7 | 254 | 44,5 |
| 600 | 600 | 220 | 12,0 | 19,0 | 122,0 | 15,6 | 920,8 | 3070 | 243 | 33,9 | 308 | 46,6 |
Tab. 14.4 Válcované UPN profily DIN 1026-1, ČSN 42 5570
A – plocha průřezu
I – moment setrvačnosti
t – tloušťka stěny
W – průřezový modul
i – poloměr setrvačnosti
m – hmotnost
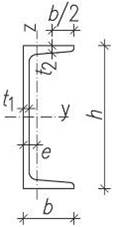
| Označení průřezu UPN | Jmenovité rozměry | m | A | Iy | Wy | iy | Iz | Wz1 | Wz2 | iz | ||||
| h | b | t1 | t2 | e | ||||||||||
| [mm] | [kg/m] | [mm2] | 106 [mm4] | 103 [mm3] | [mm] | 103 [mm4] | 103 [mm3] | 103 [mm3] | [mm] | |||||
| 50 | 50 | 38 | 5,0 | 7,0 | 13,7 | 5,59 | 712 | 0,265 | 10,6 | 19,3 | 90,9 | 3,74 | 6,64 | 11,3 |
| 65 | 65 | 42 | 5,5 | 7,5 | 14,2 | 7,09 | 903 | 0,575 | 17,7 | 25,2 | 140 | 5,03 | 9,81 | 12,2 |
| 80 | 80 | 45 | 6,0 | 8,0 | 14,5 | 8,65 | 1100 | 1,06 | 26,5 | 31,0 | 194 | 6,35 | 13,3 | 13,3 |
| 100 | 100 | 50 | 6,0 | 8,5 | 15,5 | 10,6 | 1350 | 2,05 | 41,1 | 39,1 | 291 | 8,45 | 18,8 | 14,7 |
| 120 | 120 | 55 | 7,0 | 9,0 | 16,1 | 13,3 | 1700 | 3,64 | 60,7 | 46,3 | 431 | 11,1 | 26,8 | 15,9 |
| 140 | 140 | 60 | 7,0 | 10,0 | 17,6 | 16,0 | 2040 | 6,05 | 86,4 | 54,5 | 625 | 14,7 | 35,6 | 17,5 |
| 160 | 160 | 65 | 7,5 | 10,5 | 18,4 | 18,9 | 2400 | 9,25 | 116 | 62,1 | 850 | 18,2 | 46,2 | 18,8 |
| 180 | 180 | 70 | 8,0 | 11,0 | 19,3 | 22,0 | 2800 | 13,5 | 150 | 69,6 | 1130 | 22,4 | 58,8 | 20,1 |
| 200 | 200 | 75 | 8,5 | 11,5 | 20,1 | 25,3 | 3220 | 19,1 | 191 | 77,1 | 1480 | 26,9 | 73,3 | 21,4 |
| 220 | 220 | 80 | 9,0 | 12,5 | 21,4 | 29,4 | 3740 | 26,9 | 245 | 84,8 | 1960 | 33,5 | 91,3 | 22,9 |
| 240 | 240 | 85 | 9,5 | 13,0 | 22,4 | 33,2 | 4230 | 36,0 | 300 | 92,2 | 2470 | 39,5 | 111 | 24,2 |
| 260 | 260 | 90 | 10,0 | 14,0 | 23,7 | 37,9 | 4830 | 48,2 | 371 | 100 | 3170 | 47,8 | 134 | 25,6 |
| 280 | 280 | 95 | 10,0 | 15,0 | 25,3 | 41,9 | 5340 | 62,8 | 448 | 108 | 3990 | 57,1 | 157 | 27,3 |
| 300 | 300 | 100 | 10,0 | 16,0 | 27,0 | 46,1 | 5880 | 80,3 | 535 | 117 | 49,30 | 67,6 | 183 | 29,0 |
Tab. 14.5 Válcované UPE profily DIN 1026-2, ČSN 42 5572
A – plocha průřezu
I – moment setrvačnosti
t – tloušťka stěny
W – průřezový modul
i – poloměr setrvačnosti
m – hmotnost
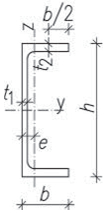
| Označení průřezu UPE | Jmenovité rozměry | m | A | Iy | Wy | iy | Iz | Wz | iz | ||||
| h | b | t1 | t2 | e | |||||||||
| [mm] | [kg/m] | [mm2] | 106 [mm4] | 103 [mm3] | [mm] | 103 [mm4] | 103 [mm3] | [mm] | |||||
| 80 | 80 | 50 | 4,0 | 7,0 | 18,2 | 7,9 | 1010 | 1,07 | 26,8 | 32,6 | 255 | 8,00 | 15,9 |
| 100 | 100 | 55 | 4,5 | 7,5 | 19,1 | 9,82 | 1250 | 2,07 | 41,4 | 40,7 | 383 | 10,6 | 17,5 |
| 120 | 120 | 60 | 5,0 | 8,0 | 19,8 | 12,1 | 1540 | 3,64 | 60,6 | 48,6 | 555 | 13,8 | 19,0 |
| 140 | 140 | 65 | 5,0 | 9,0 | 21,7 | 14,5 | 1840 | 6,00 | 85,6 | 57,1 | 788 | 18,2 | 20,7 |
| 160 | 160 | 70 | 5,5 | 9,5 | 22,7 | 17,0 | 2170 | 9,11 | 114 | 64,8 | 1070 | 22,6 | 22,2 |
| 180 | 180 | 75 | 5,5 | 10,5 | 24,7 | 19,7 | 2510 | 13,50 | 150 | 73,4 | 1440 | 28,6 | 23,9 |
| 200 | 200 | 80 | 6,0 | 11,0 | 25,6 | 22,8 | 2900 | 19,10 | 191 | 81,1 | 1870 | 34,5 | 25,4 |
| 220 | 220 | 85 | 6,5 | 12,0 | 27,0 | 26,6 | 3390 | 26,80 | 244 | 89,0 | 2470 | 42,5 | 27,0 |
| 240 | 240 | 90 | 7,0 | 12,5 | 27,9 | 30,2 | 3850 | 36,00 | 300 | 96,7 | 3110 | 50,1 | 28,4 |
| 270 | 270 | 95 | 7,5 | 13,5 | 28,9 | 35,2 | 4480 | 52,50 | 389 | 108,0 | 4010 | 60,7 | 29,9 |
| 300 | 300 | 100 | 9,5 | 15,0 | 28,9 | 44,4 | 5660 | 78,20 | 522 | 118,0 | 5380 | 75,6 | 30,8 |
Tab. 14.6 Válcované nosníky HEB DIN 1025-2
A – plocha průřezu
I – moment setrvačnosti
t – tloušťka stěny
W – průřezový modul
i – poloměr setrvačnosti
m – hmotnost
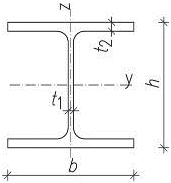
| Označení průřezu HEB | Jmenovité rozměry | m | A | Iy | Wy | iy | Iz | Wz | iz | |||
| h | b | t1 | t2 | |||||||||
| [mm] | [kg/m] | 103 [mm2] | 106 [mm4] | 103 [mm3] | [mm] | 106 [mm4] | 103 [mm3] | [mm] | ||||
| 100 | 100 | 100 | 6,0 | 10,0 | 20,4 | 2,6 | 4,497 | 89,9 | 41,6 | 1,67 | 33,4 | 25,3 |
| 120 | 120 | 120 | 6,5 | 11,0 | 26,7 | 3,4 | 8,64 | 144 | 50,4 | 3,17 | 52,6 | 30,6 |
| 140 | 140 | 140 | 7,0 | 12,0 | 33,7 | 4,3 | 15,1 | 216 | 59,3 | 5,50 | 78,5 | 35,8 |
| 160 | 160 | 160 | 8,0 | 13,0 | 42,6 | 5,43 | 24,9 | 311 | 67,8 | 8,89 | 111 | 40,5 |
| 180 | 180 | 180 | 8,5 | 14,0 | 51,2 | 6,53 | 38,3 | 426 | 76,6 | 13,5 | 151 | 45,7 |
| 200 | 200 | 200 | 9,0 | 15,0 | 61,3 | 7,81 | 57,0 | 570 | 85,4 | 20,0 | 200 | 50,7 |
| 220 | 220 | 220 | 9,5 | 16,0 | 71,5 | 9,1 | 80,9 | 736 | 94,3 | 28,4 | 258 | 55,9 |
| 240 | 240 | 240 | 10,0 | 17,0 | 83,2 | 10,6 | 113 | 938 | 103 | 39,2 | 327 | 60,8 |
| 260 | 260 | 260 | 10,0 | 17,5 | 93,0 | 11,8 | 149 | 1150 | 112 | 51,3 | 395 | 65,8 |
| 280 | 280 | 280 | 10,5 | 18,0 | 103 | 13,1 | 193 | 1380 | 121 | 65,9 | 471 | 70,8 |
| 300 | 300 | 300 | 11,0 | 19,0 | 117 | 14,9 | 252 | 1680 | 130 | 85,6 | 571 | 75,8 |
| 320 | 320 | 300 | 11,5 | 20,5 | 127 | 16,1 | 308 | 1930 | 138 | 92,4 | 616 | 75,7 |
| 340 | 340 | 300 | 12,0 | 21,5 | 134 | 17,1 | 367 | 2160 | 146 | 96,9 | 646 | 75,3 |
| 360 | 360 | 300 | 12,5 | 22,5 | 142 | 18,1 | 432 | 2400 | 155 | 101 | 676 | 74,9 |
| 400 | 400 | 300 | 13,5 | 24,0 | 155 | 19,8 | 577 | 2880 | 171 | 108 | 721 | 74,0 |
| 450 | 450 | 300 | 14,0 | 26,0 | 171 | 21,8 | 799 | 3550 | 191 | 117 | 781 | 73,3 |
| 500 | 500 | 300 | 14,5 | 28,0 | 187 | 23,9 | 1070 | 4290 | 212 | 126 | 841 | 72,7 |
| 550 | 550 | 300 | 15,0 | 29,0 | 199 | 25,4 | 1370 | 4970 | 232 | 131 | 872 | 71,7 |
| 600 | 600 | 300 | 15,5 | 20,0 | 212 | 27,0 | 1710 | 5700 | 252 | 135 | 902 | 70,8 |
| 650 | 650 | 300 | 16,0 | 31,0 | 225 | 28,6 | 2110 | 6480 | 271 | 140 | 932 | 69,9 |
| 700 | 700 | 300 | 17,0 | 32,0 | 241 | 30,6 | 2570 | 7340 | 290 | 144 | 963 | 68,7 |
| 800 | 800 | 300 | 17,5 | 33,0 | 262 | 33,4 | 3590 | 8980 | 328 | 149 | 993 | 66,8 |
| 900 | 900 | 300 | 18,5 | 35,0 | 291 | 37,1 | 4940 | 10980 | 365 | 158 | 1050 | 65,3 |
| 1 000 | 1 000 | 300 | 19,0 | 36,0 | 314 | 40,0 | 6450 | 12890 | 401 | 163 | 1080 | 63,8 |
Tab. 14.7 Válcované nosníky HEA DIN 1025-3
A – plocha průřezu
I – moment setrvačnosti
t – tloušťka stěny
W – průřezový modul
i – poloměr setrvačnosti
m – hmotnost
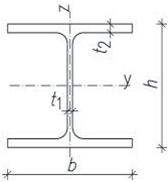
| Označení průřezu HEA | Jmenovité rozměry | m | A | Iy | Wy | iy | Iz | Wz | iz | |||
| h | b | t1 | t2 | |||||||||
| [mm] | [kg/m] | 103 [mm2] | 106 [mm4] | 103 [mm3] | [mm] | 106 [mm4] | 103 [mm3] | [mm] | ||||
| 100 | 96 | 100 | 5,0 | 8,0 | 16,7 | 2,12 | 3,49 | 72,8 | 40,6 | 1,34 | 26,8 | 25,1 |
| 120 | 114 | 120 | 5,0 | 8,0 | 19,9 | 2,53 | 6,06 | 106 | 48,9 | 2,31 | 38,5 | 30,2 |
| 140 | 133 | 140 | 5,5 | 8,5 | 24,7 | 3,14 | 10,3 | 155 | 57,3 | 3,89 | 55,6 | 35,2 |
| 160 | 152 | 160 | 6,0 | 9,0 | 30,4 | 3,88 | 16,7 | 220 | 65,7 | 6,16 | 76,9 | 39,8 |
| 180 | 171 | 180 | 6,0 | 9,5 | 35,5 | 4,53 | 25,1 | 294 | 74,5 | 9,25 | 103 | 45,2 |
| 200 | 190 | 200 | 6,5 | 10,0 | 42,3 | 5,38 | 36,9 | 389 | 82,8 | 13,4 | 134 | 49,8 |
| 220 | 210 | 220 | 7,0 | 11,0 | 50,5 | 6,43 | 54,1 | 515 | 91,7 | 19,5 | 178 | 55,1 |
| 240 | 230 | 240 | 7,5 | 12,0 | 60,3 | 7,68 | 77,6 | 675 | 101 | 27,7 | 231 | 60,0 |
| 260 | 250 | 260 | 7,5 | 12,5 | 68,2 | 8,68 | 104,5 | 836 | 110 | 36,7 | 282 | 65,0 |
| 280 | 270 | 280 | 8,0 | 13,0 | 76,4 | 9,73 | 136,7 | 1010 | 119 | 47,6 | 340 | 70,0 |
| 300 | 290 | 300 | 8,5 | 14,0 | 88,3 | 11,2 | 182,6 | 1260 | 127 | 63,1 | 421 | 74,9 |
| 320 | 310 | 300 | 9,0 | 15,5 | 97,6 | 12,4 | 229,3 | 1480 | 136 | 69,9 | 466 | 74,9 |
| 340 | 330 | 300 | 9,5 | 16,5 | 105 | 13,3 | 276,9 | 1680 | 144 | 74,4 | 496 | 74,6 |
| 360 | 350 | 300 | 10,0 | 17,5 | 112 | 14,3 | 330,9 | 1890 | 152 | 78,9 | 526 | 74,3 |
| 400 | 390 | 300 | 11,0 | 19,0 | 125 | 15,9 | 450,7 | 2310 | 168 | 85,6 | 571 | 73,4 |
| 450 | 440 | 300 | 11,5 | 21,0 | 140 | 17,8 | 637,2 | 2900 | 189 | 94,7 | 631 | 72,9 |
| 500 | 490 | 300 | 12,0 | 23,0 | 155 | 19,8 | 869,7 | 3550 | 210 | 103,7 | 691 | 72,4 |
| 550 | 540 | 300 | 12,5 | 24,0 | 166 | 21,2 | 1119 | 4150 | 230 | 108,2 | 721 | 72,1 |
| 600 | 590 | 300 | 13,0 | 25,0 | 178 | 22,6 | 1412 | 4790 | 250 | 112,7 | 751 | 70,5 |
| 650 | 640 | 300 | 13,5 | 26,0 | 190 | 24,2 | 1752 | 5470 | 269 | 117,2 | 782 | 69,7 |
| 700 | 690 | 300 | 14,5 | 27,0 | 204 | 26,0 | 2153 | 6240 | 288 | 121,8 | 812 | 68,4 |
| 800 | 790 | 300 | 15,0 | 28,0 | 224 | 28,6 | 3034 | 7680 | 326 | 126,4 | 843 | 66,5 |
| 900 | 890 | 300 | 16,0 | 30,0 | 252 | 32,0 | 4221 | 9480 | 363 | 135,5 | 903 | 65,0 |
| 1 000 | 990 | 300 | 16,5 | 31,0 | 272 | 34,7 | 5538 | 11190 | 400 | 140,0 | 934 | 63,5 |
Tab. 14.8 Rovnoramenné úhelníky ČSN 42 5541
A – plocha průřezu
I – moment setrvačnosti
t – tloušťka stěny
W – průřezový modul
i – poloměr setrvačnosti
m – hmotnost

| Označení průřezu L | e | Hmotnost | A | Iy | Wy1 | Wy2 | iy |
| [mm] | [kg\m] | [mm2] | 103 [mm4] | 103 [mm3] | 103 [mm3] | [mm] | |
| L 20x20x 3 | 6,0 | 0,879 | 112 | 4,0 | 0,285 | 0,670 | 5,98 |
| L 25x25x3 | 7,2 | 1,11 | 142 | 7,99 | 0,449 | 1,11 | 7,50 |
| L 25x25x4 | 7,6 | 1,45 | 185 | 10,1 | 0,583 | 1,34 | 7,41 |
| L 30x30x3 | 8,3 | 1,36 | 174 | 14,1 | 0,652 | 1,70 | 9,02 |
| L 30x30x4 | 8,8 | 1,78 | 227 | 18,1 | 0,853 | 2,07 | 8,94 |
| L 35x35x3 | 9,6 | 1,60 | 204 | 23,0 | 0,905 | 2,41 | 10,6 |
| L 35x35x4 | 10,0 | 2,09 | 267 | 29,7 | 1,19 | 2,96 | 10,5 |
| L 36x36x4 | 10,3 | 2,16 | 275 | 33,0 | 1,28 | 3,19 | 10,9 |
| L 40x40x3 | 10,7 | 1,84 | 235 | 34,7 | 1,18 | 3,25 | 12,2 |
| L 40x40x4 | 11,2 | 2,42 | 308 | 45,0 | 1,56 | 4,03 | 12,1 |
| L 40x40x5 | 11,6 | 2,97 | 379 | 54,5 | 1,92 | 4,70 | 12,0 |
| L 45x45x3 | 11,8 | 2,09 | 266 | 49,6 | 1,49 | 4,21 | 13,7 |
| L 45x45x4 | 12,3 | 2,74 | 349 | 64,7 | 1,98 | 5,26 | 13,6 |
| L 45x45x5 | 12,8 | 3,38 | 430 | 78,8 | 2,44 | 6,18 | 13,5 |
| L 50x50x4 | 13,5 | 3,06 | 389 | 90,2 | 2,47 | 6,66 | 15,2 |
| L 50x50x5 | 14,0 | 3,77 | 480 | 110 | 3,06 | 7,86 | 15,1 |
| L 50x50x6 | 14,4 | 4,47 | 569 | 129 | 3,62 | 8,93 | 15,1 |
| L 55x55x5 | 15,1 | 4,18 | 532 | 148 | 3,71 | 9,76 | 16,7 |
| L 55x55x6 | 15,6 | 4,95 | 631 | 174 | 4,41 | 11,1 | 16,6 |
| L 60x60x6 | 16,8 | 5,42 | 691 | 229 | 5,30 | 13,6 | 18,2 |
| L 60x60x8 | 17,7 | 7,09 | 903 | 292 | 6,91 | 16,6 | 18,0 |
| L 65x65x6 | 18,0 | 5,91 | 753 | 293 | 6,23 | 16,3 | 19,7 |
| L 65x65x8 | 18,0 | 7,73 | 985 | 376 | 8,15 | 20,0 | 19,5 |
| L 70x70x6 | 19,1 | 6,40 | 815 | 368 | 7,24 | 19,3 | 21,3 |
| L 70x70x7 | 19,6 | 7,39 | 942 | 423 | 8,38 | 21,6 | 21,2 |
| L 70x70x8 | 20,0 | 8,37 | 1070 | 475 | 9,49 | 23,7 | 21,1 |
| L 80x80x 6 | 21,6 | 7,34 | 935 | 560 | 9,60 | 25,9 | 24,5 |
| L 80x80x 8 | 22,5 | 9,63 | 1230 | 725 | 12,6 | 32,2 | 24,3 |
| L 80x80x 10 | 23,3 | 11,9 | 1510 | 877 | 15,5 | 36,6 | 24,1 |
| L 90x90x6 | 24,1 | 8,28 | 1050 | 810 | 12,3 | 33,6 | 27,7 |
| L 90x90x8 | 25,0 | 10,9 | 1390 | 1050 | 16,2 | 42,0 | 27,5 |
| L 90x90x10 | 25,8 | 13,4 | 1710 | 1280 | 19,9 | 49,4 | 27,3 |
| L 100x100x6 | 26,4 | 9,26 | 1180 | 1110 | 15,1 | 42,3 | 30,7 |
| L 100x100x8 | 27,3 | 12,2 | 1550 | 1450 | 20,0 | 53,2 | 30,6 |
| L 100x100x10 | 28,2 | 15,0 | 1920 | 1770 | 24,7 | 62,9 | 30,4 |
| L 100x100x12 | 29,0 | 13,4 | 2270 | 2070 | 29,2 | 71,4 | 30,2 |
| L 110x110x8 | 29,8 | 13,4 | 1710 | 1960 | 24,4 | 65,7 | 33,8 |
| L 110x110x10 | 30,7 | 16,6 | 2120 | 2390 | 30,2 | 78,0 | 33,6 |
| L 120x120x8 | 32,2 | 14,7 | 1870 | 2560 | 29,2 | 79,5 | 37,0 |
| L 120x120x10 | 33,1 | 18,2 | 2320 | 3140 | 36,1 | 94,8 | 36,8 |
| L 120x120x12 | 33,9 | 21,6 | 2750 | 3680 | 42,8 | 109 | 36,6 |
| L 130x130x12 | 36,4 | 23,6 | 3000 | 4730 | 50,5 | 130 | 39,7 |
| L 130x130x14 | 37,2 | 27,2 | 3470 | 5410 | 58,3 | 146 | 39,5 |
| L 140x140x10 | 37,9 | 21,4 | 2720 | 5060 | 49,5 | 133 | 43,1 |
| L 140x140x12 | 38,8 | 25,4 | 3240 | 5960 | 58,9 | 154 | 42,9 |
| L 140x140x14 | 39,6 | 29,4 | 3750 | 6830 | 68,0 | 172 | 42,7 |
| L 160x160x10 | 42,7 | 24,6 | 3130 | 7630 | 65,0 | 179 | 49,4 |
| L 160x160x12 | 43,6 | 29,3 | 3730 | 9020 | 77,5 | 207 | 49,2 |
| L 160x160x14 | 44,4 | 33,9 | 4320 | 10400 | 89,6 | 233 | 49,0 |
| L 160x160x16 | 45,3 | 38,4 | 4900 | 11600 | 102 | 257 | 48,8 |
| L 180x180x12 | 48,5 | 33,1 | 4210 | 13000 | 98,8 | 268 | 55,6 |
| L 180x180x14 | 49,3 | 38,3 | 4880 | 15000 | 114 | 303 | 55,4 |
| L 200x200x14 | 54,3 | 42,7 | 5440 | 20800 | 143 | 382 | 61,8 |
| L 200x200x16 | 55,2 | 48,5 | 6180 | 23400 | 162 | 425 | 61,6 |
| L 200x200x20 | 56,8 | 59,9 | 7630 | 28500 | 199 | 502 | 61,1 |
Tab. 14.9 Válcované trubky bezešvé kruhové ČSN EN 10210-2
D – vnější průměr
A – plocha průřezu
I – moment setrvačnosti
t – tloušťka stěny
W – průřezový modul
i – poloměr setrvačnosti
m – hmotnost
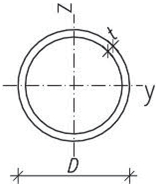
| D | t | m | A | I | W | i |
| [mm] | [mm] | [kg/m] | 102 [mm2] | 104 [mm4] | 103 [mm3] | 10 [mm] |
| 21,3 | 2,3 | 1,08 | 1,37 | 0,629 | 0,590 | 6,77 |
| 2,6 | 1,20 | 1,53 | 0,681 | 0,639 | 6,68 | |
| 3,2 | 1,43 | 1,82 | 0,768 | 0,722 | 6,50 | |
| 26,9 | 2,3 | 1,40 | 1,78 | 1,36 | 1,01 | 8,74 |
| 2,6 | 1,56 | 1,98 | 1,48 | 1,10 | 8,64 | |
| 3,2 | 1,87 | 2,38 | 2,38 | 1,27 | 8,46 | |
| 33,7 | 2,6 | 1,99 | 2,54 | 3,09 | 1,84 | 11,0 |
| 3,2 | 2,41 | 3,07 | 3,60 | 2,14 | 10,8 | |
| 4,0 | 2,93 | 3,73 | 4,19 | 2,49 | 10,6 | |
| 42,4 | 2,6 | 2,55 | 3,25 | 6,46 | 3,05 | 14,1 |
| 3,2 | 3,09 | 3,94 | 7,62 | 3,59 | 13,9 | |
| 4,0 | 3,79 | 4,83 | 8,99 | 4,24 | 13,6 | |
| 48,3 | 2,6 | 2,93 | 3,73 | 9,8 | 4,05 | 16,2 |
| 3,2 | 3,56 | 4,53 | 11,6 | 4,80 | 16,0 | |
| 4,0 | 4,37 | 5,57 | 13,8 | 5,7 | 15,7 | |
| 5,0 | 5,34 | 6,8 | 16,2 | 6,69 | 15,4 | |
| 60,3 | 2,6 | 3,70 | 4,71 | 19,7 | 6,52 | 20,4 |
| 3,2 | 4,51 | 5,74 | 23,5 | 7,78 | 20,2 | |
| 4,0 | 5,55 | 7,07 | 28,2 | 9,34 | 20,0 | |
| 5,0 | 6,82 | 8,69 | 33,5 | 11,1 | 19,6 | |
| 76,1 | 2,6 | 47,1 | 6,00 | 40,6 | 10,7 | 26,0 |
| 3,2 | 5,75 | 7,33 | 48,8 | 12,8 | 25,8 | |
| 4,0 | 7,11 | 9,06 | 59,1 | 15,5 | 25,5 | |
| 5,0 | 8,77 | 11,2 | 70,9 | 18,6 | 25,2 | |
| 88,9 | 3,2 | 6,76 | 8,62 | 79,2 | 17,8 | 30,3 |
| 5,0 | 10,3 | 13,2 | 116 | 26,2 | 29,7 | |
| 5,0 | 10,3 | 13,2 | 116 | 26,2 | 29,7 | |
| 6,3 | 12,8 | 16,3 | 140 | 31,5 | 29,3 | |
| 101,6 | 3,2 | 7,77 | 9,89 | 120 | 23,6 | 3,48 |
| 4,0 | 9,63 | 12,3 | 146 | 28,8 | 3,45 | |
| 5,0 | 11,9 | 15,2 | 177 | 34,9 | 3,42 | |
| 6,3 | 14,8 | 18,9 | 215 | 42,3 | 3,38 | |
| 8,0 | 18,5 | 23,5 | 260 | 51,1 | 3,32 | |
| 10,0 | 22,6 | 28,8 | 305 | 60,1 | 3,26 | |
| 114,3 | 3,2 | 8,77 | 11,2 | 172 | 30,2 | 39,3 |
| 4,0 | 10,9 | 13,9 | 211 | 36,9 | 39,0 | |
| 5,0 | 13,5 | 17,2 | 257 | 45,0 | 38,7 | |
| 6,3 | 16,8 | 21,4 | 313 | 54,7 | 38,2 | |
| 8,0 | 21,0 | 26,7 | 379 | 66,4 | 37,7 | |
| 10,0 | 25,7 | 32,8 | 450 | 78,7 | 37,0 | |
| 139,7 | 4,0 | 13,4 | 17,1 | 393 | 56,2 | 48,0 |
| 5,0 | 16,6 | 21,2 | 481 | 68,8 | 47,7 | |
| 6,3 | 20,7 | 26,4 | 589 | 84,3 | 47,2 | |
| 8,0 | 26,0 | 33,1 | 720 | 103 | 46,6 | |
| 10,0 | 32,0 | 40,7 | 862 | 123 | 46,0 | |
| 12,5 | 39,2 | 50,0 | 1020 | 146 | 45,2 | |
| 168,3 | 4,0 | 16,2 | 20,6 | 697 | 83 | 58,1 |
| 5,0 | 20,1 | 25,7 | 856 | 102 | 57,8 | |
| 6,3 | 25,2 | 32,1 | 1053 | 125 | 57,3 | |
| 8,0 | 31,6 | 40,3 | 1297 | 154 | 56,7 | |
| 10,0 | 39,0 | 49,7 | 1564 | 186 | 56,1 | |
| 12,5 | 48,0 | 61,2 | 1868 | 222 | 55,3 | |
| 177,8 | 5,0 | 21,3 | 27,1 | 1014 | 114 | 61,1 |
| 6,3 | 26,6 | 33,9 | 1250 | 141 | 60,7 | |
| 8,0 | 33,5 | 42,7 | 1541 | 173 | 60,1 | |
| 10,0 | 41,4 | 52,7 | 1862 | 209 | 59,4 | |
| 12,5 | 51,0 | 64,9 | 2230 | 251 | 58,6 | |
| 193,7 | 5,0 | 23,3 | 29,6 | 1320 | 136 | 66,7 |
| 6,3 | 29,1 | 37,1 | 1630 | 168 | 66,3 | |
| 8,0 | 36,6 | 46,7 | 2016 | 208 | 65,7 | |
| 10,0 | 45,3 | 57,7 | 2442 | 252 | 65,0 | |
| 12,5 | 55,9 | 71,2 | 2934 | 303 | 64,2 | |
| 14,2 | 62,9 | 80,1 | 3245 | 335 | 63,7 | |
| 16,0 | 70,1 | 89,3 | 3554 | 367 | 63,1 | |
| 219,1 | 5,0 | 26,4 | 33,6 | 1928 | 176 | 75,7 |
| 6,3 | 33,1 | 42,1 | 2386 | 218 | 75,3 | |
| 8,0 | 41,6 | 53,1 | 2960 | 270 | 74,7 | |
| 10,0 | 51,6 | 65,7 | 3598 | 328 | 74,0 | |
| 12,5 | 63,7 | 81,1 | 4345 | 397 | 73,2 | |
| 14,2 | 71,8 | 91,4 | 4820 | 440 | 72,6 | |
| 16,0 | 80,1 | 102 | 5297 | 483 | 72,0 | |
| 20,0 | 98,2 | 125 | 6261 | 572 | 70,7 | |
| 244,5 | 5,0 | 29,5 | 37,6 | 2699 | 221 | 84,7 |
| 6,3 | 37,0 | 47,1 | 3346 | 274 | 84,2 | |
| 8,0 | 46,7 | 59,4 | 4160 | 340 | 83,7 | |
| 10,0 | 57,8 | 73,7 | 5073 | 415 | 83,0 | |
| 12,5 | 71,5 | 91,1 | 6147 | 503 | 82,1 | |
| 14,2 | 80,6 | 102,7 | 6837 | 559 | 81,6 | |
| 16,0 | 90,2 | 115 | 7533 | 616 | 81,0 | |
| 20,0 | 110,7 | 141 | 8957 | 733 | 79,7 | |
| 25,0 | 135 | 172 | 10520 | 860 | 78,1 | |
| 273,0 | 5,0 | 33,0 | 42,1 | 3781 | 277 | 94,8 |
| 6,3 | 41,4 | 52,8 | 4696 | 344 | 94,3 | |
| 8,0 | 52,3 | 66,6 | 5852 | 429 | 93,7 | |
| 10,0 | 64,9 | 82,6 | 7154 | 524 | 93,1 | |
| 12,5 | 80,3 | 102 | 8697 | 637 | 92,2 | |
| 14,2 | 90,6 | 115 | 9695 | 710 | 91,6 | |
| 16,0 | 101 | 129 | 10710 | 784 | 91,0 | |
| 20,0 | 125 | 159 | 12800 | 938 | 89,7 | |
| 25,0 | 153 | 195 | 15130 | 1108 | 88,1 | |
| 323,9 | 5,0 | 39,3 | 50,1 | 6369 | 393 | 113 |
| 6,3 | 49,3 | 62,9 | 7929 | 490 | 112 | |
| 8,0 | 62,3 | 79,4 | 9910 | 612 | 112 | |
| 10,0 | 77,4 | 98,6 | 12160 | 751 | 111 | |
| 12,5 | 96,0 | 122 | 14850 | 917 | 110 | |
| 14,2 | 108,5 | 138 | 16600 | 1025 | 110 | |
| 16,0 | 121 | 155 | 18390 | 1136 | 109 | |
| 20,0 | 150 | 191 | 22140 | 1367 | 108 | |
| 25,0 | 184 | 235 | 26400 | 1630 | 106 | |
| 355,6 | 6,3 | 54,3 | 69,1 | 10550 | 593 | 124 |
| 8,0 | 68,6 | 87,4 | 13200 | 742 | 123 | |
| 10,0 | 85,2 | 109 | 16220 | 912 | 122 | |
| 12,5 | 106 | 135 | 19850 | 1117 | 121 | |
| 14,2 | 120 | 152 | 22230 | 1250 | 121 | |
| 16,0 | 134 | 171 | 24660 | 1387 | 120 | |
| 20,0 | 166 | 211 | 29790 | 1676 | 119 | |
| 25,0 | 204 | 260 | 35680 | 2007 | 117 | |
| 406,4 | 6,3 | 62,2 | 79,2 | 15850 | 780 | 141 |
| 8,0 | 78,6 | 100 | 19870 | 978 | 141 | |
| 10,0 | 97,8 | 125 | 24480 | 1205 | 140 | |
| 12,5 | 121 | 155 | 30030 | 1478 | 139 | |
| 14,2 | 137 | 175 | 33690 | 1658 | 139 | |
| 16,0 | 154 | 196 | 37450 | 1843 | 138 | |
| 20,0 | 191 | 243 | 45430 | 2236 | 137 | |
| 25,0 | 235 | 300 | 54700 | 2692 | 135 | |
| 30,0 | 278 | 355 | 63220 | 3111 | 133 | |
| 40,0 | 361 | 460 | 78190 | 3848 | 130 | |
| 457,0 | 6,3 | 70,0 | 89,2 | 22650 | 991 | 159 |
| 8,0 | 88,6 | 113 | 28450 | 1245 | 159 | |
| 10,0 | 110 | 140 | 35090 | 1536 | 158 | |
| 12,5 | 137 | 175 | 43140 | 1888 | 157 | |
| 14,2 | 155 | 198 | 48460 | 2121 | 157 | |
| 16,0 | 174 | 222 | 53960 | 2361 | 156 | |
| 20,0 | 216 | 275 | 65680 | 2874 | 155 | |
| 25,0 | 266 | 339 | 79420 | 3475 | 153 | |
| 30,0 | 316 | 402 | 92170 | 4034 | 151 | |
| 40,0 | 411 | 524 | 114900 | 5031 | 148 | |
| 508,8 | 6,3 | 77,9 | 99,3 | 31250 | 1230 | 177 |
| 8,0 | 98,6 | 126 | 39280 | 1546 | 177 | |
| 10,0 | 123 | 156 | 48520 | 1910 | 176 | |
| 12,5 | 153 | 195 | 59760 | 2353 | 175 | |
| 14,2 | 173 | 220 | 67200 | 2646 | 175 | |
| 16,0 | 194 | 247 | 74910 | 2949 | 174 | |
| 20,0 | 241 | 307 | 91430 | 3600 | 173 | |
| 25,0 | 298 | 379 | 111000 | 4367 | 171 | |
| 30,0 | 354 | 451 | 129200 | 5086 | 169 | |
| 40,0 | 462 | 588 | 162200 | 6385 | 166 | |
| 50,0 | 565 | 719 | 190900 | 7515 | 163 | |
| 610,0 | 6,3 | 93,8 | 119 | 54440 | 1785 | 213 |
| 8,0 | 119 | 151 | 68550 | 2248 | 213 | |
| 10,0 | 148 | 188 | 84850 | 2782 | 212 | |
| 12,5 | 184 | 235 | 104800 | 3435 | 211 | |
| 14,2 | 209 | 266 | 118000 | 3869 | 211 | |
| 16,0 | 234 | 299 | 131800 | 4321 | 210 | |
| 20,0 | 291 | 371 | 161500 | 5295 | 209 | |
| 25,0 | 361 | 459 | 196900 | 6456 | 207 | |
| 30,0 | 429 | 547 | 230500 | 7557 | 205 | |
| 40,0 | 562 | 716 | 292300 | 9585 | 202 | |
| 50,0 | 691 | 880 | 347600 | 11400 | 199 | |
| 711,0 | 6,3 | 109 | 139 | 86590 | 2436 | 249 |
| 8,0 | 139 | 177 | 109200 | 3071 | 249 | |
| 10,0 | 173 | 220 | 135300 | 3806 | 248 | |
| 12,5 | 215 | 274 | 167300 | 4707 | 247 | |
| 14,2 | 244 | 311 | 188700 | 5309 | 246 | |
| 16,0 | 274 | 349 | 211000 | 5936 | 246 | |
| 20,0 | 341 | 434 | 259400 | 7295 | 244 | |
| 25,0 | 423 | 539 | 317400 | 8927 | 243 | |
| 30,0 | 504 | 642 | 372800 | 10490 | 241 | |
| 40,0 | 662 | 843 | 476200 | 13400 | 238 | |
| 50,0 | 815 | 1038 | 570300 | 16040 | 234 | |
| 60,0 | 963 | 1227 | 655600 | 18440 | 231 | |
| 762,0 | 6,3 | 117 | 150 | 106800 | 2803 | 267 |
| 8,0 | 149 | 190 | 134700 | 3535 | 267 | |
| 10,0 | 185 | 236 | 167000 | 4384 | 266 | |
| 12,5 | 231 | 294 | 206700 | 5426 | 265 | |
| 14,2 | 262 | 334 | 233000 | 6120 | 264 | |
| 16,0 | 294 | 375 | 261000 | 6850 | 264 | |
| 20,0 | 366 | 466 | 321100 | 8427 | 262 | |
| 25,0 | 454 | 579 | 393500 | 10330 | 261 | |
| 30,0 | 542 | 690 | 462900 | 12150 | 259 | |
| 40,0 | 712 | 907 | 593000 | 15570 | 257 | |
| 50,0 | 878 | 1118 | 712200 | 18690 | 252 | |
| 813,0 | 8,0 | 159 | 202 | 163900 | 4032 | 285 |
| 10,0 | 198 | 252 | 203400 | 5003 | 284 | |
| 12,5 | 247 | 314 | 251900 | 6196 | 283 | |
| 14,2 | 280 | 356 | 284000 | 6990 | 282 | |
| 16,0 | 314 | 401 | 318200 | 7828 | 282 | |
| 20,0 | 391 | 498 | 391900 | 9641 | 280 | |
| 25,0 | 486 | 619 | 480900 | 11830 | 279 | |
| 30,0 | 579 | 738 | 566400 | 13930 | 277 | |
| 914,0 | 8,0 | 179 | 228 | 233700 | 5113 | 320 |
| 10,0 | 223 | 284 | 290500 | 6349 | 320 | |
| 12,5 | 278 | 354 | 359700 | 7871 | 319 | |
| 14,2 | 315 | 401 | 406300 | 8890 | 318 | |
| 16,0 | 354 | 451 | 455100 | 9959 | 318 | |
| 20,0 | 441 | 562 | 561500 | 12290 | 316 | |
| 25,0 | 548 | 698 | 690320 | 15100 | 314 | |
| 30,0 | 654 | 833 | 814800 | 17830 | 313 | |
| 1016,0 | 8,0 | 199 | 253 | 321800 | 6334 | 356 |
| 10,0 | 248 | 316 | 399900 | 7871 | 356 | |
| 12,5 | 309 | 394 | 496100 | 9766 | 355 | |
| 14,2 | 351 | 447 | 561000 | 11000 | 354 | |
| 16,0 | 395 | 503 | 628480 | 12370 | 354 | |
| 20,0 | 491 | 626 | 776300 | 15280 | 352 | |
| 25,0 | 611 | 778 | 956100 | 18820 | 350 | |
| 30,0 | 729 | 929 | 1130000 | 22250 | 349 | |
| 1067,0 | 10,0 | 261 | 332 | 463800 | 8693 | 374 |
| 12,5 | 325 | 414 | 575670 | 10790 | 373 | |
| 14,2 | 369 | 470 | 650800 | 12200 | 372 | |
| 16,0 | 415 | 528 | 729610 | 13680 | 372 | |
| 20,0 | 516 | 658 | 901800 | 16900 | 370 | |
| 25,0 | 642 | 818 | 1111000 | 20830 | 369 | |
| 30,0 | 767 | 977 | 1315000 | 24650 | 367 | |
| 1168,0 | 10,0 | 286 | 364 | 609800 | 10440 | 409 |
| 12,5 | 356 | 454 | 757400 | 12970 | 409 | |
| 14,2 | 404 | 515 | 856700 | 14670 | 408 | |
| 16,0 | 455 | 579 | 960800 | 16450 | 407 | |
| 20,0 | 566 | 721 | 1189000 | 20350 | 406 | |
| 25,0 | 705 | 898 | 1467000 | 25110 | 404 | |
| 1219,0 | 10,0 | 298 | 380 | 694000 | 11390 | 427 |
| 12,5 | 372 | 474 | 862200 | 14150 | 427 | |
| 14,2 | 422 | 537 | 975300 | 16000 | 426 | |
| 16,0 | 475 | 605 | 1094000 | 17950 | 425 | |
| 20,0 | 591 | 753 | 1354000 | 22220 | 424 | |
| 25,0 | 736 | 938 | 1672000 | 27430 | 422 |
Tab. 14.10 Válcované duté profily čtvercové ČSN EN 10210-2
D – vnější průměr
A – plocha průřezu
I – moment setrvačnosti
t – tloušťka stěny
W – průřezový modul
i – poloměr setrvačnosti
m – hmotnost
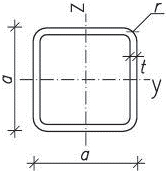
| Jmenovité rozměry | m [kg/m] |
A 102 [mm2] |
I 104 [mm4] |
W 103 [mm3] |
i [mm] |
|
| d [mm] |
t [mm] |
|||||
| 40 | 2,6 | 3,00 | 8,80 | 8,80 | 4,40 | 15,2 |
| 3,2 | 3,61 | 4,60 | 10,2 | 5,11 | 14,9 | |
| 4,0 | 4,39 | 5,59 | 11,8 | 5,91 | 14,5 | |
| 5,0 | 5,28 | 6,73 | 13,4 | 6,68 | 14,1 | |
| 50 | 2,6 | 3,81 | 4,86 | 18,00 | 7,21 | 19,3 |
| 3,2 | 4,62 | 5,88 | 21,20 | 8,49 | 19,0 | |
| 4,0 | 5,64 | 7,19 | 25,00 | 9,99 | 18,6 | |
| 5,0 | 6,85 | 8,72 | 28,90 | 11,6 | 18,2 | |
| 6,3 | 8,31 | 10,6 | 32,80 | 13,1 | 17,6 | |
| 60 | 2,6 | 4,63 | 5,90 | 32,2 | 10,70 | 23,40 |
| 3,2 | 5,62 | 7,16 | 38,2 | 12,70 | 23,10 | |
| 4,0 | 6,90 | 8,79 | 45,4 | 15,10 | 22,70 | |
| 5,0 | 8,42 | 10,70 | 53,30 | 17,80 | 22,30 | |
| 6,3 | 10,30 | 13,10 | 61,60 | 20,50 | 21,70 | |
| 8,0 | 12,50 | 16,00 | 69,70 | 23,20 | 20,90 | |
| 70 | 3,2 | 6,63 | 8,40 | 62,30 | 17,80 | 27,20 |
| 4,0 | 8,15 | 10,40 | 74,70 | 21,30 | 26,80 | |
| 5,0 | 9,99 | 12,70 | 88,50 | 25,30 | 26,40 | |
| 6,3 | 12,30 | 15,60 | 104,00 | 29,70 | 25,80 | |
| 8,0 | 15,00 | 19,20 | 120,00 | 34,20 | 25,00 | |
| 80 | 3,2 | 7,63 | 9,72 | 95 | 23,7 | 31,3 |
| 4,0 | 9,41 | 12,00 | 114 | 28,6 | 30,9 | |
| 5,0 | 11,60 | 14,70 | 137 | 34,2 | 30,5 | |
| 6,3 | 14,20 | 18,10 | 162 | 40,5 | 29,9 | |
| 8,0 | 17,50 | 22,40 | 189 | 47,3 | 29,1 | |
| 90 | 4,0 | 10,7 | 13,6 | 166 | 37,0 | 35,0 |
| 5,0 | 13,1 | 16,7 | 200 | 44,4 | 34,5 | |
| 6,3 | 116,2 | 20,7 | 238 | 53,0 | 34,0 | |
| 8,0 | 20,1 | 25,6 | 281 | 62,6 | 33,2 | |
| 100 | 4,0 | 11,9 | 15,2 | 232 | 46,4 | 39,1 |
| 5,0 | 14,7 | 18,7 | 279 | 55,9 | 39,6 | |
| 6,3 | 18,2 | 23,2 | 336 | 67,1 | 38,0 | |
| 8,0 | 22,6 | 28,8 | 400 | 79,9 | 37,3 | |
| 10,0 | 27,4 | 34,9 | 462 | 92,4 | 36,4 | |
| 120 | 5,0 | 17,8 | 22,7 | 498 | 83,0 | 46,8 |
| 6,3 | 22,2 | 28,2 | 603 | 100 | 46,2 | |
| 8,0 | 27,6 | 35,2 | 726 | 121 | 45,5 | |
| 10,0 | 33,7 | 42,9 | 852 | 142 | 44,6 | |
| 12,5 | 40,9 | 52,1 | 982 | 164 | 43,4 | |
| 140 | 5,0 | 21,0 | 26,7 | 807 | 115 | 55,0 |
| 6,3 | 26,1 | 33,3 | 984 | 141 | 54,4 | |
| 8,0 | 32,6 | 41,6 | 1195 | 171 | 53,6 | |
| 10,0 | 40,0 | 50,9 | 1416 | 202 | 52,7 | |
| 12,5 | 48,7 | 62,1 | 1653 | 236 | 51,6 | |
| 150 | 5,0 | 22,6 | 28,7 | 1002 | 134 | 59,0 |
| 6,3 | 28,1 | 35,8 | 1223 | 163 | 58,5 | |
| 8,0 | 35,1 | 44,8 | 1491 | 199 | 57,7 | |
| 10,0 | 43,1 | 54,9 | 1773 | 236 | 56,8 | |
| 12,5 | 52,7 | 67,1 | 2080 | 277 | 55,7 | |
| 14,2 | 58,9 | 75,0 | 2262 | 302 | 54,9 | |
| 16,0 | 65,2 | 83,0 | 2430 | 324 | 54,1 | |
| 160 | 5,0 | 24,1 | 30,7 | 1225 | 153 | 63,1 |
| 6,3 | 30,1 | 38,3 | 1499 | 187 | 62,6 | |
| 8,0 | 37,6 | 48,0 | 1831 | 229 | 61,8 | |
| 10,0 | 46,3 | 58,9 | 2186 | 273 | 60,9 | |
| 12,5 | 56,6 | 72,1 | 2576 | 322 | 59,8 | |
| 14,2 | 63,3 | 80,7 | 2809 | 351 | 59,0 | |
| 16,0 | 70,2 | 89,4 | 3028 | 379 | 58,2 | |
| 180 | 5,0 | 27,3 | 34,7 | 1765 | 196 | 71,3 |
| 6,3 | 34,0 | 43,3 | 2168 | 241 | 70,7 | |
| 8,0 | 42,7 | 54,4 | 2661 | 296 | 70,0 | |
| 10,0 | 52,5 | 66,9 | 3193 | 355 | 69,1 | |
| 12,5 | 64,4 | 82,1 | 3790 | 421 | 68,0 | |
| 14,2 | 72,2 | 92,0 | 4154 | 462 | 67,2 | |
| 16,0 | 80,2 | 102 | 4504 | 500 | 66,4 | |
| 200 | 5,0 | 30,4 | 38,7 | 2445 | 245 | 79,5 |
| 6,3 | 38,0 | 48,4 | 3011 | 301 | 78,9 | |
| 8,0 | 47,7 | 60,8 | 3709 | 371 | 78,1 | |
| 10,0 | 58,8 | 74,9 | 4471 | 447 | 77,2 | |
| 12,5 | 72,3 | 92,1 | 5336 | 534 | 76,1 | |
| 14,2 | 81,1 | 103 | 5872 | 587 | 75,4 | |
| 16,0 | 90,3 | 115 | 6394 | 639 | 74,6 | |
| 220 | 6,3 | 41,9 | 53,4 | 4049 | 368 | 87,1 |
| 8,0 | 52,7 | 67,2 | 5002 | 455 | 86,3 | |
| 10,0 | 65,1 | 82,9 | 6050 | 550 | 85,4 | |
| 12,5 | 80,1 | 102 | 7254 | 659 | 84,3 | |
| 14,2 | 90,1 | 115 | 8007 | 728 | 83,5 | |
| 16,0 | 100 | 128 | 8749 | 795 | 82,7 | |
| 250 | 6,3 | 47,9 | 61,0 | 6014 | 481 | 99,3 |
| 8,0 | 60,3 | 76,8 | 7455 | 596 | 98,6 | |
| 10,0 | 74,5 | 94,9 | 9055 | 724 | 97,7 | |
| 12,5 | 91,9 | 117 | 10920 | 873 | 96,6 | |
| 14,2 | 103 | 132 | 12090 | 967 | 95,8 | |
| 16,0 | 115 | 147 | 13270 | 1061 | 95,0 | |
| 260 | 6,3 | 49,9 | 63,5 | 6788 | 522 | 103 |
| 8,0 | 62,8 | 80,0 | 8423 | 648 | 103 | |
| 10,0 | 77,7 | 98,9 | 10240 | 788 | 102 | |
| 12,5 | 95,8 | 122 | 12370 | 951 | 101 | |
| 14,2 | 108 | 137 | 13710 | 1055 | 100 | |
| 16,0 | 120 | 153 | 15060 | 1159 | 99 | |
| 300 | 6,3 | 57,8 | 74 | 10550 | 703 | 120 |
| 8,0 | 72,8 | 93 | 13130 | 875 | 119 | |
| 10,0 | 90,2 | 115 | 16030 | 1068 | 118 | |
| 12,5 | 112 | 142 | 19440 | 1296 | 117 | |
| 14,2 | 126 | 160 | 21640 | 1442 | 116 | |
| 16,0 | 141 | 179 | 23850 | 1590 | 115 | |
| 350 | 8,0 | 85,4 | 109 | 21130 | 1207 | 139 |
| 10,0 | 106 | 135 | 25880 | 1479 | 139 | |
| 12,5 | 131 | 167 | 31540 | 1802 | 137 | |
| 14,2 | 148 | 189 | 35210 | 2012 | 137 | |
| 16,0 | 166 | 211 | 38940 | 2225 | 136 | |
| 400 | 10,0 | 122 | 155 | 39130 | 1956 | 159 |
| 12,5 | 151 | 192 | 47840 | 2392 | 158 | |
| 14,2 | 170 | 217 | 53530 | 2676 | 157 | |
| 16,0 | 191 | 243 | 59340 | 2967 | 156 | |
| 20,0 | 235 | 300 | 71540 | 3577 | 154 | |
Tab. 14.11 Válcované duté profily obdélníkové ČSN EN 10210-2
D – vnější průměr
A – plocha průřezu
I – moment setrvačnosti
t – tloušťka stěny
W – průřezový modul
i – poloměr setrvačnosti
m – hmotnost
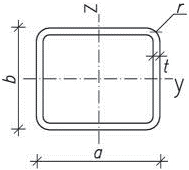
| Jmenovité rozměry | m [kg/m] |
A 103 [mm2] |
Iy 104 [mm4] |
Wy 103 [mm3] |
iy [mm] |
Iz 106 [mm4] |
Wz 103 [mm3] |
iz [mm] |
||
| a [mm] |
b [mm] |
t [mm] |
||||||||
| 50 | 30 | 2,6 | 3,00 | 3,82 | 12,2 | 4,87 | 17,9 | 5,38 | 3,58 | 11,9 |
| 3,2 | 3,61 | 4,60 | 14,2 | 5,68 | 17,6 | 6,20 | 4,13 | 11,6 | ||
| 4,0 | 4,39 | 5,59 | 16,5 | 6,60 | 17,2 | 7,08 | 4,72 | 11,3 | ||
| 5,0 | 5,28 | 6,73 | 18,7 | 7,49 | 16,7 | 7,89 | 5,26 | 10,8 | ||
| 60 | 40 | 2,6 | 3,81 | 4,86 | 23,6 | 7,86 | 22,0 | 12,4 | 6,22 | 16,0 |
| 3,2 | 4,62 | 5,88 | 27,8 | 9,27 | 21,8 | 14,6 | 7,29 | 15,7 | ||
| 4,0 | 5,64 | 7,19 | 32,8 | 10,9 | 21,4 | 17,0 | 8,52 | 15,4 | ||
| 5,0 | 6,85 | 8,73 | 38,1 | 12,7 | 20,9 | 19,5 | 9,77 | 15,0 | ||
| 6,3 | 8,31 | 10,6 | 43,4 | 14,5 | 20,2 | 21,9 | 11,0 | 14,4 | ||
| 80 | 40 | 3,2 | 5,62 | 7,16 | 57,2 | 14,3 | 28,3 | 18,9 | 9,5 | 16,3 |
| 4,0 | 6,90 | 8,79 | 68,2 | 17,1 | 27,9 | 22,2 | 11,1 | 15,9 | ||
| 5,0 | 8,42 | 10,7 | 80,3 | 20,1 | 27,4 | 25,7 | 12,9 | 15,5 | ||
| 6,3 | 10,3 | 13,1 | 93,3 | 23,3 | 26,7 | 29,2 | 14,6 | 14,9 | ||
| 8,0 | 12,5 | 16,0 | 106 | 26,5 | 25,8 | 32,1 | 16,1 | 14,2 | ||
| 90 | 50 | 3,2 | 6,63 | 8,44 | 89,1 | 19,8 | 32,5 | 35,3 | 14,1 | 20,4 |
| 4,0 | 8,15 | 10,4 | 107 | 23,8 | 32,1 | 41,9 | 16,8 | 20,1 | ||
| 5,0 | 9,99 | 12,7 | 127 | 28,3 | 31,6 | 49,2 | 19,7 | 19,7 | ||
| 6,3 | 12,3 | 15,6 | 150 | 33,3 | 31,0 | 57,0 | 22,8 | 19,1 | ||
| 8,0 | 15,0 | 19,2 | 174 | 38,6 | 30,1 | 64,6 | 25,8 | 18,4 | ||
| 100 | 50 | 3,2 | 7,13 | 9,08 | 116 | 23,2 | 35,7 | 38,8 | 15,5 | 20,7 |
| 4,0 | 8,78 | 11,2 | 140 | 27,9 | 35,3 | 46,2 | 18,5 | 20,3 | ||
| 5,0 | 10,8 | 13,7 | 167 | 33,3 | 34,8 | 54,3 | 21,7 | 19,9 | ||
| 6,3 | 13,3 | 16,9 | 197 | 39,4 | 34,2 | 63,0 | 25,2 | 19,3 | ||
| 8,0 | 16,3 | 20,8 | 230 | 46,0 | 33,3 | 71,7 | 28,7 | 18,6 | ||
| 60 | 3,2 | 7,63 | 9,72 | 131 | 26,2 | 36,7 | 58,8 | 19,6 | 24,6 | |
| 4,0 | 9,41 | 12,0 | 158 | 31,6 | 36,3 | 70,5 | 23,5 | 24,3 | ||
| 5,0 | 11,6 | 14,7 | 189 | 37,8 | 35,8 | 83,6 | 27,9 | 23,8 | ||
| 6,3 | 14,2 | 18,1 | 225 | 45,0 | 35,2 | 98,1 | 32,7 | 23,3 | ||
| 8,0 | 17,5 | 22,4 | 264 | 52,8 | 34,4 | 113 | 37,8 | 22,5 | ||
| 120 | 60 | 4,0 | 10,7 | 13,6 | 249 | 41,5 | 42,8 | 83,1 | 27,7 | 24,7 |
| 5,0 | 13,1 | 16,7 | 299 | 49,9 | 42,3 | 98,8 | 32,9 | 24,3 | ||
| 6,3 | 16,2 | 20,7 | 358 | 59,7 | 41,6 | 116 | 38,8 | 23,7 | ||
| 8,0 | 20,1 | 25,6 | 425 | 70,8 | 40,8 | 135 | 45,0 | 23,0 | ||
| 10,0 | 24,3 | 30,9 | 488 | 81,4 | 39,7 | 152 | 50,5 | 22,1 | ||
| 80 | 4,0 | 11,9 | 15,2 | 303 | 50,4 | 44,6 | 161 | 40,2 | 32,5 | |
| 5,0 | 14,7 | 18,7 | 365 | 60,9 | 44,2 | 193 | 48,2 | 32,1 | ||
| 6,3 | 18,2 | 23,2 | 440 | 73,3 | 43,6 | 230 | 57,6 | 31,5 | ||
| 8,0 | 22,6 | 28,8 | 525 | 87,5 | 42,7 | 273 | 68,1 | 30,8 | ||
| 10,0 | 27,4 | 34,9 | 609 | 102 | 41,8 | 313 | 78,1 | 29,9 | ||
| 140 | 80 | 4,0 | 13,2 | 16,8 | 441 | 62,9 | 51,2 | 184 | 46,0 | 33,1 |
| 5,0 | 16,3 | 20,7 | 534 | 76,3 | 50,8 | 221 | 55,3 | 32,7 | ||
| 6,3 | 20,2 | 25,7 | 646 | 92,3 | 50,1 | 265 | 66,2 | 32,1 | ||
| 8,0 | 25,1 | 32,0 | 776 | 111 | 49,3 | 314 | 78,5 | 31,4 | ||
| 10,0 | 30,6 | 38,9 | 908 | 130 | 48,3 | 362 | 90,5 | 30,5 | ||
| 150 | 100 | 4,0 | 15,1 | 19,2 | 607 | 81,0 | 56,3 | 324 | 64,8 | 41,1 |
| 5,0 | 18,6 | 23,7 | 739 | 98,5 | 55,8 | 392 | 78,5 | 40,7 | ||
| 6,3 | 23,1 | 29,5 | 898 | 120 | 55,2 | 474 | 94,8 | 40,1 | ||
| 8,0 | 28,9 | 36,8 | 1087 | 145 | 54,4 | 569 | 113,9 | 39,4 | ||
| 10,0 | 35,3 | 44,9 | 1282 | 171 | 53,4 | 665 | 133,1 | 38,5 | ||
| 12,5 | 42,8 | 54,6 | 1488 | 198 | 52,2 | 763 | 152,6 | 37,4 | ||
| 160 | 80 | 4,0 | 14,4 | 18,4 | 612 | 76,5 | 57,7 | 207 | 51,7 | 33,5 |
| 5,0 | 17,8 | 22,7 | 744 | 93,0 | 57,2 | 249 | 62,3 | 33,1 | ||
| 6,3 | 22,2 | 28,2 | 903 | 113 | 56,6 | 299 | 74,8 | 32,6 | ||
| 8,0 | 27,6 | 35,2 | 1091 | 136 | 55,7 | 356 | 89,0 | 31,8 | ||
| 10,0 | 33,7 | 42,9 | 1284 | 161 | 54,7 | 411 | 103 | 31,0 | ||
| 12,5 | 40,9 | 52,1 | 1485 | 186 | 53,4 | 465 | 116 | 29,9 | ||
| 180 | 100 | 4,0 | 16,9 | 21,6 | 945 | 105 | 66,1 | 379 | 75,9 | 41,9 |
| 5,0 | 21,0 | 26,7 | 1153 | 128 | 65,7 | 460 | 92,0 | 41,5 | ||
| 6,3 | 26,1 | 33,3 | 1407 | 156 | 65,0 | 557 | 111 | 40,9 | ||
| 8,0 | 32,6 | 41,6 | 1713 | 190 | 64,2 | 671 | 134 | 40,2 | ||
| 10,0 | 40,0 | 50,9 | 2036 | 226 | 63,2 | 787 | 157 | 39,3 | ||
| 12,5 | 48,7 | 62,1 | 2385 | 265 | 62,0 | 908 | 182 | 38,2 | ||
| 200 | 100 | 4,0 | 18,2 | 23,2 | 1223 | 122 | 72,6 | 416 | 83 | 42,4 |
| 5,0 | 22,6 | 28,7 | 1495 | 149 | 72,1 | 505 | 101 | 41,9 | ||
| 6,3 | 28,1 | 35,8 | 1829 | 183 | 71,5 | 613 | 123 | 41,4 | ||
| 8,0 | 35,1 | 44,8 | 2234 | 223 | 70,6 | 739 | 148 | 40,6 | ||
| 10,0 | 43,1 | 54,9 | 2664 | 266 | 69,6 | 869 | 174 | 39,8 | ||
| 12,5 | 52,7 | 67,1 | 3136 | 314 | 68,4 | 1004 | 201 | 38,7 | ||
| 16,0 | 65,2 | 83,0 | 3678 | 368 | 66,6 | 1147 | 229 | 37,2 | ||
| 120 | 6,3 | 30,1 | 38,3 | 2065 | 207 | 73,4 | 929 | 155 | 49,2 | |
| 8,0 | 37,6 | 48,0 | 2529 | 253 | 72,6 | 1128 | 188 | 48,5 | ||
| 10,0 | 46,3 | 58,9 | 3026 | 303 | 71,7 | 1337 | 223 | 47,6 | ||
| 12,5 | 56,6 | 72,1 | 3576 | 358 | 70,4 | 1562 | 260 | 46,6 | ||
| 250 | 150 | 6,3 | 38,0 | 48,4 | 4143 | 311 | 92,5 | 1874 | 250 | 62,2 |
| 8,0 | 47,7 | 60,8 | 5111 | 409 | 91,7 | 2298 | 306 | 61,5 | ||
| 10,0 | 58,8 | 74,9 | 6174 | 494 | 90,8 | 2755 | 367 | 60,6 | ||
| 12,5 | 72,3 | 92,1 | 7387 | 591 | 89,6 | 3265 | 435 | 59,6 | ||
| 14,2 | 81,1 | 103 | 8141 | 651 | 88,7 | 3576 | 477 | 58,8 | ||
| 16,0 | 90,3 | 115 | 8879 | 710 | 87,9 | 3873 | 516 | 58,0 | ||
| 260 | 180 | 6,3 | 41,9 | 53,4 | 5166 | 397 | 98,3 | 2929 | 325 | 74,0 |
| 8,0 | 52,7 | 67,2 | 6390 | 492 | 97,5 | 3608 | 401 | 73,3 | ||
| 10,0 | 65,1 | 82,9 | 7741 | 595 | 96,6 | 4351 | 483 | 72,4 | ||
| 12,5 | 80,1 | 102 | 9299 | 715 | 95,4 | 5196 | 577 | 71,3 | ||
| 14,2 | 90,1 | 115 | 10280 | 791 | 94,6 | 5719 | 635 | 70,6 | ||
| 16,0 | 100 | 128 | 11250 | 865 | 93,8 | 6231 | 692 | 69,8 | ||
| 300 | 200 | 6,3 | 47,9 | 61,0 | 7829 | 522 | 113 | 4193 | 419 | 82,9 |
| 8,0 | 60,3 | 76,8 | 9717 | 648 | 113 | 5184 | 518 | 82,2 | ||
| 10,0 | 74,5 | 94,9 | 11820 | 788 | 112 | 6278 | 628 | 81,3 | ||
| 12,5 | 91,9 | 117 | 14270 | 952 | 110 | 7537 | 754 | 80,2 | ||
| 14,2 | 103 | 132 | 15830 | 1055 | 110 | 8328 | 833 | 79,5 | ||
| 16,0 | 115 | 147 | 17390 | 1159 | 109 | 9109 | 911 | 78,7 | ||
| 350 | 250 | 6,3 | 57,8 | 73,6 | 13200 | 754 | 134 | 7885 | 631 | 104 |
| 8,0 | 72,8 | 92,8 | 16450 | 940 | 133 | 9798 | 784 | 103 | ||
| 10,0 | 90,2 | 115 | 20100 | 1149 | 132 | 11940 | 955 | 102 | ||
| 12,5 | 12 | 142 | 24420 | 1395 | 131 | 14440 | 1156 | 101 | ||
| 14,2 | 126 | 160 | 27200 | 1554 | 130 | 16050 | 1284 | 100 | ||
| 16,0 | 141 | 179 | 30010 | 1715 | 129 | 17650 | 1412 | 99,3 | ||
| 400 | 200 | 8,0 | 72,8 | 92,8 | 19560 | 987 | 145 | 6660 | 666 | 84,7 |
| 10,0 | 90,2 | 115 | 23910 | 1196 | 144 | 8084 | 808 | 83,9 | ||
| 12,5 | 112 | 142 | 29060 | 1453 | 143 | 9738 | 974 | 82,8 | ||
| 14,2 | 126 | 160 | 32380 | 1619 | 142 | 10780 | 1078 | 82,1 | ||
| 16,0 | 141 | 179 | 35740 | 1787 | 141 | 11820 | 1182 | 81,3 | ||
| 450 | 250 | 8,0 | 85,4 | 109 | 30080 | 1337 | 166 | 12140 | 971 | 106 |
| 10,0 | 106 | 135 | 36900 | 1640 | 165 | 14820 | 1185 | 105 | ||
| 12,5 | 131 | 167 | 45030 | 2001 | 164 | 17970 | 1438 | 104 | ||
| 14,2 | 148 | 189 | 50320 | 2236 | 163 | 20000 | 1600 | 103 | ||
| 16,0 | 166 | 211 | 55710 | 2476 | 162 | 22040 | 1763 | 102 | ||
| 500 | 300 | 10,0 | 122 | 155 | 53760 | 2150 | 186 | 24440 | 1629 | 126 |
| 12,5 | 151 | 192 | 65810 | 2633 | 185 | 29780 | 1985 | 125 | ||
| 14,2 | 170 | 217 | 73700 | 2948 | 184 | 33250 | 2215 | 124 | ||
| 16,0 | 191 | 243 | 81780 | 3271 | 183 | 36770 | 2451 | 123 | ||
| 20,0 | 235 | 300 | 98780 | 3951 | 182 | 44080 | 2939 | 121 | ||
Tab. 14.12 Trapézové plechy (převzato ze stránek kovprof.cz)
| Profil | t [mm] |
m [kg/m2] |
Ag [mm2] |
Iy,g 106 [mm4] |
Wy,eff+ 103 [mm3] |
Wy,eff– 103 [mm3] |
Iy,eff+ 106 [mm4] |
Iy,eff– 106 [mm4] |
podle ČSN EN 10147 |
| TR 8/100 | 0,50 | 4,30 | 529 | 0,006 | 0,95 | 0,92 | 0,004 | 0,005 | S 350G |
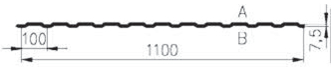 |
0,63 | 5,29 | 667 | 0,008 | 1,40 | 1,33 | 0,006 | 0,007 | S 350G |
| 0,75 | 6,46 | 794 | 0,009 | 1,87 | 1,74 | 0,007 | 0,008 | S 350G | |
| TR 19/105 | 0,63 | 5,88 | 704 | 0,041 | 4,01 | 3,96 | 0,038 | 0,040 | S 280G |
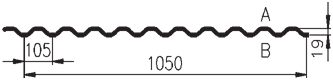 |
0,75 | 7,00 | 838 | 0,048 | 4,87 | 4,89 | 0,048 | 0,048 | S 280G |
| 0,88 | 8,21 | 984 | 0,057 | 5,73 | 5,74 | 0,057 | 0,057 | S 280G | |
| 1,00 | 9,34 | 1118 | 0,065 | 6,51 | 6,52 | 0,065 | 0,065 | S 280G | |
| TR 20/136 | 0,63 | 5,74 | – | – | – | – | – | – | S 280G |
 |
0,75 | 6,83 | – | – | – | – | – | – | S 280G |
| 0,88 | 8,02 | – | – | – | – | – | – | S 280G | |
| 1,00 | 9,11 | – | – | – | – | – | – | S 280G | |
| 1,13 | 10,29 | – | – | – | – | – | – | S 280G | |
| 1,25 | 11,38 | – | – | – | – | – | – | S 280G | |
| TR 20/137,5 | 0,63 | 5,74 | 700 | 0,040 | 2,97 | 2,95 | 0,027 | 0,036 | S 280G |
 |
0,75 | 6,83 | 833 | 0,047 | 3,74 | 3,77 | 0,035 | 0,045 | S 280G |
| 0,88 | 8,02 | 977 | 0,055 | 4,50 | 4,70 | 0,045 | 0,055 | S 280G | |
| 1,00 | 9,11 | 1110 | 0,063 | 5,20 | 5,40 | 0,055 | 0,063 | S 280G | |
| 1,13 | 10,29 | 1255 | 0,071 | 5,96 | 6,10 | 0,065 | 0,071 | S 280G | |
| 1,25 | 11,38 | 1388 | 0,079 | 6,66 | 6,74 | 0,076 | 0,079 | S 280G | |
| TR 25/175 | 0,63 | 5,58 | 689 | 0,072 | 3,97 | 4,07 | 0,051 | 0,065 | S 280G |
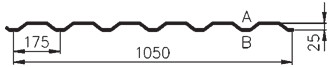 |
0,75 | 6,64 | 821 | 0,086 | 5,15 | 5,17 | 0,064 | 0,080 | S 280G |
| 0,88 | 7,80 | 963 | 0,101 | 6,22 | 6,42 | 0,081 | 0,098 | S 280G | |
| 1,00 | 8,86 | 1094 | 0,115 | 7,20 | 7,58 | 0,098 | 0,114 | S 280G | |
| 1,13 | 10,01 | 1236 | 0,129 | 8,28 | 8,56 | 0,117 | 0,129 | S 280G | |
| 1,25 | 11,08 | 1368 | 0,143 | 9,28 | 9,47 | 0,135 | 0,143 | S 280G | |
| TR 30/220 | 0,63 | 5,62 | 687 | 0,083 | 3,41 | 3,50 | 0,049 | 0,068 | S 320G |
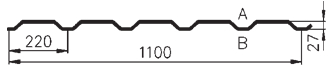 |
0,75 | 6,69 | 817 | 0,099 | 4,45 | 4,61 | 0,062 | 0,087 | S 320G |
| 0,88 | 7,84 | 959 | 0,116 | 5,71 | 5,76 | 0,077 | 0,107 | S 320G | |
| 1,00 | 8,91 | 1090 | 0,132 | 6,65 | 6,87 | 0,094 | 0,125 | S 320G | |
| 1,13 | 10,07 | 1231 | 0,149 | 7,67 | 8,11 | 0,113 | 0,146 | S 320G | |
| 1,25 | 11,14 | 1362 | 0,165 | 8,62 | 9,18 | 0,132 | 0,165 | S 320G | |
| TR 30/262,5 | 0,56 | 5,17 | 614 | 0,085 | 3,65 | 2,62 | 0,065 | 0,061 | S 320G |
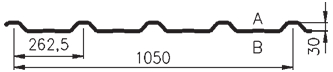 |
0,63 | 5,82 | 690 | 0,096 | 4,12 | 3,26 | 0,076 | 0,075 | S 320G |
| 0,70 | 6,46 | 767 | 0,106 | 4,58 | 3,93 | 0,088 | 0,089 | S 320G | |
| 0,75 | 6,93 | 822 | 0,114 | 4,92 | 4,43 | 0,096 | 0,099 | S 320G | |
| 0,88 | 8,13 | 964 | 0,133 | 5,79 | 5,54 | 0,117 | 0,122 | S 320G | |
| 1,00 | 9,23 | 1095 | 0,152 | 6,59 | 6,61 | 0,137 | 0,144 | S 320G | |
| TR 32/207 | 0,63 | 5,77 | 700 | 0,106 | 4,20 | 4,22 | 0,067 | 0,091 | S 320G |
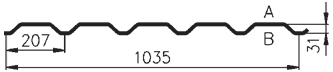 |
0,75 | 6,87 | 834 | 0,126 | 5,38 | 5,64 | 0,085 | 0,118 | S 320G |
| 0,88 | 8,06 | 978 | 0,148 | 6,50 | 7,01 | 0,107 | 0,144 | S 320G | |
| 1,00 | 9,16 | 1112 | 0,169 | 7,55 | 8,25 | 0,129 | 0,168 | S 320G | |
| 1,13 | 10,35 | 1256 | 0,190 | 8,71 | 9,33 | 0,155 | 0,190 | S 320G | |
| 1,25 | 11,45 | 1389 | 0,211 | 9,78 | 10,32 | 0,179 | 0,210 | S 320G | |
| TR 35/207 | 0,63 | 6,08 | 730 | 0,138 | 4,54 | 4,67 | 0,082 | 0,113 | S 320G |
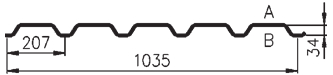 |
0,75 | 7,24 | 869 | 0,165 | 5,93 | 6,15 | 0,104 | 0,145 | S 320G |
| 0,88 | 8,49 | 1019 | 0,193 | 7,52 | 7,68 | 0,129 | 0,178 | S 320G | |
| 1,00 | 9,65 | 1158 | 0,219 | 8,75 | 9,15 | 0,157 | 0,210 | S 320G | |
| 1,13 | 10,90 | 1308 | 0,248 | 10,10 | 10,78 | 0,190 | 0,244 | S 320G | |
| 1,25 | 12,06 | 1447 | 0,274 | 11,35 | 12,13 | 0,221 | 0,274 | S 320G | |
| TR 39/333 | 0,63 | 5,97 | 718 | 0,109 | 3,20 | 2,89 | 0,095 | 0,093 | S 350G |
 |
0,75 | 7,11 | 854 | 0,129 | 3,83 | 3,84 | 0,116 | 0,121 | S 350G |
| 0,88 | 8,34 | 1002 | 0,152 | 4,51 | 4,80 | 0,140 | 0,150 | S 350G | |
| 1,00 | 9,47 | 1138 | 0,172 | 5,14 | 5,52 | 0,162 | 0,172 | S 350G | |
| 1,13 | 10,70 | 1286 | 0,194 | 5,83 | 6,24 | 0,187 | 0,194 | S 350G | |
| Pozor, nové označení stran! | 1,25 | 11,83 | 1422 | 0,215 | 6,47 | 6,90 | 0,209 | 0,215 | S 350G |
| TR 40/183 | 0,63 | 6,72 | 815 | 0,212 | 5,92 | 6,13 | 0,124 | 0,174 | S 320G |
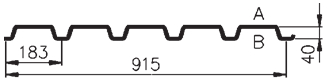 |
0,75 | 8,00 | 970 | 0,252 | 7,74 | 8,02 | 0,157 | 0,222 | S 320G |
| 0,88 | 9,38 | 1138 | 0,295 | 9,63 | 10,01 | 0,198 | 0,273 | S 320G | |
| 1,00 | 10,66 | 1293 | 0,335 | 11,21 | 11,92 | 0,242 | 0,321 | S 320G | |
| 1,13 | 12,04 | 1461 | 0,379 | 12,95 | 14,04 | 0,291 | 0,374 | S 320G | |
| 1,25 | 13,32 | 1616 | 0,419 | 14,55 | 15,64 | 0,339 | 0,415 | S 320G | |
| TR 40S/160 | 0,63 | 6,52 | 782 | 0,203 | 7,02 | 7,02 | 0,159 | 0,159 | S 320G |
 |
0,75 | 7,77 | 931 | 0,242 | 9,20 | 9,20 | 0,201 | 0,201 | S 320G |
| 0,88 | 9,11 | 1092 | 0,283 | 11,54 | 11,54 | 0,246 | 0,246 | S 320G | |
| 1,00 | 10,35 | 1241 | 0,322 | 13,84 | 13,84 | 0,289 | 0,289 | S 320G | |
| 1,13 | 11,70 | 1403 | 0,364 | 16,44 | 16,44 | 0,338 | 0,338 | S 320G | |
| 1,25 | 12,94 | 1551 | 0,402 | 18,94 | 18,94 | 0,383 | 0,383 | S 320G | |
| TR 40/160 | 0,63 | 6,47 | 782 | 0,179 | 8,84 | 8,84 | 0,179 | 0,179 | S 320G |
 |
0,75 | 7,70 | 931 | 0,213 | 10,69 | 10,69 | 0,213 | 0,213 | S 320G |
| 0,88 | 9,04 | 1093 | 0,250 | 12,67 | 12,67 | 0,250 | 0,250 | S 320G | |
| 1,00 | 10,28 | 1242 | 0,284 | 14,50 | 14,50 | 0,284 | 0,284 | S 320G | |
| 1,13 | 11,62 | 1404 | 0,321 | 16,42 | 16,42 | 0,321 | 0,321 | S 320G | |
| 1,25 | 12,86 | 1554 | 0,355 | 18,19 | 18,19 | 0,355 | 0,355 | S 320G | |
| TR 45/333 | 0,63 | 6,19 | 743 | 0,164 | 4,15 | 3,60 | 0,151 | 0,133 | S 320G |
 |
0,75 | 7,37 | 885 | 0,195 | 4,96 | 4,91 | 0,183 | 0,178 | S 320G |
| 0,88 | 8,65 | 1038 | 0,228 | 5,84 | 6,38 | 0,219 | 0,227 | S 320G | |
| 1,00 | 9,83 | 1179 | 0,260 | 6,66 | 7,30 | 0,253 | 0,260 | S 320G | |
| 1,13 | 11,10 | 1332 | 0,293 | 7,55 | 8,24 | 0,289 | 0,293 | S 320G | |
| 1,25 | 12,28 | 1473 | 0,324 | 8,37 | 9,11 | 0,324 | 0,324 | S 320G | |
| TR 50/250 | 0,63 | 6,35 | 754 | 0,295 | 5,90 | 5,90 | 0,164 | 0,208 | S 320G |
 |
0,75 | 7,55 | 898 | 0,352 | 8,04 | 8,03 | 0,212 | 0,272 | S 320G |
| 0,88 | 8,86 | 1053 | 0,413 | 10,24 | 10,57 | 0,262 | 0,347 | S 320G | |
| 1,00 | 10,07 | 1197 | 0,469 | 12,43 | 12,83 | 0,311 | 0,413 | S 320G | |
| 1,13 | 11,38 | 1352 | 0,530 | 14,99 | 15,20 | 0,365 | 0,484 | S 320G | |
| 1,25 | 12,59 | 1496 | 0,586 | 17,05 | 17,47 | 0,424 | 0,550 | S 320G | |
| TR 50/260 | 0,63 | 7,13 | 866 | 0,300 | 9,45 | 8,74 | 0,260 | 0,272 | S 320G |
 |
0,75 | 8,37 | 1016 | 0,352 | 11,21 | 10,75 | 0,317 | 0,331 | S 320G |
| 0,88 | 9,51 | 1154 | 0,400 | 12,80 | 12,67 | 0,370 | 0,386 | S 320G | |
| 1,00 | 10,74 | 1304 | 0,452 | 14,54 | 14,80 | 0,429 | 0,447 | S 320G | |
| 1,13 | 11,88 | 1442 | 0,500 | 16,15 | 16,62 | 0,484 | 0,500 | S 320G | |
| 1,25 | 14,26 | 1730 | 0,599 | 19,51 | 19,94 | 0,599 | 0,599 | S 320G | |
| TR 50/262,5 | 0,63 | 6,06 | 723 | 0,263 | 5,59 | 5,57 | 0,150 | 0,193 | S 320G |
 |
0,75 | 7,21 | 861 | 0,313 | 7,65 | 7,58 | 0,195 | 0,252 | S 320G |
| 0,88 | 8,46 | 1010 | 0,367 | 10,00 | 9,97 | 0,244 | 0,321 | S 320G | |
| 1,00 | 9,62 | 1147 | 0,417 | 12,00 | 12,33 | 0,290 | 0,386 | S 320G | |
| 1,13 | 10,87 | 1296 | 0,472 | 13,86 | 14,75 | 0,346 | 0,454 | S 320G | |
| 1,25 | 12,02 | 1434 | 0,522 | 15,60 | 16,82 | 0,400 | 0,513 | S 320G | |
| TR 55/250 | 0,75 | 7,51 | 913 | 0,412 | 11,39 | 10,59 | 0,363 | 0,376 | S 320G |
 |
0,88 | 8,81 | 1071 | 0,483 | 13,55 | 13,01 | 0,441 | 0,456 | S 320G |
| 1,00 | 10,01 | 1217 | 0,549 | 15,50 | 15,32 | 0,514 | 0,532 | S 320G | |
| 1,13 | 11,31 | 1375 | 0,621 | 17,60 | 17,87 | 0,595 | 0,615 | S 320G | |
| 1,25 | 12,51 | 1520 | 0,686 | 19,54 | 20,00 | 0,671 | 0,686 | S 320G | |
| 1,50 | 15,01 | 1824 | 0,823 | 23,57 | 23,98 | 0,823 | 0,823 | S 320G | |
| TR 56/222,5 | 0,70 | 7,52 | 915 | 0,357 | 8,13 | 8,81 | 0,294 | 0,357 | S 350G |
 |
0,75 | 8,05 | 981 | 0,382 | 8,73 | 9,44 | 0,320 | 0,382 | S 350G |
| 0,88 | 9,45 | 1150 | 0,448 | 10,29 | 11,07 | 0,388 | 0,448 | S 350G | |
| 1,00 | 10,73 | 1307 | 0,509 | 11,74 | 12,57 | 0,453 | 0,509 | S 350G | |
| 1,13 | 12,13 | 1476 | 0,575 | 13,32 | 14,19 | 0,524 | 0,575 | S 350G | |
| 1,25 | 13,41 | 1633 | 0,635 | 14,78 | 15,69 | 0,591 | 0,635 | S 350G | |
| TR 58/315 KD | 0,56 | 5,78 | 647 | 0,316 | 7,71 | 3,91 | 0,236 | 0,173 | S 320G |
 |
0,63 | 6,50 | 727 | 0,356 | 8,75 | 5,03 | 0,283 | 0,217 | S 320G |
| 0,70 | 7,22 | 808 | 0,395 | 9,77 | 6,26 | 0,324 | 0,263 | S 320G | |
| 0,75 | 7,74 | 866 | 0,423 | 10,49 | 7,18 | 0,355 | 0,298 | S 320G | |
| 0,88 | 9,08 | 1016 | 0,497 | 12,35 | 9,79 | 0,436 | 0,392 | S 320G | |
| 1,00 | 10,32 | 1154 | 0,564 | 14,09 | 12,39 | 0,512 | 0,482 | S 320G | |
| TR 59/225 | 0,75 | 8,33 | 1004 | 0,504 | 11,93 | 11,69 | 0,420 | 0,473 | S 320G |
 |
0,88 | 9,78 | 1177 | 0,591 | 14,14 | 14,34 | 0,512 | 0,574 | S 320G |
| 1,00 | 11,11 | 1338 | 0,672 | 16,13 | 16,83 | 0,599 | 0,669 | S 320G | |
| 1,13 | 12,55 | 1511 | 0,759 | 18,31 | 19,12 | 0,695 | 0,759 | S 320G | |
| 1,25 | 13,89 | 1671 | 0,839 | 20,33 | 21,14 | 0,785 | 0,839 | S 320G | |
| 1,50 | 16,67 | 2004 | 1,006 | 24,55 | 25,34 | 0,976 | 1,006 | S 320G | |
| TR 60/235 | 0,75 | 7,88 | 956 | 0,503 | 12,75 | 11,86 | 0,443 | 0,459 | S 320G |
 |
0,88 | 9,25 | 1122 | 0,590 | 15,17 | 14,58 | 0,538 | 0,557 | S 320G |
| 1,00 | 10,51 | 1275 | 0,671 | 17,36 | 17,17 | 0,627 | 0,650 | S 320G | |
| 1,13 | 11,87 | 1440 | 0,757 | 19,71 | 20,04 | 0,726 | 0,752 | S 320G | |
| 1,25 | 13,13 | 1593 | 0,838 | 21,88 | 22,38 | 0,818 | 0,838 | S 320G | |
| 1,50 | 15,75 | 1911 | 1,005 | 26,39 | 26,84 | 1,005 | 1,005 | S 320G | |
| TR 70/187 | 0,75 | 10,00 | 1173 | 0,889 | 23,43 | 23,14 | 0,889 | 0,889 | S 320G |
 |
0,88 | 11,76 | 1376 | 1,043 | 27,57 | 27,23 | 1,043 | 1,043 | S 320G |
| 1,00 | 13,37 | 1564 | 1,185 | 31,37 | 30,98 | 1,185 | 1,185 | S 320G | |
| 1,13 | 15,11 | 1768 | 1,340 | 35,47 | 35,07 | 1,340 | 1,339 | S 320G | |
| 1,25 | 16,71 | 1956 | 1,482 | 39,25 | 38,84 | 1,482 | 1,481 | S 320G | |
| 1,50 | 20,01 | 2347 | 1,778 | 47,16 | 46,73 | 1,778 | 1,777 | S 320G | |
| TR 70/200 | 0,75 | 9,33 | 1091 | 0,779 | 21,18 | 20,91 | 0,779 | 0,778 | S 320G |
 |
0,88 | 10,95 | 1280 | 0,914 | 24,92 | 24,61 | 0,914 | 0,913 | S 320G |
| 1,00 | 12,44 | 1455 | 1,038 | 28,36 | 28,00 | 1,038 | 1,037 | S 320G | |
| 1,13 | 14,09 | 1644 | 1,173 | 32,06 | 31,68 | 1,173 | 1,172 | S 320G | |
| 1,25 | 15,56 | 1819 | 1,298 | 35,48 | 35,09 | 1,298 | 1,297 | S 320G | |
| 1,50 | 18,67 | 2183 | 1,557 | 42,62 | 42,21 | 1,557 | 1,556 | S 320G | |
| TR 72/200 | 0,75 | 9,32 | 1117 | 0,837 | 19,90 | 16,56 | 0,780 | 0,718 | S 320G |
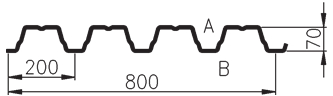 |
0,88 | 10,93 | 1310 | 0,982 | 23,64 | 20,48 | 0,943 | 0,875 | S 320G |
| 1,00 | 12,42 | 1488 | 1,115 | 26,94 | 24,27 | 1,095 | 1,025 | S 320G | |
| 1,13 | 14,02 | 1681 | 1,259 | 30,50 | 28,53 | 1,259 | 1,191 | S 320G | |
| 1,25 | 15,51 | 1859 | 1,392 | 33,79 | 32,56 | 1,392 | 1,347 | S 320G | |
| 1,50 | 18,60 | 2230 | 1,669 | 40,60 | 40,94 | 1,669 | 1,669 | S 320G | |
| TR 75/305 | 0,75 | 7,77 | 941 | 0,767 | 9,97 | 14,01 | 0,308 | 0,704 | S 320G |
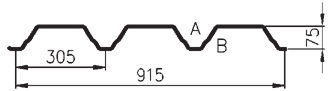 |
0,88 | 9,12 | 1104 | 0,900 | 13,62 | 17,10 | 0,379 | 0,851 | S 320G |
| 1,00 | 10,36 | 1255 | 1,022 | 17,28 | 20,05 | 0,447 | 0,990 | S 320G | |
| 1,13 | 11,71 | 1418 | 1,155 | 20,33 | 23,31 | 0,525 | 1,143 | S 320G | |
| 1,25 | 12,95 | 1568 | 1,277 | 22,91 | 26,16 | 0,599 | 1,277 | S 320G | |
| 1,50 | 15,54 | 1881 | 1,532 | 28,39 | 31,38 | 0,756 | 1,532 | S 320G | |
| TR 84/273 | 0,75 | 8,21 | 1001 | 1,024 | 18,60 | 17,95 | 1,007 | 0,951 | S 320G |
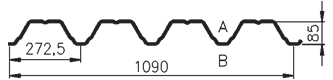 |
0,88 | 9,63 | 1175 | 1,201 | 22,28 | 21,86 | 1,201 | 1,147 | S 320G |
| 1,00 | 10,94 | 1335 | 1,364 | 25,47 | 25,57 | 1,364 | 1,331 | S 320G | |
| 1,13 | 12,36 | 1508 | 1,541 | 28,94 | 29,66 | 1,541 | 1,533 | S 320G | |
| 1,25 | 13,67 | 1668 | 1,704 | 32,16 | 33,10 | 1,704 | 1,704 | S 320G | |
| 1,50 | 16,40 | 2001 | 2,044 | 38,84 | 39,70 | 2,044 | 2,044 | S 320G | |
| TR 85/280 | 0,75 | 8,04 | 977 | 0,940 | 17,68 | 17,01 | 0,925 | 0,872 | S 320G |
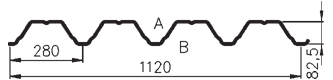 |
0,88 | 9,44 | 1147 | 1,103 | 21,19 | 20,71 | 1,103 | 1,051 | S 320G |
| 1,00 | 10,72 | 1303 | 1,253 | 24,23 | 24,24 | 1,253 | 1,221 | S 320G | |
| 1,13 | 12,11 | 1472 | 1,416 | 27,54 | 28,12 | 1,416 | 1,406 | S 320G | |
| 1,25 | 13,40 | 1628 | 1,566 | 30,59 | 31,45 | 1,566 | 1,566 | S 320G | |
| 1,50 | 16,08 | 1953 | 1,878 | 36,94 | 37,73 | 1,878 | 1,878 | S 320G | |
| TR 85K/280 | 0,75 | 8,04 | 977 | 0,940 | 17,68 | 17,01 | 0,925 | 0,872 | S 320G |
 |
0,88 | 9,44 | 1147 | 1,103 | 21,19 | 20,71 | 1,103 | 1,051 | S 320G |
| 1,00 | 10,72 | 1303 | 1,253 | 24,23 | 24,24 | 1,253 | 1,221 | S 320G | |
| 1,13 | 12,11 | 1472 | 1,416 | 27,54 | 28,12 | 1,416 | 1,406 | S 320G | |
| 1,25 | 13,40 | 1628 | 1,566 | 30,59 | 31,45 | 1,566 | 1,566 | S 320G | |
| 1,50 | 16,08 | 1953 | 1,878 | 36,94 | 37,73 | 1,878 | 1,878 | S 320G | |
| TR 89/305 | 0,75 | 8,04 | 997 | 1,134 | 17,75 | 17,99 | 1,086 | 1,051 | S 320G |
 |
0,88 | 9,43 | 1170 | 1,330 | 21,07 | 21,88 | 1,305 | 1,268 | S 320G |
| 1,00 | 10,72 | 1330 | 1,512 | 24,17 | 25,58 | 1,496 | 1,472 | S 320G | |
| 1,13 | 12,11 | 1503 | 1,708 | 27,57 | 29,65 | 1,702 | 1,695 | S 320G | |
| 1,25 | 13,40 | 1663 | 1,890 | 30,74 | 33,13 | 1,890 | 1,890 | S 320G | |
| 1,50 | 16,08 | 1997 | 2,267 | 37,40 | 39,75 | 2,267 | 2,267 | S 320G | |
| TR 90/305 | 0,75 | 8,15 | 986 | 1,119 | 18,43 | 17,31 | 0,931 | 1,038 | S 320G |
 |
0,88 | 9,56 | 1157 | 1,313 | 21,81 | 21,83 | 1,131 | 1,251 | S 320G |
| 1,00 | 10,87 | 1315 | 1,492 | 24,91 | 25,51 | 1,323 | 1,452 | S 320G | |
| 1,13 | 12,28 | 1486 | 1,686 | 28,28 | 29,57 | 1,535 | 1,673 | S 320G | |
| 1,25 | 13,58 | 1643 | 1,865 | 31,42 | 33,07 | 1,734 | 1,865 | S 320G | |
| 1,50 | 16,30 | 1972 | 2,238 | 38,01 | 39,67 | 2,158 | 2,238 | S 320G | |
| TR 92/275 | 0,75 | 9,05 | 1099 | 1,322 | 19,34 | 19,88 | 1,322 | 1,223 | S 320G |
 |
0,88 | 10,62 | 1289 | 1,550 | 23,15 | 24,21 | 1,550 | 1,477 | S 320G |
| 1,00 | 12,07 | 1465 | 1,761 | 26,59 | 28,33 | 1,761 | 1,716 | S 320G | |
| 1,13 | 13,63 | 1655 | 1,989 | 30,31 | 32,86 | 1,989 | 1,978 | S 320G | |
| 1,25 | 15,08 | 1830 | 2,199 | 33,77 | 36,70 | 2,199 | 2,199 | S 320G | |
| 1,50 | 18,09 | 2195 | 2,637 | 41,07 | 44,01 | 2,637 | 2,637 | S 320G | |
| TR 94/255 | 0,75 | 8,81 | 1075 | 1,279 | 21,42 | 20,75 | 1,259 | 1,190 | S 320G |
 |
0,88 | 10,34 | 1261 | 1,500 | 25,66 | 25,26 | 1,500 | 1,435 | S 320G |
| 1,00 | 11,75 | 1433 | 1,704 | 29,34 | 29,53 | 1,704 | 1,665 | S 320G | |
| 1,13 | 13,27 | 1619 | 1,925 | 33,34 | 34,24 | 1,925 | 1,918 | S 320G | |
| 1,25 | 14,68 | 1791 | 2,129 | 37,04 | 38,13 | 2,129 | 2,129 | S 320G | |
| 1,50 | 17,61 | 2148 | 2,553 | 44,73 | 45,73 | 2,553 | 2,553 | S 320G | |
| TR 95/305 | 0,75 | 8,20 | 952 | 1,170 | 19,73 | 19,35 | 1,171 | 1,146 | S 320G |
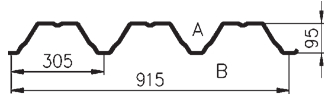 |
0,88 | 9,61 | 1127 | 1,440 | 23,75 | 23,50 | 1,417 | 1,380 | S 320G |
| 1,00 | 10,93 | 1288 | 1,660 | 27,41 | 27,44 | 1,635 | 1,600 | S 320G | |
| 1,13 | 12,35 | 1455 | 1,840 | 31,20 | 31,77 | 1,854 | 1,841 | S 320G | |
| 1,25 | 13,66 | 1623 | 2,020 | 34,65 | 35,53 | 2,050 | 2,050 | S 320G | |
| 1,50 | 16,39 | 1958 | 2,440 | 41,83 | 42,61 | 2,460 | 2,460 | S 320G | |
| TR 100/275 | 0,75 | 9,00 | 1092 | 1,521 | 22,39 | 22,18 | 1,521 | 1,415 | S 320G |
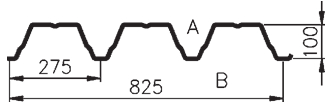 |
0,88 | 10,56 | 1281 | 1,784 | 26,65 | 26,96 | 1,784 | 1,705 | S 320G |
| 1,00 | 11,99 | 1456 | 2,026 | 30,52 | 31,49 | 2,026 | 1,978 | S 320G | |
| 1,13 | 13,55 | 1645 | 2,289 | 34,69 | 36,48 | 2,289 | 2,276 | S 320G | |
| 1,25 | 14,99 | 1819 | 2,532 | 38,55 | 40,69 | 2,532 | 2,532 | S 320G | |
| 1,50 | 17,98 | 2182 | 3,036 | 46,67 | 48,80 | 3,036 | 3,036 | S 320G | |
| TR 105/345 | 0,75 | 8,76 | 1063 | 1,593 | 19,34 | 19,72 | 1,423 | 1,474 | S 350G |
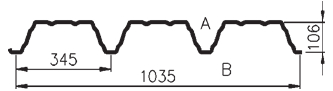 |
0,88 | 10,28 | 1248 | 1,869 | 22,90 | 24,44 | 1,715 | 1,776 | S 350G |
| 1,00 | 11,69 | 1418 | 2,123 | 26,22 | 28,51 | 1,990 | 2,060 | S 350G | |
| 1,13 | 13,21 | 1602 | 2,399 | 29,86 | 32,99 | 2,292 | 2,372 | S 350G | |
| 1,25 | 14,61 | 1772 | 2,653 | 33,24 | 37,02 | 2,574 | 2,653 | S 350G | |
| 1,50 | 17,53 | 2127 | 3,182 | 40,37 | 44,39 | 3,158 | 3,182 | S 350G | |
| TR 106/250 | 0,75 | 9,96 | 1208 | 1,866 | 25,82 | 25,63 | 1,790 | 1,740 | S 320G |
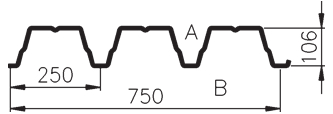 |
0,88 | 11,68 | 1418 | 2,188 | 31,02 | 31,14 | 2,140 | 2,096 | S 320G |
| 1,00 | 13,27 | 1611 | 2,486 | 35,69 | 36,37 | 2,469 | 2,432 | S 320G | |
| 1,13 | 14,99 | 1819 | 2,808 | 40,67 | 42,12 | 2,808 | 2,798 | S 320G | |
| 1,25 | 16,58 | 2012 | 3,105 | 45,19 | 46,86 | 3,105 | 3,105 | S 320G | |
| 1,50 | 19,88 | 2414 | 3,722 | 54,63 | 56,19 | 3,722 | 3,722 | S 320G | |
| TR 109/333 | 0,75 | 9,00 | – | – | – | – | – | – | S 350G |
 |
0,88 | 10,56 | – | – | – | – | – | – | S 350G |
| 1,00 | 12,00 | – | – | – | – | – | – | S 350G | |
| 1,13 | 13,56 | – | – | – | – | – | – | S 350G | |
| 1,25 | 15,00 | – | – | – | – | – | – | S 350G | |
| 1,50 | 18,00 | – | – | – | – | – | – | S 350G | |
| TR 110/333 | 0,75 | 8,84 | – | – | – | – | – | – | S 350G |
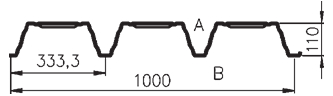 |
0,88 | 10,36 | – | – | – | – | – | – | S 350G |
| 1,00 | 11,78 | – | – | – | – | – | – | S 350G | |
| 1,13 | 13,31 | – | – | – | – | – | – | S 350G | |
| 1,25 | 14,73 | – | – | – | – | – | – | S 350G | |
| 1,50 | 17,67 | – | – | – | – | – | – | S 350G | |
| TR 115/275 | 0,75 | 9,09 | 1109 | 1,824 | 26,43 | 25,72 | 1,716 | 1,709 | S 320G |
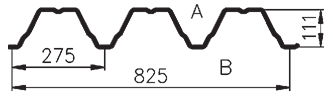 |
0,88 | 10,67 | 1301 | 2,140 | 31,86 | 31,18 | 2,113 | 2,053 | S 320G |
| 1,00 | 12,12 | 1478 | 2,431 | 36,62 | 36,35 | 2,431 | 2,378 | S 320G | |
| 1,13 | 13,70 | 1670 | 2,747 | 41,63 | 42,03 | 2,747 | 2,732 | S 320G | |
| 1,25 | 15,15 | 1848 | 3,037 | 46,16 | 46,91 | 3,037 | 3,037 | S 320G | |
| 1,50 | 18,18 | 2216 | 3,643 | 55,56 | 56,26 | 3,643 | 3,643 | S 320G | |
| TR 126/320 | 0,75 | 9,38 | 1134 | 2,690 | 31,88 | 33,72 | 2,690 | 2,690 | S 350G |
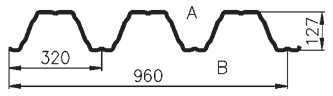 |
0,88 | 11,00 | 1331 | 3,157 | 39,52 | 40,87 | 3,157 | 3,157 | S 350G |
| 1,00 | 12,50 | 1512 | 3,588 | 46,97 | 47,18 | 3,588 | 3,588 | S 350G | |
| 1,13 | 14,13 | 1709 | 4,055 | 53,79 | 54,06 | 2,690 | 2,690 | S 350G | |
| 1,25 | 15,63 | 1891 | 4,486 | 60,44 | 60,42 | 3,157 | 3,157 | S 350G | |
| 1,50 | 18,75 | 2270 | 5,384 | 73,82 | 73,66 | 3,588 | 3,588 | S 350G | |
| TR 130/343 | 0,75 | 8,72 | 1058 | 2,258 | 26,91 | 24,15 | 1,939 | 2,115 | S 320G |
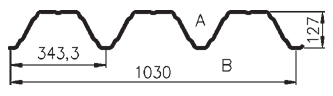 |
0,88 | 10,24 | 1241 | 2,650 | 32,07 | 30,99 | 2,345 | 2,552 | S 320G |
| 1,00 | 11,63 | 1410 | 3,011 | 36,73 | 37,50 | 2,731 | 2,950 | S 320G | |
| 1,13 | 13,14 | 1594 | 3,402 | 41,81 | 43,89 | 3,158 | 3,384 | S 320G | |
| 1,25 | 14,54 | 1763 | 3,763 | 46,53 | 48,89 | 3,559 | 3,763 | S 320G | |
| 1,50 | 17,45 | 2116 | 4,514 | 56,05 | 58,64 | 4,409 | 4,514 | S 320G | |
| TR 135/310 | 0,75 | 9,79 | 1184 | 2,982 | 28,49 | 26,92 | 2,834 | 2,744 | S 320G |
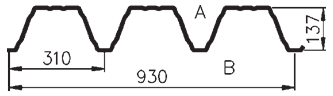 |
0,88 | 11,49 | 1389 | 3,499 | 35,32 | 34,89 | 3,388 | 3,330 | S 320G |
| 1,00 | 13,06 | 1579 | 3,976 | 42,07 | 42,54 | 3,905 | 3,852 | S 320G | |
| 1,13 | 14,76 | 1784 | 4,492 | 48,45 | 51,15 | 4,470 | 4,426 | S 320G | |
| 1,25 | 16,33 | 1974 | 4,969 | 54,03 | 59,28 | 4,969 | 4,959 | S 320G | |
| 1,50 | 19,59 | 2369 | 5,962 | 65,81 | 71,83 | 5,962 | 5,962 | S 320G | |
| TR 136/326 | 0,75 | 9,15 | 1112 | 2,592 | 29,53 | 26,47 | 2,226 | 2,435 | S 320G |
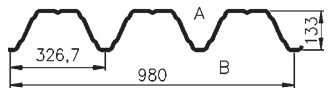 |
0,88 | 10,73 | 1305 | 3,041 | 35,18 | 33,94 | 2,692 | 2,934 | S 320G |
| 1,00 | 12,20 | 1483 | 3,455 | 40,28 | 41,09 | 3,135 | 3,390 | S 320G | |
| 1,13 | 13,78 | 1676 | 3,904 | 45,84 | 48,18 | 3,625 | 3,888 | S 320G | |
| 1,25 | 15,25 | 1854 | 4,318 | 51,01 | 53,58 | 4,086 | 4,318 | S 320G | |
| 1,50 | 18,30 | 2224 | 5,181 | 61,42 | 64,27 | 5,061 | 5,181 | S 320G | |
| TR 144/287 | 0,75 | 10,50 | 1282 | 3,641 | 41,24 | 41,50 | 3,641 | 3,641 | S 320G |
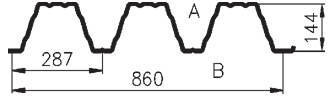 |
0,88 | 12,20 | 1505 | 4,274 | 49,00 | 49,51 | 4,274 | 4,274 | S 320G |
| 1,00 | 113,90 | 1710 | 4,858 | 56,24 | 56,89 | 4,858 | 4,858 | S 320G | |
| 1,13 | 15,70 | 1933 | 5,491 | 64,14 | 64,85 | 3,641 | 3,641 | S 320G | |
| 1,25 | 17,40 | 2139 | 6,076 | 71,47 | 72,17 | 4,274 | 4,274 | S 320G | |
| 1,50 | 20,90 | 2568 | 7,295 | 86,77 | 87,35 | 4,858 | 4,858 | S 320G | |
| TR 150/280 | 0,75 | 11,00 | 1338 | 4,000 | 42,36 | 35,59 | 3,612 | 3,760 | S 320G |
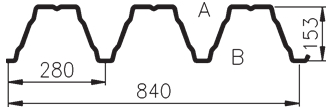 |
0,88 | 12,90 | 1570 | 4,692 | 50,23 | 45,56 | 4,354 | 4,520 | S 320G |
| 1,00 | 14,66 | 1784 | 5,331 | 57,27 | 55,24 | 5,055 | 5,218 | S 320G | |
| 1,13 | 16,57 | 2016 | 6,024 | 64,89 | 66,22 | 5,826 | 5,982 | S 320G | |
| 1,25 | 18,33 | 2230 | 6,663 | 71,98 | 75,13 | 6,546 | 6,663 | S 320G | |
| 1,50 | 21,99 | 2676 | 7,993 | 86,89 | 90,12 | 7,993 | 7,993 | S 320G | |
| TR 160/250 | 0,75 | 12,10 | 1472 | 4,708 | 48,12 | 41,20 | 4,245 | 4,421 | S 320G |
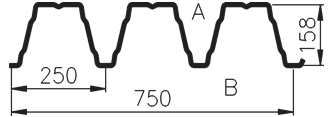 |
0,88 | 14,19 | 1727 | 5,522 | 57,06 | 52,75 | 5,119 | 5,324 | S 320G |
| 1,00 | 16,13 | 1962 | 6,274 | 65,09 | 63,88 | 5,943 | 6,146 | S 320G | |
| 1,13 | 15,22 | 2217 | 7,088 | 73,73 | 76,44 | 6,851 | 7,046 | S 320G | |
| 1,25 | 20,16 | 2452 | 7,838 | 81,76 | 85,33 | 7,698 | 7,838 | S 320G | |
| 1,50 | 24,19 | 2942 | 9,402 | 98,65 | 102,33 | 9,402 | 9,402 | S 320G | |
| TR 165/250 | 0,75 | 11,83 | 1444 | 4,588 | 45,61 | 38,34 | 4,570 | 4,315 | S 320G |
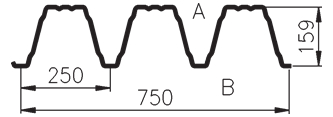 |
0,88 | 13,88 | 1695 | 5,383 | 54,36 | 49,29 | 5,383 | 5,239 | S 320G |
| 1,00 | 15,77 | 1926 | 6,117 | 62,51 | 60,03 | 6,117 | 6,059 | S 320G | |
| 1,13 | 17,82 | 2177 | 6,912 | 71,36 | 71,38 | 6,912 | 6,912 | S 320G | |
| 1,25 | 19,72 | 2408 | 7,646 | 79,46 | 81,20 | 7,646 | 7,646 | S 320G | |
| 1,50 | 23,66 | 2890 | 9,174 | 95,89 | 99,93 | 9,174 | 9,174 | S 320G | |
| TR 170/250 | 0,75 | 12,00 | 1486 | 5,129 | 52,09 | 39,60 | 4,808 | 4,633 | S 350G |
 |
0,88 | 14,08 | 1743 | 6,016 | 61,68 | 51,17 | 5,772 | 5,646 | S 350G |
| 1,00 | 16,00 | 1981 | 6,835 | 70,50 | 62,80 | 6,676 | 6,615 | S 350G | |
| 1,13 | 18,08 | 2238 | 7,722 | 80,09 | 76,13 | 7,664 | 7,639 | S 350G | |
| 1,25 | 20,00 | 2476 | 8,540 | 88,87 | 88,02 | 8,540 | 8,540 | S 350G | |
| 1,50 | 24,00 | 2970 | 10,243 | 107,23 | 109,77 | 10,243 | 10,243 | S 350G | |
| TR 200/375 | 0,75 | 11,78 | – | – | – | – | – | – | S 350G |
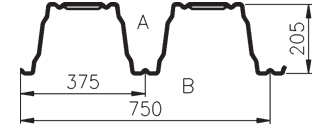 |
0,88 | 13,82 | – | – | – | – | – | – | S 350G |
| 1,00 | 15,70 | – | – | – | – | – | – | S 350G | |
| 1,13 | 17,74 | – | – | – | – | – | – | S 350G | |
| 1,25 | 19,63 | – | – | – | – | – | – | S 350G | |
| 1,50 | 23,55 | – | – | – | – | – | – | S 350G | |
| TR 200/420 | 0,75 | 10,74 | 1294 | 7,344 | 33,34 | 48,07 | 6,579 | 7,190 | S 350G |
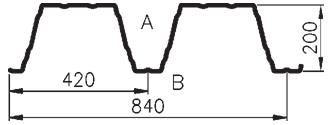 |
0,88 | 12,60 | 1518 | 8,617 | 41,23 | 59,83 | 7,913 | 8,589 | S 350G |
| 1,00 | 14,32 | 1725 | 9,792 | 49,21 | 70,69 | 9,172 | 9,792 | S 350G | |
| 1,13 | 16,18 | 1950 | 11,066 | 58,65 | 82,81 | 10,561 | 11,066 | S 350G | |
| 1,25 | 17,90 | 2157 | 12,241 | 68,19 | 94,17 | 11,860 | 12,241 | S 350G | |
| 1,50 | 21,49 | 2588 | 14,690 | 86,74 | 116,32 | 14,596 | 14,690 | S 350G | |
| Ag plocha plného průřezu (na 1m šířky) Iy,g moment setrvačnosti plného průřezu (na 1m šířky) Wy,eff průřezový modul efektivního průřezu pro únosnost (na 1m šířky, vliv smykového ochabnutí není uvažován) Iy,eff moment setrvačnosti efektivního průřezu pro deformaci (na 1m šířky, vliv smykového ochabnutí není uvažován) |
|||||||||
Tab. 14.13 Tenkostěnné profily čtvercové svařované (Jäckel) – výběr ČSN EN 10219-2
D – vnější průměr
A – plocha průřezu
I – moment setrvačnosti
t – tloušťka stěny
W – průřezový modul
i – poloměr setrvačnosti
m – hmotnost
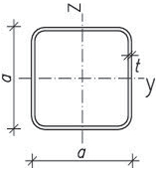
| Jmenovité rozměry | A [mm2] |
m [kg/m] |
Iy 104 [mm4] |
Wy 103 [mm3] |
iy [mm] |
Id 104 [mm4] |
|
| b [mm] |
t [mm] |
||||||
| 20 | 2,0 | 134 | 1,02 | 0,69 | 0,69 | 7,2 | 1,21 |
| 25 | 1,5 | 135 | 1,03 | 1,22 | 0,97 | 9,5 | 2,01 |
| 2,0 | 174 | 1,32 | 1,48 | 1,19 | 9,2 | 2,53 | |
| 3,0 | 241 | 1,83 | 1,84 | 1,47 | 8,7 | 3,33 | |
| 30 | 1,5 | 165 | 1,26 | 2,20 | 1,46 | 11,5 | 3,57 |
| 2,0 | 214 | 1,63 | 2,72 | 1,81 | 11,3 | 4,54 | |
| 3,0 | 301 | 2,29 | 3,50 | 2,34 | 10,8 | 6,15 | |
| 35 | 1,5 | 195 | 1,49 | 3,60 | 2,05 | 13,6 | 5,78 |
| 2,0 | 254 | 1,93 | 4,51 | 2,58 | 13,3 | 7,41 | |
| 3,0 | 361 | 2,74 | 5,95 | 3,40 | 12,8 | 10,22 | |
| 40 | 2,0 | 294 | 2,24 | 6,94 | 3,47 | 15,4 | 11,28 |
| 3,0 | 421 | 3,20 | 9,32 | 4,66 | 14,9 | 15,75 | |
| 4,0 | 535 | 4,08 | 11,07 | 5,54 | 14,4 | 19,44 | |
| 5,0 | 636 | 4,84 | 12,26 | 6,13 | 13,9 | 22,31 | |
| 45 | 2,0 | 334 | 2,54 | 10,12 | 4,50 | 17,4 | 16,30 |
| 3,0 | 481 | 3,65 | 13,78 | 6,12 | 16,9 | 22,99 | |
| 4,0 | 615 | 4,68 | 16,61 | 7,38 | 16,4 | 28,67 | |
| 50 | 2,0 | 374 | 2,84 | 14,15 | 5,66 | 19,5 | 22,63 |
| 3,0 | 541 | 4,13 | 19,47 | 7,79 | 19,0 | 32,13 | |
| 4,0 | 695 | 52,9 | 23,74 | 9,49 | 18,5 | 40,42 | |
| 5,0 | 836 | 6,37 | 27,04 | 10,82 | 18 | 47,46 | |
| 60 | 2,0 | 454 | 3,46 | 25,14 | 8,38 | 23,5 | 39,79 |
| 3,0 | 661 | 5,04 | 35,13 | 11,71 | 23,1 | 57,09 | |
| 4,0 | 855 | 6,51 | 43,55 | 14,52 | 22,6 | 72,64 | |
| 5,0 | 1040 | 7,89 | 50,49 | 16,83 | 22,1 | 86,42 | |
| 6,0 | 1203 | 9,17 | 56,07 | 18,69 | 21,6 | 98,41 | |
| 80 | 2,0 | 614 | 4,67 | 61,7 | 15,42 | 31,7 | 96,34 |
| 3,0 | 901 | 6,86 | 87,84 | 21,96 | 31,2 | 139,93 | |
| 4,0 | 1175 | 8,95 | 111,04 | 27,76 | 30,7 | 180,44 | |
| 5,0 | 1436 | 10,96 | 131,44 | 32,86 | 30,3 | 217,83 | |
| 6,0 | 1683 | 12,81 | 149,00 | 37,29 | 29,8 | 252,07 | |
| 8,0 | 2084 | 15,91 | 168,38 | 42,09 | 28,4 | 307,14 | |
| 100 | 2,0 | 774 | 5,89 | 123,01 | 24,60 | 39,9 | 190,54 |
| 3,0 | 1141 | 8,69 | 177,05 | 35,41 | 39,4 | 278,68 | |
| 4,0 | 1495 | 11,36 | 226,35 | 45,27 | 38,9 | 362,01 | |
| 5,0 | 1840 | 13,97 | 271,10 | 54,22 | 38,4 | 440,52 | |
| 6,0 | 2163 | 16,49 | 311,47 | 62,29 | 37,9 | 514,16 | |
| 8,0 | 2724 | 20,76 | 366,00 | 73,19 | 36,7 | 644,51 | |
| 10,0 | 3257 | 24,84 | 411,08 | 82,22 | 35,5 | 749,84 | |
| 110 | 4,0 | 1655 | 12,60 | 305,94 | 55,62 | 43,0 | 486,47 |
| 5,0 | 2036 | 15,50 | 367,95 | 66,90 | 42,5 | 593,60 | |
| 120 | 3,0 | 1381 | 10,47 | 312,35 | 52,06 | 47,6 | 487,72 |
| 4,0 | 1815 | 13,78 | 402,28 | 67,05 | 47,1 | 636,57 | |
| 5,0 | 2236 | 16,98 | 485,47 | 80,91 | 46,6 | 778,50 | |
| 6,0 | 2643 | 20,09 | 562,16 | 93,67 | 46,1 | 913,46 | |
| 8,0 | 3364 | 25,61 | 676,88 | 112,81 | 44,9 | 1162,95 | |
| 10,0 | 4057 | 30,85 | 776,81 | 129,47 | 4,38 | 1376,41 | |
| 12,5 | 4704 | 35,80 | 817,01 | 136,17 | 41,7 | 1550,67 | |
|
Poznámka: |
|||||||
Tab. 14.14 Tenkostěnné profily obdélníkové svařované (Jäckel) – výběr ČSN EN 10219-2
a, b – vnější průměr
A – plocha průřezu
t – tloušťka stěny
I – moment setrvačnosti
m – hmotnost
i – poloměr setrvačnosti
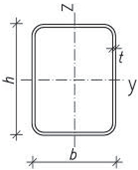
| Jmenovité rozměry | A [mm2] |
m [kg/m] |
Iy 104 [mm4] |
Wy 103 [mm3] |
iy [mm] |
Iz 104 [mm4] |
Wz 103 [mm3] |
iz [mm] |
Id 104 [mm4] |
||
| h [mm] |
b [mm] |
t [mm] |
|||||||||
| 25 | 15 | 1,5 | 105,0 | 0,80 | 0,80 | 0,64 | 8,70 | 0,36 | 0,48 | 5,8 | 0,85 |
| 30 | 15 | 2,0 | 154,0 | 1,18 | 1,54 | 1,03 | 1,00 | 0,57 | 0,67 | 5,7 | 1,34 |
| 35 | 20 | 1,5 | 150,0 | 1,15 | 2,33 | 1,33 | 12,5 | 0,80 | 0,97 | 8,00 | 2,28 |
| 2,0 | 194,0 | 1,48 | 2,87 | 1,64 | 12,2 | 1,18 | 1,18 | 7,8 | 2,87 | ||
| 40 | 10 | 2,0 | 174,0 | 1,32 | 2,60 | 1,30 | 12,2 | 0,25 | 0,49 | 3,8 | 0,83 |
| 20 | 1,5 | 165,0 | 1,26 | 3,27 | 1,63 | 14,1 | 1,10 | 1,10 | 8,2 | 2,74 | |
| 20 | 2,0 | 214,0 | 1,63 | 4,05 | 2,02 | 13,8 | 1,34 | 1,34 | 7,9 | 3,45 | |
| 20 | 3,0 | 301,0 | 2,29 | 5,21 | 2,60 | 13,2 | 1,69 | 1,69 | 7,5 | 4,57 | |
| 25 | 2,0 | 234,0 | 1,77 | 4,77 | 2,39 | 14,3 | 2,28 | 1,82 | 9,9 | 5,17 | |
| 40 | 35 | 2,0 | 274,0 | 2,09 | 6,22 | 3,11 | 15,1 | 5,06 | 2,89 | 13,6 | 9,12 |
| 2,5 | 334,0 | 2,54 | 7,33 | 3,67 | 14,8 | 5,96 | 3,40 | 13,4 | 10,97 | ||
| 50 | 20 | 1,5 | 195,0 | 1,49 | 5,77 | 2,31 | 17,2 | 1,35 | 1,35 | 8,3 | 3,69 |
| 2,0 | 254,0 | 1,93 | 7,23 | 2,89 | 16,9 | 1,67 | 1,67 | 8,1 | 4,66 | ||
| 3,0 | 361,0 | 2,74 | 9,51 | 3,81 | 16,2 | 2,13 | 2,13 | 7,7 | 6,20 | ||
| 50 | 30 | 1,5 | 225,0 | 1,71 | 7,54 | 3,01 | 18,3 | 3,42 | 2,28 | 12,3 | 7,60 |
| 2,0 | 294,0 | 2,24 | 9,54 | 3,81 | 18,0 | 4,29 | 2,86 | 12,1 | 9,77 | ||
| 2,5 | 359,0 | 2,73 | 11,30 | 4,52 | 17,7 | 5,06 | 3,37 | 11,9 | 11,74 | ||
| 3,0 | 421,0 | 3,20 | 12,83 | 5,13 | 17,5 | 5,71 | 3,81 | 11,6 | 13,50 | ||
| 4,0 | 535,0 | 4,08 | 15,25 | 6,10 | 16,9 | 6,71 | 4,47 | 11,2 | 16,53 | ||
| 50 | 35 | 2,0 | 314,0 | 2,37 | 10,69 | 4,28 | 18,5 | 6,15 | 3,51 | 14,0 | 12,71 |
| 3,0 | 451,0 | 3,44 | 14,49 | 5,80 | 17,9 | 8,27 | 4,73 | 17,8 | 12,673 17,648 |
||
| 60 | 20 | 1,5 | 225,0 | 1,71 | 9,25 | 3,08 | 20,3 | 1,61 | 1,61 | 8,5 | 4,66 |
| 2,0 | 294,0 | 2,24 | 11,68 | 3,89 | 19,9 | 1,99 | 1,99 | 8,2 | 4,643 | ||
| 3,0 | 421,0 | 3,20 | 15,62 | 5,21 | 19,3 | 2,57 | 2,57 | 7,8 | 7,87 | ||
| 60 | 40 | 1,5 | 285,0 | 2,18 | 14,39 | 4,80 | 22,5 | 7,72 | 3,86 | 16,4 | 15,97 |
| 2,0 | 374,0 | 2,84 | 18,40 | 6,14 | 22,2 | 9,83 | 4,92 | 16,2 | 20,70 | ||
| 2,5 | 459,0 | 3,49 | 22,07 | 7,36 | 21,9 | 11,74 | 5,87 | 16,0 | 25,14 | ||
| 3,0 | 541,0 | 4,13 | 25,38 | 8,46 | 21,7 | 13,45 | 6,73 | 15,8 | 29,28 | ||
| 4,0 | 695,0 | 5,29 | 30,99 | 10,33 | 21,1 | 16,31 | 8,15 | 15,3 | 36,67 | ||
| 5,0 | 836,0 | 6,37 | 35,33 | 11,78 | 20,6 | 18,48 | 9,24 | 14,9 | 42,85 | ||
| 60 | 50 | 3,0 | 601,0 | 4,58 | 30,26 | 10,09 | 22,4 | 22,80 | 9,12 | 19,5 | 42,63 |
| 70 | 30 | 2,0 | 374,0 | 2,84 | 22,22 | 6,35 | 24,4 | 5,87 | 3,91 | 12,5 | 15,45 |
| 3,0 | 541,0 | 4,13 | 30,57 | 8,74 | 23,8 | 7,90 | 5,27 | 12,1 | 21,53 | ||
| 70 | 50 | 2,0 | 454,0 | 3,46 | 31,48 | 8,99 | 26,3 | 18,76 | 7,50 | 20,3 | 37,45 |
| 4,0 | 855,0 | 6,51 | 54,67 | 15,62 | 25,3 | 32,26 | 12,90 | 19,4 | 68,07 | ||
| 5,0 | 1040,0 | 7,89 | 63,46 | 18,13 | 24,8 | 37,28 | 14,91 | 19,0 | 80,77 | ||
| 70 | 60 | 3,0 | 721,0 | 5,50 | 50,79 | 14,51 | 26,5 | 40,03 | 13,34 | 23,6 | 72,40 |
| 80 | 20 | 2,0 | 374,0 | 2,84 | 25,19 | 6,30 | 26,0 | 2,65 | 2,65 | 8,4 | 8,40 |
| 80 | 30 | 2,0 | 414,0 | 3,16 | 31,27 | 7,82 | 27,5 | 6,65 | 4,43 | 12,7 | 18,37 |
| 3,0 | 601,0 | 4,58 | 43,35 | 10,84 | 26,9 | 9,00 | 6,00 | 12,2 | 25,65 | ||
| 80 | 35 | 2,0 | 434,0 | 3,30 | 34,31 | 8,58 | 28,1 | 9,41 | 5,38 | 14,7 | 24,35 |
| 3,0 | 631,0 | 4,80 | 47,80 | 11,95 | 27,5 | 12,89 | 7,37 | 14,3 | 34,35 | ||
| 80 | 40 | 2,0 | 454,0 | 3,46 | 37,36 | 9,34 | 28,7 | 12,72 | 6,36 | 16,7 | 30,88 |
| 3,0 | 661,0 | 5,04 | 52,25 | 13,06 | 28,1 | 17,57 | 8,78 | 16,3 | 43,88 | ||
| 4,0 | 855,0 | 6,51 | 64,79 | 16,20 | 27,5 | 21,49 | 10,74 | 15,9 | 55,24 | ||
| 5,0 | 1040,0 | 7,89 | 75,11 | 18,78 | 26,9 | 24,65 | 12,32 | 15,4 | 64,97 | ||
| 6,0 | 1203,0 | 9,17 | 83,32 | 20,83 | 26,3 | 27,05 | 13,52 | 15,0 | 73,07 | ||
| 80 | 60 | 2,0 | 534,0 | 4,07 | 49,53 | 12,38 | 30,5 | 31,88 | 10,63 | 24,4 | 61,22 |
| 3,0 | 781,0 | 5,95 | 70,05 | 17,51 | 30,0 | 44,91 | 14,97 | 24,0 | 88,35 | ||
| 4,0 | 1010,0 | 7,73 | 87,92 | 21,98 | 29,4 | 56,16 | 18,72 | 23,5 | 113,13 | ||
| 5,0 | 1236,0 | 9,42 | 103,28 | 25,83 | 28,9 | 65,75 | 21,92 | 23,1 | 135,53 | ||
| 6,0 | 1443,0 | 10,99 | 116,25 | 29,06 | 28,4 | 73,63 | 24,54 | 22,6 | 155,55 | ||
| 90 | 30 | 3,0 | 661,0 | 5,04 | 59,13 | 13,14 | 29,9 | 10,09 | 6,73 | 10,9 | 29,81 |
| 90 | 40 | 3,0 | 721,0 | 5,50 | 70,49 | 15,67 | 31,3 | 19,62 | 9,81 | 16,5 | 51,41 |
| 90 | 50 | 3,0 | 781,0 | 5,95 | 81,85 | 18,19 | 32,4 | 32,75 | 13,10 | 20,5 | 76,67 |
| 4,0 | 1015,0 | 7,73 | 102,71 | 22,82 | 31,8 | 40,74 | 16,30 | 20,0 | 97,70 | ||
| 5,0 | 1236,0 | 9,42 | 120,60 | 26,80 | 31,2 | 47,45 | 18,98 | 19,6 | 116,47 | ||
| 100 | 30 | 2,0 | 494,0 | 3,76 | 55,77 | 11,15 | 33,6 | 8,22 | 5,48 | 12,9 | 24,33 |
| 100 | 40 | 3,0 | 781,0 | 5,95 | 92,34 | 18,47 | 34,4 | 21,68 | 10,84 | 16,7 | 59,06 |
| 4,0 | 1015,0 | 7,73 | 115,7 | 23,14 | 33,8 | 26,72 | 13,36 | 16,2 | 74,53 | ||
| 100 | 50 | 2,0 | 574,0 | 4,37 | 74,98 | 15,00 | 36,2 | 25,68 | 10,27 | 21,2 | 61,59 |
| 3,0 | 841,0 | 6,41 | 106,46 | 21,29 | 35,6 | 36,06 | 14,42 | 20,7 | 88,56 | ||
| 4,0 | 1095,0 | 8,34 | 134,14 | 26,83 | 35,0 | 44,95 | 17,98 | 20,3 | 112,99 | ||
| 5,0 | 1336,0 | 10,19 | 158,19 | 31,64 | 34,4 | 52,53 | 21,01 | 19,8 | 134,58 | ||
| 6,0 | 1560,0 | 11,93 | 178,75 | 35,75 | 33,8 | 58,67 | 23,47 | 19,4 | 154,20 | ||
| 8,0 | 1924,0 | 14,66 | 196,24 | 39,25 | 31,9 | 64,29 | 25,72 | 18,3 | 180,79 | ||
| 100 | 60 | 3,0 | 901,0 | 6,86 | 120,57 | 24,11 | 36,6 | 54,65 | 18,22 | 24,6 | 121,67 |
| 4,0 | 1175,0 | 8,95 | 152,28 | 30,52 | 36,0 | 68,68 | 22,89 | 24,2 | 156,27 | ||
| 5,0 | 1440,0 | 10,96 | 180,77 | 36,15 | 35,5 | 80,83 | 26,94 | 23,7 | 187,86 | ||
| 6,0 | 1680,0 | 12,81 | 205,30 | 41,06 | 34,9 | 91,20 | 30,40 | 23,3 | 216,44 | ||
| 100 | 80 | 5,0 | 1640,0 | 12,42 | 225,94 | 45,19 | 37,2 | 159,61 | 39,90 | 31,2 | 307,55 |
| 110 | 30 | 2,0 | 527,0 | 4,07 | 71,62 | 13,02 | 36,6 | 9,00 | 6,00 | 36,6 | 27,35 |
| 120 | 40 | 3,0 | 901,0 | 6,86 | 148,04 | 24,67 | 40,5 | 25,80 | 12,90 | 16,9 | 74,56 |
| 4,0 | 1175,0 | 8,96 | 186,89 | 31,15 | 39,9 | 31,92 | 15,96 | 16,5 | 94,23 | ||
| 5,0 | 1436,0 | 10,93 | 220,81 | 36,80 | 32,9 | 36,98 | 18,49 | 16,0 | 111,35 | ||
| 120 | 50 | 4,0 | 1255,0 | 9,55 | 213,82 | 35,64 | 41,3 | 53,47 | 21,39 | 20,6 | 144,22 |
| 5,0 | 1536,0 | 11,69 | 253,89 | 42,32 | 40,7 | 62,70 | 25,08 | 20,2 | 172,44 | ||
| 120 | 60 | 3,0 | 1020,0 | 7,77 | 189,12 | 31,52 | 43,0 | 64,40 | 21,47 | 25,1 | 156,34 |
| 4,0 | 1335,0 | 10,19 | 240,74 | 40,12 | 42,5 | 81,25 | 27,08 | 24,7 | 201,12 | ||
| 5,0 | 1636,0 | 12,42 | 286,97 | 47,83 | 41,9 | 95,99 | 32,00 | 24,2 | 242,23 | ||
| 6,0 | 1920,0 | 14,65 | 328,01 | 54,67 | 41,3 | 108,77 | 36,26 | 23,8 | 279,67 | ||
| 8,0 | 2404,0 | 18,34 | 375,31 | 62,55 | 39,5 | 123,98 | 41,33 | 22,7 | 339,55 | ||
| 120 | 80 | 3,0 | 1140,0 | 8,69 | 230,20 | 38,37 | 44,9 | 123,43 | 30,86 | 32,9 | 255,47 |
| 4,0 | 1495,0 | 11,39 | 194,59 | 49,10 | 44,4 | 157,29 | 39,32 | 32,4 | 331,24 | ||
| 5,0 | 1840,0 | 13,98 | 353,14 | 58,86 | 43,9 | 187,78 | 46,94 | 32,0 | 402,27 | ||
| 6,0 | 2160,0 | 16,49 | 406,00 | 67,68 | 43,3 | 215,00 | 53,82 | 31,5 | 468,54 | ||
| 8,0 | 2724,0 | 20,76 | 475,83 | 79,31 | 41,8 | 251,66 | 62,92 | 30,4 | 584,04 | ||
| 120 | 100 | 5,0 | 2036,0 | 15,50 | 419,31 | 69,88 | 45,4 | 316,27 | 63,25 | 39,4 | 582,86 |
| 6,0 | 2403,0 | 18,31 | 484,11 | 80,68 | 44,9 | 364,86 | 72,97 | 39,0 | 682,04 | ||
| 8,0 | 3044,0 | 23,19 | 576,35 | 96,06 | 43,5 | 433,83 | 86,77 | 37,8 | 861,65 | ||
|
Poznámka: |
|||||||||||
Tab. 14.15 Tabulky železobetonových desek
Návod k používání tabulek:
podle typu (jednosměrně pnutá deska nebo deska působící ve více směrech) vyhledáme v odpovídající tabulce ohybový moment v závislosti na zatížení a rozpětí desky. V tab. 3.9 v závislosti na ohybovém momentu a kvalitě materiálu vyhledáme odpovídající tloušťku desky.
Tab. 14.15.1 Jednosměrně pnuté desky M=1/8q_\text{d}\cdot\ell^2
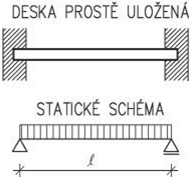 |
Rozpětí ℓ [m] | Hodnoty ohybových momentů M [kNm] | ||||||
| Návrhové zatížení qd [kN/m2] | ||||||||
| ≤ 4 | 6 | 8 | 10 | 12 | 14 | 16 | ||
| do 1,0 | 0,50 | 0,75 | 1,0 | 1,25 | 1,5 | 1,75 | 2,0 | |
| 1,2 | 0,72 | 1,08 | 1,44 | 1,80 | 2,16 | 2,52 | 2,88 | |
| 1,4 | 0,98 | 1,47 | 1,96 | 2,45 | 2,94 | 3,43 | 3,92 | |
| 1,6 | 1,28 | 1,92 | 2,56 | 3,20 | 3,84 | 4,48 | 5,12 | |
| 1,8 | 1,62 | 2,43 | 3,24 | 4,05 | 4,86 | 5,67 | 6,48 | |
| 2,0 | 2,0 | 3,0 | 4,0 | 5,0 | 6,7 | 7,0 | 8,0 | |
| 2,2 | 2,42 | 3,63 | 4,84 | 6,05 | 7,26 | 8,47 | 9,68 | |
| 2,4 | 2,88 | 4,32 | 5,76 | 7,02 | 8,64 | 10,08 | 11,52 | |
| 2,6 | 3,38 | 5,07 | 6,76 | 8,45 | 10,14 | 11,83 | 13,52 | |
| 2,8 | 3,92 | 5,88 | 7,84 | 9,80 | 11,76 | 13,72 | 15,68 | |
| 3,0 | 4,5 | 6,75 | 9,00 | 11,25 | 13,50 | 15,75 | 18,00 | |
| 3,2 | 5,12 | 7,68 | 13,24 | 12,80 | 15,36 | 17,92 | 20,48 | |
| 3,4 | 5,78 | 8,67 | 11,56 | 14,45 | 17,34 | 20,23 | 23,12 | |
| 3,6 | 6,48 | 9,72 | 12,96 | 16,20 | 19,44 | 22,68 | 25,92 | |
Tab. 14.15.2 Jednosměrně pnuté desky M=1/10q_\text{d}\cdot\ell^2
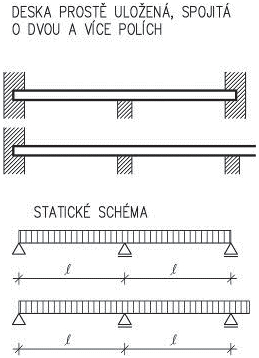 |
Rozpětí ℓ [m] | Hodnoty ohybových momentů M [kNm] | ||||||
| Návrhové zatížení qd [kN/m2] | ||||||||
| ≤ 4 | 6 | 8 | 10 | 12 | 14 | 16 | ||
| do 1,0 | 0,40 | 0,60 | 1,80 | 1,00 | 1,20 | 1,40 | 1,60 | |
| 1,2 | 0,58 | 0,86 | 1,15 | 1,44 | 1,73 | 2,02 | 2,30 | |
| 1,4 | 0,78 | 1,18 | 1,57 | 1,96 | 2,35 | 2,74 | 3,14 | |
| 1,6 | 1,02 | 1,54 | 2,05 | 2,56 | 3,07 | 3,58 | 4,10 | |
| 1,8 | 1,30 | 1,94 | 2,59 | 3,24 | 3,89 | 4,54 | 5,18 | |
| 2,0 | 1,60 | 2,40 | 3,20 | 4,00 | 4,80 | 5,60 | 6,40 | |
| 2,2 | 1,94 | 2,90 | 3,87 | 4,84 | 5,81 | 6,78 | 7,74 | |
| 2,4 | 2,30 | 3,46 | 4,61 | 5,76 | 6,91 | 8,06 | 9,22 | |
| 2,6 | 2,70 | 4,06 | 5,41 | 6,76 | 8,11 | 9,46 | 10,82 | |
| 2,8 | 3,14 | 4,70 | 6,27 | 7,84 | 9,41 | 10,98 | 12,54 | |
| 3,0 | 3,6 | 5,40 | 7,20 | 9,00 | 10,80 | 12,60 | 14,40 | |
| 3,2 | 4,1 | 6,14 | 8,19 | 10,24 | 12,29 | 14,34 | 16,38 | |
| 3,4 | 4,62 | 6,94 | 9,25 | 11,56 | 13,87 | 16,18 | 18,50 | |
| 3,6 | 5,18 | 7,78 | 10,37 | 12,96 | 15,55 | 18,14 | 20,74 | |
Tab. 14.15.3 Jednosměrně pnuté desky M=1/12q_\text{d}\cdot\ell^2
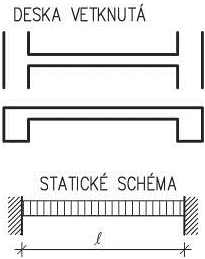 |
Rozpětí ℓ [m] | Hodnoty ohybových momentů M [kNm] | ||||||
| Návrhové zatížení qd [kN/m2] | ||||||||
| ≤ 4 | 6 | 8 | 10 | 12 | 14 | 16 | ||
| do 1,0 | 0,33 | 0,50 | 0,67 | 0,83 | 1,00 | 1,17 | 1,33 | |
| 1,2 | 0,48 | 0,72 | 0,96 | 1,20 | 1,44 | 1,68 | 1,92 | |
| 1,4 | 0,65 | 0,98 | 1,31 | 1,63 | 1,96 | 2,29 | 2,61 | |
| 1,6 | 0,85 | 1,28 | 1,71 | 2,13 | 2,56 | 2,99 | 3,41 | |
| 1,8 | 1,08 | 1,62 | 2,16 | 2,70 | 3,24 | 3,78 | 4,32 | |
| 2,0 | 1,33 | 2,00 | 2,67 | 3,33 | 4,00 | 4,67 | 5,33 | |
| 2,2 | 1,61 | 2,42 | 3,23 | 4,03 | 4,84 | 5,65 | 6,45 | |
| 2,4 | 1,92 | 2,88 | 3,84 | 4,80 | 5,76 | 6,72 | 7,68 | |
| 2,6 | 2,25 | 3,38 | 4,51 | 5,63 | 6,76 | 7,89 | 9,01 | |
| 2,8 | 2,61 | 3,92 | 5,23 | 6,53 | 7,84 | 9,15 | 10,45 | |
| 3,0 | 3,00 | 4,50 | 6,00 | 7,50 | 9,00 | 10,50 | 12,00 | |
| 3,2 | 3,41 | 5,12 | 6,83 | 8,53 | 10,24 | 11,95 | 13,65 | |
| 3,4 | 3,85 | 5,78 | 7,71 | 9,63 | 11,56 | 13,49 | 15,41 | |
| 3,6 | 4,32 | 6,48 | 8,64 | 10,80 | 12,96 | 15,12 | 17,28 | |
Tab. 14.15.4 Jednosměrně pnuté desky M=1/16q_\text{d}\cdot\ell^2
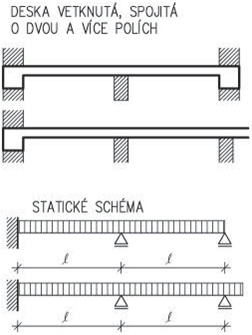 |
Rozpětí ℓ [m] | Hodnoty ohybových momentů M [kNm] | ||||||
| Návrhové zatížení qd [kN/m2] | ||||||||
| ≤ 4 | 6 | 8 | 10 | 12 | 14 | 16 | ||
| do 1,0 | 0,25 | 0,38 | 0,50 | 0,63 | 0,75 | 0,88 | 1,00 | |
| 1,2 | 0,36 | 0,54 | 0,72 | 0,90 | 1,08 | 1,26 | 1,44 | |
| 1,4 | 0,49 | 0,74 | 0,98 | 1,23 | 1,47 | 1,72 | 1,96 | |
| 1,6 | 0,64 | 0,96 | 1,28 | 1,60 | 1,92 | 2,24 | 2,56 | |
| 1,8 | 0,81 | 1,22 | 1,62 | 2,03 | 2,43 | 2,84 | 3,24 | |
| 2,0 | 1,00 | 1,50 | 2,00 | 2,50 | 3,00 | 3,50 | 4,00 | |
| 2,2 | 1,21 | 1,82 | 2,42 | 3,03 | 3,63 | 4,24 | 4,84 | |
| 2,4 | 1,44 | 2,16 | 2,88 | 3,60 | 4,32 | 5,04 | 5,76 | |
| 2,6 | 1,69 | 2,54 | 3,38 | 4,23 | 5,07 | 5,92 | 6,76 | |
| 2,8 | 1,96 | 2,94 | 3,92 | 4,90 | 5,88 | 6,86 | 7,84 | |
| 3,0 | 2,25 | 3,38 | 4,50 | 5,63 | 6,75 | 7,88 | 9,00 | |
| 3,2 | 2,56 | 3,84 | 5,12 | 6,40 | 7,68 | 8,96 | 10,24 | |
| 3,4 | 2,89 | 4,34 | 5,78 | 7,23 | 8,67 | 10,12 | 11,56 | |
| 3,6 | 3,24 | 4,86 | 6,48 | 8,10 | 9,72 | 11,34 | 12,96 | |
Tab. 14.15.5 Obousměrně pnuté desky, poměr stran 1 : 1
 |
Rozpětí ℓ [m] | Hodnoty ohybových momentů M [kNm] | ||||||
| Návrhové zatížení qd [kN/m2] | ||||||||
| ≤ 4 | 6 | 8 | 10 | 12 | 14 | 16 | ||
| 3,0 | 2,25 | 3,38 | 4,50 | 5,63 | 6,75 | 7,88 | 9,00 | |
| 3,3 | 2,72 | 4,08 | 5,44 | 6,81 | 8,17 | 9,53 | 10,89 | |
| 3,6 | 3,24 | 4,86 | 6,48 | 8,10 | 9,72 | 11,34 | 12,96 | |
| 3,9 | 3,80 | 5,70 | 7,60 | 9,51 | 11,41 | 13,31 | 15,21 | |
| 4,2 | 4,41 | 6,61 | 8,82 | 11,02 | 13,23 | 15,43 | 17,64 | |
| 4,5 | 5,06 | 7,59 | 10,13 | 12,66 | 15,19 | 17,72 | 20,25 | |
| 4,8 | 5,76 | 8,64 | 11,52 | 14,40 | 17,28 | 20,16 | 23,04 | |
| 5,1 | 6,50 | 9,75 | 13,01 | 16,26 | 19,51 | 22,76 | 26,01 | |
| 5,4 | 7,29 | 10,94 | 14,58 | 18,23 | 21,87 | 25,52 | 29,16 | |
| 5,7 | 8,12 | 12,18 | 16,25 | 20,31 | 24,37 | 28,43 | 32,49 | |
| 6,0 | 9,00 | 13,50 | 18,00 | 22,50 | 27,00 | 31,50 | 36,00 | |
| 6,3 | 9,92 | 14,88 | 19,85 | 24,81 | 29,77 | 34,73 | 39,69 | |
| 6,6 | 10,89 | 16,34 | 21,23 | 27,23 | 32,67 | 38,12 | 43,56 | |
Tab. 14.15.6 Obousměrně pnuté desky, poměr stran 1:1
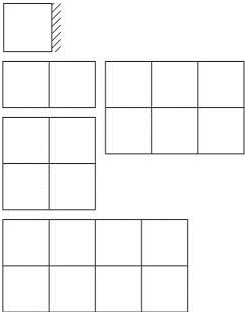 |
Rozpětí ℓ [m] | Hodnoty ohybových momentů M [kNm] | ||||||
| Návrhové zatížení qd [kN/m2] | ||||||||
| ≤ 4 | 6 | 8 | 10 | 12 | 14 | 16 | ||
| 3,0 | 3,21 | 4,82 | 6,43 | 8,03 | 9,64 | 11,25 | 12,85 | |
| 3,3 | 3,89 | 5,83 | 7,78 | 9,72 | 11,66 | 13,61 | 15,55 | |
| 3,6 | 4,63 | 6,94 | 9,25 | 11,57 | 13,88 | 16,19 | 18,51 | |
| 3,9 | 5,43 | 8,14 | 10,86 | 13,57 | 16,29 | 19,00 | 21,72 | |
| 4,2 | 6,30 | 9,45 | 12,59 | 15,74 | 18,89 | 22,04 | 25,19 | |
| 4,5 | 7,23 | 10,84 | 14,46 | 18,07 | 21,69 | 25,30 | 28,92 | |
| 4,8 | 8,23 | 12,34 | 16,45 | 20,56 | 24,68 | 28,79 | 32,90 | |
| 5,1 | 9,29 | 13,93 | 18,57 | 23,21 | 27,86 | 32,50 | 37,14 | |
| 5,4 | 10,41 | 15,62 | 20,82 | 26,03 | 31,23 | 36,44 | 41,64 | |
| 5,7 | 11,60 | 17,40 | 23,20 | 29,00 | 34,80 | 40,60 | 46,40 | |
| 6,0 | 12,85 | 19,28 | 25,70 | 32,13 | 38,56 | 44,98 | 51,41 | |
| 6,3 | 14,17 | 21,25 | 28,34 | 35,42 | 42,51 | 49,59 | 56,68 | |
| 6,6 | 15,55 | 23,33 | 31,10 | 38,88 | 46,65 | 54,43 | 62,20 | |
Tab. 14.15.7 Obousměrně pnuté desky, poměr stran 1 : 1
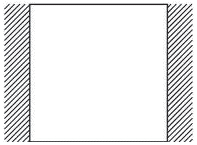 |
Rozpětí ℓ [m] | Hodnoty ohybových momentů M [kNm] | ||||||
| Návrhové zatížení qd [kN/m2] | ||||||||
| ≤ 4 | 6 | 8 | 10 | 12 | 14 | 16 | ||
| 3,0 | 2,50 | 3,75 | 5,00 | 6,25 | 7,50 | 8,75 | 10,00 | |
| 3,3 | 3,02 | 4,54 | 6,05 | 7,56 | 9,07 | 10,58 | 12,10 | |
| 3,6 | 3,60 | 5,40 | 7,20 | 9,00 | 10,80 | 12,59 | 14,39 | |
| 3,9 | 4,22 | 6,33 | 8,45 | 10,56 | 12,67 | 14,78 | 16,89 | |
| 4,2 | 4,90 | 7,35 | 9,80 | 12,25 | 14,69 | 17,14 | 19,59 | |
| 4,5 | 5,62 | 8,43 | 11,25 | 14,06 | 16,87 | 19,25 | 22,49 | |
| 4,8 | 6,40 | 9,60 | 12,79 | 15,99 | 19,19 | 22,39 | 25,59 | |
| 5,1 | 7,22 | 10,83 | 14,44 | 18,06 | 21,67 | 25,28 | 28,89 | |
| 5,4 | 8,10 | 12,15 | 16,19 | 20,24 | 24,29 | 28,34 | 32,39 | |
| 5,7 | 9,02 | 13,53 | 18,04 | 22,55 | 27,06 | 31,57 | 36,09 | |
| 6,0 | 10,00 | 14,99 | 19,99 | 24,99 | 29,99 | 34,99 | 39,98 | |
| 6,3 | 11,02 | 16,53 | 22,04 | 27,55 | 33,06 | 38,57 | 44,08 | |
| 6,6 | 12,10 | 18,14 | 24,19 | 30,24 | 36,29 | 43,33 | 48,38 | |
Tab. 14.15.8 Obousměrně pnuté desky, poměr stran 1 : 1
 |
Rozpětí ℓ [m] | Hodnoty ohybových momentů M [kNm] | ||||||
| Návrhové zatížení qd [kN/m2] | ||||||||
| ≤ 4 | 6 | 8 | 10 | 12 | 14 | 16 | ||
| 3,0 | 2,00 | 3,00 | 4,00 | 5,00 | 6,00 | 7,00 | 8,00 | |
| 3,3 | 2,42 | 3,63 | 4,84 | 6,05 | 7,26 | 8,47 | 9,68 | |
| 3,6 | 2,88 | 4,32 | 5,76 | 7,20 | 8,64 | 10,09 | 11,53 | |
| 3,9 | 3,38 | 5,07 | 6,76 | 8,45 | 10,15 | 11,84 | 13,53 | |
| 4,2 | 3,92 | 5,88 | 7,84 | 9,80 | 11,77 | 13,73 | 15,69 | |
| 4,5 | 4,50 | 6,75 | 9,00 | 11,26 | 13,51 | 15,76 | 18,01 | |
| 4,8 | 5,12 | 7,68 | 10,35 | 12,81 | 15,37 | 17,93 | 20,49 | |
| 5,1 | 5,78 | 8,67 | 11,57 | 14,46 | 17,35 | 20,24 | 23,13 | |
| 5,4 | 6,48 | 9,72 | 12,97 | 16,21 | 19,45 | 22,69 | 25,93 | |
| 5,7 | 7,22 | 10,84 | 14,45 | 18,06 | 21,67 | 25,28 | 28,89 | |
| 6,0 | 8,00 | 12,01 | 16,01 | 20,01 | 24,01 | 28,01 | 32,02 | |
| 6,3 | 8,82 | 13,24 | 17,65 | 22,06 | 26,47 | 30,89 | 35,30 | |
| 6,6 | 9,68 | 14,53 | 19,37 | 24,21 | 29,05 | 33,90 | 38,74 | |
Tab. 14.15.9 Obousměrně pnuté desky, poměr stran 1 : 1
 |
Rozpětí ℓ [m] | Hodnoty ohybových momentů M [kNm] | ||||||
| Návrhové zatížení qd [kN/m2] | ||||||||
| ≤ 4 | 6 | 8 | 10 | 12 | 14 | 16 | ||
| 3,0 | 1,50 | 2,25 | 3,00 | 3,75 | 4,50 | 5,25 | 6,00 | |
| 3,3 | 1,81 | 2,72 | 3,63 | 4,54 | 5,44 | 6,35 | 7,26 | |
| 3,6 | 2,16 | 3,24 | 4,32 | 5,40 | 6,48 | 7,56 | 8,64 | |
| 3,9 | 2,53 | 3,80 | 5,07 | 6,34 | 7,60 | 8,87 | 10,14 | |
| 4,2 | 2,94 | 4,41 | 5,88 | 7,35 | 8,82 | 10,29 | 11,76 | |
| 4,5 | 3,38 | 5,06 | 6,75 | 8,44 | 10,13 | 11,81 | 13,50 | |
| 4,8 | 3,84 | 5,76 | 7,68 | 9,60 | 11,52 | 13,44 | 15,36 | |
| 5,1 | 4,34 | 6,50 | 8,67 | 10,84 | 13,01 | 15,17 | 17,34 | |
| 5,4 | 4,86 | 7,29 | 9,72 | 12,15 | 14,58 | 17,01 | 19,44 | |
| 5,7 | 5,42 | 8,12 | 10,83 | 13,54 | 16,25 | 18,95 | 21,66 | |
| 6,0 | 6,00 | 9,00 | 12,00 | 15,00 | 18,00 | 21,00 | 24,00 | |
| 6,3 | 6,62 | 9,92 | 13,23 | 16,54 | 19,85 | 23,15 | 26,46 | |
| 6,6 | 7,26 | 10,89 | 14,52 | 21,78 | 21,78 | 25,41 | 29,04 | |
Tab. 14.15.10 Obousměrně pnuté desky, poměr stran 1:1
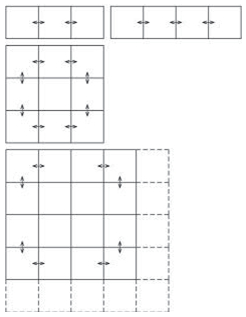 |
Rozpětí ℓ [m] | Hodnoty ohybových momentů M [kNm] | ||||||
| Návrhové zatížení qd [kN/m2] | ||||||||
| ≤ 4 | 6 | 8 | 10 | 12 | 14 | 16 | ||
| 3,0 | 3,00 | 4,50 | 6,00 | 7,50 | 9,00 | 10,50 | 12,00 | |
| 3,3 | 3,63 | 5,44 | 7,26 | 9,07 | 10,89 | 12,77 | 14,51 | |
| 3,6 | 4,32 | 6,48 | 8,64 | 10,80 | 12,95 | 15,11 | 17,27 | |
| 3,9 | 5,07 | 7,60 | 10,14 | 12,67 | 15,20 | 17,74 | 20,27 | |
| 4,2 | 5,88 | 8,82 | 11,76 | 14,69 | 17,63 | 20,57 | 23,51 | |
| 4,5 | 6,75 | 10,12 | 13,49 | 16,87 | 20,24 | 23,62 | 26,99 | |
| 4,8 | 7,68 | 11,52 | 15,35 | 19,19 | 15,20 | 26,87 | 30,71 | |
| 5,1 | 8,67 | 13,00 | 17,33 | 21,67 | 17,63 | 30,33 | 34,67 | |
| 5,4 | 9,72 | 14,57 | 19,43 | 24,29 | 20,24 | 34,01 | 38,86 | |
| 5,7 | 10,83 | 16,24 | 21,65 | 27,06 | 23,03 | 37,89 | 43,30 | |
| 6,0 | 12,00 | 17,99 | 23,99 | 29,99 | 35,99 | 41,98 | 47,98 | |
| 6,3 | 13,22 | 19,84 | 26,45 | 33,06 | 39,67 | 46,29 | 52,90 | |
| 6,6 | 14,51 | 21,77 | 29,03 | 36,29 | 43,54 | 50,80 | 58,06 | |
LITERATURA
[1] Rybicky, R. Faustformeln und Faustwerte für Konstruktionen in Hochbau. Werner-Verlag GmBH. Düsseldorf, 1997.
[2] Otron, A. The Way We Built Now, Form, Scale and Technique. Van Nostrand Reinhold (UK), 1988.
[3] Majdúch, D., Aringer, K. Oporné múry a pozemní steny. Alfa, Bratislava, 1982.
[4] Jeřábek, J. Dřevěné konstrukce. (skripta) SNTL, Praha, 1987.
[5] Kotyk, J. Střešní krytiny. SNTL, Praha, 1987.
[6] Voldřich, F., Volák, J., Kalousek, J.: Schodiště. Konstrukčně-architektonický detail. ČSVA, Praha, 1972.
[7] Hájek, V., Pavlis, J. Schodiště. SNTL, Praha,1988.
[8] Kalousek, J. Stavební konstrukce. ES ČVUT, Praha, 1989.
[9] Lorenz, K. Kovové a dřevěné konstrukce. ES ČVUT, Praha.
[10] Hořejší, J., Šafka, J. a kol. Statické tabulky. TP51 SNTL/ALFA, Praha, 1987.
[11] Lorenz, K., Kalousek, J., Vítová, M. Navrhování nosných konstrukcí Pomůcka pro architekty. Vydavatelství ČVUT, Praha, 1993.
[12] Juranka, T. Zakládání staveb. ES ČVUT, Praha, 1991.
Normy:
[13] ČSN EN 1990 (730002) Eurokód: Zásady navrhování konstrukcí, Eurocode: Basis of structural design, 2004.
[14] ČSN EN 1991-1-1 (730035) Eurokód 1: Zatížení konstrukcí – Část 1-1: Obecné zatížení – Objemové tíhy, vlastní tíha a užitná zatížení pozemních staveb, Eurocode 1: Actions on structures – Part 1-1: General actions – Densities, self-weight, imposed loads for buildings, 2004.
[15] ČSN EN 1992-1-1 ed. 2 (731201) Eurokód 2: Navrhování betonových konstrukcí – Část 1-1: Obecná pravidla a pravidla pro pozemní stavby, Eurocode 2: Design of concrete structures – Part 1-1: General reles and rules for buildings, 2011.
[16] ČSN EN 1993-1-1 (731401) Eurokód 3: Navrhování ocelových konstrukcí – Část 1-1: Obec- ná pravidla a pravidla pro pozemní stavby, Eurocode 3: Design of steel structures – Part 1-1: General rules and rules for buildings, 2006.
[17] ČSN EN 1995-1-1 (731701) Eurokód 5: Navrhování dřevěných konstrukcí – Část 1-1: Obec- ná pravidla – Společná pravidla a pravidla pro pozemní stavby, Eurocode 5: Design of timber structures – Part 1-1: General – Common rules and rules for buildings, 2006.
[18] ČSN EN 1996-1-1 (731101) Eurokód 6: Navrhování zděných konstrukcí – Část 1-1: Obecná pravidla pro vyztužené a nevyztužené konstrukce, Eurocode 6: Design of masonry structures – Part 1-1: General rules for reinforced and unreinforced masonry structures, 2013.
[19] ČSN EN 1996-2 (731101) Eurokód: 6 Navrhování zděných konstrukcí – Část 2: Volba ma- teriálů, konstruování a provádění zdiva, Eurocode 6: Design of masonry structures – Part 2: Design considerations, selection of materials and execution of masonry, 2007.
[20] ČSN 73 1201 Navrhování betonových konstrukcí pozemních staveb, Design of concrete structures of buildings, 2010.
[21] ČSN 42 5930 Štětovnice z konstrukčních ocelí válcovaných za tepla. Rozměry, Hot rolled sheet piles of structural steels. Dimensions, 1988.
[22] ČSN 42 5550 Tyče průřezu I z ocelí tříd 10 a 11 válcované za tepla. Rozměry, Hot-rolled i-sections of steel grades 10 and 11. Dimensions, (DIN 1025-1), 1970.
[23] ČSN 42 5553 Tyče průřezu IPE z konstrukčních ocelí válcované za tepla. Rozměry, (Hot rolled structural steel sections of ipe shape. Dimensions, DIN 1025-5) 1986.
[24] ČSN 42 5570 Tyče z ocelí tříd 10 a 11 válcované za tepla. Rozměry (DIN 1026-1), Hot-rolled U-sections of steel grades 10 and 11. Dimensions, 1970.
[25] ČSN 42 5572 Tyče průřezu UPE z konstrukčních ocelí válcované za tepla. Rozměry (DIN 1026-2), 1987.
[26] ČSN 42 5541 Tyče průřezu rovnoramenného L z konstrukčních ocelí válcované za tepla. Rozměry, Hot rolled equal armed L-section made of structural steels. Dimensions, 1976.
[27] ČSN EN 10210-2 Duté profily tvářené za tepla z nelegovaných a jemnozrnných konstrukčních ocelí – Část 2: Rozměry, úchylky a statické hodnoty, Hot finished structural hollow section of non-alloy and fine grain steels – Part 2: Tolerances, dimensions and sectional propertiesn, 2006.
[28] ČSN EN 10219-2 Svařované duté profily z konstrukčních nelegovaných a jemnozrnných ocelí, tvářené za studena – Část 2: Rozměry, úchylky a statické hodnoty, Cold formed welded structural hollow sections of non-alloy and fine grain steels – Part 2: Tolerances, dimensions and sectional properties, 2006.
[29] DIN 1025-2 Deutsche Institut für Normung – Warmgewalzte I – Träger – Teil 2: I – Träger, IPB – Reihe; Maße, Masse, statische Werte.
[30] DIN 1025-3 Deutsche Institut für Normung – Warmgewalzte I – Träger; Breite I – Träger, leichte Ausführung, IPBl – Reihe; Maße, Masse, statische Werte.
Internetové odkazy:
[31] www.betonstavby.cz (Betonové stavby group s.r.o. Klatovy)
[32] www.ytong.cz
[33] www.cznord.cz
[34] www.ferona.cz
[35] www.kondor.cz
[36] www.kovprof.cz
[37] www.wienerberger.cz
[38] www.heluz.cz