ČESKÁ KOMORA AUTORIZOVANÝCH INŽENÝRŮ A TECHNIKŮ ČINNÝCH VE VÝSTAVBĚ
Rada pro podporu rozvoje profese ČKAIT
Autoři: doc. Ing. Jan Masopust, CSc.
Stav: aktualizace 2021, vydání tiskem 2018
Anotace:
Pomůcka byla vydána tištěnou formou v roce 2018 a elektronickou formou byla zveřejněna v roce 2021 jako aktualizace. Je rozdělena do pěti kapitol: geotechnický průzkum, zásady navrhování základových konstrukcí – princip a ověření mezních stavů, plošné základy – druhy, hloubka založení, zatížení a návrh podle mezního stavu porušení s příkladem, návrh podle mezního stavu použitelnosti s příkladem, hlubinné základy, druhy pilot, trysková injektáž – definice, druhy, oblast použití, technologické zásady provádění, použití TI pro sanace a opravy staveb.
Obsah
ÚVOD
Předložená pomůcka vznikla v souvislosti s vydání ČSN EN 1997-1, Eurokód 7: navrhování geotechnických konstrukcí – Část 1: Obecné zásady, jež se od roku 2010 stala v České republice v podstatě jedinou platnou normou pro navrhování geotechnických konstrukcí. Tato norma má v rámci Eurokódů poněkud zvláštní postavení, které je dáno jednak značným rozsahem a rozmanitosti geotechnických konstrukcí, hlavně však tou skutečností, že tyto konstrukce jsou realizovaný v základové půdě, jež je většinou přírodním materiálem, jehož vlastnosti nejsou předepsány, jako je tomu u jiných stavebních materiálů, ale je třeba je nejprve zjistit, přičemž možnosti jejich stanovení jsou značně omezené. Při realizaci geotechnických konstrukcí dochází vždy k interakci se základovou půdou, přičemž možnosti předpovědi této interakce jsou rovněž omezené, a to nejen nejistotami ve vstupních údajích, týkajících se vlastností základové půdy, ale zejména vlivy technologickými, které lze jen obtížně předvídat, v nejlepším případě je lze kvalifikovat, jejich kvantifikace je však zcela mimo reálné možnosti.
Zakládání staveb, jakožto významná součást geotechniky, je obor, v němž se pokrok ubírá především dvěma cestami:
- hlubším a postupným poznáváním fyzikálních principů interakce ve vztahu základová půda – stavební konstrukce;
- vývojem technologií v závislosti na vývoji a výrobě stále dokonalejších strojních sestav a aplikací chemie do stavebnictví.
Tempo vývoje je určováno především druhým faktorem, který je veden obecnou snahou investorů a podnikatelů ve stavebnictví za rozvojem stále progresivnějších a produktivnějších výrobních postupů. První faktor v podstatě dohání technologický pokrok a je jím motivován.
Zakládání staveb se zabývá návrhem, stavbou a kontrolou základů staveb, popřípadě i jejich sanacemi a rekonstrukcemi. Další zájmovou oblastí jsou potom stavební jámy, které tvoří nedílnou součást základů staveb. Jejich budování bývá mnohdy náročnější než výstavba vlastních základů realizovaná ze dna těchto jam. Do oboru zakládání staveb náleží i metody zlepšování vlastností základové půdy a nejnověji též zemní konstrukce a environmentální stavby. Základy jsou nejspodnější částí stavby, jimiž stavba přichází do styku s nejpřirozenějším stavebním materiálem, kterým je základová půda, jež může být tvořena jak horninami a zeminami v přirozeném stavu, tak i uloženinami vzniklými částečně nebo i zcela lidskou činností. Jakákoliv stavba může postrádat libovolný stavební prvek či součást, přesto má vždy základy, kterými je spojena se základovou půdou. Teoretický základ nauky o zakládání staveb tvoří na jedné straně inženýrská geologie a hydrogeologie, mechanika zemin a skalních hornin, na druhé straně pak stavební mechanika a nauka o konstrukcích staveb. To však zdaleka nestačí, neboť nedílnou součástí návrhu základů je znalost o materiálech, tj. zejména o betonu a oceli a stanovení možností realizace těchto základů, což souvisí s otázkami technologickými. V neposlední řadě je třeba posoudit i ekonomii návrhu, neboť ta bývá mnohdy rozhodujícím kritériem při konečném výběru druhu a metody zakládání. Je tedy zřejmé, že při návrhu základů nelze postupovat deduktivní metodou, neboť mnohé souvislosti neumíme ani definovat, natož pak řešit. K cíli vede vesměs metoda induktivní, při níž se eliminují řešení nevhodná, a to na základě relativně jednoduchých a jasně formulovaných kritérií. Přesto, že v zakládání staveb vycházíme z moderních teoretických poznatků o fyzikálních principech chování základové půdy a stavební konstrukce, důležitou roli hraje i nadále zkušenost. Ta je ovšem nepřenosná a lze ji nabýt dlouhodobou praxí v oboru. Přesto, že zakládání staveb je komplexní disciplína využívající poznatky z mnoha vědních oborů a syntetizující je do výsledného návrhu vyhovujícího co nejlépe obecně platným, nebo i specifickým kritériím, vznikly v metodologii zakládání staveb v poslední době relativně dva vyhraněné směry, preferující tu, či onu oblast poznání. Tento trend je pochopitelný, neboť na straně jedné možnosti matematického modelování interakce základových konstrukcí se základovou půdou a na straně druhé výsledky polního i laboratorního zkoušení vlastností základových půd otevírají dříve netušené možnosti zkoumání základových konstrukcí a mění zakládání staveb, jakožto původně převážně empirickou disciplínu na vědu založenou na výpočtech. Nelze však opomenout tu skutečnost, že zakládání staveb řeší především praktické úlohy, tj. musí umožnit návrh a realizaci základů staveb na konkrétním staveništi, v reálném čase a s reálnými prostředky. Lze tedy pozorovat dva základní přístupy v tomto oboru:
- Metoda matematického modelování, kdy jsou preferovány skutečné geometrické tvary konstrukcí, vlastnosti základových půd získané běžnými i speciálními zkouškami a určité konstitutivní vztahy vyjadřující co nejlépe skutečné chování konstrukce, přičemž právě komplexností a složitostí konstitutivních vztahů se posuzuje kvalita modelu, neboť vlastní výpočetní metodou bývá vesměs metoda konečných prvků (MKP), jež sama o sobě nevytváří zásadní problém. Tím je potřeba získání vhodných vstupních parametrů výpočtu týkajících se zejména fyzikálních vlastností základových půd, přičemž instrumentace příslušných zkoušek je často obtížná nebo i nereálná. Příslušné parametry se získávají v lepším případě nepřímými zkouškami, ale častěji odborným odhadem, který se ovšem nesrovnává s „exaktním“ výpočtem, tudíž výsledek je přinejmenším nevyrovnaný a má spíše charakter parametrické studie. Druhým a zřejmě významnějším problémem tohoto přístupu je praktická nemožnost matematického modelování technologických efektů, které však bývají pro chování zvláště speciálních základů staveb rozhodující. Uvedený přístup, trpící popsanými nedostatky, je nicméně nezbytný pro mimořádně složité a rozsáhlé konstrukce.
- Inženýrský přístup, někdy nazývaný přístupem pragmatickým, při němž se preferují poznatky získané měřením na stavbách a využívá se při něm relativně jednoduchých teoretických předpokladů (např. teorie pružnosti aplikované na pružný poloprostor, jímž se modeluje základová půda). Snahou je potom nalézt významné souvislosti, které nejvíce ovlivní výsledné chování konstrukce za důsledného respektování technologických vlivů. Výsledkem je potom množství různých „koeficientů“, jimiž jsou jednoduché vzorce a rovnice doplňovány a „upřesňovány“. Ty ovšem budí nedůvěru a odmítání ze strany zastánců prvního přístupu a činí jej „nevědeckým“. Tento přístup je pro řešení úloh tvarově složitých nepřijatelný, neboť potřebná zjednodušení jsou již nepřípustná, nicméně výsledky získané touto metodikou pro běžné úlohy nejsou o nic horší než výsledky přístupu prvního.
Budoucnost oboru spočívá zřejmě v kritické syntéze obou přístupů, jejíž náznaky lze v posledním desetiletí vystopovat v příspěvcích na různých specializovaných mezinárodních konferencích, zvláště monotematických.
Předložená pomůcka je součástí řady pomůcek Profesis, kterou vydává ČKAIT s cílem pomoci autorizovaným inženýrům a technikům ve výstavbě v každodenní odborné práci. Vydání této pomůcky je však komplikováno tou skutečností, že zatímco evropská norma ČSN EN 1997-1 platí v ČR od 1. 4. 2010, národní aplikační dokument (NAD), jež může do příslušných striktně vyjmenovaných článků této normy zavést tzv. národní zkušenosti, u nás dosud vydán nebyl, zatímco naprostá většina evropských zemí tuto možnost dokonale využila. Problémy kolem NAD se v poslední době v důsledku nedosažené shody mezi zpracovatelem a posuzovatelem natolik zkomplikovaly, že vydání NAD se zřejmě nedočkáme. Jistým východiskem z tohoto stavu je vydání české normy ČSN 73 1004: Navrhování základových konstrukcí – Stanovení požadavků pro výpočetní metody v červenci 2020.
Autor bude s vděčností přijímat veškeré podněty a příspěvky týkající se předložených výpočtů tak, aby mohly být popřípadě zapracovány do příštích a inovovaných vydání.
1 GEOTECNICKÝ PRŮZKUM
Geotechnický (nebo též inženýrskogeologický) průzkum musí poskytnout dostatečné údaje o základové půdě a podzemní vodě na staveništi a v jeho okolí pro sestavení prostorového modelu geologických a hydrogeologických poměrů na staveništi a pro řádný a pravdivý popis základních vlastností základové půdy a pro věrohodné stanovení charakteristických velikostí parametrů základové půdy, jež buď samy, nebo ve formě hodnot návrhových vstupují do příslušných geotechnických výpočtů.
Geotechnický průzkum na konkrétním staveništi vychází z projektu průzkumných prací, který by měl plánovat technické práce průzkumu, rozsah a četnost zkoušek základových půd, a to zejména na základě důkladné znalosti účelu, pro nějž se provádí. Velmi často objednává tento průzkum stavebník (investor), a to v době, kdy nemá stavební záměr ujasněn a není schopen jasně formulovat problematiku, na níž by měl průzkum dát dostatečnou odpověď. V tomto případě může mít průzkum charakter tzv. předběžného s tím, že je třeba počítat s následným průzkumem podrobným. Jeho provádění je vždy vhodné konzultovat s projektantem geotechnických konstrukcí, který je schopen příslušné otázky jasně formulovat a zadat, neboť právě ten je hlavním uživatelem výsledků průzkumu a pro něj představuje jeho Závěrečná zpráva jeden z rozhodujících podkladů pro návrh geotechnické konstrukce. Často s ohledem na složitost geotechnických poměrů na staveništi bývá nutné realizovat doplňující geotechnický průzkum, jenž má za úkol vesměs upřesnit a vyjasnit některé speciální problémy.
1.1 CÍLE GEOTECHNICKÉHO PRŮZKUMU
Hlavním cílem geotechnického průzkumu je poskytnutí takových údajů o geologických a hydrogeologických poměrech staveniště a jeho okolí, jakož i o vlastnostech základové půdy, jež umožní technicky správný, ekonomicky přijatelný a časově i technologicky proveditelný návrh geotechnické konstrukce za výrazné redukce geotechnických rizik spojených s tímto návrhem i jeho realizací. Konkrétní cíle geotechnického průzkumu se mohou v podrobnostech lišit, a to jak s ohledem na jeho příslušnou etapu, tak na druh a složitost geotechnické konstrukce. Geotechnický průzkum je třeba vždy chápat jakožto jeden z nejdůležitějších podkladů, podle něhož se řídí návrh a provádění geotechnické konstrukce, nikoliv jako cíl jistého snažení a tomu je třeba jej přizpůsobit.
1.2 ETAPOVITOST GEOTECHNICKÉHO PRŮZKUMU
Při provádění geotechnického průzkumu se dodržují zásady etapovitosti, a to jednak s přihlédnutím k jednotlivým fázím přípravy stavby a její dokumentace (studie proveditelnosti, územní řízení, DSP, RDS), jednak z hlediska principu postupného zvyšování úrovně znalostí o daném geotechnickém prostředí a soustředění se na to, co je důležité.
Jednotlivé etapy geotechnického průzkumu jsou:
- předběžný průzkum;
- podrobný průzkum;
- doplňkový průzkum a sledování v průběhu realizace stavby.
Pro sanace a rekonstrukce stávajících stavebních a geotechnických konstrukcí se provádí obyčejně jednostupňový průzkum, jež má vesměs charakter průzkumu podrobného, popř. i doplňkového.
Předběžný průzkum má vždy zahrnovat důkladnou prohlídku staveniště a jeho okolí, studium archivních materiálů (rešerše např. z Geofondu) a seznámení se stavebním záměrem. Jen zcela výjimečně se provádějí odkryvné terénní práce, nicméně nepřímé průzkumné metody (geofyzikální měření) jsou relativně časté. Výsledkem předběžného průzkumu má být umožnění:
- stanovení obecné vhodnosti staveniště;
- srovnání vhodnosti několika stavenišť, pokud to přichází v úvahu;
- odhadu změn a dopadů na staveniště a jeho okolí, jež mohou být zapříčiněny plánovanými pracemi (výstavbou);
- naplánování podrobného průzkumu, popř. i doplňujícího průzkumu, jež budou následovat;
- určení zemníků, pokud to přichází v úvahu.
Podrobný průzkum zahrnuje již vesměs veškeré práce potřebné k získání co nejúplnějších poznatků o geotechnických poměrech na staveništi. Je zpravidla podkladem pro projekt DSP a musí vždy správně odhalit nejdůležitější geotechnická rizika příslušného staveniště s ohledem na druh a rozsah plánované stavby. Podrobný průzkum tedy zahrnuje:
- využití poznatků z průzkumu předchozího (předběžného);
- dostatečný rozsah odkryvných technických prací (jádrových vrtů vč. odběru vzorků zemin i podzemní vody, popř. sond kopaných);
- polních zkoušek penetračních, popř. pressiometrických vč. příslušných měření;
- geofyzikální měření, pokud jím lze vyjasnit problematiku předchozími zkouškami neřešitelnou;
- hydrogeologické zkoušky, pokud jsou jejich výsledky nezbytné a mají konkrétní uplatnění;
- laboratorní zkoušky na odebraných vzorcích zemin a hornin v takovém rozsahu, který je nutný pro správné zatřídění vrstev základové půdy a jsou-li přímo využitelné jakožto podklad pro stanovení vstupů pro geotechnické výpočty.
Podrobný průzkum musí podat informace o následujících geotechnických aspektech:
- geologické stratigrafii do potřebné hloubky;
- přírodních nebo umělých podzemních prostorách či kavernách;
- degradaci hornin, zemin nebo sypaniny;
- zlomům, puklinám a ostatním plochám diskontinuit;
- možnosti časového přetváření zemního a horninového prostředí;
- bobtnavým a prosedavým zeminám či horninám;
- přítomnosti odpadů a umělých zemních struktur;
- hydrogeologickým poměrům na staveništi a ev. vlivu výstavby na jejich změnu.
Doplňkový průzkum, který není uveden v ČSN EN 1997-1, bývá realizován v těch případech, kdy při plánovaných pracích průzkumu podrobného dojde k takové situaci, že vzniklý geotechnický problém nelze uspokojivě objasnit, nebo v případech výrazné změny ve tvaru, statickém působení, či umístění stavby. Doplňkový průzkum bývá v těchto případech podkladem pro RDS.
Vlastní geotechnický průzkum vychází tedy vždy z dosavadní prozkoumanosti staveniště, a to formou geotechnické rešerše ze stávajících podkladů, získaných nejčastěji v Geofondu, což je účelová organizace zřízená Českou geologickou službou spadající pod Ministerstvo životního prostředí. Tato organizace soustřeďuje již po několik desetiletí výsledky zejména vrtného průzkumu prováděného pro různé účely na našem území, eviduje je a vhodným způsobem je poskytuje dalším zájemcům. Dále jsou plánována průzkumná díla, což jsou zejména tzv. jádrové vrty, méně často kopané sondy. Tato průzkumná díla musí být nejen dostatečně četná s ohledem na rozsah plánovaného objektu, ale musí zejména zasahovat do dostatečné hloubky tak, aby popis a vlastnosti základové půdy byly známy v celém rozsahu její interakce s konstrukcí. V této souvislosti lze upozornit na pomůcku vydanou v rámci Profesis TP 1.9.8. Revizní protokol pro ověření dostatečnosti geotechnického průzkumu, 1. vydání (2017).
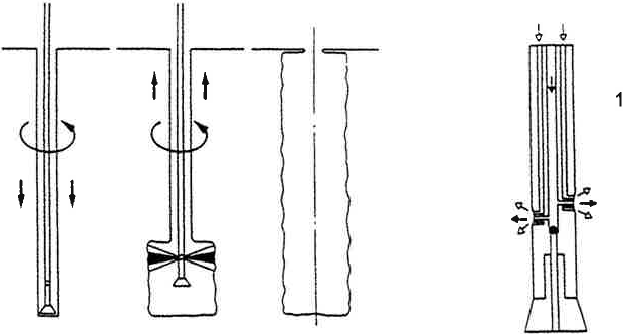
V rámci geotechnického průzkumu jsou dále plánovány zkoušky základových půd, a to jak laboratorní, pro které je třeba odebrat příslušné vzorky (porušené i tzv. neporušené) a dále zkoušky polní, k nimž v našich podmínkách řadíme např. sondy penetrační, které jsou jednak dynamické, jednak statické. Principem dynamického sondování je zarážení jistého hrotu na konci soutyčí určitými dynamickými rázy, přičemž se určuje počet úderů potřebných na zaražení o 200 mm. Někdy se měří i velikost kroutícího momentu potřebného k pootočení soutyčí v jisté hloubce; jde však pouze o údaj informativní. Na základě počtu úderů lze usuzovat na některé globální vlastnosti základové půdy, tzn. v případě zemin jemnozrnných na konzistenci a v případě zemin hrubozrnných na ulehlost. V této souvislosti je třeba upozornit na tu skutečnost, že zejména v českých geotechnických podmínkách, které se vyznačují značnou rozmanitostí, zůstávající základními průzkumnými metodami jádrové vrty a dynamická penetrace je zkouška doprovodná, upřesňující ovšem pouze v případě, že litologický profil je znám. Základem statické penetrace je kontinuální zatlačování penetrační sondy skládající se ze speciálního hrotu a sady penetračních trubek, a to konstantní rychlostí kolem 20 mm·s-1. Odpor, který základová půda klade vnikání penetrační sondy, je pak rovněž jistým měřítkem kvality a vlastností zeminy. Tento totální odpor Qt se skládá z odporu na kuželovém hrotu qst a z lokálního tření na plášti sondy fs. Opět je nutné zdůraznit, že výsledky statického penetračního sondování by se měly vždy opírat o znalost geologických poměrů na lokalitě, tj. zejména o znalost litologického profilu základové půdy.
Závěrečná zpráva o geotechnickém (inženýrskogeologickém) průzkumu, jež má obvykle část textovou a přílohy, má zhodnotit výsledky všech provedených průzkumných prací a odpovědět na všechny otázky týkající se geotechnických podmínek staveniště. V rozhodující části, týkající se přírodních poměrů zájmové oblasti a inženýrsko-geologických podmínek výstavby, je třeba uvést:
- geomorfologickou charakteristiku zájmové oblasti a stratigraficko-litologickou charakteristiku horninového prostředí, a to obvykle od nejnižší jednotky (zpravidla od předkvartérního horninového podloží);
- veškeré event. anomálie, které byly průzkumem zastiženy a ověřeny;
- hydrogeologické poměry na lokalitě (charakteristiku a mocnosti zjištěných zvodní, typ propustnosti, úrovně naražené a ustálené hladiny podzemní vody a její možné kolísání);
- historii vývoje zájmové oblasti ve smyslu antropogenních vlivů.
Na základě těchto výsledků by měl být sestaven inženýrsko-geologický model zájmového území s jasným pojmenováním a rozlišením tzv. geotechnických typů základové půdy a sestavení databáze tzv. odvozených parametrů základové půdy.
1.3 ZRÁVA O GEOTECHNICKÉM PRŮZKUMU
Každá etapa geotechnického průzkumu je uzavřena závěrečnou zprávou, jež sestává:
- z prezentace všech dostupných geotechnických informací vč. geologických jevů a relevantních údajů;
- z popisu stavby (díla), pro které byl průzkum (jeho příslušná etapa) prováděn vč. uvedení jeho konstrukčního, statického či dynamického působení;
- z vyhodnocení geotechnických informací získaných příslušným průzkumem s přihlédnutím k informacím předcházejícím (i archivním) a s uvedením předpokladů, na základě kterých se interpretovaly výsledky zkoušek.
Prezentace geotechnických informací sestává zejména:
- z účelu a rozsahu geotechnického průzkumu (jeho příslušné etapy);
- z obecného popisu morfologie staveniště vč. jejího známého či zjištěného vývoje;
- z geologie staveniště řešené nejlépe v prostorovém 3D modelu, popř. v jednotlivých dostatečně vypovídajících řezech vedených do potřebné hloubky;
- z popisu všech zjištěných, popř. pravděpodobných geologických anomálií (zlomech, tektonických pásmech, dutinách či kavernách atd.) s event. doporučením jejich následného zkoumání v rámci doplňkového průzkumu;
- z hydrogeologických poměrů na staveništi vč. prognózy kolísání hladiny podzemní vody;
- z údajů o agresivitě podzemní vody;
- z přehledu terénních a laboratorních prací;
- z přehledu odvozených hodnot geotechnických parametrů.
Závěrečná zpráva musí obsahovat souhrn tzv. odvozených vlastností základových půd (kap. 3), které jsou základním podkladem pro stanovení charakteristických hodnot geotechnických parametrů základových půd, což je ovšem práce a zodpovědnost projektanta geotechnické konstrukce. Nelze se do budoucna spokojit s takovým stavem, kdy v rámci jisté etapy geotechnického průzkumu uvádí jeho zpracovatel již přímo charakteristické velikosti parametrů základové půdy, za které považuje tzv. normové vlastnosti většinou opsané z bývalé normy ČSN 73 1001: Základová půda pod plošnými základy. Jde o jasné nepochopení základních principů Eurokódu 7, který jednoznačně stanovuje zodpovědnost v této oblasti. Rovněž tak v závěrečných zprávách často uváděná doporučení k metodě zakládání objektu a popř. i příslušné geotechnické výpočty, týkající se únosnosti základových prvků, popř. jejich sedání apod. lze chápat pouze jako informativní.
1.4 ZÁKLADOVÁ PŮDA
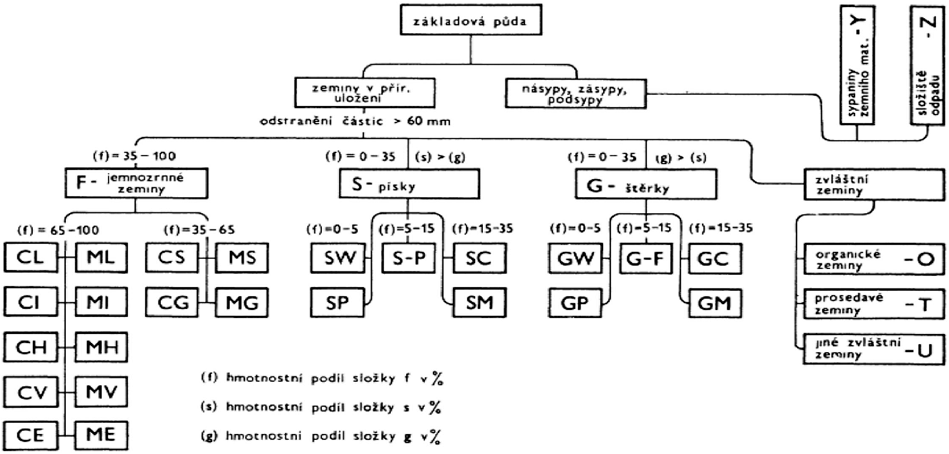
Základovou půdou se nazývá prostředí obklopující základy staveb. Tvoří ji zeminy v přirozeném uložení, jež jsou obyčejně produkty různého zvětrávání hornin a dále horniny v různém stupni porušení. Za základovou půdu se obyčejně nepokládají materiály vzniklé lidskou činností, jako jsou různé navážky, zásypy, skládky apod., pokud vlastnosti těchto materiálů nejsou zlepšeny speciálními metodami tak, aby byly pro zakládání přijatelné. Základové půdy se třídí podle různých kritérií, nicméně jeden z nejlepších systémů třídění základových půd je součástí bývalé ČSN 73 1001: Základová půda pod plošnými základy z roku 19871, obr. 1., jenž byl sestaven pro základovou půdu tvořenou zeminami. Ty se třídí zejména na základě granulometrického rozboru, kde kritériem je velikost zrn tvořících pevnou součást zemin. Podle velikosti těchto částic se rozlišují:
1 Přesto, že tato norma byla v souvislosti s definitivní platností ČSN EN 1997-1 zrušena, bude zejména její část týkající se klasifikace základových půd jistě i nadále využívána projektanty geotechnických konstrukcí
a) velmi hrubé částice
aa) balvanitá složka
ab) kamenitá složka
(b)
(cb)
> 200 mm
200 až 600 mm
b) hrubé částice
ba) štěrková složka
bb) písčitá složka
(g)
(s)
60 až 2 mm
2 až 0,06 mm
c) jemné částice
ca) prachová složka (hlína, silt)
cb) jílová složka
(f)
(m)
(c)
0,06 až 0,002 mm
< 0,002 mm
Velmi hrubé částice se obyčejně z dalšího třídění vylučují a jejich přítomnost se popisuje jako příměs, pokud (b + cb) < 20 % celkové hmotnosti zeminy, v případě většího podílu (b + cb) se popisují jako zeminy kamenité, popř. balvanité a jejich vlastnosti se popisují individuálně. Částice menší než 60 mm se třídí na základě trojúhelníkového
diagramu podle obr. 2. K podrobnému rozlišení jemnozrnných zemin, ale i zemin s podílem částic f > 15 % (g + s + f) slouží tzv. plasticita zemin, která se charakterizuje podle polohy v diagramu na obr. 3 za pomoci konzistenčních mezí wL a wp, resp. podle čísla plasticity Ip = wL – wp, přičemž základním ukazatelem je vlhkost, jež patří mezi základní laboratorní zkoušky zemin a lze ji stanovit i na porušených vzorcích. Tento diagram se používá zejména pro podrobné rozlišení jemnozrnných zemin, pro rozlišení plasticity, jež se dělí na nízkou (L), střední (I), vysokou (H), velmi vysokou (V) a extrémně vysokou (E) a dále pro stanovení jejich konzistence, pro níž se definuje stupeň konzistence IC = (wL – w) / Ip (tab. 1). Jemnozrnné zeminy (F) se dále třídí na 8 tříd (tab. 4), písky (S) a štěrky (G) pak na 5 tříd (tab. 2 a 3).
Tab. 1 Konzistence zemin
| Konzistence | Stupeň konzistence IC | Chování zeminy |
| kašovitá | < 0,05 | při sevření se protlačuje mezi prsty |
| měkká | 0,05–0,50 | dá se lehce hníst v prstech |
| tuhá pevná |
0,50–1,00 > 1,00 |
hněte se obtížně v prstech lze do ní vtisknout nehet |
| tvrdá | – | vyschlá, při úderu kladiva se drolí |
Horniny se dělí do 6 tříd (tab. 5) na základě velikosti prosté tlakové pevnosti σc, jež se dá stanovit i na vzorcích nepravidelného tvaru. Třídám R1 až R3 odpovídají skalní horniny, třídám R4 až R6 pak poloskalní horniny, přičemž třída R6 tvoří přechod mezi poloskalní horninou a zeminou vesměs pevné až tvrdé konzistence. Pro zatřídění hornin podle této tabulky jsou tedy nezbytné výsledky zkoušek prosté tlakové pevnosti σc hornin, neboť zatřídění pouze na základě subjektivního hodnocení je nedostatečné a může vést k chybám.
Obr. 1 Schéma klasifikačního systému základových půd tvořených zeminami
Obr. 2 Klasifikační diagram zemin s částicemi < 60 mm
Obr. 3 Diagram plasticity jemnozrnných zemin
Tab. 2 Třídění písčitých zemin
| Třída | Název | Symbol | Kvalitativní znaky |
| S1 | písek dobře zrněný | SW | f < 5 % (g + s + f) |
| S2 | písek špatně zrněný | SP | f < 5 % (g + s + f) a není SW |
| S3 | písek s příměsí jemnozrnné zeminy | S–F | f = 5 – 15 % (g + s + f) |
| S4 | písek hlinitý | SM | f = 15 – 35 % (g + s + f) a pod čarou A |
| S5 | písek jílovitý | SC | f = 15 – 35 % (g + s + f) a nad čarou A |
Tab. 3 Třídění štěrkovitých zemin
| Třída | Název | Symbol | Kvalitativní znaky |
| G1 | štěrk dobře zrněný | GW | f < 5 % (g + s + f) |
| G2 | štěrk špatně zrněný | GP | f < 5 % (g + s + f) a není GW |
| G3 | štěrk s příměsí jemnozrnné zeminy | G–F | f = 5 – 15 % (g + s + f) |
| G4 | štěrk hlinitý | GM | f = 15 – 35 % (g + s + f) a pod čarou A |
| G5 | štěrk jílovitý | GC | f = 15 – 35 % (g + s + f) a nad čarou A |
Tab. 4 Třídění jemnozrnných zemin
| Třída | Název | Symbol | Kvalitativní znaky |
| F1 | hlína štěrkovitá | MG | f = 35 – 65 % (g + s + f) a g > s a pod čarou A |
| F2 | jíl štěrkovitý | CG | f = 35 – 65 % (g + s + f) a g > s a nad čarou A |
| F3 | hlína písčitá | MS | f = 35 – 65 % (g + s + f) a s > g a pod čarou A |
| F4 | jíl písčitý | CS | f = 35 – 65 % (g + s + f) a s > g a nad čarou A |
| F5 | hlína s nízkou a střední plasticitou | ML, MI | f > 65 % (g + s + f) a wL < 50 % a pod čarou A |
| F6 | jíl s nízkou a střední plasticitou | CL, CI | f > 65 % (g + s + f) a wL < 50 % a nad čarou A |
| F7 | hlína s plasticitou vysokou, velmi a extrémně | MH, MV, ME | f > 65 % (g + s + f) a wL > 50 % a pod čarou A |
| F8 | jíl s plasticitou vysokou, velmi a extrémně | CH, CV, CE | f > 65 % (g + s + f) a wL > 50 % a nad čarou A |
Tab. 5 Třídění hornin na základě pevnosti
| Třída | σc [MPa] | Pevnost | Charakteristika | Příklady |
| R1 | > 150 | velmi vysoká | kladívkem lze těžko otloukat | zdravé vyvřeliny a přeměněné horniny |
| R2 | 50–150 | vysoká | kladívkem lze těžko rozbíjet | zdravé sedimenty a navětralé R1 |
| R3 | 15–50 | střední | kladívkem lze lehce rozbíjet | zdravé měkké sedimenty a navětralé R2 |
| R4 | 5–15 | nízká | lze škrábat nožem, ne nehtem | zdravé slabě zpevněné sedimenty |
| R5 | 1,5–5 | velmí nízká | lze rozdrobit rukou | zdravé velmi slabě zpevněné sedimenty |
| R6 | 0,5–1,5 | extrémně nízká | lze škrábat nehtem | zcela zvětralé sedimenty |
1.5 PŘEHLED HLAVNÍCH VLASTNOSTÍ ZÁKLADOVÝCH PŮD
Vlastnostmi základových půd se zabývá mechanika zemin, která je součástí mechaniky partikulárních látek a která představuje jeden z nejdůležitějších podkladů pro zakládání staveb. Zeminy tvoří trojfázové prostředí, v němž se uplatňuje fáze pevná – částice (zrna) zeminy, jež se navzájem více či méně dotýkají, fáze kapalná – voda a plynná – vzduch, jež tvoří výplň pórů, tj. prostor mezi zrny. Mechanické vlastnosti zemin jsou určovány podílem jednotlivých fází a (při určitém zjednodušení) možností pohybu pevných částic v rámci celku v případě určitého stavu napjatosti. Vlastnosti zeminy stejného složení (z hlediska geologického) mohou být tedy různé, studují-li se na tzv. vzorcích neporušených, tj. v přirozeném stavu, jejichž odběr je však ve skutečnosti málo reálný, nebo na vzorcích porušených (např. vrtáním, odběrem apod.). Jelikož zeminy a horniny představují ve srovnání s jinými stavebními materiály (ocel, beton, dřevo) silně nehomogenní a anizotropní prostředí, má na jejich mechanické vlastnosti vliv i velikost studovaného vzorku.
Ze vzorků porušených lze získat základní, tzv. popisné či indexové vlastnosti zemin, jako jsou velikost, tvar a složení zrn, hustota (měrná hmotnost) a vlhkost. Ostatní potřebné vlastnosti je třeba vyšetřovat na vzorcích neporušených, resp. v laboratoři připravených a homogenizovaných, aby co nejvíce odpovídaly neporušenému stavu (in situ). Kromě v předchozí kapitole popsané zrnitosti lze tedy na porušených vzorcích stanovit hustotu pevných částic ρs jako:
\begin{gathered}
\rho_\text{s}=\frac{G_\text{s}}{V_\text{s}}\space[\text{g}\cdot\text{cm}^{-3}]
\end{gathered}(1)
kde je:
Gs … hmotnost pevných částic;
Vs … objem pevných částic.
Objemová tíha zeminy v přirozeném uložení je pak dána:
\begin{gathered}
\gamma=\frac{G_\text{z}}{V_\text{z}}\space[\text{kN}\cdot\text{m}^{-3}]
\end{gathered}(2)
kde je:
Gz … tíha zeminy v přirozeném uložení;
Vz … objem zeminy v přirozeném uložení.
Objemová tíha suché zeminy (vysušené na 105 °C) je:
\begin{gathered}
\gamma_\text{d}=\frac{G_\text{s}}{V_\text{z}}\space[\text{kN}\cdot\text{m}^{-3}]
\end{gathered}(3)
přičemž objem pórů Vp = Vz – Vs, kterým lze definovat buď pórovitost
\begin{gathered}
n=\frac{V_\text{p}}{V_\text{z}}\cdot100\space\%=\frac{(\gamma_\text{s}-\gamma_\text{d})}{\gamma_\text{s}}\cdot100\space[\%]
\end{gathered}(4)
nebo číslo pórovitosti
\begin{gathered}
e=\frac{V_\text{p}}{V_\text{s}}=\frac{(\gamma_\text{s}-\gamma_\text{d})}{\gamma_\text{d}}
\end{gathered}(5)
Vzájemné vztahy mezi pórovitostí n a číslem pórovitosti e jsou pak:
\begin{gathered}
e=\frac{n}{(100-n)},&\text{resp.}&n=\frac{e}{(1+e)}\cdot100\space[\%]
\end{gathered}(6)
Číslo pórovitosti hrubozrnné zeminy je tím větší, čím je zemina kypřejší, tedy pro zeminu existuje jakési smluvní nejkypřejší uložení s číslem pórovitosti emax a po intenzivním (opět smluvním) zhutnění, při kterém se zrna ještě nedrtí pak naopak emin. Na základě těchto velikostí se definuje stupeň relativní ulehlosti hrubozrnné zeminy:
\begin{gathered}
I_\text{D}=\frac{(e_\text{max}-e)}{(e_\text{max}-e_\text{min})}
\end{gathered}(7)
a ulehlost se pojmenuje podle tab. 6.
Tab. 6 Ulehlost hrubozrnných zemin
| ID | 0–0,33 | 0,33–0,67 | 0,67–0,90 |
| ulehlost | kyprá | středně ulehlá | ulehlá |
Vlhkost zeminy v hmotnostních procentech, která je důležitým ukazatelem zejména pro zeminy jemnozrnné, je definována:
\begin{gathered}
w=\frac{G_\text{v}}{G_\text{s}}\cdot100\space\%=\frac{(\gamma-\gamma_\text{d})}{\gamma}\cdot100\space[\%]
\end{gathered}(8)
kde je:
Gv … tíha vody.
Na základě vlhkosti se určuje konzistence jemnozrnné zeminy, a to pomocí tzv. konzistenčních mezí, což jsou smluvně stanovené velikosti vlhkosti:
- wL – mez tekutosti na přechodu z konzistence kašovité do měkké;
- wP – mez plasticity na přechodu z konzistence tuhé do pevné;
- ws – mez smrštění na přechodu z konzistence pevné do tvrdé.
Interval vlhkostí, v němž zůstává zemina v plastickém stavu, je charakterizován číslem plasticity:
\begin{gathered}
I_\text{p}=w_\text{L}-w_\text{p}
\end{gathered}(9)
Konzistenci zeminy lze slovně vyjádřit (tab. 7) pomocí stupně konzistence IC, který je definován:
\begin{gathered}
I_\text{C}=\frac{(w_\text{L}-w)}{I_\text{p}}
\end{gathered}(10)
Tab. 7 Konzistence jemnozrnných zemin
| Konzistence | Stupeň konzistence IC | Chování zeminy |
| kašovitá | < 0,05 | při sevření se protlačuje mezi prsty |
| měkká | 0,05–0,50 | dá se lehce hníst v prstech |
| tuhá | 0,50–1,00 | obtížně se hněte v prstech |
| pevná | > 1,00 | lze do ní vtisknout nehet |
| tvrdá | – | vyschlá, při úderu kladiva se drolí |
Hlavní mechanické vlastnosti zemin jsou pevnost (smyková), vlastnosti deformační a propustnost. Zeminy se porušují smykem, přičemž se obecně přijímá tzv. Mohr-Coulombova hypotéza porušení, pro niž platí, obr. 4:
\begin{gathered}
\tau_\text{f}=\sigma_\text{f}\cdot\tg\varphi+c
\end{gathered}(11)
kde je:
τf … tangenciální napětí na smykové ploše (vnitřní odpor zeminy);
σf … normálové napětí působící kolmo na smykovou plochu porušení;
φ … úhel vnitřního tření zeminy;
c … soudržnost (koheze) zeminy.
Smykovou pevností zemin rozumíme obyčejně maximální, tzv. vrcholovou pevnost τf, při níž dochází k porušení, tj. k vytvoření smykové plochy. Po jejím dosažení se při dalším smyku odpor zeminy obyčejně snižuje a ustálí se na tzv. zbytkové neboli reziduální pevnosti τr, obr. 5.
V případě hrubozrnných zemin je zdrojem smykové pevnosti tření mezi zrny a pevnost je reprezentována úhlem vnitřního tření φ, obr. 6a). U zemin jemnozrnných je zdrojem smykové pevnosti vnitřní tření mezi zrny reprezentované úhlem vnitřního tření φ a dále soudržnost (koheze) c, jež tkví ve vzájemných vazbách zrn zeminy s vodou na molekulární úrovni a vyjadřuje se jako smyková pevnost při normálovém napětí σ1 = 0, obr. 6c). Pro nasycené jíly je pevnost charakterizována pouze totální soudržností cu, příslušný úhel vnitřního tření φu = 0, obr. 6b).
Obr. 4 Mohr-Coulombovo zobrazení porušení zemin
Obr. 5 Přetvárný diagram pro σ3 = konst.
Obr. 6 Mohr-Coulombova teorie porušení, a) – zeminy jemnozrnné, normálně konsolidované; b) – zeminy jemnozrnné plně saturované; c) – zeminy hrubozrnné
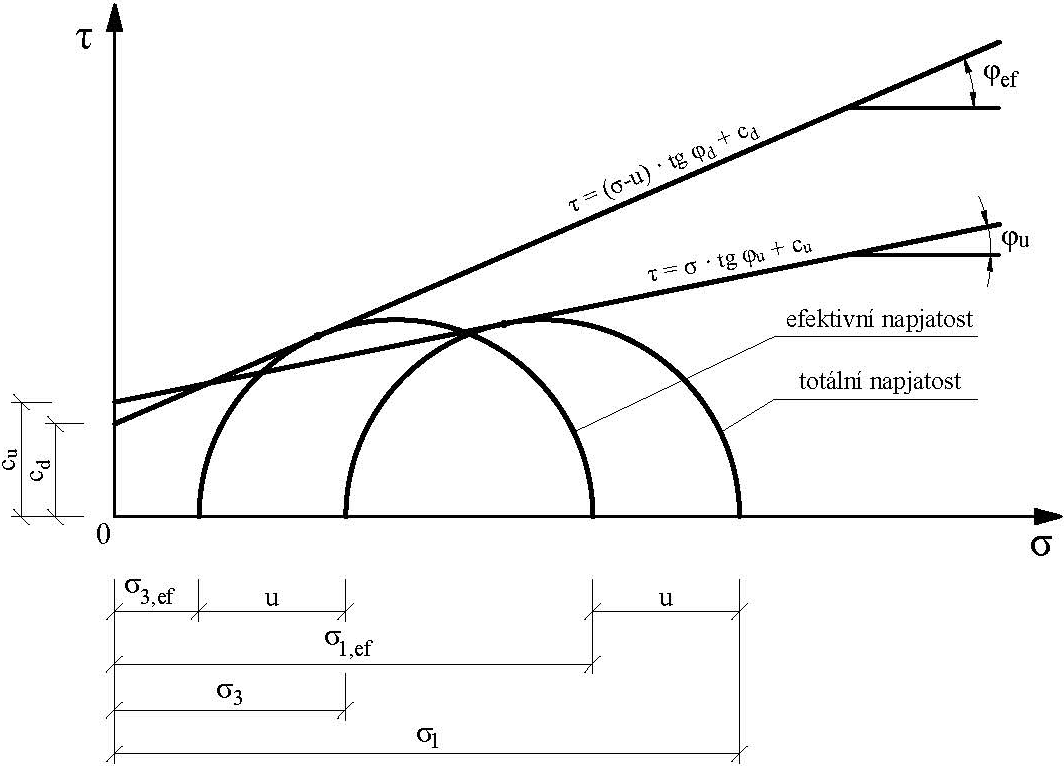
Parametry smykové pevnosti zemin se stanovují v laboratoři na tzv. neporušených vzorcích, a to buď v klasickém (krabicovém) smykovém přístroji, nebo v tzv. triaxiálním přístroji, kde však platí σ2 = σ3 a volí se obyčejně následující okrajové podmínky, při nichž se stanoví, obr. 7:
- a) pevnost zemin v totálních parametrech φu, cu, kdy se během zkoušky nemění objem vzorku zeminy ani obsah vody v pórech, mění se pouze tvar vzorku a zemina se porušuje v nekonsolidovaném stavu; výsledné parametry platí tedy pouze pro danou ulehlost a vlhkost zeminy, přičemž jejich použití je třeba tomuto stavu přizpůsobit; příslušné zkoušky se nazývají nekonsolidované, neodvodněné (UU);
- b) pevnost zemin v efektivních parametrech φef, cef, kdy ke smyku dochází až po úplné primární konsolidaci vzorku zeminy, když zatížení přenášejí pouze zrna a neutrální napětí je rovno nule; tyto parametry se využívají při návrhu sklonu svahů v zářezech, při výpočtu zemních tlaků konsolidované zeminy apod. a stanovují z konsolidovaných odvodněných zkoušek (CD) nebo ze zkoušek konsolidovaných neodvodněných s měřením pórového tlaku u (CAUP).
Obr. 7 Totální a efektivní parametry pevnosti
Základními parametry, vyjadřujícími deformaci základových půd, jsou hodnoty modulů přetvárnosti Edef a oedometrického modulu přetvárnosti Eoed. Při zatížení zeminy na velké ploše dochází ke stlačování zeminy zmenšením objemu jejich pórů, přičemž boční přetvoření εx = εy = 0. Modelem je tzv. oedometrická zkouška v přístroji oedometru, jehož princip je na obr. 8.
Obr. 8 Princip oedometru
Deformace zeminy probíhá v čase, přičemž se uvažuje pouze tzv. primární konsolidace, kdy dochází k vytlačování vody z pórů zeminy, tedy k vymizení pórových tlaků. V případě, že u = 0, je primární konsolidace ukončena a při zvětšování napětí dochází již k deformaci (drcení) zrn, tedy ke konsolidaci sekundární, obr. 9.
Obr. 9 Princip primární a sekundární konsolidace
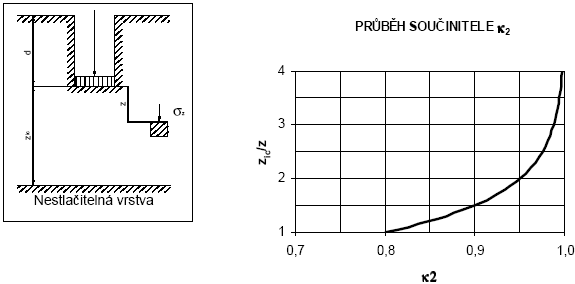
Oedometrický modul přetvárnosti se stanovuje pro příslušné intervaly zatížení (obr. 10):
\begin{gathered}
E_\text{def}=\Delta\sigma_\text{i}\cdot d\cdot(1-\nu^2)\cdot\frac{\alpha}{\Delta s_\text{i}}
\end{gathered}(13)
kde je:
d … průměr zatěžovací desky (většinou 356 mm – plocha desky 1 000 cm2),
ν … Poissonovo číslo zeminy;
Δsi … přírůstek sedání desky způsobený přírůstkem napětí Δσi po ukončení konsolidace;
α … součinitel závislý na tvaru a tuhosti desky (pro kruhovou a dokonale tuhou desku α = 0,79).
Mezi oedometrickým modulem přetvárnosti Eoed a modulem přetvárnosti (deformace) Edef je v případě předpokladu pružného poloprostoru následující vztah:
\begin{gathered}
E_\text{oed}=\frac{E_\text{def}}{\beta};&&\beta=1-2\cdot\frac{\nu^2}{(1-\nu)}
\end{gathered}(14)
Obr. 10 Stanovení velikosti edometrického modulu přetvárnosti Eoed
2 ZÁSADY NAVRHOVÁNÍ ZÁKLADOVÝCH KONSTRUKCÍ
2.1 PRINCIP MEZNÍCH STAVŮ
Zakládání staveb vychází z mezních stavů základové půdy a stavební konstrukce, přičemž rozlišujeme mezní stavy porušení (skupina 1. mezního stavu) a mezní stavy použitelnosti (skupina 2. mezního stavu). Mezní stavy porušení (1. mezního stavu) jsou:
- (EQU) – ztráta rovnováhy konstrukce nebo základové půdy uvažované jako tuhé těleso, při níž nejsou pevnost konstrukčních materiálů a základové půdy rozhodující, např. stabilita tuhého základu na skalní hornině (jde vesměs o málo časté případy);
- (STR) – vnitřní porušení či nadměrná deformace konstrukce nebo jejích prvků, pro něž je jejich pevnost rozhodující k posouzení odolnosti (rovněž málo častý případ mimořádně únosné základové půdy, kde o stabilitě rozhoduje pevnost konstrukce);
- (GEO) – porušení nebo nadměrná deformace základové půdy, pro níž je smyková pevnost základové půdy rozhodující pro posouzení odolnosti (nejčastější případ pro posouzení plošných i hlubinných základů v zeminách a poloskalních horninách);
- (UPL) – ztráta rovnováhy konstrukce nebo základové půdy nastává vlivem vztlaku vody nebo jiných svislých zatížení (jde o málo časté případy tahem zatěžovaných základů, nebo o případy vztlaku, kdy nedostatečně hmotná konstrukce je pod hladinou podzemní vody);
- (HYD) – nadzdvihování dna, vnitřní eroze a sufoze v základové půdě způsobená hydraulickým gradientem (rovněž málo časté případy, pro něž je rozhodující proudový tlak podzemní vody).
Pro všechny základové konstrukce, posuzované statickým výpočtem, se musí ověřit, že tyto, (resp. příslušné) mezní stavy nejsou překročeny, přičemž pro nejčastější případy GEO a STR platí, že návrhová hodnota (účinku) zatížení smí dosáhnout nejvýše návrhové hodnoty mezní únosnosti (k zatížení). Přitom velikost zatížení se zvyšuje souborem dílčích koeficientů typu A a únosnost získaná na základě příslušně snížených charakteristických hodnot vlastností základových půd dílčími koeficienty typu M, se redukuje dalšími dílčími koeficienty typu R podle následujícího schématu:
\begin{gathered}
A\cdot F\le\frac{U[f\cdot(\frac{\gamma}{M};\space\frac{\varphi}{M};\space\frac{c}{M}]}{R}
\end{gathered}(15)
kde je:
A … dílčí součinitelé zatížení;
Fk … zatížení charakteristické;
U … únosnost návrhová;
γk; φk; ck … charakteristické velikosti stabilitních parametrů základové půdy;
M … dílčí součitelé na parametry základové půdy;
R … dílčí součinitelé na únosnost.
Základy staveb musí obvykle splnit i mezní stavy použitelnosti, jež jsou tvořeny přetvořením konstrukce. Jelikož v případě základů staveb jde především o zatížení svislé, tlakové, jsou příslušné deformace tvořeny zejména sedáním základů, které může být rovnoměrné – pro celou konstrukci, nebo nerovnoměrné, tvořené vzájemným diferenčním sedáním sousedních základů, pootočením základu, nebo jeho průhybem. Zatímco rovnoměrné sedání nevnáší do stavební konstrukce žádné přídavné vnitřní síly, a není tudíž nebezpečné, v případě sedání nerovnoměrného je to jinak. Přípustné velikosti těchto sedání stanoví investor, popř. se posuzují podle přípustných hodnot uvedených v normě, jde tedy o velikosti doporučené, nikoliv zcela závazné.
2.2 OVĚŘENÍ MEZNÍCH STAVŮ, NÁVRHOVÉ PŘÍSTUPY
2.2.1 Ověření mezních stavů porušení
Pro ověření statické rovnováhy nebo celkového přemístění konstrukce či základové půdy (EQU) platí:
\begin{gathered}
E_\text{dst,d}\le E_\text{stb,d}+T_\text{d}
\end{gathered}(16)
kde je:
Edst,d … návrhová hodnota účinku destabilizujícího zatížení;
Estb,d … návrhová hodnota účinku stabilizujícího zatížení.
Pro ověření mezního stavu porušení nebo nadměrné deformace konstrukčního prvku nebo části základové půdy (STR a GEO), platí:
\begin{gathered}
E_\text{d}\le R_\text{d}
\end{gathered}(17)
kde je:
Ed … návrhová hodnota účinku zatížení;
Rd … návrhová hodnota mezní únosnosti k zatížení.
\begin{gathered}
E_\text{d}=E[\gamma_\text{F}F_\text{rep};\space\frac{X_\text{k}}{\gamma_\text{M}};\space a_\text{d}],\space\text{nebo}\space E_\text{d}=\gamma_\text{E}E[F_\text{rep};\space\frac{X_\text{k}}{\gamma_\text{M}};\space a_\text{d}]
\end{gathered}(18)
\begin{gathered}
R_\text{d}=R[\gamma_\text{F}F_\text{rep};\space\frac{X_\text{k}}{\gamma_\text{M}};\space a_\text{d}],\space\text{nebo}\space R_\text{d}=\frac{R[\gamma_\text{F}F_\text{rep};\space X_\text{k};\space a_\text{d}]}{\gamma_\text{R}},\space\text{nebo}\space R_\text{d}=\frac{R[\gamma_\text{F}F_\text{rep};\space\frac{X_\text{k}}{\gamma_\text{M}};\space a_\text{d}]}{\gamma_\text{R}}
\end{gathered}(19)
kde je:
γF, γE … dílčí součinitelé zatížení nebo účinku zatížení (viz tab. 8);
γM … dílčí součinitelé parametrů základové půdy (viz tab. 9);
γR … dílčí součinitelé únosnosti (viz tab. 12);
Frep … reprezentativní hodnota zatížení (viz ČSN EN 1990);
ad … návrhové hodnoty geometrických údajů (viz ČSN EN 1990).
Pro ověření vztlaku (UPL) platí:
\begin{gathered}
V_\text{dst,d}\le G_\text{stb,d}+R_\text{d}
\end{gathered}(20)
\begin{gathered}
V_\text{dst,d}=G_\text{dst,d}+Q_\text{dst,d}
\end{gathered}(21)
kde je:
Vdst,d … návrhová hodnota destabilizujícího svislého zatížení na konstrukci;
Gstb,d … návrhová hodnota stabilizujících stálých svislých zatížení pro posouzení vztlaku;
Gdst,d … návrhová hodnota destabilizujících stálých zatížení pro posouzení vztlaku;
Qdst,d … návrhová hodnota destabilizujících proměnných svislých zatížení pro posouzení vztlaku;
Rd … návrhová hodnota mezní únosnosti k zatížení.
Pro ověření odolnosti proti porušení nadzdvižením dna vlivem proudění v základové půdě (HYD) platí:
\begin{gathered}
u_\text{dst,d}\le\sigma_\text{stb,d},\space\text{nebo}\space S_\text{dst,d}\le G´_\text{stb,d}
\end{gathered}(22)
kde je:
udst,d … návrhová hodnota destabilizujícího celkového pórového tlaku vody;
σstb,d … návrhová hodnota stabilizujícího celkového svislého napětí;
Sdst,d … návrhová hodnota destabilizující průsakové síly v základové půdě;
G´stb,d … návrhová hodnota stabilizujících stálých svislých zatížení pro posouzení nadzdvihování dna (tíha nadlehčená vztlakem).
2.2.2 Návrhové přístupy pro případy porušení STR a GEO
Způsob, jakým se aplikují vztahy (17) až (19) pro nejčastější případy porušení základových konstrukcí (GEO) a (STR), se stanovuje s využitím jednoho ze tří návrhových přístupů (NP).
Návrhový přístup 1 (NP1)
Pro všechny případy posouzení základových konstrukcí s výjimkou pilot a kotev platí:
- a) Kombinace 1: A1 „+“ M1 „+“ R1,
- b) Kombinace 2: A2 „+“ M2 „+“ R1
kde: „+“ značí: „kombinuje se s …“
Pro případy osově zatížených pilot a kotev platí:
- a) Kombinace 1: A1 „+“ M1 „+“ R1,
- b) Kombinace 2: A2 „+“ (M1 nebo M2) „+“ R4.
Příslušné soubory součinitelů pro A, M jsou potom uvedeny v tab. 8 a 9 a pro R v příslušných tabulkách podle druhu základové konstrukce. V kombinaci 2 se soubor M1 používá pro výpočet únosnosti pilot a kotev a soubor M2 pak pro výpočet nepříznivých zatížení pilot vystavených např. negativnímu plášťovému tření nebo příčnému zatížení.
Tab. 8 Dílčí součinitelé zatížení γF nebo účinků zatížení γE
| Zatížení | Značka | Soubor | ||
| A1 | A2 | |||
| stálé | nepříznivé | γG | 1,35 | 1,00 |
| příznivé | 1,00 | 1,00 | ||
| proměnné | nepříznivé | γQ | 1,50 | 1,30 |
| příznivé | 0 | 0 | ||
Návrhový přístup 2 (NP2)
Pro všechny případy posouzení základových konstrukcí platí:
Kombinace: A1 „+“ M1 „+“ R2.
Tab. 9 Dílčí součinitelé parametrů základové půdy γM
| Parametr zeminy | Značka | Soubor | |
| M1 | M2 | ||
| úhel vnitřního třeníx) | γφ | 1,00 | 1,25 |
| efektivní soudržnost | γc | 1,00 | 1,25 |
| neodvodněná smyková pevnost | γcu | 1,00 | 1,40 |
| pevnost v prostém tlaku | γqu | 1,00 | 1,40 |
| objemová tíha | γγ | 1,00 | 1,00 |
| x) Tento součinitel se použije pro tg φ | |||
Návrhový přístup 3 (NP3)
Pro všechny případy posouzení základových konstrukcí platí:
Kombinace: (A1 nebo A2)x) „+“ M2 „+“ R3.
x) Dílčí součinitele typu A1 se použijí na zatížení konstrukce, A2 pak na geotechnické zatížení.
2.3 GEOTECHNICKÉ KATEGORIE
Při návrhu základů staveb se vychází na jedné straně z geotechnických poměrů na staveništi a z vlastností základových půd, na straně druhé pak z tvaru a charakteru zakládané konstrukce a ze zatěžovacích údajů. Při návrhu geotechnických konstrukcí vzniká obecně riziko, jež závisí:
- na složitosti geologických a geotechnických podmínek podloží;
- na náročnosti konstrukce, která bude s tímto podložím v interakci či konstrukce, která bude v tomto prostředí přímo situována či bude podloží využívat jako konstrukční materiál (podzemní stavby, zemní konstrukce);
- na možných následcích jejího selhání na osoby, na budované nebo sousední dílo, a to ve smyslu společenském, ekonomickém a z hlediska následků na životní prostředí.
Tyto možné následky se dělí do těchto tříd (v souladu s ČSN EN 1990 „Zásady navrhování konstrukcí“, čl. B.3.1-tab. B.1):
- Třída 1 – možné následky slabé, mající zanedbatelné vlivy na osoby nebo malé vlivy na budované nebo sousední dílo;
- Třída 2 – možné následky střední, mající mírné vlivy na osoby a/nebo významné vlivy na budované nebo sousední dílo;
- Třída 3 – možné následky značné, mající významné vlivy na osoby a/nebo velmi významné vlivy na budované nebo sousední dílo.
Posouzení rizika spojeného s návrhem geotechnické konstrukce provádí zpracovatel geotechnického návrhu v součinnosti s investorem a se zpracovatelem geotechnického průzkumu. Pokud je geotechnická konstrukce součástí většího investičního celku, též v součinnosti s generálním projektantem. Norma ČSN EN 1997-1 zavádí 3 geotechnické kategorie (GK), ty však jsou obligatorní a kritériem je zde především míra rizika, kterou zakládání daného objektu v příslušných geotechnických poměrech představuje, tedy:
- 1. GK zahrnuje pouze malé a jednoduché konstrukce se zanedbatelným rizikem, pro které platí, že základní požadavky na posouzení návrhu založení budou splněny na základě zkušeností a kvalitativního geotechnického průzkumu;
- 2. GK zahrnuje obvyklé typy konstrukcí a základů s běžným rizikem a jednoduchými základovými poměry či podmínkami zatížení; posouzení návrhu vyžaduje obvykle kvantitativní geotechnické údaje a příslušné výpočty k ujištění, že základní požadavky mezních stavů jsou splněny;
- 3. GK zahrnuje pak konstrukce, jež nespadají do 1. a 2. GK, tj. konstrukce s neobvyklým rizikem, kdy návrh a posouzení základů vyžaduje specializovaný průzkum a obvykle i polní zkoušky.
V souladu s článkem 2.1.(11) resp. (12) ČSN EN 1997-1 se může prvotně doporučená GK upřesňovat. Nižší GK lze použít při předběžných hodnoceních staveniště a při předprojektové přípravě.
Orientační doporučení hranic GK:
1. GK
- Plošné základy: skupina nenáročných staveb v jednoduchých základových poměrech.
- Piloty: nespadají do 1. GK.
- Kotvení: nespadají do 1. GK.
- Zemní konstrukce dopravních staveb (násypy, zářezy): orientační omezení výškou 3,0 m.
- Opěrné konstrukce a vyztužené zemní konstrukce: orientační omezení výškou 1,5 m, bližší specifikace viz EC 7 – Národní aplikační standard.
- Zemní konstrukce vodních staveb (nízké hráze, protipovodňové hráze, násypy a zářezy různých typů kanálů – plavební, přívodní apod.): orientační omezení pro trvalé či dočasné vzdutí hladiny vody o výšce do 2,5 m a při malém vlivu na okolí.
- Zemní konstrukce environmentálních staveb: nespadají do 1. GK.
- Tunely: nespadají do 1. GK.
2. GK
- Plošné základy: skupina nenáročných staveb ve složitých základových poměrech, resp. náročných staveb v jednoduchých základových poměrech.
- Piloty: Pro stanovení únosnosti osamělých pilot v tlaku na základě výpočtu nebo zkoušek v jednoduchých i složitých geotechnických poměrech, ne však v mimořádně složitých podmínkách, a to pro stálé i proměnné zatížení s malým až středním vlivem pro dotčené okolí (třída rizika 1 a 2). Pro stanovení únosnosti skupiny pilot v tlaku v jednoduchých geotechnických poměrech s malým až středním vlivem na okolí. Pro stanovení únosnosti osamělých i skupinových pilot v tahu v jednoduchých geotechnických poměrech s malým až středním vlivem na okolí. Pro stanovení příčné únosnosti pilot v jednoduchých geotechnických poměrech při působení zatížení v hlavě piloty s malým až středním vlivem na okolí.
- Kotvy: Pro dočasné kotvy v nikoliv mimořádně složitých geotechnických podmínkách pro zatížení stálé i proměnné s malým až středním vlivem na okolí (třída rizika 1 a 2).
- Zemní konstrukce dopravních staveb (násypy, zářezy): orientační omezení výškou: vyšší než 3,0 m.
Poznámka:
Při orientační výšce nad 6 m, resp. při nestandardním zatížení, při situování na sesuvném podloží či při využití nestandardních materiálů je třeba vycházet z 3. GK.
- Opěrné konstrukce a vyztužené zemní konstrukce: orientační omezení výškou: vyšší než 1,5 m.
Poznámka:
Při orientační výšce nad 6 m, resp. při nestandardním zatížení, při situování na sesuvném podloží či při využití nestandardních materiálů je třeba vycházet z 3. GK.
- Zemní konstrukce vodních staveb (nízké hráze, protipovodňové hráze, násypy a zářezy různých typů kanálů – plavební, přívodní apod.): orientační omezení výškou: pro trvalé či dočasné vzdutí hladiny vody vyšší než 2,5 m. Při výšce nad 15 m (přehrady), resp. i při nižších výškách, ale velmi složitých poměrech v podloží a při vysokém vlivu na okolí (třída rizika 3) je nutno postupovat podle 3. GK.
- Zemní konstrukce environmentálních staveb: nespadají do 2. GK.
- Tunely: Pro tunely v tvrdých neporušených horninách nevyžadující zvláštní opatření na vodotěsnost a nemající jiné požadavky.
3. GK
Všechny geotechnické konstrukce, které nespadají do 1. GK ani 2. GK.
Poznámka 1:
Návrh Geotechnické kategorie musí být v konečné fázi zdůvodněn – ve Zprávě o geotechnickém návrhu.
Poznámka 2:
Pro případ 1. GK osoba zodpovědná za geotechnický návrh konstrukce nemusí mít autorizaci podle zákona č. 360/92 Sb., pro obor Geotechnika.
Poznámka 3:
Autorizace pro obor geotechnika podle zákona č. 360/92 Sb., je požadována podle výše uvedené klasifikace pro geotechnický návrh konstrukcí spadajících do 2. GK a 3. GK. Výjimkou pro 2. GK může být případ zkušeného odborníka s významnou praxí v geotechnice s autorizací v příbuzném oboru (např. dopravní či vodní stavby, statika a dynamika stavebních konstrukcí apod.). Tento požadavek je též ovlivněn skutečností, že za volbu, zdůvodnění a následné použití charakteristických hodnot geotechnických parametrů zodpovídá osoba realizující geotechnický návrh.
2.4 NÁVRHOVÉ SITUACE
Při návrhu geotechnické konstrukce musí být podrobně specifikovány příslušné návrhové situace, jež musí zejména zahrnovat:
- obecnou vhodnost základové půdy obklopující základovou konstrukci;
- uspořádání a zatřídění různých vrstev a zón zemin a skalních či poloskalních hornin (tzv. geotechnických typů) a prvků stavby, které vstupují do výpočetního modelu;
- sklon a zvláštní tvary podložních vrstev;
- podzemní prostory přirozené i umělé, jejich umístění a tvar;
- v případě konstrukcí založených ve skalních horninách nebo v jejich těsném sousedství:
- střídání tvrdých a měkkých poloh;
- poruchy, pukliny, trhliny;
- dutiny, např. vyluhované a vyplněné měkkými zeminami, pokračující proces vyluhování apod.;
- zatížení, kombinaci zatěžovacích stavů;
- povahu okolního prostředí, v němž se geotechnická konstrukce navrhuje, tedy např.:
- vliv sufoze, eroze a výkopů vedoucích ke změně povrchu základové půdy;
- vliv chemické koroze;
- vliv zvětrávání;
- klimatické vlivy (promrzání, vysychání);
- změna hladiny podzemní vody vč. vlivu změn od čerpání nebo zatopení;
- přítomnost plynů v základové půdě;
- časové vlivy na změnu geotechnického prostředí;
- zemětřesení, technická seismicita, ostatní dynamické účinky;
- vliv poddolování;
- odolnost konstrukcí vůči přetvoření;
- vliv nových konstrukcí na okolní zástavbu.
Kromě toho je třeba posoudit odolnost základových konstrukcí vůči nepříznivým vlivům prostředí, což souvisí s trvanlivostí základů. Při návrhu materiálů použitých pro stavbu základů se musí zohlednit:
- v případě betonu – vliv agresivity prostředí (podzemní vody, popř. i základové půdy);
- v případě oceli – totéž, a navíc vliv běžné i elektrolytické koroze;
- v případě dřeva – vliv trouchnivění a napadení houbami a aerobními bakteriemi;
- v případě umělých hmot – účinek stárnutí a ostatní chemické degradace přísl. materiálu.
2.5 METODY NÁVRHU ZÁKLADOVÝCH KONSTRUKCÍ
Navržené základové konstrukce se ověřují jedním, nebo kombinací následujících způsobů:
- tatickým výpočtem (viz kap. 2.6);
- přijetím normativních opatření;
- experimentálními modely a zatěžovacími zkouškami;
- observační metodou (viz kap. 2.7).
Návrh přijetím normativních opatření lze použít v návrhových situacích, pro něž neexistují výpočetní modely, nebo nejsou nutné. Normativní opatření zahrnují konvenční a obvykle konzervativní pravidla návrhu vyplývající z dlouholetých zkušeností, nicméně tento způsob návrhu by měl být omezen na 1. GK a podpořen vždy výsledky geotechnického průzkumu.
Experimentální modely a zatěžovací zkoušky se naopak volí v případě 3. GK tam, kde matematické modelování není spolehlivé zejména s ohledem na nejistotu vstupních údajů a technologických vlivů. Přitom je třeba zejména zohlednit:
- rozdíly v základových poměrech (pokud existují) mezi zkouškou a skutečností;
- vliv času, zejména z hlediska doby působícího zatížení;
- vliv měřítka, zvláště jsou-li použity malé modely.
2.6 NAVRHOVÁNÍ ZÁKLADOVÝCH KONSTRUKCÍ NA ZÁKLADĚ STATICKÉHO VÝPOČTU
Nejpoužívanější metodou pro posouzení navržené základové konstrukce, zvláště v 2. GK a 3. GK, je statický výpočet, pro nějž potřebujeme vytvořit a získat:
- výpočetní model, nebo modely;
- zatížení; a to jak ve formě známých zatěžovacích sil, tak i přetvoření;
- relevantní vlastnosti základové půdy, jejich jednotlivých vrstev či geotechnických typů;
- geometrické tvary konstrukcí a ostatních komponentů výpočetního modelu;
- mezní (přípustné) velikosti deformací, šířky trhlin, vibrací apod.
Při sestavování výpočetního modelu (matematického modelu) je třeba vycházet nejdříve z modelu geologického, který řeší geologické a hydrogeologické poměry na staveništi a zde má hlavní slovo zpracovatel geotechnického průzkumu. Dále je třeba tento model přepracovat na model geotechnický, tj. doplnit jej o geotechnické typy a číselné údaje vlastností základových půd (charakteristické, či návrhové), kde do tvorby tohoto modelu již vstupuje projektant geotechnické konstrukce.
2.6.1 Výpočetní modely
Výpočetní model musí jasně popisovat chování konstrukce a základové půdy pro příslušný mezní stav. Může být sestaven z modelu:
- analytického;
- semiempirického;
- numerického.
Výpočetní model může obsahovat zjednodušení a jeho event. nepřesnost musí být vždy na straně bezpečnosti. Při sestavování výpočetního modelu je třeba vzít v úvahu, že jeho matematická preciznost je pouze jeho jednou součástí, jež nemusí být nejdůležitější pro kvalitu výsledku, neboť ta závisí na rozsahu a kvalitě geotechnického průzkumu a z něj vyplývajících vstupních údajů pro výpočet. Výpočetní modely sestávají:
- z vlastní výpočetní metody založené na analytickém modelu vč. příslušného zjednodušení;
- z úpravy výsledků výpočtu podle rozsahu jejich nejistoty a odstranění systematických chyb souvisejících se zvolenou analytickou metodou, jakož i z kritického zhodnocení získaných výsledků.
Vlastní výpočet probíhá vesměs automaticky na osobních počítačích a využívá se při něm buď vlastních, nebo jakkoliv komerčně vytvořených programů, jež jsou nabízeny širokým spektrem distributorů nebo i výrobců. V geotechnice je na místě velká opatrnost, neboť výpočetní programy jsou na straně jedné nenahraditelným nástrojem v rukou zkušených odborníků, kteří dokážou odhadnout rozsah výsledků a umějí s nimi rozumně nakládat. Pro začátečníky však na straně druhé představují často značné nebezpečí, neboť svádějí k tomu přijmout výsledky bez kritického přemýšlení. V EC 7-1 je tedy následující doporučení:
- kdykoliv je to možné, musí být výpočetní model korelován s polním pozorováním a s modelovými zkouškami, popř. se spolehlivějšími statickými výpočty;
- ve výpočetním modelu lze uplatnit i empirické vztahy; musí být však jasně stanoveno, pro které relevantní základové poměry platí.
Pokud je to možné, je třeba výpočetní model sestavit tak, aby byla zachycena interakce mezi stavbou a základovou půdou, v níž bude zohledněna skutečná tuhost základové konstrukce a vlastní stavby. Pro tuto analýzu je však třeba mít k dispozici dostatečně reprezentativní vztah mezi napětím a přetvořením v základové půdě.
2.6.2 Zatížení v geotechnickém modelu
Předpokládá se obecně, že velikosti zatížení jsou:
- známé veličiny;
- jsou dány přetvořením konstrukce;
- vyplynou z výpočtu interakce mezi základovou půdou a konstrukcí.
V geotechnických výpočtech se musí uvažovat následující zatížení:
- tíhy zemin, skalních hornin a vody;
- napětí in situ v základové půdě (např. napětí geostatické);
- tlak volné vody;
- tlak podzemní vody (hydrostatický);
- proudový tlak podzemní vody (hydrodynamický tlak);
- vlastní tíhy konstrukcí;
- užitné zatížení konstrukcí;
- zatížení větrem;
- zatížení povrchu terénu a zatížení uvnitř terénu;
- kotevní síly;
- změny vnějšího zatížení vyvolané např. výkopem základové půdy nebo změnou úrovně hladiny podzemní vody;
- zatížení od dopravy;
- pohyby zapříčiněné důlní činností;
- bobtnání a smršťování základové půdy způsobené klimatickými vlivy, vegetací apod.;
- pohyby vyvolané sesuvy půdy, skalním řícením nebo creepem apod.;
- pohyby vyvolané degradací, dekompozicí, zhutňováním a rozpouštěním;
- pohyby a zatížení od zemětřesení, výbuchů, vibrací a ostatních dynamických účinků;
- vliv změny teploty vč. zvedání mrazem;
- zatížení ledem a vodními vlnami;
- trvalé účinky předpětí v kotvách a rozpěrách.
Při stanovení velikosti zatížení se přihlíží k době jeho trvání a k jeho možným změnám. Při posuzování základových konstrukcí z hlediska 1. mezního stavu (porušení) se pro různé trvalé i dočasné návrhové situace zavádějí konkrétní velikosti dílčích součinitelů γm, jimiž se násobí charakteristické hodnoty stálých a nahodilých zatížení (tab. 8), resp. dělí parametry základové půdy (tab. 9). Pro posuzování konstrukcí z hlediska 2. mezního stavu (použitelnosti) musí být velikosti dílčích součinitelů rovny 1,0. Příslušné případy zatížení A, B, C (tab. 10) jsou podrobně definovány v ČSN EN 1990 a jsou následující:
- případ A se pro základové konstrukce uplatňuje pouze pro případy vztlaku (viz kap. 2.1 – UPL i HYD);
- případ B je rozhodující pro návrh pevnosti konstrukčních základových prvků nebo opěrných zdí (viz kap. 2.1 – STR);
- případ C je obecně nejtypičtější pro základové konstrukce (viz kap. 2.1 – GEO i EQU).
Tab. 10 Dílčí součinitelé zatížení a bezpečnosti základové půdy γm pro 1. mezní stav pro trvalé i dočasné návrhové situace
| Případ | Zatížení | Vlastnosti základové půdy | |||||
| stálé, jež působí | nahodilé | (1) tg φ | (2) cef | (3) cu | (4) σc | ||
| nepříznivě | příznivě | nepříznivě | |||||
| A | 1,00 | 0,95 | 1,50 | 1,10 | 1,30 | 1,20 | 1,20 |
| B | 1,35 | 1,00 | 1,50 | 1,00 | 1,00 | 1,00 | 1,00 |
| C | 1,00 | 1,00 | 1,30 | 1,25 | 1,60 | 1,40 | 1,40 |
| a) tangens úhlu vnitřního tření efektivního i totálního; b) efektivní soudržnost; c) totální soudržnost; d) jednoosá tlaková pevnost hornin. |
|||||||
2.6.3 Vlastnosti základových půd
Vlastnosti základových půd jsou reprezentovány jejich geotechnickými parametry potřebnými pro příslušné geotechnické výpočty, přičemž obecně existují následující 3 úrovně těchto parametrů:
- odvozené hodnoty Xo, které se získají v průběhu provádění geotechnického průzkumu jakožto hodnoty měřené na vzorcích základové půdy v laboratoři či polním měřením, a příslušně upravené standardními výpočty (ty obstará zpracovatel geotechnického průzkumu a s příslušným komentářem je uvede v závěrečné zprávě příslušné etapy tohoto průzkumu, přičemž snahou je získat vždy příslušný soubor těchto odvozených hodnot);
- charakteristické hodnoty Xk, které vycházejí z hodnot odvozených a vybírají se jako obezřetný odhad této hodnoty ovlivňující výskyt příslušného mezního stavu (za velikost charakteristických hodnot odpovídá projektant geotechnické konstrukce, neboť ten ví, resp. by měl vědět, jakým způsobem příslušný geotechnický parametr ovlivňuje příslušný geotechnický výpočet);
- návrhové hodnoty Xd se odvodí z charakteristických hodnot Xk použitím vztahu:
\begin{gathered}
X_\text{d}=\frac{X_\text{k}}{\gamma_\text{M}}
\end{gathered}(23)
Charakteristické hodnoty vstupují přímo do výpočtů 2. mezního stavu (použitelnosti). Pokud se pro určení charakteristické hodnoty příslušného parametru základové půdy použijí statistické metody, potom se charakteristická hodnota odvodí tak, že vypočtená pravděpodobnost horší hodnoty řídící výskyt uvažovaného mezního stavu není větší než 5 %. Obezřetný odhad průměrné hodnoty lze charakterizovat výběrem průměrné hodnoty omezeného souboru odvozených velikostí geotechnického parametru s pravděpodobností 95 %.
2.6.4 Mezní velikosti přetvoření
Při návrhu základových konstrukcí se musí stanovit mezní hodnoty deformací základů a musí se prokázat, že navržená konstrukce vyhovuje z hlediska 2. mezního stavu. To je důležité jak pro hodnoty celkového průměrného sedání, tak pro sedání nerovnoměrné, které je dáno relativním průhybem, úhlovým přetvořením i nakloněním základu. Mezní velikosti sedání stanoví uživatel stavby (investor), doporučené velikosti jsou pak v tab. 11. Při stanovení velikosti mezních konečných sedání sm,lim se musí vzít v úvahu:
- spolehlivost, s níž lze přijatelnou hodnotu deformace specifikovat;
- druh stavební konstrukce a konstrukčního materiálu;
- typ základu a základové půdy;
- předpokládané využití stavební konstrukce;
- zajištění bezpečnosti inženýrských sítí vstupujících do stavební konstrukce.
Při výpočtech velikostí nerovnoměrných sedání Δs / L, Δs / B je třeba vzít v úvahu:
- výskyt a rychlost sedání a pohybů základové půdy;
- náhodné a systematické proměny vlastností základové půdy;
- rozdělení zatížení;
- metodu výstavby (zejména z hlediska postupného zatěžování základové konstrukce);
- tuhost konstrukce v průběhu výstavby a po dokončení stavby.
Tab. 11 Mezní velikosti sedání
| Druh stavby | Konečné celkové průměrné sednutí sm,lim | Nerovnoměrné sednutí | ||
| Hodnota [mm] | Druh | Hodnota | Název | |
| 1. Budovy a konstrukce u nichž nevznikají vlivem nerovnoměrného sedání přídavná namáhání a není nebezpečí porušení prostupů a souvisejících konstrukcí | 120 | Δs / L | 0,003 0,006 |
RP ÚP |
| 2. Konstrukce 2.1 staticky určité 2.2 železobetonové staticky neurčité 2.3 ocelové staticky neurčité |
100 60 80 |
Δs / L | 0,005 0,002 0,003 |
ÚP ÚP ÚP |
| 3. Vícepodlažní skeletové budovy 3.1 železobet. skelety s výplňovým zdivem 3.2 ocelové skelety s výplňovým zdivem |
60 70 |
Δs / L | 0,0015 0,0025 |
RP ÚP |
| 4. Vícepodlažní budovy s nosnými stěnami 4.1 zděné z cihel a bloků se ztužujícími věnci 4.2 z velkorozměrných panelů a monol. betonu |
80 60 |
Δs / L | 0,0015 0,0015 |
RP ÚP |
| 5. Železobetonové konstrukce 5.1 Tuhé železobetonové konstrukce 5.2 Komíny do výšky 100 m 5.3 Komíny vyšší než 100 m |
200 200 100 |
Δs / B | 0,003 0,005 0,002 |
N N N |
| 6. Jeřábové dráhy | 50 | Δs / L | 0,0015 | ÚP |
| RP – relativní průhyb; ÚP – úhlové přetvoření; N – naklonění | ||||
2.7 OBSERVAČNÍ METODA
Vzhledem k tomu, že předpověď geotechnického chování konstrukce je velmi obtížná, doporučuje se pro návrh a realizaci stavby přijmout přístup známý jako „observační metoda“, která spočívá v průběžném posuzování správnosti návrhu a jeho případné korekce v průběhu výstavby. Observační metoda se uplatňuje zejména v případech složitých staveb a základových konstrukcí v takových geotechnických poměrech, kdy např. upřesňování geotechnických podkladů se již nejeví jako účelné. Před započetím výstavby se tedy musí:
- stanovit meze přijatelného chování konstrukce (zejména přípustné deformace);
- ve stadiu návrhu prokázat s jistou pravděpodobností, že chování konstrukce bude v těchto přijatelných mezích;
- naplánovat monitoring, jímž se bude průběžné chování konstrukce sledovat a jež okamžitě odhalí jakékoliv předvídané i nepředvídané anomálie; doba odezvy přístrojů pracujících v rámci monitoringu vč. vyhodnocení měření musí být natolik krátká, aby umožnila zásah do chování konstrukce v reálném a přiměřeném čase;
- vypracovat plán možných opatření, která lze přijmout, pokud monitoring odhalí chování konstrukce mimo přijatelné meze.
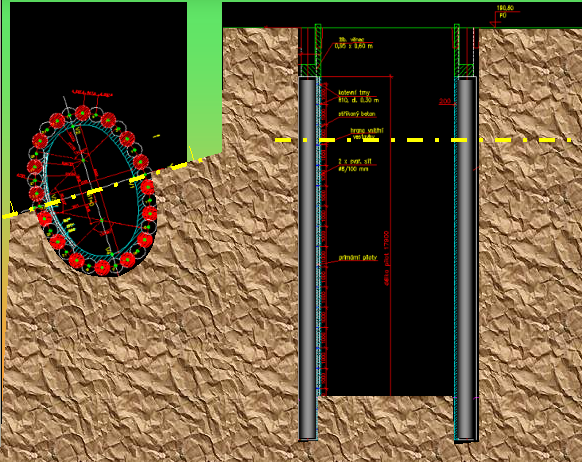
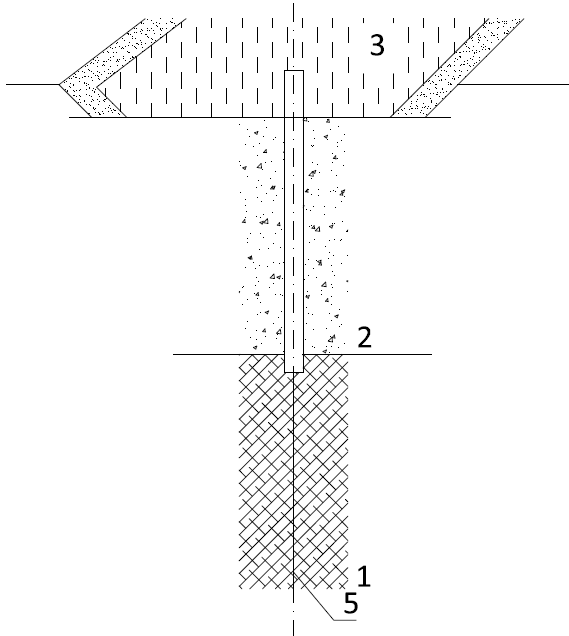
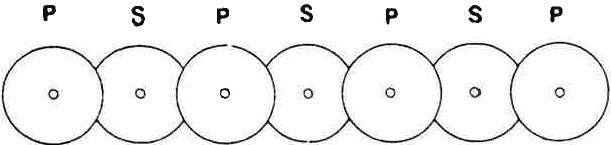
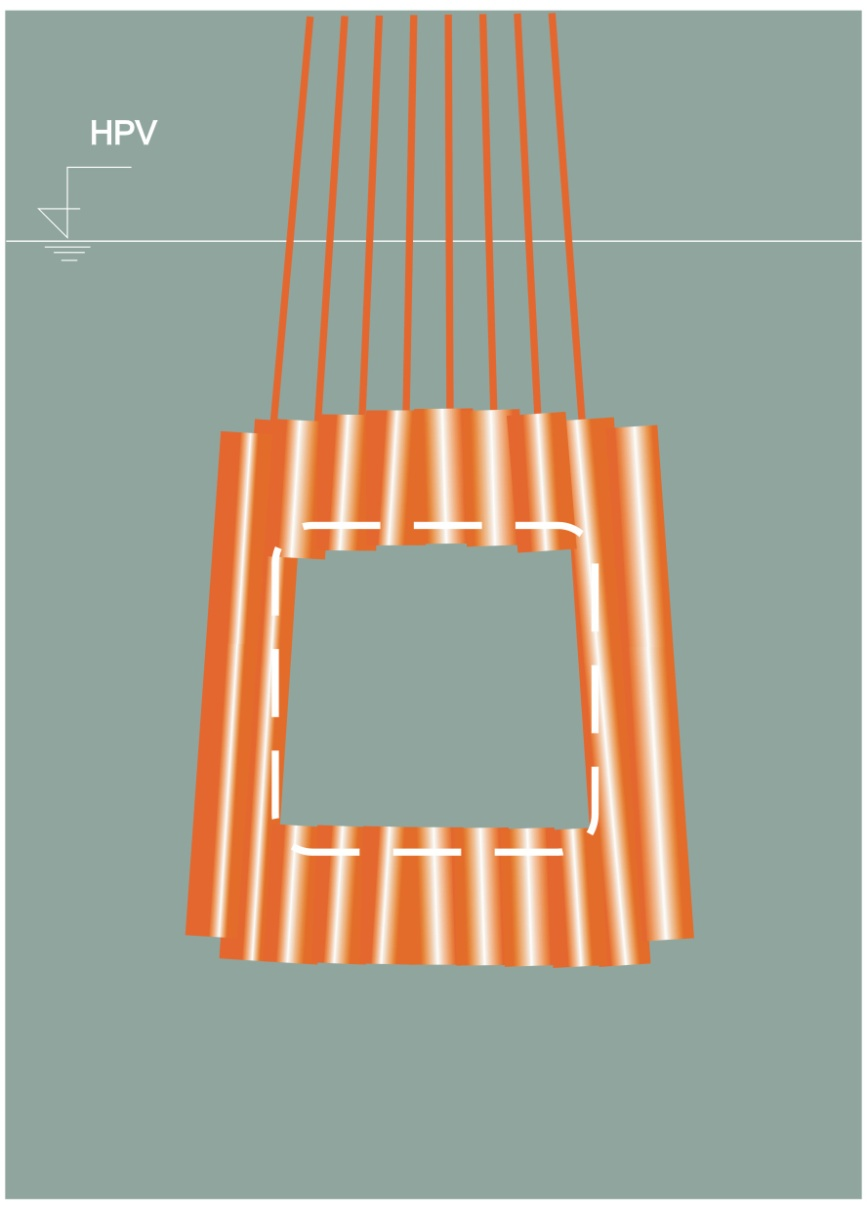
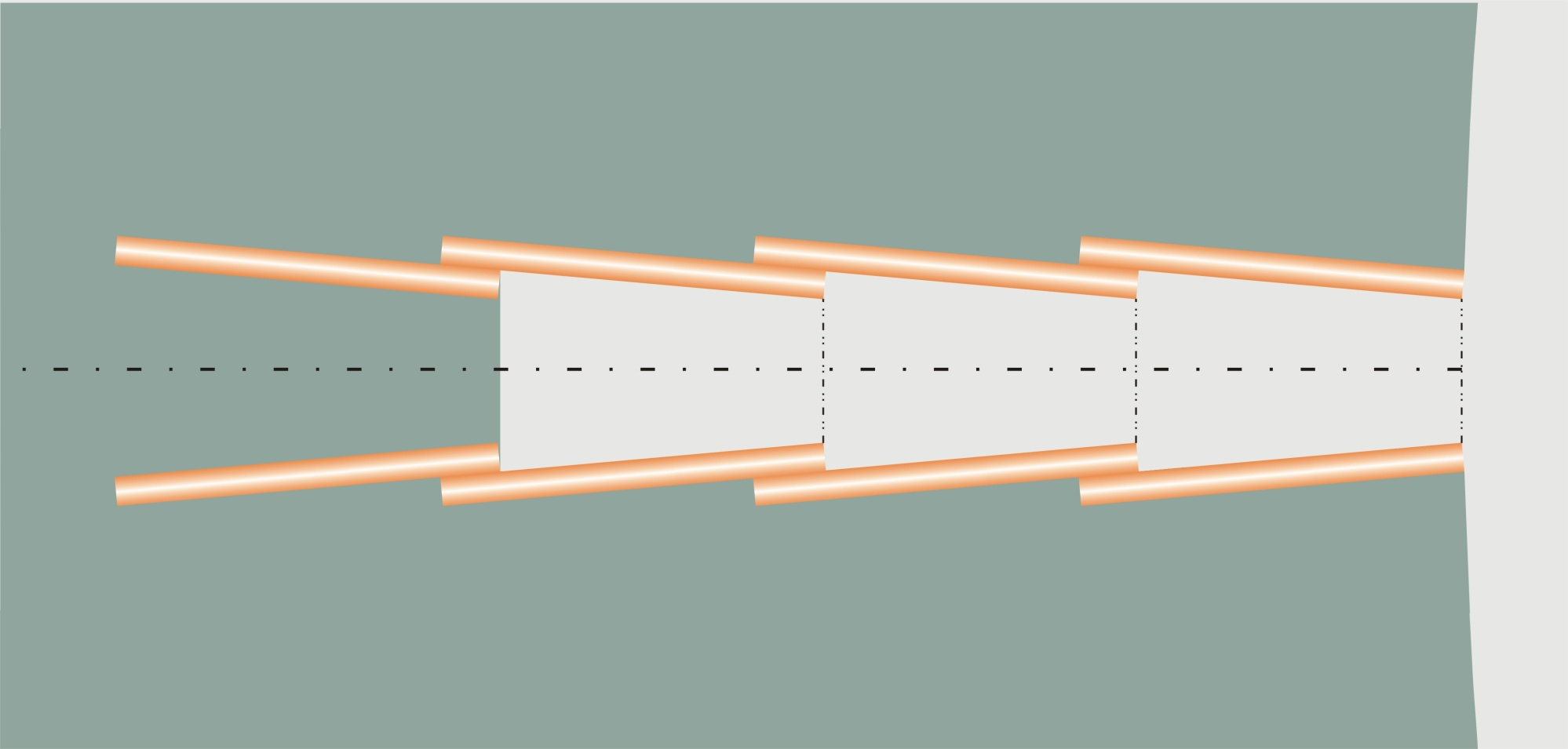
Příkladem uplatnění observační metody v praxi zakládání staveb byla výstavba šachty pro výtah v hustě zastavěném území, kdy původně navrhovanou šachtu kruhového půdorysu nebylo možné realizovat z důvodu výskytu nepřeložitelných inženýrských sítí a půdorysný tvar šachty musel být změněn na elipsu, obr. 11. Ostění šachty bylo navrženo z převrtávaných pilot průměru 750 mm osově ve vzdálenosti 620 mm. V případě, že by tvar šachty byl kruhový, namáhání pilot by bylo příznivé, působila by pouze tlaková síla ve střednici pilot o velikosti N = p · r, kde p je radiální napětí od zemního tlaku a r je poloměr šachty, a zajisté by nebylo nutné navrhovat žádné ztužující konstrukce. S ohledem na skutečně navržený půdorysný tvar – eliptický – vznikají v jeho střednici kromě sil tlakových také nezanedbatelné ohybové momenty, pro něž by bylo nutné navrhnout ztužení, např. pomocí vnitřních, příslušně dimenzovaných železobetonových věnců.
Obr. 11 Příklad uplatnění observační metody při výstavbě šachty
Bylo však využito popisované observační metody, kdy návrh těchto ztužujících věnců byl sice připraven, nicméně se zatím nerealizoval. Po provedení převrtávaných pilot a v průběhu hloubení šachty se uskutečnilo měření deformací a to formou tzv. konvergenčních měření, kdy se měří příslušné vzdálenosti mezi body na vnitřním líci obnažených pilot a z nich se potom usuzuje na celkové deformace konstrukce. Samozřejmě byly předem stanoveny tzv. varovné stavy, jež byly dány max. přípustnou deformací pilotových stěn bez ztužení. Příslušná měření na stavbě ukázala, že naměřené deformace byly vesměs hluboko pod hodnotami přípustnými, což znamenalo, že ztužující věnce se nemusely provést a došlo tak nejen ke zlevnění stavby, ale i k jejímu zrychlení.
2.8 KONTROLA ZÁKLADOVÝCH POMĚRŮ, MONITORING A ÚDRŽBA
Během výstavby se musí kontrolovat, zda zastižená základová půda a její vlastnosti odpovídají předpokladům geotechnického průzkumu a projektu. Jakékoliv zjištěné odchylky je třeba ihned zaznamenat (např. do stavebního deníku) a oznámit projektantovi. V rámci této kontroly se rovněž sleduje úroveň hladiny podzemní vody, její kolísání, průsaky do stavební jámy, do základové spáry apod. Pokud se během výstavby vyskytují změny pórových tlaků, které mohou ovlivnit provádění konstrukce či její stabilitu, monitoruje se tlak vody v pórech až do dokončení stavby a ujištění, že se tento tlak rozptýlil. Rovněž je vhodné zkontrolovat chemismus podzemní vody, zejména v těch případech, kdy na základě geotechnického průzkumu byla zjištěna její agresivita a bylo navrženo určité opatření pro ochranu základových konstrukcí proti této agresivitě. Musí se kontrolovat vliv výstavby vč. všech technologických postupů (odvodňování, injektáže, tunelování) na režim podzemních vod.
Geotechnický monitoring se musí použít:
- ke kontrole platnosti předpokladů projektu ve všech stadiích výstavby;
- k ujištění, že se konstrukce po svém dokončení chová podle požadavků projektu.
Monitoring má obsahovat následující typy měření:
- deformace základové půdy ovlivněné konstrukcí;
- velikostí zatížení;
- velikostí kontaktních napětí v základové spáře;
- pórových tlaků;
- sil a deformací v konstrukčních prvcích stavby.
Ve vztahu k příslušné geotechnické kategorii se výsledky monitoringu interpretují následujícím způsobem:
- pro 1. GK – obyčejně postačí vyhodnocení založené na vizuální prohlídce;
- pro 2. GK – obyčejně jde o vyhodnocení měření deformací (3D);
- pro 3. GK – kromě měření a vyhodnocení deformací v časovém sledu se hodnotí i síly a napětí v konstrukčních prvcích, jakož i pórové tlaky.
Pokud je to relevantní, musí se v projektu specifikovat potřebná údržba k zajištění bezpečnosti a použitelnosti základové konstrukce. Specifikace údržby má poskytnout informace:
- o kritických částech konstrukce, které vyžadují pravidelnou prohlídku;
- o pracích, které je zakázáno provádět bez předchozí revize stávající konstrukce;
- o četnosti prohlídek.
3 PLOŠNÉ ZÁKLADY
Plošné základy, jež jsou nejspodnější částí konstrukce stavby, přenášejí veškeré zatížení ze stavby do základové půdy pomocí plochy základové spáry. Ta se volí obvykle vodorovná v takové hloubce, která je optimální z hlediska únosnosti základové půdy, klimatických vlivů a technologie provádění těchto základů. V případě nutnosti návrhu šikmé základové spáry se volí příslušné odstupňování s vodorovnými úseky. Volbu druhu základu ovlivňuje velikost a způsob jeho zatížení a složení a vlastnosti základové půdy. Rozměr a tvar základu se navrhne a posuzuje vesměs výpočtem 1. a 2. mezního stavu ve smyslu ČSN EN 1997-1. Zvláštní pozornost je třeba při realizaci těchto základů věnovat kvalitě základové půdy, jakož i speciálním případům zakládání, tj. např. základům na násypech a na prosedavých zeminách (spraších), v sesuvných oblastech, v seizmických územích, základům strojů atd.
3.1 DRUHY PLOŠNÝCH ZÁKLADŮ
Plošnými základy jsou:
- základové patky, jež jsou typické pro zakládání sloupů;
- základové pasy, jež tvoří základy zdí;
- základové desky, jež tvoří souvislý základ pod celou stavbou, nebo jejím dilatačním celkem.
Někdy jsou jako zvláštní kategorie uváděny i základové rošty, jež jsou však tvořeny základovými pasy obyčejně kolmo uspořádanými, není tedy důvodu považovat je za další kategorii plošných základů.
Základové patky mají obdélníkový, výjimečně i kruhový tvar a jsou z prostého, častěji však vyztuženého betonu. Bývají vesměs monolitické, jednostupňové, výjimečně, v případě větších hloubek založení i vícestupňové. Pro zakládání sloupů montovaných železobetonových konstrukcí bývají opatřeny kalichy pro vetknutí těchto sloupů. Od dříve hojně používaných prefabrikovaných patek se ustupuje, neboť jsou dražší a obyčejně neposkytují žádné významné výhody. Pro zakládání monolitických železobetonových konstrukcí a konstrukcí ocelových jsou opatřeny kotevní výztuží. Pro potřeby posuzování plošných základů se stanovuje jejich tuhost, která souvisí nejen s jejich tvarem, ale i s deformačními vlastnostmi základové půdy.
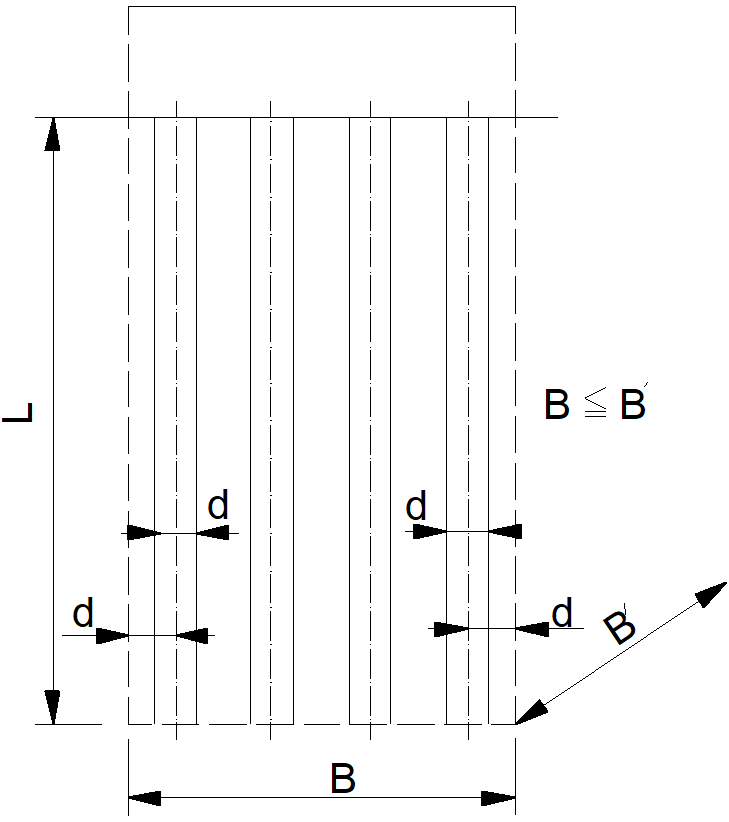
Za základové pasy se považují obdélníkové základy s poměrem L / B ≥ 6, přičemž vždy platí, že jejich šířka B ≤ L (délka). Základové pasy bývají ve směru šířky prakticky vždy tuhé, poddajné bývají naopak ve směru své délky. Základové pasy lze vést v potřebných směrech, v nichž jsou umístěny zakládané zdi. V případě málo únosné základové půdy a pravidelné rozteče nosných konstrukcí mohou základové pasy tvořit i plošné základy pod sloupy, resp. kombinace sloupů s nosnými stěnami.
Základová deska je souvislý plošný základ přenášející zatížení celého stavebního objektu nebo jeho souvislé, oddilatované části. Základové desky umožňují účinné vodorovné ztužení objektu v úrovni základové spáry, snížení kontaktního napětí při zakládání na málo únosné půdě, snížení nerovnoměrného sedání a vzájemného pootáčení svislých prvků konstrukce na málo únosném podloží a provedení celoplošné izolace suterénu stavby proti podzemní vodě.
Plošné základy spadají obyčejně do 1. GK a 2. GK, zcela výjimečně i do 3. GK. Návrh plošných základů spočívá v návrhu velikosti a tvaru plochy základové spáry vč. hloubky založení D a dále z doporučení vedoucích k ochraně základové spáry před a při provádění plošných základů. Správně navržená plocha základů se posuzuje prokázáním mezního stavu porušení (stability) a popř. prokázáním mezního stavu použitelnosti, jež vede k odbornému odhadu (výpočtu) velikosti sedání základů. V případech umístění plošného základu (vesměs patky či pasu) blízko nebo na přirozeném či umělém svahu, blízko výkopu nebo opěrné zdi, blízko vodoteče či jezera nebo nádrže a blízko hornických děl či zasypaných konstrukcí, se musí prokázat celková stabilita základové půdy (EQU).
3.2 HLOUBKA ZALOŽENÍ
Klimatické poměry v České republice ovlivňují plošné základy staveb jednak možností promrzání, jednak nadměrným vysycháním spojeným s přetvořením příslušných zemin. Z hlediska mrazu je na našem území minimální hloubka založení D = 0,80 m, v horských oblastech to může být i více. K vysychání spojeném se smršťováním základové půdy jsou citlivé jemnozrnné zeminy s velmi a extrémně vysokou plasticitou třídy F7 a F8, kde minimální hloubka založení činí D = 1,60 m. V případě dočasných nebo provizorních staveb lze zakládat i v hloubce D = 0,40 m, je však třeba mít jistotu, že klimatické vlivy tuto část objektu negativně neovlivní.
Hloubka založení D pro posouzení 1. mezního stavu je nejmenší svislá vzdálenost od (upraveného) terénu k základové spáře, jež tvoří kontakt plošného základu s geotechnickým prostředím. Pro posouzení 2. mezního stavu (použitelnosti), kdy se stanovuje zejména sedání plošných základů, je hloubka založení vztažena vždy k původnímu terénu.
3.3 NÁVRH PODLE MEZNÍHO STAVU PORUŠENÍ, PŘÍKLAD 1
Při výpočtu mezního stavu porušení (GEO) a (STR) je třeba vycházet z návrhových hodnot zatížení Fd, jež se odvozují z hodnot reprezentativních Frep, a ty pak z hodnot charakteristických Fk podle vztahů:
\begin{gathered}
F_\text{d}=\gamma_\text{F}\cdot F_\text{rep};&&F_\text{rep}=\psi\cdot F_\text{k}
\end{gathered}(24)
kde je:
γF … dílčí součinitelé zatížení jsou dány v tab. 8 a součinitel ψ se převezme z ČSN EN 1990.
kruhu, jež se pro účely výpočtu převede nejlépe na rovnoplochý čtverec), působí obecně 6 složek zatížení, tj. 3 složky silové ve směru os: Fxd, Fyd, Fzd a 3 složky momentové otáčející kolem těchto os: Mxd, Myd a Mzd, přičemž obyčejně kroutící moment kolem svislé osy z: Mzd = 0, osa z je svislá. Nejprve je třeba stanovit excentricitu e působící svislé síly Fzd vzhledem k těžišti základové spáry, resp. její složky:
\begin{gathered}
e_\text{x}=\frac{M_\text{yd}}{F_\text{zd}}\space\space\text{a}\space\space e_\text{y}=\frac{M_\text{xd}}{F_\text{zd}}
\end{gathered}pro něž musí platit:
\begin{gathered}
(\frac{e_\text{x}}{B})^2+(\frac{e_\text{y}}{L})^2\le(\frac{1}{3})^2
\end{gathered}(25)
Pokud tato podmínka není splněna, je třeba tvar plochy základové spáry změnit (jde o podmínku stability). Pro 1. mezní stav (porušení) se předpokládá konstantní průběh napětí v základové spáře σd, tudíž se počítá s tzv. efektivní plochou základové spáry:
\begin{gathered}
A_\text{ef}=B_\text{ef}\cdot L_\text{ef}
\end{gathered}kde je:
\begin{gathered}
B_\text{ef}=B-2e_\text{x};&&L_\text{ef}=L-2e_\text{y}
\end{gathered}(26)
\begin{gathered}
\sigma_\text{d}=\frac{F_\text{zd}}{A_\text{ef}}\le\frac{R_\text{d}}{\gamma_\text{RV}}
\end{gathered}(27)
kde je:
Rd … návrhová únosnost základové spáry, jež se určí a posoudí příslušnými návrhovými přístupy podle ČSN EN 1997-1. Na základě doporučení NAD se v ČR používá NP1 (viz kap. 2.2.2); v jiných zemích, např. v SRN a v Rakousku se používá NP2;
γRV … dílčí součinitel únosnosti pro plošné základy podle tab. 12.
V případě jemnozrnných zemin třídy F se návrhová únosnost posuzuje zvlášť pro tzv. neodvodněné podmínky, kdy o únosnosti v základové spáře rozhodují totální parametry základové půdy, pro něž zhruba platí: φud = 0 a pevnost je dána totální soudržností cu, potom:
\begin{gathered}
R_\text{d}=(\pi+2)\cdot c_\text{u}\cdot b_\text{c}\cdot s_\text{c}\cdot i_\text{c}+q
\end{gathered}(28)
kde je:
\begin{gathered}
q=\gamma\cdot D
\end{gathered}… tlak nadloží nad základovou spárou;
\begin{gathered}
b_\text{c}=1-\frac{2\alpha}{(\pi+2)}
\end{gathered}… vliv sklonu základové spáry α od vodorovné;
\begin{gathered}
s_\text{c}=1+0{,}2\cdot\frac{B_\text{ef}}{L_\text{ef}}
\end{gathered}… vliv tvaru základu (pro čtverec nebo kruh je sc = 1,2);
\begin{gathered}
i_\text{c}=0{,}5\cdot(1+(1-\frac{H_\text{d}}{(A_\text{ef}\cdot c_\text{u})})^\frac{1}{2})\space\space\text{pro}\space\space H_\text{d}\le A_\text{ef}\cdot c_\text{u}\space\space\text{kde}\space\space H_\text{d}=(F_\text{xd}^2+F_\text{yd}^2)^\frac{1}{2}
\end{gathered}… vliv šikmosti vyvolané vodorovným zatížením Hd.
Pro odvodněné podmínky se návrhová únosnost stanoví:
\begin{gathered}
R_\text{d}=c_\text{ef}\cdot N_\text{c}\cdot b_\text{c}\cdot s_\text{c}\cdot i_\text{c}+\gamma_1\cdot D\cdot N_\text{q}\cdot b_\text{q}\cdot s_\text{q}\cdot i_\text{q}+0{,}5\gamma_2\cdot B_\text{ef}\cdot N_\gamma\cdot b_\gamma\cdot s_\gamma\cdot i_\gamma
\end{gathered}(29)
kde je:
\begin{gathered}
N_\text{q}=e^{\pi\tg\varphi}\cdot\tg^2\cdot(45+\frac{\varphi}{2});&&N_\text{c}=(N_\text{q}-1)\cdot\cotg\varphi;&&N_\gamma=2\cdot(N_\text{q}-1)\cdot\tg\varphi30)\\\\
b_\text{c}=b_\text{q}-\frac{(1-b_\text{q})}{(N_\text{c}\cdot\tg\varphi)};&&b_\text{q}=b_\gamma=(1-\alpha\cdot\tg\varphi)^2
\end{gathered}(31)
\begin{gathered}
s_\text{q}=1+(\frac{B_\text{ef}}{L_\text{ef}})\cdot\sin\varphi;&&s_\gamma=1-0{,}3\cdot(\frac{B_\text{ef}}{L_\text{ef}});&&s_\text{c}=\frac{(s_\text{q}\cdot N_\text{q}-1)}{(N_\text{q}-1)}
\end{gathered}(32)
\begin{gathered}
i_\text{c}=i_\text{q}-\frac{1-i_\text{q})}{(N_\text{c}\cdot\tg\varphi)};&&i_\text{q}=(1-\frac{H_\text{d}}{(F_\text{zd}+A_\text{ef}\cdot c_\text{ef}\cdot\cotg\varphi)})^\text{m};&&i_\gamma=(1-\frac{H_\text{d}}{(F_\text{zd}+A_\text{ef}\cdot c_\text{ef}\cdot\cotg\varphi)})^{\text{m}+1}
\end{gathered}(33)
kde je:
\begin{gathered}
m=m_\text{x}=\frac{(2+(\frac{B_\text{ef}}{L_\text{ef}}))}{(1+(\frac{B_\text{ef}}{L_\text{ef}}))}
\end{gathered}pokud Hd je ve směru B;
\begin{gathered}
m=m_\text{y}=\frac{(2+(\frac{L_\text{ef}}{B_\text{ef}}))}{(1+(\frac{L_\text{ef}}{B_\text{ef}}))}
\end{gathered}pokud Hd je ve směru L;
\begin{gathered}
m=m_\varepsilon=m_\text{y}\cdot\cos^2\varepsilon+m_\text{x}\sin^2\varepsilon
\end{gathered}pokud Hd svírá s osou y úhel ε;
(34)
γ1 … objemová tíha zeminy nad základovou spárou;
γ2 … objemová tíha zeminy pod základovou spárou do hloubky 2,5 Bef.
Dále je třeba posoudit základovou spáru na usmyknutí dané výslednicí vodorovných sil v základové spáře Hd. Platí vztah:
\begin{gathered}
A_\text{ef}\cdot\frac{R_\text{dh}}{\gamma_\text{Rh}}=\frac{(F_\text{zd}\cdot\tg\varphi_\text{d}+c_\text{d}\cdot A_\text{ef}+S_\text{pd})}{\gamma_\text{Rh}}\ge H_\text{d}
\end{gathered}(35)
kde je:
Rdh … návrhová únosnost základové spáry ve vodorovném směru;
Spd … vodorovná návrhová složka zemního odporu uvažovaná na výšku základu;
γRh … dílčí součinitel únosnosti pro plošné základy podle tab. 12.
Tab. 12 Dílčí součinitelé únosnosti γR
| Značka | Soubor | |||
| R1 | R2x) | R3x) | ||
| únosnost | γR,v | 1,0 | 1,4 | 1,0 |
| usmyknutí | γR,h | 1,0 | 1,1 | 1,0 |
| x) podle doporučení NAD používá se pouze NP1, tedy dílčí součinitelé pro R1 | ||||
Příklad 1
Návrh základové patky v základové půdě podle obr. 12 pro charakteristické velikosti zatížení na povrchu patky: NkG = 500 kN, NkQ = 300 kN, MykG = 50 kNm, MykQ = 150 kNm, HxkQ = 80 kN. Návrh pro 1. mezní stav (porušení). Vlastnosti základové půdy jsou v tab. 13.
Tab. 13 Vlastnosti základové půdy pro příklad 1
| Vrstva | Popis | Úhel vnitřního tření [°] | Soudržnost [kPa] | Objemová tíha [kN·m-3] | Modul deformace [MPa] | Poissonovo číslo | ||
| efektivní | totální | efektivní | totální | |||||
| a | navážka (Y) | – | – | – | – | 18,0 | – | – |
| b | jíl písčitý, pevný (F6) | 20 | 0 | 12,0 | 65,0 | 21,0 | 5,0 | 0,40 |
| c | písek hlinitý (S3) | 30 | – | 5,0 | – | 19,5 | 18,0 | 0,30 |
| d | slínovec zvětralý (R5) | – | – | – | – | 22,0 | 25,0 | – |
Obr. 12 Zadání k příkladu 1
Řešení:
Vzhledem k tomu, že v případě jemnozrnných zemin rozhoduje obyčejně únosnost pro neodvodněné podmínky, bude nejprve posouzena tato krátkodobá únosnost:
1. NP1a: A1 „+“ M1 „+“ R1
Volíme patku čtvercovou B x L = 2,5 x 2,5 m, tloušťka t = 1,0 m, hloubku založení D = 1,20 m (ve vrstvě č. 2 – jílu slabě písčitém tuhém až pevném tř. F6).
a) zatížení a napětí v úrovni základové spáry:
- tíha patky
\begin{gathered}
G=2{,}5\cdot2{,}5\cdot1{,}0\cdot25=156{,}25\space\text{kN}
\end{gathered}- normálová síla v těžišti základové spáry:
\begin{gathered}
N_\text{zd}=(500+156{,}25)\cdot1{,}35+300\cdot1{,}5=1\space335{,}94\space\text{kN}
\end{gathered}- vodorovná síla v těžišti základové spáry:
\begin{gathered}
H_\text{xd}=80\cdot1{,}5=120{,}00\space\text{kN}
\end{gathered}- moment v těžišti základové spáry:
\begin{gathered}
M_\text{yd}=50\cdot1{,}35+150\cdot1{,}50+120\cdot1{,}0=412{,}50\space\text{kNm}
\end{gathered}- excentricita svislé síly v základové spáře:
\begin{gathered}
e_\text{xd}=\frac{412{,}5}{1\space335{,}94}=0{,}308\space\text{m}\lt\frac{2{,}5}{3}=0{,}83\space\text{m}
\end{gathered}- efektivní šířka základu:
\begin{gathered}
B_\text{ef}=2{,}5-2\cdot0{,}308=1{,}884\space\text{m (délka}\space L_\text{ef}=1{,}50\space\text{m)}
\end{gathered}- efektivní plocha základové spáry:
\begin{gathered}
A_\text{ef}=2{,}5\cdot1{,}884=4{,}71\space\text{m}^2
\end{gathered}- napětí v základové spáře:
\begin{gathered}
\sigma_\text{d}=\frac{1\space335{,}94}{4{,}71}=283{,}64\space\text{kPa}
\end{gathered}b) únosnost základové spáry pro neodvodněné podmínky (krátkodobá únosnost) spočte se podle rovnice (28):
- efektivní tlak nadloží:
\begin{gathered}
q=18{,}0\cdot1{,}0+0{,}2\cdot21{,}0=22{,}20\space\text{kPa}
\end{gathered}- součinitelé:
\begin{gathered}
b_\text{c}=1{,}0;\\\\
s_\text{c}=1{,}0+0{,}2\cdot\frac{1{,}88}{2{,}5}=1{,}15\\\\
i_\text{c}=0{,}5\cdot(1+(1-(\frac{120}{(65{,}0\cdot4{,}71)})^\frac{1}{2})=0{,}89
\end{gathered}\begin{gathered}
R_\text{d}=(3{,}14+2{,}0)\cdot65{,}0\cdot1{,}0\cdot1{,}15\cdot0{,}89+22{,}2=364{,}15\space\text{kPa}
\end{gathered}\begin{gathered}
\sigma_\text{d}=283{,}64\space\text{kPa}\lt\frac{364{,}15}{1{,}0}=364{,}15\space\text{kPa}\implies\space\text{vyhovuje}
\end{gathered}c) odolnost proti usmyknutí (podle rovnice (35), Spd se obyčejně zanedbává):
- únosnost ve smyku v základové spáře:
\begin{gathered}
R_\text{dh}=A_\text{ef}\cdot c_\text{ud}=4{,}71\cdot65=306{,}15\space\text{kN}
\end{gathered}- výsledek
\begin{gathered}
\frac{R_\text{dh}}{\gamma_\text{Rh}}=\frac{306{,}15}{1{,}0}=306{,}15\space\text{kN}\lt H_\text{d}=120{,}0\space\text{kN}\implies\space\text{vyhovuje}
\end{gathered}2. NP1b: A2 „+“ M2 „+“ R1
a) zatížení a napětí v úrovni základové spáry:
- normálová síla v těžišti základové spáry:
\begin{gathered}
N_\text{zd}=(500+156{,}25)\cdot1{,}0+300\cdot1{,}3=1\space046{,}25\space\text{kN}
\end{gathered}- vodorovná síla v těžišti základové spáry:
\begin{gathered}
H_\text{xd}=80\cdot1{,}3=104{,}00\space\text{kN}
\end{gathered}- moment v těžišti základové spáry:
\begin{gathered}
M_\text{yd}=50\cdot1{,}0+150\cdot1{,}30+104\cdot1{,}0=349{,}00\space\text{kNm}
\end{gathered}- excentricita svislé síly v základové spáře:
\begin{gathered}
e_\text{xd}=\frac{349{,}0}{1\space046{,}25}=0{,}333\space\text{m}\le\frac{2{,}5}{3}=0{,}83\space\text{m}
\end{gathered}- efektivní šířka základu:
\begin{gathered}
B_\text{ef}=2{,}5-2\cdot0{,}333=1{,}834\space\text{m (délka}\space L_\text{ef}=2{,}50\space\text{m)}
\end{gathered}- efektivní plocha základové spáry:
\begin{gathered}
A_\text{ef}=2{,}5\cdot1{,}834=4{,}59\space\text{m}^2
\end{gathered}- napětí v základové spáře:
\begin{gathered}
\sigma_\text{d}=\frac{1\space046{,}25}{4{,}59}=227{,}94\space\text{kPa}
\end{gathered}b) únosnost základové spáry pro neodvodněné podmínky (krátkodobá únosnost) spočte se podle rovnice (12):
\begin{gathered}
c_\text{ud}=\frac{65{,}0}{1{,}4}=46{,}43\space\text{kPa}
\end{gathered}- součinitelé:
\begin{gathered}
b_\text{c}=1{,}0;\\\\
s_\text{c}=1{,}0+0{,}2\cdot\frac{1{,}83}{2{,}5}=1{,}14\\\\
i_\text{c}=0{,}5\cdot(1+(1-(\frac{104}{(46{,}43\cdot4{,}59)})^\frac{1}{2})=0{,}86
\end{gathered}\begin{gathered}
R_\text{d}=(3{,}14+2{,}0)\cdot46{,}43\cdot1{,}0\cdot1{,}15\cdot0{,}86+22{,}2=236{,}03\space\text{kPa}
\end{gathered}\begin{gathered}
\sigma_\text{d}=227{,}94\space\text{kPa}\lt\frac{236{,}03}{1{,}0}=236{,}03\space\text{kPa}\implies\space\text{vyhovuje}
\end{gathered}c) odolnost proti usmyknutí:
- únosnost ve smyku v základové spáře:
\begin{gathered}
R_\text{dh}=A_\text{ef}\cdot c_\text{ud}=4{,}59\cdot46{,}43=213{,}11\space\text{kN}
\end{gathered}- výsledek
\begin{gathered}
\frac{R_\text{dh}}{\gamma_\text{Rh}}=\frac{213{,}11}{1{,}0}=213{,}11\space\text{kN}\gt H_\text{d}=104{,}0\space\text{kN}\implies\space\text{vyhovuje}
\end{gathered}3) Dlouhodobá únosnost (odvodněné podmínky)
NP1a: A1 „+“ M1 „+“ R1
a) zatížení a napětí v úrovni základové spáry (patka má rozměry 2,5 x 2,5 m)
- normálová síla v těžišti základové spáry:
\begin{gathered}
N_\text{zd}=(500+156{,}25)\cdot1{,}35+300\cdot1{,}5=1\space335{,}94\space\text{kN}
\end{gathered}- vodorovná síla v těžišti základové spáry:
\begin{gathered}
H_\text{xd}=80\cdot1{,}5=120{,}00\space\text{kN}
\end{gathered}- moment v těžišti základové spáry:
\begin{gathered}
M_\text{yd}=50\cdot1{,}35+150\cdot1{,}50+120\cdot1{,}0=412{,}50\space\text{kNm}
\end{gathered}- excentricita svislé síly v základové spáře:
\begin{gathered}
e_\text{xd}=\frac{412{,}5}{1\space335{,}94}=0{,}308\space\text{m}\le\frac{2{,}5}{3}=0{,}83\space\text{m}
\end{gathered}- efektivní šířka základu:
\begin{gathered}
B_\text{ef}=2{,}5-2\cdot0{,}308=1{,}884\space\text{m (délka}\space L_\text{ef}=2{,}50\space\text{m)}
\end{gathered}- efektivní plocha základové spáry:
\begin{gathered}
A_\text{ef}=2{,}5\cdot1{,}884=4{,}71\space\text{m}^2
\end{gathered}- napětí v základové spáře:
\begin{gathered}
\sigma_\text{d}=\frac{1\space335{,}94}{4{,}71}=283{,}64\space\text{kPa}
\end{gathered}b) únosnost základové spáry pro odvodněné podmínky (dlouhodobá únosnost) spočte se podle rovnice (29)
- součinitelé únosnosti:
\begin{gathered}
N_\text{q}=2{,}718^{3{,}14\tg20}\cdot\tg^2(45+\frac{20}{2})=6{,}39;&N_\text{c}=(6{,}39-1{,}0)\cdot\cotg20=14{,}80;&N_\gamma=2\cdot(6{,}39-1{,}0)\cdot\tg20=3{,}92
\end{gathered}- součinitelé tvaru základu:
\begin{gathered}
s_\text{q}=1{,}0+\frac{1{,}88}{2{,}5}\cdot\sin20=1{,}26;&s_\gamma=1{,}0-0{,}3\cdot\frac{1{,}88}{2{,}5}=0{,}77;&s_\text{c}=\frac{(1{,}26\cdot6{,}39-1{,}0)}{(6{,}39-1{,}0)}=1{,}3
\end{gathered}- součinitelé šikmosti zatížení:
\begin{gathered}
m_\text{B}=\frac{(2+\frac{1{,}88}{2{,}5})}{(1+\frac{1{,}88}{2{,}5})}=1{,}57
\end{gathered}\begin{gathered}
i_\text{q}=\frac{(1-120)}{(1\space335{,}94+4{,}71\cdot12{,}0\cdot\cotg20)})^{1{,}57}=0{,}88\\\\
i_\text{c}=0{,}88-\frac{(1-0{,}88)}{(14{,}8\cdot\tg20)}=0{,}86\\\\
i_\gamma=(1-\frac{120}{(1\space335{,}94+4{,}71\cdot12{,}0\cdot\cotg20)})^{2{,}57}=0{,}81
\end{gathered}\begin{gathered}
R_\text{d}=12{,}0\cdot14{,}8\cdot1{,}31\cdot0{,}86+22{,}2\cdot6{,}39\cdot1{,}26\cdot0{,}88+0{,}6\cdot21{,}0\cdot1{,}88\cdot0{,}77\cdot0{,}81=371{,}45\space\text{kPa}
\end{gathered}\begin{gathered}
\sigma_\text{d}=283{,}64\space\text{kPa}\lt\frac{371{,}45}{1{,}0}=371{,}45\space\text{kPa}\implies\space\text{vyhovuje}
\end{gathered}c) odolnost proti usmyknutí
- únosnost ve smyku v základové spáře:
\begin{gathered}
R_\text{dh}=(N_\text{zd}\cdot\tg\varphi_\text{d}+A_\text{ef}\cdot c_\text{ef,d})=1\space335{,}94\cdot\tg20+4{,}71\cdot12{,}0=542{,}76\space\text{kN}
\end{gathered}- výsledek
\begin{gathered}
\frac{R_\text{dh}}{\gamma_\text{Rh}}=\frac{542{,}76}{1{,}0}=542{,}76\space\text{kN}\gt H_\text{d}=120{,}0\space\text{kN}\implies\space\text{vyhovuje}
\end{gathered}4. Dlouhodobá únosnost (odvodněné podmínky) NP1b: A2 „+“ M2 „+“ R1
a) zatížení a napětí v úrovni základové spáry (patka má rozměry 2,5 x 2,5 m)
- normálová síla v těžišti základové spáry:
\begin{gathered}
N_\text{zd}=(500+156{,}25)\cdot1{,}0+300\cdot1{,}3=1\space046{,}25\space\text{kN}
\end{gathered}- vodorovná síla v těžišti základové spáry:
\begin{gathered}
H_\text{xd}=80\cdot1{,}3=104{,}00\space\text{kN}
\end{gathered}- moment v těžišti základové spáry:
\begin{gathered}
M_\text{yd}=50\cdot1{,}0+150\cdot1{,}30+104\cdot1{,}0=349{,}0\space\text{kNm}
\end{gathered}- excentricita svislé síly v základové spáře:
\begin{gathered}
e_\text{xd}=\frac{349{,}0}{1\space046{,}25}=0{,}333\space\text{m}\lt\frac{2{,}5}{3}=0{,}83\space\text{m}
\end{gathered}- efektivní šířka základu:
\begin{gathered}
B_\text{ef}=2{,}5-2\cdot0{,}333=1{,}834\space\text{m (délka}\space L_\text{ef}=2{,}50\space\text{m)}
\end{gathered}- efektivní plocha základové spáry:
\begin{gathered}
A_\text{ef}=2{,}5\cdot1{,}834=4{,}59\space\text{m}^2
\end{gathered}- napětí v základové spáře:
\begin{gathered}
\sigma_\text{d}=\frac{1\space046{,}25}{4{,}59}=227{,}94\space\text{kPa}
\end{gathered}b) únosnost základové spáry pro odvodněné podmínky (dlouhodobá únosnost)
(vliv M2):
\begin{gathered}
c_\text{d}=\frac{12{,}0}{1{,}25}=9{,}60\space\text{kPa},&\varphi_\text{d}=\arctg(\frac{\tg20}{1{,}25})=16{,}23\degree
\end{gathered}- součinitelé únosnosti:
\begin{gathered}
N_\text{q}=2{,}718^{3{,}14\tg16{,}23}\cdot\tg^2(45+\frac{16{,}23}{2})=4{,}44\\\\
N_\text{c}=(4{,}44-1{,}0)\cdot\cotg16{,}23=11{,}82\\\\
N_\gamma=2\cdot(4{,}44-1{,}0)\cdot\tg16{,}23=2{,}00
\end{gathered}- součinitelé tvaru základu:
\begin{gathered}
s_\text{q}=1{,}0+\frac{1{,}83}{2{,}5}\cdot\sin16{,}23=1{,}20\\\\
s_\gamma=1{,}0-0{,}3\cdot\frac{1{,}83}{2{,}5}=0{,}78\\\\
s_\text{c}=\frac{(1{,}21\cdot4{,}44-1{,}0)}{(4{,}44-1{,}0)}=1{,}27
\end{gathered}- součinitelé šikmosti zatížení:
\begin{gathered}
m_\text{B}=\frac{(2+\frac{1{,}83}{2{,}5})}{(1+\frac{1{,}83}{2{,}5})}=1{,}58
\end{gathered}\begin{gathered}
i_\text{q}=(1-\frac{104}{(1\space046{,}25+4{,}59\cdot9{,}6\cdot\cotg16{,}23)})^{1{,}58}=0{,}87\\\\
i_\text{c}=0{,}87-\frac{(1-0{,}87)}{(11{,}82\cdot\tg16{,}23)}=0{,}83\\\\
i_\gamma=(1-\frac{104}{(1\space046{,}25+4{,}59\cdot9{,}6\cdot\cotg16{,}23)})^{2{,}58}=0{,}79\\\\
\end{gathered}\begin{gathered}
R_\text{d}=9{,}6\cdot11{,}82\cdot1{,}27\cdot0{,}83+22{,}2\cdot4{,}44\cdot1{,}20\cdot0{,}87+0{,}5\cdot21{,}0\cdot1{,}83\cdot0{,}78\cdot0{,}79=234{,}36\space\text{kPa}
\end{gathered}\begin{gathered}
\sigma_\text{d}=227{,}94\space\text{kPa}\lt\frac{234{,}36}{1{,}0}=234{,}36\space\text{kPa}\implies\text{vyhovuje}
\end{gathered}c) odolnost proti usmyknutí
- únosnost ve smyku v základové spáře:
\begin{gathered}
R_\text{dh}=(N_\text{zd}\cdot\tg\varphi_\text{d}+A_\text{ef}\cdot c_\text{ef,d})=1\space046{,}25\cdot\tg16{,}23+4{,}59\cdot9{,}6=348{,}62\space\text{kN}
\end{gathered}- výsledek
\begin{gathered}
\frac{R_\text{dh}}{\gamma_\text{Rh}}=\frac{348{,}62}{1{,}0}=348{,}62\space\text{kN}\gt H_\text{d}=104{,}0\space\text{kN}\implies\text{vyhovuje}
\end{gathered}5. Výpočet bude proveden i pro NP2, který je charakterizován: A1 „+“ M1 „+“ R2
a) zatížení a napětí v úrovni základové spáry
- tíha patky
\begin{gathered}
G=2{,}5\cdot2{,}5\cdot1{,}0\cdot25=156{,}25\space\text{kN}
\end{gathered}- normálová síla v těžišti základové spáry:
\begin{gathered}
N_\text{zd}=(500+156{,}52)\cdot1{,}35+300\cdot1{,}5=1\space335{,}94\space\text{kN}
\end{gathered}- vodorovná síla v těžišti základové spáry:
\begin{gathered}
H_\text{xd}=80\cdot1{,}5=120{,}00\space\text{kN}
\end{gathered}- moment v těžišti základové spáry:
\begin{gathered}
M_\text{yd}=50\cdot1{,}35+150\cdot1{,}50+120\cdot1{,}0=412{,}50\space\text{kNm}
\end{gathered}- excentricita svislé síly v základové spáře:
\begin{gathered}
e_\text{xd}=\frac{412{,}5}{1\space335{,}94}=0{,}308\space\text{m}\lt\frac{2{,}5}{3}=0{,}83\space\text{m}
\end{gathered}- efektivní šířka základu:
\begin{gathered}
B_\text{ef}=2{,}5-2\cdot0{,}308=1{,}884\space\text{m (délka}\space L_\text{ef}=2{,}50\space\text{m)}
\end{gathered}- efektivní plocha základové spáry:
\begin{gathered}
A_\text{ef}=2{,}5\cdot1{,}884=4{,}71\space\text{m}^2
\end{gathered}- napětí v základové spáře:
\begin{gathered}
\sigma_\text{d}=\frac{1\space335{,}94}{4{,}71}=283{,}64\space\text{kPa}
\end{gathered}b) únosnost základové spáry pro neodvodněné podmínky (krátkodobá únosnost)
- efektivní tlak nadloží:
\begin{gathered}
q=18{,}0\cdot1{,}0+0{,}2\cdot21{,}0=22{,}20\space\text{kPa}
\end{gathered}- součinitelé:
\begin{gathered}
b_\text{c}=1{,}0;&s_\text{c}=1+0{,}2\cdot\frac{1{,}88}{2{,}5}=1{,}15\\\\
i_\text{c}=0{,}5\cdot(1+(1-(\frac{120}{(65{,}0\cdot4{,}71)})^\frac{1}{2})=0{,}89
\end{gathered}\begin{gathered}
R_d=(3{,}14+2{,}0)\cdot65{,}0\cdot1{,}0\cdot1{,}15\cdot0{,}89+22{,}2=364{,}15\space\text{kPa}
\end{gathered}\begin{gathered}
\sigma_\text{d}=283{,}64\space\text{kPa}\gt\frac{364{,}15}{1{,}4}=260{,}10\space\text{kPa}\implies\text{nevyhovuje}
\end{gathered}(součinitel γR,V pro R2 je 1,4), nutno zvětšit základ na 2,6 x 2,6 m
c) tíha nové patky
\begin{gathered}
G=2{,}6\cdot2{,}6\cdot1{,}0\cdot25=169{,}00\space\text{kN}
\end{gathered}- normálová síla v těžišti základové spáry:
\begin{gathered}
N_\text{zd}=(500+169)\cdot1{,}35+300\cdot1{,}5=1\space353{,}15\space\text{kN}
\end{gathered}- vodorovná síla v těžišti základové spáry:
\begin{gathered}
H_\text{xd}=80\cdot1{,}5=120{,}00\space\text{kN}
\end{gathered}- moment v těžišti základové spáry:
\begin{gathered}
M_\text{yd}=50\cdot1{,}35+150\cdot1{,}50+120\cdot1{,}0=412{,}50\space\text{kNm}
\end{gathered}- excentricita svislé síly v základové spáře:
\begin{gathered}
e_\text{xd}=\frac{412{,}5}{1\space353{,}15}=0{,}350\space\text{m}\lt\frac{2{,}5}{3}=0{,}83\space\text{m}
\end{gathered}- efektivní šířka základu:
\begin{gathered}
B_\text{ef}=2{,}6-2\cdot0{,}305=1{,}99\space\text{m (délka}\space L_\text{ef}=2{,}6\space\text{m)}
\end{gathered}- efektivní plocha základové spáry:
\begin{gathered}
A_\text{ef}=2{,}6\cdot1{,}99=5{,}17\space\text{m}^2
\end{gathered}- napětí v základové spáře:
\begin{gathered}
\sigma_\text{d}=\frac{1\space353{,}15}{5{,}17}=261{,}73\space\text{kPa}
\end{gathered}d) únosnost základové spáry pro neodvodněné podmínky (krátkodobá únosnost)
- efektivní tlak nadloží:
\begin{gathered}
q=18{,}0\cdot1{,}0+0{,}2\cdot21{,}0=22{,}20\space\text{kPa}
\end{gathered}- součinitelé:
\begin{gathered}
b_\text{c}=1{,}0;&s_\text{c}=1{,}0+0{,}2\cdot\frac{1{,}99}{2{,}6}=1{,}15;&i_\text{c}=0{,}5\cdot(1+(1-(\frac{120}{(65{,}0\cdot5{,}17)})^\frac{1}{2})=0{,}90
\end{gathered}\begin{gathered}
R_\text{d}=(3{,}14+2{,}0)\cdot65{,}0\cdot1{,}0\cdot1{,}15\cdot0{,}90+22{,}2=367{,}99\space\text{kPa}
\end{gathered}\begin{gathered}
\sigma_\text{d}=261{,}73\space\text{kPa}\lt\frac{367{,}99}{1{,}4}=262{,}85\space\text{kPa}\implies\text{vyhovuje}
\end{gathered}e) odolnost proti usmyknutí
- únosnost ve smyku v základové spáře:
\begin{gathered}
R_\text{dh}=A_\text{ef}\cdot c_\text{ud}=5{,}17\cdot65=336{,}05\space\text{kN}
\end{gathered}- výsledek
\begin{gathered}
\frac{R_\text{dh}}{\gamma_\text{Rh}}=\frac{336{,}05}{1{,}1}=305{,}50\space\text{kN}\gt H_\text{d}=120{,}0\space\text{kN}\implies\text{vyhovuje}
\end{gathered}f) únosnost základové spáry pro odvodněné podmínky (dlouhodobá únosnost)
- součinitelé únosnosti:
\begin{gathered}
N_\text{q}=2{,}718^{3{,}14\tg20}\cdot\tg^2(45+\frac{20}{2})=6{,}39\\\\
N_\text{c}=(6{,}39-1{,}0)\cdot\cotg20=14{,}80\\\\
N_\gamma=2\cdot(6{,}39-1{,}0)\cdot\tg20=3{,}92
\end{gathered}- součinitelé tvaru základu:
\begin{gathered}
s_\text{q}=1{,}0+\frac{1{,}99}{2{,}6}\cdot\sin20=1{,}26\\\\
s_\gamma=1{,}0-0{,}3\cdot\frac{1{,}99}{2{,}6}=0{,}77\\\\
s_\text{c}=\frac{(1{,}26\cdot6{,}39-1{,}0)}{(6{,}39-1{,}0)}=1{,}31
\end{gathered}- součinitelé šikmosti zatížení:
\begin{gathered}
m_\text{B}=\frac{(2+\frac{1{,}99}{2{,}6})}{(1+\frac{1{,}99}{2{,}6})}=1{,}57\\\\
i_\text{q}=(1-\frac{120}{(1\space353{,}15+5{,}17\cdot12{,}0\cdot\cotg20)})^{1{,}57}=0{,}88\\\\
i_\text{c}=0{,}88-\frac{(1-0{,}88)}{(14{,}8\cdot\tg20)}=0{,}86\\\\
i_\gamma=(1-\frac{120}{(1\space353{,}15+5{,}17\cdot12{,}0\cdot\cotg20)})^{2{,}57}=0{,}81
\end{gathered}\begin{gathered}
R_\text{d}=12{,}0\cdot14{,}8\cdot1{,}31\cdot0{,}86+22{,}2\cdot6{,}39\cdot1{,}26\cdot0{,}88+0{,}5\cdot21{,}0\cdot1{,}99\cdot0{,}77\cdot0{,}81=372{,}53\space\text{kPa}
\end{gathered}\begin{gathered}
\sigma_\text{d}=261{,}73\space\text{kPa}\lt\frac{372{,}53}{1{,}4}=266{,}10\space\text{kPa}\implies\text{vyhovuje}
\end{gathered}g) odolnost proti usmyknutí
- únosnost ve smyku v základové spáře:
\begin{gathered}
R_\text{dh}=(N_\text{zd}\cdot\tg\varphi_\text{d}+A_\text{ef}\cdot c_\text{ef,d})=1\space353{,}15\cdot\tg20+5{,}17\cdot12{,}0=554{,}54\space\text{kN}
\end{gathered}- výsledek
\begin{gathered}
\frac{R_\text{dh}}{\gamma_\text{Rh}}=\frac{554{,}54}{1{,}1}=504{,}13\space\text{kN}\gt H_\text{d}=120{,}0\space\text{kN}\implies\text{vyhovuje}
\end{gathered}Komentář:
- v českém NAD doporučený přístup NP1a, dává příznivější výsledky než přístup NP2, neboť v obou případech jde o kombinaci A1“+“M1, avšak NP1a se kombinuje s R1, což pro únosnost plošných základů znamená použití dílčích součinitelů únosnosti γR,v = γR,h = 1,0, zatímco v případě NP2 se využívá R2, kde γR,v = 1,4 a γR,h = 1,1;
- v případě jemnozrnných zemin je třeba vždy zvážit, není-li nutné posoudit krátkodobou (neodvodněnou) únosnost základové půdy.
3.4 NÁVRH PODLE MEZNÍHO STAVU POUŽITELNOSTI, PŘÍKLAD 2
Mezní stav použitelnosti vede k výpočtu sedání plošných základů, jež se musí provést vždy pro případy 2. GK a 3. GK. V případě 1. GK to nebývá nutné, a to s ohledem na velikost napětí v základové spáře. Sedání plošných základů se stanoví za předpokladu, že základová půda je pružný poloprostor, kde přitížení v základové spáře σ0,1 = σ0 – γ · D se do hloubky šíří v závislosti na intenzitě tohoto zatížení, jeho rozložení v základové spáře a tvaru této spáry. Průběh napětí v základové spáře již nemusí být konstantní, jako tomu bylo v případě 1. mezního stavu; stanovuje se podle zásad teorie pružnosti zejména s ohledem na tuhost základu. Stanoví se pomocná velikost k:
\begin{gathered}
k=(\frac{E_\text{b}}{E_\text{def,pr}})\cdot(\frac{t}{B})^3,\space\text{resp.}\space(\frac{E_\text{b}}{E_\text{def,pr}})\cdot(\frac{t}{L})^3
\end{gathered}(36)
kde je:
Eb … modul pružnosti betonu základu;
Edef,pr … je průměrná velikost modulu deformace základové půdy do hloubky 2B pod základovou spáru;
t … tloušťka základu;
B a L … jeho půdorysné rozměry ve směru, pro který se tuhost počítá.
Pokud k < 1, je základ poddajný a rozdělení napětí v základové spáře je třeba určit např. matematickým modelováním, bývá to zejména případ základových desek. Je-li k ≥ 1, je základ tuhý a průběh napětí je vesměs lineární. Lze jej získat superpozicí od účinků: normálová síla Fzk a příslušné momenty Mxk, Myk, přičemž přípustná jsou pouze tlaková napětí v základové spáře. Při výpočtu sedání se počítá s charakteristickými hodnotami zatížení, kdy veškeré dílčí součinitelé výpočtu γF, γM, γR jsou rovny 1. Průběh napětí od přitížení směrem do hloubky σz,i = σ0,1 · I, kde I je příčinkový součinitel sedání závislý na tvaru základu a na průběhu působícího napětí. Nejčastěji používaný součinitel I2 platný pro tzv. charakteristický bod obdélníkového základu rovnoměrně zatíženého je na obr. 13, příčinkové součinitele I platné pro jiné tvary základů a příslušné průběhy napětí v základové spáře lze najít ve všech učebnicích mechaniky zemin a zakládání staveb. Statické schéma pro výpočet sedání je potom na obr. 14.
Konečné sedání pod příslušným bodem plochy základové spáry se vypočte podle vzorce:
\begin{gathered}
s=\sum_{\text{i}=1}^\text{n}(\sigma_\text{z,i}-m\cdot\sigma_\text{or,i})\cdot\frac{h_\text{i}}{E_\text{oed,i}}
\end{gathered}(37)
kde je:
σz,i … svislá složka napětí od přitížení σ0,1 ve středu i-té vrstvy;
σor,i … původní geostatické napětí (σor,i = γ · (D + z)) ve středu i-té vrstvy;
m … opravný součinitel podle tab. 10 ČSN EN 1997-1, podle EC 7-1 m = 0,2;
hi … mocnost i-té vrstvy;
Eoed,i … charakteristická velikost oedometrického modulu přetvárnosti i-té vrstvy.
Vztah mezi modulem přetvárnosti Edef a oedometrickým modulem přetvárnosti Eoed je dán rovnicí (14).
Obr. 13 Průběh příčinkového součinitele sedání I2 pro charakteristický bod obdélníka
Pro konkrétní výpočet sedání plošného základu je třeba spočítat upravené vzdálenosti zri pomocí vzdáleností zi od základové spáry do středu i-té vrstvy podle vztahu:
\begin{gathered}
z_\text{ri}=\kappa_1\cdot\kappa_2\cdot z_\text{i}
\end{gathered}(38)
kde je:
κ1 … součinitel zohledňující hloubku založení D podle obr. 15;
κ2 … součinitel zohledňující existenci nestlačitelné vrstvy základové půdy v hloubce zr pod základovou spárou podle obr. 16.
Velikost konečného průměrného sednutí sm,lim a sednutí nerovnoměrného Δs / L, Δs / B stanovuje objednatel (investor) s přihlédnutím na charakter stavby, přičemž mezní doporučené hodnoty jsou v tab. 11.
Pro částečně nebo plně nasycené jemnozrnné zeminy se mají uvažovat 3 složky sedání:
\begin{gathered}
s_\text{celk}=s_0+s_1+s_2
\end{gathered}(39)
kde je:
s0 … sedání okamžité,
s1 … sedání konsolidační,
s2 … sedání vyvolané creepem.
Výše uvedeným způsobem lze stanovit velikosti sedání s0 a s1, pro odhad sedání s2 jsou potřebné speciální zkoušky základové půdy.
Obr. 14 Statické schéma pro výpočet konečného sedání
Obr. 15 Průběh součinitele κ1
Obr. 16 Průběh součinitele κ2
Příklad 2
Stanovení konečného sedání základové patky podle příkladu 1 (2. mezního stavu – použitelnosti). Předpokládáme existenci „nestlačitelné“ vrstvy základové půdy v hloubce zc = 8,0 m pod úrovní základové spáry.
Řešení:
Pro výpočet sedání se použijí charakteristické velikosti zatížení a průběh napětí v základové spáře podle teorie pružnosti. Budeme počítat sedání pro čtvercovou základovou patku B x L = 2,6 x 2,6 m.
a) stanovení zatížení a napětí v základové spáře
- normálová síla v těžišti základové spáry:
\begin{gathered}
N_\text{zk}=(500+169)\cdot1{,}0+3\space001{,}0=969{,}0\space\text{kN}
\end{gathered}- vodorovná síla v těžišti základové spáry:
\begin{gathered}
H_\text{xk}=80\space\text{kN}
\end{gathered}- moment v těžišti základové spáry:
\begin{gathered}
M_\text{yk}=50\cdot1{,}0+150\cdot1{,}0+80\cdot1{,}0=280{,}0\space\text{kN}
\end{gathered}- napětí v základové spáře od Nzk:
\begin{gathered}
\sigma_\text{n}=\frac{969}{2{,}6^2}=143{,}34\space\text{kPa}
\end{gathered}- napětí v základové spáře od Myk:
\begin{gathered}
\sigma_\text{m}=280\cdot\frac{6}{2{,}6^3}=\pm95{,}58\space\text{kPa}
\end{gathered}- napětí
\begin{gathered}
\sigma_1=143{,}34-95{,}58=47{,}76\space\text{kPa};&\sigma_2=143{,}34+95{,}58=238{,}92\space\text{kPa}
\end{gathered}- původní geostatické napětí v základové spáře:
\begin{gathered}
\sigma_{\text{or}{,}0}=18{,}0\cdot1{,}0+0{,}2\cdot21{,}0=22{,}2\space\text{kPa}
\end{gathered}- napětí konstantní
\begin{gathered}
\sigma_\text{a}=47{,}76-22{,}2=25{,}56\space\text{kPa}
\end{gathered}- napětí trojúhelníkové
\begin{gathered}
\sigma_\text{b}=238{,}92-47{,}76=191{,}16\space\text{kPa}
\end{gathered}- tuhost plošného základu (rovnice 36)
- průměrná velikost modulu deformace do hloubky 2 · 2,6 = 5,2 m pod základovou spárou:
\begin{gathered}
E_\text{def,pr}=\frac{(2{,}3\cdot5{,}0+2{,}9\cdot18)}{5{,}2}=12{,}25\space\text{MPa}
\end{gathered}- tuhost:
\begin{gathered}
k=(\frac{26\space500}{12{,}25})\cdot(\frac{1{,}0}{2{,}6})^3=123\gt1\space\text{... základ je tuhý}
\end{gathered}- výpočet konečného sedání bude součtem sedání tuhého základu pod charakteristickým bodem pro zatížení konstantní σa = 25,56 kPa a zatížení trojúhelníkové s pořadnicí σb = 191,16 kPa, vlastní výpočet je sestaven v tab. 14.
Tab. 14 Výpočet sedání základové patky z příkladu 2
| Číslo vrstvy | Mocnost hi [m] | zi [m] | D/zi | κ1 | zc/zi | κ2 | Zri = κ1 · κ2 · zi | σor,i [kPa] | 0,2 · σor,i [kPa] |
| 1 | 0,5 | 0,25 | 4,80 | 1,50 | 32,0 | 1,0 | 0,38 | 30,18 | 6,04 |
| 2 | 0,8 | 0,90 | 1,33 | 1,39 | 8,89 | 1,0 | 1,25 | 48,45 | 9,65 |
| 3 | 1,0 | 1,80 | 0,66 | 1,28 | 4,44 | 1,0 | 2,30 | 70,50 | 14,10 |
| 4 | 1,0 | 2,80 | 0,43 | 1,20 | 2,85 | 0,99 | 3,36 | 90,00 | 18,0 |
| 5 | 1,0 | 3,80 | 0,32 | 1,15 | 2,11 | 0,96 | 4,37 | 102,42 | 20,48 |
| 6 | 1,0 | 4,80 | 0,25 | 1,10 | 1,67 | 0,92 | 5,28 | 113,61 | 22,72 |
Pokračování tab. 14
| Sedání pro konstantní napětí σa = 25,56 kPa | Sedání pod nezatíženou hranou | ||||||||
| Číslo vrstvy | zi / B | I2 | σzi [kPa] | σzi – 0,2 · σor,i | Eoed,i [MPa] | si [mm] | IA,1 | σzi – 0,2 · σor,i | sA,i [mm] |
| 1 | 0,146 | 0,80 | 20,45 | 14,41 | 10,63 | 0,50 | 0,030 | 5,43 | 0,23 |
| 2 | 0,481 | 0,42 | 10,74 | 1,09 | 10,63 | 0,08 | 0,055 | 11,38 | 0,86 |
| 3 | 0,885 | 0,27 | 6,90 | -7,20 | 10,63 | – | 0,064 | 10,37 | 0,98 |
| 4 | 1,292 | 0,17 | 4,35 | – | 24,32 | – | 0,060 | 4,94 | 0,20 |
| 5 | 1,680 | 0,12 | 3,07 | – | 24,32 | – | 0,042 | -4,42 | – |
| 6 | 2,030 | 0,09 | 2,50 | – | 24,32 | – | 0,034 | – | – |
| sedání pod charakteristickým bodem | 0,58 mm | sedání pod bodem A | 2,27 mm | ||||||
Pokračování tab. 14
| Sedání pod zatíženou hranou | |||||
| Číslo vrstvy | zi/B | IB,1 | σzi – 0,2 · σor,i | Eoed,i [MPa] | sB,i [mm] |
| 1 | 0,146 | 0,240 | 85,72 | 10,63 | 4,03 |
| 2 | 0,481 | 0,180 | 59,17 | 10,63 | 4,45 |
| 3 | 0,885 | 0,130 | 35,60 | 10,63 | 3,35 |
| 4 | 1,292 | 0,090 | 16,41 | 24,32 | 0,67 |
| 5 | 1,680 | 0,060 | 2,46 | 24,32 | 0,10 |
| 6 | 2,030 | 0,045 | -5,52 | 24,32 | – |
| Sedání pod bodem B | 12,60 mm | ||||
Výsledky:
- sedání základové patky na hraně A:
\begin{gathered}
s_\text{A}=0{,}58+2{,}27=2{,}85\space\text{mm}
\end{gathered}- sedání základové patky na hraně B:
\begin{gathered}
s_\text{B}=0{,}58+12{,}60=13{,}18\space\text{mm}
\end{gathered}- průměrné sedání základové patky:
\begin{gathered}
s=\frac{(2{,}85+13{,}18)}{2}=8{,}02\space\text{mm}\implies\text{jistě vyhoví}
\end{gathered}- naklonění základové patky:
\begin{gathered}
\frac{\Delta s}{B}=\frac{(13{,}18-2{,}85)}{2\space600}=0{,}0039
\end{gathered}⇒ vyhoví pro staticky určité konstrukce, nevyhoví však již např. pro železobetonové a ocelové konstrukce staticky neurčité.
3.5 OCHRANA ZÁKLADOVÉ SPÁRY
Za účelem zajištění předpokládané únosnosti základové půdy a přípustného sedání plošných základů je nutné ochránit základovou spáru jak před vlivy mechanickými, tak i klimatickými. K poškození základové půdy dochází při strojním hloubení, jež musí být ukončeno v dostatečné výšce nad základovou spárou a poslední vrstva musí být odebrána ručně, nebo jen za použití malé mechanizace, a to těsně před položením podkladního betonu. V zásadě platí, že odkrýt lze pouze takovou plochu, která bude v téže směně pokryta podkladním betonem. Zatímco kvalita zeminy může být ovlivněna chůzí do hloubky až 0,20 m, zemními stroji pak na hloubku přes 0,50 m. Odstřel v horninách může nakypřit základovou půdu až na hloubku 1,0 m. Ochrana základové půdy výrazně závisí na druhu zeminy v základové spáře a na výši hladiny podzemní vody, jež musí být snížena nejméně o 0,30 m pod úroveň základové spáry. Betonáž plošných základů pod hladinu podzemní vody se nedoporučuje. V případě hrubozrnných zemin dostatečné mocnosti lze hloubit strojně až na projektovanou základovou spáru a tu následně upravit např. pomocí vibračního válce. V případě zemin jemnozrnných a hornin poloskalních platí bez výjimky výše uvedené doporučení o ručním dohloubení poslední vrstvy zeminy a okamžitém položení vrstvy podkladního betonu v tloušťce alespoň 0,10 m s tím, že výstavba vlastních základů bude bezprostředně následovat. Naprosto nepřípustný je takový postup, při němž se na vyhloubenou základovou spáru v jemnozrnných zeminách nebo poloskalních horninách rozprostírá vrstva písku nebo štěrku, byť hutněného. Ta nemá žádný význam z hlediska únosnosti, a navíc může s ohledem na svoji propustnost způsobit průnik vody (podzemní či srážkové) k zeminám v základové spáře, a tím zhoršení jejich vlastností zejména deformačních, což může vést k nepředpokládanému sedání. V případě podkopání základové spáry v těchto zeminách je třeba plombovat hubeným betonem, nikoliv pískem či štěrkem.
4 HLUBINNÉ ZÁKLADY
Volbu metody hlubinného zakládání stavby ovlivňují jak faktory přírodní, tak i ekonomické. Hlubinné základy se navrhují tam, kde v běžném dosahu plošných základů není dostatečně únosná a málo stlačitelná základová půda a je-li nutné zakládat pod hladinu podzemní vody. Také se navrhují pro omezení velikosti deformací. Často se však realizují i tam, kde plošné založení je příliš drahé, a to především s ohledem na množství spotřebovaného stavebního materiálu, hlavně betonu. Úkolem hlubinných základů je přenést zatížení do únosnějších, hlouběji uložených vrstev základové půdy, anebo výrazně omezit sedání. Přenos zatížení hlubinnými základy do základové půdy není zprostředkován pouze plochou jejich pat, nýbrž (zejména) jejich pláštěm.
4.1 DRUHY HLUBINNÝCH UÁKLADŮ, DRUHY PILOT
Prvky hlubinného zakládání jsou: studně a kesony (dnes již překonané a nepoužívané), dále piloty všeho druhu, mikropiloty, podzemní stěny (zvláště jejich lamely) a jiné speciální technologie, jako jsou kotvy, injektáž klasická, trysková atd.
Piloty jsou nejrozšířenější a nejvíce používané prvky hlubinného zakládání staveb. Mají zpravidla tvar sloupů, přičemž příčný průřez může být kruhový nebo jakkoliv hranatý a členitý, může být po délce konstantní, nebo proměnný. V evropské praxi se piloty dělí podle výrobního postupu do dvou rozsáhlých skupin (obr. 17):
- piloty typu displacement, kdy zemina z prostoru, který pilota zaujímá, není odstraněna, nýbrž je stlačena jak do stran, tak i pod patu piloty (piloty ražené);
- piloty typu replacement(non displacement), kdy je v průběhu provádění zemina odstraněna z prostoru budoucí piloty (piloty vrtané).
Obr. 17 Evropská klasifikace pilot
V České republice došlo k výraznému rozvoji pilot v šedesátých letech minulého století a v průběhu asi 40 let se ustálil takový stav na trhu pilot, kdy asi 95 % zaujaly vrtané piloty a zbytek pak tvoří předrážené piloty Franki, jež jsou v podstatě jediným reprezentantem pilot ražených. Výrazná převaha vrtaných pilot v České republice je dána hlavně geotechnickými podmínkami, jež jsou (s ohledem na velikost naší země), velmi pestré a rozmanité a (až na výjimky) jsou charakteristické tou skutečností, že v relativně malé hloubce (do 10–20 m) se na staveništích nachází skalní (poloskalní) podloží, do něhož je výhodné vrtané piloty vetknout. Tento trend v oblasti pilotových základů se zřejmě nezmění i v budoucnu, neboť v současné době se ceny vrtaných pilot ustálily na takové úrovni, kdy zcela konkurují i plošným základům a jsou dány v podstatě kubaturou spotřebovaného stavebního materiálu – betonu.
4.2 PILOTY VRTANÉ
Provádění, monitoring, dohled nad prováděním a kontrola provádění vrtaných pilot se řídí evropskou normou ČSN EN 1536+A1: Provádění speciálních geotechnických prací – Vrtané piloty (2016). Podrobně o návrhu pilot a o zkušenostech s jejich realizací zvláště v České republice pojednává ve své monografii Masopust [2]. Za vrtané piloty se považují prvky, jež jsou v zeminách prováděny vrtáním a těžením a jež mají nosný dřík, který přenáší zatížení anebo omezuje deformace. Vrtané piloty mohou mít kruhový průřez (obr. 18a), nebo mohou být tvořeny lamelami podzemních stěn (obr. 18b) za předpokladu, že je celý jejich průřez betonován najednou a jeho plocha nepřekročí 15,0 m2. Po délce mohou mít vrtané piloty průřez konstantní, nebo teleskopický, nebo mohou mít rozšířenou patu či dřík (obr. 19). Za vrtané piloty se považují prvky se štíhlostí L / D ≥ 5. Piloty mohou být navrhovány jako:
- osamělé;
- skupinové (obr. 20);
- pilotové stěny, které slouží jako pažicí a opěrné konstrukce.
Technologie provádění těchto pilot zahrnuje: vrtání, přípravné práce před betonáží, betonáž a práce dokončovací. Poněkud odlišná je technologie provádění pilot CFA.
Vrty pro piloty a vrtné nástroje
Vrty se provádějí technologií rotačně náběrového vrtání, popřípadě drapákového hloubení, jež je sice pomalejší, v balvanitých zeminách však bývá nezbytná. Obvyklými vrtnými nástroji jsou: vrtný hrnec (šapa) – obr. 21a, vhodný pro písčité a štěrkovité, suché i zvodnělé zeminy a pro poloskalní horniny, vrtný šnek (spirál) – obr. 21b, který je vhodný pro jemnozrnné zeminy, vrtací korunka – obr. 21c pro provrtávání vložek skalních hornin. Jednolanový drapák – obr. 21d se používá pro těžení balvanů a pro rozbíjení vrtných překážek je vhodné dláto – obr. 21e. Vrtné nástroje mají normalizované řezné průměry a bývají opatřeny výměnnými břity. Na výběru vhodného nástroje a jeho kvalitě závisí do značné míry rychlost a úspěšnost vrtání. Pro dosažení požadovaného vrtného postupu může dojít v průběhu vrtání k výměně nástroje, nebo ke změně technologie vrtání. Vytěžená zemina z vrtů se sype přímo na nákladní auta, nebo na terén v okolí vrtu, z něhož se později nakládá a odváží na příslušnou skládku.
Vrty pro piloty se provádějí jako nepažené, pažené pomocí ocelových pažnic a pažené pomocí pažicí suspenze, většinou jílové (bentonitové). Pokud je jisté, že v celém procesu instalace vrtané piloty zůstanou stěny i dno vrtu stabilní, smějí se provádět vrty nepažené. V průběhu vrtání je však třeba neustále kontrolovat, nevniká-li do vrtu voda a neopadávají-li stěny vrtu. Pokud ano, je třeba vrt ihned zapažit. Vrty s d > 1,0 m by měly být paženy vždy tzv. úvodní pažnicí délky 1,5–2,5 m, přesahující pracovní plošinu asi o 0,2–0,3 m. Hrubozrnné zeminy s ID < 0,5, dále jemnozrnné zeminy s IC < 0,5, vrstvy navážek a nedokonale hutněných násypů by měly být paženy vždy.
Obr. 18 Příčné průřezy vrtaných pilot: a – kruhová pilota, b – příklady lamel podzemních stěn, d – průměr piloty, b – délka lamely, w – tloušťka lamely, A – průřezová plocha dříku lamely
Obr. 19 Tvary dříků vrtaných pilot: a – konstantní průřez, b – teleskopický dřík, c – rozšířená pata, d – rozšířený dřík
Obr. 20 Skupiny pilot: a, a1, a2 – osové vzdálenosti pilot ve skupině
Obr. 21 Vrtné nástroje: a – vrtný hrnec (šapa), b – vrtný šnek (spirál), c – vrtací korunka, d – jednolanový drapák, e – dláto.
Legenda: 1 – vrtná tyč, 2 – ovladač vyklápění dna, 3 – vrtný hrnec, 4 – dno vrtného hrnce s výměnnými zuby, 5 – centrátor, 6 – tělo, 7 – závit šneku, 8 – výška závitu, 9 – řezací zuby, 10 – závěs, 11 – rolny, 12 – lopatky, 13 – břit
Pažení ocelovými pažnicemi je základní a nejvíce používanou metodou zajištění stability vrtů s d ≤ 1,50 m. Používá se jednak tzv. černých (varných) ocelových rour s tloušťkou stěny 8–12 mm, jednak speciálních spojovatelných ocelových pažnic, vesměs dvouplášťových s tloušťkou stěny 40 mm, obr. 22. Pažnice se instalují zavrtáváním rotačním způsobem za pomoci vrtné soupravy, vibrováním, popřípadě beraněním a pomocí oscilačních, tzv. dopažovacích zařízení. Za pažení vrtu se považuje takový postup, při němž pažnice postupuje spolu s hloubením vrtu, nebo toto hloubení předchází. Typické průměry pažnic varných i spojovatelných spolu s používanými průměry vrtných nástrojů (šap a spirálů) jsou v tab. 15.
Obr. 22 Spojovatelná pažnice: 1 – tělo (díl) pažnice, 2 – spoj pažnic se spojovacími šrouby, 3 – pažnicová korunka
Tab. 15 Průměry varných a spojovatelných pažnic spolu s vrtným nářadím (v mm)
| Průměr varné pažnice | 630 | 720 | 820 | 920 | 1 020 | 1 220 | 1 420 | – | 1 620 | (1 820) |
| Průměr spojovatelné pažnice | 630 | 750 | 880 | – | (1 020) 1 080 |
1 180 (1 220) |
– | 1 500 | – | 1 800 |
| Průměr vrtného nářadí | 570 | 630 | 770 | 870 | 920 | 1 070 | 1 220 | 1 350 | 1 500 | 1 700 |
Nevystačíme-li s ocelovými pažnicemi, používá se výjimečně jílová pažicí suspenze, jež zajišťuje stabilitu stěn i dna vrtu kombinovaným účinkem hydrostatického tlaku a elektrochemických jevů, v jejichž důsledku se na stěně vrtu vytvoří ochranný jílový filtrační koláč, jehož tloušťka závisí na kvalitě této suspenze a na mnoha dalších okolnostech. Je-li jílová suspenze v klidu, přejde z tekutého stavu na gel (geluje) a její pevnost ve střihu se výrazně zvětší. Mícháním přejde gel na tekutinu (sol), přičemž tyto stavy lze neustále opakovat. Tato vlastnost opakovatelných změn stavu suspenze se nazývá tixotropie. Jílová suspenze se vyrábí z jílu, vody a případně z dalších přísad v rozplavovači o obsahu 4–7 m3, obr. 23. Základní receptura této pažicí suspenze je v tab. 16. Po rozplavení se suspenze uchovává většinou v laminátových nádržích o obsahu asi 40 m3. U připravené pažicí suspenze se musí zkontrolovat, zda její vlastnosti odpovídají standardům podle tab. 17. Použitá a případně regenerovaná pažicí suspenze se smí rovněž používat. Jednou z nejdůležitějších vlastností s ohledem na betonáž pod suspenzi je její písčitost (obsah písku), který nesmí přestoupit 3 %. V případě, že je obsah písku větší, je nutné suspenzi přečistit, neboť v průběhu betonáže může dojít k provalení čerstvého betonu přes postupně se usazující vrstvu písku na jeho povrchu, a tím k přerušení dříku piloty touto pískovou vrstvou. Znečištěná suspenze je tedy čerpána z oblasti paty vrtu a hnána přes soustavu vibračních sít, kde se odstraní hrubé nečistoty. Následně se suspenze zbaví jemnějších částic v hydrocyklonech, jejichž princip je na obr. 24.
S postupujícím tlakem na ochranu životního prostředí je pažení pilot jílovou suspenzí stále na ústupu a využívá se prakticky pouze pro piloty průměru přes 1,50 m. Pro pažení lamel podzemních stěn je však využití pažicí suspenze jedinou použitelnou metodou.
Obr. 23 Rozplavovač pro přípravu pažicí suspenze, 1 – nádoba rozplavovače o obsahu cca 7 m3, 2 – elektromotor, 3 – pogumovaná míchací vrtule
Obr. 24 Schéma hydrocyklonu, 1 – vtokový nátrubek, 2 – vnitřní odtoková trubice, 3 – spodní ventil
Tab. 16 Základní receptura jílové pažicí suspenze (na 1 m3)
| Pořadí pro míchání | Množství | Doba míchání | |
| 1. voda | 975 l | – | |
| 2. uhličitan sodný (soda) | je-li pH záměsové vody 6,5–5,5 5,5–4,5 < 4,5 |
potom 1,3–2,0 kg 2,0–2,5 kg nutný jiný zdroj vody |
5 minut |
| 3. KMC (Lovosa) | 1 kg | 5 minut | |
| 4. Mletý bentonit (Sabenil) | 64 kg | 15 minut | |
Tab. 17 Vlastnosti jílové pažicí suspenze
| Vlastnosti | Parametr | Přístroj | Hodnota |
| reologické | viskozita | Marsh | 30–40 sec |
| pevnost ve stříhu | FANN 35 | min. 5,0 Pa | |
| tixotropie | FANN 35 | 4,0 Pa | |
| koloidní | filtrace | Baroid – FANN | max 8,0 mm / 7,5 min |
| tloušťka filtr. koláče | Baroid – FANN | max 1,0 mm | |
| odstoj vody | Odměrný válec | 0 % / 24 hod | |
| fyzikální | objemová hmotnost | Hustoměr | cca 1,04 g / cm3 |
| obsah písku | OT-2 | max 3,0 % | |
| chemické | hodnota pH | Indikační papírky | přes 7,5 |
| analýza filtrátu | Analytické metody | – |
Přípravné práce před betonáží
Tyto práce sestávají z čištění vrtu, kontroly jeho délky, popřípadě z čerpání podzemní vody – jen je-li to účelné a neohrozí-li se tím stabilita vrtu, dále z armování železobetonové piloty. Dno vrtu se čistí tzv. čisticí šapou s rovným dnem, uzavíratelnou, nebo s klapkami bez centrátoru, a to zejména tehdy, je-li vrtáno spirálem. Snahou musí být, aby přestávka mezi dovrtáním a zahájením betonáže byla co nejkratší. Pokud se vrty provádějí v zeminách, jejichž vlastnosti se mohou s časem zhoršovat (bobtnání, rozbřídání apod.) a nelze je v jedné směně zabetonovat, musí se čistit těsně před betonáží, a to prohloubením piloty o 1,5 m nebo o dva průměry.
Vrtané, na místě betonované piloty, se provádějí jako nevyztužené (z prostého betonu), železobetonové (vyztužené armokoši v celé své délce, nebo v části), popř. s kotevní (spojovací) výztuží. Piloty z prostého betonu se smějí navrhovat tehdy, jsou-li pouze tlačené a nenacházejí-li se v zeminách náchylných ke ztrátě stability. I ty však bývají v hlavách opatřeny kotevní výztuží, jež se však obyčejně osazuje až do čerstvého betonu jejich hlav. V ostatních případech se piloty provádějí jako železobetonové, kdy dřík piloty nebo jeho podstatná část je vyztužen armokošem, který se skládá:
- z podélné výztuže, jejíž minimální množství je dáno tab. 18;
- příčné výztuže podle tab. 18;
- pomocné výztuže.
Tab. 18 Minimální vyztužení železobetonových vrtaných pilot a příčná výztuž
| Jmenovitá průřezová plocha dříku piloty AC | Plocha podélné výztuže As | Pravoúhlé a kruhové třmínky a spirála | ≥ 6 mm a ≥ ¼ největšího průměru podélné výztuže |
| AC ≤ 0,5 m2 | As ≥ 0,5 % AC | ||
| 0,5 m2 < AC ≤ 1,0 m2 | As ≥ 0,0025 m2 | výztužné sítě jako příčná výztuž | ≥ 5 mm |
| AC > 1,0 m2 | As ≥ 0,25 % AC |
Minimální krytí výztuže u pilot s profilem d ≤ 0,6 m je 50 mm, u pilot s d > 0,6 m pak 60 mm. U pilot pažených spojovatelnými pažnicemi se krytí výztuže zvětšuje, a to obyčejně o tloušťku stěny této pažnice, jež bývá 40 mm. Výztuž vrtaných pilot se vyrábí ve formě armokoše, který musí být dostatečně tuhý, příklad je na obr. 25. Pokud to je proveditelné, zapouštějí se armokoše do vrtů vcelku, bez spojů. Je-li nutné výztuž spojovat během instalace ve vrtu, jsou přípustné tzv. lanové rychlospojky a příslušný průřez je třeba umístit mimo nejvíce namáhaný dřík.
Obr. 25 Příklad armokoše vrtané piloty: 1 – podélná nosná výztuž, 2 – distanční kruhy z ploché oceli, 3 – příčná výztuž ve formě spirály, 4 – patní kříž z ploché oceli, 5 – patní deska z plechu, 6a – distanční vložka ve formě háku, 6b – distanční kolečko z betonu, popř. z umělé hmoty
Betonáž vrtaných pilot
Beton pro betonáž vrtaných pilot musí mít vysokou odolnost proti rozměšování, vysokou plasticitu a správné složení a konzistenci, schopnost samozhutnění, a především správnou zpracovatelnost pro jeho ukládání, jakož i pro případ vytahování pažnic z čerstvého betonu. Složení betonu by mělo v zásadě odpovídat požadavkům ČSN EN 206 Beton – Část 1: Specifikace, vlastnosti, výroba a shoda. Podle této normy se stanovují zejména požadavky na třídu betonu, jež by měla být v rozmezí C16/20 až C30/37. Požadavek na vyšší třídu betonu bývá většinou nesmyslný, neboť se v pilotě vyšší pevnost betonu nevyužije, a navíc nebývá reálné vyrobit transportbeton této třídy s požadovanou zpracovatelností, která je pro betonáž vrtaných pilot zcela prioritní. Složení betonu pro vrtané piloty je dáno tab. 19 a požadované vlastnosti betonu, týkající se jeho zpracovatelnosti, jsou dány v tab. 20. Aby bylo dosaženo potřebných vlastností betonu, smějí být jako přísady do betonu použity plastifikátory, superplastifikátory a zpomalovače tuhnutí za předpokladu, že je dodrženo správné dávkování. Pokud se betonuje za nízkých teplot (pod +5 °C s klesající tendencí), smí být použity provzdušňovací přísady. Rovněž je dovoleno používat tzv. samozhutnitelné betony (hyperplastifikované), se stupněm rozlití 600–700 mm. Je však třeba správnou recepturu betonu vyzkoušet, aby nedošlo k nežádoucím jevům, jako je např. krvácení.
Tab. 19 Složení čerstvého betonu
| Obsah cementu: | |
|
≥ 325 kg/m3 ≥ 375 kg/m3 |
| Vodní součinitel v/c | < 0,60 |
| Podíl jemné frakce d < 0,125 mm (včetně cementu) Je-li: | |
|
≥ 400 kg/m3 ≥ 450 kg/m3 |
Tab. 20 Požadavky na zpracovatelnost čerstvého betonu při různých podmínkách betonáže
| Stupeň rozlití Ø [mm] | Stupeň sednutí kužele (podle Abramse) [mm] | Typické podmínky použití (příklady) |
| Ø = 500 ± 30 | H = 150 ± 30 | betonáž do sucha |
| Ø = 560 ± 30 | H = 180 ± 30 | betonáž bet. čerpadlem nebo sypákovými rourami pod vodu |
| Ø = 600 ± 30 | H = 200 ± 30 | betonáž sypákovými rourami pod pažicí suspenzi |
| Změřený stupeň rozlití (Ø) nebo sednutí kužele (H) se zaokrouhlí na 10 mm | ||
Vrtané piloty se betonují buď způsobem betonáže do sucha, nebo způsobem betonáže pod vodu (či pod pažicí suspenzi). První metoda smí být použita pouze tehdy, je-li vrt před betonáží zcela suchý. Betonáž se provádí pomocí betonážní roury (usměrňovací) s násypkou umístěné svisle ve středu vrtu tak, aby proud betonu nenarážel ani na výztuž piloty, ani na stěny vrtu. Vnitřní průměr této roury bývá min. 200 mm, musí však být větší, než je 8násobek největší použité frakce kameniva v betonu. Délku betonážní roury je třeba vyzkoušet tak, aby vytékající beton směřoval do osy vrtu a nerozměšoval se pádem o jeho stěny či o výztuž.
V případě betonáže pod vodu nebo pod pažicí suspenzi se používá metoda Contractor, při níž se dobře zpracovatelný beton ukládá pomocí licí (dříve sypákové) roury, jež slouží k zabránění rozměšování a znečištění betonu kapalinou v pilotě. Licí roura je na horním konci opatřena násypkou trychtýřovitého tvaru, jež je schopna pojmout dostatečnou zásobu betonu, aby betonáž probíhala plynule. Licí roura má zcela hladkou vnitřní stěnu a její světlost je nejméně 150 mm, resp. nejméně 6násobek největší frakce kameniva v betonu. Je opatřena vodotěsnými spoji snadno rozpojitelnými po cca 1,5 až 2,0 m. Aby se licí roura mohla v průběhu betonáže volně pohybovat, nesmí její největší příčný rozměr (vč. spojů) přesáhnout 35 % průměru vrtu, resp. 60 % vnitřního průměru armokoše (v případě vrtaných pilot) a 80 % vnitřní světlé šířky armokoše (v případě lamel podzemních stěn). Před zahájením betonáže se licí roura spustí až na dno vrtu a opatří se vhodnou zátkou (např. ve formě pohyblivého pístu), jež zamezí promíchání betonu s kapalinou ve vrtu. Naplní se zcela betonem a povytáhne se o výšku rovnající se asi průměru roury. V dalším průběhu betonáže se licí roura pozvolna povytahuje podle potřeby, ovšem tak, aby (kromě zahájení betonáže) byla v betonu ponořena vždy nejméně 1,5 m v případě pilot s d < 1,2 m, resp. 2,5 m v případě pilot s d ≥ 1,2 m a nejméně 3,0 m v případě lamel podzemních stěn, zvláště tehdy, betonují-li se více licími rourami najednou. Licí roury se zásadně zkracují shora a povytahují se zvolna, aby se zabránilo případnému sacímu efektu. Hlavy pilot (lamel podzemních stěn) se v případě betonáže pod vodu (suspenzi) vždy přebetonují na potřebnou výšku, jež je dána podmínkou, aby v úrovni projektované hlavy piloty byl kvalitní, neznečištěný beton. V průběhu betonáže se voda, popř. pažicí suspenze z vrtu odčerpává.
Součástí betonáže pilot zapažených ocelovými pažnicemi je vytahování těchto pažnic, které musí proběhnout bezprostředně po betonáži, resp. zahájeno musí být v průběhu betonáže, je-li ovšem sloupec betonu nad patou pažnic dostatečný k vyvození potřebného přetlaku, aby se zabránilo vniknutí vody nebo zeminy do vrtu nad patou pažnic a aby nedošlo k povytažení armokoše. Pažnice je třeba vytahovat zvolna a neustále sledovat hladinu betonu (např. těžkou olovnicí), jež klesá v souvislosti s plněním mezikruží betonem a může klesnout náhle v souvislosti se zaplněním event. zapažnicových kaveren. Hlavu piloty je třeba vždy dostatečně přebetonovat, aby z výše uvedených důvodů neklesla hladina čerstvého betonu po odpažení pod svoji projektovanou úroveň.
Práce dokončovací
Po betonáži piloty a vytažení pažnic obyčejně následuje prodleva, během níž se realizují ostatní piloty na staveništi. Mezi práce dokončovací náleží úprava hlavy pilot, úprava její výztuže a případné zřízení nadpilotové konstrukce, která je součástí piloty. Hlavy přebetonovaných pilot se upravují odbouráním, které musí probíhat ohleduplně, aby se zabránilo poškození zbylé části piloty. Zvláštní pozornost musí být věnována kvalitě betonu v hlavě piloty. Poškozený beton musí být odstraněn až na úroveň betonu zcela zdravého a nahrazen čerstvým betonem, který se dokonale spojí s betonem stávajícím. Na dostatečnou výšku musí být odbourán zejména beton pilot prováděných pod jílovou pažicí suspenzí.
Pokud je armokoš nad hlavou piloty zohýbán při odbourávání její znečištěné hlavy, smí být narovnán a upraven ve smyslu platných zásad nakládání s betonářskou výztuží. Je třeba zabránit zejména ohýbání výztuže za tepla a ostrým ohybům. Pokud by došlo k nepřípustnému ohybu výztuže, nebo k jejímu zeslabení, je vhodnější příslušný prut vyříznout a nahradit přivařeným prutem novým.
V této pracovní fázi se opatřují hlavy pilot prováděných z prostého betonu tzv. spojovací výztuží, tvořenou určitým počtem svislých prutů, jež se do upravené hlavy zapíchají do čerstvého betonu.
Piloty prováděné průběžným šnekem – CFA
Průběžný šnek (obr. 26) nahrazuje ve vhodných zeminách pažení a zvyšuje produktivitu práce při provádění vrtaných, na místě betonovaných pilot až několikanásobně. Stabilita stěn vrtu je tedy zajištěna pomocí zeminy, která v průběhu vrtání zůstává na závitech tohoto šneku, jehož délka odpovídá nejméně celkové délce příslušné piloty, nastavování vrtného šneku je nepřípustné. Vhodnými jsou jak zeminy hrubozrnné (s relativní ulehlostí ID > 0,4 a nestejnozrnné s d60 / d10 > 2), suché, či zvodnělé, které neobsahují velké balvany, tak zeminy jemnozrnné (kromě měkkých s IC < 0,5 a cu < 15 kPa) a kromě senzitivních jílů a spraší, pokud neobsahují tvrdé, nevrtatelné polohy, či vložky.
Piloty CFA se provádějí vesměs jako svislé. Vrtání průběžným šnekem musí být prováděno tak rychle, jak je to možné a s minimálními otáčkami vrtného nástroje, aby se na nejmenší možnou míru snížily negativní účinky vrtání na okolní zeminu. Za tím účelem musí vrtná souprava disponovat dostatečným kroutícím momentem i tažnou silou. Stoupání závitů průběžného šneku musí být u klasických CFA pilot stejné po celé délce. V první fázi se nástroj zavrtá postupně do zeminy na celkovou hloubku tak, že prakticky nedochází k nakupení zeminy kolem ohlubně vrtu. Středová roura průběžného šneku je uzavíratelná, aby se zabránilo vniku zeminy a vody do této roury. V další fázi se betonuje středovou rourou přímo pomocí betonážního čerpadla, jehož hadice je k ní již během vrtání napojena. Betonuje se příslušným tlakem čerstvého betonu, který má zpracovatelnost danou stupněm sednutí kužele podle Abramse nejméně 190–210 mm a obsahuje především oblé kamenivo. Během betonáže se průběžný šnek nesmí otáčet, nebo se otáčí ve stejném smyslu jako při vrtání. Přetlak betonu u paty piloty zajišťuje, že vzniklý prostor je betonem ihned zaplněn. V průběhu betonáže musí být k dispozici dostatečná zásoba betonu, aby dřík piloty mohl být vyplněn plynule a zcela od paty až po pracovní úroveň. Obyčejně se však betonuje i skrz vrstvu zeminy, která se při vytahování šneku kupí v okolí ohlubně vrtu. Tím se zajistí, že v úrovni projektované hlavy piloty bude kvalitní beton. Ihned po skončení betonáže a vytažení nástroje se nakupená zemina (i s event. betonem) odstraní např. nakladačem, beton v hlavě piloty se upraví a pilota se opatří armokošem, je-li to předepsáno. Ten bývá na spodním konci mírně kónický a nemá patní kříž. Zasouvá se do čerstvého betonu zprvu vlastní tíhou, dále např. tlakem vhodného zařízení (lžíce nakladače). Nesmí se vibrovat, neboť je nebezpečí roztřídění betonu. Smí se však použít poklepů příslušného zařízení, je-li k dispozici.
Obr. 26 Technologie provádění pilot průběžným šnekem (CFA): 1 – přítlačný válec, 2 – věž vrtné soupravy, 3 – pracovní plošina, 4 – výška závitu, 5 – rozrušená zemina, 6 – průběžný šnek, 7 – vnitřní roura, 8 – zátka roury, 9 – přívod betonu, 10 – vyvrtaná zemina, 11 – beton piloty
4.3 METODY STANOVENÍ OSOVÉ ÚNOSNOSTI VRTANÝCH PILOT
Osová únosnost osamělé piloty je zatížení, při kterém pilota vyhoví podmínkám na ni kladeným, tj. jak obecným podmínkám pevnostním (řešení podle 1. skupiny mezního stavu), tak i obecným podmínkám deformačním (řešení podle 2. skupiny mezního stavu). Tlaková osová únosnost osamělé vrtané piloty se stanoví buď zkouškou, nebo výpočtem. V zásadě jsou přijatelné následující návrhové postupy (EC 7-1):
- návrh na základě výsledků statických zatěžovacích zkoušek zkušebních pilot, systémových, popř. modelových, je-li v souladu s příslušnou teorií;
- návrh na základě dynamických zatěžovacích zkoušek, jehož platnost byla prokázána statickými zatěžovacími zkouškami ve srovnatelných podmínkách;
- návrh na základě empirických a analytických výpočtových metod vycházejících z pevnostních a deformačních charakteristik základové půdy, vlastností materiálu piloty a z technologie provádění, jehož platnost byla prokázána statickými zatěžovacími zkouškami ve srovnatelných podmínkách;
- návrh vycházející z pozorovaného chování srovnatelného pilotového základu prokazujícího, že tento přístup je podpořen výsledky průzkumu staveniště.
Interakce piloty a základové půdy
Vrtané piloty přenášejí vnější svislé tlakové zatížení do okolní základové půdy pláštěm a patou. Z výsledků zkoušek vyplývá, že pokud smykové napětí na plášti piloty (tzv. plášťové tření) není uměle redukováno, popř. zcela eliminováno (např. povlakem na plášti piloty), přenáší pilota postupně rostoucí vnější zatížení vždy převážně plášťovým třením, přičemž jeho průměrná velikost roste se sedáním a blíží se k maximu, které je dosaženo při sedání o velikosti 5–30 mm v závislosti na druhu základové půdy a na technologii provádění. V hrubozrnných zeminách bývá velikost limitního sedání pro mezní mobilizaci plášťového tření menší a v ulehlých materiálech se projevuje efekt dilatace, jež při dalším sedání vede k mírnému poklesu plášťového tření na velikost reziduální. Napětí na patě piloty se aktivuje pomaleji a jeho velikost roste s deformací, přičemž mezní hodnoty se dosahuje při sedání rovném 80–120 % průměru piloty d. V důležitém rozsahu odpovídajícím limitní velikosti sedání pro mobilizaci plášťového tření bývá růst napětí v patě piloty lineární ve vztahu k sedání. Popsaný mechanismus platí v relativně homogenní základové půdě, nebo i základové půdě vrstevnaté, pokud se deformační vlastnosti jednotlivých vrstev (zvláště u paty piloty) výrazně nemění. Je-li pilota vetknuta do výrazně tužší vrstvy, stoupá poměr mobilizovaného napětí v patě piloty k mobilizovanému plášťovému tření a napětí na patě piloty má vzrůstající tendenci. Je-li pilota opřena o prakticky nestlačitelnou vrstvu (např. skalní podloží tř. R1, R2), mělo by být vnější zatížení přenášeno v podstatě pouze patou piloty, neboť její sedání, nutné k mobilizaci tření na plášti by mělo být velmi omezené, resp. dané pouze stlačením železobetonového dříku piloty. Ve skutečnosti je však prognóza chování této piloty velmi riskantní, neboť závisí zcela na technologii provádění, tj. vrtání, čištění paty vrtu a způsobu betonáže. Na velikost kritického posunu piloty pro plnou aktivaci plášťového tření nemá vliv průměr piloty (na rozdíl od aktivace napětí v patě), drsnost pláště má však vliv podstatný. Na velikost mobilizovaného plášťového tření má rozhodující vliv drsnost pláště, jež je zcela ovlivněna technologií provádění a dále průměr piloty d.
K dokonalému popisu chování osamělé, vrtané, svisle zatížené piloty je třeba znát:
- pracovní diagram piloty, udávající závislost mezi zatížením hlavy piloty a její deformací (sedáním), zpravidla v čase;
- průběh normálové síly v dříku piloty pro příslušný zatěžovací stupeň (popř. průběh normálového napětí v dříku piloty s jeho délkou).
Pokud známe tyto vztahy, můžeme stanovit tzv. přenosovou funkci, jež zcela popisuje chování vrtané piloty. Analytické vyjádření obou výše uvedených vztahů, a tudíž i přenosové funkce však není reálné, neboť závisí nejen na vlastnostech základové půdy a materiálu piloty, ale především na technologických aspektech provádění, jež jsme schopni poměrně dobře kvalifikovat, jejich kvantifikace, nutná pro matematické vyjádření, je však zatím mimo naše možnosti.
4.3.1 Statické zatěžovací zkoušky
Základní metodou pro stanovení únosnosti osamělé piloty je statická zatěžovací zkouška piloty ve skutečném měřítku, neboť ta zobrazuje zcela věrohodně jak technologické aspekty provádění, tak i vlivy přírodní, tj. vlastnosti základové půdy a dostatečně modeluje časový průběh sedání. Statické zatěžovací zkoušky vrtaných pilot lze rozdělit na:
- studijní, které se provádějí na mimosystémových pilotách v předstihu před stavbou, obyčejně jako součást doplňujícího geotechnického průzkumu. Lze je provádět na modelových pilotách, které mají shodnou délku s pilotami systémovými, jsou prováděny shodnou technologií, pouze jejich profil lze zmenšit v maximálním poměru 1 : 2;
- průkazní, jež se provádějí obyčejně těsně před zahájením realizace pilot a na rozsáhlých staveništích s velkým počtem pilot. Účelem průkazních zkoušek je ověřit předpoklady projektu a popř. reagovat na změny, které v realizačním projektu nastaly. Provádějí se též na mimosystémových pilotách;
- kontrolní, které se provádějí v průběhu realizace pilot, nebo po jejich skončení, existuje-li odůvodněná pochybnost o kvalitě pilot, nebo jedná-li se o velký počet pilot na staveništi. Zkouší se obyčejně piloty systémové, které se však nesmějí přetěžovat, tzn., že mohou být zatíženy pouze silou odpovídající max. zatížení provoznímu, popř. extrémnímu.
Výsledkem statické zatěžovací zkoušky je vždy tzv. pracovní diagram piloty, jehož příklad je na obr. 27. Pro měření průběhu normálového napětí v dříku piloty s hloubkou se využívá jak strunových tenzometrů navázaných na armokoši, tak i tenzometrických tělísek, tzv. load-cells, umístěných v dříku piloty. Instrumentace zkušebních pilot se obyčejně vyplatí, neboť získané výsledky lze lépe interpretovat a popř. i extrapolovat, přičemž náklady na instrumentaci zkušebních pilot již nejsou rozhodující. Vlastní statické zatěžovací zkoušky pilot se provádějí pomocí zatěžovacích mostů, jež jsou opatřeny vnějším zatížením, popř. jsou kotveny (pro zatížení překračující cca 2,5 MN). Schéma zkušebních mostů, používaných spíše v minulosti, je na obr. 28. Jejich nevýhodou byla hlavně potřeba získání příslušného zatížení, jehož sestava na zkušebním mostu byla značně riskantní. Schéma dnes nejvíce používaného zkušebního mostu je na obr. 29. Kotvení mostu se realizuje buď pomocí tahových pilot, nebo pomocí zemních kotev, jejichž uspořádání musí odpovídat podmínkám podle obr. 30. Podrobně o statických zatěžovacích zkouškách pilot pojednává [2, 3].
Obr. 27 Příklad výsledků statické zatěžovací zkoušky vrtané piloty
Obr. 28 Schéma zatěžovacích mostů s únosností 3 – 5 MN: 1 – ocelový most, 2 – hydraulický lis/lisy, 3 – zkušební pilota, 4 – podpěry mostu, 5 – vnější zatížení (balast), 6 – ocelový příčník, 7 – kotvení zatěžovacího mostu, 8 – měřická základna, 9 – měřicí zařízení pro deformace
Obr. 29 Schéma zkušebního mostu typu „hříbek“ pro zatížení do 22 MN: 1 – ocelový zkušební most, 2 – roznášecí deska na hlavě piloty, 3 – kotvy, 4 – zkušební pilota, 5 – hydraulické lisy, 6 – ukotvení táhel kotev
Obr. 30 Údaje pro navrhování kotevních systémů pro statické zatěžovací zkoušky pilot
4.3.2 Únosnost vrtaných pilot výpočtem na základě 1. skupiny mezního stavu, příklad 3
Statické schéma výpočtu je na obr. 31. Návrhová únosnost je dána vztahem:
\begin{gathered}
U_\text{vd}=U_\text{bd}+U_\text{fd}\ge V_\text{d}
\end{gathered}(40)
kde je:
Uvd … svislá návrhová únosnost piloty;
Ubd … návrhová únosnost paty piloty;
Ufd … návrhová únosnost na plášti piloty;
Vd … svislá složka návrhového zatížení působícího v hlavě piloty.
Využívá se návrhových velikostí stabilitních parametrů jednotlivých vrstev základové půdy, jež se stanoví podle zásad ČSN EN 1997-1 z velikostí charakteristických pomocí dílčích součinitelů spolehlivosti základové půdy γm (tab. 9). Doporučuje se pro případy 1. mezního stavu výpočtu pilot použít návrhový přístup NP2, který má schéma: A1 „+“ M1 „+“ R2, kde dílčí součinitelé únosnosti vrtaných a CFA pilot jsou v tab. 21.
Obr. 31 Statické schéma piloty pro stanovení návrhové únosnosti podle 1. mezního stavu
Tab. 21 Dílčí součinitelé únosnosti γm pro piloty vrtané a CFA
| Únosnost | Značka | Soubor R2 |
| pata | γb | 1,1 |
| plášť (tlak) | γs | 1,1 |
| celková/kombinovaná (tlak) | γt | 1,1 |
| plášť v tahu | γs,t | 1,15 |
Návrhová únosnost paty piloty je dána vztahem:
\begin{gathered}
U_\text{bd}=k_1\cdot A_\text{s}\cdot R_\text{d}
\end{gathered}(41)
kde je:
As … plocha paty piloty;
Rd … návrhová únosnost paty piloty stanovená v zeminách podle vztahu:
\begin{gathered}
R_\text{d}=1{,}2\cdot c_\text{d}\cdot N_\text{c}+(1+\sin\varphi_\text{d}\cdot\gamma_1\cdot L\cdot N_\text{d}+0{,}7\cdot\gamma_2\cdot\frac{d}{2}\cdot N_\text{b})
\end{gathered}(42)
kde je:
\begin{gathered}
N_\text{c}=2+\pi&\text{pro}\space\varphi_\text{u,d}=0\\\\
N_\text{c}=(N_\text{d}-1)\cdot\cotg\varphi_\text{d}&\text{pro}\space\varphi_\text{d}\gt0\\\\
N_\text{d}=\text{exp}(\pi\cdot\tg\varphi_\text{d})\cdot\tg^2(45+\frac{\varphi_\text{d}}{2})\\\\
N_\text{b}=1{,}5\cdot(N_\text{d}-1)\cdot\tg\varphi_\text{a}
\end{gathered}k1 … součinitel, vyjadřující zvětšení únosnosti vlivem délky piloty L:
pro
\begin{gathered}
L\le2{,}0\space\text{m}&k_1=1{,}0\\\\
2{,}0\space\text{m}\lt L\le4{,}0\space\text{m}&k_1=1{,}05\\\\
4{,}0\space\text{m}\lt L\le6{,}0\space\text{m}&k_1=1{,}1\\\\
L\ge6{,}0\space\text{m}&k_1=1{,}15
\end{gathered}(43)
Návrhová únosnost na plášti je dána:
\begin{gathered}
U_\text{fd}=\sum\pi d_\text{i}\cdot h_\text{i}\cdot f_\text{si}
\end{gathered}(44)
kde tření na plášti fsi,d je dáno rovnicí:
\begin{gathered}
f_\text{sim,d}=\sigma_\text{xi}\cdot\tg(\frac{\varphi_\text{d}}{\gamma_\text{r1}})+\frac{c_\text{d}}{\gamma_\text{r2}}
\end{gathered}(45)
a kontaktní napětí v i-té vrstvě je dáno:
\begin{gathered}
\sigma_\text{xi}=k_2\cdot\sigma_\text{ori}
\end{gathered}(46)
kde je:
σori … geostatické napětí v hloubce zi
k2 … součinitel bočního zemního tlaku na plášť piloty:
pro
\begin{gathered}
z\le10{,}0\space\text{m}&k_2=1{,}0\\\\
z\gt10{,}0\space\text{m}&k_2=1{,}2
\end{gathered}Součinitel podmínek působení základové půdy γr2 se dosazuje následovně:
pro
\begin{gathered}
z\le10{,}0\space\text{m}&\gamma_\text{r2}=1{,}3\\\\
1{,}0\space\text{m}\lt z\le2{,}0\space\text{m}&\gamma_\text{r2}=1{,}2\\\\
2{,}0\space\text{m}\lt z\le3{,}0\space\text{m}&\gamma_\text{r2}=1{,}1\\\\
z\gt3{,}0\space\text{m}&\gamma_\text{r2}=1{,}0
\end{gathered}Součinitel podmínek působení γr2 vyjadřuje vliv technologie provádění pilot a je podle Sedleckého [1985]:
- γr1 = 1,0 … betonáž piloty do suchého nezapaženého vrtu do soudržných zemin;
- γr2 = 1,1 … betonáž piloty do suchého nezapaženého vrtu do nesoudržných zemin a poloskalních hornin;
- γr2 = 1,2 … betonáž piloty do vrtu zapaženého ocelovou pažnicí a pod vodu;
- γr2 = 1,25 … betonáž piloty do vrtu zapaženého pažicí suspenzí;
- γr2 = 1,5 … betonáž piloty sekundárně chráněné fólií umělé hmoty tl. 0,25 mm;
- γr2 = 1,6 … betonáž piloty sekundárně chráněné fólií z umělé hmoty při průměru d > 2,0 m.
Příklad 3
Stanovte výpočtovou únosnost osamělé vrtané piloty d = 0,90 m, L = 10,20 m prováděné technologií CFA v základové půdě podle tab. 22.
Tab. 22 Vlastnosti základové půdy podél piloty pro příklad 3
| Číslo vrstvy | Popis | od – do [m] | γ, (γ´) [kN·m-3] | φ | c [kPa] | cu [kPa] | qs [MPa] |
| 1 | navážka suchá | 0,0–1,0 | 18,0 | 32,5 | – | – | – |
| 2 | navážka zvodnělá | 1,0–2,2 | 10,0 | 32,5 | – | – | – |
| 3 | jíl | 2,2–5,2 | 8,0 | 17,5 | 10,0 | 100,0 | – |
| 4 | písek 2 | 5,2–7,8 | 10,0 | 30,0 | – | – | 7,0 |
| 5 | písek 3 | 7,8–10,2 | 10,0 | 30,0 | – | – | 11,0 |
| 6 | štěrk 4 | 10,2–15,0 | 11,0 | 35,0 | – | – | 17,5 |
| Hladina podzemní vody je v hloubce 1,0 m pod terénem | |||||||
Řešení
a) Návrhová únosnost paty:
\begin{gathered}
U_\text{bd}=K_1\cdot A_\text{s}\cdot\frac{R_\text{d}}{\gamma_\text{b}}
\end{gathered}\begin{gathered}
k_1\space\text{pro}\space L\gt6\space\text{m}\space...\space K_1=1{,}15
\end{gathered}\begin{gathered}
A_\text{s}=\pi\cdot\frac{0{,}9^2}{4}=0{,}636\space\text{m}^2
\end{gathered}\begin{gathered}
R_\text{d}=1{,}2\cdot c_\text{d}\cdot N_\text{cd}+(1+\sin\varphi)\cdot\gamma_1\cdot L\cdot N_\text{dd}+0{,}7\cdot\gamma_2\cdot\frac{d}{2}\cdot N_\text{bd}
\end{gathered}\begin{gathered}
\varphi_\text{k}=35\degree,&\varphi_\text{d}=35\degree\space\text{(koef.}\cdot\gamma\text{M}=1{,}0\space\text{pro M1)}
\end{gathered}\begin{gathered}
N_\text{dd}=\text{exp}\space(\pi\cdot\tg\varphi_\text{d})\cdot\tg^2(45+\frac{\varphi_\text{d}}{2})=33{,}21
\end{gathered}\begin{gathered}
N_\text{bd}=1{,}5\cdot(N_\text{dd}-1)\cdot\tg\varphi_\text{d}=33{,}83
\end{gathered}\begin{gathered}
N_\text{cd}=(N_\text{dd}-1)\cdot\cotg\varphi_\text{d}=46{,}00
\end{gathered}\begin{gathered}
\gamma_1=\frac{(18{,}0\cdot1{,}0+10\cdot1{,}2+3{,}0\cdot8{,}0+5{,}0\cdot10{,}0)}{10{,}2}=10{,}2\space\text{kN/m}^3
\end{gathered}\begin{gathered}
\gamma_2=10{,}0\space\text{kN/m}^3
\end{gathered}\begin{gathered}
R_\text{d}=(1+\sin35)\cdot10{,}2\cdot10{,}2\cdot33{,}21+0{,}7\cdot10{,}0\cdot\frac{0{,}90}{2}\cdot33{,}83=5\space543{,}54\space\text{kPa}
\end{gathered}\begin{gathered}
U_\text{bd}=1{,}15\cdot0{,}636\cdot\frac{5\space543{,}54}{1{,}1}=3\space685{,}95\space\text{kN}
\end{gathered}b) Návrhová únosnost pláště:
\begin{gathered}
U_\text{fd}=\pi\cdot\frac{\sum(d_\text{i}\cdot h_\text{i}\cdot f_\text{si})}{\gamma_\text{s}}
\end{gathered}- průběh geostatického napětí σori, vodorovného napětí σxi a plášťového tření fsi
hloubky 0,0–1,0 m:
\begin{gathered}
\sigma_\text{or1}=0{,}5\cdot18{,}0=9{,}0\space\text{kPa}\\\\
\sigma_\text{x1}=1{,}0\cdot9{,}0=9{,}0\space\text{kPa}\\\\
f_\text{s1}=9{,}0\cdot\tg32{,}5=5{,}73\space\text{kPa}
\end{gathered}hloubky 1,0–2,2 m:
\begin{gathered}
\sigma_\text{or2}=1{,}0\cdot18{,}0+0{,}6\cdot10{,}0=24{,}0\space\text{kPa}\\\\
\sigma_\text{x2}=1{,}0\cdot24{,}0=24{,}0\space\text{kPa}\\\\
f_\text{s2}=24{,}0\cdot\tg32{,}5=15{,}29\space\text{kPa}
\end{gathered}hloubky 2,2–5,2 m:
\begin{gathered}
\sigma_\text{or3}=1{,}0\cdot18{,}0+1{,}2\cdot10{,}0+1{,}5\cdot8{,}0=42{,}0\space\text{kPa}\\\\
\sigma_\text{x3}=1{,}0\cdot42{,}0=42{,}0\space\text{kPa}\\\\
f_\text{s3}=42{,}0\cdot\tg17{,}5+10{,}0=23{,}24\space\text{kPa}
\end{gathered}hloubky 5,2–7,8 m:
\begin{gathered}
\sigma_\text{or4}=1{,}0\cdot18{,}0+1{,}2\cdot10{,}0+3{,}0\cdot8{,}0+1{,}3\cdot10{,}0=67{,}0\space\text{kPa}\\\\
\sigma_\text{x4}=1{,}0\cdot67{,}0=67{,}0\space\text{kPa}\\\\
f_\text{s4}=67{,}0\cdot\tg30=38{,}68\space\text{kPa}
\end{gathered}hloubky 7,8–10,2 m:
\begin{gathered}
\sigma_\text{or5}=1{,}0\cdot18{,}0+1{,}2\cdot10{,}0+3{,}0\cdot8{,}0+2{,}6\cdot10{,}0+1{,}2\cdot10{,}0=92{,}0\space\text{kPa}\\\\
\sigma_\text{x5}=1{,}0\cdot92{,}0=92{,}0\space\text{kPa}\\\\
f_\text{s5}=92{,}0\cdot\tg30=53{,}11\space\text{kPa}
\end{gathered}\begin{gathered}
U_\text{fd}=\pi\cdot0{,}9\cdot\frac{(1{,}0\cdot5{,}73+1{,}2\cdot15{,}29+3{,}0\cdot23{,}24+2{,}6\cdot38{,}68+2{,}4\cdot53{,}11)}{1{,}1}=826{,}81\space\text{kN}
\end{gathered}c) Návrhová únosnost piloty:
\begin{gathered}
U_\text{pd}=3\space685{,}95+826{,}81=4\space512{,}76\space\text{kN}
\end{gathered}(tuto návrhovou únosnost je třeba posuzovat ve vztahu k návrhovému zatížení)
4.3.3 Únosnost vrtaných pilot výpočtem na základě 2. skupiny mezního stavu, příklad 4
A. Charakteristická únosnost pilot opřených o nestlačitelné podloží
Jedná se o vrtané piloty opřené patou o skalní horniny tř. R1, R2, resp. zahloubené do těchto hornin na hloubku t = 0,1 – 0,2 m. O jejich únosnosti rozhoduje zpravidla výpočtové zatížení betonového dříku, jež bývá menší, než je únosnost skalní horniny, o níž je pata piloty opřena. Se zřetelem ke ztíženým podmínkám betonáže uvažuje se s výpočtovým namáháním betonu o velikosti 25 až 33 % krychelné pevnosti betonu Rbk, tudíž únosnost těchto pilot:
\begin{gathered}
U_\text{vd}=0{,}8\cdot A_\text{s}\cdot R_\text{bk}
\end{gathered}(47)
kde je:
Rbk … charakteristická pevnost betonu v tlaku (v závislosti na jeho třídě).
V případě vrtaných, velkoprůměrových pilot se neuvažuje s efektem vzpěrné pevnosti. Při konkrétním výpočtu této únosnosti je třeba vždy uvážit vliv čistoty paty piloty, resp. reálnou možnost dosažení této čistoty. Celková deformace hlavy piloty se skládá z deformace vyvolané vlivem smykových napětí podél piloty, vlivem napětí v patě piloty a konečně z vlastní deformace betonového dříku vlivem působící síly. Okamžité sedání je dáno vztahem:
\begin{gathered}
s=I_\text{sp}\cdot V\cdot\frac{L}{(A_\text{s}\cdot E_\text{b}})
\end{gathered}(48)
kde je:
Isp … příčinkový koeficient pro sedání opřené piloty podle tab. 23;
V … působící svislá síla;
Eb … modul deformace (pružnosti) betonu.
V tab. 19 je definována tuhost piloty poměrem:
\begin{gathered}
K=\frac{E_\text{b}}{E_\text{s}}
\end{gathered}(49)
kde je:
Es … průměrná velikost sečnového modulu deformace zemin podél dříku pilot
Tab. 23 Velikosti příčinkového koeficientu Isp pro sedání opřené piloty
| K L/d |
100 | 200 | 500 | 1 000 | 2 000 | 5 000 | 10 000 |
| 3 | 0,92 | 0,97 | 0,99 | 1,00 | 1,00 | 1,00 | 1,00 |
| 5 | 0,88 | 0,92 | 0,97 | 0,98 | 0,99 | 1,00 | 1,00 |
| 10 | 0,75 | 0,84 | 0,92 | 0,96 | 0,98 | 1,00 | 1,00 |
B. Charakteristická únosnost pilot zahloubených do stlačitelného podloží
Pro stanovení charakteristické únosnosti vrtaných pilot v zeminách a poloskalních horninách je třeba řešit tvar mezní zatěžovací křivky podle obr. 32a. Pilota se nachází ve vrstevnaté zemině podle obr. 32b.
Mezní únosnost na plášti piloty je dána:
\begin{gathered}
R_\text{su}=0{,}7m\cdot\pi\cdot\sum d_\text{i}\cdot h_\text{i}\cdot q_\text{si}
\end{gathered}(50)
kde je:
hi … mocnost příslušné vrstvy zeminy podle obr. 32b;
m … dílčí koeficient vyjadřující vliv povrchu dříku piloty:
- pro betonáž do suchého vrtu a pod vodu m = 1,0;
- pro betonáž pod pažicí suspenzi m = 0,9;
- pro ochranu dříku pomocí fólie PVC, PE, tl. přes 0,7 mm, m = 0,7;
- pro ochranu dříku pomocí fólie a pletiva B-systému m = 0,5;
- pro ochranu ponechanou ocelovou pažnicí m = 0,15;
qsi … mezní plášťové tření v i-té vrstvě piloty.
Velikost mezního plášťového tření je dána vztahem:
\begin{gathered}
q_\text{si}=a-\frac{b}{(\frac{D_\text{i}}{d_\text{i}})}
\end{gathered}(51)
kde je:
a, b … regresní koeficienty [kPa] podle tab. 24;
Di … vzdálenost od hlavy piloty do poloviny i-té vrstvy (obr. 32b);
di … průměr piloty v této vrstvě.
Velikost napětí q0 na patě piloty, při deformaci odpovídající plné mobilizaci plášťového tření, je:
\begin{gathered}
q_0=e-\frac{f}{(\frac{L}{d_0})}
\end{gathered}(52)
kd eje:
e, f … regresní koeficienty [kPa] podle tab. 24;
L … délka piloty;
d0 … průměr piloty v patě.
Stanovíme-li průměrnou velikost plášťového tření podél dříku piloty qs jako vážený průměr velikostí qsi:
\begin{gathered}
q_\text{s}=\frac{(\sum d_\text{i}\cdot h_\text{i}\cdot q_\text{si})}{(\sum d_\text{i}\cdot h_\text{i})}
\end{gathered}(53)
lze určit koeficient přenosu zatížení do paty piloty β podle rovnice:
\begin{gathered}
\beta=\frac{q_0}{(q_0+4\cdot q_\text{s}\cdot\frac{L}{d_0})}
\end{gathered}(54)
a zatížení v hlavě piloty na mezi mobilizace plášťového tření:
\begin{gathered}
R_\text{y}=\frac{R_\text{su}}{(1-\beta)}
\end{gathered}(55)
Tab. 24 Velikosti regresních koeficientů pro jednotlivé typy zemin a hornin
| Zemina Hornina | Regresní koeficienty /kPa/ | ||||
| a | b | e | f | ||
| poloskalní | R 3 R 4 R 5 |
246,02 169,98 131,92 |
225,95 139,45 94,96 |
2 841,31 1 616,22 957,61 |
1 298,96 1 155,34 703,89 |
| hrubozrnné | ID = 0,5 ID = 0,7 ID = 0,9 |
62,46 91,22 154,03 |
16,06 48,44 115,88 |
268,11 490,34 1 596,70 |
174,89 445,42 1 399,88 |
| jemnozrnné | IC = 0,5 IC = 0,75 IC ≥ 1,0 |
46,39 71,85 97,31 |
20,81 64,70 108,59 |
197,74 592,67 987,60 |
150,22 617,24 1 084,26 |
Odpovídající velikost sedání je dána rovnicí:
\begin{gathered}
s_\text{y}=I\cdot\frac{R_\text{y}}{(d\cdot E_\text{s})}
\end{gathered}(56)
kde je:
I … příčinkový koeficient sedání piloty;
Es … průměrná velikost sečnového modulu deformace zemin podél dříku piloty.
Příčinkový koeficient:
\begin{gathered}
I=I_1\cdot R_\text{k}
\end{gathered}(57)
kde je:
I1 … základní příčinkový koeficient stanovený podle obr. 33;
Rk … korekční součinitel podle obr. 34, vyjadřující vliv tuhosti pilot K (rovnice 49) a štíhlostního poměru L / d.
Velikosti sečnových modulů deformace Es jsou pro jednotlivé typy zemin mocnosti vrstev zemin hi sestaveny do tab. 25, 26 a 27. Průměrný sečnový modul deformace se vypočítá jako vážený průměr:
\begin{gathered}
E_\text{s}=\frac{(\sum E_\text{si}\cdot h_\text{i})}{(\sum h_\text{i})}
\end{gathered}(58)
Obr. 33 Příčinkový koeficient sedání I1
Obr. 34 Korekční součinitel Rk
Souřadnicemi (sy; Ry) je jednoznačně určena první větev mezní zatěžovací křivky tvaru paraboly 2° o rovnici:
\begin{gathered}
s=s_\text{y}\cdot(\frac{R}{R_\text{y}})^2
\end{gathered}(59)
pro obor zatížení: 0 ≤ R ≤ Ry. Druhá větev mezní zatěžovací křivky je dána úsečkou o souřadnicích koncového bodu (s25 = 25 mm; Rbu), přičemž:
\begin{gathered}
R_\text{bu,k}=R_\text{su}+R_\text{pu}
\end{gathered}(60)
\begin{gathered}
R_\text{pu,k}=\beta\cdot R_\text{y}\cdot\frac{s_{25}}{s_\text{y}}
\end{gathered}(61)
Rovnice této druhé větve mezní zatěžovací křivky je:
\begin{gathered}
s=s_\text{y}+(s_{25}-s_\text{y})\cdot\frac{(R-R_\text{y})}{(R_\text{bu}-R_\text{y})}
\end{gathered}(62)
pro obor zatížení: Ry ≤ R ≤ Rbu.
Tab. 25 Sečnové moduly deformace Es [MPa] pro horniny poloskalní
| h [m] | d [m] | ||||||||
| 0,6 | 1,0 | 1,5 | |||||||
| R 3 | R 4 | R 5 | R 3 | R 4 | R 5 | R 3 | R 4 | R 5 | |
| 1,5 3 5 10 |
50,3 64,5 – – |
28,2 43,1 58,2 87,5 |
20,2 30,8 41,3 61,6 |
72,3 105,5 – – |
35,0 57,3 75,3 114,5 |
24,7 41,0 54,8 83,2 |
85,5 138,3 – – |
33,5 58,8 87,9 133,0 |
22,3 41,2 63,7 97,0 |
Tab. 26 Sečnové moduly deformace Es [MPa] pro zeminy hrubozrnné
| h [m] | d [m] | ||||||||
| 0,6 | 1,0 | 1,5 | |||||||
| ID | |||||||||
| 0,5 | 0,7 | 0,9 | 0,5 | 0,7 | 0,9 | 0,5 | 0,7 | 0,9 | |
| 1,5 3 5 10 |
11,0 15,5 18,8 23,8 |
13,7 20,2 26,6 36,6 |
28,3 44,5 56,1 72,1 |
12,8 18,4 22,8 29,8 |
15,8 25,0 32,5 47,8 |
30,6 47,8 69,1 93,4 |
13,0 19,4 24,5 32,6 |
15,3 24,5 36,0 54,0 |
29,0 52,5 78,2 107,3 |
Tab. 27 Sečnové moduly deformace Es [MPa] pro zeminy jemnozrnné
| h [m] | d [m] | ||||||||
| 0,6 | 1,0 | 1,5 | |||||||
| IC | |||||||||
| 0,5 | 0,75 | ≥ 1,0 | 0,5 | 0,75 | ≥ 1,0 | 0,5 | 0,75 | ≥ 1,0 | |
| 1,5 3 5 10 |
6,9 10,0 12,5 15,5 |
10,0 15,5 21,9 29,9 |
13,2 22,0 31,2 44,3 |
7,9 12,5 15,9 21,3 |
10,7 18,6 25,7 36,3 |
13,4 23,9 35,4 51,3 |
8,6 13,7 18,4 24,6 |
10,5 18,4 27,6 41,0 |
12,3 23,0 36,7 57,4 |
Příkald 4
Stanovte průběh mezní zatěžovací křivky vrtané piloty Ø 1,22 m pažené ocelovou pažnicí do hloubky 5,3 m, dovrtanou bez pažení na celkovou hloubku 8,5 m v následujícím geotechnickém profilu:
0,0–0,8: navážka (neúnosná zemina)
0,8–1,5: jílovitá hlína měkká (neúnosná zemina)
1,5–5,3: hrubý písek zvodnělý, ulehlý ID = 0,7
5,3–6,7: slín pevný IC = 1,0
6,7–9,0: slínovec zvětralý R 5
hladina podzemní vody je v hloubce 2,20 m.
Řešení:
a) geometrické údaje a mezní napětí na plášti:
z tab. 24
\begin{gathered}
\frac{D_1}{d_1}=\frac{3{,}5}{1{,}22}=2{,}87&\text{z tab. 24}&q_\text{s,1}=91{,}22-\frac{48{,}44}{2{,}87}=74{,}34\space\text{kPa}\\\\
\frac{D_2}{d_2}=\frac{6{,}1}{1{,}07}=5{,}70&&q_\text{s,2}=97{,}31-\frac{108{,}59}{5{,}70}=78{,}26\space\text{kPa}\\\\
\frac{D_3}{d_3}=\frac{7{,}6}{1{,}07}=7{,}10&&q_\text{s,3}=131{,}92-\frac{94{,}96}{7{,}10}=118{,}55\space\text{kPa}\\\\
\frac{L}{d_0}=\frac{8{,}5}{1{,}07}=7{,}94&&q_\text{s,1}=957{,}61-703{,}89=868{,}96\space\text{kPa}
\end{gathered}b) průměrné plášťové tření:
\begin{gathered}
q_\text{s}=\frac{(1{,}22\cdot3{,}8\cdot74{,}34+1{,}07\cdot1{,}4\cdot78{,}26+1{,}07\cdot1{,}8\cdot118{,}55)}{(1{,}22\cdot3{,}8+1{,}07\cdot1{,}4+1{,}07\cdot1{,}8)}=85{,}66\space\text{kPa}
\end{gathered}c) koeficient přenosu zatížení patou:
\begin{gathered}
\beta=\frac{868{,}96}{(868{,}96+4\cdot7{,}94\cdot85{,}66)}=0{,}242
\end{gathered}d) mezní síla na plášti piloty:
\begin{gathered}
R_\text{su}=0{,}7\cdot\pi\cdot1{,}0\cdot(1{,}22\cdot3{,}8\cdot74{,}34+1{,}07\cdot1{,}4\cdot78{,}26+1{,}07\cdot1{,}8\cdot118{,}55)=1\space504{,}64\space\text{kN}
\end{gathered}e) zatížení na mezi mobilizace plášťového tření:
\begin{gathered}
R_\text{y}=\frac{1\space504{,}64}{(1-0{,}242)}=1\space985{,}00\space\text{kN}
\end{gathered}f) koeficient I1 z grafu na obr. 34 pro L / d0 = 7,94 … I1 = 0,175
g) sečnové moduly deformace z tab. 25–27:
\begin{gathered}
E_\text{s1}=29{,}49\space\text{MPa},&E_\text{s2}=13{,}40\space\text{MPa}&E_\text{s3}=28{,}20\space\text{MPa}
\end{gathered}průměrná velikost:
\begin{gathered}
E_\text{s}=\frac{(3{,}8\cdot29{,}49+1{,}4\cdot13{,}40+1{,}8\cdot28{,}20)}{(3{,}8+1{,}4+1{,}8)}=25{,}94\space\text{MPa}
\end{gathered}h) tuhost: K = 26 500 / 25,94 = 1 022, z grafu na obr. 35 pro L / do = 7,94 a K = 1 021
\begin{gathered}
R_\text{k}=1{,}05,&&I=0{,}175\cdot1{,}05=0{,}184,&&d=\frac{(3{,}8\cdot1{,}22+1{,}07\cdot3{,}2)}{7{,}0}=1{,}15\space\text{m}
\end{gathered}i) sedání piloty na mezi mobilizace plášťového tření:
\begin{gathered}
s_\text{y}=0{,}184\cdot\frac{1\space985{,}0}{(1{,}15\cdot25\space940)}=0{,}0122\space\text{m}=12{,}2\space\text{m}
\end{gathered}pro sedání piloty s = 10 mm vychází:
\begin{gathered}
R_\text{k,10}=1\space985{,}0\cdot(\frac{10}{12{,}2})^\frac{1}{2}=1\space797{,}13\space\text{kN}
\end{gathered}pro sedání piloty s25 = 25 mm vychází:
\begin{gathered}
R_\text{pu,k}=0{,}242\cdot1\space985{,}0\cdot\frac{25}{12{,}2}=984{,}36\space\text{kN}\\\\
R_\text{bu,k}=1\space504{,}64+984{,}36=2\space489{,}00\space\text{kN}
\end{gathered}4.4 PŘÍČNĚ ZATÍŽENÍ PILOTY
Piloty přenášejí kromě osových zatížení též síly vodorovné a ohybové momenty. S ohledem na poměrně malé přípustné horizontální deformace se posuzují účinky osového a příčného zatížení zvlášť a výsledky se superponují při posuzování únosnosti průřezů pilot, tj. při jejich dimenzování. Příčně zatíženou pilotu lze považovat za nosník vetknutý do pružně plastického prostředí a v jistém oboru deformací jej lze řešit jako nosník omezené délky na pružném podkladě. Předpokládá se tedy lineární závislost mezi napětím a deformací podle Winklerovy hypotézy:
\begin{gathered}
\sigma_\text{z}=k_\text{h,z}\cdot u_\text{z}
\end{gathered}(63)
kde je:
kh,z … modul vodorovné reakce podloží v hloubce z [kN·m-3];
uz … příslušná vodorovná deformace pilot [m].
Velikost modulu kh závisí obecně na typu zeminy a na deformaci piloty a jeho průběh s hloubkou může mít různý tvar. V jemnozrnných zeminách a poloskalních horninách se předpokládá konstantní velikost s hloubkou a úměrnost s modulem deformace zeminy podle vztahu:
\begin{gathered}
k_\text{h}=\frac{E_\text{def}}{d}
\end{gathered}kde je:
d ≤ 1,0 m a je-li d > 1,0, potom se dosazuje d = 1,0 m.
V hrubozrnných zeminách se předpokládá lineární růst s hloubkou z podle vztahu:
\begin{gathered}
k_\text{hz}=n_\text{h}\cdot\frac{z}{d}
\end{gathered}(65)
kde je:
nh … konstanta podle tab. 28.
Tab. 28 Konstanta nh [MN·m-3] pro nesoudržné zeminy
| Zemina | nh [MN·m-3] | ||
| relativní ulehlost ID | 0,33 | 0,50 | 0,90 |
| suchý písek a štěrk | 1,5 | 7,0 | 18,0 |
| vlhký písek a štěrk | 2,5 | 4,5 | 11,0 |
V závislosti na tuhosti piloty a vlastnostech základové půdy, jakož i velikosti působícího příčného zatížení, lze rozeznat následující 2 případy deformací příčně zatížených pilot:
- osa piloty zůstává po zatížení přímá, pouze se posunuje a otáčí – tuhé piloty;
- osa piloty se po zatížení deformuje – ohebné piloty.
Z hlediska podepření pilot jako nosníků v zemině rozeznáváme tyto základní případy:
- volná hlava, volná pata – případ podepření sloupu osamělou pilotou;
- pevná hlava, volná pata – piloty v hlavě vetknuté do základového bloku, jež neumožní pootočení, nýbrž pouze posun;
- volná hlava, kloub v patě – zakotvení piloty na malou hloubku do skalního podloží, což znemožní posun v patě;
- piloty zatížené jednostranným tlakem – případ pilotových stěn.
Únosnost příčně zatížené piloty lze stanovit zkouškou nebo výpočtem. Statické zatěžovací zkoušky příčně zatížených pilot jsou jednoduché, neboť se obyčejně 2 piloty v hlavách rozpírají, což nevyžaduje instalaci zatěžovacího zařízení.
4.4.1 Výpočet příčně zatížených osamělých tuhých pilot, příklad 5
Příčně zatížené piloty se v přijatelném oboru deformací chovají jako tuhé, pokud platí vztah:
\begin{gathered}
L_\text{max}=m\cdot d
\end{gathered}kde je:
m … koeficient podle tab. 29 a 30 v závislosti na statickém schématu piloty.
Tab. 29 Koeficient m pro jemnozrnné zeminy
| Statické schéma | Koeficient m | |||
| totální koheze cu [kPa] | 10 | 30 | 60 | 100 |
| vetknutá hlava, volná pata | 6,7 | 5,5 | 4,5 | 3,5 |
| volná hlava, volná pata | 10,0 | 8,0 | 7,0 | 6,0 |
| volná hlava, kloub v patě | 9,5 | 7,5 | 6,0 | 5,0 |
Tab. 30 Koeficient m pro hrubozrnné zeminy
| Statické schéma | Koeficient m | ||
| relativní ulehlost ID | 0,5 | 0,7 | 0,9 |
| vetknutá hlava, volná pata | 5,5 | 4,2 | 3,2 |
| volná hlava, volná pata | 7,0 | 5,5 | 4,2 |
| volná hlava, kloub v patě | 5,5 | 4,2 | 3,2 |
Tuhé piloty představují staticky určitý systém a v tom případě lze pomocí příslušných podmínek rovnováhy stanovit velikost posunu v hlavě ua, pootočení střednice ψ a příslušné velikosti vnitřních sil v pilotě, na jejichž základě lze její průřez dimenzovat. Statické schéma tuhé piloty s volnou hlavou i patou je na obr. 35. Neznámou polohu bodu otáčení O, (hloubku z0) a posun hlavy vyřešíme z následujících rovnic, vyjadřujících silovou podmínku rovnováhy ve vodorovném směru a momentovou podmínku k bodu otáčení O:
\begin{gathered}
H-d\cdot\frac{u_\text{a}}{z_0}\cdot\int^\text{L}_0k_\text{hz}\cdot(z_0-z)\cdot dz=0
\end{gathered}(67)
\begin{gathered}
h\cdot(h+z_0)-d\cdot\frac{u_\text{a}}{z_0}\cdot\int_0^\text{L}k_\text{hz}\cdot(z_0-z)^2\cdot dz=0
\end{gathered}(68)
Obr. 35 Statické schéma tuhé příčně zatížené piloty
a) volná hlava, volná pata – homogenní jemnozrnná zemina
V homogenní jemnozrnné zemině se předpokládá konstantní modul vodorovné reakce podloží khz = kh = konstanta a soustava rovnic (67), (68) pak přejde na tvar:
\begin{gathered}
H-d\cdot u_\text{a}\cdot\frac{k_\text{h}}{z_0}\cdot\int_0^\text{L}(z_0-z)\cdot dz=0
\end{gathered}(69)
\begin{gathered}
H\cdot(h+z_0)-d\cdot u_\text{a}\cdot\frac{k_\text{h}}{z_0}\cdot\int_0^\text{L}(z_0-z)\cdot dz=0
\end{gathered}(70)
a řešením získáme:
\begin{gathered}
z_0=\frac{(3\cdot h+2\cdot L)}{(6\cdot h+3\cdot L)}\cdot L
\end{gathered}(71)
\begin{gathered}
u_\text{a}=2\cdot H\cdot\frac{(3\cdot h+2\cdot L)}{(k_\text{h}\cdot d\cdot L^2)}
\end{gathered}(72)
\begin{gathered}
\tg\psi=\frac{u_\text{a}}{z_0}=2\cdot H\cdot\frac{(6\cdot h+3\cdot L)}{(k_\text{h}\cdot d\cdot L^3)}
\end{gathered}(73)
Maximální ohybový moment bude v hloubce z1, pro níž je posouvající síla nulová, tedy:
\begin{gathered}
z_1^2-2\cdot z_0\cdot z_1+z_0\frac{L^2}{(3\cdot h+2\cdot L)}=0
\end{gathered}(74)
\begin{gathered}
M_\text{max}=H\cdot(h+z_1)-H\cdot(3\cdot h+2\cdot L)\cdot(3\cdot z_0-z_1)\cdot\frac{z_1^2}{(3\cdot z_0\cdot L^2)}
\end{gathered}(75)
b) Volná hlava, volná pata – homogenní hrubozrnná zemina
V homogenní hrubozrnné zemině se předpokládá lineárně rostoucí modul vodorovné reakce podloží podle (64) a soustava rovnic (67), (68) pak přejde na tvar:
\begin{gathered}
H-u_\text{a}\cdot\frac{n_\text{h}}{z_0}\cdot\int_0^\text{L}z\cdot(z_0-z)\cdot dz=0
\end{gathered}(76)
\begin{gathered}
H\cdot(h+z_0)-u_\text{a}\cdot\frac{n_\text{h}}{z_0}\cdot\int_0^\text{L}z\cdot(z_0-z)^2\cdot dz=0
\end{gathered}(77)
a řešením získáme:
\begin{gathered}
z_0=\frac{(4h+3L)}{(6h+4L)}\cdot L
\end{gathered}(78)
\begin{gathered}
u_\text{a}=6H\cdot\frac{(4h+3L)}{(n_\text{h}\cdot L^3)}
\end{gathered}(79)
\begin{gathered}
\tg\psi=\frac{u_\text{a}}{z_0}=6H\cdot\frac{(6h+4L)}{(n_\text{h}\cdot L^4)}
\end{gathered}(80)
Maximální ohybový moment bude v hloubce z1, pro níž je posouvající síla nulová, tedy:
\begin{gathered}
z_1^3-[L+\frac{L^2}{(12h+8L)}]\cdot z_1^2+\frac{L^4}{(12h+8L)}=0
\end{gathered}(81)
\begin{gathered}
M_\text{max}=H\cdot(h+z_1)-H\cdot(4L\cdot z_1^3-3\cdot z_1^4)\cdot\frac{(3h+2L)}{(3L^4)}-H\cdot\frac{z_1^3}{(3L^2)}
\end{gathered}(82)
c) Vetknutá hlava, volná pata
K výpočtu vodorovného posunu ua postačí pouze silová podmínka rovnováhy, neboť poloha bodu otáčení z0 → ∞, tudíž rovnice (69) je identicky rovna 0. V homogenní jemnozrnné zemině s kh = konst. bude:
\begin{gathered}
H-d\cdot k_\text{h}\cdot\int_0^\text{L}u_\text{a}\cdot dz=0
\end{gathered}(83)
\begin{gathered}
u_\text{a}=\frac{H}{(d\cdot k_\text{h}\cdot L)}
\end{gathered}(84)
\begin{gathered}
M_\text{max}=M_\text{a}=H\cdot(\frac{1}{2}\cdot L+\frac{3}{4}\cdot d)
\end{gathered}(85)
V homogenní hrubozrnné zemině bude:
\begin{gathered}
H-d\cdot h_\text{h}\cdot\int_0^\text{L}z\cdot dz=0
\end{gathered}(86)
\begin{gathered}
u_\text{a}=\frac{2H}{(n_\text{h}\cdot L^2)}
\end{gathered}(87)
\begin{gathered}
M_\text{max}=M_\text{a}=2H\cdot\frac{L}{3}
\end{gathered}(88)
d) Volná hlava, kloub v patě
Bod otáčení je tedy znám, neboť je v patě piloty, tudíž k řešení postačí momentová podmínka rovnováhy (rovnice 70), kde je z0 = L, tedy:
\begin{gathered}
H\cdot(h+L)-d\cdot\frac{u_a}{L}\cdot\int_0^\text{L}k_\text{hz}\cdot(L-z)^2\cdot dz=0
\end{gathered}(89)
V homogenní jemnozrnné zemině bude tedy:
\begin{gathered}
u_\text{a}=3H\cdot\frac{(h+L)}{(d\cdot k_\text{h}\cdot L^2)}
\end{gathered}(90)
\begin{gathered}
\tg\psi=\frac{u_\text{a}}{L}=3\cdot H\cdot\frac{(h+L)}{(d\cdot k_\text{h}\cdot L^3)}
\end{gathered}(91)
\begin{gathered}
z_1^2-2L\cdot z_1+2\cdot\frac{L^3}{(3h+L)}=0
\end{gathered}(92)
\begin{gathered}
M_\text{max}=H\cdot(h+z_1)-H\cdot(h+L)\cdot(3L-z_1)\cdot\frac{z_1^3}{(2\cdot L^3)}
\end{gathered}(93)
V homogenní hrubozrnné zemině bude:
\begin{gathered}
u_\text{a}=12H\cdot\frac{(h+L)}{(n_\text{h}\cdot L^3)}
\end{gathered}(94)
\begin{gathered}
\tg\psi=\frac{u_\text{a}}{L}=12H\cdot\frac{(h+L)}{(n_\text{h}\cdot L^4)}
\end{gathered}(95)
\begin{gathered}
z_1^3-\frac{3}{2L}\cdot z_1^2+\frac{L^4}{(4\cdot h+4L)}=0
\end{gathered}(96)
\begin{gathered}
M_\text{max}=H\cdot(h+z_1)-2H\cdot(2L-z_1)\cdot(h+L)\cdot\frac{z_1^3}{L^4}
\end{gathered}(97)
Příklad 5
Stanovte vnitřní síly a deformace piloty d = 0,90, L = 6,00 m v jemnozrnné zemině charakterizované cu,k = 45 kPa (φu,k = 0), zatížené vodorovnou silou Hk = 50 kN a ohybovým momentem Mk = 75 kNm
Řešení:
Jde o případ tuhé piloty v homogenní jemnozrnné zemině, neboť pro cu,k = 45 kPa a pilotu s volnou hlavou i patou vychází podle tab. 29 koeficient m = 7,5, tedy Lmax = 7,5 · 0,9 = 6,75 m > 6 m.
Soustava rovnic (66) a (67) se výrazně zjednoduší a řešením získáme:
a) polohu bodu otáčení
\begin{gathered}
z_0=L\cdot\frac{(3h+2L)}{(6h+3L)}=6{,}0\cdot\frac{(3\cdot1{,}5+2\cdot6{,}0)}{(6\cdot1{,}5+3\cdot6{,}0)}=3{,}67\space\text{m}
\end{gathered}neboť
\begin{gathered}
h=\frac{M_\text{k}}{H_\text{k}}=\frac{75}{50}=1{,}5\space\text{m}\\\\
E_\text{def}=(80-100)\cdot c_\text{u,k}=4\space500\space\text{kPa}\\\\
k_\text{h}=\frac{4\space500}{0{,}9}=5\space000\space\text{kPa}
\end{gathered}b) vodorovný posun v hlavě:
\begin{gathered}
u_\text{a}=2H\cdot\frac{(3h+2L)}{(k_\text{h}\cdot dL^2)}=2\cdot50\cdot\frac{(3\cdot1{,}6+2\cdot6{,}0)}{(5\space000\cdot0{,}9\cdot6{,}0^2)}=0{,}0102\space\text{}=10{,}2\space\text{mm}
\end{gathered}c) pootočení osy piloty:
\begin{gathered}
\tg\psi=\frac{u_\text{a}}{z_0}=2H\cdot\frac{(6h+3L)}{(k_\text{h}\cdot d\cdot L^3)}=2\cdot50\cdot\frac{(6\cdot1{,}5+3\cdot6{,}0)}{(5\space000\cdot0{,}9\cdot6{,}0^3)}=0{,}00278(\psi=0{,}16\degree)
\end{gathered}d) maximální ohybový moment je v hloubce z1, pro níž je posouvající síla nulová, tedy:
\begin{gathered}
z_1^2-2z_0\cdot z_1+\frac{(L^2\cdot z_0)}{(3h+2L)}=0...z_1^2-7{,}34\cdot z_1+8{,}00=0...z_1=1{,}33\space\text{m}\\\\
M_\text{max}=H\cdot(h+z_1)-H\cdot z_1^2\cdot(3h+2L)\cdot\frac{(3z_0-z_1)}{(3L^3\cdot z_0)}=50\cdot(1{,}5+1{,}33)-50\cdot1{,}33^2\cdot(3\cdot1{,}5+2\cdot6{,}0)\cdot\frac{(3\cdot3{,}67-1{,}33)}{(3\cdot6{,}0^2\cdot3{,}67)}=105{,}86\space\text{kNm}
\end{gathered}Poznámky:
a) V případě výpočtu příčně zatížených pilot z hlediska získání průběhu vnitřních sil pro účely dimenzování železobetonového průřezu se vychází z 1. mezního stavu a návrhového přístupu NP2. Zatížení pilot je tedy v návrhových hodnotách (viz tab. 8, soubor A1), vlastnosti základové půdy rovněž návrhové (viz tab. 9, soubor M1) a spočtená únosnost se redukuje koeficientem γRH = 1,1 (pro soubor R2);
b) v případě výpočtu příčně zatížených pilot z hlediska získání jejich deformací se vychází z výpočtu 2. mezního stavu, kdy se použije všech vstupních parametrů (zatížení i vlastností základových půd) charakteristických;
c) vlastní metoda výpočtu (rovnice z kap. 4.4) jsou v obou případech stejné
4.4.2 Výpočet příčně zatížených osamělých ohebných pilot, příklad 6
V tomto případě nevystačíme s podmínkami rovnováhy, neboť se nejedná o staticky určitý systém. Rovnice ohybové čáry piloty podle obr. 36 má potom tvar:
\begin{gathered}
E_\text{b}\cdot I\cdot(\frac{d^4u}{dz^4})+d\cdot k_\text{hz}\cdot u=0
\end{gathered}(98)
kde je:
Eb … modul pružnosti (deformace) materiálu piloty;
I … moment setrvačnosti průřezu piloty.
Obr. 36 Deformace příčně zatížené ohebné piloty
Po dvojí integraci této rovnice lze získat rovnici ohybové čáry nosníku ve známém tvaru:
\begin{gathered}
-E_\text{b}\cdot I\cdot(\frac{d^2u}{dz^2})=M_\text{z}
\end{gathered}(99)
Tuto rovnici lze přímo řešit pouze pro speciální případy uložení. Je-li pilota uložena ve vrstevnaté zemině, není modul vodorovné reakce podloží konstantní, nýbrž má obecný průběh a výchozí diferenciální rovnici ohybové čáry lze řešit přibližně – numericky řešení, přičemž jsou příslušné derivace funkce uz nahrazeny diferenčními výrazy v určitých, předem zvolených bodech. Jedná se ostatně o aplikaci metody sítí pro nosníkovou úlohu, přičemž výpočtové schéma tohoto řešení je na obr. 37. Při označení dílků 1 až n, dělících bodů 0 až n máme pro n dílků jednotné délky Δz = L / n celkem n+1 průřezů, v nichž hledáme n+1 neznámých vodorovných posunů. Okolní základová půda vzdoruje deformacím ui napětím, jehož intenzita je přímo úměrná velikosti těchto deformací (Winklerův předpoklad). Jelikož neřešíme spojitý průběh ohybové čáry, znázorníme odpor zemního prostředí diskrétními silami Pi, jež mají fyzikální význam ui násobku pérových konstant a rovnají se:
\begin{gathered}
P_\text{i}=\Delta z\cdot d\cdot k_\text{hz}\cdot u_\text{i}=C_\text{i}\cdot u_\text{i}
\end{gathered}(100)
Druhou derivaci funkce průběhu ohybové čáry v bodě i nahradíme diferenčním výrazem:
\begin{gathered}
\frac{d^2u}{dz^2_\text{(i)}}=\frac{(u_\text{i-1}-2\cdot u_\text{i}+u_\text{i+1})}{(\Delta z)^2}
\end{gathered}(101)
a získáme:
\begin{gathered}
E_\text{b}\cdot\frac{I}{(\Delta z)^2}\cdot(u_\text{i-1}-2\cdot u_\text{i}+u_\text{i+1})=M_\text{zatěžovací}-M_\text{vzdorovací}
\end{gathered}(102)
kde je:
\begin{gathered}
M_\text{zatěžovací}=H\cdot(h+z_\text{i})
\end{gathered}(103)
\begin{gathered}
M_\text{vzdorovací}=P_0\cdot z_\text{i}+P_1\cdot(z_\text{i}-1\cdot\Delta z)+P_2\cdot(z_\text{i}-2\cdot\Delta z)+...+P_\text{i}\cdot(z_\text{i}-i\cdot\Delta z)=\sum_\text{j=0}^\text{j=i}P_\text{j}\cdot(z_\text{i}-j\cdot\Delta z)
\end{gathered}(104)
Pro n+1 průřezů můžeme psát n-1 těchto lineárních rovnic o n+1 neznámých deformacích u0 až un:
\begin{gathered}
E\cdot\frac{I}{(\Delta z)^2}\cdot(u_\text{i-1}+2\cdot u_\text{i}+u_\text{i+1})=H\cdot(h+z_\text{i})-\sum_\text{j=0}^\text{j=n}C_\text{hi}\cdot u_\text{j}(z_\text{i}-j\Delta\cdot z)=0
\end{gathered}(105)
Zbývající 2 rovnice poskytují podmínky rovnováhy:
- součtová ve vodorovném směru:
\begin{gathered}
H-\sum_\text{i=0}^\text{i=n}P_\text{i}=0
\end{gathered}(106)
momentová k bodu n:
\begin{gathered}
H\cdot(h+L)-\sum_\text{i=0}^\text{i=n}P_\text{i}\cdot L\cdot(1-\frac{i}{n})=0
\end{gathered}(107)
Příklady výpočtu ohebných příčně zatížených pilot ve Winkler-Pasternakově modelu podloží jsou uvedeny v monografii [1].
Obr. 37 Výpočtové schéma ohebné, příčně zatížené piloty – Winklerův model
Příklad 6
Stanovte vnitřní síly a deformace piloty d = 0,63 m, L = 9,00 m, zatížené vodorovnou silou Hk = 70 kN a ohybovým momentem Mk = 80 kNm v geotechnickém profilu:
- 0,0–2,0: navážka hlinitá (Edef = 3,0 MPa);
- 2,0–7,0: písek slabě hlinitý, zvodnělý, středně ulehlý (ID = 0,5);
- 7,0–9,0: břidlice zvětralá tř. R5 (Edef = 7,0 MPa).
Řešení:
Jedná se o pilotu ohebnou, neboť platí m = 9,0 / 0,63 = 14,3 > 7 (viz tab. 29 a 30).
a) stanovení průběhu vodorovné reakce podloží:
0,0–2,0: navážka – průběh konstantní
\begin{gathered}
k_\text{h1}=\frac{3{,}0}{0{,}63}=4{,}76\space\text{MN/m}^3
\end{gathered}2,0–7,0: písek – průběh lineárně proměnný, nh = 4,5 MN / m3 (tab. 28);
- v hloubce 2,0 m:
\begin{gathered}
k_\text{k22}=4{,}5\cdot\frac{2{,}0}{0{,}63}=14{,}28\space\text{MN/m}^3
\end{gathered}- v hloubce 7,0 m:
\begin{gathered}
k_\text{k27}=4{,}5\cdot\frac{7{,}0}{0{,}63}=50{,}0\space\text{MN/m}^3
\end{gathered}7,0–9,0: zvětralá břidlice – průběh konstantní
\begin{gathered}
k_\text{h3}=\frac{7{,}0}{0{,}63}=11{,}11\space\text{MN/m}^3
\end{gathered}b) vlastní výpočet podle rovnic (98)–(106) pomocí programu „h-pil“, viz např. [1]
Pilota
Průměr piloty: 0,63 m
Délka piloty: 9,00 m
Modul pružnosti betonu: 26 500,00 MPa
Geologie
| Vrstva | Název | Hloubka [m] | Kh [MN/m3] | Smykový modul [MN/m] |
| 1 | navážka hlinitá | 0,00 | 4,76 | 2,38 |
| 2,00 | 4,76 | 2,38 | ||
| 2 | písek hlinitý | 2,00 | 14,28 | 7,14 |
| 7,00 | 50,00 | 25,00 | ||
| 3 | břidlice zvětralá | 7,00 | 11,11 | 5,60 |
| 9,00 | 11,11 | 5,6 |
Zatížení
Horizontální síla v hlavě piloty: 70,00 kN
Moment v hlavě piloty: 80,00 kNm
Výsledky
| Hloubka [m] | WINKLER | WINKLER-PASTERNAK | |||
| Posun [mm] | Moment [kNm] | Napětí [kPa] | Posun [mm] | Moment [kNn] | |
| 0,0 | 12,04 | 80,00 | 57,32 | 10,77 | 80,00 |
| 1,0 | 8,19 | 133,44 | 38,97 | 7,25 | 130,05 |
| 2,0 | 4,98 | 162,21 | 31,82 | 4,35 | 157,93 |
| 3,0 | 2,55 | 166,49 | 5,62 | 2,9 | 153,78 |
| 4,0 | 0,93 | 137,49 | 26,45 | 0,78 | 121,89 |
| 5,0 | -0,03 | 91,98 | -1,14 | -0,04 | -78.64 |
| 6,0 | -0,54 | 46,56 | -23,22 | 0,48 | 39,25 |
| 7,0 | -0,82 | 15,80 | -36,64 | -0,72 | 14,54 |
| 8,0 | -1,01 | 4,00 | -11,26 | -0,88 | 4,01 |
| 9,0 | -1,19 | 0,00 | -13,18 | -1,02 | 0,00 |
4.5 SKUPINY PILOT
4.5.1 Osově zatížení skupiny pilot, příklad 7
Při návrhu mimořádně zatížených pilotových základů nevystačíme s jednou pilotou a jsme nuceni navrhnout více pilot uspořádaných do skupiny, jež tvoří jeden statický celek. Piloty jsou vždy v hlavách spojeny patkou, nebo deskou, nebo alespoň nadzemní konstrukcí, přičemž tuhost výsledného systému významně ovlivňuje deformace tohoto pilotového základu. Piloty se ve skupině navrhují v minimálních osových vzdálenostech, jež jsou 2,5d v případě pilot maloprofilových (d ≤ 0,6), v případě velkoprůměrových pilot (d > 0,6 m) pak 1,7d, a to z pochopitelných důvodů, tedy ve snaze ušetřit co nejvíce na rozměrech této konstrukce. V souvislosti s návrhem skupiny pilot je třeba řešit následující úkoly:
- posoudit mezní únosnost skupinového pilotového základu (posoudit 1. mezní stav);
- stanovit velikosti příslušných deformací (sedání, pootočení, naklonění, průhyb), tedy posoudit 2. mezní stav;
- stanovit velikosti působících sil do jednotlivých pilot, a to za účelem jejich dimenzování.
Za skupinu pilot se obyčejně nepovažuje uspořádání pilot v jedné řadě, které je obvyklé pod základovými pasy nosných stěn bytových a občanských staveb, nebo pod opěrami menších mostů. Piloty se pod základy rozmisťují tak, aby každá pilota byla osově a přibližně stejně zatížena, tzn., že těžiště skupiny pilot by se mělo co nejvíce shodovat s působištěm svislé výslednice R. Tento požadavek však nelze většinou zajistit, neboť:
- zatížení se obyčejně skládá ze stálého a proměnného, přičemž tato složka mění své působiště;
- rozdělení sil do jednotlivých pilot je výrazně ovlivněno tuhostí systému, a tedy tuhostí spojující konstrukce;
- i malá nepřesnost v poloze piloty (výrobní tolerance) může způsobit významnou změnu sil do jednotlivých pilot;
- z prostorových důvodů nelze vždy uspořádat piloty pod základem nejvýhodněji.
Je-li výslednice vnějšího zatížení šikmá ve vztahu k ose pilot, vzniká též příčná složka zatížení, jež namáhá piloty ve skupině vodorovnou silou a ohybovým momentem. Piloty lze sice navrhovat jako šikmé (u velkoprůměrových pilot lze snadno zajistit sklon např. 8:1), to však bývá s ohledem na velikosti působících sil nedostatečné, a navíc svislé piloty jsou schopny přenášet příčná zatížení zcela běžně. Z toho důvodu se šikmé piloty navrhují ve skupině zřídka a většinou tehdy, je-li třeba z titulu jejich vzájemného ovlivňování zajistit jejich větší osovou vzdálenost v níže položených únosných vrstvách zemin. Piloty ve skupině se tedy vzájemně ovlivňují, přičemž míra tohoto ovlivňování je dána zhruba následujícími faktory:
- počtem pilot, jejich průměry, uspořádáním a délkou (přičemž čím jsou osové vzdálenosti menší a piloty v relativně homogenní zemině delší, tím je ovlivňování významnější);
- vlastnostmi základové půdy podél dříků pilot a pod jejich patami (přičemž čím je základová půda v oblasti pat pilot pevnější, tím je ovlivňování menší a naopak);
- celkovou průměrnou velikostí sedání skupiny pilot (čím je sedání větší, tím je i větší ovlivňování a naopak);
- tuhostí spojující základové konstrukce (patky, desky) a kvalitou základové půdy v základové spáře této konstrukce.
Teoretická analýza je založena na vytváření matematických 3D modelů v pružném, nebo jinak definovaném poloprostoru, kde se uplatní především vlivy geometrického uspořádání a prostých tuhostí jednotlivých komponentů, ovlivněných zvolenými deformačními (pružnostními) moduly kontinua.
Mezní únosnost skupinového základu svisle zatíženého
V případě centricky zatížené skupiny pilot opřených o skalní podloží (R1, R2), nebo vetknutých do poloskalního podloží (R3, R4, popř. i R5) a do ulehlých písků či štěrků (ID ≥ 0,7), je mezní návrhová únosnost skupiny pilot (1. mezní stav) dána součtem únosností jednotlivých pilot působících jako osamělé. Návrhová únosnost skupiny pilot v jemnozrnných zeminách je pak přibližně dána:
- a) součtem únosností pilot ve skupině působících jako osamělé,
- b) únosností zemního tělesa ve tvaru hranolu opsaného skupině pilot (podle obr. 38) podle vztahu:
\begin{gathered}
Z_\text{g}=0{,}5\cdot(2\cdot(B+B´))\cdot L\cdot c_\text{us}+B\cdot B´\cdot c_\text{u}\cdot N_\text{cs}
\end{gathered}(108)
kde je:
cus … průměrná velikost neodvodněné koheze zemin podél dříků pilot;
cu … neodvodněná koheze zeminy v ose zemního tělesa v hloubce 0,67L pod jeho dolní podstavou;
Ncs … koeficient únosnosti podle rovnice:
\begin{gathered}
N_\text{s}=5\cdot(1+\frac{L}{(5\cdot B)})\cdot(1+\frac{L}{(5\cdot B´)})
\end{gathered}(109)
c) rozhoduje vždy menší z obou únosností stanovených podle a), b).
Obr. 38 Schéma pro výpočet mezní únosnosti pilotové skupiny
Sedání skupinového základu svisle zatíženého
Přibližně lze sedání pravidelné skupiny pilot spojených dostatečně tuhou patkou určit:
- v případě centricky zatížené skupiny pilot opřených o skalní podloží (R1, R2), nebo vetknutých do poloskalního podloží (R3, R4, popř. i R5) a do ulehlých hrubozrnných zemin s ID ≥ 0,7 jako sedání osamělé piloty nacházející se ve stejném prostředí;
- v případě centricky zatížené skupiny pilot v ostatních typech zemin lze použít jednu z následujících metod:
- jako sedání fiktivního plošného základu v hloubce 0,67L šířky B a délky B´ (podle obr. 39), přičemž do výpočtu je třeba zahrnout vliv hloubky založení a mocnosti deformační zóny podle metodiky výpočtu sedání plošných základů;
- sedání skupiny pilot lze vypočítat ze vztahu:
\begin{gathered}
s=s_\text{y}+s_\text{p}
\end{gathered}(110)
kde je:
sy … sedání osamělé piloty na mezi mobilizace plášťového tření (rovnice 56) odečtené z mezní zatěžovací křivky osamělé piloty (obr. 32a);
sp … sedání fiktivního plošného základu v úrovni pat pilot, jehož rozměry jsou dány obvodem těchto pilot.
Fiktivní plošný základ je zatížen silou rovnající se součtu sil působících v patách pilot uvažovaných jako osamělé, přičemž podíl síly přenášené pláštěm a patou piloty se odečte z mezní zatěžovací křivky.
Výpočet sil v jednotlivých pilotách pilotové skupiny
V nejjednodušším případě pilotové skupiny se zavádějí následující předpoklady:
- piloty jsou v hlavách spojeny dostatečně tuhou deskou (patkou), jež se neprohýbá, pouze se posunuje a otáčí; v prostoru lze tedy stanovit 6 složek deformace – posuny ve směru souřadných os: vx, vy, vz, – pootočení kolem souřadných os: va, vb, vc;
- tuhost pilot je s ohledem na tuhost desky tak malá a deformace jsou tak nepatrné, že lze ve statickém schématu uvažovat s kloubovým spojením pilot jak v hlavě, tak i v patě, tudíž piloty jsou schopny přenášet pouze osové síly Ni;
- velikost osové síly Ni v i-té pilotě je přímo úměrná deformaci této piloty vi ve směru její osy, tudíž Ni = si·vi, přičemž koeficient úměrnosti si [kN·m-1] může být (po částech) konstantní, čímž lze modelovat (přírůstkovou metodou) pracovní diagram piloty;
- vliv skupinového účinku na sedání pilot je zanedbán, resp. lze jej modelovat pouze vhodnou volbou parametru (pérové konstanty) si.
V praxi se často setkáváme se skupinou pouze svislých pilot zatížených svislou silou Rx působící mimostředně s excentricitami ey a ez podle obr. 39.

Obr. 39 Statické schéma skupiny pouze svislých pilot
Pro výpočet deformací tuhé spojovací desky lze potom psát soustavu 3 lineárních rovnic:
\begin{gathered}
\begin{pmatrix}
R_\text{x}\\
R_\text{b}\\
R_\text{c}
\end{pmatrix}
=
\begin{pmatrix}
S_\text{xx},&0,&0\\
0,&S_\text{bb},&S_\text{bc}\\
0,&S_\text{cb},&S_\text{cc}
\end{pmatrix}
\cdot\begin{pmatrix}
v_\text{x}\\
v_\text{b}\\
v_\text{c}
\end{pmatrix}
\end{gathered}(111)
kde je:
\begin{gathered}
S_\text{xx}=\sum s_\text{i}\cdot p^2_\text{xi}=\sum s_\text{i}\\\\
S_\text{bb}=\sum s_\text{i}\cdot p^2_\text{bi}=\sum s_\text{i}\cdot z_\text{i}^2\\\\
S_\text{cc}=\sum s_\text{i}\cdot p^2_\text{ci}=\sum s_\text{i}\cdot(-y_\text{i})^2\\\\
S_\text{bc}=S_\text{cb}=\sum s_\text{i}\cdot p_\text{bi}\cdot p_\text{ci}=\sum s_\text{i}\cdot z_\text{i}\cdot(-y_\text{i})\\\\
\end{gathered}(112)
Deformace spojovací desky je dána třemi jejími složkami:
\begin{gathered}
v_\text{x}=\frac{R_\text{x}}{S_\text{xx}}\\\\
v_\text{b}=\frac{(S_\text{cc}\cdot R_\text{b}-S_\text{bc}\cdot R_\text{c})}{(S_\text{bb}\cdot S_\text{cc}-S_\text{bc}^2)}\\\\
v_\text{c}=\frac{(S_\text{bb}\cdot R_\text{c}-S_\text{bc}\cdot R_\text{b})}{(S_\text{bb}\cdot S_\text{cc}-S_\text{bc}^2)}
\end{gathered}(113)
Takto se přibližně řeší i obecně zatížená skupina svislých pilot, přičemž složky zatížení Ry a Rz se separují a jimi se zatíží skupina pilot zvlášť podle zásad uvedených v kap. 4.4. Výsledné účinky se potom získají superpozicí.
Jedná-li se o velkoprůměrové piloty, vetknuté do základové desky, není předpoklad o kloubovém spojení hlav pilot s deskou přijatelný. Příslušný způsob výpočtu je detailně popsán v monografii [1].
K výpočtu pilotového roštu potřebujeme znát matici tuhosti piloty, která se skládá ze 6 parametrů, z nichž 3 vyjadřují tuhost piloty vzdorující silám ve směru os: x, z, y a 3 tuhosti piloty vzdorující ohybovým momentům otáčejícím se kolem těchto souřadných os. Tuhost piloty je tedy síla (resp. moment) způsobující jednotkový posun (resp. pootočení). K jejich stanovení je třeba stanovit pružnou délku L´ podle teorie nosníku omezené délky na pružném podkladě.
V zeminách jemnozrnných za předpokladu po částech konstantního modulu vodorovné reakce podloží kh je pružná délka:
\begin{gathered}
L´=(\frac{(E_\text{b}\cdot I)}{(k_\text{h}\cdot d)})^{0{,}25}
\end{gathered}(114)
a v zeminách hrubozrnných za předpokladu lineárně se zvětšujícího modulu vodorovné reakce podloží podle rovnice (64) je pružná délka:
\begin{gathered}
L´=(E_\text{b}\cdot\frac{I}{n_\text{h}})^{0{,}20}
\end{gathered}(115)
kde je:
Eb … modul deformace betonu piloty;
I … moment setrvačnosti průřezu piloty;
kh, nh … modul vodorovné reakce podloží;
d … průměr piloty.
Tuhost piloty ve svislém směru sx vyjadřuje tedy osovou sílu potřebnou k jednotkové deformaci piloty. Tu lze stanovit z výsledků statické zatěžovací zkoušky nebo z výsledků výpočtu mezní zatěžovací křivky piloty (kap. 4.3.3). Tuhosti piloty ve směru y a z se za předpokladu dokonalého vetknutí stanoví z rovnice:
\begin{gathered}
s_\text{y,z}=\frac{(12\cdot E_\text{b}\cdot I_\text{y,z})}{(5{,}37\cdot L´^3)}
\end{gathered}(116)
Tuhost piloty proti kroucení:
\begin{gathered}
s_\text{a}=G\cdot\frac{I_\text{t}}{L}
\end{gathered}(117)
kde je:
G … smykový modul deformace betonu piloty;
It … polární moment setrvačnosti průřezu piloty;
L … délka piloty.
Ohybové tuhosti jsou pak:
\begin{gathered}
s_\text{b,c}=E_\text{b}\cdot\frac{I_\text{y,z}}{(1{,}5\cdot l´)}
\end{gathered}(118)
Vektor deformací hlavy i-té piloty bude:
\begin{gathered}
V_\text{i}=(v_\text{xi},v_\text{yi},v_\text{zi},v_\text{ai},v_\text{bi},v_\text{ci})^\text{T}
\end{gathered}(119)
a vektor sil působících v hlavě piloty:
\begin{gathered}
R_\text{i}=(R_\text{xi},R_\text{yi},R_\text{zi},R_\text{ai},R_\text{bi},R_\text{ci})^\text{T}
\end{gathered}(120)
Platí následující silové a momentové podmínky rovnováhy:
\begin{gathered}
R_\text{xi}=s_\text{xi}\cdot v_\text{xi}\\\\
R_\text{yi}=s_\text{yi}\cdot v_\text{yi}+0{,}5\cdot L´\cdot s_\text{yi}\cdot v_\text{ci}\\\\
R_\text{zi}=s_\text{zi}\cdot v_\text{zi}-1{,}5\cdot L´\cdot s_\text{zi}\cdot v_\text{bi}\\\\
R_\text{ai}=s_\text{ai}\cdot v_\text{ai}\\\\
R_\text{bi}=-1{,}5\cdot L´\cdot s_\text{zi}\cdot v_\text{zi}+(s_\text{bi}+2{,}25\cdot L´^2\cdot s_\text{zi})\cdot v_\text{bi}\\\\
R_\text{ci}=1{,}5\cdot L´\cdot s_\text{yi}\cdot v_\text{yi}+(s_\text{ci}+2{,}25\cdot L´^2\cdot s_\text{yi})\cdot v_\text{ci}
\end{gathered}(121)
Matice tuhosti i-té piloty:
\begin{gathered}
s_\text{i}=
\begin{pmatrix}
s_\text{xi}&0&0&0&0&0\\
0&s_\text{yi}&0&0&0&0{,}5\cdot L´\cdot s_\text{yi}\\
0&0&s_\text{zi}&0&-0{,}5\cdot L´\cdot s_\text{zi}&0\\
0&0&0&s_\text{ai}&0&0\\
0&0&-0{,}5\cdot L´\cdot s_\text{zi}&0&s_\text{bi}+0{,}25\cdot L´^2\cdot s_\text{zi}&0\\
0&0{,}5\cdot L´\cdot s_\text{yi}&0&0&0&s_\text{ci}+0{,}25\cdot L´^2\cdot s_\text{yii}
\end{pmatrix}
\end{gathered}(122)
A transformačné matice udávající polohu i-té piloty v globálním souřadném systému má tvar:
\begin{gathered}
T_\text{i}=
\begin{pmatrix}
p_\text{xxi}&p_\text{xyi}&p_\text{xzi}&0&0&0\\
p_\text{yxi}&p_\text{yyi}&p_\text{yzi}&0&0&0\\
p_\text{zxi}&p_\text{zyi}&p_\text{zzi}&0&0&0\\
p_\text{axi}&p_\text{ayi}&p_\text{azi}&p_\text{xxi}&p_\text{xyi}&p_\text{xzi}\\
p_\text{bxi}&p_\text{byi}&p_\text{bzi}&p_\text{yxi}&p_\text{yyi}&p_\text{yzi}\\
p_\text{cxi}&p_\text{cyi}&p_\text{czi}&p_\text{zxi}&p_\text{zyi}&p_\text{zzi}
\end{pmatrix}
\end{gathered}(123)
kde je:
\begin{gathered}
p_\text{xx}=\cos\alpha&&p_\text{xy}=-\sin\alpha\\\\
p_\text{xz}=0\\\\
p_\text{yx}=\sin\alpha\cdot\cos\omega&&p_\text{yy}=\cos\alpha\cdot\cos\omega&&p_\text{yz}=-\sin\omega\\\\
p_\text{zx}=\sin\alpha\cdot\sin\omega&&p_\text{zy}=\cos\alpha\cdot\sin\omega&&p_\text{zz}=\cos\omega
\end{gathered}\begin{gathered}
(p_\text{ax},p_\text{bx},p_\text{cx})=(p_\text{xx},p_\text{yx},p_\text{zx})\cdot
\begin{pmatrix}
0&z&-y\\
-z&0&x\\
y&-x&0
\end{pmatrix}\\\\
(p_\text{ay},p_\text{by},p_\text{cy})=(p_\text{xy},p_\text{yy},p_\text{zy})\cdot
\begin{pmatrix}
0&z&-y\\
-z&0&x\\
y&-x&0
\end{pmatrix}\\\\
(p_\text{az},p_\text{bz},p_\text{cz})=(p_\text{xz},p_\text{yz},p_\text{zz})\cdot
\begin{pmatrix}
0&z&-y\\
-z&0&x\\
y&-x&0
\end{pmatrix}
\end{gathered}(124)
Globální matice tuhosti soustavy pilot je:
\begin{gathered}
S=\sum_\text{i=1}^\text{i=n}T_\text{i}\cdot S_\text{i}\cdot T_\text{i}^\text{T}
\end{gathered}(125)
Globální deformace soustavy pilot je dána vektorem:
\begin{gathered}
v=(v_\text{x},v_\text{y},v_\text{z},v_\text{a},v_\text{b},v_\text{c})^\text{T}
\end{gathered}(126)
Zatěžovací vektor soustavy pilot (zatěžovací síly působící v těžišti soustavy pilot):
\begin{gathered}
R=(R_\text{x},R_\text{y},R_\text{z},R_\text{a},R_\text{b},R_\text{c})^\text{T}
\end{gathered}(127)
Základní rovnice:
\begin{gathered}
R=S\cdot v,\space\text{neboli}\space v=S^{-1}\cdot R
\end{gathered}(128)
Deformace jednotlivých pilot je dána vektorem:
\begin{gathered}
V_\text{i}=T_\text{i}^\text{T}\cdot v
\end{gathered}(129)
Vektor sil pro jednotlivé piloty:
\begin{gathered}
R_\text{i}=S_\text{i}\cdot v_\text{i}=S_\text{i}\cdot T_\text{i}^\text{T}\cdot v=S_\text{i}\cdot T_\text{i}^\text{T}\cdot S^{-1}\cdot R
\end{gathered}(130)
Příklad 7
Stanovení mezní únosnosti a deformace skupiny 6 ks pilot Ø 1,20 m, dlouhých 10,0 m ve dvou řadách (ve směru osy y) osově po 2,50 m v obou směrech spojených tuhou základovou patkou 4,0 x 6,5 m, tloušťky 1,50 m mostního pilíře v geotechnickém profilu:
0,0–3,0: jílovitá hlína písčitá, pevná
\begin{gathered}
(\gamma=20{,}0\space\text{kN}\cdot\text{m}^{-3},&\varphi_\text{ef,k}=25\degree,& c_\text{ef,k}=10\space\text{kPa},& c_\text{u,k}=50\space\text{kPa})
\end{gathered}3,0–8,0: jíl, tuhý
\begin{gathered}
(\gamma=20{,}5\space\text{kN}\cdot\text{m}^{-3},&\varphi_\text{ef,k}=25\degree,& c_\text{ef,k}=8\space\text{kPa},& c_\text{u,k}=40\space\text{kPa})
\end{gathered}8,0–12,0: jíl, pevný
\begin{gathered}
(\gamma=21{,}0\space\text{kN}\cdot\text{m}^{-3},&\varphi_\text{ef,k}=25\degree,& c_\text{ef,k}=8\space\text{kPa},& c_\text{u,k}=40\space\text{kPa})
\end{gathered}Zatěžovací údaje v těžišti hlav skupiny pilot:
hodnoty charakteristické
hodnoty návrhové
- svislá síla
Nk = 6 729 kN
Nd = 9 335 kN
- moment
Mz,k = 679 kNm
Mz,d = 1 019 kNm
- moment
My,k = 4 033 kNm
My,d = 6 024 kNm
- vodorovná síla
Hz,k = 170 kN
Hz,d = 255 kN
- vodorovná síla
Hy,k = 170 kN
Hy,d = 255 kN
Řešení:
a) Tab. 31 Výsledky výpočtu sil do pilot skupinového základu (viz předchozí text)
| Způsob zatížení | Maximální svislá síla max N [kN] | Minimální svislá síla min N [kN] | Moment v hlavě M1 [kNm] | Vodorovná síla v hlavě H1 [kN] |
| 1. mezní stav kloubové spojení pilot s patkou | 2 294 | 818 | 0 | 43 |
| 1. mezní stav vetknutí pilot do patky | 1 898 | 1 216 | 495 | 43 |
| 2. mezní stav kloubové spojení pilot s patkou | 1 615 | 628 | 0 | 29 |
| 2. mezní stav vetknutí pilot do patky | 1 349 | 894 | 332 | 29 |
Nadále bude počítáno s případem vetknutí hlav pilot do základové patky, jelikož jde o případ realistický s ohledem na tuhosti obou komponentů a způsob úpravy spojovací výztuže.
b) výpočet 1. mezního stavu pro osamělou pilotu (dlouhodobá únosnost – viz kap. 4.3.2)
- síla na patě
\begin{gathered}
U_\text{bd}=k_1\cdot A_\text{s}\cdot R_\text{d}...k_1=1{,}15(L\gt6\space\text{m}),A_\text{s}=1{,}13\space\text{m}^2\\\\
N_\text{d}=\text{exp}(3{,}14\cdot\tg20)\cdot\tg^2(45+\frac{20}{2})=6{,}39\\\\
N_\text{c}=5{,}39\cdot\cotg20=14{,}82\\\\
N_\text{b}=1{,}5\cdot5{,}39\cdot\tg20=2{,}94\\\\
\gamma_1=\frac{(3\cdot20{,}0+5\cdot20{,}5+2\cdot21{,}0)}{10}=20{,}45\space\text{kN}\cdot\text{m}^{-3}\\\\
R_\text{d}=1{,}2\cdot8{,}0\cdot14{,}82+(1+\sin20)\cdot20{,}45\cdot10\cdot6{,}39+21{,}0\cdot\frac{1{,}2}{2}\cdot2{,}94=1\space933{,}00\space\text{kPa}\\\\
U_\text{bd}=1{,}15\cdot1{,}13\cdot1\space933{,}0=2\space511{,}93\space\text{kN}
\end{gathered}- síla na plášti
\begin{gathered}
U_\text{fd}=3{,}14\cdot\sum d_\text{i}\cdot h_\text{i}\cdot f_\text{si}
\end{gathered}1. vrstva:
\begin{gathered}
\sigma_\text{z,0}=0;&\sigma_\text{z,3,0}=20{,}0\cdot3{,}0=60{,}0\space\text{kPa};\\\\
\sigma_\text{z,1}=30\space\text{kPa};&\sigma_\text{x,1}=1{,}0\cdot30{,}0=30{,}0\space\text{kPa};\\\\
f_\text{s,1}=30{,}0\cdot\tg(\frac{25}{1{,}0})+\frac{10}{1{,}2}=22{,}32\space\text{kPa}
\end{gathered}(koeficient technologie γr,1 = 1,0 – do sucha)
2. vrstva:
\begin{gathered}
\sigma_\text{z,3}=20{,}5\cdot3{,}0=61{,}5\space\text{kPa};&\sigma_\text{z,8,0}=20{,}5\cdot8{,}0=164{,}0\space\text{kPa};\\\\
\sigma_\text{z,2}=112{,}75\space\text{kPa};&\sigma_\text{x,2}=1{,}0\cdot112{,}75=112{,}75\space\text{kPa};\\\\
f_\text{s,1}=112{,}75\cdot\tg(\frac{20}{1{,}0})+\frac{8{,}0}{1{,}0}=49{,}05\space\text{kPa}
\end{gathered}3. vrsta:
\begin{gathered}
\sigma_\text{z,8}=21{,}0\cdot8{,}0=168{,}0\space\text{kPa};&\sigma_\text{z,10,0}=21{,}0\cdot10{,}0=210{,}0\space\text{kPA};\\\\
\sigma_\text{z,3}=189{,}0\space\text{kPa};&\sigma_\text{x,3}=1{,}0\cdot189{,}0=189{,}0\space\text{kPa};\\\\
f_\text{s,1}=189{,}0\cdot\tg(\frac{20}{1{,}0})+\frac{8{,}0}{1{,}0}=76{,}79\space\text{kPa}\\\\
U_\text{fd}=3{,}14\space\text{1{,}2}\cdot(3{,}0\cdot22{,}32+5{,}0\cdot49{,}05+2{,}0\cdot76{,}79)=1\space754{,}91\space\text{kN}
\end{gathered}Aplikujeme návrhový přístup NP2 … γR = 1,1
- návrhová únosnost
\begin{gathered}
U_\text{vd}=(2\space511{,}93+1\space754{,}91)1{,}1=3\space878{,}95\space\text{kN}\gt2\space294\space\text{kN}\implies\text{vyhovuje}
\end{gathered}c) mezní únosnost skupinového základu (krátkodobá)
- počítáme s únosností náhradního plošného základu Bef · Lef v hloubce H = L = 10,0 m
\begin{gathered}
B=2{,}5+1{,}2=3{,}7\space\text{m};&L=5{,}0+1{,}2=6{,}2\space\text{m}
\end{gathered}excentricity:
\begin{gathered}
e_\text{y}=\frac{1\space019}{9\space335}=0{,}109\space\text{m};&e_\text{z}=\frac{6\space024}{9\space335}=0{,}645\space\text{m}
\end{gathered}efektivní rozměry fiktivního základu:
\begin{gathered}
B_\text{ef}=3{,}7-2\cdot0{,}109=3{,}48\space\text{m},&L_\text{ef}=6{,}2-2\cdot0{,}645=4{,}91\space\text{m}\\\\
c_\text{us,d}=\frac{(3{,}0\cdot50{,}0+7{,}0\cdot40{,}0)}{10{,}0}=42{,}0\space\text{kPa};&c_\text{ud}=40{,}0\space\text{kPa}\\\\
N_\text{cs}=5\cdot(1+\frac{10{,}0}{(5\cdot3{,}348)})\cdot(1+\frac{10{,}0}{(5\cdot4{,}91)})=11{,}08\\\\
Z_\text{g}=0{,}5\cdot2\cdot(3{,}48+4{,}91)\cdot10{,}0\cdot42{,}0+3{,}48\cdot4{,}91\cdot40{,}0\cdot11{,}08=11\space096{,}67\space\text{kN}\\\\
Z_\text{g,d}=\frac{11\space096{,}67}{\gamma_\text{R}}=\frac{10\space590{,}34}{1{,}1}=10\space087{,}88\space\text{kN}\gt9\space335\space\text{kN}\implies\text{vyhovuje}
\end{gathered}d) 2. mezní stav pro osamělou pilotu (mezní zatěžovací křivka – viz kap. 4.3.3)
1. vrstva
\begin{gathered}
\frac{D_1}{d}=\frac{1{,}5}{1{,}2}=1{,}25;&q_\text{s,1}=97{,}31-\frac{108{,}59}{1{,}25}=10{,}44\space\text{kPa}
\end{gathered}2. vrstva
\begin{gathered}
\frac{D_2}{d}=\frac{5{,}5}{1{,}2}=4{,}58;&q_\text{s,2}=46{,}39-\frac{20{,}81}{4{,}58}=41{,}85\space\text{kPa}
\end{gathered}3. vrstva
\begin{gathered}
\frac{D_3}{d}=\frac{9{,}0}{1{,}2}=7{,}50;&q_\text{s,3}=97{,}31-\frac{108{,}59}{7{,}50}=82{,}83\space\text{kPa}
\end{gathered}pata
\begin{gathered}
\frac{L}{d}=\frac{10{,}0}{1{,}2}=8{,}33;&q_0=987{,}60-\frac{1\space084{,}26}{8{,}33}=857{,}44\space\text{kPa}
\end{gathered}únosnost pláště
\begin{gathered}
R_\text{su}=0{,}7\cdot1{,}0\cdot3{,}14\cdot1{,}2\cdot(3{,}0\cdot10{,}44+5{,}0\cdot41{,}84+2{,}0\cdot82{,}83)=1\space071{,}47\space\text{kN}
\end{gathered}průměrné plášťové tření
\begin{gathered}
q_\text{ss}=\frac{(3{,}0\cdot10{,}44+5{,}0\cdot41{,}84+2{,}0\cdot82{,}83)}{10{,}0}=40{,}62\space\text{kPa}
\end{gathered}koeficient přenosu
\begin{gathered}
\beta=\frac{857{,}44}{(857{,}44+4\cdot\frac{40{,}62}{1{,}2})}=0{,}388
\end{gathered}síla na mezi mobilizace plášťového tření
\begin{gathered}
R_\text{y}=\frac{1\space071{,}47}{(1-0{,}388)}=1\space750{,}77\space\text{kN}
\end{gathered}sečnové moduly deformace:
\begin{gathered}
E_\text{s,1}=23{,}5\space\text{MPa};&E_\text{s,2}=16{,}9\space\text{MPa};&E_\text{s,3}=16{,}5\space\text{MPa}
\end{gathered}průměrná velikost
\begin{gathered}
E_\text{ss}=\frac{(3{,}0\cdot23{,}5+5{,}0\cdot16{,}9+2{,}0\cdot16{,}5)}{10{,}0}=18{,}2\space\text{MPa}
\end{gathered}koef. sedání I1 = 0,162 (pro L / d = 8,33); Rk = 1,06 (pro k = 26 500 / 18,2 a L / d = 8,33)
\begin{gathered}
I=I_1\cdot R_\text{h}=0{,}162\cdot1{,}06=0{,}172
\end{gathered}sedání na mezi mobilizace plášťového tření
\begin{gathered}
s_\text{y}=0{,}172\cdot\frac{1\space750{,}77}{(1{,}2\cdot18\space200)}=0{,}0138\space\text{m}
\end{gathered}pro max. sílu v pilotě maxN = 1 349 kN je sedání
\begin{gathered}
s_\text{max}=13{,}8\cdot(\frac{1\space349}{1\space751})^2=8{,}19\space\text{mm}
\end{gathered}pro min. sílu v pilotě minN = 894 kN je sedání
\begin{gathered}
s_\text{min}=13{,}8\cdot(\frac{894}{1\space751})^2=3{,}60\space\text{mm}\implies\text{vyhovuje}
\end{gathered}e) 2. mezní stav sedání skupinového základu
průměrná velikost sedání v těžišti skupiny pilot
\begin{gathered}
s_\text{s}=\frac{8{,}19+3{,}60)}{2}=5{,}90\space\text{m}\implies\text{vyhovuje}
\end{gathered}max. sklon:
\begin{gathered}
\frac{\Delta s_\text{s}}{a}=\frac{(8{,}19-3{,}6)}{5\space590}=0{,}000821;&a=(2\space500^2+5\space000^2)^\frac{1}{2}=5\space590\space\text{mm};&\tg\alpha=\frac{2\space500}{5\space000}=0{,}5\space...\space\alpha=26{,}5\degree
\end{gathered}sklon základu ve směru osy y:
\begin{gathered}
\frac{\Delta s}{a_\text{y}}=0{,}000821\cdot\cos26{,}5=0{,}000733
\end{gathered}sklon základu ve směru osy z:
\begin{gathered}
\frac{\Delta s}{a_\text{z}}=0{,}000821\cdot\sin26{,}5=0{,}000365\implies\text{sklony vyhovují}
\end{gathered}Poznámka:
výsledky výpočtu sedání pilot jsou zřejmě mírně optimistické, neboť není uvažováno se spolupůsobením pilot ve skupině. Tento vliv by bylo možné odhadnout výpočtem podle výše uvedeného textu.
f) příčné zatížení pilot; vod síla v hlavě H0 = 29 kN, moment v hlavě M0 = 332 kNm
výpočet ohebné piloty podle kap. 4.4.
Průměr piloty: 1,20 m
Délka piloty: 10,00 m
Modul pružnosti betonu: 26 500,00 MPa
Geologie
| Vrstva | Nazev | Hloubka [m] | kh [MN/m3] | Smykový modul [MN/m] |
| 1 | hlína písčitá | 0,00 | 1,17 | 0,60 |
| 3,00 | 1,17 | 0,60 | ||
| 2 | jíl tuhý | 3,00 | 2,13 | 1,00 |
| 5,00 | 2,13 | 1,00 | ||
| 3 | jíl tuhý | 5,00 | 3,06 | 1,50 |
| 8,00 | 3,06 | 1,50 | ||
| 4 | jíl pevný | 8,00 | 4,62 | 2,30 |
| 10,00 | 4,62 | 2,30 |
Zatížení
Horizontální síla v hlavě piloty: 29,00 kN
Moment v hlavě piloty: 332,00 kNm
Výsledky
| WINKLER | WINKLER-PASTERNAK | ||||
| Hloubka [m] | Posun [mm] | Moment [kNm] | Napětí [kPa] | Posun [mm] | Moment [kNm] |
| 0,0 | 16,94 | 332,00 | 19,82 | 15,90 | 332,00 |
| 1,0 | 14,05 | 349,53 | 16,44 | 13,17 | 348,28 |
| 2,0 | 11,28 | 347,46 | 13,20 | 10,56 | 345,71 |
| 3,0 | 8,65 | 329,51 | 11,15 | 8,08 | 328,03 |
| 4,0 | 6,13 | 296,92 | 13,06 | 5,73 | 295,59 |
| 5,0 | 3,73 | 248,91 | 8,37 | 3,48 | 249,07 |
| 6,0 | 1,42 | 190,45 | 4,33 | 1,32 | 191,92 |
| 7,0 | -0,83 | 126,88 | -2,53 | -0,76 | 129,94 |
| 8,0 | -3,02 | 66,30 | -9,84 | -2,8 | 70,84 |
| 9,0 | -5,19 | 18,87 | -23,99 | -4,81 | -22,48 |
| 10 | -7,35 | 0,00 | -33,98 | -6,81 | 0,00 |
g) dimenzování železobetonového průřezu piloty (výsledné vnitřní síly jsou ve velikostech charakteristických, tudíž bude dimenzováno podle klasické teorie:
Beton C25/30, ocel R – 10505, min. vyztužení 10 Ø R 20 mm
\begin{gathered}
(A_\text{s}=0{,}00314\space\text{m}^2\gt A_\text{s,min}=0{,}25\%\space A_\text{b}=0{,}00283\space\text{m}^2)
\end{gathered}Železobetonový kruhový průřez, klasická teorie, čistý ohyb, ohyb a tlak nebo tah
Průřez:
D = 120 cm – průměr betonového průřezu
d = 20 mm; – profil želez
nz = 10 ks – počet želez
kryti = 100 mm – krytí k nosné výztuži
n = 15 – poměr E oceli a betonu
Zatížení:
M = 350 kNm – P = 894 kN (P < 0 je tah)
Výpočet pro:
- tlak nebo tah s velkou výstředností, beton v tahu nepůsobí;
- tlak (tah) s malou výstředností, tah v betonu nejvýše tb = +1 MPa.

Výsledky:
Typ namáhání průřezu: „velká excentricita, tlak“;
Neutrálná osa:
\begin{gathered}
x=90{,}17\space\text{deg}\\\\
e=60{,}18\space\text{cm},&f=-0{,}18\space\text{cm}
\end{gathered}Napětí při více tlačeném kraji:
Beton
\begin{gathered}
\sigma_\text{b}=-3{,}71\space\text{MPa}\implies\text{vyhovuje}
\end{gathered}Ocel
\begin{gathered}
\sigma_\text{c}=-45{,}45\space\text{MPa}
\end{gathered}Napětí při méně tlačeném kraji:
Beton
\begin{gathered}
\sigma_\text{b}=0{,}00\space\text{MPa}
\end{gathered}Ocel
\begin{gathered}
\sigma_\text{c}=45{,}11\space\text{MPa}\implies\text{vyhovuje}
\end{gathered}4.5.2 Příčně zatížené pilotové skupiny, příklad 8
Skupiny pilot spojené se základovou patkou, přenášející pouze příčné síly, vykazují shodné posuny svých hlav. Jednotlivé piloty ve skupině se však na celkovém přenosu vodorovné síly HR podílejí různými velikostmi Hi, a to s ohledem na svoji polohu ve skupině, přičemž platí:
\begin{gathered}
\frac{H_\text{i}}{H_\text{R}}=\frac{\alpha_\text{i}}{\sum\alpha_\text{i}}
\end{gathered}(131)
kde je:
Hi … vodorovná síla připadající na i-tou pilotu ve skupině;
HR … celková vodorovná síla na skupinu pilot;
αi = αL · αR zmenšovací koeficienty závisející na vzdálenosti pilot ve skupině, kde:
αL závisí na vzdálenosti pilot aL ve směru působící síly;
αR závisí na vzdálenosti pilot aR kolmo na působící sílu.
Tento poněkud zjednodušený vztah platí pro dvojose symetrickou soustavu pilot, což je ostatně obvyklý případ. Přibližně lze tímto způsobem řešit i jiné případy, jak je naznačeno na obr. 41. V případě zcela nesymetrické, obecně uspořádané soustavy pilot, nezbývá než matematické modelování, jež však naráží na známé a již vzpomenuté problémy se vstupními údaji týkajícími se vlastností základové půdy.
Pro zmenšovací koeficienty αL, αR platí následující vztahy:
\begin{gathered}
\alpha_\text{L}=0{,}25+0{,}125\cdot\frac{a_\text{L}}{d}
\end{gathered}(132)
pro obor
\begin{gathered}
2{,}0\le\frac{\alpha_\text{L}}{d}\le6{,}0
\end{gathered}pro
\begin{gathered}
\frac{\alpha_\text{L}}{d}\le2{,}0\space\text{je}\space\alpha_\text{L}=0{,}5
\end{gathered}pro
\begin{gathered}
\frac{\alpha_\text{L}}{d}\le6{,}0\space\text{je}\space\alpha_\text{L}=1{,}0
\end{gathered}Zmenšovací koeficient αR pro příčný směr s ohledem na působící sílu HR má dva tvary, a to:
\begin{gathered}
\alpha_\text{RA}=0{,}7+0{,}1\cdot\frac{\alpha_\text{R}}{d}
\end{gathered}(133)
\begin{gathered}
\alpha_\text{LZ}=0{,}25+0{,}25\cdot\frac{\alpha_\text{R}}{d}
\end{gathered}(134)
pro obor
\begin{gathered}
2{,}0\le\frac{\alpha_\text{R}}{d}\le3{,}0
\end{gathered}pro
\begin{gathered}
\frac{\alpha_\text{R}}{d}\lt2{,}0
\end{gathered}platí řešení pilotové stěny, tj. jedné řady pilot
pro
\begin{gathered}
\frac{\alpha_\text{R}}{d}\gt3{,}0\space\text{je}\space\alpha_\text{RA}=\alpha_\text{RZ}=1{,}0
\end{gathered}Jde-li o dvojose souměrnou pilotovou skupinu podle obr. 40, můžeme jednotlivé piloty ve skupině rozdělit do 4 typů: I, II, III a IV.
Obr. 40 Typy pilot ve skupině zatížené příčnou silou
\begin{gathered}
\text{pro typ I platí:}&\alpha_\text{iI}=1\cdot\alpha_\text{RA}\\\\
\text{pro typ II platí:}&\alpha_\text{iII}=1\cdot\alpha_\text{RZ}\\\\
\text{pro typ III platí:}&\alpha_\text{iIII}=\alpha_\text{L}\cdot\alpha_\text{RA}\\\\
\text{pro typ IV platí:}&\alpha_\text{iIV}=\alpha_\text{L}\cdot\alpha_\text{RZ}
\end{gathered}(135)
Dochází však také ke změně modulů vodorovné reakce podloží. V případě pilot uložených v jemnozrnné zemině platí pro stanovení pružné délky L´ vzorec (84). V případě pilot s poměrem L / L´ ≥ 4,0 se zmenšuje modul vodorovné reakce podloží podle vztahu:
\begin{gathered}
k_\text{hi}=\alpha_\text{i}^{1{,}33}\cdot k_\text{h}
\end{gathered}(136)
a pro piloty s poměrem L / L´ ≤ 2,0 platí:
\begin{gathered}
k_\text{hi}=\alpha_\text{i}\cdot k_\text{h}
\end{gathered}(137)
přičemž pro mezilehlé případy lze lineárně interpolovat. V případě pilot uložených v hrubozrnné zemině platí pro stanovení pružné délky L´ vzorec (86). V případě pilot s poměrem L / L´ ≥ 4,0 se zmenšuje modul vodorovné reakce podloží podle vztahu:
\begin{gathered}
n_\text{hi}=\alpha_\text{i}^{1{,}67}\cdot n_\text{h}
\end{gathered}(138)
a pro piloty s poměrem L / L´ ≤ 2,0 platí:
\begin{gathered}
n_\text{hi}=\alpha_\text{i}\cdot n_\text{h}
\end{gathered}(139)
rovněž lze pro mezilehlé hodnoty lineárně interpolovat.
Obr. 41 Příklady pilotových skupin vodorovně zatížených
Příklad 8
Rozdělení celkové vodorovné síly HR = 4 000 kN do jednotlivých pilot skupiny celkem 20 ks pilot d = 880 mm délky L = 10,0 m uložených v jemnozrnné zemině s kh = 6,0 MN·m-3 podle obr. 42.
Obr. 42 Zadání k příkladu 8, pilotová skupina vodorovně zatížená
Řešení:
a) podle předchozího textu označíme typy jednotlivých pilot ve skupině: (I až IV);
b) stanovení pružné délky jednotlivé piloty: Eb = 26 500 MPa, I = 0,029 m4
\begin{gathered}
L´=(26\space500\cdot\frac{0{,}029}{(6{,}0\cdot0{,}88)})^{0{,}25}=3{,}47\space\text{m}
\end{gathered}c) další pomocné údaje:
\begin{gathered}
\frac{L}{L´}=\frac{10}{3{,}47}=2{,}88
\end{gathered}\begin{gathered}
\frac{a_\text{L}}{d}=\frac{2{,}50}{0{,}88}=2{,}84\space...&\alpha_\text{L}=0{,}25+0{,}125\cdot\frac{a_\text{L}}{d}=0{,}605
\end{gathered}\begin{gathered}
\frac{a_\text{R}}{d}=\frac{2{,}20}{0{,}88}=2{,}50&...\space\alpha_\text{RA}=0{,}7+0{,}1\cdot\frac{a_\text{R}}{d}=0{,}950\\\\
&...\space\alpha_\text{RA}=0{,}25+0{,}25\cdot\frac{a_\text{R}}{d}=0{,}875
\end{gathered}d) výpočet sil do jednotlivých typů pilot – tab. 32
Tab. 32 Výpočet sil do jednotlivých typů pilot
| Typ piloty | Počet pilot n | αi | n · αi | Hi [kN] | n · Hi [kN] |
| I II III IV |
2 3 6 9 |
1 · 0,95 = 0,95 1 · 0,875 = 0,875 0,605 · 0,95 = 0,575 0,605 · 0,875 = 0,529 |
1,900 2,625 3,450 4,761 |
299 276 180 166 |
598 828 1 080 1 494 |
| Σ | 20 | 12,736 | 4 000 |
e) výsledné rozdělení sil do jednotlivých pilot:
- průměrná vodorovná síla na 1 pilotu Hpr = 4 000 / 20 = 200 kN
- 2 piloty typu I přenášejí 149,5 % Hpr
- 3 piloty typu II přenášejí 138,0 % Hpr
- 6 pilot typu III přenáší 90 % Hpr
- 9 pilot typu II přenáší 83 % Hpr
- rozdíl mezi nejvíce zatíženou pilotou typu I a nejméně zatíženou pilotou typu IV činí ΔH = 133 kN, tedy 180 % – nelze zanedbat
f) stanovení modulů horizontální deformace khi pro jednotlivé typy pilot v tab. 33
(lineární interpolací mezi hodnotami pro L / L´ = 4 a L / L´ = 2,0, a to pro L / L´ = 2,88)
Tab. 33 Stanovení velikosti khi pro jednotlivé typy pilot
| Typ piloty | αi | L / L´ = 4,0 | L / L´ = 2,0 | L / L´ = 2,88 |
| khi = αi1,33 · kh | khi = αi · kh | khi [MN·m-3] | ||
| I II III IV |
0,95 0,875 0,575 0,529 |
5,604 5,024 2,874 2,572 |
5,700 5,250 3,450 3,174 |
5,658 5,150 3,197 2,909 |
4.6 PILOTY RAŽENÉ
Jedná se o piloty typu „displacement“ instalované v základové půdě bez těžení zeminy z vrtu nebo prostoru, který pilota zaujímá, s výjimkou omezeného zvednutí terénu, vibrací, nebo prací souvisejících s odstraněním překážek a pomocných prací potřebných k instalaci ražené piloty, a to ve smyslu ČSN EN 12699: 2016 Provádění speciálních geotechnických prací – Ražené piloty. Materiálem pro ražené piloty mohou být: ocel, litina, beton (železobeton, předpjatý beton), dřevo, malta (injekční směs), nebo kombinace těchto materiálů. Piloty se v základové půdě instalují beraněním, vibrováním, šroubováním, zatlačováním, nebo kombinací těchto technologií. Přesto, že za piloty se obyčejně považují prvky průměru (nebo nejmenšího příčného rozměru) přesahujícího 300 mm, v případě ražených pilot není tato spodní hranice již stanovena. Do ražených pilot tedy podle posledního znění normy ČSN EN 14199: Provádění speciálních geotechnických prací – Mikropiloty z roku 2015 náležejí též tzv. ražené mikropiloty. Z obr. 17 vyplývá, že existují 2 rozsáhlé skupiny těchto pilot: prefabrikované a na místě betonované. Typické druhy ražených pilot jsou schematicky vyznačeny na obr. 43.
Obr. 43 Příklady ražených pilot: a – beraněná, na místě betonovaná pilota, b – šroubová, na místě betonovaná pilota, c – prefabrikovaná železobetonová (čtvercová, kruhová) pilota, d – ocelová pilota (kruhová, H-profilu), e – prefabrikovaná železobetonová kónická (kruhová, nebo čtvercová) pilota, f – na místě betonovaná pilota s rozšířenou patou (předrážená, Franki), g – na místě betonovaná s rozšířením paty, h – na místě betonovaná s ponechanou pažnicí a s rozšířením paty, i – pilota s tělesem rozšiřujícím patu v měkké zemině, j – ocelová svařovaná s rozšířením paty
Ražené, na místě betonované piloty se instalují v základové půdě beraněním, vibrováním a šroubováním, přičemž těmito metodami se nejprve provede otvor vesměs kruhového profilu, ten se zabetonuje (včetně armování) a vlastní razící roura se buď vytáhne (piloty dočasně pažené), nebo se v zemi ponechá, (trvale pažené). Do této skupiny spadá veliké množství různých druhů pilot, z nichž se v našich geotechnických podmínkách nejvíce rozšířily tzv. předrážené, na místě betonované piloty (typu Franki).
4.6.1 Technologické zásady při provádění pilot Franki
Vlastní technologie pochází z Belgie z 30. let minulého století. V současné době se u nás provádí kolem 5–10 % pilotových základů touto technologií, přičemž ovšem značná jejich část připadá na prvky štěrkové, které spadají do oblasti zlepšování vlastností základové půdy. Technologický postup výroby klasické předrážené piloty na místě betonované je znázorněn na obr. 44.
Obr. 44 Technologický postup výroby předrážené piloty Franki: a – stražení razicí roury se zátkou, b – ražení piloty skrz neúnosnou zeminu, c – vyrážení zátky, d – formování dříku vyztužené piloty, e – hotová železobetonová pilota Franki, 1 – razicí roura, 2 – beran, 3 – betonová zátka (korek), 4 – rozšířená pata piloty, 5 – armokoš
Používají se ocelové silnostěnné razicí roury vnějšího průměru 408 mm nebo 512 mm (ve světě i větší průměry), délky rour odpovídají zhruba délce pilot a jsou běžně do 12–14 m, výjimečně lze pro prodloužení pilot používat nástavců, s nimiž jsou ovšem komplikace při vytahování. Vlastní razicí souprava se skládá z podvozku vesměs housenicového, byly však vyvinuty i razicí soupravy na kolových podvozcích, dále z lafety s několikanásobným kladkostrojem pro dosažení co největší tažné síly, volnopádového vrátku a skipu pro transport betonu do razicí roury. Soupravy jsou velmi jednoduché, bez komplikovaných hydraulických okruhů a bez elektroniky, což je výhodné, uvážíme-li, jakým dynamickým účinkům jsou na staveništích vystaveny. Razicí roura se vztyčí do své provozní polohy, přičemž lze razit piloty jak svislé, tak i šikmé, běžně o sklonu do 8 : 1. Do razicí roury se prostřednictvím skipu nasype asi 0,15 m3 suchého betonu (v/c ≤ 0,30). Tento beton, k jehož výrobě se doporučuje používat drcené kamenivo frakce do 22 mm (výjimečně do 32 mm) a množství cementu přesahující 300 kg/m3, se vyrábí většinou na staveništi, neboť jeho transport by byl s ohledem na jeho vlastnosti komplikovaný.
Beton vytvoří v dolní části razicí roury tzv. „zátku“ či „korek“, jež je hutněna volným pádem beranu tvaru ocelového válce o hmotnosti 1,25–5,5 t, který může padat z výšky asi 2–4 m. Při beranění vniká razicí roura do základové půdy, přičemž přenos beranící síly je zčásti zprostředkován třením betonové zátky o vnitřní stěnu roury. Během beranění se sleduje vnik roury do základové půdy ve vztahu k počtu úderů, nebo lépe měří se velikost mechanické energie (dané součinem tíhy beranu a výšky jeho pádu) ve vztahu k vniku razicí roury, přičemž významné je to zejména na poslední 1,0 m, nebo i 2,0 m. Na základě této velikosti (a s ohledem na druh základové půdy) se usuzuje na únosnost předrážené piloty. Po dosažení únosné zeminy, resp. po splnění příslušného energetického kritéria, se razicí roura vyvěsí ve věži soupravy pomocí 2 mohutných lanových závěsů. Přidá se postupně asi 0,5–1,0 m3 betonu a dojde k fázi nazvané vyrážení „zátky“, („korku“). Přitom se formuje typická „cibule“ pod patou piloty, jež má rozhodující vliv na její únosnost, nicméně ve skutečnosti nesmí dojít k úplnému vyražení betonu z roury, neboť by hrozilo přerušení piloty či vnik zeminy nebo vody do razící roury. V další fázi se razicí roura opatří armokošem složeným z podélné výztuže Ø nejméně 14 mm, distančních kruhů (většinou z ploché oceli) a spirály. Následně se přisýpá další beton, který se hutní beranem pracujícím uvnitř armokoše při současném povytahování razicí roury. Hotová pilota se vyznačuje:
- typickou cibulovitou patou, její průměr může dosáhnout až 1,5–1,8násobku průměru dříku piloty;
- drsným pláštěm, přičemž dřík piloty mívá průměr 420–450 mm (resp. 520–550 mm);
- mimořádně kvalitním betonem, neboť ten při nízkém vodním součiniteli je hutněn tak, jako v žádné jiné betonové konstrukci, tudíž jeho pevnost dosahuje běžně 150 % (i více) krychelné pevnosti betonu odpovídající jeho třídě stanovené na základě jeho složení;
- mimořádně odolným betonem s ohledem na jeho nepropustnost a odolnost vůči agresivnímu prostředí;
- mimořádně vysokou mírou únosnosti (definovanou např. únosností v kN cenou piloty) v příznivých geotechnických podmínkách.
Předrážené piloty mají ovšem i své nevýhody:
- při jejich provádění (beranění) vznikají velké dynamické účinky, jež jsou většinou nesrovnatelně větší než např. účinky vibrování, proto jejich provádění je v intravilánech problematické a např. v hustě zastavěných centrech měst nepřichází v úvahu;
- jsou omezeny průměrem i délkou, i když délková omezení nejsou většinou rozhodující;
- jsou vhodné pouze v některých typech zemin, a to především v hrubozrnných zeminách, jež neobsahují velké balvany, popř. tvrdé (horninové) vložky, které nelze prorazit. Při jejich beranění vznikají veliké pórové tlaky zvláště pak v jemnozrnných zeminách, přičemž energetická kritéria mylně ukazují na velký odpor prostředí při beranění, který je všem dán pórovým přetlakem, který časem (s postupující primární konsolidací) vymizí a pilota svoji „únosnost“ ztrácí, což se projevuje jejím následným sedáním. Proto jsou Franki piloty v jemnozrnných zeminách méně vhodné až nevhodné, zrovna tak v horninách poloskalních, kde nemá smysl snažit se ovlivnit jejich únosnost „vetknutím“ do těchto hornin;
- v suchých jemnozrnných zeminách charakteru např. sprašových hlín vzniká nebezpečí „odsátí“ vody z již tak suchého betonu a k jeho následné nedokonalé hydrataci, jež se nakonec projeví „spálením“ betonu a jeho rozpadem. Přitom samozřejmě nelze k ražení používat beton s vyšším vodním součinitelem, neboť potom by vlastní ražení nebylo reálné. Dřík piloty lze ovšem betonovat běžným transportbetonem zpracovatelnosti podobné, jako např. pro vrtané piloty; sníží se tak ovšem charakter drsného pláště typické Franki piloty, jež má značný vliv na její únosnost;
- Franki piloty jsou vhodné především k přenášení osových zatížení (tlakových i tahových); pro příčné síly jsou méně vhodné s ohledem na průměr a pro pilotové stěny se nehodí vůbec (s ohledem na tvar jejich dříku).
Přesto lze konstatovat, že předrážené piloty Franki mají v rámci vhodných geotechnických podmínek stavenišť své pevné místo, a to především tam, kde se jedná o méně zatížené konstrukce, kde jsou cenově velice výhodné.
4.6.2 Ražené piloty typu VUIS
Před cca 30 lety se u nás a zejména pak na Slovensku prováděly ještě tzv. piloty VUIS (podle Výzkumného ústavu inžinierských stavieb Bratislava), z nichž nejrozšířenější byl tzv. typ „B“ podle obr. 45. Tyto piloty o průměru 300–450 mm byly relativně velmi levné a vyznačovaly se snadným prováděním, ovšem pouze ve vhodných zeminách, kterými byly málo až středně ulehlé písky jílovité, či hlinité a písčité jíly či hlíny. Do základové půdy se zavibrovala ocelová roura opatřená betonovou „botkou“ s přírubou. Po dosažení požadované, resp. reálně dosažitelné hloubky, se do této roury vložil armokoš a na její ústí se vzduchotěsně nasadil vzdušník s víkem, kterým se vyhloubený a zapažený otvor vybetonoval. Následně se vzdušník uzavřel a naplnil stlačeným vzduchem, který jednak beton zhutnil, jednak pomohl k vytažení vibrační roury, přičemž samozřejmě botka zůstala v patě této piloty.
Obr. 45 Vibrované na místě betonované piloty typu VUIS; a – vibrování pažnice, b – těžba jemnozrnné zeminy, c – odstranění jemnozrnné zeminy stlačeným vzduchem, d – betonáž piloty, e – vibrování se ztracenou botkou, f, g – armování a betonáž
4.6.3 Osová únosnost ražených pilot stanovená výpočtem, příklad 9
Příklad 9
Stanovte mezní únosnost (1. mezní stav) piloty Franki Ø 520 mm svislé, zatížené tlakem, v následujícím geotechnickém profilu:
0,0–1,5: násyp, navážka (Y)
1,5–5,0: jílovitá hlína písčitá, tuhá (F4)
5,0–6,5: písek, středně ulehlý, zvodnělý (S3)
6,5–10,0: štěrk písčitý, ulehlý, zvodnělý (G2)
Hladina podzemní vody v hloubce 5,50 m.
Řešení:
Navrhujeme ukončit piloty Franki ve vrstvě štěrků (G2), tj. jejich délku L = 7,50 m, vetknutí do štěrků je tmin = 1,0 m.
Pro výpočet 1. mezního stavu se opět použije NP2, tj. A1 „+“ M1 „+“ R2. Únosnost lze stanovit podle rovnice (109), uvedené např. v původní normě ČSN 73 1002 Pilotové základy z roku 1970:
\begin{gathered}
U_\text{v,d}=1{,}8\cdot\gamma_\text{f,3}\cdot A_\text{s}\cdot R_\text{tab}+1{,}6\cdot\gamma_\text{f,4}\cdot u\cdot\sum h_\text{i}\cdot f_\text{s,i}
\end{gathered}(140)
kde je:
γf,3, γf,4 … součinitelé typu zatížení podle tab. 34;
As … plocha paty piloty, která v důsledku vytvoření cibulového rozšíření může vzrůst až o 75 %;
Rtab … napětí na patě piloty v únosné základové půdě podle tab. 35;
u … obvod dříku piloty;
hi … mocnost únosné vrstvy základové půdy podél dříku piloty;
fsi … tření na plášti piloty v únosné základové půdě podle tab. 35.
a) koeficient
\begin{gathered}
\gamma_\text{f,3}=1{,}0\cdot1{,}0=1{,}0;&\gamma_\text{f,4}=1{,}0\cdot1{,}0=1{,}0
\end{gathered}b) rozšíření paty předpokládáme o 50 %:
\begin{gathered}
A_\text{s}=1{,}5\cdot3{,}14\cdot\frac{0{,}52^2}{4}=0{,}318\space\text{m}^2
\end{gathered}c) napětí v patě (štěrky – G, ID = 0,67 … Rtab = 2,0 MPa),
d) plášťové tření:
v navážce – fs1 = 0 … neúnosná zemina
v písčitém jílu (třídy F, IC = 0,5) – fs2 = 0,03 MPa
v písku (třídy S, ID = 0,67) – fs3 = 0,10 MPa
ve štěrku (třídy G, ID = 0,67) – fs4 = 0,15 MPa
e)
\begin{gathered}
U_\text{v,d}=(1{,}8\cdot1{,}0\cdot0{,}318\cdot2{,}0+1{,}6\cdot3{,}14\cdot0{,}52\cdot(3{,}5\cdot0{,}03+1{,}5\cdot0{,}10+1{,}0\cdot0{,}15))=2{,}20\space\text{MN}
\end{gathered}Poznámky:
- při aplikaci 1. mezního stavu podle NP2 je třeba pro zatížení využít koeficientů pro A1 a vypočtenou únosnost dělit koeficientem γR = 1,1 (podle tab. A.6 ČSN EN 1997-1);
- únosnost je třeba posuzovat ve vztahu k návrhovému zatížení; např. skládá-li se svislá síla ze 70 % ze zatížení stálého a 30 % ze zatížení pohyblivého, bude „zatížitelnost“ P této piloty:
\begin{gathered}
\small0{,}7\cdot1{,}35+0{,}3\cdot1{,}5=1{,}395;&\small P=\frac{2\space200}{(1{,}395\cdot1{,}1)}=1\space433{,}7\space\text{kN}
\end{gathered}Tab. 34 Součinitelé pro výpočet únosnosti pilot Franki
| Zatížení | γf,3 | γf,4 |
| tlak tah |
1,0 0 |
1,0 0,7 |
| statické dynamické |
1,0 1,0 |
1,0 0,7 |
Tab. 35 Velikosti napětí na patě Rtab a plášťové tření fs pro piloty Franki v zeminách
| Zeminy hrubozrnné | ID | Rtab [MPa] | fs [MPa] |
| štěrky (G) | > 0,67 0,33–0,67 <0,33 |
5,0 2,0 1,0 |
0,15 0,08 0,04 |
| písky (S) | >0,67 0,33–0,67 < 0,33 |
4,0 1,2 0,6 |
0,10 0,06 0,02 |
| zeminy jemnozrnné | IC | Rtab [MPa] | fs [MPa] |
| (F) | 0,25–0,5 0,5–1,0 > 1,0 |
0,50 1,50 3,00 |
0,03 0,05 0,10 |
4.7 MIKROPILOTY
Mikropiloty jsou prvky hlubinného zakládání staveb, vyznačující se svou mimořádnou štíhlostí a úspornými nároky na prostor při provádění. Byly vyvinuty právě pro účely podchycování a zesilování základů stávajících staveb v mimořádně stísněných podmínkách a postupně se jejich používání rozšířilo i na novostavby v takových podmínkách, kdy s ohledem na pracovní prostor nelze jiné metody využít. Vhodné jsou i tam, kde např. vrtané piloty nelze provádět z titulu špatně vrtatelných hornin v základové půdě. Provádění, dohled nad prováděním, monitoring a kontrola výroby mikropilot se řídí ustanoveními evropské normy ČSN EN 14199: Provádění speciálních geotechnických prací – Mikropiloty (2015), přičemž tato norma platí pro mikropiloty vrtané, vnějšího průměru do 300 mm.
Délky mikropilot ani jejich sklony nejsou omezeny. S ohledem na svou štíhlost jsou mikropiloty určeny především pro přenášení osových sil (tlakových i tahových), ačkoliv nelze vyloučit i jejich zatížení silami příčnými, pro jejichž významnější přenášení však mají malou tuhost a navrhují se tudíž ve skupinách ve formě mikropilotových roštů. Aby byla využita jejich vnitřní únosnost, daná vlastní konstrukcí mikropiloty, jsou upnuty do základové půdy injektáží. Přesto, že ve světě se využívá mnoha typů pilot malých průměrů, které lze z hlediska kritérií výše uvedené normy zařadit mezi mikropiloty, u nás se využívá prakticky pouze mikropilot:
- s trubní ocelovou výztuží, jež absolutně převládají (více než 90 % všech);
- armokošových, kde výztuž tvoří armokoš skládající se z nosných prutů a příčné výztuže, jež obyčejně obklopují menžetovou trubku z PVC nebo PE, sloužící k injektáži jejich kořenů;
- tyčových, i nichž tvoří dřík ocelová tyč Ø 50–70 mm příslušně tvarovaná (např. GEWI) a paralelní s ní je rovněž vedena manžetová trubka.
Vyjmenované mikropiloty lze dále dělit:
a) podle způsobu namáhání:
- tlakové;
- tahové;
- namáhané příčnými silami.
b) podle způsobu uvedení mikropilot do funkce:
- nepředtěžované (volné), kdy deformace potřebné k mobilizaci únosnosti mikropiloty probíhají po jejím spojení s nadzákladovou konstrukcí v plné hodnotě;
- předtížené, kdy se mikropilota před spojením se základem předtíží silou odpovídající jejímu následnému zatížení, přičemž konečné sednutí je dáno jejím pružným stlačením;
- předpjaté, kdy předtížená mikropilota je spojena s konstrukcí v zatíženém stavu; výsledné deformace jsou pak minimální.
Předtížených a předepjatých mikropilot se využívá především pro podchycování, popř. jako podpor při stěhování stávajících konstrukcí.
4.7.1 Zásady technologického postupu výroby mikropilot
Maloprofilové vrtání
Technologie vrtání maloprofilových vrtů je prakticky shodná pro výrobu mikropilot, kotev, pro klasickou i tryskovou injektáž. Maloprofilové (někdy se uvádí též středněprofilové), bezjádrové vrtání, jež se pro tyto prvky většinou používá, se odlišuje významně od vrtání rotačně náběrového, případně drapákového hloubení, jež je naopak typické pro vrtané piloty, popř. pro podzemní stěny. V současné době používané vrtné soupravy jsou plně hydraulické, montované na housenicovém podvozku a mají lafetu, která umožňuje provádět vrty prakticky pod libovolným sklonem s velkou produktivitou, jež je dána jednak dlouhými pasy vrtných trubek, jednak mechanickým zásobníkem vrtných trubek, což práci usnadňuje a zrychluje. Takovéto vrtné soupravy jsou však rozměrné a vysoké, což v mnoha případech nevyhovuje. Proto existují na druhé straně speciální vrtné soupravy, jež jsou vskutku miniaturní, mohou se pohybovat ve sklepích, projedou otvory širokými 0,80 m a mohou provádět vrty ve stísněných prostorách s pracovní výškou kolem 2,20 m.
Maloprofilové vrty pro mikropiloty, kotvy, hřebíky, injektáž a tryskovou injektáž se provádějí většinou jako bezjádrové, neboť požadavek na kontinuální odběr jádra by vedl k významnému snížení rychlosti vrtání a zdražení příslušných prvků. Podle způsobu rozrušování horniny lze maloprofilové bezjádrové vrtání pro výše uvedené účely dělit na:
- vrtání rotační (na plnou čelbu – Rotary, nebo spirálové vrtání);
- vrtání nárazové (příklepné);
- vrtání kombinované (rotačně příklepné, rotačně vibrační).
Podle způsobu výnosu rozrušené horniny ze dna vrtu lze vrtání dělit na:
- vrtání za sucha;
- vrtání výplachové (s přímým proplachem, s nepřímým proplachem).
Podle způsobu zajištění stability stěn vrtů lze maloprofilové vrty dělit na:
- nezapažené;
- pažené pomocí ocelových pažnic (vesměs spojovatelných);
- pažení pomocí suspenze (většinou jílové, nebo jílocementové, která zde navíc plní funkci vyplachování vrtů od vrtné měli, proto ji nazýváme vrtným výplachem).
Technologie vrtání se volí především s ohledem na konkrétní geotechnické podmínky na staveništi, ve vztahu k dimenzím a druhu geotechnické konstrukce a s ohledem na charakter stavebního objektu. V naší praxi přichází tedy v úvahu většinou rotační vrtání spirálem za sucha, rotační vrtání na plnou čelbu s výplachem, rotačně příklepové vrtání.
Rotační vrtání spirálem za sucha je vhodné pro vrty v jemnozrnných zeminách tuhé až pevné konzistence a v měkkých poloskalních horninách, kdy vyvrtaný materiál je vynášen spirálem na povrch. Vrtné soupravy musí disponovat dostatečným kroutícím momentem. Při práci v pevných jílech lze odpor při vrtání a tření snížit přidáním malého množství vody (do 10 l/min) k břitu vrtáku, je však třeba sledovat rychlost postupu vrtání, aby nedošlo k výrazné změně konzistence vrtaných zemin. Průběžné spirálové vrtáky se nastavují v pasech délky většinou 1,5 m. Typické průměry vrtání jsou v tab. 36.
Rotační vrtání na plnou čelbu je základní metodou provádění maloprofilových vrtů v zeminách a měkčích horninách (do třídy R4). Hlavními používanými nástroji jsou listová a valivá dláta. Listová dláta s přibírkovými stupni (2 nebo 3břitová) jsou vhodná v měkkých horninách, jako v jílovcích, břidlicích, měkkých pískovcích apod. Valivá dláta se používají ve všech typech hornin, je však třeba zvolit vhodný druh dláta a správný režim vrtání. V měkkých horninách se používají dláta zubová (s vysokými zuby). V horninách R5–R3 jsou vhodná i roubíková dláta (s vysokými roubíky ze slinutých karbidů). Čím jsou horniny tvrdší, tím je třeba používat nižších zubů, popř. nižších roubíků a volit větší přítlak při nižších otáčkách. V hrubých štěrcích se vrtá dlátem s roubíky při malém přítlaku. Vrty se provádějí výjimečně nepažené se vzduchovým výplachem, většinou však pažené a vyplachované vodním, jílovým a jílocementovým (zcela výjimečně pěnovým) výplachem. Jílový (bentonitový) výplach má prakticky stejné složení jako jílová pažicí suspenze používaná pro pažení vrtaných pilot. Příkon suspenze musí být takový, aby mezikružím mezi vrtnými trubkami a stěnou vrtu dostatečně vyplachovala vrt od vrtné měli. Nejtypičtější je ovšem výplach jílocementový, jež se používá v nestabilních zeminách (písky, štěrky) a horninách. Jeho složení (na 1 m3) je: 400 kg cementu CEM II/A-S, 55 kg aktivovaného bentonitu (Sabenil), 850 l vody. Hotový výplach se vyznačuje následujícími vlastnostmi: objemová hmotnost 1,31 t/m3, viskozita 35–38 s (Marsch), dekantace 1 % /3 hod.
Tab. 36 Doporučené minimální průměry vrtů a typy vrtných nástrojů pro mikropiloty
| Typ nástroje | Průměr nástroje podle průměru trubní výztuže mikropiloty [mm] | ||
| Ø 70/12 | Ø 89/10 | Ø 108/16 | |
| spirálový vrták | 118, 140 | 140, 180 | 180, 220 |
| listové dláto s přibírkovými stupni | 75/120 | 75/140 | 75/160 |
| valivé dláto (neagresivní prostředí) | min.118 | min.130 | min.150 |
| valivé dláto (agresivní prostředí) | min.150 | min.170 | min.190 |
| ponorné kladivo (bez pažní) | min.118 | min.133 | min.156 |
| pažnicová kolona Duplex (neagresivní prostředí) | 121 | 133 | 156 |
| pažnicová kolona Duplex (agresivní prostředí) | 133 | 156 | 191 |
Rotačně příklepné vrtání se používá jednak v tvrdých horninách, kde není třeba pažit, jednak ve štěrcích, balvanitých zeminách a ostatních horninách (kromě měkkých až tuhých soudržných zemin), kde se průběžně paží ocelovými spojovatelnými pažnicemi (systém Duplex). Vrtná drť je vynášena mezikružím na povrch pomocí stlačeného vzduchu vyráběného v kompresorech. Vlastní kladivo je buď horní, nebo ponorné. Vlastní nástroj je tvořen korunkou buď křížovou, nebo roubíkovou, jež na dno vrtu klepe a současně se otáčí. Rychlost vrtání závisí jak na otáčkách, tak na přítlaku. Při vrtání systémem Duplex, při němž se dosahuje nejvyšší produktivity práce, se současně se spodovým (ponorným) kladivem zatahuje do vrtu kolona pažnic ukončená vrtnou korunkou (většinou roubíkovou), přičemž vlastní dláto má konstantní předstih před pažnicí. Obojí se potom nastavuje v jednom dílu, což při větších průměrech nástroje a vrtné soupravě nevybavené mechanickým, či automatickým podavačem trubek činí velké potíže, neboť značná hmotnost této kolony prakticky brání ruční manipulaci. Proto je vrtání systémem Duplex typické pro velké vrtné soupravy, a nikoliv pro stísněné podmínky práce, např. ve sklepích.
Výztuž mikropilot
Výztuž mikropilot je tvořena buď ocelovými silnostěnnými trubkami (trubní mikropiloty), nebo speciálně upraveným armokošem z betonářské výztuže (mikropiloty armokošové), popř. ocelovými tvarovanými tyčemi (např. mikropiloty GEWI).
Trubky se používají většinou z oceli 11 523 a dílensky se upravují na typické délky 1 500 mm, nebo 3 000 mm s příslušnými závity a jinými úpravami. Nejtypičtější průměry výztužných trubek jsou: 70/12 mm, 89/10 mm a 108/16 mm. Samozřejmě lze použít i trubky jiných profilů, naráží to však na obtíže při výběru vhodných obturátorů a na tu skutečnost, že výztuž mikropilot existuje vesměs jako typizovaná výroba polotovarů, které lze objednat a dodat na stavbu. Na obr. 46 jsou typické díly tvořící výztuž trubní mikropiloty a v tab. 37 jsou příslušné rozměry. Perforace kořenové části výztužné trubky je tvořena 2 otvory Ø 8 mm (proti sobě), posunutými o 20 mm, přičemž je třeba dbát na dokonalé odstranění vnitřních otřepů po vrtání, jež by mohly způsobit zničení obturátoru, nebo nemožnost jeho osazení či manipulace s ním. Trubní díly jsou ve výrobně obyčejně kalibrovány pro eliminaci jejich výrobních tolerancí. Vždy dvojice těchto otvorů, tvořících budoucí injektážní etáž, je překryta gumovou manžetou tlustou 4 mm z bezvložkové hadice dlouhé 80 mm. Spodní část kořenové výztužné trubky je opatřena zátkou z pl. 3 mm. Jednotlivé díly výztužných trubek se spojují pomocí spojníků dl. 100–150 mm opatřených průběžným vnitřním plochým závitem. Hlava mikropiloty, přenášející pouze tlak, se opatřuje ocelovou deskou z plechu 20–25 mm – 200/200 až 250/250 mm s přivařeným nátrubkem, hlava mikropiloty přenášející tah se opatřuje deskou se speciálním šroubem přizpůsobeným vnitřnímu závitu konce výztužné trubky. V obou případech mají desky středový otvor Ø 30 mm pro odvzdušnění a provedení vnitřní výplně. Výztužné trubky mikropilot lze zapouštět vcelku (pokud je k tomu dostatek místa a k dispozici je např. jeřáb), nebo po částech a montovat je nad vrtem opatřeným zálivkou. V případě výztužných trubek zapouštěných v celku se připouštějí svařované spoje.
Tab. 37 Rozměry typických dílů výztužných trubek mikropilot
| Typ | Trubka A, B | Spojník C | Zátka D | Hlava na tlak E | ||||||
| trubka Ø | D | l | l1 | d1 | l2 | d1 | l3 | a | t | l3 |
| 70/12 | 70 | 3 000x) | 50,5 | 83 | 100 | 83 | 50 | 200 | 20 | 50 |
| 89/10 | 89 | 3 000x) | 58 | 114 | 150 | 114 | 75 | 250 | 20 | 75 |
| 108/16 | 108 | 3 000x) | 75,5 | 127 | 150 | 127 | 75 | 300 | 40 | 75 |
x) typické délky jsou 3 000 a 1 500 mm
Armokošové mikropiloty mají výztuž sestavenou z podélných prutů Ø 20–28 mm z oceli 10 425 nebo 10 505 ovinutých spirálou z Ø 5–6 mm. Středem armokoše prochází manžetová trubka z PVC Ø 50/3,8 mm, která je v kořenové části opatřena vždy čtveřicí vrtů Ø 6 mm překrytých gumovou manžetou z bezvložkové hadice 60/5 délky 80 mm, a to po 500 mm. Nejnižší manžeta je osazena 250 mm od konce manžetové trubky, jež je zaslepen zátkou. Vyrábějí se i speciální manžetové trubky. Armokoš se vyrábí zpravidla v jednom kuse, a tak se i osazuje, neboť jeho spojování je prakticky nereálné.
Obr. 46 Schéma typických dílů výztužných trubek mikropilot: A – perforovaná trubka, B – plná trubka, C – spojník, D – zátka, E – hlava na tlak s nátrubkem
Tyčové mikropiloty se vyrábějí z tvarované ocelové tyče Ø 50–70 mm (s nalisovaným hrubým závitem, např. GEWI) a manžetová trubka Ø 32/3,6 mm se k tyči připevňuje ovázáním manipulační páskou.
Zálivka a injektáž mikropilot
Bezprostředně po dokončení vrtu a jeho vyčištění se vrt vyplní zálivkou. V případě vrtání na vodní, jílový nebo jílocementový výplach se provede výměna výplachu za zálivku. Ta se může do vrtu čerpat přes vrtné nářadí, jinak se čerpá pomocí PVC trubky Ø 50/3,8 mm zasunuté na dno vrtu. V případě vrtu zapaženého ocelovou pažnicí se provede výměna výplachu za zálivku při dovrtání na konečnou hloubku a výztužná trubka se osazuje do pažnicové kolony, jež se ihned vytahuje za současného doplňování zálivky. Zálivka pro mikropiloty se používá cementová o složení c : v = 2,2 : 1. Na 1 m3 zálivky se dávkuje: 1 285 kg cementu CEM II/A-S a 585 l vody. Míchá se v aktivační míchačce a přepouští se do pomaluběžné míchačky, zpracovat se musí do 3 hodin. Tato cementová zálivka má následující vlastnosti: objemová hmotnost 1,87 t/m3, dekantace 1 %/1 hod, pevnost 20 MPa/7 dní a 27 MPa/28 dní. Do takto vyplněného vrtu cementovou zálivkou se zapouští výztuž mikropiloty, jež je zbavena nečistot a odmaštěna (v případě trubní výztuže), aby nebyla snížena přilnavost k cementovému kameni. Současně se zajistí krytí výztuže mikropilot, jehož minimální velikosti jsou stanoveny podle tab. 38.
Tab. 38 Minimální krytí výztuže mikropilot (mm) podle druhu prostředí a způsobu jejich namáhání
| Druh zálivky | Neagresivní prostředí | Středně agresivní prostředí | ||
| tlak | tah, ohyb | tlak | tah, ohyb | |
| cementová | 20 | 30 | 40 | 50 |
| malta | 35 | 40 | 50 | 60 |
Osová únosnost mikropilot závisí zejména na jejich upnutí do okolní základové půdy v oblasti kořene. Toto upnutí se dosáhne injektáží kořene mikropiloty. Při injektáži nejde tedy o proinjektování okolní zeminy (např. za účelem jejího zpevnění, či snížení propustnosti, jak je tomu u klasické injektáže), účelem je dosáhnout roztržení zálivky a její roztlačení radiálním směrem za pomoci injekční směsi tak, aby byla mikropilota upnuta do okolního prostředí. Injektuje se tedy zpravidla menším množstvím injektážní směsi, přičemž typické jsou opakované reinjektáže. Konečný injektážní tlak je tedy předepsán v projektu a k jeho dosažení je často nutná injektáž ve více fázích (podle druhu základové půdy). Injektuje se zásadně vzestupně (od nejspodnější etáže k vrchní etáži kořene) pomocí dvojitého obturátoru upnutého na příslušnou etáž, a to buď ve výztužné trubce (mikropiloty trubní), nebo v trubce manžetové (mikropiloty armokošové, event. ostatní). Používá se necirkulační obturátor rozpínatelný pneumaticky, popř. hydralicky. Injektuje se cementovou suspenzí o stejném složení, jako je cementová zálivka, tedy c : v = 2,2 : 1. Injektáž se provádí vysokotlakým čerpadlem podle následujícího technologického postupu:
a) 1. fáze injektáže
Při použití cementu CEM II/A-S (tř. 32,5) ji lze zahájit za 12 hodin po osazení výztuže, při použití jiných cementů, popř. malty, je třeba tuto dobu stanovit podle nárůstu pevnosti této hmoty. Dvojitý obturátor se osadí na spodní etáž a injektuje se při sledování tlaku a spotřeby. Dosáhne-li se projektem předepsaného tlaku, (např. 1,5–4,0 MPa, tab. 36), považuje se injektáž příslušné etáže za ukončenou a dvojitý obturátor se uvolní a posune na následující etáž a celý postup se opakuje. Pokud se předepsaného tlaku nedosáhne, injektuje se zpravidla 15 l směsi (v horninách skalních, poloskalních a hrubozrnných), resp. 5–10 l směsi (v zeminách jemnozrnných). V navážkách a násypech (pokud je v nich výjimečně umístěn kořen mikropiloty) i více (např. 50 l). Tlak při injektáži zpravidla zpočátku roste, potom náhle klesne, což obyčejně značí protržení zálivky a při další injektáži by měl stoupat. Po protržení zálivky je třeba tlak ihned snížit a injektovat rychlostí asi 4–7 l/min při nejpomalejším chodu čerpadla. Po ukončení 1. fáze injektáže je třeba výztužnou (manžetovou) trubku dokonale propláchnout vodou, aby byla neustále průchodná. K tomu se používá PE hadička Ø 20 mm ukončená speciální hlavou s tryskami.
b) 2. a další fáze injektáže (reinjektáž)
Při použití cementu CEM II/A-S (tř. 32,5) může následovat nejdříve za 6–10 hodin po předcházející fázi injektáže. Kritérium je stále dosažení projektem předepsaného tlaku (potom se jedná o konečnou fázi), nebo spotřeby směsi (následuje další reinjektáž). Pokud se nepodaří protrhnout zálivku ani při tlaku 8–10 MPa, považuje se injektáž této etáže za ukončenou. Pokud ani při 3. fázi injektáže (2. reinjektáži) není dosaženo projektem předepsaného tlaku, je třeba poradit se s projektantem. Zainjektovanou mikropilotu je třeba vyplnit cementovou zálivkou stejného složení (c : v = 2,2 : 1). To se provádí pomocí PE hadičky Ø 20 mm zapuštěné na dno výztužné (manžetové) trubky. Zálivku je třeba asi po 2 dnech doplnit, z titulu odstoje vody.
4.7.2 Únosnost mikropilot, příklad 10
Mikropiloty se s ohledem na své rozměry a tuhost používají především pro přenos osových sil (tlakových i tahových). Schopnost mikropilot přenášet i síly příčné a ohybové momenty závisí především na druhu a rozměrech jejich výztuže, v menší míře pak na okolní základové půdě. Osovou únosnost mikropilot lze stanovit zkouškou, nebo statickým výpočtem. Příčnou únosnost mikropilot lze stanovit statickým výpočtem únosnosti průřezu mikropilot podle zásad výpočtu ocelových, betonových, popř. spřažených konstrukcí.
Statické zatěžovací zkoušky
Statické zatěžovací zkoušky mikropilot se provádějí vesměs se stupňovitým zatížením, obdobné jako v případě pilot. Uspořádání této zkoušky je však zpravidla jednodušší a vlastní zkouška je levnější, což je dáno relativně snadno dosažitelnou silou potřebnou při této zkoušce. Typické uspořádání statické zatěžovací zkoušky je na obr. 47. Využívá se celkem tří mikropilot umístěných v řadě ve stejných osových vzdálenostech, jež jsou nejméně 20 d, kde d je průměr mikropiloty (minimální osová vzdálenost je však 1,50 m). Střední mikropilota je zkušební (jak pro tlak, tak i pro tah), krajní piloty jsou reakční. Zkušební most je ocelový z válcovaných, popř. svařovaných nosníků dimenzovaných tak, aby (jako prostý nosník) přenesl příslušná zatížení při zkoušce a jeho deformace byla v přijatelných mezích.
Obr. 47 Uspořádání statické zatěžovací zkoušky mikropiloty: A – tlaková zkouška, B – tahová zkouška, 1– zkušební mikropilota, 2 – reakční mikropiloty, 3 – zatěžovací most, 4 – hydraulický lis, 5 – měření deformací hlavy mikropiloty, 6 – táhla spojující hlavu mikropiloty s lisem
Při zatěžovací zkoušce se měří deformace hlavy mikropiloty nejméně dvěma nezávislými snímači s přesností nejméně 0,1 mm. Vlastní zkouška má obdobný průběh jako statická zatěžovací zkouška piloty, za kritérium ustálené deformace se považuje její přírůstek menší než 0,1 mm/20 minut (ČSN EN 14 199), lze však stanovit kritérium přísnější. Statické zatěžovací zkoušky (typové) lze provádět na mikropilotách nesystémových, a to v případě:
- použití nové a nevyzkoušené technologie provádění mikropilot;
- složitých geotechnických podmínek na staveništi, kdy není dostatek stávajících zkušeností;
- mimořádných požadavků na únosnost mikropilot;
- když je zřejmé, že náklady na zkoušku se zhodnotí při návrhu systémových mikropilot.
V případě mikropilot systémových lze statické zatěžovací zkoušky provádět pouze se souhlasem projektanta (zkoušky ověřovací a kontrolní), a to silami, které nepřekročí charakteristickou velikost jejich pracovního zatížení. Speciálním případem jsou mikropiloty předtěžované, popř. předpínané. Norma EN 14 199 doporučuje provádět kontrolní statické zatěžovací zkoušky systémových mikropilot následovně:
- v případě tlakových zatížení – nejméně 1 zkouška na každých 100 ks mikropilot;
- v případě tahových zatížení – nejméně 1 zkouška na každých 25 ks mikropilot.
Pro vyhodnocování výsledků statické zatěžovací zkoušky mikropiloty neexistují jednotná a předem daná kritéria, postupuje se ve smyslu Eurocódu 7 tak, že pro vnější únosnost mikropiloty (její interakci se základovou půdou) je zpravidla rozhodující 2. mezní stav (použitelnosti), kdy důležitá je deformace hlavy mikropiloty a pro vnitřní únosnost složeného průřezu (popř. pouze ocelového průřezu – v případě mikropilot trubních) je rozhodující 1. mezní stav z hlediska dimenzování tohoto průřezu.
Pokud je třeba omezit deformace mikropilot v konstrukci (např. při podchycování), navrhují se mikropiloty předtížené. Je-li nutné vyloučit, popř. omezit i pružnou deformaci, navrhují se mikropiloty předepnuté. Při předtěžování se mikropilota postupně zatíží stupni: 0,5P; 0,8P; 1,0P (kde P je její charakteristické pracovní zatížení) a nakonec se zcela odlehčí. Kritérium ustálení deformace je 0,1 mm/20 minut. V jílech bývá ovšem doba zatěžování při stupni 1,0 P i několik hodin. Takto předtížená mikropilota se bude v konstrukci deformovat pouze pružně. Předepjatá mikropilota se zatěžuje obdobně s tím rozdílem, že se do konstrukce zabuduje v zatíženém stavu, což lze realizovat např. při podchytávání stávajících základů pomocí podvleků.
Statický výpočet
a) vnější návrhová únosnost osamělé mikropiloty Umv,d:
Jedná se v podstatě o vnější únosnost její kořenové části, jež je dána:
\begin{gathered}
U_\text{mv,d}=U_\text{ms,d}+U_\text{mp,d}
\end{gathered}(141)
kde je:
Ums,d … únosnost na plášti kořene mikropiloty;
Ump,d … únosnost na patě tlačené mikropiloty v případě jejího vetknutí (popř. i opření do hornin R1 až R3 (v ostatních případech tlakových mikropilot se Ump,d zanedbává).
\begin{gathered}
U_\text{mp}=\pi\cdot\frac{d^2}{4}\cdot R_\text{d}
\end{gathered}(142)
\begin{gathered}
U_\text{ms,d}=\pi\cdot d\cdot\sum L_\text{ti}\cdot\tau_\text{i}\cdot m_\text{z}
\end{gathered}(143)
kde je:
d … průměr mikropiloty (průměr vrtu opatřeného výztuží a zálivkou);
Rd … únosnost na patě pro skalní horniny R1–R3 stanovená např. podle tab. 39;
Lti … délka kořenové části mikropiloty v příslušné únosné i-té únosné vrstvě;
ti … návrhová velikost plášťového tření v příslušné hornině podle tab. 40;
mz … koeficient, jež závisí na druhu zatížení (pro tlak mz = 1,0, pro tah mz = 0,8).
Tab. 39 Návrhové velikosti napětí Rd na patě mikropilot v horninách R1–R3
| Hornina – třída | Typické vlastnosti | Rd [MPa] |
| R1 | σCx) > 150 MPa | 8,0–10,0 |
| R2 | σCx) = 50 – 150 MPa | 4,0–6,0 |
| R3 | σCx) = 15 – 50 Mpa | 1,5–3,0 |
| x) σC je pevnost horniny v prostém tlaku | ||
Tab. 40 Návrhové velikosti plášťového tření mikropilot
| Druh základové půdy | Typické vlastnosti | Počet injektáží | Konečný injektážní tlak [MPa] | Plášťové tření τi [MPa] |
| skalní horniny R1–R4 | σf > 50 MPa | 0 | – | 0,6–1,0 |
| poloskalní horniny R5, R6 | σf < 50 MPa | 0–1 | 0,5–3,0 | 0,2–0,6 |
| štěrky písčité | 35° < φ < 45°, c = 0 | 1–2 | 1,0–2,0 | 0,15–0,20 |
| štěrky jílovité | 25° < φ < 35°, c = 10 | 1–2 | 2,0–4,0 | 0,15 |
| písky | 25° < φ < 35°, c = 0 | 2–3 | 1,5–4,0 | 0,1–0,15 |
| soudržné zeminy tvrdé | 10° < φu < 30° cu > 0,1 MPa |
1–3 | 1,5–3,0 | 0,08–0,14 |
| soudržné zeminy pevné | φu < 100 0,05 < cu < 0,15 MPa |
2–3 | 1,0–2,5 | 0,06–0,08 |
| soudržné zeminy tuhé | φu = 0 0,025 < cu < 0,05 MPa |
3–(4) | 0,5–2,0 | 0,04–0,06 |
b) vnější únosnost skupiny mikropilot:
Podobně jako u pilot je třeba stanovit velikosti sil působících do jednotlivých mikropilot ve skupině od vnějšího zatížení působícího na spojovací konstrukci v hlavách mikropilot a dále stanovit vliv tzv. skupinového účinku. Ten je v zásadě méně významný ve srovnání s pilotami, a to především s ohledem na rozměry mikropilot a na tu skutečnost, že jejich osová vzdálenost ve skupinovém základu je vesměs větší, (a / d > 5). Síly působící do jednotlivých pilot se s ohledem na tuhost spojující konstrukce stanoví obyčejně podle zásad uvedených v kap. 4.5, přičemž jejich spojení s nadzákladovou konstrukcí lze považovat vesměs za kloubové. Pokud se jedná o rozsáhlý mikropilotový základ (s počtem mikropilot 10 a větším), není uvedený postup již vhodný a je třeba přistoupit k matematickému modelování, jež je obtížné, neboť interakce mikropilot se základovou půdou není jednoduchá.
c) vnitřní osová únosnost mikropilot:
Uvažujeme-li spřažený průřez mikropiloty, je jeho únosnost v tlaku za předpokladu plné plastifikace:
\begin{gathered}
N_\text{pl,Rd}=A_\text{a}\cdot\frac{f_\text{y}}{\gamma_\text{a}}+0{,}85\cdot A_\text{c}\cdot\frac{f_\text{ck}}{\gamma_\text{c}}
\end{gathered}(144)
kde je:
Aa … plocha tlačené oceli;
Ac … plocha tlačeného cementového kamene;
fy … návrhové napětí v oceli;
fck … návrhové napětí v cementovém kameni;
γa … dílčí součinitel pro ocel;
γc … dílčí součinitel pro cementový kámen.
V případě mikropilot jakožto velmi štíhlých prvků přichází obecně v úvahu vzpěr. Kritické osové zatížení prutu uloženého v elastickém prostředí charakterizovaném modulem deformace Ez (pružnosti):
\begin{gathered}
N_\text{cr}=2\cdot((EJ)_\text{e}\cdot E_\text{z})^\frac{1}{2}
\end{gathered}(145)
\begin{gathered}
(EJ)_\text{e}=E_\text{a}\cdot J_\text{a}+0{,}85\cdot\frac{E_\text{cm}}{\gamma_\text{c}}\cdot J_\text{c}
\end{gathered}(146)
kde je:
Ea … modul pružnosti oceli;
Ecm … modul pružnosti cementového kamene;
Ja … moment setrvačnosti ocelového průřezu;
Jc … moment setrvačnosti cementového kamene.
V případě mikropilot namáhaných tahem počítáme pouze s únosností ocelové výztuže.
d) vnitřní únosnost ohýbaných mikropilot s výztužnou trubkou
Statické schéma pro výpočet je na obr. 48. Nejprve je třeba stanovit polohu neutrálné osy z rovnice:
\begin{gathered}
\frac{f_\text{y}}{\gamma_\text{c}}\cdot A_\text{a}\cdot\frac{t}{(r_\text{a}+t)}=A_\text{m}\cdot\frac{f_\text{ck}}{\gamma_\text{c}}
\end{gathered}(147)
kde je:
t … vzdálenost neutrálné osy od osy průřezu;
ra … poloměr výztužné trubky;
Am … tlačená plocha cementového kamene.
Obr. 48 Statické schéma mikropiloty s výztužnou trubkou pro výpočet ohybové únosnosti
Moment únosnosti je potom dán vztahem:
\begin{gathered}
M_\text{pl,Rd}=\frac{f_\text{y}}{\gamma_\text{c}}\cdot\frac{(J_\text{a}+A_\text{a}\cdot t^2)}{(r_\text{a}+t)}+A_\text{n}\cdot\frac{f_\text{ck}}{\gamma_\text{c}}\cdot t_0
\end{gathered}(148)
t0 … vzdálenost těžiště plochy Am od neutrálné osy.
Příklad 10
Stanovte únosnost mikropiloty s trubní výztuží Ø 108/16 mm v geotechnickém profilu:
0,0–3,0: násyp nehomogenní – navážka (Y), Edef = 4,0 MPa
3,0–6,5: jíl písčitý, tuhý (F3, IC = 0,5), Edef = 6,0 MPa
6,5–7,5: zvětralá až zvětralá břidlice (R4), Edef = 40 MPa
7,5–10,0: břidlice slabě zvětralá (R3), Edef = 500 MPa
Řešení:
a) zvolíme průměr vrtu dv, délku svislé mikropiloty L a délku injektovaného kořene Lk:
\begin{gathered}
d_\text{v}=180\space\text{mm},&L=8{,}50\space\text{m},&L_\text{k}=5{,}0\space\text{m}
\end{gathered}b) únosnost v tlaku:
- vzpěr:
\begin{gathered}
(EJ)_\text{e}=2{,}1\cdot10^5\cdot5{,}04\cdot10^{-6}+0{,}85\cdot2{,}5\cdot\frac{10^4}{1{,}35}\cdot4{,}48\cdot10^{-5}=1{,}65\space\text{MN}\cdot\text{m}^2\\\\
E_\text{z,mean}=\frac{3{,}0\cdot4{,}0+3{,}5\cdot6{,}0+1{,}0\cdot40+1\cdot500)}{8{,}5}=67{,}41\space\text{MPa}\\\\
N_\text{cr}=2\cdot(1{,}65\cdot67{,}41)^\frac{1}{2}=21{,}09\space\text{MN}
\end{gathered}– výrazně překračuje vnitřní únosnost MP, vzpěrná pevnost tedy nemá význam.
- vnější únosnost:
\begin{gathered}
U_\text{mv,d}=3{,}14\cdot\frac{0{,}18^2}{4}\cdot2\space000+3{,}14\cdot0{,}18\cdot(3\cdot50+1\cdot600+1\space800)=926{,}93\space\text{kN}
\end{gathered}- vnitřní únosnost
\begin{gathered}
N_\text{pl,Rd}=4{,}62\cdot10^{-3}\cdot5\cdot\frac{10^2}{1{,}15}+0{,}85\cdot1{,}62\cdot10^{-2}\cdot\frac{25}{1{,}35}=2{,}26\space\text{MN}\gt0{,}93\space\text{MN}
\end{gathered}rozhoduje tedy vnější únosnost.
c) únosnost v tahu
\begin{gathered}
U_\text{mvt,d}=0{,}8\cdot3{,}14\cdot0{,}18\cdot(3\cdot50+1\cdot600+1\cdot800)=700{,}85\space\text{kN}
\end{gathered}Poznámky:
- únosnost MP na plášti je závislá od dosažení příslušného konečného injekčního tlaku podle tab. 36;
- při aplikaci 1. mezního stavu podle NP2 je třeba pro zatížení využít koeficientů pro A1 a výpočtenou únosnost dělit příslušnými koeficienty γR pro R2 (podle tab. 15);
- únosnost je třeba posuzovat ve vztahu k návrhovému zatížení; např. skládá-li se svislá síla z 50% ze zatížení stálého a 50% ze zatížení pohyblivého, bude „zatížitelnost“ P této MP v tlaku:
\begin{gathered}
\small 0{,}5\cdot1{,}35+0{,}5\cdot1{,}5=1{,}425;&\small P_\text{tl}=\frac{926{,}93}{(1{,}425\cdot1{,}1)}=591{,}34\space\text{kN}&\small\text{a v tahu}&\small P_\text{tah}=\frac{700{,}85}{(1{,}425\cdot1{,}15)}=427{,}67\space\text{kN}
\end{gathered}4.7.3 Použití mikropilot
Mikropiloty jsou relativně drahé a pracné prvky speciálního zakládání staveb, jejichž využití je vázáno na takové konstrukce a případy, kdy jiné – levnější a méně technologicky náročné metody nejsou použitelné, a to jak z důvodů prostorových (naprostá většina případů), tak z důvodů geotechnických, kdy např. velkoprůměrové vrtání v daném geol. profilu není reálné. Hlavní oblast použití je tedy vázána na rekonstrukce a sanace staveb a na podchycování stávajících objektů, pro zakládání novostaveb jsou používány zřídka. S ohledem na cenu MP se vždy snažíme o takový návrh osově zatížených mikropilot, kdy vnější únosnost se blíží únosnosti vnitřní.
V případě podchycování za účelem zvýšení únosnosti stávajících základů, zejména plošných, je hlavním problémem nikoliv únosnost jednotlivých mikropilot, ale zejména možnost přenosu zatížení ze stávajících základů (nosných zdí, sloupů) do vlastních mikropilot. Na obr. 49 jsou příklady chybného a správného návrhu podchycení stávajících základů pomocí mikropilot. Příklad ad a) ukazuje zcela chybný návrh, který je však relativně častý u nezkušených projektantů. Během provrtávání stávajících plošných základů dochází nejspíše k jejich porušení, a to zejména, jedná-li se o základy z prokládaného kamene nebo prostého betonu. V průběhu dalšího vrtání dochází k proplachování vrtu a usazování měkké zeminy na stěně vrtu procházejícího stávajícím základem, a to bez praktické možnosti tento průchod jakkoliv vyčistit. V průběhu dalšího technologického postupu se vyrobí únosná mikropilota schopná přenášek řádově stovky kN podle požadavku na podchycení. Tyto síly by ovšem měly být přeneseny „třením“ v rozbitém a znečištěném průchodu skrz stávající základ, což je naprosto nereálné. Toto řešení je přijatelné v případě podchytávání kamenných mostních pilířů, kdy mikropiloty procházejí pilířem v délce několika metrů. V tomto případě může být přenos síly z mikropilot do dříku pilíře reálný, což je nutné vždy pečlivě zvážit.
Správné řešení je na obr. 49b, kdy se využije staticky naprosto jasně působící konstrukce podvleků (ocelových, nebo betonových) skrz stávající zdi a vesměs svislých mikropilot. Jejich hlavy lze opatřit hydraulickými lisy, a tak řídit event. deformace stávajících zdí.
Obr. 49 Podchycení stávající nosné zdi pomocí mikropilot: a) nesprávný návrh, b) správné řešení
Mikropiloty ve formě mikropilotových bárek se s úspěchem využívá pro podchycování nosných sloupů, např. za účelem podkopání stávajícího objektu pro vytvoření hlubšího suterénu (obr. 50). V průběhu výkopu se jednotlivé mikropiloty zavětrují za účelem vytvoření relativně tuhé konstrukce a nové sloupy se obyčejně betonují uvnitř této bárky. Mikropiloty se současně využijí pro hlubinné založení těchto nastavených sloupů.
Obr. 50 Mikropilotová bárka
Speciální případ použití mikropilot je při sanacích vrtaných pilot, kdy se jimi překlene nekvalitní, popř. přerušených dřík velkoprůměrové vrtané piloty.
4.8 KOTVY
Zemní a horninové kotvy jsou prvky speciálního zakládání staveb, kterými se přenášejí tahové síly z konstrukce do základové půdy. Skládají se z kotevní hlavy, volné délky a kořenové (kotevní) délky, jež je do základové půdy upnuta prostřednictvím injektáže. Alternativní systémy, jako jsou např. tahové piloty a mikropiloty, zavrtávané kotvy bez injektáže, rozpínací svorníky a táhla se za výše definované kotvy nepovažují. U zemních a horninových kotev musí tedy být splněny následující podmínky:
- kořenová část kotvy je v základové půdě upnuta pomocí injektážní směsi;
- tahová síla je do kotvy vnesena předpětím, tzn., že kotva musí mít volnou délku, jež svým protažením umožní vnesení kotevní síly (podle Hookova zákona).
Pro navrhování kotev platí obecná ustanovení ČSN EN 1997-1, pro provádění a monitorování kotev platí ČSN EN 1537 Provádění speciálních geotechnických prací – Horninové kotvy a pro zkoušení kotev norma ČSN EN ISO 22477-5: Zkoušení geotechnických konstrukcí.
Kotvy se dělí podle následujících kritérií:
1) podle typu kotevního táhla:
- kotvy tyčové;
- kotvy pramencové;
2) podle doby své funkce:
- kotvy dočasné (doba jejich funkce je do 2 let);
- kotvy trvalé (doba jejich funkce je více než 2 roky);
3) podle způsobu namáhání kořene:
- kotvy s kořenem taženým;
- kotvy s kořenem tlačeným.
Na obr. 51 je schéma injektované horninové kotvy s pojmenováním svých hlavních komponentů. Tak jako i jiné prvky hlubinného zakládání staveb, procházejí kotvy neustálým vývojem, což v podstatě znemožňuje podat o nich ucelenou informaci. Z mnoha různých typů kotev se v současné době v naší republice provádějí v podstatě pouze kotvy tyčové, a to z vysokopevnostních tyčí Dywidag a dále kotvy pramencové (nesprávně nazývané též jako lanové).
Technologický postup výroby kotev sestává z následujících fází:
a) provádění maloprofilových vrtů;
b) vyplnění vrtů zálivkou;
c) výroba, doprava, manipulace a osazení kotvy;
d) injektáž kořene kotvy a popř. reinjektáž, even. předinjektáž okolní základové půdy;
e) napínání kotev, zkoušení kotev, dohled a přezkušování.
Fáze a) a b) se v podstatě neliší od provádění mikropilot snad pouze s tím rozdílem, že vrty pro kotvy jsou většinou šikmé a jejich sklon se udává ve stupních od vodorovné. Průměr vrtu navrhne projektant v závislosti na únosnosti a typu kotvy a na geotechnických podmínkách na staveništi. Příklady doporučených průměrů vrtů pro kotvy jsou uvedeny v tab. 41.
Při provádění vrtů pro kotvy je třeba zaručit následující výrobní tolerance, pokud projekt nestanoví přísnější:
- poloha závrtného bodu na konstrukci s přesností 75 mm;
- odchylka osy vrtu nejvýše 2°.
Obr. 51 Schéma injektované horninové kotvy: 1 – bod ukotvení táhla v napínacím zařízení, 2 – bod ukotvení táhla v hlavě kotvy, 3 – matice táhla, popř. hlava s kuželkami, 4 – podkladní deska, 5 – podbetonování, 6 – kotvená konstrukce, 7 – průchodka, 8 – těsnicí O-kroužky, 9 – základová půda, 10 – vrt, 11 – povlaková trubka, 12 – táhlo, 13 – kotevní délka injektované části kotvy, 14 – volná délka s odpovídající výplní; le = vnější délka kotevního táhla, měřená od ukotvení táhla v hlavě k místu uchycení táhla v napínacím zařízení, ltf = volná délka ocelového táhla, ltd = kotevní délka táhla, lfree = volná délka kotvy, lfixed = délka kořene kotvy
Tab. 41 Příklady průměrů vrtů d [mm] pro kotvy podle typu kotev a základové půdy
| Druh kotvy | Zeminy jemnozrnné | Zeminy hrubozrnné | Horniny skalní a poloskalní | |||
| trvanlivost kotvy | dočasné | trvalé | dočasné | trvalé | dočasné | trvalé |
| tyčové (CPS, Dywidag) | 133 | 156 | 133 | 156 | 118 | 133 |
| pramencové do 4xLp | 156 | 175 | 133 | 156 | 133 | 156 |
| pramencové do 8xLp | 175 | 194 | 156 | 175 | 156 | 175 |
Při provádění je třeba zabránit zavalení vrtů jak během vrtání, tak i během ukládání zálivky a kotevního táhla, proto se vrty velice často paží. V případě extrémně dlouhých vrtů bývá problém s jejich vyplachováním, proto je přípustné vrty prohloubit o jistou délku, v níž se usadí vrtná měl. V jednotlivých druzích základové půdy je třeba volit vhodnou technologii vrtání. To je významné zvláště v soudržných zeminách, aby nedošlo k výrazné změně jejich konzistence na stěnách vrtu a ve zvodnělých zeminách, aby nedošlo k narušení hydrogeologických poměrů. V případě vrtání pod hladinou podzemní vody je třeba přijmout zvláštní opatření, jako je např.:
- těžký výplach (zatěžkaný popílkem, popř. barytem);
- použití speciálních vrtných zařízení s těsněným vrtným soutyčím, popř. preventrů;
- snížení hladiny podzemní vody při uvážení příslušných rizik vyplývajících např. z dodatečného sedání;
- předinjektáž základové půdy za účelem jejího utěsnění, popř. i zpevnění.
Pro zálivku kotev se – stejně jako u mikropilot – využívá vesměs cementové suspenze ve složení c : v = 2,2 : 1 až 2,3 : 1 (podle druhu cementu a jemnosti jeho mletí).
Kotvy se na stavbu dovážejí většinou jako polotovary v různém stupni dokončení (podle druhu), na stavbě se kompletují a ukládají do vrtů. Kotvy jsou zvláště náchylné na poškození v průběhu nakládání, transportu a skladování, kdy je nebezpečí, že dojde k poškození protikorozní ochrany i kořenové části kotvy. Mimořádně náročné je ukládání dlouhých kotev do vrtů, kdy je zapotřebí množství pracovníků pro manipulaci s kotvou, popř. speciálních přípravků. Před osazením kotevního táhla musí být vrt zkontrolován, zda v něm nejsou překážky, je-li dostatečně dlouhý a dokonale vyplněný zálivkou. Kotvu je třeba osadit v nejkratší možné době po dokončení zálivky, aby se zamezilo její usazení.
Pro montáž dočasných pramencových kotev na staveništi se obyčejně nejprve připraví manžetová trubka, jež je tvořena PVC trubkou Ø 32/3,6 mm, v kořenové části s injekčními otvory Ø 6 mm překrytými gumovými manžetami. Vzdálenost manžet (etáží) je 500 mm, první etáž je zpravidla umístěna 250 mm nad koncem kotvy. Na manžetovou trubku se navlékají rozpěrky (centrátory), jež mají na obvodu vybrání pro osazení jednotlivých pramenců. Centrátory mají zajistit polohu táhla kotvy ve vrtu, tedy zajistit krytí táhla cementovou suspenzí, jež musí být minimálně 10 mm (měřeno od vnějšku ochranného obalu). Jejich vzdálenosti závisí na tuhosti a hmotnosti kotvy a jsou mezi 1–3 m. Kotvy se opatřují dále deviačními kroužky, jež zajišťují správnou polohu pramenců v kotevní objímce, popř. přechod z volné délky do kořenové části. Kotva prochází zpravidla kotvenou konstrukcí prostřednictvím průchodky, což je většinou ocelová trubka trvale do konstrukce zabudovaná. Její průměr je volen s ohledem na tu skutečnost, že vrtání probíhá většinou skrz zabudovanou průchodku; (typická průchodka je z trubky Ø 168/3,6 mm). Průchodka bývá ukončena ocelovou roznášecí deskou z plechu 30 mm, rozměrů 290/290 mm, jež je součástí hlavy kotvy. Roznášecí deska bývá zabudována spolu s průchodkou. Vlastní kotevní hlava je ocelový výrobek přizpůsobený především v případě pramencových kotev počtu pramenců. Ta se montuje až při napínání kotev.
V případě tyčových kotev je kotevní hlava tvořena speciální deskou s půlkulovým vybráním pro usazení speciální matice. Hlavy trvalých kotev (jak pramencových, tak i tyčových) jsou opatřeny víkem, ochranou ve tvaru hrnce, jež je na kotevní hlavu namontován a jeho vnitřní prostor je zalit speciální antikorozní hmotou (např. epoxydehtem).
Kotvy jsou mimořádně štíhlé ocelové prvky, u nichž musí být zajištěna protikorozní ochrana, přičemž neexistuje jednoznačný způsob pro zajištění této ochrany v daném geotechnickém prostředí. V zásadě se rozlišují dva stupně této ochrany, jež odpovídají životnosti kotev. V případě dočasných kotev musí tato ochrana spolehlivě působit po dobu nejméně dvou let. V tab. 42 jsou uvedeny příklady protikorozní ochrany pro dočasné kotvy.
Provádění trvalých kotev je podmíněno:
- certifikátem výrobku – trvalá kotva příslušného provedení, vydaném příslušným zkušebním ústavem;
- certifikátem opravňujícím příslušnou firmu k realizaci těchto kotev.
Únosnost kotev je zajištěna upevněním jejich kořenové délky v základové půdě injektáží, jejímž účelem dále je:
- upnutí kořene kotvy v základové půdě tak, že je kotva schopna přenést vnášenou tahovou sílu do okolní základové půdy;
- ochrana táhla kotvy proti korozi;
- zpevnění základové půdy bezprostředně přiléhající ke kořenové části kotvy, aby se zvýšila její únosnost;
- utěsnění základové půdy bezprostředně obklopující kořenovou část kotvy, aby se omezil únik injekční směsi.
Tab. 42 Příklady protikorozních ochranných systémů pro dočasné kotvy
| 1. Kotevní délka táhla |
| Všechna instalovaná táhla by měla být opatřena nejméně 10 mm krytím cementovou injekční směsí ke stěně vrtu. Pokud je známo, že je horninové prostředí agresivní, může být ochrana táhla příslušně zvětšena například použitím jednoduché ohebné povlakové trubky na táhlo. |
| 2. Volná délka táhla |
| Ochranný systém by měl mít nízké tření, a umožnit tak pohyb táhla uvnitř vrtu. Toho může být dosaženo použitím jednoho z následujících způsobů: a) plastový povlak každého jednotlivého táhla, jehož konce jsou utěsněny proti vniknutí vody; b) plastový povlak každého jednotlivého táhla, který je zcela vyplněn protikorozní výplní; c) plastová nebo ocelová povlaková trubka společná pro všechna táhla, jejíž konce jsou utěsněny proti vniknutí vody; d) plastová nebo ocelová povlaková trubka společná pro všechna táhla zcela vyplněná protikorozní výplní; b) nebo d) jsou vhodné pro použití v agresivním prostředí. |
| 3. Přechod mezi kotevní hlavou a volnou délkou (vnitřní prostor kotevní hlavy) |
| Povlaková trubka volné délky táhla může být utěsněna k podkladní/kotevní desce, nebo kovová či plastová trubka může být k podkladní desce přivařena nebo s ní spojena. Měla by přesahovat povlakovou trubku volné délky a v případě agresivního prostředí by měla být vyplněna protikorozní výplní, cementem nebo pryskyřicí, která je použita ve spodním konci trubky. |
| 4. Kotevní hlava |
Pokud je kotevní hlava přístupná prohlídkám a je možné její ochranu obnovit, lze použít následující ochranu:
Pokud není hlava kotvy přístupná, mělo by na ni být upevněno kovové nebo plastové víko, které by mělo být při prodloužené životnosti kotvy vyplněno protikorozní výplní. Pokud je známo, že je prostředí agresivní, mělo by být kovové nebo plastové víko vyplněno protikorozní výplní. |
V případě trvalých kotev se realizuje tzv. sekundární ochrana, přičemž principem je to, že nejméně jedna souvislá vrstva z materiálu zabraňujícímu korozi, jež nepodléhá degradaci během celé životnosti kotvy, musí tvořit kotevní ochranu. Příklady této ochrany jednotlivých komponentů kotvy jsou v tab. 43.
V současné době se u nás provádějí prakticky pouze kotvy s kořenem taženým, takže jejich injektáž má stejné zásady, jako je tomu u mikropilot. Opět se injektuje vesměs cementovou suspenzí c : v = 2,3 : 1 až 2,3 : 1 a je třeba protrhnout zálivku a prostřednictvím injektáže ji roztlačit proti stěnám vrtu. Rozhodující je dosažení projektem předepsaného tlaku na příslušnou etáž, proto reinjektáže, zvláště v zeminách, jsou zcela typické.
Na rozdíl od většiny mikropilot se všechny kotvy podrobují příslušným zkouškám, jež spočívají v jasně definovaném postupu napínání, jehož účelem je:
- zjištění únosnosti kotvy a vypracování záznamu o této kotvě;
- napnutí a ukotvení táhla kotvy na jeho zaručené kotevní síle.
Tab. 43 Příklady protikorozních ochranných systémů pro trvalé kotvy
| Ověření navrhované ochrany Všechny systémy protikorozní ochrany se podrobí zkoušce (zkouškám) k prokázání účinnosti systému. Výsledky všech zkoušek se zdokumentují pro kontrolu. |
|
1. Kotevní délka táhla Protikorozní obal se může vytvořit jedním z níže uvedených způsobů:
|
Protikorozní obaly zhotovené na stavbě
|
2. Volná délka táhla Ochranný systém umožňuje volný pohyb táhla uvnitř vrtu. Toho může být dosaženo jedním z následujících způsobů:
A. společná plastová povlaková trubka vyplněná pružnou protikorozní výplní; |
|
| 3. Přechod mezi kotevní hlavou a volnou délkou Ke kotevní hlavě je přivařeno nebo je s ní pevně spojeno natřené hrdlo z ocelové nebo plastové trubky. To je připevněno přímo k povlakové trubce volné délky a je vyplněno protikorozní cementovou nebo pryskyřičnou výplní. |
|
| 4. Kotevní hlava Natřené a/nebo galvanizované kovové víko s minimální tloušťkou stěny 3 mm, nebo pevné plastové víko s minimální tloušťkou stěny 5 mm se připevní na podkladní desku a pokud je odnímatelné, je vyplněno pružnou protikorozní hmotou a utěsněno plochým těsněním. Pokud není odnímatelné, je vyplněno cementem nebo pryskyřicí. |
|
4.8.1 Kotvy tyčové
Nosná část této kotvy, přenášející tahovou sílu, je tvořena jedním táhlem z ušlechtilé oceli, jež má po celé své délce nalisován hrubý závit. Táhla se vyrábějí v délkách 12,0 m (výjimečně 14,0 m) a k nim se dodávají spojky, matice a tvarové podložky. U nás se v současné době používají tyčové kotvy Dywidag Ø 26,5 mm, 32 mm a 36 mm. Základní parametry materiálů těchto kotev jsou v tab. 44.
Tab. 44 Základní parametry materiálů tyčových kotev
| Vlastnost materiálu kotevního táhla | Kotvy Dywidag | |||||
| Ocel 835/1 030 | Ocel 1 080/1 230 | |||||
| Ø 26,5 | Ø 32 | Ø 36 | Ø 26,5 | Ø 32 | Ø 36 | |
| jmenovitý průměr [mm] | 26,5 | 32 | 36 | 26,5 | 32 | 36 |
| stoupání závitu [mm] | 13 | 16 | 18 | 13 | 16 | 18 |
| průřezová plocha A [mm2] | 551 | 804 | 1 018 | 551 | 804 | 1 018 |
| hmotnost [kg/m] | 4,48 | 6,53 | 8,27 | 4,48 | 6,53 | 8,27 |
| mezní pevnosti [kN] | 568 | 828 | 1 049 | 678 | 989 | 1 252 |
| napětí na mezi pevnosti fp [MPa] | 1 080 | 1 230 | ||||
| kotevní síla Fdov [kN] | 284 | 414 | 524 | 339 | 495 | 626 |
S ohledem na komplikace při nastavování kotev a na problémy se zapouštěním těchto prvků do základové půdy, provádějí se u nás v současné době tyčové kotvy v délkách do 12 m (resp. 14 m) tak, aby nemusely být nastavovány.
Tyčové kotvy dočasné
Dočasné tyčové kotvy se na stavbu dodávají většinou bez jakékoliv úpravy a teprve na stavbě se montují. Schéma takovéto kotvy je na obr. 52. Kotevní délka táhla (ltd) je bez jakékoliv úpravy, na volnou délku táhla (ltf) se navleče hladká ochranná flexibilní trubka, opatřená uvnitř zvláštní plastickou hmotou, umožňující prokluz mezi touto trubkou a táhlem. Po asi 2,0 m se kotva opatří centrátory, jejichž funkcí je vystředit kotvu ve vrtu. Injektáž těchto kotev se provádí buď pomocí jedné manžetové trubky umístěné paralelně s táhlem, nebo pomocí dvojice hadiček spojených přes speciální pryžové manžety s táhlem. První způsob injektáže je typický především pro pramencové kotvy a bude popsán níže. Zde bude představena jiná metoda injektáže, která byla vyvinuta v SRN v souvislosti s výrobou tyčových kotev Dywidag. V tom případě je kotevní délka táhla opatřena pryžovými manžetami, jež se montují v osových vzdálenostech po 0,5 m a hadičkami profil 10 mm pro transport injektážní směsi a pro proplachování vodou. Tyto vysokotlaké hadičky jsou z umělé hmoty, jsou flexibilní a v místě průchodu skrz pryžovou manžetu jsou opatřeny 2 otvory o průměru 3 mm. Pod spodní manžetou jsou hadičky nastaveny speciální U spojkou, do níž jsou zalepeny vteřinovým lepidlem. Podél volné délky kotvy jsou hadičky fixovány obtočením lepicí páskou. Schéma injektážního zařízení je na obr. 53. Celá tato montáž se provádí na staveništi. Připravená kotva se zapustí do vrtu, který byl před tím vypláchnut a vyplněn cementovou suspenzí.
S injektáží lze začít nejdříve za 12 hodin po osazení kotvy za předpokladu použití cementu CEM II/A-S. Při použití jiných cementů je třeba stanovit tuto dobu individuálně. Před injektáží se propláchne celý systém tak, že se jedna hadička (bývají barevně označené) připojí na přívod vody a ta se nechá volně protékat druhou hadičkou. Po tomto propláchnutí se příslušná hadička připojí k vývodu vysokotlakého čerpadla a injektážní směs se nechá volně proudit tímto systémem. Vytéká-li volně injektážní směs druhou hadičkou, ta se zaškrtí jejím prostým přehnutím, a tak je zahájena injektáž. Je zřejmé, že nelze stanovit, zda se injektuje všemi manžetami, nebo pouze některými, nicméně jedná se o způsob velmi jednoduchý, rychlý a technologicky nenáročný. Kontroluje se tlak i spotřeba injektážní směsi. V zeminách většinou při první fázi injektáže nedojde k dosažení předepsaného tlaku. Proto se injektuje množstvím, jež odpovídá asi trojnásobku objemu vrtu v kořenové části a první fáze injektáže se ukončí. V horninách obvykle již při první fázi injektáže dojde k dosažení předepsaného tlaku při malém množství injektážní směsi. Následně se celý systém propláchne vodou. Druhá fáze injektáže (1. reinjektáž) se provádí nejdříve za 10 hodin po skončení první fáze. Opět se zkontroluje průchodnost systému vodním proplachem a injektuje se stejně jako v 1. fázi. I v horninách, kde již v 1. fázi došlo k dosažení předepsaného tlaku, se doporučuje jedna reinjektáž. Takto lze (zvláště v zeminách) reinjektovat vícekrát, než je obvyklé při injektáži pomocí klasické manžetové trubky používané u pramencových kotev. Po skončení všech fází injektáže se doporučuje vždy propláchnout celý systém vodou pro eventuální další využití. Jak již bylo uvedeno, tato metoda injektáže kotev nezaručuje dokonalé proinjektování kořenové části kotvy, resp. kontrolu tohoto proinjektování. Je však natolik technologicky nenáročná (není třeba použít obturátorů), rychlá a málo pracná, že se zvláště u dočasných kotev zhusta využívá. S tímto způsobem injektáže bývají dobré výsledky v případě základových půd tvořených hrubozrnnými zeminami a horninami, naopak v případě zemin jemnozrnných nebývá mnohdy tato injektáž úspěšná.
Obr. 52 Schéma dočasné tyčové kotvy (CPS, Dywidag): 1 – šestihranná matice, 2 – kotevní deska s půlkulovým vybráním, 3 – ochrana matice, 4 – hladká trubka na volné délce táhla, 6 – centrátor, 7 – táhlo kotvy
Obr. 53 a. Schéma injekčního zařízení tyčových kotev, b. řez pryžovou manžetou 1: 1 –pryžové manžety, jež se připevní na kotevní část táhla „zaklapnutím“, 2 – injekční a proplachovací hadičky průměru 10 mm, 3 – spojka U, 4 – kotevní část táhla
Tyčové kotvy trvalé
U nás se používají zcela výjimečně, a to pouze v délkách do 12 m. Důvodem je ta skutečnost, že kotvu je nutné dovézt na staveniště již zcela smontovanou, čímž vznikají problémy s dopravou, manipulací a skladováním, jež je na staveništi prakticky vyloučené. Trvalé tyčové kotvy se montují ve speciálních dílnách, kde se provádí současně injektáž kořene speciální suspenzí a takto upravená kořenová část kotvy je mimořádně náchylná na poškození při dopravě a manipulaci. Schéma trvalé tyčové kotvy je na obr. 54.
Obr. 54 Schéma trvalé tyčové kotvy (Dywidag): 1 – šestihranná matice, 2 – kotevní deska s půlkulovým vybráním, 3 – ochrana matice, 4 – hladká trubka na volné délce táhla, 5 – vrubovaná flexibilní trubka, 6 – centrátor, 7 – táhlo kotvy, 8 – injektáž prostoru mezi táhlem 7 a trubkou 5, 9 – botka kotvy z umělé hmoty
Úprava hlavy (podkotevní ochrana) tyčových kotev (zejména trvalých) je na obr. 55.
Obr. 55 Úprava hlavy (podkotevní ochrana) tyčové kotvy: 1 – roznášecí deska, 2 – ocelová roznášecí deska s kónickým nástavcem opatřená epoxidovým nátěrem, 3 – antiko ochrana, 4 – podkladní beton, 5 – podkotevní ochrana po napnutí kotvy, 6 – ocel. demontovatelné víko, 7 – ochráněné táhlo tyčové kotvy, 8 – výplň epoxidovou pryskyřicí, 9 – gumové těsnění, 10 – ocelová průchodka s přírubou, 11 – cementová injektáž, 12 – plastová trubka na volné délce táhla, 13 – kónická ocelová trubka, 14 – kotvená konstrukce, 15 – podmazání epoxidovou pryskyřicí
Na rozdíl od dočasné kotvy je v případě trvalé kotvy opatřena kořenová část dvojitou antikorozní ochranou, přičemž první ochranu tvoří (tak jako je tomu u kotev dočasných) zálivka a injektáž v kořenové části, druhou pak (na rozdíl od kotev dočasných) speciální ochrana kořenové délky spočívající v použití vrubované flexibilní trubky z umělé hmoty a v injektáži prostoru mezi touto trubkou a táhlem kotvy speciální pryskyřicí. Touto vrubovanou flexibilní trubkou s injektáží je ve skutečnosti opatřena prakticky celá kotva (kromě hlavy) a ve volné délce je na ni navíc navlečena hladká trubka, jež má samozřejmě větší průměr než v případě kotvy dočasné. Mimořádná pozornost je věnována přechodu mezi volnou a kotevní délkou a hlavovou částí kotvy, kde výrobci používají osvědčených metod, které jsou součástí jejich „know-how“.
Technologický postup výroby těchto kotev se však v zásadě neliší od postupu výroby kotev dočasných, v předchozím textu popsaná injektáž se využívá i v tomto případě, pouze speciální pryžové manžety a centrátory jsou co do velikosti přizpůsobeny průměrům trubek kotevní ochrany.
4.8.2 Kotvy pramencové
V současné době jsou v naší republice nejrozšířenější a prakticky jediné v případě kotev trvalých. Důvodem je snazší transport a manipulace s kotvami při zapouštění, možnost využití větší délky kotev, jistou roli hraje i tradice. Vlastní pramence jsou spleteny z nízkotepelně popouštěných ocelových drátů: 1 x 5,5 mm + 6 x 5,0 mm, tudíž celkový vnější průměr pramence je kolem 15,5 mm, přičemž rozeznáváme kvalitu: Ø 15,5/1 620 MPa a Ø 15,5/1 800 MPa. Kromě toho je znám ještě typ: Ø 15,7/1 770, jež odpovídá výrobkům firmy Dywidag-Systems International, označených: 0,6″ 1 570/1 770. Hlavní vlastnosti těchto pramenců jsou v tab. 45 a jmenovité nosnosti trvalých kotev podle počtu a kvality pramenců jsou v tab. 46.
Tab. 45 Hlavní parametry ocelových pramenců
| Typ pramence | Pramenec Ø 15,5/1 620 | Pramenec Ø 15,5/1 800 | Pramenec Ø 15,7/1 770 | |
| jmenovitý průměr [mm] | 15,5 | 15,5 | 15,7 | |
| jmenovitý průřez [mm] | 141,5 | 141,5 | 150,0 | |
| zatížení a napětí | 229,2 | 255 | 265,5 | |
| na mezi pevnosti | Fm [kN] | |||
| fp [MPa] | 1 620 | 1 800 | 1 770 | |
| na mezi 0,2 | Fp0,2 [kN] | 194,8 | 217 | 235,5 |
| fp0,2 [MPa] | 1 377 | 1 532 | 1 570 | |
| na mezi 0,1 | Fp0,1 [kN] | – | 178 | – |
| fp0,1 [MPa] | – | 1 620 | – | |
| tažnost [%] | 3,0 | 3,5 | 3,5 | |
| modul pružnosti E [Gpa] | 200 10 % | 200 10 % | 195 | |
| jmenovitá hmotnost [kg·m-1] | 1,12 | 1,12 | 1,15 | |
Tab. 46 Jmenovitá únosnost trvalých kotev podle počtu a kvality pramenců Fdov [kN]
| Táhlo | 1x Ø 15,5 |
2x Ø 15,5 |
3x Ø 15,5 |
4x Ø 15,5 |
6x Ø 15,5 |
8x Ø 15,5 |
9x Ø 15,5 |
10x Ø 15,5 |
12x Ø 15,5 |
| Ocel 1 620 MPa | 120 | 240 | 360 | 480 | 720 | 960 | 1 080 | 1 200 | 1 440 |
| Ocel 1 800 MPa | 140 | 280 | 420 | 560 | 840 | 1 120 | 1 260 | 1 400 | 1 680 |
| Táhlo | 1x Ø 15,7 |
2x Ø 15,7 |
3x Ø 15,7 |
4x Ø 15,7 |
6x Ø 15,7 |
8x Ø 15,7 |
9x Ø 15,7 |
10x Ø 15,7 |
12x Ø 15,7 |
| Ocel 1 770 MPa | 142 | 284 | 426 | 568 | 852 | 1 136 | 1 278 | 1 420 | 1 562 |
Pramencové kotvy dočasné
V současné době se u nás využívá nejvíce pramenců kvality 1 570/1 770 MPa, jež se označují: Lp 15,7/1 770. Pramence se dodávají navinuté na cívkách, přičemž ve výrobně kotev je třeba porovnat kvalitu pramenců s příslušným dodacím listem či atestem. Současně je třeba zkontrolovat, nejsou-li pramence napadeny rzí. Pramence se řežou rozbrušovací pilou na příslušné délky, jež jsou nejméně o 1,0 m delší, než je uvedeno v projektu. Konce pramenců se opatří proti rozpletení omotáním speciální lepicí páskou, nebo se na řezu opatrně zavaří elektrickým obloukem. Na přechodu volné délky do kořenové části se vytvoří zátka z elastoplastu. Na volnou délku se navleče ochranná PE trubka, jež se v místě zátky přepáskuje. Pramence se v kořenové části volně spletou jako pomlázka a na konci kořenové části se vytvoří špička z plastbetonu. Takto lze splést kotvy do maximálního počtu 6 pramenců. V případě výroby kotev s více pramenci se použije skládaných kotev ze samostatných kotev o nejvýše šesti pramencích. Volná délka kotvy se výjimečně vyplňuje antikorozní (plastickou) směsí. Takto upravená kotva se obyčejně transportuje na stavbu (ve smotcích) a na staveništi se dokončí. Jde zejména o montáž manžetové trubky z PVC Ø 32/3,6 mm, jež se na stavbu dodává v délkách 4 m, přičemž spojování se provádí pomocí závitových nátrubků rovněž z PVC. Manžetová trubka vede paralelně s pramenci, je k nim připevněna pomocí izolační pásky. V případě skládaných kotev vede manžetová trubka osou skládané kotvy. Charakteristický příčný řez pramencovou kotvou je na obr. 56, podélný řez pramencem je pak na obr. 57.
Ihned po dokončení a vyčištění vrtu se v případě jeho pažení jílocementovým, nebo jiným výplachem provede jeho výměna za cementovou zálivku ve složení c : v = 2,2 : 1 až 2,3 : 1. Vrt se plní od počvy prostřednictvím PVC trubky Ø 50 mm, trubkou se pohybuje za účelem odstranění zbylé vrtné drti. Bezprostředně po vyplnění vrtu zálivkou se osadí kotva, většinou ručně za pomoci dostatečného počtu pracovníků. V případě dlouhých kotev lze též použít malé mechanizace a různých přípravků. Následuje injektáž a popř. reinjektáž kořene podrobně popsaná v kap. 5.1.7 Mikropiloty. Rozhodujícím kritériem pro ukončení injektáže, resp. reinjektáže je dosažení konečného injektážního tlaku předepsaného projektem.
Pramencové kotvy trvalé
Pro trvalé kotvy jsou v naší republice nejužívanější právě kotvy pramencové. V zásadě se využívá dvou typů těchto kotev lišících se svojí konstrukcí a antikorozní úpravou.
Pro první typ je charakteristická ta skutečnost, že každý pramenec zvlášť má svoji volnou délku a délku kořenovou. Do výrobny kotev jsou dodávány pramence potažené ve speciálním závodě pryžovým povlakem, jež je na odmaštěný pramenec nastříkán za tepla. Jednotlivé pramence jsou potom nařezány na příslušnou délku a v kořenové části je pryžový povlak odstraněn. Na takto upravený pramenec je navléknuta vrubovaná flexibilní PE trubka průměru 20 mm, jež je připáskována na začátek volné délky. Prostor mezi pramencem a PE trubkou je ve výrobně zainjektován pryskyřicí a konec kořene je upraven speciální botkou z umělé hmoty. Takto připravené jednotlivé pramence jsou dodávány na stavbu, kde se z nich montují kotvy tak, že vnitřkem je vedena klasická manžetová trubka z PE Ø 32/3,6 mm s manžetami po 500 mm, na níž jsou distanční kruhy z umělé hmoty s výřezy, do nichž se zasunou jednotlivé pramence. Montáž těchto kotev je poměrně jednoduchá, jsou však značně náchylné na poškození při transportu a manipulaci, a to ve své kořenové části.
Obr. 56 Příčný řez pramencovou kotvou: a) kořenem, b) v místě usměrňovacího prvku, v místě táhla: 1 – vrt, 2 – zálivka, 3 – pramenec, 4 – manžetová trubka, 5 – usměrňovací kus, 6 – ochranná trubka táhla, 7 – výplň pryskyřicí
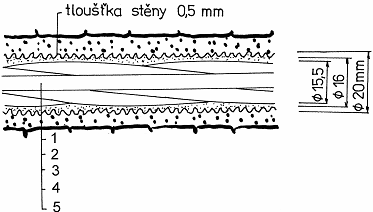
Obr. 57 Podélný řez pramencem trvalé kotvy v kořenové délce: 1 – pramenec, 2 – výplň pryskyřicí, 3 – vrubová plastová trubka, 4 – cementová zálivka (injektáž), 6 – vrt
Pro druhý typ se využívá holých pramenců Lp 15,7 mm, přičemž příslušný počet pramenců se ve vzdálenostech po asi 2 m spojí převázáním lepicí páskou. Mezi pramence se vloží dvě PE trubičky: první má průměr 10/2 mm, je ukončena 0,5–1,0 m před špičkou kotvy a slouží k plnění kořenové části kotvy; druhá má průměr 7/1,5 mm, končí na začátku kořenové části a slouží k odvzdušnění při plnění kořenové části kotvy. Následuje navléknutí PE trubky s vyřezaným závitem na volnou délku kotvy a navléknutí vrubované PE trubky na kořen, přičemž obě trubky se sešroubují a přepáskují, upraví se špička kotvy z plastbetonu. Na kotvu se připevní klasická manžetová PE trubka Ø 32/3,6 mm a kotva se vloží do vrtu vyplněného zálivkou jako v případě kotev dočasných. Plnění kořenové části se provádí většinou u zapuštěných kotev, a to pomocí kotlíků na stlačený vzduch. Plnění je ukončeno, vytéká-li cementová suspenze z odvzdušňovací hadičky. Takto se realizují kotvy s nejvýše šesti pramenci. V případě kotev s požadovanou větší únosností se skládají jednotlivé kotvy do jednoho vrtu.
Na obr. 58 je potom schéma podkotevní ochrany trvalých pramencových kotev.
Obr. 58 Úprava hlavy (podkotevní ochrana) pramencové kotvy: 1 – kotevní hlava, 2 – ocelová roznášecí deska s kónickým nástavcem opatřená epoxidovým nátěrem, 3 – antiko ochrana, 4 – podkladní beton, 5 – podkotevní ochrana po napnutí kotvy, 6 – ocelové demontovatelné víko, 7 – ochráněný kotevní pramenec, 8 – výplň epoxidovou pryskyřicí, 9 – gumové těsnění, 10 – ocelová průchodka s přírubou, 11 – cementová injektáž, 12 – plastová trubka na volné délce táhla, 13 – kónická ocelová trubka, 14 – kotvená konstrukce, 15 – podmazání z epoxidové pryskyřice
4.8.3 Zkoušení a napínání kotev
Horninové kotvy jsou prvky, jež přenášejí tahové síly, které se do nich vnášejí napínáním. Vlastní napínání lze provést nejdříve za 10 dnů po dokončení injektáže kořene a 7 dnů po osazení a případném podlití kotevní desky. Pro vlastní napínání se používá napínacího zařízení vybaveného siloměry s možností měření deformací (protažení) táhla kotvy. Napínací zařízení včetně siloměrů musí být kalibrováno v intervalu po 6 měsících. Napínací zařízení pro tyčové a pramencové kotvy by mělo napínat kotvu jako celek. Pokud se musí napínat jednotlivé pramence zvlášť, musí být vybaveno měřicím zařízením, jež v každém okamžiku umožní stanovit celkovou sílu v kotvě. Postup napínání je buď standardní (níže uvedený), nebo ve speciálních případech musí být stanoven v projektu. Zkoušky kotev prováděné na stavbě se dělí na:
- typové zkoušky;
- ověřovací zkoušky (dříve označené jako průkazní);
- kontrolní zkoušky.
4.8.3.1 Typové zkoušky, příklad 11
Typové zkoušky se obyčejně požadují před zahájením provádění kotev (dočasných i trvalých), a to na nesystémových kotvách zejména za účelem vypracování projektu kotvení. Stanoví se jimi:
- odpor proti vytažení;
- chování při tečení;
- upřesní se výrobní postup.
U typové zkoušky se často jedná o rozšířenou ověřovací zkoušku na nejméně třech kotvách. Konstrukce kotvy by měla být navržena tak, aby se mohlo dosáhnout charakteristického odporu proti vytažení kotvy Rak. Zkušební síla PP je:
\begin{gathered}
P_\text{p}=R_\text{ak}
\end{gathered}(149)
přičemž musí být dodrženy následující limitní hodnoty:
\begin{gathered}
P_\text{p}\le0{,}80\cdot P_\text{tk}=0{,}80\cdot f_\text{t}\cdot A_\text{t}\\\\
P_\text{p}\le0{,}95\cdot P_\text{t0,k1}=0{,}95\cdot f_\text{t0,1k}\cdot A_\text{t}\space\space\text{příp.}\space\space0{,}95\cdot P_\text{t0,2k}=0{,}95\cdot f_\text{t0,2k}\cdot A_\text{t}
\end{gathered}(150)
rozhodující je menší z hodnot.
Kotva má být napínána minimálně šesti napínacími cykly až po zkušební sílu PP s pozorovacími časy podle tab. 47 a obr. 59. Při každém zatěžovacím stupni se měří posun volného konce kotvy. Po každém zatěžovacím stupni se kotva odlehčí na sílu odpovídající předtížení P0, jež se obyčejně volí:
\begin{gathered}
P_0=0{,}1\cdot P_\text{p}
\end{gathered}(151)
a na tomto mezistupni se udržuje po dobu nejméně 1 min. Pozorovací čas na prvních dosažených zatěžovacích stupních se prodlouží v případě, že míra dotvarování ks nemůže být jednoznačně určena.
Tab. 47 Zatěžovací stupně a pozorovací časy u typových zkoušek
| Zatěžovací stupně | Minimální pozorovací časy [min] | |
| jemnozrnné zeminy a horniny | hrubozrnné zeminy | |
| 0,1 PP | 1 | 1 |
| 0,4 PP | 15 | 15 |
| 0,55 PP | 15 | 15 |
| 0,7 PP | 30 | 60 |
| 0,8 PP | 30 | 60 |
| 0,9 PP | 30 | 60 |
| 1,00 PP | 60 | 180 |
Charakteristický odpor proti vytažení Rak se dosáhne, když míra dotvarování ks překročí hodnotu 2,0 mm. Rozhodující je nejnižší hodnota Rak, která se dosáhne u odzkoušené kotvy. Pokud se při průzkumné zkoušce nedosáhne charakteristického odporu proti vytažení Rak, tak pro Rak platí maximálně dosažená zkušební síla PP.
K posouzení chování kotvy při zatížení slouží stanovení velikosti creepu (tečení) pod zatížením a protažení ocelového táhla kotvy. Chování při tečení je charakterizováno velikostí dotvarování ks při konstantní kotevní síle (obr. 60):
\begin{gathered}
k_\text{s}=\frac{(s_\text{b}-s_\text{a})}{\log(\frac{t_\text{b}}{t_\text{a}})}
\end{gathered}(152)
kde je:
sa … posun v hlavě kotvy v určitém čase ta
sb … posun v hlavě kotvy v určitém čase tb
ta … začátek sledovaného času
tb … konec sledovaného času
Obr. 59 Pracovní diagram na příkladu typové zkoušky trvalé kotvy v hrubozrnné zemině
Obr. 60 Křivky čas-posun ke stanovení míry dotvarování ks při zkušební síle Pp na příkladu typové zkoušky nesystémové kotvy v hrubozrnné zemině
Pozorovací časy uvedené v tab. 50 se prodlouží, když:
a) přírůstek posunů Δs ≥ 0,5 mm, a sice u
- dočasných kotev v hrubozrnných zeminách a horninách: mezi 10. min a 30. min
- dočasných kotev v jemnozrnných zeminách: mezi 20. min a 60. min
- trvalých kotev v hrubozrnných zeminách a horninách: mezi 20. min a 60. min
- trvalých kotev v jemnozrnných zeminách: mezi 60. min a 180. min
nebo
b) sklon křivky čas-posun v zobrazení podle obr. 60 roste s logaritmem času.
Pro případy a) a b) musejí být pozorovací časy prodlouženy tak, aby mohla být z lineární větve na konci křivky čas-posun na obrázku jednoznačně určena míra dotvarování. U trvalých kotev musí pozorovací čas činit včetně prodloužení v hrubozrnné zemině a hornině min. 120 min a v jemnozrnné zemině min. 720 min.
Příklad 11
Pramencové kotvy 4 x Lp 15,7 mm (ocel 1 570/1 770 MPa) v ulehlém štěrku; volná délka Ltf = 10,00 m, kořenová délka Ltb = 6,00 m, vzdálenost ukotvení táhla do napínací pistole od bodu ukotvení táhla Le = 1,00 m; realizace dvou ks typových zkoušek s výsledky podle tab. 48.
a) Stanovení zkušební síly a předtížení
\begin{gathered}
P_\text{P}\le0{,}80\cdot P_\text{tk}=0{,}80\cdot f_\text{t}\cdot A_\text{t},\space A_\text{t}=4\cdot0{,}0005792\space\text{m}^2,\space f_\text{t}=1\space770\space\text{MPa}\\\\
P_\text{P}\le0{,}80\cdot1\space770\cdot0{,}0005792=0{,}820\space\text{MN}\\\\
\text{resp.}\space P_\text{P}\le0{,}95\cdot P_\text{t0,1k}=0{,}95\cdot f_\text{t0,1k}\cdot A_\text{t}=0{,}95\cdot1\space500\cdot0{,}0005792=0{,}825\space\text{MN}
\end{gathered}rozhoduje menší, tedy Pp = 820 kN
předtížení volíme Pa = 82 kN
Při zkouškách kotev č. 1 a č. 2 byly změřeny následující velikosti protažení táhla
Tab. 48 Výsledky měření dvou kotev při typových zkouškách
| Čas t [min] | |||||||||||
| K | 1 | 2 | 5 | 10 | 15 | 20 | 30 | 45 | 60 | 75 | 120 |
| 1 | 79,20 | 79,37 | 79,65 | 79,84 | 79,98 | 80,04 | 80,15 | 80,28 | 80,35 | – | – |
| 2 | 71,50 | 71,75 | 72,04 | 72,39 | 72,76 | 72,82 | 73,09 | 73,33 | 73,58 | 73,74 | 73,96 |
| Kotva č. 1: max. zkušební síla Pp1 = 820 kN (= Pp,max) Kotva č. 2: max. zkušební síla Pp2 = 740 kN (= 0,9 · Pp,max) |
|||||||||||
b) Vyhodnocení naměřených protažení táhel:
Kotva č. 1: normální pozorovací čas pro Pp,max = 820 kN činí 60 min
Pro lineární průběh čáry dotvarování platí:
\begin{gathered}
s_{60}-s_{20}=80{,}35-80{,}04=0{,}31\space\text{mm}\lt0{,}50\space\text{mm}-\text{normální pozorovací čas}\\\\
k_\text{s,1}=\frac{(s_{60}-s_{20})}{\log(\frac{120}{20})}=\frac{(80{,}35-80{,}04)}{0{,}477}=0{,}65\lt1{,}0\implies\text{vyhovuje}\\\\
R_\text{m,1}=820\space\text{kN}
\end{gathered}Kotva č. 2: vykázala pomalé ustalování deformací již při zatěžovacím stupni
\begin{gathered}
0{,}9\cdot P_\text{p,max}=740\space\text{kN}
\end{gathered}normální pozorovací čas pro Pp = 740 kN činí 60 min
\begin{gathered}
s_{60}-s_{20}=73{,}58-72{,}82=0{,}76\space\text{mm}\gt0{,}50\space\text{mm}-\text{prodloužený pozorovací čas}\\\\
k_\text{s,2}=\frac{(s_{120}-s_{20})}{\log(\frac{120}{20})}=\frac{(73{,}96-72{,}82)}{0{,}778}=1{,}46\lt2{,}0\implies\text{vyhovuje}\\\\
R_\text{m,2}=740\space\text{kN}
\end{gathered}c) Stanovení charakteristické hodnoty mezního stavu únosnosti (kořene) kotvy proti vytržení:
\begin{gathered}
R_\text{ULS,m}=\text{min}(R_\text{m}{,}P_\text{p})=\text{min}(820,740)=740\space\text{kN}\\\\
R_\text{ULS,k}=\frac{R_\text{ULS,m}}{\xi_\text{ULS}}=740\space\text{kN}
\end{gathered}(pro n = 2 typové zkoušky kotev je ξULS = 1,0 – viz tab. A.20 změny A.1 k ČSN EN 1997-1)
Stanovení návrhové hodnoty mezního stavu únosnosti (kořene) kotvy proti vytržení:
\begin{gathered}
R_\text{ULS,d}=\frac{R_\text{ULS,k}}{\gamma_\text{a,ULS}}=\frac{740}{1{,}1}=673\space\text{kN}
\end{gathered}Pro doporučený návrhový přístup NP2 je γa,ULS = 1,1 (tab. A.19 změny A.1 k ČSN EN 1997-1).
d) Stanovení velikosti zaručené kotevní síly P0 (z výsledků provedených dvou typových zkoušek kotev s přihlédnutím k meznímu stavu únosnosti):
pro P0 platí:
\begin{gathered}
P_0\le\frac{P_\text{p}}{1{,}25},\space\text{tudíž}\space P_\text{0,max}=\frac{740}{1{,}25}=592\space\text{kN}
\end{gathered}zaručená kotevní síla může tedy nabýt max. velikosti P0,max = 592 kN
nutno zkontrolovat, zda platí:
\begin{gathered}
P_\text{0,max}\le R_\text{ULS,d},\space592\space\text{kN}\lt673\space\text{kN}\implies\text{vyhovuje}
\end{gathered}e) Stanovení únosnosti kořene kotvy proti vytržení statickým výpočtem
- průměr vrtu d = 180 mm, délka kořene Ltb = 6,0 m, char. velikost tření na plášti ve štěrku písčitém, ulehlém τi = 0,20 MPa (lze využít tab. 36), návrhový přístup NP2: A1„+“M1„+“R2
- charakteristická velikost
\begin{gathered}
R_\text{ULS,k}=3{,}14\cdot0{,}18\cdot6{,}0\cdot200=678{,}24\space\text{kN}
\end{gathered}- návrhová velikost
\begin{gathered}
R_\text{ULS,d}=\frac{R_\text{ULS,k}}{\gamma_\text{a,ULS}}=\frac{678{,}24}{1{,}1}=617\space\text{kN}
\end{gathered}f) Stanovení charakteristické únosnosti (RSLS,k) a návrhové únosnosti (RSLS,d) kotvy podle mezního stavu použitelnosti:
- postup je stejný jako v případě mezního stavu únosnosti s tím, že základní odvozené hodnoty (Rm) se odečítají pro velikosti přijatelných deformací pro mezní stav SLS.
4.8.3.2 Ověřovací zkoušky, příklad 12
Ověřovací zkouška se musí provést na každé stavbě na třech kotvách, a to v takovém místě, kde se dají na základě poměrů základové půdy očekávat nejnepříznivější výsledky. Ověřovací zkouška se má provádět před začátkem kotevních prací. K ověření předpokládané únosnosti může být provedena také během kotevních prací, když jsou k dispozici výsledky ověřovacích zkoušek stejného kotevního systému ve srovnatelné základové půdě a se stejným výrobním postupem.
U dočasných kotev se smí od ověřovací zkoušky upustit, když jsou k dispozici výsledky ověřovacích zkoušek stejného kotevního systému ve srovnatelné základové půdě a se stejným výrobním postupem. Ověřovací zkouška se však musí provést, když má být dokázán vyšší odpor proti vytažení Rak než na jiném místě.
Zkušební síla PP se prokazuje z naměřené hodnoty namáhání kotvy Pd. Pro zkušební sílu musí být dodrženy mezní hodnoty jako v případě zkoušek typových. Každá kotva má být napínána min. pěti napínacími cykly na zkušební sílu PP. Maximální zatěžovací stupně napínacích cyklů jsou uvedeny v tab. 49.
Tab. 49 Zatěžovací stupně a pozorovací časy pro ověřovací zkoušky
| Zatěžovací stupně | Minimální pozorovací časy (min) | |||
| Dočasné kotvy | Trvalé kotvy | |||
| hrubozrnná zemina a hornina | jemnozrnná zemina | hrubozrnná zemina a hornina | jemnozrnná zemina | |
| Paa) | 1 | 1 | 1 | 1 |
| 0,4 PP | 1 | 1 | 15 | 15 |
| 0,55 PP | 1 | 1 | 15 | 15 |
| 0,7 PP | 5 | 5 | 30 | 60 |
| 0,8 PP | 5 | 5 | 30 | 60 |
| 1,00 PP | 30 | 60 | 60 | 180 |
| a) Předtížení Pa by mělo ležet mezi 0,1 · Pp a 50 kN. | ||||
Při každém zatěžovacím stupni se měří posun volného konce kotvy. Po prvním dosažení zatěžovacího stupně se zatížení drží nejméně po dobu minimálních pozorovacích časů uvedených v tab. 45 na konstantní úrovni a potom se sníží na předtížení Pa. Poté se přejde se zatěžovacími mezistupni na maximální zatěžovací stupeň dalšího napínacího cyklu. Pozorovací čas na zatěžovacích mezistupních činí nejméně 1 min. Při konstantně udržované zkušební síle se během pozorovacího času měří posuny (např. po 1 min, 2 min, 3 min, 5 min, 10 min, 15 min, 20 min, 30 min, 45 min a 60 min) a výsledek se vykreslí podle obr. 61 v semilogaritmickém měřítku.
Pozorovací časy uvedené v tab. 50 se prodlouží podle stejných podmínek jako v případě typových zkoušek. Musí se dokladovat, že posuny uvedené v tab. 48, příp. míry dotvarování nejsou překročeny. Ke zjištění míry dotvarování se mají křivky čas-posun příslušného maximálního zatěžovacího stupně zobrazit podle obr. 62.
Tab. 50 Pozorovací časy a dovolené posuny, příp. míry dotvarování při zkušební síle PP pro ověřovací zkoušky
| Dočasné kotvy | Trvalé kotvy | |||
| hrubozrnná zemina a hornina | jemnozrnná zemina | hrubozrnná zemina a hornina | jemnozrnná zemina | |
| pokus s min. pozorovacím časem [min] při splnění podmínek: | ||||
| ta [min] tb [min] posun Δs = sb – sa [mm] |
10 30 ≤ 0,5 |
20 60 ≤ 0,5 |
20 60 ≤ 0,5 |
60 180 ≤ 0,5 |
| pokus s prodlouženým pozorovacím časem [min]: | ||||
| pozorovací čas tb [min] míra dotvarovánía) ks [mm] |
≥ 30 ≤ 2,0 |
≥ 60 ≤ 2,0 |
≥ 120 ≤ 2,0 |
≥ 720 ≤ 2,0 |
| a) ks z lineární koncové oblasti křivky čas-posun podle obr. 61. | ||||
Obr. 61 Křivky čas-posun ke stanovení míry dotvarování ks = (sb – sa / log (tb / ta) na příkladu ověřovací zkoušky trvalé kotvy v nesoudržné zemině
Překročí-li se u ověřovací zkoušky kotvy právě při jednom zatěžovacím stupni pod zkušební silou PP kritérium ks = 2,0 mm, musí se přípustná kotevní síla pro všechny kotvy, pro které platí ověřovací zkouška, nově určit na bázi nejnižší zkušební hodnoty. V opačném případě se musí provést další průkazní zkoušky (např. na kotvách s vylepšeným výrobním postupem).
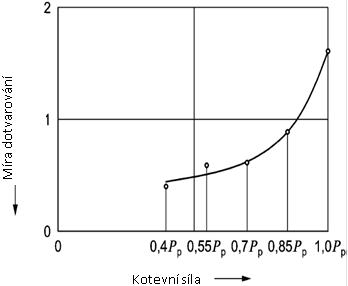
Obr. 62 Zobrazení míry dotvarování jako funkce kotevní síly
Stanovení volné délky táhla kotvy
Je třeba doložit, že se volná délka táhla Lapp, určená z výsledků zkoušek, podstatně neliší od plánované (navrhované) volné délky táhla. To se považuje za splněné, když jsou dodrženy níže uvedené podmínky pro vypočtené volné délky oceli Lapp pro sílu P = 0,70 · PP:
- horní hranice vypočtených volných délek táhel u pramencových kotev:
\begin{gathered}
L_\text{app}\le L_\text{rf}+L_\text{e}+0{,}5\cdot L_\text{tb}
\end{gathered}(153)
- horní hranice vypočtených volných délek táhel u tyčových kotev:
\begin{gathered}
L_\text{app}\le1{,}1\cdot L_\text{tf}+L_\text{e}
\end{gathered}(154)
- spodní hranice vypočtených volných délek táhel u všech typů kotev:
\begin{gathered}
L_\text{app}\ge0{,}8\cdot L_\text{tf}+L_\text{e}
\end{gathered}(155)
Uvedené hranice vypočtených volných délek táhel kotev můžou být kontrolovány přímo přes měřený posun. K tomu se posun na konci každého cyklu dělí na elastickou a trvalou složku a vynáší se do grafu. Výše uvedené hranice vypočtených volných délek táhel se k tomu přepočítají, jak vyplývá z hraničních křivek elastického posunu:
- horní hraniční křivka a pro pramencovou kotvu:
\begin{gathered}
s_\text{e1}=\frac{(P_\text{p}-P_\text{a})}{(E_\text{t}\cdot A_\text{t})}\cdot(L_\text{tf}+L_\text{e}+0{,}5\cdot L_\text{tb})
\end{gathered}(156)
- horní hraniční křivka a pro tyčovou kotvu:
\begin{gathered}
s_\text{e1}=\frac{(P_\text{p}-P_\text{a})}{(E_\text{t}\cdot A_\text{t})}\cdot(1{,}1\cdot L_\text{tf}+L_\text{e})
\end{gathered}(157)
- křivka elastických posunů plánovaných volných délek oceli:
teoretická křivka c:
\begin{gathered}
s_\text{e1}=\frac{(P_\text{p}-P_\text{a})}{(E_\text{t}\cdot A_\text{t})}\cdot(L_\text{tf}+L_\text{e})
\end{gathered}(158)
spodní hraniční křivka b:
\begin{gathered}
s_\text{e1}=\frac{(P_\text{p}-P_\text{a})}{(E_\text{t}\cdot A_\text{t})}\cdot(0{,}8\cdot L_\text{tf}+L_\text{e})
\end{gathered}(159)
Příklad 12:
Stanovení volné délky táhla kotvy č. 1 z příkladu 11
- zkušební síla Pp = 820 kN, předtížení Pa = 82 kN
- teoretická křivka a je dána vztahem:
\begin{gathered}
s_\text{e1}=\frac{(P_\text{p}-P_\text{a})}{(E_\text{t}\cdot A_\text{t})}\cdot(L_\text{tf}+L_\text{e}+0{,}5\cdot L_\text{tb})=\frac{(0{,}820-0{,}082)}{(200\space000\cdot0{,}0005792)}\cdot(10{,}0+1{,}0+0{,}5\cdot0{,}6)=0{,}0892\space\text{m}=89{,}20\space\text{mm}
\end{gathered}- teor. křivka c je dána vztahem:
\begin{gathered}
s_\text{e1}=\frac{(P_\text{p}-P_\text{a})}{(E_\text{t}\cdot A_\text{t})}\cdot(L_\text{tf}+L_\text{e})=\frac{(0{,}820-0{,}082)}{(200\space000\cdot0{,}0005792)}\cdot(10{,}0+1{,}0)=0{,}0701\space\text{m}=70{,}10\space\text{mm}
\end{gathered}- teoretická křivka b je dána vztahem:
\begin{gathered}
s_\text{e1}=\frac{(P_\text{p}-P_\text{a})}{(E_\text{t}\cdot A_\text{t})}\cdot(0{,}8\cdot L_\text{tf}+L_\text{e})=\frac{(0{,}820-0{,}082)}{(200\space000\cdot0{,}0005792)}\cdot(0{,}8\cdot10{,}0+1{,}0)=0{,}05734\space\text{m}=57{,}34\space\text{mm}
\end{gathered}4.8.3.3 Kontrolní zkoušky
Každá kotva stavebního díla (pokud neprojde zkouškou ověřovací) se podrobí zkoušce kontrolní, což je v podstatě postup napínání kotvy. Zkušební síla PP se prokazuje obdobně jako u zkoušky typové či ověřovací, samozřejmě již se znalostí únosnosti kotvy na vytržení, tedy se znalostí velikosti RULS,d, popř. RSLS,d.
Pro zkušební sílu platí opět limitní velikosti jako v případě zkoušek typových či ověřovacích. Kotvy se zatěžují od předtížení Pa s mezistupni podle tab. 51 až do zkušební síly PP a poté odlehčeny opět na úroveň předtížení Pa. Čekací doba na jednotlivých zatěžovacích stupních jsou uvedeny v této tabulce. Na každém zatěžovacím stupni se měří posuny volného konce kotev. Zkušební síla se musí udržet konstantní u nesoudržných zemin a horniny min. 5 min, u soudržných zemin min. 15 min. Při tom se měří posuny v závislosti na čase (např. po 1 min, 2 min, 3 min, 5 min, 10 min a 15 min).
Tab. 51 Zatěžovací stupně a pozorovací časy při kontrolní zkoušce
| Zatěžovací stupně | Minimální pozorovací časy [min] | |
| Dočasné a trvalé kotvy | ||
| hrubozrnné zeminy a hornina | jemnozrnné zeminy | |
| Paa) | 1 | 1 |
| 0,4 PP | 1 | 1 |
| 0,55 PP | 1 | 1 |
| 0,7 PP | 1 | 1 |
| 0,85 PP | 1 | 1 |
| 1,00 PP | 5 | 15 |
| a) Předtížení Pa by měla ležet mezi 0,1 PP a 50 kN. | ||
V této tabulce uvedené minimální pozorovací časy se prodlužují:
- pokud je v hrubozrnných zeminách a horninách přírůstek posunů mezi 2. a 5. minutou Δs > 0,20 mm;
- pokud je v jemnozrnných zeminách přírůstek posunů mezi 5. a 15. minutou Δs > 0,25 mm.
V těchto případech se v pozorování pokračuje tak dlouho, dokud nemůžou být míry dotvarování jednoznačně stanoveny. Musí se dokladovat, že posuny uvedené v tab. 52, příp. míry dotvarování nejsou překročeny. Má se dále doložit, že se při zkušební síle PP dodrží pro vypočtené volné délky táhel Lapp následující podmínky:
- horní hranice vypočtených volných délek táhel u pramencových kotev:
\begin{gathered}
L_\text{app}\le L_\text{tf}+L_\text{e}+0{,}5\cdot L_\text{tb}
\end{gathered}(160)
- horní hranice vypočtených volných délek táhel u tyčových kotev:
\begin{gathered}
L_\text{app}\le1{,}1\cdot L_\text{tf}+L_\text{e}
\end{gathered}(161)
- spodní hranice vypočtených volných délek táhel u všech typů kotev:
\begin{gathered}
L_\text{app}\ge0{,}8\cdot L_\text{tf}+L_\text{e}
\end{gathered}(162)
Tab. 52 Pozorovací časy a dovolené posuny příp. míry dotvarování při zkušební síle PP u kontrolních zkoušek
| Dočasné a trvalé kotvy | ||
| hrubozrnné zeminy a horniny | jemnozrnné zeminy | |
| pozorovací čas: ta [min] tb [min] posun: Δs = sb – sa [min] |
2 5 ≤ 0,2 |
5 15 ≤ 0,25 |
| prodloužený pozorovací čas: tb [min] míra dotvarovánía) ks [min] |
> 5 ≤ 2,0 |
> 15 ≤ 2,0 |
| a) ks z lineární koncové oblasti křivky čas-posun podle tab. 59. | ||
4.8.3.4 Elektrické zkoušky protikorozní ochrany kotev
Jedná se o měření elektrického odporu mezi kotvou a okolní základovou půdou nebo stavební konstrukcí za účelem vyšetření účinnosti použitého systému protikorozní ochrany (trvalých) kotev. Používají se 2 metody měření elektrického odporu:
- ERM I, při níž se měří izolace kotvy proti základové půdě a proti stavební konstrukci;
- ERM II, při níž se měří izolace kotvy pouze proti stavební konstrukci.
Princip metody ERM I je znázorněn na obr. 63 a 64. Při měření je kotva připojena jako kladný pól a uzemnění jako záporný pól měřeného proudového okruhu pro stejnosměrný proud o napětí 500 V. Ve fázi A se zkouší neporušenost plastového obalu na volné délce kotvy a na kořenové délce, a to v různých fázích výroby kotvy před jejím zakotvením:
- po osazení kotvy do vrtu;
- po prvé fázi injektáže;
- po skončení injektáže.
Používá se měřicího zařízení s min. rozsahem měření 10 kΩ. Pokud elektrický odpor mezi kotevním táhlem a základovou půdou je větší než 100 kΩ, je neporušenost obalu vyhovující, přičemž zcela neporušený a vodotěsný plastový obal má vykazovat odpor přes 100 MΩ.
Ve fázi B se zkouší kompletní elektrická izolace kotvy proti základové půdě a stavební konstrukci ve fázi:
- po napnutí kotvy;
- po zainjektování prostoru hlavy kotvy;
- kdykoliv v průběhu životnosti kotvy.
Pokud takto změřený elektrický odpor Rl ≥ 100 kΩ, považuje se kotva z hlediska korozní ochrany za vyhovující.
Metoda ERM II se provádí tehdy, je-li Rl < 100 kΩ, za účelem zjištění, že mezi hlavou kotvy a výztuží kotvené konstrukce není žádný přímý kontakt. Schéma této zkoušky, která se provádí při napnuté kotvě, je na obr. 65. Používá se střídavého proudu o napětí asi 40 V, přičemž měřený rozsah odporu je 0 až 200 kΩ. Jako uzemění se zpravidla používá kotevní deska, nebo výztuž kotvené konstrukce, je-li deska opatřena elektricky izolačním nátěrem. Měření je mimořádně citlivé na atmosférické vlivy a na event. bludné proudy v základové půdě. Za vyhovující kotvu se z hlediska tohoto měření pokládá ta, u níž byl změřen elektrický odpor Rll > 100 Ω.
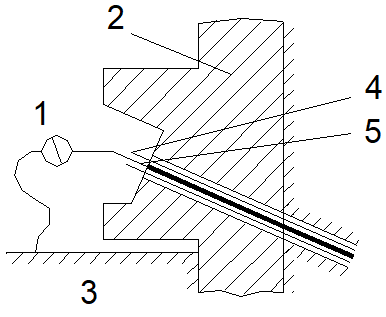
Obr. 63 Metoda ERM I před napnutím kotvy: 1 – ohmmetr, 2 – kotvená konstrukce, 3 – základová půda, 4 – PE povlaková trubka, 5 – kotevní táhlo
Obr. 64 Metoda ERM I po napnutí kotvy: 1 – ohmmetr, 2 – kotvená konstrukce, 3 – základová půda, 4 – PE povlaková trubka, 5 – kotevní táhlo, 6 – PE kotevní průchodka, 7 – podkladní deska, 8 – kotevní objímka, 9 – izolační deska
Obr. 65 Metoda ERM II po napnutí kotvy: 1 – ohmmetr
4.8.3.5 Zásady návrhu injektovaných horninových kotev
Návrh a výpočet horninových kotev vychází z potřeb kotvené konstrukce, kterou může být:
- pažicí konstrukce;
- zajištění svahů a násypů;
- podzemní prostory;
- podzemní stavby;
- základové konstrukce nadlehčované podzemní vodou;
- stavby a jejich základy přenášející tahové síly vyvolané horní stavbou nebo jejími účinky přenášenými do základů.
Předpjaté horninové kotvy se navrhují podle zásad mezních stavů popsaných v kapitole 8, ČSN EN 1997-1. Kromě mezního stavu únosnosti a použitelnosti, kdy se posuzuje porušení kotvy následkem tahového namáhání, je třeba při návrhu kotvení zvážit:
- porušení kotvy následkem namáhání příčnými silami a kroucením;
- porušení kotvy následkem koroze;
- ztráta kotevní síly následkem nadměrného posunu kotevní hlavy, nebo následkem tečení a relaxace kotvy;
- porušení, nebo nadměrná deformace části stavební konstrukce vzniklá v důsledku převzetí kotevní síly.
Návrh kotvení má vycházet zejména ze zkoušek kotev (typových a ověřovacích) a nutná jsou následující ověření a výpočty:
- ověření vnitřního odporu kotvy;
- ověření odporu kotvy proti vytažení;
- ověření použitelnosti a trvanlivosti kotvy;
- výpočet nutné volné kotevní délky;
- určení zaručené síly kotvy.
Charakteristická velikost vnitřního odporu kotvy Rlk je rovna síle na mezi pevnosti táhla:
\begin{gathered}
R_\text{1k}=P_\text{tk}=A_\text{t}\cdot f_\text{t}
\end{gathered}(163)
kde je:
At … průřezová plocha kotevního táhla;
Ft … charakteristiká pevnost kotevního táhla v tahu.
Odpor kotvy proti vytažení se určuje na základě výsledků typových, nebo ověřovacích zkoušek, nejsou-li k dispozici, potom výjimečně výpočtem na základě znalosti o geotechnických poměrech na staveništi s přihlédnutím ke zkušenostem v obdobných základových poměrech. Pro výpočet vnitřního odporu kotvy lze s opatrností použít hodnot z tab. 36, jež platí pro mikropiloty.
Charakteristický odpor kotvy proti vytažení Rak je definován jako tahová síla, která způsobuje jistou deformaci ks, nebo úbytek síly kl (podle předchozích kapitol). Musí platit:
\begin{gathered}
R_\text{ak}\le R_\text{a}
\end{gathered}(164)
přičemž za Ra se dosadí nejmenší velikost zjištěná při zkouškách. Současně se požaduje, aby:
\begin{gathered}
R_\text{ak}\ge R_\text{1k}
\end{gathered}(165)
Návrhová hodnota odporu kotvy Rd závisí na způsobu zatížení kotvy ve vyšetřovaném mezním stavu. Je-li kotva zatížena pouze tahem, je:
\begin{gathered}
R_\text{d}=\frac{R_\text{k}}{\gamma_\text{R}}
\end{gathered}(166)
kde za Rk se dosazuje menší z velikostí Rak, Rlk a γR je dílčí koeficient bezpečnosti odporu kotvy rovný 1,1 pro dočasné i trvalé kotvy.
Je-li kotva namáhána navíc střihem a ohybem, platí:
\begin{gathered}
R_\text{d}=\gamma_\text{q}\cdot P_0
\end{gathered}(167)
kde je:
γq … koeficient tahové síly, jež se pohybuje obvykle v mezích: 0,8 ≤ γq ≤ 1,1 a zohledňuje:
- relaxaci kotevního táhla;
- tečení kořene;
- posun kotvené konstrukce v oblasti hlavy kotvy;
- posun stavební konstrukce jako tuhého tělesa k počátku mezního stavu.
Průkaz mezního stavu použitelnosti kotvené konstrukce se provádí tak, že do výpočetních schémat se dosadí charakteristické hodnoty působení, vlastností základové půdy a geometrických rozměrů. Stanoví se velikosti deformací, které se porovnají s deformacemi přípustnými. Je-li vypočtený (nebo odhadovaný) posun větší než přípustný, je třeba jej zdůvodnit podrobnějším šetřením nebo zkouškami. Pokud to nevede k cíli, je třeba změnit projekt.
4.9 KLASICKÉ INJEKTÁŽE
Injektování je činnost, při níž se do základové půdy vpravuje (injektuje) injektážní směs z injektážních vrtů pod určitým (injektážním) tlakem a v určitém množství. Klasické injektáže se řídí evropskou normou ČSN EN 12715 Provádění speciálních geotechnických prací – Injektáže, jež byla vydána v roce 2000. Injektáže se dělí podle různých kritérií, nicméně v souladu s výše uvedenou normou rozeznáváme následující druhy injektáží (tab. 53).
V souvislosti s výše uvedeným dělením klasických injektáží jsou v tab. 54 uvedeny typické druhy injekčních směsí pro různé druhy základových půd.
Tab. 53 Principy a metody klasických injektáží
| Klasická injektáž | Princip injektáže | Podskupina | Metoda injektáže |
| průniková (impregnační) | |||
| penetrační | |||
| bez přetvoření základové půdy | kontaktní (injektáž puklin) | ||
| výplňová | (výplňová) | ||
| klakáž | |||
| s přetvořením základové půdy | |||
| zhutňovací injektáž |
Tab. 54 Druhy klasické injektáže a injektážní směsi pro různé druhy základových půd
| Injektované prostředí | Druh základové půdy | Injektáž bez přetvoření v hornině | Injektáž s přetvořením | ||
| průniková | kontaktní, nebo inj. puklin | výplňová | |||
| zrnité (nesoudržné) zeminy | štěrk, písčitý štěrk a hrubý písek, kx > 5 · 10-3 |
jílocementové, popř. cementové suspenze | |||
| písek 5 · 10-5 < k < 5· 10-3 |
velmi jemné suspenze (mikrodur) | jílocementové suspenze | |||
| střední až jemný písek 5 · 10-6 < k < 1 · 10-4 |
velmi jemné suspenze, chemické suspenze | ||||
| rozpukané skalní horniny | poruchy, trhliny krasové dutiny exx > 100 mm |
malty a suspenze na bázi cementu a jílocementu | malty, suspenze cementové, rozpínavé polyuretany | ||
| trhliny, pukliny 0,1 < e < 100 mm |
cementové suspenze | ||||
| vlasové pukliny e < 0,1 mm |
velmi jemné suspenze, křemičité gely, chemické směsi | ||||
| dutiny, kaverny | velké dutiny | ||||
| kx je součinitel filtrace [m · s-1]; exx je šířka puklin [mm] | |||||
Vysvětlení některých pojmů:
- injektáž bez přetvoření základové půdy zahrnuje náhradu přirozeného obsahu kapaliny (popř. plynu) v přístupných pórech a dutinách základové půdy injekční směsí bez významného přetvoření základové půdy;
- injektáž s přetvořením základové půdy zahrnuje násilné vniknutí injekční směsi způsobující deformace v základové půdě;
- při penetrační injektáži jde o vyplnění spár a diskontinuit v hornině, nebo pórů v zemině bez vzniku přetvoření; penetrační injektáž je buď impregnační (průniková), nebo injektáž kontaktní, při níž jde vyplnění spáry mezi stavební konstrukcí a horninou, nebo injektáž puklin především v horninách;
- výplňová injektáž má za úkol vyplnit dutiny větších rozměrů injekční směsí, vesměs pak zrnitou;
- klakáží nazýváme trhání horniny způsobené injektáží vody nebo injektážní směsi tlakem, jež překonává lokální tahovou pevnost horniny a původní tlak v hornině;
- zhutňovací injektáž je technologický postup způsobující přetvoření v základové půdě, při němž dochází k vtlačování injektážní směsi do základové půdy bez vzniku trhlin;
- injektážní tlak je tlak aplikovaný během injektáže měřený obyčejně za injektážním čerpadlem nebo u ústí vrtu;
- účinný tlak je skutečný tlak působící v injektovaném prostředí;
- injektážní směs je čerpatelný materiál (suspenze, roztok, emulze nebo i malta) injektovaný do základové půdy, který má jisté vlastnosti a tuhne a tvrdne v jistém čase;
- suspenze je směs kapaliny a pevných částic, jež se při tečení chová jako Binghamova kapalina, tzn. vyznačuje se jistou viskozitou, popř. i kohezí;
- stabilní suspenze se vyznačují nepatrným odstojem vody (po 2 hodinách < 5 %);
- koloidní suspenze (roztoky) jsou injektážní směsi s uměle vytvořenou soudržností, v nichž jsou pevné částice nebo molekuly dokonale rozptýleny a zůstávají trvale ve vznosu (injektážní směs se nesegreguje a má nulový odstoj vody);
- pravý roztok je kapalina vzniklá 100% rozpuštěním chemické látky ve vodě;
- malta je zrnitá směs obsahující písek (lze připustit i frakci do 4 mm);
- manžetová trubka je injektážní trubka perforovaná v určitých intervalech (etážích); otvory jsou z vnější strany překryty gumovými manžetami ve formě krátkých hadic, jež působí jako jednosměrné ventily (obr. 66);
- obturátor je zařízení vkládané do manžetové trubky nebo do vrtu s dostatečně stabilními stěnami, jímž se vrt (manžetová trubka) rozděluje na injektované části; obturátor obvykle pracuje na principu utěsnění vrtu (manžetové trubky) vlastním rozepnutím, které je aktivováno mechanicky, hydraulicky nebo pneumaticky (obr. 67);
- jednoduchý obturátor je necirkulační obturátor s jedním prstencem utěsnění (obr. 67a);
- dvojitý obturátor je zařízení skládající se z dvojice těsnění (pakrů) upevněných k injektážní trubce v předem určené vzájemné vzdálenosti používané k omezení injektáže do základové půdy mezi těmito dvěma těsnicími prvky, tj. K vymezení injektáže na příslušnou etáž (obr. 67b).
V praxi se stále používá jednodušší rozdělení klasických injektáží podle následujících kritérií:
A. podle účelu:
- těsnicí, kdy hlavním účelem je zmenšení velikosti koeficientu filtrace základové půdy, a tím snížení její propustnosti;
- zpevňovací, kdy účelem je zvýšení smykové pevnosti základové půdy, a především zvýšení jejího modulu deformace za účelem omezení přetvoření základové půdy;
- kompenzační, kdy hlavním účelem je postupné omezování deformací základové půdy zvláště v oblasti stávající zástavby, projevujících se např. při ražbě podzemních děl, nebo realizaci hlubokých výkopů.
B. podle druhu základových půd:
- injektáž hrubozrnných zemin, kdy jde především o injektáž těsnicí, s níž je spojeno i zlepšení pevnostních a deformačních charakteristik;
- injektáž jemnozrnných zemin, kdy jde především o zlepšení pevnostních a deformačních charakteristik základové půdy nebo o zvedání a dorovnávání stavebních objektů; provádí se vesměs klakáž, tzn. injektáž s výrazným přetvořením základové půdy;
- injektáž skalních a poloskalních hornin, kdy jde především o těsnění jejich puklin, spár, diskontinuit a o vyplňování puklin.
C. podle druhu injektážních směsí:
- silikátové injektážní směsi a malty, kde hlavní složkou ovlivňující výsledné vlastnosti injekční směsi je cement;
- chemické suspenze a roztoky (tvrdé a měkké gely – směsi na bázi vodního skla, organické pryskyřice – akrylátové, polyuretany, fenolické a epoxidové).
Obr. 66 Manžetová trubka z plastu: 1 – manžetová trubka, 2 – pryžová manžeta, 3 – otvor
Obr. 67 Schéma obturátorů: a) jednoduchý necirkulační, b) dvojitý necirkulační
Technologický postup provádění klasických injektáží zahrnuje následující výrobní fáze:
- vrtání maloprofilových (popř. středněprofilových) vrtů;
- vystrojení vrtů pro účely klasických injektáží;
- příprava injekční směsi;
- vlastní injektáž, popř. reinjektáže;
- monitoring a kontrola prací.
Injektování je činnost, pro jejíž kvalitní zvládnutí jsou zapotřebí dobré znalosti z inženýrské geologie, mechaniky zemin a hornin, ale současně i značná dávka inženýrského citu, který lze získat pouze praxí. Příkladem může být Ing. Jaroslav Verfl, DrSc., který celý svůj profesní život zasvětil rozvoji injektážních prací, a to především v úzkém sepětí se stavbami (přehrady a nádrže, velké vodní stavby, stavební jámy apod.). Jeho zkušenosti jsou shrnuty v monografii [6], která tvoří základní literaturu tohoto oboru.
Provádění injektážních vrtů se v podstatě neliší od provádění vrtů pro mikropiloty a kotvy, jak bylo probráno v příslušných kapitolách. Samozřejmě převažuje bezjádrové vrtání, přesto jsou v některých případech požadována jádra, a to zvláště v případě kontroly provedených injektážních prací. Zde přichází v úvahu většinou diamantové vrtání v horninách (nevyjímaje systém wire-line), v zeminách pak vrtání roubíkovými korunkami na dvojitou jádrovku.
Injektážní vrty se vesměs vystrojují manžetovými trubkami za účelem řízené injektáže. Jedná se o patent firmy Soletanche pocházející z 50. let 20. století a znamenající kvalitativní skok nejen v případě klasických injektáží, ale současně umožňující realizaci mikropilot a injektovaných kotev, a to především v zeminách. Při injektování hornin lze si představit injektáž bez použití manžetových trubek, a to v těch případech, kdy stěny vrtu jsou dostatečně stabilní v celém průběhu injektáže. Přesto i těchto případech se používají manžetové trubky, které se zapouštějí do vrtů opatřených zálivkou. Zálivka má za úkol upevnit manžetovou trubku ve vrtu, a především znemožnit odtok injekční směsi podél stěn vrtu. Kvalitou zálivky, tedy především její pevností a časovým nárůstem této pevnosti lze ovlivňovat počátek i průběh injektáže. Na rozdíl od zálivky pro mikropiloty a kotvy není potřebné, aby měla velkou pevnost a kladla velký odpor proti protržení. Na druhé straně se však ukazuje, že na trhací tlak má podstatně větší vliv pevnost okolní základové půdy než pevnost zálivky. Proto se využívá zálivky, která má mít pevnost kolem 0,5–1,0 MPa/14 dní. Pro tyto účely se hodí nejlépe jílocementová zálivka o složení c : j = 5 : 1, jež má následující složení (na 1 000 l):
- 400 kg cementu CEM II/A (popř. B – S);
- 80 kg aktivovaného bentonitu;
- 841 l vody;
a základní vlastnosti:
- objemová hmotnost γ = 1,32 t·m-3;
- viskozita Marsh 35 – 38 s;
- dekantace max. 1 % za 3 hodiny;
- pevnost v prostém tlaku 0,4 MPa/7 dní a 1,0 MPa/28 dní.
Za manžetové trubky se hodí v podstatě jakékoliv trubky (ocelové, z umělé hmoty), pokud mají hladký a pravidelný vnitřní povrch. S ohledem na unifikované obturátory se pro klasické injektáže nejvíce používají polyetylenové trubky průměru 50 / 3,9 mm s manžetami po 0,33 m (tedy 3 etáže na 1 bm). Dva injektážní otvory v trubce umístěné proti sobě a posunuté výškově o 20 mm mají průměr 8 mm a jsou překryty gumovou manžetou tl. 3,5 mm délky 80 mm. V současné době se manžetové trubky vyrábějí a odpadají tak problémy s ochranou manžet proti strhnutí (obr. 66). Podstava manžetové trubky je zaslepena, v případě, že injektáž není plánována až k ústí vrtu, použije se příslušně dlouhý nástavec z hladké trubky stejného průměru.
Pro vlastní realizaci a usměrnění injektáže se používají obturátory, které buď těsní vrt či manžetovou trubku v jednom místě, a znemožňují tak průniku směsi nad toto místo (jednoduché obturátory), nebo vymezují zdola i shora injekční etáž (dvojité obturátory). Jejich princip je na obr. 67. Jednoduchý necirkulační obturátor se používá při sestupné i vzestupné provozní injektáži hornin a při vodních tlakových zkouškách. Injektuje-li se nestabilní (cementovou) suspenzí, dochází k sedimentaci cementových zrn na dně vrtu a k zalepování puklin v hornině, které pak nelze injektovat. Tuto nevýhodu odstraňuje cirkulační obturátor, jež umožňuje propláchnutí vrtu a výměnu injektážní směsi při zachování tlaku. Má však průměr nejméně 76 mm (lépe 93 mm) a hodí se hlavně pro průzkumné práce, neboť umožňuje měření tlaku přímo ve zkoušené etáži při vyloučení tlakových ztrát vzniklých odpory při proudění v přívodním potrubí. S ohledem na jeho velikost a stále častější používání jemně mletých cementů jeho význam upadá. Dvojitý necirkulační obturátor se používá především pro injektování v zeminách přes manžetovou trubku. Původní obturátory se upínaly mechanicky – šroubováním, při němž docházelo ke stlačování a současně roztahování gumového pakru. Současně vyráběné obturátory se aktivují především pneumaticky pomocí neoprénové hadičky průměru 5 mm, a to stlačeným vzduchem z ocelové láhve. Některé obturátory lze též upínat tlakovou vodou.
Nejpoužívanější injektážní směsi na bázi silikátů se vyrábějí v aktivačních míchačkách, kde dochází k rozbití jemných částic cementu, což má za následek zvětšení plochy jejich povrchu a vede k výrazné aktivaci. Takto vyrobená směs po aktivaci trvající asi 2 minuty se přepouští do pomaloběžné míchačky, která při frekvenci otáčení lopatek asi 30x za minutu udržuje směs v pohybu. Vyrobenou jílocementovou injektážní směs lze v této míchačce udržovat po dobu asi dvou hodin. Pokud do té doby není zpracována, neměla by být přidána do nové záměsi. Chemické směsi se připravují v automatických míchacích centrech, z nichž se přepouštějí do dávkovačů. Doba jejich skladování závisí především na druhu směsi a na účinnosti příslušného reaktivu.
Vlastní injektáž se provádí pomocí čerpadel, která musí mít řiditelný tlak i množství směsi.
Čerpadla jsou:
- tlakové (Wolfholzovy) kotlíky o objemu 30 až 300 l, kde namíchaná směs se vzduchotěsně uzavře a pomocí tlakového vzduchu se rozvádí; tato zařízení se v současné době používají zcela výjimečně, např. pro injektáž zdiva malého rozsahu;
- pístová čerpadla (např. od firmy Atlas-Copco) s vyměnitelnými písty a válci;
- plunžrová čerpadla (např. od firem Hänny, Klaus Obermann, Clivio apod.).
Moderní, hydraulicky ovládaná čerpadla se vyznačují řiditelným tlakem v rozmezí 0–16 MPa a řiditelným množstvím 0–11 l/min, v případě pístových čerpadel i např. 65 l/min. Pro dopravu malt se používá šnekových čerpadel (např. od firmy Putzmeistr). Pokud se požaduje čerpání velkého množství jílocementové suspenze k výplni velkých kaveren apod., používá se klasických kalových čerpadel (např. GFMU, UZA i FLYGHT).
Pro návrh a projekt injektážních prací jsou zapotřebí následující podklady:
- geotechnické;
- geometrické (situace a výškopis staveniště a jeho okolí);
- stavební (údaje o stavebním objektu a o objektech sousedních – stavební stav, druh a hloubka založení apod.);
- údaje o podzemních inženýrských sítích;
- údaje o všech současných a následujících aktivitách na staveništi, které by mohly injekční práce ovlivnit (např. čerpání podzemní vody, její vsakování, tunelářské práce, hluboké výkopy);
- požadavky kladené na dozor, monitoring a zkoušení v době provádění injektáže a po jejím zkoušení.
Kromě toho se vždy vyplatí získat informace o jakýchkoliv zkušenostech s předchozími injektážními pracemi na staveništi nebo v jeho blízkosti, jakož i o zkušenostech s injektážními pracemi na staveništích s podobnými geotechnickými poměry. Rovněž tak je dobré seznámit se s projektovou dokumentací předchozích injektážních prací, je-li to možné.
Geotechnický průzkum má kromě základních údajů o geologické stavbě území a vlastnostech jednotlivých geotechnických typů (podle ČSN EN 1997-1):
- stanovit injektovatelnost základových půd;
- poskytnout podklady pro výběr injektážních hmot.
Injektovatelnost základových půd souvisí především s jejich propustností, která v případě skalních a poloskalních hornin závisí především na jejich puklinatosti, vrstevnatosti a ostatních plochách diskontinuit, v případě zemin pak především na granulometrickém složení a na pórovitosti. Injektovatenost skalních a poloskalních hornin se stanovuje především pomocí vodních tlakových zkoušek. Injektovatelnost hrubozrnných zemin, jako jsou štěrky a písky, se stanovuje jak na základě laboratorních, tak i polních zkoušek. V případě zkoušek laboratorních to je zejména zrnitostní rozbor a z něho vyplývající křivka zrnitosti, jednak pórovitost, jejíž stanovení je ovšem obtížné. V případě zkoušek polních jde především o čerpací zkoušky, výjimečně zkoušky vsakovací a event. o zkoušky penetrační, na jejichž základě lze odvodit ulehlost hrubozrnných zemin. V případě zemin jemnozrnných nelze hovořit o klasické injektáži, neboť póry těchto zemin jsou tak malé a nepropojené, že jejich vyplňování injektážní směsí není reálné. V těchto případech tedy klasická injektáž probíhá formou klakáže, kdy v první fázi dojde k porušení struktury zeminy a vytvoření trhlin, které se v druhé fázi vyplní injektážní směsí.
Zvláště v případech rozsáhlých projektů injektážních prací se má navrhnout zkušební injektáž na zkušebním injektážním poli, a to za účelem určení, nebo potvrzení zvolené metody injektážních prací. Toto pokusné pole má být považováno za součást průzkumu na staveništi. Má být provedeno vždy, když předběžné průzkumy a místní nebo srovnatelné zkušenosti nejsou dostatečné k potvrzení nebo posouzení efektivity navržených injektážních prací. Pokusné pole má poskytnout údaje pro realizační projekt, a to především o vzdálenosti vrtů, injektážním tlaku, spotřebě a druhu injektážní směsi.
4.9.1 Vodní tlakové zkoušky
Vodní tlakové zkoušky (dále jen VTZ) jsou základními zkouškami pro zjištění skutečné propustnosti horniny, kterou uvádíme v souladu s jejich výsledky, např. V litrech za minutu na běžný metr délky vrtu. Kromě toho se v průběhu zkoušek dá orientačně zjistit charakter puklin, jejich výplň a tlak, při němž ještě nedochází k deformaci horniny. V průběhu provádění VTZ dochází často k vypláchnutí a otevření puklin, což usnadňuje jejich následnou injektáž. VTZ lze v zásadě provádět dvojím způsobem:
- vzestupně;
- sestupně.
V případě vzestupné VTZ se vyhloubí vrt na konečnou hloubku a zkouší se jednotlivé etáže od paty vrtu, a to opět dvojím možným způsobem. První spočívá v utěsnění určitého úseku vždy od paty vrtu jednoduchým obturátorem. Měří se časová spotřeba vody při určitém tlaku. Následně se postoupí o další etáž a zkouška se opakuje. Spotřeba vody na tuto následnou etáž se stanoví jako rozdíl dvou velikostí: spotřeby vody při této zkoušce a spotřeby vody při zkoušce předcházející (samozřejmě při shodném tlaku). V druhém případě se použije dvojitý obturátor a měří se spotřeba vody na každou etáž (uzavřenou dole i nahoře) zvlášť. Vzestupný způsob VTZ je jednoduchý, nicméně nedává přesné výsledky. Především při vrtání na celkovou hloubku dochází k nepříznivému zanášení puklin vrtnou mělí, což zkresluje výsledky. Dále může docházet k úniku vody puklinami, jak je znázorněno na obr. 68.
Obr. 68 Únik vody puklinami při VTZ (podle J. Verfla), a) – vzestupná zkouška za použití jednoduchého obturátoru, b) – vzestupná zkouška za použití dvojitého obturátoru, c) – sestupná zkouška
Při sestupném uspořádání VTZ se vyhloubí vrt vždy na určitou hloubku a provede se zkouška při použití jednoduchého obturátoru u ústí vrtu. Většinou se však jedná o zkoušky hornin, nad nimiž jsou ještě pokryvné útvary. V tom případě se provede vrt většího průměru, do něhož se zacementuje ocelová roura (pažnice). Po zatvrdnutí cementové zálivky se vrt v hornině převrtá na potřebnou délku etáže a obturátor se upne u paty pažnice. Zkoušce následující etáže předchází potřeba prohloubení vrtu o další etáž, když v předchozí etáži byla po zkoušce již provedena injektáž. Sestupný způsob dává většinou podstatně přesnější výsledky, avšak za cenu pomalejšího postupu prací a nutnosti neustálého převrtávání zkušebního vrtu.
Výsledky vodních tlakových zkoušek se vynášejí nejlépe graficky do příslušného profilu vrtu kresleného v jistém měřítku. Osvědčil se ten způsob, kdy obecně přijímanými grafickými značkami se vynese geologický profil vrtu, do něhož lze zaznamenat i další anomálie (např. ztráta jádra, propad nářadí, anomálie zjištěné karotáží apod.) a vedle se vynáší ztráty vody v litrech za minutu při jistém tlaku, a to vždy v příslušném délkovém intervalu, nebo lépe v přepočtu na 1 bm hloubky vrtu. Takovýto podélný profil slouží potom jako podklad pro návrh těsnicí injektáže.
VTZ sloužily již v minulosti především ke stanovení přípustné propustnosti skalního a poloskalního podloží. Lugeon (1933) stanovil jako první kritéria pro tuto propustnost, a to v souvislosti s výstavbou přehrady Sarrans ve Francii, kde skalní podloží tvořila rozpukaná žula. Podle Lugeona nemají ztráty vody u přehrad, vyšších než 30 m, přesáhnout 1 l/min na 1 m délky vrtu při tlaku 1,0 MPa, kdežto u přehrad nižších než 30 m jsou přípustné ztráty 3x větší (při stejném tlaku). Přepočteme-li zhruba toto kritérium, získáme výslednou propustnost prostředí danou koeficientem filtrace k = (4 – 9) · 10-8 m.s-1. Jiné kritérium navrhl Jähde (1953), podle něj je přípustná ztráta 0,1–0,5 l vody na 1 bm vrtu při tlaku 0,3 MPa. Praxe ukázala, že tato kritéria jsou velmi přísná a měla by platit především pro kvalitu horniny v základové spáře přehrady a do hloubky 10–15 m pod ní. Ve větších hloubkách lze podle Verfla [6] povolit i větší ztráty vody, jak ukázal rozsáhlý výzkum zejména na přehradě Velká Morávka.
4.9.2 Injektáž skalních hornin
Účelem injektáže skalních hornin je:
- vytvoření těsnicí clony pod vodním dílem a zvětšení modulu deformace skalního podloží;
- zlepšení geotechnických vlastností hornin;
- vytvoření kontaktu podzemního díla s okolní horninou.
Základní hmotou pro injektáž puklin v horninách je cementová suspenze stabilizovaná jílem, (resp. bentonitem). Vlastní cementová suspenze vyrobená z cementu CEM I, CEM IIA (B-S) není dostatečně stabilní, a to zvláště proto, že cementová zrna mají velikost větší než asi 40–50 μm. Tato zrna v souvislosti se zmenšující se rychlostí injektované suspenze v puklinách rychle sedimentují a zalepují pukliny, které nejsou dostatečně do hloubky zaplněny. Navíc při použití necirkulačních obturátorů zrna cementu sedimentují u dna vrtu a časem prakticky znemožní injektáž. Cementová suspenze se tedy stabilizuje bentonitem, jehož množství závisí jednak na požadované pevnosti výsledného produktu a jednak na velikosti cementových zrn po jejich aktivaci. Přidáním jílu (bentonitu) pevnost suspenze výrazně klesá, proto není obyčejně žádoucí injektovat klasickou jílocementovou suspenzí, např. takovou, jejíž receptura se hodí pro zálivku a je výše uvedena, neboť její pevnost není dostatečná. Obyčejně stačí přidat kolem 10 % bentonitu do cementové suspenze s velikostí zrn kolem 90 μm, ale jsou-li zrna menší (40–50 μm), postačí kolem 2 % bentonitu k tomu, aby suspenze byla dostatečně stabilní. Viskozita příslušné suspenze se kontroluje viskozimetrem Marsh. Při použití mikromletých cementů (Mikrodur, popř. Finosol), kde až 95 % cementových zrn má velikost pod 10 μm, resp. 6 μm, je přidávání bentonitu zbytečné, směs je dostatečně stabilní a její schopnost pronikat i vlasovými trhlinami s šířkou e ≅ 0,1 mm je vynikající. Tyto materiály jsou však často mimořádně drahé a jejich použití je spíše výjimečné. Proto se i nadále na dotěsňování vlasových puklin používá směsí chemických, které se injektují vesměs v druhém pořadí.
V případě návrhu těsnicí clony pod vodním dílem je třeba vzít v úvahu, jedná-li se o gravitační přehradu nebo zemní hráz, bude-li injekční clona navázána na injektážní blok, nebo na injektážní štolu, popř. bude-li navázána na podzemní těsnicí stěnu. Praxe ukázala, že se lépe osvědčuje jednořadá, co nejdokonaleji provedená injektážní clona, která je v horní části doplněna připojovací injektáží, jež brání zbytečnému rozlití injektážní směsi z hlavní řady v horních, propustnějších úsecích. Schéma jednořadé injektáže zavázané do injektážního bloku je na obr. 69. Vrty injektážní clony jsou rozděleny do několika pořadí. Nejprve se hloubí vrty I. pořadí na celkovou navrženou hloubku, přičemž jejich osová vzdálenost bývá průměrně 10 m. Injektuje se obyčejně sestupným způsobem maximálním tlakem, který ještě nezpůsobuje deformace v horninovém prostředí. Následují vrty II. pořadí, jež se navrhují v poloviční vzdálenosti mezi vrty I. pořadí. Jejich délka je cca o 5–10 m menší. Následují pak kratší vrty III. pořadí atd., přičemž výsledná osová vzdálenost vrtů bývá kolem 1,0 m, (vrty V. pořadí), jež zasahují do hl. kolem 10 m. Při provádění jednořadé injektážní clony je třeba dbát na svislost vrtů, kterou je třeba průběžně kontrolovat (inklinometrem) a popř. upravovat (úhybovými klíny, technologií vrtání apod.).
Obr. 69 Schéma jednořadé injektážní clony: a – injektážní blok, I – vrty I. pořadí, II – vrty II. pořadí, III – vrty III. pořadí
V případě sypaných hrází, jejichž podloží je tvořeno zeminami, se jako těsnění základové půdy využívá především podzemních stěn (betonových, popř. ze samotvrdnoucí suspenze, pokud vyhoví hydraulickým gradientům). Podzemní stěna by měla zasahovat do podložní horniny, do níž by měla být připojena injektážní clonou (obr. 70). S ohledem na možné komplikace s následným provrtáváním podzemní stěny (jejíž tloušťka bývá 0,80 m) se v ní někdy ponechávají ocelové, popř. plastové trubky – průchodky, které vedou a usměrňují následné injektážní vrty.
4.9.3 Injektáž hrubozrnných zemin
Podstatou injektáže hrubozrnných (nesoudržných) zemin je co nejúplnější vyplnění jejich pórů za účelem jejich utěsnění, tj. zmenšení průměrné velikosti jejich koeficientu filtrace, přičemž v této souvislosti dochází i k jejich zpevnění, tj. zvýšení jejich smykové pevnosti a zvýšení průměrné velikosti jejich modulu deformace, což vede současně k omezení jejich deformací pod zatížením.
Injektovat hrubozrnné zeminy lze v zásadě následujícími způsoby:
- vzestupně;
- sestupně;
- pomocí manžetových trubek.
Obr. 70 Napojení injekční clony na podzemní těsnicí stěnu: 1 – skalní podloží, 2 – pokryvné útvary, 3 – těsnicí jádro (zemní hráze), 4 – podzemní stěna, 5 – injektážní vrty
Zatímco první dva způsoby jsou spíše historické, v současné době zcela dominuje injektáž pomocí manžetových trubek.
Obr. 71 Injektáž hrubozrnných zemin vzestupným způsobem: a – zaberaněná hladká trubka 1, b – zaberaněná trubka s perforací 1, 2 – přívod injektážní směsi, 3 – zainjektovaná poloha
Při vzestupném způsobu (obr. 71) se používají většinou zaberaněné ocelové silnostěnné trubky vnitřního průměru 60 až 80 mm, jež se zarazí na celkovou hloubku a vnitřek se vyčistí – vypláchnutím vodou. Horní, vyčnívající část trubky se opatří víčkem s manometrem a kohoutem, k němuž se připojí potrubí od čerpadla. Po zainjektování příslušného množství injekční směsi se trubka povytáhne asi o 0,5 m a injektáž se opakuje. Trubky kladou značný odpor proti vytažení, které má probíhat pod injektážním tlakem. Současně je třeba trubku shora zkracovat. Hlavní nevýhodou tohoto způsobu je jednak ta skutečnost, že injektážní směs často vytéká podél trubky, jednak to, že nelze reinjektovat. Proti vnikání materiálu do injektážní trubky lze její konec opatřit speciální špicí.
Při sestupném způsobu (obr. 72) se postupuje tak, že do úrovně, od níž chceme injektovat, osadíme ocelovou pažnici (do cementové zálivky) a na ni nasadíme výplachovou hlavu. Rotačním vrtáním s jílocementovým výplachem lze vynášet materiál z vrtu a po uzavření kohoutu lze injektovat. Nevýhodou je nekontrolovatelné čerpání směsi do jednotlivých hloubkových úrovní a současně nemožnost provrtání větších kamenů ve štěrcích.
Obr. 72 Injektáž hrubozrnných zemin sestupným způsobem: 1 – vrtné nářadí, 2 – výplachová hlava, 3 – uzávěr pažnice, 4 – cementace úvodní pažnice, 5 – zainjektovaná hrubozrnná zemina, 6 – injektovaný úsek
Vynález manžetových trubek v 50. letech minulého století znamenal kvalitativní skok v klasické injektáži, neboť umožnil řízenou injektáž předem stanovených etáží bez výrazného nebezpečí úniku injektážní směsi podél vrtu a současně i reinjektáže ve stejném vrtu.
Hrubozrnné zeminy se vyznačují průlinovou propustností, která souvisí především s pórovitostí a dále i s tvarem zrn (granulometrickým složením). Pórovitost hrubozrnných zemin je asi od 25 do 50 %, což znamená, že pro dokonalé utěsnění pórů je zapotřebí velkého množství injektážní směsi. Její druh a hranice použitelnosti jsou dány např. tab. 51.
V poslední době v souvislosti s vývojem a výrobou ultrajemných cementů (např. firma Dyckerhoff) pod označením Finosol F, U, X dochází ke změně náhledu na použití cementových suspenzí pro injektáž stále jemnějších zemin. Na základě jejich granulometrického rozboru je patrné, do jakých pórů mohou teoreticky vnikat. Vývoj ultrajemných cementů byl urychlen jednak požadavky ekologů, které v podstatě znemožnily použití některých organických pryskyřic (např. močovinoformaldehydových), jednak cenou a vlastnosti některých chemických směsí (např. polyuretanů). Přesto je zatím cena ultrajemných cementů značně vysoká, že ztěžuje jejich větší rozšíření.
Jak vyplývá z tab. 55, je základní směsí pro těsnicí injektáž štěrků jílocementová suspenze klasického složení uvedeného. S ohledem na velké spotřeby hmot a cenu aktivovaných bentonitů je snaha k využití levnějších přírodních jílů. Praxe ukazuje, že se hodí jíly s mezí tekutosti nejméně 90 %. Vyrobená jílocementová suspenze, popř. cemenová suspenze stabilizovaná jílem, musí mít následující vlastnosti, které je třeba zjistit a kontrolovat:
- dobrá zpracovatelnost;
- objemová stálost;
- cenová dostupnost;
- dobrá pronikací schopnost;
- dobrá čerpatelnost;
- odolnost proti erozi;
- vyhovující pevnost v tlaku.
Tab. 55 Příklad vhodnosti použití různých injektážních směsí pro injektáž hrubozrnných zemin (upraveno podle J. Verfla)
| Reologie | Suspenze (Binghamovy kapaliny) | Roztoky (Newtonovy kapaliny) | ||||
| nestabilní | stabilní | koloidní roztoky | čisté roztoky | |||
| druhy směsí | cement | cement + jíl (bentonit) | odvločko- vaný bentonit | chemické směsi | ||
| vodní sklo | organické pryskyřice | |||||
| tvrdý gel | měkký gel | |||||
| použití | pukliny a trhliny v hornině | aluviální náplavy (štěrky a písky) | jemný hlinitý písek | |||
| převládá štěrk | hrubý písek | střední písek | jemný písek | |||
| koeficient filtrace kx) | > 5 · 10-4 | > 5 · 10-5 | > 5 · 10-5 | > 5 · 10-5 1) | > 10-6 2) | |
| specifická plocha zrn Ssxx) | < 50 | < 150 | < 150 | < 400 | < 1 000 | |
| kritérium injektáže | tlak | limitované množství + tlak | ||||
| x) k xx) Ss [cm2·g-1] 1) mez daná vývojem viskozity 2) mez odpovídající normálním podmínkám pro homogenní výplně |
||||||
Zjišťování vlastností injektážních směsí pro injektáž hrubozrnných zemin:
- pevnost v prostém tlaku nebývá u směsí pro těsnění štěrků a písků rozhodující, nicméně potřeba jisté pevnosti existuje, aby byla schopna odolat určitým velikostem hydraulických gradientů a aby nedošlo k porušení její celistvosti. Pevnost v prostém tlaku se zkouší na kostkách s hranou 100 mm, popř. 70 mm, nebo na válečcích o průměru 40 mm a výšce 100 mm. Pevnost se zkouší po 14, 28 a 90 dnech;
- pevnost ve smyku čerstvé suspenze se zkouší na přístroji SNS-2, kdy jde o měření smykového odporu po obvodu rýhovaného válce ponořeného v otáčející se nádobě se suspenzí. Přístroj je schopen změřit velikost smykové pevnosti cca 100 N·m-2;
- propustnost suspenze se zkouší laboratorně v propustoměru s konstantním spádem. Volí se průměr zkušebního válečku 200 mm a jeho výška též 200 mm. Vzorek se podrobí počátečnímu hydraulickému gradientu i = 5, který se postupně zvyšuje až do protržení vzorku;
- viskozita se měří laboratorně nejlépe pomocí rotačního viskozimetru Fann, spíše však při všech příležitostech průtokovým viskozimetrem Marsh. Jedná se o základní zkoušku suspenze. Viskozimetr Marsh je trychtýř o objemu asi 1,5 l zakončený trubičkou průměru 4,8 mm a délky 50,8 mm. Měří se čas v sekundách potřebný k protečení 1 l suspenze;
- odolnost proti korozi je důležitá vlastnost zatvrdlé suspenze s ohledem na její trvanlivost. Suspenze se naleje do válcové nádoby s uzavřeným otvorem na dně o průměru 8 mm. Výška vzorku je 7 cm. V ose vzorku je v době tuhnutí suspenze skleněná trubička průměru 8 mm. Ta se po zatuhnutí suspenze odstraní a přes otvor se nechá proudit voda rychlostí cca 2 m·s-1. Zjišťuje se úbytek směsi erozí proudící vody po 1 hodině;
- odstoj vody (dekantace) vzniká v důsledku sedimentace pevných částí. Odstoj vody nesmí být veliký, aby nedocházelo k usazování cementových zrn ve vrtech, což by ztěžovalo, až znemožnilo průnik směsi do pórů zeminy. Odstoj vody se zkouší v kalibrovaných válcích objemu 1 000 cm3, a to po 24 hodinách. U stabilních směsí má být dekantace nulová.
Pro dotěsňování hrubozrnných zemin se používá chemických směsí, které se v zásadě dělí na:
- koloidní roztoky (evoluční);
- pravé roztoky (neevoluční).
V obou případech jde o kapaliny Newtonovského typu lišící se svojí viskozitou, která je ovšem důležitým faktorem s ohledem na těsnění méně propustných zemin.
Nejdůležitějšími koloidními roztoky jsou chemické směsi vyrobené na bázi vodního skla. Tuhnutí je založeno na principu gelovatění vodního skla po přidání reaktivu, kdy vznikne gel kyseliny křemičité. Tato reakce je rychlá v případě neředěného vodního skla s anorganickým reaktivem, popř. pomalá v případě ředěného vodního skla s organickým reaktivem. Vodní sklo je rozpustný alkalický křemičitan sodný Na2SiO3 nebo draselný K2SiO3, který je dodáván v konstantním složení o hustotě 38 až 40° Bé, což lze převést na hustotu pomocí vztahu:
\begin{gathered}
\rho=\frac{144{,}3}{(144{,}3-\degree\text{Bé})}\space\space[\text{g}\cdot\text{cm}^{-3}]
\end{gathered}(168)
tudíž komerčně dodávané vodní sklo má hustotu ρ = 1,357 – 1,384 g·cm-3. K inovaci chemických injektáží na bázi vodního skla došlo především koncem 60. let minulého století, kdy byly vynalezeny organické reaktivy – jako etylacetát, butylacetát, glyoxal, formamid, u nichž bylo možné dobře regulovat proces tuhnutí. Vývoj těchto reaktiv nadále pokračuje, neboť i směsi typu etylacetát, butylacetát nejsou bez problémů – jsou to hořlaviny I. stupně a při reakci s vodním sklem se vyvíjí čpavek, což nepřispívá k ochraně životního prostředí. Nejmodernější faktiva (např. ACE 1575 od firmy Borden Chemicals) tyto nevýhody nemají, jsou však mimořádně drahé. Přidávají se v množství 5–10 % do ředěného rotoku vodního skla (v poměru cca 3 : 1). Přesto však stále zůstávají chemické směsi na bázi vodního skla základními injektážními hmotami pro dotěsňování hrubozrnných zemin v druhém sledu za suspenzemi jílocementovými a pro těsnění středně a jemně zrnitých písků. V zásadě se dělí na:
- tvrdé gely vyznačující se relativně vysokou pevností (směs písku s gelem má tlakovou pevnost až 3 MPa);
- měkké (plastické) gely vyznačující se vynikající prostupností, neboť jejich viskozita se blíží vodě. Původně se používaly anorganické reaktivy (např. hlinitan sodný), dnes se spíše přikláníme k ředěnému vodnímu sklu a organickým reaktivům.
4.9.4 Injektáž jemnozrnných zemin
Jak bylo uvedeno již v úvodu k této kapitole, nejde v podstatě o injektáž podle obecně přijímané definice, neboť póry jemnozrnných zemin jsou natolik malé a zřejmě i nepropojené, že o jejich vyplňování injekční směsí nelze hovořit. O vlastnostech jemnozrnných zemin rozhoduje jak granulometrické složení, tak především obsah vody, tedy jejich vlhkost a konzistenční meze (mez tekutosti a mez plasticity), které dohromady udávají objektivní vztah pro stanovení stupně konzistence:
\begin{gathered}
I_\text{C}=\frac{(w-w_\text{P})}{(w_\text{L}-w_\text{p})}
\end{gathered}(169)
kde je:
w … aktuální vlhkost (v hmotnostních procentech);
wL … vlhkost na mezi tekutosti;
wP … vlhkost na mezi plasticity;
na jehož základě se stanovuje skutečná konzistence jemnozrnné zeminy. (tab. 56).
Tab. 56 Konzistence soudržných zemin
| Konzistence | Podrobnější rozdělení | Stupeň konzistence IC | Chování zeminy |
| kašovitá | < 0,05 | při sevření se protlačuje mezi prsty | |
| plastická | měkká | 0,05–0,50 | dá se lehce hníst v prstech |
| tuhá | 0,50–1,00 | hněte se obtížně v prstech | |
| pevná | > 1,00 | lze do ní vtisknout nehet | |
| tvrdá | – | vyschlá, drolí se po úderu kladivem |
Konsistenční meze spolu s aktuální vlhkostí současně vyjasňují, jedná-li se o hlínu, (silt), či o jíl, a to na základě Cassagrandeho diagramu plasticity zemin pro částice menší než 0,5 mm.
Z této stručné charakteristiky jemnozrnných zemin vyplývá, že tyto zeminy se vyznačují vesměs malou propustností (danou malou hodnotou koeficientu filtrace k < 10-6 m·s), tudíž obyčejně nevzniká problém utěsnění těchto zemin. Naopak však smyková pevnost těchto zemin a jejich stlačitelnost, závisející hlavně na jejich konzistenci, bývá nedostatečná a hlavním úkolem injektáže je zlepšení právě těchto základních mechanických vlastností. S ohledem na výše uvedenou nemožnost penetrace pórů těchto zemin injektážní směsí, vzniká představa o jejich injektáží taková, že do jejich struktury budou násilně zavedeny prvky, tj. proudy, lasy, pruhy apod. injektáže, které budou působit jednak napětím, které urychlí proces jejich primární konsolidace (disipací pórových tlaků spolu s vytěsňováním vody z pórů), jednak svojí větší pevností přispějí k zvýšení pevnosti skeletu jako celku. Tak vznikly první pokusy s klakáží jemnozrnných zemin, tj. trháním jejich struktury překročením jejich lokální tahové pevnosti. Tato metoda je např. pod názvem Soilfrac® patentována firmou Keller, avšak v České republice byla již dříve vícekrát použita např. pro zvedání obytného domu v Brně-Jundrově a pro zlepšení geotechnických vlastností zemin vyvolaných konsolidačním tlakem injektáže při hloubení průzkumné šachty ve Frenštátě pod Radhoštěm [6]. V poměrně velkém rozsahu bylo využito této konsolidační injektáže (nazvané tamponáží) při hloubení šachty dolu Slaný v hloubkách 500–800 m. Jako hlavní injektážní hmota se používá jílocementová suspenze o složení c : j = 4 – 6 : 1, kterou se jemnozrnná zemina klakuje.
4.9.5 Kompenzační injektáž
Kompenzační injektáž je injektáž, při níž cíleně dochází k přetvoření horninového prostředí, a to vesměs za účelem postupného omezování deformací základové půdy, zvláště v oblasti stávající zástavby, projevujících se např. při ražbě podzemních děl, nebo realizaci hlubokých výkopů, popř. při uvádění stávajících objektů do potřebné polohy (např. zvedáním). Může sem patřit i tzv. konsolidační injektáž, jejímž cílem je jednak urychlení primární konsolidace zemin vyvoláním tlakových napětí, a tím urychlením disipace vody z pórů, jednak zlepšením vlastností základové půdy, při kterém nebude docházet k nedovoleným deformacím. Termín konsolidační injektáž nepopisuje ani princip, ani metodu, proto se většinou nepoužívá. Kompenzační injektáž je v podstatě klakáží, jež vyvolává řízenou deformaci stavebních objektů (vesměs jejich zvedání). Řídit rozsah a šíření trhlin vznikajících klakáží v základové půdě je krajně obtížné. Konečného cíle bývá však dosahováno v průběhu několika fází injektáže spojených s podrobným monitoringem deformací v určitém časovém období. Konečně do oblasti kompenzačních injektáží spadají i injektáže zhutňovací, jejichž principem je vtlačování tuhé (viskózní) zrnité injektážní směsi do základové půdy s cílem posunu skeletu horniny, nebo vzniku deformace. Použití této injektáže je velmi omezené např. na velmi kypré zeminy. Injektážní směs se vtlačuje prostřednictvím injektážních trubek s otevřeným koncem (bez perforace), přičemž její konzistence je taková, že vytvoří homogenní těleso, jež nevniká do pórů základové půdy, ani nevytváří klakážní trhliny.
Kompenzační injektáže se provádějí většinou pomocí vějířů vodorovných, nebo mírně ukloněných vrtů (subhorizontálních), zasahujících pod objekty, které mají být zvedány (rovnány), popř. pod objekty, u nichž jsou očekávány deformace v důsledku následných stavebních prací (např. ražba tunelů, hloubení stavebních jam apod.). Aby bylo možné injektážní vrty vhodně situovat, provádějí se obyčejně ze šachtic realizovaných mimo tyto objekty a zasahujících do potřebných hloubek. S ohledem na potřebu několika fází řízené injektáže, využívá se vždy manžetových trubek (většinou ocelových, popř. i trubek z umělé hmoty) osazených v jílocementové zálivce. Základní hmotou pro konsolidační injektáž je cementová suspenze stabilizovaná bentonitem, přičemž výsledná hustota suspenze bývá 1,65–1,80 t·m3.
Názorným příkladem využití kompenzační injektáže při rovnání deformací stavebního objektu je zvedání železobetonového bazénu v lázeňském komplexu budov v SRN. Bazén nepravidelného půdorysu délky kolem 30 m, největší šířky asi 17 m a hloubky 1,35 m byl postaven na násypu tvořeném údajně hutněným recyklátem z betonové vozovky, který byl sypán na podložní vrstvu měkkých až kašovitých prachovitých zemin s organickými zbytky a s vrstvou rašeliny. Podloží s nepravidelným povrchem pak tvořily tuhé až pevné jíly. Bazén se v průběhu výstavby a po jeho napuštění naklonil a sedl až o 180 mm, přičemž rozdíl mezi sedáním protilehlých hran přesáhl 50 mm. Navržena byla tedy kompenzační injektáž za účelem zvednutí bazénu a vyrovnání rozdílných deformací. Jak vyplývá z obr. 73, bylo na okraji bazénu osazeno celkem 11 měřických bodů a na dně bazénu dalších 15 bodů, na nichž byly sledovány svislé deformace. Konfigurace terénu (bazén byl na násypu) umožnila realizovat injektážní vrty z výkopu, jehož průčelní stěna byla zajištěna hřebíkováním a vrstvou stříkaného betonu. Z ní bylo realizováno celkem 30 injektážních vrtů ve čtyřech úrovních zasahujících pod půdorys bazénu. Vrty délky až 35 m měly sklon 7° a 12° od vodorovné a vystrojeny byly ocelovými manžetovými trubkami. V průběhu 5,5 měsíců provádění kompenzační injektáže došlo k zatlačení celkem 200 m3 injektážní směsi a naměřené zvednutí činilo až 47 mm, přičemž došlo k dostatečnému vyrovnání více sedlé části bazénu, aniž byla jeho železobetonová konstrukce poškozena.
Obr. 73 Kompenzační injektáž při zvedání železobetonového bazénu: a – půdorysné schéma, b – charakteristický řez, 1 – měřické body, 2 – injekční vrty, 3 – pracovní plošina, 4 – bazén, 5 – násyp z recyklátu, 6 – prachovité zeminy s organickou příměsí, 7 – vrstva rašeliny, 8 – tuhý až pevný jíl
Jiným příkladem klasické kompenzační injektáže je postupné vyrovnávání poklesů zástavby ležící v poklesové kotlině raženého tunelu Mrázovka v Praze 5. Šlo především o 3 podsklepené pětipodlažní obytné domy v Ostrovského ulici, pod nimiž procházel tunel v hloubce kolem 12 m. Prognóza chování nadloží stanovená výpočtem při využití měření z ražby průzkumné štoly vedla k nepřípustným deformacím objektů (sedání až 110 mm a sklon poklesové kotliny 0,4 %), což rozhodlo o volbě této metody. Pro realizaci injektážních vrtů byly v Ostrovského ulici navrženy 2 šachty kruhového průřezu o průměru 5 m, hluboké 10,0 m, zajištěné převrtávanými pilotovými stěnami. Z nich byly prováděny vějíře injektážních vrtů ve třech úrovních, jež byly osazeny ocelovými manžetovými trubkami do jílocementové zálivky. Současně byl instalován monitoring svislých deformací, jež sestával z kombinace dvou systémů: optického měření a hydrostatické nivelace. Oba systémy byly plně automatizovány, výsledky měření byly ihned zpracovány pomocí počítače a četnost měření byla volitelná. Hydrostatická nivelace, jež byla použita uvnitř objektu s elektromagnetickými čidly na nosných stěnách a pod stropem suterénu, sestávala z 40 hadicových vodovah, kde byl snímán pohyb plováku ve skleněném válci s vodou. Pro optickou nivelaci byla použita totální stanice Leica TCA 2003 s úhlovou přesností 0,5″. Referenční body byly umístěny na odlehlé zástavbě. Schéma této kompenzační injektáže je na obr. 74. Vlastní kompenzační injektáž probíhala v následujících fázích:
- po vyražení levé boční štoly tunelu pod Ostrovského ulicí (NRTM) došlo k sednutí v maximální velikosti 15 mm. Po zatvrdnutí betonu primárního ostění štoly byla zahájena první fáze kompenzační injektáže (KI), přičemž jejím cílem byla kompenzace této deformace, zpevnění rozvolněného podloží domu tvořeného zvětralou břidlicí a též otestování funkce této injektáže. Během dvou dnů od zahájení 1. fáze (KI) došlo k zastavení poklesů domů a následně pak ke kompenzacím deformací rychlostí až 2 mm/den. Celkově byly vzniklé deformace kompenzovány až ze 69 % (tj. cca o 10–11 mm);
- ražba pravé boční štoly způsobila sedání o velikosti 10 mm na fasádě domu nad tunelovou troubou. Je zřejmé, že se zde již projevil účinek 1. fáze KI. Nastala 2. fáze KI, jež kompenzovala vzniklé deformace téměř ze 100 %;
- při následné ražbě kaloty a odstranění vnitřních bočních stěn došlo k sedání o velikosti kolem 18 mm, maximálně pak 23 mm. Ukázalo se tedy, že tyto deformace ne- jsou již pro zástavbu nebezpečné, a není tedy nutná další fáze KI.
4.9.6 Monitoring a kontrola provádění injektážních prací
Realizace injektáží je úzce spojena s dohledem, monitoringem a kontrolou, jež poskytují zpětnou vazbu a umožňují operativní změny v průběhu provádění. Dohled nad prováděním injektážních prací se stanoví již v projektové dokumentaci, přičemž sledována musí být každá etapa prací. Dohled musí být tedy organizován kontinuálně a všechna pozorování musí být porovnána s parametry a předpoklady návrhu. Pokud se výsledky pozorování výrazně liší od návrhu, musí být zjištěna příčina vzniku odchylek a návrhové parametry, nebo parametry provádění musí být upraveny s ohledem na nové podmínky. Záznamy z provádění musí obsahovat všechna data ze sledování všech etap prací.
Před zahájením prací má být provedeno zaměření a pasportizace všech objektů a zařízení, jež se pravděpodobně nacházejí v oblastech ovlivněných injektáží. Výsledky pasportizace se průběžně kontrolují v době provádění injektáží. Typ, dosah a přesnost měření prováděných v rámci monitoringu na staveništi a mimo ně musí být v projektové dokumentaci jasně specifikovány. Příslušná zařízení musí být uvedena v činnost před zahájením vlastních prací. Je vhodné využívat počítačové systémy zejména:
- k monitoringu vrtání;
- k měření, kontrole a interpretaci vrtných parametrů;
- k měření a záznamům injekčních parametrů různých směsí injektovaných v různých fázích.
Veškeré monitorované parametry musí být zaznamenávány v čase a musí být ihned k dispozici (např. tištěnou formou), současně však musí být vhodným způsobem zálohovány a skladovány na bezpečném místě.
a)
b)
Obr. 74 Kompenzační injektáž pod zástavbou v souvislosti s ražbou tunelu: a) půdorysné schéma, b) charakteristický řez
V průběhu vrtání mají být zaznamenány následující parametry, jejichž interpretace poskytne velmi cenné informace o skutečných změnách geotechnických podmínek:
- rychlost postupu vrtání;
- tlak a množství výplachu;
- odvozená vrtná energie;
- otáčky vrtného nářadí;
- kroutící moment;
- přítlak;
- hloubka vrtu.
Kvalita a konzistence injektážní směsi musí být udržována prováděním kontrolních zkoušek, jejichž cílem je sledování souladu měřených parametrů s parametry požadovanými. Minimální požadavky na realizaci rutinních testů na staveništích jsou uvedeny v tab. 57, přehled o měření parametrů různých typů injektážních směsí je v tab. 58.
Tab. 57 Kontrolní zkoušky injektážních směsí – minimální požadavky
| Suspenze | Velmi jemné suspenze | Roztoky (chemické směsi) | Malty |
| hustota | hustota | hustota | hustota |
| viskozita (Marsh) | velikost zrn | doba tuhnutí | zpracovatelnost |
| doba tuhnutí | viskozita | – | – |
| odstoj vody | odstoj vody | – | – |
4.9.7 Dokumentace injektážních prací
Injektážní práce je třeba důsledně dokumentovat, a to nejlépe v soulasu s ČSN EN 12715: Provádění speciálních geotechnických prací – Injektáže. Na staveništi musí být k dispozici následující dokumenty:
- zpráva o geotechnickém průzkumu staveniště, která obsahuje veškeré údaje použité při zpracování projektové dokumentace;
- organizační schéma, které jasně stanovuje rozhodovací pravomoci řídicího personálu zúčastněných stran;
- technologický předpis, odsouhlasený zodpovědnými zástupci zúčastněných stran, v němž jsou stanoveny cíle injekčních prací a detailně rozpracovány pracovní postupy k jejich dosažení; současná též měřitelná kritéria pro budoucí hodnocení dosažení cílů injektáže.
Technologický předpis je základním dokumentem pro zahájení prací a musí obsahovat:
- detailní výkresy vrtů stávajícího objektu, geotechnické poměry, úrovně podzemní vody, navrhované hranice stavby a hranice navržených injekčních prací;
- detailní návrh směsi, očekávaná spotřeba směsi v jednotlivých etážích každého vrtu, postup injektáže, maximální injekční tlak a očekávanou rychlost čerpání směsi;
- návrh monitoringu prováděného na staveništi, jakož i údržby a dalších prací prováděných do doby převzetí injekčních prací.
Na staveništi musí být vedena následující dokumentace:
- denní záznam o průběhu vrtání a injektování;
- měsíční výkazy s denním postupem injektážních prací a spotřebami injektážních hmot;
- závěrečná zpráva obsahující závěrečné zhodnocení injektáže vč. příslušných technických detailů, jakož i souhrnného objemu prací;
- zpráva o převzetí prací po jejich ukončení, v níž zúčastněné strany potvrdí dosažení akceptačních kritérií, definovaných v technologickém postupu.
Tab. 58 Měření parametrů injektážních směsí
| Parametr | Jednotka | Přístroj/metoda | Použití | Roztok | Suspenze | Malta |
| doba průtoku (viskozita průtoková) | [s] | Marshův kužel (průměr otvoru 4,75 mm), popř. jiné průtokové viskozimetry | laboratoř + stavba | NP | A | A |
| viskozita (dynamická) | [Pa·s] | rotační viskozimetr reometr | laboratoř + stavba | A | A | NP |
| hustota | [kg·m-3] | pyknometr, odměrná kádinka, výplachové váhy (baroid) | laboratoř + stavba | A | A | A |
| koheze, mez tečení, smyková pevnost | [Pa] | rotační viskozimetr, reometr, deska přístroj na měření koheze kasumetr, střihoměr | laboratoř | NP | A | NP |
| schopnost vázat vodu | [m3] | Baroidův filtrační přístroj (nízkotlaký) | laboratoř + stavba | NP | A | A |
| odstoj, sedimentace | [%], nebo [m3/m3/2h] | odměrný válec | laboratoř + stavba | NP | A | A |
| zpracovatel-nost | [mm] | Abramsův kužel | laboratoř + stavba | NP | NP | A |
| doba tuhnutí | [s], [hod.] | nakláněná skleněná kádinka, Vicatova jehla | laboratoř + stavba | A | A | A |
| doba tvrdnutí | [s], [hod.] | vrtulková zkouška, smykový přístroj, měření pevnosti v prostém tlaku | laboratoř + stavba | A | A | A |
| konečné ztvrdnutí deformace konečná pevnost | – [%] [MPa] | měření pevnosti v prostém tlaku, měření poměrného přetvoření, mriaxiální zkouška, modový zátěžový test | laboratoř | A | A | A |
| odolnost | – | mechanická: – průtokový test chemická | laboratoř | A | A | A |
| tixotropie | [Pa·s] | reometr, viskozimetr, hydrometr | laboratoř | NP | A | NP |
| synereze | [obj.] [%] | objem vody vyloužený ze vzorku za určitý čas | laboratoř | A | NP | NP |
| smršťování / rozpínavost | [% objemu, ev. délky] | určení meze smrštění | laboratoř + stavba | A | A | A |
| granulometrie | měření velikosti zrn | laboratoř | NP | A | A | |
| schopnost pronikání | – | injekční test injektáž do pískové kolony | stavba (laboratoř) | A | A | NP |
| A = použitelné, NP = není použitelné / obecně není používáno | ||||||
Pracovní záznamy musí obsahovat:
a) všeobecné údaje:
- data prováděných prací;
b) vrtání
- číslo a umístění, délku, průměr, směr a sklon vrtu (popř. injektážního místa);
- jméno obsluhy vrtné soupravy;
- vrtný mechanismus a metoda vrtání;
- typ vrtného výplachu;
- vystrojení vrtu (např. pažnice, manžetová injektážní trubka, typ zálivky apod.);
- zvláštní jevy zaznamenané v průběhu vrtání a instalace vystrojení (např. ztráta výplachu, ztráta zálivky apod.);
c) míchání směsi a injektáž:
- složení směsi (typ a dávkování) a její kontrolní parametry;
- objem směsi injektovaný do základové půdy (spotřeba), tlak a doba provádění každé fáze;
- interakce s ostatními vrty a zjištěné průsaky;
- jakékoli neobvyklé jevy a pozorování;
d) kontrola
- vzorkování injektážní směsi;
- počet vzorků pro laboratorní rozbor;
- rutinní kvalitativní rozbory;
- jména obsluhy a její kvalifikace.
4.10 TRYSKOVÁ INJEKTÁŽ (TI)
4.10.1 Definice, druhy TI, oblast použití TI
Trysková injektáž (TI) je metoda zlepšování vlastností základové půdy založená na rozrušení struktury základové půdy v okolí vrtu vysokou mechanickou energií tryskaného média, jejího částečného nahrazení a smíchání rozrušené základové půdy s cementačním pojivem. Technologie tryskové injektáže (dále jen TI) se vyvíjela v posledních 30–40 letech a podstatně se liší od technologie (klasické) injektáže popsané v kapitole 4.9. Provádění, zkoušení a monitoring TI se řídí ustanoveními evropské normy ČSN EN 12716: Provádění speciálních geotechnických prací – Trysková injektáž. Podle metody provádění se TI dělí následovně:
- jednofázový systém (někdy nesprávně popisovaný jako M1, R1), při němž se rozrušování zeminy, jakož i její zpevnění dosahuje jedním médiem o vysoké mechanické energii, obyčejně paprskem cementové suspenze (obr. 75);
- dvojfázový systém vzduchový (někdy nesprávně popisovaný jako M2, R2), zahrnující technologii TI, při níž rozrušování zeminy a její zpevnění se dosahuje vysokou mechanickou energií tryskaného paprsku, zpravidla cementové suspenze, za podpory stlačeného vzduchu jakožto druhého média (obr. 76). Stlačený vzduch obyčejně obaluje paprsek cementové suspenze a činí jej průraznějším;
- dvojfázový systém vodní (někdy nesprávně označovaný jako M2, R2 s vodním předřezem), zahrnující technologii TI, při níž je rozrušování zeminy dosaženo pomocí vysoké mechanické energie vodního paprsku a zpevnění nastává odděleným paprskem injekční směsi, vesměs cementové (obr. 77);
- trojfázový systém (někdy nesprávně označovaný jako M3, R3), což je technologie TI, při níž je rozrušování zeminy dosaženo vysokou mechanickou energií vodního paprsku za podpory stlačeného vzduchu a zpevnění nastává odděleným paprskem injekční směsi, vesměs cementové (obr. 78).
Obr. 75 Schéma technologie provádění jednofázové TI: 1 – monitor, 2 – kulička
Obr. 76 Schéma technologie provádění dvojfázové vzduchové TI: 1 – monitor, 2 – paprsek cementové suspenze, 3 – stlačený vzduch
Jednotlivé druhy TI se volí s ohledem na geotechnické poměry na staveništi, na geometrický tvar výsledných prvků TI, popř. konstrukcí z TI, jakož i s ohledem na výsledné vlastnosti prvků i konstrukcí z TI. Obecně platí, že čím vyšší stupeň TI, tím větší jsou výsledné rozměry jednotlivých prvků, jejichž realizace se však stává náročnější a často „agresivnější“ k zemnímu prostředí, a zvláště pak ke stavebním konstrukcím. Proto se jednotlivé metody různě kombinují za účelem dosažení nejlepšího efektu v daných geotechnických podmínkách a s ohledem na výsledné parametry jednotlivých prvků či konstrukcí. Trojfázová TI se ovšem používá zřídka, neboť pro její realizaci je třeba ve vrtném soutyčí vést 3 oddělená média (vodu, vzduch, cementovou suspenzi), což klade značné nároky jak na vlastní zařízení, tak na technologii provádění. Celkově je však třeba zdůraznit, že provádění TI je mimořádně specializovanou a náročnou technologií, jež vyžaduje speciální, kvalitní a mimořádně nákladné zařízení, kvalifikované a zodpovědné pracovníky, a zvláště dostatek zkušeností, které lze získat pouze dlouhodobou praxí. Jsme tedy většinou svědkem takového stavu, kdy jednotlivé firmy, provádějící TI, zkušenosti nepředávají, naopak je chrání jako své „know-how“ a využívají je ve snaze získat konkurenční výhodu.
Obr. 77 Schéma technologie provádění dvojfázové vodní TI: 1 – monitor, 2 – vodní paprsek, 3 – paprsek cementové suspenze
Obr. 78 Schéma technologie provádění trojfázové TI: 1 – monitor, 2 – vodní paprsek, 3 – stlačený vzduch, 4 – paprsek cementové suspenze
Pro lepší porozumění technologii provádění TI uvádíme následující pojmy a definice:
- prvek TI je objem zeminy upravené TI jedním vrtem, hlavní užívané prvky jsou:
- sloup TI – válcový prvek vytvořený pomocí TI, kdy se monitor otáčí (obr. 79a);
- lamela z TI – plošný prvek vytvořený pomocí TI, kdy se monitor neotáčí (obr. 79b);
- konstrukce z TI je sestava prvků TI, jež se částečně, nebo zcela dotýkají, či překrývají; nejvíce užívané konstrukce z TI jsou:
- stěna z TI – stěna vytvořená z jednotlivých prvků TI (obr. 80);
- deska z TI – horizontální konstrukce vytvořená pomocí spojených vertikálních sloupů TI omezené výšky (obr. 81);
- klenba z TI – konstrukce vytvořené z horizontálních, popř. mírně (od vodorovné) ukloněných sloupů TI (obr. 81);
- blok z TI – třírozměrná konstrukce vytvořená většinou ze sloupů TI;
- vrtná souprava pro TI – běžná rotačněvrtná souprava pro maloprofilové (vesměs bezjádrové) vrtání umožňující automatickou regulaci rotace a posuvu vrtného soutyčí a nářadí;
- vrtné soutyčí pro TI – vrtné soutyčí s jednoduchými, dvojitými, popř. i trojitými vnitřními kanály umožňujícími vést jednotlivá média k monitoru;
- monitor je nástroj montovaný na konec soutyčí (resp. mezi konec soutyčí a vrtný nástroj), umožňující tryskat paprsek (paprsky) tekutého média (médií) TI do základové půdy;
- tryska je speciální výměnný prvek montovaný do monitoru zprostředkující transformaci média TI ve vrtném soutyčí do paprsku tryskajícího do základové půdy; trysky jsou obyčejně vyrobeny ze slinutých karbidů, nebo ze speciální keramiky a mají různé tvary i průměry otvorů;
- pomoměr účinnosti TI je účinný dosah paprsku rozrušujícího zeminu, měřený od osy monitoru;
- vyplavený materiál je přebytek směsi částic rozrušené zeminy a média TI vznikající při jejím provádění a obvykle vytékající na povrch terénu mezikružím vrtu pro TI;
- parametry TI jsou definovány následovně:
- tlak média TI uvnitř vrtného soutyčí pro TI;
- průtok média uvnitř vrtného soutyčí pro TI;
- složení injekční směsi;
- rychlost rotace vrtného soutyčí pro TI (při provádění sloupů TI);
- rychlost vytahování (nebo i zapouštění) vrtného soutyčí pro TI;
- předřez (předtryskání) je technologický postup, při němž tryskání příslušného prvku TI je usnadněno rozrušováním zeminy pomocí vodního paprsku, nebo paprskem jiného média prováděném v předstihu;
- pořadí provádění: čerstvý – čerstvý je pořadí provádění prvků TI, při němž se následný prvek provádí ihned po předchozím, bez čekání na zatvrdnutí sousedních prvků (obr. 82);
- pořadí provádění: primární – sekundární je pořadí provádění prvků TI, při němž může být tryskání nového prvku na styku s prvkem již provedeným zahájeno až po stanovené době tvrdnutí, nebo dosažení předepsané pevnosti sousedního prvku TI provedeného v předchozím kroku (obr. 83);
- materiál prvku TI je materiál, z něhož je tvořeno těleso prvku TI. Jeho vlastnosti závisí jak na vlastnostech původní (nezlepšené) základové půdy, tak i na technologii a parametrech použité TI;
- vyztužená TI je obyčejně sloup TI vyztužený ocelovou trubkou, betonářským prutem, popř. válcovaným profilem umístěným obyčejně v ose sloupu a vkládaným buď do čerstvě vytryskaného sloupu, nebo do následného vrtu vyplněného cementovou suspenzí. V žádném případě nelze na takovýto prvek pohlížet jako na železobetonový průřez srovnatelný např. S klasickým železobetonovým sloupem.
Obr. 79 Příklady prvků z TI: a – sloup TI, b – lamela z TI
Obr. 80 Stěna z TI: a – ze sloupů TI, b – z lamel TI
Obr. 81 Deska ze sloupů TI, klenba z horizontálních, popř. mírně ukloněných sloupů TI
Obr. 82 Schéma pořadí provádění stěny ze sloupů TI: čerstvý – čerstvý
Obr. 83 Schéma pořadí provádění stěny ze sloupů TI: primární – sekundární
4.10.2 Technologie provádění TI
Před návrhem TI musí být k dispozici následující podklady:
a) geotechnické, tj. detailní popis základové půdy na staveništi s údaji o jejich geotechnických vlastnostech v rozsahu dotčeném TI. Zvláštní pozornost musí být věnována zejména:
- výskytu tuhých a pevných vrstev a čoček jemnozrnných zemin;
- bobtnavých jílů;
- vysokému obsahu organických látek v zemině;
- výskytu senzitivních jílů;
- stmeleným, nebo jakkoli zpevněným vrstvám nebo čočkám zemin;
- úrovni hladiny podzemní vody;
- výskytu napjaté hladiny podzemní vody;
- vysokému hydraulickému spádu podzemní vody;
- agresivitě podzemní vody;
- ulehlosti hrubozrnných zemin;
- výskytu kamenů a balvanů;
- výskytu dutin v základové půdě;
- výskytu chemického odpadu nebo skládek;
- granulometrickému složení základové půdy, její vlhkosti, konzistenčním mezím,
- smykové pevnosti zemin;
b) stavební (okrajové podmínky na staveništi), což jsou základy sousedních budov, podzemní stavby a inženýrské sítě, vzdušná vedení a ostatní pracovní překážky, přístupnost staveniště;
c) požadavky na ochranu životního prostředí, zvláště s ohledem na nakládání s vyplaveným materiálem;
d) přípustné deformace podchytávaných, nebo sousedních objektů.
Při projektování a provádění TI se obyčejně postupuje podle níže uvedeného seznamu činností (tab. 59), přičemž jejich uvedené pořadí nemusí nutně odpovídat časovému pořadí.
Vlastní technologický postup provádění TI sestává z následujících činností:
- vrtání (bezjádrových) maloprofilových vrtů předem určených geometrických vlastností;
- zavedení monitoru spojeného s vrtným soutyčím pro TI na dno vrtu (tento krok obyčejně odpadá, neboť monitor bývá montován na soutyčí již v průběhu vrtání);
- tryskání média rozrušujícího strukturu zeminy a pomocí pojiva zpevňujícího zeminu při současném vytahování a otáčení soutyčí s předem určenými hodnotami pro rychlost vytahování a otáčení, pro tlak a průtok každého jednotlivého média.
Strojní zařízení pro provádění TI zahrnuje:
- vrtnou soupravu, vybavenou pro TI, tj. se soutyčím pro TI, monitorem a zařízením k pohonu soutyčí, jež musí být tak uzpůsoben, aby umožnil pohyb vrtného soutyčí stanovenou rychlostí otáčení a posunu;
- míchací zařízení pro přípravu médií TI vč. jejich skladování (jde vesměs o cementovou suspenzi);
- vysokotlaké čerpadlo;
- vysokotlaká potrubí spojující čerpadlo s vrtnou soupravou;
- zařízení k měření tlaku, průtočné rychlosti a množství, rychlosti otáčení a posunu, jakož i okamžité hloubky monitoru;
- zařízení pro hospodaření s vyplaveným materiálem.
Tab. 59 Doporučený seznam činnosti při projektování a provádění TI
| Číslo | Činnost |
| 1 | Získání údajů z geotechnického průzkumu staveniště |
| 2 | Rozhodnutí o vhodnosti použití TI, předběžné zkoušky v laboratoři a na staveništi (jsou-li možné), vypracování předběžných technických specifikací |
| 3 | Získání všech potřebných povolení pro provádění TI od úřadů a ostatních účastníků |
| 4 | Stanovení geotechnické kategorie, globální návrh prvků a konstrukcí TI |
| 5 | Předběžné stanovení fází provádění |
| 6 | Zhodnocení geotechnických vlastností základových půd ve vztahu k návrhovým předpokladům |
| 7 | Posouzení proveditelnosti návrhu |
| 8 | Provedení zkušebních prvků (zkušebního pole) a příslušných zkoušek |
| 9 | Vyhodnocení výsledků provedených zkoušek |
| 10 | Volba systému TI |
| 11 | Realizační projekt TI, návrh rozměrů, umístění a orientace prvků a konstrukcí TI |
| 12 | Stanovení pracovního postupu |
| 13 | Stanovení omezujících faktorů pro postup prací |
| 14 | Změna, popř. upřesnění pracovního postupu |
| 15 | Instrukce všem zainteresovaným stranám týkající se klíčových bodů návrhu, jímž má být věnována zvláštní pozornost |
| 16 | Specifikace pro monitoring vlivů TI na sousední stavební objekty (druh a přesnost přístrojů, volba metod, četnost měření) a pokyny pro vyhodnocení výsledků |
| 17 | Stanovení mezních přípustných hodnot účinků TI na okolní zástavbu |
| 18 | Provádění TI vč. monitoringu parametrů TI |
| 19 | Dohled nad prací vč. definování kvalitativních požadavků |
| 20 | Monitorování účinků TI na okolní zástavbu a předávání výsledků měření |
| 21 | Kontrola kvality provedených prací |
Délka vrtného soutyčí vrtné soupravy, jakož i výška lafety nemá být kratší, než je délka projektovaného prvku TI. To však nelze v některých případech zaručit, např. při podchycování pomocí TI ze sklepních prostor apod. Snahou je však vždy minimalizovat přerušení při tryskání sloupů TI. Vrtné soutyčí pro TI musí být přizpůsobeno různým systémům provádění:
- pro jednofázový systém – jedním kanálem pro přívod cementové suspenze;
- pro dvojfázový systém – dvěma kanály pro transport dvou médií (suspenze a vzduchu, popř. vody a suspenze);
- pro trojfázový systém – třemi kanály pro transport všech tří médií (suspenze, vody a vzduchu).
Více kanálů prochází vždy jedním soutyčím k monitoru. Monitor pro jednotlivé systémy obsahuje:
- pro jednofázovou TI – vybavení jednou, nebo dvěma kruhovými tryskami rozmístěnými po obvodu proti sobě v různých výškách;
- pro dvojfázovou vzduchovou TI – vybavení jednou či dvěma koncentrickými tryskami (vzduch je veden mezikružím a obaluje paprsek cementové suspenze);
- pro dvojfázovou vodní TI – vybavení jedno, či více tryskami pro vysokotlaké tryskání vody a jednou, či více níže položenými tryskami pro cementovou suspenzi;
- pro trojfázovou TI – vybavení jedno či více koncentrickými tryskami pro vodní paprsek obalený stlačeným vzduchem a jednou, či více níže položenými tryskami pro cementovou suspenzi.
Vrty pro TI se provádějí jako maloprofilové stejnou technologií jako vrty pro mikropiloty, kotvy, či klasickou injektáž. Průměr vrtů je 100–200 mm, obecně platí, že pro vícefázovou TI je zapotřebí větší průměr vrtů. Vrtáno může být na vzduchový, vodní, cementový, jílocementový, popř. i pěnový výplach. Odchylka osy ohlubně vrtu by se neměla od projektované polohy lišit více než o 50 mm a sklon osy vrtu více než o 2 %. Průměr vrtů se volí takový, aby při tryskání mohl vyplavený materiál volně vytékat mezikružím mezi stěnou vrtu a vrtným soutyčím.
Míchací a čerpací stanice sestává pro různé systémy TI z těchto komponentů:
- pro jednofázový systém: skladovací zařízení na cement (obyčejně silo), aktivační míchačka, pomaloběžní míchačka (domíchávač), vysokotlaké čerpadlo;
- pro dvojfázový systém vzduchový: jako výše, a navíc výkonný kompresor se vzdušníkem;
- pro dvojfázový systém vodní: jako pro jednofázový systém, a navíc vysokotlaké čerpadlo pro tryskání vody;
- pro trojfázový systém: jako pro dvojfázový systém vodní, a navíc kompresor se vzdušníkem.
Po dovrtání do projektované hloubky se obyčejně ihned začne s tryskáním. Tryská se odspodu a při provádění sloupů se monitorem rotuje pomalými otáčkami a soutyčí se povytahuje. Toto povytahování není plynulé, nýbrž po 2–5 otáčkách monitoru dojde k náhlému povytažení monitoru o několik centimetrů (tzv. stepování). Tyto operace se provádějí automaticky a řízeny jsou přes mikroprocesor. Při jednofázové injektáži se obyčejně ihned po dovrtání na výplach, tvořený cementovou suspenzí prakticky shodného složení, jako pro TI, popř. s několikaprocentním přídavkem bentonitu, započne s tryskáním. Přívod výplachu k vrtnému nářadí se přeruší spuštěním ocelové kuličky do přívodního kanálu, která uvízne v sedle a usměrní tok suspenze vodorovným směrem přes trysku monitoru. Zvýší se příslušně tlak této suspenze a souprava se nastaví na zvolené otáčky a stepování. Tak započne proces realizace sloupu TI. Přitom se pečlivě sleduje jak průtok suspenze a její tlak, tak zejména množství a průtok vyplaveného materiálu u ústí vrtu. Tento průtok musí být pravidelný a rovnoměrný. Zjistí-li se jakákoliv anomálie v chování vyplaveného materiálu, musí být tryskání okamžitě přerušeno a vzniklá závada odhalena a odstraněna. Jedná se zejména o velmi nebezpečné ucpání mezikruží, kdy tlak tryskaného média, jež nemůže být volně rozptýlen při vyplavování, může způsobit náhlé zvednutí základové půdy spojené s negativními jevy (nadzvednutí objektů, vznik deformací, trhlin apod.). Sloup se tryská až do projektované úrovně, jež však musí být pod úrovní pracovní plošiny, neboť do její úrovně nelze efektivně tryskat, neboť není k dispozici potřebný odpor. Tento výškový rozdíl, který je ostatně potřebný též pro vhodný návrh geometrického uspořádání sloupů TI, např. při podchycování stávajících konstrukcí, by měl být nejméně 1,0 m. Vyplavený materiál je smíchaný s rozrušenou zeminou a nemůže být použit pro další tryskání. Skladuje se obyčejně ve vyhloubených jámách (je-li možné je na staveništi zřídit), tam se nechá sedimentovat a po zatuhnutí se vybagruje a odváží na skládky. Tam, kde to není možné, odváží se v tekutém stavu cisternami. Vyplavený materiál není jakkoliv závadný a nepředstavuje žádnou ekologickou zátěž. S výhodou jej lze použít např. do stabilizací. Z vyplaveného materiálu se pravidelně odebírají vzorky, u nichž se ihned (na staveništi) měří objemová hmotnost (např. baroid váhami). Ostatní vzorky se ponechávají ztvrdnout pro zkoušku pevnosti v prostém tlaku různého stáří, popř. zkoušky propustnosti.
Vlastní cementová suspenze má různé složení dané vodním součinitelem, který se pohybuje od 0,5 do 1,5 (typické složení je např. c : v = 0,8:1). Výjimečně se přidává několik % bentonitu za účelem snížení sedimentace. U vyrobené cementové suspenze se zkouší:
- hustota;
- odstoj vody (měřením po 3 hodinách ve skleněném válci o objemu 1 000 cm3 a průměru 60 mm);
- viskozita (Marsh);
- doba tuhnutí;
- pevnost v prostém tlaku na válcích s poměrem výška/průměr = 2,0, a to po 3, 7, 28 dnech, popřípadě až po 56 dnech. Není-li jinak stanoveno, volí se 4 vzorky na každých 1 000 m3 objemu sloupů TI.
Zhotovené prvky a konstrukce z TI se zkouší z hlediska stanovení a kontroly jejich geometrie a z hlediska dosažení jejich mechanických vlastností. Rozměry prvků se nejlépe stanoví pozorováním a měřením na odkopaných prvcích. To však vyžaduje rozsáhlé výkopové práce do značné hloubky, což často není možné. V případě provádění zkušebního pole by se však s výkopem mělo vždy počítat. Pokud nelze přímá pozorování provádět, mohou být příslušné údaje získány z jádrových, popř. i plnoprofilových vrtů prováděných šikmo na osu prvku. Při jádrovém vrtání lze navíc získat i vzorky pro tlakovou pevnost, popř. i propustnost. Výjimečně lze měření provádět pomocí penetračních zkoušek na nezatvrdlých pilířích. Interpretace výsledků měření je však obtížná a nejistá.
Tab. 60 Přibližný rozsah parametrů TI pro různé systémy
| Parametry TI | Jednofázový systém | Dvojfázový systém (vzduchový) | Dvojfázový systém (vodní) | Trojfázový systém |
| tlak na čerpadle inj. směsi [MPa] | 30–50 | 30–50 | > 2 | > 2 |
| průtok injekční směsi [l/min.] | 50–450 | 50–450 | 50–200 | 50–200 |
| tlak vody [MPa] | NP | NP | 30–60 | 30–60 |
| průtok vody [l/min.] | NP | NP | 50–150 | 50–150 |
| tlak vzduchu [MPa] | NP | 0,2–1,7 | NP | 0,2–1,7 |
| množství vzduchu [m3/min.] | NP | 3–12 | NP | 3–12 |
| NP = není používáno | ||||
V případě jednofázové injektáže lze získat sloupy o průměru 500–800 mm, výjimečně i větší. Tlaková pevnost sloupů je silně závislá na druhu a kvalitě základové půdy, v níž se TI provádí a na parametrech TI, jejichž používaný rozsah je v tab. 60. Ve štěrcích a píscích lze běžně dosáhnout pevnosti σd = 8,0 – 10,0 MPa, v jílovitých píscích pak σd = 4,0 – 5,0 MPa a v tuhých jílech σD = 2,0 – 3,0 MPa, je-li to vůbec reálné. V poloskalních a skalních horninách nelze jednofázovou TI úspěšně provádět. V případě dvojfázové TI bývá průměr sloupů 0,8–1,5 m a trojfázová TI umožňuje ve vhodných základových podmínkách realizovat sloupy průměru přes 1,5 m. v případě podchytávání stávajících konstrukcí se nedoporučuje používat dvojfázovou TI vzduchovou, neboť stlačený vzduch může v základové půdě vyvolat nežádoucí a náhlé deformace.
4.10.3 Oblasti použití TI
Využití technologie TI v oblasti speciálního zakládání staveb je skutečně rozsáhlé. Bez nadsázky lze o technologii TI hovořit jako o jednom z mezníků v zakládání staveb, neboť prvky z TI a konstrukce z těchto prvků umožňují elegantně a velice účinně řešit mnoho závažných a zásadních problémů v daném oboru. Technologii TI lze využít v následujících oblastech:
- pro zakládání nových staveb (jako náhrada hlubinných základů);
- pro podchycování stávajících základů a konstrukcí za účelem zvýšení únosnosti v základové spáře;
- pro podchycování stávajících základů a konstrukcí za účelem umožnění jejich odkopání, popř. podkopání;
- jako pažicí a současně i těsnicí konstrukce pro těsnění boků stavebních jam;
- pro dotěsňování jiných konstrukcí (např. štětových stěn nebo záporového pažení), při jejich napojování na stávající stavby;
- pro těsnění dna stavebních jam v propustných zeminách;
- pro dočasné zajišťování výrubu štol, kolektorů i tunelů;
- pro zlepšování vlastností základové půdy;
- pro urychlení konsolidace podloží násypů;
přičemž tento výčet není jistě konečný. Je ovšem zřejmé, že technologie TI je:
- mimořádně náročná na její zvládnutí, tj. na návrh, provádění, kontrolu a monitoring;
- relativně nebezpečná z hlediska možných rizik, a to nejen při jejím nevhodném použití;
- relativně drahá jak z hlediska nároků na nutné vybavení, tak z hlediska spotřeby hmot (např. cementu) a hospodaření s vyplaveným materiálem.
Technologie TI by měla být tedy realizována pouze zkušenými a specializovanými firmami, což dává záruku jejího správného využití, a ne komerčního zneužití, jak jsme tomu svědky např. při zbytečných a nevhodných realizacích mikropilotových základů.
Budování hlubinných základů novostaveb (obr. 84) pomocí sloupů, popř. lamel z TI, je v souvislosti se snižující se cenou těchto prvků stále častější. Je pochopitelné, že výsledný prvek TI nelze srovnávat s železobetonovým průřezem vrtané piloty, a to jak z hlediska kvality (pevnosti) betonu, tak z hlediska možnosti vyztužení, což je potřebné zvláště u prvků namáhaných kombinací ohybu s tlakem (popř. i tahem). Výjimečně lze využít hlubinných základů sestávajících ze sloupů TI na těch stavbách, kde je technologie TI uplatněna ve velké míře např. pro podchycování a současně je třeba založit hlubinně konstrukce, pro něž by se nevyplatilo instalovat novou technologii (piloty, mikropiloty).
Na obr. 85 je sestava statické zatěžovací zkoušky sloupu TI na staveništi v Brně a na obr. 86 je grafický záznam průběhu této statické zatěžovací zkoušky. Výsledky byly mimořádně uspokojivé a prokázaly, že:
- k ustalování deformací na každém zatěžovacím i odlehčovacím stupni docházelo velmi rychle, tudíž příslušná doba na každém z těchto stupňů činila vesměs 1 hod;
- celková deformace dosažená při maximálním zatížení 1 000 kN činila 3,85 mm, což svědčí o značné únosnosti tohoto prvku;
- trvalá deformace po odlehčení z 1 000 kN na 0 kN činila pouze kolem 1,0 mm, tj. Cca 25 %, tudíž zcela převládá deformace pružná (75 %), což rovněž svědčí o té skutečnosti, že zatím nedochází k výrazným plastickým deformacím, tudíž mezní únosnosti sloupu TI nebylo zdaleka dosaženo.
Obr. 84 Hlubinné zakládání pomocí sloupů TI
Obr. 85 Sestava statického zatěžovacího sloupu TI ø 800 mm dl. 10,0 m
Obr. 86 Výsledky statické zatěžovací zkoušky sloupu TI v Brně
Jednou z rozhodujících oblastí použití TI je podchytávání stávajících základů. To může být navrhováno v případě nástaveb, dostaveb a rekonstrukcí, a to jednak za účelem zvýšení únosnosti v základové spáře z titulu jejího přitížení (obr. 87), jednak za účelem umožnění (obyčejně jednostranného) výkopu podél stávajících základů zasahujícího pod stávající základovou spáru (obyčejně plošných) základů (obr. 88), popř. V kombinaci obou požadavků. Hlavní výhodou zesilování stávajících základů podchycováním pomocí sloupů TI je skutečnost, že při vhodném geometrickém uspořádání není třeba budovat žádné „spojovací“ konstrukce zprostředkující přenos zatížení ze stávajících základů do podchycovacích prvků, neboť sloupy TI obyčejně přímo podepírají stávající základovou spáru. Lze též regulovat potřeby podchycení, a to jak půdorysným uspořádáním prvků TI, tak jejich délkou. Při využití miniaturních vrtných souprav lze podchycovat konstrukce i z úrovně suterénu apod. Jedná se ovšem o technologii velmi náročnou na organizaci práce a na její monitoring, neboť např. i při krátkodobém ucpání vrtu hrozí reálné nebezpečí „nadzvednutí“ stávajících základů a poškození objektu. Při této práci je třeba vždy zajistit podrobný stavebně-technický průzkum stávajících objektů a pasportizaci stávajícího stavu tak, aby po skončení práce nevznikly zbytečné dohady o míře zavinění při případném poškození konstrukcí. Současně je třeba zajistit přístup do všech sousedních (např. sklepních) prostor tak, aby průběh provádění TI mohl být neustále monitorován a popř. dočasně přerušen, nebo upraven.
Technologie TI v podstatě jako jediná umožňuje ve vhodných podmínkách prohloubení výkopu prakticky těsně podél stávajících základů, a to v souvislosti s jejich podchycením. Podle stavebního stavu stávajícího základového, resp. suterénního zdiva, podle charakteru základové půdy a podle potřebné výšky podchytávání se volí geometrické uspořádání sloupů TI, resp. nutnost kotvení, nebo i rozepření této konstrukce tak, aby byla zajištěna její stabilita. Lze konstatovat, že právě podchytávání pomocí sloupů TI umožnilo výstavbu hlubokých suterénů v prolukách mezi mělčeji založenými objekty s maximálním využitím příslušného prostoru např. pro podzemní parking, či pro jiná zázemí novostaveb. Při postupujícím výkopu lze těleso tvořené sloupy TI upravovat (např. osekáním, nebo naopak dobetonováním), popř. opatřit vrstvou se zednickou úpravou (např. stříkaným betonem s hlazeným povrchem) tak, aby tato vrstva sloužila přímo jako podklad pro svislou izolaci.
Obr. 87 Podchycování stávajících základů pomocí sloupů TI za účelem zvýšení jejich únosnosti
Konstrukce ze sloupů TI lze využít pro utěsnění dna stavebních jam, popř. šachtic (obr. 89), kdy se s výhodou využívá různých průměrů sloupů, jež se vzájemně překrývají, a vytvoří tak dostatečně těsné dno šachty. I v případě rozsáhlých stavebních jam jejich pažicí stěny nezasahují do nepropustného podloží, jež se nachází příliš hluboko, využívá se těsnění dna pomocí mělce, nebo hluboce umístěné desky z TI. Těchto konstrukcí bylo ve velké míře využito při výstavbě hlubokých těsněných stavebních jam v Berlíně v posledním desetiletí 20. století.
Obr. 88 Podchycování stávajících základů pomocí sloupů TI za účelem umožnění jednostranného odkopání podchycených základů
Příklad možného využití sloupů TI pro urychlení konsolidace stlačitelných zemin pod nově budovanými násypy je na obr. 90. Jedná se spíše o možnost než o masové využití těchto prvků, jež jsou dražší než štěrkové pilíře, které jsou pro tyto účely nejtypičtější. Naopak ovšem těsnicí konstrukce podél vodotečně zavázaná do nepropustného podloží je výhodná, a to zejména tam, kde lze očekávat kolize s inženýrskými sítěmi a podzemní těsnicí stěna není reálná.
Značné využití nalézá TI při dočasném zajišťování podzemních staveb, a to jak obyčejně mělce pod povrchem budovaných štol (kolektorů), tak i v případě tunelů, kde nahrazují tzv. deštníky prováděné z ocelových trubek. Na obr. 91 je příklad využití svislých sloupů TI prováděných z povrchu a vymezujících tvar budoucí štoly za účelem dočasné ochrany při výrubu. Toto zajištění je velmi účinné, nicméně je drahé a vyzžívá se poměrně zřídka, většinou pak v případě havárií.
Podstatně více je však využívána metoda schematicky vyznačená na obr. 92, 93, kdy se realizuje klenba ze subhorizontálních sloupů vrtaných z podzemí pomocí speciálních vrtných souprav. Tato metoda byla úspěšně vyzkoušena např. při výstavbě kolektoru v centru Prahy.
Při výstavbě tunelu Blanka a provozního úseku metra V. A.
Obr. 89 Těsnění dna stavebních jam a šachtic
Obr. 90 Sloupy TI budované za účelem urychlení konsolidace stlačitelných zemin pod násypem
Obr. 91 Dočasné zajištění výrubu štoly pomocí soustavy svislých sloupů TI
Obr. 92 Schéma vytváření subhorizontálních „deštníků“ ze sloupů TI za účelem zajištění výrubu podzemních děl
Obr. 93 Půdorysné schéma obálky „deštníků“ ze sloupů TI
Zhotovené prvky a konstrukce z TI se zkouší z hlediska stanovení a kontroly jejich geometrie a z hlediska dosažení jejich mechanických vlastností. Rozměry prvků se nejlépe stanoví pozorováním a měřením na odkopaných prvcích. To však vyžaduje rozsáhlé výkopové práce do značné hloubky, což často není možné. V případě provádění zkušebního pole by se však s výkopem mělo vždy počítat. Pokud nelze přímá pozorování provádět, mohou být příslušné údaje získány z jádrových, popř. i plnoprofilových vrtů prováděných šikmo na osu prvku. Při jádrovém vrtání lze navíc získat i vzorky pro tlakovou pevnost, popř. i propustnost. Výjimečně lze měření provádět pomocí penetračních zkoušek na nezatvrdlých pilířích. Interpretace výsledků měření je však obtížná a nejistá.
V případě jednofázové injektáže lze získat sloupy o průměru 500–700 mm, výjimečně i větší. Tlaková pevnost sloupů je silně závislá na druhu a kvalitě základové půdy, v níž se TI provádí a na parametrech TI, jejichž používaný rozsah je v tab. 60. Ve štěrcích a píscích lze běžně dosáhnout pevnosti σd = 8,0 – 10,0 MPa, v jílovitých píscích pak σd = 4,0 – 5,0 MPa a v tuhých jílech σD = 2,0 – 3,0 MPa, je-li to vůbec reálné. V poloskalních a skalních horninách nelze jednofázovou TI úspěšně provádět. V případě dvojfázové TI bývá průměr sloupů 0,8–1,2 m a trojfázová TI umožňuje ve vhodných základových podmínkách realizovat sloupy průměru kolem 1,5 m.
5 PŘÍLOHY
5.1 SEZNAM SOUVISEJÍCÍCH ČSN
| Označení | Název | Účinnost od |
| ČSN 73 0020 | Terminologie spolehlivosti stavebních konstrukcí a základových půd | 2010-04-01 |
| ČSN ISO 2394 | Obecné zásady spolehlivosti konstrukcí | 2016-11-01 |
| ČSN EN 1990 | Zásady navrhování konstrukcí | 2004-04-01 |
| ČSN EN 1991-1 (1 až 7) | Zatížení konstrukcí | 2004-04-01 |
| ČSN EN 1992-1-1 | Navrhování betonových konstrukcí – Část 1-1: Obecná pravidla a pravidla pro pozemní stavby | 2007-06-01 |
| ČSN EN 1992-1-1 ed. 2 | Navrhování betonových konstrukcí – Část 1-1: Obecná pravidla a pravidla pro pozemní stavby | 2019-01-12 |
| ČSN EN 1992-2 | Navrhování betonových konstrukcí – Část 2: Betonové mosty a konstrukční zásady | 2007-06-01 |
| ČSN EN 1993-1-1 | Navrhování ocelových konstrukcí – Část 1-1: Obecná pravidla a pravidla pro pozemní stavby | 2007-01-01 |
| ČSN EN 1993-2 | Navrhování ocelových konstrukcí – Část 2: Ocelové mosty | 2008-08-01 |
| ČSN EN 1996-1-1+A1 | Navrhování zděných konstrukcí – Číst 1-1: Obecná pravidla pro vyztužené a nevyztužené konstrukce | 2007-06-01 |
| ČSN EN 1997-1 | Navrhování geotechnických konstrukcí – Část 1: Obecná pravidla | 2006-10-01 |
| ČSN EN 1997-2 | Navrhování geotechnických konstrukcí – Část 2: Průzkum a zkoušení základové půdy | 2008-04-01 |
| ČSN EN 1998-1 | Navrhování konstrukcí odolných proti zemětřesení – Část 1: Obecná pravidla, seismická zatížení a pravidla pro pozemní stavby | 2006-10-01 |
| ČSN EN 1998-2 | Navrhování konstrukcí odolných proti zemětřesení – Část 2: Mosty | 2007-06-01 |
| ČSN EN 1998-3 | Navrhování konstrukcí odolných proti zemětřesení – Část 3: Hodnocení a zesilování pozemních staveb | 2007-06-01 |
| ČSN EN 1536+A1 | Provádění speciálních geotechnických prací – Vrtané piloty | 2016-04-01 |
| ČSN EN 1537 | Provádění speciálních geotechnických prací – Injektované horninové kotvy | 2001-05-01 |
| ČSN EN 1538+A1 | Provádění speciálních geotechnických prací – Podzemní stěny | 2016-04-01 |
| ČSN EN 12063 | Provádění speciálních geotechnických prací – Štětové stěny | 2000-04-01 |
| ČSN EN 12699 | Provádění speciálních geotechnických prací – Ražené piloty | 2016-12-01 |
| ČSN EN 12715 | Provádění speciálních geotechnických prací – Injektáže | 2021-12-01 |
| ČSN EN 12716 | Provádění speciálních geotechnických prací – Trysková injektáž | 202-06-01 |
| ČSN EN 14199 | Provádění speciálních geotechnických prací – Mikropiloty | 2020-10-01 |
| ČSN EN 14475 | Provádění speciálních geotechnických prací – Vyztužené zemní konstrukce | 2006-06-01 |
| ČSN EN 14490 | Provádění speciálních geotechnických prací – Hřebíkování zemin | 2010-11-01 |
| ČSN EN 14679 | Provádění speciálních geotechnických prací – Hloubkové zlepšování zemin | 2006-10-01 |
| ČSN EN 14731 | Provádění speciálních geotechnických prací – Hloubkové zhutňování zemin vibrováním | 2006-05-01 |
| ČSN EN 15237 | Provádění speciálních geotechnických prací – Svislé drény | 2007-09-01 |
| ČSN 73 0037 | Zemní tlak na stavební konstrukce | 1992-01-01 |
| ČSN 73 0039 | Navrhování objektů na poddolovaném území. Základní ustanovení | 1915-01-01 |
| ČSN 73 0040 | Zatížení stavebních konstrukcí technickou seismicitou a jejich odezva | 2019-04-01 |
| ČSN 73 0601 | Ochrana staveb proti radonu z podloží | 2019-03-01 |
5.2 LITERATURA
[1] MASOPUST, J. Vrtané piloty. Praha: Čeněk a Ježek, 1994, 263 s.
[2] MASOPUST, J. Zakládání staveb, 1. díl. Praha: Nakladatelství ČVUT, 2015, 166 s.
[3] MASOPUST, J., GLISNÍKOVÁ, V. Zakládání staveb, modul M01. Brno: Akademické nakladatelství CERM, s.r.o., 2007, 182 s.
[4] MASOPUST, J. Navrhování základových a pažicích konstrukcí. Příručka k ČSN EN 1997-1. Praha: Informační centrum ČKAIT, 2012, 220 s.
[5] TURČEK, P. a kol. Zakládání staveb. Bratislava: JAGA, 2005, 302 s.
[6] VERFEL, J. Injektování hornin a výstavba podzemních stěn. MÚS Bradlo, Bratislava, 1992, 511 s.