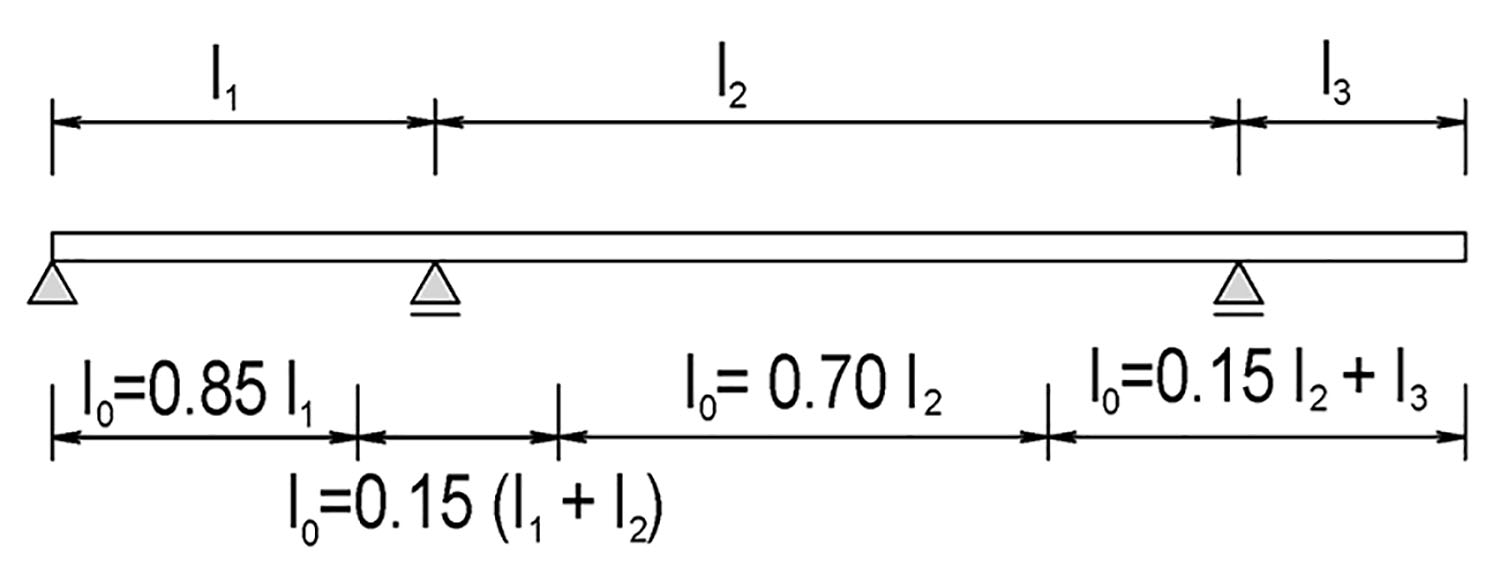Autoři: Ing. Jiří Šmejkal, CSc., prof. Ing. Jaroslav Procházka, CSc.
Stav: kontrola 2022, vydání 2017
Anotace:
Tabulkový přehled základní problematiky navrhování betonových a železobetonových konstrukcí včetně základních tabulek a návrhových pomůcek. V tabulkách je průběžně aktualizovaná verze návrhového standardu pro navrhování betonových a železobetonových konstrukcí. Tabulky obsahují vše potřebné pro návrh běžných konstrukcí pozemních staveb.
Obsah:
Úvod
V rámci evropské unie platí technické standardy v oblasti navrhování stavebních konstrukcí. Pro navrhování betonových a železobetonových konstrukcí platí základní norma ČSN EN 1992-1-1 s upřesňujícím národním dokumentem. Návrhová norma je značně nepřehledná, což je dáno především množstvím vzorců s řadou univerzálních součinitelů, které lze upravovat v rámci národní přílohy. Relativně časté změny, opravy a upřesnění v základní normě a její národní příloze vedou k nepřehlednosti problematiky navrhování betonových konstrukcí. Zjednodušená tabulková forma základní problematiky má za cíl získat přehled a rychlé orientování v celé problematice navrhování železobetonových konstrukcí pro běžné konstrukce pozemních staveb. Problém neustálých úprav základních dokumentů vede k elektronické formě vydání této publikace, která umožňuje její průběžnou aktualizaci s upozorněním na měněné parametry.
Tabulkový přehled problematiky navrhování betonových konstrukcí navazuje na publikaci pro navrhování železobetonových konstrukcí Navrhování betonových konstrukcí. Příručka k ČSN EN 1992-1-1 a ČSN EN 1992-1-2 prof. Ing. Jaroslava Procházky, CSc. a kol., kde jsou podrobně vysvětleny všechny vzorečky a návrhové postupy včetně příkladů.
Tabulkový přehled je určen projektantům konstrukcí pozemních staveb, kteří problematiku znají. S tabulkami a návrhovými pomůckami nemusí kontrolovat aktuálnost textu normy a národní přílohy, popřípadě aktuální upřesnění názorů na metodiku návrhu jednotlivých problémů.
Autor děkuje za odbornou pomoc a podporu při tvorbě těchto tabulek prof. Ing. Jaroslavu Procházkovi, CSc. Autor také děkuje předem všem čtenářům za upozornění na nedopatření popřípadě i na tiskové chyby, které se v pomůcce vyskytly a zároveň se za ně omlouvá.
Značení v Eurokódech
Nejčastější označení
| A | plocha | E | modul pružnosti |
| G | stálé zatížení, modul pružnosti ve smyku | F | zatížení |
| L | rozpětí | ||
| Q | proměnné zatížení | M | ohybový moment |
| I | moment setrvačnosti | S | statický moment |
| N | normálová síla | R | odolnost |
| T | krouticí moment | V | posouvající síla |
| a | vzdálenost | b | šířka |
| c | betonová krycí vrstva | d | průměr |
| e | výstřednost | f | pevnost materiálu |
| g | rovnoměrné zatížení | h | výška průřezu |
| r | poloměr | s | vzdálenost |
| t | tloušťka | w | šířka trhliny |
| x | vzdálenost neutrální osy | z | rameno vnitřních sil |
Řecká písmena
| α, β | úhel, poměr, součinitel | γ | dílčí součinitel spolehlivosti |
| ε | poměrná deformace | θ | sklon tlačené diagonály |
| λ | štíhlostní poměr | ν | Poissonův součinitel |
| ρ | objemová hmotnost | součinitel redukce pevnosti betonu | |
| stupeň vyztužení | τ | smykové napětí | |
| ϕ | průměr výztuže | φ | součinitel dotvarování |
| ψ | součinitel, kterým se definují reprezentativní hodnoty proměnného zatížení |
Indexy
| b | soudržnost | eff | efektivní, účinná hodnota |
| k | charakteristická hodnota | d | návrhová hodnota |
| c | beton, tlak | s | betonářská výztuž |
| E | účinek zatížení | R | odolnost |
| t | tah | l | podélný |
| y | mez kluzu | m | ohybový, průměrný |
Konvence v označování vnitřních sil a průřezových charakteristik
1 Beton
Tab. 1.1 Charakteristiky betonu podle ČSN EN 1992-1-1, hodnoty v MPa
| Parametr | C12/15 | C16/20 | C20/25 | C25/30 | C30/37 | C35/45 | C40/50 | C45/55 | C50/60 |
| fck | 12,00 | 16,00 | 20,00 | 25,00 | 30,00 | 35,00 | 40,00 | 45,00 | 50,00 |
| fck,cube | 15,00 | 20,00 | 25,00 | 30,00 | 37,00 | 45,00 | 50,00 | 55,00 | 60,00 |
| fcm | 20,00 | 24,00 | 28,00 | 33,00 | 38,00 | 43,00 | 48,00 | 53,00 | 58,00 |
| fcd | 8,00 | 10,67 | 13,33 | 16,67 | 20,00 | 23,33 | 26,67 | 30,00 | 33,33 |
| fctm | 1,60 | 1,90 | 2,20 | 2,60 | 2,90 | 3,20 | 3,50 | 3,80 | 4,10 |
| fctk,0.05 | 1,10 | 1,30 | 1,50 | 1,80 | 2,00 | 2,20 | 2,50 | 2,70 | 2,90 |
| fctd | 0,73 | 0,87 | 1,00 | 1,20 | 1,33 | 1,47 | 1,67 | 1,80 | 1,93 |
| Ecm | 27000 | 29000 | 30000 | 31000 | 33000 | 34000 | 35000 | 36000 | 37000 |
| εc1[‰] | 1,80 | 1,90 | 2,00 | 2,10 | 2,20 | 2,25 | 2,30 | 2,40 | 2,45 |
| fbd dobré podmínky | 1,65 | 1,95 | 2,25 | 2,70 | 3,00 | 3,30 | 3,75 | 4,05 | 4,35 |
| fbd špatné podmínky | 1,16 | 1,37 | 1,58 | 1,89 | 2,10 | 2,31 | 2,63 | 2,84 | 3,05 |
| fyd/ fcd*) | 54,35 | 40,75 | 32,62 | 26,08 | 21,74 | 18,64 | 16,30 | 14,49 | 13,04 |
| Poměrné deformace betonu v tlaku \varepsilon_\text{cu1}=\varepsilon_\text{cu2}=\varepsilon_\text{cu3}=0{,}35\%, \varepsilon_\text{c2}=0{,}2\%, \varepsilon_\text{c3}=0{,}175\%, n=2^*) platí pro výztuž B500 | |||||||||
Tab. 1.2 Povinné údaje specifikace betonu podle ČSN EN 206+A1
| C fck/fck,cube … požadovaná pevnostní třída – charakteristické pevnosti válcová/krychelná |
| X.. …stupeň vlivu prostředí (X0, XC.., XD.., XS.., XF.., XA..) |
| Cl.. …maximální obsah chloridů (% podíl chloridových iontů – součtově ve všech složkách betonu – k hmotnosti cementu) |
| Dmax …maximální zrno kameniva použitého pro výrobu daného betonu |
| S.. …stupeň konzistence čerstvého betonu, stanovený buď metodou sednutí kužele S1-S5, nebo metodou stupně zhutnitelnosti C0-C3, případně metodou rozlití F1-F6. Stupeň konzistence je nutno volit s ohledem na předpokládaný způsob ukládání a zpracování čerstvého betonu |
Tab. 1.3 Součinitel dotvarování φ (∞, t0) v pro třídu cementu N
| Stáří při vnesení zatížení | Relativní vlhkost 50 % (vnitřní prostředí) | |||||
| jmenovitý rozměr h_0=2A_\text{c}/u… Ac plocha průřezu, u obvod vystavený vysýchání | ||||||
| Beton | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 | |
| 7 dní | C20/25 | 3,714 | 3,349 | 3,167 | 3,049 | 2,971 |
| C25/30 | 3,421 | 3,085 | 2,917 | 2,809 | 2,737 | |
| C30/37 | 3,055 | 2,764 | 2,619 | 2,525 | 2,464 | |
| 28 dní | C20/25 | 2,858 | 2,578 | 2,438 | 2,347 | 2,287 |
| C25/30 | 2,633 | 2,374 | 2,245 | 2,162 | 2,106 | |
| C30/37 | 2,352 | 2,128 | 2,016 | 1,896 | 1,896 | |
| Stáří při vnesení zatížení | Relativní vlhkost 80 % (vnitřní prostředí) | |||||
| jmenovitý rozměr h_0=2A_\text{c}/u… Ac plocha průřezu, u obvod vystavený vysýchání | ||||||
| Beton | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 | |
| 7 dní | C20/25 | 2,682 | 2,528 | 2,450 | 2,407 | 2,377 |
| C25/30 | 2,471 | 2,329 | 2,257 | 2,217 | 2,189 | |
| C30/37 | 2,233 | 2,110 | 2,048 | 2,014 | 1,990 | |
| 28 dní | C20/25 | 2,064 | 1,946 | 1,886 | 1,853 | 1,829 |
| C25/30 | 1,902 | 1,793 | 1,737 | 1,707 | 1,685 | |
| C30/37 | 1,719 | 1,626 | 1,576 | 1,550 | 1,531 | |
Tab. 1.4 konečná hodnota poměrného smrštění vyvozeného vysýcháním betonu \varepsilon_{\text{cd}\infty}[\text{‰}]
| Relativní vlhkost 50 % (vnitřní prostředí) | |||||
| jmenovitý rozměr h_0=2A_\text{c}/u… Ac plocha průřezu, u obvod vystavený vysýchání | |||||
| beton | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 |
| C20/25 | -0,485 | -0,414 | -0,397 | -0,393 | -0,388 |
| C25/30 | -0,471 | -0,404 | -0,384 | -0,384 | -0,379 |
| C30/37 | -0,458 | -0,325 | -0,376 | -0,376 | -0,372 |
| Relativní vlhkost 80 % (vnitřní prostředí) | |||||
| jmenovitý rozměr h_0=2A_\text{c}/u | |||||
| beton | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 |
| C20/25 | -0,282 | -0,232 | -0,232 | -0,230 | -0,227 |
| C25/30 | -0,279 | -0,242 | -0,233 | -0,231 | -0,228 |
| C30/37 | -0,278 | -0,243 | -0,234 | -0,232 | -0,229 |
| Platí pro třídu cementu N | |||||
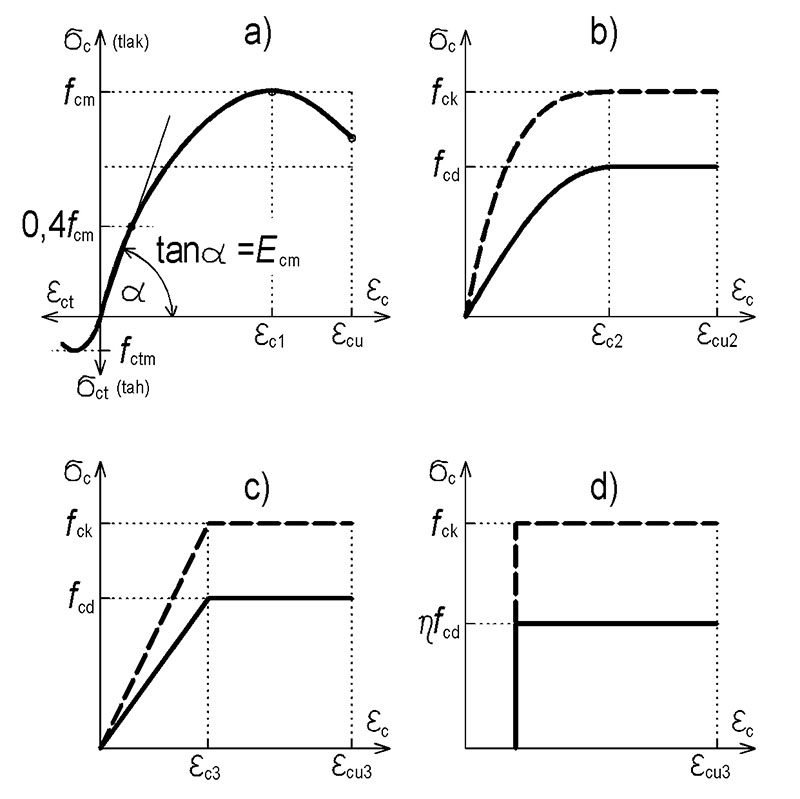
Pracovní diagram betonu v tlaku
Obr 1.1 Pracovní diagram betonu v tlaku
a) pracovní diagram betonu pro analýzu konstrukcí (použití 0,4fcm pro definici Ecm)
b) parabolicko-rektangulární pracovní diagram pro beton namáhaný tlakem
c) bilineární pracovní diagram
d) obdélníkové rozdělení napětí betonu v tlaku – pro dimenzování:
λ = 0,8 a η = 1,0 pro betony do třídy C50/60
λ = 0,8 – (fck – 50)/400 a η=1,0 – (fck – 50)/500 pro betony vyšších tříd a η = 1,0
2 Betonářská výztuž
Tab. 2.1 Charakteristiky betonářské výztuže podle ČSN EN 10080 a ČSN 420139
Pracovní diagram betonářské výztuže
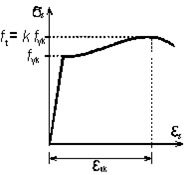
Pracovní diagram oceli s vyznačenou mezí kluzu fyk (ocel za tepla válcovaná).
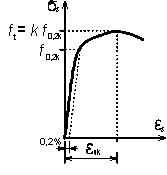
Pracovní diagram oceli bez vyznačené meze kluzu, s tzv. smluvní mezí kluzu f0,2 (ocel za studena tvářená).
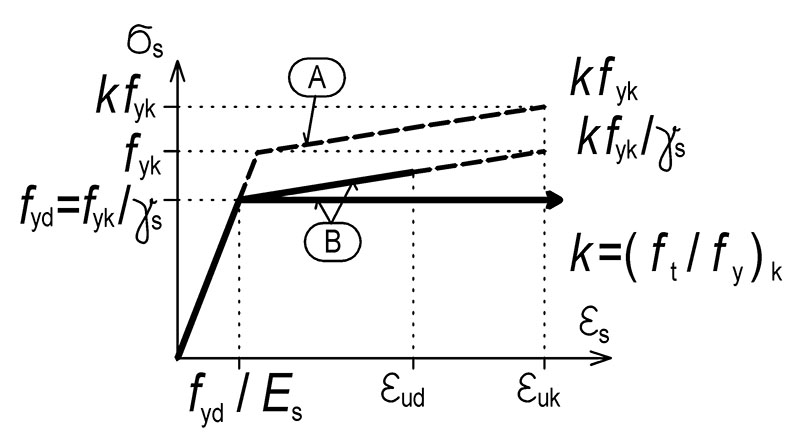
Idealizovaný diagram betonářské oceli se stoupající větví (A) – charakteristické hodnoty a s vodorovnou větví a stoupající větví návrhové hodnoty (B).
Obr. 2.1 Pracovní diagramy betonářské výztuže
3 Vlivy prostředí
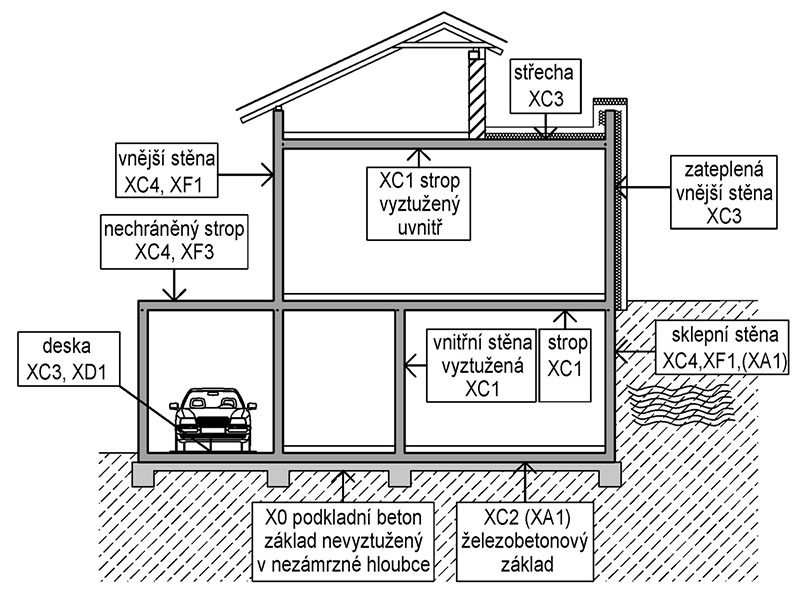
Obr. 3.1 Vlivy prostředí
Tab. 3.1 Vlivy prostředí
| Označení stupně | Popis prostředí | Informativní příklady | ||||||
| 1. bez nebezpečí koroze nebo narušení | ||||||||
| X0 | beton bez výztuže – všechny vlivy mimo působení mrazu, obrusu nebo chemicky agresivního prostředí beton s výztuží ve velmi suchém prostředí | betonové základy bez výztuže, prostý beton ve vnitřním prostředí, minimální třída betonu C12/15 | ||||||
| Vliv | Popis prostředí | Min. třída | Informativní příklady | |||||
| 2. koroze vlivem karbonatace XC | ||||||||
| XC1 | suché nebo stále mokré | C20/25 | beton uvnitř budov s nízkou vlhkostí, beton trvale ponořený ve vodě | |||||
| XC2 | mokré, občas suché | C25/30 | základové konstrukce, vodojemy | |||||
| XC3 | středně mokré, vlhké | C30/37 | vnitřní povrchy s velkou vlhkostí nebo venkovní chráněné proti dešti | |||||
| XC4 | střídavě mokré a suché | C30/37 | vnější povrchy vystavené srážkám | |||||
| 3. koroze vlivem chloridů, ne však z mořské vody XD | ||||||||
| XD1 | středně mokré, vlhké | C30/37 | stavební části dopravních ploch | |||||
| XD2 | mokré, občas suché | C30/37 | plavecké bazény | |||||
| XD3 | střídavě mokré a suché | C35/45 | vozovky, parkoviště | |||||
| 4. působení mrazu a rozmrazování XF | ||||||||
| XF1 | mírně nasycen vodou bez rozmrazovacích prostředků | C30/37 | svislé povrchy vystavené dešti a mrazu | |||||
| XF2 | mírně nasycen vodou s rozmrazovacími prostředky | C25/30a) | svislé povrchy vystavené dešti a mrazu a rozmrazovacím prostředkům | |||||
| XF3 | značně nasycen vodou bez rozmrazovacích prostředků | C30/37 a) | vodorovné povrchy vystavené dešti a mrazu | |||||
| XF4 | značně nasycen vodou s rozmrazovacími prostředky | C30/37 a) | vodorovné povrchy vystavené dešti a mrazu a rozmrazovacím prostředkům | |||||
| a) Minimální provzdušnění 4 % | ||||||||
| 5. chemické působení XA | ||||||||
| XA1 | slabě agresivní chemické prostředí | C30/37 | nádrže čistíren odpadních vod, žumpy, septiky, základy staveb | |||||
| XA2 | středně agresivní chemické prostředí | C30/37 b) | základy v agresivním prostředí | |||||
| XA3 | vysoce agresivní chemické prostředí | C35/45 b) | průmyslové čistírny, sklady chemikálií, silážní jámy, chladicí věže | |||||
| b) Síranovzdorný cement | ||||||||
| 6. koroze vlivem mechanického působení – obrus XM | ||||||||
| XM1 | mírné nebo střední namáhání obrusem | C30/37 | průmyslové podlahy, vozidla s pneumatikami | |||||
| XM2 | silné namáhání obrusem | C30/37 | průmyslové podlahy pojíždění celogumovými koly vysokozdvižných vozíků | |||||
| XM3 | velmi silné namáhání obrusem | C35/45 | podlahy pojížděné ocelovými nebo umělohmotnými koly, pásy, silné proudění vody | |||||
| Chemická charakteristika | Zkušební metoda | XA1 | XA2 | XA3 | ||||
| podzemní voda | ||||||||
| SO4-2 mg/litr | EN 196-2 | ≥ 200 a ≤ 600 | > 600 a ≤ 3 000 | > 3 000 a ≤ 6 000 | ||||
| pH | ISO 4316 | ≥ 5,5 a ≤ 6,5 | > 4,5 a ≤ 5,5 | > 4,0 a ≤ 4,5 | ||||
| CO2 mg/litr agresivní | EN 13577 | ≥ 15 a ≤ 40 | > 40 a ≤ 100 | > 100 do nasycení | ||||
| NH4+ mg/litr | ISO 7150-1,-2 | ≥ 15 a ≤ 30 | > 30 a ≤ 60 | > 60 a ≤ 100 | ||||
| Mg2+ mg/litr | ISO 7980 | ≥ 300 a ≤ 1 000 | > 1 000 a ≤ 3 000 | > 3 000 do nasycení | ||||
| zemina | ||||||||
| SO4-2 mg/kg | EN 196-2 | ≥ 2 000 a ≤ 3 000 | > 3 000 a ≤ 12 000 | > 12 000 a ≤ 24 000 | ||||
| kyselost ml/kg | DIN 4030-2 | > 200 | ||||||
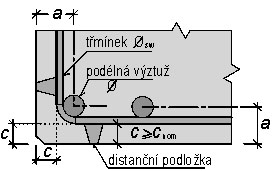
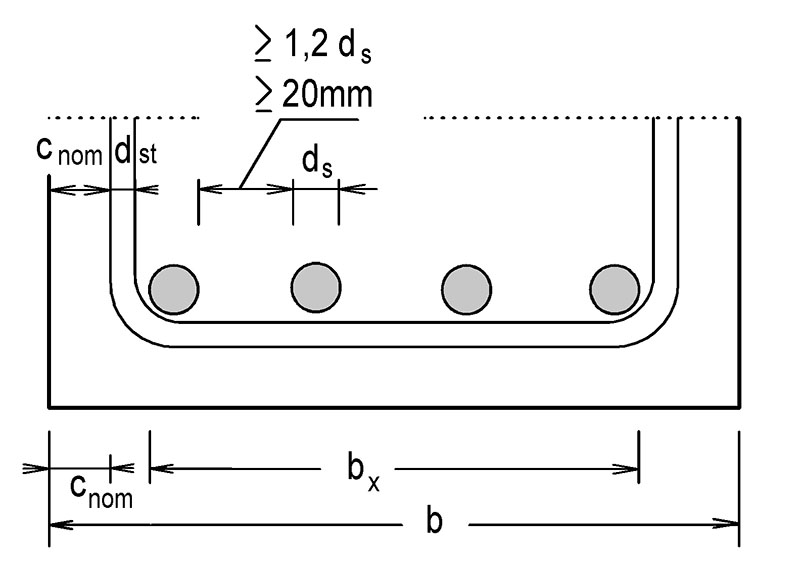
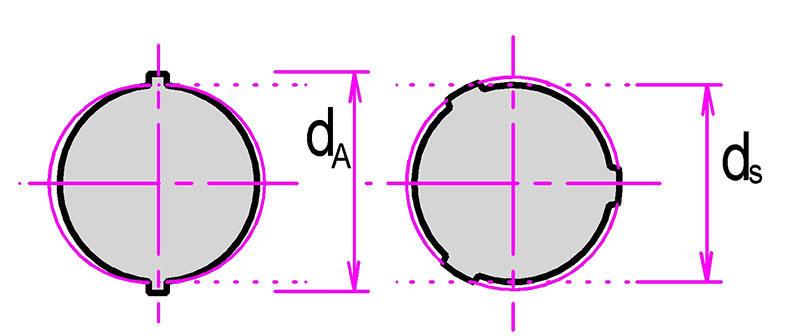
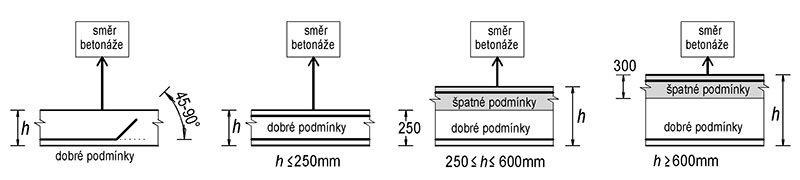
Obr. 3.2 Betonová krycí vrstva
Betonová krycí vrstva cnom = cmin + Δcdev cmin = max
(cmin,b ; cmin,dur +Δcdur,g – Δcdur,st – Δcdur,add; 10 mm)
Δcdev obvykle 10 mm pro monolit a 5 mm pro prefabrikát. Hodnoty cdur,g = Δcdur,st = Δcdur,add = 0 obvykle se nepoužívají, bližšíviz ČSN EN 1992-1-1.
Při betonáži na nerovné povrchy cnom ≥ 45 mm.
Při betonáži na zeminu cnom ≥ 75 mm.
Pokud je horní líc namáhán obrusem, je nutné zvětšit hodnotu cmin o 5 mm (XM1), o 10 mm (XM2) a o 15 mm pro XM3.
Tab. 3.2 Betonová krycí vrstva (S4-50 let, z hlediska koroze výztuže)
| Vliv prostředí | Minimální třídy betonu | Minimální bet. krycí vrstva | Monolitická konstrukce cnom [mm] | Prefabrikovaná konstrukce cnom [mm] | ||
| XC1 | C20/25 | 15 | 25 | Nejméně však Ø+10 mm | 20 | Nejméně však Ø+5 mm |
| XC2 | C25/30 | 25 | 35 | 30 | ||
| XC3 | C30/37 | 25 | 35 | 30 | ||
| XC4 | C30/37 | 30 | 40 | 35 | ||
| XD1 | C30/37 | 35 | 45 | 40 | ||
| XD2 | C35/45 | 40 | 50 | 45 | ||
| XD3 | C35/40 | 45 | 55 | 50 | ||
| U deskových konstrukcí lze betonovou krycí vrstvu zredukovat o 5 mm. Pro beton o dvě třídy vyšší než minimální lze zmenšit betonovou krycí vrstvu o 5 mm. Životnost 100 let – zvětšení betonové krycí vrstvy o 10 mm, pro trvale zasypané povrchy zvětšit o 10 mm. Podrobněji viz ČSN EN 1992-1-1. |
||||||
4 Návrh průřezu namáhaného ohybem
4.1 Jednostranně vyztužený průřez
Tab. 4.1 Návrh a posouzení jednostranně vyztuženého průřezu
| Návrh výztuže Poměrný ohybový moment \mu_\text{Ed}=\frac{M_\text{Edi}}{b\cdot d^2\cdot f_\text{cd}}=\frac{M_\text{Ed}-N_\text{Ed}\cdot z_\text{s1}}{b\cdot d^2\cdot f_\text{cd}}, z tab. 4.2 nebo výpočtem \omega_1=1-\sqrt{1-2\cdot\mu_\text{Ed}} Mechanický stupeň vyztužení \omega_1=\frac{A_\text{s}}{b\cdot d}\cdot\frac{f_\text{yd}}{f_\text{cd}} Staticky nutná plocha výztuže A_\text{s}=\omega_1\cdot\frac{b\cdot d}{f_\text{yd}/f_\text{cd}}+\frac{N_\text{Ed}}{f_\text{yd}} Výška tlačené oblasti x=d\cdot\xi\le\xi_\text{bal,1}\cdot d reps. x=d\cdot\xi\le\xi_\text{max}\cdot d (doporučeno) Rameno vnitřních sil z=d\cdot\zeta |
Posouzení výztuže (Při ručním výpočtu uvažujeme obvykle obdélníkové rozdělení napětí v tlačené části průřezu) Výška tlačené oblasti x=\frac{A_\text{s}\cdot f_\text{yd}}{0{,}8\cdot b\cdot f_\text{cd}} Rameno vnitřních sil z=(d-0{,}4x) M_\text{Rd}=A_\text{s}\cdot z\cdot f_\text{yd}=0{,}8\cdot b\cdot x\cdot z\cdot f_\text{cd}\ge M_\text{Ed} Kontrola výšky tlačené oblasti \xi=\frac{x}{d}=\frac{\varepsilon_\text{c2}}{\varepsilon_\text{c2}-\varepsilon_\text{s1}}\le\xi_\text{bal,1} resp. \xi=\frac{x}{d}\le\xi_\text{max} Pro betonu do třídy C50/60 \xi_\text{bal,1}=0{,}617 při ovinutí tlačené zóny betonu třmínky \xi_\text{max}=0{,}450 bez ovinutí tlačené zóny betonu Označení podle obr. 4.1 |
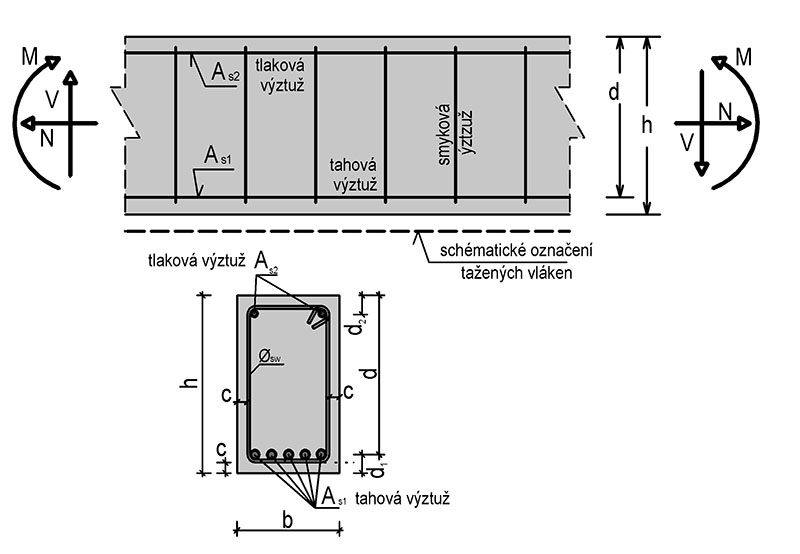
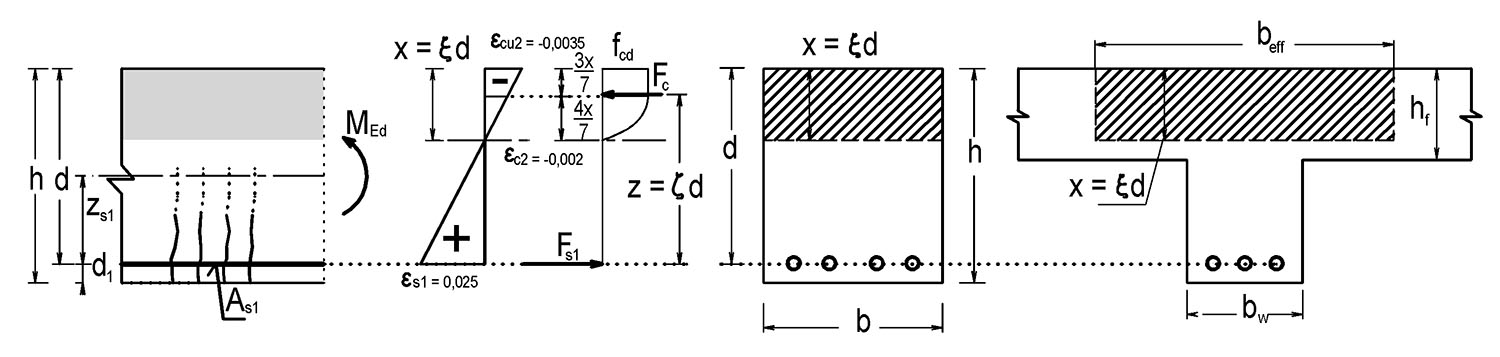
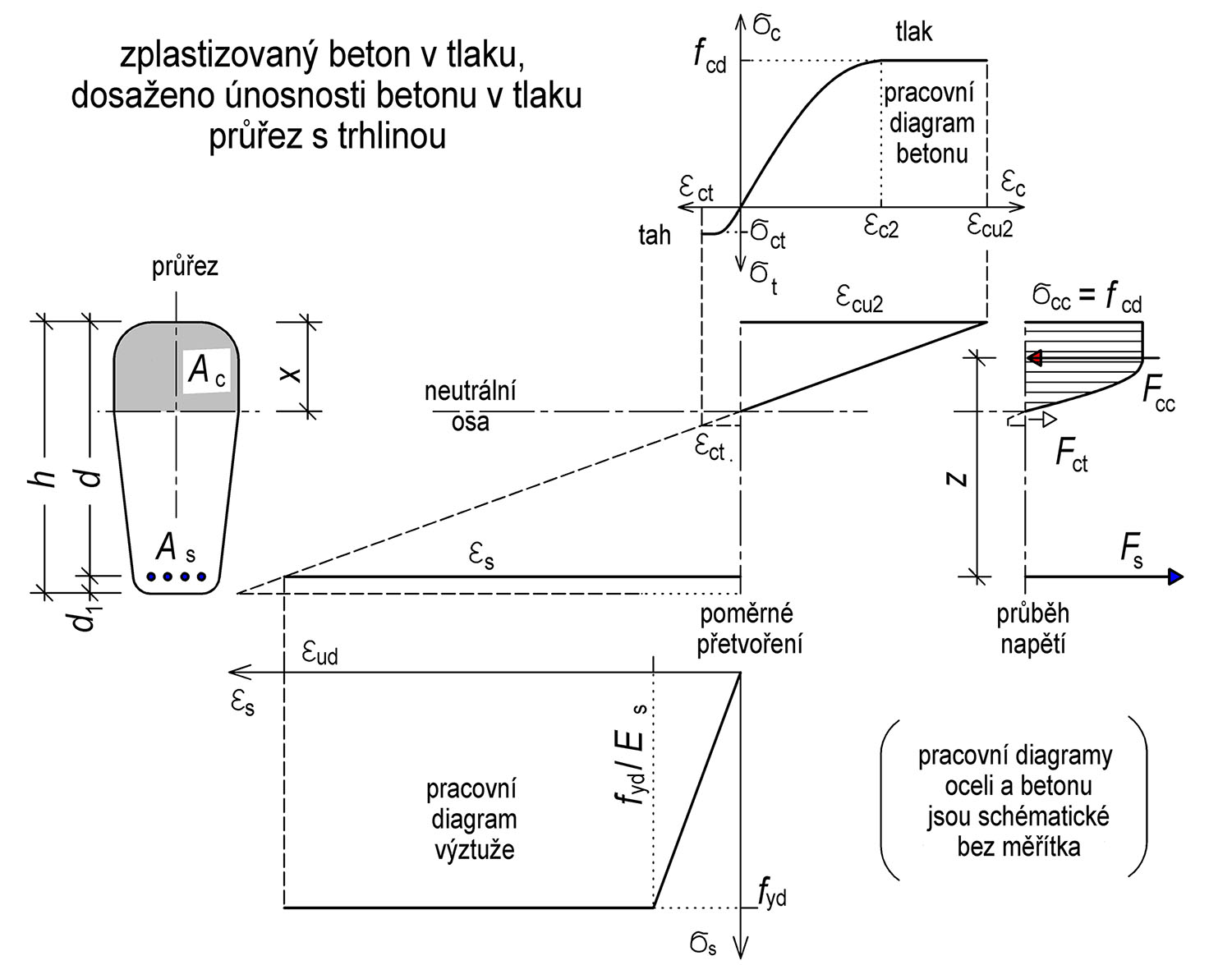
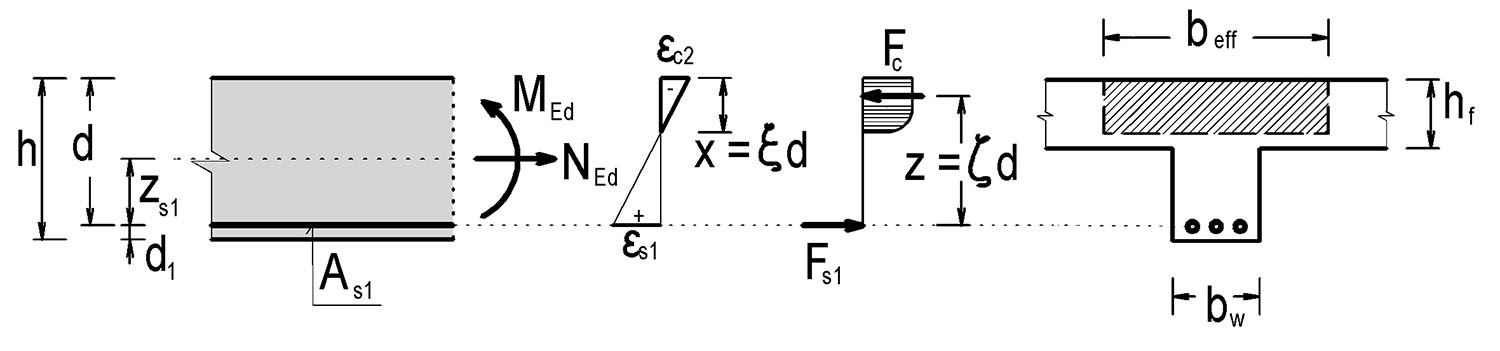
Obr. 4.1 Principy návrhu a posouzení jednostranně vyztuženého průřezu
Obr. 4.2 Jednostranně vyztužený průřezu
Tab. 4.2 Jednostranně vyztužený průřez pro parabolicko-rektangulární rozdělení napětí v betonu tlaku a pro výztuž se stoupající horní větví v pracovním diagramu
| μEds [-] | ω1 [-] | ξ = x/d [-] | ζ = z/d [-] | εc2 [‰] | εs1 [‰] | σsd [MPa] | β [-] | ka = ax/x [-] |
| 0,01 | 0,0101 | 0,0300 | 0,995 | -0,8 | 25,0 | 456,5 | 0,34 | 0,346 |
| 0,02 | 0,0202 | 0,0440 | 0,990 | -1,2 | 25,0 | 456,5 | 0,46 | 0,353 |
| 0,03 | 0,0305 | 0,0550 | 0,984 | -1,5 | 25,0 | 456,5 | 0,56 | 0,360 |
| 0,04 | 0,0409 | 0,0660 | 0,979 | -1,8 | 25,0 | 456,5 | 0,62 | 0,368 |
| 0,05 | 0,0514 | 0,0760 | 0,974 | -2,1 | 25,0 | 456,5 | 0,68 | 0,377 |
| 0,06 | 0,0620 | 0,0860 | 0,968 | -2,4 | 25,0 | 456,5 | 0,72 | 0,387 |
| 0,07 | 0,0727 | 0,0970 | 0,963 | -2,7 | 25,0 | 456,5 | 0,75 | 0,396 |
| 0,08 | 0,0836 | 0,1070 | 0,957 | -3,0 | 25,0 | 456,5 | 0,78 | 0,405 |
| 0,09 | 0,0946 | 0,1180 | 0,951 | -3,3 | 25,0 | 456,5 | 0,80 | 0,413 |
| 0,10 | 0,1057 | 0,1305 | 0,946 | -3,5 | 23,0 | 454,9 | 0,81 | 0,416 |
| 0,11 | 0,1170 | 0,1445 | 0,940 | -3,5 | 20,4 | 452,5 | 0,81 | 0,416 |
| 0,12 | 0,1285 | 0,1586 | 0,934 | -3,5 | 18,3 | 450,4 | 0,81 | 0,416 |
| 0,13 | 0,1401 | 0,1729 | 0,928 | -3,5 | 16,5 | 448,7 | 0,81 | 0,416 |
| 0,14 | 0,1518 | 0,1875 | 0,922 | -3,5 | 15,0 | 447,2 | 0,81 | 0,416 |
| 0,15 | 0,1638 | 0,2022 | 0,916 | -3,5 | 13,6 | 445,9 | 0,81 | 0,416 |
| 0,16 | 0,1759 | 0,2172 | 0,910 | -3,5 | 12,4 | 444,7 | 0,81 | 0,416 |
| 0,17 | 0,1882 | 0,2324 | 0,903 | -3,5 | 11,4 | 443,7 | 0,81 | 0,416 |
| 0,18 | 0,2007 | 0,2478 | 0,897 | -3,5 | 10,5 | 442,8 | 0,81 | 0,416 |
| 0,19 | 0,2134 | 0,2635 | 0,890 | -3,5 | 9,6 | 442,0 | 0,81 | 0,416 |
| 0,20 | 0,2263 | 0,2794 | 0,884 | -3,5 | 8,9 | 441,3 | 0,81 | 0,416 |
| 0,21 | 0,2395 | 0,2957 | 0,877 | -3,5 | 8,2 | 440,7 | 0,81 | 0,416 |
| 0,22 | 0,2528 | 0,3122 | 0,870 | -3,5 | 7,6 | 440,1 | 0,81 | 0,416 |
| 0,23 | 0,2665 | 0,3291 | 0,863 | -3,5 | 7,1 | 439,5 | 0,81 | 0,416 |
| 0,24 | 0,2804 | 0,3462 | 0,856 | -3,5 | 6,5 | 439,0 | 0,81 | 0,416 |
| 0,25 | 0,2946 | 0,3638 | 0,849 | -3,5 | 6,0 | 438,5 | 0,81 | 0,416 |
| 0,26 | 0,3091 | 0,3817 | 0,841 | -3,5 | 5,6 | 438,1 | 0,81 | 0,416 |
| 0,27 | 0,3239 | 0,4000 | 0,834 | -3,5 | 5,1 | 437,7 | 0,81 | 0,416 |
| 0,28 | 0,3391 | 0,4187 | 0,826 | -3,5 | 4,8 | 437,3 | 0,81 | 0,416 |
| 0,29 | 0,3546 | 0,4379 | 0,818 | -3,5 | 4,4 | 437,0 | 0,81 | 0,416 |
| 0,30 | 0,3705 | 0,4576 | 0,810 | -3,5 | 4,1 | 436,7 | 0,81 | 0,416 |
| 0,31 | 0,3869 | 0,4778 | 0,801 | -3,5 | 3,7 | 436,4 | 0,81 | 0,416 |
| 0,33 | 0,4211 | 0,5201 | 0,784 | -3,5 | 3,2 | 435,8 | 0,81 | 0,416 |
| 0,35 | 0,4576 | 0,5651 | 0,765 | -3,5 | 2,6 | 435,3 | 0,81 | 0,416 |
| 0,37 | 0,4968 | 0,6136 | 0,745 | -3,5 | 2,2 | 434,8 | 0,81 | 0,416 |
4.2 Oboustranně vyztužený průřez
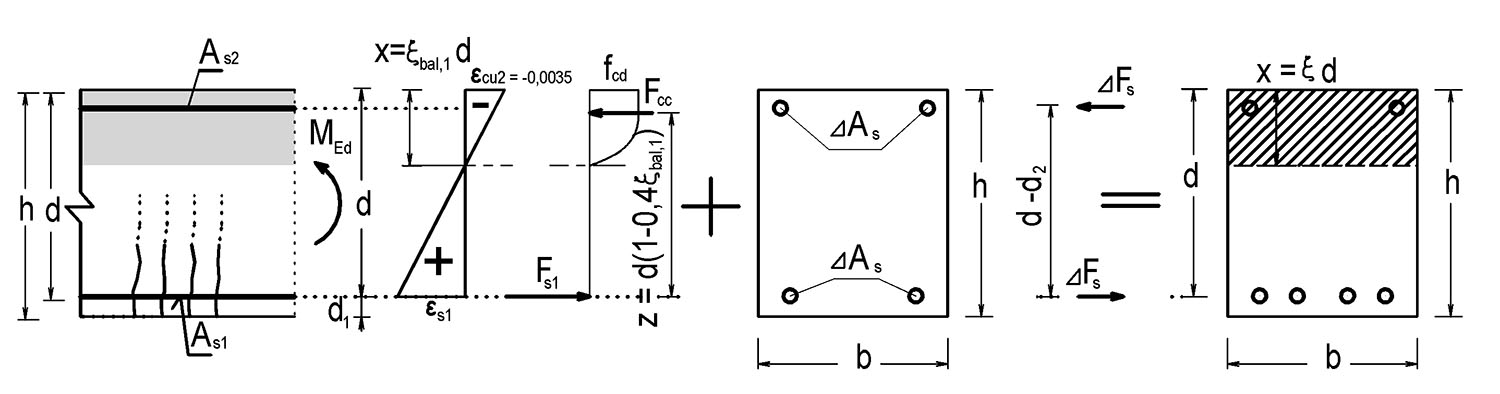
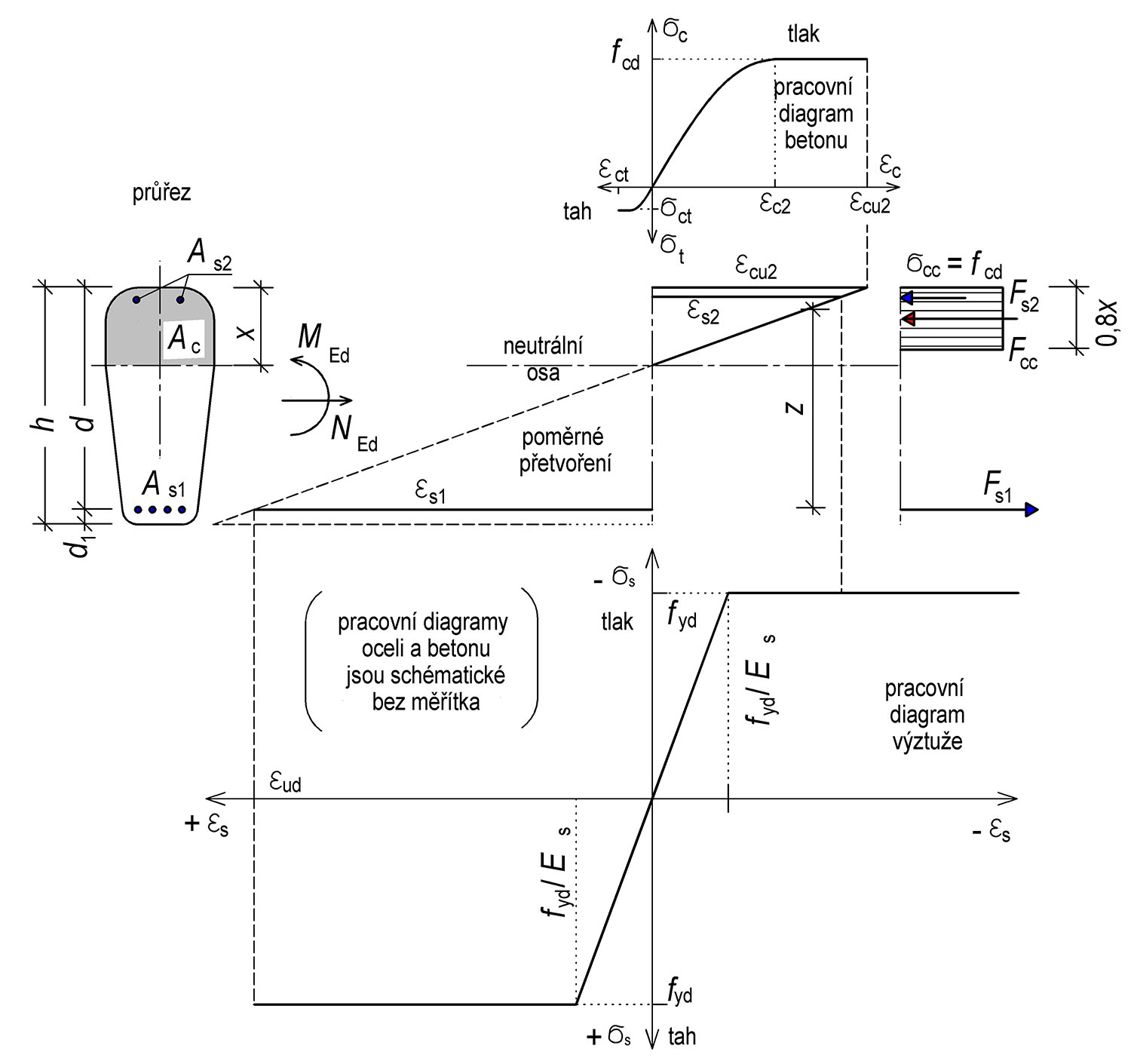
Obr. 4.3 Principy návrhu a posouzení oboustranně vyztuženého průřezu
Obr. 4.4 Oboustranně vyztužený průřezu
\begin{gathered}
M_\text{Ed}\le M_\text{Rd}=F_\text{s2}\cdot(d-d_2)+F_\text{cc}(d-k_\text{a}\cdot x)
\end{gathered}Tab. 4.3 Návrh a posouzení oboustranně vyztuženého průřezu
| Návrh výztuže pomocí tabulek \mu_\text{Ed}=\frac{M_\text{Edi}}{b\cdot d^2\cdot f_\text{cd}}=\frac{M_\text{Ed}-N_\text{Ed}\cdot z_\text{s1}}{b\cdot d^2\cdot f_\text{cd}} Z tab. 4.4 stanovíme ω1 a ω2 Staticky nutná plocha výztuže v tažené části A_\text{s1}=\omega_1\cdot\frac{b\cdot d}{f_\text{yd}/f_\text{cd}}+\frac{N_\text{Ed}}{f_\text{yd}} Staticky nutná plocha tlačené výztuže A_\text{s2}=\omega_2\frac{b\cdot d}{f_\text{yd}/f_\text{cd}} Výška tlačené oblasti x=d\cdot\xi\le\xi_\text{bal,1}\cdot d Rameno vnitřních sil z=d\cdot\zeta Proměnné viz obr. 4.3 |
Návrh a posouzení výztuže Tažená výztuž A_\text{s1}+A_\text{s1,max}+\Delta A_\text{s1} Tlačená výztuž A_\text{s2}=\Delta A_\text{s1}=\Delta M_\text{Ed}/((d-d_2)\cdot f_\text{yd}) Maximální únosnost pro jednostranně vyztužený průřez A_\text{s1}:M_\text{Rd,1}=A_\text{s}\cdot d\cdot(1-0{,}4\xi_\text{bal,1})\cdot f_\text{yd} Pro tlačenou a část tažené výztuže A_\text{s2}=\Delta A_\text{s1}:\Delta M_\text{Rd}=\Delta A_\text{s}\cdot(d-d_2)\cdot f_\text{yd} Celková únosnost M_\text{Rd}=M_\text{Rd,1}+\Delta M_\text{Rd}\ge M_\text{Ed} Musí být splněny podmínky pro x\le\xi_\text{bal,1}\cdot d maximální výška tlačené oblasti x\ge\xi_\text{bal,2}\cdot d_2 poloha horní výztuže |
Tab. 4.4 Návrhová tabulka pro oboustranně vyztužený průřez pro ξlim = 0,6170;
\begin{gathered}
\varepsilon_\text{s1}=2{,}17 \text{ ‰}\space\text{ a }\space\varepsilon_\text{c}=-3{,}50 \text{ ‰}
\end{gathered}| d2/d = 0,05 | d2/d = 0,10 | d2/d = 0,15 | d2/d = 0,20 | |||||
| εs2,lim = -3,22 ‰ | εs2,lim = -2,93 ‰ | εs2,lim = -2,65 ‰ | εs2,lim = -2,37 ‰ | |||||
| μEds | ω1 | ω2 | ω1 | ω2 | ω1 | ω2 | ω1 | ω2 |
| 0,38 | 0,5090 | 0,0090 | 0,5090 | 0,0090 | 0,5100 | 0,0100 | 0,5100 | 0,00100 |
| 0,39 | 0,519 | 0,0190 | 0,5200 | 0,0200 | 0,5210 | 0,0210 | 0,5230 | 0,0230 |
| 0,40 | 0,5300 | 0,0300 | 0,5310 | 0,0310 | 0,5330 | 0,0330 | 0,5350 | 0,0350 |
| 0,41 | 0,5400 | 0,0400 | 0,5420 | 0,0420 | 0,5450 | 0,0540 | 0,5480 | 0,0480 |
| 0,42 | 0,5510 | 0,0510 | 0,5540 | 0,0540 | 0,5570 | 0,0570 | 0,5600 | 0,0600 |
| 0,43 | 0,5610 | 0,0610 | 0,5650 | 0,0650 | 0,5690 | 0,0690 | 0,5730 | 0,0730 |
| 0,44 | 0,5720 | 0,0720 | 0,5760 | 0,0760 | 0,5800 | 0,0800 | 0,5850 | 0,0850 |
| 0,45 | 0,5820 | 0,0820 | 0,5870 | 0,0870 | 0,5920 | 0,0920 | 0,5980 | 0,0980 |
| 0,46 | 0,5930 | 0,0930 | 0,5980 | 0,0980 | 0,6040 | 0,1040 | 0,6100 | 0,1100 |
| 0,47 | 0,6030 | 0,1030 | 0,6090 | 0,1090 | 0,6160 | 0,1160 | 0,6230 | 0,1230 |
| 0,48 | 0,6140 | 0,1140 | 0,6200 | 0,1200 | 0,6270 | 0,1270 | 0,6350 | 0,1350 |
| 0,49 | 0,6240 | 0,1240 | 0,6310 | 0,1310 | 0,6390 | 0,1390 | 0,6480 | 0,1480 |
| 0,50 | 0,6350 | 0,1350 | 0,6420 | 0,1420 | 0,6510 | 0,1510 | 0,6600 | 0,1600 |
| 0,51 | 0,6450 | 0,1450 | 0,6540 | 0,1540 | 0,6630 | 0,1630 | 0,6730 | 0,1730 |
| 0,52 | 0,6560 | 0,560 | 0,6650 | 0,1650 | 0,6740 | 0,1740 | 0,6850 | 0,1850 |
| 0,53 | 0,6660 | 0,1660 | 0,6760 | 0,1760 | 0,6860 | 0,1860 | 0,6980 | 0,1980 |
| 0,54 | 0,6770 | 0,1770 | 0,6870 | 0,1870 | 0,6980 | 0,1980 | 0,7100 | 0,2100 |
| 0,55 | 0,6880 | 0,1880 | 0,6980 | 0,1980 | 0,7100 | 0,2100 | 0,7230 | 0,2230 |
| 0,56 | 0,6980 | 0,1980 | 0,7090 | 0,2090 | 0,7210 | 0,2210 | 0,7350 | 0,2350 |
| 0,57 | 0,7090 | 0,2090 | 0,7200 | 0,2200 | 0,7330 | 0,2330 | 0,7480 | 0,2480 |
| 0,58 | 0,7190 | 0,2190 | 0,7310 | 0,2310 | 0,7450 | 0,2450 | 0,7600 | 0,2600 |
| 0,59 | 0,7300 | 0,2300 | 0,7410 | 0,2420 | 0,7570 | 0,2570 | 0,7730 | 0,2730 |
| 0,60 | 0,7400 | 0,2400 | 0,7540 | 0,2540 | 0,7690 | 0,2690 | 0,7850 | 0,2850 |
Tab. 4.5 Maximální počet výztužných prutů v trámu/průvlaku
| Šířka trámu b [mm] | Šířka bx [mm] | Průřez výztužných prutů ø v [mm]/počet výztužných prutů | ||||||||||
| ø 8 | ø 10 | ø 12 | ø 14 | ø 16 | ø 18 | ø 20 | ø 22 | ø 25 | ø 28 | ø 32 | ||
| 100 | 26 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 150 | 76 | 3 | 3 | 3 | 2 | 2 | 2 | 2 | 2 | 1 | 1 | 1 |
| 200 | 126 | 5 | 4 | 4 | 4 | 4 | 3 | 3 | 3 | 2 | 2 | 2 |
| 250 | 176 | 7 | 6 | 6 | 5 | 5 | 4 | 4 | 4 | 3 | 3 | 3 |
| 300 | 226 | 8 | 8 | 7 | 7 | 6 | 6 | 5 | 5 | 4 | 4 | 3 |
| 350 | 276 | 10 | 9 | 9 | 8 | 8 | 7 | 6 | 6 | 5 | 5 | 4 |
| 400 | 326 | 12 | 11 | 10 | 10 | 9 | 8 | 7 | 7 | 6 | 5 | 5 |
| 450 | 376 | 14 | 13 | 12 | 11 | 11 | 10 | 9 | 8 | 7 | 6 | 5 |
| 500 | 426 | 15 | 14 | 13 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 |
| třmínek ø sw | průměr třmínků ≤ 8 mm | ≤ 10 mm | ≤ 12 mm | |||||||||
Světlá vzdálenost prutů a musí být taková, aby beton mohl být řádně uložen a zhutněn tak, aby byla dosažena odpovídající soudržnost výztuže s betonem. Světlá vzdálenost ve vodorovném a svislém směru mezi jednotlivými rovnoběžnými pruty nebo mezi vodorovnými vrstvami nemá být menší než největší z následujících hodnot:
4.3 T-průřez
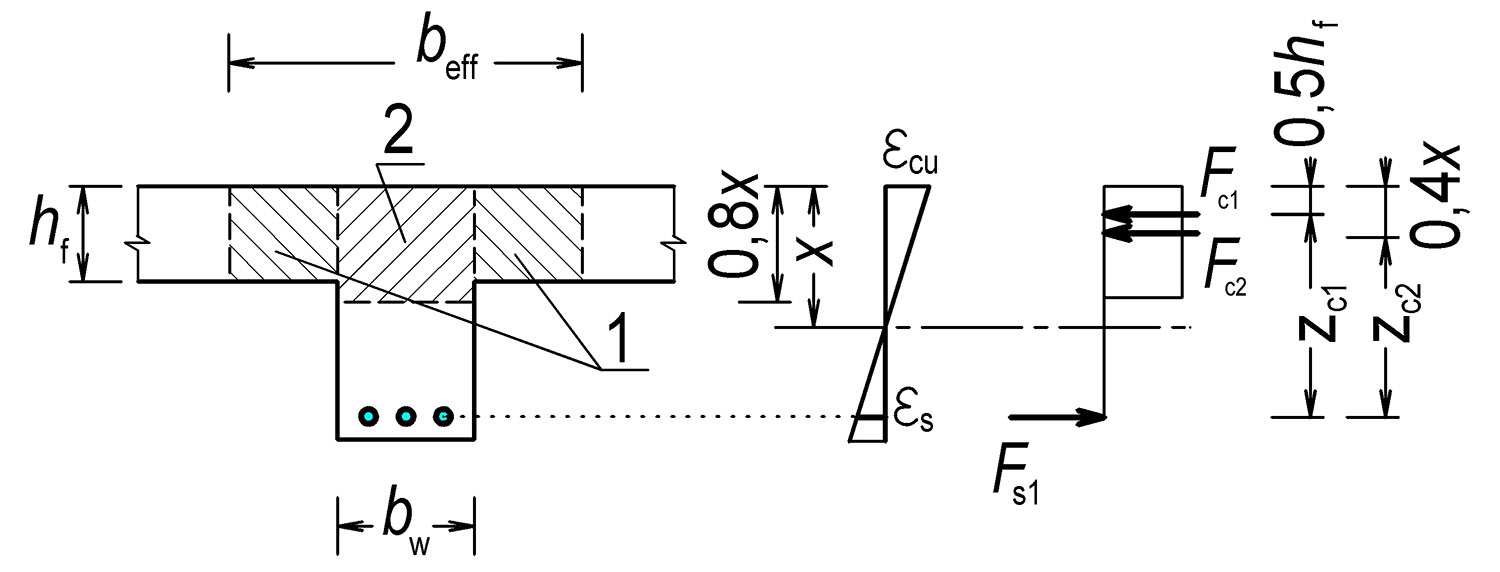
Tab. 4.6 Návrh T-průřezu
Neutrální osa jde deskou
Návrh stejný jako u obdélníkového průřezu
Neutrální osa jde stojinou
Stanovíme maximální únosnost části přírub (1)
z_\text{c1}=d-0{,}5h_\text{f}
M_\text{Rd,1}=(b_\text{eff}-b_\text{w}\cdot h_\text{f}\cdot f_\text{cd}\cdot z_\text{c1}
Stanovíme únosnost obdélníkového průřezu (2)
z_\text{c2}=d-0{,}4x, M_\text{Rd,2}=0{,}4x\cdot b_\text{w}\cdot f_\text{cd}\cdot z_\text{c2}
Celková únosnost T-průřezu
M_\text{Rd}=M_\text{Rd,1}+M_\text{Rd,2}
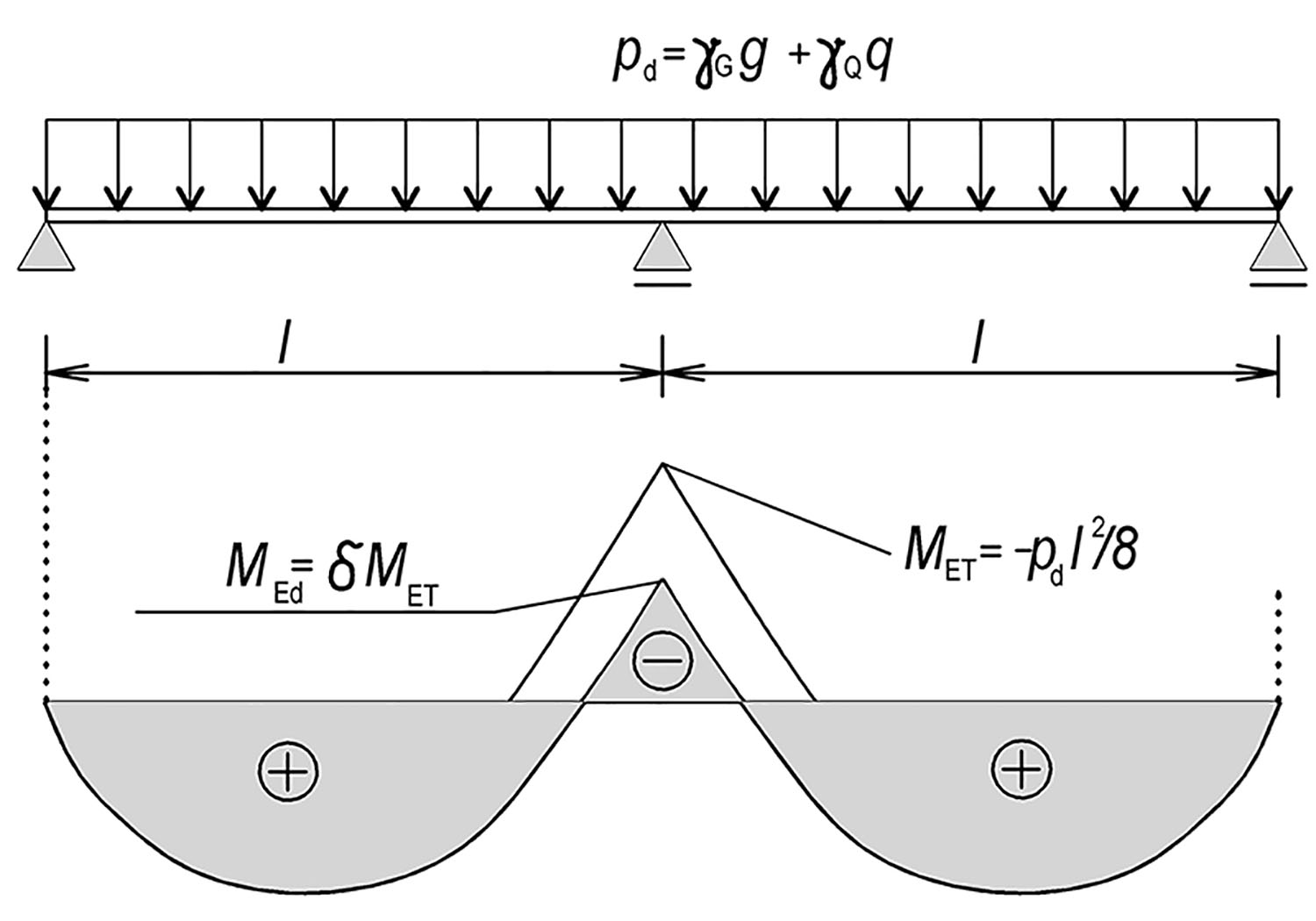
4.4 Redistribuce vnitřních sil
U spojitých nosníků nebo desek, které jsou převážně namáhány ohybem a mají poměr délek přilehlých rozpětí v rozmezí od 0,5 do 2,0 lze redistribuovat ohybové momenty
\delta\ge0{,}44+\frac{1{,}25\cdot x_\text{u}}{d} (pro betony do C50/60 včetně)
kde je
xu … vzdálenost neutrální osy od tlačeného okraje stanovená v MSÚ po redistribuci.
Musí být splněna podmínka
Pro výztuž duktility A …….\delta\ge0{,}80
Pro výztuž duktility B a C …\delta\ge0{,}70
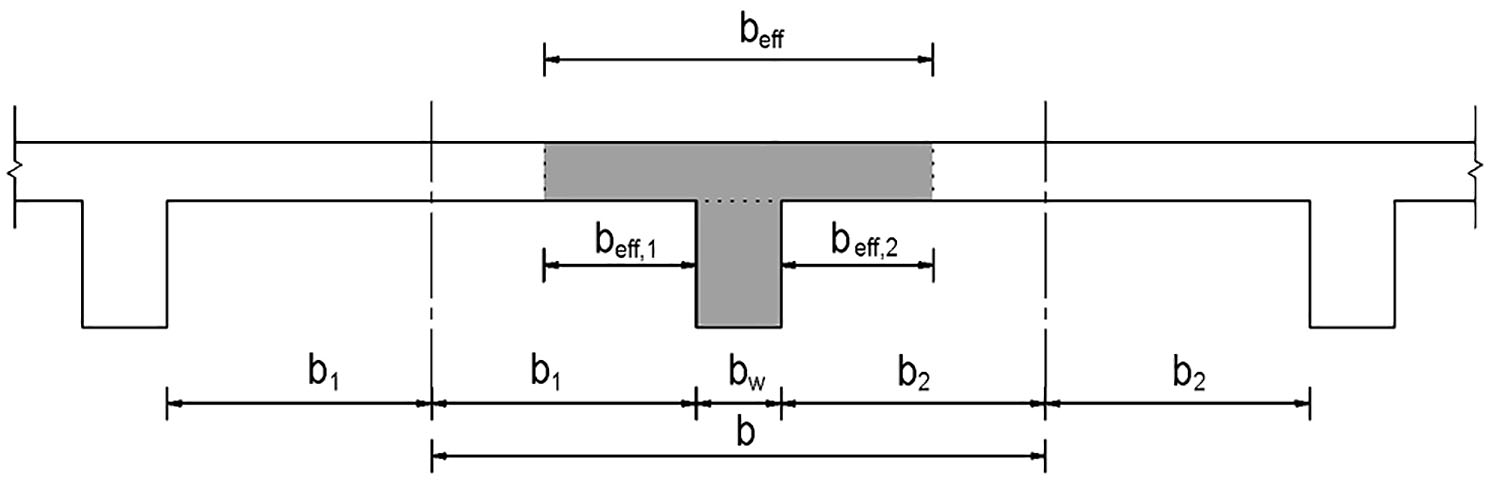
4.5 Spolupůsobící šířka desky
b_\text{eff}=\sum b_\text{eff,i}+b_\text{w}\le b,
kde
b_\text{eff,i}=0{,}2b_\text{i}+0{,}1l_0\le0{,}2l_0
b_\text{eff,i}\le b_\text{i}
Při výpočtu vnitřních sil lze uvažovat jednu šířku desky po celé délce nosníku.
U T-průřezů postupujeme stejně jako u obdélníkových průřezů, pokud neutrální osa prochází horní deskou.
4.6 Rozhodující vnitřní síly
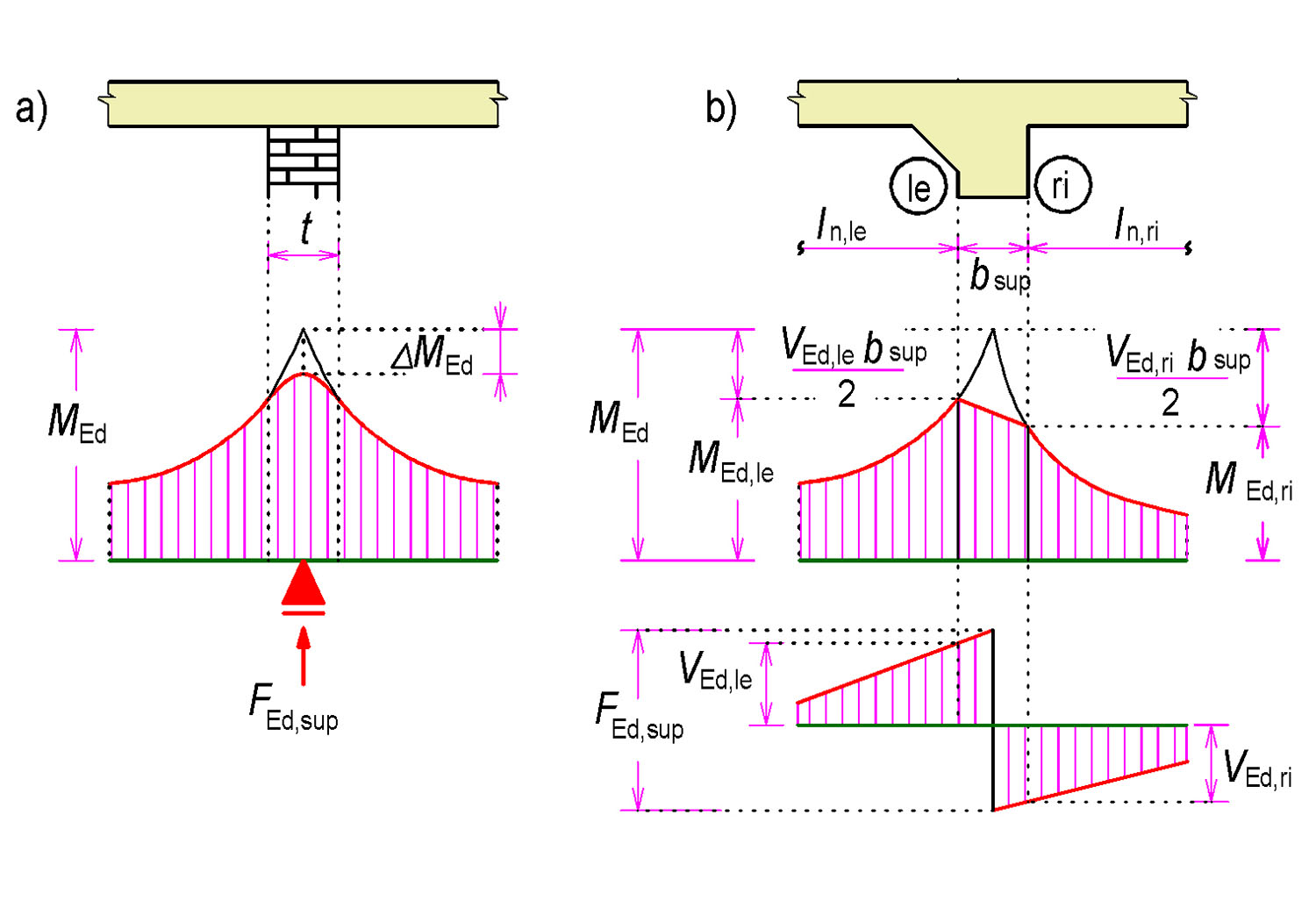
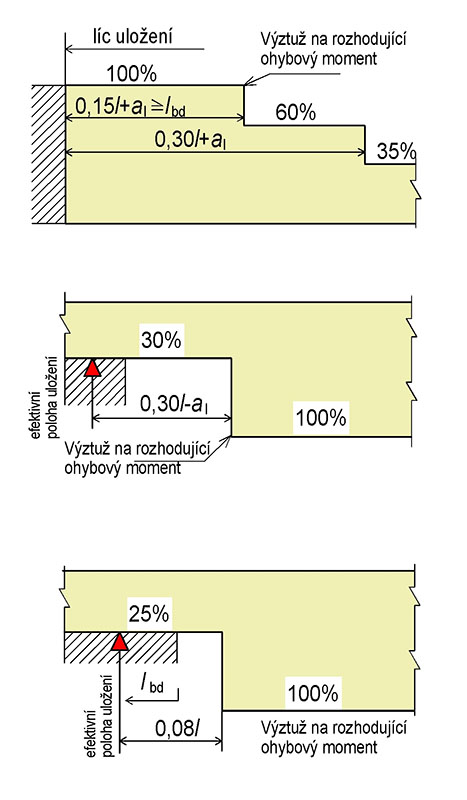
Tab. 4.7 Rozhodující ohybový moment nad podporou
a) Redukce návrhového momentu u podpory umožňující volné pootočení.
M_\text{Ed,le}=M_\text{Ed}+\frac{V_\text{Ed,le}\cdot b_\text{sup}}{2}\ge0{,}65\cdot\frac{1}{12}\cdot q_\text{le}\cdot l_\text{n,le}^2
M_\text{Ed,ri}=M_\text{Ed}+\frac{V_\text{Ed,ri}\cdot b_\text{sup}}{2}\ge0{,}65\cdot\frac{1}{12}\cdot q_\text{ri}\cdot l_\text{n,ri}^2
kde \frac{1}{12}\cdot q_\text{ri}\cdot l_\text{n,ri}^2 je moment v plném vetknutí
qle a qri jsou zatížení nosníku z levé resp. pravé strany podpory
b) Redukce ohybového momentu u podpory monoliticky spojené s podporou.
4.7 Minimální a maximální vyztužení
Tab. 4.8 Minimální a maximální vyztužení ohýbaného prvku
| Minimální plocha výztuže | A_\text{s,min}=0{,}26\cdot\bigg(\frac{f_\text{ctm}}{f_\text{yk}}\bigg)\cdot b_\text{t}\cdot d ne méně však než A_\text{s,min}=0{,}0013\cdot b_\text{t}\cdot d fctm viz tab.1.1, fyk viz tab. 2.1, bt je šířka průřezu, d je účinná výška průřezu a h je celková výška průřezu |
| Maximální vyztužení | Průřezová plocha tahové a tlakové výztuže nemá překročit hodnotu: 0{,}04\cdot A_\text{c}, kde A_\text{c}=b\cdot h |
5 Návrh průřezu namáhaného posouvající silou
5.1 Prvky bez smykové výztuže
Únosnost betonového průřezu
\begin{gathered}
V_\text{Rd,c}=[0{,}18/\gamma c\cdot k\cdot(100\rho_\text{l}f_\text{ck})^{1/3}+0{,}15\cdot\sigma_\text{cp}]\cdot b_\text{w}\cdot d
\end{gathered}Minimální únosnost
\begin{gathered}
V_\text{Rd,c}=(v_\text{min}+0{,}15\sigma_\text{cp})\cdot b_\text{w}\cdot d
\end{gathered}Poznámka:
Bez smykové výztuže mohou být navrhovány pouze desky a málo namáhané ohýbané prvky.
\begin{gathered}
k=1+\sqrt{\frac{200}{d}}\le2{,}0
\end{gathered}vliv výšky průřezu [mm]
\begin{gathered}
\rho_\text{l}=\frac{A_\text{sl}}{b_\text{w}d}\le0{,}02
\end{gathered}vliv vyztužení tahovou výztuží
\begin{gathered}
\sigma_\text{cp}=N_\text{Ed}/A_\text{c}<2{,}0\cdot f_\text{cd}[\text{MPa}]
\end{gathered}vliv normálové síly v průřezu (NEd > 0 pro tlak)
\begin{gathered}
v_\text{min}=0{,}035k^{3/2}\cdot f_\text{ck}^{1/2}
\end{gathered}(fck viz tab. 1.1)
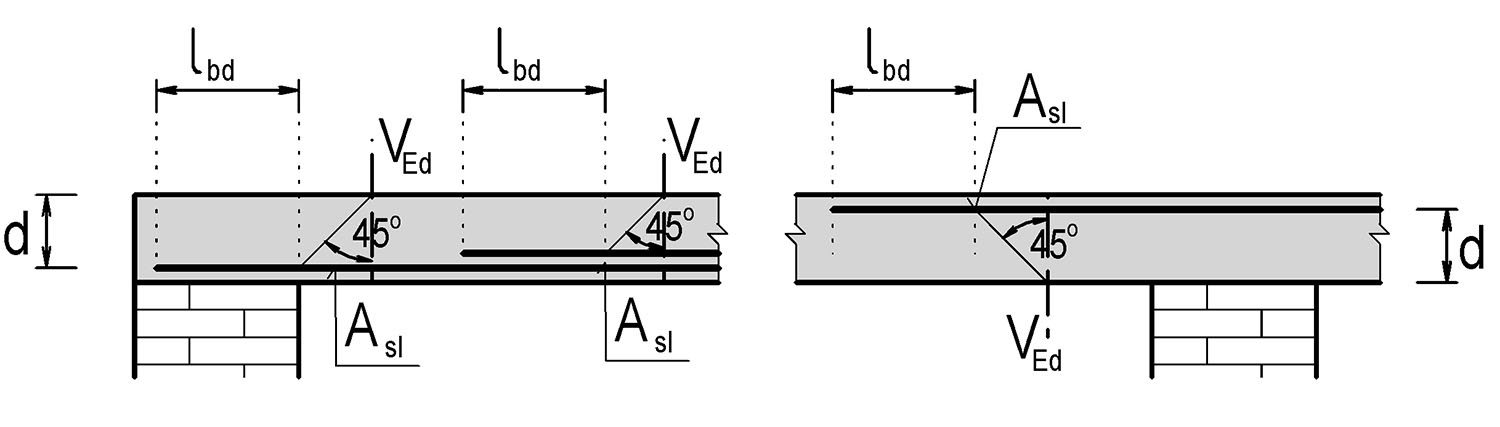
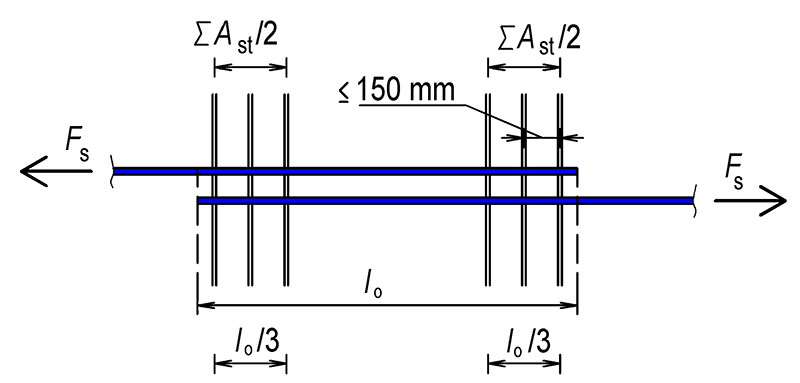
Obr. 5.1 Započitatelná tahová výztuž
5.2 Rozhodující posouvající síla
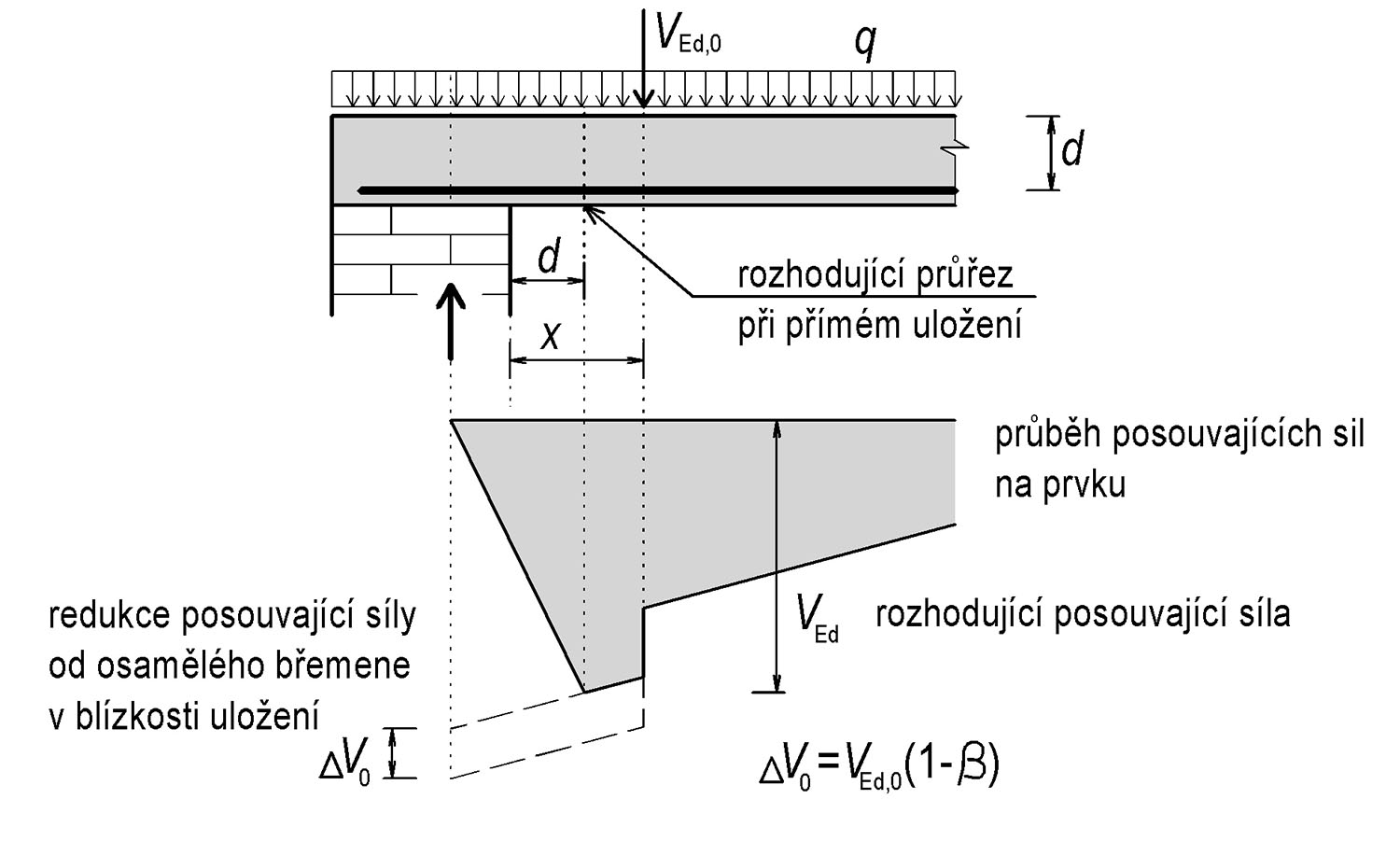
Při přímém uložení lze redukovat posouvající sílu součinitelem β, pokud je blízko uložení (ve vzdálenosti av od líce uložení).
Pokud platí
0{,}5d\le a_\text{v}\le2d
pak součinitel β má hodnotu
\beta=a_\text{v}/(2d)\ge0{,}25
Přitom musí být splněna podmínka
V_\text{Ed}\le0{,}5b_\text{w}\cdot d\cdot v\cdot f_\text{cd}\\
v=0{,}6\cdot(1-f_\text{ck}/250)
a u prvků se smykovou výztuží navíc podmínka
V_\text{Ed}\le A_\text{sw}\cdot f_\text{ywd}\cdot\sin\alpha
kde je
fywd … návrhová únosnost smykové výztuže
fcd – viz tab.1.1
5.3 Prvky se smykovou výztuží
Tab. 5.1 Únosnost smykově vyztuženého průřezu
| Únosnost tlačených betonových diagonál | Staticky nutná plocha smykové výztuže |
| V_\text{Rd,max}=v\cdot b_\text{w}\cdot z\cdot f_\text{cd}\cdot\frac{\cot\theta+\cot\alpha}{1+\cot^2\theta} Podmínka 1\le\cot\theta\le2{,}5 Pro \cot\theta=0{,}5, tedy minimální sklon, je minimální únosnost V_\text{Rd,max}=0{,}345\cdot vf_\text{cd}\cdot b_\text{w} v=0{,}6(1-f_\text{ck}/250), fck v MPa Pro tažený prvek je doporučená hodnota \cot\theta=1{,}0 Pro ohýbaný prvek je doporučená hodnota \cot\theta=1{,}2 |
a_\text{sw}=\frac{V_\text{Ed}}{f_\text{ywd}\cdot z\cdot\sin\alpha\cdot/\cot\theta+\cot\alpha)} Únosnost svislých třmínků V_\text{Rd,s}=\frac{A_\text{sw}\cdot f_\text{ywd}}{s}\cdot z\cdot\cot\theta kde je A_\text{se}=n\cdot(\pi\phi_\text{sw}^{2/4}) plocha všech větví jednoho třmínku; s … osová vzdálenost třmínků v podélném směru; z … cot θ průmět šikmé smykové trhliny. |
| Pokud je nutná smyková výztuž, pak s výjimkou desek musí přenést celou posouvající sílu |V_\text{Ed}|\le V_\text{Rd,s} | |
Konstrukční zásady pro smykově vyztužené průřezy
Smyková výztuž může svírat se střednicí konstrukčního prvku úhel α mezi 45°a 90°.
Třmínky musí být účinně zakotveny. Třmínky musí tvořit nejméně 50 % potřebné smykové výztuže.
Stupeň smykového vyztužení ρw musí splňovat podmínky
\rho_\text{w}=\frac{A_\text{sw}}{s\cdot b_\text{w}\cdot\sin\alpha}\ge\rho_\text{w,min} a současně \rho_\text{w}=\frac{A_\text{sw}}{s\cdot b_\text{w}\cdot\sin\alpha}\le\frac{0{,}5\cdot v\cdot f_\text{cd}}{f_\text{ywd}}
kde je
ρw … stupeň smykového vyztužení;
ρw ³ ρw,min;
Asw … plochy smykové výztuže v rozsahu délky s;
s … vzdálenost smykové výztuže měřená ve střednici prvku;
bw … šířka stojiny prvku;
α … úhel, který svírá smyková výztuž se střednicí prvku a
\begin{gathered}
v=0{,}60[1-f_\text{cd}/250]
\end{gathered}fywd … návrhová únosnost smykové výztuže.
Minimální stupeň smykového vyztuženíρw,min se stanoví ze vztahu
\rho_\text{w,min}=\frac{0{,}08\sqrt{f_\text{ck}}}{f_\text{yk}} kde fck; fyk se dosazuje v MPa
Tab. 5.2 Minimální stupeň smykového vyztuženíρw,min
| fck [MPa] | 16 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| ρw,min [%] | 0,061 | 0,071 | 0,082 | 0,093 | 0,103 | 0,112 | 0,121 | 0,130 |
Maximální podélná vzdálenost s mezi třmínky (smykovými výztužnými sestavami) nesmí přesáhnout sl,max.
\begin{gathered}
s_\text{l,max}=0{,}75d(1+\cot\alpha)\le400\text{ mm}
\end{gathered}vzdálenost ohybů nesmí přesáhnout
\begin{gathered}
s_\text{b,max}=0{,}6d(1+\cot\alpha)
\end{gathered}příčná vzdálenost větví třmínkové výztuže nesmí přesáhnout
\begin{gathered}
s_\text{t,max}=0{,}75d\le600\text{ mm}
\end{gathered}kde je
d … účinná výška trámu a a úhel který svírá smyková výztuž se střednicí prvku.
5.4 Smyk v pracovní spáře
Tab. 5.3 Smyk v pracovní spáře
Smyk v pracovní spáře
v_\text{Edi}\le v_\text{Rdi}
v_\text{Edi}=\beta\cdot\frac{V_\text{Ed}}{z\cdot b_\text{i}}
kde β je poměr podélné síly v dobetonované části k celkové síle
Pro velmi hladký povrch c ≤ 0,1, μ = 0,5
Pro hladký povrch c = 0,20, μ = 0,6
Pro zdrsněný povrch c = 0,40, μ = 0,7
Pro zazubený povrch c = 0,50, μ = 0,9
Smyková únosnost v pracovní spáře
v_\text{Rdi}=c\cdot f_\text{ctd}+\mu\cdot\sigma_\text{n}+\rho\cdot f_\text{yd}(\mu\cdot\sin\alpha+\cos\alpha)\le0{,}5v\cdot f_\text{cd}
v=0{,}60\bigg[1-\frac{f_\text{ck}}{250}\bigg],\rho=\frac{A_\text{s}}{A_\text{i}},
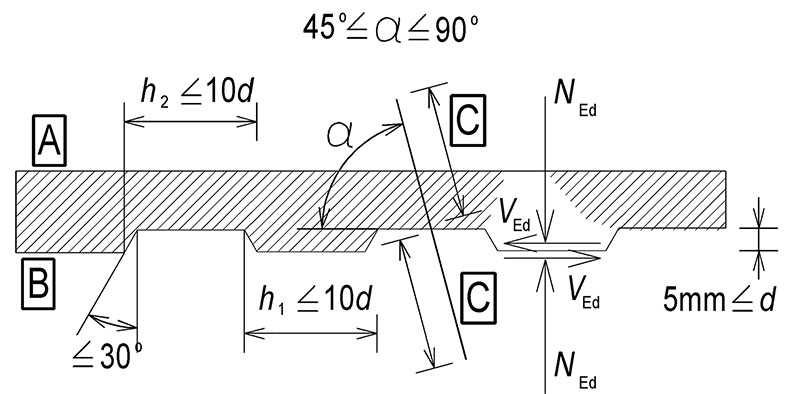
sklon spřahovací výztuže 45o ≤ α ≤ 90o kde jsou
c, μ … součinitelé definující vliv drsnosti horního líce prvku v pracovní spáře;
σn … normálové napětí v průřezu;
Ai …plocha styčné spáry;
As … plocha výztuže procházející spárou.
Obr. 5.3 Smyk ve vodorovné pracovní spáře
5.5 Smyk mezi horní přírubou a stojinou
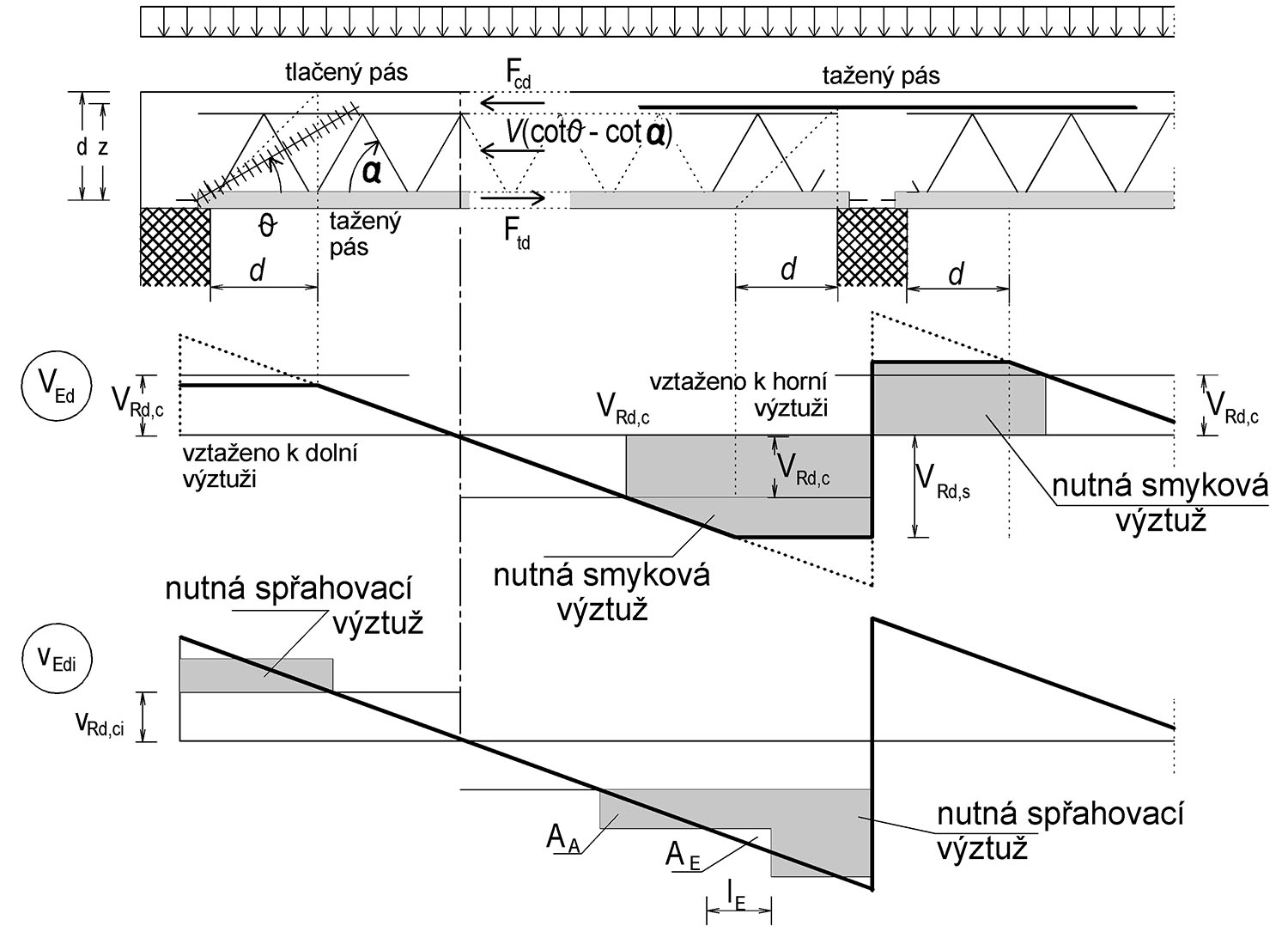
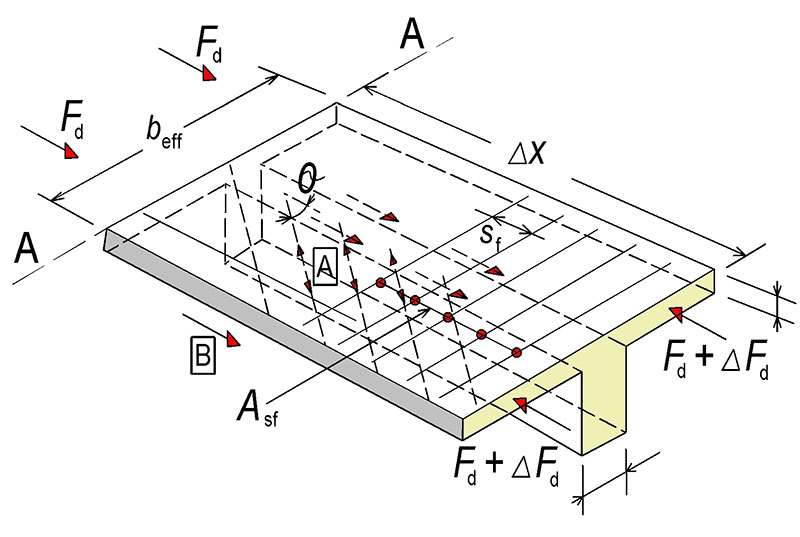
Obr. 5.4 Smyk mezi horní přírubou a stojinou
Při posouzení tlačeného pasu
\begin{gathered}
\Delta F_\text{d}=\frac{\Delta M_\text{Ed}}{z}\cdot\frac{A_\text{ca}}{A_\text{cc}}\approx\frac{M_\text{Ed}}{z}\cdot\frac{b_\text{a}}{b_\text{eff}}
\end{gathered}Při posouzení taženého pasu
\begin{gathered}
\Delta F_\text{d}=\frac{\Delta M_\text{Ed}}{z}\cdot\frac{A_\text{sa}}{A_\text{s}}
\end{gathered}Podélné smykové napětí
\begin{gathered}
v_\text{Ed}=\Delta F_\text{d}/(h_\text{f}\cdot\Delta\chi)
\end{gathered}kde je
z … rameno vnitřních sil;
Aca … plocha horní pásnice;
Acc … plocha tlačené části;
As … celková plocha výztuže;
Asa … plocha výztuže v horní pásnici oddělená posuzovaným řezem;
ba … šířka pásnice za posuzovaným řezem;
hf … tloušťka desky.
5.6 Třmínky
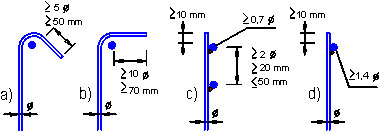
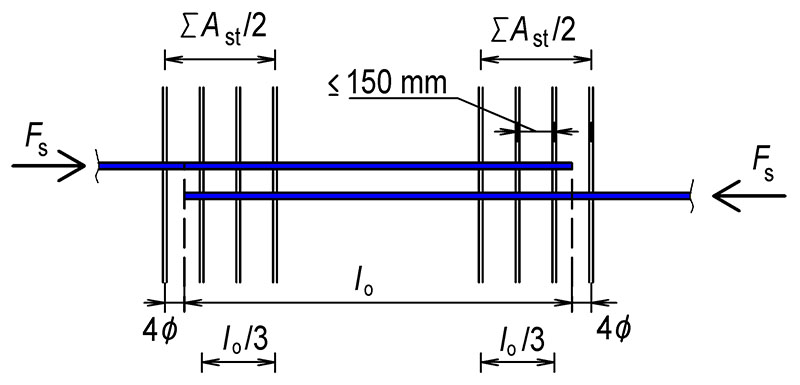
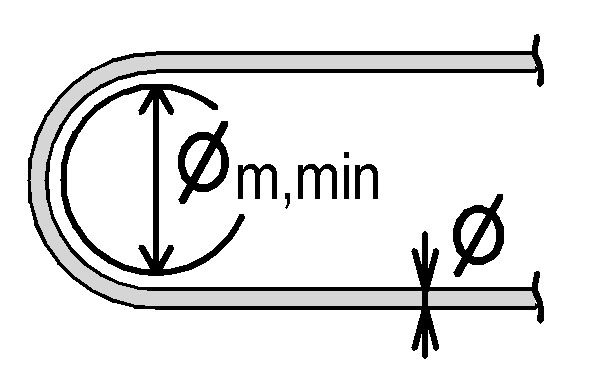
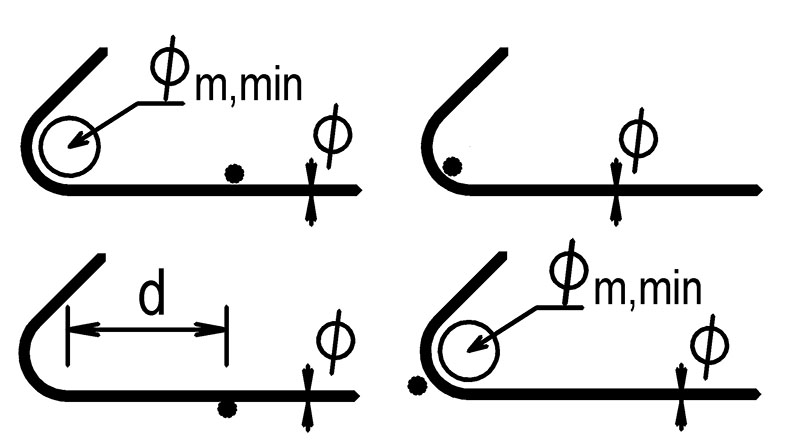
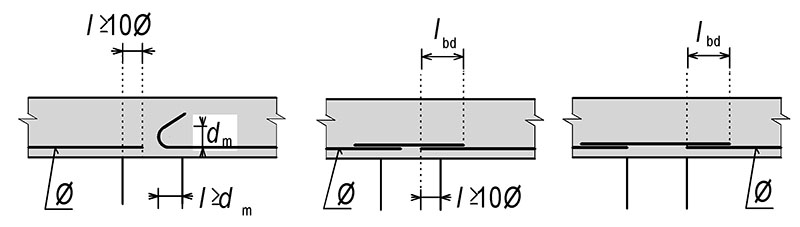
Obr. 5.5 Koncová úprava třmínků
Koncové úpravy c) a d) jsou pro příčně přivařené pruty. Pozor svařování pouze podle ČSN EN ISO 17660-1.
Poznámka:
Při kótování výztuže nutno do délky háku započítat i zakřivenou část prutu.
Tab. 5.4 Plocha smykové výztuže
| Vzdálenost třmínků v mm | Plocha smykové výztuže ass[mm2/m] pro dvoustřižné třmínky | ass [mm2/m] pro čtyřstřižné třmínky | Počet třmínků na 1 bm | ||||||
| ø 6 | ø 8 | ø 10 | ø 12 | ø 14 | ø 10 | ø 12 | ø 14 | ||
| 50 | 1130 | 2011 | 3142 | 4524 | 6158 | 6283 | 9048 | 12320 | 20 |
| 75 | 754 | 1340 | 2094 | 3015 | 4104 | 4188 | 6030 | 8208 | 13,33 |
| 100 | 565 | 1005 | 1571 | 2262 | 3079 | 3142 | 4524 | 6158 | 10 |
| 125 | 452 | 804 | 1257 | 1810 | 2463 | 2513 | 3619 | 4926 | 8 |
| 150 | 377 | 671 | 1048 | 1509 | 2054 | 2095 | 3017 | 4107 | 6,67 |
| 200 | 283 | 503 | 785 | 1131 | 1539 | 1571 | 2262 | 3079 | 5 |
| 250 | 226 | 402 | 628 | 905 | 1232 | 1257 | 1810 | 2463 | 4 |
6 Kroucení
6.1 Prvky namáhané kroucením
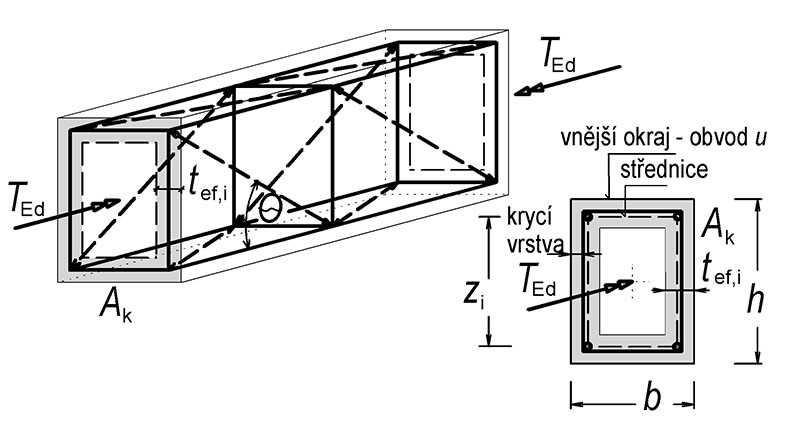
Obr. 6.1 Průřez namáhaný kroucením
kde je
Ak … plocha omezená střednicemi spojených stěn průřezu včetně vnitřních otvorů;
τt,i … smykové napětí od kroucení v i-té stěně;
tef,i … účinná tloušťka stěny, která je rovna A/u, ale nemá být menší než dvojnásobek vzdálenosti, mezi lícem prvku a středem podélné výztuže;
A … celková plocha průřezu uvnitř vnějšího okraje A = b∙h;
uk … vnější obvod průřezu – plochy Ak;
zi … délka střednice i-té stěn.
Plocha svislých třmínků \sum A_\text{swt}
\begin{gathered}
\frac{\sum A_\text{swt}\cdot f_\text{ywd}}{s_\text{wt}}=\frac{T_\text{Ed}}{2A_\text{k}\cdot\cot\theta}
\end{gathered}Plocha podélné výztuže \sum A_\text{sl}
\begin{gathered}
\frac{\sum A_\text{sl}\cdot f_\text{yd}}{u_\text{k}}=\frac{T_\text{Ed}}{2A_\text{k}}\cot\theta
\end{gathered}Podélnou výztuž rozdělit po celém obvodu průřezu.
Doporučený sklon tlačené diagonály
θ = 45o
Současné namáhání posouvající silou a krouticím momentem
\begin{gathered}
T_\text{Ed}/T_\text{Rd,max}+V_\text{Ed}/V_\text{Rd,max}\le1{,}0
\end{gathered}kde
\begin{gathered}
T_\text{Rd,max}=2v\cdot1\cdot f_\text{cd}\cdot A_\text{k}\cdot t_\text{ef,i}\cdot\sin\theta\cos\theta
\end{gathered}6.2 Konstrukční zásady
Třmínky pro zachycení účinků kroucení mají být uzavřené, kotvené přesahem nebo koncovými háky a mají svírat úhel 90°se střednicí prvku. Podélná vzdálenost třmínků pro zachycení účinků kroucení nemá překročit hodnotu u/8, kde u je vnější obvod průřezu. Podélné vložky mají být uspořádány tak, aby v každém rohu průřezu byla alespoň jedna vložka; ostatní vložky se rozdělí pravidelně podél vnitřního obvodu třmínků v osových vzdálenostech nepřesahujících 350 mm.
7 Protlačení
7.1 Maximální únosnost tlačené diagonály
\begin{gathered}
v_\text{Ed}\le v_\text{Rd,max}\\\\
v_\text{Rd,max}=0{,}4\cdot v\cdot f_\text{cd}\\\\
v=0{,}6\cdot[1-f_\text{ck}/250]\\\\
v_\text{Ed}=\beta\cdot V_\text{Ed}/(u_0\cdot d)
\end{gathered}kde je
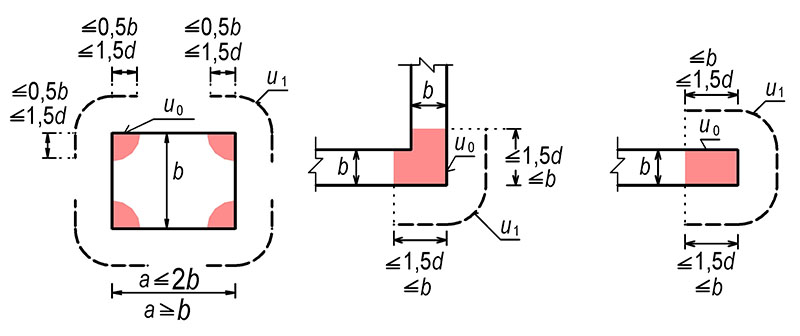
u0 … kontrolovaný obvod v líci zatěžované plochy (sloupu);
fck – viz tab.1.1.
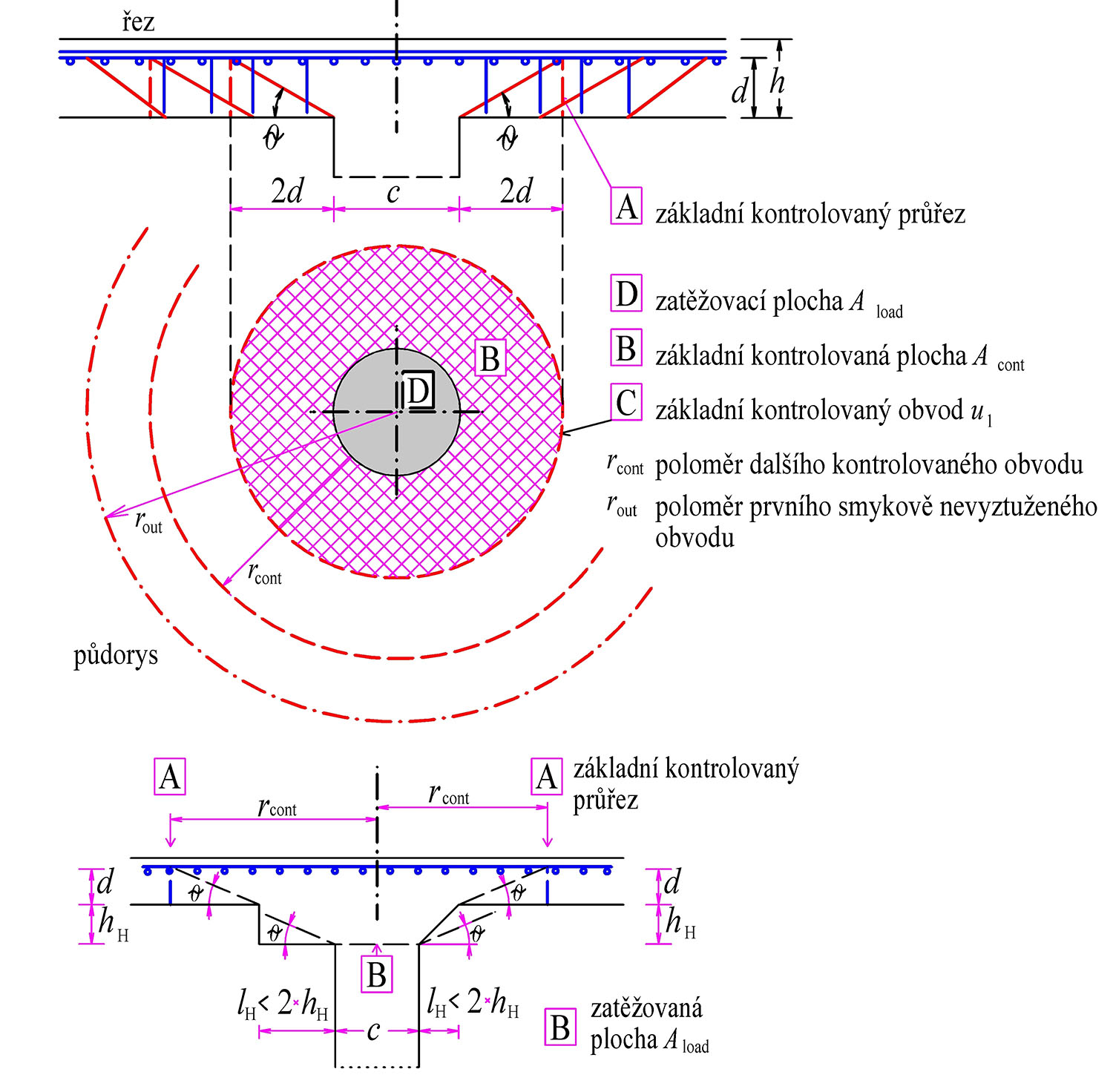
Obr. 7.1 Průřez namáhaný protlačením
7.2 Únosnost desky bez smykové výztuže na protlačení
\begin{gathered}
v_\text{Ed}\le v_\text{Rd}\\\\
v_\text{Rd,c}=C_\text{Rd,c}k\cdot(100\rho_\text{l}f_\text{ck})^{1/3}/\gamma c+0{,}1\sigma_\text{cp}\ge v_\text{min}+0{,}1\sigma_\text{cp}\\\\
v_\text{min}=0{,}035\cdot k^{3/2}\cdot f_\text{ck}^{1/2}\\\\
C_\text{Rd,c}=0{,}18/\gamma c=0{,}12\text{ a }\gamma c=1{,}5\\\\
k=1+\sqrt{200/d},\rho_\text{l}=\sqrt{\rho_\text{ly}\cdot\rho_\text{lz}}\le0{,}02
\end{gathered}scy; scz jsou normálová napětí v betonu v kritickém průřezu ve směru os y a z
\begin{gathered}
(\text{MPa, tlak}>0)\\\\
s_\text{cp}=0{,}5s_\text{cy}+s_\text{cz}
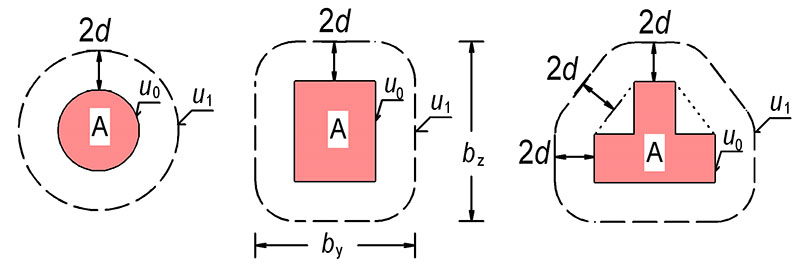
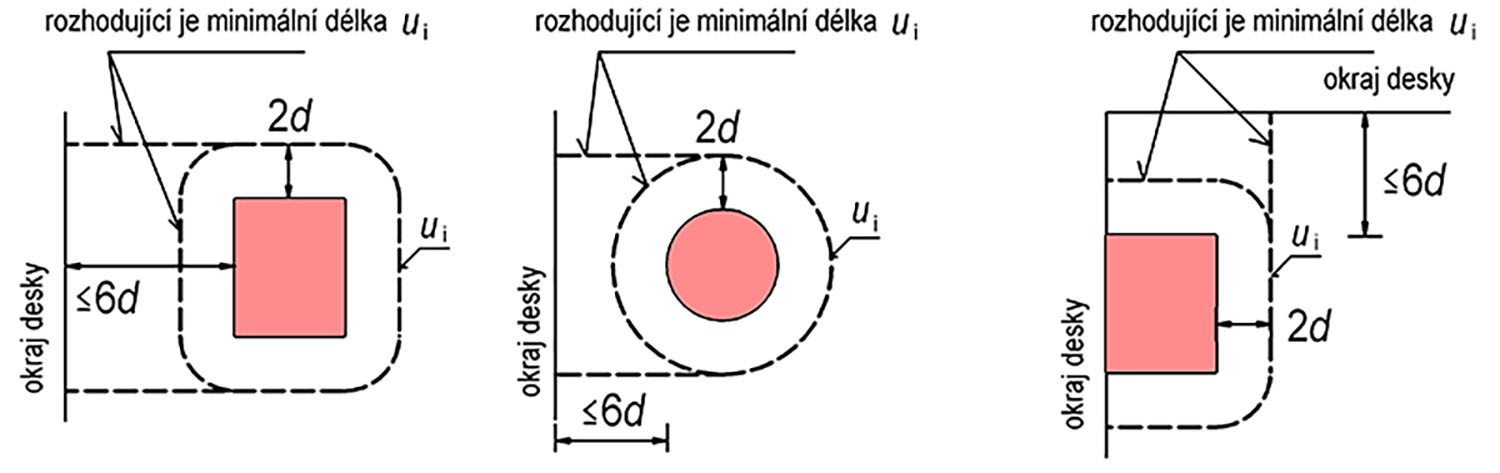
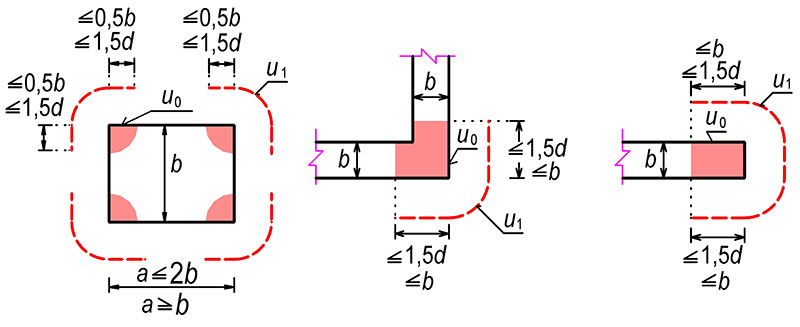
\end{gathered}Typické tvary kontrolovaných obvodů u1
Obr. 7.2 Typické tvary kontrolovaných obvodů v blízkosti okraje desky
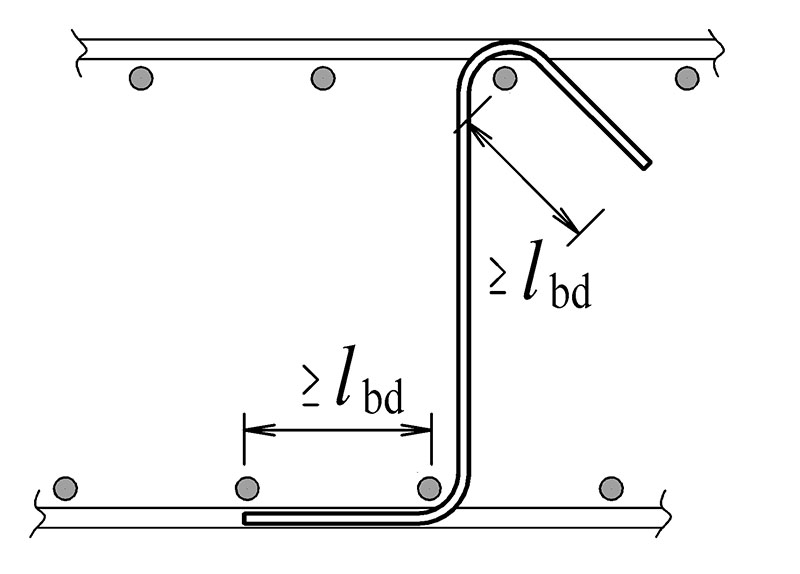
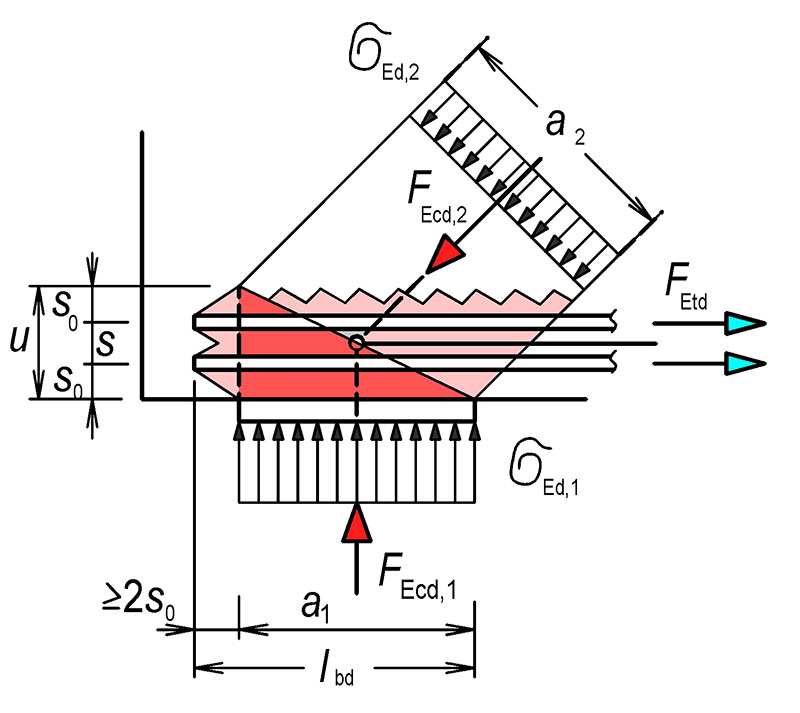
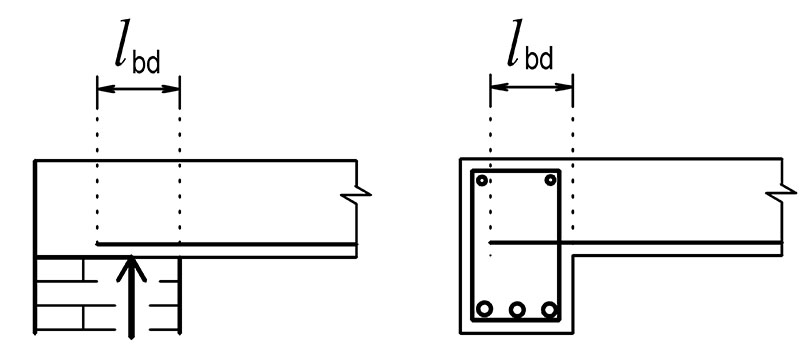
lbd je návrhová kotevní délka
Obr. 7.3 Dostatečně zakotvená smyková výztuž – příklad
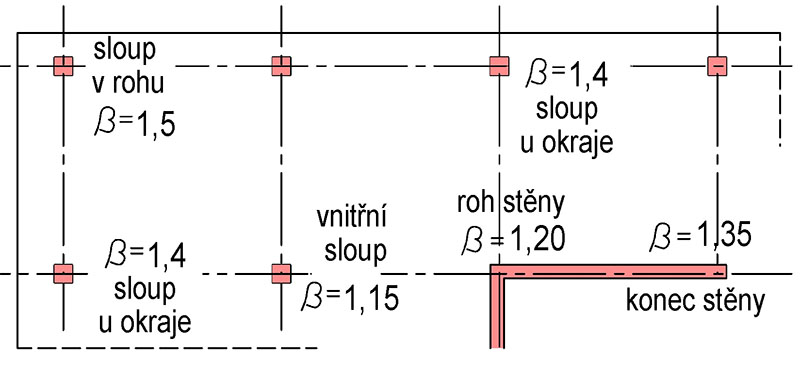
Obr. 7.4 Součinitel β excentrického zatížení styčné plochy pro pravidelné a řádně prostorově ztužené nosné systémy
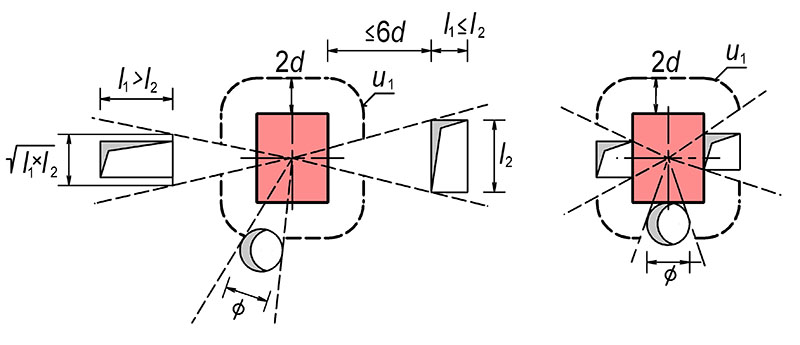
Obr. 7.5 Vliv prostupů v blízkosti zatěžované plochy (redukce délky všech kontrolovaných obvodů)
Obr. 7.6 Omezení délky kontrolovaných obvodů
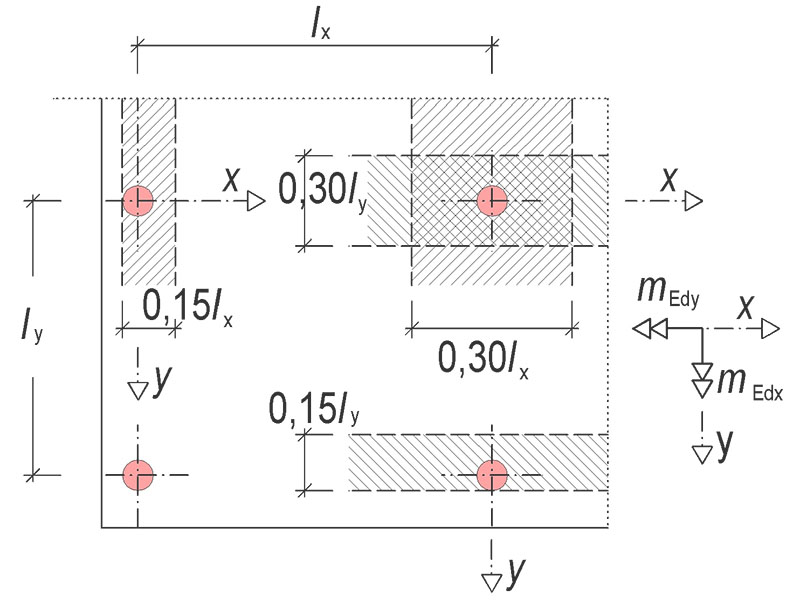
Tab. 7.1 Minimální vyztužení deskového prvku namáhaného na protlačení
| Umístění sloupu | ηz | Šířka pruhu | ηy | Šířka pruhu | ||
| Tah při horním líci desky | Tah při spodním líci desky | Tah při horním líci desky | Tah při spodním líci desky | |||
| Vnitřní sloup | 0,125 | 0 | 0,3ly | 0,125 | 0 | 0,3ly |
| Krajní sloup „z“ | 0,25 | 0 | 0,15ly | 0,125 | 0,125 | na 1 m šířky desky |
| Krajní sloup „y“ | 0,125 | 0,125 | na 1 m šířky desky | 0,25 | 0 | 0,15ly |
| Rohový sloup | 0,5 | 0,5 | na 1 m šířky desky | 0,5 | 0,5 | na 1 m šířky desky |
\begin{gathered}
m_\text{Ed,z}=\eta_\text{z}\cdot V_\text{Ed}\space\text{ a }\space m_\text{Ed,y}=\eta_\text{y}\cdot V_\text{Ed}
\end{gathered}Obr. 7.7 Minimální vyztužení
7.3 Únosnost desky se smykovou výztuží na protlačení
\begin{gathered}
v_\text{Ed}=\beta\frac{V_\text{Ed}}{u_\text{i}d}
\end{gathered}Maximální únosnost v prvním kontrolovaném obvodu u1 ve vzdálenosti 2d od zatěžované plochy
\begin{gathered}
\beta\cdot V_\text{Ed}\le V_\text{Rd,amx}=k_\text{max}\cdot v_\text{Rd,c}\cdot u_1\cdot d\space\text{ resp. }\space v_\text{Ed,1}=\beta\cdot V_\text{Ed}/(u_1d)\le k_\text{max}\cdot v_\text{Rd,c}
\end{gathered}νRdc viz kap. 7.2
Pro spolehlivě zakotvenou smykovou výztuž platí:
kmax pro desky h = 200 mm;
kmax pro desky h ≥ 700 mm (mezilehlé hodnoty lze interpolovat).
Únosnost smykově vyztuženého průřezu v_\text{Ed}\le v_\text{Rd,cs}
\begin{gathered}
v_\text{Rd,cs}=0{,}75v_\text{Rd,c}+1{,}5(d/s_\text{r})A_\text{sw}f_\text{ywd,ef}(1/(u_1\cdot d))\sin\alpha\le\bold{k_\text{max}\cdot v_\text{Rd,c}}
\end{gathered}kde je
Asw … plocha smykové výztuže v jednom kontrolovaném obvodu okolo sloupu [mm2];
vRd,c … návrhová únosnost betonového průřezu v prvním kontrolovaném obvodu bez smykové výztuže viz kap 7.2;
sr …radiální vzdálenost obvodů smykové výztuže [mm2];
fywd,ef … účinná návrhová pevnost smykové výztuže na protlačení podle vztahu
\begin{gathered}
f_\text{ywd,ef}=250+0{,}25d\le f_\text{ywd}\text{MPa}
\end{gathered}d … průměrná účinná výška desky v ortogonálních směrech [mm];
α … úhel, který svírá smyková výztuž s rovinou desky.
1,5 (d/sr) počet prvků smykové výztuže v oblasti mezi vyšetřovaným a předchozím kontrolovaným obvodem. Při maximálních vzdálenostech sr = 0,75d vychází dva prvky smykové výztuže v radiálním směru. Pokud bude vzdálenost sr menší než 0,75d, je nutné počet vždy zaokrouhlit nahoru na celé prvky.
Únosnost v každém následujícím kontrolovaném obvodu ui ve vzdálenosti 2d od poslední smykové výztuže
\begin{gathered}
v_\text{Rd,cs}=0{,}75v_\text{Rd,c}+1{,}5(d/s_\text{r})A_\text{sw}f_\text{ywd,ef}(1/(u_\text{i}\cdot d))\sin\alpha\le\bold{k_\text{max}\cdot v_\text{Rd,c}}
\end{gathered}Únosnost prvního smykově nevyztuženého průřezu
\begin{gathered}
\beta V_\text{Ed}\le V_\text{Rd,out}=v_\text{Rd,c}\cdot u_\text{out}\cdot d
\end{gathered}Únosnost v prvním následujícím smykově nevyztuženém kontrolovaném obvodu uout ve vzdálenosti 1,5d od poslední smykové výztuže.
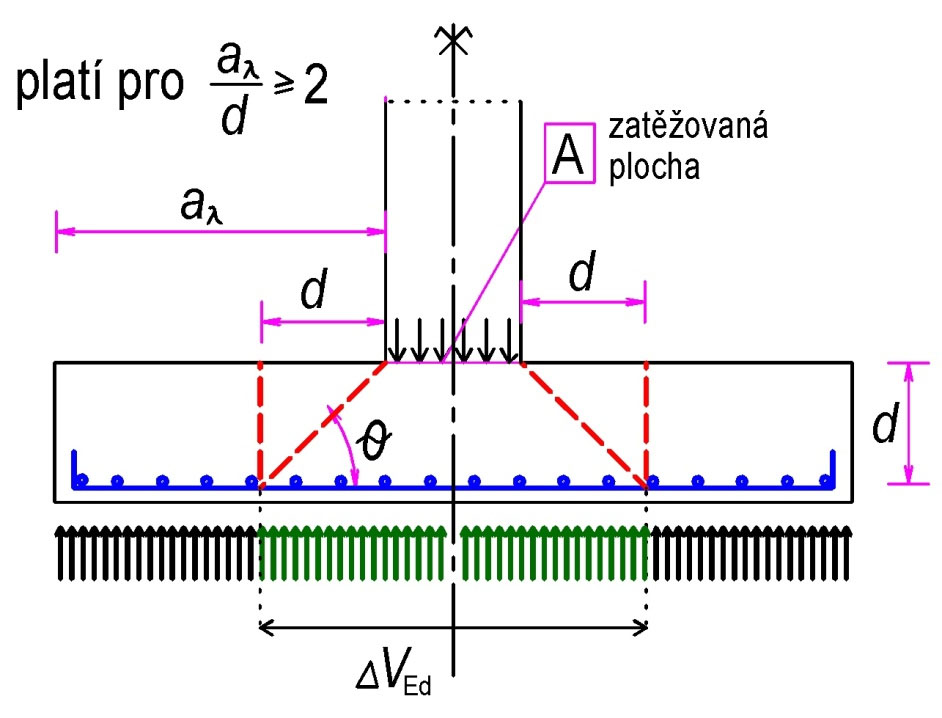
7.4 Poddajné základové patky
Pro poddajné patky lze uvažovat první kontrolovaný obvod ve vzdálenosti d od líce sloupu. Za poddajné patky lze považovat patky, u nichž je vzdálenost od okraje patky od líce sloupu větší než 2d.
U základových patek nelze použít zjednodušujícího součinitele β. Vliv excentricity zatížení lze řešit sektorovým modelem.
Poznámka:
Sektorový model řeší protlačení základové patky pouze v nejvíce namáhané části, smyková výztuž se konstrukčně umístí v celém kontrolovaném obvodustejná.
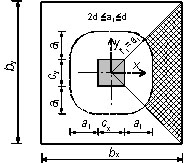
Obr. 7.9 Sektorový model oblasti namáhané protlačením
Obr. 7.10 Konstrukční vyztužení smykovou výztuží oblasti namáhané protlačením
7.5 Principy smykového vyztužení oblasti namáhané protlačením
Asw,min jedna větev smykové výztuže 0,3d až 0,5d od líce styčné plochy.
Maximální vzdálenost smykové výztuže v radiálním směru je 0,75d a nejméně 2 větve smykové výztuže ve vzdálenostech do 2,0d V tangenciálním směru je maximální vzdálenost větví smykové výztuže 1,5d v prvním kontrolovaném obvodu a 2,0d v následujících kontrolovaných obvodech.
Minimální množství smykové výztuže v kontrolovaném obvodu
\begin{gathered}
\sum A_\text{sw}\ge0{,}08\sqrt{f_\text{ck}}/f_\text{yk}
\end{gathered}fck viz tab. 1.1
fyk viz tab. 2.1
Návrh smykových trnů vždy podle metodiky výrobce.
8 Interakce normálové síly a ohybového momentu
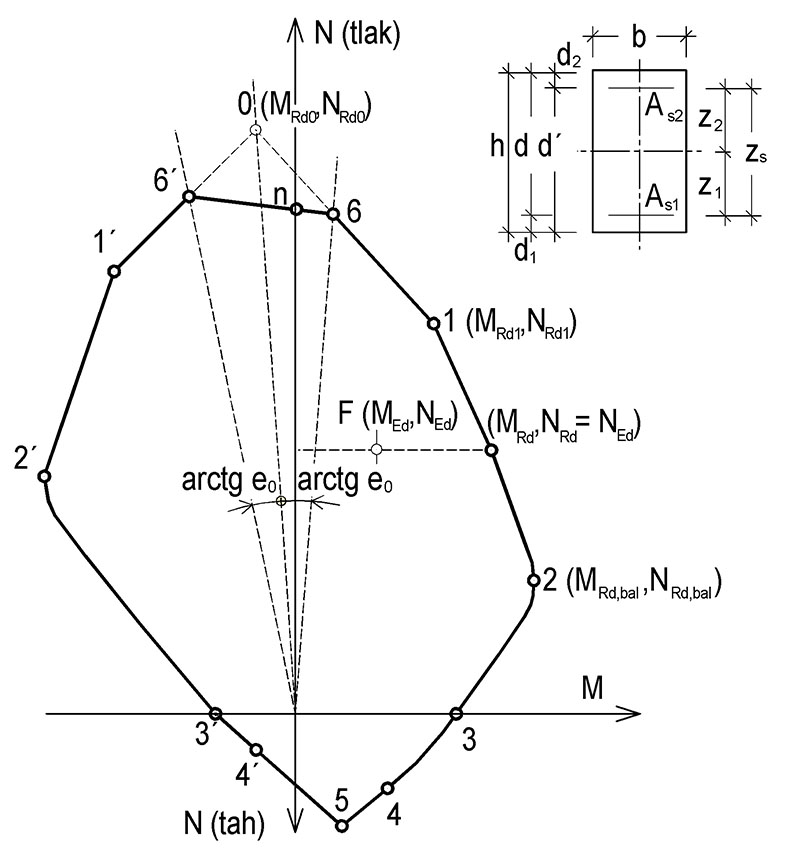
8.1 Interakční diagram
Obr. 8.1 Interakční diagram
fcd viz tab. 1.1
fyd viz tab. 2.1
\sigma_\text{s},\sigma_\text{s1},\sigma_\text{s2} jsou napětí ve výztuži
\lambda=0{,}80
\xi_\text{bal,1}\text{ a }\xi_\text{bal,2} viz kap. 4.1 a kap. 4.2
Bod 0 Porušení při rovnoměrném rozdělení přetvoření při tlačeném betonu po celé výšce průřezu:
N_\text{Rd0}=-(bhf_\text{cd}+\sum A_\text{s}\sigma_\text{s})\\
M_\text{Rd0}=(A_\text{s2}t_2-A_\text{s1}z_1)\sigma_\text{s},\sigma_\text{s}=\varepsilon_\text{c2}E_\text{s}\le f_\text{yd}
Bod 1 Neutrální osa prochází těžištěm výztuže As1:
N_\text{Rd1}=-(\lambda\xi_\text{bal,1}bdf_\text{cd}+\Delta F_\text{s})\\
M_\text{Rd1}=\lambda bdf_\text{cd}0{,}5(h-\lambda d)+F_\text{s2}z_2\\
d\ge\xi_\text{bal,2}d_2\Rightarrow\sigma_\text{s2}=f_\text{yd},\lambda=0{,}80
Bod 2 Neutrální osa prochází vnitřní částí průřezu:
N_\text{Rd,bal}=-(\lambda\xi_\text{bal,1}bdf_\text{cd}+\Delta F_\text{s})\\
M_\text{Rd,bal}=\lambda\xi_\text{bal,1}bdf_\text{cd}0{,}5(h-\lambda\xi_\text{bal,1}d)+F_\text{s}z_1+F_\text{s2}z_2\\
\xi_\text{bal,1}d\ge\xi_\text{bal,2}d_2\Rightarrow\sigma_\text{s1}=\sigma_\text{s2}=f_\text{yd},\lambda=0{,}80
Bod 3 Mez únosnosti při namáhání prostým ohybem:
N_\text{Rd}=0
M_\text{Rd}= mez únosnosti při namáhání ohybem, výztuž tažená As1, tlačená As2
Bod 4 Neutrální osa prochází těžištěm výztuže As2:
N_\text{Rdt,bal}=F_\text{s1}\\
M_\text{Rdt,bal}=F_\text{s1}z_1
Bod 5 Neutrální osa prochází společným těžištěm výztuže As1:
N_\text{Rdt0}=F_\text{s1}+F_\text{s2}\\
M_\text{Rdt0}=F_\text{s1}z_1-F_\text{s2}z_2
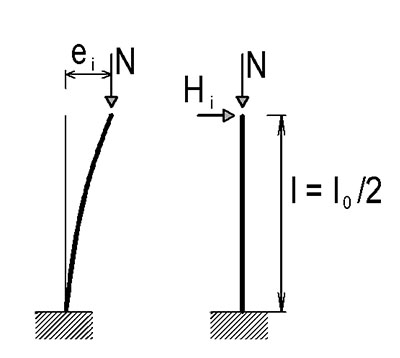
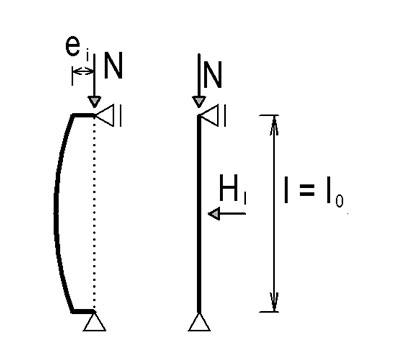
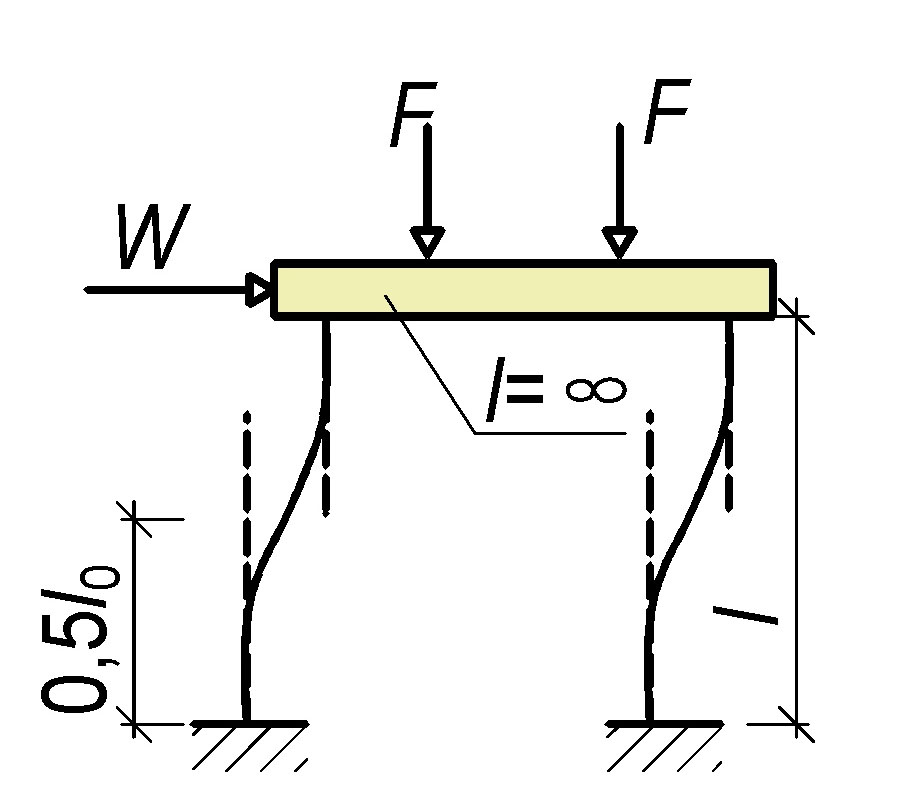
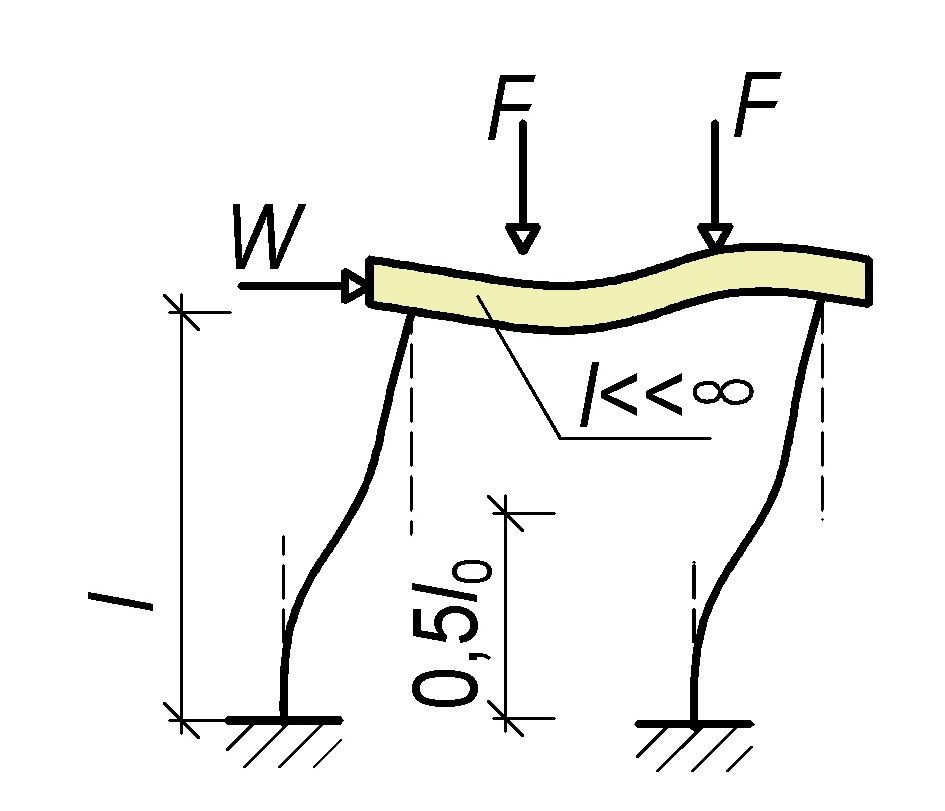
Geometrické imperfekce e_\text{i}\ge\frac{l_0}{400}
Pro osamělé prvky
Excentricita e_\text{i}=\theta_\text{i}\frac{l_0}{2},\theta_\text{i}=\frac{\alpha_\text{m}\cdot\alpha_\text{h}}{200}\\
\alpha_\text{h}=2/\sqrt{l};2/3\le\alpha_\text{h}\le1\text{ a }\alpha_\text{m}=\sqrt{0{,}5(1-1/m)}
m je počet svislých prvků přispívající k danému účinku
příčná síla H_\text{i}=\theta_\text{i}N pro neztužené prvky
příčná síla H_\text{i}=\theta_\text{i}N pro ztužené prvky
Minimální excentricita tlačených prvků
e_\text{f}=M_\text{Ed}/N_\text{Ed}\ge\text{max}(\frac{b}{30};20\text{mm}) a současně e_\text{i}\ge\frac{l_0}{400}
b je menší rozměr obdélníkového průřezu
9 Štíhlé prvky
9.1 Vzpěrná délka
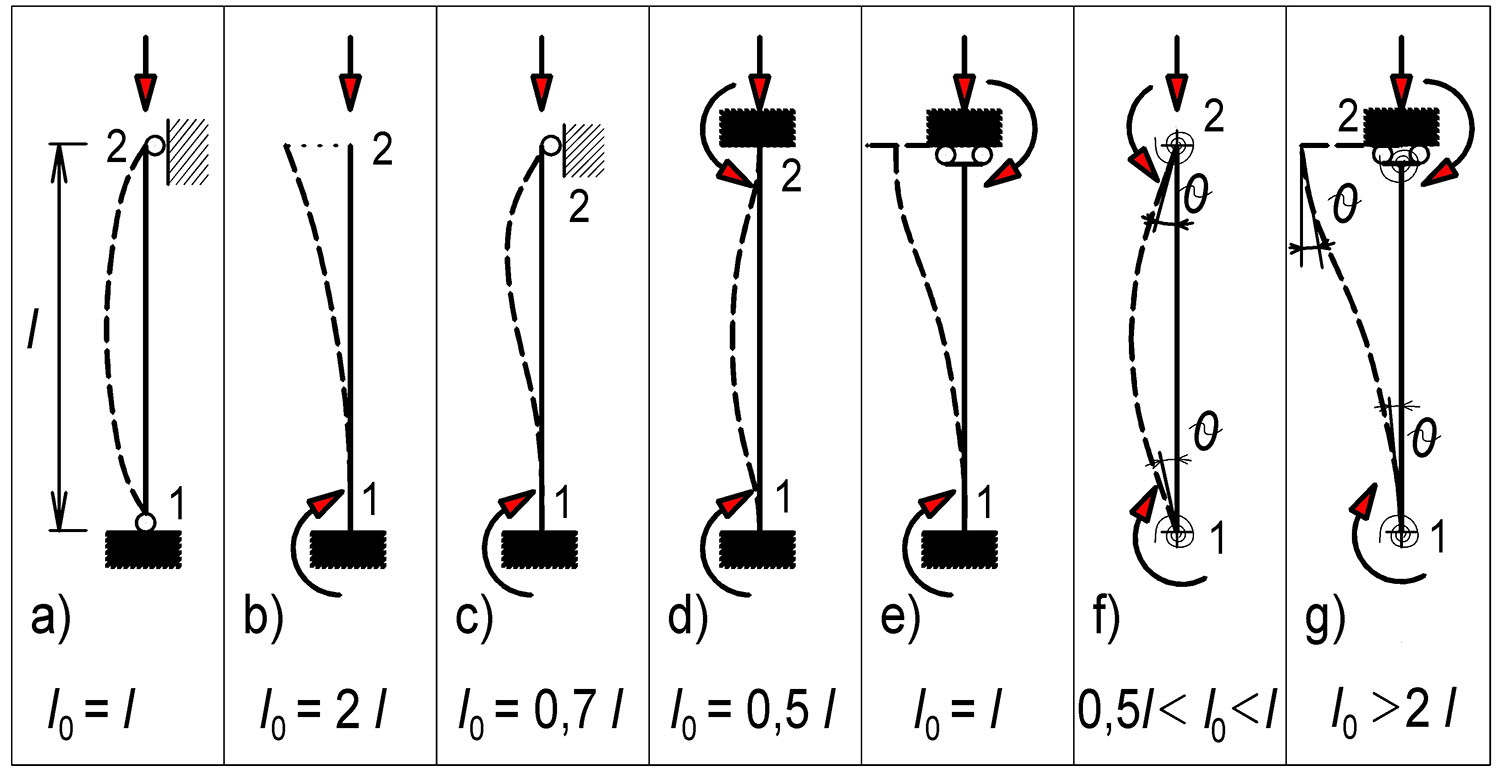
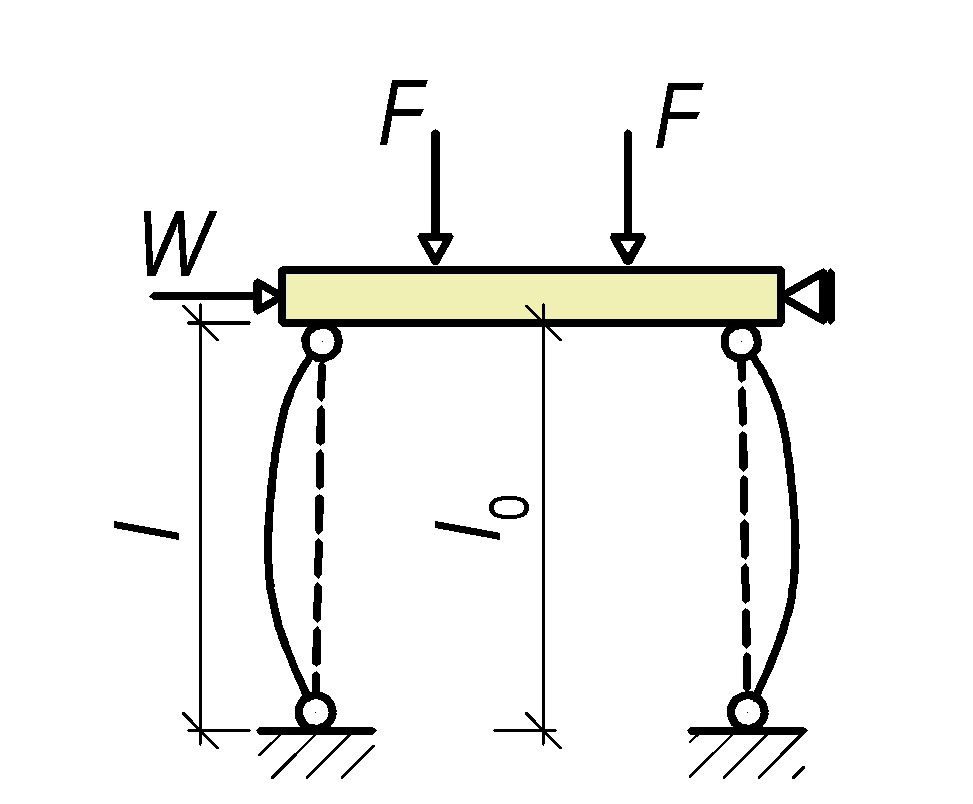
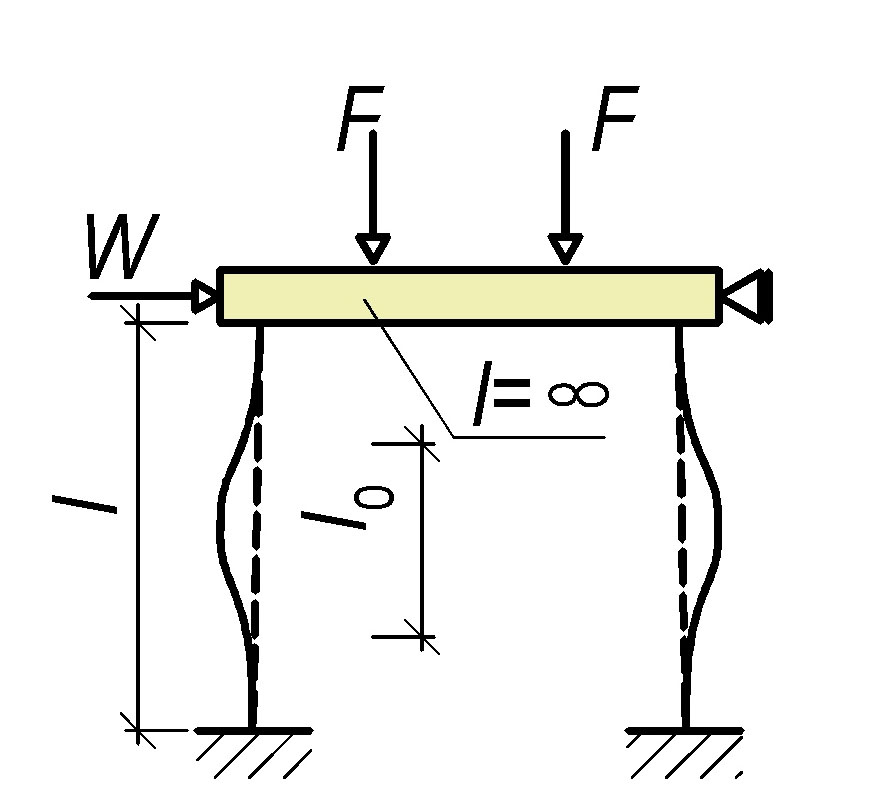
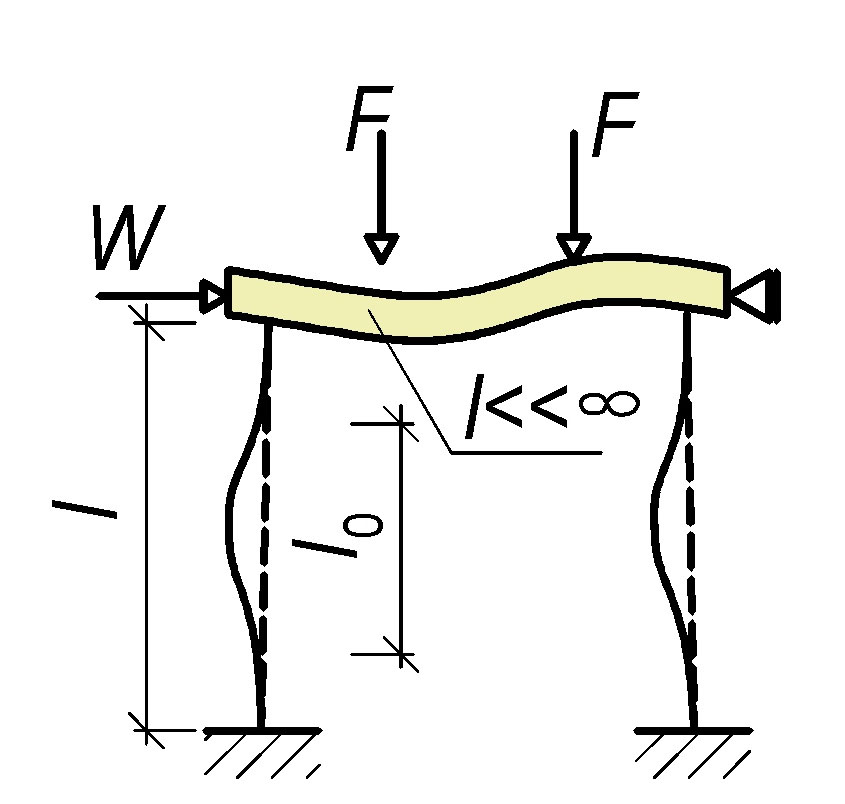
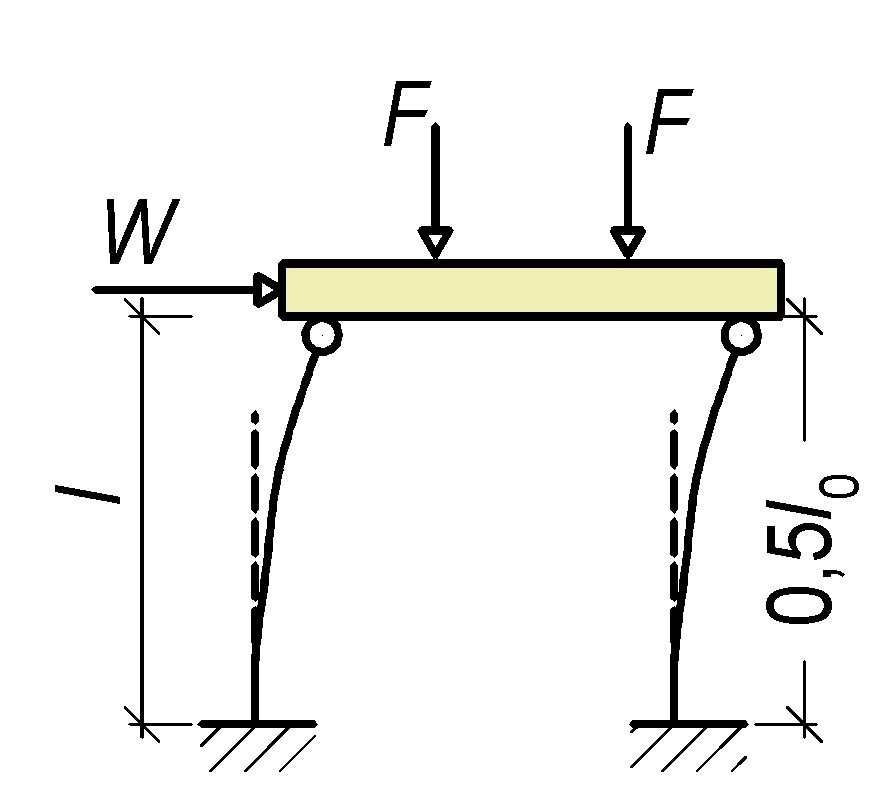
Tab. 9.1 Vzpěrná délka
Pokud nebudou sloupy dokonale vetknuté, je nutné provést výpočet rámové konstrukce.
U pravidelných rámů lze stanovit účinnou délku následovně:
l_0=l\text{max}\bigg\{\bigg[\sqrt{1+10\frac{k_1k_2}{k_1+k_2}}\bigg];\bigg[\bigg(1+\frac{k_1}{1+k_1}\bigg)\bigg(1+\frac{k_2}{1+k_2}\bigg)\bigg];10\text{mm}\bigg\} |
Tab. 9.2 Hodnoty součinitele β pro stanovení účinné délky l0sloupů ztužených rámů
(vzpěrná délka je l0 = β l, kde l je světlá výška tlačeného prvku)
| Uložení sloupu ve vrcholu | Uložení sloupu v patě | ||
| 1 – tuhé | 2 | 3 – poddajné | |
| 1 – tuhé | 0,75 | 0,80 | 0,90 |
| 2 | 0,80 | 0,85 | 0,95 |
| 3 – poddajné | 0,90 | 0,95 | 1,00 |
| Typy uložení: 1 – Sloup je ve styčníku monoliticky spojen s průvlaky provedenými ve dvou na sebe kolmých směrech, jejichž výška je rovna nejméně rozměru sloupu v uvažované rovině. Pokud je sloup spojen se základem, pak má být navržen na moment splňující výše uvedenou podmínku. 2 – Sloup je ve styčníku monoliticky spojen s průvlaky provedenými ve dvou na sebe kolmých směrech, jejichž výška je menší než rozměr sloupu v uvažované rovině, ne však menší než je polovina tohoto rozměru. 3 – Sloup je ve styčníku spojen s prvky poskytujícími pouze malý odpor proti pootočení. |
|||
9.2 Kritérium štíhlosti
Tab. 9.3 Kritérium štíhlosti
| \lambda=\frac{l_0}{i}\le\lambda_\text{lim}=\frac{20ABC}{\sqrt{n}}=\frac{10{,}78}{\sqrt{n}} \lambda<\lambda_\text{lim} masivní sloup, \lambda\ge\lambda_\text{lim} štíhlý sloup |
A=1/(1+0{,}2\varphi_\text{ef}) jinak A=0{,}7 |
| \phi_\text{ef}=\phi_{(\infty,\text{t0})}\frac{M_\text{0Eqp}}{M_\text{0Ed}} | |
| omezení maximální štíhlosti \lambda_\text{lim}\le75 a \lambda_\text{lim}=16/\sqrt{n} pro |n|\le0{,}41 n viz tab. 9.5 |
B=\sqrt{(1+2\omega)} kde \omega=A_\text{s}f_\text{yd}/(A_\text{c}f_\text{cd}) jinak B=1{,}1 |
| pro ztužené sloupy C=1{,}7-r_\text{m} kde r_\text{m}=M_{01}/M_{02} jinak C=0{,}7
Poznámka: |
|
| pro obdélníkové sloupy \lambda=\frac{3{,}46\cdot l_0}{h} | pro kruhové sloupy \lambda=\frac{4{,}0\cdot l_0}{d} |
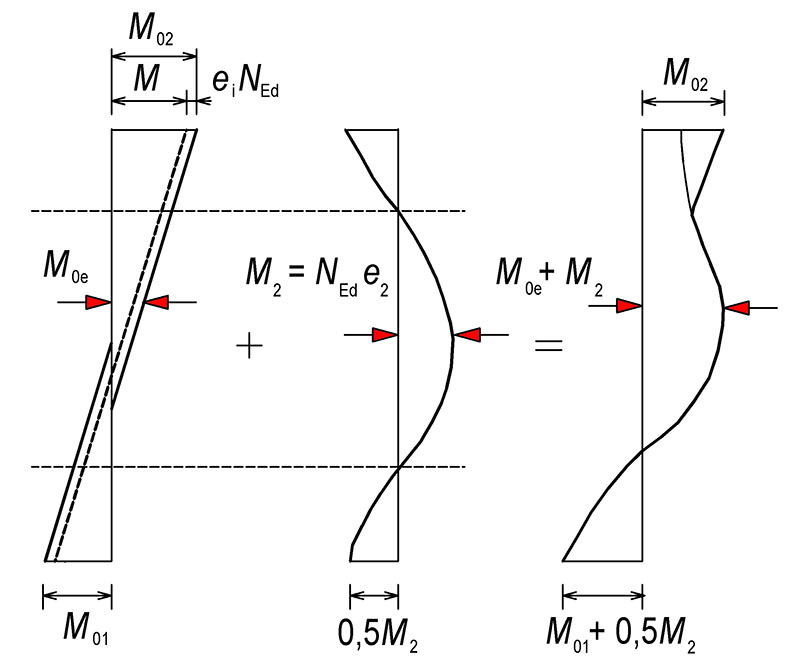
Tab. 9.4 Účinky 2. řádu
Pro štíhlé prvky stanovíme momenty 1. řádu s vlivem imperfekcí
M_{02}=\text{max}(|M_\text{top}|;|M_\text{bot}|+e_\text{i}N_\text{Ed})\text{ a}\\
M_{01}=\text{min}(|M_\text{top}|;|M_\text{bot}|+e_\text{i}N_\text{Ed}).
Momenty M01 a M02 mají stejné znaménko, pokud vyvozují tah na stejné straně sloupu.
Ekvivalentní koncový ohybový moment .
M_\text{0Ed}=\text{max}(0{,}6M_{02}+0{,}4M_{01};0{,}4M_{02})+e_\text{i}|N_\text{Ed}|.
Návrhový moment štíhlého sloupu
M_\text{Ed}=\text{min}(M_{02};M_\text{0Ed}+M_2;M_{01}+0{,}5M_2).
Návrhový ohybový moment 2. řádu M_2=N_\text{Ed}\cdot e_2, kde e2 je příčná deformace vyvozená účinky druhého řádu.
9.3 Analýza štíhlých prvků – Metoda jmenovité křivosti
Tab. 9.5 Metoda jmenovité křivosti
| Křivost 1/r=K_\text{r}\cdot K_\phi\cdot f_\text{yd}/(0{,}45d\cdot E_\text{s}); kde d je účinná výška, popřípadě d=h/2+i_\text{s} pokud není výztuž soustředěna na protilehlých stranách; is je poloměr setrvačnosti celé výztuže; E_\text{s}=200\text{ GPa}. |
Opravný součinitel závisející na normálové síle K_\text{r}=\frac{(n_\text{u}-n)}{(n_\text{u}-n_\text{bal})}\le1 Poměrná návrhová normálová síla n=|N_\text{Ed}|/A_\text{c}f_\text{cd}\le1\\ n_\text{u}=1+\omega, kde je \omega=A_\text{s,est}f_\text{yd}/(A_\text{c}f_\text{cd}); As,est … odhadnutá průřezová plocha veškeré výztuže; Ac … průřezová plocha betonu; nbal = 0,4 (hodnota n při maximální únosnosti). fcd viz tab. 1.1 fyd viz tab. 2.1 |
|
| Účinek dotvarování K_\varphi=1+\beta\cdot\varphi_\text{ef} |
\varphi_\text{ef}=\frac{\varphi(\infty,t_0)M_\text{0Eqp}}{M_\text{0Ed}}\\ \beta=0{,}35+\frac{f_\text{ck}}{200}-\frac{\lambda}{150} | \varphi(\infty,t_0) je konečný součinitel dotvarování M0Eqp je ohybový moment 1. řádu pro kvazistálé zatížení. M0Ed je ohybový moment 1. řádu od návrhové kombinace zatížení. fck viz tab. 1.1 λ je štíhlost prvku |
| Excentricita e_2=0{,}1\frac{K_\text{r}K_\varphi f_\text{yd}}{0{,}45d\cdot E_\text{s}}l_0^2 | kde je d … účinná výška průřezu Es … modul pružnosti výztuže cca 200 GPa |
|
| Ohybový moment 2. řádu | M_2=N_\text{Ed}\cdot e_2 | |
| Návrhový ohybový moment | M_\text{Ed}=\text{max}(M_{02};M_\text{0Ed}+M_2;M_{01}+0{,}5M_2) | |
| Pokud platí A_\text{s,req}\approx A_\text{s,est}, posoudí se konstrukční ustanovení pro návrh výztuže sloupů a dokončí se návrh. Pokud je požadovaná výztuž větší než původně odhadnutá, opraví se vztah pro ω a provede se nový výpočet. |
||
9.4 Analýza štíhlých prvků – Metoda jmenovité tuhosti
Tab. 9.6 Metoda jmenovité tuhosti
| Metoda je citlivá na vstupní odhadnuté množství výztuže, výpočet je nutné provádět iteračně, až vstupní hodnota množství výztuže bude odpovídat vypočtenému množství výztuže. | |
| Jmenovitá tuhost EI=K_\text{c}E_\text{cd}I_\text{c}+K_\text{s}E_\text{s}I_\text{s}, kde je Ecd … návrhová hodnota modulu pružnosti betonu pro staticky neurčité konstrukce E_\text{cd,ef}=E_\text{cd}/(1+\varphi_\text{ef})\\ E_\text{cd}=E_\text{cm}/\gamma_\text{cE}; γcE = 1,2 je součinitel spolehlivosti; Ic … moment setrvačnosti betonového průřezu vztažený k těžišťové ose; Is … moment setrvačnosti výztuže vztažený k těžišťové ose betonového průřezu; Kc … opravný součinitel zohledňující zejména účinky trhlin a dotvarování betonu; Ks … opravný součinitel zohledňující příspěvek výztuže; fck, fcd viz tab. 1.1 fyd viz tab. 2.1 |
Při vyztužení \rho\ge0{,}002 platí K_\text{s}=1, K_\text{c}=\frac{k_1k_2}{1+\varphi_\text{ef}}, k_1=\sqrt{\frac{f_\text{ck}}{20}}, k_2=\frac{|N_\text{Ed}|}{A_\text{c}f_\text{cd}}\cdot\frac{\lambda}{170}\le0{,}2 |
| Při vyztužení \rho\ge0{,}01 platí K_\text{s}=0, K_\text{c}=0{,}3/(1+0{,}5\varphi_\text{ef}). Součinitel dotvarování φef \varphi_\text{ef}=\varphi(\infty,t_0)M_\text{0Eqp}/M_\text{0Ed} Vliv dotvarování může být zanedbán (φef´= 0), pokud jsou splněny tři následující podmínky: \varphi(\infty,t_0)\le2, \lambda\le75 a M_\text{0Ed}/N_\text{Ed}\ge h. Přitom musí být mechanický stupeň vyztužení nejméně \omega=\frac{A_\text{s}f_\text{yd}}{A_\text{c}f_\text{cd}}=0{,}25 M_\text{0Eqp} je ohybový moment prvního řádu od kvazistálé kombinace zatížení; M_\text{0Ed} je ohybový moment prvního řádu od návrhové kombinace zatížení. |
|
| Celkový návrhový moment zahrnující v sobě moment 2. řádu M_\text{Ed}=M_\text{0Ed}\bigg[1+\frac{\beta}{(N_\text{B}/|N_\text{Ed}|-1)}\bigg] Eulerovo kritické břemeno je N_\text{B}=\pi^2EI/l_0^2; součinitel rozdělení momentů \beta=\pi^2/c_0; kde c0 = 8 konstantní průběh momentu; c0 = 9,6 parabolický průběh; c0 = 12 symetrický trojúhelníkový průběh. |
|
| Návrh výztuže průřezu na vnitřní síly NEd a MEd | |
9.5 Sloupy – konstrukční zásady
- Podélnou výztuž sloupů tvoří nejméně čtyři pruty ø12mm, u kruhového průřezu nejméně 6 profilů a u polygonálního průřezu – nejméně v každém rohu jeden prut.
- Minimální plocha podélné výztuže A_\text{s,min}=0{,}1\cdot N_\text{Ed}/f_\text{yd}\ge0{,}002\cdot A_\text{c}, A_\text{s,max}=0{,}04\cdot A_\text{c}.
- Maximální plocha podélné výztuže mimo stykování A_\text{s,max}=0{,}04\cdot A_\text{c}, v místě stykování až dvojnásobek.
- Osová vzdálenost příčné výztuže s po délce sloupu musí být menší než scl,max
scl,max ≤ 15-ti násobek nejmenšího průměru podélných prutů,
scl,max ≤ menší z rozměrů sloupu a
scl,max ≤ 300 mm.
- Podélné pruty jsou zajištěny proti vybočení třmínkem, pokud se nacházejí ve vzdálenosti do 150 mm od rohu třmínku.
- V místě styku podélných prutů a pod uložením desky (průvlaku) v délce 2b (b je menší rozměr sloupu) je nutné třmínky zhustit.
- U třmínků s pravoúhlým hákem je nutno prodloužit hák na 15ø.
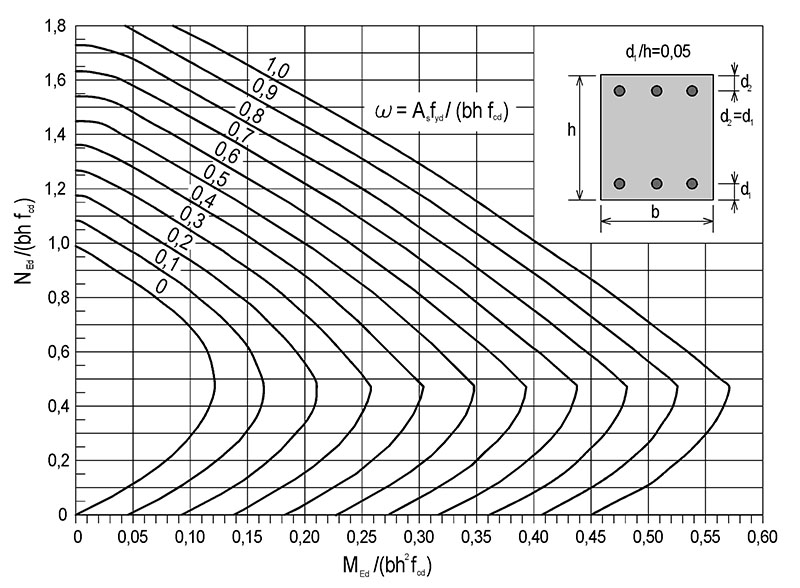
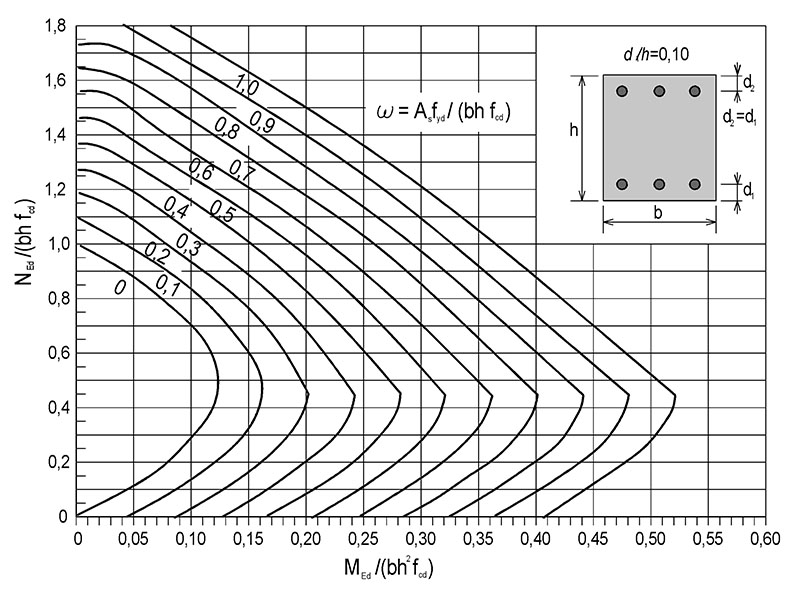
9.6 Nomogramy pro návrh průřezů souměrně vyztužených sloupů
1) Vypočteme poměrné hodnoty:
normálové síly N_\text{Ed}/(b\cdot h\cdot f_\text{cd}) a ohybového momentu M_\text{Ed}/(b\cdot h^2\cdot f_\text{cd});
vzdálenost těžiště výztuže od okraje průřezu d_1/h=d_2/h.
2) Z příslušného grafů odečteme hodnotu \omega=A_\text{s}\cdot f_\text{yd}/(b\cdot h\cdot f_\text{cd}), mezi grafy lze interpolovat.
3) Stanovíme plochu veškeré výztuže v průřezu A_\text{s,req}=\omega\cdot b\cdot h\cdot f_\text{cd}/f_\text{yd}.
4) Překontrolujeme podmínku minimálního a maximálního vyztužení.
Obr. 9.5 Nomogram pro návrh průřezu souměrně vyztuženého sloupu
Obr. 9.6 Nomogram pro návrh průřezu souměrně vyztuženého sloupu
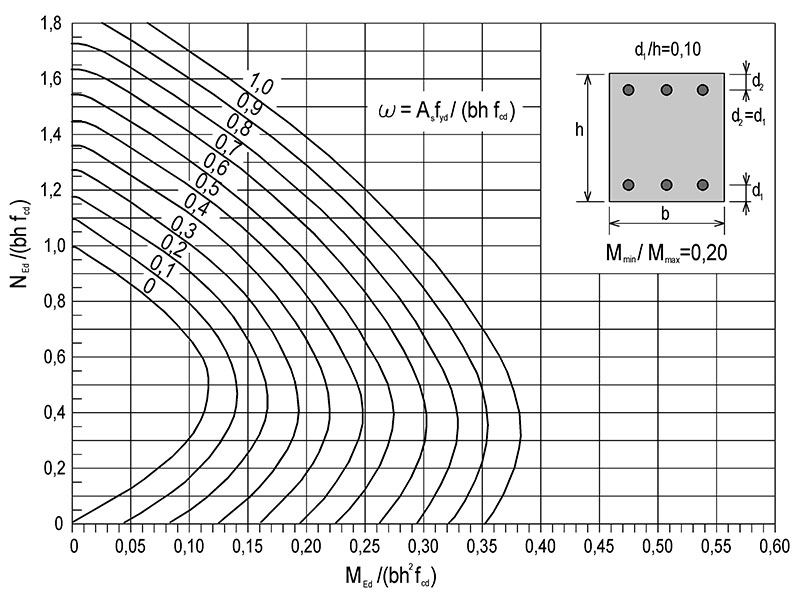
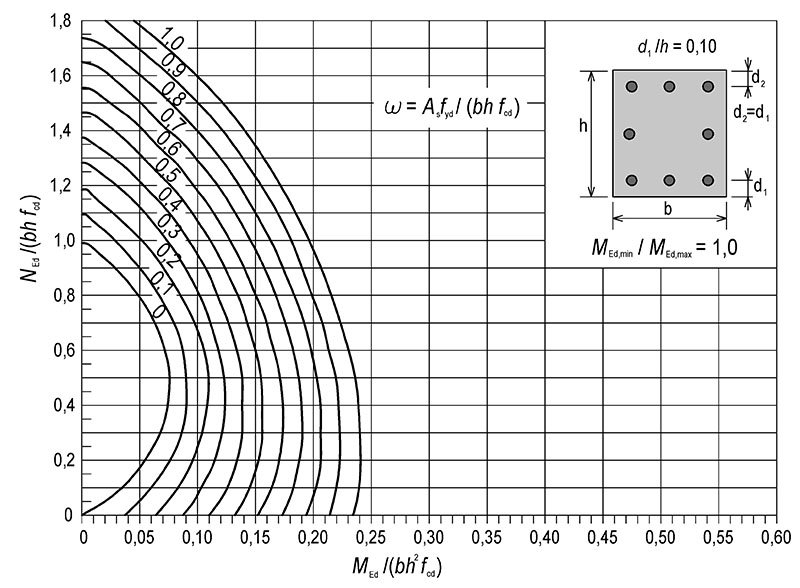
9.7 Nomogramy pro návrh průřezů – normálová síla působí mimo osy souměrnosti (ohyb ve dvou směrech)
1) Vypočteme poměrné hodnoty:
normálové síly N_\text{Ed}/(b\cdot h\cdot f_\text{cd});
ohybového momentu m_\text{x}=M_\text{Edx}/(b\cdot h^2\cdot f_\text{cd};
a m_\text{y}=M_\text{Edy}/(b\cdot h^2\cdot f_\text{cd}).
2) Určíme:
Mmax = max (mx; my);
Mmin = min (mx; my);
vypočteme poměr Mmin/Mmax a vzdálenost těžiště výztuže od okraje průřezu d_1/h=d_2/h.
3) Z příslušného grafů odečteme hodnotu \omega=A_\text{s}\cdot f_\text{yd}/(b\cdot h\cdot f_\text{cd}), mezi grafy lze interpolovat.
4) Stanovíme plochu veškeré výztuže v průřezu A_\text{s,req}=\omega\cdot b\cdot h\cdot f_\text{cd}/f_\text{yd}.
5) Překontrolujeme podmínku minimálního a maximálního vyztužení.
Obr. 9.7 Nomogram pro návrh průřezu souměrně vyztuženého sloupu namáhaného šikmým ohybem
Obr. 9.8 Nomogram pro návrh průřezu souměrně vyztuženého sloupu namáhaného šikmým ohybem
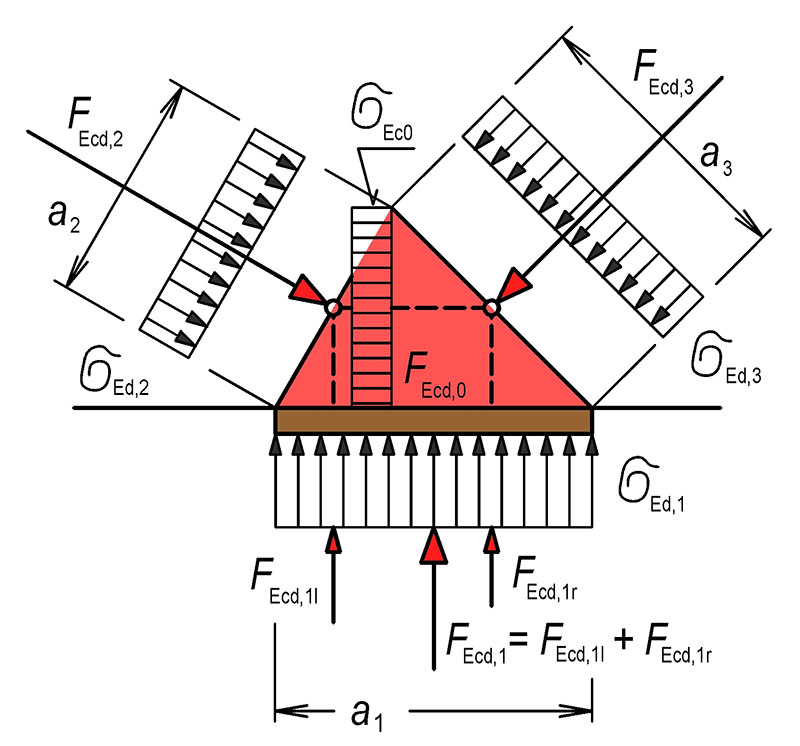
10 Lokální modely – poruchové oblasti
Tab. 10.1 Styčníky modelů náhradní příhradoviny
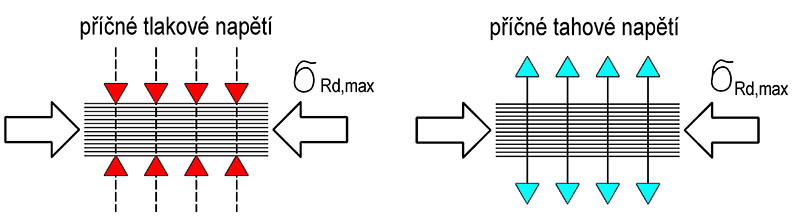
Únostnost \sigma_\text{Rd,max}=f_\text{cd}
Únostnost \sigma_\text{Rd,max}=0{,}6\cdot v'\cdot f_\text{cd} kde v'=1-\frac{f_\text{ck}}{250}
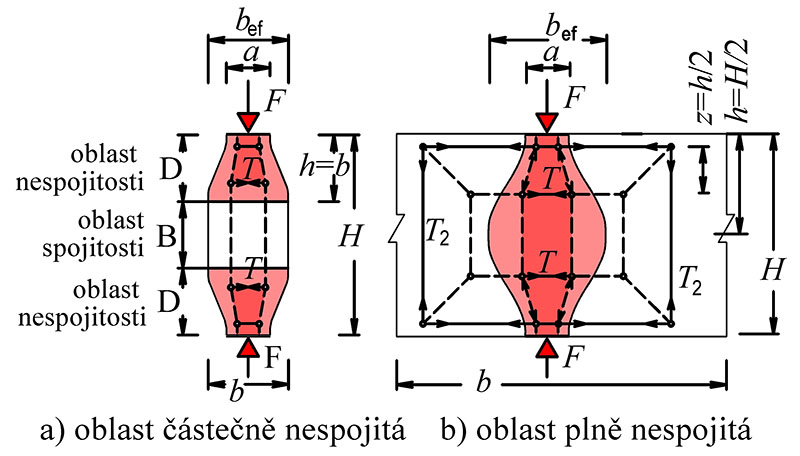
Tab. 10.2 Příčné tahy v betonových vzpěrách
Částečná nespojitost
T=\frac{1}{4}\cdot\frac{b-a}{b}\cdot F, b\le\frac{H}{2} a b_\text{ef}=b
Úplná nespojitost
T=\frac{1}{4}\cdot\big(1-0{,}7\frac{a}{h}\big)\cdot F\\
b>\frac{H}{2} a b_\text{ef}=0{,}5H+0{,}65a
Pro pozemní stavby lze uvažovat zjednodušeně
T=0{,}22\cdot F
10.1 Jednoduché oblasti
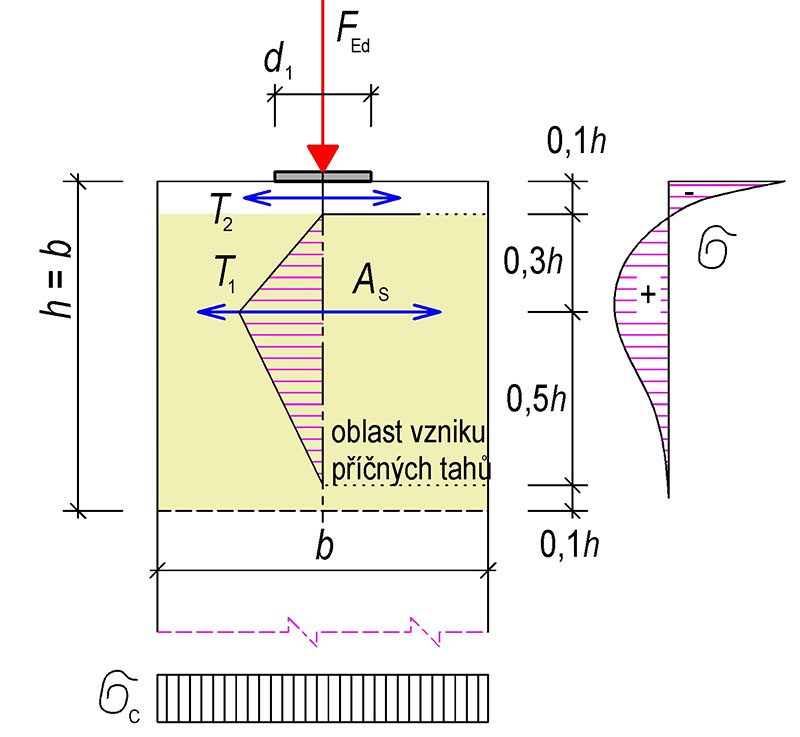
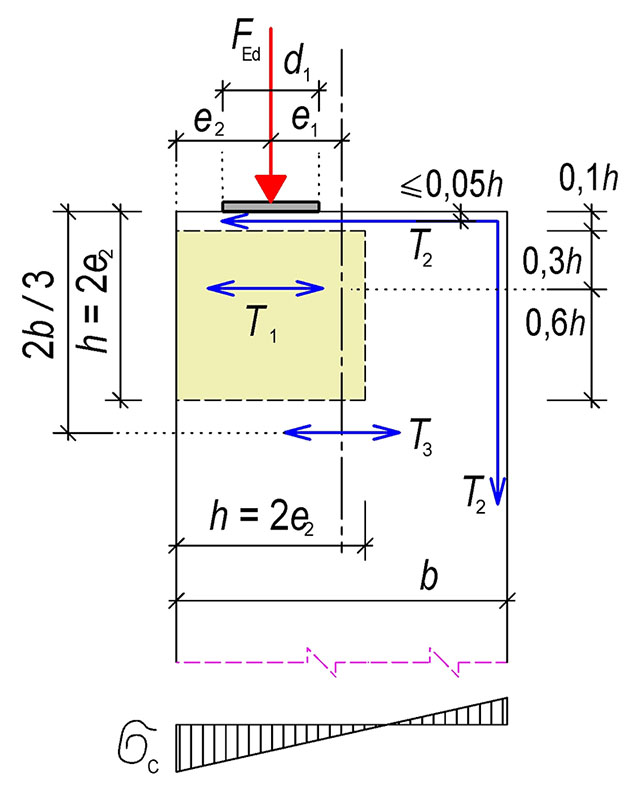
Tab. 10.3 Osamělé břemeno
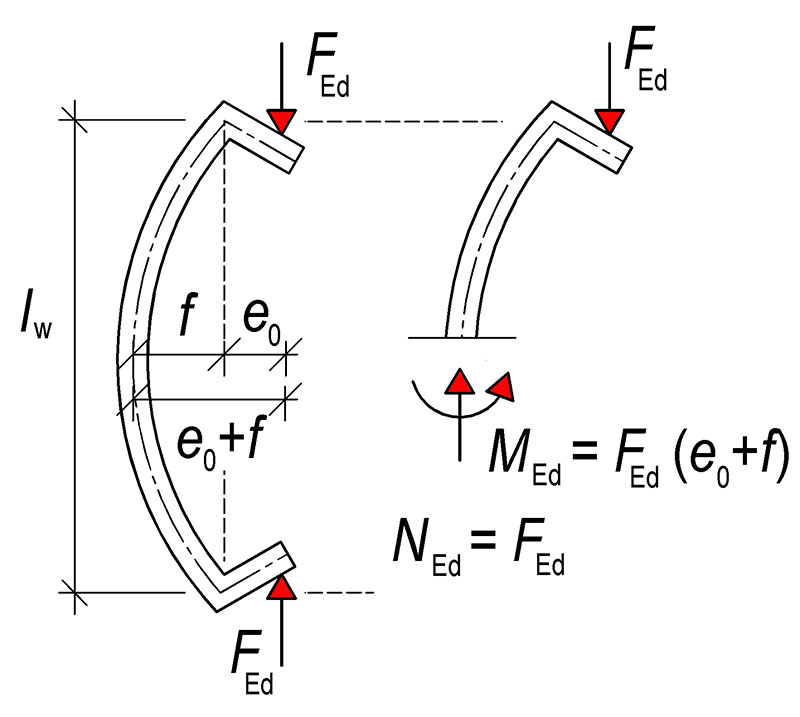
Příčný tah při centrickém zatížení stěny
T_1=0{,}25\cdot\big(1-\frac{d_1}{b}\big)\cdot F_\text{Ed}
T_2\approx0{,}1\cdot F_\text{Ed} konstrukční vyztužení, proti roztržení líce prvku
Příčný tah při excentrickém zatížení stěny lze konzervativně stanovit podle vztahu
T_1=0{,}25\cdot\big(1-\frac{d_1}{h}\big)\cdot F_\text{Ed}\ge0{,}1\cdot F_\text{Ed}\\
T_2=0{,}25\cdot\big(\frac{e_1}{b}-\frac{1}{6}\big)\cdot F_\text{Ed}\ge0{,}1\cdot F_\text{Ed}\\
T_3\approx0{,}3\cdot T_2
Tab. 10.4 Změna průřezu
10.2 Konzoly
Tab. 10.5 Návrh výztuže přímo uložené konzoly
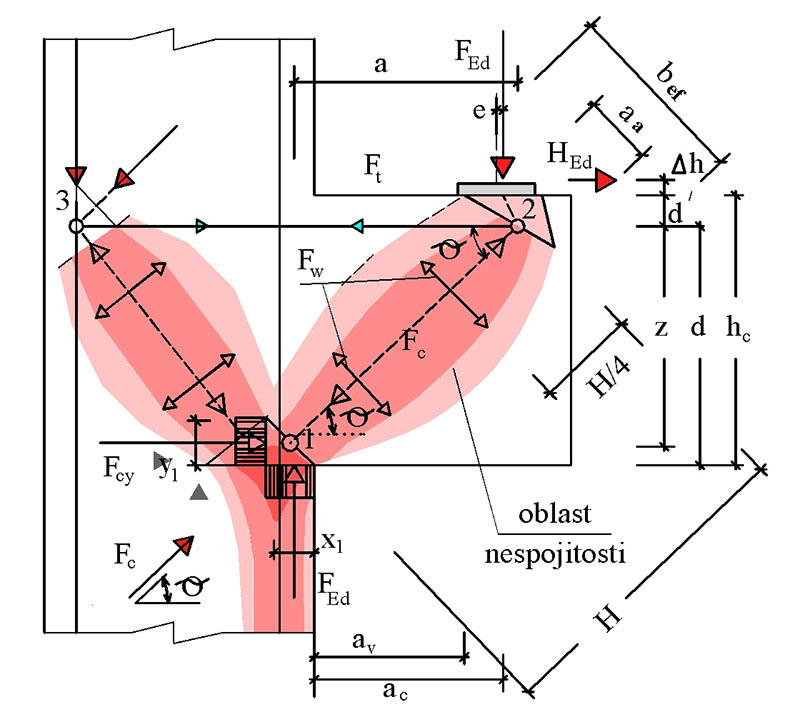
Obr. 10.1 Model náhradní příhradoviny konzoly
Vodorovné třmínky u krátkých konzol by měly být větší než 25 % hlavní tahové výztuže. Svislé třmínky u dlouhých konzol by měly přenést minimálně sílu 0,5FEd.
Svislé třmínky
F_\text{wv}=0{,}44\cdot\cot\theta\cdot F_\text{Ed}
Vodorovné třmínky
F_\text{wh}=0{,}44\cdot F_\text{Ed}=0{,}44\frac{F_\text{t}}{\cot\theta}
Šířka styčníku 1
x_1=\frac{F_\text{Ed}}{\sigma_\text{Rd,max}\cdot b}
Rameno vnější síly
a=a_\text{c}+0{,}5x_1+\frac{H_\text{Ed}}{F_\text{Ed}}(d'+\Delta h)
Výška styčníku 1
y_1=d-\sqrt{d^2-2x_1(a+H_\text{Ed}/F_\text{Ed}(d'+\Delta h))}
Hlavní tahová síla
F_\text{t}=F_\text{Ed}\cdot\frac{a}{z}+H_\text{Ed}(1+(d'+\Delta h)/z)
Hlavní tahová výztuž
A_\text{s,main}=\frac{F_\text{t}}{f_\text{yd}}
Síla v betonové vzpěře
F_\text{c}=\frac{F_\text{Ed}}{\sin\theta}
Únosnost betonové vzpěry
\sigma_\text{Rd,max}=0{,}6\cdot v'\cdot f_\text{cd}
fcd viz tab. 1.1
fcd viz tab. 2.1
b je šířka konzoly
θ je sklon tlačené diagonály
10.3 Nepřímo uložené konzoly
Tab. 10.6 Návrh výztuže nepřímo uložené konzoly
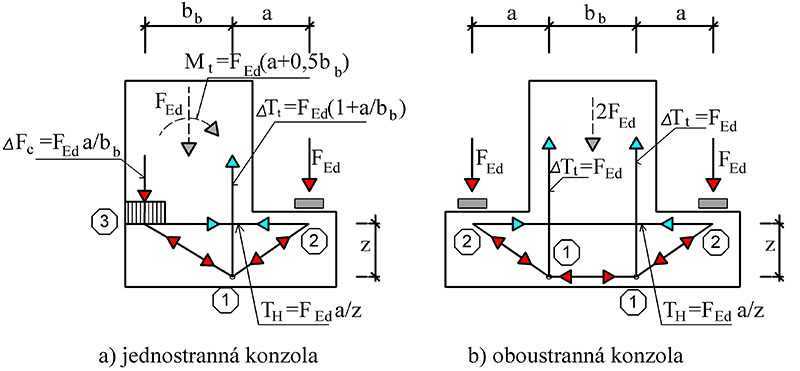
Obr. 10.2 Modely náhradní příhradoviny nepřímo uložené konzoly
Styčník 1 (CCT popřípadě CTT) uvažujeme nad třmínkovou výztuží nosníku, účinná výška d je tak snížena (oproti přímo uloženým konzolám) o betonovou krycí vrstvu a průměr třmínkové výztuže nosníku. Účinná výška konzoly je d=h-d'-c_\text{nom}+\text{\O}_\text{sw,nosnik}.
Øsw,nosnik je průměr třmínků nosníku,
cnom je betonová krycí vrstva viz tab. 3.2
d‘ je vzdálenost těžiště výztuže od taženého okraje
10.4 Ozuby trámů a průvlaků
Tab. 10.7 Návrh řešení oblasti ozubu – model A
Hlavní svislé táhlo u líce ozubu T_{23}=F_\text{Ed}+H_\text{Ed}\cdot\frac{z_\text{k}}{z}, plocha výztuže A_\text{s}=(T_{23}+H_\text{Ed}\cdot\frac{z_\text{k}}{z})/f_\text{yd}
Účinná výška ozubu je d_\text{k}=h_\text{k}-d_\text{k}'=h_\text{k}-(c_\text{nom}+\text{\O}_\text{sw}+2{,}5\text{\O}) (předpoklad 2 vrstvy výztuže ve vzdálenosti 4ø
Rameno vnitřních sil z_\text{k}=d_\text{k}-\Delta y-0{,}5\cdot y_2=d_\text{k}-a_\text{d},
kde \Delta y=c_\text{nom}+\text{\O}_\text{sw} a y2 je výška styčníku 2.
Rameno vnějších sil – reakce a=a_\text{c}+c_\text{nom}+0{,}5\cdot x_2+H_\text{Ed}/F_\text{Ed}\cdot(d_\text{k}'+\Delta h);
kde x2 je šířka styčníku 2
kde \Delta a je vodorovná vzdálenost těžiště navržených třmínků (táhla T23) od bočního líce prvku:
\Delta a=c_\text{nom}+0{,}5\cdot x_2.
Do hodnoty ac je doporučeno započítat vliv \Delta\approx15\text{K }25\text{ mm} nepřesnosti výroby a montáže prvku podle ČSN EN 13760.
Hodnota aH zohledňuje působení vodorovné síly a_\text{H}=\frac{H_\text{Ed}}{A}(d_\text{k}+\Delta h).
Výška styčníku 2 je y_2=(d_\text{k}-\Delta y)-\sqrt{(d_\text{k}-\Delta y)^2-4\cdot0{,}5\cdot X}
kde X=(a-H_\text{Ed}/F_\text{Ed}\cdot(d_\text{k}'+\Delta h))\cdot F_\text{Ed}/(b\cdot\sigma_\text{Rd,max}).
Síla v hlavním vodorovném táhle T_{14}=\frac{A\cdot a+H_\text{Ed}\cdot(z_\text{k}+d\text{k}'+\Delta h)}{z_\text{k}}
Hlavní tahová výztuž (obvykle ve formě smyček) A_\text{s14}=T_{14}/f\text{yd}
Stanovíme výztuž v následujících táhlech T45 a T67 a T_{45}=T_{23}=T_{67} a A_\text{s}=t_{23}/f_\text{yd}
Sklon tlačené diagonály \theta_1{...}\cot\theta_1=a/z_\text{k}
Síla v betonové diagonální vzpěře F_{12}=F_\text{Ed}/\sin\theta_1
Překontrolujeme únosnost betonové vzpěry podle vztahu \sigma_\text{Rd,max}=0{,}6\cdot v'\cdot f_\text{cd}.
Výztuž na přenesení příčných tahů v betonové vzpěře:
vodorovná T_\text{wh}=0{,}44\cdot F_\text{Ed}\ge0{,}25\cdot F_{14}
svislá T_\text{wv}=2T\cdot\cos\theta_1=0{,}44F_\text{c}\cos\theta_1=0{,}44F_\text{Ed}\cdot\cot\theta_1\ge0{,}5F_\text{Ed}.
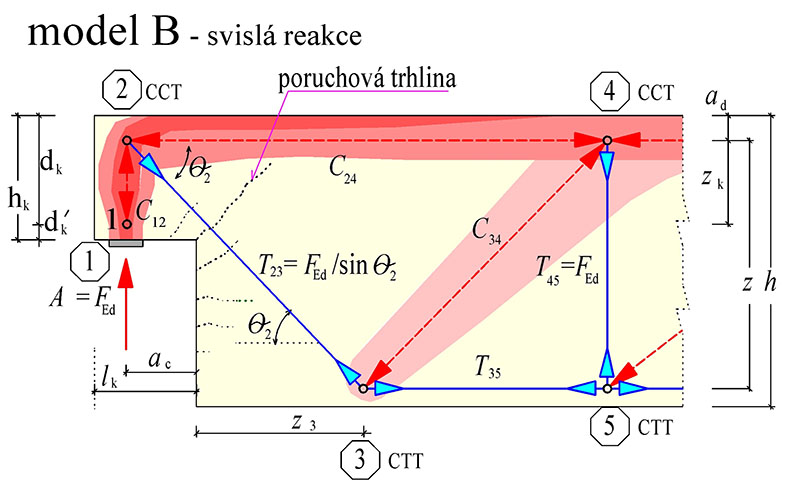
Tab. 10.8 Návrh řešení oblasti ozubu – model B
OZUBY – model B
Stanovíme sklon šikmé výztuže θ2. Optimální sklon je kolmý na poruchovou trhlinu, sklon je dán geometrií navržené výztuže. Na začátku můžeme vycházet ze sklonu 45o, po navržení výztuže sklon upřesníme a posouzení opakujeme se skutečným sklonem táhla T23. Síla v táhle T_{23}=A/\sin\theta_2.
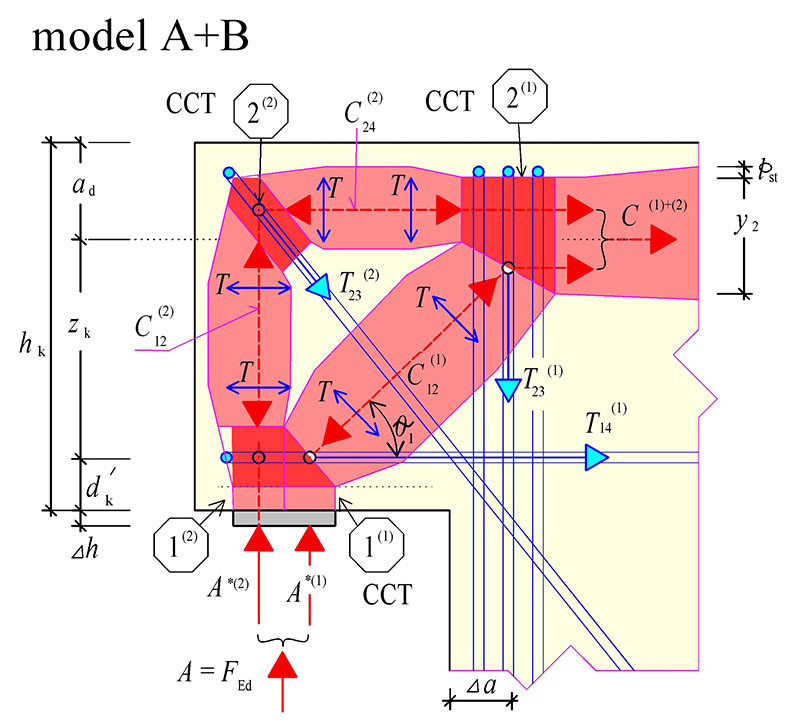
Tab. 10.9 Návrh řešení oblasti ozubu – kombinovaný model A a B
OZUBY – kombinovaný model A a B
Tlaková síla při horním líci ozubu pro stanovení výšky styčníku 2(1) je součtem tlakových sil v betonových vzpěrách obou modelů A a B:
C^{(1)+(2)}=C_{12}^{(1)}\cdot\cos\theta_1+C_{24}^{(2)}
Výška tlačeného pásu při horním líci (ve styčníku 2(1)) y_2=C^{(1)+(2)}/(\sigma_\text{Rd,max}\cdot b)
kde je
σRd,max … návrhová únosnost betonu v tlaku ve styčníku CCT;
b … šířka ozubu.
Ostatní postup je shodný s předchozími modely.
10.5 Malý kruhový prostup
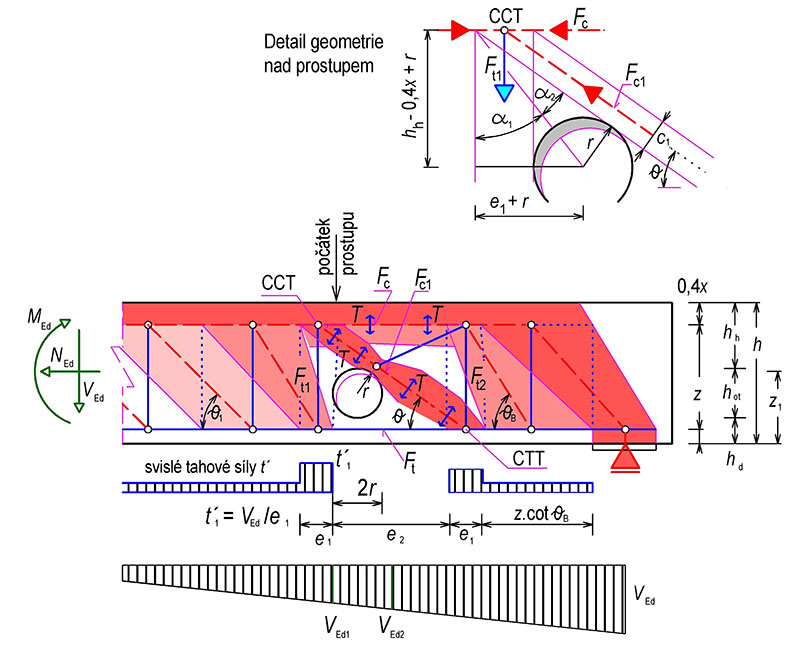
Tab. 10.10 Návrh řešení oblasti nosníku s malým kruhovým prostupem
Obr. 10.6 Model náhradní příhradoviny oblasti malého kruhového otvoru
Síla v taženém dolním pasu F_\text{t}=\frac{M_\text{Ed2}+N_\text{Ed2}\cdot z_1}{z}+\frac{|V_\text{Ed2}|}{\tan\alpha}+N_\text{Ed2}
Síla v tlačeném horním pasu F_\text{c}=\frac{-M_\text{Ed2}-N_\text{Ed2}\cdot z_1}{z}-|V_\text{Ed}|\cdot\cot\alpha
Táhlo před prostupem
A_\text{s1}=\frac{F_\text{t1}}{f_\text{ywd}}=\frac{|V_\text{Ed1}|}{f_\text{ywd}}
Úhel sklonu tlačené diagonály
\alpha=90\degree-(\alpha_1+\alpha_2)\\
\alpha_1=\text{arctg}\bigg(\frac{e_1+r}{h_\text{h}-0{,}4x+r}\bigg)\\
\alpha_2=\text{arcsin}\bigg(\frac{r}{\sqrt{(e_1+r)+(h_\text{h}-0{,}4x+r)^2}}\bigg)
Šířka betonové vzpěry
c_1=e_1\cdot\sin\alpha
Napětí v betonové vzpěře
\sigma_\text{c}=\frac{|V_\text{Ed1}|}{b\cdot c_1\cdot\sin\alpha}\le\sigma_\text{Rd,max}
Příčné tahy v betonové vzpěře
Vodorovná síla T_\text{wh}=0{,}44\cdot V_\text{Ed}
Svislá síla T_\text{wv}=0{,}44\cdot V_\text{Ed}\cdot\cot\alpha
10.6 Další poruchové oblasti
11 Mezní stavy použitelnosti
11.1 Omezení napětí
| Beton | Pokud je v tlačeném betonu při charakteristické kombinaci omezeno napětí hodnotou 0,6·fck (v prostředí XD, XF a XS), nevzniknou nežádoucí podélné trhliny. Lineární dotvarování betonu lze uvažovat, pokud napětí betonu v tlaku splňuje podmínku |\sigma_\text{c}|\le0{,}45f_\text{ck}. |
| Výztuž | Nepřijatelně široké trhliny nevzniknou, pokud při charakteristické kombinaci zatížení nepřekročí tahové napětí v betonářské výztuži hodnotu 0,8·fyk. Je-li napětí ve výztuži vyvozeno vynuceným přetvořením, je možno použít podmínku \sigma_\text{s}\le1{,}0f_\text{yk}. |
11.2 Průřezové charakteristiky
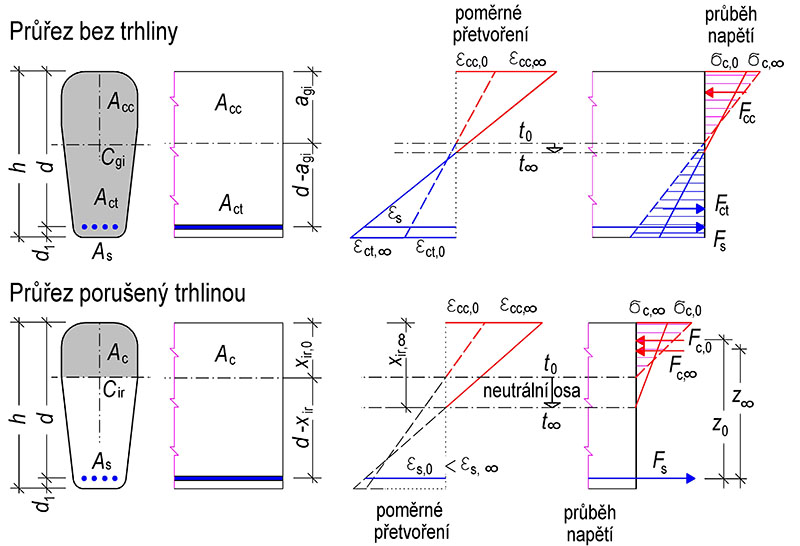
Tab. 11.1 Stanovení průřezových charakteristik – průřez bez trhliny a průřez porušený trhlinou
Průřez bez trhliny
Plocha ideálního průřezu
A_\text{i}=A_\text{c}+(\alpha_\text{e}-1)(A_\text{s1}+A_\text{s2})
vzdálenost těžiště ideálního průřezu od horního okraje
a_\text{gi}=[A_\text{c}\cdot a_\text{c}+(\alpha_\text{e}-1)(A_\text{s1}\cdot d)]/A_\text{i}
moment setrvačnosti ideálního průřezu vztažený k těžišti průřezu
I_\text{i}=I_\text{c}+A_\text{c}(a_\text{gi}-a_\text{c})^2+(\alpha_\text{e}-1)[A_\text{s1}(d-a_\text{gi})^2+A_\text{s2}(a_\text{gi}-d_2)^2]
kde je
Ac … plocha betonové části průřezu;
Ic … moment setrvačnosti betonového průřezu; (pro obdélníkový průřez I_\text{c}=1/12\cdot b\cdot h^3);
As1 … průřezová plocha tažené nebo méně tlačené (dolní) betonářské výztuže;
As2 … průřezová plocha tlačené nebo méně tažené (horní) betonářské výztuže;
ac … vzdálenost těžiště betonového průřezu od tlačeného nebo méně taženého okraje průřezu;
αe = Es/Ecm
Es = 200 000 MPa,
Ecm viz tab. 1.1
Napětí v krajních betonových vláknech při působení ohybového momentu a normálové síly (zavádíme tah +, tlak –)
v horních vláknech \sigma_\text{c2}=\frac{N_\text{kd}}{A_\text{i}}-\frac{M_\text{kdi}a_\text{gi}}{I_\text{i}}
v dolních vláknech \sigma_\text{c2}=\frac{N_\text{kd}}{A_\text{i}}+\frac{M_\text{kdi}(h-a_\text{gi})}{I_\text{i}}
Napětí ve výztuži, je před vznikem trhliny velmi malé.
Průřez porušený trhlinou
Velikosti tlačené části průřezu xir
x_\text{ir}=[A_\text{cc}\cdot a_\text{c}+(\alpha_\text{e}-1)(A_\text{s1}\cdot d+A_\text{s2}\cdot d_2)]/A_\text{ir}
pro obdélníkový průřez
x_\text{ir}=\frac{\alpha_\text{e}}{b}(A_\text{s1}+A_\text{s2})\bigg[-1+\sqrt{1+\frac{2b}{\alpha_\text{e}}\frac{A_\text{s1}d+A_\text{s2}d_2}{(A_\text{s1}+A_\text{s2})^2}}\bigg]
Plocha ideálního průřezu s trhlinou
(A_\text{ir}=A_\text{cc}+\alpha_\text{e}\cdot(A_\text{s1}+A_\text{s2});I_\text{ir} kde A_\text{cc}=bx_\text{ir};\\
I_\text{ir}=\frac{1}{3}bx_\text{ir}^3+\alpha_\text{e}[A_\text{s1}(d-x_\text{ir})^2+A_\text{s2}(x_\text{ir}-d_2)^2]
Napětí v krajních tlačených vláknech betonu určíme ze vztahu:
\sigma_\text{c}=\frac{N_\text{kd}}{A_\text{ir}}+N_\text{kd}(x_\text{ir}-e)\frac{x_\text{ir}}{I_\text{ir}}
Napětí ve výztuži vypočteme ze vztahů:
\sigma_\text{s1}=\bigg[\frac{N_\text{kd}}{A_\text{ri}}+N_\text{kd}(x_\text{ir}-e)\frac{x_\text{ir}-d}{I_\text{ir}}\bigg]\alpha_\text{e}\\
\sigma_\text{s2}=\bigg[\frac{N_\text{kd}}{A_\text{ri}}+N_\text{kd}(x_\text{ir}-e)\frac{x_\text{ir}-d_2}{I_\text{ir}}\bigg]\alpha_\text{e}
11.3 Šířka trhlin
Tab. 11.2 Maximální šířka trhliny podle vlivu prostředí
| Šířka trhlin | w_\text{k}=s_\text{r,max}\cdot(\varepsilon_\text{sm}-\varepsilon_\text{cm}) |
| Třída prostředí | Železobetonové konstrukce pro kvazistálou kombinaci zatížení |
| X0, XC1 | 0,41) |
| XC2, XC3, XC4 | 0,32) |
| XD1, XD2, XS1 až XS3 | 0,2 |
| 1) Není-li jiný požadavek, v prostředí X0 a XC1 není výpočet wmax nutný. Pro stupně vlivu prostředí X0, XC1 nemá šířka trhliny vliv na trvanlivost, uvedená hodnota má vést k obecně přijatelnému vzhledu. 2) V případě staveb kategorie použitelnosti A až D (viz EN 1991-1-1) a není-li jiný požadavek (například vodonepropustnost a podobně) předpokládá se, že omezená šířka trhlin je zajištěna minimálním množstvím výztuže a výpočet wmax pak není nutný. |
|
Tab. 11.3 Stanovení maximální šířky trhlin
Stanovení maximální šířky trhlin w_\text{k}=s_\text{r,max}\cdot(\varepsilon_\text{sm}-\varepsilon_\text{cm})
Maximální vzdálenost trhlin
Rozdíl přetvoření
(\varepsilon_\text{sm}-\varepsilon_\text{cm})=\bigg[\sigma_\text{s}-k_\text{t}\frac{f_\text{ct,eff}}{\rho_\text{p,eff}}(1+\alpha_\text{E}\rho_\text{p,eff})\bigg]/E_\text{s}\ge0{,}6\cdot\sigma_\text{s}/E_\text{s}
f_\text{ct,eff}=0{,}5\cdot f_\text{ctm} pro vznik trhlin v raných stádiích betonu
Tab. 11.4 Součinitele pro stanovení šířky trhlin
| k | Vliv nerovnoměrného rozdělení vnitřních rovnovážných napětí vedoucích ke zmenšení sil vyplývajících z omezeného přetvoření | h\le300\text{ mm} | 1,0 | |
| h\le800\text{ mm} | 0,65 | |||
| kt | Vliv doby trvání zatížení | krátkodobé | 0,6 | |
| dlouhodobé | 0,4 | |||
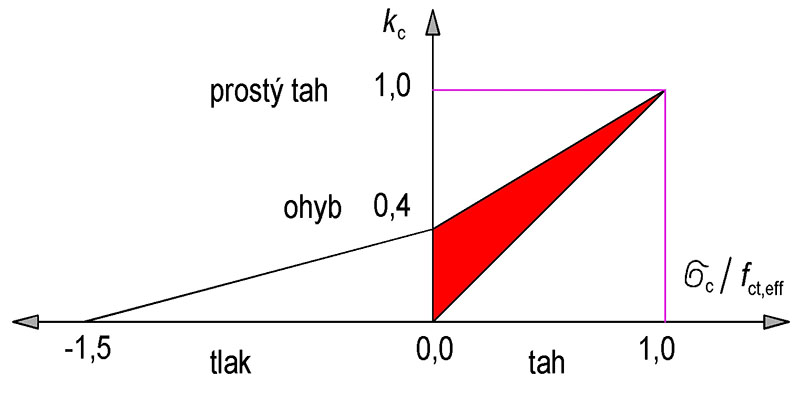
| kc | Vliv napětí v průřezu před vznikem trhlin a změna ramene vnitřních sil. | tah | 1,0 | |
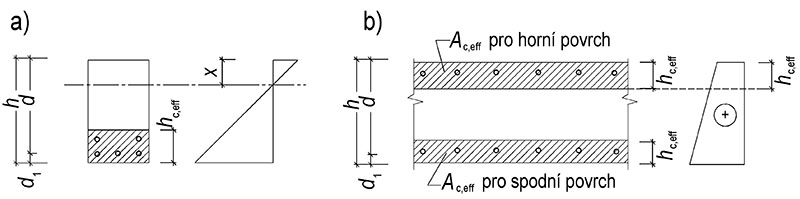
| ohyb s normálovou sílou – obdélníkové průřezy | k_\text{c}=0{,}4\bigg[1-\frac{\sigma_\text{c}}{k_1(h/h^{*})f_\text{ct,eff}}\bigg] | |||
| ohyb s normálovou silou – přilehlé desky | k_\text{c}=0{,}9\frac{F_\text{cr}}{A_\text{ct}f_\text{ct,eff}}\ge0{,}5 | |||
| k1 | Vliv účinků normálových sil na rozdělení napětí – pro stanovení kc, h* = h pro h ≤ 1 a h* = 1 pro h > 1 m | tlak | 1,5 | |
| tah | 2h*/3h | |||
| k1 | Vliv vlastností soudržné výztuže | velká soudržnost | 0,8 | |
| k2 | Vliv rozdělení poměrného přetvoření | tah | 1,0 | |
| ohyb | 0,5 | |||
| mimostředný tah | k_2=(\varepsilon_1+\varepsilon_2)/(2\cdot\varepsilon_1) | |||
| k3 | Součinitel vyjadřující vliv poškozené soudržnosti betonu a výztuže v bezprostřední blízkosti trhliny, c v [mm] | k_3=3{,}4\cdot(25/c)^{2/3}\le3{,}4 | ||
| k4 | Součinitel vyjadřující vztah mezi soudržností a pevností betonu v tahu | 0,425 | ||
| kde je Act … je plocha betonu v tažené části průřezu těsně před vznikem trhlin; Fcr … absolutní hodnota tahové síly v přilehlé desce před vznikem trhlin vyvozená momentem na mezi vzniku trhlin. |
||||
11.4 Výpočet pomocí tabulek
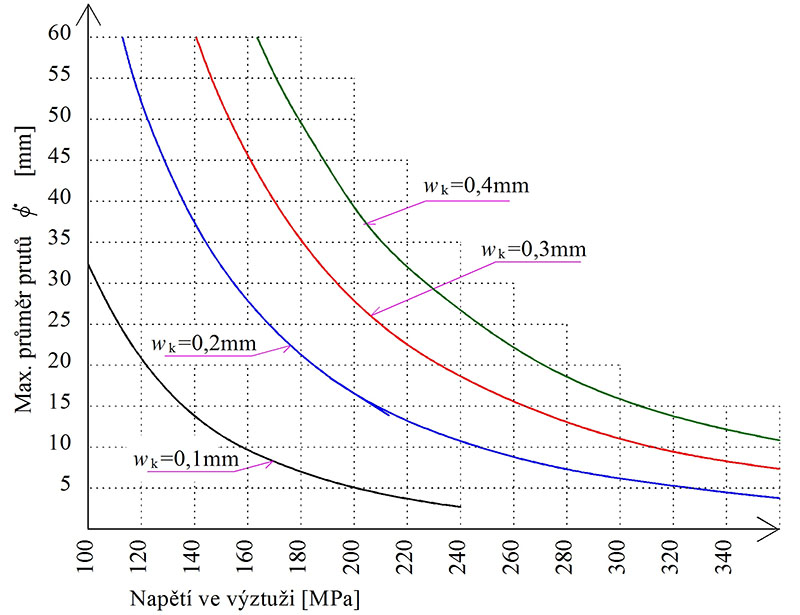
Tab. 11.5 Tabulky pro stanovení maximálního průměru výztuže (wk je šířka trhlin v mm)
| Napětí ve výztuži [MPa] | Maximální průměr prutů v [mm] | Maximální průměr prutů [mm] | Napětí ve výztuži v [MPa] | ||||||
| wk = 0,4 | wk = 0,3 | wk = 0,2 | wk = 0,1 | wk = 0,4 | wk = 0,3 | wk = 0,2 | |||
| 100 | 168,8 | 123,4 | 77,9 | 32,4 | 6 | 452,2 | 380,1 | 295,2 | |
| 120 | 115,4 | 83,8 | 52,3 | 20,7 | 8 | 402,0 | 339,2 | 265,2 | |
| 140 | 83,5 | 60,3 | 37,1 | 13,8 | 10 | 366,1 | 309,7 | 243,1 | |
| 160 | 62,9 | 45,1 | 27,3 | 9,6 | 12 | 338,6 | 287,0 | 226,1 | |
| 180 | 48,9 | 34,8 | 20,8 | 6,8 | 14 | 316,7 | 268,9 | 212,4 | |
| 200 | 38,9 | 27,6 | 16,2 | 4,8 | 16 | 298,8 | 254,0 | 201,0 | |
| 220 | 31,6 | 22,2 | 12,8 | 3,4 | 18 | 283,6 | 241,3 | 191,3 | |
| 240 | 26,1 | 18,2 | 10,3 | 2,4 | 20 | 270,6 | 230,5 | 183,0 | |
| 260 | 21,9 | 15,1 | 8,4 | 22 | 259,3 | 221,1 | 175,7 | ||
| 280 | 18,5 | 12,7 | 6,9 | 25 | 244,8 | 208,9 | 166,4 | ||
| 300 | 15,8 | 10,8 | 5,7 | 28 | 232,6 | 198,6 | 158,4 | ||
| 320 | 13,7 | 9,2 | 4,8 | 32 | 218,9 | 187,0 | 149,4 | ||
| 340 | 11,9 | 8,0 | 4,0 | Přibližná oprava maximálního napětí (tabulka jen pro první odhad) \sigma_\text{s}\le\sigma_\text{s}^{*}\cdot\sqrt{(f_\text{ct,eff}/2{,}9)} |
|||||
| 360 | 10,4 | 6,9 | 3,4 | ||||||
| Oprava pro ohýbaný prvek \text{\o}=\text{\o}_\text{s}^{*}\cdot\frac{1{,}6\cdot k\cdot k_\text{c}\cdot h_\text{cr}}{k_2\cdot h_\text{c,eff}}\cdot\frac{f_\text{ct,eff}}{2{,}9} |
Oprava pro tažený prvek \text{\o}=\text{\o}_\text{s}^{*}\cdot\frac{k\cdot h_\text{cr}}{4\cdot(h-d)}\cdot\frac{f_\text{ct,eff}}{2{,}9} |
||||||||
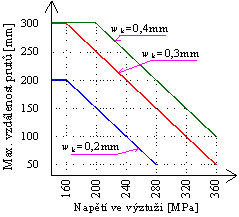
Obr. 11.1 Maximálního průměru výztuže v závislosti na napětí ve
Součinitele viz tab. 11.4
kde je
h … výška průřezu;
d … účinná výška průřezu;
hcr … výška tlačené části průřezu před vznikem trhlin.
Tab. 11.6 Maximální vzdálenost výztužných prutů v závislosti na napětí a šířce trhlin (wk je šířka trhlin v mm)
| Napětí ve výztuži [MPa] | Maximální vzdálenost prutů výztuže | ||
| wk = 0,4 mm | wk = 0,3 mm | wk = 0,2 mm | |
| 160 | 300 | 300 | 200 |
| 200 | 300 | 250 | 150 |
| 240 | 250 | 200 | 100 |
| 280 | 200 | 150 | 50 |
| 320 | 150 | 100 | – |
| 360 | 100 | 50 | – |
11.5 Minimální plocha výztuže – přímý výpočet
Tab. 11.7 Vzorce pro výpočet šířky trhlin
| Pro rané trhliny u tažených prvků Maximální hodnota z obou vztahů |
A_\text{s,min}=\frac{s_3\cdot f_\text{cf,eff}\cdot(k\cdot A_\text{ct}-0{,}4\cdot A_\text{c,eff})}{2\cdot E_\text{s}\cdot w_\text{k}}\pm\sqrt{\bigg(\frac{s_3\cdot f_\text{cf,eff}\cdot(k\cdot A_\text{ct}-0{,}4\cdot A_\text{c,eff})}{2\cdot E_\text{s}\cdot w_\text{k}}\bigg)^2+\frac{0{,}17\cdot\phi\cdot A_\text{c,eff}\cdot f_\text{ct,eff}\cdot(k\cdot A_\text{ct}-0{,}4\cdot A_\text{c,eff})}{E_\text{s}\cdot w_\text{k}}} |
| A_\text{s,min}=\frac{0{,}3\cdot s_3\cdot f_\text{ct,eff}\cdot k\cdot A_\text{ct}}{E_\text{s}\cdot w_\text{k}}\pm\sqrt{\bigg(\frac{0{,}3\cdot s_3\cdot f_\text{ct,eff}\cdot k\cdot A_\text{ct}}{E_\text{s}\cdot w_\text{k}}\bigg)^2+\frac{0{,}204\cdot\phi\cdot A_\text{c,eff}\cdot f_\text{ct,eff}\cdot k\cdot A_\text{ct}}{E_\text{s}\cdot w_\text{k}}} | |
| Pro rané trhliny u ohýbaných prvků Maximální hodnota z obou vztahů |
A_\text{s,min}=\frac{0{,}2\cdot s_3\cdot f_\text{cf,eff}\cdot(k\cdot A_\text{ct}-A_\text{c,eff})}{E_\text{s}\cdot w_\text{k}}\pm\sqrt{\bigg(\frac{0{,}2\cdot s_3\cdot f_\text{cf,eff}\cdot(k\cdot A_\text{ct}-A_\text{c,eff})}{E_\text{s}\cdot w_\text{k}}\bigg)^2+\frac{0{,}068\cdot\phi\cdot A_\text{c,eff}\cdot f_\text{ct,eff}\cdot(k\cdot A_\text{ct}-A_\text{c,eff})}{E_\text{s}\cdot w_\text{k}}} |
| A_\text{s,min}=\frac{0{,}12\cdot k\cdot s_3\cdot f_\text{cf,eff}\cdot A_\text{ct}}{E_\text{s}\cdot w_\text{k}}\pm\sqrt{\bigg(\frac{0{,}12\cdot k\cdot s_3\cdot f_\text{cf,eff}\cdot A_\text{ct}}{E_\text{s}\cdot w_\text{k}}\bigg)^2+\frac{0{,}041\cdot\phi\cdot A_\text{c,eff}\cdot f_\text{ct,eff}\cdot k\cdot A_\text{ct}}{E_\text{s}\cdot w_\text{k}}} | |
| Ověření šířky trhlin od zatížení | w_\text{k}=\bigg(s_3\frac{0{,}34\cdot k_2\cdot\phi\cdot A_\text{c,eff}}{A_\text{s1}}\bigg)\cdot\frac{1}{E_\text{s}}\cdot\bigg(\sigma_\text{s}-0{,}4\cdot\frac{f_\text{ct,eff}\cdot A_\text{c,eff}}{A_\text{s1}}-0{,}4\cdot\alpha_\text{e}\cdot f_\text{ct,eff}\bigg) S podmínkou \bigg(\sigma_\text{s}-0{,}4\cdot\frac{f_\text{ct,eff}\cdot A_\text{c,eff}}{A_\text{s1}}-0{,}4\cdot\alpha_\text{e}\cdot f_\text{ce,eff}\bigg)\ge0{,}6\cdot\sigma_\text{s} |
11.6 Omezení průhybů
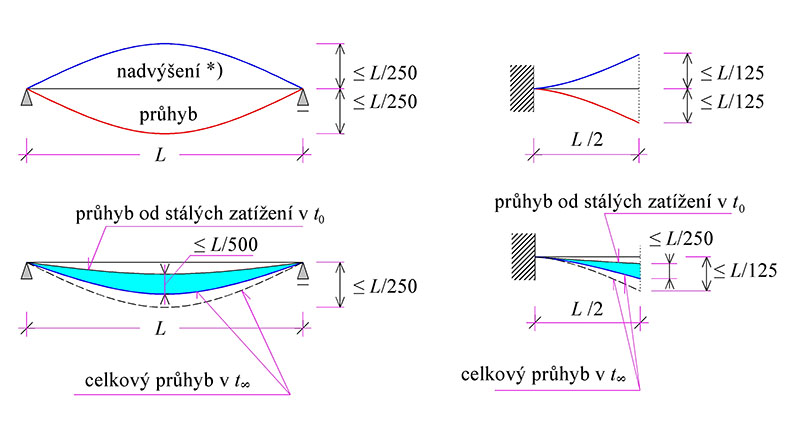
Průhyb vypočtený při kvazi-stálém zatížení nemá překročit hodnotu 1/250 rozpětí. Pro kompenzaci celého průhybu nebo jeho části lze použít nadvýšení, které nemá překročit hodnotu 1/250 rozpětí.
Průhyb od zatížení po zabudování prvku vypočtený při kvazi-stálém zatížení nemá překročit hodnotu 1/500 rozpětí
Obr. 11.2 Maximálního průhyby ohýbaných prvků
11.7 Vymezující ohybová štíhlost
Tab. 11.8 Vymezující ohybová štíhlost
| Vymezují ohybová štíhlost | \frac{l}{d}\le\lambda_\text{d}, kde \lambda_\text{d}=\kappa_\text{c1}\kappa_\text{c2}\kappa_\text{c3}\lambda_\text{d,tab}, | |||||
| \lambda_\text{d,tab}=\Bigg\lang{\begin{matrix} K\Big[11+1{,}5\sqrt{f_\text{ck}}\frac{\rho_\text{o}}{\rho}+3{,}2\sqrt{f_\text{ck}}\Big(\frac{\rho_\text{o}}{\rho}-1\Big)^{3/2}\Big]\space\text{pro}\space\rho\le\rho_\text{o},\\\\ K\Big[11+1{,}5\sqrt{f_\text{ck}}\frac{\rho_\text{o}}{\rho-\rho'}+\frac{1}{12}\sqrt{f_\text{ck}}\frac{\rho'}{\rho_\text{o}}\Big]\space\text{pro}\space\rho\gt\rho_\text{o}, \end{matrix}} | ||||||
| κc1 | κc1 = 0,8 pro T-průřezy s poměrem šířky příruby k šířce žebra větší než 3, κc1 = 1,0 v ostatních případech; | |||||
| κc2 | nosníky a nosníkové desky κc2 = 7/l pro l > 7,0 m, κc2 = 1,0 pro l ≤ 7,0 m; | |||||
| κc3 | \kappa_3=\frac{310}{\sigma_\text{s}}{=}\mathllap{\&}\frac{500}{f_\text{yk}}\frac{A_\text{s,prov}}{A_\text{s,req}} | A_\text{s,prov} … plocha výztuže v extrémně namáhaném průřezu o rozměrech b a h; A_\text{s,req}… průřezová plocha výztuže v průřezu potřebná k přenesení extrémního momentu. |
||||
| ρ0 | referenční stupeň vyztužení \rho_0=10^{-3}\sqrt{f_\text{ck}}, kde fck je v MPa viz tab. 1.1 | |||||
| ρ | požadovaný stupeň vyztužení tahovou výztuží | |||||
| ρ‘ | požadovaný stupeň vyztužení tlakovou výztuží | |||||
| Součinitel K – Nosná soustava pro beton C30/37 | K | λd,tab pro silně namáhaný beton ρ = 1,5 % | λd,tab pro slabě namáhaný beton (desky) ρ = 0,5 % | |||
|
1,0 | 14 | 20 | |||
|
1,3 | 18 | 26 | |||
|
1,5 | 20 | 30 | |||
|
1,2 | 17 | 24 | |||
|
0,4 | 6 | 8 | |||
|
Poznámka: U desek nosných ve dvou směrech se má posouzení provést pro kratší z rozpětí deskového pole. U desek lokálně podepřených se při posouzení má uvažovat delší z rozpětí deskového pole. |
||||||
11.8 Výpočet přetvoření
Tab. 11.9 Výpočet přetvoření
| Ohybová poddajnost průřezu bez trhlin | C_\text{I}=\frac{1}{E_\text{c,eff}I_\text{i}} kde je Ii … moment setrvačnosti průřezu bez trhliny; při \alpha_\text{e}=E_\text{s}/E_\text{c,eff} |
|
| Ohybová poddajnost průřezu s trhlinami | C_\text{II}=\frac{1}{E_\text{c,eff}I_\text{ir}} kde je Iir … je moment setrvačnosti průřezu s trhlinou; při \alpha_\text{e}=E_\text{s}/E_\text{c,eff} |
|
| Modul pružnosti betonu | E_\text{c,eff}=\frac{E_\text{cm}}{1+\varphi(\infty,t_0)} a pro krátkodobé účinky E_\text{c,eff}=E_\text{cm} | |
| Součinitel ζ udávající míru spolupůsobení betonu mezi trhlinami | \zeta=1-\beta\cdot\bigg(\frac{\sigma_\text{sr}}{\sigma_\text{s}}\bigg)^2 \zeta=0 pro průřezy bez trhlin Poznámka: Hodnotu 0 je nutné pečlivě zvážit, doporučeno je uvažovat hodnotu nejméně 0,5. |
β = 1,0 při jednorázovém krátkodobě působícím zatížení; β = 0,5 při dlouhodobě působícím nebo mnohonásobně opakovaném zatížení; σs je napětí v tahové výztuži vypočtené pro průřez s trhlinami; σsr je napětí v tahové výztuži vypočtené pro průřez s trhlinami při zatížení způsobujícím vznik prvních trhlin. Poměr σsr/σs lze při prostém ohybu nahradit poměrem Mcr/Mkd. |
| Křivost od přímého zatížení | \frac{1}{r_\text{m}}=M_\text{kd}\cdot[(1-\zeta)\cdot C_\text{I}+\zeta\cdot C_\text{II}] | |
| Křivost od smršťování | \frac{1}{r_\text{cs}}=\varepsilon_\text{cs}\cdot\alpha_\text{e}\cdot\bigg[(1-\zeta)\cdot\frac{S_\text{i}}{I_\text{i}}+\zeta\cdot\frac{S_\text{ir}}{I_\text{ir}}\bigg],\space\alpha_\text{e}=E_\text{s}/E_\text{c,eff} a \varepsilon_\text{cs} je poměrné přetvoření od celkového smršťování, průřezové charakteristiky bez trhliny Si, Ii a s trhlinou Sir, Iir. | |
| Průhyb nosníku | f I je průhyb nosníku při uvažování plného působení betonu v tahu, f II je průhyb nosníku, u kterého beton v tahu nepůsobí. |
|
Tab. 11.10 Tabulka pro zjednodušení řešení
Zjednodušené řešení
f_\text{s}=k\cdot l^2\cdot\frac{1}{r_\text{ms}};
kde \frac{1}{r_\text{ms}} křivost ve středu nosníku (ve vetknutí konzoly) od zatížení, popřípadě od smršťování
E_\text{c,eff}=\frac{E_\text{cm}}{(1+\varphi_\text{i})}
je součinitel dotvarování.
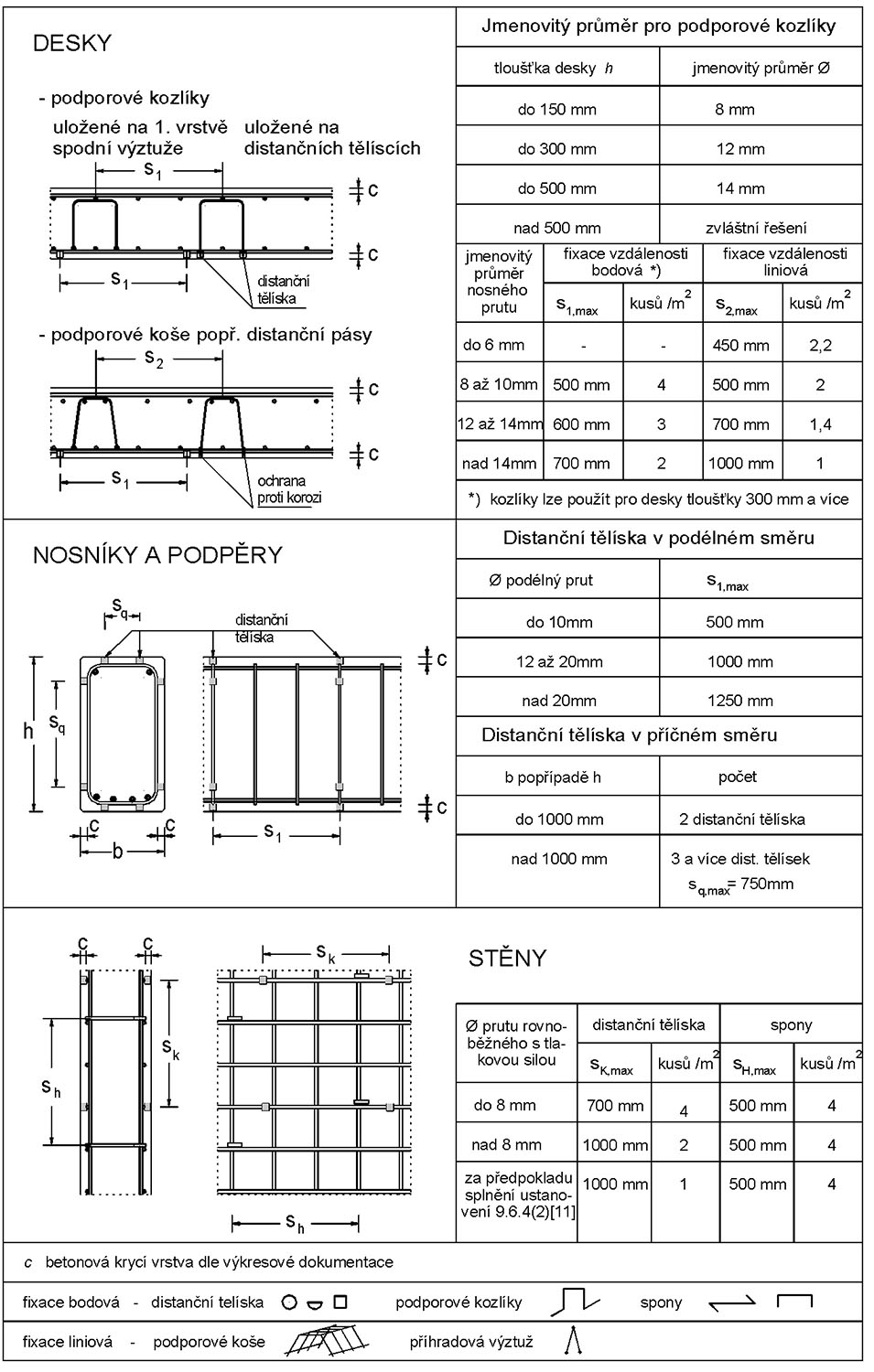
12 Konstrukční zásady a tabulky
12.1 Průřezové charakteristiky betonářské výztuže
Tab. 12.1 Průřezové charakteristiky betonářské výztuže
| Jmenovitý průměr [mm] | 6 | 8 | 10 | 12 | 14 | 16 | 20 | 25 | 28 | 32 |
| průřezová plocha [mm2] | 28,3 | 50,3 | 78,5 | 113,1 | 154 | 201 | 314 | 491 | 616 | 804 |
| hmotnost [kg/m] | 0,222 | 0,335 | 0,617 | 0,888 | 1,21 | 1,58 | 2,47 | 3,85 | 4,83 | 6,31 |
| výztuž ve svitcích 0,5 – 3,0 Mg | dodávaná v délce 12 – 15 m | |||||||||
Tab. 12.2 Průřezová plocha výztuže as při plošném vyztužování [mm2/m]
| Osové vzdálenosti prutů | Průřez výztuže [mm]/plocha výztuže v mm2/m | ||||||||||
| [mm] | ø 6 | ø 8 | ø 10 | ø 12 | ø 14 | ø 16 | ø 18 | ø 20 | ø 22 | ø 25 | ø 28 |
| 50 | 565 | 1005 | 1571 | 2262 | 3079 | 4021 | 5089 | 6283 | 7603 | 9817 | 12315 |
| 60 | 471 | 838 | 1309 | 1885 | 2566 | 3351 | 4241 | 5236 | 6336 | 8181 | 10263 |
| 70 | 404 | 718 | 1122 | 1616 | 2199 | 2872 | 3635 | 4488 | 5430 | 7012 | 8796 |
| 80 | 353 | 628 | 982 | 1414 | 1924 | 2513 | 3181 | 3927 | 4752 | 6136 | 7697 |
| 90 | 314 | 559 | 873 | 1257 | 1710 | 2234 | 2827 | 3491 | 4224 | 5454 | 6842 |
| 100 | 283 | 503 | 785 | 1131 | 1539 | 2011 | 2545 | 3142 | 3801 | 4909 | 6158 |
| 110 | 257 | 457 | 714 | 1028 | 1399 | 1828 | 2313 | 2856 | 3456 | 4462 | 5598 |
| 120 | 236 | 419 | 654 | 942 | 1283 | 1676 | 2121 | 2618 | 3168 | 4091 | 5131 |
| 130 | 217 | 387 | 604 | 870 | 1184 | 1547 | 1957 | 2417 | 2924 | 3776 | 4737 |
| 140 | 202 | 359 | 561 | 808 | 1100 | 1436 | 1818 | 2244 | 2715 | 3506 | 4398 |
| 150 | 188 | 335 | 524 | 754 | 1026 | 1340 | 1696 | 2094 | 2534 | 3272 | 4105 |
| 160 | 177 | 314 | 491 | 707 | 962 | 1257 | 1590 | 1963 | 2376 | 3068 | 3848 |
| 170 | 166 | 296 | 462 | 665 | 906 | 1183 | 1497 | 1848 | 2236 | 2887 | 3622 |
| 180 | 157 | 279 | 436 | 628 | 855 | 1117 | 1414 | 1745 | 2112 | 2727 | 3421 |
| 190 | 149 | 265 | 413 | 595 | 810 | 1058 | 1339 | 1653 | 2001 | 2584 | 3241 |
| 200 | 141 | 251 | 393 | 565 | 770 | 1005 | 1272 | 1571 | 1901 | 2454 | 3079 |
| 210 | 135 | 239 | 374 | 539 | 733 | 957 | 1212 | 1496 | 1810 | 2337 | 2932 |
| 220 | 129 | 228 | 357 | 514 | 700 | 914 | 1157 | 1428 | 1728 | 2231 | 2799 |
| 230 | 123 | 219 | 341 | 492 | 669 | 874 | 1106 | 1366 | 1653 | 2134 | 2677 |
| 240 | 118 | 209 | 327 | 471 | 641 | 838 | 1060 | 1309 | 1584 | 2045 | 2566 |
| 250 | 113 | 201 | 314 | 452 | 616 | 804 | 1018 | 1257 | 1521 | 1963 | 2463 |
Tab. 12.3 Průřezová plocha As výztuže podle počtu prutů [mm2]
| Průřez výztuže | Počet prutů/plocha výztuže v mm2 | ||||||||||
| [mm] | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| ø 6 | 28 | 57 | 85 | 113 | 141 | 170 | 198 | 226 | 254 | 283 | 311 |
| ø 8 | 50 | 101 | 151 | 201 | 251 | 302 | 352 | 402 | 452 | 503 | 553 |
| ø 10 | 79 | 157 | 236 | 314 | 393 | 471 | 550 | 628 | 707 | 785 | 864 |
| ø 12 | 113 | 226 | 339 | 452 | 565 | 679 | 792 | 905 | 1018 | 1131 | 1244 |
| ø 14 | 154 | 308 | 462 | 616 | 770 | 924 | 1078 | 1232 | 1385 | 1539 | 1693 |
| ø 16 | 201 | 402 | 603 | 804 | 1005 | 1206 | 1407 | 1608 | 1810 | 2011 | 2212 |
| ø 18 | 254 | 509 | 763 | 1018 | 1272 | 1527 | 1781 | 2036 | 2290 | 2545 | 2799 |
| ø 20 | 314 | 628 | 942 | 1257 | 1571 | 1885 | 2199 | 2513 | 2827 | 3142 | 3456 |
| ø 22 | 380 | 760 | 1140 | 1521 | 1901 | 2281 | 2661 | 3041 | 3421 | 3801 | 4181 |
| ø 25 | 491 | 982 | 1473 | 1963 | 2454 | 2945 | 3436 | 3927 | 4418 | 4909 | 5400 |
| ø 28 | 616 | 1232 | 1847 | 2463 | 3079 | 3695 | 4310 | 4926 | 5542 | 6158 | 6773 |
| ø 32 | 804 | 1608 | 2413 | 3217 | 4021 | 4825 | 5630 | 6434 | 7238 | 8042 | 8847 |
| ø 40 | 1257 | 2513 | 3770 | 5027 | 6283 | 7540 | 8796 | 10053 | 11310 | 12566 | 13823 |
12.2 Kotvení betonářské výztuže
Tab. 12.4 Základní kotevní délka – výpočet
| Základní kotevní délka | l_\text{b,rqd}=\frac{\phi}{4}\cdot\frac{\sigma_\text{sd}}{f_\text{bd}} fbd viz tab. 1.1, \sigma_\text{sd} je napětí ve výztuži |
||||||||||
| Návrhová kotevní délka | l_\text{bd}=\alpha_1\cdot\alpha_2\cdot\alpha_3\cdot\alpha_4\cdot\alpha_5\cdot l_\text{b,rqd}\ge l_\text{b,min} | ||||||||||
| Minimální kotevní délka výztuže v tahu | l_\text{b,min}=\text{max}[0{,}3l_\text{b,rqd};10\phi;100\text{ mm}] | ||||||||||
| v tlaku | l_\text{b,min}=\text{max}[0{,}6l_\text{b,rqd};10\phi;100\text{ mm}] | ||||||||||
| Ovlivňující činitel | Způsob kotvení | Prut betonářské výztuže | |||||||||
| tažený | tlačený | ||||||||||
| Tvar prutů | přímý prut | \alpha_1=1{,}0 | \alpha_1=1{,}0 | ||||||||
| jiný než přímý prut | \alpha_1=0{,}70 pokud c_\text{d}\gt3\cdot\phi jinak \alpha_1=1{,}0 |
\alpha_1=1{,}0 | |||||||||
| Betonová krycí vrstva | přímý prut | \alpha_2=1-0{,}15\cdot(d_\text{d}-\phi)/\phi přitom 0{,}70\le\alpha_2\le1{,}0 | \alpha_2=1{,}0 | ||||||||
| jiný než přímý prut | \alpha_2=1-0{,}15\cdot(d_\text{d}-3\cdot\phi)/\phi přitom 0{,}70\le\alpha_2\le1{,}0 | \alpha_2=1{,}0 | |||||||||
| Ovinutí příčnou nepřivařenou výztuží | všechny způsoby | \alpha_3-1-K\cdot\lambda přitom 0{,}70\le\alpha_3\le1{,}0 | \alpha_3=1{,}0 | ||||||||
| Ovinutí přivařenou příčnou výztuží | všechny způsoby | \alpha_4=0{,}70 | \alpha_4=1{,}0 | ||||||||
| Účinek ovinutí příčným tlakem | všechny způsoby | \alpha_5=1-0{,}04\cdot p přitom 0{,}70\le\alpha_5\le1{,}0 | – | ||||||||
| Součinitel množství stykovaných prutů k celkové ploše výztuže | % stykovaných prutů | < 25 % | 33 % | 50 % | > 50 % | ||||||
| a6 přesněji \alpha_6=(\rho_1/25)^{0{,}5} |
1 | 1,15 | 1,4 | 1,5 | |||||||
| Součinitel \lambda=(\sum A_\text{st}-\sum A_\text{st,min})/A_\text{s} kde je As … plocha jednoho kotveného prutu; ΣAst … průřezová plocha příčné výztuže v oblasti kotevní délky; ΣAst,min … průřezová plocha minimální příčné výztuže Ast = 0,25As pro nosníky; Ast = 0 pro desky. Při stykování přesahem místo ΣAst,min je nutno uvažovat hodnotu 1,0*As(σsd/fyd); p … příčný tlak za mezního stavu únosnosti v MPa; ρ1 … procento přesahem stykované výztuže na délce 0,65lo od středu uvažovaného přesahu. Přitom platí, že součin \alpha_2\cdot\alpha_3\cdot\alpha_5\ge0{,}70. |
|||||||||||
| Hodnoty K pro nosníky a desky | Hodnoty cd pro nosníky a desky | ||||||||||
| Ovinutí příčnou nepřivařenou výztuží | Pro přímé pruty c_\text{d}=\text{min}(a/2;c_1;c) |
Pro pruty s ohyby nebo háky c_\text{d}=\text{min}(a/2;c_1) |
Pro pruty se smyčkou c_\text{d}=c |
||||||||
Tab. 12.5 Základní kotevní délka lb,rqd v počtu profilů kotveného prutu při \sigma_\text{sd}=f_\text{yd} (výztuž B500)
Tab. 12.6 Základní kotevní délka lb,rqd v [mm] prutu při \sigma_\text{sd}=f_\text{yd} (pro výztuž B500)
| Třída betonu | Podmínky soudržnosti | Základní kotevní délka v mm pro průřez výztužných prutů | |||||||||
| ø 6 | ø 8 | ø 10 | ø 12 | ø 14 | ø 16 | ø 18 | ø 20 | ø 22 | ø 25 | ||
| C12/15 | dobré | 395 | 527 | 659 | 791 | 922 | 1054 | 1186 | 1318 | 1449 | 1647 |
| špatné | 565 | 753 | 941 | 1129 | 1318 | 1506 | 1694 | 1882 | 2070 | 2353 | |
| C16/20 | dobré | 334 | 446 | 557 | 669 | 780 | 892 | 1003 | 1115 | 1226 | 1394 |
| špatné | 478 | 637 | 796 | 956 | 1115 | 1274 | 1433 | 1593 | 1752 | 1991 | |
| C20/25 | dobré | 290 | 386 | 483 | 580 | 676 | 773 | 870 | 966 | 1063 | 1208 |
| špatné | 414 | 552 | 690 | 828 | 966 | 1104 | 1242 | 1380 | 1518 | 1725 | |
| C25/30 | dobré | 242 | 322 | 403 | 483 | 564 | 644 | 725 | 805 | 886 | 1006 |
| špatné | 345 | 460 | 575 | 690 | 805 | 920 | 1035 | 1150 | 1265 | 1438 | |
| C30/37 | dobré | 217 | 290 | 362 | 435 | 507 | 580 | 652 | 725 | 797 | 906 |
| špatné | 311 | 414 | 518 | 621 | 725 | 828 | 932 | 1035 | 1139 | 1294 | |
| C35/45 | dobré | 198 | 264 | 329 | 395 | 461 | 527 | 593 | 659 | 725 | 823 |
| špatné | 282 | 376 | 471 | 565 | 659 | 753 | 847 | 941 | 1035 | 1176 | |
| C40/50 | dobré | 174 | 232 | 290 | 348 | 406 | 464 | 522 | 580 | 638 | 725 |
| špatné | 248 | 331 | 414 | 497 | 580 | 663 | 745 | 828 | 911 | 1035 | |
| C45/55 | dobré | 161 | 215 | 268 | 322 | 376 | 429 | 483 | 537 | 590 | 671 |
| špatné | 230 | 307 | 383 | 460 | 537 | 613 | 690 | 767 | 843 | 959 | |
| C50/60 | dobré | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 | 550 | 625 |
| špatné | 214 | 286 | 357 | 428 | 500 | 571 | 643 | 714 | 785 | 892 | |
| C55/67 | dobré | 145 | 193 | 242 | 290 | 338 | 386 | 435 | 483 | 531 | 604 |
| špatné | 207 | 276 | 345 | 414 | 483 | 552 | 621 | 690 | 759 | 863 | |
| C60/75 a vyšší | dobré | 140 | 187 | 234 | 281 | 327 | 374 | 421 | 468 | 514 | 584 |
| špatné | 200 | 267 | 334 | 401 | 468 | 534 | 601 | 668 | 735 | 835 | |
12.3 Stykování prutů betonářské výztuže
Tab. 12.7 Stykování přesahem
Stykování přesahem
l_0=\alpha_1\cdot\alpha_2\cdot\alpha_3\cdot\alpha_4\cdot\alpha_5\cdot\alpha_6l_\text{b,rqd}\\
l_0\gt l_\text{0,min}\\
l_\text{0,min}\ge\text{max}[0{,}3\alpha_6l_\text{b,rqd};15\phi;200\text{ mm}]
Stykovat nelze v oblasti plastických kloubů. V oblasti styku musí být provedena příčná výztuže.
Součinitelé \alpha_1\cdot\alpha_2\cdot\alpha_3\cdot\alpha_4\cdot\alpha_5\cdot\alpha_6 – viz tab. 12.4
12.4 Ohýbání výztuže za studena
Tab. 12.8 Ohýbání výztuže
| Profil | Minimální průměr vnitřního zakřivení | \phi_\text{m,min}=\frac{F_\text{bt}}{f_\text{cd}}\cdot\bigg[\frac{1}{2\cdot\phi}+\frac{1}{a_\text{b}}\bigg] Nutné především pro návrh smyček (vzdálenost mezi smyčkami, vliv blízkosti líce prvku) |
|
| ø ≤ 16 mm | \phi_\text{m,min}=4\space\varnothing | ||
| ø >16 | \phi_\text{m,min}=7\space\varnothing | ||
| Pro dynamická namáhání | \phi_\text{m,min}=15\space\varnothing | ||
| Výztužné sítě – nejmenší průměr zakřivení \varphi_\text{m,min}=5\phi | |||
| Výztužné sítě pro d ≥ 3 øje nejmenší průměr 5 ø pro d < 3 ø je nejmenší průměr 20 ø |
|||
12.5 Kotvení výztuže nad podporami
Tab. 12.9 Kotvení dolní výztuže nad podporami
Tab. 12.10 Stykování tažených výztužných prutů(výztuž B500, cd > 3ø, plné využití výztuže)
| Beton | Průměr ø | Délka přesahu v mm | |||||||
| dobré podmínky soudržnosti | špatné podmínky soudržnosti | ||||||||
| množství stykované výztuže v % | množství stykované výztuže v % | ||||||||
| < 25 % | 33 % | 50 % | > 50 % | < 25 % | 33 % | 50 % | > 50 % | ||
| C20/25 | 6 | 290 | 333 | 406 | 435 | 414 | 476 | 580 | 621 |
| 8 | 386 | 444 | 541 | 580 | 552 | 635 | 773 | 828 | |
| 10 | 483 | 556 | 676 | 725 | 690 | 794 | 966 | 1035 | |
| 12 | 580 | 667 | 812 | 870 | 828 | 952 | 1159 | 1242 | |
| 14 | 676 | 778 | 947 | 1014 | 966 | 1111 | 1353 | 1449 | |
| 16 | 773 | 889 | 1082 | 1159 | 1104 | 1270 | 1546 | 1656 | |
| 20 | 966 | 1111 | 1353 | 1449 | 1380 | 1587 | 1932 | 2070 | |
| 25 | 1208 | 1389 | 1691 | 1812 | 1725 | 1984 | 2415 | 2588 | |
| 32 | 1546 | 1778 | 2164 | 2319 | 2208 | 2540 | 3092 | 3313 | |
| C25/30 | 6 | 242 | 278 | 338 | 362 | 345 | 397 | 483 | 518 |
| 8 | 322 | 370 | 451 | 483 | 460 | 529 | 644 | 690 | |
| 10 | 403 | 463 | 564 | 604 | 575 | 661 | 805 | 863 | |
| 12 | 483 | 556 | 676 | 725 | 690 | 794 | 966 | 1035 | |
| 14 | 564 | 648 | 789 | 845 | 805 | 926 | 1127 | 1208 | |
| 16 | 644 | 741 | 902 | 966 | 920 | 1058 | 1288 | 1380 | |
| 20 | 805 | 926 | 1127 | 1208 | 1150 | 1323 | 1610 | 1725 | |
| 25 | 1006 | 1157 | 1409 | 1510 | 1438 | 1653 | 2013 | 2157 | |
| 32 | 1288 | 1481 | 1804 | 1932 | 1840 | 2116 | 2576 | 2761 | |
| C30/37 | 6 | 217 | 250 | 304 | 326 | 311 | 357 | 435 | 466 |
| 8 | 290 | 333 | 406 | 435 | 414 | 476 | 580 | 621 | |
| 10 | 362 | 417 | 507 | 543 | 518 | 595 | 725 | 776 | |
| 12 | 435 | 500 | 609 | 625 | 621 | 714 | 870 | 932 | |
| 14 | 507 | 583 | 710 | 761 | 725 | 833 | 1014 | 1087 | |
| 16 | 580 | 667 | 812 | 870 | 828 | 952 | 1159 | 1242 | |
| 20 | 725 | 833 | 1014 | 1087 | 1035 | 1190 | 1449 | 1553 | |
| 25 | 906 | 1042 | 1268 | 1359 | 1294 | 1488 | 1812 | 1941 | |
| 32 | 1159 | 1333 | 1623 | 1739 | 1656 | 1905 | 2319 | 2484 | |
| C35/45 | 6 | 198 | 227 | 277 | 296 | 282 | 325 | 395 | 423 |
| 8 | 264 | 303 | 369 | 395 | 376 | 433 | 527 | 565 | |
| 10 | 329 | 379 | 461 | 494 | 471 | 541 | 659 | 706 | |
| 12 | 395 | 455 | 553 | 593 | 565 | 649 | 791 | 847 | |
| 14 | 461 | 530 | 646 | 692 | 659 | 758 | 922 | 988 | |
| 16 | 527 | 606 | 738 | 791 | 753 | 866 | 1054 | 1129 | |
| 20 | 659 | 758 | 922 | 988 | 941 | 1082 | 1318 | 1412 | |
| 25 | 823 | 947 | 1153 | 1235 | 1176 | 1353 | 1647 | 1765 | |
| 32 | 1054 | 1212 | 1476 | 1581 | 1506 | 1732 | 2108 | 2259 | |
| C40/50 | 6 | 174 | 200 | 243 | 261 | 248 | 286 | 348 | 373 |
| 8 | 232 | 267 | 325 | 348 | 331 | 381 | 464 | 497 | |
| 10 | 290 | 333 | 406 | 435 | 414 | 476 | 580 | 621 | |
| 12 | 348 | 400 | 487 | 522 | 497 | 571 | 696 | 745 | |
| 14 | 406 | 467 | 568 | 609 | 580 | 667 | 812 | 870 | |
| 16 | 464 | 533 | 649 | 696 | 663 | 762 | 928 | 994 | |
| 20 | 580 | 667 | 812 | 870 | 828 | 952 | 1159 | 1242 | |
| 25 | 725 | 833 | 1014 | 1087 | 1035 | 1190 | 1449 | 1553 | |
| 32 | 928 | 1067 | 1299 | 1391 | 1325 | 1524 | 1855 | 1988 | |
| C45/50 | 6 | 161 | 185 | 225 | 242 | 230 | 265 | 322 | 345 |
| 8 | 215 | 247 | 301 | 322 | 307 | 353 | 429 | 460 | |
| 10 | 268 | 309 | 376 | 403 | 383 | 441 | 537 | 575 | |
| 12 | 322 | 370 | 451 | 483 | 460 | 529 | 644 | 690 | |
| 14 | 376 | 432 | 526 | 564 | 537 | 617 | 751 | 805 | |
| 16 | 429 | 494 | 601 | 644 | 613 | 705 | 859 | 920 | |
| 20 | 537 | 617 | 751 | 805 | 767 | 882 | 1074 | 1150 | |
| 25 | 671 | 772 | 939 | 1006 | 959 | 1102 | 1342 | 1438 | |
| 32 | 859 | 988 | 1202 | 1288 | 1227 | 1411 | 1718 | 1840 | |
Základní kotevní délka lb,rqd v [mm] prutu při \sigma_\text{sd}=f_\text{yd} (pro výztuž B500)
Tab. 12.11 Rozdělení tahových sil ohýbaného prvku
Tab. 12.12 Rozdělení tahových sil ohýbaného prvku
Pro prostý nosník, krajní a vnitřní pole spojitého nosníku a pro konzoly s rovnoměrným zatížením lze podle uvedených schémat s ohledem na využití výztuže stanovit délku kratší výztuže v poli a nad podporou.
Přitom je nutné respektovat, že minimálně 25 % spodní výztuže nosníků a 50 % spodní výztuže desek musí zůstat u spodního povrchu od podpory k podpoře a musí být zakotvena za líci skutečných podpor tak, aby přenesla sílu F_\text{td}=|V_\text{Ed}|\cdot a_1/z.
Dolní výztuž v poli
Při rozdělení výztuže – 50 % na celé rozpětí l01 a 50 % kratší výztuže
Maximální vzdálenost kratší výztuže od uložení
0\le x_{50}=0{,}=0{,}067l_0-a_1-l_\text{b,min}\le0{,}5l_0-a_1-l_\text{bd}
kde je l0 … rozpětí prostého nosníku nebo vzdálenost mezi nulovými body pole spojitého nosníku l_0=l_{01}=l_{02};
al … posun tahové síly ve výztuži z důvodu šikmé smykové trhliny a_1=z\cdot(\cot\theta-\cot\alphaú/2 u smykově vyztužených prvků a a_1=d u smykově nevyztužených prvků.
Dále d je účinná výška průřezu, lbmin je minimální kotevní délka a lbd je návrhová kotevní délka
Minimální délka kratší výztuže (50+50) je l_{50}=0{,}87\cdot l_0+2\cdot(a_1+l_\text{b,min})\ge2\cdot(a_1+l_\text{bd})
Parametry uložení kratší výztuže (25+75 … 75 % na celé rozpětí):
Maximální vzdálenost kratší výztuže od uložení
0\le x_{25}=0{,}25l_0-a_1-l_\text{b,min}\le0{,}5l_0-a_1-l_\text{bd}
Minimální délka kratší výztuže (25+75) je l_{25}=0{,}50\cdot l_0+2\cdot(a_1+l_\text{b,min})\ge2\cdot(a_1+l_\text{bd})
Horní výztuž nad vnitřní podporou a pro výztuž konzol
Při rozdělení 50 % na celé rozpětí (s patřičným zakotvením) a 50 % kratší výztuže platí parametry uložení
x_{50}=0{,}707l_\text{k}-a_1-l_\text{b,min}\ge l_\text{k}-a_1-l_\text{bd}
Příslušná délka horní výztuže (obvykle poloviční délka při stejném rozpětí polí a stejném zatížení)
l_\text{k50}=0{,}3l_\text{k}+a_1+l_\text{b,min}\ge l_\text{bd}+a_1
Při rozdělení 33 % na celé rozpětí s příslušným zakotvením) a 33 % kratší a následujících 33 % nejkratší výztuže platí parametry uložení
x_{33}=0{,}82\cdot l_\text{k}-a_1-l_\text{b,min}\ge l_\text{bd}+a_1\\
x_{66}=0{,}58\cdot l_\text{k}-a_1-l_\text{b,min}\ge0{,}18l_\text{k}+a_1+l_\text{bd}
Příslušná délka horní výztuže (obvykle poloviční délka při stejném rozpětí polí a stejném zatížení)
l_\text{k33}=0{,}18\cdot l_\text{k}+a_1+l_\text{b,min}\ge l_\text{bd}+a_1\\
l_\text{k66}=0{,}42\cdot l_\text{k}+a_1+l_\text{b,min}\ge l_\text{k33}+l_\text{bd}+a_1
12.6 Doporučené uspořádání výztuže nosníků
Tab. 12.13 Doporučené uspořádání výztuže
kde je
b_1\ge\text{max}\big(\frac{l_1}{4};\frac{l_2}{4};l_\text{s}\big);\\
b_2\ge\text{max}\big(\frac{l_1}{5};\frac{l_2}{5};l_\text{s}\big);\\
a_1\le\frac{l_1}{10};\\
a_2\le\frac{l_2}{10}.
Přitom musí být řádně zakotveno minimálně 25 % dolní výztuže nosníků a 50 % spodní výztuže desek za lícem podpory tak, aby přenesla minimální sílu F_\text{td}=|V_\text{Ed}|\cdot a_1/z.
Pro konzoly a vnitřní podpory spojitých nosníků
Horní výztuž
Pro vnitřní pole spojitých nosníků
Dolní výztuž
Pro prosté nosníky
Dolní výztuž
kde je
l … efektivní (účinná) délka prvku (například nosníku, desky);
lbd … návrhová kotevní délka betonářské výztuže;
al … posun tahové síly ve výztuži z důvodu šikmé smykové trhliny u smykově vyztužených prvků.
a_1=z\cdot(\cot\theta-\cot\alpha)/2
Platí pro zatížení Qk ≤ Gk, pouze pro rovnoměrné zatížení.
13 Požární odolnost
13.1 Železobetonové nosné stěny
Tab. 13.1 Nejmenší rozměry a osové vzdálenosti výztuže nosných železobetonových stěn
| Normová požární odolnost | Nejmenší rozměry [mm] tloušťka stěny/osová vzdálenost | |||
| m fi = 0,35 | m fi = 0,7 | |||
| stěna ohřívaná z jedné strany | stěna ohřívaná ze dvou stran | stěna ohřívaná z jedné strany | stěna ohřívaná ze dvou stran | |
| REI 30 | 100/10* | 120/10* | 120/10* | 120/10* |
| REI 60 | 110/10* | 120/10* | 130/10* | 140/10* |
| REI 90 | 120/20* | 140/10* | 140/25 | 170/25 |
| REI 120 | 150/25 | 160/25 | 160/35 | 220/35 |
| REI 180 | 180/40 | 200/45 | 210/50 | 270/55 |
| REI 240 | 230/55 | 250/55 | 270/60 | 350/60 |
| *Obvykle rozhoduje betonová krycí vrstva podle ČSN EN 1992-1-1. | ||||
13.2 Železobetonové trámy
Tab. 13.2 Nejmenší rozměry bmin a osové vzdálenosti a pro prostě podepřené železobetonové trámy
| Normová požární odolnost | Nejmenší rozměry [mm] | ||||
| Možné kombinace a a bmin, kde je a … průměrná osová vzdálenost výztuže; bmin … šířka trámu. |
tloušťka stojiny bw | ||||
| třída WA | |||||
| R 30 | bmin = 80 / a = 25 | bmin = 120 / a = 20 | bmin = 160 / a = 15* | bmin = 200 / a = 15* | 80 |
| R 60 | bmin = 120 / a = 40 | bmin = 160 / a = 35 | bmin = 200 / a = 30 | bmin = 300 / a = 25 | 100 |
| R 90 | bmin = 150 / a = 55 | bmin = 200 / a = 45 | bmin = 300 / a = 40 | bmin = 400 / a = 35 | 110 |
| R 120 | bmin = 200 / a = 65 | bmin = 240 / a = 60 | bmin = 300 / a = 55 | bmin = 500 / a = 50 | 130 |
| R 180 | bmin = 240 / a = 80 | bmin = 300 / a = 70 | bmin = 400 / a = 65 | bmin = 600 / a = 60 | 150 |
| R 240 | bmin = 280 / a = 90 | bmin = 350 / a = 80 | bmin = 500 / a = 75 | bmin = 700 / a = 70 | 170 |
| asd = a + 10 mm (viz. poznámka níže) | |||||
| asd je osová vzdálenost od bočního líce trámu pro rohové výztužné pruty (nebo předpínací výztuž nebo dráty) u trámů s jednou vrstvou výztuže. Pro hodnoty bmin větší než hodnoty uvedené ve sloupci 4, není zvětšení asd požadováno. *Obvykle rozhoduje krytí předepsané ČSN EN 1992-1-1. | |||||
Tab. 13.3 Nejmenší rozměrybmin a osové vzdálenosti a výztuže pro železobetonové spojité trámy
| Normová požární odolnost | Nejmenší rozměry [mm] | ||||
| Možné kombinace a a bmin, kde je a … průměrná osová vzdálenost výztuže; bmin … šířka trámu |
šířka stěny bw | ||||
| třída WA | |||||
| R 30 | bmin = 80 / a = 15* | 160/12* | 80 | ||
| R 60 | bmin = 120 / a = 25 | 200/12* | 100 | ||
| R 90 | bmin = 150 / a = 35 | 250/25 | 110 | ||
| R 120 | bmin = 200 / a = 45 | 300/35 | 450/35 | 500/30 | 130 |
| R 180 | bmin = 240 / a = 60 | 400/50 | 550/50 | 600/40 | 150 |
| R 240 | bmin = 280 / a = 75 | 500/60 | 650/60 | 700/50 | 170 |
| asd = a + 10 mm | *Rozhoduje krytí podle ČSN EN 1992-1-1. | ||||
| asd je osová vzdálenost od bočního líce trámu pro rohové výztužné pruty u trámů s pouze jednou vrstvou výztuže. Pro větší hodnoty bmin než v tabulce, není zvětšení asd požadováno. | |||||
13.3 Železobetonové desky
Tab. 13.4 Nejmenší rozměry hsa osové vzdálenosti a pro železobetonové plné desky
| Normová požární odolnost | Nejmenší rozměry v mm | |||
| Tloušťka desky hs v mm | Osová vzdálenost výztuže ai | |||
| působící v jednom směru | působící ve dvou směrech | |||
| ly/lx £ 1,5 | 1,5 < ly/lx £ 2 | |||
| REI 30 | 60 | 10* | 10* | 10* |
| REI 60 | 80 | 20 | 10* | 15* |
| REI 90 | 100 | 30 | 15* | 20 |
| REI 120 | 120 | 40 | 20 | 25 |
| REI 180 | 150 | 55 | 30 | 40 |
| REI 240 | 175 | 65 | 40 | 50 |
| lx a lyjsou rozpětí pravoúhlých desek působících ve dvou směrech, kde ly je větší rozpětí. Osová vzdálenost a pro desky působící ve dvou směrech se vztahuje na desky podepřené po celém obvodě. Jiné případy se řeší jako desky působící v jednom směru. *Obvykle rozhoduje krytí předepsané ČSN EN 1992-1-1. |
||||
13.4 Železobetonové sloupy
Tab. 13.5 Nejmenší rozměrybmin a osové vzdálenosti a železobetonových sloupů pravoúhlého nebo kruhového průřezu
| Normová požární odolnost | Mechanický stupeň vyztužení w | Nejmenší rozměry [mm] šířka sloupu bmin/osová vzdálenost výztuže a | |||
| n = 0,15 | n = 0,3 | n = 0,5 | n = 0,7 | ||
| R 30 | 0,100 0,500 1,000 | 150/25* 150/25* 150/25* | 150/25* 150/25* 150/25* | 200/30 : 250/25* 150/25* 150/25 | 300/30 : 350/25* 200/30 : 250/25* 200/30 : 300/25 |
| R 60 | 0,100 0,500 1,000 | 150/30 : 200/25* 150/25* 150/25* | 200/40 : 300/25* 150/35 : 200/25* 150/30:200/25* | 200/40:400/25* 250/35:350/25* 250/40:400/25 | 500/25* 350/40 : 550/25* 300/50 : 600/30 |
| R 90 | 0,100 0,500 1,000 | 200/40 : 250/25* 150/35 : 200/25* 200/25* | 300/40:400/25* 200/45:300/25* 200/40:300/25* | 500/50:550/25* 300/45:550/25* 250/40:550/25* | 550/40:600/25* 500/50:600/40 500/50:600/45 |
| R 120 | 0,100 0,500 1,000 | 250/50 : 350/25* 200/45:300/25* 200/40:250/25* | 400/50:550/25* 300/45:550/25* 250/50:400/25* | 550/25* 450/50:600/25 450/45:600/30 | 550/60:600/45 500/60:600/50 600/60 |
| R 180 | 0,100 0,500 1,000 | 400/50:500/25* 300/45:450/25* 300/35:400/25* | 500/60:550/25* 450/50:600/25* 450/50:550/25* | 550/60:600/30 500/60:600/50 500/60:600/45 | (1) 600/75 (1) |
| R 240 | 0,100 0,500 1,000 | 500/60:550/25* 450/45:500/25* 400/45:500/25* | 550/40:600/25* 550/55:600/25* 500/40:600/30 | 600/75 600/70 600/60 | (1) (1) (1) |
| *Obvykle rozhoduje krytí předepsané ČSN EN 1992-1-1. (1) Vyžaduje šířku větší než 600 mm. Zde je nutné podrobné posouzení vzpěru. n=N_\text{0Ed,fi}/(0{,}7\cdot(A_\text{c}f_\text{cd}+A_\text{s}f_\text{yd})) je poměr zatížení při požární situaci a při běžné teplotě; kde je N0Ed,fi … normálová síla pro požární situaci (výpočet 1. řádu). |
|||||
14 Výztužné sítě
Tab. 14.1 Obvyklé výztužné sítě B500A– standardní sítě ČR
| Výztužné sítě KARI B500A | průřez mm2 | rozměr sítě v m | hmotnost v kg | vzdálenosti prutů v mm | průměry prutů | |
| ø | po okraji | |||||
| podél. příčně | podél. příčně | celá síť 1m2 | podél. příčně | podél. příčně | podél. příčně | |
| KA16 | 125/125 | 3,00 2,00 | 11,88/1,98 | 100/100 | 4/4 | |
| KA17 | 84/84 | 8,12/1,35 | 150/150 | |||
| KA18 | 62/62 | 5,94/0,99 | 200/200 | |||
| KD35 | 196/196 | 3,00 2,00 | 18,48/3,08 | 100/100 | 5/5 | |
| KD36 | 98/98 | 9,24/1,54 | 200/200 | |||
| KD37 | 131/131 | 12,63/2,10 | 150/150 | |||
| KH20 | 188/188 | 3,00 2,00 | 18,20/3,03 | 150/150 | 6/6 | |
| KH30 | 283/283 | 26,64/4,44 | 100/100 | |||
| KH31 | 141/141 | 13,32/2,22 | 200/200 | |||
| KY49 | 503/503 | 3,00 2,00 | 47,4/7,90 | 100/100 | 8/8 | |
| KY50 | 335/335 | 32,39/5,40 | 150/150 | |||
| KY51 | 251/251 | 23,70/3,95 | 200/200 | |||
| KY86 | 335/335 | 6,00/2,40 | 75,84/5,27 | 150/150 | 8/8 | |
| KY81 | 503/503 | 5,00/2,15 | 85,91/7,99 | 100/100 | 8/8 | |
Tab. 14.2 Obvyklé výztužné sítě B500A – standardní sítě Rakousko
| Výztužné sítě KARI B500A | průměry mm2 | rozměr sítě v m | hmotnost v kg | vzdálenosti prutů v mm | průměry prutů | |
| ø | po okraji | |||||
| podél. příčně | podél. příčně | celá síť 1m2 | podél. příčně | podél. příčně | podél. příčně | |
| A60 | 283/65 | 6,00 2,40 | 39,31/2,73 | 100/300 | 6/5 | |
| A70 | 385/79 | 52,46/3,64 | 100/300 | 7/5,5 | ||
| A82 | 528/110 | 72,24/5,02 | 100/300 | 8,2/6,5 | ||
| AQ42 | 138/138 | 6,00 2,40 | 31,39/2,18 | 100/100 | 4,2/4,2 | |
| AQ50 | 196/196 | 44,35/3,08 | 100/100 | 5/5 | ||
| AQ55 | 237/237 | 53,86/3,74 | 100/100 | 5,5/5,5 | ||
| AQ60 | 283/283 | 63,94/4,44 | 100/100 | 6/6 | ||
| AQ65 | 332/332 | 74,88/5,20 | 100/100 | 6,5/6,5 | ||
| AQ70 | 385/385 | 86,98/6,04 | 100/100 | 7/7 | ||
| AQ76 | 453/453 | 102,53/7,12 | 100/100 | 7,6/7,6 | ||
| AQ80 | 503/503 | 113,76/7,90 | 100/100 | 8/8 | ||
| AQ82 | 528/528 | 119,52/8,30 | 100/100 | 8,2/8,2 | ||
| AQ90 | 636/636 | 143,71/9,98 | 100/100 | 9/9 | ||
Tab. 14.3 Obvyklé výztužné sítě B500A – standardní sítě Německo
| průměry mm2 | rozměr sítě v m | hmotnost v kg | vzdálenosti prutů v mm | průměry prutů | ||
| ø | po okraji | |||||
| podél. příčně | podél. příčně | celá síť 1m2 | podél. příčně | podél. příčně | podél. příčně | |
| Q188A | 188/188 | 6,00 2,30 | 41,7/3,02 | 150/150 | 6/6 | |
| Q257A | 257/257 | 56,8/4,12 | 150/150 | 7/7 | ||
| Q335A | 335/335 | 74,3/5,38 | 150/150 | 8/8 | ||
| Q424A | 424/424 | 84,4/6,12 | 150/150 | 9/9 | 4 x ø7+4 x ø7 | |
| Q524A | 524/524 | 100,9/7,31 | 150/150 | 10/10 | 4 x ø7+4 x ø7 | |
| Q636A | 636/636 | 6,00/2,35 | 132/9,36 | 100/125 | 9/10 | 4 x ø7+4 x ø7 |
| R188A | 188/113 | 6,00 2,30 | 33,6/2,43 | 150/250 | 6/6 | |
| R257A | 257/113 | 41,2/2,99 | 150/250 | 7/6 | ||
| R335A | 335/113 | 50,2/3,54 | 150/250 | 8/6 | ||
| R424A | 424/201 | 67,2/4,87 | 150/250 | 9/8 | 2 x ø8+2 x ø8 | |
| R524A | 524/201 | 75,7/5,49 | 150/250 | 10/8 | 2 x ø8+2 x ø8 | |
14.1 Stykování výztužných sítí
Tab. 14.4 Stykování výztužných sítí
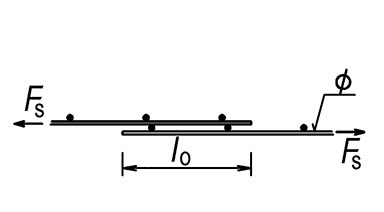
styk podélné výztuže
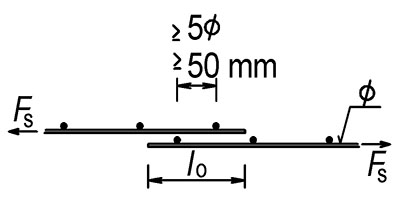
styk příčné výztuže
| Dobré podmínky kotvení výztuže | ||||||||||||||
| Beton | Styk přesahem v podélném směru v mm | Styk přesahem v příčném směru v mm | ||||||||||||
| C20 /25 | C25 /30 | C30 /37 | C35 /45 | C40 /45 | C45 /50 | C50 /55 | C20 /25 | C25 /30 | C30 /37 | C35 /45 | C40 /45 | C45 /50 | C50 /55 | |
| Q188A | 290 | 250 | 220 | 200 | 200 | 200 | 200 | 290 | 250 | 220 | 200 | 200 | 200 | 200 |
| Q257A | 340 | 290 | 260 | 230 | 210 | 200 | 200 | 340 | 290 | 260 | 230 | 210 | 200 | 200 |
| Q335A | 380 | 330 | 290 | 260 | 240 | 220 | 210 | 380 | 330 | 290 | 260 | 240 | 220 | 210 |
| Q424A | 430 | 370 | 330 | 290 | 270 | 250 | 230 | 500 | ||||||
| Q524A | 500 | 430 | 390 | 340 | 310 | 290 | 270 | 500 | ||||||
| Q636A | 510 | 440 | 390 | 350 | 320 | 300 | 280 | 570 | 480 | 430 | 380 | 350 | 350 | 350 |
| Špatné podmínky kotvení výztuže | ||||||||||||||
| Beton C | Styk přesahem v podélném směru v mm | Styk přesahem v příčném směru v mm | ||||||||||||
| C20 /25 | C25 /30 | C30 /37 | C35 /45 | C40 /45 | C45 /50 | C50 /55 | C20 /25 | C25 /30 | C30 /37 | C35 /45 | C40 /45 | C45 /50 | C50 /55 | |
| Q188A | 410 | 350 | 320 | 280 | 260 | 240 | 220 | 410 | 350 | 320 | 280 | 260 | 240 | 220 |
| Q257A | 480 | 410 | 370 | 320 | 300 | 280 | 260 | 480 | 410 | 370 | 320 | 300 | 280 | 260 |
| Q335A | 550 | 470 | 420 | 370 | 340 | 320 | 290 | 550 | 470 | 420 | 370 | 340 | 320 | 290 |
| Q424A | 610 | 520 | 470 | 420 | 380 | 350 | 330 | 610 | 520 | 500 | 500 | 500 | 500 | 500 |
| Q524A | 720 | 610 | 550 | 490 | 450 | 410 | 390 | 720 | 610 | 550 | 500 | 500 | 500 | 500 |
| Q636A | 730 | 620 | 560 | 500 | 460 | 420 | 390 | 810 | 690 | 620 | 550 | 500 | 500 | 500 |
15 Distanční prvky
Tab. 15.1 Distanční prvky
16 Změny v ČSN EN 1992-1-1 76653.včetně NA
16.1 Změny 2015 – ČSN EN 1992-1-1 (Omezení únosnosti v protlačení (viz kap. 8))
Maximální hodnota únosnosti v protlačení by měla být omezena nejen maximální únosností betonové diagonály vztahem \nu_\text{Rd,max}=0{,}4\cdot \nu \cdot f_\text{cd}, ale i maximální únosností smykově vyztuženého průřezu. Proto bylo doplněno kritérium maximální únosnosti v prvním kontrolovaném obvodu.
\begin{gathered}
\nu_\text{Rd,cs}=0{,}75\nu_\text{Rd,c}+1{,}5(d/s_\text{r})A_\text{sw}f_\text{ywd,eff}(1/(u_1d))\sin\alpha\le k_\text{max}\cdot \nu_\text{Rd,c}
\end{gathered}kde je
Asw … plocha jednoho prutu smykové výztuže kolem sloupu [mm2];
νRd,c … návrhová smyková únosnost při protlačení [MPa] bez smykové výztuže;
sr … radiální vzdálenosti prutů smykové výztuže [mm];
fywd,eff … účinná návrhová pevnost smykové výztuže při protlačení daná vztahem;
fywd,eff = 250 + 0,25 d ≤ fywd [MPa];
d … průměrná účinná výška průřezu v ortogonálních směrech [mm];
α … úhel mezi smykovou výztuží a rovinou desky;
kmax … součinitel, kterým se omezuje maximální únosnost v protlačení při použití smykové výztuže (doporučené hodnota je 1,5).
16.2 Změny 2016 – ČSN EN 1992-1-1
Změny v základní normě pro navrhování železobetonových konstrukcí ČSN EN 1992-1-1 Eurokód 2: Navrhování betonových konstrukcí – Část 1-1: Obecná pravidla a pravidla pro pozemní stavby
| článek | původní | nové znění |
| 7.3.4(2) | \rho_\text{p,eff}=(A_\text{s}+\xi_1A_\text{p}')/A_\text{c,eff} | \rho_\text{p,eff}=(A_\text{s}+\xi_1^2A_\text{p}')/A_\text{c,eff} |
| 7.3.4(5) | 1,3násobku tloušťky stěny | 1,3násobku výšky stěny |
16.3 Změny v národní příloze 2016
článek
nové znění – úprava
5.3.6(1)
Hodnota kλ = 1,0 se uvažuje pro λ ≤ 3,0 a hodnota kλ = 1,5 se uvažuje pro λ ≥ 6,75.
5.8.3.1
Maximální hodnota limitní štíhlosti pro osamělé prvky
λlim ≤ 75 (5.13a CZ)
λlim = 25 pro |n| ≥ 0,41 (5.13b CZ)
kde n = NEd/(Ac∙fcd) je poměrná normálová síla.
5.8.5(1)
Zjednodušené metody pro stanovení účinků 2. řádu
V ČR je doporučeno používat především metodu (b) – metodu jmenovité křivosti.
6.2.3(2)
Sklon tlačené diagonály
V ČR hodnotu cot θ se doporučuje volit v závislosti na namáhání prvku a případném jeho předpětí následovně:
- Pro ohýbané prvky s významnou tahovou normálovou silou je doporučená hodnota cot θ = 1 (resp. θ = 45°).
- Pro ohýbané prvky s významnou tlakovou normálovou silou a předpjaté prvky je doporučená hodnota v intervalu 1,0 ≤ cot θ ≤ 2,5 resp. (45°≤ θ ≤ 21,8°).
- Pro ohýbané prvky bez působení významné normálové sily je doporučená hodnota v intervalu 1,0 ≤ cot θ ≤ 1,75 resp. (45° ≤ θ ≤ 30°).
6.2.4(4)
Styk mezi stěnou a přírubami
Doporučená hodnota cot θt se v ČR uvažuje následovně:
cot θt = 1,2 pro tlačené příruby (θf = 40°),
cot θt = 1,0 pro tažené příruby (θf = 45°).
6.4.5(1)
Únosnost ve smyku při protlačení desek a základů se smykovou výztuží
Doporučená hodnota kmax se v ČR uvažuje následovně:
U desek se smykovou výztuží spolehlivě zakotvenou v úrovni horní i dolní výztuže a se svařovanými smykovými mřížkami dostatečně zakotvenými při obou lících deskového prvku se uvažuje:
kmax = 1,45 při h = 200 mm, kmax = 1,70 při h ≥ 700 mm,
mezilehlé hodnoty lze interpolovat;
u základů se smykovou výztuží se uvažuje kmax = 1,5.
Při použití certifikovaných výrobků pro smykovou výztuž uvažuje se hodnota kmax podle příslušného evropského technického osvědčení – viz 6.4.5 článek normy ČSN EN 1992-1-1[2]
7.3.3(2)
(Tabulka 7.3 zůstává beze změn)
Omezení šířky trhlin bez přímého výpočtu (wk je šířka trhlin v mm)
| Napětí ve výztuži2) [MPa] | Maximální průměr prutů [mm] | |||
| wk=0,4 mm | wk=0,3 mm | wk=0,2 mm | wk=0,1 mm | |
| 120 | 116 | 84 | 52 | 21 |
| 160 | 63 | 45 | 27 | 10 |
| 200 | 36 | 28 | 16 | 5 |
| 240 | 26 | 18 | 10 | – |
| 280 | 19 | 13 | 7 | – |
| 320 | 14 | 9 | 5 | – |
| 360 | 10 | 7 | – | – |
| 400 | 8 | 5 | – | – |
1) Hodnoty v tabulce vycházejí z následujících předpokladů:
betonová krycí vrstva c= 36 mm (průměrná hodnota k3ˑc při betonové krycí vrstvě 25 a 50 mm); fct,eff = 2,9 MPa; k = 1,0; kc = 0,4; kt = 0,4; hcr = 0,5h; hc,eff =2,5(h – d) = 0,1h; k1 = 0,8; k2 = 0,5; k4 = 0,425; k3 = 3,4(25/c)2/3 ≤ 3,4 a (\varepsilon_\text{sm}-\varepsilon_\text{cm})=0{,}6\cdot\sigma_\text{s}/E_\text{s}
Součinitele viz tab. 11.4
2) Při odpovídající kombinaci účinků zatížení.
Oprava tabulkových hodnot – maximální průměr prutu
Ohyb (alespoň část průřezu je tlačena): \phi=\phi_\text{s}^*\cdot\frac{k\cdot k_\text{c}\cdot h_\text{cr}}{5\cdot k_2\cdot(h-d)}\cdot\frac{f_\text{ct,eff}}{2{,}9}; (7.6CZ)
Tah (rovnoměrný prostý tah) \phi=\phi_\text{s}^*\cdot\frac{k\cdot h_\text{cr}}{4\cdot(h-d)}\cdot\frac{f_\text{ct,eff}}{2{,}9}; (7.7CZ)
kde je
ϕs … maximální upravený průměr prutu;
ϕs* … maximální průměr prutu uvedený v tabulce 7.2 CZ;
h … celková výška průřezu;
hcr …výška tlačené oblasti bezprostředně před vznikem trhliny při uvažování charakteristických hodnot předpětí a osových sil při kvazi–stálé kombinaci zatížení;
d … účinná výška průřezu vztažená k těžišti krajní vrstvy výztuže.
Pokud je celý průřez namáhán tahem, pak (h – d) je minimální vzdálenost od těžiště vrstvy výztuže k povrchu betonu (při nesymetrické výztuži se uvažují vzdálenosti ke každému povrchu betonu).
Poznámka:
Tabulky jsou sestaveny pro betonovou krycí vrstvu výztuže 36 mm; slouží tedy pro přibližný návrh minimální průřezové plochy výztuže, popř. pro orientační posouzení šířky trhliny.
7.3.4(3)
Výpočet šířky trhlin
V ČR se uvažuje pro hodnoty k3 = 3,4(25/c)2/3 ≤ 3,4 a k4 = 0,425,
kde c je tloušťka betonové krycí vrstvy výztuže v mm
8.3(2)
Přípustné vnitřní průměry zakřivení při ohýbání prutů Pro pruty a dráty
| Nejmenší vnitřní průměr zakřivení pro háky, třmínky a smyčky (viz obr. 8.1) | Nejmenší vnitřní průměr zakřivení pro ohyby a jiné ohýbané pruty | |||
| Průměr prutu mm | Nejmenší betonová krycí vrstva c ve směru kolmém na rovinu ohybu | |||
| ø ≤ 16 | ø > 16 | c ≥ 100 mm a současně c ≥ 7ø | c < 50 mm a současně c < 3ø | c ≤ 50 mm nebo c ≤ 3ø |
| 4ø | 7ø | 10ø | 15ø | 20ø |
Pro ohýbanou svařovanou výztuž a sítě
| Nejmenší vnitřní průměr zakřivení | |||||
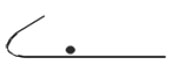 |
nebo |
 |
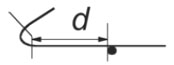 |
nebo |
 |
| 5ø | d ≥ 3ø : 5ø d < 3ø nebo svary v oblasti zakřivení: 20ø |
||||
|
Poznámka: |
|||||
Poznámka:
Při zpětném ohýbání výztuže (za studena) platí:
- Průřez zpětně ohýbané výztuže může být maximálně 14 mm.
- Při statickém namáhání musí být vnitřní průměr zakřivení zpětně ohýbané výztuže minimálně 6ø . Únosnost zpětně ohýbané výztuže je nutné redukovat na 80 %.
- Při dynamickém namáhání musí být vnitřní průměr zakřivení zpětně ohýbané výztuže minimálně 15ø , rozkmit napětí musí být menší než 50 MPa.
- V místě zpětného ohybu je únosnost betonové tlačené diagonály omezena na 0,3VRd,max, pokud je prvek vyztužen smykovou výztuží kolmou k ose prvku, a 0,2VRd,max pro prvek se skloněnou smykovou výztuží. Doporučená hodnota sklonu tlačené diagonály je q = 40°.
Při ohýbání za tepla ≥ 500°C je nutné uvažovat mez kluzu fyk = 250 MPa.
6.2.1(8)
doplnění
Úprava pro rozhodující posouvající sílu
Posouzení na VRd,c a VRd,s může být provedeno ve vzdálenosti d od líce podpory jen u prvků namáhaných převážně rovnoměrným zatížením a při jejich přímém uložení. U nepřímého uložení se všechny hodnoty VRd,c, VRd,s a VRd,max posoudí v ose uložení
6.2.3(8)
doplnění
Úprava redukce posouvající síly v blízkosti uložení
Redukce posouvající síly součinitelem β lze použit pouze u přímého uložení. U krátkých konzol vyšetřovaných pomocí modelů náhradní příhradoviny se posouvající síla neredukuje.U krátkých konzol konstrukcí pozemních staveb nemusí být smyková výztuž umístěna jen ve střední části délky 0,75 av, lze ji umístit rovnoměrně po celé délce tlačené betonové diagonály.
6.4.2(2)
Zjednodušení stanovení kontrolovaného obvodu u poddajných základových konstrukcí
Pro základové desky a poddajné základové patky (l ≥ 2,0) je možné zjednodušeně uvažovat kontrolovaný obvod ve vzdálenosti d. Štíhlost základové patky je podle vztahu l = al /d, kde al je nejmenší vzdálenost mezi lícem zatěžovací plochy a okrajem základové konstrukce.
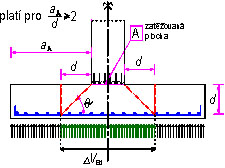
2,06.4.5(4)
Únosnost ve smyku při protlačení desek a základů se smykovou výztuží
Uložení smykové výztuže podle obr. 6.22 B normy ČSN EN 1992-1-1 [2] se nedoporučuje.
6.5.3(3)
Příčná tahová síla u betonových vzpěr
Příčná tahová síla T může být přenesena betonem, pokud vyvolaný tah < 0,5 fctd;
pokud vyvolaný tah ≥ 0,5fctd ale zároveň < fctd, pak postačí minimální konstrukční vyztužení prvku.
Pokud vyvolaný tah v betonu ≥ fctd je nutné navrhnout výztuž zachycující vznikající příčné tahy.
6.5.3(4)
Příčná tahová síla u místně zatížených ploch
Pokud není pro přenos příčných tahů navržena výztuž, musí zatěžující břemeno splňovat podmínku FRdu ≤ 0,5∙fcd Ac0 .
7.3.3(1)
Omezení šířky trhlin
Ustanovení článku platí pouze pro desky v prostředí XC0 a XC1.
7.3.4(2)
Výpočet šířky trhlin
Pokud u železobetonových konstrukcí při kvazistálé kombinaci nevznikají trhliny, ale vznikají při časté nebo charakteristické kombinaci, uvažuje se při výpočtu trhlin při kvazistálém zatížení napětí ve výztuži σs,stanovené v průřezu porušeném trhlinou při tomto kvazistálém zatížení. Pokud při kvazistálé kombinaci zatížení působí v průřezu tlaková normálová síla zajišťující tlakové napětí v celém průřezu, pak lze považovat šířku trhliny při této kombinaci za nulovou.
7.3.4(3)
Výpočet šířky trhlin
Hodnota maximální vzdálenosti trhlin podle vztahu (7.14) má být větší, než podle vztahu (7.11) jinak se má použít hodnota maximální vzdálenosti trhlin podle vztahu (7.11).
7.4.2(2)
Případy, kdy lze od výpočtu průhuby upustit
Při stupních vyztužení ρ < 0,5% doporučuje se stanovit průhyb výpočtem. Platnost vztahů (7.16a) a ( 7.16b) se doporučuje omezit stupněm vyztužení ρ = 0,5 %.
Dále vztahy (7.16a) a (7.16b) jsou stanoveny pro As,prov ≈ As,req ; při větším množství použité výztuže nedávají dostatečně přesné hodnoty l/d, proto při hodnotách As,prov≥ 1,5 As,req je doporučeno stanovit průhyb výpočtem.
Vztahy (7.16a) a (7.16b) platí převážně pro rovnoměrné zatížení včetně lehkých přemístitelných příček; při zatížení osamělými břemeny, včetně těžších příček, není doporučeno vztahy používat.
Pokud napětí v betonu při kvazistálé kombinaci zatížení překročí hodnotu 0,45 fck (nelineární dotvarování viz článek 3.1.4(4) – výpočet ø podle vztahu (3.7)), je třeba početně ověřit přetvoření prvku (nelze použít článek 7.4.2).
7.4.3(3)
Posouzení průhybů výpočtem
Pokud v konstrukci při uvažované kombinaci zatížení (např. kvazistálé) nevznikají trhliny, je třeba při výpočtu průhybu vzít v úvahu poškození konstrukce trhlinami od potencionálně vyšších zatížení, které na konstrukci mohou působit.
8.4.4(1)
Návrhová kotevní délka
V případě kotvení výztuže v oblasti příčných tahů se doporučuje uvažovat vliv příčného tahu obdobně jako u působení příčného tlaku s tím, že hodnota příčného tahu se dosazuje se záporným znaménkem. Pro součinitel α5 se uvažuje s rozšířeným omezením 0{,}7\le\alpha_5\le1{,}5.
Taženou výztuž není vhodné kotvit v tažené části průřezu. Pokud je nutné nosnou výztuž v tažené části průřezu ukončit, musí se stykovat např. přesahem; délka přesahu se uvažuje hodnotou l0 podle pravidel článku 8.7.3 normy. Pokud některé výztužné pruty v tažené části průřezu je možné ukončit, zakotví se podle pravidel o kotvení výztuže.
9.4
Desky lokálně podepřené, základové konstrukce
Pro zajištění spolehlivého přenosu posouvající síly do podpor se doporučuje posoudit desky v oblasti podepření na minimální ohybové momenty mEd podle následujících vztahů:
mEd,z = ηz∙VEd a mED,y = ηy∙VEd .
| Umístění sloupu | ηz | Šířka pruhu | ηy | Šířka pruhu | |||
| Tah při horním líci desky | Tah při spodním líci desky | Tah při horním líci desky | Tah při spodním líci desky | ||||
| Vnitřní sloup | 0,125 | 0 | 0,3 ly | 0,125 | 0 | 0,3 lz | |
| Krajní sloup „z“ | 0,25 | 0 | 0,15 ly | 0,125 | 0,125 | na 1 m šířky desky | |
| Krajní sloup „y“ | 0,125 | 0,125 | na 1 m šířky desky | 0,25 | 0 | 0,15 lz | |
| Rohový sloup | 0,5 | 0,5 | na 1 m šířky desky | 0,5 | 0,5 | na 1 m šířky desky | |
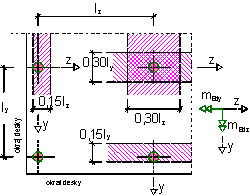 |
kde je VEd … reakce ve sloupu v [kN]; mEd,y, mEd,z … měrné ohybové momenty v [kNm/m] podle obrázku; ηy, ηz … součinitelé ohybových momentů podle tabulky.
Poznámka: |
||||||
9.5.3(3)
Příčná výztuž
U konstrukčních prvků vystavených riziku nehodové události (výbuch, apod.) se osová vzdálenost příčné výztuže scl,max redukuje z 300 mm na 150 mm, dále pruty umístěné mezi rohovými pruty zajištěnými příčnou výztuží, musí být zajištěny příčnou výztuží (sponami, třmínky apod.) ve vzdálenosti 2 scl,max, tedy po výšce ob jednu řadu základní příčné výztuže.
17 Literatura
[1] ČSN EN 1990: Zásady navrhování konstrukcí. Praha: ČSNI 03/2004.
[2] ČSN EN 1991-1-1: Zatížení konstrukcí – Obecná zatížení – Část 1-1: Objemové tíhy, vlastní tíha a užitná zatížení budov, Praha:ČNI 3/2004.
[3] ČSN EN 1991-1-2: Zatížení konstrukcí – Obecná zatížení – Část 1-2: Zatížení konstrukcí při požáru, Praha: ČNI 8/2004, Oprava 1 12/2006.
[4] ČSN EN 1992-1-1: Navrhování betonových konstrukcí – Obecně – Část 1-1: Obecná pravidla pro pozemní a inženýrské stavby, Praha: ČNI 11/2006. Oprava 1 7/2009.
[5] ČSN EN 1992-1-2: Navrhování betonových konstrukcí – Obecně – Část 1-2: Navrhování na účinky požáru, Praha: ČNI 11/2006.
[6] ČSN EN 206: Beton Specifikace, vlastnosti, výroba a shoda, Praha: ČNI 2014.
[7] ČSN EN 10080: Ocel pro výztuž do betonu. Svařitelná žebírková betonářská ocel – Všeobecně, Praha: ČNI 12/2005.
[8] ČSN 42 0139: Ocel pro výztuž do betonu. Svařitelná žebírková betonářská ocel – Všeobecně, Praha: ČNI 12/2007.
[9] ČSN EN ISO 17660-1,2: Svařování betonářské oceli – Část 1: Nosné svarové spoje, Část 2: Nenosné svarové spoje, Praha: ČNI 7/2007.
[10] PROCHÁZKA J., ŠMEJKAL J., VÍTEK J., L, VAŠKOVÁ J. Navrhování betonových konstrukcí. Příručka k ČSN EN 1992-1-1 a ČSN EN 1992-1-2. Praha: IC ČKAIT, 2010, (2. vydání 2013), ISBN 978-80-87438-03-9.
[11] ŠMEJKAL J. Železobetonové konstrukce I. Skriptum FAV ZČU Plzeň, 2010, ISBN 978-80-7043-943-2.
[12] HANZLOVÁ H., Šmejkal J. Betonové a zděné konstrukce 1. Základy navrhování betonových konstrukcí. Skriptum ČVUT, Praha, 2013, ISBN 978-80-01-05323-2.
[13] KOHOUTKOVÁ A., PROCHÁZKA J., ŠMEJKAL J. Modelování a vyztužování betonových prvků. Lokální modely železobetonových konstrukcí. Skriptum ČVUT, Praha. (1. vydání 2013), (1. dotisk 2014). ISBN 978-80-01-05329-4.
[14] ALBERT A., Bautabelle für Ingenieure mit Berechnungshinweisen und Beispielen. 21. Auflage 2014, Bundesanzeiger Verlag GmbH Köln, ISBN 978-3-8462-0304-0.